A Cross-Linguistic Pressure for
Uniform Information Density in Word Order
Thomas Hikaru Clark1 Clara Meister2 Tiago Pimentel3 Michael Hahn4
Ryan Cotterell2 Richard Futrell5 Roger Levy1
1MIT, USA 2ETH Z¨urich, Switzerland 3University of Cambridge, UK
4Saarland University, Germany 5UC Irvine, USA
thclark@mit.edu meistecl@inf.ethz.ch tp472@cam.ac.uk
mhahn@lst.uni-saarland.de ryan.cotterell@inf.ethz.ch
rfutrell@uci.edu rplevy@mit.edu
Abstract
While natural languages differ widely in both
canonical word order and word order flex-
ibility, their word orders still follow shared
cross-linguistic statistical patterns, often at-
tributed to functional pressures. In the effort to
identify these pressures, prior work has com-
pared real and counterfactual word orders. Yet
one functional pressure has been overlooked in
such investigations: The uniform information
density (UID) hypothesis, which holds that in-
formation should be spread evenly throughout
an utterance. Here, we ask whether a pres-
sure for UID may have influenced word order
patterns cross-linguistically. To this end, we
use computational models to test whether real
orders lead to greater information uniformity
than counterfactual orders. In our empirical
study of 10 typologically diverse languages,
we find that: (i) among SVO languages, real
word orders consistently have greater unifor-
mity than reverse word orders, and (ii) only
linguistically implausible counterfactual or-
ders consistently exceed the uniformity of real
orders. These findings are compatible with
a pressure for information uniformity in the
development and usage of natural languages.1
1
Introduction
Human languages differ widely in many respects,
yet there are patterns that appear to hold consis-
tently across languages. Identifying explanations
for these patterns is a fundamental goal of lin-
guistic typology. Furthermore, such explanations
may shed light on the cognitive pressures under-
lying and shaping human communication.
1Code for reproducing our experiments is available at
https://github.com/thomashikaru/word-order-uid.
This work studies the uniform information den-
sity (UID) hypothesis as an explanatory princi-
ple for word order patterns (Fenk and Fenk, 1980;
Genzel and Charniak, 2002; Aylett and Turk,
2004; Jaeger, 2010; Meister et al., 2021). The
UID hypothesis posits a communicative pressure
to avoid spikes in information within an utter-
ance, thereby keeping the information profile of
an utterance relatively close to uniform over time.
While the UID hypothesis has been proposed as
an explanatory principle for a range of linguistic
phenomena, e.g., speakers’ choices when faced
with lexical and syntactic alternations (Levy and
Jaeger, 2006), its relationship to word order pat-
terns has received limited attention, with the
notable exception of Maurits et al. (2010).
Our work investigates the relationship be-
tween UID and word order patterns, differing
from prior work in several ways. We (i) use Trans-
former language models (LMs) (Vaswani et al.,
2017) to estimate information-theoretic operation-
alizations of information uniformity; (ii) analyze
large-scale naturalistic datasets of 10 typologi-
cally diverse languages; and (iii) compare a range
of theoretically motivated counterfactual gram-
mar variants.
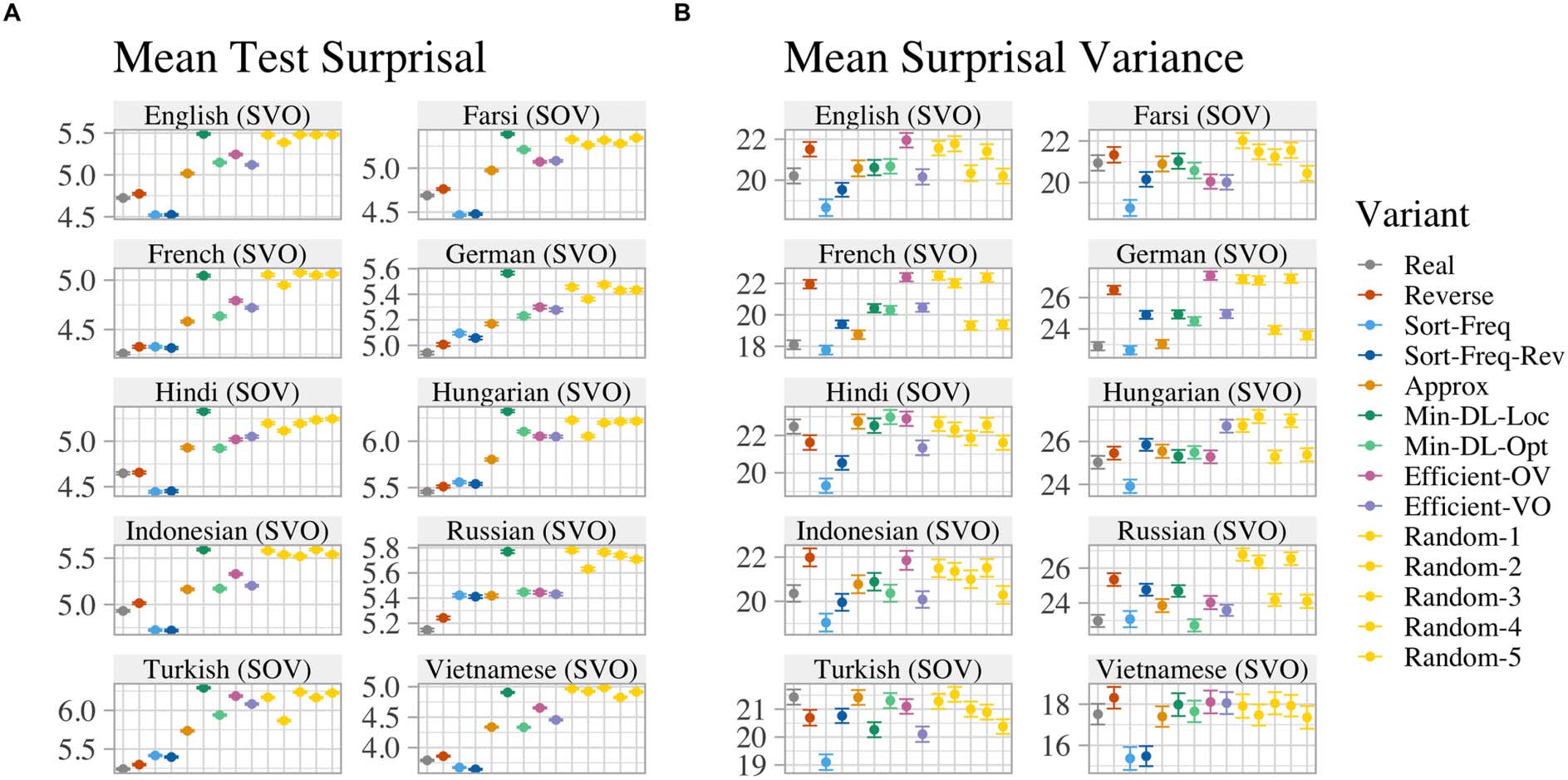
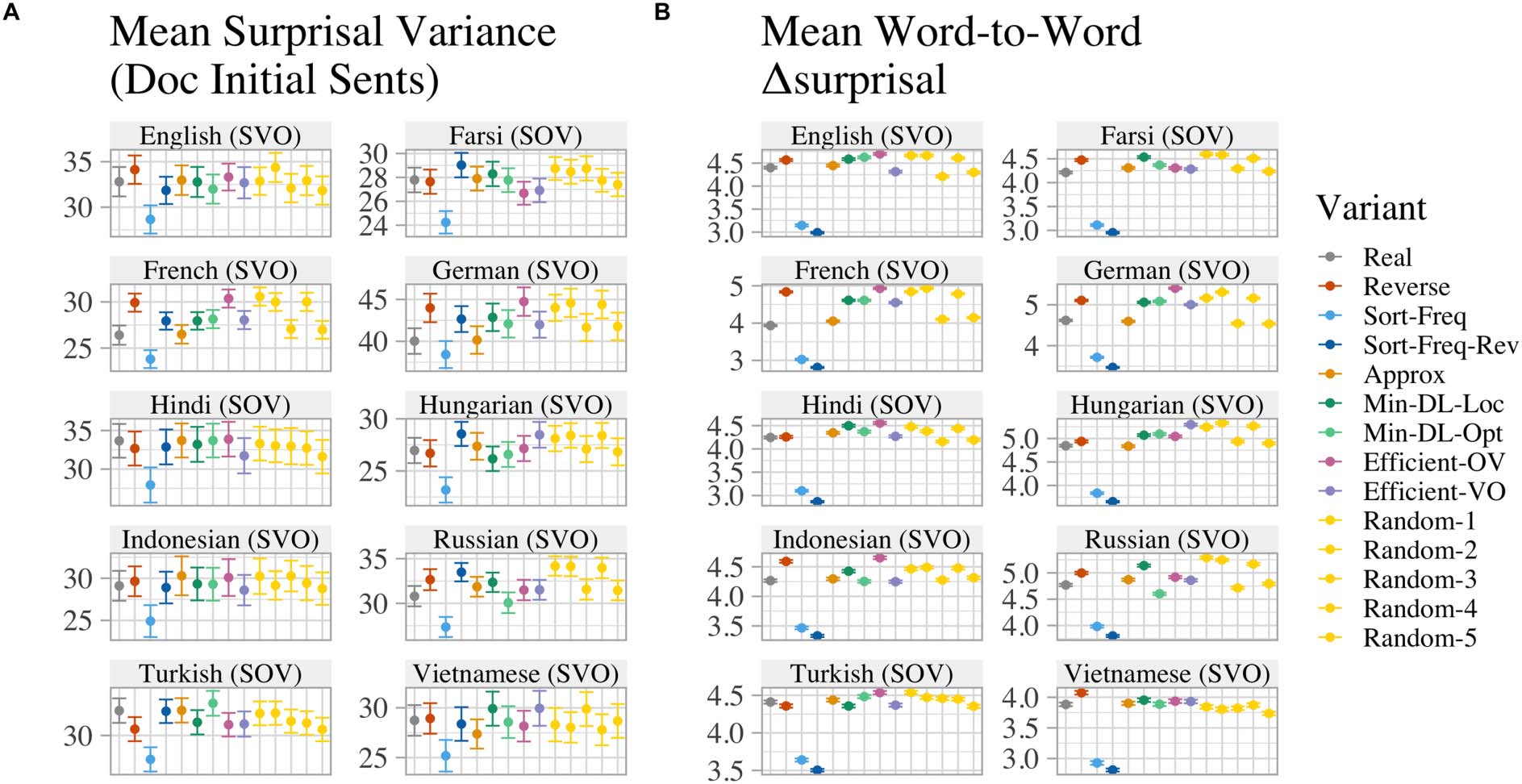
Experimentally, we find that among SVO lan-
guages, the real word order has a more uniform
information density than nearly all counterfac-
tual word orders; the only orders that consistently
exceed real orders in uniformity are generated
using an implausibly strong bias for uniformity,
at the cost of expressivity. Further, we find that
counterfactual word orders that place verbs be-
fore objects are more uniform than ones that place
objects before verbs in nearly every language.
Our findings suggest that a tendency for uniform
information density may exist in human language,
1048
Transactions of the Association for Computational Linguistics, vol. 11, pp. 1048–1065, 2023. https://doi.org/10.1162/tacl a 00589
Action Editor: Mark-Jan Nederhof. Submission batch: 9/2022; Revision batch: 1/2023; Published 8/2023.
c(cid:2) 2023 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
8
9
2
1
5
4
4
9
5
/
/
t
l
a
c
_
a
_
0
0
5
8
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
with two potential sources: (i) word order rules,
with SVO order generally being more uniform
than SOV; and (ii) choices made by speakers,
who use the flexibility present in real languages to
structure information more uniformly at a global
level (and not only in a small number of isolated
constructions).
2 Functional Pressures in Language
2.1 Linguistic Optimizations
A number of
linguistic theories link cross-
linguistic patterns to functional pressures. For
example, both the grammatical rules of a lan-
guage and speakers’ choices (within the space of
grammatically acceptable utterances) are posited
to reflect a trade-off between effort and robust-
ness: Shorter and simpler structures are easier to
produce and comprehend, but longer and more
complex utterances can encode more information
(Gabelentz, 1901; Zipf, 1935; Hawkins, 1994,
2004, 2014; Haspelmath, 2008). Another such
functional pressure follows from the principle of
dependency length minimization (DLM), which
holds that, in order to minimize working memory
load during comprehension, word orders should
place words in direct dependency relations close
to each other (Rijkhoff, 1986, 1990; Hawkins,
1990, 1994, 2004, 2014; Grodner and Gibson,
2005; Gibson, 1998, 2000; Bartek et al., 2011;
Temperley and Gildea, 2018; Futrell et al., 2020).
A growing body of work has turned to informa
tion theory, the mathematical theory of commu-
nication (Shannon, 1948), to formalize principles
that explain linguistic phenomena (Jaeger and
Tily, 2011; Gibson et al., 2019; Pimentel et al.,
2021c). One such principle is that of uniform
information density.
2.2 Uniform Information Density
According to the UID hypothesis, speakers tend
to spread information evenly throughout an utter-
ance; large fluctuations in the per-unit information
content of an utterance can impede communi-
cation by increasing the processing load on the
listener. Speakers may modulate the information
profile of an utterance by selectively producing
linguistic units such as optional complementizers
in English (Levy and Jaeger, 2006; Jaeger, 2010).
A pressure for UID in speaker choices has also
been studied in specific constructions in other
languages, though with mixed conclusions (Zhan
and Levy, 2018; Clark et al., 2022).
Formally, the information conveyed by a lin-
guistic signal y, e.g., an utterance or piece of
text, is quantified in terms of its surprisal s(·),
which is defined as y’s negative log-probability:
s(y) def= − log p(cid:2)(y). Here, p(cid:2) is the underlying
probability distribution over sentences y for a
language (cid:2). Note that we do not have access to
the true distribution p(cid:2), and typically rely on a
language model with learned parameters θ to es-
timate surprisal values with a second distribu-
tion pθ.
Surprisal can be additively decomposed over
the units that comprise a signal. Explicitly, for
a signal y that can be expressed as a series of
linguistic units (cid:3)y1, . . . , yN (cid:4), where yn ∈ V and
V is a set vocabulary of words or morphemes,
the surprisal of a unit yn is its negative log-
probability given prior context: s(yn) = − log
p(cid:2)(yn | y
which disproportionately increases in the pres-
ence of larger surprisal values.4 Note that for all
of these operationalizations, lower values corre-
spond to greater uniformity.5
4This metric suggests a super-linear processing cost for
surprisal.
5We note that, while a fully uniform language would
have value 0 for UIDv and UIDlv, it would not for UIDp(y),
so the metrics are not directly comparable.
3 Counterfactual Language Paradigm
Following prior work that has used counterfac-
tual languages to study the functional pressures
at play in word order patterns, we investigate to
what degree a language’s word order shows signs
of optimization for UID. In this approach, a
corpus of natural language is compared against
a counterfactual corpus containing minimally
changed versions of the same sentences, where
the changes target an attribute of interest, e.g.,
the language’s word order. For example, several
studies of DLM have compared syntactic depen-
dency lengths in real and counterfactual corpora,
generated by permuting the sentences’ word or-
der either randomly (Ferrer-i-Cancho, 2004; Liu,
2008) or deterministically by applying a counter-
factual grammar (Gildea and Temperley, 2010;
Gildea and Jaeger, 2015; Futrell et al., 2015b,
2020). Similarly, we will compare measures of
UID in real and counterfactual corpora to investi-
gate whether real languages’ word orders exhibit
more uniform information density than alterna-
tive realizations.
3.1 Formal Definition
We build on the counterfactual generation proce-
dure introduced by Hahn et al. (2020) to create
parallel corpora. This procedure operates on sen-
tences’ dependency parses. Formally, a depen-
of a sentence y is a directed tree
dency parse
with one node for every word, where each word
in y, with the exception of a designated root
word, is the child of its (unique) syntactic head;
see Zmigrod et al. (2020) for a discussion of the
role of the root constraint in dependency tree
annotation. Each edge in the tree is annotated
with the syntactic relationship between the words
connected by that edge; see Figure 1 for an ex-
ample. Here we use the set of dependency re-
lations defined by the Universal Dependencies
(UD) paradigm (de Marneffe et al., 2021), though
1050
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
8
9
2
1
5
4
4
9
5
/
/
t
l
a
c
_
a
_
0
0
5
8
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
allowed by this formalism, the grammars which
we borrow from Hahn et al. (2020) enforce two
additional simplifying constraints. First, the rela-
tive positioning (left or right) between the head
and dependent of a particular relation is fixed.
Second, the relative ordering of different rela-
tions on the same side of a head is also fixed. We
denote grammars which satisfy both constraints
as consistent. Notably, natural languages violate
both of these assumptions to varying degrees. For
example, even in English—a language with rel-
atively strict word order—adverbs can generally
appear before or after their head. While these sim-
plifications mean that the formalism cannot per-
fectly describe natural languages, it provides a
computationally well-defined method for inter-
vening on many features of word order. In par-
ticular, the consistent grammars of Hahn et al.
(2020) are parameterized by a set of scalar weights
corresponding to each possible syntactic relation;
the ordering function thus reduces to sorting each
head’s dependents based on their weight values.
Notably, Hahn et al. (2020) also introduced a
method for optimizing these grammars for vari-
ous objective functions by performing stochastic
gradient descent on a probabilistic relaxation of
the grammar formalism; we use several of these
grammars (described in §3.2) in our subsequent
analysis.
Creating Counterfactual Word Orderings.
The above paradigm equips us with the tools
necessary for systematically altering sentences’
word orderings, which in turn, enables us to create
counterfactual corpora. Notably, the large corpora
we use in this study contain sentences as strings,
not as their dependency parses. We therefore de-
fine our counterfactual grammar intervention as
the output of a (deterministic) word re-ordering
function f : Y → Y, where Y def= V ∗ is the set of
all possible sentences that can be constructed us-
ing a language’s vocabulary V.6 This function
takes as input a sentence from our original lan-
guage and outputs a sentence with the counter-
factual word order defined by a given ordering
function g. We decompose this function into two
steps:
f(y) = linearize(parse(y), g)
(4)
6For notational brevity, we leave the dependency of V
on (cid:2) implicit as it should be clear from context.
Figure 2: Pseudo-code to linearize a dependency tree
according to a grammar’s ordering function g. In
this code, each node contains a word and its syntac-
tic dependents.
we follow Hahn et al. (2020) in transforming
dependency trees such that function words are
treated as heads, leading to representations closer
to those of standard syntactic theories; see also
Gerdes et al. (2018).
Tree Linearization. While syntactic relation-
ships are naturally described hierarchically, sen-
tences are produced and processed as linear strings
of words. Importantly, there are many ways to
’s nodes into a
linearize a dependency parse
string y. Concretely, a grammar under our for-
malism is defined by an ordering function (see
Kuhlmann, 2010) g(·, ·) which takes as arguments
a dependency parse and a specific node in it, and
returns an ordering of the node and its depen-
dents. For each node, its dependents are arranged
from left to right according to this ordering; any
node without dependents is trivially an ordered
set on its own. This process proceeds recursively
to arrive at a final ordering of all nodes in a de-
pendency tree, yielding the final string y. Pseudo-
based on an
code for the linearization of a tree
ordering function g is given in Figure 2.
Simplifying Assumptions. One consequence of
this formalism is that all counterfactual orders
correspond to projective trees,
trees with
no crossing dependencies. While projectivity is
a well-attested cross-linguistic tendency, human
languages do not obey it absolutely (Ferrer-i-
Cancho et al., 2018; Yadav et al., 2021). Within
the space of projective word order interventions
i.e.,
1051
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
8
9
2
1
5
4
4
9
5
/
/
t
l
a
c
_
a
_
0
0
5
8
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
8
9
2
1
5
4
4
9
5
/
/
t
l
a
c
_
a
_
0
0
5
8
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
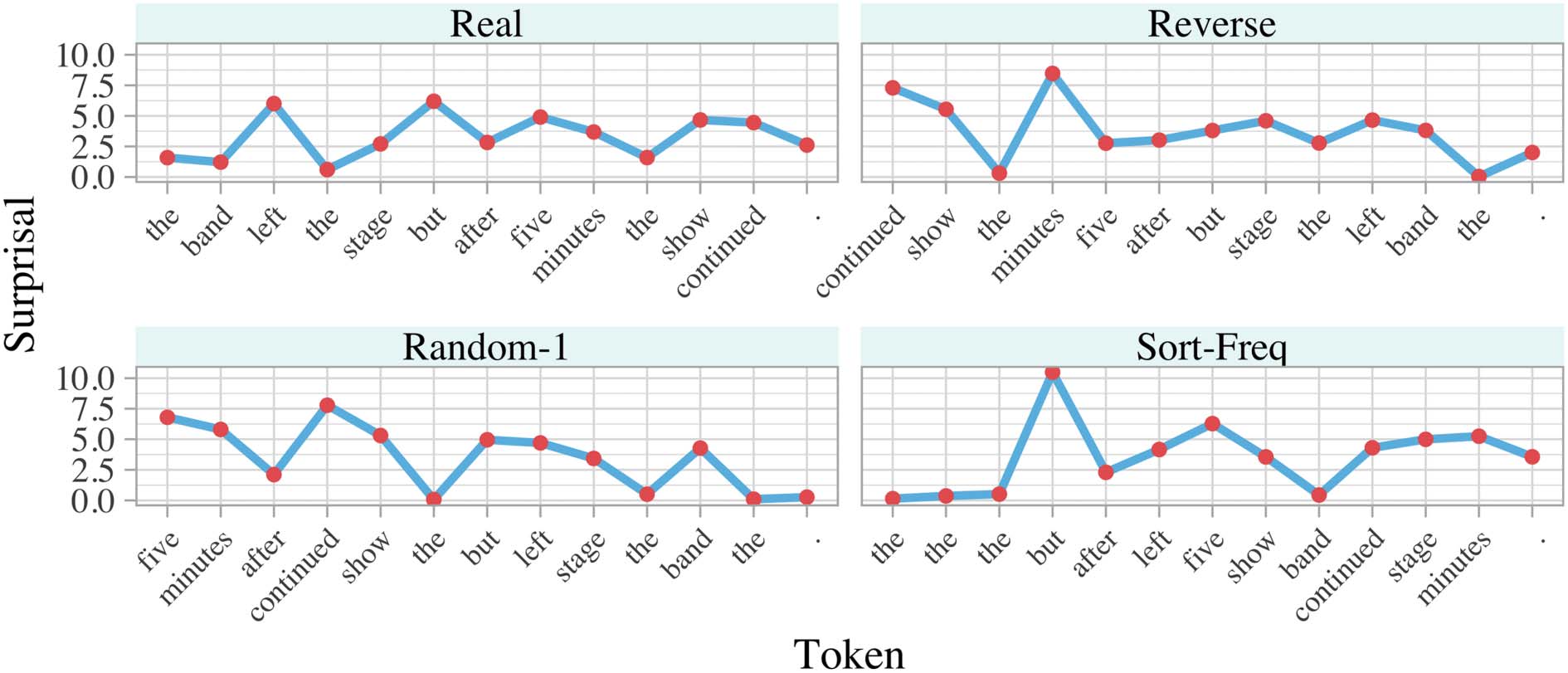
Figure 3: The same source sentence according to 4 real and counterfactual orderings.
We use a state-of-the-art parser (Straka and
Strakov´a, 2017) to implement parse : Y → T
where T is the set of all dependency parses. Spe-
cifically, we define parse(y) = argmax ∈T
| y) for a learned conditional probability
p(
distribution over possible parses p(· | y). We
then obtain the linearized form of the resulting
tree by supplying it and the ordering function g
to linearize, as defined above. Collectively,
the outputs of this process (parallel datasets dif-
fering only in word order) are referred to as
variants. Importantly, f here is a determinis-
tic function; one could instead consider f to be
probabilistic in nature, with each sentence y hav-
. We dis-
ing a distribution over tree structures
cuss the implications of this choice in §4.
3.2 Counterfactual Grammar Specifications
In addition to the original REAL word order,
we explore the following theoretically motivated
counterfactual grammars for each language. Ex-
ample sentences from several of these grammars
are shown in Figure 3.
Consistent Approximation to Real Order. AP-
PROX is a consistent approximation to the real
word order within our formalism; it uses an order-
ing function parameterized by weights that were
fitted to maximize the likelihood of observed
word orders for each language, as reported by
Hahn et al. (2020). This variant captures most of
the word order features of a real language while
allowing for a fair comparison to deterministic
counterfactual grammars that do not model the
flexibility of real language. From the perspective
of the UID hypothesis, we expect this variant
to be less uniform that REAL because it has less
flexibility to accommodate speakers’ choices that
optimize for UID.
Consistent Random Grammars. We include
variants RANDOM1 through RANDOM5, which use
ordering functions parameterized by randomly
assigned weights. This means that for a given
random grammar, each dependency relation has
a fixed direction (left or right), but that the di-
rections of these relations lack the correlations
observed in natural language (Greenberg, 1963).
Random grammars with the same numerical in-
dex share weights across languages.
Consistent Grammars Optimized for Effi-
ciency. We include two consistent grammars
that are optimized for the joint objective of par-
seability (how much information an utterance
provides about
its underlying syntactic struc-
ture) and sentence-internal predictability, as re
ported by Hahn et al. (2020), one with OV order
(EFFICIENT-OV) and one with VO order (EFFICIENT-
VO). For example, the EFFICIENT-OV grammar for
English would give a plausible version of a con-
sistent and efficient grammar in the counterfac-
tual world where English has verbs after objects.
Grammars Optimized for Dependency Length
Minimization. From the same work we also
take consistent grammars that are optimized for
1052
DLM, denoted as MIN-DL-OPT. While lineariza-
tions produced by these grammars are not gua-
ranteed to minimize dependency length for any
particular sentence, they minimize the expected
average dependency length of a large sample of
sentences in a language. In addition, we include
MIN-DL-LOC, an inconsistent grammar that applies
the projective dependency-length minimization
algorithm of Gildea and Temperley (2007) at the
sentence level, leading to sentences with minimal
DL but without the constraint of consistency.
Frequency-sorted Grammars. SORT-FREQ is an
inconsistent grammar which orders words in a
sentence from highest to lowest frequency, ig-
noring dependency structure altogether. We use
this ordering as a heuristic baseline for which
we expect UID to hold relatively strongly: Low-
frequency elements, which tend to have higher
surprisal even if solely from their less frequent
usage (Ellis, 2002), are given more context, and
thus should have smaller surprisals than if they
occurred early; more conditioning context tends
to reduce the surprisal of the next word (Luke and
Christianson, 2016). We also test SORT-FREQ-REV,
ordering words from least to most frequent, which
for analogous reasons we expect
to perform
poorly in terms of UID. However, both of these
orderings lead to massive syntactic ambiguity
by introducing many string collisions—any two
sentences containing the same words in differ-
ent orders would be linearized identically. This
eliminates word order as a mechanism for ex-
pressing distinctions in meaning, so these orders
are implausible as alternatives to natural
lan-
guages (Mahowald et al., 2022).
Reverse Grammar. Finally, we also include the
REVERSE variant, where the words in each sentence
appear in the reverse order of the original. This
variant preserves all pairwise distances between
words within sentences and has identical depen-
dency lengths as the original order, thus isolating
the effect of linear order on information density
from other potential influences. Notably, if the
original language happens to be perfectly consis-
tent, then REVERSE will also satisfy consistency;
in practice, this is unlikely to hold with natural
languages.
3.3 UID and Counterfactual Grammars
Let p(cid:2)(y) be the probability distribution over
sentences y for a language of interest (cid:2). We can
define a language’s UID score as the expected
value of its sentences’ UID scores, where we
overload the UID function to take either a sen-
tence y or an entire language (cid:2):
UID((cid:2)) def=
(cid:3)
y∈Y
p(cid:2)(y) UID(y)
(5)
sentence-level UID can be UIDv(y),
where
UIDlv(y), or UIDp(y). In practice, we estimate this
language-level UID score using a Monte-Carlo
estimator, taking the mean sentence-level UID
score across a held-out test set S(cid:2) of sentences
y in language (cid:2), where we assume y ∼ p(cid:2):
(cid:4)UID((cid:2)) def=
1
|S(cid:2)|
(cid:3)
y∈S(cid:2)
UID(y)
(6)
Similarly,
entropy, H) of this language is computed as:
the expected surprisal (or Shannon
H((cid:2)) def= −
(cid:3)
y∈Y
p(cid:2)(y) log p(cid:2)(y)
(7)
We evaluate how well a language model pθ
approximates p(cid:2) by its cross-entropy:
H(p(cid:2), pθ) = −
(cid:3)
y∈Y
p(cid:2)(y) log pθ(y)
(8)
where a smaller value of H implies a better
model. Again using a Monte Carlo estimator,
we measure cross-entropy using the held-out test
set S(cid:2):
(cid:5)H(p(cid:2), pθ) = − 1
|S(cid:2)|
(cid:3)
y∈S(cid:2)
log pθ(y)
(9)
This is simply the mean surprisal that the model
assigns to a corpus of naturalistic data.
These computations can also be applied to
counterfactual variants of a language. Let (cid:2)f
stand for a language identical to (cid:2), but where
its strings have been transformed by f; this lan-
guage’s distribution over sentences would be
y(cid:10)∈Y p(cid:2)(y(cid:10)) {y = f(y(cid:10))}. Since
p(cid:2)f(y) =
entropy is non-increasing over function transfor-
mations (by Jensen’s inequality), it follows that:
(cid:2)
H((cid:2)) ≥ H((cid:2)f)
(10)
1053
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
8
9
2
1
5
4
4
9
5
/
/
t
l
a
c
_
a
_
0
0
5
8
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Further, if our counterfactual generation function
f is a bijection—meaning that each input string
gets mapped to a distinct output string and each
output string has an input that maps to it—then
we can create a second function f−1 : Y →
Y, which would generate (cid:2) from (cid:2)f. Then, the
following holds:
H((cid:2)) ≥ H((cid:2)f) ≥ H((cid:2)f−1◦ f) = H((cid:2))
(11)
i.e., it must be that H((cid:2)) = H((cid:2)f). Reversing a
sentence is an example of a bijective function,
and thus Equation (11) holds necessarily for the
pair of REAL and REVERSE variants; the counter-
factual generation procedure thus should not pro-
duce differences in mean surprisal between these
variants. At the same time, bijectivity does not
necessarily hold for our other counterfactual trans-
formations and is violated to a large degree when
mapping to SORT-FREQ and SORT-FREQ-REV. Thus
in general, we can only guarantee Inequality 10.
Crucially, however, the transformation f might
change the UID score of such a language, al-
lowing us to evaluate the impact of word order
on information uniformity. As a simple example,
consider the language (cid:2)1 that places a uniform
distribution over only four strings: aw, ax, by,
and bz. In this language, the first and second
symbols always have 1 bit of surprisal, and the
end of the string has 0 bits of surprisal. If the
counterfactual language (cid:2)2 is the reverse of (cid:2)1, we
have a uniform distribution over the strings wa,
xa, yb, and zb. Here, the first symbol always has
2 bits of surprisal, and the second symbol and
end of sentence always have zero bits, as their
values are deterministic for a given initial sym-
bol. While the mean surprisal per symbol is the
same for (cid:2)1 and (cid:2)2, (cid:2)1 has more uniform infor-
mation density than (cid:2)2.
4 Limitations
4.1 Use of Counterfactual Grammars
Real Word Orders Are not Consistent. The
consistent grammars borrowed from Hahn et al.
(2020) assume that the direction of each syntactic
relation, as well as the relative ordering of de-
pendents on the same side of a head, are fixed.
This is not generally true of natural languages. We
address this difference by including the variant AP-
PROX as a comparison to the counterfactual vari-
ants, which are constrained by consistency, and
by including REVERSE as a comparison to REAL,
both of which are not constrained by consistency.
Automatic Parsing Errors. Another issue is
that the dependency parses extracted for each
original sentence as part of the counterfactual
generation pipeline may contain parsing errors.
These errors may introduce noise into the coun-
in the
terfactual datasets that
original sentences, and may cause deviations from
the characteristics that we assume our counter-
factual grammars should induce. For example,
MIN-DL-LOC only produces sentences with mini-
mized dependency length if the automatic parse is
correct.
is not present
Deterministic Parsing. Finally, our counter-
factual generation procedure assumes a determin-
istic mapping from sentences to dependency trees
as one of its steps. However, multiple valid parses
of sentences are possible in the presence of syn-
tactic ambiguity. In such cases, we always select
the most likely structure according to the parser,
which learns these probabilities based on its train-
ing data. Therefore, this design choice could lead
to underrepresentation of certain syntactic struc-
tures when applying a transformation. However,
we note that the variants REAL, REVERSE, SORT-
FREQ, and SORT-FREQ-REV do not depend on de-
pendency parses and so are unaffected by this
design choice.
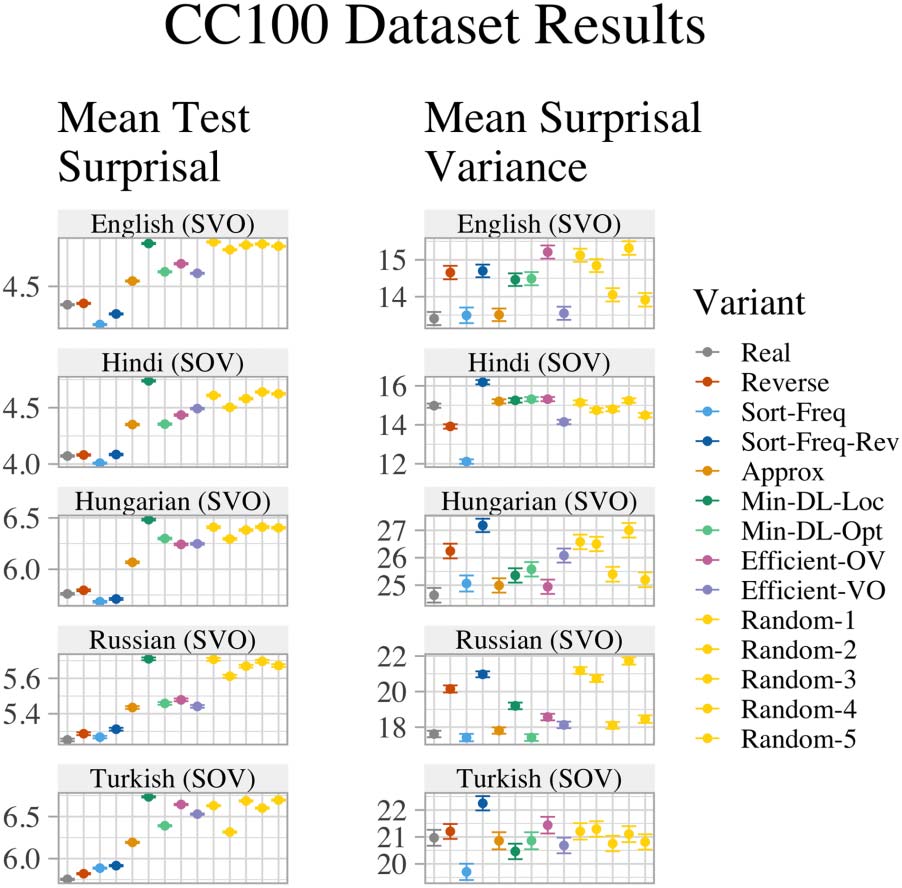
4.2 Choice of Dataset
Properties of language can vary across genres and
domains. When drawing conclusions about hu-
man language in general, no single dataset will
be completely representative. Due to the amount
of data required to train LMs, we use written
corpora in this work, and use the term speaker
loosely to refer to any language producer regard-
less of modality. To address potential concerns
about the choice of dataset in this study, we con-
ducted a supplementary analysis on a subset of
languages using a different web corpus, which we
report in §7.5.
4.3 Errors and Inductive Biases
Model Errors. Language model quality could
impact the estimated values of our UID metrics
UIDv, UIDp, and UIDlv. To see why, consider a
model pθ that—rather than providing unbiased
1054
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
8
9
2
1
5
4
4
9
5
/
/
t
l
a
c
_
a
_
0
0
5
8
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
estimates of p(cid:2)—is a smoothed interpolation be-
tween p(cid:2) and the uniform distribution:
pθ(yn | y