A Constraint-Based Hypergraph Partitioning
Approach to Coreference Resolution
∗
Emili Sapena
Universitat Polit`ecnica de Catalunya
∗∗
Llu´ıs Padr ´o
Universitat Polit`ecnica de Catalunya
†
Jordi Turmo
Universitat Polit`ecnica de Catalunya
This work is focused on research in machine learning for coreference resolution. Coreference
resolution is a natural language processing task that consists of determining the expressions in
a discourse that refer to the same entity.
The main contributions of this article are (i) a new approach to coreference resolution
based on constraint satisfaction, using a hypergraph to represent the problem and solving it
by relaxation labeling; and (ii) research towards improving coreference resolution performance
using world knowledge extracted from Wikipedia.
The developed approach is able to use an entity-mention classification model with more
expressiveness than the pair-based ones, and overcome the weaknesses of previous approaches
in the state of the art such as linking contradictions, classifications without context, and lack
of information evaluating pairs. Furthermore, the approach allows the incorporation of new
information by adding constraints, and research has been done in order to use world knowledge
to improve performances.
RelaxCor, the implementation of the approach, achieved results at the state-of-the-art level,
and participated in international competitions: SemEval-2010 and CoNLL-2011. RelaxCor
achieved second place in CoNLL-2011.
1. Introduction
Coreference resolution is a natural language processing (NLP) task that consists of
determining which mentions in a discourse refer to the same entity or event. A men-
tion is a referring expression that has an entity or event as a referent. By referring
expression we mean noun phrases (NP), named entities (NEs), embedded nouns, and
pronouns (all but pleonastic and interrogative ones) whose meaning as a whole is a
∗ TALP Research Center, Universitat Polit`ecnica de Catalunya. E-mail: esapena@lsi.upc.edu.
∗∗ TALP Research Center, Universitat Polit`ecnica de Catalunya. E-mail: padro@lsi.upc.edu.
† TALP Research Center, Universitat Polit`ecnica de Catalunya. E-mail: turmo@lsi.upc.edu.
Submission received: 12 March 2012; revised submission received: 14 September 2012; accepted for
publication: 13 November 2012.
doi:10.1162/COLI a 00151
© 2013 Association for Computational Linguistics
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
[[FC Barcelona]0 president Joan Laporta]1 has warned [Chelsea]2 off [star striker Lionel
Messi]3.
Aware of [[Chelsea]2 owner Roman Abramovich]4’s interest in [the young Argentine]3,
[Laporta]1 said last night: “[I]1 will answer as always, [Messi]3 is not for sale and [we]0
do not want to let [him]3 go.”
Figure 1
Example of coreference resolution. All the mentions are annotated with a subscript indicating
their coreference chain. Boldfaced mentions refer to the entity Lionel Messi.
reference to an entity or event in the real world, which is what we call referent. In
this article, we do not deal with coreference involving events, and focus only on entity
correference.
Coreference chains or entities are groups of referring expressions that have the
same referent. Thus, a coreference chain is formed by all mentions in a discourse that
refer to the same real entity. Given an arbitrary text as input, the goal of a coreference
resolution system is to find all the coreference chains. A partial entity is a set of
mentions considered coreferential during resolution.
Figure 1 shows the mentions of a newspaper article and their corresponding coref-
erence chains. Note that the difficulty of coreference resolution lies in the variety of
necessary knowledge sources. For instance, morphological and syntactic analysis is
needed to detect mentions, and semantic/world knowledge to know that Messi is a
star striker and a young Argentine.
Coreference resolution is a mandatory step in order to understand natural language.
In this sense, dealing with such a problem becomes important for tasks in which the
higher their comprehension of the discourse, the better such systems will perform—
tasks such as machine translation (Peral, Palomar, and Ferr´andez 1999), question an-
swering (Morton 2000), summarization (Azzam, Humphreys, and Gaizauskas 1999),
and information extraction.
One of the possible directions to follow in coreference resolution research is
the incorporation of new information such as world knowledge and discourse co-
herence. In some cases, this information cannot be expressed in terms of pairs of
mentions—that is, it is information that involves either several mentions at once or
partial entities. Furthermore, an experimental approach in this field should over-
come the weaknesses of previous state-of-the-art approaches, such as linking contra-
dictions, classifications without context, and a lack of information when evaluating
pairs.
This article presents an approach for coreference resolution based on constraint
satisfaction that represents the problem in a hypergraph and solves it by relaxation
labeling. One of the main goals of developing such an approach is the incorporation
of world knowledge and discourse coherence in order to improve performance while
addressing the problems mentioned previously.
The article is structured as follows. Section 2 summarizes the state of the art of
machine learning approaches to coreference resolution, highlighting their most rele-
vant parts with their corresponding issues. Section 3 defines our proposed approach
and Section 4 provides details about the implementation and the training methods.
The experiments and error analysis are described in Section 5. Section 6 presents our
approach to incorporate world knowledge in order to improve coreference resolution
performance. Experiments and a detailed error analysis are also included. Finally, we
discuss the conclusions of this article in Section 7.
848
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
2. Coreference Resolution: State of the Art
In this section we summarize the main machine-learning–based approaches to corefer-
ence resolution. For a wider study, we refer the reader to Mitkov (2002).
A coreference resolution system receives plain text as input, and returns the same
text with coreference annotations as output. Most existing coreference resolution sys-
tems can be considered instances of this general process, which consists of three main
steps: mention detection, characterization of mentions, and resolution (see Figure 2).
The first step is the detection of mentions, where text processing is needed in order
to find the boundaries of the mentions in the input text. Next, in the second step, the
identified mentions are characterized by gathering all the available knowledge about
them and their possible compatibility. Typically, machine learning systems introduce all
the knowledge by means of feature functions. Finally, the resolution itself is performed
in the third step. A generalization of the inner architecture of the resolution step is
difficult given the diversity of approaches and algorithms used for resolution. Even
so, the diverse approaches in current systems have at least two main processes in the
resolution: classification and linking.
(cid:1)
(cid:1)
Classification. This process evaluates the compatibility of elements in
order to corefer. The elements can be mentions or partial entities. A typical
implementation is a binary classifier that assigns class CO (coreferential)
or NC (not coreferential) to a pair of mentions. It is also very typical to use
confidence values or probabilities associated with the class. Classifiers can
also use rankers and constraints.
Linking. The linking process links mentions and partial entities in order
to form the final entities. This process may range from a simple heuristic,
such as single-link, to an elaborate algorithm such as clustering or graph
partitioning. The input of the linking process includes the output of the
classification process: classes and probabilities.
2.1 Classification Models
The models found in the state of the art for the classification process are: mention pairs,
rankers, and entity-mention.
Mention pairs. Classifiers based on the mention-pair model determine whether two
mentions corefer or not. To do so, a feature vector is generated for a pair of mentions
using a set of features. Given these features as input, the classifier returns a class:
CO (coreferent), or NC (not coreferent). In many cases, the classifier also returns a
confidence value about the decision taken. The class and the confidence value of each
Figure 2
Architecture of a coreference resolution system.
849
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Figure 3
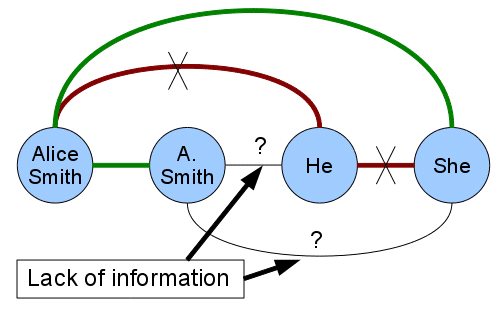
A pairwise classifier does not have enough information to classify pairs (A. Smith, he) and (A.
Smith, she).
evaluated pair of mentions will be taken into account by the linking process to obtain
the final result.
The mention-pair model has two main weaknesses: a lack of contextual infor-
mation and contradictions in classifications. Figure 3 shows an example of lack of
information. The figure is a representation of a document with four mentions (Alice
Smith, A. Smith, he, she). The edges between mentions represent the classification in
a mention-pair model; green means that the classifier returns the CO class, and red
(also marked with an X) returns the NC class. In this case, the lack of information is
due to the impossibility of determining the gender of A. Smith. Next, Figure 4 shows
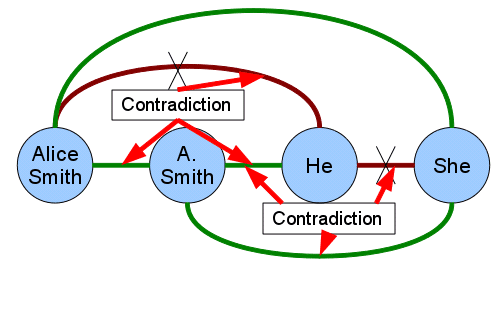
a possible scenario with contradictions. In this scenario, the classifier has determined
that the pairs (A. Smith, he) and (A. Smith, she) corefer, which causes contradictions
when generating the final coreference chains given that the pairs (Alice Smith, he) and
(he, she) do not corefer.
Rankers. The rankers model overcomes the lack of contextual information found using
mention-pairs. Instead of directly considering whether mi and mj corefer, more perspec-
tive can be achieved by looking for the best candidate from a group of mentions to
corefer with an active mention. Rankers can still fall in contradictions, however, and
need to rely on the linking process to solve that.
Entity-mention. The entity-mention model classifies a partial entity and a mention, or
two partial entities, as coreferent or not. In some models, a partial entity even has its
Figure 4
Green edges mean that both mentions corefer, and red edges mean the opposite. An
independent classification of (A. Smith, he) and (A. Smith, she) produces contradictions.
850
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
own properties or features defined in the model in order to be compared with the
mentions. Due to the information that a partial entity gives to the classifier, in most
cases this model overcomes the lack of information and contradiction problems of the
mention-based models. For example, a partial entity may include the mentions Alice
Smith and A. Smith, whose genders are “female” and “unknown” respectively. In this
case, the partial entity is more likely to be linked with the subsequent mention she than
with he (Figures 3 and 4). The features used for entity-mention models are almost the
same as those used for mention-based models. The only difference is that the value of
an entity feature is determined by considering the particular values of the mentions
belonging to it.
2.2 Resolution
The coreference resolution engines in the state of the art can be classified into three
paradigms depending on their resolution process (i.e., combinations of classification
and linking processes):
(cid:1)
(cid:1)
(cid:1)
Backward search approaches classify mentions with previous ones,
looking for the best antecedents. In this case, the linking step is typically
an heuristic that links mention pairs classified as positive (single-link).
Two-step approaches perform the resolution in two separate steps. The
first step is to classify all of the elements, and then the second step is a
linking process using algorithms such as graph partitioning or clustering
to optimize the results given the classification output.
One-step approaches directly run the linking process while classification
is performed on-line. In this manner, mention-group and entity-mention
models can be easily incorporated.
Figure 5 summarizes the classification of several systems in the state of the art,
up to 2011. Recently, the CoNLL-2012 shared task (Pradhan et al. 2012) offered an
evaluation framework similar to that of CoNLL-2011. The second column specifies
which resolution step is used. The third column shows the classification model used
by the system, and the fourth column identifies the algorithm followed in the linking
process.
More details about supervised machine learning systems can be found in Ng (2010).
3. A Constraint-Based Hypergraph Partitioning Approach to Coreference Resolution
One of the possible directions to follow in coreference resolution research is the incorpo-
ration of new information such as world knowledge and discourse coherence. In some
cases, this information cannot be expressed in terms of pairs of mentions, that is, it is
information that involves either several mentions at once or partial entities. Therefore,
an experimental approach in this field needs the expressiveness of the entity-mention
model as well as the mention-pair model in order to use the most typical mention-pair
features. Furthermore, such an approach should overcome the weaknesses of previous
state-of-the-art approaches, such as linking contradictions, classifications without con-
text, and a lack of information when evaluating pairs. Also, the approach would be
more flexible if it could incorporate knowledge both automatically and manually.
851
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Approach
Resolution
Classification Model
Linking process
Aone and Bennett (1995)
McCarthy and Lehnert (1995)
Soon, Ng, and Lim (2001)
Ponzetto and Strube (2006)
Yang, Su, and Tan (2006)
Ng and Cardie (2002)
Ng (2005)
Ng (2007)
Ji, Westbrook, and Grishman (2005)
Bengtson and Roth (2008)
Stoyanov et al. (2009)
Ng (2009)
Uryupina (2009)
Yang et al. (2003)
Denis and Baldridge (2008)
Yang et al. (2008)
Rahman and Ng (2011b)
Luo et al. (2004)
Luo (2007)
Klenner and Ailloud (2008)
Nicolae and Nicolae (2006)
Denis and Baldridge (2007)
Klenner (2007)
Finkel and Manning (2008)
Bean et al. (2004)
Cardie and Wagstaff (1999)
Ng (2008)
Culotta, Wick, and McCallum (2007)
Finley and Joachims (2005)
Cai and Strube (2010)
Yang et al. (2004)
McCallum and Wellner (2005)
Haghighi and Klein (2007)
Poon and Domingos (2008)
backward
search
mention pairs
heuristic
rankers
entity-
mention
two step
mention pairs
one step
entity-
mention
global
optimization
clustering
graph partitioning
global
optimization
clustering
hypergraph partitioning
clustering
graph partitioning
global
optimization
Figure 5
A classification of coreference resolution approaches in state-of-the-art machine-learning systems.
Given these prerequisites, we define an approach based on constraint satisfaction
that represents the problem in a hypergraph and solves it by relaxation labeling, re-
ducing coreference resolution to a hypergraph partitioning problem with a given set of
constraints. The main strengths of this system are:
(cid:1)
(cid:1)
(cid:1)
Modeling the problem in terms of hypergraph partitioning avoids linking
contradictions and errors caused by a lack of information or context.
Constraints are compatible with the mention-pair and entity-mention
models, which let us incorporate new information. Moreover, constraints
can be both automatically learned and manually written.
Relaxation labeling is an iterative algorithm that performs function
optimization based on local information. It first determines the entities of
the mentions in which it has more confidence, mainly solving the problem
of lack of information for some pairs and the lack of context. The iterative
resolution facilitates the use of the entity-mention model.
The rest of this section describes the details of the approach. Section 3.1 describes
the problem representation in a (hyper)graph. Next, Section 3.2 explains how the
852
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
knowledge is represented as a set of constraints, and Section 3.3 explains how attach-
ing influence rules to the constraints means that the approach incorporates the entity-
mention model. Finally, Section 3.4 describes the relaxation labeling algorithm used for
resolution.
3.1 Graph and Hypergraph Representations
The coreference resolution problem consists of a set of mentions that have to be
mapped to a minimal collection of individual entities. By representing the problem
in a hypergraph, we are reducing coreference resolution to a hypergraph partitioning
problem. Each partition obtained in the resolution process is finally considered
an entity.
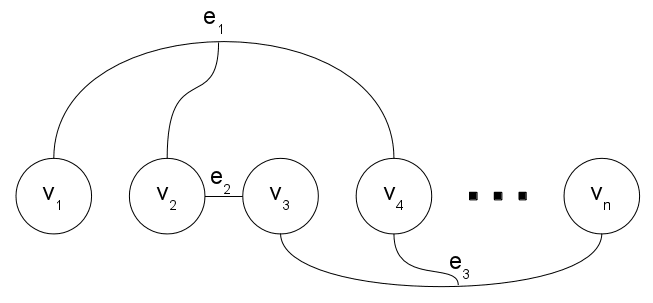
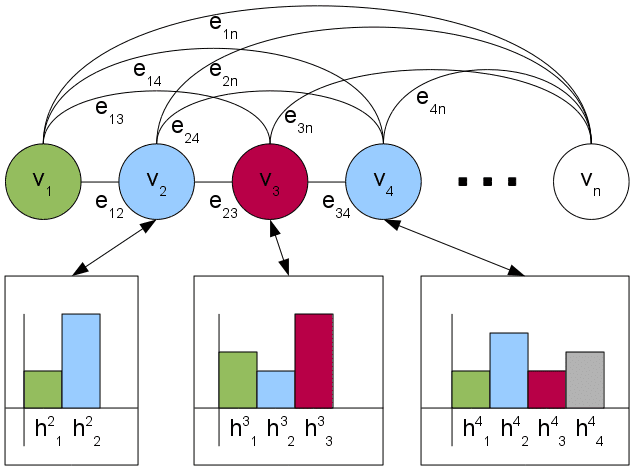
The document mentions are represented as vertices in a hypergraph. Each of
these vertices is connected by hyperedges to other vertices. Hyperedges are assigned
a weight that indicates the confidence that adjacent mentions corefer. The larger the
hyperedge weight in absolute terms, the more reliable the hyperedge. In the case of the
mention-pair model, the problem is represented as a graph where edges connect pairs
of vertices.
Let G = G(V, E) be an undirected hypergraph, where V is a set of vertices and E is
a set of hyperedges. Let m = (m1, . . . , mn) be the set of mentions of a document with n
∈ V.
mentions to resolve. Each mention mi in the document is represented as a vertex vi
∈ E is added to the hypergraph for each group (g) of vertices (v0, . . . , vN)
A hyperedge eg
affected by a constraint, as shown in Figure 6. The subset of hyperedges that incide on
vi is E(vi).
A subset of constraints Cg
⊆ C restricts the compatibility of a group of mentions. Cg
is used to compute the weight value of the hyperedge eg. Let w(eg) ∈ W be the weight
of the hyperedge eg:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
(cid:1)
w(eg) =
λk
k∈Cg
(1)
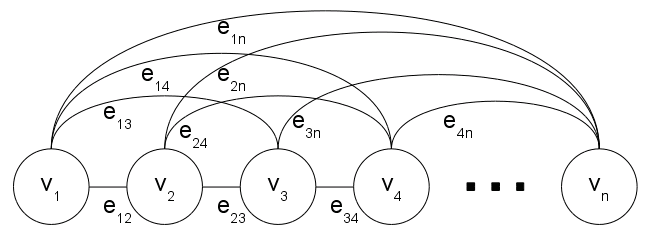
where λk is the weight associated with constraint k. The graph representing the mention-
pair model is a subcase of the hypergraph where |g| = 2. Figure 7 illustrates a graph. For
simplicity, in the case of the mention-pair model, an edge between mi and mj is called
eij. In addition, sometimes wij is used instead of w(eij).
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6
Example of hypergraph representing the mentions of a document connected by hyperedges
(mention-group model).
853
Computational Linguistics
Volume 39, Number 4
Figure 7
Example of graph representing the mentions of a document connected by edges (mention-pair
model).
DIST SEN 1(0,1) & GENDER YES(0,1) & ¬ FIRST(0) &
MAXIMALNP(0) & MAXIMALNP(1) &
SRL ARG 0(0) & SRL ARG 0(1) &
TYPE P(0) & TYPE P(1)
Figure 8
Example of a mention-pair constraint (N = 2).
DIST SEN 1(0,1) & DIST SEN 1(1,2) &
AGREEMENT YES(0,1,2) & ALIAS YES(0,2) &
SRL ARG 0(0) & SRL ARG 0(1) & SRL ARG 0(2) &
TYPE E(0) & TYPE S(1) & TYPE E(2)
Figure 9
Example of a mention-group constraint (N = 3).
3.2 Constraints as Knowledge Representation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
In this approach, knowledge is a set of weighted constraints where each constraint
contributes a piece of information that helps to determine the coreferential relations
between mentions. A constraint is a conjunction of feature-value pairs that are evaluated
over all the pairs or groups of mentions in a document. When a constraint applies to a
set of mentions, a corresponding hyperedge is added to the hypergraph, generating the
representation of the problem explained in Section 3.1 (Figure 6).
Let N be the order of a constraint, that is, the number of mentions expected by the
constraint (|g|). A pair constraint has order N = 2, and a group constraint has N > 2.
The mentions evaluated by a constraint are numbered from 0 to N − 1 in the order they
are found in the document.
Figures 8 and 9 show examples of constraints for N = 2 and N = 3, respectively.
The constraint in Figure 8 requires that: The distance between the mentions is just
one sentence, their genders match, m0 is not the first mention of its sentence, m0 is
a maximal NP (the next parent node in the syntactic tree is the sentence itself), m1
also is a maximal NP, both mentions are ARG0 in semantic role labeling, and both
mentions are pronouns.1 The constraint in Figure 9 applies to three mentions and
requires that: The distance between consecutive mentions is one sentence, all three
mentions agree in both gender and number, m0 and m2 are aliases, all three mentions
are ARG0 in their respective sentences, and m0 and m2 are named entities and m1 is
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 The argument system used is due to PropBank (Kingsbury and Palmer 2003).
854
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
a common NP.2 There are many examples of negative constraints, that is, constraints
that restrict mentions from being in the same entity. For instance GENDER NO(0,1)
& TYPE P(0) & TYPE P(1) expresses that m1 and m0 are pronouns and do not match
in gender.
Each constraint has a weight that determines the hyperedge weight of the hyper-
graph (see Equation (1)). A constraint weight is a value that, in absolute terms, reflects
the confidence of the constraint. Moreover, this weight is signed, and the sign indicates
whether the adjacent mentions corefer (positive) or not (negative). The use of negative
information is not very extensive in state-of-the-art systems, but given the hypergraph
representation of the problem, where most of the mentions are interconnected, the
negative weights contribute information that cannot be obtained using only positive
weights. Moreover, in our experiments, the use of negative weights accelerates the
convergence of the resolution algorithm. The training process that determines the
weight of each constraint is explained in Section 4.3.
3.3 Entity-Mention Model Using Influence Rules
We have explained how groups of mentions satisfying a constraint are connected by
hyperedges in the hypergraph. This section explains how the entity-mention model
is definitively incorporated to our constraint-based hypergraph approach. The entity-
mention model takes advantage of the concept of an entity during the resolution pro-
cess. This means that each mention belongs to an entity during resolution, and this
information can be used to make new decisions.
In order to incorporate the entity-mention model into our approach, we define
the influence rule, which is attached to a constraint. An influence rule expresses the
conditions that the mentions must meet during resolution before the influence of the
constraint takes effect.
An influence rule consists of two parts: condition and action.
(cid:1)
(cid:1)
The condition of an influence rule is a conjunction of coreference relations
that the mentions must satisfy before the constraint has influence. This
condition is specified by joining mentions into groups, where each
group represents a partial entity specified by a subscript. For instance,
(0, 1)A, (2)B means that mentions 0 and 1 belong to entity A and mention 2
belongs to entity B (A (cid:7)= B).
The action of an influence rule defines the desired coreference relation
and determines which mentions are influenced. It is expressed in the
same terms as the condition, specifying the mentions that are influenced
and the entity to which they should belong. For instance, an action can
be (3)B. This action indicates that mention 3 is influenced in order to
belong to entity B.
Figure 10 shows an example of an N = 4 constraint with an influence rule attached.
The constraint specifies the feature functions that the involved mentions must meet,
such as semantic role arguments, sentence distances, and agreements. The influence rule
then determines that when mentions 0 and 2 belong to the same entity, and mention 1
2 Feature functions used in our experiments are explained in detail in Section 4.2.
855
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Constraint:
SRL ARG 0(0) & SRL ARG 1(1) & SRL ARG 0(2) & SRL ARG 1(3) &
DIST SEN 0(0,1) & DIST SEN 1(1,2) & DIST SEN 0(2,3) &
AGREEMENT YES(0,2) & AGREEMENT YES(1,3)
Influence rule: (0, 2)A, (1)B
Example:
Charlie0 called Bob1.
He2 invited him3 to the party.
⇒ (3)B
Figure 10
Artificial example of an entity-mention constraint. It takes advantage of the partial entities
during resolution. If mentions 0 and 2 tend to corefer, the structure indicates that mentions 1
and 3 may corefer in a different entity.
belongs to a different entity, mention 3 is influenced in order to belong to the same entity
as mention 1. This figure also contains some text to help understand why this kind of
constraint may be useful. A mention-pair approach could easily make the mistake of
classifying mentions 2 and 3 as coreferent. This is an example of introducing information
about discourse coherence using an entity-mention model.
In order to retain consistency with the mention-pair model, all the constraints used
in this approach are assigned a default influence rule that depends on the sign of the
edge weight. In the case that the weight is positive, the last mention is influenced
to belong to the same entity as the first mention, and a negative weight causes the
opposite. Figure 11 shows the default influence rules for mention-pair constraints with
both positive and negative weights.
Note that when influence rules are used, a hyperedge is added for each subset of
constraints that applies to the same group of mentions and has the same influence rule.
In the case that some constraints apply to the same group of mentions but have different
influence rules, a hyperedge is added to the graph for each influence rule. Therefore, in
⊆ C refers to the constraints that apply to the group and share the same
Equation (1), Cg
influence rule.
3.4 Relaxation Labeling
Relaxation is a generic name for a family of iterative algorithms that perform function
optimization based on local information. They are closely related to neural nets and
gradient steps. Relaxation labeling has been successfully used in engineering fields to
solve systems of equations, in Artificial Intelligence for computer vision (Rosenfeld,
Hummel, and Zucker 1976), and in many other AI problems. The algorithm has also
been widely used to solve NLP problems such as part-of-speech tagging (Padr ´o 1998),
chunking, knowledge integration, semantic parsing (Atserias 2006), and opinion mining
(Popescu and Etzioni 2005).
Description
Default influence rule for a
mention-pair constraint (positive weight)
Default influence rule for a
mention-pair constraint (negative weight)
Example of an influence rule for an
entity-mention constraint
Conditions
Action
(0)A
(0)A
(0, 2)A, (1)B
(1)A
(1)B
(3)B
Figure 11
Default influence rules for mention-pair constraints.
856
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
Figure 12
Representation of Relax solving a graph. The vertices representing mentions are connected by
weighted edges eij. Each vertex has a vector hi of probabilities to belong to different partitions.
The figure shows h2, h3, and h4.
Relaxation labeling (Relax) solves our weighted constraint-based hypergraph par-
titioning problem by dealing with (hyper)edge weights as compatibility coefficients.3 In
this manner, each vertex is assigned to a partition satisfying as many constraints as
possible. In each step, the algorithm updates the probability of each vertex belonging
to a partition. This update is performed by transferring the probabilities of adjacent
vertices proportional to the edge weights.
Let V = {v1, v2, . . . , vn
} be a set of variables. In our approach, each vertex (vi) in the
hypergraph is a variable in the algorithm. Let Li be the number of different labels that
are possible for vi. The possible labels of each variable are the partitions that the vertex
can be assigned. Note that the number of partitions (entities) in a document is a priori
unknown, but it is at most the number of vertices (mentions) because, in an extreme
case, each mention in a document could refer to a different entity. Therefore, a vertex
with index i can be in the first i partitions (i.e., Li = i).
The aim of the algorithm is to find a weighted labeling such that global consistency
is maximized. A weighted labeling is a weight assignment for each possible label of
each variable: H = (h1, h2, . . . , hn), where each hi is a vector containing a weight for
each possible label of vi; that is, hi = (hi
2, . . . , hi
). As relaxation is an iterative process,
Li
these weights (of between 0 and 1) vary in time. We denote the probability for label l of
variable vi at time step t as hi
l when the time step is not relevant. Note
that the label assigned to a variable at the end of the process is the one with the highest
weight (max(hi)). Figure 12 shows an example.
l(t), or simply hi
1, hi
Maximizing global consistency is defined as maximizing the average support for
each variable, which is defined as the weighted sum of the support received by each of
× Sil, where Sil is the support received by that pair
its possible labels—that is,
from the context.
Li
l=1 hi
(cid:2)
l
The support for a variable-label pair (Sil) expresses the compatibility of the as-
signment of label l to variable vi compared with the labels of neighboring variables,
according to the edge weights. Although several support functions may be used (Torras
3 For the rest of this section, there is no distinction between edges and hyperedges.
857
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
1989), we chose the following (Equation (2)), which defines the support as the sum of
the influences of the incident edges.
(cid:1)
Sil =
Inf (e)
e∈E(vi )
(2)
where Inf (e) is the influence of edge e. The influence of an edge is defined by its
weight and the influence rules attached to the constraints involved with this edge (see
Section 3.3). An influence rule determines how the current probabilities for the same
label of adjacent vertices (hj
l) are combined.
The pseudo-code for the relaxation algorithm can be found in Figure 13. It consists
of the following steps:
1.
2.
3.
4.
Start with a random labeling, or with a better-informed initial state.
For each variable, compute the support that each label receives from the
current weights of adjacent variable labels following Equation 2.
Normalize support values between −1 and 1. Supports are divided by a
ScaleFactor. In case that after that a support is higher than 1 or −1 then its
value is cutted to 1 or −1, respectively. Given that constraint weights are
between 1 and −1 and a group of mentions is not generally affected by
more than 10 constraints, ScaleFactor is empirically set to 8 in our
experiments.
Update the weight of each variable label according to the support obtained
by each of them (that is, increase weight for labels with high support
[greater than zero], and decrease weight for those with low support
[less than zero]) according to the update function:
hi
l(t + 1) =
(cid:2)
l(t) × (1 + Sil)
hi
Li
k=1 hi
k(t) × (1 + Sik)
(3)
Initialize:
H := H0,
Main loop:
Repeat
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
For each variable vi
For each possible label l for vi
(cid:2)
e∈E(vi ) Inf (e)
Sil =
End for
Normalize supports between -1 and 1
For each possible label l for vi
(t)×(1+Sil )
hi
k
hi
l(t + 1) =
(t)×(1+Sik )
hi
l
(cid:2)Li
k=1
End for
End for
Until no more significant changes
Figure 13
Relaxation labeling algorithm.
858
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
There are many functions that can be used to calculate the support (Torras
1989). The one we chose was also used by Padr ´o (1998) and M`arquez,
Padr ´o, and Rodr´ıguez (2000).
5.
Iterate the process until the convergence criterion is met. The usual
criterion is to wait for no more changes in an iteration, or a maximum
change below some epsilon parameter (Equation (4)). But there is also a
maximum number of iterations where the process is stopped. This number
is a constant and does not depend on the size of the document.
max(hi
l(t + 1) − hi
l(t)) ≤ |(cid:4)| ∀i, l
(4)
Each combination of labels for the graph vertices is a partitioning (Ω). The resolution
which optimizes the goodness function F(Ω, W),
process searches the partitioning Ω∗
which depends on the edge weights W. In this manner, Ω∗
is optimal if:
F(Ω∗
, W) ≥ F(Ω, W), ∀Ω
(5)
A partitioning Ω is directly obtained from the weighted labeling H assigning to
each variable the label with maximum probability. The supports and the weighted
labeling depend on the edge weights (Equation (2)). To satisfy Equation (6) is equivalent
to satisfying Equation (5). Many studies have been done towards the demonstration of
the consistency, convergence, and cost reduction advantages of the relaxation algorithm
(Rosenfeld, Hummel, and Zucker 1976; Hummel and Zucker 1983; Pelillo 1997). For
instance, Hummel and Zucker (1983) prove that maximizing average consistency
(left-hand-side term of Equation (6) produces labelings satisfying Equation (5) when
only binary constraints are used. Although there is no formal proof for higher order
constraints, the presented algorithm (that forces a stop after a number of iterations) has
proven useful for practical purposes in our case.
Li(cid:1)
l=1
∗i
h
l
× Sil
≥
Li(cid:1)
l=1
hi
l
× Sil
∀h, ∀i
(6)
Note that because the weight update for each label is independent of the others,
the algorithm can be straightforward parallelized. In the following, there are some
examples of the Relax implementation of the edge influences (Inf (e)) given the influence
rules attached to the constraints.
The simplest example is when mention m0 has a direct influence over mention
⇒ (1)A. This is determined by
m1. The influence rule attached to the constraint is (0)A
Equation (7) and is the kind of influence used in the mention-pair model.
Inf (e) = w(e) × h0
l
(7)
The next example requires that mention m0 and mention m1 tend to corefer during
⇒ (2)A.
the resolution in order to influence mention m2. The influence rule is (0, 1)A
In this case, the influence of the edge representing this influence rule is given by
Equation (8). Mentions m0 and m1 are tending to corefer (belong to the same entity: l)
when their values for label l are tending to 1 (and the other labels are tending to 0). In
this case, multiplying h0
l achieves a value close to 1, and the influence is almost
l and h1
859
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Figure 14
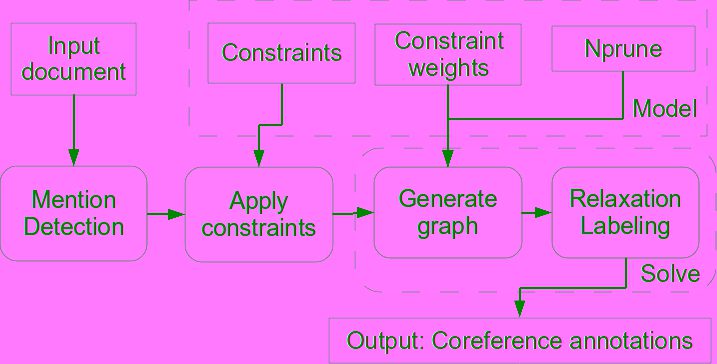
RELAXCOR resolution process.
the weight of the edge. In other cases when the coreference between m0 and m1 is not
clear (or they are clearly not coreferent), at least one of the values of h0
l is not
close to 1 and the value of their product rapidly decreases, so the influence of the edge
also decreases.
l and h1
Inf (e) = w(e) × h0
l
× h1
l
(8)
Following the previous example, now suppose that in order for m0 to influence m2
l is negated
l ), as is shown in Equation (9). The corresponding
it is required that m1 does not belong to the same entity as m0. In this case, h1
using its complementary value (1 − h0
influence rule is (0)A, (1)B
⇒ (2)A.
Inf (e) = w(e) × h0
l
× (1 − h1
l )
(9)
The complexity of the influence rules can be increased arbitrarily and, theoretically,
any number of mentions and entities can be involved. This last example (Equation (10))
⇒ (3)B, an influence rule requiring m0 and m2 to
shows how to represent (0, 2)A, (1)B
belong to the same entity, while m1 belongs to a different one in order to influence m3.
Inf (e) = w(e) × h1
l
× (1 − h0
l
× h2
l )
(10)
4. RelaxCor
RELAXCOR is the coreference resolution system implemented in this work to perform
experiments and test the approach explained in Section 3. This section explains the
implementation and training methods, before the experiments and error analysis are
presented in the following sections. RELAXCOR is programmed in Perl and C++, is open
source, and is available for download from our research group’s Web site.4
The resolution process of RELAXCOR is shown in Figure 14. First, the mention
detection system determines the mentions of the input document and their boundaries.
The mention detection system is explained in Section 4.1. Alternatively, true mentions
can be used when available, allowing this step to be skipped. Next, for each pair or
group of mentions (depending on the model), the set of feature functions calculate their
values, and the set of model constraints is applied. The set of feature functions used
4 http://nlp.lsi.upc.edu.
860
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
by RELAXCOR and its knowledge sources are explained in Section 4.2. A (hyper)graph
is then generated using the applied constraints and their weights. Finally, relaxation
labeling is executed to find the partitioning that maximizes constraint satisfaction.
The training and development processes used in this work are described in Sec-
tions 4.3 and 4.4. The former explains the method for training the mention-pair model,
and the latter concerns the entity-mention model.
4.1 Mention Detection
RELAXCOR includes a mention detection system that uses part-of-speech and syntactic
information. Syntactic information may be obtained from dependency parsing or con-
stituent parsing. The system extracts one candidate mention for every:
(cid:1)
(cid:1)
(cid:1)
(cid:1)
Noun phrase (NP).
Pronoun.
Named Entity.
Capitalized common noun or proper name that appear two or more times
in the document. For instance, the NP an Internet business is a mention, but
also Internet is added in the case that the word is found once again in the
document.
The head of every candidate mention is then determined using part-of-speech
tags and a set of rules from Collins (1999) when constituent parsing is used, or using
dependency information otherwise. In case some NPs share the same head, the larger
NP is selected and the rest are discarded. Also, mention repetitions with exactly the
same boundaries are discarded. Note that a mention detection system in pipeline
configuration with the resolution process acts as a filter and the main objective at this
point is to achieve as much recall as possible.
4.2 Knowledge Sources and Features
The system gathers knowledge using a set of feature functions that interpret and evalu-
ate the input information according to some criteria. Given a set of mentions numbered
from 0 to N − 1 following the order found in the document, each feature function
evaluates their compatibility in a specific aspect. RELAXCOR includes features from
all linguistic layers: lexical, syntactic, morphological, and semantic. Moreover, some
structural features of the discourse have also been used, such as distances, quotes, and
sentential positions. A feature function with only one argument indicates that it offers
information about only one mention. For example, REFLEXIVE(0) indicates that mention
0 is a reflexive pronoun. Figure 15 shows an exhaustive list of the features used and a
brief description of each one.
We use decision trees for constraint acquisition (see Section 4.3.2). Because the use
of binary features favors a better performance in this type of learning (Rounds 1980;
Safavian and Landgrebe 1991), all of the used feature functions are binary. The original
sources that had a list of possible values have been binarized by a set of feature functions
that each represent a different value. Even in numerical cases, there is a set of binary
features representing the most important specific values, and the rest are placed in
ranges.
861
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
n
o
i
t
i
s
o
p
d
n
a
e
c
n
a
t
s
i
D
l
a
c
i
x
e
L
l
a
c
i
g
o
l
o
h
p
r
o
M
c
i
t
c
a
t
n
y
S
c
i
t
n
a
m
e
S
Distance between X and Y in sentences:
DIST SEN 0(X,Y): same sentence, DIST SEN 1(X,Y): consecutive sentences
DIST SEN L3(X,Y): less than 3 sentences
Distance between X and Y in phrases:
DIST PHR 0(X,Y), DIST PHR 1(X,Y), DIST PHR L3(X,Y)
Distance between X and Y in mentions:
DIST MEN 0(X,Y), DIST MEN L3(X,Y), DIST MEN L10(X,Y)
APPOSITIVE(X,Y): One mention is in apposition with the other.
IN QUOTES(X): X is in quotes or inside a NP or a sentence in quotes.
FIRST(X): X is the first mention in the sentence.
STR MATCH(X,Y): String matching of X and Y
PRO STR(X,Y): Both are pronouns and strings match
PN STR(X,Y): Both are proper names and strings match
NONPRO STR(X,Y): String matching like in Soon, Ng, & Lim (2001) and mentions are not pronouns.
HEAD MATCH(X,Y): String matching of NP heads.
TERM MATCH(X,Y): String matching of NP terms.
HEAD TERM(X): mentions head matches with the term.
The number of the mentions match:
NUMBER YES(X,Y,…), NUMBER NO(X,Y), NUMBER UN(X,Y)
The gender of both mentions match:
GENDER YES(X,Y,…), GENDER NO(X,Y), GENDER UN(X,Y)
Agreement: Gender and number of all mentions match:
AGREEMENT YES(X,Y,…), AGREEMENT NO(X,Y), AGREEMENT UN(X,Y)
Closest Agreement: X is the first agreement found looking backward from Y:
C AGREEMENT YES(X,Y), C AGREEMENT NO(X,Y), C AGREEMENT UN(X,Y)
THIRD PERSON(X): X is 3rd person.
PROPER NAME(X): X is a proper name.
NOUN(X): X is a common noun.
ANIMACY(X,Y,…): Animacy of mentions match.
REFLEXIVE(X): X is a reflexive pronoun.
POSSESSIVE(X): X is a possessive pronoun.
TYPE P/E/N(X): X is a pronoun (p), NE (e) or nominal (n).
DEF NP(X): X is a definite NP.
DEM NP(X): X is a demonstrative NP.
INDEF NP(X): X is an indefinite NP.
NESTED(X,Y): One mention is included in the other.
SAME MAXIMALNP(X,Y): Both mentions have the same NP parent or they are nested.
MAXIMALNP(X): X is not included in any other NP.
EMBEDDED(X): X is a noun and is not a maximal NP.
C COMMANDS(X,Y): X C-Commands Y.
BINDING POS(X): Condition A of binding theory.
BINDING NEG(X): Conditions B and C of binding theory.
COORDINATE(X): X is a coordinate NP.
Semantic class of the mentions match (the same as Soon, Ng, and Lim (2001))
SEMCLASS YES(X,Y,…), SEMCLASS NO(X,Y), SEMCLASS UN(X,Y)
One mention is an alias of the other:
ALIAS YES(X,Y,…), ALIAS NO(X,Y), ALIAS UN(X,Y)
PERSON(X): X is a person.
ORGANIZATION(X): X is an organization.
LOCATION(X): X is a location.
SRL ARG N/0/1/2/X/M/L/Z(X): SRL argument of X.
SAME SRL ARG(X,Y,..): All mentions are the same argument (ARG0, ARG1, etc.).
SRL SAMEVERB(X,Y,…): The mentions have a semantic role for the same verb.
SRL SAME ROLE(X,Y,…): The same semantic role (agent, patient, etc.)
SAME SPEAKER(X,Y,…): The same speaker.
Figure 15
Feature functions used by RELAXCOR.
4.3 Training and Development for the Mention-Pair Model
This section describes the training and development process for the implementation of
RELAXCOR using the mention-pair model and the graph representation. The training
process applies a machine learning algorithm over the training data to obtain a set
of constraints. A weight is then assigned to each constraint, taking into account the
precision of the constraint finding coreferent mentions.
A machine learning process is applied to obtain the set of constraints. Constraints
can also be added writing them by hand. Adding manual constraints is expensive,
862
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
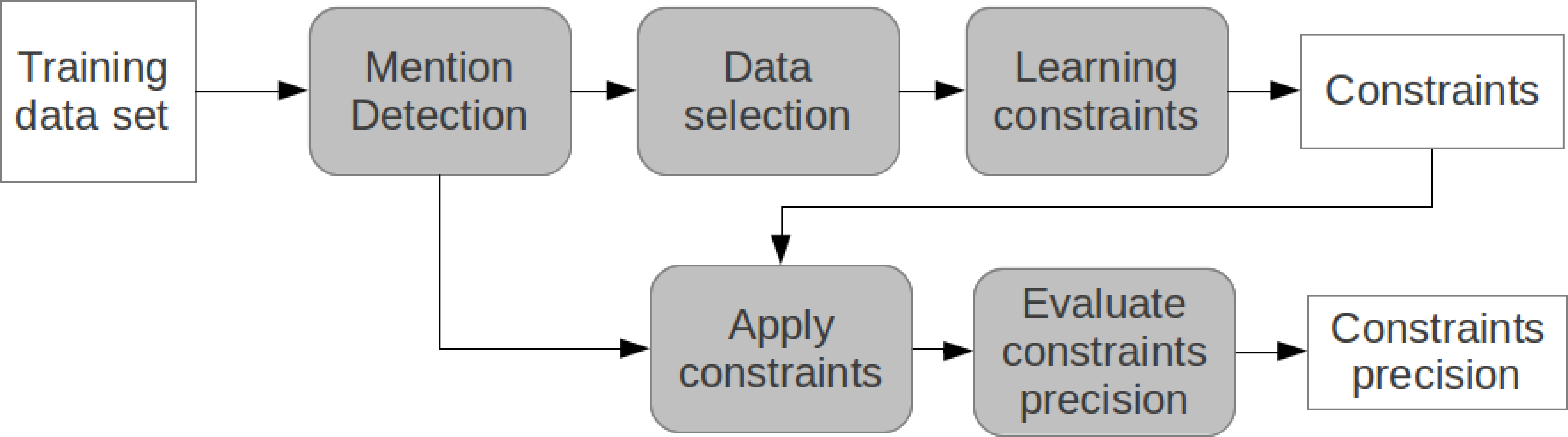
Figure 16
RELAXCOR training process.
however, given that it takes a group of linguistic experts many hours devoted to this
task. An alternative option is to use constraints from other coreference resolution
systems, such as the ones used in Lee et al. (2011). Our experiments are based on
automatically learned constraints.
Figure 16 shows the training process. First, a data selection process unbalances
the training data set and then a machine learning process obtains the constraints.
The learned constraints are then applied to the training data set and their precision
is evaluated. The precision of each constraint determines its weight. The develop-
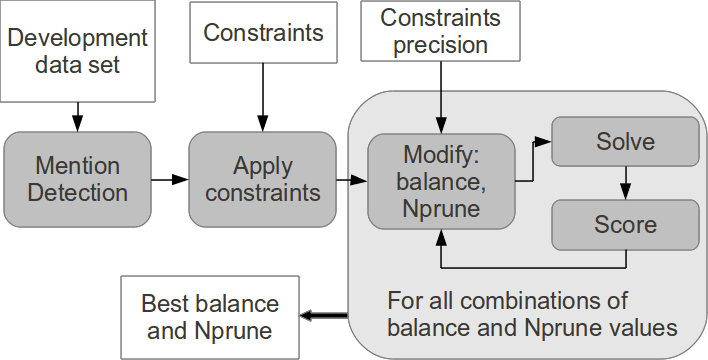
ment process optimizes two parameters—balance and Nprune—in order to achieve max-
imum performance given a measure for the task. Figure 17 shows the development
process.
4.3.1 Data Selection. Generating an example for each possible pair of mentions in the
training data produces an unbalanced data set in which more than 99% of the examples
are negative (not coreferent). This bias towards negative examples makes the task of the
machine learning algorithms difficult. Many classifiers simply learn to classify every
example as negative, which achieves an accuracy of 99% but is not at all useful. In
the case of decision trees and rule induction, this imbalance is also counterproductive.
In addition, some corpora have more examples than the maximum affordable by the
learning algorithm, given our computational resources. In this case, it is necessary to
reduce the number of examples.
In order to reduce the amount of negative examples, a data selection process similar
to clustering is run using the positive examples as the centroids. We define the distance
between two examples as the number of features with different values. A negative
example is then discarded if the distance to all the positive examples is always greater
than a threshold, D. The value of D is empirically chosen depending on the corpora
and the computational resources available.
Figure 17
RELAXCOR development process.
863
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
4.3.2 Learning Constraints. Constraints are automatically generated by learning a deci-
sion tree and then extracting rules from its leaves using C4.5 software (Quinlan 1993).
The algorithm generates a set of rules for each path from the learned tree, then checks
whether the rules can be generalized by dropping conditions. These rules become our
set of constraints. Other studies have successfully used similar processes to extract
rules from a decision tree that are useful in constraint satisfaction algorithms (M`arquez,
Padr ´o, and Rodr´ıguez 2000).
The weight assigned to a constraint (λk) is its precision over the training data (Pk),
but shifted by a balance value:
λk = Pk
− balance
(11)
The precision here refers to the positive class, that is, the ratio between the number
of positive examples and the number of examples where the constraint applies. Note
that the data selection process (Section 4.3.1) discards some negative examples to learn
the constraints, but the weight of the constraints is calculated with the precision of the
constraint over the whole training data.
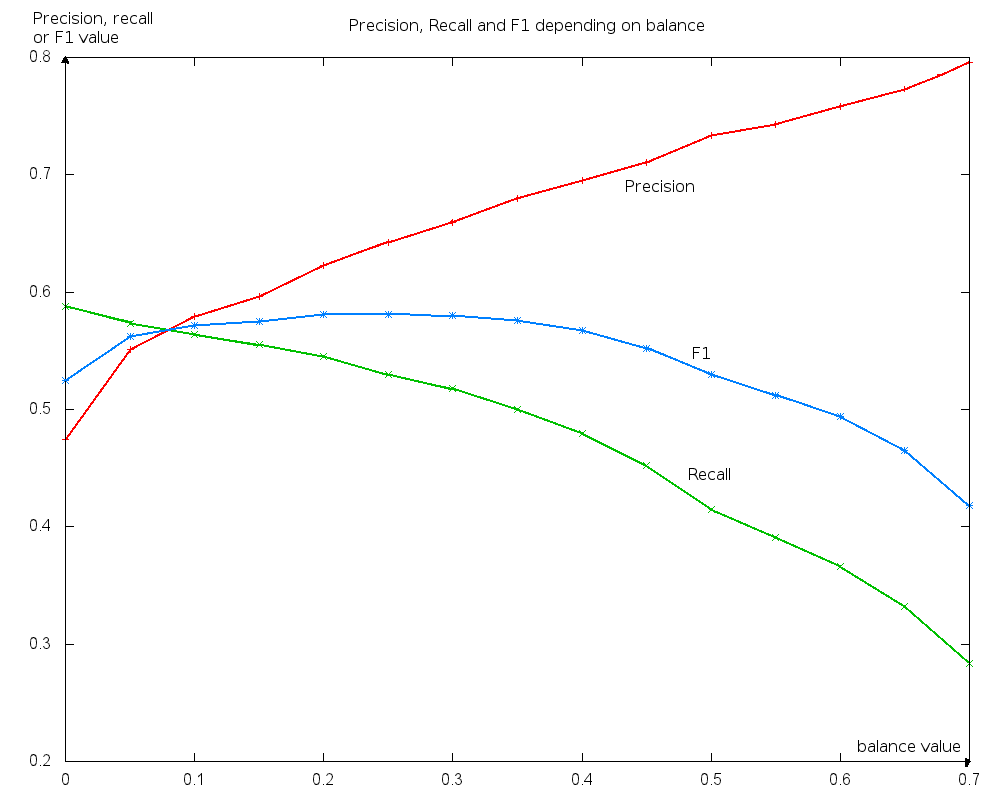
The balance parameter adjusts the constraint weights to improve the balance be-
tween precision and recall. On the one hand, a high balance value causes most of the
constraints to have a negative weight, with only the most precise having a positive
weight. In this case, the system is precise but the recall is low, given that many rela-
tions are not detected. On the other hand, a low value for balance causes many low-
precision constraints to have a positive weight, which increases recall but also decreases
precision (see Figure 18). The correct value for balance is thus a compromise solution
found in the development process, optimizing performance for a specific evaluation
measure.
Figure 18
The figure shows MUC’s precision (red), recall (green), and F1 (blue) for each balance value in
this experiment. Corpus: ACE-2002.
864
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
4.3.3 Pruning. As explained in Section 3.2, when a constraint applies to a set of mentions,
a corresponding hyperedge is added to the hypergraph. In the case of the mention-
pair model with automatically learned constraints, the most typical case is that each
pair of mentions satisfy at least one constraint, which produces an edge for each pair
of mentions. There are three main issues to take into account when the problem is
represented by an all-connected graph:
(cid:1)
(cid:1)
(cid:1)
The weight of an edge depends on the weights assigned to the constraints
according to Equation (1). Note that the calculation of edge weights is
independent of the graph adjacency. This implies that the larger the
number of adjacencies, the smaller the influence of a constraint.
Consequently, resolution has different results for large and small
documents.
Regarding the second issue, it is notable that some kinds of mention pairs
are very weakly informative—for example, pairs such as (pronoun,
pronoun). Many stories or discourses have a few main characters (entities)
that monopolize the pronouns in the document. This produces many
positive training examples for pairs of pronouns matching in gender and
person, which may lead the algorithm to produce large coreferential
chains joining all these mentions, even for stories where there are many
different characters.
Finally, the computational cost of solving an all-connected graph by
relaxation labeling is O(n3). This cost is easily deduced by examining the
algorithm in Figure 13. First, there is a loop for each variable vi, and the
number of variables is the number of mentions: n. Inside this, there is
another loop for each label l of vi, and the number of labels for vi is Li = i.
The cost for these two loops is O( n2
2 ). Inside the second loop, the support
is calculated. The calculation of the support Sil for a vertex vi and label l
is an iteration over the incident edges E(vi), which is equal to n in an
all-connected graph. Thus, the adjacency of the vertices depends on the
size of the document. Therefore, the final computation cost of the
algorithm is O( n3
2 ), or O(n3) taking out the constant value.
The pruning process turns E(vi) into a constant value Nprune. For each vertex’s
incidence list E(vi), only a maximum of Nprune edges remain and the others are pruned.
In particular, the process keeps the Nprune/2 edges with the largest positive weight and
the Nprune/2 with the largest negative weight. The value of Nprune is chosen empirically
by maximizing performance over the development data. After pruning, (i) the contribu-
tion of the edge weights does not depend on the size of the document; (ii) most edges of
the less informative pairs are discarded, avoiding further confusion without limitation
on distance or other restrictions that cause a loss of recall; and (iii) computational costs
are reduced from O(n3) to O(n2), given that the innermost loop has a constant number
of iterations (Nprune).
4.3.4 Reordering. Usually, the vertices of the graph would be placed in the same order
as the mentions are found in the document (chronological order). In this manner, vi
corresponds to mi. As suggested by Luo (2007), however, there is no need to generate
the model following that order. In our approach, the first variables have a lower number
865
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
of possible labels. Moreover, an error in the first variables has more influence on the
performance than an error in later ones. It is reasonable to expect that placing named
entities at the beginning is helpful for the algorithm, given that named entities are
usually the most informative mentions.
Reordering only affects the number of possible labels of the variables. The chrono-
logical order of the document is taken into account by the constraints, regardless of the
graph representation. Our experiments (Sapena, Padr ´o, and Turmo 2010a) confirm that
placing named entity mentions first, then nominal mentions, and finally the pronouns,
increases the precision considerably. Inside each of these groups, the order is the same
as in the document.
4.4 Training and Development for the Entity-Mention Model
The training process for the entity-mention model is, in theory, exactly the same as for
the mention-pair model, but with predefined influence rules and groups of N mentions
instead of pairs. For each combination of influence rule and N, the training process has
the same steps as explained in previous sections: Learn constraints, apply them to the
training data, calculate the weights, and perform the development process to find the
optimal balance value. The positive examples are those that satisfy the final condition
of the influence rule, and the rest are negative examples. A machine-learning process to
discover group constraints has a considerable cost, however, if all the training data need
to be evaluated. The number of combinations increases exponentially as the number
of implied mentions increases. Moreover, the ratio of positive to negative examples
is extremely low, and a data selection process like the one used for pair constraints
(Section 4.3.1) has a high computational cost.
For these reasons, the group constraints of our experiments are obtained using
only the examples that the mention-pair model could not solve. Thus, after training
and running RELAXCOR over an annotated data set using just pair constraints, its
errors are now used as examples for training the entity-mention model. The type of
errors are those in which three mentions (N = 3) corefer (0, 1, 2)A, but the mention-
pair model has determined that just two of them corefer and discarded the third one
(for example: (0, 1)A, (2)B). Each time an error like this is found, the three mentions
correspond to a positive example (corefer) and all other combinations of three men-
tions between mentions 0 and 2 are considered negative examples. The influence rules
⇒
for the constraints learned this way are (0, 1)A
(0)A, depending on which mention was wrongly classified by the mention-pair
model.
⇒ (1)A, and (1, 2)A
⇒ (2)A, (0, 2)A
Note that when an entity-mention model has been trained this way, the resolution
system is executed using both the mention-pair and entity-mention models at the
same time.
Alternatively, constraints for the entity-mention model can be added manually
by writing them. Figure 19 shows an example of a manually written entity-mention
constraint (i.e., a group constraint with an influence rule). This kind of constraint has
great potential to take advantage of the structure of discourses. The example shows
how the algorithm can benefit from knowing that nested mentions have some kind of
relation. In the case that two coreferring mentions are related with two other mentions
with the potential to corefer, the entity-mention model can use this information to find
more coreference relations.
The rest of the training and development process is conducted in the same way
as for the mention-pair model. The weights of group constraints are obtained by
866
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
The Technical University of Catalonia, sometimes called UPC-Barcelona Tech, is
the largest engineering university in Catalonia, Spain. The objectives of the UPC
are based on internationalization, as it is [[Spain]0’s technical university with the
highest number of international PhD students]1 and [[Spain]2’s university with
the highest number of international master’s degree students]3…
Constraint: PN STR(0,2) & HEAD MATCH(1,3) & NESTED(0,1) & NESTED(2,3)
Influence rule: (0, 2)A, (1)B
⇒ (3)B
Figure 19
Example of a manually written group constraint using an influence rule to take advantage of
the entity-mention model. The constraint expects four mentions where: two of them are proper
names and match in their complete strings, the other two match in their heads, mention 0 is
inside mention 1, and mention 2 is inside mention 3. The influence rule says that when mentions
0 and 2 belong to the same entity (A) but mention 1 belongs to another one (B), then mention 3
should belong to entity B in order to corefer with mention 1. (Text source: Wikipedia.
Annotations were manually done for this example.)
evaluating their precision over the training data, and the balance value is determined by
a development process. In our experiments, however, the number of group constraints
is typically lower than the number of pairwise ones, so there is no need for pruning.
4.5 Related Work
In Section 2, we introduced an overview of many approaches, with their classification
models and resolution processes (see Figure 5). Our approach can be classified simi-
larly as a one-step resolution that uses the entity-mention model for classification and
conducts hypergraph partitioning for the linking process. This classification matches
that of the COPA system described in Cai and Strube (2010). Both approaches represent
the problem in a hypergraph, where each mention is a vertex, and use hypergraph
partitioning in order to find the entities. The differences between these two approaches
are substantial, however. The most significant differences are as follows:
(cid:1)
(cid:1)
(cid:1)
Hypergraph generation. RELAXCOR adds hyperedges to the hypergraph
for each group of mentions that satisfy a constraint, whereas COPA adds
a hyperedge for each group of mentions that satisfy a feature. Note that
the addition of hyperedge weights representing features cannot take
advantage of the nonlinear combinations offered by constraints. Actually,
in order to incorporate some nonlinearity, COPA needs combined features
to introduce information such as mention type (pronoun, proper name,
etc.) or distances.
Resolution algorithm. RELAXCOR uses relaxation labeling in order to
satisfy as many constraints as possible. In fact, the hypergraph is just a
representation of the problem. COPA uses recursive 2-way partitioning, a
hypergraph partitioning algorithm. COPA’s main contribution is not the
resolution algorithm, but the hypergraph representation of the problem.
Computational costs. RELAXCOR needs to train a decision tree in order to
extract a set of rules to use them as soft constraints. These constraints are
then applied to the training data to calculate their weight. COPA does not
867
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
use constraints, which reduces the computational cost of the training
process. On the other hand, the cost of the resolution algorithm is O(n3) for
COPA whereas it is O(n2) in RELAXCOR thanks to the pruning process.
5. Experiments and Results
Several experiments have been performed on coreference resolution in order to test
our approach. This section includes a short explanation and result analysis of the
most significant experiments. First, there is an explanation of a set of experiments to
evaluate the performance of coreference resolution and mention detection. The scores
are compared with the state of the art in diverse corpora, measures, and languages.
Next, our participation in Semeval-2010 and CoNLL-2011 shared tasks is explained in
detail with performance, comparisons, and error analysis. Finally, a set of experiments
using the entity-mention model are described.
The framework used in our experiments consists of widely used corpora and mea-
sures to facilitate replication and comparison. Corpora used are ACE 2002 (NIST 2003),
the same portion of OntoNotes v2.0 used in Semeval-2010 (Recasens et al. 2010), and the
same portion of OntoNotes v4.0 used in CoNLL Shared Task 2011 (Pradhan et al. 2011).
Regarding the measures, we used MUC (Vilain et al. 1995), B3 (Bagga and Baldwin
1998), and two variants of CEAF (Luo 2005): mention-based (CEAFm) and entity-based
(CEAFe).
5.1 Mention Detection
The performance of the mention detection system achieves a good recall, higher than
90%, but a low precision, as published in Sapena, Padr ´o, and Turmo (2011) and repro-
duced in Table 1. The OntoNotes corpora have been used for this experiment, as they
were used in CoNLL-2011. Given that the mention detection in a pipeline combination
acts as a filter, recall should be kept high, as a loss of recall at the beginning would result
in a loss of performance in the rest of the process. At this point, however, the precision is
not a priority as long as it remains reasonable, given that the coreference resolution pro-
cess is able to determine that many mentions are singletons. Moreover, the evaluation
of precision on the OntoNotes corpora only take into account mentions included in a
coreference chain, not singletons. The RELAXCOR output, however, includes singletons.
This means that the precision value is not really evaluating the precision of the mention
detection system. A fair evaluation of mention detection should be performed in a
corpus with annotations of every referring expression, but such a corpus is not available
as far as we know.
The most typical error made by the system is to include extracted NPs that are
not referential (e.g., predicative and appositive phrases) and mentions with incorrect
boundaries. The incorrect boundaries are mainly due to errors in the predicted syntactic
Table 1
Mention detection results on OntoNotes (Corpus: CoNLL-2011 Shared Task).
OntoNotes
Recall
Precision
Development
Test
92.45
92.39
27.34
28.19
F1
42.20
43.20
868
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
Table 2
Results on ACE-phase02.
Metric:
Model
RELAXCOR
MaxEnt+ILP (Denis 2007)
Rankers (Denis 2007)
bnews
npaper
nwire
Global
CEAF
CEAF
F1
69.5
–
65.7
F1
67.3
–
65.3
F1
72.1
–
68.1
F1
P
69.7
66.2
67.0
85.3 66.8
81.4 65.6
79.8 66.8
F1
74.9
72.7
72.7
B3
R
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
column and some mention annotation discrepancies. Furthermore, the coreference an-
notation of OntoNotes used in CoNLL-2011 included verbs as anaphors of some verbal
nominalizations. But verbs are not detected by our mention detection system, so most
of the missing mentions are verbs. The methodology of the mention detection system is
explained in Section 4.1.
5.2 State-of-the-Art Comparison
RELAXCOR performance has been compared several times with other published results
from state-of-the-art systems. We claimed Sapena, Padr ´o, and Turmo (2010a) to have
the best performance for the ACE-phase02 corpus, using true mentions in the input and
evaluating with the CEAF and B3 measures. The table comparing scores with the best
results found at that moment is reproduced as Table 2.
The approach is also compared with the state of the art in two competitions:
SemEval-2010 (Sapena, Padr ´o, and Turmo 2010b) and CoNLL-2011 (Sapena, Padr ´o, and
Turmo 2011). RELAXCOR achieved one of the best performances in SemEval-2010, but
contradictory results across measures prevented the organization from determining a
Figure 20
RELAXCOR (sapena) achieved the second position in the official closed track (CoNLL-2011).
869
Computational Linguistics
Volume 39, Number 4
Table 3
Results of RELAXCOR on development data (SemEval-2010).
–
CEAF
MUC
language
R
P
ca
es
en-closed
en-open
69.7
70.8
74.8
75.0
69.7
70.8
74.8
75.0
F1
69.7
70.8
74.8
75.0
R
P
27.4
30.3
21.4
22.0
77.9
76.2
67.8
66.6
F1
40.6
43.4
32.6
33.0
R
67.9
68.9
74.1
74.2
B3
P
96.1
95.0
96.0
95.9
F1
79.6
79.8
83.7
83.7
winner. In addition, RELAXCOR achieved second position in the CoNLL-2011 Shared
Task; Figure 20 reproduces the official table of results. Following sections describe the
shared tasks in detail.
Finally, the performance of RELAXCOR is again compared with two other state-of-
the-art systems in M`arquez, Recasens, and Sapena (2012).
5.2.1 SemEval-2010. The goal of SemEval-2010 task 1 (Recasens et al. 2010) was to eval-
uate and compare automatic coreference resolution systems for six different languages
in four evaluation settings and using four different evaluation measures. This complex
scenario aimed at providing insight into several aspects of coreference resolution, in-
cluding portability across languages, relevance of linguistic information at different
levels, and behavior of alternative scoring measures. The task attracted considerable
attention from a number of researchers, but only six teams submitted results. Moreover,
participating systems did not run their systems for all the languages and evaluation
settings, thus making direct comparisons among all the involved dimensions very
difficult.
RELAXCOR participated in the SemEval task for English, Catalan, and Spanish
(Sapena, Padr ´o, and Turmo 2010b). At the time, the system was not ready to detect
mentions. Thus, participation was restricted to the gold-standard evaluation, which
included the manual annotated information and also provided the mention boundaries.
RELAXCOR results for development and test data sets are shown in Tables 3 and 4,
respectively. The version of RELAXCOR used in SemEval had a balance value fixed to
0.5, which proved to be an inadequate value. Thus, the results have high precision but
a very low recall. This situation produced high scores with the CEAF and B3 measures,
due in part to the annotated singletons. The system was penalized by measures based
on pair-linkage, however, particularly MUC. Although RELAXCOR had the highest
Table 4
Results of RELAXCOR on test data (SemEval-2010).
–
CEAF
MUC
language
R
P
F1
R
P
F1
R
B3
P
Information: closed Annotation: gold
ca
es
en
70.5
66.6
75.6
70.5
66.6
75.6
70.5
66.6
75.6
29.3
14.8
21.9
77.3
73.8
72.4
42.5
24.7
33.7
68.6
65.3
74.8
95.8
97.5
97.0
BLANC
R
P
BLANC
56.0
53.4
57.0
81.8
81.8
83.4
59.7
55.6
61.3
F1
79.9
78.2
84.5
Information: open Annotation: gold
en
75.8
75.8
75.8
22.6
70.5
34.2
75.2
96.7
84.6
58.0
83.8
62.7
870
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
precision scores (even with MUC), the recall was low enough to finally obtain low
scores for F1.
Regarding the test scores of the comparison with other participants (Recasens et al.
2010), RELAXCOR obtained the best performance for Catalan (CEAF and B3), English
(closed: CEAF and B3; open: B3), and Spanish (B3). Moreover, RELAXCOR was the most
precise system under all metrics in all languages, except for CEAF in English-open and
Spanish. This confirms the robustness of the results of RELAXCOR, but also highlights
the necessity of searching for a balance value other than 0.5 to increase the recall of the
system without losing much by way of precision. Indeed, the idea of using development
(Section 4.3) to adapt the balance value occurred after these results were obtained.
The incorporation of WordNet to the English run of RELAXCOR was the only
difference between our implementation in the English-open and English-closed tasks.
The scores were slightly higher when using WordNet, but not significantly so (75.8%
vs. 75.6% for CEAF and 34.2% vs. 33.7% for MUC). Analyzing the MUC scores, note
that the recall improves (from 21.9% to 22.6%), while the precision decreases a little
(from 74.4% to 70.5%), which corresponds to the information and noise that WordNet
typically provides.
More recent results of RELAXCOR on the same corpora are published in M`arquez,
Recasens, and Sapena (2012).
5.2.2 CoNLL-2011. The CoNLL-2011 Shared Task was based on the English portion of
the OntoNotes 4.0 data5 (Pradhan et al. 2011). As is customary for CoNLL tasks, there
was a closed and an open track. For the closed track, systems were limited to using the
distributed resources, in order to allow a fair comparison of algorithm performance,
whereas the open track allowed for almost unrestricted use of external resources in
addition to the provided data. About 65 different groups demonstrated interest in the
shared task by registering on the task Web page. Of these, 23 groups submitted system
outputs on the test set during the evaluation week. Eighteen groups submitted only
closed track results, three groups only open track results, and two groups submitted
both closed and open track results.
RELAXCOR participated in the closed track CoNLL task (Sapena, Padr ´o, and Turmo
2011). All the knowledge required by the feature functions was obtained from the
annotations of the corpus, and no external resources were used with the exception of
WordNet, gender and number information, and sense inventories. All of these were
allowed by the task organization and are available on their Web site.
The results obtained by RELAXCOR can be found in Tables 5 and 6. Due to the
lack of annotated singletons, mention-based metrics B3 and CEAF produce lower scores
(near 60% and 50%, respectively) than typically achieved with different annotations and
mapping policies (usually near 80% and 70%). Moreover, the requirement that systems
use automatic preprocessing and do their own mention detection increases the difficulty
of the task, which obviously decreases the scores in general. The official ranking score
was the arithmetic mean of the F-scores of MUC, B3, and CEAFe.
The MUC measure is link-based and does not take singletons into account, anyway.
Thus, it is the only one comparable with the state of the art at this point. The results
obtained with the MUC scorer show an improvement in RELAXCOR’s recall, a feature
that needed improvement given the remarkably low SemEval-2010 results with MUC.
Note that these improvements in MUC scores, specially in recall, are mainly due to
5 CoNLL-2011 Shared Task Web site: http://conll.bbn.com.
871
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Table 5
RELAXCOR results on the development data set (CoNLL-2011).
Measure
Recall
Precision
F1
Mention detection
mention-based CEAF
entity-based CEAF
MUC
B3
(CEAFe+MUC+B3)/3
92.45
55.27
47.20
54.53
63.72
–
27.34
55.27
40.01
62.25
73.83
–
42.20
55.27
43.31
58.13
68.40
56.61
Table 6
RELAXCOR official test results (CoNLL-2011).
Measure
Recall
Precision
F1
Mention detection
mention-based CEAF
entity-based CEAF
MUC
B3
BLANC
(CEAFe+MUC+B3)/3
92.39
53.51
44.75
56.32
62.16
69.50
–
28.19
53.51
38.38
63.16
72.08
73.07
–
43.20
53.51
41.32
59.55
67.09
71.10
55.99
the introduction of the balance value in the development process but also to many
other refinements done in the whole process such as new feature functions and bug
fixing.
RELAXCOR achieved second position in the official closed track results, as shown
in Figure 20. The final column shows the official ranking score. The difference from
the system in first place is 1.8 points, which is statistically significant, whereas the
difference to third position is just 0.03 points and is not significant. The winning
system—Stanford (Lee et al. 2011)—does not use machine learning but combines
many heuristics to join mentions and partial entities, starting with the most precise
ones. It is thought that the difference between RELAXCOR and Stanford’s system is
mainly due to their use of sophisticated handwritten heuristics instead of our auto-
matically learned constraints. Note that Lee et al. (2011) solve coreferences by applying
first the most precise constraints. RELAXCOR also solves first the most precise con-
straints given that these ones have the highest weights and are the most influencing
ones.
5.3 Languages
Sapena, Padr ´o, and Turmo (2010b), and M`arquez, Recasens, and Sapena (2012) show the
performance of our approach for English, Catalan, and Spanish. The scores for Spanish
and Catalan do not seem as good as for English, because the system was originally
designed with the English language in mind. As a result, it does not include language-
specific features for Spanish and Catalan, such as whether a mention is an elliptical
subject or not. Despite this, RELAXCOR scores for Catalan and Spanish are the best
among the state of the art.
872
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
Table 7
Comparison of RELAXCOR results using just the mention-pair model (N = 2) with those also
using the entity-mention model (N = 3) (Corpus: SemEval-2010).
Measure
Precision Recall
2 CEAFm
=
N
MUC
B3
CEAFe
3 CEAFm
=
N
MUC
B3
CEAFe
81.73
72.92
91.87
81.95
82.02
73.01
91.59
82.10
81.73
54.17
82.87
90.47
82.02
54.28
83.12
90.63
F1
81.73
62.17
87.14
86.00
82.02
62.27
87.15
86.15
5.4 Experiments with the Entity-Mention Model
Constraints for the entity-mention model are automatically obtained using the training
data examples that the mention-pair model could not solve, with predefined influence
rules and limited to N = 3. The training process is explained in Section 4.4. Experiments
with the entity-mention model are conducted using both models at the same time. The
goal of the experiments is to improve the performance of the mention-pair model itself.
Table 7 shows the experimental results using the SemEval-2010 English corpus. The
table compares the entity-mention results (RELAXCOR using N = 3 constraints with
influence rules, including the whole set of N = 2 constraints) with those using mention-
pairs (RELAXCOR using just N = 2 constraints). The entity-mention model outperforms
the mention-pair model. The number of really useful examples (i.e., mentions wrongly
classified by the mention-pair model but correctly classified by the entity-mention
model), however, is low. Consequently, the difference in their scores is not significant.
The N = 3 constraints have a good precision and also an acceptable recall, although
most of the mentions affected by these constraints were already affected and correctly
solved by the mention-pair model. Further research is needed in order to find more
useful constraints, either by writing more elaborate group constraints or finding a better
system that automatically finds them.
These results may be somewhat justified, because the entity-mention model uses
the same feature functions and, consequently, the same information as the mention-
pair model. In fact, only the new information is that information already included in
the conditions of the influence rules, which take into account the entities assigned to
each mention during resolution. In addition, group constraints can also include, in an
implicit way, information about the structure of the discourse. It seems clear, however,
that this new information is either minimal or not relevant enough. Figure 21 shows an
example of a learned entity-mention constraint.
Constraint: GENDER NO (0,1) = 0 & STR MATCH(0,1) = 0 & ORGANIZA-
TION(0) = 0 & POSSESSIVE(1) & NUMBER NO(1,2) = 0 & NUMBER UN(1,2)
= 0 & DIST SEN L3(0,1) & DIST SEN L3(0,2)
Influence rule: (0, 2)A
⇒ (1)A
Figure 21
Example of a learned N = 3 constraint.
873
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Even though the obtained performance does not significantly outperform the
mention-pair model, we can draw some positive conclusions from these experiments.
First of all, the approach is ready to use either model (mention-pair or entity-mention)
in a constructive way. As soon as new feature functions specific to entity-mention
models appear, the results will reflect this. One research line to follow in this field is the
incorporation of feature functions following discourse theories, such as focusing and
centering. Another research line is the introduction of world knowledge using these
models, as explained in the next section.
6. Adding World Knowledge to Coreference Resolution
Often, common sense and world knowledge is essential to resolve coreferences. For
example, we can find coreferential mentions in any newspaper, such as {Obama, USA
President}, {Messi, Barcelona striker}, or {Beirut, the Lebanese capital}.
In order to know the importance of the coreference links that are missed due to
a lack of world knowledge, the partial and total scores of RELAXCOR on the test data
set of OntoNotes 2.0 (the same data set used for the English task in SemEval-2010) are
shown in Table 9 for each mention class described in Table 8. Analyzing the table, we
observe that PN N, CN P, and CN N are the classes with the lowest recall, especially
PN N and CN N. In addition, PN N and CN N have the lowest precision. The final
column shows the number of mentions corresponding to the class of that row and the
percentage representing the total number of coreferent mentions. Note that these three
classes together represent 27% of coreferent mentions.
According to M`arquez, Recasens, and Sapena (2012), Stoyanov et al. (2009), and
Pradhan et al. (2007), these results can be roughly generalized to any other system
using similar information, and even other languages. Therefore, these classes require
attention in order to improve global performance, and the fact that lexical, morpholog-
ical, syntactic, and semantic levels are not very useful to deal with them encourages
the research on adding world knowledge to coreference resolution systems. In state-
of-the-art systems, we can find some attempts to add world knowledge to coreference
resolution, using Wikipedia (Ponzetto and Strube 2006; Uryupina et al. 2011) or YAGO
and Freenet (Rahman and Ng 2011a).
Table 8
Description of the mention classes for English documents.
Class
PN E
PN P
Description
NPs headed by a Proper Name that Exactly match (excluding case and the
determiner) at least one preceding mention in the same coreference chain.
NPs headed by a Proper Name that Partially match (i.e., head match or overlap,
excluding case) at least one preceding mention in the same coreference chain.
PN N NPs headed by a Proper Name that do Not match any preceding mention in
the same coreference chain.
Same definitions as in PN E, PN P, and PN N,
but referring to NPs headed by a Common Noun.
First- and second-person pronouns that corefer with a preceding mention.
Gendered third-person pronouns that corefer with a preceding mention.
Ungendered third-person pronouns that corefer with a preceding mention.
CN E
CN P
CN N
P 1∪2
P 3G
P 3U
874
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
Table 9
Results of RELAXCOR in English OntoNotes from SemEval-2010 without world knowledge.
measure
class
Pre
Rec
F1
quantity
PN E
PN P
PN N
CN E
CN P
CN N
P 1∪2
P 3G
P 3U
99.7
94.5
5.3
97.3
87.3
22.6
74.5
88.8
78.1
74.4
83.0
91.8
99.4
77.9
1.3
71.8
36.0
2.5
61.2
85.0
59.3
59.9
83.0
84.6
99.6
85.4
2.1
82.6
51.0
4.5
67.2
86.9
67.4
66.4
83.0
88.1
356 (18%)
222 (12%)
75 (04%)
149 (08%)
172 (09%)
278 (14%)
134 (07%)
187 (10%)
356 (18%)
MUC
MUC
CEAFm
B3
This section presents our approach to incorporating world knowledge to corefer-
ence resolution, represented in Figure 22. The nature of our model allows the integration
of world knowledge encoded not only as features, but also as constraints, which is a
more expressive and natural way.
The work presented in this section is intended as a proof-of-concept for the ability
of RELAXCOR to absorb knowledge from heterogeneous sources. Results show that
although the algorithm is able to successfully handle the added knowledge, the per-
formance is hardly increased due to the noisy nature of the knowledge automatically
extracted from Wikipedia.
The approach proceeds in two phases. First, given a document, the world know-
ledge potentially useful for the resolution of coreferences is acquired from Wikipedia,
and second, this knowledge is incorporated to RELAXCOR using two alternative
models: feature functions and constraints. These phases are described in Sections 6.1
and 6.2, respectively. Finally, Section 6.3 describes our experiments and analyzes their
results.
6.1 Acquiring World Knowledge
Our methodology to acquire world knowledge useful for coreference resolution consists
of finding the real-world entities occurring in the document (i.e., Entity Linking) and
extracting information related to them from Wikipedia.
Figure 22
Process to add information from Wikipedia to coreference resolution.
875
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
6.1.1 Entity Linking. One approach to finding real-world entities mentioned in a docu-
ment is to select the NE mentions of that document and to disambiguate them in order
to determine which entities in the real world—in our case, which Wikipedia entries—
are referred to by the mentions. Using every NE mention in a document, however, may
add noise to the process of coreference resolution. For instance, consider a document
with Bill Clinton and, some sentences later, Clinton. If we try to get information about
Clinton from Wikipedia, we obtain a page about the English family name Clinton with
a lot of non-relevant information that may lead to erroneous results. Given that Bill
Clinton appears in the same document, it seems more convenient to select the most
informative NE mention and discard the less informative ones, like Clinton, which are
probably pointing to the same real-world entity. This is why we just take into account
the most informative NE mentions, called MI mentions from now on.
We obtain MI mentions as follows: We build cliques formed by groups of mentions
where the ALIAS function is true for all the pairs, and all mentions in the group belong
to the same class (Person, Organization, or Location). Finally, the longest NE mention
from each group is selected as an MI mention.
After this selection process, each MI mention is disambiguated by using Google as
an information retrieval system to find the most relevant pages in Wikipedia. The query
is generated from the MI mention as the mention head plus all nouns, proper names,
and adjectives that appear immediately before it. From the results provided by Google,
we select as the real world entity for the MI mention the first URL that corresponds to
a Wikipedia entry and includes the head of the MI mention (or a string that matches as
an alias) in the title or in the first sentence of the first paragraph.6 If no result is found,
we assume that the MI mention does not exist in Wikipedia.
6.1.2 Information Extraction. For each Wikipedia entry obtained in the entity disambigua-
tion step, we extract information from the description, the infobox, and the categories
of the entry, and also from other Wikipedia pages linking to that entry, as found in
the “What Links Here” section. Concretely, we extract all names (i.e., official names,
nicknames, and aliases), as well as properties indicating the most descriptive aspects or
qualities of the entity.
The first paragraph of a Wikipedia entry is considered the description of the entry.
The description typically starts with the complete name of the entity, some aliases,
and the most descriptive properties of the entity. After preprocessing the text, the
first NE is extracted as the official name. Next, a set of patterns are used to extract
aliases (e.g., “sometimes called
NP-
From the infobox, all the contents of the following fields are extracted: fullname,
name, office, title, profession, company name, playername, occupation, nickname,
official name, native name, settlement type, type. In addition, all categories associ-
ated with the entry are also extracted as properties.
Finally, from each page that links to the current entry following the “What Links
Here” section, those sentences including the link are selected. From each one of them,
the anchor text used to link the entry is extracted as a name. In addition, the following
6 We also discard special Wikipedia pages, such as disambiguation pages or pages with names that do not
contain the character “:”.
7 We extract as properties both the NP (e.g., “American politician”) and its head (e.g., “politician”) in order
to get more general properties as well.
876
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
expressions are extracted as properties using patterns: the set of nouns and adjectives
to the left of the anchor text, the set of NPs in apposition to the link, and the set of NPs
denoting a property of a list of entries in which one of them is the current one (e.g.,
“
We take the frequency of the extracted expression as the confidence value associated
with each expression—the most repeated expressions are the most reliable. In order to
avoid incorrect information as much as possible, we define a threshold below which
all the extracted names and properties are discarded.
6.2 Incorporating World Knowledge to the Models
Two approaches for the incorporation of the knowledge extracted from Wikipedia have
been studied. The first is to add some feature functions for the mention-pair model that
evaluate whether a pair of mentions may corefer according to Wikipedia’s information,
similar to other state-of-the-art studies (Ponzetto and Strube 2006; Rahman and Ng
2011a). The second approach adds a set of constraints to the hypergraph connecting
groups of mentions, using the entity-mention model.
6.2.1 Feature Functions. In this approach, new feature functions are added to evaluate
pairs of mentions, and some learned constraints may use them as any other feature
function. These feature functions are only applied to pairs < MI, X >, where MI is a MI
mention and X is any other mention but a pronoun, and use the information extracted
from Wikipedia to determine their value. Concretely, the feature functions used in our
experiments are the following ones:
(cid:1)
(cid:1)
WIKI ALIAS(MI, X): returns true if the head of X is another MI mention of
the same entry as MI, or X matches one of the names extracted from
Wikipedia for MI.
WIKI DESC(MI, X): returns true if all the X terms are included in one of the
properties extracted from Wikipedia for MI.
6.2.2 Constraints. In this approach, world knowledge is incorporated by adding con-
straints relating the mentions that may corefer given the extracted information about the
entities. In this case, the features of the previous model are now replaced by constraints.
In addition, other constraints can be added to take advantage of the entity-mention
model. The following is a list of constraints used in our experiments:
(cid:1)
(cid:1)
(cid:1)
Constraint cAlias is added for each pair of mentions that satisfy the same
conditions as WIKI ALIAS.
Constraint cDesc is added for each pair of mentions that satisfy the same
conditions as WIKI DESC.
Constraint cWiki3, a N = 3 constraint, is added for each combination of
three mentions (0, 1, 2) where 0 is a MI mention, 1 is a NE mention alias of
0, and 2 is a nominal mention or a NE mention that satisfies WIKI ALIAS
or WIKI DESC with 0. This constraint tries to link the nominal mention
with the closest NE mention that may corefer. The influence rule is
⇒ (2)A, that is, 2 is influenced when 0 and 1 corefer.
(0, 1)A
877
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
(cid:1)
Constraint cStructWiki3, an N = 3 constraint, is added for each
combination of three mentions (0, 1, 2) where 0 is an MI mention, 1 is an
NP that satisfies WIKI ALIAS or WIKI DESC with 0, and 2 is an NE mention
alias of 0. In addition, the three mentions have the same syntactic function
and are found in consecutive sentences. The influence rule associated with
⇒ (1)A, that is, 1 is influenced when 0 and 2 corefer.
this constraint is (0, 2)A
Figure 23 shows examples of the constraints cWiki3 and cStructWiki3. The idea
behind cWiki3 is to link the nominal mention (2, The organization) with a closer men-
tion in the document than the MI mention (0, the Organization of Petroleum Exporting
Countries). Linking nearest mentions may take advantage of information given by other
constraints, such as syntactic patterns. When the Organization of Petroleum Exporting
Countries is tending to corefer with OPEC, mention The organization is influenced by
both mentions. The second case, cStructWiki3, takes advantage of a typical discourse
structure where the same entity is the subject of some consecutive sentences. First
mention 0, Google Inc., is the MI mention, whereas 2 (Google) is just an alias. Between
them we find a nominal mention (The company), which we expect to solve using world
knowledge. Both N = 3 constraints are expected to have high precision but low recall.
Note that cAlias and cWiki are equivalent to the feature functions of the previous
model. The difference is that, in the case of constraints, they are always applied when
WIKI ALIAS and WIKI DESC are true, and so their weight is added to the edge weight
of that pair in the hypergraph. In the model using feature functions, however, the
constraints learned by the model may or may not include those features.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
6.3 Experiments and Results
The experiments consist of the execution of RELAXCOR using each one of the models
to incorporate information. RELAXCOR + features incorporates the new features to the
original model and repeats the training process from the beginning. Constraints are
learned using these new feature functions mixed with all the others (a detailed list of
features is in Section 4.2). RELAXCOR + constraints incorporates the new constraints. In
this case, the learning process uses the constraints already learned for RELAXCOR and
adds the new constraints to the model. The training process is then applied normally to
compute the weight of the constraints using their precision in the training files.
Table 10 shows the results obtained when adding world knowledge compared with
the results of RELAXCOR without world knowledge. The first three columns list the
cWiki3
Output from the Organization of Petroleum Exporting Countries is already…
As a result, the effort by some oil ministers to get OPEC to approve…
The organization is scheduled to meet in Vienna…
cStructWiki3
Google Inc. is offering new applications…
The company is going to…
Predictably, Google has highlighted user profiles…
Figure 23
Examples of the application of N = 3 constraints cWiki3 and cStructWiki3.
878
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
Table 10
Results of RELAXCOR on English OntoNotes 2.0 from SemEval-2010 with world knowledge.
The baseline is RELAXCOR using mention-pair model, features, is RELAXCOR using features
WIKI ALIAS and WIKI DESC, and constraints stands for RELAXCOR with the set of constraints
in Section 6.2.2. Gains over the baseline are boldfaced and losses are in italics.
baseline
features
constraints
measure
class
Pre
Rec
F1
Pre
Rec
F1
Pre
Rec
F1
PN E
PN P
PN N
CN E
CN P
CN N
P 1∪2
P 3G
P 3U
99.7
94.5
5.3
97.3
87.3
22.6
74.5
88.8
78.1
74.4
83.0
91.8
99.4
77.9
1.3
71.8
36.0
2.5
61.2
85.0
59.3
59.9
83.0
84.6
99.6
85.4
2.1
82.6
51.0
4.5
67.2
86.9
67.4
66.4
83.0
88.1
100
92.9
15.0
97.3
90.2
32.1
76.9
87.6
76.2
75.9
83.4
92.6
98.0
76.6
4.0
72.5
43.0
3.2
59.7
86.6
54.8
59.6
83.4
84.5
99.0
84.0
6.3
83.1
58.3
5.9
67.2
87.1
63.7
66.8
83.4
88.4
100
93.6
14.8
97.3
89.2
31.0
77.1
87.6
76.1
75.4
83.5
92.3
99.2
78.8
5.3
72.5
43.0
3.2
60.4
86.6
55.3
60.3
83.5
84.7
99.6
85.6
7.8
83.1
58.0
5.9
67.8
87.1
64.1
67.0
83.5
88.4
MUC
MUC
CEAFm
B3
results of RELAXCOR using the mention-pair model, as explained in Section 4, the next
three columns are the results of RELAXCOR adding the features of Section 6.2.1, and the
final three columns are the scores for RELAXCOR with the constraints of Section 6.2.2.
Note that the main improvements are focused around PN N, CN P, and CN N, as
expected. Moreover, the global scores also improve, but the global improvements are
not statistically significant.
Although there are improvements in our target classes (PN N, CN P, and CN N),
there are some collateral effects that decrease the performance for other classes such
as PN P and P 3U (ungendered pronouns: it). The latter is a strong decrease and, given
that the class P 3U represents 18% of the total coreferent mentions, this affects the global
results. This decrease in pronoun classification performance is related to the balance
value learned in the development process. One possible solution would be to have a
different balance value depending on the class.
Another phenomenon to take into account in the case of RELAXCOR + features is
that the improvement in global scores is in precision but not in recall. This is because
the development process is optimizing scores for the CEAF measure, which encourages
precision more than recall compared with the MUC scorer.
The improvements achieved seem too few given the necessary effort to extract the
knowledge. In general terms, we have found that, although performance is slightly
improved on average, few new coreference relations are found, taking into account
the expected potential for improvement. Moreover, some of these new relations do not
change the final output and, even worse, many of them are incorrect. In addition, some
coreferences that were correctly solved before this process are now incorrectly classified.
In particular, the recall of ungendered pronouns has decreased considerably.
Finally, it is interesting to remark that these improvements are achieved thanks to a
reduced number of mentions in test documents that end up having an actual Wikipedia-
influenced constraint (e.g., fewer than 1% of the mentions in features model). Thus, better
extraction procedures or a knowledge source more suitable for entities appearing in the
target documents should yield larger improvements.
879
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
More details on the extraction process and a detailed error analysis can be found in
Sapena (2012). The error analysis shows how the extracted knowledge was often redun-
dant (i.e., used only in cases where the algorithm already produced the right answer)
or noisy (due to errors in the entity disambiguation or information extraction steps).
Thus, we think that the experiments show that RELAXCOR is able to incorporate world
knowledge into the resolution model in an easy and natural way, and that further work
is required on acquiring more accurate and useful knowledge to feed the coreference
resolution process.
7. Conclusions
In this work, we defined an approach based on constraint satisfaction that represents
the problem in a hypergraph and solves it by relaxation labeling, reducing coreference
resolution to a hypergraph partitioning problem under a set of constraints. Our ap-
proach manages mention-pair and entity-mention models at the same time, and is able
to introduce new information by adding as many constraints as necessary. Furthermore,
our approach overcomes the weaknesses of previous approaches in state-of-the-art
systems, such as linking contradictions, classifications without context, and a lack of
information in evaluating pairs.
The presented system, RELAXCOR, achieved state-of-the-art results using only the
mention-pair model without new knowledge. Moreover, experiments with the entity-
mention model showed how it is able to introduce knowledge in a constructive way.
Although it is clearly necessary to incorporate world knowledge to move forward
in the field of coreference resolution, the process required to introduce such information
in a constructive way has not yet been found. In this work, we tested a methodology
that identified the real-world entities referred to in a document, extracted information
about them from Wikipedia, and then incorporated this information in two different
ways in the model. It seems that neither of the two forms work very well, however, and
that the results and errors are in the same direction: The slight improvement of the few
new relationships is offset by the added noise. Other state-of-the-art systems have better
improvements than ours (Ponzetto and Strube 2006; Uryupina et al. 2011; Rahman and
Ng 2011a), but these also seem too modest given the large amount of information used
and the room for improvement outlined in the Introduction.
The problem seems to lie with the extracted information rather than the model used
to incorporate it. The extracted information is biased in favor of the more famous and
popular entities (those in Wikipedia, and having larger entries). This causes the system
to find more information about these entities, including false positives, and causes an
imbalance against entities with little or no information in Wikipedia. Moreover, it is not
possible to use negative information in the absence of complete information.
Therefore, we believe that research in this field should focus on the extraction of
more reliable and concise information, so that the information added, no matter how
minimal, should always be constructive and avoid false positives. On the other hand,
we would need to find some process of reasoning to expand the scope of the information
obtained using logic and common sense. Only then could the full potential of the
knowledge base be exploited.
Acknowledgments
This research was supported by the Spanish
Science and Innovation Ministry, via the
KNOW2 project (TIN2009-14715-C04-04) and
from the European Community’s Seventh
Framework Programme (FP7/2007-2013)
under grant agreement number 247762
(FAUST).
880
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
References
Aone, C. and S. W. Bennett. 1995. Evaluating
automated and manual acquisition
of anaphora resolution strategies.
In Proceedings of the Annual Meeting of the
Association for Computational Linguistics
(ACL 1995), pages 122–129.
Atserias, J. 2006. Towards Robustness in
Natural Language Understanding.
Ph.D. thesis, Departamento de
Lenguajes y Sistemas Inform´aticos,
Euskal Herriko Unibertsitatea,
Donosti, Spain.
Azzam, S., K. Humphreys, and
R. Gaizauskas. 1999. Using coreference
chains for text summarization.
In Proceedings of the Workshop on
Coreference and its Applications,
pages 77–84, Stroudsburg, PA.
Bagga, A. and B. Baldwin. 1998. Algorithms
for scoring coreference chains. In
Proceedings of the Linguistic Coreference
Workshop at LREC, pages 563–566,
Granada.
Bean, D., E. Riloff, S. Dumais, D. Marcu, and
S. Roukos. 2004. Unsupervised learning of
contextual role knowledge for coreference
resolution. In Proceedings of the Annual
Conference of the North American Chapter of
the Association for Computational Linguistics
(NAACL-HLT 2004), pages 297–304,
Boston, MA.
Bengtson, E. and D. Roth. 2008.
Understanding the value of features for
coreference resolution. In Proceedings of the
Conference on Empirical Methods in Natural
Language Processing (EMNLP 2008),
pages 294–303, Waikiki, HI.
Cai, J. and M. Strube. 2010. End-to-end
coreference resolution via hypergraph
partitioning. In Proceedings of the
23rd International Conference on
Computational Linguistics, pages 143–151,
Beijing.
Cardie, C. and K. Wagstaff. 1999. Noun
phrase coreference as clustering.
In Proceedings of the 1999 Joint SIGDAT
Conference on Empirical Methods in
Natural Language Processing and Very
Large Corpora (EMNLP-VLC 1999),
pages 82–89, College Park, MD.
Collins, M. 1999. Head-Driven Statistical
Models for Natural Language Parsing.
Ph.D. thesis, University of Pennsylvania.
Culotta, A., M. Wick, and A. McCallum.
2007. First-order probabilistic models for
coreference resolution. In Proceedings of the
Annual Conference of the North American
Chapter of the Association for Computational
Linguistics (NAACL-HLT 2007),
pages 81–88, Rochester, NY.
Denis, P. 2007. New Learning Models for
Robust Reference Resolution. Ph.D. thesis,
University of Texas at Austin.
Denis, P. and J. Baldridge. 2007. Joint
determination of anaphoricity and
coreference resolution using integer
programming. Proceedings of the Annual
Conference of the North American Chapter of
the Association for Computational Linguistics
(NAACL-HLT 2007), pages 236–243,
Rochester, NY.
Denis, P. and J. Baldridge. 2008. Specialized
models and ranking for coreference
resolution. Proceedings of the Conference on
Empirical Methods for Natural Language
Processing (EMNLP 2008).
Finkel, J. R. and C. D. Manning. 2008.
Enforcing transitivity in coreference
resolution. In Proceedings of the Annual
Meeting of the Association for Computational
Linguistics (ACL 2008), pages 45–48,
Columbus, OH.
Finley, T. and T. Joachims. 2005. Supervised
clustering with support vector machines.
ACM International Conference Proceedings
Series, 119:217–224.
Haghighi, A. and D. Klein. 2007.
Unsupervised coreference resolution
in a nonparametric bayesian model.
In Proceedings of the Annual Meeting of the
Association of Computational Linguistics
(ACL 2007), pages 848–855.
Hummel, R. A. and S. W. Zucker. 1983. On
the foundations of relaxation labeling
processes. IEEE Transactions on Pattern
Analysis and Machine Intelligence,
5(3):267–287.
Ji, H., D. Westbrook, and R. Grishman.
2005. Using semantic relations to refine
coreference decisions. Proceedings of the
Conference on Human Language Technology
and Empirical Methods in Natural Language
Processing (HLT-EMNLP 2005),
pages 17–24, Prague.
Kingsbury, P. and M. Palmer. 2003.
Propbank: the next level of treebank.
In Proceedings of Treebanks and Lexical
Theories, V¨axj ¨o.
Klenner, M. 2007. Enforcing consistency on
coreference sets. In Proceedings of the
Conference on Recent Advances in Natural
Language Processing (RANLP 2007),
pages 323–328, Borovets.
Klenner, M. and ´E. Ailloud. 2008. Enhancing
Coreference Clustering. In Proceedings of
the Second Workshop on Anaphora Resolution
(WAR II, 2008), pages 31–40, Bergen.
881
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
Lee, H., Y. Peirsman, A. Chang,
N. Chambers, M. Surdeanu, and
D. Jurafsky. 2011. Stanford’s multi-pass
sieve coreference resolution system at the
CoNLL-2011 shared task. In Proceedings of
the Fifteenth Conference on Computational
Natural Language Learning: Shared Task,
pages 28–34, Portland, OR.
Luo, X. 2005. On coreference resolution
performance metrics. Proceedings of the
Joint Conference on Human Language
Technology and Empirical Methods in Natural
Language Processing (HLT-EMNLP 2005),
pages 25–32, Vancouver.
Luo, X. 2007. Coreference or not: A twin
model for coreference resolution. In
Proceedings of the Annual Conference of the
North American Chapter of the Association for
Computational Linguistics (NAACL-HLT
2007), pages 73–80, Rochester, NY.
Luo, X., A. Ittycheriah, H. Jing,
N. Kambhatla, and S. Roukos. 2004.
A mention-synchronous coreference
resolution algorithm based on the bell
tree. In Proceedings of the Annual Meeting
of the Association for Computational
Linguistics (ACL 2004), pages 135–142,
Barcelona.
M`arquez, L., L. Padr ´o, and H. Rodr´ıguez.
2000. A machine learning approach for
POS tagging. Machine Learning Journal,
39(1):59–91.
M`arquez, L., M. Recasens, and E. Sapena.
2012. Coreference resolution: An empirical
study based on SemEval-2010 shared
task 1. Journal on Language Resources and
Evaluation, Special Issue on SemEval-2010.
doi:10.1007/s510579-012-9194-z.
McCallum, A. and B. Wellner. 2005.
Conditional models of identity uncertainty
with application to noun coreference.
Advances in Neural Information Processing
Systems, 17:905–912.
McCarthy, J. F. and W. G. Lehnert. 1995.
Using decision trees for coreference
resolution. Proceedings of the Fourteenth
International Conference on Artificial
Intelligence, pages 1,050–1,055.
Mitkov, Ruslan. 2002. Anaphora Resolution.
Longman.
Morton, T. S. 2000. Using coreference in
question answering. NIST Special
Publication SP, pages 685–688.
Ng, V. 2005. Machine learning for coreference
resolution: From local classification to
global ranking. In Proceedings of the Annual
Meeting of the Association for Computational
Linguistics (ACL 2005), pages 157–164,
Ann Arbor, MI.
882
Ng, V. 2007. Shallow semantics for
coreference resolution. In Proceedings of the
International Joint Conference on Artificial
Intelligence (IJCAI 2007), pages 1,689–1,694,
Hyderabad.
Ng, V. 2008. Unsupervised models for
coreference resolution. In Proceedings of the
Conference on Empirical Methods in Natural
Language Processing (EMNLP 2008),
pages 640–649, Waikiki, HI.
Ng, V. 2009. Graph-cut-based anaphoricity
determination for coreference resolution.
In Proceedings of the Annual Conference of the
North American Chapter of the Association for
Computational Linguistics (ACL 2009),
pages 575–583, Suntec.
Ng, V. 2010. Supervised noun phrase
coreference research: The first fifteen
years. In Proceedings of the Annual Meeting
of the Association for Computational
Linguistics (ACL 2010), pages 1,396–1,411,
Uppsala.
Ng, V. and C. Cardie. 2002. Improving
machine learning approaches to
coreference resolution. In Proceedings
of the Annual Meeting of the Association for
Computational Linguistics (ACL 2002),
pages 104–111, Philadelphia, PA.
Nicolae, C. and G. Nicolae. 2006. Best
Cut: A graph algorithm for coreference
resolution. Proceedings of the Conference on
Empirical Methods for Natural Language
Processing (EMNLP 2006), pages 275–283,
Sydney.
NIST, US. 2003. The ACE 2003 Evaluation
Plan. US National Institute for Standards
and Technology (NIST), pages 1–8.
Padr ´o, L. 1998. A Hybrid Environment for
Syntax–Semantic Tagging. Ph.D. thesis,
Departamento de Llenguatges i Sistemes
Inform`aics, Universitat Polit´ecnica de
Catalunya.
Pelillo, M. 1997. The dynamics of nonlinear
relaxation labeling processes. Journal
of Mathematical Imaging and Vision,
7(4):309–323.
Peral, J., M. Palomar, and A. Ferr´andez.
1999. Coreference-oriented interlingual
slot structure & machine translation.
In Proceedings of the Workshop on
Coreference and its Applications,
pages 69–76, Stroudsburg, PA.
Ponzetto, S. P. and M. Strube. 2006.
Exploiting semantic role labeling,
WordNet and Wikipedia for
coreference resolution. In Proceedings
of the Human Language Technology
Conference of the North American Chapter
of the Association of Computational
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sapena, Padr ´o, and Turmo
Constraint-Based Hypergraph Partitioning Coreference Resolution
Linguistics (NAACL 2006), pages 192–199,
New York, NY.
Poon, H. and P. Domingos. 2008. Joint
unsupervised coreference resolution
with Markov Logic. In Proceedings of the
Conference on Empirical Methods in Natural
Language Processing (EMNLP 2008),
pages 650–659, Waikiki, HI.
Popescu, A. M. and O. Etzioni. 2005.
Extracting product features and opinions
from reviews. In Proceedings of the
Conference on Human Language Technology
and Empirical Methods in Natural Language
Processing (HLT-EMNLP 2005),
pages 339–346, Vancouver.
Pradhan, S., A. Moschitti, N. Xue,
O. Uryupina, and Y. Zhang. 2012.
CoNLL-2012 shared task: Modeling
multilingual unrestricted coreference in
OntoNotes. In Proceedings of the Conference
on Computational Natural Language Learning
(CoNLL 2012), pages 1–40, Jeju Island.
Pradhan, S., L. Ramshaw, M. Marcus,
M. Palmer, R. Weischedel, and N. Xue.
2011. CoNLL-2011 shared task: Modeling
unrestricted coreference in OntoNotes.
In Proceedings of the Conference on
Computational Natural Language Learning
(CoNLL 2011), pages 1–27, Portland, OR.
Pradhan, S. S., L. Ramshaw, R. Weischedel,
J. MacBride, and L. Micciulla. 2007.
Unrestricted coreference: Identifying
entities and events in OntoNotes. In
Proceedings of the International Conference
on Semantic Computing (ICSC 2007),
pages 446–453.
Quinlan, J. R. 1993. C4.5: Programs for
Machine Learning. Morgan Kaufmann.
Rahman, A. and V. Ng. 2011a. Coreference
resolution with world knowledge. In
Proceedings of the Annual Meeting of the
Association for Computational Linguistics
(ACL 2011), pages 814–824, Portland, OR.
Rahman, A. and V. Ng. 2011b. Narrowing
the modeling gap: A cluster-ranking
approach to coreference resolution.
Journal of Artificial Intelligence Research,
40(1):469–521.
Recasens, M., L. M`arquez, E. Sapena, M. A.
Mart´ı, M. Taul´e, V. Hoste, M. Poesio,
and Y. Versley. 2010. SemEval-2010
Task 1: Coreference resolution in
multiple languages. In Proceedings of
the International Workshop on Semantic
Evaluations (SemEval-2010), pages 1–8,
Uppsala.
Rosenfeld, R., R. A. Hummel, and
S. W. Zucker. 1976. Scene labelling by
relaxation operations. IEEE Transactions
on Systems, Man and Cybernetics,
6(6):420–433.
Rounds, E. M. 1980. A combined
nonparametric approach to feature
selection and binary decision tree design.
Pattern Recognition, 12(5):313–317.
Safavian, S. R. and D. Landgrebe. 1991.
A survey of decision tree classifier
methodology. IEEE Transactions on
Systems, Man and Cybernetics,
21(3):660–674.
Sapena, E. 2012. A Constraint-Based
Hypergraph Partitioning Approach to
Coreference Resolution. Ph.D. thesis,
Universitat Politecnica de Catalunya.
Sapena, E., L. Padr ´o, and J. Turmo. 2010a.
A global relaxation labeling approach to
coreference resolution. In Proceedings
of the International Conference on
Computational Linguistics (COLING 2010),
pages 1,086–1,094, Beijing.
Sapena, E., L. Padr ´o, and J. Turmo. 2010b.
RelaxCor: A global relaxation labeling
approach to coreference resolution.
In Proceedings of the ACL Workshop on
Semantic Evaluations (SemEval-2010),
pages 88–91, Uppsala.
Sapena, E., L. Padr ´o, and J. Turmo. 2011.
RelaxCor participation in CoNLL shared
task on coreference resolution.
In Proceedings of the Fifteenth Conference
on Computational Natural Language
Learning: Shared Task, pages 35–39,
Portland, OR.
Soon, W. M., H. T. Ng, and D. C. Y. Lim.
2001. A machine learning approach to
coreference resolution of noun phrases.
Computational Linguistics, 27(4):521–544.
Stoyanov, V., N. Gilbert, C. Cardie, and
E. Riloff. 2009. Conundrums in noun
phrase coreference resolution: Making
sense of the state-of-the-art. In Proceedings
of the Joint Conference of the Annual
Meeting of the ACL and the International
Joint Conference on Natural Language
Processing (ACL-IJCNLP 2009),
pages 656–664, Suntec.
Torras, C. 1989. Relaxation and neural
learning: Points of convergence and
divergence. Journal of Parallel and
Distributed Computing, 6:217–244.
Uryupina, O. 2009. Detecting anaphoricity
and antecedenthood for coreference
resolution. Procesamiento del Lenguaje
Natural, pages 113–120.
Uryupina, O., M. Poesio, C. Giuliano, and
K. Tymoshenko. 2011. Disambiguation and
filtering methods in using Web knowledge
for coreference resolution. In Proceedings of
883
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 39, Number 4
the International Florida Artificial Intelligence
Research Society Conference, pages 317–322,
Palm Beach, FL.
Vilain, M., J. Burger, J. Aberdeen,
D. Connolly, and L. Hirschman. 1995.
A model-theoretic coreference scoring
scheme. In Proceedings of the Message
Understanding Conference (MUC-6),
pages 45–52, Arlington, VA.
Yang, X., J. Su, J. Lang, C. L. Tan, T. Liu, and
S. Li. 2008. An entity-mention model for
coreference resolution with inductive logic
programming. In Proceedings of the Annual
Meeting of the Association for Computational
Linguistics (ACL 2008), pages 843–851,
Columbus, OH.
Yang, X., J. Su, and C. L. Tan. 2006.
Kernel-based pronoun resolution with
structured syntactic knowledge.
Proceedings of the 21st International
Conference on Computational Linguistics and
the 44th Annual Meeting of the Association for
Computational Linguistics (COLING-ACL
2006), pages 41–48, Sydney.
Yang, X., J. Su, G. Zhou, and C. L. Tan.
2004. An NP-cluster based approach to
coreference resolution. In Proceedings of the
International Conference on Computational
Linguistics (COLING 2004), pages 226–232,
Geneva.
Yang, X., G. Zhou, J. Su, and C. L. Tan. 2003.
Coreference resolution using competition
learning approach. In Proceedings of
the Annual Meeting of the Association for
Computational Linguistics (ACL 2003),
pages 176–183, Sapporo.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
9
4
8
4
7
1
8
0
2
3
3
5
/
c
o
l
i
_
a
_
0
0
1
5
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
884