What Evidence Supports Special Processing for Faces? - Am MIT spezialisierte KI-Forschung

What Evidence Supports Special Processing for Faces?
A Cautionary Tale for fMRI Interpretation

Rosemary A. Cowell1 and Garrison W. Cottrell2

Abstrakt

■ We trained a neurocomputational model on six categories of
photographic images that were used in a previous fMRI study
of object and face processing. Multivariate pattern analyses of
the activations elicited in the object-encoding layer of the model
yielded results consistent with two previous, contradictory fMRI
Studien. Findings from one of the studies [Haxby, J. V., Gobbini,
M. ICH., Furey, M. L., Ishai, A., Schouten, J. L., & Pietrini, P. Distrib-
uted and overlapping representations of faces and objects in
ventral temporal cortex. Wissenschaft, 293, 2425–2430, 2001] war
interpreted as evidence for the object-form topography model.
Findings from the other study [Spiridon, M., & Kanwisher, N.

How distributed is visual category information in human occipito-
temporal cortex? Eine fMRT-Studie. Neuron, 35, 1157–1165, 2002]
were interpreted as evidence for neural processing mecha-
nisms in the fusiform face area that are specialized for faces.
Because the model contains no special processing mechanism
or specialized architecture for faces and yet it can reproduce
the fMRI findings used to support the claim that there are spe-
cialized face-processing neurons, we argue that these fMRI
results do not actually support that claim. Results from our
neurocomputational model therefore constitute a cautionary tale
for the interpretation of fMRI data. ■

EINFÜHRUNG

What is the nature of the representations in visual cor-
tex that underlie object processing? Empirical research
has attempted to address this fundamental question for
more than half a century, using a wide range of experi-
mental techniques. Kürzlich, two contrasting theoretical
frameworks for understanding the functional organization
of ventral visual cortex have emerged: The first is a mod-
ular view of object processing (z.B., Kanwisher, 2010;
Spiridon & Kanwisher, 2002; Kanwisher, McDermott, &
Chun, 1997), and the second is a “distributed processing”
account (z.B., OʼToole, Jiang, Abdi, & Haxby, 2005;
Hanson, Matsuka, & Haxby, 2004; Haxby et al., 2001; Ishai,
Ungerleider, Martin, Schouten, & Haxby, 1999).

According to the modular view, there is cortical spe-
cialization for specific domains of visual recognition:
Human inferotemporal cortex contains discrete regions
dedicated to distinct object categories, such as faces
(Kanwisher et al., 1997; McCarthy, Chip, Gore, & Allison,
1997), places (Epstein & Kanwisher, 1998), body parts
(Downing, Jiang, Schumann, & Kanwisher, 2001), and word
Formen (Cohen et al., 2002; Petersen, Fuchs, Snyder, & Rachel,
1990). Such regions are proposed to have a selective role
in the perception of a restricted object category and to
employ qualitatively distinct processing mechanisms
(Kanwisher, 2010; Spiridon & Kanwisher, 2002). In ADDI-

1University of Massachusetts Amherst, 2Universität von Kalifornien
San Diego

tion, it has been suggested that such modules may have
evolutionary as well as developmental origins (Kanwisher,
2010).

Im Gegensatz, distributed processing theories of visual
recognition claim that object representations are distrib-
uted across a broad expanse of inferotemporal cortex.
The object form topography account, proposed by Haxby
and colleagues (Haxby et al., 2001; Ishai, Ungerleider,
Martin, & Haxby, 2000; Ishai et al., 1999), posits that
ventral temporal cortex contains a continuous represen-
tation of object form, with a topological organization
that reflects the distinctions between object categories.
Arguing against the modular view, Ishai et al. (1999) sug-
gest that the topology arises because information char-
acteristic of objects within a category clusters together
in cortex, producing a region that responds maximally
to that category; this gives the appearance of a module,
belying the continuous, distributed nature of the cortical
Darstellungen.

Both the modular and distributed processing views
of object processing have been supported primarily by
data from fMRI studies, in which participants view pictures
of objects and faces while the hemodynamic response
in their ventral visual cortex is measured (z.B., Downing
et al., 2001; Haxby et al., 2001; Ishai et al., 1999; Kanwisher
et al., 1997; McCarthy et al., 1997). In diesem Artikel, Wir
focus on the debate over the existence of an anatomical
module for faces by using a neurocomputational model
to replicate studies in which multivoxel pattern analy-
Schwester (MVPA) was used to interpret the fMRI data. Unlike

Zeitschrift für kognitive Neurowissenschaften 25:11, S. 1777–1793
doi:10.1162/jocn_a_00448

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

F
/

T
T

ich
T
.

:
/
/

H
T
T
P
:
/
D
/
Ö
M
w
ich
N
T
Ö
P
A
R
D
C
e
.
D
S
F
ich
R
Ö
l
M
v
e
H
R
C
P
H
A
D
ich
ich
R
R
e
.
C
C
T
.
Ö
M
M
/
J
e
Ö
D
u
C
N
Ö
/
C
A
N
R
A
T
R
ich
T
ich
C
C
l
e
e
–
P
–
D
P
D
2
F
5
/
1
2
1
5
/
1
1
7
1
7
/
7
1
1
7
9
7
4
7
5
/
9
1
8
3
7
7
Ö
9
C
8
N
2
_
9
A
/
_
J
0
Ö
0
C
4
N
4
8
_
A
P
_
D
0
0
B
4
j
4
G
8
u
.
e
P
S
T
D
Ö
F
N
B
0
j
7
S
M
e
ICH
P
T
e
M
L
ich
B
B
e
R
R
A
2
R
0
2
ich
3
e
S

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

traditional univariate analyses of fMRI data, MVPA examines
patterns of activation across voxels in a search for com-
binations that maximally discriminate between behavioral
Bedingungen. daher, MVPA allows for the possibility of
discovering a combinatorial representational code, welche
is likely to be utilized by the brain if representations are
truly distributed. Using a neurocomputationally plausible
model of object processing (Cowell, Huber, & Cottrell,
2009), we perform MVPA on the activation patterns in
the layer of the model where stimulus representations
reside. Our aim is to assist in the interpretation of fMRI
results by examining the necessity of possible schemes of
neural representation (z.B., modular vs. distributed) für
producing particular patterns of BOLD activation. Der
method we present allows us to check whether the repre-
sentational assumptions that are made in interpreting
MVPA results are necessary to produce the data reported
in empirical studies.

We examine the studies of Spiridon and Kanwisher
(2002) and Haxby et al. (2001). In line with the idea that
MVPA may be used to investigate both distributed and
modular hypotheses, the authors of these two studies
drew opposing conclusions from their results. Haxby
et al. (2001) found that information about the category
membership of an object was distributed across visual
Kortex, rather than confined to regions that were maxi-
mally active in response to that category, and therefore
argued in favor of distributed object representations.
Spiridon and Kanwisher (2002) also found that information
was distributed but that the information in “face-selective”
regions was more exclusively useful for making category
decisions about faces than was the case for any other
object-selective region. Das ist, the “house-selective”
region was not as selective in its utility for categorizing
Häuser, nor was the “bottle-selective” region superior in
its categorization of bottles, und so weiter. The authors took
this as evidence for specialized processing of faces by
face-selective neurons.

We trained our neurocomputational model on six cate-
gories of the photographic images used by Haxby et al.
(2001). MVPA of the activation patterns elicited in the
object-encoding layer demonstrated that both the Haxby
et al. (2001) results and the Spiridon and Kanwisher
(2002) results were replicated by our model. Weil
the model contains no special processing mechanism
or specialized architecture for faces and yet the above
finding from Spiridon and Kanwisher (2002) was none-
theless produced in the model, we argue that this re-
sult from Spiridon and Kanwisher (2002) cannot be
used to support the claim that there are specialized face-
processing neurons in the fusiform face area (FFA).1 Der
findings from our neurocomputational model therefore
constitute a cautionary tale for the interpretation of fMRI
Daten. Darüber hinaus, this study introduces a novel compu-
tational method for testing the necessity of cognitive
hypotheses for explaining fMRI data from studies of object
Verarbeitung.

METHODEN

A Neurocomputational Model of Object
Processing in Visual Cortex

To simulate fMRI data, we require a model that is, An
some level, neurocomputationally plausible. Weil
the target data are responses of voxels—each of which
contains several million neurons (Logothetis, 2008)—
we opt for a level of analysis in which the architecture
and processing algorithm mimic cortical connectivity
and processing across networks of neurons rather than
in single units. An appropriate model is the Kohonen net-
arbeiten (Kohonen, 1982), in which the learning algorithm is
a computational abstraction of cortical mechanisms such
as Hebbian learning and lateral inhibition. A Kohonen
network self-organizes, meaning that learning is unsuper-
vised, lending it biological plausibility. Learning of the
feedforward weights is strongly influenced by lateral con-
nectivity between units in the network (Kohonen, 1982,
1984); this architecture produces representations that
preserve the similarity structure of the stimulus inputs,
as in representations seen in mammalian sensory and
motorischer Kortex (z.B., Krubitzer & Calford, 1992; Cynader,
Swindale, & Matsubara, 1987; Swindale, Matsubara, &
Cynader, 1987; Aitkin, Merzenich, Irvine, Clarey, & Nelson,
1986; Lemon, 1981). This makes the network particularly
well suited to our purposes, because stimulus represen-
tations are spatially situated across units and subsets of
those units that are defined by stimulus preference are
often spatially contiguous, similar to category-selective
voxels seen in fMRI studies. These subsets of units can
be used for MVPA, analogous to the subsets of voxels used
in the fMRI studies. Darüber hinaus, because of this prop-
erty, the method can potentially create a model “FFA,”
unlike a backpropagation network in which the hidden
unit representations are fully combinatorial without
any spatial localization. Zusätzlich, a Kohonen network
offers a system of representation that is somewhere
between distributed, in that all inputs are connected to
all representational units, and localized, in that lateral in-
hibition constrains representations to be somewhat local-
ized in space. Daher, the network representations mimic
those observed in fMRI studies of object-processing areas,
possessing both distributed and localized properties, Und
the model has the potential to reproduce MVPA findings
from both the “distributed account” and the “modular
account”. By analyzing the activation patterns that the
model contains, we can investigate whether both sets of
results can emerge from a system of representation in
which no modules are explicitly assumed.

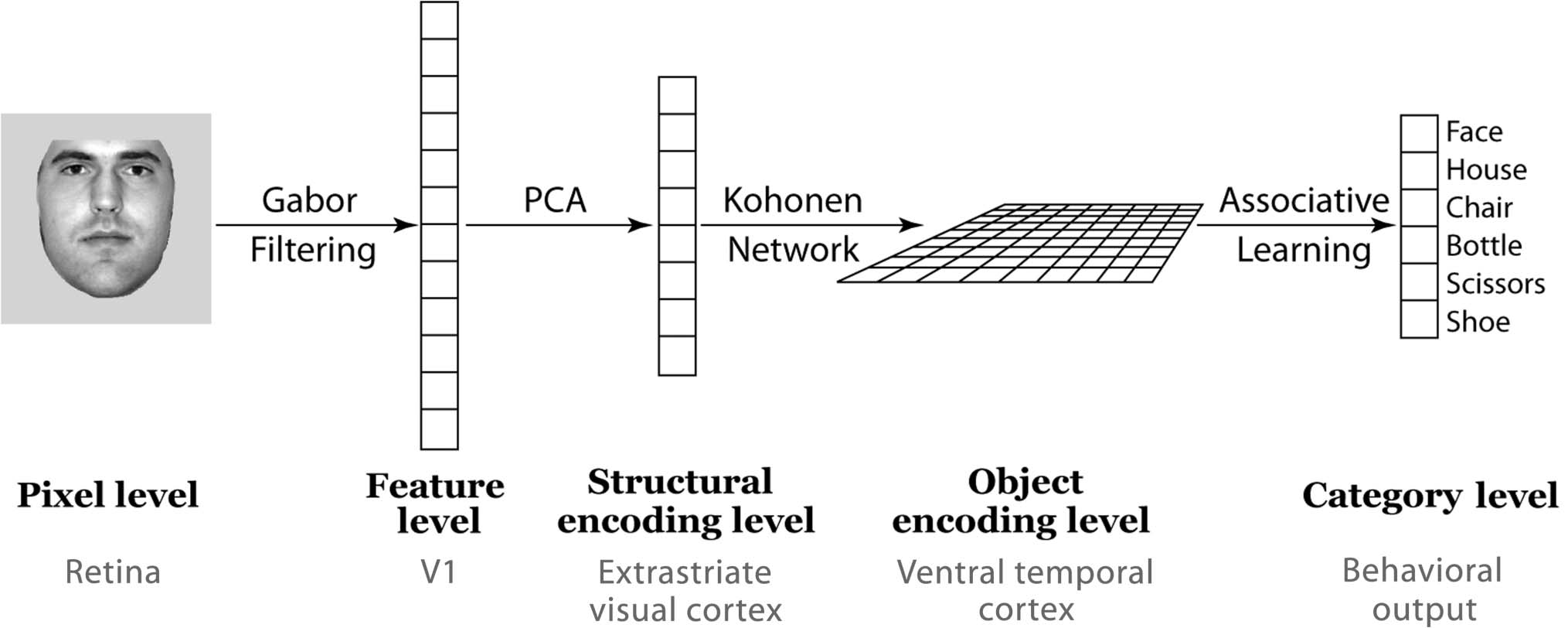
Figur 1 shows the model architecture. Erste, input im-
ages are filtered using Gabor wavelets, modeling the re-
ceptive fields in V1. The Gabor filter outputs are reduced
in dimensionality by principal component analysis (PCA),
a process that can be accomplished by Hebbian learn-
ing (Sänger, 1989). Processing in these two early stages
echoes the dimensionality expansion and reduction of

1778

Zeitschrift für kognitive Neurowissenschaften

Volumen 25, Nummer 11

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

F
/

T
T

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

T
T

F
/

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

Figur 1. Model architecture. Photographic images are Gabor filtered, and then the filter outputs are reduced in dimensionality through PCA.
For each stimulus, projections onto the top 20 PCs are passed as inputs to the two-dimensional Kohonen network at the object encoding level
of the model. In a final layer, units in the object encoding level are connected to six category-level output units, via weights that are adjustable
through the delta rule. The activations of units at the category level are used to determine network behavior (d.h., categorization performance)
during training to criterion. Activations of units in the object encoding level are used for the MVPA simulations.

stimulus representations that are thought to occur in stri-
ate and extrastriate visual cortex (Sänger, 1989; Daugman,
1985). At the next stage of the model, the stimulus repre-
sentations resulting from Gabor filtering and PCA are
input to a Kohonen network, in which topographically
arranged representations of objects develop. In the final
stage, representations in the topographic layer are asso-
ciated, via the delta rule, with output nodes corresponding
to six object categories, as a test of whether the informa-
tion in the representation layer is sufficient to distinguish
the categories.

The use of a Kohonen network at the hidden layer is a
departure from previous models of face and object process-
ing we have developed (Tong, Joyce, & Cottrell, 2008;
Dailey & Cottrell, 1999), in which the hidden layer was
trained with the backpropagation algorithm. The Kohonen
network introduces two key properties not possessed by
a backpropagation network. Erste, the learning of object
representations in the model is unsupervised and neuro-
computationally plausible. Zweite, units in the Kohonen
network occupy a fixed position relative to their neighbors
within a two-dimensional grid, and object representations
are arranged topographically across them, making it possi-
ble to find the units that are “selective for” a given object
category.

The network is trained by presenting a series of stimuli
and incrementally updating the weights from the struc-
tural encoding level to the object-encoding units at each
presentation. The topography of stimulus representa-
tions emerges in the network owing to the neighborhood
function governing the weight updates: the most active
unit updates its weights most strongly to move closer
to the stimulus; neighboring units in the grid are also

updated in the direction of the stimulus, but less strongly;
and the weights of distant units are not updated. Con-
sequently, neighboring units learn similar weight values
and come to represent items that are close in stimulus
Raum.

MVPA of Simulated Data

We replicated the fMRI studies by treating the activations
of units at the object encoding level as responses of vox-
els in an fMRI data set. We performed MVPA using corre-
lation, measuring the discriminability of object categories
by comparing the similarity of the representations elic-
ited by each category. As in Spiridon and Kanwisher
(2002) and Haxby et al. (2001), we analyzed the activation
patterns not only across all voxels (Einheiten) that were re-
sponsive to objects but also across smaller subsets of
those units. The subsets were defined, as in the fMRI
Studien, as populations of units that were more strongly
activated by one particular stimulus category than the
Andere, providing a computational equivalent of “face-
selective” or “house-selective” regions in cortex.

Visual Categorization Training

Stimuli

We used grayscale photographic stimuli from the fMRI
study of Haxby et al. (2001). Stimuli belonged to six
categories: faces, Häuser, chairs, bottles, scissors, Und
shoes. This set comprised all the object categories of
Haxby et al. (2001) except cats2 and scrambled images.
All images were scaled and cropped to 64 × 64 pixels.

Cowell and Cottrell

1779

Wir verwendeten 240 training images, 40 from each category,
with each category set containing 10 exemplars pictured
from four different views. An additional 48 Bilder (eight
per category: two distinct exemplars from four different
Ansichten) were assigned to a holdout set for testing classi-
fication performance after every 10 training epochs.

Image Preprocessing

Stimuli were filtered using Gabor wavelets to transform
the images into representations suitable for object recog-
Nation (Dailey & Cottrell, 1999). The Gabor filters were
applied to 1,024 points in each image, evenly spaced on
A 32 × 32 grid. This resulted in a vector of size 40,960
(1,024 sample points, at which eight orientations and
five scales of the filter were applied), and we reduced the
dimensionality of the patterns by performing PCA on
alle 288 images used in the study. For each image, we re-
tained the projections onto the first 20 principal compo-
nents to use as input to the Kohonen network. We did
not normalize the vectors produced by the PCA to have
equal variance (a common step for backpropagation net-
funktioniert) because unnormalized vectors enabled better
learning in the Kohonen layer.

Training the Neural Network

Twelve networks were trained to classify objects into six
categories. Learning of feedforward weights from the
input units to the object-encoding units was unsupervised,
das ist, it was independent from the learning of weights
from the object-encoding units to the output units. Unlike
backpropagation, the only effect of the object-encoding-
to-output weights on the input-to-object-encoding weights
was that all training was terminated according to classifica-
tion accuracy at the output units. All units in the model
were sigmoidal. The weights from input units to object-
encoding units were trained by the Kohonen learning rule
as follows:

wjiðt þ 1Þ ¼ wjiðtÞ þ f ðdistÞ (cid:2) ðai − wjiÞ

ð1Þ

in which wji is the weight from input i to unit j, ai is the
activation of input i, and f is a neighborhood weighting
function on the learning rate. The neighborhood func-
tion is centered on the most active unit and is given by
the following:

f ðdistÞ ¼ ηe

ð Þ2

− dist
G

ð2Þ

scaled by a factor of 10 in the exponential. The weights
from object-encoding units to output units were trained
using a delta rule with learning rate of 0.01. The object-
encoding layer was a square grid with sides of length 40,
50, 60, oder 70 Einheiten.

Classification accuracy was assessed after every 10 train-
ing epochs by recording the responses at the output
nodes to stimuli in the holdout set. Training of each
network was terminated when classification accuracy
exceeded 85% on three successive presentations of the
holdout set, but not before at least 40 training epochs
were completed.

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

Procedures for MVPA of Empirical Data

Haxby et al. MVPA Methods

Participants viewed grayscale photographic images of eight
categories: faces, Häuser, cats, bottles, shoes, scissors,
chairs, and phase-scrambled images. For each participant,
fMRI data were screened to find “object-selective” voxels,
in which the BOLD signal to the different object categories
differed significantly, as assessed by the omnibus effect of
seven regressors used to model the seven meaningful
categories. Only object-selective voxels were used in sub-
sequent MVPA. Data for each participant were split into
halves: odd- and even-numbered scans. The discriminabil-
ity of brain images was determined by examining the simi-
larity of activation patterns in the halves, with similarity
measured as the voxelwise correlation between the pat-
Seeschwalben. For the pairwise category comparison between, für
Beispiel, faces and shoes, the correlation between the
mean response to faces on odd runs and that to faces on
even runs was compared with the correlation between the
mean response to faces on odd runs and that to shoes on
even runs. If the face–face (innerhalb)-category correlation
was higher than the face–shoe (between-category) cor-
relation, the discrimination was scored as correct. In
fact, there are four binary comparisons to be made for
each pairwise category discrimination: faceodd–faceeven
versus faceodd–shoeeven, faceodd–faceeven versus faceeven–
shoeodd, shoeodd–shoeeven versus faceodd–shoeeven, Und
shoeodd–shoeeven versus faceeven–shoeodd. Averaging over
four binary comparisons yields a possible score of 0%,
25%, 50%, 75%, oder 100%, for each pairwise category dis-
crimination. The overall discriminability of a category was
determined by averaging over all seven pairwise category
comparisons involving that category (z.B., for faces: face–
house, face–cat, face–shoe, usw.).

/
J

T
T

F
/

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

where dist is the distance from unit i to the maximally
active unit in the grid and η is the learning rate, welche
starts at 1 and reduces over epochs, as η = epoch(−0.2).
G is a Gaussian width parameter that decreases over
the first 50 Epochen, as G = 0.5 + 10*Epoche(−0.3). Ac-
tivations of sigmoidal units in the Kohonen layer were

Spiridon and Kanwisher MVPA Methods

These authors used MVPA procedures very similar to those
of Haxby et al., except for the way in which scan data were
split into halves. Spiridon and Kanwisher (2002) assayed
three different splits: Erste, they divided the scan data so
that brain images in the halves had been evoked by the

1780

Zeitschrift für kognitive Neurowissenschaften

Volumen 25, Nummer 11

identical set of images (the “identical images” condition);
zweite, the halves of scan data were evoked by images
of the same individuals in each category, but the individ-
uals were not pictured from the same views in each half
(“different views”); and third, the sets of images evoking
responses in the halves of data contained different exem-
plars of each object category (“different exemplars”).
Daher, the within-category correlation ( WCC) zwischen
the halves of the data measured either the reliability of
brain responses to a given stimulus, the reliability of re-
sponses to different views of the same individual, oder der
reliability of brain responses to different individuals from
the same category. Importantly for our purposes, Spiridon
and Kanwisher (2002) found no significant differences
between the accuracy of pairwise category discriminations
across the three conditions.

Procedures for MVPA of Simulated Data

Recording Activation Patterns

For all trained networks, we recorded the activation pat-
terns in the object-encoding units elicited by all 240 train-
ing stimuli on the final epoch of training.3

Assigning Images to “Scans”

In the fMRI studies, participants viewed blocks of 12
(Haxby et al.) oder 16 (Spiridon and Kanwisher) photo-
graphic images from a single category. Because the
hemodynamic response is slow, the activation of voxels
by any individual image was temporally smeared across
the block such that the activation pattern recorded for a
particular category on any scan was an amalgamation of
the brain responses elicited by all images in that block. In
Kontrast, in our simulations, we were able to extract the
precise activation pattern elicited by each photographic
Bild. To approximate the data averaging in the fMRI
Studien, we assigned stimulus images within each category
to blocks and averaged across all patterns within a block.
In each simulated “scan,” there was one such block per
category.

In Summe, we used activation patterns caused by 240 stim-
uli, umfassend 40 from each category, consisting of
10 individual exemplars pictured from four different view-
points. (Jedoch, only for chairs and shoes were the four
viewpoints consistent across individual exemplars; für
other categories, each exemplar was pictured from four
viewpoints, but not necessarily the same four viewpoints
as used for other exemplars). We assigned the 40 Bilder
from each category to four scans of 10 images using a
protocol that approximated those of the fMRI studies. In
simulations, each “scan” contained two views each of five
individuals. For each category, we randomly assigned five
individuals to Scans 1 Und 2, and the other five individuals
to Scans 3 Und 4. Zusätzlich, for all categories, we con-
strained Scans 1 Und 3 to contain only two of the four

views per individual and Scans 2 Und 4 to contain the
other two views.

Dividing the Data

For each category, we divided the activation patterns
corresponding to the four scans into halves (two sets
of two) and averaged over each half to obtain the two
averaged activation patterns for measuring correlations.
To split the scans, we used both the “different views”
and the “different exemplars” methods of Spiridon and
Kanwisher (2002). For “different views,” we assigned
Scans 1 Und 3 to the first half and Scans 2 Und 4 to the
second half, so that each half was generated by images of
all possible individuals but only half of all possible views
(albeit that not all categories comprised a standard set of
four views). For “different exemplars,” we assigned Scans
1 Und 2 to the first half and Scans 3 Und 4 to the second
half, so that each half contained all views of any individ-
ual but only half of all individuals. In all simulations, Wir
ran the analysis with both types of split then averaged
the discrimination scores from the two analyses into a
single score. Allgemein, we found that the type of split
did not dramatically affect discrimination accuracy.

Determining Visually Active and
Category-selective Units

We tested the object-encoding layer units in our model
for visual activity and category selectivity with methods
very similar to those of the fMRI studies, before perform-
ing MVPA. For Simulations 1–3 (replicating Haxby et al.,
2001), we included all object-selective units. To determine
object selectivity for each unit, we performed a one-way
ANOVA on the unitʼs responses to each category and
examined the omnibus effect of the six conditions (d.h.,
categories), using an uncorrected significance level of
P < 10−6 as our criterion. ( We found that, in a typical simulation, slightly more than 90% of model units passed this criterion.) Spiridon and Kanwisher (2002) first screened voxels to exclude any voxels that were not visu- ally active, that is, possessed activations that were not sig- nificantly different from zero for any object category. In Simulation 4, we did the same with all object-encoding units and found that, unsurprisingly, all units were visually active. Next, we determined the category selectivity of each unit by performing an independent samples t test comparing the responses to the maximally activating object category with the responses to all other categories. We used the p values derived in this t test to rank order the voxels in terms of selectivity, to determine the “most selective” units (see below). Selection of Units In Simulation 1, we used all object-selective units. In Simu- lation 2, we used all object-selective units except those Cowell and Cottrell 1781 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f / t . u s e r o n 1 7 M a y 2 0 2 1 that were maximally activated by one of the two categories being discriminated. For example, when discriminating houses and scissors, we used all object-selective units ex- cept those maximally activated by either house images or scissor images. The units maximally activated by a given category were defined as those among the object-selective units (i.e., among units whose responses differed signifi- cantly by object category) for which the mean activation caused by that category was higher than the mean activa- tions caused by all other categories. We report the over- all discriminability of each category; for example, for “houses,” this is the average across all pairwise discrimina- tions involving the category “houses” (houses vs. faces, houses vs. bottles, etc.). In Simulation 3, we included only object-selective units that were maximally activated by a single category, with “maximally activated” being determined as in Simulation 2. We then used these six sets of units—maximally activated by each of the six categories—to perform six separate analyses. The number of units in the object-encoding grid that qualified as maximally activated by each category was not equal across categories. Simulation 4 replicated a finding from Spiridon and Kanwisher (2002), which involved an analysis similar to Simulation 3 but with the number of category-selective voxels fixed at 30 for all categories. For each category, we selected the 30 units for which the independent sam- ples t test measuring category selectivity had yielded the smallest p values. Following Spiridon and Kanwisher (2002), for all nonpreferred categories in each set of 30 units, we excluded all discriminations involving the preferred category. For example, in the “house units” analysis, we excluded all pairwise discriminations involving houses in the calculation of mean overall discrimination accuracy, doing so for all overall category discrimination scores except “house” (for which it is not possible to exclude all pairwise discriminations involving houses and still compute a score). Discrimination Accuracy Empirical BOLD data contain considerable noise, arising from both internal sources within the brains of scanned participants and external sources, such as variability in scanner measurements. Because of such noise, activation patterns in the halves of the scan data elicited by the same object category (such as faceeven–faceodd or shoeeven– shoeodd) produce voxelwise correlations considerably less than 1. This is true even in the “identical images” condi- tion, in which brain responses in the halves of the scan data are elicited by the exact same set of images. In con- trast, in the neurocomputational model, there is no noise: Each time a particular image is presented to the same trained network, the exact same activation pattern results. Consequently, if input images are assigned to “scans” in the halves of the simulated data according to the “identical images” protocol, all WCCs are 1. On the other hand, if input images are assigned to the halves of simulated data using a scheme similar to the “different views” or “differ- ent exemplars” conditions of Spiridon and Kanwisher (2002), natural variability in network responses to different instances of the same category produces WCCs of less than 1, which are more in line with those of fMRI data. Therefore, we divided the activation patterns such that the two data halves did not contain identical images, yielding WCC and between-category correlation (BCC) values that varied from −1 to +1. We determined category discriminability by averaging over pairwise category discrimination scores, each of which was derived from four binary comparisons of WCC and BCC values. However, we modified the procedure for comparing correlation values from that used in the fMRI studies. Because the simulated activation patterns contained far less noise than empirical BOLD data, the WCC values were consistently higher than the BCC values, and so, averaging across the four binary comparisons of within- versus between-correlations consistently yielded scores of 100%. To avoid this ceiling effect, we derived a probabilistic pairwise category discrimination score from the WCC and BCC values as follows: PðcorrectÞ ¼ 1 4 (cid:2) X i within eβri within þ eβri;j eβri between ! þ within eβri within þ eβrj;i eβri between ð3Þ where i = 1, 2 is the pair of categories being compared; if i = 2, then j = 1, whereas if i = 1, then j = 2. Thus, i,j is the correlation between patterns elicited by rbetween category i in the first half of the data and category j in j,i is the correla- the second half of the data, and rbetween tion between patterns elicited by category i in the second half of the data and category j in the first half of the data. The constant β = 2 and was chosen such that discrimina- tion was at 95% for high WCC and low BCC values, before applying it to the network data. Probability of correct choice was used as a proxy for accuracy of a pairwise category discrimination. Exploratory Analyses BCC and WCC To determine which properties of the simulated object representations were driving the simulated MVPA results, we examined separately the two correlation values—BCC and WCC—that contribute to pairwise discriminations. To calculate BCC and WCC, activation patterns to all stimuli in a category were split into halves and averaged, as for the calculation of discrimination accuracy. For BCC values, the averaged patterns from the halves of the data were compared for all 15 pairings of two different cate- gories (face–house, face–chair, face–bottle, …, house– chair, house–bottle, etc.). There were two ways of making each comparison, for example, faces in the first half of 1782 Journal of Cognitive Neuroscience Volume 25, Number 11 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . / f u s e r o n 1 7 M a y 2 0 2 1 the data versus houses in the second half (face1–house2), as well as faces in the second half versus houses in the first half (face2–house1), and two ways of splitting the activa- tion patterns into halves (“different views” and “different exemplars”). The mean BCC reported for each category is the average across all five pairwise comparisons involv- ing that category, across both comparison types and both split types. Mirroring the calculation of discrimina- tion accuracy in Simulation 4 (in which we followed the procedure of Spiridon & Kanwisher, 2002; see Selection of Units), for all nonpreferred categories in each set of 30 units, we excluded all BCCs involving the preferred category. To determine each WCC value, we compared the average patterns elicited by that category in the two halves of the data. 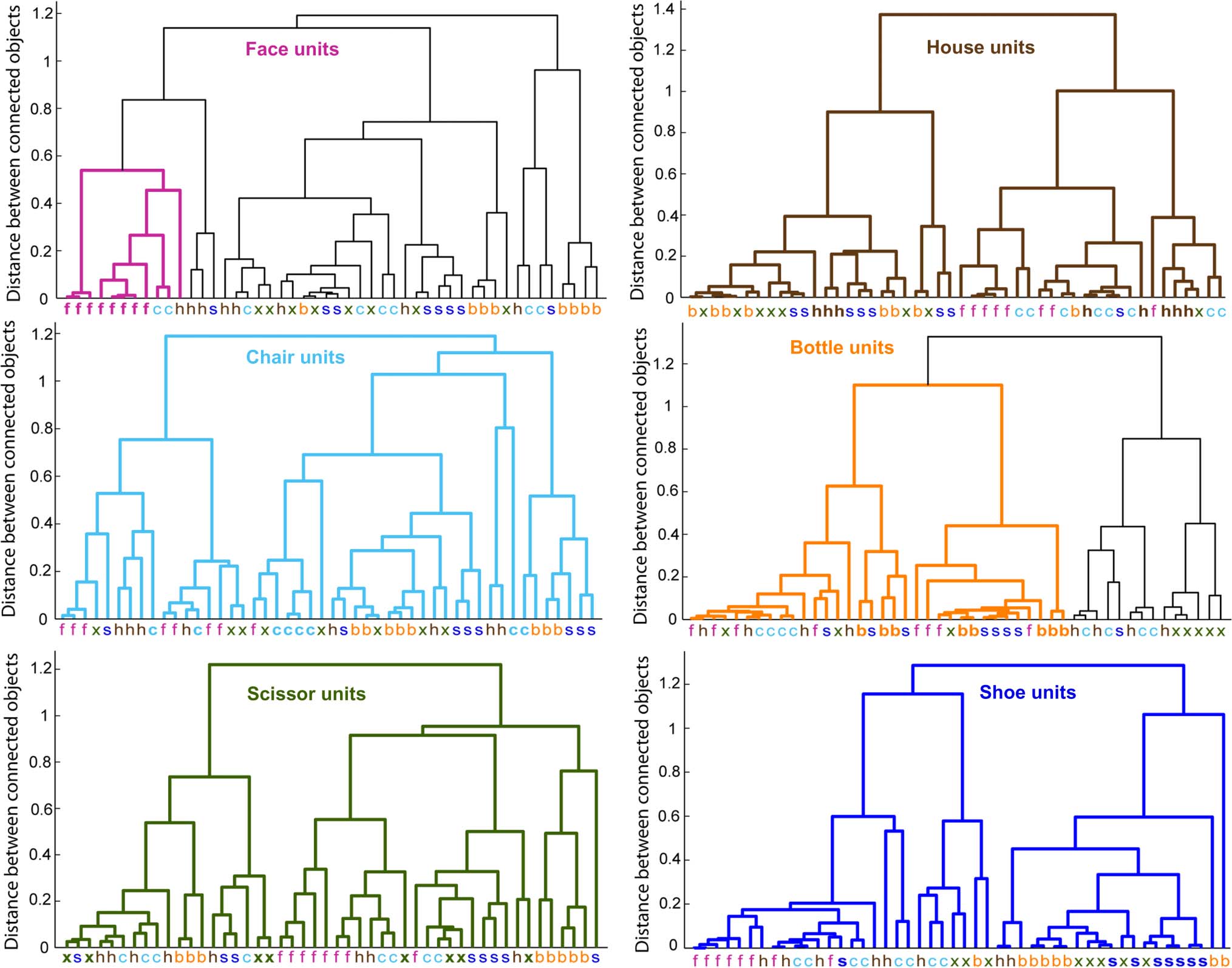Dendrograms To visualize the similarity of activation patterns in the dif- ferent categories, we performed a hierarchical cluster analysis and plotted dendrograms using the MATLAB func- tion dendrogram. Assuming some similarity space for all objects in a data set, a dendrogram depicts the clustering of objects in that space by using inverted U-shaped lines to connect objects in a hierarchical tree. We quantified dis- tance as one minus the correlation between two activation patterns (using the MATLAB function pdist with method “correlation”) to mirror the similarity metric used in Simu- lation 4. We then used these distances to link similar pairs of objects into binary clusters (containing two objects) before linking these clusters to each other and to other objects, creating progressively bigger clusters until all activation patterns in the data set were linked together in a tree (using the MATLAB function linkage). Each tree was plotted as a dendrogram. The height of each inverted U indicates the distance between the objects, or groups of objects, that are connected by the two arms of the U. Where the two objects connected by an inverted U con- tain more than one activation pattern, the height of the U represents the average of distances between all possible pairs of objects across the groups. RESULTS Using a neurocomputationally plausible model (Figure 1), we trained 100 networks to classify photographic im- ages into six object categories. To ensure that the network properties we investigated were not dependent on net- work size, we tested 25 networks at each of four sizes4 for the object representation layer: 40 × 40, 50 × 50, 60 × 60, and 70 × 70 units. Ninety-nine networks reached a prespecified performance criterion after between 40 and 200 training epochs; one network failed to reach criterion within a prespecified limit and so was replaced by an ad- ditional, successful simulation, giving 100 networks in the final data set. 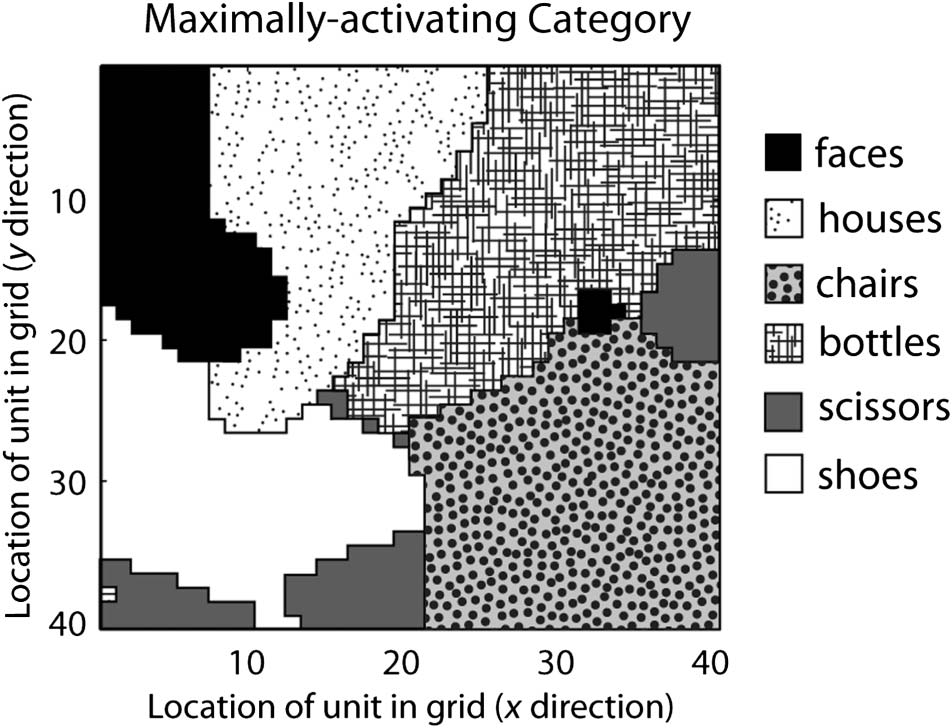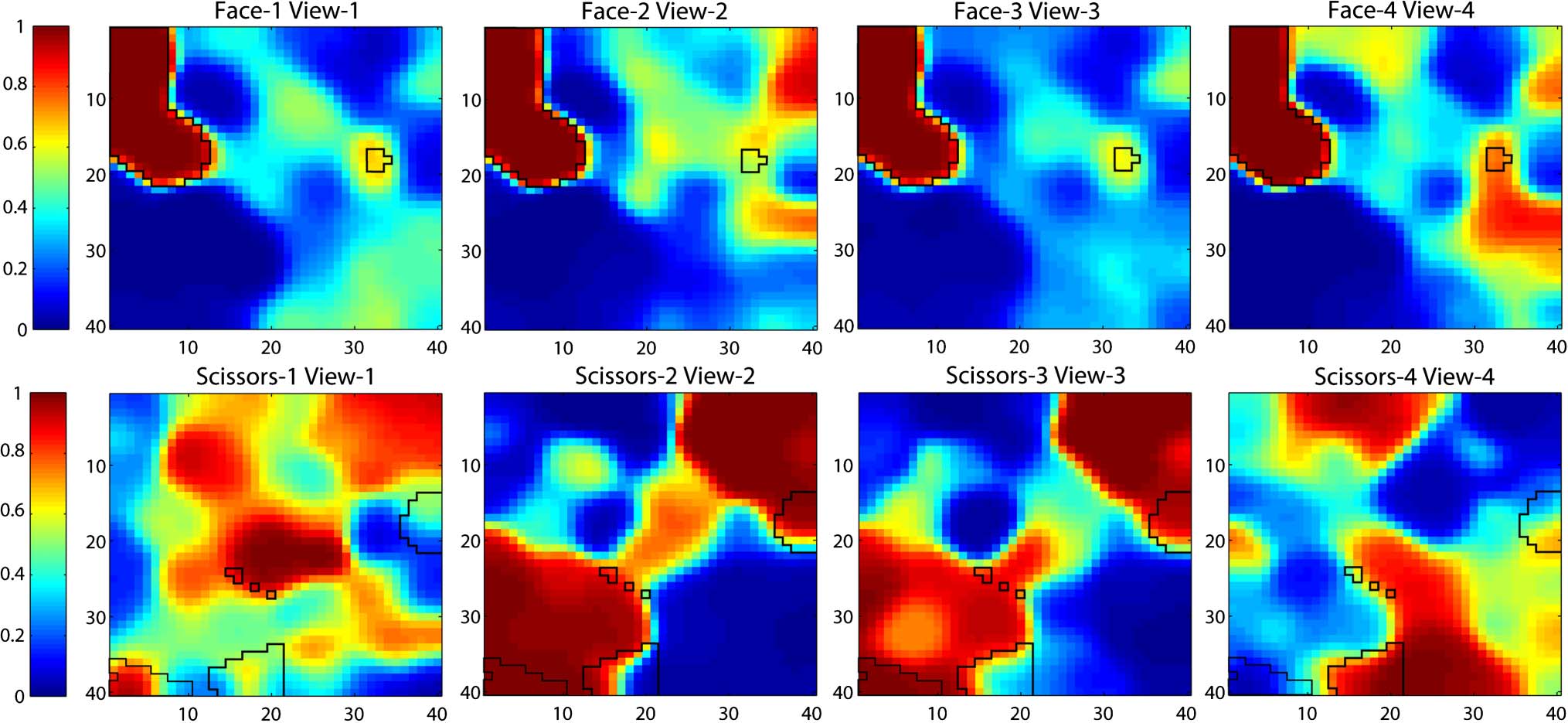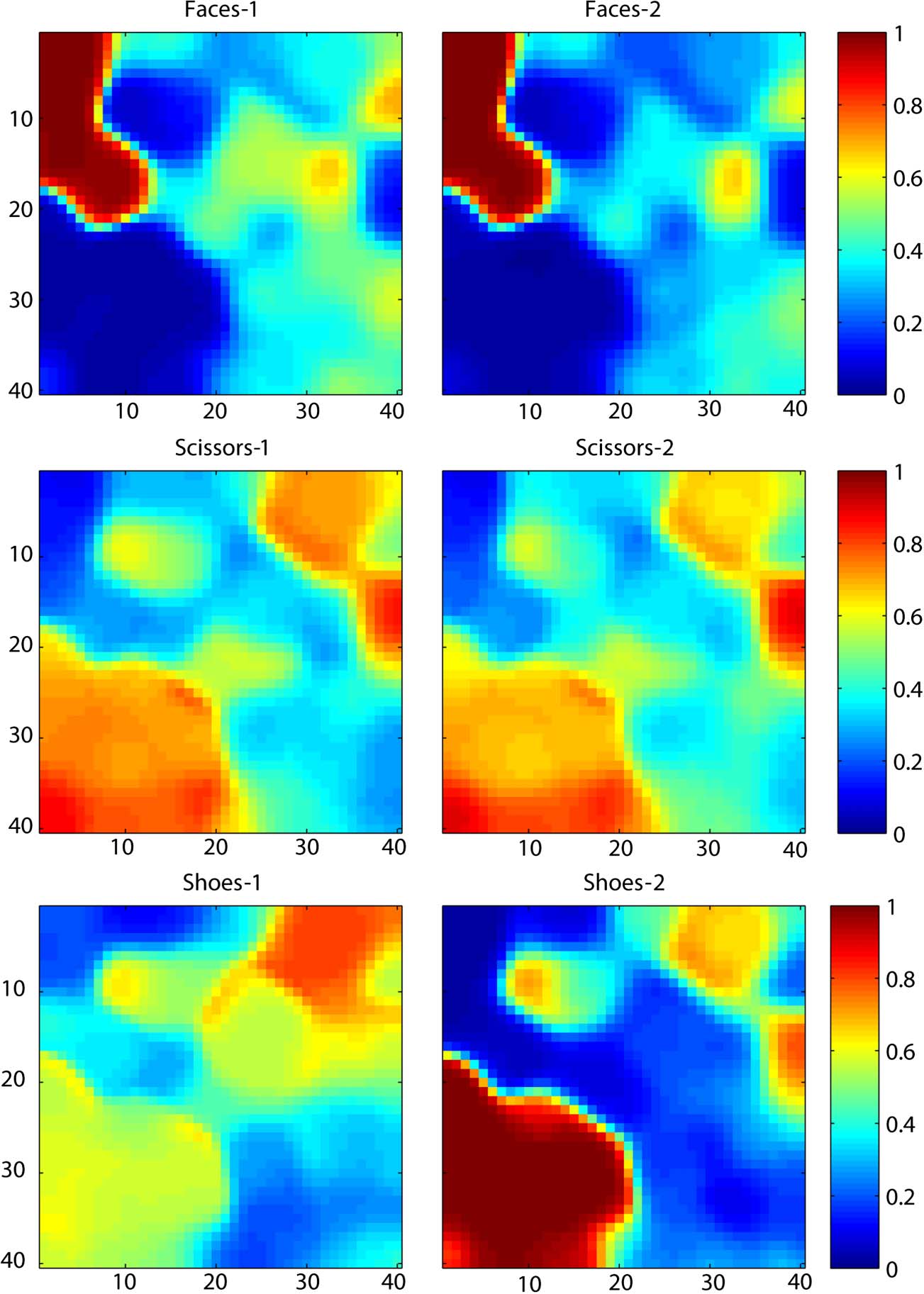On completion of training, a topographic organization of object representations was typically seen across units in the object-encoding layer: Units that were maximally active to a particular object category tended to be spatially clustered in the two-dimensional grid of units. Figure 2 shows the category preference elicited by each unit in the object encoding layer in a typical simula- tion; Figure 3 shows the average activation value elicited in each unit by the set of patterns in each category. Figure 2 reflects numerical category preferences: Each unit is coded according to the category that elicited the numerically high- est average activation in it, regardless of whether that ac- tivation value was statistically significantly higher than the activation caused by other categories. Units were subject to selectivity tests analogous to those used by the fMRI authors before being entered into MVPA simulations; there- fore, in any given simulation, only a subset of the units shown in each patch may have been included in the MVPA. Simulation 1: Category Discrimination Using All Object-selective Voxels The first finding reported by Haxby et al. (2001) was that activation patterns across all object-selective voxels in ventral temporal cortex contained sufficient information to perform pairwise category discriminations between the object categories viewed, with an overall accuracy level of 96%. In addition, Haxby et al. (2001) found that the pairwise discrimination of activation patterns elicited by stimuli from two different categories was most accurate when one of the two categories was faces. Activation pat- terns caused by houses were also well discriminated from other categories. Pairwise discriminations for scissors, shoes, and bottles were, on average, less accurate. D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . f / u s e r o n 1 7 M a y 2 0 2 1 Figure 2. Category preferences of units in the object encoding layer, in a typical network size of 40 × 40 units trained on six object categories. Each unit in the layer is depicted by a textured square at the x–y position corresponding to its location in the model; texture indicates the object category that maximally activates the unit. Category preference for each unit is taken as the category that elicited the numerically highest activation in the unit, when comparing the activation patterns obtained by averaging all stimuli in each category. Cowell and Cottrell 1783 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . 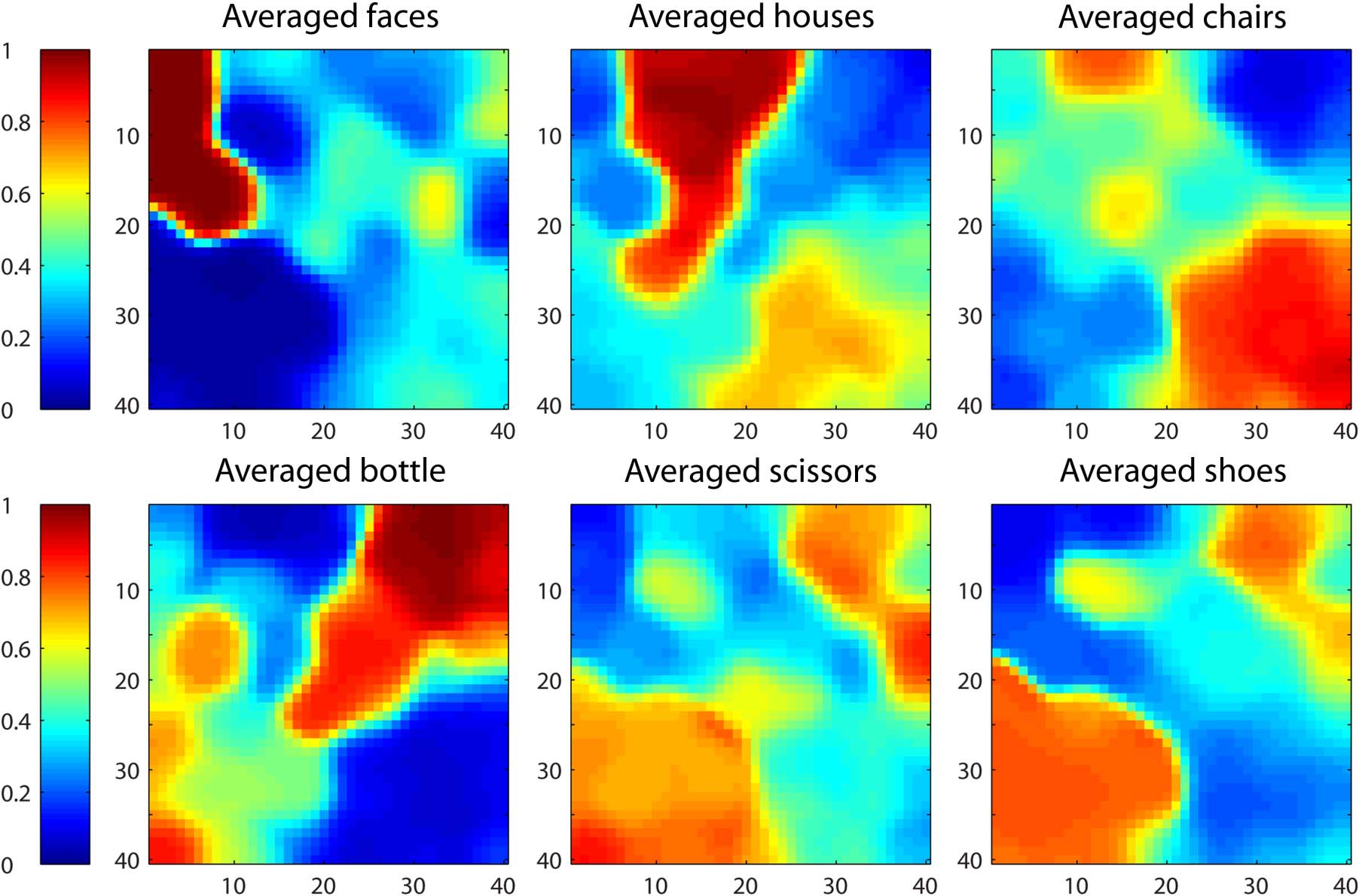f / u s e r o n 1 7 M a y 2 0 2 1 Figure 3. Activation of all units in the grid (for the same 40 × 40 network depicted in Figure 2), averaged over all stimulus patterns in a given category. As in Figure 2, each unit is depicted by a square at its x–y position in the model. High activations are shown in red, whereas low activations are in blue, as indicated by the scale at the left. Having trained networks to classify the six categories, we extracted activation patterns elicited in the object- encoding units by images from each category. In this analysis, which included all object-selective units, we performed MVPA on the model activation patterns using the methods of Haxby et al. (2001) for analyzing BOLD activation patterns. Simulated activation patterns, like human brain images, contained sufficient information to produce accurate pairwise discrimination of the six object categories included in our study (Table 1, top row). Overall accuracy was 85% with the parameters we used to determine discrimination performance (see Methods). In addition, we obtained a very similar qualita- tive trend in the accuracy of pairwise discriminations across object categories: Patterns elicited by faces were the most accurately discriminated from other categories, Table 1. Mean ± SEM Pairwise Category Discrimination Accuracy for Each of the Six Object Categories in Simulation 1 (“All Category-selective Units”), Simulation 2 (“Minus Units Maximally Active…”), and Simulation 3 (“Units Maximally Active to…”) Percent Correct Discrimination Region Faces Houses Chairs Bottles Scissors Shoes All category-selective units 91.0 ± 0.06 87.3 ± 0.09 87.2 ± 0.08 83.7 ± 0.1 81.1 ± 0.1 80.0 ± 0.06 Minus units maximally active to 90.8 ± 0.12 85.3 ± 0.19 88.1 ± 0.14 85.8 ± 0.15 80.8 ± 0.13 80.5 ± 0.09 compared categories Units maximally active to: Faces Houses 92.4 ± 0.07 80.1 ± 0.22 80.2 ± 0.35 82.9 ± 0.19 76.8 ± 0.26 73.7 ± 0.28 86.5 ± 0.16 86.2 ± 0.35 86.2 ± 0.17 81.3 ± 0.15 80.4 ± 0.15 79.7 ± 0.12 Small objects 88.0 ± 0.09 85.0 ± 0.15 84.3 ± 0.09 83.5 ± 0.13 81.7 ± 0.16 80.2 ± 0.08 In each row, responses of only those units belonging to a particular subset of units in the object encoding layer (defined on the left) were included in the analysis. 1784 Journal of Cognitive Neuroscience Volume 25, Number 11 Table 2. Average Pairwise Category Discrimination Accuracies, from Simulations 1–3 (Column 1), Haxby et al. (2001) (Column 2), and Spiridon and Kanwisher (2002) (Column 3) Region All category-selective units Minus units maximally active to compared categories Units maximally active to: Faces Houses Small objects Scores are averages across all six object categories. Average Percent Correct Discrimination Simulations Haxby et al. (2001) Spiridon and Kanwisher (2002) 85.0 85.2 81.0 83.4 83.8 95.0 93.8 83.0 92.7 93.2 96.0 – – – – whereas scissors, shoes, and bottles were the most poorly discriminated classes. This simulation also closely approximates an analysis performed by Spiridon and Kanwisher (2002). These authors noted that, if the same set of images are used to generate the brain patterns in both halves of the data between which correlations were measured, good cate- gory discrimination performance may simply reflect the reliability of BOLD responses to low-level features, rather than the presence of category-level information. To estab- lish the presence of category information, Spiridon and Kanwisher replicated the analysis of Haxby et al. using different stimuli from the same category to generate each half of the data; like Haxby et al., they found good dis- crimination performance. In Simulation 1, we followed Spiridon and Kanwisherʼs procedure for dividing the data, using nonidentical image sets to generate the halves (see Methods). Our finding of good classification performance despite nonidentical images sets therefore resembles the Spiridon and Kanwisher (2002) result. Moreover, Spiridon and Kanwisher replicated the finding of Haxby et al. that faces and houses were more accurately discriminated than other object categories (as did OʼToole et al., 2005, in a reanalysis of the data from Haxby et al., 2001) and argued that this indicated a “special” status for faces and houses in visual cortex. However, we were able to simulate this result in a computational model whose architecture and processing algorithms confer no special status on faces or houses. There was no face or house module in the model and no special process employed to learn these category representations. Simulation 2: Category Discrimination Using Nonmaximally Active Voxels We replicated a second finding of Haxby et al. (2001): Information about a particular object category is not con- tained solely in the cortical region responding maximally to that category. Haxby et al. assessed pairwise category discrimination using patterns of brain responses from which the voxels maximally responsive to the two cate- gories being discriminated had been removed. For example, in the discrimination of houses and shoes, all voxels maximally activated by houses or by shoes were removed from the analysis. Category identification was still possible based on patterns containing only non- maximal responses; the overall accuracy of pairwise dis- criminations (94%) was only slightly reduced relative to the case where all object-selective cortex was included in the analysis (96%). We replicated this analysis in the model and also found that good discrimination per- formance was maintained (Table 1, second row). We found overall discrimination accuracy of 85% when units maximally active to the object classes being discriminated were removed (Table 2, second row), compared with 85% when all responses were included (Simulation 1; Table 2, first row). Again, this analysis was very similar to one performed by Spiridon and Kanwisher (2002). In that study, the authors reported that the overall category discrimination accuracy obtained using all visually active voxels was not substantially altered by the removal of face-selective or house-selective voxels from the patterns analyzed. Simulation 3: Category Discrimination Using Only Maximally Active Voxels In this simulation, we replicated a third result from Haxby et al. (2001): Voxels in regions that are maximally respon- sive to a particular object category contain sufficient in- formation about other object categories to discriminate between those categories. In their analysis, Haxby et al. took sets of voxels that were maximally (and differentially) activated by one category: faces, houses, or a category defined as “small man-made objects” (i.e., chairs, bottles, scissors, and shoes). For each set of category-selective voxels, they determined the discriminability of all pairs of object categories, finding good overall performance in Cowell and Cottrell 1785 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f / t . u s e r o n 1 7 M a y 2 0 2 1 each region, ranging from 83% to 94%. We replicated this analysis using simulated activation patterns and similarly found good discrimination performance, ranging from 81% to 84% across the three regions (Table 1, rows 3– 5; Table 2, rows 3–5), indicating that units in the object representation layer in the model carry information about the type of object being viewed even when they respond maximally to other categories. Simulation 4: Category Discrimination Using Maximally Active Voxels, with Number of Units Held Constant On the basis of the three simulations described, Haxby et al. concluded that many different object categories— including those with limited biological significance during our evolutionary history, such as scissors and shoes—are represented robustly in the ventral temporal cortex by distinct patterns of responses that are overlapping and distributed in nature. They suggested that the information representing each category was not restricted to a small region in which voxels responded maximally to that cate- gory but, instead, that submaximal responses outside that region are also an integral part of the category representa- tion. Moreover, they argued that voxels responding maxi- mally to one particular category (such as faces or houses) also contribute to the representation of other object cate- gories, rather than possessing a specialized, category- specific function. Spiridon and Kanwisherʼs (2002) study was very simi- lar to that of Haxby et al. (2001), but contrary to Haxby et al., they interpreted their results in favor of cortical specialization for face and place processing. One im- portant analysis that provided evidence in favor of spe- cialization for faces involved a modified replication of the third Haxby et al. analysis simulated above. In this analysis, Spiridon and Kanwisher (2002) investigated whether cortical regions specialized for processing object categories other than faces and houses could be found if the category-selective region was not constrained to be a spatially contiguous set of voxels (finding a cluster of voxels maximally active to faces or houses is a typical constraint in localizing the FFA and the parahippocampal place area, but such clusters typically do not exist for other object categories). They tested for the existence of distributed selective regions by examining discrimina- tion performance within the set of 30 voxels “most selec- tive” for each category, choosing those voxels without heed to their location in the cortex. Their analysis was therefore very similar to Simulation 3, except that the size of the set of voxels was equated across category- selective regions. Spiridon and Kanwisher (2002) found that patterns across face-selective voxels produced better accuracy on face discriminations than on discriminations involving other stimulus classes and, critically, that this preferred-category advantage was not true for any other set of 30 voxels (e.g., in the shoe-selective cluster, dis- crimination of shoes was not superior to that of other categories). The authors took this as evidence for spe- cialized neural processing for faces that does not exist for other man-made categories. We replicated this analysis, choosing only the 30 most category-selective units in the object representation layer of the model for each category-selective region (see Methods). As seen in Table 3, we find a qualitatively similar pattern of results: In the face-selective units, face discriminations are more accurate than those of other categories, but this preferred-category advantage does not exist in any other category-selective region. The simulation of this finding provides a key insight for inter- preting the original finding from the empirical fMRI data. In the model used to simulate the activation pat- terns, we assumed no anatomical module for faces in Table 3. Mean ± SEM Pairwise Category Discrimination Accuracy, Simulation 4 Percent Correct Discrimination D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . f / Faces Houses Chairs Bottles Scissors Shoes 30 units most selective for: Faces Houses Chairs Bottles 85.4 ± 0.96 74.9 ± 0.62 79.0 ± 0.92 81.2 ± 0.64 72.0 ± 0.57 69.3 ± 0.61 81.9 ± 0.53 81.8 ± 0.74 82.9 ± 0.77 74.5 ± 0.41 75.1 ± 0.54 75.3 ± 0.59 80.3 ± 0.73 84.9 ± 0.43 76.5 ± 0.84 76.7 ± 0.63 77.1 ± 0.68 74.9 ± 0.46 82.3 ± 0.74 76.1 ± 0.66 76.7 ± 0.89 79.0 ± 0.52 78.9 ± 0.62 76.2 ± 0.67 Scissors 82.2 ± 0.46 81.3 ± 0.54 75.0 ± 0.91 83.6 ± 0.4 76.5 ± 0.53 80.3 ± 0.67 Shoes 80.7 ± 0.63 80.9 ± 0.58 78.7 ± 0.66 85.0 ± 0.46 84.9 ± 0.57 69.3 ± 0.56 In each row, activation patterns across only the 30 most selective units for the indicated category were used in the analysis. The highest accuracy for each set of units (i.e., in each row) is underlined. Cells on the diagonal are indicated in bold, for clarity. If any set of category-selective units possesses a preferred-category discrimination advantage, the cell on the diagonal contains the highest discrimination accuracy in the row, and is therefore shown in bold and underlined. This is true only for face-selective units, as in Spiridon and Kanwisher (2002). u s e r o n 1 7 M a y 2 0 2 1 1786 Journal of Cognitive Neuroscience Volume 25, Number 11 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f . 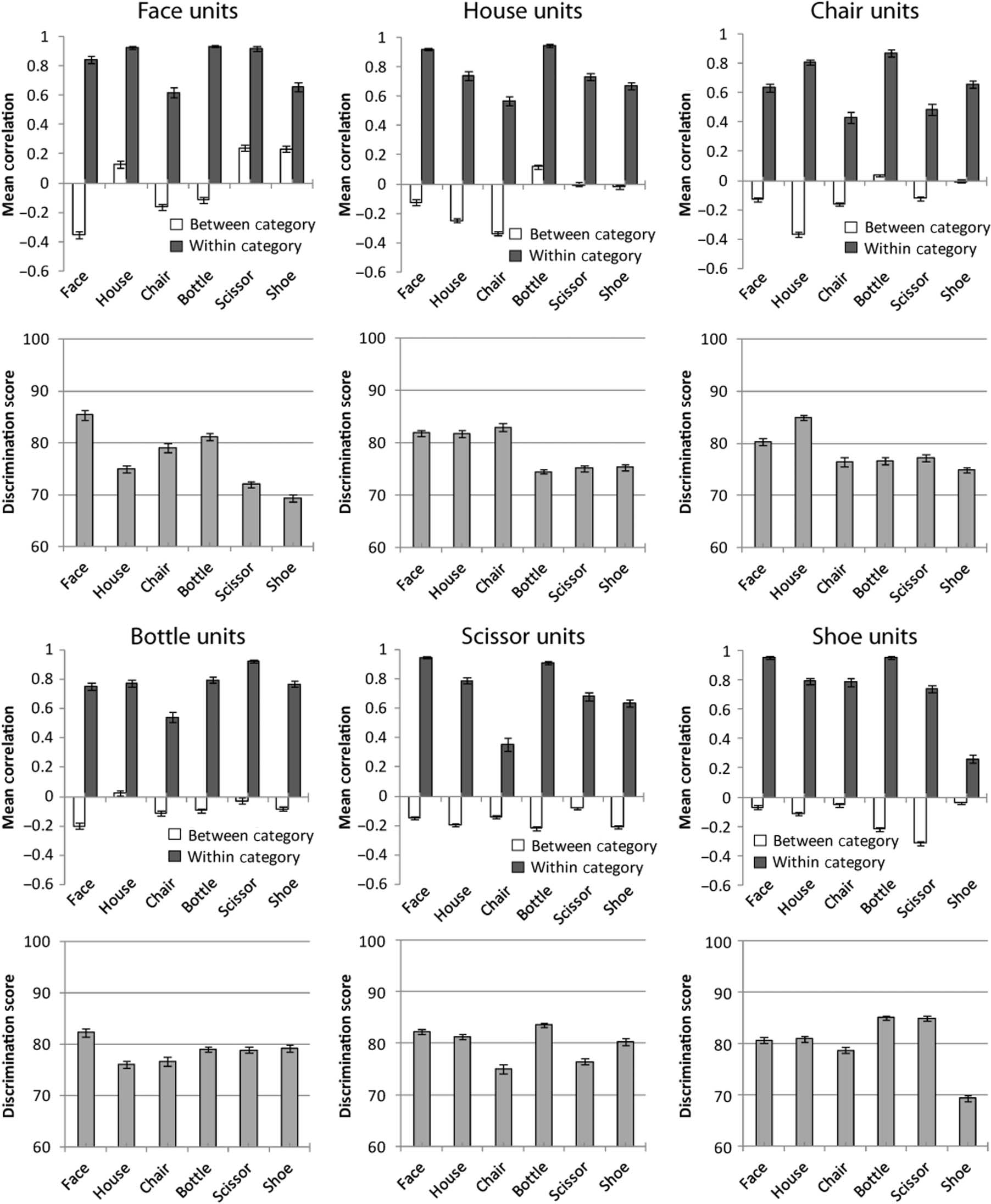t / Figure 4. WCC and BCC values for activation patterns in the object encoding layer of the model. For each set of 30 units used in Simulation 4— the units maximally selective for faces, houses, chairs, bottles, scissors, and shoes—the upper plot (row 1 or 3) shows the WCC and BCC values for each class of stimulus, and the lower plot (row 2 or 4) shows the discrimination accuracy for that stimulus class. Discrimination accuracy is based on WCC and BCC values, according to Equation 3. Higher WCC and lower BCC lead to better discrimination scores. the network architecture, nor did we implement any specialized processing mechanism for faces that differed from the mechanism used to learn about and generate activation patterns for other object categories. Yet, the pattern of better face discrimination in the face-selective units emerged spontaneously. Postulation of a specialized processing mechanism for faces is therefore not necessary to explain this result in the empirical fMRI data. Assuming that brain patterns, like the activation patterns in our neurocomputational model, reflect the natural similarity space in which the stimuli viewed by human participants reside (Kriegeskorte et al., 2008; OʼToole et al., 2005), Cowell and Cottrell 1787 u s e r o n 1 7 M a y 2 0 2 1 this pattern of results emerges simply on the basis of the inherent properties of the stimuli themselves, and the topographic manner in which the brain (and our model) represents these properties. in the same category) for each object category, (2) con- structing dendrograms to depict the similarity of object activation patterns, and (3) visually examining plots of simulated activation patterns. BCC and WCC Exploratory Analyses of Simulation 4 To determine what properties of the object representa- tions in the network allowed us to replicate the results from Spiridon and Kanwisher, we explored the modelʼs representations by (1) examining the BCCs (the similarity of patterns in one category to patterns in other categories) and WCCs (the similarity of patterns elicited by objects The accuracy of a category discrimination increases as the WCC of activation patterns increases or as the BCC of the activation patterns decreases (see Methods, Equation 3). For example, in a pairwise discrimination between faces and shoes, the higher the correlation between activation patterns caused by faces in the halves of the data (the WCC) or between activation patterns caused by shoes in D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f . t / u s e r o n 1 7 M a y 2 0 2 1 Figure 5. Dendrograms showing the clustering of activation patterns elicited by individual stimuli across the six sets of 30 category-selective units defined in Simulation 4. Dendrogram leaves (x axis) are labeled and color-coded according to the category of the activation pattern (f = faces, h = houses, c = chairs, b = bottles, x = scissors, and s = shoes). In each dendrogram, the smallest possible cluster of patterns that contains all eight exemplars belonging to the preferred category is shown in color, with thickened lines. For all sets of units except face and bottle units, this cluster includes all 48 stimuli; that is, for all categories except faces and bottles, the patterns elicited by stimuli in a given category were not highly similar across the units that were maximally activated by that category. For bottle units, the cluster encompassing all eight bottles contains 34 of the 48 the stimuli, that is, there were 26 nonbottle stimuli that elicited patterns that were at least as similar to the bottles as some bottles were to each other, suggesting relatively poor clustering of bottle patterns in terms of similarity. For face units, the cluster encompassing all eight faces contains only 11 of 48 stimuli, suggesting a tight clustering of face patterns. 1788 Journal of Cognitive Neuroscience Volume 25, Number 11 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . f / u s e r o n 1 7 M a y 2 0 2 1 Figure 6. Activation of units in the object encoding layer of the model, elicited by individual face (top row) and scissor (bottom row) stimuli. Each plot is generated by a unique exemplar pictured from a unique view. The black polygons delineate the regions of units that responded maximally to faces (top row) and scissors (bottom row). Activation patterns elicited by different scissor stimuli exhibit much more variability than activation patterns elicited by different face stimuli. two halves of the data, the better the discrimination of faces and shoes. In contrast, the higher the correlation be- tween faces in one half of the data and shoes in the other half of the data (the BCC), the poorer the discrimination of faces and shoes. Figure 4 shows, for each subregion of the grid analyzed in Simulation 4 (i.e., the six sets of 30 units most selective for each category), the mean WCC and BCC values for activation patterns elicited by stimuli in the six categories. In Figure 4, for each set of 30 units, the WCC and BCC values (first and third rows) are shown directly above the discrimination accuracy (second and fourth rows) for each category of activation patterns. Categories with high WCCs and low BCCs yielded good discrimination scores, but the BCC value tended to have a greater influ- ence on discrimination accuracy. For example, in face units, although houses, bottles, and scissors have slightly higher WCC values than face stimuli, none of these cate- gories have a low value of BCC as faces do. Therefore, the superior discrimination of faces in the face units seems largely driven by the fact that activation patterns caused by faces are the most distinct from other categoriesʼ activa- tion patterns. The powerful influence of the BCC is also observed for chair patterns across face units: Good dis- crimination accuracy is obtained despite low WCC values, presumably owing to the relatively low BCC values for chairs in these units. Thus, the modelʼs account of the finding by Spiridon and Kanwisher—an advantage in face-selective voxels for the discrimination of faces over other categories, which does not exist for any other category—is that face patterns across the face units are maximally distinct from the patterns of other categories, whereas this is not true for preferred-category patterns in any other set of units. Dendrograms To visualize how face representations across face- selective units are self-similar and distinct from other categories, we constructed dendrograms depicting the clustering (i.e., similarity) of activation patterns elicited by individual stimuli across the six sets of 30 category- selective units from Simulation 4 (Figure 5). The six sepa- rate dendrograms, one for each set of category-selective units, include patterns generated by a single, typical model simulation. In each dendrogram, eight example activation patterns from the 40 stimuli per category were randomly chosen for inclusion, because it was not possible to depict more than eight stimuli per category in a single plot. Dendrograms connect objects according to similarity in a hierarchical tree. The height of the inverted U connecting each pair of objects (or object groups) indicates the simi- larity of those objects. The dendrograms in Figure 5 show that, for all sets of units except face and bottle units, stim- uli in the preferred category are no more similar to each other and no more distinct from other categories than stimuli in the nonpreferred categories. For activation pat- terns across the bottle units, bottle patterns are somewhat self-similar and distinct from other categories, in that all bottle patterns reside within a subcluster of the dendro- gram that contains about two thirds of the patterns. For activation patterns across the face units, faces are even more self-similar and distinct: All eight face patterns fall Cowell and Cottrell 1789 within a subcluster that contains only 11 of the 48 patterns. The distinctiveness of a category can be quantified in terms of “cluster purity,” which we define as the proportion of leaves corresponding to preferred category patterns within the smallest cluster that contains all eight preferred cate- gory patterns in the dendrogram. For face units, the mean cluster purity was 0.68 (across all dendrograms generated for all 100 simulated networks). For house, chair, bottle, scissor, and shoe units, the mean cluster purities were 0.22, 0.18, 0.24, 0.18, and 0.2, respectively. The dendro- grams in Figure 5 possess “purity” values representative of the mean cluster purity for each set of 30 category- selective units. In summary, only across face units did we consistently find that activation patterns elicited by stimuli from the preferred category were well separated into a relatively category-pure cluster. Activation Patterns We plotted the simulated activation patterns to visualize the properties of the stimulus representations (Figures 3, 6, and 7). In Figures 6 and 7, all plots are taken from a single simulation (network size = 40 × 40 units), which was also used to generate Figures 2 and 3; the regions of maximal response to faces and scissors in Figure 6 can therefore be compared with the map of category prefer- ences in Figure 2. Whereas faces elicit remarkably consis- tent activation patterns across different individuals and different views, the activation patterns elicited by scissors vary considerably, leading to higher WCCs for faces than for scissors and other nonface categories. However, this effect is diluted in the MVPA results by the fact that, before calculating WCCs, patterns in each category are Figure 7. Mean activation of units in the object encoding layer of the model, in each half of the data, for the face, scissor, and shoe categories. Activation patterns were assigned to the halves of the data according to the “different views” protocol. Regions of the grid that are activated highly by faces tend not to be activated by shoes or scissors, and vice versa, whereas activation patterns elicited by shoes and scissors tend to include many units in common. D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . / t f u s e r o n 1 7 M a y 2 0 2 1 1790 Journal of Cognitive Neuroscience Volume 25, Number 11 averaged into halves, removing much inter-individual and inter-view variability. It is therefore more instructive to examine plots of activation patterns that have been aver- aged across halves of the data. Figure 7 shows mean activation values across patterns in the halves of the data, for the face, scissor, and shoe stimuli. Two important properties of the representations are evident. First, for shoes, even when averaged across half of the stimuli in the category, the two resulting aver- age activation patterns are remarkably different, a fact likely to lead to low WCC values and poor discrimination accuracy. Second, regions of the grid that are activated by faces are in general not activated by scissors or shoes, and vice versa; in contrast, many regions of the grid ac- tivated by scissors are also activated by shoes. In other words, patterns caused by faces are quite distinct from patterns caused by other categories, eliciting high values only in units that do not contribute to the representa- tions of other categories; this is not true for scissor and shoe patterns. This unique property of face representa- tions in the model accounts for the high BCCs for faces. Moreover, we note that this is particularly true in the portion of the grid that is maximally activated by faces (the top-left corner in Figures 2 and 6), that is, the area from which the subset of 30 most-selective face units were drawn in Simulation 4. DISCUSSION We used a model of object processing in visual cortex to simulate MVPA results from two fMRI studies: Spiridon and Kanwisher (2002) and Haxby et al. (2001). The model employs a neurocomputationally plausible mecha- nism to govern the unsupervised development of visual object representations into a topographically organized map. We developed a method for analyzing the activa- tion patterns elicited by objects from different categories across the topographic object-encoding layer of the mod- el, in a manner analogous to the MVPA procedures of the fMRI studies. Replicating Haxby et al., we demonstrated that activation patterns in the model contain sufficient information to perform pairwise category discrimination under three conditions: using all object-selective units in the object-encoding layer, using only object-selective units that were not maximally activated by the categories taking part in the discrimination, and using subsets of object-selective units that were maximally activated by a single category or group of categories. Replicating Spiridon and Kanwisher (2002), we demonstrated that, for activa- tion patterns across the 30 units most selective for faces, faces were better discriminated than any other category, and this preferred-category discrimination advantage did not exist for any other set of 30 units most selective for a particular object category. The successful replication of these empirical results indicates that the object representations of the model share important properties (in particular, the similarity relationships that determine category discriminability) with object representations in the ventral temporal cortex measured with fMRI. Moreover, the method we devised for analyzing simulated activation patterns is a viable ap- proach for predicting the discriminability of brain pat- terns. The approach is therefore suitable for testing the ability of theoretical assumptions concerning neural architecture and neural processing mechanisms to explain patterns of fMRI data. Three of the empirical results we simulated have been interpreted as evidence for distributed object processing (Simulations 1–3), and the fourth as evidence for a spe- cialized face-processing module (Simulation 4). In simulat- ing key findings on both sides, the present computational study offers an explanation for the contradiction that seems to be posed by the empirical data. In the model, there was neither an anatomical module for the category of faces nor any specialized processing mechanism or distinct representational assumptions for faces. Rather, the MVPA results that arose in the model were driven by the inherent similarity properties of the face and object stimuli themselves, in combination with a neurocom- putationally plausible learning rule that produced topog- raphy in the model representations mimicking that seen in visual cortex. The simulations therefore demonstrate that it is not necessary to posit specialized neural mecha- nisms to account for the finding by Spiridon and Kanwisher (2002) that there is a face-discrimination advantage across voxels maximally activated by faces, whereas there is no such preferred-category discrimination advantage across voxels maximally activated by other categories. Examination of the WCC and BCC values for activation patterns in the different categories revealed that pairwise category discriminability in the model was most strongly influenced by the presence of low BCCs. Face patterns across face-selective units showed particularly low BCCs, meaning activation patterns caused by faces were the most distinct from other categoriesʼ activation patterns, likely making an important contribution to the result observed in Simulation 4. This account of the simulated data was corroborated by the hierarchical cluster analysis carried out on individual stimulus activation patterns from the model: Only across face units did we consistently find that activation patterns elicited by stimuli from the preferred category (faces) were well separated into a rela- tively category-pure cluster (Figure 5). Finally, in line with the notion that facesʼ distinctiveness as a stimulus class drove the result seen in Simulation 4, the plots of Figure 7 indicated that patterns caused by faces were quite distinct from patterns caused by other classes of stimuli, eliciting high values only in units that do not contribute to the representations of other categories. We note that the extreme distinctiveness of face rep- resentations in the model also seems likely to be a prop- erty of the neural representations of faces. In the fMRI literature, category-selective voxels are often defined as those that respond more than twice as strongly to the Cowell and Cottrell 1791 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j / . t f u s e r o n 1 7 M a y 2 0 2 1 preferred category than to other categories (Kanwisher, 2010; Spiridon & Kanwisher, 2002). What the present computational study shows is that the superior dis- criminability of faces in face-preferring regions of cortex might emerge simply on the basis of the raw stimulus properties themselves, provided that ventral temporal cortex representations reflect stimulus similarity space to some extent (an idea finding support in OʼToole et al., 2005, and Kriegeskorte et al., 2008). We emphasize that our simulations cannot rule out a “face module” account of the fMRI data. However, a stimulus similarity explanation that does not appeal to cortical modules is a more parsimonious account, given that a specialized face-processing module is not neces- sary to explain the empirical results. Moreover, our re- sults are in line with those of another computational study by Jiang et al. (2006), in which a shape-based ac- count of object processing that assumes no face-specific processes can account for both behavioral findings (such as the face-inversion and “configural” effects) and a series of fMRI results indicating face selectivity in the FFA. A key demonstration made by the present study is that these photographic images of everyday objects do not constitute a well-controlled stimulus set. Our simulation experiment deliberately eschews not only any specialized architecture or processing mechanism for faces but also many aspects of everyday learning and experience that are different for faces than for other classes of object (e.g., more time spent looking at faces or lifelong practice with subordinate-level, rather than category-level, dis- criminations). This choice was made to isolate and test the ability of the raw stimulus properties inherent in the images presented to human participants to account for the MVPA findings. Because of the simplicity of the model, some properties of the representations measured in ven- tral temporal cortex with fMRI are not reflected in our si- mulated activation patterns, for example, the finding that there are many more voxels selective for faces and houses than for other classes of object (e.g., see Figure 6, Spiridon & Kanwisher, 2002). It is remarkable that, despite the discrepancy between the object representations in our networks and those measured with fMRI for this seemingly important property, the MVPA results are in accord. In- deed, one would have expected that having fewer voxels for faces would make it more difficult to obtain this result. This demonstrates that the relative number of voxels selec- tive for the various object categories is not a property of the representations that is necessary to account for the MVPA findings; stimulus properties alone can provide an explanation. The stimuli used by both Haxby et al. (also used in this study) and Spiridon and Kanwisher were not standardized in terms of within- and between-category similarity; they simply reflected the inherent variability in similarity that exists across real-world object categories. Sets of images such as these cannot be used to test whether there are specialized neural processing mechanisms for faces that do not apply to other categories, because any appearance in the fMRI data of qualitative differences in the neural representations of faces might simply be attributable to inherent “properties” of faces as a class of visual stimulus (namely, that faces are in general highly similar to each other and very different from objects in other categories). In summary, the novel computational technique that we present constitutes a valuable tool for the interpretation of fMRI data in terms of hypotheses concerning neuro- cognitive architecture and mechanisms. The present result offers a cautionary tale for the interpretation of MVPA results: It can be difficult to determine the consequences of a particular neurocognitive theory for patterns of brain activation in fMRI without explicit simulation of the hy- pothesized mechanisms. However, when the assumptions of a neurocognitive theory are instantiated in a concrete computational model and the consequences of those as- sumptions are simulated, it is possible to determine which inferences regarding neurocognitive mechanisms can and cannot be drawn from the empirical data. Reprint requests should be sent to Rosemary A. Cowell, Psy- chology Department, Tobin Hall, University of Massachusetts, Amherst, MA 01003, or via e-mail: rcowell@psych.umass.edu. Notes 1. This is not to say that there may not be other data that can support this claim. 2. We also trained a set of networks on seven categories includ- ing cats and performed MVPA on those networks. The MVPA results for the six categories we report were not qualitatively (or substantially quantitatively) affected by the addition of cats. We did not include cats in the simulations we report because net- works did not perform well behaviorally at categorizing cats, likely because of the greater variability in viewing angle from which images in this set were pictured, relative to the more restricted range of viewing angles within other stimulus categories. 3. We replicated all MVPA simulations reported here using a set of novel stimuli. The novel images had been used only as holdout images to test categorization performance during training; net- worksʼ weights had never been updated in response to the presentation of these stimuli. All qualitative aspects of the MVPA results we report for training stimuli were the same using these novel stimuli. We report the results from analyses with training stimuli because this afforded a larger stimulus set with which to perform MVPA (because many more items were required for the training set than for the holdout set). 4. All of the qualitative patterns of results that emerged in the MVPA results averaged over four network sizes were also evident in at least three of the four network sizes examined indepen- dently. The vast majority of the qualitative patterns we report were in fact evident in all four network sizes tested. REFERENCES Aitkin, L. M., Merzenich, M. M., Irvine, D. R., Clarey, J. C., & Nelson, J. E. (1986). Frequency representation in auditory cortex of the common marmoset (Callithrix jacchus jacchus). Journal of Comparative Neurology, 252, 175–185. 1792 Journal of Cognitive Neuroscience Volume 25, Number 11 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f / t . u s e r o n 1 7 M a y 2 0 2 1 Cohen, L., Lehericy, S., Chochon, F., Lemer, C., Rivaud, S., & Dehaene, S. (2002). Language-specific tuning of visual cortex? Functional properties of the visual word form area. Brain, 125, 1054–1069. Cowell, R. A., Huber, D. E., & Cottrell, G. W. (2009). Virtual brain reading: A connectionist approach to understanding fMRI. Proceedings of the 31st Annual Conference of the Cognitive Science Society (pp. 212–217), Washington, DC. Cynader, M. S., Swindale, N. V., & Matsubara, J. A. (1987). Functional topography in cat area 18. Journal of Neuroscience, 7, 1401–1413. Dailey, M. N., & Cottrell, G. W. (1999). Organization of face and object recognition in modular neural network models. Neural Networks, 12, 1053–1074. Daugman, J. G. (1985). Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. Journal of the Optical Society of America A—Optics Image Science and Vision, 2, 1160–1169. Downing, P. E., Jiang, Y. H., Shuman, M., & Kanwisher, N. (2001). A cortical area selective for visual processing of the human body. Science, 293, 2470–2473. Epstein, R., & Kanwisher, N. (1998). A cortical representation of the local visual environment. Nature, 392, 598–601. Hanson, S. J., Matsuka, T., & Haxby, J. V. (2004). Combinatorial codes in ventral temporal lobe for object recognition: Haxby (2001) revisited: Is there a “face” area? Neuroimage, 23, 156–166. Haxby, J. V., Gobbini, M. I., Furey, M. L., Ishai, A., Schouten, J. L., & Pietrini, P. (2001). Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science, 293, 2425–2430. Ishai, A., Ungerleider, L. G., Martin, A., & Haxby, J. V. (2000). The representation of objects in the human occipital and temporal cortex. Journal of Cognitive Neuroscience, 12 (Suppl. 2), 35–51. Ishai, A., Ungerleider, L. G., Martin, A., Schouten, J. L., & Haxby, J. V. (1999). Distributed representation of objects in the human ventral visual pathway. Proceedings of the National Academy of Sciences, U.S.A., 96, 9379–9384. Jiang, X., Rosen, E., Zeffiro, T., Vanmeter, J., Blanz, V., & Riesenhuber, M. (2006). Evaluation of a shape-based model of human face discrimination using fMRI and behavioral techniques. Neuron, 50, 159–172. Kanwisher, N. (2010). Functional specificity in the human brain: A window into the functional architecture of the mind. Proceedings of the National Academy of Sciences, U.S.A., 107, 11163–11170. Kanwisher, N., McDermott, J., & Chun, M. M. (1997). The fusiform face area: A module in human extrastriate cortex specialized for face perception. Journal of Neuroscience, 17, 4302–4311. Kohonen, T. (1982). Self-organized formation of topologically correct feature maps. Biological Cybernetics, 43, 59–69. Kohonen, T. (1984). Self-organization and associative memory. Berlin: Springer-Verlag. Kriegeskorte, N., Mur, M., Ruff, D. A., Kiani, R., Bodurka, J., Esteky, H., et al. (2008). Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron, 60, 1126–1141. Krubitzer, L. A., & Calford, M. B. (1992). Five topographically organized fields in the somatosensory cortex of the flying fox: Microelectrode maps, myeloarchitecture, and cortical modules. Journal of Comparative Neurology, 317, 1–30. Lemon, R. N. (1981). Variety of functional organization within the monkey motor cortex. Journal of Physiology, 311, 521–540. Logothetis, N. K. (2008). What we can do and what we cannot do with fMRI. Nature, 453, 869–878. McCarthy, G., Puce, A., Gore, J. C., & Allison, T. (1997). Face-specific processing in the human fusiform gyrus. Journal of Cognitive Neuroscience, 9, 605–610. OʼToole, A. J., Jiang, F., Abdi, H., & Haxby, J. V. (2005). Partially distributed representations of objects and faces in ventral temporal cortex. Journal of Cognitive Neuroscience, 17, 580–590. Petersen, S. E., Fox, P. T., Snyder, A. Z., & Raichle, M. E. (1990). Activation of extrastriate and frontal cortical areas by visual words and word-like stimuli. Science, 249, 1041–1044. Sanger, T. D. (1989). Optimal unsupervised learning in a single-layer linear feedforward neural network. Neural Networks, 2, 459–473. Spiridon, M., & Kanwisher, N. (2002). How distributed is visual category information in human occipito-temporal cortex? An fMRI study. Neuron, 35, 1157–1165. Swindale, N. V., Matsubara, J. A., & Cynader, M. S. (1987). Surface organization of orientation and direction selectivity in cat area 18. Journal of Neuroscience, 7, 1414–1427. Tong, M. H., Joyce, C. A., & Cottrell, G. W. (2008). Why is the fusiform face area recruited for novel categories of expertise? A neurocomputational investigation. Brain Research, 1202, 14–24. D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 1 2 1 5 / 1 1 7 1 7 / 7 1 1 7 9 7 4 7 5 / 9 1 8 3 7 7 o 9 c 8 n 2 _ 9 a / _ j 0 o 0 c 4 n 4 8 _ a p _ d 0 0 b 4 y 4 g 8 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . / t f u s e r o n 1 7 M a y 2 0 2 1 Cowell and Cottrell 1793 What Evidence Supports Special Processing for Faces? Bild

PDF Herunterladen