Transactions of the Association for Computational Linguistics, 1 (2013) 291–300. Action Editor: Chris Callison-Burch.
Submitted 5/2013; Published 7/2013. C(cid:13)2013 Verein für Computerlinguistik.
291
Large-scale Word Alignment Using Soft Dependency Cohesion Constraints Zhiguo Wang and Chengqing Zong National Laboratory of Pattern Recognition Institute of Automation, Chinesische Akademie der Wissenschaft {zgwang, cqzong}@nlpr.ia.ac.cn Abstract Dependency cohesion refers to the observation that phrases dominated by disjoint dependency subtrees in the source language generally do not overlap in the target language. It has been verified to be a useful constraint for word alignment. Jedoch, previous work either treats this as a hard constraint or uses it as a feature in discriminative models, which is ineffective for large-scale tasks. In diesem Papier, we take dependency cohesion as a soft constraint, and integrate it into a generative model for large-scale word alignment experiments. We also propose an approximate EM algorithm and a Gibbs sampling algorithm to estimate model parameters in an unsupervised manner. Experiments on large-scale Chinese-English translation tasks demonstrate that our model achieves improvements in both alignment quality and translation quality. 1 Introduction Word alignment is the task of identifying word correspondences between parallel sentence pairs. Word alignment has become a vital component of statistical machine translation (SMT) Systeme, since it is required by almost all state-of-the-art SMT systems for the purpose of extracting phrase tables or even syntactic transformation rules (Koehn et al., 2007; Galley et al., 2004). During the past two decades, generative word alignment models such as the IBM Models (Brown et al., 1993) and the HMM model (Vogel et al., 1996) have been widely used, primarily because they are trained on bilingual sentences in an unsupervised manner and the implementation is freely available in the GIZA++ toolkit (Oh und Ney, 2003). Jedoch, the word alignment quality of generative models is still far from satisfactory for SMT systems. In den vergangenen Jahren, discriminative alignment models incorporating linguistically motivated features have become increasingly popular (Moore, 2005; Taskar et al., 2005; Riesa and Marcu, 2010; Saers et al., 2010; Riesa et al., 2011). These models are usually trained with manually annotated parallel data. Jedoch, when moving to a new language pair, large amount of hand-aligned data are usually unavailable and expensive to create. A more practical way to improve large-scale word alignment quality is to introduce syntactic knowledge into a generative model and train the model in an unsupervised manner (Wu, 1997; Yamada and Knight, 2001; Lopez and Resnik, 2005; DeNero and Klein, 2007; Pauls et al., 2010). In diesem Papier, we take dependency cohesion (Fuchs, 2002) into account, which assumes phrases dominated by disjoint dependency subtrees tend not to overlap after translation. Instead of treating dependency cohesion as a hard constraint (Lin and Cherry, 2003) or using it as a feature in discriminative models (Cherry and Lin, 2006B), we treat dependency cohesion as a distortion constraint, and integrate it into a modified HMM word alignment model to softly influence the probabilities of alignment candidates. We also propose an approximate EM algorithm and an explicit Gibbs sampling algorithm to train the model in an unsupervised manner. Experiments on a large-scale Chinese-English translation task demonstrate that our model achieves improvements in both word alignment quality and machine translation quality. The remainder of this paper is organized as follows: Abschnitt 2 introduces dependency cohesion
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
292
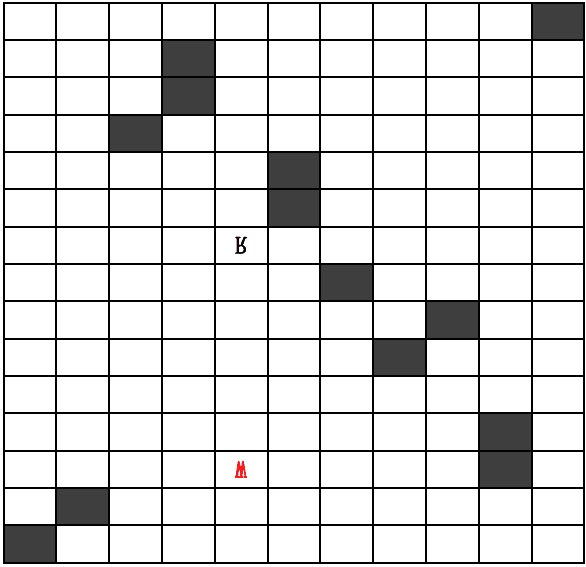
constraint for word alignment. Abschnitt 3 presents our generative model for word alignment using dependency cohesion constraint. Abschnitt 4 describes algorithms for parameter estimation. We discuss and analyze the experiments in Section 5. Abschnitt 6 gives the related work. Endlich, we conclude this paper and mention future work in Section 7. 2 Dependency Cohesion Constraint for Word Alignment Given a source (foreign) sentence 𝒇1𝐽=𝑓1,𝑓2,…,𝑓𝐽 and a target (English) sentence 𝒆1𝐼=𝑒1,𝑒2,…,𝑒𝐼, the alignment 𝓐 between 𝒇1𝐽and 𝒆1𝐼 is defined as a subset of the Cartesian product of word positions: 𝓐∈{(𝑗,𝑖):𝑗=1,…,𝐽;𝑖=1,…,𝐼} When given the source side dependency tree 𝑇, we can project dependency subtrees in 𝑇 onto the target sentence through the alignment 𝓐. Dependency cohesion assumes projection spans of disjoint subtrees tend not to overlap. Let 𝑇(𝑓𝑖) be the subtree of 𝑇 rooted at 𝑓𝑖, we define two kinds of projection span for the node 𝑓𝑖: subtree span and head span. The subtree span is the projection span of the total subtree 𝑇(𝑓𝑖), while the head span is the projection span of the node 𝑓𝑖 itself. Following Fox (2002) and Lin and Cherry (2003), we consider two types of dependency cohesion: head-modifier cohesion and modifier-modifier cohesion. Head-modifier cohesion is defined as the subtree span of a node does not overlap with the head span of its head (parent) node, while modifier-modifier cohesion is defined as subtree spans of two nodes under the same head node do not overlap each other. We call a situation where cohesion is not maintained crossing. Using the dependency tree in Figure 1 as an example, given the correct alignment “R”, the subtree span of “有/have” is [8, 14] , and the head span of its head node “之一/one of” is [3, 4]. They do not overlap each other, so the head-modifier cohesion is maintained. Ähnlich, the subtree span of “少数/few” is [6, 6], and it does not overlap the subtree span of “有/have”, so a modifier-modifier cohesion is maintained. Jedoch, when “R” is replaced with the incorrect alignment “W”, the subtree span of “有/have” becomes [3, 14], and it overlaps the head span of its head “之一/one of”, so a head-modifier crossing occurs. In der Zwischenzeit, the subtree spans of the two nodes “有/have” and “少数/few” overlap each other, so a modifier-modifier crossing occurs. Fuchs (2002) showed that dependency cohesion is generally maintained between English and French. To test how well this assumption holds between Chinese and English, we measure the dependency cohesion between the two languages with a manually annotated bilingual Chinese-English data set of 502 sentence pairs1. We use the head-modifier cohesion percentage (HCP) and the modifier-modifier cohesion percentage (MCP) to measure the degree of cohesion in the corpus. HCP (or MCP) is used for measuring how many head-modifier (or modifier-modifier) pairs are actually cohesive. Tisch 1 lists the relative percentages in both Chinese-to-English (ch-en, using Chinese side dependency trees) and English-to-Chinese (en-ch, using English side dependency trees) directions. As we see from Table 1, dependency cohesion is 1 The data set is the development set used in Section 5. 澳洲是与北韩有的邦交少数国家。之一AustraliaisoneofthefewcountriesthathavediplomaticrelationswithNorthKorea.123456789101112131415 Figure 1: A Chinese-English sentence pair including the word alignments and the Chinese side dependency tree. The Chinese and English words are listed horizontally and vertically, jeweils. The black grids are gold-standard alignments. For the Chinese word “有/have”, we give two alignment positions, where “R” is the correct alignment and “W” is the incorrect alignment.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
293
generally maintained between Chinese and English. So dependency cohesion would be helpful for word alignment between Chinese and English. Jedoch, there are still a number of crossings. If we restrict alignment space with a hard cohesion constraint, the correct alignments that result in crossings will be ruled out directly. In the next section, we describe an approach to integrating dependency cohesion constraint into a generative model to softly influence the probabilities of alignment candidates. We show that our new approach addresses the shortcomings of using dependency cohesion as a hard constraint. 3 A Generative Word Alignment Model with Dependency Cohesion Constraint The most influential generative word alignment models are the IBM Models 1-5 and the HMM model (Brown et al., 1993; Vogel et al., 1996; Oh und Ney, 2003). These models can be classified into sequence-based models (IBM Models 1, 2 and HMM) and fertility-based models (IBM Models 3, 4 Und 5). The sequence-based model is easier to implement, and recent experiments have shown that appropriately modified sequence-based model can produce comparable performance with fertility-based models (Lopez and Resnik, 2005; Liang et al., 2006; DeNero and Klein, 2007; Zhao and Gildea, 2010; Bansal et al., 2011). So we built a generative word alignment model with dependency cohesion constraint based on the sequence-based model. 3.1 The Sequence-based Alignment Model According to Brown et al. (1993) and Och and Ney (2003), the sequence-based model is built as a noisy channel model, where the source sentence 𝒇1𝐽 and the alignment 𝒂1𝐽 are generated conditioning on the target sentence 𝒆1𝐼. The model assumes each source word is assigned to exactly one target word, and defines an asymmetric alignment for the sentence pair as 𝒂1𝐽=𝑎1,𝑎2,…,𝑎𝑗,…,𝑎𝐽, where each 𝑎𝑗∈[0,𝐼] is an alignment from the source position j to the target position 𝑎𝑗, 𝑎𝑗=0 means 𝑓𝑗 is not aligned with any target words. The sequence-based model divides alignment procedure into two stages (distortion and translation) and factors as: 𝑝(𝒇1𝐽,𝒂1𝐽|𝒆1𝐼)=∏𝑝𝑑(𝑎𝑗|𝑎𝑗−1,𝐼)𝑝𝑡(𝑓𝑗|𝑒𝑎𝑗)𝐽𝑗=1 (1) where 𝑝𝑑 is the distortion model and 𝑝𝑡 is the translation model. IBM Models 1, 2 and the HMM model all assume the same translation model 𝑝𝑡(𝑓𝑗|𝑒𝑎𝑗). Jedoch, they use three different distortion models. IBM-Modell 1 assumes a uniform distortion probability 1/(I+1), IBM-Modell 2 assumes 𝑝𝑑(𝑎𝑗|𝑗) that depends on word position j and HMM model assumes 𝑝𝑑(𝑎𝑗|𝑎𝑗−1,𝐼) that depends on the previous alignment 𝑎𝑗−1. Kürzlich, tree distance models (Lopez and Resnik, 2005; DeNero and Klein, 2007) formulate the distortion model as 𝑝𝑑(𝑎𝑗|𝑎𝑗−1,𝑇), where the distance between 𝑎𝑗 and 𝑎𝑗−1 are calculated by walking through the phrase (or dependency) tree T. 3.2 Proposed Model To integrate dependency cohesion constraint into a generative model, we refine the sequence-based model in two ways with the help of the source side dependency tree 𝑇𝑓. Erste, we design a new word alignment order. In the sequence-based model, source words are aligned from left to right by taking source sentence as a linear sequence. Jedoch, to apply dependency cohesion constraint, the subtree span of a head node is computed based on the alignments of its children, so children must be aligned before the head node. Riesa and Marcu (2010) propose a hierarchical search procedure to traverse all nodes in a phrase structure tree. Ähnlich, we define a bottom-up topological order (BUT-order) to traverse all words in the source side dependency tree 𝑇𝑓. In the BUT-order, tree nodes are aligned bottom-up with 𝑇𝑓 as a backbone. For all children under the same head node, left children are aligned from right to left, and then right children are aligned from left to right. Zum Beispiel, the BUT-order for the following dependency tree is “C B E F D A H G”. AHGFEDCB ch-en en-ch HCP MCP HCP MCP 88.43 95.82 81.53 91.62 Tisch 1: Cohesion percentages (%) of a manually annotated data set between Chinese and English.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
294
For the sake of clarity, we define a function to map all nodes in 𝑇𝑓 into their BUT-order, and notate it as BUT(𝑇𝑓)=𝜋1,𝜋2,…,𝜋𝑗,…,𝜋𝐽, where 𝜋𝑗 means the j-th node in BUT-order is the 𝜋𝑗-th word in the original source sentence. We arrange alignment sequence 𝒂1𝐽 according the BUT-order and notate it as 𝒂[1,𝐽]=𝑎𝜋1,…,𝑎𝜋𝑗,…,𝑎𝜋𝐽, where 𝑎𝜋𝑗 is the aligned position for a node 𝑓𝜋𝑗. We also notate the sub-sequence 𝑎𝜋𝑖,…,𝑎𝜋𝑗as 𝒂[𝑖,𝑗]. Zweite, we keep the same translation model as the sequence-based model and integrate the dependency cohesion constraints into the distortion model. The main idea is to influence the distortion procedure with the dependency cohesion constraints. Assume node 𝑓ℎ and node 𝑓𝑚 are a head-modifier pair in 𝑇𝑓, where 𝑓ℎ is the head and 𝑓𝑚 is the modifier. The head-modifier cohesion relationship between them is notated as 𝒽ℎ,𝑚∈{𝑐𝑜ℎ𝑒𝑠𝑖𝑜𝑛,𝑐𝑟𝑜𝑠𝑠𝑖𝑛𝑔}. When the head-modifier cohesion is maintained 𝒽ℎ,𝑚=𝑐𝑜ℎ𝑒𝑠𝑖𝑜𝑛, otherwise 𝒽ℎ,𝑚=𝑐𝑟𝑜𝑠𝑠𝑖𝑛𝑔. We represent the set of head-modifier cohesion relationships for all the head-modifier pairs in 𝑇𝑓 as: 𝑯 = {𝒽ℎ,𝑚 | ℎ∈[1,𝐽], 𝑚∈[1,𝐽], ℎ≠𝑚, 𝑓ℎ and 𝑓𝑚 are a head-modifier pair in 𝑇𝑓} The set of head-modifier cohesion relationships for all the head-modifier pairs taking 𝑓ℎ as the head node can be represented as: 𝓱ℎ = {𝒽ℎ,𝑚 | 𝑚∈[1,𝐽], 𝑚≠ℎ, 𝑓ℎ and 𝑓𝑚 are a head-modifier pair in 𝑇𝑓} Obviously, 𝑯=⋃𝓱ℎ𝐽ℎ=0. Ähnlich, we assume node 𝑓𝑘 and node 𝑓𝑙 are a modifier-modifier pair in 𝑇𝑓. To avoid repetition, we assume 𝑓𝑘 is the node sitting at the position after 𝑓𝑙 in BUT-order and call 𝑓𝑘 as the higher-order node of the pair. The modifier-modifier cohesion relationship between them is notated as 𝓂𝑘,𝑙∈{𝑐𝑜ℎ𝑒𝑠𝑖𝑜𝑛,𝑐𝑟𝑜𝑠𝑠𝑖𝑛𝑔}. When the modifier-modifier cohesion is maintained 𝓂𝑘,𝑙=𝑐𝑜ℎ𝑒𝑠𝑖𝑜𝑛, otherwise 𝓂𝑘,𝑙=𝑐𝑟𝑜𝑠𝑠𝑖𝑛𝑔. We represent the set of modifier-modifier cohesion relationships for all the modifier-modifier pairs in 𝑇𝑓 as: 𝑴 = {𝓂𝑘,𝑙 | 𝑘∈[1,𝐽], 𝑙∈[1,𝐽], 𝑘≠𝑙, 𝑓𝑘 and 𝑓𝑙 are a modifier-modifier pair in 𝑇𝑓} The set of modifier-modifier cohesion relationships for all the modifier-modifier pairs taking 𝑓𝑘 as the higher-order node can be represented as: 𝓶𝑘 = {𝓂𝑘,𝑙 | 𝑙∈[1,𝐽], 𝑙≠𝑘, 𝑓𝑘 and 𝑓𝑙 are a modifier-modifier pair in 𝑇𝑓} Obviously, 𝑴=⋃𝓶𝑘𝐽𝑘=0. With the above notations, we formulate the distortion probability for a node 𝑓𝜋𝑗 as 𝑝𝑑(𝑎𝜋𝑗,𝓱𝜋𝑗,𝓶𝜋𝑗|𝒂[1,𝑗−1]). According to Eq. (1) and the two improvements, we formulated our model as: 𝑝(𝒇1𝐽,𝒂[1,𝐽]|𝒆1𝐼,𝑇𝑓)=𝑝(𝒂[1,𝐽],𝑯,𝑴,𝒇1𝐽,|𝒆1𝐼,𝑇𝑓) ≈∏𝑝𝑑(𝑎𝜋𝑗,𝓱𝜋𝑗,𝓶𝜋𝑗|𝒂[1,𝑗−1])𝑝𝑡(𝑓𝜋𝑗|𝑒𝑎𝜋𝑗)𝜋𝑗∈𝐵𝑈𝑇(𝑇𝑓) (2) Hier, we use the approximation symbol, because the right hand side is not guaranteed to be normalized. In der Praxis, we only compute ratios of these terms, so it is not actually a problem. Such model is called deficient (Brown et al., 1993), and many successful unsupervised models are deficient, z.B., IBM model 3 and IBM model 4. 3.3 Dependency Cohesive Distortion Model We assume the distortion procedure is influenced by three factors: words distance, head-modifier cohesion and modifier-modifier cohesion. daher, we further decompose the distortion model 𝑝𝑑 into three terms as follows: 𝑝𝑑(𝑎𝜋𝑗,𝓱𝜋𝑗,𝓶𝜋𝑗|𝒂[1,𝑗−1]) =𝑝(𝑎𝜋𝑗|𝒂[1,𝑗−1])𝑝(𝓱𝜋𝑗|𝒂[1,𝑗])𝑝(𝓶𝜋𝑗|𝒂[1,𝑗],𝓱𝜋𝑗) ≈𝑝𝑤𝑑(𝑎𝜋𝑗|𝑎𝜋𝑗−1,𝐼)𝑝ℎ𝑐(𝓱𝜋𝑗|𝒂[1,𝑗])𝑝𝑚𝑐(𝓶𝜋𝑗|𝒂[1,𝑗]) (3) where 𝑝𝑤𝑑 is the words distance term, 𝑝ℎ𝑐 is the head-modifier cohesion term and 𝑝𝑚𝑐 is the modifier-modifier cohesion term. The word distance term 𝑝𝑤𝑑 has been verified to be very useful in the HMM alignment model. Jedoch, in our model, the word distance is calculated based on the previous node in BUT-order rather than the previous word in the original sentence. We follow the HMM word alignment model (Vogel et al., 1996) and parameterize 𝑝𝑤𝑑 in terms of the jump width: 𝑝𝑤𝑑(𝑖|𝑖′,𝐼)=𝑐(𝑖−𝑖′)∑𝑐(𝑖′′−𝑖′)𝑖′′ (4) where 𝑐() is the count of jump width.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
295
The head-modifier cohesion term 𝑝ℎ𝑐 is used to penalize the distortion probability according to relationships between the head node and its children (modifiers). daher, we define 𝑝ℎ𝑐 as the product of probabilities for all head-modifier pairs taking 𝑓𝜋𝑗 as head node: 𝑝ℎ𝑐(𝓱𝜋𝑗|𝒂[1,𝑗])=∏𝑝ℎ(𝒽𝜋𝑗,𝑐|𝑓𝑐,𝑒𝑎𝜋𝑗,𝑒𝑎𝑐)𝒽𝜋𝑗,𝑐∈𝓱𝜋𝑗 (5) where 𝒽𝜋𝑗,𝑐∈{𝑐𝑜ℎ𝑒𝑠𝑖𝑜𝑛,𝑐𝑟𝑜𝑠𝑠𝑖𝑛𝑔} is the head-modifier cohesion relationship between 𝑓𝜋𝑗 and one of its child 𝑓𝑐, 𝑝ℎ is the corresponding probability, 𝑒𝑎𝜋𝑗and 𝑒𝑎𝑐 are the aligned words for 𝑓𝜋𝑗 and 𝑓𝑐. Ähnlich, the modifier-modifier cohesion term 𝑝𝑚𝑐 is used to penalize the distortion probability according to relationships between 𝑓𝜋𝑗 and its siblings. daher, we define 𝑝𝑚𝑐 as the product of probabilities for all the modifier-modifier pairs taking 𝑓𝜋𝑗 as the higher-order node: 𝑝𝑚𝑐(𝓶𝜋𝑗|𝒂[1,𝑗])=∏𝑝𝑚(𝓂𝜋𝑗,𝑠|𝑓𝑠,𝑒𝑎𝜋𝑗,𝑒𝑎𝑠)𝓂𝜋𝑗,𝑠∈𝓶𝜋𝑗 (6) where 𝓂𝜋𝑗,𝑠∈{𝑐𝑜ℎ𝑒𝑠𝑖𝑜𝑛,𝑐𝑟𝑜𝑠𝑠𝑖𝑛𝑔} is the modifier-modifier cohesion relationship between 𝑓𝜋𝑗 and one of its sibling 𝑓𝑠, 𝑝𝑚 is the corresponding probability, 𝑒𝑎𝜋𝑗 and 𝑒𝑎𝑠 are the aligned words for 𝑓𝜋𝑗 and 𝑓𝑠. Both 𝑝ℎand 𝑝𝑚 in Eq. (5) and Eq. (6) are conditioned on three words, which would make them very sparse. To cope with this problem, we use the word clustering toolkit, mkcls (Och et al., 1999), to cluster all words into 50 classes, and replace the three words with their classes. 4 Parameter Estimation To align sentence pairs with the model in Eq. (2), we have to estimate some parameters: 𝑝𝑡, 𝑝𝑤𝑑, 𝑝ℎ and 𝑝𝑚. The traditional approach for sequence-based models uses Expectation Maximization (EM) algorithm to estimate parameters. Jedoch, in our model, it is hard to find an efficient way to sum over all the possible alignments, which is required in the E-step of EM algorithm. daher, we propose an approximate EM algorithm and a Gibbs sampling algorithm for parameter estimation. 4.1 Approximate EM Algorithm The approximate EM algorithm is similar to the training algorithm for fertility-based alignment models (Oh und Ney, 2003). The main idea is to enumerate only a small subset of good alignments in the E-step, then collect expectation counts and estimate parameters among the small subset in M-step. Following with Och and Ney (2003), we employ neighbor alignments of the Viterbi alignment as the small subset. Neighbor alignments are obtained by performing one swap or move operation over the Viterbi alignment. Obtaining the Viterbi alignment itself is not so easy for our model. daher, we take the Viterbi alignment of the sequence-based model (HMM model) as the starting point, and iterate the hill-climbing algorithm (Brown et al., 1993) many times to get the best alignment greedily. In each iteration, we find the best alignment with Eq. (2) among neighbor alignments of the initial point, and then make the best alignment as the initial point for the next iteration. The algorithm iterates until no update could be made. 4.2 Gibbs Sampling Algorithm Gibbs sampling is another effective algorithm for unsupervised learning problems. As is described in the literatures (Johnson et al., 2007; Gao and Johnson, 2008), there are two types of Gibbs samplers: explicit and collapsed. An explicit sampler represents and samples the model parameters in addition to the word alignments, while in a collapsed sampler the parameters are integrated out and only alignments are sampled. Mermer and Saraçlar (2011) proposed a collapsed sampler for IBM Model 1. Jedoch, their sampler updates parameters constantly and thus cannot run efficiently on large-scale tasks. Stattdessen, we take advantage of explicit Gibbs sampling to make a highly parallelizable sampler. Our Gibbs sampler is similar to the MCMC algorithm in Zhao and Gildea (2010), but we assume Dirichlet priors when sampling model parameters and take a different sampling approach based on the source side dependency tree. Our sampler performs a sequence of consecutive iterations. Each iteration consists of two sampling steps. The first step samples the aligned position for each dependency node according to the BUT-order. Concretely, when sampling the aligned
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
296
position 𝑎𝜋𝑗(𝑡+1) for node 𝑓𝜋𝑗 on iteration 𝑡+1, the aligned positions for 𝒂[1,𝑗−1] are fixed on the new sampling results 𝒂[1,𝑗−1](𝑡+1)on iteration 𝑡+1, and the aligned positions for 𝒂[𝑗+1,𝐽] are fixed on the old sampling results 𝒂[𝑗+1,𝐽](𝑡) on iteration 𝑡. daher, we sample the aligned position 𝑎𝜋𝑗(𝑡+1) as follows: 𝑎𝜋𝑗(𝑡+1) ~ 𝑝(𝑎𝜋𝑗|𝒂[1,𝑗−1](𝑡+1),𝒂[𝑗+1,𝐽](𝑡),𝑓1𝐽,𝑒1𝐼)=𝑝(𝒇1𝐽,𝒂̂𝑎𝜋𝑗|𝒆1𝐼)∑𝑝(𝒇1𝐽,𝒂̂𝑎𝜋𝑗|𝒆1𝐼)𝑎𝜋𝑗∈{0,1,…,𝐼} (7) where 𝒂̂𝑎𝜋𝑗=𝒂[1,𝑗−1](𝑡+1)∪𝑎𝜋𝑗∪𝒂[𝑗+1,𝐽](𝑡), the numerator is the probability of aligning 𝑓𝜋𝑗 with 𝑒𝑎𝜋𝑗 (the alignments for other nodes are fixed at 𝒂[1,𝑗−1](𝑡+1)and 𝒂[𝑗+1,𝐽](𝑡)) calculated with Eq. (2), and the denominator is the summation of the probabilities of aligning 𝑓𝜋𝑗 with each target word. The second step of our sampler calculates parameters 𝑝𝑡, 𝑝𝑤𝑑, 𝑝ℎ and 𝑝𝑚 using their counts, where all these counts can be easily collected during the first sampling step. Because all these parameters follow multinomial distributions, we consider Dirichlet priors for them, which would greatly simplify the inference procedure. In the first sampling step, all the sentence pairs are processed independently. So we can make this step parallel and process all the sentence pairs efficiently with multi-threads. When using the Gibbs sampler for decoding, we just ignore the second sampling step and iterate the first sampling step many times. 5 Experiments We performed a series of experiments to evaluate our model. All the experiments are conducted on the Chinese-English language pair. We employ two training sets: FBIS and LARGE. The size and source corpus of these training sets are listed in Table 2. We will use the smaller training set FBIS to evaluate the characters of our model and use the LARGE training set to evaluate whether our model is adaptable for large-scale task. For word alignment quality evaluation, we take the hand-aligned data sets from SSMT20072, which contains 2 http://nlp.ict.ac.cn/guidelines/guidelines-2007-SSMT(English).doc 505 sentence pairs in the testing set and 502 sentence pairs in the development set. Following Och and Ney (2003), we evaluate word alignment quality with the alignment error rate (AER), where lower AER is better. Because our model takes dependency trees as input, we parse both sides of the two training sets, the development set and the testing set with Berkeley parser (Petrov et al., 2006), and then convert the generated phrase trees into dependency trees according to Wang and Zong (2010; 2011). Our model is an asymmetric model, so we perform word alignment in both forward (ChineseEnglish) and reverse (EnglishChinese) directions. 5.1 Effectiveness of Cohesion Constraints In Eq. (3), the distortion probability 𝑝𝑑 is decomposed into three terms: 𝑝𝑤𝑑, 𝑝ℎ𝑐 and 𝑝𝑚𝑐. To study whether cohesion constraints are effective for word alignment, we construct four sub-models as follows: (1) wd: 𝑝𝑑=𝑝𝑤𝑑; (2) wd-hc: 𝑝𝑑=𝑝𝑤𝑑∙𝑝ℎ𝑐; (3) wd-mc: 𝑝𝑑=𝑝𝑤𝑑∙𝑝𝑚𝑐; (4) wd-hc-mc: 𝑝𝑑=𝑝𝑤𝑑∙𝑝ℎ𝑐∙𝑝𝑚𝑐. We train these four models with the approximate EM and the Gibbs sampling algorithms on the FBIS training set. For approximate EM algorithm, we first train a HMM model (mit 5 iterations of IBM model 1 Und 5 iterations of HMM model), then train these four sub-models with 10 iterations of the approximate EM algorithm. For Gibbs sampling, we choose symmetric Dirichlet priors identically with all hyper-parameters equals 0.0001 to obtain a sparse Dirichlet prior. Dann, we make the alignments produced by the HMM model as the initial points, and train these sub-models with 20 iterations of the Gibbs sampling. AERs on the development set are listed in Table 3. We can easily find: 1) when employing the head-modifier cohesion constraint, the wd-hc model yields better AERs than the wd model; 2) Train Set Source Corpus # Words FBIS FBIS newswire data Ch: 7.1M En: 9.1M LARGE LDC2000T50, LDC2003E14, LDC2003E07, LDC2004T07, LDC2005T06, LDC2002L27, LDC2005T10, LDC2005T34 Ch: 27.6M En: 31.8M Table 2: The size and the source corpus of the two training sets.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
297
when employing the modifier-modifier cohesion constraint, the wd-mc model also yields better AERs than the wd model; Und 3) when employing both head-modifier cohesion constraint and modifier-modifier cohesion constraint together, the wd-hc-mc model yields the best AERs among the four sub-models. So both head-modifier cohesion constraint and modifier-modifier cohesion constraint are helpful for word alignment. Tisch 3 also shows that the approximate EM algorithm yields better AERs in the forward direction than reverse direction, while the Gibbs sampling algorithm yields close AERs in both directions. 5.2 Comparison with State-of-the-Art Models To show the effectiveness of our model, we compare our model with some of the state-of-the-art models. All the systems are listed as follows: 1) IBM4: The fertility-based model (IBM model 4) which is implemented in GIZA++ toolkit. The training scheme is 5 iterations of IBM model 1, 5 iterations of the HMM model and 10 iterations of IBM model 4. 2) IBM4-L0: A modification to the GIZA++ toolkit which extends IBM models with ℓ0-norm (Vaswani et al., 2012). The training scheme is the same as IBM4. 3) IBM4-Prior: A modification to the GIZA++ toolkit which extends the translation model of IBM models with Dirichlet priors (Riley and Gildea, 2012). The training scheme is the same as IBM4. 4) Agree-HMM: The HMM alignment model by jointly training the forward and reverse models (Liang et al., 2006), which is implemented in the BerkeleyAligner. The training scheme is 5 iterations of jointly training IBM model 1 Und 5 iterations of jointly training HMM model. 5) Tree-Distance: The tree distance alignment model proposed in DeNero and Klein (2007), which is implemented in the BerkeleyAligner. The training scheme is 5 iterations of jointly training IBM model 1 Und 5 iterations of jointly training the tree distance model. 6) Hard-Cohesion: The implemented “Cohesion Checking Algorithm” (Lin and Cherry, 2003) which takes dependency cohesion as a hard constraint during beam search word alignment decoding. We use the model trained by the Agree-HMM system to estimate alignment candidates. We also build two systems for our soft dependency cohesion model: 7) Soft-Cohesion-EM: the wd-hc-mc sub-model trained with the approximate EM algorithm as described in sub-section 5.1. 8) Soft-Cohesion-Gibbs: the wd-hc-mc sub-model trained with the Gibbs sampling algorithm as described in sub-section 5.1. We train all these systems on the FBIS training set, and test them on the testing set. We also combine the forward and reverse alignments with the grow-diag-final-and (GDFA) heuristic (Koehn et al., 2007). All AERs are listed in Table 4. We find our soft cohesion systems produce better AERs than the Hard-Cohesion system as well as the other systems. Tisch 5 gives the head-modifier cohesion percentage (HCP) and the modifier-modifier cohesion percentage (MCP) of each system. We find HCPs and MCPs of our soft cohesion systems are much closer to the gold-standard alignments. To evaluate whether our model is adaptable for large-scale task, we retrained these systems using the LARGE training set. AERs on the testing set are listed in Table3 6. Compared with Table 4, Wir 3 Tree-Distance system requires too much memory to run on our server when using the LARGE data set, so we can’t get the result. forward reverse GDFA IBM4 42.90 42.81 44.32 IBM4-L0 42.59 41.04 43.19 IBM4-Prior 41.94 40.46 42.44 Agree-HMM 38.03 37.91 41.01 Tree-Distance 34.21 37.22 38.42 Hard-Cohesion 37.32 38.92 38.92 Soft-Cohesion-EM 33.65 34.74 35.85 Soft-Cohesion-Gibbs 34.45 33.72 34.46 Tisch 4: AERs on the testing set (trained on the FBIS data set). EM Gibbs forward reverse forward reverse wd 26.12 28.66 27.09 26.40 wd-hc 24.67 25.86 26.24 24.39 wd-mc 24.49 26.53 25.51 25.40 wd-hc-mc 23.63 25.17 24.65 24.33 Tisch 3: AERs on the development set (trained on the FBIS data set).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
T
l
A
C
_
A
_
0
0
2
2
8
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
298
find all the systems yield better performance when using more training data. Our soft cohesion systems still produce better AERs than other systems, suggesting that our soft cohesion model is very effective for large-scale word alignment tasks. 5.3 Machine Translation Quality Comparison We then evaluate the effect of word alignment on machine translation quality using the phrase-based translation system Moses (Koehn et al., 2007). We take NIST MT03 test data as the development set, NIST MT05 test data as the testing set. We train a 5-gram language model with the Xinhua portion of English Gigaword corpus and the English side of the training set using the SRILM Toolkit (Stolcke, 2002). We train machine translation models using GDFA alignments of each system. BLEU scores on NIST MT05 are listed in Table 7, where BLEU scores are calculated using lowercased and tokenized data (Papineni et al., 2002). Although the IBM4-L0, Agree-HMM, Tree-Distance and Hard-Cohesion systems improve word alignment than IBM4, they fail to outperform the IBM4 system on machine translation. The BLEU score of our Soft-Cohesion-EM system is better than the IBM4 system when using the FBIS training set, but worse when using the LARGE training set. Our Soft-Cohesion-Gibbs system produces the best BLEU score when using both training sets. We also performed a statistical significance test using bootstrap resampling with 1000 Proben (Koehn, 2004; Zhang et al., 2004). Experimental results show the Soft-Cohesion-Gibbs system is significantly better (P<0.05) than the IBM4 system. The IBM4-Prior system slightly outperforms IBM4, but it’s not significant. 6 Related Work There have been many proposals of integrating syntactic knowledge into generative alignment models. Wu (1997) proposed the inversion transduction grammar (ITG) to model word alignment as synchronous parsing for a sentence pair. Yamada and Knight (2001) represented translation as a sequence of re-ordering operations over child nodes of a syntactic tree. Gildea (2003) introduced a “loosely” tree-based alignment technique, which allows alignments to violate syntactic constraints by incurring a cost in probability. Pauls et al. (2010) gave a new instance of the ITG formalism, in which one side of the synchronous derivation is constrained by the syntactic tree. Fox (2002) measured syntactic cohesion in gold standard alignments and showed syntactic cohesion is generally maintained between English and French. She also compared three variant syntactic representations (phrase tree, verb phrase flattening tree and dependency tree), and found the dependency tree produced the highest degree of cohesion. So Cherry and Lin (2003; 2006a) used dependency cohesion as a hard constraint to restrict the alignment space, where all potential alignments violating cohesion constraint are ruled forward reverse HCP MCP HCP MCP IBM4 60.53 63.94 56.15 64.80 IBM4-L0 60.57 62.53 66.49 65.68 IBM4-Prior 66.48 74.65 67.19 72.32 Agree-HMM 75.52 66.61 73.88 66.07 Tree-Distance 81.37 74.69 78.00 71.73 Hard-Cohesion 98.70 97.43 98.25 97.84 Soft-Cohesion-EM 85.21 81.96 82.96 81.36 Soft-Cohesion-Gibbs 88.74 85.55 87.81 84.83 gold-standard 88.43 95.82 81.53 91.62 Table 5: HCPs and MCPs on the development set. FBIS LARGE IBM4 30.7 33.1 IBM4-L0 30.4 32.3 IBM4-Prior 30.9 33.2 Agree-HMM 27.2 30.1 Tree-Distance 28.2 N/A Hard-Cohesion 30.4 32.2 Soft-Cohesion-EM 30.9 33.1 Soft-Cohesion-Gibbs 31.6* 33.9* Table 7: BLEU scores, where * indicates significantly better than IBM4 (p<0.05). forward reverse GDFA IBM4 37.45 39.18 40.52 IBM4-L0 38.17 38.88 39.82 IBM4-Prior 35.86 36.71 37.08 Agree-HMM 35.58 35.73 39.10 Hard-Cohesion 35.04 37.59 37.63 Soft-Cohesion-EM 30.93 32.67 33.65 Soft-Cohesion-Gibbs 32.07 32.68 32.28 Table 6: AERs on the testing set (trained on the LARGE data set).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
t
l
a
c
_
a
_
0
0
2
2
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
299
out directly. Although the alignment quality is improved, they ignored situations where a small set of correct alignments can violate cohesion. To address this limitation, Cherry and Lin (2006b) proposed a soft constraint approach, which took dependency cohesion as a feature of a discriminative model, and verified that the soft constraint works better than the hard constraint. However, the training procedure is very time-consuming, and they trained the model with only 100 hand-annotated sentence pairs. Therefore, their method is not suitable for large-scale tasks. In this paper, we also use dependency cohesion as a soft constraint. But, unlike Cherry and Lin (2006b), we integrate the soft dependency cohesion constraint into a generative model that is more suitable for large-scale word alignment tasks. 7 Conclusion and Future Work We described a generative model for word alignment that uses dependency cohesion as a soft constraint. We proposed an approximate EM algorithm and an explicit Gibbs sampling algorithm for parameter estimation in an unsupervised manner. Experimental results performed on a large-scale data set show that our model improves word alignment quality as well as machine translation quality. Our experimental results also indicate that the soft constraint approach is much better than the hard constraint approach. It is possible that our word alignment model can be improved further. First, we generated word alignments in both forward and reverse directions separately, but it might be helpful to use dependency trees of the two sides simultaneously. Second, we only used the one-best automatically generated dependency trees in the model. However, errors are inevitable in those trees, so we will investigate how to use N-best dependency trees or dependency forests (Hayashi et al., 2011) to see if they can improve our model. Acknowledgments We would like to thank Nianwen Xue for insightful discussions on writing this article. We are grateful to anonymous reviewers for many helpful suggestions that helped improve the final version of this article. The research work has been funded by the Hi-Tech Research and Development Program ("863" Program) of China under Grant No. 2011AA01A207, 2012AA011101, and 2012AA011102 and also supported by the Key Project of Knowledge Innovation Program of Chinese Academy of Sciences under Grant No.KGZD-EW-501. This work is also supported in part by the DAPRA via contract HR0011-11-C-0145 entitled "Linguistic Resources for Multilingual Processing". References Mohit Bansal, Chris Quirk, and Robert Moore, 2011. Gappy Phrasal Alignment By Agreement. In Proc. of ACL 2011. Peter F. Brown, Stephen A. Della Pietra, Vincent J. Della Pietra and Robert L. Mercer, 1993. The mathematics of statistical machine translation: Parameter estimation. Computational Linguistics, 19 (2). pages 263-311. C. Cherry and D. Lin, 2003. A probability model to improve word alignment. In Proc. of ACL '03, pages 88-95. C. Cherry and D. Lin, 2006a. A comparison of syntactically motivated word alignment spaces. In Proc. of EACL '06, pages 145-152. C. Cherry and D. Lin, 2006b. Soft syntactic constraints for word alignment through discriminative training. In Proc. of COLING/ACL '06, pages 105-112. John DeNero and Dan Klein, 2007. Tailoring word alignments to syntactic machine translation. In Proc. of ACL '07, pages 17. C. Dyer, J. Clark, A. Lavie and N.A. Smith, 2011. Unsupervised word alignment with arbitrary features. In Proc. of ACL '11, pages 409-419. Heidi J. Fox, 2002. Phrasal cohesion and statistical machine translation. In Proc. of EMNLP '02, pages 304-3111. Michel Galley, Mark Hopkins, Kevin Knight, Daniel Marcu, 2004. What's in a translation rule? In Proc. of NAACL '04, pages 344-352. J. Gao and M. Johnson, 2008. A comparison of Bayesian estimators for unsupervised Hidden Markov Model POS taggers. In Proc. of EMNLP '08, pages 344-352. Daniel Gildea, 2003. Loosely Tree-Based Alignment for Machine Translation. In Proc. of ACL'03, pages 80-87.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
2
8
1
5
6
6
6
5
5
/
/
t
l
a
c
_
a
_
0
0
2
2
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
300
K. Hayashi, T. Watanabe, M. Asahara and Y. Matsumoto, 2011. Third-order Variational Reranking on Packed-Shared Dependency Forests. In Proc. of EMNLP '11. M. Johnson, T. Griffiths and S. Goldwater, 2007. Bayesian inference for PCFGs via Markov chain Monte Carlo. In Proc. of NAACL '07, pages 139-146. Philipp Koehn, 2004. Statistical significance tests for machine translation evaluation. In Proc. of EMNLP'04. P. Koehn, H. Hoang, A. Birch, C. Callison-Burch, M. Federico, N. Bertoldi, B. Cowan, W. Shen, C. Moran and R. Zens, 2007. Moses: Open source toolkit for statistical machine translation. In Proc. of ACL '07, Demonstration Session, pages 177-180. Percy Liang, Ben Taskar and Dan Klein, 2006. Alignment by agreement. In Proc. of HLT-NAACL 06, pages 104-111. D. Lin and C. Cherry, 2003. Word alignment with cohesion constraint. In Proc. of NAACL '03, pages 49-51. Adam Lopez and Philip Resnik, 2005. Improved HMM alignment models for languages with scarce resources. In ACL Workshop on Building and Using Parallel Texts '05, pages 83-86. Cos¸kun Mermer and Murat Saraçlar, 2011. Bayesian word alignment for statistical machine translation. In Proc. of ACL '11, pages 182-187. R.C. Moore, 2005. A discriminative framework for bilingual word alignment. In Proc. of EMNLP '05, pages 81-88. F.J. Och, C. Tillmann and H. Ney, 1999. Improved alignment models for statistical machine translation. In Proc. of EMNLP/WVLC '99, pages 20-28. Franz Josef Och and Hermann Ney, 2003. A systematic comparison of various statistical alignment models. Computational Linguistics, 29 (1). pages 19-51. K. Papineni, S. Roukos, T. Ward and W.J. Zhu, 2002. BLEU: a method for automatic evaluation of machine translation. In Proc. of ACL '02, pages 311-318. Adam Pauls, Dan Klein, David Chiang and Kevin Knight, 2010. Unsupervised Syntactic Alignment with Inversion Transduction Grammars. In Proc. of NAACL '10. Slav Petrov, Leon Barrett, Romain Thibaux and Dan Klein, 2006. Learning accurate, compact, and interpretable tree annotation. In Proc. of ACL 2006. Jason Riesa and Daniel Marcu, 2010. Hierarchical search for word alignment. In Proc. of ACL '10, pages 157-166. Jason Riesa, Ann Irvine and Daniel Marcu, 2011. Feature-Rich Language-Independent Syntax-Based Alignment for Statistical Machine Translation. In Proc. of EMNLP '11. Darcey Riley and Daniel Gildea, 2012. Improving the IBM Alignment Models Using Variational Bayes. In Proc. of ACL '12. M. Saers, J. Nivre and D. Wu, 2010. Word alignment with stochastic bracketing linear inversion transduction grammar. In Proc. of NAACL '10, pages 341-344. A. Stolcke, 2002. SRILM-an extensible language modeling toolkit. In ICSLP '02. B. Taskar, S. Lacoste-Julien and D. Klein, 2005. A discriminative matching approach to word alignment. In Proc. of EMNLP '05, pages 73-80. Ashish Vaswani, Liang Huang, and David Chiang, 2012. Smaller alignment models for better translations: unsupervised word alignment with the l0 norm. In Proc. ACL'12, pages 311–319. Stephan Vogel, Hermann Ney and Christoph Tillmann, 1996. HMM-based word alignment in statistical translation. In Proc. of COLING-96, pages 836-841. D. Wu, 1997. Stochastic inversion transduction grammars and bilingual parsing of parallel corpora. Computational Linguistics, 23 (3). pages 377-403. Zhiguo Wang, Chengqing Zong, 2010. Phrase Structure Parsing with Dependency Structure, In Proc. of COLING 2010, pages 1292-1300. Zhiguo Wang, Chengqing Zong, 2011. Parse Reranking Based on Higher-Order Lexical Dependencies, In Proc. Of IJCNLP 2011, pages 1251-1259. Kenji Yamada and Kevin Knight, 2001. A syntax-based statistical translation model. In Proc. of ACL '01, pages 523-530. Ying Zhang, Stephan Vogel, and Alex Waibel. 2004. Interpreting BLEU/NIST scores: How much improvement do we need to have a better system? In Proc. of LREC. Shaojun Zhao and Daniel Gildea, 2010. A fast fertility hidden Markov model for word alignment using MCMC. In Proc. of EMNLP '10, pages 596-605.