The Structure of Ontogenies in a
Model Protocell
Eran Agmon*,**
Alexander J. Gates**
Randall D. Beer**
Indiana University
Abstract Emergent individuals are often characterized with respect
to their viability: their ability to maintain themselves and persist
in variable environments. As such individuals interact with an
Umfeld, they undergo sequences of structural changes that
correspond to their ontogenies. Letzten Endes, individuals that adapt
to their environment, and increase their chances of survival, persist.
This article provides an initial step towards a more formal treatment
of these concepts. A network of possible ontogenies is uncovered
by subjecting a model protocell to sequential perturbations and
mapping the resulting structural configurations. The analysis of this
network reveals trends in how the protocell can move between
configurations, how its morphology changes, and how the role of
the environment varies throughout. Viability is defined as expected
life span given an initial configuration. This leads to two notions of
adaptivity: a local adaptivity that addresses how viability changes in
plastic transitions, and a global adaptivity that looks at longer-term
tendencies for increased viability. To demonstrate how different
protocell-environment pairings produce different patterns of ontogenic
ändern, we generate and analyze a second ontogenic network for
the same protocell in a different environment. Endlich, the mechanisms
of a minimal adaptive transition are analyzed, and it is shown that
these rely on distributed spatial processes rather than an explicit
regulatory mechanism. The combination of this model and analytical
techniques provides a foundation for studying the emergence of
viability, ontogeny, and adaptivity in more biologically realistic systems.
Schlüsselwörter
Protocell, autopoiesis, ontogeny, viability,
adaptivity
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1 Einführung
Biological individuals are a special class of physical systems that counter the universal trend towards
disintegration. In any given moment, a physical system has a structural configuration—the spatial
arrangement of components from which it is constituted. The states and locations of these compo-
nents unfold dynamically, and whereas most configurations tend towards a uniform equilibrium,
biological individuals are a unique subclass of physical systems that persist as individuals. The theory
* Contact author.
** Cognitive Science Program, and School of Informatics and Computing, Indiana University, Bloomington, IN 47406. Email: agmon.eran@
gmail.com (E.A.), ajgates@indiana.edu (A.J.G.), rdbeer@indiana.edu (R.D.B.)
© 2016 Massachusetts Institute of Technology Artificial Life 22: 499–517 (2016) doi:10.1162/ARTL_a_00215
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
of autopoiesis argues this viability comes from their closure of production; as a result of their
intrinsic dynamics and material exchange with the environment, biological individuals produce
and distribute the materials needed to stabilize themselves [18].
An individual and its environment form a coupled system, with the state of the individual in part
determining the state of the environment, and the state of the environment in part determining the
state of the individual. Daher, from the perspective of the individual, the exact state of the envi-
ronment is unknown; stattdessen, the environment appears as a probability distribution over possible
perturbations to the individualʼs state. These perturbations, together with the individualʼs intrinsic
Dynamik, determine the individualʼs subsequent states. Daher, a perturbation can have one of three
consequences: The individual can be unaffected (a robust transition), it can be changed to a different
viable configuration (a plastic transition), or it can cross into the set of nonviable configurations and
disintegrate (a destructive transition) [2].
An individual that remains viable for any length of time experiences a sequence of perturbations
that induce a corresponding sequence of configurational changes. In diesem Artikel, we refer to an un-
broken trajectory through the set of viable configurations as an ontogeny; when the trajectory crosses
the boundary of viability into a nonviable region, closure of production is broken and the ontogeny
ends. Different sequences of perturbations have the potential to induce different ontogenies. Wenn die
set of possible perturbations is known, one can in principle map the entire network of possible
transitions that an individual can undergo, by exposing copies of the same individual to all sequences
of perturbations and recording the resulting sequences of configurational change.
Viability is often defined as a biological individualʼs capacity to sustain its function. This is tra-
ditionally treated as a binary notion: Either the individual is currently viable or it is not. Zum Beispiel,
W. R. Ashby postulated a set of essential variables that need to be maintained within a viable region
for a system to persist [3]. Autopoiesis also proposes a binary notion: Either a system persists
through closure of production, or it disintegrates. More recently, the binary notion of viability
has been extended to a more graded notion [5, 10]. This extension focuses not on whether a system
is inside or outside of a viable region, but on its temporal distance to the boundary. In diesem Artikel, Die
viability of any configuration is measured as the average number of environmental perturbations it is
from disintegration, weighted by the probability of those perturbations.
Adaptivity is associated with increases in an individualʼs viability resulting from interactions with
its environment [4, 10]. Some have suggested that adaptivity requires an explicit regulatory mecha-
nism [8, 10]. Jedoch, as an operationally defined notion, adaptivity should be neutral with respect
to the mechanism by which it is achieved. Stattdessen, by adopting an operational definition of adap-
tivity, the mechanisms underlying adaptive change become an interesting target of inquiry, eher
than presumed a priori. This generalization allows for examples of adaptivity that arise from more
implicit, systemic processes rather than only those with explicit, dedicated mechanisms.
Developing an account of ontogeny, viability, and adaptivity requires theoretical models to dem-
onstrate how these notions can be quantified. Simple models, insbesondere, allow for unambiguous
definitions and computations. There is a long history of building such models. These include
particle-based models of basic autopoiesis [24], particle-based models capable of self-replication
[15], models of the origins of protocells [19], models exploring the interrelations of autopoiesis
and behavior [11], reaction-diffusion systems that support emergent individuals [25], lattice-based
models of metabolism-boundary co-construction [21], emergence of organization in lambda cal-
culus [12], emergence of organization in the Game of Life [7], and models with metabolism, self-
replication, and membrane synthesis [13]. Jedoch, despite the abundance of models, most served
merely as demonstrations for a particular concept and were not analyzed further.
In diesem Artikel, the relationship between viability, ontogeny, and adaptivity is investigated in the
context of a model protocell that we recently proposed [1]. After reviewing the model (Abschnitt 2)
and describing an environment in which we place it (Abschnitt 3), the article is organized as follows.
Abschnitt 4 builds upon a framework for exploring ontogenies as a network structure [6]. Applying this
methodology reveals a rich complexity of ontogenic structure, which we characterize through a
combination of graph-theoretic, morphology-based, and statistical measures. In Section 5, viability
500
Artificial Life Volume 22, Nummer 4
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
is measured for all configurations across the ontogenic network, and increases in the measure allow
us to identify trends of adaptive change. In Section 6, a second ontogenic network is derived from a
new environment; comparing it with the original ontogenic network demonstrates a more general
understanding of how ontogenies unfold through the space of viable configurations. Endlich, In
Abschnitt 7, the mechanism of a particular adaptive transition is analyzed in detail.
2 A Model of Emergent Individuality
For a model to fully address the emergence of individuality, the modeled individual must emerge
from lower-level processes rather than being hardcoded into the model. The model itself can only
define primitives that do not have any of the individual-level properties of interest. To accomplish this
within a spatial chemical system, individuals need to exhibit metabolism-boundary co-construction
[2]. Mit anderen Worten, they need to synthesize their own components via a metabolism, and separate
themselves from an environment by constructing and maintaining an emergent boundary. Während
such emergence has been explored in systems with abstract physics, such as the Game of Life
[6], the model described here moves towards a more realistic chemistry.
The continuous-time spatial model of molecular concentration dynamics considered here was
first introduced in [1]. Since it serves as an exemplar system for the analytical methods proposed
in this work, we only offer a brief overview of this model. The physics of this model include the
Diffusion, repulsion, chemical reactions, and decay of four molecular species: membrane (M ), auto-
catalyst (A ), food (F ), and water (W ). The chemical reactions are such that A is produced from an
autocatalytic reaction between A and F, while M molecules are produced by a reaction in which A
catalyzes the conversion of F to M. Both A and M also decay at a constant rate. Considered indi-
vidually, molecular concentrations diffuse across a two-dimensional lattice at a constant rate. Wie-
immer, the presence of repulsion between molecular types breaks the traditional symmetries. Based on
the behavior of phospholipid bilayers, the model implements anisotropic repulsion between mem-
brane molecules M and both A and W. This requires the introduction of an additional state variable, u,
which defines the orientation of M at every lattice site and behaves with its own dynamic of alignment
with neighboring membrane orientations. The combination of alignment dynamics and anisotropic
repulsion supports the self-assembly of membrane sheets. Hier, we utilize a 40 × 40 toroidal lattice.
Each lattice point has the five state variables (M, A, F, W, and u), resulting in an 8000-dimensional
coupled dynamical system. For specific details of the modelʼs implementation, including the forms of
the reaction, Diffusion, and repulsion equations, and the relevant parameter values, refer to [2].
The model displays two distinct types of equilibrium points: the uniform equilibrium point with
zero concentrations of both A and M (Figure 1a), and stable inhomogeneities in which positive
concentrations of A and M are maintained (Figure 1b). A configuration is considered stable when
the average temporal derivatives of A and M over the entire lattice satisfy the stabilization criteria
(Gleichung 2 in the Appendix). Even though these configurations are equilibrium points, they are still
chemically active, with positive diffusion and reaction rates. It was demonstrated that, in the latter
class of equilibrium points, M was necessary to contain A at concentrations high enough that A
could continuously construct both A and M faster than their molecular decay. Daher, these config-
urations exhibit metabolism-boundary co-construction [2].
Throughout this work, we study the ontogeny of a particular configuration labeled SC (stable con-
figuration), shown as the rightmost snapshot of Figure 1b, and on the right side of Figure 2. Due to uʼs
initialization and subsequent dynamics, SC has broken symmetries across both its horizontal and vertical
axes (with the horizontal broken symmetry more visibly apparent than the vertical broken symmetry).
3 Environment as Perturbation
From the individualʼs point of view, an environment is a probability distribution over a set of
perturbations. We first consider an environment E1, which consists of perturbations that increase
Artificial Life Volume 22, Nummer 4
501
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figur 1. Sequential snapshots of transients unfolding towards the modelʼs two types of equilibrium points (depicted in
the rightmost snapshots). These diagrams show the spatial concentrations of autocatalyst (Rot), membrane (Blau), Und
food (Grün); water has been removed for clarity. (A) Most initial conditions unfold to a uniform attractor, with zero
concentrations of M and A. (B) Some initial conditions unfold to stable inhomogeneous configurations, with nonzero
concentrations of M and A, which engage in metabolism-boundary co-construction. The stable configuration at t =
18,000 is SC, which provides the starting point for this articleʼs exploration of ontogenic networks. The time of each
snapshot (top right of each image) highlights the differences in time scale between the two sequences.
the concentration of either autocatalyst (A ) or membrane (M ) in the local neighborhoods of nine
distinct focal points. These locations are specified relative to the given configuration according to an
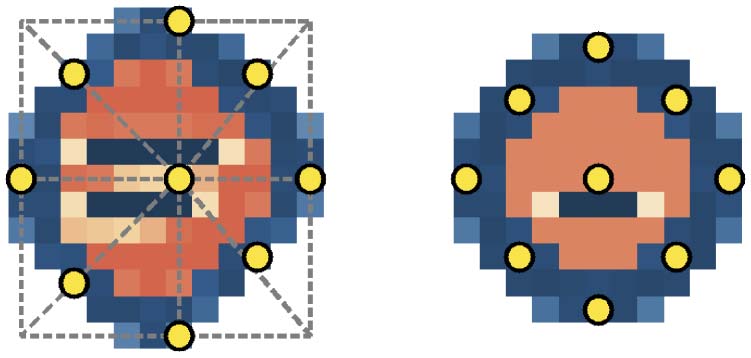
algorithm that guarantees placement on the configuration (Figur 2). The increase in concentration is
Þ2=2j 2, Wo |xij − xf| ist der
determined by a Gaussian function of the form G xi j
Euclidean distance (in numbers of lattice sites) from the focal point xf to the given cell xij, a is the
magnitude of the function, and a constant j 2 = 2.0. Four different magnitudes of a = [0.5, 1, 1.5, 2]
werden verwendet. In Summe, the environment E1 consists of 72 possible perturbations (9 locations × 2 molec-
ular species × 4 magnitudes), each of which occurs with a uniform probability.
− xi j −xf
D
J
¼ ae
(cid:1)
(cid:3)
J
Once a perturbation is applied, it instantaneously displaces the system in state space. The system
dynamics then unfold towards a limit set, resulting in one of three classes of possible outcomes: Die
uniform state, the same viable configuration, or a different viable configuration. Examples of these
three possibilities are illustrated in Figure 3.
To determine the identity of the resulting configuration, C, a comparison metric is used within
the 3200-dimensional state space of M and A molecular concentrations (40 × 40 lattice sites for two
molecule types). The structural distance from each previously observed configuration, C 0, is found
by taking the summed absolute difference between the configurationsʼ states. If this value is suffi-
ciently low, then we consider the configurations equivalent. The comparison metric is defined in
Gleichung 3 in the Appendix.
Figur 2. In E1, the locations of the nine perturbations are determined relative to a configuration. The diagram on the
left shows how this is done: A box encapsulates the configuration, and focal points are centered on the lattice cells
according to intersections with the boxʼs lines. For SC, this produces the nine points shown on the right. E2 (described
in Section 6) uses the same nine absolute locations, shown here on SC, for all of its subsequent perturbations.
502
Artificial Life Volume 22, Nummer 4
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figur 3. Three perturbations from environment E1 applied to SC. The perturbations increase the membrane concen-
tration with the same amplitude a = 2, as shown in yellow. Following perturbation, the system undergoes transients that
stabilize in different attractor classes. The top branch shows a robust transition that returns to the original configuration,
the middle branch shows a plastic transition that brings the system to a different stable configuration, and the bottom
branch shows a destructive transition.
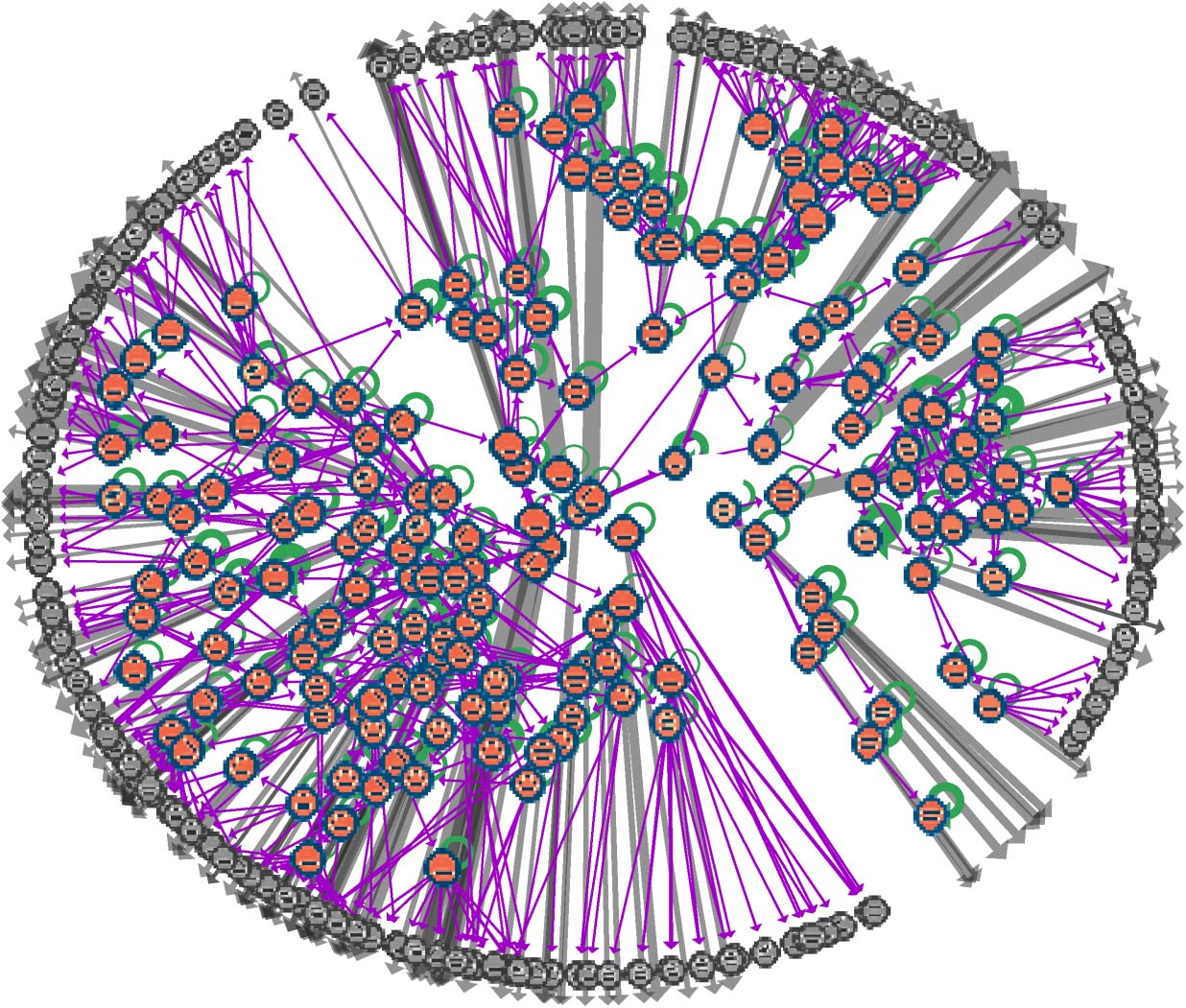
4 Ontogenic Networks
Typical environments are the source of repeated perturbations that induce a sequence of changes to
an individualʼs structure. A single trajectory through the set of viable configurations is an ontogeny.
Different perturbations have the potential to induce different plastic transitions, resulting in different
ontogenic trajectories. The structure of all possible ontogenies defines an ontogenic network, in which
the viable configurations and death state constitute the networkʼs nodes, and each environmental
perturbation is a directed edge (see the Appendix for extended definition). Given a specific indi-
vidualʼs configuration in a specific environment, the full ontogenic network is obtained by exhaus-
tively characterizing the configurationʼs response to every environmental perturbation. Der Prozess
is then repeated for all subsequent configurations until closure is achieved (d.h., every transition re-
sults in either a previously characterized configuration or death) [6].
The full ontogenic network formed by SCʼs repeated exposure to environment E1 is a multigraph
with a set of reachable configurations as its nodes, each of which is the source for 72 directed edges.
Following each perturbation, the system was given sufficient time to stabilize before the next per-
turbation was applied. The network was generated by a breadth-first search that exposed all config-
urations to E1 as they were discovered. As the frontier of the search expanded from SC, it uncovered
an exponentially increasing number of configurations. Due to computational limitations,1 the search
was terminated at a uniform depth of 17 edges from SC, resulting in a total of 268 discovered con-
figurations. The combination of a breadth-first search with truncation at a uniform depth fully char-
acterizes the local search space around SC. Of these configurations, 114 are at a depth of 17, Und
their outgoing transitions were left unsearched. These configurations will be termed the unsearched
frontier, and are excluded from this sectionʼs analysis. This leaves 154 configurations whose transi-
tions were fully characterized.
As a first step towards characterizing the structure of this network, we focus on the relationships
between the 154 searched configurations. We reduce the full ontogenic network by first combining edges
according to equivalence classes of transition, and second by considering the death state with all destruc-
tive transitions separately from the rest of the network. The resulting reduced ontogenic network (ON1)
is shown in Figure 4. SCʼs initial asymmetry is propagated through all configurations in ON1. In theory,
mirrored initial conditions can yield ontogenies identical to ON1, but with mirrored configurations.
Remarkably, this pairing of a simple configuration and environment generates an extensive onto-
genic network, rich with features. The systemʼs many stable configurations (represented in Figure 4
by the morphological structure of A and M concentrations) are shown as nodes, while the death
state is shown by the surrounding black ellipse. The directed edges in ON1 reflect the probability for
1 At the time of writing, the search of each ontogenic network required approximately one and a half months of running time.
Artificial Life Volume 22, Nummer 4
503
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figur 4. The ontogenic network ON1 captures the structure of all possible ontogenies starting at SC in environment E1,
truncated to a search depth of 17 transitions from SC. All configurationsʼ morphologies are shown as nodes, während die
death state is depicted as a black ellipse. Configurations on the unsearched frontier are shown in grayscale. Directed
edges capture the transitions between configurations and are categorized as robust (green self-loops), plastic (purple
edges), and destructive (gray edges). Edge width represents the log probability for each transition.
a transition to occur given a random perturbation from the environment, with robust transitions
shown as green self-loops, plastic transitions shown as directed purple edges between configurations,
and destructive transitions shown in gray.
ʼs searched configurations reveals that they vary widely in their
A statistical analysis of ON1
response to perturbations from E
1. It is interesting to note that all configurations have nonzero
probabilities of both destruction and survival in this environment. For each configuration, eins
can calculate its robustness (the probability of undergoing a robust transition, Gleichung 6), its plas-
ticity (the probability of undergoing a plastic transition, Gleichung 7), and its fragility (the probability
of undergoing a destructive transition, Gleichung 8). (Equations are found in the Appendix.) Specif-
isch, for the configurations of ON1, robustness occurs in the range [0.0, 0.79], plasticity occurs in
the range [0.0, 0.82], and fragility occurs in the range [0.10, 0.96]. The outdegree distribution of the
network reflects the number of different plastic options available for viable configurations. Das
distribution has a range of [0, 9] with a mean of 3.49, which reflects the fact that the average viable
configuration can undergo plastic transitions to three or four other configurations following a per-
turbation. Weiter, 30% of plastic transitions are bidirectional—a number that indicates the network
has many more bidirectional edges than found in a random graph. In der Tat, this hypothesis is sup-
ported by a p-value ≪ 0.001 when comparing ON1 with an ensemble of 1000 random graphs with
the same number of nodes and degree distribution.
The graph-theoretic structure of the viable configurations in ON1 reflects several interesting
characteristics of ontogenies starting at configuration SC in environment E1. Erste, the number of
viable configurations increases exponentially with minimum path length from SC. Zweite, ON1 has
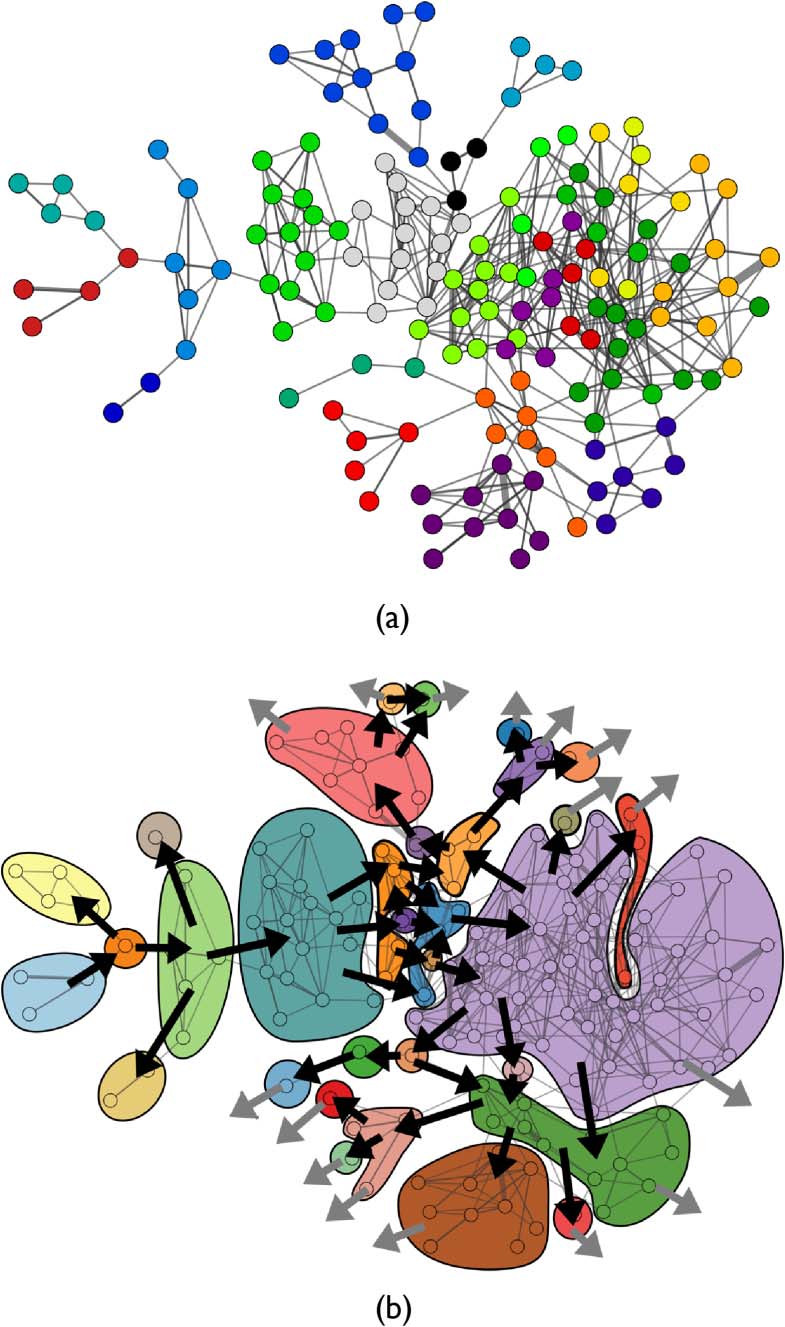
several distinct clusters as highlighted by InfoMap network community detection [22] (Figure 5a).
These graph-theoretic clusters reflect sets of configurations for which transitions are more likely to
504
Artificial Life Volume 22, Nummer 4
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
remain within the set than leave it. Dritte, there are several configurations that function as bottle-
necks for the network in the sense that ontogenies must pass through those configurations to reach
different areas of the network. These configurations are determined by high values of betweenness
centrality [20].
Strongly connected components (SCCs) found in the current ON1 demonstrate irreversibility,
branching, and attractors (Figure 5b). SCCs are sets of configurations in which all configurations
are mutually reachable [20]. Es gibt 32 SCCs in ON1. The presence of multiple SCCs indicates
irreversibility—if the system moves from one SCC to another, it cannot return. Branching is illus-
trated by diverging paths from the SCCs. If an individual exits an SCC along one branch, the alter-
natives can no longer be explored. Endlich, those SCCs with no outgoing connections are attractors in
the sense that if an ontogeny enters one of these sets, it is guaranteed to remain there until death.
The analysis of ontogenies is further enriched by considering their morphologies—their unique
spatial arrangements of molecular concentrations. Recall that each configuration defines a point in
the 3200-dimensional state space of M and A molecular concentrations. Due to their high dimen-
sionality, these configurations are projected onto a 2-dimensional manifold using the IsoMap mani-
fold identification technique [23] including the whole set of other configurations as neighbors.
The resulting projection is shown in Figure 6. This projection is indicative of morphological clus-
tering with many points tightly grouped and relatively large distances between the groups. Specific
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 5. Two copies of ON1 (with the same layout as Figure 4). (A) ON1ʼs nodes are colored by cluster membership in
InfoMap communities. (B) Strongly connected components are shown as colored regions, with arrows indicating the
direction of ontogenic change. Gray arrows indicate transitions to the unsearched frontier.
Artificial Life Volume 22, Nummer 4
505
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figur 6. ON1ʼs stable configurations, clustered according to morphological similarity. Each point is a single configura-
tionʼs morphological state projected onto a two-dimensional space determined by two IsoMap components. Different
colors represent clusters detected by K-means clustering. An exemplar configuration from each cluster illustrates the
clusterʼs unique morphological features.
partitions of configurations can be identified using K-means clustering [17]. The resulting eight clus-
ters are shown using different colors in Figure 6. Comparison of the exemplar configurations from
each cluster, identified by their central position relative to the clusterʼs mean, demonstrates how the
clusters vary along several qualitative dimensions: the size of the configuration, the shape of the
outer membrane, the thickness of the outer membrane, and the number and arrangement of internal
membrane structures.
Further graph-theoretic analysis reveals how morphological features change as ontogenies unfold in
ON1 as a function of individual plastic transitions, graph-theoretic path length from SC, and cluster-
ing. Erste, plastic transitions are much more likely to occur between morphologically similar configu-
rations. A Bayesian BEST test [16] between the distribution of all inter-configuration distances using
the Euclidean metric and the distribution of configuration distances for those linked by a plastic tran-
sition shows that the average difference was 3.25, which fell in a 95% highest-density interval (HDI)
von [3.16, 3.34]. Weil 0 falls outside the HDI, there is credible evidence that the distributions have
different means. Außerdem, the distribution of credible effect sizes is slightly left-skewed, with a
mode of 2.18 und ein 95% HDI of [2.11, 2.25], which again suggests a credible effect. Zweite, a reliable
pattern of growth occurs in ON1; the size of morphologies increases with increasing graph-theoretic
path length from SC. Endlich, there is a strong correspondence between the morphological clusters and
the InfoMap clusters previously identified in ON1 as reflected by a normalized mutual information [9]
value of 0.67 between the two clusterings. daher, as an ontogeny unfolds and an individual falls
into a graph-theoretic cluster, it also tends to maintain its morphological features by remaining within
a corresponding morphological cluster.
To proceed in the case of SC in E
1, we return to the full ontogenetic network and classify each of
Die 72 perturbations by their probabilities of inducing a robust, destructive, or plastic transition when
applied to a random configuration from the set of viable configurations in ON1. The resulting clas-
sification is visualized in Figure 7a according to barycentric coordinates for the three probabilities.
Hier, each point (arrow or circle) represents one of the 72 perturbations, and the inverse distance
between the point and each vertex reflects the associated probability of a transition in that equiva-
lence class; a point directly on a vertex denotes 100% of transitions falling in that category.
506
Artificial Life Volume 22, Nummer 4
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
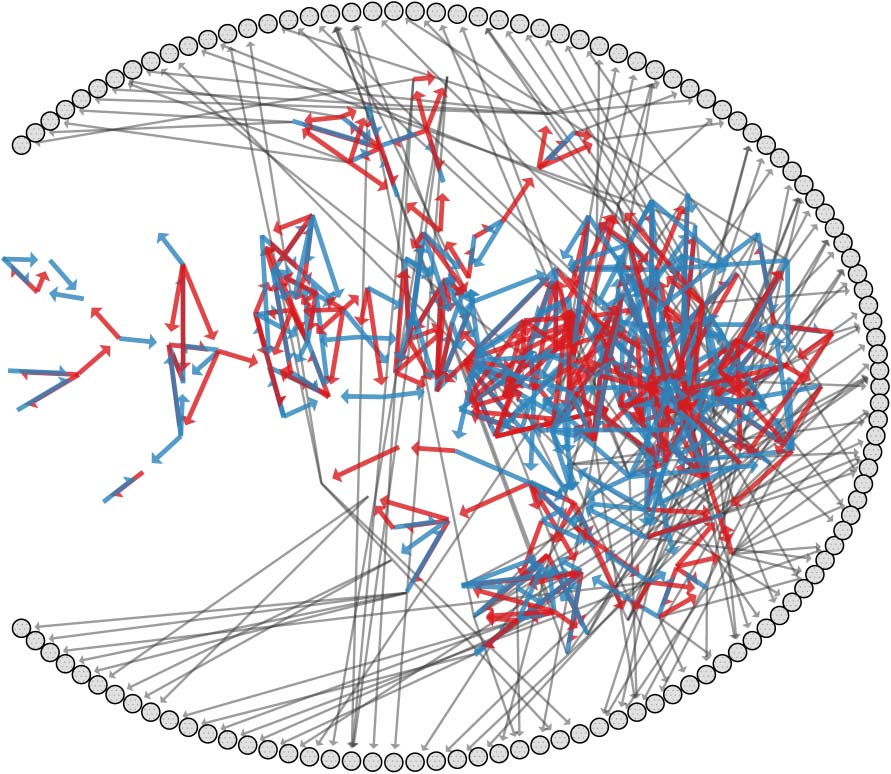
Figur 7. Environment E1 ʼs 72 perturbations positioned according to their probabilities of inducing a robust, destructive,
or plastic transition when applied to a random configuration from ON1. (A) Perturbations are shown in barycentric
coordinates with markers illustrating their location, type, and size. Arrows indicate the perturbation location on the
outer membrane, and circles indicate perturbations to the central position. Color indicates molecular type, entweder
membrane (Blau) or autocatalyst (Rot). The perturbationʼs magnitude is shown by the darkness of the marker,
with darker markers indicating larger magnitudes. (B) Histograms categorize the probability of perturbations inducing
a destructive, robust, or plastic transition conditioned on (upper ) the perturbations type and magnitude or (lower )
location.
Inspection of Figure 7a reveals that perturbations can vary widely in their consequences.
Vor allem, all perturbations but one are destructive to at least one configuration, but none of the
72 perturbations are destructive to all configurations. There is a gradated tradeoff between per-
turbationsʼ probabilities of inducing a robust transition versus inducing a destructive transition. A
small subset of perturbations are associated with a large tendency to induce plastic transitions.
These results can be further subdivided according to the location and magnitude of the applied
perturbation as shown in Figure 7b. In the first row of the subfigure, three normalized histograms
are shown, which categorize perturbations based on outcome, molecular type (membrane in blue,
autocatalyst in red), and magnitude (light to dark color ). As one would expect, robust transitions are
primarily associated with small perturbations, while destructive transitions are associated with large
perturbations. Plastic transitions occur more frequently for perturbations to membrane concentra-
tions than to autocatalyst concentrations, regardless of magnitude. The second row of the subfigure
illustrates three additional histograms categorizing perturbations based on outcome and location.
These diagrams indicate that plastic transitions result more often from perturbations to the center
and north east locations, while destructive transitions are slightly biased to perturbations on the
north west.
5 Quantifying Viability and Adaptivity
Viability is an individualʼs ability to maintain itself, and is a consequence of well-matched configu-
rations and environments. While some sequences of perturbations applied to an individual yield long
Artificial Life Volume 22, Nummer 4
507
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
ontogenies, the same individual exposed to different perturbations can result in shorter-lived ontog-
enies. The viability of a configuration is here defined as the expected life span over all of its possible
ontogenies [2]. Two notions of adaptivity follow from this definition. Local adaptivity is the change
in viability resulting from a plastic transition; an adaptive transition increases a systemʼs viability, Und
a maladaptive transition reduces it. Global adaptivity is the tendency for an individualʼs viability to
increase with longer ontogenies; positive global adaptivity is the tendency for viability to increase
im Laufe der Zeit, and negative global adaptivity is the tendency for viability to decrease over time.
The above notion of viability can be quantified by considering the ontogenic network as a tran-
sition matrix for a Markov chain. As a consequence of this, death becomes an absorbing state and
most configurations are transients. Finding the average number of transitions from each transient
state to an absorbing state is a well-studied problem [14], and gives our measure of viability
(Gleichung 9 in the Appendix). The lower bound on this measure is 1, which occurs when all per-
turbations bring the configuration to death within one step. The existence of an immortal config-
uration would give an upper bound of infinite viability.
In order to calculate viability for ON1, all configurations on the unsearched frontier are assigned
to transition directly to death. This gives a conservative lower bound for the actual viability of all
searched configurations. The analysis of ON1 reveals a wide range of viabilities, aus 1.0588 Zu
6.3046 with an average of 3.3516, reflecting the fact that the average configuration is 3 random
perturbations away from death. Given the viabilities for each configuration, the adaptivity of a tran-
sition is calculated from the difference in viability across the transition (Gleichung 10 in the Appendix).
Our analysis identified a surprising abundance of adaptive transitions (Figur 8). In der Tat, 40% of the edges
are locally adaptive, which means just under half of the plastic transitions produce an increase in viability.
It is important to note that robustness, plasticity, fragility, and viability are all distinct notions, Und
highlight different features of configurations. This is demonstrated by the fact that configurations
identified as extreme examples of these measures are all distinct from one another (Figur 9). Der
most viable configuration is not the most robust, and the least viable configuration is not the most
fragile. Unlike robustness or fragility, which are instantaneous measures, viability is a consequence of
how configurations are embedded within the full ontogenic network. The viability of a configuration
depends on the structure with which it is connected to other configurations with plastic transitions,
and the viabilities of those configurations.
Figur 8. The network layout is the same as in previous figures. Viability is shown by the darkness of the green nodes,
locally adaptive transitions are blue, and locally maladaptive transitions are red.
508
Artificial Life Volume 22, Nummer 4
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
A
R
T
l
/
_
A
_
0
0
2
1
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figur 9. The configurations identified as extreme examples of robustness, plasticity, fragility, and viability in ON1
demonstrate that all of these notions are distinct. To provide a scale for the structural differences in this figure, Die
minimum is 9.86 (between the most plastic and the most viable configurations) and the maximum is 68.37 (zwischen
the most robust and the least plastic configurations).
Remarkably, ontogenies from SC also display global adaptivity. A correlation analysis found that a
configurationʼs graph-theoretic path length from SC is positively correlated with its viability (r-value
−8 ). This means that longer-lived ontogenies beginning at SC will generally
von 0.4622, P < 10
experience an increase in their viability. Note that viability is a forward-looking measure, not based
on how long it took to survive up to a given configuration, but rather on how long it is expected to
survive from that configuration. This global trend is configuration specific; each configuration in ON1
can have a different global adaptivity, and can even be globally maladaptive.
6 Comparative Analysis of Ontogenic Networks
The structure of ontogenies depends on the particular pairing of an individual and its environment.
If the individualʼs initial configuration is changed, we would expect to obtain a different ontogenic
network. Likewise, if the environment is changed, we would also expect a different ontogenic net-
work with its own unique properties. Such networks are all instances of a general set of possible
ontogenic networks. To gain a broader understanding of this set, it is useful to consider multiple
ontogenic networks and compare their structures. In this section, we compare ON1 with one addi-
tional ontogenic network, ON2 (Figure 10), according to their graph-theoretic properties, morphol-
ogies, and the features of interactions between the protocell and its environment.
2 are identical in all but one feature: Whereas the locations of E
The second ontogenic network, ON2, is obtained by exposing SC to a new environment, E
2. The
ʼs pertur-
environments E
ʼs per-
bations are determined relative to the protocell (as depicted in Figure 2), the locations of E
turbations remain fixed in space (at positions denoted in the left of Figure 2). The distinction
between environments with spatially relative and those with spatially absolute perturbations is im-
portant. Environments with spatially relative perturbations, such as E1, track the individual so that it
cannot avoid the perturbations. In contrast, environments with spatially fixed perturbations, such as
E
2, allow individuals to adjust their position relative to those perturbations.
1 and E
2
1
The procedures by which the two ontogenic networks were obtained were identical except for
two minor differences. First, due to computational limitations, the search of ON2 was terminated at
a depth of 7 transitions from SC rather than 17. Second, the stabilization criteria for two of the
configurations in ON2 was slightly relaxed by reducing the convergence window to 700 time steps.
There are three distinctions that can be drawn between the graph-theoretic structures of ON1 and
ON2 that reflect key variations in the resulting ontogenies. First, ON2 contains many more config-
urations (387) than ON1 (268), even though the search depth of ON2 is substantially less than that of
ON1. Given its higher rate of growth with search depth, if ON2 had been searched to the same
depth as ON1, its size would far exceed the size of ON1. Second, in ON2, all branches rooted at
SC extend to the unsearched frontier. In contrast, in ON1 only one branch from SC extends to the
Artificial Life Volume 22, Number 4
509
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figure 10. The ontogenic network ON2 captures the structure of all possible ontogenies starting at SC in environment E2,
truncated to a search depth of 7 transitions from SC. All configurationsʼ morphologies are shown as nodes, while the
death state is depicted as a black ellipse. Configurations on the unsearched frontier are shown in grayscale. Directed
edges capture the transitions between configurations and are categorized as robust (green self-loops), plastic (purple
edges), and destructive (gray edges). Edge width represents the log probability for each transition.
unsearched frontier. Third, ON2 exhibits more irreversibility than ON1; ON2 contains 102 strongly
connected components, as compared with 32 in ON1. Since there are many small SCCs in ON2,
when a plastic transition occurs, the protocell is less likely to have the option to return to a prior
configuration.
Configurations in ON2 are on average less robust, less plastic, and more fragile than in ON1
(Table 1). Configurations in ON2 are also less viable, and the transitions are less adaptive (only
34% of ON2ʼs edges are adaptive, compared to 40% of edges in ON1). However, these conclusions
may be confounded both by the reduced search depth and by the increased size of ON2ʼs un-
searched frontier.
Table 1. Statistics for four properties of configurations from ON1 compared with configurations from ON2.
ON1
Mean
0.4715
Robust
Plastic
0.1682
Destructive
Viability
0.0481
3.3516
Range
[0.0, 0.7917]
[0.0, 0.8194]
[0.0972, 0.9583]
[1.0588, 6.3046]
ON2
510
Mean
0.3752
0.1012
0.4762
2.1180
Range
[0.0, 0.7222]
[0.0, 0.6944]
[0.2222, 0.9444]
[1, 3.6241]
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
Figure 11. Ontogenic networks ON1 and ON2ʼs combined morphologies, projected onto a two-dimensional space
determined by two IsoMap components. ON1 is shown in blue, ON2 is shown in green, and the morphologies shared
by both ontogenies are shown in orange. The original starting configuration, SC, is labeled.
A comparison of ON1 and ON2
ʼs morphologies shows that they explore different regions of
morphology space. The 641 total configurations uncovered by either ON1 or ON2 can be differen-
tiated by their structures. Indeed, the IsoMap decomposition for all 312 searched configurations
(Figure 11) clearly illustrates this separation. The distinction between the configurations in ON1
and ON2 is also visible in the comparison of morphological features: We see more configurations
with only a single internal membrane structure, there are some morphologies with three internal
membrane structures, and many have diagonal membrane structures (one of these is shown in
Figure 12). As with ON1, these configurations cluster according to morphological similarity. Inter-
estingly, there were only 14 configurations shared by the two networks. Of these 14, four include SC
and its three immediate progeny, while the others occur within a search depth of 5 in ON1 and 4 in
ON2. Only six plastic transitions exist within both networks amongst these 14 configurations, and
only two transitions are shared that do not involve SC. This comparison suggests that as the search
procedure expands beyond the unsearched frontiers, the reachable morphologies will continue to
diverge in their features.
The two ontogenic networks also differ in their patterns of morphological change and in the
consequences of these changes. For example, ON1ʼs configurations show a reliable increase in size,
while the size of configurations in ON2 varies widely. The configurations in ON2 range in size from
Figure 12. The internalization of perturbations by a large configuration in ON2. The nine fixed perturbation locations
from E2 are denoted by yellow dots.
Artificial Life Volume 22, Number 4
511
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
slightly smaller than SC to approximately the same size as the largest configuration uncovered in
ON1. The possibility of engulfment is a consequence of increased size in E
2. Because the perturbations
are fixed in space, their effects become increasingly internalized as a configuration grows in size
(Figure 12). In contrast, engulfment is impossible in E
1, the
perturbations simply move further away. This ability of an individual to modify the impact of an
environmental perturbation on it is a first step towards two-way environment-individual interaction.
1. As a configuration grows in size in E
7 Mechanisms of Adaptivity
This model provides an excellent opportunity to investigate the mechanisms underlying adaptivity.
Previous formulations of adaptivity have assumed an explicit regulatory subsystem [3, 10]. This
mechanism is designed to monitor the systemʼs internal state relative to its boundary of viability
and use this information to bring the system to more viable states. Models that implement this a
priori assumption cover only a subset of possible mechanisms of adaptivity. In contrast, this articleʼs
model demonstrates an emergent type of adaptivity. Analyzing the processes involved here can
provide insights not previously possible.
As a first step towards understanding the mechanisms of emergent adaptivity, we examine a
minimally adaptive scenario embedded within ON1. An adaptive transition requires an environment
of at least two perturbations, one that increases viability, and another that reduces it. Taken to its
extreme, one perturbation would bring an initial configuration to death, and the other perturbation
would bring it to a second, immortal configuration. Multiple instances of this exact scenario are
found embedded within ON1 when environment E
1 is restricted to only two perturbations.
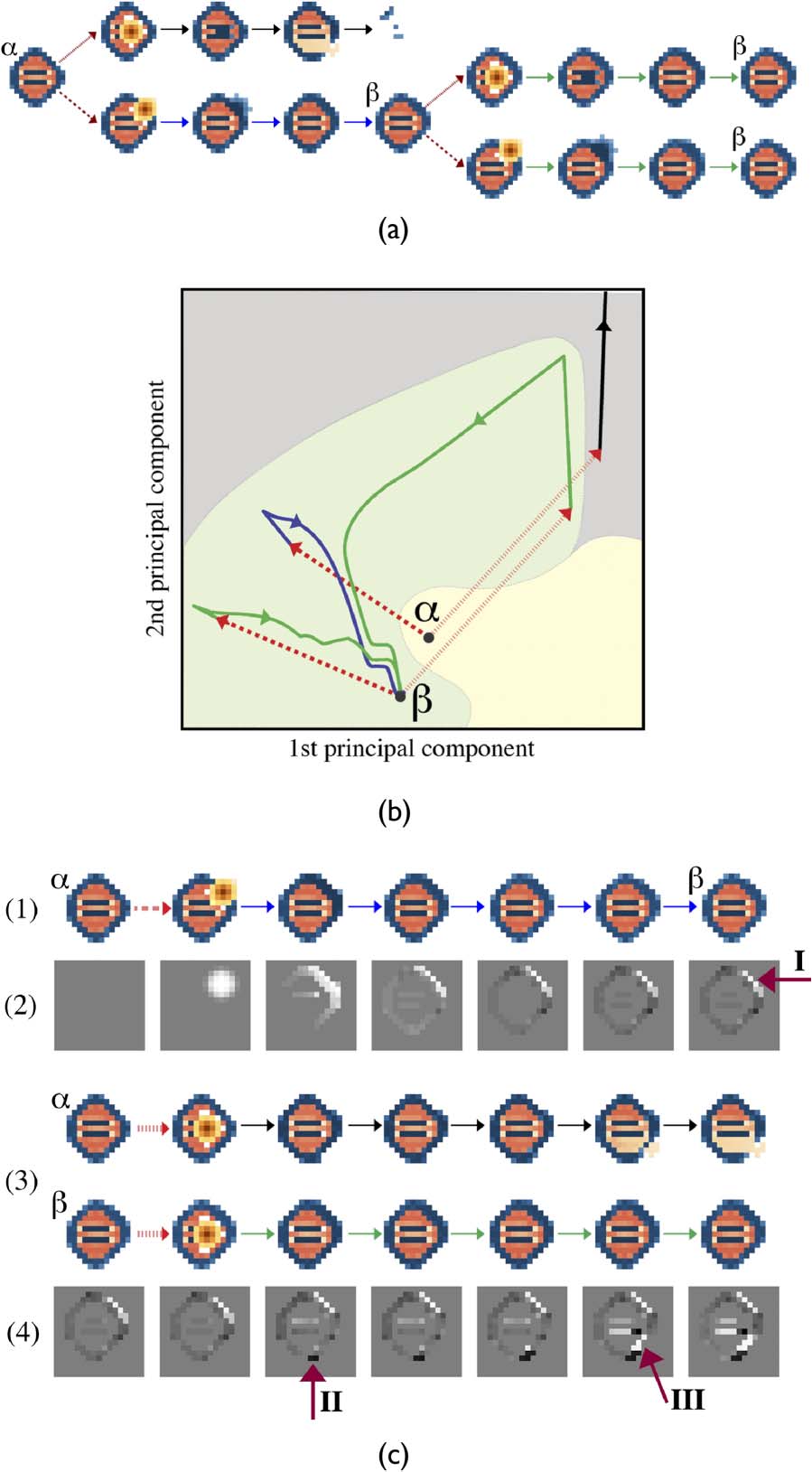
The chosen example of a minimally adaptive scenario is shown in Figure 13a. The scenario begins
with configuration a, which is subjected to the two perturbations. The perturbations are placed at
different locations, but otherwise have the same magnitude and are both to the membrane field. On
the top branch, a disintegrates, whereas on the bottom branch it undergoes a plastic transition to
configuration h. Then h is subjected to the same two perturbations, both of which result in robust
transitions. In this minimal context, h can survive all perturbations, whereas a can survive only half
of them. The transition from a to h is therefore adaptive.
One way to analyze this scenario is to utilize dynamical systems theory to characterize the sys-
temʼs phase space (Figure 13b). For visualization, the high-dimensional state space is projected onto
the top two principal components. This makes trajectories appear to overlap, even though no over-
lap is possible in the full dynamics. Configurations a, h, and death are equilibrium points, each
surrounded by a basin of attraction. The real basins of attraction are not visualizable, so faux basins
of attraction are added to represent a hypothetical division of phase space. The two classes of per-
turbations (dashed red lines) instantaneously displace the system within the state space. Whereas
perturbations to a move the system either to deathʼs basin of attraction or to hʼs basin of attraction,
when applied to h they displace the system within the same basin of attraction. Given this analysis,
adaptivity is explained by the congruence between the two configurationsʼ basins of attractions and
the available perturbations. The position of the equilibrium points and the shapes of their basins are
such that the perturbed states fall outside aʼs basin, yet remain within hʼs.
A more detailed investigation of mechanism needs to address the specific physico-chemical in-
teractions that take place during this adaptive transition. A spatial analysis is here approached by
taking sequential snapshots of transient configurations throughout the minimally adaptive scenario
and identifying the critical differences in their morphologies (Figure 13c). First, we look at the adap-
tive transition from a to h (Figure 13c(1)) and the divergence from a that occurs throughout this
transition (Figure 13c(2)). The sequence begins with a, at which there is no difference. Next, the
perturbation displaces the membrane field, seen as a circular difference in the top right. Further
down the sequence, the membrane concentration spreads around the boundary. While the northeast
side of the configuration remains at increased concentrations, the rest of the boundary is slightly
lower from its initial concentrations; this trait stabilizes at h. The most obvious difference between
512
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13. A minimally adaptive scenario and its analysis. (a) Configuration a branches off into two transients following
the application of two perturbations, one of which leads to disintegration, and the other to a plastic transition resulting in
h. Then h is perturbed by the same two perturbations and recovers, proving it has adapted. (b) The same sequence of
events shown in state space projected onto the top two principal components. Faux basins of attraction (yellow, green,
gray regions) are added for explanatory purposes. Perturbations are indicated by the two classes of dashed red lines.
Transients are shown as trajectories, with the destructive transition as a black trajectory, the adaptive plastic transition
as a blue trajectory, and the robust transitions as green trajectories. (c) The scenario is analyzed as sequences of
spatiotemporal configurations: (1) The transition from a to h. (2) The difference from aʼs membrane field for the
corresponding sequence in (1); the figure is gray where membrane concentrations are the same as a, white where they
are more than a, and black where they are less than a. (3) Both a and hʼs responses to the second perturbation. (4) The
difference between membrane concentrations for the two sequences in (3). Where membrane concentrations are
the same in these sequences, the figure is gray; where the transient following h has a higher membrane concentration,
the figure is white; and where it has lower concentration, the figure is black.
stable configuration h and a is a local increase in membrane concentration, which makes h rounder
and thickens its boundary (arrow I).
Next, we examine how these morphological differences allow h to survive a perturbation that a
does not survive (Figure 13c(3)). The difference between these two sequences shows where the
relevant divergences begin (Figure 13c(4)). The sequence begins with the initial difference between
Artificial Life Volume 22, Number 4
513
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
a and h. When the perturbations are applied to both configurations, they do not appear in the difference
plot, because the perturbations are spatially aligned. Later, the behavior begins to diverge. The obvious
difference between their initial structures (arrow I) is not where the fatal divergence begins. Instead, a
region on the bottom of a (arrow II), which bulges out and to the right, is the important feature. This
growth draws aʼs membrane downward, reducing the membrane concentration in the southeast
boundary (arrow III). This opens up a tear in aʼs membrane, from which autocatalyst pours out and
ultimately brings about disintegration, whereas hʼs morphology allows it to stay intact and restabilize.
In contrast with previous formulations of adaptivity, we see that no explicit regulatory mechanism is
found during this emergent adaptive transition. Adaptivity is the result of distributed processes, and is
better explained by their emergent spatiotemporal dynamics. The analysis demonstrates that local
changes in chemical distributions, such as thickening membranes, have consequences for subsequent
behavior. In dynamical systems terms, adaptivity is determined by the shape of configurationsʼ basins
of attraction, and how interactions with the environment move a system through the phase space. A
transition is adaptive if it brings the individual to a configuration with a more accommodating basin.
8 Discussion
Ontogenies result from the interplay between an individualʼs configurations and its environment.
Here, we mapped the space of all possible ontogenies for a model protocell in a specific environ-
ment by exposing it to sequential perturbations and measuring its responses. The resulting ontogenic
network contained rich structure as uncovered by a combination of statistical and graph-theoretic
methods, including bottlenecks that constrain ontogenic change and branches that reflect irreversible
transitions. The set of configurational morphologies was found to cluster according to morpholog-
ical similarity, and these clusters roughly corresponded to those identified in the network topology.
Exploration of the same protocell exposed to a second environment generated a different ontogenic
network with distinct properties. This second network displayed a different branching structure,
demonstrated increased irreversibility, and expanded towards a different region of morphology space
with unique morphological features.
The viability of individual configurations was quantified as the average expected life span of the
protocell. Two notions of adaptivity then followed from this definition of viability: Local adaptivity
measured the change in viability resulting from plastic transitions, and global adaptivity measured
long-term trends in viability. Surprisingly, the first ontogenic network (ON1) had an abundance of
locally adaptive transitions, and even displayed global adaptivity. Finally, the mechanisms of a min-
imally adaptive scenario were analyzed, demonstrating how adaptivity can be achieved by distributed
processes without requiring an explicit regulatory mechanism.
The combination of this model and analytical techniques provides a foundation for studying the
emergence of viability, ontogeny, and adaptivity in more biologically realistic systems. One natural
extension along these lines re-conceptualizes viable configurations as members of dynamically richer
limit sets. Another recognizes that environments also include sequential perturbations that occur on
similar or faster time scales compared to an individualʼs intrinsic dynamics; these environments
would prevent the system from stabilizing at a limit set before the next perturbation arrives and
require a new, more continuous conceptualization of ontogenic change. Further, biological indi-
viduals and environments are structurally coupled [18], allowing an individualʼs behavior to induce
correlations with its environment which affect future interactions. All of these factors need to be
considered in a generalization of adaptivity to real-world biological individuals.
Acknowledgments
We would like to thank Simon McGregor and Pedro A. M. Mediano for pointing out an error in an
earlier draft of this paper. This work was supported by NSF grant IIC-1216739 to R.D.B., by Lilly
Endowment, Inc., through its support for the Indiana University Pervasive Technology Institute, and
by the Indiana METACyt Initiative. The software is freely available at https://github.com/eagmon/
co-construction_base.
514
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
References
1. Agmon, E., Gates, A. J., Churavy, V., & Beer, R. D. (2014). Quantifying robustness in a spatial model
of metabolism-boundary co-construction. In H. Sayama, J. Rieffel, S. Risi, R. Doursat, & H. Lipson (Eds.),
Artificial Life 14: Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems
(pp. 514–521). Cambridge, MA: MIT Press.
2. Agmon, E., Gates, A. J., Churavy, V., & Beer, R. D. (2016). Exploring the space of viable configurations
in a model of metabolism-boundary co-construction. Artificial Life, 22(2), 153–171.
3. Ashby, W. R. (1954). Design for a brain. New York: Wiley.
4. Barandiaran, X., & Moreno, A. (2008). Adaptivity: From metabolism to behavior. Adaptive Behavior, 16(5),
325–344.
5. Barandiaran, X. E., & Egbert, M. D. (2014). Norm-establishing and norm-following in autonomous
agency. Artificial Life, 20(1), 5–28.
6. Beer, R. D. (2014). The cognitive domain of a glider in the Game of Life. Artificial Life, 20(2), 183–206.
7. Beer, R. D. (2015). Characterizing autopoiesis in the Game of Life. Artificial Life, 21(1), 1–19.
8. Bich, L., Mossio, M., Ruiz-Mirazo, K., & Moreno, A. (2016). Biological regulation: Controlling the
system from within. Biology & Philosophy, 31(2), 237–265.
9. Danon, L., Daz-Guilera, A., Duch, J., & Arenas, A. (2005). Comparing community structure identification.
Journal of Statistical Mechanics: Theory and Experiment, 2005(09), P09008.
10. Di Paolo, E. A. (2005). Autopoiesis, adaptivity, teleology, agency. Phenomenology and the Cognitive Sciences,
4(4), 429–452.
11. Egbert, M. D., & Di Paolo, E. (2009). Integrating autopoiesis and behavior: An exploration in
computational chemo-ethology. Adaptive Behavior, 17(5), 387–401.
12. Fontana, W., & Buss, L. W. (1994). The arrival of the fittest: Toward a theory of biological organization.
Bulletin of Mathematical Biology, 56(1), 1–64.
13. Gánti, T. (2003). Chemoton theory: Theory of living systems. New York: Springer Science & Business Media.
14. Grinstead, C. M., & Snell, J. L. (1998). Introduction to probability. Providence, RI: American Mathematical
Society.
15. Hutton, T. J. (2007). Evolvable self-reproducing cells in a two-dimensional artificial chemistry. Artificial Life,
13(1), 11–30.
16. Kruschke, J. K. (2013). Bayesian estimation supersedes the t test. Journal of Experimental Psychology: General,
142(2), 573–603.
17. Lloyd, S. (1982). Least squares quantization in pcm. IEEE Transactions on Information Theory, 28(2), 129–137.
18. Maturana, H. R., & Varela, F. J. (1980). Autopoiesis and cognition: The realization of the living. Netherlands:
Springer.
19. Mavelli, F., & Ruiz-Mirazo, K. (2007). Stochastic simulations of minimal self-reproducing cellular
systems. Philosophical Transactions of the Royal Society B: Biological Sciences, 362(1486), 1789–1802.
20. Newman, M. E. (2003). The structure and function of complex networks. SIAM Review, 45(2), 167–256.
21. Ono, N., & Ikegami, T. (1999). Model of self-replicating cell capable of self-maintenance. In Advances in
artificial life (pp. 399–406). Berlin Heidelberg: Springer.
22. Rosvall, M., & Bergstrom, C. T. (2008). Maps of random walks on complex networks reveal community
structure. Proceedings of the National Academy of Sciences of the U.S.A., 105(4), 1118–1123.
23. Tenenbaum, J. B., De Silva, V., & Langford, J. C. (2000). A global geometric framework for nonlinear
dimensionality reduction. Science, 290(5500), 2319–2323.
24. Varela, F. G., Maturana, H. R., & Uribe, R. (1974). Autopoiesis: The organization of living systems,
its characterization and a model. Biosystems, 5(4), 187–196.
25. Virgo, N. D. (2011). Thermodynamics and the structure of living systems. Ph.D. thesis, University of Sussex.
Artificial Life Volume 22, Number 4
515
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
Appendix
The Structure of Ontogenies in a Model Protocell
A full ontogenic network is a multigraph (ON = (C, E, R)) with a set of nodes C, a set of edges E,
and a set of edge labels identified by the set of perturbations R. This network is generated by
applying perturbations (R) with a probability distribution (P ) to configurations in C. The search
begins with an initial configuration C1 and the death state C0. By applying perturbations r 2 R to
C1, new configurations in C are uncovered. The same set of perturbations are applied recursively to
all uncovered configurations until closure is achieved (i.e., every transition results in either a pre-
viously characterized configuration or death).
A response to perturbation, f, is a deterministic function that maps a stable configuration, Ci , and
a perturbation, r 2 R, to a new stable configuration, Cj:
f Ci ; r
ð
Þ ¼ Cj
(1)
In this article, we consider a configuration stable when the average temporal derivatives of auto-
catalyst (A ) and membrane (M ) over the entire lattice satisfies the following equation:
1
2
X
X
(cid:4)
(cid:4)
(cid:1)
_m xij ; tk
(cid:3)
(cid:4)
(cid:4) < (cid:2)1
m 2 A; Mf
g
xi j
(2)
Here, the first sum is over the two molecular species, A and M, and the second sum is over all lattice
sites, xij . Also, tk is the time, and (cid:2)1 is the upper limit for what is considered stable. In this article we
used tk 2 [t, t + 1000], and (cid:2)
= 0.05. These parameters were selected to be very stringent, with (cid:2)
1
1
being orders of magnitude less than the summed concentrations of observed morphologies, and t =
1000 being much longer than it takes for the average temporal derivatives of transient dynamics to
dip below (cid:2)1.
In order to determine whether a configuration is distinct from previous configurations, a metric is
required. We utilize the structural distance from each previously observed configuration Ck 2 C.
Structural distance is found by taking the summed absolute difference between the configurationsʼ
states:
(cid:3)
(cid:1)
d Cj ; Ck
¼
X
X
(cid:1)
(cid:4)
(cid:4)
mCj
t; xij
(cid:3)
(cid:1)
t; xij
(cid:3)
(cid:4)
(cid:4)
− mCk
m 2 A; Mf
g
xij
(3)
If this sum satisfies d(Cj , Ck) < (cid:2)
= 1.0, then we consider configuration Cj equivalent to Ck.
The value (cid:2)2 = 1.0 was selected because it was far less than the distances between observed stable
configurations.
2 with (cid:2)
2
Much of the analysis in this article is applied to a reduced, weighted ontogenic network, in which
edges from the full network are combined according to equivalence classes of transition outcomes.
In a reduced ontogenic network, the weight of a directed edge between a configuration Ci and a
configuration Cj is the probability of transitioning from Ci to Cj given the available perturbations.
This is determined by the following equation:
Wi → j ¼
X
r 2R
p rð ÞyCi ;r ;Cj
(4)
Here Wi → j is the weight from Ci to Cj. It is determined by taking the sum of all transitions from i to
j that occur on applying perturbations r from R, weighted by their respective probabilities, p(r ). Our
delta function, yCi ;r ;Cj, is equal to 1 if there is a transition f(Ci, r ) = Cj, and 0 if there is no transition.
516
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. Agmon et al.
The Structure of Ontogenies in a Model Protocell
This process determines a transition matrix, W, between all configurations in C:
(cid:5)
(cid:6)
1
0
W d W v
W ¼
(5)
Here, W v is the transition matrix between all viable configurations (C1:n), and W d is the transition
matrix from those viable configurations to death (C0). The probability of transitioning from C0 to
any C1:n is 0, and probability of transitioning from C0 to itself is 1.
The robustness, R, of a configuration Ci is its diagonal entry in W v:
Ri ¼ W v
ii
(6)
The plasticity, P, of a configuration Ci is the sum over all off-diagonal entries of row i within W v:
Pi ¼
X
j≠i
W v
ij
The fragility, F, of a configuration Ci is its probability of transitioning to C0:
Fi ¼ W d
i
(7)
(8)
The viability, Vi , of configuration Ci , is defined as the average number of perturbations it takes
before reaching the death state, C0. This value is obtained by treating the transition matrix W as a
Markov process with an absorbing state corresponding to C0, and calculating the average number of
transitions from all transient states to the absorbing state:
V ¼ I − W v
ð
−1 (cid:2) 1
Þ
(9)
The vector of viabilities, V, is determined by the fundamental matrix (I − W v)
vector the same length as V whose entries are all 1.
−1 and 1 is a column
The local adaptivity of the transition from Ci to Cj is the resulting change in viability:
ACi → Cj ¼ Vj − Vi
(10)
Artificial Life Volume 22, Number 4
517
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
2
4
4
9
9
1
6
6
6
0
6
8
a
r
t
l
/
_
a
_
0
0
2
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3