The MODES Toolbox:
Measurements of Open-Ended
Dynamics in Evolving Systems
Abstract Building more open-ended evolutionary systems can
simultaneously advance our understanding of biology, artificial life,
and evolutionary computation. Um dies zu tun, Jedoch, we need a
way to determine when we are moving closer to this goal. Wir
propose a set of metrics that allow us to measure a systemʼs ability to
produce commonly-agreed-upon hallmarks of open-ended evolution:
change potential, novelty potential, complexity potential, Und
ecological potential. Our goal is to make these metrics easy to
incorporate into a system, and comparable across systems so that we
can make coherent progress as a field. Zu diesem Zweck, we provide
detailed algorithms (including C++ implementations) for these
metrics that should be easy to incorporate into existing artificial life
Systeme. Außerdem, we expect this toolbox to continue to grow as
researchers implement these metrics in new languages and as the
community reaches consensus about additional hallmarks of open-
ended evolution. Zum Beispiel, we would welcome a measurement
of a systemʼs potential to produce major transitions in individuality.
To confirm that our metrics accurately measure the hallmarks we
are interested in, we test them on two very different experimental
Systeme: NK landscapes and the Avida digital evolution platform. Wir
find that our observed results are consistent with our prior knowledge
about these systems, suggesting that our proposed metrics are
effective and should generalize to other systems.
Emily L. Dolson*
Michigan State University
BEACON Center for the Study of
Evolution in Action
Department of Computer Science
and Engineering
Program in Ecology, Evolutionary
Biology, and Behavior
dolsonem@msu.edu
Anya E. Vostinar
Grinnell College
Department of Computer Science
vostinar@grinnell.edu
Michael J. Wiser
Michigan State University
BEACON Center for the Study of
Evolution in Action
Program in Ecology, Evolutionary
Biology, and Behavior
mwiser@msu.edu
Charles Ofria
Michigan State University
BEACON Center for the Study of
Evolution in Action
Department of Computer Science
and Engineering
Program in Ecology, Evolutionary
Biology, and Behavior
ofria@msu.edu
Schlüsselwörter
Open-ended evolution, digital evolution,
phylogenetic metrics, evolutionary
Dynamik, complexity
1 Einführung
A central goal of the field of artificial life is to build evolving systems that capture the full range of
dynamics found in natural systems. Such systems should be capable of producing evolutionary out-
comes such as sophisticated navigation behaviors, novel cooperative strategies, complex ecosystems,
* Korrespondierender Autor.
© 2019 Massachusetts Institute of Technology
Artificial Life 25: 50–73 (2019) doi:10.1162/artl_a_00280
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
and major evolutionary transitions, to name but a few. Researchers seek such open-ended systems for a
number of reasons:
1. For biologists, access to systems exhibiting complex and nuanced evolutionary processes
allows rapid experimentation and facilitates developing a deep intuition for underlying
mechanisms [47].
2. For evolutionary computation researchers, insights from open-ended evolving systems will
allow researchers to break complexity barriers, expanding the classes of engineering
problems that evolutionary algorithms can solve [22, 37] and producing more general
forms of evolved intelligence.
3. For artificial life researchers, it is concerning that there may be dynamics of fundamental
importance to biology that artificial life systems do not exhibit. The existence of such
dynamics suggests that we are not building evolving systems as innovative as those
found in nature, be it due to limited memory, limited time, or simply an insufficient
understanding of the necessary components. Identifying these missing factors should
allow us to better understand life as it is and to better explore life as it could be.
While various artificial life systems have reproduced individual dynamics—such as the evolution
of complex traits [29], cooperative behaviors [20], and coexistence of diverse ecotypes [14]—these
accomplishments have been in highly controlled circumstances. The overarching goal of open-ended
evolution research is to create a system where all of these dynamics emerge more organically, as in
nature. Zusätzlich, replicating this process would provide substantial insights into our own origins,
including the evolution of human brains. In der Tat, harnessing a more open-ended set of evolutionary
dynamics could help us spur breakthroughs in the evolution of general artificial intelligence.
Open-ended evolution is a many-faceted concept. A number of patterns are considered to be hall-
marks of open-ended evolution [46], most notably the continual production of novelty [3, 28], un-
constrained increases in diversity [4], ongoing increases in complexity [26, 29], and shifts in
individuality such as those often associated with major transitions in evolution [34]. There is a growing
consensus in the field that all of these dynamics are important pieces of the open-ended evolution
puzzle [46]. Zusätzlich, we have previously suggested that there is a fifth necessary and even simpler
dynamic: continuous change in the information content of components in the population [17].
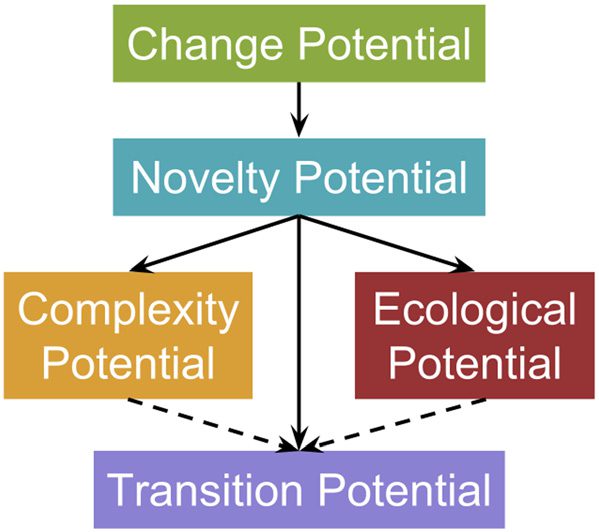
These five properties of a system fit into a hierarchy, wie in der Abbildung gezeigt 1. For novelty to exist,
there must be some degree of change in the information within a population. While this observation
is trivially true, many evolutionary algorithms suffer from premature convergence, the absence of
nontrivial change. Daher, it remains an important prerequisite to define and explicitly address.
Figur 1. Relationships between the metrics. Originally published in [17]. Solid lines with arrows indicate metrics that are
prerequisites for other metrics.
Artificial Life Volume 25, Nummer 1
51
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Ähnlich, complexity and diversity can only increase indefinitely if novel members of the population
continue to be generated. Endlich, transitions in individuality typically involve multiple organisms
coming together into a single individual, building from complex and diverse progenitors. All of these
dynamics capture different subsets of interesting behavior that evolving systems might exhibit, Und
we propose they are all necessary (but perhaps not sufficient) in a fully open-ended system.
To draw conclusions about what factors of a system promote or inhibit these dynamics, we need
methods for measuring the extent to which each dynamic is present. Wichtig, these methods
must be applicable across a wide variety of systems. Some progress has been made toward this end
with evolutionary activity statistics [7, 12], an approach to isolating and quantifying the adaptive
component of an evolving system, separating out the non-adaptive dynamics. Evolutionary activity
statistics require that the user decide on two things ahead of time: a definition for components (mean-
ingful individual pieces of a system) and a way of filtering noise out of the system (typically by
contrasting with a shadow population that evolves with selective pressures turned off ).
Thus far, components have needed to be defined for each system on a case-by-case basis. In
artificial life systems, alleles or genotypes are typically used as components, while in the fossil record,
whole species were used as components [7]. This flexibility to choose different components is valu-
able, as it allows for the study of open-ended evolution at different scales of organization. Jedoch,
it also means that care must be taken when comparing evolutionary activity statistics across systems.
Hier, we suggest a component definition that should work for any system in which genomes are
composed of elements that collectively determine fitness (see Section 3.1.2). Beachten Sie, dass, although this
component definition will not work with every system, we will suggest other approaches with
broader compatibility.
Due to the critical role of stochasticity in evolution, most evolving systems are noisy. In order to
make behavioral generalizations, we need a way to distinguish evolutionary signal from this noise.
In the original description of evolutionary activity statistics, a specific method was proposed for
dies tun: For each run of a system, there should be a corresponding shadow run in which any out-
come of selection is replaced with a random choice. Dynamics observed in the shadow run can then
be subtracted out from those in the main run. While this control can be highly informative, es ist
challenging to implement in many systems and requires researchers to be able to isolate all selective
events in the system. Zum Beispiel, when evolutionary activity statistics were applied to the fossil
record, a different filter had to be used: the assumption that any species that was successful enough
to have made it into the fossil record was probably evolutionarily successful for a substantial amount
of time. In diesem Artikel, we build on this idea to propose a filter for evolutionary activity that can be
more easily implemented across a variety of systems (see Section 3.1.1).
Evolutionary activity statistics classify evolving systems based on how open-ended they are.
Jedoch, it is relatively easy to create a system that falls into the most open-ended class while still
failing to further our goals for open-ended evolution research or to match our subjective under-
standing of what we would expect from a truly open-ended system [33]. In der Tat, there is debate
over whether open-endedness is even quantifiable [45]. Darüber hinaus, it is our opinion that most efforts
to define systems as either open-ended or not have largely been unproductive; open-endedness is
likely better thought of as a continuum than as a binary. While there is much debate over what would
constitute a fully open-ended system, there is consensus in the field that we are not particularly close
to building such a system.1 Our goal in this article is to extend evolutionary activity statistics into
easy-to-use diagnostic criteria that quantitatively measure key hallmarks of open-ended evolution.
We want researchers to be able to isolate the effects of experimental settings on these hallmarks,
keeping such results relevant across experimental platforms. In this way, we hope to spur a more
1 This line of thought originally led us to conceptualize the metrics described here in terms of possible barriers a system might encounter
that would prevent it from being open-ended [17]. Jedoch, our attempts to measure these barriers align closely with dynamics that
have since been identified as hallmarks of open-ended evolution. Letzten Endes, these perspectives are two sides of the same coin, and both
are useful frames through which to view open-endedness. For simplicity, we phrase this article in terms of hallmarks rather than
barriers.
52
Artificial Life Volume 25, Nummer 1
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
consistent and comparable march toward true open-endedness, adding new metrics to this toolbox
as the community reaches a consensus on the features that we should promote.
In the rest of this article we will introduce the MODES (Measurements of Open-ended Dynam-
ics in Evolving Systems) toolbox and explore the behavior of the metrics it contains in the context
of two evolving systems: NK landscapes [25] and the Avida digital evolution platform [36].
2 Hintergrund
2.1 Evolutionary Activity
Evolutionary activity statistics attempt to quantify the extent to which adaptive dynamics are occurring
in a population. In most applications, evolutionary activity has been measured as the length of time that
components exist in the population beyond what would be expected in the absence of selection [6, 7,
13]. This measure was chosen because it translates easily across systems and represents a universal
measure of evolutionary success. In earlier work, a measure of selective sweeps was used instead of
component existence time [5], but this metric could not be easily generalized across systems.
Multiple facets of evolutionary activity are used in the interpretation of evolutionary activity sta-
tistics: the activity of new components (Anew), der Mittelwert (or median) cumulative activity of compo-
nents in the population ( (cid:1)Acum), and the diversity of components in the population (D). Based on the
long-term behavior of these quantities, systems that exhibit qualitatively similar dynamics have been
grouped together into a class of evolutionary dynamics. Anfänglich, three possible classes were de-
scribed: no evolutionary activity, bounded evolutionary activity, and unbounded evolutionary activ-
ität. Over time, additional classes have been added to more precisely reflect the types of systems
observed. For ease of referring to these classes, Tisch 1 merges together all prior additions to
the original classification system of which we are aware.
Tisch 1. All previously described classes of evolutionary dynamics as measured with evolutionary activity statistics.
Median2
evolutionary
Aktivität ((cid:1)Acum)
null
unbounded
Change
Novelty
(Anew)
Diversity (oder
ecology) (D)
Type of
evolutionary
Complexity
dynamics Described in
?
?
null
null
bounded
bounded
None
Bedau et al. [6]
bounded
bounded
Uncreative
Skusa and
Bedau [42]
bounded
positive
positive
bounded
bounded
Bounded
Bedau et al. [6]
bounded
positive
positive
unbounded
bounded
Unbounded Bedau et al. [6]
unbounded
positive
positive
bounded
unbounded
positive
positive
unbounded
?
?
Unbounded Channon [12]
Unbounded Channon [12]
Klasse
1
2
3
4A
4B
4C
Notes. For each class, we show the response of all quantities measured for evolutionary activity statistics and in our
proposed metrics (novelty and diversity should behave equivalently between the two systems). Note that we expect
bounded evolutionary activity to imply bounded complexity, as any scenario in which complexity is growing without
bound should imply that evolutionary activity is too. Question marks indicate that the value of a given metric is not
specified in the description for a class of evolutionary activities. Higher-numbered classes are generally believed to fall
further along the continuum of open-endedness than lower-numbered classes. In principle, classes 4b and 4c could each
be further split into subclasses based on whether complexity is bounded or unbounded. Likewise, classes 1 Und 2 could
be further subdivided based on whether change is 0 or positive. In the absence of further data on the behavior of real-
world systems, it is unclear how helpful such increased precision would be.
Artificial Life Volume 25, Nummer 1
53
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
According to the original formulation of evolutionary activity statistics, in order for a system to
be categorized among the most open-ended systems (originally class 3, now class 4), it must exhibit
unbounded growth in summed evolutionary activity across all components in the population [6] (sehen
Tisch 1). Technically, this growth could happen either because of an unbounded increase in the
number of components (Diversität) or because of an unbounded increase in the average evolutionary
activity of components in the population. The latter case was originally thought not to occur [7];
Jedoch, when such a case was observed, Channon suggested that class 3 open-ended dynamics
should be broken up into three subcategories. These subcategories depend on whether the growth
in evolutionary activity was driven by diversity, per-component evolutionary activity, or a combina-
tion of both [12] (siehe Tabelle 1).
In parallel, Skusa and Bedau refined the classification in a different way [42], inserting a new second
class in which evolutionary activity was unbounded but no novel components came into being (sehen
Tisch 1). Such a situation would describe purely ecological dynamics. This observation may seem sur-
prising at first—shouldnʼt unbounded evolutionary activity involve adaptation? Jedoch, when evo-
lutionary activity is measured as the existence time of a component, evolutionary activity statistics draw
no distinction between stabilizing selection and selection favoring changes to the status quo [13]. Daher,
pressure for multiple eco-types to continue existing in their current form (d.h., ecology) will show up as
evolutionary activity above and beyond what is observed in the shadow run.
Tatsächlich, the presence of a single component under stabilizing selection will trivially cause the mean
evolutionary activity to increase indefinitely; such a component will sit in the population, increasing
the populationʼs activity counter despite being quickly lost from the shadow population. This be-
havior casts doubt on how we should interpret class 4b, sowie. To remedy this concern, Channon
suggested that we should look for unbounded growth in median (rather than mean) per-component
evolutionary activity [13]. This adjustment is a drastic improvement, but it still does not eliminate the
possibility that systems exhibiting class 4b evolutionary dynamics are not doing quite what we would
expect. If at least 51% of the components in the population are under stabilizing selection—as
would be expected in an ecological system—the rest of the population could still be behaving like
a class 3 System. While such a system would still be interesting for ecological studies, our under-
standing of it would not be well served by conflating it with systems that are exhibiting open-ended
adaptive evolution.
How can we know whether evolutionary activity is driven by stabilizing selection rather than
more interesting dynamics? If every component is experiencing directional (as opposed to stabiliz-
ing) Auswahl, the change metric we propose here should theoretically be comparable to the number
of components.2 In contrast, if most of the population is under stabilizing selection, the change
metric should be very low.
Letzten Endes, our change metric (described in the next section) is in keeping with the original evo-
lutionary activity measure, which sought to quantify the acquisition of new genetic information [5].
Aus diesem Grund, in our suite of metrics, we replace the concept of evolutionary activity with change.
We believe that this framing will be easier to measure and interpret with little loss of information
(although of course we encourage the use of other measures of evolutionary activity where appro-
priate). Our change metric does have the downside that it is not possible to classify it usefully as
bounded or unbounded. Because we seek only to compare systems and identify progress toward
higher levels of open-endedness, this limitation should not be a problem for us.
2.2 Prior Work Using MODES
Soros [43] used a preliminary version of our framework [17] to study open-ended evolution in the
artificial life system Chromaria. Agents in Chromaria are colorful circles controlled by compositional
2 The original formulation of evolutionary activity statistics used the mean rather than the median, but Channon [13] makes a compelling
argument for using the median instead. Using median rather than mean does not change any of the intuitions for how we expect this metric
to behave and reduces. Using median rather than mean the risk of non-intuitive behavior due to outliers. Jedoch, the change metric may
often be lower than the number of components, because not every component will change during every measurement period.
54
Artificial Life Volume 25, Nummer 1
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
pattern-producing networks (CPPNs) that must find a region of the world that matches their color
in order to reproduce. These agents can be classified into species based on their patterns of color-
ation, and change and novelty can be assessed by measuring the emergence of new species. Eco-
logical interactions in Chromaria occur as a result of individuals planting themselves in the world,
which alters the color environment that subsequent agents must navigate. Daher, Soros was able to
measure the ecology of Chromaria through a series of visual snapshots of the world, as well as by
measuring the number of species that occur over the course of a run. zuletzt, she measured com-
plexity in terms of the number of elements in the CPPNs controlling the agents.
Using these MODES-inspired metrics, Soros [43] investigated three hypothesized necessary con-
ditions for open-ended evolution: (1) some sort of minimal criterion [44] must be met before re-
production, (2) when new types of individuals evolve, it should create new ways to satisfy the
minimal criterion, Und (3) individuals should be responsible for making decisions about how they
interact with the world. By measuring hallmarks of open-ended evolution under various controls that
removed these conditions, Soros [43] found strong evidence that all of the conditions are indeed
necessary for change and novelty (let alone ecology and complexity) in Chromaria. These experi-
ments perfectly illustrate the kind of hypothesis-driven research that we hope a further formalization
of our metrics will enable. Zusätzlich, they serve as an example of the range of approaches that can
be taken to translate these concepts between systems.
2.3 Applying MODES to Biology
Since many hypotheses about open-ended evolution involve comparisons with the biosphere, es ist
critical that MODES metrics are applicable not only to digital systems, but are also relevant to ex-
perimental biological systems. To confirm that they are, we consider how we would apply them to a
well-studied wet lab experiment. The long-term evolution experiment (LTEE) [30] is an exemplar of
experimental evolution, consisting of 12 populations of the bacteria E. coli, which have been evolving
independently for more than 60,000 generations [21]. As detailed in [46], the LTEE exhibits many
hallmarks of open-ended evolution, including the criteria we propose here. Because fitness within
the LTEE is best described by an unbounded power law function [31, 53], the system demonstrates
change as defined by the change metric: Populations continue to change in nontrivial ways over
Zeit. Weiter, studies of individual populations within the LTEE have shown numerous examples
of the generation of novelty, including exploration of new areas of the fitness landscape [47], repeat-
ed selective sweeps [32], and new diversity arising after such sweeps [9]. Toward the ecology metric,
several populations within the LTEE demonstrate frequency-dependent fitness dynamics [27, 32,
39, 40], which are necessarily cases of ecological interactions. Included in these cases of frequency
dependence is a special case [9, 10, 48] driven by cross-feeding and specialization on different re-
sources [49]. Because each population in the LTEE descends from a single ancestor present at the
start of the experiment, all ecological complexity in any population must have arisen during the
course of the experiment, and thus demonstrates ecology as defined by the ecological metric.
The complexity metric is inherently harder to quantify in a biological system than in a computational
eins, but recent large-scale genome sequencing from the LTEE [47] offers the promise of being able
to measure complexity at the genome level over the course of the experiment. Because our metrics
can theoretically be applied to a well-studied and open-ended biological system, they can be used to
compare dynamics in a broad range of systems and enable the field of artificial life to move forward
in quantifiable steps to open-ended evolution.
3 Metrics
Like the original evolutionary activity statistics [6], the metrics we present here can operate on a wide
range of units. Oft, these units will be genotypes or phenotypes, but in other cases they may be
higher-level taxonomic groups, such as species. To highlight this agnosticism, Bedau et al. referred to
these units as components. We will use the same terminology where applicable.
Artificial Life Volume 25, Nummer 1
55
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
3.1 Overarching Techniques
We use two broad techniques to ensure that our metrics can focus on the most relevant and mean-
ingful information in an evolving population. Zusätzlich, we describe a technique for determining
whether a metric is bounded or unbounded.
3.1.1 Filtering Out Noise
In any evolving population, mutations continually produce new maladapted components that are
then purged from the population via natural selection. All of the MODES metrics assume that some
form of filtering has been applied beforehand, to prevent maladapted components from over-
whelming the hallmarks that we are measuring. Hier, we describe a persistence filter that we use
in our experiments. Jedoch, shadow runs [6] are also a viable filter option, and there are likely
further useful filtering techniques that have not yet been invented.
To focus only on the adaptive products of evolution, we limit our analysis to those components
whose descendants persist for a substantial number of generations. We refer to this technique as a
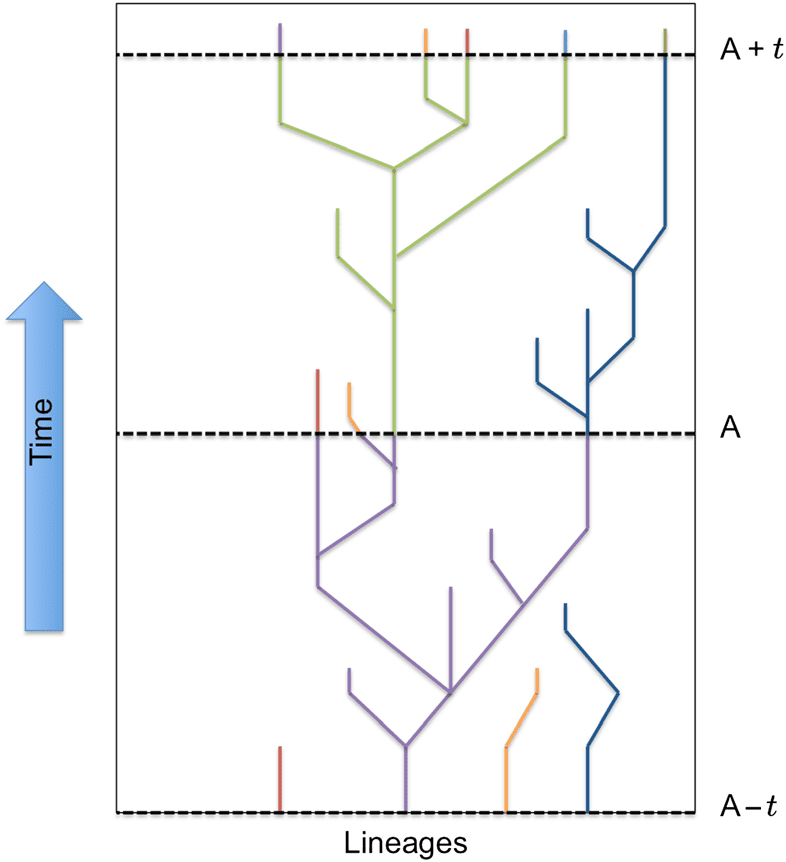
persistence filter. We mark each organism with a lineage ID at a given timepoint A, as demonstrated in
Figur 2 (where color indicates lineage ID). The lineage IDs are passed on to offspring for the
next t generations, where t is a predetermined number of generations indicating the length of our
filtering process (hereafter referred to as the filter length). At timepoint A + T, we determine
which components from the population at A have descendants at A + T. At this point, those
components are considered persistent ; in the example in Figure 2 the individuals at the bases of
the green and blue lineages are considered persistent at timepoint A + T. These are the individuals
that would be evaluated in the MODES metrics. This filtering leads to a delay in counting a com-
ponent in a metric until t generations later, but enables us to avoid an apparent increase in metrics
due to drift via mutation. Zum Beispiel, the red and orange components from timepoint A would
not be considered in our metrics, because their lineages do not persist to timepoint A + T.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 2. An illustrative example of how we filter components for persistent lineages. At timepoint A, the purple lineage
has proven to be persistent and therefore the original component from A − t will be considered meaningful. Ähnlich, Die
green and blue lineages persist to timepoint A + T, and so the original green and blue components will be considered
meaningful as they existed at timepoint A.
56
Artificial Life Volume 25, Nummer 1
E. L. Dolson et al.
The MODES Toolbox
How large should t be? The correct value depends on our goals. If we are interested in evolution
on a shorter time scale, we may only want to filter out deleterious mutants, which will likely survive
only a few generations. In this case, a relatively small value of t should suffice. In der Tat, prior open-
ended evolution research has used what is effectively a persistence filter with t = 1 as a supplemental
filtering technique [13]. If we are interested in a broader time scale, Jedoch, we may want to filter
out neutral mutants too and measure only adaptive evolution. In this case, coalescence theory can
inform our choice of t. In an asexual population without diversity-preserving forces, the population
will periodically coalesce, das ist, neutral clades will die out, resulting in a new most recent common
ancestor of the current population. If we take a snapshot of such a population at any given point in
time and let the population continue evolving for long enough, a single individual from the snapshot
will eventually be a common ancestor of the entire extant population. We define the coalescence
time here as the amount of time that this process takes, although it should be noted that coalescence
time is more commonly thought of retrospectively.
If we want to filter out all neutral mutants that do not go on to play a critical role in evolution, Es
would be ideal to choose a value for t that falls above the expected distribution for coalescence
mal. If we did so, then we could be confident that any individuals that made it past the filter
represented a meaningful part of the evolutionary history of the population. If only a single individ-
ual makes it through the filter, that individual must be along the line of descent for the entire pop-
ulation. Multiple individuals making it through the filter would be evidence of ecological dynamics
promoting their coexistence.
The median coalescence time for a well-mixed asexual population of N haploid individuals under
no selective pressure is 2N generations [18]. Bedauerlicherweise, the expected distribution of coalescence
times is exponential, meaning that we would have to choose a potentially impractically large value for
t if we want to guarantee that it is rare to get through the filter by chance. Jedoch, the presence of
selective pressure dramatically reduces expected coalescence time. Since most systems in which peo-
ple study open-ended evolution do have selective pressure of some form, in practice relatively low
values of t yield still effective filters.
For a meaningful comparison across populations, we must filter them using consistent values of
T. We always expect filters with lower t values to let more individuals through, and it is challenging
to separate this effect from changes in the underlying dynamics of the system. Zusätzlich, t must
be measured in units of generations to ensure consistency in the amount of filtering that occurs.
Researchers studying systems that use a different time scale need only calculate the average generations
within the population to measure t.
In evaluating results, one should strive to use consistent values of t relative to population size and
be aware that, all else being equal, increasing selective pressure will reduce the number of taxa that
get through the filter.
This effect brings up an important distinction between this filtering technique and the shadow
run traditionally used with evolutionary activity statistics. Whereas shadow runs filter out the effect
of neutral processes, the persistence filter does not do so entirely. We view this reduced filtering
primarily as an advantage—drift can be an important part of the evolutionary process—but there
may also be situations where it is undesirable. Our metrics are unable to distinguish between class 1
Und 2 dynamics or between class 3 and 4b dynamics (siehe Tabelle 1), although they are able to distin-
guish between useful subcategories within those classes (as discussed in Section 3.2.1 below).
3.1.2 Identifying Meaningful Sites in Genomes
Because genomes are such a common unit of taxonomic organization to use as components in open-
ended evolution research, we present a technique for filtering noise out of genomes. Although this
step is not necessary for using the MODES metrics, it will improve the signal-to-noise ratio in a
variety of common use cases and simplify the calculation of complexity. We recommend its use
where applicable.
While a genome may have descendants in t generations, if t is small this persistent genome may
not be phenotypically different from another persistent genome in the population. To ensure that
Artificial Life Volume 25, Nummer 1
57
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
we are not separately counting genomes that differ only in noncoding regions, we use an additional
filter in which we determine which sites in the genome contain information about the environment.
In calculating all of the following metrics, we first reduce the genome to its meaningful sites.
This approach can easily be extended to any system in which the genome is made up of a set of
elements that collectively determine fitness. Whether or not a genomic position is meaningful can be
approximated by measuring the overall fitness3 effect of either removing it or changing it to a null
alternative that is known to not contribute information. If removing the site resulted in a lower
overall fitness, that implies that the site contained information (d.h., was meaningful). Umgekehrt,
if removing the site increased or had no effect on fitness, we can conclude that it is most likely
not meaningful. We can then define a component as the sequence of meaningful sites in a genome
rather than the whole genome. By doing so, we avoid treating functionally identical components as
distinct.
When should we remove sites, and when should we replace them with a null alternative? A null
alternative should be used in cases where changing the structure of the genome changes the meaning
of other sites. Zum Beispiel, in Avida it is critical that we replace instructions with nulls rather than
completely removing them, because information can be encoded in the number of instructions be-
tween two other instructions. A more accurate technique would be to examine the fitness effect of
substituting all possible alternative elements and calculate the potential entropy at that site. Wann
null substitutions are not possible, this technique is an effective method.
A caveat to this technique is that, in practice, there are interactions between sites. By only knock-
ing out a single site at a time, we miss these interactions. How to best remedy this situation is an
open question, as measuring all possible combined effects is computationally intractable. In vielen
Fälle, measuring pairwise interactions is possible and may be worthwhile. This issue will reduce the
efficacy of this approach at reducing noise, because some functionally equivalent genomes will be
classified as different. When used for calculating the complexity metric, it may cause fragile genomes
to appear more complex than robust ones.
Beachten Sie, dass, although identifying informative sites can be computationally intensive, we would
need to do so anyway to calculate the complexity metric. Daher, this additional layer of filtering is
effectively free.
3.1.3 Determining Boundedness
In the design of these metrics, we have primarily focused on determining the effect that small
changes to a system have on the extent to which that system exhibits hallmarks. Jedoch, Sie
can also be used to classify systems in much the same way that evolutionary activity statistics do.
As described in Table 1, this classification requires determining whether diversity is increasing with-
out bound. Zusätzlich, it would be informative to determine whether complexity is growing without
bound. In früheren Arbeiten, the definition of boundedness in this context has been stated in terms of
the limit of the supremum of diversity as time goes to infinity [7]. While this is an excellent theo-
retical definition, taking limits of empirical data as time goes to infinity is generally not practical.
Previous applications of evolutionary activity statistics seem to determine boundedness based on
whether or not a line on a graph appears to be plateauing. This technique has the potential to be
misleading [52].
Stattdessen, we advocate the use of statistics to determine what mathematical model best fits the
observed data. We can then classify the pattern as bounded or unbounded based on the limit of
the best-fitting mathematical model. Such an approach has previously been used to demonstrate that
fitness is following an unbounded growth pattern in a long-term wet lab evolution experiment with
E. coli [31, 53].
3 As defined in the system being studied. If the system does not have a fitness definition, average lifetime reproductive output can be used.
58
Artificial Life Volume 25, Nummer 1
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
3.2 MODES Metrics
The MODES Toolbox
3.2.1 Change Metric
Our first metric focuses on whether the genetic makeup of the population is changing in a nontrivial
Weg. This metric will be above zero during adaptive evolution, including situations where the pop-
ulation is returning to previous states, perhaps due to environmental cycling. In the work presented
Hier, we use persistence filter (explained above) to ensure that we mark a component as new only if
its lineage persists for a full t generations. Jedoch, a different filtering technique (z.B., a shadow
run) could be used instead. For this comparison, we first find the components from persistent lin-
eages from generation A by determining which components have descendants in generation A + T.
In the example shown in Figure 2, the components at the roots of the green and blue lineages would
count as persistent. We then compare these components with those found to have been from per-
sistent lineages in the previous time point (z.B., we would compare the roots of the blue and green
lineages with the root of the purple lineage in Figure 2). In this way, we create a sliding window to
observe change in the population. Note that the example in the figure assumes the resolution at
which data are collected (d.h., the number of generations between timepoints) is equal to the value
of t, but this does not need to be the case. It may be desirable to have a very long length t but still
gather data frequently. In such a case, each timepoint is individually filtered by looking ahead t gen-
erations, but change is calculated by comparing the set of persistent taxa in the current time point
with the set of persistent taxa in the previous timepoint.
For those who find it helpful, the change metric can be formalized with the following equation:
change ¼
(cid:2)
X
c2F
0
1
if c 2 F
0
ansonsten
(1)
0
where F
components from the current timepoint that passed the filter, and c is a component in F.
is the set of components from the previous timepoint that passed the filter, F is the set of
While there is no change metric in the original conception of evolutionary activity statistics, Wir
expect that it will provide similar information to cumulative evolutionary activity [6]. Change must
be positive in systems exhibiting class 3 or higher evolutionary dynamics, as these systems must all
exhibit positive novelty. Klasse 1 systems may or may not exhibit change; an evolving system that
stagnates (z.B., many genetic algorithms) would have zero change, whereas a completely neutral sys-
tem where all change was caused by drift would sometimes have a nonzero amount of change (von-
pending on the value of t ). Klasse 2 systems would have nonzero change if they were cycling between
fixed states, but not if they were purely the result of stabilizing selection.
3.2.2 Novelty Metric
The novelty metric measures how many components have evolved in the population that have never
been seen previously in the experiment. For this metric we again filter out components that do not
have descendants in t generations, enabling us to focus on meaningful novelty. As with change, Wir
could have used a different filtering technique instead. To measure novelty, we simply count how
many components from persistent lineages have never been in a previous timepointʼs persistent
component pool. It is possible with this metric for a component to evolve but not persist, Und
therefore not be recorded in the permanent history, but then evolve and persist at a later point
and be counted as novel. Once a component has been counted as novel, Jedoch, it is part of
the permanent history and will never be counted in the novelty metric again. Daher, while a compo-
nent could be delayed in being counted as novel, or not counted if it never persists, it will not be
counted twice. Our novelty metric is functionally equivalent to Anew in evolutionary activity
Statistiken [6].
Artificial Life Volume 25, Nummer 1
59
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
The novelty metric can be formalized with the following equation:
novelty ¼
(cid:2)
X
c2F
0
1
if c 2 S
ansonsten
(2)
where S is the set of all components that have ever passed the filter, F is the set of components from
the current timepoint that passed the filter, and c is a component in F.
3.2.3 Complexity Metric
The complexity metric measures the maximum complexity of any component found in the entire
Bevölkerung. There is still debate over how to best measure complexity, and not all approaches are
usable for all component types. Hier, we recommend an information-theoretic approach, welche
works well with the components described in Section 3.1.2 über. Once the meaningful sites have
been identified, they can simply be counted to get a measurement of complexity; the value of the
complexity metric at a given timepoint is the highest observed count of informative sites across all
components in the population that make it through the filter. This metric is somewhat crude and can
be improved by using more advanced information-theoretic techniques where all possible mutations
are considered at each site. Im Idealfall, epistatic interactions between sites would also be considered by
measuring the fitness effects of knocking out combinations of genes. Bedauerlicherweise, doing so is
often not possible in practice.
There is no equivalent to the complexity metric in evolutionary activity statistics. Jedoch, als
many believe growth in complexity to be an important hallmark of open-ended evolution [46], Wir
feel it is a critical addition. Insbesondere, it would be interesting to find nontrivial systems that exhibit
unbounded growth in complexity. We suspect that such growth could only occur in systems exhi-
biting class 4b or 4c evolutionary dynamics, as bounded evolutionary activity should imply bounded
complexity (although the converse is not true).
3.2.4 Ecological Metric
The ecological metric measures the amount of information in the population as a whole. While com-
ponents may not individually contain increasing amounts of information (as measured by the com-
plexity metric), they could still be increasingly diverse and therefore contain increased information
collectively in the population. Im Idealfall, we would measure this collective information by tracking the
origin of each piece of information across all components in the population and counting the unique
pieces of information. Bedauerlicherweise, this approach is not computationally practical for many sys-
Systeme. As a proxy, we can look at the diversity of post-filter genotypes (reduced to informative sites,
where possible). Complex ecologies in which multiple subsets of the population are using different
information about the environment to survive are likely to be characterized by a relatively balanced
distribution of individuals across the various successful phenotypes. Daher, we use Shannon entropy
[41], a popular metric of diversity that also measures evenness, to measure the diversity of the per-
sistent genotypes and calculate the ecological metric. This metric is equivalent to D in evolutionary
activity statistics [6].
The equation for Shannon entropy is
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
ecology ¼ −
X
c2F
P cð Þ log2 P cð Þ
D
Þ
(3)
where c is a component in F, the set of components at the current time step that passed the filter.
P(C) is the proportion of F occupied by component c. This value gets higher when the number of
60
Artificial Life Volume 25, Nummer 1
E. L. Dolson et al.
The MODES Toolbox
components in F increases and when the components occupy more equal proportions of the
Bevölkerung.
4 Experimental Systems
We used two radically different experimental systems in order to ensure both that these metrics can
be broadly applied and that they produce meaningfully consistent results. For both systems, we used
genomes as components.
4.1 NK Landscape
To begin a systematic examination of MODES metrics, we used a simple NK model [25]. An NK
model uses two parameters, N and K, to randomly generate a fitness landscape. N specifies the
number of sites in the genome, each of which is a 0 or a 1. The fitness landscape specifies the effect
of a given value at a given site on the fitness of the bit-string organism. This fitness effect depends
on the values at the K subsequent adjacent sites. Daher, K tunes the ruggedness of the landscape; niedrig
values of K produce smooth landscapes with few peaks, whereas high values produce landscapes
with many peaks. We chose to use NK models because they are a well-understood system for study-
ing general questions about evolutionary dynamics.
4.1.1 Experimental Treatments
Our basic treatment used N = 20 (d.h., 20 bits in an individual) and K = 3 (the fitness contribution
of each bit was influenced by three other bits). We used a population size of 200 and a per-site
mutation rate of 0.05, with tournament selection and a tournament size of 2. In addition to this
baseline treatment, we tested the effects of eight experimental treatments: High K tests the effect
of a highly rugged landscape (K = 10) where fitness is effectively randomized whenever a mutation
occurs. High N tests the effect of longer bit-string genomes (N = 100; mutation rate was adjusted to
0.01 to keep the whole-genome mutation rate consistent with the base condition), allowing for a
higher potential complexity. Low Mutation and High Mutation test the effects of more extreme mu-
tation rates (0.005 Und 0.1 jeweils); we expect the mutation rate to be important for finding new
areas of the fitness landscape and thus our novelty metric. Small Pop and Large Pop vary the popu-
lation size (Zu 20 Und 1000 jeweils); in small populations we expect more drift in the population,
allowing more change, while in a large population we expect stronger selection and consequently that
a higher percentage of changes along the line of descent are beneficial. Endlich, we included two
special treatments: In Oscillating Environment, the fitness function was toggled between two prede-
fined NK landscapes every 500 generations, allowing us to see the effect of changing selective pres-
sures where the population was not able to stay on a single peak. In Fitness Sharing organisms that
were too similar to each other detracted from each otherʼs fitness, creating a pressure to explore
multiple portions of the landscape at the same time and, ideally, maintain a high diversity. Wir verwendeten
the fitness sharing equations described by Goldberg et al. [19], with a sharing threshold of 50 und ein
a of 1. For all experiments, we used a filter length (T ) equal to the population size.
4.2 Avida
The Avida digital evolution platform is a popular artificial life system for studying evolutionary
Dynamik [36]. Avida consists of a population of self-replicating digital organisms with circular ge-
nomes composed of assembly-code-like instructions. Over the course of their lifetimes, organisms
in Avida execute the code in their genome. The population is initially seeded with a single hand-
coded organism that inefficiently copies itself and does nothing else. Each organism lives in its own
cell in a toroidal grid. When an organism copies itself, its offspring is placed in a different cell, über-
writing any previous occupant of that cell. Daher, there is pressure for individuals to reproduce
quickly, before others copy over them. During the replication process, mutations are probabilistically
introduced. Daher, the system contains inheritance, Variation, und Auswahl, causing evolution by
Artificial Life Volume 25, Nummer 1
61
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
natural selection to occur. Optionally, tasks can be added to the environment in Avida. Diese sind
computational problems that organisms can perform for a reward in the form of additional CPU
cycles that allow organisms to execute their code faster.
4.2.1 Experimental Treatments
To understand how MODES metrics will behave in a full-featured artificial life system, we tested
them in Avida under a variety of scenarios. For all experiments, we used a well-mixed population in
order to speed up the expected rate of coalescence. All other parameters in Avida were left at their
default values. We ran experiments in two different environments. The empty environment has no
tasks—all evolution is focused entirely on optimizing the efficiency with which organisms can self-
replicate. The Logic 9 Umfeld, which has been used in many prior experiments (z.B., [29]),
contains tasks for all nontrivial one- and two-input Boolean logic functions.
Artificial life systems necessarily have constraints on the amount of time and memory we can give
ihnen. It is important in open-ended evolution research to determine whether these constraints are
imposing practical limitations on the dynamics the system exhibits [54]. To do so, we ran experi-
ments in each environment at three different population sizes: 500, 1000, Und 2000. In each con-
dition, wir rannten 30 replicate runs of Avida.
Zusätzlich, to understand how sensitive our metrics are to the choice of the filter length (T ), Wir
conducted some additional experiments in the empty environment in which we varied t. Allgemein,
since our Avida runs are so long, we aim to filter neutral mutants out with our persistence filter,
rather than just deleterious mutants. At each of the three population sizes, we tried t values of 500,
1000, Und 2000. To ensure that we always have data from a filter length larger than the population
Größe, we also included a condition with a population size of 2000 and a t of 4000.
4.3 Implementation Details
If not implemented with care, these metrics can become computationally intractable in the context
of the long experiments that open-ended evolution research often entails. Insbesondere, RAM
requirements can become prohibitive. We provide a few high-level approaches to mitigating these
difficulties.
The largest memory cost is imposed by the novelty metricʼs requirement that we keep track of
every taxon that has ever passed the persistence filter. Because we only need to know when we
encounter a repeat taxon (rather than storing an archive of all taxa we have encountered), we can
dramatically reduce this cost by using a Bloom filter [8]. Although this approach does introduce a
(tunable) risk of false negatives (d.h., misclassifying a novel taxon as not novel), this risk only makes
the metrics more conservative.
The next largest cost is imposed by needing to keep track of the phylogeny over time. Zusätzlich
to standard phylogenetic pruning techniques (such as removing all taxa that do not have extant de-
scendants), we can safely remove all taxa that died before the current generation minus t. 4 Das
optimization prevents the tree from growing without bound over the course of the experiment.
zuletzt, it is helpful to be aware that increasing t will reduce computational demands by increasing
the percentage of taxa that will be filtered out. With these optimizations, MODES metrics can be
implemented with minimal overhead.
4.4 Statistical Methods
We assessed significance using Kruskal-Wallis tests followed by post hoc Wilcox tests comparing
each treatment with the baseline condition. To correct for multiple comparisons, we used a
4 An important caveat is that this approach will only work with a strictly increasing unit of time. In many systems (including Avida ) Die
average generation is not guaranteed to consistently increase. To support such systems, our implementation of the metrics allows for
time to be tracked using two units at once, one corresponding to generation, and one that is guaranteed to be strictly increasing.
62
Artificial Life Volume 25, Nummer 1
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Bonferroni correction. Effect size measurements determine whether a treatment has a meaningful
impact on a variable. Because standard deviations varied wildly among conditions, we used Glassʼs D
as our measure of effect size [24]. As a general guideline for interpreting Glassʼs D, a value of 0.2 Ist
generally thought to be low, while a value of 0.8 is generally thought to be high (although this guide-
line is context dependent). All analyses and statistics for this article were conducted using the R
statistical computing language (Ausführung 3.4.4) [38] and the ggplot2 plotting library [50]. Distributions
of final metric values are visualized using raincloud plots [2]. Statistical code and supplemental
statistical information is freely available [15].
4.5 Code Availability
A C++ implementation of the MODES toolbox is available as part of the Empirical library [35]. Der
library is header only, and designed to be as easy to integrate into existing systems as possible. Code
reliability is ensured with a suite of unit tests automatically run when code is added. As a proof of
this concept, the Avida experiments presented in this article were carried out using a lightly modified
version of Avida that incorporated this implementation of our metrics [11]. All code used in this
article is open source and freely available [11, 15, 35].
5 Results and Discussion
To ensure that these metrics are capturing the dynamics that we want them to, we tested them on a
range of variants of our basic NK model and a range of conditions in Avida. The preliminary results
for each metric are presented here.
5.1 Change Metric
In the baseline and low mutation-rate conditions for the NK landscape, change is close to 0 (sehen
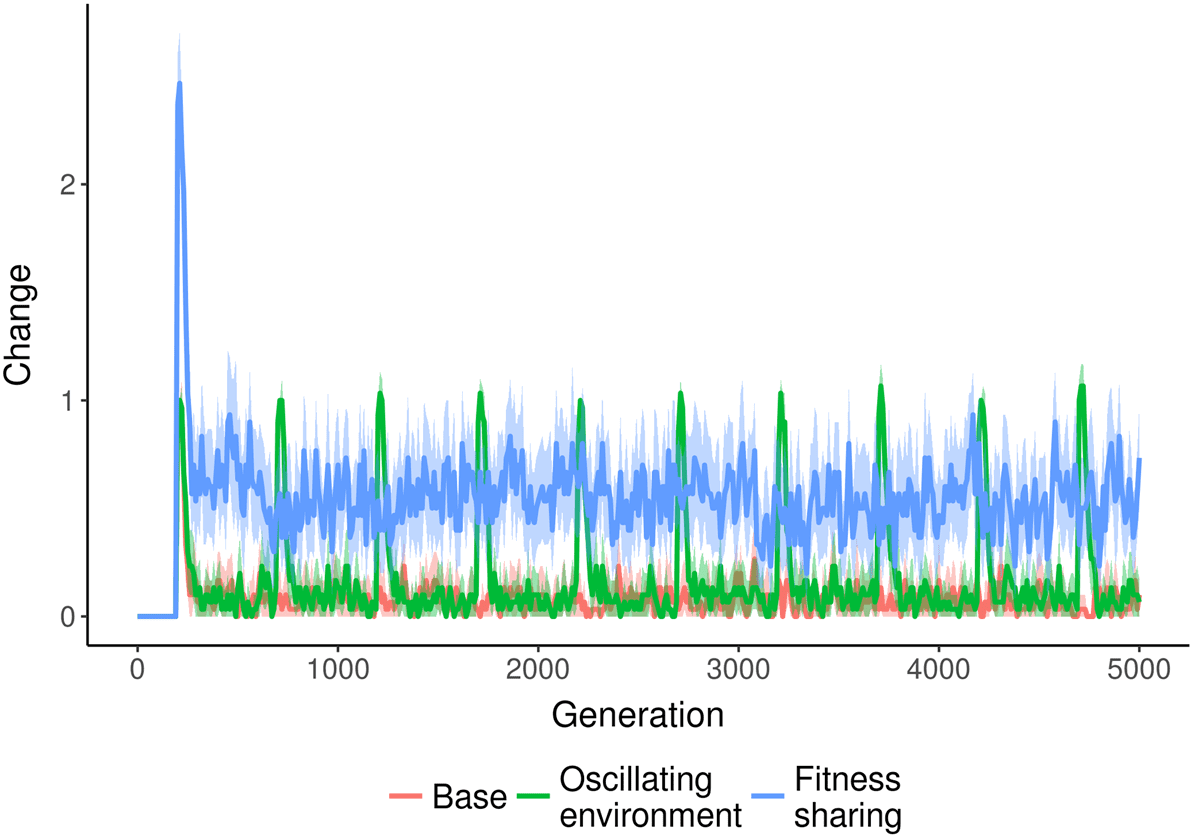
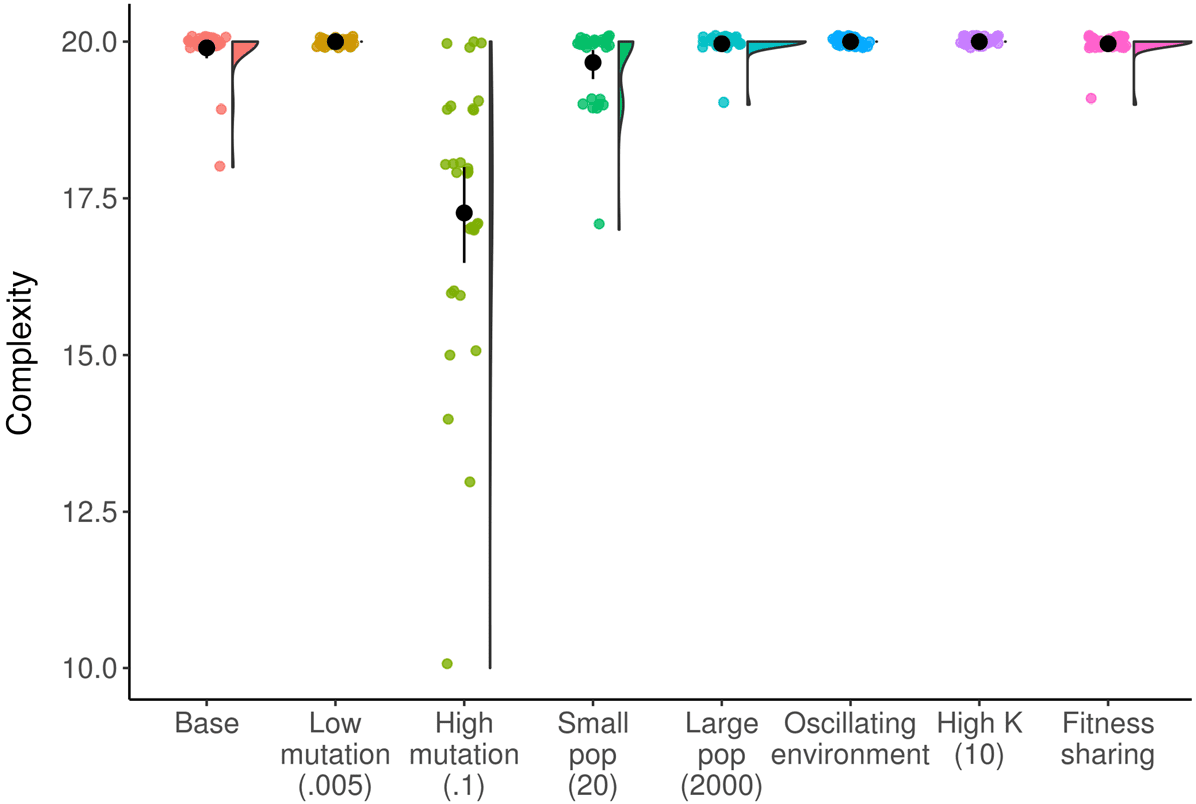
Figuren 3 Und 4), indicating that our metrics are capable of detecting the stagnation typical of many
genetic algorithms. As shown in Figure 3, several environmental changes increase the amount of
Figur 3. Amount of change over time in varying NK landscape environments. Fitness sharing increases the amount of
change in the population over time. Umgekehrt, a routinely changing environment leads to spikes in change that quickly
drop as the population converges again. Shaded region represents a bootstrapped 95% confidence interval around the
mean.
Artificial Life Volume 25, Nummer 1
63
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
A
R
T
l
/
_
A
_
0
0
2
8
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
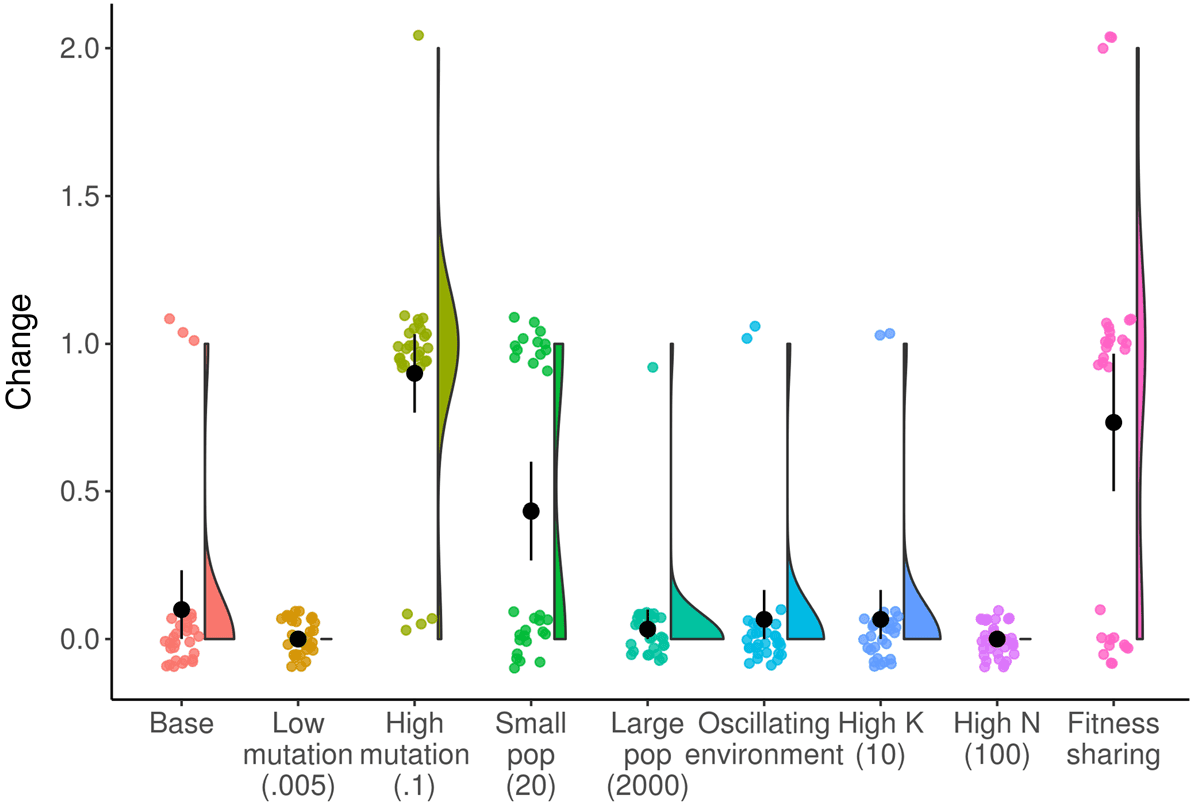
Figur 4. Raincloud plot of change at final generation across NK landscape treatments. Environmental conditions that
increase the amount of change at the final timepoint include: increasing the mutation rate, decreasing the population size,
and implementing fitness sharing. Black circle and line indicate mean and bootstrapped 95% confidence interval.
meaningful change found in the NK landscape populations over time. When negative frequency
dependence is introduced via fitness sharing, the amount of change increases and remains higher
than the baseline over time. Umgekehrt, when the environment changes frequently, there is an initial
spike of increased change that quickly drops back down to the baseline value.
The majority of environmental conditions we tested in the NK landscape system produced dy-
namics over time qualitatively similar to the baseline treatment. In Abbildung 4 we show the amount of
meaningful change in populations at the final timepoint in more environmental conditions. A higher
mutation rate leads to increased meaningful change ( P < 0.0001, Wilcoxon test; Glassʼs D = 0.80),
because mutations are necessary to create any meaningful change in this system. A smaller popula-
tion size produces more meaningful change ( p = 0.004, Wilcoxon test; Glassʼs D = 0.33), because a
small population cannot hold as many different genomes at one time and therefore there are more
genomes that can arise that are different than what is in the previous population. Finally, fitness
sharing produces increased meaningful change ( p < 0.0001, Wilcoxon test; Glassʼs D = 0.63), be-
cause it creates a constant pressure for the population to adapt away from whatever is the current
dominant genotype.
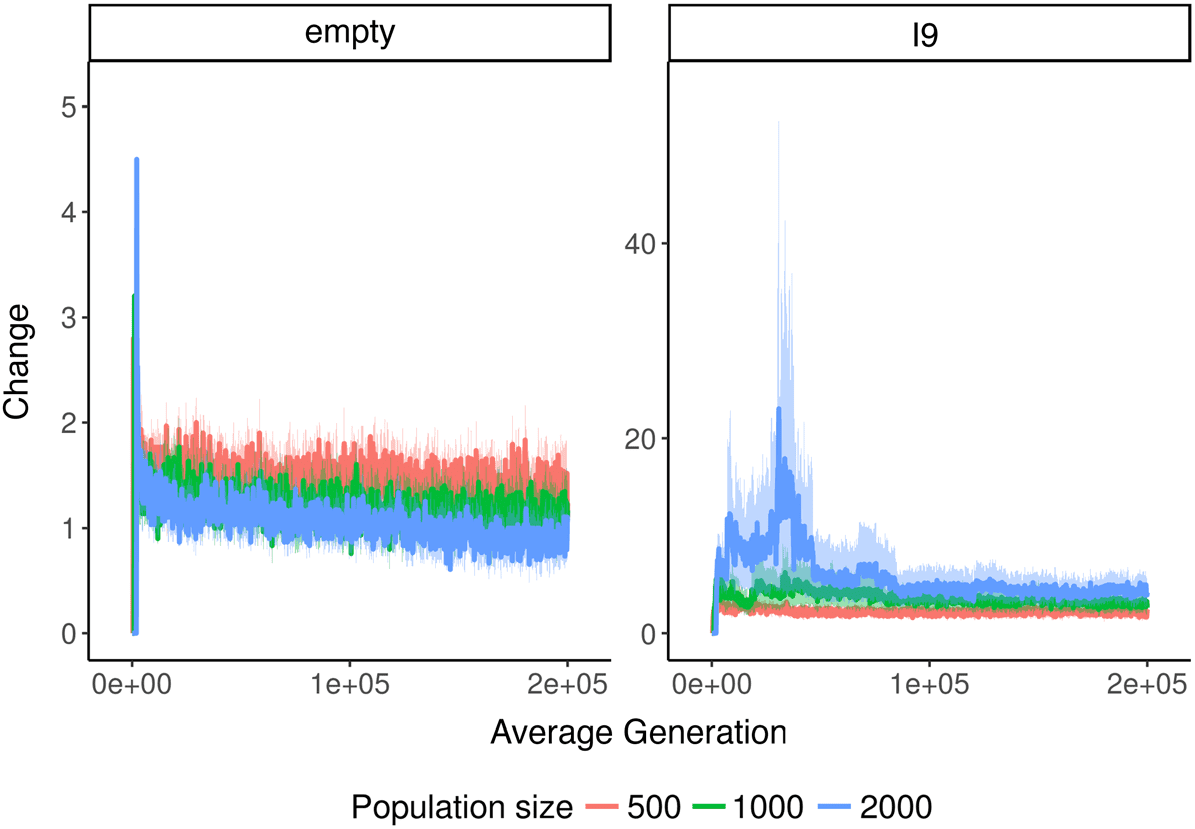
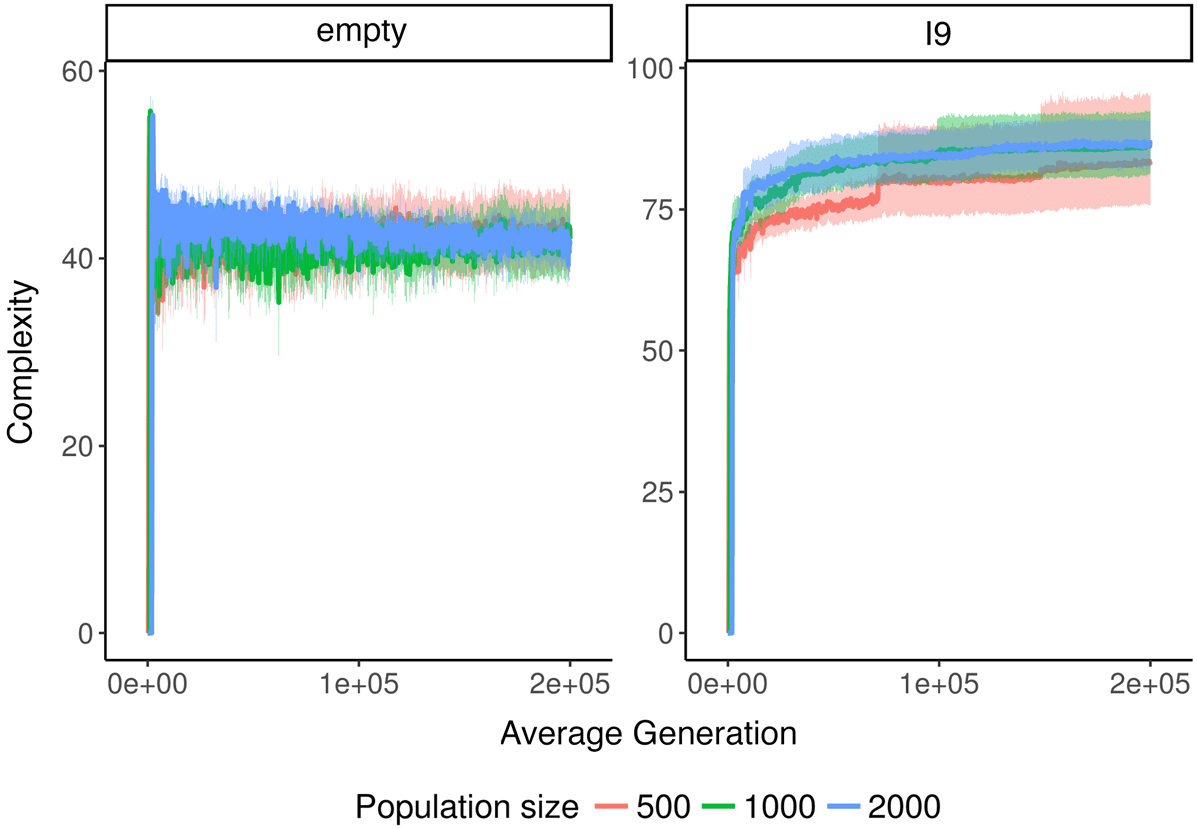
In Avida, there is always at least a little change (see Figure 5). This observation is consistent with
previous findings that fitness in Avida increases indefinitely [51], as an increase in fitness implies
both change and novelty. Based on coalescence theory, we would expect change in the empty
environment to usually be less than or equal to one, because it is a single-niche environment. During
each interval, either a fitter genotype will arise and sweep the population or the current fittest
genotype will remain dominant. Because our value of t is not higher than the maximum expected
coalescence interval, we should also expect to see the occasional timepoint with change greater than
one. Our data are roughly consistent with this expectation. In addition, there is a subtle downward
trend in the change data, likely due to the progressively increasing difficulty of finding beneficial
mutations.
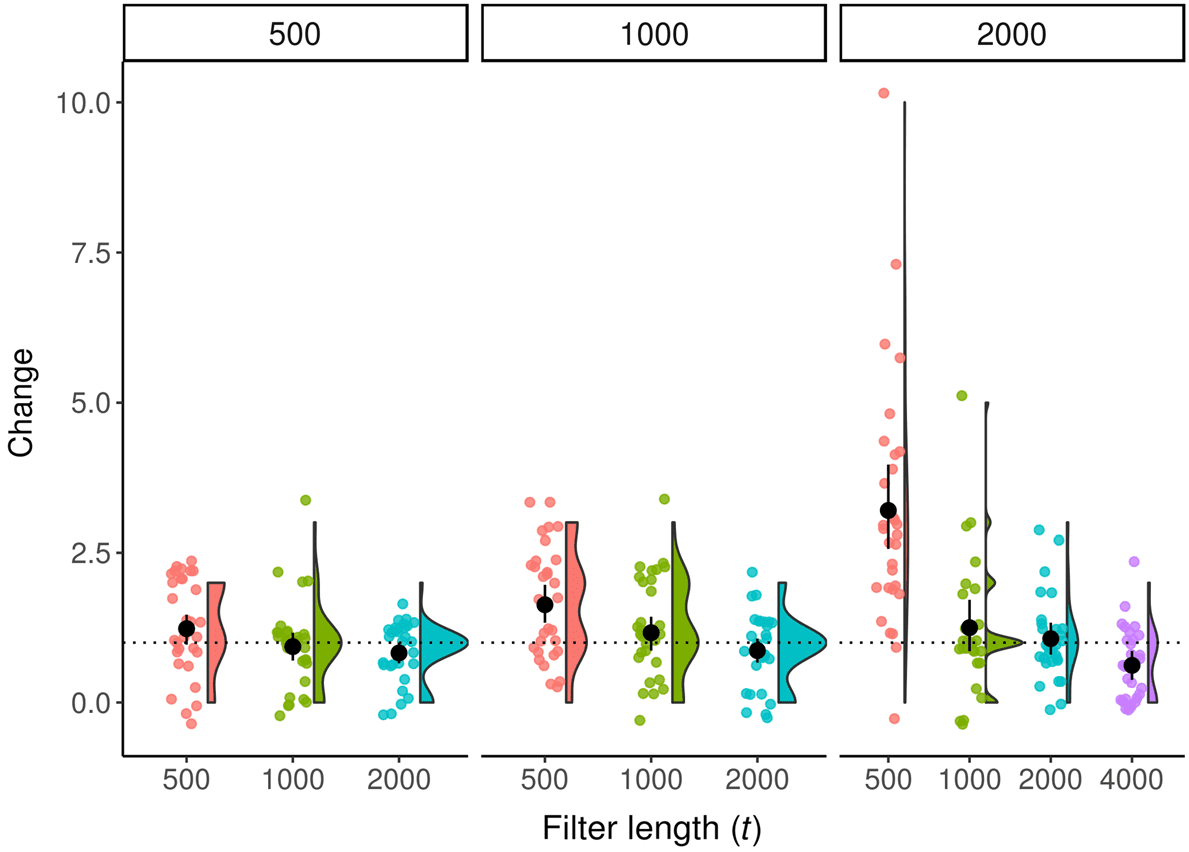
As expected, increasing the filter length t decreases the amount of change observed, because
fewer taxa are able to get through the filter (see Figure 5). In general, using a value of t equal to
the population size seems to yield an adequate filter. The confidence interval for the mean of these
conditions always overlaps 1, indicating that a substantial amount of filtering is occurring. Using
lower values of t begins to lead to substantial increases in the variance of observed change. Using
64
Artificial Life Volume 25, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Figure 5. Raincloud plot of change at final generation across multiple population sizes and filter lengths in Avida in the
empty environment. Labels along the top indicate population size. Black circle and lines indicate mean and bootstrapped
95% confidence interval. Horizontal bar indicates change = 1, the expected average change in the empty environment.
a higher value of t does further reduce noise, but with diminishing returns. In the empty environ-
ment, population size does not appear to have much effect on change, implying (unsurprisingly) that
population size does not exert pressure on evolutionary dynamics in this environment.
In the Logic 9 environment, however, there is a slight increase in change as population size
increases, particularly early in the experiment (see Figure 6). Additionally, change is generally a little
higher in the Logic 9 environment than the empty environment. This distinction is an unexpected
benefit of using a value of t too low to guarantee coalescence. Logic 9 is a single-niche environment,
Figure 6. Change over time across different environments and population sizes in Avida. Note that the y axes have
different scales. In general, change is much higher in the Logic 9 environment. Filter length, t, is equal to population size.
Artificial Life Volume 25, Number 1
65
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
so if we chose a large enough value of t, we would expect change to always be less than or equal to 1.
However, Logic 9 is a more complex environment than the empty environment, which increases the
odds that multiple lineages will be able to keep evolutionary pace with other for a substantial amount
of time. Thus, at the values of t we used, our change metric is able to reflect the fact that more is
going on in the Logic 9 environment than the empty environment.
While change is a metric often not considered in discussions of open-ended evolution, these
results show that the amount of meaningful change can reflect differences in the environment
and evolution of the populations and is likely a necessary dynamic for open-ended evolution.
Our change metric responds in intuitive ways to variations in parameter settings, suggesting that
it is a reliable indicator of the dynamics we designed it to capture.
5.2 Novelty Metric
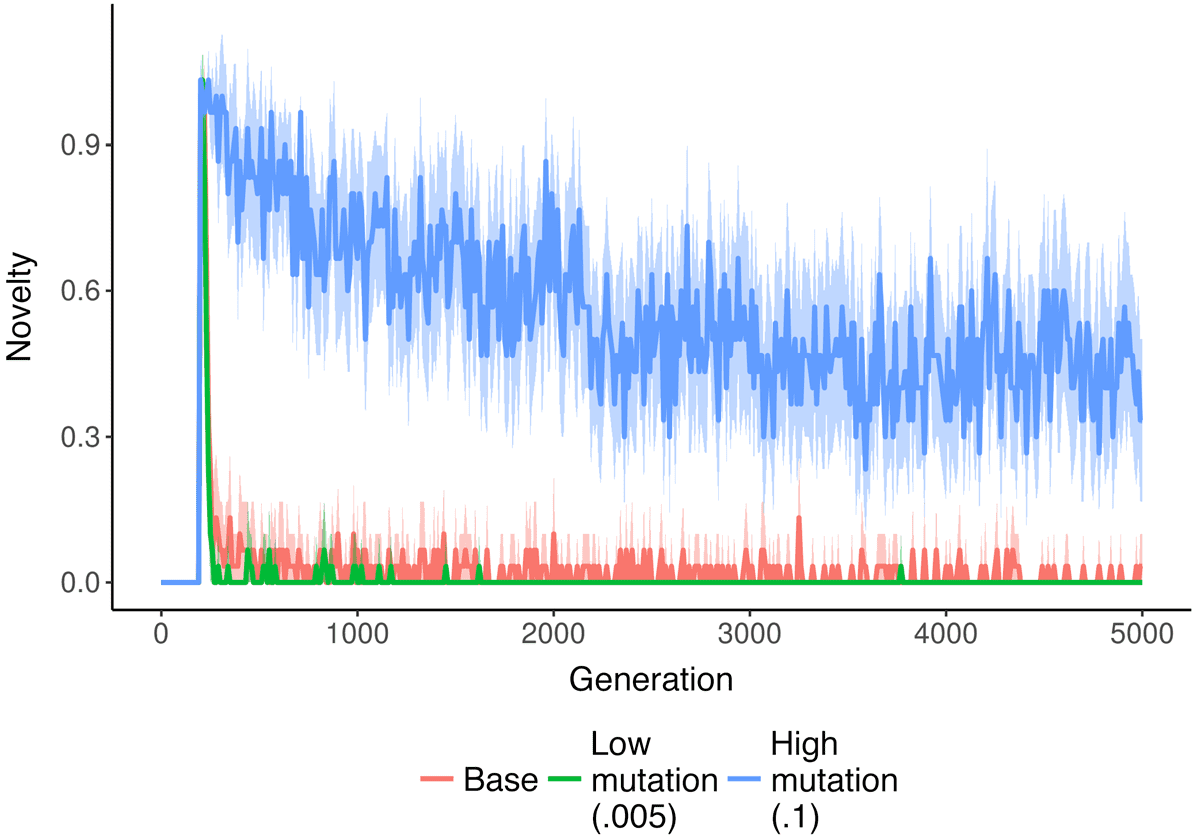
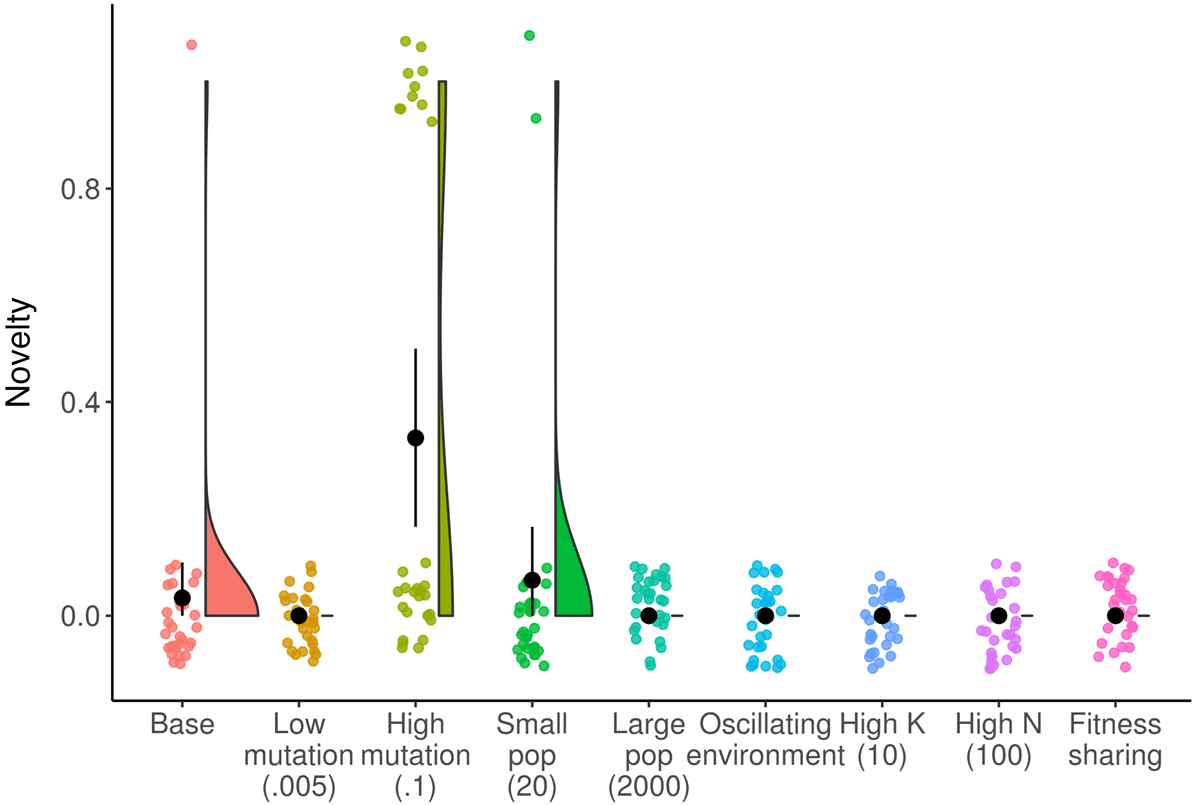
As shown in Figure 7, a higher mutation rate increases the amount of novelty generated by the NK
landscape system. This result is to be expected, because more mutations make it easier to cross
fitness valleys and otherwise traverse the fitness landscape. Even at a high mutation rate, novelty
does start to decrease over time as the search space is explored.
We again found that the majority of treatments had a qualitatively similar trajectory over time,
and therefore in Figure 8 we show only the final novelty value. As predicted, the baseline treatment
has, with the exception of one replicate, stopped producing meaningful novelty by the final time-
point. Indeed, the only environment still reliably producing meaningful novelty is the high-mutation-
rate condition ( p = 0.003, Wilcoxon test; Glassʼs D = 0.3). High mutation rates produce ongoing
novelty by shifting the mutation-selection balance so that drift is able to preserve novel lineages for
longer than t. Notably, fitness sharing does not increase the final novelty ( p = 0.333, Wilcoxon test),
presumably because it is promoting cycling among previously discovered genomes.
Like NK landscapes, Avida shows gradually declining novelty over time (although novelty in
Avida declines more slowly) [15]. This trend presumably reflects the declining availability of bene-
ficial mutations. Interestingly, the novelty and change graphs from Avida look almost identical,
implying that there is little cycling among previously discovered solutions. This result, too, is
Figure 7. Amount of novelty over time in NK landscape with varying mutation rate. The novelty metric measures the
number of completely new meaningful genomes that have lineages that persisted since the previous timepoint. As the
mutation rate increases, more novelty is continuously produced. However, at all mutation rates the novelty decreases
over time. Shaded region represents a bootstrapped 95% confidence interval around the mean.
66
Artificial Life Volume 25, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Figure 8. Raincloud plot of novelty at final generation across NK landscape treatments. Black circles and lines indicate
mean and bootstrapped 95% confidence interval. At the final timepoint, little meaningful novelty is found in our baseline
populations. Only increasing the mutation rate increases novelty, implying that other conditions with high change are
simply promoting cycling among a fixed set of genotypes.
consistent with the previously observed indefinite fitness increases in Avida [51]—if the population
is always getting fitter, genotypes from earlier in the run would be unlikely to survive in the present.
These results highlight the power of the novelty metric to identify environments and populations
that have the potential to be open-ended due to the high number of new genotypes being consis-
tently discovered. Novelty is likely necessary, but not sufficient, for open-ended evolution, because if
nothing new is being produced by a population, neither the complexity nor the ecological metric can
be nonzero.
5.3 Complexity Metric
In an NK landscape population, organisms cannot evolve to be more complex than N. As a result,
the complexity increases over time and then saturates. High mutation rate ( p < 0.0001, Wilcoxon
test; Glassʼs D = −2.6) and small population size ( p < 0.0001, Wilcoxon test; Glassʼs D = −0.23)
reduce complexity because they shift the mutation-selection balance to make staying on a fitness
peak more challenging (see Figure 9). All other treatments were able to achieve maximal complexity
fairly reliably. Note that, due to the roughness of our complexity metric, this merely indicates the
presence of an individual on a fitness peak. We cannot distinguish between higher and lower peaks.
The high-N treatment was, unsurprisingly, able to attain a drastically higher complexity due to its
increased upper bound on complexity.
The NK landscape results demonstrate that the complexity metric correctly identifies a system
that is not able to continuously produce more complex solutions. Once the maximum complexity
allowed by the genome length is reached, no higher value is possible.
In Avida, the complexity metric reveals a stark difference between the empty and Logic 9 envi-
ronments (see Figure 10). In the empty environment, there is a rapid rise in complexity followed by a
decrease and leveling out. This behavior is likely due to the strong pressure in Avida to become a
more efficient self-replicator by optimizing code. Over time, simpler solutions are selected for, all
else being equal. In the Logic 9 environment, on the other hand, there is an ongoing upward tra-
jectory in complexity. While Logic 9 still rewards efficiency, algorithms that can make maximally
efficient use of the tasks are complex. These results are consistent with other measurements of
complexity in Avida over time [1].
Artificial Life Volume 25, Number 1
67
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Figure 9. Raincloud plot of complexity at final generation across NK landscape treatments. Black circles and lines indicate
mean and bootstrapped 95% confidence interval. Note that we have excluded the high-N condition from this graph
because it throws off the axes. Most of the treatments reach the maximum complexity allowed by the genome length
(20 or 100) and cannot continue to increase. High mutation rate and smaller populations decrease the final complexity
achieved by the populations on average.
In the biosphere, complexity appears to be growing without bound [26], although there is debate
over the mechanisms behind this process. In this situation, building a nontrivial system that exhibits
such behavior is a worthwhile goal for open-ended evolution research. Unbounded growth in
complexity is only possible in a system with a sufficiently complex environment such that there
is always new information to be integrated into the genome.
Figure 10. Complexity in Avida over time across different environments and population sizes. Note that y axes have
different scales. In general, complexity appears to continue increasing in the Logic 9 environment, whereas it drops and
then stabilizes in the empty environment. Filter length, t, is equal to population size.
68
Artificial Life Volume 25, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Figure 11. Raincloud plot of ecology at final generation across NK landscape treatments. Black circles and lines indicate
mean and bootstrapped 95% confidence interval. Fitness sharing is the only condition that reliably produces ecology.
5.4 Ecology Metric
Across both of our systems, the only condition that creates a multi-niche environment is the fit-
ness sharing condition in NK landscapes. Accordingly, that is the only condition in which we ob-
serve ecology significantly above the baseline ( p < 0.0001, Wilcoxon test; Glassʼs D = 0.91) (see
Figure 11). Because fitness sharing specifically rewards organisms with less common genotypes, it
promotes a stably high ecology value over time. This result demonstrates the tradeoff inherent in
fitness sharing in that it leads to higher ecology at the expense of lower complexity. Interestingly,
in the Avida data, we see a consistent low level of ecology across all conditions [15]. We hypoth-
esize that this slight increase over NK landscapes is due to the noise introduced by Avidaʼs variable
generation times.
Ecology is an extremely powerful force in nature, leading to feedback cycles of ever-increasing
diversity. Like complexity, diversity seems to be growing without bound in the biosphere [23]. Thus,
it will be important to see what mechanisms are important for promoting it in artificial life systems,
too.
6 Conclusions
We have proposed a suite of metrics that quantify the presence of four generally accepted hallmarks
of evolution. These metrics build on prior work with evolutionary activity statistics and are largely
compatible with them. Additionally, we have proposed techniques for reducing noise in these
statistics. By testing them on two very different well-understood evolutionary systems, we have
demonstrated that our metrics respond in an intuitive way to the dynamics these systems exhibit.
Thus, these metrics should also be useful in understanding the extent to which novel systems exhibit
hallmarks of open-ended evolution. Moreover, we can use them to understand the impact of incre-
mental changes to a system. By breaking the seemingly monolithic problem of designing an open-
ended evolutionary system into smaller, measurable pieces, we facilitate improved use of the scientific
method. One of the primary goals in building an open-ended evolutionary system is to understand
the underlying components that are necessary to do so. By measuring the effects that controlled
changes to a system have on this suite of metrics, we can more productively work toward these
goals.
Artificial Life Volume 25, Number 1
69
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
Going forward, it will be interesting to see how a wider variety of artificial life systems respond to
the metrics in the MODES toolbox. In particular, further investigation into the differences between
using a shadow run as a filter and using the persistence filter described here would be worthwhile.
Ultimately, these two techniques capture sufficiently different information that it may be valuable to
use each in turn.
For a long time, the field of open-ended evolution has been plagued by a lack of data that can be
meaningfully compared across systems. We believe that the MODES toolbox will help remedy this
problem by making useful metrics easily accessible. As new hallmarks of open-ended evolution are
identified and new techniques of reducing noise are developed, we encourage contributions to the
toolbox. It may also be worthwhile to complement these high-level metrics that screen for the pres-
ence of hallmarks of open-ended evolution with a suite of lower-level metrics that provide more
mechanistic insight into why hallmarks are or are not being observed [16]. By working together
as a community of users, researchers, and developers we can dramatically increase the rate at which
open-ended evolution research progresses.
Acknowledgments
We thank members of the artificial life community for feedback on the initial ideas for the MODES
toolbox. We further thank the MSU Digital Evolution Lab for helpful feedback on this manuscript.
This research was supported by the National Science Foundation (NSF) through the BEACON
Center (Cooperative Agreement DBI-0939454), a Graduate Research Fellowship to E.D. (Grant
No. DGE-1424871), and NSF Grant No. DEB-1655715 to C.O. Michigan State University pro-
vided computational resources through the Institute for Cyber-Enabled Research. Any opinions,
findings, and conclusions or recommendations expressed in this material are those of the author(s)
and do not necessarily reflect the views of the NSF or MSU.
References
1. Adami, C., Ofria, C., & Collier, T. C. (2000). Evolution of biological complexity. Proceedings of the National
Academy of Sciences of the U.S.A., 97(9), 4463–4468.
2. Allen, M., Poggiali, D., Whitaker, K., Marshall, T. R., & Kievit, R. (2018). Raincloud plots: A multi-
platform tool for robust data visualization. PeerJ Preprints, 6: e27137v1.
3. Banzhaf, W., Baumgaertner, B., Beslon, G., Doursat, R., Foster, J. A., McMullin, B., de Melo, V. V.,
Miconi, T., Spector, L., Stepney, S., & White, R. (2016). Defining and simulating open-ended novelty:
Requirements, guidelines, and challenges. Theory in Biosciences, 135(3), 131–161.
4. Bedau, M. A., & Bahm, A. (1994). Bifurcation structure in diversity dynamics. In R. Brooks & P. Maes
(Eds.), Artificial Life IV: Proceedings of the Fourth International Workshop on the Synthesis and Simulation of Living
Systems (pp. 258–268). Cambridge, MA: MIT Press.
5. Bedau, M. A., & Packard, N. H. (1992). Measurement of evolutionary activity, teleology, and life. In I. C.
Langton, C. Taylor, D. Farmer, & S. Rasmussen (Eds.), Artificial Life II (pp. 431–461). Redwood City, CA:
Addison-Wesley.
6. Bedau, M. A., Snyder, E., Brown, C. T., & Packard, N. H. (1997). A comparison of evolutionary activity in
artificial evolving systems and in the biosphere. In P. Husbands & I. Harvey (Eds.), Proceedings of the Fourth
European Conference on Artificial Life, ECAL97 (pp. 125–134). Cambridge, MA: MIT Press.
7. Bedau, M. A., Snyder, E., & Packard, N. H. (1998). A classification of long-term evolutionary dynamics. In
C. Adami, R. K. Belew, H. Kitano, & C. E. Taylor (Eds.), Artificial life VI: Proceedings of the Sixth International
Conference on Artificial Life (pp. 228–237). Cambridge, MA: MIT Press.
8. Bloom, B. H. (1970). Space/time trade-offs in hash coding with allowable errors. Communications of the
ACM, 13(7), 422–426.
9. Blount, Z. D., Barrick, J. E., Davidson, C. J., & Lenski, R. E. (2012). Genomic analysis of a key innovation
in an experimental Escherichia coli population. Nature, 489(7417), 513–518.
10. Blount, Z. D., Borland, C. Z., & Lenski, R. E. (2008). Historical contingency and the evolution of a key
innovation in an experimental population of Escherichia coli. Proceedings of the National Academy of Sciences of the
U.S.A., 105(23), 7899–7906.
70
Artificial Life Volume 25, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
11. Bryson, D., Baer, B., Ofria, C., Barrick, J., Vostinar, A., Goldsby, H., Zaman, L., Chandler, C., Goings, S.,
Dolson, E., Vogel, M., Covert, A., Wright, G., Nahum, J., Misevic, D., Wagner, A., Rupp, M., Yilmaz, E.,
Pakanati, A., & Biswas, R. (2018). Code for using MODES metrics in Avida. Available at https://doi.org/
10.5281/zenodo.1439479.
12. Channon, A. (2001). Passing the ALife test: Activity statistics classify evolution in Geb as
unbounded. In J. Kelemen & P. Sosk (Eds.), Advances in artificial life (pp. 417–426). Berlin, Heidelberg:
Springer.
13. Channon, A. (2003). Improving and still passing the ALife test: Component-normalised activity
statistics classify evolution in Geb as unbounded. In R. K. Standish, M. A. Bedau, & H. A. Abbass
(Eds.), Proceedings of the Eighth International Conference on Artificial Life, ICAL 2003 ( pp. 173–181).
Cambridge, MA: MIT Press.
14. Cooper, T. F., & Ofria, C. (2003). Evolution of stable ecosystems in populations of digital organisms. In
R. K. Standish, M. A. Bedau, & H. A. Abbass (Eds.), Artificial life VIII: Proceedings of the Eighth International
Conference on Artificial Life (pp. 227–232). Cambridge, MA: MIT Press.
15. Dolson, E. (2018). Data, code, and supplemental figures for the MODES toolbox. Available at https://
doi.org/10.5281/zenodo.2345140.
16. Dolson, E., Lalejini, A., Jorgensen, S., & Ofria, C. (2018). Quantifying the tape of life: Ancestry-based
metrics provide insights and intuition about evolutionary dynamics. In T. Ikegami, N. Virgo, O. Witkowski,
M. Oka, R. Suzuki, & H. Iizuka (Eds.), The 2018 Conference on Artificial Life: A hybrid of the European Conference
on Artificial Life (ECAL) and the International Conference on the Synthesis and Simulation of Living Systems (ALIFE)
(pp. 75–82). Cambridge, MA: MIT Press.
17. Dolson, E., Vostinar, A., & Ofria, C. (2015). Whatʼs holding artificial life back from open-ended evolution?
The Winnower, Sept.
18. Fu, Y.-X., & Li, W.-H. (1999). Coalescing into the 21st century: An overview and prospects of coalescent
theory. Theoretical Population Biology, 56(1), 1–10.
19. Goldberg, D. E., Richardson, J., & Grefenstette, J. J. (1987). Genetic algorithms with sharing for
multimodal function optimization. In Genetic algorithms and their applications: Proceedings of the Second International
Conference on Genetic Algorithms (pp. 41–49). Hillsdale, NJ: Lawrence Erlbaum.
20. Goldsby, H. J., Dornhaus, A., Kerr, B., & Ofria, C. (2012). Task-switching costs promote the evolution of
division of labor and shifts in individuality. Proceedings of the National Academy of Sciences of the U.S.A., 109(34),
13686–13691.
21. Good, B. H., McDonald, M. J., Barrick, J. E., Lenski, R. E., & Desai, M. M. (2017). The dynamics of
molecular evolution over 60,000 generations. Nature, 551(7678), 45–50.
22. Hara, A., & Nagao, T. (1999). Emergence of the cooperative behavior using ADG; automatically defined
groups. In W. Banzhaf, J. M. Daida, A. E. Eiben, M. H. Garzon, V. G. Honavar, M. J. Jakiela, & R. E. Smith
(Eds.), Proceedings of the 1st Annual Conference on Genetic and Evolutionary Computation, Vol. 1 (pp. 1039–1046).
San Francisco: Morgan Kaufmann.
23. Harmon, L. J., & Harrison, S. (2015). Species diversity is dynamic and unbounded at local and continental
scales. The American Naturalist, 185(5), 584–593.
24. Hedges, L. V. (1981). Distribution theory for Glassʼs estimator of effect size and related estimators. Journal
of Educational Statistics, 6(2), 107–128.
25. Kauffman, S., & Levin, S. (1987). Towards a general theory of adaptive walks on rugged landscapes. Journal
of Theoretical Biology, 128(1), 11–45.
26. Korb, K. B., & Dorin, A. (2011). Evolution unbound: Releasing the arrow of complexity. Biology &
Philosophy, 26(3), 317–338.
27. Le Gac, M., Plucain, J., Hindr, T., Lenski, R. E., & Schneider, D. (2012). Ecological and evolutionary
dynamics of coexisting lineages during a long-term experiment with Escherichia coli. Proceedings of the National
Academy of Sciences of the U.S.A., 109(24), 9487–9492.
28. Lehman, J., & Stanley, K. O. (2011). Abandoning objectives: Evolution through the search for novelty
alone. Evolutionary Computation, 19(2), 189–223.
29. Lenski, R. E., Ofria, C., Pennock, R. T., & Adami, C. (2003). The evolutionary origin of complex features.
Nature, 423(6936), 139–144.
Artificial Life Volume 25, Number 1
71
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
30. Lenski, R. E., Rose, M. R., Simpson, S. C., & Tadler, S. C. (1991). Long-term experimental evolution in
Escherichia coli. I. Adaptation and divergence during 2,000 generations. The American Naturalist, 138(6),
1315–1341.
31. Lenski, R. E., Wiser, M. J., Ribeck, N., Blount, Z. D., Nahum, J. R., Morris, J. J., Zaman, L., Turner, C. B.,
Wade, B. D., Maddamsetti, R., Burmeister, A. R., Baird, E. J., Bundy, J., Grant, N. A., Card, K. J., Rowles,
M., Weatherspoon, K., Papoulis, S. E., Sullivan, R., Clark, C., Mulka, J. S., & Hajela, N. (2015). Sustained
fitness gains and variability in fitness trajectories in the long-term evolution experiment with Escherichia coli.
Proceedings of the Royal Society of London B: Biological Sciences, 282(1821), 20152292.
32. Maddamsetti, R., Lenski, R. E., & Barrick, J. E. (2015). Adaptation, clonal interference, and
frequency-dependent interactions in a long-term evolution experiment with Escherichia coli. Genetics,
200(2), 619–631.
33. Maley, C. C. (1999). Four steps toward open-ended evolution. In W. Banzhaf, J. M. Daida, A. E. Eiben,
M. H. Garzon, & V. G. Honavar (Eds.), Proceedings of the 1st Annual Conference on Genetic and Evolutionary
Computation, Vol. 2 of GECCOʼ99 (pp. 1336–1343). San Francisco: Morgan Kaufmann.
34. Maynard Smith, J., & Szathmáry, E. (1997). The major transitions in evolution. Oxford: Oxford University Press.
35. Ofria, C., Dolson, E., Lalejini, A., Fenton, J., Jorgensen, S., Miller, R., Moreno, M. A., Stredwick, J., Zaman,
L., Schossau, J., Gillespie, L., C G, N. & Vostinar, A. (2018). Empirical, Oct. Available at https://doi.org/
10.5281/zenodo.1439475.
36. Ofria, C., & Wilke, C. O. (2004). Avida: A software platform for research in computational evolutionary
biology. Artificial Life, 10(2), 191–229.
37. Potter, M. A., & De Jong, K. A. (2000). Cooperative coevolution: An architecture for evolving coadapted
subcomponents. Evolutionary Computation, 8(1), 1–29.
38. R Core Team. (2017). R: A language and environment for statistical computing. Vienna: R Foundation for Statistical
Computing.
39. Ribeck, N., & Lenski, R. E. (2015). Modeling and quantifying frequency-dependent fitness in microbial
populations with cross-feeding interactions. Evolution, 69(5), 1313–1320.
40. Rozen, D. E., & Lenski, R. E. (2000). Long-term experimental evolution in Escherichia coli. VIII. Dynamics
of a balanced polymorphism. The American Naturalist, 155(1), 24–35.
41. Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27(3),
379–423.
42. Skusa, A., & Bedau, M. A. (2003). Towards a comparison of evolutionary creativity in biological and
cultural evolution. Artificial Life, 8, 233–242.
43. Soros, L. (2018). Necessary conditions for open-ended evolution. Electronic Theses and Dissertations, Jan.
44. Soros, L., & Stanley, K. (2014). Identifying necessary conditions for open-ended evolution through the
artificial life world of Chromaria. In H. Sayama, J. Rieffel, S. Risi, R. Doursat, & H. Lipson (Eds.),
ALIFE 14: Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems
(pp. 793–800). Cambridge, MA: MIT Press.
45. Stanley, K. O., & Soros, L. B. (2016). The role of subjectivity in the evaluation of open-endedness.
Presentation delivered in OEE2: The Second Workshop on Open-Ended Evolution, at ALIFE 2016,
in Cancún, Mexico, 4–8 July 2016.
46. Taylor, T., Bedau, M., Channon, A., Ackley, D., Banzhaf, W., Beslon, G., Dolson, E., Froese, T.,
Hickinbotham, S., Ikegami, T., McMullin, B., Packard, N., Rasmussen, S., Virgo, N., Agmon, E., Clark, E.,
McGregor, S., Ofria, C., Ropella, G., Spector, L., Stanley, K. O., Stanton, A., Timperley, C., Vostinar, A., &
Wiser, M. (2016). Open-ended evolution: Perspectives from the OEE workshop in York. Artificial Life,
22(3), 408–423.
47. Tenaillon, O., Barrick, J. E., Ribeck, N., Deatherage, D. E., Blanchard, J. L., Dasgupta, A., Wu, G. C.,
Wielgoss, S., Cruveiller, S., Mdigue, C., Schneider, D., & Lenski, R. E. (2016). Tempo and mode of genome
evolution in a 50,000-generation experiment. Nature, 536(7615), 165–170.
48. Turner, C. B., Blount, Z. D., & Lenski, R. E. (2015). Replaying evolution to test the cause of extinction of
one ecotype in an experimentally evolved population. PLoS ONE, 10(11), e0142050.
49. Turner, C. B., Blount, Z. D., Mitchell, D. H., & Lenski, R. E. (2015). Evolution and coexistence in
response to a key innovation in a long-term evolution experiment with Escherichia coli. bioRxiv, June.
72
Artificial Life Volume 25, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
E. L. Dolson et al.
The MODES Toolbox
50. Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. New York: Springer-Verlag.
51. Wiser, M. J. (2015). An analysis of fitness in long-term asexual evolution experiments. Ph.D. thesis, Michigan State
University.
52. Wiser, M. J., Dolson, E. L., Vostinar, A., Lenski, R. E., & Ofria, C. (2018). The boundedness illusion:
Asymptotic projections from early evolution underestimate evolutionary potential. PeerJ Preprints, 6:
e27246v2.
53. Wiser, M. J., Ribeck, N., & Lenski, R. E. (2013). Long-term dynamics of adaptation in asexual populations.
Science, 342(6164), 1364–1367.
54. Zaman, L. (2018). Investigating open-ended coevolution in digital organisms. In T. Ikegami, N. Virgo,
O. Witkowski, M. Oka, R. Suzuki, & H. Iizuka (Eds.), The 2018 Conference on Artificial Life: A hybrid of the
European Conference on Artificial Life (ECAL) and the International Conference on the Synthesis and Simulation of
Living Systems (ALIFE) (pp. 258–259). Cambridge, MA: MIT Press.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
2
5
1
5
0
1
6
6
7
1
1
6
a
r
t
l
/
_
a
_
0
0
2
8
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Artificial Life Volume 25, Number 1
73