The Cognitive Domain of a Glider
in the Game of Life
Randall D. Beer*
Indiana University
Abstract This article examines in some technical detail
the application of Maturana and Varelaʼs biology of cognition to a
simple concrete model: a glider in the game of Life cellular
automaton. By adopting an autopoietic perspective on a glider,
the set of possible perturbations to it can be divided into destructive
and nondestructive subsets. From a gliderʼs reaction to each
nondestructive perturbation, its cognitive domain is then mapped.
Zusätzlich, the structure of a gliderʼs possible knowledge of its
immediate environment, and the way in which that knowledge is
grounded in its constitution, are fully described. The notion of
structural coupling is then explored by characterizing the paths of
mutual perturbation that a glider and its environment can undergo.
Endlich, a simple example of a communicative interaction between
two gliders is given. The article concludes with a discussion of the
potential implications of this analysis for the enactive approach to
Erkenntnis.
Schlüsselwörter
Autopoiesis, enaction, cognitive domain,
structural coupling, cellular automata
A version of this paper with color figures is
available online at http://dx.doi.org/10.1162/
artl_a_00125. Subscription required.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1 Einführung
Since the publication of its original manifesto over 20 years ago [28], interest in what has come to be
known as the enactive approach to cognition has been steadily growing [10, 22, 24]. This approach is
grounded—historically, conceptually, and even terminologically—in earlier work by Maturana and
Varela (henceforth MV) on the biology of cognition [15, 16, 25]. Bedauerlicherweise, MVʼs framework
can be difficult to understand, requiring a fundamental shift in perspective that many find strange on
first reading. Even among experts, there are a number of disagreements of interpretation that have
not yet been fully resolved. Daher, it would seem that a detailed analysis of a concrete example of
MVʼs framework in action could be very beneficial to ongoing work in enactive cognitive science.
Such is the goal of this article.
There is a long history of developing computational models of the concept of autopoiesis that
serves as the foundation of MVʼs biology of cognition [3, 9, 17–19, 27, 29, 33]. There have even
been attempts to engineer physical autopoiesis [13]. Jedoch, the focus of most of this work has
been on simply demonstrating that autopoiesis can be produced; there has been very little systematic
mathematical analysis of such models. More importantly for our purposes here, most work on
modeling autopoiesis has not directly engaged the behavioral and cognitive implications of MVʼs
biology of cognition, although there are important recent exceptions [6–8, 23]. Building on a pre-
vious proposal [1], the central aim of this article is to rigorously and exhaustively characterize the
* Cognitive Science Program, 1900 E. 10th Street, 840 Eigenmann, Indiana University, Bloomington, IN 47406. Email: rdbeer@indiana.edu
© 2014 Massachusetts Institute of Technology
Artificial Life 20: 183–206 (2014) doi:10.1162/ARTL_a_00125
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
complete cognitive domain of a glider in the game of Life, as well as the structure of the interactions
in which it can participate with its environment.
This article is organized as follows. Abschnitt 2 introduces the key concepts and terminology of
MVʼs framework that we will be exploring. Abschnitt 3 then reviews the game of Life cellular auto-
maton and argues for the utility of considering gliders from an autopoietic perspective. Abschnitt 4
characterizes the cognitive domain of a glider by enumerating its reaction to all possible perturba-
tions that it can receive from its immediate environment. In Section 5, we examine the structure of
the different response classes that result from these perturbations and how this structure is
grounded in a gliderʼs constitution. Abschnitte 6 Und 7 then begin a characterization of the ways in
which a glider and its environment can interact over time, while Section 8 presents a preliminary
investigation of communicative interactions between gliders. Endlich, we conclude in Section 9 with a
discussion of some of the broader issues raised by this analysis and suggest some directions for
future work.
2 Autopoiesis and Cognition
Let us begin with a brief introduction to the key concepts of MVʼs framework that we will need in
dieser Artikel. This section makes no claim to being exhaustive and, in the interests of clarity, viele
subtleties are purposely simplified or ignored. For more complete presentations, see the original
Literatur [15, 16, 25] or more recent discussions [24].
With one crucial exception, MVʼs framework derives from a fairly traditional perspective on
Wissenschaft, albeit one expressed in a somewhat idiosyncratic language. Scientists can only study systems
that can be distinguished in some way from the general background of experience; MV call such a
system a simple unity. Zum Beispiel, a sealed pressure vessel containing a gaseous mixture is a simple
unity. Simple unities have properties (z.B., Volumen, temperature, pressure, and color ) that can be
measured and manipulated, as well as relations between these properties (z.B., the ideal gas law
and Planckʼs law of blackbody radiation). But scientists can also treat such a system as a composite
unity by further decomposing it into a collection of components (z.B., the molecular constituents of
the gas and vessel) with their own properties and relations. Scientific explanation typically involves
building bridges between the properties and relations of a unity and the properties and relations of
its components (z.B., the derivation via statistical mechanics of the ideal gas law and the quantum
mechanical derivation of Planckʼs law).
MV make an important distinction between the organization of a composite unity and its structure. A
composite unityʼs organization is given by the abstract relations between its components that are
essential to its being the particular kind of unity that it is. A composite unityʼs structure, on the
andererseits, is given by the actual components and relations between them that constitute a concrete
instance of that unity. Zum Beispiel, for a system to be a pressure vessel, the molecules of the vessel
must satisfy relations of integrity and containment with respect to the molecules of the gas; diese
relations define its organization. Im Gegensatz, the additional component properties and relations
necessitated by any concrete realization of a pressure vessel constitute its structure. Zum Beispiel,
the types, Positionen, orientations, and velocities of the molecular constituents of an actual pressure
vessel are part of its structure. Note that MV argue that any scientifically explainable composite unity
must be a structure-determined system; its behavior must be determined ultimately by the complete set of
concrete properties and relations of its particular instantiation.
The structure of a composite unity is always changing, both as a result of its own intrinsic
dynamics and as a result of any external perturbations that are applied to it. Zum Beispiel, the types,
Positionen, orientations, and velocities of the gas molecules in a pressure vessel are in constant flux as
they careen about the container, colliding with one another, ricocheting off the walls of the vessel,
and making and breaking chemical bonds. Zusätzlich, we can externally perturb the vessel by heat-
ing it or pumping additional gas into it. As long as a unityʼs organization is maintained in the pres-
ence of such changes, they are termed nondestructive. Im Gegensatz, a structural change is destructive if it
184
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
destroys a unityʼs organization. Zum Beispiel, a pressure vessel may lose its integrity as a result of a
corrosive chemical reaction with the gas it contains or because it has been heated to the point of
melting. In this case, the unity disintegrates, losing its identity as an instance of the abstract class of
which it was previously a member.
So far, so traditional. The crucial deviation of MVʼs framework from a traditional perspective on
science is its recognition of the role of the observer within the framework. On MVʼs view, a unity
such as a pressure vessel is not given a priori. Eher, it arises as a distinction made in language
among a community of observers. Although by no means unique in modern science (consider
quantum mechanics), making explicit the role of the observer in science takes out an enormous
explanatory loan. Glücklicherweise, MV proceed to fully repay this loan by systematically constructing
an account of the observer within their framework. This construction proceeds in two steps. Erste,
MV provide a theory of living systems. Dann, they provide a theory of cognition built upon this
biological foundation.
Given MVʼs perspective on science, it should not be surprising that their account of life consists
not of a list of necessary properties or components, but rather a specification of the organization
that is unique to living systems. MV call this organization autopoietic, which literally means “self-
producing.” The basic idea is that an autopoietic system consists of a network of processes that
produce components whose interactions serve to generate and maintain the very network of pro-
cesses that produced them. The canonical example of an autopoietic system is a living cell, welche
consists of a set of spatiotemporally organized molecular components that participate in biochemical
reactions that produce those very components and maintain their spatiotemporal organization.
Loosely speaking, a living cell is like a pressure vessel in which the reactions between the gas and
the container are such as to preserve the vesselʼs integrity even in the face of natural degradation and
external assault. Natürlich, a living system can actively maintain its autopoietic organization in the
face of structural change only within limits. If those limits are exceeded, autopoiesis is lost and the
unity disintegrates.
MV call the set of all interactions that an autopoietic system can participate in without loss of
identity its cognitive domain. This is a somewhat unusual and controversial use of the term “cognitive”
(a more neutral term would be “domain of interactions”). Trotzdem, MVʼs use of this term is
grounded in the idea that the only way an entity can “know” a given environmental configuration is
for that entity to undergo a nondestructive change in structure as a result of interacting with that
configuration without disintegration. In this way, perception is conceptualized as a perturbative
rather than an instructive interaction, because how an entityʼs structure changes in response to a
given environmental perturbation depends as much on the entityʼs structure at the time of the inter-
action as it does on the structure of the perturbation itself. Daher, to MV, cognition is the process of
identity-preserving action within an environment. An interesting consequence of this definition is
Das, strictly speaking, all living systems are cognitive systems; nervous systems are not essential for
Erkenntnis. Jedoch, by introducing the potential for massive structural variation in a metabolically
nonessential way, nervous systems obviously greatly expand the range of perturbations that an
entity can compensate for without loss of identity.
As long as an entity persists in some environment, its structural changes must necessarily
exhibit a congruence with those of that environment; if they did not, the entity would disinte-
grate. Likewise, the structural changes of the environment depend on both its own internal
dynamics and the perturbations induced by the entities with which it interacts. MV call this process
of congruent structural change structural coupling. When an entityʼs environment contains other
entities, then they can become structurally coupled with one another, with the actions of each
serving as a source of perturbations to the others. As long as they participate in this interlocking
chain of mutual perturbations, these entities generate a new consensual domain of communicative
interactions in which each orients the others to future possibilities for action within their respective
cognitive domains.
In MVʼs framework, communicative interactions within a consensual domain form the basis for
linguistic interactions that ultimately make possible a community of observers who can distinguish in
Artificial Life Volume 20, Nummer 2
185
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
language the simple and composite unities that science tries to explain [14]. Jedoch, MVʼs account
of language is beyond the scope of this article. What we will attempt to do here is to concretize the
notions of cognitive domain and structural coupling by analyzing in depth their application to a
simple model.
3 Glider Autopoiesis
The game of Life (GoL) is a two-dimensional cellular automaton invented by John Conway and
popularized by Martin Gardner in the pages of Scientific American [2, 11, 21]. If we define sij to be
the binary state of the (ith, jth) cell in an unbounded rectangular lattice L and let Aij give the number
of 1s in that cellʼs Moore neighborhood (the eight cells directly surrounding it), then the individual
cell update rule for GoL can be written as
(cid:1)
¼ f sðkÞ
ij
; AðkÞ
ij
sðkþ1Þ
ij
(cid:3)
(
≡ 1 Wenn
0
(cid:1)
ij ¼ 1∧ AðkÞ
sðkÞ
(cid:3)
ij ¼ 2
∨ AðkÞ
ij ¼ 3
ansonsten
where k is a nonnegative integer and ∧ and ∨ denote conjunction and disjunction, jeweils.
: L→L be a function that updates the entire lattice by simultaneously applying f
Weiter, let f
to every cell in parallel. We will use the notation f k to denote the kth iteration of this function,
and the notation LðkÞ
ich; j with bounds on i and j to denote the state of a subset of the lattice at iteration
k. Daher, GoL is a discrete-time, discrete-space dynamical system.
When we as external observers watch a randomly initialized GoL lattice evolve over time, we will
typically witness a great deal of complicated activity, which quickly settles down into a much sparser
set of localized spatiotemporal patterns that persist, propagate, and interact. The term glider in GoL is
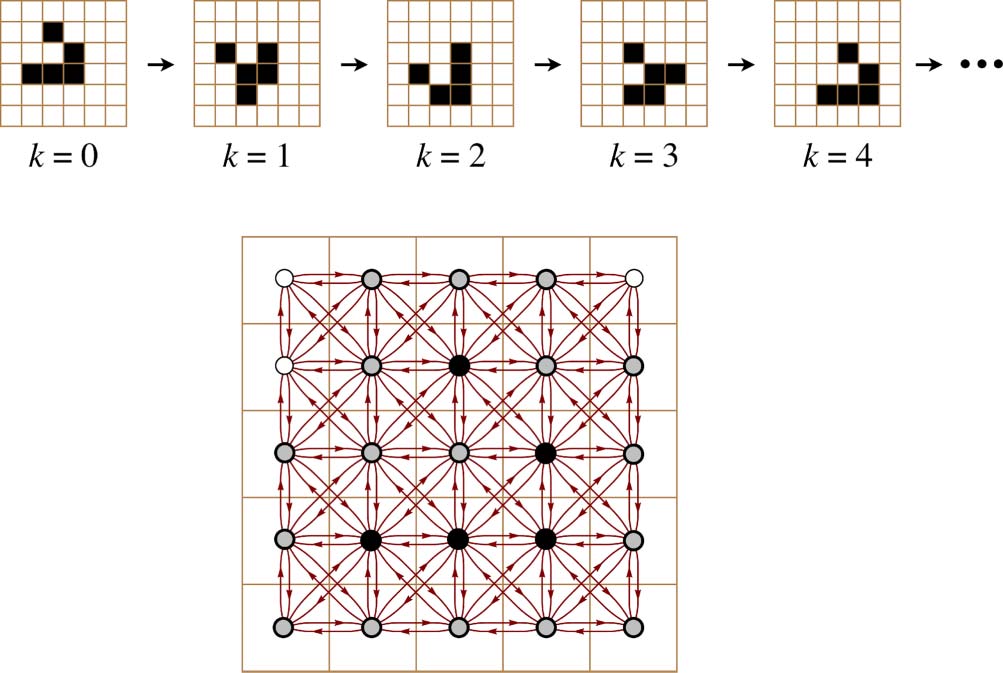
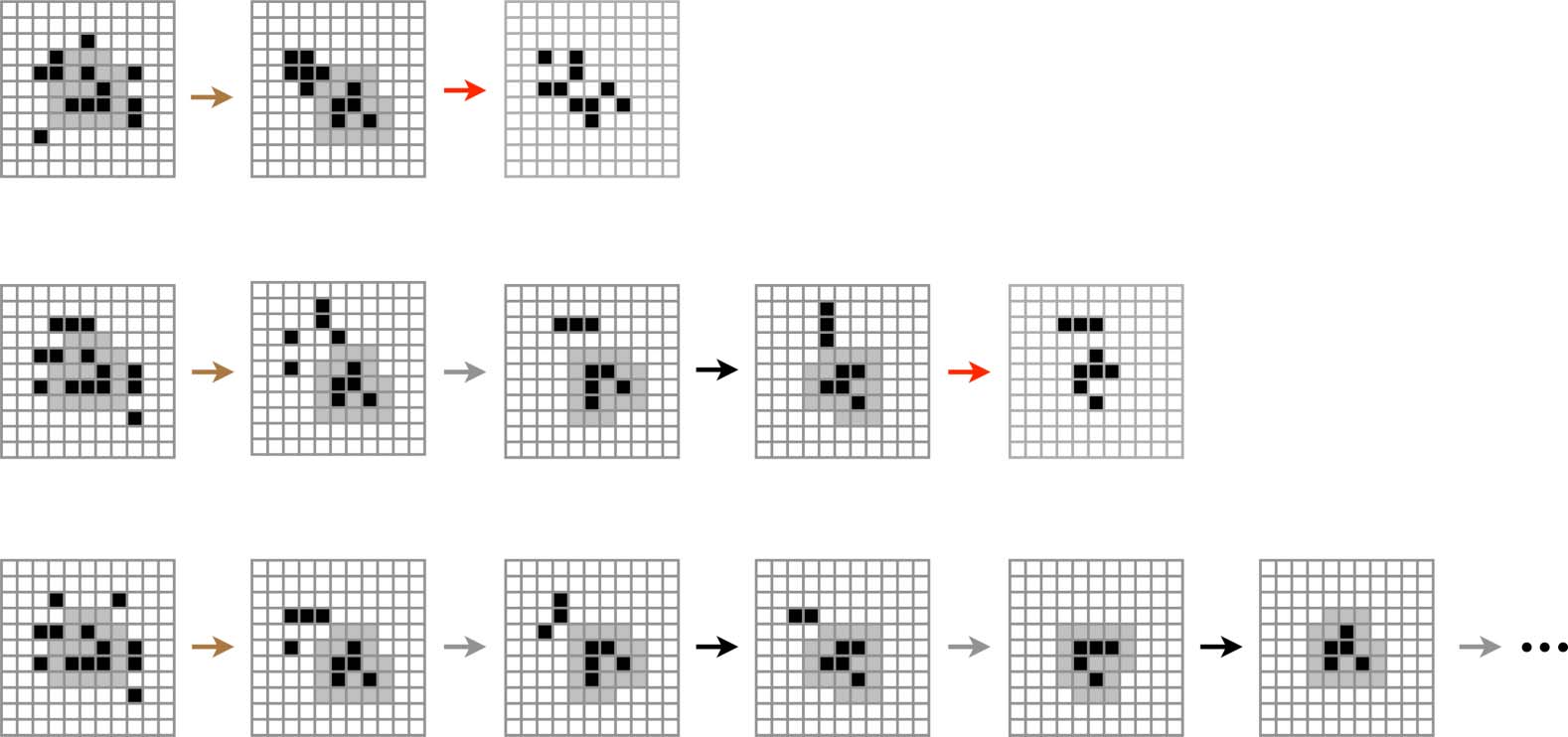
used to refer to particular patterns such as those shown at the top of Figure 1. A glider is the
simplest instance of a general class of patterns called spaceships, which are periodic structures that
move through the lattice at some velocity. As a spatiotemporal pattern, a glider can be distinguished
by the following three properties: (1) It is a nonempty 3 × 3 pattern (2) that repeats every four updates
Figur 1. A glider in the game of Life. Top: Four iterations in the movement of a glider. Bottom: The lattice cell states
constituting the k = 0 glider configuration (black nodes) depend upon the surrounding lattice cell states in their Moore
neighborhoods (gray nodes) in order to make the proper transition to the k = 1 configuration.
186
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
(3) shifted by 1 cell in both the horizontal and vertical directions. Daher, we can say that a glider
centered at location (ich, J ) exists in L at iteration k if the following set of equations is satisfied:
(cid:1)
iþDi;jþDj ¼ f 4 LðkÞ
LðkÞ
iþDi(cid:2)1; jþDj(cid:2)1
(cid:3)
;
−1≤Di; Dj≤1
The four different sign assignments correspond to movement in the four possible diagonal
directions ↗, ↘, ↙, and ↖. For each of the possible sign assignments, the resulting nine equations
can be completely written out in terms of cell states at iteration k and nested applications of f.
There are nine cells in a 3 × 3 block and thus only 29 = 512 möglich 3 × 3 patterns. By checking
alle, we find that there are a total of 16 nonempty patterns that satisfy these equations, all of
which are rotations or reflections of the k = 0 and k = 1 patterns shown at the top of Figure 1. Es ist
important to emphasize that this spatiotemporal definition of a glider only makes sense against a
local background of inactive cells. If any of the patterns in Figure 1 were surrounded by a field
of active cells, not only would the resulting configuration be unrecognizable as a glider by an external
observer, but it would fail to propagate or otherwise behave as one.
In a previous article [1], I suggested that spatiotemporal patterns such as gliders can also be
interpreted as self-producing systems within a GoL lattice and thus may provide a simple model
of a physical autopoietic system. The ideal way to test this proposal would be to provide a formal
characterization of the organization of a glider and then examine the extent to which this organiza-
tion satisfies MVʼs definition of autopoiesis. This is the focus of ongoing work. For the purposes of
dieser Artikel, I will simply describe the autopoietic formulation of a glider sketched in [1] so that we
can focus here on exploring the cognitive implications of this formulation.
From an autopoietic perspective, we can think of a glider as consisting of configurations of
components (the states of the underlying lattice cells) that participate in a network of processes
(the GoL update rules acting over four iterations through the overlapping Moore neighborhoods
of these components) that regenerate the very configurations of components whose interactions
are necessary to maintain that network. Although the term “glider” is normally only applied to par-
ticular configurations of ON cells, it is easy to see that this definition is incomplete from an auto-
poietic perspective. In order for the ON cells (black nodes in the bottom of Figure 1) to undergo the
transitions necessary for the preservation of a glider, all of the other cells in their Moore neighbor-
hoods (gray nodes) must be OFF. Because the states and transitions of these OFF cells codetermine
and are codetermined by the ON cells, they must be considered a fundamental part of a gliderʼs
constitutive network of processes. Zusätzlich, they form a kind of spatial boundary that delineates a
glider from its surroundings. Daher, in this article, a glider will be defined as the 16 possible rotations
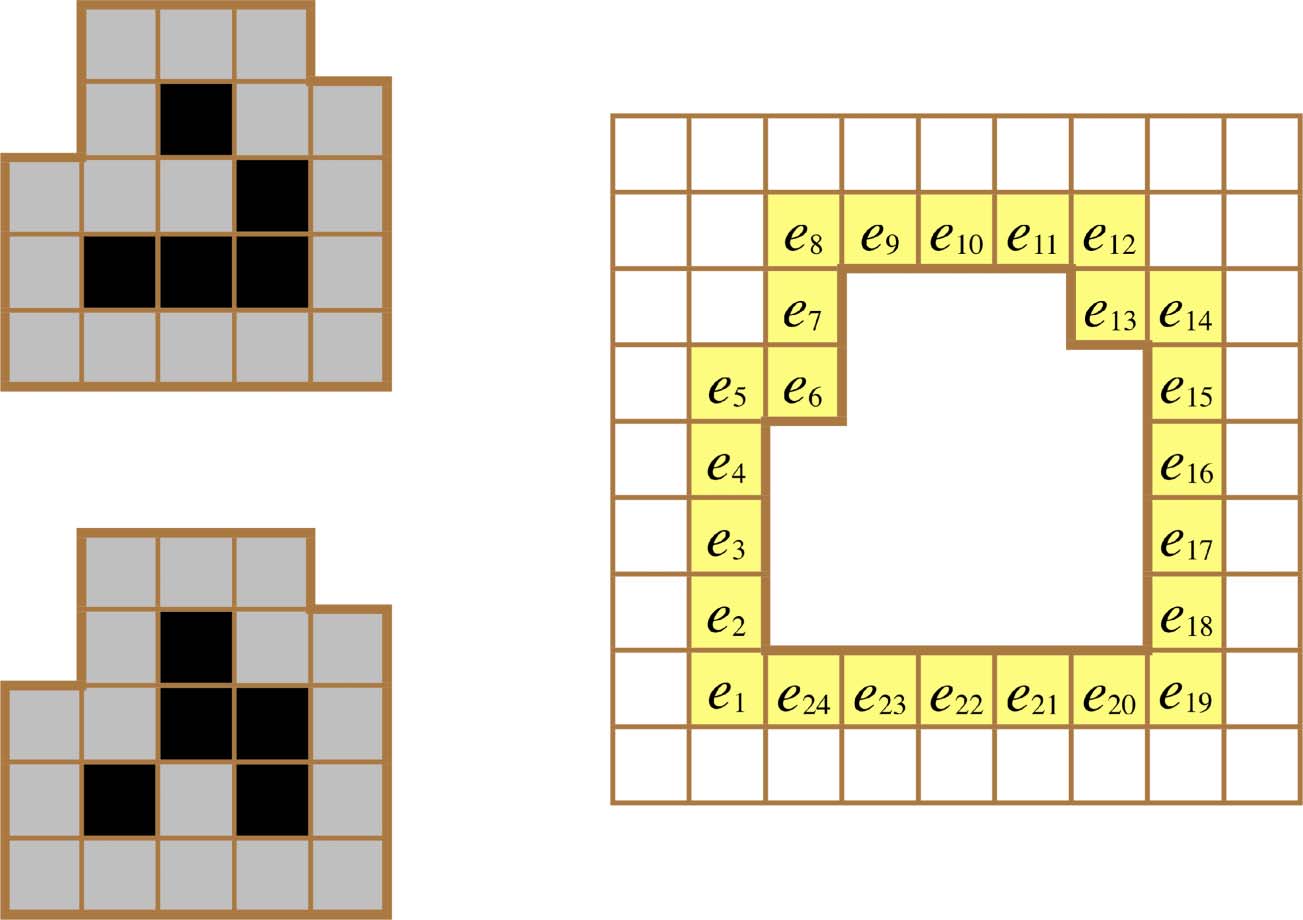
and reflections of the two canonical patterns shown on the left side of Figure 2. We will use G to
refer to this set of possible glider configurations.
M
For later reference, we introduce the naming convention Au
for these glider configurations.
There are two basic forms A: W (the wedge shape) and R (the rocket shape). Each form can have
four different orientations u: 0, k/2, k, and −k/2. Zusätzlich, each orientation can occur with
two different chiralities m: R (right-handed) and L (left-handed). One interesting observation to
make is that these three features—form, orientation, and chirality—are emergent properties of a
glider; they do not exist at the level of the individual cells that constitute it. Higher-level glider fea-
tures, such as the direction of glider movement, can be derived from these fundamental properties.
4 Cognitive Domain
In an empty environment, gliders undergo an endlessly repeating sequence of state changes deter-
mined by their own intrinsic dynamics (Figur 1). Jedoch, a nonempty environment can perturb
Artificial Life Volume 20, Nummer 2
187
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
Figur 2. The canonical W (left top) and R (left bottom) glider states and a labeling of the cells in their immediate
Umfeld (in the electronic version, the yellow lattice cells are at the right).
this sequence in various ways. Recall that in MVʼs framework, an entityʼs cognitive domain is the set
of all interactions in which it can participate without loss of identity. The goal of this section is to
completely characterize the cognitive domain of a glider.
Es gibt 24 environment cells immediately surrounding a glider (Figur 2, Rechts). We will call this
set of 24 cells a gliderʼs 1-environment and postpone a more general discussion of larger envi-
ronments until Section 7. Since each of the cells in the 1-environment can be either 0 oder 1, Dort
Sind 224 possible perturbations P that a glider can undergo. For reasons that will become clear
shortly, we will refer to these as microperturbations. The consequences of each microperturbation
depend on the glider form, but not on its orientation or chirality (since the effect will be the same
after the appropriate rotation or reflection of both the glider and its environment). Daher, we can
impose all 224 possible microperturbations on each of the two canonical W0
R configurations
in an otherwise empty environment and use symmetry to fill in the consequences for the remaining
14 configurations.
R and R0
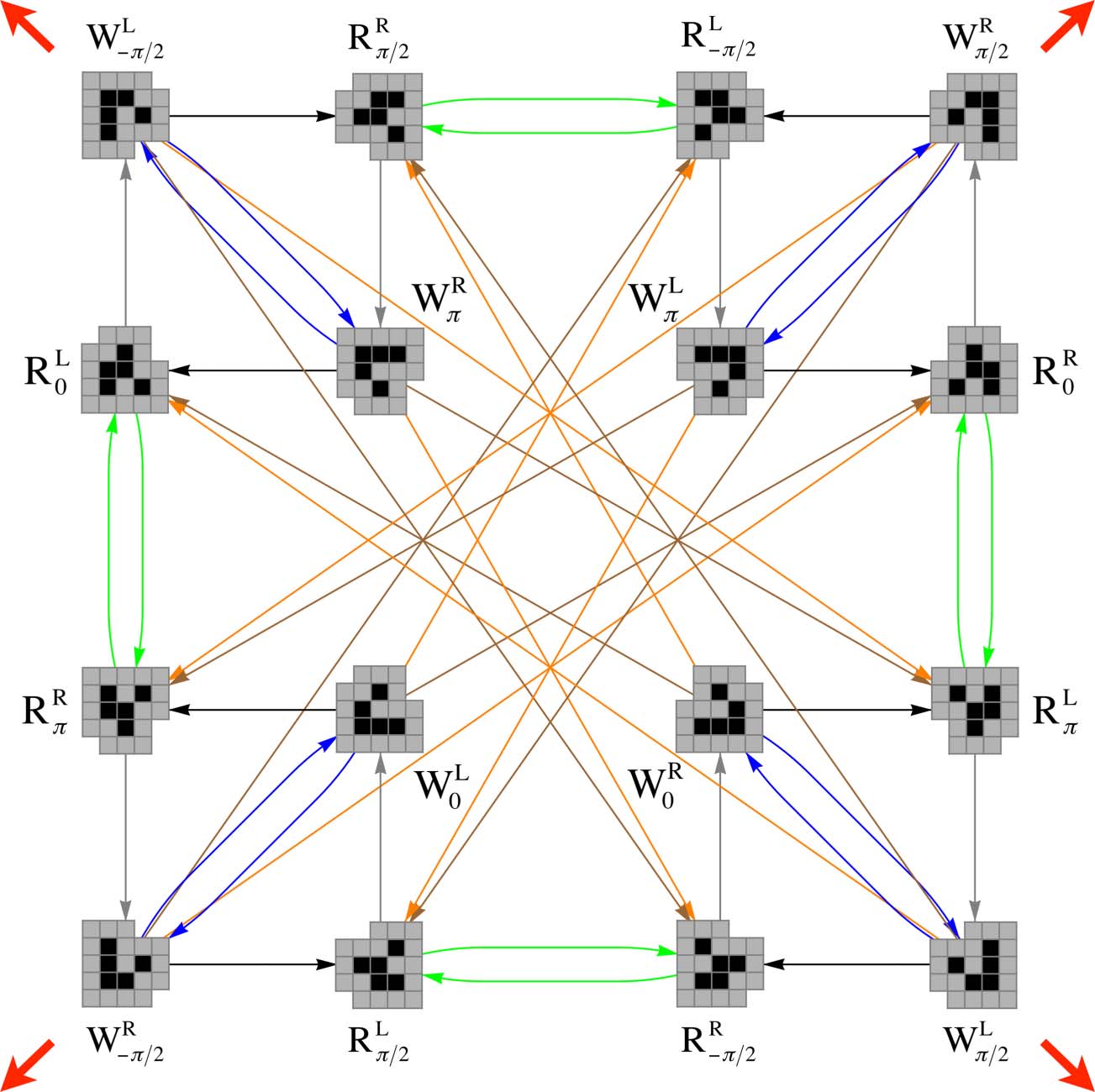
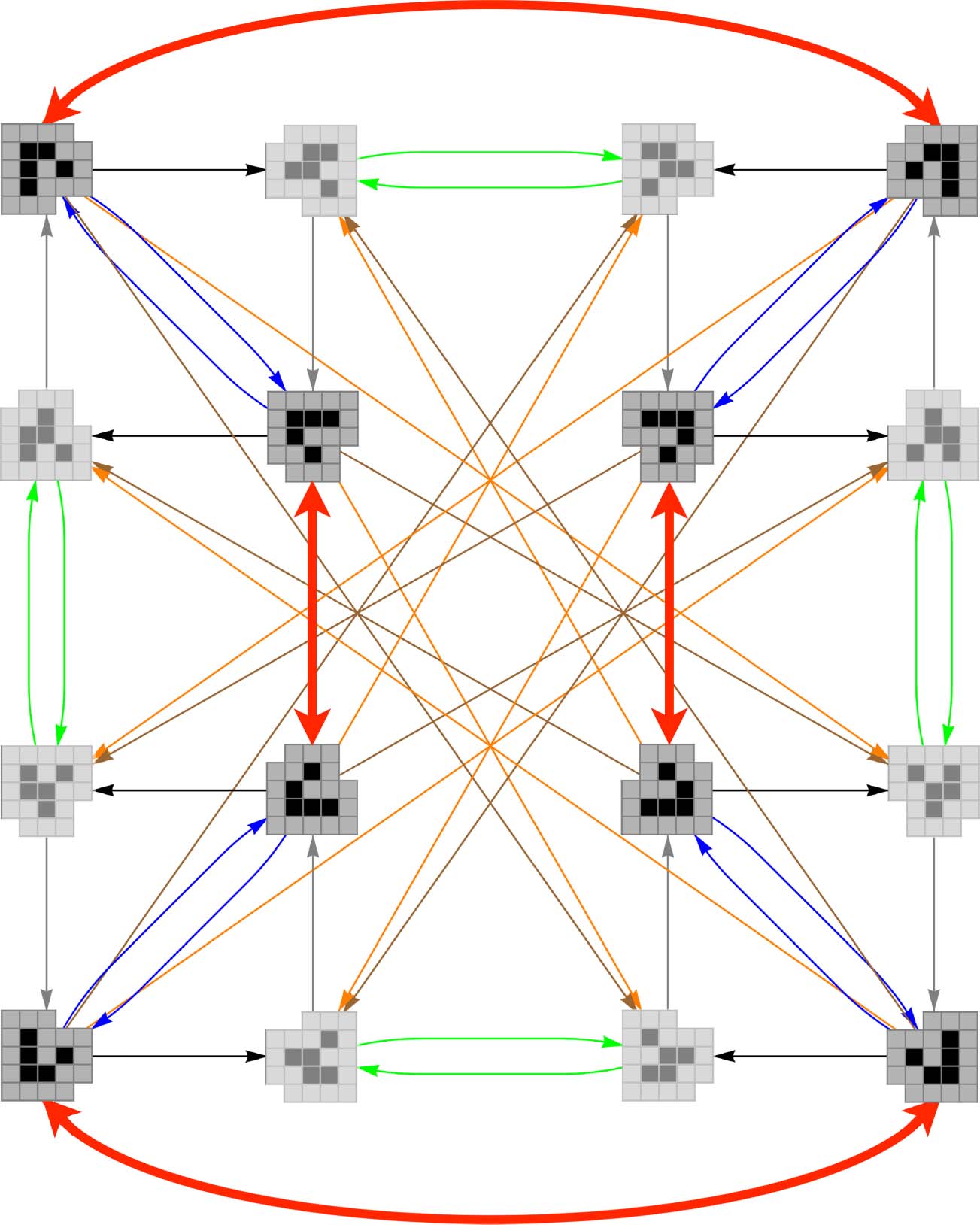
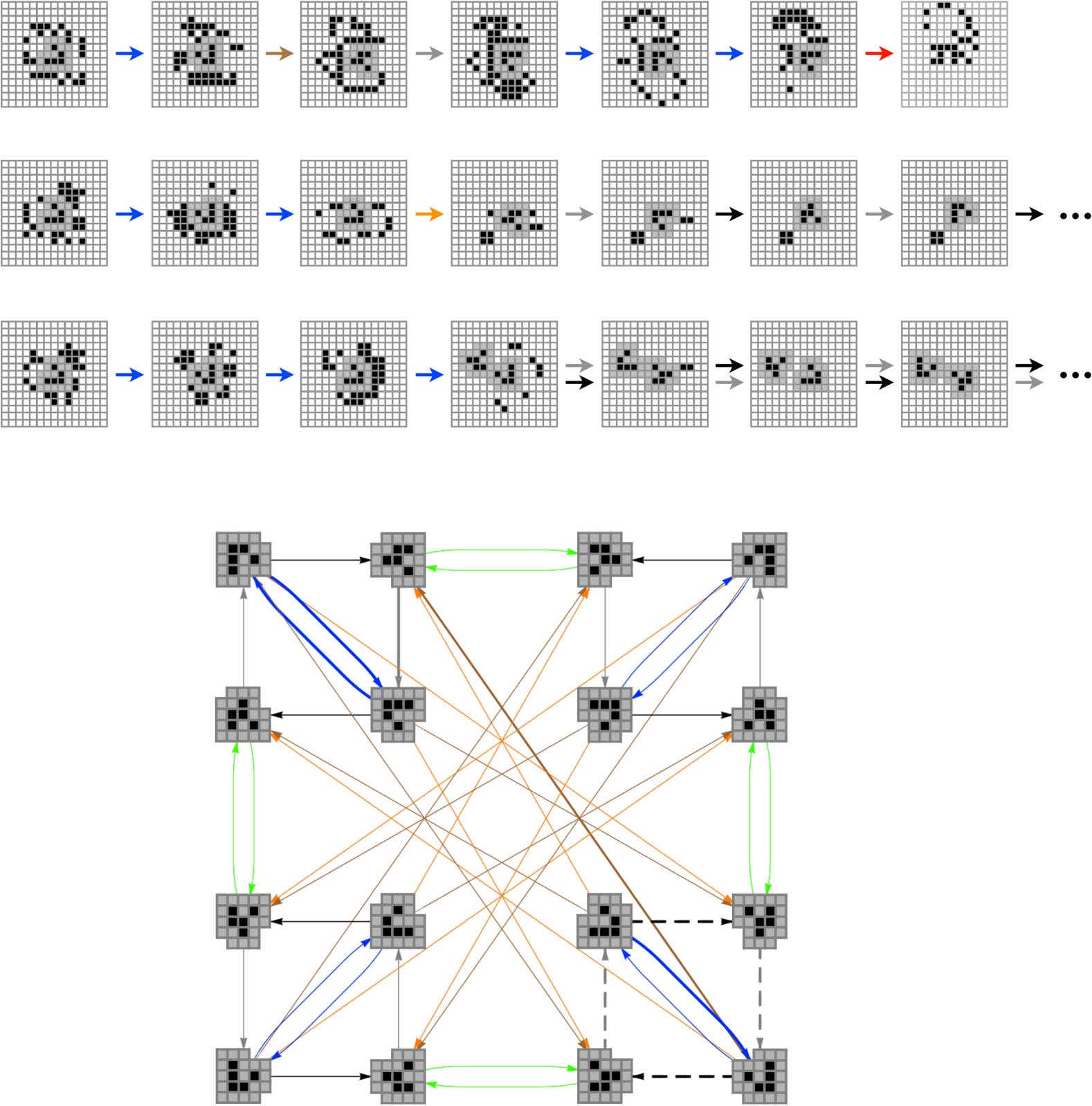
The results of this exhaustive microperturbation study are shown as an interaction graph in
Figur 3. Of all perturbations, 99.57% are lethal for the W form and 99.87% are lethal for the R form.
The remaining perturbations induce transitions from one glider state to another and thus preserve
the gliderʼs identity while changing its structure. These perturbations fall into classes C that we will
refer to as macroperturbations and that we will label by the color of the corresponding arc in Figure 3.
Daher, C = {BLACK, BROWN, BLUE, ORANGE, GRAY, GREEN}. Two microperturbations fall into the same
macroperturbation class if they perturb the same initial glider state into the same subsequent glider
L
R configuration into a Wk/2
state. Zum Beispiel, all microperturbations that transform a W0
configuration fall into the BLUE class. The BLUE class also contains all microperturbations that
produce an equivalent transformation under rotational and/or reflectional symmetry. Zum Beispiel,
L configu-
all microperturbations that produce a transformation from a Wk/2
ration (which are just k/2 rotations of the W0
configurations, jeweils) are also
included in the BLUE class.
R configuration to a Wk
L
R and Wk/2
Note that the BLACK and GRAY macroperturbations are special because they include the 0-perturbation,
das ist, they are equivalent to the transition that a glider state would undergo in the absence of any
environmental perturbation. We call perturbations in these two classes null perturbations because
188
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
they have no effect on the glider. If we focus on only the BLACK and GRAY arcs in Figure 3, Wir
observe four distinct BLACK → GRAY → BLACK → GRAY 4-cycles, corresponding to unperturbed
gliders moving along the four diagonal directions marked in red, in the electronic verison. Pertur-
bations in the other classes trigger transitions within or between these different 4-cycles.
We can think of this interaction graph as defining a new parameterized function F : G×C→G
that maps one glider state to another depending upon the class of perturbation applied. Für
R . Because encountering some classes of per-
Beispiel, we can say that F(W0
turbations in some states is lethal for a glider, F is only a partial function. In order to make it
a total function, we define an additional state ∅ to represent the absence of a glider, extend the
domain of F to G∪f∅g(cid:3)C→G∪f∅g, and define ∅ to be absorbing, das ist, F(∅; C) = ∅ for all
possible perturbation classes c∈C (once a glider is dead, its stays dead).
R; ORANGE) = Rk/2
Beachten Sie, dass, although the function F on glider states is ultimately grounded in the lattice update
function f on cell states defined in Section 2, the two are not identical. The function f describes the
microdynamics of the constituents of a glider, and the cognitive map F describes the macrodynamics
of glider entities as they undergo transformations in response to environmental perturbations.
Whereas f applies to any lattice configuration, the function F can only be applied to a glider when
one is actually present in the lattice. Daher, the cognitive domain can be interpreted as a new
emergent domain of description.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3. The cognitive domain of a glider. Each glider configuration is labeled as described in the main text, Und
transitions between them are colored according to the class of the perturbations that produce that transition. Im
electronic version, red arrows indicate the direction of motion of each of the four BLACK → GRAY → BLACK → GRAY 4-cycles
through the lattice.
Artificial Life Volume 20, Nummer 2
189
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
Because the glider organization is preserved by all perturbations within its cognitive domain,
we can also characterize the various classes of perturbations by the glider properties that they
maintain invariant:
1. Form is preserved by BLUE and GREEN perturbations only; all other perturbations swap it.
2. Chirality is preserved by GRAY and ORANGE perturbations only; all other perturbations
swap it.
3. Orientation is preserved by BROWN perturbations only; GRAY, BLUE, and ORANGE
perturbations rotate by (cid:2)k/2, whereas BLACK and GREEN perturbations rotate by k.
4. BLACK perturbations have no invariants, simultaneously swapping form and chirality and
rotating by k.
Endlich, the direction of glider motion is preserved by BLACK, GRAY, and BLUE perturbations,
whereas BROWN and ORANGE perturbations reverse the direction of motion, and GREEN perturbations
can reflect about either the horizontal or the vertical axis, depending on the chirality and orientation
of the R form to which they are applied.
5 Glider Epistemology
Each macroperturbation class contains many microperturbations. What features do all micro-
perturbations in a given macroperturbation class share? How does a glider distinguish between
microperturbations falling into different macroperturbation classes, but fail to distinguish between
microperturbations in the same class? Recall that, according to MV, for an entity to “know” a
given environmental configuration is for it to undergo a nondestructive change in structure as
a result of interacting with that configuration without disintegration. Because we as scientific
observers stand outside the GoL lattice, we can simultaneously consider the relationship between
all possible environmental configurations and all possible glider states. daher, we can char-
acterize the sets of distinctions that a glider can and cannot make about the state of its immediate
environment and how those distinctions are grounded in the particular way that a glider maintains
its identity. In this sense, we are in a position to completely understand the “epistemology” of
a glider.
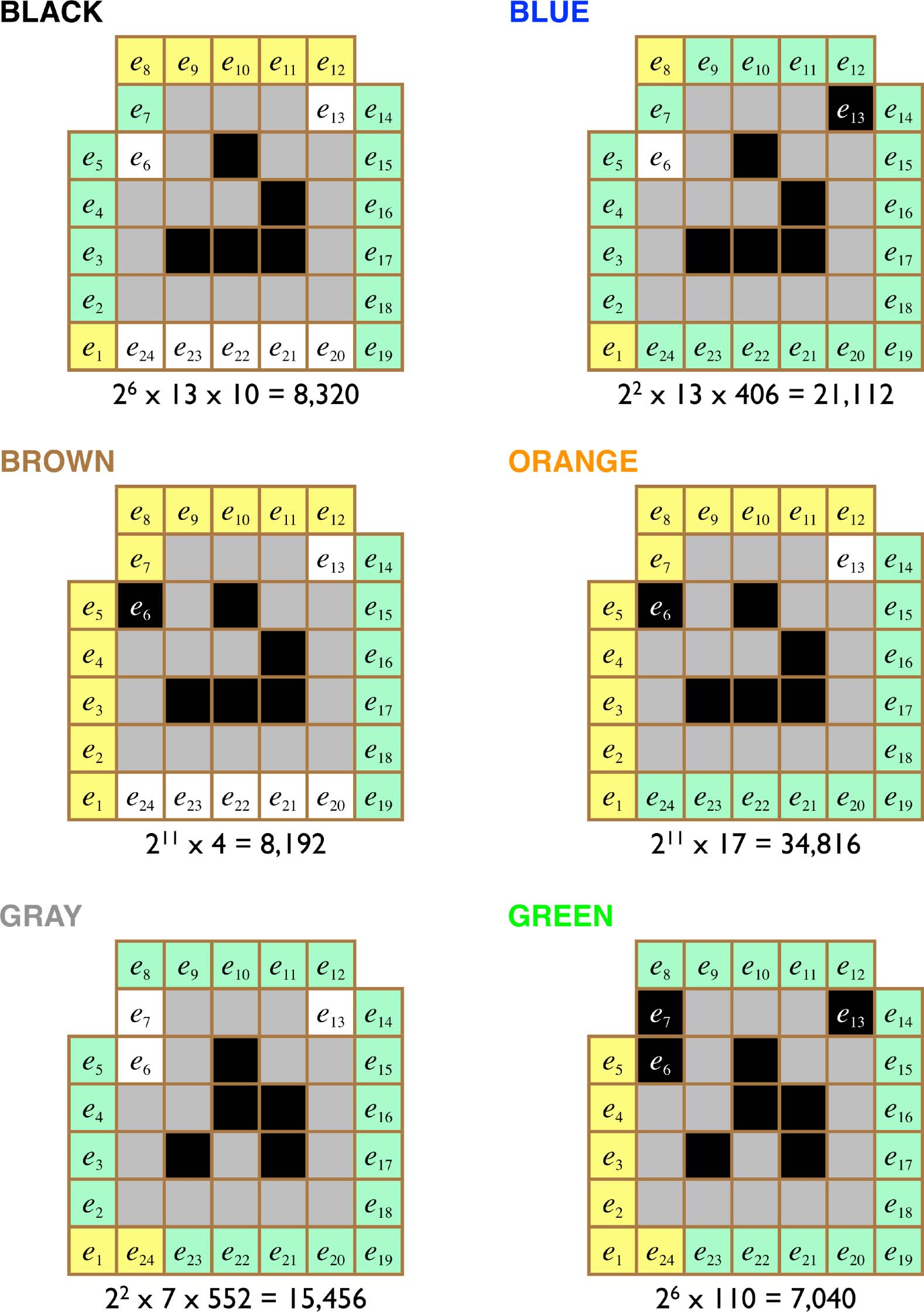
By simply enumerating the effect of each microperturbation from the exhaustive perturbation
study described in the previous section, we find that, of the 224 = 16,777,216 possible micro-
perturbations to a glider, 16,683,428 destroy it. Daher, the vast majority of immediate environmental
configurations are fundamentally unknowable by a glider. Der 93,788 remaining configurations
are knowable depending on the gliderʼs form, with the following breakdown. For the W form,
es gibt 8,320 BLACK perturbations, 8,192 BROWN perturbations, 21,112 BLUE perturbations, Und
34,816 ORANGE perturbations, for a total of 72,440 survivable perturbations. For the R form, Dort
Sind 15,456 GRAY perturbations and 7,040 GREEN perturbations, for a total of 22,496 survivable
perturbations. Interessant, 1,148 perturbations are shared by both the BLACK and GRAY classes; A
gliderʼs response to these perturbations depends entirely on the state it is in when they are encoun-
tered. Ansonsten, all of these classes are disjoint. Zum Beispiel, any BLUE perturbation is lethal to the
R form, and any GREEN perturbation is lethal to the W form.
In von Uexküllʼs terms [30], these classes form a gliderʼs Umwelt. From the 224 Umwelt
configurations that we can distinguish, a glider can distinguish only the six classes in C: Micro-
perturbations from within the same macroperturbation class produce the same glider state and
thus the same response to a subsequent perturbation. Außerdem, the structure of these classes
may appear nonsensical to us. We normally describe biological organisms interacting with their
environments in terms of such categories as “terrain,” “food,” “predator,” and so on, but no such
categories are apparent here. Jedoch, our task is not to evaluate the significance of these classes
190
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
to us, but rather to understand how a gliderʼs organization and structure make them significant to
Es. We do this by characterizing the structure of each class and showing how this structure derives
from the constraints that must be satisfied for a glider to maintain its existence in response to
a perturbation.
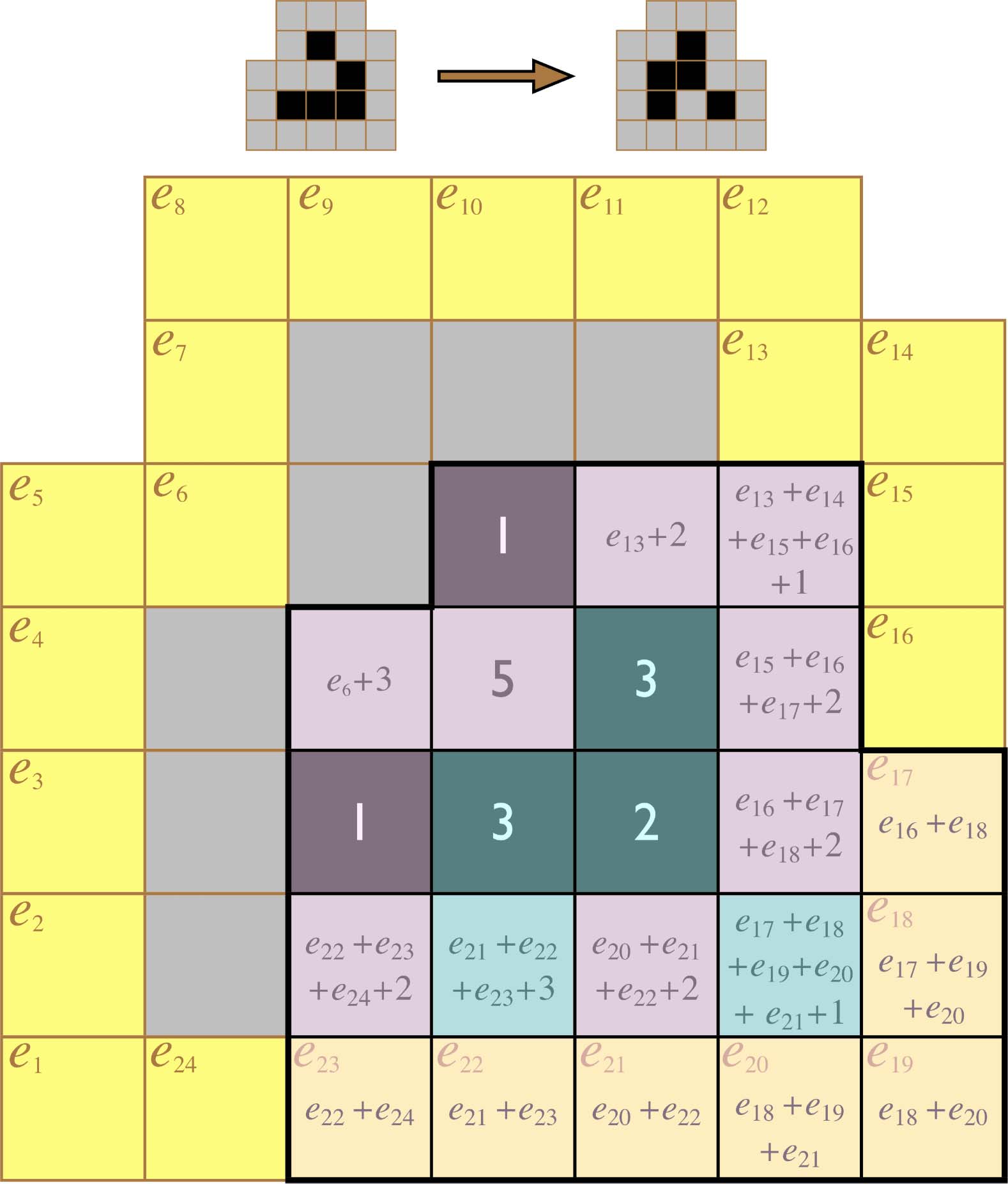
The structure of each class is summarized in Figure 4. Each image in this figure shows the
initial glider state and a representation of the constraints required to make the named transition
geschehen. The following environmental cell coloring convention is used. Black and white environ-
mental cells are constrained to be either ON or OFF, jeweils, in order for the given transi-
tion to take place. Green environment cells are partially constrained; although no single pattern
of activity is required for these cells, only a subset of the possible patterns is permissible. Yellow
environmental cells are completely unconstrained. Interessant, we can see that different transi-
tions are sensitive to different combinations of environmental cells; in effect, different sensory
surfaces emerge at different locations around the glider, depending on its state and the immediate
situation. Außerdem, it turns out that nonlocal integration across these sensory surfaces is
required for all of the nonnull transitions: At least two nonadjacent patterns of ON cells are
necessary for these transitions to take place.
–e24
For a BLACK transition from a W-form glider to take place, environment cells e6, e13, and e20
must be OFF. Cells e1 and e8–e12 can take on any value. Endlich, cells e2–e7 must take on one of
13 patterns, and cells e14–e19 must take on one of 10 patterns. This gives a total class membership
von 26 × 13 × 10 = 8,320 perturbations.
For a BLUE transition from a W-form glider to take place, cell e6 must be OFF and cell e13 must be
–e13 must take on one of 13 patterns, Und
ON. Cells e1 and e8 can take on any value. Endlich, cells e2
the remaining 15 green cells must take on one of 406 patterns. This gives a total class membership of
22 × 13 × 406 = 21,112 perturbations.
For a BROWN transition from a W-form glider to take place, cell e6 must be ON and cells e13 and
e20–e24 must be OFF. Cells e1–e5 and e7–e12 can take on any value. Endlich, cells e14–e19 must take on
one of four possible patterns. This gives a total class membership of 211 × 4 = 8,192 perturbations.
For an ORANGE transition from a W-form glider to take place, cell e6 must be ON and cell e13 must
–e24 must take on one of 17 anders
be OFF. Cells e1
patterns. This gives a total class membership of 211 × 17 = 34,816 perturbations.
–e12 can take on any value. Cells e14
–e5 and e7
For a GRAY transition from an R-form glider to take place, cells e6, e7, and e13 must be OFF. Cells
e1 and e24 can take on any value. Cells e2–e5 must take on one of 7 possible values and cells e14–e23
must take on one of 552 possible values. This gives a total class membership of 22 × 7 × 552 =
15,456 perturbations.
Endlich, for a GREEN transition from an R-form glider to take place, cells e6, e7, and e13 must be
–e23 must take on one of 110
ON. Cells e1
patterns. This gives a total class membership of 26 × 110 = 7,040 perturbations.
–e5 and e24 can take on any value. Cells e8
–e12 and e14
Nächste, we illustrate the process of deriving the structure of a perturbation class from the con-
straints that must be satisfied for a glider to make the required state transition in response to per-
turbations from that class. Consider the BROWN transition shown at the top of Figure 5. To begin, Wir
draw the initial glider state, with its ON cells in black, its OFF cells in gray, and its environment cells
in yellow to indicate that they can in principle take on any value (bottom of Figure 5). We then
superimpose a transparent image of the target glider state, with its ON cells in blue and its OFF
cells in pink, in the proper position. Endlich, for every cell in the target glider state, we fill in the
number of ON cells in its Moore neighborhood. Some of these sums are known exactly, and others
are known only symbolically because they depend on the unknown states of the environment. Wir
wish to solve for the set of environmental states that allow this transition to take place. Beachten Sie, dass,
since they do not enter into the neighbor sums of any cell in the target glider states, we can already
–e12 can take on any value without affecting a BROWN transi-
see that environment cells e1
tion, which is why they remain yellow in the electronic version of Figure 4.
–e5 and e7
We next write down the full set of equations that must be satisfied for each cell in the initial state
to have the correct value in the target state. Since we can immediately verify that each cell with a
Artificial Life Volume 20, Nummer 2
191
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4. The structure of the six perturbation classes distinguished by a glider. In the electronic version, in order for each
of the named transitions to occur, environment cells shown in black and white must be ON and OFF, jeweils, while
green cells are partially constrained and yellow cells are unconstrained. The cardinality of each class is given below the
corresponding diagram, with powers of 2 accounting for the unconstrained yellow cells and each remaining factor
accounting for the allowable patterns of a distinct subset of partially constrained green cells.
192
Artificial Life Volume 20, Nummer 2
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
numerical neighbor count will make the proper transition, we will not consider these states
weiter. For the nonnumerical cell counts, we reason as follows. Consider the cell with neighbor-
hood count e6 + 3. This cell is OFF in the initial state and should remain OFF in the target state.
The only way that this cell can fail to remain OFF is for this sum to equal 3. This gives rise to the
inequality e6 + 3 6¼ 3. Similar reasoning (with conditionals arising for environment states that
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 5. In the electronic version, neighborhood counts involved in determining the membership of the BROWN
perturbation class. The original W state is shown in black and gray, surrounded by its immediate environment in yellow.
The R state resulting from a BROWN perturbation is shown in its proper position as a transparent overlay, with its ON
cells colored blue and its OFF cells colored pink. The neighborhood counts of each cell in the new R state are shown as
an integer when they are known, and as a symbolic expression involving unknown environment states otherwise.
Artificial Life Volume 20, Nummer 2
193
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
become part of the target glider because their initial states are unknown) gives rise to the following
set of constraint equations:
(cid:4)
(cid:4)
e16 þ e18 6¼
e6 þ 3 6¼ 3
e13 þ 2 6¼ 3
e13 þ e14 þ e15 þ e16 þ 1 6¼ 3
e15 þ e16 þ e17 þ 2 6¼ 3
e16 þ e17 þ e18 þ 2 6¼ 3
e17 þ e18 þ e19 þ e20 þ e21 þ 1 ¼ 3
e20 þ e21 þ e22 þ 2 6¼ 3
e21 þ e22 þ e23 þ 3 ¼ 3
e22 þ e23 þ e24 þ 2 6¼ 3
3;
e17 ¼ 0
2; 3;
e17 ¼ 1
3;
e18 ¼ 0
2; 3;
e18 ¼ 1
3;
e19 ¼ 0
2; 3;
e19 ¼ 1
3;
e20 ¼ 0
2; 3;
e20 ¼ 1
3;
e21 ¼ 0
2; 3;
e21 ¼ 1
3;
e22 ¼ 0
2; 3;
e22 ¼ 1
3;
e23 ¼ 0
2; 3;
e23 ¼ 1
e17 þ e19 þ e20 6¼
e18 þ e19 þ e21 6¼
e21 þ e23 6¼
e18 þ e20 6¼
e22 þ e24 6¼
e20 þ e22 6¼
(cid:4)
(cid:4)
(cid:4)
(cid:4)
(cid:4)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
Our next step is to simplify this set of equations as much as possible. Two trivial simplifica-
tions are immediately obvious. Since all environment cells must take on the value 0 oder 1, the only
= 1, which is why this cell is black in
way that the constraint e6 + 3 6¼ 3 can be satisfied is if e6
= 0, Und
Figur 4. Likewise, the only way that the constraint e13 + 2 6¼ 3 can be satisfied is if e13
knowing this value removes e13 from the other equation in which it appears. Another simplifica-
tion comes from the constraint e21 + e22 + e23 +3 = 3, which can only be true if e21 = e22 = e23 = 0.
This conclusion then triggers a chain of other simplifications that result in the conclusion that
e20 = e24 = 0, which is why all of these cells are white in Figure 4. Endlich, we can simplify the
conditional inequalities by observing that the sum of the values of two environment cells can
never equal 3, so that any assertion of this fact is redundant. Applying all of these simplifications
–e19, welches ist
leaves us with the following set of unconditional constraints for the values of e14
why they are green in the electronic version of Figure 4:
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
e14 þ e15 þ e16 6¼ 2
e15 þ e16 þ e17 6¼ 1
e16 þ e17 þ e18 6¼ 1
e16 þ e17 þ e18 6¼ 3
e17 þ e18 þ e19 ¼ 2
Solving this set of equations gives the four possible patterns that these cells can take on in a
BROWN perturbation: {e14, e15, e16, e17, e18, e19} = {0, 1, 0, 1, 1, 0}, {0, 0, 1, 1, 0, 1}, {1, 1, 1, 1,
0, 1}, {1, 1, 1, 0, 1, 1}.
194
Artificial Life Volume 20, Nummer 2
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
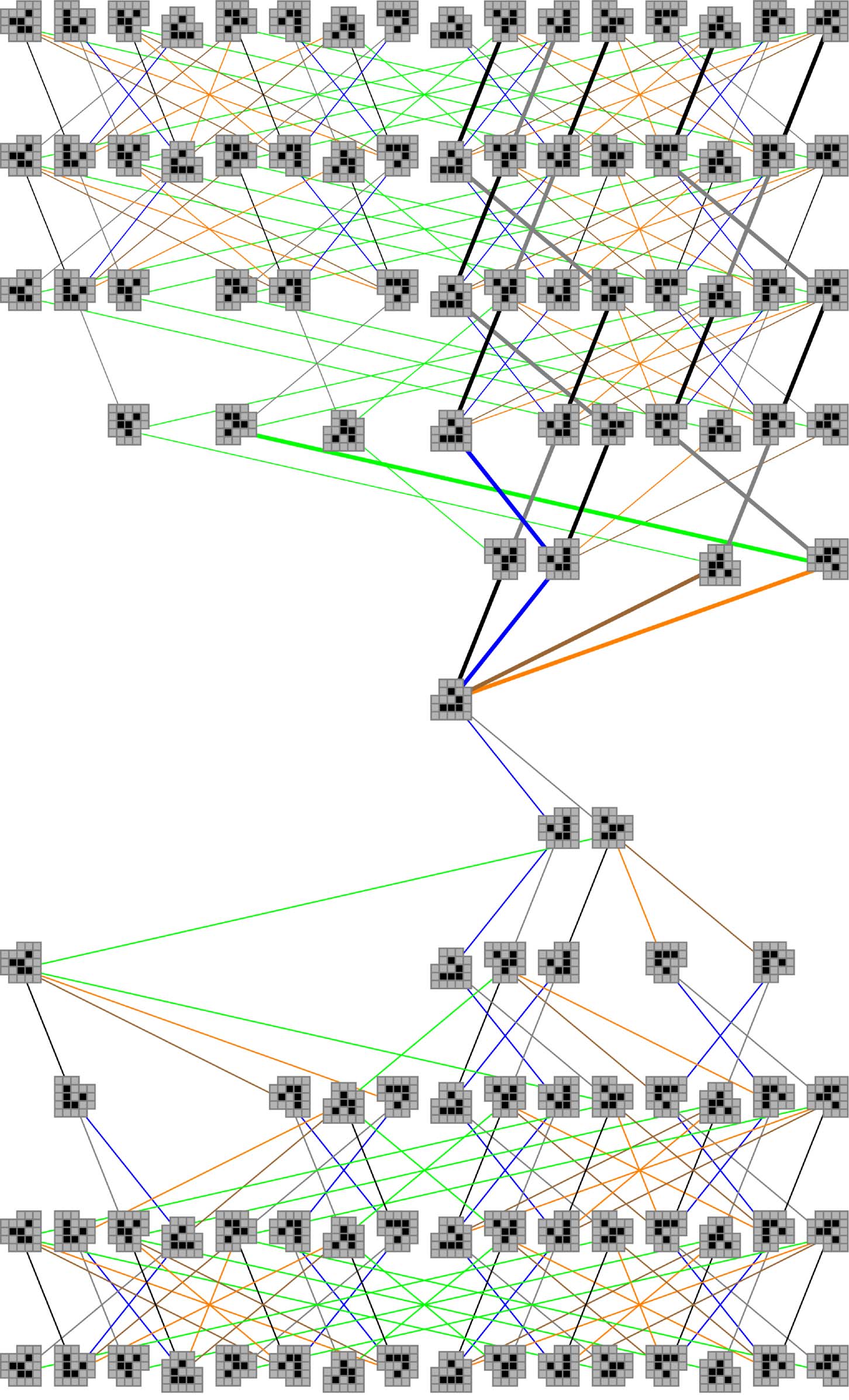
Figur 6. All behavioral trajectories through the canonical W state, from five steps in the past through five steps in the
future. Thick lines indicate the subset of behavioral trajectories that result from structural coupling.
Artificial Life Volume 20, Nummer 2
195
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
Similar calculations can be made for the other five perturbation classes. In each case, folgen-
ing the procedure just outlined, a set of explicit constraint equations can be derived that
describe which subsets of environmental cells must take on fixed values, which can take on
any of a constrained set of values, and which can take on any value in order for a given transi-
tion to take place. Außerdem, the process of deriving these constraint equations illuminates
how they are grounded in the requirement that a glider maintain its identity in response to each
class of perturbation.
6 Behavioral Trajectories
To this point, we have only considered the one-step effect of individual 1-environment perturba-
tions on a glider. Jedoch, im Laufe der Zeit, a persisting glider will undergo a sequence of state changes
as a result of the interaction between its own internal dynamics and the sequence of perturbations
that it experiences. We will call such sequences behavioral trajectories, because an observer would
interpret them as actions that the glider is taking (turning to the left, moving one step to the right,
usw.). What can we say about the structure of such behavioral trajectories? In diesem Abschnitt, Wir
will characterize the dynamics of a glider driven by imposed sequences of 1-environment macro-
perturbations. This will prepare us for an examination in Section 7 of how MVʼs concept of structural
coupling can be applied to the situation where a glider and its environment are in a relationship of
mutual perturbation.
Formally, this involves studying the dynamics of iterates of the cognitive map F, das ist, F k( g0;
c0,…,ck−1), where g0 denotes an initial glider state drawn from G, and c0,…,ck−1 denotes a sequence
of perturbation classes, each of which is drawn from C. Daher, Zum Beispiel, F 2( W0
R; BLUE,
ORANGE) = R0
R; BLUE, GREEN, …) = ∅ for all k > 1. The latter fate can be avoided
by applying only BLACK, BROWN, BLUE, or ORANGE perturbations to W-states and applying only GRAY
or GREEN perturbations to R-states.
L, but F k(W0
Since behavioral trajectories are just paths through the cognitive domain, it is useful to visu-
alize the structure of these paths for a particular glider state by unrolling the interaction graph
R, from five iterations in
im Laufe der Zeit. Figur 6 shows all paths through the canonical wedge state W0
the past to five iterations in the future. Each path through this layered graph represents a valid
behavioral trajectory. An analogous graph can be constructed for any glider state in the cognitive
Domain. Note that paths can both diverge and converge, depending upon the sequence of per-
turbations encountered. Note also that iteration 4 includes all 16 glider states. Daher, Dort
always exists a sequence of perturbations of length at most 4 that can take a glider from one state
R →
to any other state. An example of a transition that requires a minimum of four steps is W0
L, which can only be accomplished by a length-4 perturbation sequence such as {BLUE, BROWN,
Wk
GREEN, GRAY}. An important consequence of this fact is that the path structure from iteration 4 Zu
iteration 5 repeats indefinitely into the future (and similarly for the path structure from iteration −4
to iteration −5 into the past).
How a glider responds to a given perturbation depends on the state it is in at the time, which in
turn depends at least in part on the sequence of perturbations that it has previously experienced.
Daher, as a glider encounters and survives a particular sequence of perturbations, dependencies build
up between the gliderʼs state and that sequence. Our formalization of a gliderʼs cognitive domain
allows us to pose and answer a variety of interesting questions about the structure of these depen-
dencies for a glider, both in forward and backward time.
The kinds of forward questions that we can address include the following:
(1) Given an initial glider state and a sequence of k perturbations, what state does it end up in? Der
answer to this question is simply F k( g0; c0,…,ck−1). Zum Beispiel, we noted above that F4(W0
R; BLUE,
BROWN, GREEN, GRAY) = Wk
L.
196
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
Figur 7. The effect of a {BLUE, BROWN, GREEN, GRAY} perturbation sequence on a gliderʼs cognitive domain. In the electronic
Ausführung, R-states are destroyed, and W-states are transformed as shown by the red arrows.
(2) Given a sequence of k perturbations, how does what state a glider ends up in depend on what
state it started in? This question is answered by studying Fk( G; c0,…,ck−1) as a function of g.
Zum Beispiel,
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
F 4ðg; BLUE; BROWN; GREEN; GRAYÞ ¼
8
>>>>>>>>>>>>>< >>>>>>>>>>>>>:
−k=2
WL
k
WL
WL
0
WL
k=2
WR
k
WR
WR
0
WR
k=2
∅
−k=2
−k=2
if g ¼ WR
0
if g ¼ WR
k=2
if g ¼ WR
k
if g ¼ WR
if g ¼ WL
0
if g ¼ WL
k=2
if g ¼ WL
k
if g ¼ WL
ansonsten
−k=2
Artificial Life Volume 20, Nummer 2
197
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
This sequence reflects W-form gliders about either their horizontal or vertical axes, depending
on their orientation (red arrows in the electronic version of Figure 7) while destroying all R-form
gliders.
(3) Given an initial glider state, how does what state a glider ends up in depend on what sequence of
perturbations it encounters? This question is answered by studying F k( g0; C k) as a function of the
possible length-k perturbations Ck. Zum Beispiel,
(cid:5)
F 2 WR
0 ; C 2
(cid:6)
¼
8
>>>>>>>>>>>>>>>< >>>>>>>>>>>>>>>:
k=2
WL
RR
0
WR
0
RR
k=2
RL
0
WL
−k=2
RR
k
WR
k
RL
−k=2
∅
if C 2 ¼ fBLACK; GRAYg
if C 2 ¼ fBLACK; GREENg
if C 2 ¼ fBLUE; BLUEg
if C 2 ¼ fBLUE; BROWNg
if C 2 ¼ fBLUE; ORANGEg
if C 2 ¼ fBROWN; GRAYg
if C 2 ¼ fBROWN; GREENg
if C 2 ¼ fORANGE; GRAYg
if C 2 ¼ fORANGE; GREENg
ansonsten
Natürlich, all of these forward questions are just special cases of the general question of how the
state a glider ends up in at a given time depends on where it starts and the sequence of perturbations
it encounters, das ist, F k( G; C k) for arbitrary k, G, and C k, which in turn is really just a question about
the structure of all possible forward paths through the cognitive domain.
The kinds of backward questions that we can address include the following:
(1) What initial state g leads to a given final state gf after a given sequence of perturbations, das ist,
{G|Fk( G; c0,…,ck−1) = gf}? Zum Beispiel, {G|F4( G; {BLUE, BROWN, GREEN, GRAY}) = Wk
R}.
(2) What sequence of perturbations leads from a given initial state to a given final state, das ist, {C k|F k
( g0; Ck) = gf}? Zum Beispiel, {C 4|F4(W0
L} = {{BLUE, BROWN, GREEN, GRAY}, {BLACK,
GREEN, GRAY, BLUE}}. Noch einmal, these are just special cases of the general question of how knowing
a gliderʼs state in the present constrains its possible past states and perturbation sequences, das ist,
{G, C k|F k( G; C k) = gf}, which is really just a question about the structure of all possible backward paths
through the cognitive domain.
R; C 4) = Wk
L} = {W0
Daher, given F, it is relatively straightforward to answer any particular instance of these forward
and backward questions. But can we say anything more general about the structure of dependencies
in a gliderʼs behavioral trajectories? Tatsächlich, information theory [4] can be used to quantify the
information that observing a given glider state now gives us about the gliderʼs possible pasts and
futures. Um dies zu tun, we must be explicit about the universe of possible perturbations that
we wish to study. There are four possibilities: (1) the set of all sequences of microperturbations;
(2) the subset of all sequences of microperturbations that preserve glider identity; (3) the set of
all sequences of macroperturbations; (4) the subset of all sequences of macroperturbations that
preserve glider identity. We have mostly focused on (4) in this article, and we will continue to do so
here by assuming a uniform distribution over nonlethal sequences of macroperturbations. Aber es ist so
important to understand that other choices are possible and that different choices will in general
produce different results.
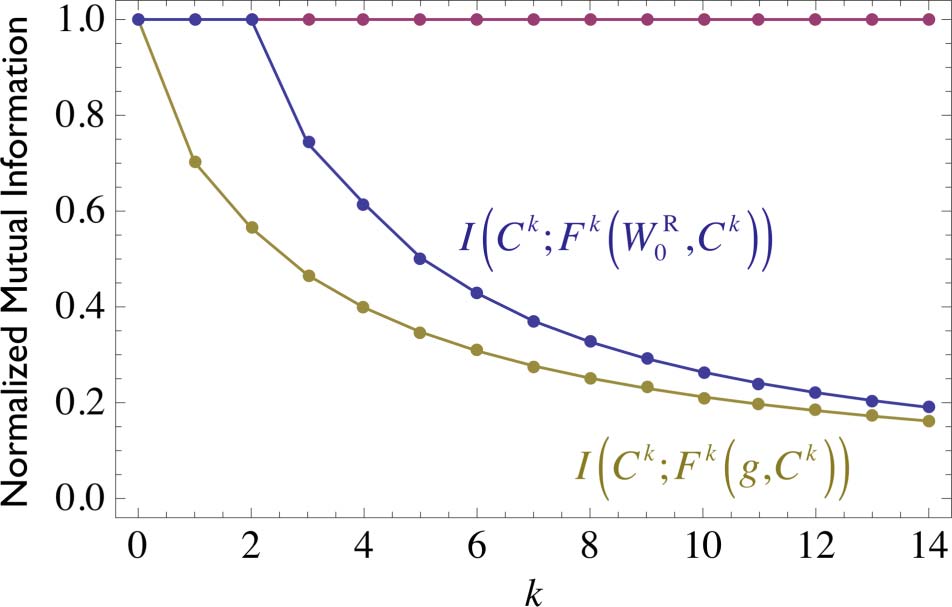
As an example of the application of information theory to characterize the dependence between a
gliderʼs state changes and the sequence of environmental perturbations it encounters, suppose we
198
Artificial Life Volume 20, Number 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
R and we want to quantify the information that a measurement
know that a glider began in state W0
of its state after k iterations carries about the sequence of perturbations it has encountered in the
interim. This is given by the mutual information I(C k; F k(W0
R, C k)), where the mutual information
between two random variables X and Y can be defined in terms of their entropies and conditional
entropies as I(X; Y ) = H(Y ) − H(Y|X ). From this point on we will normalize everything by H(X )
(which just equals log|Ck| in our case, since we are assuming a uniform distribution over nonlethal
paths of length k). Auch, because Y is a function of X in our case, H(Y|X ) = 0 and we are left
with I(C k; F k(W0
R, C k )). If we plot this information as a function of k (Blau
curve in the electronic version of Figure 8), we see that the initially complete information about
perturbation paths begins to fall steadily toward a limiting form (yellow curve) as paths begin to
converge at k = 3. This limiting form is given by I(C k; F k( G, C k )), the path information available in
a state measurement at iteration k when the initial state is unknown, which can be derived in closed
bilden. Similar calculations can be done to characterize the informational relationships for any of the
forward or backward questions described in this section.
R, C k )) = H(F k(W0
7 Structural Coupling
The analysis in the previous section treated each 1-environment perturbation as if it were com-
pletely independent of the preceding one. Although we as external observers can impose such
perturbation sequences on a glider, this is clearly not the case within GoL itself, since environ-
mental states must follow the same underlying laws of “physics” as glider states. Zusätzlich, just
as the environment perturbs the entity, so does the entity in turn perturb the environment. Recall
that MV use the term structural coupling to refer to the mutual selection that occurs between a
surviving entity and its environment of paths of structural change from among the possible paths
of each. How might we apply this concept of structural coupling to the interactions that gliders
can undergo with their environments?
Let us begin by fully analyzing the simplest possible scenario. Suppose that we impose one of
the allowable 1-environment perturbations on a particular glider state as an initial condition in
an otherwise empty lattice, and then subsequently allow the state of the environment to evolve
“naturally” rather than manually imposing additional allowable perturbations. This scenario is the
natural extension of the one studied in the previous section. Examples of it are shown in Figure 9.
Figur 8. The information about the sequence of environmental perturbations a glider has encountered that is available
in a measurement of that gliderʼs state at iteration k. In the electronic version, the blue curve averages over all macro-
perturbation class sequences from the canonical W state, whereas the yellow curve averages over all macroperturbation
class sequences from all possible initial states. Note that the blue curve asymptotically approaches the yellow one. The magenta
curve considers only structurally coupled paths from the canonical W state (thick lines in Figure 6). Note that the state of a
structurally coupled glider retains perfect information about the sequence of perturbations that it has encountered.
Artificial Life Volume 20, Number 2
199
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
Figur 9. Three examples of structurally coupled interactions that, although they all begin with a BROWN perturbation,
evolve in very different ways.
Note that in order to perform this analysis, we need to switch our focus from macroperturbation
classes to a consideration of microperturbations, because two microperturbations in the same class will
in general evolve to different subsequent environment states. Figur 9 shows three examples of initial
BROWN perturbations with very different eventual fates. The glider in the top example survives only
one step, in the middle example survives three steps, and in the third example survives indefinitely.
In order to provide a broader picture of the consequences of structural coupling in this
scenario, let us revisit the macroperturbation pathway graph shown in Figure 6. Recall that this
graph shows all the possible paths to depth 5 in the future and the past for the canonical wedge
R shown, only five survive to level 5 im
state. Of the 208 possible forward paths from W0
presence of structural coupling, with one surviving only to level 2 (thick lines in Figure 6). Notiz
Das, beyond level 2, only null macroperturbation paths survive (alternating gray and black lines).
Note also that these structurally coupled paths do not converge. Das impliziert das, unlike in the
case of unconstrained perturbation sequences, there is no loss of information about the past for
structurally coupled paths. This can be seen in Figure 8 (magenta line in the electronic version),
where a measurement of the glider state at any time provides perfect information about the
sequence of macroperturbations the glider has experienced to that point. This result is perhaps
somewhat surprising and would certainly not be expected to be true for arbitrary environments.
Jedoch, it is true for the kinds of interactions that develop between a glider and all possible
1-environments in an otherwise initially empty lattice.
Wie oben erwähnt, macroperturbations do not tell the entire story in the presence of structural
coupling. Just because some initially BROWN perturbations survive until level 5, that does not mean
R
they all do, as we have already seen in Figure 9. In der Tat, of the 72,440 microperturbations of W0
that survive to level 1, nur 4,458 survive to level 2, nur 2,362 survive to level 5, and only 2,241
R, with similar results. Daher,
survive beyond level 10. A similar analysis can be performed on R0
structural coupling strongly constrains the interactions that a glider will engage in without loss of
Identität. It selects from all possible trajectories of glider–environment dynamics only those that are
consistent with a gliderʼs ongoing existence—or, from the perspective of the glider, it selects a
subset of the possible paths through its cognitive domain.
To reiterate, the specific results we have described so far in this section apply only to the sim-
plified scenario of structural coupling between a glider and all possible 1-environment initial states in
an otherwise empty lattice. Obviously, larger sets of cells can impact a glider over longer periods of
Zeit, and we would ideally also like to examine structural coupling in such larger environments.
Bedauerlicherweise, this is impractical to do in any exhaustive way. Der 24 cells of the 1-environment are
200
Artificial Life Volume 20, Number 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
surrounded by 32 cells of what we can call the 2-environment, und so weiter. Allgemein, the l-environment
8ich + 16 = 4l 2 +
contains 8l + 16 cells, and therefore the total (1,l )-environment contains Ai − 1
20l cells with 24l 2+20l possible initial environment states for a given glider state. Even in finite
lattices with periodic boundary conditions, this number of initial states very quickly becomes
computationally infeasible.
l
A preliminary study of a sample of the (1,2)-environments has revealed a variety of interesting
behavioral trajectories, several examples of which are shown in Figure 10. The top example undergoes
A {BLUE, BROWN, GRAY, BLUE, BLUE} sequence of perturbations before disintegrating. This sequence of
perturbations drives the gliderʼs state along a path through its cognitive domain (solid bold arcs in
the graph at the bottom of Figure 10) that is very different from the path it would follow in an empty
Umfeld (dashed arcs in graph). The middle example undergoes a {BLUE, BLUE, ORANGE}
sequence before entering into a {GRAY, BLACK, GRAY BLACK, …} null perturbation loop that persists
forever, leaving behind a static square pattern called a block. The bottom example begins on a
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 10. Three examples of structurally coupled interactions from a preliminary study of (1,2)-environments. The path
through a gliderʼs cognitive domain corresponding to the uppermost interaction is shown at the bottom, with dashed
lines indicating the path the glider would have followed in isolation and thick lines indicating its structurally coupled path.
Artificial Life Volume 20, Nummer 2
201
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
Figur 11. The simplest nontrivial example of a communicative interaction between two gliders supported by some
surrounding environmental scaffolding.
{BLUE, BLUE, BLUE} sequence before spawning a second glider whose boundary initially overlaps with
its own. Both gliders then enter into null perturbation loops, moving away from one other and
persisting forever.
Even this preliminary study of the trajectories of structural coupling has revealed some intriguing
general patterns. Erste, the trajectories that survive to a given iteration are always a tiny fraction of the
possible perturbation sequences. Zusätzlich, of the trajectories that do survive to a given iteration,
many fall into similar sequences after initial transients have passed. Zum Beispiel, a glider eventually
leaving behind a single block, as shown in the middle example in Figure 10, occurs frequently.
Außerdem, some sequences of nonnull perturbation classes seem to occur much more frequently
als andere. Zum Beispiel, sequences of BLUE perturbations are quite common. Daher, although the
combinatorics are daunting, it is clear that a more complete study of the trajectories of structural
coupling might yield interesting insights into the structure of the set of all possible lives that a glider
can live in a periodic lattice of a given size.
8 Communicative Interactions and Consensual Domains
Once we begin to consider larger environments, it becomes possible for one glider to encounter
another. In der Tat, we have already seen an example of this in the bottom sequence in Figure 10. Recall
Das, for MV, entity-entity perturbations are communicative interactions that serve to orient entities
within their respective cognitive domains to new possibilities for action. When these communicative
interactions are mutual and ongoing, the participating agents generate a new consensual domain of
coordinated orientations. Can gliders in GoL be used to explore any of these ideas?
It is relatively easy to see that two gliders can only directly interact when their boundaries partially
Überlappung, since it is only then that the ON cells of each glider intersect the 1-environment of the
andere. It is also straightforward to enumerate all such overlaps and examine their consequences.
In many cases, one or both participating gliders disintegrate after one step. Jedoch, there are some
instances in which both gliders survive the interaction, sometimes overlapping for multiple steps.
Bedauerlicherweise, the interactions between two such gliders are always null perturbations (d.h., BLACK
or GRAY); from the perspective of each glider it is as if the other one is not even present. Tatsächlich, Das
will always be the case, Weil, as pointed out in Section 5, nonnull perturbations require nonlocal
patterns of ON cells and two gliders can perturb one another only locally. Daher, no nontrivial
communicative interactions are possible between two gliders in an otherwise empty lattice.
L
instead of Rk
Nonnull communicative interactions can occur in more complex environments containing either
more than two gliders or additional environmental scaffolding. A simple example of the latter is
R glider interact with one another and a nonempty
R and an R0
shown in Figure 11, where a W0
R glider experiences a BLUE perturbation, causing it to transition
Umfeld. Here the central W0
R glider experiences a GREEN perturbation,
to state Wk/2
R . From this point on, both gliders not only persist
causing it to transition to state Rk
but also maintain an ongoing interaction through their overlapping boundaries, jointly moving
toward the lower right corner of the lattice 90° out of phase. Daher, due to their initial
communicative interaction, their joint states have fallen into a coordinated pattern of action
that defines a consensual domain. Bedauerlicherweise, all communicative interactions beyond the first one
correspond to null perturbations.
L. Gleichzeitig, the R0
L instead of Wk/2
202
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
This brief exploration has demonstrated that nontrivial communicative interaction between
gliders is possible, but much more work needs to be done to determine whether the chains of such
nontrivial interactions required to generate an interesting consensual domain can occur. Im Idealfall, Wir
would like a configuration in which at least two gliders surrounded by appropriate environmental
scaffolding could engage in a recurring sequence of nontrivial communicative interactions. Dann wir
could characterize each gliderʼs path through its cognitive domain as a consequence of its com-
municative interactions with the other glider. We could also examine the structure of the resulting
consensual domain that their sequence of joint states defines. Bedauerlicherweise, the challenge here is
the same as for structural coupling. We need to search the space of GoL configurations for
those with desired properties in the face of daunting combinatorics. One interesting idea might
be to try to adapt some of the glider-manipulation technology that GoL enthusiasts have developed
over the years for changing the phase or direction of motion of a glider (www.conwaylife.com/wiki).
Jedoch, in every case so far examined, this technology destroys the original glider and then creates
another one with the desired properties several iterations later, violating the fundamental autopoietic
constraint of maintaining an identity.
9 Diskussion
The central goal of this article has been to illustrate in some technical detail how many of the key
ideas underlying MVʼs biology of cognition play out in a simple concrete model. Erste, we presented
a conception of a glider in the game of Life as a spatiotemporal pattern of ON and OFF cells that
participate in a closed network of interactions that generate and maintain that very same pattern.
This definition of a glider also specifies a boundary, which in turns defines an immediate environ-
ment that serves as an interface between the glider and the rest of the lattice. Zweite, by explicitly
enumerating the consequences to a glider of every possible perturbation of its immediate envi-
ronment, we completely described the structure of a gliderʼs cognitive domain as the set of all
nondestructive interactions into which it can enter. Dritte, we found that this cognitive domain
divides the nondestructive perturbations into six classes, which form a gliderʼs Umwelt, und das
the structure of each perturbation class can be derived explicitly from the constraints that a glider
must satisfy in order to maintain its existence. Vierte, we characterized the interlocking sequences
of mutual perturbation that occur during structural coupling between a glider and its environment
and demonstrated how the tools of information theory can be used to quantify the resulting chains
of dependencies. Endlich, we suggested how one might be able to explore consensual domains in this
model by presenting a very simple example of a communicative interaction between two gliders.
One point to emphasize about our analysis is that the state change a glider undergoes at each
point in time is codetermined by its own internal dynamics and the perturbations that it receives
from its environment. Although the very limited number of states that a glider can be in may
obscure this fact, an external perturbation alone cannot in general uniquely determine its next state.
Zum Beispiel, the same BLUE perturbation that merely reorients a glider in a W state completely
destroys a glider in an R state. Another important manifestation of this point is the significant
imbalance in robustness to perturbation between W states (which can survive 72,440 distinct
microperturbations) and R states (which can survive only 22,496).
An important issue that deserves a deeper exploration is how best to define the possible states of
a glider. There are at least three possibilities. Erste, if we grant significance to the absolute coordinates
of each lattice cell, then there are 16 possible gliders centered about every cell in the lattice, for a
total of 16NM possible glider states in a periodic N × M lattice and an infinite number of possible
glider states in an unbounded lattice. Zweite, if we grant significance only to relative positions within
the lattice (d.h., we abstract over translational symmetry), then we obtain the 16 possible glider states
that we have used in this article (Figur 3). The argument for this definition is that, although the
absolute coordinate system we impose on the lattice would seem to be completely arbitrary, Die
orientation and chirality of a glider are relevant to how we as external observers describe how a
Artificial Life Volume 20, Nummer 2
203
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
glider relates to its environment. Endlich, if we also remove the significance of orientation and
chirality from our definition of glider state (d.h., we also abstract over rotational and reflectional
symmetries), then we are left with only two states: W and R. This is arguably the appropriate
definition of a gliderʼs intrinsic state, seit, from an internal perspective, a glider has no way of
determining its orientation or chirality. From this internal perspective, the six macro perturbation
classes that we have explored in this article collapse to only four (BLUE, GREEN, GRAY, and BLACK/
BROWN/ORANGE), and the gliderʼs cognitive domain becomes much simpler. Jedoch, as mentioned
über, the distinction between W and R forms still has important behavioral consequences.
The distinction we drew in Section 4 between the microdynamics of lattice cells (as defined by f )
and the macrodynamics of glider states (as defined by F ) nicely illustrates a point that has been
emphasized previously [1]: If we are only interested in the behavioral dynamics of an agent whose
existence we are willing to take for granted, then this behavioral dynamics can be characterized
by the tools of dynamical systems theory. Außerdem, such a behavioral characterization can
often be performed in relative isolation from an account of the constitutive processes that underlie
this behavioral dynamics, as we have done here, Zum Beispiel, in Section 6 (although this may not
always be the case [6]). This observation justifies the abstractions that are common in situated,
embodied, and dynamical approaches to behavior and cognition. Jedoch, if we wish to understand
why an agentʼs behavioral dynamics has the particular structure that it does or we wish to probe an
agentʼs behavior at the limits of its viability, then we must consider at least some aspects of its
underlying constitution.
Allgemeiner, how might the key ideas of the enactive approach to cognition manifest
themselves in this simple model? At its core, enaction is about a self-sustaining entity bringing forth,
through its history of structural coupling with its environment, a world of significance and a value-
laden point of view on that world [26, 28, 31]. The analysis in this article has demonstrated how the
closed network of processes that constitute a glider classify environmental configurations into non-
destructive and destructive subsets that are respectively “good” and “bad” for the glider. Zusätzlich,
we have seen how a gliderʼs constitution further classifies the nondestructive perturbations into
six subclasses according to which structural changes it undergoes in response. These categories
do not preexist as objective properties of the GoL universe. Eher, they are induced by the exis-
tence of a glider. This brings a subjective or phenomenal aspect into even this simple model. A
particularly key feature of this simple model of enaction is that it allows us to analyze an agent from
both the “inside” and the “outside” simultaneously, making it possible to reconcile the subjective
and objective perspectives in a way that we currently find extremely difficult to do with ourselves.
Daher, although much work remains to be done, at least some of the key ideas of the enactive
approach might be usefully explored in this simple model.
Interessant, Di Paolo [5] has questioned the sufficiency of the sorts of autopoietic ideas that
we have examined here for enaction. Insbesondere, he argues that a merely autopoietic system is
incapable of exhibiting the graded norms of better and worse; only the binary norm of survival
versus disintegration is implied by autopoiesis. Di Paolo suggests that the concept of adaptivity—“the
capacity of an organism to regulate itself with respect to the boundaries of its own viability”—must be
explicitly added to autopoiesis in order to fully capture the sense-making required for true enaction.
Although full justice cannot be done to this debate here, it is worth pointing out how careful con-
sideration of simple models can illuminate otherwise subtle conceptual issues such as this.
It is certainly true that a gliderʼs constitution fundamentally distinguishes between destructive and
nondestructive perturbations. But it does much more than that. Within the class of nondestructive
perturbations, a glider further distinguishes subclasses according to the state within its cognitive
domain that results from each such perturbation. This is a simple consequence of structural
degeneracy: The same organization can be realized by multiple structures. Natürlich, the structural
degeneracy of a glider is quite mild, but this degeneracy can be astronomical in more complicated
entities. These differences in state in turn have consequences for the gliderʼs sensitivity to sub-
sequent perturbations and thus implicitly constitute different valuations of its situation. A glider
prospers in (d.h., maintains its structural coupling with) precisely those environments to whose
204
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
spatiotemporal structure its autopoietic dynamics is matched. A persisting autopoietic system there-
fore necessarily behaves as if it is changing its future responses as a consequence of its past inter-
Aktionen. The fact that these conclusions follow directly from MVʼs original autopoietic framework
suggests that the necessity of adding an explicit notion or process of adaptivity to that framework
may require further discussion. In der Tat, this observation is nothing more than a reiteration of the
central lesson of work on learning without synaptic plasticity: Dynamics alone is sufficient for
adaptivity; no explicit adaptive process is required [12, 20, 32].
As simple as it is, the game of Life has turned out to provide a rich medium for exploring some
of the key ideas underlying MVʼs biology of cognition and the enactive approach that has grown out
davon. Natürlich, this simple model cannot do adequate justice to the full range of topics in this
Literatur. At best, it can perhaps serve as a starting point for concretely grounding the conceptual
analysis that lies at the foundations of this approach. Daher, there are many directions for future
Entwicklung. Erste, it would be very interesting to formalize the argument sketched in Section 3
that a glider is in fact a legitimate model of autopoiesis by mathematically characterizing the form
of its organizational closure and showing that it satisfies MVʼs definition within the GoL lattice.
Zweite, much more work remains to be done on describing the set of possible trajectories of
structural coupling and the interlocking chains of dependence between glider and environment
that they produce. Dritte, in order to further explore the notion of a consensual domain it will be
necessary to find longer chains of nonnull communicative interactions between sets of gliders and
their shared environment. Vierte, it would be worthwhile to apply the analysis in this article to other
self-producing/maintaining patterns in the game of Life and other cellular automata in order to
catalog the different possible cognitive domains and the trajectories of structural coupling in which
they can engage. Endlich, it will ultimately be important to extend this analysis to more complicated
and realistic models of autopoiesis that would more completely capture the many facets of the
enactive approach to cognition.
Danksagungen
I would like to thank Eran Agmon, Xabier Barandiaran, Mike Beaton, Ezequiel Di Paolo,
Mathew Egbert, Eduardo Izquierdo, Marieke Rohde, and Paul Williams for discussion and feedback
on a earlier draft of this article. This work was supported in part by NSF grants IIS-0916409
and IIC-1216739.
Verweise
1. Beer, R. D. (2004). Autopoiesis and cognition in the game of Life. Artificial Life, 10(3), 309–326.
2. Berlekamp, E. R., Conway, J. H., & Guy, R. K. (1982). Winning ways for your mathematical plays: Volumen 2.
New York: Academic Press.
3. Bourgine, P., & Stewart, J. (2004). Autopoiesis and cognition. Artificial Life, 10(3), 327–345.
4. Cover, T. M., & Thomas, J. A. (2006). Elements of information theory (2nd ed.). Hoboken, NJ: Wiley.
5. Di Paolo, E. (2005). Autopoiesis, adaptivity, teleology, Agentur. Phenomenology and the Cognitive Sciences, 4(4),
429–452.
6. Egbert, M. D., & Barandiaran, X. E. (2011). Quantifying normative behaviour and precariousness in
adaptive agency. In T. Lenaerts, M. Giacobini, H. Bersini, P. Bourgine, M. Dorigo, & R. Doursat (Hrsg.),
Proceedings of the 11th European Conference on Artificial Life (S. 210–218). Cambridge, MA: MIT Press.
7. Egbert, M. D., Barandiaran, X. E., & Di Paolo, E. A. (2010). A minimal model of metabolism based
chemotaxis. PLoS Computational Biology, 6(2), e1001004. doi:10.1371/journal.pcbi.1001004
8. Egbert, M. D., & Di Paolo, E. A. (2009). Integrating behavior and autopoiesis: An exploration in
computational chemo-ethology. Adaptive Behavior, 17(5), 387–401.
9. Fontana, W., & Buss, L. W. (1994). The arrival of the fittest: Toward a theory of biological organization.
Bulletin of Mathematical Biology, 56(1), 1–64.
10. Froese, T., & Ziemke, T. (2009). Enactive artificial intelligence: Investigating the systemic organization of
life and mind. Artificial Intelligence, 173(3–4), 466–500.
Artificial Life Volume 20, Nummer 2
205
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
R. D. Beer
The Cognitive Domain of a Glider in the Game of Life
11. Gardner, M. (1983). Wheels, Life and other mathematical amusements. New York: W. H. Freeman.
12. Izquierdo, E., Harvey, ICH., & Beer, R. D. (2008). Associative learning on a continuum in evolved dynamical
neural networks. Adaptive Behavior, 16(6), 361–384.
13. Luisi, P. L. (2006). The emergence of life: From chemical origins to synthetic biology. Cambridge, Vereinigtes Königreich: Cambridge
Universitätsverlag.
14. Maturana, H. R. (1978). Biology of language: The epistemology of reality. In G. A. Müller & E. Lenneberg
(Hrsg.), Psychology and biology of language and thought: Essays in honor of Eric Lenneberg (S. 27–63). New York:
Academic Press.
15. Maturana, H. R., & Varela, F. J. (1980). Autopoiesis and cognition. Dordrecht, Die Niederlande: D. Reidel.
16. Maturana, H. R., & Varela, F. J. (1987). The tree of knowledge. Boston: Shambhala.
17. Mavelli, F., & Ruiz-Mirazo, K. (2007). Stochastic simulations of minimal self-reproducing cellular systems.
Philosophical Transactions of the Royal Society B: Biological Sciences, 362(1486), 1789–1802.
18. McMullin, B. (2004). Thirty years of computational autopoiesis: Eine Rezension. Artificial Life, 10(3), 277–295.
19. Ono, N., & Ikegami, T. (2000). Self-maintenance and self-reproduction in an abstract cell model. Zeitschrift für
Theoretical Biology, 206(2), 243–253.
20. Phattanasri, P., Chiel, H. J., & Beer, R. D. (2007). The dynamics of associative learning in evolved model
circuits. Adaptive Behavior, 15(4), 377–396.
21. Poundstone, W. (1984). The recursive universe. New York: William Morrow.
22. Stewart, S., Gapenne, O., & Di Paolo, E. (Hrsg.). (2010). Enaction: Toward a new paradigm for cognitive science.
Cambridge, MA: MIT Press.
23. Suzuki, K., & Ikegami, T. (2009). Self-repairing and mobility of a simple cell model. In J. Pollack, M. Bedau, P.
Husbands, T. Ikegami, & R. A. Watson (Hrsg.), Artificial Life IX: Proceedings of the Ninth International Conference
on the Simulation and Synthesis of Living Systems (S. 421–426). Cambridge, MA: MIT Press.
24. Thompson, E. (2007). Mind in life. Cambridge, MA: MIT Press.
25. Varela, F. J. (1979). Principles of biological autonomy. New York: North Holland.
26. Varela, F. J. (1988). Structural coupling and the origin of meaning in a simple cellular automaton. In E. E.
Sercarz, F. Celada, N. A. Mitchison, & T. Tada (Hrsg.), The semiotics of cellular communication in the immune system
(S. 151–161). Berlin: Springer-Verlag.
27. Varela, F. J., Maturana, H. R., & Uribe, R. (1974). Autopoiesis: The organization of living systems, its
characterization and a model. BioSystems, 5(4), 187–196.
28. Varela, F. J., Thompson, E., & Rosch, E. (1991). The embodied mind. Cambridge, MA: MIT Press.
29. Virgo, N. (2011). Thermodynamics and the structure of living systems. Unpublished doctoral dissertation, Universität
of Sussex, Brighton, Vereinigtes Königreich.
30. von Uexküll, J. (1934). A stroll through the worlds of animals and men: A picture book of invisible worlds.
Reprinted in 1957 in C. L. Schiller (Transl. & Ed.), Instinctive behavior: The development of a modern concept
(S. 5–80). International Universities Press.
31. Weber, A., & Varela, F. J. (2002). Life after Kant: Natural purposes and the autopoietic foundation of
biological individuality. Phenomenology and the Cognitive Sciences, 1(2), 97–125.
32. Yamauchi, B., & Beer, R. D. (1994). Sequential behavior and learning in evolved dynamical neural networks.
Adaptive Behavior, 2(3), 219–246.
33. Zeleny, M. (1977). Self-organization of living systems: A formal model of autopoiesis. International Journal of
General Systems, 4(1), 13–28.
206
Artificial Life Volume 20, Nummer 2
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
A
R
T
l
/
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
2
0
2
1
8
3
1
6
6
4
5
1
8
A
R
T
l
/
_
A
_
0
0
1
2
5
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3