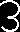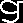Steven Jan
University of Huddersfield
School of Music and Humanities
Queensgate, Huddersfield
HD1 3DH United Kingdom
s.b.jan@hud.ac.uk
Meme Hunting with
the Humdrum Toolkit:
Principles, Problems,
and Prospects
Einführung: Theorizing a Memetics of Music
[A meme is] a unit of cultural transmission, oder
a unit of imitation. . . . Examples of memes are
tunes, Ideen, catch-phrases, clothes fashions,
ways of making pots or of building arches. Nur
as genes propagate themselves in the gene pool
by leaping from body to body via sperms or
Eier, so memes propagate themselves in the
meme pool by leaping from brain to brain via a
Verfahren . . . [Das], in the broad sense, can be
called imitation. (Dawkins 1989, 2nd ed.,
P. 192)
So wrote Dawkins over a quarter of a century ago,
drawing together various strands of nature–culture
analogizing from the previous two centuries and
more and recasting them in the crucible of his
powerful selfish gene hypothesis—the notion that,
ultimately, the driving force of evolution is the sin-
gle gene, whose phenotypic effects (d.h., those on
the organism’s morphology and behavior) influence
the reproductive prospects of that gene in ways
that justify Dawkins’s metaphor of apparent selfish
intentionality.
In its use of music as the first example of a
meme substrate, Dawkins’s definition is a provoca-
tive invitation to the development of a memetics of
music—a subdiscipline of musicology that would
attempt systematically to apply the insights of
Universal Darwinism (Plotkin 1995) to the me-
dium of music to trace pattern transmission and
evolution over time. Such an application has strong
intuitive attraction: schließlich, music appears to sup-
port discrete, ‘‘digital’’ patterns within the fluid,
‘‘analog’’ continuity of the sound stream—on a
smooth continuum from pointed instances of intra-
and inter-composer quotation to the myriad stan-
dardized cliche´ s and gestures that are the ‘‘connec-
tive tissue’’ of a musical style. In what is
essentially a memetic study (he terms it ‘‘referen-
tial analysis’’), Cope offers a formalization of this
continuum moving from ‘‘quotations’’ and ‘‘para-
phrases’’ through ‘‘likenesses’’ to ‘‘frameworks’’
and ‘‘commonalities’’ (2003, P. 11), and he de-
scribes his software, Sorcerer, that can detect such
inter-composer references.
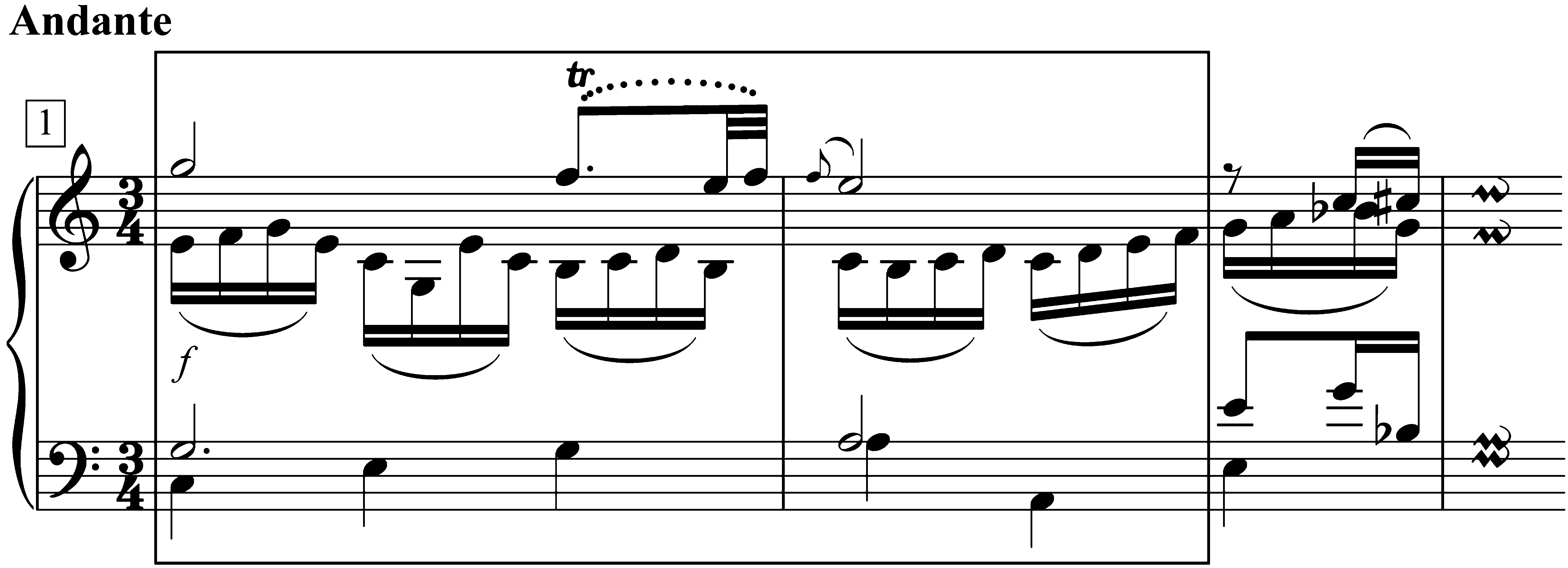
Nearer to the former than to the latter end of
this continuum, an example of cadence-pattern rep-
lication such as that shown in Figure 1 schlägt vor
that what was probably imitated from J. C. Bach (A
common figure in his style) was a closed and cogni-
tively salient unit for Mozart. Es ist, Dawkins would
argue, a selfish meme that hijacked Mozart’s neu-
ronal mechanisms in the service of its own replica-
tion.
It appears that, in brief, a memetics of music
would need to address the following three broad
conceptual issues (for fuller treatments, see Jan
2000A, 2000B, 2002, Und 2003):
1. The ontological basis of the musical meme,
perhaps in terms of an analogy with the ge-
notype–phenotype distinction in biology, al-
though its application to memetics is still
controversial (Blackmore 1999, P. 63).
2. The nature of the musical meme, or how the
continuum of musical elements is seg-
mented into discrete particles that can be
related, by presumed replication, to equiva-
lent particles in other contexts. This issue
also encompasses the replication of musical
memes at different hierarchic locations.
3. The evolutionary dynamic of musical
memes, accounting for the continuous
change of musical style over time as a con-
sequence of the differential transmission
and survival of mutant memes.
Computermusikjournal, 28:4, S. 68–84, Winter 2004
(cid:1) 2004 Massachusetts Institute of Technology
One problem with exploring the second and third
points above is the sheer volume of music that
68
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1. Replicated Pat-
terns in Works of J. C.
Bach and Mozart. (A) J. C.
Bach, Keyboard Concerto
in E-flat Major, Op. 7, NEIN.
5 (C 59;
1770), ICH, mm. 52–55; (B)
Mozart, Die Entfu¨ hrung
aus dem Serail, KV 384
(1782), NEIN. 11, ‘‘Martern
aller Arten,’’ mm. 13-15.
(A)
(B)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
must be investigated for statistically significant
conclusions to be drawn from it—although sugges-
tive conclusions may often be drawn from non-
empirical studies. Clearly, computer-aided study is
a viable method of making the empirical investiga-
tion of such a corpus of music manageable. For as-
sistance with the development of a theory of
memetics and the investigation of memes in mu-
sic, one software package in particular seems the
most suitable currently available—the virtues of
Cope’s Sorcerer program notwithstanding—namely
the Humdrum Toolkit, conceived and developed
seit 1989 by David Huron (1997, 2002).
This article investigates some uses of the Hum-
drum Toolkit in shaping and empirically testing as-
pects of a theory of musical memetics. It begins
Jan
69
with a discussion of the psychological processes
that affect pattern perception—and therefore what
patterns might constitute a musical meme. After a
brief overview of the Humdrum Toolkit, two case
Studien, using contrasting but related methodolo-
gies, are investigated to determine to what extent
certain patterns are propagated in the music of the
late 18th and early 19th centuries and how Hum-
drum might be used to detect them. Endlich, Die
prospects for computer-aided memetic analysis us-
ing Humdrum are assessed.
Pattern Replication in Music: A Gestalt/
Implication-Realization Perspective
In formulating a memetics of music, our starting
point must be to define what we understand by
Dawkins’s ‘‘unit of cultural transmission . . . of im-
itation’’ (Punkt 2 in the list in the previous section),
because memetics is fundamentally a discipline
that studies particulate entities in a variety of sub-
strates and their movement between brains via ex-
ternal media, such as scores, sound waves, Und
Aufnahmen. Such a definition is clearly fundamental
for implementing investigations of the memetic
paradigm in computerized searches. Zu diesem Zweck,
and in a further subdivision of point 2, one might
propose three hypotheses:
(1) In a stream of musical information, memes
acquire definition from their surrounding informa-
tion as a result of partly learned but principally in-
nate attributes of human perceptual and cognitive
architecture—Meyer’s level of laws (1989, S. 13–
14). If incoming information is subject to this filter,
then only certain privileged configurations—those
‘‘which . . . approach the ideal of indivisible parti-
culateness’’ (Dawkins 1989, P. 33; emphasis his)—
will be able to pass through and be consciously
attended to or stored in memory, both essential
preconditions for memetic transmission and evolu-
tion.
(2) As multiparametric ‘‘molecules’’ made up of a
number of ‘‘atoms’’ of cultural information—indi-
vidual pitches, Rhythmen, and other uniparametric
entities—musical memes appear to exist at several
structural-hierarchic levels. The Schenkerian
model offers a useful perspective, terminology, Und
graphic symbology to describe them, Aber, in an in-
version of the Schenkerian orthodoxy, it appears
that memes at higher hierarchic levels are gener-
ated and expressed by patterns at lower levels.
Other theoretical models have been formulated to
explain this relationship between shallow-
middleground-level structure and surface-level pat-
terning, including Narmour’s distinction between
style structures and style forms/shapes (1977, S.
173–174; 1990, P. 30ff), and the broadly comparable
schema–feature dualism invoked by Gjerdingen
(1988, S. 45–46). Neither of these models appears
incompatible with a memetic perspective.
(3) The cultural salience of a meme—the attri-
bute that affects its propensity to imitation, its fe-
cundity, as Dawkins calls it (1989, P. 17)—and its
differential fitness—its fecundity as compared with
that of its memetic alleles or rivals—appear to be
partly a function of its relationship to its antece-
dent (d.h., the form from which it derives). A more
chromatic, rhythmically syncopated consequent
(mutation) of a given antecedent may, up to a cer-
tain degree of variation, be more likely to be imi-
tated than the antecedent itself—although simpler
versions may sometimes be more memorable. Der
element of variation is generally to be found in the
surface elements of the meme, the underlying
structure assuring the sameness of the two pat-
Seeschwalben. Daher, as a general principle, a consequent
mutant meme is essentially the same meme as its
antecedent if the structural level above that which
is modified remains unaltered.
Although a complete computer-aided empirical
testing of the above hypotheses—and others devel-
oped from the list in the introduction—is beyond
the scope of this article, a preliminary exploration
of them might use two distinct but related method-
ologies, illustrated later in the two case studies us-
ing the Humdrum Toolkit.
The first methodology identifies a natural candi-
date pattern and then evaluates its prevalence in a
given idiom or dialect (Meyer 1989, S. 23–24) ac-
cording to the criterion of fit against the template
pattern. If matches are found, then the pattern is,
by definition, a meme, existing in the form of sev-
eral copies. It may then be fruitful to modify the
70
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
original template pattern in the light of the original
search to locate other patterns that, while structur-
ally similar to the template, nevertheless manifest
certain evolutionary deviations from it.
The second methodology synthesizes an artificial
candidate pattern to predict what types of configu-
rations are likely to attain memetic status. Dann,
attempts are made to locate real instances of the
candidate in a given repertory. As with the first
methodology, the hierarchic location and evolu-
tionary profile of such figures may also be an ele-
ment of the search strategy.
It is well known that issues pertinent to the first
hypothesis above were effectively theorized by
members of the Gestalt school of psychology in the
1920s and 1930s. In a reinvigoration of this tradi-
tion, their work informs two avenues of music-
theoretical investigation developed during the last
twenty years. Much of Lehrdahl and Jackendoff
(1983) relies on the insights of Gestalt psychology
for the formulation of metrical and grouping well-
formedness and preference rules. Temperley’s more
recent model (2001) of grouping structure in mu-
sic—a development of the preference-rule method-
ology of Lehrdahl and Jackendoff—also draws on
Gestalt insights but, unlike Lehrdahl and Jacken-
doff, subjects them to empirical testing via com-
puter models.
Perhaps the most comprehensive application of
Gestalt principles to music analysis, Jedoch, Ist
Narmour’s implication-realization (hereafter ‘‘i-r’’)
Modell (1977, 1984, 1989, 1990, 1992, 1999), welche
draws strongly on the groundwork of Meyer (1956,
1973, 1989). Reviewing Gestalt grouping principles
and categorizing them into innate and acquired
phenomena, Narmour notes that
the separate registral and intervallic aspects of
small intervals . . . are said to be implicatively
governed from the bottom up by the Gestalt
laws of similarity, proximity, und gemeinsam
Richtung. . . . [W]hat is important to notice
about the invocation of such Gestalt laws is
(1) that they have been shown to be highly re-
sistant to learning and thus may be innate . . .
(2) unlike the notoriously interpretive, holisti-
cally supersummative, top-down Gestalt laws
of ‘‘good’’ continuation, ‘‘good’’ figure, Und
‘‘best’’ organization . . . the Gestalt laws of
Ähnlichkeit, proximity, and common direction
are measurable, formalizable, and thus open to
empirical testing. (1989, S. 46–47)
It seems sensible to begin a computerized inves-
tigation of the grouping and ‘‘closural’’ structure of
music with the bottom-up Gestalt principles of
Ähnlichkeit, proximity, and common direction, als
implemented in the i-r model. The top-down laws
of good continuation, good figure, and best organi-
zation are less consistent, being culturally condi-
tioned and therefore variable aspects of perception
and cognition. The benefit of these insights to me-
metic research is that we can use the i-r model to
predict what forms memes are likely to take, Und
then we can use these criteria to help design com-
puterized search tools to locate them in real musi-
cal contexts—the second pattern-searching
methodology discussed above.
In brief, the i-r model offers a means of assessing
the bottom-up, note-to-note implicative flux of a
passage and identifying its points of procession and
closure at various hierarchical levels. Narmour pro-
poses a number of basic i-r functions, to which he
applies a distinctive terminology and symbology.
His fundamental premise is that, in melodic mo-
tion, an interval of a perfect fourth or smaller mov-
ing in a given registral direction implies a
continuation of similar intervallic magnitude in
the same direction (a phenomenon termed process
and symbolized by ‘‘P’’); whereas an interval of a
perfect fifth or larger moving in a given registral di-
rection implies a continuation of smaller interval-
lic magnitude in the opposite direction (termed
reversal, ‘‘R’’). Most importantly for this study,
these implicative potentials may not be fulfilled,
being terminated by durational interference (‘‘d’’),
harmonic interruption (‘‘h’’), or metric (beat) differ-
entiation (‘‘b’’), which serve to define the bound-
aries of a perceptual/cognitive grouping (Narmour
1989, S. 45–51; 1990).
Although Narmour’s theory is not universally ac-
cepted, in their evaluation of the predictive power
of the i-r model (using the Humdrum Toolkit as
Jan
71
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
their analytic engine), Thompson and Stainton con-
clude that ‘‘a combination of these principles can
predict much of how Bach and Schubert composed
(or ‘realized,’ in Narmour’s terminology) notes fol-
lowing implicative intervals. . . . [C]omposers may
be abiding by some basic rules, learned or innate,
regarding melodic expectancy’’ (1996, P. 33). Wenn die
results of this and other studies (such as Schellen-
berg 1996) are to be believed, then a Gestalt per-
spective, refined by the precepts of the i-r model,
would appear to be a fundamental element in both
pure and empirical memetic research.
It is worth noting that effective use of the toolkit
in its ‘‘raw’’ state requires a degree of facility with
UNIX that many musicologists without technical
backgrounds are unable or unwilling to devote time
to acquiring. Andreas Kornsta¨ dt’s JRing program
(2001) circumvents this difficulty by providing a
graphical front-end to the Humdrum tools which
should increase their accessibility, albeit with the
loss of some flexibility. The investigations de-
scribed below, Jedoch, use Humdrum in its origi-
nal form.
Overview of the Humdrum Toolkit
The Humdrum Toolkit is a suite of software tools
for UNIX systems. It encapsulates a central UNIX
design philosophy in that, although each of the
über 70 tools is fairly modest in its individual ef-
fects, great analytical sophistication can be
achieved by connecting several tools in pipelines.
The tools can also be incorporated into shell scripts
to facilitate the processing of lengthy pipelines and
expedite large processing tasks.
Beyond the tools themselves, Humdrum provides
a syntax for representing music—that is, a series of
formal conditions that stipulate how music may be
represented in a manner comprehensible by the
Werkzeuge. The default representation scheme is
‘‘**kern,’’ which provides a means of encoding the
fundamental elements of common-practice West-
ern notation. Im Wesentlichen, pitches are represented by
their letter names (CC–BB, C–B, (Mitte) c–b, cc–
bb, usw.), rhythm values are indicated by integers
(‘‘4’’ (cid:2) quarter-note, ‘‘8.’’ (cid:2) dotted eighth-note,
usw.), and parts/voices are organized in spines (tab-
separated columns of data), with leftmost spines
representing lower parts and rightmost representing
upper parts. Each horizontal line of the **kern
Punktzahl, called a data record, represents a simultane-
ity in the music, being divided into as many data
tokens as there are spines (Figure 3c later in this ar-
ticle shows two bars of music represented in
**kern). More detailed overviews of Humdrum
and the **kern encoding are given in Huron (1997,
2002).
Pattern Searching with Humdrum
In investigating musical memes, two of the Hum-
drum tools have particular significance. Der
broadly similar patt and pattern tools, as their
names imply, are pattern-locating utilities. Beide
tools search the representation of the music under
investigation using a template that defines the pat-
tern sought. Templates use UNIX regular expres-
sion syntax to stipulate what the target file may or
may not contain in order for a positive (d.h., A
match or hit; see Temperley 2001, P. 74) to be reg-
istered.
The chief difference between patt and pattern
is in the latter’s implementation of record-count
metacharacters, d.h., characters that specify how
many records containing a sought pattern may oc-
cur in the target file for a positive to be registered—
namely one or more (specified by ‘‘(cid:3)’’), zero or
mehr (‘‘*’’), or zero or one (‘‘?’’). Patt does not sup-
port record-count metacharacters, Dolmetschen
them as literals.
A useful feature of patt is its echo option,
which is not supported by pattern. This shows
the results of the search by displaying only those
segments of the **kern score containing the found
pattern. An alternative option is to specify that
patt tag the score under investigation by the in-
sertion of an additional rightmost ‘‘**patt’’ spine,
which places a user-specified keyword (wie zum Beispiel
‘‘meme’’) at those points in the encoding where the
sought pattern occurs. Pattern, by contrast, sim-
ply outputs a list of line numbers indicating where
the pattern is found, and the researcher must then
peruse the input to locate these occurrences.
72
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The essence of a successful search using patt or
pattern lies in designing a parsimonious and effi-
cient template. Having provisionally formulated
such a template, it is essential to test it out on pas-
sages—either synthetic examples or extracts taken
from real pieces—in which the sought pattern is
known to exist. This is to verify that the template
will not register a false negative, d.h., will fail to
find an instance of the pattern, despite its occurring
in the music. Such a test may also indicate if the
template would record a false positive, d.h., würde
register a pattern match for configurations that the
musician’s judgment would reject as unconvincing.
Given these two potential problem classes, it is un-
wise to begin investigations of real repertories
without such simulations conducted in controlled
and circumscribed conditions.
Meme Hunting with the Humdrum Toolkit:
Principles and Problems
I now describe two case studies that illustrate the
application of Humdrum to some of the theoretical
problems outlined above and exemplify the two
methodologies for computer-aided pattern replica-
tion analysis outlined in the second section.
Case Study 1: The ‘‘Glass Harmonica’’ Pattern
A pattern occurs in mm. 1–2 of Mozart’s Adagio in
C Major for Glass Harmonica, KV 356 (617A) aus
1791, that is essentially a chromatically altered
interrupted cadence. We might hypothesize that
figures such as this derive from evolutionarily sim-
pler forms—those outlining a diatonic interrupted
cadence and, ultimately, those outlining a perfect
cadence (with or without a terminal 4ˆ –3ˆ appoggia-
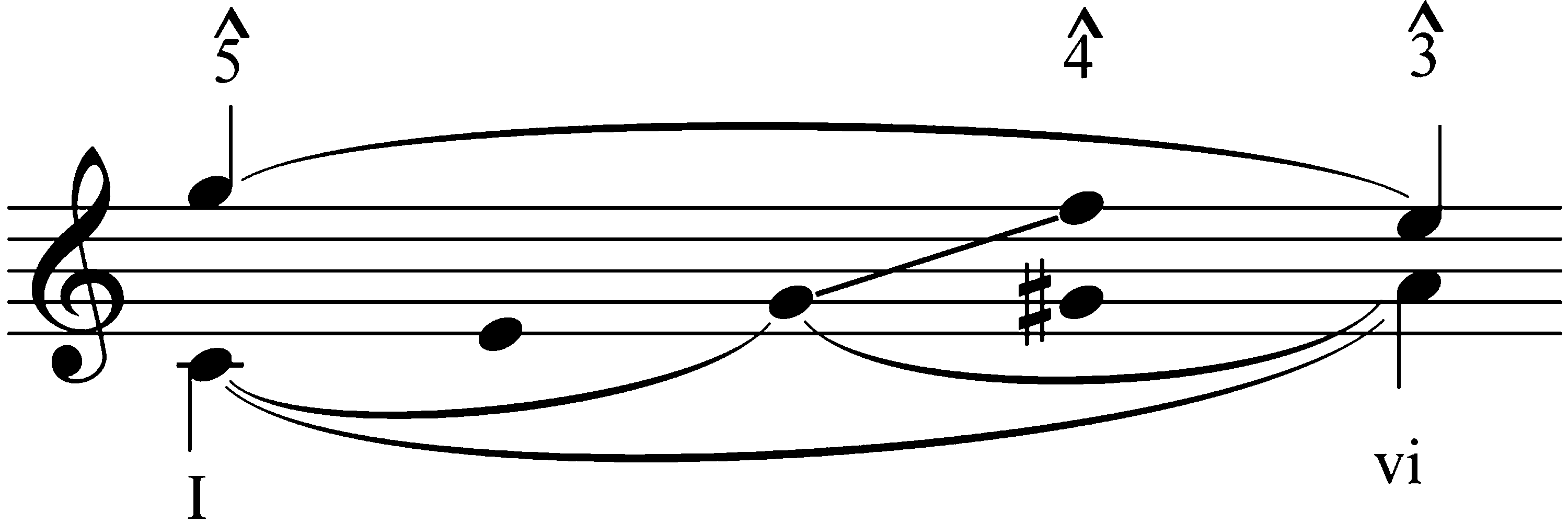
tura)—such as are represented in Figure 2.
This distinctive figure seems a good starting
point for a study following the first pattern-
searching methodology, and it might well be a
meme in the non-trivial (‘‘strong’’) sense of having
been propagated within the dialect of the European
late 18th century. (The trivial—‘‘weak’’—sense as-
cribes memetic status to it on the grounds that the
pattern is replicated in contemporary musical cul-
ture in the minds of present-day listeners to the
Adagio.)
My segmentation of the music is based on the
fact that, as well as exemplifying a clear melodic
Verfahren, the figure clearly satisfies all three of Nar-
mour’s criteria for closure (d.h., termination of im-
plicative potential). Erste, in Figure 3a, the left-hand
dotted half-note in m. 2 creates durational interfer-
enz; zweite, the unit is harmonically interrupted
owing to the resolution of the vii7/vi in the fourth
beat of m. 1 to vi in the first beat of m. 2; and fi-
schließlich, the rest in the right hand in m. 2 effects met-
ric (beat) differentiation. This segmentation also
satisfies Temperley’s ‘‘PSPR 1 (Gap Rule)’’ and
‘‘PSPR 3 (Metrical Parallelism Rule)’’ (2001, S. 68–
71), the latter on account of the recurrence of the
unit in the same metrical position at mm. 5, 21,
Und 25.
Figur 3 shows three representations of these
Maßnahmen, the first a score with an overlaid i-r anal-
ysis, the second a voice-leading reduction showing
foreground and shallow-middleground elements (Zu
which I shall return later), and the third a **kern
encoding.
When designing a template to search for the
‘‘Glass Harmonica’’ pattern, we begin with the
premise that it is likely to be independent of key,
and therefore the search process must be conducted
in terms of scale degree and not absolute pitch. Der
repertoire under investigation must be converted
Zu, and the template conceived in terms of, Die
Humdrum ‘‘**deg’’ representation. The encoding
in Figure 3c appears as in Figure 4 when converted
to **deg, in which all rhythmic information is re-
moved (numbers being used instead to indicate
scale degrees) and in which ‘‘(cid:3)’’ and ‘‘(cid:4)’’ indicate
chromatically raised and lowered versions, bzw-
aktiv, of the diatonic pitch. Zusätzlich, data are
propagated downwards into null (leer) tokens to
indicate the effect of the ditto command.
Having arrived at a **deg version of the pattern,
a patt template suitable for locating the configura-
tion shown in Figure 4, which might be stored as a
file called glass.patt, may be extrapolated from
Es, wie in der Abbildung gezeigt 5.
This template would only locate examples of the
Jan
73
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 2. (A) Diatonic per-
fect cadence in Mozart,
Clarinet Quintet in A Ma-
jor, KV 581 (1789), III,
mm. 1–8; (B) Diatonic in-
terrupted cadence in Mo-
zart, Divertimento in F
Major, KV 138 (125C;1772),
II, mm. 1-3.
(A)
(B)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
pattern in the tonic key, unless they occurred in a
passage whose departure from the tonic was so ex-
tensive or significant as to warrant a new key tan-
dem interpretation (z.B., ‘‘*G:’’) indicating the
changed tonal center (and therefore the status of
the new local tonic note as 1ˆ , as far as deg is con-
cerned). To locate examples in the dominant key—
the most probable other key in which the pattern
might occur—then an analogous ‘‘transposed’’ tem-
plate would have to be employed.
For ease of use, the commands that implement
this search may be placed in a shell script,
memefinder1.ksh. The script is available online at
mitpress2.mit.edu/e-journals/Computer-Music-
Journal/memefinder.tgz. If this archive is not ex-
panded automatically, the Unix command tar
xzvf memefinder.tgz will extract its contents.
Memefinder1.ksh repeats its operations on all
.krn files in the current directory, rendering it
suitable for searches of a large repertory. The find-
ings are successively appended to a single memere-
sults file that may be inspected by the researcher
after processing is completed. The operation of the
script is summarized in Figure 6.
In conducting a search for the pattern it seems
reasonable to restrict an initial investigation to Vi-
ennese music of the late 18th century. It was de-
cided to use those string quartets of Haydn and
Mozart that are publicly available from the
CCARH Muse Data Web site (www.musedata.org),
which contains the vast majority of Haydn’s quar-
tets (apart from some of the early works) and all of
74
Computermusikjournal
Figur 3. Three representa-
tions of Mozart, Adagio in
C Major for Glass Har-
monica, KV 356 (617A;
1791), mm. 1–2.
(A) Implication-
Realization Analysis;
(B) Voice-Leading Reduc-
tion; (C) **Kern Encoding.
(A)
(B)
(C)
Mozart’s quartets, together with a small selection
of various other chamber works of Mozart.
A patt search using memefinder1.ksh and the
template glass.patt produced the results shown
in Table 1.
The examples from Mozart’s KV 298 and KV 478
are the most salient, being clearly demarcated by
durational interference, harmonic interruption, Und
metric (beat) differentiation. The passages from
Mozart’s KV 458 and Haydn’s Op. 71, NEIN. 1 Sind, von
Kontrast, relatively open, ‘‘processive’’ tonicizations
of vi in the context of larger descending I–vi–IV se-
quences (possibly itself memetic) and lack the de-
marcation engendered by Narmour’s three closural
Kriterien. Our musical judgment might be inclined
to reject these latter examples for not representing
clear examples of the pattern. As for its ‘‘strong’’
memetic status, we might reserve judgment on the
‘‘Glass Harmonica’’ pattern at this stage, insisting
Jan
75
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4. The **deg ver-
sion of Figure 3c.
Figur 5. The glass.patt
template for the ‘‘Glass
Harmonica’’ pattern.
The template shown in Figure 7, glass.pattern,
is designed to find versions of the pattern that, al-
though broadly based on the middleground struc-
ture shown in Figure 3b, synchronize the two
component linear strata in various ways. Eins
might in particular speculate on a possible variable
alignment of the upper-voice 4ˆ against its support-
ing harmony, or the omission of the diatonic lower-
voice 5ˆ ; both seem likely evolutionary alterations.
The use of record-count metacharacters in the tem-
plate—essential to account for these two scenar-
ios—necessitates the use of pattern as the search
tool.
If such a pattern template is derived from a
patt template to account for unpredictable surface
elaborations of an underlying structure, then it will
lose some of the precision of the patt template
owing to its use of record-count metacharacters to
account for the unknown extra elements—the dim-
inutions that are symptomatic of memetic evolu-
tionary change. Although Humdrum pattern
searches are in principle suitable for locating stable
middleground patterns beneath a changing fore-
Boden, such searches inevitably increase the
chance of producing false positives. By this, we are
referring to patterns that, although perhaps appear-
ing to be descended from the antecedent at the
foreground level, do not correspond at the middle-
ground level, and are therefore—according to the
rule given under point 3 in the second section—not
consequents of the given antecedent. As may be
seen by comparing Figure 5 with Figure 7, all but
the first line of the pattern template contain vari-
ously the ‘‘(cid:3),’’ ‘‘*,’’ and ‘‘?’’ symbols or the Bool-
that a copy be found in the work of another com-
poser, thus implying connection in a nexus of imi-
Station.
As noted earlier, after a preliminary search based
on the configuration of a candidate pattern, it may
be instructive to revisit the search template and
consider ways of modifying it to account for vari-
ants that are derived from the antecedent form dur-
ing the course of a diachronic-evolutionary process.
As mentioned, it might be hypothesized—accord-
ing to the rule given under point 3 in the second
section of this article—that such variants will re-
tain the shallow-middleground-level structure of
the meme (Figure 3b) but will manifest a degree of
variability in the foreground-level patterning that
generates that middleground structure. Such vari-
ability of surface patterning might, zum Beispiel, af-
fect the rhythmic synchronization of components
of the pattern.
76
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 6. Flowchart illus-
trating the operation of
Memefinder1.ksh.
Tisch 1. Search Results (ICH) for the ‘‘Glass Harmonica’’ Pattern
Haydn
String Quartet in B-Flat major, Op. 71, NEIN. 1 (1793), III
Mozart
Flute Quartet in A major, KV 298 (1778/1786?), II
String Quartet in B-Flat major KV 458 (‘‘Hunt’’; 1784), II
Piano Quartet in G minor KV 478 (1785), II
Pattern found in
mm. 37–38
Pattern found in
mm. 5–6
mm. 4–5; 24–25
mm. 1–2
ean OR operator (‘‘|’’). Clearly, any modifier that
allows for a multiplicity of often very loosely de-
fined elements, the absence of an element, or ‘‘al-
ternativity’’ between elements, will tend to register
as positives a great variety of middleground struc-
tures.
Humdrum ultimately cannot ‘‘know’’ the
structural-hierarchic location of a given pitch (Zu
my knowledge, no software yet available can per-
form Schenkerian analysis); patt and pattern do
not have the higher-order algorithms necessary for
diese Aufgabe. This type of complex determination,
which often vexes seasoned Schenkerians, must be
the task of the researcher. Jedoch, given that
middleground elements often have greater metrical
(accentual) and durational (agogic) weight than ele-
ments at the foreground level, then searches may
be adjusted to account for these factors. The posi-
tion of the bar line—which often directly precedes
a structurally important pitch—can easily be fac-
tored into a search template. Aus diesem Grund, Die
template shown in Figure 7 adds barline signifiers
(‘‘^(cid:2)’’) before ‘‘^1.*5$’’ and before ‘‘^6.*4$’’ be-
cause these elements are markers of pitches inter-
preted, in Figure 3b, as having middleground status.
Trotzdem, the second of these components of
the template is qualified by a metacharacter in
such a way as to make its presence non-obligatory.
Glass.pattern deliberately casts the net widely,
yet this lack of precision has its advantages: Die
template registers a positive for the decorated and
syncopated version of the pattern in mm. 25–26 of
Mozart’s Adagio that glass.patt cannot detect.
Owing to this attribute, and because a middle-
ground 3ˆ /vi may not necessarily directly follow a
bar line, use of this template necessitates a subse-
Jan
77
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 7. Der
glass.pattern template
for the ‘‘Glass Harmonica’’
pattern.
of the pattern, from the opening of the slow move-
ment of Haydn’s String Quartet in F major, Op. 74,
NEIN. 2. Given the distinct instances of the pattern
in Mozart’s KV 298, 478, Und 356 (617A), und darin
work of Haydn’s, we are now justified in regarding
it as a meme in the ‘‘strong’’ sense, for it is a par-
ticulate unit that would appear to have been trans-
mitted (spontaneous generation aside) by imitation
from Mozart to Haydn (or to Haydn by means of
some other nexus of imitation).
The passage from Haydn’s Op. 74, NEIN. 2 dem-
onstrates the attributes mentioned above in
connection with likely evolutionary variants of
the pattern (d.h., variable alignment of the upper-
voice 4ˆ against its supporting harmony and omis-
sion of the diatonic lower-voice 5ˆ ). In finding a
passage that glass.patt missed but which our
musical judgment tells us is a clear example of the
unit, glass.pattern appears to strike an appro-
priate balance between an overly narrow and an
overly broad specification of the sought configura-
tion.
Case Study 2: The ‘‘I-R Process’’ Pattern
To begin, one must devise a musical pattern that
contains some combination of realized and/or de-
nied implications and satisfies one or more of Nar-
mour’s criteria for closure. Figur 8 zeigt ein
suitable pattern.
This simple shape (which may exist, as indicated
by the permutation slashes [‘‘/’’] in the example, In
a variety of chromatic and rhythmic forms) is de-
marcated before its initial pitch and closed after its
terminal pitch by rests, which enforce closure by
quent manual interpretation of the results. Ulti-
mately, in making such judgments, one is treading
the fine line between false positives and false nega-
tives: sifting and eliminating false positives arising
from a less-discriminating template makes more
effort for the researcher (undermining, to some de-
gree, the benefits of computer-assisted investiga-
tionen); Jedoch, false negatives are more serious,
compromising the integrity of a set of results.
Using this revised template, glass.pattern, A
pattern search using memefinder1.ksh (Figur 6)
produced the results shown in Table 2.
The second search found an additional example
Tisch 2. Search Results (II) for the ‘‘Glass Harmonica’’ Pattern
Haydn
String Quartet in B-Flat major, Op. 71, NEIN. 1 (1793), III
String Quartet in F major, Op. 74, NEIN. 2 (1793), II
Mozart
Flute Quartet in A major, KV 298 (1778/1786?), II
String Quartet in B-Flat major, KV 458 (‘‘Hunt’’) (1784), II
Piano Quartet in G minor, KV 478 (1785), II
Pattern found in
mm. 37–38
mm. 1–2; 5–6; 75–76
Pattern found in
mm. 5–6
mm. 4–5; 24–25
mm. 1–2
78
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 8. Candidate pat-
tern.
metric (beat) differentiation, establishing it as a dis-
crete perceptual/cognitive unit. As a rising scale
pattern, it exemplifies Narmour’s notion of process,
the implication of the initial motion c–d(flat) Sein
realized by continuation of the ascent to e(flat) Und
then f(sharp). Further continuation to g is sup-
pressed owing to the durational interference of the
dotted quarter-note (or longer) F(sharp) and/or the
metric (beat) differentiation of the rest, which neu-
tralizes the implicative charge and closes the
grouping. Clearly, the pattern is not as distinctive
or salient as that of Figure 3—it is a ‘‘commonal-
ity’’ on Cope’s continuum—but its closural attrib-
utes nevertheless allow it to exist as a meme.
It is most efficient to conceive this ‘‘I-R Process’’
pattern in terms of its intervallic structure and (als
indicated by the permutations in Figure 8) to allow
for a variable sequence of major and minor seconds,
so the pattern essentially represents a tetrachord
starting on any degree of the diatonic or chromatic
scale. One could specify more accurately its inter-
vallic structure, but for present purposes, a wide
variety of configurations will be accommodated;
später, finer distinctions will be made. In conceiving
a template, it is again necessary to convert the mu-
sical information to a representation independent
of absolute pitch: most parsimonious would be to
use the melodic interval or ‘‘**mint’’ representa-
tion, which indicates the direction of motion (‘‘(cid:3)’’
(cid:2) hoch, ‘‘(cid:4)’’ (cid:2) down), interval category (‘‘M’’ for ma-
jor, ‘‘m’’ for minor, usw.), and interval size of a me-
lodic progression. Figur 9 shows the pattern in
both **kern and **mint representations.
An appropriate template file must contain regu-
lar expressions capable of identifying patterns in
which the terminal pitch is a quarter note or longer
followed by a rest. Without this capacity, patterns
that terminate on note values shorter than a quar-
ter note and/or with no terminal rest—and which
are therefore not, in Narmour’s view, closed by
durational interference and/or metric (beat) differ-
entiation—will also be recorded as positives. An
the basis of our working hypothesis, such patterns
may not have sufficient end-closure for indepen-
dent memetic existence.
To find patterns that match the sought interval-
lic criteria and closural properties, it is necessary to
use the Humdrum assemble tool vertically to
align the original **kern spine against the derived
**mint spine (the result resembling Figure 9), Und
then to devise a template that can distinguish be-
tween the presence of integers in the **kern spine
(which signify rhythmic values) and integers in the
**mint spine (which signify intervallic steps).
A suitable template, i-r_process.pattern, Ist
shown in Figure 10. In the penultimate line, Es
specifies that the first ‘‘4,’’ ‘‘4.,’’ ‘‘2,’’ or ‘‘2.’’ to be
encountered must be followed directly by a pitch.
Das ist, it must be only a **kern quarter note,
dotted quarter-note, half-note, or dotted half-note
and not, daher, a **mint intervallic signifier,
the desired values of which are specified at the end
of this line by ‘‘((\(cid:3)M2)|(\(cid:3)m2)).’’ For this
suchen, pattern must be used, because record-
count metacharacters are employed in several lines
of the template, including ‘‘*’’ in lines 2, 4, 6, Und 8
to account for the presence of any null data tokens
interspersed between **mint signifiers. Diese, In
this context, would indicate the presence in other
spines of rhythmic values shorter than those of the
sought pattern.
As with the first case study, the pertinent com-
mands may be placed in a shell script,
memefinder2.ksh (also available at mit-
press2.mit.edu/e-journals/Computer-Music-Journal/
memefinder.tgz), a variant of memefinder1.ksh
(siehe Abbildung 6). Unlike memefinder1.ksh, Jedoch,
this script extracts each spine of the input file in
turn and subjects it individually to the actions of
pattern to ensure that the sought pattern exists
within a single spine and is not spread ‘‘diagonally’’
across two or more parts. The operation of the
script is summarized in Figure 11.
Using the same repertoire as that employed for
the first case study, a pattern search using meme-
finder2.ksh and the i-r_process.pattern tem-
plate produced the results shown in Table 3. To
Jan
79
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 9. **kern and
**mint encodings of the
‘‘I-R Process’’ pattern in
Figur 8. (A) **kern
encoding; (B) **mint
encoding.
(A)
(B)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
distinguish between the various forms of this figure
(which the i-r_process.pattern template spe-
cifically did not), values in square brackets after bar
numbers indicate the internal interval classes of
the particular pattern, the careted superscript be-
fore these indicating its starting scale degree.
Ignoring rhythmic factors for present purposes,
all intervallic variants of this pattern appear to be
memes in the ‘‘strong’’ sense. Every type found in
the Haydn movement also occurs in the three Mo-
zart examples, suggesting their connection in a
nexus of imitation—albeit a very broad one, gegeben
that this is such a basic figure, and one surely not
restricted to Haydn and Mozart. Correlating this
observation with initial scale degree, we see that
7ˆ1–2–2 and 5ˆ2–2–1 are common patterns in this
sample. Trotzdem, there is clearly insufficient
evidence to extrapolate wider conclusions about
the prevalence of this pattern and its variants in
the dialect as a whole, given the small size of the
results group and the distorting effect of intra-work
repetition. Darüber hinaus, one should perhaps be careful
not to make too much of such fine structural dis-
tinctions, owing to the limited number of configu-
rations available within the diatonic tetrachord, A
function of the intervallic characteristics of the
major and minor modes.
Abschluss: Prospects
It seems clear that there is much to commend the
use of the Humdrum Toolkit in developing a the-
ory of memetics. The following conclusions can be
drawn from the above investigations. Erste, a theory
of musical memetics will be complex and multifac-
80
Computermusikjournal
Figur 10. Der
i-r_process.pattern
Vorlage.
Figur 11. Flow chart illus-
trating the operation of
Memefinder2.ksh.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
Figur 10
Figur 11
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Jan
81
Tisch 3. Search Results for the ‘‘I-R Process’’ Pattern
Haydn
Pattern found in
String Quartet in F-Sharp minor, Op. 50, NEIN. 4 (1787), ICH
mm. 5 [1ˆ2–2–1; 3ˆ2–1–2], 15 [7ˆ1–2–2], 120 ((cid:2) M. 5) [1ˆ2–2–1;
Mozart
String Quartet in F major, KV 158 (1773), III
String Quartet in A major, KV 464 (1785), IV
String Quartet in D major KV 575 (1789), ICH
3ˆ2–1–2]
Pattern found in
mm. 28 [5ˆ2–2–1], 29 [7ˆ1–2–2]
M. 4 [2ˆ2–1–2]
mm. 6 [7ˆ1–2–2; 5ˆ2–2–1], 14 [7ˆ1–2–2; 5ˆ2–2–1], 122 ((cid:2) M. 6)
[7ˆ1–2–2; 5ˆ2–2–1], 130 ((cid:2) M. 14) [7ˆ1–2–2; 5ˆ2–2–1]
eted, requiring for its formulation both synchronic-
structural and diachronic-evolutionary
perspectives. Computers offer sophisticated means
of facilitating research in both dimensions.
Zweite, one of the central problems in develop-
ing a theory of musical memetics is the necessity
to formulate a robust, psychologically valid model
of pattern perception. Narmour’s i-r model, und das
Gestalt principles upon which it is based, are argu-
ably the best candidates at present.
Dritte, two useful strategies for verifying the me-
metic status of candidate patterns are 1) to identify
a natural candidate pattern and then evaluate its
prevalence in a given repertory; Und 2) to synthe-
size an artificial candidate pattern using Gestalt/i-r
principles and then attempt to locate real instances
of it in a given repertory.
Vierte, the Humdrum Toolkit’s patt and pat-
tern utilities are powerful tools for searching rep-
resentations of musical information and locating
memes and are amenable to both the above strate-
gies. The regular expression syntax they implement
is well suited to memetic investigations on ac-
count of its flexibility and precision.
Endlich, the results of such searches may be used
both qualitatively and quantitatively. Das ist, Sie
can foster analytical and critical discussion of spe-
cific musical works and the memes they contain,
and they can facilitate statistical evaluation of the
frequency and distribution of memes within idioms
and dialects.
I hope to have shown that it is in the nature of
computer-aided research that, perhaps more impor-
tant than making a complex task more managea-
ble, the highly structured approach required by the
enterprise forces the researcher to interrogate as-
sumptions, to rethink methodologies, and to refine
the hypotheses upon which the investigation is
based. In considering the prospects for this re-
suchen, three issues in particular deserve mention.
The Geographical Distribution of Memes and the
Generic Mapping Tools
The second part of the last point above suggests
that memes might be tracked as they spread geo-
graphically. A mechanism for implementing this
already exists, für, as described in Aarden and Hu-
ron (2001), Humdrum can be integrated with Wes-
sel’s and Smith’s Generic Mapping Tools (verfügbar
online at gmt.soest.hawaii.edu). This linkage
might, in theory, permit the detailed memetic pro-
filing of musical styles, allowing their transmission
and evolution over time to be charted.
The Humdrum Simil Tool
As suggested earlier, the ‘‘Glass Harmonica’’ meme
might be regarded as a mutation of a normative di-
atonic V–I or, less modified, a V–vi progression (Feige-
ure 2). The concept of mutation can usefully be
described in terms of the notion of edit-distance,
das ist, the number of changes (additions, deletions,
and substitutions) required to move from the ante-
cedent to the consequent form. This scale, Die
Damerau-Levenshtein edit distance metric, has al-
82
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
ready been implemented by Keith Orpen in the
Humdrum simil tool (Orpen and Huron 1992) Und
may prove useful in memetic research.
Investigating the Hierarchic Location of Memes
A third development—touched upon in the first
case study—would be to search for patterns at
deeper levels of structure. The patterns examined
here have been short figures of foreground orienta-
tion based on simple shallow-middleground-level
frameworks. The use of record-count metacharac-
ters with pattern facilitates the identification of
more distributed, ‘‘virtual’’ configurations that, Wenn
replicated, can still be regarded as memetic.
Danksagungen
I am grateful to Michael Clarke for his constructive
comments on an earlier version of this article and
to the two anonymous reviewers who suggested
further improvements.
Verweise
Aarden, B., and D. Huron. 2001. ‘‘Mapping European
Folksong: Geographical Localization of Musical Fea-
tures.’’ Computing in Musicology 12:169–183.
Blackmore, S. J. 1999. The Meme Machine. Oxford: Ox-
ford University Press.
Cope, D. 2003. ‘‘Computer Analysis of Musical Allu-
sions.’’ Computer Music Journal 27(1):11–28.
Dawkins, R. 1989. The Selfish Gene, 2nd ed. Oxford: Ox-
ford University Press.
Gjerdingen, R. Ö. 1988. A Classic Turn of Phrase: Musik
and the Psychology of Convention. Philadelphia: Uni-
versity of Pennsylvania Press.
Huron, D. 1997. ‘‘Humdrum and Kern: Selective Feature
Encoding.’’ In E. Selfridge-Field, Hrsg. Beyond MIDI: Der
Handbook of Musical Codes. Cambridge, Massachu-
Einstellungen: MIT Press, S. 375–401.
Huron, D. 2002. ‘‘Music Information Processing Using
the Humdrum Toolkit: Concepts, Beispiele, and Les-
sons.’’ Computer Music Journal 26(2):11–26.
Jan, S. 2000A. ‘‘Replicating Sonorities: Towards a Memet-
ics of Music.’’ Journal of Memetics—Evolutionary
Models of Information Transmission 4(1). Verfügbar
online at jom-emit.cfpm.org/2000/vol4/jan_s.html.
Jan, S. 2000B. ‘‘The Memetics of Music and Its Implica-
tions for Psychology.’’ In J. Sloboda et al., Hrsg. Proceed-
ings of the Sixth International Conference on Music
Perception and Cognition. Keele, Vereinigtes Königreich: Universität
Keele Department of Psychology.
Jan, S. 2002. ‘‘The Selfish Meme: Particularity, Replica-
tion, and Evolution in Musical Style.’’ International
Journal of Musicology 8:9–76.
Jan, S. 2003. ‘‘The Evolution of a ‘Memeplex’ in Late Mo-
zart: Replicated Structures in Pamina’s ‘Ach ich
fu¨ hl’s.’ ’’ Journal of the Royal Musical Association
128(2):330–370.
Kornsta¨ dt, A. 2001. ‘‘The JRing System for Computer-
Assisted Musicological Analysis.’’ Proceedings of the
Second Annual International Symposium on Music
Information Retrieval. Bloomington: Indiana Univer-
sity Press, S. 93–98.
Lerdahl, F., and R. Jackendoff. 1983. A Generative The-
ory of Tonal Music. Cambridge, Massachusetts: MIT
Drücken Sie.
Meyer, L. B. 1956. Emotion and Meaning in Music. Chi-
cago: University of Chicago Press.
Meyer, L. B. 1973. Explaining Music: Essays and Explora-
tionen. Chicago: University of Chicago Press.
Meyer, L. B. 1989. Style and Music: Theory, Geschichte, Und
Ideology. Philadelphia: University of Pennsylvania
Drücken Sie.
Narmour, E. 1977. Beyond Schenkerism: The Need for
Alternatives in Music Analysis. Chicago: Universität
Chicago Press.
Narmour, E. 1984. ‘‘Toward an Analytical Symbology:
The Melodic, Harmonic, and Durational Functions of
Implication and Realization.’’ In M. Baroni and L. Cal-
legari, Hrsg. Musical Grammars and Computer Analy-
Schwester: Atti del Convegno. Florence: Olschki, S. 83–114.
Narmour, E. 1989. ‘‘The ‘Genetic Code’ of Melody: Cog-
nitive Structures Generated by the Implication-
Realization Model.’’ In S. McAdams and I. Delie` ge,
Hrsg. Music and The Cognitive Sciences. London: Har-
wood, S. 45–63.
Narmour, E. 1990. The Analysis and Cognition of Basic
Melodic Structures: The Implication-Realization
Modell. Chicago: University of Chicago Press.
Narmour, E. 1992. The Analysis and Cognition of Me-
lodic Complexity: The Implication-Realization Model.
Chicago: University of Chicago Press.
Narmour, E. 1999. ‘‘Hierarchical Expectation and Musi-
cal Style.’’ In D. Deutsch, Hrsg. The Psychology of Mu-
sic, 2nd ed. San Diego, Kalifornien: Academic Press, S.
441–472.
Jan
83
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Orpen, K. S., and D. Huron. 1992. ‘‘Measurement of Sim-
ilarity in Music: A Quantitative Approach for Non-
Parametric Representations.’’ Computers in Music
Forschung 4:1–44.
Plotkin, H. 1995. Darwin Machines and the Nature of
Knowledge: Concerning Adaptations, Instinct and the
Evolution of Intelligence. London: Penguin.
Schellenberg, E. G. 1996. ‘‘Expectancy in Melody: Tests
of the Implication-Realization Model.’’ Cognition
58:75–125.
Temperley, D. 2001. The Cognition of Basic Musical
Structures. Cambridge, Massachusetts: MIT Press.
Thompson, W. F., and M. Stainton. 1996. ‘‘Using Hum-
drum to Analyze Melodic Structure: An Assessment of
Narmour’s Implication-Realization Model.’’ Comput-
ing in Musicology 10:24–33.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
/
2
8
4
6
8
1
8
5
4
2
2
3
0
1
4
8
9
2
6
0
4
2
7
2
8
4
0
3
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
84
Computermusikjournal