SOCIAL NETWORKS AND RESEARCH OUTPUT
Lorenzo Ductor, Marcel Fafchamps, Sanjeev Goyal, and Marco J. van der Leij*
Abstract—We study how knowledge about the social network of an individ-
ual researcher, as embodied in his coauthor relations, helps us in developing
a more accurate prediction of his or her future productivity. Wir finden
that incorporating information about coauthor networks leads to a mod-
est improvement in the accuracy of forecasts on individual output, over and
above what we can predict based on the knowledge of past individual out-
put. Zweite, we find that the informativeness of networks dissipates over
the lifetime of a researcher’s career. This suggests that the signaling content
of the network is quantitatively more important than the flow of ideas.
ICH.
Einführung
G OOD recruitment requires an accurate prediction of a
candidate’s potential future performance. Sports clubs,
academic departments, and business firms routinely use past
performance as a guide to predict the potential of applicants
and to forecast their future performance. In diesem Papier, Die
focus is on researchers.
Social interaction is an important aspect of research activ-
ität: researchers discuss and comment on each other’s work,
they assess the work of others for publication and for
prizes, and they join together to coauthor publications. Sci-
entific collaboration involves the exchange of opinions and
ideas and facilitates the generation of new ideas. Access
to new and original ideas in turn may help researchers be
more productive. It follows that other things being equal,
individuals who are better connected and more central in
their professional network may be more productive in the
future.
Network connectedness and centrality arise out of links
created by individuals and thus reflect their individual charac-
teristics: ability, sociability, and ambition, Zum Beispiel. Seit
the ability of a researcher is imperfectly known, the existence
of such ties may be informative.
These considerations suggest that someone’s collaboration
network is related to his or her research output in two ways:
the network serves as a conduit of ideas and signals individual
Qualität. The first channel suggests a causal relationship from
Received for publication August 27, 2011. Revision accepted for publi-
cation May 3, 2013. Editor: Philippe Aghion.
* Ductor: Massey University; Fafchamps: University of Oxford and Mans-
field College; Goyal: University of Cambridge and Christ’s College; van der
Leij: CeNDEF, University of Amsterdam; De Nederlandsche Bank; and Tin-
bergen Institute.
We thank the editor and two anonymous referees for a number of help-
ful comments. We are also grateful to Maria Dolores Collado, Markus
Mobius, and conference participants at SAEe (Vigo), Bristol, Stern (NYU),
Microsoft Research, Cambridge, MIT, Alicante, Oxford, Tinbergen Insti-
tute, Stockholm University, and City University London for useful com-
gen. L.D. gratefully acknowledges financial support from the Spanish
Ministry of Education (Programa de Formacion del Profesorado Univer-
sitario). S.G. thanks the Keynes Fellowship for financial support. M.L.
thanks the Spanish Ministry of Science and Innovation (project SEJ2007-
62656) and the NWO Complexity program for financial support. The views
expressed are our own and do not necessarily reflect official positions of De
Nederlandsche Bank.
A supplemental appendix is available online at http://www.mitpress
journals.org/doi/suppl/10.1162/REST_a_00430.
network to research output, whereas the second does not.
Determining causality would clarify the importance of the
two channels. Bedauerlicherweise, as is known in the literature on
social interactions (Manski, 1993; Moffit, 2001), identifying
network effects in a causal sense is difficult in the absence of
randomized experiments.
In diesem Papier, we take an alternative route: we focus on
the predictive power of social networks in terms of future
research output. Das ist, we investigate how much current
and past information on collaboration networks contributes
to forecasting future research output. Causality in the sense of
prediction informativeness is known as Granger causality and
is commonly analyzed in the macroeconometrics literature;
Zum Beispiel, Stock and Watson (1999) investigate the predic-
tive power of unemployment rate and other macroeconomics
variables on forecasting inflation.1
Finding that network variables Granger-cause future out-
put does not constitute conclusive evidence of causal network
effects in the traditional sense. dennoch, it implies that
knowledge of a researcher’s network can potentially be
used by an academic department in making recruitment
decisions.
We apply this methodology to evaluate the predictive
power of collaboration networks on future research out-
put, measured in terms of future publications in economics.
We first ask whether social network measures help predict
future research output beyond the information contained
in individual past performance. We then investigate which
specific network variables are informative and how their
informativeness varies over a researcher’s career.
Our first set of findings is about the information value of
Netzwerke. We find that including information about coauthor
networks leads to an improvement in the accuracy of forecasts
about individual output over and above what we can predict
based on past individual output. The effect is significant but
modest; the root mean squared error in predicting future pro-
ductivity falls from 0.773 Zu 0.758 and the R2 increases from
0.395 Zu 0.417. We also observe that several network vari-
fähig, such as productivity of coauthors, closeness centrality,
and the number of coauthors, have predictive power. Of those,
the productivity of coauthors is the most informative network
statistic among those we examine.
Zweite, the predictive power of network information
varies over a researcher’s career: it is more powerful for
young researchers but declines systematically with career
Zeit. Im Gegensatz, information on recent past output remains
a strong predictor of future output over an author’s entire
Karriere. Infolge, fourteen years after the onset of a
1 A few examples of applications that have determined the appropriateness
of a model based on its ability to predict are Swanson and White (1997),
Sullivan, Timmermann, and White (1999), Lettau and Ludvigson (2001),
Rapach and Wohar (2002) and Hong and Lee (2003).
The Review of Economics and Statistics, Dezember 2014, 96(5): 936–948
© 2014 by the President and Fellows of Harvard College and the Massachusetts Institute of Technology. Veröffentlicht unter einer Creative Commons Namensnennung 3.0
Unportiert (CC BY 3.0) Lizenz.
doi:10.1162/REST_a_00430
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
SOCIAL NETWORKS AND RESEARCH OUTPUT
937
researcher’s publishing career, networks do not have any
predictive value on future research output over and above
what can be predicted using recent and past output alone.
Our third set of findings is about the relation between
author ability and the predictive value of networks. Wir
partition individual authors in terms of past productivity
and examine the extent to which network variables pre-
dict their future productivity. We find that the predictive
value of network variables is nonmonotonic with respect
to past productivity. Network variables do not predict the
future productivity of individuals with below-average initial
productivity. They are somewhat informative for individu-
als in the highest past-productivity tier group. But they are
most informative about individuals in between. Tatsächlich, für
these individuals, networks contain more information about
their future productivity than recent research output. Taken
together, these results predict that academic recruiters would
benefit from gathering and analyzing information about the
coauthor network of young researchers, especially for those
who are relatively productive.
This paper is a contribution to the empirical study of
social interactions. Traditionell, economists have studied the
question of how social interactions affect behavior across
well-defined groups, paying special attention to the diffi-
culty of empirically identifying social interaction effects.
(For an overview of this work, sehen, z.B., Moffitt (2001) Und
Glaeser and Scheinkman, 2003.) In den vergangenen Jahren, interest
has shifted to the ways by which the architecture of social
networks influences behavior and outcomes.2 Recent empir-
ical papers on network effects include Bramoullé, Djebbari
and Fortin (2009), Calvó-Armengol, Patacchini, and Zenou
(2009), Conley and Udry (2010), and Fafchamps, Goyal, Und
van der Leij (2010).
This paper is also related to a more specialized litera-
ture on research productivity. Two recent papers, Azoulay,
Zivin, and Wang (2010) and Waldinger (2010), both use
the unanticipated removal of individuals as a natural experi-
ment to measure network effects on researchers’ productivity.
Azoulay et al. (2010) study the effects of the unexpected death
of superstar life scientists. Their main finding is that coau-
thors of these superstars experience a 5% Zu 8% decline in
their publication rate. Waldinger (2010) studies the dismissal
of Jewish professors from Nazi Germany in 1933 Zu 1934. His
main finding is that a fall in the quality of a faculty has sig-
nificant and long-lasting effects on the outcomes of research
students. Our paper quantifies the predictive power of net-
work information over and above the information contained
in past output.
Der Rest der Arbeit ist wie folgt gegliedert. Section II
lays out the empirical framework. Section III describes the
data and defines the variables. Section IV presents our find-
ings. Section V checks the robustness of our main findings.
Abschnitt VI schließt ab.
2 For a survey of the theoretical work on social networks see Goyal (2007),
Jackson (2008), and Vega-Redondo (2007).
II. Empirical Framework
It is standard practice in most organizations to look at
the past performance of job candidates as a guide to their
future output. This is certainly true for the recruitment and
promotion of researchers, possibly because research output—
journal articles and books—is publicly observable.
The practice of looking at past performance appears to
rest on two ideas. The first is that a researcher’s output
largely depends on ability and effort. The second is that
individuals are aware of the relationship between perfor-
mance and reward and consequently exert effort consistent
with their career goals and ambition. This potentially cre-
ates a stable relationship between ability and ambition, An
the one hand, and individual performance, andererseits.
Given this relationship, it is possible to (imperfectly) predict
future output on the basis of past output. In diesem Papier, Wir
start by asking how well past performance predicts future
output.
We then ask if future output can be better predicted if we
include information about an individual’s research network.
Social interaction among researchers takes a variety of forms,
some of it more tangible than others. Our focus is on social
interaction, reflected in the coauthorship of a published paper,
a concrete and quantifiable form of interaction. Coauthorship
of academic articles in economics rarely involves more than
four authors, so it is likely that coauthorship entails personal
interaction. Darüber hinaus, given the length of papers and the
duration of the review process in economics, it is reasonable
to suppose that collaboration entails communication over
an extended period of time. These considerations—personal
interaction and sustained communication—in turn suggest
several ways by which someone’s coauthorship network can
reveal valuable information on their future productivity. Wir
focus on two: research networks as a conduit of ideas and
coauthorship as a signal about unobserved ability and career
objectives.
Consider first the role of research networks as a conduit for
Ideen. Communication in the course of research collaboration
involves the exchange of ideas, so we expect that a researcher
who is collaborating with highly creative and productive peo-
ple has access to more new ideas. This in turn suggests that a
researcher who is close to more productive researchers may
have early access to new ideas. As early publication is a key
element in the research process, early access to new ideas can
lead to greater productivity. These considerations lead us to
expect that other things being equal, an individual who is in
close proximity to highly productive authors will on average
have greater future productivity.
Proximity need not be immediate, Jedoch: if A coauthors
with B and B coauthors with C, then ideas may flow from A to
C through their common collaborator B. The same argument
can be extended to larger network neighborhoods. It follows
that authors who are more central in the research network
are expected to have earlier and better access to new research
Ideen.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
938
THE REVIEW OF ECONOMICS AND STATISTICS
As a first step, we look at how the productivity of an
individual, say i, varies with the productivity of his or her
coauthors. We then examine whether i’s future productivity
depends on the past productivity of the coauthors of his or
her coauthors. Endlich, we generalize this idea to i’s central-
ity in the network in terms of how close a researcher is to all
other researchers (closeness) or how critical a researcher is
to connections among other researchers (betweenness)—the
idea being that centrality gives privileged access to ideas that
can help a researcher’s productivity.
Access to new ideas may open valuable opportunities, Aber
it takes ability and effort to turn a valuable idea into a publica-
tion in an academic journal. It is reasonable to suppose that the
usefulness of new ideas varies with ability and effort. Im Par-
besonders, a more able researcher is probably better able than a
less able researcher to turn the ideas accessed through the net-
work into publications. Since ability and industriousness are
reflected in past performance, we expect the value of a social
network to vary with past performance. To investigate this
possibility, we partition researchers into different-tier groups
based on their past performance and examine whether the
predictive power of having productive coauthors and other
related network variables varies systematically across tier
groups.
The second way by which network information may help
predict future output is that the quantity and quality of one’s
coauthors is correlated with, and thus can serve as a signal
für, an individual’s hidden ability and ambition. Given the
commitment of time and effort involved in a research col-
laboration, it is reasonable to assume that researchers do not
casually engage in a collaborative research venture. Somit
when a highly productive researcher forms and maintains a
collaboration with another, possibly more junior, Forscher
ich, this link reveals positive attributes of i that could not be
inferred from other observable data. Over time, Jedoch,
evidence on i’s performance accumulates, and residual uncer-
tainty about i’s ability and industriousness decreases. Wir
therefore expect the signal value of network characteristics
to be higher at the beginning of a researcher’s career and to
fall afterward.
Our empirical strategy is based on these ideas. Since our
focus is on predictive power, we worry that overfitting may
bias inference. To avoid this, we divide the sample into two
halves—one used to obtain parameter estimates and the other
to assess the out-of-sample predictive power of these esti-
Kumpels. We thus begin by randomly dividing the authors into
two equal-size groups. The first half of the authors is used
to estimate a regression model of researcher output. We then
use the estimated coefficients obtained from the model fitted
on the first half of the authors to predict researcher output for
the authors in the second half of the data. We compare these
predictions with actual output.
The purpose of this procedure is to assess the out-of-sample
prediction performance of the model. The reason for using
out-of-sample predictions is that in-sample errors are likely
to understate forecasting errors. As Fildes and Makridakis
(1995) stated, “The performance of a model on data out-
side that used in its construction remains the touchstone for
its utility in all applications” regarding predictions. Ein anderer
drawback of in-sample tests is that they tend to reject the null
hypothesis of predictability. Mit anderen Worten, in-sample tests
of predictability may spuriously indicate predictability when
there is none.3
The rest of this section develops some terminology and
presents the regressions more formally. We begin by describ-
ing the first step of our procedure and then explain how we
assess prediction performance. The dependent variable of
interest is a measure yit of the future output of author i at
time t, defined in more detail in section 3. This measure takes
into account the number of articles published, the length of
each article, and the ranking of the journal where the article
appears.
We first study predictions of yit based on past output and a
set of controls xit. Control variables include cumulative output
since the start of i’s career until t − 5; career time dummies;
year dummies; and the number of years since i’s last publi-
cation. Career time dummies are included to capture career
cycle effects—that researchers publish less as they approach
retirement. We then examine by how much recent research
output and network characteristics improve the prediction.
We also compare the accuracy of the prediction when we use
only past output and when we combine it with recent network
characteristics.
The order of the regression models we estimate is as fol-
lows. We start with benchmark model 0, which examines the
predictive power of the control variables xit:
Modell 0
yi,t+1 = xitβ + εit.
We then include recent individual output yi,t as additional
regressor. This yields model 1:
Modell 1
yi,t+1 = xitβ + yitγ1 + εit.
In model 2 we investigate the predictive power of network
variables zi,T:
Modell 2
yi,t+1 = xitβ + zitγ2 + εit.
i’s coauthors up
Network variables include the number of
to time t, the productivity of these coauthors, and different
network centrality measures detailed in the data section. Wir
estimate model 2 first with one network variable at a time,
then include network variables simultaneously.
Endlich,
in model 3 we ask if network variables zit
improve the prediction of future output over and above
3 Arguments in favor of using out-of-sample predictions can be found
in Ashley, Granger, and Schmalensee (1980) who state that “a sound and
natural approach” to testing predictability “must rely primarily on the out-
of-sample forecasting performance of models relating the original series of
interest” (P. 1149). Along with Fair and Shiller (1990), they also conjecture
that out-of-sample inference is more robust to model selection biases and
to overfitting or data mining.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
SOCIAL NETWORKS AND RESEARCH OUTPUT
939
the prediction obtained from model 1, das ist, from past
productivity:
We also consider an unrestricted model with only network
Information, model 2’:
Modell 3
yi,t+1 = xitβ + yitγ1 + zitγ2 + εit.
Here too we first consider one network variable at a time to
ascertain which network characteristics have more predictive
power. We also estimate model 3 with several network vari-
ables together to evaluate the overall information contained
in the network.
Models 0, 1, Und 2 are nested in model 3. A compari-
son of models 1 Und 2 allows us to investigate the relative
information content of recent individual output and recent
social network. A comparison of models 1 Und 3 examines
whether social network variables have explanatory power
over and above the information contained in recent individual
output.
For models 2 Und 3, we consider both regressions with a
single network variable and regressions with multiple net-
work variables. In the latter case, since our ultimate purpose
is to predict research output, we need a criterion to select a
parsimonious set of regressors, so as to avoid overfitting. To
select among social network regressors, we use the Bayesian
information criterion (BIC). We find that in our case, Die
lowest values of the BIC are obtained when all the network
variables are included, which is why our final specification
of the multivariate model includes them all.
The previous models are called restricted models because
we are imposing the constraint that the lagged productiv-
ity variables since the start of i’s career until t − 5 have
the same effect on future productivity. Darüber hinaus, in these
Modelle, we consider only five-year network variables: jede
network variable is computed assuming that a link between
author i and her coauthor has a predictive effect that lasts
for five years. These restricted models are simple to esti-
mate and allow us to compare the predictive power of
network variables and recent output. But we may be able to
improve the predictions of the restricted models by relaxing
the constraint that productivity lags have the same coeffi-
cient. Ähnlich, the predictive power of the network variables
might increase if we include several lags of the network
Variablen.
To see whether this is the case, we also estimates ver-
sions of models 1, 2, Und 3 that include several lags of the
productivity and network variables. The number of lags of
the productivity and network variables is selected using the
BIC. We call these the unrestricted models. The benchmark
unrestricted model, Modell 1, contains thirteen lags of the
productivity variable and a new set of control variables xit:
career dummies, time dummies, and years since the last pub-
lication. This model examines the predictive power of past
output:
Model 2’
yi,t+1 = xitβ +
T(cid:2)
s=0
zit−sθs + εit,
where T is the maximum lag length of the network variable
selected using the BIC criteria. Zum Beispiel, in T = 14 Wir
include lags from zit−14 to zit – zit−14 in the network variable
obtained combining all joint publications from t −14 to t, Und
zit is the network variable computed using the joint publica-
tions at period t. A comparison of models 1’ and 2’ provides
insights about the importance of past networks, relativ zu
past output.
The unrestricted model 3, model 3’, combines all past
output and past network information:
Model 3’
yi,t+1 = xitβ +
12(cid:2)
s=0
yit−sγs +
T(cid:2)
s=0
zit−sθs + εit.
We also estimate models 2’ and 3’ with multiple network
Variablen. A comparison of models 1’ and 3’ allows us to
examine the explanatory power of network variables over
and above knowledge of past output.
This describes the first step of our analysis. In the sec-
ond step, we evaluate the predictive accuracy of the different
Modelle. To this effect, we compare, in the second half of the
Daten, the actual research output yi,t+1 to the predictions(cid:3)yi,t+1
obtained by applying to authors in the second half of the data
the regression coefficients of restricted models 0 Zu 3 Und
unrestricted models 1’ to 3’ obtained from the first half of the
Daten. To evaluate the prediction accuracy of (cid:3)yi,t+1, we report
the root-mean-squared errors (RMSE) defined as
RMSE =
(cid:4)
1
N
(cid:2)
ich,T
(yi,t+1 −(cid:3)yi,t+1)2.
If the introduction of an explanatory variable in (cid:3)yi,t+1
decreases the out-of-sample RMSE, this variable contains
useful information that helps predict researchers’ future
productivity.
In order to assess whether forecasts from two models are
significantly different, we use a test described by Diebold and
Mariano (1995). This test is based on the loss differential of
forecasting the future output of an individual i, di,T. As we
measure the accuracy of each forecast by a squared error loss
Funktion (RMSE), we apply the Diebold-Mariano test to a
squared loss differential, das ist,
di,t = ε2
Ai,T
− ε2
Bi,T,
Model 1’
yi,t+1 = xitβ +
12(cid:2)
s=0
yit−sγs + εit.
where A is a competing model and B is the benchmark model.
To determine if one model predicts better, we test the
null hypothesis, H0 : E[di,T] = 0, against the alternative,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
940
THE REVIEW OF ECONOMICS AND STATISTICS
H1 : E[di,T] (cid:2)= 0. Under the null hypothesis, the Diebold-
Mariano test is
D(cid:5)
ˆV (D)/N
(cid:2) N(0, 1),
where d = n−1
(cid:6)
di,T, is the average loss differential and
ich,T
√
ˆV (D) is a consistent estimate of the asymptotic (long-run)
nd. We adjust for serial correlation by using a
variance of
Newey-West type estimator of ˆV ( ¯d).4
III. Data
The data used for this paper are drawn from the EconLit
database, a bibliography of journals in economics compiled
by the editors of the Journal of Economic Literature. Aus
this database, we use information on all articles published
zwischen 1970 Und 1999. These data are the same as those ana-
lyzed by Goyal, van der Leij, and Moraga-González (2006),
Fafchamps et al. (2010), van der Leij and Goyal (2011), Und
Ductor (2014).
A. Definition of variables
The output qit of author i in year t is defined as
(cid:2)
qit =
journal qualityj,
j∈Sit
(1)
where Sit is the set of articles j of individual i published in
year t. When available, the journal quality variable is taken
from the work of Kodrzycki and Yu (2006, hereafter KY).5
Bedauerlicherweise, KY do not include in their analysis all the
journals in the EconLit database. To avoid losing information
and minimizing measurement error in research output, Wir
construct a prediction of the KY quality index of journals not
included in their list.6 The actual KY journal quality index is
used whenever available.
(cid:6)
T −t(cid:6)
4 Formally, ˆV ( ¯d) =
where wm(T ) is the Bartlett Kernel function:
ich(ˆγ0 + 2
τ=1
wm(T ) =
(cid:7) (cid:8)
(cid:9)
1 − τ
M(T )
0,
Wenn 0 ≤ τ
M(T )
ansonsten,
≤ 1,
wm(T ) ˆγτ), and ˆγτ = ˆCov(di,T, di,t−τ),
We are interested in predicting future output. In economics,
the annual number of papers per author is small and affected
by erratic publication lags. We therefore need a reasonable
time window over which to aggregate output. The results
presented here are based on a three-year window, but our
findings are insensitive to the use of alternative window length
(z.B., five years).7 Our dependent variable of interest is thus
the output of author i in years t + 1, T + 2, T + 3:
q f
Es
= qi,t+1 + Qi,t+2 + Qi,t+3
(2)
Unsurprisingly, q f
i has a long upper tail. To avoid our
results from being entirely driven by a handful of highly
productive individuals, we log the dependent variable as
follows:8
(cid:8)
(cid:9)
yi,t+1 = ln
1 + q f
Es
.
The analysis presented in the rest of the paper uses yi,t+1 as
dependent variable.
We expect recent productivity to better predict output over
the next three years than older output. To capture this idea,
we divide past output into two parts in the restricted models:
cumulative output until period t − 5, which captures i’s his-
torical production and is used as control variable, and output
from t − 4 until t, which represents i’s recent productivity
and is expected to be a strong predictor of future output. Wir
it from t to t − 4 als
define recent output qr
qr
Es
= qit + Qi,t−1 + Qi,t−2 + Qi,t−3 + Qi,t−4.
Control variables in the restricted models xit
include
it from the start ti0 of i’s career until t − 5:
cumulative output qc
qc
Es
= qi,ti0
+ . . . Qi,t−6 + Qi,t−5,
where ti0 is the year in which individual i obtained his or
her first publication. We use ln(1 + qc
ich,T) als
regressors, since the distribution of both variables presents
fat tails. We also include the number of years rit with no
published article since i’s last article was published:
ich,T) and ln(1 + qr
(cid:7)
rit =
if qit > 0
0
ri,t−1 + 1 ansonsten.
Und
ri,ti0
= 0.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
and m(T ), also known as the truncation lag, is a number growing with T ,
the number of periods in the panel. The truncation lag has been chosen by
the BIC.
5 We do not consider citations because they often materialize long after a
paper has been published. This means that authors at the beginning of their
career often have a small citation record, Also, for them at least, citations have
little predictive power.
6 Um dies zu tun, we regress the KY index on commonly available information
of each journal listed in EconLit, such as the number of published articles per
Jahr, the impact factor, the immediacy index, the Tinbergen Institute Index,
an economics dummy, interaction terms between the economics dummy
and the impact factor, and various citation measures. Estimated coefficients
from this regression are then used to obtain a predicted KY journal quality
index for journals not in their list. Since most of the journals that KY omitted
are not highly ranked, their predicted quality index is quite small.
Variable rit is used as proxy for leave or retirement from aca-
demics: the longer someone has not published, the more likely
he or she has retired or left research. Other controls include
career time dummies cit and year dummies t. To summarize,
xit = {qc
Es, rit, cit, T}.
7 The predictive power of network variables is slightly higher under a five
years window. Results are available in the online appendix.
8 We have considered alternative nonlinear models in which the dependent
variable does not have to be transformed, such as Poisson, nonnegative
binomial, and zero inflated nonnegative binomial models. In terms of out-of-
sample RMSE, the specification that provides the best forecast is ln(X + 1),
which is the one we report here. See the online appendix for more details.
SOCIAL NETWORKS AND RESEARCH OUTPUT
941
In the unrestricted models 1’ and 3’, we relax the constraint
Es. In these models, we consider thirteen
it and qc
imposed in qr
lags of the productivity variable:
(cid:10)
yi,t−s = ln
1 + Qi,t−s + Qi,t−s−1 + Qi,t−s−2
(cid:11)
∀s = 0, . . . , 12.
Within the giant component, we consider, the following
two global proximity measures:9
• Closeness centrality Cc
ich,t is the inverse of the average
distance of a node to other nodes within the giant
component and is defined as
Control variables in the unrestricted models are the same
as in the restricted models but excluding past output.
Next we turn to the network variables. Given that we wish
to investigate whether network characteristics have predictive
power over and above that of recent productivity, Netzwerk
variables must be constructed in such a way that they do
not contain information outside the time window of qr
Es. Wir
therefore define the five-year coauthorship network Gt,5 bei
time t over the same time window as qr
it for the restricted
Modelle, das ist, using all joint publications from year t − 4
to t. At time t, two authors i and j are said to have a link gij,T
in Gt,5 if they have published in an EconLit journal in years
t − 4 to t. Ansonsten, gij,t = 0.
For unrestricted models 2’ and 3’, we introduce different
coauthorship networks, Gt,S, where s determines the number
of years that a link between author i and her coauthor j lasts.
Zum Beispiel, in network Gt,10, we assume that the effects
from a collaboration last during ten years, from t − 9 to t.
The set of network statistics that we construct from Gt,s is
motivated by the theoretical discussion of section II. Some
of the network statistics we include in our analysis are, An
a priori grounds, more correlated with access to new scien-
tific ideas; others are included because they are thought to
have a high signaling potential. Measures of network topol-
ogy such as centrality and degree reflect network proximity
and thus belong primarily to the first category, while other
Maßnahmen, such as the productivity of coauthors, are likely to
have greater signaling potential.
Based on these observations, the list of network variables
that we use in the analysis is as follows. We say that there is
a path between i and j in Gt,s if gij,t = 1 at some period from
t − (s − 1) to t or there exists a set of distinct nodes j1, . . . , jm,
such that gij1,t = gj1j2,t = . . . = gjmj,t = 1. The length of such
a path is m + 1. The distance d(ich, J; Gt,S) is the length of the
shortest path between i and j in Gt,S. We use the following
standard definitions:
• (First-order) degree is the number of coauthors that i
has in period t − (s − 1) to t, n1i,t = |Ni(Gt,S)|, Wo
Ni(Gt,S) = {J : gij,t = 1}.
• (Second-order) degree is the number of nodes at distance
ich (Gt,S)|, Wo
2 from i in period t−(s−1) to t, n2i,t = |N 2
ich (Gt,S) = {k : D(ich, k; Gt,S) = 2}.
N 2
• Giant component: The giant component in Gt,s is the
largest subset of nodes such that there exists a path
between each pair of nodes in the giant component and
no path to a node outside. We create a dummy vari-
able that takes value 1 if an author belongs to the giant
component and 0 ansonsten.
nt − 1
D(ich, J; Gt,S)
,
Cc
ich,T
=
(cid:6)
J(cid:2)=i
where nt is the size of the giant component in year t in
the coauthorship network Gt,S. Because Cc
ich,t has fat tails,
we use ln(1 + Cc
ich,T) as a regressor instead.
• Betweenness centrality Cb
ich,t is the frequency of the short-
est paths passing through node i and is calculated
als
Cb
ich,T
=
(cid:2)
J(cid:2)=k:J,k(cid:2)=i
τi
J,k(Gt,S)
τj,k(Gt,S)
,
where τi
J,k(Gt,S) is the number of shortest paths between
j and k in Gt,s that pass through node i, and τj,k(Gt,S) Ist
the total number of shortest paths between j and k in Gt,S.
In the regression analysis, we similarly use ln(1 + Cb
ich,T)
as regressor.
Nächste, we define regressors that capture the productivity of
coauthors and that of coauthors of coauthors. We apply the
ln(X + 1) transformation to them as well:
• Productivity of coauthors is defined as the output of
coauthors of author i from t − (s − 1) to t,
=
q1
Es
(cid:2)
qr
jt
j∈Ni(Gt,S)
jt is the output of j from period t − (s − 1) Zu
where qr
period t (excluding papers that are coauthored with i).
• Productivity of coauthors of coauthors is the output of
coauthor of coauthors of author i from t − (s − 1) to t,
=
q2
Es
(cid:2)
qr
kt,
k∈N 2
ich (Gt,S)
kt is the output of k from t − (s − 1) to t exclud-
where qr
ing papers that are coauthored with the neighbors of i,
Ni(Gt,S).
We also include a dummy variable that takes the value 1
jt in
for author i if one of i’s coauthors in Gt,s has an output qr
the top 1% of the distribution of qr
Es.
In the restricted models, all the network variables are
obtained using Gt,5, das ist, combining all joint publications
9 For a careful discussion on the interpretation of centrality measures, sehen
Wasserman and Faust (1994).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
942
THE REVIEW OF ECONOMICS AND STATISTICS
Table 1.—Summary Statistics
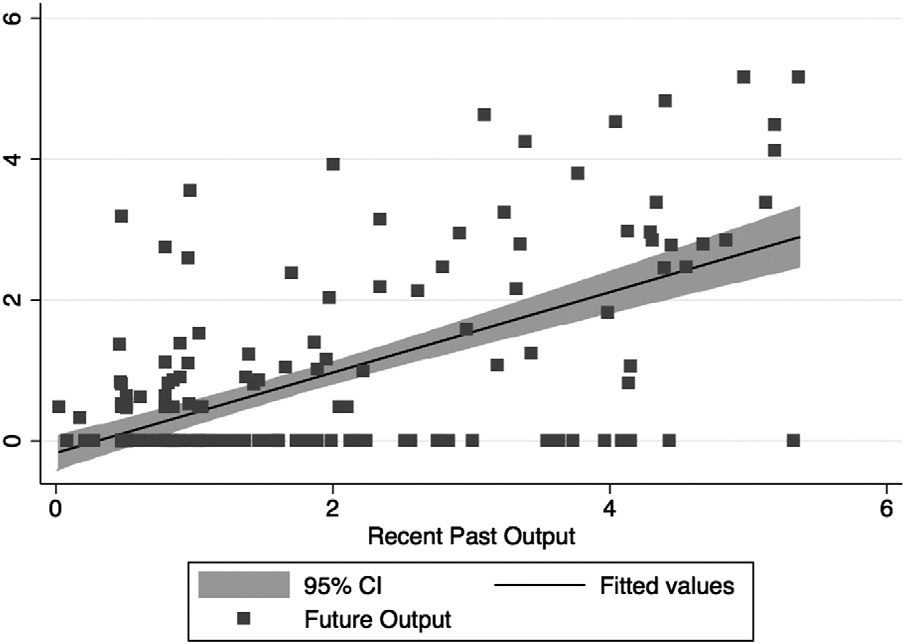
Figure 1.—A Scatter Plot of Future Output and Recent Past Output
Mean
SD
Correlations
Output
Future productivity
Past stock output
Recent past output
Network variables
.41
1.62
.62
.99
1.44
1.20
Degree
Degree of order 2
Giant component
Closeness centrality
Betweenness centrality
Coauthors’ productivity
Coauthors of coauthors’ prod.
Working with top 1%
Number of observations
Number of authors
.58
.90
.10
.01
.50
.59
.58
.01
1,697,415
75,109
1.21
3.12
.30
.02
2.29
1.40
1.58
.11
1,697,415
75,109
1
.44
.69
.55
.46
.47
.48
.48
.58
.54
.34
1,697,415
75,109
Network variables are computed assuming that a link between two authors lasts during five years
(five-year network variables). The number of observations used to obtain the statics for future output
Ist 1,335,428, for recent past output it is 1,230,335, and for past stock output it is 1,132,248. All the
correlations coefficients are obtained using the same number of observations, 872,344.
from t − 4 to t. Im Gegensatz, in the unrestricted models, Wir
include network variables obtained using different periods of
the coauthorship networks, from Gt,1 to Gt,15. The number of
network periods is selected according to the BIC.
B. Descriptive Statistics
Tisch 1 provides summary statistics of the variables
included in the analysis. Column 1 provides the mean value
of each variable, column 2 the standard deviation, and col-
umn 3 correlations between the different variables and future
productivity.
For the restricted model, we excluded observations rela-
tive to authors in the earliest stage of their career, for which
cit < 6. The reason is that these authors have not yet estab-
lished a publication record and network, so there is little
information on which to form predictions of future output.
This assumption is relaxed in the unrestricted models, where
we consider the full sample, 1,335,428 observations, after
replacing the missing lagged productivity and network vari-
ables by 0s. The rationale for doing so is that authors who
have just started their career have no past output and coau-
thorship, hence the value of their lagged productivity and
network variables is truly 0.
We draw attention to some distinctive features of the data.
First, we observe that the variance in future output qf
it is
large, with a standard deviation 2.41 times larger than the
mean. There is a high, positive correlation of 0.69 between
recent output qr
it. Figure 1 shows a scatter
plot and a linear regression line with the confidence interval
between qf
jt for 1,000 random selected observations.
This visually confirms that, as anticipated, recent past output
has a strong predictive power on future output.
jt and future output qf
it and qr
Second, we observe a high correlation between qf
it and
several five-year network variables such as coauthors’ output
q1
it, author degree, and closeness and betweenness central-
ity. The network variable most highly correlated with future
productivity is the productivity of i’s coauthors, q1
it, with a
correlation coefficient of 0.58. Other network variables such
as degree, closeness, and betweenness centrality are also
highly correlated with future output qf
it. Figure 2 shows the
relationship between some five-year network variables and
future output.
IV. Empirical Findings
We have seen a reasonably strong correlation between
future output and recent past output, but also between future
output and the characteristics of i’s recent coauthorship net-
work. We now turn to a multivariate analysis and estimate the
different models outlined in section II. We start by present-
ing the results on the predictive power of recent past output.
We then examine the relation between the productivity of
an individual author and the predictive power of network
variables.
A. Predicting Future Output
Table 2 presents the prediction results for model 0, the
it, rit, cit, t}; model 1,
baseline model with controls xit = {qc
which includes recent output qr
it; and model 2, which includes
a network variable, one per regression. Column 1 presents the
R2 of the regression on the in-sample data for each model.
Column 2 shows the out-of-sample RMSE for each model.
Column 3 compares the RMSE of model 1/model 2 with the
benchmark model, model 0. Column 4 shows the coefficient
of each regressor.
Recent output qr
it explains slightly less than half of the
variation in future output qf
it—
around 51% of the total variation—remains unexplained after
we take qr
it into account. The question is whether we can
improve on this using network variables.
it. Half of the variation in qf
We begin by examining the predictive power of the differ-
ent network variables when one network variable is added to
controls xit. This is achieved by comparing the results from
the model 2 regressions with model 0. Results, presented in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
r
e
s
t
_
a
_
0
0
4
3
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SOCIAL NETWORKS AND RESEARCH OUTPUT
943
Figure 2.—Scatter Plots of Future Productivity on Closeness Centrality and Coauthors’ Productivity
6
4
2
0
2
−
5
4
3
2
1
0
.04
.06
.08
Closeness Centrality
.1
0
2
4
6
Coauthors’ productivity
8
95% CI
Future Output
Fitted values
95% CI
Future Output
Fitted values
Table 2.—Prediction Accuracy: Restricted Models 1 and 2
Table 3.—Prediction Accuracy: Restricted Models 1 and 3
R2
RMSE
RMSE
Differential
Coefficients
R2
RMSE
RMSE
Differential
Coefficients
Model 0
Past output
Model 1
Recent past output
Model 2
Degree
Degree of order 2
Giant component
Closeness
Betweenness
Coauthors’ productivity
Coauthors of coauthors’
productivity
Working with a top 1%
.28
.49
.38
.36
.35
.36
.38
.41
.39
.36
.789
.665
.728
.744
.748
.743
.734
.715
.727
.746
–
15.72%∗∗∗
7.73%∗∗∗
5.70%∗∗∗
5.20%∗∗∗
5.83%∗∗∗
6.97%∗∗∗
9.38%∗∗∗
7.86%∗∗∗
5.45%∗∗∗
.22∗∗∗
.49∗∗∗
.29∗∗∗
.10∗∗∗
1.05∗∗∗
22.96∗∗∗
.11∗∗∗
.30∗∗∗
.24∗∗∗
1.75∗∗∗
Model 0
Past output
Model 1
Recent past output
Model 3
Degree
Degree of order 2
Giant component
Closeness
Betweenness
Coauthors’ productivity
Coauthors of coauthors’
productivity
Working with a top 1%
.28
.49
.50
.50
.50
.50
.50
.50
.50
.50
.789
.665
.660
.660
.662
.660
.657
.660
.660
.660
–
15.72%∗∗∗
16.35%∗∗∗
16.35%∗∗∗
16.10%∗∗∗
16.35%∗∗∗
16.73%∗∗∗
16.35%∗∗∗
16.35%∗∗∗
16.35%∗∗∗
.22∗∗∗
.49∗∗∗
.09∗∗∗
.03∗∗∗
.27∗∗∗
13.89∗∗∗
.06∗∗∗
.09∗∗∗
.07∗∗∗
.59∗∗∗
Significant at ∗∗∗1%, ∗∗5%. Model 0 includes career time dummies, year dummies, number of years
since the last publication, and cumulative productivity from the first publication till t − 5. Model 1 adds
to model 0 recent output. Model 2 adds to model 0 one of the network variables. Each network variable
is computed assuming that a link from a collaboration lasts during five years (five-year network variable).
The number of in-sample observations is 436,440.
Significant at ∗∗∗1%, ∗∗5%. Model 0 includes career time dummies, year dummies, number of years
since the last publication, and cumulative productivity from the first publication until t − 5. Model 1 adds
to model 0 recent output. Model 3 adds to model 1 one of the network variables. Each network variable is
computed assuming that the effects from a collaboration last during five years (five-year network variable).
The number of in-sample observations is 436,440.
table 2, show that coauthors’ productivity q1
it, closeness cen-
trality Cc
i,t, and the productivity q2
it of coauthors of coauthors
are statistically significant and help predict future output.
However, the predictive power is much less than recent out-
put, for example, coauthors’ productivity reduces the RMSE
by 9.38% whereas recent output reduces the RMSE by
15.72%.
We then combine recent output qr
it and network variables
in model 3. Results presented in table 3 show that the same
network variables remain significant once we include qr
it as
regressor. Being significant does not imply that network vari-
ables are very informative, however. For this, we have to
examine the improvement in prediction that they represent.
We compare multivariate model 3, that is, with multiple
network variables in the regression, to model 1. Table 4
shows that the R2 of model 3 is greater than the R2 obtained
under model 1. This means that network information taken
Table 4.—Prediction Accuracy of the Restricted Multivariate
Models
Model 0
Model 1
Multivariate model 2
Multivariate model 3
R2
.278
.493
.433
.509
RMSE
RMSE Differential
.789
.665
.700
.654
–
15.72%∗∗∗
11.28%∗∗∗
17.11%∗∗∗
Significant at ∗∗∗1%. These restricted models include only five-year network variables. The number of
in-sample observations is 436,440.
in combination with recent output yields a more accurate
prediction than a prediction based on past output alone. The
gain in explanatory power is small, however: the R2 rises
from 0.49 in model 1 to 0.51 in model 3. In line with this, the
RMSE declines from 0.67 down to 0.65 when we incorpo-
rate network information. This small difference is statistically
significant, as shown by the Diebold-Mariano test.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
r
e
s
t
_
a
_
0
0
4
3
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
944
THE REVIEW OF ECONOMICS AND STATISTICS
Table 5.—Prediction Accuracy: Unrestricted Models 1’ and 2’
Model 1’
Recent past output
Lag Length
13
R2
.39
RMSE
RMSE Differential
Coefficients
.773
–
.44∗∗∗
Model 2’
Degree
Degree of order 2
Giant component
Closeness
Betweenness
Coauthors’ productivity
Coauthors of coauthors’ production
Working with a top 1%
.24
.23
.23
.24
.26
.29
.27
.24
Significant at ∗∗∗1% , ∗∗5%. Model 1’ includes career time dummies, year dummies, number of years since the last publication, and thirteen lags of the productivity variable. Model 2’ contains career time dummies,
year dummies, number of years since the last publication, and several lags of a network variable. The maximum lag length for each model is selected using the BIC. For the network variables, the maximum possible
lag length considered is 15. The coefficients presented in the table correspond to the first lag of the variable. The number of in-sample observations is 667,423.
−11.38%∗∗∗
−12.16%∗∗∗
−12.29%∗∗∗
−11.51%∗∗∗
−9.83%∗∗∗
−7.76%∗∗∗
−9.57%∗∗∗
−11.51%∗∗∗
.10∗∗∗
.05∗∗∗
.96∗∗∗
1.42
.07∗∗
.11∗∗∗
.09∗∗∗
.45∗∗∗
.861
.867
.868
.862
.849
.833
.847
.862
15
14
15
15
15
12
15
14
Model 1’
Past output
Table 6.—Prediction Accuracy: Unrestricted Models 1’ and 3’
Lag Length
13
R2
.39
RMSE
RMSE Differential
Coefficients
.773
–
.44∗∗∗
Model 3’
Degree
Degree of order 2
Giant component
Closeness
Betweenness
Coauthors’ productivity
Coauthors of coauthors’ productivity
Working with a top 1%
.40
.40
.40
.40
.40
.41
.41
.40
Significant at ∗∗∗1%, ∗∗5%. Model 1’ includes career time dummies, year dummies, number of years since the last publication, and thirteen lags of the productivity variable. Model 3’ adds to model 1’ several lags
of a network variable. The maximum lag length is selected using the BIC criteria. For the network variables, the maximum possible lag length considered is 15. The coefficients presented in the table correspond to the
first lag of the variable. The number of in-sample observations is 667,423.
.65%∗∗∗
.65%∗∗∗
.65%∗∗∗
.78%∗∗∗
.78%∗∗∗
1.55%∗∗∗
1.16%∗∗∗
.78%∗∗∗
.14∗∗∗
.06∗∗∗
.58∗∗∗
2.35∗∗
.02
.09∗∗∗
.07∗∗∗
.39∗∗∗
.768
.768
.768
.767
.767
.761
.764
.767
6
5
8
10
9
12
11
13
Table 7.—Prediction Accuracy of the Unrestricted Multivariate
Models
Lags
R2
RMSE
RMSE Differential
13
15
8
0.395
Model 1’
0.322
Multivariate model 2’
Multivariate model 3’
0.417
Significant at ∗∗∗1%. For multivariate model 3, we consider eight lags for each network variable and
thirteen lags of the output. The lag length is selected according to the BIC; for the multivariate models,
we considered as candidate models only those where each network variable has the same number of lags.
The number of in-sample observations is 667,423
–
−5.30%∗∗∗
1.94%∗∗∗
0.773
0.814
0.758
Table 5 presents the prediction results for the benchmark
unrestricted model 1’ and model 2’. Model 1’ contains thir-
teen lags of the productivity variable and the same control
variables as in the restricted models except past output. Model
2’ includes the control variables without past output and sev-
eral lags of a network variable. Column 1 presents the lag
length of each variable; the rest of the columns are analogous
to table 2. The predictions obtained from the unrestricted
models are consistent with their restricted versions. The net-
work variable with the highest predictive power is coauthors’
productivity with an RMSE 7.76% greater than the past out-
put model, model 1’. Similar results obtain on the effects of
networks when we compare models 1’ and 3’, as preported in
table 6. As shown in table 7, the predictive power of network
over and above information of past output is slightly higher
when we consider the unrestricted version, that is, when we
include several lags of the network variables. In the restricted
multivariate models, the RMSE is reduced by 1.65% when
we add network variables to past and recent output, while in
the unrestricted version, the reduction is around 1.94%.
From this we conclude that network variables contain pre-
dictive information over and above what can be predicted on
the basis of past output, but this information gain is modest.
B. Networks and Career Cycle
Next we estimate the predictive power of network vari-
ables for different career time cit. The RMSE of restricted
models 0, 1 and multivariate models 2 and 3 (with multiple
network variables included in the regression) as well as the
RMSE of unrestricted models 1’ and multivariate Models 2’
and 3’ are plotted in Figures 3 and 5, respectively. Career
age cit is on the horizontal axis, while RMSE is measured
on the vertical axis. Unsurprisingly, the figures show that
the predictive accuracy of all the models improves (reflected
in the decline in RMSE) with career time. This is primarily
because the control variables xit, particularly cumulative out-
put qc
it, reveal more information about individual ability and
preferences over time.
To examine whether the relative predictive gain of net-
work variables varies with career time, we report in figures 4
and 6 the difference in RMSE between multivariate mod-
els 2 and 3 versus model 1 and the difference in RMSE
between their unrestricted versions, respectively. We note a
marked decline in the difference between models 1’ and 3’
over the course of a researcher’s career. After time t = 14,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
r
e
s
t
_
a
_
0
0
4
3
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SOCIAL NETWORKS AND RESEARCH OUTPUT
945
Figure 3.—RMSE Out-of-Sample Across Career Time:
Restricted Models
Figure 5.—RMSE Out-of-Sample across Career Time:
Unrestricted Models
9
.
8
.
7
.
6
.
5
.
5
10
15
20
5
t
RMSE M0
RMSE MV2
RMSE M1
RMSE MV3
10
t
RMSE M1’
RMSE MV3’
15
20
RMSE MV2’
Figure 4.—RMSE % Difference across Career Time:
Restricted Models
Figure 6.—RMSE % Difference across Career Time:
Unrestricted Models
5
0
5
−
0
1
−
9
.
8
.
7
.
6
.
5
.
2
0
2
−
4
−
6
−
5
10
15
20
t
5
10
t
15
20
RMSE % Diff. MV2 M1
RMSE % Diff. MV3 M1
RMSE % Diff. MV2’ M1’
RMSE % Diff. MV3’ M1’
According to the Diebold-Mariano test, the difference between the RMSE of multivariate model 3 and
model 1 is statistically significant for every career time year.
According to the Diebold-Mariano test, the differences between the RMSE of multivariate model 3’ and
model 1’ are insignificant for t = 12 and from t = 14 to t = 20.
the prediction accuracy of models with or without network
variables becomes virtually indistinguishable. The Diebold-
Mariano test shows that the differences between multivariate
model 3’ and model 1’ are not statistically significant from
t = 14 to t = 20. In the restricted models, figure 4, the decline
in the predictive power of network variables is not observed
until t = 15.10 This indicates that for senior researchers, net-
work variables contain little information over and above the
information contained in past and recent output.
What does this pattern in the data suggest about the relative
importance of the two potential ways in which networks may
10 The fact that the predictive power of networks is still significant for
mature authors in the restricted model analysis might be a consequence of
including inactive authors in the sample—those who do not publish regu-
larly. As an inactive author matures, future output and network variables
are both more likely to be 0 due to the reduction of output prior to retire-
ment, so the predictive power of networks does not dissipate. Indeed, we
find that if we restrict the analysis to active authors—authors with positive
recent output—the predictive power of networks in the restricted model is
negligible after the authors have more than fifteen years of experience.
matter: flow of ideas and signaling? As time passes, the
publication record of a researcher builds up. Since ability,
research ambition, and other personality traits are relatively
stable over time, this accumulating evidence ought to pro-
vide a more accurate estimate of the type of the person.
Hence, it should become easier to judge his or her abil-
ity and research ambition on the basis of the publication
record alone. Based on this, we would expect that the sig-
naling value of networks decreases over time, and hence that
network variables have less and less additional predictive
power.
Research networks can, however, be important conduits of
valuable research ideas as well. Unlike the signaling value
of networks, access to new research ideas remains important
throughout a researcher’s career. Thus, if network variables
help predict future output because they capture access to
new ideas, their predictive value should remain relatively
unchanged over a researcher’s career. This is not what we
observe, leaving signaling as a stronger contender as the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
r
e
s
t
_
a
_
0
0
4
3
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
946
THE REVIEW OF ECONOMICS AND STATISTICS
possible channel by which network variables help predict
future productivity.
not shown here to save space, are available in the online
appendix.
C. Network Information across Productivity Categories
In this section we examine whether the predictive power
of network information varies systematically with recent out-
put qr
it. This analysis is predicated on the idea that it takes
talent and dedication to transform the new ideas conveyed
by the research network into publishable output. Conse-
quently, we expect the predictive power of network variables
to increase with ability, and hence with qr
it, at least over a
certain range.
To investigate this possibility, we divided the observations
into five tier groups on the basis of their recent output qr
it.
The top category includes authors in the top 1% in terms of
qr
it. The second top category includes authors in the 95–99
percentiles of qr
it. The third category covers authors in the
90–94 percentiles, the fourth includes authors in the 80–89
percentiles, and the last category is for authors in the 50–79
percentiles.11
Figure 7 shows the RMSE % difference between mod-
els 1 and 2 versus model 0 across the different categories.
The RMSE % differences are always positive because the
restricted benchmark model, model 0, is nested in models
2 and 1; thus, it is very likely that models 2 and 1 have a
predictive power greater than model 0. For the most pro-
ductive authors, those above the 99th percentile, network
variables have predictive power in explaining future research
output but much less than recent output. For the next cat-
egory of researchers, those in the 95–98 percentile range,
network information has greater predictive power. Even more
striking, for researchers in the third category, the 90–94
percentile range, network variables are better at predicting
future research output than qr
it! All the models have sta-
tistically significant predictive power across the different
tiers.
By contrast, network information has little but significant
predictive power for low-productive individuals (those in the
50–79 percentile range). This suggests that for researchers
with low ability or research ambition, having published with
high-quality coauthors has little informative content regard-
ing their future output—perhaps because they are unable to
take advantage of the access to information and research ideas
that good coauthors provide.
Similar patterns are observed when we compare RMSE of
unrestricted model 2’ versus model 1’.
V. Robustness
We have conducted an extensive investigation into the
robustness of our results to various assumptions made
in constructing the variables used in the estimation. The
results of this analysis are summarized here; the details,
In the analysis so far, we have used accumulated pro-
ductivity from t + 1 to t + 3 as the variable qit we seek
to predict (see equation [2]). The rationale for doing so is
that the distant future is presumably harder to predict than
the immediate future, and we want to give the model a fair
chance. Yet in economics, there are long lags between the
submission and publication of a paper and wide variation in
these lags across papers and journals. Publication lags thus
introduce additional variation in the variable we are trying
to predict and may thus lead us to underestimate the predic-
tive power of network information. To check whether this
is affecting our results, we repeat the analysis using average
future productivity over a five-year window instead of three
years:
q f
it
= qi,t+1 + qi,t+2 + qi,t+3 + qi,t+4 + qi,t+5,
and, as before, we use ln(1+qf
it) as the variable we seek to pre-
dict. Results are similar to those reported here except that the
predictive power of network variables is larger using a five-
year window. In particular, network variables are even more
useful than past output to forecast the future performance
of a researcher, that is, multivariate model 2’ outperforms
model 1’.
Next we investigate whether results are sensitive to our
definition of output qit. We examine whether different results
obtain if we correct for article length and number of coau-
thors. Results show that the predictive power of network
variables is unaffected.12
Finally, the main specification used so far is a linear model
estimated by OLS in which the dependent variable is a loga-
rithmic transformation of future research output, ln(qf
+ 1).
it
We are concerned that the model might be misspecified by
restricting ourselves to OLS applied to this particular func-
tional form. We therefore repeat the analysis with nonlinear
regression models frequently used to study research output
or citations, such as the Poisson model, the negative bino-
mial model, and the zero-inflated negative binomial model.
Results show that the in-sample log likelihood is higher for
the (zero-inflated) negative binomial model than for the lin-
ear model applied to the ln(y + 1)-transformation. However
the out-of-sample RMSE is lowest for the linear model. As
the linear model is also easy to interpret and evaluate, we use
it as our main specification.
We also consider panel data models. Fixed-effect models
are not useful to predict the productivity of junior researchers
so we do not pursue them further.13 We also investigate the
predictive power of vector autoregressive (VARs) models
where past network variables affect future output and past
output influences future network variables. We estimate such
11 We do not consider authors below the median because the median recent
output is 0.
12 See the online appendix for more details.
13 Results from panel data regressions are available in the online appendix.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
r
e
s
t
_
a
_
0
0
4
3
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SOCIAL NETWORKS AND RESEARCH OUTPUT
947
Figure 7.—RMSE % Difference between Restricted Models across Productivity Tiers
Tier 1 (>99%)
Tier 2 (95−98%)
Betweenness
Coauthors’ productivity
Coauthors’ coauthors prod.
Degree
Degree of order 2
Top 1%
Betweenness
Coauthors’ productivity
Coauthors’ coauthors prod.
Degree
Degree of order 2
Top 1%
0
.5
1
1.5
2
2.5
3
3.5
4
4.5
0
.5
1
1.5
2
Modell 1
Modell 1
Tier 3 (90−94%)
Tier 4 (80−89%)
Betweenness
Betweenness
Coauthors’ productivity
Coauthors’ productivity
Coauthors’ coauthors prod.
Coauthors’ coauthors prod.
Degree
Degree of order 2
Top 1%
Modell 1
Degree
Degree of order 2
Top 1%
Modell 1
0
.5
1
1.5
2
0
.5
1
1.5
2
Tier 5 (50−79%)
Betweenness
Coauthors’ productivity
Coauthors’ coauthors prod.
Degree
Degree of order 2
Top 1%
Modell 1
0
.5
1
1.5
2
VAR models using a seemingly unrelated regressions (SUR)
Ansatz, allowing for correlation in the error terms across
the two equations. The lag length of each equation is selected
using the BIC criteria. The SUR regressions should in prin-
ciple lead to more efficient predictions as long as the two
equations do not include the same set of lagged variables, A
conditions that is fulfilled here. Results show that the pre-
dictions generated by the unrestricted SUR model 3 verwenden
feasible generalized least squares (FGLS) hardly differ from
the unrestricted model 3 estimated using simple OLS. Dort-
Vordergrund, the SUR model does not outperform, out of sample, Die
simple OLS.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
948
THE REVIEW OF ECONOMICS AND STATISTICS
VI. Abschluss
In diesem Papier, we have examined whether a researcher’s
coauthor network helps predict their future output. Under-
lying our study are two main ideas. The first idea is that a
collaboration resulting in a published article reveals valuable
information about an author’s ability and research ambitions.
This is particularly true for junior researchers whose type
cannot be fully assessed from their cumulative output. Der
second idea is that professional research networks provide
access to new research ideas. These ideas can subsequently
be turned into published papers provided the researcher
possesses the necessary ability and dedication.
To investigate these ideas, we examine coauthorship in
economics. Our focus is not on statistical significance or
causality but rather on predictive power. Aus diesem Grund,
we adopt a methodology that eliminates data mining and
minimizes the risk of pretesting bias. To this effect, wir rannten-
domly divide the data into two halves. Parameter estimates
are obtained with one-half and predictions are judged by how
well they perform in the other half of the sample.
We find that information about someone’s coauthor net-
works leads to a modest improvement in the forecast accuracy
of their future output over and above what can be predicted
from their past output. The network variables that have the
most information content are the productivity of coauthors,
closeness centrality, and the number of past coauthors. Diese
results are robust to alternative specifications and variable
definitions.
We investigate whether the predictive power of network
variables is stronger for more talented researchers, as would
be the case if taking advantage of new ideas requires talent
and dedication. We find that the predictive value of network
variables is nonmonotonic with respect to past productiv-
ität. Network variables do not predict the future productivity
of individuals with below-average initial productivity. Sie
are somewhat informative for individuals in the highest
past productivity tier group. But they are most informative
about individuals in between. Tatsächlich, for these individu-
als, networks contain more information about their future
productivity than recent research output.
The work presented here leaves many questions unan-
swered. Insbesondere, we do not claim to have identified a
causal effect of coauthorship or network quality on future out-
put. If anything, the signaling hypothesis is based on a reverse
causality argument, and it receives the most support from our
Analyse. Jedoch, we also find evidence that network con-
nections are most useful to talented researchers. This result
is consistent with a causal relationship between the flow of
research ideas and future output, with the caveat that talent
is needed to turn ideas into publishable papers.
VERWEISE
Ashley, Richard, Clive W. J. Granger, and Richard Schmalensee, “Adver-
tising and Aggregate Consumption: An Analysis of Causality,”
Econometrica 48 (1980), 1149–1167.
Azoulay, Pierre, Joshua Graff Zivin, and Jialan Wang, “Superstar Extinc-
tion,” Quarterly Journal of Economics 25 (2010), 549–589.
Bramoullé, Yann, Habiba Djebbari, and Bernard Fortin, “Identification of
Peer Effects through Social Networks,” Journal of Econometrics
150:1 (2009), 41–55.
Calvó-Armengol, Antoni, Eleonora Patacchini, and Yves Zenou, “Peer
Effects and Social Networks in Education,” Review of Economic
Studien 76:4 (2009), 1239–1267.
Conley, Timothy G., and Christopher R. Udry, “Learning about a New
Technologie: Pineapple in Ghana,” American Economic Review 100
(2010), 35–69.
Diebold, Francis, and Roberto Mariano, “Comparing Predictive Accuracy,”
Journal of Business and Economic Statistics 13 (1995), 253–263.
Ductor, Lorenzo, “Does Co-Authorship Lead to Higher Academic Produc-
tivity?” Oxford Bulletin of Economics and Statistics (2014), doi:
10.1111/obes.12070.
Fafchamps, Marcel, Sanjeev Goyal, and Marco J. van der Leij, “Match-
ing and Network Effects,” Journal of the European Economic
Association 8:1 (2010), 203–231.
Fair, Ray C., and Robert J. Shiller, “Comparing Information in Forecasts
from Econometric Models,” American Economic Review 80 (1990),
375–389.
Fildes, Robert, and Spyros Makridakis, “The Impact of Empirical Accu-
racy Studies on Time Series Analysis and Forecasting,” International
Statistical Review 63 (1995), 289–308.
Glaeser, Edward, and Jose A. Scheinkman, “Nonmarket Interactions,” in M.
Dewatripoint, L. Hansen, and S. Turnovsty, Hrsg., Advances in Eco-
nomics and Econometrics: Theory and Applications, Eighth World
Congress (Cambridge: Cambridge: Universitätsverlag, 2003).
Goyal, Sanjeev, Connections: An Introduction to the Economics of Networks
(Princeton, NJ: Princeton University Press, 2007).
Goyal, Sanjeev, Marco J. van Der Leij, and Jos Luis Moraga-González,
“Economics: An Emerging Small World,” Journal of Political
Economy 114:2 (2006), 403–412.
Hong, Yongmiao, and Tae-Hwy Lee, “Inference on Predictability of For-
eign Exchange Rates via Generalized Spectrum and Nonlinear Time
Series Models,” Review of Economics and Statistics 85:4 (2003),
1048–1062.
Jackson, M. O., Social and Economic Networks (Princeton, NJ: Princeton
Universitätsverlag, 2008).
Kodrzycki, Yolanda K., and Pingkang Yu, “New Approaches to Ranking
Economics Journals” (Boston: Federal Reserve Bank of Boston,
2006).
Lettau, Martin, and Sydney Ludvigson, “Consumption, Aggregate Wealth,
and Expected Stock Returns,” Journal of Finance 56:3 (2001),
815–849.
Manski, Charles F., “Identification of Endogenous Social Effects: Der
Reflection Problem,” Review of Economic Studies 60:3 (1993),
531–542.
Moffitt, Robert A., “Policy Interventions, Low-Level Equilibria, and Social
Interaktionen,” in S. Durlauf and P. Jung, Hrsg., Social Dynamics
(Cambridge, MA: MIT Press, 2001).
Rapach, David E., and Mark E. Wohar, “Testing the Monetary Model
of Exchange Rate Determination: New Evidence from a Cen-
tury of Data,” Journal of International Economics 58:2 (2002),
359–385.
Stock, James H., and Mark W. Watson, “Forecasting Inflation,” Journal of
Monetary Economics 44 (1999), 293–335.
Sullivan, Ryan, Allan Timmermann, and Halbert White, “Data-Snooping,
Technical Trading Rule Performance, and the Bootstrap,” Journal of
Finance 54:5 (1999), 1647–1691.
Swanson, Norman R., and Halbert White, “A Model Selection Approach to
Real-Time Macroeconomic Forecasting Using Linear Models and
Artificial Neural Networks,” this review 79:4 (1997), 540–550.
van der Leij, Marco J., and Sanjeev Goyal, “Strong Ties in a Small World,”
Review of Network Economics 10:2 (2011), 1.
Vega-Redondo, F., Complex Social Networks (Cambridge: Cambridge
Universitätsverlag, 2007).
Waldinger, Fabian, “Quality Matters: The Expulsion of Professors and
the Consequences for PhD Student Outcomes in Nazi Germany,”
Journal of Political Economy 118:4 (2010), 787–831.
Wasserman, Stanley, and Katherine Faust, Social Network Analysis: Meth-
ods and Applications (Cambridge: Cambridge University Press,
1994).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
R
e
S
T
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
9
6
5
9
3
6
2
0
1
2
4
9
5
/
R
e
S
T
_
A
_
0
0
4
3
0
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3