Roberto Oboe
Department of Mechanical and Structural
Maschinenbau
University of Trento
Via Mesiano 77, 38050 Trient, Italien
roberto.oboe@unitn.it
http://www.ing.unitn.it/~oboer/
A Multi-Instrument, Force-
Feedback Keyboard
When playing a musical instrument, a player per-
ceives not only the sound generated, but also the
haptic interaction, arising during the contact be-
tween player and instrument. Such haptic interac-
tion, based on the sense of touch, involves several
senses in the player: tactile, kinesthetic (d.h., medi-
ated by end organs located in muscles, tendons, Und
joints and stimulated by bodily movements and ten-
sionen), proprioceptive (d.h., von, relating to, or being
stimuli arising within the organism), usw. By its na-
tur, the haptic interaction is bidirectional, and this
is exploited by musical instrument players, who can
better correlate their actions on the instrument to
the sound generated. Zum Beispiel, by paying atten-
tion to the interaction force between key and finger,
arising during the descent of the key, pianists can
detect the re-triggering of the escapement mecha-
nisms and, im Gegenzug, can adjust the key motion to ob-
tain the fastest repetition of the note.
Roughly speaking, haptic information allows the
player to perceive the “state” of the mechanism be-
ing manipulated through the key. By using this
knowledge about the state of the mechanism and
correlating it with the sound generated, the player
learns a strategy to obtain desired tones. This tight
correspondence between acoustic response and
touch response, Jedoch, is lost in many electronic
Instrumente (z.B., in standard commercial synthe-
sizers), in which sound generation is related only to
the key attack velocity and pressure. In this type of
synthetic instrument, the touch feedback is inde-
pendent of the instrument being simulated. Für in-
Haltung, the interaction with different instruments
like harpsichord, piano, or pipe organ gives the same
haptic information to the player. This constitutes a
significant limitation for the musician, who loses
expressive control of the instrument and, im Gegenzug, von
the generated sound.
Computermusikjournal, 30:3, S. 38–52, Fallen 2006
© 2006 Massachusetts Institute of Technology.
This consideration led to several research activi-
Krawatten, aimed at the realization of an active keyboard,
in which actuators connected to the keys are driven
in such a way that the haptic interaction experi-
enced is the same as if the player were interacting
with the keyboard of the real instrument being em-
ulated by the synthesizer (Bäcker 1988; Cadoz,
Lisowski, and Florens 1990; Gillespie 1992; Gille-
spie and Cutkosky 1992; Cadoz, Luciani, and Flo-
rens 1993; Gillespie 1994). Such haptic displays are
usually referred to as “virtual mechanisms,” be-
cause they are designed for the reproduction of the
touch feedback that a user would experience when
interacting with an actual multi-body mechanism.
A very simple example of virtual mechanism is the
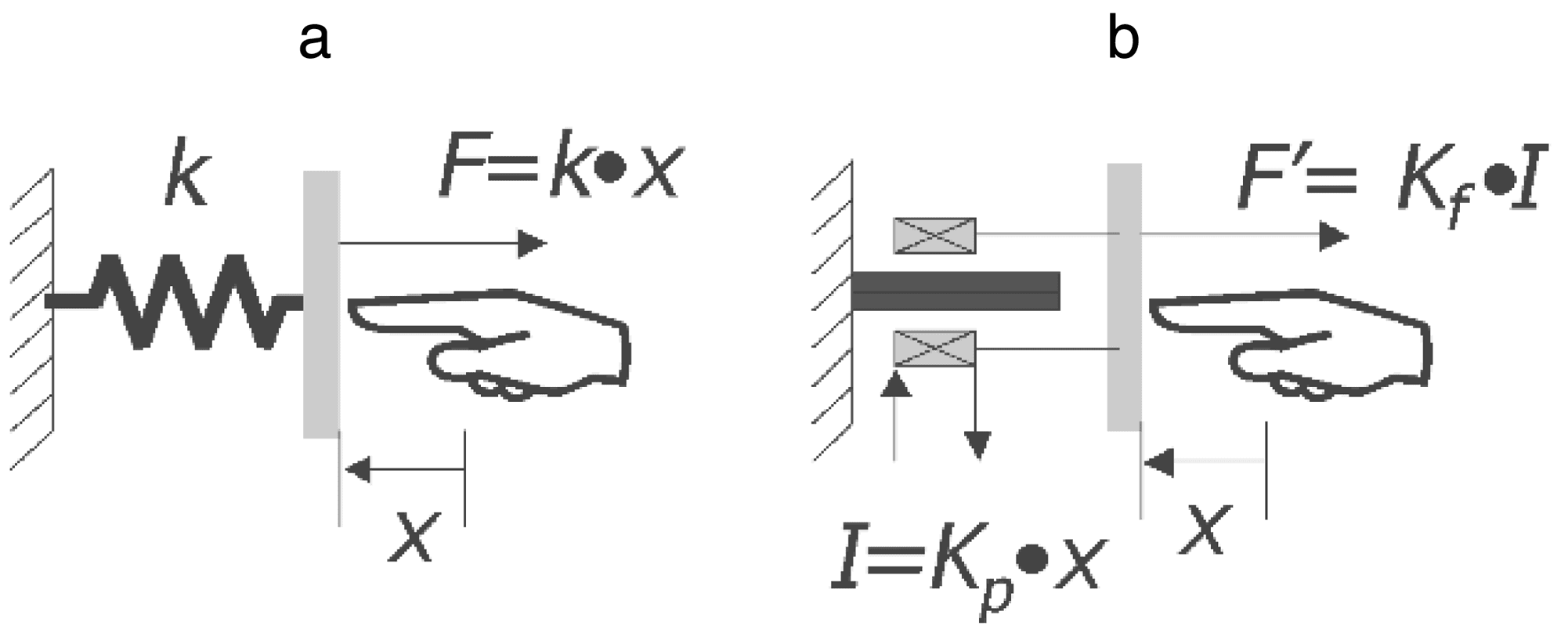
“virtual spring” shown in Figure 1.
Figure 1a shows the actual mechanism, realized
by a spring, anchored to a wall on one side and to a
plate on the other. Pushing the plate, a force propor-
tional to the displacement x is percevied. In Abbildung
1B, the virtual mechanism is shown. Hier, Die
spring has been replaced by a linear motor. By sens-
ing the position of the plate and driving the motor
with a current proportional to such displacement,
the force perceived by the user is again proportional
to the displacement, as if the user were pushing the
system with the real spring. Following the same
principle, a damping mechanism can be simulated
by generating a force proportional to the velocity of
the plate, while an inertial term can be added by
sending to the motor a current proportional to plate
acceleration.
This very simple example can be extended to
multi-body mechanisms, composed of several parts,
which interact with one another in terms of im-
pacts, constraints, usw. In such a case, the motion of
each part of the virtual mechanism must be calcu-
lated by a dynamic simulator, which incorporates
all the characteristics of the real mechanism and
computes the interaction forces among the parts. Es
is worth noting that, at times, an overly detailed
38
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
C
Ö
M
J
.
.
2
0
0
6
3
0
3
3
8
P
D
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1. Virtual spring.
description of the real mechanism leads to a bulky
dynamic simulator, not suitable for real-time imple-
mentation, as is required in haptic interaction.
Darüber hinaus, it is usually difficult to tune the parame-
ters of the dynamic simulator, especially when the
mechanism to be simulated contains several non-
linear components, such as nonlinear dampers or
constraints.
Among all the possible keyboard-operated instru-
gen, the grand piano has by far the most compli-
cated mechanism (Topper and Wills 1987). Der
grand piano action, in fact, is composed of dozens of
components and this, as we mentioned, has im-
peded the realization of a real-time dynamic simula-
tor for it. A remarkable work by Gillespie and
Cutkosky (1992) shows how it is possible to imple-
ment a very detailed model of the piano action and
tune it by matching simulation and experimental
results, the latter obtained by accurately measuring
all dynamic and kinematic variables on an actual
piano mechanism. Jedoch, the obtained model,
even if it results in good agreement with experimen-
tal data, can run only offline. Given these consider-
ations, several researchers have focused their work
on the reproduction of only one or a few specific
behaviors of the mechanism. Zum Beispiel, Bäcker
(1988) proposes the simulation of user-programmable
inertial and viscous characteristics to adapt the key-
board to the player’s taste.
Gillespie (1992, 1994), andererseits, hat
studied the modeling of a simplified piano action,
composed of only two bodies: the key and the
hammer. Even with this very simple model, es ist
possible to reproduce part of the hammer motion,
composed of three different phases: contact with
the key, fly, and return on the key. This model,
Jedoch, does not take into account the impact of
the hammer with the string and the effect of es-
capement, even if such characteristics are very
useful in regaining the previously mentioned corre-
spondence between acoustic response and haptic
interaction.
This article presents the preliminary results ob-
tained by the MIKEY (Multi-Instrument active
KEYboard) Projekt. The project is aimed at the real-
ization of a multi-instrument active keyboard with
realistic touch feedback. Insbesondere, the instru-
ments to be emulated are the grand piano, the harp-
sichord, and the Hammond organ. Given the
previous consideration, it is clear that some tradeoff
between model accuracy and real-time operability
had to be made at the beginning of the project, espe-
cially for the grand piano. The research presented
here started from the work of Gillespie and has
been improved by adding some additional features,
namely the hammer-string impact, various state-
dependent hammer-key impacts, and the escape-
ment effect. Auch, to improve the quality of the
haptic feedback, a direct-drive, low-friction motor
has been used. Endlich, particular attention has been
paid to the cost of the overall system, by using inex-
pensive devices for sensing, actuation, and real-time
Berechnung.
After introducing the models used in the dynamic
simulator, the article describes the experimental
setup realized. The experimental results obtained
are then reported and compared with those obtained
with a standard piano keyboard. Comments on the
results presented conclude the article.
Modeling the Mechanisms
The realization of a realistic haptic interaction with
an active keyboard requires an accurate model of
the mechanism to be emulated. In diesem Abschnitt,
three different mechanisms emulated by the MIKEY
system are described, pointing out the simplifica-
tion operated on the complete model to achieve a
dynamic simulation that runs in real time. Der
three models considered are the grand piano, Die
harpsichord, and the Hammond organ.
Oboe
39
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
C
Ö
M
J
.
.
2
0
0
6
3
0
3
3
8
P
D
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
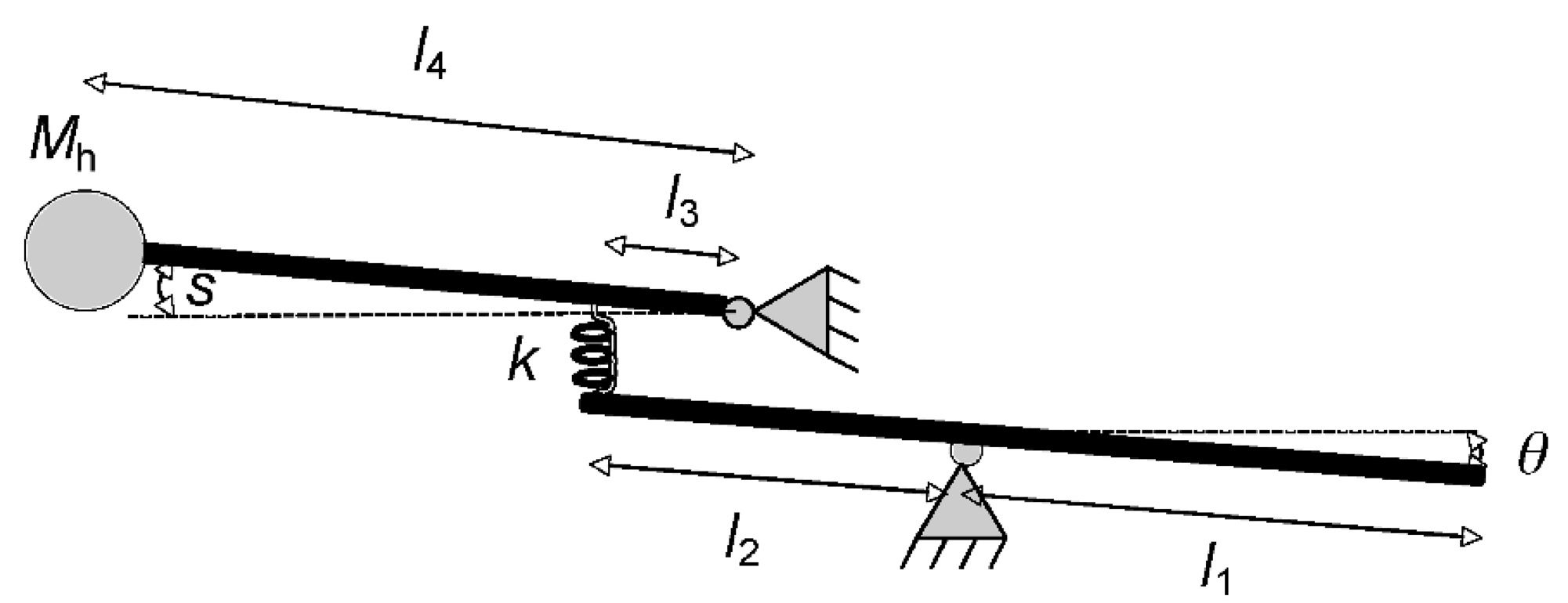
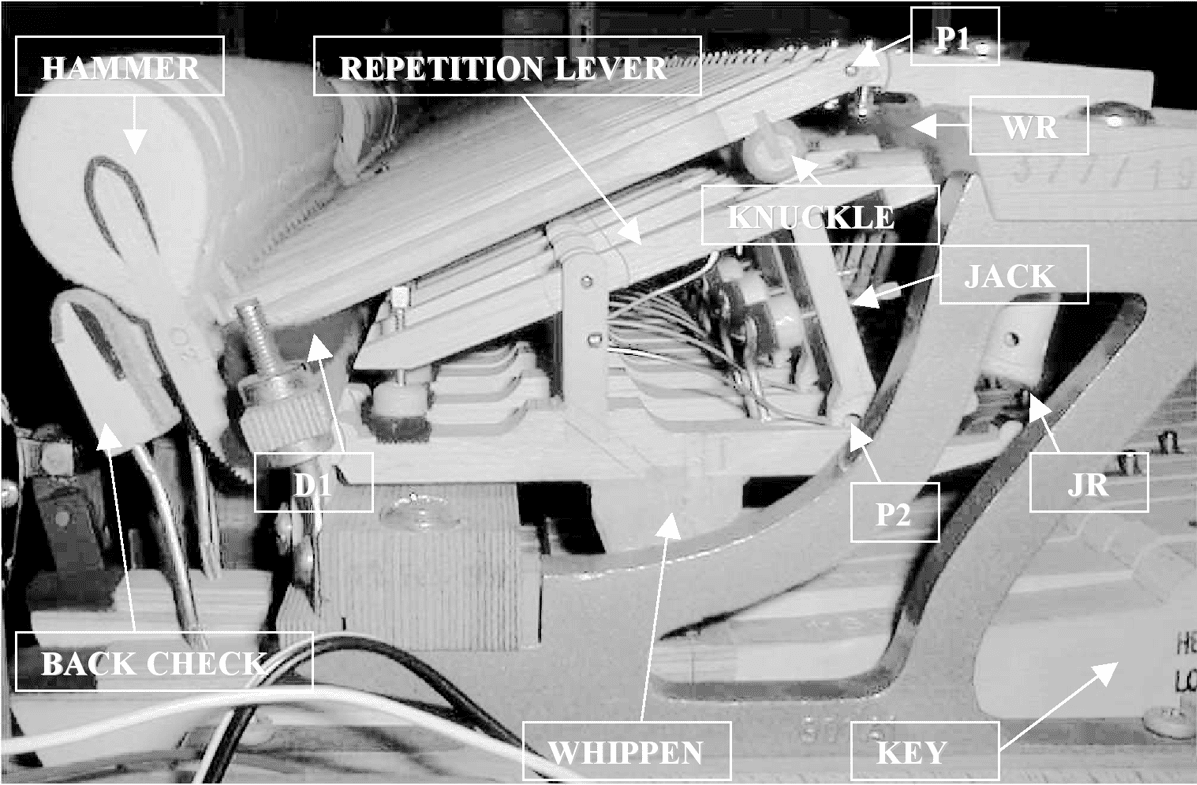
Figur 2. Grand piano
Aktion.
Figur 3. Simplified model
of the piano action.
Grand Piano Action
A typical grand piano action is shown in Figure 2.
As previously mentioned, this is a mechanism com-
posed of several parts, with characteristics that are
not always easily described with simple models.
This is the case, zum Beispiel, with the “soft” parts,
like felts, exhibiting non-linear stiffness and high
values of internal friction (d.h., energy dissipation).
The parts composing the mechanism are briefly de-
scribed here (referring to Figure 2). The hammer is
free to rotate around the pivot P1 and rests on a soft
damper D1. When the key is pressed, the whippen
goes up and the jack stays in its position, thanks to
the action of a spring. Gleichzeitig, the ham-
mer swings up, pushed by the jack and the repeti-
tion lever, both in contact with the rubber-covered
knuckle. When the key is pressed further, the repe-
tition lever is stopped against the regulator WR, Und
only the jack remains in contact with the hammer.
Endlich, the jack is stopped by the regulator JR at
one end and starts to rotate clockwise around the
pivot P2, losing contact with the hammer.
If the key descent is fast enough, the hammer
reaches the string (which is not shown in Figure 2,
but which lies horizontally above the action). Der
impact with the string has quite complicated dy-
namics, but they can be summarized as a finite-
time impact with a loss of energy. Literature in this
field says that the impact time is roughly one eighth
of the period of the note’s waveform, and about 20
percent of the hammer energy is lost during impact
(Fletcher and Rossing 1991). The hammer, Dann,
bounces back, and it may impact different parts of
die Aktion, according to the key position. If the key
is still completely lowered, the hammer tail impacts
the back-check and dissipates all its energy, without
touching the whippen. (No haptic feedback is gener-
ated by this impact.) Should the key be raised a
little (enough to have the jack back in its position
and ready for repetition), the hammer hits the whip-
pen, Und, according to the mutual velocity, may or
may not bounce back toward the string. The haptic
feedback perceived by the player in this phase is
similar to that experienced when a ball hits a pad,
rebounds, and hits the pad again. Owing to the dis-
sipation of energy occurring during the impact, nur
one rebound usually occurs. Endlich, should the key
be in its rest position, the hammer hits both the
whippen and a rest felt D1. The hammer rebounds
Und, because this lowers the downward force acting
on the whippen, the latter moves upward, so a little
downward motion of the key can be observed at the
front of the key (nearest the player).
This qualitative description of the piano action
behavior has an analytical counterpart. So far, Gille-
spie and Cutkosky (1992) have developed the most
accurate dynamic model of the piano action. Wie-
immer, owing to limitations in computational power,
the equations of their model could be integrated
only off-line. Real time experiments performed by
Gillespie (1994) were based on a simplified model of
the piano key, composed of the key and the hammer.
The simplified model, reported in Figure 3, consid-
ers a hammer swinging around a pivot and interact-
ing with the key through a spring-like contact.
The simplified model is fully described by the
40
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
C
Ö
M
J
.
.
2
0
0
6
3
0
3
3
8
P
D
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
contact stiffness k, the lengths l1 and l2, the hammer
mass Mh and inertia Ih = Mhl4
2, the length l4, und das
distance between hammer pivot and contact point
l3. As a further simplification, all rotational motions
are approximated as linear; as a result, the force ex-
changed between key and hammer is
F
hk
=
θ
k l
(
2
−
l s
),
3
(1)
where s and q represent the hammer and key angu-
lar position, jeweils.
It is worth noting that Equation 1 considers a
spring with negligible length, and it is applicable
only when the spring results to be compressed, d.h.,
Wann
θ −
l
(
2
l s
)
3
>
0
.
(2)
When Equation 2 is not satisfied, this means that
the hammer is in free fall, d.h., its motion is driven
only by gravity.
The dynamic simulator of the simplified model,
Dann, accounts for two sub-models, dazugehörigen
to the conditions of contact and no-contact between
the hammer and the key, jeweils. Its behavior
can be properly represented by a hybrid dynamic
System (Brockett 1993), describing the hammer mo-
tion with a continuous time differential equation,
in which one term (the spring force) depends on a
switching function that indicates the occurrence of
contact between hammer and key.
Given these considerations, hammer motion is
described by the following equations:
ICH
˙˙( )
θ
T
H
=
h s
θ
( , )
=
h s
θ
( , )(
θ
kl l
(
2
3
T
( )
−
−
l s t M l g
3
( )))
H
4
1
0
Wenn
Wenn
(
(
θ
l
2
θ
l
2
T
( )
T
( )
−
−
l s t
( ))
3
l s t
( ))
3
≥
<
0
0
,
(3)
where g represents the gravity acceleration and the
second equation is simply the Heaviside function of
the spring compression, thus representing the
switch between contact and no-contact conditions.
As for the haptic feedback, the force to be gener-
ated by an actuator replacing the hammer in the
mechanism of Figure 2 should be equal to Equation
4, which is a modified version of Equation 1:
f
haptic
=
h s
θ
θ
k l
( , )( (
2
−
l s
))
3
(4)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
It is worth noting that this model includes nei-
ther the escapement nor the hammer-string impact
modeling. Also, no friction or damping is considered
in the model, resulting in an overestimated hammer
speed and non-dissipative impacts between hammer
and key. Indeed, both dynamic simulation (i.e., the
computation of the motion of each part of the
mechanism) and haptic feedback cannot be accu-
rately reproduced with such a simplified model. On
the other hand, even if it can be expected that the
present limitations in computational power will be
partially removed by technological improvements,
the high cost of the devices needed for the real-time
computation is still a major impediment to the real-
ization of a commercial product in which all the
characteristics of the piano action are incorporated
in a real-time dynamic simulator.
Given the above considerations, it is clear that
some trade-offs are necessary in the design of a low-
cost active keyboard with realistic haptic feedback.
In the MIKEY project, we wanted to have a system
in which the angular position and the velocity of
the hammer could be accurately computed to pro-
vide an input to a sound synthesizer. In addition, we
wanted to have the most important haptic effects to
be reproduced at the player’s hand, namely the es-
capement, the hammer rebounds on the key, the
key weight, and the variable inertia of the system
(the latter two both changing when the hammer is
not in contact with the whippen or the repetition
lever is engaged).
The solution adopted to satisfy both requirements
is twofold. First, the dynamic simulator for the
hammer motion described herein has been en-
riched, by modeling the dissipative impacts of the
hammer with the string or the whippen and by set-
ting l3 as a control variable, whose value depends on
the state of the repetition mechanism. Second, the
haptic feedback is generated by adding the interac-
tion force computed by using the improved dy-
namic model (i.e., not accounting for impacts) to a
set of position-dependent events, like impacts and
escapement.
In particular, the dynamic simulator computes
the angular position of the hammer according to the
following modified version of Equation 3:
Oboe
41
⎧
⎨
⎩
I
˙˙( )
θ
t
h
=
h s
θ
( , )
l kl s t
( )
3
(
2
−
θ
l
3
t
( ))
+
B
k
d
dt
l s t
( )
(
2
−
θ
l
3
t
( ))
−
−
B t M l g
˙ ( )
θ
θ
h
4
h s
θ
( , )
=
1
0
if
if
(
(
l s t
( )
2
l s t
( )
2
−
−
θ
l
3
θ
l
3
t
( ))
t
( ))
≥
<
0
0
,
(5)
=
l
3
l
3
l
3
long
short
if rep
if rep
=
=
0
1
where Bq represents the friction of the hammer
joint, and the dissipation of energy in the impact be-
tween key and hammer has been modeled like vis-
cous friction Bk. The flag rep represents the state of
the repetition mechanism, set to 1 when the repeti-
tion lever is engaged. Clearly, should the repetition
lever be engaged, this results in a varied ratio be-
tween key and hammer speed, to be considered by
the dynamic simulator and to be haptically repro-
duced. This is accounted for in the simulator (Equa-
tion 5) by changing the length l3, depending on the
repetition lever state, the latter determined by the
position of the key.
This model, though containing more details of
the actual mechanisms than does that of Equation
3, does not take into account some very important
facts of the grand piano action. The first one is the
impact between hammer and string. For this reason,
during the free fly phase, the dynamic simulator
(Equation 5) evaluates the occurrence of hammer–
string impact. If such impact occurs, the angular ve-
locity of the simulated hammer is set so that it
bounces back with 90 percent of the velocity it had
before the impact. (This corresponds to an energy
loss of about 20 percent.) The impact duration, as
mentioned before, is about one eighth of the note
period in the actual piano, but it has been set to zero
in the dynamic simulator to simplify the implemen-
tation, because this choice has no consequences on
the perceived force.
Another aspect not considered by Equation 5 is
that, as mentioned before, when the hammer flies
back to the whippen, it may or may not impact on
it, depending on the position of the key. This has
been considered in the dynamic simulator, which
“stops” the simulated hammer in correspondence
to a simulated back-check if the key is fully pressed.
Regarding the haptic feedback, a preliminary con-
sideration should be made on the reproduction of
the inertial terms and key weight. In the MIKEY
project, to have a keyboard with limited size, the
whippen is removed, and only the key is left. The
force generated by the motor is applied on the back
of the key, i.e., where the whippen interacts with
the key in the actual mechanism, as will be shown
in the next section. Because the whippen is always
in contact with the key in the actual mechanism,
this means that part of the force to be generated by
the motor should be used to emulate the weight and
the inertia of the whippen. An alternative solution
that leads to smaller actuators is to replace the
whippen with some properly placed weights, as will
be shown later.
Regarding the haptic reproduction of the interac-
tion between the key and whippen with the ham-
mer, it is worth noting that Equation 5 represents a
rather simplified model of the actual mechanism,
leading to the following haptic force:
f
haptic
2
=
θ
( , )
h s
k l s t
( )
(
2
−
θ
l
t
( ))
3
+
B
k
d
dt
l s t
( )
(
2
−
θ
l
t
( )) .
3
(6)
Equation (6), however, does not take into account
all the nonlinear terms in friction, arising during
impacts, nor does it take into account the effects of
the repetition lever engagement, which is perceived
as a force that increases while the jack is sliding un-
der the soft surface of the knuckle, and then rapidly
decreases as the key is further pressed.
All the above considerations can be summarized
by the following equation, representing the force to
be applied at the key rear end, in order to have the
correct haptic feedback:
f t
( )
h
=
+
t G X t
f
( )
( )
haptic
2
+
+
˙˙( ),
θ
t
I
x
(7)
where G represents a user-selectable simulated
gravity effect (i.e., a user can program each key to
have different weights), and X accounts for extra
terms like the escapement or impacts. As for the
term Ix, this represents an additional inertial term,
which can be used to reproduce the haptic percep-
tion of keys with different inertia.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
42
Computer Music Journal
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎨
⎩
⎧
⎨
⎩
⎛
⎝
⎜
⎞
⎠
⎟
Figure 4. Simplified model
of escapement showing
force v. position.
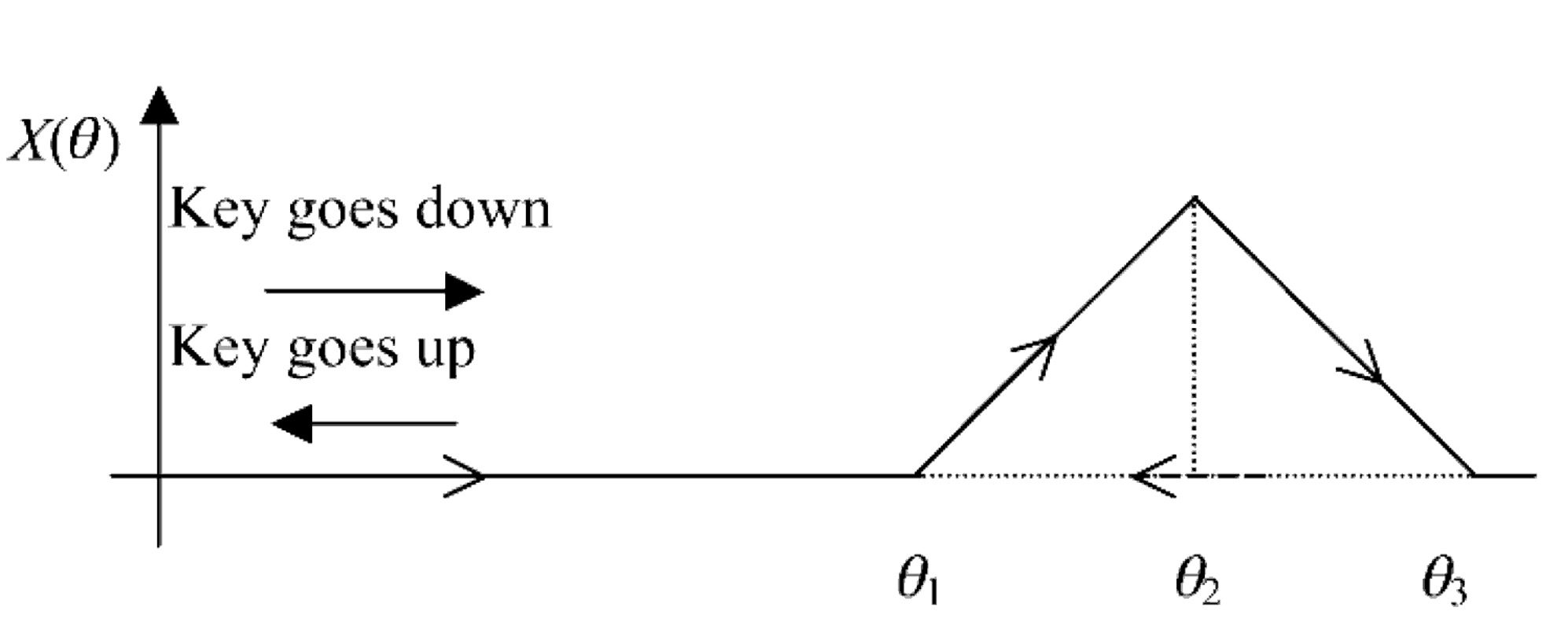
Figure 5. Management of
inversions during the es-
capement phase.
As for the extra terms X, we first consider the dif-
ferent types of hammer–key impacts and the corre-
sponding haptic effects. When the key is completely
pressed, the hammer head is stopped by the back
check, and no haptic feedback must be generated. If
the key is completely up, the impact is between the
hammer link and the rest damper. This is a dissipa-
tive event, in which the energy remaining after the
impact is a small part of the original one. Also, to
avoid multiple rebounds, when the hammer veloc-
ity goes below a certain threshold, its value is set to
zero after the impact. When the key is in any other
position, the hammer-key impact occurs at the
contact point, which can be modeled as a spring-
damper element, with a highly nonlinear damping
ratio and stiffness. To avoid complex modeling, the
force impulse to be haptically reproduced is com-
puted by considering the impact as a partially dissi-
pative event, in which the intensity of the force
impulse depends on the relative velocity between
hammer and key, and the energy of the hammer
(i.e., its speed) after the impact is a fraction of that
before the impact. Of course, amplitude and dura-
tion of the force pulse depend on the relative speed
of hammer and key. In MIKEY, to simplify the sys-
tem, the duration has been estimated experimen-
tally, and the amplitude is determined on the basis
of the observed reduction in absolute speed after the
impact in the actual keyboard.
Finally, X contains a term depending on the key
position q, which accounts for the escapement. This
is essentially a nonlinear spring that intervenes
when the key reaches the position corresponding to
the contact of the whippen with the regulator. After
the contact, the player perceives an increased resis-
tance of the key, which suddenly drops when the
second regulator forces the jack to slide under the
knuckle. A simplified model of this sequence has
been incorporated in the escapement model used in
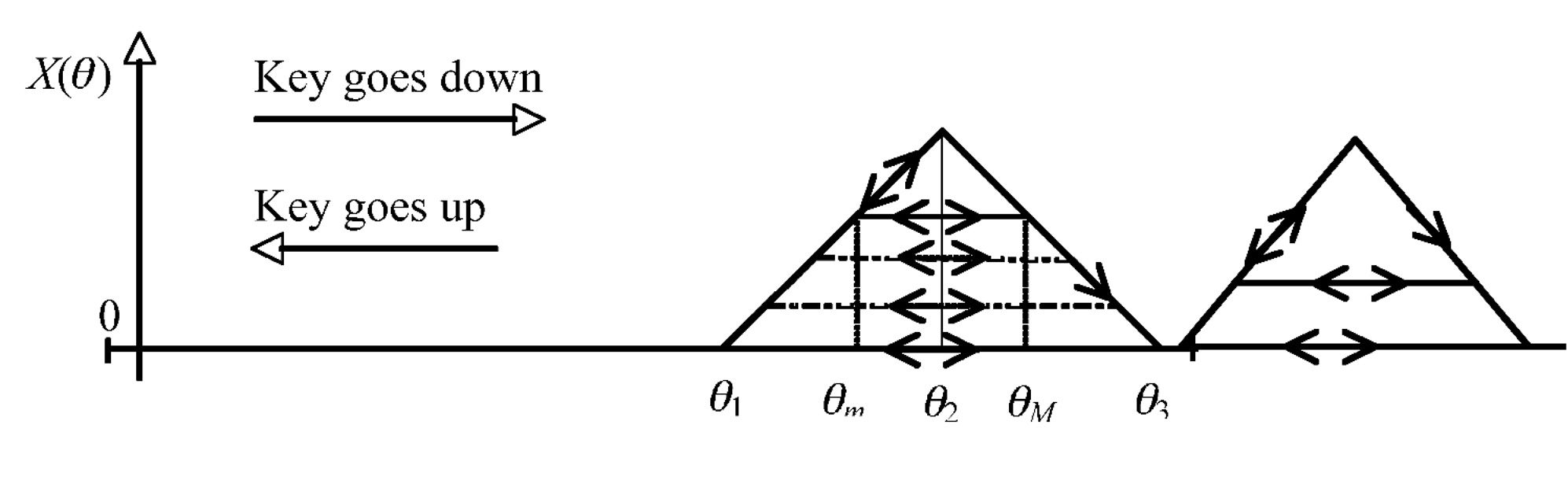
MIKEY system and it is shown in Figure 4.
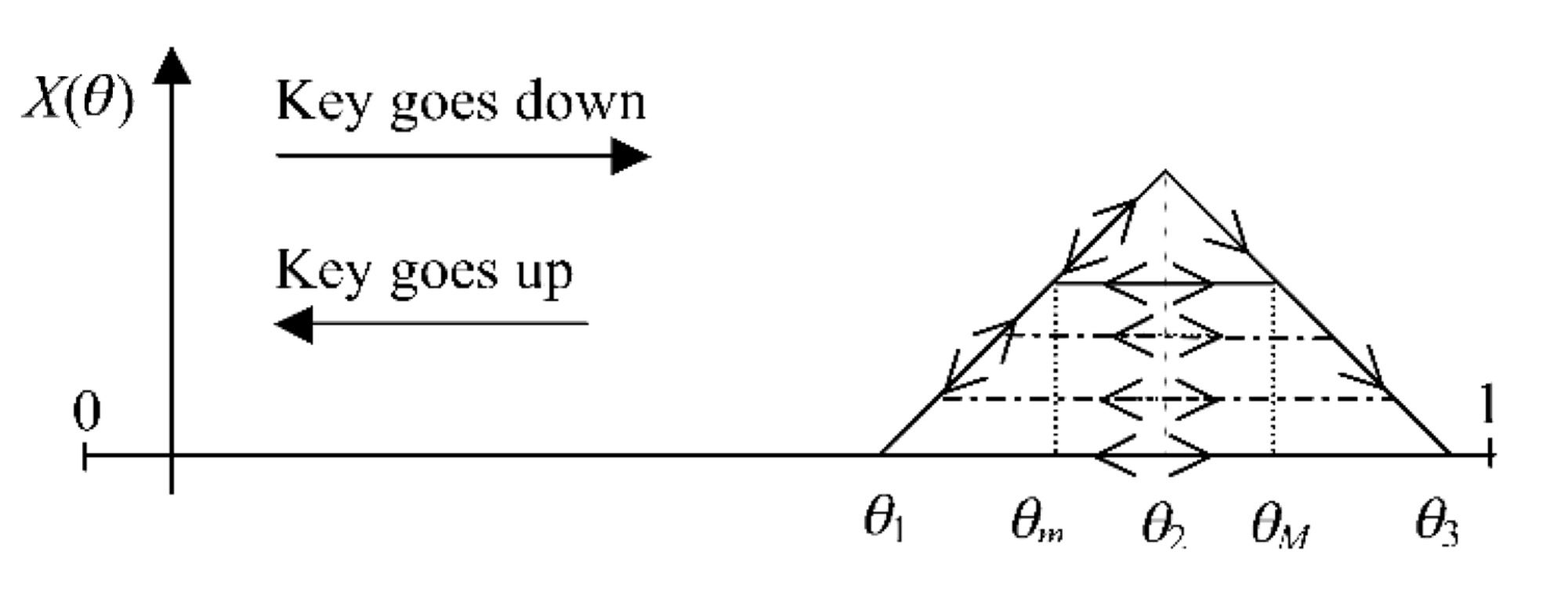
When the key reaches the position q1, the force
applied by the actuator linearly increases until it
reaches q2. At this point, the force linearly decreases,
until it reaches zero in q3. On the way back to the
origin, the force is held at zero, because the jack re-
load is an event that does not generate haptic feed-
back. A problem arises when the key goes up (i.e., it
inverts its motion) during escapement. A solution
proposed here is to consider the trajectories shown
in Figure 5.
If the inversion occurs between q1 and q2, the
force goes down with the position. Once the escape-
ment peak is passed, if an inversion in motion oc-
curs (e.g., at the point qM in Figure 5), the force is
kept constant, at the value it had at moment of in-
version, until the key gets to the position qm in
which the force of the positive slope is equal. Then,
should the position decrease further, the force de-
creases with it. If during the motion from qM to qm
another inversion occurs, the force is kept constant
until the key position gets again to qM. With this
simple model, the force perceived during escape-
ment first increases and then rapidly decreases, as if
a trigger were pushed. Furthermore, the sliding of
the jack under the knuckle during re-loading of the
escapement is modeled as a constant force, which
allows handling, in a simple way, the possible inver-
sion of motion in this phase.
The simple model of the escapement is of course
linked to the dynamic simulator, which is informed
of the state of the jack and, in turn, may alter the
value of the mechanical advantage between key and
Oboe
43
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Double-plectrum
harpsichord mechanism.
Figure 7. Harpsichord jack:
(a) key going down; (b) re-
turn to rest position.
(a)
(b)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
hammer motion accordingly. Experimental results
reported in the next section and informal tests with
performers confirm that a quite realistic haptic
feedback is obtained by adding the various contribu-
tions described in Equation 7.
Harpsichord
Many harpsichords have two strings for each key,
with a row of jacks for each set of strings. (A harp-
sichord mechanism with two jacks is shown in
Figure 6.) Stops, or registers, allow the player to
move unwanted sets of jacks slightly out of reach of
the strings, thus making possible different volumes
and combinations of tone colors. One set of strings
may sound an octave above normal pitch
(Humphries 2002).
In Figure 7a, a jack is shown, with the string be-
tween a damper and the plectrum. When the key
goes down, the string is pushed against the elastic
plectrum, and the force perceived increases as the
key goes down until the plectrum plucks the string.
After this event, the force approaches a very low
value. Then, the key is raised and the plectrum eas-
ily slides aside, under the action of the string (see
Figure 7b), so that the mechanism is ready to pluck
the string again.
The haptic feedback for harpsichords is very simi-
lar to the escapement in the grand piano action,
with a position-dependent force that increases as
the key is pressed until a threshold position, corre-
sponding to the string’s plucking. If the key is
pressed further, the force rapidly decreases. This be-
havior is similar to that of the escapement in the
grand piano, so it has been emulated by using the
function reported in Figure 5. Of course, actual
thresholds and forces have been tuned experimen-
tally on an actual harpsichord. As for such multi-
string systems, their haptic feedback has been
obtained by simply putting together several plec-
trum simulations, each of them with different (pos-
sibly non-overlapping) thresholds, as shown in
Figure 8.
In addition to the position-dependent force, a vis-
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
cous term can be added to the motor command to
simulate the friction of the real key, resulting in the
following commanded force:
˙ ( )
+θ
t B t X t
θ
( ( )).
=
f
harp( )
(8)
It is worth noting that the harpsichord exhibits a
smaller key inertia relative to that of the grand pi-
ano. Such a difference can be totally handled by the
actuators, or it can be obtained by properly placing
(and removing) additional weights on the keys, ac-
44
Computer Music Journal
Figure 8. Multi-plectrum
harpsichord, force to be
generated versus position.
Figure 9. Hammond organ.
cording to the instrument to be emulated. Of course,
the use of additional weights reduces the flexibility
of the system but greatly reduces its cost, because
the force to be generated by the motor (and thus its
size and cost) does not include the inertial term,
which can be quite high when playing a fortissimo
note on the grand piano.
Hammond Organ
The last keyboard-operated instrument considered
in the MIKEY project is the Hammond organ,
shown in Figure 9. This instrument was conceived
with the goal of giving the player the same haptic
feedback as in electrically controlled pipe organs.
In such instruments, electrically actuated pneu-
matic valves are turned on by a small switch
placed under each key. The perceived force is the
same as if a spring were placed under the key, with
a very small inertia and weight for the key itself.
This means that the force to be generated by the ac-
tuator in the virtual keyboard must be proportional
to key position. Should the key in the virtual key-
board have a higher weight and inertia than the de-
sired one, the motor must apply a force to emulate a
negative inertial term and weight. This solution,
however, may lead to unstable behavior, so it is
preferable to have removable weights mounted on
each key.
Given these considerations, the force to be gener-
ated by the motor in the most general case (i.e.,
without removable weights) should be expressed as
f
t
hammond( )
=
˙ ( )
θ
+
k t B t
θ
( )
−
(cid:2)
˙ ( ),
(cid:2)
θ
G J t
−
(9)
where DG and DJ account for the reduction of per-
ceived weight and inertia, respectively. As in the
harpsichord, the viscous term B is added, in order to
take account of friction that is usually present in
the real keyboard.
Experimental Setup
An important issue in designing a realistic simulator
is to tune its parameters, in order to closely emulate
the behavior of the actual system. For this reason,
the first part of the experimental activity has been
devoted to the collection of data from a real grand
piano keyboard to be used in model tuning.
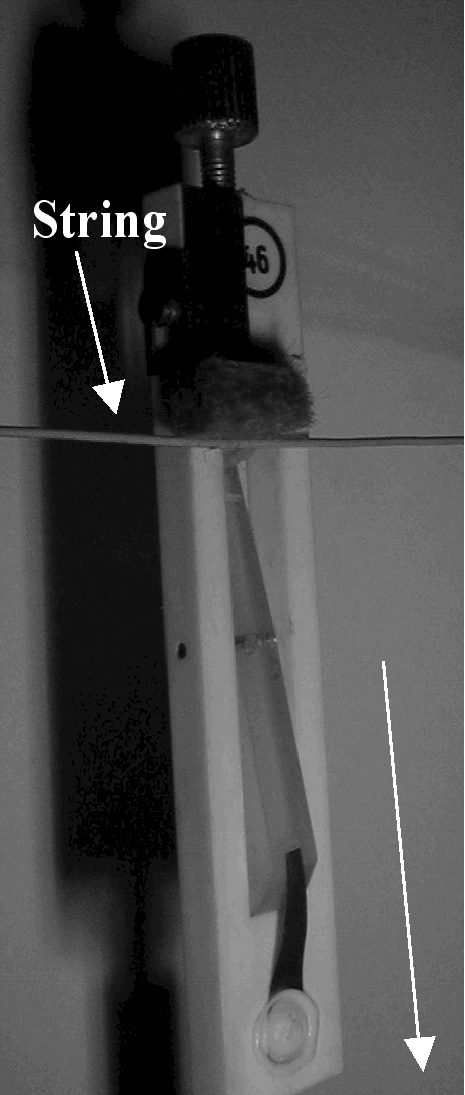
Key position is measured with a simple reflective
linear position sensor, placed under the front part of
the key (i.e., near the player). Hammer position is
sensed by placing an infrared LED on the hammer
stem, with its light beam pointing to a 37-mm
position-sensitive detector (PSD) from Hamamatsu
Photonics, which in turn produces an analog signal
proportional to the hammer position (see Figure 10).
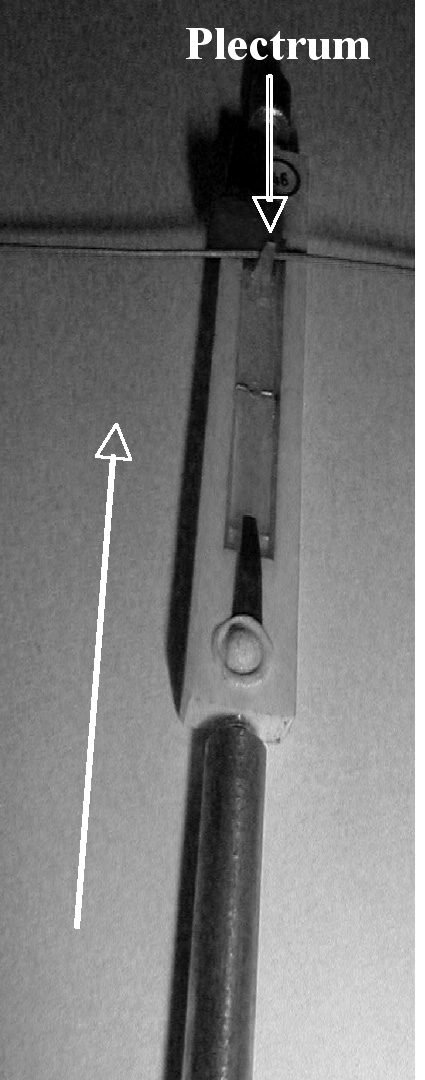
The force exerted on the key is measured by using
a piezo-resistive sensor placed on the front part of
the key, as shown in Figure 11. Additionally, a
simple detector for determining when the hammer
is no longer in contact with the whippen has been
realized by covering both the hammer and the whip-
pen with a thin layer of conducting material, thus
realizing an electrical switch that opens when the
hammer leaves the whippen.
Using this modified keyboard, it is possible to es-
timate several parameters, such as the hammer in-
ertia and the energy loss occurring in the impacts
against the whippen and the rest felt. As an ex-
ample, Figure 12 reports the recorded hammer posi-
Oboe
45
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10. Hammer posi-
tion sensing.
Figure 11. Force sensor.
Figure 12. Hammer re-
bounds on the whippen.
Figure 11
0.058
0.056
0.054
0.052
0.05
0.048
0.046
]
m
[
n
o
i
t
i
s
o
p
Hammer rebounds
hammer position
T
a
s
tion, released from the position at which it impacts
on the string. From the observed decay of the ampli-
tude and the oscillation period, the equivalent stiff-
ness and damping ratio can be easily obtained.
Furthermore, the same keyboard has been used in
validating the simulator by comparing the simu-
lated hammer trajectory with the actual one, under
the action of the same input (as will be described
later).
The second part of the experimental activity uses
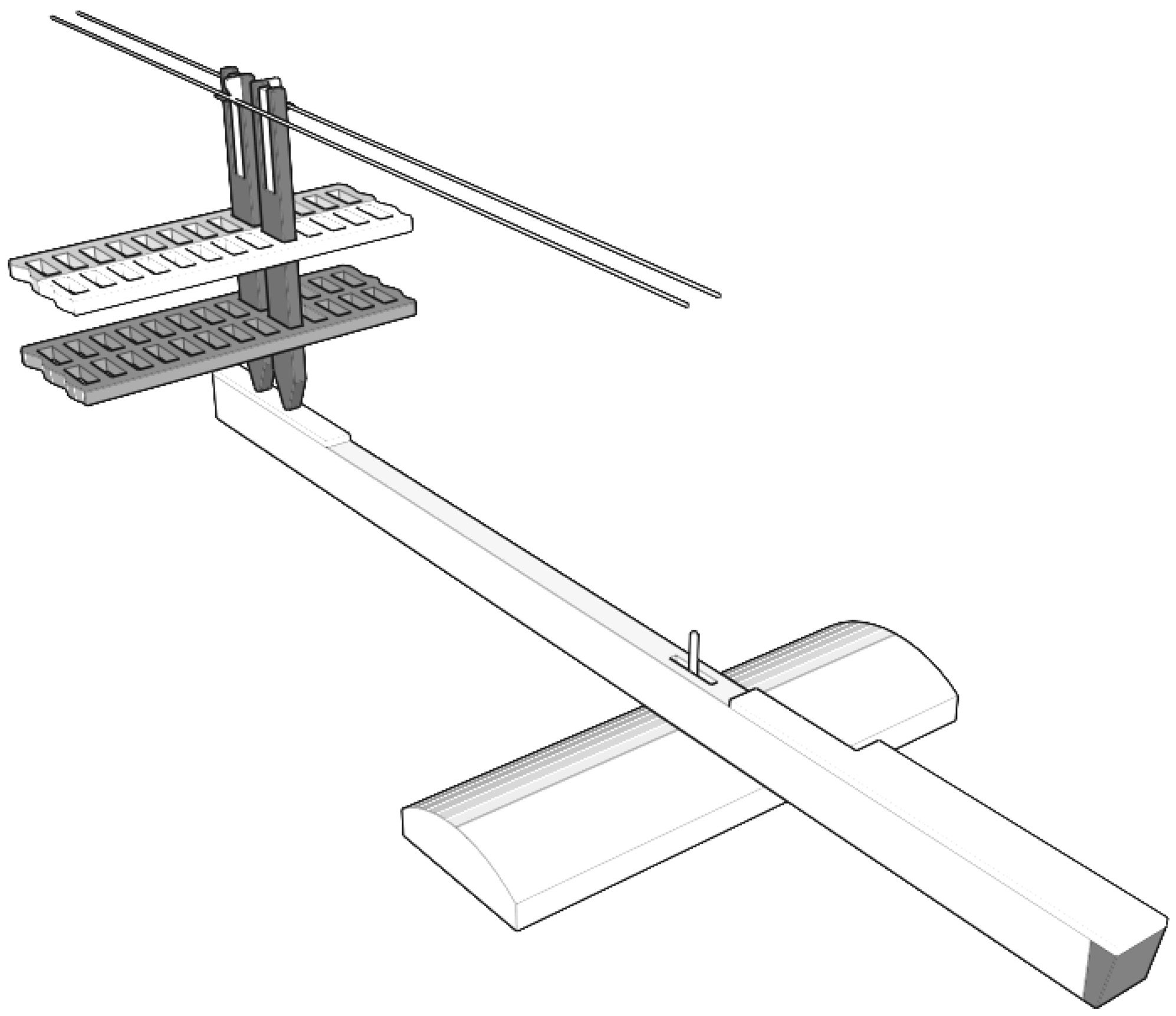
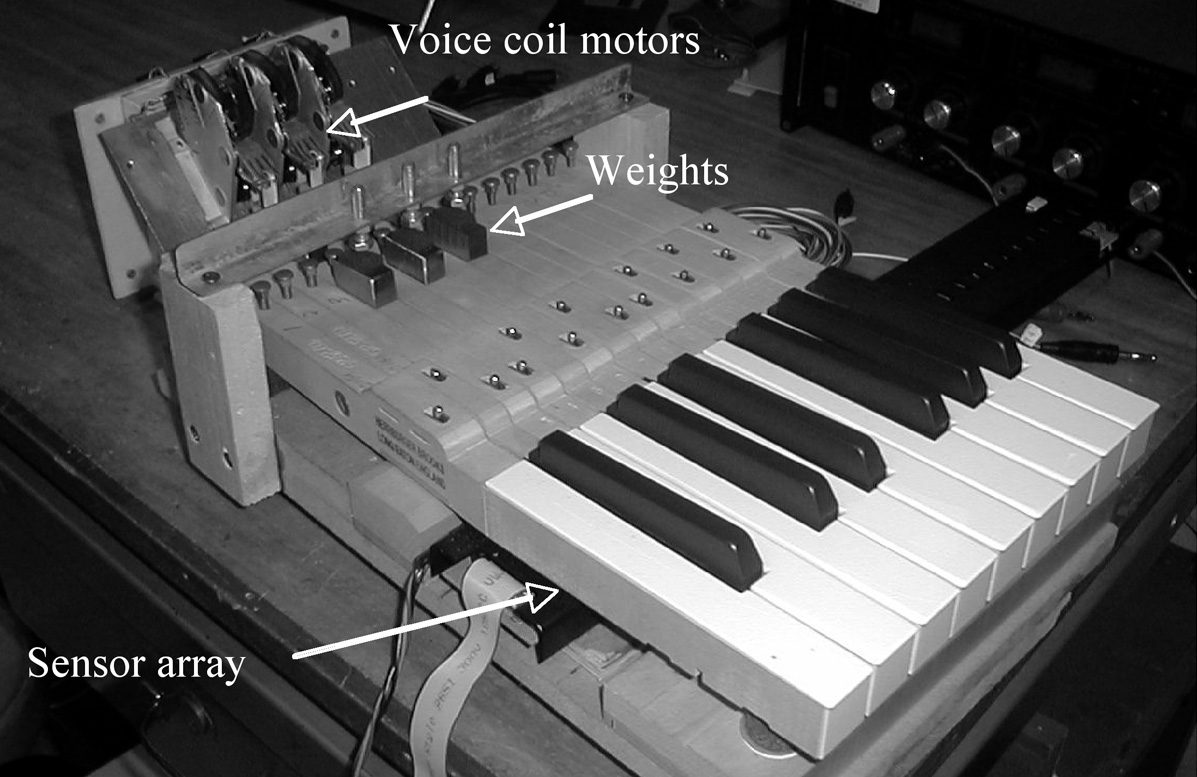
a different keyboard, the active one, shown in Fig-
ure 13. It represents only a small section of a com-
0.044
0.9
0.95
1
1.05
1.1
time [sec]
1.15
1.2
1.25
1.3
Figure 12
plete piano keyboard, and only three keys are con-
nected to rotational voice coils motors through rigid
links and low friction ball bearings, as shown in de-
tail in Figure 14. The motors, which have been re-
moved from standard hard disk drives (U4-class
disks, made by Seagate), have a very low friction
and inertia, so that the force applied to the key can
be considered directly proportional to the current
applied to the motor, thus avoiding the use of ex-
pensive force sensors. The torque constant is about
46
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13. MIKEY key-
board.
Figure 14. Detail of the
MIKEY keyboard.
Figure 15. Block diagram
of the key-control unit.
Figure 13
Figure 14
0.007 Nm/A, and the generated torque can be con-
sidered proportional to the applied current, up to
the frequency of the first mechanical resonant mode
of the voice coil motor (VCM), around 3 kHz. The
rated current is around 500 mA, and the peak cur-
rent is 2 A (which is allowed for less than 100 msec).
Key position is measured by using a low-cost reflec-
tive sensor, placed under the front of the key. Its
output is roughly linear, and its range is normalized
between 0 and 1 by an automated tuning procedure.
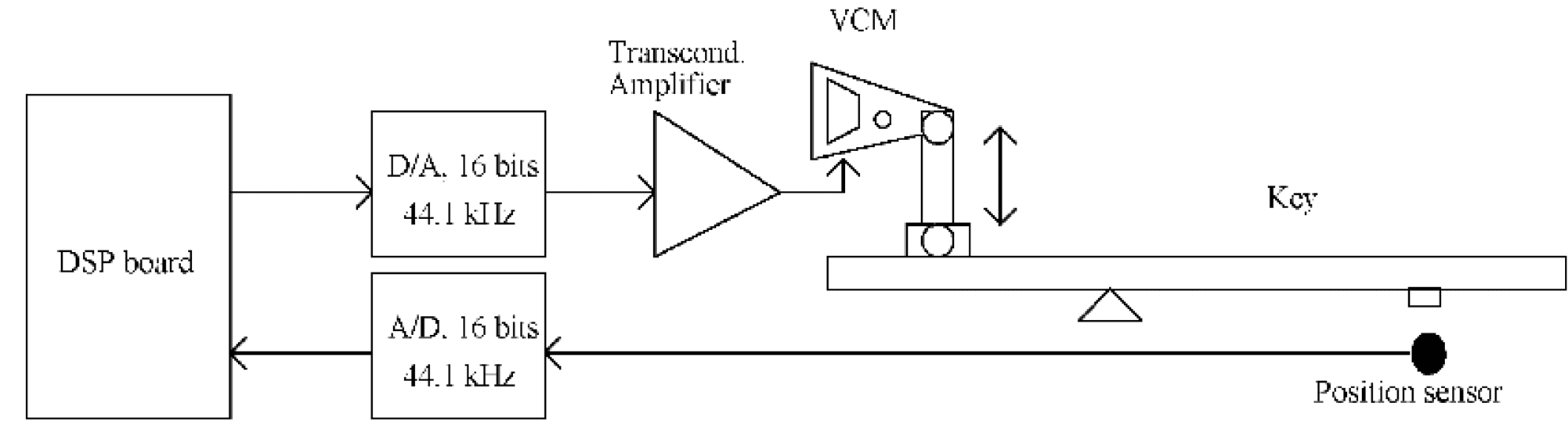
According to the block diagram of Figure 15, each
sensor’s output is sampled by a 16-bit, 44.1-kHz
A/D converter, which sends the digital data to a dig-
ital signal processor (DSP) board built around a Mo-
torola 56000 series chip. To obtain key velocity and
acceleration, position data are filtered through
multi-sample differentiators (Bibbero 1977). The
force to be generated by the motor is computed in
real time by the DSP and sent to a 16-bit, 44.1-kHz
D/A converter. Its output constitutes the input of a
linear trans-conductance amplifier (i.e., an amplifier
that generates an output current that is proportional
to the voltage applied at its input), realized with a
high-power operational amplifier and capable of
forcing a current up to 2 A into the voice coil motor,
with a bandwidth of 40 kHz.
Note that in Figure 14, some weights have been
added to the original key structure. Their masses
and positions have been chosen to get the same in-
ertia and weight of the key as with the whippen.
This solution is required to limit the request of
force to be generated by the motor. For instance, it
is useless and power-consuming to use the motor to
generate the gravitational effect originally due to
the whippen, since this constant term can be easily
replaced by a properly placed weight. Finally, in Fig-
ure 13, key regulators are shown. They have been
added to provide a mechanical stop to the key that
otherwise could pop off the keyboard in case of for-
tissimo action, since the “natural” stop, provided
by the whippen, has been removed.
It is worth noting that the system consists of low-
cost and readily available components. In particular,
the voice-coil motor has been obtained from a hard
disk drive and can be produced at very low cost
(about US$ 2 per motor). The A/D-D/A converters have been realized with a low-cost single chip codec, usually adopted in PC sound boards (about $1 per key). The transconductance amplifier is also
derived from hard-disk current drivers (SV123 by
STMicroelectronics, $1 per channel). Finally, the DSP used is an outdated device, easily replaceable with present microcontrollers (typically ranging around $4 per chip). As a result, the overall cost for
the hardware of each key is below $10.
Oboe
47
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 16. Generated force
of a full key dip and
release.
Figure 17. Generated force
of a half key dip and
release.
Experimental Results
An active keyboard is designed to generate a haptic
feedback as close as possible to that of a real key-
board. In addition, when the piano action is emu-
lated, the dynamic simulator should compute the
hammer position accurately to give meaningful in-
formation to the sound synthesizer.
The first type of experiment is usually carried out
with a group of expert performers, but this has not
been done in the MIKEY project, because the first
tests with performers were quite biased by the fact
that no sound was generated when acting on the key,
so the correlation between haptic perception and
generated sound was lost. For this reason, the exper-
imental results for the grand piano and the harpsi-
chord first show the force commands generated by
the dynamic simulator, pointing out the events that
have haptic relevance. For the grand piano, we then
show the agreement between actual and simulated
hammer motion under the same key motion. No ex-
perimental results are presented for the Hammond
organ, as the haptic force is trivially obtained by
generating a force proportional to key position.
Grand Piano
The force generated by the motor is the sum of sev-
eral components that in turn depend on the state of
the key, its escapement, etc., as stated by Equation
7. Figure 16 shows the profile of the force generated
by the motor when the key is completely down and
the hammer bounces back from the string. At time
t1, the key descent starts, and the force generated is
relative to the viscous term. After awhile, the es-
capement phase starts, the force rises, and then goes
rapidly to zero at t2, when the key stops. The key re-
mains down until t3, when it is released by the
player. When going up, the key is under the action
of a viscous force. When it reaches its final rest posi-
tion, the hammer rebounds on the rest felt at t4, and
a small key rebound is observed.
A typical experiment to perceive the haptic feed-
back owing to the rebound of the hammer on the
key involves pushing the key down to a middle po-
sition (before the escapement region) by placing a
Grand piano-escapement
t
3
t
4
t
2
0.1
0.2
0.3
0.4
0.5
time [sec]
0.6
0.7
0.8
0.9
1
Grand piano-hammer rebound
t
5
t
6
t
7
0.6
0.5
0.4
0.3
0.2
0.1
0
]
A
[
t
n
e
r
r
u
c
M
C
V
0. 1
0. 2
t
1
0. 3
0
Figure 16
0.5
0.4
0.3
0.2
0.1
0
0. 1
]
A
[
t
n
e
r
r
u
c
M
C
V
0. 2
t
1
t
2
t
3
t
4
0. 3
0
0.1
0.2
0.3
0.4
0.5
time [sec]
0.6
0.7
0.8
0.9
1
Figure 17
constraint under the key itself. In this case, the ef-
fect of the hammer impact is to pull up the key.
This can be observed in Figure 17, where the force
generated in the above-mentioned conditions is re-
ported. From t1 to t2, the key goes from the rest posi-
tion to the constraint. The corresponding force is
caused by inertial and viscous effects. Meanwhile,
the dynamic simulator computes the hammer posi-
48
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 18. Position re-
sponse of the hammer
motion.
0.06
0.05
0.04
]
m
[
n
o
i
t
i
s
o
p
0.03
0.02
0.01
0
0.01
0.06
0.05
0.04
]
m
[
n
o
i
t
i
s
o
p
0.03
0.02
0.01
0
0.01
Virtual hammer position
Virtual key position
string position
virtual hammer
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
Actual hammer position
string position
hammer position
0.012
0.01
0.008
0.006
0.004
0.002
0
virtual key
escapement ends
escapement begins
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
?3
x 10
Actual key position
escapement ends
escapement begins
12
10
8
6
4
2
0
]
m
[
n
o
i
t
i
s
o
p
]
m
[
n
o
i
t
i
s
o
p
2.6
2.8
3
3.2
3.4
3.6
3.8
2
time [sec]
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
tion. The hammer leaves the key and, after a short
flight, impacts the key at time t3. The force impulse
ends at t4. When the key is released at t5, the force
represents a viscous effect until at t6 the hammer re-
bounds on the rest felt, causing a motion of the key
that ends at t7. Note that the final rebound is
smaller when the key is only half pressed, because
the simulator accounts for the smaller energy of the
hammer at the time of impact with the rest felt.
The behavior of the dynamic simulator has been
with the actual one under the same key motion.
This type of validation experiment is used to con-
firm the correctness of the inertial, kinematic, and
friction parameters used in the mathematical model
of the key. To implement this type of experiment, it
is necessary to move the keys of both keyboards
(the standard and the active one) with a servo actua-
tor, programmed to generate a typical profile. (This
is obtained by recording the key motion while a
player was playing on the standard keyboard.)
validated in two ways. The first type of test was
aimed at comparing the simulated hammer motion
Figure 18 illustrates the experimental results
obtained, confirming that the dynamic simulator
Oboe
49
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 19. Force response
of the hammer motion.
Virtual hammer position
Actual hammer position
]
m
[
n
o
i
t
i
s
o
p
]
N
[
e
c
r
o
f
0.6
0.5
0.4
0.3
0.2
0.1
0
0. 1
0.2
0
0. 2
0. 4
0. 6
0. 8
1
1. 2
1. 4
1. 6
1. 8
string position
virtual hammer
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
Input force virtual
input force
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
]
m
[
n
o
i
t
i
s
o
p
]
N
[
e
c
r
o
f
0.6
0.5
0.4
0.3
0.2
0.1
0
0. 1
0.2
0
0. 2
0. 4
0. 6
0. 8
1
1. 2
1. 4
1. 6
1. 8
string position
actual hammer
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
Input force actual
input force
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
2.6
2.8
3
3.2
3.4
3.6
3.8
time [sec]
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
designed correctly replicates the behavior of the ac-
tual mechanism. It is worth noting, however, that
this result does not provide much information on the
force perceived by the player, because the dynamic
simulator does not take into account the key iner-
tia, but only its angular position (and derivatives).
Thus, the second type of experiment was aimed at
showing that the actual and the simulated hammer
have similar motion when the same force was ap-
plied to the key. This has been realized by first
recording the force exerted by the player on the ac-
tual keyboard and then by applying the same force
(by using a force-controlled actuator) to the key of
the MIKEY keyboard. The results obtained are re-
ported in Figure 19, and they confirm that the vir-
tual mechanism closely replicates the behavior of
the grand piano action from the point of view of the
dynamic response.
Harpsichord
The force to be generated by the motor in the vir-
tual harpsichord is shown in Figures 20 and 21. In
50
Computer Music Journal
Figure 20. Generated force
from the single-plectrum
harpsichord.
Figure 21. Generated force
from the double-plectrum
harpsichord.
Harpsichord-single plectrum
Harpsichord-double plectrum
0.5
0.4
0.3
0.2
0.1
0
]
A
[
t
n
e
r
r
u
c
M
C
V
t
5
t
6
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
]
A
[
t
n
e
r
r
u
c
M
C
V
0. 1
0
t
1
t
2
t
3
0.1
0.2
t
4
0.3
0.4
0.5
time [sec]
0.6
0.7
0.8
0.9
1
0.05
0
0.1
0.2
0.3
0.4
0.5
time [sec]
0.6
0.7
0.8
0.9
1
Figure 20, a single-jack harpsichord is considered.
The key descent starts at time t1, and the force ap-
plied to the key emulates a viscous friction. At t2,
the plectrum engages with the string and plucks it.
This event ends at t3. At t4, the key is completely
down and stops. At t5, the key is raised, and a vis-
cous effect is generated until the key gets back to
the rest position at t6.
In Figure 21, the force for a double-jack harpsi-
chord is reported. It is worth noting that the two
virtual plectrums are purposely set with a large gap
to show two distinct spikes during key descent.
Conclusion
The realization of a multi-instrument active key-
board may require the design of a complex dynamic
simulator, in which all parts composing the real
mechanism are included. This approach, however,
is very expensive in terms of computation and may
be unsuitable for real-time operation. In the MIKEY
project, we have demonstrated that it is possible to
have a realistic feedback and good accuracy in dy-
namic simulation (e.g., in evaluating the hammer
position in grand piano) by using a simplified dy-
namic simulator that generates a set of events (e.g.,
impacts and states). In turn, such events generate a
set of haptic feedbacks. As a result, the MIKEY sys-
tem is capable of generating the haptic feedback for
three different keyboard-operated instruments. Ex-
perimental results confirm that such feedback
contains many of the characteristics of the real in-
strument. Moreover, the system has been realized
by using low-cost electronics, demonstrating that a
mass production of an active keyboard is now pos-
sible with the proposed approach.
Acknowledgments
The author wishes to thank Generalmusic s. p. a.
and Professor Giovanni De Poli for providing sup-
port to this research, and Dr. Stefano Piovan, Dr.
Alesandro Canova, and Dr. Federica Andriollo for
their assistance in experimental activities.
References
Baker, R. 1988. “Active Touch Keyboard.” United States
Patent No. 4,899,631.
Bibbero, R. J. 1977. Microprocessors in Instruments and
Control. New York: Wiley.
Brockett R. W. 1993 “Hybrid Models for Motion Control
Systems.” In H. Trentelman and J. C. Willems, eds.
Perspectives in Control. Boston, Massachussetts:
Birkhauser, pp. 29–54.
Oboe
51
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cadoz, C., L. Lisowski, and J.-L. Florens. 1990. “Modular
Feedback Keyboard.” Proceedings of the 1990 Interna-
tional Computer Music Conference. San Francisco,
California: International Computer Music Association,
pp. 379–382.
Gillespie, B. 1994. “The Virtual Piano Action: Design and
Implementation.” Proceedings of the 1994 Interna-
tional Computer Music Conference. San Francisco,
California: International Computer Music Association,
pp. 167–170.
Cadoz, C., A. Luciani, and J-L. Florens. 1993. “CORDIS-
Gillespie, B., and M. Cutkosky. 1992. “Dynamical Model-
ANIMA: A Modeling and Simulation System for Sound
and Image Synthesis—The General Formalism.” Com-
puter Music Journal 17(1):19–29.
Fletcher, N. H., and T. D. Rossing. 1991. The Physics of
Musical Instruments. New York: Springer-Verlag.
Gillespie, B. 1992. “The Touchback Keyboard.” Proceed-
ing of the Grand Piano Action.” Proceedings of the
1992 International Computer Music Conference. San
Francisco, California: International Computer Music
Association, pp. 77–80.
Humphries, C. 2002. The Piano Handbook. San Fran-
cisco, California: Backbeat Books.
ings of the 1992 International Computer Music Confer-
ence. San Francisco, California: International
Computer Music Association, pp. 447–448.
Topper, T., and B. Wills. 1987. “The Computer Simula-
tion of Piano Mechanisms.” International Journal of
Modelling and Simulation 7(4):135–139.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
0
3
3
8
1
8
5
4
5
9
8
/
c
o
m
j
.
.
2
0
0
6
3
0
3
3
8
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
52
Computer Music Journal