RESEARCH ARTICLE - Am MIT spezialisierte KI-Forschung

RESEARCH ARTICLE

The ha-index: The average citation h-index

Department of Marketing, Innovation, and Organization, Faculty of Economics and Business Administration,
Ghent University, Ghent, Belgien

Yves Fassin

Keine offenen Zugänge

Tagebuch

Schlüsselwörter: bibliometrics, Zitat, h-index, indicator, journal

ABSTRAKT

The ranking and categorizations of academic articles of a data set have traditionally been
based on the distribution of their total citations. This ranking formed the basis for the definition
of the h-index. As an alternative methodology, the ranking of articles of a data set can be
performed according to the distribution of the average citations of the articles. Applying this
same principle to the h-index itself leads to an average h-index, the ha-index: the largest
number of papers ha published by a researcher who has obtained at least ha citations per year
on average. The new ha-index offers more consistency, increased selectivity, and fairer
treatment of younger scholars compared to the classic h-index. With its normalized time
aspect, the method leads to better acknowledgment of progress. The evolution of the h-indices
over time shows how the ha-index reaches its full potential earlier and offers more stability
im Laufe der Zeit. The average citation ha-index partly solves the problem of the temporality of the
h-index. The ha-index can also be applied to academic journals. Insbesondere, the application
of the ha-index to journals leads to more stability as they reach their limit sooner. The ha-index
offers a response to the inflation of h-index levels.

EINFÜHRUNG

The mathematical elegance and the arithmetic convenience of the h-index have been the
major motivations for the widespread adoption of this indicator in the evaluation of science.
It has become especially popular in applications concerning individual researchers. Defined
as “the highest number of papers a scientist has that have each received at least that number of
citations” (Ball, 2005; Hirsch, 2005), the h-index combines publication and citation counts,
the most widely used proxies for productivity and impact. Jedoch, several bibliometric
scholars have pointed to imperfections, and criticism has led to the proposal of alternatives
that have not, Jedoch, succeeded in dethroning the h-index. In a recent ISSI newsletter, A
new indicator was proposed (Fassin, 2020B) based on the ranking of articles of the data set
according to the distribution of the average citations, rather than on the total citation distribu-
tion. The same principle as for the h-index is then applied, leading to a new ha-index: Die
largest number of papers ha published by a researcher who have obtained at least ha citations
per year on average. In diesem Papier, a more in-depth analysis is realized that expands on the
rationale behind this metric and positions it within existing h-index variants.

The structure of the paper is as follows. A literature study examines the criticism of the
h-index and its proposed alternatives. From a systematization of the h-index variants, Die
new ha-index is defined, followed by the practical application of the ranking of articles accord-
ing to total citations and average citations. The ha-index is then applied to individual

Zitat: Fassin, Y. (2023). Der
ha-index: The average citation h-index.
Quantitative Science Studies. Advance
Veröffentlichung. https://doi.org/10.1162/qss
_a_00259

DOI:
https://doi.org/10.1162/qss_a_00259

Peer Review:
https://www.webofscience.com/api
/gateway/wos/peer-review/10.1162
/qss_a_00259

zusätzliche Informationen:
https://doi.org/10.1162/qss_a_00259

Erhalten: 17 Juli 2022
Akzeptiert: 8 April 2023

Korrespondierender Autor:
Yves Fassin
yves.fassin@ugent.be

Handling-Editor:
Vincent Larivière

Urheberrechte ©: © 2023 Yves Fassin.
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International (CC BY 4.0)
Lizenz.

Die MIT-Presse

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

researchers and to academic journals and compared to the existing indices. Its characteristics
and its advantages are described. Particular attention is given to the evolution of the ha- Und
h-indices over time, with applications.

2. LITERATURE STUDY OF THE h-INDEX

In a very short period, the h-index has been widely accepted as a measure of scientific per-
formance and research achievement (Ball, 2005, 2007; Zhang, Thijs, & Glänzel, 2011). Es ist
easily computable and provides a synthetic metric that combines the number of papers and
their citations, the two traditional elements for evaluating researchers. Its simplicity allows
comparison between scientists in a balanced way (Hirsch, 2005), even if other indicators
are useful as complementary information and necessary for adding context (Wendl, 2007),
as pointed out in the Leiden Manifesto for research metrics (Hicks, Wouters et al., 2015).

Strong criticisms have underlined the drawbacks and imperfections of the h-index (see e.g.,
Bouyssou & Marchant, 2011; Costas & Bordons, 2007; Waltman & van Eck, 2012; Wendl,
2007). Many bibliometric scholars advocate the use of multiple indicators and remain skep-
tical about the potential of any indicator to assess a scientist’s work in one single metric. Sogar
if it has become, in a very short time, the most popular of all bibliometric indicators, according
to Bornmann and Leydesdorff (2018, P. 1,122), the h-index could be “the wrong type of sum-
mary statistics.” Major imperfections concern problems of inadequate differentiation and
selectivity and defective stability, due to their sharp and continuous increase over the years.
A major drawback of the h-index is its time dependence. The h-index does not take into
account any normalization of citation impact regarding the publication year or discipline.

As a consequence, the h-index engenders unfairness in assessment, as it has been privileg-
ing past achievements over recent contributions. Zusätzlich, different databases lead to differ-
ent h-indices for the same researcher or group; h-indices should therefore be used with caution
for formal academic purposes (Teixeira da Silva & Dobranszki, 2018).

2.1.

Imperfections and Drawbacks of the h-Index

The h-index does not signal a contribution to seminal papers with extraordinarily high citation
counts (Vinkler, 2010), nor does it fully reflect a scientist’s accomplishment (Bras-Amorós,
Domingo-Ferrer & Torra, 2011). An author who has published only one or several foundational
papers is not rewarded by the h-index calculation, whereas modestly performing scientists
with a larger number of moderately cited publications are unfairly favored (Dorogovtsev &
Mendes, 2015).

The h-index values career achievement. It is subject to the principle of cumulative advan-
tage, which in science means that scientists benefit from recognition from peers and prestige
from published research (Allison, Long, & Krauze, 1982; Merton, 1968; Price, 1976; Wendl,
2007). By definition, the h-index cannot decrease (Hirsch, 2005). Older, more well-established
researchers benefit from the lasting impact of publications from their early years and keep
receiving new additional citations that can help to further increase their h-index (Rousseau,
Egghe, & Waffen, 2018). Darüber hinaus, papers that have earned sufficient citations in their first years
but are not cited any more are still categorized in the researcher’s h-index, even if they no
longer have any impact. It is impossible for junior academics to reach that same level in a
few years of academic research. In social sciences especially, it may take more than 5 Jahre
to accumulate a significant number of citations (Harzing, Alakangas, & Adams, 2014). Younger
scholars have to build a portfolio of citable articles.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

There has been a substantial increase in the number of academic publications and citations
over recent decades. This growth has resulted in the exponential growth of database collec-
tions such as the Web of Science (Hu, Leydesdorff, & Rousseau, 2020). As a consequence, Wir
have noticed inflation of the figures of the h-indices of all researchers and all journals. Das
phenomenon has diminished the significance and differentiation power of the h-index. Thresh-
olds are rising, so it takes a few years for a new or recent paper to enter the existing h-core of a
journal or a data set of a field. Once above a certain level of h-index, it is difficult for a junior
scholar to achieve a further quick increase of the h-index; this requires different papers with
substantial references, and the researcher’s h-index is by definition limited to the number of
published articles. Not only are citations important, but also the number of papers—so both
elements that define the h-index constitute constraints for young researchers. The h-index is
clearly a measure of a researcher’s past accomplishments (Penner, Pan et al., 2013), not of
their future achievements or potential. The h-index is, daher, not the most appropriate indicator
for junior researchers (Harzing et al., 2014).

Redner (1998) observed that many papers obtain their citations over a limited period of
popularity and then are no longer cited. The h-index tends to progress linearly during the most
productive time of a researcher’s career; it can then benefit from additional citations over a few
Jahre. Later, the increase in the h-index often results from citations to older publications close
to the h-point (Schreiber, 2015). Then the h-index for authors tends to stabilize at the end of
their productive careers. Jedoch, the h-indices of retired researchers do not decrease, even if
they have little more impact. That inherent limitation of the size of the data set does not matter
for academic journals or fields that can pursue a rise in their h-index.

This phenomenon of the exponential rise of the h-index of all researchers over the years
(Hu, Leydesdorff, & Rousseau, 2020) makes the comparison of higher h-indices more difficult
than at the time of its launch, where Hirsch suggested that an h-index of 20 nach 20 years of
research activity is a sign of success and exceptional h-indices of 40 outstanding (Ball, 2007).
The same concerns for age arise for the h-index of journals. In der Zwischenzeit, the h-index of the
journals Nature and Science has exploded from 150 Zu 1,300 in less than 15 Jahre (Braun,
Glänzel, & Schubert, 2006). Econometric analysis tends to indicate that journal rankings
reward older journals: The longer the existence of a journal, the more articles it publishes
and the more likely a higher h-index becomes (Hudson, 2013; Ritzberger, 2008).

Another drawback of the h-index is the difficulty of comparing researchers from different
disciplines (Batista, Campiteli et al., 2006). The h-index is “sensitive to differences in
co-authorship patterns” between disciplines (Ryan, 2016, P. 578). The various fields adopt
different publication practices with a varying number of publications and a different number
of citations and, as a consequence, this results in a wide variation in the h-index.

2.2. Alternatives to the h-Index

The different critiques of the h-index have led to a huge number of alternatives. Bornmann,
Mutz et al. (2011) performed a meta-analysis of studies on h-index variants; their comparative
Analyse, and especially the correlation between the h-index and 37 variants, concludes that
most variants offer little added value over the h-index and are mostly redundant. A more recent
comprehensive study on the h-index and its variants, realized by Bihari, Tripathi, and Deepak
(2021), grouped the h-index variants into seven categories.

Some bibliometric scholars suggest counting the citations of the papers belonging to the
h-core selection; others propose counting the top-cited papers in the corresponding fields,
not only the h-core papers (Bornmann & Leydesdorff, 2018; Bras-Amorós et al., 2011). To

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

better acknowledge exceptional contributions, Egghe suggested the g-index of a set of articles,
defined as the highest rank g such that these g articles together received at least g2 citations
(Egghe, 2006A, 2006B). Jin, Liang et al. (2007) advance the R-index, as the square root of the
total number of citations received by articles belonging to the h-core.

A number of variants of the h-index have been proposed, such as Kosmulski’s h(2)-index,
equal to h2 as the highest rank such that the first h2 articles each received at least (h2)2 citations
(Kosmulski, 2006). Analogously, an h3-index has been defined (Fassin & Rousseau, 2019). Der
w-index indicates that a researcher has published w papers, with at least 10w citations each
(Wu, 2010).

2.3. Normalization

Several proposals have been made to improve the fairness of the h-index. A number of variants
of the h-index have suggested normalized alternatives that answer the distorting effects of the
researcher’s age or career length, multiple authorship, or scientific field.

2.3.1. Career length

To take into account the career length, Hirsch (2005) proposed an age-normalized variant
of the h-index, namely the m-quotient, defined as h/n, where n defines the number of years
since the researcher’s first publication. As a complement to the R-index, Jin et al. (2007) put
forward the AR-index, as the square root of the age-normalized total number of citations
received by articles belonging to the h-core.

Schreiber (2015) presented the application of the h-index restricted to time windows. Er
described “the timed h-index ht(5j) for publications from the year y and the previous t (5, oder
alternatively, 10) years in dependence to the length t of the utilized time window” (Schreiber,
2015, P. 150). Jedoch, in this time window approach, older major researchers who do not
publish any more completely disappear from the classification.

2.3.2. Multiple authorship and differences between fields

A number of other proposals for alternatives or variants to the h-index have focused on the
interdisciplinary character. To tackle these unequal characteristics between fields, bibliometri-
cians have focused on the number of authors. In der Tat, fields with a higher number of articles
per researcher often work with larger (often international) teams and have more multiauthor
Papiere (Batista et al., 2006). According to this reasoning, corrections for multiple authorship
somewhat compensate for interdisciplinary differences. To reduce the effects of coauthorship,
Batista et al. (2006) proposed the Individual h-index hI obtained by dividing the standard
h-index by the average number of authors in the articles contributing to the h-index.

A more fine-grained alternative, the normalized individual h-index, hInorm, was introduced
by Harzing (2007) in the Publish or Perish program (PoP)1. The procedure of calculation for
this hInorm is to first normalize the number of citations for each paper by dividing the number of
citations by the number of authors for that paper, and only then to calculate the hInorm as the
h-index of the normalized citation counts.

Multiple authorship has generated a huge debate between full-counting and fractional,
reduced, or adapted counting formulas (Berker, 2018). Where full-counting privileges con-
firmed researchers who have published many papers with their network partners, fractional
counting may be too penalizing for teams and especially for the leading authors and for the

1 www.harzing.com.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

corresponding authors. Several authors have, daher, proposed different alternatives of
adapted fractional counting with different methods of paper credit assignment (for a short over-
view, see Fassin (2020A)). The contribution of each author assigned with weighted factors can
vary according to their role and position in the authorship list, but is not as diluted as with total
fractional counting.

2.3.3.

Field normalization

Bornmann and Leydesdorff (2018) argue that h-index values are only comparable after proper
field normalization. Several schemes for normalizing the citation counts have been proposed
in recent years, based on percentiles (Leydesdorff & Bornmann, 2011), percentile rank classes
(Leydesdorff, Bornmann et al., 2011), or variable h-type percentiles categories (Fassin, 2018).
The HF-rating constitutes another attempt to cope with the interdisciplinary comparison
(Fassin, 2020A).

To accommodate the issues of both disciplinary (multiple authorship) and career length,
Harzing et al. (2014) proposed the individual, average annual increase of the h-index called
hI,annual, or hIa. It is also calculated in the PoP program. It is defined as the hIn-index divided by
the number of years of activity of the researcher. This criterion is also questionable; some bib-
liometric scholars propose the time that has elapsed between the researcher’s first article, oder
since their PhD (Harzing et al., 2014).

3. SYSTEMATIZATION OF THE h-INDEX VARIANTS

Tatsächlich, to schematize the procedures for defining the h-index variants, we can distinguish three
different operations: the ranking of the articles, the normalization or adjustments for age or
career length, and the normalization of multiple authorship. The different h-index variants pro-
posed depend on the order of calculation in the procedure.

The classic h-index executes the ranking only according to the article citations, without any
normalization. The m-quotient corrects the h-index for age after ranking. Batista et al.’s (2006)
hI-index corrects for multiple authorship after ranking. Harzing et al.’s (2014) hInorm-index first
corrects for multiple authorship to normalize and then proceeds with the ranking (Ryan, 2016).

When drawing up a matrix of the variants on the basis of the order of calculation of the
Operationen, in Table 1, one comes to a gap. Curiously, an alternative with a correction for
age followed by the ranking and determination of an h-index variant has not yet been
vorgeführt.

The ranking of a data set in the declining order of total citations formed the basis for the
definition of the h-index. Jetzt, the principle applied to define the h-index can also be applied
to the average citation ranking. When ranking all papers of a researcher according to the aver-
age citation per paper, an average citation h-index can be defined: the ha-index.

Tisch 1. Order of calculation

Multiple age correction

m = h

a= (Hirsch)

Ranking first

Ranking second

Multiple authorship correction

=
hI = h avg na

(Batista et al.)

hInorm (Harzing et al.)

Double correction

hIa = hIn/a (Harzing)

–

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Assuming N publications ( pk)k=1,…,N with ck citations and age ak and (na)k coauthors for the

kth publication:

ha is the largest number of papers published by a researcher that have each obtained at least
N
ha citations per year on average: arg maxk2

≥k

ck
ak

H, hIn and ha are obtained by ranking the citations or adapted ratios of citations. The units for
ranking of the three h-indices differ. The h-index is obtained by ranking the citations of all pub-
lications, hIn by ranking the number of citations divided by the number of authors for each pub-
lication taken individually, and ha by ranking the number of citations divided by the number of
years since publication, also for each publication. This gives for h, hIn and ha respectively:

ck ; ck
Þ
nað

; Und

ck
ak

The order of the various publications will differ in the different orderings.

m and hI are directly derived from the h-index.

m ¼ h =a

hIa ¼ hIn=a

hI ¼ hIn= a v g na

It is curious that this ha variant has not been proposed yet, probably because the h-index is
an integer, but the average citations per paper are not integer numbers. In all honesty, we came
across this finding not from the drawing up of the matrix, but indirectly from the study of the
evolution of citations of publications over their lifetime. In the following section, Wir
demonstrate how the average number of citations per year is an acceptable criterion for the
normalization of the age effect.

We could round the ha-index down to the integer below, as for the original h-index; Wie-
immer, the classic procedure of rounding up to the higher step if > 0.5 is preferable in this case2.
In der Tat, the Web of Science takes into account the current incomplete year in the calculation
of the average citations per year, which penalizes papers during most of the year. The average
can exceed the threshold by the end of the year, but then diminishes as the unit for the new
year is added to the denominator.

4. THE TIME DEPENDENCE OF THE h-INDICES

Citations increase over time, and also the h-index and h-type indices rise over the years. Der
h-index is time dependent; it never declines and can at its maximum reach the number of
articles published. In der Praxis, for senior researchers, it rarely reaches more than 50% of the
number of publications, as all authors have written articles that do not get citations. Der Profi-
posed ha-index rests upon the criterion of average citations per year as if the citations grow in a
linear way. To what extent is this average citation per year representative of the citation pattern
of academic publications? At an individual level too, citations of academic articles fluctuate
significantly during the lifetime of an article and do not evolve in a linear pattern.

The evolution of a successful article’s citations can be presented graphically in a simplified
Weg, as a diachronous cumulative curve (Hu, Li, & Rousseau, 2020). The cumulative citation
curve has the shape of an S-curve (Bejan & Lorente, 2012) with three successive periods of

2 Als Beispiel, for five publications with average citations of 4.25, 3.5, 3.25, 3, Und 2 the ha-index will be 3
Weil 3 ≤ 3.25 ≤ 4. With the rounding up, the ha-index for five publications with average citations of
4.25, 3.75, 3.65, 3.5, Und 2 the ha index will be 4 Weil 3 ≤ 4 (replacing 3.5) ≤ 4.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

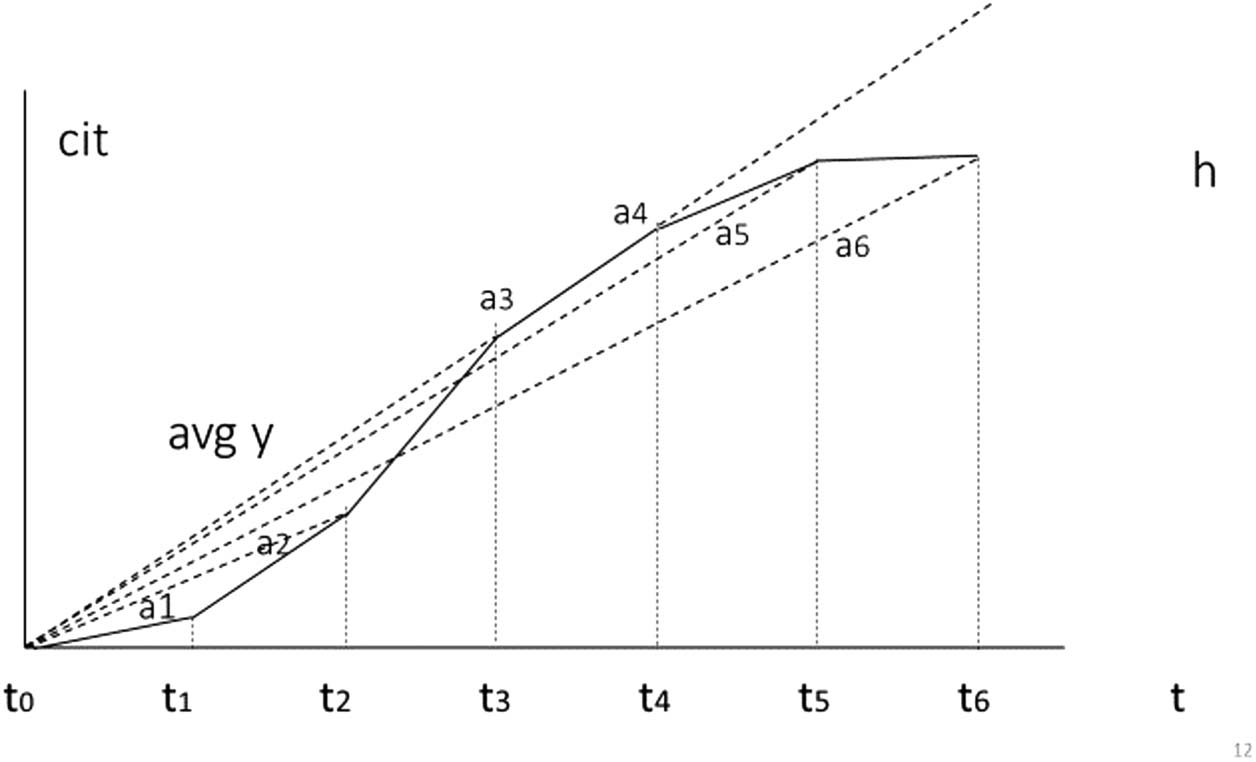
Figur 1. Cumulative citation curve and average citations.

increasing growth rate, to reach the average (avg y) after 15–20 years. The growth rate of cita-
D
tions a iþ1
will continue for an additional 5–10 years at a slower pace with less than half
D
iþ1
T
the average of the previous period, and will then gradually decrease further to remain stable or
even decline to zero once the article is no longer cited.

Þ−ai
Þ−ti

In this simplified graph (Figur 1) of cumulative citations over time, the average is deter-
mined by the angle of the line drawn from the center of the axes to the point of the citation
at a certain time. This average moves up from 0 to a1 at t1 and to a2 at t2; at t3 it reaches its
maximum average ay, where it stabilizes for a period t3 until t4 and then declines to a5 at t5
and to a6 at t6.

The average citation defined at a certain time varies; it is lower for the first years until the
article reaches its peak. The assumption of the average number of citations leads to a tempo-
rary underestimation of the future potential of younger articles during the first years, but on an
overall evaluation, as a moving average, it represents a good approximation, as the averages
a3, a4, and a5 stabilize and decline only slowly to a6 after 25 Jahre. Once that average gets
below ha, the article can fall out of the ha-core, with a possible limited negative impact on the
researcher’s ha-index.

This time evolution of the citations of a senior researcher’s publications impacts the
ha-index, which will stabilize and ultimately slowly decline once the articles are no longer
cited. In contrast with the h-index, the ha-index is less time independent.

5. ERGEBNISSE: A PRACTICAL APPLICATION

To illustrate our proposal, we carry out two comparative analyses: the first at the level of cita-
tion distribution of a field, the second at the individual level.

5.1. Comparative Analysis at the Field Level

An example has been worked out on a homogeneous data set composed of all 67,052 articles
in the field of entrepreneurship3. For this sample, the citation distribution tables and curves of

3 Retrieved from the Web of Science (version Clarivate) by the query TS=entrepreneur*, field TOPIC (title,

abstract, author key words, keywords plus), for all years (1956–2019).

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Quantitative Science Studies

academic articles are executed, Erste, on the basis of the total citations, und zweitens, by applying
the ranking on the basis of average citations per year. The two rankings show middling differ-
ences but higher variations for the most cited recent articles. Nearly 75% of the articles of the
top 10% decile of the ha-ranking also belong to the top 10% of the h-ranking. Some 70% of the
top 1% percentile are common to both rankings, Aber 30% fall out of the 1% percentile in one of
those rankings. The Spearman rank correlation of the 12,500 most cited entrepreneurship arti-
cles between their ranking according to the total citations count and their ranking according to
the average citation per year reveals a moderate correlation of 0.634.

It should be noticed that the selection of the ha-articles may differ from the selection accord-
ing to rank in the h-index or h2-index. The ha-core can include articles that are not in the
h2-core and vice versa. The top of the ranking of articles also differs between both rankings
(siehe Tabelle 2). Although four of the five first-ranked articles in entrepreneurship research are the

Tisch 2.

Comparison of the rankings of the h-core and ha-core of entrepreneurship

Authors
Teece

Shane & Venkataraman

Uzzi

Mollick

Lumpkin & Dess

Zott, Amit, & Massa

Connelly et al.

Anderson et al.

Davidsson & Honig

Greenwood et al.

Authors

Shane & Venkataraman

Uzzi

Teece

Lumpkin & Dess

Harvey

Müller

Slater & Narver

Shane

Desphandes et al.

Sarasvathy

J
SMJ

AMR

ASQ

JBV

AMR

JBV

AMA

AMR

ASQ

SMJ

AMR

JMK

Betriebssystem

JMK

AMR

Year
2007

2000

1997

2014

1996

2011

2014

2003

2011

Year

2000

1997

2007

1996

1989

1983

1995

2000

1993

2001

TC
3,439

4,621

4,461

945

3,315

1,284

1,118

778

1,741

951

4,621

4,461

3,439

3,315

2,265

1,968

1,878

1,868

1,815

1,800

AVC
245.6

220.1

185.9

135.0

132.6

128.4

111.8

111.1

96.7

95.1

AVC

220.1

185.9

245.6

132.6

70.8

51.8

72.2

89.0

64.8

90.0

r avg
1

r cit
3

r avg

r cit

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

same in both rankings, only five other articles join the top 10 in both rankings. The six other
most cited articles are in the top 65 of the best average citation, but they were all published
Vor 2001. Four of the six remaining articles with the best average were published after 2010
and are placed 21, 31, 51, Und 77 in the citation ranking. Lower ranked articles show more
differences in ranking.

Well-cited articles climb gradually in the overall ranking, but it takes them 5–10 years to
reach the top 10% decile or h-core, whereas they start in higher deciles in the average citation
ranking. This average citation ranking allows a smoother transition, thanks to a unique overall
temporal normalization. It compensates for the lower number of citations that newer publica-
tions can logically achieve.

In der Praxis, the overall average citation distribution of any data set can be considered a
good approximation; consequently, it can be put forward as a unique time-independent crite-
rion. The overall average citation ranking can be proposed as a more accurate way to perform
the ranking of a specific data set of articles.

5.2. A Comparative Analysis at the Individual Level

To illustrate the effect of the different variants of the h-index discussed in the scheme in
Tisch 1, a comparative analysis has been performed.

A number of data are retrieved and their indices are calculated for some scholars in different
scientific fields. Tisch 3 presents the WoS data of those scholars: number of papers in WoS − n,
total citations in WoS − TC, the number of years the scholar has been active (number of years
since their first publications) j, the average number of authors aa; then their indices h, M, hI, Und
hInorm, hIa, AR, G, w, and ha are computed on those WoS data. The asterisk * signals the presence
of an article in ha-core; the ratio ha/h is calculated in the last column. The sample consists of a
dozen management scholars, a group of scholars in family firms and entrepreneurship research,
members of the CYFE Center for Young and Family Enterprises at the University of Bergamo
(with some of their coauthors), and the three leading scholars in entrepreneurship. They present
a mix of established, well-known, midcareer, or younger scholars to offer a diversity of profiles.
Zusätzlich, to study a comparison over different fields, the indices are calculated for a few
bibliometric scholars, for a few top researchers in various fields such as medicine and plant
Wissenschaften, and for physicist Ed Witten, the scientist with the highest h-index (Ball, 2005; Hirsch,
2005) and Jorge Hirsch for his impactful work in bibliometrics4. Just as the h-indices, so too do
the ha-indices depend on the size and citation patterns over the disciplines. The ha-index of the
field of entrepreneurship is 54; es ist 30 for bibliometrics and exceeds 100 for medicine, Physik,
and plant sciences.

The last column in Table 3 presents the ratio between the ha-index and the h-index,
showing a great dispersion, even if there is a high correlation between both indices.
Well-established authors have a lower ratio ha/h than midcareer or younger scholars, welche
underlines the selectivity of the ha-index.

Tisch 4 displays the ranking of those 16 entrepreneurship scholars on the basis of various
data and indices presented in Table 3. The following lines with the additional authors from

4 With the increased multidisciplinarity of sciences, many scholars publish in different fields of research (für
example Jorge Hirsch in physics and in bibliometrics). In such cases, three different h- and ha-indices can be
berechnet: one in each discipline and one for their total oeuvre. This means that the general rule of cleaning
the data first must be followed, depending on the objective of the evaluation.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Tisch 3.

Indices of a selection of scholars (retrieved in September 2020)

F
ENT

ENT

N
125

225

BIBL

334

BIBL

Author
SZ

ADM

AVG

TC
24,147

12,438

2,812

15,626

2,497

7,915

2,410

823

867

j
29

347

406

408

1,074

8,157

5,026

190

aa
2.42

3.35

3.69

1.85

3.00

2.39

3.16

3.38

2.82

3.75

3.82

3.44

2.77

3.17

3.67

4.33

2.57

1.40

4.20

3.33

H
66

M
2.28

hI
27.2

hInorm
52

2.14

18.5

2.23

7.9

1.12

24.9

1.57

7.3

0.84

15.9

1.56

0.87

2.13

0.92

1.38

0.56

0.33

1.00

0.75

0.60

7.9

3.8

6.0

3.2

2.9

2.6

4.7

1.9

0.8

0.7

2.59

17.1

0.25

0.18

0.33

2.9

1.2

1.8

1.88

144

3.35

76.8

120

7.09

1.46

11.1

6.94

119

3.31

17.1

11.10

1.17

1.9

hIa
1.8

1.3

1.2

1.1

0.5

1.0

0.7

1.5

0.4

0.6

0.4

0.3

0.7

0.5

0.4

1.6

0.3

0.2

2.8

0.6

1.1

0.4

AR
37.0

G
125

32.4

106

19.5

28.3

17.3

18.4

15.4

9.4

9.9

8.3

8.8

7.9

7.0

4.5

3.1

3.9

22.9

18.1

3.0

2.2

57.9

315

27.6

172

44.8

201

12.5

w
26

ha
19

ha/h
0.29

0.31

0.45

0.26

0.50

0.26

0.36

0.54

0.35

0.42

0.45

0.56

0.31

0.50

0.67

0.27

0.80

0.40

0.17

0.22

0.14

0.18

0.33

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

PHY

361

102,280

MED

420

31,566

PLS

489

46,818

1,201

Auth: author’s initials; F: field; N: number of papers in WoS; TC: total citations in WoS; j: the number of years the scholar has been active (since their first
publications); aa average number of authors; h-index; m-quotient (h/y); hI and hInorm-indices; individual hIa-index; AR-index; g-index; w-index; the new ha (* für
an article in ha-core); the ratio ha/h.

other disciplines give their respective rankings through (individual) interpolation in this short
entrepreneurship list to emphasize comparison. Tisch 4 is completed with the HF-ratings of the
scholars, divided into tiers of authors of comparable categories.

The differences between the absolute values of the h-indices change significantly over the
various indices. Even if there is a high correlation between the h-index and the ha-index,
changes in the order can be noted when comparing the rankings, especially for the middle

Quantitative Science Studies

The ha-index

Tisch 4.

Ranking of a selection of scholars following various indices

Author
SZ

ADM

AVG

F
ENT

ENT

BIBL

PHY

MED

PLS

N
2

TC
1

H
1

M
1

hI
1

hInorm
1

hIa
1

AR
1

G
1

w
1

ha
1

HF
AAA

AAA

BBB

CCC

BBC

BBB

AAA

BBB

AAA

BBB

Legend: siehe Tabelle 3, and in addition: HF-rating based on full citation count.

category but also for some top-ranked authors. Jedoch, some of the absolute differences are
smaller than their sole ranking may suggest. Although it is difficult to draw significant results
from such a small sample, the analysis of the comparative rankings presents some indications.

The h-index ranking of most scholars lies in between the citation ranking and the produc-
tivity ranking. The m-quotient and the hIa-index offer the widest divergence from the h-index
ranking. The AR ranking lies in between the h- and ha-indices, except for authors with few
papers but one exceptional highly cited paper, such as Hirsch in bibliometrics.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

The ha-index improves the position of midcareer researchers with 15–20 years of activity;
they benefit from the increase in the number of publications that have accumulated sufficient
citations, and from the increase in their average citations. Older scholars still benefit from the
citations but not from continuous growth, which makes their ha-indices stagnate.

In the m-quotient, the number of years of activity (j ) plays an overarching role; it can seri-
ously distort the index, especially if the most important articles are not published at the begin-
ning of the author’s career. A suggestion for refinement is to take a different time-space into
consideration: Die (average) time that has elapsed since the most cited publication(S) as single,
Erste, or corresponding author. With increased precision, ha is calculated with the year average
citation per publication and takes this asymmetry in time into account.

5.3. Multiple Authorship and Field Normalization

Likewise, the same objection of imprecision applies to the multiple authorship correction,
where the hI-index considers the average number of publications in the h-core. In manchen Fällen,
a publication with many authors (even up to 20) ranked just within the h-core considerably
reduces the hI-index, whereas the more fine-grained method of the hInorm would have replaced
this publication with a single-authored article.

The application of corrections for both age and multiple authorship in the hIa-index also
takes into account different career stages but suffers from the same problem related to the cor-
rect choice of the number of years.

The hInorm variant and the hI-indices have been presented as indices that allow interdisci-
plinary comparison, where the average number of authors is used as a proxy for different
scientific fields. This assumption is based upon the observation that scholars in life sciences
publish many more publications with large teams than social scientists who publish mostly as
single authors or, nowadays, in small teams of two to four researchers.

By comparing entrepreneurship scholars with scholars of other fields, it has been shown
that this generalization is not as correct as previously imagined. Although the top authors in
physics and in plant sciences largely exceed the entrepreneurship scholars in the h-index rank-
ing, the difference is attenuated in other rankings, especially in the hInorm- and ha-indices.
Jedoch, a top scholar in bibliometrics would fall into the subtop of entrepreneurship for sev-
eral indices yet subtop researchers in life sciences may surpass the top entrepreneurship
scholars. This comparison shows the importance of the differences in size, Alter, collaboration,
and publication practices in different scientific fields and their evolution over time.

Normalization for multiple authorship remains a difficult exercise. For the interdisciplinary
comparison, a bibliometric normalization performed directly on the total distribution of the
field is to be preferred. The HF-rating is based on such a normalization (Fassin, 2020A). Wo
this method does not provide an exact ranking, it supplies tiers of authors of comparable cat-
egories. In this categorization, all top authors of the various disciplines achieve the same AAA
rating, including Hirsch in bibliometrics for his impactful article, even though he has written a
limited number of articles.

In the next section, we examine the evolution of the h- and ha-indices over the years, pre-

senting evidence of greater stability, one of the main advantages of the ha-index.

6. THE EVOLUTION OF RESEARCHERS’ ha- AND h-INDEX OVER THE YEARS

Tisch 5 displays a few examples of the evolution of the ha-index (left part of the table) Und
the h-index (right part) over the years 1960–2020 for researchers of different fields

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Q
u
A
N

T
ich
T

ich

T
ich
v
e
S
C
e
N
C
e
S
u
D
e
S

ich

Tisch 5.

Examples of evolution of ha-indices (links) and h-indices (Rechts) im Laufe der Zeit

Author
SZ

PDG

1960

95
2

2000
3

5
5

10
11

15
15

2020
19

1960

95
6

2000
15

5
18

10
35

15
53

2020
66

115

125

132

144

105

1
3

T
H
e

H
A
–
ich
N
D
e
X

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Figur 2.

Evolution of the h-index over time.

(entrepreneurship, bibliometrics, and physics) and with different experience and age (most of
the authors are those mentioned in Fassin (2020A)). Figuren 2 Und 3 present the graphs of those
evolutions over time.

The first authors are the three major scholars in entrepreneurship research: Mike Wright
(MW ), Scott Shane (SS), and Shaker Zahra (SZ). The rise of their ha-index from 2005 Zu
2020 amounts to between 50 Und 70% of the rise of their h-index, after more than 20 Jahr
careers. A researcher who has been active for 15 Jahre, Thomas Zellweger (TZ), has doubled
his h-index in the last 5 Jahre, and his ha-index has increased by 50%. Younger authors Minola
(TM) and Campopiano (GC), with about 10 years of research experience, are still expanding
their h- and ha-indices. In bibliometrics, Lutz Bornmann (LB) also stabilizes his ha-index
around 12 compared to his h-index of 44, reflecting the smaller size of the field. Es ist interessant
to notice the evolution of the top physics researchers who were selected in Nature’s article
when launching the h-index: Witten (EW ), Anderson (PA), and DeGennes (PDG) (Ball,
2005, 2007). The peaks of their ha-indices rose to respectively 33, 20, Und 16 after 30–40 years
of academic research. Seit 2005, their ha-indices have stabilized and can even decline,
whereas their h-index has still risen by 20%.

Figur 3.

Evolution of the ha-index over time.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

The graphs perfectly illustrate the time dependence of the h-index and the stabilization that
the ha-index provides over time during the maturity phase. They also elucidate the differences
between fields and between ages. For senior and retired researchers (the physicists), Die
h-curve is concavely increasing in function of time towards an asymptotic value, und das
ha-index shows a stabilization followed by a slight decline. Compared to the classic h-index,
the ha-index has a time limit and reaches its full potential at an earlier stage.

7. ADVANTAGES OF THE AVERAGE CITATION ha-INDEX

Wie bereits erwähnt, the selection of the ha-articles differs from the selection according to rank in the
h-index or h2-index. This ha-index offers advantages. Compared to the classic h-index, Die
average ha-index offers better selectivity and allows better differentiation, more stability, Und
a quicker acknowledgment of potential.

The ha-index will help to better distinguish those articles that have an impact or that sustain a
certain interest. Consider two scholars with equal h-indices of 10: One has accumulated 10 oder
more citations for his 10 publications 10 years ago, with the following citations distribution (50,
30, 20, 20, 15) and five articles with 10 citations; der Zweite, a younger researcher, has a citations
distribution (25, 20, 16, 12, 10) and five other articles with 10 citations published in the last three
Jahre. The first scholar’s ha-index will select only two articles; the second scholar’s ha-index will
Sei 4 oder 5 if two or three of the articles with 10 citations were published only 2 years ago.

The average ha-index is lower in number and more selective than the high levels attained
today by the classic h-index. The number of articles in the ha-core lies more in the same range
as the h2-index, although, in general, they rank somewhat higher. Only those articles that
sustain a higher growth rate over a longer period will remain in the ha-core. An increase in
the h-index demands two conditions: All papers in the h-core have at least one additional
Zitat, which is usually the case, but also that one of the papers outside the h-core reaches
the level of h + 1 citations, usually the next paper closest to the h-threshold or a more recent
paper with high growth rate. An increase in the ha-index requires more than one additional
citation for the existing papers, and especially for the potential papers: If the difference is 1, Es
will need as many citations as the number of years since its publication; if the difference is only
a fraction, it will necessitate the number of years, multiplied by the fraction of the difference. In
this sense, the selectivity of the ha-index is much wider, although not as wide as for the
h2-index, where the number of extra citations required for an increase of the h2-index
increases exponentially. An additional advantage relates to another critique of the h-index;
this stricter criterion prevents manipulation of the ha-index through self-citations.

Tatsächlich, the ha-index allows the differentiation of articles according to their citation evolution
pattern. Foundational papers continue to be quoted extensively and survive in the ha-core
and in the h2-core. Older papers gradually decline over the years, but a basis of older papers
persists: Those highly cited papers that have accumulated a sufficient reserve of citations for
the next years. Older publications that continue to receive a reasonable number of citations
maintain their place in the ha-core, which means they still have an impact. Older papers with
reasonably high cumulative citations retain their place in the h-core, but will slowly disap-
pear from the ha-core once their contributions lose impact. Older, lower cited articles cannot
enter the ha-core, even if they belong to the h-core. Recently published younger papers with
potential can quickly enter the ha-core, a few years before gathering sufficient citations to
reach the threshold of the h-core and certainly many years before the h2-core. The earlier
detection of potential papers helps to acknowledge the visibility of younger researchers. Es
can also highlight important recent contributions of established researchers.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

The ha-index is more stable, as it does not increase as much as the h-index. Contrary to the
h-index, which cannot decline, the ha-index can stagnate and decline, for older scholars,
when older publications around the ha-index no longer receive many citations, whereas those
articles around the h-core can enter the h-index in the long run with a few additional citations.
Those articles around the ha-core have to arouse sustainable interest. This new indicator com-
bines career achievement with potential, recognizing experience and recent contributions. In
fact, as some scholars contend, a combination of metrics can give more guidance. Mit
respect to the ha-index, the ratio between the ha- and h-indices also provides valuable
Information.

The ha-index does not solve all the drawbacks of the h-index; the major shortcoming of the
h-index is that it does not signal the existence of an exceptional contribution. This condition is
not fulfilled yet with the ha-index. The g-index or the AR-index adds this information on excess
citations to a certain extent. The alternative solution is to mark the presence of a paper in the
ha-core of the data set of the field under study with an asterisk (*) added to the researcher’s
ha-index (siehe Tabelle 3), following the suggestion for the HF-rating (Fassin, 2020A).

A characteristic of the ha-index is its ease of calculation. As it is lower than the h-index, A
preselection can be restricted to the h-core (or even, in many cases, the upper half of the
h-core). The ranking of the h-core articles according to the average citation per paper provides
a temporary provisional figure; the final ha-core can be determined after an additional check
with a limited number of already highly cited recent papers of the h-core that can be interpo-
lated in that provisional ranking. Harzing’s PoP program proposes an automatic selection
choice for classification following the average citation per paper based on Google Scholar
citations. Scopus and Web of Science, which are more selective in their selection of citations,
do not provide this choice option yet.

In the following section, we extend the application of the ha-index to academic journals.

8. THE AVERAGE CITATION ha-INDEX FOR ACADEMIC JOURNALS
The same principle for the h-index can be applied to academic journals to define the journal’s
ha-index. Data sets of journals group much larger numbers of articles than citation distributions
of individual scientists. They are also more homogeneous, with smooth transitions, wohingegen
data sets of individual researchers may present huge differences between their most cited
Papiere. Infolge, journals present a wider citation distribution with a smoother citation dis-
tribution curve. This makes the application and comparison of ha-indices even more useful.

Applied to Scientometrics (SCIM), the ha-index advances towards 22 by the end of 2020,

whereas its h-index reaches 118 and the h2-index 18.

In Table 6, the ha-index of some journals in bibliometrics and in management are compared
with their h-, h2-, and h3-indices, and with the average number of citations per paper. Der
journals display a variety of profiles and different levels of h-indices. The selection of manage-
ment journals contains three of the top five management journals. The table also includes the
data for the two leading journals Science and Nature, which exceed the level of 200 for their
ha-indices, compared to 1,300 for their h-indices.

The asymmetry of the composition of the h2-core and ha-core for journals is illustrated in
the Supplementary material for an example of a journal data set. The ha-core includes more
recent articles than the h2-core.

Tisch 7 exhibits the evolution of various h- and ha-indices over time, aus 1985 Zu 2020,
and also yearly from 2015 Zu 2020, for three different journals with different profiles and

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Tisch 6.
on January 13, 2021)

Comparison of h- and ha-indices of bibliometrics and management journals (Retrieved

SCIM

JOI

JDOC

MJLIS

JASIS

JASST

JIS

JDIS

AMJ

AMR

SMJ

ASQ

JMS

JBE

N
6,367

1,038

3,555

282

3,376

3,870

2,349

3,249

2,458

3,013

2,949

3,727

2,950

8,557

Wissenschaft

Natur

> 150,000

> 200,000

avg cit
18.4

22.6

8.9

4.4

21.8

22.2

11.4

3.7

avg cit

156.2

182.4

153.2

105

69.5

48.3

30.8

n/a

H
118

110

114

363

330

316

284

235

183

180

1,311

1,336

h2
18

h3
7

ha
22

200

210

SCIM: Scientometrics; JOI: Journal of Informetrics; JDOC: Journal of Documentation; MJLIS: Malaysian Journal of
Library and Information Science; JASIS: Journal of the Association for Information Systems; JASST: Journal of the
Association for Information Science and Technology; JIS: Journal of Information Science: JDIS: Journal of Data
and Information Science Management; AMJ: Academy of Management Journal; AMR: Academy of Management
Rezension; SMJ: Strategic Management Journal; ASQ: Administrative Science Quarterly; RP: Research Policy; JMS:
Journal of Management Studies; JBE: Journal of Business Ethics.

different levels of h-indices: the Journal of Business Ethics, the Academy of Management
Rezension (the most cited journal in management research), and a leading journal in biblio-
metrics, Scientometrics, to analyze an example in a smaller discipline.

The same observation applies to the journals’ ha-indices, which reveal more stability than
the h-index as their increase is slower; especially for higher indices, the increase by one unit
per year of existence is a severe criterion. Although the ha-index of journals will not decrease,
they approach the asymptotic limit of the parabolic form of their evolution sooner. Younger
journals, such as JBE and SCIM, have not yet reached this limit. JBE’s h-index continues to rise
von 14 units per year, somewhat less than 10%; its ha-index rises by one unit per year on

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Tisch 7.

The evolution of the journals’ ha-, h-, h2, and h3-indices

1985

1990
2

1995
3

2000
4

2005
4

2010
10

2015
16

2020
31

2015
16

2016
19

2017
21

2018
25

2019
28

2020
31

1985

1990

1995

2000

2005

2010

2015

2020

2015

2016

2017

2018

2019

2020

118

185

105

262

180

330

118

105

261

118

274

133

289

145

300

102

159

317

108

180

330

118

1985

1990

1995

2000

2005

2010

2015

2020

2015

2016

2017

2018

2019

2020

1985

1990

1995

2000

2005

2010

2015

2020

2015

2016

2017

2018

2019

2020

ha
JBE

AMR

SCIM

JBE

AMR

SCIM

JBE

AMR

SCIM

JBE

AMR

SCIM

JBE: Journal of Business Ethics; AMR: Academy of Management Review; SCIM: Scientometrics.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

average. SCIM’s h-index continues to rise by 5% a year, which is around five units a year. Der
rise of the ha-index is somewhat slighter, but in absolute values, it increases only once every 2
Jahre. AMR has reached a higher level of 37 for its ha-index and, due also to its smaller size, Es
is closer to its natural limits, but its h-index is still progressing at a rate of around 5%.

9. LIMITATIONS AND FURTHER RESEARCH

First of all, it is worth repeating that metrics and indicators are not substitutes for a more
comprehensive assessment of scientific contributions (Teixeira da Silva & Dobranszki,
2018); h-related indices depend on citations, which are reliant on the theme and the content
of the article, and also on the size of the specific topic in the field. Metrics should be com-
plemented with qualitative information and context as recommended by the Leiden Mani-
festo for research metrics (Hicks et al., 2015) and by the San Francisco Declaration on
Research Assessment5 (DORA).

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

5 See sfdora.org.

Quantitative Science Studies

The ha-index

The ha-index has been presented as an integer number in the same way as the index
values of the h-index are also restricted to integers. Jedoch, the numbers taken into
account, namely average citations per year, are not integers. An alternative is to adopt a
kind of interpolated version of the h-index (Rousseau, 2006). Jedoch, as the ha-index is,
just as the h-index, a Probably Approximately Correct (PAC) indicator (Rousseau, 2016), Die
ha-index does not need the precision suggested by the interpolated version. Auch, the choice
of an average citation is an approximation, as the linear growth of citations does not hold
exactly.

The application of the integer number can have consequences for young scholars in less
popular research areas: When all their articles have average citations lower than 1, they would
obtain an ha of 0, and an ha of 1 when their actual average citations are higher than 1 Aber
lower than 2. This makes comparison and differentiation rather difficult. The suggestion is
to use the figure with one decile for ha-indices of lower than 3. For ha-indices lower than 1,
the ha will be defined by the best average citation per year of the researchers’ articles limited to
1; for ha-indices between 1 Und 2, the ha will be defined with the second best average citation
per year; or by the third best average citation per year when three articles have more than two
citations per year.

Time remains a critical factor in bibliometrics. As the time elapsed is still a major determi-
nant of the publication record and the number of citations, by analogy with the h-index
(Schreiber, 2015; Schubert & Glänzel, 2007) it might be interesting to introduce a recent
0-index for the last five or 10 Jahre, especially to compare the work of younger scholars.
ha

The recent growth rate of an article during its first 5–15 years is higher than its average
citation per year. Such a criterion increases selectivity. This means that articles selected to join
the higher averages group certainly deserve their place in the ha-core. Mention has also been
made of another observation that can slightly affect the count: the imprecision in the calcula-
tion due to the inclusion of the current year6.

Future work on the ha-index should explore the theoretical foundations to support the prac-
tical advantages of the new indicator, following the theoretical work on the h-index and its
alternatives by Bertoli-Barsotti and Lando (2015, 2017), Egghe and Rousseau (2006), Und
Glänzel (2006) and mathematical approaches on stochastics (Burrell, 2007).

Insights into the pattern of citation distribution merit further research. It would be advisable
to conduct more empirical research in other sciences, such as in health and life sciences, mit
different citation patterns and higher immediacy in referencing than in management or social
Wissenschaften. If the average citation in the first year is highest, recent papers could obtain a dis-
proportionate advantage, although this would rapidly decrease. The use of the WoS average,
which also counts the incomplete ongoing year in the denominator, could be a mitigating
factor that could compensate for that advantage. Similar empirical research could be
performed based on Google Scholar data with their higher levels of h-indices. Auch, andere
h-related indices could be integrated into the comparative empirical analysis. Another avenue
for further research could investigate in depth the evolution of the ha- and h-indices over time
in more and more varied scientific disciplines.

6 The analysis of JBE would award an ha-index of 28 by the end of 2019, and when using the average citations
of the WoS in May 2020, mit einer (incomplete) additional year it drops to 26. This approximative nature is
an additional argument to round the figure when using the data as extracted from the Web of Science. In diesem
case it would award JBE an ha-index of 27.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

10. CONCLUSION

The present analysis of the comparison of the categorizations of academic articles based on
total citations or average citations offers new insights into bibliometrics. The overall average
citations categorization based on the complete data set seems to propose a better method, als es
offers more consistency over time and provides a fairer evaluation than the overall total cita-
tions categorization. It gives a more precise view of the researcher’s sustained impact and, als es
provides greater acknowledgment of progress through the inclusion of more recent contribu-
tionen, it is in favor of younger scholars. With its normalized time aspect, it mitigates other
h-index variants and allows a better comparison—to a certain degree—between articles from
different periods of publication. It can partially alleviate some of the unfair outcomes of the
h-index as it distinguishes progress in an earlier phase. The average citation ha-index partly
solves the problem of the temporality of the h-index7.

The comparison between variants of the h-index also questions the validity of the correc-
tion for multiple authorship as a proxy for interdisciplinary comparison and suggests that nor-
malization be performed at the level of the total citation distribution of the field. It also suggests
better alternatives of adapted fractional counting for multiauthorship.

With its increased selectivity and better differentiation, the proposed new ha-index offers a
valuable informative alternative to the h-index. It responds to the inflation of levels of
h-indices. Außerdem, it brings us closer to the more comparable figures of the original
h-index at the time of its launch. The ha-index reaches its full potential earlier than the h-index.
It offers stability over time, especially in the application of the ha-index to larger data sets, solch
as those for academic journals, where the ha-index reaches its limit sooner. It has the same
ease of calculation as the h-index. This new indicator combines achievement with potential
and recognizes experience as well as recent contributions.

ACKNOWLEDGMENTS

The author thanks Professor Ronald Rousseau for his fruitful feedback and suggestions in the
development of this paper, especially for the mathematical formulation of the ha-index and for
the observation for cases of lower ha-index. He also thanks the editor and the anonymous
reviewers for their suggestions.

COMPETING INTERESTS

The author has no competing interests.

FUNDING INFORMATION

The author received no funding.

DATA AVAILABILITY

The indices are calculated from data of the Web of Science. For legal reasons, data from
Clarivate’s Web of Science cannot be made openly available.

7 I owe this nice formulation to an anonymous reviewer, whom I wish to thank.

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

VERWEISE

Allison, P. D., Long, J. S., & Krauze, T. K. (1982). Cumulative advan-
tage and inequality in science. American Sociological Review,
47, 615–625. https://doi.org/10.2307/2095162

Ball, P. (2005). The index aims for fair ranking of scientists. Natur,
436(7053), 900. https://doi.org/10.1038/436900a, PubMed:
16107806

Ball, P. (2007). Achievement index climbs the ranks. Natur,
448(7155), 737. https://doi.org/10.1038/448737a, PubMed:
17700666

Batista, P. D., Campiteli, M. G., Kinouchi, O., & Martinez, A. S.
(2006). Is it possible to compare researchers with different scien-
tific interests? Scientometrics, 68(1), 179–189. https://doi.org/10
.1007/s11192-006-0090-4

Bejan, A., & Lorente, S. (2012). The physics of spreading ideas.
International Journal of Heat and Mass Transfer, 55(4), 802–807.
https://doi.org/10.1016/j.ijheatmasstransfer.2011.10.029

Berker, Y. (2018). Golden ratio as a substitute for geometric and har-
monic counting to determine multi-author publication credit.
Scientometrics, 114(3), 839–857. https://doi.org/10.1007
/s11192-017-2632-3

Bertoli-Barsotti, L., & Lando, T. (2015). On a formula for the h-index.
Journal of Informetrics, 9(4), 762–776. https://doi.org/10.1016/j
.joi.2015.07.004

Bertoli-Barsotti, L., & Lando, T. (2017). A theoretical model of the
relationship between the h-index and other simple citation indi-
cators. Scientometrics, 111, 1415–1448. https://doi.org/10.1007
/s11192-017-2351-9, PubMed: 28596626

Bihari, A., Tripathi, S., & Deepak, A. (2021). A review on h-index
and its alternative indices. Journal of Information Science. https://
doi.org/10.1177/01655515211014478

Bornmann, L., & Leydesdorff, L. (2018). Count highly-cited papers
instead of papers with h citations: Use normalized citation
counts and compare “like with like”! Scientometrics, 115(2),
1119–1123. https://doi.org/10.1007/s11192-018-2682-1,
PubMed: 29628536

Bornmann, L., Mutz, R., Hug, S. E., & Daniel, H.-D. (2011). A mul-
tilevel meta-analysis of studies reporting correlations between
the h-index and 37 different h-index variants. Journal of Infor-
metrics, 5(3), 346–359. https://doi.org/10.1016/j.joi.2011.01.006
Bouyssou, D., & Marchant, T. (2011). Ranking scientists and depart-
ments in a consistent manner. Journal of the American Society for
Information Science and Technology, 62(9), 1761–1769. https://
doi.org/10.1002/asi.21544

Braun, T., Glänzel, W., & Schubert, A. (2006). A Hirsch-type index
for journals. Scientometrics, 69(1), 169–173. https://doi.org/10
.1007/s11192-006-0147-4

Bras-Amorós, M., Domingo-Ferrer, J., & Torra, V. (2011). A biblio-
metric index based on the collaboration distance between cited
and citing authors. Journal of Informetrics, 5(2), 248–264. https://
doi.org/10.1016/j.joi.2010.11.001

Burrell, Q. L. (2007). Hirsch’s h-index: A stochastic model. Zeitschrift für
Informetrics, 1(1), 16–25. https://doi.org/10.1016/j.joi.2006.07.001
Costas, R., & Bordons, M. (2007). The h-index: Advantages, limita-
tions and its relation with other bibliometric indicators at the
micro level. Journal of Informetrics, 1(3), 193–203. https://doi
.org/10.1016/j.joi.2007.02.001

Dorogovtsev, S. N., & Mendes, J. F. (2015). Ranking scientists.
Nature Physics, 11(11), 882–883. https://doi.org/10.1038
/nphys3533

Egghe, L. (2006A). An improvement of the h-index: The g-index.

ISSI Newsletter, 2(1), 8–9.

Egghe, L. (2006B). Theory and practice of the g-index. Sciento-
metrics, 69(1), 131–152. https://doi.org/10.1007/s11192-006
-0144-7

Egghe, L., & Rousseau, R. (2006). An informetric model for the
Hirsch-index. Scientometrics, 69(1), 121–129. https://doi.org/10
.1007/s11192-006-0143-8

Fassin, Y. (2018). A new qualitative rating system for scientific
publications and a fame index for academics. Journal of the
Association for Information Science and Technology, 69(11),
1396–1399. https://doi.org/10.1002/asi.24059

Fassin, Y. (2020A). The HF-rating as a universal complement to the
h-index. Scientometrics, 125, 965–990. https://doi.org/10.1007
/s11192-020-03611-5

Fassin, Y. (2020B). The average citation ha-index. ISSI Newsletter,

16(4), 64–67.

Fassin, Y., & Rousseau, R. (2019). The h(3)-index of academic
journals. Malaysian Journal of Library & Information Science,
24(2), 41–53. https://doi.org/10.22452/mjlis.vol24no2.3

Glänzel, W. (2006). On the h-index—A mathematical approach to a
new measure of publication activity and citation impact. Sciento-
metrics, 67, 315–321. https://doi.org/10.1007/s11192-006-0102-4
Harzing, A. W. (2007). Publish or perish. Retrieved from https://

www.harzing.com/.

Harzing, A., Alakangas, S., & Adams, D. (2014). hIa: An individual
annual h-index to accommodate disciplinary and career length
differences, Scientometrics, 99(3), 811–821. https://doi.org/10
.1007/s11192-013-1208-0

Hicks, D., Wouters, P., Waltman, L., de Rijcke, S., & Rafols, ICH.
(2015). Bibliometrics: The Leiden Manifesto for research metrics.
Natur, 520(7548), 429–431. https://doi.org/10.1038/520429a,
PubMed: 25903611

Hirsch, J. E. (2005). An index to quantify an individual’s scientific
research output. Proceedings of the National Academy of
Sciences USA, 102, 16569–16572. https://doi.org/10.1073/pnas
.0507655102, PubMed: 16275915

Hudson, J. (2013). Ranking journals. Economic Journal, 123(570),

202–222. https://doi.org/10.1111/ecoj.12064

Hu, X., Li, X., & Rousseau, R. (2020). Describing citations as a func-
tion of time. Journal of Data and Information Science, 5(2), 1–12.
https://doi.org/10.2478/jdis-2020-0011

Hu, X., Leydesdorff, L., & Rousseau, R. (2020). Exponential growth
in the number of items in the WoS. ISSI Newsletter, 16(2), 32–38.
Jin, B., Liang, L., Rousseau, R., & Egghe, L. (2007). The R- Und
AR-indices: Complementing the h-index. Chinese Science Bulle-
tin, 52(6), 855–863. https://doi.org/10.1007/s11434-007-0145-9
Kosmulski, M. (2006). A new Hirsch-type index saves time and works
equally well as the original h-index. ISSI Newsletter, 2(3), 4–6.
Leydesdorff, L., & Bornmann, L. (2011). Integrated impact indica-
tors compared with impact factors: An alternative research
design with policy implications. Journal of the American Society
for Information Science and Technology, 62(11), 2133–2146.
https://doi.org/10.1002/asi.21609

Leydesdorff, L., Bornmann, L., Mutz, R., & Opthof, T. (2011). Turn-
ing the tables on citation analysis one more time: Principles for
comparing sets of documents. Journal of the American Society for
Information Science and Technology, 62(7), 1370–1381. https://
doi.org/10.1002/asi.21534

Merton, R. K. (1968). The Matthew effect in science: The reward
and communication systems of science are considered. Wissenschaft,
159(3810), 56–63. https://doi.org/10.1126/science.159.3810.56,
PubMed: 5634379

Quantitative Science Studies

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The ha-index

Price, D. de Solla. (1976). A general theory of bibliometric and
other cumulative advantage processes. Journal of the American
Society for Information Science, 27(5), 292–306. https://doi.org
/10.1002/asi.4630270505

Penner, O., Pan, R. K., Petersen, A. M., Kaski, K., & Fortunato, S.
(2013). On the predictability of future impact in science. Scien-
tific Reports, 3(1), 3052. https://doi.org/10.1038/srep03052,
PubMed: 24165898

Redner, S. (1998). How popular is your paper? An empirical study
of the citation distribution. European Physical Journal B—
Condensed Matter and Complex Systems, 4(2), 131–134.
https://doi.org/10.1007/s100510050359

Ritzberger, K. (2008). A ranking of journals in economics and
related fields. German Economic Review, 9(4), 402–430.
https://doi.org/10.1111/j.1468-0475.2008.00446.x

Rousseau, R. (2006). Simple models and the corresponding h- Und
g-index. E-LIS: ID 6153. Verfügbar unter https:// hdl.handle.net
/10760/7501.

Rousseau, R. (2016). Citation data as a proxy for quality or scientific
influence are at best PAC (probably approximately correct).
Journal of the Association for Information Science and Tech-
nology, 67(12), 3092–3094. https://doi.org/10.1002/asi.23525
Rousseau, R., Egghe, L., & Waffen, R. (2018). Becoming metric-wise:

A bibliometric guide for researchers. Chandos Publishing.

Ryan, J. C. (2016). A validation of the individual annual h-index
(hIa): Application of the hIa to a qualitatively and quantitatively
different sample. Scientometrics, 109(1), 577–590. https://doi
.org/10.1007/s11192-016-1972-8

Schreiber, M. (2015). Restricting the h-index to a publication and
citation time window: A case study of a timed Hirsch index. Jour-
nal of Informetrics, 9(1), 150–155. https://doi.org/10.1016/j.joi
.2014.12.005

Schubert, A., & Glänzel, W. (2007). A systematic analysis of
Hirsch-type indices for journals. Journal of Informetrics, 1(3),
179–184. https://doi.org/10.1016/j.joi.2006.12.002

Teixeira da Silva, J. A., & Dobranszki, J. (2018). Multiple versions
of the h-index: Cautionary use for formal academic purposes.
Scientometrics, 115, 1107–1113. https://doi.org/10.1007
/s11192-018-2680-3

Vinkler, P. (2010). Indicators are the essence of scientometrics and
bibliometrics. Scientometrics, 85(3), 861–866. https://doi.org/10
.1007/s11192-010-0159-y

Waltman, L., & van Eck, N. J. (2012). The inconsistency of the
h-index. Journal of the American Society for Information Science
and Technology, 63(2), 406–415. https://doi.org/10.1002/asi
.21678

Wendl, M. C. (2007). H-index: However ranked, citations need
Kontext. Natur, 449, 403. https://doi.org/10.1038/449403b,
PubMed: 17898746

Wu, Q. (2010). The w-index: A measure to assess scientific impact
by focusing on widely cited papers. Journal of the American Soci-
ety for Information Science and Technology, 61(3), 609–614.
https://doi.org/10.1002/asi.21276

Zhang, L., Thijs, B., & Glänzel, W. (2011). The diffusion of
H-related literature. Journal of Informetrics, 5(4), 583–593.
https://doi.org/10.1016/j.joi.2011.05.004

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

1
0
1
1
6
2
Q
S
S
_
A
_
0
0
2
5
9
2
1
5
0
5
1
5
Q
S
S
_
A
_
0
0
2
5
9
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Quantitative Science Studies

22 RESEARCH ARTICLE image

PDF Herunterladen