RESEARCH ARTICLE
Authorship in top-ranked mathematical
and physical journals: Role of gender on
self-perceptions and bibliographic evidence
Keine offenen Zugänge
Tagebuch
1Department of Computer Science, Communication and Economy, Hochschule für Technik und Wirtschaft Berlin,
Berlin, Deutschland
2Amazon Development Center, Berlin, Deutschland
Helena Mihaljevic´1
and Lucía Santamaría2
Zitat: Mihaljević, H., & Santamaría,
L. (2020). Authorship in top-ranked
mathematical and physical journals:
Role of gender on self-perceptions and
bibliographic evidence. Quantitative
Science Studies, 1(4), 1468–1492.
https://doi.org/10.1162/qss_a_00090
DOI:
https://doi.org/10.1162/qss_a_00090
Erhalten: 13 April 2020
Akzeptiert: 4 August 2020
Korrespondierender Autor:
Helena Mihaljevic´
helena.mihaljevic@htw-berlin.de
Handling-Editor:
Ludo Waltman
Urheberrechte ©: © 2020 Helena Mihaljević
and Lucía Santamaría. Veröffentlicht unter
eine Creative-Commons-Namensnennung 4.0
International (CC BY 4.0) Lizenz.
Die MIT-Presse
Schlüsselwörter: bibliometric data analysis, gender bias, peer review, scholarly communication, statistical
modeling
ABSTRAKT
Despite increasing rates of women researching in math-intensive fields, publications by female
authors remain underrepresented. By analyzing millions of records from the dedicated bibliographic
databases zbMATH, arXiv, and ADS, we unveil the chronological evolution of authorships by
women in mathematics, Physik, and astronomy. We observe a pronounced shortage of female
authors in top-ranked journals, with quasistagnant figures in various distinguished periodicals
in the first two disciplines and a significantly more equitable situation in the latter. Zusätzlich,
we provide an interactive open-access web interface to further examine the data. To address
whether female scholars submit fewer articles for publication to relevant journals or whether
they are consciously or unconsciously disadvantaged by the peer review system, we also study
authors’ perceptions of their submission practices and analyze around 10,000 responses,
collected as part of a recent global survey of scientists. Our analysis indicates that men and
women perceive their submission practices to be similar, with no evidence that a significantly
lower number of submissions by women is responsible for their underrepresentation in
top-ranked journals. According to the self-reported responses, a larger number of articles
submitted to prestigious venues correlates rather with aspects associated with pronounced
research activity, a well-established network, and academic seniority.
1.
EINFÜHRUNG
A strong publication record ranks among the most powerful determinants of academic career
success in many disciplines, exerting significant influence on decisions about tenure, funding,
and promotions (Krantz, 2007; McGrail, Rickard, & Jones, 2006). While monographs and edited
books predominantly drive research in the humanities and social sciences, in math-intensive
fields, the most relevant deliverable is the peer-reviewed article in a scholarly journal.
Analyses of the dedicated mathematics and astrophysics databases zbMATH and ADS show that
this type of publication constitutes over 80% of their indexed content from 1970 to date. Zeitschrift
articles have effectively become not only a vehicle for communicating knowledge in these
Bereiche, promoting the exchange of ideas and advancing science, but also a tool for research
assessment, a development that is not without criticism (Hicks, Wouters, et al., 2015; Taubes,
1993). It is not just the number of authored articles that matters, but especially the venues where
they appear and their perceived quality, which are often used as a proxy for the relevance of the
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
content published therein. Depending on the type of sought position, associated institution, Und
seniority level, the “rank” of the journals where researchers publish can be decisive for the
fate of their pursued careers (Kelsky, 2017; Martin, 2019).
Despite the steady increase in their participation in math-intensive fields, women remain
underrepresented as authors in the most prestigious topical journals (Bendels, Müller, et al.,
2018; Mihaljevic´-Brandt, Santamaría, & Tullney, 2016; Westen, Jacquet, et al., 2013). Nach
to the multidisciplinary study of Holman, Stuart-Fox, and Hauser (2018) that covers 36 Million
authorships from PubMed and the arXiv, many Science, Technologie, Maschinenbau, Mathematik,
und Medizin (STEMM) research specialties, including surgery, computer science, Physik, Und
mathematics “will not reach gender parity this century.” Yet it is difficult to determine whether
female scholars submit fewer articles for publication to relevant venues or whether they are
consciously or unconsciously disadvantaged by the peer review system.
The refereeing process, which varies significantly among publishers and journals, is typically a
Komplex, often opaque, and potentially unfair mechanism (Schmied, 2006), albeit regarded as nec-
essary for the vetting of knowledge claims (Lee, Sugimoto, et al., 2013). It typically consists of
various steps, such as an initial review by an editor, the selection of external reviewers, Die
decision whether to blind the process, the communication of referee reports, and the subsequent
acceptance or rejection. Most academic publishers do not make their processes fully transparent
(Prager, Kammern, et al., 2018) and neither is it common practice to report on potential biases
and measures on how to overcome them. Welcome exceptions are the recent initiatives by
medical journal The Lancet (Clark & Horton, 2019) and science journal Nature (Natur, 2020)
to increase diversity and transparency. Zusätzlich, publication and peer review practices differ
considerably among scientific disciplines. These comprise, but are not limited to, the typical
number of referees; the average time delay from submission to publication; the communication
style between editors, reviewers, and authors; and the degree of blindness during the process. In
this study we will essentially focus on peer-reviewed publications in top-ranked journals in
mathematics and physics, including astrophysics.
Mathematics is a relatively small field with even narrower subfields. Journals of high perceived
quality within the community ideally base their decisions on manuscript acceptance on
Littlewood’s precepts of novelty, correctness, and interest (Krantz, 1997, P. 125). The thorough
examination of proofs is a key expectation of peer review in the discipline. Linked to it is the
assumption that all statements in a peer-reviewed paper can be regarded as true, despite the fact
that such a requirement is often extremely hard to fulfill within reasonable time and effort (Geist,
Löwe, & Van Kerkhove, 2010, S. 160–163; Grcar, 2013; Krantz, 2007, P. 1510). Aside from
some exceptions, such as extremely prestigious journals like the Annals of Mathematics or
particularly difficult research results where additional expertise might be sought, a common prac-
tice is to engage a single referee in the peer review process (Andersen, 2017; Krantz, 2007). Der
London Mathematical Society, which publishes many top-ranked journals in particular in pure
Mathematik, refers to the referee in singular form in its Author Guidelines, noting that “in math-
ematics it is common for the Referee to know the Authors personally,” thus “fine judgement” is
required to handle potential biases (London Mathematical Society Guide to Authors, 2020). Der
survey of mathematical journal editors in Geist et al. (2010) stresses that “the mathematical peer
review is largely a communication between an editor and one referee based on trust due to a
personal relationship.” The standard to which proofs in submissions are scrutinized by the
reviewer is not homogeneous across journals, ranging from cases where all claims in a demon-
stration are fully checked by the peer to others where the responsibility for mathematical correct-
ness is placed mostly on the author (Nathanson, 2008). The promptness and thoughtfulness with
which a manuscript is handled might depend on the reputation of the author, the perceived
Quantitative Science Studies
1469
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
novelty of the topic, or other potentially nonobjective considerations (Krantz, Kuperberg, & Transporter
der Poorten, 2003). Given that the correctness of proofs is so important to accept or reject a man-
uscript, the fact that peer review in mathematics lacks homogeneity and relies substantially on the
authors’ credit and the level of trust between editors and reviewer(S) merits a thorough investiga-
tion of the potential existence of structural biases. Although a large body of research on the peer
review system has been published in the past decades, so far only one systematic study exists that
focuses on the particularities of mathematics, namely that by Geist et al. (2010); vgl. Andersen
(2017) and Auslander (2008).
Physics is a larger research field that spans numerous subfields with very different organiza-
tional styles, from small theoretical groups that operate in a way closely resembling that of math-
ematicians, to big-science collaborations that involve thousands of researchers around a
common experiment. Many physics papers, most significantly in the fields of astrophysics and
high-energy physics, appear first as preprints, which has been shown to increase the number
of citations (Gentil-Beccot, Mele, & Brooks, 2009). The arXiv has long been used to communicate
research results and establish priority claims, in fact relegating journals to outlets for “secondary
distribution, archiving, and peer-review” (Brooks, 2009). Peer review in physics is a relatively
modern practice. Originally, traditional authoritative German journals such as Annalen der
Physik did not seek external referees and published based on the sole opinion of an identifiable
editor instead (Lalli, 2016). Peer review became standard within the English-speaking world
around the mid-20th century and it was only towards the late 20th century that it “came to be
seen as a process central to scientific practice” (Balduin, 2018). The currently established process
in most physics journals involves the selection of two referees “in parallel” from a curated pool of
reviewers (Gordon, 1979). If reports on a manuscript conflict, the staff editor normally seeks an
adjudicating referee. Rejection decisions might involve the journal’s editor-in-chief and editorial
board. Physics fields organized around small research groups do operate within the triangular
relationship authors–editor–referees. Jedoch, scholarly communication in large collaborative
disciplines such as high-energy physics, observational astronomy, or gravitational physics differs
significantly. Big-science collaborations that rely on access to large facilities to perform research
“increasingly resemble organizations in themselves” (Birnholtz, 2008). Typically, all of their
members, in a growing number that often creeps into the thousands, are listed as authors on
any paper published by the collaboration: sehen, Zum Beispiel, Schmied (2016) for astronomy and
Pritychenko (2016) for nuclear and particle physics. Credit attribution in such a setting poses a
distinct set of challenges: There is no differentiation for the first or last author as most significant
contributor (Birnholtz, 2008) and acknowledgment of individual ownership is ambiguous or
directly impossible (Birnholtz, 2006). The peer review process in big-science disciplines entails
the particularity that manuscripts have generally been internally reviewed and vetted ahead of
Vorlage; sometimes finding external reviewers with comparable expertise and no conflicts of
interest becomes arduous for journal editors (A. Day, persönliche Kommunikation, Juni 21, 2020).
From the exposition above, it becomes apparent that professional networks, personal connec-
tionen, and trust relationships are pivotal elements in scholarly communication in mathematics and
Physik. According to the norms of modern science though, truth-claims cannot be judged on the
basis of personal or social attributes of their authors. This includes race, nationality, religion, affilia-
tion, Klasse, and of course gender. Und doch, at the core of the discussion is the recognition that “the
institution of science is part of a larger social structure with which it is not always integrated” (Merton,
1973). Folglich, we consider the entire process from manuscript submission until final decision
on acceptance or rejection an excellent use case for the assessment of the impersonal character of
Wissenschaft. Jedoch, only a few studies exist that investigate the complete peer review mechanism
comprehensively, mainly due to lack of access to extensive data from academic publishers.
Quantitative Science Studies
1470
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
For this reason it is convenient to consider additional perspectives on the intricacies of the
publication process. The authors’ perceptions of their own submission practices provide one such
important source of information. In diesem Artikel, we analyze the answers of almost 10,000
worldwide scientists from the physical sciences and mathematics who participated in an online
snowball-sampled survey and answered the following question: “During the last five years, Wie
many articles have you submitted to journals that are top-ranked in your field?” We show that the
respondents’ gender does not play a significant role in their perceived submission practices.
Stattdessen, a higher number of manuscripts submitted to top-ranked journals correlates rather with
factors associated with pronounced research activity, a well-established network, and academic
seniority, such as being a journal editor, member of a grant committee, or conducting research
abroad.
Außerdem, we use bibliographic databases to analyze the distribution of authors’ gender in
selected journals in mathematics, astronomy and astrophysics, and theoretical physics. Wir
compute and model longitudinal trends in the proportion of publications authored by women
im Laufe der Zeit. Our analysis shows that the percentage of female authors in top-ranked astronomy
and astrophysics journals has grown steadily over recent decades, reaching numbers well com-
parable to their overall presence in the discipline. This is in stark contrast to most high-profile
journals in mathematics and even more so in theoretical physics. Zusätzlich, we provide an
interactive open-access web interface that allows us to examine all journals indexed in the
dedicated databases zbMATH and ADS and the arXiv preprint server similarly.
Although our two analyses of survey responses and bibliographic data are not directly com-
parable, it is useful to discuss their implications for the existence of potential imbalances in the
peer review process in mathematics and physics altogether. This is even more the case given that
the respondents’ perceptions of their own submission practices are very similar across disciplines,
which is in discrepancy with the measured outcomes in the considered topical journal
publications.
1.1. Related Work
The situation of women in academia, especially in the so-called “hard sciences,” is a massively
researched topic. The literature that examines its causes presents contradictory conclusions, yet
the one mostly agreed-upon fact is that women are underrepresented in all math-intensive fields
at the level of college, graduate studies, and the professoriate: see Ceci, Ginther, et al. (2014),
Ceci and Williams (2011), Hill, Corbett, and Rose (2010), Kahn and Ginther (2017), and Wang
and Degol (2016) for reviews. More controversial is the debate about the underlying causes.
Arguments based on early biological differences in mathematical ability among the sexes do
not seem to be supported by current experimental evidence (Hutchison, Lyons, & Ansari,
2018; Kersey, Csumitta, & Cantlon, 2019); Genau genommen, sociocultural influences rather than biolog-
ical factors appear more likely to have an impact (Andreescu, Gallian, et al., 2008; Wang &
Degol, 2016). Regardless, gender segregation concerning career preferences already manifests
by high school and continues through college major choices. By graduation, men outnumber
women in nearly every STEM field; particularly in physics, engineering, and computer science
the latter earn a mere 20% of bachelor’s degrees (Hill et al., 2010). Perceptions and unconscious
beliefs about gender in mathematics and science seem to play a role in women’s choices, als
evidenced by their underrepresentation in fields believed to emphasize brilliance as key to suc-
Prozess (Meyer, Cimpian, & Leslie, 2015). Once in possession of a doctorate in a math-intensive
field, there is no clear consensus about the existence of biases in academic interviewing, hiring,
and promotion. For astronomers in the United States, zum Beispiel, no gender differences are
found in career outcomes, the proportion of graduates starting postdocs and the proportion of
Quantitative Science Studies
1471
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
those hired into long-term positions being comparable for men and women (Perley, 2019). In
fact, Ceci et al. (2014) argue that more pipeline leakage is observed in life and social science
fields, where women are already prevalent, than in math-intensive ones, where they are under-
represented but in which the number of women holding assistant professorships is commensu-
rate with that of men.
One potential reason for the dearth of women in math-intensive fields that is supported by
data is the fact that female researchers publish fewer papers on average than their male counter-
Teile (Larivière, Ni, et al., 2013) and are less likely to be listed as either first or last author (Westen
et al., 2013). This extends to top-ranked journals, as evidenced in Bendels et al. (2018)’s analysis
of publications spanning various scientific fields from the Nature Index (Natur, 2014).
Discipline-specific studies report analogous findings in high-rank serials in mathematics
(Mauleón & Bordons, 2012). Female mathematicians are significantly underrepresented in the
most prestigious journals: The amount of publications by women has remained in the single-digit
percentage range over the last decades, despite the fact that they have been entering the field at a
higher rate over that time period (Mihaljevic´-Brandt et al., 2016). Whether women submit fewer
manuscripts is difficult to confirm in the absence of transparent statistics on submission rates.
What seems to hold is that women are underrepresented when it comes to being invited to
submit to prestigious venues, as shown in statistics of commissioned authors to journals in the
life and physical sciences (Conley & Stadmark, 2012).
The topic of whether the peer review system is intrinsically biased against women is highly
disputed, with some studies challenging its robustness, albeit without consistent outcomes. A
comprehensive review from an epistemiological perspective is that of Lee et al. (2013), WHO
characterize and examine the empirical, methodological, and normative claims of bias in peer
Rezension. Results showing lack of evidence for bias in peer review in science are quoted for in-
stance in Fox, Verbrennungen, and Meyer (2016), who conclude that gender, seniority, and geographic
location affect the particularities of the refereeing process but not its outcome. Squazzoni,
Bravo, et al. (2020) find no evidence of gender imbalance in the acceptance rates of 145 journals
in biomedicine, life, physical, and social sciences, yet their conclusions emphasize the com-
plexity of the problem, as distortions are extremely difficult to account for. Ceci and Williams
(2011) argue that there is “no sex discrimination in publishing” and conclude that the critical
variable for bias in peer review is not gender per se, but rather access to resources, which cor-
relates with the former because women are more likely to work as adjuncts or at teaching-intensive
institutions with limited means. Upon analysis of diverse sources in math-intensive disciplines,
Ceci et al. (2014) agree that “manuscript reviewing and grant funding are gender neutral.”
Per contra, divergent conclusions can also be found in the literature. Recent analyses of jour-
nals in the physical and life sciences hint at the existence of gender- and geography-based
biases: IOP Publishing (2018) shows that women are less likely to receive acceptance for pub-
lication in half of the subdisciplines covered by their 50+ journals and are less frequently invited
to review. An evaluation of submissions to the eLife journal by Murray, Siler, et al. (2019) reveals
a homophilic effect between the gender and the affiliation country of gatekeepers (editors and
referees) and authors regarding the outcome of the review. Given the underrepresentation of
women in editorial boards (Topaz & Sen, 2016) and reviewer pools (Lerback & Hanson,
2017), it is not unrealistic to suspect that the chances of manuscript acceptance for female
authors might be lessened, even if this mechanism occurs at a subconscious level. Helmer,
Schottdorf, et al. (2017) reach similar conclusions in their analysis of the Frontiers journals, stres-
sing the need for increased efforts to fight against subtler forms of gender bias and not just focus
on numerical underrepresentation alone. A reasonable strategy to limit bias in peer review is the
implementation of the double-blind strategy. Tomkins, Zhang, and Heavlin (2017A) confirm that
Quantitative Science Studies
1472
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
single-blind reviews confer a notable advantage to papers with famous authors and authors
from high-prestige institutions in conference proceedings, the standard publication outlet in
computer science. A meta-analysis indicates that the overall effect against women can be con-
sidered statistically significant (Tomkins, Zhang, & Heavlin, 2017B), followed by the recommen-
dation that double-blind reviewing be implemented as a means to control for biases.
Most of the existing literature on bias in peer review concerns the natural, medical, and life
Wissenschaften. Comparatively few articles are devoted to mathematics and physics, even though pub-
lication practices vary considerably, a fact that would merit further field-specific analyses. To the
best of our knowledge, no systematic studies exist that look into hidden biases possibly introduced
by publication practices in large collaborations, such as those in experimental physics. The lack of
homogeneity in peer review for mathematics and its implications for the publication rates of un-
derrepresented groups is likewise seldom addressed. Regarding the potential implementation of
double-blind mechanisms in mathematics and physics, editors doubt that every single author
identity can be successfully hidden in such small fields (Palus, 2015). Almost no journal in these
areas currently offers double-blind review in any case, which is regarded as difficult to manage
and maintain. To what extent the lack of double-blindness is hindering women and other un-
derrepresented groups in mathematics and the physical sciences remains largely unknown.
This article addresses the scarcity of targeted studies on gender bias in scholarly communi-
cation in mathematics and the physical sciences by looking at discipline-specific bibliographical
databases to select and study publications in distinguished topical journals. Zusätzlich, Wir
leverage the responses to a global survey of scientists by specifically selecting answers from
mathematicians, physicists, and astronomers to questions about their perceived submission
practices to top-ranked journals in their disciplines. The data offers novel insights into (A) Die
ways that female and male scientists perceive to behave regarding prestigious publication
venues and (B) the evidence provided by publication rates split by gender obtained from the
bibliographical sources themselves.
2. DATA AND METHODOLOGY
2.1. Selection of Journals and Perceived Quality
The quality of academic journals is often estimated by one of the available rankings that try to
infer scientific prestige from various metrics, in particular citations. Perhaps the most widespread
of them is the Journal Impact Factor ( JIF) (Garfield, 2006), with the Eigenfactor (Westen, Bergstrom,
& Bergstrom, 2010) and the CiteScore (da Silva & Memon, 2017) as known alternatives. In some
disciplines, journals are categorized using manually compiled lists, usually curated by field-
specific academic organizations, as for instance the so-called ERA indicator developed by the
Excellence in Research for Australia. For a review of bibliometric indices see, Zum Beispiel,
Roldan-Valadez, Salazar-Ruiz, et al. (2018).
Aside from the convenience of having an accessible categorization to assess quality, it is by
no means clear that journal rankings can encapsulate said information meaningfully. Against the
JIF numerous well-argued critiques have been formulated on the basis of both technical issues,
such as its concrete definition and implementation (Kiesslich, Weineck, & Koelblinger, 2016),
which is problematic because the calculation is based on the arithmetic mean of a highly skewed
distribution of citations, and of interpretative concerns (Larivière & Sugimoto, 2019). Ähnlich,
concerns about potential biases have been raised against the ERA indicators (Haslam & Koval,
2010; Vanclay, 2011), which eventually led to their discontinuation. A consensus seems to be
emerging that research quality should not be measured based just on the one-dimensional scale
of a journal ranking (Callaway, 2016; DORA, 2012; Shanta, Sharma, & Pradhan, 2013; Verma,
Quantitative Science Studies
1473
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
2015). This development is in agreement with the views of the majority of the mathematical
Gemeinschaft, namely that “citation data provide only a limited and incomplete view of research
Qualität, and the statistics derived from citation data are sometimes poorly understood and
misused” (Adler, Ewing, & Taylor, 2009). In astrophysics, a field characterized by the pattern
of communicating results as preprints ahead of publication, survey data showed that researchers
rate “the quality of the journal as perceived by the scientific community” as more important than
the JIF (Polydoratou & Moyle, 2007).
Entsprechend, we have decided to refrain from employing any such ranking scheme in our
analyses and instead leverage expert domain knowledge to select and prioritize some topical
journals above others. For every analyzed discipline we justify our choices in the respective sub-
sections under Subsection 3.2. Our selection of journals is intended to be representative of
top-ranked outlets across disciplines and in agreement with the views of the respective scientific
communities. Trotzdem, readers are encouraged to query the entire database used in this
study to analyze publication statistics from their journals of interest in mathematics, astronomy
and astrophysics, and theoretical physics using the custom web interface provided at http://
gender-publication-gap.f4.htw-berlin.de/journals/.
2.2. Data Sources
Our analysis is based on two distinct types of data sources: (A) bibliographic records of published
articles in mathematics, astronomy and astrophysics, and theoretical physics, enriched by in-
ferred author gender labels, Und (B) answers from participants in a global survey of scientists,
carried out in 2018 by the American Institute of Physics as part of an international and interdis-
ciplinary project (“A Global Approach to the Gender Gap in Mathematical, Computing, Und
Natural Sciences: How to Measure It, How to Reduce It?”, https://gender-gap-in-science.org/).
2.2.1. Bibliographic records
The data on published journal articles stems from three bibliographic repositories managed by
scientific organizations with (partially, mindestens) open-access data policies. All three are regarded
as high-quality, curated, comprehensive bibliographic collections for the respective disciplines,
and have often served as data basis for specialized scientometric analyses (Brisbin & Whitcher,
2018; Caplar, Tacchella, & Birrer, 2017; Mihaljevic´-Brandt et al., 2016; Schmied, 2016).
1. Mathematik: Zentralblatt MATH (zbMATH https://zbmath.org), founded in 1931, ist der
longest standing and one of the two most comprehensive abstracting and reviewing
services in pure and applied mathematics. Edited by the nonprofit institution FIZ
Karlsruhe, a member of the Leibniz Association, its contents will be made freely accessible
In 2021. It places high value on its completeness, containing about 4 million bibliographic
entries with reviews or abstracts drawn from about 3,000 journals and 180,000 books. Es ist
author database comprises 950,000 author profiles. Every year, etwa 120,000
mathematical publications are indexed, and about 100 new journals and 3,000 Forschung
monographs and conference proceedings are added to the database (Hulek, 2016). For all
practical purposes, regardless of the subfield within mathematics and its applications,
every relevant publication can be found in zbMATH (Hansen, 2018). Our analyses
of zbMATH entries capture the database at the end of July 2019.
2. Astronomy and astrophysics: The SAO/NASA Astrophysics Data System (ADS, https://ui
.adsabs.harvard.edu) is a digital library for research in astronomy and astrophysics operated
by the Smithsonian Astrophysical Observatory under a NASA grant. It is the main discovery
platform for scientific literature used by the community of astronomers and astrophysicists,
Quantitative Science Studies
1474
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
providing both disciplinary completeness and enriched data features (Accomazzi, Kurtz,
et al., 2018). The ADS maintains three bibliographic databases covering publications in
astronomy and astrophysics, Physik, and the arXiv e-prints. For our analyses in astrophys-
ics we have restricted ourselves to the first one, which contains over 2.5 million publica-
tionen, 1.1 million of which are peer-reviewed. About 25,000 new entries are added yearly
to the collection. The coverage of major journals of astronomy is complete, and those
account for a large fraction of the research contained in the database (Santamaría, 2018).
We analyze data from ADS as of at the end of March 2018.
3. Theoretical physics: The arXiv (https://arxiv.org), funded by Cornell University, the Simons
Foundation, and member institutions, provides open access to electronic preprints in
various fields, most notably physics. Contrary to mathematics and astronomy and astro-
Physik, where curated databases such as zbMATH and ADS ensure access to a mostly
complete corpus of bibliometric metadata, no comparable repository exists for the entire
field of theoretical physics. Standard publication practices of physicists, especially in the-
oretical subfields, include the upload of preprints to the arXiv prior to or concurrently with
manuscript submission. Tatsächlich, this is so common that in fields such as high-energy phys-
ics, many peer-reviewed journals allow direct submissions from the arXiv via the e-print
number. This preprint repository is “an indispensable mode of scientific exchange”
(Jackson, 2002), “covering the majority of publications in subfields like astronomy, astro-
Physik, and nuclear and particle physics” (Larivière, Sugimoto, et al., 2014). Weil
arXiv e-prints do not include standardized information on the posterior appearance in
peer-reviewed journals, we have cross-referenced the data with CrossRef (https://www
.crossref.org) to enrich the information on serials as well as on authors’ first names that
we use for gender inference. Trotzdem, it should be noted that the analyzed content
of selected journals from physics taken from the arXiv might differ from the full published
records. We base our study on data gathered from the arXiv at the end of July 2019.
2.2.2. Survey responses
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Answers to the question about the perception of submission practices were collected
through the “2018 Global Survey of Mathematical, Natural, and Computing Scientists”
(http://statisticalresearchcenter.org/global18), developed within the aforementioned Gender Gap
in Science project with the goal of obtaining a broader picture of the status of mathematicians
and scientists worldwide. The questionnaire addressed the researchers’ impressions of their early
Jahre, university studies, doctoral studies, and professional careers.
Data was sampled via a snowball method that targeted affiliates and contacts from partner-
ing institutions of the project. Due to the far-reaching network of 11 professional societies and
scientific organizations it was possible to reach almost 30,000 respondents across the globe.
The main reason for the choice of a snowball sampling technique was the lack of a single
network to reach all targets; thus the creation of a statistically representative sample was
not feasible. This poses certain limitations on the proper interpretation of the collected data,
most notably the fact that answers cannot be assumed to be representative of the (sub-)popu-
lations as a whole. Eher, they should be considered indicators of trends observed among
participating individuals in the survey.
Our analyses are based on the replies of participants with at least a Master’s degree that are
primarily working in mathematics, Physik, or astronomy and that entered a valid answer to
the question: “During the last five years, how many articles have you submitted to journals that
are top-ranked in your field?” This selection yields 9,984 responses.
Quantitative Science Studies
1475
Authorship in top-ranked mathematical and physical journals
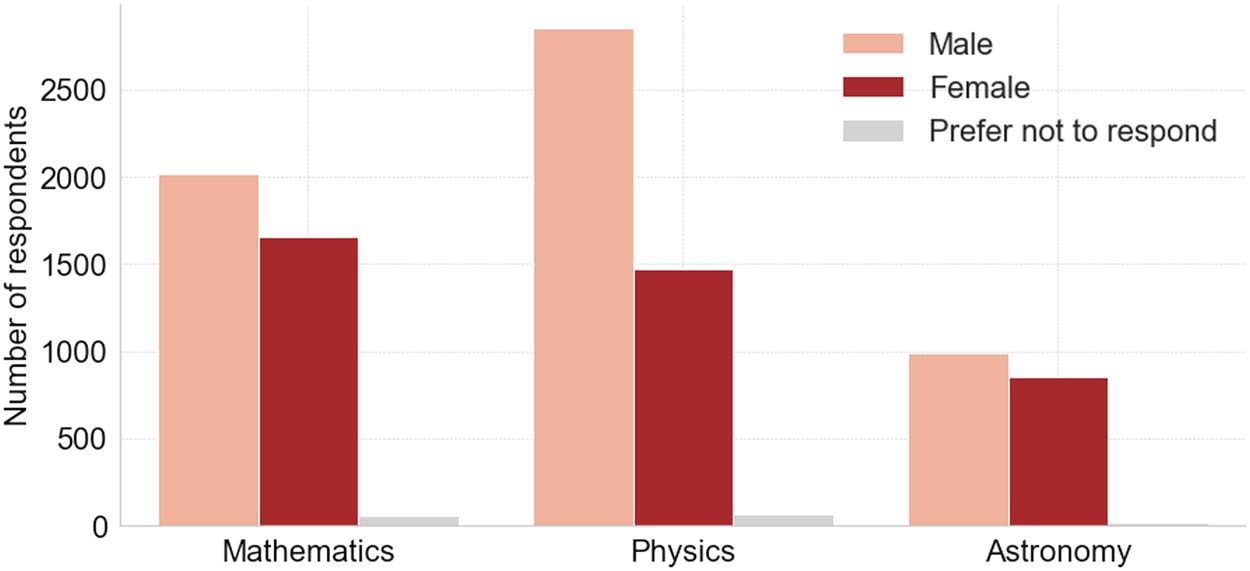
Figur 1. Total number of survey respondents broken down by discipline and gender.
Figur 1 shows the number of respondents per discipline and gender. Physicists are the largest
Gruppe, mit 4,392 answers, while mathematicians amount to 3,734 and astronomers to 1,858. In
Physik, women make up about 34% of all participants, whereas they reach 45% in astronomy
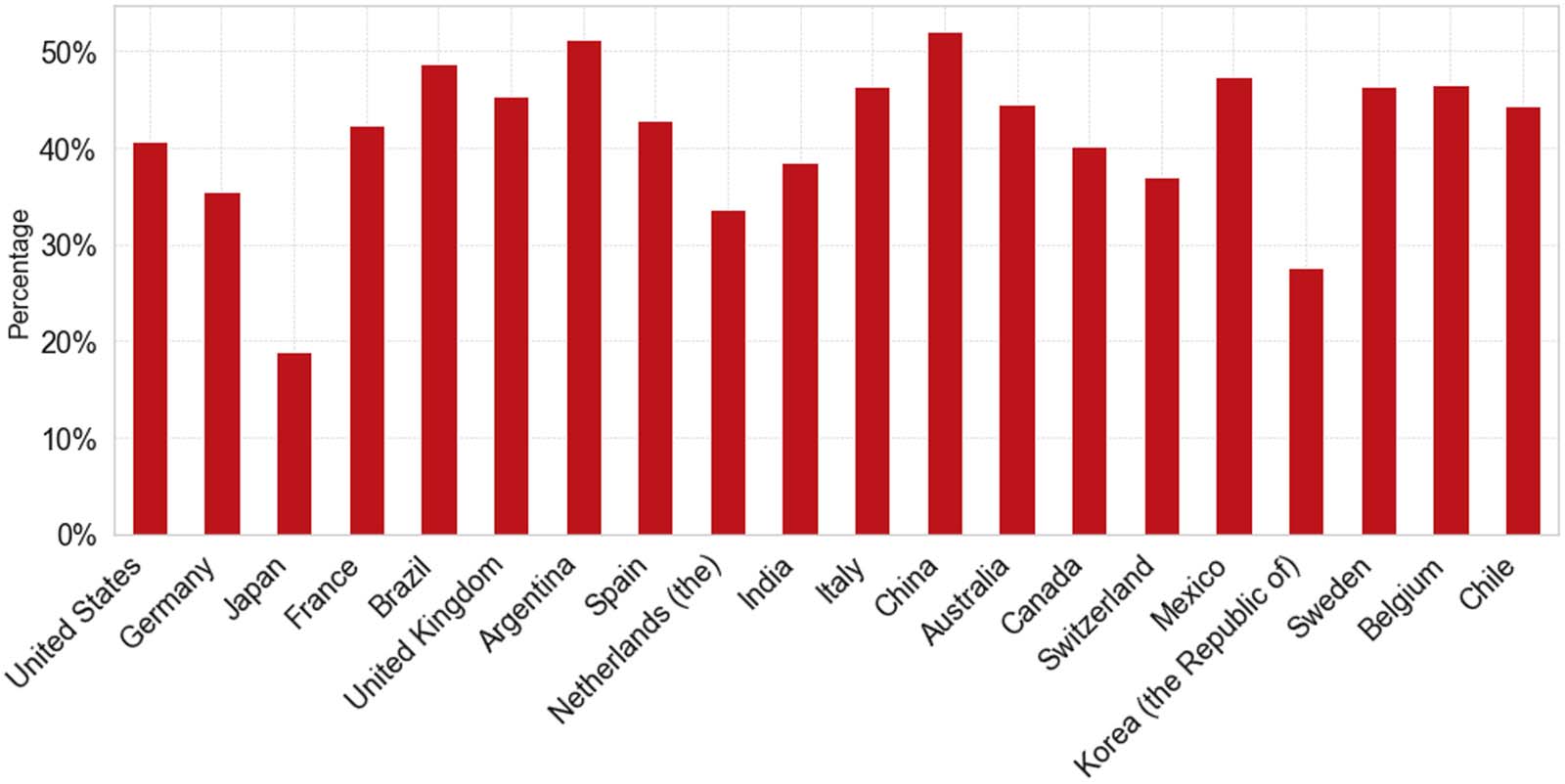
and mathematics. The gender breakdown is also country-dependent. As shown in Figure 2,
women represent 35% Zu 50% of all survey respondents in the majority of countries, mit dem
notable exceptions of Japan and South Korea, where their proportion is much smaller. Gesamt,
the percentage of women in the data set is significantly larger than in their respective disciplines,
estimated from the figures of the UNESCO Institute for Statistics (http://data.uis.unesco.org),
which report less than 30% of scientific researchers worldwide being women, vgl. by the propor-
tions of active authors per discipline over time (https://gender-publication-gap.f4.htw-berlin.de
/cohorts/authors). Women were possibly more inclined to respond to a survey that they perceived
to deal with gender issues, even though the call explicitly stated that the entire scientific commu-
nity was encouraged to contribute.
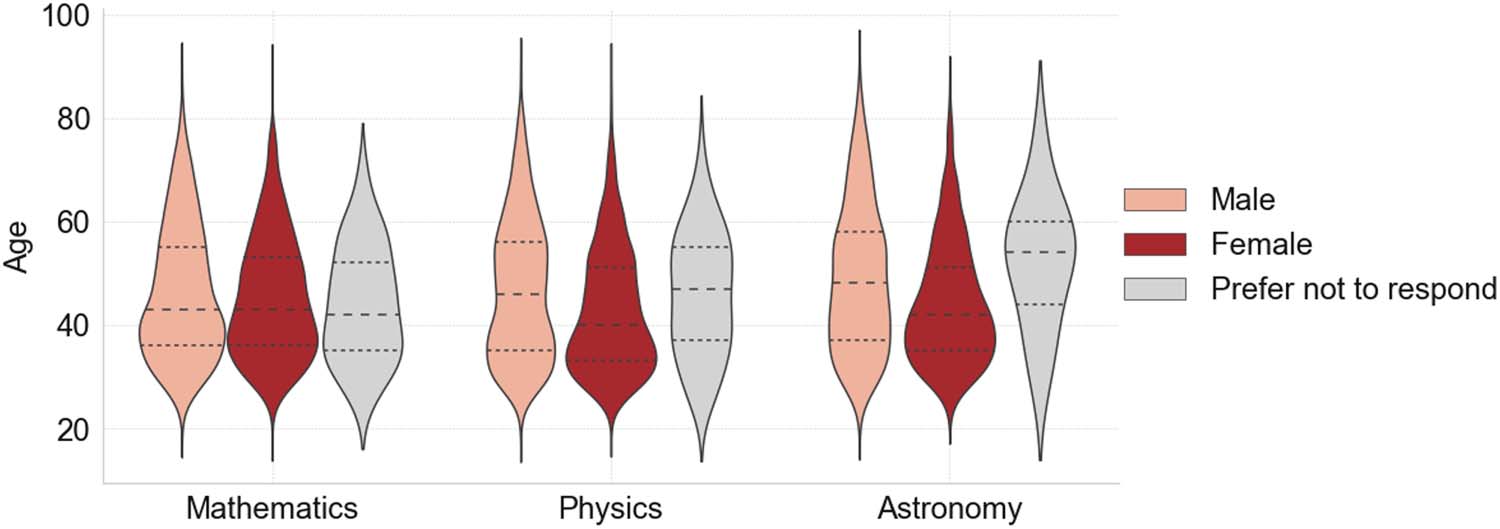
In Abbildung 3 we show the age distribution broken down by gender and discipline. Note that the
median lies between 40 Und 50 years in all three fields. Whereas in physics and astronomy female
respondents tend to be younger than their male counterparts, in mathematics the age distribution
Figur 2. Percentage of female survey respondents from mathematics, astronomy, and physics per country.
Quantitative Science Studies
1476
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
Figur 3. Age distribution of survey respondents broken down by gender and discipline. Dashed
lines indicate the quartiles, the middle line marks the median.
is almost gender independent. In physics, we observe a second bulge in the range of 45 Zu 55 Jahre,
which indicates that the survey was answered by comparatively more female than male physicists
in the second half of their academic career, a fact that might be relevant for the correct interpre-
tation of the data.
2.3. Gender Inference
Bibliographic metadata does not include the authors’ gender, hence this information needs to be
inferred. Usually, an author’s name is the only piece of information capable of providing an in-
dication. In our analyses we have combined assessments from different gender assignment
services maximizing the recall (d.h., the proportion of names that can be assigned a gender), while
keeping the error rate under a certain threshold. Our algorithm is based on the benchmark of
Santamaría and Mihaljevic´ (2018), where we compared five dedicated web services and software
packages. Roughly speaking, in our first stage we use the results from Gender API (https://Geschlecht
-api.com) featuring a high probability score. For names leading to gender assignments with
probability values between 75 Und 90 in Gender API we combine responses with those from
genderize.io (https://genderize.io). All remaining unidentified first names are processed with
Python package gender guesser (https://github.com/lead-ratings/gender-guesser), which attains
high precision but low recall. For authors without a first name but with last names contained
in a curated list of Soviet surnames (https://en.wikipedia.org/wiki/List_of_surnames_in_Russia),
we apply surname-ending rules to infer the gender. It is also important to note that more than
70% of the first names of authors in ADS are abbreviated as initials; thus direct gender inference
via first names would hardly be useful. daher, we have trained an algorithm which clusters
authorships into author profiles and increases the percentage of identifiable authorships
enormously (Mihaljevic´ & Santamaría, 2020).
Following the gender assignment procedure, all author names are tagged with a “female,”
“male,” or “unknown” qualifier. The percentage of nonlabeled records is generally large and pri-
marily affects names from certain regions; zum Beispiel, authors of Chinese ancestry are more often
assigned unknown labels due to loss of gender marking during transliteration. In our gender anal-
yses we remove all authorships labeled as “unknown,” which in itself introduces a selection bias.
An agnostic estimation of the incurred error would assume that the percentage of men and women
in the “unknown” group mimics the ratio between the groups identified as male and female.
Yet we know from our previous studies that the proportion of women in the group of authors
labeled unknown is smaller than the share of identified women (Mihaljevic´-Brandt et al.,
2016). This means that “unknown” names are more likely to be men than women. We conclude
Quantitative Science Studies
1477
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
that our estimated percentage of women among all authorships when removing unknown authors
is always an upper bound with respect to the entire data set of authors. When possible, we have
added error regions to our plots to reflect this fact.
Numerous challenges arise in connection with automated gender recognition (AGR). To name
a few, the association of a name with gender is not unique and also depends on the cultural and
regional context; hence relying solely on the first name can be error-prone and lead to biases
towards certain countries. Außerdem, all AGR approaches that build on names or other phys-
iological features, such as facial images or voice, assume a binary gender paradigm that reinforces
noninclusive preconceptions. Despite these (and other) critiques, we have performed a name-
based gender inference because academia is notoriously not gender agnostic and because
gender disparities are indeed observed and need to be explained. We have discussed various
concerns related to AGR in Mihaljevic´, Tullney, et al. (2019) and would welcome ideas towards
more inclusive schemas, preferably based on self-identification. Those would allow fairer,
sustainable, and statistically significant analyses of bibliographic corpora in terms of gender.
2.4. Authorships
Academic publications are authored by one or more people (d.h., authors); formally speaking, Wir
consider each one-to-many pairing of publication and author as one instance of authorship. Für
Beispiel, an article authored by three individuals yields three different authorships.
Authorships might be counted in various ways: They can be weighted equally, regardless of
the total number of authors in the paper and with no distinction on the order of appearance. Das
leads to a counting scheme that does not discriminate between authorship in single-author versus
large-collaboration articles. Alternativ, one can incorporate the importance of individual pub-
lications by computing so-called fractional authorships, where each authorship is assigned a
weight of 1/n, with n being the total number of authors. Zum Beispiel, in the example above,
the weight would be 1/3. Außerdem, analyses might consider only one specific position in
the list of authors as relevant, and often it is the first or the last slot that is particularly significant.
The sensible choice of a counting schema for authorships is field-specific and depends on the
peculiarities of each discipline. In mathematics there are few large collaborations, most articles
being written by a handful of authors. In that situation, statistics on publication patterns remain
roughly unchanged when using equal or fractional authorship counts. This is not the case in other
fields such as astronomy or high-energy physics, where sizable collaborations abound; hence for
those it makes more sense to proceed using fractional authorships.
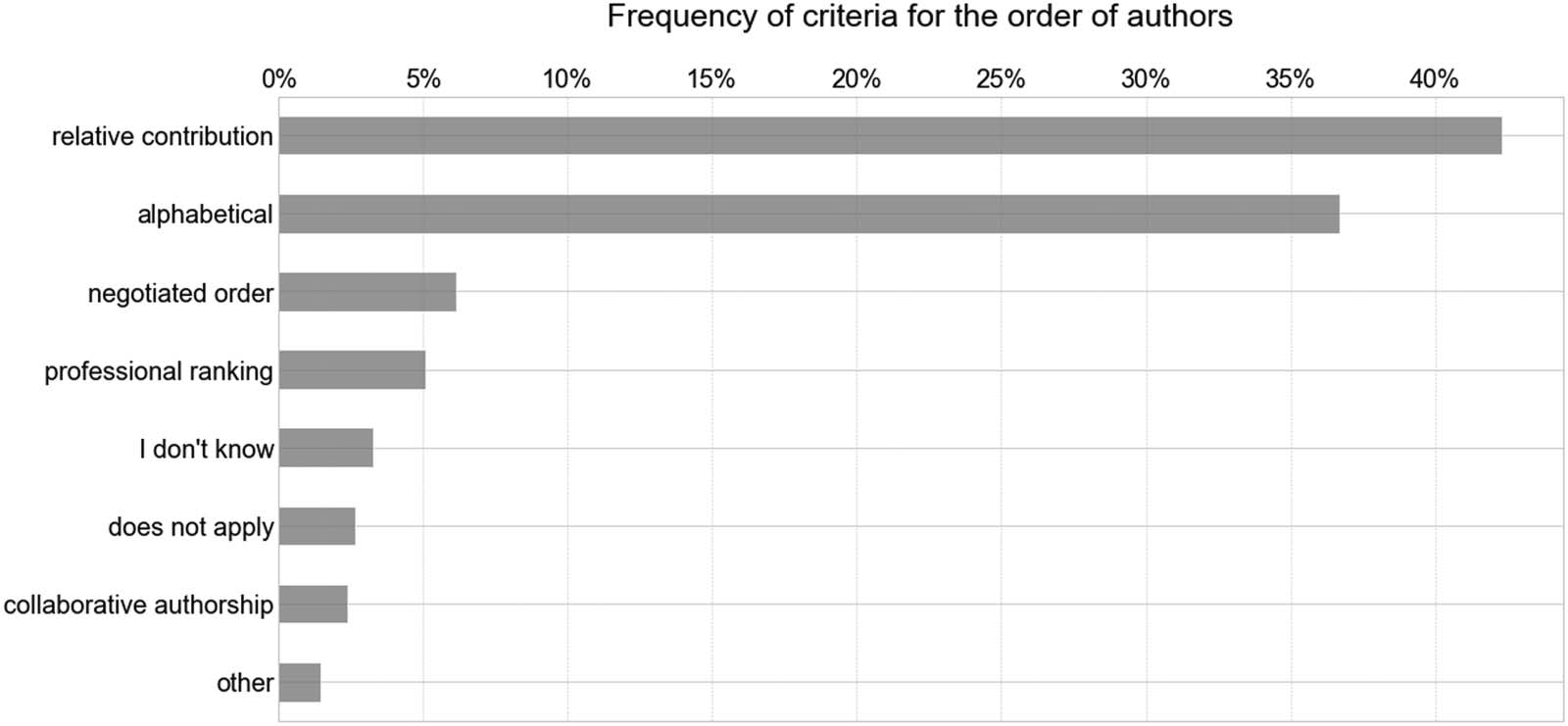
The global survey of scientists yields further insights on name ordering practices, speziell
the following question: “In your field, which criteria are usually used to determine who will be the
Erste, Mitte, or last author?” Almost half of the 10,219 respondents answered with “relative
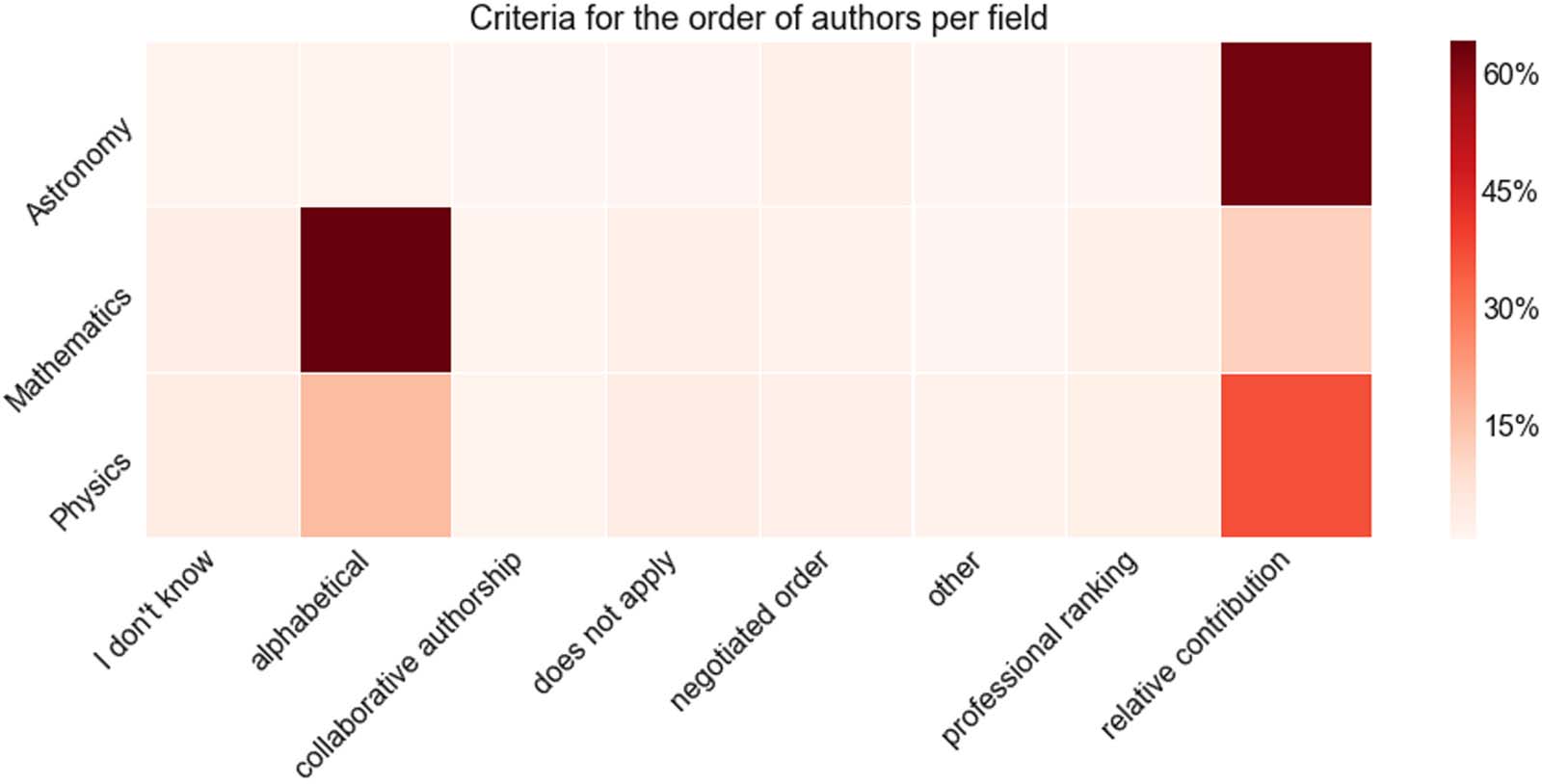
contribution,” followed by “alphabetical ordering.” Details are displayed in Figure 4.
Conventions regarding the assignment of author order in a publication vary per discipline: In
mathematics the dominant criterion is alphabetical, but this is uncommon elsewhere, sogar
almost unheard of in astronomy. In the physical sciences it is mostly the relative contribution that
determines the author list order, at least within small research groups. Tatsächlich, astronomy has its
particular unspoken publication policies, whereby whoever did (or claims to have done) most of
the work becomes first author, usually followed by a few major contributors. Equal (smaller)
contributors are listed next in alphabetical order. Generally speaking, when subsequent authors
are not alphabetical, the order reflects the importance of their contributions. Both first and leading
(second or third) authors play important roles. Large collaborations on the other side abide to the
rules described in Section 1 and also tend to favor alphabetical ordering, sometimes inserting a
Quantitative Science Studies
1478
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
Figur 4. Distribution of answers to the question “In your field, which criteria are usually used to determine who will be the first, Mitte, oder
last author?” from the global survey of scientists.
handful of leading authors at the forefront. Siehe Abbildung 5 for actual numbers obtained from the
global survey’s respondents.
3. ERGEBNISSE
3.1. Self-reported Publication Practices: Perceptions on Submission to Top Journals
In the global survey of scientists the following question was asked: “During the last five years, Wie
many articles have you submitted to journals that are top-ranked in your field?” Respondents were
expected to provide a number between 0 Und 30; larger values were clustered together. 9,984
researchers in astronomy, mathematics and physics who hold at least a Master’s degree provided
a valid answer to this question, among them 3,981 Frauen, 5,861 men, Und 142 individuals who
Figur 5. Heatmap displaying the distribution of answers to the question “In your field, which criteria are usually used to determine who will
be the first, Mitte, or last author?” from the global survey of scientists, broken down by academic discipline.
Quantitative Science Studies
1479
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
Q
S
S
_
A
_
0
0
0
9
0
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Authorship in top-ranked mathematical and physical journals
did not disclose their gender. The respondents had the possibility to choose between “Female,”
“Male,” and “prefer not to respond.” They could also select none of them.
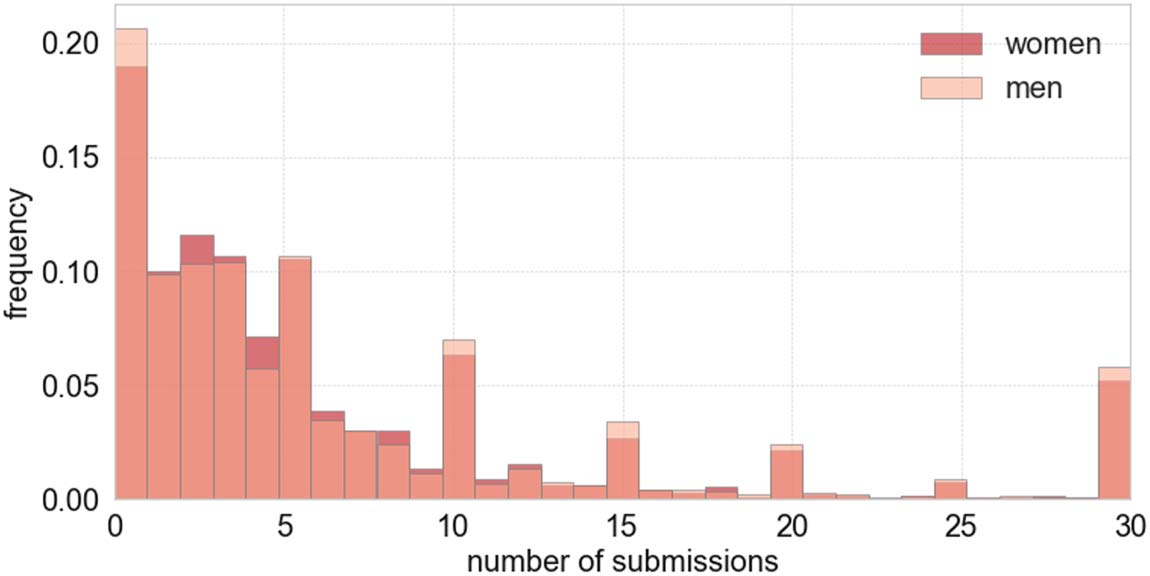
The majority of respondents quoted a small number: the median amounted to four submissions
in the last 5 Jahre, regardless of gender. The mean values in all three groups were very much alike,
mit 6.21 for women, 6.5 for men, Und 6.64 in the unlabeled group. Figur 6 displays the histo-
gram of responses by women and men split by gender. Note that peaks at multiples of five most
likely indicate a rounding effect on the participants’ side. Both distributions are similar, with a
slight shift of answers from women towards lower numbers of submitted articles to what they
consider top-ranked journals, except for the answer that no article was submitted to such a
journal. Correspondingly, a somewhat higher proportion of men is visible in the long tail.
As a first assessment of the effect of gender on the perceived number of submissions, we test the
null hypothesis that there is no statistical difference between the self-reported rates of women and
men. For this purpose we use the nonparametric Mann-Whitney U test and compute two so-
called “rank scores,” (d.h., the number of times a score from group A precedes in rank order a
score from group B, und umgekehrt (controlling for the minimum possible value for the rank
sum)). This is appropriate to decide whether two data sets have been sampled from populations
with the same distribution. We apply the test to the following data sets: (A) total answers of all
women and all men, (B) answers subdivided by discipline, Und (C) answers subdivided by world
region. We set a significance level (cid:1) = 0.05 and apply the Bonferroni correction, yielding (cid:1) =
0.017 for the subgroup analysis (B) Und (cid:1) = 0.004 in case (C), jeweils.
In almost all scenarios, the null hypothesis cannot be rejected using the applied test method.
The only exception occurs in subgroup analysis (C) for the region “Northern Europe” with a
p value <0.0019 based on 715 respondents. However, the effect size is rather small, with the
Rank-Biserial correlation having a very low value of 0.13. The Rank-Biserial correlation equals
the difference of the proportions of the two rank sums, where the proportion is meant with respect
to the number of all possible comparisons between groups 1 and 2. This indicator can have a
maximum value of 1, in which case in all pairwise comparisons between both groups the score
of one of them would be smaller than the other’s. A correlation value close to 0, on the other hand,
implies that the effect is very small, as is the case here.
To complete the picture we have built a multivariate linear model using an ordinary least
squares (OLS) fit to predict the logarithm of the number of articles submitted to top-ranked
Figure 6. Histogram of the number of publications submitted to top-ranked journals in the last 5 years
as self-reported by the respondents to the global survey’s question “During the last five years, how
many articles have you submitted to journals that are top-ranked in your field?” Dark (light) bars
encode answers from women (men).
Quantitative Science Studies
1480
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
journals in the last 5 years (the target variable) taking the following attributes as independent
variables:
(cid:129) highest academic degree (Master’s/Doctoral)
(cid:129) primary discipline (Astronomy/Physics/Mathematics)
(cid:129) gender (Female/Male/Prefer not to respond)
(cid:129) age
(cid:129) country
(cid:129) parent or guardian of children ( Yes/No)
(cid:129) number of total/successful grant applications in the last 5 years
(cid:129) participation in 14 types of academic activities (e.g., journal editor, supervision of graduate
students)
We have applied a logarithmic transform to the target variable to achieve a roughly normal
distribution and have preprocessed the data by removing rows with missing values and replacing
rare countries by dummy values. To test for multicollinearity among all predictor variables, we
have performed a fivefold cross validation as follows: For each predictor, we use the remaining
ones to fit a tree-based ensemble model. Depending on the type of target (categorical/numerical)
we either fit a classifier with accuracy as the loss function or a regression by minimizing the mean
squared error. Furthermore, we introduce additional random variables, which serve as baseline to
estimate the impact of the predictors. For each of the target variables, we evaluate the fivefold
validation score, which measures the goodness of fit and thus the collinearity of the variable with
other predictors of the initial OLS model, and we analyze the relevance of the most important
ones. The procedure does not show significant mutlicollinearity for the variable gender. The most
important predictor of gender is age, followed by the randomly distributed variables with almost
the same values for feature importance. The variable age, however, shows mutlicollinearity with
the highest academic degree and with being the parent or guardian of children. Thus, we have
excluded age as a predictor in the OLS model for the number of articles submitted to top journals.
The resulting OLS model is overall significant, yielding an adjusted R2 value of 0.422, which
means that the model explains around 42% of the variation in the data. Such an R2 can be
considered satisfactory for this kind of fit, as our data clearly do not include all relevant predictors,
such as place of work, teaching load, or the exact meaning of “renowned” or “top-ranked” jour-
nals, that could explain the amount of submissions. We can look at the model’s coefficients to
estimate the effect of gender on the number of submitted articles while controlling for the other
predictors. As suggested by the previous exploration, while gender is statistically significant for
the overall model, its effect is comparatively small and yields an increase of around 6% for men
versus women when controlling for the other predictors. The difference is measured for the
overall median number of four submissions. The relative difference decreases to 5% or 4%, when
taking five or 10 submissions, respectively, as the baseline. Conversely, the field of expertise has a
much greater impact. When controlling for the other variables, submission numbers in mathe-
matics and physics are predicted to be significantly lower than in astronomy. In particular, math-
ematicians are found to submit merely half as many articles as astronomers. The country of
residence also plays a role: For example, Japan has the largest negative contribution in the result-
ing linear model. Indeed, in all three disciplines, 50% of the respondents from Japan claim to have
submitted one or no manuscripts to a top-ranked journal. This might be an indication that the term
top-ranked is understood differently across countries, possibly due to varying ranking schemes.
Among the factors that correlate positively with submissions is the holding of certain academic
functions associated with strong research activity and a solid network, such as conducting
Quantitative Science Studies
1481
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
research abroad, delivering talks, and co-organizing conferences, or with seniority and academic
prestige, as is typically the case for scientists who serve as journal editors, supervise graduate
students or are members of grant committees. It is worth noting that a restricted model (based
on highest academic degree, primary field, gender, age, country, parenting of children) that does
not take into account the latter set of predictors associated with overall academic success results
in only slightly higher impact of the respondents’ gender, indicating that gender is not strongly
correlated with such variables and thus not implicitly encoded.
We deduce that the selected female and male survey participants perceive their submission
practices to journals they consider to be top-ranked in a similar way, with no evidence that
women appreciate major differences with respect to men. What matters much more for the
regression model, beyond the discipline-specific differences, is strong research activity, a
network, and overall academic success. A closer look at the data further indicates that the
proportion of women and men among those who participate in committees or pursue active
international collaborations is very similar among the survey respondents.
3.2. Bibliographic Analysis of Top-Ranked Journals
In all three disciplines analyzed in this article, the proportion of women among actively publishing
researchers has steadily increased in recent decades. Using data from the bibliographic services
zbMATH, ADS, and arXiv we estimate that the proportion of authorships by women in mathematics
and astronomy has grown from around 6% in 1970 to around 25% nowadays. The temporal trend
in theoretical physics papers from the arXiv is less positive, yielding percentages around 5% in the
early 1990s towards 20% nowadays. The figures are considerably lower, with proportions between
8% and 16%, in subfields other than astrophysics, as can be explored at our website.
In this section we analyze aggregated publication statistics in various high-ranked journals
grouped by discipline. The selection was primarily driven by recommendations of senior
researchers, taking into account additional field-specific information that we spell out in the
following subsections. In all figures, dots represent the percentage of fractional authorships attrib-
uted to women among all authorships with inferred gender (i.e., after removing unknown gender
assignments). Solid curves are the result of fitting a locally weighted scatter plot smoothing regres-
sion (LOWESS) model to the data. We count fractional authorships; however, the trends remain
roughly the same when considering full or first authorships.
3.2.1. Mathematics
In the course of the professionalization of mathematics during the 19th century numerous national
mathematical societies were formed, the oldest being the Moscow Mathematical Society, founded
in 1864 (Cooke, 2011, p. 73). Akin to academic institutions, professional societies soon estab-
lished their own journals, in which some of the most profound works of the discipline are still
published today. We have thus decided to consider nine prestigious mathematical journals that
are (co-)published by national societies. We have selected an additional nine journals that are
particularly favored in certain subfields of mathematics and can be used as a proxy for what is
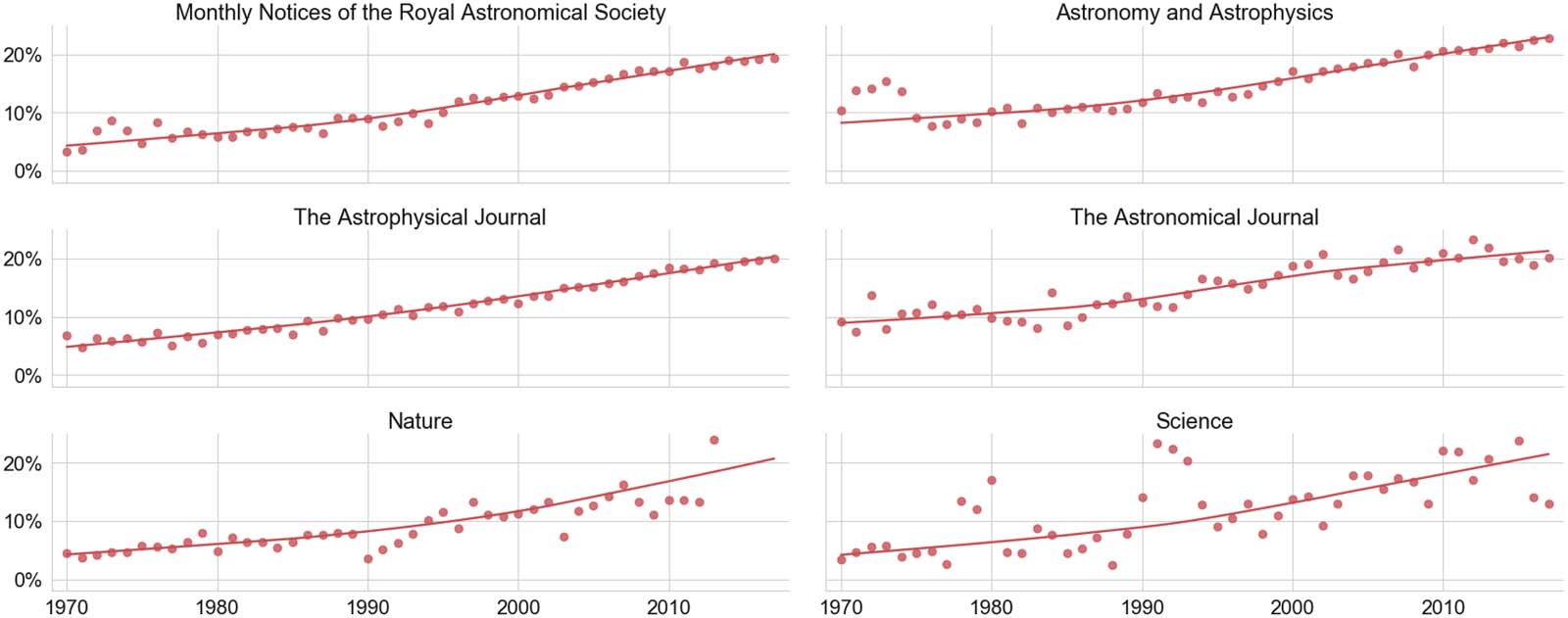
considered high-quality research in those areas. All journal names are listed in Figure 7.
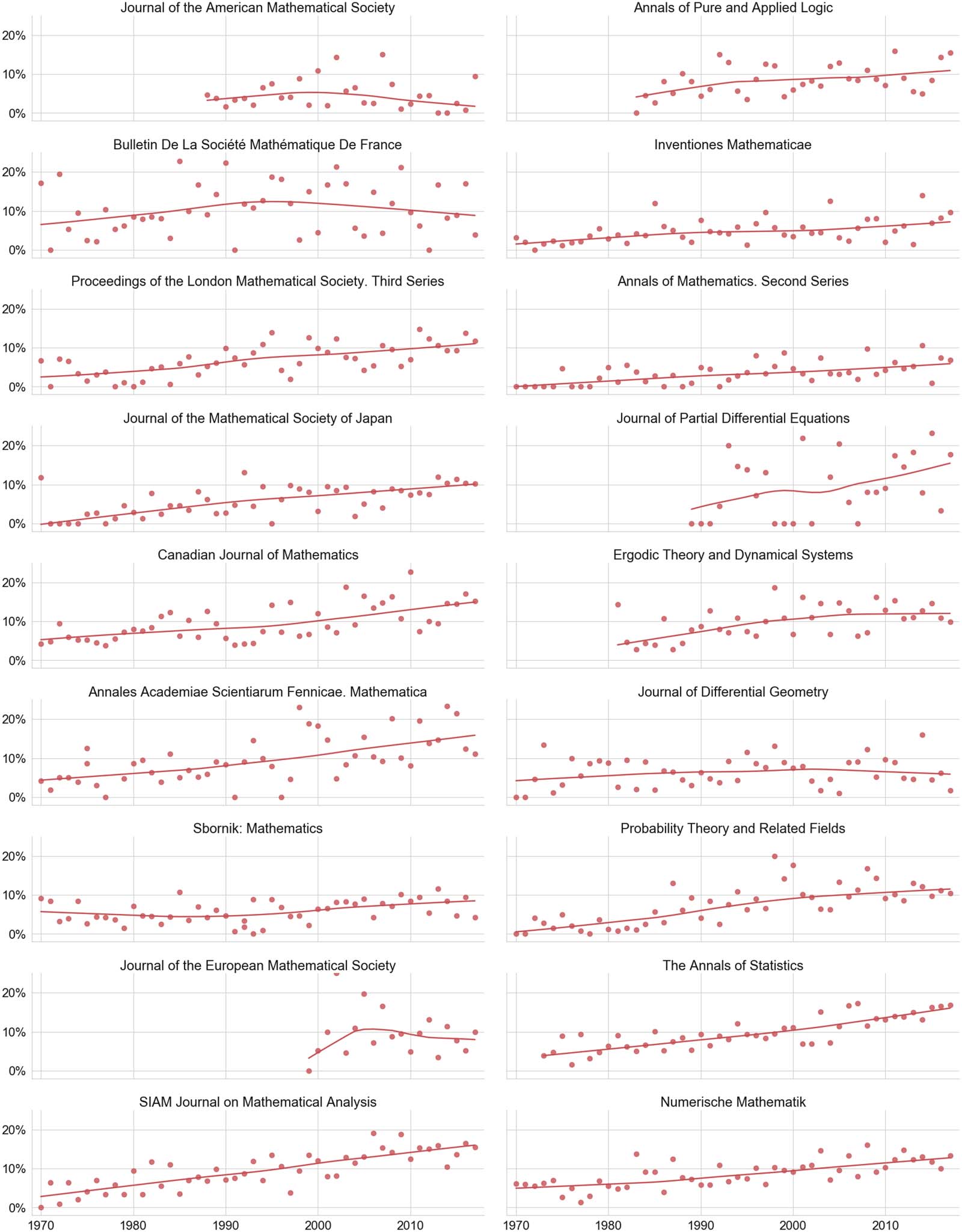
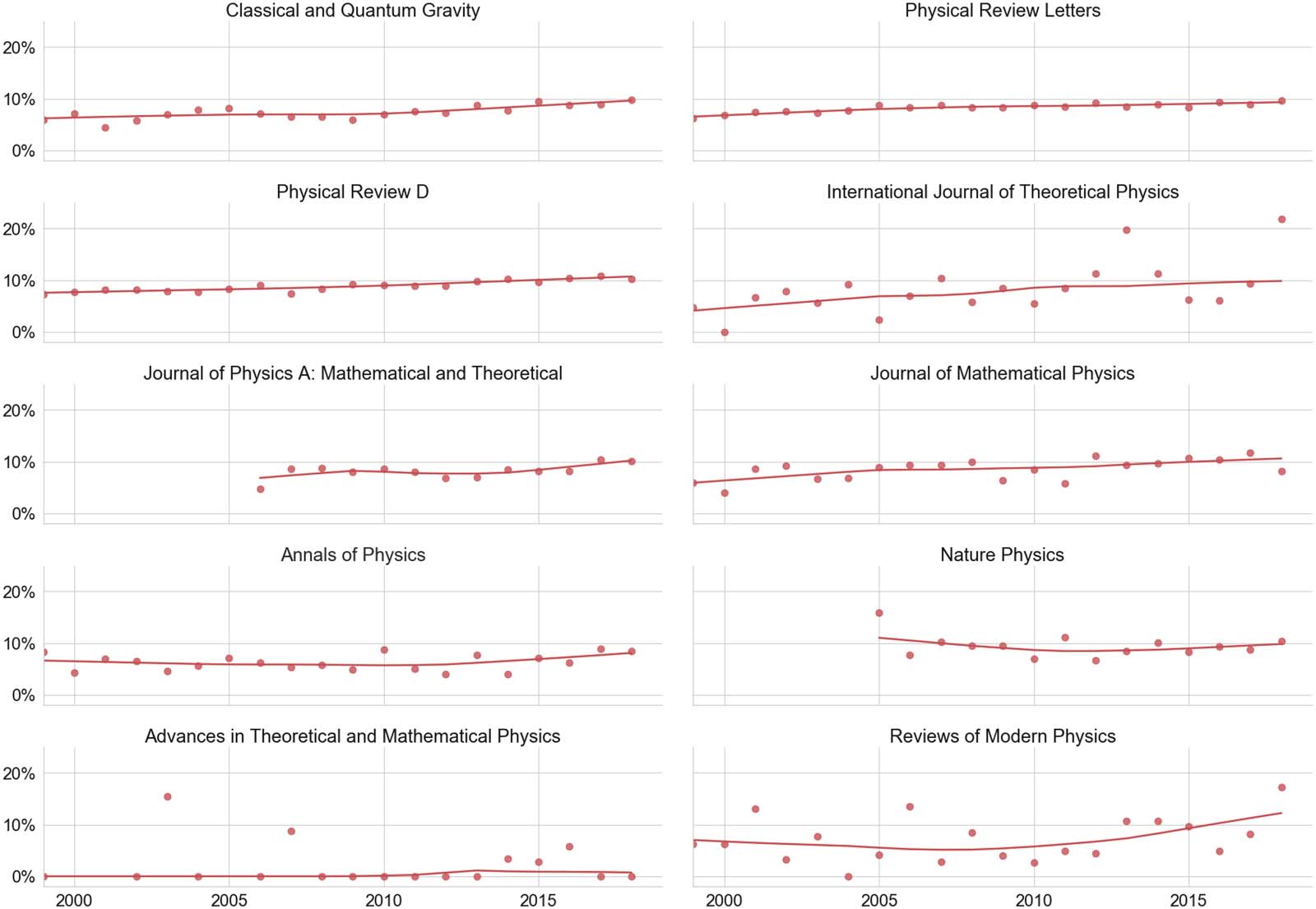
Figure 7 displays percentages of fractional authorships from women in distinguished mathe-
matics journals since 1970. In all considered serials the numbers are predominantly constrained
below 20%. A solid half of the society journals displayed on the left column show a positive
tendency over time. The Bulletin de la Société Mathématique de France shows a rather noisy
behavior and no clear chronological trend, with proportions of women ranging from almost
0% to over 20%. The average share is around 10%, similar to the Journal of the European
Quantitative Science Studies
1482
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Percentage of fractional authorships from women in top-ranked mathematics journal per year since 1970.
Mathematical Society. The lowest percentages are found in the Journal of the American
Mathematical Society, where the proportion of women is around 5% or less and shows no no-
ticeable increase over time. Topical journals in the right column are arranged roughly following
the MSC 2010 (http://msc2010.org/msc2010final2-Aug10.pdf). The last three journals, which
mainly feature work in areas of applied mathematics, display a rising development over time
with shares above 10% in recent years. Except for the Journal of Differential Geometry, all jour-
nals reveal a slight positive trend. The particularly renowned journals Inventiones Mathematicae
Quantitative Science Studies
1483
Authorship in top-ranked mathematical and physical journals
and Annals of Mathematics, which for the most part publish work in pure mathematics, stand out
with numbers predominantly in the single-digit range.
In addition to the few selected journals shown above, we wish to obtain a more comprehen-
sive picture of the correlation between journal quality and gender distribution of their authors by
looking at a larger data set. As baseline for journals representing international mathematical
research, we employ the Mathematics Subject Classification (MSC 2010), a tree-like, three-level
alphanumerical scheme used by researchers, publishers, and the two main reviewing services in
mathematics to label publications according to their subject matter. For every journal we
compute the percentage of articles primarily classified into a core MSC class, namely between
03 and 65. A serial is considered a core mathematics journal if said percentage is larger than 90%.
Journals indexed cover-to-cover in zbMATH are included in this group too, based on the expert
opinion of their editorial board. Finally, all articles published before 1970 are also tagged as core
mathematics, as that was the focus of the indexing service back then. This “Core Math” selection
comprises 1,716 journals and around 2.9 million authorships.
Rather than using standard but questionable journal rankings to differentiate among perceived
quality of mathematics serials, we adopt the internal ranking schema used by zbMATH instead.
This journal categorization, which consists of a handful of labels, is updated on a regular basis by
zbMATH’s editorial staff, which comprises experts from most mathematical disciplines and
engages in active communication with zbMATH’s reviewer community to reflect the relevance
of the journals’ content. Editorial prioritization can certainly change over time, and a journal that
was not considered particularly valuable 20 years ago may well have a different reputation today.
However, experience shows that the corresponding fluctuations are rather small in mathematics,
so that we can assume a relatively high stability in this classification. This selected group of 175
“priority” serials, named “Core Math Priority,” is given preferential treatment due to their assumed
novelty and special relevance. The latter is deemed to contain only prominent publication venues
of proven quality. To give an estimate of the relative volume, articles in “Core Math Priority”
contribute almost 900,000 authorships and make up about 25% of the “Core Math” data set in
the last 10 years.
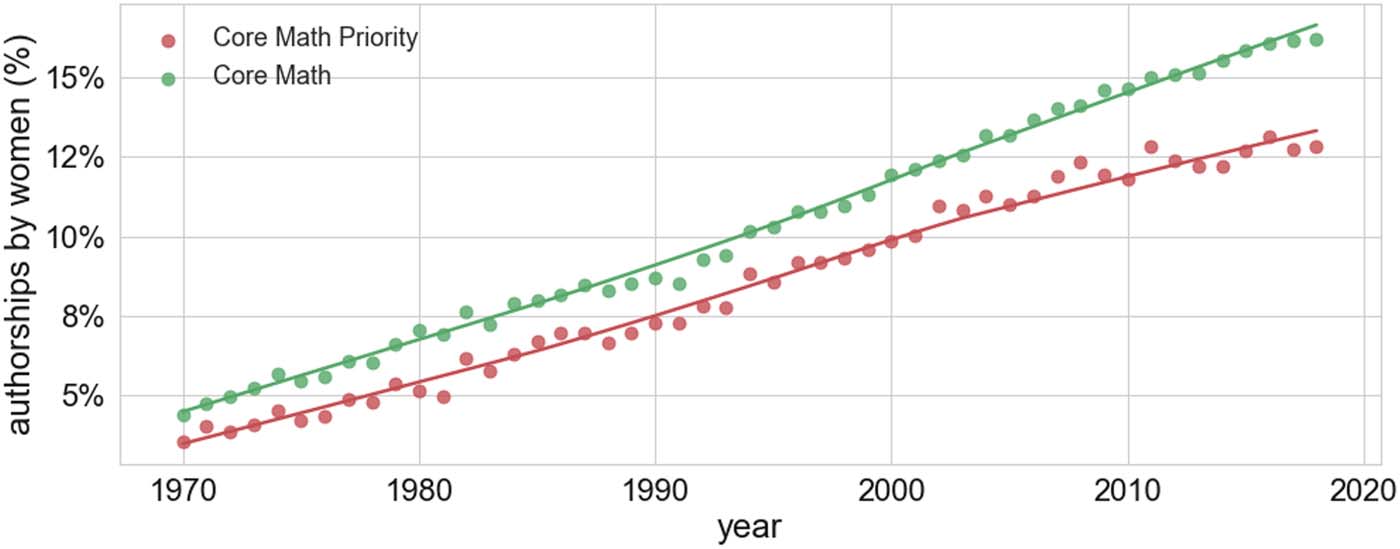
All 18 journals presented in Figure 7 belong to the Core Math Priority data set. In Figure 8 we
observe that the proportion of authorships from women has been growing steadily in both the Core
Math and Core Math Priority data sets, which confirms the trend from Figure 7. However, a gap
remains between the percentage of women publishing in top-ranked journals and their overall
representation as scientific authors in the entire field of mathematics.
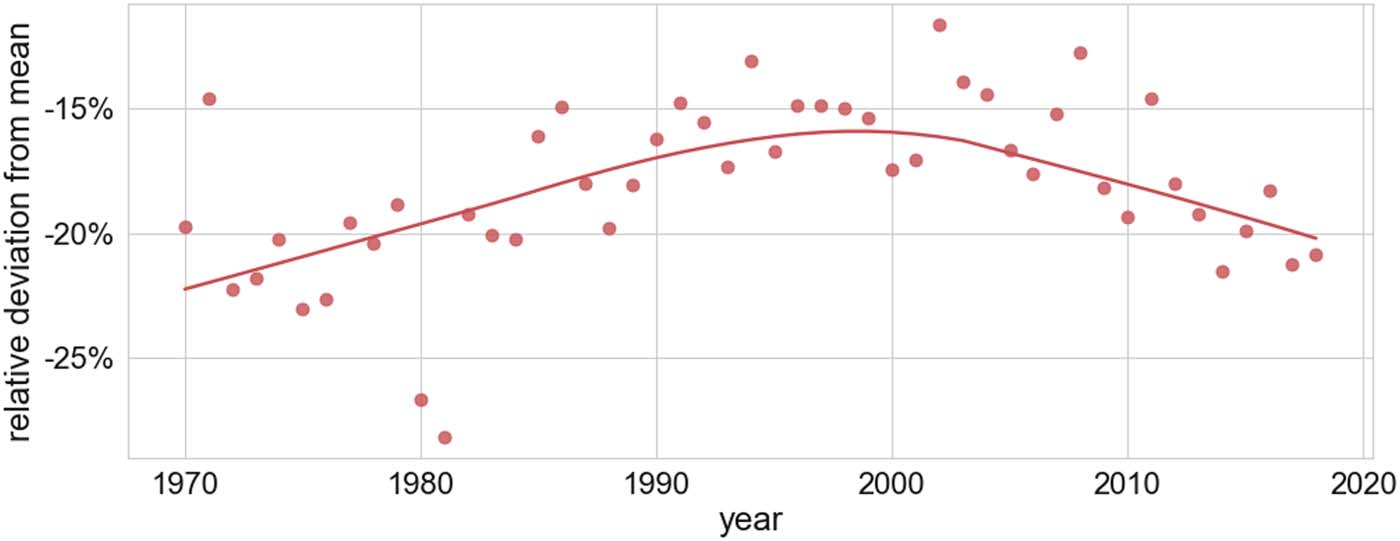
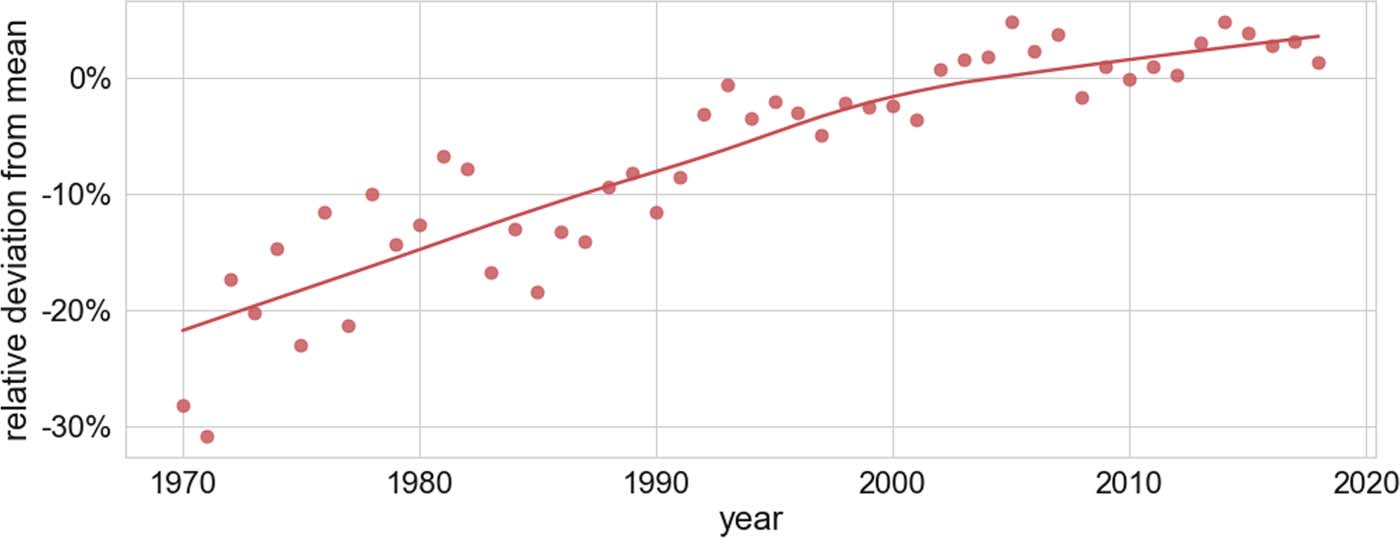
To quantify the chronological evolution of the gap shown in Figure 8 more accurately, we
have calculated the relative deviation from the mean per year; that is, for each year we measure
the difference between the proportions of female authorships in both data sets and normalize it by
dividing by the proportion of women in the Core Math baseline set. The relative deviation from
the mean is displayed in Figure 9. Starting with a relative deviation of almost −25%, the gap be-
comes progressively narrower until the early 2000s, reaching a relative deviation of −10% to
−15%. However, this trend does not seem to carry on: Since 2010, the values have declined
and are back in the range of almost −20%.
3.2.2. Astronomy and astrophysics
In contrast to mathematics and its plethora of prestigious journals, there seems to be a consensus
that the six serials showcased in Figure 10 encompass the vast majority of noteworthy research in
astronomy and astrophysics (Caplar et al., 2017). This list comprises the five journals covered in
Caplar et al. (2017) plus The Astronomical Journal, which the senior astronomers consulted
Quantitative Science Studies
1484
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
Figure 8. Percentage of fractional authorships from women in the Core Math (green) and the Core Math Priority (red) data sets per year since
1970, fitted using the LOWESS smoothing.
considered a distinguished publication venue as well. Figure 10 displays the percentage of frac-
tional authorships from women in said journals since 1970. Using first author counts yields very
similar results, with slightly fewer female first authors in Science but overall exhibiting the same
trends.
Unlike in mathematics and theoretical physics, authored contributions from female astrono-
mers and astrophysicists in top-ranked journals have clearly increased since the 1970s. All six
analyzed serials present female percentages around 20% in recent years, with a continuous
increment and comparable little noise.
As mentioned, these six journals cover the majority of the publications in astronomy and
astrophysics. To quantify this more precisely, we attempt to extract from ADS those journals with
a specific focus in astronomy or astrophysics. To this extent, we implement a simple method: We
create the “Astro” data set by considering all serials that contain “astro” in their name, plus Nature
and Science, as they also publish high-quality research in the field. The advantage of this straight-
forward approach is that it works in most languages, thus enabling a country-agnostic selection.
We find that the six manually selected journals shown in Figure 10 cover the majority, meaning
about 70%, of the publications in the Astro data set. Figure 11 illustrates a noteworthy phenom-
enon: In the 1970s and 1980s, when the six journals accounted for about 50% of all publications
in astronomy and astrophysics, female authorships were underrepresented when compared to all
Astro journals. But in recent years the proportion of authorships by women in top journals no
Figure 9. Relative deviation of the annual share of fractional authorships from women in the Core
Math Priority data set from that in Core Math, fitted using LOWESS smoothing.
Quantitative Science Studies
1485
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
Figure 10. Percentage of fractional authorships from women in prestigious astronomy and astrophysics journals per year since 1970.
longer deviates from the overall mean in the negative direction. In fact, women’s share in the six
renowned journals nowadays even slightly exceeds their proportions in the entire Astro data set.
3.2.3. Theoretical physics
Theoretical physicists consulted for this analysis suggested that the 10 journals listed in
Figure 12 can be regarded as highly prestigious while offering a broad insight into different
specialization areas. Figure 12 displays the percentage of fractional authorships from women
in them over the past 20 years, according to indexed records in the arXiv. When using first author
counts instead, the obtained results are very similar, showing more noise for first authors in
Reviews of Modern Physics but overall exhibiting the same trends.
The situation in theoretical physics appears to be static all throughout the 2000s and 2010s, with
average percentages of women barely reaching 10% and displaying little to no rising tendency. A
minor exception is the International Journal of Theoretical Physics, which shows an upward shift
but overall rather low figures for women’s contributions. The situation in Advances in Theoretical
and Mathematical Physics is rather dismal, showing practically no female representation.
It should be kept in mind that the development in physics, especially if astrophysics is excluded
from the consideration, is not as positive as in the other disciplines. Nevertheless, the trends in
these journals remain clearly behind the development of the proportion of women in the total
number of physics articles indexed in the arXiv. It is important to remark that our statistics for
Figure 11. Relative deviation of the annual share of fractional authorships from women in the top six
astronomy and astrophysics journals with respect to the entire Astro data set, fitted using LOWESS smoothing.
Quantitative Science Studies
1486
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 12. Percentage of fractional authorships from women in top theoretical physics journals per year since 1999.
theoretical physics are based on arXiv data, meaning that only submissions to the preprint service
rather than the final published records are considered. Although the practice of submitting
preprints to the arXiv is widespread in physics, we cannot guarantee that our data basis is
comprehensive for all journals displayed above. Nevertheless, we argue that the general evolution
in the discipline can be roughly captured by using the arXiv data as proxy for publications in
theoretical physics.
3.2.4. Additional resources
Apart from the results shown above, further adhoc analyses of journals and gender can be
informed by the resources displayed in our visualization website. In http://gender-publication
-gap.f4.htw-berlin.de/journals/collection it is possible to group selected journals (e.g., the most
representative serials in a given discipline), and study how the contributions of female authors in
that collection have evolved over time. We encourage the interested reader to take advantage of
this feature to inform their own understanding of publication dynamics in their field.
4. CONCLUSIONS
Motivated by the undeniable role that high-impact publications play in the making or breaking of
academic careers, we have analyzed the gender distribution of authorships in prestigious math-
ematics, physics, and astronomy journals in the past 50 years. Dedicated open-access biblio-
graphic databases and a custom gender inference algorithm allow us to perform this analysis
at scale rather than manually. All other factors being equal, the expectation is that the proportion
of women among all authors should roughly resemble the percentage of established female re-
searchers in the profession, a number that has been steadily growing and that is estimated to be
currently above 20% on average in mathematics and astronomy and astrophysics, and between
Quantitative Science Studies
1487
Authorship in top-ranked mathematical and physical journals
10% and 20% in other theoretical physical sciences. Remarkably, several of the analyzed jour-
nals in the most mathematical disciplines exhibit meager female representation and no signs of
turnaround over the last couple of decades. The situation in astronomy and astrophysics, to the
contrary, aligns better with the supposition that male and female authors are to be published in
top-ranked journals at a comparable rate.
A search for potential causes for this phenomenon leads us to ask whether submission rates to
prominent venues in mathematics and theoretical physics differ significantly when broken down
by gender (i.e., perhaps women are underrepresented in the aforementioned journals because
they do not submit as many manuscripts for consideration as men). A second explanation might
lie in the process of peer review itself, which in the case of these disciplines favors close interac-
tions and trust relationships between editors and reviewers. Maybe structural biases against
women hinder their acceptance rates in high-ranked journals, which are known to be already
very stringent. It is almost impossible to establish to which extent any of these hypotheses may
account for the lack of female representation in top mathematics and physics journals, as relevant
submission and acceptance rates are hard to obtain from academic publishers.
Alternative data sources that could shed light on this topic include self-reports such as classical
survey methods. We have leveraged the 2018 Global Survey of Mathematical, Natural, and
Computing Scientists to obtain answers from almost 10,000 mathematicians, physicists, and as-
tronomers about their submission practices to top-ranked journals in their disciplines. Our anal-
ysis of their responses indicates that women and men report similar numbers of submitted articles
in the past 5 years, with no major statistically significant differences in subgroup analyses broken
down by disciplines or world regions. Therefore, the first of the two conjectures mentioned in the
above paragraph is at least not supported by the survey’s data.
The comparison of responses from the global survey regarding self-reported number of sub-
missions to prestigious journals with the actual publication statistics from selected top-ranked
serials results in a conflicting picture for mathematics and theoretical physics. On one side, there
is no statistically significant difference between women and men regarding perceptions of their
own publication practices; both quote comparable figures for their manuscript submission rates,
as shown in Subsection 3.1. Per contra, such reports do not harmonize with the observed per-
centage of authorships from women in the selected top journals in mathematics and theoretical
physics, as exposed in Subsection 3.2. The answers to the survey cannot explain the low number
of women that are published in these renowned venues, as for instance the percentage of women
in multiple distinguished mathematics serials is shown to be comparatively smaller than the over-
all ratio of female mathematicians in the complete field. The gap between female-authored pub-
lications in very prestigious journals and in the totality of core mathematics journals, that had
been closing before the 2000s, has astonishingly grown larger again ever since. We don’t observe
a similar phenomenon in astronomy and astrophysics. Coincidentally, a major difference be-
tween peer review in both fields is a missing homogeneous standard for acceptance criteria in
the former, which leaves room for factors such as author’s prestige or institutional pedigree to
affect the decision-making process, consciously or unconsciously. This could be one of the ways
in which women are at a disadvantage regarding high-impact publications in small fields. One of
the rare self-evaluations by one of the major publishers in physics suggests at least a gender- and
workplace-based bias in physics (IOP Publishing, 2018).
However, it cannot be concluded from the survey results that peer review in top-ranked
mathematics and theoretical physics journals discriminates against women. Ultimately, the
global survey and the bibliographic databases cannot be directly aligned with each other:
Because participation in the survey was not randomized but built on snowball sampling, its
Quantitative Science Studies
1488
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
results cannot be considered representative of the entire population of researchers and
scholars. For instance, it might be plausible to expect that female respondents to the survey
are among those that submit to renowned venues comparatively more frequently. According
to the survey answers, a higher number of manuscripts submitted to top-ranked journals cor-
relates with factors associated with pronounced research activity, a well-established network,
and academic seniority. While these aspects do not significantly depend on gender among the
surveyed scientists, this might well be a confounding factor in the overall population of re-
searchers in these disciplines, as suggested by, for example, Ceci and Williams (2011).
Additionally, the survey question itself does not provide a definition of what a “top-ranked”
journal is, leaving that characterization to the individual perceptions of respondents, which
potentially induces gender-related as well as other types of bias, such as the use of a country-
specific scheme for the ranking of journals, as suggested by the consistently lower numbers in
responses from scientists from Japan. Similarly, an unbalanced distribution of authorship in top-
ranked journals at the country level and, even more granularly at the institutional level, is to be
expected. We were only able to investigate these superficially, as the coverage of affiliations, from
which entities such as countries and institutions can be extracted, was not suffiently ensured by
zbMATH. Moreover, a certain bias was present towards larger publishers such as Springer and
Elsevier; this is a topic to be addressed in depth elsewhere. Nonetheless, the survey encodes
the impressions of a sizable number of actual scientists and this confers its significance despite
the lack of statistical representation.
As it could not be ruled out that potential biases in the peer review process in mathematics
and physics are a cause for the underrepresentation of female authors in top-ranked journals,
we recommend increasing the transparency in the submission and acceptance practices of
scholarly communicators as well as implementing any measures to alleviate conscious and
unconscious biases. The onus is on academic publishers to conduct and make available their
own investigations on rejection and publication rates in relation to the gender, as well as other
potentially important social and demographic features, of their submitting authors.
ACKNOWLEDGMENTS
We sincerely thank the anonymous reviewers for their critical feedback that helped improve
and clarify this manuscript.
AUTHOR CONTRIBUTIONS
Both authors contributed equally to the analysis and writing of the manuscript.
FUNDING INFORMATION
This work is informed by the authors’ participation in the project “A Global Approach to the
Gender Gap in Mathematical, Computing, and Natural Sciences: How to Measure It, How to
Reduce It?” funded by the International Science Council (ISC).
DATA AVAILABILITY
This research has made use of NASA’s Astrophysics Data System Bibliographic Services and FIZ
Karlsruhe’s service zbMATH. The authors thank the managing editors of ADS and zbMATH for
granting access to the database records.
Quantitative Science Studies
1489
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
REFERENCES
Accomazzi, A., Kurtz, M. J., Henneken, E. A., Grant, C. S.,
Thompson, D. M., … Templeton, M. R. (2018). New ADS func-
tionality for the curator. EPJ Web of Conferences, 186, 08001.
DOI: https://doi.org/10.1051/epjconf/201818608001
Adler, R., Ewing, J., & Taylor, P. (2009). Citation statistics: A report
from the International Mathematical Union (IMU) in coopera-
tion with the International Council of Industrial and Applied
Mathematics (ICIAM) and the Institute of Mathematical Statistics
(IMS). Statistical Science, 24(1), 1–14. DOI: https://doi.org/10.1214
/09-STS285
Andersen, L. E. (2017). On the nature and role of peer review in
mathematics. Accountability in Research, 24(3), 177–192. DOI:
https://doi.org/10.1080/08989621.2016.1274885
Andreescu, T., Gallian, J. A., Kane, J. M., & Mertz, J. E. (2008).
Cross-cultural analysis of students with exceptional talent in math-
ematical problem solving. Notices of the American Mathemathical
Society, 55(10), 1248–1260.
Auslander, J. (2008). On the roles of proof in mathematics. In B. Gold
& R. A. Simons (Eds.), Proof and other dilemmas: Mathematics and
philosophy (pp. 61–78). Mathematical Association of America.
DOI: https://doi.org/10.5948/UPO9781614445050.005
Baldwin, M. (2018). Scientific autonomy, public accountability, and
the rise of “peer review” in the Cold War United States. Isis, 109(3),
538–558. DOI: https://doi.org/10.1086/700070
Bendels, M. H. K., Müller, R., Brueggmann, D., & Groneberg, D. A.
(2018). Gender disparities in high-quality research revealed by
Nature Index journals. PLOS ONE, 13(1), 1–21. DOI: https://doi
.org/10.1371/journal.pone.0189136, PMID: 29293499,
PMCID: PMC5749692
Birnholtz, J. (2006). What does it mean to be an author? The inter-
section of credit, contribution, and collaboration in science.
Journal of the American Society for Information Science and
Technology, 57(13), 1758–1770. DOI: https://doi.org/10.1002
/asi.20380
Birnholtz, J. (2008). When authorship isn’t enough: Lessons from
CERN on the implications of formal and informal credit attribution
mechanisms in collaborative research. The Journal of Electronic
Publishing, 11(1). DOI: https://doi.org/10.3998/3336451.0011.105
Brisbin, A., & Whitcher, U. (2018). Women’s representation in
mathematics subfields: Evidence from the arXiv. The Mathematical
Intelligencer, 40(1), 38–49. DOI: https://doi.org/10.1007/s00283
-017-9761-7
Brooks, T. C. (2009). Organizing a research community with SPIRES:
Where repositories, scientists and publishers meet. Information Services
& Use, 29(2–3), 91–96. DOI: https://doi.org/10.3233/ISU-2009-0596
Callaway, E. (2016). Beat it, impact factor! Publishing elite turns
against controversial metric. Nature, 535(7611), 210–211. DOI:
https://doi.org/10.1038/nature.2016.20224, PMID: 27411614
Caplar, N., Tacchella, S., & Birrer, S. (2017). Quantitative evaluation
of gender bias in astronomical publications from citation counts.
Nature Astronomy, 1, 0141. DOI: https://doi.org/10.1038/s41550
-017-0141
Ceci, S. J., Ginther, D. K., Kahn, S., & Williams, W. M. (2014). Women
in academic science: A changing landscape. Psychological Science
in the Public Interest, 15(3), 75–141. DOI: https://doi.org/10.1177
/1529100614541236, PMID: 26172066
Ceci, S. J., & Williams, W. M. (2011). Understanding current causes
of women’s underrepresentation in science. Proceedings of the
National Academy of Sciences, 108(8), 3157–3162. DOI: https://
doi.org/10.1073/pnas.1014871108, PMID: 21300892, PMCID:
PMC3044353
Clark, J., & Horton, R. (2019). What is The Lancet doing about
gender and diversity? The Lancet, 393(10171), 508–510. DOI:
https://doi.org/10.1016/s0140-6736(19)30289-2, PMID:
30739674
Conley, D., & Stadmark, J. (2012). A call to commission more women
writers. Nature, 488(7413), 590. DOI: https://doi.org/10.1038
/488590a, PMID: 22932370
Cooke, R. (2011). The history of mathematics: A brief course. New York:
Wiley.
da Silva, J. A. T., & Memon, A. R. (2017). CiteScore: A cite for sore eyes,
or a valuable, transparent metric? Scientometrics, 111(1), 553–556.
DOI: https://doi.org/10.1007/s11192-017-2250-0
DORA. (2012). San Francisco declaration on research assessment.
Retrieved from https://sfdora.org/read/
Fox, C. W., Burns, C. S., & Meyer, J. A. (2016). Editor and reviewer
gender influence the peer review process but not peer review
outcomes at an ecology journal. Functional Ecology, 30(1),
140–153. DOI: https://doi.org/10.1111/1365-2435.12529
Garfield, E. (2006). The history and meaning of the journal impact
factor. JAMA, 295(1), 90–93. DOI: https://doi.org/10.1001
/jama.295.1.90, PMID: 16391221
Geist, C., Löwe, B., & Van Kerkhove, B. (2010). Peer review and knowl-
edge by testimony in mathematics. In PhiMSAMP: Philosophy of
mathematics: Sociological aspects and mathematical practice
(pp. 155–178). London: College Publications.
Gentil-Beccot, A., Mele, S., & Brooks, T. C. (2009). Citing and reading
behaviours in high-energy physics. Scientometrics, 84(2), 345–355.
DOI: https://doi.org/10.1007/s11192-009-0111-1
Gordon, M. (1979). Peer review in physics. Physics Bulletin, 30(3),
112–113. DOI: https://doi.org/10.1088/0031-9112/30/3/017
Grcar, J. F. (2013). Errors and corrections in mathematics literature.
Notices of the American Mathemathical Society, 60(4), 418–425.
DOI: https://doi.org/10.1090/noti988
Hansen, S. (2018). Two databases in the rough. Retrieved from
https://hacklibraryschool.com/2018/07/16/databases-in-the
-rough/. Accessed July 27, 2020.
Haslam, N., & Koval, P. (2010). Possible research area bias in the
Excellence in Research for Australia (ERA) draft journal rankings.
Australian Journal of Psychology, 62(2), 112–114. DOI: https://
doi.org/10.1080/00049530903334489
Helmer, M., Schottdorf, M., Neef, A., & Battaglia, D. (2017).
Gender bias in scholarly peer review. eLife, 6, e21718. DOI:
https://doi.org/10.7554/eLife.21718, PMID: 28322725, PMCID:
PMC5360442
Hicks, D., Wouters, P., Waltman, L., de Rijcke, S., & Rafols, I. (2015).
Bibliometrics: The Leiden Manifesto for research metrics. Nature,
520(7548), 429–431. DOI: https://doi.org/10.1038/520429a,
PMID: 25903611
Hill, C., Corbett, C., & Rose, A. (2010). Why so few? Women in science,
technology, engineering, and mathematics. Washington, DC:
American Association of University Women.
Holman, L., Stuart-Fox, D., & Hauser, C. E. (2018). The gender gap in
science: How long until women are equally represented? PLOS
Biology, 16(4), 1–20. DOI: https://doi.org/10.1371/journal.pbio
.2004956, PMID: 29672508, PMCID: PMC5908072
Hulek, K. (2016). zbMATH – looking to the future. EMS Newsletter,
2016-12, 3–7. DOI: https://doi.org/10.4171/NEWS/101/15
Hutchison, J. E., Lyons, I. M., & Ansari, D. (2018). More similar than
different: Gender differences in children’s basic numerical skills are
the exception not the rule. Child Development, 90(1), e66–e79.
DOI: https://doi.org/10.1111/cdev.13044, PMID: 29484644
Quantitative Science Studies
1490
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
IOP Publishing. (2018). Diversity and inclusion in peer review at IOP
Publishing. Retrieved from www.ioppublishing.org/wp-content
/uploads/2018/09/J-VAR-BK-0818-PRW-report-final2.pdf
Jackson, A. (2002). From preprints to e-prints: The rise of electronic pre-
print servers in mathematics. Notices of the American Mathematical
Society, 49(1), 23–32.
Kahn, S., & Ginther, D. (2017). Women and STEM ( Working Paper
No. 23525). National Bureau of Economic Research. DOI: https://
doi.org/10.3386/w23525
Kelsky, K. (2017). The professor is in: The career-math of publishing.
Retrieved from https://community.chronicle.com/news/1874-the
-professor-is-in-the-career-math-of-publishing. Accessed June 14,
2020.
Kersey, A. J., Csumitta, K. D., & Cantlon, J. F. (2019). Gender similar-
ities in the brain during mathematics development. NPJ Science of
Learning, 4(1). DOI: https://doi.org/10.1038/s41539-019-0057-x,
PMID: 31728205, PMCID: PMC6841948
Kiesslich, T., Weineck, S. B., & Koelblinger, D. (2016). Reasons for
journal impact factor changes: Influence of changing source items.
PLOS ONE, 11(4), e0154199. DOI: https://doi.org/10.1371/journal
.pone.0154199, PMID: 27105434, PMCID: PMC4841562
Krantz, S. G. (1997). A primer of mathematical writing. Being a disqui-
sition on having your ideas recorded, typeset, published, read, and
appreciated. Providence, RI: American Mathematical Society.
Krantz, S. G. (2007). How to write your first paper. Notices of the
American Mathematical Society, 54(11), 1507–1511.
Krantz, S. G., Kuperberg, G., & van der Poorten, A. (2003). Three views
of peer review. Notices of the American Mathematical Society,
50(6), 678–682.
Lalli, R. (2016). “Dirty work,” but someone has to do it: Howard P.
Robertson and the refereeing practices of Physical Review in the
1930s. Notes and Records: the Royal Society Journal of the
History of Science, 70(2), 151–174. DOI: https://doi.org/10.1098
/rsnr.2015.0022
Larivière, V., Ni, C., Gingras, Y., Cronin, B., & Sugimoto, C. R. (2013).
Bibliometrics: Global gender disparities in science. Nature, 504
(7479), 211–213. DOI: https://doi.org/10.1038/504211a, PMID:
24350369
Larivière, V., & Sugimoto, C. R. (2019). The journal impact factor: A
brief history, critique, and discussion of adverse effects. In Springer
handbook of science and technology indicators (pp. 3–24).
Springer International Publishing. DOI: https://doi.org/10.1007/978
-3-030-02511-3
Larivière, V., Sugimoto, C. R., Macaluso, B., Milosevic´, S., Cronin, B.,
& Thelwall, M. (2014). arXiv e-prints and the journal of record: An
analysis of roles and relationships. Journal of the American Society
for Information Science and Technology, 65, 1157–1169. DOI:
https://doi.org/10.1002/asi.23044
Lee, C. J., Sugimoto, C. R., Zhang, G., & Cronin, B. (2013). Bias in peer
review. Journal of the American Society for Information Science and
Technology, 64(1), 2–17. DOI: https://doi.org/10.1002/asi.22784
Lerback, J., & Hanson, B. (2017). Journals invite too few women to
referee. Nature, 541(7638), 455–457. DOI: https://doi.org/10.1038
/541455a, PMID: 28128272
London Mathematical Society. (2020). London Mathematical
Society guide to authors. Retrieved from https://www.lms.ac.uk
/sites/lms.ac.uk/files/Publications/AuthorGuide.pdf. Accessed
June 14, 2020.
Martin, K. (2019). Some career advice for postdocs and grad students.
Retrieved from https://math.ou.edu/~kmartin/career-ad.html.
Accessed June 14, 2020.
Mauleón, E., & Bordons, M. (2012). Authors and editors in mathe-
matics journals: A gender perspective. International Journal of
Gender, Science and Technology, 4(3), 267–293. Retrieved from
http://genderandset.open.ac.uk/index.php/genderandset/article
/viewArticle/236
McGrail, M. R., Rickard, C. M., & Jones, R. (2006). Publish or perish:
A systematic review of interventions to increase academic publica-
tion rates. Higher Education Research & Development, 25(1), 19–35.
DOI: https://doi.org/10.1080/07294360500453053
Merton, R. K. (1973). The normative structure of science. In N. W.
Storer (Ed.), The sociology of science: Theoretical and empirical
investigations (pp. 267–278). Chicago, London: University of
Chicago Press.
Meyer, M., Cimpian, A., & Leslie, S.-J. (2015). Women are underrep-
resented in fields where success is believed to require brilliance.
Frontiers in Psychology, 6, 235. DOI: https://doi.org/10.3389/fpsyg
.2015.00235, PMID: 25814964, PMCID: PMC4356003
Mihaljevic´, H., & Santamaría, L. (2020). Disambiguation of author
entities in ADS using supervised learning and graph theory methods.
Mihaljevic´, H., Tullney, M., Santamaría, L., & Steinfeldt, C. (2019).
Reflections on gender analyses of bibliographic corpora. Frontiers
in Big Data, 2, 29. DOI: https://doi.org/10.3389/fdata.2019.00029
Mihaljevic´-Brandt, H., Santamaría, L., & Tullney, M. (2016). The
effect of gender in the publication patterns in mathematics.
PLOS ONE, 11(10), 1–23. DOI: https://doi.org/10.1371/journal
.pone.0165367, PMID: 27780266, PMCID: PMC5079651
Murray, D., Siler, K., Larivière, V., Chan, W. M., Collings, A. M., …
Sugimoto, C. R. (2019). Author-reviewer homophily in peer review.
bioRxiv. DOI: https://doi.org/10.1101/400515
Nathanson, M. B. (2008). Desperately seeking mathematical truth.
Notices of the American Mathematical Society, 55(7), 773.
Nature. (2014). Introducing the index. Nature, 515(7526), S52–S53.
DOI: https://doi.org/10.1038/515s52a, PMID: 25390142
Nature. (2020). Nature will publish peer review reports as a trial.
Nature, 578(7793), 8. DOI: https://doi.org/10.1038/d41586-020
-00309-9, PMID: 32025024
Palus, S. (2015). Is double-blind review better? APS News, 24(9).
Retrieved from https://www.aps.org/publications/apsnews/201510
/letters.cfm
Perley, D. A. (2019). Gender and the career outcomes of Ph.D. astron-
omers in the United States. Publications of the Astronomical Society
of the Pacific, 131(1005), 114502. DOI: https://doi.org/10.1088
/1538-3873/ab0cc4
Polydoratou, P., & Moyle, M. (2007). Exploring aspects of scientific
publishing in astrophysics and cosmology: The views of scientists.
In M.-A. Sicilia & M. D. Lytras (Eds.), Metadata and semantics
(pp. 179–190). Cham: Springer. DOI: https://doi.org/10.1007/978
-0-387-77745-0_17
Prager, E. M., Chambers, K. E., Plotkin, J. L., McArthur, D. L.,
Bandrowski, A. E., … Graf, C. (2018). Improving transparency
and scientific rigor in academic publishing. Brain and Behavior,
9(1), e01141. DOI: https://doi.org/10.1002/brb3.1141
Pritychenko, B. (2016). Fractional authorship in nuclear physics.
Scientometrics, 106(1), 461–468. DOI: https://doi.org/10.1007/s11192
-015-1766-4
Roldan-Valadez, E., Salazar-Ruiz, S. Y., Ibarra-Contreras, R., &
Rios, C. (2018). Current concepts on bibliometrics: A brief review
about impact factor, eigenfactor score, CiteScore, SCImago jour-
nal rank, source-normalised impact per paper, h-index, and alter-
native metrics. Irish Journal of Medical Science (1971–), 188(3),
939–951. DOI: https://doi.org/10.1007/s11845-018-1936-5
Santamaría, L. (2018). Mining 50 years of astronomy and astrophysics
publications data. Retrieved from https://gender-gap-in-science
.org/2018/03/17/mining-50-years-of-astronomy-and-astrophysics
-publications-data/. Accessed July 27, 2020.
Quantitative Science Studies
1491
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Authorship in top-ranked mathematical and physical journals
Santamaría, L., & Mihaljevic´, H. (2018). Comparison and benchmark
of name-to-gender inference services. PeerJ Computer Science,
4, e156. DOI: https://doi.org/10.7717/peerj-cs.156
Shanta, A., Sharma, S., & Pradhan, A. (2013). Impact factor of a
scientific journal: Is it a measure of quality of research? Journal
of Medical Physics, 38(4), 155. DOI: https://doi.org/10.4103/0971
-6203.121191, PMID: 24672148, PMCID: PMC3958993
Smith, G. H. (2016). Trends in multiple authorship among papers in
astronomy. Publications of the Astronomical Society of the Pacific,
128(970), 124502. DOI: https://doi.org/10.1088/1538-3873/128
/970/124502
Smith, R. (2006). Peer review: A flawed process at the heart of
science and journals. Journal of the Royal Society of Medicine,
99(4), 178–182. DOI: https://doi.org/10.1258/jrsm.99.4.178,
PMID: 16574968, PMCID: PMC1420798
Squazzoni, F., Bravo, G., Dondio, P., Farjam, M., Marusic, A., …
Grimaldo, F. (2020). No evidence of any systematic bias against
manuscripts by women in the peer review process of 145 scholarly
journals. Preprint. DOI: https://doi.org/10.31235/osf.io/gh4rv
Taubes, G. (1993). Measure for measure in science. Science, 260(5110),
884–886. DOI: https://doi.org/10.1126/science.8493516, PMID:
8493516
Tomkins, A., Zhang, M., & Heavlin, W. D. (2017a). Reviewer bias in
single- versus double-blind peer review. Proceedings of the
National Academy of Sciences, 114(48), 12708–12713. DOI:
https://doi.org/10.1073/pnas.1707323114, PMID: 29138317,
PMCID: PMC5715744
Tomkins, A., Zhang, M., & Heavlin, W. D. (2017b). Single versus
double blind reviewing at WSDM 2017. CoRR, abs/1702.00502.
http://arxiv.org/abs/1702.00502
Topaz, C. M., & Sen, S. (2016). Gender representation on journal
editorial boards in the mathematical sciences. PLOS ONE, 11(8),
1–21. DOI: https://doi.org/10.1371/journal.pone.0161357,
PMID: 27536970, PMCID: PMC4990198
Vanclay, J. K. (2011). An evaluation of the Australian Research
Council’s journal ranking. Journal of Informetrics, 5(2), 265–274.
DOI: https://doi.org/10.1016/j.joi.2010.12.001
Verma, I. M. (2015). Impact, not impact factor. Proceedings of the
National Academy of Sciences, 112(26), 7875–7876. DOI: https://
doi.org/10.1073/pnas.1509912112, PMID: 26080449, PMCID:
PMC4491750
Wang, M.-T., & Degol, J. L. (2016). Gender gap in science, technology,
engineering, and mathematics (STEM): Current knowledge, implica-
tions for practice, policy, and future directions. Educational
Psychology Review, 29(1), 119–140. DOI: https://doi.org/10.1007
/s10648-015-9355-x, PMID: 28458499, PMCID: PMC5404748
West, J. D., Bergstrom, T. C., & Bergstrom, C. T. (2010). The
Eigenfactor MetricsTM: A network approach to assessing scholarly
journals. College & Research Libraries, 71(3), 236–244. DOI:
https://doi.org/10.5860/0710236
West, J. D., Jacquet, J., King, M. M., Correll, S. J., & Bergstrom, C. T.
(2013). The role of gender in scholarly authorship. PLOS ONE, 8(7).
DOI: https://doi.org/10.1371/journal.pone.0066212, PMID:
23894278, PMCID: PMC3718784
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
4
1
4
6
8
1
8
7
1
0
4
7
q
s
s
_
a
_
0
0
0
9
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Quantitative Science Studies
1492