RESEARCH ARTICLE
Impact factor volatility due to a single paper:
A comprehensive analysis
Manolis Antonoyiannakis1,2
1Department of Applied Physics & Applied Mathematics, Columbia University, 500 W. 120th St., Mudd 200,
New York, New York 10027
2American Physical Society, Editorial Office, 1 Research Road, Ridge, New York 11961-2701
Schlüsselwörter: bibliostatistics, citation distributions, impact factor, science of science, volatility
ABSTRAKT
We study how a single paper affects the impact factor (IF) of a journal by analyzing data from
3,088,511 papers published in 11639 journals in the 2017 Journal Citation Reports of
Clarivate Analytics. We find that IFs are highly volatile. Zum Beispiel, the top-cited paper of
381 journals caused their IF to increase by more than 0.5 points, while for 818 journals the
relative increase exceeded 25%. Einer in 10 journals had their IF boosted by more than 50% von
their top three cited papers. Because the single-paper effect on the IF is inversely proportional
to journal size, small journals are rewarded much more strongly than large journals for a
highly cited paper, while they are penalized more for a low-cited paper, especially if their IF is
hoch. This skewed reward mechanism incentivizes high-IF journals to stay small to remain
competitive in rankings. We discuss the implications for breakthrough papers appearing in
prestigious journals. We question the reliability of IF rankings given the high IF sensitivity to a
few papers that affects thousands of journals.
Keine offenen Zugänge
Tagebuch
Zitat: Antonoyiannakis, M. (2020).
Impact factor volatility due to a single
Papier: A comprehensive analysis.
Quantitative Science Studies, 1(2),
639–663. https://doi.org/10.1162/
qss_a_00037
DOI:
https://doi.org/10.1162/qss_a_00037
Erhalten: 04 November 2019
Akzeptiert: 31 Dezember 2019
Korrespondierender Autor:
Manolis Antonoyiannakis
ma2529@columbia.edu
Handling-Editor:
Ludo Waltman
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
INTRODUCTION AND MOTIVATION
1.
The effect of a journal’s scale (d.h., Größe) on its citation average cannot be overstated. Kürzlich,
we showed (Antonoyiannakis, 2018) that citation averages, such as impact factors (IFs), Sind
scale dependent in a way that drastically affects their rankings, and which can be understood
and quantified via the Central Limit Theorem: For a randomly formed journal of scale n, Die
ffiffiffi
N
range of its IF values (measured from the global citation average) scales as 1/
. While actual
journals are not completely random, the Central Limit Theorem explains to a large extent their
IF scale behavior, and allows us to understand how the balance in IF rankings is tipped in two
important ways: (A) Only small journals can score a high IF; Und (B) large journals have IFs that
asymptotically approach the global citation average as their size increases, via regression to
der Mittelwert.
P
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Urheberrechte ©: © 2020 Manolis
Antonoyiannakis. Published under a
Creative Commons Attribution 4.0
International (CC BY 4.0) Lizenz.
Die MIT-Presse
At a less quantitative level, the scale dependence of citation averages has been noted ear-
lier, by Amin and Mabe (2004), Campbell (2008), and Antonoyiannakis and Mitra (2009). Noch
it is almost always neglected in practice. Journal size is thus never accounted or controlled for
in IF rankings, whether by standardization of citation averages (a rigorous approach; sehen
Antonoyiannakis, 2018), or by the grouping of journals in size categories, much like their
grouping in subject categories, a procedure widely accepted due to different citation practices
across subjects of research. Stattdessen, IFs for journals of all sizes are lumped together in rankings
such as the Journal Citation Reports ( JCR) or the Impact Factor Quartile rankings of Clarivate
Impact factor volatility due to a single paper
Analytics, or in ad hoc lists of competitively ranked journals used by faculty hiring and tenure
committees, usw. The problem spills over into university rankings and even in national rankings
of citation indicators, which generally do not control for the size of a cohort (department, Re-
search field, usw.) in comparing citation averages.
Perhaps the best demonstration of how sensitive citation averages are to scale is to study
how they are affected by a single paper. Usually, we take it for granted that averages are
scale independent. Jedoch, underlying this certainty is the assumption that a sum over n
terms grows (more or less) linearly with scale n. In most cases, this assumption is valid. Aber
for research papers in scholarly journals the assumption can break down, because the huge
variation in annual citations per paper—from zero to several thousand—can cause the
average to spike abruptly and grow nonlinearly when a highly cited paper is published in
a small journal. While this effect dies out with increasing scale, it routinely plagues IF rank-
ings, because most scholarly journals are small enough that the effect is present. Zusamenfassend, Wir
need to dispel the notion that size normalization is equivalent to size independence for
citation averages.
Also, how volatile are IFs, and other citation averages in general? A single research article can
tip the balance in university rankings (Bornmann & Marx, 2013; Waltman, van Eck, et al., 2011)
and even affect national citation indicators (Aksnes & Sivertsen, 2004) when citation averages
werden verwendet, due to the skewed nature of citation distributions. It is also known that in extreme
situations, a single paper can strongly boost a journal’s IF (Dimitrov, Kaveri, & Bayry, 2010;
Foo, 2013; Milojevic´, Radicchi, & Bar-Ilan, 2017; Moed, Colledge, et al., 2012; Rossner,
Van Epps, & Hill, 2007). More recently, Liu, Liu, et al. (2018) studied the effect of a highly cited
paper on the IF of four different-sized journals in particle physics and found that “the IFs of low
IF and small-sized journals can be boosted greatly from both the absolute and relative perspec-
tives.” While cautionary remarks have been raised recently at the assumption of size indepen-
dence of citation averages (Antonoyiannakis, 2018; Cope & Kalantzis, 2014; Leydesdorff,
Bornmann, & Adams, 2019; Lyu & Shi, 2019; Prathap, 2019), the overwhelming majority of
researchers, bibliometricians, administrators, Verlag, and editors continue to use them with-
out realizing or acknowledging the problem.
In diesem Papier, we show how pervasive the scale sensitivity of citation averages is, by ana-
lyzing the volatility of IFs due to a single paper for all 11,639 journals listed in the 2017 JCR.
Our paper is structured as follows. Erste, we introduce the volatility index as the IF change, Δf
(C)—or relative change, Δfr(C)—when a single paper cited c times is published by a journal of
IF f and size N. Zweite, we study theoretically how Δf(C) depends on c, F, and N, and obtain
analytic expressions for the volatility in the general case but also for two special cases: Wann
the new paper is cited well above or well below the journal average. We discuss the impli-
cations for editorial decisions from the perspective of improving a journal’s position in IF rank-
ings. Dritte, we analyze data from the 11639 journals in the 2017 JCR. We provide summary
statistics for the journals’ IF volatility due to their own top-cited paper. We discuss the impli-
cations for publishing breakthrough papers in high-profile journals. We also discuss the
reliability of IF rankings, and provide recommendations for more meaningful and statistically
viable comparisons of journals’ citation impact.
The high volatility values from real journal data demonstrate that ranking journals by IFs
constitutes a nonlevel playing field, Weil, depending on size, the IF gain for publishing
an equally cited paper can span up to four orders of magnitude across journals. It is there-
fore critical to consider novel ways of comparing journals based on solid statistical
grounds.
Quantitative Science Studies
640
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact factor volatility due to a single paper
2. METHODEN
2.1. How a Single Paper Affects the IF: An Example from Four Journals
We are now ready to analyze the effect of a single paper on a journal’s IF. Anfänglich, let the journal
have an IF equal to f1, which is the ratio of C1 citations to the biennial publication count N1. Der
additional paper causes the IF denominator to increase by 1, and the numerator by c.
Before we study the general case, let us first consider one example, to get an idea of what is
geht weiter. In Table 1 we list four journals whose sizes range from 50 Zu 50,000, but their IFs are
the same. The numbers are fictitious but realistic: As one can confirm from the JCR, es gibt
journals with size and IFs sufficiently close to the values in the table.
Journal B is 10 times larger than A. When a highly cited paper (c = 100) is published by A,
the IF changes by Δf(100) = 1.902. When the same paper is published by B, the change is 10
times smaller: Δf(100) = 0.194. daher, to compete with journal A—to obtain the same IF
increase Δf(C)—journal B needs to publish 10 equally highly cited papers. Likewise, for every
paper of c = 100 that A publishes, C needs to publish 100 equally cited papers to obtain the
same IF increase. And for every paper of c = 100 that journal A publishes, journal D needs to
publish 1,000 equally cited papers to compete.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
To sum up, the IF increase is inversely proportional to journal size. Publication of the same
highly cited paper in any of the journals A, B, C, or D produces widely disparate outcomes, als
the corresponding IF increase spans four orders of magnitude, aus 0.0019 Zu 1.902. Mit
such a high sensitivity to scale, the comparison of IFs of these four journals is no level playing
field: Small journals disproportionately benefit from highly cited papers.
The above example considers a highly cited paper. As we will shortly see, there is a suffi-
cient number of highly cited papers to cause hundreds of journals every year to jump up con-
siderably in IF rankings due to one paper. And even further, there are many journals of
sufficiently small size and small IF that even a low or moderately cited paper can produce
a big increase in their IF. daher, IF volatility due to a single paper (or a handful of papers)
is a much more common pattern than is widely recognized, which is why this behavior of IFs
goes beyond academic interest. To understand this fully, let us now consider the general case.
2.2. The General Case: Introducing the IF Volatility Index
The initial IF is
f1 ¼ C1
N1
;
(1)
Tisch 1. A hypothetical but realistic scenario. Four journals, A, B, C, and D, have the same IF but different sizes, when they each publish a
paper that brings them c = 100 citations. The IF gain spans four orders of magnitude—both in absolute, Δf(C), and relative, Δfr(C), terms—
because it depends not only on the additional paper, but also on the size of each journal
Zeitschrift
A
B
C
D
Size N1
50
500
5,000
Citations C1
150
1,500
15,000
50,000
150,000
Initial IF f1
3
New paper c
100
Final IF f2
4.902
3
3
3
100
100
100
3.194
3.019
3.002
Quantitative Science Studies
Δf(C) f2
– f1
Δfr(C) (f2
− f1)/f1
1.902
0.194
0.019
0.0019
63.4%
6.45%
0.65%
0.06%
641
Impact factor volatility due to a single paper
so that when the new paper is published by the journal, the new IF becomes
The change (volatility) in the IF caused by this one paper is then
f2 ¼ C1 þ c
N1 þ 1
:
so that
Δf cð Þ ≡ f2 − f1 ¼ C1 þ c
N1 þ 1
− C1
N1
;
Δf cð Þ ¼ c − f1
N1 þ 1
≈ c − f1
N1
;
(2)
(3)
(4)
≫ 1, which applies for all but a few journals that
where the approximation is justified for N1
publish only a few items per year. Also, the IF volatility, Δf(C), depends both on the new paper
(d.h., on c) and on the journal (size N1 and citation average f1) in which it is published.
We can also consider the relative change in the citation average caused by a single paper,
which is probably a more pertinent measure of volatility. Zum Beispiel, if a journal’s IF jumps
aus 1 Zu 2, then this is bigger news than if it jumped from 20 Zu 21. The relative volatility is
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Δfr cð Þ ≡ f2 − f1
f1
¼ c − f1
D
f1 N1 þ 1
Þ
≈ c − f1
f1N1
¼ c − f1
C1
;
(5)
Wo, wieder, the approximation is justified when N1
simplified for highly cited papers (c ≫ f1) als
Δfr cð Þ ≈ c
C1
; when c ≫ f1:
≫ 1. The above equation can be further
(6)
Let us now return to Δf(C) and make a few remarks.
(A) For c > f1, the additional paper is above average with respect to the journal, and there is
a benefit to publication: Δf(C) > 0 and the IF increases (d.h., f2 > f1).
(B) For c < f1, the new paper is below average with respect to the journal, and publishing it
invokes a penalty: Δf(c) < 0 as the IF drops (i.e., f2 < f1).
(c) For c = f1, the new paper is average, and publishing it makes no difference to the IF.
(d) The presence of N1 in the denominator means that the benefit or penalty of publishing
an additional paper decays rapidly with journal size. This has dramatic consequences.
Let us now consider two special cases of interest:
Case 1
The new paper is well above average relative to the journal (i.e., c ≫ f1). Here,
Δf cð Þ ¼ c−f1
N1 þ 1
c
N1 þ 1
≈ c
N1
≈
;
(7)
≫ 1. The volatility Δf(c)
where the last step is justified because in realistic cases we have N1
depends on the paper itself and on the journal size. The presence of N1 in the denominator
means that publishing an above-average paper is far more beneficial to small journals than to
large journals. For example, a journal A that is 10 times smaller than a journal B will have a 10
times higher benefit upon publishing the same highly cited paper, even if both journals had the
Quantitative Science Studies
642
Impact factor volatility due to a single paper
same IF to begin with! The editorial implication here is that it pays for editors of small journals
to be particularly watchful for high-performing papers. From the perspective of competing in IF
rankings, small journals have two conflicting incentives: Be open to publishing risky and po-
tentially breakthrough papers on the one hand, but not publish too many papers lest they lose
their competitive advantage due to their small size.
For c ≪ N1, we get Δf(c) ≈ 0 even for large c. So, when large journals publish highly cited
papers, they have a tiny benefit in their IF. For example, when a journal with N1 = 2,000 pub-
lishes a paper of c = 100, the benefit is a mere Δf(100) = 0.05. For a very large journal of N1 =
20,000, even an extremely highly cited paper of c = 1,000 produces a small gain Δf(1000) =
0.05.
But for small and intermediate values of N1, the value of Δf(c) can increase appreciably.
This is the most interesting regime for journals, which tend to be rather small: Recall that “90%
of all journals publish 250 or fewer citable items annually” (Antonoyiannakis, 2018).
Case 2
The new paper is well below average relative to the journal (i.e., c ≪ f1). (For journals of, say,
f1
≤ 2, the condition c ≪ f1 implies c = 0.) Here,
Δf cð Þ ¼ c − f1
N1 þ 1
≈ −
f1
N1 þ 1
≈ − f1
N1
;
(8)
≫ 1. The penalty Δf(c) depends now only on the journal
because in realistic cases we have N1
parameters (N1, f1), and it is greater for small, high-IF journals. The editorial implication is that
editors of small and high-IF journals need to be more vigilant in pruning low-performing pa-
pers than editors of large journals. Two kinds of papers are low-cited, at least in the IF citation
window: (a) archival, incremental papers, and (b) some truly groundbreaking papers that may
appear too speculative at the time and take more than a couple years to be recognized.
For f1
≪ N1, we get Δf(c) ≈ 0. Very large journals lose little by publishing low-cited papers.
The take-home message from the above analysis is two-fold. First, with respect to increasing
their IF, it pays for all journals to take risks. Because the maximum penalty for publishing
below-average papers (≈ f1/N1) is smaller than the maximum benefit for publishing above-
average papers (≈ c/N1), it is better for a journal’s IF that its editors publish a paper they are
on the fence about if what is at stake is the possibility of a highly influential paper. Some of
these papers may reap high citations to be worth the risk: Recall that c can lie in the hundreds
or even thousands.
However, the reward for publishing breakthrough papers is much higher for small journals.
For a journal’s IF to seriously benefit from groundbreaking papers, the journal must above all
remain small, otherwise the benefit is much reduced due to its inverse dependence with size.
To the extent that editors of elite journals are influenced by IF considerations, they have an
incentive to keep a tight lid on their acceptance decisions and reject many good papers, and
even some potentially breakthrough papers they might otherwise have published. We wonder
whether the abundance of prestigious high-IF journals with small biennial sizes, N2Y < 400,
and especially their size stability over time, bears any connection to this realization. In other
words, is “size consciousness” a reason why high-IF journals stay small? We claim yes. As
Philip Campbell, former Editor-in-Chief of Nature put it, “The larger the number of papers,
the lower the impact factor. In other words, worrying about maximizing the impact factor turns
Quantitative Science Studies
643
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
what many might consider a benefit—i.e. more good papers to read—into a burden.”
(Campbell, 2008).
To recap, why are high-IF journals incentivized to stay small to remain competitive in IF
rankings? Because once a journal reaches a high IF, it is much easier to sustain it by staying
small than by expanding in size. Eq. (4) explains why. For every above-average paper (of fixed
citation count, for simplicity of argument) published, the IF increases but by a smaller amount
as the journal grows, so the returns diminish. At the same time, for every below-average
paper published, the IF drops. With increasing journal size, it gets harder to keep raising
the IF but easier to slip into a lower IF, because low-cited papers are far more abundant than
highly cited papers. It is a matter of risk.
The incentive for high-IF journals to stay small may disproportionately affect groundbreak-
ing papers, because they entail higher risk. How so? First, it is hard to identify such papers
before publication. Many groundbreaking papers face controversy in the review process
and are misjudged by referees who may be too conservative or entrenched to realize their
transformative potential. Obviously, no editor wishes to publish unrealistic or wrong papers.
The editors hedge their bets, so to speak, and take chances in accepting controversial papers.
(Needless to say, this is where editorial skill and competence, coupled with outstanding and
open-minded refereeing, can make a difference.) But editors of small, high-IF journals can
afford fewer risks than editors of large, moderate-IF journals, as explained in the previous
paragraph—which pushes them to be more conservative and accept a smaller fraction of
these controversial papers. Second, even if it were possible to know the groundbreaking papers
beforehand, editors of small, high-IF journals would still be incentivized by IF arguments to
reject some of them, because such papers are less likely to be top-cited in the 2-year IF window.
Indeed, Wang, Veugelers, and Stephan (2017) reported on the increased difficulty of transfor-
mative papers to appear in prestigious journals. They found that “novel papers are less likely to
be top cited when using short time-windows,” and “are published in journals with Impact
Factors lower than their non-novel counterparts, ceteris paribus.” They argue that the increased
pressure on journals to boost their IF “suggests that journals may strategically choose to not
publish novel papers which are less likely to be highly cited in the short run.” To sum up: If
a small journal fine-tunes its risk level and publishes only some controversial (i.e., potentially
groundbreaking) papers, its IF will benefit more, statistically speaking, than if it published them all.
Why worry about intellectually risky papers? Because they are more likely to lead to major
breakthroughs (Fortunato, Bergstrom, et al., 2018). It was in this spirit that the Physical Review
Letters Evaluation Committee recommended back in 2004 that steps be taken to “educate ref-
erees to identify cutting edge papers worth publishing even if their correctness cannot be de-
finitively established,” and that “[r]eferee training should emphasize that a stronger attempt be
made to accept more of the speculative exciting papers that really move science forward”
(Cornell, Cowley, et al., 2004). Granting agencies have reached a similar understanding.
For example, an effort to encourage risk in research is the NIH Common Fund Program, es-
tablished in 2004 and supporting “compelling, high-risk research proposals that may struggle
in the traditional peer review process despite their transformative potential” (NIH News
Release, 2018). These awards “recognize and reward investigators who have demonstrated
innovation in prior work and provide a mechanism for them to go in entirely new, high-impact
research directions.” (Collins, Wilder, & Zerhouni, 2014). Europe’s flagship program for fund-
ing high-risk research, the European Research Council, was established in 2007 and “target[s]
frontier research by encouraging high-risk, high-reward proposals that may revolutionize sci-
ence and potentially lead to innovation if successful.” (Antonoyiannakis, Hemmelskamp, &
Kafatos, 2009).
Quantitative Science Studies
644
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
2.3. How the IF Volatility Index Depends on the Parameters f
1, N
1, and c
We now analyze graphically how Δf(c) depends on its parameters, namely, the IF of the jour-
nal f1, the biennial publication count N1, and the annual citation count c of a single paper.
First, let us briefly comment on the dependence of Δf(c) on f1. IFs f1 range typically from
0.001–200, but are heavily concentrated in low-to-moderate values (Antonoyiannakis, 2018):
The most commonly occurring value (the mode) is 0.5, while 75% of all journals in the 2017
JCR have IF < 2.5. Because our chief aim here is to study the effects of a single paper on ci-
tation averages, we are mostly interested in high c values (c > 100, sagen), in which case the
effect of f1 on Δf(C) or on Δfr(C) can be usually ignored, as can be seen from Eq. (7) and Eq. (6)
jeweils. For smaller c values relative to f1, the effect of f1 is to simply reduce the size of
Δf(C) by some amount, but is otherwise of no particular interest.
Let us now look at the dependence of Δf(C) on N1 and c. The journal biennial size N1 ranges
from 20–60,000 and is heavily centered at small sizes (Antonoyiannakis, 2018), which has im-
portant implications, as we shall see. As for c, it ranges from 0–5,000 in any JCR year, and its
distribution follows a power law characteristic of the Pareto distribution for c ≥ 10 (Tisch 2).
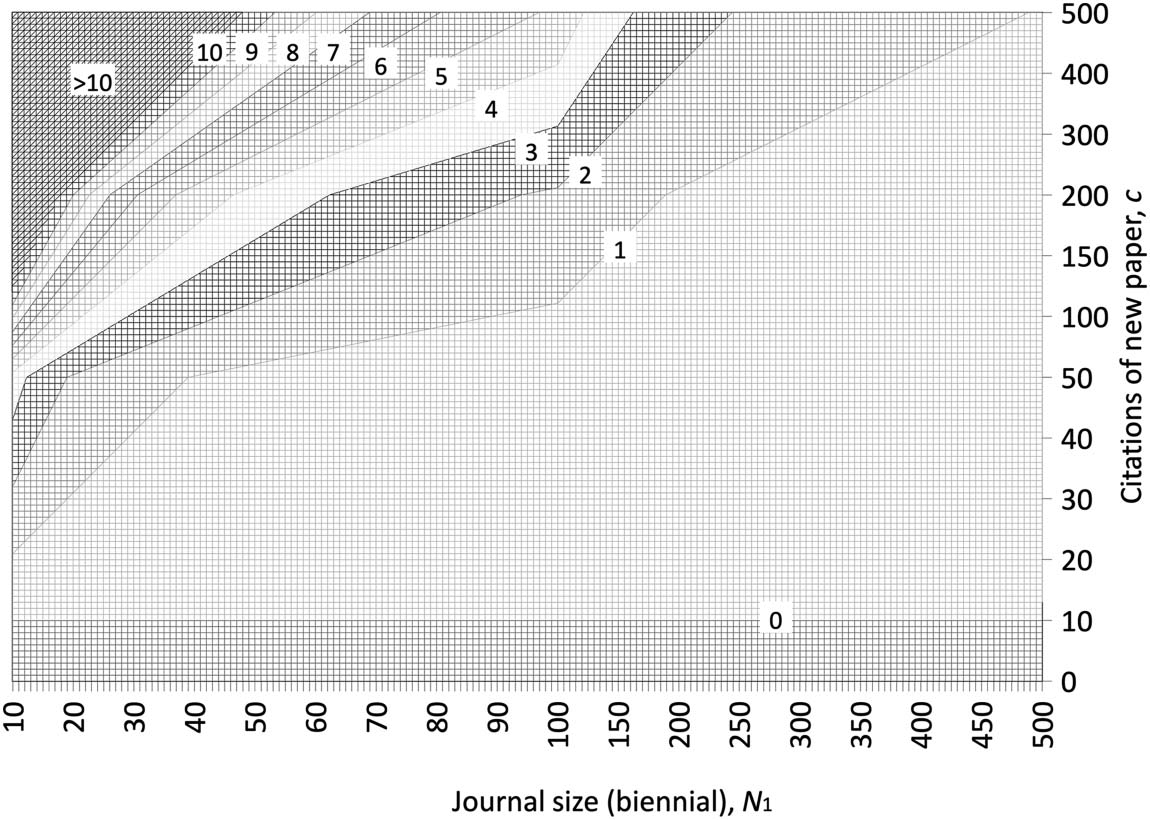
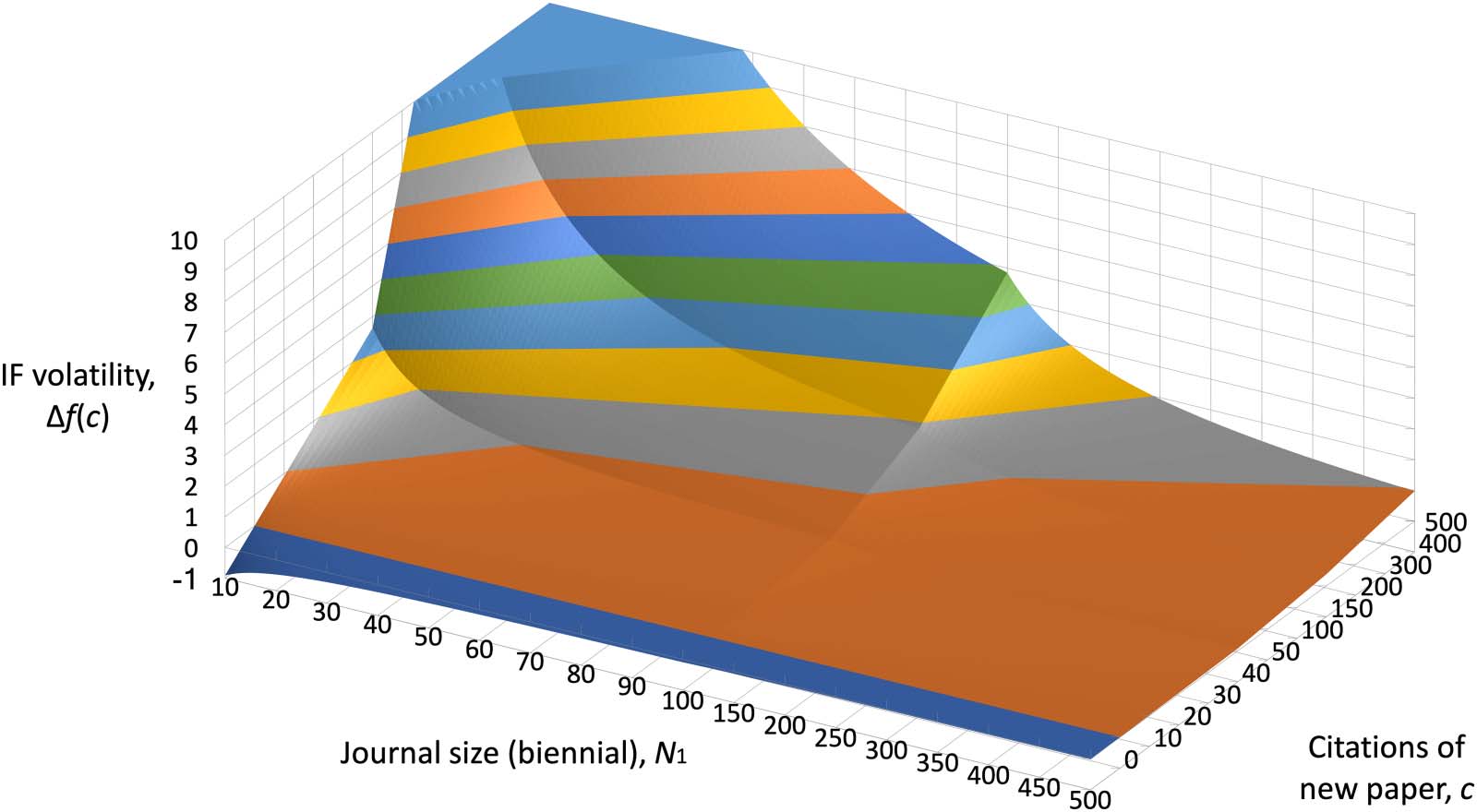
Figur 1 is a 3D surface plot of Δf(C) vs. N1 and c, for a fixed f1 = 10. Figur 2 is a projection of
Figur 1 in 2D (d.h., a contour plot), for more visual clarity. The main features of the plots are:
(cid:129) For a given c value, Δf(C) decreases rapidly with N1, as expected from Eq. (4), Weil
the two quantities are essentially inversely proportional for c ≫ f1.
(cid:129) For realistic values of N1, C, the volatility Δf(C) can take high values. Zum Beispiel, für 20
≤ 100 Und 20 ≤ c ≤ 500 we have 0.5 < Δf(c) < 25. Think about it: A single paper can
≤ N1
raise the IF of these journals by several points! This is impressive.
Why are these parameter values realistic? Because small journals abound, while there are
thousands of sufficiently cited papers that can cause an IF spike. Indeed, 25% of the 11,639
Table 2. Number of papers cited at least ct times. Publication years = 2015–2016, Citation year =
2017. JCR data
Citation
threshold, ct
0
No. papers cited
at least ct times
3,088,511
Citation
threshold, ct
200
No. papers cited
at least ct times
302
1
2
5
10
20
30
40
50
100
2,138,249
1,490,683
570,744
176,718
43,030
18,485
10,016
6,222
1,383
300
400
500
1,000
1,500
2,000
2,500
3,000
4,000
139
80
56
14
7
6
5
2
0
Quantitative Science Studies
645
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
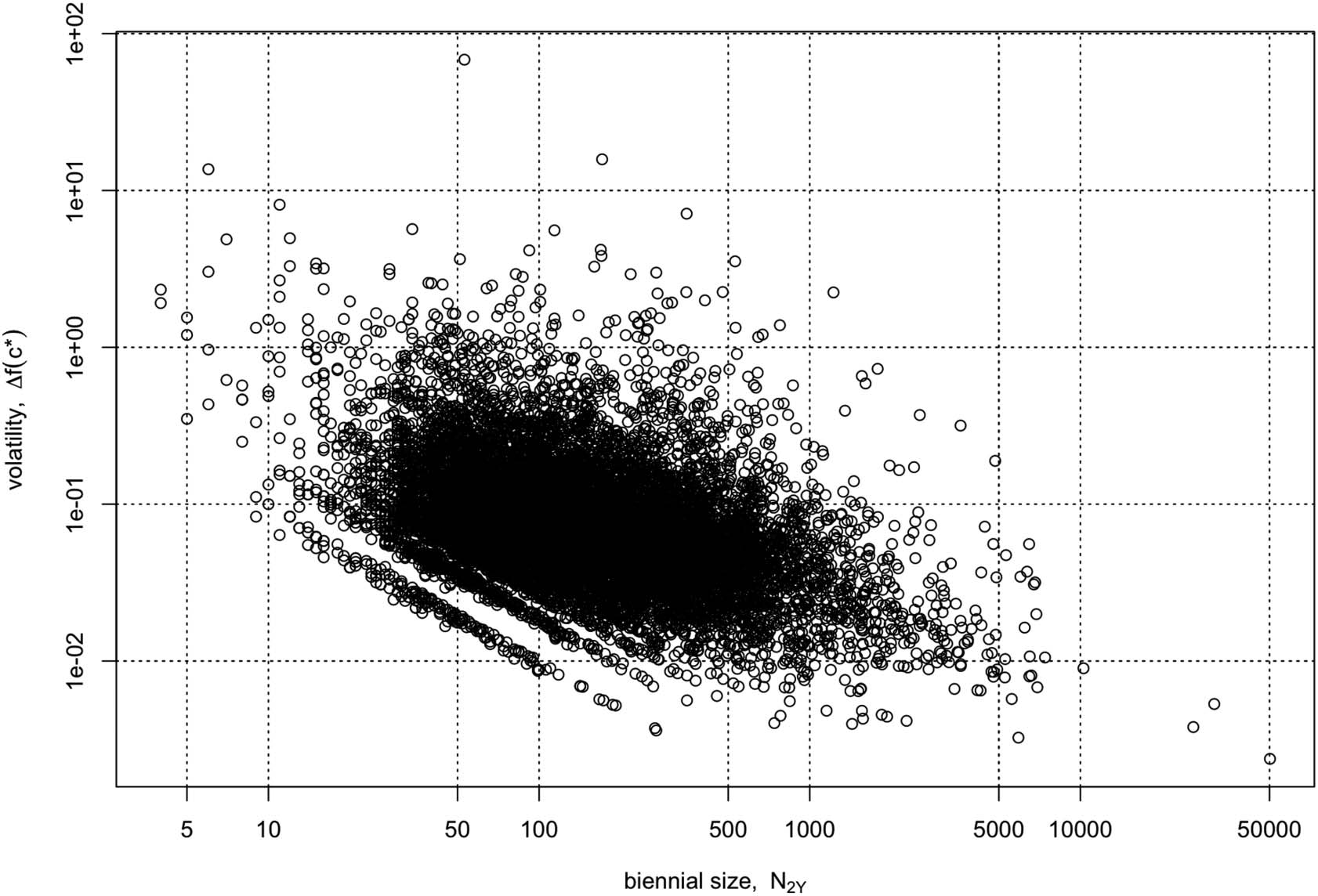
Figure 1. 3D surface plot of IF volatility Δf(c) vs. (biennial) journal size N1 and citation count c of the new paper, for a journal whose IF was
f1 = 10 before publishing the paper. The range of N1 values plotted here covers 90% of all journals, while 50% of all journals publish ~130 or
fewer citable items biennially (Antonoyiannakis, 2018). So, for thousands of journals a paper cited c ~ 100 can cause Δf(c) > 1. The IF of the
journal has little effect on Δf(C) as long as c ≫ f1. See Eq. (4).
journals in our data set publish fewer than 68 items biennially (N1 < 68), while 50% of journals
publish fewer than 130 items, and 75% of journals publish fewer than 270 items. The range of
N1 values plotted here (10–500) spans 90% of all journals (Antonoyiannakis, 2018). At the
same time, 6,222 papers in our data set were cited at least 50 times, 1,383 papers were cited
at least 100 times, 302 papers were cited at least 200 times, etc. (Table 2).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Same data as in Figure 1 but in a contour plot. Changes in gray level denote crossing
integer values of Δf(c) as shown in the plot. As journal size decreases, the IF volatility Δf(c)
increases.
Quantitative Science Studies
646
Impact factor volatility due to a single paper
As these plots demonstrate, small journals (N1
≤ 500) enjoy a disproportionate benefit upon
publishing a highly cited paper, compared to larger journals. Small journals are abundant.
Highly cited papers are relatively scarce, but nevertheless exist in sufficient numbers to cause
abrupt IF spikes for hundreds of small journals.
But an additional effect is also at work here, and it can cause IF spikes for thousands of
journals: a medium-cited paper published in a small and otherwise little-cited journal.
Given the high abundance of medium-cited papers (e.g., more than 176,000 papers in our
≤ 1), jour-
data set are cited at least 10 times) and low-IF journals (e.g., 4,046 journals have f1
nals that would otherwise have had a negligible IF can end up with small or moderate IF. This
is a much more commonly occurring effect than has been realized to date.
3. RESULTS
Now that we understand the IF volatility in theory, let us look at some real journal data. We
have analyzed all journals listed in the 2017 JCR of Clarivate Analytics.
At this point, we could continue to study the effect of a hypothetical paper on the IFs of
actual journals, using JCR data for IFs and journal sizes. For example, we could ask the
question, “How does the IF of each journal change by incorporation of a paper cited c =
100 times?” and calculate the corresponding volatility Δf(100). While such a calculation
would be of value, we adopt a different approach, in order to stay firmly anchored on actual
data from both journals and papers, and avoid hypotheticals. We ask the question “How did
the IF (citation average) of each journal change by incorporation of its most cited paper,
which was cited c* times in the IF 2-year time-window?” We thus calculate the quantity
Δf(c*), where c* is no longer constant and set equal to some constant hypothetical value,
but varies across journals.
First, a slight change in terminology to avoid confusion. We study the effect of a journal’s
top-cited paper on its citation average f when its biennial publication count is N2Y. So, our
journal’s initial state has size N1 = N2Y
− 1 and citation average f1, which we denote as f*.
Our journal’s final state has N2 = N2Y and f2 = f, upon publication of the top-cited paper that
was cited c* times. We study how Δf(c*) and Δfr(c*) behave using JCR data.
Now, some technical details. The analysis was carried out in the second half of 2018.
Among the 12,266 journals initially listed in the 2017 JCR, we removed the several hundred
duplicate entries, as well as the few journals whose IF was listed as zero or not available. We
thus ended up with a master list of 11,639 unique journal titles that received a 2017 IF as of
December 2018. For each journal in the master list we obtained its individual Journal Citation
Report, which contained the 2017 citations to each of its citable papers (i.e., articles and re-
views) published in 2015–2016. We were thus able to calculate the citation average f for each
journal, which approximates the IF and becomes identical to it when there are no “free” or
“stray” citations in the numerator—that is, citations to front-matter items such as editorials,
letters to the editor, commentaries, etc., or citations to the journal without specific reference
of volume and page or article number. We will thus use the terms “IF” and “citation average”
interchangeably, for simplicity. Collectively, the 11,639 journals in our master list published
3,088,511 papers in 2015–2016, which received 9,031,575 citations in 2017 according to the
JCR. This is our data set.
For the record, for 26 journals the top-cited paper was the only cited paper, in which case
f* = 0. Also, for 11 journals none of their papers received any citations, in which case f = f* =
Quantitative Science Studies
647
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
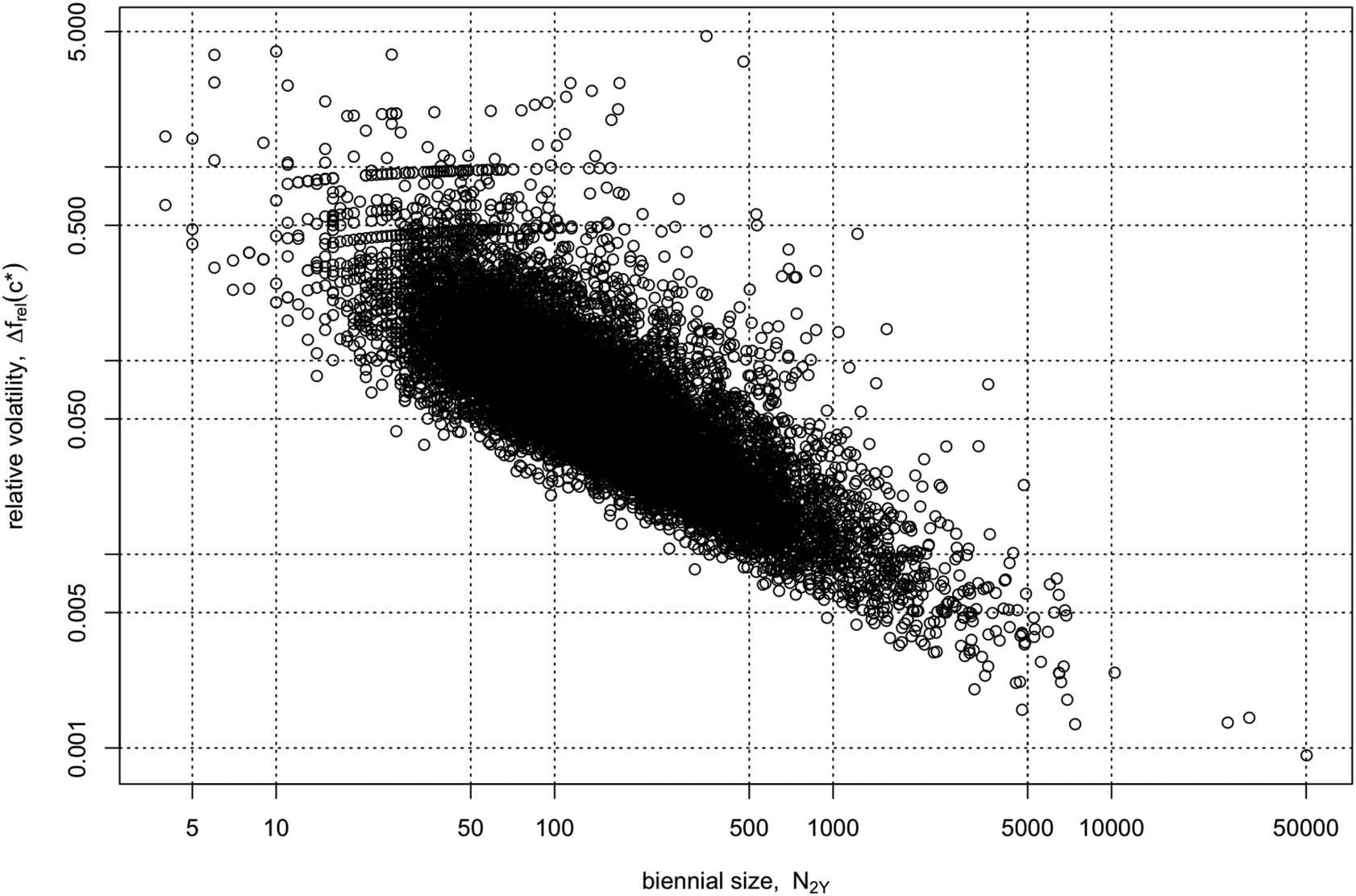
Figure 3.
IF volatility, Δf(c*), vs. journal (biennial) size, N2Y, for 11,639 journals in the 2017 JCR.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4.
IF relative volatility, Δfr(c*) vs. journal (biennial) size, N2Y, for 11,639 journals in the 2017 JCR.
Quantitative Science Studies
648
Impact factor volatility due to a single paper
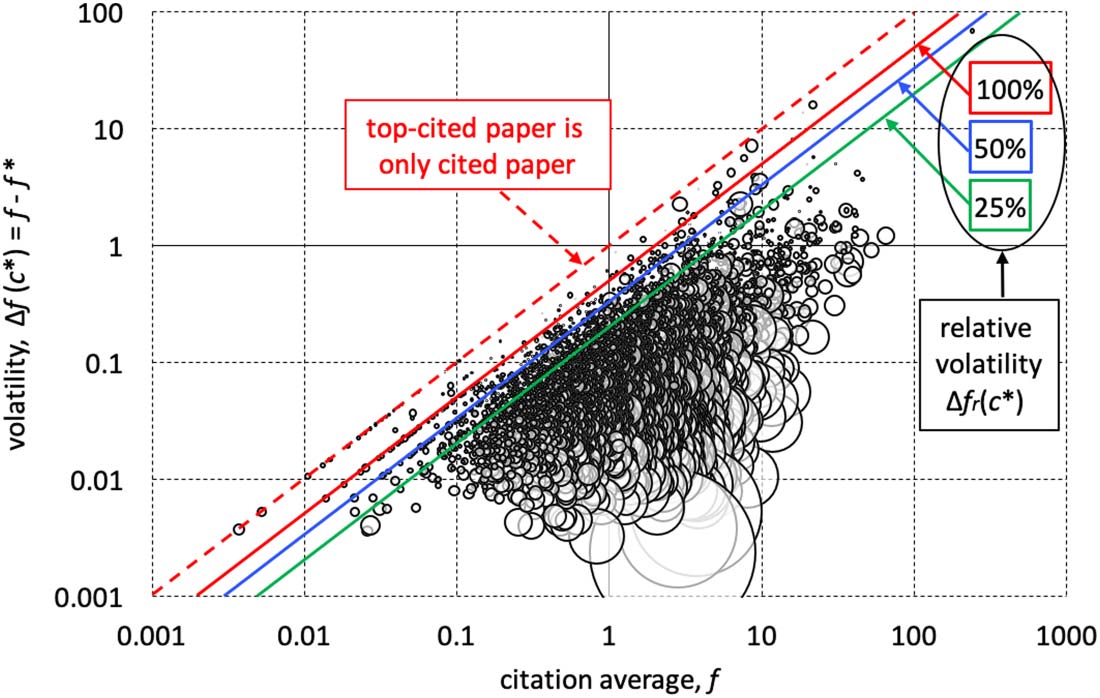
IF volatility, Δf(c*), vs. citation average, f, for 11,639 journals in the 2017 JCR. Bubble
Figure 5.
size shows journal size. The dashed line corresponds to the top-cited paper having all the journal’s
citations, which occurs for 26 journals. The three parallel lines labeled “100%,” “50%,” and “25%”
denote relative volatility values Δfr(c*)—that is, relative IF boost—caused by the top-cited paper.
Thus, data points above the 25% line describe the 818 journals whose top-cited paper boosted their
IF by more than 25%. As expected from the Central Limit Theorem, increasing journal size causes
the volatility to drop (larger bubbles “fall” to the bottom) and the IF to approach the global citation
average μ = 2.9.
0! (These journals were however allocated an IF, so they did receive citations to the journal
and year, or to their front matter.) None of these 37 journals is depicted in our log-log plots.
In Figures 3 and 4 we plot the volatility Δf(c*) and relative volatility Δfr(c*), respectively, vs.
journal size N2Y. In Figure 5 we plot the volatility Δf(c*) vs. the journal citation average, f, in a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
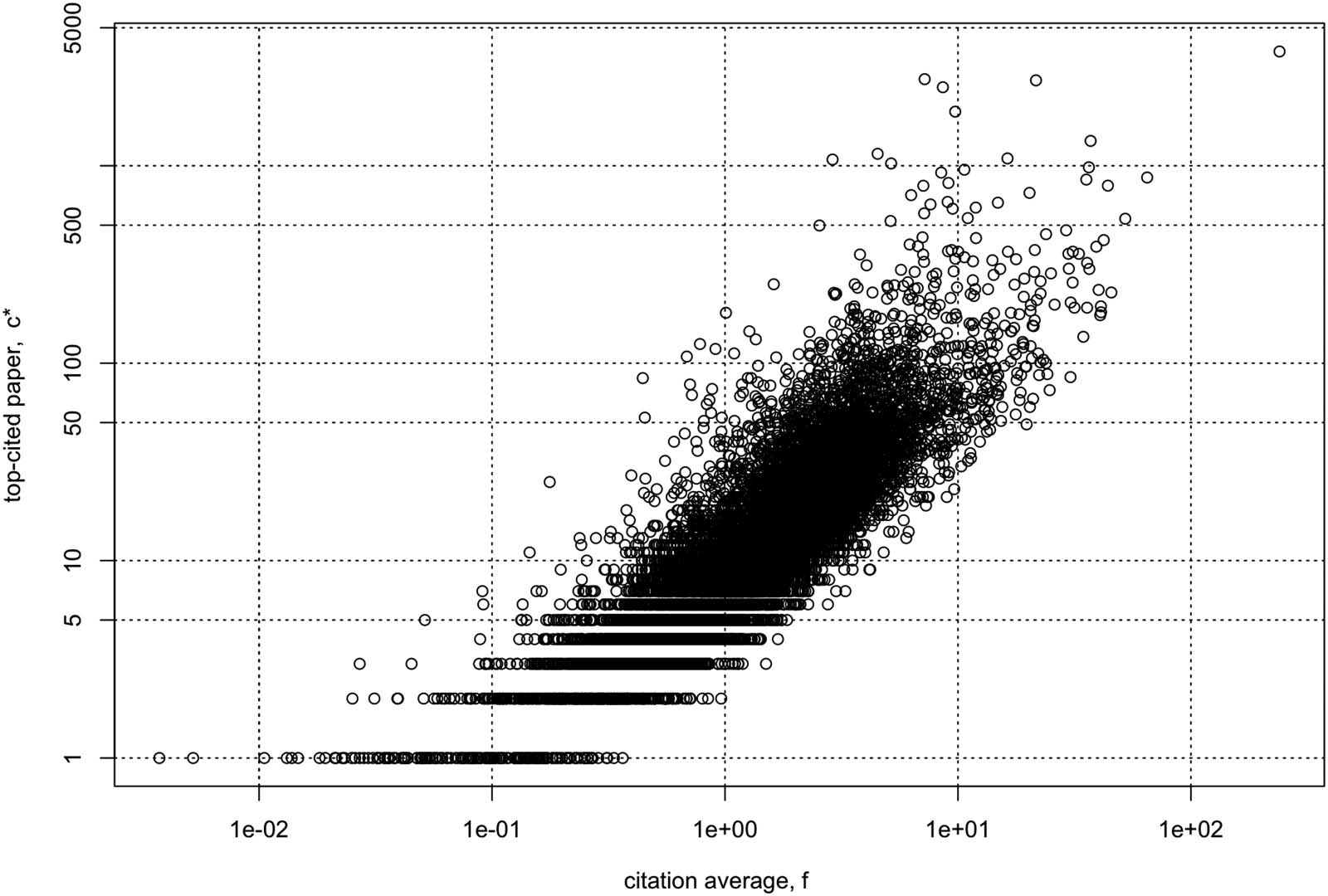
Figure 6. Citations of top-cited paper, c*, vs. citation average, f, for 11,639 journals in the 2017 JCR.
Quantitative Science Studies
649
Impact factor volatility due to a single paper
Table 3. Top 50 journals in volatility Δfr(c*) due to their top-cited paper. Publication years = 2015–2016, Citation year = 2017. JCR data.
11,639 journals and 3,088,511 papers in data set
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Journal
CA-CANCER J CLIN
J STAT SOFTW
LIVING REV RELATIV
PSYCHOL INQ
ACTA CRYSTALLOGR C
ANNU REV CONDEN MA P
ACTA CRYSTALLOGR A
ADV PHYS
PSYCHOL SCI PUBL INT
ACTA CRYSTALLOGR B
NAT ENERGY
INT J COMPUT VISION
NAT REV MATER
MOL BIOL EVOL
EPILEPSY CURR
LIVING REV SOL PHYS
PURE APPL CHEM
PROG SOLID STATE CH
PROG QUANT ELECTRON
ADV OPT PHOTONICS
SOLID STATE PHYS
GENET MED
IEEE IND ELECTRON M
MATER TODAY
ACTA NEUROPATHOL
J METEOROL SOC JPN
PROG OPTICS
J BIOL ENG
ANNU REV NEUROSCI
ENDOCR REV
CLIN MICROBIOL REV
Quantitative Science Studies
Δf(c*)
68.27
15.80
13.67
8.12
7.12
5.67
5.57
4.96
4.88
4.19
4.15
3.83
3.65
3.53
3.43
3.30
3.27
3.18
3.17
3.16
3.03
3.00
2.93
2.93
2.93
2.81
2.67
2.58
2.56
2.52
2.48
c*
3,790
2,708
87
97
2,499
209
637
85
49
710
420
656
228
1,879
53
47
525
57
55
106
19
818
89
260
650
247
32
103
114
123
184
Δfr(c*)
40%
271%
273%
105%
474%
35%
271%
19%
33%
199%
11%
74%
9%
57%
218%
44%
175%
52%
43%
18%
379%
49%
42%
15%
25%
130%
103%
101%
22%
21%
14%
f
240.09
f*
171.83
21.63
18.67
15.82
8.62
21.82
7.62
30.42
19.71
6.30
42.24
9.03
45.55
9.73
5.00
10.75
5.14
9.25
10.60
20.79
3.83
9.10
9.86
22.62
14.84
4.98
5.27
5.13
14.10
14.70
20.49
5.82
5.00
7.70
1.50
16.15
2.05
25.45
14.83
2.11
38.09
5.20
41.90
6.20
1.57
7.45
1.87
6.07
7.43
17.63
0.80
6.10
6.93
19.69
11.91
2.16
2.60
2.55
11.54
12.19
18.02
N2Y
53
171
6
11
351
34
114
12
7
169
92
170
51
530
15
12
160
16
15
28
6
271
28
82
218
87
11
39
40
44
67
650
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
Table 3. (continued )
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Journal
J HUM RESOUR
IND ORGAN PSYCHOL-US
ADV CATAL
GIGASCIENCE
J ACAD MARKET SCI
CHINESE PHYS C
THYROID
INT J CANCER
NAT PROTOC
ALDRICHIM ACTA
JAMA-J AM MED ASSOC
REV MOD PHYS
SURF SCI REP
NAT REV GENET
ANNU REV ASTRON ASTR
AUTOPHAGY
GEOCHEM PERSPECT
EUR HEART J-CARD IMG
MOBILE DNA-UK
Δf(c*)
2.38
2.35
2.33
2.33
2.29
2.25
2.25
2.24
2.21
2.10
1.99
1.99
1.96
1.95
1.93
1.93
1.92
1.91
1.90
c*
156
42
13
240
198
1,075
792
2,746
614
28
851
191
55
235
88
606
9
574
91
Δfr(c*)
61%
53%
64%
53%
43%
350%
46%
45%
23%
43%
6%
6%
12%
5%
9%
26%
144%
36%
54%
f
6.27
6.75
6.00
6.71
7.57
2.90
7.10
7.20
11.92
7.00
35.57
35.82
17.70
40.17
24.21
9.49
3.25
7.16
5.43
f*
3.89
4.40
3.67
4.38
5.28
0.64
4.85
4.96
9.72
4.90
33.57
33.83
15.74
38.22
22.27
7.56
1.33
5.25
3.53
N2Y
64
16
4
101
84
477
350
1,224
274
11
410
79
20
101
34
310
4
298
46
bubble plot where bubble size is proportional to journal size. In Figure 6 we plot the citation
count of the top-cited paper, c*, vs. journal citation average, f. In Tables 3 and 4 and 7 and 8 we
identify the top 100 journals in decreasing volatility Δf(c*) and relative volatility Δfr(c*), respec-
tively. In Tables 5 and 6 we show the frequency distribution of Δf(c*) and Δfr(c*), respectively.
Our key findings are as follows.
1. High volatilities are observed for hundreds of journals. For example
(a) Δf(c*) > 0.5 für 381 journals,
(B) Δf(c*) > 0.25 für 1,061 journals, usw.
Relative volatilities are also high for hundreds of journals. Zum Beispiel
(C) Δf(c*) > 50% für 231 journals,
(D) Δfr(c*) > 25% für 818 journals, usw.
Quantitative Science Studies
651
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact factor volatility due to a single paper
Tisch 4. Top 51–100 journals in volatility Δf(c*) due to their top-cited paper. Publication years = 2015–2016, Citation year = 2017. JCR data.
11,639 journals and 3,088,511 papers in data set
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
Zeitschrift
NAT REV DRUG DISCOV
MULTIVAR BEHAV RES
EARTH SYST SCI DATA
MAT SCI ENG R
NAT CHEM
BONE RES
ANNU REV IMMUNOL
NPJ COMPUT MATER
PROG PART NUCL PHYS
PHOTOGRAMM ENG REM S
J AM SOC ECHOCARDIOG
WIRES DEV BIOL
J SERV RES-US
NANO-MICRO LETT
JAMA ONCOL
WORLD PSYCHIATRY
ADV APPL MECH
NEURAL NETWORKS
NAT REV MICROBIOL
EXERC IMMUNOL REV
KIDNEY INT SUPPL
APPL MECH REV
PROG ENERG COMBUST
NEW ASTRON REV
EMBO MOL MED
BEHAV BRAIN SCI
LANCET NEUROL
NAT PHOTONICS
NAT BIOTECHNOL
PHYS LIFE REV
NAT REV NEUROSCI
Δf(c*)
1.82
1.80
1.76
1.65
1.65
1.64
1.63
1.63
1.63
1.60
1.59
1.58
1.57
1.57
1.57
1.56
1.55
1.54
1.53
1.52
1.51
1.51
1.51
1.50
1.49
1.47
1.44
1.44
1.42
1.40
1.40
Quantitative Science Studies
c*
181
176
133
60
450
89
101
62
76
225
399
114
94
137
367
82
11
434
203
34
23
55
73
21
292
46
285
367
358
40
191
Δfr(c*)
5%
102%
27%
9%
7%
16%
8%
25%
17%
114%
34%
43%
36%
29%
11%
10%
48%
28%
5%
29%
82%
29%
6%
25%
18%
31%
6%
5%
5%
18%
5%
F
41.14
3.56
8.29
20.36
23.89
11.92
22.57
8.09
10.98
3.00
6.21
5.21
5.98
7.02
16.40
17.86
4.80
7.05
f*
39.32
1.76
6.54
18.71
22.24
10.28
20.94
6.45
9.35
1.40
4.62
3.64
4.41
5.46
14.83
16.29
3.25
5.51
30.46
28.94
6.68
3.36
6.73
5.17
1.85
5.22
24.76
23.25
7.50
9.59
6.21
25.08
31.14
29.80
9.17
31.63
6.00
8.10
4.74
23.63
29.70
28.38
7.77
30.23
N2Y
78
97
72
25
259
48
49
34
41
140
248
70
57
84
225
42
5
279
114
19
14
33
33
10
191
28
181
234
232
23
115
652
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact factor volatility due to a single paper
Tisch 4. (Fortsetzung )
Zeitschrift
J PHOTOCH PHOTOBIO C
Δf(c*)
1.39
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
CIRCULATION
NAT REV IMMUNOL
ANNU REV BIOPHYS
ACTA NUMER
EUR HEART J
ACTA PHYS SLOVACA
GENOM PROTEOM BIOINF
BIOCHEM MEDICA
ANNU REV FLUID MECH
ANNU REV EARTH PL SC
EUR J HEART FAIL
ACTA ASTRONOM
PSYCHOTHER PSYCHOSOM
DIALOGUES HUM GEOGR
LANCET INFECT DIS
J ECON GROWTH
J URBAN TECHNOL
100
REV MINERAL GEOCHEM
c*
69
1,089
194
52
23
729
13
109
128
70
70
338
65
70
22
336
37
61
40
Δfr(c*)
10%
9%
3%
13%
16%
7%
133%
26%
62%
10%
14%
15%
57%
18%
32%
8%
25%
91%
17%
F
14.88
16.32
41.07
11.65
9.64
20.29
2.33
6.47
3.47
14.67
10.76
9.75
3.60
8.27
5.29
f*
13.49
14.93
39.69
10.30
8.30
18.95
1.00
5.14
2.15
13.36
9.44
8.44
2.30
6.98
4.00
N2Y
40
776
112
31
11
532
9
78
95
43
46
252
48
49
14
17.76
16.49
250
6.40
2.66
8.58
5.13
1.39
7.32
25
47
26
1.38
1.38
1.35
1.34
1.33
1.33
1.33
1.32
1.32
1.32
1.31
1.31
1.29
1.29
1.28
1.28
1.27
1.26
2.
If we look at the top few cited papers per journal—as opposed to the single top-cited
paper—then the IF sensitivity to a handful of papers becomes even more dramatic. Für
Beispiel, the IF was boosted by more than 50% von
(A)
(B)
(C)
the top two cited papers for 710 journals,
the top three cited papers for 1,292 journals,
the top four cited papers for 1,901 journals, usw.
Also, 10% of journals had their IF boosted by more than 50% by their top three cited papers!
3. Highest volatility values occur for small journals. This agrees with our earlier finding
that smaller journals benefit the most from a highly cited paper. By “small journals” we
≤ 500. Zum Beispiel, 97 of the top 100 journals ranked by volatility (Tables 3
mean N2Y
Und 4), and all the top 100 journals ranked by relative volatility (Tables 7 Und 8) Kneipe-
lish fewer than 500 papers biennially (N2Y
≤ 500).
Quantitative Science Studies
653
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact factor volatility due to a single paper
Tisch 5. Number of journals whose change in IF (Δf(C)) due to their highest-cited paper was greater
than the threshold in the first column. Zum Beispiel, 381 journals had their IF boosted more than 0.5
points by their most cited paper. Publication years = 2015–2016, Citation year = 2017. Data from
JCR. Total number of papers in data set is 3,090,630, published in 11,639 journals
Volatility, Δf(c*) (threshold)
0.1
NEIN. journals above threshold
3,881
% all journals
33.3%
0.25
0.5
0.75
1
1.5
2
3
4
5
10
50
1,061
381
221
140
73
41
21
11
7
3
1
9.1%
3.3%
1.9%
1.2%
0.6%
0.4%
0.2%
0.1%
0.1%
0.03%
0.01%
4. Above the limit of N2Y
≈ 500, journal size starts to become prohibitively large for a
journal’s IF to profit from highly cited papers. Notice how the maximum values of
Δf(c*) and Δfr(c*) follow a downward trend with journal size above this limit.
5. For some journals, an extremely highly cited paper causes a large volatility Δf(c*).
Consider the top two journals in Table 3. The journal CA-A Cancer Journal for
Clinicians published in 2016 a paper that was cited 3,790 times in 2017, accounting
for almost 30% of its IF citations that year, with a corresponding Δf(c*) = 68.3. Without
this paper, the journal’s citation average would have dropped from f = 240.1 to f* =
171.8. Ähnlich, the Journal of Statistical Software published in 2015 a paper cited
2,708 times in 2017, capturing 73% of the journal’s citations that year. Without this
Papier, the journal’s citation average would have dropped from f = 21.6 to f* = 5.8.
Although such extreme volatility values are rare, they occur every year.
6. A paper need not be exceptionally cited to produce a large IF boost, provided the jour-
nal is sufficiently small. Consider the journals ranked #3 Und #4 in Table 3, nämlich,
Living Reviews in Relativity and Psychological Inquiry. These journals’ IFs were strongly
boosted by their top-cited paper, even though the latter was much less cited (c* = 87
Und 97, jeweils) than for the top two journals. This is because journal sizes were
smaller also (N2Y = 6 Und 11). Such occurrences are common, because papers cited
dozens of times are much more abundant than papers cited thousands of times, Und
there are also plenty of very small journals. In der Tat, within the top 100 journals ranked
by volatility (Tables 3 Und 4) es gibt 19 journals whose top-cited paper received
fewer than 50 citations and yet caused a significant volatility Δf(c*) that ranged from
1.6 Zu 4.8. High values of relative volatility Δfr(c*) due to low-cited or moderately cited
papers are even more common. Für 75 of the 100 journals in Tables 7 Und 8, Die
Quantitative Science Studies
654
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact factor volatility due to a single paper
Tisch 6. Number of journals whose relative change in IF (Δfr(C)) due to their highest-cited paper was
greater than the threshold in the first column. Zum Beispiel, 3,421 journals had their IF boosted more
als 10% by their most cited paper. Publication years = 2015–2016, Citation year = 2017. Data
from JCR. Total number of papers in data set is 3,090,630, published in 11,639 journals
Relative volatility, Δfr(c*) (threshold)
10%
NEIN. journals above threshold
3,403
% all journals
29.2%
20%
25%
30%
40%
50%
60%
70%
75%
80%
90
100%
200
300%
400%
1,218
10.5%
818
592
387
231
174
140
127
124
101
50
14
5
1
7.0%
5.1%
3.3%
2.0%
1.5%
1.2%
1.1%
1.1%
0.9%
0.4%
0.12%
0.04%
0.01%
top-cited paper received fewer than 10 citations and yet caused Δfr(c*) to range from
90% Zu 395%.
7. High volatilities are observed across the IF range. Siehe Abbildung 5. Zum Beispiel, Δf(c*) >
0.5 for f ~ 1–40. High relative volatilities (Δfr(c*) > 25%) are also observed across the
IF spectrum. Jedoch, as expected from the Central Limit Theorem, with increasing
journal size the IF approaches the global citation average μ = 2.9, is less sensitive to
outliers and volatility drops: Large bubbles “fall” to the bottom.
8. The top-cited paper captures a sizable fraction of the journal’s citations for journals
across the IF range. Siehe Abbildung 5. The dashed line with unity slope corresponds to
the situation when the top-cited paper has all the journal’s citations (so that f* = 0
and Δf(c*) = f ). This line can never be reached in a log-log plot of data, although there
Sind 26 journals with f* = 0 and another 11 journals with f = 0, as we mentioned earlier.
But note how many journals are close to that line and how they extend across the IF
range. Zum Beispiel, 818 journals have Δfr(c*) > 25% (data points above the green
Linie). Another example: Among the 142 journals whose top-cited paper captures more
als 50% of the journal’s citations, their IF ranges from f = 0.1–21.6 while their size
ranges from N2Y = 31–477.
9. Broadly speaking, the citation count of the top-cited paper correlates with the IF. Sehen
Figur 6. But note the spread of highly cited papers across journals. Zum Beispiel,
papers with c* ≥ 50 appear in many journals of small-to-moderate IF, 0.5 < f 2.5.
Quantitative Science Studies
655
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
Table 7. Top 50 journals in relative volatility Δfr(c*) due to their top-cited paper. Publication years = 2015–2016, Citation year = 2017. JCR
data. 11,639 journals and 3,088,511 papers in data set
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Journal
ACTA CRYSTALLOGR C
COMPUT AIDED SURG
ETIKK PRAKSIS
SOLID STATE PHYS
CHINESE PHYS C
LIVING REV RELATIV
J STAT SOFTW
ACTA CRYSTALLOGR A
AFR LINGUIST
AM LAB
ZKG INT
EPILEPSY CURR
REV INT ECON
REV BRAS ORNITOL
ACTA CRYSTALLOGR B
REV ESP DERECHO CONS
DIABETES STOFFWECH H
ITINERARIO
CENTAURUS
HITOTSUB J ECON
ACROSS LANG CULT
Z ETHNOL
TURK PSIKOL DERG
PALAEONTOGR ABT B
THEOR BIOL FORUM
PURE APPL CHEM
CAL COOP OCEAN FISH
PROBUS
NETH Q HUM RIGHTS
MECH ENG
GEOCHEM PERSPECT
Quantitative Science Studies
Δf(c*)
7.12
0.88
0.15
3.03
2.25
13.67
15.80
5.57
0.26
0.04
0.06
3.43
1.13
0.37
4.19
0.03
0.03
0.05
0.07
0.07
0.08
0.08
0.08
0.31
0.11
3.27
0.60
0.23
0.28
0.05
1.92
c*
2,499
9
4
19
1,075
87
2,708
637
3
5
7
53
107
32
710
2
2
2
2
2
2
2
2
6
2
525
16
5
8
6
9
Δfr(c*)
474%
395%
381%
379%
350%
273%
271%
271%
264%
247%
230%
218%
215%
210%
199%
196%
195%
192%
189%
189%
188%
188%
188%
184%
183%
175%
167%
154%
151%
148%
144%
f
8.62
1.10
0.19
3.83
2.90
18.67
21.63
7.62
0.36
0.05
0.09
5.00
1.66
0.55
6.30
0.04
0.05
0.08
0.11
0.11
0.12
0.12
0.13
0.47
0.17
5.14
0.96
0.38
0.46
0.09
3.25
f*
1.50
0.22
0.04
0.80
0.64
5.00
5.82
2.05
0.10
0.01
0.03
1.57
0.53
0.18
2.11
0.01
0.02
0.03
0.04
0.04
0.04
0.04
0.04
0.17
0.06
1.87
0.36
0.15
0.19
0.04
1.33
N2Y
351
10
26
6
477
6
171
114
11
136
110
15
94
85
169
76
59
37
27
27
26
26
24
19
18
160
26
21
28
109
4
656
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
Table 7. (continued )
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Journal
AFR NAT HIST
ACTA PHYS SLOVACA
J METEOROL SOC JPN
ENVIRON ENG RES
J RUBBER RES
J AFR LANG LINGUIST
FORKTAIL
MEAS CONTROL-UK
PHOTOGRAMM ENG REM S
HEREDITAS
DEV ECON
EVOL EQU CONTROL THE
APPL LINGUIST REV
CCAMLR SCI
PSYCHOL INQ
JPN J MATH
PROG OPTICS
MULTIVAR BEHAV RES
J BIOL ENG
Δf(c*)
0.35
1.33
2.81
0.78
0.11
0.44
0.15
0.38
1.60
0.25
0.23
0.55
0.58
0.43
8.12
0.38
2.67
1.80
2.58
c*
2
13
247
80
4
7
6
19
225
5
6
34
25
3
97
6
32
176
103
Δfr(c*)
140%
133%
130%
129%
127%
124%
115%
114%
114%
113%
111%
110%
109%
108%
105%
105%
103%
102%
101%
f
0.60
2.33
4.98
1.38
0.20
0.80
0.28
0.71
3.00
0.47
0.44
1.05
1.12
0.83
15.82
0.73
5.27
3.56
5.13
f*
0.25
1.00
2.16
0.60
0.09
0.36
0.13
0.33
1.40
0.22
0.21
0.50
0.54
0.40
7.70
0.36
2.60
1.76
2.55
N2Y
5
9
87
102
35
15
40
49
140
19
25
61
42
6
11
15
11
97
39
10. Note the parallel lines of negative slope at the bottom left corner of Figure 3. All these
lines have slope equal to −1 in a log-log plot of Δf(c*) vs. N2Y, a feature that is readily
≫ 1 usually). The
explained from Eq. (4), whence Δf(c*) ~ (c* − f*)/N2Y (because N2Y
offset of the parallel lines is equal to log(c* − f*), which for c* ≫ f* is roughly equal to
log(c*). Therefore, the Δf(c*) data points for all journals whose highest cited paper was
cited c* times must fall on the same line, irrespective of their IF, as long as c* ≫ f*. The
parallel lines are therefore simply lines of increasing c* value, starting from c* = 1, 2,
3, etc., as we move from the bottom left to the top right of the figure. When the in-
equality c* ≫ f* no longer holds, a broadening of the parallel lines occurs and they
overlap, exactly as we see in Figure 3. Because of the highly skewed citation distribu-
tion of papers, the parallel lines become less populated as c* increases, that is, for
higher values of Δf(c*).
We have studied how a journal’s top-cited paper affects its IF. Could the effect work the
other way around, the journal affecting citations to its papers? If such an effect were strong, the
source journal would have boosted all its papers indiscriminately, and the IF volatility would
Quantitative Science Studies
657
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
Table 8. Top 51–100 journals in relative volatility Δfr(c*) due to their top-cited paper. Publication years = 2015–2016, Citation year = 2017.
JCR data. 11,639 journals and 3,088,511 papers in data set
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
Journal
MANUF ENG
NUCL ENG INT
DEUT LEBENSM-RUNDSCH
NEW REPUBLIC
JCT COATINGSTECH
ANDAMIOS
FR CULT STUD
ACTES RECH SCI SOC
CEPAL REV
J HELL VET MED SOC
LANGAGES
BER LANDWIRTSCH
ANTHROPOS
REV FAC AGRON LUZ
AFR STUD-UK
FR HIST
MED GENET-BERLIN
REV ROUM LINGUIST
ACM T INFORM SYST SE
ETHICAL PERSPECT
PEDAGOG STUD
TRAV GENRE SOC
SECUR REGUL LAW J
PULP PAP-CANADA
ATLANTIS-SPAIN
J HISTOTECHNOL
STUD E EUR THOUGHT
ETHIOP J HEALTH DEV
Z ARZNEI- GEWURZPFLA
INDOGER FORSCH
EARTH SCI HIST
Δf(c*)
0.01
c*
2
Δfr(c*)
99%
0.01
0.02
0.01
0.01
0.03
0.02
0.05
0.02
0.03
0.05
0.02
0.02
0.04
0.02
0.02
0.06
0.04
0.91
0.02
0.05
0.02
0.02
0.05
0.02
0.02
0.02
0.02
0.03
0.05
0.05
1
3
1
1
2
1
3
1
2
3
1
1
2
1
1
3
2
21
1
2
1
1
2
1
1
1
1
1
2
2
99%
98%
98%
98%
97%
97%
97%
97%
97%
96%
96%
96%
96%
96%
96%
96%
96%
96%
96%
95%
95%
95%
95%
95%
95%
95%
95%
95%
95%
95%
f
0.03
0.01
0.05
0.02
0.02
0.06
0.03
0.09
0.03
0.07
0.11
0.04
0.04
0.08
0.04
0.04
0.13
0.09
1.86
0.04
0.09
0.05
0.05
0.10
0.05
0.05
0.05
0.05
0.05
0.11
0.11
f*
0.01
0.01
0.02
0.01
0.01
0.03
0.02
0.05
0.02
0.04
0.05
0.02
0.02
0.04
0.02
0.02
0.07
0.04
0.95
0.02
0.05
0.02
0.02
0.05
0.03
0.03
0.03
0.03
0.03
0.06
0.06
Quantitative Science Studies
N2Y
159
145
133
110
86
71
65
64
62
58
57
55
53
49
49
48
47
47
22
46
43
42
42
41
40
40
40
39
38
37
37
658
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
Table 8. (continued )
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
Journal
CIV SZLE
PSYCHOANAL STUD CHIL
TIJDSCHR RECHTSGESCH
TRAIT SIGNAL
SOCIOL FORSKNIN
MIL OPER RES
J POLYNESIAN SOC
AIBR-REV ANTROPOL IB
AFR ASIAN STUD
HIST LINGUIST
RLA-REV LINGUIST TEO
SCANDIA
ROM J POLIT SCI
GORTERIA
FORSCH INGENIEURWES
OBSERVATORY
J URBAN TECHNOL
EAST EUR COUNTRYSIDE
100
SOCIOLOGUS
Δf(c*)
0.03
c*
1
Δfr(c*)
95%
0.05
0.03
0.03
0.09
0.03
0.10
0.06
0.06
0.07
0.18
0.04
0.11
0.04
0.32
0.04
1.27
0.09
0.05
2
1
1
3
1
3
2
2
2
5
1
3
1
8
1
61
2
1
94%
94%
94%
94%
94%
93%
93%
93%
93%
93%
93%
92%
92%
92%
91%
91%
91%
90%
f
0.05
0.11
0.06
0.06
0.18
0.06
0.20
0.13
0.13
0.14
0.37
0.07
0.23
0.08
0.67
0.09
2.66
0.18
0.10
f*
0.03
0.06
0.03
0.03
0.09
0.03
0.10
0.07
0.07
0.07
0.19
0.04
0.12
0.04
0.35
0.05
1.39
0.10
0.05
N2Y
37
36
35
35
34
31
30
30
30
29
27
27
26
25
24
23
47
22
21
be low for all journals. Therefore, at least for the thousands of journals of high (absolute or
relative) volatility, citations to the top-cited paper are mainly article driven and not journal
driven.
4. CONCLUSIONS
Our paper has two core messages. First, we demonstrate how strongly volatile IFs are due to a
single or a few papers, and how frequently this occurs: Thousands of journals are seriously
affected every year. Second, we demonstrate the skewed reward mechanism that affects jour-
nals’ IFs disproportionately for an equally cited paper, depending on journal size.
The above findings corroborate our earlier finding (Antonoyiannakis, 2018) that IFs are
scale dependent and particularly volatile for small journal sizes, as explained by the
Central Limit Theorem. This point is pertinent because 90% of all journals publish no more
than 250 citable items annually, a regime where single-paper effects are at play as IFs are
susceptible to sufficiently highly cited papers, of which there are thousands.
Quantitative Science Studies
659
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
Compared to large journals, small journals have (a) much more to gain by publishing a
highly cited paper, and (b) more to lose by publishing a little-cited paper. The penalty for a
zero-cited paper can be easily exceeded by the reward of a highly cited paper. So, in terms of
IF, it pays for a small journal to “fine tune” its risk level: publish a few potentially groundbreak-
ing papers, but not too many. This upper limit to how many risky papers an elite, high-IF jour-
nal can publish before it begins to compromise its IF imparts a conservative mindset to the
editor: Reject most but a few of the intellectually risky and innovative submissions, and the
journal’s IF can still benefit massively if some of them pay off. Such an ulterior motive—where
the editor is conscious of the journal’s size while assessing an individual paper at hand—
makes it even harder for transformative papers to appear in elite journals.
The reliability of IF rankings (and citation averages in general) is compromised by the
high IF volatility due to a handful of papers, observed for thousands of journals each year.
Three examples: (a) In 2017, the top-cited paper of 381 journals raised their IF by 0.5;
(b) 818 journals had their IF boosted by more than 25% by their top-cited paper; and (c)
one in 10 journals (1,292 journals) had their IF boosted by more than 50% by their top three
cited papers.
Given this high sensitivity to outliers, does it make sense to compare two journals by their
IF? In our view, such a comparison is at best incomplete and at worst misleading. Why incom-
plete? Because unless we know the underlying citation distributions and can thus ascertain
that the averages (IFs) are not swayed by a few outliers, we cannot safely use IFs as represen-
tatives of both journals. And because most journals are small and have highly skewed citation
distributions with outliers, IF comparisons are more often misleading, because under these
conditions, the mean (average) is a poor measure of central tendency, as per standard statis-
tical practice (Adler, Ewing, & Taylor, 2009; Bornmann & Mutz, 2011; Calver & Bradley,
2009; De Veaux, Velleman, & Bock, 2014, pp. 57–58; Seglen, 1992; Wall, 2009).
So, the volatility of IFs is not of academic but of practical interest. It is not an exclusive
feature of a few journals or a statistical anomaly that we can casually brush off, but an every-
day feature inherent in citation averages, affecting thousands of journals each year. It casts
serious doubt on the suitability of the IF as a journal-defining quantity, and on the merits of
ranking journals by IF. And it is a direct consequence of the Central Limit Theorem.
It is therefore prudent to consider ways of comparing journals based on more solid statis-
tical grounds. The implications may reach much further than producing ranked lists aimed at
librarians—which was the original objective of Eugene Garfield when he proposed the IF—
and affect research assessment and the careers of scientists.
4.1. What to Do?
Many alternatives to the IF have been proposed to date. Here we share our own recommen-
dations for how to remedy the problem, along three lines of thought.
1. Use metrics that are less sensitive to outliers than IFs. At a minimum, use citation medians
instead of citation averages or IFs, as has been proposed by Aksnes & Sivertsen (2004),
Rossner et al. (2007), Wall (2009), Calver & Bradley (2009), Antonoyiannakis (2015a,
2015b), and Ioannidis & Thombs (2019).
A median shows the midpoint or “center” of the distribution. When statisticians wish to
describe the typical value of a skewed distribution, they normally report the median (De
Veaux, Velleman, & Bock, 2014), together with the interquartile distance (the distance
Quantitative Science Studies
660
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact factor volatility due to a single paper
between the 1st and 3rd quartiles) as a measure of the spread. Note that citation distributions
are typically highly skewed, which makes the use of medians more suitable for their descrip-
tion. Citation medians are far less sensitive to outlier papers and much less susceptible to gam-
ing than citation averages (IFs). On a practical note, as of 2017, the JCR of Clarivate Analytics
list the citation median per article type (research article and review article) for each journal,
facilitating the wide dissemination of medians. (Cautionary note: On more occasions than we
would have liked, the JCR citation medians contained errors in article type that needed cor-
rection before use.)
2. Use standardized averages to remove the scale dependence from “bare” citation
averages.
A bare average is prone to fluctuations from outliers, but the Central Limit Theorem al-
lows us to standardize it and remove the scale dependence. So, instead of the bare citation
average (or IF), f, we have proposed (Antonoyiannakis, 2018) the standardized average, or Φ
index:
Φ ¼ f − μ
p
σs=
ffiffiffiffiffiffiffiffi
s
N2Y
;
(9)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
s, σ
where μ
s are the global average and standard deviation of the citation distribution of all
papers in the subject of the journal in question. The quantities μ
s need to be found
for each research subject before a journal’s Φ index can be calculated. For example, if we
were to treat, for simplicity, all 3,088,511 papers published in all journals in 2015–2016 as
belonging to a single subject, then μ = 2.92, σ = 8.12, and we can use Eq. (9) to standard-
ize the citation average of any journal. Here, f and N2Y are the journal’s citation average
(IF) and biennial size, as usual. The Φ index is readily applicable to all citation averages,
for instance in university rankings. More details will be provided in a forthcoming
publication.
s and σ
3. Resist the one-size-fits-all mindset (i.e., the limitations of a single metric). Think of
scholarly journals as distributions of widely varying papers, and describe them as such.
In line with this thinking, Larivière et al. (2016) suggested that journals display their full
citation distribution, a recommendation adopted by several publishers so far. In a welcome
development, the Clarivate Analytics JCR now display citation distributions for all journals
that receive an IF. However, plots of citation distributions can be overwhelming in practice
(too much information) and do not allow easy comparison across journals. So, again we
turn to statistical practice and ask how statisticians describe distributions. Typically, they
use a five-number summary of various percentiles, which is graphically displayed as a
box plot and includes outlier information (De Veaux et al., 2014; Krzywinski & Altman,
2014; Spitzer, Wildenhain, et al., 2014). We believe that use of box plots and, more gen-
erally, percentiles (Bornmann, Leydesdorff, & Rüdiger, 2013), leads to responsible, informa-
tive, and practical comparisons of citation impact across journals and other collections of
papers.
NOTE
This is an extended version of an article (Antonoyiannakis, 2019) presented at the 17th
International Conference of the International Society for Scientometrics and Informetrics,
Rome, Italy.
Quantitative Science Studies
661
Impact factor volatility due to a single paper
ACKNOWLEDGMENTS
I am grateful to Jerry I. Dadap for stimulating discussions, and to Richard Osgood Jr. and Irving
P. Herman for encouragement and hospitality. This work uses data, accessed through Columbia
University, from the Web of Science and Journal Citation Reports (2017) with explicit consent
from Clarivate Analytics.
AUTHOR CONTRIBUTIONS
Manolis Antonoyiannakis: Conceptualization, Data curation, Formal analysis, Methodology,
Writing.
COMPETING INTERESTS
The author is an Associate Editor of Physical Review B and Physical Review Research, and a
Bibliostatistics Analyst at the American Physical Society. He is also an Editorial Board member
of the Metrics Toolkit, a volunteer position. He was formerly an Associate Editor of Physical
Review Letters and Physical Review X. The manuscript expresses the views of the author and
not of any journals, societies, or institutions where he may serve.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
FUNDING INFORMATION
This research did not receive any specific grant from funding agencies in the public, commer-
cial, or not-for-profit sectors.
DATA AVAILABILITY
The data that support the findings of this study are openly available in the Figshare server at
https://doi.org/10.6084/m9.figshare.11977881.v2. This includes a file with two Excel sheets,
one for the theoretical study of volatility (Figures 1–2) and another sheet for the data analytics
study of 11,639 journals from the 2017 JCR (Figures 3–6 and Tables 3–8).
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
q
s
s
_
a
_
0
0
0
3
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
REFERENCES
Adler, R., Ewing, J., & Taylor, P. (2009). Citation Statistics. A report
from the International Mathematical Union (IMU) in cooperation
with the International Council of Industrial and Applied Mathematics
(ICIAM) and the Institute of Mathematical Statistics (IMS). Statistical
Science, 24(1), 1–14. https://doi.org/10.1214/09-STS285
Aksnes, D. W., & Sivertsen, G. (2004). The effect of highly cited
papers on national citation indicators. Scientometrics, 59,
213–224. https://doi.org/10.1023/B:SCIE.0000018529.58334.eb
Amin, M., & Mabe, M. (2004). Impact factors: Use and abuse.
International Journal of Environmental Science and Technology,
1, 1–6.
Antonoyiannakis, M. (2015a). Median Citation Index vs.
Journal Impact Factor. APS March Meeting. Available from:
http://meetings.aps.org/link/BAPS.2015.MAR.Y11.14
Antonoyiannakis, M. (2015b). Editorial: Highlighting impact and the
impact of highlighting: PRB editors’ suggestions. Physical Review
B, 92, 210001. https://doi.org/10.1103/PhysRevB.92.210001
Antonoyiannakis, M. (2018). Impact factors and the Central Limit
Theorem: Why citation averages are scale dependent. Journal of
Informetrics, 12, 1072–1088. https://doi.org/10.1016/j.joi.2018.08.011
Antonoyiannakis, M. (2019). How a single paper affects the impact
factor: Implications for scholarly publishing. Proceedings of the
17th Conference of the International Society of Scientometrics
and Informetrics, vol. II, pp. 2306–2313. Available from https://
bit.ly/32ayyW4
Antonoyiannakis, M., Hemmelskamp, J., & Kafatos, F. C. (2009).
The European Research Council takes flight. Cell, 136, 805–809.
https://doi.org/10.1016/j.cell.2009.02.031
Antonoyiannakis, M., & Mitra, S. (2009). Editorial: Is PRL too large
to have an “impact”? Physical Review Letters, 102, 060001.
https://doi.org/10.1103/PhysRevLett.102.060001
Bornmann, L., Leydesdorff, L., & Rüdiger, M. (2013). The use of
percentiles and percentile rank classes in the analysis of biblio-
metric data: Opportunities and limits. Journal of Informetrics, 7,
158–165. https://doi.org/10.1016/j.joi.2012.10.001
Bornmann, L., & Marx, W. (2013). How good is research really?
Measuring the citation impact of publications with percentiles in-
creases correct assessments and fair comparisons. EMBO
REPORTS, 14, 226–230. https://doi.org/10.1038/embor.2013.9
Bornmann, L., & Mutz, R. (2011). Further steps towards an ideal
method of measuring citation performance: The avoidance of ci-
tation (ratio) averages in field-normalization. Journal of
Informetrics, 5(1), 228–230. https://doi.org/10.1016/j.
joi.2010.10.009
Quantitative Science Studies
662
Impact factor volatility due to a single paper
Calver, M. C., & Bradley, J. S. (2009). Should we use the mean ci-
tations per paper to summarise a journal’s impact or to rank jour-
nals in the same field? Scientometrics, 81(3), 611–615. https://
doi.org/10.1007/s11192-008-2229-y
Campbell, P. (2008). Escape from the impact factor. Ethics in
Science and Environmental Politics, 8, 5–7. https://doi.org/
10.3354/esep00078
Collins, F. S., Wilder, E. L., & Zerhouni, E., (2014). NIH Roadmap/
Common Fund at 10 years. Science, 345(6194), 274–276. https://
doi.org/10.1126/science.1255860
Cope, B. & Kalantzis, M. (2014). Changing knowledge ecologies
and the transformation of the scholarly journal. In B. Cope and
A. Philips (Eds.), The Future of the Academic Journal (2nd ed.,
pp. 9–83). Chandos Publishing, Elsevier Limited. https://doi.org/
10.1533/9781780634647.9
Cornell, E., Cowley, S. Gibbs, D., Goldman, M., Kivelson, S., …
Ushioda, K. (2004). Physical Review Letters Evaluation Committee
Report, http://publish.aps.org/reports/PRLReportRev.pdf
De Veaux, R. D., Velleman, P. D., & Bock, D. E. (2014). Stats: Data
and models (3rd ed.). Pearson Education Limited.
Dimitrov, J. D., Kaveri, S. V., & Bayry, J. (2010). Metrics: Journal’s
impact factor skewed by a single paper. Nature, 466, 179. https://
doi.org/10.1038/466179b
Foo, J. Y. A. (2013). Implications of a single highly cited article on a
journal and its citation indexes: A tale of two journals.
Accountability in Research, 20, 93–106. https://doi.org/
10.1080/08989621.2013.767124
Fortunato, S., Bergstrom, C. T., Borner, K., Evans, J. A., Helbing, D.,
… Barabasi, A. L. (2018). Science of science. Science, 359,
1007. https://doi.org/10.1126/science.aao0185
Ioannidis, J. P. A., & Thombs, B. D. (2019). A user’s guide to inflated
and manipulated impact factors. European Journal of Clinical
Investigation, 49(9), 1–6. https://doi.org/10.1111/eci.13151
Krzywinski, M., & Altman, N. (2014). Visualizing samples with box
plots. Nature Methods, 11, 119–120. https://doi.org/10.1038/
nmeth.2813
Larivière, V., Kiermer, V., MacCallum, C. J., McNutt, M., Patterson,
M., … Curry, S. (2016). A simple proposal for the publication of
journal citation distributions, BioRxiv, 062109. https://doi.org/
10.1101/062109
Leydesdorff, L., Bornmann, L., & Adams, J. (2019). The integrated
impact indicator revisited (I3*): A non-parametric alternative to
the journal impact factor. Scientometrics, 119, 1669–1694.
https://doi.org/10.1007/s11192-019-03099-8
Liu, W. S., Liu, F., Zuo, C., & Zhu, J. W. (2018). The effect of pub-
lishing a highly cited paper on a journal’s impact factor: A case
study of the Review of Particle Physics. Learned Publishing 31,
261–266. https://doi.org/10.1002/leap.1156
Lyu, G., & Shi, G. (2019). On an approach to boosting a journal’s
citation potential. Scientometrics, 120, 1387–1409. https://doi.
org/10.1007/s11192-019-03172-2
Milojevic´, S., Radicchi, F., & Bar-Ilan, J. (2017). Citation success
index—An intuitive pair-wise journal comparison metric.
Journal of Informetrics, 11(1), 223–231. https://doi.org/10.1016/
j.joi.2016.12.006
Moed, H. F., Colledge, L., Reedijk, J., Moya-Anegon, F., Guerrero-
Bote, V., Plume, A., & Amin, M. (2012). Citation-based metrics
are appropriate tools in journal assessment provided that they are
accurate and used in an informed way. Scientometrics, 92,
367–376. https://doi.org/10.1007/s11192-012-0679-8
NIH News Release. (2018). 2018 NIH Director’s awards for High-
Risk, High-Reward Research program announced, https://www.
nih.gov/news-events/news-releases/2018-nih-directors-awards-
high-risk-high-reward-research-program-announced
Prathap, G. (2019). Scale-dependent stratification: A skyline-shore-
line scatter plot. Scientometrics, 119, 1269–1273. https://doi.org/
10.1007/s11192-019-03038-7
Rossner, M., Van Epps, H., & Hill, E. (2007). Show me the data.
Journal of Cell Biology, 179, 1091–1092. http://jcb.rupress.org/
content/179/6/1091
Seglen, P. O. (1992). The skewness of science. Journal of the
American Society for Information Science, 43(9), 628–638.
https://doi.org/10.1002/(SICI)1097-4571(199210)43:9<628::
AID-ASI5>3.0.CO;2-0
Spitzer, M., Wildenhain, J., Rappsilber, J., & Tyers, M. (2014).
BoxPlotR: A web tool for generation of box plots. Natur
Methoden, 11, 121–122. https://doi.org/10.1038/nmeth.2811
Wall, H. J. (2009). Don’t get skewed over by journal rankings. Der
B.E. Journal of Economic Analysis and Policy, 9, 34. https://doi.
org/10.2202/1935-1682.2280
Waltman, L., van Eck, N. J., van Leeuwen, T. N., Visser, M. S., &
van Raan, A. F. J. (2011). Towards a new crown indicator: Ein
empirical analysis. Scientometrics, 87, 467–481. https://doi.org/
10.1007/s11192-011-0354-5
Wang, J., Veugelers, R., & Stephan, P. (2017). Bias against novelty
in science: A cautionary tale for users of bibliometric indicators.
Research Policy, 46, 1416–1436. https://doi.org/10.1016/j.
respol.2017.06.006
Quantitative Science Studies
663
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
1
2
6
3
9
1
8
8
5
7
9
8
Q
S
S
_
A
_
0
0
0
3
7
P
D
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3