RESEARCH ARTICLE

Connected from the outside: The role of U.S.
regions in promoting the integration of the
European research system

Keine offenen Zugänge

Tagebuch

Emanuele Rabosio1

, Lorenzo Righetto1

, Alessandro Spelta2

, and Fabio Pammolli1,3

1Human Technopole, Center for Analysis, Decisions and Society, Milano, Italien
2Università di Pavia, Dipartimento di Scienze Economiche e Aziendali, Pavia, Italien
3Politecnico di Milano, Dipartimento di Ingegneria Gestionale, Milano, Italien

Zitat: Rabosio, E., Righetto, L.,
Spelta, A., & Pammolli, F. (2020).
Connected from the outside: Die Rolle
of U.S. regions in promoting the
integration of the European research
System. Quantitative Science Studies,
1(2), 894–917. https://doi.org/10.1162/
qss_a_00034

DOI:
https://doi.org/10.1162/qss_a_00034

Erhalten: 22 Februar 2019
Akzeptiert: 27 Januar 2020

Korrespondierender Autor:
Emanuele Rabosio
emanuele.rabosio@fht.org

Handling-Editor:
Vincent Larivière

Schlüsselwörter: EU R&D integration, patent coinventorship network, resistance distance

ABSTRAKT

Considerable efforts have been deployed by the European Union to create an integrated
Forschung & Development area. In diesem Papier, we focus on the structure and evolution of the
European collaboration network as reflected by patent data. We study patent networks
representing collaborations between inventors located in different geographic areas. Existing
studies seem to indicate an increasing integration of the European research system, but none of
them has investigated which regions contribute most to this integration. We analyze the patent
coinventorship network to measure network-based distances between regions through
multiple metrics, in order to evaluate the role of different areas for the integration of the EU R&D
System. We study changes of the average closeness between European regions belonging to
different countries. Insbesondere, we perform a counterfactual exercise, simulating the impact
on EU integration of the removal of countries and individual regions. Our findings reveal an
important contribution from U.S. regions in favoring EU integration. Insbesondere, the size
and the density of the U.S. System, together with the presence of a few regional hubs, play a key
role in reducing the distances between European regions.

1.

EINFÜHRUNG

Achieving strong integration between member countries is a primary goal for the European
Union (EU). In research & Entwicklung (R&D), specific policies have been implemented
(Nedeva & Stampfer, 2012; Scherngell & Barber, 2011). The Framework Programs for
Research and Technological Development are an example of such policies.

The EU R&D system has been analyzed in depth in the literature, with contrasting results.
Hoekman, Frenken, and Tijssen (2010) and Miguelez and Moreno (2013) have found that the
bias to collaborate within the same EU country has diminished over time. Morescalchi,
Pammolli, et al. (2015) have underlined that this decrease has stopped since the mid-1990s.
Chessa, Morescalchi, et al. (2013), darüber hinaus, have highlighted that the EU integration growth
might have been driven by trends toward globalization of research more than by the aforemen-
tioned EU-specific efforts.

In this paper we study a related, though different, Problem. Tatsächlich, we aim to understand
which countries and regions contribute most to the integration of the European R&D system.

Urheberrechte ©: © 2020 Emanuele Rabosio,
Lorenzo Righetto, Alessandro Spelta,
and Fabio Pammolli. Published under a
Creative Commons Attribution 4.0
International (CC BY 4.0) Lizenz.

Die MIT-Presse

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

Our study includes both the EU and the U.S., to shed light on the role that relevant external
agents play in European integration. To the best of our knowledge, ours is the first attempt to
tackle this issue.

Networks of innovators (Orsenigo, Pammolli, & Riccaboni, 2001; Owen-Smith, Riccaboni,
et al., 2002; Powell & Grodal, 2005) can be analyzed to assess interregional connections. Wir
focus on the patent coinventorship network (Chessa et al., 2013; Morescalchi et al., 2015),
where nodes are regions, and edges are weighted by the number of coinventions occurring
between regions.

We employ the resistance distance (Klein & Randić, 1993) to measure distances within the
Netzwerk. Resistance distance takes into account the path(S) that must be covered on the net-
work to join two nodes. Auch, the resistance distance between two nodes of a network repre-
sents the expected time that a random walk needs to move from the first node to the second
eins (von Luxburg, Radl, & Hein, 2010). In unserem Fall, this measure can be considered as a proxy
of the velocity of the information flow (Stephenson & Zelen, 1989) along the network, welche
takes into account not only the shortest paths between the nodes (Goddard & Oellermann,
2011) but also longer ones, because information may flow indirectly on the network also
on these paths (Bozzo & Franceschet, 2013).

To evaluate the contribution of individual countries and regions to EU integration (d.h., their
integration capability), we first define an indicator of EU integration on the basis of the close-
ness centrality between EU regions belonging to different countries in the technological col-
laboration network. Dann, the integration capability of a country or region is quantified by
measuring the difference in the indicator value when that same country or region is removed
from the network. Our analyses are focused on patent data and therefore, as discussed in
Arora, Belenzon, and Patacconi (2018), Arora, Belenzon, et al. (2019), and Arora, Fosfuri,
and Gambardella (2004), are biased toward development activities rather than toward research
Aktivitäten. As a consequence, the knowledge flows that we are investigating are more related
to technological knowledge than to scientific knowledge.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1.1. Summary of the Results

Our main findings are the following:

(cid:129) The countries exhibiting the largest contribution to EU R&D integration are Germany
und die Vereinigten Staaten, with the latter being more relevant than most EU countries.
(cid:129) In diesem Kontext, we find that a considerable fraction of the regions that are most relevant
for EU R&D integration are located in the United States, rather than within EU borders.
(cid:129) The smallest EU countries turn out to be those benefiting most from the U.S. contribution

to establish an indirect connection to other EU countries.

1.2. Paper Structure

The paper is organized as follows. Abschnitt 2 summarizes the previous studies on the border
and distance effects on the intensity of collaborations. Abschnitt 3 describes the Regpat data set
that has been employed in this work, and introduces the indicator we use to measure the in-
tegration capability. Abschnitt 4 shows a set of analyses on the coinventor network. Erste, Wir
propose some descriptive statistics and pictures, to provide an initial understanding of the
structure of the network (section 4.1). Zweite, the integration capability of countries (section 4.2)
and individual regions (section 4.3) is analyzed. Dritte, the previous results are deepened to

Quantitative Science Studies

895

The role of U.S. regions in promoting the integration of the European research system

understand which EU countries rely most on the United States to connect to other EU
Länder (section 4.4). Endlich, section 5 concludes the paper.

2. BACKGROUND

In den vergangenen Jahren, several studies have analyzed the effects of geography on R&D collaborations.
Insbesondere, the intensity of R&D collaborations between regions (d.h., their “R&D closeness”)
has been studied based on geographical distance and on belonging to the same country. Der
intuition suggests that in a globalized world, where low transport costs, ICT facilities, Und
widespread knowledge of the English language are making communication between widely
separated people easier, geographical factors should play a marginal role in determining the
collaboration intensity between two regions (Frenken, Hoekman, et al., 2009; Singh & Marx,
2013). Jedoch, the analyses proposed so far in the literature, relying on different data and
Werkzeuge, have produced conflicting conclusions.

Among the papers supporting a decrease in the importance of geographical factors over
Zeit, Brun, Carrère, Guillaumont, et al. (2005) consider the trade scenario; the authors pro-
pose a gravity model generated from data of the United Nations Commodity Trade Statistics,
where the effect of physical distance on the trade volume between countries is shown to di-
minish over time. Waltman, Tijssen, and van Eck (2011), in contrast, consider Web of Science
(WoS) data on scientific publications, and compute for each paper the greatest distance be-
tween the addresses of the authors; they observe that, in spite of differences between scientific
sectors, there is a clear trend of increasing distance over time.

Other studies, Jedoch, claim alternative evidence. Ponds (2009) studies international col-
laborations employing a probit regression on copublication data involving Dutch institutions;
he finds that these collaborations grow, but at the same pace as the national ones. Maisonobe,
Eckert, et al. (2016) build a copublication network between cities using data from the Science
Citation Index Expanded, and find that in most countries domestic collaborations grow faster
than international ones.

In the EU, an increase in collaborations between countries might be favored not only by the
trend toward globalization of research, but also by the specific policies undertaken. Hoekman
et al. (2010) apply a gravity model to copublication data from WoS, finding that the bias to-
ward collaborating with partners from the same EU country decreases over time, while the bias
toward cooperators that are geographically close does not. Miguelez and Moreno (2013) em-
ploy a gravity model to study the patent regional coinventor network; similar to Hoekman
et al. (2010), they find that the importance of belonging to the same country diminishes over
Zeit, while the distance effect actually grows. Chessa et al. (2013) propose difference-in-
differences estimates on four regional networks, concluding that integration between EU coun-
tries is growing, but no more than one would expect due to research globalization trends.
Morescalchi et al. (2015) claim, through a gravity model on patent regional networks, that dis-
tance and country effects within the EU decreased only until the mid-1990s. Another gravity
model for patent data is introduced by Cappelli and Montobbio (2016), who share the view that
the effects of distance and national borders within the EU are decreasing over time. Endlich,
Doria Arrieta, Pammolli, and Petersen (2017), using publications data, show that the 2004/
2007 EU enlargement has had a negative impact on cross-border collaborations.

The above results, though conflicting in some respects, show signs of a pattern toward high
R&D integration within the EU, while the effectiveness of European policies has not been fully

Quantitative Science Studies

896

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

Tisch 1. Basic statistics on the Regpat data set

# patents

# Regionen

# Länder

# coinvented patents with inventors from different regions

# coinvented patents with inventors from different regions

that are also coassigned

3,175,990

5,520

48

1,171,993

112,915

demonstrated. In this work we study EU integration from a different point of view. We intro-
duce a different way to measure the R&D closeness between regions, not relying only on the
intensity of direct collaborations (z.B., number of coinventorships or coauthorships) but con-
sidering also indirect connections. The introduction of an indirect measure allows us to under-
stand which countries and regions provide the greatest contribution to EU integration, fostering
the connection of EU countries and regions.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

3. DATA AND METHODS

3.1. Data

The data employed in this study are drawn from the OECD Regpat database (Marsch 2018 ver-
sion), containing all patent applications filed with the European Patent Office (EPO). Each pat-
ent is associated with its inventors, whose geographic location, in terms of NUTS3 regions, Ist
also known. Tisch 1 reports some basic statistics related to the Regpat data set. Note that only
9.6% of the patents that are coinvented by inventors coming from different regions are also
coassigned to multiple institutions. This happens because many coinventor relations are re-
ferred to inventors working in different subsidiaries of multinational firms. daher, Die
coinventorship network reflects for a relevant part the organization of work between firms
and their subsidiaries. Trotzdem, we are interested in patterns of knowledge flows between regions,
so we maintain that the embedding of new knowledge in the collaborating regions is relevant
irrespectively of institutional boundaries.

The data set globally contains 5,520 Regionen, but in our analyses we consider just those
belonging to the EU-15 countries1 (1,067 Regionen) und die Vereinigten Staaten (3,144 Regionen).
We restrict the analysis to the EU-15 countries because they have been part of the
European Union for the longest time, and thus have been more significantly involved in its
policies. The remaining EU countries have been in the Union only since 2004 oder später (d.h.,
no more than 17.1% of the total time span considered in this work), which to us appears to be
too little to include them in a study on EU R&D integration.2 In Figure 1 we plot the number of
patents by year from 1980 Zu 2014, considering patents including at least one U.S. inventor
and patents including at least one EU-15 inventor; in both cases the number is steadily
increasing.

1 Österreich (AT), Belgien (BE), Denmark (DK), Finland (FI), Frankreich (FR), Deutschland (DE), Greece (GR), Ireland
(IE), Italien (IT), Luxembourg (LU), Niederlande (NL), Portugal (PT), Spanien (ES), Schweden (SE), Großbritannien
(Vereinigtes Königreich).

2 We have also performed experiments considering the EU-28 instead of the EU-15, and the results do not

show remarkable differences with respect to those obtained using EU-15.

Quantitative Science Studies

897

The role of U.S. regions in promoting the integration of the European research system

Figur 1. Number of patents by year, aus 1980 Zu 2014.

These data are used to build the coinventor geographic network, referred to specific time
periods. In these networks nodes are constituted by NUTS3 regions, while the weight wij(T)
of the edge joining the nodes i and j in the network at time t is given by the number of
coinventions happened between the i and j regions in the time period t. In our work the
time period t will be represented by one of the intervals 1980–1989, 1990–1999, 2000–2009,
and 2010–2014, or by individual years. Tisch 2 shows the number of edges and the sum of
the weights in the networks related to 1980–1989, 1990–1999, and 2000–2009; we omit the
latest period (2010–2014) because it is shorter. Like the number of patents, the values of these
indicators are remarkably also growing with time.

3.2. Methoden

In this section we illustrate the main methods and techniques used to carry out the analyses.
Erste, the resistance distance is introduced (section 3.2.1). Dann, we describe our measures
of integration capability (section 3.2.2) and how we use null models to support our claims
(section 3.2.3). Endlich, changepoint detection is explained (section 3.2.4).

3.2.1. Resistance distance

The distance dij between two nodes i and j of the network, representing how difficult the in-
formation flow is between the corresponding regions, is measured as the resistance distance
(Klein & Randić, 1993), which is defined as the effective (electrical) resistance between the two
nodes when each edge is associated with a conductance equal to its weight. Let L be the
Laplacian matrix3 of the network and L+ its Moore–Penrose pseudoinverse. The resistance dis-
tance dij between nodes i and j is computed as follows (Bozzo & Franceschet, 2013):
þ
dij ¼ L
ii

þ
þ L
jj

− 2L

(1)

þ
ij

In der Praxis, to avoid infinite values for pairs of nodes belonging to disconnected components,
we work with the closeness cij, defined as the reciprocal of the resistance distance: cij = 1
dij

.

3 The Laplacian matrix of a network with adjacency matrix M is defined as D − M, where D is the diagonal

matrix whose (ich, ich) entry is the degree of the ith node (Goddard & Oellermann, 2011).

Quantitative Science Studies

898

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

Tisch 2. Number of edges and sum of the weights in the coinventor networks

Period
1980–1989

1990–1999

2000–2009

# edges
28,310

76,886

137,158

Sum of weights
236,904

848,988

2,013,473

We remark again the importance of evaluating the closeness between pairs of nodes with a
messen, like the inverse of the resistance distance, which takes into account multiple paths
joining the nodes, and not just first-order interactions. Erste, using a measure considering mul-
tiple paths joining the nodes recognizes that knowledge may also flow on the network in an
indirect, mediated way. Zweite, as we will explain in section 3.2.2, this allows us to measure
the contribution that nodes (d.h., Regionen) and sets of nodes (d.h., Länder) provide to the close-
ness of other nodes.

Note that a possible alternative closeness measure taking paths into account, as mentioned
in the introduction, is the inverse of the shortest-path distance, where the shortest-path dis-
tance between two nodes is the sum of the inverses of the weights of the edges lying on the
shortest path joining the two nodes. Jedoch, this measure is less suitable than the inverse of
the resistance distance in our scenario, because it considers only the shortest paths, neglecting
the fact that information may also flow on the network on other, longer paths.

3.2.2. Evaluation of the integration capability

The level of integration within the EU is assessed using the average cross border closeness (cid:1)C,
which is the average of the closenesses between all the pairs of regions belonging to different
EU countries:

P

(cid:1)c ¼

ich;jð

Þ:ich;j2 different EU countriescij
Þ : ich; J 2 different EU countries

J

J

ich; jð

(2)

Note that the value of (cid:1)c may be restricted to specific pairs of countries, thus measuring the
integration level between these pairs of countries.

To assess the contribution of a subset of the nodes of the network to the average cross-border
closeness (d.h., to the integration), we compute the percentage closeness loss that happens when
this subset is excluded from the network. We will exclude sets of nodes to evaluate the contri-
bution of the countries, and single nodes to evaluate the contribution of specific hubs (intended
as very relevant regions, characterized by many connections). The percentage closeness loss
associated with a region/country represents the integration capability of that region/country.

Let S be a subset of the nodes of the network. Typically, S may represent a country or a
single node. The quantity (cid:1)cS indicates the average cross-border closeness measured consider-
ing the cijs computed using paths involving the whole network, but averaged only on the re-
gions not included in S:

P

(cid:1)cS ¼

ich;jð

Þ:ich;j2= S∧i;j2different EU countriescij
Þ : ich; j 2= S∧i; J 2 different EU countries

J

ich; jð
J

(3)

Zum Beispiel, if the subset S contains the German nodes, then these nodes are not considered
in the averaging process, but the paths used to compute the cijs are allowed to pass through

Quantitative Science Studies

899

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

Deutschland; daher, we are evaluating the capability of Germany to connect regions belong-
ing to other countries.

The quantity (cid:1)cSj, in contrast, denotes the value obtained measuring (cid:1)c once the subset S has
been removed from the network, therefore excluding S from both the average and the paths
used in the computation of the cijs. (cid:1)cSj can be computed through Eq. (3), but determining the
cijs exploiting only the paths not transiting from the nodes in S. Zum Beispiel, if the subset S
again contains the German nodes, the German nodes are not considered in the average and
are not allowed to appear in the paths used in the computation of the closeness between the
pairs of nodes.

The percentage closeness loss pclS associated with subset S, representing the contribution
of subset S to European integration, is measured as the percentage of closeness that is lost
when S is removed from the network:

pclS ¼

(cid:1)cS − (cid:1)cSj
(cid:1)cS

(4)

Note that the numerator of Eq. (4) is always not negative.

Endlich, to analyze in greater depth the contribution of the United States to European inte-
gration also shortest paths are computed. The shortest path between two nodes s and t of a
network is the path between s and t such that the sum of the weights of the constituent edges is
minimized (Goddard & Oellermann, 2011). In more detail, we will consider the shortest paths
between EU nodes belonging to different countries, counting how many American nodes are
contained in these paths.

Notice that, in summary, the percentage closeness loss represents the ability of a set of
nodes to make other nodes of the network closer. daher, it is a measure for sets of nodes
that is related to two other traditional centrality measures defined instead for individual nodes:
betweenness and current-flow betweenness. The betweenness of a node is the number of
shortest paths crossing that node, while current-flow betweenness measures the extent to
which a node lies on paths between other nodes. Betweenness considers only the shortest
paths while current-flow betweenness takes into account all the paths, although longer paths
give a lesser contribution. Percentage closeness loss considers all the paths, not only the short-
est ones; daher, it is a measure referred to sets of nodes that is more similar to current-flow
betweenness.

3.2.3. Null models

To better appreciate the percentage closeness losses obtained on our networks we sometimes
compare them with those measured on null models, where the null model of a network is
another network obtained by keeping some elements constant and randomizing other ones.
In more detail, we will use three classes of null models:

(cid:129) Gravity-based null model (Expert, Evans, et al., 2011). This model is used to check whether
the detected patterns are simple effects of gravitylike forces, depending on spatial distance
and on a concept of mass. Let gij be the geographical distance between the regions asso-
ciated with nodes i and j, and Mi and Mj the masses of the nodes. The weight wNM
of the
edge (ich, J ) in the null model is defined as wNM
ich;jjgij ¼ g wij)/
P
ij
ich;jjgij ¼ g MiMj). The weight of the edge (ich, J ) grows with the mass of i and j, and with
(
the weights that in the real network are associated with the nodes geographically at the
same distance of i and j. This null model preserves neither the weights of the edges nor

= MiMjf( gij), with f( G) = (

P

ij

Quantitative Science Studies

900

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

the strength of the nodes, but maintains the total weight of the network. In our framework
the spatial distances are continuous, so it is necessary to divide them into bins. We con-
sider the mass of a node as the total number of patents produced in the corresponding
region in the time frame of interest.

(cid:129) Null model where the edges within the United States are randomly reshuffled. We con-
sider two variants of this null model: one that does not preserve the strength of the
Knoten, and one that approximately preserves it (Rubinow & Spurns, 2011). Zum Beispiel,
if in the real network the edge between Boston and Los Angeles is 100, in the null model
this weight can be assigned to the edge between Portland and Memphis. In the first var-
iant all the U.S. nodes obtain approximately the same strength. Both the variants pre-
serve the weights of the edges, which are reshuffled. The two variants of this null model
are dubbed US-INT and US-INT-STR, jeweils.

(cid:129) Null model where the EU-US connections are randomly reshuffled. We consider two
variants of this null model: The first preserves the strength (of the EU-US connections)
just for the EU nodes, while the second (etwa) preserves it for both EU and U.S.
Knoten (Rubinow & Spurns, 2011). Zum Beispiel, if in the real network the edge between
Paris and Santa Clara has weight 200, in the null model this weight can be assigned to
the edge between Paris and Anchorage. Both variants preserve the weights of the EU-US
edges, which are reshuffled. The two variants of this null model are dubbed EU-US and
EU-US-STR, jeweils.

3.2.4. Changepoint detection

In order to better appreciate the yearly variations of the percentage closeness loss we use a
technique named changepoint detection (Killick, Fearnhead, & Eckley, 2012), which identifies
the time instants (changepoints) corresponding to abrupt changes in a function. Identifying the
changepoints splits the function in sections, and in particular we split the yearly percentage
closeness loss function where the regression line changes the most. This is achieved by finding
the sections of the function such that the sum of the residual errors of the regressions in each
section is minimized.

Let x1, … , xn be the points of the function that we are studying, and let SSx1,…,xi be the
residual error associated with the regression line approximating the function in the points
x1, … , xi. The changepoint detection procedure finds the time instants m1, … , mk minimizing
the following metric:

J ¼ SSx1;…;xm1−1

þ SSxm1

;…;xm2 −1

þ … þ SSxmk

;…;xn

(5)

Note that adding more changepoints keeps reducing the metric value. To cope with this prob-
lem, the procedure rejects further candidates when the decrease of the value of J provided by
the new candidate is lower than a given threshold. In this work the threshold has been set to
twice the variance of the function, meaning that we stop adding changepoints when the
subsequent new one would increase the R2 determination coefficient of the regression by
less than 2/n.

4. ERGEBNISSE

In this section we show the results of our analyses on the coinventorship network. We begin by
providing some preliminary statistics and pictures (section 4.1), and then we analyze the in-
tegration capability of countries (section 4.2) and of individual regions (section 4.3). Endlich,

Quantitative Science Studies

901

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

we study in more detail the impact of the United States on the closeness of the individual EU
countries to the other EU countries (section 4.4).

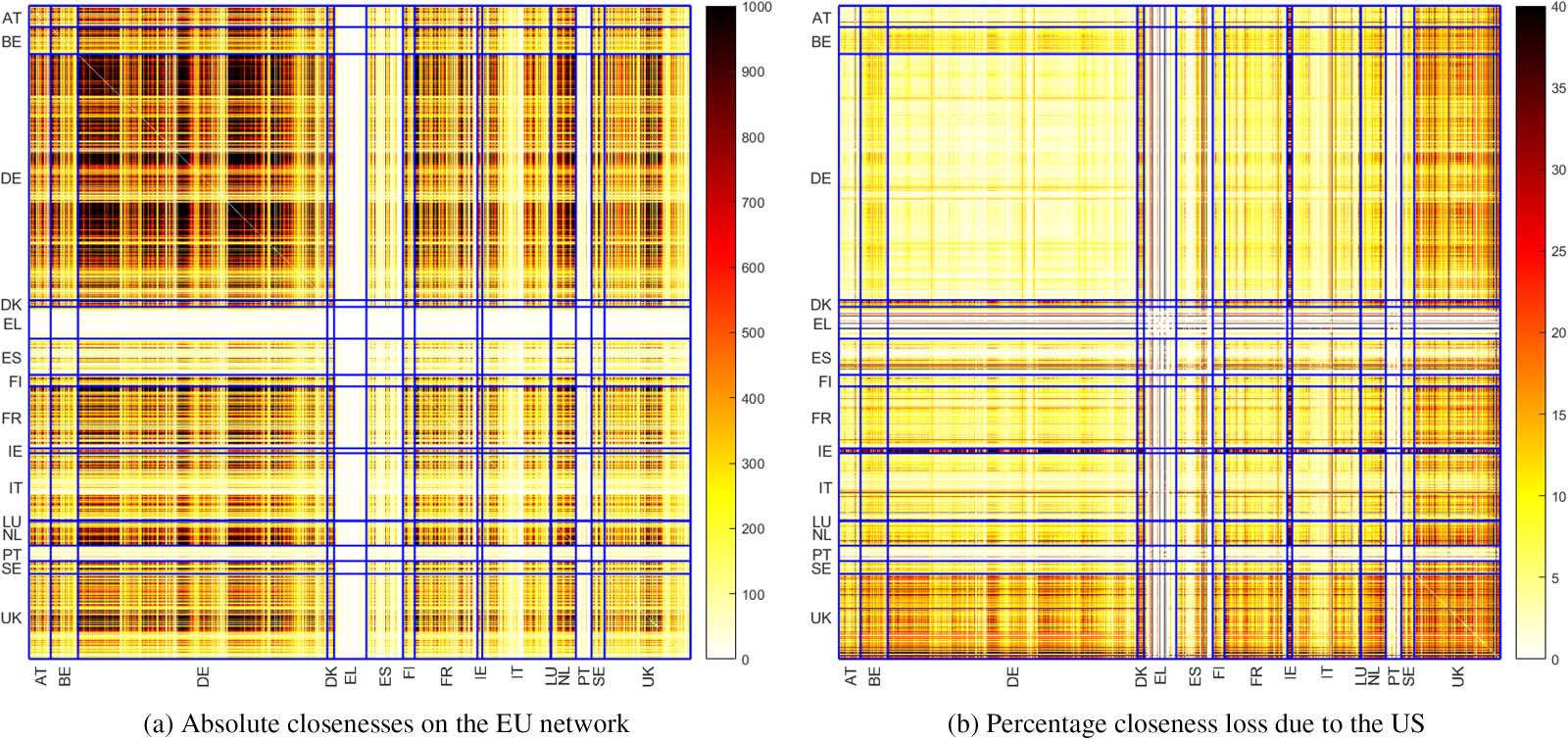
4.1. Descriptives

In this section we show some preliminary statistics and illustrations to provide an initial un-
derstanding of the structure of the coinventor network. Insbesondere, we want to highlight the
features of the national subnetworks and of the hubs.

Tisch 3 contains some statistics related to the national subnetworks in the 2000–2009 pe-
Riod. For each country we report the number of nodes, the number of nodes with 250 or more
patents, and the average closeness (computed as the inverse of the resistance distance) Sei-
tween the pairs of nodes associated with 250 or more patents. We have computed this average
considering only the nodes associated with a certain number of patents because the other ones
are not likely to appear in effective paths joining EU regions belonging to different countries.
The average closeness between U.S. nodes is 78% greater than that of the EU (see the last two
lines of the table).

We can also see the greater number of connections existing in the U.S. subnetwork with
respect to the EU ones pictorially in Figure 2, where the network contains a node for each

Tisch 3. Statistics related to the national subnetworks in the 2000–2009 period

Country
Österreich

Belgien

Denmark

Finland

Frankreich

Deutschland

Greece

Ireland

Italien

Luxembourg

Niederlande

Portugal

Spanien

Schweden

Vereinigtes Königreich

Vereinigte Staaten

EU

# Knoten
35

# nodes ≥ 250 patents
13

Average closeness between
nodes ≥ 250 patents
328.29

44

11

19

101

402

52

8

110

1

40

25

59

21

139

3,144

1,067

12

9

5

41

161

0

4

38

1

20

1

8

11

43

171

367

967.63

1,063.58

1,152.65

1,049.89

1,611.08

/

341.95

418.95

/

878.54

/

249.71

525.56

597.95

1,953.46

1,100.22

Quantitative Science Studies

902

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The role of U.S. regions in promoting the integration of the European research system

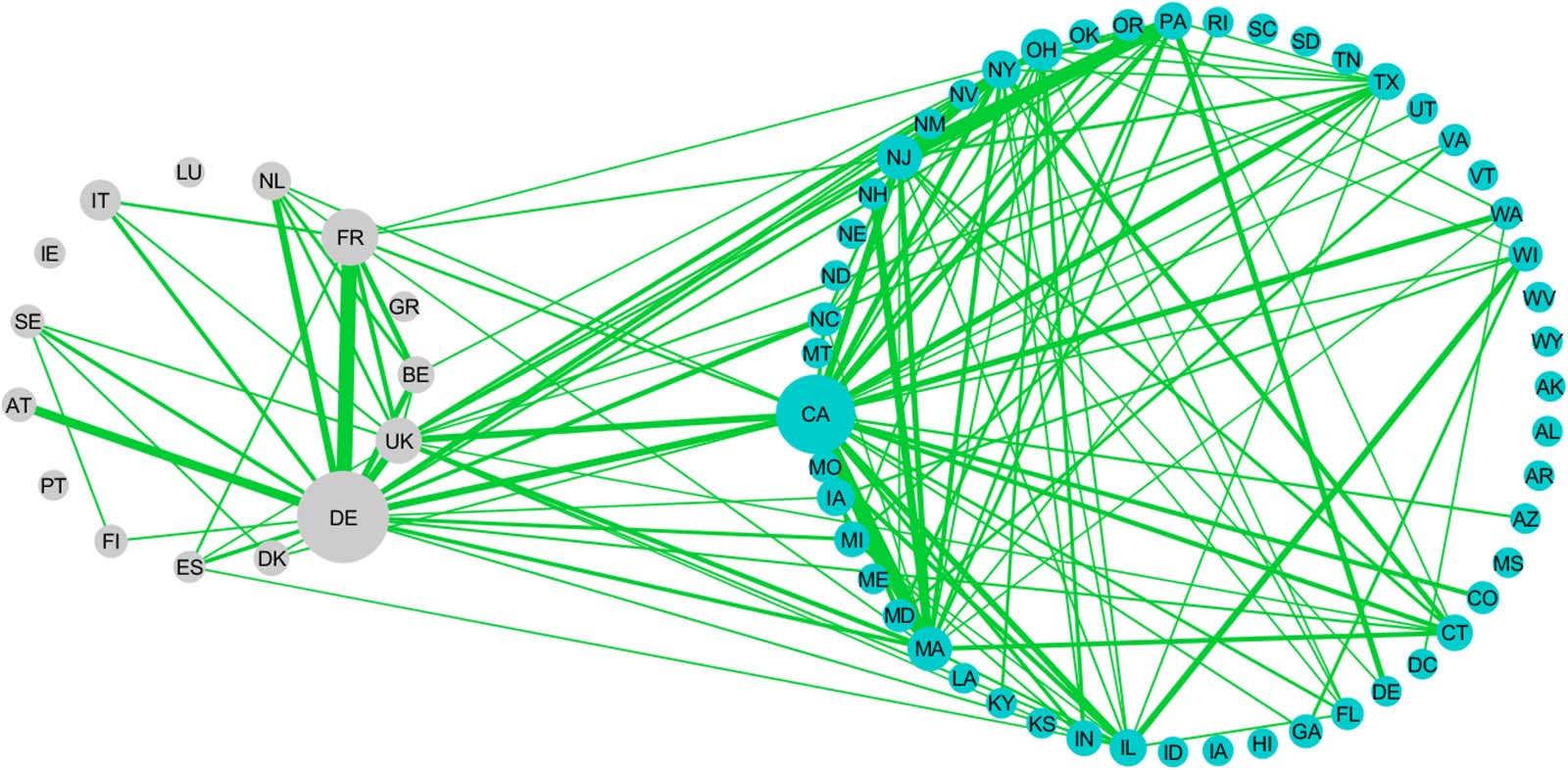
Figur 2.
weights of the edges in the national subnetworks, while the edge thickness is proportional to the number of coinventions.

EU-US coinventorship network. Nodes are EU countries (grau) und wir. Staaten (Blau). The node size is proportional to the sum of the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

country, but we have decided to decompose the United States into the component states; nur
the edges representing at least 500 coinventions are included. The edge thickness is propor-
tional to the number of coinventions and the size of the nodes is proportional to the sum of the
weights in the national subnetwork. The figure allows us to appreciate the links between the
UNS. Staaten, whereas the EU countries are less connected.

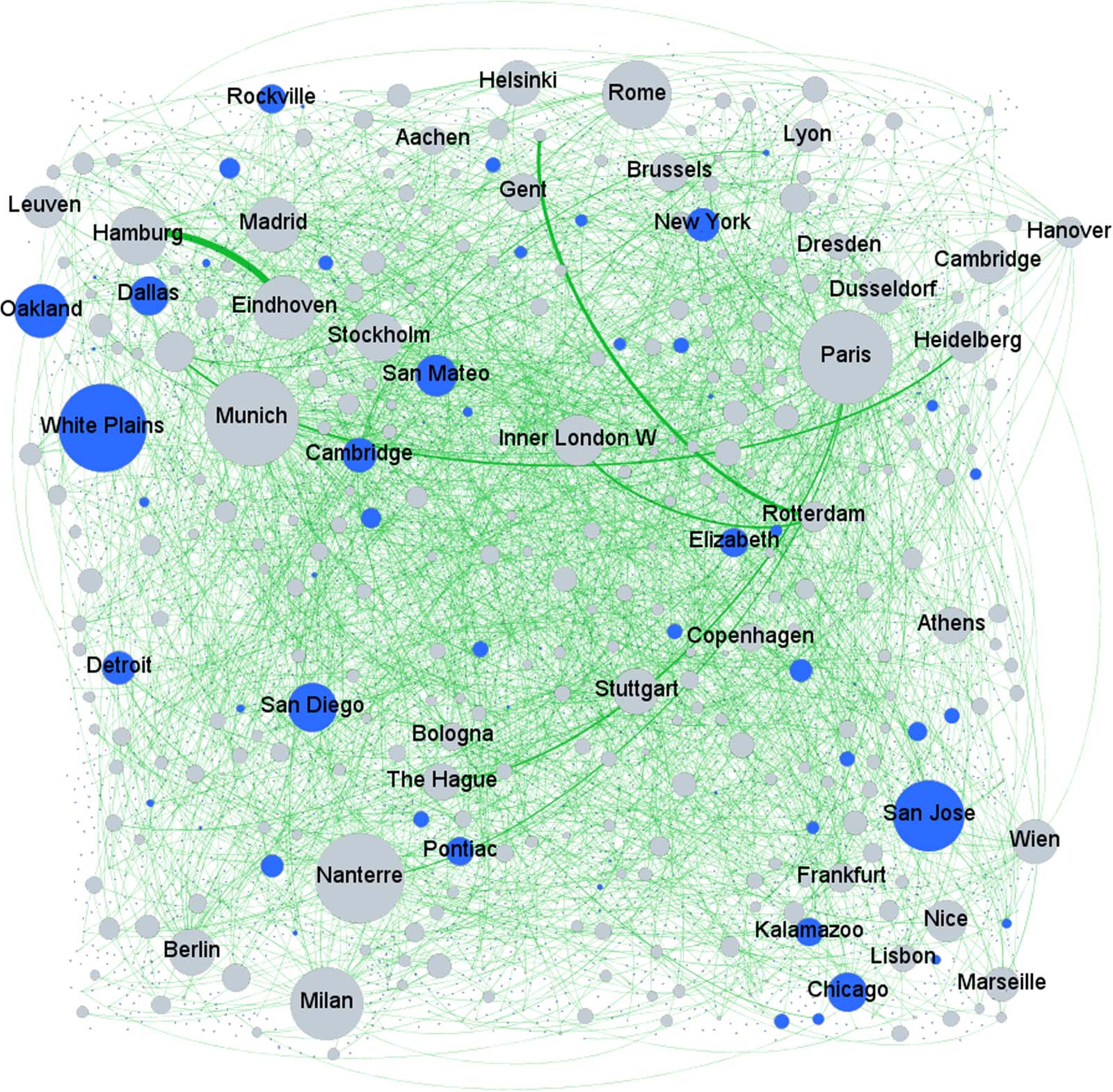
Endlich, Figur 3 represents the shortest paths connecting EU nodes belonging to different
countries in the 2000–2009 period. The figure shows the edges that are part of at least one
shortest path joining two regions belonging to different EU countries. The edge thickness
grows with the edge weight, while the node size grows with the betweenness, computed con-
sidering only the shortest paths joining EU nodes belonging to different countries. The figure is
quite difficult to read due to the size of the network, but in any case allows us to understand
Das, even when considering only the paths joining different EU regions, there emerge a sig-
nificant share of relevant hubs that are within the United States and not in the EU itself.

Summarizing, this preliminary analysis suggests that the U.S. subnetwork contains many
nodes associated with a relevant number of patents, and that these nodes are more connected
between each other than happens in the European national subnetworks. So it seems plausible
that the U.S. subnetwork as a whole might provide a faster, though indirect, connection be-
tween EU regions. Darüber hinaus, we can note that there are several nodes from both the EU and
the United States that are crossed by many shortest paths joining EU nodes belonging to dif-
ferent countries. Wieder, it seems worthwhile to investigate the relative importance of U.S. Und
EU hubs in making the EU R&D system more integrated.

4.2. The Integration Capability of the Countries

In this section we will use the procedure described in section 3.2 to show which countries
(among the EU countries and the United States) have the greatest integration capability; Das
Ist, contribute the most to increasing the closeness between the EU regions belonging to differ-
ent countries.

To measure the integration capability of a country, the formulas of section 3.2 are applied
considering the subset S to be excluded as the set of the nodes belonging to that country. In

Quantitative Science Studies

903

The role of U.S. regions in promoting the integration of the European research system

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 3. EU-US network representing the shortest paths between EU regions belonging to different countries. EU regions are grey, while U.S.
regions are blue. The node size is proportional to the betweenness computed considering only the shortest paths joining EU nodes belonging
to different countries, while the edge thickness is proportional to the edge weight.

this way the value resulting from Eq. (4) gives the percentage closeness loss due to the removal
of the country; the greater this percentage, the greater the integration capability of the country.

Tisch 4 shows the integration capability for each EU country and for the United States. Der
analyzed years are divided into four periods: 1980–1989, 1990–1999, 2000–2009, and 2010–2014.
The main feature that emerges from the table is that Germany and the United States are by far
the countries with the greatest capability to connect the EU countries. Notice that the United
States exhibits a large contribution to European R&D integration, greater than that shown by the
European countries themselves. On the one hand this is due to the larger population—the
population of the United States is, zum Beispiel, almost five times that of France—providing
more possibilities to establish collaborations, but on the other hand it indicates that the
United States plays a fundamental role in the European R&D system. In der Tat, a large pop-
ulation alone is not enough to develop joint R&D projects.

We want now to understand whether the measured integration capabilities are just the re-
sult of simple gravitylike forces (d.h., mass and distance effects), or are due to more complex

Quantitative Science Studies

904

The role of U.S. regions in promoting the integration of the European research system

Tisch 4. Percentage of the average cross-border closeness within the EU that is lost by excluding the
United States or the individual EU countries from the coinventor network

1980–1989
0.6452

1990–1999
0.4743

2000–2009
0.6208

2010–2014
0.7867

Country
Österreich

Belgien

Denmark

Finland

Frankreich

1.2581

0.4091

0.1573

2.8053

Deutschland

11.0070

Greece

Ireland

Italien

Luxembourg

Niederlande

Portugal

Spanien

Schweden

Vereinigtes Königreich

USA

0.0292

0.0808

0.7154

0.2478

1.726

0.0207

0.0896

1.0132

3.2244

7.4903

1.6850

0.4994

0.5247

3.1101

1.6606

0.5785

0.4984

3.3041

10.3100

10.5810

1.4251

0.4519

0.3668

2.8239

9.3136

0.0314

0.1452

0.8928

0.2378

1.5439

0.0304

0.3417

0.8602

2.7337

0.0882

0.2163

0.9290

0.2688

1.4793

0.0874

0.7870

0.9544

2.6222

10.4740

10.7590

0.0639

0.2317

1.068

0.2895

1.2793

0.1040

0.8800

1.0464

2.3039

9.9570

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Dynamik (z.B., different propensity to long-distance collaborations). To this aim, the gravity
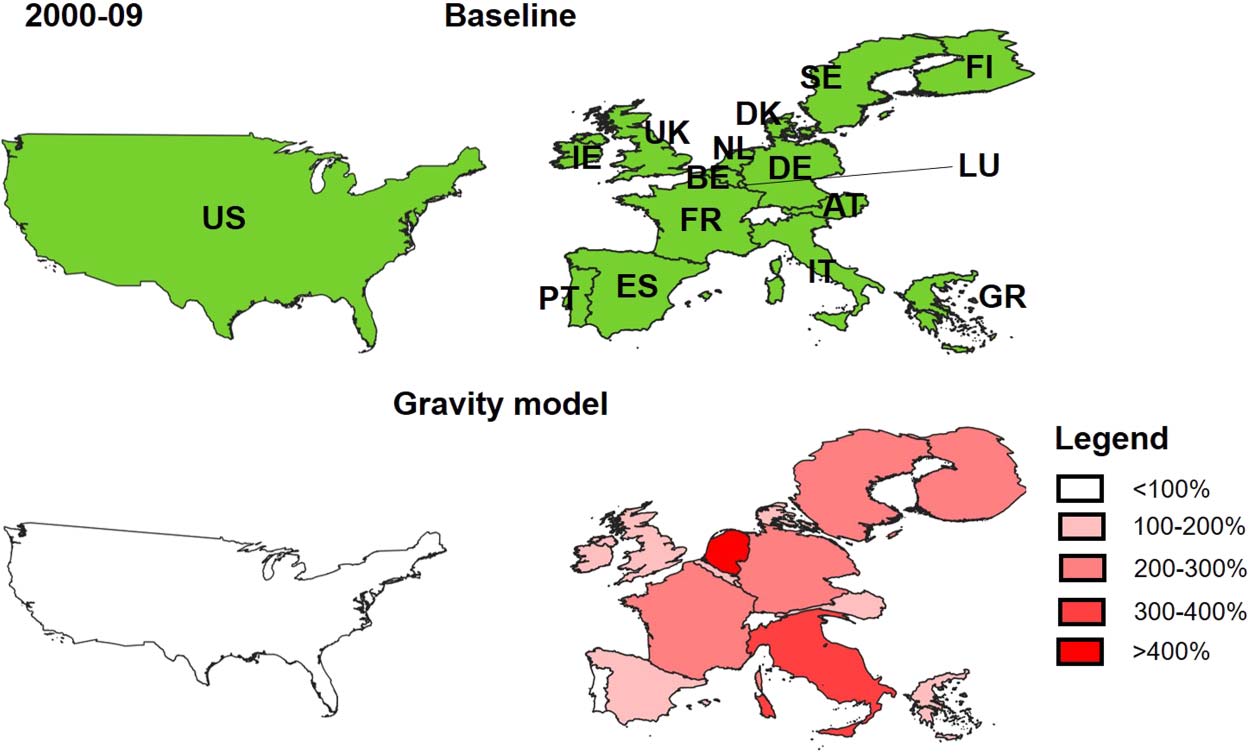
null model, introduced in section 3.2, is employed. The integration capabilities observed using
the gravity model are in Table 5, reported as differences with respect to the values observed
in the real network, while Figure 4 provides a pictorial representation of the comparison be-
tween the real network and the gravity null model referred to the 2000–2009 period. We note
that when the gravity model is used, almost all the European countries show an integration
capability that is greater than that observed in the real network (d.h., they contribute to
European integration less than is expected due to simple mass-distance effects); zum Beispiel,
Germany would be 2.5 times more important if R&D collaborations only depended on mass
and distance. Im Gegensatz, the United States exhibits an integration capability that is greater than
the amount due to gravity.

In order to further investigate the role of the United States in the EU R&D system and try to
understand the nature of the connections linking Europe and the United States, we make use of
a more straightforward measure of distance along the network (d.h., shortest paths) and we
employ null models disrupting some portions of the network (internal U.S. network and EU-
US connections) to assess their relative importance.

In the first place, we have determined all the shortest paths joining EU regions belonging
to different countries, and classified them on the basis of the number of U.S. regions that are
enthalten. The second column of Table 6 reports the shortest paths statistics related to the real
network in the 2000–2009 period (for brevity, the other periods follow a similar pattern). UNS.

Quantitative Science Studies

905

The role of U.S. regions in promoting the integration of the European research system

Tisch 5. Percentage of the average cross-border closeness within the EU that is lost by excluding the
United States or the individual EU countries from the coinventor network on the gravity null model.
The results are reported as differences with respect to the real coinventor network

Country
Österreich

Belgien

Denmark

Finland

Frankreich

1980–1989
+0.4191

1990–1999
+0.6404

2000–2009
+0.5965

2010–2014
+0.8478

+0.1100

+0.0951

+0.4314

+5.4822

+0.2641

+0.3354

+0.7692

+4.9078

+0.2400

+0.4880

+0.9484

+3.9589

+0.4878

+0.5462

+0.8673

+5.1109

Deutschland

+16.7832

+17.8759

+16.2197

+15.9801

Greece

Ireland

Italien

Luxembourg

Niederlande

Portugal

Spanien

Schweden

Vereinigtes Königreich

USA

+0.0130

+0.0042

+2.0169

+0.0022

+4.3309

−0.0087

+0.1805

+1.4089

+3.0774

−3.4335

+0.0341

+0.0379

+2.4311

−0.0179

+4.5983

+0.0063

+0.1970

+1.4092

+2.2613

−3.1522

+0.0036

+0.1101

+2.3147

+0.1055

+5.9839

−0.0167

+0.0560

+1.5709

+1.1042

−2.4052

+0.0140

+0.1464

+1.8654

+0.2347

+5.1791

−0.0204

+0.1986

+1.5873

+0.9792

−2.0788

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
Q
S
S
/
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

1
2
8
9
4
1
8
8
5
7
7
4
Q
S
S
_
A
_
0
0
0
3
4
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 4. Regular and thematic map of the countries under study (EU-15 + US). In the latter case,
the deformation and the color code represent the ratio between the percentage loss in the average
closeness within the EU when links are rewired according to a gravity-law null model (see text for
Einzelheiten) over observations in the 2000–2009 period. Zum Beispiel, countries in white have less im-
portance in the null model case with respect to the observed one.

Quantitative Science Studies

906

The role of U.S. regions in promoting the integration of the European research system

Tisch 6. Percentage of shortest paths between EU regions belonging to different countries, including U.S. Regionen, classified by number of U.S.
regions included in the 2000–2009 period, in the real network and null models. The data values related to the null models are expressed as
differences with respect to the real network. The double asterisks (**) indicate that all the differences, except one, are statistically significant
at p < 0.01 % sp ≥1 USA node % sp 1 USA node % sp 2 USA nodes % sp 3 USA nodes % sp >3 USA nodes

Real network
57.7635

5.0215

18.9355

9.7906

24.0159

US-INT
−24.3377**

+22.5199**

−13.3102**

−9.5757**

−23.9717**

US-INT-STR
+6.7447**

−2.4165**

−11.9037**

+11.9008**

+9.1641**

EU-US
−52.4168**

−2.9377**

−18.6610**

−9.4098**

−21.4084**

EU-US-STR
+2.0894**

+15.4171**

+1.7815**

+0.5475

−15.6567**

regions participate in more than half of the intra-EU cross-border shortest paths, thus confirming
the importance of the United States in the EU R&D system. Interessant, as we sensed from
Figur 2, many shortest paths include several U.S. Knoten (24% of the shortest paths include
more than three U.S. Knoten), and this confirms that since the U.S. subnetwork contains many
internal connections, the most convenient way to link two EU regions is often to move to the U.S.
subnetwork, cover “cheap” paths inside this subnetwork, and find the most appropriate node to exit.

Let us consider the two classes of nongravity null models introduced in section 3.2: Der erste
class randomizes the connections inside the United States, while the second one randomizes the
connections between EU and U.S. Knoten. Daher, the first class allows us to evaluate the relevance
to the EU integration of the connections internal to the United States, while the latter permits us to
assess the importance of the EU-U.S. connections. Columns 3 Zu 6 of Table 6 contain the results
of the shortest path analysis for the null models (2000–2009 period), while Table 7 zeigt die
percentage closeness loss for the null models. All the values reported for the null models are
obtained by repeating the random generation of the models 100 times and then averaging the
measurements. The tables indicate the differences with respect to the results obtained with the
real network. We have performed a t-test to evaluate the statistical significance of the differ-
zen; all the values in Tables 6 Und 7 are statistically significant with p-values << 0.01, except for one value in Table 6. Regarding the class of null models reshuffling the U.S. internal connections, the first variant preserves just the weights of the network, while the second one also maintains the strengths of the nodes (i.e., it preserves the hubs within the U.S. subnetwork). First, we note that the U.S. integration capability in terms of resistance distance remains almost constant in both variants. Table 7. Percentage of the average cross-border closeness within the EU that is lost by excluding the United States from the coinventor network on the null models, expressed as difference with respect to the values observed on the real network. The double asterisks (**) indicate that all the differences are statistically significant at p < 0.01 1980–1989 1990–1999 2000–2009 2010–2014 US-INT −0.4737** −0.4150** −0.1736** −0.2280** US-INT-STR −0.0065** −0.0034** −0.0201** −0.0219** EU-US −3.2818** −2.8326** −1.9164** −2.4482** EU-US-STR −0.3502** −0.7904** −0.8137** −0.8394** 907 Quantitative Science Studies l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. regions in promoting the integration of the European research system This happens because the U.S. subnetwork has many nodes and edges, and therefore reshuf- fling the connections leaves, in both cases, good paths between the pairs of U.S. nodes; this confirms that the great number of connections in the U.S. subnetwork helps join the EU regions. However, the second null model exhibits a performance that is more similar to that of the real case, thus suggesting that the presence of strong U.S. hubs facilitating the links is also important. When we analyze the effect of null models on shortest paths, which are more sensitive than the resistance distance to changes in the network, these considerations are reinforced: On the first null model, the number of shortest paths transiting from the United States falls with respect to the real situation, while on the second null model it even grows. This behavior seems to indi- cate again the importance of the hubs, confirming the intuitive evidence of Figure 3. The growth of the number of shortest paths with U.S. nodes in the second null model is probably due to the fact that once the hubs are preserved, a more balanced distribution of the weights to the edges helps find better paths. The relevance of the U.S. hubs is confirmed also by the last class of null models: those reshuf- fling the EU-US connections. The first null model of this class does the reshuffling by preserving the strength of the transatlantic connections just for the EU nodes, while the second one preserves this strength also for the U.S. nodes. The second null model behaves similarly to the real situa- tion, while in the first one the U.S. contribution to EU integration decreases; this suggests that it is not enough to connect to the U.S. network, it must be done through the right access points. Finally, we conduct a finer-grained temporal analysis to shed further light on the variations of the U.S. contribution that emerged in the four decades by using yearly networks. We want to assess whether the U.S. integration capability has evolved over time following a steady trend, or the tendency has changed through time. To do this, we employ changepoint detec- tion analysis. In brief, this method allows us to retrieve the optimal set of linear slope change- points to model the observed data (see section 3.2.4 for details), thus discovering the possible changes in the trend of the magnitude of the U.S. integration capability. We apply the method to the pattern of yearly percentage closeness loss in the EU network due to collaborations with the United States, with the aim of identifying the years in which the trend of growth or decrease of the U.S. contribution to the EU integration has changed significantly. 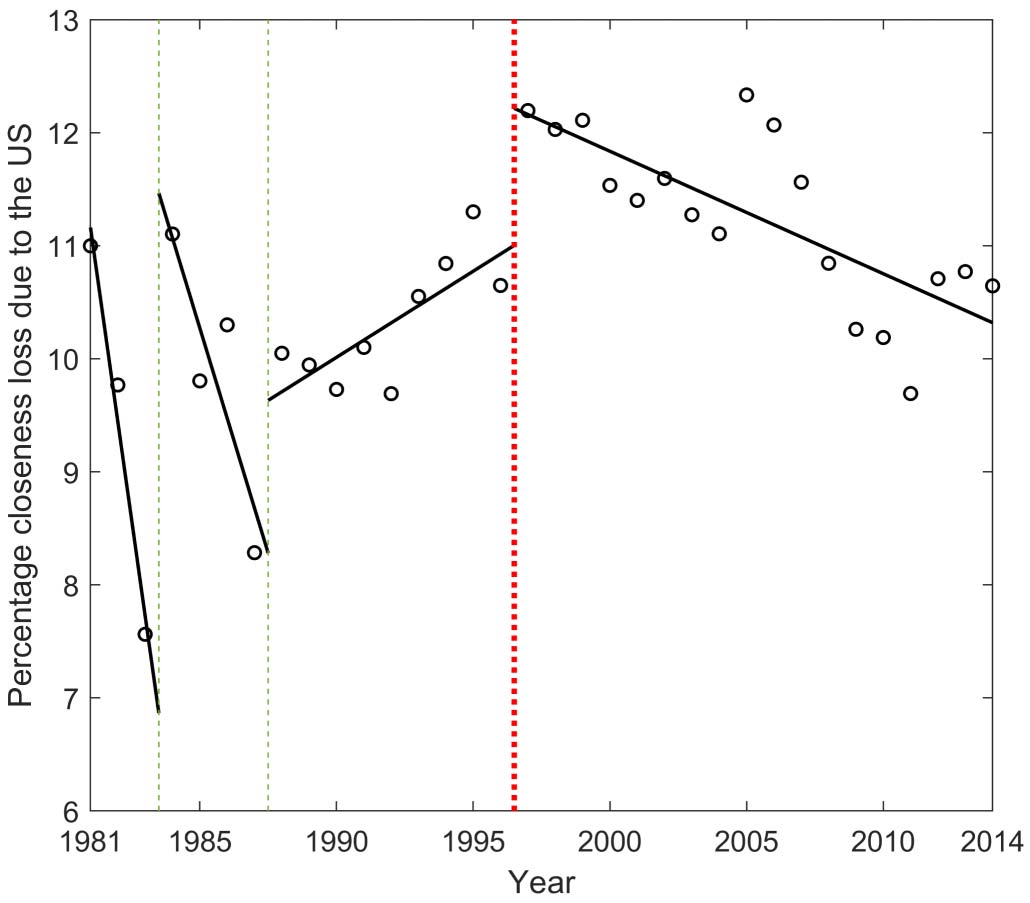We have considered the years from 1981 to 2014, omitting 1980, which is associated with few data. The resulting plot is in Figure 5(a). The changepoint associated with the greatest reduction of the residual error of the regression is detected in 1997 (highlighted in red in Figure 5); then, two more changepoints are identified in 1983 and 1987. Interestingly, before 1997 the U.S. contribution shows, globally, a positive trend, while after 1997 there is a long period with a clearly negative trend. Figure 5(b) shows the R2 and p-values of the discovered regressions; note that the last two regressions, which are those of greatest interest, are significant at p < 0.05. It can be seen that the latter result is consistent with the evidence shown by Chessa et al. (2013), who have highlighted that EU integration, in the same case of coinventorship, has ex- perienced growth starting in the years before 2000. Also, they find that the integration level has subsequently stabilized. Our changepoint detection analysis identifies a clear inversion of the tendency in the U.S. contribution to EU integration in the same period, which then started to decrease. Therefore, the growth of the EU integration level found by Chessa et al. (2013) seems to be reflected in a progressive emancipation of the EU from the U.S. R&D system. In this respect, we point out the possible role of EU policies, characterized by increasing financing of R&D programs, fostering intra-EU collaborations. Summarizing this section, we find that Germany and the United States provide the highest contribution to connect the EU countries. In particular, the United States has a more significant Quantitative Science Studies 908 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. regions in promoting the integration of the European research system l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5. (a) Yearly percentage closeness loss due to the United States, between 1981 and 2014. The dashed vertical lines indicate the identified changepoints, while the regression lines in the sections delimited by the changepoints are in solid black. (b) R2 and p-values of the discovered regressions. impact than most European countries. Our analyses indicate that two important factors that make the United States able to help connect the EU regions are represented by the high num- ber of links in the internal U.S. network and the presence of U.S. hubs: To connect two EU nodes it is enough that these two nodes are close to two distinct American nodes, which may then usually be easily linked through a path within the U.S. subnetwork especially, due to the help of effective internal hubs. Finally, we observe that the U.S. contribution to EU integration seems to have been decreasing since 1997. 4.3. The Integration Capability of the Hubs In this section we appraise the integration capability of individual hubs. Studying individual nodes is interesting, because they are much more similar in terms of population than the coun- tries, thus leading to less biased analysis results. Quantitative Science Studies 909 The role of U.S. regions in promoting the integration of the European research system Table 8. Percentage of the average cross-border closeness that is lost by excluding the 10 EU and 10 U.S. (italicized) main hubs from the coinventor network (closenesses between pairs of nodes including a node in the same country of the hub not considered in the computation) Region (a) 1980–1989 Integration capability Aachen Berlin Munich Biberach Wuppertal Houston, TX San Jose, CA Milan Stockholm Mettmann Vienna Paris Cambridge, MA Oakland, CA San Mateo, CA San Diego, CA Chicago, IL Elizabeth, NJ San Francisco, CA White Plains, NY (c) 2000–2009 Cambridge, MA Munich San Jose, CA Berlin Helsinki San Diego, CA Aachen 0.6701 0.5640 0.4052 0.3431 0.3106 0.3037 0.2956 0.2743 0.2620 0.2542 0.2295 0.2191 0.2152 0.1549 0.1545 0.1427 0.1337 0.1256 0.1245 0.1159 0.4612 0.4480 0.3727 0.3527 0.3179 0.3155 Region (b) 1990–1999 Rockville, MD Cambridge, MA Munich San Diego, CA Paris Cincinnati, OH San Jose, CA Berlin Rotterdam Bad Homburg Stockholm Hamilton, OH Helsinki Norristown, PA Houston, TX Milan Cambridge Nanterre Raleigh, NC San Mateo, CA (d) 2010–2014 Cambridge, MA San Jose, CA Munich Aachen Helsinki Stockholm l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Integration capability 0.3738 0.3360 0.3272 0.3133 0.3038 0.2872 0.2758 0.2753 0.2691 0.2436 0.2364 0.2287 0.2221 0.2211 0.2163 0.2095 0.2047 0.2036 0.1516 0.1424 0.4432 0.4220 0.3957 0.3648 0.3193 0.3090 0.2980 0.31316 Frankfurt Quantitative Science Studies 910 The role of U.S. regions in promoting the integration of the European research system Table 8. (continued ) Region Stockholm Madrid Houston, TX Paris Brussels Barcelona Lyon San Mateo, CA Oakland, CA Cincinnati, OH Norristown, PA Raleigh, NC Chicago, IL Integration capability 0.3023 Region Berlin Integration capability 0.2919 0.2828 0.2375 0.2332 0.2219 0.2187 0.2167 0.2159 0.1735 0.1597 0.1573 0.1572 0.1371 San Diego, CA Malmo Barcelona Lyon Houston, TX San Mateo, CA Paris Oakland, CA Raleigh, NC Midland, OH Cincinnati, OH Norristown, NJ 0.2805 0.2765 0.2658 0.2648 0.2636 0.2432 0.2326 0.1832 0.1713 0.1696 0.1528 0.1228 It must be noticed that the integration capability of a node may derive from two different factors: the ability to connect foreign regions, and the ability to connect regions of the same country with the outside. The American hubs can benefit only from the first factor, since we are considering just cross-border EU links. To evaluate the integration capability of an individual region, the procedures of section 3.2 are applied considering this region as the subset S to be excluded in Eqs. (3)–(4). Eqs. (3)–(4) actually result in evaluating both the ability to connect foreign regions and the ability to connect regions of the same country to the outside. We are also interested in evaluating the first factor alone, and to this end we consider, in the numerator and denominator of Eq. (3), only the pairs of regions not belonging to the same country of the hub. We begin by conducting a comparison between EU and U.S. hubs in terms of the ability to connect foreign regions, and then we an- alyze the European hubs considering also their ability to connect regions of the same country to the outside. We have considered for each analyzed time period an initial set of nodes with 30 EU regions and 30 U.S. regions chosen as those with the greatest current-flow betweenness, where the current-flow betweenness has been computed considering only the paths joining regions belonging to different EU countries. Table 8 shows for the four time periods mentioned above the percentage closeness loss for the EU and U.S. main hubs considering only the ability to connect foreign regions, while Table 9 repeats the evaluation only for the EU hubs appraising also the ability to connect nodes of the same country of the hub to the outside. The main evidence that arises from Table 8 is that the effect of the U.S. hubs is comparable to that of EU hubs, and even stronger in the period 1990–1999. This further supports our pre- vious considerations regarding the importance of the United States in the EU R&D system: The strong American hubs may act as entry and exit points in the U.S. subnetwork, and then also facilitate the connections inside the subnetwork. Quantitative Science Studies 911 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. regions in promoting the integration of the European research system Table 9. Percentage of the average cross-border closeness within EU that is lost by excluding the 10 EU main hubs from the coinventor network Region (a) 1980–1989 Milan Munich Paris Vienna Nanterre Outer London West Versailles Stockholm Lyon Kingston (c) 2000–2009 Milan Helsinki Berlin Munich Paris Stockholm Vienna Lyon Madrid Cambridge Integration capability Region Integration capability (b) 1990–1999 3.7978 1.7139 1.6977 1.3557 1.1936 1.1713 1.1591 1.0759 1.0603 0.9804 1.6807 1.3161 1.2280 1.2156 1.0897 1.0891 0.9037 0.8546 0.8383 0.8237 Milan Paris Munich Berlin Helsinki Stockholm Nanterre Lyon Versailles Vienna (d) 2010–2014 Helsinki Milan Stockholm Berlin Munich Paris Lyon Barcelona Grenoble Vienna 2.4952 1.2713 1.2369 1.1325 1.1146 1.0069 0.9880 0.9754 0.9564 0.8853 1.3885 1.3720 1.2719 1.2344 1.1829 1.0439 0.9194 0.9027 0.8606 0.7824 The most recurrent European hub is Munich, while other important regions are Berlin and Aachen. Regarding the United States, the main hub seems to be Cambridge, MA, with an im- portant role played by San Jose, CA; a very relevant integration capability is shown also by Houston, TX in 1980–1989 and Rockville, MD in 1990–1999. As a further insight about the U.S. hubs, we can analyze their main IPC patent classes. The most frequent class is Medical/ Veterinary for Cambridge and Rockville, Computing for San Jose and Drilling/ Mining for Houston. Therefore, with the exception of Houston in 1980–1989, it appears that the integration capability of the U.S. has been driven by regions focused on ICT and life science fields. Table 9, instead, takes into account also the ability to connect regions of the same country with the outside. In this table new regions emerge, for instance Milan and Vienna. These Quantitative Science Studies 912 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. 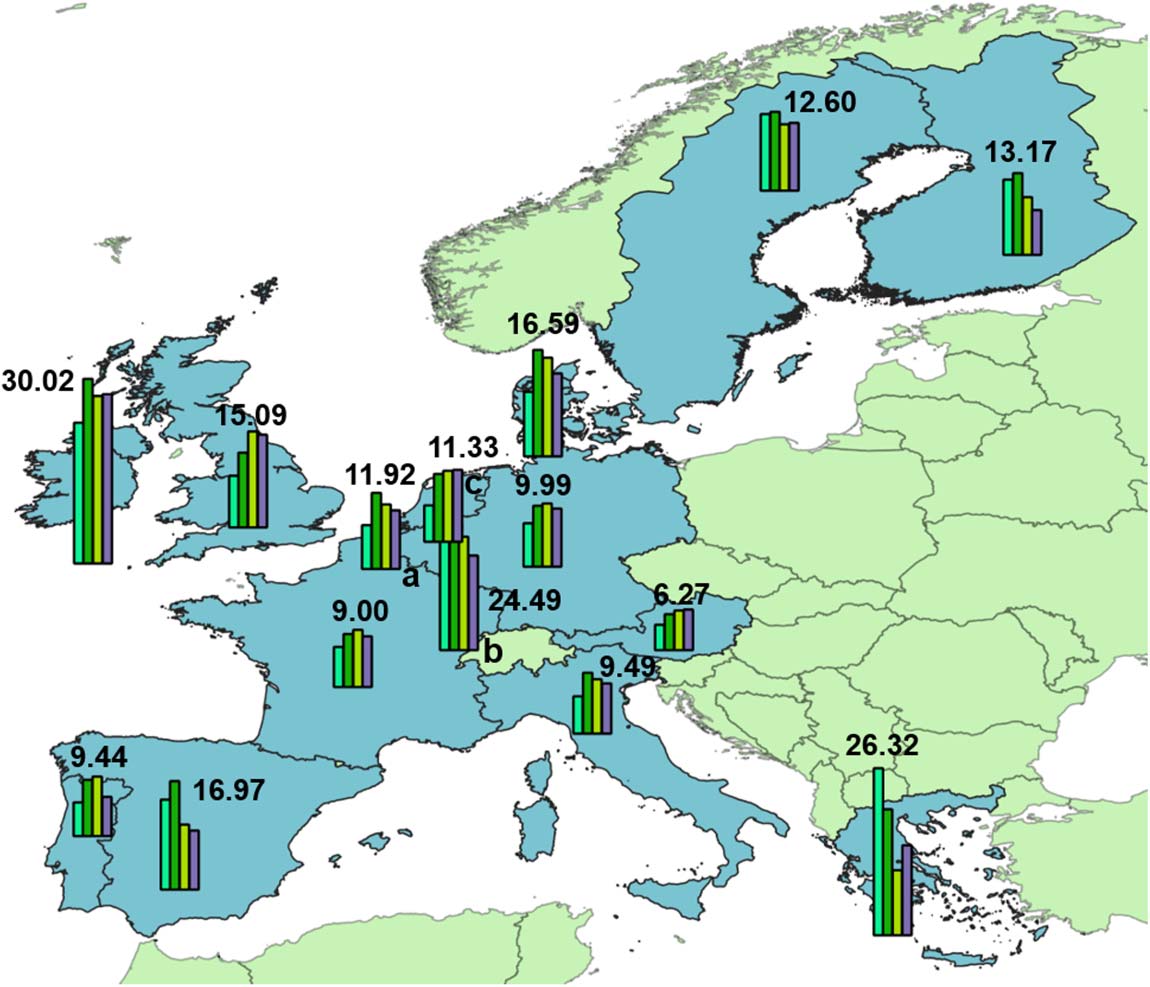regions in promoting the integration of the European research system Table 10. For each EU country, percentage of the average cross-border closeness toward the other EU countries that is lost by excluding the United States from the coinventor network Country Austria Belgium Denmark Finland France Germany Greece Ireland Italy Luxembourg Netherlands Portugal Spain Sweden UK 1980–1989 4.4958 1990–1999 5.7493 2000–2009 6.2671 2010–2014 6.0019 7.2856 10.7555 11.6032 6.6648 7.0774 26.3186 21.9114 6.0771 21.4734 6.2872 5.4839 15.2605 12.6027 8.1891 11.9208 16.5860 13.1692 8.4478 9.5578 19.8067 30.0243 9.4906 24.4928 10.5942 8.8667 16.9715 12.4948 11.7321 10.2429 15.8985 9.2353 8.9996 9.9859 10.3177 27.4674 8.5954 17.9527 11.1229 9.4384 10.3864 10.5493 15.0948 9.1578 13.2177 7.1949 8.0087 9.1361 14.1905 28.0969 7.9810 14.9668 11.3276 6.2752 9.4545 10.9270 14.4985 regions play an important role in their national subnetworks. It is interesting to note that the contribution of Milan has diminished over time, suggesting that the other Italian regions may have become more capable to connect autonomously with foreign EU countries. 4.4. Impact of the United States on the Closeness of the Individual EU Countries to the Other EU Countries The previous section has highlighted the very relevant role of the United States in strengthening the connections between European countries. In this section we look further into this issue by trying to understand which European countries most need the United States to become close to the other ones. In order to evaluate the impact of the United States on the closeness of a specific EU coun- try to the other EU countries we evaluate again the percentage closeness loss. In this case Eq. (3) must consider only the pairs of nodes involving a region of the country of interest, and the subset S of the network to be excluded is represented by the American nodes. In this way Eq. (4) results in the contribution of the United States to the closeness of the country under analysis to the other EU countries. Table 10 shows the numerical results in the usual four time periods, while Figure 6 gives a graphical intuition of the proportion of the U.S. contribution to the different countries. It is possible to notice that the countries benefiting the most from U.S. collaborations are the smal- lest ones: Actually, these countries, due to their size, need more external collaborations to Quantitative Science Studies 913 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. regions in promoting the integration of the European research system l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . Figure 6. Graphical representation of the results in Table 10. The four columns over each country show the percentage closeness loss due to the United States for that country, in the four time periods: 1980–1989 (blue), 1990–1999 (green), 2000–2009 (yellow), 2010–2014 (purple). The number indicated above each country represents the highest value measured in the four periods. In the figure, ‘a’ indicates Belgium, ‘b’ indicates Luxembourg and ‘c’ indicates The Netherlands. / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. Heatmaps showing the closenesses between the EU regions with and without the United States, in the 2000–2009 period. Figure 7 (a) depicts the starting situation with the absolute closenesses measured on the network including only the EU; the absolute closeness values reported in the legend are the inverses of the resistance distance, as explained in section 3.2. Figure 7(b) represents the percentage closeness loss between pairs of EU regions due to the United States; the values in the legend in this case are therefore percentages. White indicates low values, while dark red indicates high values. Quantitative Science Studies 914 The role of U.S. regions in promoting the integration of the European research system carry out R&D projects. This confirms the findings of Waltman et al. (2011), according to which peripheral countries are more prone to start long-distance collaborations. An exception is represented by the UK, but such an exception was expected given the well-known strong relationship of this country with the United States. Figure 7 deepens the results shown in Table 10 and Figure 6, by proposing a heatmap of the percentage closeness loss due to the United States between pairs of EU regions. In more detail, the heatmap showing the percentage closeness loss is in Figure 7(b), while for the sake of completeness Figure 7(a) reports the starting situation, with the absolute closenesses computed on the network including only the EU. As in Table 10, it can be noticed that the most periph- eral countries benefit most from the U.S. contribution; in addition, Figure 7(b) underlines that the connections between pairs of peripheral countries are the ones helped most. Another pe- culiarity highlighted by Figure 7(b) is that the diagonal of the heatmap is very light, meaning that the connections between pairs of regions within the same EU country do not need the mediation of the U.S. to be established. Finally, note that Germany, which provides a very relevant contribution to EU integration (see the previous sections), does not seem to benefit that much from the help of the United States to become connected to the other EU countries. This may be due to the fact that Germany, as is clear from Figure 7(a), has a high closeness to the other countries also on the network containing only the EU countries, and so does not need the U.S. to create connections. 5. CONCLUSIONS In this work we have studied the patent coinventor network and used indirect distance mea- sures to investigate the contribution of individual countries and regions to European R&D in- tegration, that is, their integration capability. The analysis has been carried out on a network encompassing both the EU and United States, in order to ascertain also possible contributions from the United States to European integration. After having proposed some descriptive statistics and pictures for the coinventor network, we have analyzed the contribution to EU integration provided by countries and regions by computing the amount of network-based closeness between European regions belonging to different countries that is lost when specific subsets of the nodes of the network are removed. We can summarize the main conclusions of this work as follows: (cid:129) The countries that contribute most to connecting regions across EU countries are Germany and the United States. In particular, the United States proves to be more rel- evant in joining EU countries than most of the EU countries themselves. The integration capability of the United States is more than the country would have had if the collab- orations were driven exclusively by gravitylike effects, while the integration capability of almost all the EU countries is lower than that due to gravity. Moreover, our analyses indicate that an important factor that makes the United States able to foster the connec- tion of EU regions is represented by the high number of links in the U.S. subnetwork: To connect two EU nodes on the coinventor network it is enough that these two nodes are close to two distinct American hubs, which may then usually be easily linked through a “fast” path within the United States. Also, the connections within the U.S. subnetwork are facilitated by the presence of strong internal hubs. In addition, the U.S. contribution to EU integration seems to have been decreasing since 1997, in conjunction with re- newed efforts by the EU in support of European technological collaborations. Quantitative Science Studies 915 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. regions in promoting the integration of the European research system (cid:129) There are strong regional hubs in terms of integration capability in both Europe and the United States. Some European hubs, especially German ones, are able to connect re- gions of foreign countries. Other European hubs, the most notable example being Milan, have a remarkable effect on the average cross-border closeness, but their contri- bution is especially in the connection of nodes of their same country with the outside. (cid:129) The role of the United States in promoting integration with other EU countries is stronger for the smallest EU countries, probably because these countries, due to their size, need more external collaborations to carry out R&D projects. A first natural development of our work consists in using the techniques introduced in this paper to analyze the role that other external countries besides the United States, such as Japan, play in EU integration. Moreover, in the introduction we claimed that patents are more related to development activities than to research activities, and thus our coinventorship network is biased toward the flow of technological knowledge. It would be interesting to delve into the more scientific part of knowledge flow, building a collaboration network using scientific publication data. It would be interesting also to repeat the study using the regional coassignment network, which shows the connections between the regions where the headquarters of companies and institutions are located. This alternative analysis might highlight different trends, and compar- ing these results with those obtained on the coinventorship network—which more naturally describes the relationships of knowledge exchange between regions—might lead to further intriguing insight. In addition, the coassignment network might also be used to investigate the contribution of different institutional types (e.g., companies vs. public research organiza- tions) to EU R&D integration. Finally, another possible extension to our study regards the evaluation of the integration capability of a region through a mathematical model with weights to be learned from data; such weights would allow us to understand the relevance of various effects (e.g., the size of the nodes), to the integration capability. AUTHOR CONTRIBUTIONS Emanuele Rabosio: Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing—original draft, Writing—review & editing. Lorenzo Righetto: Formal anal- ysis, Methodology, Visualization, Writing—review & Editing. Alessandro Spelta: Methodology, Writing—Review & editing. Fabio Pammolli: Conceptualization, Methodology, Supervision, Writing—review & editing. COMPETING INTERESTS The authors have no competing interests. FUNDING INFORMATION No funding has been received for this research. DATA AVAILABILITY This research work was carried out using the Regpat data set (March 2018 version), publicly available from OECD. Quantitative Science Studies 916 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The role of U.S. regions in promoting the integration of the European research system REFERENCES Arora, A., Belenzon, S., & Patacconi, A. (2018). The decline of science in corporate R&D. Strategic Management Journal, 39(1), 3–32. https://doi.org/10.1002/smj.2693 Arora, A., Belenzon, S., Patacconi, A., & Suh, J. (2019). The chang- ing structure of American innovation: Some cautionary remarks for economic growth ( Working Paper No. 25893). National Bureau of Economic Research. https://doi.org/10.3386/w25893 Arora, A., Fosfuri, A., & Gambardella, A. (2004). Markets for tech- nology: The economics of innovation and corporate strategy. Cambridge, MA: MIT Press. Bozzo, E., & Franceschet, M. (2013). Resistance distance, closeness, and betweenness. Social Networks, 35(3), 460–469. https://doi. org/10.1016/j.socnet.2013.05.003 Brun, J.-F., Carrère, C., Guillaumont, P., & de Melo, J. (2005). Has distance died? Evidence from a panel gravity model. World Bank Economic Review, 19(1), 99–120. https://doi.org/10.1093/wber/lhi004 Cappelli, R., & Montobbio, F. (2016). European integration and knowledge flows across European regions. Regional Studies, 50(4), 709–727. https://doi.org/10.1080/00343404.2014.931572 Chessa, A., Morescalchi, A., Pammolli, F., Penner, O., Petersen, A. M., & Riccaboni, M. (2013). Is Europe evolving toward an in- tegrated research area? Science, 339(6120), 650–651. https://doi. org/10.1126/science.1227970 Doria Arrieta, O. A., Pammolli, F., & Petersen, A. M. (2017). Quan- tifying the negative impact of brain drain on the integration of European science. Science Advances, 3(4). https://doi.org/ 10.1126/sciadv.1602232 Expert, P., Evans, T. S., Blondel, V. D., & Lambiotte, R. (2011). Uncovering space-independent communities in spatial networks. Proceedings of the National Academy of Sciences of the United States of America, 108(19), 7663–7668. https://doi.org/10.1073/ pnas.1018962108 Frenken, K., Hoekman, J., Kok, S., Ponds, R., van Oort, F., & van Vliet, J. (2009). Death of distance in science? A gravity approach to re- search collaboration. In A. Pyka & A. Scharnhorst (Eds.), Inno- vation Networks: New Approaches in Modelling and Analyzing, pp. 43–57. Berlin, Heidelberg: Springer. https://doi.org/10.1007/ 978-3-540-92267-4_3 Goddard, W., & Oellermann, O. R. (2011). Distance in graphs. In Structural Analysis of Complex Networks, pp. 49–72. Boston, MA: Birkhäuser. https://doi.org/10.1007/978-0-8176-4789-6_3 Hoekman, J., Frenken, K., & Tijssen, R. J. (2010). Research collabo- ration at a distance: Changing spatial patterns of scientific collab- oration within Europe. Research Policy, 39(5), 662–673. https:// doi.org/10.1016/j.respol.2010.01.012 Killick, R., Fearnhead, P., & Eckley, I. A. (2012). Optimal detection of changepoints with a linear computational cost. Journal of the American Statistical Association, 107(500), 1590–1598. https:// doi.org/10.1080/01621459.2012.737745 Klein, D. J., & Randić, M. (1993). Resistance distance. Journal of Mathematical Chemistry, 12(1), 81–95. https://doi.org/10.1007/ BF01164627 Maisonobe, M., Eckert, D., Grossetti, M., Jégou, L., & Milard, B. (2016). The world network of scientific collaborations between cities: Domestic or international dynamics? Journal of Informetrics, 10(4), 1025–1036. https://doi.org/10.1016/j. joi.2016.06.002 Miguelez, E., & Moreno, R. (2013). Do labour mobility and techno- logical collaborations foster geographical knowledge diffusion? The case of European regions. Growth and Change, 44(2), 321–354. https://doi.org/10.1111/grow.12008 Morescalchi, A., Pammolli, F., Penner, O., Petersen, A. M., & Riccaboni, M. (2015). The evolution of networks of innovators within and across borders: Evidence from patent data. Research Policy, 44(3), 651–658. https://doi.org/10.1016/j.respol. 2014.10.015 Nedeva, M., & Stampfer, M. (2012). From “science in Europe” to “European science”. Science, 336(6084), 982–983. https://doi. org/10.1126/science.1216878 Orsenigo, L., Pammolli, F., & Riccaboni, M. (2001). Technological change and network dynamics: Lessons from the pharmaceutical industry. Research Policy, 30(3), 485–508. https://doi.org/ 10.1016/S0048-7333(00)00094-9 Owen-Smith, J., Riccaboni, M., Pammolli, F., & Powell, W. W. (2002). A comparison of U.S. and European university-industry re- lations in the life sciences. Management Science, 48(1), 24–43. https://doi.org/10.1287/mnsc.48.1.24.14275 Ponds, R. (2009). The limits to internationalization of scientific research collaboration. Journal of Technology Transfer, 34(1), 76–94. https://doi.org/10.1007/s10961-008-9083-1 Powell, W. W., & Grodal, S. (2005). Networks of innovators. In The Oxford Handbook of Innovators, pp. 56–85. https://doi.org/ 10.1093/oxfordhb/9780199286805.003.0003 Rubinov, M., & Sporns, O. (2011). Weight-conserving characteriza- tion of complex functional brain networks. NeuroImage, 56(4), 2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069 Scherngell, T., & Barber, M. J. (2011). Distinct spatial characteris- tics of industrial and public research collaborations: Evidence from the fifth EU framework programme. Annals of Regional Science, 46(2), 247–266. https://doi.org/10.1007/s00168-009- 0334-3 Singh, J., & Marx, M. (2013). Geographic constraints on knowledge spillovers: Political borders vs. spatial proximity. Management Science, 59(9), 2056–2078. https://doi.org/10.1287/mnsc.1120.1700 Stephenson, K., & Zelen, M. (1989). Rethinking centrality: Methods and examples. Social Networks, 11(1), 1–37. https://doi.org/ 10.1016/0378-8733(89)90016-6 von Luxburg, U., Radl, A., & Hein, M. (2010). Getting lost in space: Large sample analysis of the commute distance. In Proc. of NIPS 2010, 24th Annual Conference on Neural Information Processing Systems. Curran Associates, Inc. Waltman, L., Tijssen, R. J., & van Eck, N. J. (2011). Globalisation of science in kilometres. Journal of Informetrics, 5(4), 574–582. https://doi.org/10.1016/j.joi.2011.05.003 Quantitative Science Studies 917 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 1 2 8 9 4 1 8 8 5 7 7 4 q s s _ a _ 0 0 0 3 4 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

PDF Herunterladen