FORSCHUNG
Parcellation-induced variation of empirical and
simulated brain connectomes at group and
subject levels
Justin W. M. Domhof1,2, Kyesam Jung1,2, Simon B. Eickhoff1,2, and Oleksandr V. Popovych1,2
1Institute of Neuroscience and Medicine, Brain and Behaviour (INM-7), Research Centre Jülich, Jülich, Deutschland
2Institute for Systems Neuroscience, Medical Faculty, Heinrich Heine University Düsseldorf, Düsseldorf, Deutschland
Schlüsselwörter: Parcellations, Modeling, Ruhezustand, Graphentheorie, Structure-function relationship
Keine offenen Zugänge
Tagebuch
ABSTRAKT
Recent developments of whole-brain models have demonstrated their potential when
investigating resting-state brain activity. Jedoch, it has not been systematically investigated
how alternating derivations of the empirical structural and functional connectivity, serving as
the model input, from MRI data influence modeling results. Hier, we study the influence from
one major element: the brain parcellation scheme that reduces the dimensionality of brain
networks by grouping thousands of voxels into a few hundred brain regions. We show graph-
theoretical statistics derived from the empirical data and modeling results exhibiting a high
heterogeneity across parcellations. Außerdem, the network properties of empirical brain
connectomes explain the lion’s share of the variance in the modeling results with respect to the
parcellation variation. Such a clear-cut relationship is not observed at the subject-resolved
level per parcellation. Endlich, the graph-theoretical statistics of the simulated connectome
correlate with those of the empirical functional connectivity across parcellations. Jedoch,
this relation is not one-to-one, and its precision can vary between models. Our results imply
that network properties of both empirical connectomes can explain the goodness-of-fit of
whole-brain models to empirical data at a global group level but not at a single-subject level,
which provides further insights into the personalization of whole-brain models.
ZUSAMMENFASSUNG DES AUTORS
The structural and functional connectivities of the brain, which reflect the anatomical
connections of axonal bundles and the amount of coactivation between brain regions,
jeweils, only weakly correlate with each other. In order to enhance and investigate this
relationship, large-scale whole-brain dynamical models were involved in this branch of
Forschung. Jedoch, how the definitions of the brain regions parcellated according to a so-
called brain atlas influence these models has so far not been systematically assessed. In diesem
Artikel, we show that this influence can be large, and link group-averaged, atlas-induced
deviations to network properties extracted from both types of connectivity. Zusätzlich, Wir
demonstrate that the same association does not apply to subject-specific variations. Diese
results may contribute to the further personalization of the whole-brain models.
Zitat: Domhof, J. W. M., Jung, K.,
Eickhoff, S. B., & Popovych, Ö. V.
(2021). Parcellation-induced variation
of empirical and simulated brain
connectomes at group and subject
levels. Netzwerkneurowissenschaften, 5(3),
798–830. https://doi.org/10.1162/netn_a
_00202
DOI:
https://doi.org/10.1162/netn_a_00202
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00202
Erhalten: 2 Februar 2021
Akzeptiert: 27 Mai 2021
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Oleksandr V. Popovych
o.popovych@fz-juelich.de
Handling-Editor:
Alex Fornito
Urheberrechte ©: © 2021
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Structure-function relationship:
The correspondence between
structural and functional
Konnektivität.
Structural connectivity:
Reflection of the physical,
anatomical connections throughout
das Gehirn.
Funktionale Konnektivität:
Reflection of synchronized
coactivations throughout the brain.
Dynamical whole-brain model:
A model that simulates brain activity
on the basis of the structural
connectivity in order to replicate the
functional connectivity.
Brain atlas or parcellation:
A description of the delineation of
the brain into distinct regions.
Granularity:
The number of brain regions in a
parcellation.
Empirical structural connectivity:
Structural connectivity derived from
(dwMRI) Daten.
Empirical functional connectivity:
Functional connectivity derived from
(fMRT) Daten.
EINFÜHRUNG
The structure-function relationship in the human brain has been a topic of interest in many
neuroimaging studies (Suárez, Markello, Betzel, & Misic, 2020). Hier, the structural connec-
tivity (SC) and functional connectivity (FC), which reflect the physical connections and pat-
terns of synchronized coactivation throughout the brain, jeweils, do not exhibit a perfect
association (Honey et al., 2009). One effort to close this gap in the structure-function relation-
ship involves the employment of dynamical whole-brain models that use SC as prior knowl-
edge to simulate resting-state brain activity (Honey et al., 2009). These models indeed
successfully explain an additional amount of variance beyond the direct comparison of SC
and FC (Honey et al., 2009). They also demonstrate that the brain at rest operates at a state
of maximal metastability (Deco, Kringelbach, Jirsa, & Ritter, 2017). Other studies even sug-
gested that the vast parameter space of the models can be exploited to reproduce resting-state
brain activity on a personalized level (Ritter, Schirner, McIntosh, & Jirsa, 2013; Sanz-Leon,
Knock, Spiegler, & Jirsa, 2015; Zimmermann et al., 2018).
Throughout the past decade, the workflow associated with dynamical whole-brain models
investigating resting-state brain activity has matured (Bansal, Nakuci, & Muldoon, 2018; Deco,
Jirsa, & McIntosh, 2011; Popovych, Manos, Hoffstaedter, & Eickhoff, 2019). When these
models are derived and validated using magnetic resonance imaging (MRT) Daten, region-based
SC and FC are typically calculated from diffusion-weighted MRI (dwMRI) and functional MRI
(fMRT) Sequenzen, jeweils, so that the computations remain tractable (Bandettini, Wong,
Hinks, Tikofsky, & Hyde, 1992; Kwong et al., 1992; Ogawa et al., 1992; Popovych et al.,
2019; Yeh, Jones, Liang, Descoteaux, & Connelly, 2021). The reconstruction of these connec-
tomes requires the use of a so-called brain parcellation or brain atlas, which describes which
voxels should be included in which brain region. Over the years, many brain atlases have
been constructed upon conceptually distinct underpinnings, where each of these methodolo-
gies incorporates its own biological knowledge and assumptions (z.B., the number of parcels
or granularity) into the parcellation (Amunts & Zilles, 2015; Eickhoff, Polizist, & Yeo, 2018;
Eickhoff, Yeo, & Genon, 2018).
Because region-based SC and FC are reconstructed on the basis of a particular brain par-
cellation, it to a large extent determines the SC and FC matrices. The used brain parcellation
may thus exert a substantial influence on the results of region-based neuroimaging studies.
Earlier works examined the influence of parcellations on graph-theoretical measures derived
from region-based SC and FC (Wang et al., 2009; Zalesky et al., 2010) and on direct SC-FC
comparisons (Messé, 2020). The impact of the granularity of a brain atlas on modeling results
was also investigated for the Desikan-Killiany atlas (Desikan et al., 2006) and variations of it,
wherein the brain regions were split into a number of smaller subregions (Proix et al., 2016).
Trotzdem, a systematic investigation of the influence of the brain parcellation is, to the best
of our knowledge, currently lacking when it comes to dynamical whole-brain models replicat-
ing resting-state brain activity.
Hier, we investigate this influence by using the methodology outlined in Figure 1. We first
extracted the SCs and FCs, henceforth referred to as the empirical SCs and empirical FCs, Re-
spectively, from the MRI data of 200 healthy subjects using 19 freely available state-of-the-art
brain parcellations (Figur 1, Grün). We constructed the models corresponding to the SC and
two qualitatively different models for the local dynamics of individual brain regions that were
based on phase oscillators and a neural mass model (Figur 1, Blau). By comparing between
the two models, we could evaluate whether any observed effects were model-dependent. Der
resting-state brain activity was individually simulated for every combination of parcellation,
Netzwerkneurowissenschaften
799
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Figur 1. Summary of the methods used in this study. Connectome extraction (Grün) umfaßt
the construction of the empirical structural (SC) and functional connectivity (FC) von dem
diffusion-weighted (dwMRI) and functional magnetic resonance imaging (fMRT) Daten, jeweils.
Both connectomes serve as input for the modeling stage (Blau), where the model parameters are
optimized to maximize the correlation between simulated and empirical data (dotted arrow).
Graph-theoretical metrics were extracted from the empirical and simulated connectomes (Rot)
and regressed with the model fitting results (orange).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Simulated functional connectivity:
Functional connectivity simulated by
a dynamical whole-brain model.
Goodness-of-fit:
The maximized fit between the
empirical functional connectivity
and the functional connectivity
simulated by a dynamical whole-
brain model.
Modell, and subject. Then FCs were derived from the simulated brain activity, which will
henceforth be referred to as simulated FCs. The correlations between the simulated and em-
pirical FCs were calculated and maximized through model parameter variations to quantify
how well the models could reproduce the empirical FCs (Figur 1, Blau). Endlich, we compared
the maximized correlations or goodness-of-fits with graph-theoretical measures calculated
from the empirical SC and FC (Figur 1, red and orange), so that any observation regarding
the modeling results could be interpreted in terms of the properties of the empirical networks
used to construct and validate our models.
We found large deviations in the goodness-of-fit as brain parcellations vary. Zusätzlich,
most of the group-averaged interparcellation variance in the goodness-of-fit could be attributed
to variations in the graph-theoretical metrics. Such a well-pronounced relationship was prac-
tically absent when we considered within-parcellation, interindividual differences. Endlich, Wir
show that the models (inaccurately) map the empirical SC to a simulated functional network
that has similar network properties as the empirical FC. Our investigation therefore illustrates
how the results produced by a dynamical whole-brain modeling workflow are influenced by
the brain parcellation, and reveals some of its current limitations and open issues. The reported
results are relevant when considering personalized models of resting-state brain dynamics in
the framework of precision medicine.
MATERIALS AND METHODS
In this study, we systematically investigated the influence of the brain atlas on the validation of
dynamical whole-brain models by using the methodology outlined in Figure 1. Erste, we ex-
tracted the empirical SC and FC matrices corresponding to a particular parcellation from the
dwMRI and fMRI data, jeweils (Figur 1, Grün). The result of the empirical SC reconstruc-
tion comprised two matrices: one with the number of streamlines and one with the average
length of the streamlines between each pair of brain regions, which are referred to as the actual
structural connectivities (SCs) and the path lengths (PLs), jeweils. The empirical FC matrix
contained the Pearson correlation coefficients across the BOLD response time series extracted
from the fMRI data.
Netzwerkneurowissenschaften
800
Influence of parcellation on large-scale whole-brain modeling results
Subsequently, the empirical SC and PL matrices were fed to the model as prior knowledge,
while the empirical FC matrix was compared with the simulated FC matrix produced by the
model simulations (Figur 1, Blau). Two models (a phase oscillator and a neural mass model)
were used for the acquisition of the simulation results, and we simulated both models for a broad
range of global parameter settings to maximize the fit between the empirical and simulated FC.
We also extracted some graph-theoretical metrics from the empirical SC and PL and the
empirical and simulated FC matrices (Figur 1, Rot). To be specific, we determined the degree
distribution and the modularity of the empirical SC and both types of FC to characterize their
centrality and segregation, jeweils. Zusätzlich, we calculated the closeness centrality
distribution and the global efficiency of the PL matrix as representations of its centrality and
Integration, jeweils. The latter two metrics calculated from the PL matrix are based on the
streamline path lengths between brain regions and allow a natural interpretability of the
obtained quantities (siehe unten). Außerdem, we calculated the clustering coefficients from
the empirical SC and FC and the characteristic path lengths from the empirical PL and FC
matrices. These latter two metrics can also be used to compare our results with the literature
investigating the influence of the brain parcellation on graph-theoretical metrics extracted from
empirical SC and FC (Wang et al., 2009; Zalesky et al., 2010).
Endlich, we sought to find correlations between the model simulation results and the extracted
graph-theoretical metrics using univariate and multivariate regression approaches (Figur 1,
orange). In the remainder of this section, we discuss the procedures employed at each step in
detail. The source code of our analyses and connectome data have been made available else-
Wo (https://jugit.fz-juelich.de/inm7/public/parcellation-modelling and https://doi.org/10
.25493/81EV-ZVT; Domhof, 2021; Domhof, Jung, Eickhoff, & Popovych, 2021).
Extraction of Empirical Connectomes
Empirical connectomes were extracted for 200 (96 Männer, Alter 28.5 ± 3.5 Jahre) healthy, unre-
lated subjects from the HCP S1200 release dataset (https://www.humanconnectomeproject.org;
Van Essen et al., 2012, 2013) verwenden 19 different brain parcellations. The local ethics committee
of the HCP WU-Minn gave its approval for the study and written, informed consent was given by
all subjects. Hier, we discuss the extraction of empirical SC and PL from dwMRI data and
empirical FC from fMRI data, and present the brain atlases for which we extracted the region-
based connectomes.
SC extraction from dwMRI. For the extraction of the empirical SC matrices from dwMRI data, Wir
used a workflow developed in-house that consisted of four stages: (1) preprocessing of dwMRI
Bilder, (2) calculation of the whole-brain tractography ( WBT), (3) transformation of the atlas
Bilder, Und (4) reconstruction of the empirical SC. The workflow included functions from
the ANTs (Tustison et al., 2010), FreeSurfer (Dale, Fischl, & Sereno, 1999), FSL (Jenkinson,
Beckmann, Behrens, Woolrich, & Schmied, 2012), and MRtrix3 (Tournier et al., 2019) Software
packages. Computations were performed on the JURECA high-performance computing cluster
(Jülich Supercomputing Centre, 2018).
(1) In the preprocessing stage, we used FreeSurfer functions to perform the following opera-
tions on the T1-weighted images: bias field correction, tissue segmentation, cortical (surface)
reconstruction, volume-surface conversion, and surface deformation. We also used FreeSurfer
functions to correct the dwMRI images with regard to head motions and eddy current distortions,
while MRtrix3 functions were employed to denoise them and perform bias field correction. Der
dwMRI images were then registered to the T1-weighted images using the linear and nonlinear
transformation functions included in FSL; afterwards, tissue segmentation was performed for
Netzwerkneurowissenschaften
801
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
these images as well. (2) Subsequently, WBT was calculated using exclusively MRtrix3 func-
tionen. A multi-shell, multi-tissue constrained algorithm (Jeurissen, Tournier, Dhollander,
Connelly, & Sijbers, 2014) estimated the response functions for spherical deconvolution, welche
were subsequently used to determine the fiber-oriented distributions from the dwMRI data. Der
WBT was then completed through a second-order integration over the fiber-oriented distribu-
tions using a probabilistic algorithm (Tournier, Calamante, & Connelly, 2010), where we used
10M streamlines and the following other tracking parameter settings: step size = 0.625 mm, ein-
gle = 45°, min. length = 2.5 mm, max. length = 250 mm, FOD amplitude for terminating tract =
0.06, max. attempts per seed = 50, max. number of sampling trials = 1,000, and downsampling =
3 mm. (3) Nächste, the images of the brain atlases used in this study (siehe unten) were linearly and
nonlinearly transformed from the standard space (in which they were all sampled) to the native
space using FSL functions. (4) Endlich, we reconstructed the empirical SCs and PLs for all pairs of
parcels included in a particular parcellation by using the MRtrix3 function tck2connectome.
FC extraction from fMRI. To construct the empirical FC matrix, BOLD signals of the resting-
state brain activity were first extracted from fMRI data that were preprocessed using the
ICA-FIX approach as provided by the HCP repository (Griffanti et al., 2014), which eliminated
the motion parameter but not the global signal effect from the images. Hier, the brain atlas
images were used to calculate the mean voxel intensity across each parcel per volume result-
ing in one BOLD signal time series per parcel. Individual time series were linearly detrended
and z-scored before we constructed the empirical FC matrix by calculating the Pearson cor-
relation coefficients across the time series for each pair of parcels. Four resting-state fMRI ses-
sions were available in the HCP dataset for every subject (two phase encoding directions
scanned on two days), each one comprising 1,200 volumes sampled with a repetition time
von 720 MS. We thus calculated four different empirical FCs per subject that were used for
the validation of our models.
In our study, we performed the whole workflow outlined in Figure 1 für die
Brain parcellations.
19 parcellations included in Table 1. As the aim of this study is to compare the modeling re-
sults for a variety of brain atlases, we ensured their comparability such that only cortical areas
were considered and that all parcellations had similar volumes and were sampled to the
MNI152 nonlinear template space (Grabner et al., 2006). For more details on the preprocess-
ing of the used atlases, see the Supplementary Method.
Graph-Theoretical Analysis of Empirical Connectomes
The empirical SC, PL, and both the empirical and the simulated FC matrices were subjected to
graph-theoretical analyses in order to extract data variables portraying the properties of the
networks they represent. In these analyses, the connectivity matrices represented a (Netzwerk)
graph in which the brain regions were the nodes and the individual matrix elements were
undirected weighted edges between them. Since self-connections inferred from the empirical
SC and FC extraction procedures did not influence the model simulation results (siehe unten),
we removed them from the connectivity matrices prior to the graph-theoretical analyses by
setting their diagonal elements to 0. From the empirical SC and both types of FC matrices,
we extracted the (weighted) degree distribution and the modularity. We selected these mea-
sures because they characterized respectively the network centrality and segregation (Rubinow
& Spurns, 2010) when only the signal transmission efficiencies within the network were taken
into account. The PL matrix may also provide information about the network properties from
the point of view of signal transmission latencies. Hier, we used the closeness centrality
Netzwerkneurowissenschaften
802
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Tisch 1. Overview of the used brain parcellation schemes with the index for reference in this study, the number of parcels after image
Verarbeitung, and associated publications. In addition to this table, we have included a Supplementary Data Sheet that includes (a number of
statistics of ) the connectomes that were extracted through the use of these parcellations.
Index
1
Name
MIST
NEIN. of parcels
31
Urchs et al. (2019)
Refs.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Craddock
Shen 2013
Schäfer
Harvard-Oxford
Desikan-Killiany
von Economo-Koskinas
AAL (Ausführung 2)
Destrieux
Brainnetome
56
103
167
38
56
108
160
79
156
100
200
48
96
70
86
92
150
210
Craddock, James, Holtzheimer, Hu, and Mayberg (2012)
Shen, Tokoglu, Papademetris, and Constable (2013)
Schaefer et al. (2018)
Desikan et al. (2006); Frazier et al. (2005);
Goldstein et al. (2007); Makris et al. (2006)
Desikan et al. (2006)
Scholtens, de Reus, de Lange, Schmidt, and van den Heuvel
(2018); von Economo and Koskinas (1925)
Rolls, Joliot, and Tzourio-Mazoyer (2015);
Tzourio-Mazoyer et al. (2002)
Destrieux, Fischl, Dale, and Halgren (2010)
Fan et al. (2016)
distribution and the global efficiency as indicators of network centrality and integration,
jeweils.
The degree for empirical SC and both types of FC and closeness centrality for empirical PL
indicate how strongly and how quickly a node may influence the network dynamics, bzw-
aktiv. Entsprechend, the global efficiency describes (for empirical PL) how quickly signals may
be integrated throughout the network, and the modularity portrays (for empirical SC and both
types of FC) to what extent the network is segregated into separate modules that have many or
strong intramodular and few or weak intermodular connections.
Besides the modularity and the global efficiency, we also calculated the clustering coeffi-
cient as a measure of segregation from the empirical SC and FC and the characteristic path
length as a measure of integration from the empirical PL and FC matrices. Even though the
modularity and global efficiency are more state-of-the-art techniques, the calculation of the
clustering coefficient and characteristic path length enabled the comparison of our study with
Netzwerkneurowissenschaften
803
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
the literature investigating the influence of the brain parcellation on the graph-theoretical mea-
sures of empirical SC and FC (Wang et al., 2009; Zalesky et al., 2010).
In the remainder of this section, we explain in detail how and why these particular metrics
were calculated. Any calculations were carried out using the Python programming language
(Python Software Foundation, https://www.python.org/) in combination with the SciPy
(Virtanen et al., 2020), NumPy (van der Walt, Colbert, & Varoquaux, 2011), and NetworkX
(Hagberg, Swart, & S Chult, 2008) modules.
Degree distribution. Let a symmetric N × N coupling matrix W determine how the N network
nodes are connected by undirected, weighted edges. Hier, the assumption of symmetry is
justified because the empirical SC and empirical and simulated FC matrices inferred from
WBT and (simuliert) BOLD signal time series correlations, jeweils, are symmetric as well.
The degree dj of node j can be calculated by taking the sum over the jth row of W leading to N
values for the entire network corresponding to the number of parcels included in the used brain
parcellation. We actually used the degree as opposed to other measures of centrality because of
this simple summation: It makes the degree distribution easy to calculate and straightforwardly
interpretable with respect to the neurobiology of the brain (Rubinow & Spurns, 2010). Der
degrees could be directly calculated from the empirical SC matrices. The empirical and
simulated FCs were first thresholded at 0, and the Fisher Z-transforms (Fischer, 1915, 1921) von
the positive elements were subsequently calculated before determining the degrees.
To compare the degree distributions across parcellations, we fitted them to the gamma
(Gamma(X|k, θ)) parametric probability distribution. The gamma distribution is defined for pos-
itive real numbers (x > 0) by the following equation:
D
Gamma xjk; θ
Þ ¼
1
θkΓ kð Þ
(cid:1)
xk−1 exp − x
θ
(cid:3)
;
(1)
where Γ(X) represents the gamma function and k and θ are free parameters commonly referred to
as the shape and scale parameter, jeweils. The former determines to what extent the distri-
bution function has a shape resembling an exponential decay or a bell curve, and the latter
scales the probabilities with respect to the x-axis (see Figure S1 in the Supplementary Results
for an illustration). The fitting result for SC and FC matrices comprised the fitted shape and scale
parameters denoted by DegreeSC=FC
scale , jeweils. In addition to these fitted
Parameter, we also calculated the Kolmogorov-Smirnov statistics between the fitted cumulative
gamma distributions and the cumulative empirical degree distributions, and the mean and the
standard deviation of the degree.
shape and DegreeSC=FC
We used the gamma distribution to characterize the degree distribution for several reasons.
Erste, we acknowledge that the degree can practically assume semi-infinite values because
it cannot be smaller than 0 for the empirical SC as well as for the thresholded and Fisher
Z-transformed empirical and simulated FC. Dann, modeling the distribution by the gamma
distribution is more applicable to this situation than, Zum Beispiel, by the Gaussian distribution.
Insbesondere, the shape parameter of the gamma distribution may reflect the variable concen-
trations of degrees close to 0 that are observed for the different parcellations; see the
Supplementary Data Sheet. Zweite, studies investigating the influence of the brain parcella-
tion on graph-theoretical measures extracted from empirical SC and FC have used the trun-
cated power law model to characterize degree distributions (Wang et al., 2009; Zalesky et al.,
2010). The truncated power law model essentially is an unnormalized version of the gamma
distribution (see Wang et al., 2009; Zalesky et al., 2010; and Equation 1). daher, Die
parameters of the gamma distribution and the truncated power law model are practically
Netzwerkneurowissenschaften
804
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
the same. Using the gamma distribution to characterize the degree distribution thus enhances
the comparability of our study with the literature. Trotzdem, we deviate from the use of the
(unnormalized) truncated power law model as the normalization condition enables the com-
parison of the fitting errors between the empirical and fitted distributions across parcellations.
The latter is our third and final reason to use the gamma distribution to model the degree
distributions. In sum, the gamma distribution suits the problem at hand given that the degrees
can only assume values larger than or equal to 0. Zusätzlich, it enables the comparison of all
the fitting results across parcellations, and enhances the comparability of our results with the
Literatur.
Modularity. The modularity of a network was obtained by maximizing its expression (Rubinow
& Spurns, 2011):
Modularity ¼
1
wþ
XN
XN
(cid:1)
W
i¼1
j¼1
(cid:3)
δMi;Mj
−
þ
ij
− e
þ
ij
1
wþ þ w−
XN
XN
i¼1
j¼1
(cid:3)
(cid:1)
−
W
ij
− e
−
ij
δMi;Mj
:
(2)
ij and W −
Here i and j both represent the number of a particular network node. Zusätzlich, W
ij
þ
ij = Wij and
ij , and e(cid:2)
are the positive and negative elements of W, jeweils (d.h., if Wij > 0, then W
W −
ij = −Wij). Then w
is defined by
represents the total sum over W (cid:2)
ij = 0; otherwise W
ij = 0 and W −
(cid:2)
þ
ij
þ
P
(cid:2)
e
ij
¼
N
j¼1 W (cid:2)
N
i¼1 W (cid:2)
ij
P
ij
w(cid:2)
:
(3)
Endlich, Mi denotes the module to which node i belongs and δMi;Mj is the Kronecker delta,
meaning δMi;Mj = 1 if Mi = Mj and δMi;Mj = 1 ansonsten. By changing the modular structure
of the network (d.h., changing Mi), the modularity can be maximized. Since evaluating all pos-
sible module configurations is too computationally expensive, we used the Louvain algorithm
to solve this optimization problem (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008).
The modularity was selected from other measures of segregation (z.B., the clustering coef-
ficient and local efficiency) because of its more sophisticated design, especially in light of the
negative correlations an FC matrix can have (Rubinow & Spurns, 2010, 2011). Zusätzlich, Es
allows for an in-depth examination of the modular network structure after the maximization
has been performed, zum Beispiel, to determine the strength of community structure for a given
Netzwerk (Newman & Girvan, 2004).
Closeness centrality. Signals propagating throughout the network from one node to another
can traverse several edges that have associated weights representing the cost of crossing them.
The minimal cost of traveling between nodes i and j is termed the shortest path length lij. Für
the empirical PL matrix, the calculated shortest path length literally estimated the minimal dis-
tance that the signals have to cover along the white matter fibers connecting two brain regions.
The closeness centrality Lj of node j is then defined as the inverse of the mean shortest path
length between that node and all other nodes in the network (Rubinow & Spurns, 2010):
Lj ¼ N − 1
N
i¼1 lij
P
; Wo
lii ¼ 0:
(4)
We calculated the closeness centrality for all nodes to determine the network’s closeness cen-
trality distribution. Subsequently, we fitted this distribution to the gamma probability distribution
(1) because also the closeness centrality could not assume values below 0, which resulted in the
fitted gamma distribution shape and scale parameters denoted by Centr:PL
scale,
shape and Centr:PL
Netzwerkneurowissenschaften
805
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
jeweils. Just as with the degree distribution, we also calculated the root-mean-square errors
between the fitted cumulative gamma distributions and the cumulative empirical closeness cen-
trality distributions, and the mean and the standard deviation of the closeness centrality.
Also the degree or betweenness centrality could have been used to analyze the empirical PL
Matrix (Rubinow & Spurns, 2010). Trotzdem, we selected the closeness centrality as opposed
to these alternatives. The degree calculated on the basis of the empirical PL does not have the
same neurobiological interpretation as with the empirical SC and both types of FC (see above).
The betweenness centrality has the disadvantage that it discards any information about the
shortest path lengths themselves (Rubinow & Spurns, 2010).
Global efficiency. The global efficiency of a network was also defined in terms of the shortest
path lengths (Rubinow & Spurns, 2010):
Efficiency ¼
1
N
XN
i¼1
P
N
j¼1 l−1
ij
N − 1
; Wo
lii ¼ 0:
(5)
It can thus be interpreted as the mean of the inverted shortest path lengths across all pairs of
network nodes. An alternative measure of integration is the characteristic path length (Rubinow
& Spurns, 2010), but it has been argued that global efficiency may be superior when investi-
gating brain networks (Achard & Bullmore, 2007).
Clustering coefficient. For weighted graphs, which we consider in our study, several variants of
the clustering coefficient exist. We use the expression of the clustering coefficient proposed by
Utopie, Saramäki, Kertész, and Kaski (2005):
Cluster ¼
P
XN
N
j¼1
i¼1
1
N
P
(cid:4)
^
N
W ij
k¼1
D
di di − 1
^
W ik
Þ
(cid:5)1=3
^
W jk
:
(6)
^
Wij = Wij /max(W) are the elements of the connectivity matrix normalized by their max-
Hier,
imum and di represents the degree of node i.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
The clustering coefficient is a rather simple measure of segregation and its expression has
not been optimized for FC matrices. daher, we consider the modularity to be a more ac-
curate statistic for network segregation. Trotzdem, as previous work studying the influence
of brain parcellations on graph-theoretical measures extracted from empirical connectomes
included this measure (Wang et al., 2009; Zalesky et al., 2010), we have added it to our cal-
culations. We calculated the clustering coefficient from the empirical SC matrix and from the
thresholded and Fisher’s Z-transformed empirical FC matrix (see also the case with the degree).
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Characteristic path length. The characteristic path length is obtained by averaging the shortest
path length across all pairs of nodes (Rubinow & Spurns, 2010):
Char: PL ¼
P
N
j¼1 lij
N − 1
1
N
XN
i¼1
; Wo
lii ¼ 0:
(7)
Analogous to the modularity and the clustering coefficient describing the network segregation,
the global efficiency and the characteristic path length are both measures of network integra-
tion. Wie oben erwähnt, the global efficiency is superior in brain network research (Achard &
Bullmore, 2007). Jedoch, we also included the characteristic path length to ameliorate the
comparability of our work with other studies investigating the influence of the brain parcellation
on region-based SC and FC by means of this metric (Wang et al., 2009; Zalesky et al., 2010).
We calculated the characteristic path length associated with the structural connectivity by
Netzwerkneurowissenschaften
806
Influence of parcellation on large-scale whole-brain modeling results
using the PL matrix. For the functional connectivity we used the thresholded and Fisher
Z-transformed empirical FC matrix with inverted elements. The latter inversion was done after
the Z-transformation to convert the functional association strengths to estimations of the link
lengths, where link strengths and lengths are inversely related (Rubinow & Spurns, 2010).
Model Simulations
In the modeling stage of our workflow, the brain was once again seen as a network of brain
Regionen (network nodes) parcellated according to a given brain atlas. We subsequently used a
system of coupled oscillators to model the collective dynamics of the mean-field activities of the
individual brain regions. The coupling between network nodes was defined by the extracted
empirical SC, where the SC matrix determined how strongly one region influenced the other.
The PL matrix was used to evaluate the latency in the signal propagation between the nodes.
By simulating the dynamics of the whole-brain models, we sampled the activity time series of
the N nodes included in the network. We subsequently correlated these time series with one
another and constructed a simulated FC matrix. Endlich, the similarity between the simulated
and the empirical FC matrices was quantified by vectorizing the upper triangular parts of both
matrices excluding the diagonal and subsequently calculating the Pearson correlation coeffi-
cient between the resulting two vectors. By exploring the parameter space of the model via a
grid search, the maximal similarity between the empirical and simulated FC matrices could
be found, which is henceforth also referred to as the goodness-of-fit of the model.
In this study, we modeled the local dynamics of the brain regions from different perspec-
tives by considering two different models. The first model was the Kuramoto system of coupled
phase oscillators (Kuramoto, 1984), and the other was an ensemble of Wilson-Cowan type
neural mass models (Wilson & Cowan, 1972). These two models were chosen because of their
major conceptual differences, which increased the likelihood of finding cross-model devia-
tionen. These models have also been used in previous studies investigating the brain’s
structure-function relationship by dynamical whole-brain models (Deco, Jirsa, McIntosh,
Spurns, & Kötter, 2009; Messé, Rudrauf, Benali, & Marrelec, 2014; Ponce-Alvarez et al.,
2015).
In the Kuramoto model (Kuramoto, 1984), the mean-field activity of
Phase oscillator model.
brain region i 2 {1, 2, …, N} (N is the number of brain regions in a given parcellation) is as-
sumed to oscillate with a region-specific frequency fi, and the dynamics of its phase φ
ich(T) Sind
governed by the differential equation
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Phi
i tð Þ ¼ 2πfi þ
(cid:1)
(cid:4)
j t − τij
(cid:5)
(cid:3)
− φ
i tð Þ
þ σpνi tð Þ:
(8)
Cij sin φ
XN
j¼1
ich(T) is independent Gaussian white noise with zero mean and unit variance, and σ
Here ν
p =
0.17 is the noise intensity. Außerdem, Cij and τ
ij represent the individual coupling strength
and delay values between brain regions, jeweils. These were derived from the empirical
SC and PL matrices via
8
<
Cij ¼
:
0
G :
SCij
N SCh
i
if
i ¼ j
otherwise
8
<
and τij ¼
:
0
τ :
PLij
PLh
i
if
i ¼ j
otherwise
:
(9)
Here, the operator h·i returns the mean over all elements of the matrix, and G and τ are scaling
factors referred to as the global coupling and global delay.
Network Neuroscience
807
Influence of parcellation on large-scale whole-brain modeling results
Although the Kuramoto model has been used in different paradigms in relation to large-scale
whole-brain models (e.g., Messé et al., 2014 vs. Ponce-Alvarez et al., 2015), we adopted the
approach wherein the ultraslow phase dynamics of the BOLD signals was directly modeled by
φi(t). Then the simulated BOLD signals cos(φi (t)) were used for the calculation of the simulated FC
matrix. The region-specific oscillation frequencies fi in the range [0.01, 0.1] Hz were derived from
the empirical BOLD signal time series via spectral density estimation. For this analysis, we subjected
those signals to Welch’s method (welch function implemented in the SciPy module; Virtanen
et al., 2020) while using a 1,024 time-points-long Hamming window function with 95% (927 time
points) overlap between segments. We used the frequencies corresponding to the largest peaks
in the spectra and heterogenized them a little by adding Gaussian white noise with zero mean
and 0.002 Hz standard deviation. Finally, G and τ were considered to be free parameters and
were optimized in order to maximize the similarity between empirical and simulated FC.
Neural mass model. The neural mass model used in this study was a Wilson-Cowan model
(Wilson & Cowan, 1972) adapted from the paper by Deco et al. (2009). It models the inter-
action between the excitatory and inhibitory neuron ensembles of the ith brain region, where
their mean firing rates Ei(t) and Ii(t), that is, the proportion of cells firing within a unit of time,
respectively, are modeled via the following coupled differential equations:
_
Ei tð Þ ¼ −Ei tð Þ þ κS
μ
E
XN
(cid:4)
CijEj t − τij
(cid:5)
j¼1
!
− cEIIi tð Þ þ Ib
þ σnνi tð Þ
and
μ
E
_
Ii tð Þ ¼ −Ii tð Þ þ κS cIEEi tð Þ
ð
Þ þ σnνi tð Þ:
E and μ
In these equations, μ
I are the decay time constants of the excitatory and inhibitory
activity, respectively. Both populations received the same zero-mean, independent Gaussian
white noise of intensity σn. Parameters cEI and cIE regulate the inhibition of the excitatory cells
by the inhibitory pool and the excitation of the inhibitory cells by the excitatory pool, respec-
tively. S(x) is a sigmoid function defined by
1
Þ
Þ
ð
1 þ exp −λ x−γð
1
Þ
1 þ exp λγð
S xð Þ ¼
(12)
−
;
where λ and γ determine its width and the position of its inflexion point, respectively.
Additionally, Ib is a constant external input to the excitatory neurons, and κ = (1 + exp(λγ))/
exp(λγ) scales S(x) such that κS(x) = 1 as x → ∞. Finally, Cij and τij have the same interpretations
and similar associated expressions as with the Kuramoto model (9):
8
<
Cij ¼
:
cEE
G :
SCij
i
N SCh
if
i ¼ j
otherwise
8
<
and τij ¼
:
0
τ :
PLij
PLh
i
if
i ¼ j
otherwise
;
(13)
where cEE is a parameter scaling the self-excitation of the excitatory pool.
We set the model parameters to the values listed in Table 2. As for the Kuramoto model,
parameters G and τ were regarded as free parameters and were varied to maximize the similarity
between the empirical and simulated FC matrix. The considered parameter configurations
resulted in a low activity state of disconnected nodes (G = 0) and generation of limit-cycle
oscillations with an alpha-band frequency when the individual regions were coupled (G > 0).
The modeled alpha oscillations have been shown to be dominant in EEG of human resting-state
brain activity (Fraga González et al., 2018; Spitoni, Di Russo, Cimmino, Bozzacchi, & Pizzamiglio,
2013) and to interact with BOLD responses (Mayhew, Ostwald, Porcaro, & Bagshaw, 2013).
Netzwerkneurowissenschaften
808
(10)
(11)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Tisch 2.
Parameter settings of the neural mass model
Parameter
M
E
μI
Ib
Wert
20 MS
20 MS
0.100 MS
Parameter
λ
γ
σ
N
Wert
20.000
0.300
0.002
Parameter
cEE
cEI
cIE
Wert
1.000
1.500
0.000
Simulating the neural mass model yielded neuronal signal time series that are not directly
comparable with the empirical BOLD responses extracted from fMRI data. To account for this,
the neuronal signals of the excitatory pool were converted to BOLD responses by the Balloon-
Windkessel model from Friston, Harrison, and Penny (2003), a procedure that has also been
used elsewhere (Havlicek et al., 2015). The resulting (simuliert) BOLD signals were subse-
quently used to construct the simulated FC matrix.
Implementation, Simulation, and parameter variation. The Python (Python Software Foundation,
https://www.python.org/) and C++ (Standard C++ Foundation, https://isocpp.org/) programming
languages were selected for the implementation of the model simulations; Hier, we also used the
SciPy (Virtanen et al., 2020) and Numpy (van der Walt et al., 2011) modules. Simulation and
analysis computations were carried out on the JURECA high-performance computing cluster
(Jülich Supercomputing Centre, 2018). The temporal integration of both models as well as the
neuronal to BOLD signal conversion followed Heun’s method. For both models, we optimized
the free parameters by simulating the models using a dense grid of 64 × 48 parameter points for
the global coupling and delay, jeweils, and subsequently selecting the parameters maxi-
mizing the correlation between the empirical and simulated FC (goodness-of-fit). Regarding the
phase oscillator model, the global coupling and delay were varied using G 2 {0.000, 0.015,
0.030, …, 0.945} and τ 2 {0 S, 1 S, 2 S, …, 47 S}. For every parameter setting, we then simulated
70 min of network dynamics with a 60-ms integration time step and disregarded the first 10 min
so that the initial conditions did not influence the results. For the neural mass model we used G 2
{0.000, 0.018, 0.036, …, 1.134} and τ 2 {0.0 MS, 1.5 MS, 3.0 MS, …, 70.5 MS} for the global
coupling and delay, sampled 510 s of network activity with an integration step size of 2 MS
and removed the first 150 s prior to analysis. The differences in the simulation parameters (sim-
ulated time and integration time step size) between both models were adapted to the ultraslow
timescale and alpha frequency oscillations of the phase oscillators and the neural mass model,
jeweils. The simulations above were performed individually for each combination of the
200 Fächer, Die 2 Modelle, und das 19 considered parcellations listed in Table 1.
Analyse
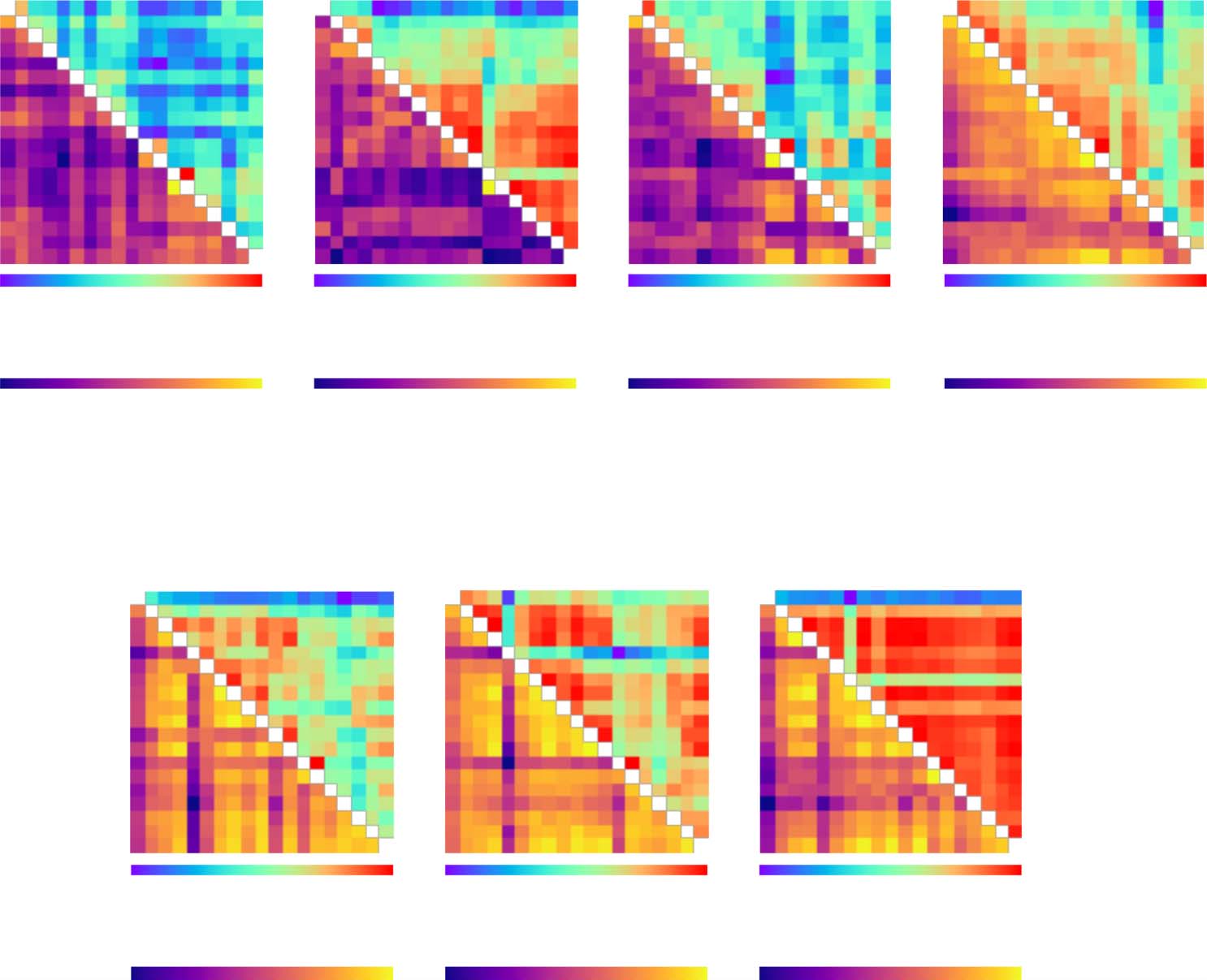
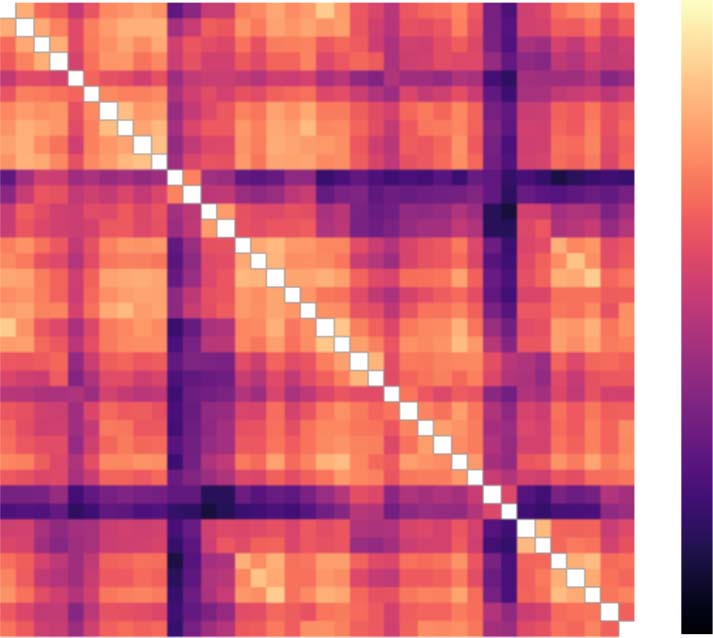
Analysis of interparcellation variations. We observed differences across brain parcellations when
examining the graph-theoretical measures and goodness-of-fit. We determined whether these
deviations were consistent across subjects; mit anderen Worten, we assessed whether altering the
parcellation changes the patterns of the values across all subjects. Zu diesem Zweck, we gathered
the values of the considered graph-theoretical measure for the individual subjects into separate
data vectors for each parcellation and calculated the Pearson correlation coefficient corre-
sponding to each pair of vectors and thus parcellations. The same approach was used to inves-
tigate goodness-of-fit correlations across subjects for different models, where separate data
vectors were constructed for every combination of brain atlas and model for local dynamics
to also assess the effect of the model in this respect.
Netzwerkneurowissenschaften
809
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Dann, we studied whether covariations between the graph-theoretical metrics and the
goodness-of-fit existed by combining principal component analysis with ordinary least squares
regression. We built a dataset with the granularities (number of parcels N ), the median values
across subjects of 13 considered graph-theoretical measures extracted from the empirical SC,
PL, and FC matrices, and the Pearson correlation coefficient between the empirical SC and
empirical FC such that we obtained a 15 × 19 matrix in which each row was associated with
one of those statistics and each column held the values of those metrics for a particular par-
cellation from Table 1. The dataset was z-scored to ensure the comparability of the individual
metrics to one another and subsequently decomposed into the scores and loadings corre-
sponding to the principal components (PCs) through the use of singular value decomposition
as performed by the linalg.svd function in NumPy (van der Walt et al., 2011). Endlich, Die
scores of the PCs were regressed with the median values of the goodness-of-fit across subjects
for every brain atlas for both model types separately. Hier, we considered both a univariate
and a multivariate approach, in which we used the scores of only the first PC and those of
multiple PCs, jeweils, to explain the variance in the goodness-of-fit for varying brain par-
cellation via ordinary least squares regression.
Detection of within-parcellation, between-subject correlations. We checked whether the covaria-
tions found between the group-averaged graph-theoretical measures and the goodness-of-fit
across parcellations were also present when considering intraparcellation, interindividual var-
iations. Somit, we investigated whether graph-theoretical metrics could also explain interin-
dividual differences when considering a specific parcellation in isolation. Erste, we wielded the
same approach from the previous paragraph for this investigation. For each brain atlas, Wir
built a 14 × 800 data matrix, in which each row corresponded to one of the data variables
mentioned in the previous paragraph excluding the granularity and each column held the
values of these statistics for a specific subject and fMRI session pair. For the HCP dataset used
in our study, four resting-state fMRI sessions were available for each subject, which led to the
200 (Fächer) × 4 (fMRI sessions) = 800 columns in the datasets. In order to keep the matrix
dimensions the same also for the SC matrices, the same SC characteristics were repeated in the
dataset for the individual fMRI sessions per subject. We calculated the z-scored dataset, extracted
the first PC, and regressed its scores with the goodness-of-fits of the individual subjects.
We also checked whether a multivariate approach could substantially improve the explained
interindividual variance in the goodness-of-fit across subjects for a given brain parcellation. To
do so, we directly regressed the z-scored dataset with the goodness-of-fits of the individual
subjects and sessions via (multivariate) ordinary least squares regression for the two models
separately.
ERGEBNISSE
In this study, we investigated the effect of the brain atlas on the goodness-of-fit of dynamical
whole-brain models. For this inquiry, we first extracted the empirical SC, PL, and FC matrices
from the dwMRI and fMRI data of 200 subjects included in the HCP S1200 release dataset using
Die 19 parcellations in Table 1 and subsequently subjected them to graph-theoretical analyses.
Nächste, we sampled the modeling results associated with those empirical SC and FC matrices
for the Kuramoto system (8–9) of coupled phase oscillators (Kuramoto, 1984) and the ensemble
(10–13) of Wilson-Cowan type neural mass models (Wilson & Cowan, 1972). Endlich, we inves-
tigated through principal component analysis and linear regressions whether differences in net-
work properties could explain the variance in modeling results.
Netzwerkneurowissenschaften
810
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Parcellation-Induced Heterogeneity of Empirical Connectomes
We found a high variability in the graph-theoretical network properties of the empirical SC for
varying parcellations (Figur 2). Notiz, Jedoch, that the shape and scale parameters of the
degree distributions of the empirical SC should be considered with some reservation as they
may not fully capture all differences in these distributions across parcellations; sehen
Supplementary Data Sheet. Trotzdem, we on average obtained better fit with the gamma
distribution for all approximated network metrics than with the Gaussian distribution.
The shape parameter of the degree distribution of the empirical SC, zum Beispiel, had a me-
dian value ranging from 1.1 for the von Economo-Koskinas atlas (atlas index 16) Zu 8.1 für die
Craddock parcellation with 56 parcels (atlas index 6) (Figure 2A). Its scale parameters exhib-
ited an opposing trend with respect to the variation of the parcellation when compared with
the shape parameters: Relatively large values for the shape parameter were accompanied by
relatively small values for the scale parameter when considering an individual atlas
(Figure 2B). This opposing trend was also observed for the shape parameter and scale param-
eters describing the closeness centrality distribution of the empirical PL matrix (Figure 2E–F).
The modularities derived from the empirical SC matrix showed an increasing trend when the
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 2. Heterogeneity of graph-theoretical properties of empirical structural networks across parcellations. (A–D) Statistics extracted
from the structural connectivity (SC) matrices, which are the shape (A) and scale (B) parameters of the degree distributions, the modularities
(C), and the clustering coefficients (D). (E–H) Statistics extracted from the path length (PL) matrices, which are the shape (E) and scale (F)
parameters of the closeness centrality distributions, the global efficiencies (G), and the characteristic path lengths (H). Dots and lines depict
the medians and interquartile ranges across subjects, jeweils. The atlas indices on the vertical axes correspond to those in Table 1, welche
contains the information about the used parcellations. Abkürzungen: Centr. = closeness centrality, Char.PL = characteristic path length.
Netzwerkneurowissenschaften
811
Influence of parcellation on large-scale whole-brain modeling results
number of parcels grew (Figure 2C). Andererseits, the clustering coefficients showed an
opposing trend (Figure 2D). This is a rather striking observation, because both measures reflect
network segregation. Jedoch, the modularity is calculated through a consideration of the
entire network (Gleichung 2); whereas the clustering coefficient is determined on a node-by-
node basis (Gleichung 6). These findings therefore demonstrate that parcellations with higher
granularities may yield structural networks that contain more pronounced subnetworks, Aber
have fewer triplets of nodes that are strongly interconnected. The decreasing trend of the
(raw) clustering coefficient with increasing granularity was also observed in other studies in-
vestigating the empirical SC (Zalesky et al., 2010). Simple dependencies on the granularity
were found neither for the parameters of the degree distribution (Figure 2A–B) nor for the
graph-theoretical metrics derived from the empirical PL matrix (Figure 2E–H).
Analogous to the modularity and the clustering coefficient, the global efficiency and char-
acteristic path length of the PL matrix also exhibited opposing trends (Figure 2G–H). Diese
opposing trends were expected: Longer characteristic path lengths reflect slower integration
of signals throughout the network, which agrees with a lower global efficiency. Zusätzlich
to the fitted gamma distribution parameters of the degree and closeness centrality distributions
shown in Figure 2A–B and Figure 2E–F, jeweils, we also calculated the means and stan-
dard deviations of the degrees and closeness centralities and the Kolmogorov-Smirnov statis-
tics characterizing the qualities of the gamma distribution fittings; these are included in the
Supplementary Results (Figure S2A–F).
The shape parameter of the degree distribution of the empirical FC matrix exhibited similar
variations across parcellations when compared with its structural counterpart (Figure 2A vs.
Abbildung 3A), though using the Craddock parcellation with 38 parcels (atlas index 5) und das
Schaefer parcellation with 100 parcels (atlas index 11) did result in some notably larger values
for this statistic (Abbildung 3A). The scale parameter, andererseits, seemed to mostly depend
on the granularity (number of brain regions) of the parcellations (Abbildung 3B). Just as with the SC
Matrix, the modularity and the clustering coefficient of the FC matrix exhibited opposing trends,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3. Heterogeneity of graph-theoretical properties of the empirical functional connectivity (FC) across parcellations. (A–E) Statistics ex-
tracted from the empirical FC matrices, which are the shape (A) and scale (B) parameters of their degree distributions, their modularities (C),
their clustering coefficients (D), and their characteristic path lengths (E). (F) Pearson correlation coefficients corresponding to the
structure-function relationship between the upper triangular parts (excluding diagonal) of the empirical SC and FC matrices. Dots and lines
depict the medians and interquartile ranges across subjects, jeweils. The atlas indices on the vertical axes correspond to those in Table 1,
which contains the information about the used parcellations. Abkürzungen: Char.PL = characteristic path length.
Netzwerkneurowissenschaften
812
Influence of parcellation on large-scale whole-brain modeling results
and again appeared to mostly depend on the granularity (Figure 3C–D). The characteristic path
length calculated from the empirical FC did not exhibit such a general trend (Figure 3E). We also
calculated the strength of the structure-function relationship as given by the Pearson correlation
coefficient between the empirical SC and FC matrices ( ρSC,FC). It seemed to demonstrate simi-
larities with the scale parameters of the degree distributions of the empirical SC and the scale
parameters of the closeness centrality distributions and the global efficiencies of the PL matrix as
the parcellation varies (Figure 2B, E, F, Figure 3D).
So far, we observed trends for some graph-theoretical statistics that exhibited large depen-
dencies on the parcellation granularity. We therefore investigated this effect in more detail.
The literature shows that (graph-theoretical) statistics extracted from empirical SC and FC
may be inversely related to the number of parcels included in a parcellation (Messé, 2020;
Zalesky et al., 2010). We therefore plotted the median of each considered measure as a func-
tion of the inverted number of parcels for each parcellation, which revealed high dependen-
cies on the granularity for some statistics (Figure 4A–N). In der Tat, the modularity and clustering
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Scatterplots of all the measures shown in Figure 2 (A–H), Figur 3 (I–N), and Figure 6A (O–P) as a function of the inverse of the
Figur 4.
number of parcels included in the considered parcellations. Each dot corresponds to a particular atlas and the dashed lines show the least
squares linear regressions between these points. The coefficients of determination are also displayed in each plot. Abkürzungen: Centr. =
closeness centrality, Char.PL = characteristic path length, Num. = number of.
Netzwerkneurowissenschaften
813
Influence of parcellation on large-scale whole-brain modeling results
coefficient reflecting the segregation of the empirical SC and FC are highly influenced by the
parcellation granularity (Figure 4C, D, K, L). The structure-function relationship ρ
SC,FC is also
governed by the number of regions to a large extent (Figure 4N), which is in agreement with
the results of Messé (2020). Jedoch, most of the other network properties only weakly to
moderately correlate with parcellation granularity. In addition to the inverted relationship,
we checked whether the granularity effect could be modeled better by a linear dependence
on the number of parcels. The opposite was true: A linear treatment of the granularity effect
did not lead to higher explained variances, and for many measures it even resulted in lower
coefficients of determination.
To investigate how the considered measures depend on the parcellations beyond the gran-
ularity effect, we regressed this effect out by fitting the data to an inverse relationship ( y = a/N +
B) and examined the residuals. Wie erwartet, the residuals of the modularities and clustering
coefficients exhibited differences between brain atlases that had a lower scale than the raw data;
see for example Figure 4C, D, K, I vs. Figure S5C, D, K, I in the Supplementary Results. The other
residuals still exhibited differences across parcellations of the same magnitude; see Figure S3,
Figure S4, and Figure S5A–N in the Supplementary Results. In sum, even though the granularity
of a parcellation can greatly influence some of the network statistics extracted from the empirical
Daten, the observed parcellation-induced deviations typically go beyond such a simple relation-
ship. We further analyze this dependence below (Interparcellation Variations of Empirical
Connectomes and Modeling Results section).
Subsequently, we investigated how the graph-theoretical network properties of the individual
subjects correlated between each pair of the considered brain atlases; see Materials and
Methoden (Analyse) for details of this analysis. Following this procedure, we evaluated whether
the interindividual differences in the empirical network statistics exhibited similar patterns
between the parcellations used for the extraction of the empirical connectomes. We found that
these correlations were highest for the global efficiency and characteristic path length of the
empirical PL matrix (Figure 5D), for the modularity, Clusterkoeffizient, and characteristic
path length of the empirical FC matrices (Figure 5F, G), and for the correlation between
empirical SC and FC (Figure 5G). Such correspondences were generally lower for the parameters
of the degree and closeness centrality distributions (Figure 5A, C, E), and the modularity and
clustering coefficient of the empirical SC (Figure 5B). These network metrics of the corre-
sponding connectivity matrices are thus sensitive to a selected brain parcellation. At the indi-
vidual level, network segregation properties of the empirical FC and network integration
statistics thus seemed to be influenced much less by the brain parcellation than measures
reflecting the centrality and the network segregation of empirical SC.
Parcellation-Induced Heterogeneity of Modeling Results
In this section we present the results of the model simulations for all brain atlases in Table 1 Und
the two considered whole-brain models of coupled phase oscillators (8–9) and neural mass
Modelle (10–13). For each combination of subject, parcellation, and model, the optimal values
of the global coupling and delay parameters were found by maximizing the Pearson correlation
between the empirical and simulated FC matrices, which provided the goodness-of-fit of the
model illustrated in Figure 6A for both models. For varying parcellations we observed a high
variability of the fitting results, implying that the extent of correspondence between simulated
and empirical FC strongly depended on the selected parcellation. Hier, the MIST parcellation
mit 31 parcels, the Desikan-Killiany atlas, the von Economo-Koskinas atlas, and the AAL atlas
yielded the highest goodness-of-fits independently of the model type (Figure 6A, atlas indices 1,
Netzwerkneurowissenschaften
814
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 5. Cross-correlations across subjects of the network statistics derived from the empirical structural and functional connectomes for
different parcellations. The correlations between parcellations were calculated for (A) the shape (upper triangle) and scale (lower triangle)
parameters of the degree distributions of the empirical SC matrix, (B) the modularities (upper triangle) and clustering coefficients (lower tri-
angle) of the empirical SC, (C) the shape (upper triangle) and scale (lower triangle) parameters of the closeness centrality distributions of the
empirical PL matrix, (D) the global efficiencies (upper triangle) and characteristic path lengths (lower triangle) of the empirical PL matrix, (E) Die
shape (upper triangle) and scale (lower triangle) parameters of the degree distribution of the empirical FC matrix, (F) the modularities (upper
triangle) and clustering coefficients (lower triangle) of the empirical FC, Und (G) the characteristic path lengths of the empirical FC (upper
triangle) and the Pearson correlation between the empirical SC and FC (lower triangle). The atlas indices correspond to those in Table 1,
which contains the information about the used parcellations. Abkürzungen: Centr. = closeness centrality, Char.PL = characteristic path length.
16, 17, Und 18, jeweils). Interessant, the interindividual variance of the goodness-of-fit
had approximately the same range as the structure-function relationship between the empirical
SC and FC matrices (Figur 3). It also appeared as if the patterns of the goodness-of-fit versus
parcellations were similar to each other for different models (Figure 6A).
To quantify the mentioned similarity, we considered the medians of the goodness-of-fit
calculated over all subjects corresponding to the phase oscillators and regressed them across
parcellations with those of the neural mass model. This resulted in a regression with a coef-
ficient of determination of 0.88 (Figure 6C), suggesting a model-independent impact of a
given brain parcellation on the (group-averaged) goodness-of-fit. As with the graph-theoretical
Maßnahmen, we investigated the effect of granularity on the goodness-of-fit by plotting its
median across subjects against the inverse of the number of parcels included in the parcella-
tionen. The corresponding plots exhibited moderate correlations (Figure 4O–P), bei dem die
Netzwerkneurowissenschaften
815
Influence of parcellation on large-scale whole-brain modeling results
Figur 6. Goodness-of-fit of the whole-brain models based on coupled phase oscillators and neuronal mass models and their interrelations
for the considered parcellation schemes. (A) Maximized correlations (goodness-of-fit) between the empirical and simulated FC matrices for the
brain parcellation schemes and models investigated in this study as indicated on the vertical axes. Dots and lines depict the medians and
interquartile ranges across subjects, jeweils. (B) Correlations across subjects of the goodness-of-fit of the model between the considered
parcellations and models. Tisch 1 contains the parcellation information corresponding to the atlas indices used in the plots. (C) Scatterplot of
the medians of the goodness-of-fit corresponding to the phase oscillator (x-axis) and neural mass model (y-axis) across subjects. Each dot
corresponds to a particular parcellation, the purple line portrays the linear regression between both types of goodness-of-fit, and the black
dashed line corresponds to x = y.
impact of granularity on the fitting results for the phase model is much smaller than that for the
neural mass model. To quantify the parcellation-induced influence on the goodness-of-fit be-
yond the dependence on the granularity, the effect of the (inverted) granularity was regressed
out. The residual goodness-of-fits exhibited variations across parcellations that had similar
magnitudes as the original data; see for example Figure 4O–P versus Figure S5O–P in the
Supplementary Results. Zusätzlich, the agreement between models was further enhanced;
see Figure 6C versus Figure S6C. Abschließend, the granularity influences the goodness-of-fit
to a limited extent, implying that the parcellation-induced deviations cannot exclusively be
explained by this quantity.
The goodness-of-fit was also correlated across individual subjects between the considered
parcellations and models to evaluate how similar the patterns of the model fitting over all
subjects were for different parcellations and models; see Materials and Methods (Analyse) für
details of this analysis. The results showed relatively high correspondence of the fitting patterns
across individual subjects for many of the parcellation combinations for the same as well as for
different models, which is illustrated in Figure 6B. Trotzdem, we also observed generally
lower correlations for the Schaefer and also the Harvard-Oxford atlases, both within and across
Modelle (Figure 6B, atlas indices 11–14). Note that we did not find such clear, generally
decreased values when considering the correlations of the empirical graph-theoretical statistics
across parcellations (Figur 5). For the empirical FC matrices, the Craddock atlas with 38 parcels
could however be distinguished in this respect (Figure 5E–F, atlas index 5), and only a slight
indication of a lower correlation could be found for the scale parameter of the degree
Netzwerkneurowissenschaften
816
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
distribution of the empirical FC for the Schaefer atlas with 100 parcels and Harvard-Oxford
atlas with 48 parcels (Figure 5E, atlas indices 11 Und 13).
Taken together, the modeling results as represented by the goodness-of-fit between empir-
ical and simulated FC showed pronounced heterogeneity with respect to the variation of the
brain atlas. Zusätzlich, we found that the intersubject variability of the fitting results exhib-
ited similar patterns for most of the considered parcellations, although we also observed some
exceptions for which this correspondence is limited (the Schaefer and Harvard-Oxford atlases).
Interparcellation Variations of Empirical Connectomes and Modeling Results
To understand the effects observed at the group level, the patterns of the extracted graph-
theoretical statistics across parcellations (Figur 2, Figur 3, median values) were compared
with one another and with those obtained for the goodness-of-fit of both models (Figure 6A,
median values). Significant correlations were observed for some of the tested combinations,
which are shown in Figure 7A. This in particular concerned the correlations of the inverted
number of parcels with the subject medians of the modularities and clustering coefficients of
both the empirical SC and FC, the scale parameters of the degree distributions of the empirical
FC, and the correlations between empirical SC and FC (Abbildung 7A, top row/first column). In
such a way the dependencies of these measures on granularity were demonstrated, welche
were already observed in Figure 4. Außerdem, the scale parameters of the degree distribu-
tions of the empirical SC and the structure-function relationship between the empirical SC and
FC exhibited significant correlations with the fitting results for both models. Interessant, Die
modularity of the empirical FC significantly anticorrelated with fitting results for the neural
mass model (d.h., smaller modularity implies better fitting), but not for the phase model
(Abbildung 7A).
We thus found that the network properties of the empirical connectomes (Figur 2, Figur 3)
and the quality of the model validation as given by the goodness-of-fit of the simulated FC to the
empirical FC (Figur 6) in some cases demonstrated a pronounced and significant correlation
with one another across parcellations (Abbildung 7A). To quantify this relationship further, we com-
bined principal component analysis with ordinary least squares linear regression to take into
account the contributions from all graph-theoretical statistics; see Materials and Methods
(Analyse) for details of this analysis. The first principal component (PC1) extracted from the
group-averaged graph-theoretical statistics was found to explain 48% of the variance in the data
variables across parcellations (Figure 7D), and the signs of its relative loadings (Figure 7B) war
in accordance with previous results (see e.g., Abbildung 7A). Subsequently, we regressed the PC1
scores with the medians of the goodness-of-fit calculated across subjects for every brain atlas.
We found that this PC explained about 19% Und 49% of the interparcellation variance in the
goodness-of-fit for the phase oscillators and the neural mass models, jeweils (Figure 7C).
We again observed stronger contribution of empirical data to the fitting results of the neuronal
mass model; see also Figure 4O, P.
The second principal component (PC2) explained an additional 35% of the variance in the
data variables (Figure 7D). We included this component in the linear regression model, welche
made it multivariate. This improved the association between the data variables and the
goodness-of-fit to 77% Und 81% of explained variance for the phase oscillator and neural mass
Modell, jeweils (Figure 7E). Including more principal components in the linear regression
model led to an even better explanation of the goodness-of-fit variance by the empirical data
(Figure 7D, E). Notiz, Jedoch, that using too many PCs in the regression may lead to an over-
fitting for the considered 19 parcellations. Endlich, we investigated the effect of the granularity on
Netzwerkneurowissenschaften
817
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
N
e
N
_
A
_
0
0
2
0
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 7. Relationship between the interparcellation variations of the empirical graph-theoretical metrics and the goodness-of-fit. (A)
Cross-correlations among the inverted granularities, the graph-theoretical measures of the empirical connectomes (network propertties de-
picted in Figure 2 and Figure 3), the structure-function relationship, and the goodness-of-fit of the models to the empirical data. The corelation
was calculated across parcellations between the median values over all subjects. Significant correlations are highlighted by colors ( P < 0.05,
two-sided, Bonferroni corrected). (B) Loadings of the first (PC1) and the second (PC2) principal components of the group-averaged
graph-theoretical metrics, that is, the contributions of the original empirical data variables to PC1 and PC2. (C) Regressions of the PC1 scores
with the medians of the goodness-of-fit between empirical (eFC) and simulated (sFC) functional connectivity. The medians were calculated
across subjects for each considered parcellation for the phase oscillator (red) and the neural mass model (blue) as indicated in the legend
together with the fraction of the explained variance. The symbols stand for the individual parcellations from Table 1. (D) Cumulative amount of
explained variance in the group-averaged graph-theoretical measures as a function of the number of included PCs. (E) Fraction of the inter-
parcellation variance of the goodness-of-fit being explained by the (multivariate) linear regression model as a function of the number of PCs
included in the model. Other abbreviation: a.u. = arbitrary unit, cumul. = cumulative, expl. = explained, var. = variance.
these results by regressing this effect out of all the quantities used in this investigation while
following the same procedure as described above. The results of this inquiry are shown in
Figure S7 in the Supplementary Results, and they demonstrate that after the removal of the
granularity effect already the first principal component sufficed to get approximately the same
Network Neuroscience
818
Influence of parcellation on large-scale whole-brain modeling results
associations between the data variables and the goodness-of-fit as observed in Figure 7 for two
PCs. Also the difference between models was inverted and reduced.
With these results, we demonstrated that most of the interparcellation variation observed in
the modeling results at the group level (Figure 6A) could be explained by the network prop-
erties of and the relationship between empirical SC and FC used to inform and validate the
models. Furthermore, we showed which metrics derived from the empirical connectomes con-
tributed positively and negatively to the goodness-of-fit of the simulated FC produced by the
model to the empirical FC (Figure 7B). Lastly, our results confirm that the parcellation exerts an
influence on the graph-theoretical measures and the goodness-of-fits that can only be partially
explained by the granularity. This especially becomes evident when considering the high PC1
loading of the inverse of the number of parcels in relation to the relatively low association of
this PC with the modeling results (Figure 7B, D); see also Figure S7 in the Supplementary
Results, where the granularity was regressed out.
Interindividual Differences of Empirical Connectomes and Modeling Results
As shown above, the group averages of the graph-theoretical statistics and the modeling results
obtained using different brain atlases are tightly related to one another (Figure 7). Nevertheless,
as dynamical whole-brain models seem to be a promising model-based approach for studying
interindividual differences (Ritter et al., 2013; Sanz-Leon et al., 2015; Zimmermann et al.,
2018), we investigated whether the within-parcellation, between-subject variances observed
in our modeling results could also be attributed to variations of the data variables extracted from
the empirical SC and FC. To do so, we adopted the approach from the previous section, where,
for each individual parcellation, we built a separate dataset containing the corresponding
graph-theoretical network properties; see Materials and Methods (Analysis) for details. Using
this dataset, we initially checked how individual empirical graph-theoretical statistics correlated
with the interindividual variability of the goodness-of-fit, and found no clear correspondences
except for the structure-function relationship ρSC,FC (Figure S8). It is interesting to observe here
that ρ
SC,FC correlated negatively with the goodness-of-fit of the models to the empirical data for
most of the considered parcellations. Given that this bivariate approach did not yield positive
results in the form of clear (anti)correlations for the investigated network metrics, we resorted
to multivariate analyses.
As before, we calculated the PC1 of the consequent dataset of z-scored individual data
variables (network properties) and subsequently regressed the PC1 scores with the corre-
sponding goodness-of-fits of the model across individual subject-session pairs for every
one of the considered brain atlases. The obtained results showed that the amount of variance
in the modeling results across subjects explained by PC1 was low (<3%; see Figure S9A in the
Supplementary Results), even though the data variables extracted using different parcellations
exhibited similar covariations as reflected by the PC1 loadings and corresponding correlations,
which exhibited some form of clustering (Figure S9B–C). Because of the weak explanatory
power observed at this approach (Figure S9A), the used methodology based on the principal
component analysis of network properties of empirical connectomes might be inappropriate
to assess interindividual differences in the model validation.
We therefore employed a different approach, where the z-scored data variables representing
the network properties of empirical SC and FC were directly regressed with the z-scored
goodness-of-fits of the models across individual subjects via multivariate ordinary least squares
regression. The regression results obtained for individual parcellations indicated a variable
amount of explained between-subject variance in the goodness-of-fit for different parcellations
Network Neuroscience
819
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
(Figure 8A). The strongest influences of the empirical connectomes on the interindividual vari-
ations in the goodness-of-fit were observed for the von Economo-Koskinas, AAL, and
Brainnetome atlases (indices 16, 17, and 19 in Figure 8A, respectively), which however still
did not exceed 40% of explained variance. For other parcellations based on, for example, the
Schaefer or Harvard-Oxford atlases (indices 11–14 in Figure 8A), the results of the model fitting
for an individual subject practically did not depend on the network properties of the used em-
pirical connectomes. Interestingly, in most cases the phase oscillators exhibited a somewhat
stronger dependence on the considered data variables (Figure 8A, red bars), which contrasts
with the interparcellation variation of the medians (Figure 7E). We observed low consistency
between parcellations and between models regarding the regression coefficients assigned to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Relationship between the interindividual variations of the empirical graph-theoretical metrics and modeling results for different
parcellations. (A) Amounts of within-parcellation, between-subject variance in the modeling results (goodness-of-fit to empirical data) being
explained via multivariate ordinary least squares linear regression utilizing the z-scored graph-theoretical statistics of the empirical connectomes
per parcellation. Modeling results were sampled by using the systems of coupled phase oscillators (red) and neural mass models (blue). (B–C)
Regression coefficients corresponding to the data variables (network properties) depicted in Figure 2 and Figure 3 for four selected brain parcella-
tions as indicated in the legend and for the phase oscillators (B) and the neural mass models (C) leading to the regression results in panel A. The
abbreviations MIST (103), Shen (156), Sch. (100), and EK (86) correspond to the parcellations in Table 1 and in panel A with indices 3, 10, 11, and
16, respectively. (D) Pearson correlation coefficients across the regression coefficients per pair of brain parcellation and model type. Table 1
contains the parcellation information corresponding to the atlas indices. Abbreviations: coef. = coefficient, corr. = correlation.
Network Neuroscience
820
Influence of parcellation on large-scale whole-brain modeling results
the corresponding data variable by this multivariate regression analysis (Figure 8B–C). This is
reflected by the Pearson correlations across the coefficients per model and parcellation pair
illustrated in Figure 8D, which shows a clustering that is inconsistent across models.
Taken together, these results demonstrated that the contributions of the graph-theoretical
statistics derived from the empirical connectomes to the interindividual differences in the
modeling results were limited.
Network Properties of Simulated Functional Connectomes
We established that between-parcellation variances in the model fitting results could largely
be explained by the variation of the network properties taken from the empirical SC and FC
(Figure 7). However, we also found that such a relationship was hardly applicable to the ex-
planation of the intraparcellation, between-subject variations. In this case, for any parcellation,
the interindividual differences in the goodness-of-fit only weakly to moderately correlated with
the graph-theoretical properties of empirical networks for individual subjects (Figure 8).
Here we evaluate how similar the empirical FC matrices were in terms of the graph-
theoretical statistics to the simulated ones that provided the best fits based on Pearson’s cor-
relation. To do so, the simulated FC matrices were subjected to the same graph-theoretical
analyses as the empirical FCs; see Figure 9A–D, I–L for results. The medians of the network
properties calculated across subjects for the empirical and simulated FCs were correlated with
each other over all considered parcellations. The results showed that relationships between
the network properties of the empirical and simulated FCs existed, which indicated that the
models on average preserved most of the considered network properties of the empirical func-
tional connectome; only the characteristic path length exhibited low coefficients of determi-
nations for both models (Figure 9E–H, M–P). The results for the clustering coefficient have not
been shown in Figure 9 as they resembled those of the modularity. We also found that the
empirical and simulated functional networks agreed with each other to very different extents
for the two considered models except for the shape parameter of the degree distribution
(Figure 9E, M). More variance in the scale parameters of the degree distributions of the simu-
lated FC across parcellations could be explained by that of the empirical FC when the phase
oscillators rather than the neural mass models were used for the generation of the former
(Figure 9F, N). The opposite is true for the modularity and characteristic path length; here,
the neural mass model led to more explained variance (Figure 9G–H, O–P). From these results,
we can conclude that the accuracy of the transformation of the empirical SC to simulated FC
by the considered dynamical whole-brain models can depend on the model used for the sim-
ulation of the local mean activity of the brain regions. These findings furthermore indicated
that, even though different models may lead to comparable goodness-of-fits (Figure 6C), the
correspondence of the network structures of the simulated FCs to those of the empirical ones
may vary considerably across models.
Finally, we investigated how the latter analysis performed at the level of individual subjects
and individual parcellations. Hence, we correlated the network properties derived from the
empirical and simulated FCs across subjects for each individual parcellation. The obtained
results, illustrated in Figure 10A–D, revealed that the highest correspondences between the
network properties of the empirical and simulated FC could be found for the modularity
and characteristic path length (Figure 10G–H). No general patterns could be found as to which
model led to higher explained variances between empirical and simulated FC (Figure 10E–H).
Still, we observed relatively large deviations of the explained variance between the two con-
sidered models for the individual parcellations, where the largest differences between the
Network Neuroscience
821
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Phase oscillator
Neural mass (BOLD)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
t
.
Figure 9. Relationship between the graph-theoretical statistics of empirical and simulated FC matrices at the group level. Network properties
of the simulated FCs providing the best fits to the empirical FC and the scatterplots of the corresponding median values calculated across
subjects are illustrated for phase oscillator model (A–F) and neural mass model (G–L). The shape (A, E, I, M) and scale (B, F, J, N) parameters
of the degree distributions, the modularities (C, G, K, O) and the characteristic path lengths (D, H, L, P) are depicted for the parcellations in
Table 1, where dots and lines in panels A–D and I–L depict the medians and interquartile ranges across subjects, respectively. Symbols, col-
ored lines, and black lines in the scatterplots (E–H) and (M–P) of the simulated network metrics versus empirical ones stand for individual
parcellations, regression lines, and the diagonal x = y, respectively.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
models could reach around 20% of explained variance (Figure 10E–H, differences between
red and blue bars).
These results show that network properties of the empirical and simulated FCs could be a
good measure of the model validation, and allow us to distinguish different models at the level
of individual subjects (Figure 10) as well as at the group level (Figure 9). This seemed not to be
the case for the correlative model fitting, where the models were practically indistinguishable
at the group level and could be differentiated only at the subject levels. The latter claim can be
seen in the amount of variance in the goodness-of-fit that is explained by the network
Network Neuroscience
822
Influence of parcellation on large-scale whole-brain modeling results
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
Figure 10. Relationship between the graph-theoretical statistics of empirical and simulated FC matrices at the subject level. (A–D) Scatterplots
of the shape (A) and scale (B) parameters of the degree distributions, the modularities (C), and the characteristic path length (D) of the empirical
and simulated (by neural mass model) FCs within a single parcellation as given by the von Economo-Koskinas atlas (index 16 in Table 1). Every
dot represents a subject-session pair, the colored lines depict the ordinary least squares linear regression solution, and the black lines corre-
spond to x = y. (E–H) Proportion of intersubject variance of the network properties of the best-fit simulated FCs generated by the phase oscillators
(red) and the neural mass model (blue) that is explained by the network properties of the empirical FCs for a given parcellation indicated on the
horizontal axes. Table 1 contains the parcellation information corresponding to the atlas indices used in the plots. Other abbreviations: expl. =
explained, var. = variance.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
properties derived from the empirical data when comparing between- and within-parcellation
variations (see Figure 7, Figure 8).
DISCUSSION
In this study, we used a selection of 19 parcellations constructed through 10 different
approaches. They were selected with an attempt to balance between parcellations derived
from functional data, comprising the atlases described by Craddock et al. (2012), Shen
et al. (2013), Schaefer et al. (2018), and Urchs et al. (2019), and structural information, con-
stituting the other parcellations included in Table 1. Furthermore, the investigated parcella-
tions were compiled using distinct methodologies such as boundary detection algorithms,
Network Neuroscience
823
Influence of parcellation on large-scale whole-brain modeling results
histological stainings, and diverse clustering approaches (see the Supplementary Method for
details). While more brain parcellations are available in the literature and were used for data-
driven analyses (Dadi et al., 2020; Messé, 2020; Schaefer et al., 2018), the tested parcellations
and the variation regarding the number of parcels in them are representative for the state-of-
the-art brain parcellations, and can support the derived conclusions concerning the reported
relationship between the model simulation results and the empirical data.
Influence of Parcellation on Graph-Theoretical Statistics and Goodness-of-Fit
Significant (anti)correlations were found across parcellations when comparing the parcellation
granularity with individual graph-theoretical statistics and the goodness-of-fit of the whole-
brain models (Figure 7). This clearly evidenced the granularity substantially affecting the
network properties of the empirical FC and SC and the model fitting results regardless of the
method used to construct the parcellation. Still, as the parcellation varied, graph-theoretical
statistics as well as the goodness-of-fit exhibited pronounced variations (Figure 2, Figure 3,
Figure 4, Figure 6) that persisted after we corrected for the effect of the granularity (Figure
S3, Figure S4, Figure S6, Figure S5). We were not able to reliably distinguish between results
derived from e.g. functionally and structurally derived parcellations, even after the granularity
correction was performed. Hence, as parcellation-induced variances in the goodness-of-fit
were shown to be related to the variations in the empirical SC and FC, the question still remains
how the parcellations induce the pronounced differences in the graph-theoretical statistics.
The reported parcellation-induced variances emphasize the importance of a well-advised
selection of the parcellations in region-based neuroimaging studies using graph theory or
whole-brain models to analyse the data. A recent study by Messé (2020) already showed this
to be true when examining the structure-function relationship of the brain from a statistical
perspective. Also studies by Wang et al. (2009) and Zalesky et al. (2010) demonstrated the
prominent influence the brain parcellation may have on the network properties of the empir-
ical FC and SC, respectively. Our study added further modern graph-theoretical measures to
the analysis for both empirical SC and FC as well as simulated FC. In sum, these findings can
complement other considerations (e.g., the biological interpretation of the atlas) in the selec-
tion of the proper parcellation for the study at hand. After all, the question concerning an op-
timal parcellation is a difficult problem given many possible parcellation techniques and
optimization criteria.
Important Factors With Respect to Model Fitting
We found that most of the interparcellation variance in the goodness-of-fit at the group level
could be explained by the graph-theoretical statistics derived from the empirical SC and FC
(Figure 7). By examining the PC1 and PC2 loadings in Figure 7B, the graph-theoretical mea-
sures associated with a high goodness-of-fit can be identified. Here, the PC1 loadings clearly
reflected the effect of granularity in the graph-theoretical statistics and demonstrated that a
finer granularity leads to a lower goodness-of-fit. The loadings of PC2, which explained a large
amount of variance in the modeling results for both models, did not exhibit such a general
relation. The parameters of the degree and closeness centrality distributions as well as the
global efficiency are heavily loaded onto this PC. Here, the shape parameters of all the fitted
gamma distributions exhibited negative loadings, implying that a small shape parameter leads
to a high goodness-of-fit (see also Figure S7). Given Equation 1 and Figure S1, this implies that
the modeling workflow prefers that most nodes have a low centrality and a select few nodes
have a high centrality for the empirical SC as well as FC, because then the density is high close
to 0 and decreases with incrementing degree. The positive PC2 loading of the global
Network Neuroscience
824
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
efficiency, furthermore, implies that the whole-brain models can replicate the functional net-
works better if the structural networks facilitate the integration of signals.
The network architecture of the brain itself is believed to comprise a multilevel modular
structure and a heterogeneity with respect to the degree of individual nodes (Avena-
Koenigsberger, Misic, & Sporns, 2018; van den Heuvel & Sporns, 2019). Although the modu-
larity did not exhibit a strong relationship with the goodness-of-fit other than their shared
dependence on the granularity (Figure 7, Figure S7), our results show that dynamical whole-
brain models indeed favor such a heterogeneity in the degree distribution. After all, the
goodness-of-fit was ameliorated by a higher diversity with regard to the degree distribution
in the SC and FC (as illustrated in Figure S10A–E).
Within-Parcellation, Between-Subject Variances, and the Personalization of Whole-Brain Models
Previous studies suggested that dynamical whole-brain models are able to simulate the resting-
state brain activity on a personalized level (Bansal et al., 2018; Deco et al., 2017; Ritter et al.,
2013; Sanz-Leon et al., 2015; Zimmermann et al., 2018). How this personalization is achieved
is not known. In this study, we have provided evidence that interindividual differences in the
goodness-of-fit do not reliably relate to the subject-specific deviations in the graph-theoretical
measures (Figure 8, Figure S9). In addition, we have shown that the network structures of the
simulated FC map onto those of the empirical FC when considering group averages, but not
within-parcellation, interindividual variances (Figure 9, Figure 10). Taken together, the person-
alization of whole-brain models does not seem to use subject-specific deviations in the net-
work properties. How personalization of whole-brain models then actually is achieved
requires further investigation.
To account for the interindividual variations of the modeling results, other data variables may
for example be considered out of the class of the considered network properties. In such investi-
gations, special attention must be paid to the limitations in the reconstruction of the structural con-
nectome. Studies namely have shown substantial amounts of inaccuracies (e.g., false positives or
negatives) infecting the empirical SC when it is extracted from dwMRI data (Bassett, Brown,
Deshpande, Carlson, & Grafton, 2011; Lindquist, 2020; Maier-Hein et al., 2017; Schilling
et al., 2019; Sotiropoulos & Zalesky, 2019). These inaccuracies can have a systematic effect on
the network properties of the empirical SC (Zalesky et al., 2016). In order to reduce these inaccu-
racies, the whole-brain tractography should be calculated with high density by state-of-the-art
techniques, as we did in this study, which can enhance its reproducibility (Roine et al., 2019).
The patterns of the intersubject differences in the graph-theoretical statistics and the modelling
results may vary across parcellations (Figure 5, Figure 6B), which implies that the network struc-
tures of the empirical connectomes and the modeling results depend on the used parcellation
also at the level of individual subjects. This is a relevant implication as it may have consequences
for computational modeling studies investigating clinical traits (Cabral, Hugues, Kringelbach, &
Deco, 2012; Saenger et al., 2017). Observed differences between groups and individual subjects
may deviate when another parcellation is used and may therefore reflect artefacts induced
through the use of a particular parcellation rather than actual deviations in the structure-function
relationship of distinct cohorts, as also discussed by Betzel and Bassett (2017).
Perspectives and Outlook
Further brain parcellations, datasets, models, and (graph-theoretical) analyses variations might
be considered to verify and confirm the obtained results, especially when more computation-
ally powerful resources become available. In the end, the simulations and optimizations of
Network Neuroscience
825
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
dynamical whole-brain models are computationally costly. The computational costs also in-
hibit the estimation of biases in the model simulation results via, for example, null models.
Future studies should be devoted to devising strategies that could estimate these biases without
a full evaluation of the model dynamics through simulations.
Related to these computational costs is the notion that our results can contribute to the de-
velopment of informed expectations concerning the quality of the model validation for a given
brain parcellation. For this, a few network properties of the empirical connectomes calculated
for this parcellation can be examined before running time- and resource-consuming model
simulations. Additionally, this concept may be exploited to distinguish between data-induced
and model-induced deviations in the modeling results. Such an investigation may estimate to
what extent the empirical data already predicted the differences in modeling results between,
for example, healthy and clinical cohorts; the contribution of the model is consequently rep-
resented by the remaining between-group variance.
Finally, the inaccurate mappings of empirical SC to simulated FC by both tested models for
local, mean-field activity highlight their current limitations with respect to the replication of
empirical resting-state brain dynamics. How well other types of models can replicate the empirical
FC on the basis of the empirical SC remains to be seen and should be investigated further. Such
an investigation would typically comprise the application of the framework of this study to other
model types such as the Jansen-Rit model (Jansen & Rit, 1995; Jansen, Zouridakis, & Brandt,
1993), the (reduced) Wong-Wang model (Deco & Kringelbach, 2014; Hansen, Battaglia,
Spiegler, Deco, & Jirsa, 2015; Wong & Wang, 2006), different types of limit-cycle oscillators
(Deco et al., 2018; Deco et al., 2017; Ghosh, Rho, McIntosh, Kötter, & Jirsa, 2008), and a more
recently developed neural mass model that incorporates plasticity dynamics (Abeysuriya et al.,
2018). Taken together, this implies that, even though the tested models yield results that are
related to the empirical data in terms of more than one statistic, they are far from perfect and
hence there is room for improvement.
ACKNOWLEDGMENTS
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
We thank M. Kollmann for his consultation on the manuscript and S. Zhang for his consultation
on the parcellation image processing. This study was made possible through the Portfolio Theme
Supercomputing and Modeling for the Human Brain of the Helmholtz Association (https://www
.helmholtz.de/en), and through the European Union’s Horizon 2020 Research and Innovation
Program. The funders had no role in study design, data collection and analysis, decision to
publish, or preparation of the manuscript. Also, the authors gratefully acknowledge the com-
puting time granted through JARA on the supercomputer JURECA at Forschungszentrum
Jülich.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00202.
We provide three types of supporting information. The Supplementary Method contains a
summary on the construction of the parcellation schemes that we used in our study, i.e. what
methodology was applied to what type of data to construct them. In addition, it discloses how
each brain parcellation image was modified in order to enhance the comparability between
parcellations. The Supplementary Data Sheet includes depictions of the empirical SC, PL and
FC matrices acquired through the use of the same brain parcellations. In addition, the data
sheet displays statistics derived from the empirical connectomes. Finally, the Supplementary
Results contains figures that were used to support the main results.
Network Neuroscience
826
Influence of parcellation on large-scale whole-brain modeling results
AUTHOR CONTRIBUTIONS
Justin Domhof: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Software; Validation; Visualization; Writing – original draft; Writing – review & editing. Kyesam
Jung: Data curation; Methodology; Software; Writing – review & editing. Simon Eickhoff:
Conceptualization; Funding acquisition; Project administration; Supervision; Validation;
Writing – review & editing. Oleksandr Popovych: Conceptualization; Funding acquisition;
Methodology; Project administration; Resources; Supervision; Validation; Writing – original
draft; Writing – review & editing.
FUNDING INFORMATION
Simon Eickhoff, Horizon 2020 (https://dx.doi.org/10.13039/501100007601), Award ID:
785907. Simon Eickhoff, Horizon 2020 (https://dx.doi.org/10.13039/501100007601), Award
ID: 945539. Simon Eickhoff, Horizon 2020 (https://dx.doi.org/10.13039/501100007601),
Award ID: 826421.
REFERENCES
Abeysuriya, R. G., Hadida, J., Sotiropoulos, S. N., Jbabdi, S.,
Becker, R., Hunt, B. A. E., … Woolrich, M. W. (2018). A biophys-
ical model of dynamic balancing of excitation and inhibition in
fast oscillatory large-scale networks. PLoS Computational
Biology, 14(2), e1006007. https://doi.org/10.1371/journal.pcbi
.1006007, PubMed: 29474352
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economical
brain functional networks. PLoS Computational Biology, 3(2), e17.
https://doi.org/10.1371/journal.pcbi.0030017, PubMed:
17274684
Amunts, K., & Zilles, K. (2015). Architectonic mapping of the human
brain beyond Brodmann. Neuron, 88(6), 1086–1107. https://doi
.org/10.1016/j.neuron.2015.12.001, PubMed: 26687219
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018).
Communication dynamics in complex brain networks. Nature
Reviews Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn
.2017.149, PubMed: 29238085
Bandettini, P. A., Wong, E. C., Hinks, R. S., Tikofsky, R. S., & Hyde,
J. S. (1992). Time course EPI of human brain function during task
activation. Magnetic Resonance in Medicine, 25(2), 390–397.
https://doi.org/10.1002/mrm.1910250220, PubMed: 1614324
Bansal, K., Nakuci, J., & Muldoon, S. F. (2018). Personalized brain
network models for assessing structure–function relationships.
Current Opinion in Neurobiology, 52, 42–47. https://doi.org/10
.1016/j.conb.2018.04.014, PubMed: 29704749
Bassett, D. S., Brown, J. A., Deshpande, V., Carlson, J. M., &
Grafton, S. T. (2011). Conserved and variable architecture of
human white matter connectivity. NeuroImage, 54(2), 1262–1279.
https://doi.org/10.1016/j.neuroimage.2010.09.006, PubMed:
20850551
Betzel, R. F., & Bassett, D. S. (2017). Multi-scale brain networks.
NeuroImage, 160, 73–83. https://doi.org/10.1016/j.neuroimage
.2016.11.006, PubMed: 27845257
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks.
Journal of Statistical Mechanics, 2008(10), P10008. https://doi
.org/10.1088/1742-5468/2008/10/P10008
Cabral, J., Hugues, E., Kringelbach, M. L., & Deco, G. (2012).
Modeling the outcome of structural disconnection on resting-state
functional connectivity. NeuroImage, 62(3), 1342–1353. https://doi
.org/10.1016/j.neuroimage.2012.06.007, PubMed: 22705375
Craddock, R. C., James, G. A., Holtzheimer, P. E., Hu, X. P., &
Mayberg, H. S. (2012). A whole brain fMRI atlas generated via
spatially constrained spectral clustering. Human Brain Mapping,
33(8), 1914–1928. https://doi.org/10.1002/hbm.21333, PubMed:
21769991
Dadi, K., Varoquaux, G., Machlouzarides-Shalit, A., Gorgolewski,
K. J., Wassermann, D., Thirion, B., & Mensch, A. (2020). Fine-grain
atlases of functional modes for fMRI analysis. NeuroImage, 221,
117126. https://doi.org/10.1016/j.neuroimage.2020.117126,
PubMed: 32673748
Dale, A. M., Fischl, B., & Sereno, M. I. (1999). Cortical surface-based
analysis: I. Segmentation and surface reconstruction. NeuroImage,
9(2), 179–194. https://doi.org/10.1006/nimg.1998.0395, PubMed:
9931268
Deco, G., Cabral, J., Saenger, V. M., Boly, M., Tagliazucchi, E.,
Laufs, H., … Kringelbach, M. L. (2018). Perturbation of whole-
brain dynamics in silico reveals mechanistic differences between
brain states. NeuroImage, 169, 46–56. https://doi.org/10.1016/j
.neuroimage.2017.12.009, PubMed: 29225066
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., & Kötter, R. (2009).
Key role of coupling, delay, and noise in resting brain fluctua-
tions. PNAS, 106(25), 10302–10307. https://doi.org/10.1073
/pnas.0901831106, PubMed: 19497858
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging concepts
for the dynamical organization of resting-state activity in the
brain. Nature Reviews Neuroscience, 12(1), 43–56. https://doi
.org/10.1038/nrn2961, PubMed: 21170073
Deco, G., & Kringelbach, M. (2014). Great expectations: Using
whole-brain computational connectomics for understanding
neuropsychiatric disorders. Neuron, 84(5), 892–905. https://doi
.org/10.1016/j.neuron.2014.08.034, PubMed: 25475184
Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017). The
dynamics of resting fluctuations in the brain: Metastability and its
Network Neuroscience
827
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
dynamical cortical core. Scientific Reports, 7(1), 3095. https://doi
.org/10.1038/s41598-017-03073-5, PubMed: 28596608
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., … Killiany, R. J. (2006). An automated labeling system
for subdividing the human cerebral cortex on MRI scans into gyral
based regions of interest. NeuroImage, 31(3), 968–980. https://doi
.org/10.1016/j.neuroimage.2006.01.021, PubMed: 16530430
Destrieux, C., Fischl, B., Dale, A., & Halgren, E. (2010). Automatic
parcellation of human cortical gyri and sulci using standard an-
atomical nomenclature. NeuroImage, 53(1), 1–15. https://doi.org
/10.1016/j.neuroimage.2010.06.010, PubMed: 20547229
Domhof, J. (2021). Parcellation modelling, https://jugit.fz-juelich.de
/inm7/parcellation-modelling
Domhof, J. W. M., Jung, K., Eickhoff, S. B., & Popovych, O. V.
(2021). Parcellation-based structural and resting-state functional
brain connectomes of a healthy cohort [Dataset]. EBRAINS.
https://doi.org/10.25493/81EV-ZVT
Eickhoff, S. B., Constable, R. T., & Yeo, B. T. T. (2018). Topographic
organization of the cerebral cortex and brain cartography.
NeuroImage, 170, 332–347. https://doi.org/10.1016/j.neuroimage
.2017.02.018, PubMed: 28219775
Eickhoff, S. B., Yeo, B. T. T., & Genon, S. (2018). Imaging-based
parcellations of the human brain. Nature Reviews Neuroscience,
19(11), 672–686. https://doi.org/10.1038/s41583-018-0071-7,
PubMed: 30305712
Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., … Jiang, T.
(2016). The human Brainnetome Atlas: A new brain atlas based on
connectional architecture. Cerebral Cortex, 26(8), 3508–3526.
https://doi.org/10.1093/cercor/bhw157, PubMed: 27230218
Fisher, R. A. (1915). Frequency distribution of the values of the
correlation coefficient in samples from an indefinitely large popu-
lation. Biometrika, 10(4), 507–521. https://doi.org/10.2307
/2331838
Fisher, R. A. (1921). On the “probable error” of a coefficient of cor-
relation deduced from a small sample. Metron, 1, 3–32. Retrieved
from https:// hekyll.services.adelaide.edu.au/dspace/ bitstream
/2440/15169/1/14.pdf
Fraga González, G., Smit, D. J. A., van der Molen, M. J. W., Tijms,
J., Stam, C. J., de Geus, E. J. C., & van der Molen, M. W. (2018).
EEG resting state functional connectivity in adult dyslexics using
phase lag index and graph analysis. Frontiers in Human
Neuroscience, 12, 341. https://doi.org/10.3389/fnhum.2018
.00341, PubMed: 30214403
Frazier, J. A., Chiu, S., Breeze, J. L., Makris, N., Lange, N., Kennedy,
D. N., … Biederman, J. (2005). Structural brain magnetic reso-
nance imaging of limbic and thalamic volumes in pediatric bipolar
disorder. American Journal of Psychiatry, 162(7), 1256–1265.
https://doi.org/10.1176/appi.ajp.162.7.1256, PubMed:
15994707
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302. https://doi.org/10
.1016/S1053-8119(03)00202-7, PubMed: 12948688
Ghosh, A., Rho, Y., McIntosh, A. R., Kötter, R., & Jirsa, V. K. (2008).
Noise during rest enables the exploration of the brain’s dynamic
repertoire. PLoS Computational Biology, 4(10), e1000196. https://
doi.org/10.1371/journal.pcbi.1000196, PubMed: 18846206
Goldstein, J. M., Seidman, L. J., Makris, N., Ahern, T., O’Brien,
L. M., Caviness, V. S., … Tsuang, M. T. (2007). Hypothalamic
abnormalities in schizophrenia: Sex effects and genetic vulnera-
bility. Biological Psychiatry, 61(8), 935–945. https://doi.org/10
.1016/j.biopsych.2006.06.027, PubMed: 17046727
Grabner, G., Janke, A. L., Budge, M. M., Smith, D., Pruessner, J., &
Collins, D. L. (2006). Symmetric atlasing and model based seg-
mentation: An application to the hippocampus in older adults.
Medical Image Computing and Computer-Assisted Intervention,
9(Pt 2), 58–66. https://doi.org/10.1007/11866763_8, PubMed:
17354756
Griffanti, L., Salimi-Khorshidi, G., Beckmann, C. F., Auerbach, E. J.,
Douaud, G., Sexton, C. E., … Smith, S. M. (2014). ICA-based
artefact removal and accelerated fMRI acquisition for improved
resting state network imaging. NeuroImage, 95, 232–247. https://
doi.org/10.1016/j.neuroimage.2014.03.034 , PubMed:
24657355
Hagberg, A., Swart, P., & S Chult, D. (2008). Exploring network
structure, dynamics, and function using NetworkX (Technical
Report No. LA-UR-08-05495; LA-UR-08-5495). Retrieved from
https://www.osti.gov/biblio/960616-exploring-network-structure
-dynamics-function-using-networkx
Hansen, E. C. A., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switching
behavior of the resting state. NeuroImage, 105, 525–535. https://doi
.org/10.1016/j.neuroimage.2014.11.001, PubMed: 25462790
Havlicek, M., Roebroeck, A., Friston, K., Gardumi, A., Ivanov, D.,
& Uludag, K. (2015). Physiologically informed dynamic causal
modeling of fMRI data. NeuroImage, 122, 355–372. https://doi
.org/10.1016/j.neuroimage.2015.07.078, PubMed: 26254113
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. PNAS, 106(6),
2035–2040. https://doi.org/10.1073/pnas.0811168106, PubMed:
19188601
Jansen, B. H., & Rit, V. G. (1995). Electroencephalogram and visual
evoked potential generation in a mathematical model of coupled
cortical columns. Biological Cybernetics, 73(4), 357–366. https://
doi.org/10.1007/BF00199471, PubMed: 7578475
Jansen, B. H., Zouridakis, G., & Brandt, M. E. (1993). A
neurophysiologically-based mathematical model of flash visual
evoked potentials. Biological Cybernetics, 68(3), 275–283.
https://doi.org/10.1007/BF00224863, PubMed: 8452897
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W., &
Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. https://doi
.org/10.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A., & Sijbers, J.
(2014). Multi-tissue constrained spherical deconvolution for im-
proved analysis of multi-shell diffusion MRI data. NeuroImage,
103, 411–426. https://doi.org/10.1016/j.neuroimage.2014.07
.061, PubMed: 25109526
Jülich Supercomputing Centre. (2018). JURECA: Modular super-
computer at Jülich Supercomputing Centre. Journal of Large-
Scale Research Facilities, 4(A132). https://doi.org/10.17815/jlsrf
-4-121-1
Kuramoto, Y. (1984). Chemical oscillations, waves, and turbulence.
Berlin: Springer. https://doi.org/10.1007/978-3-642-69689-3
Kwong, K. K., Belliveau, J. W., Chesler, D. A., Goldberg, I. E.,
Weisskoff, R. M., Poncelet, B. P., … Turner, R. (1992).
Dynamic magnetic resonance imaging of human brain activity
Network Neuroscience
828
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
during primary sensory stimulation. PNAS, 89(12), 5675–5679.
https://doi.org/10.1073/pnas.89.12.5675, PubMed: 1608978
Lindquist, M. (2020). Neuroimaging results altered by varying anal-
ysis pipelines. Nature, 582(7810), 36–37. https://doi.org/10.1038
/d41586-020-01282-z, PubMed: 32433631
Maier-Hein, K. H., Neher, P. F., Houde, J.-C., Côté, M.-A.,
Garyfallidis, E., Zhong, J., … Descoteaux, M. (2017). The chal-
lenge of mapping the human connectome based on diffusion
tractography. Nature Communications, 8(1), 1349. https://doi
.org/10.1038/s41467-017-01285-x, PubMed: 29116093
Makris, N., Goldstein, J. M., Kennedy, D., Hodge, S. M., Caviness,
V. S., Faraone, S. V., … Seidman, L. J. (2006). Decreased volume
of left and total anterior insular lobule in schizophrenia.
Schizophrenia Research, 83(2), 155–171. https://doi.org/10
.1016/j.schres.2005.11.020, PubMed: 16448806
Mayhew, S. D., Ostwald, D., Porcaro, C., & Bagshaw, A. P. (2013).
Spontaneous EEG alpha oscillation interacts with positive and
negative BOLD responses in the visual–auditory cortices and
default-mode network. NeuroImage, 76, 362–372. https://doi
.org/10.1016/j.neuroimage.2013.02.070, PubMed: 23507378
Messé, A. (2020). Parcellation influence on the connectivity-based
structure–function relationship in the human brain. Human Brain
Mapping, 41(5), 1167–1180. https://doi.org/10.1002/ hbm
.24866, PubMed: 31746083
Messé, A., Rudrauf, D., Benali, H., & Marrelec, G. (2014). Relating
structure and function in the human brain: Relative contributions
of anatomy, stationary dynamics, and non-stationarities. PLoS
Computational Biology, 10(3), e1003530. https://doi.org/10
.1371/journal.pcbi.1003530, PubMed: 24651524
Newman, M. E. J., & Girvan, M. (2004). Finding and evaluating
community structure in networks. Physical Review E, 69(2),
026113. https://doi.org/10.1103/PhysRevE.69.026113, PubMed:
14995526
Ogawa, S., Tank, D. W., Menon, R., Ellermann, J. M., Kim, S. G.,
Merkle, H., & Ugurbil, K. (1992). Intrinsic signal changes accom-
panying sensory stimulation: Functional brain mapping with mag-
netic resonance imaging. PNAS, 89(13), 5951–5955. https://doi
.org/10.1073/pnas.89.13.5951, PubMed: 1631079
Onnela, J.-P., Saramäki, J., Kertész, J., & Kaski, K. (2005). Intensity
and coherence of motifs in weighted complex networks. Physical
Review E, 71(6), 065103. https://doi.org/10.1103/PhysRevE.71
.065103, PubMed: 16089800
Ponce-Alvarez, A., Deco, G., Hagmann, P., Romani, G. L., Mantini,
D., & Corbetta, M. (2015). Resting-state temporal synchroniza-
tion networks emerge from connectivity topology and heteroge-
neity. PLoS Computational Biology, 11(2), e1004100. https://doi
.org/10.1371/journal.pcbi.1004100, PubMed: 25692996
Popovych, O. V., Manos, T., Hoffstaedter, F., & Eickhoff, S. B.
(2019). What can computational models contribute to neuroim-
aging data analytics? Frontiers in Systems Neuroscience, 12, 68.
https://doi.org/10.3389/fnsys.2018.00068, PubMed: 30687028
Proix, T., Spiegler, A., Schirner, M., Rothmeier, S., Ritter, P., & Jirsa,
V. K. (2016). How do parcellation size and short-range connec-
tivity affect dynamics in large-scale brain network models?
NeuroImage, 142, 135–149. https://doi.org/10.1016/j
.neuroimage.2016.06.016, PubMed: 27480624
Ritter, P., Schirner, M., McIntosh, A. R., & Jirsa, V. K. (2013). The
Virtual Brain integrates computational modeling and multimodal
neuroimaging. Brain Connectivity, 3(2), 121–145. https://doi.org
/10.1089/brain.2012.0120, PubMed: 23442172
Roine, T., Jeurissen, B., Perrone, D., Aelterman, J., Philips, W.,
Sijbers, J., & Leemans, A. (2019). Reproducibility and intercorre-
lation of graph theoretical measures in structural brain connectiv-
ity networks. Medical Image Analysis, 52, 56–67. https://doi.org
/10.1016/j.media.2018.10.009, PubMed: 30471463
Rolls, E. T., Joliot, M., & Tzourio-Mazoyer, N. (2015). Implementation
of a new parcellation of the orbitofrontal cortex in the automated
anatomical labeling atlas. NeuroImage, 122, 1–5. https://doi.org
/10.1016/j.neuroimage.2015.07.075, PubMed: 26241684
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Rubinov, M., & Sporns, O. (2011). Weight-conserving characteriza-
tion of complex functional brain networks. NeuroImage, 56(4),
2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069,
PubMed: 21459148
Saenger, V. M., Kahan, J., Foltynie, T., Friston, K., Aziz, T. Z.,
Green, A. L., … Deco, G. (2017). Uncovering the underlying
mechanisms and whole-brain dynamics of deep brain stimula-
tion for Parkinson’s disease. Scientific Reports, 7(1), 9882. https://
doi.org/10.1038/s41598-017-10003-y, PubMed: 28851996
Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015).
Mathematical framework for large-scale brain network modeling
in The Virtual Brain. NeuroImage, 111, 385–430. https://doi.org
/10.1016/j.neuroimage.2015.01.002, PubMed: 25592995
Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N.,
Holmes, A. J., … Yeo, B. T. T. (2018). Local-global parcellation of
the human cerebral cortex from intrinsic functional connectivity
MRI. Cerebral Cortex, 28(9), 3095–3114. https://doi.org/10.1093
/cercor/bhx179, PubMed: 28981612
Schilling, K. G., Nath, V., Hansen, C., Parvathaneni, P., Blaber, J.,
Gao, Y., … Landman, B. A. (2019). Limits to anatomical accuracy
of diffusion tractography using modern approaches. NeuroImage,
185, 1–11. https://doi.org/10.1016/j.neuroimage.2018.10.029,
PubMed: 30317017
Scholtens, L. H., de Reus, M. A., de Lange, S. C., Schmidt, R., & van
den Heuvel, M. P. (2018). An MRI Von Economo–Koskinas atlas.
NeuroImage, 170, 249–256. https://doi.org/10.1016/j
.neuroimage.2016.12.069, PubMed: 28040542
Shen, X., Tokoglu, F., Papademetris, X., & Constable, R. T. (2013).
Groupwise whole-brain parcellation from resting-state fMRI data
for network node identification. NeuroImage, 82, 403–415.
https://doi.org/10.1016/j.neuroimage.2013.05.081, PubMed:
23747961
Sotiropoulos, S. N., & Zalesky, A. (2019). Building connectomes
using diffusion MRI: Why, how and but. NMR in Biomedicine,
32(4), e3752. https://doi.org/10.1002/nbm.3752, PubMed:
28654718
Spitoni, G. F. P., Di Russo, F., Cimmino, R. L., Bozzacchi, C., &
Pizzamiglio, L. (2013). Modulation of spontaneous alpha brain
rhythms using low-intensity transcranial direct-current stimula-
tion. Frontiers in Human Neuroscience, 7, 529. https://doi.org
/10.3389/fnhum.2013.00529, PubMed: 24027517
Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020).
Linking structure and function in macroscale brain networks.
Network Neuroscience
829
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Influence of parcellation on large-scale whole-brain modeling results
Trends in Cognitive Sciences, 24(4), 302–315. https://doi.org/10
.1016/j.tics.2020.01.008, PubMed: 32160567
Tournier, J.-D., Calamante, F., & Connelly, A. (2010). Improved
probabilistic streamlines tractography by 2nd order integration
over fibre orientation distributions. Proceedings of the
International Society for Magnetic Resonance in Medicine
(ISMRM), 18.
Tournier, J.-D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T.,
Pietsch, M., … Connelly, A. (2019). MRtrix3: A fast, flexible and
open software framework for medical image processing and vi-
sualisation. NeuroImage, 202, 116137. https://doi.org/10.1016/j
.neuroimage.2019.116137, PubMed: 31473352
Tustison, N. J., Avants, B. B., Cook, P. A., Zheng, Y., Egan, A.,
Yushkevich, P. A., & Gee, J. C. (2010). N4ITK: Improved N3 bias
correction. IEEE Transactions on Medical Imaging, 29(6), 1310–1320.
https://doi.org/10.1109/TMI.2010.2046908, PubMed: 20378467
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, O., Delcroix, N., … Joliot, M. (2002). Automated anatomical
labeling of activations in SPM using a macroscopic anatomical par-
cellation of the MNI MRI single-subject brain. NeuroImage, 15(1),
273–289. https://doi.org/10.1006/nimg.2001.0978, PubMed:
11771995
Urchs, S., Armoza, J., Moreau, C., Benhajali, Y., St-Aubin, J.,
Orban, P., & Bellec, P. (2019). MIST: A multi-resolution parcellation
of functional brain networks. MNI Open Research, 1, 3. https://doi
.org/10.12688/mniopenres.12767.2
van den Heuvel, M. P., & Sporns, O. (2019). A cross-disorder con-
nectome landscape of brain dysconnectivity. Nature Reviews
Neuroscience, 20(7), 435–446. https://doi.org/10.1038/s41583
-019-0177-6, PubMed: 31127193
van der Walt, S., Colbert, S. C., & Varoquaux, G. (2011). The
NumPy array: A structure for efficient numerical computation.
Computing in Science Engineering, 13(2), 22–30. https://doi.org
/10.1109/MCSE.2011.37
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J., Yacoub,
E., & Ugurbil, K. (2013). The WU-Minn Human Connectome
Project: An overview. NeuroImage, 80, 62–79. https://doi.org/10
.1016/j.neuroimage.2013.05.041, PubMed: 23684880
Van Essen, D. C., Ugurbil, K., Auerbach, E., Barch, D., Behrens, T. E. J.,
Bucholz, R., … Yacoub, E. (2012). The Human Connectome
Project: A data acquisition perspective. NeuroImage, 62(4),
2222–2231. https://doi.org/10.1016/j.neuroimage.2012.02.018,
PubMed: 22366334
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy,
T., Cournapeau, D., … van Mulbregt, P. (2020). SciPy 1.0:
Fundamental algorithms for scientific computing in Python.
Nature Methods, 17(3), 261–272. https://doi.org/10.1038
/s41592-019-0686-2, PubMed: 32015543
von Economo, C., & Koskinas, G. N. (1925). Die Cytoarchitektonik
der Hirnrinde des erwachsenen Menschen. Wien: Springer.
Retrieved from https://wwwzb.fz-juelich.de/contentenrichment
/inhaltsverzeichnisse/ bis2009/ Economo,Constantinvon
-DieCytoarchitektonik-1925.pdf
Wang, J., Wang, L., Zang, Y., Yang, H., Tang, H., Gong, Q., … He,
Y. (2009). Parcellation-dependent small-world brain functional
networks: A resting-state fMRI study. Human Brain Mapping,
30(5), 1511–1523. https://doi.org/10.1002/ hbm.20623,
PubMed: 18649353
Wilson, H. R., & Cowan, J. D. (1972). Excitatory and inhibitory inter-
actions in localized populations of model neurons. Biophysical
Journal, 12(1), 1–24. https://doi.org/10.1016/S0006-3495(72)
86068-5, PubMed: 4332108
Wong, K.-F., & Wang, X.-J. (2006). A recurrent network mechanism of
time integration in perceptual decisions. Journal of Neuroscience,
26(4), 1314–1328. https://doi.org/10.1523/JNEUROSCI.3733-05
.2006, PubMed: 16436619
Yeh, C.-H., Jones, D. K., Liang, X., Descoteaux, M., & Connelly, A.
(2021). Mapping structural connectivity using diffusion MRI:
Challenges and opportunities. Journal of Magnetic Resonance
Imaging, 53(6), 1666–1682. https://doi.org/10.1002/jmri.27188,
PubMed: 32557893
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel,
M. P., & Breakspear, M. (2016). Connectome sensitivity or spec-
ificity: Which is more important? NeuroImage, 142, 407–420.
https://doi.org/10.1016/j.neuroimage.2016.06.035, PubMed:
27364472
Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yücel, M.,
Pantelis, C., & Bullmore, E. T. (2010). Whole-brain anatomical
networks: Does the choice of nodes matter? NeuroImage, 50(3),
970–983. https://doi.org/10.1016/j.neuroimage.2009.12.027,
PubMed: 20035887
Zimmermann, J., Perry, A., Breakspear, M., Schirner, M., Sachdev,
P., Wen, W., … Solodkin, A. (2018). Differentiation of
Alzheimer’s disease based on local and global parameters in person-
alized Virtual Brain models. NeuroImage: Clinical, 19, 240–251.
https://doi.org/10.1016/j.nicl.2018.04.017, PubMed: 30035018
Network Neuroscience
830
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
3
7
9
8
1
9
6
0
5
4
2
n
e
n
_
a
_
0
0
2
0
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3