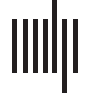FORSCHUNG
Säuglingsfunktionsnetzwerke werden staatlich moduliert
von Bewusstsein und zirkadianem Rhythmus
Rachel J. Smith1
, Ehsan Alipourjeddi1, Cristal Garner2, Amy L. Maser3,
Daniel W. Shrey2,4, und Beth A. Lopour1
1Abteilung für Biomedizintechnik, Universität von Kalifornien, Irvine, CA, USA
2Abteilung für Neurologie, Kinderkrankenhaus von Orange County, Orange, CA, USA
3Abteilung für Psychologie, Kinderkrankenhaus von Orange County, Orange, CA, USA
4Abteilung für Pädiatrie, Universität von Kalifornien, Irvine, Irvine, CA, USA
Keine offenen Zugänge
Tagebuch
Schlüsselwörter: Funktionale Konnektivität, Graphentheorie, Kreuzkorrelation, Elektroenzephalographie,
Ruhezustandsnetzwerke, Pädiatrie
ABSTRAKT
Funktionale Konnektivitätsnetzwerke sind wertvolle Werkzeuge für die Untersuchung der Entwicklung, Erkenntnis,
und Krankheiten im Gehirn von Säuglingen. Bei Erwachsenen, Solche Netzwerke werden durch den Zustand von moduliert
Bewusstsein und der zirkadiane Rhythmus; Jedoch, Es ist nicht bekannt, ob das Gehirn von Säuglingen vernetzt ist
weisen ähnliche Variationen auf, Angesichts der einzigartigen zeitlichen Eigenschaften des Säuglingsschlafs und des zirkadianen Schlafs
Musterung. Um das zu erwähnen, Wir haben funktionale Konnektivitätsnetzwerke analysiert, die daraus berechnet wurden
Langzeit-EEG-Aufzeichnungen (durchschnittliche Dauer 20.8 Std) aus 19 gesunde Säuglinge. Netzwerke waren
themenspezifisch, wie Intersubjektkorrelationen zwischen gewichteten Adjazenzmatrizen waren
niedrig. Jedoch, innerhalb einzelner Fächer, Sowohl Schlaf- als auch Wachnetzwerke waren stabil
Zeit, mit stärkerer funktioneller Konnektivität im Schlaf als im Wachzustand. Rektor
Die Komponentenanalyse ergab das Vorhandensein zweier dominanter Netzwerke; Visuelle Schlafbewertung
bestätigte, dass diese mit Schlaf und Wachheit korrespondierten. zuletzt, Wir haben dieses Netzwerk gefunden
Stärke, Grad, Clusterkoeffizient, und die Weglänge variierte erheblich mit der Tageszeit,
wenn entweder im Wachzustand oder im Schlaf auf Gruppenebene gemessen. Zusammen, diese Ergebnisse
legen nahe, dass die Modulation gesunder funktioneller Netzwerke über ca. 24 Stunden erfolgt und robust ist
und wiederholbar. Die Berücksichtigung solcher zeitlichen Periodizitäten kann die physiologische Situation verbessern
Interpretation und Verwendung der funktionellen Konnektivitätsanalyse zur Untersuchung der Gehirnfunktion
Gesundheit und Krankheit.
ZUSAMMENFASSUNG DES AUTORS
Bei Erwachsenen, Funktionelle Konnektivitätsnetzwerke werden durch den Bewusstseinszustand moduliert und
der zirkadiane Rhythmus. Wir untersuchten, ob die Gehirnnetzwerke von Säuglingen ähnliche Merkmale aufwiesen
Variationen, Angesichts der einzigartigen zeitlichen Eigenschaften des Säuglingsschlafs und der zirkadianen Muster.
Funktionelle Konnektivitätsnetzwerke wurden aus ca. 24-Stunden-EEG-Aufzeichnungen berechnet 19
gesunde Säuglinge. Wir fanden heraus, dass Netzwerke themenspezifisch waren und eine stärkere Wirkung zeigten
Verbindungen im Schlaf im Vergleich zum Wachzustand. Innerhalb von Fächern, sowohl schlafen als auch wachen
Netzwerke traten im Laufe der Zeit erneut auf. Jedoch, Netzwerkstärke, Grad, Clusterkoeffizient,
und die Weglänge variierte erheblich mit der Tageszeit, wenn es im Wachzustand gemessen wird
oder auf Gruppenebene schlafen. Zusammen, Diese Ergebnisse legen nahe, dass die Modulation bei gesunden Säuglingen erfolgt
Funktionelle Netzwerke erfolgen über 24-Stunden-Zeiträume und sind robust und wiederholbar.
Zitat: Schmied, R. J., Alipourjeddi, E.,
Garner, C., Maser, A. L., Shreya, D. L. W.,
& Lopour, B. A. (2021). Säuglingsfunktionell
Netzwerke werden je nach Zustand moduliert
Bewusstsein und zirkadianer Rhythmus.
Netzwerkneurowissenschaften, 5(2), 614–630.
https://doi.org/10.1162/netn_a_00194
DOI:
https://doi.org/10.1162/netn_a_00194
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00194
Erhalten: 28 August 2020
Akzeptiert: 22 Marsch 2021
Korrespondierender Autor:
Beth A. Lopour
beth.lopour@uci.edu
Handling-Editor:
Mark Kramer
Urheberrechte ©: © 2021
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
Säugling:
Ein pädiatrisches Fachgebiet liegt typischerweise zwischen
3 Und 12 Monate alt.
Bewusstseinszustand:
Der Bekanntheitsgrad des Subjekts;
Hier, Wir studieren speziell die Staaten
von Wachheit und Schlaf.
Ultradiane Periodizitäten:
Schwankungen im Netzwerk
Merkmale mit größeren Perioden
als 1 Std. und weniger als 24 Std, wie zum Beispiel
der Schlafzyklus.
EINFÜHRUNG
Messungen der funktionellen Konnektivität im Gehirn von Säuglingen können wertvolle Erkenntnisse darüber liefern
neuronale Entwicklung, Erkenntnis, und Krankheit. Ein Großteil unseres Wissens über die Gehirnnetzwerke von Säuglingen
stammt aus der funktionellen Magnetresonanztomographie (fMRT) Studien (Gao et al., 2017), aber EEG ist
zunehmend zur Untersuchung solcher Fragen herangezogen, da es den Vorteil einer funktionsfähigen Probenahme hat
Netzwerke mit hoher zeitlicher Auflösung über lange Zeiträume. Zum Beispiel, EEG-basierte Funktion-
Funktionelle Netzwerke spiegeln die Netzwerksegregation wider, die während der pränatalen Entwicklung auftritt, mit
Neugeborene weisen Netzwerkknoten im Frontal- und Parieto-Occipitallappen auf (Omidvarnia et al.,
2014; Tóth et al., 2017). Diese Netzwerke entwickeln sich im Laufe der Kindheit langsam weiter, mit einzigartig
frequenzspezifische Konnektivität für Kleinkinder, Kleinkinder, Kinder, und Jugendliche (Chu et al.,
2014). EEG-basierte funktionelle Netzwerke sind auch mit kognitiven Funktionen verbunden, wie sus-
fesselte die Aufmerksamkeit des Säuglings (Xie, Modell, & Richards, 2019), und Netzwerkschwingungen im Schlaf sind
korreliert mit dem Motor, Sprache, und soziale Entwicklung bei Kleinkindern (Seite, Lustenberger, &
Fröhlich, 2018). Als Krankheitsmarker, Zur Charakterisierung wurde eine funktionale Konnektivitätsanalyse verwendet-
akterisieren infantile Epilepsie (Shrey et al., 2018) und den Beginn einer Autismus-Spektrum-Störung vorhersagen
(Righi et al., 2014).
Um diese funktionellen Netzwerke genau zu beurteilen, Der Bewusstseinszustand des Subjekts muss sein
berücksichtigt. Bei Erwachsenen, Im Wachzustand gemessene funktionelle Netzwerke zeigten eine höhere Dichte-
sität und niedrigerer Clustering-Koeffizient als diejenigen, die während des Schlafs gemessen werden (Chu et al., 2012), solch
dass Netzwerke im Schlaf Small-World-Eigenschaften aufweisen (Ferri et al., 2008). Im Gegensatz, Säugling
Netzwerke weisen im Schlaf eine größere Stärke auf als im Wachzustand, für beide gesunden Sub-
Patienten und Menschen mit Epilepsie (Smith et al., 2020). Darüber hinaus, Die Netzwerkeigenschaften sind a
Funktion des jeweiligen Schlafstadiums. Bei Neugeborenen, Studien fanden heraus, dass dies stark ist, Kurzstreckenfunk-
Während des aktiven Schlafs konzentrieren sich die funktionellen Verbindungen im Hinterhauptslappen, mit im weiteren Sinne
Während des ruhigen Schlafs überwiegen verteilte Fernverbindungen (Tokariev et al., 2019;
Tokariev, Altes Haus, & Verehrung, 2016). Trotz der weit verbreiteten Zugänglichkeit des EEG und seines breiten Spektrums
Einsatz bei jungen Menschen, Keine früheren Studien zu Säuglingsschlafnetzwerken umfassten eine Analyse des Nacht-EEG
Aufnahmen. Die meisten haben sich auf kurze Clips verlassen, Dauer ca. 3–20 Minuten, aufgezeichnet während des Tagesschlafs.
Nur eine Studie (Smith et al., 2020) beinhaltete einen direkten Vergleich der Netzwerke im Schlaf und
Wachsamkeit. Das Schließen dieser Wissenslücke ist entscheidend für das Verständnis der Rolle dieses funktionalen Netzes-
Werke spielen in Gesundheit und Krankheit.
Über die Merkmale hinaus, die mit jedem einzelnen Bewusstseinszustand verbunden sind, Merkmale
Das EEG weist über verschiedene Zeiträume hinweg Periodizitäten auf. Ultradiane Periodizitäten im EEG-Signal
Merkmale, wie z. B. Frequenzbandleistung, wurden bei Erwachsenen gut untersucht (Aeschbach et al.,
1999; Kaiser, 2008). Es ist bekannt, dass EEG-basierte funktionelle Netzwerke bei der Messung stabil sind
über mehrere Minuten im Schlaf oder Wachzustand, trotz der schnellen visuellen Variabilität der Zeitreihen
(Chapeton, Es sagte, & Zaghloul, 2017; Kramer et al., 2011). Jedoch, auf funktionalen Netzwerken basierend
im intrakraniellen EEG zeigen eine starke zirkadiane Modulation graphentheoretischer Messungen, wie zum Beispiel
der Clusterkoeffizient und die Pfadlänge (Geier, Lehnertz, & Bialonski, 2015; Kuhnert, Elch, &
Lehnertz, 2010). Dies erweist sich als vielversprechender Marker zur Unterstützung der Anfallsvorhersage, als Schwingungen
Es wurde gezeigt, dass Störungen der funktionellen Netzwerkeigenschaften über Stunden und Tage hinweg mit einem Festfressen korrelieren-
bei Patienten mit Epilepsie eingesetzt (Anastasiadou et al., 2016; Baud et al., 2018; Karoly et al., 2017;
Kuhnert et al., 2010; Mitsis et al., 2020). Jedoch, Ultradiane und zirkadiane Periodizitäten des Säuglings
Funktionelle Netzwerke müssen noch untersucht werden. Angesichts der Tatsache, dass sich die Schlafzyklen von Säuglingen deutlich unterscheiden
Schlafmuster von Erwachsenen, sowohl im elektrografischen Erscheinungsbild als auch in der zirkadianen Musterung, die Netzwerke
kann eine Modulation über Zeitskalen aufweisen, die kürzer als sind 24 Std, oder gar nicht. Diese unbekannt
Zeitliche Periodizitäten können die Untersuchung der Gehirnnetzwerke von Säuglingen weiter erschweren.
Netzwerkneurowissenschaften
615
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
Wir gehen davon aus, dass sowohl der Bewusstseinszustand als auch die Tageszeit einen signifikanten Einfluss haben
Auswirkungen auf spontane funktionelle Netzwerke bei Säuglingen. daher, Unser übergeordnetes Ziel ist es, ca. 24 Stunden zu nutzen
EEG-Aufzeichnungen von gesunden Probanden, um diese Effekte zu entschlüsseln, damit sie erklärt werden können
in zukünftigen Studien. Um dies zu tun, Wir machen uns den nichtzirkadianen Säuglingsschlafzyklus zunutze, welche
ermöglicht es uns, Wach- und Schlafphasen sowohl tagsüber als auch nachts aufzuzeichnen. Wir
Beschreiben Sie zunächst die funktionalen Netzwerke, die mit Schlaf- und Wachzuständen verbunden sind, beurteilen Sie die inter-
Themenvariabilität in diesen landesspezifischen Netzwerken, und identifizieren Sie graphentheoretische Maße, die
trennt die beiden Staaten. Dann zeigen wir, dass die Messung jedes Schlaf- oder Wachnetzwerks erfolgt
stabil und wiederholbar innerhalb eines einzelnen Subjekts. zuletzt, Wir zeigen die zirkadiane Variation der Funktion-
tionale Konnektivitätsstärke und graphische theoretische Maße bei der Bewertung auf Gruppenebene.
Diese Arbeit erweitert unser Verständnis der physiologischen Funktionsschwankungen des Gehirns von Säuglingen-
funktionale Konnektivität, Dies hat das Potenzial, als Grundlage für Entwicklungsuntersuchungen zu dienen-
ment, Erkenntnis, und Krankheit.
METHODEN
Probandenrekrutierung und EEG-Aufzeichnung
Diese prospektive Studie wurde vom Institutional Review Board of the Children’s genehmigt
Krankenhaus von Orange County. Die Probanden wurden ab Juni rekrutiert und eingewilligt 2017 Zu
Februar 2019 und über Nacht einer Langzeit-Video-EEG-Aufzeichnung unterzogen, um eine Form auszuschließen
einer pädiatrischen Epilepsie, sogenannte infantile Krämpfe. Wenn bei dem Säugling keine infantile Diagnose gestellt wurde
Krämpfe, Sie wurden als Kontrollsubjekt eingestuft. Klinische Daten wurden zum Zeitpunkt der Erhebung erhoben
Einschreibung. Die Probanden galten als „gesunde“ Kontrollen, wenn sie (A) zeigte ein normales EEG re-
Schnur, (B) keine Epilepsie-Diagnose erhalten, (C) hatte keine bekannten neurologischen Erkrankungen,
Und (D) waren altersentsprechend normal (wie mit dem Vineland Adaptive bewertet
Verhaltensskalen, 33. Auflage, Spatz, Cicchetti, & Saulnier 2016). Neunzehn Kanäle von
EEG-Daten wurden abgetastet 200 Hz mit Impedanzen unten 5 kΩ.
Ein zertifizierter Schlaftechnologe am Kinderkrankenhaus von Orange County führt manuelles Delin durch-
Zeiträume der Wachheit gegessen, schnelle Augenbewegung (REM) schlafen, und Non-REM-Schlaf
Stufen (N1, N2, N3) in allen EEG-Aufzeichnungen gemäß der American Academy of
Richtlinien zur Schlafmedizin. Für unsere Analyse, Die Schlaf- und Wachphasen waren getrennt-
anhand dieser Markierungen bewertet. Zum Vergleich mit dem automatischen Schlaf-Staging (siehe Sektion
Wiederkehr von Netzwerkzuständen und Übereinstimmung mit der manuellen Schlafeinstufung), wir haben uns zusammengeschlossen
N1, N2, N3, und REM-Schlafstadien in eine „Schlaf“-Kategorie eingeteilt.
EEG-Vorverarbeitung
EEG-Daten wurden offline auf den gemeinsamen Durchschnitt zurückgeführt. Effektiv sein, diese Referenzierung
Das Schema beruht auf einer weitgehenden Abdeckung des Kopfes durch Elektroden; bei Erwachsenen, Dies kann bedeuten, dass
Verwendung von High-Density-EEG. Jedoch, Säuglingsköpfe sind deutlich kleiner als die von Erwachsenen,
Dadurch wird eine umfassendere Abdeckung gewährleistet, als dies normalerweise möglich ist 19 Elektroden. In ADDI-
tion, das hier verwendete Konnektivitätsmaß (Kreuzkorrelation gemessen bei Zeitverzögerungen ungleich Null; sehen
Abschnitt Funktionale Konnektivität) Es wurde festgestellt, dass die Wahl der Referenz nur einen minimalen Einfluss hatte-
enz, mit gemeinsamem Durchschnitt, bipolar, und gemeinsame Referenzierungsschemata, die ähnliche Referenzen bereitstellen-
Ergebnisse (Anastasiadou et al., 2019).
Artefaktzeiträume wurden mit einem automatischen Extremwertartefaktdetektor identifiziert,
ähnlich zu zuvor veröffentlichten Methoden (Durka et al., 2003; Moretti et al., 2003).
Speziell, Um Artefakte zu identifizieren, haben wir die Daten breitbandig und bandpassgefiltert (1.5–40 Hz,
Butterworth-Filter, ausgewählt, um den Einstellungen der klinischen EEG-Anzeige/-Analyse zu entsprechen), subtrahiert
Schlafinszenierung:
Visuelle Kategorisierung des EEG in
Wachsamkeit, schnelle Augenbewegung
(REM) schlafen, und Non-REM-Schlaf
Stufen 1–3; auch Schlafbewertung genannt.
Kreuzkorrelation:
Bivariat, amplitudenbasiert
Synchronisationsmaßnahme, berechnet
als Skalarprodukt zweier EEG-Signale
da ein Signal zeitlich verschoben ist.
Netzwerkneurowissenschaften
616
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
der Mittelwert von jedem Kanal, und berechnete die Standardabweichung jeder Null-Mittelwert-Zeit
Serie. Als Artefakte wurden Zeitpunkte definiert, in denen der Absolutwert der Spannung überschritten wurde
eine Schwelle von 7.5 Standardabweichungen über dem Mittelwert in einem einzelnen Kanal. Wir haben uns entschieden
diesen Schwellenwert, da er die beste Übereinstimmung zwischen automatisch erkannten Systemen ergab
und visuell identifizierte Artefakte in einem früheren Datensatz (Smith et al., 2017). Um sicherzustellen, dass das Ganze
Artefakt wurde markiert, ein Puffer von 0.9 s wurde zu beiden Seiten jedes zusammenhängenden Zeitsatzes hinzugefügt
Punkte mit extremen Amplitudenwerten. Die während der EEG-Impedanzprüfungen aufgezeichneten Daten waren
auch als Artefakt markiert. Für die Konnektivitätsanalyse, Es wurde ein breitbandiger Bandpassfilter angewendet
das rohe, erneut referenzierte Daten (0.5–55 Hz, Butterworth-Filter). Ein-Sekunden-Epochen, die enthielten
Artefaktdaten wurden nach dem Filtern aus allen Kanälen entfernt.
Funktionale Konnektivität
Wir haben funktionale Konnektivitätsnetzwerke durch Kreuzkorrelation mit der Methode devel berechnet-
von Kramer et al. (2009) und Chu et al. (2012) und zuvor auf EEG-Daten von Säuglingen angewendet
(Shrey et al., 2018). Wir haben uns für die Kreuzkorrelation entschieden, weil es sich um ein einfaches bivariates Maß handelt
sehr empfindlich gegenüber linearen Änderungen der EEG-Aktivität (David, Cosmelli, & Friston, 2004; Jalili,
Barzegaran, & Knyazeva, 2014) und hat sich als vergleichbar mit anderen Maßnahmen erwiesen
der Synchronisation (Jalili et al., 2014; Quian Quiroga et al., 2002). Obwohl Kreuzkorrelation
ist im Allgemeinen unempfindlich gegenüber nichtlinearen Wechselwirkungen im EEG, Wir haben uns für dieses schnelle und
direktes lineares Maß für die Synchronisation, da es keine nichtlineare Metrik gibt
Es hat sich gezeigt, dass es tatsächliche Änderungen der Kopplungsstärke zuverlässig misst und gleichzeitig Störeinflüsse berücksichtigt-
Aufgrund von Änderungen anderer Signaleigenschaften kommt es zu Synchronisationsstörungen (David et al., 2004;
Pereda et al., 2001).
Die Berechnung der funktionalen Konnektivität wurde wie in Shrey et al. beschrieben durchgeführt. (2018);
Wir fassen es hier kurz zusammen. Die Daten wurden in 1-s-Epochen unterteilt, und die EEG-Signale in jedem
Epoche (einer von jedem Kanal) wurden so normalisiert, dass sie einen Mittelwert von Null und eine Einheitsvarianz aufweisen. Für
jede Epoche, Wir haben die Kreuzkorrelation zwischen jedem Kanalpaar berechnet und identifiziert
das Maximum des Absolutwerts der Kreuzkorrelation. Epochen, in denen das Maximum
Kreuzkorrelationswerte, die bei einer Zeitverzögerung von Null auftraten, wurden ausgeschlossen, da sie wahrscheinlich ein Ergebnis waren
der Volumenleitung (Chu et al., 2012). Eine teilweise Korrelation mit der gemeinsamen Durchschnittsreferenz-
Es wurde eine Referenzzeitreihe durchgeführt, um zu testen, ob die Referenz die Korrelationsmessung induziert-
sicher zwischen den Kanälen (Shrey et al., 2018). Wenn es einen großen Unterschied zwischen den
Teilkorrelation und der Korrelationswert zwischen den Kanälen, die gemessene Korrelation
Es wurde angenommen, dass die Epoche auf einen Verweis auf ein Artefakt zurückzuführen war, und die Epoche wurde daraus entfernt
weitere Analyse (Unterstützende Informationstabelle S1). Z-Werte wurden für das Nichtartefakt berechnet-
tuelle Epochen, indem der Wert des Fisher-transformierten Korrelationskoeffizienten durch den geschätzten Wert dividiert wird
Standardabweichung, unter Berücksichtigung der Autokorrelation jeder Kanalepoche (Chu et al.,
2012; Kramer et al., 2009). Diese Methode hebt die Autokorrelationskomponente der Zeit auf
Reihen, die falsche Korrelationen erzeugen würden. Die Z-Werte wurden mit einer Basislinie verglichen
Verteilung, die durch Permutations-Resampling erstellt wurde. Permutations-Resampling wurde durchgeführt von
Auswählen zweier zufälliger 1-s-Datenepochen aus der Zeitreihe, die mindestens voneinander entfernt sind
1 S, Berechnen der maximalen Kreuzkorrelation zwischen den Kanälen, und Iterieren dieses Verfahrens
500 mal (Nichols & Holmes, 2003). Die standardisierten Korrelationswerte aus allen Iterationen
wurden sortiert und die Signifikanzschwelle wurde als der Wert definiert, der dem entspricht
95Perzentil der Verteilung für jedes Elektrodenpaar. Für jede Epoche, Korrelationswerte
zwischen Kanalpaaren, die diesen Schwellenwert überschritten, wurden als signifikant angesehen, Und
Diesen Verbindungen wurde der Wert eins zugewiesen; Verbindungen, die dies nicht überschreiten
Netzwerkneurowissenschaften
617
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
Dem Schwellenwert wurde der Wert Null zugewiesen. Also für p EEG-Kanäle, der Ausgang der Verbindung-
Die Produktivitätsberechnung für jede Epoche war eine binäre Matrix der Dimension p × p.
Epochenübergreifend, Konnektivitätsdaten wurden in einem dreidimensionalen Array Q gespeichert, bei dem die
Binärwert an Position Q(ich, J, k) stellte die Verbindung zwischen Elektrode i und Elektrode dar
j in der Epoche k. Anschließend wurde die Gesamtverbindungsstärke zwischen zwei Kanälen berechnet
Bruchteil der Zeitreihenepochen, in denen ein signifikanter Zusammenhang zwischen ihnen bestand. Für
Wachsamkeit, Bei dieser Berechnung wurden die Nw-binären Konnektivitätsmatrizen verwendet, die mit übereinstimmten
Zeiten des Wachwerdens, basierend auf der manuellen Schlafbestimmung. Zum Schlafen, die als Schlaf markierten Ns-Epochen
(N1, N2, N3, und REM) wurden benutzt. Weil Nw und Ns für jedes Fach ungleich waren, Wir
führte einen Bootstrapping-Vorgang durch. Für jede Iteration, Wir haben eine Zufallsstichprobe durchgeführt 11,000
Epochen (Nsamp) mit Ersatz aus jedem Schlaf-/Wachzustand; wir haben uns entschieden 11,000 Epochen sein-
denn dies war die kürzeste Dauer eines einzelnen Schlaf-Wach-Zustandes bei allen Patienten. Wir verwendeten
Diese Werte werden verwendet, um funktionale Konnektivitätsnetzwerke zu berechnen, die mit Wachheit verbunden sind, Qm
w ,
und Schlaf, Qm
w(ich, J) =
S (ich, J) = (1/Nsamp) (cid:1)k2sleep Q(ich, J, k). Wir haben diese Berechnung durchgeführt
(1/Nsamp) (cid:1)k2wake Q(ich, J, k) und Qm
für 1,000 Iterationen und dann gemittelt, um das Wachnetz Qw und das Schlafnetz zu erhalten-
n¼1 Qm
Arbeitsfragen für jedes Fach, wo Qw(ich, J) = (1/1,000)
S .
Wir haben die Netzwerkstärke bewertet, indem wir einen proportionalen Schwellenwert auf die Konnektivitätswerte angewendet haben
(Garrison et al., 2015). Speziell, Wir haben den Durchschnitt der Stärksten berechnet 10% der Verbindung-
Funktionen im Wach- und Schlafnetzwerk. Es wurde das Benjamini-Hochberg-Verfahren verwendet
ggf. für Mehrfachvergleiche korrekt (Benjamini & Hochberg, 1995).
S . Dies stellte eine Iteration dar, gekennzeichnet durch das hochgestellte m. Speziell, Qm
w und Qs(ich, J) = (1/1,000)
m¼1 Qm
P1;000
P1;000
Netzwerkstärke:
Ausmaß der Synchronisierung zwischen
Knoten, hier definiert als die
Prozentsatz der 1-s-Epochen, in denen
zwei Knoten sind signifikant
in Verbindung gebracht.
Graphentheoretische Maße
Studien zur funktionalen Konnektivität werden oft durch komplexe Netzwerkanalysen ergänzt, weil
Es liefert leicht berechenbare Maße mit biophysiologischer Bedeutung (Rubinow & Spurns,
2010). Wir haben drei gewichtete graphentheoretische Maße berechnet, die das Funktional zusammenfassen
Konnektivitätsnetzwerke, die in dieser Studie berechnet wurden. Erste, Wir haben den Grad für jeden Knoten berechnet
Summieren der Gewichte der Verbindungen, die zu diesem Knoten gehören (Bullmore & Spurns, 2009;
Rubinow & Spurns, 2010). Der Grad hängt mit unserer Messung der Netzwerkstärke zusammen,
Dies ist ein wichtiger Marker zur Unterscheidung von Schlaf und Wachheit (Smith et al., 2020)
und kann auch ein Indikator für pathologische Netzwerke sein (Shrey et al., 2018). Jedoch, Die
Die gewichtete Berechnung des Grades hat einen Vorteil gegenüber der Stärke, da keine Dreschmaschine erforderlich ist-
alt, um das Netzwerk zu binarisieren. Zweite, Der Clusterkoeffizient ist als Bruchteil von a definiert
Knotennachbarn, die auch untereinander Nachbarn sind, und sollen das Niveau von quantifizieren
funktionelle Trennung im Gehirnnetzwerk (Rubinow & Spurns, 2010; Watt & Strogatz, 1998).
Im gewichteten Netzwerkfall, Der Clustering-Koeffizient wird aus der „Intensität“ und abgeleitet
„Kohärenz“ eines Untergraphen anhand von Maßen seines geometrischen und arithmetischen Mittels (Utopie
et al., 2005). Vor der Berechnung des Clustering-Koeffizienten, Wir haben die Adjazenzmatrix normalisiert
indem jedes Element durch den maximalen Verbindungswert im Netzwerk dividiert wird (Antoniou &
Tsompa, 2008; Onnela et al., 2005). Dritte, Wir haben die kürzeste Pfadlänge berechnet, welche re-
Ports die minimale Summe der Kantenlängen für einen Pfad von einem Knoten zu einem anderen (Antoniou &
Tsompa, 2008; Rubinow & Spurns, 2010; Stam & Reijneveld, 2007). In unserem Fall, weil wir
Gehen Sie davon aus, dass der Informationsfluss mit höheren Verbindungswerten zunimmt, Wir haben die Kante definiert
Längen als Kehrwert der Kantengewichte. Daher, die minimale Summe dieser Umkehrkanten
Gewichte maximieren die Verbindungsstärke zwischen jedem Elektrodenpaar (Rubinow &
Spurns, 2010). Die kürzeste Pfadlänge ist eine der gebräuchlichsten Metriken zur Beurteilung der Funktionsfähigkeit
Integration (Rubinow & Spurns, 2010). Ähnlich der Berechnung des Clustering-Koeffizienten, Wir
Netzwerkneurowissenschaften
618
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
normalisierte die Adjazenzmatrix, bevor die Umkehrung berechnet und die kürzeste ermittelt wurde
Pfade zwischen Knoten im Netzwerk (Antoniou & Tsompa, 2008; Onnela et al., 2005).
Wir haben diese Maße aufgrund des Clustering-Koeffizienten und der charakteristischen Pfadlänge gewählt
wurden bereits früher zur Charakterisierung des Gehirns von Neugeborenen und Säuglingen verwendet (Omidvarnia et al.,
2014; Tymofiyeva et al., 2012). Clustering-Koeffizienten nehmen in niedrigeren Frequenzbändern ab und
Anstieg in höheren Frequenzbändern während der Entwicklung (Chu et al., 2014; Omidvarnia et al.,
2014; Tymofiyeva et al., 2012). Die Pfadlänge nimmt zu und die Clusterkoeffizienten nehmen mit ab
anhaltende Aufmerksamkeit bei Säuglingen (Xie et al., 2019), und das Verhältnis zwischen dem Clustering-Koeffizienten
und die Pfadlänge weisen darauf hin, dass das Gehirn des Säuglings Kleinwelteigenschaften aufweist (Gao et al.,
2011; Tymofiyeva et al., 2012). Darüber hinaus, Veränderungen im Gehirnzustand wirken sich auf graphentheoretische Messungen aus-
sicher bei Erwachsenen, mit höheren Clusterkoeffizienten (Chu et al., 2012) und größer klein-
Weltlichkeit (Ferri et al., 2008) Während dem Schlafen. Wichtig, solche globalen Diagrammeigenschaften
kann im Säuglings-EEG zuverlässig gemessen werden, wie aus einer Test-Retest-Zuverlässigkeitsstudie hervorgeht (Transporter
der Velde, Herzen, & Kemner 2019), um sie für unsere Analyse geeignet zu machen.
Zeitvariable funktionale Konnektivitätsmessung
Analyse zeitlich variierender Veränderungen in den Funktionszusammenhängen, Wir haben das binäre p × p gemittelt
Matrizen über Fenster aufeinanderfolgender Epochen hinweg. Qn sei die gemittelte p × p-Matrix
über ein Fenster von n 1-s-Epochen. Der Wert von Qn(ich, J ) gibt den Anteil der Epochen an
wobei die Verbindung zwischen Kanal i und Kanal j von Bedeutung war, analog zum
Werte von Qw und Qs für Wachheit und Schlaf, jeweils. Für unsere Analyse, wir haben nachgerechnet
Q300, die gemittelte Konnektivitätsmatrix in einem Fenster von 300 S, und dieses Fenster wurde nach innen verschoben
30-s-Schritte (90% Überlappung). Wir haben eine Fenstergröße von gewählt 300 Weil es Netzwerke gab
In zwei getrennten Studien wurde gezeigt, dass es über diesen Zeitraum stabil ist (Chu et al., 2012;
Shrey et al., 2018).
Wiederkehr von Netzwerkzuständen und Übereinstimmung mit der manuellen Schlafeinstufung
Wir stellten die Hypothese auf, dass es unterschiedliche Gehirnzustände gibt (z.B., Schlaf oder Wachheit) verbunden wäre
mit verschiedenen funktionalen Netzwerken und dass das funktionale Netzwerk einem einzigen zugeordnet ist
Der Zustand wäre im Laufe der Zeit relativ konstant. daher, Wir haben die Hauptkomponente Anal verwendet-
ysis (PCA) um die Menge funktionaler Netzwerke zu identifizieren, die einen Großteil der Var ausmachten-
ance im Laufe der Zeit, unter der Annahme, dass Zustandsübergänge die größte Ursache für diese Varianz wären.
Dadurch können wir auch beurteilen, wie viele Netzwerkzustände in den Daten aufgetreten sind und ob die Zustände
trat im Laufe der Zeit immer wieder auf.
Durchführung einer PCA in den funktionalen Konnektivitätsnetzwerken im Laufe der Zeit, Wir haben zuerst Q300 berechnet
in 300-er Fenstern mit 90% Überlappung, wie im Abschnitt „Zeitvariable Funktion“ beschrieben
Konnektivitätsmessung. Anschließend haben wir die Werte für alle eindeutigen Verbindungen in Q300 platziert
(171 Kanalpaare insgesamt, ausgenommen Selbstverbindungen) in einen Spaltenvektor c umgewandelt und normalisiert
Es soll einen Mittelwert von Null und eine Einheitsvarianz haben. Wir haben p aufeinanderfolgende Vektoren verkettet, wo p de-
Notiert die Anzahl der Fenster, die im Datensatz verfügbar waren, in Matrix C eingefügt und subtrahiert
der Mittelwert aus jeder Zeile, um sicherzustellen, dass die Verteilung der Verbindungen für jedes Kanalpaar gewährleistet ist
war Null-Mittelwert. Wir haben eine PCA für diese normalisierte funktionale Konnektivitätszeitreihe C durchgeführt
um die latenten Netzwerke zu ermitteln, die die größte Varianz in den Daten erklärten. Wir berechnen dann-
den zeitlichen Verlauf der ersten Hauptkomponente, was das relative Gewicht darstellt
dieser Komponente als Funktion der Zeit zugeordnet.
Sobald die Netzwerkzustände identifiziert wurden, Wir haben ihre physiologische Bedeutung bestimmt durch
Vergleich mit dem visuellen Schlafstadium des EEG. Wir gingen davon aus, dass es so sein würde
Hauptkomponentenanalyse:
Technik zur Dimensionsreduktion
basierend auf der Eigenzerlegung von
die Kovarianzmatrix.
Netzwerkneurowissenschaften
619
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
Gaußsches Mischungsmodell:
Parametrisches Modell, das davon ausgeht
Daten können durch a dargestellt werden
gewichtete Summe einer endlichen Anzahl von
Gaußsche Verteilungen.
Netzwerkstabilität:
Variabilität des Funktionalen
Netzwerk innerhalb eines einzigen Staates von
Bewusstsein; stabile Netzwerke sind
im Laufe der Zeit stark korreliert.
Übergänge zwischen zwei verschiedenen Zuständen, likely representing wakefulness and sleep, so we fit a
two-component Gaussian mixture model (GMM) to the principal component time series. Wir
then calculated normalized probability distribution functions (PDFs) for the two GMM distri-
butions. The threshold to separate the states was defined as the intersection of the two PDFs.
To avoid finding intersections at the extreme tails of the distributions, we calculated the PDF
ratio and identified the index where this ratio was closest to 1:
(cid:2)
(cid:4)
(cid:2)
(cid:2)
−1
(cid:2)
thresholdIndex ¼ min PDF1
PDF2
(cid:2)
(cid:3)
(cid:2)
(cid:2)
(cid:2)
:
The principal component value associated with this index was the threshold that best distin-
guished the two states. We used this value to separate the networks from all time points into
two states, and we compared these results to visual sleep scoring done by a certified EEG sleep
technician.
Calculation of Network Stability
We assessed network stability of the functional connectivity measurement by performing 2-D
correlations between independent average connectivity networks during wakefulness or sleep.
We first concatenated all epochs during sleep (Ns) or wakefulness (Nw) and then calculated
Ns/n or Nw/n sequential, nonoverlapping measurements of Qn where n is the size of the win-
dow. Then a 2-D correlation was calculated between each successive measurement of Qn
and this was repeated for window sizes n ranging from 10 s to 200 S. The mean of the cor-
relation values was recorded for each window size for each subject. The mean and 95% con-
fidence interval of the average correlation coefficient values for all subjects were then plotted
as a function of n.
Calculation of Circadian Changes in Functional Networks
zuletzt, Wir haben untersucht, ob es zirkadiane Modulationen im funktionellen Konnektiv gibt-
ity-Netzwerke. Für diese Analyse, Schlaf und Wachheit wurden je nach Mensch getrennt analysiert-
Manuelle EEG-Schlafbewertung. Für Wachheit und Schlaf, Wir haben vier Kennzahlen berechnet (der Mittelwert
Netzwerkstärke und die drei graphentheoretischen Maße) als Funktion der Zeit mit Q300
(siehe Abschnitt Zeitvariable funktionale Konnektivitätsmessung). Nächste, die Werte von jedem von
Diese vier Metriken waren mit dem 24-Stunden-Tracking verknüpft (zirkadian) Uhrzeit entsprechend der
Beginn ihrer Q300-Epoche. Wir haben dies für jedes Subjekt im Datensatz durchgeführt, dadurch erhält man a
Verteilung der Werte über die Fächer für jedes der 1,440 zirkadiane Zeitpunkte (jede Minute
im 24-Stunden-Format). Anschließend haben wir den Mittelwert aller Probanden für jeden 1-Minuten-Block berechnet
Zeit; wenn der 1-Minuten-Block weniger als fünf Datenpunkte enthielt, Die Daten wurden berücksichtigt
unzureichend und dieser Zeitpunkt wurde verworfen. Zur Beurteilung der statistischen Signifikanz, wir haben zusammengefasst
alle Datenpunkte von 11 BIN zu 1 PM als „Tages“-Verteilung und wir haben alle Daten aggregiert
Punkte ab 11 PN an 1 AM als „Nacht“-Verteilung. Ähnlich wie bei den Probenahmemethoden
Wird im Abschnitt „Funktionale Konnektivität“ verwendet, Wir haben zufällig Beobachtungen mit Ersatz ausgewählt
aus der Tages- und Nachtzeit für 1,000 Iterationen. Mit jeder Iteration, wir haben nachgerechnet
die Differenz zwischen den Mittelwerten der Verteilungen (tagsüber im Vergleich zur Nacht), Und
Wir haben getestet, ob das Konfidenzintervall der resultierenden Differenzverteilung enthalten ist 0.
ERGEBNISSE
Themendemografie
In Summe, 19 gesunde Probanden (15 weiblich, 4 Männer) wurden zwischen Juni für die Studie rekrutiert
2017 und Februar 2019, and all were included in our analysis. The mean age of the subjects
Netzwerkneurowissenschaften
620
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
N
e
N
_
A
_
0
0
1
9
4
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Zirkadiane Dynamik in funktionellen Konnektivitätsnetzwerken bei Säuglingen
War 6.3 months (+/− 3.1 months, Standardabweichung). The recordings lasted 20.8 hr on average
(+/− 7.8 Std, Standardabweichung). Recording durations are listed for every subject in Supporting
Information Table S2.
Sleep Is Associated with Stronger Functional Connections
Sleep was associated with stronger functional connections, as evidenced by the averaged con-
nectivity networks Qw and Qs across all subjects (Figure 1A) and the individual subject results
(Figure 1B). We also tested whether specific connection pairs were consistently stronger in
wakefulness or sleep; to do this, we compared the distribution of connection strengths for
one electrode pair during wakefulness to the distribution during sleep in a pairwise fashion
(n = 19 Fächer). In 48 of the 171 possible connections, wakefulness revealed stronger con-
nectivity values (Abbildung 1C, top) (two-tailed Wilcoxon sign-rank test, adjusted via Benjamini–
Hochberg procedure, adj. P < 0.05). In 55 of the 171 possible connections, sleep connectivity
values were significantly stronger than wakefulness (Figure 1C, bottom) (two-tailed Wilcoxon
sign-rank test, adjusted via Benjamini–Hochberg procedure, adj. p < 0.05). The strongest con-
nections in the averaged network were typically associated with sleep rather than wakefulness;
although a number of connections were statistically stronger during wakefulness than sleep,
these connections were typically weak, with strengths <0.04 (Figure 1D).
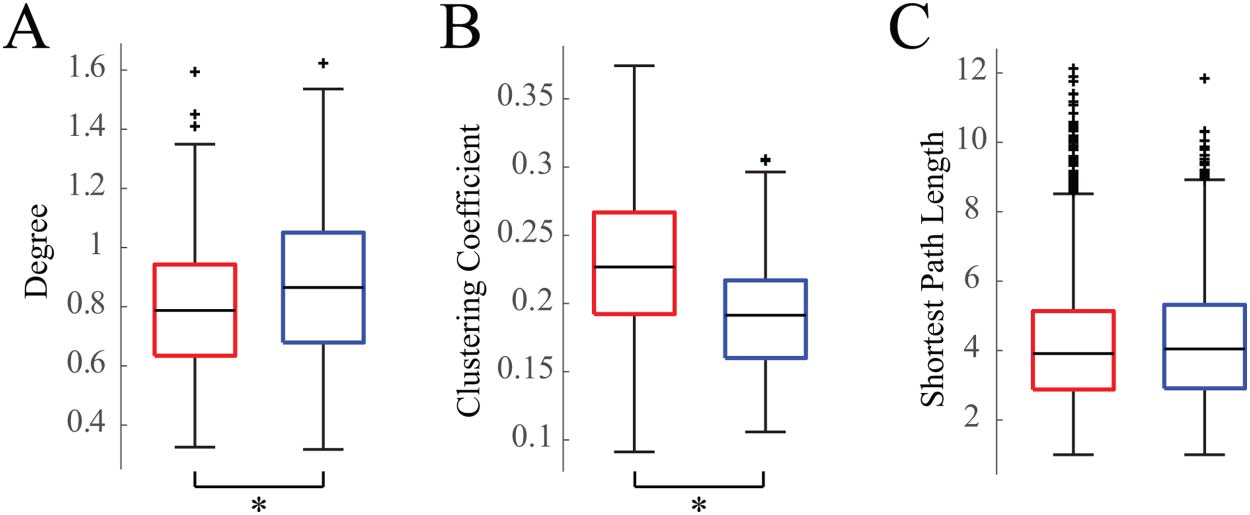
Functional Network Structures Are Subject Specific
We then measured the similarity of the functional connectivity network structure within and
across subjects, as well as within and across sleep/wake states (Figure 2). Across all subjects,
the within-sleep distribution of correlation coefficients was statistically significantly higher
than the within-wakefulness distribution, and both were significantly higher than the across-
state distribution ( Wilcoxon rank-sum test, p < 0.05). However, Cohen’s effect size value
between the within-wakefulness and across-state distributions suggested low practical signif-
icance (d = 0.233). All effect sizes are reported in Supporting Information Table S3. Within-
subject across-state correlations (e.g., comparing subject 1 sleep to subject 1 wakefulness)
were higher than across-subject within-state correlations (e.g., comparing sleep networks
(A) Average functional connectivity networks for wakefulness and sleep. For visualization, an edge is drawn if the connection value
Figure 1.
exceeds an absolute threshold of 0.075. (B) Mean connection strength for individual subjects (calculated as the average strength of the stron-
gest 10% of connections) is higher during sleep. (C) Network maps showing connections that were statistically significantly greater in wake-
fulness (top) or sleep (bottom). (D) Box plots of mean connection strength for connections that were significantly different between wakefulness
and sleep (shown in subfigure C).
Network Neuroscience
621
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Figure 2. Box plot showing 2-D correlations within and across weighted connectivity matrices for
each subject. We first compared networks across subjects within a state, for example, Subject 1
Wake to Subject 2 Wake, and the analogous comparisons during sleep; n = 171 observations each.
Then we compared across subjects and across states, for example, Subject 1 Wake to Subject 2
Sleep; n = 171 observations. Lastly, we calculated the 2-D correlation between the sleep and wake
networks within single subjects, for example, Subject 1 Wake to Subject 1 Sleep; n = 19 observa-
tions. All distributions are statistically significantly different from one another ( Wilcoxon rank-sum
test, p < 0.05).
across all subjects). This indicates that, while state-specific functional network structure com-
monalities are seen across subjects, the network structures are also patient-specific.
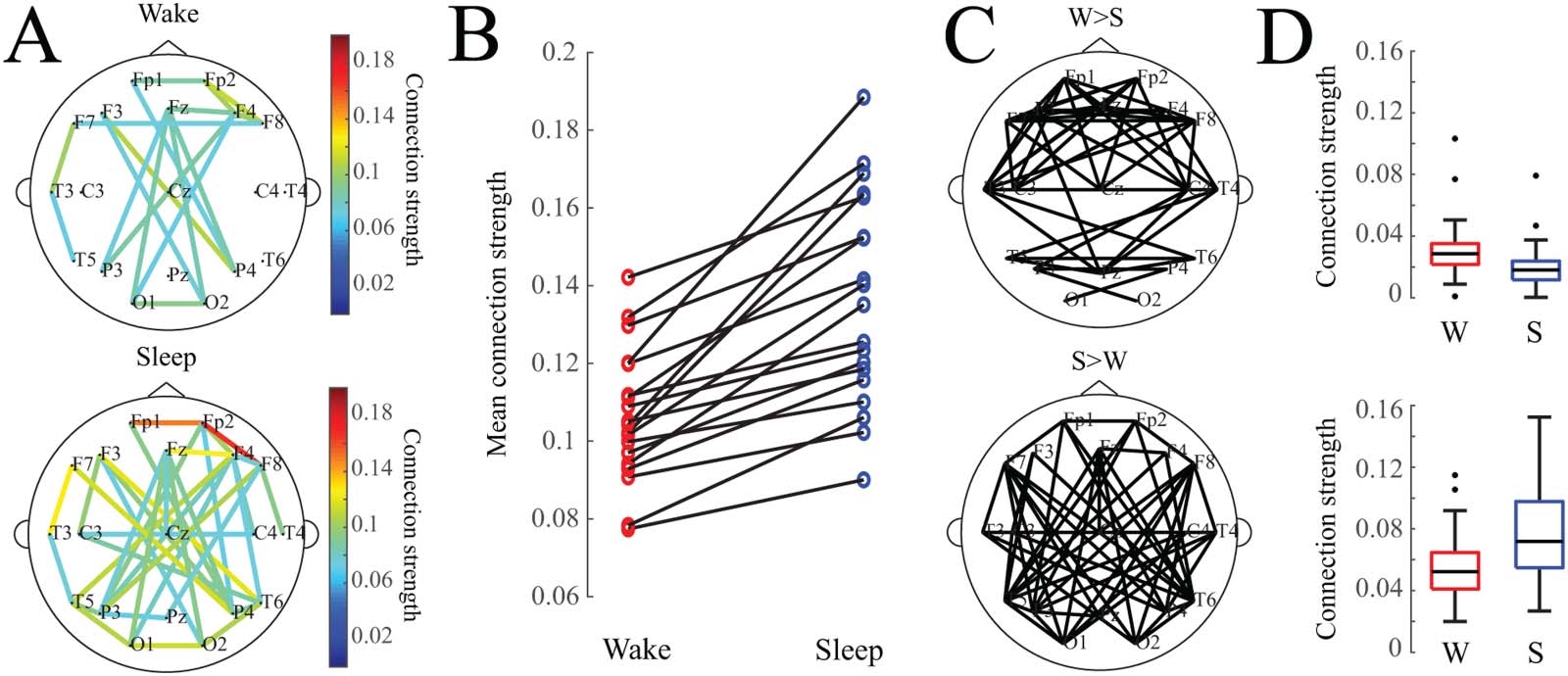
Network Structure Is More Segregated During Wakefulness
We calculated three standard weighted graph theoretical measures on the average functional
connectivity maps for sleep and wakefulness for each subject. Consistent with our finding that
networks tended to be stronger during sleep than during wakefulness, the node degree was
significantly greater in sleep than in wakefulness (Figure 3A) ( Wilcoxon rank-sum test, p <
0.05, Cohen’s d = 0.34). The clustering coefficient was significantly greater in wakefulness
compared to sleep (Figure 3B) ( Wilcoxon rank-sum test, p < 0.05, Cohen’s d = 0.78).
Lastly, we found that the shortest average path length was not significantly different between
sleep and wakefulness (Figure 3C) ( Wilcoxon rank-sum test, p < 0.05, Cohen’s d = 0.03).
Figure 3. Box plots of weighted graph theoretical measures. (A) Degree, (B) clustering coefficients,
and (C) shortest path lengths of wakefulness (red) and sleep (blue) networks for all 19 subjects.
Asterisk denotes p values less than 0.05.
Network Neuroscience
622
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
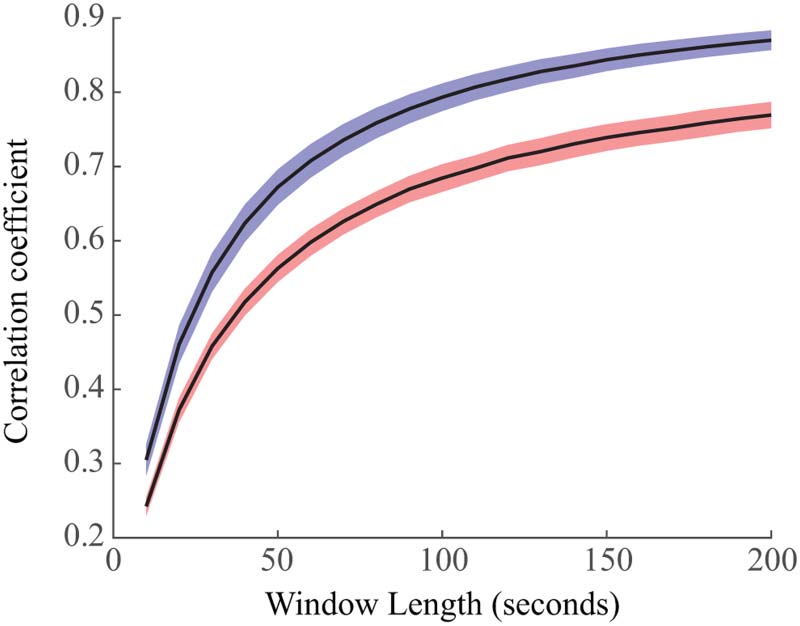
Figure 4. Stability of functional connectivity networks in wakefulness (red) and sleep (blue). We
calculated the 2-D correlation between independent averaged connectivity networks from windows
of data of varying size. We found that sleep exhibited more stable networks, with nonoverlapping
confidence intervals for the means for all window sizes.
Functional Networks Are More Stable in Sleep Than Wakefulness
We then calculated the stability of each subject’s functional connectivity networks within a
given brain state (Figure 4). Here, stability was assessed using the correlation coefficient be-
tween networks calculated from independent windows of data. Higher correlation coefficients
indicated greater similarity between networks and thus, higher stability. For each subject, we
calculated the mean correlation coefficient for each window size and then calculated the 95%
confidence interval for the mean correlation coefficients across all subjects. We found that
sleep networks were significantly more stable than networks derived from EEG during wake-
fulness (Figure 4). The confidence intervals for the mean of the stability distributions did not
overlap for any window size, indicating statistical significance over all tested window sizes.
Functional Networks Associated with Sleep and Wakefulness Recur over Hours and Days
Our analysis thus far has shown that an individual subject’s functional network remains stable
throughout each period of wakefulness or sleep. However, this analysis did not test whether
the networks recur, that is, whether the functional network of one sleep period matches that of
another sleep period within the same person. To address this, we used PCA to determine the
latent variable that described the most variance in the connectivity data; we hypothesized that
this variance would be due to transitions between wakefulness and sleep. If the networks re-
main stable for each state over multiple sleep/wake cycles, the time series of the first principal
component, which signifies the weight of that component in the functional connectivity time
series, should oscillate between two values.
We performed PCA on all functional connectivity network time series as outlined in section
Recurrence of Network States and Correspondence to Manual Sleep Staging. A representative
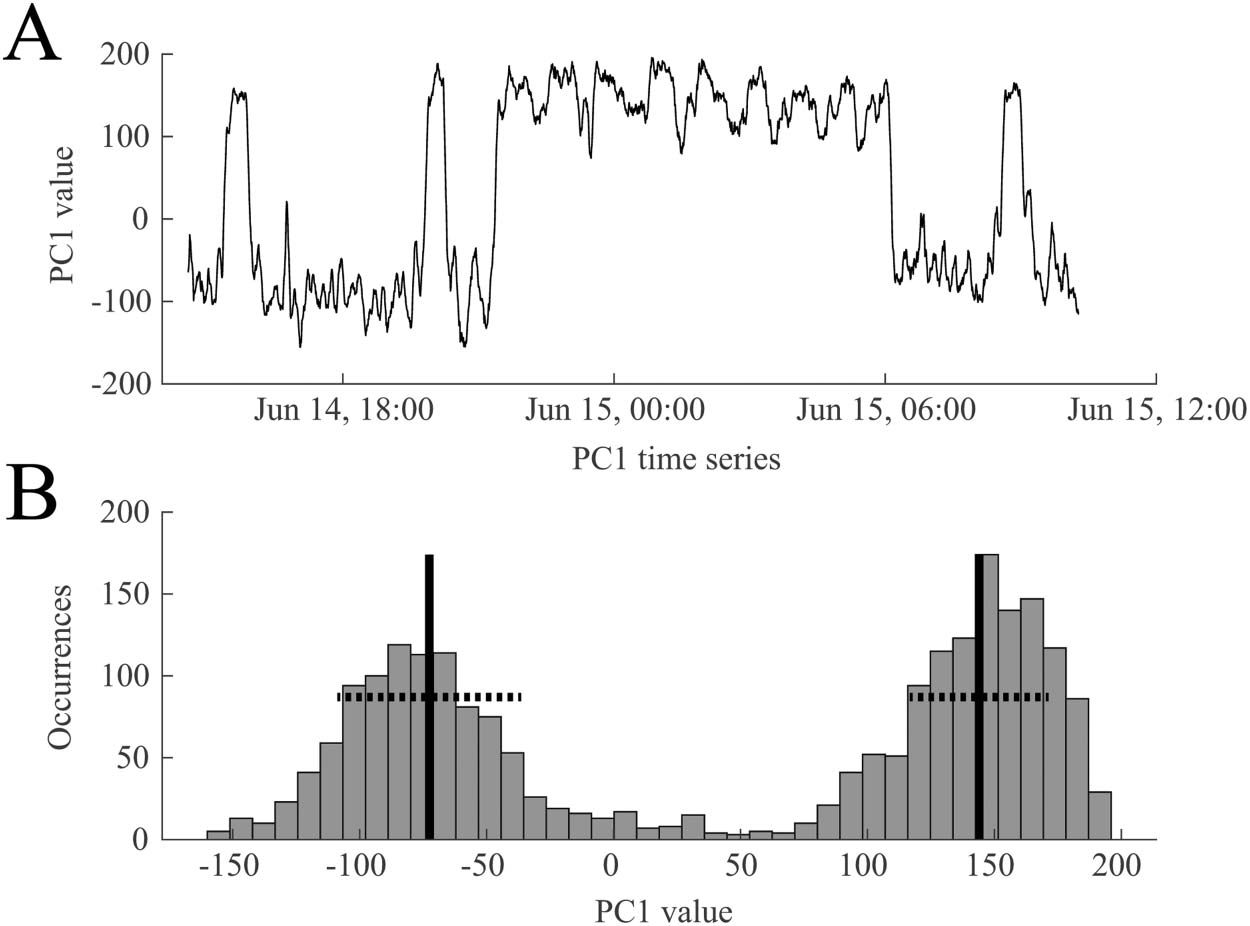
example of a time series from the first principal component (PC1) is shown in Figure 5A, dem-
onstrating the bimodal nature of the signal. This suggests that the brain is switching between
two functional network states over the course of 1 day. This was also reflected in the histogram
of the first principal component, which we fit with a two-component GMM (Figure 5B).
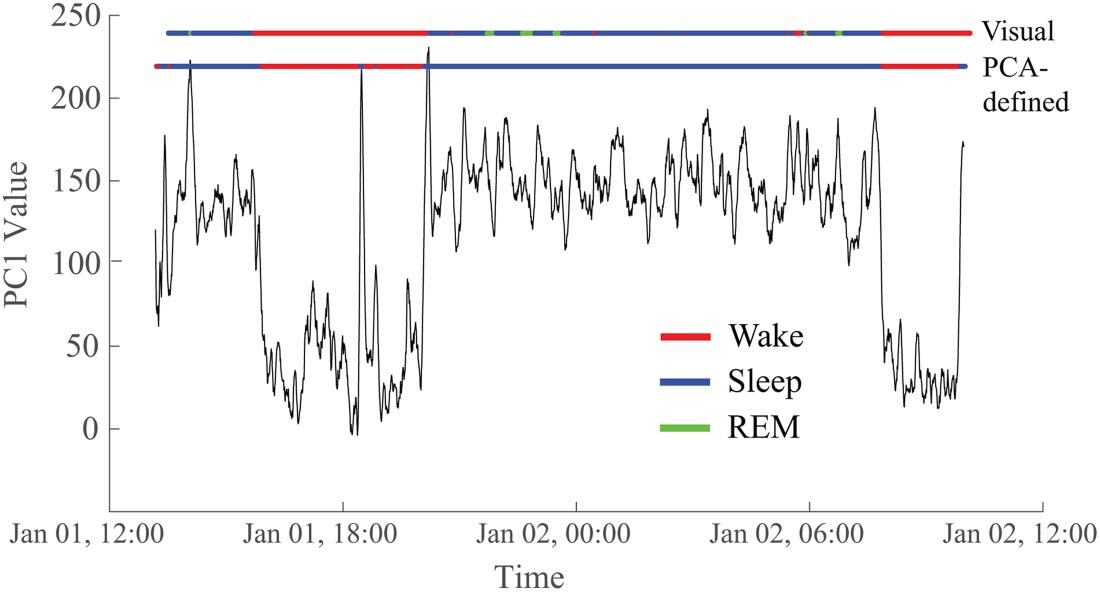
To determine whether the two reoccurring states evident in the PCA results corresponded
to wakefulness and sleep, we compared the GMM output to visual sleep staging (Figure 6).
We found a high correspondence between the two states uncovered via PCA (defined by a
Network Neuroscience
623
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
Figure 5. A representative example of the time course of the first principal component (PC1), re-
flecting how much weight is assigned to PC1 in the functional connectivity time series. (A) PC1
oscillates between two states during ~18 hr of EEG data. (B) The bimodal nature of PC1 is reflected
in its histogram. A two-component Gaussian mixture model was derived from these values and used
to classify the two states. The black vertical lines indicate the means of the two distributions, and the
dashed horizontal lines denote one standard deviation. Data are from Subject 1.
threshold applied to the GMM) and the visually identified sleep and wake stages. Across
subjects, the median percentage of correspondence was 91.2% (Supporting Information
Table S4), confirming our hypothesis that the PCA-determined states reflected wakefulness
and sleep.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. The two states derived from the PC1 time series correspond to visually marked sleep and
wakefulness in the EEG. In this representative example, the correspondence is 95.1%. The top hor-
izontal line (“Visual”) is colored to indicate the sleep/wake state based on visual markings. Red
indicates the subject is awake, blue is non-REM sleep, and green is REM sleep. The bottom hori-
zontal line (“PCA-defined”) reflects the values of the first principal component after thresholding
based on the Gaussian mixture model, with red representing wakefulness and blue representing
sleep. Data are from Subject 5.
Network Neuroscience
624
Circadian dynamics in infant functional connectivity networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
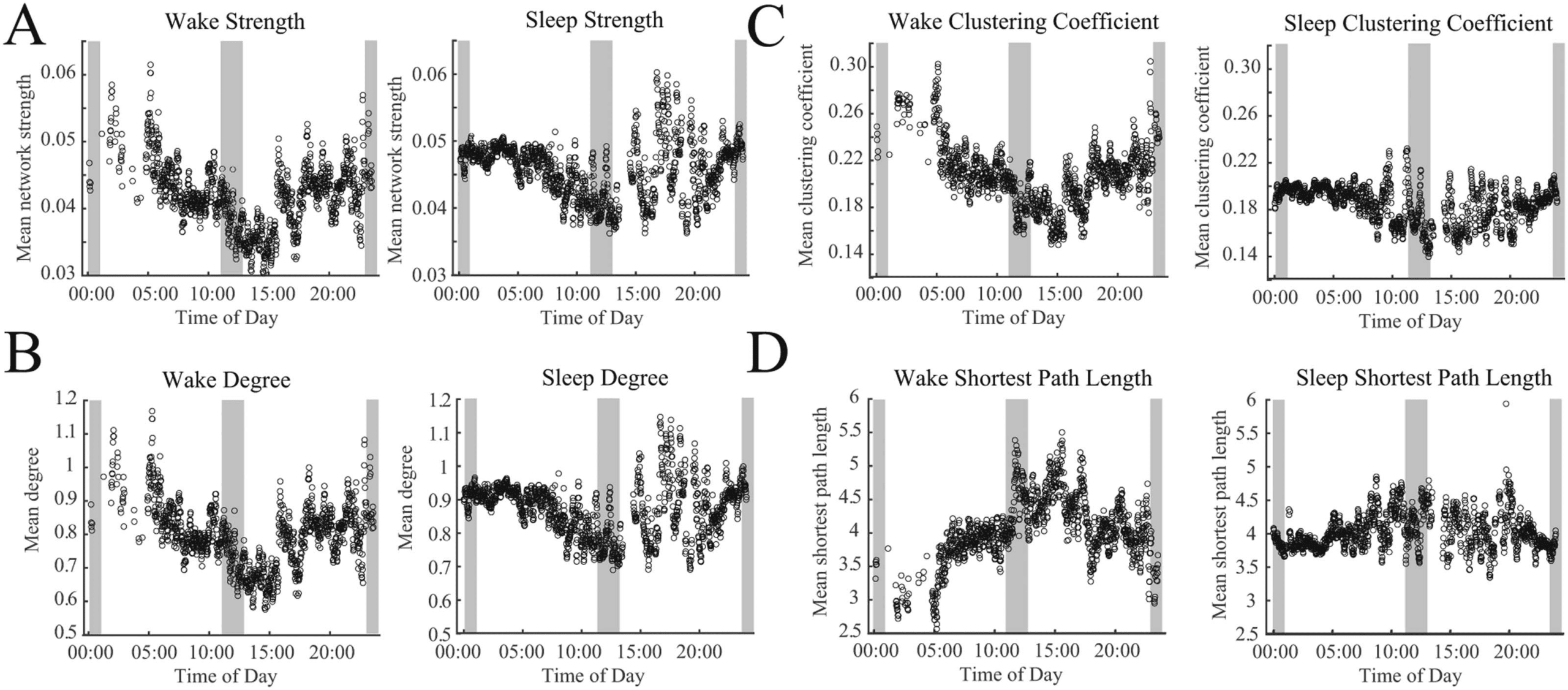
Figure 7. Circadian patterns emerge in both wakefulness and sleep for network strength and graph theoretical metrics. Twenty-four hour
periodicities are shown for (A) the network strength, defined as the mean of all connections, (B) network degree, (C) clustering coefficient,
and (D) the shortest path length. Each subfigure shows data recorded during wakefulness (left) and sleep (right). Gray shaded regions mark
daytime (11:00–13:00) and nighttime (23:00–01:00) hours.
EEG Functional Networks Exhibit Circadian Variation
When subjects were awake, the mean network strength was significantly decreased during the
daytime and was increased at nighttime (Figure 7A; 95% confidence interval does not include
0). Similar patterns were seen for the network degree (Figure 7B) and the clustering coefficient
(Figure 7C). The shortest path length showed the opposite trend (Figure 7D). Similar patterns
were observed using data collected when subjects were sleeping, although the modulation
over 24 hr was less dramatic. However, all trends in graph theoretical measures were signif-
icantly different between daytime and nighttime hours (Figure 7B–7D; 95% confidence inter-
val does not include 0). This indicated that, in addition to the significant differences between
sleep and wake functional networks, the time of day modulated the network within each state.
We noted that the sleep measurements during the daytime exhibited high amounts of vari-
ability, and, in general, there was higher variance in the measurements when subjects were
asleep during the daytime or awake at nighttime. However, this may be partially due to the
low number of data points in some time periods, as the high variance did not occur when there
were a large number of data points in the 1-min windows (Supporting Information Figure S1). A
larger cohort or more EEG data per subject would be needed to robustly quantify this variance.
DISCUSSION
In this study, we report characteristics of functional connectivity networks based on long-term EEG
recordings from 19 healthy infants. We first showed that functional connectivity networks associ-
ated with sleep and wakefulness exhibited statistically significant differences both in strength and
structure. We also showed that, although sleep and wakefulness were associated with stable net-
works, those networks were highly individualized. Within-subject comparisons of sleep to wake-
fulness were more similar than comparisons across subjects within the same state of
Network Neuroscience
625
Circadian dynamics in infant functional connectivity networks
Topology metrics:
Graph theoretical measurements of
network characteristics, such as
degree, clustering coefficient, and
shortest path length.
consciousness. Furthermore, state-specific networks recurred over multiple periods of sleep and
wakefulness within each subject, as revealed by the correspondence of PCA-derived networks to
visual sleep scoring. Lastly, we showed that circadian rhythms significantly modulated network
properties in a relatively stereotyped fashion. This suggests that the time of day during which a
recording is obtained may significantly impact measurements of functional connectivity, which
bears relevance for both cognitive and clinical studies involving functional networks.
The analysis of infant EEG, which is visually distinct from adult EEG, is a unique aspect of
this study. The vast majority of EEG functional connectivity studies focus on healthy adult data
(Stevens, 2009); thus, this study fills a critical need by reporting basic characteristics of healthy
EEG-based functional networks as a baseline for studying conditions specific to the
neonatal/infant period, including early-onset epilepsies and neurodevelopmental conditions
(Righi et al., 2014; Shrey et al., 2018). Infant EEG poses unique advantages and disadvantages
in comparison with adult recordings. On one hand, it enables study of circadian dynamics and
network characteristics separately for sleep and wakefulness because infant sleep cycles do
not always coincide with diurnal rhythms. On the other hand, the EEG patterns associated with
sleep and wakefulness in infant EEG rapidly evolve as the infant grows and develops. Wakeful
background activity in infant EEG is slower than adult EEG, and rhythms become faster with
age (Fisch, 1999; Rowan & Tolunsky, 2003). The emergence of critical patterns, such as the
posterior dominant rhythm and the mu rhythm, occurs at around 3 and 4–6 months of age,
respectively (Laoprasert, 2011; Stern, 2005). Moreover, the structural connectivity in the infant
brain is constantly changing and developing (Barkovich et al., 2006; Tymofiyeva et al., 2012),
whereas structural connectivity in adults is relatively static. This age dependence could partially
explain the subject-specific nature of the networks observed in our study, but we found no sig-
nificant correlations in our strength and topology metrics (Supporting Information Figure S2),
and subject-specific networks were also reported in adults (Chu et al., 2012). While researchers
have advanced the study of the relationship between structure and function in the brain (Pernice
et al., 2011; Ponten et al., 2010), further work is needed to examine this relationship in the
developing brain. Overall, we expect that the functional connections underlying infant neural
activity will differ from adults.
We found that functional networks were stronger during sleep than wakefulness, and they
were less clustered when the subject was awake (Burroughs et al., 2014; Kuhnert et al., 2010;
Mitsis et al., 2020). The networks were significantly stronger during sleep when compared to
wakefulness in all subjects (Figure 1B); however, we note that the effects of thresholding net-
works, even with a proportional threshold, is an active area of research and will require further
investigation (Chapeton et al., 2017; Garrison et al., 2015). To reduce the bias introduced by
thresholding the network graphs, we calculated graph theoretic properties of the networks on
the weighted adjacency matrices. The degree was significantly higher in the functional net-
works derived from sleep, consistent with our finding of overall stronger networks in sleep.
The clustering coefficient of the normalized networks was higher in awake networks, indicat-
ing greater functional segregation during wakefulness (Rubinov & Sporns, 2010; Watts &
Strogatz, 1998). Interestingly, the shortest path length, calculated as the inverse of the normal-
ized connection strength, was not significantly different between the two states, indicating sim-
ilar levels of functional integration in wakefulness and sleep (Watts & Strogatz, 1998).
We found that the awake and sleep networks were more similar within a single subject than
the awake or asleep networks across subjects. The subject-specific nature of these functional
networks was also described in a long-term intracranial EEG study in adults (Kramer et al.,
2011), as well as in a previous study by our group in a cohort of pediatric epilepsy patients
(Shrey et al., 2018). This may indicate a need for a paradigm shift in the analysis of functional
Network Neuroscience
626
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
connectivity networks. Most functional network studies have focused on finding common net-
works and pathways that facilitate specific functions or the resting state. However, the unique-
ness of functional networks has become a recent area of investigation in the fMRI community
and may deserve further attention in EEG functional network analysis (Chapeton et al., 2017;
Chen et al., 2008; D’Esposito, 2019; Dubois & Adolphs, 2016; Fingelkurts & Fingelkurts,
2011; Finn et al., 2020; Gonzalez-Castillo et al., 2015; Kramer et al., 2011). A comparison
of functional connectivity networks may require attention to both elements: the common path-
ways underlying the activity of interest, as well as the individuality of the subject’s unique func-
tional network.
The stability of functional connectivity networks in EEG is a function of the timescale used to
measure them. We found that the binary connectivity matrices in 1-s epochs were highly variable,
but stable networks were identified over the course of 200–500 s (Chu et al., 2012; Shrey et al.,
2018). However, these networks become unstable again at the timescale of hours due to brain
state transitions and circadian rhythms. This multilevel stability is assumed in our study, but further
investigation is needed to define characteristic timescales of stability in functional connectivity
networks in the human brain (Kuhnert et al., 2010). This is perhaps related to the concept that
EEG amplitude modulations do not have a characteristic scale and exhibit a fractal nature
(Hardstone et al., 2012; Linkenkaer-Hansen et al., 2001; Smith et al., 2017). This fractal nature
may be transferred to functional networks (Lehnertz et al., 2017), mathematically suggesting that
brain activity is changing in an organized way that may not have a characteristic timescale.
Several limitations of our study should be addressed in future investigations of healthy func-
tional connectivity networks. First, our EEG recordings were an average of 20.8 hr, and a lim-
ited number of recordings were longer than 24 hr. Thus, circadian patterns were assessed on
the group level rather than an individual level. Future studies could include longer, multiday
EEG recordings to analyze true subject-specific assessments of circadian patterns. Second, we
used an automatic algorithm to remove artifacts in our data, as it was infeasible to visually
confirm all artifacts due to the long recording durations. Therefore, some artifacts may have
escaped detection/removal while other artifact-free data may have been erroneously removed.
This could have contributed to the differences seen in the wake and sleep networks because
artifacts are more frequent during wakefulness; on the other hand, the results reported here
mirror those obtained with visually marked artifacts (Shrey et al., 2018). Lastly, although there
are many advantages to analyzing data from a cohort of infants, the limited age range reduces
the generalizability to other pediatric populations, and we did not have enough subjects to
discern network properties specific to each age or developmental stage. Note, though, that
a preliminary analysis revealed no modulation in strength or topology metrics as a function
of age (Supporting Information Figure S2). Future studies should increase the number of sub-
jects and broaden the age range.
The importance of this study lies in generating functional connectivity networks derived
from ~24-hr recordings of normal EEG data in infants. In addition to imparting knowledge
of how physiological functional networks are modulated throughout the day and within wak-
ing and sleep states, this will facilitate understanding of changes in network topology due to
pediatric diseases such as epilepsy and autism (Righi et al., 2014; Shrey et al., 2018). Seizure
forecasting in epilepsy has largely relied on prediction of seizure onset with several minutes of
data, but it has been shown that modulations in functional networks due to physiological pro-
cesses such as waking and sleeping can mask “pre-seizure” changes (Kuhnert et al., 2010;
Mitsis et al., 2020; Schelter et al., 2011). Accounting for these physiological fluctuations in
seizure prediction models may improve their accuracy and ultimately improve care for patients
suffering from epilepsy.
Network Neuroscience
627
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
ACKNOWLEDGMENTS
The authors thank the EEG technologists at the Children’s Hospital of Orange County (CHOC)
for their help in acquiring the EEG data. The authors also thank Dr. Michael Nunez and Derek
Hu for helpful discussions regarding the manuscript. This study was funded by a CHOC PSF
Tithe grant.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00194.
AUTHOR CONTRIBUTIONS
Rachel June Smith: Conceptualization; Data curation; Formal analysis; Investigation;
Methodology; Project administration; Software; Writing – original draft. Ehsan Alipourjeddi:
Data curation; Formal analysis; Investigation; Software; Writing – review & editing. Cristal
Garner: Data curation. Amy L. Maser: Data curation. Daniel W. Shrey: Conceptualization;
Data curation; Funding acquisition; Methodology; Supervision; Writing – review & editing.
Beth A. Lopour: Conceptualization; Funding acquisition; Investigation; Methodology;
Project administration; Resources; Supervision; Writing – review & editing.
FUNDING INFORMATION
Daniel W. Shrey, Children’s Hospital of Orange County, Award ID: PSF Tithe Grant.
REFERENCES
Aeschbach, D., Matthews, J. R., Postolache, T. T., Jackson, M. A.,
Giesen, H. A., & Wehr, T. A. (1999). Two circadian rhythms in
the human electroencephalogram during wakefulness. American
Journal of Physiology, 277(6), 1771–1779. https://doi.org/10
.1152/ajpregu.1999.277.6.R1771, PubMed: 10600925
Anastasiadou, M., Hadjipapas, A., Christodoulakis, M.,
Papathanasiou, E. S., Papacostas, S. S., & Mitsis, G. D. (2016).
Epileptic seizure onset correlates with long term EEG functional
brain network properties. Proceedings of the Annual
International Conference of the IEEE Engineering in Medicine
and Biology Society, EMBS, 2016-Octob, 2822–2825. https://
doi.org/10.1109/EMBC.2016.7591317
Anastasiadou, M. N., Christodoulakis, M., Papathanasiou, E. S.,
Papacostas, S. S., Hadjipapas, A., & Mitsis, G. D. (2019).
Graph theoretical characteristics of EEG-based functional brain
networks in patients with epilepsy: The effect of reference choice
and volume conduction. Frontiers in Neuroscience, 13(March),
1–18. https://doi.org/10.3389/fnins.2019.00221, PubMed:
30949021
Antoniou, I. E., & Tsompa, E. T. (2008). Statistical analysis of
weighted networks. Discrete Dynamics in Nature and Society,
2008. https://doi.org/10.1155/2008/375452
Barkovich, A. J., Miller, S. P., Bartha, A., Newton, N., Hamrick, S. E. G.,
Mukherjee, P., … Vigneron, D. B. (2006). MR imaging, MR
spectroscopy, and diffusion tensor imaging of sequential studies in
neonates with encephalopathy. American Journal of Neuroradiology,
27(3), 533–547, PubMed: 16551990
Baud, M. O., Kleen, J. K., Mirro, E. A., Andrechak, J. C., King-
Stephens, D., Chang, E. F., & Rao, V. R. (2018). Multi-day rhythms
modulate seizure risk in epilepsy. Nature Communications, 9(1),
1–10. https://doi.org/10.1038/s41467-017-02577-y, PubMed:
29311566
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov-
ery rate: A practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society. Series B, 57(1), 289–300.
https://doi.org/10.1111/j.2517-6161.1995.tb02031.x
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Burroughs, S. A., Morse, R. P., Mott, S. H., & Holmes, G. L. (2014).
Brain connectivity in West syndrome. Seizure: European Journal
of Epilepsy, 23(7), 576–579. https://doi.org/10.1016/j.seizure
.2014.03.016, PubMed: 24794162
Chapeton, J. I., Inati, S. K., & Zaghloul, K. A. (2017). Stable func-
tional networks exhibit consistent timing in the human brain.
Brain, 140(3), 628–640. https://doi.org/10.1093/brain/aww337,
PubMed: 28364547
Chen, A. C. N., Feng, W., Zhao, H., Yin, Y., & Wang, P. (2008).
EEG default mode network in the human brain: Spectral regional
field powers. NeuroImage, 41(2), 561–574. https://doi.org/10
.1016/j.neuroimage.2007.12.064, PubMed: 18403217
Chu, C. J., Leahy, J., Pathmanathan, J., Kramer, M. A., & Cash, S. S.
(2014). The maturation of cortical sleep rhythms and networks
Network Neuroscience
628
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
over early development. Clinical Neurophysiology, 125(7),
1360–1370. https://doi.org/10.1016/j.clinph.2013.11.028,
PubMed: 24418219
Chu, C. J., Kramer, M. A., Pathmanathan, J., Bianchi, M. T.,
Westover, M. B., Wizon, L., & Cash, S. S. (2012). Emergence
of stable functional networks in long-term human electroenceph-
alography. The Journal of Neuroscience, 32(8), 2703–2713.
https://doi.org/10.1523/ JNEUROSCI.5669-11.2012, PubMed:
22357854
D’Esposito, M. (2019). Are individual differences in human brain
organization measured with functional MRI meaningful?
Proceedings of the National Academy of Sciences of the
United States of America, 116(45), 22432–22434. https://doi.org
.org/10.1073/pnas.1915982116, PubMed: 31619565
David, O., Cosmelli, D., & Friston, K. J. (2004). Evaluation of differ-
ent measures of functional connectivity using a neural mass
model. NeuroImage, 21(2), 659–673. https://doi.org/10.1016/j
.neuroimage.2003.10.006, PubMed: 14980568
Dubois, J., & Adolphs, R. (2016). Building a science of individual
differences from fMRI. Trends in Cognitive Sciences, 20(6),
425–443. https://doi.org/10.1016/j.physbeh.2017.03.040,
PubMed: 28363838
Durka, P. J., Klekowicz, H., Blinowska, K. J., Szelenberger, W., &
Niemcewicz, S. (2003). A simple system for detection of EEG ar-
tifacts in polysomnographic recordings. IEEE Transactions on
Biomedical Engineering, 50(4), 526–528. https://doi.org/10
.1109/TBME.2003.809476, PubMed: 12723066
Ferri, R., Rundo, F., Bruni, O., Terzano, M. G., & Stam, C. J. (2008).
The functional connectivity of different EEG bands moves to-
wards small-world network organization during sleep. Clinical
Neurophysiology, 119(9), 2026–2036. https://doi.org/10.1016/j
.clinph.2008.04.294, PubMed: 18571469
Fingelkurts, A. A., & Fingelkurts, A. A. (2011). Persistent operational
synchrony within brain default-mode network and self-
processing operations in healthy subjects. Brain and Cognition,
75(2), 79–90. https://doi.org/10.1016/j.bandc.2010.11.015,
PubMed: 21172727
Finn, E. S., Glerean, E., Khojandi, A. Y., Nielson, D., Molfese, P. J.,
Handwerker, D. A., & Bandettini, P. A. (2020). Idiosynchrony:
From shared responses to individual differences during naturalis-
tic neuroimaging. NeuroImage, 215(April), 116828. https://doi
.org/10.1016/j.neuroimage.2020.116828, PubMed: 32276065
Fisch, B. J. (1999). Fisch and Spehlmann’s EEG primer: Basic prin-
ciples of digital and analog EEG (3rd ed.). Elsevier.
Gao, W., Gilmore, J. H., Giovanello, K. S., Smith, J. K., Shen, D.,
Zhu, H., & Lin, W. (2011). Temporal and spatial evolution of
brain network topology during the first two years of life. PLoS
ONE, 6(9). https://doi.org/10.1371/journal.pone.0025278,
PubMed: 21966479
Gao, W., Lin, W., Grewen, K., & Gilmore, J. H. (2017). Functional
connectivity of the infant human brain: Plastic and modifiable.
Neuroscientist, 23(2), 169–184. https://doi.org/10.1177
/1073858416635986, PubMed: 26929236
Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable, R. T.
(2015). The (in)stability of functional brain network measures
across thresholds. NeuroImage, 118, 651–661. https://doi.org/10
.1016/j.neuroimage.2015.05.046, PubMed: 26021218
Geier, C., Lehnertz, K., & Bialonski, S. (2015). Time-dependent
degree-degree correlations in epileptic brain networks: From assor-
tative to dissortative mixing. Frontiers in Human Neuroscience,
9(August), 1–11. https://doi.org/10.3389/fnhum.2015.00462,
PubMed: 26347641
Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015).
Tracking ongoing cognition in individuals using brief, whole-
brain functional connectivity patterns. Proceedings of the
National Academy of Sciences of the United States of America,
112(28), 8762–8767. https://doi.org/10.1073/pnas.1501242112,
PubMed: 26124112
Hardstone, R., Poil, S. S., Schiavone, G., Jansen, R., Nikulin, V. V.,
Mansvelder, H. D., & Linkenkaer-Hansen, K. (2012). Detrended
fluctuation analysis: A scale-free view on neuronal oscillations.
Frontiers in Physiology, 3(450), 75–87. https://doi.org/10.3389
/fphys.2012.00450, PubMed: 23226132
Jalili, M., Barzegaran, E., & Knyazeva, M. G. (2014). Synchronization
of EEG: Bivariate and multivariate measures. IEEE Transactions on
Neural Systems and Rehabilitation Engineering, 22(2), 212–221.
https://doi.org/10.1109/ TNSRE.2013.2289899, PubMed:
24216751
Kaiser, D. (2008). Ultradian and circadian effects in electroenceph-
alography activity. Biofeedback, 36(4), 148.
Karoly, P. J., Ung, H., Grayden, D. B., Kuhlmann, L., Leyde, K.,
Cook, M. J., & Freestone, D. R. (2017). The circadian profile of
epilepsy improves seizure forecasting. Brain, 140(8), 2169–2182.
https://doi.org/10.1093/brain/awx173, PubMed: 28899023
Kramer, M. A., Eden, U. T., Lepage, K. Q., Kolaczyk, E. D., Bianchi,
M. T., & Cash, S. S. (2011). Emergence of persistent networks in
long-term intracranial EEG recordings. Journal of Neuroscience,
31(44), 15757–15767. https://doi.org/10.1523/JNEUROSCI.2287
-11.2011, PubMed: 22049419
Kramer, M. A., Eden, U. T., Cash, S. S., & Kolaczyk, E. D. (2009).
Network interference with confidence from multivariate time se-
ries. Physical Review E, 79(6). https://doi.org/10.1103/PhysRevE
.79.061916, PubMed: 19658533
Kuhnert, M. T., Elger, C. E., & Lehnertz, K. (2010). Long-term variabil-
ity of global statistical properties of epileptic brain networks. Chaos,
20(4). https://doi.org/10.1063/1.3504998, PubMed: 21198096
Laoprasert, P. (2011). Atlas of pediatric EEG (1st ed.). McGraw-Hill.
Lehnertz, K., Geier, C., Rings, T., & Stahn, K. (2017). Capturing
time-varying brain dynamics. EPJ Nonlinear Biomedical
Physics, 5, 2. https://doi.org/10.1051/epjnbp/2017001
Linkenkaer-Hansen, K., Nikouline, V. V, Palva, J. M., & Ilmoniemi,
R. J. (2001). Long-range temporal correlations and scaling behavior
in human brain oscillations. The Journal of Neuroscience, 21(4),
1370–1377. https://doi.org/10.1002/anie.201106423, PubMed:
22170851
Mitsis, G. D., Anastasiadou, M. N., Christodoulakis, M.,
Papathanasiou, E. S., Papacostas, S. S., & Hadjipapas, A.
(2020). Functional brain networks of patients with epilepsy ex-
hibit pronounced multiscale periodicities, which correlate with
seizure onset. Human Brain Mapping, 41(8), 2059–2076.
https://doi.org/10.1002/hbm.24930, PubMed: 31977145
Moretti, D. V., Babiloni, F., Carducci, F., Cincotti, F., Remondini,
E., Rossini, P. M., … Babiloni, C. (2003). Computerized
Network Neuroscience
629
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circadian dynamics in infant functional connectivity networks
processing of EEG-EOG-EMG artifacts for multi-centric studies in
EEG oscillations and event-related potentials. International
Journal of Psychophysiology, 47(3), 199–216. https://doi.org
/10.1016/S0167-8760(02)00153-8, PubMed: 12663065
Nichols, T., & Holmes, A. (2003). Nonparametric permutation tests for
functional neuroimaging. Human Brain Function, 25(August 1999),
887–910. https://doi.org/10.1016/B978-012264841-0/50048-2
Omidvarnia, A., Fransson, P., Metsäranta, M., & Vanhatalo, S.
(2014). Functional bimodality in the brain networks of preterm
and term human newborns. Cerebral Cortex, 24(10), 2657–2668.
https://doi.org/10.1093/cercor/bht120, PubMed: 23650289
Onnela, J. P., Saramäki, J., Kertész, J., & Kaski, K. (2005). Intensity
and coherence of motifs in weighted complex networks. Physical
Review E - Statistical, Nonlinear, and Soft Matter Physics, 71(6),
1–4. https://doi.org/10.1103/ PhysRevE.71.065103, PubMed:
16089800
Page, J., Lustenberger, C., & Fröhlich, F. (2018). Social, motor, and
cognitive development through the lens of sleep network dynam-
ics in infants and toddlers between 12 and 30 months of age.
Sleep, 41(4), 1–10. https://doi.org/10.1093/sleep/zsy024,
PubMed: 29506060
Pereda, E., Rial, R., Gamundi, A., & González, J. (2001).
Assessment of changing interdependencies between human
electroencephalograms using nonlinear methods. Physica D:
Nonlinear Phenomena, 148(1–2), 147–158. https://doi.org/10
.1016/S0167-2789(00)00190-1
Pernice, V., Staude, B., Cardanobile, S., & Rotter, S. (2011). How
structure determines correlations in neuronal networks. PLoS
Computational Biology, 7(5). https://doi.org/10.1371/journal
.pcbi.1002059, PubMed: 21625580
Ponten, S. C., Daffertshofer, A., Hillebrand, A., & Stam, C. J. (2010).
The relationship between structural and functional connectivity:
Graph theoretical analysis of an EEG neural mass model.
NeuroImage, 52, 985–994. https://doi.org/10.1016/j.neuroimage
.2009.10.049, PubMed: 19853665
Quian Quiroga, R., Kraskov, A., Kreuz, T., & Grassberger, P.
(2002). Performance of different synchronization measures in
real data: A case study on electroencephalographic signals.
Physical Review E - Statistical Physics, Plasmas, Fluids, and
Related Interdisciplinary Topics, 65(4), 14. https://doi.org/10
.1103/PhysRevE.65.041903, PubMed: 12005869
Righi, G., Tierney, A. L., Tager-Flusberg, H., & Nelson, C. A. (2014).
Functional connectivity in the first year of life in infants at risk for
autism spectrum disorder: An EEG study. PLoS ONE, 9(8), 1–8.
https://doi.org/10.1371/journal.pone.0105176, PubMed: 25140874
Rowan, A. J., & Tolunsky, E. (2003). Primer of EEG with a mini-atlas.
Butterworth-Heinemann.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52,
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Schelter, B., Feldwisch-Drentrup, H., Ihle, M., Schulze-Bonhage,
A., & Timmer, J. (2011). Seizure prediction in epilepsy: From
circadian concepts via probabilistic forecasting to statistical
evaluation. Proceedings of the Annual International Conference
of the IEEE Engineering in Medicine and Biology Society, EMBS,
1624–1627. https://doi.org/10.1109/ IEMBS.2011.6090469,
PubMed: 22254634
Shrey, D. W., Kim McManus, O., Rajaraman, R., Ombao, H., Hussain,
S. A., & Lopour, B. A. (2018). Strength and stability of EEG functional
connectivity predict treatment response in infants with epileptic
spasms. Clinical Neurophysiology, 129(10), 2137–2148. https://
doi.org/10.1016/j.clinph.2018.07.017, PubMed: 30114662
Smith, R. J., Sugijoto, A., Rismanchi, N., Hussain, S. A., Shrey, D. W.,
& Lopour, B. A. (2017). Long-range temporal correlations reflect
treatment response in the electroencephalogram of patients with
infantile spasms. Brain Topography, 30(6). https://doi.org/10.1007
/s10548-017-0588-5, PubMed: 28905146
Smith, R. J., Hu, D. K., Shrey, D. W., Rajaraman, R., Hussain, S. A.,
& Lopour, B. A. (2020). Computational characteristics of interic-
tal EEG as objective markers of epileptic spasms. BioRxiv. https://
doi.org/10.1101/2020.11.13.380691
Sparrow, S. S., Cicchetti, D. V., & Saulnier, C. A. (2016). Vineland
adaptive behavior scales (3rd ed.). Pearson.
Stam, C. J., & Reijneveld, J. C. (2007). Graph theoretical analysis of com-
plex networks in the brain. Nonlinear Biomedical Physics, 1(3), 1–19.
https://doi.org/10.1186/1753-4631-1-3, PubMed: 17908336
Stern, J. M. (2005). Atlas of EEG patterns (2nd ed.). Lippincott
Williams & Wilkins.
Stevens, M. C. (2009). The developmental cognitive neuroscience of
functional connectivity. Brain and Cognition, 70(1), 1–12. https://
doi.org/10.1016/j.bandc.2008.12.009, PubMed: 19185406
Tokariev, A., Roberts, J. A., Zalesky, A., Zhao, X., Vanhatalo, S.,
Breakspear, M., & Cocchi, L. (2019). Large-scale brain modes
reorganize between infant sleep states and carry prognostic infor-
mation for preterms. Nature Communications, 10(1). https://doi
.org/10.1038/s41467-019-10467-8, PubMed: 31197175
Tokariev, A., Vanhatalo, S., & Palva, J. M. (2016). Analysis of infant
cortical synchrony is constrained by the number of recording
electrodes and the recording montage. Clinical Neurophysiology,
127(1), 310–323. https://doi.org/10.1016/j.clinph.2015.04.291,
PubMed: 26122070
Tóth, B., Urbán, G., Háden, G. P., Márk, M., Török, M., Stam, C. J.,
& Winkler, I. (2017). Large-scale network organization of EEG
functional connectivity in newborn infants. Human Brain
Mapping, 38(8), 4019–4033. https://doi.org/10.1002/ hbm
.23645, PubMed: 28488308
Tymofiyeva, O., Hess, C. P., Ziv, E., Tian, N., Bonifacio, S. L.,
McQuillen, P. S., … Xu, D. (2012). Towards the “baby connec-
tome”: Mapping the structural connectivity of the newborn brain.
PLoS ONE, 7(2). https://doi.org/10.1371/journal.pone.0031029,
PubMed: 22347423
ven der Velde, B., Haartsen, R., & Kemner, C. (2019). Test-retest reli-
ability of EEG network characteristics in infants. Brain and Behavior,
9(5), 1–10. https://doi.org/10.1002/brb3.1269, PubMed: 30912271
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
“small-world” networks. Nature, 393(6684), 440–442. https://
doi.org/10.1038/30918, PubMed: 9623998
Xie, W., Mallin, B. M., & Richards, J. E. (2019). Development of
brain functional connectivity and its relation to infant sustained
attention in the first year of life. Developmental Science, 22(1),
1–18. https://doi.org/10.1111/desc.12703, PubMed: 29968370
Network Neuroscience
630
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
2
6
1
4
1
9
2
6
5
7
0
n
e
n
_
a
_
0
0
1
9
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3