FORSCHUNG
Consistency of Regions of Interest as nodes
of fMRI functional brain networks
Onerva Korhonen
1,2
, Heini Saarimäki
1
, Enrico Glerean
1
1
, Mikko Sams
, and Jari Saramäki
2
1Department of Neuroscience and Biomedical Engineering, School of Science, Aalto University, Espoo, Finland
2Department of Computer Science, School of Science, Aalto University, Espoo, Finland
Schlüsselwörter: Functional magnetic resonance imaging, Functional brain networks, Node definition,
Region of Interest, Anatomical atlas, Brain parcellation
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Keine offenen Zugänge
Tagebuch
ABSTRAKT
The functional network approach, where fMRI BOLD time series are mapped to networks
depicting functional relationships between brain areas, has opened new insights into the
function of the human brain. In this approach, the choice of network nodes is of crucial
importance. One option is to consider fMRI voxels as nodes. This results in a large number
of nodes, making network analysis and interpretation of results challenging. A common
alternative is to use predefined clusters of anatomically close voxels, Regions of Interest
(ROIs). This approach assumes that voxels within ROIs are functionally similar. Weil
these two approaches result in different network structures, it is crucial to understand what
happens to network connectivity when moving from the voxel level to the ROI level. Wir
show that the consistency of ROIs, defined as the mean Pearson correlation coefficient
between the time series of their voxels, varies widely in resting-state experimental data.
Therefore the assumption of similar voxel dynamics within each ROI does not generally
hold. Weiter, the time series of low-consistency ROIs may be highly correlated, resulting
in spurious links in ROI-level networks. Based on these results, we recommend that
averaging BOLD signals over anatomically defined ROIs should be carefully considered.
ZUSAMMENFASSUNG DES AUTORS
Network methods have opened new insights on structure and functional dynamics of the
human brain. Jedoch, constructing functional brain networks is far from trivial—the
neuroscientific community still lacks a standard definition of the nodes of brain networks.
In the present article, we consider the two most commonly used approaches: using either
imaging voxels or predefined Regions of Interest (ROIs) as nodes of the network. Wir
investigate what happens when voxel-level signals are averaged for obtaining ROI-level
Netzwerke. We introduce the concept of ROI consistency to characterize the similarity of the
dynamics of voxels in an ROI. With the help of consistency, we show that although voxels
in an ROI are assumed to behave similarly, this assumption does not hold for all ROIs.
In the functional brain network approach (Spurns, 2013A, 2013B; Wig, Schlaggar, & Petersen,
2011), the brain is depicted as a collection of nodes and links. Each node represents a brain
area that is supposed to be functionally homogeneous, and links represent anatomical or func-
tional connections between nodes. Studies of structural features of networks constructed from
functional magnetic resonance imaging (fMRT) data have opened new insights on the dynamics
Zitat: Korhonen, O., Saarimäki, H.,
Glerean, E., Sams, M., & Saramäki J.
(2017). Consistency of regions of
interest as nodes of fMRI functional
brain networks. Netzwerkneurowissenschaften,
1(3), 254–274. https://doi.org/10.1162/
netn_a_00013
DOI:
https://doi.org/10.1162/netn_a_00013
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00013
Erhalten: 05 Januar 2017
Akzeptiert: 19 April 2017
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Onerva Korhonen
onerva.korhonen@aalto.fi
Handling-Editor:
Xinian Zuo
Urheberrechte ©: © 2017
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
Consistency of ROIs as nodes of fMRI functional brain networks
Spurious link:
A connection that is not in reality
present in the underlying data but
appears in the extracted network.
Functional homogeneity:
Every voxel of an ROI is performing
some particular function and
therefore has (grob) ähnlich
Dynamik, yielding strongly
correlated voxel time series.
and function of the brain (for reviews, see Bassett & Bullmore, 2009; Papo, Zanin, Pineda-
Pardo, Boccaletti, & Buldú, 2014; Spurns, 2013B).
Jedoch, the reliability of fMRI network analysis and the factors that affect it have lately be-
come a subject of discussion (Andellini, Cannatà, Gazzellini, Bernardi, & Napolitano, 2015;
Aurich, Alves Filho, da Silva, & Franco, 2015; Braun et al., 2012; Shehzad et al., 2009; Shirer,
Jiang, Price, Ng, & Greicius, 2015; Telesford et al., 2010). One of the critical questions is how
to choose what the nodes represent. The anatomical locations and the number of nodes have
been reported to affect properties of brain networks, such as small-worldness or scale-freeness
(de Reus & Van den Heuvel, 2013; Spurns, 2013A, 2013B; Wang et al., 2009; Zalesky et al.,
2010).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
It would be natural to consider single neurons as network nodes, linked by synaptic connec-
tionen. Jedoch, this micro-level approach is not an option for studying the whole human brain,
because of the excessive number of neurons and the lack of resolution of imaging methods
(de Reus & Van den Heuvel, 2013). Daher, network studies of the brain are currently limited to
the mesoscopic and macroscopic levels. For fMRI, these are the level of imaging voxels and
the level of Regions of Interest (ROIs) that are collections of voxels defined on the basis of, für
Beispiel, anatomical landmarks.
In the voxel-level approach, the nodes are voxels, cubical volume elements with 2–8 mm
edges that form a regular grid covering the brain. The BOLD signal associated with each voxel
is directly given by the fMRI measurement (Stanley et al., 2013). In the ROI-level approach, Die
nodes are ROIs that comprise tens to hundreds of voxels. An ROI’s signal is typically computed
by averaging the BOLD signals of its voxels (Stanley et al., 2013). ROIs are usually defined us-
ing an anatomical atlas, based on structural MR images or histological investigations (sehen, z.B.,
Stanley et al., 2013). Data-driven methods that cluster voxels based on resting-state functional
Konnektivität (z.B., Craddock, James, Holtzheimer, Hu, & Mayberg, 2012; Nelson et al., 2010;
Power et al., 2011; Shen, Tokoglu, Papademetris, & Polizist, 2013; for a review see Sporns,
2013B; Wig, Schlaggar, & Petersen, 2011),
ICA, and dual regression (Beckmann, Mackay,
Filippini, & Schmied, 2009), or combination of anatomical, functional, and connectivity data
(Fan et al., 2016; Glasser et al., 2016) have also been suggested for defining ROIs. Jedoch,
despite promising results, these methods are used only infrequently.
The main benefits of the ROI approach are increased signal-to-noise ratio (SNR) and de-
creased computational cost. Weiter, one can expect that cognitive functions cover brain areas
larger than single voxels (Shen et al., 2013; Wig et al., 2011). daher, the ROI approach
may characterize true brain activity better than voxels with functionally arbitrary boundaries.
Jedoch, areas related to cognitive functions may not necessarily match with the anatomical
boundaries that define ROIs: The same function may be distributed across multiple anatomical
Bereiche, or one anatomical area may contain several functionally distinct subareas (Papo, Zanin,
& Buldú, 2014; Stanley et al., 2013). Daher, the main disadvantage of the ROI approach is the
possible loss of information that results from averaging signals of voxels that represent different
functions for producing the ROI signal (Stanley et al., 2013).
Andererseits, if the functional network is constructed with voxels as nodes, problems
arise from the numbers of nodes and links that represent correlations between voxel time
Serie. Because of computational limitations, one has to heavy-handedly threshold correlation
matrices to reduce the number of links. This results in sparse networks where much information
has been discarded.
255
Thresholding:
Discarding weak links in order to
make the backbone of a network
more visible.
Netzwerkneurowissenschaften
Consistency of ROIs as nodes of fMRI functional brain networks
Hubs:
Most central nodes of a network, über
which most of the information
flowing in the network is transmitted.
In both approaches, some information is deliberately discarded. But do they retain similar
Information? There is some evidence that moving from the voxel level to the ROI level changes
network properties. Hayasaka & Laurienti (2010) found that ROI-level networks are less robust
against fragmentation than voxel-level networks at low network densities. Weiter, ROI-level
networks showed less small-world properties, and had different degree distributions and less
stable hubs. Tohka, Er, and Evans (2012) reported similar results in structural brain networks
that were based on the thickness of cortical gray matter. daher, one may ask whether voxel-
level and ROI-level networks provide comparable views on the underlying brain function.
In diesem Artikel, we ask what happens to network connectivity when moving from the voxel-
level network to the ROI level, where in both cases links represent zero-lag correlations. In
besondere, we focus on whether voxels of an ROI display coherent dynamics, as they should
if the ROIs match with underlying functional areas. Zu diesem Zweck, we introduce the concept of
ROI consistency that quantifies the similarity of the signals of voxels that comprise the ROI, von-
fined as their mean Pearson correlation coefficient. With the help of resting-state fMRI data of
13 subjects measured in-house as well as 28 subjects from the Autism Brain Imaging Data Ex-
ändern (ABIDE) initiative, we show that consistency varies widely across ROIs. Therefore voxel
dynamics within ROIs are not always coherent. We then show that this variation is reflected in
network properties: Signals of voxels in non-consistent ROIs are not correlated between ROIs,
and less consistent ROIs are less central as nodes of the functional brain network.
ERGEBNISSE
Voxel Time Series Within ROIs Are on Average Correlated, but Not Uniformly
We begin by considering the functional homogeneity of voxels within ROIs—in the ROI ap-
proach, it is assumed that voxels within an ROI are functionally more similar and thereby
have more strongly correlated time series than voxels in different ROIs. For defining ROIs, Wir
use three different atlases: the anatomical Harvard-Oxford (HO) and Automated Anatomical
Labeling (AAL) atlases as well as the Brainnetome atlas that is based on structural and func-
funktionale Konnektivität.
For testing the homogeneity assumption, we calculated the distribution of Pearson corre-
lation coefficients between the time series of pairs of voxels that are in the same ROI. Das
distribution was calculated across all ROIs and therefore covered the whole cerebral cortex
and subcortical structures. In HO and AAL, also cerebellum was included; the Brainnetome
atlas does not contain cerebellar ROIs. As a reference, we computed a similar distribution for
pairs of voxels that reside in different ROIs.
; Brainnetome: r = 0.29 vs. r = 0.073, t = 83.05, P (cid:2) 10−5
Correlations are on average stronger within ROIs than in the reference (d.h., voxels in differ-
ent ROIs) in all investigated parcellations: Their distribution has a higher mean (HO: r = 0.20
vs r = 0.073, Student’s t = 49.81, P (cid:2) 10−5
; AAL: r = 0.19 vs. r = 0.067, t = 50.00,
P (cid:2) 10−5
; the p value has
been calculated using a permutation-based two-tailed t test; Glerean et al., 2016) and is more
strongly right-skewed than the approximately normal reference distribution (Figur 1). Wie-
immer, there is a large overlap between the two distributions, and a significant number of small
and negative correlations is present in both distributions. Daher, the functional uniformity of
ROIs is far from perfect.
One might expect the connectivity-based Brainnetome parcellation to show stronger func-
tional homogeneity of ROIs than the anatomical HO and AAL. Surprisingly, this is not the case:
Although the mean of the within-ROI correlation distribution is sligthly higher in Brainnetome
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
256
Consistency of ROIs as nodes of fMRI functional brain networks
j
T
ich
S
N
e
D
j
T
ich
l
ich
B
A
B
Ö
R
P
j
T
ich
S
N
e
D
j
T
ich
l
ich
B
A
B
Ö
R
P
Ö
H
L
A
A
j
T
ich
S
N
e
D
j
T
ich
l
ich
B
A
B
Ö
R
P
e
M
Ö
T
e
N
N
ich
A
R
B
within-ROI
Referenz
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
-1.0
-0.5
0.0
0.5
1.0
within-ROI
Referenz
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
-1.0
-0.5
0.0
0.5
1.0
within-ROI
Referenz
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
-1.0
-0.5
0.0
Correlation
0.5
1.0
Figur 1. Voxel time series are on average more strongly correlated within ROIs than between
ROIs but the correlation is not perfect. Distributions of Pearson correlation coefficients between
voxel time series within (Blau) and between (Grün, Referenz) ROIs in HO, AAL, and Brainnetome.
Although the within-ROI correlation distribution is more skewed to the right, the distributions largely
Überlappung, and small and negative correlations exist also within ROIs. Correlation distributions are
calculated across all ROIs from the pooled data of 13 Fächer.
than in other parcellations, the overlap of the within-ROI and reference correlation distribu-
tions is equally large in all parcellations.
In order to investigate to what extent our results generalize to other datasets, we repeated
all analysis of this article on a second, independet dataset, the ABIDE data (Di Martino et al.,
2014). The results obtained using the ABIDE data were highly similar to those obtained
using the in-house dataset and presented in this Results section. A detailed description of the
results obtained using the ABIDE dataset can be found in Supplementary Results (Korhonen,
Saarimäki, Glerean, Sams, & Saarimäki, 2017).
Spatial smoothing, a commonly used method in the preprocessing of fMRI data, makes the
time series of neighboring voxels more similar, and is therefore expected to affect the results
presented above. We repeated all analysis of this article for data that were smoothed with
Netzwerkneurowissenschaften
257
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Consistency of ROIs as nodes of fMRI functional brain networks
three Gaussian kernels with different full widths at half maximum. Although spatial smoothing
increased all correlations between voxel time series, it has no qualitative effects on the results;
Zum Beispiel, correlation distributions are as equally broad after spatial smoothing as without
Es (for a detailed description of the effects of spatial smoothing, see Supplementary Results;
Korhonen et al., 2017).
The Consistency of ROIs Varies Across the Brain
The consistency of an ROI (Phi), defined as the mean Pearson correlation coefficient of the time
series of voxels belonging to the ROI, is a simple measure of the ROI’s functional cohesion. In
order to evaluate the variation of consistency between ROIs, we calculated consistency distri-
butions for each parcellation from the pooled data of all 13 Fächer (Figur 2). Obwohl
the maximum observed ROI consistency is high (HO: φmax = 0.89; AAL: φmax = 0.66;
Brainnetome: φmax = 0.75), the consistency distribution is broad, peaking at low consistency
Werte (HO: φ = 0.22; AAL: φ = 0.18; Brainnetome: φ = 0.25). This indicates that in all three
atlases, a significant number of ROIs contain collections of voxels that are not functionally
uniform in the resting state.
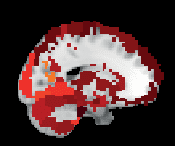
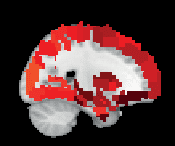
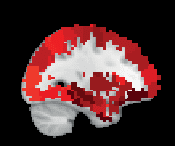
To investigate in more detail how consistency is distributed among ROIs, wir haben nachgerechnet
the mean consistency for each ROI across subjects. Visualization of the mean consistency
on a brain template (Figur 3) demonstrates what the broad consistency distribution means in
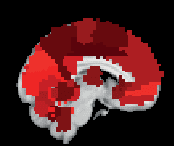
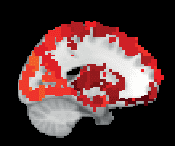
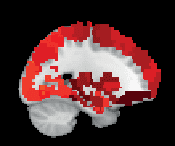
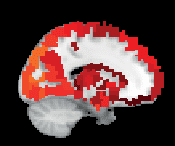
üben: The most consistent ROIs have twice the consistency of the least consistent ones.
The identity of the most consistent ROIs varies across subjects only slightly. In HO, the most
coherent ROIs include the left and right supracalcarine, cuneal, and intracalcarine cortices as
well as the cerebellar areas Vermis Crus II and Vermis VIIb. In the case of the supracalcarine
cortices and the cerebellar areas, the high consistency is probably explained by the size of the
ROIs, since all these areas are small (containing 10 voxels or less).
HO
AAL
Brainnetome
5.0
4.0
3.0
2.0
1.0
j
T
ich
S
N
e
D
j
T
ich
l
ich
B
A
B
Ö
R
P
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
0.0
0.0
0.2
0.4
0.6
0.8
1.0
ROI consistency
Figur 2. Consistency of ROIs is widely distributed. The consistency distributions has been cal-
culated from the pooled data of 13 Fächer.
Netzwerkneurowissenschaften
258
1.0
0.8
0.6
0.4
0.2
0.0
C
Ö
N
S
ich
S
T
e
N
C
j
Consistency of ROIs as nodes of fMRI functional brain networks
Ö
H
L
A
A
e
M
Ö
T
e
N
N
ich
A
R
B
Figur 3. ROI consistency is not anatomically uniform. We have visualized the mean consistency
across 13 subjects on a template brain. ROIs colored with yellow and orange are those with highest
consistency, while low-consistency ROIs are colored with black. See the main text for the details
of the identity of these ROIs. Areas colored with gray-white scale (white matter and, in the case of
Brainnetome, cerebellum) are not included in this study.
In AAL, the most consistent ROIs include left and right cuneal cortex and right Heschl’s
gyrus as well as the small cerebellar ROIs Vermis_1_2 and Vermis_10. In Brainnetome, Die
most consistent ROIs include several subsections of the left and right cuneal cortex and right
medial superior occipital gyrus.
For the least consistent ROIs, intersubject variation is larger.
In HO, the least consistent
ROIS include the right frontal orbital cortex, right and left frontal pole, right precentral gyrus,
and superior division of left lateral occipital cortex. In AAL, among the least consistent ROIs
are left and right hippocampus, left and right inferior temporal gyrus, and left frontal superior
orbital gyrus.
In Brainnetome, the least consistent ROIs include left and right orbital gyrus
(6_3), left and right fusiform gurys, and left and right hippocampus.
Netzwerkneurowissenschaften
259
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Consistency of ROIs as nodes of fMRI functional brain networks
ROIs of different parcellations do not perfectly match with each other. Jedoch, it is in-
teresting to see that same ROIs, in particular cuneal cortices, are among the most consistent
ROIs in all three parcellations. For sizes, mean consistency values, and consistency ranks of
all ROIs, see Supplementary Table (Korhonen et al., 2017).
In terms of mean consistency, the differences between the three parcellations investigated
are small. Taking into account the individual variation of structure and function of the brain,
one might expect to see more variation in consistency between subjects in Brainnetome than
in HO and AAL. In order to test this hypothesis, we calculated the standard deviation of con-
sistency across subjects for each ROI. Jedoch, we found no significant difference between
the standard deviations of consistency in different parcellations.
In HO and AAL parcellations, ROI consistency is partially explained by its size, das ist,
the number of voxels within the ROI (Figur 4). Consistency is highest for small ROIs and de-
creases with increasing ROI size (HO: Pearson correlation coefficient r = −0.35, P (cid:2) 10−5
;
AAL: r = −0.38, P (cid:2) 10−5
). This decrease saturates for ROIs larger than a few hundred voxels.
Jedoch, for ROIs of any size, there is a lot of variation around the mean. In Brainnetome, In
Kontrast, ROI consistency and size do not correlate (r = 0.017, p = 0.35).
We also investigated whether head motion explains some part of the individual differences
in ROI consistency. Jedoch, we did not find significant correlation between ROI consistency
and subjects’ head motion, measured in terms of framewise displacement.
Low ROI Consistency Predicts Low Voxel-Level Correlations Between Pairs of ROIs
One of the aims of this paper is to understand how the consistency of ROIs relates to their net-
work properties. We begin by looking at the voxel level, and define the voxel-level correlation
between two ROIs as the mean Pearson correlation coefficient between time series of voxels
within the ROIs (see Equation 3). We expect that the voxel-level correlation is strong only if
the ROIs are consistent enough. This is motivated as follows: A strong voxel-level correlation
means that many pairs of voxels in both ROIs must have similar time series. This means that in
each ROI, there must be a lot of similarly behaving voxels, resulting in high consistency. As the
limiting case, (cid:3)C (ICH, J)(cid:4)vox = 1 if and only if the time series of all voxels in both ROIs are equal
(xi = xj∀i ∈ I, j ∈ J and xi = xi(cid:7) ∀i, ich(cid:7) ∈ I). In order to test this hypothesis, we investigate voxel-
level correlations between two ROIs as a function of the mean consistency of the ROI pair.
As we hypothesized, our data indicate that high mean consistency is a prerequisite for a
strong voxel-level correlation between two ROIs (Figur 5, links). Jedoch, it is clear that there is
a lot of variation: Voxel-level correlation correlates only moderately with ROI consistency (HO:
Pearson correlation r = 0.29, P (cid:2) 10−5
; Brainnetome: r = 0.28,
P (cid:2) 10−5
). Despite this variation, voxel-level correlations are never strong between low-
consistency ROIs, and all data points are located below the identity line ((cid:3)C (ICH, J)(cid:4)vox = φ).
; AAL: r = 0.17, P (cid:2) 10−5
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Low-Consistency ROIs May Have High ROI-Level Correlations
Nächste, we investigated how ROI consistency relates to correlations at the ROI level. To this
end, for pairs of ROIs, we calculated the ROI-level correlations (see Equation 4) as a function
of their mean consistency. In HO and Brainnetome, ROI-level correlations depend on con-
sistency clearly less than the voxel-level correlations (Figur 5, Rechts; HO: Pearson correlation
Netzwerkneurowissenschaften
260
Consistency of ROIs as nodes of fMRI functional brain networks
Ö
H
j
C
N
e
T
S
ich
S
N
Ö
C
ICH
Ö
R
L
A
A
j
C
N
e
T
S
ich
S
N
Ö
C
ICH
Ö
R
e
M
Ö
T
e
N
N
ich
A
R
B
j
C
N
e
T
S
ich
S
N
Ö
C
ICH
Ö
R
1.0
0.8
0.6
0.4
0.2
0.0
1.0
0.8
0.6
0.4
0.2
0
100 200 300 400 500 600 700
800
900
0.0
0
1.0
0.8
0.6
0.4
0.2
0.0
0
100
200
300
400
500
600
700
50
100
ROI size
150
200
Figur 4. The size dependence of the average ROI consistency (Linie) and its variation (shadowed
Bereich) show that, in HO and AAL, small ROIs have on average higher consistency. This dependency
is less visible for ROIs larger than 100 voxels. Jedoch, the variation of consistency is large for
In
all ROI sizes. daher, the size of an ROI is not the only factor that affects its consistency.
Brainnetome, ROI size and consistency are not correlated. The consistency of each ROI has been
pooled across 13 Fächer, binned on the basis of ROI size, and then bin-averaged.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
r = −0.14, P (cid:2) 10−5
tency and ROI-level correlation are negatively correlated ( r = −0.24, P (cid:2) 10−5
; Brainnetome: r = −0.00057, p = 0.92), whereas in AAL ROI consis-
).
As seen in Figure 5 (Rechts), there are pairs of low-consistency ROIs that nevertheless display
strong ROI-level correlations. From the functional point of view, this situation is not straight-
forward to interpret: If strong ROI-level correlations are taken as a sign of a strong functional
relationship, how can this relationship be real if the ROIs themselves are nonuniform and lack
consistency?
As one possible reason for these spurious-looking correlations, let us assume that signals of
voxels in ROIs I and J share a common component, but their pairwise correlations are weak
because of components unique to the signal of each voxel. In this case, the consistency of both
Netzwerkneurowissenschaften
261
Consistency of ROIs as nodes of fMRI functional brain networks
Ö
H
N
Ö
ich
T
A
l
e
R
R
Ö
C
1.0
0.5
0.0
0.0
1.0
0.5
L
A
A
N
Ö
ich
T
A
l
e
R
R
Ö
C
0.0
0.0
1.0
e
M
Ö
T
e
N
N
ich
A
R
B
N
Ö
ich
T
A
l
e
R
R
Ö
C
0.5
0.0
Voxel level
ROI level
0.5
1.0
0.0
0.5
1.0
0.5
1.0
0.0
0.5
1.0
150
120
C
Ö
u
N
T
90
60
30
0
150
120
C
Ö
u
N
T
90
60
30
0
500
400
300
200
C
Ö
u
N
T
100
0
0.0
0.5
1.0
0.0
0.5
1.0
Mean consistency of ROI pair
Figur 5. Averaging of voxel signals may induce spuriously strong ROI-level correlations between
ROIs that have low consistency. Links: The relationship between voxel-level correlation and the mean
ROI consistency for each ROI pair. Voxel-level correlation correlates with consistency, and all data
points are located below the identity line. Rechts: The same relationship for ROI-level correlations
and mean ROI consistency. ROI-level correlations are not correlated with consistency, and strong
ROI-level correlations also exist between ROIs that have low consistency and weak voxel-level
correlation. In order to produce the heatmaps, the consistency and voxel and ROI-level correlations
have been averaged across 13 Fächer.
ROIs is low. Dann, the time series of the ROIs are obtained as averages over the time series of
their voxels (see Equation 1). This averaging amplifies signal components shared by all voxels
within the ROI and suppresses components unique to each voxel. daher, the time series
of ROIs I and J consist mostly of the shared signal component and are strongly correlated.
The signal component shared by each voxel in the ROIs I and J may be either noise or
true signal. Ähnlich, the suppressed signal components may be either true signal components
unique to single voxels or independent noise. Based on the results visualized in Figure 5, Es
is not possible to say for sure whether the links between low-consistency ROIs are spurious
or whether they are true correlations that have become visible when noisy signal components
have been suppressed. Jedoch, this result suggests that extra care is needed when interpreting
Netzwerkneurowissenschaften
262
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Consistency of ROIs as nodes of fMRI functional brain networks
1.0
0.8
0.6
0.4
0.2
0.0
N
Ö
ich
T
A
l
e
R
R
R
Ö
C
l
e
v
e
l
–
ICH
Ö
R
HO
AAL
Brainnetome
-0.2
-0.2
0.0
0.2
0.4
0.6
0.8
Voxel-level correlation
Figur 6. ROI-level correlations are stronger than the voxel-level correlations between the same
ROIs. This is because averaging the voxel signals in order to obtain the ROI time series suppresses
individual signal components of each voxel and amplifies components shared among voxels (für
details and discussion, see the main text). Averaging and binning as in Figure 4.
the ROI-level correlations, since any artifactual signal shared between voxels can induce spu-
rious ROI-level correlations between ROIs that have low consistency.
For a concrete example of the effects of amplification and suppression of voxel-level signal
components when moving to the ROI level, we investigated ROI-level correlations as a func-
tion of voxel-level correlations (Figur 6). We observed that in all investigated parcellations,
on average ROI-level correlations increase faster than the increasing voxel-level correlations:
Pairs of ROIs that correlate only moderately at the voxel level can appear highly correlated at
the ROI level. Zum Beispiel, an ROI pair that has a voxel-level correlation of r = 0.2 can have
an ROI-level correlation as high as r = 0.6. Das ist, Natürlich, a direct result of the averaging
of voxel signals in order to obtain the ROI time series.
Weiter, the relationship between ROI-level and voxel-level correlations is nonlinear and
saturates already at rather low voxel-level correlation values. daher, pairs of ROIs that
appear to have similar correlations at the ROI level may in fact clearly differ at the voxel level.
Consistency of an ROI Predicts Its Network Properties
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Degree:
The number of neighbors a node has.
Strength:
The sum of the weights of the links
attached to a node.
The typical way of obtaining functional brain networks from correlation matrices is to threshold
them so that only the strongest links are retained. We next threshold the ROI-level networks,
in order to investigate whether the consistency of an ROI affects its network properties. Für
the thresholded networks, we calculate the mean degree (k) and strength (S) of ROIs across
Fächer. We observe that both the degree and the strength (Figur 7) increase with increasing
consistency in networks thresholded to low and intermediate densities. Zum Beispiel, at d =
0.25%, the Pearson correlation coefficient for degree is in HO r = 0.39, P (cid:2) 10−5
, in AAL
r = 0.27, P (cid:2) 10−5
, and in Brainnetome r = 0.53, P (cid:2) 10−5
, and the Pearson correlation
coefficient for strength is in HO r = 0.39, P (cid:2) 10−5
, und in
Brainnetome r = 0.53, P (cid:2) 10−5
, in AAL r = 0.28, P (cid:2) 10−5
.
Über, we showed that ROI-level correlations between pairs of ROIs appear rather inde-
pendent of their consistencies. This may appear at odds with the degree and strength increasing
Netzwerkneurowissenschaften
263
Consistency of ROIs as nodes of fMRI functional brain networks
A
Ö
H
e
e
R
G
e
D
ICH
Ö
R
40
30
20
10
0
0.07
40
30
20
10
0
0.07
70
60
50
40
30
20
10
0
0.07
L
A
A
e
e
R
G
e
D
ICH
Ö
R
e
M
Ö
T
e
N
N
ich
A
R
B
e
e
R
G
e
D
ICH
Ö
R
B
H
T
G
N
e
R
T
S
ICH
Ö
R
25
20
15
10
5
20.0
15.0
10.0
5.0
4.5
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.75
0.5
0.25
j
T
ich
S
N
e
D
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
0
0.07
25
20
15
10
5
0
0.07
40
30
20
10
0
0.07
H
T
G
N
e
R
T
S
ICH
Ö
R
H
T
G
N
e
R
T
S
ICH
Ö
R
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
ROI consistency
ROI consistency
Figur 7. Degree and strength of ROIs increase with consistency. For degree (A), this behavior is
mostly visible only at low and intermediate network densities, whereas strength (B) and consistency
correlate even for high densities. Averaging and binning as in Figure 4.
with consistency; Jedoch, the independence of ROI-level correlations on consistency shows
in full correlation matrices. When the correlation matrices are thresholded to retain only the
strongest links, it becomes evident that these strongest links often connect to high-consistency
ROIs.
In networks thresholded to higher densities, degree and strength are more independent
of consistency. In HO and AAL, at the network density of d = 20%, no correlation is present
between neither ROI consistency and degree (HO: Pearson correlation coefficient r = −0.055,
p = 0.81; AAL: r = −0.039, p = 0.13) nor ROI consistency and strength (HO: r = 0.098,
p = 3.2 × 10−5
; AAL: r = 0.049, p = 0.057). In Brainnetome, a weak correlation between
consistency and degree remains at density of d = 20 (r = 0.23, P (cid:2) 10−5
), and consistency
and strength are correlated both at density d = 20 (r = 0.036, P (cid:2) 10−5
) and in the full
Netzwerk (r = 0.19, P (cid:2) 10−5
).
DISKUSSION
Variation in Consistency of ROIs Points Towards Differences in Their Functional Homogeneity
The common approach of averaging over voxel time series in order to obtain representative
time series for entire ROIs does not account for possible variations and inhomogeneities within
the ROI. daher, to measure the level of such inhomogeneities, we introduced the concept
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
264
Consistency of ROIs as nodes of fMRI functional brain networks
of ROI consistency (Phi) that is defined as the mean Pearson correlation coefficient between the
time series of voxels in the ROI. This measure is simple to calculate and easy to interpret. Wenn ein
ROI has high consistency, one can assume that the averaged time series accurately represent
the underlying voxel dynamics. Andererseits, low consistency can be seen as indicative
of functional inhomogeneity in the ROI.
Earlier, measures similar to ROI consistency have been used to quantify multiple aspects of
the human brain function. Zum Beispiel, Li et al. (2002) have suggested that the consistency of
the hippocampus could be used as an early-stage biomarker for Alzheimer’s disease.
We investigated ROI consistency in three different atlases: the anatomical HO and AAL
atlases and Brainnetome atlas that is based on structural and functional connectivity. We found
that distribution of consistencies across ROIs is broad in all these atlases. The most consistent
ROIs are twice as consistent as the least consistent ones. This is in line with earlier observations
(Baumgartner, Somorjai, Summers, & Richter, 1999; Craddock et al., 2012): Voxel time series
within an activated brain area are not always strongly correlated. Weiter, the anatomical
distribution of consistency is not uniform. In contrast to what one might expect, we found no
significant difference between the Brainnetome atlas and the anatomical atlases in terms of
mean consistency of ROIs.
What Does Consistency Say About the Properties and Functional Role of an ROI?
It is tempting to interpret the consistency as a measure of the goodness of an ROI: ROIs with
high consistency are well-defined, whereas low consistency indicates inaccuracies in the ROI
definition.
In der Tat, a measure similar to mean consistency across ROIs has been used to
quantify the overall accuracy of a parcellation (Craddock et al., 2012; Stanley et al., 2013;
Thirion et al., 2006; see also Gordon et al., 2014 for a different definition of ROI homogene-
ity based on network connectivity). Jedoch, this interpretation, although useful, is probably
oversimplified.
The nonuniform anatomical distribution of consistency opens the question of its depen-
dency on time and task. Does the consistency of an ROI vary in time and how is it determined
at a given moment? One plausible hypothesis is that active brain areas have higher consistency
than currently inactive areas. This would also explain the dependency between consistency
and degree of ROI at low-to-intermediate network densities. More active ROIs that should
have higher consistency also have stronger momentary functional connections to other active
ROIs and thus have a higher degree.
The concept of regional homogeneity (ReHo) (Zang, Jiang, Lu, Er, & Tian, 2004; see also
Jiang & Zuo, 2016 for a review on how ReHo has been used) is based on an assumption similar
to the above hypothesis on the increased consistency of active brain regions.
In the ReHo
Rahmen, active voxels are identified by their increased similarity to their neighbors. Das
similarity is calculated in a cubic neighborhood that includes the voxel itself and its neighbors
in terms of faces (7 voxels); faces and edges (19 voxels); or faces, edges, and corners (27 voxels).
Despite minor technical differences—in ReHo, Kendall’s coefficient of concordance is used to
quantify the similarity of voxel time series—the similarity of ReHo and ROI consistency is
obvious: If we define an ROI that covers the ReHo neighborhood of a voxel, the consistency
of this ROI is proportional to the ReHo value of the centroid voxel.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
ReHo has been used to quantify the changes in local connectivity not only in single voxels
(2015) calculated ReHo using a two-dimensional
but also in brain areas.
Jiang et al.
Netzwerkneurowissenschaften
265
Consistency of ROIs as nodes of fMRI functional brain networks
reconstruction of the cortex, and averaged the ReHo values across voxels within function-
ally defined subareas in the ventral visual system, the prefrontal cortex, and the posteromedial
Kortex. The differences of the mean ReHo between the subareas, obtained during resting state,
reflected the different roles of these subareas in hierarchical information processing.
Despite the obvious similarities between consistency and ReHo, the purpose of these two
measures is different. ReHo is a voxel-level measure that is always calculated across the im-
mediate neighborhood of a voxel. Originally, ReHo was designed to localize activity to a
handful of voxels that may be spatially separated (Zang et al., 2004), and it can be used also
to construct functional brain networks at the level of voxels (Jiang et al., 2015). Im Gegensatz,
consistency is a property of a collection of voxels (ROI) and can be used to quantify how well
the average signal of these voxels represent the original voxel-level dynamics. daher, Die
usage of consistency is by definition limited to cases where activated brain areas—and nodes
of functional brain networks—are assumed to be larger than single voxels. As consistency is
by definition an ROI-level measure, it is natural that it relates to properties of ROI-level brain
Netzwerke, Zum Beispiel, node centrality measures and strength of links.
Bearing these differences between ReHo and consistency in mind, it is logical that an ROI
with low consistency can still contain voxels that have high ReHo; this is the case if the ROI
Wenn
definition is not accurate and the ROI contains subareas of internally correlated voxels.
the boundary between these subareas is sharp enough, even the mean ReHo of this low-
consistency ROI can be high. Ähnlich, an ROI with high consistency can contain low-ReHo
voxels: One can expect to find these at least at the boundaries of the ROI where the ReHo
neighborhood contains voxels from different ROIs.
Task-induced changes in the consistency of an ROI could also reveal its functional role,
similar to the mean ReHo in the study of Jiang et al. (2015). Auf der einen Seite, if an ROI consists
of functionally different subareas, some tasks may require synchronous activation of them all,
yielding high consistency. Andererseits, in some conditions these subareas may activate
at different times, which results in lower consistency. daher, the application of the concept
of consistency beyond single ROIs, such as to resting state or task-related networks,may reveal
dynamics of coactivation and separation of different subnetworks.
High values of test-retest reliability have been reported for several measures of local con-
nectivity, in particular for ReHo (Zuo & Xing, 2014; Zuo et al., 2013). In der vorliegenden Studie, Wir
do not investigate the test-retest reliability of consistency: When consistency is used to evalu-
ate the level of within-ROI homogeneity, low consistency values measured in one resting-state
session can be viewed as a sufficient counterexample to the assumption of homogeneous voxel
dynamics within an ROI. Jedoch, when task-dependency of consistency is investigated and,
insbesondere, if one assumes that high consistency is indicative of increased activity, it is impor-
tant to address the question of the test-retest reliability of the measure. Mit anderen Worten, Vor
investigating the changes of consistency between rest and task, it might be good to ensure that
consistency is stable between different resting-state sessions of the same subject. This investi-
gation should also address the possible effects of preprocessing on the test-retest reliability, als
Zuo et al. (2013) have done for ReHo.
The Consistency of ROIs Is Affected by Their Shape and Size and the Level of Spatial Smoothing
There are multiple factors that can explain the consistency of an ROI. Erste, even if one assumes
that perfectly consistent and static ROIs exist, atlases have typically been constructed at group
level and do not perfectly match any individuals. Because of this, an ROI may overlap with
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
266
Consistency of ROIs as nodes of fMRI functional brain networks
many true functional subareas that are internally coherent, and following this, small ROIs are
less likely to consist of several subareas. Similar results have been obtained by Gordon et al.
(2014) using a network-level homogeneity measure. Außerdem, adjacent voxels are known
to be more strongly correlated (Alexander-Bloch et al., 2013; Salvador et al., 2005). Dort-
Vordergrund, small ROIs should be more consistent. Zusätzlich, the shape of an ROI may affect its
consistency as well: Small, spherical ROIs should be most consistent.
Interessant, we found that consistency depends on ROI size in the anatomical atlases but
not in Brainnetome. In Brainnetome, ROIs are on average smaller than in HO and AAL and
the variation of ROI size is also smaller, which may explain this difference between atlases
(Gordon et al., 2014). Jedoch, it is also possible that in the connectivity-based Brainnetome
atlas, ROI consistency is less explained by size and more by other features such as the func-
tionality of the ROI.
Spatial smoothing is commonly used in the preprocessing of fMRI data. We found that
spatial smoothing increases the consistency of practically every ROI. Jedoch, smoothing
does not make the consistency distribution significantly more narrow. Even when smoothing
is applied, the consistency values of the least consistent ROIs are only half of those of the most
consistent ROIs.
From the viewpoint of voxel signals, the effects of spatial smoothing are qualitatively sim-
ilar to those of averaging voxel signals in order to obtain ROI time series: Any shared signal
components are amplified, whereas individual components are suppressed. daher, spatial
smoothing increases the correlations between all voxel time series. This increase is strongest
for voxels that are less than a full width at half maximum (FWHM) apart, which is typically the
case for voxels within the same ROI. Abschließend, one may argue that spatial smoothing is
redundant when constructing ROI-level networks: Noise suppression is already taken care of
when the voxel-level signals are averaged to ROI-level signals, and smoothing basically only
results in a baseline shift in ROI consistencies.
Averaging of Voxel Signals May Produce Spuriously High ROI-Level Correlations
We demonstrated that there are pairs of low-consistency ROIs that have strong ROI-level cor-
Beziehungen; in general, ROI-level correlations are scattered and do not appear to depend on ROI
consistency. Im Gegensatz, the mean consistency of an ROI pair determines an upper limit for
their voxel-level correlation. The existence of spuriously high ROI-level correlations is ex-
plained by the amplification of shared voxel-level signal components when the voxel signals
are averaged in order to obtain the ROI time series. Gleichzeitig, averaging suppresses
individual components.
Averaging related to moving from the voxel level to the ROI level can be seen from two
different angles. Erste, if we assume that ROIs represent functionally uniform groups of voxels
that have an underlying common signal component, then the individual voxel-level signal
components can be considered as noise. In this case, averaging acts as a filter that suppresses
noisy signal components and increases the signal-to-noise ratio (SNR). Andererseits,
individual voxel-level signal components can also reflect true underlying neural activity, Und
ROI-wide shared components can be caused by physiological noise or external noise. Should
this be the case, averaging of the voxel signals would cause a loss of information. Jedoch,
proving any of the above points of view would require more detailed modeling of changes in
SNR when voxel signals are averaged to obtain the ROI time series.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
267
Consistency of ROIs as nodes of fMRI functional brain networks
As moving from the voxel level to the ROI level changes the link structure of the network,
one may expect to see differences in other network properties as well. In der Tat, Hayasaka &
Laurienti (2010) have demonstrated that voxel and ROI-level functional brain networks differ
from each other in terms of several network metrics such as degree distribution, characteristic
path length, and local and global efficiency. These metrics naturally depend on the link struc-
ture of the network and may therefore have been affected by the structural changes caused
by averaging voxel signals. Based on their results, Hayasaka & Laurienti (2010) decided to
recommend against using anatomical ROIs as nodes of functional brain networks.
The voxels used in the acquisition and analysis of fMRI data are artificially defined, Und
it is reasonable to assume that the true functional areas in the brain are larger than voxels
(Shen et al., 2013; Wig et al., 2011). daher, coarse-graining of voxels into well-defined
larger-scale regions can yield more accurate results than voxel-level analyses. Jedoch, Wir
have shown that all ROIs are not equally consistent. daher, when working with ROIs, eins
should be careful in interpreting results and aware of possible problems, such as spuriously
high correlations between inconsistent ROIs.
MATERIALS AND METHODS
Subjects
Thirteen healthy, right-handed subjects (11 females, 2 Männer, Alter 25.1 ± 3.9, Mittelwert ± SD)
participated in the study of emotion processing. All subjects had normal or corrected-to-normal
vision, and none of them reported a history of neurological or psychiatric disease. All subjects
were volunteers, gave written, informed consent according to the Declaration of Helsinki,
and were compensated for their participation. The study was approved by the Research Ethics
Committee of Aalto University.
Data Acquisition
Functional magnetic resonance imaging (fMRT) data were acquired with a 3T Siemens Magne-
tom Skyra scanner in the AMI Centre (Aalto Neuroimaging, Aalto University, Espoo, Finland).
A whole-brain T2*-weighted EPI sequence was measured with the following parameters: TR =
, Voxelgröße = 3.1 × 3.1 × 4.0 mm
1.7S, 33 axial slices, TE = 24 MS, flip angle = 70
, Matrix
Größe 64 × 64 × 33, FOV = 256 × 256 mm
. Data from an approximately 6 min (215 time points)
resting-state session were used in this study. During the resting state, subjects were asked to
lay still with their eyes open, fixating to a gray background image, and avoid falling asleep.
◦
3
2
Besides fMRI, anatomical MR images with isotropic 1 × 1 × 1 mm3
voxel size were also
acquired using a T1-weighted MP-RAGE sequence.
Preprocessing of the Data
The fMRI data were preprocessed with FSL (Jenkinson, Beckmann, Behrens, Woolrich, & Schmied,
2012; Smith et al., 2004; Woolrich et al., 2004) and with an in-house MatLab toolbox, BraMiLa
(https://version.aalto.fi/gitlab/BML/bramila). The preprocessing pipeline be-
gan with removal of the three first frames of each subject’s data in order to eliminate the error
caused by scanner transient effect (leaving 212 time points for further analysis), slice timing cor-
rection, motion correction by MCFLIRT (Jenkinson, Beckmann, Behrens, Woolrich, & Schmied,
2002), and extraction of white matter and cerebrospinal fluid (CSF). Functional data were
coregistered to the anatomical image with FLIRT (7 df), further registered to MNI152 2 mm
Netzwerkneurowissenschaften
268
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Consistency of ROIs as nodes of fMRI functional brain networks
standard template (12 df), and resampled to voxels of 4 × 4 × 4 mm
detrended, and signals from white matter and CSF were regressed out from the data.
. Signals were linearly
3
Regressing out from the data, the global signal (GS) decreases motion-related variance of
the data (Power et al., 2014). Jedoch, removal of GS may also distort correlation patterns in
the network (Fuchs, Zhang, Snyder, & Rachel, 2009; Gotts et al., 2013). daher, es gibt kein
general consensus among the fMRI community whether GS should be regressed out. Im
present work, we decided not to regress out GS. The potential effect of GS on our data would
be increased ROI consistency (siehe unten), since GS is shared among all voxels and therefore
may increase voxel-level correlations. Jedoch, we observed a wide range of ROI consistency
Werte, including very low consistencies.
In order to control for motion artifacts, expansion of motion parameters was extracted
out from the data with linear regression (36 Volterra expansion-based signals; Power et al.,
2014). Head motion has been reported as a source of artifacts in connectivity studies (Power,
Barnes, Snyder, Schlaggar, & Petersen, 2012). daher, we calculated the framewise displace-
ment for each subject. Jedoch, as the framewise displacement of all the subjects was under
the suggested threshold of 0.5 mm, we did not perform any scrubbing. Weiter, in later analy-
sis we also investigated whether differences in head motion could explain differences in ROI
consistency.
In order to further avoid artifacts, voxels that were located at the edge between brain and
skull where the signal power was less than 2% of the individual subject’s mean signal power
were excluded from further analysis.
Spatial Smoothing
Our standard preprocessing pipeline did not include spatial smoothing. Jedoch, in order
to investigate how this commonly used preprocessing method would affect our results, Wir
repeated all analysis with data that had been smoothed with a Gaussian kernel. We used three
different kernel sizes: full width at half maximum (FWHM) von 5 mm, 8 mm, Und 12 mm. Für
Einzelheiten, see Supplementary Methods (Korhonen et al., 2017).
Atlas-Based Regions of Interest
After preprocessing (and spatial smoothing when applied), the cerebral cortex as well as sub-
cortical structures and the cerebellum were divided into ROIs. For defining the ROIs, we used
three different brain parcellations: the commonly used anatomical HO and AAL atlases as well
as the Brainnetome atlas that is based on structural and functional connectivity.
The ROIs were defined so that each voxel belonged to one ROI only. The time series of
ROIs were defined as averages of the time series of the voxels within the ROIs:
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
XI =
1
NI
xi,
∑
i∈I
(1)
where I is the focal ROI, NI is its size defined as the number of constituent voxels, and xi is
the time series of voxel i.
Harvard-Oxford atlas. HO atlas ( http://neuro.debian.net/pkgs/fsl-harvard-
oxford-atlases.html; Desikan et al., 2006) is a probabilistic atlas that is based on the
Netzwerkneurowissenschaften
269
Consistency of ROIs as nodes of fMRI functional brain networks
macroanatomical boundaries of the brain. In der vorliegenden Studie, we used 138 ROIs from the
HO atlas at a probability level of 30% (meaning that each voxel belongs to the ROI it has been
associated with in 30% or more of the subjects in the group used to create the parcellation).
Ninety-six of these ROIs were located at the cerebral cortex, 15 of them covered subcortical
gray matter, Und 27 were located in the cerebellum. Note that one of the cerebellar ROIs of
the HO atlas (ROI 120, Vermis Crus I) is not defined at the probability level of 30% und war
therefore excluded from the present study.
In the HO atlas, the distribution of ROI sizes is broad: in the case of our in-house data, Die
number of voxels in an ROI varied between 5 Und 857, median ROI size being 88 (for sizes of
all ROIs, see Supplementary Table; Korhonen et al., 2017).
ROIs of the AAL (Tzourio-Mazoyer et al., 2002) atlas
Automated Anatomical Labeling atlas.
have been obtained by parcellating a spatially normalized high-resolution single-subject struc-
tural volume based on the main sulci. Dann, a label has been automatically assigned to each
of the ROIs. In der vorliegenden Studie, we used 116 ROIs from the AAL parcellation. Ninety of these
ROIs were located at the cerebral cortex, while 8 of them consisted of subcortical gray matter,
Und 18 covered the cerebellar cortex.
As in the HO atlas, in AAL the size of ROIs varied across a wide range. In the case of our
in-house data, the number of voxels in an ROI varied between 4 Und 607, with a median of
157 (for further details, see Supplementary Table; Korhonen et al., 2017).
The Brainnetome atlas (Fan et al., 2016) is based on in vivo structural and
Brainnetome atlas.
functional connectivity measured using multimodal neuroimaging techniques. In the present
Studie, we used 246 ROIs from the Brainnetome atlas, 210 of which were located at the cere-
bral cortex and 36 covered subcortical gray matter. Note that the Brainnetome atlas does not
include ROIs located in the cerebellum.
In Brainnetome, the size of ROIs varied less than in HO or AAL: In the case of our in-house
Daten, the minimum number of voxels in an ROI was 5 and the maximum number of voxels in
an ROI was 186, with a median of 63. Also, Brainnetome ROIs were smaller than ROIs of HO
or AAL.
Network Extraction
We study functional brain networks at two different scales: at the level of voxels and at the
level of ROIs. At the voxel level, nodes of the network represent single voxels of the cortical
gray matter, whereas at the ROI level whole ROIs are used as network nodes. At both lev-
els, network extraction begins with calculating the weighted adjacency matrix A between all
nodes so that its element Ai,j indicates the strength of connection between nodes i and j of
the network. To define the connection strength, we calculate the Pearson correlation coeffi-
cients between time series of each i-j pair. Pearson correlation is commonly used to quantify
functional connections between nodes of brain networks (see Braun et al., 2012; Wig et al.,
2011). This procedure yields a full, symmetric, weighted adjacency matrix that, after removing
1
2 N(N − 1) independent real-valued elements where N denotes
the diagonal values, contains
the number of network nodes.
We performed most of our analyses on the full adjacency matrix, using zero-lag correla-
tions between all nodes of the network. Jedoch, for the analysis of the relationship between
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
270
Consistency of ROIs as nodes of fMRI functional brain networks
consistency, Grad, and strength of an ROI (siehe unten), the network was thresholded to a set
of densities (0.25, 0.5, 0.75, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 10, 15, Und 20%). To obtain
a network with a density d, links weaker than the 1 − dth percentile were removed from the
network by setting the corresponding elements in A to zero. Thresholded networks were an-
alyzed as weighted, instead of transforming the thresholded adjacency matrix into a binary
eins. The range of densities was chosen to emphasize low densities, where network structure
is most sensitive to small changes in link weights.
The neuroscientific interpretation of negative correlations between brain areas has been
subject to dispute. It has been argued that negative correlations are less reliable than positive
ones and should thus be excluded from analysis (Schwarz & McGonigle, 2011; Shehzad et al.,
2009). Gleichzeitig, others have argued that negative correlations have a true neurobiolog-
ical meaning (Fox et al., 2009; Wig et al., 2011). Negative correlations are indeed included in
our analysis of full matrices, das ist, calculations of distributions of correlations between time
series of voxels in same and different ROIs, and studies of the relationship between consis-
tency and voxel and ROI-level correlations. Im Gegensatz, for thresholded networks that are used
to investigate the relationship between consistency and network measures, the thresholding
method automatically excludes negative correlations since only the strongest d% of links are
accepted at each density d.
The Consistency of ROIs
In order to quantify the amount of variation between the time series of the voxels within an
ROI, we define the ROI consistency as
Phi(ICH) =
1
NI(NI − 1) ∑
ich,ich(cid:7)∈I
C(xi, xi(cid:7) ),
(2)
where I denotes the focal ROI, NI is the number of voxels in I, C(xi, xi(cid:7) ) denotes the Pearson
correlation coefficient between the time series xi and xi(cid:7) of voxels i and i(cid:7)
that belong to I,
and the summation is done over all voxel pairs within I. The interpretation of consistency is
straightforward: If an ROI contains many voxels with nonuniform dynamics, φ is low, indicating
that the ROI time series is a poor approximation of voxel dynamics. Im Gegensatz, an ideal ROI
where all voxels have identical time series would reach the theoretical maximum value of
φ = 1.
Negative values of consistency are possible only in theory. They arise only when the ROI
consists of pairs of voxels with signals anticorrelated with each other and independent of the
signals of the rest of voxels in the ROI. In der Praxis, there are only a few significant negative
correlations between signals of voxels within an ROI (siehe Abbildung 1), and we did not observe
any negative consistency values.
Time Series Correlations at the Voxel and ROI Levels
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
In the present article, we ask whether consistency predicts the connectivity of an ROI. Das tun wir
this by investigating the relationship between the mean consistency and correlation between
an ROI pair at two levels. The voxel-level correlation between two ROIs is defined as the mean
correlation between the time series of voxels within the ROIs, averaged over all possible voxel
pairs:
Netzwerkneurowissenschaften
(cid:3)C (ICH, J)(cid:4)vox =
1
NI NJ
∑
i∈I
∑
j∈ J
C(xi, xj).
(3)
271
Consistency of ROIs as nodes of fMRI functional brain networks
The ROI-level correlation between two ROIs is simply defined as the Pearson correlation
between the time series of the ROIs:
C(ICH, J)ROI = C(XI, XJ),
(4)
where XI and XJ are the ROI time series, computed as averages of voxel time series within I
and J (see Equation 1).
Relationship Between ROI Consistency and Network Measures
In order to investigate the role of an ROI as a network node, we utilized two commonly used
network measures: the degree k and the strength s of an ROI. These measures are commonly
used to identify the hubs of the functional brain network (Rubinow & Spurns, 2010).
The degree of an ROI is defined as the number of its neighbors, das ist, the number of other
ROIs to which it is directly connected by a link. The degree offers a rough estimate of how
central a node is in the network: Nodes with many neighbors can be seen as more important
for information flow than nodes with less neighbors.
The strength of an ROI is defined as the sum of the weights of the links of the ROI. Daher, Es
quantifies the amount of connectivity of the ROI. Like the degree, the strength of an ROI can
be used to estimate its centrality; unlike the degree, it accounts for link weights too. Jedoch,
because strength mixes topology (existence of links) with link weights, interpretation is not
always straightforward: An ROI with a few strong links can have the same strength as an ROI
with many weaker links.
As discussed above, high ROI consistency is expected to be related to strong voxel-level
correlations. It is also natural to assume that strong voxel-level correlations give rise to strong
ROI-level correlations. Thereby, a natural hypothesis would be that ROIs that have high con-
sistency are connected by strong links. Infolge, these ROIs can be expected to have high
Stärke, zu. In a thresholded network, higher strength may also indicate larger number of
links with above-threshold weight, giving rise to higher degree as well. We have investigated
these relationships in networks thresholded to different densities.
ABIDE Data
In order to ensure that our results are not caused by any property specific to our in-house
dataset, we repeated all our analysis for a second, independent dataset. This dataset, referred
to as the ABIDE data, was part of the Autism Brain Imaging Data Exchange I (ABIDE I) Projekt
(Di Martino et al., 2014) and consisted of 28 healthy controls. For details of the ABIDE data,
see Supplementary Methods (Korhonen et al., 2017).
ACKNOWLEDGMENTS
We acknowledge the computational resources provided by the Aalto Science-IT project. Wir
thank Rainer Kujala for inspiring discussions and for comments on the manuscript, and Marita
Kattelus and Athanasios Gotsopoulos for their help in data acquisition.
BEITRÄGE DES AUTORS
Onerva Korhonen: Konzeptualisierung: Lead; Formale Analyse: Lead; Untersuchung: Lead; Meth-
odology: Lead; Software: Lead; Visualisierung: Lead; Writing – original draft: Lead; Writing –
Rezension & Bearbeitung: Lead. Heini Saarimäki: Datenkuration: Lead; Ressourcen: Lead; Writing –
Rezension & Bearbeitung: Supporting. Enrico Glerean: Software: Equal; Writing – review & Bearbeitung:
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
272
Consistency of ROIs as nodes of fMRI functional brain networks
Supporting. Mikko Sams: Konzeptualisierung: Equal; Aufsicht: Lead; Writing – review &
Bearbeitung: Supporting.
Jari Saramäki: Konzeptualisierung: Lead; Aufsicht: Lead; Writing –
original draft: Supporting; Writing – review & Bearbeitung: Lead.
VERWEISE
Alexander-Bloch, A. F., Vértes, P. E., Stidd, R., Lalonde, F., Clasen,
(2013). The anatomical dis-
L., Rapoport, J., . . . Gogtay, N.
tance of functional connections predicts brain network topology
in health and schizophrenia. Hirnrinde, 3(1), 127–138.
Andellini, M., Cannatà, V., Gazzellini, S., Bernardi, B., &
(2015). Test-retest reliability of graph metrics
Napolitano, A.
of resting state MRI functional brain networks: Eine Rezension. Zeitschrift
of Neuroscience Methods, 253, 183–192.
Aurich, N. K., Alves Filho, J. O., da Silva, A. M. M., & Franco, A. R.
(2015). Evaluating the reliability of different preprocessing steps
to estimate graph theoretical measures in resting state fmri data.
Frontiers in Neuroscience, 9, 48.
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
Gesundheit und Krankheit. Curr Opin Neurol., 22(1653), 340–347.
Baumgartner, R., Somorjai, R., Summers, R., & Richter, W.
(1999). Assessment of cluster homogeneity in fMRI data using
Kendall’s coefficient of concordance. Magnetic Resonance Imag-
ing, 17(10), 1525–1532.
Beckmann, C. F., Mackay, C. E., Filippini, N., & Schmied, S. M. (2009).
Group comparison of resting-state fMRI data using multi-subject
ICA and dual regression. NeuroImage, 47(Suppl. 1), S148.
Braun, U., Plichta, M. M., Esslinger, C., Sauer, C., Haddad, L.,
Grimm, O., . . . Meyer-Lindenberg, A.
(2012). Test–retest reli-
ability of resting-state connectivity network characteristics using
fMRI and graph theoretical measures. NeuroImage, 59(2), 1404–
1412.
Craddock, R. C., James, G. A., Holtzheimer, P. E., Hu, X. P., &
Mayberg, H. S. (2012). A whole brain fMRI atlas generated via
spatially constrained spectral clustering. Kartierung des menschlichen Gehirns,
33(8), 1914–1928.
de Reus, M. A., & Van den Heuvel, M. P. (2013). The parcellation-
based connectome: Limitations and extensions. NeuroImage,
80, 397–404.
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., . . . Killiany, R. J.
(2006). An automated la-
beling system for subdividing the human cerebral cortex on MRI
scans into gyral based regions of interest. NeuroImage, 31(3),
968–980.
Di Martino, A., Yan, C.-G., Li, Q., Denio, E., Castellanos, F. X.,
Alaerts, K., . . . Milham, M. P. (2014). The autism brain imaging
data exchange: Towards a large-scale evaluation of the intrinsic
brain architecture in autism. Molekulare Psychiatrie, 19(6), 659–
667.
Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., . . . Jiang, T.
(2016). The human Brainnetome atlas: A new brain atlas based
on connectional architecture. Hirnrinde, 26(8).
Fuchs, M. D., Zhang, D., Snyder, A. Z., & Rachel, M. E. (2009). Der
global signal and observed anticorrelated resting state brain net-
funktioniert. Journal of Neurophysiology, 101(6), 3270–3283.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Glasser, M., Coalson, T., Robinson, E., Hacker, C., Harwell, J.,
(2016). A multi-modal parcel-
Yacoub, E., . . . Van Essen, D.
lation of human cerebral cortex. Natur, 536, 171–178.
Glerean, E., Pan, R. K., Salmi, J., Kujala, R., Lahnakoski, J. M.,
Roine, U., . . . Jääskeläinen, ICH. P.
(2016). Reorganization of
functionally connected brain subnetworks in high-functioning
autism. Kartierung des menschlichen Gehirns, 37(3), 1066–1079.
Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F., Kelley,
W. M., & Petersen, S. E. (2014). Generation and evaluation of a
cortical area parcellation from resting-state correlations. Zerebral
Kortex, 26(1), 288–303.
Gotts, S., Saad, Z., Jo, H. J., Wallace, G., Cox, R., & Martin, A.
(2013). The perils of global signal regression for group compar-
isons: A case study of autism spectrum disorders. Grenzen in
Human Neuroscience, 7, 356.
Hayasaka, S., & Laurienti, P. J.
(2010). Comparison of charac-
teristics between region- and voxel-based network analyses in
resting-state fMRI data. Neurobild, 50(2), 499–508.
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W.,
& Schmied, S. M.
Improved optimisation for the robust
and accurate linear registration and motion correction of brain
Bilder. NeuroImage, 17(2), 825–841.
(2002).
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W.,
& Schmied, S. M. (2012). FSL. NeuroImage, 62(2), 782–790.
Jiang, L., Xu, T., Er, Y., Hou, X.-H., Wang, J., Cao, X.-Y., . . . Zuo,
X.-N. (2015). Toward neurobiological characterization of func-
tional homogeneity in the human cortex: Regional variation,
morphological association and functional covariance network
organization. Brain Structure and Function, 220(5), 2485–2507.
(2016). Regional homogeneity: A multi-
modal, multiscale neuroimaging marker of the human connec-
tome. The Neuroscientist, 22(5), 486–505.
Jiang, L., & Zuo, X.-N.
Korhonen, O., Saarimäki, H., Glerean, E., Sams M., & Saramäki, J.
(2017). Supplemental material for “Consistency of regions of
interest as nodes of
functional brain networks.”
Netzwerkneurowissenschaften, 1(3), 254–274. https://doi.org/10.1162/
netn_a_00013
fMRT
Li, S.-J., Li, Z., Wu, G., Zhang, M.-J., Franczak, M., & Antuono,
P. G. (2002). Alzheimer disease: Evaluation of a functional MR
imaging index as a marker. Radiology, 225(1), 253–259.
Nelson, S. M., Cohen, A. L., Power, J. D., Wig, G. S., Miezin,
(2010). A parcella-
F. M., Wheeler, M. E., . . . Petersen, S. E.
tion scheme for human left lateral parietal cortex. Neuron, 67(1),
156–170.
Papo, D., Zanin, M., & Buldú, J. (2014). Reconstructing functional
brain networks: Have we got the basics right? Frontiers in Human
Neurowissenschaften, 8, 107.
Papo, D., Zanin, M., Pineda-Pardo, J. A., Boccaletti, S., & Buldú,
J. M. (2014). Functional brain networks: Great expectations, hart
Netzwerkneurowissenschaften
273
Consistency of ROIs as nodes of fMRI functional brain networks
times and the big leap forward. Phil. Trans. R. Soc. B, 369(1653),
20130525.
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &
(2012). Spurious but systematic correlations in
Petersen, S. E.
functional connectivity MRI networks arise from subject motion.
NeuroImage, 59(3), 2142–2154.
Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
(2011). Functional network
Church, J. A., . . . Petersen, S. L.
organization of the human brain. Neuron, 72(4), 665–678.
Power, J. D., Mitra, A., Laumann, T. O., Snyder, A. Z., Schlaggar,
B. L., & Petersen, S. E.
(2014). Methods to detect, character-
ize, and remove motion artifact in resting state fMRI. NeuroIm-
Alter, 84, 320–341.
Rubinow, M., & Spurns, Ö. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.
Salvador, R., Suckling, J., Coleman, M. R., Pickard, J. D., Menon,
D., & Bullmore, E.
(2005). Neurophysiological architecture of
functional magnetic resonance images of human brain. Zerebral
Kortex, 15(9), 1332–1342.
Schwarz, A. J., & McGonigle, J.
(2011). Negative edges and soft
thresholding in complex network analysis of resting state func-
tional connectivity data. NeuroImage, 55(3), 1132–1146.
Shehzad, Z., Kelly, A. C., Reiss, P. T., Gee, D. G., Gotimer,
K., Uddin, L. Q.,
(2009). The resting
Gehirn: Unconstrained yet reliable. Hirnrinde, 19(10),
2209–2229.
. Milham, M. P.
.
.
Shen, X., Tokoglu, F., Papademetris, X., & Polizist, R. T.
(2013). Groupwise whole-brain parcellation from resting-state
fMRI data for network node identification. NeuroImage, 82,
403–415.
Shirer, W. R., Jiang, H., Price, C. M., Ng, B., & Greicius, M. D.
(2015). Optimization of RS-fMRI pre-processing for enhanced
signal-noise separation, test-retest reliability, and group discrim-
ination. NeuroImage, 117, 67–79.
Schmied, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F.,
Behrens, T. E. J.,
. . . Matthews, P. M.
Johansen-Berg, H.,
(2004). Advances in functional and structural MR image anal-
ysis and implementation as FSL. NeuroImage, 23(Suppl. 1),
S208–S219.
Spurns, Ö.
(2013A). The human connectome: Origins and chal-
Längen. NeuroImage, 80, 53–61.
Spurns, Ö.
(2013B). Network attributes for segregation and inte-
gration in the human brain. Aktuelle Meinung in der Neurobiologie,
23(2), 162–171.
Stanley, M. L., Moussa, M. N., Paolini, B. M., Lyday, R. G., Burdette,
J. H., & Laurienti, P. J. (2013). Defining nodes in complex brain
Netzwerke. Front. Comput. Neurosci., 7(169), 10–3389.
Telesford, Q. K., Morgan, A. R., Hayasaka, S., Simpson, S. L., Barret,
W., Kraft, R. A., . . . Laurienti, P. J.
(2010). Reproducibility of
graph metrics in fmri networks. Frontiers in Neuroinformatics, 4,
117.
Thirion, B., Flandin, G., Pinel, P., Roche, A., Ciuciu, P., & Polina,
J.-B. (2006). Dealing with the shortcomings of spatial normaliza-
tion: Multi-subject parcellation of fMRI datasets. Menschliches Gehirn
Mapping, 27(8), 678–693.
Tohka, J., Er, Y., & Evans, A. C.
(2012). The impact of sampling
density upon cortical network analysis: Regions or points. Mag-
netic Resonance Imaging, 30(7), 978–992.
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M.
(2002). Automated
anatomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
NeuroImage, 15(1), 273–289.
Wang, J., Wang, L., Zang, Y., Yang, H., Tang, H., Gong, Q., . . .
Er, Y.
(2009). Parcellation-dependent small-world brain func-
tional networks: A resting-state fMRI study. Human Brain Map-
ping, 30(5), 1511–1523.
Wig, G. S., Schlaggar, B. L., & Petersen, S. E.
(2011). Concepts
and principles in the analysis of brain networks. Annals of the
New York Academy of Sciences, 1224(1), 126–146.
Woolrich, M. W.,
Jbabdi, S., Patenaude, B., Chappell, M.,
Makni, S., Behrens, T., . . . Schmied, S. M. (2004). Bayesian analysis
of neuroimaging data in FSL. NeuroImage, 45(1), S173–S186.
Zalesky, A., Fornito, A., Harding, ICH. H., Cocchi, L., Yücel, M.,
(2010). Whole-brain anatomi-
Pantelis, C., & Bullmore, E. T.
cal networks: Does the choice of nodes matter? NeuroImage,
50(3), 970–983.
Zang, Y., Jiang, T., Lu, Y., Er, Y., & Tian, L.
(2004). Regional ho-
mogeneity approach to fMRI data analysis. NeuroImage, 22(1),
394–400.
Zuo, X.-N., & Xing, X.-X. (2014). Test-retest reliabilities of resting-
state fMRI measurements in human brain functional connec-
tomics: A systems neuroscience perspective. Neurowissenschaften &
Bioverhaltensberichte, 45, 100–118.
Zuo, X.-N., Xu, T., Jiang, L., Yang, Z., Cao, X.-Y., Er, Y., . . .
Milham, M. P.
(2013). Toward reliable characterization of
functional homogeneity in the human brain: Vorverarbeitung,
imaging resolution and computational space.
scan duration,
NeuroImage, 65, 374–386.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
l
ich
T
.
e
D
u
/
N
e
T
N
/
A
R
T
ich
C
e
–
P
D
F
/
1
/
3
/
2
5
4
/
1
0
9
2
0
4
0
/
N
e
T
N
_
A
_
0
0
0
1
3
.
P
D
F
B
j
G
u
e
S
T
Ö
N
0
7
S
e
P
T
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
274