FORSCHUNG
Dynamic core-periphery structure of information
sharing networks in entorhinal cortex
and hippocampus
Nicola Pedreschi1,2, Christophe Bernard2, Wesley Clawson2, Pascale Quilichini2,
Alain Barrat1,3, and Demian Battaglia2
1Aix-Marseille University, Université de Toulon, CNRS, CPT, Turing Center for Living Systems, Marseille, Frankreich
2Aix-Marseille University, Inserm, INS, Institut de Neurosciences des Systèmes, Marseille, Frankreich
3Tokyo Tech World Research Hub Initiative (WRHI), Institute of Innovative Research, Tokyo Institute of Technology, Japan
Keine offenen Zugänge
Tagebuch
Schlüsselwörter: Temporal networks, Informationstheorie, Hippocampus, Entorhinal cortex, Cell
assemblies, Dynamic functional connectivity
ABSTRAKT
Neural computation is associated with the emergence, reconfiguration, and dissolution of
cell assemblies in the context of varying oscillatory states. Hier, we describe the complex
spatiotemporal dynamics of cell assemblies through temporal network formalism. We use a
sliding window approach to extract sequences of networks of information sharing among
single units in hippocampus and entorhinal cortex during anesthesia and study how global
and node-wise functional connectivity properties evolve through time and as a function of
changing global brain state (theta vs. slow-wave oscillations). Erste, we find that information
sharing networks display, at any time, a core-periphery structure in which an integrated core
of more tightly functionally interconnected units links to more loosely connected network
leaves. However the units participating to the core or to the periphery substantially change
across time windows, with units entering and leaving the core in a smooth way. Zweite, Wir
find that discrete network states can be defined on top of this continuously ongoing liquid
core-periphery reorganization. Switching between network states results in a more abrupt
modification of the units belonging to the core and is only loosely linked to transitions
between global oscillatory states. Dritte, we characterize different styles of temporal
connectivity that cells can exhibit within each state of the sharing network. While inhibitory
cells tend to be central, we show that, ansonsten, anatomical localization only poorly
influences the patterns of temporal connectivity of the different cells. Außerdem, cells can
change temporal connectivity style when the network changes state. Insgesamt, diese
findings reveal that the sharing of information mediated by the intrinsic dynamics of
hippocampal and entorhinal cortex cell assemblies have a rich spatiotemporal structure,
which could not have been identified by more conventional time- or state-averaged analyses
of functional connectivity.
ZUSAMMENFASSUNG DES AUTORS
It is generally thought that computations performed by local brain circuits rely on complex
neural processes, associated with the flexible waxing and waning of cell assemblies, das ist,
an ensemble of cells firing in tight synchrony. Although cell assembly formation is inherently
and unavoidably dynamical, it is still common to find studies in which essentially “static”
approaches are used to characterize this process. In der vorliegenden Studie, we adopt instead a
temporal network approach. Avoiding usual time-averaging procedures, we reveal that hub
neurons are not hardwired but that cells vary smoothly their degree of integration within the
Zitat: Pedreschi, N., Bernard, C.,
Clawson, W., Quilichini, P., Barrat, A., &
Battaglia, D. (2020). Dynamic
core-periphery structure of information
sharing networks in entorhinal cortex
and hippocampus. Netzwerk
Neurowissenschaften, 4(3), 946–975.
https://doi.org/10.1162/netn_a_00142
DOI:
https://doi.org/10.1162/netn_a_00142
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00142
Erhalten: 17 Januar 2019
Akzeptiert: 16 April 2020
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Corresponding Authors:
Alain Barrat
alain.barrat@cpt.univ-mrs.fr
Demian Battaglia
demian.battaglia@univ-amu.fr
Handling-Editor:
Olaf Sporns
Urheberrechte ©: © 2020
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
N
e
N
_
A
_
0
0
1
4
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Cell assembly:
Group of cells firing repeatedly in a
coordinated manner and serving as a
functional entity for neuronal
information processing; das ist, a set
of cells “working together.”
Temporal network:
A time series of snapshots of the
instantaneous network of
communication between the
elements of the network.
assembly core. Außerdem, our temporal network framework enables the definition of
alternative possible styles of “hubness.” Some cells may share information with a multitude
of other units but only in an intermittent manner, as “activists” in a flash mob. Im Gegensatz,
some other cells may share information in a steadier manner, as resolute “lobbyists.” Finally,
by avoiding averages over preimposed states, we show that within each global oscillatory
state rich switching dynamics can take place between a repertoire of many available network
Staaten. We thus show that the temporal network framework provides a natural and effective
language to rigorously describe the rich spatiotemporal patterns of information sharing
instantiated by cell assembly evolution.
EINFÜHRUNG
Since its early definitions (Abeles, 1982; Hebb, 1949), the notion of cell assembly, loosely
defined as a group of neurons with coordinated firing within a local or distributed circuit, hat
been associated with information processing. According to a widely accepted view (sehen, z.B.,
Varela, Lachaux, Rodriguez, & Martinerie, 2001), neuronal representations and, more gener-
ally, computations are constructed via the dynamic integration of the information conveyed by
the spiking activity of different cells. The recruitment of a cell assembly goes thus well beyond
the mere coactivation of an ensemble of cells frequently firing together. It corresponds indeed
to the instantiation of an actual transient functional network allowing information to be shared
between neurons and fed into novel informational constructs suitable for further processing
(Buzsáki, 2010).
In this sense, it appears quite natural to describe the flexible creation, transformation, Und
dissolution of groups of information-exchanging neurons as a dynamic network whose nodes
and edges evolve through time, reflecting the recruitment (or the dismissal) of neurons into
(or out of) the integrated assembly. Trotzdem, cell assemblies at the level of neuronal
microcircuits—and, insbesondere, in the hippocampal formation, involved in spatial navigation
and episodic memory (Buzsáki & Moser, 2013)—have been most often characterized in terms
of sets of nodes frequently coactivating in time (Mao, Hamzei-Sichani, Aronov, Froemke, &
Yuste, 2001; Müller, Ayzenshtat, Carrillo-Reid, & Yuste, 2014) or repeatedly activating in se-
quences (Ikegaya et al., 2004; Malvache, Reichinnek, Villette, Haimerl, & Cossart, 2016). Solch
“static” catalogues of patterns of firing partially fail at highlighting that the temporally coordi-
nated firing of nodes gives rise to a dynamics of functional links (Aertsen, Gerstein, Habib, &
Palm, 1989; Bonifazi et al., 2009; Clawson et al., 2019), das ist, to a temporal network (Holme,
2015; Holme & Saramäki, 2012; Masuda & Holme, 2017).
The temporal network framework has recently emerged in order to take into account that
for many systems, a static network representation is only a first approximation. Studies of
temporally resolved data in communication and social networks have in particular uncov-
ered features such as broad distributions of contact or intercontact times (burstiness) zwischen
individuals (Barabási, 2005; Cattuto et al., 2010), multiple temporal and structural scales
(Darst et al., 2016; Laurent, Saramäki, & Karsai, 2015; Saramäki & Moro, 2015), and a rich
array of intrinsically dynamical structures that could not be unveiled within a static network
Rahmen (Galimberti, Barrat, Bonchi, Cattuto, & Gullo, 2018; Gauvin, Panisson, & Cattuto,
2014; Kobayashi, Takaguchi, & Barrat, 2019; Kovanen, Karsai, Kaski, Kertész, & Saramäki,
2011).
In the neuroscience field, emphasis has been recently put on the need to upgrade
“connectomics” into “chronnectomics,” to disentangle temporal variability from intersubject
and intercohort differences (Calhoun, Müller, Pearlson, & Adalı, 2014; Hutchison et al., 2013).
Netzwerkneurowissenschaften
947
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
N
e
N
_
A
_
0
0
1
4
2
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Information sharing network:
A weighted network in which the
weight of an edge linking two
neurons represents the amount of
mutual information between the
activities of these neurons.
Hippocampus:
A characteristically folded neural
structure belonging to the limbic
System. Crucial for spatial navigation
and memory, the hippocampus has
various anatomical subdivisions,
such as hippocampus CA1 (first zone
of “cornu ammonis”).
Entorhinal cortex:
An area of the brain serving as the
main interface between the
hippocampus and the neocortex.
It is involved in functions such as
memory and space-time integration
and is critically affected in
pathologies like Alzheimers disease.
Global oscillatory states:
Alternative modes of collective
oscillation of neural activity (slower,
∼1 Hz, as in the slow oscillation
state; or faster, ∼5–8 Hz),
widespread across multiple brain
Regionen, which can be detected in
neural recordings.
Network states:
Discrete states of the evolution of the
network in terms of its structure and
rate change of connectivity.
Connectivity profile:
For each neuron, a description of its
main connectivity (and connectivity
Variation) properties within a
Netzwerkstatus.
Netzwerkneurowissenschaften
Jedoch, a majority of dynamic network studies have so far considered large-scale brain-wide
networks of interregional connectivity (Thompson, Brantefors, & Fransson, 2017) und nur
fewer have addressed information sharing networks at the level of microcircuits, in vitro or
in silico (Orlandi, Soriano, Alvarez-Lacalle, & Erzähler, 2013; Poli, Pastore, & Massobrio, 2015;
Stetter, Battaglia, Soriano, & Geisel, 2012), and even more rarely in vivo (Clawson et al., 2019).
Hier, we propose to embrace a temporal network perspective when describing dynamic
information sharing within and between cell assemblies. Concretely, we analyze high-density
electrophysiological recordings in the hippocampus and medial entorhinal cortex of the rat,
allowing to follow in parallel the spiking activity of several tens of single units in different
brain regions and layers. We focus on recordings performed during anesthesia, guaranteeing
long and stable recordings of intrinsic cell assembly dynamics over several hours (Quilichini,
Sirota, & Buzsáki, 2010). In der Tat, even during anesthesia, the spatiotemporal complexity of
firing is not suppressed but a wide repertoire of cofiring ensembles and associated information
processing modes can be found (Clawson et al., 2019). Außerdem, with the used anes-
thesia protocol, we observe a characteristic stochastic alternation between two global brain
oscillatory states, respectively dominated by slow oscillations (SO) and theta (THE) oscillations
(see Methods). Such experimental condition is therefore particularly suitable to probe the de-
pendence of cell assembly dynamics on the currently active global oscillatory state (Clawson
et al., 2019), which is expected to be a major modulator of information processing in the hip-
pocampus formation (Buzsáki & Moser, 2013; Klausberger et al., 2003) and cortical circuits in
allgemein (Gilbert & Sigman, 2007; Varela et al., 2001). Using a sliding window approach, Wir
extract temporal networks of information sharing between cells, and we develop methods to
investigate how their connectivity properties evolve in time.
At the level of whole network organization, we pay attention to whether connectivity struc-
ture changes continuously—as in the case of many social or communication networks
(Cattuto et al., 2010; Miritello, Lara, Cebrian, & Moro, 2013; Saramäki & Moro, 2015)—or
rather undergoes switching between different discrete network states—as recently observed
for instance in an animal social network (Gelardi, Fagot, Barrat, & Claidière, 2019)—possibly
in relation to transitions between global oscillatory states. We find that switching between
discrete network states does spontaneously occur during anesthesia. Remarkably, we identify
a multiplicity of states of connectivity between single neurons, with rich switching dynamics
ongoing even in the absence of a change in the global oscillatory state. The sharing network
Konnektivität, Jedoch, is never frozen, but keeps fluctuating within each of the network states.
More specifically, at any time, the instantaneous information sharing network displays a core-
periphery organization (Della Rossa, Dercole, & Piccardi, 2013; Kojaku & Masuda, 2018), In
which a limited number of neurons form a tightly mutually connected core, while a majority
of other neurons are more peripheral. Individual neurons through time modulate their degree
of integration within the sharing network and may “float” between the core and the periph-
ery, transiently leaving or getting engaged into the core, giving rise to what we call a liquid
core-periphery architecture.
At the level of single nodes, the neighborhood of each neuron is constantly evolving. Most
importantly, neurons that have at the time aggregated level similar static connectivities, having
connections for a comparable overall amount of time, can strongly differ in their temporal
connectivity profile. Zum Beispiel, some neurons may form links that remain active for a limited
amount of time but in an uninterrupted way. Other neurons may instead repeatedly connect
and disconnect to others, sharing information in an intermittent and sporadic fashion. Wir
thus define for each neuron its specific temporal connectivity profile, which summarizes its
948
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
N
e
N
_
A
_
0
0
1
4
2
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Connectivity styles:
Typical classes of connectivity
profiles that reoccur over the time of
a recording and across all recordings.
dynamic patterns of attachment in the evolving core-periphery sharing network. We then use
an unsupervised classification approach to identify temporal connectivity style archetypes and
show that neurons can adopt different styles in different network states, possibly associated
with variations of their role in information processing (see Discussion).
Going beyond averaged network analyses with suitable time-resolved metrics allows thus
an unprecedented precision in characterizing the functional organization of information shar-
ing. Cell assemblies are not anymore seen as rigidly defined groups of cells but as dynamic
Netzwerke, restlessly exchanging flows of information between core and periphery and contin-
uously modifying their extent and reach toward cells in different anatomical locations. In other
Wörter, the adoption of a temporal network framework makes it possible to witness and seize
the inner life of cell assemblies while it unfolds and gives rise to emergent computations.
ERGEBNISSE
Information Sharing Dynamics Can Be Described as a Temporal Network
Single unit recordings of neuronal activity were acquired simultaneously from the CA1 region
in the hippocampus and in the mEC (Figure 1A and Supporting Figure S1) für 16 rats under
anaesthesia (18 recordings for 16 rats). Following Clawson et al. (2019), we constructed time-
resolved weighted networks of functional connectivity, adopting a sliding window approach.
Within each 10-s-long time window, we took connection weights (functional links) zwischen
pairs of neurons (network nodes) to be proportional to the amount of shared information (Kirst,
Timme, & Battaglia, 2016) between their firing rates. Only links whose strength exceeded a
general significance threshold were kept (see Methods). We then slide the time window by 1 S,
in order to achieve a 90% overlap between consecutive windows. In Figure 1B, we represent
the temporal network construction procedure. Based on the data segments in each of three
windows centered at times ta, tb, and tc, we extract an N × N matrix for each time window,
where N is the number of neurons and in which the element (ich, J) corresponds to the shared
information between nodes i and j. Each such matrix, in network terms, is interpreted as the
adjacency matrix of a weighted graph G of N nodes. Even if the used functional connectivity
metric is in principle pseudodirected (because of the presence of a time lag between putative
sender and receiver node), we found that asymmetries between reciprocal connections were
very small (see Methods), especially for the stronger connections, and chose therefore to sym-
metrize the adjacency matrix for most analyses. This procedure thus maps each multichannel
recording of length T seconds to a time series of T network representations, obtaining finally
a temporal network of information sharing among neurons, formed by the temporal succes-
sion of these T network snapshots. Cartoon representations of the temporal network snapshots
G(ta), G(tb), and G(tc) in the three highlighted time windows are shown in Figure 1C. Some
actual network frames of a specific recording, together with a diagram describing emergence
and disappearance of links (edge activity plot), can be seen in Figure 2.
On the top of Figure 1B we also present the characteristic switching between global oscil-
latory states observed in our recordings. Analysis of the local field potentials recorded simul-
taneously to single unit activity allowed identifying a spontaneous stochastic-like alternation
between epochs belonging to a first SO global state (light blue color) spectrally dominated by
< 1 Hz oscillations and epochs in a second THE global state, characterized by the presence
of high power in a 4–8 Hz spectral band. In the following we will relate the temporal network
reconfiguration dynamics to these global oscillatory state transitions.
We carried on our study by analyzing in parallel the evolution of the weighted temporal
network structure and of the corresponding unweighted temporal network. To this aim we
Network Neuroscience
949
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
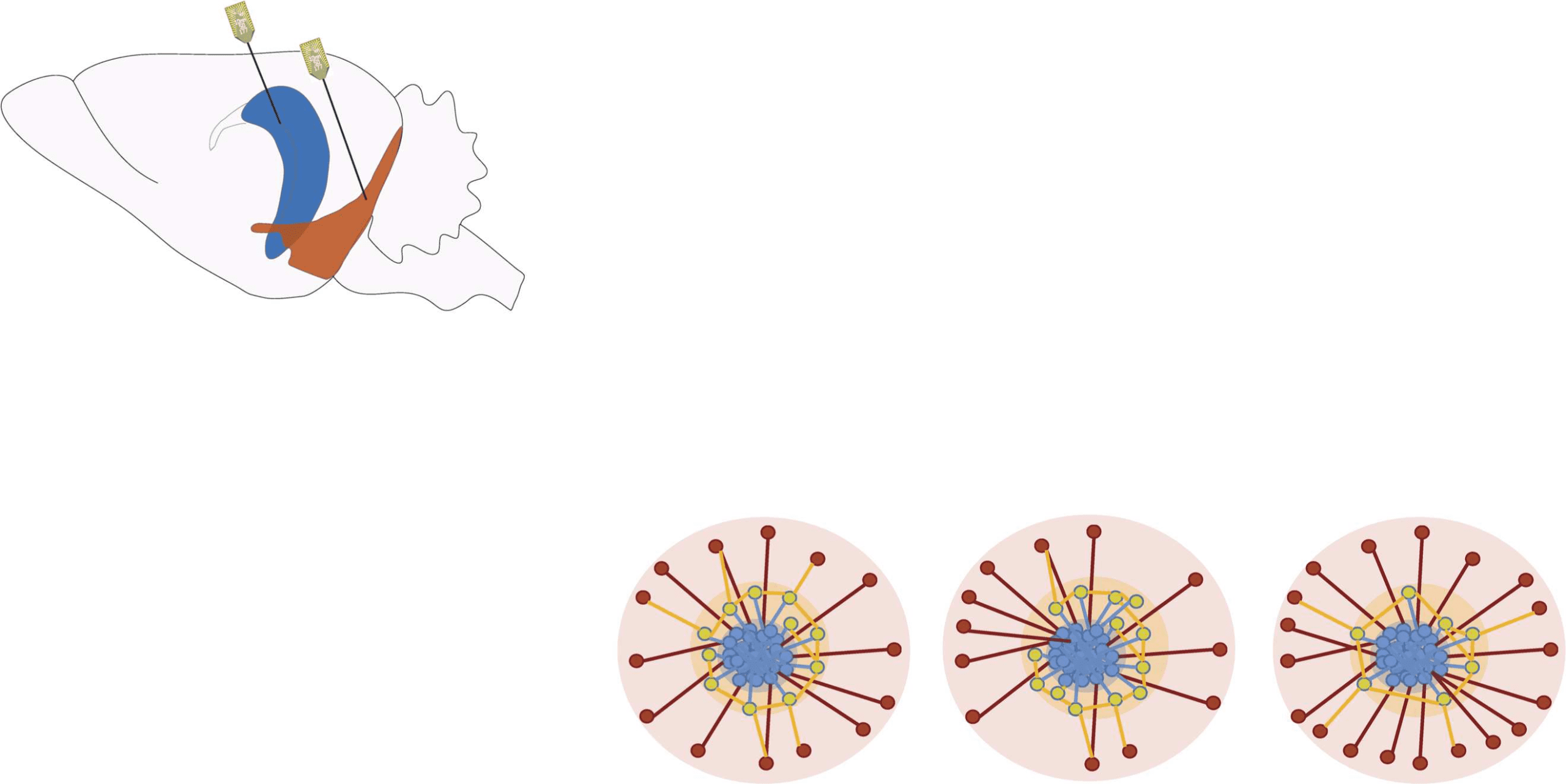
Figure 1. Recordings and feature vectors. (A) Approximate recording locations in mEC (orange)
and CA1 (blue) during anesthesia. (B) An example of LFP signal recorded by the channels in CA1
and in mEC; below the LFPs are two examples of single-unit activity from the same recording. The
intervals ta, tb, and tc are examples of time windows in which the corresponding network time-
frames are constructed. The horizontal bar above the recordings represents the global oscillation
states: in light blue the slow oscillations and in darker blue the theta oscillations.
(C) Illustrative
sketches of the two features computed for each node at each time-frame: On the left, in the green
box, we illustrate the Jaccard index, which quantifies the overlap between two sets. Here we con-
sider the local Jaccard indices between the neighborhoods of each node i ∈ [1, N] in successive
time frames (e.g., Ji(ta) is the Jaccard index for node i between times ta − 1 and ta): these quantities
carry information on how little or how radically the neighborhoods of i change across time, and we
call them liquidity. The center and right panels are a schematic representation of the core-periphery
organization of the network and the intuitive explanation of the coreness C values of the nodes: core
(blue) nodes have high values of coreness C ∼ 1, whereas peripheral (red) nodes have low values,
C ∼ 0; the yellow area surrounding the core is the core-skin, i.e., nodes whose coreness values are
higher than 0 and lower than 1. When a node is disconnected from the rest of the network (when it
has no neighbors), its coreness is exactly zero. (D) At each time frame, we obtain feature vectors of
the coreness and liquidity values of all neurons i ∈ [1, N], schematized by the two colorful vectors
(yellow, blue, and red for coreness and green for liquidity). The analyses were performed both for
unweighted networks, in which links are either present or absent, and for weighted networks, in
which the links are characterized by a weight given by the amount of shared information between
the nodes. For weighted networks, liquidity is measured by the cosine similarity instead of the
Jaccard index (see Methods), and a weighted coreness is computed for each node.
Network Neuroscience
950
Dynamic core-periphery networks in entorhinal cortex and hippocampus
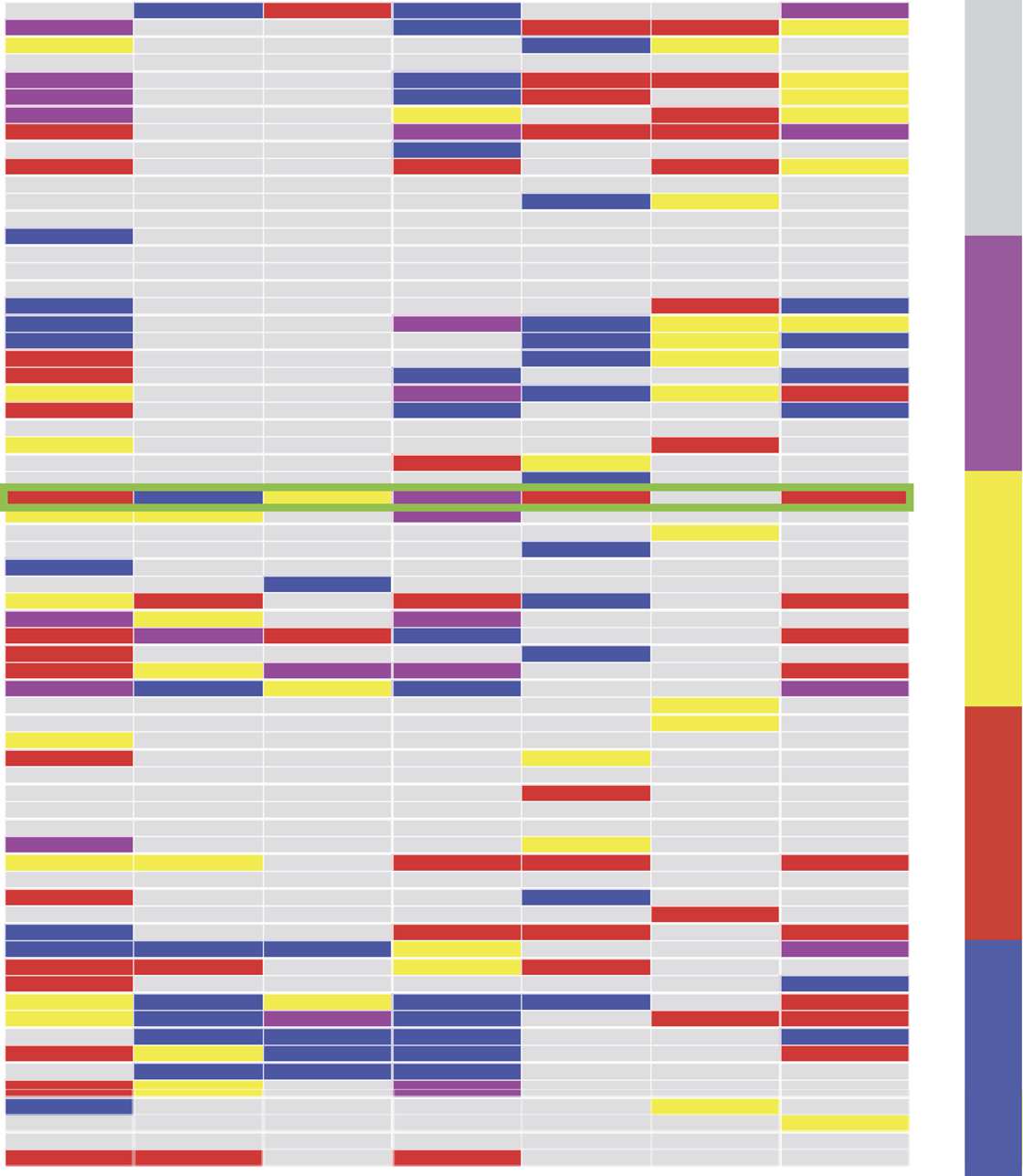
Figure 2. Temporal network visualization. Evolution of the information sharing temporal net-
work computed for one of the recordings, represented using the visualization toolbox TACOMA
(http://tacoma.benmaier.org/about.html). The six networks on the top plots represent
six snapshots of the network’s evolution at the corresponding times: Each black dot represents a
neuron whose activity has been recorded at the corresponding time. The bottom panel displays the
temporal network’s edge activity plot: Each row of the plot represents the activity of one edge of the
network, i.e., a black dot on a row means that the corresponding edge on the vertical axis is active
(a nonzero element of the network’s adjacency matrix) at the corresponding time on the horizontal
axis. The edges are ordered on the vertical axis by increasing value of their first activation time.
defined for each time window a binarized version of the network snapshot, whose adjacency
matrix is only composed of zeros and ones: The adjacency matrix element is 0 (no link is
present in the unweighted network) when two nodes are not connected (i.e., MI below thresh-
old) and it is equal to 1 when they are (MI above threshold, see Methods). By comparing
weighted and unweighted analyses we could assess whether the network changes involve ac-
tual evolutions of the structures of the links or rather correspond only to weight modulations
on a stable link structure. To quantify the dynamics of the network, we focused on two main
aspects—translated into corresponding temporal network features in both weighted and un-
weighted versions—aimed at answering two different questions. First, are the connections of
the network stable in time, or rapidly changing? Second, does the network have a clear and
specific structural organization, and if so, is it persistent in time or unstable and only transient?
In order to answer the first question, we quantified, for each neuron i, how much its neigh-
borhood changed between successive time windows (Gelardi et al., 2019; Miritello et al.,
2013; Stehlé, Charbonnier, Picard, Cattuto, & Barrat, 2013; Valdano et al., 2015). To this aim
we computed for each i and at each time t the cosine similarity Θi(t) between the neighbor-
hoods of i (the subgraphs composed only by the edges involving i) at time t − 1 and at time
t. To analyze the unweighted temporal networks, we instead used the Jaccard index Ji(t) be-
tween these successive neighborhoods (see side jargon boxes for precise definitions). Values
of these quantities close to or equal to 1 suggest that the node has not changed neighbors in
successive time windows: hence its neighborhood shows low liquidity (elsewhere, it would be
said that the node shows high “loyalty,” Valdano et al., 2015). On the contrary, values close
951
cosine similarity Θi(t):
The cosine similarity between a node
i’s neighborhoods at times t − 1 and t
is defined as
Θi(t) ≡
∑j wij(t − 1)wij(t)
q∑j wij(t − 1)2
q∑j wij(t)2
,
where wij(t) is the weight of the link
between nodes i and j at time t.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Jaccard index Ji(t):
The local Jaccard index for node i at
time t (Figure 1C) is defined as
Ji(t) ≡
|νi(t − 1) ∩ νi(t)|
|νi(t − 1) ∪ νi(t)|
,
where νi(t − 1) and νi(t) are the
neighborhoods of node i at times
t − 1 and t, respectively. Ji(t) = 0
when νi(t − 1) and νi(t) are two
disjoint sets of nodes, while Ji(t) = 1
when the two sets are identical.
coreness coefficient Ci(t):
In a static, unweighted, undirected
network, the coreness Ci of node
i ∈ [1, N] is a real number between 0
and 1, interpreted as follows: When
Ci ∼ 1 the node belongs to the core
of the network, i.e., a set of tightly
connected nodes; when Ci ≃ 0 the
node belongs instead to the network’s
periphery, i.e., is only loosely linked
to the rest of the network.
to or equal to 0 mean that the neuron has completely changed neighbors between subsequent
times: Its neighborhood is highly liquid. At each time t, the set of cosine similarity values
Θi(t), i ∈ [1, N] and the Jaccard index values Ji(t), i ∈ [1, N] (for the unweighted case) form
the time-dependent feature vectors Θ(t) and J(t), each of dimension N (Figure 1D).
In order to answer the second question and probe for the presence of specific network ar-
chitectures, we considered the core-periphery organization of the graph. This way of charac-
terizing the information sharing network snapshots was suggested to us by the visual inspection
of their spatial embeddings, some of which are represented in Figure 2. We thus computed
the coreness coefficient Ci(t) of each node i in each snapshot t, using the definition of core-
ness introduced by Della Rossa et al. (2013), which quantifies how peripheral or centrally
integrated each node is in the network (see Methods and side jargon box). We thus obtain a
time-dependent vector C(t) of dimension N by computing at each time t the coreness Ci(t)
for each node i ∈ [1, N] in the network of time window t. The computation of coreness coeffi-
cient can also be performed for weighted networks (Della Rossa et al., 2013), yielding a time
series of vectors {Cw(t)|t ∈ [0, T]} (with Cw(t) = {Ci
w(t), i ∈ [1, N]}).
Information Sharing Networks Have a Soft Core-Periphery Architecture
In order to investigate the core-periphery organization of the information sharing networks,
we looked at the distributions of the instantaneous coreness values Ci(t) over all neurons and
time frames. A weighted coreness distribution from a representative recording is shown in
Figure 3A (see Supporting Figure S2 for equivalent unweighted coreness analyses). Figure 3B
moreover displays instantaneous distributions of the weighted coreness, for the same recording
and for several time frames. We found that, within each time frame, a majority of neurons
had low coreness values, that is, they were peripheral nodes in the instantaneous sharing
network (red color in the cartoons of Figure 3A), while fewer neurons had high coreness values.
Interestingly, in most recordings there was not a sharp separation between core and periphery.
On the contrary, we generically observed the presence of a smooth distribution spanning all
possible coreness values. The transition between core and periphery was thus smooth, without
gaps but with neurons displaying gradually less tight links with the core, without yet being
fully peripheral. We note that such smooth distributions are actually encountered in many
systems (Della Rossa et al., 2013), a strict distinction between a very central core and a very
loose periphery being only a schematic idealized vision and real networks displaying typically
hierarchies of scales and local connectivities.
We moreover compared this empirical soft core-periphery structure with one of three dif-
ferent null models, that is, randomized versions of the data that preserve, at each time slice,
increasing amounts of the empirical data structure (see Methods): The first null model preserves
only the numbers of nodes and edges at each time step; the second preserves in addition the
degree of each node at each time; the third shuffles randomly link weights over an otherwise
fully preserved connectivity structure. As shown by Supporting Figure S3, the distributions of
node coreness were strongly modified for all three null models, with substantially reduced or
suppressed counts of nodes with large coreness values with respect to the empirical distribu-
tions. This means that null models do not display the core-periphery structure found in actual
data, in particular no core is found in these null models. Therefore, the empirically found
core-periphery structure is not due to simple local properties (which are preserved in some of
the randomized versions) but encodes nontrivial higher order correlations.
Network Neuroscience
952
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
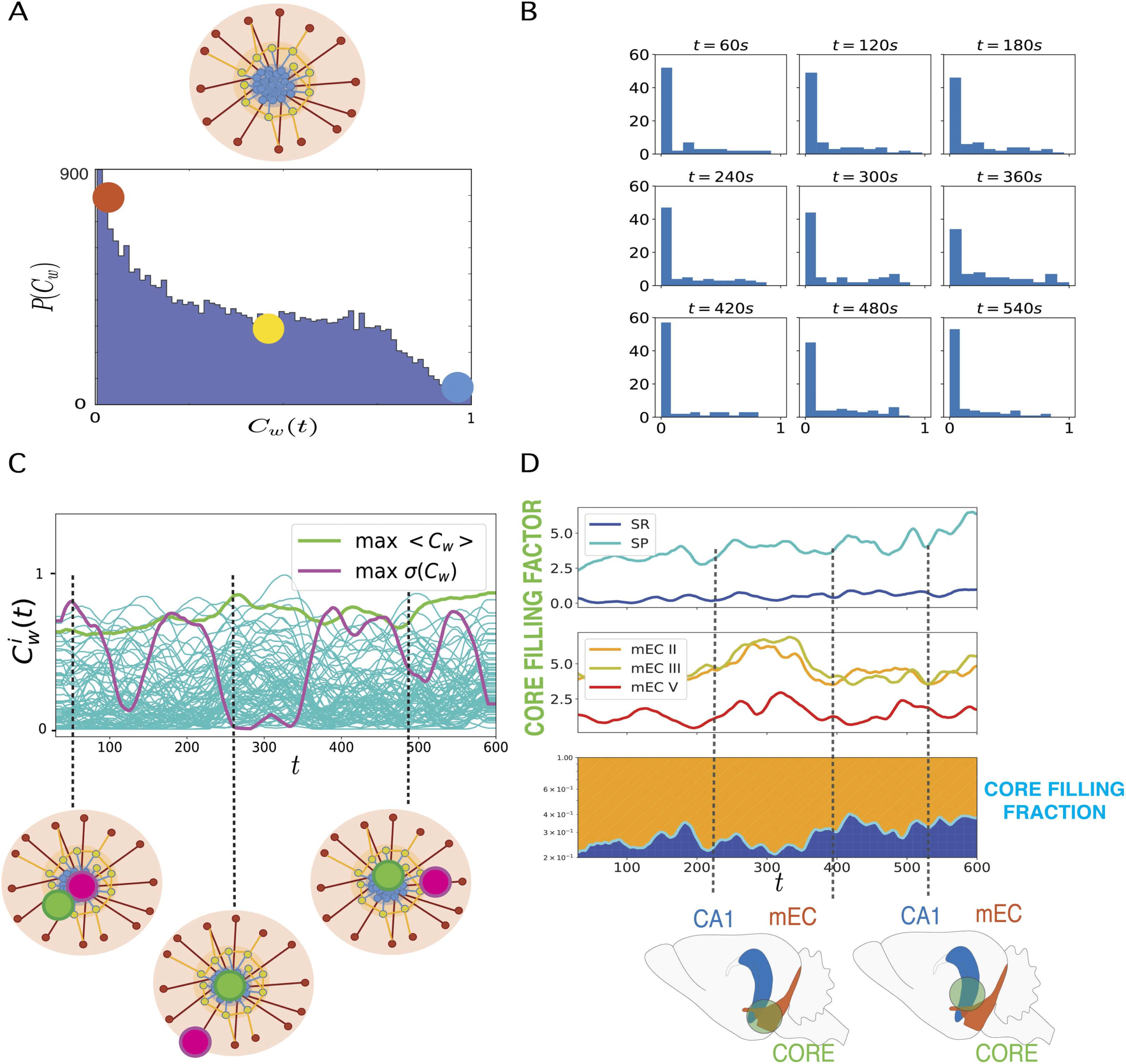
The analyses of Figure 3A and 3B indicate that at any time frame the sharing network has
a soft core-periphery architecture, but they do not inform us about how individual neurons
evolve in time within this architecture.
In order to follow dynamic changes in the coreness
of individual neurons, we studied the time evolution of this feature for each neuron of each
recording. In Figure 3C we plot the coreness Ci
w(t) versus time, for each node i ∈ [1, N] of a
representative recording. The two highlighted lines in the figure represent the coreness evolu-
tion of two particular nodes. In light green, we show the instantaneous coreness of the node
with maximum average coreness hCi
w(t)iT (averaged over the recording length T). The fig-
ure shows clearly that this neuron’s instantaneous coreness is always large: The corresponding
neuron is persistently part of the network’s core throughout the whole recording. This contrasts
with the purple line, which displays the instantaneous coreness of the neuron with largest core-
ness standard deviation (σ(hCi
w(t)iT)): The curve fluctuates from high to low coreness values,
indicating that the corresponding neuron switches several times between central core positions
in the network and more peripheral ones. The contrast between these two behaviors is high-
lighted in the cartoon at the bottom of Figure 3C. Note that even in the randomized versions
of the data, coreness values of a given node fluctuate (see Supporting Figure S3) as, in partic-
ular, disconnected nodes have zero coreness. The range of fluctuations is however reduced
with respect to the original data, since the maximum coreness values are themselves much
smaller.
The continuous range of observed instantaneous coreness values and the fluctuations in
individual coreness values indicate that the set of most central neurons changes in time. We
thus examined whether some regions were contributing more than others to this core. To this
aim, we define the core, at each time frame, as the set of neurons whose instantaneous coreness
lies above the 95th percentile of the distribution (in histograms such as those in Figure 3B). In
Figure 3D we then plot the core filling factors of the CA1 and mEC layers (top and center plots,
respectively). We define the core filling factor of each region as the percentage of the overall
number of neurons of the recording located in that region that belong to the core. We plot
the time evolution core filling factors separately for neurons located in different hippocampal
CA1 layers (light and dark blue lines, top panel) and for neurons in different medial entorhinal
cortex (mEC) layers (red, orange, and yellow lines, center panel). The figure illustrates that the
core filling factors vary substantially through time. In the example shown here (corresponding
to the same recording as in Figure 3C), the core filling factor of CA1 stratum pyramidale (SP)
neurons belonging to the core increases from ∼ 2% to near 7% during the recording.
The results of Figure 3D indicate that the core is not restricted to neurons belonging to
a specific region, but is generally composed of both neurons belonging to EC and neurons
belonging to CA1. We remind indeed that our networks are networks of functional connectivity
and do not have to reflect necessarily the underlying anatomical connectivity (for which it
would be unlikely that our recordings pick up monosynaptically connected cells between
different regions). However, the participation of CA1 and EC neurons to the core is changing
through time and, as a result, the core is sometimes “more on the EC side” or “more on the
CA1 side” (see lower cartoons in Figure 3D). To visualize the relative fractions of core neurons
belonging to the two different regions, we computed and show in the bottom panel of Figure 3D
the normalized core filling regional fractions: The fraction of core nodes belonging either to
EC (orange) or CA1 (blue)—the sum of these two fractions adding up to 1. The orange and
blue bands change thickness through time, reflecting in this recording a progressive shift from
a low to a higher involvement of CA1 neurons in the core. This variation of the multiregional
core composition may reflect changes in the way the different regions control information
integrative processes (see Discussion).
Network Neuroscience
953
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Dynamic core-periphery structure. (A) Top: Cartoon representing the core-periphery
organization of the network with core nodes colored in blue and peripheral nodes in red. Bottom:
Histogram of the values of the instantaneous weighted coreness Ci(t) of each neuron at each time
of a recording: The most frequent values of Ci
w(t) are close to 0 (red dot), hence coreness values
typical of peripheral nodes, whereas coreness values of core nodes, Ci(t) ∼ 1 are rare (blue dot).
(B) Histograms of instantaneous weighted coreness values of the neurons in several individual time-
frames (every 60 s). The different histograms show that the picture of a majority of neurons with low
coreness value and few neurons with high coreness hold at all times. The core-periphery organiza-
tion of the information sharing network is thus persistent in time. (C) Plot of the temporal evolution
of the weighted coreness Ci
w(t) of each node i in a specific recording: The green line highlights the
evolution of the coreness of the node with highest average coreness hCw(t)imax (time average over
the whole recording); the purple line corresponds to the node whose coreness fluctuates the most
(node of maximum variance of Ci
w(t)). We show below this plot a cartoon of the core-periphery
organization of the network, where we illustrate how the former node steadily belongs to the core,
while the latter node evolves several times from the core to the periphery and back. (D) Plots of
the core filling factor (top and center panels) and of the core filling fraction (bottom) of the different
layers of hippocampus (HPC) and medial entorhinal cortex (mEC). The core filling factor of each
layer is the percentage of nodes of each layer that are located in the core (nodes above the 95th
percentile of coreness values).
In the bottom panel, the green line represents the separation be-
tween the fraction of core nodes located either in the mEC layers (orange) or in the HPC (blue): the
core filling fraction. The cartoon below the core filling fraction plot illustrates how the neurons that
belong to the core at different times can be located in different anatomical structures.
Network Neuroscience
954
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Network States
As previously mentioned and summarized in Figure 1C, for each recording and each time win-
dow t, we computed for each neuron i ∈ [1, N] several temporal network properties, tracking
notably the “liquidity” of its neighborhood (Jaccard index and cosine similarity) and its posi-
tion within the core-periphery architecture (weighted and unweighted instantaneous coreness
values). To investigate how these properties change dynamically at the global network level,
we computed for each of these four quantities the correlation between their values at different
times, obtaining four correlation matrices of size T × T. For instance, the element (t, t′) of
the unweighted liquidity correlation matrix is given by the Pearson correlation between the N
values of the Jaccard coefficient computed at t {Ji(t), i ∈ [1, N]} and the N values computed
at t′ {Ji(t′), i ∈ [1, N]} (see Methods for definition). In Figure 4A, we show these four corre-
lation matrices for a representative recording, two for the unweighted features (above, Jaccard
index and unweighted coreness), and two for the weighted ones (below, cosine similarity and
weighted coreness).
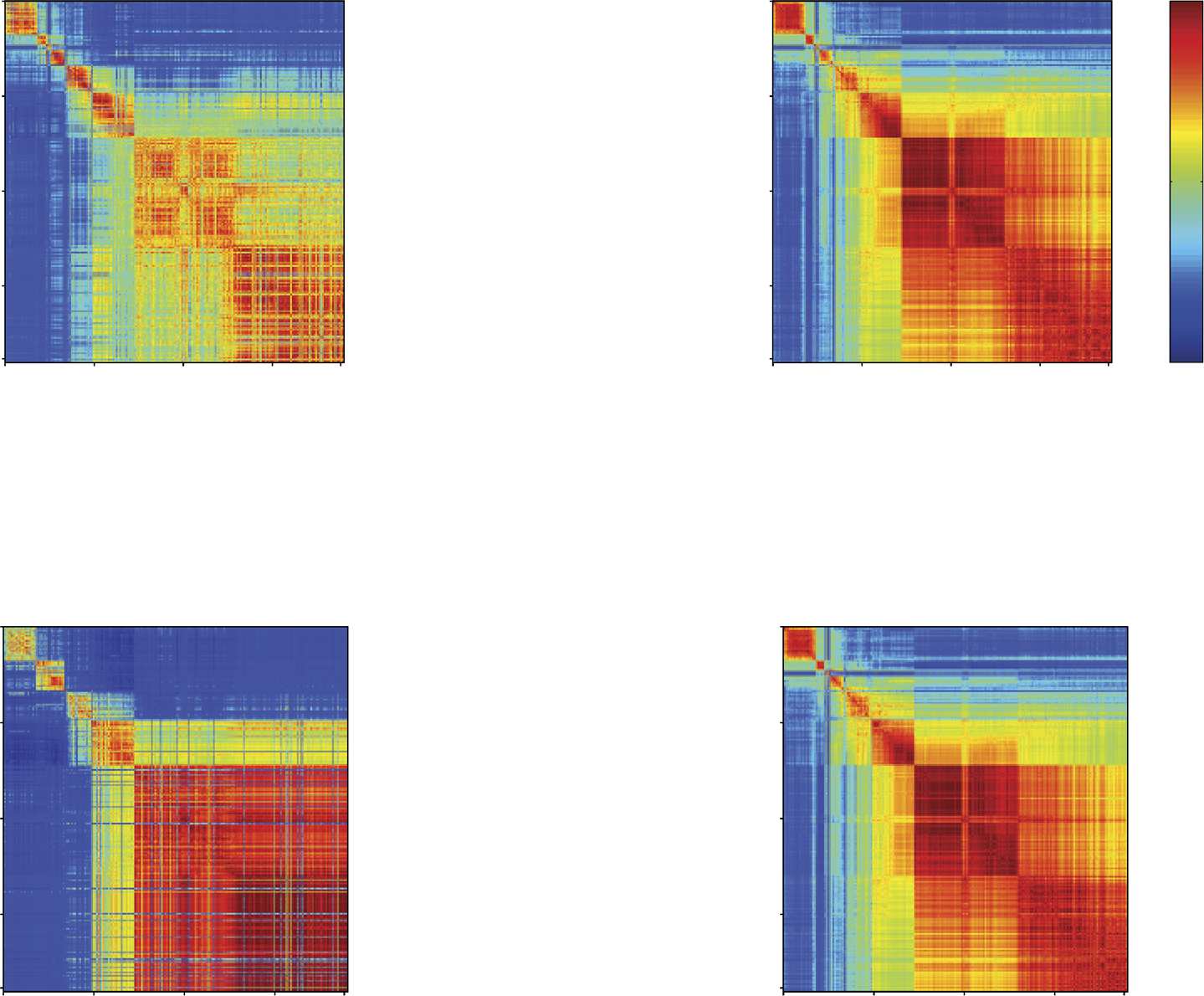
The block-wise structure of these correlation matrices suggests the existence of epochs in
time where neurons’ feature values are strongly correlated (red blocks on the diagonal). In the
case of Figure 4A, mostly diagonal blocks are observed, with low correlation values outside
the blocks, meaning that the network configurations are similar during each epoch but very
different in different epochs. In other cases, we sometimes observe as well off-diagonal blocks,
indicating that the network might return to a configuration close to one previously observed
(we show an example of this behavior in Supporting Figure S4, as well as an example in
which only one epoch is observed). Each block on the diagonal (epoch in which the node
properties are strongly correlated) can be interpreted as a network connectivity configuration
associated with specific liquidity and coreness assignments of the various neurons. We call
these configurations network states.
To quantitatively extract such discrete network states, we use the time series of the feature
vectors Θ(t), J(t), Cw(t), and C(t). We concatenate these vectors two by two at each time,
obtaining two 2N-dimensional feature vectors: The first one contains at each time the values of
the unweighted liquidity and coreness of all nodes ({J(t), C(t)}), and the second one contains
the corresponding weighted values ({Θ(t), Cw(t)}). We then perform in each case (weighted
and unweighted) an unsupervised clustering of these T 2N-dimensional feature vectors. As
a result of this clustering procedure, as shown in Figure 4A, we obtain a sequence of states
(temporal clusters of the feature vectors) that the network finds itself in at different times (yellow
state spectrum for the unweighted case, red for the weighted case).
We also observe that these states are not a mere artificial construction. Our procedure
would segment the temporal network into states even if discretely separated clusters did not
exist, but we explicitly checked that, for all recordings but two, clustering was meaningful:
Supporting Figure S5A shows indeed that clustering quality was in a large majority of cases
well above chance level (see Methods). Furthermore, when repeating the same analysis on the
three null model, as shown in Supporting Figure S6A, we found that the quality of the cluster-
ing performed on the features vectors to extract the network states decreased sensibly for the
randomized networks (Supporting Figure S6B). This shows that empirical temporal networks
display a nonrandom level of structuration into connectivity states.
We compared the network states spectra found for the weighted and unweighted case by
computing the mutual information between the two sequences of states for each recording,
normalized by the largest entropy among the entropies of the two distinct sequences. Such
Network Neuroscience
955
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
relative mutual information is bounded in the unit interval and quantifies the fraction of infor-
mation that a state sequence carries about the other (reaching the unit value when the two state
sequences are identical, and being zero if the two sequences are statistically independent). We
compute this quantity for each recording and display the distribution of values obtained as a
light green boxplot on the left of Figure 4B. This boxplot shows that the mutual information
values between the weighted and unweighted network states sequences of a recording are
concentrated around a median approaching 0.8. Therefore, the spectra of network states ex-
tracted by the weighted and unweighted analyses are generally matching well, indicating the
robustness of their extraction procedure. Most importantly, the high degree of matching be-
tween weighted and unweighted analyses confirms that network state changes correspond to
actual connectivity reorganizations (as revealed by unweighted analyses) and not just to weight
modulations on top of a fixed connectivity.
One may also wonder whether network state changes really depend on changes of local
connectivity properties (as we implicitly assumed with our use of node-specific features) or
can be already explained by variations of global network properties. We therefore consid-
ered as well the time evolution of several global features (see Supporting Figure S7A): the
node-averaged cosine similarity (Jaccard index in the unweighted case); the node averaged
coreness; the sum over all weights of all edges (number of edges in the unweighted case). We
then extracted network states based now on these global features (see Methods) and compared
the resulting state spectra with the original ones. Computing the amount of mutual information
between spectra based on global and local features, we found that some degree of correlation
exists, not surprisingly since the numbers of links and nodes themselves fluctuate in time, in
a way preserved by null models and thus contributing to state switching dynamics. However,
as shown by Supporting Figure S7B, for both weighed and unweighted state extraction anal-
yses, the relative mutual information between global and local features-based states is of the
order of only ∼40%. Furthermore, the mutual information between weighed and unweighted
global features-based states drops to ∼50%, while it approached ∼80% for local features-
based states. Together, these reduced values indicate that the consideration of local features
genuinely provides additional information on top of global features fluctuations and that this
information is useful to determine more consistent states.
As previously discussed, the system undergoes switching between two possible global brain
states during the anesthesia recordings: These global states are associated with different oscilla-
tory patterns, dominated by either theta (THE) or slow (SO) oscillations. We studied the relation
between changes in the network state and global oscillatory state switching. To this aim, we
computed the normalized mutual information between network state sequences (weighted or
unweighted) and global state sequences. The distributions of the values obtained are shown as
boxplots on the right of Figure 4B, for both weighted (red) and unweighted (yellow) network
state sequences. In both cases, we detect positive, although low, values of the relative mutual
information with global oscillatory states, with a median value close to ∼ 0.3. This indicates
that some coordination between global oscillatory state and network state switching exists but
that oscillatory state switching does not well explain network state switching. A very simple
reason for this poor correlation is that, while there are just two main global oscillatory states
(see, however, Discussion), the number of network states is not a priori limited. In fact, the
statistics of the number of network states in the different recordings, shown in Figure 4C, indi-
cate that in many recordings we could extract at least three network states and sometimes up
to seven. Therefore, network state switching can occur within each oscillatory global state.
Nevertheless, it is possible that each given network state would tend to occur mostly within
one specific global oscillatory state. To check whether this is the case, we computed for each
Network Neuroscience
956
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
network state the fraction of times that this state occurred during THE or SO epochs. We show
in Figure 4D the histograms of these time fractions, measured over the set of all network states.
The light blue histogram corresponds to the fractions of time a network state manifested itself
during the THE state (the dark blue histogram gives the same information but for the SO state).
Both histograms are markedly bimodal, indicating that a majority of states occur during either
the THE or the SO states, but not in both. In other words, network states are to a large degree
oscillatory state specific. Therefore, the global oscillatory states do not fully determine the
observed coreness and liquidity configurations (there may be several network states for each
of the oscillatory states), but most network states can be observed only during one specific
global oscillatory state and not during the other.
Connectivity Profiles and Styles
To refine our analysis, we now investigate and characterize the temporal network properties
at the level of single neurons within each of the detected network states. In order to do so,
we computed, for each node and in each state, a set of dynamical features averaged over
all time frames assigned to the specifically considered state. We focus here on the weighted
features, since the weighted and unweighted analyses provide similar results. The state-specific
connectivity profile of a given neuron i in a given state included first the following:
its state-averaged weighted coreness value;
its state-averaged cosine similarity value.
Note that analogous time-resolved features were already used for network state extraction,
but that we consider here state-averaged values. We also computed four additional network
state-specific features, defined as follows for each node i ∈ [1, N] in a state h spanning the set
of times Th (see explanatory cartoons in Figure 5A):
the state-averaged strength hsi(t)it∈Th ≡ h∑j wij(t)it∈Th, hence the state-averaged total
instantaneous weight of the connections of i;
the activation number ni
a, the number of times that the strength of node i changes from
0 to a nonzero value within the state, hence it gives the number of time that i changes
its connectivity from being isolated to being connected to at least one other neuron;
the total connectivity time τi, the number of time frames within Th in which i is connected
to at least one other neuron;
the Fano factor Φi ≡ σ(h∆tiih)
a periods in which i is connected to at least
h∆tiih
one other neuron has a certain duration ∆ti (the sum of these durations is τi), and Φi,
the ratio of the variance and the average of the different connectivity durations of i over
the state h, quantifies whether these durations are of similar value or are very diverse.
; each of the ni
Each neuron’s temporal properties within a given state are thus summarized by the values of
these overall six features, which define the neuron’s state-specific connectivity profile as a six-
dimensional vector. Normalizing all the features to have values between 0 and 1, connectivity
profiles can be visually represented as radar plots (Figure 5B) in which the value of each feature
is plotted on the corresponding radial axis.
After computing the connectivity profile of each node, in each network state and in each
recording, we performed an unsupervised clustering (using K-means clustering) over all these
six-dimensional connectivity profiles in order to identify categories of these profiles, which
Network Neuroscience
957
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4.
Liquidity and coreness network states. (A) For each recording, the feature vectors of liquidity and coreness described in Figure 1D
are combined at each time, obtaining time-dependent vectors of dimension 2N: {J(t), C(t)} in the unweighted case, {Θ(t), Cw(t)} for the
weighted case. K-means clustering of these vectors yields for each recording a sequence of network states visited by the network (center
panels). We show on both sides of the network state sequences the correlation matrices (C.M.) of the various feature vectors (unweighted
coreness and Jaccard, weighted coreness and cosine similarity): Each element (t, t∗) of a matrix is the Pearson correlation coefficient between
the corresponding feature vectors computed at times t and t∗. For instance, the cosine similarity C.M. has as element (t, t∗) the Pearson
correlation between the list of values of the cosine similarity (weighted liquidity) of nodes at times t and t∗, {Θi(t), i = 1, . . . , N} and
{Θi(t∗), i = 1, . . . N}. (B) Left panel: Distribution of the values of the mutual information between the weighted and unweighted network
states spectra of all recordings: The mutual information between the two spectra is high, showing that the two spectra are highly correlated
for all recordings. Right panel: Distribution of the values of mutual information between the weighted network states spectrum and the global
oscillating states spectrum (red boxplot) for all recordings (yellow boxplot: same for the unweighted network states spectra). (C) Statistics of
the number of network states in the different recordings. In many recordings this number is larger than 2, and it can reach values as large
as 7. (D) Histograms showing the percentage of states having probability p to occur during a specific global oscillation state, slow (blue) or
theta (light blue). Both histograms are bi-modal, hence the majority of states are strongly global-state-specific; the blue histogram shows an
abundance of states (∼ 23%) most likely to occur during the slow global oscillations.
we call connectivity styles. With this approach we uncovered the existence of four general
connectivity styles that a neuron can manifest within a network state:
Core style (or “streamers”), a class of nodes of high average coreness, average strength,
average cosine similarity, total connectivity time, and low activation number na and Fano
Network Neuroscience
958
Dynamic core-periphery networks in entorhinal cortex and hippocampus
factor Φ: overall, a class of rather central neurons with numerous stable connections that
are persistently connected within a state (blue representative polygon in Figure 5B). A
behavior similar to that of a speaker of an assembly, continuously conveying information
to the same, and many, people: a “streamer” of information;
Peripheral style (or “callers”), nodes with high activation number and total connectivity
time but low strength, Fano factor, and coreness: a class of peripheral nodes that are
periodically connected in numerous events of similar connectivity durations and low
weights within a state, whose connections are neither completely liquid nor completely
stable (red representative polygon in Figure 5B). A behavior similar to a customer or guest
regularly making short calls to trusted core members to be updated on the latest news:
aka, a “caller.”
Bursty and regular core-skin style (or “freelancer helpers” and “staff helpers”), two
classes of connectivity profiles both characterized by nodes with intermediate coreness
and strength and high values of cosine similarity and total connectivity time, whose dif-
ference lies in the values of the Fano factor Φ: the former (yellow representative polygon
in Figure 5B) displaying high values of Φ can therefore be interpreted as a class of nodes
that have stable connections, that are active for a long time yet with highly varying con-
nectivity times; the latter (purple representative polygon in Figure 5B) is characterized
instead by low values of the Fano factor, hence the connectivity durations of these nodes
do not fluctuate much. The behaviors of these neurons can be assimilated to the one
of external experts assisting core staff in a company, with either regular work schedules
(the regular core-skin neurons could then be seen as “staff helpers”) or sporadically and
irregularly (the bursty core-skin neurons could then be seen as “freelancer helpers”).
Note that we also identified (and subsequently discarded) an additional “junk” cluster with
relatively fewer elements (9.7% of the total number of connectivity profiles computed for all
neurons in all recordings) and small values of all features. We thus removed these cases,
as usual in unsupervised clustering applications (Forsyth, 2018), to better discriminate the
remaining “interesting” classes listed above.
Overall each connectivity profile (one for each neuron in each possible network state in the
associated recording) was categorized as belonging to one of the above connectivity styles,
according to the output cluster label assigned by the unsupervised clustering algorithm. How-
ever, a substantial diversity of connectivity profiles subsists within each of the clusters. We
therefore considered as well a soft classification scheme, which quantifies the degree of re-
lation of each individual connectivity profile with the tendencies identified by each of the
different connectivity style clusters. Concretely, we trained a machine learning classifier to
receive as input a connectivity profile and predict the connectivity style assigned to it by this
unsupervised clustering. In this way, after training, the classifier assigned to each connectivity
profile a four-dimensional vector whose elements represented the probabilities of belonging
to any one of the four possible connectivity styles (see Methods for details). In Figure 5C, each
connectivity profile is represented as a dot with as coordinates the soft classification labels pro-
duced by the classifier, that is, the probabilities that each given connectivity profile belongs
to the periphery, core-skin (summing the probabilities for the bursty and regular subtypes), or
core connectivity styles. This plot reveals, on the one hand, the existence of a gap between
core (blue) and periphery (red) connectivity profiles: In other words, connectivity profiles that
are likely to be classified as of the “streamer” type are very unlikely to be classified as being
of the “caller” type, stressing the radical difference between these two connectivity styles. On
the other hand, both the core and the periphery connectivity styles display some mixing with
the core-skin style, as made clear by the almost continuous paths of connectivity profiles
Network Neuroscience
959
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
from the core (blue) to the core-skin (yellow) and from the core-skin to the periphery (red).
This means that there is a continuum spectrum of connectivity profiles interpolating between
“streamers” and “helpers” on one side and “helpers” and “callers” on the other. The poly-
gons shown in Figure 5B are on the contrary archetypal (in the sense introduced by Battaglia,
Karagiannis, Gallopin, Gutch, and Cauli [2013]). These archetype profiles manifest in an ex-
treme manner the tendencies inherent to their connectivity style. This is reflected by the fact
that they lie at the vertices of the bounded soft membership space represented in Figure 5C.
They display thus strong similarity to just one connectivity style, which they epitomize even
better than the centroids of the associated connectivity style cluster, having near zero chance
of being misclassified (cluster centroids are shown for comparison in Supporting Figure S5B).
We finally checked whether the different connectivity styles were adopted more or less
frequently by neurons in specific anatomical locations or of specific types (excitatory or in-
In Figure 5D, we plot the number of connectivity profiles assigned to each style
hibitory).
(colors as in Figure 5B), separating them by anatomical layer and by brain region. However,
since we recorded unequal numbers of cells in the different layers (see Supporting Figure S1),
we also accounted for the different numbers of cells and recordings per layer and estimated
chance-level expectations for the connectivity style counts in each layer: this allowed us to
detect significant over- or underrepresentation of certain styles at different locations. The num-
bers of “streamers” (core), “staff helpers” (regular core-skin), and “callers” (periphery) profiles
were compatible with chance levels at all the recorded locations. We only detected over-
representations (green upward triangles) of “freelancer helpers” (bursty core-skin) in stratum
radiatum (SR) of CA1 and Layer II of medial entorhinal cortex, and an underrepresentation
(red downward triangle) of this style in Layer III of medial entorhinal cortex (see Discussion for
possible interpretations). These moderate deviations from chance levels suggest that the con-
nectivity styles adopted by different neurons (and thus their centrality in the core-periphery
architecture of information sharing networks) are only poorly affected by their anatomical lo-
cation in the hippocampal formation circuit, in apparent contrast with the widespread belief
that the “hubness” of neurons should be strongly determined by structural and developmental
factors (Cossart, 2014).
We found however a stronger interrelation between cell type and connectivity styles
(Figure 5D, bottom). We still found representatives of any of the connectivity styles among both
excitatory and inhibitory neurons. However we found that the fraction of inhibitory (resp., ex-
citatory) neurons among the core neurons was significantly above (resp., below) chance level.
Conversely, the fraction of inhibitory (resp., excitatory) neurons among the peripheral neurons
was significantly below (resp., above) chance level (see Discussion).
Connectivity Profiles Are Network State–Dependent and Not Only Node-Dependent
We have computed connectivity profiles per neuron and per network state, in order to enable
the detection of a possible network state dependency of the temporal properties of the neurons’
connectivity. However, the state specificity of this computation does not prevent a priori a
neuron to always assume the same connectivity profile across all possible network states in
which it participates. It is thus an open question whether connectivity profiles are only node-
dependent (for a given neuron, the same in every state) or, more generally, state-dependent
(for a given neuron, possibly different across different network states).
To answer this question, we checked whether network state transitions are associated with
connectivity style modifications at the level of individual neurons. We found that changes in
the connectivity style of a neuron upon a change of state are the norm rather than the exception.
We computed for every neuron the index η, quantifying the diversity of connectivity styles that
Network Neuroscience
960
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
wih, average liquidity hΘiih, average strength hsiih, connectivity number ni
Figure 5. Connectivity profiles. (A) Cartoons illustrating the features: The strength si(t) of a node i at time t measures the global importance
of node i’s connections (the cartoon shows a comparison of low vs. high values of si(t)); its liquidity, hence the cosine similarity (Jaccard
index in the unweighted case) between successive neighborhoods (the cartoon illustrates a change between the neighborhood of i at successive
times); its coreness; the connectivity number ni
a and total connectivity time τi of node i in a state: τi represents the number of time frames
in which neuron i is connected to at least one other neuron, and ni
a is the number of times that i switches from being disconnected to being
connected to at least one other neuron; the Fano factor quantifies the fluctuations of the durations of the ni
a periods in which i is connected.
(B) The connectivity profile of each neuron i in a state h is a 6-dimensional vector whose components are its state-averaged features: average
coreness hCi
a, total connectivity time τi, Fano factor Φi. Clustering
of all the connectivity profiles yields four connectivity styles that we represent here as radar plots. We identify four main styles: core (blue),
periphery (red), bursty core-skin (yellow), and regular core-skin (magenta), with different distinctive values of the different features composing
the connectivity profile. Shown here are radar plots for the connectivity profile of archetypal cells in each of the connectivity styles (see Results
for details). (C) 3D plot of the connectivity styles space: The three axes are the probabilities of the connectivity profile of a node in a network
state to belong to the periphery, core-skin, or core, respectively. (D) Histograms of the layer location (top plot) of the neurons exhibiting each
connectivity style (identified by the same color as panel B), and histograms of cell type (inhibitory and excitatory, bottom plot) populations
per connectivity style. A green upward arrow means that the connectivity style of the corresponding color is statistically overrepresented in
the corresponding layer or cell type, whereas a red downward arrow means that the connectivity style is underrepresented in that layer or cell
type.
Network Neuroscience
961
Dynamic core-periphery networks in entorhinal cortex and hippocampus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Network state specificity of connectivity profiles. (A) Histogram of the connectivity-style-
switching probability η of nodes, in the weighted (red) and unweighted (yellow) cases, computed
for each neuron in each recording. η is defined (see Methods) as the ratio between the number of
transitions between different connectivity styles in subsequent states of a neuron during the whole
recording and the maximum value between the total number of connectivity styles and number
of network states observed in the recording.
(B) Visualization as a weighted, directed graph of
the cross–network state connectivity style transition matrix. The color of an edge corresponds to
the color of the node from which it emanates. The width of an edge from connectivity style A
to connectivity style B is proportional to the probability of a neuron to switch from a connectivity
profile of connectivity style A in a state to a profile of connectivity style B in the next state. (C) Matrix
representation of the changes in connectivity styles of the neurons when the network changes state.
Each element (s, n) of the matrix is colored according to the connectivity style to which node n’s
connectivity profile belongs in state s. (D) Connectivity profile transitions of node n = 28, whose
evolution is characterized by transitions between profiles belonging to different styles, highlighting
how a given node can display radically different dynamical behaviors in different states.
a neuron assumes across the different network state transitions occurring during a recording.
Such an index is bounded in the range 0 ≤ η ≤ 1 and assumes the null value if the neuron
always remains in the same connectivity style (no style transitions); it takes the unit value if
the neuron changes connectivity style every time that a network state transition occurs, and it
assumes intermediate values if style transitions occur for some of the network state transitions
but not for all (see Methods). The distribution of the observed values of this η index is shown in
Figure 6A. This distribution is bimodal, with a first peak occurring around η ∼ 0.5 and a second
at η ∼ 1 (computed according to either unweighted or weighed network state transitions).
This means that almost no neuron was associated with a network state-independent, fixed
connectivity style. On the contrary, a large number of neurons changed connectivity style in
Network Neuroscience
962
Dynamic core-periphery networks in entorhinal cortex and hippocampus
at least roughly half of the network state transitions (first mode of the distribution), and many
changed style at almost each state transition (second mode of the distribution of η).
Figure 6B is a graph representation of the transition matrix between connectivity styles,
computed over all the observed connectivity style transitions. We plot here a weighted, di-
rected graph, in which the two connectivity styles “regular” and “bursty core-skin” have been
merged for simplicity into a single category. The width of each colored edge corresponds to
the value of the transition rate from the class of the same color. The transition rate is defined
as the probability that a node characterized by one of the three connectivity styles in one net-
work state switches to one of the other two connectivity styles in the successive network state.
Consistent with Figure 5C, we find that edges of large weight connect the core-skin to the pe-
riphery and to the core in both directions: high transition rates are found between these styles.
The edges connecting core and periphery are sensibly smaller. We can thus conclude that it
is largely more likely that neurons of a core connectivity profile switch to a core-skin profile
in the following network state than to a peripheral profile, and vice versa: Direct transitions
between core profiles and periphery profiles are not very likely to occur, although they are
not impossible. More complete transition graphs and tables (including as well the core-skin
class separation into “bursty” and “regular,” and the “junk” classes) are shown in Supporting
Figure S8. Individual neurons can thus float through the core-periphery architecture, descend-
ing from core towards periphery and ascending back into the core, via crossing the core-skin
styles.
The overall behavior of neurons’ switching styles between states is illustrated in Figures 6C
and 6D for a specific recording. The former is a matrix whose element (i, s) has the color of the
connectivity style exhibited by node i in state s. In this plot we highlight the row corresponding
to the state-wise evolution of a specific selected node, whose successive connectivity profiles
in the successive network state are shown in Figure 6D.
Connectivity Profiles Only Poorly Depend on Firing Rate
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
In our recordings we observed a diversity of firing rates between different single units. While
the median firing rate was close to ∼ 1 Hz, some neurons had, at specific moments, high
rates approaching 40 Hz, despite the anesthesia conditions.
Importantly, firing rates were
also changing across the different network states. To check whether variations of temporal
connectivity features compiled in the state-specific connectivity profiles of different neurons
could simply be explained by these firing rate variations, we constructed scatterplots of state-
specific coreness, liquidity, strength, number of activations, Fano factors, and total time of
activation for the different neurons against their firing rate, averaged over the corresponding
state. These scatterplots are shown in Supporting Figure S5C.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The degree of correlation between firing rate and connectivity features was at best mild.
Cells with larger than median firing rate tended to have slightly less liquid neighborhoods on
average, but the range of variation was broad and largely overlapping with the one of liquidity
values for lower firing rate neurons. Other features, such as total time of activation, displayed
an even weaker dependence on firing rate, while some others, such as the connectivity number,
tended to be inversely correlated with firing, but, once again, in a rather weak manner (the
correlation coefficient is ρ = −0.14).
Overall, the analyses of Supporting Figure S5C indicate that the structure of information
sharing networks is shaped by the coordination of firing between units more than by the firing
rates of individual cells.
Network Neuroscience
963
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Relations Between Connectivity Styles and Active Information Storage
We focused in this study on the dynamics of links of information sharing. Information sharing
can be seen as a generalized measure of cross-correlation between the firing activity of two
In Clawson et al. (2019), we analyzed as well active
different single units (see Methods).
information storage (Lizier, Atay, & Jost, 2012), a complementary measure, which can be seen
as a generalized autocorrelation of the firing activity of a single node (or, equivalently, to a self-
loop of information sharing connectivity). While information sharing quantifies the amount
of information in common between the present activity of a neuron and the past activity of
another, information storage is meant to capture the amount of information in the present
activity of a neuron that was already conveyed by its past activity (see Methods). In this sense,
neurons with a large value of information storage would functionally act as “memory buffers”
repeating in time the same information content (cf. Discussion).
In Clawson et al. (2019)
we found that information storage, as information sharing, is state-dependent and that some
cells, which we called therein “storage hubs,” display particularly large values of storage. We
checked here whether high storage cells manifest some preferential connectivity style.
We show in Supporting Figure S9 distributions of information storage values, separated ac-
cording to the connectivity style assumed by different neurons in each different network state.
We found that high storage is not associated exclusively with specific styles of connectivity.
On the contrary, cells with high storage could be found for any of the connectivity styles. The
overall larger storage values were found for core streamers cells. However, we could find high
storage cells even among the core-skin helpers and the periphery callers. Interestingly, distri-
butions of storage for core-skin and periphery styles were bimodal, including a peak at high
storage values (see Discussion for possible interpretations).
DISCUSSION
We have described here the internal organization of assemblies of neurons dynamically ex-
changing information through time, using a temporal network framework and developing ad-
equate tools for their analysis. In line with our previous study (Clawson et al., 2019), we found
a coexistence of organization, such as the existence of discrete network states, and freedom,
such as the liquid continuous reorganization of network neighborhoods within each state. The
rich information sharing dynamics we revealed in our anesthesia recordings in hippocam-
pus and entorhinal cortex cannot be explained merely in terms of transitions between global
brain states (here, alternations between “REM-sleep”-like THE epochs and SO epochs). On
the contrary, we found that each of the global state gives access to wide repertoires of possible
networks of information sharing between neurons. These network state repertoires are largely
global state-specific and are robustly identified using both weighted and unweighted network
characterizations.
We extracted here functional connectivity networks evaluating information sharing—that
is, time-lagged mutual information—between the firing of pairs of single units. This choice was
motivated by the fact that mutual information is relatively simpler to evaluate than other more
sophisticated and explicitly directed measures of information transfer (Schreiber, 2000), which
require larger amounts of data to be properly estimated. Using a simpler measure was thus bet-
ter suited to our need to estimate connectivity within short windows, to give rise to a temporal
network description. Although mutual information is a symmetric measure, the introduction of
a time lag makes our metric “pseudodirected” because information cannot causally propagate
from the future to the past. Therefore, sharing of information between the past activity of a
node i and the present activity of another node j could be indicative of a flow of information
Network Neuroscience
964
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
from i to j. When computing time-lagged mutual information between all directed pairs of
single units in our recording, we found however only a very mild degree of asymmetry. As
shown in Supporting Figure S8, most strong information sharing connections were very close
to symmetric, indicative of time-lagged mutual information peaking near zero-lag for these
connections. This finding corresponds to the early intuition that members of a cell assembly
share information via their tightly synchronized firing (Abeles, 1982; Hebb, 1949). Supporting
Figure S8 also shows that some of the more weakly connected pairs of neurons displayed a
varying degree of directional asymmetry, with the strongest imbalance found for cells with
a core connectivity style. However, the strengths of nodes with unbalanced pseudodirected
sharing were orders of magnitude smaller than for balanced nodes. Our choice to ignore asym-
metries thus appears well justified, as is the choice to use lagged mutual information rather
than more complex directed metrics.
A striking architectural property of the measured information sharing networks was their
core-periphery architecture. Such architecture was preserved at every time frame (as shown
in Figure 3B), although the coreness of individual neurons changed smoothly through time
even within states. This preservation of a global functional architecture despite the variation
of the specific realizations and participant neurons is reminiscent of “functional homeostasis”
observed in highly heterogeneous circuits that must nevertheless perform a crucial function
in a stable and efficient manner (Kispersky, Gutierrez, & Marder, 2011; Marder & Goaillard,
2006). What is important is that, at any time, a functional separation between “streamers,”
“helpers,” or “callers” exists, however which neurons specifically assume these roles and the
exact location of these neurons within the anatomical circuit (cf. Figure 5D) appear to be less
important.
Core-periphery organizations have been found in many social, infrastructure, communica-
tion, and information processing networks, with various types of coreness profiles, that is,
strong or gradual separations between the innermost core and the most peripheral nodes
(Della Rossa et al., 2013; Holme, 2005; Kojaku & Masuda, 2018; Puck Rombach, Porter,
Fowler, & Mucha, 2014). The dynamics of this type of structure has however barely been
tackled in temporal networks (Galimberti et al., 2018).
In neuroscience, such architecture
has been identified in larger-scale networks of interregional functional connectivity, during
both task and rest (Avena-Koenigsberger, Misic, & Sporns, 2017; Bassett et al., 2013; Battiston,
Guillon, Chavez, Latora, & Fallani, 2018; de Pasquale, Corbetta, Betti, & Penna, 2018), in line
with the general idea that cognition requires the formation of integrated coalitions of regions,
merging information streams first processed by segregated subsystems (Deco, Tononi, Boly, &
Kringelbach, 2015; Tononi, Edelman, & Sporns, 1998). Here, we find that a similar architecture
is prominent at the completely different scale of networks between single units within local
microcircuits in the hippocampal formation. The core-periphery architecture of information
sharing thus reflects dynamic information integration and segregation. Cells belonging to the
core form an integrated ensemble, within which strong flows of information are continually
streamed and echoed. At the opposite end of the hierarchy of connectivity styles, peripheral
neurons are segregated and perform transient “calls” toward “streamer” neurons in the core to
get updated and share their specific information contents.
Following Buzsáki (2010), a “syntax of information processing” would be enforced by
the spatiotemporal organization of neuronal firing. Our dynamic core-periphery architecture
is also ultimately determined by the coordinated firing patterns of many neurons. The fact
that these coordinated firing patterns invariantly translate into networks with a core-periphery
architecture can be seen as a proxy for the existence of a syntactic organization of information
Network Neuroscience
965
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
flows. In this self-organized syntax, peripheral neurons are in the ideal functional position to
act as “readers” of the contents streamed by the integrated cell assembly formed by core neu-
rons. Transitions between network states may act as the equivalent of bar lines, parsing the flow
of information into “words” or longer sentence blocks, spelled with an irregular tempo. In the
vision of Buzsáki (2010), roles such as the one of reader or chunking into informational words
would be a by-product of neuronal firing organization. We thus stress here once again that even
in our case the real “stuff” out of which sharing functional networks are made are spiking pat-
terns at the level of the assembly. The network representation provides however a natural and
intuitive visualization of the dynamics of these patterns. Coordinated firing events—and not
single neuron firing properties, cf. the poor correlations in Supporting Figure S5—are mapped
into network structures and changes of firing pattern into changes of connectivity style within
the network. The logical syntax of assembly firing is thus translated into a dynamic topological
architecture of sharing networks, which is easier to study and characterize.
In order to interpret the functional role of this emergent core-periphery organization, one
should elucidate the information processing roles played by individual neurons within this
network organization. An entire spectrum of possible roles may exist, mirroring the smooth
separation subsisting between core and periphery. Communication between core and periph-
ery can be helped by core-skin neurons, which sporadically connect to the core, transiently
expanding its size. Speculatively, such breathing of the integrated core may be linked to fluctu-
ating needs in terms of information processing bandwidth, analogous to dynamic memory al-
location in artificial computing systems. The possible algorithmic role of neurons with different
connectivity styles could be investigated using metrics from the partial information decompo-
sition framework (Wibral, Priesemann, Kay, Lizier, & Phillips, 2017). Beyond pseudodirected
sharing, it may be possible to identify neurons acting as active memory buffers displaying large
information storage (Lizier et al., 2012); neurons actively transfering information to others, as-
sociated with large transfer entropy (Schreiber, 2000); or, yet, neurons combining received
inputs into new, original representations, associated with positive information modification
values (Lizier, Flecker, & Williams, 2013). As previously said, we could at least quantify infor-
mation storage. In particular, as shown in Supporting Figure S9, subgroups of core-skin helpers
and periphery callers existed with high storage values, approaching the ones of storage hubs
within the core. Therefore, at least some of the core-skin or periphery cells transiently con-
nected to the core may play the role of ancillary memory units, “flash drives” sporadically
plugged in when needed to write or read specific information snippets. Unfortunately, the
number of coordinated firing events observed in our recordings was not sufficient for a reason-
able estimation of transfer or modification, beyond storage. We can nevertheless hypothesize
that core neurons are the workhorses of information modification, shaping novel informational
constructs via their integrated firing.
We found that the bursty core-skin style—the “freelancer helper” role—was over-represented
in SR of CA1 and Layer 2 of EC. SR receives inputs from hippocampus CA3 that are believed to
be linked to retrieval of previously encoded associations (Hasselmo & Stern, 2013; Schomburg
et al., 2014). CA3, an associative memory module crucial for retrieval, receives inputs on its
turn from layer 2 of EC. The overrepresentation of the bursty core-skin style in SR and Layer 3
of EC may thus be compliant with our intuition of “helpers” as additional on-demand storage
resources, plugged to the core when needed to read the specific contents buffered by their spik-
ing. On the contrary, Layer 3 of EC, which sends inputs to stratum lacunosum-moleculare of
CA1, would rather mediate encoding than retrieval (Douchamps, Jeewajee, Blundell, Burgess,
& Lever, 2013; Schomburg et al., 2014). Correspondingly, in Layer 3 of EC the overrepre-
sentation of freelancer helpers observed in Layer 2 is replaced by an underrepresentation,
966
Encoding and retrieval:
Two components of the memory
functions exerted by the
hippocampus (and possibly different
parts of it), with encoding
corresponding to the “writing” of an
internal memory and retrieval to the
“reading” of existing memories.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
consistently with the complementary functions that inputs from these EC layers are postulated
to play.
We also found an excess of inhibitory interneurons among core style cells (Figure 5D).
Inteneurons tended to exhibit larger firing rates than excitatory cells, but we showed that core-
ness is not significantly affected by firing rate (Supporting Figure S5C). Therefore, this excess is
rather to be linked to a key functional role of interneurons in mediating cell assembly forma-
tion. Their central position within the core of the information sharing network may allow them
to efficiently control the recruitment of new neurons into the integrated core and orchestrate
their coordinated firing, as already discussed in the literature (Bonifazi et al., 2009; Quilichini
et al., 2012).
Remarkably, however, in a majority of cases, the connectivity style adopted by a neuron
was only poorly affected by its anatomical localization or by its cell type. Apart from the few
exceptions just discussed above, the distribution of the different styles through the different
In particular, the fact of
anatomical regions and layers was indeed close to chance levels.
being localized within a specific layer of CA1 or EC did not affect in a significant way the
probability of belonging to the core or to the periphery. Furthermore, a majority of neurons
switched between different styles when network state changed (Figure 6), indicating that con-
nectivity styles and, in particular, core membership are not hardwired. In contrast, it is often
thought that the function that a neuron plays is affected by its individual firing and morphol-
ogy properties, as well as by details of its synaptic connections within the circuit (Booker &
Vida, 2018). In this dominating view, functional hubness would thus be the garland reserved
for a few elite cells, selected because of their extreme technical specialization, largely deter-
mined by their developmental lineage (Cossart, 2014). Here—further elaborating on Clawson
et al. (2019)—we propose a more “democratic” view in which core membership and, more
in general, connectivity style would be dynamically appointed, such that the total number of
neurons that are elected into the core at least once is much larger than the currently active core
members at specific times. The core composition can indeed be radically reorganized when
the network states switch and can fluctuate between alternative majorities of hippocampal or
entorhinal cortex neurons (Figure 3D).
Such a democratic system implies a primacy of collective dynamics at the neuronal pop-
ulation level, flexibly shaping coordinated firing ensembles, on technical specialization and
“blood” origins at the single neuron level. Switching network states may reflect transitions
between alternative attractors of firing dynamics (Amit, 1989) implementing alternative firing
correlations. Discrete state switching coexists however with more liquid fluctations of core
attachment, which would rather suggest a complex but not random dynamics at the edge of
instability (Maass, Natschlager, & Markram, 2002; Marre, Yger, Davison, & Fregnac, 2009).
State transitions and flexible core-periphery reorganization are also poorly determined by
global oscillations, despite the important role played by oscillations in information routing
(Buzsáki, 2006; Womelsdorf et al., 2007). Even if global oscillatory modes do not “freeze” in-
formation sharing patterns they nevertheless affect them, with different oscillatory states giving
rise to alternative repertoires of possible information sharing networks (Figure 4D). Compu-
tational modeling of spiking neural circuits may help in the future to reach a mechanistic
understanding of how ongoing collective oscillations interact with discrete attractor switch-
ing, metastable transients, and plasticity to give rise to liquid core-periphery architectures of
information sharing.
We have started here applying a temporal network language to describe the internal life
of cell assemblies along their emergence, expansion and contraction, and sudden transfor-
mations. We chose here to focus on an anesthesia condition in which intrinsic information
Network Neuroscience
967
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
processing is not suppressed but considerably “slowed down” with respect to behavior, for
methodological convenience (possibility to use long time windows for network estimation). In
Clawson et al. (2019), we performed related analyses of information dynamics in natural sleep
as well, again finding discrete state switching not only in the hippocampal formation but also
in the prefrontal cortex. It will be interesting to consider in the future comparisons with ad-
ditional conditions, as well as more detailed investigations of relations between network state
In perspective, for instance,
dynamics and oscillatory dynamics or, even, actual behavior.
our method could be extended to recordings in pathological conditions—such as epilepsy, in
which intrinsic assembly dynamics is altered (Muldoon, Soltesz, & Cossart, 2013)—relating
temporal network properties’ alterations to the degree of cognitive deficits. Furthermore, it
may be possible to relate network state transitions within consistent oscillatory epochs (e.g.,
THE) to changes of the cross-frequency coupling between theta and gamma oscillations, since
multiple gamma oscillations types are known to exist and be linked to alternative cognitive
processes (Schomburg et al., 2014). To cope, however, with the much faster timescales rel-
evant for behavioral tasks, we should modify our network estimation approach to avoid the
use of too-short windows. Nevertheless, information sharing networks could be estimated first
in a state-resolved manner, by pooling together firing events based on the similarity of the
conditions in which they occur—for example, transient phase relations and synchrony levels
(Palmigiano, Geisel, Wolf, & Battaglia, 2017) or coactivation patterns (Malvache et al., 2016;
Miller et al., 2014)—rather than strict temporal contiguity. State-specific network frames could
then be reallocated to specific times, depending on which “state” the system is visiting at dif-
ferent times, thus reconstructing an effective temporal network with the same time resolution
as the original recordings (see, e.g., Thompson et al., 2017, for an analogous approach used at
the macroscale of fMRI signals). In this way it would become possible to link temporal network
reconfiguration events to actual behavior, hence probing their direct functional relevance.
METHODS
Animal Surgery
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In this work we used a portion of the data (12 of 18 experiments) initially published by
Quilichini et al. (2010), which includes local field potentials (LFPs) and single-unit record-
ings obtained from the dorsomedial entorhinal cortex of anesthetized rats. Seven additional
simultaneous recordings in both mEC and dorsal HPC under anesthesia were included in this
study, previously analyzed by Clawson et al. (2019). Details of anatomical locations and num-
bers of cells included can be found in Supporting Figure S1 and Supporting Table S1.
All experiments were in accordance with experimental guidelines approved by the Rutgers
University (Institutional Animal Care and Use Committee) and Aix-Marseille University Ani-
mal Care and Use Committee. We performed experiments on 12 male Sprague Dawley rats
(250 to 400 g; Hilltop Laboratory Animals) and 7 male Wistar Han IGS rats (250 to 400 g;
Charles Rivers Laboratories). We performed acute experiments anesthetizing these rats with
urethane (1.5 g/kg, intraperitoneally) and ketamine/xylazine (20 and 2 mg/kg, intramuscularly),
with additional doses of ketamine/xylazine (2 and 0.2 mg/kg) being supplemented during the
electrophysiological recordings to avoid recovery from anesthesia. The body temperature was
monitored and kept constant with a heating pad. The head was secured in a stereotaxic frame
(Kopf) and the skull was exposed and cleaned. Two miniature stainless steel screws, driven
into the skull, served as ground and reference electrodes. To reach the mEC, we performed
one craniotomy from bregma: −7.0 mm anteroposterior (AP) and +4.0 mm mediolateral (ML);
to reach the CA1 area of HPC, we performed one craniotomy from bregma: 3.0 mm AP and
+2.5 mm ML. The probes were mounted on a stereotaxic arm. We recorded the dorsomedial
Network Neuroscience
968
Dynamic core-periphery networks in entorhinal cortex and hippocampus
portion of the mEC activity using a NeuroNexus CM32-4×8-5 mm-Buzsaki32-200-177 probe
(in eight experiments), a 10-mm-long Acreo single-shank silicon probe with 32 sites (50-mm
spacing) arranged linearly (in five experiments), or a NeuroNexus H32-10mm-50-177 probe
(in five experiments), which was lowered in the EC at 5.0 to 5.2 mm from the brain sur-
face with a 20◦ angle. We recorded HPC CA1 activity using a H32-4×8-5mm-50-200-177
probe (NeuroNexus Technologies) lowered at 2.5 mm from the brain surface with a 20◦ angle
(in four experiments), a NeuroNexus H16-6mm-50-177 probe lowered at 2.5 mm from the
brain surface with a 20◦ angle (in two experiments). The online positioning of the probes was
assisted by the presence of unit activity in cell body layers and the reversal of theta oscillations
when passing from L2 to L1 for the mEC probe and the presence in SP of either unit activity or
ripples (80 to 150 Hz) for the HPC probe.
At the end of the recording, the animals were injected with a lethal dose of pentobarbital Na
(150 mg/kg, intraperitoneally) and perfused intracardially with 4% paraformaldehyde solution.
We confirmed the position of the electrodes (DiI was applied on the back of the probe before
insertion) histologically on Nissl-stained 40-mm section.
Data Collection and Spike Sorting
Extracellular signal recorded from the silicon probes was amplified (1,000), bandpass-filtered
(1 Hz to 5 kHz), and acquired continuously at 20 kHz with a 64-channel DataMax Sys-
tem (RC Electronics ora 258-channel Amplipex) or at 32 kHz with a 64-channel DigitalLynx
(NeuraLynx at 16-bit resolution). We preprocessed raw data using a custom-developed suite
of programs (Csicsvari, Hirase, Czurka, Mamiya, & Buzsaki, 1999). After recording, the signals
were downsampled to 1250 Hz for the LFP analysis. Spike sorting was performed automatically
using KLUSTAKWIK (http://klustakwik.sourceforge.net, Harris, Henze, Csicsvari,
Hirase, & Buzsáki, 2000), followed by manual adjustment of the clusters, with the help of
autocorrelogram, cross-correlogram (CCG), and spike waveform similarity matrix (KLUSTERS
software package; https://klusta.readthedocs.io/en/latest/, Hazan, Zugaro, &
Buzsáki, 2006). After spike sorting, we plotted the spike features of units as a function of time
and discarded the units with signs of significant drift over the period of recording. More-
over, we included in the analyses only units with clear refractory periods and well-defined
clusters.
Recording sessions were divided into brain states of THE and SO periods. The epochs
of stable theta (THE) or slow oscillations (SO) were visually selected from the ratios of the
whitened power in the THE band ([3 6] Hz in anesthesia) and the power of the neighboring
bands of EC Layer 3 LFP, which was a layer present in all of the 18 anesthesia recordings.
We determined the layer assignment of the neurons from the approximate location of their
somata relative to the recording sites (with the largest amplitude unit corresponding to the pu-
tative location of the soma), the known distances between the recording sites, and the histo-
logical reconstruction of the recording electrode tracks. To assess the excitatory or inhibitory
nature of each of the units, we calculated pairwise cross-correlograms between spike trains
of these cells. We determined the statistical significance of putative inhibition or excitation
(trough or peak in the [+2:5] ms interval, respectively) using well-established nonparametric
tests and criteria used for identifying monosynaptic excitations or inhibitions (Quilichini et al.,
2010), in which each spike of each neuron was jittered randomly and independently on a
uniform interval of [5:5] ms a thousand times to form 1,000 surrogate datasets and from which
the global maximum and minimum bands at 99% acceptance levels were constructed.
Network Neuroscience
969
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Information Sharing Networks
We estimated time-resolved information sharing networks following the same procedures as
In particular, we used time-lagged mutual information between bi-
Clawson et al. (2019).
narized spike trains as a measure of the amount of shared information. Information sharing
between each pair of neurons (i, j)i,j=1,...,N is defined as the time-lagged mutual information
MI[i(t), j(t − λ)] between the firing patterns extracted for the relative neurons in a 10-s-long
time window:
Ishared(j −→ i) = ∑
λ
Ishared(i −→ j) = ∑
λ
MI[i(t), j(t − λ)] ,
MI[j(t), i(t − λ)] ,
(1)
(2)
where the time lag λ varies in the range 0 ≤ λ ≤ 0.5Tθ, Tθ being the phase of the THE cycle
(THE oscillations have higher frequency than slow oscillations). We subtract a significance
threshold, that is, the 95th percentile of MI computed on reshuffled binarized spike trains (400
iterations), setting to zero non-significant terms. The information sharing network is defined by
an adjacency matrix A(i, j)i,j=1,...,N, whose element A(i, j) corresponds to Ishared(i −→ j). It is
therefore a weighted, directed network. The time window is then shifted by 1 s to extract the
information sharing network at the next time-step, assuring a 90% overlap with the previous
time window for the computation of the information theoretic measures.
In order to study the effect of asymmetries in the adjacency matrices of our information
sharing networks, we compute the asymmetry coefficient ∆S% for each neuron in each state
h, defined as follows:
∆S%i
h =
out − si,h
si,h
out + si,h
si,h
in
in
,
∀i = 1, . . . , N .
(3)
∆S%i
h thus represents the ratio between the amount of information that neuron i outputs
to other neurons during state h (si,h
out = ∑t=1,...,Th ∑j wij) and the amount of information that
is conveyed to neuron i by its neighbors during state h (si,h
h = 1
means that for neuron i in state h, si,h
in = 0, therefore it is a perfect sender of information,
whereas if ∆S%i
h = 0,
then si,h
out = si,h
in and therefore the amount of information that neuron i conveys to its neighbors
during the state h is equal to the amount of information that it receives. As shown in Supporting
Figure S10, the asymmetries in the adjacency matrices of the information sharing networks
have a negligible effect. We thus neglect the aforementioned asymmetries and consider the
networks to be undirected.
out = 0 and the neuron is therefore a perfect receiver. If ∆S%i
in = ∑t=1,...,Th ∑j wji). ∆S%i
h = −1, si,h
Active Information Storage
Information sharing can be seen as a generalized form of cross-correlation where the time-
lagged mutual information captures all types of linear and nonlinear correlations. Analogously,
one can evaluate a generalized autocorrelation functional, known under the name of active
information storage (Lizier et al., 2012). Following Clawson et al. (2019), we evaluated active
information storage of a given neuron, within a given time window as
Istorage(i) = ∑
λ
MI[i(t), i(t − λ)] ,
(4)
970
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
where the time lag λ varies once again in the range 0 ≤ λ ≤ 0.5Tθ. The values of storage
whose distributions are shown in Supporting Figure S9 are averages for each neuron over all
the time windows whose associated connectivity profile match a specific connectivity style
(see below for definitions of connectivity profiles and styles).
Network Features
As described in the main text, we consider the cosine similarity and Jaccard coefficient be-
tween the neighborhoods of each node in successive times. See the jargon boxes for the precise
definitions.
We also consider the definition of coreness Ci of node i in a network introduced by
Della Rossa et al. (2013), see the jargon box in the main text. To compute the coreness of
neurons at each time frame we used the implementation of the method available at https://
core-periphery-detection-in-networks.readthedocs.io/en/latest/index.
html.
Null Models
We compare the results obtained in the empirical data to those achieved by repeating the pre-
sented analysis on three different null models obtained by different randomization procedures
of the original networks:
Random null model: Temporal network obtained by generating at each time step t an
Erdös-Rényi random graph with the same number of nodes and edges as the original
data.
Degree-preserving null model: Temporal network generated by randomizing at each
time t the edges of the original network at the corresponding time, preserving the degree
(number of connections) of each node. To this aim we use the method of Maslov and
Sneppen (2002).
Neighborhood-preserving null model: A temporal network whose adjacency matrix at
time t is obtained by a systematic reshuffling of the weights of the experimental data
temporal network; this preserves the neighborhood (set of neighbors) of each node at
each time. This randomization procedure therefore leaves the unweighted structure
unchanged.
Network States
The two pairs of feature vectors computed at each time t, two vectors for the unweighted
case and two for the weighted one, are merged into two 2 × N-dimensional vectors, one
containing the unweighted features (Jaccard and unweighted coreness) and the other formed by
the weighted ones (cosine similarity and weighted coreness). For each recording we therefore
have two series of length T (T varies for different recordings), of weighted and unweighted
feature vectors. In order to investigate the existence of recurring epochs of stable (correlated)
liquidity and topology configuration of the network (the network states), we perform a K-means
clustering on the feature vector time series. As a result of the clustering we obtain for each
recording two sets (one for the weighted analysis, one for the unweighted one) of network
states of specific liquidity (Jaccard index, for unweighted networks, or cosine similarity, for
weighted networks) and core-periphery organization (unweighted or unweighted coreness) of
the system (Figure 4A).
Network Neuroscience
971
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Network States Obtained From Global Network Features
We consider six global network features, three for the unweighted case and three for the
weighted case: the node-averaged cosine similarity (Jaccard index in the unweighted case); the
node averaged coreness (weighted and unweighted); and the sum over all weights of all edges
(number of edges in the unweighted case). These features are computed at each time t and
merged in two 3-dimensional vectors, yielding two time series of length T for each recording
(where T varies for each recording). As for the local network feature vectors, we perform a
K-means clustering on each (unweighted and weighted) feature vector time series: As a result,
we obtain for each recording the two sets of global unweighted and weighted network states,
corresponding to the epochs of similar organization of the network in terms of node-averaged
liquidity, core-periphery structure, and connectivity.
Clustering Connectivity Profiles: Connectivity Styles
As shown in Figure 5B, we represent the connectivity behavior of a neuron in a network state
with a radar plot whose radial axes correspond to the six features defined in the Results section,
which are averages of temporal properties over the network state. We therefore compute one
6-dimensional connectivity profile for each neuron, in each network state, for each recording.
We investigate the existence of typical connectivity profiles across different recordings: this
corresponds to searching for common radar plot shapes for neurons of different network states
of different recordings. We therefore perform a K-means clustering on all the connectivity
profiles computed for each neuron, in each network state, in each recording: We obtain four
cluster of connectivity profiles, which name connectivity styles. These connectivity styles are
shown in Figure 5B and interpreted in the Results and Discussion sections.
Unsupervised Classification for Soft Labeling of Connectivity Profile
We use the K-nearest-neighbor unsupervised classification method, trained on the connectivity
style labels of all the connectivity profiles, to obtain a soft classification of each neuron’s con-
nectivity profile. Each neuron’s state-averaged connectivity profile’s soft label is represented by
a 4-dimensional normalized vector: Each component of this vector represents the probability
of the connectivity profile to belong to the corresponding connectivity style (core, periphery,
bursty core-skin, regular core-skin). The connectivity styles shown in Figure 5B correspond to
the connectivity profiles of maximum probability to belong to the connectivity style of the cor-
responding color, that is, of maximum soft label component of the corresponding connectivity
style. The soft classification of connectivity profiles is graphically represented in Figure 5C by
plotting the connectivity profiles’ vectors of connectivity style soft labels in a 3-dimensional
space. In order to achieve a clearer visual representation, the probabilities of belonging to the
regular core-skin or the bursty core-skin connectivity styles have been summed into a single
component of the soft label vector.
Cross–Network State Connectivity Profile Transition Rate
The cross–network state connectivity profile transition rate ηi of neuron i is defined as
ηi ≡
# pro f ile transitions o f node i
max(# global classes, # network − states)
.
(5)
It quantifies the tendency of neuron i to switch, often or rarely, between connectivity profiles
belonging to different connectivity styles in different states: When ηi = 1, neuron i switches
connectivity style at every change of network state; when ηi = 0, neuron i is always in the
same connectivity style.
Network Neuroscience
972
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic core-periphery networks in entorhinal cortex and hippocampus
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00142.
AUTHOR CONTRIBUTIONS
Nicola Pedreschi: Conceptualization; Investigation; Methodology; Software; Visualization;
Writing - Original Draft; Writing - Review & Editing. Christophe Bernard: Data curation;
Resources; Writing - Review & Editing. Wesley Clawson: Data curation; Formal analysis;
Resources; Writing - Review & Editing. Pascale Quilichini: Data curation; Resources;
Writing - Review & Editing. Alain Barrat: Conceptualization; Methodology; Supervision;
Writing - Original Draft; Writing - Review & Editing. Demian Battaglia: Conceptualization;
Methodology; Supervision; Writing - Original Draft; Writing - Review & Editing.
FUNDING INFORMATION
Nicola Pedreschi, H2020 Marie Skłodowska-Curie Actions (http://dx.doi.org/10.13039/
100010665), Award ID: 713750. Nicola Pedreschi, Regional Council of Provence-Alpes-Côte
d’Azur and A*MIDEX, Award ID: ANR-11-IDEX-0001-02. Alain Barrat, Agence Nationale
de la Recherche (http://dx.doi.org/10.13039/501100001665), Award ID: ANR-19-CE46-0008.
Christophe Bernard, H2020 Marie Skłodowska-Curie Actions (http://dx.doi.org/10.13039/
100010665), Award ID: 765549. Wesley Clawson, H2020 Marie Skłodowska-Curie Actions
(http://dx.doi.org/10.13039/100010665), Award ID: 765549. Demian Battaglia, Centre Na-
tional de la Recherche Scientifique (http://dx.doi.org/10.13039/501100004794), Award ID:
INFINITI (Braintime Project). Alain Barrat, Centre National de la Recherche Scientifique
(http://dx.doi.org/10.13039/501100004794), Award ID: INFINITI (Braintime project). Pascale
Quilichini, CURE, Award ID: Epilepsy Taking Flight Award.
REFERENCES
Abeles, M.
(1982). Local cortical circuits, an electrophysiological
study. Berlin, Germany: Springer.
Aertsen, A. M., Gerstein, G. L., Habib, M. K., & Palm, G. (1989).
Dynamics of neuronal firing correlation: modulation of “effective
connectivity.” Journal of Neurophysiology, 61(5), 900–917.
Amit, D. J. (1989). Modeling brain function: The world of attractor
neural networks. New York, NY: Cambridge University Press.
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2017). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017.149
Barabási, A. L. (2005). The origin of bursts and heavy tails in human
dynamics. Nature, 435, 207–211.
Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha,
P. J., & Grafton, S. T. (2013). Task-based core-periphery organ-
ization of human brain dynamics. PLoS Computational Biology,
9(9), e1003171.
Battaglia, D., Karagiannis, A., Gallopin, T., Gutch, H. W., & Cauli,
(2013). Beyond the frontiers of neuronal types. Frontiers in
B.
Neural Circuits, 7, 13. https://doi.org/10.3389/fncir.2013.00013
Battiston, F., Guillon, J., Chavez, M., Latora, V., & Fallani, F. D. V.
(2018). Multiplex core-periphery organization of the human
Journal of the Royal Society Interface, 15(146),
connectome.
20180514. https://doi.org/10.1098/rsif.2018.0514
Bonifazi, P., Goldin, M., Picardo, M. A., Jorquera, I., Cattani, A.,
(2009). GABAergic hub neurons
Bianconi, G., . . . Cossart, R.
orchestrate synchrony in developing hippocampal networks. Sci-
ence, 326(5958), 1419–1424. https://doi.org/10.1126/science.
1175509
Booker, S. A., & Vida, I. (2018). Morphological diversity and con-
nectivity of hippocampal interneurons. Cell and Tissue Research,
373(3), 619–641. https://doi.org/10.1007/s00441-018-2882-2
Buzsáki, G. (2006). Rhythms of the brain. New York, NY: Oxford
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
University Press.
Buzsáki, G. (2010). Neural syntax: Cell assemblies, synapsembles,
and readers. Neuron, 68(3), 362–385. https://doi.org/10.1016/j.
neuron.2010.09.023
Buzsáki, G., & Moser, E. I. (2013). Memory, navigation and theta
rhythm in the hippocampal-entorhinal system. Nature Neuro-
science, 16(2), 130–138. https://doi.org/10.1038/nn.3304
Calhoun, V. D., Miller, R., Pearlson, G., & Adalı, T.
(2014). The
chronnectome: Time-varying connectivity networks as the next
frontier in fMRI data discovery. Neuron, 84(2), 262–274.
Cattuto, C., Van den Broeck, W., Barrat, A., Colizza, V., Pinton,
J.-F., & Vespignani, A.
(2010). Dynamics of person-to-person
interactions from distributed RFID sensor networks. PLoS ONE,
5(7), 1–9. https://doi.org/10.1371/journal.pone.0011596
Network Neuroscience
973
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
Dynamic core-periphery networks in entorhinal cortex and hippocampus
Clawson, W., Vicente, A. F., Ferraris, M., Bernard, C., Battaglia, D.,
& Quilichini, P. P. (2019). Computing hubs in the hippocampus
and cortex. Science Advances, 5(6).
Cossart, R. (2014). Operational hub cells: A morpho-physiologically
diverse class of GABAergic neurons united by a common func-
tion. Current Opinion in Neurobiology, 26, 51–56. https://doi.
org/10.1016/j.conb.2013.12.002
Csicsvari, J., Hirase, H., Czurka, A., Mamiya, A., & Buzsaki, G.
(1999). Oscillatory coupling of hippocampal pyramidal cells and
interneurons in the behaving rat. Journal of Neuroscience, 19(1),
274–287. https://doi.org/10.1523/jneurosci.19-01-00274.1999
Darst, R. K., Granell, C., Arenas, A., Gómez, S., Saramäki, J., &
Fortunato, S. (2016). Detection of timescales in evolving com-
plex systems. Scientific Reports, 6, 39713. https://doi.org/10.
1038/srep39713
Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L.
(2015).
Rethinking segregation and integration: Contributions of whole-
brain modelling. Nature Reviews Neuroscience, 16(7), 430–439.
https://doi.org/10.1038/nrn3963
Della Rossa, F., Dercole, F., & Piccardi, C. (2013). Profiling core-
periphery network structure by random walkers. Scientific Re-
ports, 3, 1467.
de Pasquale, F., Corbetta, M., Betti, V., & Penna, S. D. (2018). Cor-
tical cores in network dynamics. NeuroImage, 180, 370–382.
https://doi.org/10.1016/j.neuroimage.2017.09.063
Douchamps, V., Jeewajee, A., Blundell, P., Burgess, N., & Lever,
(2013). Evidence for encoding versus retrieval scheduling
C.
Journal
in the hippocampus by theta phase and acetylcholine.
of Neuroscience, 33(20), 8689–8704. https://doi.org/10.1523/
jneurosci.4483-12.2013
Forsyth, D. (2018). Probability and statistics for computer science.
Berlin, Gemany: Springer.
Galimberti, E., Barrat, A., Bonchi, F., Cattuto, C., & Gullo, F. (2018).
In Pro-
Mining (maximal) span-cores from temporal networks.
ceedings of the 27th ACM international Conference on Informa-
tion and Knowledge Management (pp. 107–116).
Gauvin, L., Panisson, A., & Cattuto, C. (2014). Detecting the com-
munity structure and activity patterns of temporal networks: A
non-negative tensor factorization approach. PLoS ONE, 9(1),
e86028.
Gelardi, V., Fagot, J., Barrat, A., & Claidière, N. (2019). Detecting
social (in)stability in primates from their temporal co-presence
network. Animal Behaviour, 139, 239.
Gilbert, C. D., & Sigman, M. (2007). Brain states: Top-down influ-
ences in sensory processing. Neuron, 54(5), 677–696. https://
doi.org/10.1016/j.neuron.2007.05.019
Harris, K. D., Henze, D. A., Csicsvari, J., Hirase, H., & Buzsáki,
G. (2000). Accuracy of tetrode spike separation as determined
by simultaneous intracellular and extracellular measurements.
Journal of Neurophysiology, 84(1), 401–414. https://doi.org/10.
1152/jn.2000.84.1.401
Hasselmo, M. E., & Stern, C. E. (2013). Theta rhythm and the en-
coding and retrieval of space and time. NeuroImage, 85(Pt. 2),
656–666. https://doi.org/10.1016/j.neuroimage.2013.06.022
Hazan, L., Zugaro, M., & Buzsáki, G. (2006). Klusters, NeuroScope,
NDManager: A free software suite for neurophysiological data
processing and visualization. Journal of Neuroscience Methods,
155(2), 207–216. https://doi.org/10.1016/j.jneumeth.2006.01.017
Hebb, D. (1949). The organization of behavior: A neuropsycholog-
ical theory. New York, NY: Wiley.
Holme, P.
(2005). Core-periphery organization of complex net-
works. Physical Review E, 72, 046111. https://doi.org/10.1103/
PhysRevE.72.046111
Holme, P. (2015). Modern temporal network theory: A colloquium.
European Physical Journal B, 88(9), 234.
Holme, P., & Saramäki, J. (2012). Temporal networks. Physics Re-
ports, 519(3), 97–125. https://doi.org/10.1016/j.physrep.2012.
03.001
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Chang, C.
(2013). Dy-
namic functional connectivity: Promise, issues, and interpreta-
tions. Neuroimage, 80, 360–378.
Ikegaya, Y., Aaron, G., Cossart, R., Aronov, D., Lampl, I., Ferster,
D., & Yuste, R. (2004). Synfire chains and cortical songs: Tem-
poral modules of cortical activity. Science, 304(5670), 559–564.
https://doi.org/10.1126/science.1093173
Kirst, C., Timme, M., & Battaglia, D.
(2016). Dynamic informa-
tion routing in complex networks. Nature Communications, 7(1),
11061. https://doi.org/10.1038/ncomms11061
Kispersky, T., Gutierrez, G. J., & Marder, E. (2011). Functional con-
nectivity in a rhythmic inhibitory circuit using Granger causal-
ity. Neural Systems and Circuits, 1(1), 9. https://doi.org/10.1186/
2042-1001-1-9
Klausberger, T., Magill, P. J., Márton, L. F., Roberts,
J. D. B.,
Cobden, P. M., Buzsáki, G., & Somogyi, P. (2003). Brain-state-
and cell-type-specific firing of hippocampal interneurons in vivo.
Nature, 421(6925), 844–848. https://doi.org/10.1038/nature01374
(2019). The structured
backbone of temporal social ties. Nature Communications, 10(1),
220.
Kobayashi, T., Takaguchi, T., & Barrat, A.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Kojaku, S., & Masuda, N. (2018). Core-periphery structure requires
something else in the network. New Journal of Physics, 20(4),
043012. https://doi.org/10.1088/1367-2630/aab547
Kovanen, L., Karsai, M., Kaski, K., Kertész, J., & Saramäki, J. (2011).
Temporal motifs in time-dependent networks. Journal of Statisti-
cal Mechanics, P11005.
Laurent, G., Saramäki, J., & Karsai, M. (2015). From calls to com-
munities: A model for time-varying social networks. European
Physial Journal B, 88, 301.
Lizier, J. T., Atay, F. M., & Jost, J. (2012). Information storage, loop
motifs, and clustered structure in complex networks. Physical
Review E, 86(2), 026110. https://doi.org/10.1103/physreve.86.
026110
Lizier, J. T., Flecker, B., & Williams, P. L.
(2013). Towards a
synergy-based approach to measuring information modification.
2013 IEEE Symposium on Artificial Life, 43–51. https://doi.org/
10.1109/alife.2013.6602430
Maass, W., Natschlager, T., & Markram, H. (2002). Real-time com-
puting without stable states: A new framework for neural com-
putation based on perturbations. Neural Computation, 14(11),
2531–2560. https://doi.org/10.1162/089976602760407955
Malvache, A., Reichinnek, S., Villette, V., Haimerl, C., &
(2016). Awake hippocampal reactivations project
Cossart, R.
Network Neuroscience
974
Dynamic core-periphery networks in entorhinal cortex and hippocampus
onto orthogonal neuronal assemblies. Science, 353(6305),
1280–1283. https://doi.org/10.1126/science.aaf3319
Mao, B.-Q., Hamzei-Sichani, F., Aronov, D., Froemke, R. C., &
(2001). Dynamics of spontaneous activity in neocor-
Yuste, R.
tical slices. Neuron, 32(5), 883–898. https://doi.org/10.1016/
s0896-6273(01)00518-9
Marder, E., & Goaillard, J.-M. (2006). Variability, compensation and
homeostasis in neuron and network function. Nature Reviews
Neuroscience, 7(7), 563–574. https://doi.org/10.1038/nrn1949
Marre, O., Yger, P., Davison, A. P., & Fregnac, Y. (2009). Reliable
recall of spontaneous activity patterns in cortical networks. Jour-
nal of Neuroscience, 29(46), 14596–14606. https://doi.org/10.
1523/jneurosci.0753-09.2009
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topol-
ogy of protein networks. Science, 296(5569), 910–913. https://
doi.org/10.1126/science.1065103
Masuda, N., & Holme, P. (Eds.).
(2017). Temporal network epi-
demiology. Singapore: Springer.
Miller, J.-e. K., Ayzenshtat, I., Carrillo-Reid, L., & Yuste, R. (2014).
Visual stimuli recruit intrinsically generated cortical ensembles.
Proceedings of the National Academy of Sciences, 111(38),
E4053–E4061. https://doi.org/10.1073/pnas.1406077111
Miritello, G., Lara, R., Cebrian, M., & Moro, E. (2013). Limited com-
munication capacity unveils strategies for human interaction. Sci-
entific Reports, 3(1), 1950. https://doi.org/10.1038/srep01950
Muldoon, S. F., Soltesz, I., & Cossart, R. (2013). Spatially clustered
neuronal assemblies comprise the microstructure of synchrony
in chronically epileptic networks. Proceedings of the National
Academy of Sciences, 110(9), 3567–3572. https://doi.org/10.
1073/pnas.1216958110
Palmigiano, A., Geisel, T., Wolf, F., & Battaglia, D.
Orlandi, J. G., Soriano, J., Alvarez-Lacalle, E., & Teller, S.
(2013).
Noise focusing and the emergence of coherent activity in neuronal
cultures. Nature Physics, 9(9). https://doi.org/10.1038/nphys2686
(2017). Flex-
ible information routing by transient synchrony. Nature Neuro-
science, 20(7), 1014–1022. https://doi.org/10.1038/nn.4569
Poli, D., Pastore, V. P., & Massobrio, P. (2015). Functional connec-
tivity in in vitro neuronal assemblies. Frontiers in Neural Circuits,
9, 57. https://doi.org/10.3389/fncir.2015.00057
Puck Rombach, M., Porter, M., Fowler, J., & Mucha, P. J.
(2014).
Core-periphery structure in networks. SIAM Journal on Applied
Mathematics, 74, 167.
Quilichini, P., LeVanQuyen, M., Ivanov, A., Turner, D., Carabalona,
A., Gozlan, H., . . . Bernard, C. (2012). Hub GABA neurons me-
diate gamma-frequency oscillations at ictal-like event onset in
the immature hippocampus. Neuron, 74(1), 57–64. https://doi.
org/10.1016/j.neuron.2012.01.026
(2010).
Quilichini, P., Sirota, A., & Buzsáki, G.
Intrinsic circuit
organization and theta-gamma oscillation dynamics in the
Journal of Neuroscience, 30(33),
entorhinal cortex of the rat.
11128–11142. https://doi.org/10.1523/jneurosci.1327-10.2010
(2015). From seconds to months: An
overview of multi-scale dynamics of mobile telephone calls.
European Physical Journal B, 88, 164.
Saramäki, J., & Moro, E.
Schomburg, E. W., Fernandez-Ruiz, A., Mizuseki, K., Berenyi, A.,
Anastassiou, C. A., Koch, C. & Buzsáki, G. (2014). Theta phase
segregation of
input-specific gamma patterns in entorhinal-
hippocampal networks. Neuron, 84(2), 470–485. https://doi.
org/10.1016/j.neuron.2014.08.051
Schreiber, T.
(2000). Measuring Information Transfer.
Phys-
ical Review Letters, 85(2), 461–464. https://doi.org/10.1103/
physrevlett.85.461
Stehlé, J., Charbonnier, F., Picard, T., Cattuto, C., & Barrat, A.
(2013). Gender homophily from spatial behavior in a primary
school: A sociometric study. Social Networks, 35(4), 604–613.
https://doi.org/10.1016/j.socnet.2013.08.003
Stetter, O., Battaglia, D., Soriano, J., & Geisel, T. (2012). Model-free
reconstruction of excitatory neuronal connectivity from calcium
imaging signals. PLoS Computational Biology, 8(8), e1002653.
https://doi.org/10.1371/journal.pcbi.1002653
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static
to temporal network theory: Applications to functional brain con-
nectivity. Network Neuroscience, 1, 69.
Tononi, G., Edelman, G. M., & Sporns, O. (1998). Complexity and
coherency: Integrating information in the brain. Trends in Cog-
nitive Sciences, 2(12), 474–484. https://doi.org/10.1016/s1364-
6613(98)01259-5
Valdano, E., Poletto, C., Giovannini, A., Palma, D., Savini, L., &
Colizza, V. (2015). Predicting epidemic risk from past temporal
contact data. PLoS Computational Biology, 11(3), 1–19. https://
doi.org/10.1371/journal.pcbi.1004152
Varela, F., Lachaux, J.-P., Rodriguez, E., & Martinerie, J.
(2001).
The brainweb: Phase synchronization and large-scale integra-
tion. Nature Reviews Neuroscience, 2(4), 229–239. https://doi.
org/10.1038/35067550
Wibral, M., Priesemann, V., Kay, J. W., Lizier, J. T., & Phillips, W. A.
(2017). Partial information decomposition as a unified approach
to the specification of neural goal functions. Brain and Cognition,
112, 25–38. https://doi.org/10.1016/j.bandc.2015.09.004
Womelsdorf, T., Schoffelen,
J.-M., Oostenveld, R., Singer, W.,
(2007). Modulation
Desimone, R., Engel, A. K., & Fries, P.
of neuronal interactions through neuronal synchronization. Sci-
ence, 316(5831), 1609–1612. https://doi.org/10.1126/science.
1139597
Network Neuroscience
975
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
9
4
6
1
8
6
7
4
0
4
n
e
n
_
a
_
0
0
1
4
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3