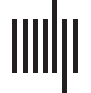FORSCHUNG
Modular co-organization of functional
connectivity and scale-free dynamics in the
human brain
Alexander Zhigalov1,2,3∗
, Gabriele Arnulfo1,4, Lino Nobili5, Satu Palva1, and J. Matias Palva1
1Neuroscience Center, University of Helsinki, Finland
2BioMag laboratory, HUS Medical Imaging Center, Helsinki University Central Hospital, Finland
3Department of Computer Science, University of Helsinki, Finland
4Department of Informatics, Bioengineering, Robotics and System Engineering, University of Genova, Italien
5Claudio Munari Epilepsy Surgery Centre, Niguarda Hospital, Italien
Keine offenen Zugänge
Tagebuch
Schlüsselwörter: Scale-free dynamics, Functional connectome, Modular networks, Neuronal avalanches,
Long-range temporal correlations
ABSTRAKT
Scale-free neuronal dynamics and interareal correlations are emergent characteristics of
spontaneous brain activity. How such dynamics and the anatomical patterns of neuronal
connectivity are mutually related in brain networks has, Jedoch, remained unclear. Wir
addressed this relationship by quantifying the network colocalization of scale-free neuronal
activity—both neuronal avalanches and long-range temporal correlations (LRTCs)—and
functional connectivity (FC) by means of intracranial and noninvasive human resting-state
electrophysiological recordings. We found frequency-specific colocalization of scale-free
dynamics and FC so that the interareal couplings of LRTCs and the propagation of neuronal
avalanches were most pronounced in the predominant pathways of FC. Several control
analyses and the frequency specificity of network colocalization showed that the results were
not trivial by-products of either brain dynamics or our analysis approach. Crucially, scale-free
neuronal dynamics and connectivity also had colocalized modular structures at multiple
levels of network organization, suggesting that modules of FC would be endowed with
partially independent dynamic states. These findings thus suggest that FC and scale-free
dynamics—hence, putatively, neuronal criticality as well—coemerge in a hierarchically
modular structure in which the modules are characterized by dense connectivity, avalanche
propagation, and shared dynamic states.
ZUSAMMENFASSUNG DES AUTORS
The framework of criticality has been suggested to explain the scale-free dynamics of
neuronal activity in complex interaction networks. Jedoch, the in vivo relationship between
scale-free dynamics and functional connectivity (FC) has remained unclear. We used human
intracranial and noninvasive electrophysiological measurements to map scale-free dynamics
and connectivity. We found that the propagation of fast activity avalanches and the interareal
coupling of slow, long-range temporal correlations—two key forms of scale-free neuronal
dynamics—were nontrivially colocalized with the strongest functional connections. Most
importantly, scale-free dynamics and FC exhibited similar modular network structures. FC
and scale-free dynamics, and possibly also neuronal criticality, appear to co-emerge in a
modular architecture in which the modules are characterized internally by shared dynamic
Staaten, avalanche propagation, and dense functional connectivity.
Zitat: Zhigalov, A., Arnulfo, G.,
Nobili, L., Verehrung, S., & Verehrung, J. M.
(2017). Modular co-organization of
functional connectivity and scale-free
dynamics in the human brain. Netzwerk
Neurowissenschaften, 1(2), 143–165.
https://doi.org/10.1162/netn_a_00008
DOI:
https://doi.org/10.1162/netn_a_00008
zusätzliche Informationen:
http://www.mitpressjournals.org/doi/
suppl/10.1162/netn_a_00008
Erhalten: 21 November 2016
Akzeptiert: 19 Februar 2017
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Alexander Zhigalov
alexander.zhigalov@helsinki.fi
Handling-Editor:
Michael Breakspear
Urheberrechte ©: © 2017
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
N
e
N
_
A
_
0
0
0
0
8
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
Funktionale Konnektivität:
Defined as the correlation between
neurophysiological time series
Scale-free dynamics:
Any fractally self-similar—that is,
power-law scaled—dynamics of a
System
Neuronal avalanche:
A cascade of neuronal activity with
power-law size and lifetime
distributions
Long-range temporal correlations:
Functional correlations characterized
by power-law decay of the
autocorrelation function
Criticality:
The state of a dynamical system at a
boundary between two qualitatively
different types of dynamics
Neuronal oscillations:
Transiently rhythmic neuronal
population activities
Resting-state:
An experimental paradigm in which
the participant does not receive any
stimulation or task
VERMISSEN:
An invasive, presurgical technique in
which local field potentials are
recorded intracerebrally to identify
the areas where epileptic seizures
originate
Netzwerkneurowissenschaften
The human connectome is a comprehensive map of how brain regions are mutually con-
nected and is fundamentally important for understanding neuronal communication and brain
dynamics in both health and disease (Fornito, Zalesky, & Breakspear, 2015). Although func-
funktionale Konnektivität (FC) in the human brain was initially characterized as a stationary network
(Rachel, 2009), recent empirical (Zalesky, Fornito, Cocchi, Gollo, & Breakspear, 2014) Und
theoretical (Deco, Jirsa, & McIntosh, 2013) studies have complemented this view by revealing
considerable connectivity pattern fluctuations that are systematic beyond simply represent-
ing noise in weak stationary connectivity (Hansen, Battaglia, Spiegler, Deco, & Jirsa, 2015;
Mitra, Snyder, Blazey, & Rachel, 2015). Such dynamic connectivity has been observed at a
range of temporal scales from milliseconds to minutes (Larson-Prior et al., 2013). It has, nev-
ertheless, remained unclear how these static and dynamic patterns of FC are related to the
actual dynamical states of the brain and to the statistical patterns of activity propagation asso-
ciated with this scale-free dynamics (Kopell, Gritton, Whittington, & Kramer, 2014).
−3 to 10
The ubiquity of scale-free dynamics in neuronal activity suggests that neuronal systems
could operate at a critical state (Chialvo, 2010). Critical neuronal dynamics are char-
zum Beispiel, by the power-law scaling of neuronal activity avalanches at fast
acterized,
−1 s) timescales (Beggs & Plenz, 2003), as well as by power-law long-range
(10
temporal correlations (LRTCs) in neuronal fluctuations at slow (101 Zu 103 S) timescales
(Linkenkaer-Hansen, Nikouline, Verehrung, & Ilmoniemi, 2001). Jedoch, the hierarchically mod-
ular rather than homogeneous structural connectivity of the brain may expand our concept
of criticality from the system operating near a critical point into the system operating in an
extended critical region or, more specifically, in a Griffiths phase (Hilgetag & Hutt, 2014;
Moretti & Munoz, 2013). Andererseits, it is important to note that several kinds of
noncritical processes are also associated with power-law LRTCs; somit, observations of scale-
free dynamics do not, per se, indicate criticality (sehen, z.B., E. J. Friedman & Landsberg, 2013;
Schwab, Nemenman, & Mehta, 2014).
Whether scale-free brain dynamics and/or neuronal criticality are related to FC has re-
ceived attention only recently (Ciuciu, Abry, & Er, 2014). Avalanche-like large-amplitude
propagating patterns in BOLD signals have a connectivity structure similar to that of FC
(Tagliazucchi, Balenzuela, Fraiman, & Chialvo, 2012). In die gleiche Richtung, slow amplitude fluc-
tuations of neuronal oscillations are characterized by both LRTCs (Linkenkaer-Hansen et al.,
2001) and long-range interareal correlations with neuroanatomical structures similar to those
of fMRI resting-state networks (Brookes et al., 2011). Somit, these converging, albeit indi-
rect, relationships suggest that critical dynamics and the functional connectome could be
linked, but in a manner that hitherto has been unclear. Recent computational-modeling
studies have further elucidated this link by suggesting, on the one hand, that the modu-
lar network architecture of resting-state FC emerges specifically when the system is poised
at a critical state (Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013) Und, auf dem anderen,
that avalanches in a modular system propagate preferentially within connectivity modules
(Russo, Herrmann, & de Arcangelis, 2014).
We advance here two hypotheses. Erste, we posit that neuronal avalanches propagate pref-
erentially along the predominant pathways of FC and within the modules of the functional
connectome. Zweite, we suggest that these modules are also endowed with partially inde-
pendent dynamic states, which are reflected in stronger interareal correlations of LRTC ex-
ponents within the modules than between them. To test these hypotheses, we assessed the
relationship between scale-free dynamics and FC by using intracranial stereotactic electroen-
cephalography (VERMISSEN) and magnetoencephalography (MEG). To ensure that the hypotheses
144
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
N
e
N
_
A
_
0
0
0
0
8
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
were testable, we also performed several lines of control analyses to establish that the indices
of dynamics and connectivity could be estimated independently. We characterized scale-free
dynamics by connectomes of avalanche propagation patterns and interareal correlations in the
LRTC scaling exponents, and compared the connection strengths and modular organizations in
these connectomes with those in connectomes of FC measured by the phase synchronization
(Vinck, Oostenveld, van Wingerden, Battaglia, & Pennartz, 2011) and amplitude correlations
(Brookes, Woolrich, & Barnes, 2012) of ongoing neuronal oscillations. We show that both
neural dynamics and FC have, in a frequency-specific and nontrivial manner, similar con-
stellations of strongest connections and shared modular structures, which provides empirical
evidence that neuronal connectivity and scale-free dynamics are intimately linked.
ERGEBNISSE
In our MEG and SEEG data, a neuronal avalanche was defined as a set of suprathreshold
peaks in waves of broadband (1–120 Hz) ongoing activity occurring in consecutive time bins
(Figure 1A). The statistical properties of avalanches can be described by the distributions of
their sizes—that is, the total numbers of peaks in each avalanche—and lifetimes—that is,
the durations of the avalanches.
In this study we used time bin widths of 8 Und 16 ms for
the MEG and SEEG data, jeweils, and thresholds of two, three, and four standard devia-
tionen (SDs) to characterize the propagation of neuronal avalanches in different scaling regimes
(Zhigalov, Arnulfo, Nobili, Verehrung, & Verehrung, 2015). To evaluate the overall statistical nature of
these avalanches, we first assessed the goodness of fit between the size distribution data and
). Der
a truncated power-law model by computing the Kolmogorov–Smirnov distance (DKS
largest DKS for the different thresholds was 0.04 (p > 0.85) suggesting that the distributions
were approximated well by the truncated power-law function (Figure 1B). The scaling ex-
ponents of the avalanche sizes were estimated using the maximum-likelihood approach (sehen
Materials and Methods). We found similar mean power-law scaling exponents in the MEG and
SEEG data, with values close to 1.5 at the three-SD threshold (Abbildung 1C). We also assessed
the avalanche branching ratios at different thresholds and observed values close to 1 at three
SDs in both the MEG and SEEG data. The scaling exponent of 1.5 and branching ratio of 1
(Abbildung 1C) correspond to a critical branching process and are well in line with a body of prior
observations on neuronal avalanche dynamics (D. Plenz, 2012).
To corroborate the truncated power-law fitting of the distributions of avalanche sizes, Wir
applied a likelihood ratio test to compare the truncated power-law model with an exponential
Modell. The results showed that the truncated power-law model outperformed the exponential
Modell (P < 0.001, log-likelihood ratio test) for all subjects and thresholds.
The distributions of the avalanche lifetimes were biased by the numbers of samples and
were less robust than the size distributions in individual subjects. To assess the lifetime
distributions, we thus concatenated avalanches across subjects. Consistent with the prior
experimental and theoretical literature, the power-law exponents of the avalanche lifetimes
were near 2 at the three-SD threshold, where a size distribution exponent of 1.5 was found
(Zhigalov, Arnulfo, Nobili, Palva, & Palva, 2017, Figure S1).
Finally, we assessed the scaling function for the shapes of
the neuronal avalanches
(Figure 1D), by averaging avalanches within ranges of lifetimes (Figure 1D, upper panel) and
then rescaling the functions by normalizing the lifetimes (Figure 1D, lower panel). At rescaling,
a collapse of the avalanche shapes was observed, which is again well in line with previous
studies (Beggs & Timme, 2012; N. Friedman et al., 2012) and further supports the hypothesis
that the neuronal avalanches observed here arose from a critical process.
Critical branching:
A stochastic process characterized by
a nearly constant mean population
size—that is, without dying out or
explosive growth
Network Neuroscience
145
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Power-law scaling neuronal activity avalanches reveal signatures of critical dynamics.
(A) We used a parcellation (top panel) comprising 219 neuroanatomically labeled cortical parcels in
an individual cortical anatomy as the basis for all analyses. Neuronal avalanches were detected
in multichannel MEG (colored lines in middle panel; for simplicity, only the MEG data are plotted
in this figure) and SEEG recordings, where avalanches (black bars at bottom) were defined as sets of
uninterrupted time bins containing one or more suprathreshold peaks (black dots). The avalanche
time series—that is, the numbers of events per time bin—are depicted with the black bars. The first
and second time bins used in the avalanche propagation connectome are marked with blue and
orange dots, respectively.
(B) Example of avalanche size distributions for the different thresholds
and a time bin width of 8 ms in the MEG data. The distributions are approximated well by trun-
cated power laws for the thresholds of two (red line), three (green line), and four (blue line) SDs.
In contrast, the avalanche sizes for surrogate data follow an exponential distribution (gray line).
(C) Mean power-law scaling exponents and branching ratios for the three thresholds (error bars in-
dicate the standard deviations for each mean) in the MEG data. (D) Avalanches exhibit a universal
scaling function, a hallmark of a critical process; graphs show the average shapes of the neuronal
avalanches associated with different lifetimes (upper panel) and the collapse after normalization
of the lifetimes (lower panel). (E) MEG group-level neuronal avalanche propagation connectomes
represent the probabilities of avalanche propagation (color scale) from each parcel to each other
parcel for the threshold of three SDs.
We characterized the spatial-propagation patterns of neuronal avalanches by compiling a
connectome of the empirical probabilities with which the activity peaks of the cortical parcels
in the first time bin were followed by activity peaks of the parcels in the second time bin
(Figure 1E and Zhigalov et al., 2017, Figure S2; see Materials and Methods).
Construction of Functional Connectivity and LRTC Connectomes
We hypothesized that the neuronal avalanches observed in MEG and SEEG (Figure 2A) would
propagate preferentially between brain areas coupled by FC. To test this hypothesis, we mea-
sured electrophysiological FC by means of the pairwise phase synchronization and amplitude
correlations (Figures 2B and 2C) of narrow-band neuronal oscillations. Furthermore, to assess
the interareal relationships of scale-free dynamics per se—that is, to measure how local
Network Neuroscience
146
Co-localization of cortical connectivity and scale-free dynamics
Figure 2. Avalanche propagation and the connectomes of interareal relationships in local LRTCs
have overall structures similar to those of the functional connectomes of phase synchroniza-
tion and amplitude correlations in both MEG and SEEG. (A) Avalanche propagation connec-
tomes represent the probabilities (color scale) of avalanche propagation from parcel to parcel.
(B) Phase-synchronization-based functional connectome at 16 Hz (color scale, showing mean
weighted phase-lag indices).
(C) Amplitude-correlation-based functional connectome at 16 Hz
(color scale, showing mean Pearson correlation coefficients of the orthogonalized amplitude time
series). (D) Connectome of interareal correlations in the local LRTCs at 16 Hz (color scale, showing
Pearson correlation coefficients across subjects). The top and bottom panels represent the MEG and
SEEG connectomes, respectively. Gray areas in the adjacency matrices (bottom panels) indicate
parcel–parcel connections not sampled in the present SEEG subject cohort.
dynamical states were correlated among all cortical regions—we obtained LRTC connectomes
(Figure 2D) by correlating across subjects the LRTC scaling exponents of orthogonalized am-
plitude time series for all pairs of parcels. The LRTC exponents are proportional to the system’s
proximity to the critical point (Poil, Hardstone, Mansvelder, & Linkenkaer-Hansen, 2012), and
hence, if brains behaved like a “single” near-critical system, this connectome should be uni-
form. However, already a visual inspection of the LRTC connectome (see Figure 2D) showed
that, like the other connectomes, it was highly nonhomogeneous, and although many brain
areas were significantly correlated in both MEG (r > 0.54, P < 0.05, Pearson’s correlation test)
and SEEG (r > 0.39, P < 0.05, Pearson’s correlation test), also a considerable fraction of re-
gions were below these nominal significance thresholds. Hence, at least among some subsets
of cortical areas, the local dynamics were only weakly correlated.
Avalanche Propagation Has Connectivity Patterns Similar to Those of FC
To test the hypothesis of colocalized avalanche propagation pathways and FC, we first mea-
sured the connection-level similarity—that is, the edge similarity—of avalanche propagation
with phase synchronization and amplitude correlations by means of the Pearson correlations
of these connectomes (see Materials and Methods). For phase-correlation-based FC, the re-
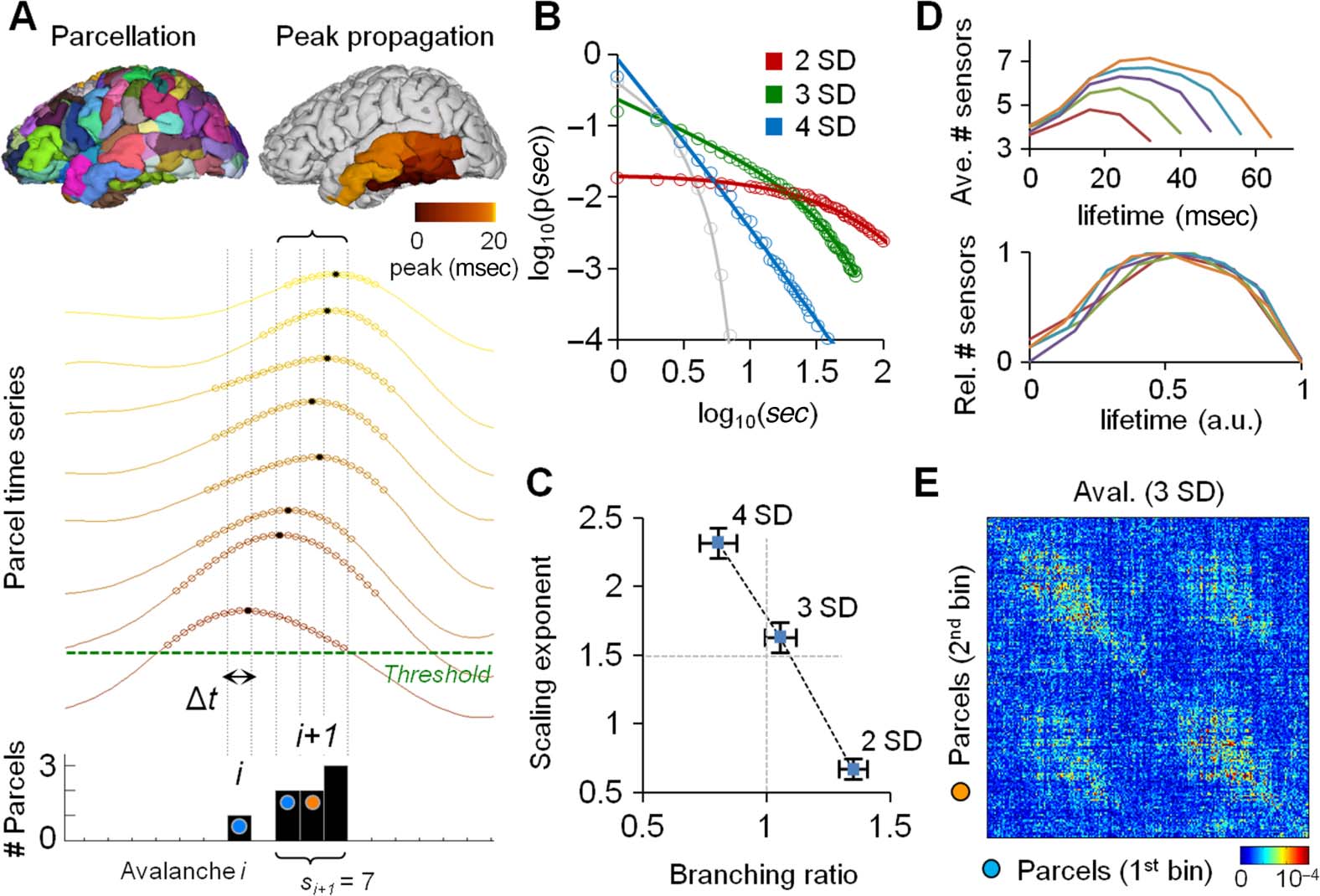
sults showed that the edge similarity was highly significant (well above the 99.9% confidence
intervals of the surrogate data, corresponding to uncorrected p < 0.001) between avalanche
propagation at three SDs and phase synchronization. This relationship was found in a limited
range of frequencies around the α and β bands (i.e., 8–14 Hz and 15–30 Hz, respectively;
Figure 3A, green lines), with peaks at around 16 Hz in MEG and at around 32 Hz in SEEG.
The similarity between phase correlations and avalanche propagation at both two and four
Network Neuroscience
147
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
SDs was much weaker (p < 0.001, Wilcoxon test) in both the α and β bands than at three
SDs, and significant only at four SDs in the β band (Figure 3A, blue lines) in MEG. The edge
similarity between avalanche propagation and the phase connectomes was also highly signif-
icant in SEEG (Figure 3A), but the differences between thresholds were not significant in SEEG
(p > 0.26, Wilcoxon test).
Similar to the phase-correlation FC, amplitude-correlation-based FC was also significantly
correlated with avalanche propagation at three SDs for frequencies up to ~30 Hz in MEG and
up to ~60 Hz in SEEG (Abbildung 3B, green lines). The spectral profiles of these similarities were,
Jedoch, distinct from those for phase FC in extending to the lowest frequencies (4−8 Hz),
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
N
e
N
_
A
_
0
0
0
0
8
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3. Avalanche propagation and functional connectivity (both phase and amplitude FC) Sind
colocalized in both MEG and SEEG. (A, B) The colocalization of broadband avalanche propaga-
tion at two (red line), three (green line), and four (blue line) SDs and of the narrow-band phase-
synchronization (A) or amplitude-correlation (B) connectomes was measured with edge similarity
(see Materials and Methods) for each frequency band in the MEG (top panels) and SEEG (bottom
panels) Daten. The gray-shaded areas indicate the surrogate-data-derived (see Materials and Methods)
confidence interval of 99.9%, corresponding to a significance criterion of p < 0.001.
Network Neuroscience
148
Co-localization of cortical connectivity and scale-free dynamics
even clearly peaking at 8 Hz (in MEG). This suggests that the amplitudes but not the phase
couplings of 4- to 8-Hz oscillations are associated with the propagation pathways of broad-
band avalanches. The similarity was again significantly greater for avalanche propagation at
three SDs than at two or four SDs (Figure 3B) across the entire range of frequencies in MEG
(p < 0.001, Wilcoxon test), whereas these differences in SEEG were not significant. These data
thus suggest that neuronal avalanches indeed propagate preferentially between brain areas that
are coupled by phase synchronization and/or amplitude correlations.
Avalanche Propagation Is Phenomenologically Distinct and Analysis-Wise Separable From Phase
Synchronization and Amplitude Correlations
To corroborate that the avalanche propagation and phase or amplitude connectomes can be
estimated independently, and hence to ensure that the hypotheses tested above were falsifi-
able, we performed two types of control analyses (see Materials and Methods).
In the first
approach, we deleted from the narrow-band data all data segments in which the broadband
amplitude exceeded the avalanche detection threshold—that is, all data used in the avalanche
analyses—and recomputed the phase and amplitude connectomes. Evaluation of their simi-
larity with the original avalanche propagation connectome revealed high similarity that was
not significantly different from what we had obtained with the uncut data (p > 0.99, KS test;
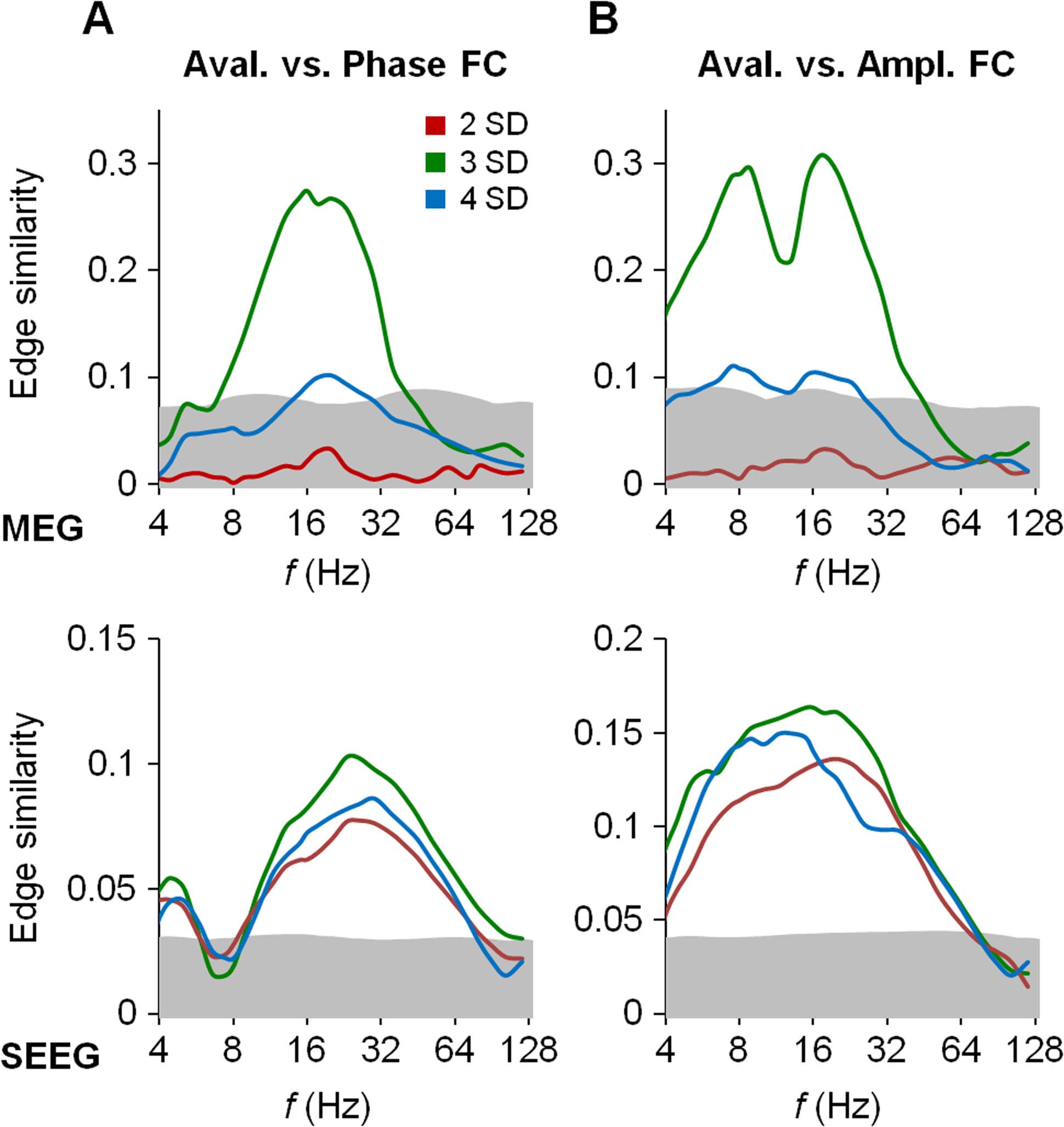
Figure 4A, durchgehende Linien). Reversing this analysis, we estimated the phase-synchronization and
amplitude-correlation connectomes by only using the suprathreshold data. Hier, the simi-
larity of the suprathreshold functional connectomes with the original avalanche propagation
connectome (Figure 4A, gestrichelt) was at chance level. These analyses thus show that the
similarity of FC and avalanche propagation does not arise from temporally colocalized time
windows in the data: avalanches neither bias the quantification of FC nor are trivially produced
by concurrent FC.
To corroborate these insights, in the second approach, we swapped all the time windows of
suprathreshold avalanche segments between random parcel pairs, and thereby systematically
reordered the avalanche propagation connectome. We then refiltered the data and recomput-
ing the phase-synchronization and amplitude-correlation connectomes. Their similarity with
the original avalanche propagation connectome did not decrease significantly much below
the original values (p > 0.99, KS test; Figure 4B, durchgehende Linien). Andererseits, the reordered
avalanche propagation connectome was uncorrelated with the functional connectomes esti-
mated from the same reordered data (Figure 4B, gestrichelt). Although this result was not
surprising, in the sense that the original correlation of FC and avalanches was broken by re-
organizing the avalanches, this analysis confirmed the first one and showed conclusively that
the bias that the avalanche segments impose on FC estimates from the same data is negligible,
and hence that the avalanches and FC can be estimated independently.
These data, together with the prior findings of (ich) avalanche–FC correlations being dis-
tinct for amplitude and for phase FC; (ii) avalanche–FC correlations being spectrally limited,
whereas FC is not (see below and in Figure 6); Und (iii) avalanches at two SDs not being more
similar to FC than at three SDs, thus strongly suggest that the broadband avalanches are neuro-
physiologically and phenomenologically distinct from the multitude of phase-/amplitude-
coupled narrow-band oscillations.
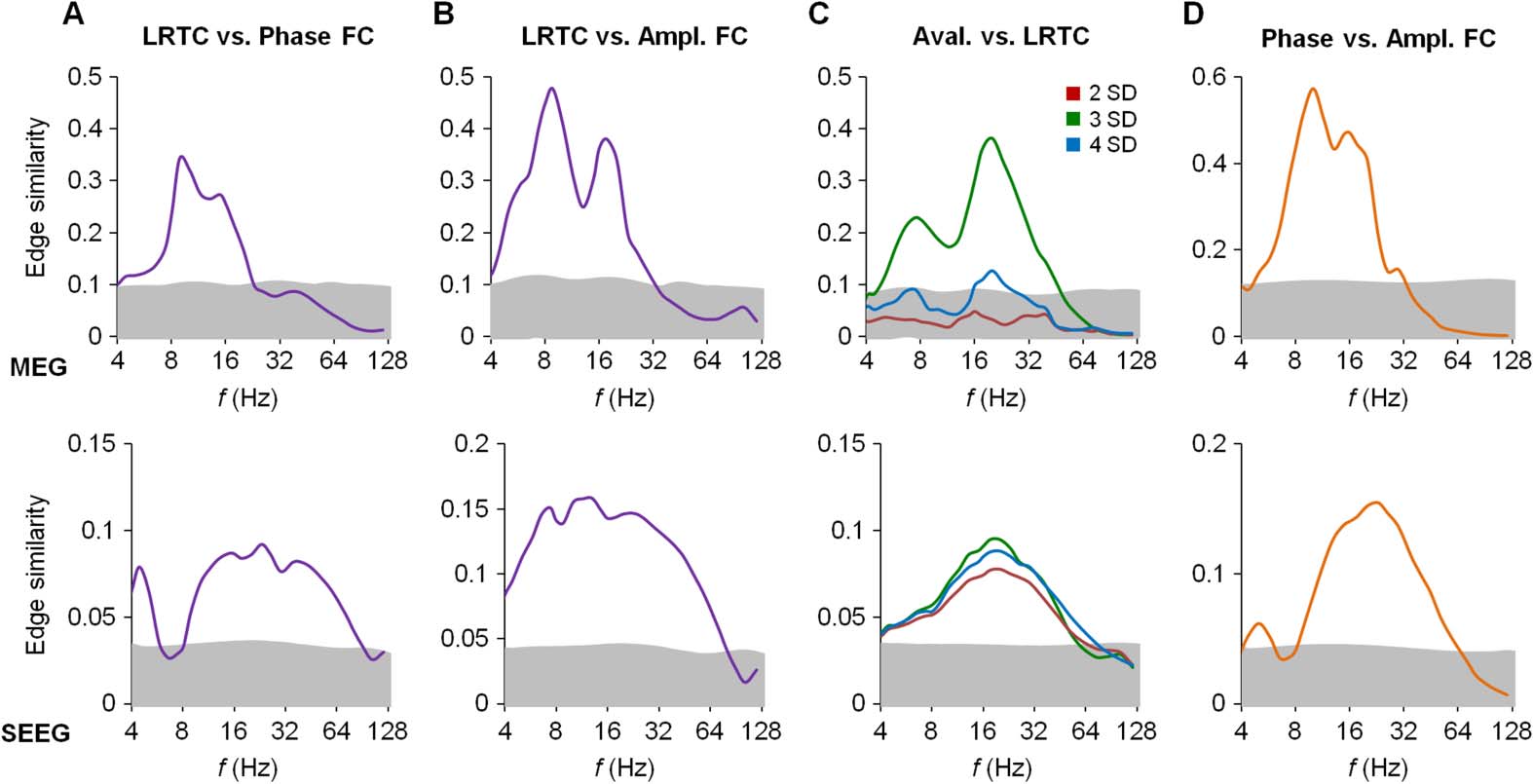
Interareal Correlations in LRTCs Are Similar to Those of FC
We then assessed how the interareal relationships in local LRTCs were correlated with the
patterns of FC. Zu diesem Zweck, we first estimated the edge similarity between the LRTC and
Netzwerkneurowissenschaften
149
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
N
e
N
_
A
_
0
0
0
0
8
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
N
e
N
_
A
_
0
0
0
0
8
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4. Avalanche propagation is phenomenologically distinct and analysis-wise separable from
both phase synchronization and amplitude correlations. (A) Edge similarity of the avalanche con-
nectome at three SDs with the phase-synchronization (left panel) and amplitude-correlation (Rechts
panel) connectomes estimated for subthreshold (durchgehende Linien) and suprathreshold (dashed line) seg-
gen. The result that the subthreshold similarity (durchgehende Linien) is close to the original similarity
between avalanche propagation at three SDs and FC (dotted lines; see Figures 3A and 3B) zeigt an
that the avalanche segments in the data are irrelevant to the estimation of FC. The suprathreshold
Ähnlichkeit (gestrichelt) being well inside the 99.9% confidence limits (gray areas) indicates that FC
during the avalanche segments does not have a structure similar to that of avalanche propagation.
(B) Edge similarity of the avalanche connectome at three SDs with the phase-synchronization (links
panel) and amplitude-correlation (right panel) connectomes (durchgehende Linien), estimated from data in
which all suprathreshold segments were swapped across random pairs of parcels prior to estimation
of the phase/amplitude connectomes. The result that this similarity is again close to the original
similarity estimates (dotted lines) indicates that the avalanches have a negligible contribution to the
FC estimates. When the reorganized avalanches were detected from the same data (gestrichelt),
their similarity was well below the confidence limits (gray area).
Netzwerkneurowissenschaften
150
Co-localization of cortical connectivity and scale-free dynamics
Figur 5. LRTC and functional connectivity (both phase and amplitude FC) are colocalized in
both the MEG and SEEG data.
(A, B) The colocalization of the LRTC and narrow-band phase-
synchronization (A) and amplitude-correlation (B) connectomes was measured with edge similarity
(see Materials and Methods) for each frequency band in the MEG (top panel) and SEEG (bottom
panel) Daten.
(C) Edge similarity between avalanche propagation at two (red lines), three (Grün
lines), and four (blue lines) SDs and the LRTC connectomes. (D) Edge similarity between the phase
and amplitude connectomes. The gray-shaded areas indicate the surrogate-data-derived (see Ma-
terials and Methods) confidence interval of 99.9%, corresponding to a significance criterion of
P < 0.001.
phase/amplitude connectomes and found robustly significant, but again band-limited, sim-
ilarities (Figures 5A and 5B) with spectral profiles akin to those found for avalanche prop-
agation (see Figures 3A and 3B). Finally, the comparison of avalanche propagation at three
SDs with the LRTC connectomes also revealed significant similarity in both the MEG and the
SEEG data (Figure 5C). The similarity was significantly larger for the avalanche propagation
at three than at two and four SDs in the MEG data (p < 0.001, Wilcoxon test). Moreover,
the phase-synchronization and amplitude-correlation connectomes were clearly correlated in
both MEG and SEEG (Figure 5D), with 16 and 32 Hz as the modal frequencies, respectively.
Throughout these similarity estimates, and also in the mutual correlation of phase and ampli-
tude FC, the frequency band of significant correlations extended to ~60 Hz in SEEG and only to
~30 Hz in MEG, which is likely attributable to the approximately millimeter versus approx-
imately centimeter spatial scales across which SEEG and MEG measure coherent neuronal
population activity.
These findings together thus show that scale-free brain dynamics, including both power-
law-scaled, millisecond-range activity avalanches and LRTCs spanning hundreds of seconds,
are intimately linked with the architecture of FC in human cortex.
LRTCs of Phase Synchrony Show Strong Similarity to FC
The findings so far converged on the idea that two facets of critical dynamics, avalanche prop-
agation and interareal coupling of local LRTCs, were colocalized with phase- and amplitude-
correlation-based functional connectivity. To corroborate this finding with an independent
index of critical dynamics, we estimated LRTCs in the momentary dynamics of phase
Network Neuroscience
151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
synchrony with phase detrended fluctuation analysis (DFA; Botcharova, Farmer, & Berthouze,
2014) between all pairs of cortical parcels in the MEG data. The adjacency matrices of the
phase DFA LRTC scaling exponents were thus directly comparable with those of FC. We found
phase DFA and FC to be highly significantly similar for both phase and amplitude FC (well
above the 99.9% confidence intervals) in the α and β frequency bands and to have profiles
similar to those of the avalanche propagation and functional connectomes (Figure 3). These
observations show that temporal correlations and spatiotemporal interactions are linked at
different timescales, which consolidates the prior findings (see Figures 4 and 5) and overall
suggests that the underlying system is poised at criticality.
Alpha–Beta-Range Oscillations Form a Cortical Core for the Dynamics–Connectivity Association
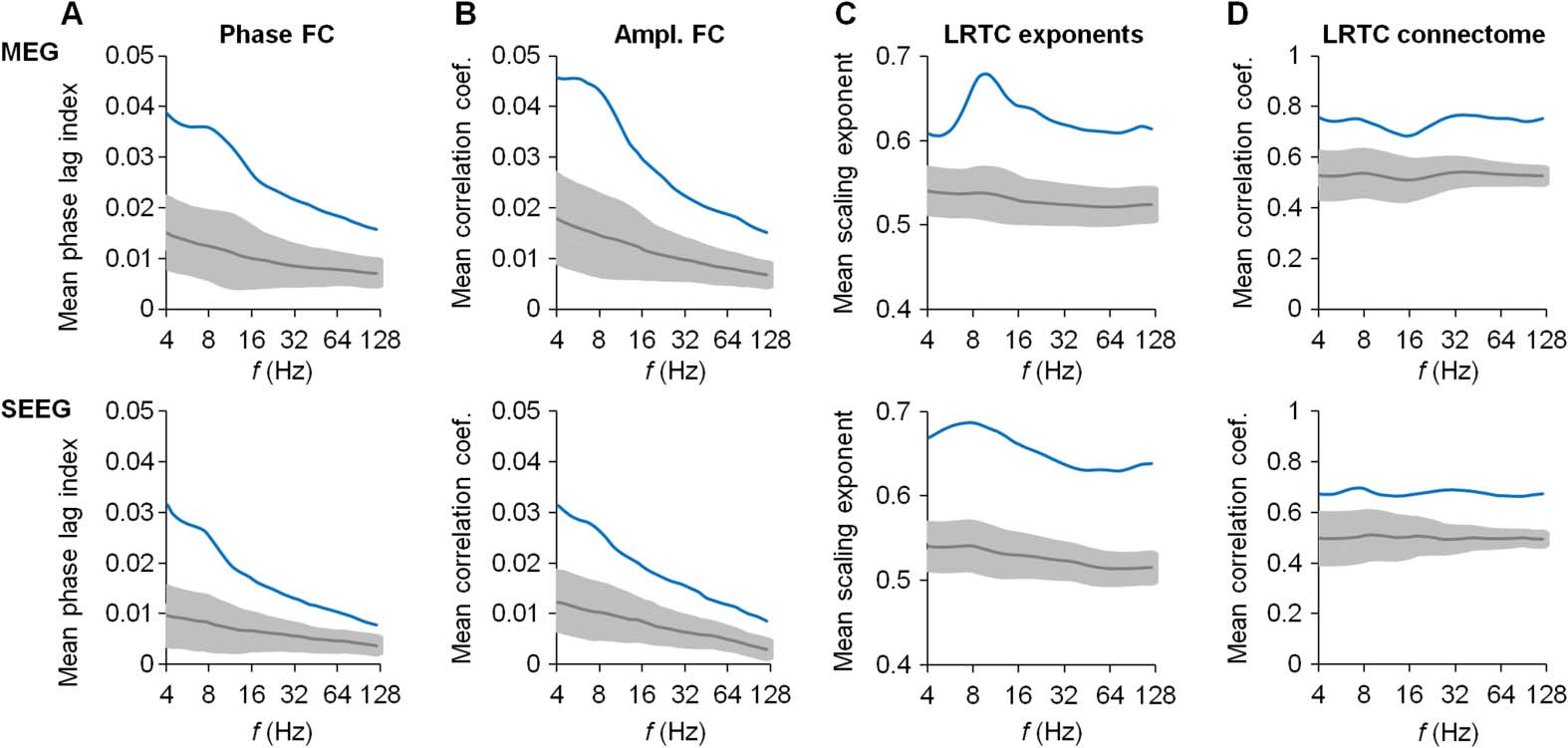
The association of scale-free dynamics and FC was found in a relatively narrow frequency
range around the α and β frequency bands. Does this reflect a “special” and nontrivial emer-
gent phenomenon or a trivial “by-product” of the scale-free dynamics being automatically
associated with connectivity?
To address this question, we asked whether either FC or LRTCs were correspondingly more
prevalent in this α/β range than in the surrounding bands. We first assessed the connection
strengths of the phase-, amplitude-, and LRTC-correlation connectomes across the frequency
range. For the phase and amplitude connectomes, the mean correlation strengths exhibited
subtle peaks, at 9 Hz in MEG and at 7 Hz in SEEG, but overall they decreased monotonically as
a function of frequency (Figures 6A and 6B) and remained well above the 99.9% confidence
limits of the corresponding surrogate values throughout the studied frequency range. Both
phase- and amplitude-based forms of FC thus appear robust for frequencies between 4 and
128 Hz. Similar averaging of the local LRTC scaling exponents (Figure 6C) showed that the
LRTCs also peaked at around 10 Hz in MEG and at 8 Hz in SEEG, but again were well above
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Highly significant FC and LRTCs are observed throughout the analyzed frequency range.
(A, B) Mean connection strengths (blue lines) of the phase (A) and amplitude (B) connectomes as a
function of frequency in the MEG (top panels) and SEEG (bottom panels) data. Gray lines indicate the
corresponding mean values for the surrogate data, and the gray-shaded areas show the confidence
limits of 99.9%. (C) LRTC scaling exponents (blue lines) averaged across all parcels peak at 10 Hz
in the MEG (top panel) and at 8 Hz in the SEEG (bottom panel) data, respectively. (D) Mean con-
nection strengths (blue lines) of the LRTC connectome as a function of frequency in the MEG (top
panel) and the SEEG (bottom panel) data.
Network Neuroscience
152
Co-localization of cortical connectivity and scale-free dynamics
the surrogate confidence limits from 4 to 128 Hz. Significant scale-free dynamics are thus not
unique to any single frequency band.
In the same vein, the interareal correlations of LRTC
exponents were essentially constant and highly significant across the studied frequency range
(Figure 6D). Hence, just as FC was a salient characteristic of all frequency bands, also scale-
free dynamics and the interareal structure of LRTCs characterized the 8- to 32-Hz range over
which most of the salient dynamics–FC coupling was found, as well as the 4- to 8-Hz and 32- to
128-Hz ranges over which the dynamics–FC correlations were much weaker or insignificant.
Together with the previous analyses (see Figure 5), these results thus show that significant
FC and scale-free dynamics in the human brain can be mutually coupled or uncoupled in
a frequency-dependent manner, which indicates that this coupling is nontrivial and neither
automatic nor epiphenomenal.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
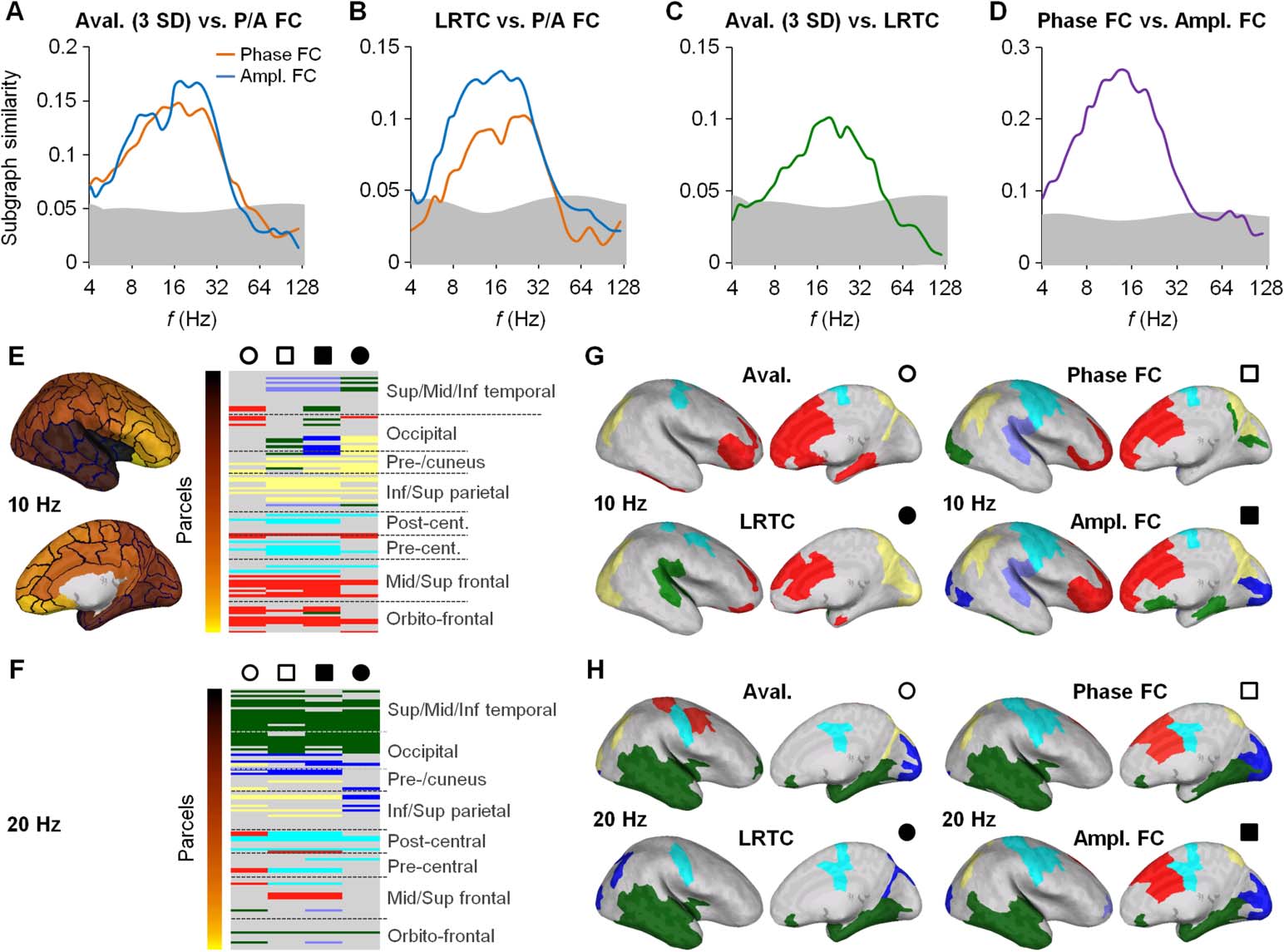
Figure 7. Neuronal criticality and functional connectivity (FC) have similar modular structures
in the MEG data.
(A) The colocalization of the modular structures in the connectomes was as-
sessed with a subgraph similarity measure (see Materials and Methods). The modular structure of
the avalanche propagation connectome at three SDs was highly significantly similar to the modular
structures of the phase and amplitude connectomes from about 4 to 40 Hz. (B) The spectral pro-
files of subgraph similarity between LRTC and the phase/amplitude connectomes are comparable
to those of the avalanche propagation connectome. (C) Subgraph similarity between the avalanche
propagation connectome at three SDs and the LRTC connectome. (D) Subgraph similarity between
the phase and amplitude connectomes. The shaded areas in all graphs indicate the 99.9% con-
fidence intervals. (E, F) A large fraction of parcels have similar subgraph assignments among the
avalanche propagation, phase, amplitude, and LRTC connectomes; hence, these connectomes ex-
hibit similar modular structures at both 10 and 20 Hz. Lavender, green, blue, yellow, cyan, and
red colors indicate the subgraph identities. The inflated brains illustrate the color codes for the
parcels scale. (G, H) Neuroanatomical visualization of matching subgraphs (functional modules)
in the avalanche propagation connectome and the phase, amplitude, and LRTC connectomes at
10 and 20 Hz, respectively. The circle and square symbols indicate correspondences between the
subgraphs in the plane (E, F) and neuroanatomical (G, H) representations.
Network Neuroscience
153
Co-localization of cortical connectivity and scale-free dynamics
Shared Modular Structures of Avalanche Propagation, LRTCs, and Functional Connectivity
The similarity between avalanche propagation pathways, interareal correlations of LRTCs, and
functional connectomes indicated a significant connection-level colocalization of these net-
works. We addressed next whether scale-free dynamics and FC had similar modular structures
in the MEG data. The SEEG data were excluded from this analysis because their sparse spatial
coverage did not allow for robust detection of the functional modules.
We identified network modules, subgraphs, by using agglomerative hierarchical clustering
of the connectomes of scale-free dynamics and FC (see Figure 2), and then measured the simi-
larity of these modular structures by quantifying the overlap among the subgraph assignments
(see Materials and Methods). The results showed that the modular structures of both avalanche
propagation at three SDs (Figure 7A) and the interareal correlations of LRTCs (Figure 7B) had
highly significant subgraph similarities with both phase- and amplitude-based FC. This colo-
calization of network modules was found in a limited frequency range up to 40 Hz, with the
greatest values again being between 8 and 30 Hz (Figures 7A and 7B). For completeness, we
also measured the subgraph similarity between avalanche propagation at three SDs and LRTCs
(Figure 7C), as well as between the levels of phase and amplitude FC (Figure 7D), and found
that both were robust in the 8- to 32-Hz range. In this frequency range, scale-free dynamics
and FC thus had both internally and mutually shared modular structures.
To identify the cortical regions that composed the shared functional modules in these con-
nectomes, we used consensus mapping of the parcel-subgraph neighborhoods obtained with
the hierarchical clustering (see Materials and Methods). This analysis showed that the most
consistently shared modules were localized to sensorimotor, visual, temporal, and prefrontal
areas (ps < 0.05, permutation test; see the cyan, blue, green, and red modules, respectively, in
Figures 7E– 7H).
DISCUSSION
large numbers of nonlinearly interacting elements. At
Criticality governs the spatiotemporal dynamics of numerous natural and artificial sys-
the critical
tems composed of
operating point,
the system exhibits long-range correlations with power-law decay con-
currently across all temporal and spatial scales (Bak, Tang, & Wiesenfeld, 1988; Chialvo,
2010). Brains have been proposed to operate near the critical point (Beggs & Plenz, 2003;
Linkenkaer-Hansen et al., 2001) or in an extended critical region (Hilgetag & Hutt, 2014;
Moretti & Munoz, 2013), which has fundamental implications for neurophysiological phe-
nomena and neuronal information processing across the scales from neurons to brain sys-
tems. Neuronal criticality has primarily been operationalized with two hallmark phenomena,
millisecond-range neuronal avalanches (D. Plenz, 2012) and long-range temporal correlations
spanning hundreds of seconds (Linkenkaer-Hansen et al., 2001), although power-law char-
acteristics have also been reported for several other forms of spatiotemporal brain dynamics
(Kitzbichler, Smith, Christensen, & Bullmore, 2009). Conversely, although scale-free dynam-
ics are an indisputable characteristic of brain activity, whether they arise from criticality or
other mechanisms has remained a matter of debate (Touboul & Destexhe, 2010).
Much of our understanding of spatiotemporal brain dynamics has arisen from studies of
hemodynamic and electrophysiological FC, which have shown that hierarchically modular ar-
chitectures of neuronal interactions govern both resting-state brain activity (Mitra et al., 2015)
and ongoing activity during task performance (de Pasquale et al., 2012).
It is theoretically
conceivable and predicted by computational models (Haimovici et al., 2013) that neuronal
Network Neuroscience
154
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
criticality and FC—concurrent, yet distinct and dissociable, network phenomena—would be
related. However, very few prior experimental studies have aimed at elucidating this relation-
ship (Pajevic & Plenz, 2009; Rubinov, Sporns, Thivierge, & Breakspear, 2011).
In this study, we sought to bridge this gap by quantifying the interareal relationships
of scale-free dynamics and FC. Toward this end, we used both meso- and macro-scale
electrophysiological recordings of human resting-state brain activity, with invasive SEEG
(Arnulfo, Hirvonen, Nobili, Palva, & Palva, 2015) and noninvasive MEG (S. Palva & Palva,
2012), respectively. We first found that at the level of the strongest connections, avalanche
propagation was well colocalized with both phase-synchronization-based and amplitude-
correlation-based FC. To investigate how these interactions were coupled with scale-free
dynamics, we estimated the interareal correlations of local LRTCs and found that these cor-
relations were also colocalized with both avalanche propagation and FC. Scale-free neuronal
dynamics and FC thus have a shared backbone of interareal relationships.
Both functional (Gallos, Makse, & Sigman, 2012; Meunier, Lambiotte, & Bullmore, 2010)
and structural (Hagmann et al., 2008) connectivity have hierarchically modular network or-
ganizations. As the second step in this study, we assessed the modularity in our estimates
of critical dynamics and found that both the propagation of neuronal avalanches and the in-
terareal correlations of LRTCs exhibited modular structures, and that these structures were
neuroanatomically similar to those of FC. This strongly suggests that neuronal communities
characterized by strong internal phase synchronization and amplitude correlations are also
characterized by preferentially internal avalanche propagation and correlated local LRTCs.
Beyond linking scale-free dynamics and connectivity, this finding also indicates that the brain
can be envisioned as a constellation of mutually coupled and hierarchically organized mod-
ules distributed to distinct neuroanatomical substrates and to different frequency bands, rather
than as a homogeneous critical-state system.
Overall, these observations strongly suggest that FC and scale-free neuronal dynamics, and
hence, putatively, neuronal criticality as well, are intimately related, which opens new avenues
for studies aiming to understand the physiological interactions between these phenomena.
Spatial Domains of Scale-Free Dynamics Revealed by Interareal LRTC Relationships
Neuronal criticality is often considered in the context of models or physical systems that have
a relatively homogeneous spatial structure of their interacting elements (N. Friedman et al.,
2012; D. Plenz & Thiagarajan, 2007). In contrast, human brains have a markedly nonhomo-
geneous and hierarchically modular large-scale structure (Gallos et al., 2012; Meunier et al.,
2010), which theoretically has a major influence on the emergence of criticality in neuronal ac-
tivity, by transforming the system from having a critical point into exhibiting a critical regime—
that is, a Griffith’s phase (Hilgetag & Hutt, 2014; Moretti & Munoz, 2013). One key implica-
tion of modular structural connectivity is that it could allow for topologically distant modules
of the network to have semi-independent dynamics. In this study, the finding that the interareal
relationships of LRTC scaling exponents were clearly nonhomogeneous provides evidence for
this theory and opens the possibility that different brain systems could have distinct operating
points (or regimes).
We found also that both the interareal relationships and modular structures of neuronal
avalanches and LRTCs had colocalized neuroanatomical bases. This finding complements
prior studies that have shown that scale-free dynamics observed at the meso- and macro-
scales with SEEG and MEG, respectively, are phenomenologically very similar (Zhigalov et al.,
Network Neuroscience
155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
2015) and that the avalanche and LRTC scaling exponents are corrected at both spatial scales
(J. M. Palva et al., 2013).
Frequency Specificity in the Dynamics–Connectivity Association
The connectivity patterns of oscillations in and around the α (8–14 Hz) and β (15–30 Hz)
bands have been suggested to provide a “cortical core” (de Pasquale et al., 2012) or “hubs”
(Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012) for neuronal integration and resting-state
network dynamics. We found here that the strongest similarities between scale-free dynamics
and FC were observed specifically in this frequency range. Likewise, the similarity between
neuronal avalanches and LRTC was also maximal in this frequency range, and an even stronger
similarity was found for both interareal phase synchronization and amplitude correlations (see
Figure 5D). The α and β oscillations in the resting state thus appear to be central for both
neuronal integration and the connectivity–dynamics association. Importantly, the lack of such
association at the lower frequencies (4–7 Hz) was not explained by a lack of FC or by ev-
idence for power-law scale-free dynamics therein, because highly significant FC as well as
LRTCs were observed in this frequency range (see Figure 6). This shows that the association of
FC and scale-free dynamics is neither trivial nor automatic in brain dynamics, but rather is a
unique dynamic property of a subset of frequency bands in ongoing brain activity.
Possible Confounders
Two sources of circularity could theoretically confound our analyses of the similarities between
broadband avalanche propagation and narrow-band phase synchronization or amplitude cor-
relations. As a conceptual confound, one may argue that the broadband avalanche events
and the narrow-band oscillations actually reflect the dynamics of a single underlying neuronal
process, which would lead to artificial or trivial colocalization of their connectomes. As a
technical confound, the estimates of narrow-band FC could be biased by the putatively large-
amplitude avalanche events, and conversely, the avalanche detection might pick up momentar-
ily large-amplitude oscillations because both phenomena were estimated from the same data.
Such “technical” cross-bias in the estimators of avalanche propagation and FC could render
the estimators mutually and artificially correlated by design. However, control analyses (see
Figure 4) showed that (i) the rare avalanche-like events in ongoing brain activity have a negli-
gible impact on estimates of FC, and (ii) both avalanche propagation and FC can be estimated
independently of each other. Thus, no technical circularity prevented our testing the hypothe-
sized relationship between avalanches and connectivity. Moreover, because (iii) narrow-band
FC during the avalanches was uncorrelated with the avalanche propagation estimated from
the same data, the propagating broadband avalanche events appear to be distinct neurophys-
iological phenomena from the interareal phase or amplitude couplings of narrow-band oscil-
lations. Finally, the finding that the avalanche propagation patterns detected at two SDs were
less similar to FC than were those detected at three SDs constitutes strong evidence that the
avalanche–connectivity relationship is not a trivial by-product of avalanches simply reflecting
phase-lagged connectivity, because if this were the case, the two-SD avalanches should be
closer in similarity to the FC estimates (which effectively correspond to the “0-SD” data) than
the avalanches at three SDs.
Clinical Implications
lines of evidence have shown that abnormalities in neuronal scaling laws are
Several
biomarkers of a number of brain diseases.
In major depressive disorder, the LRTC scaling
exponents for central/frontal theta oscillations are lower than those among healthy controls,
Network Neuroscience
156
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
whereas posterior α oscillations exhibit no abnormalities (Linkenkaer-Hansen et al., 2005). In
schizophrenia, the LRTC scaling exponents are suppressed in both the α and β bands over
parietotemporal areas (Nikulin, Jonsson, & Brismar, 2012). Similarly, in autism spectrum disor-
ders (Lai et al., 2010) and Alzheimer’s disease (Montez et al., 2009), lower-than-normal LRTC
scaling exponents are a robust characteristic. Conversely, in epileptic patients, the epilepto-
genic zone exhibits greater β-band LRTC exponents than do the surrounding cortical regions
(Monto, Vanhatalo, Holmes, & Palva, 2007). These findings are well in line with our discovery
that different brain systems are capable of operating concurrently in distinct dynamic regimes.
The intriguing, and possibly functionally essential, implication is that abnormal dynamics
affecting only specific brain systems and/or frequency bands could be predictive of corre-
sponding pathological states and mental symptoms. Neuroanatomical specificity in critical
dynamics is also salient in the relationship between healthy neuronal and behavioral fluc-
tuations, in which neuronal criticality only in well-delineated brain systems is predictive of
behavioral scaling laws (J. M. Palva et al., 2013). Future studies should thus examine the pos-
sibility of modulating cortically well-localized dynamics noninvasively—for example, by using
neurofeedback (Ros et al., 2016; Zhigalov, Kaplan, & Palva, 2016).
MATERIALS AND METHODS
Data Acquisition and Preprocessing
We analyzed resting-state invasive stereotactic-electroencephalography (SEEG) recordings from
a cohort of 27 epileptic patients (18 males, nine females; ages 16–21 years) and noninvasive
magnetoencephalography (MEG) data recorded from 14 healthy subjects (seven males, seven
females; ages 18–27 years).
Resting-state SEEG was collected for 10 min with eyes closed and without external distur-
bance using a 192-channel SEEG amplifier system (NIHON-KOHDEN NEUROFAX-110) at a
sampling rate of 1 kHz. The number of electrode contacts along each penetrating shaft varied
from eight to 15. These contacts were 2 mm long and 0.8 mm thick and had an intercontact
distance of 1.5 mm (DIXI medical, Besancon, France). The anatomical positions and amounts
of electrodes varied according to surgical requirements (Cardinale et al., 2013). We excluded
from further analyses all contacts that were located within the epileptic focus or that exhibited
epileptiform activity such as interictal spikes (Zhigalov et al., 2015). The MEG data were col-
lected in a resting-state condition for 10 min while the subjects looked at a fixation point on the
monitor screen. We recorded 306-channel (204 planar gradiometers and 102 magnetometers)
MEG (Elekta Neuromag Ltd.) at a sampling rate of 600 Hz.
The SEEG study was approved by the Ethics Committee of the Niguarda “Ca’ Granda” Hos-
pital, and the MEG study was approved by the Ethics Committee of Helsinki University Central
Hospital. The subjects gave written informed consent for participation in research studies
and for publication of the data. The studies were performed according to the Declaration of
Helsinki.
SEEG and MEG Preprocessing
The location of each SEEG electrode contact was extracted with submillimeter accuracy from
postimplant cone-beam computerized tomography scans (Arnulfo, Narizzano, Cardinale, Fato,
& Palva, 2015) and was subsequently coregistered to the Freesurfer
(http://surfer.nmr.
mgh.harvard.edu/) geometrical space. We used a “closest-white-matter” referencing scheme
for the SEEG, in which electrode contacts in gray matter were referenced to the closest
Network Neuroscience
157
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
contacts in the underlying white matter (Arnulfo, Narizzano, et al., 2015). The MEG data were
corrected for extracranial noise and for cardiac and eye blink artifacts by using the signal
space separation method (Taulu, Simola, & Kajola, 2005) and independent-component anal-
ysis (Bell & Sejnowski, 1995), respectively. For cortical surface reconstructions, T1-weighted
anatomical images were recorded with a 1.5-T magnetic resonance imaging (MRI) scanner
(Siemens). The FreeSurfer software was used for automatic volumetric segmentation of the
MRI data, surface reconstruction, flattening, and cortical parcellation. The MNE software
(www.martinos.org/mne/) was used to create three-layer boundary element conductivity mod-
els and cortically constrained source models with fixed-orientation dipoles, and for comput-
ing the forward and inverse operators (Hamalainen & Ilmoniemi, 1994). The MEG sensor time
series were filtered in multiple frequency bands using a broadband finite impulse response
filter and Morlet’s wavelets. The filtered time series were inverse-transformed and collapsed
into time series of 219 cortical parcels derived from the individual MRI scans (Daducci et al.,
2012) by applying collapsing operators that maximized individual reconstruction accuracy
(Korhonen, Palva, & Palva, 2014).
Phase-Synchronization and Amplitude-Correlation Connectomes
To eliminate artificial interactions caused directly by volume conduction and signal mixing,
we used linear-mixing-insensitive metrics for assessing interareal phase and amplitude inter-
actions. Prior to the analyses, the time series were filtered using a bank of 31 Morlet’s wavelets
with logarithmically spaced central frequencies ranging from 4 to 120 Hz. The phase syn-
chronization between each pair of cortical parcels (MEG) or electrode contacts (SEEG) was
estimated by the weighted phase lag index q (Vinck et al., 2011), as it is implemented in the
Fieldtrip toolbox (Oostenveld, Fries, Maris, & Schoffelen, 2011):
(cid:2)
q=
(cid:2)
(cid:3)
(cid:2)
∑ω Pxy (ω)
(cid:4)
(cid:4)
Pxy(ω)
∑ω
(cid:4)
(cid:4)
2 − ∑ω
(cid:3)
2 − ∑ω
Pxy(ω)
(cid:2)
Pxy(ω)
(cid:3)
2
(cid:3)
2 ,
where Pxy is the imaginary part of the cross-spectral density
Pxy(ω) = im
(cid:6)
E [xnyn−m]e
−jωm
,
(cid:5)
N
∑
m=1
(1)
(2)
and x and y are time series containing N samples; E[·] is the expectation operator, and im()
denotes the imaginary part of a complex number.
The amplitude–amplitude correlations were assessed with the Pearson correlation coeffi-
cient. The narrow-band time series were orthogonalized for each pair of cortical parcels or
electrode contacts by using linear regression (Brookes et al., 2012), and the correlation coef-
ficient, r, was computed for the amplitude envelopes of the orthogonalized time series,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:9)(cid:2)
E
AX
⎛
⎝
− μ
r =
(cid:3) (cid:10)
AX
σ
AX
σ
AY|X
AY|X
− μ
AY|X
(cid:11)(cid:12)
(cid:9)(cid:10)
E
+
(cid:11) (cid:2)
− μ
AY
AY
(cid:3)(cid:12)
⎞
(cid:15)
⎠
2,
(3)
AX|Y
− μ
AX|Y
σ
|Y
AX
σ
AY
where AX, AY and AX|Y, AY|X are the amplitude envelopes of the original and orthogonalized
time series, respectively; μ denotes the mean; and σ is the standard deviation.
Network Neuroscience
158
Co-localization of cortical connectivity and scale-free dynamics
The orthogonalization was defined as
Y|X
= Y − X
(cid:2)
+
Y
X
(cid:3)
,
(4)
where X and Y are the narrow-band time series, and X
orthogonalization X|Y is done similarly (Brookes et al., 2012).
+
denotes the pseudo-inverse of X. The
Neuronal Avalanche Propagation Connectome
The neuronal avalanche propagation connectome was constructed by utilizing the concept
of critical branching processes (Zapperi, Baekgaard Lauritsen, & Stanley, 1995), in which the
activity in successive time bins propagates from one active group of neurons to another in an
avalanche (Beggs & Plenz, 2003). Neuronal avalanches were detected in broadband-filtered
(1–120 Hz), source-reconstructed MEG and SEEG time series that were normalized by subtract-
ing the mean and dividing by the standard deviation. The time series were then transformed
into binary point processes by detecting suprathreshold peaks above threshold T (Zhigalov et al.,
2015). These binary sequences (or sequences of events) were converted into avalanche time
series by summing the events across the channels in time bins Δt. A neuronal avalanche is
defined as a cluster of events in successive time bins, where the beginning and end of the
avalanche are defined by single time bins with no events (Figure 1A). The avalanche size dis-
tributions are typically fit well by a power law or a truncated power law, depending on the
parameters T and Δt (Beggs & Plenz, 2003; Zhigalov et al., 2015). Using these avalanche
data, we defined the avalanche propagation connectome to be constructed by the empirical
probability with which suprathreshold peaks of neuronal activity would “transits” from the
subset of channels in the first time bin to the subset of channels in the second time bin of each
avalanche (Figures 1A and 1E). There are several approaches to assessing the network struc-
ture of activity propagation patterns using all time bins of an avalanche (Leleu & Aihara, 2015;
Pajevic & Plenz, 2009). However, we assessed the propagation pathways by using only the first
two bins of each avalanche (Beggs & Plenz, 2003) in order to sample the “source” and “target”
parcels in the least ambiguous manner, because later bins might contain peaks that had orig-
inated from nonsuccessive bins. The avalanche propagation connectome was constructed for
each subject separately from suprathreshold peaks of neuronal activity detected for the thresh-
olds of two, three, and four SDs and a constant time bin width of 8 or 16 ms in MEG or SEEG,
respectively (Figure 1B). The different time bin widths for MEG and SEEG were necessary to
attain comparable scaling exponents of the neuronal avalanche sizes (Zhigalov et al., 2015).
Goodness of fit was assessed by computing the Kolmogorov–Smirnov (KS) distance between
the cumulative distribution functions (CDF) of the data and of a truncated power-law model
(Klaus, Yu, & Plenz, 2011),
DKS
= max |CDFdata
− CDFmodel
| .
The corresponding p-value was estimated as follows:
⎛
p = exp
⎝−2
(cid:5)(cid:5)
(cid:16)
N2 / 2N + 0.12 +
0.11(cid:16)
N2 / 2N
(cid:6)
⎞
(cid:6)
2
⎠ ,
DKS
where N denotes the number of samples.
(5)
(6)
The scaling exponents were estimated using the maximum likelihood method
(Clauset, Shalizi, & Newman, 2009). Statistical comparison between the truncated power-law
and exponential models has been done by applying the log-likelihood ratio test (Clauset et al.,
Network Neuroscience
159
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
2009; Klaus et al., 2011). A truncated power-law model is considered to outperform an ex-
ponential model if the log-likelihood ratio is positive and the difference between the model
likelihoods is significant (p < 0.05). The probability functions of the truncated power-law and
exponential distributions are expressed as
pt (s) = Ct s
−α
−λs,
e
(7)
(8)
where p(s) denotes the probability of observing an avalanche of size s, Ct and Ce are normal-
ization constants, and α and λ are the parameters of the power-law and exponential functions,
respectively.
pe (s) = Cee
−λs,
The log-likelihood ratio between the two distributions is defined as
LLR(s) = l(α, λ|s) − l({λ}|s),
(9)
where l() denotes the log-likelihood functions, and α and λ are the parameters of the models.
The p-value for the LLR test is defined as follows:
p = erfc
(cid:17)
(cid:18)
,
|LLR|
√
2πσ2
(10)
where σ2= 1
n
n
∑
i= 1
[(l ({α,λ} | si
) − l({α,λ}|s)/n) − (l ({λ} | si
) − l({λ}|s)/n)]2.
LRTC Connectomes
We used detrended fluctuation analysis (DFA) to assess the scaling exponents of the long-
range temporal correlations (LRTCs; Linkenkaer-Hansen et al., 2001; J. M. Palva et al., 2013;
Peng, Havlin, Stanley, & Goldberger, 1995). In DFA, the time series X is normalized to a zero
(X (i) − (cid:4)X(cid:5)), then segmented into time
mean and integrated over the samples, Y(k)= ∑k
windows of various sizes τ. Each segment of the integrated data is locally fitted to a linear
function Uτ, and the mean-squared residual F(τ) is computed,
i= 1
F(τ) =
(cid:19)
(cid:20)
(cid:20)
(cid:21) 1
N
N
∑
k= 1
[Yτ (k) − Uτ(k)]2,
(11)
where N is the number of samples in segment τ.
The scaling exponent η is defined as the coefficient of the linear regression of the function
F(τ) plotted in double logarithmic coordinates. The optimal fitting range, in terms of the
linearity of the slope, was limited to 3–300 s for the present dataset.
The LRTC connectome was computed for the amplitude envelopes of the wavelet-filtered
time series using the Pearson correlation coefficient at the group level between the exponents
of each cortical parcel i (η
j was assessed with the time series of parcel j
i
orthogonalized to the parcel i (Brookes et al., 2012),
) and j (η#
j
), where η#
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:22)
(cid:2)
η
i
E
=
Aij
Network Neuroscience
− μη
(cid:17)
(cid:3)
(cid:18)(cid:23)
η#
j
− μη#
j
i
ση
ση#
j
i
.
(12)
160
Co-localization of cortical connectivity and scale-free dynamics
As in the estimation of amplitude–amplitude correlations, orthogonalization was used to
eliminate the pairwise effects of linear signal mixing on the LRTC estimates, and hence to allow
for assessment of the relationship between local cortical scaling exponents without artificial
coupling of these regions (Blythe, Haufe, Muller, & Nikulin, 2014).
Surrogates
To assess the statistical significance of the results, we generated comparable surrogate data
and applied the analyses above to these data. The surrogate time series were derived from the
original ones so that the signal of each channel was circularly shifted by a random number of
samples (Zhigalov et al., 2015). This approach provides more accurate statistical inference for
neuronal avalanches than does the conventional phase-shuffling method (Prichard & Theiler,
1994). The circular shift breaks spatial correlations but essentially fully preserves the tempo-
ral autocorrelation structure. For SEEG, the surrogate data were obtained by circular-shifting
the white-matter-referenced gray-matter recordings and used as is. For MEG, the surrogate
data were obtained by first circular-shifting the original source-reconstructed MEG parcel
time series and then forward and re-inverse modeling these data (Korhonen et al., 2014).
This approach is essentially equivalent to the one proposed by Shahbazi and colleagues
(Shahbazi, Ewald, Ziehe, & Nolte, 2010) and accurately reconstructed the net residual signal
mixing present after the MEG measurement (forward modeling) and after the partial separation
of the original cortical sources achieved by source modeling (inverse modeling).
Control Analyses for the Avalanche Propagation Connectome
To assess whether the avalanche propagation and phase-synchronization or amplitude-
correlation connectomes can be estimated independently, we performed several lines of
control simulations. We assessed the impacts of suprathreshold events—that is, neuronal
avalanches—on FC in MEG using two approaches. In the first approach (see Figure 4A), we
deleted all suprathreshold data segments above three SDs and recomputed the phase and am-
plitude connectomes (see Figure 4A, solid lines). This deletion was carried out separately for
each parcel pair in these connectomes by using logical disjunction (i.e., the OR operation)
of the avalanche segments in these parcels. We also recomputed the phase and amplitude
connectomes for the complement of these data—that is, by using only the suprathreshold seg-
ments (see Figure 4A, dashed lines). The suprathreshold, subthreshold, and original functional
phase/amplitude connectomes were compared with the avalanche propagation connectome
using the edge similarity index (Eq. 14 below). Any statistical difference between the edge
similarities at multiple frequencies was assessed with the KS test.
In the second approach (see Figure 4B), we swapped all time windows of the suprathresh-
old avalanche segments above three SDs between randomly assigned parcel pairs. This opera-
tion thus randomly reordered the avalanche propagation connectome. Because the segments
were only partially overlapping between the parcel time series, we again used disjunction
to combine avalanche segments within the pairs of parcels. After the segment swaps, the
time series were refiltered to account for the filter-related temporal spreading of the large-
amplitude avalanche events. Using these data, we then recomputed the phase and amplitude
connectomes and assessed their edge similarity with the original avalanche connectome (see
Figure 4B, solid lines). To assess how independently the avalanches and FC can be measured,
we also reanalyzed the avalanche propagation patterns from these data and compared this
swapped avalanche propagation connectome with the swapped phase and amplitude connec-
tomes using the edge similarity index (see Figure 4B, dashed lines).
Network Neuroscience
161
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
Estimation of the Branching Ratio
The branching ratio (p) was estimated by computing the ratio of the number of events in
the second time bin to the number of events in the first time bin of a neuronal avalanche
(Beggs & Plenz, 2003; Shriki et al., 2013).
p = 1
N
∑N
i= 1
(2)
i
(1)
i
n
n
,
(13)
(1)
i
(2)
i
where n
avalanche, respectively; N is the total number of avalanches.
and n
are the numbers of events in the first and second time bins of the ith
Phase DFA
In addition to classical avalanche and amplitude LRTC measures, we characterized crit-
icality in the LRTCs with moment-to-moment fluctuations of interareal phase synchrony
(Botcharova et al., 2014). The phase time series between pairs of cortical parcels (MEG) or con-
tacts (SEEG) were extracted from the complex-valued narrow-band-filtered data (4–120 Hz).
DFA (see the LRTC Connectome section above) was applied to the first time derivatives of the
phase differences. The resulting connectome represented the LRTC scaling exponents of phase
synchrony between each pair of cortical parcels.
Control Analysis for the LRTC Connectome
To assess whether the connection strengths (connectome values) have a specific frequency
profile that might explain the profile of connectome similarity, we estimated the connection
strengths for the phase, amplitude, and LRTC connectomes for the entire range of frequencies
(4–120 Hz). The connection strengths were estimated as a mean for the connectome (adja-
cency matrix) for each frequency (see Figure 6).
Edge and Subgraph Similarity Indices
The edge similarity index was defined as the Pearson correlation between two adjacency ma-
trices (connectomes),
he = E [(A − μ
) (B − μ
σ
B
A
A
σ
B)]
,
(14)
where A and B are inflated adjacency matrices (column vectors).
The modular structure of the connectomes was detected using agglomerative hierarchical
clustering (Bellec, Rosa-Neto, Lyttelton, Benali, & Evans, 2010). The number of clusters per
hemisphere, K = 7, provided a reasonable division of the connectomes into functional mod-
ules. As a result of clustering, each cortical parcel n (N = 219) was associated with a unique
subgraph (or cluster) identity (In ∈ [1, K]). The subgraph similarity index was defined as the
Jaccard similarity coefficient between matched subgraph identities,
hs= IA
IA
∩ IB
∪ IB
,
(15)
where IA and IB are the vectors of cluster identifies computed for the A and B adjacency
matrices, respectively.
Network Neuroscience
162
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
Consensus Mapping of Subgraph Identities
Consensus mapping was applied to assess the shared subgraphs of the connectomes. The
subgraph identities (see the previous section) of all four connectomes at a certain frequency
(e.g., 10 Hz; see Figures 7E and 7G) were iteratively reordered to maximize overlap between
the subgraphs. To do this, the vectors of subgraph identities of size [N × 1] were transformed
into binary arrays of size [N × K], where N is the number of parcels (N = 219) and K is the
number of subgraph identities (K = 7). Nonzero items of the array represented associations
between a parcel (row) and its subgraph identity (column), so that each row contained only one
nonzero item. The binary arrays of subgraph identities were assessed for all four connectomes.
The columns of these arrays were iteratively reordered to maximize the sum of the element-
wise product between the four arrays. The reordered binary arrays were then wrapped back to
the subgraph identity vectors and visualized (e.g., Figures 7E and 7G).
ACKNOWLEDGMENTS
This study was supported by the Academy of Finland, Grant Nos. 253130 and 256472 (to
J.M.P.) and 1126967 (to S.P.); by the Helsinki University Research Funds and European Union
Seventh Framework Programme (FP7/2007-2013) under Grant Agreement No. 29 604102
(Human Brain Project); and by the Italian Ministry of Health, Targeted Research Grant No.
RF-2010-2319316 (to L.N.).
AUTHOR CONTRIBUTIONS
Alexander Zhigalov: Data curation; Formal analysis; Methodology; Software; Visualization;
Writing – original draft; Writing – review & editing
Gabriele Arnulfo: Data curation; Methodology; Validation
Lino Nobili: Data curation
Satu Palva: Project administration; Resources
J. Matias Palva: Conceptualization; Funding acquisition; Project administration; Resources;
Supervision; Writing – review & editing
REFERENCES
Arnulfo, G., Hirvonen, J., Nobili, L., Palva, S., & Palva, J. M. (2015).
Phase and amplitude correlations in resting-state activity in hu-
man stereotactical eeg recordings. NeuroImage, 112, 114–127.
Arnulfo, G., Narizzano, M., Cardinale, F., Fato, M. M., & Palva,
J. M. (2015). Automatic segmentation of deep intracerebral elec-
trodes in computed tomography scans. BMC Bioinformatics, 16,
99. doi:10.1186/s12859-015-0511-6
Bak, P., Tang, C., & Wiesenfeld, K. (1988). Self-organized criticality.
Physical Review A, 38, 364–374.
Beggs, J. M., & Plenz, D. (2003). Neuronal avalanches in neocorti-
cal circuits. Journal of Neuroscience, 23, 11167–11177.
Beggs, J. M., & Timme, N. (2012). Being critical of criticality in the
brain. Frontiers in Physiology, 3, 163. doi:10.3389/fphys.2012.
00163
Bell, A. J., & Sejnowski, T. J. (1995). An information-maximization
approach to blind separation and blind deconvolution. Neural
Computation, 7, 1129–1159.
Bellec, P., Rosa-Neto, P., Lyttelton, O. C., Benali, H., & Evans,
(2010). Multi-level bootstrap analysis of stable clusters
A. C.
in resting-state fmri. NeuroImage, 51, 1126–1139. doi:10.1016/
j.neuroimage.2010.02.082
Blythe, D. A., Haufe, S., Muller, K. R., & Nikulin, V. V. (2014). The
effect of linear mixing in the EEG on hurst exponent estimation.
NeuroImage, 99, 377–387. doi:10.1016/j.neuroimage.2014.05.
041
Botcharova, M., Farmer, S. F., & Berthouze, L. (2014). Markers of
criticality in phase synchronization. Frontiers in Systems Neuro-
science, 8, 176. doi:10.3389/fnsys.2014.00176
Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D., Hale, J. R.,
Investigating the
Stephenson, M. C., . . . Morris, P. G.
electrophysiological basis of resting state networks using mag-
netoencephalography. Proceedings of the National Academy of
Sciences, 108, 16783–16788. doi:10.1073/pnas.1112685108
(2011).
Brookes, M. J., Woolrich, M. W., & Barnes, G. R.
(2012). Mea-
suring functional connectivity in MEG: A multivariate approach
insensitive to linear source leakage. NeuroImage, 63, 910–920.
doi:10.1016/j.neuroimage.2012.03.048
Network Neuroscience
163
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
Cardinale, F., Cossu, M., Castana, L., Casaceli, G., Schiariti, M. P.,
Miserocchi, A., . . . Lo Russo, G.
(2013). Stereoelectroen-
cephalography: Surgical methodology, safety, and stereotactic
application accuracy in 500 procedures. Neurosurgery, 72, 353–
366. doi:10.1227/NEU.0b013e31827d1161
Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature
Physics, 6, 744–750.
Ciuciu, P., Abry, P., & He, B. J. (2014). Interplay between functional
connectivity and scale-free dynamics in intrinsic fmri networks.
NeuroImage, 95, 248–263. doi:10.1016/j.neuroimage.2014.03.
047
Clauset, A., Shalizi, C., & Newman, M. (2009). Power-law distri-
butions in empirical data. SIAM Review, 51, 661–643.
Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun,
L., Gigandet, X., . . . Thiran, J. P. (2012). The connectome map-
per: An open-source processing pipeline to map connectomes
with MRI. PLoS ONE, 7, e48121. doi:10.1371/journal.pone.
0048121
de Pasquale, F., Della Penna, S., Snyder, A. Z., Marzetti, L., Pizzella,
V., Romani, G. L., & Corbetta, M. (2012). A cortical core for dy-
namic integration of functional networks in the resting human
brain. Neuron, 74, 753–764. doi:10.1016/j.neuron.2012.03.
031; 10.1016/j.neuron.2012.03.031
Deco, G., Jirsa, V. K., & McIntosh, A. R.
(2013). Resting brains
never rest: Computational insights into potential cognitive archi-
tectures. Trends in Neurosciences, 36, 268–274. doi:10.1016/j.
tins.2013.03.001
Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connectomics
of brain disorders. Nature Reviews Neuroscience, 16, 159–172.
doi:10.1038/nrn3901
Friedman, E. J., & Landsberg, A. S. (2013). Hierarchical networks,
power laws, and neuronal avalanches. Chaos, 23, 013135. doi:
10.1063/1.4793782
Friedman, N., Ito, S., Brinkman, B. A., Shimono, M., DeVille, R. E.,
Dahmen, K. A., . . . Butler, T. C. (2012). Universal critical dynam-
ics in high resolution neuronal avalanche data. Physical Review
Letters, 108, 208102.
Gallos, L. K., Makse, H. A., & Sigman, M. (2012). A small world
of weak ties provides optimal global integration of self-similar
modules in functional brain networks. Proceedings of the Na-
tional Academy of Sciences, 109, 2825–2830. doi:10.1073/pnas.
1106612109
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6, e159. doi:10.1371/
journal.pbio.0060159
Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges at
criticality on a model of the human connectome. Physical Review
Letters, 110, 178101.
Hamalainen, M. S., & Ilmoniemi, R. J.
Interpreting mag-
netic fields of the brain: Minimum norm estimates. Medical and
Biological Engineering and Computing, 32, 35–42.
(1994).
Hansen, E. C., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switch-
ing behavior of the resting state. NeuroImage, 105, 525–535.
doi:10.1016/j.neuroimage.2014.11.001
Hilgetag, C. C., & Hutt, M. T. (2014). Hierarchical modular brain
connectivity is a stretch for criticality. Trends in Cognitive Sci-
ences, 18, 114–115. doi:10.1016/j.tics.2013.10.016
Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel, A. K.
(2012). Large-scale cortical correlation structure of spontaneous
oscillatory activity. Nature Neuroscience, 15, 884–890. doi:10.
1038/nn.3101; 10.1038/nn.3101
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., & Bullmore, E.
(2009). Broadband criticality of human brain network synchro-
nization. PLoS Computational Biology, 5, e1000314. doi:10.
1371/journal.pcbi.1000314
Klaus, A., Yu, S., & Plenz, D.
(2011). Statistical analyses sup-
port power law distributions found in neuronal avalanches. PLoS
ONE, 6, e19779. doi:10.1371/journal.pone.0019779
Kopell, N. J., Gritton, H. J., Whittington, M. A., & Kramer, M. A.
(2014). Beyond the connectome: The dynome. Neuron, 83,
1319–1328. doi:10.1016/j.neuron.2014.08.016
Korhonen, O., Palva, S., & Palva, J. M.
(2014). Sparse weight-
ings for collapsing inverse solutions to cortical parcellations
optimize M/EEG source reconstruction accuracy. Journal of Neu-
roscience Methods, 226C, 147–160. doi:10.1016/j.jneumeth.
2014.01.031; 10.1016/j.jneumeth.2014.01.031
Lai, M. C., Lombardo, M. V., Chakrabarti, B., Sadek, S. A., Pasco,
(2010). A shift to ran-
G., Wheelwright, S. J., . . . Suckling, J.
domness of brain oscillations in people with autism. Biological
Psychiatry, 68, 1092–9. doi:10.1016/j.biopsych.2010.06.027
Larson-Prior, L. J., Oostenveld, R., Della Penna, S., Michalareas, G.,
Prior, F., Babajani-Feremi, A., . . . WU-Minn HCP Consortium.
(2013). Adding dynamics to the human connectome project with
MEG. NeuroImage, 80, 190–201. doi:10.1016/j.neuroimage.
2013.05.056
Leleu, T., & Aihara, K. (2015). Unambiguous reconstruction of net-
work structure using avalanche dynamics. Physical Review E, 91,
022804. doi:10.1103/PhysRevE.91.022804
Linkenkaer-Hansen, K., Monto, S., Rytsala, H., Suominen, K.,
Isometsa, E., & Kahkonen, S. (2005). Breakdown of long-range
temporal correlations in theta oscillations in patients with major
depressive disorder. Journal of Neuroscience, 25, 10131–10137.
doi:10.1523/JNEUROSCI.3244-05.2005
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., & Ilmoniemi,
R. J.
(2001). Long-range temporal correlations and scaling be-
havior in human brain oscillations. Journal of Neuroscience, 21,
1370–1377.
Meunier, D., Lambiotte, R., & Bullmore, E. T. (2010). Modular and
hierarchically modular organization of brain networks. Frontiers
in Neuroscience, 4, 200. doi:10.3389/fnins.2010.00200
Mitra, A., Snyder, A. Z., Blazey, T., & Raichle, M. E.
(2015). Lag
threads organize the brain’s intrinsic activity. Proceedings of the
National Academy of Sciences, 112, E2235–E2244.
Montez, T., Poil, S. S., Jones, B. F., Manshanden, I., Verbunt, J. P.,
(2009). Altered
van Dijk, B. W., . . . Linkenkaer-Hansen, K.
temporal correlations in parietal alpha and prefrontal
theta
oscillations in early stage alzheimer disease. Proceedings of the
Network Neuroscience
164
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Co-localization of cortical connectivity and scale-free dynamics
National Academy of Sciences, 106, 1614–1619. doi:10.1073/
pnas.0811699106
dynamics in spontaneous brain activity. Cerebral Cortex. Ad-
vance online publication. doi:10.1093/cercor/bhw285
Monto, S., Vanhatalo, S., Holmes, M. D., & Palva, J. M.
(2007).
Epileptogenic neocortical networks are revealed by abnormal
temporal dynamics in seizure-free subdural EEG. Cerebral Cor-
tex, 17, 1386–1393. doi:10.1093/cercor/bhl049
Moretti, P., & Munoz, M. A. (2013). Griffiths phases and the stretch-
ing of criticality in brain networks. Nature Communications, 4,
2521. doi:10.1038/ncomms3521
Nikulin, V. V., Jonsson, E. G., & Brismar, T.
(2012). Attenuation
of long-range temporal correlations in the amplitude dynamics
of alpha and beta neuronal oscillations in patients with schizo-
phrenia. NeuroImage, 61, 162–169. doi:10.1016/j.neuroimage.
2012.03.008
Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J. M.
(2011).
Fieldtrip: Open source software for advanced analysis of MEG,
EEG, and invasive electrophysiological data. Computational In-
telligence and Neuroscience, 2011, 156869. doi:10.1155/2011/
156869
Pajevic, S., & Plenz, D.
(2009). Efficient network reconstruction
from dynamical cascades identifies small-world topology of neu-
ronal avalanches. PLoS Computational Biology, 5, e1000271.
doi:10.1371/journal.pcbi.1000271
Palva, J. M., Zhigalov, A., Hirvonen, J., Korhonen, O., Linkenkaer-
Hansen, K., & Palva, S.
(2013). Neuronal long-range temporal
correlations and avalanche dynamics are correlated with behav-
ioral scaling laws. Proceedings of the National Academy of Sci-
ences, 110, 3585–3590. doi:10.1073/pnas.1216855110
Palva, S., & Palva, J. M. (2012). Discovering oscillatory interaction
networks with M/EEG: Challenges and breakthroughs. Trends in
Cognitive Sciences, 16, 219–230. doi:10.1016/j.tics.2012.02.
004
Peng, C. K., Havlin, S., Stanley, H. E., & Goldberger, A. L. (1995).
Quantification of scaling exponents and crossover phenomena
in nonstationary heartbeat time series. Chaos, 5, 82–87. doi:10.
1063/1.166141
Plenz, D. (2012). Neuronal avalanches and coherence potentials.
European Physical Journal Special Topics, 205, 259–301. doi:10.
1140/epjst/e2012-01575-5
Plenz, D., & Thiagarajan, T. C.
(2007). The organizing prin-
ciples of neuronal avalanches: Cell assemblies in the cortex?
Trends in Neurosciences, 30, 101–110. doi:10.1016/j.tins.2007.
01.005
Poil, S. S., Hardstone, R., Mansvelder, H. D., & Linkenkaer-Hansen,
K. (2012). Critical-state dynamics of avalanches and oscillations
jointly emerge from balanced Excitation/Inhibition in neuronal
networks. Journal of Neuroscience, 32, 9817–9823.
Prichard, D., & Theiler, J. (1994). Generating surrogate data for time
series with several simultaneously measured variables. Physical
Review Letters, 73, 951–954.
Raichle, M. E.
(2009). A brief history of human brain mapping.
Trends in Neurosciences, 32, 118–126. doi:10.1016/j.tins.2008.
11.001
Ros, T., Frewen, P., Théberge, J., Michela, A., Kluetsch, R., Mueller,
(2016). Neurofeedback tunes scale-free
A., . . . Lanius, R. A.
Rubinov, M., Sporns, O., Thivierge, J. P., & Breakspear, M. (2011).
Neurobiologically realistic determinants of self-organized criti-
cality in networks of spiking neurons. PLoS Computational Biol-
ogy, 7, e1002038. doi:10.1371/journal.pcbi.1002038
Russo, R., Herrmann, H. J., & de Arcangelis, L. (2014). Brain mod-
ularity controls the critical behavior of spontaneous activity. Sci-
entific Reports, 4, 4312. doi:10.1038/srep04312
Schwab, D. J., Nemenman, I., & Mehta, P. (2014). Zipf’s law and
criticality in multivariate data without fine-tuning. Physical Re-
view Letters, 113, 068102.
Shahbazi, F., Ewald, A., Ziehe, A., & Nolte, G. (2010). Construct-
ing surrogate data to control for artifacts of volume conduction
IFMBE Proceedings, 28,
for functional connectivity measures.
207–210. doi:dx.doi.org/10.1007/978-3-642-12197-5_46
Shriki, O., Alstott, J., Carver, F., Holroyd, T., Henson, R. N., Smith,
M. L., . . . Plenz, D. (2013). Neuronal avalanches in the resting
Journal of Neuroscience, 33, 7079–
MEG of the human brain.
7090. doi:10.1523/JNEUROSCI.4286-12.2013
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain FMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3, 15.
doi:10.3389/fphys.2012.00015
Taulu, S., Simola, J., & Kajola, M. (2005). Applications of the signal
space separation method. IEEE Transactions on Signal Processing,
53, 3359–3372. doi:10.1109/TSP.2005.853302
Touboul, J., & Destexhe, A. (2010). Can power-law scaling and neu-
ronal avalanches arise from stochastic dynamics? PLoS ONE, 5,
e8982. doi:10.1371/journal.pone.0008982
Vinck, M., Oostenveld, R., van Wingerden, M., Battaglia, F.,
& Pennartz, C. M.
(2011). An improved index of phase-
synchronization for electrophysiological data in the presence of
volume-conduction, noise and sample-size bias. NeuroImage,
55, 1548–1565. doi:10.1016/j.neuroimage.2011.01.055
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
of the National Academy of Sciences, 111, 10341–10346. doi:
10.1073/pnas.1400181111
Zapperi, S., Baekgaard Lauritsen, K., & Stanley, H. E.
(1995).
Self-organized branching processes: Mean-field theory for
avalanches. Physical Review Letters, 75, 4071–4074.
Zhigalov, A., Arnulfo, G., Nobili, L., Palva, S., & Palva, J. M. (2015).
Relationship of fast- and slow-timescale neuronal dynamics in
Journal of Neuroscience, 35, 5385–
human MEG and SEEG.
5396. doi:10.1523/JNEUROSCI.4880-14.2015
Zhigalov, A., Arnulfo, G., Nobili, L., Palva, S., & Palva, J. M. (2017).
Supplemental material for “Modular co-organization of func-
tional connectivity and scale-free dynamics in the human brain.”
Network Neuroscience, 1(2). doi.org/10.1162/netn_a_00008
Zhigalov, A., Kaplan, A., & Palva, J.
(2016). Modulation of crit-
ical brain dynamics using closed-loop neurofeedback stimula-
tion. Clinical Neurophysiology, 127, 2882–2889. doi:10.1016/
j.clinph.2016.04.028
Network Neuroscience
165
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
1
4
3
1
0
9
1
9
3
8
n
e
n
_
a
_
0
0
0
0
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3