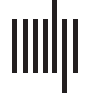FORSCHUNG

Principles underlying the input-dependent
formation and organization of memories

Juliane Herpich 1,2 and Christian Tetzlaff1,2

1Department of Computational Neuroscience, Third Institute of Physics – Biophysics, Georg-August-University,
Göttingen, Deutschland
2Bernstein Center for Computational Neuroscience, Georg-August-University, Göttingen, Deutschland

Schlüsselwörter: Synaptic plasticity, Memory, Memory interaction, Synaptic scaling, Inhibition

Keine offenen Zugänge

Tagebuch

ABSTRAKT

The neuronal system exhibits the remarkable ability to dynamically store and organize
incoming information into a web of memory representations (Artikel), which is essential for
the generation of complex behaviors. Central to memory function is that such memory items
must be (1) discriminated from each other, (2) associated to each other, oder (3) brought into a
sequential order. Jedoch, how these three basic mechanisms are robustly implemented in
an input-dependent manner by the underlying complex neuronal and synaptic dynamics is
still unknown. Hier, we develop a mathematical framework, which provides a direct link
between different synaptic mechanisms, determining the neuronal and synaptic dynamics
of the network, to create a network that emulates the above mechanisms. Combining
correlation-based synaptic plasticity and homeostatic synaptic scaling, we demonstrate
that these mechanisms enable the reliable formation of sequences and associations between
two memory items still missing the capability for discrimination. We show that this
shortcoming can be removed by additionally considering inhibitory synaptic plasticity.
Daher, the here-presented framework provides a new, functionally motivated link between
different known synaptic mechanisms leading to the self-organization of fundamental
memory mechanisms.

ZUSAMMENFASSUNG DES AUTORS

Higher-order animals are permanently exposed to a variety of environmental inputs that
have to be processed and stored such that the animal can react appropriately. Thereby, Die
ongoing challenge for the neuronal system is to continuously store novel and meaningful
stimuli and, dependent on their content, to integrate them into the existing web of
knowledge or memories. The smallest organizational entity of such a web of memories is
described by the functional relation of two interconnected memories: they can be either
unrelated (discrimination), mutually related (association), or unidirectionally related
(sequence). Jedoch, the neuronal and synaptic dynamics underlying the formation of
such structures are mainly unknown. To investigate possible links between physiological
mechanisms and the organization of memories, in this work, we develop a general
mathematical framework enabling an analytical approach. Thereby, we show that the
well-known mechanisms of synaptic plasticity and homeostatic scaling in conjunction with
inhibitory synaptic plasticity enables the reliable formation of all basic relations between
two memories. This work provides a further step in the understanding of the complex
dynamics underlying the organization of knowledge in neural systems.

Zitat: Herpich, J., & Tetzlaff, C.
(2019). Principles underlying the
input-dependent formation and
organization of memories. Netzwerk
Neurowissenschaften, 3(2), 606–634.
https://doi.org/10.1162/netn_a_00086

DOI:
https://doi.org/10.1162/netn_a_00086

zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00086

Erhalten: 26 Juli 2018
Akzeptiert: 21 Marsch 2019

Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.

Korrespondierender Autor:
Christian Tetzlaff
tetzlaff@phys.uni-goettingen.de

Handling-Editor:
Sarah Muldoon

Urheberrechte ©: © 2019
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz

Die MIT-Presse

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Input-dependent formation and organization of memories

Synaptic plasticity:
General term for all kind of different
biological mechanisms adapting the
weights of synapses. Often they
depend on neuronal activities.

Cell assembly:
A group of neurons being strongly
interconnected and essentially active
together.

EINFÜHRUNG

Learning and memorizing various pieces of information from the environment are vital func-
tions for the survival of living beings. Zusätzlich, the corresponding neuronal system has to
learn the environmental relations between these different pieces. Dafür, the neuronal sys-
tem has to form memory representations of the information and to organize them accordingly.
Jedoch, the neuronal and synaptic dynamics determining the organization of these repre-
sentations are widely unknown.

The synaptic-plasticity-and-memory hypothesis relates the formation of memory represen-
tations to the underlying neuronal and synaptic mechanisms (Martin, Grimwood, & Morris,
2000; Martin & Morris, 2002). Namely, a to-be-learned piece of information activates via an
environmental stimulus a certain population of neurons triggering synaptic plasticity. Synaptic
plasticity, im Gegenzug, changes the weights of the synapses between the activated neurons such that
these neurons become strongly interconnected and form a memory representation—so-called
Hebbian cell assembly (CA)—of the presented information (Hebb, 1949; Palm, 1981; Buzsaki,
2010; Palm, Knoblauch, Hauser, & Schütz, 2014). Besides the formation of a memory repre-
sentation, the newly learned piece of information is also related to already stored information
(Hebb, 1949; Wickelgren, 1999; Tse et al., 2007, 2011). Thereby, the relations or functional
organizations between different memory representations can be organized in three different,
fundamental ways: they can be unrelated (discrimination), mutually related (association), oder
unidirectionally related (sequence). Jedoch, although the link between the formation of a sin-
gle memory representation and the underlying neuronal and synaptic mechanisms is already
well established (Garagnani, Wennekers, & Pulvermüller, 2009; Tetzlaff, Kolodziejski, Timme,
Tsodyks, & Wörgötter, 2013; Litwin-Kumar & Doiron, 2014; Zenke, Agnes, & Gerstner, 2015),
it is largely unknown which mechanisms enable the self-organized formation of relations
between memory representations.

In this theoretical study, we have developed the first theoretical framework enabling one to
analyze the ability of diverse neuronal and synaptic mechanisms to form memory representa-
tions and, in addition, to form the different types of memory-relations. Thereby, our analysis
indicates that the interaction of correlation-based synaptic plasticity with homeostatic synaptic
scaling is not sufficient to form all types of memory relations, although it enables the forma-
tion of individual memory representations (Tetzlaff et al., 2013; Tetzlaff, Dasgupta, Kulvicius,
& Wörgötter, 2015). Jedoch, our analysis shows that, if the average level of inhibition within
the memory representations is significantly lower than the average level in the remaining net-
arbeiten, the neuronal system is able, on the one hand, to form memory representations and,
andererseits, to organize them into the fundamental types of memory relations in an
input-dependent, self-organized manner.

Correlation-based synaptic plasticity:
Synaptic plasticity mechanisms
adapting synaptic weights depending
on the correlation of the pre- Und
postsynaptic neuronal activities.

Homeostatic plasticity:
Synaptic plasticity mechanism
adapting the synaptic weights such
that neuronal systems maintain a
desired average activity level.

Several theoretical studies (Tetzlaff et al., 2013; Litwin-Kumar & Doiron, 2014; Zenke et al.,
2015; Tetzlaff et al., 2015; Chenkov, Sprekeler, & Kempter, 2017) investigated the formation
of individual memory representations in neuronal systems indicating correlation-based synap-
tic plasticity as essential mechanism. Zusätzlich, homeostatic plasticity, as synaptic scaling
(Turrigiano, Leslie, Desai, Rutherford, & Nelson, 1998), is required to keep the system in an
adequate dynamic regime (Dayan & Abbott, 2001; Tetzlaff, Kolodziejski, Timme, & Wörgötter,
2011; Zenke, Hennequin, & Gerstner, 2013). Further studies indicate that synaptic plasticity
and homeostatic plasticity also yield the formation of sequences of representations (Chenkov
et al., 2017; Lazar, Pipa, & Triesch, 2009; Tully, Lindn, Hennig, & Lansner, 2016). Wie-
immer, it remains unclear whether the interaction of synaptic and homeostatic plasticity also
enables the formation of further memory relations as described above. Interessant, several

Netzwerkneurowissenschaften

607

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Input-dependent formation and organization of memories

theoretical studies (Wickelgren, 1999; Palm, 1982; Byrne & Huyck, 2010) indicate that a
neural system with the ability to form all described memory relations has an algorithmic
advantage to process the stored information. Außerdem, the neuronal dynamics resulting
from interconnected memory representations match experimental results on the psychological
(Roma, Pinkoviezky, Rubin, & Tsodyks, 2013) and single-neuron level (Griniasty, Tsodyks, &
Amit, 1993; Amit, Brunel, & Tsodyks, 1994). Jedoch, these studies consider neural systems
after completed learning; daher, it is unclear how neuronal systems form the required relations
between memory representations in a self-organized manner.

We consider a neuronal network model with plastic excitatory connections, which are gov-
erned by the interaction of correlation-based and homeostatic plasticity. As already shown in
previous studies, this interaction enables the self-organized formation of individual memory
Darstellungen (Tetzlaff et al., 2013, 2015). Similar to these studies, we use methods from the
scientific field of nonlinear dynamics (Glendinning, 1994; Izhikevich, 2007) to derive the under-
lying mechanisms yielding the self-organized formation of the relations between memory
Darstellungen. Daher, we analyze the ability of the plastic network to form different types of
relations between two memory representations—namely, discrimination, Sequenzen, and as-
sociation. Please note that this is a high-dimensional problem of the order of N2 (given N neu-
rons). To reduce complexity, standard approaches such as mean-field analysis are not feasible,
as they obliterate the different memory representations involved. Daher, we developed a new
theoretical framework by considering the mean equilibrium states of the relevant system vari-
ables and by comparing them to constraints given for the different memory-relations. Thereby,
we map the constraints on the long-term average activity level of the neuronal populations
beteiligt, reducing the problem to a two-dimensional one, which can be analyzed graphically
and analytically. By this framework, we optimized the parameters of the system and identi-
fied that correlation-based and homeostatic plasticity do not suffice to form all three types of
memory relation. Stattdessen, if the average inhibitory level within the memory representations is
below control level, memory representations can be formed, maintained, and related to each
andere. Zusätzlich, we show that the required state can also be reached in a self-organized,
dynamic way by the interplay between excitatory and inhibitory synaptic plasticity. Daher, Die
here-presented results provide a next step to understanding the complex dynamics underlying
the formation of memory relations in neuronal networks.

ERGEBNISSE
In our work, we analyze the ability of two neuronal populations p ∈ {1, 2} to become memory
representations and, in parallel, to reliably build up different functional organizations such as
discrimination, sequence, and association (Tisch 1). Allgemein, the external input to popula-
tion p should trigger synaptic changes within the population such that it becomes a memory
representation of its specific input. Individual input events can have different amplitude, dura-
tion, and probability of occurrence (Figure 1Ai); Jedoch, synaptic changes are slow compared
with the presentation of single input events such that the average over all input events deter-
mines the formation of a memory representation (Figure 1Aii). Daher, throughout this study, Wir
consider the average input stimulation a population receives, whereby a reduced number of
input events and/or reduced amplitudes and shorter durations map to a lower average input
(compare Figure 1, A with B).

Given two populations of neurons, dependent on the input properties, connections be-
tween the populations should also be altered to form the neuronal substrate underlying the
diverse functional organizations described above. In accordance to the synaptic-plasticity-
and-memory hypothesis (Martin et al., 2000; Hebb, 1949), we define a neuronal population

Netzwerkneurowissenschaften

608

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Input-dependent formation and organization of memories

Tisch 1.
Populationen. The different functional organizations are defined based on the average excitatory synaptic weights (cid:3) ˜ω
(cid:3) ˜ω

Synaptic weight-dependent definition of memory and different forms of functional organization of two interconnected neuronal
(cid:4), Und

(cid:4) at equilibrium in relation to the average inhibitory synaptic weights ( ˜θ).

(cid:4), (cid:3) ˜ω

(cid:4), (cid:3) ˜ω

21

11

22

12

functional organization

abbreviation

color code

Memory representation

(cid:2) ˜ω11(cid:4)
< ˜θ (cid:2) ˜ω22(cid:3) < ˜θ (cid:2) ˜ω21(cid:3) − (cid:2) ˜ω12(cid:3) − > ˜θ

> ˜θ

< ˜θ < ˜θ > ˜θ

> ˜θ

< ˜θ > ˜θ

< ˜θ > ˜θ

none

discrimination

sequence 12

sequence 21

association

bistable

various

nm

Rabatt

s12

s21

asc

bs

grau

Blau

Gelb

Grün

Rot

pink

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

as being a memory representation if its neurons are strongly interconnected. Mit anderen Worten,
the average excitatory synaptic strength between all neurons within the population has to be
larger than the average inhibitory synaptic strength. Daher, because of the dominant excitation,
neuronal activity within the population will be amplified. We define the relation between two
memory representations in a similar manner based on the relation of excitation and inhibition
between the corresponding neuronal populations: in general, if the average excitatory synaptic
strength from one population to the other is larger than the average inhibitory synaptic strength,
an increased level of activity in the former population triggers an increased activation in the
letztere. This can be different for both directions such that, zum Beispiel, the net connection from
Bevölkerung 1 Zu 2 can be excitatory and inhibitory from 2 Zu 1. This case is defined as a sequence
aus 1 Zu 2. Ähnlich, an association is present if both connections are excitatory-dominated,
and a discrimination consists of both directions being zero or inhibition-dominated.

To analyze the self-organized formation of memory representations and their functional
organization, we consider a plastic recurrent neuronal network model N consisting of rate-
coded neurons being interconnected via plastic excitatory and static inhibitory connections
(Figure 2A). Within the recurrent network are two distinct populations of neurons (p ∈ {1, 2};
black and yellow dots, jeweils) within each the neurons receive the same external input
(red layer E ). All remaining neurons are summarized as background neurons B (Blau)
˜Fex
P
such that the neuronal network can be described as the interaction of three different neuronal
Populationen.

All excitatory connections within the recurrent layer are plastic regarding the interaction of
fast correlation-based synaptic plasticity and slow homeostatic synaptic scaling (Tetzlaff et al.,
2011; Tetzlaff, Kolodziejski, Timme, & Wörgötter, 2012). Please note that previous studies
indicate that this interaction yields the reliable formation of individual memory representations
(Tetzlaff et al., 2013, 2015). The resulting changes in synaptic weights between postsynaptic
neuron i and presynaptic neuron j is thus regulated by

(cid:2)

(cid:3)

˙ω

ich,j = μFi Fj + γ

FT − Fi

ω2
ich,J

(1)

609

Synaptic weights:
The average transmission efficacy
of a synapse quantified as a single
number, which can be adapted
by synaptic plasticity.

Netzwerkneurowissenschaften

✗
✓

Input-dependent formation and organization of memories

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 1. Given that the synaptic changes are slow, the average input determines the synaptic
Dynamik. (A) Individual presentations or events of one specific input shown to a corresponding
population of neurons can have different duration, Amplitude, and probability of occurrence (ich).
Jedoch, compared with the duration of a single event, synaptic changes are in general slow.
daher, the average input strength (ii), considered here, mainly influences the long-term dynam-
ics of the neuronal system (Figure 2A). (B) Daher, different duration, Amplitude, and/or probability of
occurrence map to a different average input triggering different synaptic dynamics.

with neural activities Fi and Fj, μ being the timescale of synaptic plasticity, γ the timescale of
synaptic scaling, and the target firing rate FT of the homeostatic process.

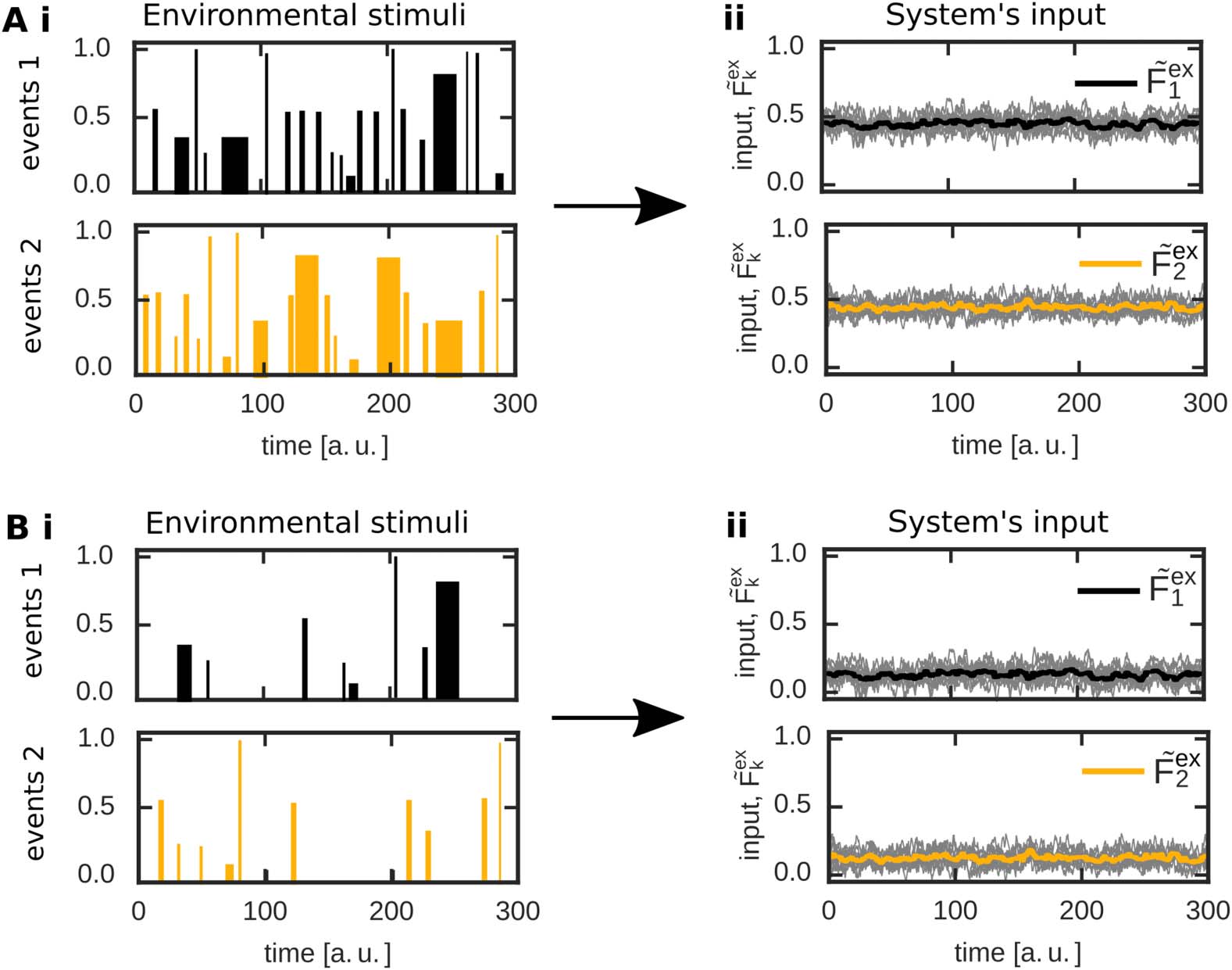
Daher, an external input to populations 1 Und 2 alters neural activities within the correspond-
ing populations and, Außerdem, triggers changes in the corresponding synaptic weights (sehen
Figure 2C for an example). In the first phase, all neurons of the network receive a noisy in-
put (Figure 2C, panel i) such that neural activities (panel ii) and synaptic weights (panels iii
and iv) are at base level. At t = 10, both populations 1 Und 2 receive a strong external
Eingang (panel i). In more detail, each neuron in a specific population receives an input from
10 input neurons each modeled by its own Ornstein-Uhlenbeck process (grey lines; Gelb
and black line indicate the average). The mean of these processes is the same for all input neu-
rons transmitting to one population ( ˜Fex
2 = 0.75 for pop. 2). After a brief
transition phase, the system reaches a new equilibrium state. Hier, for both populations the
intrapopulation synapses are stronger than the average inhibitory synaptic weights ( ˜θ; panel iii),
indicating the formation of two memory representations. Außerdem, the excitatory synapses
connecting both populations are adapted and also become stronger than the average inhibi-
tion level (panel iv). This implies that both populations or memory representations are strongly
linked with each other; daher, an association has been formed. daher, given a certain

1 = 0.9 for pop. 1 and ˜Fex

Netzwerkneurowissenschaften

610

Input-dependent formation and organization of memories

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1 and ˜Fex

Figur 2. The formation of interconnected memory representations in a plastic neural network.
(A) In a recurrent network N , two neuronal populations (1: black; 2: Gelb) receive specific ex-
ternal inputs of average amplitudes ˜Fex
2 . All remaining neurons of the network (Blau) Sind
combined to a background population B and serve as control neurons receiving noisy external
inputs. Each population p ∈ {1, 2, B} is described by its mean intra-population-synaptic weight
(cid:5) ∈ {1, 2, B}\P) via a set of
˜ωpp, its mean activity ˜Fp, and its connections to other populations (P
synapses with average synaptic strength ˜ω
P(cid:5) P. (B) The abstraction of the neuronal network model
yields a low-dimensional one described by the mean equilibrium activities (Fp) and correspond-
ing mean equilibrium synaptic weights (wp(cid:5)P). Hier, the external input (Rot) combines inputs from
background neurons and external inputs given in the complete network model (A). (C) In the net-
work model (A), changing the amplitude of the external input to neuronal populations 1 (black) Und
2 (Gelb) at t = 10 yields increased average activities within the populations and background neu-
rons (Blau), triggering synaptic changes. Gray lines indicate single neuron/synapse dynamics. Nach
a brief period, all system variables reach an equilibrium state. This state is matched very well by
the theoretical analysis (green lines) considering the abstract model (B). (ich) Inputs; (ii) average activ-
ities of each population; (iii) average intrapopulation synaptic weights; (iv) average interpopulation
synaptic weights. The average input amplitudes are determined by two Ornstein-Uhlenbeck pro-
cesses with mean ˜Fex

1 = 0.9 and ˜Fex

2 = 0.75.

stimulus, the equilibrium state of the synaptic weights determines the functional organization
of the corresponding memory representations.

Memory Representation and Functional Organization

As the impact of single synapses on the overall network dynamics is small, we will consider
in the following the equilibrium states of the average synaptic weights of inter- and intrapop-
ulation synapses (indicated by (cid:3)X(cid:4)). Daher, these synaptic states determine whether a neuronal
population is a memory representation, and how several of these representations are function-
ally organized (discrimination, sequence, or association).

Netzwerkneurowissenschaften

611

Input-dependent formation and organization of memories

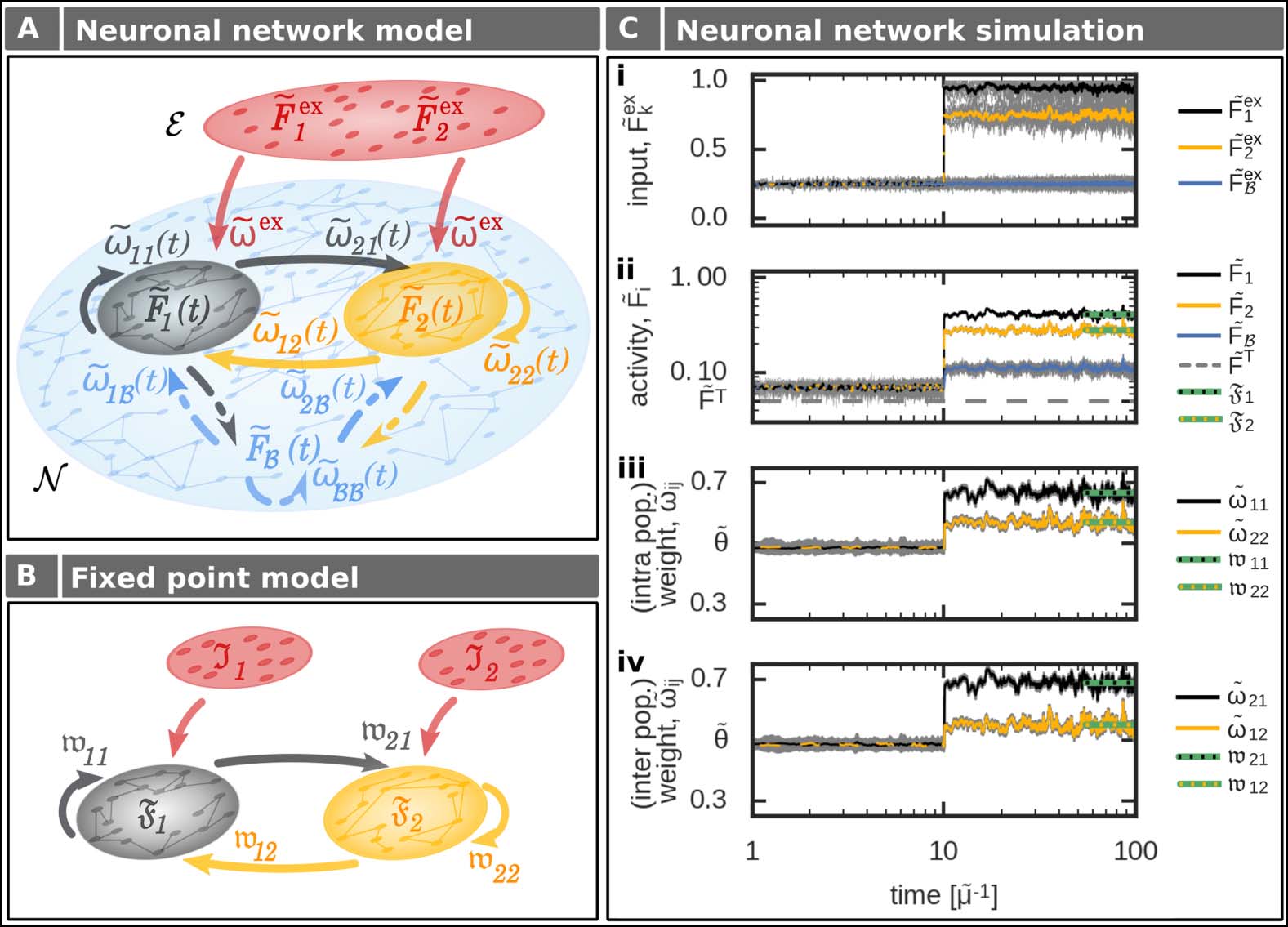
daher, as long as the average recurrent or intrapopulation excitatory synaptic weight
(cid:3) ˜ωpp(cid:4) of neuronal population p is weaker than the average inhibitory synaptic strength ˜θ,
an external input to the population will lead to an average decrease in population activity
( ˜x indicates the normalized variable of x; see Methods). Daher, the neuronal population does
not serve as a memory representation and the system state is defined as no memory state
(nm; Tisch 1, Figure 3Ai, left panel, grey area). Im Gegensatz, if the average recurrent excitatory
synaptic weight is at the equilibrium state above the level of inhibition (Figure 3Ai, left panel,
white area), the neuronal population reacts with an increased activity level to an external
input and, daher, it serves as a memory representation (memory state). Mit anderen Worten,
the neuronal population p has to fulfill the following condition to be classified as a memory
representation:

˜θ < (cid:3) ˜ωpp(cid:4). (2) Given that both neuronal populations p ∈ {1, 2} are a stable memory representation (Figure 3Ai, left panel, white area), they can form different functional organizations (discrimina- tion, sequences, or association). Thereby, the average interpopulation synaptic weights (cid:3) ˜ω (cid:4) p(cid:5) p (p, p ) define the different functional organizations, dependent on their rela- tion to the average inhibitory synaptic weight strength ˜θ (Table 1). Thus, for two interconnected memories 1 and 2, we can define four different functional organizations with different weight- dependent conditions (Figure 3Ai, right panel): (cid:5) ∈ {1, 2}, p (cid:6)= p (cid:5) discrimination: both average interpopulation synaptic weights are weaker than the in- hibitory weights (blue, disc) (cid:3) ˜ω 12 (cid:4), (cid:3) ˜ω 21 (cid:4) < ˜θ; (3) sequence 21: average interpopulation synaptic weight from memory 1 to memory 2 is stronger than inhibitory weights, while the interpopulation synaptic weight from 2 to 1 is weaker (green, s21) (cid:3) ˜ω 12 (cid:4) < ˜θ < (cid:3) ˜ω (cid:4); 21 (4) sequence 12: interpopulation synaptic weight from memory 1 to memory 2 is weaker than the inhibitory weights, while the interpopulation synaptic weight from 2 to 1 is stronger (yellow, s12) (cid:3) ˜ω 21 (cid:4) < ˜θ < (cid:3) ˜ω (cid:4); 12 (5) association: both average interpopulation synaptic weights are stronger than the average inhibitory synaptic weight (red, asc) ˜θ < (cid:3) ˜ω (cid:4), (cid:3) ˜ω (cid:4). 21 12 (6) Assessing under which input condition the plastic neuronal network is Full-network analysis. able to form memory representations and diverse functional organizations, the whole set of differential equations, which represents a mathematical problem of the order of n2 (with n neurons), has to be solved numerically for each input condition ( ˜Fex 2 ). Thereby, each sim- ulation runs until the system reaches its equilibrium state. In this equilibrium state, excitatory synaptic weights are analyzed and compared with the inhibitory synaptic weights (Figure 3Aii, right panels) enabling a classification according to the functional organizations (Figure 3Aiii). This classification can be mapped to the inputs providing the resulting functional organization dependent on the specific external inputs (Figure 3Di,ii). Note, for better comparison with the population model (see the next section), the results (Figure 3Di) are mapped to the population 1 , ˜Fex Network Neuroscience 612 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3. Definition and analysis of the input-dependent formation of functional organizations (FO) between two neuronal populations. For details see main text and Table 1. (Ai) The different FOs are defined based on the average synaptic weights. (Aii) Solving numerically the complete network dynamics, which is of a n2-order dimension, for different external inputs (left) yields average excitatory synaptic weights (lines indicate constraints as in Ai). (Aiii) These average synaptic weights (Aii) can be analyzed regarding the weight-dependent conditions of FOs (Ai). Color code of dots as areas in Ai. (B) Considering the dependency of the intrapopulation synaptic weight (wpp, blue curve; Equation 9) on its respective activity (Fp) in equilibrium enables the mapping of the weight-dependent memory conditions on the 2d-activity space. Grey space: no memory representation; white space: memory representation. (Ci) Conditions for the different FOs of two memories in the mapped −activity space of the neuronal populations (Equations 12–17). (Cii) Within this 2d-space one can calculate the fixed point of the F1 population activities F1, F2 by the intersection of the equations FFP 1 and FFP 2 given an input stimulation I1, I2 (here, I1 = 0.95, I2 = 0.4). (Ciii) By comparing the resulting fixed point from (Cii) with the FO-conditions (Ci), we can obtain the respective FO. (D) Given the results in the weight (A) or activity space (C), we can assess for each input case the resulting FO. Used parameters: ˜θ = 0.5, ˜FT = 0.05, n(cid:3) = 20. − F2 Network Neuroscience 613 Input-dependent formation and organization of memories input space defined below (Figure 3Dii, Equation 7). The whole analysis is computationally ex- pensive and, furthermore, it does not provide additional insights into the relation between the synaptic dynamics and the ability to form diverse functional organizations. Thus, in the follow- ing, we provide a different approach to solve this complex, high-dimensional mathematical problem. To reduce the complexity of the system, in the following, Population model at equilibrium. we derive a method that directly calculates the mean state variables of the memory-related neuronal populations p ∈ {1, 2} at equilibrium (Figure 2B). For this we combine the inputs a population receives from the external layer E ( ˜Fex ˜ωex) with the inputs from the background p neurons in B ( ˜FB ˜ω p,B) to Ip = ˜Fex p ˜ωex + nB nex p ˜FB ˜ω p,B (7) with nB being the number of neurons belonging to the background population B, and nex p being the number of input neurons. Please note that we use Equation 7 only for transferring the results of the full network simulations to the input space I1, I2 (Figure 3Dii) to enable comparison with the results from the population model (Figure 3Diii). For the population model derived in the following, we directly consider different levels of I1 and I2. Given the input stimulation Ip, we consider that the firing rate ˜Fi of each neuron i ∈ p of a population p is close to the mean firing rate of this particular population (cid:3) ˜Fp(cid:4). By this, we receive the mean neuronal activity of population p at equilibrium Fp ≈ (cid:3) ˜Fp(cid:4) ≈ ˜Fi (Equa- tion 38). With the equilibrium activities of the neuronal populations p and p(cid:5), in turn, we can calculate the respective equilibrium synaptic weights wp(cid:5)p from population p to population p(cid:5) (Equation 39): (cid:4) wp(cid:5)p = FpFp(cid:5)(1 − ˜FT) Fp(cid:5) − ˜FT and the equilibrium synaptic weights of each population p itself (cid:5) (cid:6) (cid:6) (cid:7) F2 p(1 − ˜FT) Fp − ˜FT . wpp = (8) (9) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Activity-dependent constraints of memory representation and functional organization. Given the rel- ation between average population activities and synaptic weights in equilibrium (Equations 8 and 9), next, we map the weight-dependent conditions for memory representations (Equation 2) and functional organizations (Equations 3–6) onto the average population activities (Figure 3B). Thus, the fixed point or equilibrium equation of the synaptic dynamics (Equation 9; blue curve in Figure 3B) yields two activity-dependent conditions of a neuronal population p to become a memory representation: Network Neuroscience √ ˜θ2 + ˜θ D 2(1 − ˜FT) Fp >

√

˜θ2 − ˜θ
D
2(1 − ˜FT)

Fp < , (10) (11) 614 Input-dependent formation and organization of memories with D = ˜θ2 − 4 ˜FT(1 − ˜FT). Thus, we can define two open intervals (Figure 3B, white regimes) for the population activity leading to a representation of the respective memory by: and (cid:2) (cid:3) lowerF := ˜FT, F with F := √ ˜θ2 − ˜θ D 2(1 − ˜FT) , upperF := (F, 1) with F := √ ˜θ2 + ˜θ D 2(1 − ˜FT) . (12) (13) Note that below the target firing rate ˜FT the interaction of synaptic plasticity and scaling does not have a fixed point (Figure 3B, hatched regime; Equation 1). Furthermore, in the regime F < Fp < F no proper memory representation can be formed (equivalent to wpp ≤ ˜θ). This activity regime is defined as the no memory state nm := [F, F] (Figure 3B, grey regime) with size |nm|= ˜θ D/(1 − ˜FT). √ As we consider the interaction of two interconnected neuronal populations 1 and 2, we receive four distinct activity regimes enabling the formation of two memory representations (Figure 3Ci). These regimes are defined by all possible combinations of lowerF and upperF in both dimensions of F1 and F2. In other words, these activity regimes are separated by the no memory phase (nm) in both dimensions (Figure 3Ci, grey regimes). Similarly, with Equation 8, we can map the diverse conditions of the functional organiza- tions (Equations 3–6) onto different activity-dependent conditions. In general, the condition wp(cid:5)p < ˜θ becomes (cid:8) (cid:9) and wp(cid:5)p > ˜θ to

Fp < ˜θ2 1 − ˜FT 1 − ˜FT Fp(cid:5) (cid:8) Fp >

˜θ2
1 − ˜FT

1 −

˜FT
Fp(cid:5)

(cid:9)

.

(14)

(15)

To distinguish between both cases (which determines the functional organization between two
memories 1 Und 2), we define two separatrices:

S21 := F1 =

S12 := F2 =

˜θ2
1 − ˜FT
˜θ2
1 − ˜FT

(cid:10)

(cid:10)

1 −

1 −

(cid:11)

(cid:11)

,

.

˜FT
F2
˜FT
F1

(16)

(17)

Daher, S21 represents w21 = ˜θ in the activity-space (Figure 3Ai, Ci, red curves) while S12 repre-
sents w12 = ˜θ (Figure 3Ai, Ci, black curves). The relation of each activity level according to its
separatrix determines the actual functional organization:

Discrimination. When both activities F1 and F2 are below the respective separatrix S21
and S12 (Figure 3Ci, blue area), the system is in an discriminatory functional organization.

Sequence. The system establishes a sequence from memory 1 to memory 2, when the
activity F1 is above the corresponding separatrix S21 while the activity F2 stays below
separatrix S12 (Figure 3Ci, green area, s21) and vice versa for a sequence from memory 2
to memory 1 (yellow area, s12).

Netzwerkneurowissenschaften

615

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Input-dependent formation and organization of memories

Association. Both memories are organized in an associational entity when both neuronal
activities F1 and F2 are above their respective separatrix (Figure 3Ci, red area).

To obtain which functional organization the system
Functional organizations in activity-space.
forms for a given external input, we have to calculate the input-dependent average population
activities F1 and F2 in the equilibrium state. Dafür, for each pair of inputs I1 and I2, we derive
the fixed point conditions for both populations (Gleichung 43) dependent on the activity of the
1 (F2), black curve; FFP
other population (Figure 3Cii; FFP
2 (F1), yellow curve). The intersection
between both fixed point conditions (FFP
1 = FFP
2 ) determines the fixed point of the whole
System (green dot). The relation of the corresponding activities F1 and F2 of this intersection to
the separatrices determines the functional organization (Figure 3Ciii). This can be expressed in the
input space (Figure 3Diii). Daher, the interaction of synaptic plasticity and scaling enables the
formation of sequences in both directions and associations. Außerdem, there is a regime of
input values in which no memory representation is formed.

Comparing the analytical results from the population model (Figure 3Diii) with the results
from the full network analysis (Figure 3Dii) indicates that the population model matches the
full network quite well. Especially, the inherent property of a system to form different functional
organizations is precisely predicted by the population model. Remarkably, already the map-
ping of the weight-dependent conditions on the activity space (Figure 3Ci) provides sufficient
information to assess the possible organizations of memories for a given system (not requiring
the evaluation of the system’s fixed points).

Both analysis methods (Figure 3A and C)
Synaptic-plasticity-induced formation of associations.
indicate that the interaction of synaptic plasticity and scaling enables the formation of se-
quences and associations between two memory representations (Figure 3D). Interessant, für
very low external input stimulations I1 and I2, the system forms an association. This is mainly
due to the quadratic weight-dependency of synaptic scaling (Gleichung 1) such that for low
population activities synaptic scaling dominates the synaptic dynamics and drives the synaptic
weights to high values (up-scaling). This is in contrast to the synaptic-plasticity-and-memory hy-
pothesis (Martin et al., 2000; Hebb, 1949), which states that the processes of correlation-based
synaptic plasticity dominates learning. Along this line, synaptic scaling should mainly regulate
the synaptic dynamics in an homeostatic manner (Turrigiano & Nelson, 2004). Mit anderen Worten,
the synaptic weights should mainly increase with increasing neuronal activities. To deter-
(cid:13)
Fmin = 2 ˜FT
mine the regime in which this behavior is present, we consider the activity level
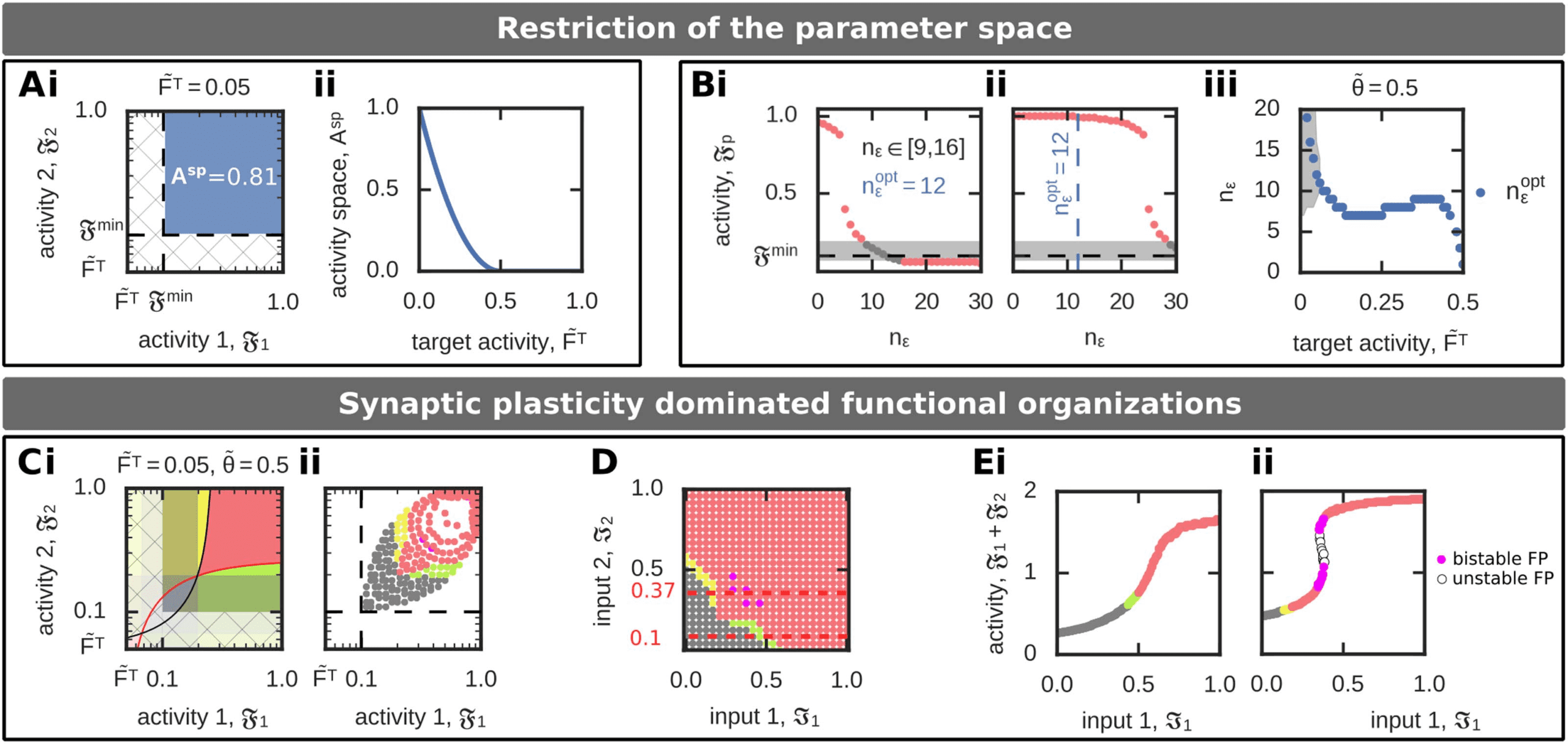
yielding the local minimum of the synaptic weight function (Gleichung 9; Abbildung 3B). Below Fmin
(Fp ∈ ( ˜FT, Fmin)), the dynamics are dominated by synaptic scaling and should be avoided.
Daher, the plausible activity regime is in the

(cid:12)

[Fmin, 1] × [Fmin, 1] − activity space

(18)

(Figure 4Ai, blue space) as in this space the synaptic weight dynamics are dominated by
correlation-based synaptic plasticity. This regime exists as long as the target activity ˜FT is below
restricting the target activity parameter to ˜FT ∈ (0, 0.5) (Figure 4Aii).
0.5

ASP = (1 − 2 ˜FT)2

(cid:2)

(cid:3)

The activity regime lowerF (Gleichung 12), which enables a proper formation of
Theorem 1
memory representations, is not part of the correlation-based dominated activity space (18) für
synaptic plasticity.

Netzwerkneurowissenschaften

616

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Input-dependent formation and organization of memories

Proof. Assume that the upper bound F of lowerF is smaller than the lower bound Fmin for
the synaptic plasticity dominated activity regime (Gleichung 18). It follows that the condition
(cid:2)
˜FT(1 − ˜FT) > 0 is true for ˜FT ∈ (0, 0.5) and by this lowerF (cid:6)∈ Asp.

Daher, to assure that the activity regime lowerF cannot be reached by the system, we have
to change the mapping between neuronal activity and inputs such that no reasonable input
pair I1, I2 yields population activities within lowerF. This activity-input mapping is mainly
determined by the inflexion point (cid:5) of the activity function (Equations 33 Und 43). Hier, Wir
specify the inflexion point in units of n(cid:2) ((cid:5) = n(cid:2)umax) with n(cid:2) being the number of maximally
active presynaptic neurons (with maximally strong synapses; see Methods). Erste, we analyze
the resulting population activities Fp and corresponding functional organizations for different
N(cid:2) given no external inputs (I1 = I2 = 0; Figure 4Bi). For n(cid:2) > 12, the population activities are
below Fmin, which triggers up-scaling yielding a scaling-induced formation of an association.
Please note that the system analyzed beforehand (Figur 3) has n(cid:2) = 20. For n(cid:2) < 9, neurons are too easy to excite such that activities are independent of the input nearby the maximum, yielding the functional organization of association. For 9 ≤ n(cid:2) ≤ 16, the system is in the no- memory state. Thus, to prevent the input-independent association of two interconnected neu- ronal populations, we consider the inflexion point to be in the regime 9 ≤ n(cid:2) ≤ 16. Thereby, n(cid:2) opt = 12 yields activities nearby the lower minimum activity level Fmin defined above. The same analysis for maximal external input stimulation (I1 = I2 = 1; Figure 4Bii) shows that for n(cid:2) opt = 12 the system can nearly reach its maximal firing rate of Fp = 1 such that the whole activity space [Fmin, 1] can be reached by the system. Please note that for n(cid:2) > 24, the system
cannot reach high activity levels, and for n(cid:2) > 27 the system is not able to form memory rep-
resentations, although it is maximally stimulated by the external input. Außerdem, as can be
opt depends on the target firing rate ˜FT (Figure 4Biii).
expected from Figure 4A, the value of n(cid:2)

Im Folgenden (Figure 4C–E), we will consider n(cid:2) = 12 and ˜FT = 0.05, was impliziert
that an association is only be formed by synaptic dynamics dominated by correlation-based
synaptic plasticity. The activity regime yielding scaling-dominated learning (hatched area in
Figure 4Ci) is theoretically possible; Jedoch, the adapted activity-input mapping assures that
this regime cannot be reached for given external inputs (Figure 4Cii and D). In the resulting
System, low inputs I1, I2 lead to a no-memory state (grau), while in a small regime sequences
are formed (yellow and green). Thereby, the sequence is formed from the population receiving
a stronger input to the population receiving the weaker input. If both inputs are strong, ein
association between the memory representations is being built (Rot). Note that there is a small
bimodal regime with two long-term equilibrium states both being an association (pink; see two
exemplary cross sections in Figure 4E).

After optimizing the activity-input mapping
Parameter-dependency of functional organizations.
by n(cid:2) such that the formation of diverse functional organizations is dominated by synaptic
plasticity, in the following, we will analyze which kind of functional organizations can be
formed by the system dependent on the different system parameters. Thereby, we will focus
on the target activity ˜FT and the average level of inhibition ˜θ.

Allgemein, as the no-memory state implies that neuronal populations can exist that do
not encode information (or have “forgotten” this information), this state has a large influence
on the overall system properties. As described above, the size of this state is given by |nm| =
√
D/(1 − ˜FT) with D = ˜θ2 − 4 ˜FT(1 − ˜FT). Daher, the discriminant D or rather ˜FT and ˜θ define
˜θ
whether the no-memory state can exist in a given system (Figur 5). Zusätzlich, as the relation
of the activity levels to the separatrices (Equations 16 Und 17) define which kind of functional

Netzwerkneurowissenschaften

617

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Input-dependent formation and organization of memories

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

− F2

Synaptic plasticity dominated functional organization (FO) of two interconnected memories. (A, B) The regime ASP, in which
Figur 4.
synaptic plasticity dominates the synaptic dynamics, depends on the target firing rate ˜FT (A) and inflexion point (cid:5) = n(cid:2)umax (B). (A) Der
−activity phase space (Ai, blue space) leading to synaptic plasticity dominated FOs decreases with increasing target firing
area of the F1
rate ˜FT (Aii). (B) The inflexion point (measured in n(cid:2)) determines the activity-input mapping such that for the same input different activities
opt, Fp ≈ Fmin. (Bi): Input: I1 = I2 = 0. (Bii): Input: I1 = I2 = 1.
Und, daher, different FOs are realized. If the inflexion point equals n(cid:2)
(Biii) The value of n(cid:2)
opt (Blau) depends on the target firing rate ˜FT. The grey area specifies all n(cid:2) that yield to the no-memory state. (C–E) Eins
example of synaptic plasticity dominated formation of FOs. Used parameters: ˜FT = 0.05, N(cid:2) = 12. (C) Although the system implies regimes
of scaling-dominated synaptic dynamics (hatched area; ich), the activity-input mapping excludes that the system can reach these by external
−input phase space, color-coded according to the respective FOs, shows that associations can only be
inputs (ii). (D) The resulting I1
formed for stronger inputs (compare to Figure 3Diii). (E) The sum of both population activities (F1 + F2) for a fixed input I2 shows for some
cases the existence of two equilibrium states encoding associations (pink). (NEIN): Input: I2 = 0.1. (Eii): Input: I2 = 0.37. Color code see Table 1.

− I2

(cid:12)

(cid:12)

(cid:13)(cid:13)

Fp ∈

Fmin, 1

organization is present (see above), the separatrices have to be within the synaptic plasticity
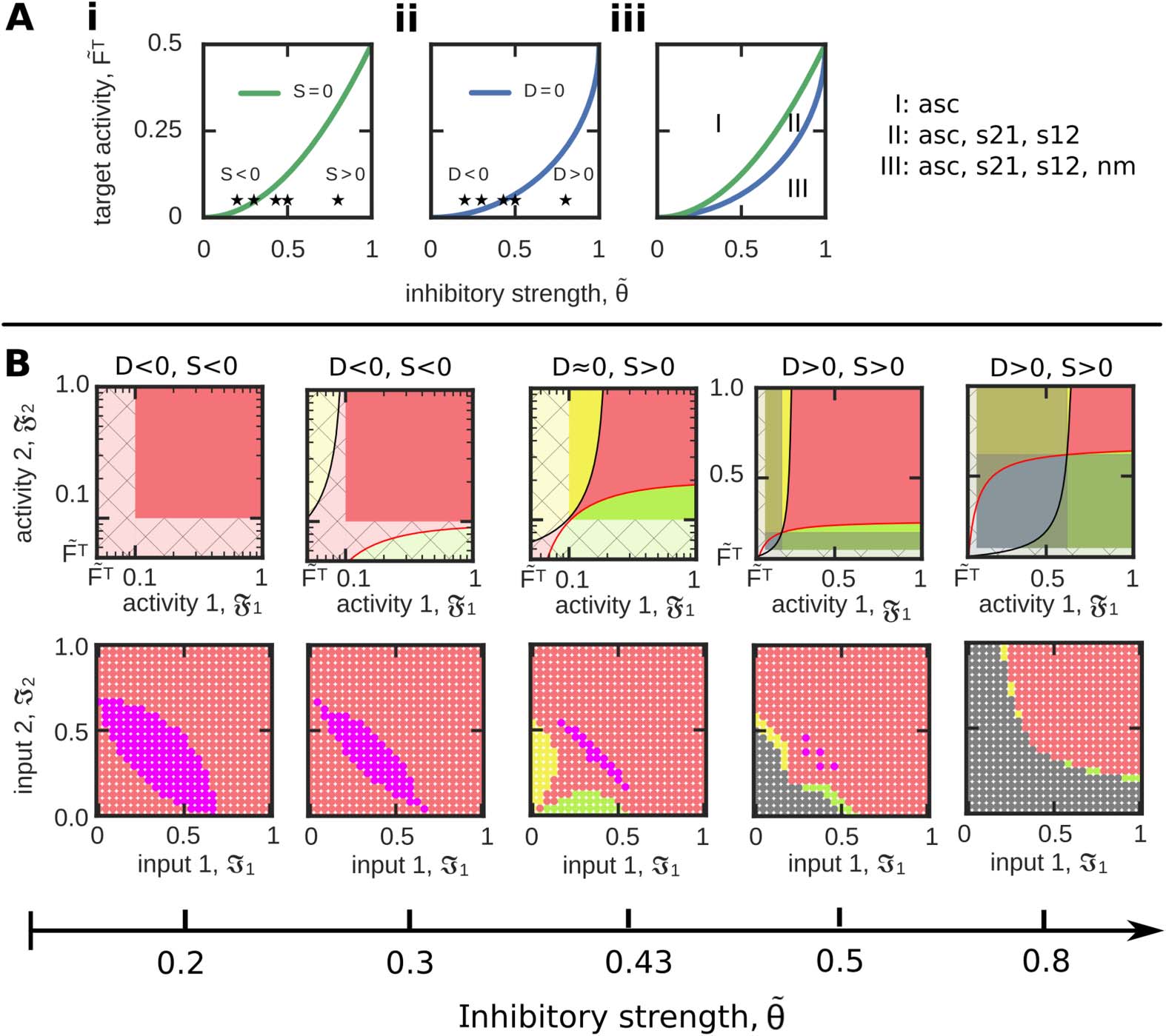
to enable the formation of sequences (s12: F1 < dominated activity regime S21, F2 > S12; s21: F1 > S21, F2 < S12) and discrimination (disc: F1 < S21, F2 < S12). As S12 (S21) increase with F1 (F2), the maximum difference S between the lower activity level of synaptic plasticity dominated dynamics and the separatrix is given for F1 = 1 (F2 = 1) such that S = S12[F1 = 1] − Fmin = ˜θ2 − 2 ˜FT. (19) Thus, the ˜FT- ˜θ-dependency of D (Figure 5Ai) and S (Figure 5Aii) determines the potential of the system to form diverse functional organizations (Figure 5Aiii). Interestingly, there are three functionally different system configurations: for D < 0, S < 0, the system can only form asso- ciations (regime I in Figure 5Aiii; first and second column in Figure 5B). If D < 0, S > 0, Die
system can form either associations or sequences (s12 as well as s21; regime II; third column).
And if D > 0, S > 0, associations, Sequenzen, and the no-memory state can be formed and
reached by the system (regime III; fourth and fifth column). Daher, this analysis shows that with
larger average inhibitory weight ˜θ and smaller target activity level ˜FT the system receives a
larger repertoire of functional organizations. Jedoch, this analysis also shows that the func-
tional organization of discrimination cannot be formed in a long-term manner. Although for

Netzwerkneurowissenschaften

618

Input-dependent formation and organization of memories

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

3
2
6
0
6
1
0
9
2
7
1
2
N
e
N
_
A
_
0
0
0
8
6
P
D

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 5. Quantification of the system ability to form different FOs dependent on the parame-
ters ˜FT and ˜θ. (A) The measure S (ich; Grün) indicates whether sequences can be formed, während die
measure D (ii; Blau) specifies the existence of no-memory states. (iii) Both measures together sepa-
rate the ˜FT − ˜θ−parameter phase space into three distinct regimes. Please see main text for details.
(B) For a constant target activity ( ˜FT = 0.05), we show several examples of resulting functional or-
ganizations for different values of inhibition ˜θ (asterisks in (A)) in activity (top row) and input space
(bottom). Color code see Table 1.

large values of inhibition both separatrices intersect; daher, both activity levels could be simul-
taneously below their corresponding separatrix (sehen, zum Beispiel, blue area in fifth column in
Figure 5B), the resulting area of discrimination cannot be reached by any inputs I1, I2, Weil
in all these cases the neuronal populations cannot serve as memory representations (grau).

Theorem 2 Correlation-based synaptic plasticity in combination with an activity-dependent
postsynaptic synaptic scaling term lacks the formation of functionally unrelated memories
(discrimination).

Proof. The constraints for a discrimination of two memories can be summarized by two in-
equations regarding the mean synaptic weights of the neuronal population model:

Netzwerkneurowissenschaften

w12 < θ < w11 ⇒ F1 > F2,

(20)

619

Input-dependent formation and organization of memories

Und

w21 < θ < w22 ⇒ F1 < F2. (21) We easily see that the first condition (Equation 20) is in contradiction to the second condition (Equation 21) and, thus, the discrimination of two interconnected memories is excluded. (cid:2) Thus, a neuronal system with correlation-based synaptic plasticity and a postsynaptic-activity- dependent synaptic scaling is not able to form two excitatory relations in between two memory representations that are weaker than the average inhibition. This analysis reveals that applying such a learning rule globally for the neuronal network dynamics is not sufficient to distinguish the two different processes of memory formation and discrimination. Thus, it seems that this learning rule has to be augmented by at least one additional adaptive process that decouples these two processes. 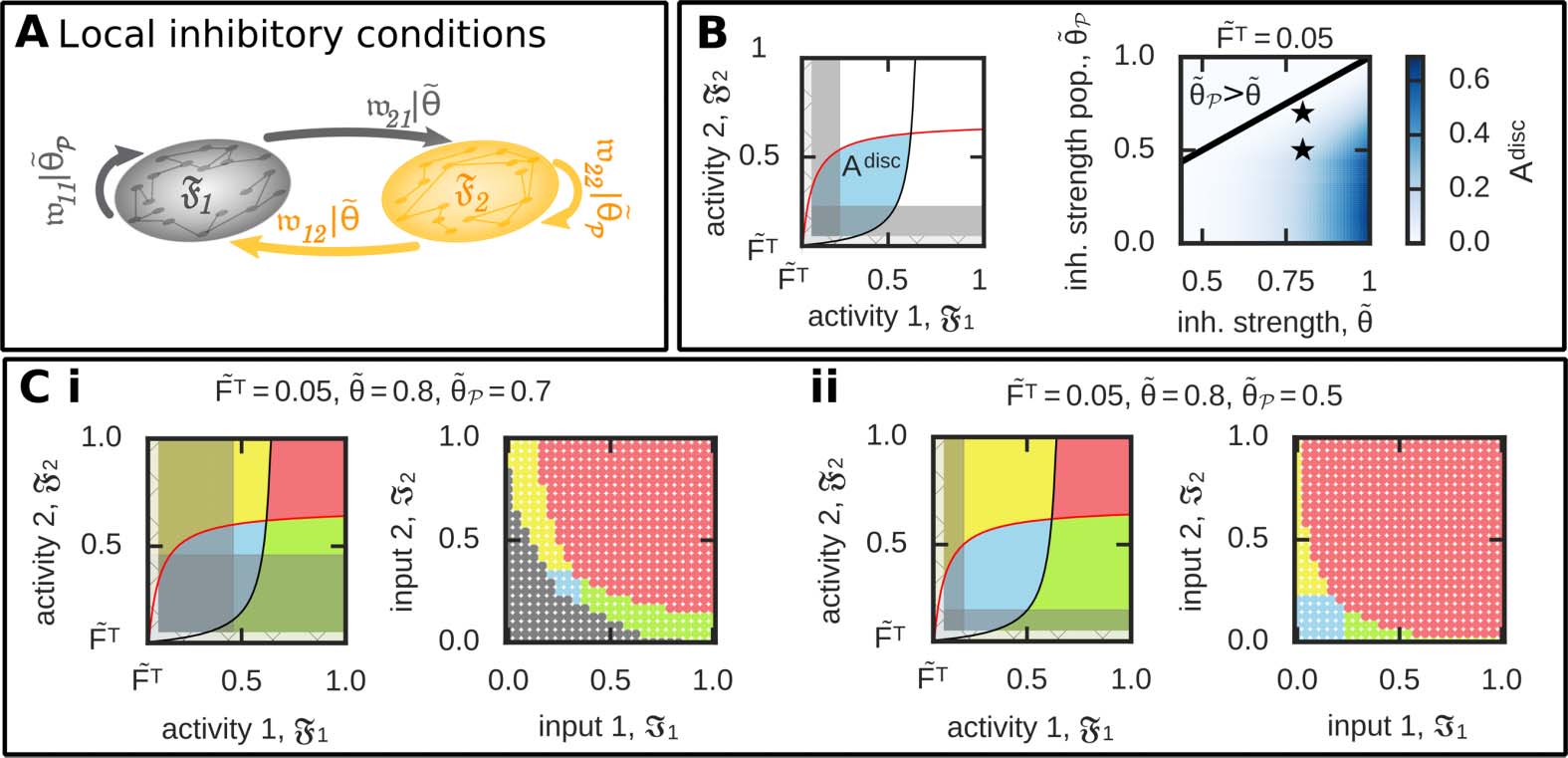Local Inhibition Enables the Functional Organization of Discrimination The ability to form a discriminatory relation between memory representations is functionally very important for a neuronal system, as it implies that not all memories, which are anatom- ically connected with each other, have to be functionally connected with each other. Thus, to overcome the lack of discriminatory functional organizations of memories, we have to “decouple” the discrimination condition from the memory condition (see above). For this, we introduce a different inhibitory synaptic weight strength ( ˜θP = 1 n2 p − j,i) within the neuronal populations compared with the inhibitory synaptic weight strength for all other connections ( ˜θ, Figure 6A). In other words, the parameter ˜θ is different for the discrim- ination condition as for the memory condition (which is now ˜θP ). To quantify the influence ∑i,j∈p ˜w l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 6. Considering different levels of inhibition level for connections within the neuronal pop- ulations compared with all others enables the formation of two discriminated memory representa- tions. (A) We consider a different average inhibitory synaptic weight within the neuronal populations ( ˜θp) compared with all others ( ˜θ). (B) Left: To quantify the effect of different inhibition levels, we calculate the area of discrimination states (Adisc; blue) not being “covered” by the no-memory states (grey) in the F1-F2-activity space. Right: Adisc dependency on different relations between ˜θp and ˜θ. (C) Given a lower level of inhibition within the populations than otherwise provides the neural sys- tem the ability to form all functional organizations as indicated here by two examples (asterisked in (B)); (i) ˜θ = 0.8, ˜θp = 0.7; (ii) ˜θ = 0.8, ˜θp = 0.5. Color code see Table 1. Network Neuroscience 620 Input-dependent formation and organization of memories of this new parameter on the potential to form two discriminated memory representations, we calculate the size of the activity space leading to discrimination (Figure 6B, left). In general, if inhibition within the populations is weaker than for all other connections ( ˜θP < ˜θ), the system can form memories being in a discrimination (Figure 6B, right). Please note that the other functional organizations are still maintained such that all different types can be obtained (Figure 6C). Interestingly, the state of discrimination is being formed if the inputs presented to both populations are weak. A weak input means that, among others, the probability of oc- currence is low, which implies that the chance of both inputs being presented simultaneously is very low (Figure 1). In other words, if both inputs are only accidentally shown simulta- neously, the neuronal system should discriminate their memory representations. Vice versa, if the inputs are often shown together (as for high input levels), the system should associate the representations as the interplay between synaptic plasticity, scaling, and inhibition does (Figure 6C). 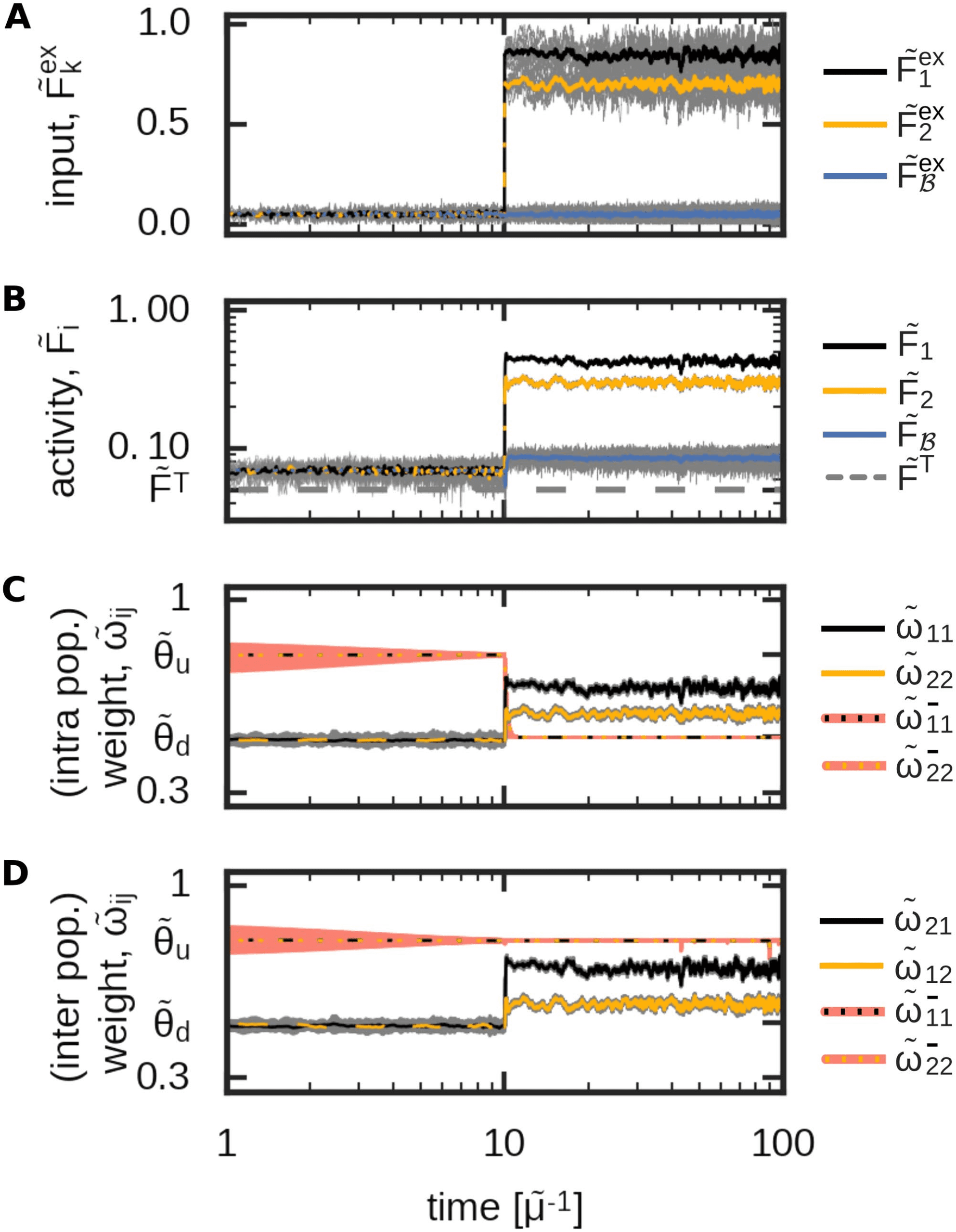Although in the analysis above we predefined different levels of inhibition, these different levels can also be obtained by the system in a self-organized manner by considering inhibitory synaptic plasticity (see Figure 7 for an example of discrimination). Similar to excitatory synaptic plasticity, the here-used example of inhibitory synaptic plasticity depends on the correlation of pre- and postsynaptic firing. In addition, the inhibitory synaptic plasticity rule is multiplied by two additional constrains. First, a minimum activity level θF for the pre- and postsynaptic firing rates introduces a threshold for inhibitory synaptic plasticity to occur ˙˜ω− j,i ∝ ˜Fi ˜FjH(∑F − θF), (22) with ˙˜ω− j,i being the strength of the inhibitory synapse connecting the presynaptic neuron i with the postsynaptic neuron j, ∑F := ˜Fi + ˜Fj, and H being the Heaviside step function. Second, the difference in the pre- and postsynaptic firing rates (ΔF := | ˜Fi |) provides an abstract measure for the noncorrelation of firing due to large deviations in their firing rates. − ˜Fj ˙˜ω− j,i ∝ ˜Fi ˜FjH(δF − ΔF). (23) Here, δF describes a tolerance range for such a variation in the firing rates. According to these conditions, the inhibitory synaptic weights converge either to an up-state (θu), if the sum of neuronal activities is smaller than its threshold ( ∑ F < θF) and/or the difference in the pre- and postsynaptic activities is above its tolerance range (ΔF > δF), oder
a down-state (θd), if the sum of neuronal activities is larger than its threshold ( ∑ F > θF)
and the difference in the pre- and postsynaptic activities is smaller than its tolerance
range (ΔF < δF). This type of inhibitory synaptic plasticity (Equation 44) together with plastic excitatory synapses governed by the interaction of correlation-based synaptic and homeostatic plasticity enables the reliable formation of memory representations and, in addition, provides the system the ability to form all basic functional organizations. In other words, our analyses indicate that a self-organized neural network can form all types of functional organizations if the interaction of synaptic plasticity and scaling are complemented by further adaptive processes. Network Neuroscience 621 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . 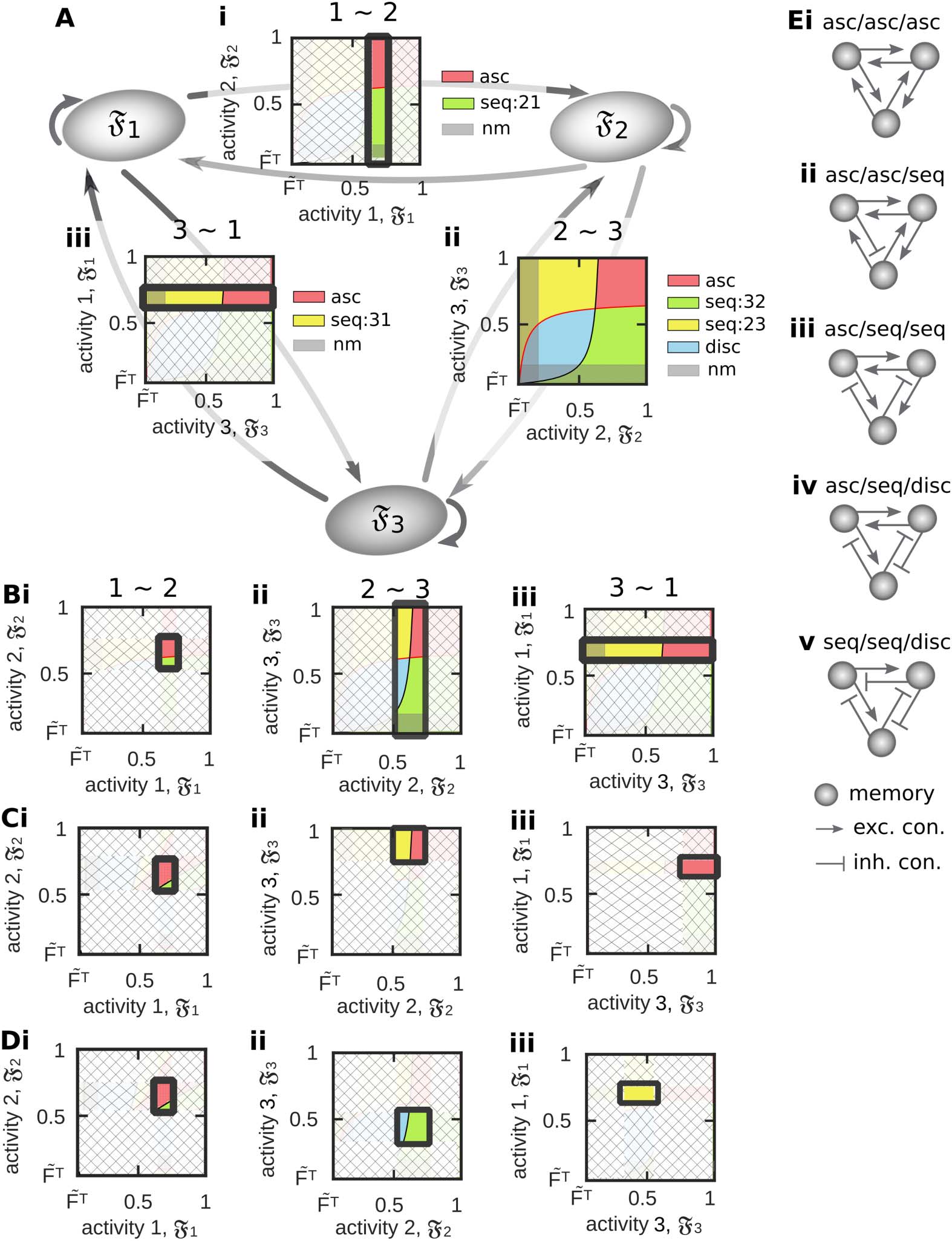t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories Generalization of the Interaction Between Multiple Memory Representations The analyses shown before are focused on the functional organization between two memory representations. However, given the results from these analyses, we can infer which types of functional organizations can be formed between three memory representations (Figure 8A). For this, we have to consider the space of possible functional organizations for different lev- (cid:5) ∈ {1, 2, 3} between two neuronal populations (e.g., resulting els of activities Fp and Fp (cid:5) , p, p from the interaction between synaptic plasticity and scaling and different levels of inhibition as l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 7. An exemplary inhibitory plasticity rule enables the self-organized formation of a dis- criminatory functional organization. The development of the input-driven dynamics of the complete neural network (Figure 2) with inhibitory plasticity (Equation 44). (A) The average input amplitudes are determined by two Ornstein-Uhlenbeck processes with mean ˜Fex 2 = 0.7. (B) Av- erage activities of each population; (C) average intrapopulation excitatory and inhibitory synaptic weights; (D) average interpopulation excitatory and inhibitory synaptic weights. 1 = 0.85 and ˜Fex Network Neuroscience 622 Input-dependent formation and organization of memories l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 8. By considering the results from analyzing the relations between two memory represen- tations, we can infer possible functional organizations between three neuronal populations. (A) If we assume that the external input can constrain the activity of a neuronal population to a specific ∈ [0.65, 0.8] restricts its value, constraining for instance the average activity of population 1 to F1 relation to populations 2 (i) and 3 (iii), while the relation between population 2 and 3 is not limited ∈ [0.5, 0.75]), (ii; compare to Figure 6Cii, left). (B) If the activity of population 2 is also constrained (F2 the relation between population 2 and 3 becomes also limited (ii). (C, D) If the activity of population 3 ∈ [0.3, 0.55]), the functional organiza- ∈ [0.75, 1]; D: F3 is also limited to a certain interval (C: F3 tions between all three populations are determined. (E) Different possible functional organizations for the examples shown in C and D. Color code see Table 1. Network Neuroscience 623 Input-dependent formation and organization of memories shown in Figure 6Cii, left). This space implies that if two populations are in a specific functional organization, the activity levels of the corresponding populations are determined to specific intervals that in turn, constrain the functional organization between these populations and a third one. In other words, if we constrain the activity level of population 1 by the external input ∈ [0.65, 0.8], the spaces of functional organiza- onto, without loss of generality, the interval F1 tions between population 1 and 2 (Figure 8Ai) and between population 1 and 3 (Figure 8Aii) are limited onto specific regimes such that only a subset of functional organizations can be realized. As long as we do not constrain the activity levels of population 2 and 3, these two populations are able to form all types of functional organizations (Figure 8Aii). If we also con- ∈ [0.5, 0.75]), the functional strain the activity level of, for example, the second population (F2 organization between population 1 and 2 is basically specified (association) and the space of functional organizations between population 2 and 3 is limited. Now, if also the activity ∈ [0.3, 0.55] level of the third population is constrained (F3 in D), all three possible interactions between the three memory representations are defined. By the above described procedure, we can infer which functional organizations between three memory representations can be reliably formed (see Figure 8E for examples given in C and D). Numerical simulations are required to confirm these results. However, we expect that, by ap- plying procedures as described above, the here-developed framework can be extended to inves- tigate the ability of diverse plasticity mechanisms to form different types of webs of memories. ∈ [0.75, 1] in Figure 8C and F3 DISCUSSION General Framework In the present work, we have developed a mathematical framework to investigate the ability of adaptive neural networks to form in a dynamic, input-dependent manner diverse functional organizations of interconnected memories. In contrast to previous studies focusing only on a subset of possible functional organizations (Chenkov et al., 2017; Tully et al., 2016; Griniasty et al., 1993; Abbott & Blum, 1996; Leibold & Kempter, 2006; Herrera-Aguilar, Larralde, & Aldana, 2012), we consider here all possible organizations between two memory represen- tations. Thereby, we define the functional organizations dependent on the relation between the excitatory and inhibitory synaptic weights of the neuronal network. By introducing a population description, we are able to transfer the resulting high-dimensional problem to a low-dimensional problem considering average synaptic weights and activities of the neuronal populations involved. In addition, by considering the long-term equilibrium dynamics, we could further reduce the system complexity with the input stimulation being a system param- eter. Finally, we could map the resulting dynamics onto the two-dimensional activity space which is sufficient to solve this complex problem of memory interactions (Figure 3). Thus, we gain an easily accessible understanding of the possible states the system can reach as well as of the underlying principles arising from the considered plasticity mechanisms and their limita- tions. Given the generality of the complete framework, it can be commonly used to investigate the effect of diverse plasticity mechanisms on the formation and interaction between memory representations. Analysis of the Interplay Between Synaptic Plasticity and Synaptic Scaling Given this general mathematical framework, we analyzed the effect of the interplay of correlation-based synaptic plasticity with homeostatic synaptic scaling on the formation of func- tional organizations of memory. This type of interplay is a quite general formulation of synaptic dynamics (Tetzlaff et al., 2011; Abbott & Nelson, 2000), which is sufficient to form individ- ual memory representations (Tetzlaff et al., 2013, 2015). We have shown that these types of Network Neuroscience 624 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories mechanisms provide a neural network the ability to form several types of functional organi- zation of memory representations such as sequences and associations (Figures 4 and 5). Fur- thermore, our method shows that correlation-based plasticity with scaling does not enable the formation of two stable memory representations being in a discriminated state. This shortcoming is due to the purely correlation-based formulation of synaptic plasticity and, by this, mathematically couples the condition for memory formation with the condition of discrimination. Interestingly, the correlation-independent dynamics triggered by synaptic scaling are not sufficient to decouple the conditions. However, these dynamics enable the formation of sequences providing a further functional role of synaptic scaling besides synaptic stabilization (Tetzlaff et al., 2011; Zenke et al., 2013; Zenke, Gerstner, & Ganguli, 2017) and homeostatic regulation of neuronal activities (Turrigiano & Nelson, 2004; Abbott & Nelson, 2000). On the basis of our results, we expect that similar mathematical models of synaptic dy- namics, which consist of correlation-based plasticity and a homeostatic term dependent on the postsynaptic activity level (e.g., Oja’s rule (Oja, 1982) or BCM rule (Bienenstock, Cooper, & Munro, 1982)) are also not able to form memory representations in a discriminated state. Thus, a further factor determining the synaptic dynamics of the network is required to enable the functional organization of discrimination. Local Variations of Inhibition We have shown that local variations in the level of inhibition could serve as such a factor enabling the discrimination between memory representations and other functional organiza- tions (Figure 6). Thereby, the average inhibitory synaptic strength within a memory represen- tation has to be weaker than all other inhibitory synaptic weights. This is in contrast to the idea of an inhibition, which balances the strong excitation within interconnected groups of neurons (Litwin-Kumar & Doiron, 2014; Vogels, Sprekeler, Zenke, Clopath, & Gerstner, 2011). However, despite the local differences in the balance of inhibition and excitation, the network-wide levels of excitation and inhibition can still be in a balanced state (van Vreeswijk & Sompolinsky, 1998; Denève & Machens, 2016). Furthermore, this type of inhibitory weight structure could emerge from an anti-Hebbian-like inhibitory plasticity rule as discovered in the memory-related hippocampus (Woodin, Ganguly, & Poo, 2003). Possible Extensions of Synaptic Dynamics Besides inhibition, other mechanisms could be the additional factor yielding all functional organizations. For instance, spike-timing-dependent plasticity (STDP; Gerstner, Kempter, van Hemmen, & Wagner, 1996; Bi & Poo, 1998; Markram, Gerstner, & Sjöström, 2011) adapts the synaptic weights according to the correlation of pre- and postsynaptic spiking dynam- ics. By considering detailed models of this mechanism (van Rossum, Bi, & Turrigiano, 2000; Song, Miller, & Abbott, 2000; Shouval, Bear, & Cooper, 2002; Graupner & Brunel, 2012), the influence of time-dependent properties of the stimuli, as correlations, on the formation of functional organizations of multiple memory representations can be investigated. Previous studies already indicated that STDP together with other plasticity mechanisms can reliably form memory representations (Litwin-Kumar & Doiron, 2014; Zenke et al., 2015); however, the interaction between such memory representations and the ability to form diverse functional organizations given the mechanism of STDP remains unclear. For a more detailed understand- ing, the theoretical framework presented in this study could be used. For this, the framework has to be adapted such that it takes the dynamics of STDP and spikes into account. This requires Network Neuroscience 625 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories differential equations describing the dynamics of populations of neurons of a certain size, given synaptic plasticity. In a recent study (Schwalger, Deger, & Gerstner, 2017), the authors derive a mathematical model of populations of a certain number of spiking neurons, which also con- siders the dynamics of short-term synaptic plasticity (Schmutz, Gerstner, & Schwalger, 2018). However, a mathematical model describing the dynamics of a population of spiking neurons (of fixed size) with STDP, which would be essential to extend the here-presented framework by time-dependent properties of stimuli, is still missing. This methodical gap could be at least partially circumvented by extending the rate-dependent synaptic plasticity model. For instance, spike-timing-dependent triggered LTD (Bi & Poo, 1998; van Rossum et al., 2000), in contrast to firing rate-dependent LTD (Bienenstock et al., 1982; Sjöström, Turrigiano, & Nelson, 2001; Malenka & Bear, 2004), could be a measure of uncor- related spike trains decoupling the memory from the discrimination condition. In more detail, the LTP part of STDP can be interpreted as a measure of the probability that the pre- and post- synaptic neurons fire correlated spikes during a small time window (Dayan & Abbott, 2001), described here in the rate-model by the correlation-based LTP-term, whereas the amount of uncorrelated spike pairs triggering LTD could be described in the here-used rate-model by the difference between the pre- and postsynaptic firing rates. We expect that considering such a difference term would be sufficient to enable the formation of memory representations (by correlation-based LTP) in a discrimination state (by non-correlation-based LTD). This has to be verified in subsequent studies. However, given a population model incorporating detailed dynamics of correlation-based synaptic plasticity, the here-presented framework can be extended to investigate the influence of more complex stimulus protocols on the formation of diverse functional organizations. In a more realistic scenario, different stimuli could be presented in a probabilistic manner de- termined by different sources (hidden causes). The detection of several independent hidden sources from a stream of stimuli is a complex problem humans or cell cultures are able to solve (Mesgarani & Chang, 2012; Isomura, Kotani, & Jimbo, 2015). Several theoretical studies mainly focusing on neuronal networks with a feed-forward structure indicate that the dynamics of synaptic plasticity enables the solving of such types of problems (Dayan & Abbott, 2001; Bell & Sejnowski, 1995; Hyvärinen & Oja, 2000; Isomura & Toyoizumi, 2016; Pehlevan, Mohan, & Chklovskii, 2017; Isomura & Toyoizumi, 2018). Thus, we suppose that plastic feed-forward and recurrent connections enable the neuronal system to detect hidden sources by the feed- forward dynamics and forms memory representations of these by the recurrent synapses. Given relations between these sources, the synapses connecting the memory representations could represent the strength of these relations. Of course, if the number of sources increases, due to the increase in combinations of different functional organizations (Figure 8), the here-derived theoretical framework has to be adjusted. For instance, by measuring the mutual information or transfer entropy (Brunel & Nadal, 1998; MacKay, 2003; Vicente, Wibral, Lindner, & Pipa, 2011) conditioned on the input between representations, one could extract the formed func- tional organization given different stimulus protocols. Beyond the scope of reliably forming memory representations of environmental stimuli, it is still unclear how to maintain these representations for a long duration (Dudai, 2004, 2012). Similar to previous studies (Tetzlaff et al., 2013, 2015), also here the interplay between synap- tic plasticity and scaling yields the slow decay of synaptic weight structures after withdraw- ing the stimuli (see Supporting Information Figure S1 for different rates of synaptic dynamics; Herpich & Tetzlaff, 2019). However, as long as the average synaptic weight remains larger than control, the corresponding neurons and synapses resemble a memory representation of the Network Neuroscience 626 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories stimulus. Prolonging the lifetime of such a memory can be done by the diverse mechanisms of consolidation as synaptic (Frey & Morris, 1997; Clopath, Ziegler, Vasilaki, Büsing, & Gerstner, 2008; Redondo & Morris, 2011; Li, Kulvicius, & Tetzlaff, 2016) or sleep-induced consolida- tion (Tetzlaff et al., 2013; Diekelmann & Born, 2010; Nere, Hashmi, Cirelli, & Tononi, 2013). We expect that similar mechanisms can also consolidate the intermemory synaptic weights maintaining the whole functional organization. However, under which conditions memory representations as well as the interconnections are consolidated requires further experimental and theoretical studies. Please note that there is a multitude of studies indicating the existence of additional factors influencing synaptic plasticity. For instance, neuromodulatory transmitters, such as acetylcholine, noradrenaline, serotonin, and dopamine, can serve as a third factor (Frémaux & Gerstner, 2016; Gu, 2002). However, with the mathematical framework developed in this study, it is now possi- ble to investigate in more detail the effect of such factors on the formation, maintenance, and organization of memory representations in neuronal circuits. Furthermore, given the under- standing of the organization between two memory representations, now one can extend this framework to investigate the self-organized formation of webs of memories and the emergence of complex behavior. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 MATERIALS AND METHODS Neuronal Network Model We consider a recurrent neuronal network model consisting of a set N of n rate coded neurons (N := Nn = {1, . . . , n}, Figure 2A, dots). The neurons are interconnected via an all-to- all connectivity for the excitatory as well as for the inhibitory connections. Note that, if not stated otherwise, the inhibitory connections are constant while the excitatory synapses are plastic. Within the recurrent network, we define two distinct subsets of neurons P1 and P2 as neural population 1 (black dots) and neural population 2 (yellow dots). For simplicity, both neural populations have the same number of neurons (|P1| = |P2| = nP ). Furthermore, we assume no overlap between both neuronal populations (P1 ∩ P2 = ∅). Neurons that are not part of neuronal population P1 or P2 are summarized as background neurons (B := N \(P1 ∪ P2)), with size |B|= n − 2nP ). Thus, we can describe the neuronal network model as the interaction of three different neuronal populations p ∈ {P1, P2, B} =: P. All neurons i of a neuronal population p receive a population-p-specific input stimulation defined by Fex p via nex P different neurons k connected via constant excitatory synapses ωex. All these input neurons k are summarized to a population-p-specific input Ep ∈ E . Furthermore, each single neuron k ∈ Ep of the external input layer provides an external input stimulus of average strength Iex is k defined by the population-p-specific stimulation parameter Fex (see Equation 37). Note, we p P equal to nP to consider the same order of magnitude for input populations as for the set nex populations themselves. k ωex onto the interconnected neurons of the neuronal network N , where Fex := Fex k Neuron model. We consider point neurons with each neuron i ∈ p ⊂ N of the network sum- ming up its incoming inputs from the interconnected excitatory (Figure 2A, blue connections), inhibitory, and input neurons (red connections) to its overall neuron-specific input current (φ i). The inputs are transmitted via the synapses, thus, the neuron specific input current integrates the separate inputs of the neurons (Fj) proportional to the respective synaptic weights (ω i,j): ω i,jFj i = ∑ φ j∈N + (cid:17) (cid:15)(cid:16) (cid:14) i network exc. ω− − ∑ i,jFj j∈N − (cid:17) (cid:15)(cid:16) (cid:14) i network inh. , [φ] = 1pA. Iex k + ∑ k∈Ep (cid:14) (cid:15)(cid:16) (cid:17) external exc. (24) 627 Network Neuroscience Input-dependent formation and organization of memories , N − i ∈ N are the sets of indices for the excitatory, inhibitory, and externally inter- Here, N + i i,j ([ω] = connected presynaptic neurons j to the postsynaptic neuron i, whereby, ω −1) the respective presynaptic neu- 1pC) are the respective synaptic weights, and Fj ([F] = 1s ron’s activity. In contrast to the plastic excitatory synaptic weights, all inhibitory synapses (θ := ω− i,j = constant) are constant. Although any neuron can have only either excitatory or inhibitory outgoing connections, similar to previous studies (Tetzlaff et al., 2013, 2015), we merge both distinct neuronal sets for the excitatory and inhibitory neurons to one neuronal population generalized by N = N + . This approach is a simplification of the used model by assuming that an excitatory and an inhibitory neuron have a similar connectivity. This leads to the following input current (φ i) onto one neuron i belonging to population p: i = N − i,j and ω− i i = ∑ φ j∈N (ω i,j − θ)Fj + ∑ k∈Ep Iex k , θ, ωex ∈ R+. (25) We can further specify this input current in respect to the presynaptic neuron’s affiliation to a neuronal population p ∈ {P1, P2, B}: i = ∑ φ p∈P ∑ j∈p (ω i,j − θ)Fj + ∑ k∈Ep Iex k . This neuron specific input drives its respective membrane potential (ui) described by: τ ˙ui = −ui + Rφ i, τ, R ∈ R+, [u] = 1mV. (26) (27) Here, τ ([τ] = 1s) is the time constant for the membrane potential and set to τ = 1s and R = 0.1nΩ, ([R] = 1nΩ) is the membrane resistance. The membrane potential ui is nonlinearly transformed to a neural firing rate (Fi): Fi = Fmax 1 + exp [β((cid:5) − ui)] , Fmax, β, (cid:5) ∈ R+, [F] = 1Hz, (28) −1) being the steepness, and with Fmax = 100Hz being the maximal firing rate, β ([β] = 1mV (cid:5) ([(cid:5)] = 1mV) being the inflexion point of the sigmoid. Thus, the neuronal activity for each ∈ [0, Fmax]). To simplify the description of the neuron i takes values between 0 and Fmax (Fi neuronal dynamics, we combine Equation 27 and Equation 28 to: τ ˙Fi = (Fmax − Fi)Fi Fmax (cid:18) (cid:10) log Fmax Fi (cid:11) (cid:19) − 1 + β(Rφ i − (cid:5)) . (29) All excitatory synapses within the recurrent network Synaptic plasticity and synaptic scaling. are plastic and change proportional to the activity-dependent Hebbian learning rule (H; Hebb, 1949; Bliss & Lømo, 1973) H : (0, Fmax)2 → R+, (Fi, Fj) (cid:15)→ μFi Fj, μ ∈ R+, (30) with time constant μ. This correlation learning rule leads to unbounded synaptic weight dy- namics. Thus, we include synaptic scaling (S; Turrigiano et al., 1998; Turrigiano & Nelson, 2004) as a homeostatic mechanism S : (0, Fmax) × R+ → R, (Fi, ω i,j) (cid:15)→ γ(FT − Fi)ω2 i,j, γ, FT ∈ R+, (31) with the time constant γ and target firing rate FT. This scaling mechanism decreases (increases) the synaptic weight if the postsynaptic activity is above (below) the target firing rate. Note that Network Neuroscience 628 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories 60s on the timescale of minutes while γ = 1 Hebbian dynamics are in general faster than scaling dynamics, thus, γ (cid:16) μ. Therefore, we set μ = 1 90·60s on timescale of hours. Combining the correlation-based Hebbian learning term additive with the postsynaptic activity-dependent ∝ H + S), we get the following learning rule for the synaptic weights synaptic scaling term ( ˙ω (Tetzlaff et al., 2011, 2012): i,j ˙ω i,j = μFi Fj + γ(FT − Fi)ω2 i,j. (32) In the following, we give an interpretation for Constraining parameters of the activity function. the parameters like the inflexion point and steepness of the sigmoidal shaped activity func- tion (Equation 28). To specify the inflexion point of the neuronal activities, we define the maximal evoked membrane potential (umax) of a neuron i by only one incoming synapse (ω ij) to the postsynaptic neuron j. Therefore, we set the pre- and postsynaptic neuronal ac- tivities to the maximal activity level of (Fj = Fi = Fmax) and, by this, calculate the fixed synaptic weight, using Equation 32, and define it as the maximal synaptic weight (ωmax := (cid:20) μ(Fmax)2/(γ(Fmax − FT)). Equation 27 specifies the maximal network internal (∑ Iex k = 0) evoked membrane potential of umax := RFmax(ωmax − ˜θ). Using this quality of umax, we in- terpret the inflexion (cid:5) of a neuron i as the number (n(cid:2)) of such maximally wired presynaptic neurons. This leads to (cid:5) = n(cid:2)umax. For the determination of the precise value for n(cid:2) = 12 see the Results section. To specify the steepness of the neuronal activity function, we have to consider their maximal and minimal possible evocable membrane potential and choose a steepness parameter β because of two different constraints: (1) the activity for the minimal membrane potential has to take on higher values as the target firing rate FT to prevent unstable weight dynamics, and (2) for a maximal evoked membrane potential the neurons have to take on the maximal firing rate of Fmax. One specific parameter for the steepness of the activity function that fulfill these two conditions is β = 0.00035mV −1 for all neurons. Normalized Neuronal Network Model In the following, to reduce complexity, we normalize the neuronal activities of all neurons i ∈ N according to the maximal neural firing rate ( ˜Fi := Fi/Fmax) and all synaptic weights to the maximal excitatory synaptic weight ( ˜ω i,j/ωmax; ˜θ := θ/ωmax). Thus, the external input stimulation is also normalized to ˜Iex k /(Fmaxωmax). By this, we map the (normalized) neuronal activity ˜Fi and the (normalized) excitatory synaptic weight ˜ω (cid:19) i,j := ω k = Iex i,j to [0, 1] ∈ R: (cid:10) (cid:11) (cid:18) τ ˙˜Fi = (1 − ˜Fi) ˜Fi log − 1 + β(Rφ i − (cid:5)) , 1 ˜Fi for the neuronal activity with ⎛ ⎞ φ i = Fmaxωmax ⎝ ∑ p∈P ∑ j∈p ( ˜ω i,j − ˜θ) ˜Fj + ∑ k∈Ep ⎠, ˜Iex k and for the synaptic weight with τω ˙˜ω i,j = ˜Fi ˜Fj + ˜FT − ˜Fi 1 − ˜FT ˜ω2 i,j, (cid:10) (cid:25) τω = ˜μ −1 = Fmax Fmaxμγ(1 − ˜FT) (cid:11)−1 . (33) (34) (35) (36) 629 Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories Numerical Simulation and Stimulation Protocol Each neuronal simulation starts with a tuning phase, where each of the n = 100 neurons of P = 10 different input neurons of the input layer E . the network receive input noise from nex For the simulations in Figure 2 and Figure 3 the noise for the input neurons is determined by N (0.25, 0.025) · Fmax. In all remaining simulations, we applied input noise of N (0.05, 0.025)· Fmax. Subsequent to this tuning phase (t = 10), all neurons k of the external input layer Ep that are connected to neurons i ∈ p fire according to an Ornstein-Uhlenbeck process: ˙˜Fex k = δ( ˜Fex p (cid:14) − ˜Fex k ) (cid:17) (cid:15)(cid:16) drift + , σ ζ k dt (cid:14) (cid:15)(cid:16) (cid:17) diffusion ζ k ∼ N (0, 1) (37) p . For values used for the inputs ˜Fex with a drift term with constant δ = 0.025 and an arbitrary population specific equilibrium level for the firing rate of ˜Fex p , a normal distributed diffusion term with constant σ = 0.0125 and an k (t = 0) = ˜Fex initial firing rate of ˜Fex p , please see captions of corresponding figures. Please note, as the comparison to the population model at equilibrium that is based on the average activities and average synaptic weights indicates (Figure 3), we expect that the specific type of noise does not significantly influence the results. We apply the input stimulation over time, by this we simulate the whole activity and synaptic weight dynamics until the system reaches an equilibrium state. Numerically, we solve the differential equations of the normalized model (Equations 33–35; with ˜Iex k ) for the synaptic −3[μ−1] = 1ms) weight dynamics and activity dynamics with the euler method (Δt = 1 μ(Fmax)2/(γ(Fmax − FT) and (cid:5) = n(cid:2)umax and parameters provided in Table 2; ωmax = with umax = RFmax(ωmax − ˜θ) and n(cid:2) = 20 for Figures 2, 3 and n(cid:2) = 12 for Figure 7. All i,j(t = 0) ∼ N ( ˜θ, 0.025) initial synaptic weights are distributed around the balanced state ˜ω and activities around ˜Fi(t = 0) ∼ N (0.07, 0.005). In our model we also consider autapses ω ii. k = ˜ωex ˜Fex 60 10 (cid:20) Analysis of the System’s Equilibrium State As the different functional organizations of two interconnected neuronal populations are de- fined at the system’s equilibrium state, we can reduce our problem to an analytical calculation of the average neuronal activities and synaptic weights at equilibrium state. Because of the homogeneous external input stimulation of all neurons i belonging to one neuronal popula- tion p and the underlying full connectivity of the network, we make the assumption that the Table 2. Used Parameters. Network model Neuron model Syn. plast. & syn. scal. parameter value parameter n nP nB nex P ˜ωex ˜θ τ R Fmax β 100 neurons 10 neurons n − 2nP 10 neurons 1 0.5 parameter μ γ ˜FT value −1 1 60 s −1 1 5400 s 0.05[Fmax] value −1 1s 0.1nΩ 100[Hz] 0.00035 1 mV Network Neuroscience 630 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories fixed firing rate of each neuron i of a population p ( ˜F particular population (Fp) at fixed point state ∗ i ) approaches the mean firing rate of the Fp := n−1 p ∑ i∈p ∗ ˜F i ≈ ˜F ∗ i . (38) Using these average activities (Fp) of both neuronal populations p at stable state, we can cal- culate the respective average excitatory synaptic weights at the system’s stable state (cid:5) (cid:6) (cid:6) (cid:7) FpFp(cid:5) 1 − ˜FT (cid:13) (cid:12) (39) wp(cid:5) p = Fp(cid:5) − ˜FT . l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 This approach, reduces the problem to analytically calculate the average activities (Fp) of the neuronal populations p ∈ {P1, P2} dependent on the external input stimulation. Therefore, we calculate the mean population specific external input current onto one neuron i of popu- lation p as ˜Iex p := ∑k∈E i,i∈p ˜Iex k . We easily see that the input current onto each neuron i of a neuronal population p is inde- pendent of the neuronal dynamics and is only defined by the average qualities of each neuronal population at the system’s stable state. Thus, the fixed mean input onto a neuronal population p (Qp) is given by: ⎛ Qp ≈ Fmaxωmax ⎝nP ˜Iex p + ∑ p(cid:5)∈P ∑ j∈p (cid:2) (cid:3) wpp(cid:5) − ˜θ Fp(cid:5) ⎞ ⎠ ⎛ = Fmaxωmax ⎝nP ˜Iex p + ∑ p(cid:5)∈P (cid:2) (cid:3) nP wpp(cid:5) − ˜θ Fp(cid:5) ⎞ ⎠ Eq 39 = FmaxωmaxnP ⎛ ⎛ (cid:4) ⎝ ˜Iex p + ∑ p(cid:5)∈P ⎝ (cid:12) 1 − ˜FT (cid:13) FpFp(cid:5) Fp − ˜FT ⎞ ⎠ Fp(cid:5) ⎞ ⎠ . − ˜θ (40) We further reduce the complexity of the model to enable a fixed point analysis, while adding the fixed input from the background neurons onto one neuronal population p at stable state ˜IpB := nP (n − 2nP ) (cid:12) wpB − ˜θ (cid:13) FB (41) p ), proportionally to the size of the external input layer := ˜IpB/nP ). This leads to the total input current onto one neuronal population p ∈ to the external input stimulation ( ˜Iex (Δ ˜Iex p {P1, P2}), as: ⎛ Qp = FmaxωmaxnP ⎝Ip + ∑ p(cid:5)∈{P1,P2} ⎛ (cid:4) ⎝ (cid:12) 1 − ˜FT (cid:13) FpFp(cid:5) Fp − ˜FT ⎞ ⎠ Fp(cid:5) ⎞ ⎠ , − ˜θ (42) p + Δ ˜Iex with Ip := ˜Iex p . This expression of the input current onto each neuronal population p at stable state allows us to numerically calculate the respective average activity of each population at the system’s stable state: (cid:10) (cid:10) (cid:11) (cid:11) FFP p := (1 − Fp)Fp log 1 Fp − 1 + β(RQp − (cid:5)) != 0 in a two dimensional parameter-phase space of (IP1 − IP2 − space). (43) 631 Network Neuroscience Input-dependent formation and organization of memories Inhibitory Synaptic Plasticity In the last section of this study, we introduce inhibitory synaptic plasticity. This specific plas- ticity rule depends on a threshold (θF) for the sum of pre- and postsynaptic activity levels (∑ F := ˜Fi + ˜Fj) and on a tolerance range (δF) for the difference in the pre- and postsynaptic |) leading the inhibitory synaptic weight ( ˜ω− firing rates (ΔF := | ˜Fi j,i) converge either to an up- (θu) or down-state (θd). The synaptic weight converge to: − ˜Fj an up-state (θu), if the sum of neuronal activities is smaller than its threshold (∑ F < θF) and/or the difference in the pre- and postsynaptic activities increases its tolerance range (ΔF > δF),
a down-state (θd), if the sum of neuronal activities is greater than its threshold (∑ F > θF)
and the difference in the pre- and postsynaptic activities is smaller than its tolerance
range (ΔF < δF). These conditions lead to the following learning rule on the inhibitory synaptic plasticity: (cid:8) ˙˜ω− j,i = ˜Fi ˜Fj ρu( ˜θu − ˜ω− ji )H (cid:5)[H(ΔF − δF) + H(θF − ∑ F)] (cid:9) (44) + ρd( ˜θd − ˜ω− ji )H(δF − ΔF)H(∑ F − θF) , with ρu, ρd being the learning rates towards the up- and down-state and H side function with H we set θu = 0.8, θd = 0.5, θF = 2Fmin, δF = 0.05, and ρd = ρu = 1. an adapted Heavi- (cid:5)(0) = 0 to express the and/or condition for the up-state. In our simulations (cid:5) ACKNOWLEDGMENTS The authors thank the International Max Planck Research School for Physics of Biological and Complex Systems, Niedersächsisches Voraband University of Göttingen, for a Stipend to Juliane Herpich. AUTHOR CONTRIBUTIONS Juliane Herpich: Conceptualization; Formal analysis; Investigation; Methodology; Visualiza- tion; Writing - Original Draft. Christian Tetzlaff: Conceptualization; Funding acquisition; Methodology; Project administration; Supervision; Validation; Writing - Review & Editing. FUNDING INFORMATION Christian Tetzlaff, H2020 Future and Emerging Technologies (http://dx.doi.org/10.13039/ 100010664), Award ID: 732266. Christian Tetzlaff, Deutsche Forschungsgemeinschaft (http:// dx.doi.org/10.13039/501100001659), Award ID: SFB-1286, Project C1. REFERENCES Abbott, L., & Nelson, S. (2000). Synaptic plasticity: Taming the beast. Nature, 3, 1178–1183. Abbott, L. F., & Blum, K. I. (1996). Functional significance of long- term potentiation for sequence learning and prediction. Cerebral Cortex, 6, 406–416. Amit, D. J., Brunel, N., & Tsodyks, M. (1994). Correlations of cor- tical Hebbian reverberations: Theory versus experiment. Journal of Neuroscience, 14(11), 6435–6445. Bell, A. J., & Sejnowski, T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Computation, 7, 1129–1159. Bi, G. Q., & Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. Journal of Neuroscience, 18, 10464–10472. Network Neuroscience 632 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories Bienenstock, E. L., Cooper, L. N., & Munro, P. W. (1982). Theory for the development of neuron selectivity: Orientation specificity and binocular interaction in visual cortex. Journal of Neuro- science, 2(1), 32–48. Bliss, T., & Lømo, T. (1973). Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit fol- lowing stimulation of the perforant path. Journal of Physiology, 232(2), 331–356. Brunel, N., & Nadal, information, Fisher information, and population coding. Neural Computation, 10, 1731–1757. (1998). Mutual J. P. Buzsaki, G. (2010). Neural syntax, cell assemblies, synapsembles, and readers. Neuron, 68, 362–385. Byrne, E., & Huyck, C. (2010). Processing with cell assemblies. Neurocomputing, 74, 76–83. Chenkov, N., Sprekeler, H., & Kempter, R. (2017). Memory replay in balanced recurrent networks. PLoS Computational Biology, 13, e1005359. Clopath, C., Ziegler, L., Vasilaki, E., Büsing, L., & Gerstner, W. (2008). Tag-trigger-consolidation: A model of early and late long- term potentiation and depression. PLoS Computational Biology, 4, e10000248. Dayan, P., & Abbott, L. (2001). Theoretical Neuroscience - Compu- tational and Mathematical Modeling of Neural Systems. The MIT Press, Cambridge, Massachusetts. Denève, S., & Machens, C. K. (2016). Efficient codes and balanced networks. Nature Neuroscience, 19, 375–382. Diekelmann, S., & Born, J. (2010). The memory function of sleep. Nature Reviews Neuroscience, 11, 114–126. Dudai, Y. (2004). The neurobiology of consolidation, or, how stable is the engram? Annual Review of Psychology, 55, 51–86. Dudai, Y. (2012). The restless engram: Consolidation never end. Annual Review of Neuroscience, 35, 227–247. Frémaux, N., & Gerstner, W. (2016). Neuromodulated spike-timing- dependent plasticity, and theory of three-factor learning rules. Frontiers in Neural Circuits, 9, 85. Gu, Q. (2002). Neuromodulatory transmitter systems in the cortex and their role in cortical plasticity. Neuroscience, 111(4), 815–835. Hebb, D. (1949). The Organization of Behavior. Wiley, New York. Herpich, J., & Tetzlaff, C. (2019). Supporting Information for “Princi- ples underlying the input-dependent formation and organization of memories.” Network Neuroscience, 3(2), 606–634. https:// doi.org/10.1162/netn_a_00086 Herrera-Aguilar, J. L., Larralde, H., & Aldana, M. (2012). Pattern recognition in neural networks with competing dynamics: Coex- istence of fixed-point and cyclic attractors. PLoS One, 7, e42348. Hyvärinen, A., & Oja, E. (2000). Independent component analysis: Algorithms and applications. Neural Networks, 13, 411–430. Isomura, T., Kotani, K., & Jimbo, Y. (2015). Cultured cortical neurons can perform blind source separation according to the free-energy principle. PLoS Computational Biology, 11, e1004643. Isomura, T., & Toyoizumi, T. (2016). A local learning rule for inde- pendent component analysis. Scientific Reports, 6, 28073. Isomura, T., & Toyoizumi, T. (2018). Error-gated Hebbian rule: A lo- learning rule for principal and independent component cal analysis. Scientific Reports, 8, 1835. Izhikevich, E. (2007). Dynamical Systems in Neuroscience: The Ge- ometry of Excitability and Bursting. Cambridge, MA: MIT Press. Lazar, A., Pipa, G., & Triesch, J. (2009). SORN: a self-organizing recurrent neural network. Frontiers in Computational Neuro- science, 3, 23. Leibold, C., & Kempter, R. (2006). Memory capacity for sequences in a recurrent network with biological constraints. Neural Com- putation, 18, 904–941. Li, Y., Kulvicius, T., & Tetzlaff, C. Induction and consoli- dation of calcium-based homo- and heterosynaptic potentiation and depression. PLoS One, 11(8), e0161679. (2016). Litwin-Kumar, A., & Doiron, B. (2014). Formation and maintenance of neuronal assemblies through synaptic plasticity. Nature Com- munications, 5, 5319. MacKay, D. J. C. (2003). Information theory, inference, and learning algorithms. Cambridge, UK: Cambridge University Press. Frey, U., & Morris, R. (1997). Synaptic tagging and long-term Malenka, R. C., & Bear, M. F. (2004). LTP and LTD: An embarrass- potentiation. Nature, 385, 533–536. ment of riches. Neuron, 44, 5–21. Garagnani, M., Wennekers, T., & Pulvermüller, F. (2009). Recruit- ment and consolidation of cell assemblies for words by way of Hebbian learning and competition in a multi-layer neural net- work. Cognitive Computation, 1, 160–176. Gerstner, W., Kempter, R., van Hemmen, J. L., & Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature, 383, 76–81. Glendinning, P. (1994). Stability, instability and chaos: An introduc- tion to the theory of nonlinear differential equations. Cambridge, UK: Cambridge University Press. Graupner, M., & Brunel, N. (2012). Calcium-based plasticity model explains sensitivity of synaptic changes to spike pattern, rate, and dendritic location. Proceedings of the National Academy of Sci- ences of the United States of America, 109(10), 3991–3996. Griniasty, M., Tsodyks, M., & Amit, D. (1993). Conversion of tempo- ral correlations between stimuli to spatial correlations between attractors. Neural Computation, 5, 1–17. Markram, H., Gerstner, W., & Sjöström, P. (2011). A history of spike- timing-dependent plasticity. Frontiers in Synaptic Neuroscience, 3. Martin, S. J., Grimwood, P. D., & Morris, R. G. M. (2000). Synaptic plasticity and memory: An evaluation of the hypothesis. Annual Review of Neuroscience, 23, 649–711. Martin, S. J., & Morris, R. G. M. (2002). New life in an old idea: The synaptic plasticity and memory hypothesis revisited. Hippocam- pus, 12, 609–636. Mesgarani, N., & Chang, E. F. (2012). Selective cortical representa- tion of attended speaker in multi-talker speech perception. Na- ture, 485, 233–236. Nere, A., Hashmi, A., Cirelli, C., & Tononi, G. (2013). Sleep- dependent synaptic down-scaling (I): Modeling the benefits of sleep on memory consolidation and integration. Frontiers in Neuro- logy, 4(143). Oja, E. (1982). Simplified neuron model as a principal component analyzer. Journal of Mathematical Biology, 15(3), 267–273. Network Neuroscience 633 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Input-dependent formation and organization of memories Palm, G. (1981). Towards a theory of cell assemblies. Biological Cybernetics, 39, 181–194. Palm, G. (1982). Neural assemblies: An alternative approach to artificial intelligence. Springer-Verlag, Berlin. Palm, G., Knoblauch, A., Hauser, F., & Schütz, A. (2014). Cell as- semblies in the cerebral cortex. Biological Cybernetics, 108(5), 559–572. Pehlevan, C., Mohan, S., & Chklovskii, D. B. (2017). Blind nonneg- ative source separation using biological neural networks. Neural Computation, 29, 2925–2954. Redondo, R., & Morris, R. G. M. (2011). Making memories last: The synaptic tagging and capture hypothesis. Nature Reviews Neuro- science, 12, 17–30. Romani, S., Pinkoviezky, I., Rubin, A., & Tsodyks, M. (2013). Scal- ing laws of associative memory retrieval. Neural Computation, 25, 2523–2544. Schmutz, V., Gerstner, W., & Schwalger, T. (2018). Mesoscopic population equations for spiking neural networks with synaptic short-term plasticity. arXiv, 1812.09414. Schwalger, T., Deger, M., & Gerstner, W. (2017). Towards a theory of cortical columns: From spiking neurons to interacting neu- ral populations of finite size. PLoS Computational Biology, 13, e1005507. Shouval, H. Z., Bear, M. F., & Cooper, L. N. (2002). A unified model of NMDA receptor-dependent bidirectional synaptic plas- ticity. Proceedings of the National Academy of Sciences of the United States of America, 99, 10831–10836. Sjöström, P. J., Turrigiano, G. G., & Nelson, S. B. (2001). Rate, tim- ing, and cooperativity jointly determine cortical synaptic plastic- ity. Neuron, 32, 1149–1164. Song, S., Miller, K. D., & Abbott, L. F. (2000). Competitive heb- bian learning through spike-timing-dependent synaptic plasticity. Nature Neuroscience, 3, 919–926. Tetzlaff, C., Dasgupta, S., Kulvicius, T., & Wörgötter, F. (2015). The use of hebbian cell assemblies for nonlinear computation. Scientific Reports, 5, 12866. Tetzlaff, C., Kolodziejski, C., Timme, M., Tsodyks, M., & Wörgötter, F. (2013). Synaptic scaling enables dynamically distinct short- and long-term memory formation. PLoS Computational Biology, 9(10), e1003307. Tetzlaff, C., Kolodziejski, C., Timme, M., & Wörgötter, F. (2011). Synaptic scaling in combination with many generic plasticity mechanisms stabilizes circuit connectivity. Frontiers in Compu- tational Neuroscience, 5, 47. Tetzlaff, C., Kolodziejski, C., Timme, M., & Wörgötter, F. (2012). Analysis of synaptic scaling in combination with hebbian plasticity in several simple networks. Frontiers in Computational Neuroscience, 6, 36. Tse, D., Langston, R., Kakeyama, M., Bethus, I., Spooner, P., Wood, E., . . . Morris, R. (2007). Schemas and memory consolidation. Science, 316. Tse, D., Takeuchi, T., Kakeyama, M., Kajii, Y., Okuno, H., Tohyama, C., . . . Morris, R. (2011). Schema-dependent gene activation and memory encoding in neocortex. Science, 333(891). Tully, P. J., Lindn, H., Hennig, M. H., & Lansner, A. (2016). Spike- based bayesian-hebbian learning of temporal sequences. PLoS Computational Biology, 12, e1004954. Turrigiano, G., Leslie, K., Desai, N., Rutherford, L., & Nelson, S. (1998). Activity-dependent scaling of quantal amplitude in neo- cortical neurons. Nature, 391, 892–896. Turrigiano, G., & Nelson, S. (2004). Homeostatic plasticity in the developing nervours system. Nature Reviews Neuroscience, 5, 97–107. van Rossum, M. C., Bi, G. Q., & Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. Journal of Neuroscience, 20, 8812–8821. van Vreeswijk, C., & Sompolinsky, H. (1998). Chaotic balanced state in a model of cortical circuits. Neural Computation, 10, 1321–1371. Vicente, R., Wibral, M., Lindner, M., & Pipa, G. (2011). Transfer entropy-a model-free measure of effective connectivity for the neurosciences. Journal of Computational Neuroscience, 30, 45–67. Vogels, T. P., Sprekeler, H., Zenke, F., Clopath, C., & Gerstner, W. (2011). Inhibitory plasticity balances excitation and inhibi- tion in sensory pathways and memory networks. Science, 334, 1569–1573. Wickelgren, W. A. (1999). Webs, Cell Assemblies, and chunking in neural nets: Introduction. Canadian Journal of Experimental Psychology, 53(1), 118. Woodin, M. A., Ganguly, K., & Poo, M.-m. (2003). Coincident pre- and postsynaptic activity modifies GABAergic synapses by postsynaptic changes in Cl- transporter activity. Neuron, 39, 807–820. Zenke, F., Agnes, E. J., & Gerstner, W. (2015). Diverse synaptic plas- ticity mechanisms orchestrated to form and retrieve memories in spiking neural networks. Nature Communications, 6, 6922. Zenke, F., Gerstner, W., & Ganguli, S. (2017). The temporal paradox of hebbian learning and homeostatic plasticity. Current Opinion in Neurobiology, 43, 166–176. Zenke, F., Hennequin, G., & Gerstner, W. (2013). Synaptic plastic- ity in neural networks needs homeostasis with a fast rate detector. PLoS Computational Biology, 9, e1003330. Network Neuroscience 634 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 2 6 0 6 1 0 9 2 7 1 2 n e n _ a _ 0 0 0 8 6 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3

PDF Herunterladen