FORSCHUNG
Dynamic properties of simulated brain network
models and empirical resting-state data
Amrit Kashyap1 and Shella Keilholz
1
1Abteilung für Biomedizintechnik, Georgia Tech and Emory University, Atlanta, GA, USA
Schlüsselwörter: Resting-state fMRI, Brain network modeling, Dynamics, Dynamic functional connectivity
ABSTRAKT
Brain network models (BNMs) have become a promising theoretical framework for
simulating signals that are representative of whole-brain activity such as resting-state fMRI.
Jedoch, it has been difficult to compare the complex brain activity obtained from
simulations to empirical data. Previous studies have used simple metrics to characterize
coordination between regions such as functional connectivity. We extend this by applying
various different dynamic analysis tools that are currently used to understand empirical
resting-state fMRI (rs-fMRI) to the simulated data. We show that certain properties correspond
to the structural connectivity input that is shared between the models, and certain dynamic
properties relate more to the mathematical description of the brain network model. Wir
conclude that the dynamic properties that explicitly examine patterns of signal as a function
of time rather than spatial coordination between different brain regions in the rs-fMRI signal
seem to provide the largest contrasts between different BNMs and the unknown empirical
dynamical system. Our results will be useful in constraining and developing more realistic
simulations of whole-brain activity.
ZUSAMMENFASSUNG DES AUTORS
The development of more sophisticated models of the brain will allow us to address some of
the most challenging questions in neuroscience, such as how the physical structure of the
brain can give rise to behavior, Bewusstsein, and memory. Our focus in this manuscript is
on simulating the relatively slow brain signals that coordinate information transfer across
large scales in the brain and that can be measured using fMRI. Previous measures used
averaged measures of functional connectivity in the simulated brain signals to compare with
the empirical signal. In order to extend previous findings, we use dynamic analysis
techniques developed for these fMRI signals to understand more transient events that occur
naturally during normal brain activity. We show that these dynamic properties are better in
differentiating models from each other and from the measured brain activity. These results will
be useful in constraining and developing more realistic simulations of whole-brain activity.
Keine offenen Zugänge
Tagebuch
Zitat: Kashyap, A., & Keilholz, S.
(2019). Dynamic properties of
simulated brain network models and
empirical resting-state data. Netzwerk
Neurowissenschaften, 3(2), 405–426.
https://doi.org/10.1162/netn_a_00070
DOI:
https://doi.org/10.1162/netn_a_00070
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00070
Erhalten: 13 Juni 2018
Akzeptiert: 11 September 2018
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Shella Keilholz
shella.keilholz@bme.gatech.edu
Handling-Editor:
Olaf Sporns
EINFÜHRUNG
Urheberrechte ©: © 2018
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
The complex activity patterns produced by the brain are critical for understanding behavior
and the function of the central nervous system. To explain its complexity, studies have used
resting-state fMRI (rs-fMRI) scans and functional connectivity (FC) analysis to describe the co-
ordination between different brain regions of interest (ROIs) during rest, Aufgabe, and other be-
havioral paradigms (Smith et al., 2009). In den vergangenen Jahren, analysis of FC data has moved beyond
looking at average statistical relationships maintained over the course of a long scan (average
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamic properties of simulated brain network models
Resting-state fMRI (rs-fMRI):
Brain activity measured with fMRI
while participants lie still with their
eyes open and allow their minds to
freely wander. The term “resting
state” is used to highlight the contrast
with task-based fMRI, Wo
participants are actively engaged
in a known, well-defined task.
Funktionale Konnektivität:
The definition of a network based
on coordinated activity between
different regions. There are two types
of functional connectivity: average or
static functional connectivity, welche
is estimated across long scans, Und
dynamic or transient functional
Konnektivität,which is calculated
over short time segments.
Regions of interest:
The cortical sheet is parcellated into
many different nonoverlapping
regions of interest. They cover the
ganzes Gehirn, and each of these
regions corresponds to areas that
are thought to functionally process
similar types of information, das ist,
visual area 1 (V1) and motor area 1
(M1).
Structural connectivity:
The structural network defined by the
white matter tracks between different
cortical areas. This is usually
constructed from diffusion-weighted
MRI and is averaged across many
individuals.
Brain network model:
A network-based model that is used
to simulate spontaneous brain
Aktivität. It is composed of two main
components, the structural network
and the activity of each node based
on its neighbors.
Dynamic analysis techniques:
Different computational algorithms
that are applied to resting-state data
in order to understand transient
features that occur during the scan.
They primarily are used to analyze
network-based coordination that
changes on a moment-to-moment
basis.
FC) to dynamic analysis methods that assume the coordination of brain activity changes on
a moment-to-moment basis (Hutchison et al., 2013; Keilholz, Caballero-Gaudes, Bandettini,
Deco, & Calhoun, 2017; Shakil, Lee, & Keilholz, 2016). The anatomical connections of the
brain are assumed to remain constant on these short timescales so that the time-varying co-
ordinated activity plays out over the same framework of structural connectivity (SC) based on
white matter connections over time (Cabral, Kringelbach, & Deco, 2017; Deco, Kringelbach,
Jirsa, & Ritter, 2017; Shen, Hutchison, Bezgin, Everling, & McIntosh, 2015). The brain’s activ-
ity can be modeled as interactions of ROIs connected by a structural network, where the activity
of eachROI is a function of the local state of processing plus the delayed activity of its network
neighbors (Breakspear, 2017; Sanz-Leon, Knock, Spiegler, & Jirsa, 2015). The resulting set of
differential equations form a dynamical system that can be used as a generative model to sim-
ulate activity across the whole brain for a given state vector of ROI activity. Daher, dynamic FC
can be thought of as the brain’s trajectory across the phase space of the underlying dynamical
System (Cabral et al., 2017; Deco et al., 2013).
Numerical simulations of this network of ROIs, known as the brain network model (BNM)
(Sanz-Leon et al., 2015), simulate spovntaneous neural activity in the absence of external stimuli.
Without explicit external stimuli, as in rs-fMRI, there exists no time-locked measure or event
that would allow for straightforward comparison across modalities. Stattdessen, researchers have
used measures that summarize activity throughout the brain, such as average FC, estimated
through Granger causality or correlation, along with distance metrics or graph theoretic analy-
sis to quantify similarity across modalities (Cabral, Hugues, Spurns, & Deco, 2011; Liang et al.,
2015; Senden, Reuter, van den Heuvel, Goebel, & Deco, 2017). At least 12 different BNMs
have successfully reproduced the most prominent features of average FC (Cabral, Hugues,
Kringelbach, & Deco, 2012; Cabral et al., 2011; Cabral et al., 2017; Hugues, Battaglia, Spiegler,
Deco, & Jirsa, 2015; Sanz-Leon et al., 2015; Senden et al., 2017). Newer studies have tried to
develop more complex BNMs to describe transient features observed in resting state, wie zum Beispiel
spontaneous switching between two FC states during rest in order to more faithfully simulate
natural brain activity (Cabral et al., 2017; Deco et al., 2018; Hansen et al., 2015). Jedoch,
as BNMs have become more sophisticated, dynamic analysis methods for rs-fMRI have also
become more developed, leading to the question of which dynamical properties of rs-fMRI
BNMs can reproduce. Many dynamic analysis methods have been applied to rs-fMRI and pro-
vide complementary views of the brain activity (Hutchison et al., 2013; Keilholz et al., 2017).
The replication of these dynamic features using a generative model would provide new in-
sight on how they might arise and what they could represent. Gleichzeitig, more stringent
constraints based on dynamic rather than average rs-fMRI features would provide better dis-
crimination between different models and between different parameterizations of the same
Modell.
The following study compares the dynamics observed in rs-fMRI to the results of the same
analysis methods applied to two BNMs (Figur 1). We simulate two different types of BNMs
with delayed inputs, the Kuramoto oscillator model and the Firing Rate model, and then ap-
ply four of the most common dynamic analysis techniques to compare features found in the
simulated data with those found in rs-fMRI scans (Cabral et al., 2012; Cabral et al., 2011). Wir
chose the Kuramoto and the Firing Rate models because they have been shown to be robust,
have relatively few parameters to optimize, and exhibit different dynamical properties that we
expect to lead to differences in analysis output (Cabral et al., 2017; Deco, Jirsa, & McIntosh,
2010). Darüber hinaus, the Firing Rate model is more simplistic in the dynamics it can reproduce, Und
we expect it to serve as a contrast to the more complex Kuramoto model (Cabral et al., 2017).
To characterize the models and compare them with empirical data, we chose four analysis
Netzwerkneurowissenschaften
406
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamic properties of simulated brain network models
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
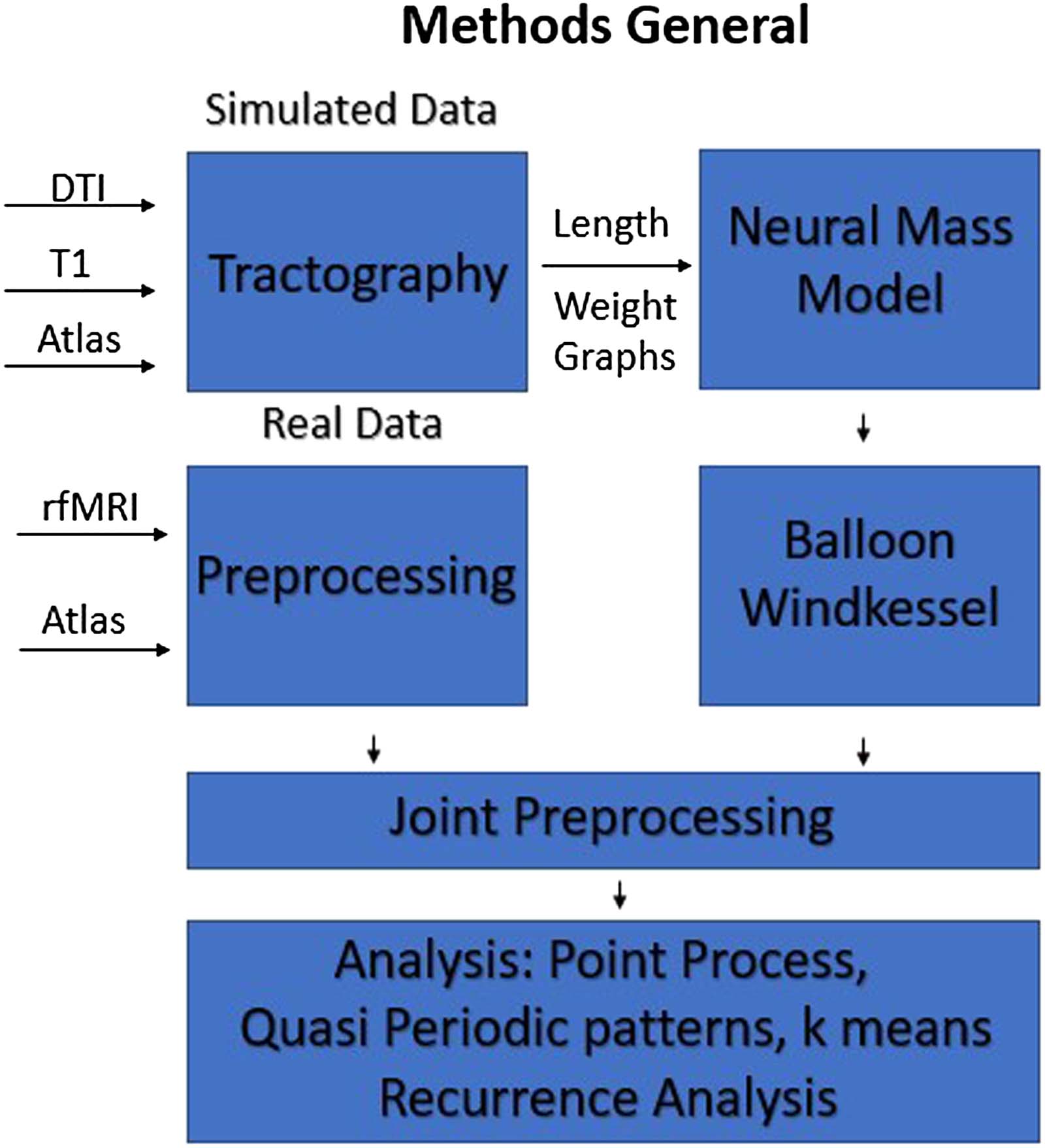
Figur 1. General workflow. We used DTI data to generate the length and weight matrix between
ROIs of our specified atlas. Using this structural connectome, we generate data using the different
neural mass models and transformed into the BOLD signal via the Balloon-Windkessel model. To
compare with empirical fMRI data, scans from HCP were preprocessed and parcellated using the
same atlas. The final preprocessing of filtering, globale Signalregression, and normalization was done
jointly for all sets of data. The final data were then analyzed with each of the different dynamic
analysis techniques.
techniques that test the signal for states, repeating events, or trajectories that are representa-
tive of its higher order spatiotemporal structure. We chose these techniques in order to span
the spectrum of analyzing the signal by the patterns in the spatial domain and patterns in the
temporal domain. Zusätzlich, we simulated models at different parameter settings in order to
understand how dynamics evolve as a function of the parameter. We used this to evaluate how
well the analysis techniques compared with average FC in guiding model selection.
Dynamic Analysis Techniques
1. Point process or neural avalanche theory, which models the fMRI signal as a combina-
tion of discrete neural events or avalanches. An event in an ROI is observed when the
signal crosses a threshold, and then quantifies coactivation of these events between differ-
ent ROIs (Caballero et al., 2010; Liu & Duyn, 2013; Natalia, Gaudes, Dryden, Francis,
& Gowland, 2012; Tagliazucchi, Balenzuela, Fraiman, & Chialvo, 2012).
Netzwerkneurowissenschaften
407
Dynamic properties of simulated brain network models
2. Repeated or quasiperiodic spatiotemporal patterns (QPP), which identifies a unique
spatiotemporal pattern that is particularly prominent in the default mode network
(DMN) and the task positive network (TPN). This pattern is extracted by iteratively using a
spatiotemporal template of fixed length to correlate with the signal, finding the peaks
in the correlation vector, and then averaging all the highest peaks to determine the
next template (Belloy et al., 2018; Majeed et al., 2011; Majeed, Magnuson, & Keilholz,
2009; Thompson, Pan, Magnuson, Jaeger, & Keilholz, 2014; Yousefi, Schienbein, Schumacher,
& Keilholz, 2018).
3. K-means clustering on windowed functional connectivity, which identifies discrete pe-
riods in time when the spatial patterns of correlated brain activity are relatively stable.
Sliding window functional connectivity matrices are clustered using k-means in order to
identify the clusters in dynamic functional connectivity (Allen et al., 2014).
4. Recurrence quantification analysis (RQA), which identifies repeated spatial signatures
as a function of time (Webber & Marwan, 2015). In this method, the spatial pattern at
each time point is correlated with the spatial pattern at all other time points, und das
results are then quantified using information theory for repeated time signatures.
Brain Network Models (Neural Mass Models)
1. Kuramoto model: A model where the trajectory of each neural mass is modeled as an
oscillator and the phases of each oscillator are synchronized based on network input
and perturbed by random noise.
2. Firing Rate model: Each neural mass is modeled by a single parameter that represents
the aggregate firing rate of the population, and it decays with a certain time constant and
increases its activity based on network input and random noise.
All BNMs are simulated on the same structural network but are different from each other
on how they describe the evolution as a system of differential equations. Darüber hinaus, since both
models have been shown to reproduce average functional connectivity, we hypothesize that the
BNMs will show convergence on properties that relate more to their structural connectivity and
divergence on properties that describe more their transient dynamical nature. This comparison
also allows us to identify which elements of the BNMs explain particular dynamic processes
observed in rs-fMRI, providing insight into the potential neurophysiological sources of types
of dynamics. The results will identify metrics that enable the development of more realistic
models as well as provide guidance toward the underpinnings of relevant signatures in rs-fMRI
Daten.
ERGEBNISSE
Comparisons to Average Functional Connectivity
We first demonstrate that the simulated models reproduce common metrics in brain network
modeling: average FC and power spectrum (Figur 2). The ordering of the ROIs seen in the fig-
ure is shown in Supplementary Table 1 (see Kashyap & Keilholz, 2019) and is from Cabral et al.
(2011). The BNMs were simulated using the same structural connectivity as an input, ran-
domly initialized and numerically integrated to evolve the state space according to each
specific model. To approximate the BOLD signal, they are then passed through the Balloon-
Windkessel model that converts neural signal to its hemodynamical response (see Methods).
The methodology and parameter values are similar to those described in Cabral et al. (2011)
and Cabral et al. (2012), and comparable reproduction of results are shown in Supplementary
Figur 1 (Kashyap & Keilholz, 2019). We also simulated at very high and low global coupling
Netzwerkneurowissenschaften
408
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamic properties of simulated brain network models
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
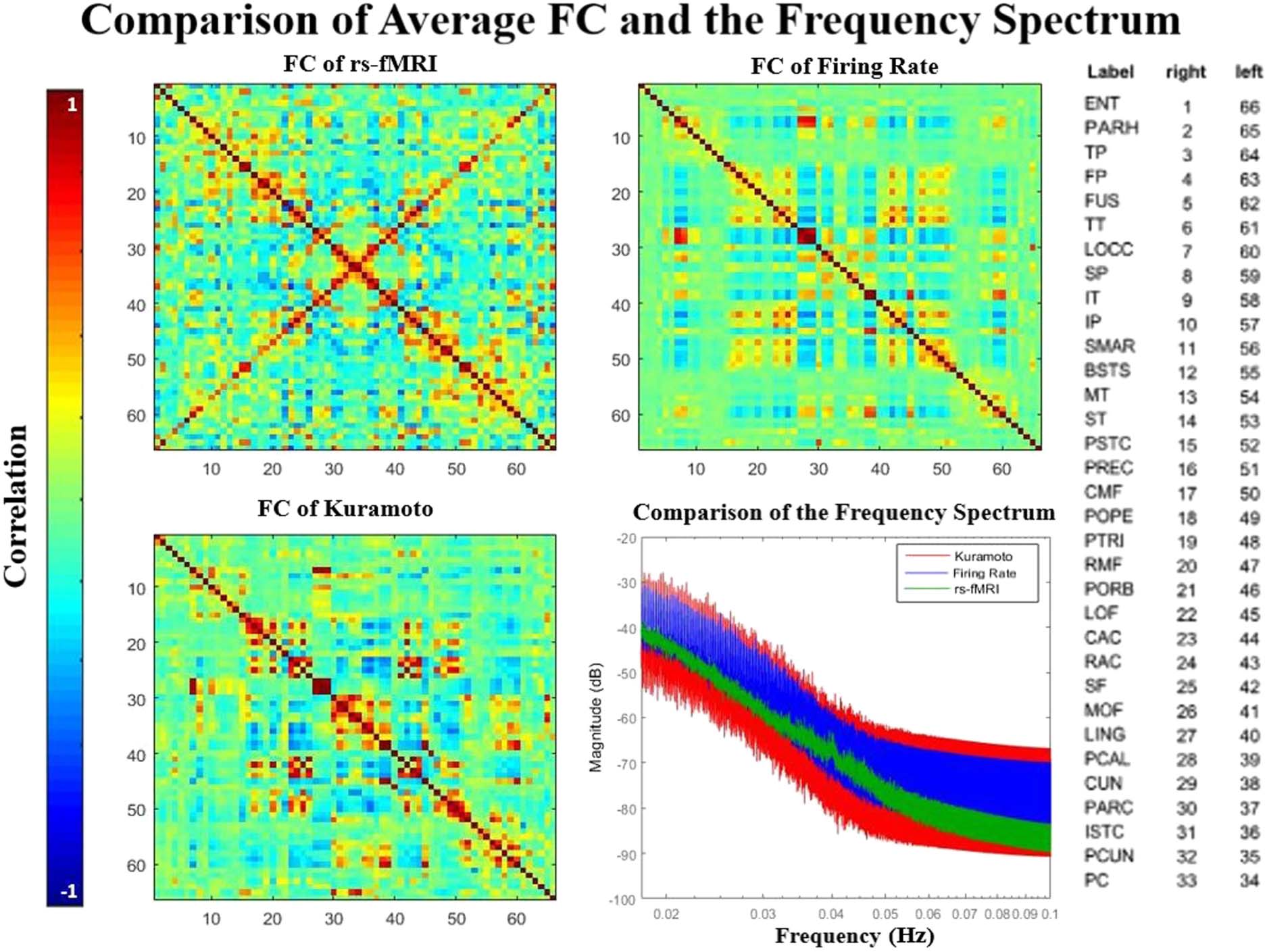
Figur 2. Comparison of the average functional connectivity between the rs-fMRI signals and the two simulated models.Correlation between
the matrix for empirical data and the Firing Rate simulation is 0.5; correlation between empirical and Kuramoto matrices is 0.37. Both modeled
matrices and the empirical data exhibit similar structure such as the coordination between hemispheres, which can be seen in the symmetry of
the matrix. The mean frequency spectrum of all ROIs is plotted (bottom right) and shows that the real signal falls within range of both models.
All power spectra exhibit a ( 1
F )n trend.
levels to study the effect of parameterization on the other metrics. To quantify the similarity
between the simulated FC matrices and the empirical FC matrix, we calculated the corre-
lation between the two, a method that is extensively used in previous studies (Cabral et al.,
2011; Cabral et al., 2017; Senden et al., 2017). Correlation was 0.37 between Kuramoto and
rs-fMRI FC matrices, Und 0.5 between Firing Rate and rs-fMRI FC matrices. These are in the
range of values reported in earlier literature in other BNMs [0.3, 0.7] (Cabral et al., 2011;
Senden et al., 2017). Wie erwartet, these correlation values are higher values than at very high
and low global coupling levels (Supplementary Figure 2, Kashyap & Keilholz, 2019). Power
spectra were calculated for each ROI independently, then averaged (Figur 2, bottom right).
When plotted on a log-log plot, the BOLD signal has a characteristic ( 1
F )n distribution. Der
power exponent has been reported in literature as 0.88, comparable to the 0.9 measured here
for empirical unfiltered rs-fMRI (Bullmore et al., 2000). The empirical slope falls well within
the distribution of the simulated power spectrums. The two simulated models had a slope
von 0.74 (Kuramoto) Und 0.7 (Firing Rate) before preprocessing, comparable to a previous re-
port of 0.78 using a different BNMs but not as good as the current best of 0.91 (Ritter, 2017;
Ritter, Schirner, McIntosh, & Jirsa, 2013).
Netzwerkneurowissenschaften
409
Dynamic properties of simulated brain network models
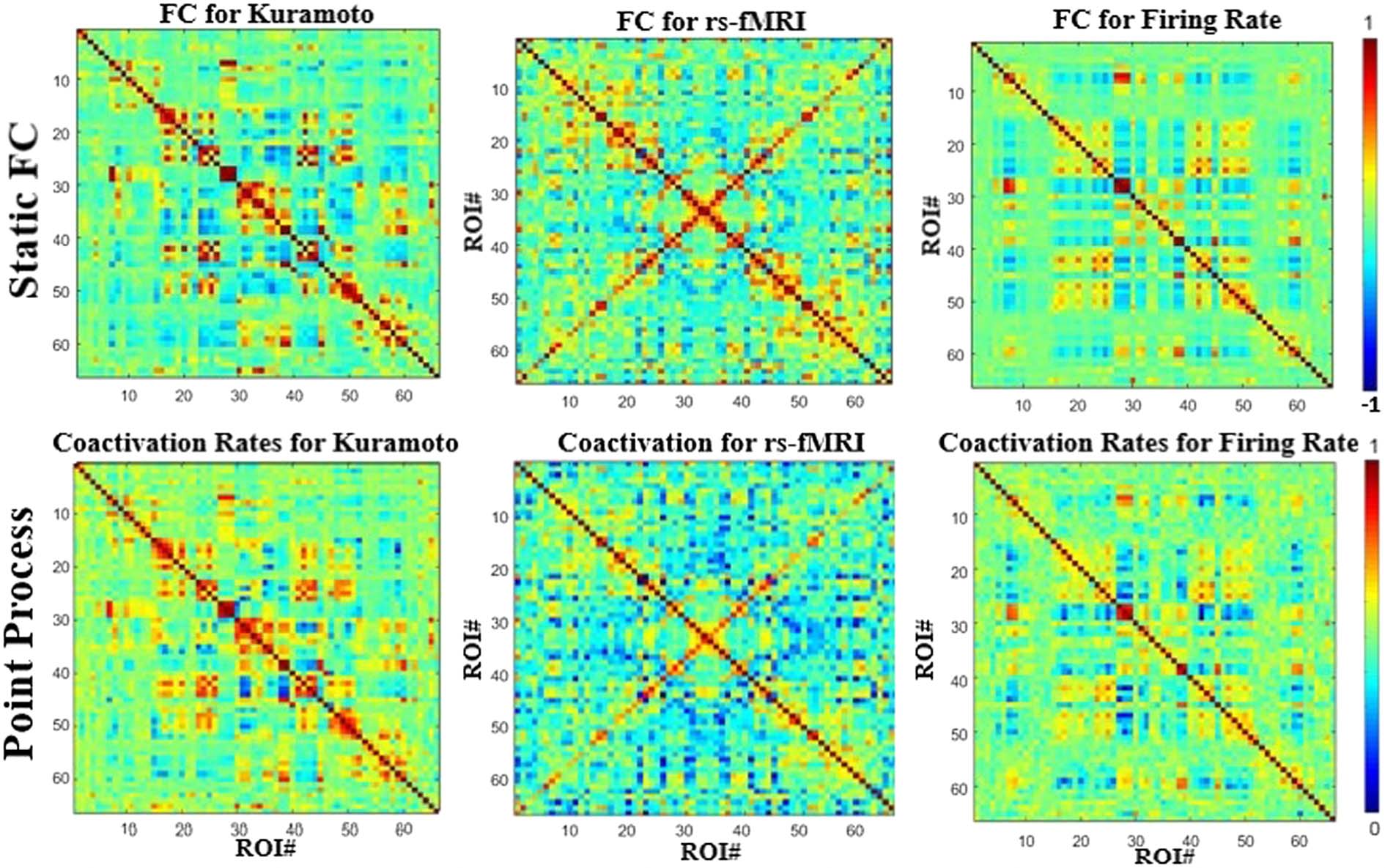
Point Process/Neural Avalanche
In coactivation analysis based on the point process approach, all ROIs that cross a certain
activation threshold (see Methods; Tagliazucchi et al., 2012) are examined at each time point
to identify coactivation patterns. The bottom row of Figure 3 shows the coactivation data ob-
tained for the Kuramoto simulation, the Firing Rate simulation, and empirical rs-fMRI data.
Each value in the matrix represents the fraction of co-occurrences between two ROIs. Der
matrices are compared with the respective average FC matrices (Figur 3, top row), and all
three signals show a high degree of correlation (>0.9) between the two different analysis
Techniken. This is because average FC can be calculated by a handful of events, wie gezeigt
by Tagliazucchi et al. (2012). Darüber hinaus, from Supplementary Figure 2 (Kashyap & Keilholz,
2019), point process/coactivation rates seem to behave identically at different parameter set-
tings, further suggesting they are measuring similar structure in the data. The Firing Rate coac-
tivation rates are again closer to the coactivation rates of the empirical data than the Kuramoto
Modell, which is similar to the results observed with the average FC anaylsis.
Quasiperiodic Pattern Algorithm Comparison
The quasiperiodic pattern (QPP) finding algorithm estimates a recurring spatiotemporal pattern
that occurs throughout resting and task states. It consists of a characteristic pattern dominated
by the activation and inhibition of the regions that correspond to the default mode network
(DMN) and task positive network (TPN) in a specific temporal sequence (Majeed et al., 2011;
Majeed et al., 2009; Yousefi et al., 2018). The QPP templates obtained from the real data and
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3. Coactivation rates (point process) between the different modalities compared with those from static or average functional con-
nectivity. The resulting maps are almost identical between different modalities and have a correlation of over 0.9 between each respective
dataset.
Netzwerkneurowissenschaften
410
Dynamic properties of simulated brain network models
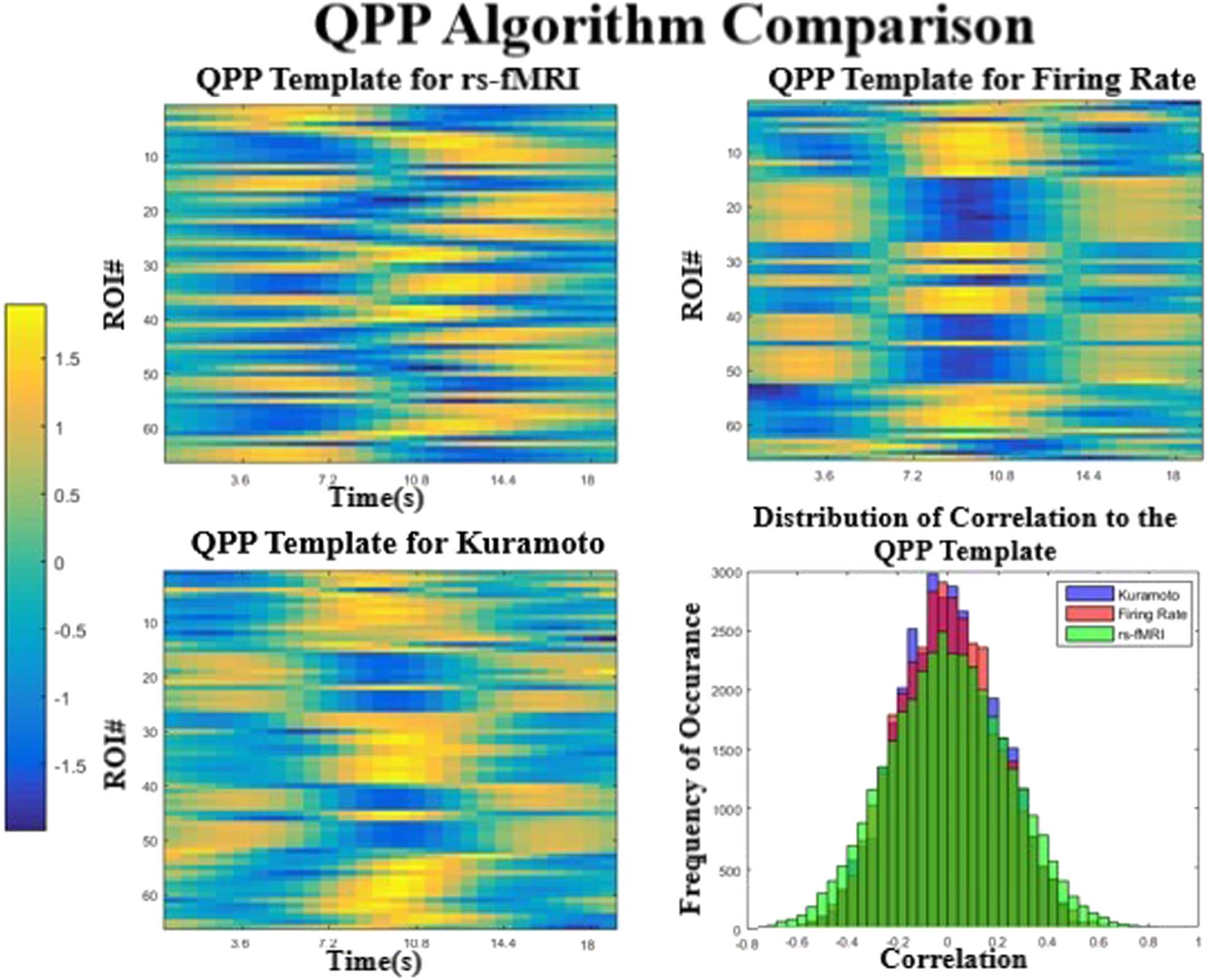
from each simulation are shown in Figure 4 in a simplified format, where the color bar shows
the level of activation or deactivation in each ROI as a function of time. For better visualization,
please see the supplementary videos (Kashyap & Keilholz, 2019) that show the pattern as it
evolves over a surface representation of the brain. The pattern in the rs-fMRI data is consistent
with the QPP templates obtained previously (Majeed et al., 2011; Yousefi et al., 2018).
The QPP templates from the two models are very similar to each other (Figur 4 top right
and bottom left, correlation of 0.81), but have important differences from the empirical QPP
(Figur 4, top left, correlation of 0.34, 0.33). Tatsächlich, the pattern in the simulated models seems
to indicate a simple flip between two states, where a subset of ROIs is first active and then in-
active. The boxy nature of the plot is due to the spatial ordering of the ROIs that was originally
defined by their subnetwork connectivity, suggesting that these subcomponents are activating
and deactivating together. The QPP obtained from the real data is more complex and demon-
strates time lags between areas in addition to the alternation of states, suggesting that the power
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
N
e
N
_
A
_
0
0
0
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4. Comparison of the QPPs obtained for each model and the real data. The two simulated models (top right and bottom left) produce
templates that are similar to each other but less similar to the template extracted from rs-fMRI. The correlation values to the template are
plotted in a histogram (bottom right), which shows that the real signal has more extreme values than either model. All three are significantly
different from each other (P < 0.0001) in a Komogorov-Smirnov test.
Network Neuroscience
411
Dynamic properties of simulated brain network models
in the BOLD signal cyclically flows through a certain order of ROIs. The relative lengths of
the simulated and the observed patterns are different as well. The QPP from the real data is
approximately 20 s in length, in agreement with previous reports (Majeed et al., 2011; Yousefi
et al., 2018). In contrast, both of the models give QPPs that are ∼12–13 s in length, despite
the use of identical windows and the similar frequency content of the signals.
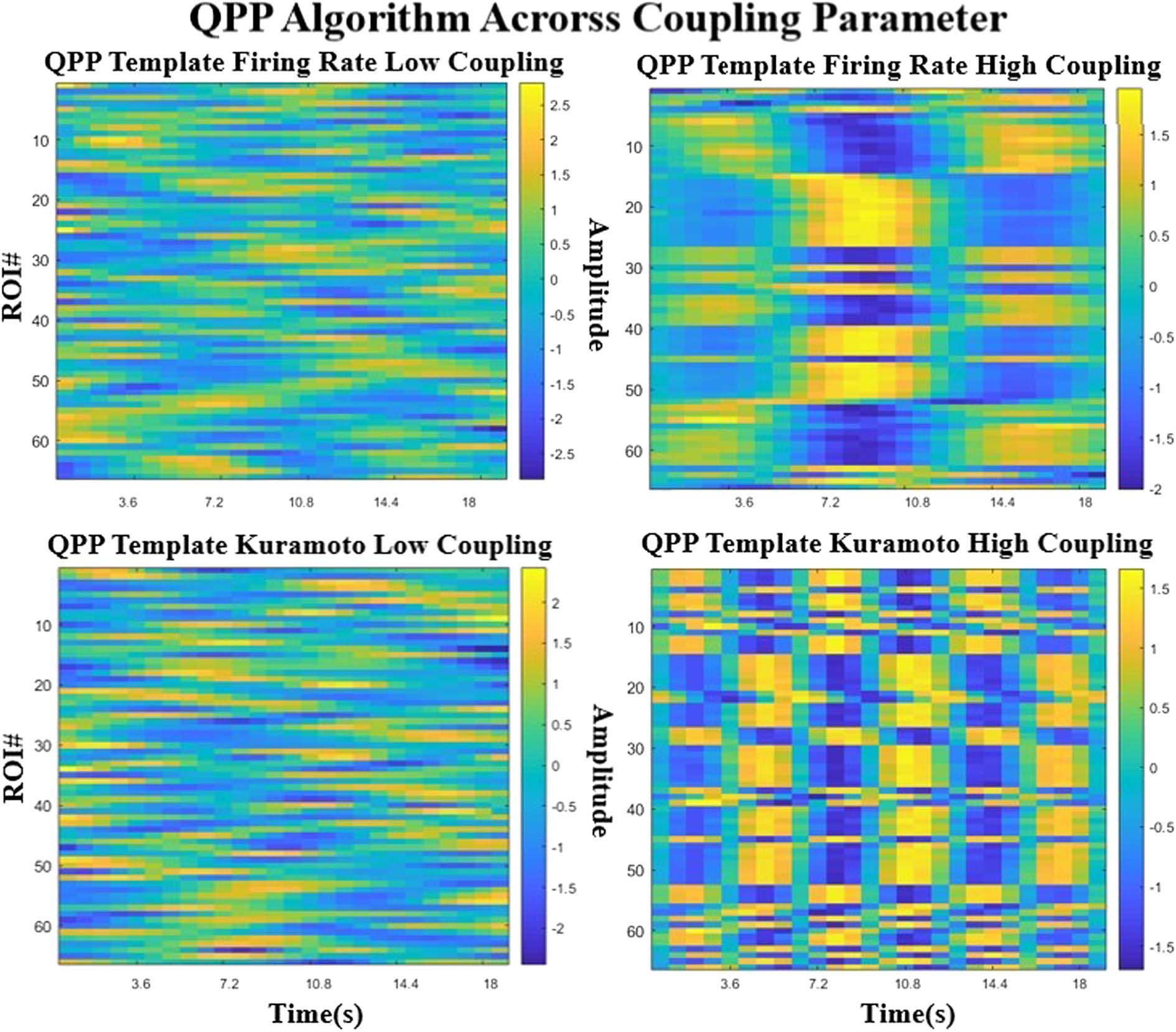
At low and high global coupling (Figure 5), the QPP pattern transitions from an unstructured
noise-like template to a structured signal. The number of repeated patterns for a given window
seems to depend on the strength of the coupling parameter for the Kuramoto model, where at
higher coupling the pattern seems to shorten and repeat more often. For the Firing Model, the
template pattern emerges from unstructured noise after a certain coupling strength.
The correlation vector represents how correlated the QPP template is with the scan at every
time point. The distribution of the values are displayed using histograms (Figure 4, bottom
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Comparison of the QPPs obtained for each model across different coupling strengths. The left column represents low global
coupling and the right column, higher global coupling. The top row is the Firing Rate model and the bottom row is the Kuramoto model. As
coupling strength seems to increase, the pattern goes from a random unstructured signal to a highly boxlike structure.
Network Neuroscience
412
Dynamic properties of simulated brain network models
right), in order to compare different modalities. The flatter distribution of the resting-state fMRI
shows that the template occurs more often significantly and at higher correlations in the real
scan than either of the templates.
K-Means on Sliding Windowed Matrices
To identify FC states that occur at different time points in the BOLD signal, we used k-means
analysis to compare the sliding windowed FC of the real and simulated data. After k-means
clustering (k = 7), we examined both the spatial composition of the resulting clusters (or states)
and metrics that describe how the brain transitions between them (Allen et al., 2014). We
have also explored cluster numbers k = 8 and 9; these are shown in Supplementary Figure 3
(Kashyap & Keilholz, 2019). The results are similar across all metrics and all models. This is
due to the number of actual clusters seen per individual simulation (Supplementary Figure 3,
right column; Kashyap & Keilholz, 2019), which is constant across cluster numbers, suggesting
that the methodology is measuring the intrinsic dynamic structure seen within the data, rather
than arbitrarily dividing up the segments.
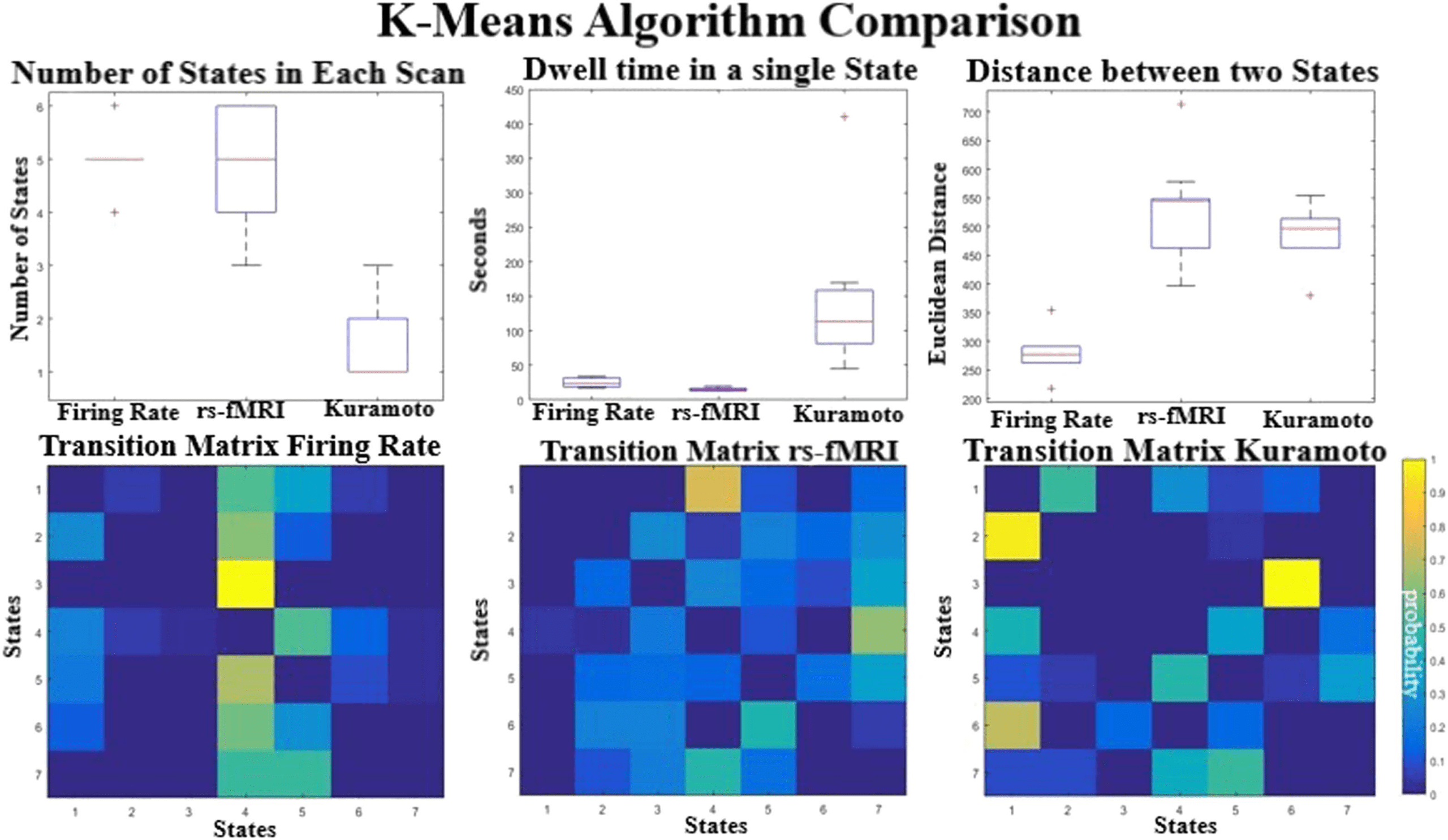
The top row in Figure 6 quantifies for each individual scan or simulation, starting at different
initial conditions (N = 30), how many of unique states are visited, how long they dwell in each
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. The top row shows the average number of states seen in an individual run (top left), the average dwell time in each state (top
middle), and the mean distances between the centroids (top right).The transition matrices between the different k-means centroids are shown
on the bottom row. The values reflect the number of raw occurrences divided by the total number of transitions giving the probability of
transitioning from one state to another. Self-transitions are set to 0.
Network Neuroscience
413
Dynamic properties of simulated brain network models
state, and how far apart (L2 Norm distance between cluster centers) these visited states are on
average. The Firing Rate and the rs-fMRI each have an average of five states per individual
scan and transition at similar rates, but the average distance between centroids is almost twice
as large in the rs-fMRI states compared with the simulated data. Visually the Firing Rate cen-
troids look very similar (Supplementary Figure 4, Kashyap & Keilholz, 2019), suggesting that
the diversity of states encountered is still very low. The Kuramoto model produces states with
similar distances between centroids as empirical data, but each instantiation seems to have
fewer states compared with rs-fMRI. Most runs (66%) result in only a single state, but under
certain initial conditions the Kuramoto model can exhibit transitions between two to three dif-
ferent states. The model also seems to dwell in these states longer than in the rs-fMRI and Firing
Rate. The transition matrix for the empirical data shows that transitions are more evenly dis-
tributed between states than in the simulated data (Figure 6, bottom row). The empirical rs-fMRI
data have more transitions between states than in either simulated model. The Kuramoto and
the Firing Rate are roughly around the same complexity seen in the transition matrices but far
less than seen in the empirical signal. We quantified this by measuring the sparsity fraction
by counting the number of transitions and dividing by the total number of possible transitions
(Firing Rate has 0.55 transitions, Kuramoto has 0.52, and rs-fMRI has 0.86).
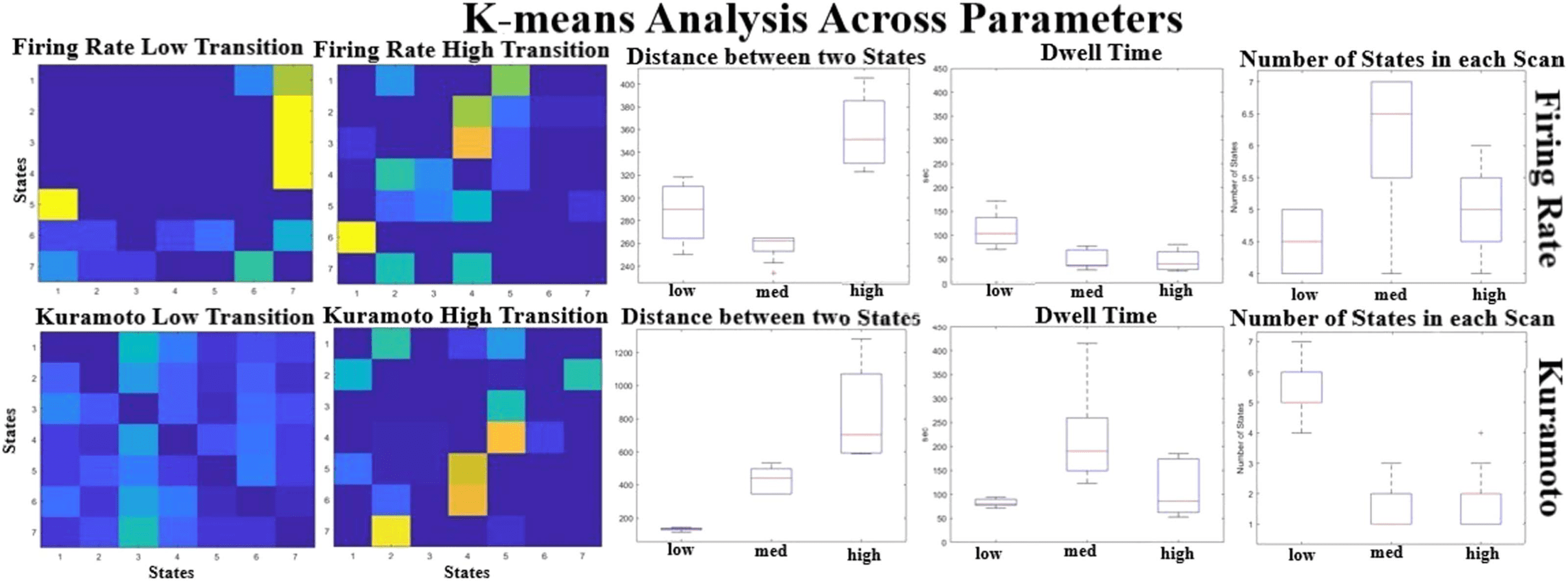
Varying the coupling strength also affected the state dynamics seen in the models. Figure 7
shows that the distance between the states increases as a function of coupling strength, espe-
cially for the Kuramoto model, suggesting that stable dynamical states seem to be moving apart
from each other. The other parameters seem to have a nonlinear relationship with the coupling
parameters as the dynamics of the system changes. None of the models have the complexity
seen in rs-fMRI in terms of number of distinct states and large distances between their centers,
but the one that seems the closest to the real signal is the Kuramoto model at medium coupling
levels. Even though the BNMs seem to produce some state transition properties, these BNMs
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. K-means analysis across parameters. The transition matrices for the Firing Rate (top) and the Kuramoto (bottom) are given at different
coupling parameters. The distance between cluster centers (middle) seems to be increasing as a function of coupling strength, suggesting that
the states are diverging and are having more state-like dynamics for higher coupling strengths. The number of states seems relatively the same
even at higher coupling strengths, suggesting that the models are limited to how much variety they can produce.
Network Neuroscience
414
Dynamic properties of simulated brain network models
clearly have much simpler dynamics as compared with the rs-fMRI even when varying the
parameters.
Recurrence Quantification Analysis (RQA)
Figure 8 shows the reccurance plots for the empirical and simulated BOLD signal. These plots
are calculated by correlating the pattern of activity at each time point with the pattern from
every other time point. Diagonal lines that are parallel to the main diagonal represent repeating
transistions that are seen throughout the scan, whereas vertical or horizontal blocks represent
dwell periods during the scan. A cursory inspection of the three recurrence plots (Figure 8,
top row) shows that the two models have far less repeating structure than seen in rs-fMRI. This
relation is quantified by the bottom three plots that show the recurrence rate (left), entropy of
diagonal lines (middle), and average length of diagonal lines (right). The reccurence rate seems
to be much higher in the Kuramoto and empirical signal than in the Firing Rate model. How-
ever, the entropy and length of the lines (related to how different the states are and how long
they linger) clearly separate the three datasets (bottom and right). Entropy and line length are
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
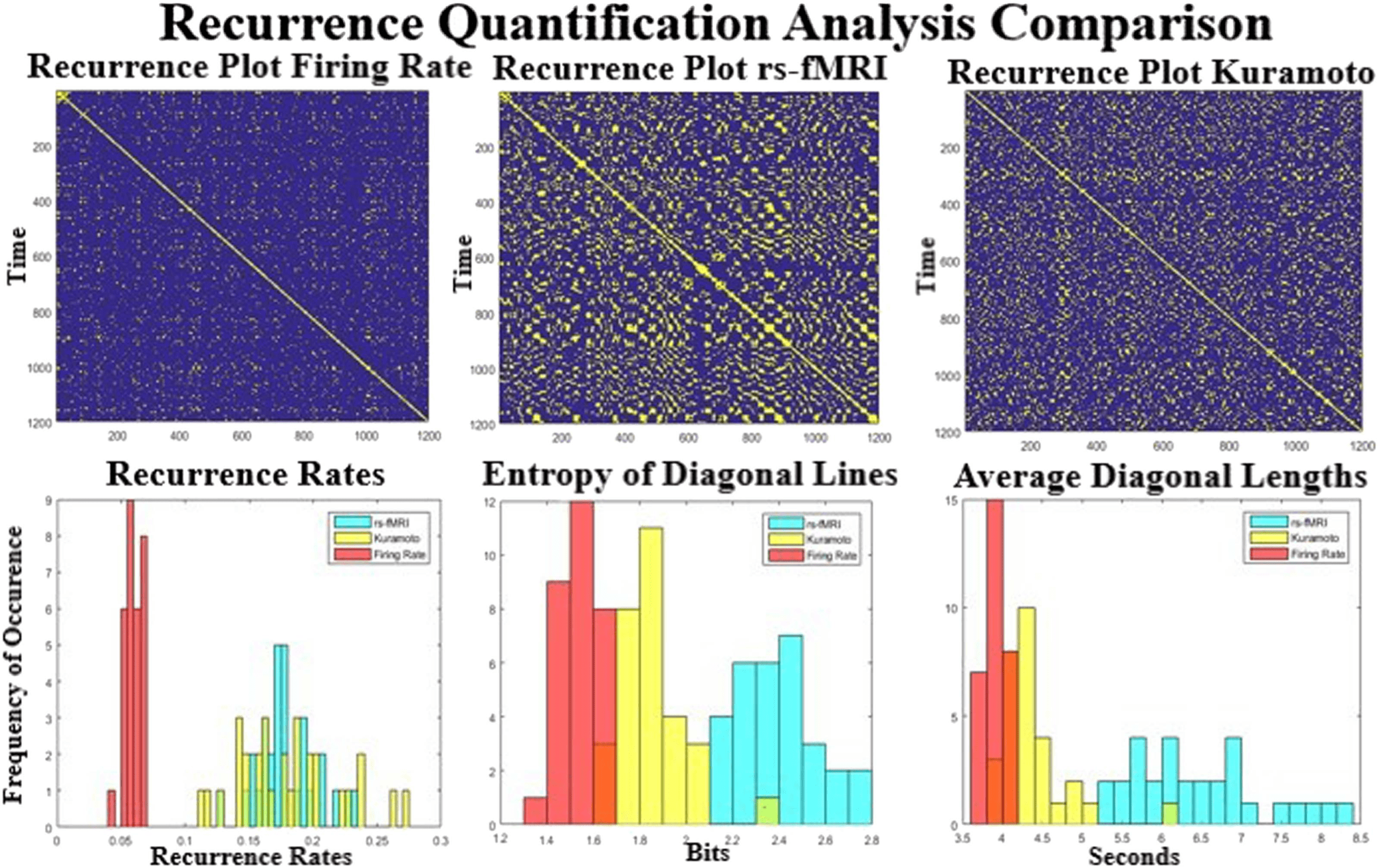
Figure 8. Comparison of the recurrent quantification analysis (RQA) between the simulated and real datasets. The top row shows three scans
of recurrent plots thresholded at 0.3 for the three datasets. The bottom row shows the distribution of three different RQA techniques over all
scans. The bottom left shows the recurrence rate, which is much higher for the Kuramoto and rs-fMRI model than for the Firing Rate simulation.
The recurrence rate is a measure of repeated states seen in the dynamics of the rs-fMRI signal. The middle and the right plots quantify how
much similar trajectories occur during the scan. The measured rs-fMRI signal shows much more variance between different trajectories and is
of much longer duration.
Network Neuroscience
415
Dynamic properties of simulated brain network models
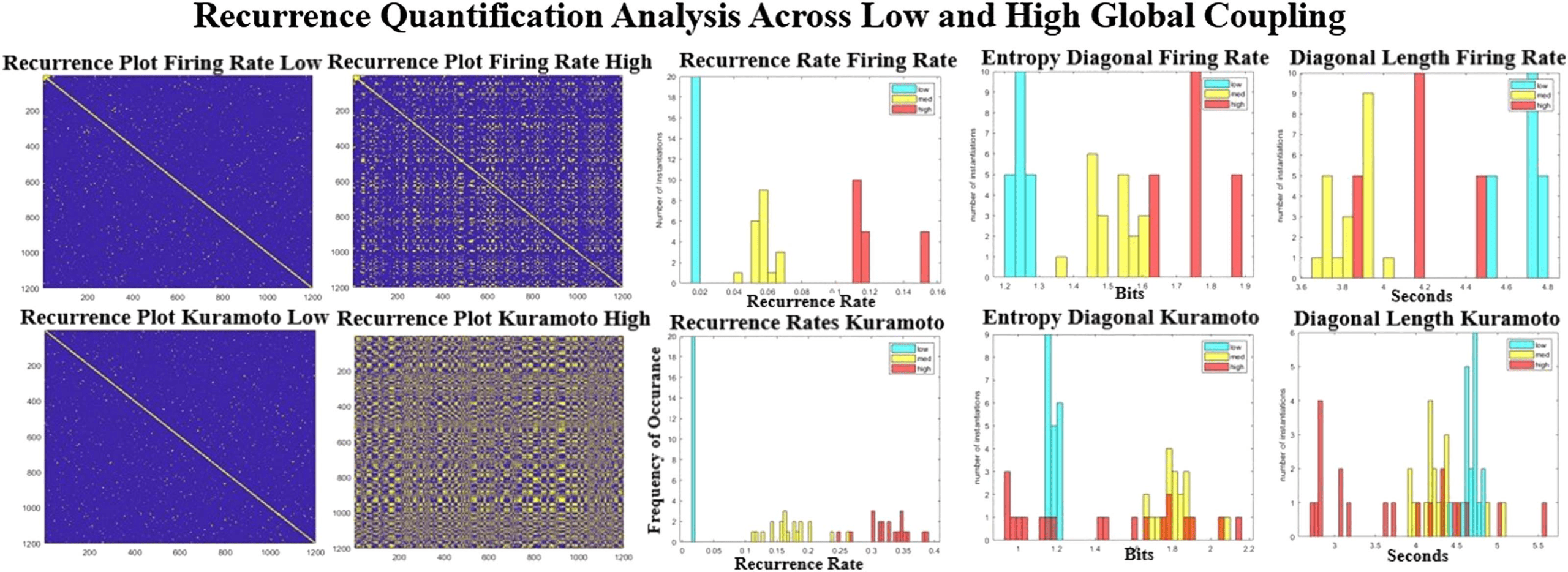
Figure 9. Recurrence quantification analysis across different parameters. Left are the recurrence plots at high and low global coupling for
Kuramoto (bottom row) and Firing Rate (top row). The recurrence rate that quantifies the number of events increases monotonically (center
column) as a function of coupling strength. The entropy and the lengths of the diagonal lines seem to have a nonlinear relationship. Neither
of the right two metrics are as high, as seen in the resting dataset (Figure 8).
highest in the real data and lowest in the Firing Rate simulation, with the Kuramoto simulation
residing in between. The low entropy values for the Firing Rate data signify that the model does
not have as many repeated trajectories as compared with the other modalitites.
Changing the global parameters has some very linear effects, as can be seen in Figure 9. At
low coupling parameters the reccurence plot shows almost no structure, and at high coupling
more and more structure emerges. The reccurence rate that is most related to the number of
events seen in reccurance plots is almost linear (Figure 6B, middle column) for both models.
At higher levels of coupling there seems to be a larger spread in the models (entropy rate,
Figure 9, right from middle column), as they seem to be more a function of initial condition
than at low levels of coupling. The entropy levels and the average diagonal length seem to
be much higher in rest than all of the models, suggesting longer, slower repeated trajectories
in the real signal. Overall the technique is able to separate the emprical data and the models
pretty robustly and shows a clear difference between the more simpler Firing Rate model and
the more complex Kuramoto model, and at least one of the measures seems to vary linearly
with the parameter selection.
DISCUSSION
Average Functional Connectivity and Power Spectra
From previous studies using multiple models and parameterizations, it appears that certain
properties of the simulated signal are most reliant upon the underlying structural connectivity
rather than the model of activity used at each node (Bullmore & Sporns, 2009; Stam et al.,
2016). In our study, these properties should be similar across models (which share identical
structural connectivity) and in the real data. Average functional connectivity analysis is one
of these properties. The structural connectivity matrices derived from diffusion tensor imaging
and the respective functional connectivity estimates derived from resting-state fMRI have a
correlation value of 0.45 as measured through our methodology, which is similar to what has
Network Neuroscience
416
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
been described before (Bullmore & Sporns, 2009). In fact, all three dynamical systems produce
signals where functional connectivity is highly correlated with the structural input, leading to
suggest that average functional connectivity is closely related to the underlying connectome.
There are known differences between SC and FC; for example, an edge in FC between two
nodes can be the result of a third process that drives the two structurally disconnected regions.
However, most of the edges between the ROIs can be described as a function of how many
white matter tracks run between them (Stam et al., 2016). Moreover, the frequency spectrum
and the characteristic ( 1
f )n distribution are similar for both BNMs and the empirical rs-fMRI,
suggesting that the spectrum is a property of the underlying structure of the network. The Firing
Rate model reproduces the average FC better than the Kuramoto model, which might be due
to overfitting since it has fewer parameters to optimize compared with the Kuramoto model.
This matches well with previous reported literature where the Firing Rate model has produced
FC matrices that have a large correlation (corr. = 0.8) by tweaking the input SC to maximize
similarity to the output FC (Senden et al., 2017).
Coactivation Patterns/Point Process
The coactivation analysis also showed a shared feature across the empirical and simulated
data. For all three datasets, coactivation patterns were strongly correlated with average func-
tional connectivity. This is likely because functional connectivity is driven by processes that
activate certain subnetworks of the SC together (Smith et al., 2009). This further strengthens
the notion that SC and average FC are closely related. The global coupling parameter affects
the coactivation rates in a similar way as for average FC, where low levels of coupling result in
a very uncoordinated system, and high levels result in global networks that are highly active.
Since the model parameters were chosen to fit average FC best, and it is easier to fit the Fir-
ing Rate model, it once again reproduces measures that are more faithful to empirical rs-fMRI
compared with the Kuramoto model, probably for the same reason that it can better match the
average FC of the empirical data. Regardless of the coupling parameters used, the coactivation
patterns are similar to the average FC for both models.
QPPs
The successful detection of quasiperiodic patterns in both BNMs indicates that these network
models capture at least some of the dynamical features of the brain’s activity. Unlike the pre-
vious sections of spatial metrics where the naïve Firing Rate model performed better than the
Kuramoto model, the QPP templates for the two models are indistinguishable. On the other
hand, there are substantial differences compared with the real QPP. The real QPP is more com-
plex, with gradual switching at different time lags in different areas. The real QPP template is
also longer in length than the ones from the BNMs, as the simulated model starts repeating itself
before the end of the template. The length of the spatiotemporal pattern seems to be a function
of the coupling parameter, especially in the Kuramoto model, where increased coupling leads
to faster repetitions of the patterns. The overall spatial shape of the pattern (i.e., the areas in-
volved in activation and deactivation) are quite similar across models and parameterizations,
though none are as complex as the patterns in empirical data. We believe the incorporation
of aspects of neural field models and Connectome Harmonics (Atasoy, Donnelly, & Pearson,
2016; Sanz-Leon et al., 2015) into the existing BNMs may result in a more accurate repro-
duction of the spatial propagation because it would take into account surface propagation
was well as network propagation. It could also be possible that the difference in QPP tem-
plates results from the unidirectionality of certain white matter connections or other properties
that cannot be captured using standard tractography.
Network Neuroscience
417
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
K-Means Analysis
Some dynamic properties appear to arise more from the complex interactions linked to the
unique temporal description of activity in each ROI than from the underlying structural con-
nectivity. These properties are likely to be different for each BNM, and from previous literature,
the Kuramoto model has outperformed the Firing Rate model (Cabral et al., 2017). The k-means
algorithm on the windowed FC matrices revealed a complex network of states in the rs-fMRI
data that each demonstrated distinct spatial patterns of connectivity between ROIs along with
a complex web of transitions between them. In the Firing Rate model there are a similar num-
ber of states compared with rs-fMRI, but the distances between the states are much smaller
compared with rs-fMRI, suggesting that it is more appropriate to consider the Firing Rate states
as representing a single state artificially divided into multiple components. The state descrip-
tion in the Firing Rate model echoes previous findings because it is known that stable attractor
states cannot be produced with only a linear set of differential equations (Cabral et al., 2017).
The Kuramoto model at very low levels of coupling has similarly many states that are close
together. But at higher values the Kuramoto model, for some initial conditions, can produce
transitions between states that are as spatially distinct as the rs-fMRI but limited to fewer states
and a simpler transition matrix than the empirical signal. This suggests that BNMs can repro-
duce at least some of the dynamic states observed in rs-fMRI, although current models do
not recapitulate the rich variety observed in empirical data. The Kuramoto model under cer-
tain parameters does better than the Firing Rate model and can produce complex state-like
behavior.
Recurrence Analysis
Recurrence analysis quantifies elements in the temporal structure of the data similar to cluster-
ing analysis on short FC matrices. Therefore, we predicted it to depend more on the dynamic
description of the data rather than the shared spatial connectivity input. The Firing Rate model
again exhibited the least complexity, the rs-fMRI data exhibited the most, and the Kuramoto
model fell in between the two for the normal parameters. The empirical data have repeated
trajectories that occur more often and are longer than either observed in the simulated BNMs.
Out of the dynamic analysis metrics that were examined, the RQA metrics separated the three
datasets the most effectively, whereas the average functional connectivity analysis exhibited the
fewest differences. Moreover, the recurrence rate that quantifies the number of repeated tem-
poral events seems to linearly depend on the coupling parameters for a certain range. This
relationship is similar to average FC, which at low levels of coupling shows no structure and at
higher levels of coupling shows increased network structure (Supplementary Figure 2, Kashyap
& Keilholz, 2019). Average FC and recurrence analysis both use correlation, except that one
uses the space across rows that spans the ROIs, whereas the other uses the space of the columns
that represent single time points in the BOLD data. Average FC, which examines coordination
between ROIs, reveals a static network related to the input SC. Recurrence analysis that exam-
ines the time domain reveals properties that seem to be most unique to the formulation of each
BNM. Recurrence analysis also is quick to compute and therefore could be a good addition to
average FC as a metric for model selection, which is a very computationally intensive process.
Together they can ensure that the model has roughly similar network component structure
compared with rs-fMRI based on average FC, and similar temporal structure recurrence rates.
Overall Discussion
The goal of our exploratory study was to find better dynamic metrics to compare empirical
rs-fMRI and the brain network models. We have chosen two different BNMs at three different
Network Neuroscience
418
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
parameterizations to provide an axis of contrast between the simpler Firing Rate model and
the more complex Kuramoto model, which has been shown to reproduce more complex dy-
namic trajectories (Cabral et al., 2017). The dynamic analysis techniques can be ordered in
how much they analyze the structure in the spatiotemporal BOLD signal as a function of spa-
tial coordination between regions or repeated temporal trajectories. The ordering in Table 1 is
not strict, but loosely goes from techniques that observe spatial patterns to those that observe
temporal patterns. These two components seem to correspond to the two main components in
the formulation of BNM: the structural network that provides input from connected ROIs and
a description of the evolution of the state variables.
The Firing Rate model outperforms the Kuramoto model on metrics that are more closely
linked with spatial patterns, whereas the Kuramoto performs better on metrics that are linked
with the temporal structure observed in rs-fMRI. We believe that the performance on spatial
metrics, such as average FC and point process, is due to the Firing Rate model being easier to
fit to the rs-fMRI because of its fewer parameters. Moreover, since average FC and the SC are
similar, it is probably an easier task to match the FC output that is very closely related to the SC
input. The temporal metrics reveal that the Kuramoto model has much richer dynamics than
the Firing Rate model and is closer in reproducing features seen in rs-fMRI. Moreover, these
differences are more likely due to the differences in the differential equation formulation of
the BNM since it defines the network evolution. The BNMs seemed to perform also similarly
between the QPP and the point process metric, suggesting that it might be an invariant property
of all BNMs.
Limitations
Our modeling approach makes many simplifying assumptions that do not capture the true
complexity of the brain. In the construction of the structural connectome, we assumed that
all connections were bidirectional. This is a limitation of using tractography to build the struc-
tural network, since tractography cannot distinguish unidirectional connections. Moreover,
estimates of fiber density for connections between regions that have very sharp angles or be-
tween regions that are spatially far apart are far lower than the true connectivity between these
regions (Bullmore & Sporns, 2009). In our generative models we also assumed a homogeneity
in the response of ROIs, in both their neural description, as well as their transformation us-
ing the hemodynamic Balloon-Windkessel model. Moreover, we did not simulate subcortical
structures that are known to play a crucial role in the operation of the central nervous system.
All these factors might change the association between dynamic metrics and the simulated
BNM signal.
Table 1. Comparison between models across different analysis techniques.
Analysis technique
Static FC
Firing rate
Better
Kuramoto
Worse
Point process
Better
Worse
QPP
Tied
Tied
K-means
Worse
Better
RQA
Worse
Better
Metric
Correlation between average FC of rs-fMRI
and models (Figure 2)
Correlation between point process matrices of
rs-fMRI and models (Figure 3)
Correlation between the shape of extracted
spatiotemporal signal between rs-fMRI and
models and their rate of occurrence (Figure 4)
Number of distinct states and diversity of state
transitions (Figure 6)
Average number of repeated temporal transitions
and the entropy of those transitions (Figure 8)
Network Neuroscience
419
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
We also examined only a single parameterization for only two BNMs. There are a variety of
BNMs, some of which are likely to exhibit more complex dynamics than either the Kuramoto
or the Firing Rate model (Sanz-Leon et al., 2015). Even different parameterizations of a sin-
gle model can give rise to vastly different behavior (Hansen et al., 2015). We chose to focus
on the Kuramoto and Firing Rate models because of their relative simplicity, their thorough
characterization, and the expectation that they would have dissimilar dynamic properties.
There are also numerous dynamic analysis methods available for rs-fMRI (Keilholz et al.,
2017). We chose to focus on a few of the most common ones, but future work should certainly
examine the use of other types of analysis to produce even more sensitive metrics. Moreover,
our study does not look at methods to test these metrics and use the established correlation
as distance function. We have also not explored the entire space of parameterization, so it
is possible that these models can produce more realistic signals; however, based on previous
results establishing these as close to optimum, the results are probably a realistic representation
of their capabilities.
Conclusion
We believe that either of the two more-temporal metrics, namely RQA or k-means, would be
the most appropriate in evaluating BNMs in the future. The k-means approach is a stronger
criterion to evaluate on, because the cluster centers as well as the state transitions between
the model and the empirical signal would have to match in order to reproduce resting-state
dynamics. However, the RQA approach is less computationally intensive and can used to
quickly check the diversity in the temporal structure of the simulation and to assist the selection
of parameters in the model. The QPP algorithm would be useful in evaluating properties of
the network structure, as it seems to be common between the BNM. It probably would be
more useful to evaluate models that incorporate more biophysical plausibility such as neural
field models and connectome harmonics. The average FC and the point process do not reveal
processes that are much more complex than the SC input, but they useful in the way they are
currently used to sweep the parameters and bias the system.
From the dynamic analysis perspective, the most distinguishable metric in rs-fMRI seems
to be predicting the temporal structure of the signal. We already know how the different ROIs
are connected as a network, but it is still a mystery how the signal evolves. BNM provides
a mathematical framework for exactly how this signal might evolve, so it is appropriate to
evaluate them by characterizing their temporal dynamics.
METHODS
Structural Connectome
Using Human Connectome Project’s diffusion-weighted images (spin echo TR 5520 ms, TE
89.5 ms, flip angle 78, voxel 1.25 mm) from five random subjects (Van Essen et al., 2013), we
generated one average structural connectome. Tractography was performed using the freely
available software MRtrix with maximum fiber length set to 250 mm (Tournier, Calamante,
& Connelly, 2012) and parcellated using the Desikan-Killiany atlas (Desikan et al., 2006). For
each subject, their respective T1w images (TR 2,400 ms, TE 2.14, voxel size 0.7 mm) were
aligned to the standard space; then the using the warping matrix we transformed the diffusion-
weighted images. Probabilistic tractography then was run between each ROI and then pruned
to generate 10 million fibers. To generate the estimates for the length and weight matrices
from the tractography, we used the same methodology as Hagmann et al. (2008). The length
between two ROIs was defined as the average fiber length of all fibers that went between them,
Network Neuroscience
420
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
and the weight was the number of fibers going between two ROIs normalized by the surface
area of the receiving ROI. The atlas provides 84 cortical and subcortical ROIs, but we selected
the same 66 cortical regions as in Cabral et al. (2011) for comparison to previous work. The
resulting matrices are shown in Supplementary Figure 5 (Kashyap & Keilholz, 2019). There are
a few important differences between our tractography, the one from Hagmann et al. (2008),
and the ideal tractography. Our current tractography, due to longer fiber lengths, has more
interhemispheric connections than the one presented in Hagmann et al. (2008). However,
tractography is less sensitive to longer connections (Fornito, Zalesky, & Breakspear, 2013) and
therefore the between-hemispheric connections were scaled by a factor of 4 to offset the known
issue. Tractography is also less sensitive to fibers with sharp angles than to fibers with more
straight angles, so for example it results in less connections between the two primary visual
areas (ROIs 27–29) that have the sharpest bend in the corpus callosum (Fornito et al., 2013).
The final weight matrix was normalized using the matrix norm function to be unit norm. The
length matrix was divided by the mean conduction velocity 5.45 m/s to get the delay matrix.
This set the mean delay to 11 ms in accordance with Cabral et al. (2011).
Brain network models describe the BOLD signal as the coupling of n distinct neural
BNMs.
populations corresponding to different cortical regions. Each population is connected via a
weight matrix obtained from structural connectivity that describes the strength of the connec-
tion between nodes. In general each of these n areas are modeled by a differential equation for
each node: dn(t)
dt = f (N(t), W, L), where N(t) is the time series of all the nodes/ROIs, W is the
weight matrix, L is the length matrix, and for given random initial conditions for n0, the time
series n(t) can be solved for by using the Euler integration method (Sanz-Leon et al., 2015).
The time series n(t) is the state variable and is representative of a measurable property of the
neural mass such as firing rate. Some variants use more than one variable to represent the state
of the neural mass, but in this paper we consider two models that only use one state variable,
namely the Firing Rate and the Kuramoto models. Table 2 shows the mathematical description
as well as the values of the parameters used in the simulations.
The Kuramoto model is derived from an assumption that each neural population is in a
closed periodic trajectory in phase space that represents its computational processing (Cabral
et al., 2011). It has been shown that it can then be modeled by a phasic oscillator that can be
described by a single parameter, theta, that represents its location within a 2pi cycle. Inputs
into these phasic oscillators perturb its trajectory, but it stays within its limit cycle. Each of these
oscillators couples via the network and is driven to the same angle and thus synchronizes the
oscillators as a function of the difference between the angles of neighboring oscillators.
The Firing Rate model assumes that the mean firing rate of the neural populations is dis-
tributed in a Gaussian manner. This assertion is in accordance with the central limit theorem,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Parameter
name
Firing Rate
Kuramoto
Differential equations that
were simulated via Euler
method with a time step
of 0.1 ms
τ0
dt = −rn(t)
drn
N
∑
+ k
c1
p=1
+σn(t)
Cnprp(t − τnp)
dθn
dt = ωn + k
N
∑
p=1
−θn(t)) + σn(t)
cnp sin(θp(t − τnp)
Table 2. Parameters
State variables
r(t) – mean
firing rate
θ(t) – oscillator
phase
Cnp –
structural
network
weight
K = 0.9
(scale of
Cnp)
K = 13
(scale of
Cnp)
Tnp –
structural
network
delays
11 ms set
for mean
σn –
SD of
Gaussian
white noise
ωn –
oscillator
frequency
c1 –
first eigenvalue
of weight
matrix
τ0 –
relaxation
constant
2 rad/s
N/A
calculated
20 ms
11 ms set
for mean
2 rad/s
Randomly
initialized as
N ∼ (60 Hz,
2 Hz)
N/A
N/A
Network Neuroscience
421
Dynamic properties of simulated brain network models
which states that the sum of uncorrelated random processes converges to a Gaussian proba-
bility distribution, even if the individual processes are highly non-Gaussian. Inputs into this
neural mass shift the mean firing rate to a higher firing rate. The mass shifted from its equilib-
rium tries to relax at the rate proportional to its own firing rate, keeping the system stable via
negative feedback.
For each model, the differential equations were numerically integrated with a time step
function of 0.1 ms for a duration of 15 min to match the length of an HCP rs-fMRI scan. The
first 20 s are thrown away to avoid transient effects from initial conditions. The choices for
the values for all the parameters given in Table 2 follow previous work by Cabral et al. (2012)
and Cabral et al. (2011), except that the values for k are slightly different than the ones in the
paper to account for differences in the structural connectivity matrix. The values were slightly
smaller for the Kuramoto (13 instead of 18) because there were more numerous connections in
the newer tractography. The low coupling models were simulated for the Firing Rate at k = 0.3.
The Kuramoto model had a low coupling of 3. The high coupling models were simulated at
k = 60 for Kuramoto and k = 0.999 for Firing Rate. We simulated 30 individual runs at param-
eterization values from previous studies, and 20 runs each at high and low global coupling
levels. Simulations of functional connectivity and the intermediate steps with the original
Hagmann matrices and the comparisons with Cabral et al. (2011) are given in Supplementary
Figure 1 (Kashyap & Keilholz, 2019).
In order to compare the neural simulated data with the hemodynamic
Converting to BOLD.
response measured from fMRI, we have to convert the high-frequency activity down to the
low-frequency hemodynamic response. This is performed with the Balloon-Windkessel model,
which is a quadruple differential equation model that in a neuronal input and calculates the
blood flow and blood volume and uses that to estimate the fraction of the oxygenated blood
to the deoxygenated blood (Friston, Harrison, & Penny, 2003; Stephan, Weiskopf, Drysdale,
Robinson, & Friston, 2007). Supplementary Figure 6 (Kashyap & Keilholz, 2019) shows the im-
pulse response of the Balloon-Windkessel model, which looks roughly like the canonical hemo-
dynamic response function. We used the same constants for our Balloon model as those given
in Friston et al. (2003). After passing the output of the BNMs through the Balloon-Windkessel
model, it was then downsampled to the same sampling rate as the rs-fMRI data (0.72 s).
For the rs-fMRI data we used 30 individual HCP scans (gradient echo
Pre-processing rs-fMRI.
EPI, TR 720 ms, TE 33.1 ms, flip angle 52, voxel 2 mm) that are each roughly 15 min long. The
data came from the minimally processed pipeline and then were ICA denoised using the 300
ICA vectors that HCP provides. We then applied the same Desikan-Killiany atlas as used in the
tractography onto the data and obtained the mean time series for each ROI. From then on, the
same processing pipeline was applied for the simulated data and the real data, in order to keep
the processing as similar as possible. These steps in order were z-scoring each time series, then
band passing filtering the signal from 0.01 to 0.25 Hz, then global signal regression using a
linear regression model, and then applying a final z-score step. These steps were selected in
accordance with Cabral et al. (2011).
Dynamic Analysis Techniques
To compare the dynamics of the rs-fMRI signal and the BNMs, we selected analysis techniques
that are commonly used and characterized the signal at different spatial and temporal scales.
Table 3 shows a quick comparison of the different techniques that were applied.
Network Neuroscience
422
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
The point process assumes that activity in an area triggers neural avalanches in regions
that are involved in the information processing (Tagliazucchi et al., 2012). The signal is only
interpretable at either its high levels of activation or very low levels of activation when it is coor-
dinating information transfer with other elements in the network. Later models explicitly write
out the mathematical formulation using impulse response and solve for a sparse representa-
tion of these coactivation patterns, which are thought to be unique computational trajectories
across the brain (Karahano˘glu & Van De Ville, 2015; Liu & Duyn, 2013). But in this analysis,
we use Tagliazucchi’s methodology by quantifying when different ROIs cross the same thresh-
old over time. We implemented this approach by recording when the activity at a certain ROI
crosses a certain threshold and then counting how many other ROIs cross the same threshold
within three time steps (0.72 s) of the original crossing. We normalize the co-occurrence rates
to get a fraction by dividing by the total number of crossings at each ROI. We applied this
analysis with two different thresholds, one at the mean of the signal and one at 1 standard
deviation away, which for our normalized signals were at 0 and 1, respectively. Prior work
that has shown that average functional connectivity is primarily driven by coactivation events
(Tagliazucchi et al., 2012).
A second approach examines the quasiperiodic patterns of BOLD signal propagation over
the course of the scan. The QPP algorithm identifies the most prominent repeating spatiotem-
poral pattern in the signal (Majeed et al., 2011; Majeed et al., 2009). In brief, the algorithm
chooses a random chunk of the rs-fMRI data (20 s of data) and correlates it with the entire scan
(Majeed et al., 2011). Time points with high correlation to the random chunk indicate repeated
occurrences and are averaged together to form the new template. This process is iterated until
the template converges. Since we use a random seed point as the original template, repeated
runs of the algorithm produce QPPs with different phases. Therefore, in order to compare the
patterns from the rs-fMRI and the simulated models, the QPP was circularly shifted to the point
where maximum correlation occurred.
Sliding window correlation followed by k-means clustering was applied to examine the
brain states and transitions in each set of data (Allen et al., 2014). Using a sliding window
length of 60 × 0.72 s, the Pearson correlation was calculated pairwise for all ROIs. The window
was then advanced by one time point and the process was repeated until the window reached
the end of the scan. This value is around the range used in previous work (Allen et al., 2014).
Table 3. Dynamic analysis techniques
Analysis technique
Point process/
neural avalanche
Quasiperiodic
pattern
Recurrent
quantification analysis
K-means clustering
of FC matrices
Description
FC is driven by discrete
events in rs-fMRI when
different ROIs coactivate
together
A specific spatiotemporal
pattern observed in rs-fMRI
that repeats itself over the
length of the scan
A sequence of similar ROI
activity and/or trajectories
that appear to repeat over time
Multiple stable FC states that
transition between each other
State variable
Level of activity
of a single ROI
Spatial scale
Very similar to average
FC and the SC input
Temporal scale
Coordination is seen in the
shortest scales (∼ 1 s)
Phase during the
spatiotemporal pattern
template
Specific nodes go
through a sequence of
activation and inactivation
Pattern (20 s) Occur
(2/3 per min)
Level of activity across
the whole network at a
single point in time
Windowed FC matrices
at ∼ 45 s
Repeating firing patterns
over time
Local networks embedded
in the larger SC that
coordinate processing for
a stable period of time
Medium (∼ 10 − 20 s)
Longest (45 s–1 min)
Network Neuroscience
423
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
Correlation values were Fisher-transformed to better approximate a normal distribution and
the k-means algorithm was applied to cluster the data into seven groups using Manhattan
distance based on previous studies (Allen et al., 2014). Clustering was repeated 30 times, and
the best resulting clustering was chosen based on minimizing the total distance from the cluster
centroids and the feature vectors in order to mitigate the effects of randomly choosing the
centroid locations.
Recurrent analysis was performed by calculating correlation of the spatial pattern of activ-
ity pairwise across all time points. We then thresholded the values at 0.3, based on literature
search, and created recurrent plots (Bassett, Nelson, Mueller, Camchong, & Lim, 2012; Cabral
et al., 2014). These metrics were calculated using freely available MATLAB toolbox (Ouyang,
Li, Dang, & Richards, 2008), and their distribution for each type of data was plotted. Recur-
rence rate, entropy rate, and average diagonal length were measured. The recurrence rate is the
rate that similar states occur throughout the scan, as seen in Equation 1. Entropy rate quanti-
fies the difference between repeated states, as seen in Equation 2. The average diagonal length,
Equation 3, measures how long these trajectories occur. Collectively they give us an insight
into how often similar states occur, how different they are from each other, and how long each
of these spatiotemporal trajectories persists.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
RR =
1
N2
∑N
i,j=1 R(i, j), where R is the recurrent plot.
L =
∑N
l=lmin lP(l)
∑N
l=lmin P(l)
, where P(I) is the frequency of diagonal length I.
ENTROPY = − ∑N
l=lmin P(l) ln(P(l)), where P(l) is the frequency of diagonal length l.
(1)
(2)
(3)
ACKNOWLEDGMENTS
We would like to thank the help of Dr. Constantine Dovrolis, who provided invaluable help
and insight with developing and debugging our initial brain network models. We would also
like to thank members of the Keilholz Lab, specifically Behnaz Yousefi and Anzar Abbas, who
provided their expertise in the quasiperiodic patterns algorithm, and Dr. Jacob Billings, who
helped set up all the servers and the data from the Human Connectome Project that were used
in this manuscript.
AUTHOR CONTRIBUTIONS
Amrit Kashyap: Conceptualization; Data curation; Formal analysis; Funding acquisition; Inves-
tigation; Methodology; Project administration; Resources; Software; Validation; Visualization;
Writing – original draft; Writing – review & editing. Shella Keilholz: Conceptualization; Data
curation; Formal analysis; Funding acquisition; Investigation; Methodology; Project adminis-
tration; Resources; Supervision; Validation; Visualization; Writing – original draft; Writing –
review & editing.
FUNDING INFORMATION
Shella Keilholz, Georgia Institute of Technology (http://dx.doi.org/10.13039/100006778), Award
ID: GT FIRE. Amrit Kashyap, National Institutes of Health (http://dx.doi.org/10.13039/100000002),
Award ID: TL1 TR000456-11. Shella Keilholz, National Institutes of Health (http://dx.doi.org/
10.13039/100000002), Award ID: R01MH111416.
Network Neuroscience
424
Dynamic properties of simulated brain network models
REFERENCES
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele,
T., & Calhoun, V. D. (2014). Tracking whole-brain connectivity
dynamics in the resting state. Cerebral Cortex, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352
Atasoy, S., Donnelly, I., & Pearson, J. (2016). Human brain networks
function in connectome-specific harmonic waves. Nature Commu-
nications, 7(21), 10340. https://doi.org/10.1038/ncomms10340
Bassett, D. S., Nelson, B. G., Mueller, B. A., Camchong, J., &
Lim, K. O. (2012). Altered resting state complexity in schizo-
phrenia. NeuroImage, 59(3), 2196–2207. https://doi.org/10.1016/
j.neuroimage.2011.10.002
Belloy, M. E., Naeyaert, M., Abbas, A., Shah, D., Vanreusel, V.,
van Audekerke, J., . . . Verhoye, M. (2018). Dynamic resting state
fMRI analysis in mice reveals a set of Quasi-Periodic Patterns
and illustrates their relationship with the global signal. Neuro-
Image, 180(Pt. B), 463–484. https://doi.org/10.1016/j.neuroimage.
2018.01.075
Breakspear, M. (2017). Dynamic models of large-scale brain activ-
ity. Nature Neuroscience, 20(23), 340. https://doi.org/10.1038/
nn.4497
Bullmore, E., Long, C., Suckling, J., Fadili, J., Calvert, G., Zelaya,
F., . . . Brammer, M. (2000). Colored noise and computational
inference in neurophysiological (fMRI) time series analysis: Re-
sampling methods in time and wavelet domains. Human Brain
Mapping, 12(2), 61–78.
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10, 186. https://doi.org/10.1038/nrn2575
Caballero, G. C., Petridou, N., Dryden, I. L., Bai, L., Francis, S. T.,
& Gowland, P. A. (2010). Detection and characterization of
single-trial fMRI BOLD responses: Paradigm free mapping. Hu-
man Brain Mapping, 32(9), 1400–1418. https://doi.org/10.1002/
hbm.21116
Cabral, J., Hugues, E., Kringelbach, M. L., & Deco, G. (2012). Mod-
eling the outcome of structural disconnection on resting-state
functional connectivity. NeuroImage, 62(3), 1342–1353. https://
doi.org/10.1016/j.neuroimage.2012.06.007
Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of local
network oscillations in resting-state functional connectivity. Neuro-
Image, 57(1),130–139. https://doi.org/10.1016/j.neuroimage.2011.
04.010
Cabral, J., Kringelbach, M. L., & Deco, G. (2014). Exploring the
network dynamics underlying brain activity during rest. Progress
inNeurobiology, 114, 102–131. https://doi.org/10.1016/j.pneurobio.
2013.12.005
Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional
connectivity dynamically evolves on multiple time-scales over
a static structural connectome: Models and mechanisms. Neuro-
Image, 160, 84–96. https://doi.org/10.1016/j.neuroimage.2017.
03.045
Deco, G., Cabral, J., Saenger, V. M., Boly, M., Tagliazucchi, E.,
Laufs, H., . . . Kringelbach, M. L. (2018). Perturbation of whole-
brain dynamics in silico reveals mechanistic differences between
brain states. NeuroImage, 169, 46–56. https://doi.org/10.1016/
j.neuroimage.2017.12.009
Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017). The
dynamics of resting fluctuations in the brain: Metastability and
its dynamical cortical core. Scientific Reports, 7(1), 3095. https://
doi.org/10.1038/s41598-017-03073-5
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2010). Emerging con-
cepts for the dynamical organization of resting-state activity in
the brain. Nature Reviews Neuroscience, 12, 43. https://doi.org/
10.1038/nrn2961
Deco, G., Ponce-Alvarez, A., Mantini, D., Romani, G. L., Hagmann,
P., & Corbetta, M. (2013). Resting-state functional connectivity
emerges from structurally and dynamically shaped slow linear
fluctuations. Journal of Neuroscience, 33(27), 11239. https://doi.
org/10.1523/JNEUROSCI.1091-13.2013
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., . . . Killiany, R. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021
Fornito, A., Zalesky, A., & Breakspear, M. (2013). Graph analysis of
the human connectome: Promise, progress, and pitfalls. Neuro-
Image, 80, 426–444. https://doi.org/10.1016/j.neuroimage.2013.
04.087
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302. https://doi.org/10.
1016/S1053-8119(03)00202-7
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://doi.
org/10.1371/journal.pbio.0060159
Hansen, E. C. A., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switch-
ing behavior of the resting state. NeuroImage, 105, 525–535.
https://doi.org/10.1016/j.neuroimage.2014.11.001
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013). Dynamic
functional connectivity: Promise,
issues, and interpretations.
NeuroImage, 80, 360–378. https://doi.org/10.1016/j.neuroimage.
2013.05.079
Karahano˘glu, F. I., & Van De Ville, D. (2015). Transient brain activ-
ity disentangles fMRI resting-state dynamics in terms of spatially
and temporally overlapping networks. Nature Communications,
6, 7751. https://doi.org/10.1038/ncomms8751
Kashyap, A., & Keilholz, S. (2019). Supporting information for
“Dynamic properties of simulated brain network models and
resting-state data.” Network Neuroscience, 3(2),
empirical
405–426. https://doi.org/10.1162/netn_a_00070
Keilholz, S., Caballero-Gaudes, C., Bandettini, P., Deco, G., &
Calhoun, V. (2017). Time-resolved resting-state functional mag-
netic resonance imaging analysis: Current status, challenges, and
new directions. Brain Connectivity, 7(8), 465–481. https://doi.
org/10.1089/brain.2017.0543
Network Neuroscience
425
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamic properties of simulated brain network models
Liang, L., Deng, B., Wang, J., Wang, R., Wei, X., Yu, H., . . .
Yang, C. (2015). Granger causality analysis in the neural mass
model. 2015 34th Chinese Control Conference (CCC), 28AD,
4641–4645. https://doi.org/10.1109/ChiCC.2015.7260356
Liu, X., & Duyn, J. H. (2013). Time-varying functional network
information extracted from brief instances of spontaneous brain
activity. Proceedings of
the National Academy of Sciences,
110(11), 4392–4397. https://doi.org/10.1073/pnas.1216856110
Majeed, W., Magnuson, M., Hasenkamp, W., Schwarb, H.,
Schumacher, E. H., Barsalou, L., & Keilholz, S. D. (2011). Spa-
tiotemporal dynamics of low frequency bold fluctuations in rats
and humans. NeuroImage, 54(2), 1140–1150. https://doi.org/10.
1016/j.neuroimage.2010.08.030
Majeed, W., Magnuson, M., & Keilholz, S. D. (2009). Spatiotem-
poral dynamics of low frequency fluctuations in BOLD fMRI of
the rat. Journal of Magnetic Resonance Imaging, 30(2), 384–393.
https://doi.org/10.1002/jmri.21848
Natalia, P., Gaudes, C. C., Dryden, I. L., Francis, S. T., & Gowland,
P. A. (2012). Periods of rest in fMRI contain individual sponta-
neous events which are related to slowly fluctuating spontaneous
activity. Human Brain Mapping, 34(6), 1319–1329. https://doi.
org/10.1002/hbm.21513
Ouyang, G., Li, X., Dang, C., & Richards, D. A. (2008). Using
recurrence plot for determinism analysis of EEG recordings in
genetic absence epilepsy rats. Clinical Neurophysiology, 119(8),
1747–1755.
Ritter, P. (2017). Multimodal simulations based on realistic struc-
tural connectivity using the virtual brain platform. Organization
for Human Brain Mapping, Vancouver, Canada Center.
Ritter, P., Schirner, M., McIntosh, A. R., & Jirsa, V. K. (2013). The
virtual brain integrates computational modeling and multimodal
neuroimaging. Brain Connectivity, 3(2), 121–145. https://doi.org/
10.1089/brain.2012.0120
Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math-
ematical framework for large-scale brain network modeling in
the virtual brain. NeuroImage, 111, 385–430. https://doi.org/10.
1016/j.neuroimage.2015.01.002
Senden, M., Reuter, N., van den Heuvel, M. P., Goebel, R., &
Deco, G. (2017). Cortical rich club regions can organize state-
dependent functional network formation by engaging in oscil-
latory behavior. NeuroImage, 146, 561–574. https://doi.org/10.
1016/j.neuroimage.2016.10.044
Shakil, S., Lee, C.-H., & Keilholz, S. D. (2016). Evaluation of sliding
window correlation performance for characterizing dynamic func-
tional connectivity and brain states. NeuroImage, 133, 111–128.
https://doi.org/10.1016/j.neuroimage.2016.02.074
Shen, K., Hutchison, R. M., Bezgin, G., Everling, S., & McIntosh,
A. R. (2015). Network structure shapes spontaneous functional
connectivity dynamics. Journal of Neuroscience, 35(14), 5579.
https://doi.org/10.1523/JNEUROSCI.4903-14.2015
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E., . . . Beckmann, C. F. (2009). Correspondence of
the brain’s functional architecture during activation and rest. Pro-
ceedings of the National Academy of Sciences, 106(31), 13040.
https://doi.org/10.1073/pnas.0905267106
Stam, C. J., van Straaten, E. C. W., Van Dellen, E., Tewarie, P., Gong,
G., Hillebrand, A., . . . Van Mieghem, P. (2016). The relation be-
tween structural and functional connectivity patterns in complex
brain networks. International Journal of Psychophysiology, 103,
149–160. https://doi.org/10.1016/j.ijpsycho.2015.02.011
Stephan, K. E., Weiskopf, N., Drysdale, P. M., Robinson, P. A.,
& Friston, K. J. (2007). Comparing hemodynamic models with
DCM. NeuroImage, 38(3-3), 387–401. https://doi.org/10.1016/
j.neuroimage.2007.07.040
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3, 15.
https://doi.org/10.3389/fphys.2012.00015
Thompson, G.
Jaeger, D., &
J., Pan, W.-J., Magnuson, M. E.,
Keilholz, S. D. (2014). Quasi-periodic patterns (QPP): Large-scale
dynamics in resting state fMRI that correlate with local infraslow
electrical activity. NeuroImage, 84, 1018–1031. https://doi.org/
10.1016/j.neuroimage.2013.09.029
Tournier, J. D., Calamante, F., & Connelly, A. (2012). MRtrix: Diffu-
sion tractography in crossing fiber regions. International Journal
of Imaging Systems and Technology, 22(1), 53–66. https://doi.
org/10.1002/ima.22005
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E., Yacoub,
E., Ugurbil, K., & WU-Minn HCP Consortium. (2013). The WU-
Minn Human Connectome Project: An overview. NeuroImage,
80, 62–79.
Webber, C. L., & Marwan, N. (Eds.). (2015). Recurrence quantifi-
cation analysis: Theory and best practices. Cham, Switzerland:
Springer.
Yousefi, B., Shin, J., Schumacher, E. H., & Keilholz, S. D. (2018).
Quasi-periodic patterns of intrinsic brain activity in individuals and
their relationship to global signal. NeuroImage, 167, 297–308.
https://doi.org/10.1016/j.neuroimage.2017.11.043
Network Neuroscience
426
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
4
0
5
1
0
9
2
6
5
6
n
e
n
_
a
_
0
0
0
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3