FORSCHUNG
Computation is concentrated in rich clubs
of local cortical networks
Samantha P. Faber
1, Nicholas M. Timme
2, John M. Beggs
3, and Ehren L. Newman 1
1Department of Psychological and Brain Sciences, Indiana University Bloomington, Bloomington, IN, USA
2Abteilung für Psychologie, Indiana University-Purdue University Indianapolis, Indianapolis, IN, USA
3Department of Physics, Indiana University Bloomington, Bloomington, IN, USA
Schlüsselwörter: Cortical networks; Effective connectivity; Neural computation; Rich clubs; Transfer
entropy; Informationstheorie
Keine offenen Zugänge
Tagebuch
ABSTRAKT
To understand how neural circuits process information, it is essential to identify the
relationship between computation and circuit organization. Rich clubs, highly
interconnected sets of neurons, are known to propagate a disproportionate amount of
information within cortical circuits. Hier, we test the hypothesis that rich clubs also perform
a disproportionate amount of computation. To do so, we recorded the spiking activity of on
average ∼300 well-isolated individual neurons from organotypic cortical cultures. We then
constructed weighted, directed networks reflecting the effective connectivity between the
Neuronen. For each neuron, we quantified the amount of computation it performed based on
its inputs. We found that rich-club neurons compute ∼160% more information than neurons
outside of the rich club. The amount of computation performed in the rich club was
proportional to the amount of information propagation by the same neurons. This suggests
that in these circuits, information propagation drives computation. In Summe, our findings
indicate that rich-club organization in effective cortical circuits supports not only information
propagation but also neural computation.
ZUSAMMENFASSUNG DES AUTORS
Here we answer the question of whether rich-club organization in functional networks of
cortical circuits supports neural computation. To do so, we combined network analysis with
information theoretic tools to analyze the spiking activity of hundreds of neurons recorded
from organotypic cultures of mouse somatosensory cortex. We found that neurons in rich
clubs computed significantly more than neurons outside of rich clubs, suggesting that rich
clubs do support computation in cortical circuits. In der Tat, the amount of computation that
we found in the rich clubs was proportional to the amount of information they propagate,
suggesting that in these circuits, information propagation drives computation.
EINFÜHRUNG
The idea that neurons propagate information and that downstream neurons integrate this infor-
mation via neural computation is foundational
to our understanding of how the brain
processes, and responds to, die Welt. Noch, the determinants of such computations remain
largely unknown. Advances in data acquisition methods, offering increasingly comprehensive
recordings of the activation dynamics that play out atop of neural circuits, together with ad-
vances in data analytics, now make it possible to empirically study the determinants of neural
Zitat: Faber, S. P., Timme, N. M.,
Beggs, J. M., & Newman, E. L. (2019).
Computation is concentrated in rich
clubs of local cortical networks.
Netzwerkneurowissenschaften, 3(2), 384–404.
https://doi.org/10.1162/netn_a_00069
DOI:
https://doi.org/10.1162/netn_a_00069
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00069
https://github.com/NewmanMemLab/
synergyInRichClubs
Erhalten: 29 Marsch 2018
Akzeptiert: 30 August 2018
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Samantha P. Faber
samfaber@indiana.edu
Handling-Editor:
Martijn van den Heuvel
Urheberrechte ©: © 2018
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
N
e
N
_
A
_
0
0
0
6
9
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computation in rich clubs
Information:
The reduction in uncertainty,
typically measured in bits.
Computation:
The process of integrating multiple
sources of information to produce an
output.
Information propagation:
The transfer of unmodified
information from one spiking neuron
to another.
Rich club:
A set of neurons with strong
connections that connect to each
other more than expected by chance.
Berechnung. Using these tools, we addressed the fundamental question of where, relativ zu
information flow in local cortical networks, the majority of neural computation takes place.
Although there is no agreed upon definition of “computation,” in its simplest form, com-
putation refers to the process of integrating multiple sources of information to produce a new
output. This is in contrast to information propagation which is simply the passing of (unmod-
ified) information from a source to a receiver. Neural computation is the systematic transfor-
mation of information received by a neuron (determined by analyzing its output with respect
to its inputs) based on the input of multiple upstream neurons (Timme et al., 2016). This type
of computation can be detected empirically when the activity of upstream neurons accounts
for the activity of a downstream neuron better when considered jointly than when treated as
independent sources of variance. Because computation is the information gained beyond what
was already accounted for by the upstream neurons when they are treated independently, es ist
not a given that strong sources of information propagation necessarily lead to a large amount
of computation. Analytical tools adapted from Shannon’s information theory make it possible
to track such computation as well as information propagation in networks of spiking neurons
(Strong et al., 1998; Borst & Theunissen, 1999; Schreiber, 2000; Williams & Beer, 2010).
The determinants of strong computation in neural circuits remain poorly understood.
Previously, Timme et al. ( 2016) used these tools to show that computation does not vary sys-
tematically with the number of inputs received by a neuron, as might be intuited. Eher, com-
putation correlates with the number of outputs of the upstream neurons. This counterintuitive
finding suggested that the amount of computation a neuron performs may be better predicted
by its position in the broader topographic structure of the circuit than by the local connectivity.
The relationship between computation and the strength of inputs, Jedoch, remains unknown.
To understand the determinants of maximal computation in neural circuits, es ist wichtig
determine how computation varies as a function of the topology of the functional networks
along which information propagates and within which computation is performed. This raises
the question of what topological conditions support computation.
Local cortical networks, like many complex networks, contain “rich clubs,” that is, the most
strongly connected neurons interconnect with a higher probability than would be expected
by chance. The existence of a rich club in a functional network predicts that a select set of
highly integrated nodes handles a disproportionately large amount of traffic. In der Tat, im
local networks of cortical circuits, 20% of the neurons account for 70% of the information
propagation (Nigam et al., 2016). Als solche, rich clubs represent a conspicuous topographic
landmark in the flow of information across neural circuits.
Daher, here we addressed the critical question: What is the role of the rich club with respect
to neural computation? We tested among three possible hypotheses. Erste, computation is con-
stant throughout the topology of a network: predicting that rich clubs do not perform more
or less computation than would be expected by chance. Zweite, computation grows with in-
creasing information availability: predicting that rich clubs are rich in computation given their
high information density. Dritte, computation decreases with increasing information availabil-
ität: predicting that rich clubs are computationally poor.
Organotypic culture:
A cell culture, derived from tissue,
that retains many of the structural
and functional properties of the
intact tissue.
To test these hypotheses, we recorded the spiking activity of hundreds of neurons from
organotypic cultures of mouse somatosensory cortex and assessed the distribution of com-
putation inside versus outside of rich clubs of information propagation (Figur 1). The results
demonstrate that rich-club neurons perform 160% more computation than neurons outside of
the rich club, accounting for the majority of network computation (∼88%). Throughout the
Netzwerkneurowissenschaften
385
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
N
e
N
_
A
_
0
0
0
6
9
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computation in rich clubs
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
N
e
N
_
A
_
0
0
0
6
9
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
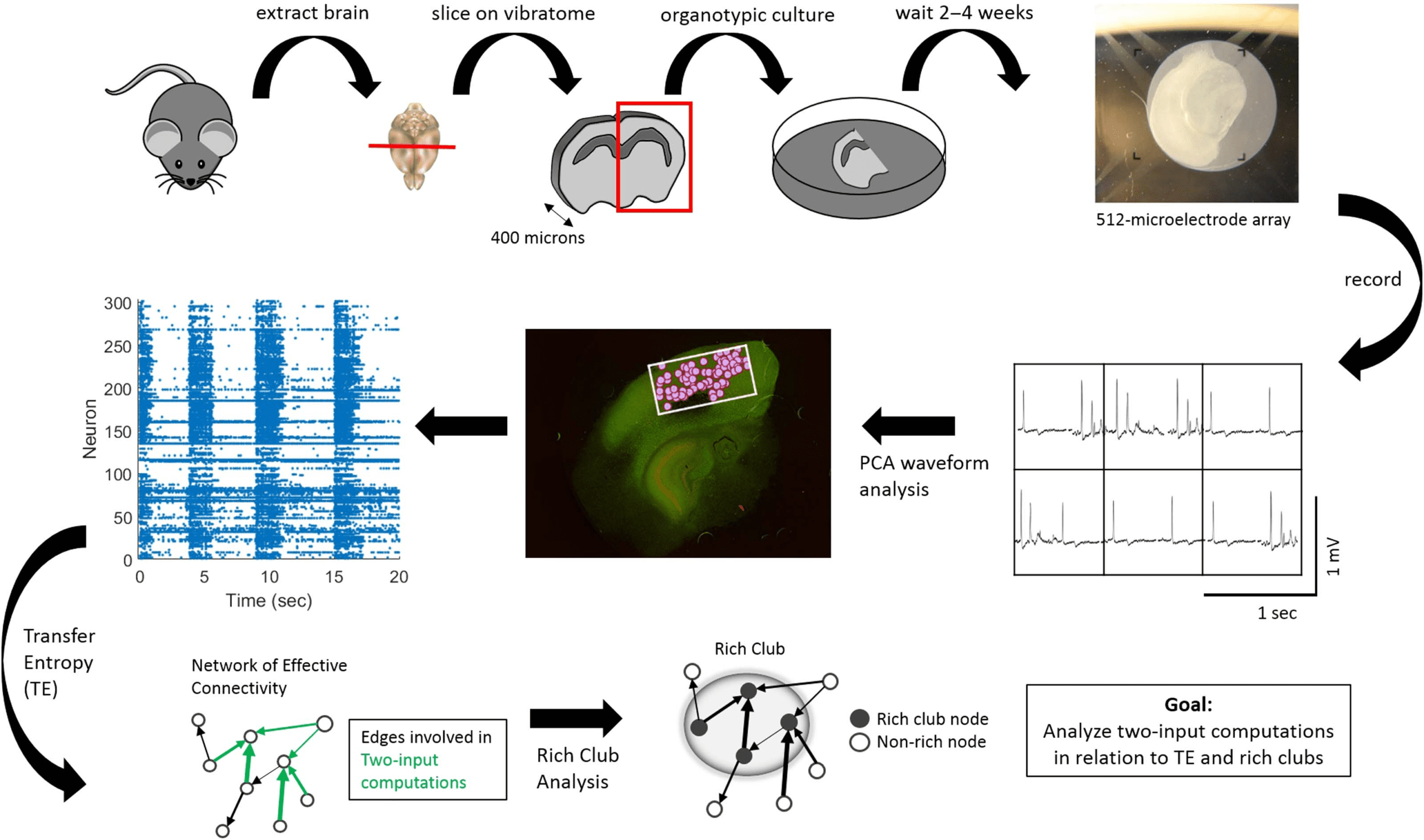
Figur 1.
Experimental and data analysis procedure. (Top row, left to right) Brains were extracted from mouse pups and sliced using a vibra-
tome. Slices containing somatosensory cortex were organotypically cultured for up to 2 Zu 4 weeks. Cultures were then placed on a recording
array and recorded for 1 Std. (Middle row, right to left) Recordings yielded neuron-spiking dynamics at each electrode—waveforms at six example
electrodes shown—which were sorted using principal component analysis in order to isolate individual cells based on their distinct waveforms.
Once cells were isolated and localized (pink circles) within the recording area (white rectangle), their corresponding spike trains could be
determined. (Bottom Row, left to right) Spike trains were then used to compute transfer entropy (DER), at multiple timescales, between each
neuron pair in a recording. This resulted in networks of effective connectivity. Computations occurring at neurons receiving two connections
were then calculated using partial information decomposition. A rich-club analysis was used to detect collections of hub neurons that connect
to each other. Endlich, we examined the relationship between TE within a triad and two-input computations as well as between two-input
computations and rich clubs.
Netzwerke, computation occurs proportionally to information propagation (d.h., the two are cor-
related) although at a slightly reduced rate (∼3% decrease) inside of rich clubs. Wichtig,
Jedoch, rich clubs contained more computation than would be expected given the correlation
between propagation and computation. These results show that rich clubs are computation-
ally dense. Daher, rich clubs support elevated amounts of both computation and propagation
relative to the rest of the network.
ERGEBNISSE
To study the relationship between information processing and the functional network struc-
ture of cortical microcircuits, we recorded spiking activity of between 98 Und 594 Neuronen (me-
dian = 310) simultaneously from 25 organotypic cultures of mouse somatosensory cortex. Wir
then quantified the information transfer from each neuron to every other neuron at timescales
relevant for synaptic transmission (up to 14 MS; Mason et al., 1991; Swadlow, 1994) verwenden
386
Timescale:
The range of time in which delays
between spiking neurons were
berücksichtigt.
Netzwerkneurowissenschaften
Computation in rich clubs
Transfer entropy:
An information theoretic measure
that quantifies the amount of directed
information transfer between two
spiking neurons.
Synergy:
A measure that quantifies the
information gained by considering
the spiking of two neurons jointly
compared to independently.
transfer entropy (DER; Schreiber, 2000). TE was selected for its ability to detect nonlinear
interactions and deal with discrete data, such as spike trains. The range of timescales, spanning
0.05–14 ms, was discretized into three subwindows (0.05-3, 1.6–6.4, and 3.5–14 ms) to im-
prove the sensitivity to functional interactions across these delays. This resulted in 75 Netzwerke
(25 recordings at three timescales). Because TEA→B quantifies how much information is gained
about whether neuron B will spike in the next moment obtained by knowing whether A is now
spiking, it provides a directional, weighted effective connection. Significant T values (abhalten-
mined by comparing to the distribution of TE values obtained when we shuffled the respective
spike trains) were kept and used to build a graph of the circuit’s functional network. The graph
was then used to identify all possible triads in which two transmitting neurons have significant
connections to a common receiver neuron. Daher, the same neuron often participated in many
triads, the number of which was correlated with the degree of the neuron. Triads were then
used to analyze neural computation. Our analysis of neural computation was predicated on
the idea that nonlinear integration of multiple inputs implements a form of computation (sehen
also Timme et al., 2016). Daher, we quantified neural computation as the additional information
regarding the future state of the receiver that was gained beyond what the transmitting neurons
offered individually (after accounting for the redundancy between the transmitting neurons
and the past state of the receiver itself). We did this using a partial information decomposi-
tion approach (PID; Williams & Beer, 2010) to calculate synergy. PID is currently the only
method available that is capable of quantifying the computation that occurs in the multiway
interactions of neuronal triads. We focused on triads as the computational unit, rather than
higher order configurations, for several reasons. Erste, they represent the minimal (fundamen-
tal) computational unit, on which higher order units depend. Zweite, they have previously
been demonstrated to account for the vast majority of information gained when considering
higher order interactions (Timme et al., 2016). And third, calculating synergy for an interaction
with even a single additional input (3 inputs total) is much more computationally intensive and
does not offer significantly greater explanatory power.
All TE and synergy values were normalized by the entropy of the receiver neuron in order to
cast them in terms of the proportion of the receiver neuron’s capacity that is accounted for by
the transmitting neuron, or by computation, jeweils. Because of this, all TE and synergy
values are in terms of bits per bit. All results are reported as medians with 95% bootstrap confi-
dence intervals (computed using 10,000 Iterationen) presented in brackets. The three timescales
at which TE was computed follow the same pattern of results and are therefore combined for
ease of presentation; separate results for each timescale are reported in the Supporting Infor-
mation (Faber, Timme, Beggs, & Newman, 2019).
Computation and Information Propagation Vary Widely in Cortical Microcircuits
When building the networks, we found that 0.52% [0.38%, 1.1%] of all possible directed
connections between neurons were significant at the α = 0.001 Ebene (z.B., 480 von 81,510
possible connections, oder 0.59%, were significant in a network of 286 Neuronen). To consider
the amount of information that was used in two-input computations, we defined information
propagation as the sum of the two inputs (TE values) converging on a neuron. Across neurons,
the distribution of propagation values was approximately lognormal (shown in Figure 2), con-
sistent with previously observed distributions of both structural (Song et al., 2005; Lefort et al.,
2009; Ikegaya et al., 2012) and functional connectivity (für eine Rezension, see Buzsáki & Mizuseki,
2014). This lognormality indicates that there exists a long tail of large propagation values such
that a few neurons propagate particularly large amounts of information. Concretely, we found
that the strongest 8.5% [8%, 9.7%] of neurons propagated as much information as the rest of
Netzwerkneurowissenschaften
387
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
N
e
N
_
A
_
0
0
0
6
9
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Computation in rich clubs
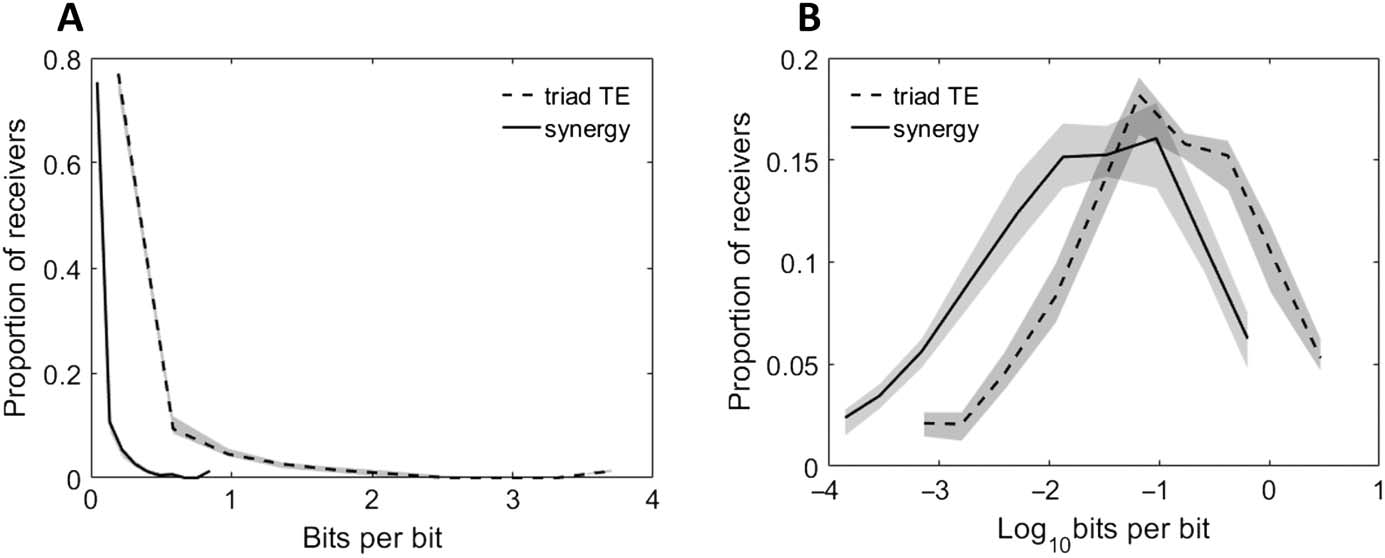
Figur 2. Distributions of neuron computation (synergy) and propagation (triad TE) are highly
varied. Histograms of synergy and triad TE values for all receivers in all networks at all timescales.
(A) Distributions of measured values. (B) Distributions of log-scaled values to emphasize variabil-
ität. Solid and dashed lines depict the median across networks, and shaded regions depict 95%
bootstrap confidence intervals around the median.
the neurons combined. Within a network, the difference between the neurons that received
the most versus the least information commonly spanned 3.9 [3.6, 4.1] orders of magnitude.
Computation (measured as synergy), like propagation, varied in a lognormal fashion
(Figur 2). The top 8.4% [8%, 9.3%] of neurons computed the same amount of information
as the rest of the neurons combined. The synergy typically spanned 4.1 [3.8, 4.2] orders of
magnitude over neurons in individual networks. Vor allem, computation was reliably smaller
−14) indicating
than propagation (0.11 vs. 0.025; Zs.r. = −7.5, n = 75 Netzwerke, p = 5.3 × 10
that despite finding substantial computation, most information was accounted for by neuron-
to-neuron propagation. The variability in computation motivated us to test the hypothesis that
the dense interconnectivity of rich clubs serves as a hub, not only for propagation, but also for
Berechnung.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
N
e
N
_
A
_
0
0
0
6
9
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
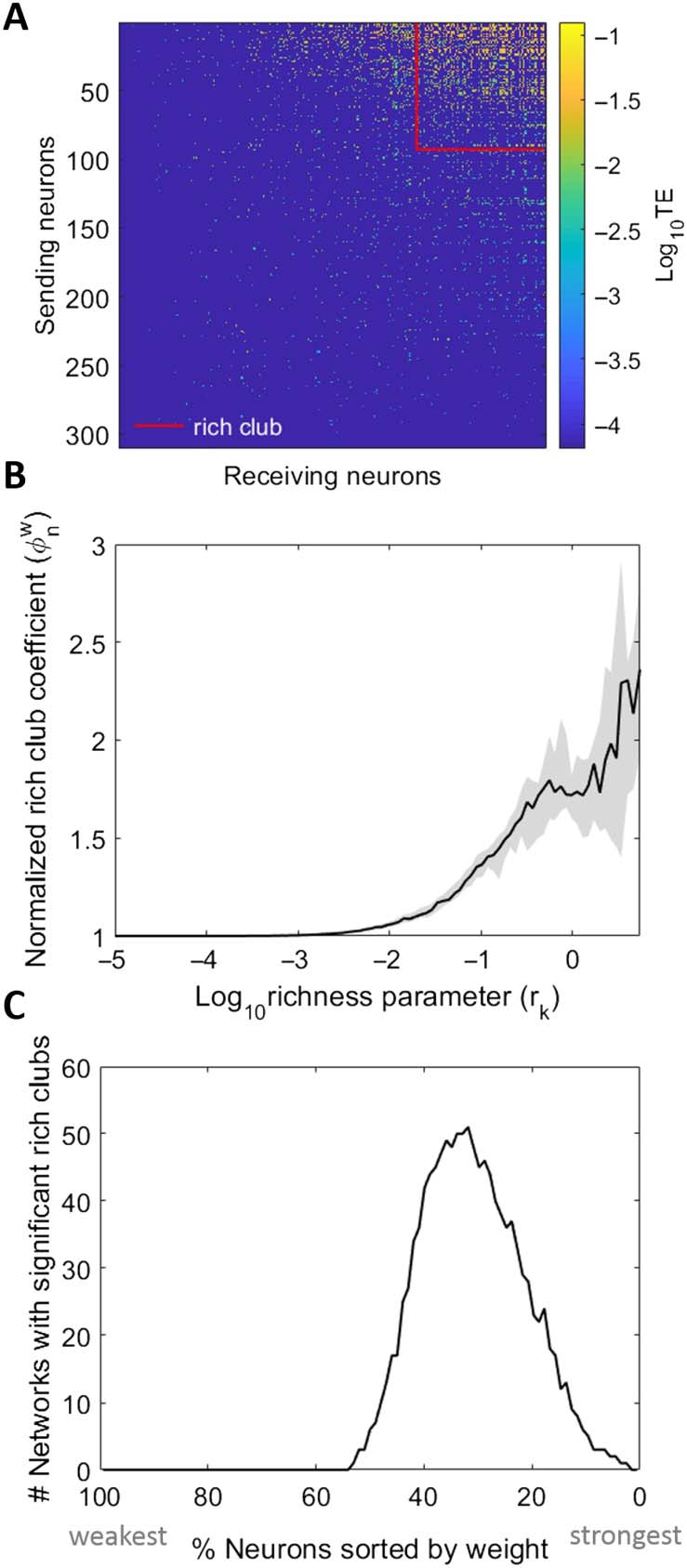
Rich Clubs Perform a Majority of the Network-Wide Computation
In every network, we found significant rich clubs at multiple richness parameter (R) levels (d.h.,
thresholds) wie in der Abbildung gezeigt 3. The richness parameter was defined as the sum of incoming
and outgoing TE edge weights of each neuron. Rich clubs were computed at every kth value
of r by dividing the sum of all weights for nodes with r ≥ rk by the sum of the n largest
weights in the network, where n is the number of edges between neurons with r ≥ rk. Der
resulting rich-club coefficients approach one when the strongest edges connect the neurons in
the subsets defined by r ≥ rk. These rich-club coefficients are then normalized by coefficients
from null distributions in order to quantify how much rich clubs differ from those expected by
chance (see Supporting Information Methods for more detail, Faber et al., 2019). The more the
normalized rich-club coefficient diverges from one, the richer the rich club (Abbildung 3B).
When comparing the observed rich-club coefficients with those from null distributions, Wir
also calculated p values to establish significance of the rich clubs. We found significant rich
clubs at multiple richness parameter levels, which typically consisted of the top 10%–50% of
the neurons in each network (Figure 3C). The median number of thresholds that resulted in
significant rich-club coefficients was four per network.
To ensure that the detection of rich clubs was not biased by the spatial sampling of the
recording apparatus, we compared the distances between rich-club neurons (defined as the
Netzwerkneurowissenschaften
388
Computation in rich clubs
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
N
e
N
_
A
_
0
0
0
6
9
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3. Networks reliably show rich clubs. (A) Adjacency matrix of a representative 310-neuron
network with rich clubs. Rich club of top 30% of neurons depicted. Neurons sorted in order of
increasing richness from left to right and bottom to top. TE values are log scaled. (B) Normalized,
weighted rich-club coefficients for all networks. X-axis is log-scaled richness parameter level, Wo
the richness parameter is the sum of the weighted connections for each neuron. Solid line represents
median across all networks; shaded region is 95% bootstrap confidence interval around the median.
In order for a rich club to be recruited into the synergy analysis, coefficients were required to be
significant (P < 0.01) when compared with those from randomized networks. (C) The number of
networks, out of the 75 analyzed, with significant rich clubs at each threshold. The majority of
networks had significant rich clubs composed of the top 50% to 10% of the network.
top 30% of neurons in a network) to the distances between all neurons in the network. We
found that there were no significant differences between the two distributions of distances
(Kolmogorov–Smirnov tests revealed that 75 out of 75 networks had distributions that were
not significantly different at the α = 0.01 level).
We investigated the relationship between these rich clubs and computation (measured as
synergy) by using multiple approaches. In the first approach, we asked if the mean normalized
Network Neuroscience
389
Computation in rich clubs
synergy-per-triad (where the mean was taken over all triads in a network, for each network) was
significantly greater for triads with receivers inside, versus outside, of a single, representative
rich club from each network. The representative rich club for each network was selected at
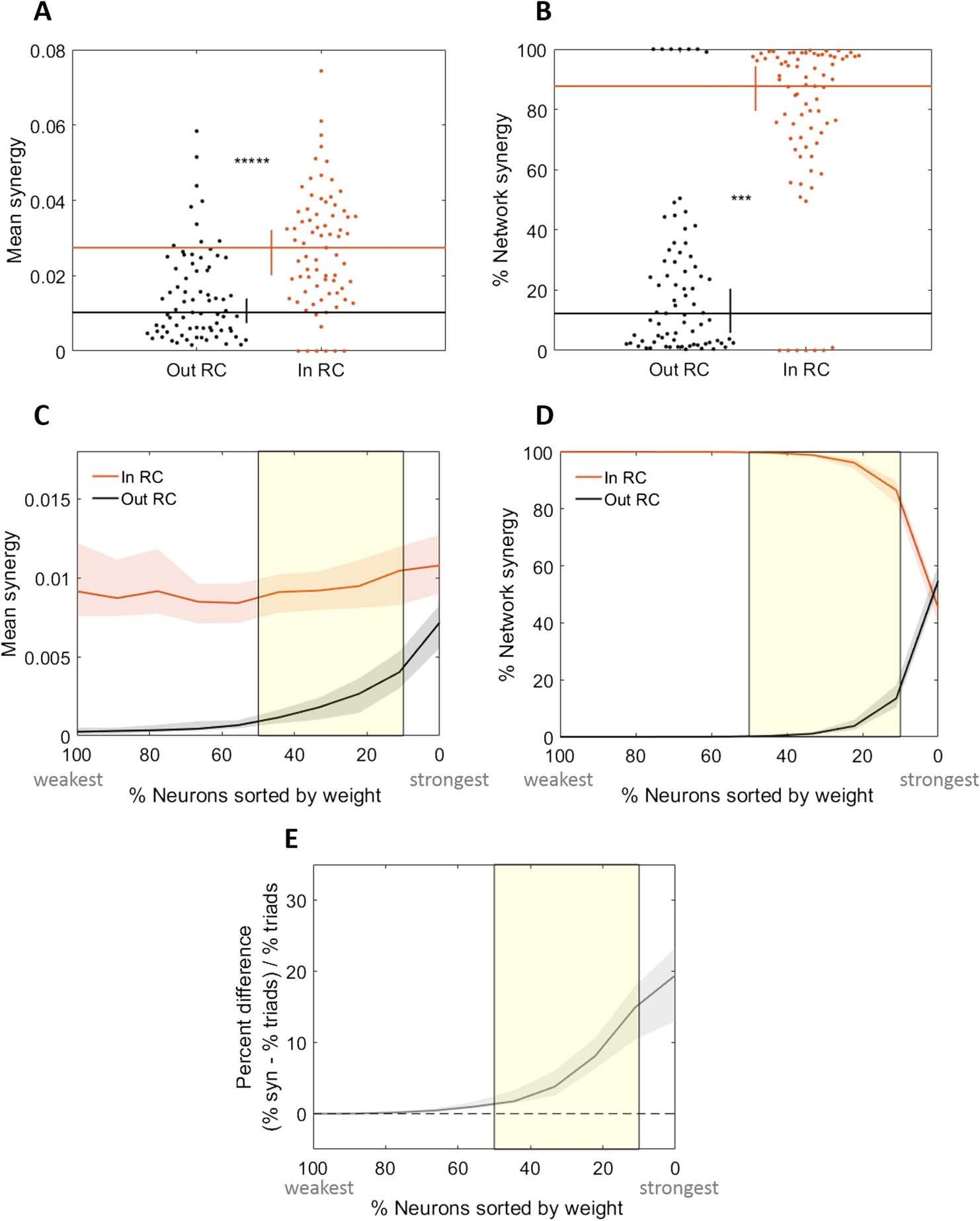
random from among the significant ones. Indeed, we found that mean synergy was 270%
−13;
greater inside of the rich club (0.027 vs. 0.01, Zs.r. = 7.2, n = 75 networks, p = 5.2 × 10
Figure 4). We next asked what percentage of the network-wide computation was performed
inside of the rich club and found that in these representative rich clubs, 87.7% [79.5%, 94.3%]
of all synergy in a network was performed by rich-club neurons (Figure 4B).
A concern that arises when considering whether synergy is stronger inside of rich clubs
identified with information theoretic measures, such as TE, is that the rich clubs are defined
as having high TE and thus may cause high concentrations of computation for trivial reasons.
To test this, we used a spike-time shuffling analysis that preserved TE but disrupted the joint
firing statistics between transmitters of a triad. This allowed us to compute the null distribution
of synergy that would be expected given the TE that comprised each rich club (see Supporting
Information for methods, Faber et al., 2019). Although this analysis demonstrated that high
TE in the rich club can be sufficient to generate a null distribution of synergy that is greater
inside versus outside of the rich club (significant in two of the three timescales, see Supporting
Information for full details, Faber et al., 2019), the actual synergy levels observed in the rich club
here were reliably even greater than the null distributions. When we Z-scored the observed
synergy values by the values of the null distribution of synergy, the median Z-scored synergy
−9). The
values across networks was 13.31 (Zs.r. = 5.76, n = 75 networks, p = 8.6 × 10
individual Z-scored synergy values were significant at the α = 0.05 level in 88% (66 of 75) of
the networks. The results of these analyses demonstrate that the computation observed in the
rich club is not a simple consequence of the magnitude of the TE values that comprise the rich
clubs in these networks.
Our second approach to quantify synergy with respect to the rich club examined how syn-
ergy varied as a function of the richness levels. The results of these analyses recapitulate the
findings reported above. That is, across levels, richer neurons consistently had greater mean
synergy-per-triad (Figure 4C). Similarly, at most thresholds, rich neurons accounted for a major-
ity of the network-wide synergy (Figure 4D). However, because the richest neurons are likely
to participate in a larger number of triads, rich clubs would be expected to perform a large per-
centage of the network-wide synergy even if the mean synergy-per-triad was not significantly
greater than that found elsewhere in the network. Thus, we also asked how the percentage
of network-wide synergy varied as a function of the percentage of triads that are included in
the rich club. As shown in Figure 4E, the share of synergy performed by the richest neurons
was consistently greater than the percentage of above threshold triads. Notably, the percent
difference drops off as the threshold decreases, reflecting that as the rich clubs become less
rich, they have less relative amounts of synergy.
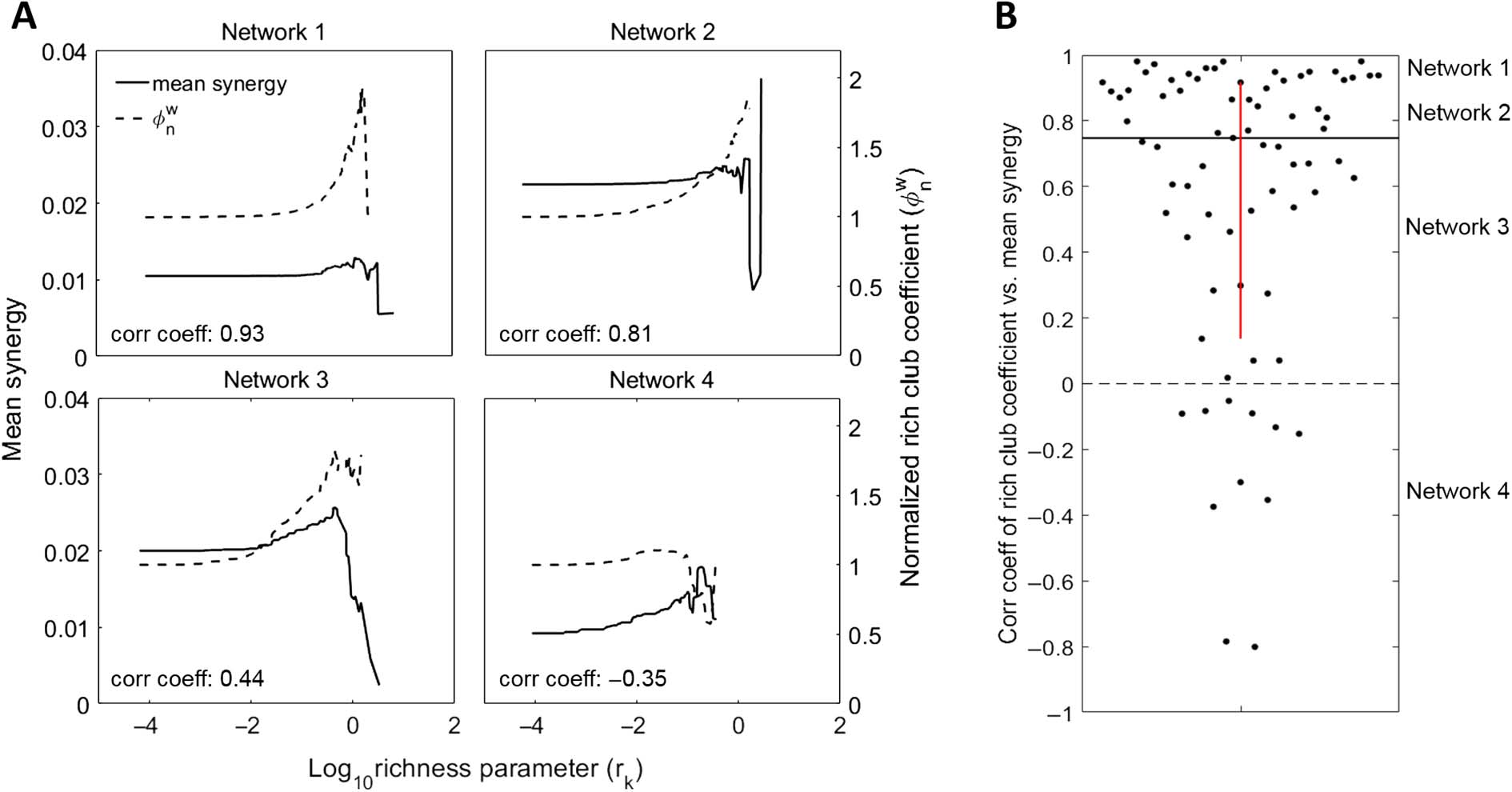
Our third approach compared the relationship between the strength of the rich club for
any given threshold, as indicated by the normalized rich-club coefficient, with the amount
of synergy taking place in that rich club. Specifically, we correlated the normalized rich-club
coefficient with the mean normalized synergy of triads inside of the rich club across thresholds
for each network separately and asked if there was a consistent trend across networks (Figure 5).
In most networks, synergy and normalized rich-club coefficient were positively correlated (64
of 75 networks) such that the median correlation coefficient of 0.75 [0.66, 0.84] was signif-
−11; Figure 5B). These
icantly greater than zero (Zs.r. = 6.6, n = 75 networks, p = 2.9 × 10
results indicate that rich-club strength was strongly predictive of mean synergy.
Network Neuroscience
390
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Rich-club neurons compute more than non–rich-club neurons. (A) Triads with receivers
in the rich club (RC) have median mean normalized synergy (compute more) than those with re-
ceivers outside the rich club. (B) Triads with receivers in the rich club perform a significantly larger
percentage of the total network computation than triads with receivers outside the rich club. Dis-
tributions shown here are complementary; values sum to 1. (C–E) Comparison of key metrics at all
possible rich-club thresholds. The thresholds have been aligned over networks based on the number
of neurons in the network that are included at each threshold. The highest (most stringent) thresholds
are on the right with the lowest percent of neurons in the rich club. (C) At all significant rich-club
levels (indicated by the yellow shaded region), triads with receivers in the rich club have greater
median mean synergy than those with receivers outside the rich club. (D) The percentage of network
synergy is plotted as a function of rich-club level. At all significant rich-club levels, a greater per-
centage of network synergy occurs in the rich clubs than outside the rich clubs. Distributions shown
here are complementary; values sum to 1. (E) The percent difference in the percentage of network
synergy and the percentage of network triads in the rich club is plotted as a function of rich-club
level. Positive values reflect a larger relative percentage of synergy than percentage of triads. At all
significant rich-club levels, a greater percentage of synergy is accounted for by a smaller percentage
of triads in the rich clubs. Significance indicators: *****p < 1 × 10
−9; ***p < 1 × 10
−6.
Network Neuroscience
391
Computation in rich clubs
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Normalized rich-club coefficient correlates with synergy. (A) Normalized rich-club coefficients and mean normalized synergy
at increasing richness levels for four representative networks. Negative correlations are observed in networks that have poor rich clubs, or
in which the mean synergy decreases as we consider fewer, richer neurons. The second case is observed in networks whose top neurons
participate in many triads with synergy values that are highly variable. (B) Distribution of correlation coefficients for correlations between
rich-club coefficients and mean triad synergy at all richness levels. Most network rich-club coefficients are positively correlated with mean
triad synergy. This shows that rich clubs are predictive of increased synergy levels.
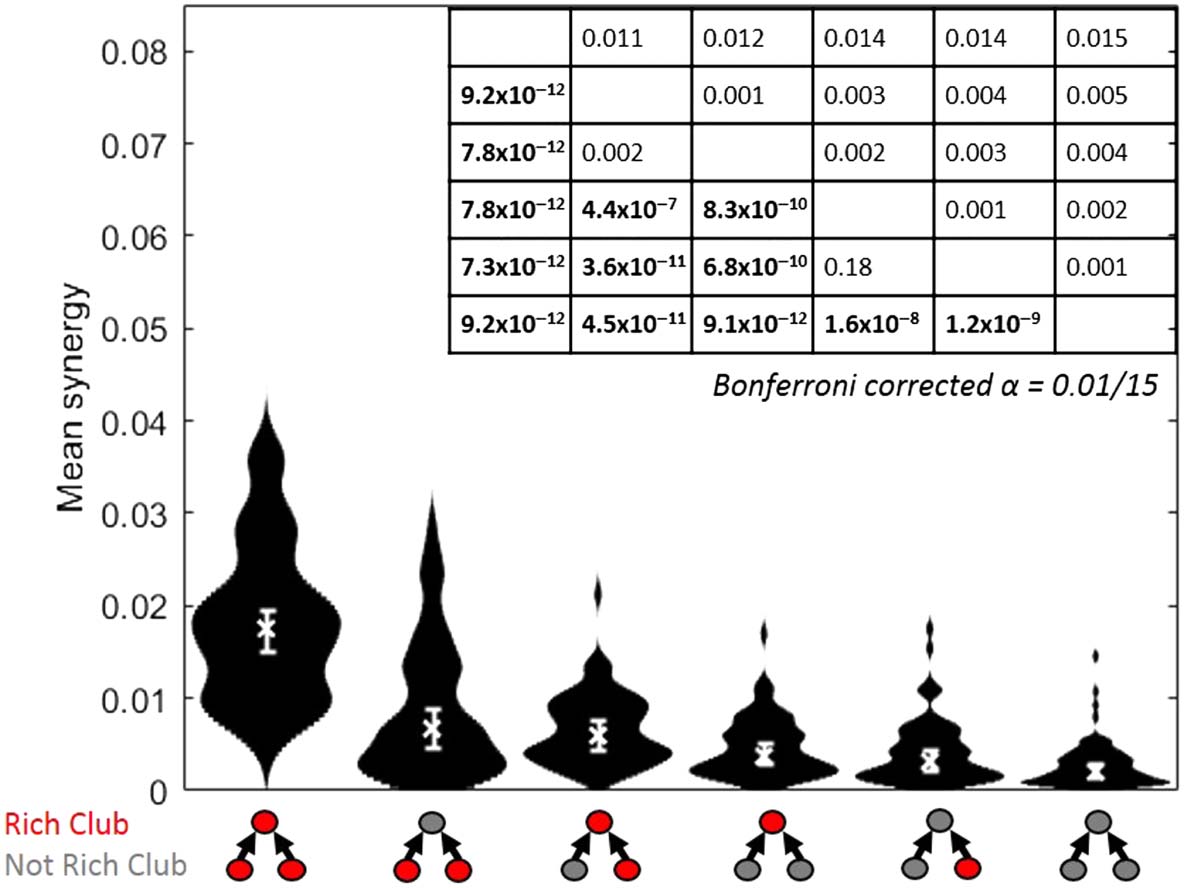
Finally, we asked how mean synergy depends on which triad members were in the rich
club. The analyses described above categorize a triad as inside of the rich club if the receiver
is a member of the rich club. Here, we calculated the mean normalized synergy separately for
each of the six possible alignments of the triad members to the rich club. The results, shown
in Figure 6, demonstrate that the single configuration with the largest mean synergy occurred
in triads for which all three members were in the rich club. The two configurations with the
next greatest mean synergy both had two members in the rich club. Configurations with one
member in the rich club had the next greatest mean synergy. Triads that had no neurons in the
rich club had the lowest mean synergy. Consistent with the above results, this pattern indicates
that the greater the involvement in the rich club, the greater the mean synergy.
Stable Computation-to-Propagation Ratio Accounts for the High Density of Computation in Rich Clubs
Our results show that rich-club neurons both propagate a majority of the information (Nigam
et al., 2016) and perform a majority of the computation in the network. A possible explana-
tion for the co-localization of information propagation and computation is that propagation
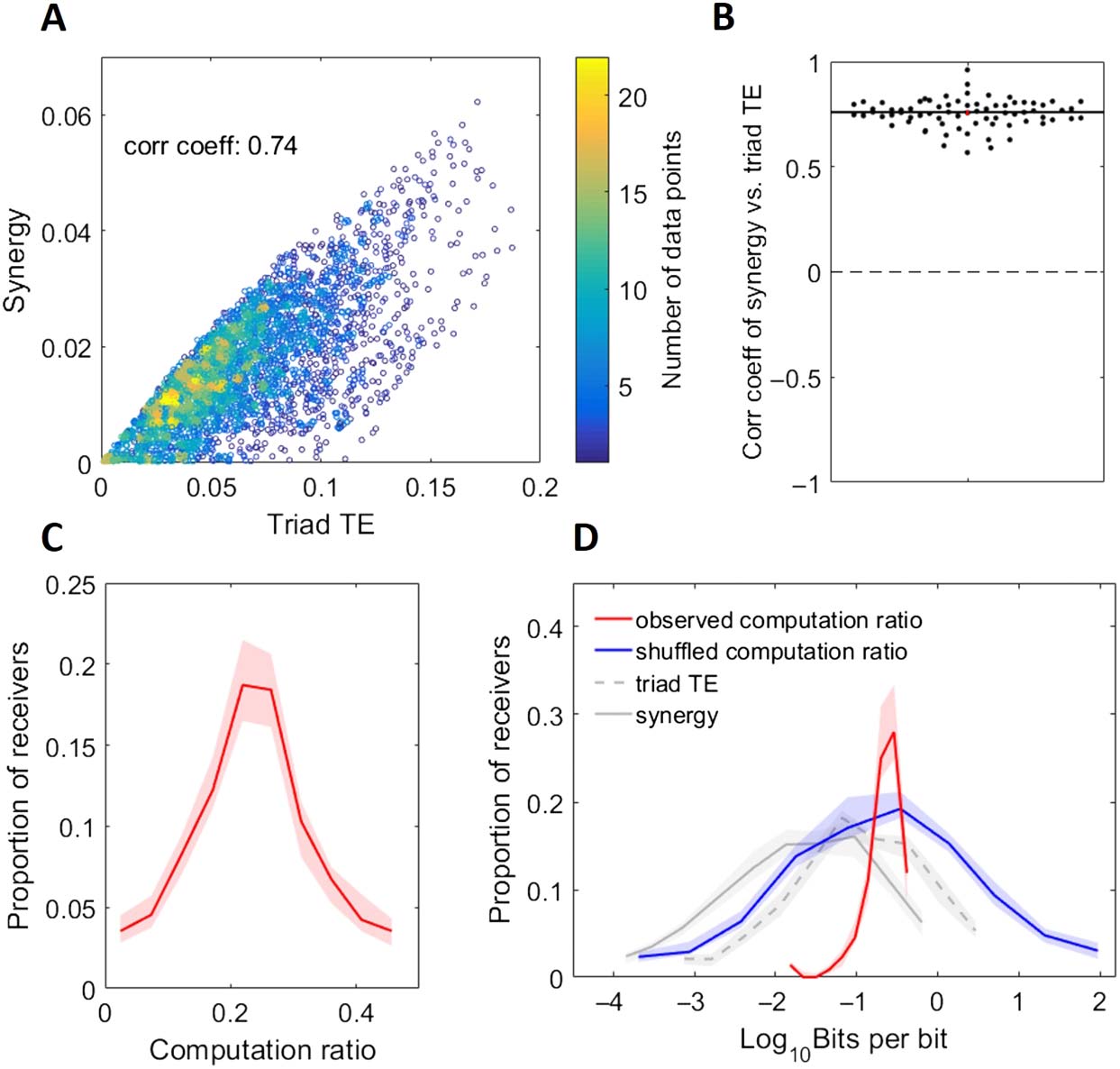
drives computation. To investigate this, we asked how correlated information propagation and
computation (measured as synergy) were across triads for each network. In every network,
the amount of information being propagated in a triad was strongly correlated with synergy
−14;
( ρ = 0.76 [0.74 0.77], minimum ρ = 0.57, Zs.r. = 7.52, n = 75 networks, p = 5.3 × 10
Figure 7 and 7B).
Seeing that computation and propagation were highly correlated across triads, we asked
what range of computation ratios (i.e., computation/propagation) occurred across networks.
Network Neuroscience
392
Computation in rich clubs
Figure 6. Greater computation (synergy) is performed by triads with greater numbers of neurons
in the rich club. Distributions of mean synergy for each of all possible triad interactions with the
rich club. Triads that have all members in the rich club have the greatest synergy. Triads with both
transmitters in the rich club, and a single transmitter and the receiver in the rich club, have similar
amounts of synergy. Triads with only the receiver in the rich club have more synergy than triads
with a single transmitter in the rich club. All triads with any member in the rich club have more
synergy than triads with no members in the rich club. Medians, denoted by “x,” and 95% bootstrap
confidence intervals are shown. Table shows Bonferroni–Holm corrected p values (lower diagonal)
and differences of medians (upper diagonal) of pairwise comparisons between the conditions,
which are sorted by median mean synergy. Significant p values are boldface. Distributions shown
have n = 75 data points.
As shown in Figure 7C and 7D, the computation ratio was highly stereotyped over networks
with a median of 0.239 [0.237, 0.241]. In contrast to the 3.9 [3.6, 4.1] and 4.1 [3.8, 4.2] or-
ders of magnitude over which triad TE and synergy varied, respectively, the computation ratio
varied by 1.57 [1.46, 1.62] orders of magnitude. By way of comparison, randomizing the align-
ment of synergy to triad TE across triads results in computation ratios that span 5.8 [5.3, 6.3]
orders of magnitude. The significant reduction in variance over what would be expected by
−14) suggests that the computation ratio
chance (Zs.r. = −7.5, n = 75 networks, p = 5.3 × 10
is a relatively stable property of neural information processing in such networks.
The implication of a stable computation ratio across triads is that information propagation
will reliably be accompanied by computation, thereby accounting for the high density of com-
putation in propagation-dense rich clubs. Because the computation ratio allows computation
to be predicted from propagation, it is informative to ask if this ratio varies as a function of rich-
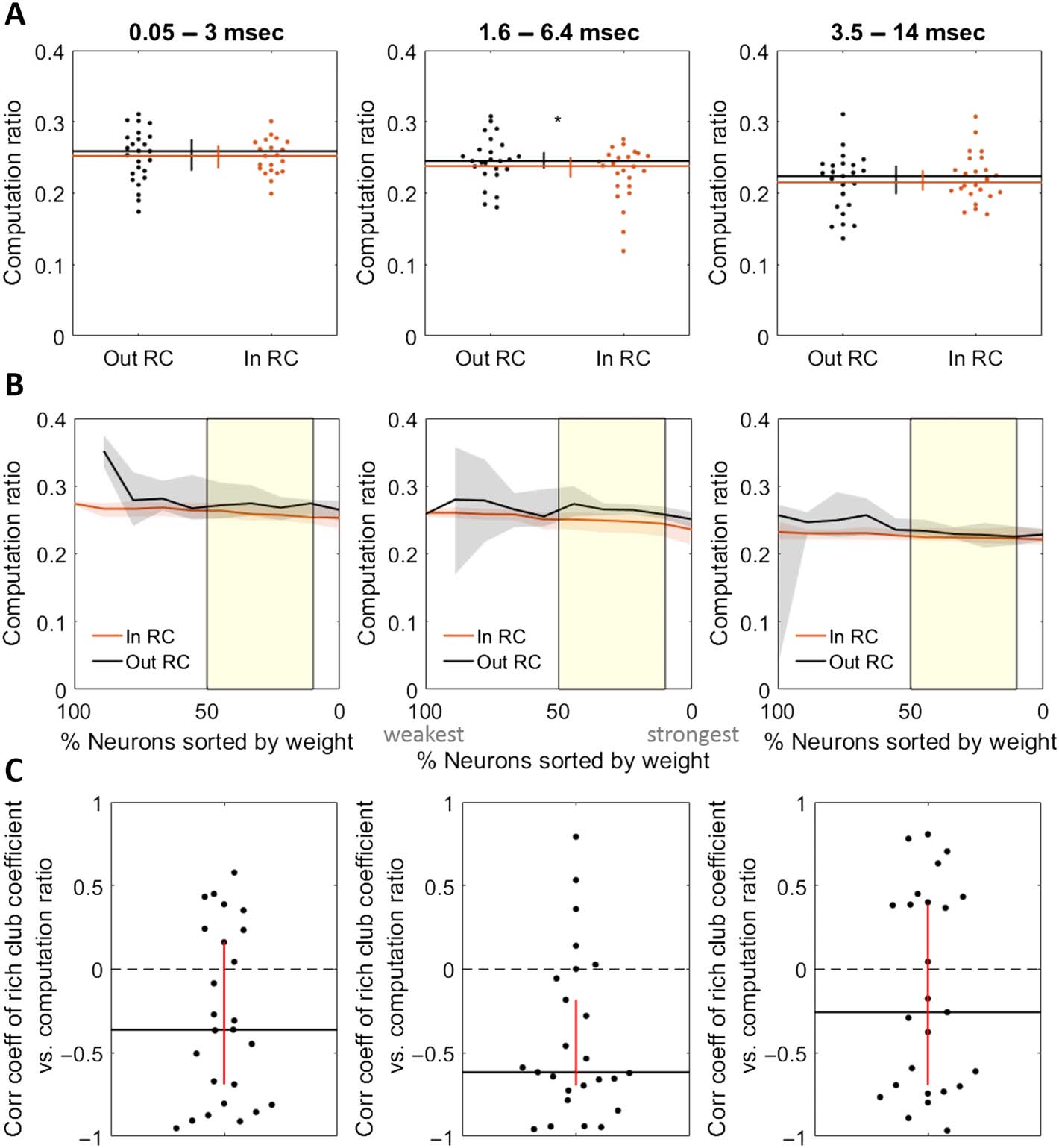
club membership. We found that the computation ratio was not substantially different for triads
inside, versus outside, of rich clubs (0.252 vs. 0.259 at the 0.05–3 ms timescale, Zs.r. = −1.58,
n = 25 networks, p = 0.11; 0.238 vs. 0.245 at the 1.6–6.4 ms timescale, Zs.r. = −2, n = 25
networks, p = 0.045; and 0.215 vs. 0.224 at the 3.5–14 ms timescale, Zs.r. = 0.97, n = 25 net-
works, p = 0.33; Figure 8). The difference was only marginally significant for the 1.6–6.4 ms
timescale (Figure 8B, center). We also tested whether the rich-club coefficient was correlated
with the computation ratio across thresholds and found that it was significantly negatively
correlated at the 0.05–3 ms timescale (ρ = −0.36 [−0.69, 0.16], Zs.r. = −2.38, n = 25 net-
works, p = 0.017; Figure 8C, left) and at the 1.6–6.4 ms timescale (ρ = −0.62 [−0.70, −0.18],
Network Neuroscience
393
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Propagation is highly predictive of computation. (A) Scatterplot of synergy (computation)
versus triad TE (propagation) in a representative network with 3,448 triads. Colorbar depicts point
density. Also shown is the correlation coefficient. (B) Distribution of network correlations between
synergy and triad TE. This shows that computation was strongly, positively correlated with propaga-
tion across all networks. (C) Histogram of computation ratio values for all receivers in all networks.
(D) Histogram of log-scaled computation ratio values for all receivers in all networks. Gray lines
are replotted here from Figure 2 for ease of comparison. The blue line represents the distribution of
computation ratios that results from shuffling the alignment of triad synergy to TE. Thus, the span of
observed computation ratios is significantly smaller than what we might have observed by chance.
For C and D, Solid and dashed lines depict the medians across networks, and shaded regions depict
95% bootstrap confidence intervals around the medians.
Zs.r. = −3.2, n = 25 networks, p = 0.001; Figure 8C center), but not at the 3.5–14 ms timescale
(ρ = −0.26 [−0.69, 0.39], Zs.r. = −0.98, n = 25 networks, p = 0.33; Figure 8C right). This
negative correlation suggests that the computation ratio decreases at high levels of propaga-
tion at the shortest timescales. However, computation ratios were only slightly reduced (∼3%)
compared with the substantially greater computation values found in the rich club (∼160%),
thereby leaving rich clubs overall dense in computation (see Figure 10).
To demonstrate that the result of synergy in the rich club cannot be fully explained by a
simple correlation between incoming weight of the receiver and synergy, we asked if there was
greater synergy in the rich clubs after the correlation between connection strength and synergy
had been regressed out. To do this, we performed a regression between summed incoming
connection strength and synergy across triad receivers for a given network and then collected
the residual synergy for each triad after accounting for the summed incoming connections. We
then asked if the residual synergy values were still significantly greater in the rich club than
outside and found that they were (Zs.r. = 6.29, n = 75 networks, p = 3.24 × 10
−10).
Network Neuroscience
394
Computation in rich clubs
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
Figure 8. Rich-club membership is not strongly predictive of the ratio of computation to propa-
gation (computation ratio). (A) Mean computation ratio for triads with receivers inside versus out-
side the rich club at the 0.05–3 ms timescale (left), the 1.6–6.4 ms timescale (center), and the
3.5–14 ms timescale (right). (B) Computation ratio for triads with receivers inside versus outside the
rich club at all significant rich club levels (indicated by the yellow shaded region) at the 0.05–3 ms
timescale (left), the 1.6–6.4 ms timescale (center), and the 3.5–14 ms timescale (right). (C) Coefficient
distribution for correlations between mean computation ratio and normalized rich-club coefficient
at all richness levels, for each network, at the 0.05–3 ms timescale (left), the 1.6–6.4 ms timescale
(center), and the 3.5–14 ms timescale (right). Significance indicators: *p < 0.05.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Operationalization of Computation Was Not Critical for Present Results
To investigate whether our findings are robust to the method of quantifying computation, we
implemented two alternate methods of identifying computation to test if the same results were
obtained. In the first, we used an alternate implementation of partial information decompo-
sition (PID). Unlike the standard PID approach, which effectively computes the upper bound
on synergy (by assuming maximum redundancy between transmitters), this alternate imple-
mentation effectively computes the lower bound of synergy (by assuming no redundancy be-
tween transmitters). When using this approach, we find the same pattern of results. That is,
mean synergy-per-triad is significantly greater inside versus outside of the rich clubs (0.011
Network Neuroscience
395
Computation in rich clubs
−7; Supporting Information Figure S9,
vs. 0.006; Zs.r. = 5.14, n = 75 networks, p = 2.7 × 10
Faber et al., 2019), and computation is significantly, positively correlated with information
propagation (ρ = 0.57 [0.42, 0.61]; Zs.r. = 7.4, n = 75 networks, p = 7.59 × 10
−14).
Our second alternate method of identifying computation estimated the input-output trans-
fer functions of individual neurons as described by Chichilnisky ( 2001). In the prior analyses,
using PID, we took synergy as evidence of computation because it quantifies how much more
information is carried by multiple neurons when considered together than the sum of informa-
tion carried by the same neurons when considered individually. Similarly, in this analysis, we
took nonlinear input-output functions as evidence of computation because they indicate that
a neuron does not simply echo its inputs but, rather, responds based on patterns of upstream
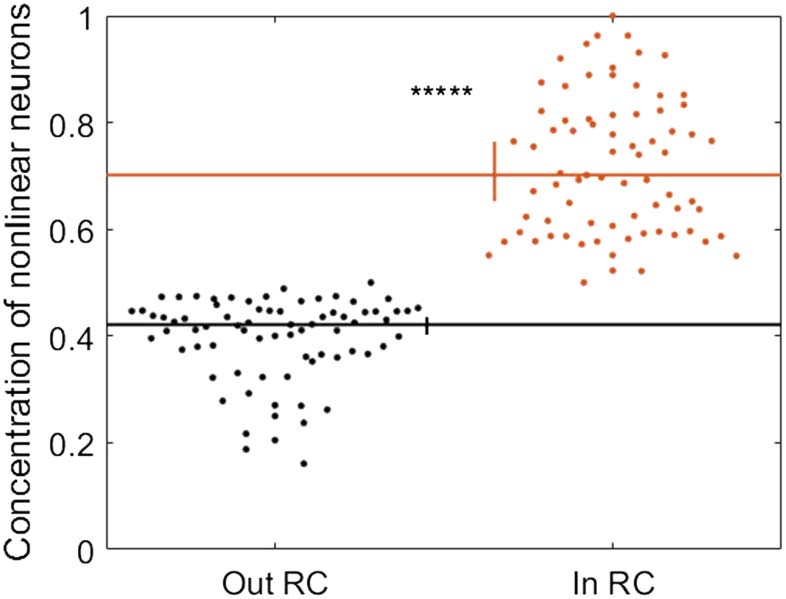
inputs. Accordingly, we performed a median split across neurons based on the linearity of their
estimated input-output functions. Those with the most nonlinear functions were identified as
neurons that likely perform more computation. Comparing this classification with the normal-
ized synergy values obtained via PID, we found that neurons with nonlinear transfer functions
were also found to have significantly greater amounts of synergy than those with linear transfer
−10). As such, use of
functions (0.109 vs. 0.034; Zs.r. = 6.22, n = 75 networks, p = 4.79 × 10
this classification regime provides an independent, yet related, approach to identifying com-
putation. Consistent with our main results, the concentration of neurons exhibiting nonlinear
transfer functions was significantly greater inside versus outside of the rich clubs (70.1% vs.
42.1%; Zs.r. = 7.47, n = 75 networks, p = 7.73 × 10
−14; Figure 9).
The information theoretic approaches used here to track computation and propagation by/to
a receiving neuron are designed to control for the ability of the receiver to account for its
own spiking before attributing variance to sending neurons by conditionalizing on the prior
state of the receiver. Defining the prior state of the receiver is a parameter-dependent process
(e.g., the duration and lag of a window in the past must be defined). Here, we used the same
window of time to define the past of the receiver as we do the sender. A concern with this
approach, however, is that we may be underestimating the information storage of the neuron
with use of short windows. To assess the influence this may have on our results, we repeated
our analysis with transmitter spike trains for which the timing of each spike was jittered by
a random amount drawn from a uniform distribution with a mean of zero and a width of
three times the duration of the past. This disrupts the short-term interactions but preserves the
Figure 9. Alternative measure of neural computation reveals results that correspond to those ob-
tained using PID. Neurons with nonlinear transfer functions are represented more inside rich clubs
than they are outside rich clubs. Significance indicators: *****p < 1 × 10
−9.
Network Neuroscience
396
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
long-term structure, effectively providing a null distribution of values that would be expected
given the long-term spiking dynamics alone. By subtracting these values from those obtained
from nonjittered spike trains, we were able to assess what effects these values may have had
on our findings. We found that after subtracting these residuals, all results held (Supporting
Information Figure S11, Faber et al., 2019).
DISCUSSION
Our goal in this work was to test the hypothesis that neural computation in cortical circuits
varies in a systematic fashion with respect to the functional organization of those circuits.
Specifically, we asked if neurons in rich clubs perform more computation than those outside of
the rich clubs. To answer this question, we recorded the spiking activity of hundreds of neurons
in organotypic cultures simultaneously and compared the information processing qualities of
individual neurons to their relative position in the broader functional network of the circuit. We
found that neurons in rich clubs computed ∼160% more than neurons outside of rich clubs.
The amount of computation that we found in the rich club was proportional to the amount of
information they propagate, suggesting that in these circuits, information propagation drives
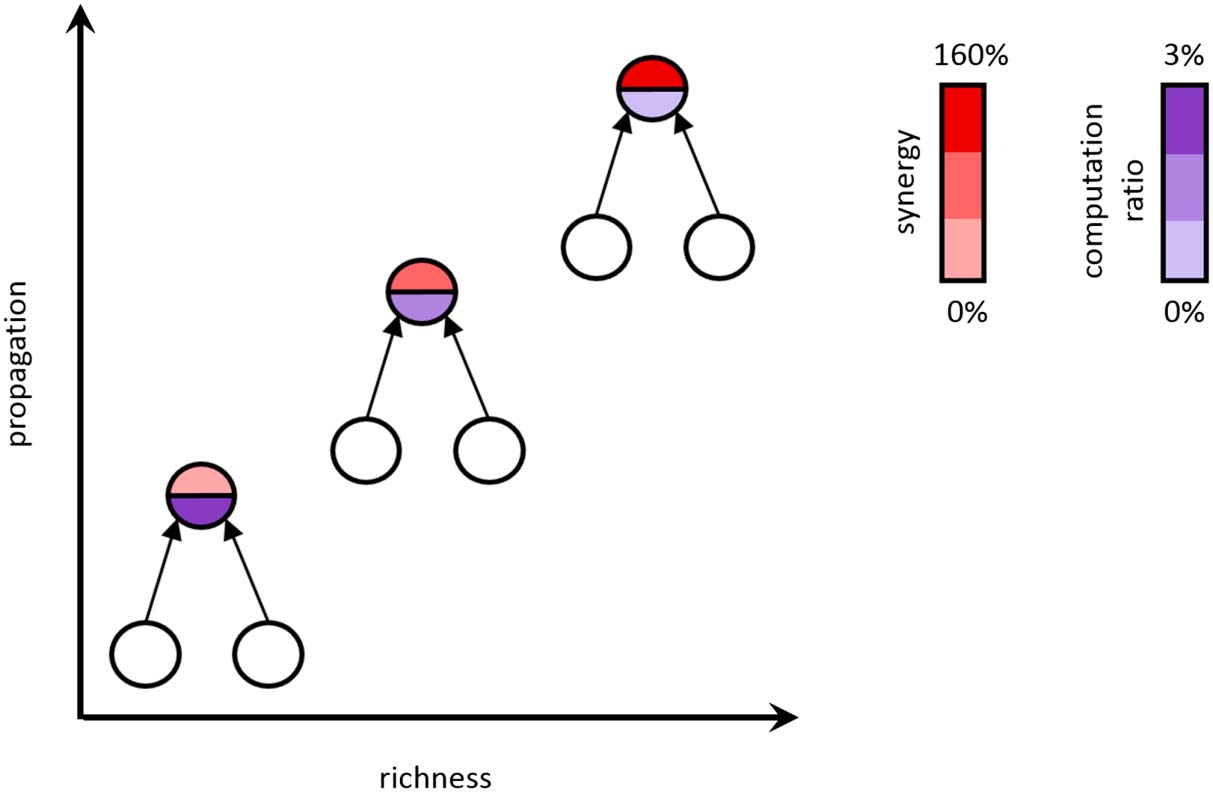
computation. These results are summarized in Figure 10.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Finding Computation in Organotypic Cortical Networks
What does it mean for organotypic cultures to process information? In a neural circuit that has
no clear sensory inputs, it is easy to imagine that all spiking is either spontaneous or in response
to upstream spontaneous spiking. Spontaneous spikes contribute to what, in an information
theoretic framework, is considered entropy. When the spiking of upstream neurons allows us
to predict future spiking, one colloquially says that those neurons carry information about
the future state of the circuit. This is technically accurate because that prediction effectively
reduces the uncertainty of the future state of the system. This is what TE, used in this work,
formally measures. The cause of the upstream spiking, whether spontaneous or sensory driven,
does not change this logic. As in systems with intact sensory inputs, the neurons in organotypic
cultures process information by integrating received synaptic inputs. Although we argue that in
Figure 10.
Summary of major findings. Synergy (computation) increases with propagation and node
richness by an average of 160%, and the computation ratio (amount of computation performed
relative to propagation) decreases by 3%.
Network Neuroscience
397
Computation in rich clubs
this respect information processing by organotypic cultures is like the cortical circuits of intact
animals, we recognize that important differences accompany the lack of true sensory input. For
example, the spatiotemporal structure of the spontaneous spiking that drives activity in cultures
is likely fundamentally different from that driven by sensory experience. Understanding how
that structure influences information processing will be important to investigate as technologies
enabling high temporal resolution recordings of hundreds of neurons in vivo mature.
With regard to building an understanding of the drivers of neural computation, the present
work substantially builds on previous work that showed that computation was positively cor-
related with the number of outgoing connections (i.e., out degree) of the upstream neurons
(Timme et al., 2016). Although the rich-club membership of those neurons was not analyzed,
it is reasonable to assume that neurons with high degree would be included in rich clubs. In
that respect, our findings are consistent with the previous report. The work of Timme et al.
( 2016), however, looked only at degree and did not analyze edge weights. Here, we found a
strong correlation between synergy and information propagation (i.e., summed edge weights
contributing to computation), indicating that computation is strongly dependent on weight.
This substantially alters our understanding of computation as it shows that beyond the pattern
of connections constituting a network, computation is sensitive to the quantity of the informa-
tion relayed across individual edges.
Rich Clubs as a Home for Computation
Prior work on rich clubs convincingly argued that rich clubs play a significant role in the rout-
ing of network information (van den Heuvel & Sporns, 2011; Harriger et al., 2012; van den
Heuvel et al., 2013; Nigam et al., 2016). For example, Nigam et al. ( 2016) showed, using the
same data, that the top 20% richest neurons transmit ∼70% of network information. Here,
we showed that information propagation is directly related to computation. Combining this
discovery with the previous knowledge that rich clubs perform large amounts of information
propagation accounts for the high densities of computation we observed in the cortical circuit
rich clubs. Although the precise mechanism of how computation is derived from propagation
is unknown, one possibility is that it is the result of what one might consider to be “informa-
tion collisions.” This idea is based on the finding of Lizier et al. ( 2010) who demonstrated that
the dominant form of information modification (i.e., computation) in cellular automata is the
result of collisions between the emergent particles (see also Adamatzky & Durand-Lose, 2012;
Bhattacharjee et al., 2016; Sarkar, 2000). In the context of our circuits, the idea is that com-
putation arises when packets of information embedded in the outgoing spike trains of sending
neurons collide onto the same receiving neuron in sufficient temporal proximity to alter the
way the receiver responds to those inputs. The density of propagating information in rich clubs
would proportionately increase the likelihood of such collisions, and thereby increase the
amount (and number) of computation(s) performed by the rich club (Flecker et al., 2011).
Operationalizing Information Computation and Propagation
Our primary analyses used synergy as a proxy for computation among triads consisting of a pair
of transmitting neurons and a single receiving neuron, following the methods of Timme et al.
( 2016). Synergy, as a measure of the information gained when the pair of transmitters is consid-
ered jointly over the combined information carried by the neurons individually, provides an
intuitively appealing measure of computation (see Timme et al., 2016, for a comprehensive
discussion of this relationship). Synergy is a product of partial information decomposition (PID)
(Williams & Beer, 2010). However, PID is not the only information theoretic tool available for
quantifying neural computation. Our use of PID was motivated by several factors: (a) it can
Network Neuroscience
398
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
detect linear and nonlinear interactions; (b) it is capable of measuring the amount of informa-
tion a neuron computes based on simultaneous inputs from other neurons; and (c) it is currently
the only method capable of quantifying how much computation occurs in an interaction in
which three variables predict a fourth as done here (the future state of the receiver is predicted
from the past state of the receiver and two other transmitters).
Concerns have been raised about how PID calculates the redundancy term in that it results
in an overestimation of redundancy and consequently, synergy (Bertschinger et al., 2014; Pica
et al., 2017). Here, we addressed this concern by demonstrating that an alternate implementa-
tion of PID that minimizes redundancy (and thus synergy) nonetheless yields the same pattern
of results. Going further, we also used a noninformation theoretic approach to identify neurons
that likely perform substantial computation by finding those neurons with nonlinear input-
output transfer functions, following the methods of Chichilnisky ( 2001). This, like our other
analyses, showed that the concentration of computation was greater inside of the rich clubs.
Our primary analyses used TE as a proxy for information propagation. A strength of TE is
that it makes it possible to quantify the mutual information between a sending and receiving
neuron after accounting for variance in the receiving neuron spiking that was predictable from
its prior state. However, the window used to define the prior state is parameter dependent (e.g.,
duration, lag from the present). Here, we defined this window so as to match the window that
was used to define the sender state (spanning 0.05–3 ms, 1.6–6.4 ms, or 3.5–14 ms for our three
timescales, respectively). By doing so, we maintain clear bounds on the timescale at which
the functional dynamics were analyzed (selected a priori to span timescales at which synaptic
communication occurs). A risk of using this window size, rather than a longer size, is that it
may underestimate the variance in the receiver spiking that can be accounted for by the prior
state of the receiver (i.e., without considering the sending neuron) and, thus, result in larger
propagation or synergy values. To assess the impact this may have had on our results, following
the precedent set by others (Dragoi & Buzsáki, 2006; Nigam et al., 2016) we performed a
control analysis in which we jittered the spiking at short time scales and quantified the residual
propagation and synergy. By subtracting these residual values from our original (nonjittered)
values, we were able to assess what effects these values may have had on our findings. We
found that after subtracting these residuals, all results held.
Organotypic Cultures as a Model System
The goal of the present work was to better understand information processing in local cortical
networks. To do this, we used a high-density 512-microelectrode array in combination with
organotypic cortical cultures. This approach allowed us to record spiking activity at a temporal
resolution (20 kHz; 50 microseconds) that matched typical synaptic delays in cortex (1–3 ms;
Mason et al., 1991). The short interelectrode spacing of 60 microns was within the range of
most monosynaptic connections in cortex (Song et al., 2005). This spacing means that the
spiking of most cells is picked up by multiple sites, and there are few gaps where cells are
too far from electrodes to be recorded. The large electrode count allowed us to simultane-
ously sample hundreds of neurons, revealing complex structures like the rich club. While the
cortical layers in organotypic cultures can differ in some respects from those seen in vivo
(Staal et al., 2011), organotypic cultures nevertheless exhibit very similar synaptic structure and
electrophysiological activity to that found in vivo (Caeser et al., 1989; Bolz et al., 1990; Götz
& Bolz, 1992; Plenz & Aertsen, 1996; Klostermann & Wahle, 1999; Ikegaya et al., 2004; Beggs
& Plenz, 2004). The distribution of firing rates in these cultures is lognormal, as seen in vivo
(Nigam et al., 2016), and the strengths of functional connections are lognormally distributed,
Network Neuroscience
399
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
similar to the distribution of synaptic strengths observed in patch clamp recordings (Song et al.,
2005, reviewed in Buzsáki & Mizuseki, 2014). These features suggested that organotypic cor-
tical cultures serve as a reasonable model system for exploring local cortical networks, while
offering an unprecedented combination of large neuron count, high temporal resolution, and
dense recording sites that cannot currently be matched with in vivo preparations.
Relevance to Cognitive Health
The increased computation in rich clubs described here may help to explain the functional
importance of rich clubs as well as the role of rich clubs in healthy neural functioning. Prior
work has shown that cognitively debilitating disorders, including Alzheimer’s disease, epilepsy,
and schizophrenia, are associated with diminished rich-club organization (van den Heuvel &
Sporns, 2011; van den Heuvel et al., 2013; Braun et al., 2015). An implication of our present
findings is that such diminished rich-club organization would lead to commensurately dimin-
ished neural computation. This could account for the impairments observed in such disorders
which include loss of memory, consciousness, or mental cohesiveness. Future studies should
make use of in vivo methods to explore the relationship between computation and behavior.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Conclusions
The present work demonstrates, for the first time, that synergy is significantly greater inside,
versus outside, of rich clubs. Given this, we conclude that rich clubs not only propagate a
large percentage of information within cortical circuits but are also home to a majority of
the circuit-wide computation. We also showed that computation was robustly correlated with
information propagation, from which we infer that computation is driven by information avail-
ability. Finally, we found that the ratio of computation to propagation was slightly, although
significantly, reduced in rich clubs, suggesting that cortical circuits, like human-engineered
distributed-computing architectures, may face a communication versus computation trade-off.
These results substantially increase what is known regarding computation by cortical circuits.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
MATERIALS AND METHODS
To answer the question of whether rich-club neurons perform more computation than do non-
rich-club neurons in cortical circuits, we combined network analysis with information theo-
retic tools to analyze the spiking activity of hundreds of neurons recorded from organotypic
cultures of mouse somatosensory cortex. Because of space limitations, here we provide an
overview of our methods and focus on those steps that are most relevant for interpreting our
results. A comprehensive description of all our methods can be found in the Supporting Infor-
mation (Faber et al., 2019). All procedures were performed in strict accordance to guidelines
from the National Institutes of Health and approved by the Animal Care and Use Committees
of Indiana University and the University of California, Santa Cruz.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Electrophysiological Recordings
All results reported here were derived from the analysis of electrophysiological recordings
of 25 organotypic cultures prepared from slices of mouse somatosensory cortex. One hour
long recordings were performed at 20 kHz by using a 512-channel array of 5-μm-diameter
electrodes arranged in a triangular lattice with an interelectrode distance of 60 μm (span-
ning approximately 0.9 mm by 1.9 mm). Once the data were collected, spikes were sorted
using a principal component analysis approach (Ito et al., 2014; Litke et al., 2004; Timme
Network Neuroscience
400
Computation in rich clubs
Effective connectivity:
Time-directed statistical
dependencies of one spiking
neuron on another.
et al., 2014) to form spike trains of between 98 and 594 (median = 310) well-isolated individ-
ual neurons, depending on the recording.
Network Construction
Networks of effective connectivity, representing global activity in recordings, were constructed
following Timme et al. ( 2014, 2016). Briefly, weighted effective connections between neurons
were established using transfer entropy (TE; Schreiber, 2000). We computed TE at timescales
spanning 0.05–14 ms to capture neuron interactions at timescales relevant to synaptic trans-
mission. This was discretized into three logarithmically spaced bins of 0.05–3 ms, 1.6–6.4 ms,
and 3.5–14 ms, and separate effective networks were constructed for each timescale, resulting
in three networks per recording (75 networks total). Only significant TE, determined through
comparison to the TE values obtained with jittered spike trains (α = 0.001; 5, 000 jitters), were
used in the construction of the networks. TE values were normalized by the total entropy of
the receiving neuron so as to reflect the percentage of the receiver neuron’s capacity that can
be accounted for by the transmitting neuron.
Quantifying Computation
Computation was operationalized as synergy, as calculated by the PID approach described by
Williams and Beer ( 2010, 2011). PID compares the measured TE between neurons TE(J → I)
and TE(K → I) with the measured multivariate TE between neurons TE({J, K} → I) to
estimate terms that reflect the unique information carried by each neuron, the redundancy
between neurons, and the synergy (i.e., gain over the sum of the parts) between neurons.
Redundancy was computed as per Supporting Information Equations S8–S10 (Faber et al.,
2019). Synergy was then computed via the following:
Synergy ({J, K} → I) = TE ({J, K} → I) − TE (J → I)
(1)
−TE (K → I) + Redundancy({J, K} → I)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
t
.
As with TE, synergy was normalized by the total entropy of the receiving neuron. Although
there are other methods for calculating synergy (Bertschinger et al., 2014; Pica et al., 2017;
Wibral et al., 2017; Lizier et al., 2018), we chose this measure because it is capable of detecting
linear and nonlinear interactions, and it is currently the only measure that has detailed how one
can quantify how much synergy occurs in an interaction in which three variables (here, receiver
past and pasts of the two transmitters) predict a fourth (receiver future). Note that we chose not
to consider higher order synergy terms, for systems with more than two transmitting neurons,
because of the increased computational burden it presented (the number of PID terms increases
rapidly as the number of variables increases). However, based on bounds calculated for the
highest order synergy term by Timme et al. ( 2016), it was determined that the information
gained by including an additional input beyond two either remained constant or decreased.
Thus, it was inferred that lower order (two-input) computations dominated.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Alternate Methods of Quantifying Computation
To establish that our results are not unique to our approach for quantifying computation, we
implemented two alternate methods. The first also uses PID but sets redundancy to be the
smallest possible value. Effectively, in this approach synergy is computed as follows:
Synergy ({J, K} → I) = argMax [ TE({J, K} → I) − TE (J → I) − TE (K → I) , 0 ]
(2)
Network Neuroscience
401
Computation in rich clubs
Consequently, synergy is minimized or set to zero when the sum of TE(J → I) and
TE(K → I) is greater than TE({J, K} → I). The second alternate method identifies neurons
that perform the most computation as those with nonlinear input-output transfer functions.
The transfer functions are calculated following the methods of Chichilnisky ( 2001). Briefly, for
each neuron, the pattern of inputs across neurons and time that drive the neuron to spike were
estimated using a spike triggered average (STA) of the state of all neurons over a 14-ms window
prior to each spike. The strength of input to that neuron over time was then estimated by con-
volving the STA with the time-varying state of the network. Finally, the input-output transfer
function was established by computing the probability that the neuron fired at each level of
input. We then fit both a line and a sigmoid to the resulting transfer function to extract the
summed squared error (SSE) that results from each. We categorized neurons with the lowest
SSE from the sigmoid fit relative to the SSE from the linear fit as the neurons that perform the
most computation.
Rich-Club Analyses
Weighted rich clubs were identified using a modified version of the rich_club_wd.m func-
tion from the Matlab Brain Connectivity toolbox (Rubinov & Sporns, 2010; van den Heuvel &
Sporns, 2011), adapted according to Opsahl et al. ( 2008) to compute rich clubs with weighted
richness parameter levels. To establish the significance of a rich club at a given threshold, we
computed the ratio between the observed rich-club coefficient and the distribution of those
observed when the edges of the network were shuffled. Shuffling was performed according to
the methods of Maslov and Sneppen ( 2002).
To test if synergy was greater for rich-club neurons, our first approach randomly selected
one of the thresholds—at which the rich club was identified as significant—separately for each
network and considered all neurons above that threshold to be in the rich club. Our second
approach swept across all possible thresholds, irrespective of the significance of the associated
rich club, to assess the influence of varying the “richness” of the neurons treated as if in the
rich club. The third approach asked if the results of the second approach were correlated with
the strength of the rich club, as quantified via the normalized rich-club coefficient, to assess
if the strength of the observed effects varied with how much stronger the rich club was than
expected by chance.
Statistics
All results are reported as medians followed by the 95% bootstrap confidence limits (computed
using 10,000 iterations), reported inside of square brackets. Similarly, the median is indicated in
figures and the vertical bar reflects the 95% bootstrap confidence limits. Comparisons between
conditions or against null models were performed using the nonparametric Wilcoxon signed-
rank test, unless specified otherwise. The threshold for significance was set at 0.05, unless
indicated otherwise in the text.
ACKNOWLEDGMENTS
We thank Olaf Sporns, Randy Beer, and Benjamin Dann for helpful comments and discussion.
AUTHOR CONTRIBUTIONS
Samantha P. Faber: Conceptualization; Formal analysis; Investigation; Methodology; Project
administration; Software; Validation; Visualization; Writing – original draft; Writing – review &
editing. Nicholas M. Timme: Data curation; Formal analysis; Methodology; Resources;
Network Neuroscience
402
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
Software; Supervision; Writing – review & editing. John M. Beggs: Conceptualization; Data
curation; Funding acquisition; Investigation; Methodology; Project administration; Resources;
Software; Supervision; Validation; Writing – review & editing. Ehren L. Newman: Concep-
Investigation; Methodology; Project
tualization; Formal analysis; Funding acquisition;
administration; Resources; Supervision; Validation; Visualization; Writing – original draft;
Writing – review & editing.
FUNDING INFORMATION
Ehren L. Newman, Whitehall Foundation (http://dx.doi.org/10.13039/100001391), Award
ID: 17-12-114. John M. Beggs, National Science Foundation (http://dx.doi.org/10.13039/
100000001), Award ID: 1429500. John M. Beggs, National Science Foundation (http://dx.doi.
org/10.13039/100000001), Award ID: 1513779. Samantha P. Faber, National Science Founda-
tion (http://dx.doi.org/10.13039/100000001), Award ID: 1735095; Samantha P. Faber, Indiana
Space Grant Consortium.
REFERENCES
Adamatzky, A., & Durand-Lose, J. (2012). Collision-based comput-
ing In G. Rozenberg, T. Bäck, & J. N. Kok (Eds.), Handbook of
Natural Computing (pp. 1949–1978). Berlin: Springer.
Beggs, J. M., & Plenz, D. (2004). Neuronal avalanches are diverse
and precise activity patterns that are stable for many hours in cor-
tical slice cultures. Journal of Neuroscience, 24, 5216–5229.
Bertschinger, N., Rauh, J., Olbrich, E., Jost, J., & Ay, N. (2014).
Quantifying unique information. Entropy, 16(4), 2161–2183.
Bhattacharjee, K., Naskar, N., Roy, S., & Das, S. (2016). A survey of
cellular automata: Types, dynamics, non-uniformity and applica-
tions. arXiv:1607.02291.
Bolz, J., Novak, N., Götz, M., & Bonhoeffer, T. (1990). Formation of
target-specific neuronal projections in organotypic slice cultures
from rat visual cortex. Nature, 346, 359–362.
Borst, A., & Theunissen, F. (1999). Information theory and neural
coding. Nature Neuroscience, 2, 947–957.
Braun, U., Muldoon, S. F., & Bassett, D. S. (2015). On human brain
networks in health and disease. eLS. Chichester, UK: John Wiley
& Sons.
Buzsáki, G., & Mizuseki, K. (2014). The log-dynamic brain: how
skewed distributions affect network operations. Nature Reviews
Neuroscience, 15, 264–278.
Caeser, M., Bonhoeffer, T., & Bolz, J. (1989). Cellular organization
and development of slice cultures from rat visual cortex. Experi-
mental Brain Research, 77, 234–244.
Chichilnisky, E. J. (2001). A simple white noise analysis of neuronal
light responses. Network: Computation in Neural Systems, 12(2),
199–213.
Dragoi, G., & Buzsáki, G. (2006). Temporal encoding of place se-
quences by hippocampal cell assemblies. Neuron, 50(1), 145–157.
Faber, S. P., Timme, N. M., Beggs, J. M., & Newman, E. L. (2019).
Supporting information for “Computation is concentrated in rich
clubs of local cortical networks.” Network Neuroscience, 3(2),
384–404. https://doi.org/10.1162/netn_a_00069
Flecker, B., Alford, W., Beggs, J. M., Williams, P. L., & Beer, R. D.
(2011). Partial information decomposition as a spatiotemporal
filter. Chaos, 21(3), 037104.
Götz, M., & Bolz, J. (1992). Formation and preservation of cortical
layers in slice cultures. Journal of Neurobiology, 23, 783–802.
Harriger, L., van den Heuvel, M. P., & Sporns, O. (2012). Rich club
organization of macaque cerebral cortex and its role in network
communication. PLoS One, 7(9), e46497.
Ikegaya, Y., Aaron, G., Cossart, R., Aronov, D., Lampl, I., Ferster, D.,
& Yuste, R. (2004). Synfire chains and cortical songs: Temporal
modules of cortical activity. Science, 304, 559–564.
Ikegaya, Y., Sasaki, T., Ishikawa, D., Honma, N., Tao, K., Takahashi,
N., . . . Matsuki, N. (2012). Interpyramid spike transmission stabi-
lizes the sparseness of recurrent network activity. Cerebral Cortex,
23, 293–304.
Ito, S., Yeh, F. C., Hiolski, E., Rydygier, P., Gunning, D. E., Hottowy,
P., . . . Beggs, J. M. (2014). Large-scale, high-resolution multi-
electrode- array recording depicts functional network differences
of cortical and hippocampal cultures. PLoS One, 9, e105324.
Klostermann, O., & Wahle, P. (1999). Patterns of spontaneous ac-
tivity and morphology of interneuron types in organotypic cortex
and thalamus-cortex cultures. Neuroscience, 92, 1243–1259.
Lefort, S., Tomm, C., Floyd Sarria, J. C., & Petersen, C. C. H. (2009).
The excitatory neuronal network of the c2 barrel column in
mouse primary somatosensory cortex. Neuron, 61, 301–316.
Litke, A., Bezayiff, N., Chichilnisky, E., Cunningham, W., Dabrowski,
W., Grillo, A., . . . Kachiguine, S. (2004). What does the eye tell
the brain? Development of a system for the large-scale recording
of retinal output activity. IEEE Transactions on Nuclear Science,
51, 1434–1440.
Lizier, J. T., Prokopenko, M., & Zomaya, A. Y. (2010). Information
modifications and particle collisions in distributed computation.
Chaos, 20(3), 037109.
Lizier, J. T., Bertschinger, N., Jost, J., & Wibral, M. (2018). Information
decomposition of target effects from multi-source interactions: Per-
spectives on previous, current and future work. Entropy, 20(4), 307.
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topol-
ogy of protein networks. Science, 296, 910–913.
Mason, A., Nicoll, A., & Stratford, K. (1991). Synaptic transmission
between individual pyramidal neurons of the rat visual cortex
in vitro. Journal of Neuroscience, 11, 72–84.
Network Neuroscience
403
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Computation in rich clubs
Nigam, S., Shimono, M.,
Ito, S., Yeh, F. C., Timme, N.,
Myroshnychenko, M., Beggs, J. M. (2016). Rich-club organiza-
tion in effective connectivity among cortical neurons. Journal of
Neuroscience, 36(4), 670–684.
Opsahl, T., Colizza, V., Panzarasa, P., & Ramasco, J. J. (2008).
Prominence and control: The weighted rich-club effect. Physical
Review Letters, 101, 168702.
Pica, G., Piasini, E., Chicharro, D., & Panzeri, S. (2017). Invari-
ant components of synergy, redundancy, and unique information
among three variables. Entropy, 19(9), 451.
Plenz, D., & Aertsen, A. (1996). Neural dynamics in cortex-striatum
co-cultures—II. Spatiotemporal characteristics of neuronal activ-
ity. Neuroscience, 70, 893–924.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52,
1059–1069.
Sarkar, P. (2000). A brief history of cellular automata. ACM Com-
puting Surveys, 32(1), 80–107.
Schreiber, T. (2000). Measuring information transfer. Physical Re-
view Letters, 85, 461–464.
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., & Chklovskii, D. B.
(2005). Highly non-random features of synaptic connectivity in
local cortical circuits. PLoS Biology, 3, e68.
Staal, J. A., Alexander, S. R., Liu, Y., Dickson, T. D., & Vickers, J. C.
(2011). Characterization of cortical neuronal and glial alterations
during culture of organotypic whole brain slices from neonatal
and mature mice. PLoS One, 6, e22040.
Strong, S. P., Koberle, R., de Ruyter van Steveninck, R. R., & Bialek,
W. (1998). Entropy and information in neural spike trains. Phys-
ical Review Letters, 80(1), 197–200.
Swadlow, H. A.
(1994). Efferent neurons and suspected inter-
neurons in motor cortex of the awake rabbit: Axonal properties,
sensory receptive fields, and subthreshold synaptic inputs. Journal
of Neurophysiology, 71, 437–453.
Tang, A., Jackson, D., Hobbs, J., Chen, W., Smith, J. L., Patel, H.,
. . . Beggs, J. M. (2008). A maximum entropy model applied to
spatial and temporal correlations from cortical networks in vitro.
Journal of Neuroscience, 28, 505–518.
Timme, N. M., Ito, S., Myroshnychenko, M., Yeh, F. C., Hiolski, E.,
Litke, A. M., & Beggs, J. M. (2014). Multiplex networks of cortical
and hippocampal neurons revealed at different timescales. PLoS
One, 9, e115764.
Timme, N. M., Ito, S., Myroshnychenko, M., Nigam, S., Shimono, M.,
Yeh, F.-C., . . . Beggs, J. M. (2016). High-degree neurons feed cor-
tical computations. PLoS Computational Biology, 12(5), e1004858.
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza-
tion of the human connectome. Journal of Neuroscience, 31(44),
15775–15786.
van den Heuvel, M. P., Sporns, O., Collin, G., Scheewe, T., Mandl,
R. C., Cahn, W., . . . Kahn, R. S. (2013). Abnormal rich club
organization and functional brain dynamics in schizophrenia.
JAMA Psychiatry, 70(8), 783–792.
Wibral, M., Priesemann, V., Kay, J. W., Lizier, J. T., & Phillips, W. A.
(2017). Partial information decomposition as a unified approach
to the specification of neural goal functions. Brain and Cognition,
112, 25–38.
Williams, P. L., & Beer, R. D. (2010). Nonnegative decomposition
of multivariate information. arXiv, 1004, 2515.
Williams, P. L., & Beer, R. D. (2011). Generalized measures of
information transfer. arXiv, 1102, 1507.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
2
3
8
4
1
0
9
2
5
7
8
n
e
n
_
a
_
0
0
0
6
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
404