FORSCHUNG - Am MIT spezialisierte KI-Forschung

FORSCHUNG

High-resolution data-driven model
of the mouse connectome

Joseph E. Knox1,2, Kameron Decker Harris

Hongkui Zeng

1, Julie A. Harris1, Eric Shea-Brown 1,2, and Stefan Mihalas

2,3, Nile Graddis1, Jennifer D. Whitesell
1,2

1Allen Institute for Brain Science, Seattle, Washington, USA
2Applied Mathematics, Universität Washington, Seattle, Washington, USA
3Computer Science and Engineering, Universität Washington, Seattle, Washington, USA

Schlüsselwörter: Connectome, Whole-brain, Mouse

Keine offenen Zugänge

Tagebuch

ABSTRAKT

Knowledge of mesoscopic brain connectivity is important for understanding inter- Und
intraregion information processing. Models of structural connectivity are typically
constructed and analyzed with the assumption that regions are homogeneous. We instead
use the Allen Mouse Brain Connectivity Atlas to construct a model of whole-brain
connectivity at the scale of 100 µm voxels. The data consist of 428 anterograde tracing
experiments in wild type C57BL/6J mice, mapping ﬂuorescently labeled neuronal
projections brain-wide. Inferring spatial connectivity with this dataset is underdetermined,
since the approximately 2 × 105 source voxels outnumber the number of experiments.
To address this issue, we assume that connection patterns and strengths vary smoothly
across major brain divisions. We model the connectivity at each voxel as a radial basis
kernel-weighted average of the projection patterns of nearby injections. The voxel model
outperforms a previous regional model in predicting held-out experiments and compared
with a human-curated dataset. This voxel-scale model of the mouse connectome permits
researchers to extend their previous analyses of structural connectivity to much higher
levels of resolution, and it allows for comparison with functional imaging and other datasets.

ZUSAMMENFASSUNG DES AUTORS

Anatomical tracing experiments can provide a wealth of information regarding connectivities
originating from the injection sites. Jedoch, it is difﬁcult to integrate all this information
into a comprehensive connectivity model. In this study we construct a high-resolution model
of the mouse brain connectome using the assumption that connectivity patterns vary
smoothly within brain regions, and we present several extensions of this model. We believe
that this higher resolution connectome will be of great use to the community, enabling
comparisons with other data modalities, such as functional imaging and gene expression,
as well as for theoretical studies.

EINFÜHRUNG

Brain network structure, across many spatial scales, plays an important role in facilitating and
constraining neural computations. Models of structural connectivity have been used to inves-
tigate the relationship with functional connectivity, to compare brain structures across species,
and more (Laramée & Boire, 2015; Sethi, Zerbi, Wenderoth, Fornito, & Fulcher, 2017; Stafford
et al., 2014; X.-J. Wang & Kennedy, 2016). Jedoch, most of our knowledge of neuronal
network connectivity is limited to either a detailed description of small systems (Bock et al.,

Zitat: Knox, J. E., Harris, K. D.,
Graddis, N., Whitesell, J. D., Zeng, H.,
Harris, J. A., Shea-Brown, E., &
Mihalas, S. (2019). High-resolution
data-driven model of the mouse
connectome. Netzwerkneurowissenschaften,
3(1), 217–236. https://doi.org/
10.1162/netn_a_00066

DOI:
https://doi.org/10.1162/netn_a_00066

zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00066
https://github.com/AllenInstitute/
mouse_connectivity_models

Erhalten: 4 April 2018
Akzeptiert: 31 Juli 2018

Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.

Corresponding Authors:
Kameron Decker Harris
kamdh@uw.edu
Stefan Mihalas
stefanm@alleninstitute.org

Handling-Editor:
Marcus Kaiser

Urheberrechte ©: © 2018
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz

Die MIT-Presse

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

2011; Glickfeld, Andermann, Bonin, & Reid, 2013; Kleinfeld et al., 2011; White, Southgate,
Thomson, & Brenner, 1986) or a coarse description of connectivity between larger regions
(Felleman & Van Essen, 1991; Spurns, 2010). In between these two extremes is mesoscopic
structural connectivity: a coarser scale than that of single neurons or cortical columns but
ﬁner than whole-brain regions (Bohland et al., 2009). Facilitated by new tracing techniques,
image-processing algorithms, and high-throughput methods, mesoscale data with partial to full
brain coverage exist in animals such as the ﬂy (Jenett et al., 2012; Shih et al., 2015) and mouse
(G˘am˘anu¸t et al., 2018; Oh et al., 2014; Zingg et al., 2014), and such data are being collected
from other model organisms such as rat (Bota, Dong, & Swanson, 2003) and marmoset (Majka
et al., 2016).

We present a scalable regression technique for constructing spatially explicit mesoscale
connectivity from anterograde tracing experiments. Konkret, our model estimates the pro-
jection strength between every pair of approximately 2 × 105 cubic voxels, jede 100 µm wide,
in the Allen Mouse Brain Common Coordinate Framework (CCF v3). The CCF is a fully an-
notated reference atlas space with structure/region delineations. We use data from the Allen
Mouse Brain Connectivity Atlas (Oh et al., 2014), a large dataset of viral tract-tracing exper-
iments performed across many regions of the mouse brain. All of the data processing scripts
are publicly available at https://github.com/AllenInstitute/mouse_connectivity_models (Knox,
2018).

In these mesoscale anterograde tracing experiments, a tracer virus (recombinant adeno-
associated virus) is ﬁrst injected into the brain. The virus infects neurons at the site of injection
and causes them to express enhanced green ﬂuorescent protein (eGFP) in their cytoplasm,
including throughout the entire length of their axons. Brains and labeled axons are imaged
with blockface serial two-photon tomography (Ragan et al., 2012) throughout the entire rostral-
to-caudal extent of the brain, resulting in an aligned stack of 2-D images that can easily be
transformed to 3-D space. Each brain contains one source injection only. Every image series
is registered to the 3-D CCF, using a combination of global afﬁne and local transformations
(Kuan et al., 2015).

Combining many experiments with different injection sources in the same 3-D space re-
veals the set of pathways that connect those sources throughout the brain, the ingredients of a
“connectome.” This requires combining data across multiple animals, which appears justiﬁed
at the mesoscale (Bohland et al., 2009; Oh et al., 2014). Previous mouse connectome models
were constructed with the assumption that regions are homogeneous (G˘am˘anu¸t et al., 2018;
Oh et al., 2014; Ypma & Bullmore, 2016). While these have proven useful, they depend on
predeﬁned regional parcellations and describe connectivity at a region-limited level of reso-
lution. Hier, we go beyond the regional approach and construct a model of the whole-brain
connectivity at the scale of 100 µm voxels. Previously, K. D. Harris, Mihalas, and Shea-Brown
(2016) formulated a regularized, structured regression problem for inferring voxel connectiv-
ität. This model was applied to Allen Mouse Brain Connectivity Atlas data in the visual cortex,
outperforming a regional model in prediction of held-out experiments.

Hier, we extend the voxel approach from the visual cortex to the full mouse brain, while
also simplifying the mathematical model for computational efﬁciency. Our model relaxes the
assumption of homogeneity of connections within a region and instead assumes smoothness
across major brain divisions. We model the connectivity at each source voxel as the weighted
average of the projection patterns of nearby injections, where the weights are a monotonically
decreasing nonlinear function of distance to the injection centroid. We ﬁt the parameters of

218

Voxel:
A 3-D cubic volume element;
the generalization of a pixel.

Major brain divisions:
The set of 12 major brain divisions
from the 3-D Allen Mouse Brain
Reference Atlas: isocortex, olfactory,
Bereiche, hippocampus, cortical
subplate, striatum, pallidum,
thalamus, hypothalamus, midbrain,
pons, medulla, and cerebellum
(also called coarse structures).

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

Connection strength:
The sum of the connection weights
from all voxels in a source region R
to all voxels in a target region R
denoted WR
21.

Coarse structures:
See major brain divisions.

the model using nested cross-validation with held-out injection experiments. The new voxel-
scale model generally outpredicts a homogeneous regional model, as measured both by
cross-validation error and when compared with a human-curated dataset.

ERGEBNISSE

Spatial Method to Infer a Voxel Connectome

We consider the problem of ﬁtting a weighted, gerichtet, adjacency matrix that contains the
connection strength between any pair of points in the brain. We use n cubic voxels, 100 µm
across, to discretize the brain volume. Our goal is then to ﬁnd a matrix W ∈ Rn×n
that ac-
≥0
curately captures voxel-voxel connection strength. We assume there exists some underlying
matrix W that is common across animals. Each experiment can be thought of as an injection
X, and its projections Y, where X, Y ∈ Rn
, and we want to ﬁnd W so that Y ≈ WX, das ist,
we want to solve a multivariate regression problem. The details of all procedures are found in
Methoden.

:,i and W

We adopt a spatial weighting technique to combine information from multiple experiments
into one matrix, the outline of which is shown in Figure 1. As in K. D. Harris et al. (2016),
we assume that the connectivity from any given source voxel varies smoothly as a function
of distance: Columns W
:,j should be similar if the distance between voxels i and
j is small. We make the mathematically simplifying assumption that the projections we ob-
serve from a given experiment come from the center of mass of the injection ce. This allows
us to employ kernel regression to approximate the connectivity from a given voxel v as the
distance-weighted sum of injections in the major brain division containing v. We also expect
the connectivity could change sharply between the boundaries of high-level brain structures.
Zum Beispiel, we know that projections arising from the thalamus and hypothalamus can be
very different, even though some areas within these divisions are near each other at the borders.
To account for this, we chose a partition of the brain into 12 nonoverlapping major brain divi-
sions or coarse structures deﬁned in the CCF. The major brain divisions are isocortex, olfactory
Bereiche, hippocampal formation, cortical subplate, striatum, pallidum, thalamus, hypothalamus,
midbrain, pons, medulla, and cerebellum.

Voxel-Scale Model Compared With a Regionally Homogeneous Model

Previously, Oh et al. (2014) obtained a regional mouse connectome by integrating the injection
and projection data over regions and ﬁtting a region-by-region matrix with nonnegative least
squares. Hier, we recomputed this matrix (see Methods) and compared it with a regionalized

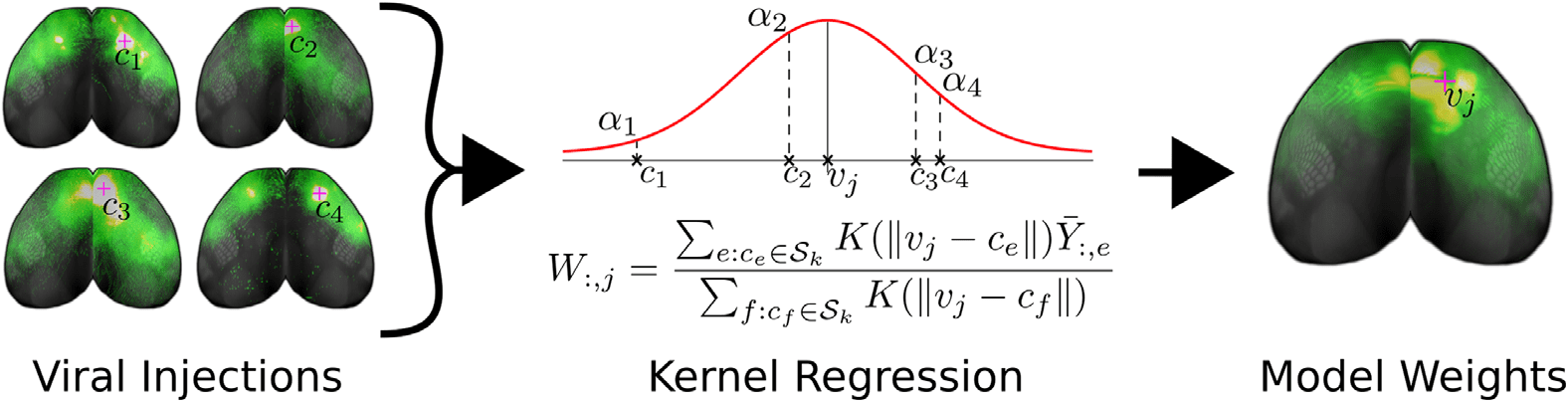
Figur 1. Cartoon illustrating our method of connectome inference. We combine the information
from viral tracing experiments with different injection sites into a model of voxel structural con-
nectivity. To predict the weight of projections Wij from the jth voxel vj to the ith voxel, we take
an average of nearby injections where the eth experiment’s projection ¯Yie is weighted by a factor
proportional to K((cid:5)vj − ce(cid:5)), ce is that injection’s center of mass, and K(·) is the kernel.

Netzwerkneurowissenschaften

219

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

Regions:
The set of 291 intermediate brain
structures from 3-D Allen Mouse
Brain Reference Atlas (also called
summary structures).

version of the voxel connectivity. To avoid confusion between the two models, we call the
regional connectome the homogeneous model, because it assumes homogeneity across ana-
tomical structures. We call our new model, when it has been averaged over regions, Die
regionalized voxel model. Zusamenfassend, wir haben uns entschieden 291 gray matter regions, which are interme-
diate level in the CCF, and recomputed the homogeneous model. The abbreviations of all
CCF regions mentioned in this paper are given in Table S1 (Knox et al., 2019). To generate
the regionalized voxel model, voxel connectivity was integrated and averaged over regions to
produce regionalized weights (see Methods for details).

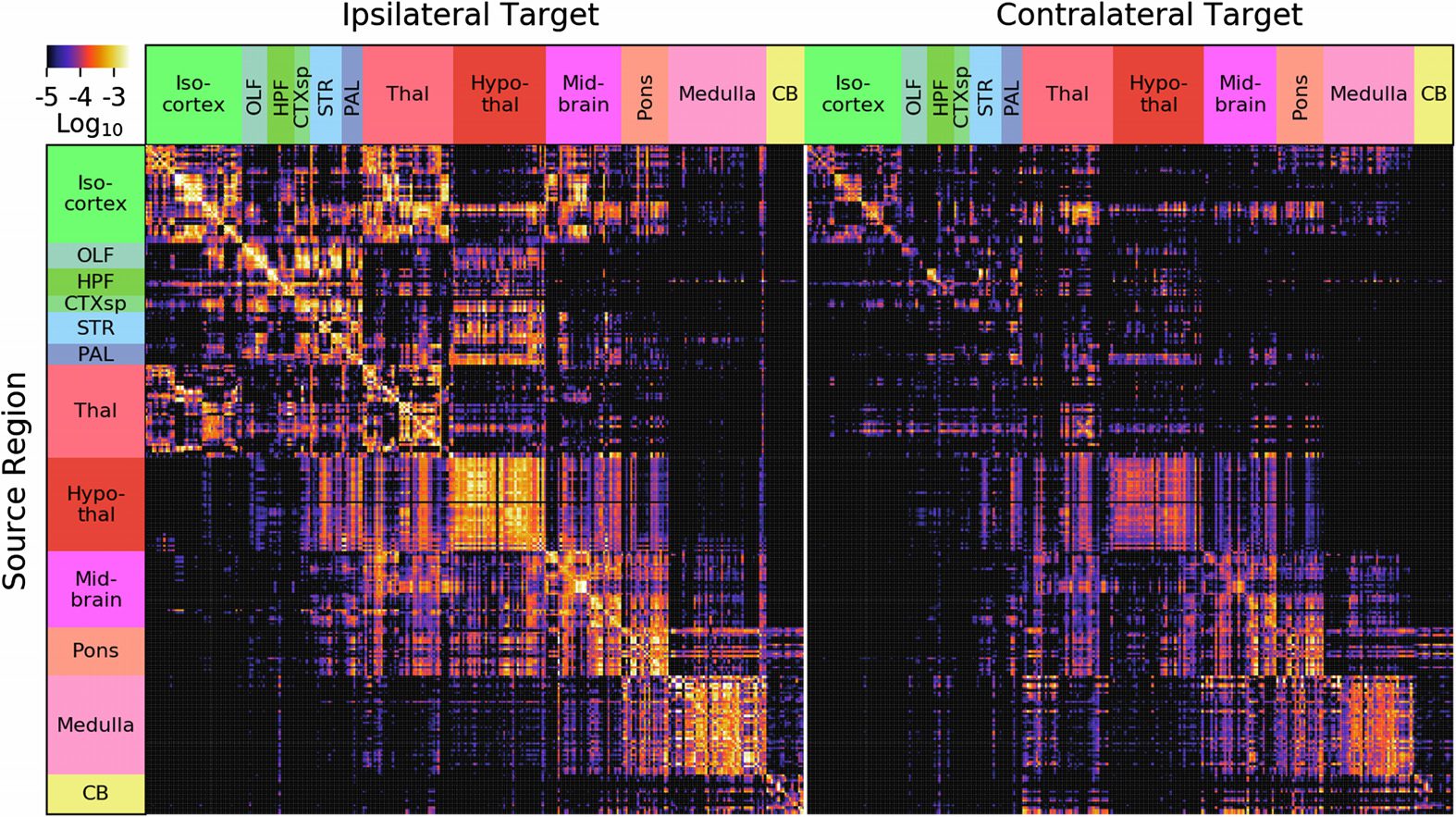
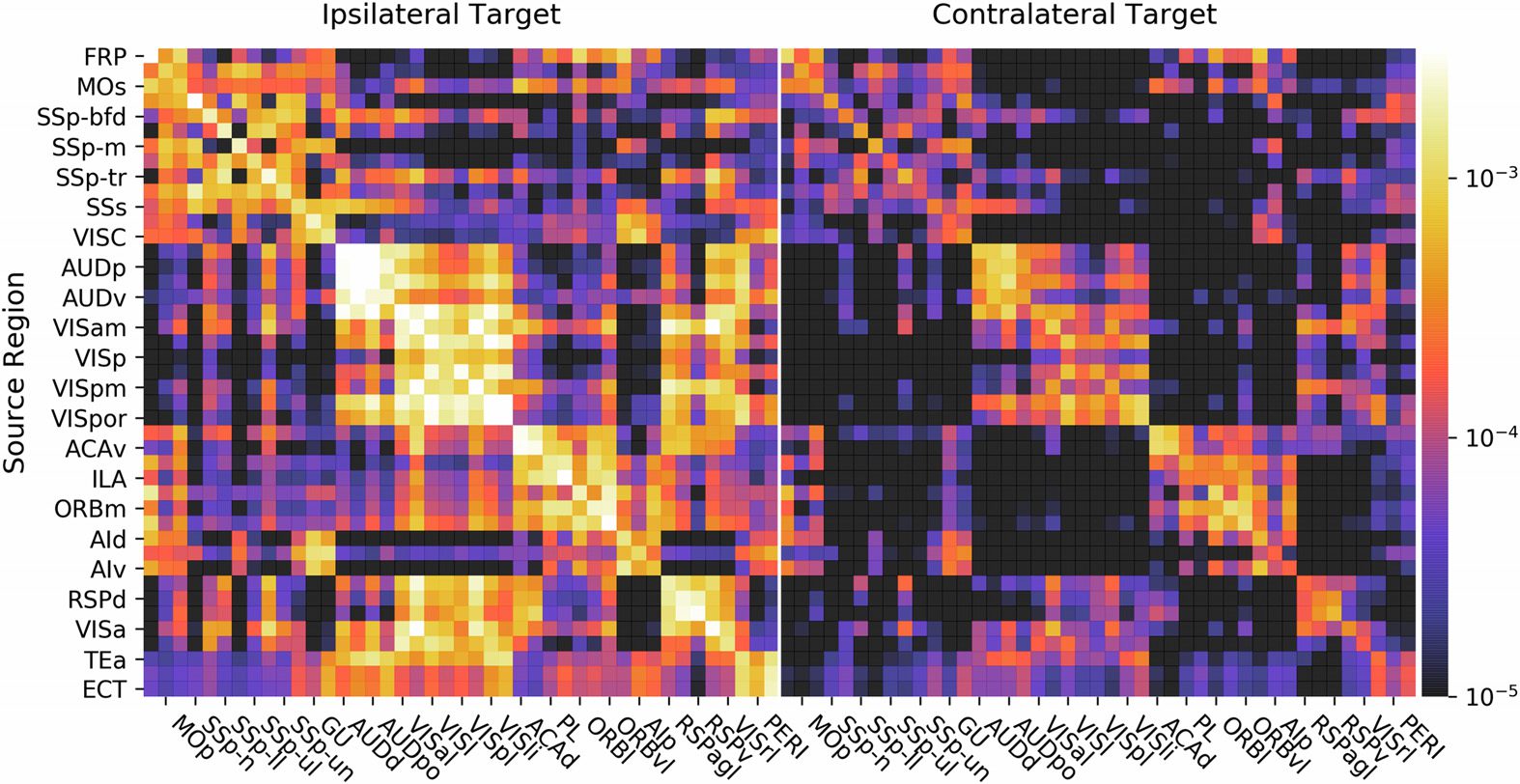
In Abbildung 2, there is a depiction of the whole-brain regionalized weights and, in Abbildung 3,
the regionalized weights for isocortex. Beachten Sie, dass, for visualization purposes, we depict sources
as rows and targets as columns (W(cid:2)

), the opposite of our mathematical convention.

A number of features are evident in Figures 2 Und 3. Erste, there are patterns that arise from
our smoothness assumption. The predicted projection patterns from a certain source voxel are
distance-weighted averages of injections nearby that voxel (see Methods and Figure 1). Dort-
Vordergrund, the method we employ smooths in the source space only. The vertical banded structures
(Zum Beispiel, the column near the right side of the medulla division in Figure 2) are due to
smoothing in source but not target regions, which makes the rows of W(cid:2)
corresponding to
nearby source voxels similar. In Abbildung 3, note that the rows PERI, ECT, and TEa (the bottom
three rows) and AUDv (upper middle) match closely. All four of these regions are very close
to each other on the posterior, ventrolateral part of the cortex, so that smoothing causes them
to be correlated. Also notice that, while the rows corresponding to these regions as sources
are very similar, the columns corresponding are not nearly as much so. This highlights that our
model interpolates only in the sources and not the targets.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 2. Whole-brain normalized connection density obtained from the regionalized voxel
Modell. We show 291 gray matter regions divided into 12 major brain divisions. For visualization
Zwecke, sources are shown on the rows and targets on the columns, the opposite convention as the
mathematics in the text (W(cid:2)
is pictured). The similarity between rows, for example in hypothalamus,
is driven both by biological similarity and as a result of the model’s interpolation in the sources. Der
similarity between columns is the result of correlations in the data, as the model does not interpolate
in target space.

Normalized connection density:
The connection strength from R
R

2 divided by the product of their

1 Zu

sizes:

WR
|R1||R2| .
21

Netzwerkneurowissenschaften

220

High-resolution model of the mouse connectome

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 3.
show sources as rows and targets as columns (W(cid:2)

Isocortex normalized connection density from the regionalized voxel model. Wieder, Wir

is pictured) for visualization.

The second feature that is evident is the presence of blocks of strongly interconnected re-
gions. These correspond to modules in the network, or regions that are more highly connected
to each other than they are to the rest of the network. This is explored further in J. A. Harris
et al. (2018).

In Table 1, we show the results of comparing homogeneous and voxel models. We ﬁt the
models using nested leave-one-out cross-validation. This allows us to evaluate both the voxel-
scale and regionalized models’ error when predicting held-out data. We report mean squared
error relative to the average squared norm of the prediction and data, which can be between
0 Und 200%. See Equation 4 and the description in the Methods. The model validation and
training errors (goodness of ﬁt, shown in parentheses) are reported at both voxel (Voxel MSErel)
and regional (Region MSErel) levels. Zusätzlich, we compare model performance using a
subset of experiments in which a given source region received at least three replicate injections.
Without another injection, the only information about that region’s projections would come
from our smoothness assumption interpolating nearby regions’ patterns. The computed relative
error MSErel for this dataset of replicated injections we call the “power to predict” (Region PTP),
and it tends to be lower than Region MSErel across divisions.

From Table 1, we see that the relative training and validation errors are higher when evalu-
ating error in the voxel space. This makes sense, because this error captures mistakes we make
in predicting spatial patterns of projections at the voxel, subregional level. That task is much
more difﬁcult than predicting regional patterns. The lowest voxel errors are in isocortex, hy-
pothalamus, and olfactory areas, whereas the highest are in cerebellum, thalamus, and cortical
subplate. At the regional level we compare both the homogeneous model and the regionalized
voxel model, which uses the voxel connectome to make a prediction that is then integrated
across each region. At the regional level, our voxel model has lower regional validation errors
than the homogeneous model in 11/12 major brain divisions. The training error is lower in 7/12
Fälle, since assuming smoothness is less biased than regional homogeneity. The regional PTP
of the voxel model is lower than the PTP of the homogeneous model in 10/12 Fälle. Ergebnisse
for training PTP are better for the regionalized model in 6/12.

Netzwerkneurowissenschaften

221

High-resolution model of the mouse connectome

Tisch 1. Table of cross-validated model errors, comparing the voxel model and the regionally
homogeneous model. In each case the training error is in parentheses. Voxel MSErel refers to relative
Fehler, Gleichung 4, at the voxel level. This measure approximates the data normalized MSE for small
= 200%, which is achieved if either Ytrue or Ypred is
Fehler, but is bounded to maximum of MSErel
0 and the other is not (see Methods). Region MSErel is the error found after regionalizing the voxel
model prediction. PTP (“power to predict”) computes MSErel for only those held-out experiments
where there was another injection in that region which was not used for ﬁtting.

Major division

Modell

Isocortex

Olfactory areas

Hippocampus

Cortical subplate

Striatum

Pallidum

Thalamus

Hypothalamus

Midbrain

Pons

Medulla

Kleinhirn

Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous
Voxel
Homogeneous

Voxel MSErel
66%
–
82%
–
92%
–
114%
–
103%
–
100%
–
115%
–
69%
–
89%
–
98%
–
96%
–
177%
–

(22%)
–
(17%)
–
(20%)
–
(40%)
–
(8%)
–
(5%)
–
(14%)
–
(46%)
–
(32%)
–
(9%)
–
(33%)
–
(9%)
–

Region MSErel
(11%)
34%
(20%)
37%
(6%)
41%
(9%)
50%
(17%)
56%
(51%)
46%
(47%)
95%
(2%)
111%
(2%)
45%
(23%)
53%
(3%)
64%
(3%)
85%
(10%)
77%
(12%)
92%
(32%)
48%
(5%)
62%
(14%)
42%
(14%)
44%
(6%)
66%
(27%)
89%
(18%)
51%
(3%)
58%
(2%)
78%
(4%)
90%

Region PTP

32%
33%
40%
44%
52%
48%
93%
99%
40%
53%
45%
74%
70%
86%
37%
77%
37%
39%
61%
87%
49%
54%
75%
63%

(9%)
(17%)
(6%)
(9%)
(17%)
(51%)
(25%)
(2%)
(1%)
(24%)
(7%)
(2%)
(12%)
(12%)
(9%)
(7%)
(13%)
(14%)
(6%)
(27%)
(21%)
(2%)
(7%)
(5%)

Allgemein, we ﬁnd the highest errors (for either model) in cortical subplate, which is the
smallest major division and has the largest distance between injections. The voxel and regional
test errors are correlated with the mean minimum distance between voxels and injection cen-
ters of mass within each major brain division (correlation coefﬁcients of 0.50 Und 0.68, bzw-
aktiv). We ﬁnd the smallest errors are in isocortex, which has the largest number of replicated
experiments. The summary statistics of our data by major brain division are summarized in
Table S2 (Knox et al., 2019).

Visualizing Voxel-Scale Connectivity: Cortico-Cortical Virtual Injections
Visualization of our model faces two challenges: The matrix W contains n × n = O(1011)
entries, and represents dense connectivities between 3-D spatial structures. In order to address
these challenges, we generated “virtual injections,” which are just the predicted projections
from a given source voxel of interest. These virtual injections allow us to visualize the average
projections from voxels of our choosing. This process is efﬁcient, because the matrix W is
formed from m rank one components, so we never have to form the entire matrix. Standard
Werkzeuge, such as volume rendering and projection, can then be applied to visualize the model’s
Vorhersagen.

Netzwerkneurowissenschaften

222

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

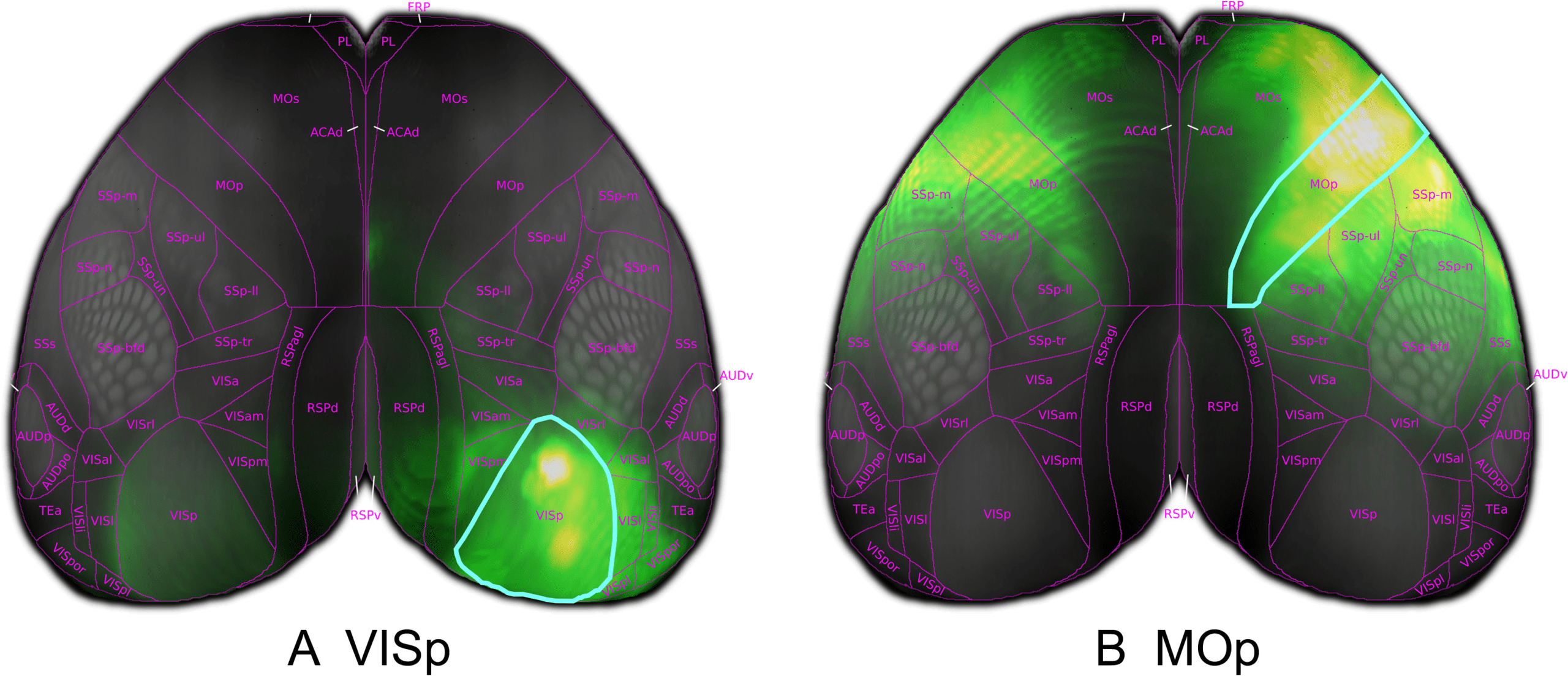
Figur 4. Model predicted cortico-cortical projections from virtual injections into the entire primary visual area (VISp) and primary motor
Bereich (MOp).

In order to visualize model predictions in the isocortex we make use of a curved cortical
coordinate system. This coordinate system deﬁnes two dimensions over the surface of the
cortex and one that is composed of steepest-descent paths from the pia surface to white matter.
By projecting model predictions along these paths, we can generate 2-D cortical projection
maps that are faithful to the boundaries of isocortical regions.

We display two such projections in Figure 4. Hier, we visualize the average over the
columns of the matrix W corresponding to the projections from two isocortical regions, marked
by a cyan outline. We observe strong ipsilateral projections to nearby areas, as expected from
the experimental data. Zum Beispiel, primary visual area VISp has a number of local projections
to higher visual areas, Figure 4A, and primary motor cortex MOp exhibits strong connectivity
to secondary motor and somatosensory areas, Figure 4B. We also observe weaker contralateral
projections across the midline in a similar pattern to the ipsilateral hemisphere.

Weight Distribution and Its Distance Dependence

We compared multiple models for the distribution of connection weights: lognormal (as has
been reported in Markov et al., 2014; Q. Wang, Spurns, & Burkhalter, 2012), inverse gamma,
exponential, and normal. We separately construct these models for ipsilateral and contralat-
eral connections for the entire brain and for connections within isocortex. For all these weight
distributions, the best ﬁt is for a lognormal distribution, as selected by Bayesian information
criterion (BIC). The BIC is a pseudo-likelihood that penalizes the number of model parameters.
See Table S3 (Knox et al., 2019). Jedoch, the results from the Kolmogorov-Smirnov test show
that the ﬁtted lognormal distributions fail to be statistically similar to the weight distributions
for any division of the connections at α = 0.05 signiﬁcance. Zusätzlich, the logarithmically
transformed weights fail to pass the Shapiro-Wilk test for normality at the same level of signiﬁ-
Abbruch. This is because the log-transformed weights, depicted on the right-hand side of Figure 5,
exhibit a skewed distribution.

Netzwerkneurowissenschaften

223

High-resolution model of the mouse connectome

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

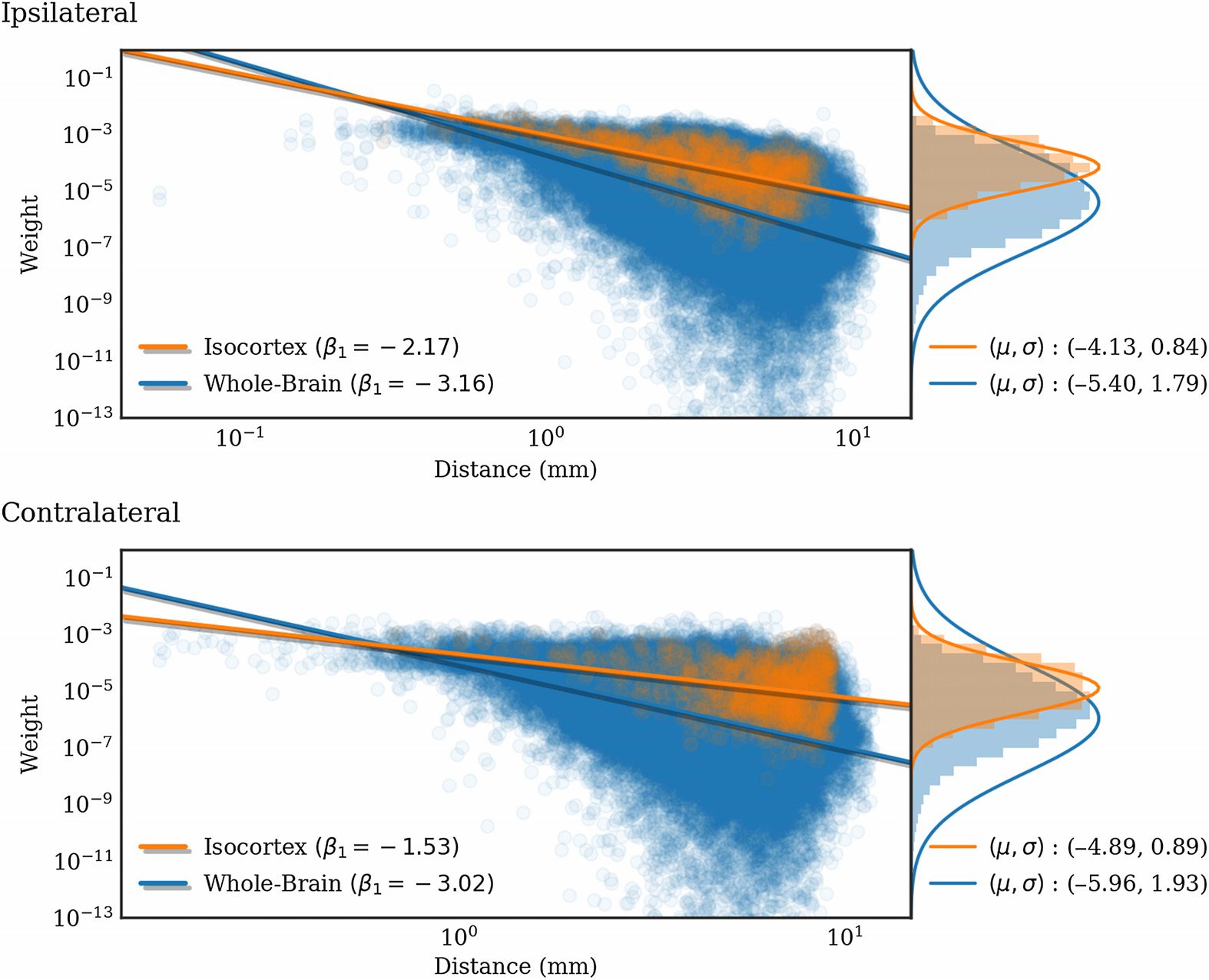
Figur 5. Normalized connection density produced by the regionalized voxel model (log scale)
plotted against interregion distance for 291 regions in the whole-brain (Blau) and for only cortico-
(weight) =
cortical connections (orange). The lines are linear least squares of the form log10
β
0. The histograms on the right side show the distributions of weights as well as
1 log10
(weight) distribution. Note that the standard deviations are biased because
Gaussian ﬁts of the log10
of small weight outliers.

(Distanz) + β

We have previously seen that a heterogeneous set of connections can be better ﬁt by a mix-
ture of lognormal distributions (Oh et al., 2014). In a similar manner, we ﬁnd the logarithmically
transformed weights are best ﬁt by a multiple component Gaussian mixture model (GMM). Sehen
Table S4 (Knox et al., 2019). The number of components was selected to minimize the BIC.
This resulted in a ﬁve-component GMM for the whole brain, and a two- to three-component
GMM for cortico-cortical connections. With the exception of two components in each of the
whole-brain mixture models, the components have similar valued weights, suggesting that dif-
ferent regions contribute to a nonhomogeneous distribution of connection weights across the
Gehirn. Jedoch, it could also be the case that the empirical distribution of log-transformed
weights is well modeled by a skewed unimodal distribution.

In Abbildung 5, we show the dependence of extant connection weights on distance. We com-
pared an exponential (Ercsey-Ravasz et al., 2013) and a power law ﬁt. Using the Levenberg-
Marquardt algorithm to ﬁt each nonlinear least squares problem, the root mean squared training
Fehler (RMSE) was found to be slightly smaller for the power-law ﬁt, but similar for both.

Model Performance Compared With Anatomical Data

To evaluate how closely the model predictions aligned with experimental data, we compared
the model weights from the homogeneous model and the regionalized voxel models with

Netzwerkneurowissenschaften

224

High-resolution model of the mouse connectome

Wild type mouse (C57BL/6J):
Mice of strain C57BL/6J that have not
been genetically altered.

Figur 6. Fraction of whole-brain projection volume from cortical sources explained by model
weights for the regionalized voxel model (Rot) and the homogeneous model (cyan). Each of the
37 cortical source regions is plotted on the x-axis, and the transparent points are for individual
experiments. Darker points and lines indicate the mean and 95% conﬁdence interval across all
injections delivered to that source.

projection data for each of the 128 injections into the isocortex in wild type mice from the
Allen Mouse Brain Connectivity Atlas. For each injection experiment, we calculated the frac-
tion of explained variance for the two models by taking the square of the Pearson correlation
between the experimental normalized projection volume and the model weights in each of the
291 Regionen. Figur 6 shows the fraction of explained variance for each experiment grouped
by source structure. Although the mean predicted variance across all sources was similar be-
tween the two models, the regionalized voxel model performed better overall (Mittelwert ± SD
regionalized: 0.87 ± 0.13, homogeneous: 0.84 ± 0.17, P < 0.0001, paired t test), but note that each model outperformed the other for some sources. To further explore the relationship between the model prediction and the experimental data, we also compared the predicted weights from both models with experimental data from a subset of experiments in which injection sites were more than 95% contained within a single source region. There were 36 experiments that met this criterion. Of these, 35 were in the isocortex and 1 was in the hippocampus, and this set contained in the following 10 sources (see Table S1, Knox et al., 2019): AUDp (1), ENTl (1), MOp (3), MOs (1), RSPd (1), SSp-bfd (1), SSp-m (4), SSp-n (1), SSs (1), and VISp (22). Note that in VISp we include four injections using the pan-excitatory Cre line Emx1-IRES-Cre mice, which have very similar projection patterns as wild type mice (J. A. Harris et al., 2018). Twelve of these experiments were manually checked for segmentation errors in the regions where nonzero projections were automatically ﬂagged. When these manually annotated data were available, we multiplied the normalized projection volume by 1 for true positives or 0 for true negatives. See Figure S1 (Knox et al., 2019) and the description in Methods. For each of these 10 sources, we plotted the normalized projection volume from the experimental data along with the predicted weights from both models for targets in the ipsilateral isocortex. Figure 7 shows the plot for VISp, where we had a total of 22 experiments of which eight were checked for true positives/true negatives at all cortical targets. Four injections into Emx1- IRES-Cre mice were included in the plot for VISp, although these were not used to ﬁt the model. Only the eight experiments that were manually checked are included in the plot in the ﬁgure. The weights predicted by the regionalized voxel model were higher overall, but generally agreed with the experimental data as well as the homogeneous model predictions. Network Neuroscience 225 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 2 1 7 1 0 9 2 3 7 3 n e n _ a _ 0 0 0 6 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 High-resolution model of the mouse connectome l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 1 2 1 7 1 0 9 2 3 7 3 n e n _ a _ 0 0 0 6 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. Normalized projection volume for VISp projections to ipsilateral (top) and contralateral (bottom) cortical targets in log scale. The raw data are compared with model predictions. Normal- ized projection volume from individual manually validated experiments (gray) and the mean and 95% conﬁdence interval for each target are plotted as black diamonds. Note that many conﬁdence intervals are smaller than the markers. Corresponding weights for VISp projections to each cortical target from the homogeneous model (cyan) and the regionalized voxel model (red) are overlaid. The biggest difference between the two models was that the regionalized voxel model correctly predicted nonzero weights for several targets that were missed by the homogeneous model. All of the ipsilateral targets of VISp that had a weight of 0 in the homogeneous model were veriﬁed true positives in at least three of the eight experiments plotted in Figure 7. All of the contralateral targets except SSp-ll were veriﬁed true positives in at least two out of the eight experiments. The regionalized voxel model predicted nonzero weights for all of these true positive targets that were assigned a weight of 0 by the homogeneous model. Contralateral SSp-ll was a true negative in all eight experiments and was incorrectly assigned a weight by the regionalized voxel model but not the homogeneous model. Both models predicted small but nonzero weights for several other targets that were true negatives (ipsilateral: FRP, AId, AIp, and AIv; contralateral: FRP, SSp-n, SSp-m, SSp-ul, GU, VISC, PL, ILA, AId, AIp, AIv). Across all 10 sources that were checked, the regionalized voxel model tended to predict nonzero weights for connections that were assigned 0 weight in the homogeneous model. Overall, we found the predictions of the regionalized voxel model to be more consis- tent with the data than the homogeneous model. Even when the predicted weight from the Network Neuroscience 226 High-resolution model of the mouse connectome regionalized voxel model was incorrect, it was not off by a large margin. The homogeneous model often performs well, but when its predictions differ from the experimental data they are sometimes off by a very large margin. For example, the homogeneous model predicts zero weight for projections from ACAv to the caudoputamen (CP), but the experimental data show that CP is in fact the strongest projection target of ACAv with a normalized projection volume of 4.4 and 5.0 (unitless) in the two available experiments (compared with 0.05 ± 0.28, mean ± SD for all targets of ACAv across the two experiments). The homogeneous model makes the same error for SSp-ll, again assigning zero weight to projections in CP when the experimen- tal data show that CP is the highest weight target of SSp-ll (normalized projection volume in CP = 3.2 ± 1.1, mean normalized projection volume in all targets = 0.03 ± 0.2, n = 3 exper- iments). This is reﬂected in the standard deviation for the fraction explained variance (0.17 for the homogeneous model vs. 0.14 for the regionalized voxel model), and is well illustrated in Figure 6, where the homogeneous model performs well overall, but very poorly for projections from SSp-ll and ACAv. DISCUSSION In this study, we infer whole-brain connectivity at 100 µm voxel resolution from a set of brain- wide anterograde viral tracing experiments in young adult wild type C57BL/6J mice (Oh et al., 2014, http://connectivity.brain-map.org). The central assumption of extant voxel methods is that brain-wide projections from nearby neurons within a brain region vary smoothly. Such a method, and its application to the visual system, has been described by K. D. Harris et al. (2016). Eventually, we hope to improve those mathematical methods to solve the original source- and target-smoothed nonnegative regression problem at whole-brain scale. However, the current implementation of that problem is computationally costly and does not scale to the whole brain. These considerations led us to develop the simpler method presented here. Our approach makes two simplifying assumptions (see Methods): First, we assume the in- jection is delivered into just the center of mass voxel, rather than the entire injection volume. This is the opposite extreme of the regionally homogeneous assumption. Second, we perform interpolation in only the source space, rather than also in the target space. With these changes, the model of K. D. Harris et al. (2016) becomes, essentially, the method we present here, be- cause of the well-known “kernel trick” (Wahba, 1990). This connection is inexact because of boundary effects, the particular choice of kernel, and the use of Nadaraya-Watson rather than regression coefﬁcients. The tracing data that forms the basis of this study is based on anterograde viral tracers (Oh et al., 2014). The viral tracing methods used to generate the Allen Mouse Brain Connectivity Atlas dataset result in two limitations affecting our ability to resolve connections. One limita- tion comes from the size of the injections, which have a typical radius of 0.3 mm. Table S2 (Knox et al., 2019) provides the volume distribution through different brain regions. An even stronger limit comes from the distances between a voxel and the center of mass of an injec- tion being typically 0.5 mm. Table S2 reports this average in the “injection distance” column. This distance is the consequence of the number of injections (491, of which we select 428 as described in Methods) being much smaller than the number of source voxels (2.5 × 105). The connections originating from a voxel have to be inferred from sources on average 0.5 mm away, which average information over a radius of 0.3 mm. Spatial averaging is thus necessary for these data. Voxel models were ﬁt and analyzed separately for a set of 12 major brain divisions. These structures represent a coarse level of anatomical parcelation of mammalian brains and have Network Neuroscience 227 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 1 2 1 7 1 0 9 2 3 7 3 n e n _ a _ 0 0 0 6 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 High-resolution model of the mouse connectome qualitatively different connection patterns. One could also take an agnostic approach and hope that the data reveal where these differences arise. Perhaps using a total variation or similar reg- ularization that allows for piecewise constant patterns, or working with a factored W = LR and clustering the factors into different regions, could provide a tractable approach to this. Non- negative matrix factorizations can also be interpreted as another way to ﬁnd network modules, as was proposed in K. D. Harris et al. (2016). However, this both increases the mathematical difﬁculty and could require more experiments than are currently available. We compared the voxel and homogeneous models’ ability to predict held-out injection ex- periments. Although the errors for both are relatively high (but see the Supporting Information (Knox et al., 2019) for a comparison with log-transformed errors), the voxel model on average performs better. However, if the homogeneous model is ﬁt with 10 µm data, it can outperform the regionalized voxel model ﬁt with 100 µm data (see the Supporting Information). We be- lieve a good method to evaluate the model’s performance is to compare the predicted weights with a human-curated ground truth metric. We were able to make this comparison for a subset of injections well contained in 10 of 43 cortical sources. By comparing the models’ predictions with experiments, we found two main differences between the regionalized voxel model and the homogeneous model. First, and most importantly, the regionalized voxel model predicts very weak but nonzero connections that the homogeneous model assigns zero weight. This is due to the inherent tendencies of the models to increase sparsity (homogeneous model) or to decrease sparsity (regionalized voxel model). We veriﬁed some of the connections that were detected by the regionalized voxel model and not the homogeneous model as true positives, but others were true negatives that were incorrectly assigned a nonzero weight by the regional- ized voxel model. Occasionally, the homogeneous model assigns a zero weight to very strong connections as with the projections to CP from ACAv and SSp-ll (Figure 6), but the regionalized voxel model is less susceptible to this type of error since it tends to decrease sparsity. The other main difference between the two models was in the prediction of weights for small target structures. Because the regionalized voxel model is a linear smoother, it will tend to overpredict weak connections for targets near regions with high connectivity. Some examples of this behavior can be seen in Figure 7 where projection weight to AUDv, for example, is overestimated by the regionalized voxel model, likely because of its spatial position between AUDp and TEa which both receive strong projections from VISp. In choosing the appropriate model for an application, it is therefore important to consider that weak connections have higher uncertainty, and whether false positives or false negatives have a greater inﬂuence on the results. We would like to emphasize that when analyzing this connectivity, especially from a graph theoretical perspective, one also has to be mindful of the correlations between connections originating from nearby sources that are introduced by the method. The spatial resolution of the connectivity is presented at 100 µm resolution. However, at source level, the average distance to the closest injection is typically 0.5 mm (see Table S2, Knox et al., 2019), which limits the resolution. Also, many graph statistics may not be well suited for studying such explicitly spatial graphs as ours. Among multiple models for unimodal weight distributions, we found the lognormal being the best ﬁt, in accordance with previous studies (e.g., Markov et al., 2014; Q. Wang et al., 2012), despite failing the Kolmogorov-Smirnov test. Following this analysis, we found that a mixture of normal distributions was an even better ﬁt for the distribution of log weights (as in Oh et al., 2014). A possible explanation for this is that the mixture results from combining Network Neuroscience 228 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 2 1 7 1 0 9 2 3 7 3 n e n _ a _ 0 0 0 6 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 High-resolution model of the mouse connectome heterogeneous neuronal populations each with lognormal statistics, or that the log-transformed distribution is skewed. We analyzed the distance dependence of the connection weights and found that a power law dependence is a marginally better ﬁt than exponential (Ercsey-Ravasz et al., 2013), similar to the result of Rubinov, Ypma, Watson, and Bullmore (2015). It is interesting that the power is close to −2 for the cortex (ipsilateral), which can be roughly approximated as a 2-D “sheet,” and close to −3 for the entire brain, which is 3-D. However, the weak scaling we observe only holds over roughly 1.5 orders of magnitude, so we prefer not to speculate too much about this result. The voxel model enables quantitative characterization of the structural connectivity of the mouse brain. It is a signiﬁcant improvement over the previously published homogeneous lin- ear model (Oh et al., 2014), with easily tractable mathematics compared with the earlier voxel proposal (K. D. Harris et al., 2016). It offers improved predictions at region level, but, more importantly, it provides the connectivity at a much higher spatial resolution. This new model provides the necessary basis for studies of large-scale network structure, enabling discovery of general organizational rules for brain-wide systems that consist of both local and long-distance connections. For example, J. A. Harris et al. (2018) performed an analysis of modularity in the wild type cortical subnetwork, employing the regionalized voxel model we present here. They found that the cortical network divides into 1–14 modules, depending on the clustering pa- rameters, but found six stable modules that were characterized as prefrontal, anterolateral, somatomotor, visual, medial, and temporal. A better understanding of such structural rules will lead to more accurate predictions of the directions of information ﬂow, constrained by anatomy, and can be used by researchers interested in questions of structure-function relation- ships in the mouse brain. METHODS Summary of Data The data were taken from 491 experiments using wild type C57BL/6J mice. These data are available from the Allen Mouse Brain Connectivity Atlas at http://connectivity.brain-map.org/ (Oh et al., 2014). The brain is divided into a set of s = 12 major brain divisions at a high level of the CCF ontology. These major brain divisions are isocortex, olfactory areas, hippocam- pal formation, cortical subplate, striatum, pallidum, thalamus, hypothalamus, midbrain, pons, medulla, and cerebellum. We also consider a ﬁner partition (lower in the ontology) into a set of r = 291 regions. The major brain divisions form a disjoint partition of the brain, as do the regions. These regions are each contained within a given major brain division. We curated experiments to exclude those in which infected cell bodies are located in mul- tiple major brain divsions. For example, we removed experiments with large injection volumes spanning multiple subcortical major brain divisions and subcortical injections with substantial leakage of the tracer in the overlying cortex. Additionally, we removed four experiments hav- ing very little to no long-distance projections (small projection volume outside of the injection location). Overall, of the 491 experiments, we removed 63 experiments resulting in a total of m = 428 included experiments. We summarize these experiments used to ﬁt our connectome in Table S2 (Knox et al., 2019). In our mathematical framework, the brain is a subset of R3 that is discretized into a col- lection of n cubic voxels. Subsets of these voxels then correspond to the major brain division {Si}s i=1. Each voxel i maps to a location in the brain, which we denote i=1 and regions {Ri}r Network Neuroscience 229 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 1 2 1 7 1 0 9 2 3 7 3 n e n _ a _ 0 0 0 6 6 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 High-resolution model of the mouse connectome by vi ∈ R3. Each injection tracing experiment produces an image stack (i.e., a 3-D image) of ﬂuorescently labeled neurons and axons throughout the brain. The ﬂuorescence signal is re- ported as injection density (fraction of ﬂuorescing pixels per voxel for voxels in the annotated injection site) and projection density (fraction of ﬂuorescing pixels per voxel outside of the injection site). For the eth experiment, let X:,e and Y:,e denote the length n vectors of injection density and projection density, respectively. We also compute voxel coordinates of the center of mass of the injection density ce ∈ R3. For our estimator, we also compute the normalized projection density, normalizing by the sum of the injection density, and denote this ¯Y:,e. Note that ¯Y:,e = (Y:,e + X:,e)/ ∑v Xve, since we also include the injection pattern in the normalized projection density. Thus, the experimental data are this collection {(X:,e, Y:,e, ¯Y:,e, ce)}m e=1, of length n vectors as well as the injection centers of mass for each experiment. Multivariate Nonparametric Regression to Infer Voxel Connectivity We consider the problem of ﬁtting a nonnegative, weighted adjacency matrix W ∈ Rn×n that ≥0 is common across animals. Entry Wij is the estimated projection density of neurons in voxel j to voxel i, if one unit of injection density were delivered to voxel j. Each experiment consists of an injection X, and its projections Y, and we would like to ﬁnd W so that so that Y ≈ WX. Uncovering the unknown W from multiple experiments (X:,e, Y:,e) for e = 1, . . . , m is then a multivariate regression problem. The unknown matrix W is a linear operator that takes images of the brain (injections) and returns images of the brain (projections). Unlike the earlier work by K. D. Harris et al. (2016), we make two crucial simplifying approximations: First, we assume that in experiment e the injection is delivered to precisely one voxel, the injection center of mass ce. This removes the more difﬁcult credit assignment problem of which voxels within each injection site contribute which projections. The method of K. D. Harris et al. (2016) solved this problem by linear regression, essentially “dividing out” the injection correlations across experiments. Second, we assume that projections vary smoothly as we change the source voxel, that is, the columns of W are smooth functions of the column voxel. However, we do not explicitly assume that the incoming projections to a target voxel vary smoothly as we move the target voxel, or smoothness in the rows. Smoothness in target space leads to dependencies among the output variables of the multivariate regression problem, making it a so-called structured regression problem, which is generally more difﬁcult to solve. Note that, because the data tend to produce patterns of projections that are spatially smooth, and because we enforce smoothness in the source space, some target smoothness will arise naturally. Nadaraya-Watson connectome estimator. With these simplifying assumptions, we can now state the model. Our data are now the pairs of center of mass voxels ce and normalized injec- tion densities ¯Y:,e, which we assume arise from an injection of one unit of virus to the center of mass. Kernel regression is a standard nonparametric method for estimating a smooth univari- ate or multivariate function. For simplicity, we use the Nadaraya-Watson estimator (Nadaraya, 1964; Watson, 1964) to estimate the connectivity: l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 1 2 1 7 1 0 9 2 3 7 3 n e n _ a _ 0 0 0 6 6 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Wij = ∑e:ce∈Sk ∑ f :c f ∈Sk K((cid:5)vj − ce(cid:5)) ¯Yie K((cid:5)vj − c f (cid:5)) = ∑ e:ce∈Sk ¯Yieαej , where αej = Network Neuroscience K((cid:5)vj − ce(cid:5)) ∑ f :c f ∈Sk K((cid:5)vj − c f (cid:5)) , (1) (2) 230 High-resolution model of the mouse connectome and k is the unique index such that vi ∈ Sk, that is, we only average over injections in the major brain division containing the source voxel. Furthermore, we can construct the matrices ¯Y = [ ¯Y (cid:2) :,1, ¯Y (cid:3) αej , A = :,2, . . . , ¯Y:,m] so that the connectome is written compactly as a rank m matrix W = ¯YA, where ¯Y ∈ Rn×m and A ∈ Rm×n . Note that each column in A, the coefﬁcients αej, has entries that sum to 1. The Nadaraya-Watson estimator, Equation (1), has a number of nice properties: It does not require any ﬁtting, because the coefﬁcients αej are given explicitly in terms of the center of masses and kernel, Equation (2). For nonnegative data, it will produce a nonnegative connec- tivity matrix, which we require. Furthermore, it forms a compressed rank m representation of W that is only as large as the data. However, it does suffer some drawbacks; for example, it is well known that the Nadaraya-Watson estimator is biased for data that are not sampled uniformly and near boundaries. Note also that experiments with center of masses ce ∈ Sk do not have any inﬂuence outside of Sk. This is because we do not want to average over experiments in vastly different brain areas. Therefore, the coefﬁcients αe,k are decoupled across major brain divisions. Essentially, we ﬁt a different model for each major brain division. Choice of spatial kernel. We use a Gaussian radial basis function kernel: (cid:4) Kσ(d) = exp − (cid:5) , d2 2σ2 (3) where σ > 0 is a hyperparameter setting the length scale or bandwidth of the kernel function.
The length scale σ is ﬁt using nested cross-validation in the model selection phase. We search
over σ ∈ [4, 50] In 11 logarithmically spaced increments, where σ is in units of 100 µm voxels.
Note that while the kernel, Gleichung 3, has inﬁnite support, we do not evaluate it on points
outside the coarse structure of interest.

To evaluate the performance of the model, Wir
Evaluating performance via cross-validation.
employ nested leave-one-out cross-validation. In the inner loop, we ﬁt m − 1 different models
on sets of m − 2 experiments in order to perform model selection, wherein we ﬁt the hyper-
parameter σ of the kernel function K. The best model is then evaluated against the held-out
experiment from the outer loop, and this process is repeated m times. The performance metric
we choose to use is mean square error relative to the average squared norm of the prediction
and left-out data:

MSErel

= 2(cid:5)Ypred − Ytrue(cid:5)2
F
F + (cid:5)Ytrue(cid:5)2
F

(cid:5)Ypred(cid:5)2

(4)

This choice of normalization prevents experiments with small (cid:5)Y(cid:5) from dominating the error,
more heavily weighting experiments with larger signal (K. D. Harris et al., 2016).

The relative error in Equation (4) is approximately equal to the usual relative mean square
F when Ypred is close to Ytrue, and this is not too small. To see

Fehler (cid:5)Ypred − Ytrue(cid:5)2

F/(cid:5)Ytrue(cid:5)2

Radial basis function:
A monotonically decreasing,
nonnegative function of distance.

Frobenius norm:
The two norm of a matrix viewed as
a vector: (cid:5) A (cid:5)F =

∑ij A2
ij.

(cid:6)

Netzwerkneurowissenschaften

231

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

Das, let Ypred = Ytrue + δ where (cid:5)δ(cid:5)F ≤ (cid:6) Und (cid:5)Ytrue(cid:5)F = O(1). Dann, dropping the superscript
“true” for clarity,

MSErel

2(cid:5)δ(cid:5)2
F
F + (cid:5)Y(cid:5)2
F

(cid:5)Y + δ(cid:5)2

2(cid:5)δ(cid:5)2
F
F + (cid:5)δ(cid:5)2
F

2(cid:5)Y(cid:5)2

(cid:5)δ(cid:5)2
F
(cid:5)Y(cid:5)2
F

⎞

⎟
⎠ =

⎛

⎜
⎝

1
1 + (cid:5)δ(cid:5)2
F
2(cid:5)Y(cid:5)2
F

(cid:13)

(cid:5)δ(cid:5)2
F
(cid:5)Y(cid:5)2
F

(cid:14)

1 − O((cid:6)2)

Jedoch, if Y is close to 0, our metric can be different. Zum Beispiel, if Ypred = 1 and Ytrue =
= 2(1 − 0.25)2/(12 + (0.25)2) = 106%. The usual relative mean square
0.25, then MSErel
error would be (1 − 0.25)2/(0.25)2 = 900%. If either Ytrue or Ypred is 0 and the other is not,
then MSErel

= 200%, its maximum value.

Consider a set of experiments {(ce, ¯Y:,e)}M

e=1, where ce is the center of mass of the eth injec-
tion. Let C ∈ Rn×m
be the matrix of injection center indicators, with entries Cie = 1{ce=vi}. Von-
ﬁne the kernel matrix Ac ∈ Rm×m
as the kernel evaluated at the centers of mass; then this is just
Ac = AC. Thus the model prediction of the center of mass projections is WC = ¯Y AC = ¯Y Ac.

We can perform leave-one-out cross-validation efﬁciently after computing the coefﬁcients
predicts that
has the eth diagonal entry

Ac for a given set of data. If we leave out experiment e, the new model W(−e)
the projections from ce are ˆY = W(−e)C:,e = ¯YA(−e)
equal to 0 and the corresponding column renormalized to sum to 1. daher,

, where A(−e)

(A(−e)
C

)ij =

⎧
⎪⎪⎪⎨
⎪⎪⎪⎩

(Ac)ij,
(Ac)ij
1−(Ac)ee ,
0,

J (cid:7)= e,

j = e and i (cid:7)= j,
i = j = e.

Extending the above result to compute the leave-one-out predictions for all of the experiments,
we ﬁnd that these are equal to ¯Y ACV

, Wo
⎧
⎨

(ACV

C )ij =

⎩

(Ac)ij
1−(Ac)jj ,
0,

ich (cid:7)= j,
i = j.

Daher, once we compute the coefﬁcients Ac, we set the diagonals equal to 0 and renormalize
the columns to obtain ACV
. The leave-one-out cross-validation relative error of the voxel model
is then

2(cid:5) ˆY − ¯Y(cid:5)2
F
F + (cid:5) ¯Y(cid:5)2
(cid:5) ˆY(cid:5)2
F

(5)

where ˆY = ¯Y ACV

are the leave-one-out predictions.

Regionalized and Homogeneous Models
The application of Equation (1) results in a very large n × n voxel-scale connectivity matrix.
Recall that we deﬁned a parcellation of the brain into r regions R. We would like to be able to
compare this with extant regional connectomes, which are smaller r × r matrices. With this,
we can deﬁne the regional projection matrix, Π ∈ Rr×n

, with entries:

Πij = 1{vj∈Ri}.

Das ist, the ith row of Π has ones in entries corresponding to voxels in region i. daher,
for some vector x ∈ Rn
corresponding to a voxel image of the brain, the vector xR = Π x

Netzwerkneurowissenschaften

232

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

has entries corresponding to the sum of x over regions. Außerdem, consider another matrix
Π† ∈ Rn×r

, with entries:

Π†

ij =

1{vi∈Rj}
|Rj|

Wo |Rj| is the number of voxels in region j. Then Π†, operating from the left on a length r
vector, spreads the entries evenly over all of the voxels in a given region. Operating from the
Rechts, it averages over the voxels in a region. Note that Π Π† = Ir, so it is a right inverse of Π
and in fact is a Moore-Penrose pseudoinverse.

With this notation, it becomes simple to convert voxel vectors and matrices into regional
ones. We refer to the sum of the connection weights between two regions as the connection
strength between the regions. Daher, the regional connection strength is given by

WR = Π W Π(cid:2)

Jedoch, these regions may be vastly different sizes, in which case a measure normalized
by source and/or target region size is more appropriate. We deﬁne the normalized projection
density as the connection strength between two regions divided by the size of the source and
target region. In this case, the matrix becomes

WR,norm density = Π†(cid:2) W Π†.

Endlich, our last normalization only normalizes by the size of the source region, which we call
normalized connection strength:

WR,norm strength = Π W Π†.

This normalization is necessary to compare directly with the homogeneous model.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

Normalized connection strength:
The connection strength from R
R

1 Zu
2 divided by the size of the source

region:

WR
21
|R1|

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

As in Oh et al. (2014), one could also ﬁt a regional
Fitting a homogeneous regional model.
model where connection strengths are ﬁxed across regions by working directly with data that
have been regionalized. We performed this for comparison and refer to the result as the homo-
geneous model. Let XR = Π X and YR = Π Y. Then the model ﬁt to these regional data is
found via nonnegative least squares as

Whomog = arg min
W (cid:8)≥0

(cid:5)W(cid:8)XR − YR(cid:5)2
F.

(6)

Note that the output Whomog is a normalized connection strength, since entry (ich, J) ist der
expected volume of ﬂuorescence in region i per unit of virus in region j.

Let ˆY ∈ Rn

be the voxel
Comparing the regionalized voxel model to the homogeneous model.
prediction; we can compute the regionalized prediction ˆYR ∈ Rr
by projecting the voxel
predictions into the regional space: ˆYR = Π ˆY. It is important to note that although the com-
parison between the regionalized voxel model and the homogeneous model are done in the
same space Rr
, the predictions themselves are slightly different. The regionalized voxel predic-
tions ˆYR
:,e are the predicted result of a unit injection into the center of mass of the injection ce,
whereas the regional prediction ˆYR
:,e = Whomog X:,e is the regional prediction of the projection
from the full injection X:,e.

Netzwerkneurowissenschaften

233

High-resolution model of the mouse connectome

To check individual experiments for segmentation er-
Manual checks of regional projections.
rors, we used the interactive projection experiment detail view page of the Allen Mouse Brain
Connectivity Atlas (z.B., http://connectivity.brain-map.org/projection/experiment/100141219).
We ﬁrst set the “projection volume” threshold to 0 so that all targets were displayed, then se-
lected the bar graph for all ipsilateral and contralateral targets to align the raw image viewer
für jede. The viewer automatically centers on the area with the highest signal in each anatom-
ical region. Jedoch, when no projections were initially apparent we checked several sec-
tions rostral and caudal to the initial location as well as the surrounding region. Target regions
that contained eGFP-expressing axons were labeled 1 (true positive). If no projections were
observed the target was assigned a 0 (true negative). In cases where there were a small num-
ber of axons that appeared to be passing ﬁbers without branches or boutons, we assigned
the target a 0. Most segmentation errors were caused by tissue edges or blood vessels that
were detected by the automatic segmentation algorithm. See Figure S1 (Knox et al., 2019).
The following manually validated experiments were used to compare model weights to exper-
imental data: 100141219, 100147853, 309113907, 479756361, 500836840, 500837552,
522409371, 546103149, 112424813, 117298988, 126908007, Und 180916954. Der Erste
eight are the VISp injections plotted in Figure 7.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

ACKNOWLEDGMENTS

This work was supported by the Allen Institute for Brain Science. The authors wish to thank
the Allen Institute founder, Paul G. Allen, for his vision, encouragement, and support. Addi-
tionally, the project described was supported in part by the National Institute on Aging of the
Nationale Gesundheitsinstitute. Its contents are solely the responsibility of the authors and do not
necessarily represent the ofﬁcial views of the National Institutes of Health. We would like to
thank Lydia Ng and Nathan Gouwens for assistance with the cortical ﬂattening.

SUPPORTING INFORMATION

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

All of the data used to construct these models are available at http://connectivity.brain-map.
org. The data used in this analysis were cached in March 2017. The curved coordinate
system is described in http://help.brain-map.org/download/attachments/2818171/Mouse_
Common_Coordinate_Framework.pdf, with the speciﬁc data available from http://download.
alleninstitute.org/informatics-archive/current-release/mouse_ccf/cortical_coordinates/ccf_2017.
All code used to build this model is available from https://github.com/AllenInstitute/mouse_
connectivity_models (Knox, 2018).

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

BEITRÄGE DES AUTORS

Joseph E. Knox: Formale Analyse;
Untersuchung; Methodik; Software; Visualisierung;
Writing – original draft; Writing – review & Bearbeitung. Kameron Decker Harris: Conceptualiza-
tion; Formale Analyse; Untersuchung; Methodik; Software; Visualisierung; Writing – original
Entwurf; Writing – review & Bearbeitung. Nile Graddis: Software; Writing – review & Bearbeitung. Jennifer
D. Whitesell: Validierung; Visualisierung; Writing – original draft; Writing – review & Bearbeitung.
Hongkui Zeng: Aufsicht. Julie A. Harris: Datenkuration; Aufsicht; Validierung; Writing –
Rezension & Bearbeitung. Eric Shea-Brown: Konzeptualisierung; Aufsicht; Writing – review & edit-
ing. Stefan Mihalas: Konzeptualisierung; Aufsicht; Writing – original draft; Writing – review
& Bearbeitung.

Netzwerkneurowissenschaften

234

High-resolution model of the mouse connectome

FUNDING INFORMATION

Julie A. Harris, National Institute on Aging (http://dx.doi.org/10.13039/100000049), Award ID:
R01AG047589. Kameron Decker Harris, Directorate for Mathematical and Physical Sciences
(http://dx.doi.org/10.13039/100000086), Award ID: 1122106. Eric Shea-Brown, Directorate
for Mathematical and Physical Sciences (http://dx.doi.org/10.13039/100000086), Award ID:
1514743. Kameron Decker Harris, Big Data for Genomics & Neuroscience Training Grant,
Award ID: 1T32CA206089-01A1.

VERWEISE

Bock, D. D., Lee, W.-C. A., Kerlin, A. M., Andermann, M. L., Hood,
G., Wetzel, A. W., . . . Reid, R. C. (2011). Network anatomy and
in vivo physiology of visual cortical neurons. Natur, 471(7337),
177–182. https://doi.org/10.1038/nature09802

Bohland, J. W., Wu, C., Widerhaken, H., Bokil, H., Bota, M., Breiter, H. C.,
. . . Mitra, P. P. (2009). A proposal for a coordinated effort for
the determination of brainwide neuroanatomical connectivity in
model organisms at a mesoscopic scale. PLoS Computational
Biology, 5(3), e1000334. https://doi.org/10.1371/journal.pcbi.
1000334

Bota, M., Dong, H.-W., & Swanson, L. W. (2003). From gene net-
works to brain networks. Naturneurowissenschaften, 6(8), 795–799.
https://doi.org/10.1038/nn1096

Ercsey-Ravasz, M., Markov, N. T., Lamy, C., Van Essen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A predic-
tive network model of cerebral cortical connectivity based on a
distance rule. Neuron, 80(1), 184–197. https://doi.org/10.1016/
j.neuron.2013.07.036

Felleman, D. J., & Van Essen, D. C. (1991). Distributed hierarchical
processing in the primate. Hirnrinde, 1(1), 1–47. https://
doi.org/10.1093/cercor/1.1.1

G˘am˘anu¸t, R., Kennedy, H., Toroczkai, Z., Ercsey-Ravasz, M.,
Van Essen, D. C., Knoblauch, K., & Burkhalter, A. (2018). Der
mouse cortical connectome, characterized by an ultra-dense cor-
tical graph, maintains speciﬁcity by distinct connectivity proﬁles.
Neuron, 97(3), 698–715.e10. https://doi.org/10.1016/j.neuron.
2017.12.037

Glickfeld, L. L., Andermann, M. L., Bonin, V., & Reid, R. C. (2013).
Cortico-cortical projections in mouse visual cortex are func-
tionally target speciﬁc. Naturneurowissenschaften, 16(2), 219–226.
https://doi.org/10.1038/nn.3300

Harris, J. A., Mihalas, S., Hirokawa, K. E., Whitesell, J. D., Knox,
J., Bernard, A., . . . Zeng, H. (2018). The organization of intra-
cortical connections by layer and cell class in the mouse brain.
bioRxiv:292961. https://doi.org/10.1101/292961

Harris, K. D., Mihalas, S., & Shea-Brown, E. (2016). High resolution
neural connectivity from incomplete tracing data using nonnega-
tive spline regression. In D. D. Lee, M. Sugiyama, U. V. Luxburg,
ICH. Guyon, & R. Garnett (Hrsg.), Advances in Neural Information
Processing Systems 29.

Jenett, A., Rubin, G. M., Ngo, T.-T. B., Shepherd, D., Murphy, C.,
Dionne, H., . . . Zugates, C. T. (2012). A GAL4-driver line
resource for Drosophila neurobiology. Cell Reports, 2(4),
991–1001. https://doi.org/10.1016/j.celrep.2012.09.011

Kleinfeld, D., Bharioke, A., Blinder, P., Bock, D. D., Briggman,
K. L., Chklovskii, D. B., . . . Sakmann, B. (2011). Large-scale
automated histology in the pursuit of connectomes. Zeitschrift für
Neurowissenschaften, 31(45), 16125–16138. https://doi.org/10.1523/
JNEUROSCI.4077-11.2011

Knox, J.

(2018). Python package providing mesoscale connectiv-
ity models for mouse, Github, https://github.com/AllenInstitute/
mouse_connectivity_models

Knox, J. E., Decker Harris, K., Graddis, N., Whitesell, J. D., Zeng, H.,
Harris, J. A., . . . Mihalas, S. (2019). Supporting information for
“High-resolution data-driven model of the mouse connectome.”
Netzwerkneurowissenschaften, 3(1), 217–236. https://doi.org/10.1162/
netn_a_00066

Kuan, L., Li, Y., Lau, C., Feng, D., Bernard, A., Sunkin, S. M.,
. . . Ng, L. (2015). Neuroinformatics of the Allen Mouse Brain
Connectivity Atlas. Methoden, 73, 4–17. https://doi.org/10.1016/
j.ymeth.2014.12.013

Laramée, M.-E., & Boire, D. (2015). Visual cortical areas of the
mouse: Comparison of parcellation and network structure with
primates. Frontiers in Neural Circuits, 8, 149. https://doi.org/10.
3389/fncir.2014.00149

Majka, P., Chaplin, T. A., Yu, H.-H., Tolpygo, A., Mitra, P. P.,
Wójcik, D. K., & Rosa, M. G. P. (2016). Towards a comprehen-
sive atlas of cortical connections in a primate brain: Mapping
tracer injection studies of the common marmoset into a reference
digital template. Zeitschrift für Vergleichende Neurologie, 524(11),
2161–2181. https://doi.org/10.1002/cne.24023

Markov, N. T., Ercsey-Ravasz, M. M., Ribeiro Gomes, A. R., Lamy,
C., Magrou, L., Vezoli, J., . . . Kennedy, H. (2014). A weighted
and directed interareal connectivity matrix for macaque cerebral
Kortex. Hirnrinde, 24(1), 17–36. https://doi.org/10.1093/
cercor/bhs270

Nadaraya, E. A. (1964). On estimating regression. Theory of Prob-

ability and Its Applications, 9(1), 141–142.

Oh, S. W., Harris, J. A., Ng, L., Winslow, B., Cain, N., Mihalas, S.,
(2014). A mesoscale connectome of the mouse
. . . Zeng, H.
Gehirn. Natur, 508(7495), 207–214. https://doi.org/10.1038/
nature13186

Ragan, T., Kadiri, L. R., Venkataraju, K. U., Bahlmann, K., Sutin, J.,
Taranda, J., . . . Osten, P. (2012). Serial two-photon tomography
for automated ex vivo mouse brain imaging. Nature Methods,
9(3), 255–258. https://doi.org/10.1038/nmeth.1854

Rubinow, M., Ypma, R.

J. F., Watson, C., & Bullmore, E. T.
(2015). Wiring cost and topological participation of the mouse

Netzwerkneurowissenschaften

235

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
2
1
7
1
0
9
2
3
7
3
N
e
N
_
A
_
0
0
0
6
6
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

High-resolution model of the mouse connectome

brain connectome. Proceedings of the National Academy of
Wissenschaften, 112(32), 10032–10037. https://doi.org/10.1073/pnas.
1420315112

Sethi, S. S., Zerbi, V., Wenderoth, N., Fornito, A., & Fulcher, B. D.
(2017). Structural connectome topology relates to regional BOLD
signal dynamics in the mouse brain. Chaos: An Interdisciplinary
Journal of Nonlinear Science, 27(4), 047405. https://doi.org/10.
1063/1.4979281

Shih, C.-T., Spurns, O., Yuan, S.-L., Su, T.-S., Lin, Y.-J., Chuang,
C.–C., . . . Chiang, A.–S.
(2015). Connectomics-based analy-
sis of information ﬂow in the Drosophila brain. Aktuelle Biologie,
25(10), 1249–1258. https://doi.org/10.1016/j.cub.2015.03.021
Spurns, Ö. (2010). Networks of the brain. Cambridge, MA: MIT Press.
Stafford, J. M., Jarrett, B. R., Miranda-Dominguez, O., Mills, B. D.,
Cain, N., Mihalas, S., . . . Fair, D. A. (2014). Large-scale topol-
ogy and the default mode network in the mouse connectome.
Verfahren der Nationalen Akademie der Wissenschaften, 111(52),
18745–18750.

Wahba, G. (1990). Spline models for observational data. Philadelphia,

PA: SIAM.

Wang, Q., Spurns, O., & Burkhalter, A. (2012). Netzwerkanalyse
of corticocortical connections reveals ventral and dorsal pro-

cessing streams in mouse visual cortex. Zeitschrift für Neurowissenschaften,
32(13), 4386–4399. https://doi.org/10.1523/JNEUROSCI.6063-
11.2012

Wang, X.-J., & Kennedy, H. (2016). Brain structure and dynamics
across scales: In search of rules. Current Opinion in Neurobiol-
Ogy, 37(Suppl. C), 92–98. https://doi.org/10.1016/j.conb.2015.
12.010
Watson, G. S.

(1964). Smooth regression analysis. Sankhy ¯a: Der
Indian Journal of Statistics, Series A (1961–2002), 26(4), 359–372.
(1986).
The structure of the nervous system of the nematode Caenorhab-
ditis elegans. Philosophical Transactions of the Royal Society of
London B: Biological Sciences, 314(1165), 1–340. https://doi.
org/10.1098/rstb.1986.0056

White, J. G., Southgate, E., Thomson, J. N., & Brenner, S.

Ypma, R. J. F., & Bullmore, E. T. (2016). Statistical analysis of
tract-tracing experiments demonstrates a dense, complex corti-
cal network in the mouse. PLoS Computational Biology, 12(9),
e1005104. https://doi.org/10.1371/journal.pcbi.1005104

Zingg, B., Hintiryan, H., Gou, L., Song, M., Bay, M., Bienkowski,
M., . . . Dong, H.-W. (2014). Neural networks of the mouse neo-
Kortex. Cell, 156(5), 1096–1111. https://doi.org/10.1016/j.cell.
2014.02.023