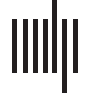FORSCHUNG - Am MIT spezialisierte KI-Forschung

FORSCHUNG

Time-varying whole-brain functional network
connectivity coupled to task engagement

1,2

Hua Xie
Vince D. Calhoun

, Javier Gonzalez-Castillo
, Gang Chen

3,4

, Daniel A. Handwerker
3,4

, Eswar Damaraju

, Xiangyu Liu

, Peter A. Bandettini

,
1
, and Sunanda Mitra

2,5

1Department of Electrical and Computer Engineering, Texas Tech University, Lubbock, TX, USA
2Section on Functional Imaging Methods, National Institute of Mental Health, Nationale Gesundheitsinstitute,
Bethesda, MD, USA
3The Mind Research Network, Albuquerque, NM, USA
4Department of Electrical and Computer Engineering, University of New Mexico, Albuquerque, NM, USA
5Functional MRI Facility, National Institute of Mental Health, Nationale Gesundheitsinstitute, Bethesda, MD, USA
6Scientiﬁc and Statistical Computing Core, National Institute of Mental Health, Nationale Gesundheitsinstitute,
Bethesda, MD, USA

Schlüsselwörter: Whole-brain connectivity pattern, Cognitive marker, Task-evoked connectivity dynamics,
Cognitive dynamics, Brainwide integration

ABSTRAKT

Brain functional connectivity (FC), as measured by blood oxygenation level-dependent
(BOLD) signal, ﬂuctuates at the scale of 10s of seconds. It has recently been found that
whole-brain dynamic FC (dFC) patterns contain sufﬁcient information to permit identiﬁcation
of ongoing tasks. Hier, we hypothesize that dFC patterns carry ﬁne-grained information that
allows for tracking short-term task engagement levels (d.h., 10s of seconds long). To test this
Hypothese, 25 subjects were scanned continuously for 25 min while they performed and
transitioned between four different tasks: Arbeitsgedächtnis, visual attention, math, and rest.
Erste, we estimated dFC patterns by using a sliding window approach. Nächste, we extracted two
engagement-speciﬁc FC patterns representing active engagement and passive engagement by
using k-means clustering. Dann, we derived three metrics from whole-brain dFC patterns to
track engagement level, das ist, dissimilarity between dFC patterns and engagement-speciﬁc
FC patterns, and the level of brainwide integration level. Endlich, those engagement markers
were evaluated against windowed task performance by using a linear mixed effects model.
Signiﬁcant relationships were observed between abovementioned metrics and windowed
task performance for the working memory task only. These ﬁndings partially conﬁrm our
hypothesis and underscore the potential of whole-brain dFC to track short-term task
engagement levels.

ZUSAMMENFASSUNG DES AUTORS

In this study, we hypothesized that whole-brain dynamic functional connectivity (FC) patterns
carry ﬁne-grained information that allows for tracking short-term task engagement levels.
We derived three task engagement markers from whole-brain dynamic FC pattern, das ist,
dissimilarity between dynamic FC patterns and high/low-engagement FC patterns, sowie
brainwide integration level. We employed a linear mixed effects model to relate those task
engagement markers with short-term task performance, and conﬁrmed our hypothesis with
the working memory task.

Keine offenen Zugänge

Tagebuch

Zitat: Xie, H., Gonzalez-Castillo, J.,
Handwerker, D. A., Bandettini, P A.,
Calhoun, V. D., Chen, G., Damaraju, E.,
Liu, X., & Mitra, S. (2019). Time-varying
whole-brain functional network
connectivity coupled to task
engagement. Netzwerkneurowissenschaften,
3(1), 49–66. https://doi.org/10.1162/
netn_a_00051

DOI:
https://doi.org/10.1162/netn_a_00051

zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00051

Erhalten: 18 Oktober 2017
Akzeptiert: 16 Marsch 2018

Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.

Korrespondierender Autor:
Hua Xie
oliver.xie@ttu.edu

Handling-Editor:
Shella Keilholz

Urheberrechte ©: © 2018
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz

Die MIT-Presse

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

Funktionale Konnektivität:
Functional connectivity refers to
statistical dependency between
signals from spatially distributed
Gehirnregionen.

Spatial independent
component analysis:
Spatial ICA decomposes
four-dimensional fMRI data into
spatially independent maps and time
courses.

K-means clustering:
K-means clustering is an
unsupervised clustering method with
the aim to partition data into k
clusters so that each observation
belongs to the cluster with the
highest similarity, and the cluster
centroid serves as a prototype of the
cluster.

Task-evoked functional
connectivity dynamics:
Temporal evolution of functional
connectivity reconﬁguration during
task performance.

EINFÜHRUNG

Funktionale Konnektivität (FC) analyses of resting-state functional magnetic resonance imag-
ing (fMRT) data have consistently revealed sets of spatially distributed and temporally cor-
related brain regions, which correspond to canonical functions such as vision, audition,
Sprache, Erinnerung, and attention (Smith et al., 2009). Spontaneous ﬂuctuations of FC during
rest over short timescales (z.B., seconds to minutes), commonly referred to as FC dynamics
(Hutchison et al., 2013), are believed to be primarily driven by neuronal phenomena, als
evidenced by studies using simultaneous fMRI and electrophysiological recordings (Chang
et al., 2013). Darüber hinaus, mounting evidence emphasizes the potential biological and cogni-
tive signiﬁcance of blood oxygenation level-dependent (BOLD) fMRI FC dynamics evaluated
on the brain as a whole (z.B., considering all possible region-to-region connections). Along
those lines, Allen et al. (2014) proposed a pipeline to investigate whole-brain dynamic FC
(dFC) during rest, also called dynamic functional network connectivity (dFNC). The pipeline
studies the time-varying connectivity between pairs of timecourses coming from independent
networks/components, using a combination of spatial independent component analysis (ICA),
and k-means clustering of sliding window correlation matrices. The identiﬁed FC states were
suggested to reﬂect shifts in ongoing cognition during rest. This approach has recently been
shown to be highly replicable (Abrol et al., 2017), predictive of mental illness (Rashid et al.,
2016), and correlate with multimodal imaging modalities (Allen, Eichele, Wu, & Calhoun,
2013).

Subsequently, others have studied task modulation of FC patterns. Shirer and colleagues
(2012) reported that subject-driven cognitive states (d.h., episodic memory, Musik, subtraction,
and rest) could be correctly classiﬁed using whole-brain FC patterns estimated with a window
Länge (WL) as short as 30–60 s. Similarly high clustering accuracy has been achieved by using
k-means to segment task-evoked dFC patterns to identify the underlying cognitive task at both
individual (Gonzalez-Castillo et al., 2015) and group levels (Xie et al., 2017). Trotzdem,
it remains an open question whether and how task-evoked FC dynamics can be used beyond
task identiﬁcation. More speciﬁcally, we are interested to investigate whether spontaneous FC
ﬂuctuations during the performance of the task can be related to behavioral ﬂuctuations.

Initial evidence suggests that task-evoked FC dynamics accompanying demanding tasks
may indeed carry such detailed information (Gonzalez-Castillo & Bandettini, 2017). Noch, Wie
to extract behaviorally relevant features from whole-brain dFC patterns remains a matter of
debate. Zum Beispiel, Shine et al. (2016) focused on the level of brainwide information inte-
gration during an N-back working memory task, and reported that more integrated FC conﬁg-
urations, as reﬂected by a higher between-module connectivity, were associated with better
task performance. Somehow contradictorily, Sadaghiani and colleagues (2015) found that it
was a more modular—and therefore less integrated—network structure that led to improved
perceptual efﬁciency for a continuous auditory detection task. Given the discrepancy, we are
interested to evaluate how brain network structure reorganizes according to short-term task
engagement level from a graph-theoretic perspective.

Zusätzlich, an alternative approach would be to compute representative whole-brain FC
patterns that describe how the brain is functionally organized during periods of high and
low engagement (HE/LE) during a given task, and use some measure of dissimilarity between
windowed dFCs and those HE/LE representative patterns to track short-term engagement level
indexed by task performance. Here we make several claims, which lead to the following
testable hypothesis.

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

Brain segregation/integration:
Connections occur primarily within
or across functional networks.

Claim 1: Short-term task engagement levels, das ist, the amount of mental effort dedicated

to the task, are encoded in whole-brain FC dynamics.

Claim 2: The resting whole-brain FC pattern can be regarded as a non-task-speciﬁc marker of
low engagement/passive engagement during task performance. Such a low-engagement
FC (LE-FC) representative pattern is obtained here as the k-means centroid associated
with resting periods, which serves as a prototype FC pattern for rest.

Claim 3: Task-related whole-brain FC patterns can be regarded as task-speciﬁc markers of high
engagement/active engagement with a given task. Such task-speciﬁc high-engagement
FC (HE-FC) representative patterns are estimated here using k-means centroids for active
tasks.

Hypothesis: The distance between windowed dFCs and HE-FC/LE-FC patterns reﬂects ongo-
ing changes in the task engagement levels, as reﬂected in variations in short-term task
Leistung (z.B., faster/more accurate responses). dFC during a given window is ex-
pected to indicate better performance if it is more similar to the HE-FC pattern, while
higher similarity to the LE-FC pattern may indicate worse performance.

To test this hypothesis, we used a continuous multitask dataset, part of which was published
In (Gonzalez-Castillo et al., 2015) to test a different hypothesis, and also incorporated addi-
tional data with the same experimental design collected as the follow-up. We tested three task
engagement markers derived from whole-brain dFC patterns, das ist, brainwide integration
level as well as distance between dFC patterns and HE/LE-FC patterns. We ﬁrst estimated dFC
from ICA time courses in terms of windowed whole-brain functional network connectivity
patterns (WL = 45 S). Dann, we estimated the temporal evolution of global brain integration
levels as indexed by each dFC’s participation coefﬁcient. We applied k-means algorithm to
extract representative HE/LE-FC patterns as deﬁned above. Cluster labels were assigned based
on the experimental paradigm, and distance-to-centroid metrics were computed for all avail-
able windowed connectivity estimates. Endlich, we evaluated if those three engagement mark-
ers correlated well with windowed behavioral measures of task engagement (z.B., windowed
reaction time, RT). Siehe Abbildung 1 for a schematic of the analysis pipeline to compute distance-
to-centroid metrics.

We performed these analyses separately on the three available active tasks: 2-back working
Erinnerung (Erinnerung), mental calculation (math), and visual attention (Video). In this exploratory
arbeiten, we were only able to partially conﬁrm our hypothesis for one of the three tasks available,
namely the 2-back memory task. As we shall discuss, the negative ﬁndings for the math and
video task are probably due to task engagement not being the primary variance contributor to
the behavioral metrics available for these two tasks.

ERGEBNISSE

Clustering Accuracy Versus Behavior

The average response accuracy, missing rate and RT within each window calculated following
the previously used procedures (Gonzalez-Castillo et al., 2015), are reported in Table 1, welche
shows overall high task compliance across three active tasks.

The average clustering accuracy describing the overall agreement between k-means par-
titions and ground truth task engagement across all 24 participants is 78.52%, suggesting in
general the k-means algorithm could successfully group dFC patterns according to ongoing
tasks despite the algorithm not being provided with any information about task timing.

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

Figur 1. Schematic of the analysis pipeline. (A) dFC patterns were ﬁrst computed using the win-
(B) Unsupervised k-means clustering was
dowed time series, obtained via group ICA, as input.
then applied on the vectorized dFCs to obtain representative HE-FC or LE-FC patterns. (C) Distance
between task-dFCs and the corresponding task-speciﬁc HE-FC pattern deﬁned as dist(task_dFC,HE)
are plotted against RT. A signiﬁcant positive relationship between the two variables should be
observed if our hypothesis holds.

To gain intuition of how clustering relates to behavior, we now focus on three representative
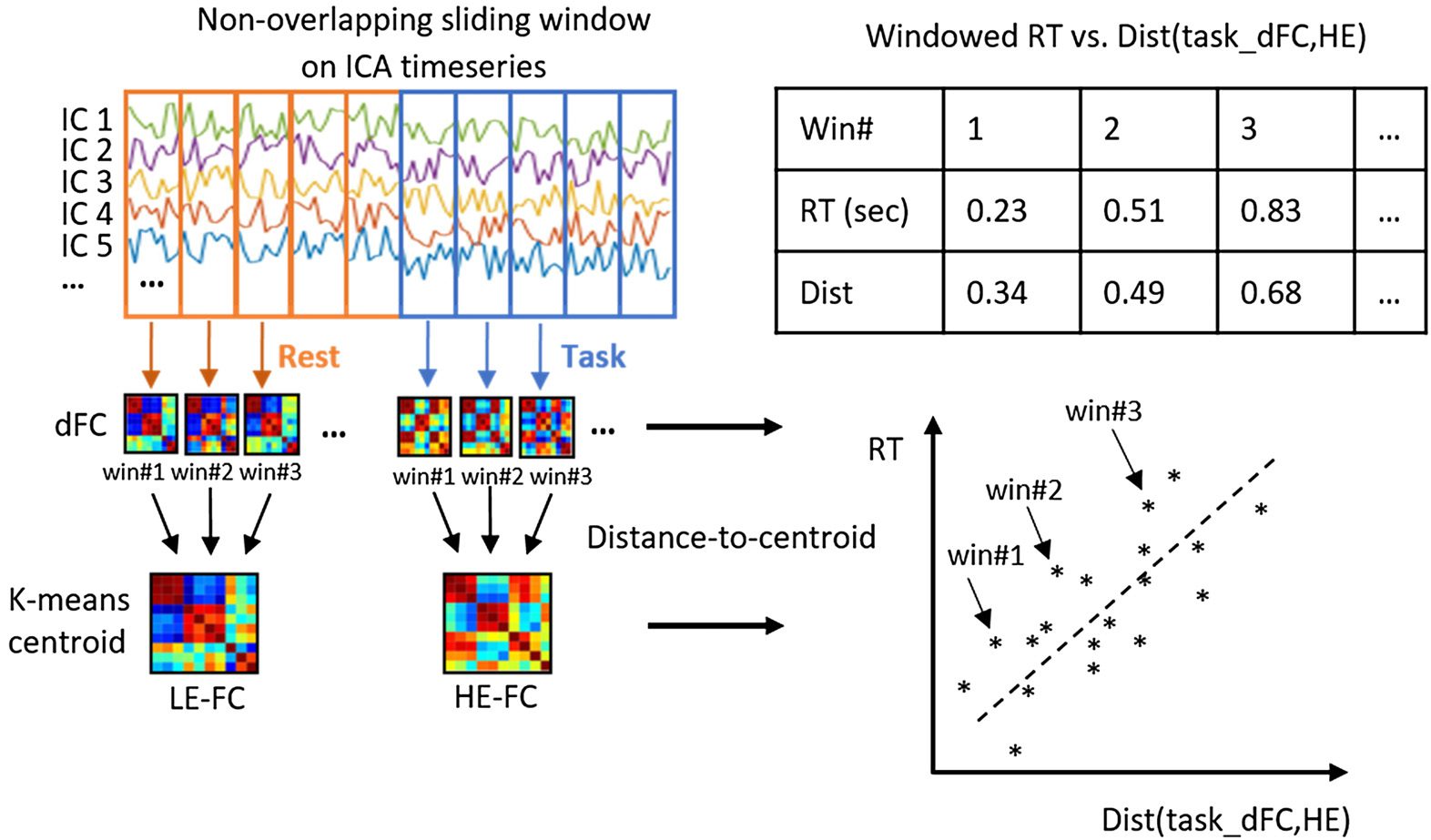
Fächer (SBJ 1, 22, Und 11) with different performance levels (z.B., good, Mittel, and bad
Leistung). Figure 2A shows a 2D visualization of dFCs and their cluster assignments (als
colors) for a subject with overall good task performance obtained with multidimensional scal-
ing (MDS). Ähnlich, Figure 2B shows the same result for a representative subject with mediocre
performance and Figure 2C for one with bad overall task performance. For subjects with good
Leistung (Figure 2A), dFCs appear to be highly organized according to the ongoing task,
so that dFCs associated with a given task (as indicated by color) cluster together, and sepa-
rate from those associated with the other tasks. Tatsächlich, for such a subject, k-means produces
100% clustering accuracy. As for a mediocre performer shown in Figure 2B, the equivalent 2D
projection shows how the general 4-group structure is mostly preserved (yet with a few out-
liers present), leading to a clustering accuracy of 84.38%. For bad performers (Figure 2C), Die
2D projection of dFCs becomes much less structured, reﬂecting weaker task modulation and
leading to poor k-means clustering accuracy (53.12% for the subject depicted in Figure 2C).

We observed that clustering accuracy correlated with overall task performance across all
tasks as previously reported (Gonzalez-Castillo et al., 2015). We next tested if that would be the

Tisch 1. Average and standard deviation of RT, response accuracy, and missing rate

RT (S)
Accuracy (%)
Missing (%)

Memory
1.00 ± 0.37
93.30 ± 5.55
13.23 ± 14.78

Math
2.27 ± 0.35
94.39 ± 4.98
1.53 ± 2.54

Video
1.34 ± 0.18
66.63 ± 16.38
30.50 ± 15.08

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 2. Multidimensional scaling (MDS) 2D projection of dFCs from three subjects with differ-
ent overall task performance (A, B, and C), and clustering accuracy vs. RT for each subject during
the working memory task (D). The dFCs are color coded based on the task. Ausruhen: gray dot; mem-
ory: blue crosshair; Video: yellow dot; math: green dot. (A) Thema 1 is a good subject with well
distinguishable dFNC structure leading to very high overall clustering accuracy (100%). (B) Thema
22 is a mediocre performer with a few outliers leading to relatively high overall clustering accuracy
(84.38%). (C) Thema 11 is a bad performer, and the lack of structure led to degraded overall clus-
tering accuracy (53.12%). (D) Clustering accuracy was correlated with average RT for the memory
Aufgabe. Each cross-represented a subject.

case on a task-by-task basis. We found that the memory clustering accuracy was signiﬁcantly
correlated with subject’s average task performance metrics: RT (r = −0.77; pFDR < 0.001; d f = 22, shown in Figure 2D), missing rate (r = −0.62; pFDR < 0.001; d f = 22), and re- sponse accuracy (r = 0.43; pFDR = 0.019; d f = 22) using Spearman correlation (see also Figure 2A–C). All p values have been false discovery rate (FDR) corrected for multiple com- parisons. We failed to ﬁnd an equivalent signiﬁcant relationship between clustering accuracy and average behavioral metrics for the other two active tasks. Tracking Short-Term Engagement Level Clustering accuracy provides a limited picture of the behavioral signiﬁcance of the clustering structure. To further understand the behavioral interpretation of whole-brain dFC, we eval- uated three candidate metrics derived from whole-brain dFC, that is, dist(task_dFC, HE), dist(task_dFC, LE), and mean participation coefﬁcient (BT). dist(task_dFC, HE) and dist(task_dFC, LE) refer to the distance of each windowed dFCs to its corresponding high-/ Network Neuroscience 53 Functional network connectivity coupled to task engagement Linear mixed effect analysis: Linear mixed effects analysis is extension of linear regression models for data that are collected in groups that has both random and ﬁxed effects. Likelihood ratio test: A likelihood ratio test is a statistical test used for comparing the goodness of ﬁt of two models (full vs. reduced model). low-engagement FC pattern (termed as HE-FC and LE-FC respectively) for a given subject and task. These distance measures reﬂect the overall dissimilarity between each dFC and engagement-speciﬁc FC patterns. Besides, we also computed the mean participation coefﬁ- cient (BT) for each dFC by using brain connectivity toolbox (Rubinov & Sporns, 2010; https:// sites.google.com/site/bctnet/ ), which quantiﬁes the degree that a given brain region connects across different modules/networks. An overall higher BT represents higher between-module connectivity, hence marks a more globally integrated brain state. As previously mentioned, task performance was evaluated in terms of window-averaged RT, response accuracy, and missing rate. Our goal is to determine the relationship between before-mentioned dFC-derived metrics and task performance, for example, dist(task_dFC, HE) versus windowed RT. To further evaluate those relationships, a linear mixed effects (LME) model was formulated on the group level by treating subject and window as random effects (Bates et al., 2014). The p values were computed using likelihood ratio tests, by comparing the goodness of ﬁt of a full model and a reduced model (one with the ﬁxed effect, e.g., BT, in question and one without). The t values were obtained from the full LME model (df = 177). The results of 2-back memory task are reported in Table 2. Eight out of nine relations were proven signiﬁcant, and there was a considerable trend toward signiﬁcance between BT and missing rate (p = 0.090). These results suggest that as task performance degrades, dFCs appear more similar to the LE-FC pattern, and less similar as the task-speciﬁc HE-FC pattern. Moreover, an increased brain integration level (BT) was found to be associated with improved task performance. Those relations were true only for the working memory task, as no consistently signiﬁcant relation was found that correlated task performance for either the math or the video. Results of math and video task can be found in Supporting Information Table S1 ( Xie, Gonzalez-Castillo, Handwerker, Bandettini, Calhoun, Chen, Damaraju, Liu, & Mitra, 2019). 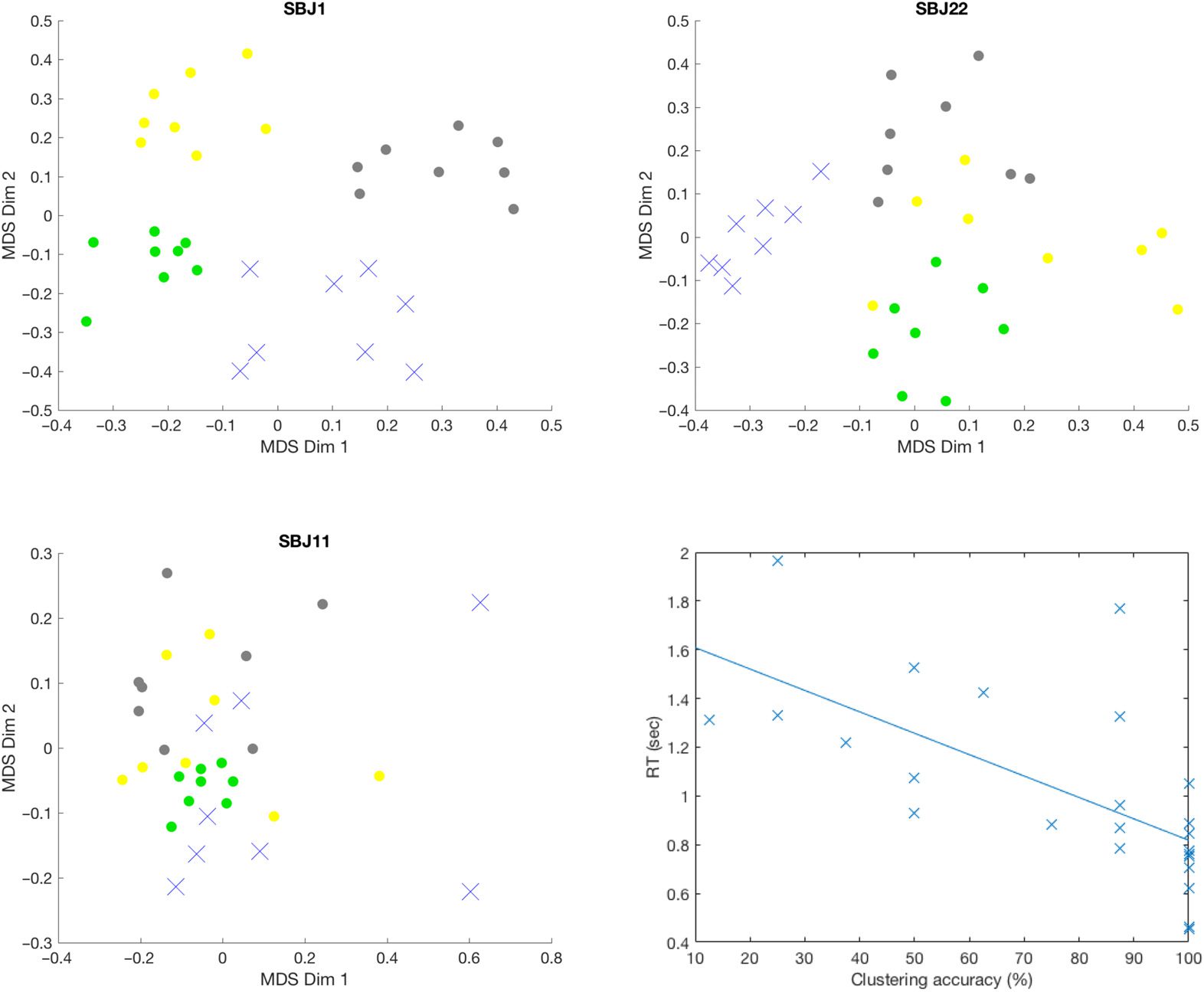Group-Level HE/LE-FC Contrast Pattern In this section, we focused on the difference between the HE-FC and LE-FC patterns during the 2-back task in order to pinpoint potential key FC links for engagement level. After obtain- ing the HE-FC and LE-FC matrices, each of which contains 61 independent components (ICs), we computed the difference between each subject’s HE-FC and LE-FC pattern, that is, FC(HE,subN) – FC(LE,subN), and performed a one-sample one-sided t test for each of 61 × 60/2 = 1, 830 links. We retained links that were signiﬁcant at an FDR-corrected p value of 0.01. We also assigned network labels by computing the spatial overlap between ICs and eight canonical networks from the Shen atlas (Shen, Tokoglu, Papademetris, & Constable, 2013). For seven ICs with almost equal overlap with more than one canonical network in the Shen atlas, the IC labels were manually determined by visually checking the ICs’ spatial patterns and compared against previous studies (Allen et al., 2014; Xie et al., 2017). This yielded two group-level engagement-speciﬁc FC contrast patterns that were consistent across subjects, that is, the active-engagement (HE > LE) and passive-engagement (LE > HE)
contrast as shown in Figure 3. If a link appears signiﬁcant in the active-engagement contrast,

Tisch 2. Results for 2-back memory task

t value (p value)
dist(WM_dFC,HE)
dist(WM_dFC,LE)
BT

RT
2.82 (0.005)
−3.93 (< 0.001) 2.68 (0.027) Response accuracy −2.47 (0.014) 4.28 (< 0.001) 2.35 (0.020) Missing rate 3.30 (0.001) −3.93 (< 0.001) −1.72 (0.090) Network Neuroscience 54 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 1 4 9 1 0 9 2 2 8 3 n e n _ a _ 0 0 0 5 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Functional network connectivity coupled to task engagement l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 4 9 1 0 9 2 2 8 3 n e n _ a _ 0 0 0 5 1 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. FC contrast maps between HE-FC and LE-FC during 2-back working memory task and (A) Active-engagement FC contrast (HE >
spatial maps of ICs highlighted in two contrast maps.
LE ). Only links that were signiﬁcant at a FDR-corrected p value of 0.01 were kept. The IC index is
also displayed along the diagonal cell. The task-positive network (TPN) for working memory task
(IC 64, 77, 78, 84, Und 98) are highlighted by the rectangle. (B) Passive-engagement FC contrast
(LE > HE). IC 34 Und 88 pointed at by arrows are ventral anterior angular cortex (vACC) and PCC,
jeweils, which are more coupled to TPN during passive engagement. (C) A composite spatial
map of task-positive ICs. (D) The spatial map of IC 34 (vACC). (E) The spatial map of IC 88 (PCC).

Netzwerkneurowissenschaften

Functional network connectivity coupled to task engagement

it indicates a stronger link is associated with improved task performance. Umgekehrt, a signiﬁ-
cant link in the passive-engagement contrast suggests that stronger coupling between those ICs
could be detrimental to task performance. Figure 3A reveals clusters among fronto-parietal ICs
with signiﬁcantly increased connectivity during the active engagement of the working mem-
ory task. Figure 3B shows a higher number of connections within default mode, sowie
an increased number of links between fronto-parietal and default-mode ICs during the passive
engagement period.

To better interpret the results in Figure 3A and 3B, we sorted the ICs associated with the
working memory task by matching the ICs’ spatial maps with the activation map generated from
NeuroSynth (Yarkoni et al., 2011; http://neurosynth.org/) using the term “working memory”
(see Supporting Information Figure S1, Xie et al., 2019). Five task-positive ICs were identiﬁed
in this manner, namely IC 64, 77, 78, 84, Und 98 as shown in Figure 3C. These ICs include
portions of the inferior frontal gyrus, superior parietal lobule, dorsolateral prefrontal cortex, Und
inferior parietal lobule. Darüber hinaus, two default-mode ICs (d.h., IC 34 Und 88) were signiﬁcantly
coupled with task-positive ICs during the passive engagement condition (highlighted by the
arrows in Figure 3B), were identiﬁed as ventral anterior angular cortex (vACC) and posterior
cingulate cortex (PCC) as shown in Figure 3D and 3E.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

DISKUSSION

In this study, we successfully replicated the relationship observed by Gonzalez-Castillo et al.
(2015) between k-means clustering accuracy and subject overall task performance, and our
results also suggest the integrity of the clustering structure of dFCs reﬂects individual’s task
Leistung (Figur 2) while using a group ICA approach rather than an atlas-based approach.
We extended the earlier work by further hypothesizing that short-term engagement level (d.h.,
the amount of effort dedicated to the task during a short period of time) may be encoded in
the whole-brain dFC. We tested three engagement markers extracted from whole-brain dFC
patterns, namely dissimilarity between dFCs and FC patterns representing active engagement
(high-engagement FC or HE-FC); dissimilarity between dFCs and FC patterns representing
passive engagement (low-engagement FC or LE-FC); and the level of brainwide integration
level indexed by mean participation coefﬁcients. Those metrics were used to relate to the short-
term engagement level reﬂected by windowed task performance through a mixed effects
Modell. Experimental results only partially conﬁrmed our initial hypothesis. Insbesondere, Die
expected relationship was only observed for the working memory task, but not for the math
and video tasks.

Behavioral Relevance of Whole-Brain dFC

An increasing number of studies has focused on the behavioral relevance of whole-brain dFC
(Cohen, 2017). In the current study, we showed that for the memory task (siehe Tabelle 2), worse
task performance was associated with dFCs with lower similarity to HE-FC patterns, and higher
similarity to LE-FC patterns, as well as smaller participation coefﬁcients (less integrated brain
conﬁguration). This suggests that the degree of deviation of dFCs from the HE-FC patterns (FC
pattern of active engagement) and LE-FC patterns (FC pattern of passive engagement) sowie
as the degree of global FC integration may indeed reﬂect the extent of task engagement, als
originally hypothesized, although only limited to the conﬁnes of the memory task.

When focusing on the global FC pattern, we showed that higher similarity to HE-FC patterns
was associated with better short-term task performance. This is in line with previous stud-
ies showing that decreased dFC variability is related to improved task performance including

Netzwerkneurowissenschaften

Functional network connectivity coupled to task engagement

increased accuracy (Elton & Gao, 2015) and more stable response times (Hutchison &
Morton, 2015).
Mit anderen Worten, the fact that reduction in dFC variability associated with
better task performance highlights the importance of maintaining a stable brain functional
organization that is optimized for a given task (HE-FC pattern) for successful task performance.
The remaining dFC variability during task performance may reﬂect some degree of residual
mind wandering and loss of focus as suggested by Elton and Gao (2015). Andererseits,
we quantiﬁed task disengagement level by using the similarity between dFC patterns and
non-task-speciﬁc LE-FC (rest k-means centroids). Using a 64-task dataset, Cole and colleagues
noted that task-evoked FC changes from rest are often similar to one another, indicating the
existence of a task-general network architecture (Cole, Bassett, Power, Mutiger, & Petersen,
failure of evoking such task-general network architecture may signal dis-
2014). Somit,
engagement from task, and result in dFCs with higher similarity to the rest FC pattern.

When switching our attention to speciﬁc FC links and networks, careful examination re-
vealed ﬁve frontal-parietal ICs (IC 64, 77, 78, 84, Und 98) showing group-level increase dur-
ing active engagement of working memory than passive engagement (Figure 3C). Using the
meta-analysis tool NeuroSynth ( Yarkoni et al., 2011), we observed how those task-positive
ICs showed considerable overlap with the so-called canonical “working memory” regions,
such as dorsolateral prefrontal cortex and superior parietal lobule (Meyer & Lieberman, 2012).
Darüber hinaus, stronger connectivity was also found between those task-positive ICs and ventral an-
terior angular cortex and PCC, part of default-mode network, during the passive-engagement
condition (Figure 3D and 3E). Mit anderen Worten, greater decoupling between the task-positive
and default-mode network is expected during active-engagement period. This observation is
in line with studies linking the strength of the anticorrelation between those two networks
with cognitive performance. Zum Beispiel, stronger anticorrelation between task-positive and
default-mode network was found to be associated with faster reaction times ( Thompson et al.,
(2016) also found that
2013) and less variable reaction times (Kelly et al., 2008). Wang et al.
reduced anticorrelation between the default-mode and attention networks was associated with
more frequent eyelid closure. Although the underlying mechanism remains to be further elu-
cidated, one explanation involves the competition between internally and externally oriented
Erkenntnis (Boveroux et al., 2010).

When turning our attention to global integration levels as a way to track task engagement,
we were able to successfully replicate the ﬁndings in Shine et al. (2016) using Pearson’s cor-
relation instead of multiplication of temporal derivatives (MTD) as a connectivity index. MTD
is calculated as the window-averaged dot product of ﬁrst-order derivatives of two time se-
Ries. Our result supports the original claim by Shine et al. (2016) that a globally integrated
and coordinated brain functional topology, as reﬂected by higher participation coefﬁcients,
might facilitate communication among brain areas that would otherwise remain segregated
during active working memory task performance. Darüber hinaus, our result evidences the robust-
ness of the link between global network integration level and working memory cognitive per-
formance against different dFC measures as well as parcellation schemes (group ICA in current
study vs. Gordon atlas in Shine et al., 2016). It is worth noting that the relationship between
task performance and brainwide integration/segregation level might depend on the under-
lying cognitive context. During the preparation phase of a visual discrimination task,
Ekman et al.
(2012) reported that an enhanced integration level among task-relevant regions
and a reduced integration level within task-irrelevant areas. The difference in the cognitive
context could explain the discrepancy between the conclusion of Shine et al. (2016) Und
Sadaghiani et al. (2015), in which Sadaghiani and collegues found that a more modular brain
organization was linked with better auditory detection task performance. Given the complex

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

nature of the working memory task, it recruits more brain regions that are widely distributed
across the brain compared with those an auditory detection task would, which may lead to the
opposite conclusion.

A recent study by Schultz and Cole (2016) showed that subjects with higher performance on
tasks such as language, relational reasoning, and memory had smaller static FC reconﬁguration
between such tasks and rest. Mit anderen Worten, Schultz and Cole concluded that task FC patterns
of good performers were more similar to their rest FC pattern than those of bad performers. Es
was argued by the authors that individuals with less FC reconﬁguration might modify network
connectivity more efﬁciently to achieve task goals. Although our results may seem to contra-
dict Schultz and Cole, we focused on the dynamical aspects of FC and window-to-window
performance ﬂuctuation, whereas they studied static connectivity patterns by using complete
scans and their relation to intersubject performance differences. The distance between a rest
and task FC map is less relevant to our measure of behavior than the relative distance of a
speciﬁc window’s FC pattern and to HE/LE-FC patterns. Als solche, observed discrepancies could
simply be a result of the difference in temporal scale and analysis-level (intrasubject in
ours vs. across-subject in theirs) across both works.

Post Hoc Analysis on Negative Findings for Math and Video Tasks

We failed to ﬁnd a signiﬁcant linear relationship between windowed connectivity and behav-
ioral metrics for the math and the visual search (Video) Aufgabe. We performed a series of post hoc
analyses in order to better understand what might have led to such negative results. Diese
analyses are discussed in this section.

To evaluate our hypothesis, variability in behavioral metrics should be driven primarily by
task engagement levels. Post hoc evaluation of behavioral metrics following our negative
results for the math and video task suggests otherwise.
Insbesondere, our data suggests (sehen
Figures S2 and S3 in the Supporting Information, Xie et al., 2019) that intertrial variability
of our behavioral metrics were confounded by other factors, such as trial difﬁculty. Despite
our efforts to account for overall intersubject differences in performance (d.h., adopting a LME
Modell), these additional confounds remain present, potentially masking window-to-window
task engagement levels.

The visual search task involves free viewing a natural scene (a prerecording of a live ﬁsh
tank without ﬁxation), target directed saccades (look for the emergent red crosshair), and target
identiﬁcation (decide whether the target is a clown ﬁsh). Als solche, reaction times for this task
can be divided into saccade latency, target localization latency, and identiﬁcation latency
(Castelhano, Pollatsek, & Cave, 2008). The stimuli are perceived faster and more accurately
when they are near the target of an upcoming saccade (Shepherd, M., Findlay, & Hockey,
1986), hence the saccade latencies would be heavily inﬂuenced by the foveal location prior
to the appearance of the target (which is independent of task engagement), but expected to be
highly variable across trials.

For the math task, subjects were asked to select the correct answer from two given options.
Math trials involved addition and/or subtraction of three numbers between 1 Und 10. Eins
robust phenomenon in mathematical cognition is known as the problem size effect, welche
refers to the fact that solution latencies (reaction time) and error rate increase with larger
operands (Ashcraft & Guillaume, 2009). Another potential confounding factor in the math
task is intertrial alternations between retrieval or calculation strategies (Van Beek et al., 2014).

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

Both of these confounds may have played an important role determining solution latencies,
therefore masking task engagement levels.

Andererseits, the memory task is less prone to the confounding effects of the above-
mentioned factors, as in our study the number complexity (Sternberg, 1969), and strength
(Froeberg, 1907) of stimuli, intertrial interval, and memory load remained constant through-
out the task. Unlike the math and video tasks (Figures S2 and S3, zusätzliche Informationen,
Xie et al., 2019), no relationship between individual’s RT and group-averaged RT was observed
for the memory task, which supports the lack of systematic intertrial difﬁculty differences.
Tatsächlich, working memory and attentional engagement have been comprehensively studied
together in the past, and led to a long list of signiﬁcant ﬁndings and theories (Awh & Jonides,
2001; Hampson, Driesen, Skudlarski, Gore, & Polizist, 2006).

Zusammenfassend, our initial hypothesis set was conﬁrmed for one of the three candidate tasks.
Post hoc detailed evaluation of behavioral metrics for the math and video tasks (those leading
to negative results) suggests that their behavioral metrics may not cleanly reﬂect task engage-
ment, impeding evaluation of our hypotheses. In der Zwischenzeit, we believe the results pre-
sented here provide evidence in support of our original claim that dFC patterns may contain
information that goes beyond task identiﬁcation, and could be a valuable index for tracking
task engagement levels.

Limitations and Future Directions

Our study has some important limitations, most of which result from its exploratory nature. Als
mentioned earlier, this study used data acquired under a paradigm previously used (Gonzalez-
Castillo et al., 2015; Xie et al., 2017). This was done so that results could be better interpreted
within the context of those previous studies, as well as for the previously reported good sep-
aration of these tasks via dFC. With hindsight, two of the three tasks were not well suited for
our goals, as their recorded behavioral metrics were not driven primarily by ﬂuctuations in
engagement level. To reliably use behavioral metrics like reaction time as a proxy for task per-
formance requires control for confounding factors such as perceived difﬁculty, engagement
strategies, and ﬁxation location. Although the memory task results presented here support our
initial hypothesis, it would be desirable to also show that the effects observed here are gen-
eralizable across tasks. To address this question of generality, we believe that tasks such as
gradual onset continuous performance task (gradCPT; Rosenberg et al., 2016) could constitute
good candidates for future studies. The gradCPT task consists of stimuli that gradually transition
between images of cities and mountains, and participants are instructed to respond when they
perceive city scenes (which occur randomly 90% of the time) leading to frequent behavioral
Zusätzlich, behavioral
measures not contaminated by any of the abovementioned factors.
measurements other than reaction time or accuracy that are more directly related to engage-
ment level, such as pupil diameter, could be helpful as complementary behavioral logs.

Zusätzlich, although k-means clustering together with the sliding window approach has
proven to be an effective method to study FC dynamics (Allen et al., 2014; Wang et al., 2016;
Xie et al., 2017), we are aware of the ongoing debate on the accuracy of dFC estimation
based on sliding window (Abrol et al., 2017; Laumann et al., 2016; Liégeois et al., 2017).
One criticism of window-based approach is the arbitrary choice of WL (Lindquist, Xu, Nebel,
& Caffo, 2014). In unserem Fall, no optimal a priori WL exists given the different intertrial inter-
vals for the different tasks. Excessively long WL may increase stability of dFC estimation, Aber
may hamper our ability to analyze FC and behavioral dynamics. Too short of a WL may lead

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

to inaccurate estimation of FC dynamics and engagement level. We believe WL = 30TRs =
45 s constitutes a plausible middle ground to accommodate both factors. It should be noted
that optimal WL is recommended to be 50 s without knowledge about the true dFC timescale
(Hindriks et al., 2016), and a recent study comparing various WLs identiﬁed 45 s as an op-
timal choice (Vergara et al., 2017). Future studies should consider alternative dFC methods,
such as dynamic condition correlation (Lindquist et al., 2014), dynamic coherence ( Yaesoubi
et al., 2015), and sparse dictionary learning ( Yaesoubi, Adali, & Calhoun, 2018). It would be
interesting to evaluate our approach against different parcellation schemes as well.

METHODEN

Subjects and Experimental Paradigm
The dataset consisted of two datasets with a total number of 25 Fächer (Alter 26.25 ± 5.15 Jahre,
9 men). The ﬁrst dataset with 17 subjects was previously studied (Gonzalez-Castillo et al.,
2015, verfügbar unter https://central.xnat.org, project ID: FCStateClassif ), and the second dataset
with additional 8 subjects was later collected for another study by using a similar protocol.
Functional runs of the subjects were obtained on a Siemens 7 Tesla MRI scanner using a
32-element receive coil (Nova Medical) with a gradient recalled, single shot, echo planar
Bildgebung (gre-EPI) sequence with TR = 1.5 S, TE = 25 MS; FA = 50◦
, 40 interleaved slices;
FOV = 192 mm; in-plane resolution, 2 × 2 mm; slice thickness, 2 mm.

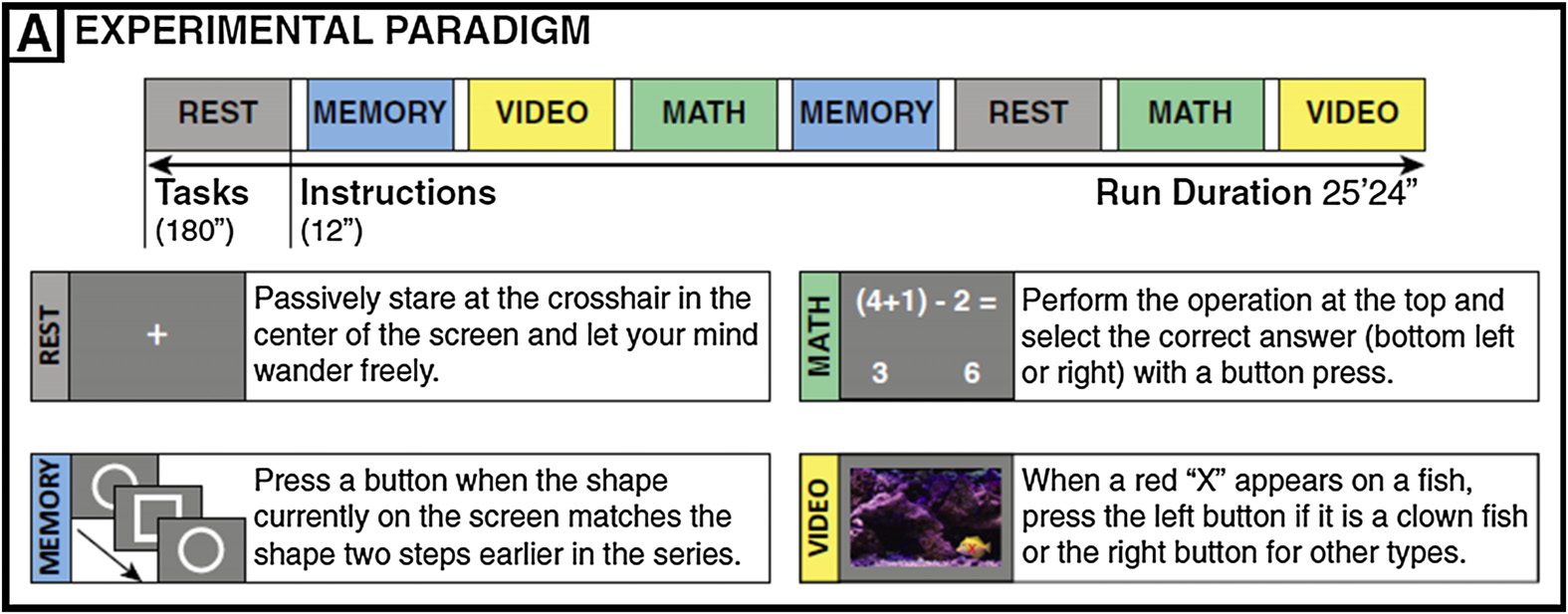
The subjects were scanned continuously for approximately 25 min (1,017 TRs) as they en-
gaged and transitioned between four different mental tasks (math, Erinnerung, Video, and rest) als
shown in Figure 4. Each task block lasted for 120 TRs (180 S). There were instructions between
every two task blocks for 8 TRs (12 S). Each task was repeated twice, and the order of task blocks
was randomized so that each task was followed by a different task. Below is a summary of
four task paradigms.

During the resting-state scan, subjects were asked to passively ﬁxate on the crosshair in the

center of the screen.

For the memory task, subjects were shown a continuous sequence of ﬁve different geometric
shapes that appeared in the center of the screen every 3 S (shapes appeared on the screen for
2.6 S, followed by a blank screen for 0.4 S). Subjects were asked to press the button when
the current shape matched that of two shapes before. There was a total number of 60 Erinnerung
trials per block.

Figur 4. Experimental paradigm from Gonzalez-Castillo et al. (2015).

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

For the math task, the subjects were instructed to choose one correct answer among two
choices for a math operation involving subtraction and addition of three numbers between
1 Und 10. The operation remained on the screen for 4 s followed by a blank screen for 1 S. Dort
was a total number of 36 math trials per block.

For the video (visual search) Aufgabe, a short video clip of ﬁsh swimming in a ﬁsh tank was pre-
gesendet, and subjects were asked to identify whether the ﬁsh highlighted by a red crosshair is a
clown ﬁsh by pressing left button (or right button if the target ﬁsh is not a clown ﬁsh). Each cue
(d.h., the red crosshair) lasted for 0.2 S, and there was a total number of 16 trials per task block.

Data Preprocessing

With a combination of toolboxes (SPM and AFNI) and customized code developed by the
Mind Research Network, the imaging data underwent the following preprocessing steps:
removal of the ﬁrst four volumes; slice timing correction using middle slice as the reference
slice; Bewegungskorrektur; despiking (3dDespike) to mitigate the impact of outliers; detrend-
ing (3dDetrend up to eighth order given the relatively long scan time); spatial normalization
to Montreal Neurological Institute space; spatial smoothing with a Gaussian kernel with
FWHM = 4 mm; Und, ﬁnally, intensity normalization to percentage signal change.

Postprocessing and Functional Network Connectivity Estimation

The group ICA was performed using the GIFT toolbox (http://mialab.mrn.org/software/gift/ )
with the model order (number of components) equal to 100. Principal components analysis
was adopted to retain 120 principal components (PC) at the single-subject level and the expec-
tation maximization algorithm was applied to retain 100 PCs at the group level. The Infomax
ICA algorithm was repeated 20 times using ICASSO (http://www.cis.hut.ﬁ/projects/ica/icasso)
with random initialization, and aggregate spatial maps were estimated as the modes of the
component clusters. Subject-speciﬁc time courses and spatial maps were estimated using the
GICA1 back reconstruction method (Erhardt et al., 2011). A subset of 61 ICs were manually
identiﬁed for further analysis based on the expectations that ICs should exhibit peak activations
in gray matter, and should have time courses dominated by low-frequency or task-frequency
ﬂuctuations (Allen et al., 2014). Time courses underwent motion-related variance regression
(motion parameters and the ﬁrst derivatives), and then were band pass ﬁltered with a sixth-
order Butterworth band-pass ﬁlter (0.0222–0.18 Hz). The upper cut-off frequency was chosen
to be 0.18 Hz to avoid confounds arising from task motor responses, Zum Beispiel, one button
press was required every 5 s during math task. The low cut-off frequency was set according
to the WL (45 S) to remove spurious ﬂuctuations as suggested by Leonardi and Van De Ville
(2015). The time courses were shifted by 6 s or 4 TRs to approximately account for hemo-
dynamic delay and segmented with nonoverlapping windows with WL (45 S) yielding a total
number of 32-windowed time series (8 for each task) for each subject. On average, each win-
dow contains 15 trials for working memory task, 9 for math task, Und 4 for visual search task.
The dFCs were calculated as Pearson’s correlation of those windowed time series, on which
Fisher transformation was then applied. One subject (SBJ 15) was dropped because of high
similarity across all dFCs.

K-Means Clustering
K-means clustering was applied on the dFCs as an unsupervised vector quantization tool to
explore the intrinsic structures of FC dynamics for each individual. The number of clusters was
set to four, and Pearson’s correlation was used as a distance measure. The maximum number

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

of iterations for the k-means algorithm was set to 1,000 to ensure the algorithm converges, Und
k-means++ (Arthur & Vassilvitskii, 2007) was used to choose initial cluster centroid positions.
The distance-to-centroid was recorded after convergence and later correlated with windowed
behavioral measures.

Window-by-Window Participation Coefﬁcients

This part of analysis was performed to validate the ﬁndings in (Shine et al., 2016), which used a
slightly different connectivity measure rather than Pearson’s correlation coefﬁcients. The whole
analysis was carried out using brain connectivity toolbox (Rubinow & Spurns, 2010; https://
sites.google.com/site/bctnet/ ).

Erste, the Louvain modularity algorithm for community detection was employed to estimate
time-varying community structure by iteratively maximizing the modularity statistics. The goal
is to further parcellate the ICs into communities so that the within-module connectivity is
stronger than the between-module connectivity. The Louvain modularity (Blondel, Guillaume,
Lambiotte, & Lefebvre, 2008) was repeated 500 times for each dFC and a consensus
partition was achieved with the consensus clustering algorithm introduced in (Lancichinetti
& Fortunato, 2012). Dann, the participation coefﬁcient (BT), which measures the between-
module connectivity strength, was computed for each window using Equation 1:

BiT = 1 − ∑N
s=1

(cid:3)2

(cid:2) κisT
κiT

(1)

where BiT is the participation coefﬁcient of IC i for window T; κisT is the strength of the positive
connections of IC i belonging to the module s for window T; κiT is the total strength of all
positive connections of IC i for window T; and N is the total number of modules detected
with the Louvain modularity algorithm. Somit, the participation coefﬁcient is between zero
(all links are within its own module) and one (links are uniformly distributed among all the
modules), as detailed by Guimera and Amaral (2005).

Endlich, the participation coefﬁcients were averaged across all the ICs of each window to
achieve mean window-by-window mean participation coefﬁcients (BT), which represented
the level of global integration for window T and were later correlated with average behavioral
measures for that window.

Group-Level Linear Mixed Effects Analysis

LME analysis has been used to conduct group analysis for fMRI studies, as this method
can address issues such as repeated measurements per person, missing data, and multiple
subject-grouping, and therefore leads to increased statistical power as well as controls for
within-individual variation (Beckmann, Jenkinson, & Schmied, 2003; Chen, Saad, Britton, Pine,
& Cox, 2013).

For this study, we used R (R 3.4.2) and lme4 package (Bates et al., 2014) to perform the LME
Analyse. The behavioral metrics (z.B., windowed RT) were expressed as a linear combination
of a set of independent variables. The ﬁxed effects were metrics derived from whole-brain win-
dowed FC matrices,
Zum Beispiel, distance-to-centroid or windowed mean participation
coefﬁcient. The random effects included intercepts for subjects (within-subject variation) Und
windows (within-window variation as all subjects go through the same experimental paradigm).
All variables were z scored before the LME analysis. The p values were computed by likeli-
hood ratio tests, das ist, comparing the full model with the ﬁxed effect in question against
a reduced model without the ﬁxed effect, to determine which model better ﬁts the data. Der

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

t values were obtained from the full LME model. Darüber hinaus, framewise displacement (FD;
Power, Barnes, Snyder, Schlaggar, & Petersen, 2012) was used as a proxy for head motion, Und
windowed FD was included in both models as a ﬁxed effect to rule out the possibility that
effect was merely driven by head motion.

Group-Level Contrast Pattern

We compared the group-level FC patterns associated with high-engagement (HE) and low-
engagement (LE) level by using a one-sample t test. More speciﬁcally, the difference between
k-means centroid labeled as memory and rest was computed on the subject level, yielding
A 61 × 61 matrix and 61 × 60/2 = 1,830 FC links for each subject. We performed a one-
sample one-tailed t test on a given link of all 24 Fächer, followed by FDR to correct for
multiple comparison, and we only kept the links with FDR-corrected p value smaller than
0.01. Two group-level contrast patterns were generated, namely active-engagement (HE > LE)
contrast and passive-engagement (LE > HE) Kontrast. A signiﬁcant link in active-engagement
contrast indicates the strength of the link is stronger for the HE condition. A signiﬁcant link
in passive-engagement contrast means the coupling between the two nodes is stronger during
the LE condition, hence weaker coupling (or stronger decoupling) is to be expected during the
HE condition.

The network labels were assigned by computing the spatial overlap between IC’s spatial
maps and the spatial masks of eight canonical networks from the Shen atlas (Finn et al., 2015;
Shen, Tokoglua, Papademetrisa, & Constablea, 2013), and the one network with maximum
overlap was chosen. For seven ICs that were shared equally by more than one network, Die
network assignment was determined by visual inspection and comparison with previous
Studien (Allen et al., 2014; Xie et al., 2017).

To identify the task-positive ICs, the activation pattern of working memory was obtained
from NeuroSynth ( Yarkoni et al., 2011; http://neurosynth.org/) using the keyword “working
memory.” Neurosynth exported a whole-brain z-score map representing the likelihood that a
voxel being activated associated with working memory from 901 Studien. The working memory
activation pattern generated by NeuroSynth can be found in Supporting Information Figure S1
(Xie et al., 2019).

BEITRÄGE DES AUTORS

Hua Xie: Konzeptualisierung; Formale Analyse; Untersuchung; Methodik; Software; Writing –
original draft; Writing – review & Bearbeitung. Javier Gonzalez-Castillo: Konzeptualisierung; Data
Kuration; Formale Analyse; Untersuchung; Methodik; Ressourcen; Aufsicht; Writing –
original draft; Writing – review & Bearbeitung. Daniel A. Handwerker: Datenkuration; Aufsicht;
Writing – review & Bearbeitung. Peter A. Bandettini: Akquise von Fördermitteln; Aufsicht; Writing –
Rezension & Bearbeitung. Vince D. Calhoun: Akquise von Fördermitteln; Aufsicht; Writing – review &
Bearbeitung. Gang Chen: Formale Analyse; Writing – review & Bearbeitung. Eswar Damaraju: Formal
Analyse. Xiangyu Liu: Writing – review & Bearbeitung. Sunanda Mitra: Akquise von Fördermitteln;
Aufsicht; Writing – review & Bearbeitung.

FUNDING INFORMATION

Peter A. Bandettini, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025),
Award ID: ZIAMH002783. Vince D. Calhoun, National Institute of Mental Health (http://
dx.doi.org/10.13039/100000025), Award ID: R01EB020407. Vince D. Calhoun, National

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

Institute of General Medical Sciences (http://dx.doi.org/10.13039/100000057), Award ID:
P20GM103472. Vince D. Calhoun, Nationale Wissenschaftsstiftung (US), Award ID: 1539067.
Portions of this study used the high-performance computational capabilities of the HPC Biowulf
Cluster at the National Institutes of Health, Bethesda, MD (http://hpc.nih.gov).

VERWEISE

Abrol, A., Damaraju, E., Müller, R. L., Stephen, J. M., Claus, E. D.,
Mayer, A. R., & Calhoun, V. (2017). Replicability of time-varying
connectivity patterns in large resting state fMRI samples. Neuro-
Image, 163, 160–176. https://doi.org/10.1016/j.neuroimage.
2017.09.020

Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T.,
& Calhoun, V. D. (2014). Tracking whole-brain connectivity dy-
namics in the resting state. Hirnrinde, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352

Allen, E., Eichele, T., Wu, L., & Calhoun, V. (2013). EEG signa-
tures of functional connectivity states. Kartierung des menschlichen Gehirns,
1, 2012. https://doi.org/10.1007/s10548-017-0546-2

Arthur, D., & Vassilvitskii, S. (2007). K-Means++: The advantages
of careful seeding. Proceedings of the Eighteenth Annual ACM-
SIAM Symposium on Discrete Algorithms, 8, 1027–1025. https://
doi.org/10.1145/1283383.1283494
Ashcraft, M. H., & Guillaume, M. M.

(2009). Kapitel 4 mathe-
matical cognition and the problem size effect. In Psychology of
Learning and Motivation (1st ed., Bd. 51). Sonst. https://doi.
org/10.1016/S0079-7421(9)51004-3

Awh, E., & Jonides,

(2001). Overlapping mechanisms of
attention and spatial working memory. Trends in Cognitive Sci-
zen, 5(3), 119–126. https://doi.org/10.1016/S1364-6613(00)
01593-X

Bates, D., Mächler, M., Bolker, B. M., & Walker, S. C. (2014).
Fitting linear mixed-effects models using lme4. arXiv Preprint,
arXiv:1406.

Beckmann, C. F., Jenkinson, M., & Schmied, S. M. (2003). Allgemein
multilevel linear modeling for group analysis in FMRI. Neuro-
Image, 20(2), 1052–1063. https://doi.org/10.1016/S1053-8119
(03)00435-X

Blondel, V. D., Guillaume, J. L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Jour-
nal of Statistical Mechanics: Theory and Experiment, 2008(10).
https://doi.org/10.1088/1742-5468/2008/10/P10008

Castelhano, M. S., Pollatsek, A., & Cave, K. R.

Boveroux, P., Vanhaudenhuyse, A., Bruno, M.-A., Noirhomme,
Q., Lauwick, S., Luxen, A., & Degueldre, C. (2010). Breakdown
of within- and between-network resting state during propofol-
induced loss of consciousness. Anesthesiology, 113(5), 1038–1053.
(2008). Typicality
aids search for an unspeciﬁed target, but only in identiﬁca-
tion and not in attentional guidance. Psychonomic Bulletin and
Rezension, 15(4), 795–801. https://doi.org/10.3758/PBR.15.4.795
Chang, C., Liu, Z., Chen, M. C., Liu, X., & Duyn, J. H. (2013).
EEG correlates of time-varying BOLD functional connectivity.
NeuroImage, 72, 227–236. https://doi.org/10.1016/j.neuroimage.
2013.01.049

Chen, G., Saad, Z. S., Britton, J. C., Pine, D. S., & Cox, R. W.
(2013). Linear mixed-effects modeling approach to FMRI group
Analyse. NeuroImage, 73, 176–190. https://doi.org/10.1016/
j.neuroimage.2013.01.047

Cohen, J. R. (2017). The behavioral and cognitive relevance of time-
varying, dynamic changes in functional connectivity. Neuro-
Image. https://doi.org/10.1016/j.neuroimage.2017.09.036

Cole, M. W., Bassett, D. S., Power, J. D., Mutiger, T. S., & Petersen,
Intrinsic and task-evoked network architectures
S. E.
of thev human brain. Neuron, 83(1), 238–251. https://doi.org/
10.1016/j.neuron.2014.05.014

(2014).

Ekman, M., Derrfuss, J., Tittgemeyer, M., & Fiebach, C. J.

(2012).
Predicting errors from reconﬁguration patterns in human brain
Netzwerke. Proceedings of the National Academy of Sciences of
the United States of America, 109, 16714–16719. https://doi.
org/10.1073/pnas.1207523109/-/DCSupplemental.www.pnas.org/
cgi/doi/10.1073/pnas.1207523109

Elton, A., & Gao, W. (2015). Task-related modulation of func-
tional connectivity variability and its behavioral correlations. Hu-
man Brain Mapping, 36(8), 3260–3272. https://doi.org/10.1002/
hbm.22847

Erhardt, E. B., Rachakonda, S., Bedrick, E. J., Allen, E. A., Adali, T., &
Calhoun, V. D. (2011). Comparison of multi-subject ICA meth-
ods for analysis of fMRI data. Kartierung des menschlichen Gehirns, 32(12),
2075–2095. https://doi.org/10.1002/hbm.21170

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
Chun, M. M., . . . Todd Constable, R.
(2015). Functional con-
nectome ﬁngerprinting: Identifying individuals using patterns of
brain connectivity. Naturneurowissenschaften, 18(Oktober), 1–11.
https://doi.org/10.1038/nn.4135

Gonzalez-Castillo, J., & Bandettini, P. A.

Froeberg, S. (1907). The Relation Between the Magnitude of Stim-
ulus and the Time of Reaction. New York: Columbia University.
(2017). Task-based dy-
namic functional connectivity: Recent ﬁndings and open ques-
tionen. NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.
08.006

Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A.
(2015). Tracking ongoing cognition in individuals using brief,
whole-brain functional connectivity patterns. Verfahren der
National Academy of Sciences of the United States of America,
112(28), 8762–8767. https://doi.org/10.1073/pnas.1501242112
Guimera, R., & Amaral, L. A. N. (2005). Cartography of com-
plex networks: Modules and universal roles. Journal of Statistical
Mechanics: Theory and Experiment, (2), 1–13. https://doi.org/
10.1088/1742-5468/2005/02/P02001

Hampson, M., Driesen, N. R., Skudlarski, P., Gore, J. C., & Polizist,
R. T. (2006). Brain connectivity related to working memory

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

Leistung. Zeitschrift für Neurowissenschaften, 26(51), 13338–13343.
https://doi.org/10.1523/JNEUROSCI.3408-06.2006

Hindriks, R., Adhikari, M. H., Murayama, Y., Ganzetti, M., Mantini,
D., Logothetis, N. K., & Deco, G. (2016). Can sliding-window
correlations reveal dynamic functional connectivity in resting-
state fMRI? NeuroImage, 127, 242–256. https://doi.org/10.1016/
j.neuroimage.2015.11.055

Hutchison, R. M., & Morton, J. B. (2015). Tracking the brain’s
Zeitschrift für
functional coupling dynamics over development.
Neurowissenschaften, 35(17), 6849–6859. https://doi.org/10.1523/
JNEUROSCI.4638-14.2015

Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini,
P. A., Calhoun, V. D., Corbetta, M., . . . Chang, C. (2013).
Dynamic functional connectivity: Promise, issues, and inter-
pretations. NeuroImage, 80, 360–378. https://doi.org/10.1016/
j.neuroimage.2013.05.079

Kelly, A. C., Uddin, L. Q., Biswal, B. B., Castellanos, F. X., &
Milham, M. P.
(2008). Competition between functional brain
networks mediates behavioral variability. NeuroImage, 39(1),
527–537. https://doi.org/10.1016/j.neuroimage.2007.08.008
Lancichinetti, A., & Fortunato, S. (2012). Consensus clustering in
complex networks. Scientiﬁc Reports, 2. https://doi.org/10.1038/
srep00336

Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton,
C., Adeyemo, B., . . . Petersen, S. E. (2016). On the stability of
BOLD fMRI correlations. Hirnrinde, 1–14. https://doi.org/
10.1093/cercor/bhw265

Leonardi, N., & Van De Ville, D.

(2015). On spurious and real
ﬂuctuations of dynamic functional connectivity during rest. Neu-
roImage, 104, 430–436. https://doi.org/10.1016/j.neuroimage.
2014.09.007

Liégeois, R., Laumann, T. O., Snyder, A. Z., Zhou, H. J., & Yeo,
B. T. T. (2017). Interpreting temporal ﬂuctuations in resting-state
functional connectivity MRI. bioRxiv, (2014). https://doi.org/10.
1101/135681

Lindquist, M. A., Xu, Y., Nebel, M. B., & Caffo, B. S. (2014). Evalu-
ating dynamic bivariate correlations in resting-state fMRI: A com-
parison study and a new approach. NeuroImage, 101, 531–546.
https://doi.org/10.1016/j.neuroimage.2014.06.052

Meyer, M. L., & Lieberman, M. D.

(2012). Social working mem-
ory: Neurocognitive networks and directions for future research.
Grenzen in der Psychologie, 3(DEC), 1–11. https://doi.org/10.3389/
fpsyg.2012.00571

Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &
Petersen, S. E. (2012). Spurious but systematic correlations in
functional connectivity MRI networks arise from subject mo-
tion. NeuroImage, 59(3), 2142–2154. https://doi.org/10.1016/
j.neuroimage.2011.10.018

Rashid, B., Arbabshirani, M. R., Damaraju, E., Cetin, M. S.,
Müller, R., Pearlson, G. D., & Calhoun, V. D. (2016). Classiﬁ-
cation of schizophrenia and bipolar patients using static and dy-
namic resting-state fMRI brain connectivity. NeuroImage, 134,
645–657. https://doi.org/10.1016/j.neuroimage.2016.04.051
Rosenberg, M. D., Finn, E. S., Scheinost, D., Papademetris, X., Shen,
X., Polizist, R. T., & Chun, M. M. (2016). A neuromarker of
sustained attention from whole-brain functional connectivity.
Naturneurowissenschaften, 19(1), 165.

Rubinow, M., & Spurns, Ö. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Sadaghiani, S., Polina, J.-B., Kleinschmidt, A., & D'Esposito, M.
(2015). Ongoing dynamics in large-scale functional connectiv-
ity predict perception. Proceedings of the National Academy of
Sciences of the United States of America, 112(27), 8463–8468.
https://doi.org/10.1073/pnas.1420687112

Schultz, D. H., & Cole, M. W. (2016). Higher intelligence is associ-
ated with less task-related brain network reconﬁguration. Zeitschrift
der Neurowissenschaften, 36(33), 8551–8561. https://doi.org/10.1523/
JNEUROSCI.0358-16.2016

Shen, X., Tokoglu, F., Papademetris, X., & Polizist, R. T. (2013).
Groupwise whole-brain parcellation from resting-state fMRI data
for network node identiﬁcation. NeuroImage, 82, 403–415.
https://doi.org/10.1016/j.neuroimage.2013.05.081

Shepherd, M., Findlay, J. M., & Hockey, R. J.

(1986). The rela-
tionship between eye movements and spatial attention. Der
Quarterly Journal of Experimental Psychology, 38(3), 475–491.
Shine, J. M., Bissett, P. G., Glocke, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., . . . Poldrack, R. A. (2016). The dynamics of
functional brain networks: Integrated network states during cog-
nitive task performance. Neuron, 92(2), 544–554. https://doi.
org/10.1016/j.neuron.2016.09.018

Shirer, W. R., Ryali, S., Rykhlevskaia, E., Menon, V., & Greicius,
M. D. (2012). Decoding subject-driven cognitive states with
whole-brain connectivity patterns. Hirnrinde, 22(1), 158–165.
https://doi.org/10.1093/cercor/bhr099

Schmied, S. M., Fuchs, P. T., Müller, K. L., Glahn, D. C., Fuchs, P. M.,
Mackay, C. E., . . . Beckmann, C. F. (2009). Correspondence
of the brain’s functional architecture during activation and rest.
Proceedings of the National Academy of Sciences of the United
States of America, 106(31), 13040–5. https://doi.org/10.1073/
pnas.0905267106

Sternberg, S.

(1969). Memory-scanning: Mental processes re-
vealed by reaction-time experiments. American Scientist, 57(4),
421–457.

Thompson, G. J., Magnuson, M. E., Merritt, M. D., Schwarb, H.,
Pan, W. J., Mckinley, A., . . . Keilholz, S. D. (2013). Short-time
windows of correlation between large-scale functional brain
networks predict vigilance intraindividually and interindividu-
ally. Kartierung des menschlichen Gehirns, 34(12), 3280–3298. https://doi.org/
10.1002/hbm.22140

Van Beek, L., Ghesquiér, P., De Smedt, B., & Lagae, L. (2014).
The arithmetic problem size effect in children: an event-related
potential study. Grenzen der menschlichen Neurowissenschaften, 8, 1–11.
https://doi.org/10.3389/fnhum.2014.00756

Vergara, V. M., Mayer, A. R., Damaraju, E., & Calhoun, V. D. (2017).
The effect of preprocessing in dynamic functional network con-
nectivity used to classify mild traumatic brain injury. Brain and
Behavior, 7(10), 1–11. https://doi.org/10.1002/brb3.809

Wang, C., Ong, J. L., Patanaik, A., Zhou, J., & Chee, M. W. L.
(2016). Spontaneous eyelid closures link vigilance ﬂuctuation
with fMRI dynamic connectivity states. Verfahren des Nationalen
Academy of Sciences of the United States of America, 113(34),
9653–9658. https://doi.org/10.1073/pnas.1523980113

Xie,H.,Calhoun, V.D.,Gonzalez-Castillo,J.,Damaraju,E.,Miller,R.,
Bandettini, P. A., & Mitra, S. (2017). Whole-brain connectivity

Netzwerkneurowissenschaften

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Functional network connectivity coupled to task engagement

dynamics reﬂect both task-speciﬁc and individual-speciﬁc mod-
ulation: A multitask study. NeuroImage. https://doi.org/10.1016/
j.neuroimage.2017.05.050

Xie, H., Gonzalez-Castillo, J., Handwerker, D. A., Bandettini, P. A.,
Calhoun, V. D., Chen, G., Damaraju, E., Liu, X., & Mitra, S.
(2019). Supporting information for “time-varying whole-brain
functional network connectivity coupled to task engagement.”
Netzwerkneurowissenschaften, 3(1), 49–66. https://doi.org/10.1162/
netn_a_00051

Yaesoubi, M., Adali, T., & Calhoun, V. D. (2018). A window-
less approach for capturing time-varying connectivity in fMRI

data reveals the presence of states with variable rates of change.
Kartierung des menschlichen Gehirns, (November 2017), 1–11. https://doi.org/
10.1002/hbm.23939

Yaesoubi, M., Allen, E. A., Müller, R. L., & Calhoun, V. D. (2015).
Dynamic coherence analysis of resting fMRI data to jointly
capture state-based phase, frequency, and time-domain infor-
mation. NeuroImage, 120, 133–142. https://doi.org/10.1016/
j.neuroimage.2015.07.002

Yarkoni, T., Poldrack, R. A., Nichols, T. E., Van Essen, D. C., &
Wager, T. D. (2011). Large-scale automated synthesis of human
functional neuroimaging data. Nature Methods, 8(8), 665–670.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
1
4
9
1
0
9
2
2
8
3
N
e
N
_
A
_
0
0
0
5
1
P
D