FORSCHUNG
Predicting longitudinal brain atrophy
in Parkinson’s disease using a
Susceptible-Infected-Removed
agent-based model
Alaa Abdelgawad1*, Shady Rahayel1,2*, Ying-Qiu Zheng3, Christina Tremblay1,
Andrew Vo1, Bratislav Misic1†
, and Alain Dagher1†
Keine offenen Zugänge
Tagebuch
*Equal contribution.
†Equal contribution.
1The Neuro (Montreal Neurological Institute-Hospital), McGill-Universität, Montreal, Kanada
2Centre for Advanced Research in Sleep Medicine, Hôpital du Sacré-Cœur de Montréal, Montreal, Kanada
3Wellcome Centre for Integrative Neuroimaging, Centre for Functional Magnetic Resonance Imaging of the Brain,
Universität Oxford, John Radcliffe Hospital, Oxford, Großbritannien
Schlüsselwörter: MRT, Alpha-synuclein, Brain networks, Neurodegeneration
ABSTRAKT
Parkinson’s disease is a progressive neurodegenerative disorder characterized by accumulation
of abnormal isoforms of alpha-synuclein. Alpha-synuclein is proposed to act as a prion
in Parkinson’s disease: In its misfolded pathologic state, it favors the misfolding of normal
alpha-synuclein molecules, spreads trans-neuronally, and causes neuronal damage as it
accumulates. This theory remains controversial. We have previously developed a Susceptible-
Infected-Removed (SIR) computational model that simulates the templating, propagation,
and toxicity of alpha-synuclein molecules in the brain. In this study, we test this model with
longitudinal MRI collected over 4 years from the Parkinson’s Progression Markers Initiative
(1,068 T1 MRI scans, 790 Parkinson’s disease scans, Und 278 matched control scans). Wir
find that brain deformation progresses in subcortical and cortical regions. The SIR model
recapitulates the spatiotemporal distribution of brain atrophy observed in Parkinson’s disease.
We show that connectome topology and geometry significantly contribute to model fit. Wir
also show that the spatial expression of two genes implicated in alpha-synuclein synthesis
and clearance, SNCA and GBA, also influences the atrophy pattern. We conclude that the
progression of atrophy in Parkinson’s disease is consistent with the prion-like hypothesis
and that the SIR model is a promising tool to investigate multifactorial neurodegenerative
diseases over time.
ZUSAMMENFASSUNG DES AUTORS
It has been suggested that neurodegenerative diseases are caused by abnormal generation,
propagation, and accumulation of neurotoxic protein isoforms. In the case of Parkinson’s
Krankheit, the culprit is alpha-synuclein, which has been shown in animal models to exhibit
prion-like properties. We devised a Susceptible-Infected-Removed agent-based model of
synucleinopathy, in which we simulate the fates of normal and misfolded alpha-synuclein
molecules moving along a brain network. We show that the progression of brain atrophy
in Parkinson’s disease over the first 2 years following diagnosis can be simulated by our
Modell. We conclude that the pattern of brain atrophy in Parkinson’s disease is shaped by a
Zitat: Abdelgawad, A., Rahayel, S.,
Zheng, Y.-Q., Tremblay, C., Vo, A., Misic,
B., & Dagher, A. (2023). Predicting
longitudinal brain atrophy in Parkinson’s
disease using a Susceptible-Infected-
Removed agent-based model. Netzwerk
Neurowissenschaften, 7(3), 906–925. https://doi
.org/10.1162/netn_a_00296
DOI:
https://doi.org/10.1162/netn_a_00296
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00296
Erhalten: 2 Mai 2022
Akzeptiert: 20 November 2022
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Alain Dagher
alain.dagher@mcgill.ca
Handling-Editor:
Martijn van den Heuvel
Urheberrechte ©: © 2023
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Agent-based model of Parkinson’s disease
combination of the connectome and regional expression of genes that control the clearance
and synthesis of alpha-synuclein. Our work supports the prion-like model of neurodegeneration
in Parkinson’s disease.
EINFÜHRUNG
Parkinson’s disease (PD) is characterized by the pathological intracellular aggregation of mis-
folded alpha-synuclein (aSyn) into Lewy bodies and neurites (Dickson et al., 2009; Spillantini
et al., 1997). In the brain, these deposits often appear in a stereotypical fashion, emerging in
the olfactory bulb and caudal brainstem and then ascending towards the midbrain, limbic
Bereiche, and cerebral cortex (Braak et al., 2003; Braak, Ghebremedhin, Rüb, Bratzke, & Del
Tredici, 2004). This spatiotemporal distribution pattern of pathology has led to the hypothesis
that misfolded aSyn may harbor prion-like properties (Brundin & Melki, 2017), allowing it to
spread between cells and impose its misfolded conformation onto native endogenous,
otherwise normal aSyn from the recipient cell (Peng, Trojanowski, & Lee, 2020). In der Tat,
the injection of synthetic aSyn preformed fibrils or brain lysates from patients with a synuclei-
nopathy has demonstrated the local formation of aSyn pathology and its propagation through
brain networks in wild-type and transgenic mice, rats, and nonhuman primates (Henrich et al.,
2020; Luk et al., 2012; Masuda-Suzukake et al., 2013; Rey et al., 2018; Rey et al., 2016;
Uemura, Uemura, Luk, Lee, & Trojanowski, 2020; Watts et al., 2013).
In humans, the evidence for a prion-like behavior of pathological aSyn has so far been indi-
rect. Zum Beispiel, in patients who received fetal mesencephalic neuronal transplants, Lewy-
related pathology could be observed inside cells that were grafted a decade earlier (Kordower,
Chu, Hauser, Freeman, & Olanow, 2008; Li et al., 2008), suggesting that pathology spread to
the grafts from the surrounding milieu. Auch, using MRI-derived volume deformation and cor-
tical thinning as proxy measures of tissue atrophy, the pattern of brain changes observed in de
novo PD patients was shown to significantly overlap with the brain’s connectivity pattern
(Pandya et al., 2019; Tremblay et al., 2021; Zeighami et al., 2015). Jedoch, other studies
have also shown that the distribution of aSyn pathology is not solely explainable by brain
connectivity and that other cell-autonomous factors play a role in shaping aSyn pathology
(Gonzalez-Rodriguez, Zampese, & Surmeier, 2020; Henrich et al., 2020; Surmeier, Obeso,
& Halliday, 2017). Daher, the mechanisms underlying the accumulation and propagation of
pathological aSyn in PD remain unclear.
One way to understand these mechanisms is through computational modeling. Wir haben
recently developed an agent-based Susceptible-Infected-Removed (SIR) model that simulates
the fate of individual aSyn proteins in the brain to recreate, based on cell-autonomous factors
and brain connectivity, the atrophy pattern seen in PD (Zheng et al., 2019). The local factors in
this case are expression of the genes SNCA and GBA, which we take as proxies of synthesis
and clearance of aSyn. Using this model, we previously recreated the pattern of atrophy
observed at baseline in de novo PD patients from the Parkinson’s Progression Markers Initia-
tiv (PPMI) cohort and demonstrated that both structural connectivity and gene expression
contributed to model accuracy (Zheng et al., 2019). We subsequently used the same model
to demonstrate that gene and connectivity factors also underpinned the propagation of path-
ologic aSyn injected into different brain regions of wild-type mice (Rahayel, Misic, et al.,
2022). Darüber hinaus, we also demonstrated that the brain atrophy seen in patients with isolated
REM sleep behavior disorder, a prodromal state of PD and dementia with Lewy bodies
(Postuma et al., 2019), could also be recreated with the model (Rahayel, Tremblay, et al.,
907
Alpha-synuclein:
An abundant neuronal protein that
may become misfolded and toxic in
Parkinson’s disease.
Lewy bodies:
Abnormal neuronal inclusions that
are a hallmark of Parkinson’s disease
neuropathology.
Prions:
Misfolded protein isoforms that were
discovered as the cause of
Creutzfeldt-Jakob disease but may
also be implicated in common
neurodegenerative diseases.
Susceptible-Infected-Removed (SIR)
Modell:
A computational model often used in
infectious disease epidemiology.
SNCA:
The gene for alpha-synuclein.
GBA:
The gene for glucocerebrosidase, A
lysosomal enzyme important for
protein degradation.
REM sleep behavior disorder:
A condition characterized by moving
or talking during sleep, which may
be a prodrome of Parkinson’s
Krankheit.
Netzwerkneurowissenschaften
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Agent-based model of Parkinson’s disease
Deformation-based morphometry:
A method to derive voxel-wise brain
atrophy from a single T1-weighted
MRI scan.
MDS-UPDRS:
A clinical scale used to assess
symptom severity in Parkinson’s
Krankheit.
2022). Jedoch, it remains unknown whether the propagation of aSyn in the brain also shapes
the progression of brain atrophy in PD over several years.
In this study, our objective was to investigate whether the agent-based SIR model could
recreate the longitudinal patterns of brain atrophy in PD patients from the PPMI cohort over
4 Jahre. We used deformation-based morphometry to measure the progression of tissue defor-
mation (atrophy) in PD patients versus controls over 1, 2, Und 4 Jahre. We then applied the
agent-based SIR model to assess whether SNCA and GBA gene expression and structural
features of the connectome significantly contributed to recreating the atrophy patterns. Wir
found that the agent-based SIR model recreated the atrophy observed longitudinally in PD
and that both gene expression and connectivity are significant contributors to the distribution
of atrophy.
METHODEN
Teilnehmer
Longitudinal data from 790 PD patients and 278 healthy control participants were included
from the PPMI database (https://www.ppmi-info.org), for a total of 1,068 MRI scans and
associated clinical measures. The PPMI is a longitudinal observational international study
aimed at assessing progression markers of PD and includes a comprehensive set of clinical
and MRI measures acquired in patients with de novo PD and in healthy controls (Marek
et al., 2018).
To be included in the PPMI, PD patients (A) had at least two features among resting tremor,
bradykinesia, and rigidity or either asymmetric resting tremor or asymmetric bradykinesia; (B)
had a diagnosis of PD for less than 2 Jahre; (C) had a baseline Hoehn and Yahr stage of I or II;
(D) had a dopamine transporter binding deficit confirmed using single photon emission com-
puted tomography; (e) were not expected to require medications for PD within six months of
the baseline assessment; (F ) were at least 30 Jahre alt; Und (G) did not have dementia. Für
healthy controls, a Montreal Cognitive Assessment score below 27 or a first-degree relative
with a clinical diagnosis of idiopathic PD led to exclusion. The longitudinal follow-up of PPMI
now extends to approximately 5 Jahre; for this study, only the participants with MRI acquisition
performed at baseline and at either 1, 2, and/or 4 years were considered for analysis because
of the limited number of scans acquired at 3 Jahre (three participants) Und 5 Jahre (zwei
Teilnehmer). The PPMI investigators obtained informed consent from all participants. Das
research using derived data was approved by the Research Ethics Board of the McGill Univer-
sity Health Center.
Clinical Measures
At each visit, patients underwent the Movement Disorders Society-Unified Parkinson’s Disease
Rating Scale (MDS-UPDRS; Goetz et al., 2007), the Montreal Cognitive Assessment
(Nasreddine et al., 2005), the REM Sleep Behavior Disorder Screening Questionnaire, An
which a score ≥5 indicates probable REM sleep behavior disorder (Stiasny-Kolster et al.,
2007), the Geriatric Depression Scale, the State-Trait Anxiety Inventory, and the Scales for
Outcomes in Parkinson’s Disease-Autonomic.
Cognitive Assessment
In addition to the aforementioned evaluation, every patient also underwent a comprehensive
cognitive assessment that included the Symbol-Digit Modalities Test; the Letter-Number
Netzwerkneurowissenschaften
908
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Agent-based model of Parkinson’s disease
Sequencing test; the Benton Judgment of Line Orientation test; the semantic and phonemic
fluency tasks; and the total recall, delayed recall, and recognition tasks from the Hopkins
Verbal Learning Test-Revised (Weintraub et al., 2015).
MRI Acquisition
T1-weighted MRI brain images were acquired at different sites across the United States,
Kanada, and Europe, with the following parameters: repetition time = 2,300 MS; Echozeit =
2.98 MS; Sichtfeld = 256 mm; flip angle = 9; and voxel size = 1 mm3. The acquisition pro-
tocols are available on the PPMI website (https://www.ppmi-info.org/study-design/research
-documents-and-sops/).
Deformation-Based Morphometry
Deformation-based morphometry (DBM) was performed on the baseline and longitudinal T1-
weighted scans of PD patients and controls to derive whole-brain individual atrophy maps.
Speziell, the maps represent the deformation needed for each voxel to be normalized to
the template space. DBM was done using the default parameters available in the CAT12 tool-
box in SPM12 (https://www.neuro.uni-jena.de/cat). This resulted in a set of processed image
files for each participant that included a voxel-wise whole-brain map of Jacobian determi-
nants, which was used as the measure of local brain tissue atrophy after the application of
a 2-mm full width at half maximum isotropic smoothing kernel. Images were visually
inspected at each step and excluded if abnormal or if the quality rating score was below
80%. The image quality rating score is an aggregate measurement generated by the CAT12
processing pipeline; it integrates several metrics of image quality, namely noise-to-contrast
Verhältnis, coefficient of joint variation, inhomogeneity-to-contrast ratio, and root-mean-squared
voxel resolution into a single value ranging from 0 Zu 1 (d.h., the higher the score, the better
the image quality).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
Substantia nigra:
A nucleus in the midbrain containing
dopamine neurons; it is affected early
in Parkinson’s disease.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Brain Parcellation
The normalized smoothed Jacobian determinants maps were next parcellated using a previ-
ously used atlas made of 42 cortical and subcortical brain regions from the left hemisphere for
which regional SNCA and GBA expression as well as structural connectome features were
verfügbar (Zheng et al., 2019). This atlas included 34 cortical regions derived from the
Desikan-Killiany Atlas (Desikan et al., 2006) Und 7 subcortical regions, namely the putamen,
Schwanz, pallidum, thalamus, hippocampus, amygdala, and accumbens, available as part of
the FreeSurfer processing stream (https://surfer.nmr.mgh.harvard.edu). Because of its impor-
tance in PD, the substantia nigra was additionally included based on the segmentation avail-
able from a 7T MRI basal ganglia atlas (https://www.nitrc.org/projects/atag; Keuken et al.,
2014). Using FLIRT (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FLIRT), the 42-region atlas was then
linearly registered to the individual deformation maps and a set of 42 regional deformation
values were extracted for each map using the MarsBaR region of interest toolbox for SPM
(https://marsbar.sourceforge.net). Note that the atlas only included regions from the left hemi-
sphere due to the SNCA and GBA gene expression for the right hemisphere being available for
only two of the six postmortem brains in the Allen Human Brain Atlas (Hawrylycz et al., 2012).
We also tested the model on one hemisphere to avoid possible errors associated with the
detection of interhemispheric white matter connections with deterministic streamline tracto-
graphy (siehe unten).
Netzwerkneurowissenschaften
909
Agent-based model of Parkinson’s disease
Regional Atrophy Quantification
A W-score approach was used to account for the normal effects of age and sex on brain
morphometry (La Joie et al., 2012; Tremblay et al., 2020). The regional deformation values from
each PD patient’s MRIs were converted into age- and sex-corrected W-scores based on the
values observed in the 157 controls available at baseline. There was no significant difference
in age and sex between the controls (Alter: 60.1 ± 11.9, 66% männlich) at baseline and the PD group
at each follow-up timepoint (baseline age: 60.9 ± 10.0, 63% männlich; Jahr 1 Alter: 60.9 ± 9.3, 63%
männlich; Jahr 2 Alter: 60.9 ± 9.3, 63% männlich; Jahr 4 Alter: 64.4 ± 9.9, 69% männlich). Only the values
from controls seen at baseline were used for standardization because of the limited number of
controls who underwent follow-up MRI. The W-score formula was the following:
Wscore ¼ PDraw value − PDpredicted based on HC
SDresiduals in HC
;
where the predicted value for a PD patient based on control data was given by (β1 × age + β2 ×
Sex + β3). Mit anderen Worten, this yielded regional deformation values that represented the differ-
ence between a PD patient’s deformation value and the deformation value that is expected for
their age and sex. Hier, W-scores are essentially z-scores corrected for age and sex (La Joie
et al., 2012). In this work, only age and sex were used as control variables, whereas all other
clinical and cognitive measures were exclusively used for characterizing the PD group at base-
line and over time. The individual W-scores were then averaged between patients for a given
region, resulting in a set of 42 regional W-scores for baseline and each of the three follow-up
timepoints. The baseline W-score was then subtracted from the average W-score seen at each
follow-up timepoint to yield a W-score difference over time (d.h., atrophy progression over 1, 2,
Und 4 Jahre). These were inverted for interpretability: A positive W-score indicated atrophy pro-
gression, whereas a negative W-score difference represented volume expansion. The three sets
von 42 atrophy difference values, one for the difference between baseline and every follow-up
timepoint, were the observed patterns of atrophy progression to which we compared the pattern
of simulated atrophy generated in silico by the agent-based SIR model. An overview of the ana-
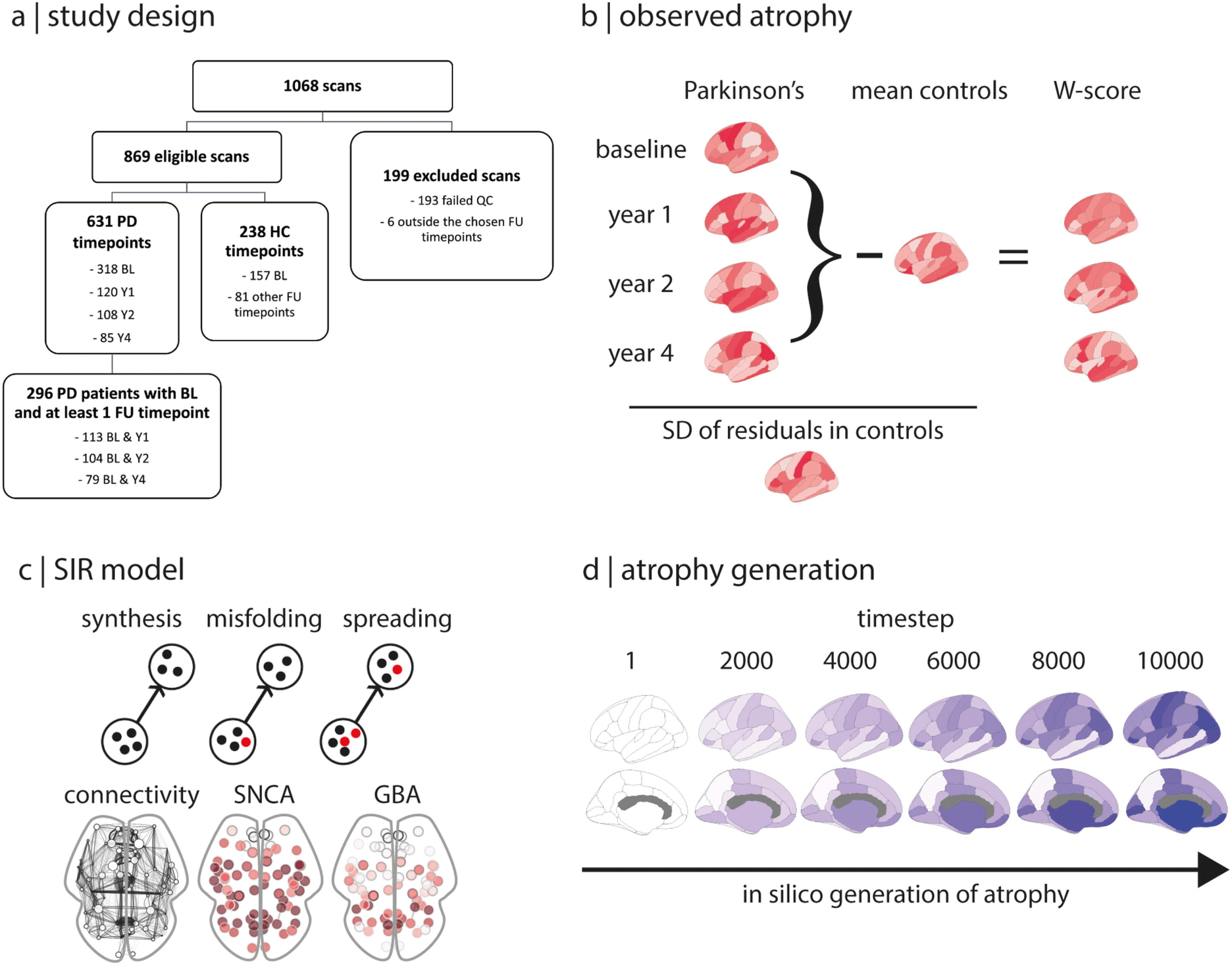
lytical steps is presented in Figure 1.
Agent-Based SIR Model
Overview of the model. The agent-based SIR model is a computational model based on infec-
tious disease epidemiology; Jedoch, instead of studying the propagation of an infection in a
Bevölkerung, it simulates the propagation of aSyn in a brain network. In our model, the agents
are aSyn molecules, which can belong to one of three compartments: “susceptible” when rep-
resenting the normal protein, “infected” when representing the misfolded protein, Und
“removed” when representing a protein that is no longer active in the region. This model
has been shown to accurately recreate the distribution of pathology in non-transgenic mice
injected with preformed aSyn fibrils as well as the atrophy pattern observed in patients with
PD (at baseline), isolated REM sleep behavior disorder, and frontotemporal dementia (Rahayel,
Misic, et al., 2022; Rahayel, Tremblay, et al., 2022; Shafiei et al., 2021; Zheng et al., 2019).
This model of disease spread starts by injecting pathology in one seed region and allowing it to
propagate through brain networks constrained by regional characteristics such as gene expression
and connectivity. When applied to aSyn, this model uses the regional expression of the SNCA and
GBA genes as indices of the local synthesis and degradation of aSyn agents, jeweils, und das
connectivity strength between brain regions based on diffusion MRI to modulate the spread of
agents between regions. The transition between compartments is determined by a set of rules that
guide the interactions between agents and their local environment. All Infected agents are deemed
Netzwerkneurowissenschaften
910
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Agent-based model of Parkinson’s disease
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1. Overview. (A) Study design. (B) Deformation-based morphometry was performed on each scan. W-scored parcellated maps were
generated for each follow-up timepoint by correcting the atrophy maps for the effects of age and sex seen in controls. The baseline W-scored
map was subtracted from each of the follow-up W-scored maps to generate progression maps of atrophy at 1, 2, Und 4 Jahre, yielding three
maps of brain atrophy progression in PD. The spread of alpha-synuclein pathology in the brain was simulated with the agent-based SIR model
based on structural connectivity and gene expression of SNCA and GBA. (D) The propagation of agents and the resulting atrophy was sim-
ulated over 10,000 timesteps, with a brain atrophy map generated at each timestep. The observed atrophy maps were compared with the
simulated brain atrophy maps. BL = baseline; FU = follow-up; HC = healthy controls; PD = Parkinson’s disease; QC = quality control; SD =
Standardabweichung; SIR = Susceptible-Infected-Removed.
to be infectious, and every susceptible agent can turn into an Infected agent when it encounters an
infected agent. Susceptible and infected agents can travel between brain regions to spread pathol-
Ogy. Both susceptible and infected agents in a region have a probability of turning into removed
agents, either by being degraded inside the region or by spreading to a connected area.
In this study, pathology was initiated in the substantia nigra and its propagation through the
brain was simulated over a total of 10,000 Iterationen. At each iteration, an atrophy value was
calculated in every brain region, derived from the combined effects of the local accumulation
of infected agents and the ongoing deafferentation between brain regions (cell death). To
Netzwerkneurowissenschaften
911
Agent-based model of Parkinson’s disease
assess whether the SIR model and its gene expression and connectivity parameters signifi-
cantly recreated atrophy progression in PD, the atrophy resulting from aSyn spread was sim-
ulated in silico for the 42 brain regions and compared with the patterns of atrophy progression
observed between baseline and 1, 2, Und 4 years in PD patients. Mit anderen Worten, following the
initiation of pathology in the substantia nigra, the model used information about structural
connectivity and regional gene expression to modulate the behavior of aSyn agents and sim-
ulate the local accumulation of aSyn pathology and atrophy.
The model was implemented as five different modules (production of normal aSyn, clear-
ance of normal and misfolded aSyn, misfolding of normal aSyn, propagation of normal and
misfolded aSyn, accrual of atrophy), which are described in the following sections.
In the model, the synthesis of aSyn inside every region was mod-
Production of normal aSyn.
ulated based on the regional gene expression of SNCA, which was extracted using abagen
(Markello et al., 2021), verfügbar unter https://abagen.readthedocs.io/, für die 42 regions based
on the six postmortem brains from the Allen Human Brain Atlas (Hawrylycz et al., 2012).
The values were averaged across samples to yield an expression vector of synthesis that
was inserted back into the model (Zheng et al., 2019). The synthesis rate in region i is given
as the probability of new agent synthesis per unit time, αi:
αi ¼ Φ0;1 SNCAexpression
D
Þ;
ich
where Φ0,1(·) is the normal cumulative distribution function. The increment of normal agents in
region i is given by αi SiΔt, where Δt is the total time and Si is the region size. The time incre-
ment used for the main analyses was set at Δt = 0.1, but peak correlation fits were robust with
values from 0.1 Zu 0.9 (see Supplementary Figure 1 in the Supporting Information).
Clearance of normal and misfolded aSyn. Ähnlich, the degradation of aSyn inside each region
was dependent on the regional gene expression of GBA, which was also extracted from the
Allen Human Brain Atlas. The clearance rate of both normal and misfolded agents in region i
per unit time occurred with the probability distribution βi:
βi ¼ Φ0;1 GBAexpression
D
Þ;
ich
where Φ0,1(·) is the normal cumulative distribution function. The probability of an agent
still being active after total time Δt is given by limδ τ →0(1 − βδτ)Δt/δτ = e−βΔt. Mit anderen Worten,
as the degradation rate increases, the probability of an agent to remain active in the region
decreases. Entsprechend, the proportion of cleared agents within timestep Δt is 1 − e−βΔt.
(cid:1)
Infected agents can promote misfolding of
Misfolding of normal aSyn (infection transmission).
susceptible agents and turn them into infected agents. The probability of a susceptible agent
Mi , where Mi is the population of
that survived clearance of not becoming infected is 1 − γ0
ich
infected agents in region i and γ0
i is the baseline likelihood that a single misfolded agent turns a
susceptible agent into an infected agent. The baseline likelihood γ0
i is given by 1/Si, where Si is
the region size. Entsprechend, the probability per unit time that a susceptible agent surviving
clearance in region i turns into an infected agent due to the action of at least one of the Mi
Þ
infected agents present in region i is given by γi = 1 − eMi
. As for the previous module,
the probability that a susceptible agent remains susceptible after total time Δt is given
D
ln 1−γ0
ich
(cid:3)
Netzwerkneurowissenschaften
912
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Agent-based model of Parkinson’s disease
(cid:1)
(cid:3)
Mi Δt=δτ
δτ
by limδτ → 0 1 − γ0
ich
becomes infected after total time Δt is given by 1 − e−γ0
the population of normal proteins Ni in region i is the following:
i Mi Δt , whereas the probability that a susceptible agent
i Mi Δt. Infolge, the increment of
= e−γ0
ΔNi ¼ αiSiΔt − 1 − e−βi Δt
Ni:
(cid:1)
(cid:3)
After each timestep, the populations of susceptible (Ni) and infected agents (Mi) are respec-
tively updated as follows:
ΔNi ¼ αiSiΔt − 1 − e−βi Δt
(cid:1)
(cid:1)
(cid:3)
Ni − e−βi Δt
(cid:3)
(cid:4)
1 − e−γ0
i Mi Δt
(cid:5)
Ni;
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(cid:1)
ΔMi ¼ e−βi Δt
(cid:3)
(cid:4)
1 − e−γ0
i Mi Δt
(cid:5)
Ni − 1 − e−βi Δt
(cid:1)
(cid:3)
Mi:
Propagation of normal and misfolded aSyn. Every susceptible and infected agent has a probabil-
ity to spread to other brain regions via fiber tracts (edges in the network). To implement this in
the model, we used a previously created structural connectivity matrix of the complete inter-
regional connection strength values for the same 42 regions used for quantifying atrophy
(Zheng et al., 2019). The structural connectivity matrix was created from the preprocessed
diffusion-weighted and T1-weighted MRI images from 1,027 healthy participants from the
Human Connectome Project (2017 Q4; 1,200-subject release). The diffusion data were recon-
structed in the individual T1 spaces using generalized q-sampling imaging with a diffusion
sampling ratio of 1.0 to generate voxel-wise maps of quantitative anisotropy and spin distri-
bution function. Deterministic streamline tractography was then performed in native space
using DSI Studio (https://www.nitrc.org/projects/dsistudio) with an angular cutoff of 55, a step
size of 0.5 mm, a minimum length of 20 mm, and a maximum length of 400 mm to reconstruct
100,000 streamlines for every region. Group-level matrices of connectivity strength and dis-
tance were then generated. The connectivity matrix represents the density of streamlines
(streamline counts) between each region pair normalized by the target region volume (voxel
counts). This connectivity strength was measured with every region entered as the tractogra-
phy seed region to generate a whole-brain structural connectivity profile that covers the 42
regions used for atrophy measurement. For each subject, the connectivity profiles were
concatenated to form a 42 × 42 matrix where every element represents the connection
strength between every pair of regions, with self-connections set to 0. A group-consensus
approach was then performed by averaging the connectivity profiles and keeping 35% von
the most commonly occurring edges across all subjects. This group-level matrix of structural
connectivity was used in the SIR model for computing the probability of an agent spreading
between regions (siehe unten). To ensure that findings were not due to the density threshold of
retained connections, we repeated the analyses using different matrix densities (Supplemen-
tary Table 1 in the Supporting Information). In addition to this connection strength matrix, Wir
also generated a group-level connectivity distance matrix based on the mean Euclidean dis-
tance of corresponding streamlines between every pair of regions. This distance matrix was
also used to modulate the mobility pattern of agents between regions as explained below.
At each timestep, every agent can either remain in region i or enter the edges (d.h., fiber
tracts connecting two regions) with probabilities:
Pregioni
→ regioni
¼ ρi;
Pregioni
→ edgeij
D
¼ 1 − ρi
Þ wijP
jwij
;
Netzwerkneurowissenschaften
913
Agent-based model of Parkinson’s disease
where wij is the undirected connection strength between region i and region j and ρi is the prob-
ability of an agent to remain in region i. This probability was set to 0.5 for every region. Der
choice of ρi led to negligible differences when simulating atrophy (Supplementary Figure 1 In
the Supporting Information). Ähnlich, for susceptible and infected agents in an edge, the prob-
ability of leaving the edge to enter another region per unit time is given by these probabilities:
Pedgeij
→ regionj
¼
1
lij
;
Pedgeij
→ edgeij
¼ 1 −
1
lij
;
where lij is the length (Euclidean distance) of the edge between regions i and j. The increments in
quantity of normal and misfolded agents Ni and Mi in region i after a total time Δt are as follows:
ΔNi ¼
ΔMi ¼
X
1
J
lji
X
1
J
lji
D
NjiΔt − 1 − ρi
ÞNiΔt;
D
MjiΔt − 1 − ρi
ÞMiΔt;
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
where Nij and Mij represent the populations of normal and infected agents in the edge between
regions i and j respectively. Nij and Mij are updated as follows:
D
ΔNij ¼ 1 − ρi
D
ΔMij ¼ 1 − ρi
Þ wijP
jwij
Þ wijP
jwij
NiΔt −
MiΔt −
1
lij
1
lij
NijΔt;
MijΔt:
Accrual of atrophy. Tissue loss was modeled as the result of two processes: the direct toxicity
from the accumulation of infected agents in region i and the deafferentation due to neuronal
death in regions connected with region i. The incremental atrophy at time t over Δt in region i
is given by the following:
(cid:4)
ΔLi tð Þ ¼ k1 1 − e−ri tð ÞΔt
(cid:5)
þ k2
X
J
wjiP
jwji
(cid:4)
1 − e−rj t−1ð
ÞΔt
(cid:5)
;
where ri (T ) represents the proportion of misfolded agents in region i at time t, k1 is the weight
(impact) of aSyn accumulation on tissue loss, and k2 is the weight (impact) of deafferentation from
neighboring regions on tissue loss. Both k1 and k2 were set to 0.5 such that accumulation of infected
agents and deafferentation had equal effect on the growth of the atrophy simulated by the model.
Statistical Analyses
Demographics and clinical variables. The demographics and clinical variables were compared
between PD patients and controls at baseline and between PD patients at each follow-up time-
point versus baseline. Student’s two-sample t tests and Mann-Whitney U tests were respec-
tively used for normally and non-normally distributed continuous variables. Chi-square tests
were used for comparing groups on categorical variables.
Longitudinal progression of atrophy. To examine the progression of brain atrophy in PD patients,
we performed linear mixed-effect modeling to investigate whether the effect of time was sig-
nificant over the regional deformation values at each timepoint, namely at baseline and after 1,
Netzwerkneurowissenschaften
914
Agent-based model of Parkinson’s disease
2, Und 4 years of follow-up. This resulted in a set of 42 separate models, one for each brain
region. A random intercept was assigned to each patient, while the fixed effect was the inter-
action of time with the age-and-sex corrected W-scored DBM values. The Benjamini-
Hochberg procedure was used to control the false discovery rate (Benjamini, Drai, Elmer,
Kafkafi, & Golani, 2001), and a regional deformation change was considered significant when
the p value was below 0.05.
Fit between observed and modeled pathology. The SIR model was run for a total of 10,000 iter-
ations after injecting pathology into the substantia nigra. The propagation speed, v, welche
models the protein spreading rate, was set to 1. Variation in propagation speed values ranging
aus 0.1 Zu 10 resulted in negligible difference in model fit (Supplementary Figure 1 im
zusätzliche Informationen). The model fit between simulated atrophy and observed atrophy
progression was measured using Spearman’s rank coefficient correlations by correlating the
simulated atrophy at each of 10,000 timesteps to the atrophy progression between baseline
and each follow-up timepoint. The peak fit between simulated and atrophy progression
patterns corresponded to the highest correlation coefficient between the two metrics.
Null models. To investigate the impact of gene expression and connectivity on the spread of
pathologic aSyn, we generated null models in which gene expression or connectivity were
randomized and compared the spatial patterns thus obtained to the true peak fits between true
and simulated atrophy (Markello & Misic, 2021). For the connectome null models, the impact
of topology and/or geometry was investigated using both rewired and repositioned null
Modelle. In rewired null networks, using the Maslov-Sneppen algorithm in the Brain Connec-
tivity Toolbox (https://sites.google.com/site/bctnet), pairs of connectivity strength between
brain regions were randomly shuffled in the structural connectivity matrix while preserving
the network’s original degree sequence and density; the rewiring per edge parameter was
set to 100. In repositioned null networks, the spatial position of regions was randomly shuffled
while preserving the network’s original degree sequence and connection profile. For gene
expression null models, the values of either SNCA or GBA regional expression were randomly
reassigned to each region. For these null models, we additionally used randomly shuffled gene
expression values that preserved spatial autocorrelation between regions. This was done by
shuffling the gene expression in the BrainSMASH toolbox (Burt, Helmer, Shinn, Anticevic,
& Murray, 2020) using the distance matrix used in the SIR model. In every case, the shuffled
connectivity of gene expression data was inserted back into the model and used to simulate
the spread of agents. For each null model (d.h., rewired, repositioned, SNCA, and GBA null
Modelle), the randomization was repeated 500 times to generate distributions of null peak fits.
The original peak fit between the observed and simulated atrophy patterns was then compared
using one-sample t tests to the average peak fit distributions of the null models.
ERGEBNISSE
Teilnehmer
A total of 1,068 T1-weighted scans from 790 PD patients and 278 controls were obtained from
the PPMI cohort (Figur 1). Of these, 199 scans were rejected: 193 failed quality control, Und 6
scans were acquired outside the follow-up timepoints investigated in this study (d.h., sie waren
acquired 3 Und 5 years after baseline). This yielded a total of 869 scans from 631 PD patients
Und 238 Kontrollen. For the PD group, there were 318 scans at baseline, 120 scans at one year,
108 scans at 2 Jahre, Und 85 scans at 4 Jahre. Only patients with a scan at baseline and at one
follow-up timepoint were kept for further analysis, leaving samples of 113 patients between
baseline and one year, 104 patients between baseline and 2 Jahre, Und 79 patients between
Netzwerkneurowissenschaften
915
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Agent-based model of Parkinson’s disease
baseline and 4 Jahre. The complete sample of 157 healthy control participants at baseline was
used as the control dataset due to the small number of scans at the follow-up timepoints.
At baseline, there were no significant differences in age, Sex, and education between PD
patients and controls (Tisch 1). Jedoch, PD patients had significantly higher scores on the
MDS-UPDRS-I, MDS-UPDRS-II, MDS-UPDRS-III, Geriatric Depression Scale, and Scales for
Outcomes in Parkinson’s Disease-Autonomic. There was also a significantly higher percentage
of probable REM sleep behavior disorder in PD patients, as well as lower scores on the
Montreal Cognitive Assessment, Symbol-Digit Modalities Test, and the total recall, delayed
recall, and recognition tasks from the Hopkins Verbal Learning Test-Revised. In PD patients,
scores gradually worsened at each follow-up timepoint on the MDS-UPDRS-I, MDS-UPDRS-II,
MDS-UPDRS-III, and the Scales for Outcomes in Parkinson’s Disease-Autonomic.
Brain Atrophy Progresses Over 4 Years in PD
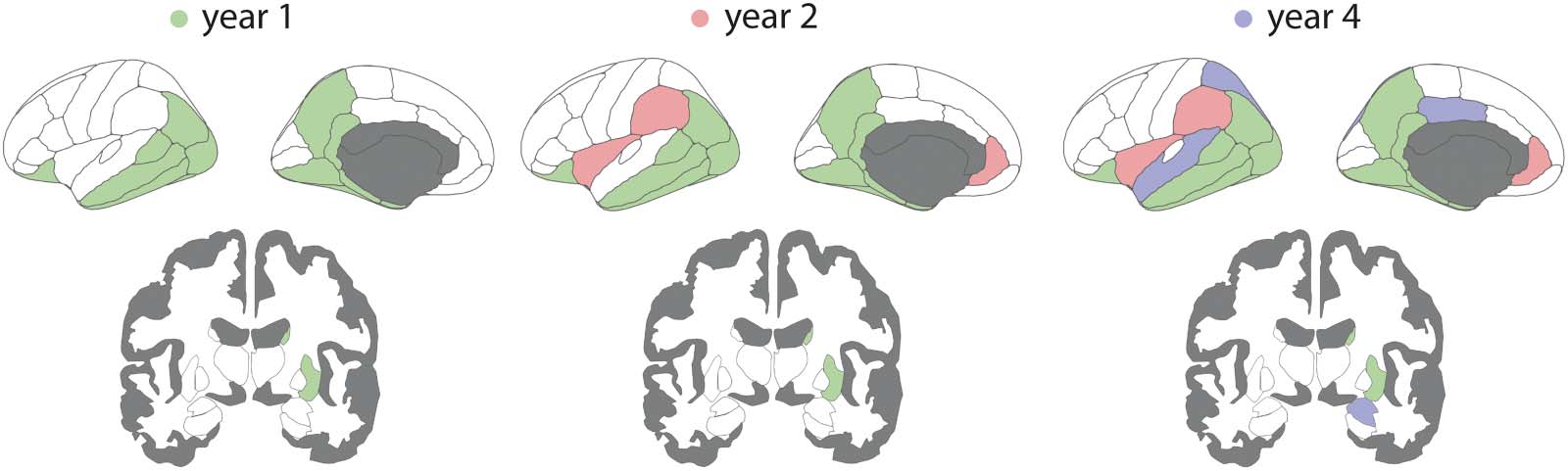
Using linear mixed-effect models, 23 of the 42 left hemisphere brain regions showed signifi-
cant progression of deformation in PD over 4 Jahre, while controlling for age and sex (Figur 2,
and Supplementary Table 2 in the Supporting Information). Speziell, between baseline and
Jahr 1, atrophy progressed in 14 Regionen, including the striatum, the temporal areas (d.h.,
middle and inferior temporal cortices, entorhinal cortex, parahippocampal gyrus, banks of
the superior temporal sulcus, lingual, and fusiform gyri), the isthmus of the cingulate cortex,
the precuneus and inferior parietal cortex, the lateral occipital cortex, and the lateral orbito-
frontal cortex. Nach 2 years of follow-up, the rostral anterior cingulate cortex, supramarginal
Kortex, temporal pole, and insula also started showing significant deformation. Nach 4 years of
follow-up, atrophy was now additionally present in the posterior cingulate cortex, superior
parietal cortex, superior temporal cortex, nucleus accumbens, and amygdala. Unlike the other
Regionen, the insula demonstrated tissue expansion both at baseline and increasing with time.
This tissue expansion may represent an increase in cerebrospinal fluid volume in the perisyl-
vian area. These results confirm previous analyses of this dataset using slightly different
methodology (Tremblay et al., 2021).
The Agent-Based SIR Model Recreates Atrophy Progression
Nächste, we used the agent-based SIR model to simulate the spread of aSyn in the 42 regions and
compared the pattern of atrophy simulated by the model with the patterns of atrophy progres-
sion observed in PD patients between baseline and 1 Jahr, 2 Jahre, Und 4 years of follow-up.
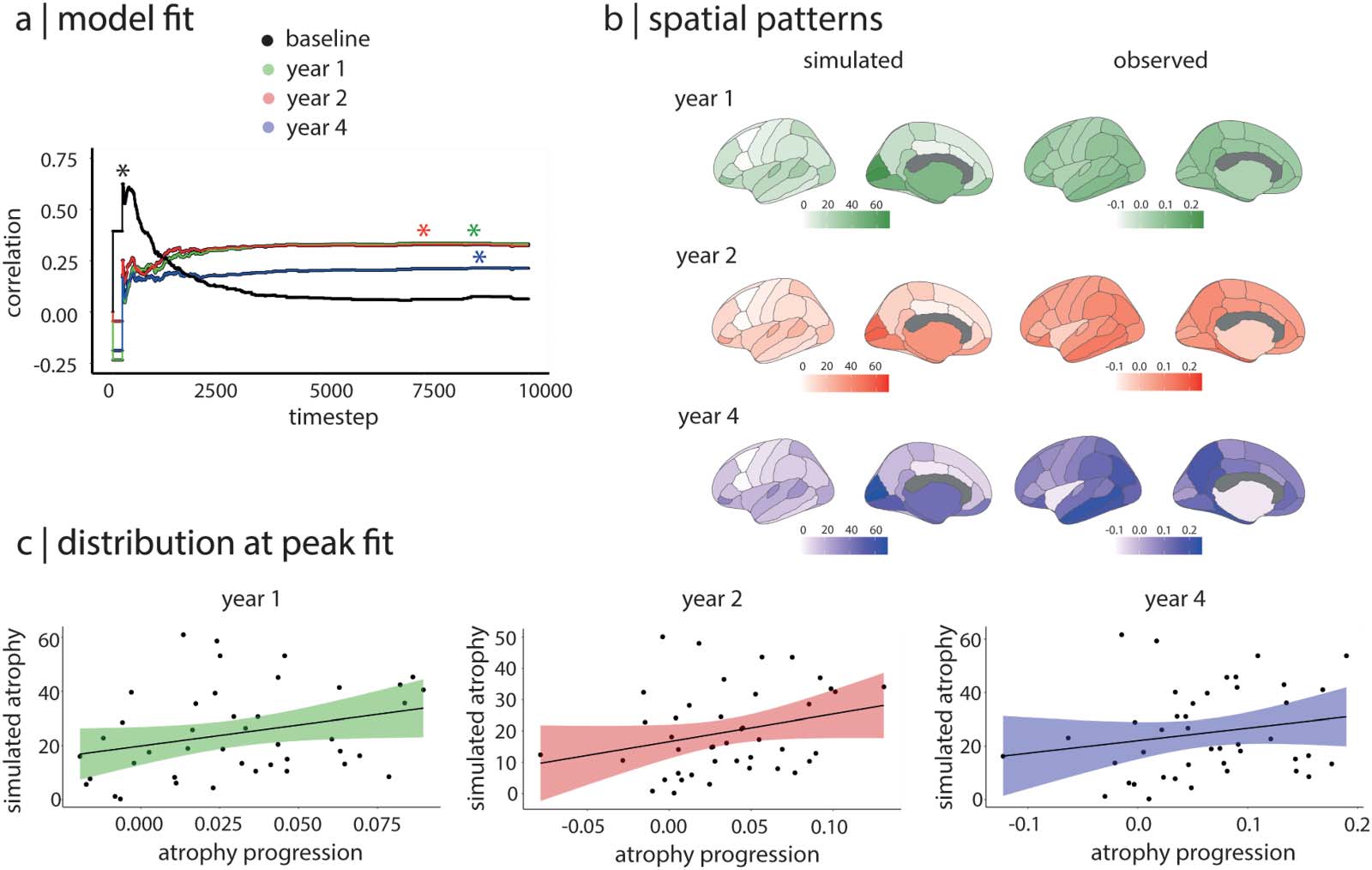
We found that the atrophy pattern simulated by the model significantly recreated the atrophy
progression patterns observed longitudinally in PD (Figur 3). Speziell, the peak correlation
between the simulated atrophy pattern and the progression of atrophy in PD was r = 0.34 (p =
0.03) bei 1 Jahr ( Y1) and r = 0.33 (p = 0.03) bei 2 Jahre ( Y2, Figure 2B); in contrast to the atrophy
seen at baseline, whose peak fit occurred at timestep 228, the peak correlation fits for the 1-
and 2-year atrophy progression were reached at much later timesteps (d.h., between timesteps
7,000 Und 9,000), once the system has reached its equilibrium state. The simulated atrophy
generated by the model did not recreate the pattern of atrophy progression seen between base-
line and 4 Jahre (r = 0.21, p = 0.18). To test the robustness of these results, we repeated the
same analyses using structural connectivity matrices containing 20%, 30%, Und 40% of the
most frequently occurring edges instead of the 35% density used for the main findings. Ergebnisse
were similar (Supplementary Table 1 in the Supporting Information). Taken together, Das
demonstrates that the agent-based SIR model recreates the progression of brain atrophy taking
place over 1 Und 2 years in PD.
Netzwerkneurowissenschaften
916
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
N
e
N
_
A
_
0
0
2
9
6
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
T
N
e
w
Ö
R
k
N
e
u
R
Ö
S
C
e
N
C
e
ich
Tisch 1. Demographics and clinical characteristics of patients and controls. Data are shown as mean (Standardabweichung). The performance in PD patients at the
follow-up timepoint was statistically compared with their performance at baseline. aunpaired t test, a*paired t test, bchi-square test, cMann-Whitney U test. BJLO =
Benton Judgment of Line Orientation; GDS = Geriatric Depression Scale; HC = healthy controls; HVLT-R = Hopkins Verbal Learning Test-Revised; LNS = Letter-Number
Sequencing; MDS-UPDRS = Movement Disorders Society-Unified Parkinson’s Disease Rating Scale; MoCA = Montreal Cognitive Assessment; PD = Parkinson’s disease;
RBD = REM sleep behavior disorder; SCOPA-AUT = Scales for Outcomes in Parkinson’s Disease-Autonomic; SDMT = Symbol-Digit Modalities Test; STAI = State-Trait
Anxiety Inventory.
Variables
Alter
Baseline
PD (n = 318) HC (n = 157)
60.1 (11.9)
60.9 (10.0)
Sex (% männlich)
201 (63%)
103 (66%)
Education, Jahre
15.77 (2.94)
16.06 (2.94)
MDS-UPDRS-III
18.52 (7.82)
1.14 (2.19)
MDS-UPDRS-II
5.20 (4.06)
0.41 (0.97)
MDS-UPDRS-I
3.51 (2.70)
2.44 (2.64)
P
0.41A
0.68B
0.31A
<0.001a
<0.001c
<0.001c
<0.001c
1-year follow-up
p
<0.001a*
PD (n = 113)
60.7 (9.5)
2-year follow-up
p
<0.001a*
PD (n = 104)
62.4 (9.4)
4-year follow-up
p
<0.001a*
PD (n = 79)
64.6 (9.8)
72 (64%)
15.4 (2.8)
65 (63%)
15.2 (2.6)
54 (68%)
15.5 (2.9)
21.5 (10.0)
0.001a*
23.3 (11.4)
<0.001a*
23.4 (10.4)
<0.001a*
7.1 (4.6)
4.8 (3.2)
2.5 (2.7)
<0.001c
<0.001c
0.43c
0.24a*
7.3 (4.8)
5.0 (3.1)
2.4 (2.7)
92.0 (7.2)
<0.001c
<0.001c
0.93c
0.14a*
9.3 (5.7)
6.4 (4.0)
2.2 (2.1)
92.5 (7.7)
<0.001c
<0.001c
0.72c
0.31a*
GDS
STAI
2.27 (2.40)
1.13 (2.24)
93.52 (7.90)
94.31 (7.14)
0.29a
92.2 (7.2)
SCOPA-AUT
9.27 (5.94)
3.78 (3.92)
Probable RBD (% cases)
120 (38%)
33 (21%)
MoCA
SDMT
LNS
BJLO
27.4 (2.1)
28.3 (1.1)
41.52 (9.34)
46.9 (11.1)
10.73 (2.72)
10.93 (2.64)
25.68 (4.18)
26.36 (3.75)
Semantic fluency
14.52 (4.59)
14.96 (4.15)
Phonemic fluency
13.27 (4.73)
14.04 (4.45)
HVLT-R, total recall
24.8 (5.0)
26.0 (4.5)
HVLT-R, delayed recall
8.57 (2.48)
9.27 (2.26)
HVLT-R, recognition
11.24 (1.19)
11.51 (0.82)
<0.001c
<0.001b
<0.001c
<0.001a
0.46a
0.06c
0.12c
0.09a
0.01a
0.002c
0.006c
10.3 (5.6)
<0.001c
10.8 (5.4)
<0.001c
12.3 (6.2)
<0.001c
32 (28%)
27.1 (2.6)
41.7 (10.2)
10.8 (2.5)
0.27c
0.67a*
0.08a*
25.2 (4.3)
<0.01c
14.3 (4.0)
13.8 (4.4)
24.6 (5.4)
8.6 (2.6)
11.3 (1.4)
0.85c
0.02a*
0.28a*
0.91c
0.27c
38 (37%)
27.1 (2.3)
41.0 (10.1)
10.8 (2.8)
25.7 (4.1)
14.7 (4.1)
34 (43%)
27.5 (2.6)
40.1 (11.3)
10.6 (3.3)
26.2 (3.6)
14.3 (4.6)
0.16c
0.11a*
0.37a*
0.19c
0.66c
0.64c
0.02a*
0.12a*
0.75c
0.84c
13.9 (4.6)
<0.01a*
14.7 (4.6)
<0.001a*
24.5 (5.7)
8.5 (2.5)
11.3 (1.7)
0.04a*
0.76c
0.03c
24.8 (6.0)
8.5 (3.2)
11.3 (0.9)
0.05a*
0.25c
0.25c
9
1
7
A
g
e
n
t
-
b
a
s
e
d
m
o
d
e
l
o
f
P
a
r
k
i
n
s
o
n
s
’
d
i
s
e
a
s
e
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Agent-based model of Parkinson’s disease
Figure 2. Regional atrophy progression in PD over 4 years. Brain deformation maps showing the regions with significant atrophy progression
at each timepoint compared with baseline. Only the left hemisphere is shown. Color reflects the first occurrence of a significant effect. PD =
Parkinson’s disease.
Brain Connectivity Shapes the Progression of Atrophy
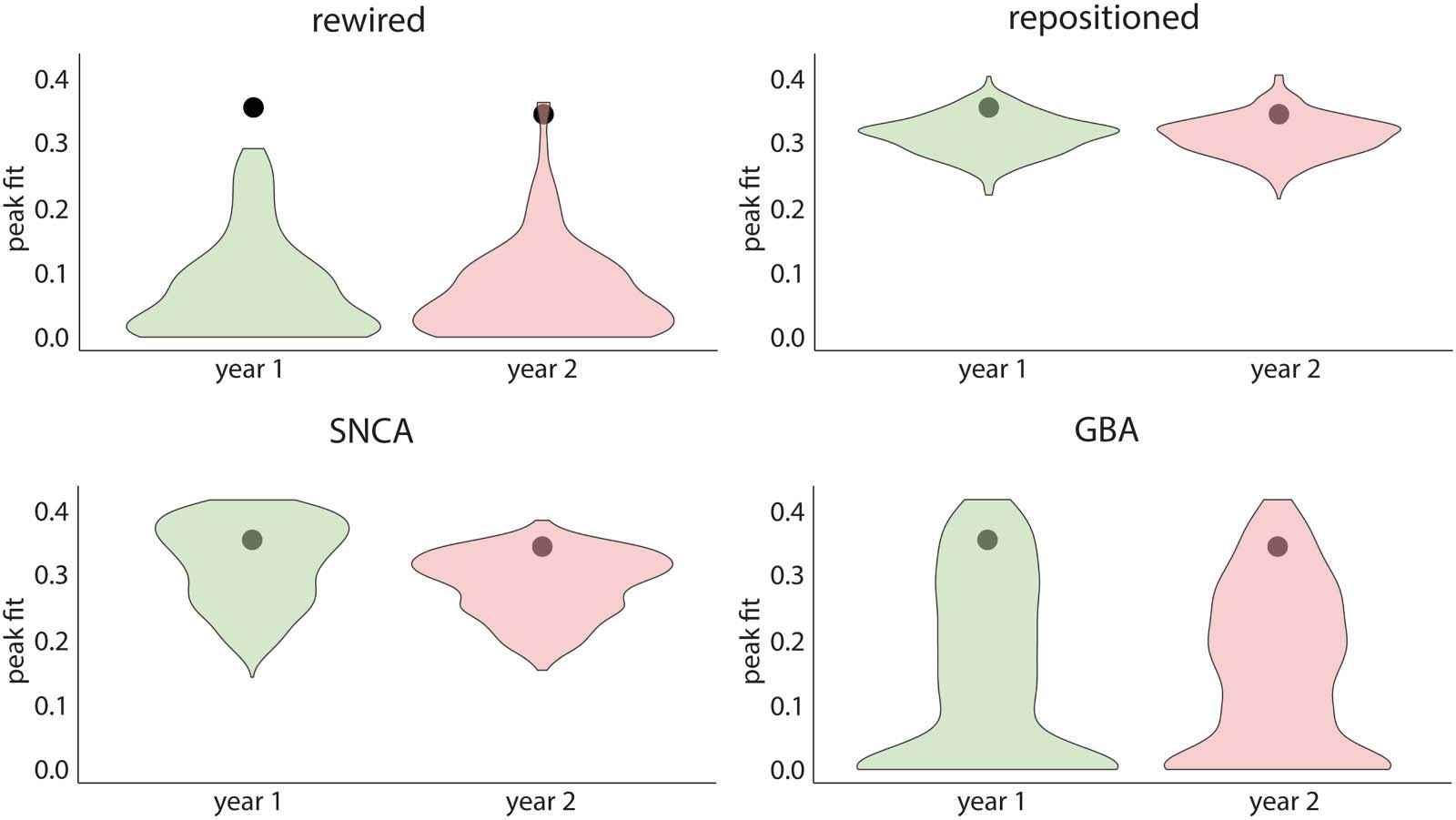
To investigate whether the connectome’s architecture shaped the progression of atrophy in
PD, we generated sets of 500 rewired and 500 repositioned null models in which the connec-
tome’s topology or geometry was randomized. For the rewired models, the peak fits were
always significantly lower than the peak fit obtained with the true connectivity matrix (p <
0.0001 for every follow-up timepoint; Figure 4). Using repositioned models to randomize
the physical position of brain regions, we also observed that the peak fit was significantly dis-
rupted at every timepoint (p < 0.0001; Figure 4). Similar results were found when using other
network densities (Supplementary Figure 1 in the Supporting Information). Taken together, this
demonstrates that both the brain’s structural connectivity pattern and the physical properties of
the connectome contribute to shaping the progression of brain atrophy in PD.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. The SIR model recreates the progression of atrophy in PD. (A) Distributions of the correlations between simulated atrophy and
observed atrophy progression over the 10,000 simulation timesteps. The asterisks indicate the peak correlation between atrophy patterns;
the y-axis represents the Spearman correlation coefficient. (B) Brain plots showing the patterns of simulated atrophy at the peak fit and the
patterns of observed atrophy progression for each follow-up timepoint. (C) Relationships between simulated atrophy at the peak fit and
observed atrophy progression for each follow-up timepoint. PD = Parkinson’s disease.
Network Neuroscience
918
Agent-based model of Parkinson’s disease
Structural connectivity and gene expression shape atrophy progression in PD. Distributions of null peak correlation fits between
Figure 4.
simulated atrophy and observed atrophy progression when randomly shuffling the connectivity between regions (rewired null models), the
spatial embedding of regions (repositioned null models), and the local expression of SNCA or GBA. The black circle refers to the true corre-
lation between simulated atrophy and observed atrophy progression. PD = Parkinson’s disease.
Gene Expression Shapes the Progression of Atrophy
To investigate whether regional gene expression shaped the progression of atrophy in PD, the
expression of SNCA or GBA was randomized across brain regions while accounting for spatial
autocorrelation. The fit between the simulated and observed patterns of atrophy progression
was significantly disrupted at baseline and at 1 and 2 years when randomizing SNCA (p <
0.0001) or GBA (p < 0.0001) (Figure 4). This suggests that local synthesis and clearance of
aSyn, as indexed by regional SNCA and GBA expression, also contribute to shaping atrophy
in PD.
DISCUSSION
The prion-like model of PD makes three predictions: (a) misfolded aSyn isoforms act as a
template to misfold normal aSyn molecules; (b) abnormal aSyn molecules propagate trans-
synaptically via the connectome; and (c) accumulation of misfolded aSyn leads to progressive
tissue damage in vulnerable regions. We previously developed an agent-based SIR model that
simulates the prion-like propagation of aSyn pathology in the brain and recreates atrophy pat-
terns seen at baseline in PD and isolated REM sleep behavior disorder (Rahayel, Tremblay,
et al., 2022; Zheng et al., 2019). However, it remains unknown whether the progression of
atrophy in PD also follows the constraints imposed by a prion-like spread. In this study, we
simulated the propagation of alpha-synuclein pathology in the brain and compared the
resulting patterns with maps of atrophy progression over 1, 2 and 4 years in patients with PD.
Three main observations were made: first, atrophy increased significantly over 4 years,
being found in the striatum early on and involving a greater number of cortical regions as dis-
ease progresses. Second, the SIR model recreated in silico the pattern of atrophy observed
longitudinally in PD patients. Third, the SIR model demonstrated that both cell-autonomous
factors, here SNCA and GBA gene expression levels, and non-cell-autonomous factors,
namely the topology and geometry of the connectome, both shape the spatiotemporal
Network Neuroscience
919
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Agent-based model of Parkinson’s disease
progression of atrophy in PD. These findings further support the theory of PD as a propagating
synucleinopathy.
Using age- and sex-corrected measures of brain deformation, we found that 55% of brain
regions showed significant atrophy in PD at some point over the 4-year follow-up. The regions
with the strongest progression of atrophy over 4 years were the putamen and caudate and the
middle and inferior temporal cortices. Atrophy in cortical regions such as the rostral anterior
cingulate cortex and supramarginal cortex appeared after 2 years, whereas the limbic struc-
tures (i.e., amygdala and nucleus accumbens) and the superior parietal, posterior cingulate,
and superior temporal cortices started showing atrophy after 4 years of follow-up. This atrophy
pattern involving basal ganglia first, followed by mostly posterior cortical regions, was also
described in a large cohort from the ENIGMA consortium (Laansma et al., 2021), which
included PD patients with overall more advanced disease than our de novo cohort. Note that
ENIGMA included the PPMI MRI scans used here, although they accounted for only 15% of
the 2,357 PD patients included. Interestingly, the substantia nigra, in which signal changes
have been associated with parkinsonism in PD (Gaurav et al., 2021), was atrophied at baseline
but did not show any atrophy progression during the follow-up years, suggesting that this
region may have already reached maximum tissue loss at the time of clinical diagnosis, at least
in terms of detectable volume deformation.
PD is pathologically characterized by the accumulation of misfolded aSyn in Lewy bodies
and Lewy neurites (Spillantini et al., 1997). Two theories currently exist to explain the
aSyn-related pathogenesis in the brain: the prion-like protein propagation and the selective
vulnerability hypotheses (Brundin & Melki, 2017; Surmeier et al., 2017). According to the
prion-like hypothesis, pathologic aSyn imposes its misfolded conformation onto native pro-
teins that can then spread trans-synaptically, a hypothesis that is supported by several studies
in animals (Luk et al., 2012; Masuda-Suzukake et al., 2013; Rahayel, Misic, et al., 2022). More
recently, MRI studies performed in humans have shown that the pattern of atrophy observed in
de novo patients with PD overlaps with known structural and functional networks (Pandya
et al., 2019; Tremblay et al., 2021; Zeighami et al., 2015), suggesting that brain connectivity
is a critical determinant of atrophy in synucleinopathies. However, there is also evidence that
connectivity alone does not completely explain the pattern of Lewy-related pathology
(Henrich et al., 2020), and that intrinsic factors may govern the selective vulnerability of
certain regions or cell types (Fu, Hardy, & Duff, 2018; Gonzalez-Rodriguez et al., 2020). While
several factors relating to cellular energetics and neurotransmitter metabolism have been
proposed (Giguere, Burke Nanni, & Trudeau, 2018), the concentration of normal aSyn and
the expression of SNCA are also markers of cell vulnerability (Luna et al., 2018).
Our model explicitly incorporates normal aSyn production and breakdown, and random-
izing these values degrades its ability to replicate observed atrophy, as does randomizing
connectivity values. Applied to de novo PD patients, the SIR model has previously demon-
strated that SNCA and GBA expression and brain connectivity both significantly influence
the distribution of atrophy in the brain of patients with PD or isolated REM sleep behavior
disorder (Rahayel, Tremblay, et al., 2022; Zheng et al., 2019). Furthermore, the same model
was recently used to predict the spread of pathologic aSyn injected in different brain regions of
wild-type mice (Rahayel, Misic, et al., 2022). However, no study had yet applied the agent-
based model to the analysis of atrophy progression in PD.
We found that the increase in brain atrophy observed at 1 and 2 years was significantly
recreated by the model. The use of null networks in which either gene expression or brain
connectivity were randomized shows that the atrophy depends upon both connectivity and
Network Neuroscience
920
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Agent-based model of Parkinson’s disease
gene expression. This is in line with similar studies showing that pathology and atrophy occur
along brain networks in other neurodegenerative diseases such as frontotemporal dementia
(Brown et al., 2019; Shafiei et al., 2021; Zhou, Gennatas, Kramer, Miller, & Seeley, 2012),
Alzheimer’s disease (Raj et al., 2015; Vogel et al., 2020; Vogel et al., 2021), and amyotrophic
lateral sclerosis (Meier et al., 2020). In contrast to other computational models, which gener-
ally simulate the spread of abnormal proteins by relying on a connectivity-based diffusion
mechanism, our agent-based model generates a pattern of propagation and atrophy that also
takes local vulnerability into account by simulating the synthesis and degradation of aSyn as
individual agents.
The progression of atrophy occurring after 4 years could not be replicated by the model.
This may be due to the lower number of scans acquired at the four-year timepoint (79 versus
104 at 2 years) causing reduced statistical power. Also, attrition bias may be present whereby
the group of PD patients still in the study at year 4 had milder disease (Tremblay et al., 2021).
Another possibility is that neuron and synapse loss over time modified neuronal connectivity,
leading to inaccuracies in modeling later spread of pathology using a healthy connectome.
Future studies could integrate measures of ongoing loss of connectivity and integrate this into
the SIR model.
Regional aSyn concentration was modulated in the SIR model to assess regional vulnera-
bility to pathology accumulation. Shuffling the expression level of either SNCA or GBA
resulted in significantly disrupted fit between observed and simulated data, suggesting the
importance of expression of both genes in shaping the spatial pattern of disease spread longi-
tudinally. In other words, regional variations in synthesis and clearance of aSyn, as indexed by
SNCA and GBA expression, contribute to the PD atrophy progression pattern in our model.
This is consistent with the fact that mutations in these genes are risk factors for genetic forms
of PD (Gan-Or, Liong, & Alcalay, 2018; Konno, Ross, Puschmann, Dickson, & Wszolek, 2016;
Riboldi & Di Fonzo, 2019).
Similarly, the randomization of connectome topology (via rewired null models) and spatial
organization (via spatial null models) resulted in disrupted fit between observed and simulated
data. While this is consistent with trans-neuronal propagation of a toxic agent, it can also be
explained by other forms of connectivity-related co-atrophy. For example, interconnected
areas may share local properties that render them similarly vulnerable to neurodegeneration.
These could include glucose metabolism, gene expression, neuronal cell count and shape,
synaptic spine density, and other cytoarchitectonic features (Fulcher & Fornito, 2016; Richiardi
et al., 2015; Scholtens, Schmidt, de Reus, & van den Heuvel, 2014), which may all influence
local vulnerability.
This study has some limitations. First, the PD patients recruited as part of the PPMI study are
younger and have less cognitive impairment than the more general population of PD patients
(Marek et al., 2018). Nonetheless, PPMI represents the largest longitudinal dataset of PD
patients with MRI acquisition and clinical assessments. Second, while the agent-based SIR
model included an effect of deafferentation on atrophy, it did not account for the effect of cell
loss on synthesis and propagation of agents. Indeed, ongoing cell loss due to the spread of
agents might be expected to modify the parameters of the model. For example, the substantia
nigra is a source of propagating aSyn in our model, having both high SNCA expression and
widespread connectivity (Zheng et al., 2019); however, severe cell loss in this region could
impact the spread of pathology in later stages of PD, something our model does not incorpo-
rate. Future studies should aim at better characterizing the impact of ongoing neurodegener-
ation by generating a PD-specific structural connectome to assess its influence on the spread of
Network Neuroscience
921
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Agent-based model of Parkinson’s disease
aSyn. Third, gene expression was investigated only for SNCA and GBA because of their known
importance in aSyn synthesis and degradation; future studies should perform a more thorough
evaluation of the different genes that may impact aSyn spread. Finally, our model does not
consider the synergy between aSyn accumulation and autophagy-lysosomal dysfunction or
mitochondrial failure (Hou, Watzlawik, Fiesel, & Springer, 2020; Senkevich & Gan-Or,
2020), which may also display regional variance.
In conclusion, we showed that brain atrophy progresses in PD into patterns that could be
recreated by the agent-based SIR model, a computational model that generates in silico the
propagation of aSyn and brain atrophy using gene expression and connectivity. This compu-
tational model may represent a promising tool for better understanding the mechanisms under-
lying the progression of atrophy in neurodegenerative diseases.
DATA AVAILABILITY
W-score deformation maps at each year can be found at https://github.com/alaaabdel
/Longitudinal_DBM_Data. The SIR model simulator can be accessed at https://github.com
/yingqiuz/SIR_simulator. Any further data are available from the corresponding author upon
request.
AUTHOR CONTRIBUTIONS
Alaa Abdelgawad: Conceptualization; Formal analysis; Software; Visualization; Writing –
original draft. Shady Rahayel: Conceptualization; Formal analysis; Investigation; Supervision;
Visualization; Writing – original draft. Ying-Qiu Zheng: Conceptualization; Formal analysis;
Methodology; Software. Christina Tremblay: Software; Supervision; Validation. Andrew Vo:
Investigation; Methodology. Bratislav Misic: Conceptualization; Formal analysis; Investigation;
Methodology; Supervision; Writing – original draft. Alain Dagher: Conceptualization; Data
curation; Formal analysis; Funding acquisition; Investigation; Methodology; Project adminis-
tration; Resources; Supervision; Writing – original draft; Writing – review & editing.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
t
.
FUNDING INFORMATION
Alaa Abdelgawad, Jeanne-Timmins Costello Fellowship, McGill University. Alain Dagher,
CIHR Institute of Neurosciences, Mental Health, and Addiction (https://dx.doi.org/10.13039
/501100000034). Alain Dagher, Michael J. Fox Foundation for Parkinson’s Research (https://
dx.doi.org/10.13039/100000864). Alain Dagher, Alzheimer’s Association (https://dx.doi.org
/10.13039/100000957). Alain Dagher, W. Garfield Weston Foundation (https://dx.doi.org/10
.13039/501100000243). Alain Dagher, Healthy Brain for Healthy Lives Initiative (McGill Uni-
versity). Shady Rahayel, Fonds de recherche du Québec–Société et Culture (https://dx.doi.org
/10.13039/100008240). Shady Rahayel, Fonds de recherche du Québec–Santé. Shady
Rahayel, Canadian Institutes of Health Research.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
REFERENCES
Benjamini, Y., Drai, D., Elmer, G., Kafkafi, N., & Golani, I. (2001).
Controlling the false discovery rate in behavior genetics research.
Behavioural Brain Research, 125(1–2), 279–284. https://doi.org
/10.1016/S0166-4328(01)00297-2, PubMed: 11682119
Braak, H., Del Tredici, K., Rüb, U., de Vos, R. A. I., Jansen Steur,
E. N. H., & Braak, E. (2003). Staging of brain pathology related
to sporadic Parkinson’s disease. Neurobiology of Aging, 24(2),
197–211. https://doi.org/10.1016/S0197-4580(02)00065-9,
PubMed: 12498954
Braak, H., Ghebremedhin, E., Rüb, U., Bratzke, H., & Del Tredici,
( 2 0 0 4 ) . S t a g e s i n t h e d e v el o p m e n t of P a r k i n s o n ’ s
K .
disease-related pathology. Cell and Tissue Research, 318(1),
121–134. https://doi.org/10.1007/s00441-004-0956-9, PubMed:
15338272
Network Neuroscience
922
Agent-based model of Parkinson’s disease
Brown, J. A., Deng, J., Neuhaus, J., Sible, I. J., Sias, A. C., Lee, S. E.,
… Seeley, W. W. (2019). Patient-tailored, connectivity-based
forecasts of spreading brain atrophy. Neuron, 104(5), 856–868.
https://doi.org/10.1016/j.neuron.2019.08.037, PubMed:
31623919
Brundin, P., & Melki, R. (2017). Prying into the prion hypothesis
for Parkinson’s disease. Journal of Neuroscience, 37(41),
9808–9818. https://doi.org/10.1523/JNEUROSCI.1788-16.2017,
PubMed: 29021298
Burt, J. B., Helmer, M., Shinn, M., Anticevic, A., & Murray, J. D.
(2020). Generative modeling of brain maps with spatial autocor-
relation. NeuroImage, 220, 117038. https://doi.org/10.1016/j
.neuroimage.2020.117038, PubMed: 32585343
Desikan, R. S., Segonne, F., Fischl, B., Quinn, B. T., Dickerson,
B. C., Blacker, D., … Killiany, R. J. (2006). An automated labeling
system for subdividing the human cerebral cortex on MRI scans
into gyral based regions of interest. NeuroImage, 31(3), 968–980.
https://doi.org/10.1016/j.neuroimage.2006.01.021, PubMed:
16530430
Dickson, D. W., Braak, H., Duda, J. E., Duyckaerts, C., Gasser, T.,
Halliday, G. M., … Litvan, I. (2009). Neuropathological assess-
ment of Parkinson’s disease: Refining the diagnostic criteria.
Lancet Neurology, 8(12), 1150–1157. https://doi.org/10.1016
/S1474-4422(09)70238-8, PubMed: 19909913
Fu, H., Hardy, J., & Duff, K. E. (2018). Selective vulnerability in
neurodegenerative diseases. Nature Neuroscience, 21(10),
1350–1358. https://doi.org/10.1038/s41593-018-0221-2,
PubMed: 30250262
Fulcher, B. D., & Fornito, A. (2016). A transcriptional signature of
hub connectivity in the mouse connectome. Proceedings of the
National Academy of Sciences, 113(5), 1435–1440. https://doi
.org/10.1073/pnas.1513302113, PubMed: 26772314
Gan-Or, Z., Liong, C., & Alcalay, R. N. (2018). GBA-associated Par-
kinson’s disease and other synucleinopathies. Current Neurology
and Neuroscience Reports, 18(8), 44. https://doi.org/10.1007
/s11910-018-0860-4, PubMed: 29884970
Gaurav, R., Yahia-Cherif, L., Pyatigorskaya, N., Mangone, G.,
Biondetti, E., Valabregue, R., … Lehericy, S. (2021). Longitudinal
changes in neuromelanin MRI signal in Parkinson’s disease: A
progression marker. Movement Disorders, 36(7), 1592–1602.
https://doi.org/10.1002/mds.28531, PubMed: 33751655
Giguere, N., Burke Nanni, S., & Trudeau, L. E. (2018). On cell loss
and selective vulnerability of neuronal populations in Parkin-
son’s disease. Frontiers in Neurology, 9, 455. https://doi.org/10
.3389/fneur.2018.00455, PubMed: 29971039
Goetz, C. G., Fahn, S., Martinez-Martin, P., Poewe, W., Sampaio,
C., Stebbins, G. T., … LaPelle, N. (2007). Movement Disorder
Society-sponsored revision of the Unified Parkinson’s Disease
Rating Scale (MDS-UPDRS): Process, format, and clinimetric test-
ing plan. Movement Disorders, 22(1), 41–47. https://doi.org/10
.1002/mds.21198, PubMed: 17115387
Gonzalez-Rodriguez, P., Zampese, E., & Surmeier, D. J. (2020).
Selective neuronal vulnerability in Parkinson’s disease. Progress
in Brain Research, 252, 61–89. https://doi.org/10.1016/ bs.pbr
.2020.02.005, PubMed: 32247375
Hawrylycz, M. J., Lein, E. S., Guillozet-Bongaarts, A. L., Shen, E. H.,
Ng, L., Miller, J. A., … Jones, A. R. (2012). An anatomically com-
prehensive atlas of the adult human brain transcriptome. Nature,
489(7416), 391–399. https://doi.org/10.1038/nature11405,
PubMed: 22996553
Henrich, M. T., Geibl, F. F., Lakshminarasimhan, H., Stegmann, A.,
Giasson, B. I., Mao, X., … Surmeier, D. J. (2020). Determinants of
seeding and spreading of alpha-synuclein pathology in the brain.
Science Advances, 6(46), eabc2487. https://doi.org/10.1126
/sciadv.abc2487, PubMed: 33177086
Hou, X., Watzlawik, J. O., Fiesel, F. C., & Springer, W. (2020).
Autophagy in Parkinson’s disease. Journal of Molecular Biology,
432(8), 2651–2672. https://doi.org/10.1016/j.jmb.2020.01.037,
PubMed: 32061929
Keuken, M. C., Bazin, P. L., Crown, L., Hootsmans, J., Laufer, A.,
Muller-Axt, C., … Forstmann, B. U. (2014). Quantifying
inter-individual anatomical variability in the subcortex using 7
T structural MRI. NeuroImage, 94, 40–46. https://doi.org/10
.1016/j.neuroimage.2014.03.032, PubMed: 24650599
Konno, T., Ross, O. A., Puschmann, A., Dickson, D. W., &
Wszolek, Z. K. (2016). Autosomal dominant Parkinson’s disease
caused by SNCA duplications. Parkinsonism and Related Disor-
ders, 22(Suppl. 1), S1–S6. https://doi.org/10.1016/j.parkreldis
.2015.09.007, PubMed: 26350119
Kordower, J. H., Chu, Y., Hauser, R. A., Freeman, T. B., & Olanow,
C. W. (2008). Lewy body-like pathology in long-term embryonic
nigral transplants in Parkinson’s disease. Nature Medicine, 14(5),
504–506. https://doi.org/10.1038/nm1747, PubMed: 18391962
La Joie, R., Perrotin, A., Barre, L., Hommet, C., Mezenge, F.,
Ibazizene, M., … Chetelat, G. (2012). Region-specific hierarchy
between atrophy, hypometabolism, and beta-amyloid (Abeta)
load in Alzheimer’s disease dementia. Journal of Neuroscience,
32(46), 16265–16273. https://doi.org/10.1523/JNEUROSCI.2170
-12.2012, PubMed: 23152610
Laansma, M. A., Bright, J. K., Al-Bachari, S., Anderson, T. J., Ard, T.,
Assogna, F., … ENIGMA-Parkinson’s Study. (2021). International
multicenter analysis of brain structure across clinical stages of
Parkinson’s disease. Movement Disorders, 36(11), 2583–2594.
https://doi.org/10.1002/mds.28706, PubMed: 34288137
Li, J. Y., Englund, E., Holton, J. L., Soulet, D., Hagell, P., Lees, A. J.,
… Brundin, P. (2008). Lewy bodies in grafted neurons in subjects
with Parkinson’s disease suggest host-to-graft disease propaga-
tion. Nature Medicine, 14(5), 501–503. https://doi.org/10.1038
/nm1746, PubMed: 18391963
Luk, K. C., Kehm, V., Carroll, J., Zhang, B., O’Brien, P., Trojanowski,
J. Q., & Lee, V. M. (2012). Pathological alpha-synuclein transmis-
sion initiates Parkinson-like neurodegeneration in nontransgenic
mice. Science, 338(6109), 949–953. https://doi.org/10.1126
/science.1227157, PubMed: 23161999
Luna, E., Decker, S. C., Riddle, D. M., Caputo, A., Zhang, B., Cole,
T., … Luk, K. C. (2018). Differential alpha-synuclein expression
contributes to selective vulnerability of hippocampal neuron sub-
populations to fibril-induced toxicity. Acta Neuropathologica,
135(6), 855–875. https://doi.org/10.1007/s00401-018-1829-8,
PubMed: 29502200
Marek, K., Chowdhury, S., Siderowf, A., Lasch, S., Coffey, C. S.,
Caspell-Garcia, C., … Parkinson’s Progression Markers Initiative.
(2018). The Parkinson’s Progression Markers Initiative (PPMI):
Establishing a PD biomarker cohort. Annals of Clinical and Trans-
lational Neurology, 5(12), 1460–1477. https://doi.org/10.1002
/acn3.644, PubMed: 30564614
Network Neuroscience
923
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Agent-based model of Parkinson’s disease
Markello, R. D., Arnatkeviciute, A., Poline, J. B., Fulcher, B. D.,
Fornito, A., & Misic, B. (2021). Standardizing workflows in
imaging transcriptomics with the abagen toolbox. eLife, 10,
e72129. https://doi.org/10.7554/eLife.72129, PubMed:
34783653
Markello, R. D., & Misic, B. (2021). Comparing spatial null models
for brain maps. NeuroImage, 236, 118052. https://doi.org/10
.1016/j.neuroimage.2021.118052, PubMed: 33857618
Masuda-Suzukake, M., Nonaka, T., Hosokawa, M., Oikawa, T.,
Arai, T., Akiyama, H., … Hasegawa, M. (2013). Prion-like spread-
ing of pathological alpha-synuclein in brain. Brain, 136(Pt. 4),
1128–1138. https://doi.org/10.1093/ brain/awt037, PubMed:
23466394
Meier, J. M., van der Burgh, H. K., Nitert, A. D., Bede, P., de Lange,
S. C., Hardiman, O., … van den Heuvel, M. P. (2020). Connectome-
based propagation model in amyotrophic lateral sclerosis. Annals
of Neurology, 87(5), 725–738. https://doi.org/10.1002/ana
.25706, PubMed: 32072667
Nasreddine, Z. S., Phillips, N. A., Bedirian, V., Charbonneau, S.,
Whitehead, V., Collin, I., … Chertkow, H. (2005). The Montreal
Cognitive Assessment, MoCA: A brief screening tool for mild
cognitive impairment. Journal of the American Geriatrics Society,
53(4), 695–699. https://doi.org/10.1111/j.1532-5415.2005
.53221.x, PubMed: 15817019
Pandya, S., Zeighami, Y., Freeze, B., Dadar, M., Collins, D. L.,
Dagher, A., & Raj, A. (2019). Predictive model of spread of
Parkinson’s pathology using network diffusion. NeuroImage,
192, 178–194. https://doi.org/10.1016/j.neuroimage.2019.03
.001, PubMed: 30851444
Peng, C., Trojanowski, J. Q., & Lee, V. M. (2020). Protein transmis-
sion in neurodegenerative disease. Nature Reviews Neurology,
16(4), 199–212. https://doi.org/10.1038/s41582-020-0333-7,
PubMed: 32203399
Postuma, R. B., Iranzo, A., Hu, M., Hogl, B., Boeve, B. F., Manni,
R., … Pelletier, A. (2019). Risk and predictors of dementia and
parkinsonism in idiopathic REM sleep behaviour disorder: A mul-
ticentre study. Brain, 142(3), 744–759. https://doi.org/10.1093
/brain/awz030, PubMed: 30789229
Rahayel, S., Misic, B., Zheng, Y. Q., Liu, Z. Q., Abdelgawad, A.,
Abbasi, N., … Luk, K. C. (2022). Differentially targeted seeding
reveals unique pathological alpha-synuclein propagation pat-
terns. Brain, 145(5), 1743–1756. https://doi.org/10.1093/brain
/awab440, PubMed: 34910119
Rahayel, S., Tremblay, C., Vo, A., Zheng, Y. Q., Lehericy, S., Arnulf,
I., … Dagher, A. (2022). Brain atrophy in prodromal synucleino-
pathy is shaped by structural connectivity and gene expression.
Brain, 145(9), 3162–3178. https://doi.org/10.1093/ brain
/awac187, PubMed: 35594873
Raj, A., LoCastro, E., Kuceyeski, A., Tosun, D., Relkin, N., Weiner,
M., & Alzheimer’s Disease Neuroimaging Initiative. (2015).
Network diffusion model of progression predicts longitudinal
patterns of atrophy and metabolism in Alzheimer’s disease. Cell
Reports, 10(3), 359–369. https://doi.org/10.1016/j.celrep.2014
.12.034, PubMed: 25600871
Rey, N. L., George, S., Steiner, J. A., Madaj, Z., Luk, K. C.,
Trojanowski, J. Q., … Brundin, P. (2018). Spread of aggregates
after olfactory bulb injection of alpha-synuclein fibrils is asso-
ciated with early neuronal loss and is reduced long term. Acta
Neuropathologica, 135(1), 65–83. https://doi.org/10.1007
/s00401-017-1792-9, PubMed: 29209768
Rey, N. L., Steiner, J. A., Maroof, N., Luk, K. C., Madaj, Z.,
Trojanowski, J. Q., … Brundin, P. (2016). Widespread transneur-
onal propagation of alpha-synucleinopathy triggered in olfactory
bulb mimics prodromal Parkinson’s disease. Journal of Experi-
mental Medicine, 213(9), 1759–1778. https://doi.org/10.1084
/jem.20160368, PubMed: 27503075
Riboldi, G. M., & Di Fonzo, A. B. (2019). GBA, Gaucher disease,
and Parkinson’s disease: From genetic to clinic to new therapeu-
tic approaches. Cells, 8(4), 364. https://doi.org/10.3390
/cells8040364, PubMed: 31010158
Richiardi, J., Altmann, A., Milazzo, A.-C., Chang, C., Chakravarty,
M. M., Banaschewski, T., … IMAGEN Consortium. (2015).
Correlated gene expression supports synchronous activity in
brain networks. Science, 348(6240), 1241–1244. https://doi.org
/10.1126/science.1255905, PubMed: 26068849
Scholtens, L. H., Schmidt, R., de Reus, M. A., & van den Heuvel,
M. P. (2014). Linking macroscale graph analytical organization to
microscale neuroarchitectonics in the macaque connectome.
Journal of Neuroscience, 34(36), 12192–12205. https://doi.org
/10.1523/JNEUROSCI.0752-14.2014, PubMed: 25186762
Senkevich, K., & Gan-Or, Z. (2020). Autophagy lysosomal path-
way dysfunction in Parkinson’s disease; evidence from human
genetics. Parkinsonism and Related Disorders, 73, 60–71.
https://doi.org/10.1016/j.parkreldis.2019.11.015, PubMed:
31761667
Shafiei, G., Bazinet, V., Dadar, M., Manera, A. L., Collins, D. L.,
Dagher, A., … GENetic Frontotemporal dementia Initiative
(GENFI). (2021). Global network structure and local transcrip-
tomic vulnerability shape atrophy in sporadic and genetic
frontotemporal dementia. bioRxiv. https://
behavioral variant
doi.org/10.1101/2021.08.24.457538
Spillantini, M. G., Schmidt, M. L., Lee, V. M., Trojanowski, J. Q.,
Jakes, R., & Goedert, M. (1997). Alpha-synuclein in Lewy bodies.
Nature, 388(6645), 839–840. https://doi.org/10.1038/42166,
PubMed: 9278044
Stiasny-Kolster, K., Mayer, G., Schafer, S., Moller, J. C., Heinzel-
Gutenbrunner, M., & Oertel, W. H. (2007). The REM sleep
behavior disorder screening questionnaire—A new diagnostic
instrument. Movement Disorders, 22(16), 2386–2393. https://
doi.org/10.1002/mds.21740, PubMed: 17894337
Surmeier, D. J., Obeso, J. A., & Halliday, G. M. (2017). Selective
neuronal vulnerability in Parkinson disease. Nature Reviews
Neuroscience, 18(2), 101–113. https://doi.org/10.1038/nrn.2016
.178, PubMed: 28104909
Tremblay, C., Abbasi, N., Zeighami, Y., Yau, Y., Dadar, M., Rahayel,
S., & Dagher, A. (2020). Sex effects on brain structure in de novo
Parkinson’s disease: A multimodal neuroimaging study. Brain,
143(10), 3052–3066. https://doi.org/10.1093/ brain/awaa234,
PubMed: 32980872
Tremblay, C., Rahayel, S., Vo, A., Morys, F., Shafiei, G., Abbasi, N.,
… Dagher, A. (2021). Brain atrophy progression in Parkinson’s
disease is shaped by connectivity and local vulnerability. Brain
Communications, 3(4), fcab269. https://doi.org/10.1093
/braincomms/fcab269, PubMed: 34859216
Uemura, N., Uemura, M. T., Luk, K. C., Lee, V. M., & Trojanowski,
J. Q. (2020). Cell-to-cell transmission of tau and alpha-synuclein.
Network Neuroscience
924
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Agent-based model of Parkinson’s disease
Trends in Molecular Medicine, 26(10), 936–952. https://doi.org
/10.1016/j.molmed.2020.03.012, PubMed: 32371172
Vogel, J. W., Iturria-Medina, Y., Strandberg, O. T., Smith, R., Levitis, E.,
Evans, A. C., … Swedish BioFinder Study. (2020). Spread of patho-
logical tau proteins through communicating neurons in human
Alzheimer’s disease. Nature Communications, 11(1), 2612.
https://doi.org/10.1038/s41467-020-15701-2, PubMed: 32457389
Vogel, J. W., Young, A. L., Oxtoby, N. P., Smith, R., Ossenkoppele,
R., Strandberg, O. T., … Hansson, O. (2021). Four distinct trajec-
tories of tau deposition identified in Alzheimer’s disease. Nature
Medicine, 27(5), 871–881. https://doi.org/10.1038/s41591-021
-01309-6, PubMed: 33927414
Watts, J. C., Giles, K., Oehler, A., Middleton, L., Dexter, D. T.,
Gentleman, S. M., … Prusiner, S. B. (2013). Transmission of
multiple system atrophy prions to transgenic mice. Proceedings
of the National Academy of Sciences, 110(48), 19555–19560.
https://doi.org/10.1073/pnas.1318268110, PubMed: 24218576
Weintraub, D., Simuni, T., Caspell-Garcia, C., Coffey, C., Lasch, S.,
Siderowf, A., … Parkinson’s Progression Markers Initiative.
(2015). Cognitive performance and neuropsychiatric symptoms
in early, untreated Parkinson’s disease. Movement Disorders,
30(7), 919–927. https://doi.org/10.1002/mds.26170, PubMed:
25737166
Zeighami, Y., Ulla, M., Iturria-Medina. Y., Dadar, M., Zhang, Y.,
Larcher, K. M.-H., … Dagher, A. (2015). Network structure of
brain atrophy in de novo Parkinson’s disease. eLife, 4,
e08440. https://doi.org/10.7554/eLife.08440, PubMed:
26344547
Zheng, Y. Q., Zhang, Y., Yau, Y., Zeighami, Y., Larcher, K., Misic, B.,
& Dagher, A. (2019). Local vulnerability and global connectivity
jointly shape neurodegenerative disease propagation. PLOS
Biology, 17(11), e3000495. https://doi.org/10.1371/journal.pbio
.3000495, PubMed: 31751329
Zhou, J., Gennatas, E. D., Kramer, J. H., Miller, B. L., & Seeley,
W. W. (2012). Predicting regional neurodegeneration from
the healthy brain functional connectome. Neuron, 73(6),
1216–1227. https://doi.org/10.1016/j.neuron.2012.03.004,
PubMed: 22445348
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
3
9
0
6
2
1
5
4
7
8
5
n
e
n
_
a
_
0
0
2
9
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
925