FORSCHUNG
Dynamical interactions reconfigure the
gradient of cortical timescales
P. Sorrentino1,2*
M. Quarantelli6, G. Sorrentino2,5†
, G. Rabuffo1*, F. Baselice3, E. Troisi Lopez4,5, M. Liparoti4,5,
, C. Bernard1†
, and V. Jirsa1†
1Institut de Neurosciences des Systèmes, Aix-Marseille University, Marseille, Frankreich
2Institute of Applied Sciences and Intelligent Systems, National Research Council, Pozzuoli, Italien
3Department of Engineering, Parthenope University of Naples, Naples, Italien
4Department of Motor Sciences and Wellness, Parthenope University of Naples, Naples, Italien
5Institute for Diagnosis and Cure Hermitage Capodimonte, Naples, Italien
6Biostructure and Bioimaging Institute, National Research Council, Naples, Italien
*Co-First Authors.
†Co-Senior Authors.
Schlüsselwörter: Brain dynamics, Cortical gradients, Cortical timescales, Dynamical networks, Edge
Konnektivität
ABSTRAKT
The functional organization of the brain is usually presented with a back-to-front gradient of
timescales, reflecting regional specialization with sensory areas (back) processing information
faster than associative areas (front), which perform information integration. Jedoch,
cognitive processes require not only local information processing but also coordinated activity
across regions. Using magnetoencephalography recordings, we find that the functional
connectivity at the edge level (between two regions) is also characterized by a back-to-front
gradient of timescales following that of the regional gradient. Unerwartet, we demonstrate a
reverse front-to-back gradient when nonlocal interactions are prominent. Daher, the timescales
are dynamic and can switch between back-to-front and front-to-back patterns.
ZUSAMMENFASSUNG DES AUTORS
Cortical gradients have been proposed as a general gauge of brain interareal variability. In line
with the expected sensory-to-associative hierarchical organization, brain regions fall, An
average, along a back-to-front axis of variance of both structural and functional features.
Jedoch, brain activity is dynamic and nonlinear, with large-scale interactions constantly
reconfiguring over time. Analyzing a large cohort of magnetoencephalographic recordings in
humans at the single-trial level, we discover a much richer repertoire of cortical timescales.
Vor allem, a front-to-back gradient of timescales is observed when interactions across regions
give rise to an emergent state of information exchange, which we uniquely capture by using
edge-wise connectivity measures.
EINFÜHRUNG
The human brain constantly scans the environment in search of relevant incoming stimuli, Und
appropriately reconfigures its large-scale activation according to environmental requests. Der
functional organization subtending these abilities, Jedoch, is not understood. One way to
Keine offenen Zugänge
Tagebuch
Zitat: Sorrentino, P, Rabuffo, G.,
Baselice, F., Troisi Lopez, E., Liparoti,
M., Quarantelli, M., Sorrentino, G.,
Bernard C., & Jirsa, V. (2023).
Dynamical interactions reconfigure the
gradient of cortical timescales. Netzwerk
Neurowissenschaften, 7(1), 73–85. https://doi
.org/10.1162/netn_a_00270
DOI:
https://doi.org/10.1162/netn_a_00270
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00270
Erhalten: 24 April 2022
Akzeptiert: 14 Juli 2022
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
P. Sorrentino
ppsorrentino@gmail.com
Handling-Editor:
Richard Betzel
Urheberrechte ©: © 2022
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
N
e
N
_
A
_
0
0
2
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamical interactions reconfigure the gradient of cortical timescales
Brain dynamics:
The study of the temporal evolution
of the brain activity, einschließlich der
information flow across brain regions
and the variation of their statistical
dependences.
Co-activation time series:
A time series obtained as the
element-wise product of any pair of
regional signals. Note that its time-
average defines the Pearson’s
correlation.
Auto-mutual information:
Mutual Information between a signal
and its time-delayed copy.
synthetically represent the functional organization among brain areas is by conceptualizing
the brain as a network, whereby areas are represented as nodes, and structural connections
or functional communication among them are represented as edges (Spurns, 2013). Das
approach led to the identification of a number of invariant features in the large-scale organi-
zation of the brain. From the functional point of view, large-scale patterns of interactions
among areas are nonstationary and reorganize over time (Bassett et al., 2011; Deco et al.,
2011; Pedersen et al., 2017; Sorrentino, et al., 2021A). It has been hypothesized that healthy
resting-state brain dynamics is tightly linked to the constant readiness to stimuli that vary
across multiple timescales (Friston et al., 1995; McIntosh et al., 2008). Entsprechend, the loss
of efficient dynamics has been linked to brain disorders and clinical symptoms (Sorrentino
et al., 2021A). Brain adaptability requires the quick acquisition of information from the envi-
ronment, its integration and interpretation. Converging evidence suggests that a set of commu-
nication channels with intrinsic operational times is present, which results in spatiotemporally
nested activities (Deco et al., 2009; Pillai & Jirsa, 2017). In this line of thinking, it has been
shown in both human and macaque that, regardless of the presence of a stimulus, areas that
are hierarchically lower in information processing operate at higher speed as compared to
associative areas (which integrate information) (Gao et al., 2020; Müller et al., 2020; Murray
et al., 2014, 2017; Shafiei et al., 2020). Somit, the cortex appears to be organized along a
back-to-front gradient of timescales.
Such a gradient exclusively refers to local information processing at the regional level (net-
work nodes). Jedoch, Erwerb, integration and interpretation of inputs are distributed and
dynamical processes, relying on the reconfiguring interactions (functional edges) occurring
between regions. Somit, we hypothesized that the corresponding timescales should also be
present between regions.
To test our hypothesis, we used source-reconstructed magnetoencephalographic (MEG)
data from a cohort of 58 healthy young subjects, based on the Automated Anatomical Labeling
(AAL) atlas, and we analyzed the time-resolved correlations between all pairs of brain regions,
as a proxy of the dynamical interactions.
ERGEBNISSE
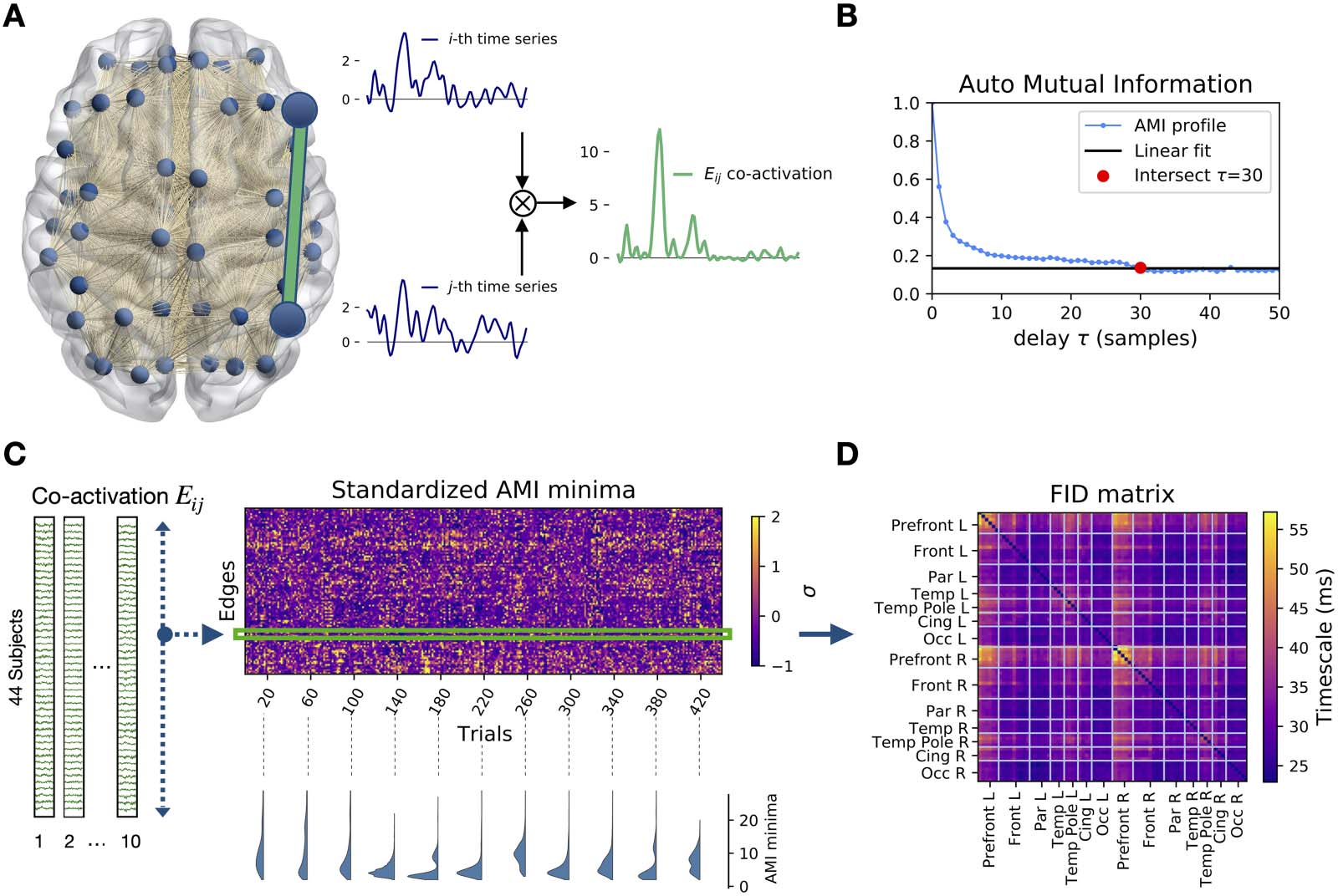
For each edge in the brain network we defined a time series as the co-activations of the MEG
signals at the extremal nodes (Figure 1A) (see Materials and Methods). We used auto-mutual
Information (AMI) to measure the amount of statistical dependence between any co-activation
time series and its time-delayed copy (MacKay, 2019). Repeating this operation for several
delays, a profile of information decay was drawn for each edge of the brain network (Figure 1B).
For short time delays, the high value of the AMI indicates little information loss. The AMI drops
(loss of information) as the time delay increases. A fast/slow characteristic decay time indicates
fast/slow information loss.
AMI edge decay times are organized according to a characteristic spatiotemporal pattern
(Abbildung 1C, top right). The trial-specific distributions of the decay times can be both multimodal
and unimodal, showing that the brain can dynamically rearrange into subnetworks operating
at different timescales (examples are shown in Figure 1C, bottom right). Averaging across trials,
we define the functional information decay (FID) Matrix (Figure 1D), which reveals a temporal
hierarchy of the edges. Considering the edges with the lowest and highest retention of infor-
mation in the FID matrix, we identify two subnetworks: the short- and long-term storage net-
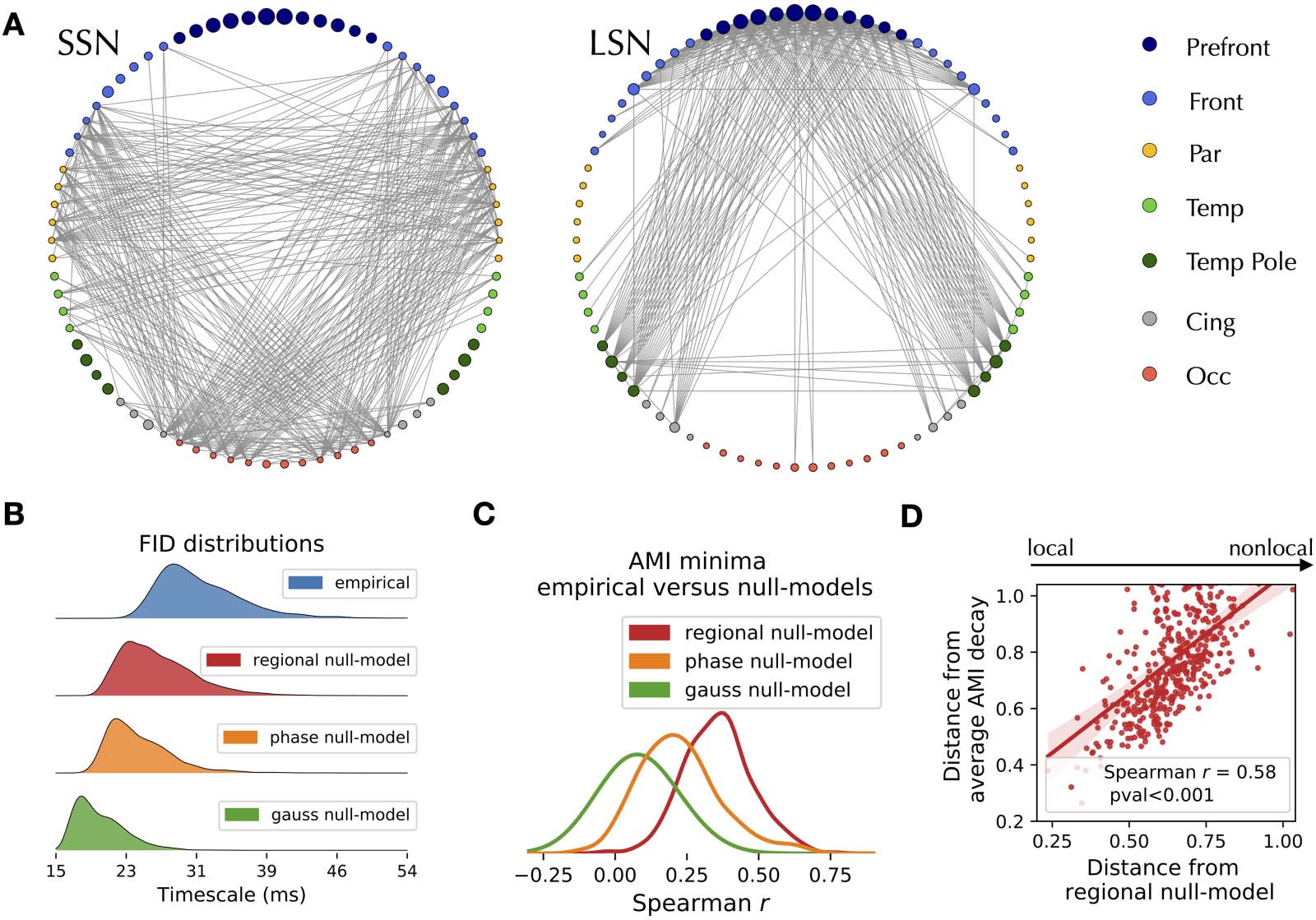
arbeiten (SSN, Figure 2A, links, and LSN Figure 2A, Rechts, jeweils). The SSN spans regions
related to stimulus processing, while the LSN mainly involves regions related to higher
Netzwerkneurowissenschaften
74
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
N
e
N
_
A
_
0
0
2
7
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Dynamical interactions reconfigure the gradient of cortical timescales
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
N
e
N
_
A
_
0
0
2
7
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1. Auto-mutual information analysis of the edge time series in MEG data. (A) The preprocessed magnetoencephalography (MEG)
dataset consists of N = 78 source-reconstructed signals, one for each brain region. We define the edge time series Eij(T) (Grün) as the
element-wise product of nodal z-scored signals at i and j (Blau). (B) Each point in the plot represents the mutual information between the
co-activation time series and its τ-delayed copy. The red dot represents the delay at which the AMI reaches a minimal level (defined by a
linear fit of the AMI tail). Notice that each time step τ corresponds to 3.9 MS, given the sample frequency of 256 Hz. (C) For each of the 44
Fächer, the time series are split into ten, 10-s-long segments (Epochen). For each trial, the τ corresponding to the AMI minima is computed. In
the carpet plot, the minima are standardized across edges for each trial separately. The example minima distributions (bottom) in randomly
selected epochs show that multimodality can emerge naturally (D) Averaging over the standardized AMI minima, we obtain the N × N FID
Matrix, where rows and columns are regions, and the matrix elements are the average minima across trials. For each couple of brain regions,
this matrix describes the typical time that the information is preserved in the corresponding co-activation signal.
Magnetoencephalography:
A device that measures the very
small magnetic fields induced by
neuronal activity.
Information storage:
A measure of how long information is
retained by a signal. It is defined as
the shortest time-delay that
minimizes the Auto-Mutual
Information of a signal. This measure
defines a characteristic timescale for
the signal.
Surrogates:
Obtained from the original data by
destroying specific feature. Wenn ein
measure of interest cannot be
obtained from the surrogate data,
then the destroyed feature is deemed
necessary for the measure of interest
to occur.
Netzwerkneurowissenschaften
cognitive functions (Tisch 1). We conclude that the hierarchy of timescales, consistent with the
previously described nodal hierarchy, is manifest at the edge level (on average). Average infor-
mation storage at the edge level ranges from 16 Zu 55 MS. Jedoch, at the single-trial level, Wir
find a larger range, with decays varying between 3.9 Zu 277 MS.
The average edge decay times vary smoothly across the brain, spanning between the SSN
and the LSN (Figure 2B, Blau). Edge decay time may capture nonlocal interactions between
regions or merely reflect local nodal processes. To distinguish between the two possibilities,
we generate three null models to disrupt or disregard dynamic interactions between regions:
(1) Gaussian surrogates, where the observed nodal autocorrelations (d.h., the power spectrum)
are imposed on otherwise independent processes; (2) phase-randomized surrogates preserving
both the regional autocorrelations and the pairwise static correlations (d.h., preserving static
functional connectivity while disrupting the dynamics); Und (3) regional null models, Wo
the edge decay times are defined as the geometric mean of the AMI decay times estimated
from nodal time series (τij =
). None of the three null models reproduces the empirical
decay-distribution (Figure 2B). We conclude that edge time delays characterize dynamical
interactions between regions.
ffiffiffiffiffiffiffiffi
τ iτ j
P
To test whether the topographical organization of the edge decay times emerges from local
or distributed processes, we correlate the empiric AMI decays with the decays retrieved by the
75
Dynamical interactions reconfigure the gradient of cortical timescales
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
N
e
N
_
A
_
0
0
2
7
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 2. Topography of delays and surrogate analysis. (A) The edges with the fastest (links) and slowest (Rechts) decay times split into a short-
storage and a long-storage network (SSN and LSN) at the trial-averaged level. (B) Distributions of the average edge AMI decays in the original
(Blau), regional (Rot), Phase (orange), and Gaussian (Grün) null models show that the long decay times of information depend on the dynamics
of the edges and are not explained by nodal spectral features or by static correlations alone. (C) Distribution of the correlation between the
decay times of each trial with the corresponding null models. (D) The x-axis measures the distance (1 minus the Spearman’s correlation) von
each trial from the null model, which is used to represent the amount of nonlocal interactions in each trial. The y-axis represents the distance
from the FID matrix (averaged across empirical trials). Each dot represents a trial.
null models. At the trial-averaged level, the FID matrices derived from the null models correlate
with the empirical ones (Spearman’s rs = 0.89, rs = 0.94, rs = 0.95, for the Gaussian, Phase-
randomized, and regional null models, jeweils, P < 0.001 for all cases). However, a greater
variability of the correlations exists at the single-trial level (Figure 2C), with trials that do not
show significant correlations with the corresponding null models. The regional null model is
the closest one to the empirical data, thus we selected it for further analyses. Since the regional
null model only retained local properties, we classified each empirical trial according to its
distance from the corresponding null model (defined as 1 minus the Spearman’s correlation
coefficient in Figure 2D). Hence, a trial that is distant from its null model is one that possesses
prominent nonlocal features. Notably, the more an empirical trial has nonlocal interactions, the
more it is distant from the empirical (average) FID matrix (rs = 0.58; Figure 2D). To summarize,
we have discovered a set of trials that possess significant nonlocal (edge) properties, which
makes the topography of timescales deviate from the average configuration.
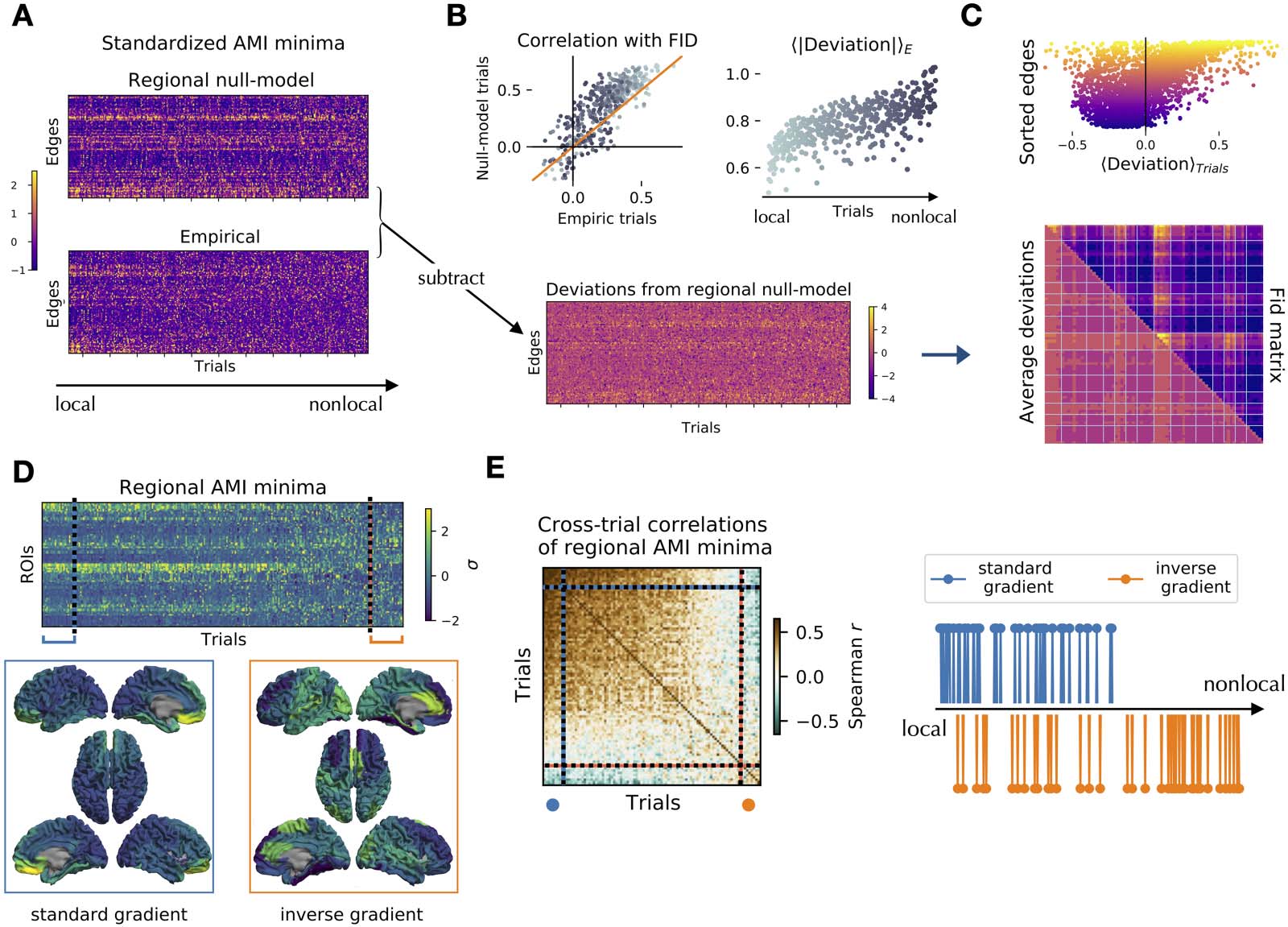
Strikingly, the corresponding trial in the null model recovers the empirical average topog-
raphy (Figure 3A; delays are standardized along the edges within each trial). In fact, the cor-
relation between the empirical trial and the empirical FID matrix is lower than the correlation
between the corresponding surrogate trial and the empirical FID matrix (Figure 3B, top left.
Note that most correlations fall above the diagonal, represented by the orange line. Local-
to-nonlocal trials are represented in colors from dark to light gray). Subtracting the standard-
ized empirical delays from the null model ones (Figure 3B, bottom), we show that the
Network Neuroscience
76
Dynamical interactions reconfigure the gradient of cortical timescales
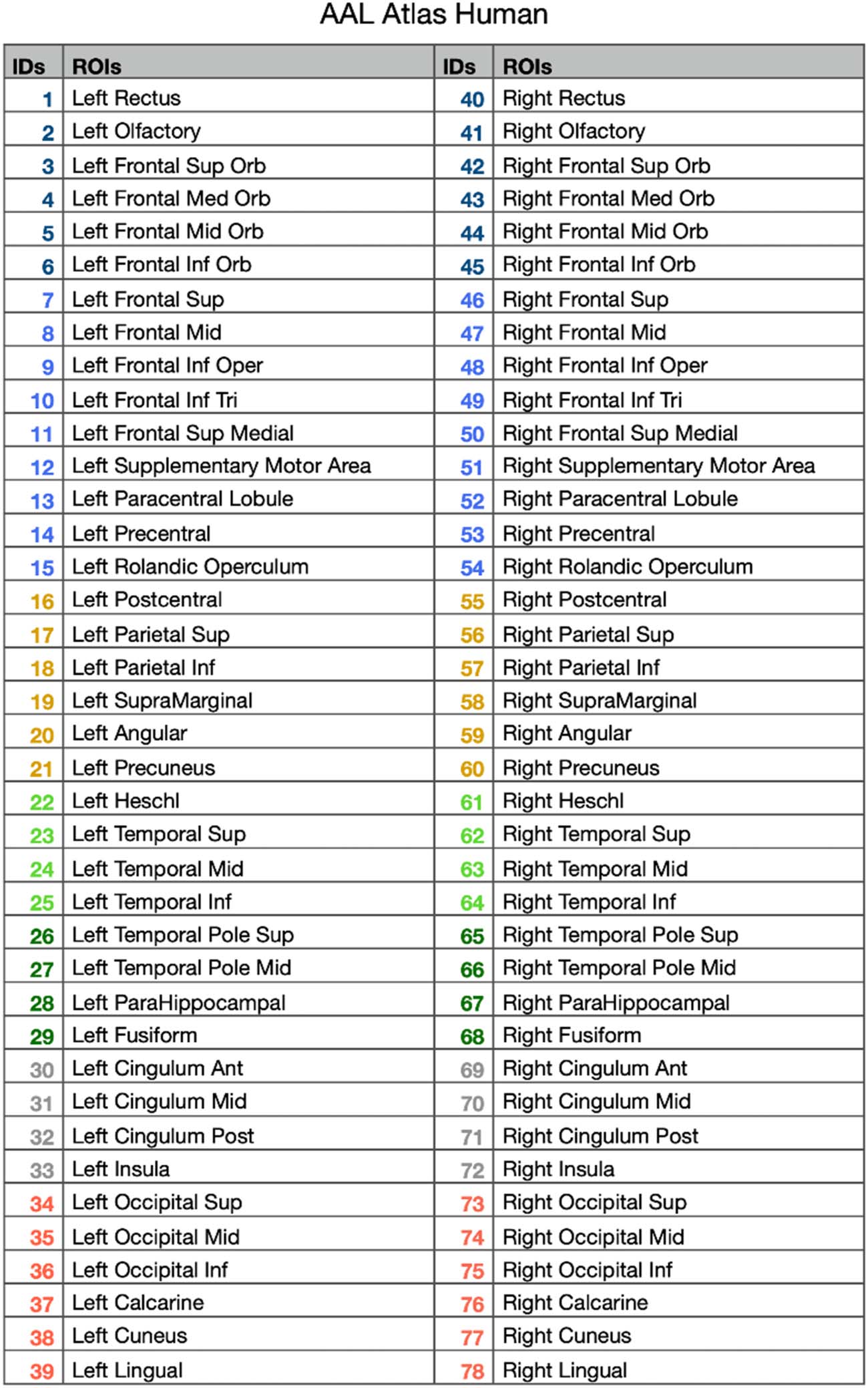
Table 1.
List of regions of AAL Atlas
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Note. Each region number is colored according to the lobe. Color codes are reported in Figure 2A. ROIs =
regions of interest.
magnitude of the deviation from the null model is higher for nonlocal trials (Figure 3B, top
right). Averaging the deviations across trials, we show high correlation between the average
FID matrix and the average deviation matrix (Figure 3C, bottom; rs = 0.79). That is, the edges
manifesting faster dynamics than expected from the regional null model (negative average
deviations) are roughly corresponding to the LSN, while slower than expected edges (positive
average deviations) generally belong to the SSN (Figure 3C, top; edges are sorted according to
Network Neuroscience
77
Dynamical interactions reconfigure the gradient of cortical timescales
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Trial-specific topography of edge and nodal timescales. (A) Standardized edge decay times (AMI minima) of the regional null model
(top) and the empirical trials (bottom). The trials (matrix columns) are sorted according to a local-to-nonlocal axis, with the highest (lowest)
correlation between the empirical and null model trials in the first (last) columns. (B) Bottom: the empirical minima (panel A, bottom) are
subtracted from the null model minima (panel A, top) to define the trial-specific deviations from the null model. Top left: correlation among
the FID matrix (trial average of the empirical AMI minima) and the trial-specific AMI minima in the empirical (x-axis) and null model (y-axis).
Most trials are above the diagonal (orange), showing that the null model retrieves the empirical average topography of timescales better than
the empirical single trials. Dots represent local and nonlocal trials from light to dark gray. Top right: the average edge deviations (in absolute
value) progressively increase when nonlocal interactions take place. (C) While the decays of the SSN edges (purple) are consistently slower
than the FID matrix (top, negative deviation), the LSN edges (yellow) vary more, and both slower and faster decays are observed (widespread
deviations along the x-axis). Overall, the pattern of deviations across trials (bottom, lower triangular matrix) has a similar topography to the
average FID matrix (bottom, upper triangular matrix) with Spearman’s rs = 0.79. (D) Standardized nodal decay times (AMI minima) of empiric
trials sorted by their similarity to the trial average (top). The trials with highest similarity show the known back-to-front gradient of timescales
(bottom, left). The furthest trials from the mean display an inverse gradient (bottom, right). (E) Correlation matrix of the regional AMI minima
(for the nodal timescales) between all pairs of trials. The trials are sorted as in panel D. The correlation matrix displays two major blocks
corresponding to the standard and inverse-gradient trials. The standard-gradient trials correspond to the trials defined as local based on the
edge decay times (the strongest 10% of these are represented as blue dots in the right panel). The inverse-gradient trials (orange dots, repre-
senting approximately 10% of the total) are predominantly nonlocal.
trial-average delay. Color map as in Figure 1D). We note that LSN (Figure 3C, top; yellow) edges are
characterized by higher deviation variability as compared to the SSN ones (Figure 3C, top; purple).
We then explore the relationship between nonlocal interactions and the known nodal gra-
dient of timescales (Gao et al., 2020; Kiebel et al., 2008; Murray et al., 2014). Computing the
AMI decay times of the nodal time series and sorting trials in growing order of similarity with
the trial-average pattern, we recover the well-established back-to-front gradient of timescales
(Figure 3D, bottom left). Remarkably, the trials that are the least similar to the average reveal an
inverse front-to-back gradient (Figure 3D, bottom right). The matrix of cross-trials correlations
(Figure 3E, left) shows that standard- and inverse-gradient trials are similar to themselves and
anticorrelated to each other. Finally, most of the trials with an inverse front-to-back gradient
are dominated by nonlocal higher order interactions between regions (Figure 3E, right;
Network Neuroscience
78
Dynamical interactions reconfigure the gradient of cortical timescales
Source-reconstruction:
A procedure to estimate the activity
at a given location that has generated
the signals recorded by the sensors.
Cortical gradient:
A continuous axis of variance of a
brain feature across the cortex.
Spearman’s rs = 0.42 between the degree of nonlocality as observed from edge analysis and
the distance from the average nodal gradient). All the results of the manuscript were replicated
on the Desikan-Killiany-Tourville (DKT) atlas and selecting different epochs for each subject
(see Supporting Information Figure S4). Furthermore, the results could not be replicated based
on random surrogates that had been linearly mixed according to subject-specific lead field
matrices (see Supporting Information Figure S1). This makes it unlikely that our results could
be explained by volume conduction alone. However, the reader should keep in mind that
source-reconstruction is a complex, ill-posed problem and, as such, some uncertainty remains
for the source estimates.
DISCUSSION
Cortical gradients provide an organizational framework for capturing the topography of large-
scale cortical organization, identifying the major axes of variance in cortical features such as
gene expression, cell densities, axonal connectivity (Fulcher et al., 2019), and neuronal time-
scales (Kiebel et al., 2008), among others. However, brain activity is ever changing and the
topography of functional features is expected to vary accordingly. Analyses of functional gra-
dients based on trial average might hide this variability. Furthermore, the classical focus on the
nodal features, that is, on region-specific signals, could disregard the impact of potential emer-
gent phenomena on the gradient flexibility.
Utilizing edge-wise analyses, our results reveal that nonlocal interactions play a key role in
shaping whole-brain activity and are associated with variability in the cortical gradients of
timescales. In fact, in addition to the classical back-to-front gradient, which mostly reflects
local information processing, nonlocal interactions were associated with an inverse front-to-
back gradient. We propose that interactions between brain regions encode information
beyond the purely nodal activity, and that such information is retained according to edge-
specific characteristic lifetimes. Hence, edge-wise analyses can be seen as complementary
to node-wise analyses. However, to correctly interpret the results of the edge time series as
a genuine manifestation of nonlocal interactions, it is important to demonstrate that the results
cannot be derived from static nodal properties alone (Novelli & Razi, 2022). To this end, we
tested our results against three null models, each preserving nodal and/or static correlation
features, while disrupting the temporal structure of the interactions. The surrogates were not
always capable of conveying all the information contained in the edge time series. This
allowed us to distinguish moments when nonlocal interactions were occurring, from moments
where they were not. Hence, we could classify the trials on an axis of increasing “nonlocality,”
according to the distance from the null models (Figure 3). On the one hand, when the edge
time series did not beat the nulls (i.e., the observations were entirely explained by nodal null
models), the standard back-to-front gradient was observed. On the other hand, if nonlocal
interactions were present (i.e., edge time series beat the nulls), the gradient rearranged itself
across the cortex (Figure 3B–D). Remarkably, in a number of trials, the topography of time-
scales anticorrelated with the standard gradient (Figure 3E), giving rise to an inverse front-
to-back gradient.
The presence of nonlocal interactions in a subset of trials can be interpreted within the
integration/segregation hypothesis (Shine et al., 2016), which suggests that the brain alternates
moments in which the processing of information is local to moments of collective processing.
If this is the case, our technique can be used as an alternative measure of network integration
(Wang et al., 2021). Furthermore, we suggest that these moments of emergent nonlocal inter-
actions along the edges might be related to increased presence of traveling waves (Roberts
Network Neuroscience
79
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical interactions reconfigure the gradient of cortical timescales
et al., 2019) and/or large-scale bursts of activity, such as neuronal avalanches (Shriki et al.,
2013; Sorrentino et al., 2021b). The distribution of the average information decays revealed
two subnetworks with short (SSN) and long (LSN) storage capability. This result is in line with
multiple models (Engel et al., 2001) and experimental evidence (Buschman & Miller, 2007)
showing that processing of external stimuli involves (bottom-up) perception and abstraction,
as well as (top-down) interpretation according to expectations (priors), embodied in the inter-
nal brain state (Engel et al., 2001). For further considerations on the neurophysiological under-
pinnings of the SSN and LSN networks, please refer to the Supporting Information section
Detailed analysis of the average edge topography. Interestingly, single-trial analysis of the
decay times revealed a spontaneous and dynamic clusterization of timescales (i.e., multimo-
dality; Figure 1C), which lends itself for further topographical characterization in future studies.
In conclusion, the dynamic rearrangement of cortical gradients speaks to a dialectic inter-
action between top-down and bottom-up processes, which remains open to interpretation
while stressing once again the relevance of distributed dynamic brain processes underpinning
cognition.
MATERIALS AND METHODS
Participants
Fifty-eight right-handed and native Italian speakers were considered for the analysis. To be
included in this study, all participants had to satisfy the following criteria: (1) to have no sig-
nificant medical illnesses and not to abuse substances or use medication that could interfere
with MEG/EEG signals; (2) to show no other major systemic, psychiatric, or neurological ill-
nesses; and (3) to have no evidence of focal or diffuse brain damage at routine MRI. The study
protocol was approved by the local Ethics Committee. All participants gave written informed
consent.
MRI Acquisition
Three-dimensional T1-weighted brain volumes were acquired at 1.5 Tesla (Signa, GE
Healthcare) using a 3D magnetization-prepared gradient-echo BRAVO sequence (TR/TE/TI
8.2/3.1/450 ms, voxel 1 × 1 × 1 mm3, 50% partition overlap, 324 sagittal slices covering
the whole brain).
MEG Acquisition
Subjects underwent magnetoencephalographic examination in a 163-magnetometers MEG
system placed in a magnetically shielded room (AtB Biomag UG, Ulm, Germany). The prepro-
cessing was done similarly as in Sorrentino et al. (2018). In short, the position of four coils and
of four reference points (nasion, right and left preauricular point and apex) were digitized
before acquisition using Fastrak (Polhemus). The brain activity was recorded for 7 min, with
eyes closed, with a ∼1.5-min-long break at 3.5 minutes, so as to minimize the chances of
drowsiness. During the break, the patients were waiting inside the shielded room and they
were informed that there was a pause, and that they were allowed to adjust their position if
they felt the need to do so. Hence, the head position was recorded at the start of each segment.
The data were sampled at 1024 Hz, and a fourth-order Butterworth band-pass filter was
applied to select components between 0.5 and 48 Hz. During the acquisitions, electrocardio-
gram (ECG) and electrooculogram (EOG) were also recorded (Gross et al., 2013). These steps
were done using Matlab 2019a and the Fieldtrip toolbox 2014 (Oostenveld et al., 2011).
Network Neuroscience
80
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical interactions reconfigure the gradient of cortical timescales
Preprocessing
Principal component analysis was performed to reduce the environmental noise (de
Cheveigné & Simon, 2008; Sadasivan & Narayana Dutt, 1996). Noisy channels were removed
manually through visual inspection of the whole dataset by an experienced rater. Supervised
independent component analysis was performed to eliminate the ECG (and the EOG) compo-
nent from the MEG signals (Barbati et al., 2004). Trials that did not contain artifacts (either
system related or physiological) or excessive environmental noise were selected.
Source Reconstruction
The data were coregistered to the native MRI. A modified spherical conductor model was used
as a forward model (Nolte, 2003). The voxels in the MRI were labeled according to the AAL
atlas (Tzourio-Mazoyer et al., 2002) and the DKT atlas (Alexander et al., 2019). We used the
cortical regions for a total of 78 areas of interest (66 for the DKT). Subsequently, a linearly
constrained minimum variance beamformer was used to compute 78 (for the AAL) time series
(one per area of interest) at a sampling frequency of 1024 Hz (Van Veen et al., 1997).
Reconstructed sources were again visually inspected by an experienced rater. Of the initial
58 subjects, 44 had enough artifact-free acquisitions and were selected for further analysis.
The source-reconstructed signals were downsampled to 256 Hz.
Edge-Centric Approach to MEG
In this work, we adopted an edge-centric approach that, rather than focusing on the local
activity of the regions (nodes), represents the dynamics of the interactions between couples
of brain regions (Esfahlani et al., 2020). This allowed us to characterize the whole-brain net-
work activity in terms of dynamical nonlocal interactions, highlighting the relational properties
of each couple of nodes. Given any couple of nodes i and j and their respective source-
reconstructed signals Xi (t ) and Xj (t ), we defined a characteristic time series Eij for the edge
ij as the product of the z-scored signals, that is,
Eij tð Þ ¼ Xi tð Þ − Xˉ
σ Xið
Þ
i
:
Xj tð Þ − Xˉ
(cid:3) (cid:4)
σ Xj
j
;
where Xˉ and σ(X ) denote the mean and variance of the signals, respectively. One can interpret
the edge co-activation time series as the unfold in time of the pairwise correlations. In fact, the
average of the above expression over time corresponds to the Pearson correlation between the
signals at nodes i and j. The edge time series were further analyzed by information theoretic
measures, aiming at characterizing the information storage capability of each functional edge.
Estimation of Information Decay Time Through Mutual Information
Shannon Entropy, defined as
H Xð Þ ¼ −
X
xi
PX xið
ð
Þ log PX xið
Þ
Þ;
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
quantifies the uncertainty over the possible outcomes xi of a random variable X with proba-
bility distribution PX. If the uncertainty over future outcomes of X decreases as we measure the
outcome yi of another random variable Y, we conclude that X and Y represent two processes
that are not independent. The new resulting uncertainty over X is then defined by
ð
H XjY ¼ yi
Þ ¼ −
X
xi
ð
PXY xijyi
Network Neuroscience
Þlog PXY xijyi
ð
ð
Þ
Þ ¼ −
X
xi
Þ
PXY xi; yi
ð
Þ
PY yið
log
(cid:5)
(cid:6)
Þ
PXY xi; yi
ð
Þ
PY yið
;
81
Dynamical interactions reconfigure the gradient of cortical timescales
with PXY (xi, yi) denoting the joint probability distribution of the pair (X, Y ). The weighted sum
over all possible outcomes of Y defines the conditional entropy, that is, the uncertainty of X
conditioned on Y
PY yið
Þ H XjY ¼ yi
ð
Þ ¼ −
ð
PXY xi; yi
Þ log
(cid:6)
Þ
(cid:5)
PXY xi; yi
ð
Þ
PY yið
X
xi ;yi
¼ H X; Yð
Þ − H Yð Þ;
H XjYð
Þ ¼ −
X
yi
where
H X; Yð
Þ ≡
X
xi ;yi
ð
PXY xi; yi
Þ log PXY xi; yi
ð
ð
Þ:
Þ
Mutual information:
Reduction in uncertainty about one
observed signal given the knowledge
of another reference signal.
The reduction in uncertainty (or, equivalently, the increase of information) over X given by
the knowledge of Y is measured by the mutual information (MI)
I X; Yð
Þ ¼ H Xð Þ − H XjYð
Þ ¼ H Xð Þ þ H Yð Þ − H X; Yð
Þ:
Unlike other measures, such as partial autocorrelation, MI statistical dependencies that take
into account nonlinear interactions, which are ubiquitously found in brain data (Paluš, 1996;
Stam, 2005). In order to quantify the time span before the information in a signal X(t ) is lost, we
rely on the AMI, that is, the MI between the signal and its time-delayed copy Y = X (t − τ ).
According to previous works on M/EEG (Gómez et al., 2007; Jeong et al., 2001), a stable esti-
mate of the probability distribution of any real-valued signal X(t ) is obtained by dividing the
data into 64 bins. The joint probability distribution for the pair (X(t ), X(t − τ )), needed for the
evaluation of the AMI, is given by a 64 × 64 contingency matrix, which is the joint histogram
of the two variables. The AMI decays as a function of the delay τ, from a maximal value at τ = 0
to a relatively stable lower value as τ → ∞. The more gentle (“slower”) the decay, the longer
the information lasts in the signal. It should be mentioned that there exists no unique estimator
for information storage. We chose AMI since we were interested in an interval estimate, rather
than a point estimate (see, e.g., Wibral et al., 2014). The same algorithm was used to compute
the nodal decay times based on the nodal time series.
Information Storage Capability of the Functional Edges
For each co-activation signal Eij, we estimated the AMI profile (Figure 1B) and we evaluated
the time delay τ corresponding to the AMI reaching a stable minimum, that is, when the orig-
inal signal and its τ-delayed versions have become maximally independent. For all the edges,
the decay times occurred within a maximum of 48 time steps (128 time steps in total). There-
fore, in order to have a steady estimate of the baseline, we fitted the last 80 points of every AMI
profile to a straight line, so as to find the stable minimum. Then, we found the τ corresponding
to the moment where the AMI decay falls within a threshold, defined as 1 standard deviation
from the stable minimum. Examples of the estimate of the AMI minimum for different edges, at
the single-epoch level, are shown in Supporting Information Figure S2. An analysis for different
thresholds (number of standard deviations around the stable minimum) is found in Supporting
Information Figure S3. Averaging across all the trials (10 time windows of 10 s each across 44
subjects), we found the N × N FID matrix (where N = 78 is the number of brain regions), con-
taining the decay times for each edge (Figure 1D). The AMI analysis of the coactivations shows
that the decay times are different among edges, as revealed by the histogram in Figure 2B
(blue). Selecting the edges from either the left or right tails of the distribution leads to the
appearance of two topographically organized subnetworks (Figure 2A).
Network Neuroscience
82
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical interactions reconfigure the gradient of cortical timescales
Surrogate Analysis
Leakage analysis. We designed surrogate analysis to exclude that linear mixing alone might
spuriously generate the patterns observed in the FID matrix. To this end, we generated for each
subject N Gaussian time series, with N = number of regions. Then, the subject-specific lead-
field matrix was used to reconstruct the sensor signals for each subject. White noise correlated
as 1/sensor distance, was added to the sensor time series with SNR = 12. Following this step,
the sensor time series were inverted and new surrogate source-level time series were gener-
ated. On these source-level surrogates, we have computed the edge time series and the FID
matrix as described previously.
Time-shuffled and phase-randomized surrogates. First, we sought to investigate if the observed
decay times might be derived by the spectral nodal properties alone. To this end, we generated
N Gaussian processes, with N = number of regions, we fourier-transformed them, and we mul-
tiplied the resulting power spectra by the power spectra of the observed time series. Finally, we
antitransformed and obtained surrogate time series that are independent Gaussian processes
endowed with the same spectral power as the original data (Gaussian surrogates). Secondly,
we sought to investigate if the time decays convey a dynamical feature of the time series or,
alternatively, if they can be explained by static correlations. Hence, starting from the original
data, we generated surrogates preserving not only the nodal spectral properties but also the
cross-spectrum (static functional connectivity). To this end, we shifted by a random phase
(extracted from a unimodal distribution) each frequency of the Fourier-transformed nodal sig-
nals. The same shift was uniformly applied to each region. Hence, we obtained new surrogates
that preserve the functional connectivity while not showing the dynamic of the original data.
ACKNOWLEDGMENTS
The authors thank Michele Allegra for insightful discussions.
SUPPORTING INFORMATION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00270.
AUTHOR CONTRIBUTIONS
Pierpaolo Sorrentino: Conceptualization; Data curation; Formal analysis; Funding acquisition;
Investigation; Methodology; Supervision; Validation; Visualization; Writing – original draft;
Writing – review & editing. Giovanni Rabuffo: Conceptualization; Formal analysis; Funding
acquisition; Investigation; Methodology; Validation; Visualization; Writing – original draft;
Writing – review & editing. Fabio Baselice: Formal analysis; Methodology; Writing – review
& editing. Emahnuel Troisi Lopez: Data curation; Investigation; Methodology; Writing – review
& editing. Marianna Liparoti: Methodology; Validation; Visualization. Mario Quarantelli: Val-
idation; Writing – original draft. Giuseppe Sorrentino: Data curation; Funding acquisition;
Investigation; Writing – original draft; Writing – review & editing. Christophe Bernard: Formal
analysis; Methodology; Writing – review & editing. Viktor Jirsa: Formal analysis; Funding
acquisition; Investigation; Methodology; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
The work was supported by the University of Naples Parthenope “Ricerca locale” grant, by the
grant ANR-17-CE37-0001-CONNECTOME, by the European Union’s Horizon 2020 Research
Network Neuroscience
83
Dynamical interactions reconfigure the gradient of cortical timescales
and Innovation Programme under grant agreement No. 945539 (SGA3) Human Brain Project
and VirtualBrainCloud No. 826421.
REFERENCES
Alexander, B., Loh, W. Y., Matthews, L. G., Murray, A. L., Adamson,
C., Beare, R., … Thompson, D. K. (2019). Desikan-Killiany-
Tourville atlas compatible version of M-CRIB neonatal parcellated
whole brain atlas: The M-CRIB 2.0. Frontiers in Neuroscience,
13, 34. https://doi.org/10.3389/fnins.2019.00034, PubMed:
30804737
Barbati, G., Porcaro, C., Zappasodi, F., Rossini, P. M., & Tecchio, F.
(2004). Optimization of an independent component analysis
approach for artifact identification and removal in magnetoen-
cephalographic signals. Clinical Neurophysiology, 115(5),
1220–1232. https://doi.org/10.1016/j.clinph.2003.12.015,
PubMed: 15066548
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of human
brain networks during learning. Proceedings of the National
Academy of Sciences, 108(18), 7641–7646. https://doi.org/10
.1073/pnas.1018985108, PubMed: 21502525
Buschman, T. J., & Miller, E. K. (2007). Top-down versus bottom-up
control of attention in the prefrontal and posterior parietal corti-
ces. Science, 315(5820), 1860–1862. https://doi.org/10.1126
/science.1138071, PubMed: 17395832
de Cheveigné, A., & Simon, J. Z. (2008). Denoising based on spatial
filtering. Journal of Neuroscience Methods, 171(2), 331–339.
https://doi.org/10.1016/j.jneumeth.2008.03.015, PubMed:
18471892
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging concepts
for the dynamical organization of resting-state activity in the
brain. Nature Reviews Neuroscience, 12(1), 43–56. https://doi
.org/10.1038/nrn2961, PubMed: 21170073
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., & Kötter, R. (2009).
Key role of coupling, delay, and noise in resting brain fluctua-
tions. Proceedings of the National Academy of Sciences of the
United States of America, 106(25), 10302–10307. https://doi
.org/10.1073/pnas.0901831106, PubMed: 19497858
Engel, A. K., Fries, P., & Singer, W. (2001). Dynamic predictions:
Oscillations and synchrony in top–down processing. Nature
Reviews Neuroscience, 2(10), 704–716. https://doi.org/10.1038
/35094565, PubMed: 11584308
Esfahlani, F. Z., Jo, Y., Faskowitz, J., Byrge, L., Kennedy, D. P.,
Sporns, O., & Betzel, R. F. (2020). High-amplitude cofluctuations
in cortical activity drive functional connectivity. Proceedings of
the National Academy of Sciences, 117(45), 28393–28401.
https://doi.org/10.1073/pnas.2005531117, PubMed: 33093200
Friston, K. J., Tononi, G., Sporns, O., & Edelman, G. M. (1995).
Characterising the complexity of neuronal interactions. Human
Brain Mapping, 3(4), 302–314. https://doi.org/10.1002/ hbm
.460030405
Fulcher, B. D., Murray, J. D., Zerbi, V., & Wang, X.-J. (2019).
Multimodal gradients across mouse cortex. Proceedings of the
National Academy of Sciences, 116(10), 4689–4695. https://doi
.org/10.1073/pnas.1814144116, PubMed: 30782826
Gao, R., van den Brink, R. L., Pfeffer, T., & Voytek, B. (2020). Neu-
ronal timescales are functionally dynamic and shaped by cortical
microarchitecture. ELife, 9, e61277. https://doi.org/10.7554/eLife
.61277, PubMed: 33226336
Gómez, C., Hornero, R., Abásolo, D., Fernández, A., & Escudero, J.
(2007). Analysis of the magnetoencephalogram background
activity in Alzheimer’s disease patients with auto-mutual infor-
mation. Computer Methods and Programs in Biomedicine,
87(3), 239–247. https://doi.org/10.1016/j.cmpb.2007.07.001,
PubMed: 17686545
Gross, J., Baillet, S., Barnes, G. R., Henson, R. N., Hillebrand, A.,
Jensen, O., … Schoffelen, J.-M. (2013). Good practice for
conducting and reporting MEG research. NeuroImage, 65,
349–363. https://doi.org/10.1016/j.neuroimage.2012.10.001,
PubMed: 23046981
Jeong, J., Gore, J. C., & Peterson, B. S. (2001). Mutual information
analysis of the EEG in patients with Alzheimer’s disease. Clinical
Neurophysiology, 112(5), 827–835. https://doi.org/10.1016
/S1388-2457(01)00513-2, PubMed: 11336898
Kiebel, S. J., Daunizeau, J., & Friston, K. J. (2008). A hierarchy of
time-scales and the brain. PLoS Computational Biology, 4(11),
e1000209. https://doi.org/10.1371/journal.pcbi.1000209,
PubMed: 19008936
MacKay, D. J. C. (2019). Information theory, inference, and learning
algorithms. Cambridge, UK: Cambridge University Press.
McIntosh, A. R., Kovacevic, N., & Itier, R. J. (2008). Increased brain
signal variability accompanies lower behavioral variability in
development. PLoS Computational Biology, 4(7), e1000106.
https://doi.org/10.1371/journal.pcbi.1000106, PubMed:
18604265
Müller, E. J., Munn, B., Hearne, L. J., Smith, J. B., Fulcher, B.,
Arnatkevičiūtė, A., … Shine, J. M. (2020). Core and matrix
thalamic sub-populations relate to spatio-temporal cortical con-
nectivity gradients. NeuroImage, 222, 117224. https://doi.org/10
.1016/j.neuroimage.2020.117224, PubMed: 32795658
Murray, J. D., Bernacchia, A., Freedman, D. J., Romo, R., Wallis,
J. D., Cai, X., … Wang, X. J. (2014). A hierarchy of intrinsic time-
scales across primate cortex. Nature Neuroscience, 17(12),
1661–1663. https://doi.org/10.1038/nn.3862, PubMed:
25383900
Murray, J. D., Bernacchia, A., Roy, N. A., Constantinidis, C., Romo,
R., & Wang, X.-J. (2017). Stable population coding for working
memory coexists with heterogeneous neural dynamics in pre-
frontal cortex. Proceedings of the National Academy of Sciences,
114(2), 394–399. https://doi.org/10.1073/pnas.1619449114,
PubMed: 28028221
Nolte, G. (2003). The magnetic lead field theorem in the
quasi-static approximation and its use for magnetoencephalogra-
phy forward calculation in realistic volume conductors. Physics
in Medicine and Biology, 48(22), 3637–3652, https://doi.org/10
.1088/0031-9155/48/22/002, PubMed: 14680264
Network Neuroscience
84
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dynamical interactions reconfigure the gradient of cortical timescales
Novelli, L., & Razi, A. (2022). A mathematical perspective on
edge-centric brain functional connectivity. Nature Communica-
tions, 13(1), 2693. https://doi.org/10.1038/s41467-022-29775-7,
PubMed: 35577769
Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J.-M. (2011). Field-
Trip: Open source software for advanced analysis of MEG, EEG,
and invasive electrophysiological data. Computational Intelli-
gence and Neuroscience, 2011, 156869. https://doi.org/10
.1155/2011/156869, PubMed: 21253357
Paluš, M. (1996). Nonlinearity in normal human EEG: Cycles,
temporal asymmetry, nonstationarity and randomness, not chaos.
Biological Cybernetics, 75(5), 389–396. https://doi.org/10.1007
/s004220050304, PubMed: 8983161
Pedersen, M., Omidvarnia, A., Walz, J. M., Zalesky, A., & Jackson,
G. D. (2017). Spontaneous brain network activity: Analysis of its
temporal complexity. Network Neuroscience, 1(2), 100–115.
https://doi.org/10.1162/NETN_a_00006, PubMed: 29911666
Pillai, A. S., & Jirsa, V. K. (2017). Symmetry breaking in space-time
hierarchies shapes brain dynamics and behavior. Neuron, 94(5),
1010–1026. https://doi.org/10.1016/j.neuron.2017.05.013,
PubMed: 28595045
Roberts, J. A., Gollo, L. L., Abeysuriya, R. G., Roberts, G., Mitchell,
P. B., Woolrich, M. W., & Breakspear, M. (2019). Metastable
brain waves. Nature Communications, 10(1), 1056. https://doi
.org/10.1038/s41467-019-08999-0, PubMed: 30837462
Sadasivan, P. K., & Narayana Dutt, D. (1996). SVD based technique
for noise reduction in electroencephalographic signals. Signal
Processing, 55(2), 179–189. https://doi.org/10.1016/S0165-1684
(96)00129-6
Shafiei, G., Markello, R. D., Vos de Wael, R., Bernhardt, B. C.,
Fulcher, B. D., & Misic, B. (2020). Topographic gradients of
intrinsic dynamics across neocortex. ELife, 9, e62116. https://
doi.org/10.7554/eLife.62116, PubMed: 33331819
Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., Moodie, C. A., & Poldrack, R. A. (2016).
The dynamics of functional brain networks: Integrated network
states during cognitive task performance. Neuron, 92(2),
544–554. https://doi.org/10.1016/j.neuron.2016.09.018,
PubMed: 27693256
Shriki, O., Alstott, J., Carver, F., Holroyd, T., Henson, R. N. A.,
Smith, M. L., Coppola, R., Bullmore, E., & Plenz, D. (2013). Neu-
ronal avalanches in the resting MEG of the human brain. Journal
of Neuroscience, 33(16), 7079–7090. https://doi.org/10.1523
/JNEUROSCI.4286-12.2013, PubMed: 23595765
Sorrentino, P., Rucco, R., Baselice, F., De Micco, R., Tessitore, A.,
Hillebrand, A., … Sorrentino, G. (2021a). Flexible brain dynam-
ics underpins complex behaviours as observed in Parkinson’s
disease. Scientific Reports, 11(1), 4051. https://doi.org/10.1038
/s41598-021-83425-4, PubMed: 33602980
Sorrentino, P., Rucco, R., Jacini, F., Trojsi, F., Lardone, A., Baselice,
F., … Sorrentino, G. (2018). Brain functional networks become
more connected as amyotrophic lateral sclerosis progresses: A
source level magnetoencephalographic study. NeuroImage: Clin-
ical, 20, 564–571, https://doi.org/10.1016/j.nicl.2018.08.001,
PubMed: 30186760.
Sorrentino, P., Seguin, C., Rucco, R., Liparoti, M., Troisi Lopez, E.,
Bonavita, S., … Zalesky, A. (2021b). The structural connectome
constrains fast brain dynamics. ELife, 10, e67400. https://doi.org
/10.7554/eLife.67400, PubMed: 34240702
Sporns, O. (2013). The human connectome: Origins and chal-
lenges. NeuroImage, 80, 53–61. https://doi.org/10.1016/j
.neuroimage.2013.03.023, PubMed: 23528922
Stam, C. J. (2005). Nonlinear dynamical analysis of EEG and MEG:
Review of an emerging field. Clinical Neurophysiology, 116(10),
2266–2301. https://doi.org/10.1016/j.clinph.2005.06.011,
PubMed: 16115797
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, O., Delcroix, N., Mazoyer, B., & Joliot, M. (2002). Auto-
mated anatomical labeling of activations in SPM using a macro-
scopic anatomical parcellation of the MNI MRI single-subject
brain. NeuroImage, 15(1), 273–289. https://doi.org/10.1006
/nimg.2001.0978, PubMed: 11771995
Van Veen, B. D., Van Drongelen, W., Yuchtman, M., & Suzuki, A.
(1997). Localization of brain electrical activity via linearly con-
strained minimum variance spatial filtering. IEEE Transactions on
Biomedical Engineering, 44(9), 867–880. https://doi.org/10.1109
/10.623056, PubMed: 9282479
Wang, R., Liu, M., Cheng, X., Wu, Y., Hildebrandt, A., & Zhou, C.
(2021). Segregation, integration, and balance of large-scale rest-
ing brain networks configure different cognitive abilities. Pro-
ceedings of the National Academy of Sciences, 118(23),
e2022288118. https://doi.org/10.1073/pnas.2022288118,
PubMed: 34074762
Wibral, M., Lizier, J. T., Vögler, S., Priesemann, V., & Galuske, R.
(2014). Local active information storage as a tool to understand
distributed neural information processing. Frontiers in Neuroin-
formatics, 8, 1. https://doi.org/10.3389/fninf.2014.00001,
PubMed: 24501593
Network Neuroscience
85
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
7
3
2
0
7
2
0
4
5
n
e
n
_
a
_
0
0
2
7
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3