REPORT
The Bayesian Mutation Sampler Explains
Distributions of Causal Judgments
Ivar R. Kolvoort1,2, Nina Temme1, and Leendert van Maanen3
1Abteilung für Psychologie, University of Amsterdam, Amsterdam, Die Niederlande
2Institute for Logic, Language, and Computation, University of Amsterdam, Amsterdam, Die Niederlande
3Department of Experimental Psychology, Utrecht University, Utrecht, Die Niederlande
Keine offenen Zugänge
Tagebuch
Schlüsselwörter: causal reasoning, causal judgments, priors, sampling, response distributions, conservatism
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
ABSTRAKT
One consistent finding in the causal reasoning literature is that causal judgments are rather
Variable. Insbesondere, distributions of probabilistic causal judgments tend not to be normal
and are often not centered on the normative response. As an explanation for these response
distributions, we propose that people engage in ‘mutation sampling’ when confronted with a
causal query and integrate this information with prior information about that query. Der
Mutation Sampler model (Davis & Rehder, 2020) posits that we approximate probabilities
using a sampling process, explaining the average responses of participants on a wide variety of
tasks. Careful analysis, Jedoch, shows that its predicted response distributions do not match
empirical distributions. We develop the Bayesian Mutation Sampler (BMS) which extends the
original model by incorporating the use of generic prior distributions. We fit the BMS to
experimental data and find that, in addition to average responses, the BMS explains multiple
distributional phenomena including the moderate conservatism of the bulk of responses, Die
lack of extreme responses, and spikes of responses at 50%.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
EINFÜHRUNG
Causal reasoning is a core facet of human cognition. Dealing with causal relationships in the
world and using them to our advantage is a crucial part of our abilities. Causal cognition ties
into most (if not all) judgments and decisions (z.B., Hagmayer & Osman, 2012; Rottman &
Hastie, 2014). Most of what we do and think is at least partly based on the perception of
and reasoning about causes and effects in the world. This makes it an important aim in cog-
nitive science to understand how we think and reason about causes and effects.
The current work addresses probabilistic causal reasoning. An example of this is when
someone tries to judge the probability that they will be late for work after hearing on the radio
that there has been a traffic accident nearby. To make such a judgment one needs to use their
knowledge of a causal system. In this case such knowledge could be represented as X → Y →
Z, where X stands for a traffic accident, Y for a traffic jam, and Z for being late for work. In einem
typical probabilistic causal reasoning experiment people are first taught about a particular
causal system (for example X → Y → Z ), after which they are asked to make certain inferences,
d.h., compute certain (conditional) probabilities. An example of such an inference is “what is
the probability of Z (being late for work) given that X (a traffic accident) passiert?”. Diese
experiments provide a window into how participants make use of causal information to come
Zitat: Kolvoort, ICH. R., Temme, N., &
van Maanen, L. (2023). The Bayesian
Mutation Sampler Explains Distributions
of Causal Judgments. Open Mind:
Discoveries in Cognitive Science, 7,
318–349. https://doi.org/10.1162
/opmi_a_00080
DOI:
https://doi.org/10.1162/opmi_a_00080
Supplemental Materials:
https://doi.org/10.1162/opmi_a_00080
Erhalten: 11 November 2022
Akzeptiert: 25 April 2023
Konkurrierende Interessen: The authors
declare no conflict of interests.
Korrespondierender Autor:
Ivar R. Kolvoort
ivarrenzokolvoort@gmail.com
Urheberrechte ©: © 2023
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
The Bayesian Mutation Sampler
Kolvoort et al.
to a specific judgment. The current work will focus on using cognitive modelling to understand
how people make such judgments using their causal knowledge.
Over the last decades so-called causal Bayesian networks1 (CBNs; Pearl, 2009; Spirtes
et al., 2000) have achieved remarkable success in modeling human behavior across a variety
of tasks related to causal learning, categorization, reasoning and inference (z.B., Ali et al.,
2011; Bramley et al., 2015; Cheng, 1997; Coenen et al., 2015; Fernbach & Erb, 2013; Griffiths
& Tenenbaum, 2005, 2009; Hagmayer, 2016; Hayes et al., 2014; Holyoak et al., 2010;
Krynski & Tenenbaum, 2007; Lee & Holyoak, 2008; Lu et al., 2008; Meder et al., 2014;
Rehder, 2014; Rehder & Burnett, 2005; Shafto et al., 2008; Steyvers et al., 2003; Waldmann
& Hagmayer, 2006). These models provide a concise representation of causal systems and a
particular formal logic that specifies how one can learn, draw inferences, and update causal
knowledge based on interventions in the system.
CBNs, as models of human cognition, are often understood as explanations on the compu-
tational level (Marr, 1982). Das ist, they provide an account of what problem needs to be
solved, but not how to solve them. This is because formal computations with CBN models
tend to be computationally expensive and so are thought not be feasible as a way for us
humans to solve problems. Instead of directly doing these Bayesian computations, recent work
in the cognitive sciences has argued that people use sampling to solve such computationally
intensive problems in a variety of domains (Bonawitz et al., 2014; Dasgupta et al., 2017;
Hertwig & Pleskac, 2010; Lieder et al., 2012; Vul et al., 2014; Zhu et al., 2020). This sampling
approach to cognition proposes that we solve problems by way of first drawing samples, entweder
from memory or an internal generative model, and then generating judgments based on the
information in these samples. In this way we can reason about probabilities without the need
to explicitly represent probabilities. Often the sampling approach is modelled using Markov
chain Monte Carlo (MCMC) processes (see Dasgupta et al., 2017). Davis and Rehder (2020)
applied this sampling approach to the domain of causal cognition, developing a model that
samples over possible states of a CBN to make causal judgments. This so-called Mutation
Sampler model (MS) provides an algorithmic level explanation (Marr, 1982) as it describes
how humans reason causally. It proposes a sampling mechanism for how we generate causal
judgments and has been successful in explaining average responses on a variety of tasks
(Davis & Rehder, 2020).
Jedoch, while accounts of average responses abound, the common observation of sub-
stantial variability in causal judgments has received less attention and is often left unexplained
(Davis & Rehder, 2020; Kolvoort et al., 2021, 2022; Rehder, 2014, 2018; Rottman & Hastie,
2016). This is an unfortunate gap in the literature, as variability in behavior can be informative
of the cognitive mechanisms involved and so can help constrain the development of theories
(z.B., as has been done in the domain of decision-making; Ratcliff, 1978). In diesem Papier, we will
analyze the distributional predictions of the MS and ultimately extend it with the incorporation
of priors to provide an explanation of some of the observed variability in causal judgments.
Sampling Theory and the Mutation Sampler
The MS is a sampling model of causal reasoning that accounts for many observed behavioral
phenomena including deviations from the normative CBN model (Davis & Rehder, 2017,
2020; Rehder & Davis, 2021). Before discussing the model in more detail, es ist wichtig
note that the original authors argue for four psychological principles to govern causal
1 Also known as causal graphical models, graphical probabilistic models, or causal Bayes’ nets.
OPEN MIND: Discoveries in Cognitive Science
319
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
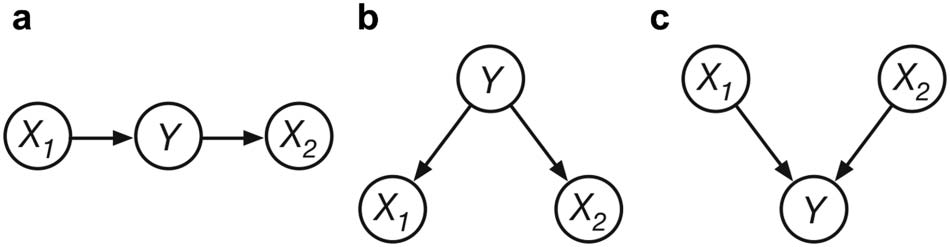
Figur 1. Three-variable causal networks. The circles represent causal variables, the arrows rep-
resent causal relationships. Throughout this manuscript we will use Y to refer to the middle variable,
and Xi to refer to a terminal variable. (A) Chain structure. (B) Common cause structure. (C) Common
effect structure.
reasoning and that the MS is but one formalization of these principles. We will refer to these
principles in this section, for a more detailed discussion on these psychological claims and the
exact formalization of the MS we refer to the original paper (Davis & Rehder, 2020).
The MS proposes that people engage in sampling over states of a causal network to make
inferences and as such describes the process by which people generate causal judgments. Das
proposal is built on the psychological claim that people reason about concrete cases and not
about abstract probabilities (Principle 1). The concrete cases here are causal networks instan-
tiated with particular values, d.h., they are particular casual network states (siehe Abbildung 1 für
three-variable causal networks). These concrete cases or causal network states are obtained
from memory or through simulations using an internal generative model. Subsequently these
samples are used to compute inferences based on the relative frequencies of certain events in
the chain of generated samples.
The MS generates a sequence of samples of a causal system using a Metropolis-Hastings
MCMC sampling algorithm (Davis & Rehder, 2020). The sampler starts in one of two proto-
typical states, with equal probability. The prototypical states are states in which the causal
variables are either all present or all absent (d.h., for 3-variable causal networks, [X1 = 1, Y =
1, X2 = 1] Und [X1 = 0, Y = 0, X2 = 0]). Nächste, a new state is proposed from the states that differ
only in value of a single variable from the current state, d.h., the current state is ‘mutated’. Das
implements the idea that people tend to only make small adjustments to the cases they are
considering currently (Principle 2). Whether the next sample is this proposal state or is the
current state is determined by the transition probability. The transition probability is defined
by the relative likelihood of the proposal and current state (Hastings, 1970). If the proposal
state is more probable than the current state, the next sample will be the proposed state with
probability 1. If the proposal state is less probable than the current state, the probability of the
next sample being the proposed state is determined by the ratio of the joint probabilities of the
proposed and current state. Due to the transitions being defined by probabilities this is a
stochastic process.
The chain of samples generated by this scheme converges to reflect the actual normative
joint distribution when the number of samples becomes sufficiently large. Das bedeutet, dass
judgments based on a large number of samples approximate the true probabilities. Jedoch,
people do not respond normatively and nor does the MS. Two factors contribute to the non-
normativity of judgments based on the mutation sampling process: (1) the starting point of the
process is biased (to prototypical states) Und (2) the number of samples (or ‘chain length’) Ist
limited.
Both these factors, limited sampling and biased starting points, lead to a probability distri-
bution that overestimates the likelihood of states where more variables have the same value.
Das ist, it is biased towards prototypical states (siehe Abbildung 3 in Davis & Rehder, 2020). Since a
OPEN MIND: Discoveries in Cognitive Science
320
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
chain of samples always starts at a prototypical state and has limited opportunity to reach
states that are very different from these prototypical states (due to limited number of samples),
the predicted probability distribution places more probability density on states based on their
closeness to the prototypical states. This effect is stronger when the number of samples taken
is small.
Davis and Rehder (2020) provide psychological justifications for these aspects of their
model that lead to non-normative responding. With regard to the biased starting points, Davis
and Rehder suggest that “prototypes readily come to mind as plausible states at which to start
sampling because, if one ignores the details of the causal graph such as the strength, Richtung,
or functional form of the causal relations, they are likely to be viewed as having relatively high
joint probability” (Principle 3; Davis & Rehder, 2020, S. 6). Assuming generative causal links,
this is the case because a prototypical state is always consistent with the causal relationships in
that there are no cases in which effects are absent while their causes are present and vice
versa. Darüber hinaus, these prototype states are generally high probability states and so are good
starting points for convergence. Taken together, when we start thinking about a causal system
we start in a simple state, that is likely to be remembered or generated as it occurs often and is
consistent with all causal relationships in the network.
The second aspect of the MS that leads to non-normative responding is that the chains of
samples are of limited length (Principle 4). Other work on sampling approaches to cognition
has shown that using only a limited number of samples can be rational when taking into
account costs associated with taking more samples (see Dasgupta et al., 2017; Hertwig &
Pleskac, 2010; Vul et al., 2014) As such the MS can be viewed as part of the new resource-
rational analysis modeling paradigm in which the rational use of limited resources is a guiding
principle (Lieder & Griffiths, 2020).
Davis and Rehder (Davis & Rehder, 2020; Rehder & Davis, 2021) fitted the MS to data
from a variety of experiments concerning causal reasoning, categorization, and intervention.
They found that the model fits better to participant responses than standard CBNs. Darüber hinaus,
the model is able to account for multiple systematic reasoning errors, d.h., deviations from the
normative CBN model, by virtue of the limited sampling and biased starting point mecha-
nisms. Zum Beispiel, the distorted joint distribution that the MS produces is able to account
for Markov violations and failures to explain away, two hallmark behavioral phenomena in
causal reasoning (Kolvoort et al., 2021, 2022; Park & Sloman, 2013; Rehder, 2018; Rehder &
Burnett, 2005; Rottman & Hastie, 2014, 2016). In addition to using existing data, Davis and
Rehder (2020) ran an experiment that presented participants with causal graphs and asked
them to generate data that they thought would be consistent with the causal structure. Der
data participants generated matched the distorted joint distributions produced by the MS.
Taken together, the tested predictions of the MS seem to be in very good accord with exper-
imental data.
Jedoch, not all aspects of the of predictions have been scrutinized. As the MS posits that
the transitions from one state to another in the generation of a chain of samples are stochastic,
it predicts not just a mean response (like the CBN estimate), but a full distribution of responses
to an inference. This is in line with the MS being a process-model, since it models the process
by which people generate causal judgments it should also produce the variability in responses
seen on a variety of tasks (Davis & Rehder, 2020). Jedoch, following the literature on causal
cognition at large, these distributional predictions have not yet received proper attention. Der
aim of the current paper is to assess these distributional predictions and use the distributional
phenomena in empirical data to guide further development of the MS.
OPEN MIND: Discoveries in Cognitive Science
321
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
.
/
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
The rest of this paper is structured in two main parts. In the first part we analyze the distri-
butions predicted by the MS and find that it cannot explain certain distributional phenomena
observed in causal reasoning tasks. Zusätzlich, we provide theoretical arguments against the
(resource-)rationality of the model, leading us to extend the model using priors in the second
Teil. In the second part we introduce the Bayesian Mutation Sampler and test its distributional
Vorhersagen. We conclude with a general discussion concerning both the theoretical and
empirical advances made in this paper.
ANALYZING THE MS AND DISTRIBUTIONAL PHENOMENA
The nature of the MS as a process-model makes it a useful tool to assess distributional phe-
nomena in addition to the mean phenomena that have been extensively studied (see Kolvoort
et al., 2021). It has been observed multiple times that causal judgments vary substantially
(Davis & Rehder, 2020; Kolvoort et al., 2021; Rehder, 2014, 2018; Rottman & Hastie,
2016). The MS has not been used to study distributional properties of responses. The authors
did present a figure indicating a qualitative similarity between the variability of responses in
Experiments 1A and 1B by Rottman and Hastie (2016) and the variability of the predicted
responses by the MS with a mean chain length of 36 (siehe Abbildung 9 in Davis & Rehder,
2020). Jedoch, this value for the chain length is far from the average best fitting parameter
(which was 12.7) that the authors found for a range of causal reasoning experiments (Davis &
Rehder, 2020). daher, many questions remain regarding the predicted distributions of the
MS. Hier, we aim to assess these predictions under a range of different chain lengths.
To this end we simulated responses using the MS with multiple chain lengths using the
same causal parameters2 as in Experiment 1A by Rottman and Hastie. We chose these param-
eters since the MS was fitted to that experiment originally and they are intended to theoreti-
cally neutral (Rottman & Hastie, 2016). Figur 2 present the results of the simulations together
with empirical data from a recent causal reasoning experiment (Kolvoort et al., 2022). Diese
data are causal probabilistic judgments, where participants had to judge the probability of a
causal variable being present conditional on information about other causal variables in the
Netzwerk (z.B., P(X1 = 1|Y = 1)). The experiment is described in more detail in a later section, für
now it suffices to note that it used similar methods, including the exact same causal parame-
ters, as Experiment 1A by Rottman and Hastie (2016).
Mutation Sampler Predicts Extreme Responses and No ‘Moderate’ Conservatism
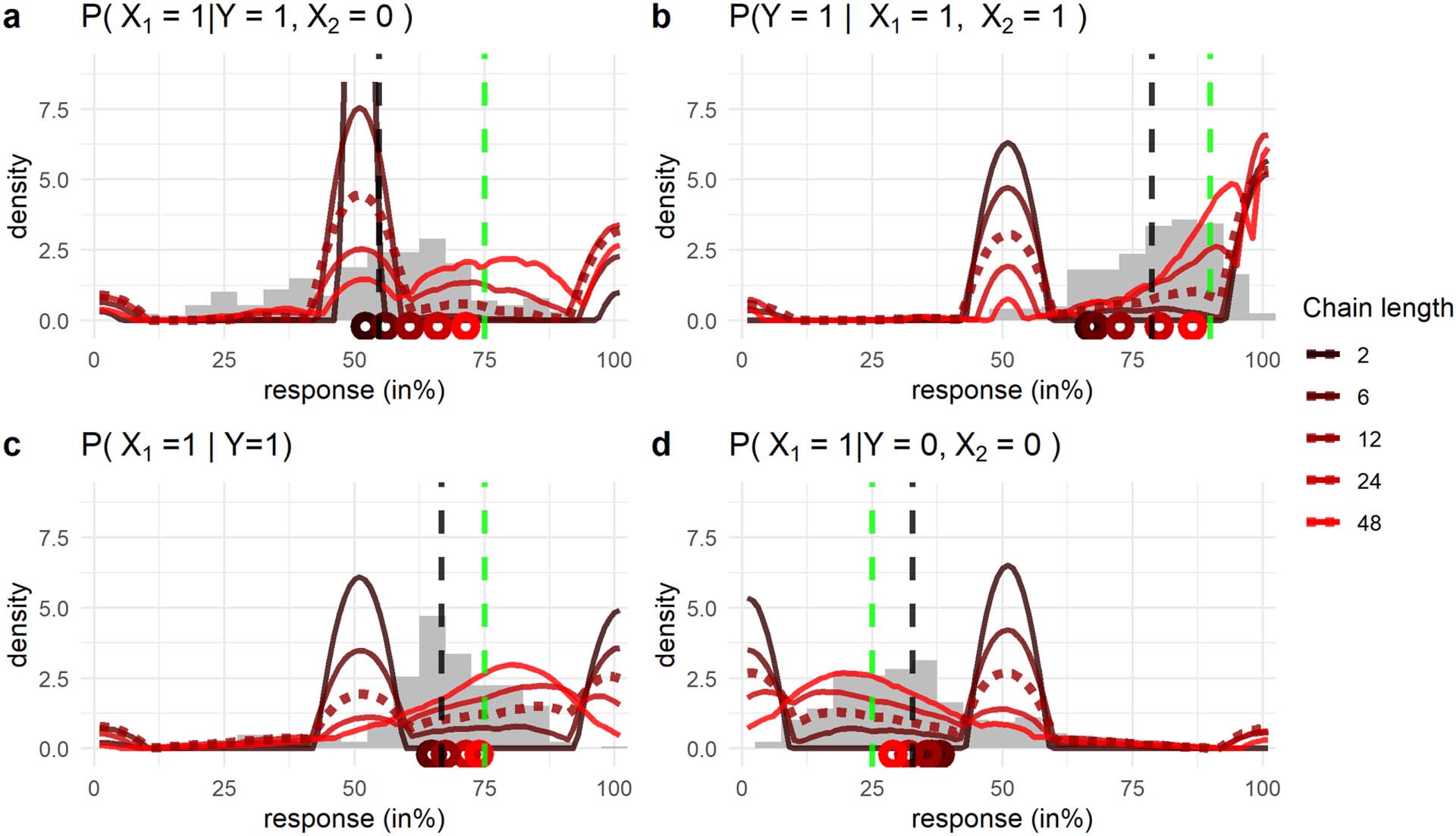
Let us take the predictions of the MS with chain length 12 (dashed red lines in Figure 2) as a
starting point for our discussion, seit 12 is close to the mean chain length found for causal
reasoning tasks (Davis & Rehder, 2020). What immediately stands out in Figure 2 is that the
MS with a chain length of 12 predicts three peaks of responses for each inference at 0%, 50%
Und 100%. Spikes of responses at 50% have been reported in the literature on causal judg-
gen (Kolvoort et al., 2021; Rottman & Hastie, 2016). To the contrary, the peaks at 0% Und
100% seem not to correspond to empirical data. Tatsächlich, it is known that participants behave
2 The chain and common cause structure had the same causal parameters, with base rates of .5 for all vari-
fähig. The effects in the network had a probability of 75% when their parent was present and 25% when it was
nicht. In the common effect structure, the two causes combined by way of a Noisy-OR gate (Cheng, 1997) mit
causal strengths of 50% and with base rates of 50%. This meant that the effect had a 0% probability if no causes
were present, 50% when one cause was present, Und 75% when both causes were present (hence the base rate
War .43 for the effect).
OPEN MIND: Discoveries in Cognitive Science
322
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Figur 2. Predictions of the Mutation sampler and data from Kolvoort et al. (2022) on four different inferences. (A) P(X1 = 1|Y = 1, X2 = 0); (B) P(Y =
1|X1 = 1, X2 = 1); (C) P(X1 = 1|Y = 1); (D) P(X1 = 1|Y = 0, X2 = 0). Plots A–D: The inferences were about a common cause structure where X1 and X2 refer
to the two effects, and Y refers to the common cause. A state of 1 (z.B., Y = 1) indicated a variable was present, a state of 0 indicated the variable was
absent. Grey histograms are the participant responses. The red lines indicate predictions of the MS with different chain lengths. The dashed red line
are the predictions with chain length of 12, close to the mean found by Davis and Rehder (2020). The predicted response distributions were
generated by simulating 10,000 responses with the MS and smoothing the result using kernel density estimation. Vertical dashed black lines indicate
mean participant response. Dashed green lines indicate the normative answer. The colored circles on the x axis indicate mean predictions.
conservatively and tend to avoid the extremes of the scale (Kolvoort et al., 2021, 2022;
Rottman & Hastie, 2016). This makes the predictions at 0% Und 100% rather surprising.
To understand these predictions we have to take a closer look at the mechanisms causing
these peaks. zuerst, the peak at 50%. These peaks are due to the MS defaulting to a 50%
response for conditional probability queries when the causal network states required for the
calculation are not reached at any point by the stochastic sampling process. Throughout this
manuscript we will use Y to refer to middle variable, and Xi to refer to a terminal variable (sehen
Figur 1). Let us say the required inference is P(X1 = 1|Y = 1, X2 = 0) as in Figure 2A. In diesem
case the sampler needs to visit the states [X1 = 1, Y = 1, X2 = 0] Und [X1 = 0, Y = 1, X2 = 0] Zu
compute the inference based on the relative frequency of these states in the chain. This com-
putation is done using the (Kolmogorov) definition of conditional probability:
(cid:1)
(cid:3)
P X1 ¼ 1│Y ¼ 1; X2 ¼ 0
¼
P X1 ¼ 1; Y ¼ 1; X2 ¼ 0
D
D
P X1 ¼ 1; Y ¼ 1; X2 ¼ 0
Þ
Þ
Þ þ P X1 ¼ 0; Y ¼ 1; X2 ¼ 0
D
From which we can get an estimate for the conditional probability based on sample frequencies:
(cid:1)
P^ X1 ¼ 1│Y ¼ 1; X2 ¼ 0
(cid:3)
¼
N X1 ¼ 1; Y ¼ 1; X2 ¼ 0
D
D
Þ
N X1 ¼ 1; Y ¼ 1; X2 ¼ 0
Þ þ N X1 ¼ 0; Y ¼ 1; X2 ¼ 0
D
(1)
Þ
where N stands for the number of samples of that causal state. Now if the required states on the
right-hand side of Equation 1 are not visited their frequencies (or probabilities) are zero. In diesem
OPEN MIND: Discoveries in Cognitive Science
323
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
case Equation 1 would reduce to 0
Zu 50%3.
0 which cannot be computed and instead the MS defaults
The predicted peaks at 0% Und 100% come about similarly as the peak at 50%, however in
this case only one of the two required states is not visited. Let us again consider the inference
P(X1 = 1|Y = 1, X2 = 0), which requires the state A: [X1 = 1, Y = 1, X2 = 0] and B: [X1 = 0, Y = 1,
X2 = 0] to be visited by the sampler. In the case where state A is not visited, Gleichung 1 sim-
Þ and we get a response at 0%. When state B is not visited by the
plifies to
Þ
sampler, Gleichung 1 simplifies to P X1¼1;Y ¼1;X2¼0
Þþ0 and we get a predicted response at 100%.
P X1¼1;Y ¼1;X2¼0
0
0þP X1¼0;Y ¼1;X2¼0
D
D
D
To gain insight in how often the MS generates ‘default’ responses at 0%, 50%, oder 100% Wir
can estimate how often a particular network state is expected to be visited. We do this by
simulating 10,000 chains of samples. Let us again regard P(X1 = 1|Y = 1, X2 = 0) (Figure 2A),
which requires visits to the states A: [X1 = 1, Y = 1, X2 = 0] and B: [X1 = 0, Y = 1, X2 = 0] to be
computed (see Equation 1). We find that with a chain length of 12, the proportion of trials on
which state A is not visited by the sampler is 0.49, the proportion where state B is not visited is
0.72, and the proportion of trials where neither is visited is 0.39. As a direct result, we see
more responses predicted at 100% than at 0% in Figure 2A, as it is more likely for state B
to not be visited than state A. Only in 18% of the trials does the sampler actually reach both
state A and B, meaning that in only 18% of the judgments a probability estimate is computed
by comparing the nonzero frequencies of states A and B in the chain of samples. We will refer
to these as ‘computed’ responses to contrast them from what we will refer to as ‘default’
responses at 0%, 50%, oder 100% which occur when at least one state (A or B) was not visited
by the sampler. The other 82% of the time the MS predicts such default responses at 0%, 50%,
oder 100%, which is why we observe large peaks in the dashed line at 0%, 50%, Und 100% In
Figur 2.
Let us now look at the effect of different chain lengths. As the predicted peaks at 0%, 50%
Und 100% by the MS are all due to certain network states not being visited by the sampling
Verfahren, the number of samples drawn, d.h., the chain length, determines the size of these pre-
dicted peaks. Fewer samples drawn increases the probability that certain states are not visited
and so larger peaks are predicted4. This effect of the chain length on predicted response dis-
tributions can be seen from the multiple red lines in Figure 2: Longer chain lengths, indicated
by brighter red lines, have smaller peaks and provide a mean estimate that is closer to the
normative answer. To assess the effect of chain length on the amount of default and computed
responses we again simulated 10,000 runs with the MS, this time using chain lengths ranging
aus 2 Zu 48 (Tisch 1).
As mentioned before, smaller chain lengths make it less likely that the required causal net-
work states to compute an inference are visited by the sampler. With a chain length of two, Die
darkest red lines in Figure 2, the two states required to compute the inference are never both
visited and the MS predicts responses to be exclusively at 0%, 50%, oder 100%. From Table 1 Wir
can indeed see that the P(X1 = 1|Y = 1, X2 = 0) inference was never computed in 10,000 runs
with a chain length of 2. For larger chain lengths these peaks are present as well albeit with a
3 Davis and Rehder (2020) implemented this mechanism by initializing the number of visits to each network
state with 10−10. When the required states for an inference are not visited Equation 1 then simplifies to 10−10/[10−10 +
10−10] = .5.
4 The joint distribution of the causal variables also ties into this, since if there is a network state that has a
small normative probability, it will be harder for the sampler to reach as well. This makes it that we observe the
largest peaks in Figure 2A, where the query refers to a state where Y = 1 and X2 = 0, an unlikely state.
OPEN MIND: Discoveries in Cognitive Science
324
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Tisch 1.
Predicted responses of the Mutation Sampler for the inference P(X1 = 1|Y = 1, X2 = 0).
Chain length
2
6
12
24
48
Computed
0.0
0.0605
0.182
0.418
0.729
Probability of response
0%
0.0177
0.0599
0.0936
0.0870
0.0309
50%
0.927
0.667
0.392
0.146
0.0228
100%
0.0554
0.213
0.332
0.349
0.218
Probabilities are calculated by running the Mutation Sampler 10,000 times using the causal param-
eters of the common cause network in Experiment 1A in Rottman and Hastie (2016). ‘Computed’
refers to responses that are computed by comparing the relative frequency of network states. Wir
contrast these with ‘default’ responses at 0%, 50%, oder 100%.
smaller magnitude. Even with a chain length of 48, which is at the high end of the range of
chain lengths found previously (Davis & Rehder, 2020), the MS still predicts a substantial pro-
portion of extreme responses at 0 Und 100%. Zum Beispiel, for the inference P(X1 = 1│Y = 1,
X2 = 0) the MS predicts responses at 100% for all chain lengths simulated (Figure 2A and
Tisch 1). Even with a chain length of 48 the MS still predicts 22% of responses to be an
extreme response of 100%. For each chain length above 2 the probability of an extreme
response is at least 24% (Tisch 1). These predictions of the MS are not borne out, multiple
studies have found participants to avoid the extremes of the scale in causal reasoning studies
(z.B., Kolvoort et al., 2021, 2022; Rottman & Hastie, 2016).
Figur 2 illustrates another aspect of the MS predictions that do not match the empirical
Daten. We know that when the chain lengths are larger the predicted response peaks at 0%,
50%, Und 100% decrease while the proportion of computed responses increases (Tisch 1).
Regarding these computed responses, when the number of samples, d.h., the chain length,
tends to infinity the predicted responses will tend towards the normative CBN point prediction.
Somit, the mean prediction will get closer to the normative response with increasing chain
lengths. One can see this happening from the red circles on the x axis indicating the mean
predicted response in Figure 2. This indicates that there is a tradeoff in the predicted distribu-
tions of the MS between the peaks at 0%, 50%, 100% and a peak of computed responses that
gets closer to the normative response when chain lengths increase.
Based on this tradeoff the MS can predict mean conservatism by varying chain lengths.
With very low chain lengths, the mean response is close to 50% as most responses will be
default responses at 50%. At large chain lengths the mean response will approach the norma-
tive response. With more moderate chain lengths the mean response will lie in between 50%
and the normative response (see circles on x axis in Figure 2). This observation is consistent
with the literature, as mean participant responses tend to be conservative and lie between 50%
and the normative answer. Jedoch, it is not just the mean response that is between 50% Und
the normative answer. Typically, the bulk of responses tends to lie between 50% and the nor-
mative answer (Kolvoort et al., 2022; Rottman & Hastie, 2016). This however is inconsistent
with the MS prediction, as the MS only predicts mean conservatism by trading off default
responses (mainly at 50%) for computed responses (near the normative response). It is not able
to predict the bulk of moderately5 conservatism responses in between 50% and the normative
5 One can interpret 50% responses as ‘extreme’ conservatism.
OPEN MIND: Discoveries in Cognitive Science
325
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
answer that have been found in experiments (Kolvoort et al., 2021, 2022; Rottman & Hastie,
2016). Relatedly, the model can predict some variability in responses that is similar to the
empirical distributions (see predicted distributions with chain lengths 24 Und 48 In
Figur 2), however when it does so the mean predicted response tends to be off and there
are still peaks that are not present in participant’s responses. The mechanics of the MS lead
to distributions that cannot mimic empirical responses in terms of certain distributional phe-
gegeben. To serve as an complete explanation of the cognitive process, the MS should be able
to predict distributional behavioral phenomena in addition to mean phenomena.
This analysis of response distributions brought to light two important aspects of the data that
the MS currently does not account for. The first is that it predicts extreme responses with a wide
range of chain lengths. These responses are not observed in experiments, where people shy
away from the extreme ends of the scale (Kolvoort et al., 2021, 2022; Rottman & Hastie,
2016). The second issue has to do with participant’s conservatism: the bulk of responses is
zwischen 50% and the normative answer (Kolvoort et al., 2022; Rottman & Hastie, 2016).
The mutation sampler can predict mean conservatism, but seemingly only by balancing the
size of the peaks at 0%, 50%, Und 100% with computed responses. It does not predict the bulk
of responses to be in between the normative answer and 50%.
Forming Judgments Based on Samples
To better understand how we could resolve the issues of the MS we identified above we con-
sider the process of forming judgments based on samples. The most straightforward manner in
which people can form probability judgments based on a set of samples is by calculating the
relative frequency of an event occurring in the samples and taking this as an estimate of a
probability of the occurrence of that event (Zhu et al., 2020). To illustrate this, imagine a sce-
nario in which someone repeatedly throws tennis balls at beer bottles causing some to break.
To estimate the probability that the bottle breaks with the next throw, we can compute the
frequency of the bottle breaking in samples where a tennis ball is thrown:
Relative frequency ¼
Nbreaks
Nbreaks þ Ndoes not break
¼ Nbreaks
Nthrows
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Also, zum Beispiel, if bottles break 12 times in 20 throws, the relative frequency of the bottle
breaking is 12/20 = 0.6. Dann, someone using the relative frequency approach would judge
the probability of a bottle breaking as 0.6. This entails that a judgment is completely based on
the incoming information and the judgment would approach the true probability when the
number of samples tends to infinity. The MS uses this relative frequency method, computing
judgments directly from the relative frequency of samples.
Problems with the relative frequency approach arise when we look at what happens when
the number of samples is limited or small. According to the relative frequency method one could
judge the probability of an event that is only witnessed once to be occurring 100% of the time.
Das ist, if one observes a bottle to break after only one throw, one would judge the probability of
a ball causing a bottle to break to be 100%. The reverse is also the case, the relative frequency
method would lead one to judge anything that has not been directly observed yet to occur with a
0% probability. These extreme judgments are psychologically implausible. A more psycholog-
ically plausible model is to include prior information. The use of prior information can stop us
from making extreme responses when we have little information to go by.
Besides preventing extreme judgments there is a more normative argument for the use of
priors. The use of priors matches our decision-making in that it allows for gradual adjustments
OPEN MIND: Discoveries in Cognitive Science
326
The Bayesian Mutation Sampler
Kolvoort et al.
in the face of consistent evidence. When more and more tennis balls consistently break bottles, A
judgment of 100% becomes more reasonable. This illustrates that people are sensitive to the
amount of information obtained. When incorporating prior information, the amount of evidence
vorgeführt (here the number of samples of throws, or ‘likelihood’ in Bayesian terms) does directly
impact one’s judgment because we can weigh it relative to our prior information (z.B., our esti-
mate gradually moves to 100% after seeing bottles break consistently). Im Gegensatz, der Verwandte
frequency approach would be insensitive to the amount of information learned from sampling.
Based on the previous theoretical arguments and the problems the MS has with predicting
empirical response distributions, we propose the Bayesian Mutation Sampler (BMS) als
account of how people make causal judgments. The BMS is a process-model of causal rea-
soning combining mutation sampling (Davis & Rehder, 2020) with a generic Bayesian
approach using priors to make probability judgments from samples (Zhu et al., 2020). Wir
expect that the incorporation of priors will help in explaining the distributional behavioral phe-
nomena discussed in previous sections.
In the next section, we will give a detailed overview of the BMS and subsequently will test
whether it is an improvement over the MS, particularly in terms of the prediction of distribu-
tional properties, by fitting both models to experimental causal reasoning data.
THE BAYESIAN MUTATION SAMPLER
The BMS posits that when making causal probabilistic judgments people engage in sampling
by way of mutation sampling (Davis & Rehder, 2020). This includes the principles of limited
sampling and biased starting points, which bias judgments away from the normative CBN
response. Jedoch, instead of using the relative frequency method to form judgments based
on samples (as in the MS), the BMS incorporates prior information.
The type of prior information that people use for judgments and decision-making varies.
Many causal reasoning studies attempt to exclude the use of prior information regarding causal
model parameters (z.B., Kolvoort et al., 2022; Rehder, 2014; Rottman & Hastie, 2016). Wie-
immer, even if researchers are successful in stopping participants from using prior information
concerning causal parameters, it is likely that people still inherit priors relevant to the exper-
imental task from similar everyday activities or in some way or another have expectations con-
cerning the experimental task (see Hemmer et al., 2015; Marchant et al., 2021; Sanborn et al.,
2021; Tauber et al., 2017; Welsh & Navarro, 2012). When specific task-related information is
not present people can still use priors that reflect a lack of information.
The BMS posits that reasoners use a generic prior that encodes what they think to be likely
answers to a causal probabilistic query before sampling. This prior gets updated based on the
information in the samples. In Bayesian terms, the prior is updated using the information in the
Proben (the likelihood) to produce a posterior distribution. Subsequently probability
judgments are based on this posterior distribution. Following Zhu et al. (2020), we take it that
people respond using the expected value of this distribution (see also Jazayeri & Shadlen,
2010).
Incorporating the Symmetric Beta Prior
Following Zhu et al. (2020) we use symmetric Beta distributions as priors in the BMS, as they
can reflect a lack of information in various ways and because they can be naturally incorpo-
rated into sample frequencies to form judgments.
OPEN MIND: Discoveries in Cognitive Science
327
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
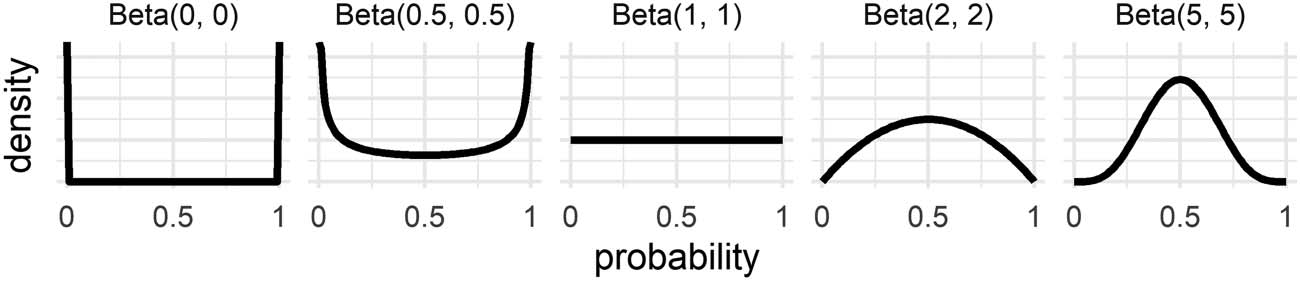
Figur 3.
tributions will be used as prior distributions in the BMS.
Symmetric Beta(β, β) distributions, using β = 0, 0.5, 1, 2, Und 5. Symmetric Beta dis-
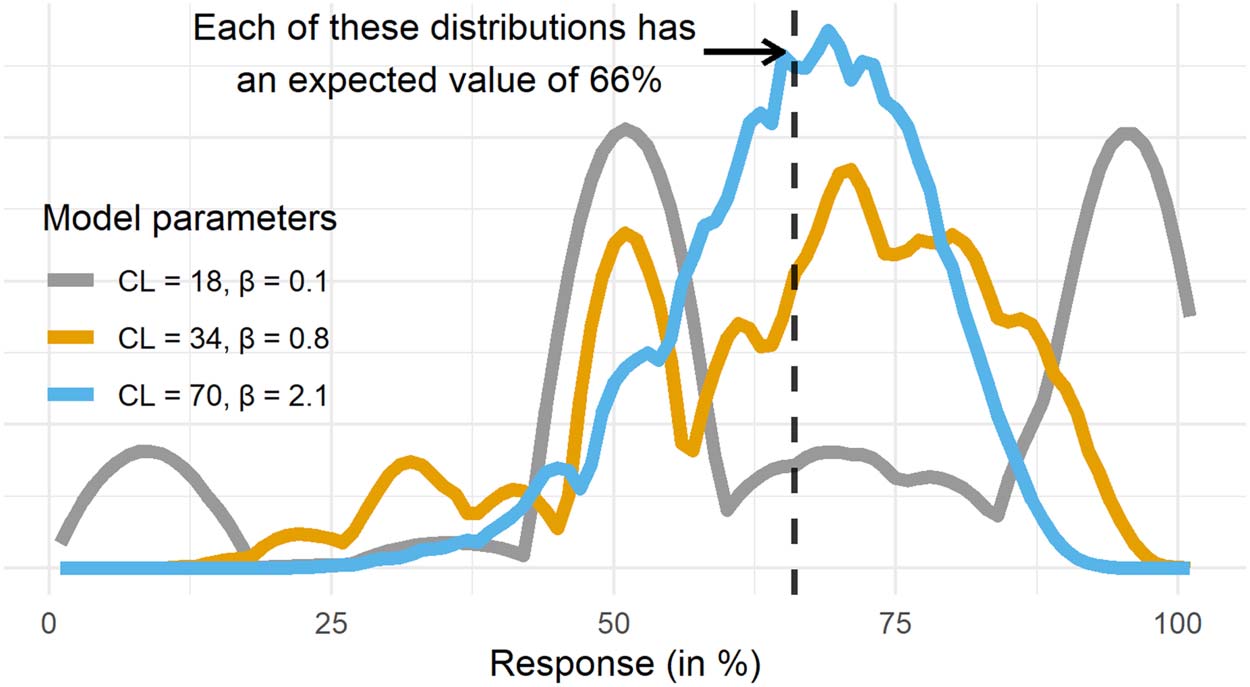
Figur 3 plots symmetric Beta(β, β) distributions with values for β as the shape parameters.
The Beta(1, 1) distribution is the uniform distribution, assigning equal probability mass to each
probability p (aus 0 Zu 1). For β > 1 the beta distributions assign more probability mass to the
center of the scale, d.h., probabilities around .5. β < 1 shows the opposite pattern, where more
probability is assigned to the extreme ends of the scale. In this way using the symmetric Beta
distributions allows the BMS to account for various levels of conservatism.
For all β > 0 the incorporation of the prior moves a response closer to 50% than when just
using the relative frequency method. The only symmetric Beta distribution that would not
introduce conservatism in this sense is the Beta(0, 0) distribution where all the probability mass
is at the extremes of the range, bei 0 Und 1. Using the Beta(0, 0) distribution is equivalent to
using the relative frequency method of forming judgments from samples. This entails that
the BMS with β set to 0 is equivalent to the standard MS and so the BMS is a generalization of
the MS.
By using the Beta(β, β) distribution as a prior, the expected value of the posterior distribution
can be determined without computing the posterior distribution itself. We can compute the
expected value directly by adding β as ‘pseudo-observations’ to Equation 1 as in Equation 2
(for the derivation of Equation 2 we refer to Appendix A in Zhu et al., 2020)6.
(cid:1)
(cid:3)
^P BMS X1 ¼ 1│Y ¼ y; X2 ¼ x
(2)
¼
N X1 ¼ 1; Y ¼ y; X2 ¼ x
D
Þ þ β
N X1 ¼ 1; Y ¼ x; X2 ¼ y
D
Þ þ N X1 ¼ 0; Y ¼ x; X2 ¼ x
D
Þ þ 2β
In Equation 2 ^P BMS refers to the estimate of the probability of an event predicted by the BMS, N
stands for the number of samples (in a chain of generated samples), and Xi, Y refer to causal
variables and x, y refer to their respective states. The β refers to the Beta(β, β) prior used, Wo
both shape parameters of the Beta distribution are equal to β.
Testing the BMS
In order to validate whether the BMS provides a better explanation of response distributions
than the MS, while still being able to predict mean responses as accurately as the MS, we fitted
both models to data from a recent causal reasoning experiment (Kolvoort et al., 2022).
Here we provide a brief description of the experimental data, for a more detailed discussion
we refer to the original paper (Kolvoort et al., 2022). The experiment consisted of three exper-
imental domains, each comprising a learning phase and a testing phase. In the learning phase
6 While conceptually different, our approach is computationally equivalent to one which would assign a prior
probability to all the possible network states instead of to likely correct responses to queries. Das ist, if we would
add β visits to all system states in Equation 1 we would get Equation 2.
OPEN MIND: Discoveries in Cognitive Science
328
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
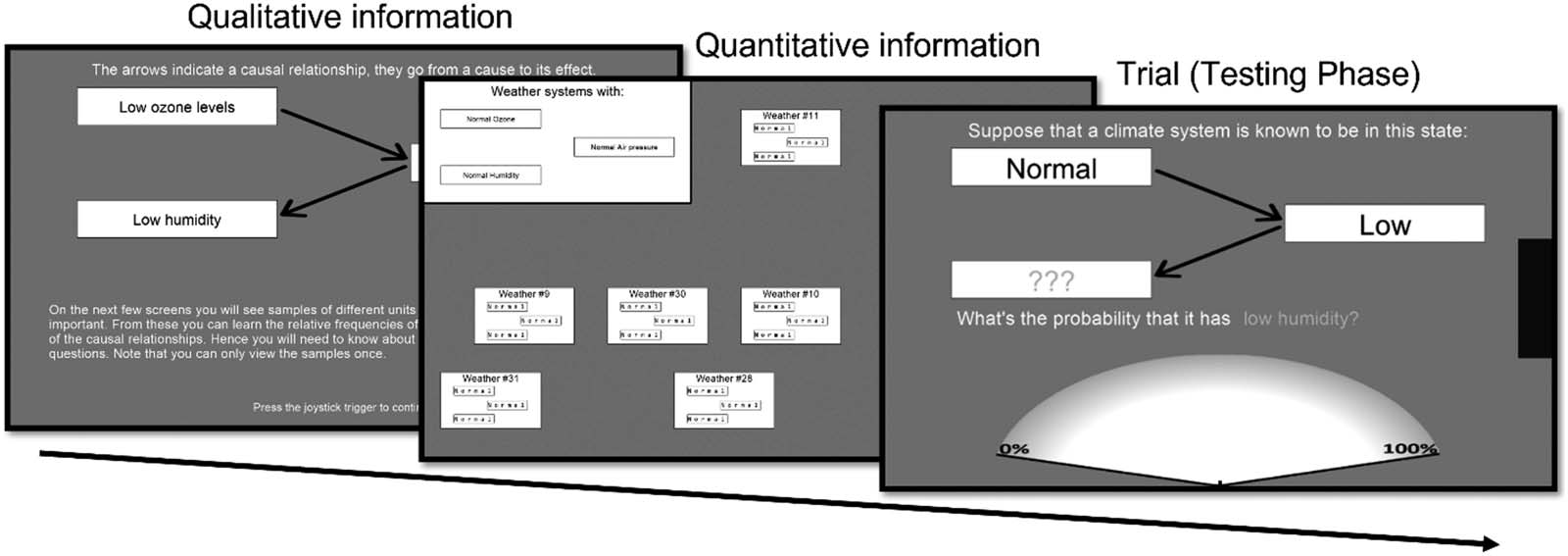
Figur 4. Overview of experiment in Kolvoort et al. (2022) with screenshots. First participants are taught about a particular causal system,
receiving both qualitative (screen 1) and quantitative (screen 2) information on the causal variables, causal relationships, and causal strengths.
Nächste, participants are asked to respond to (conditional) probability queries (screen 3).
participants learned a specific causal structure, about which they were asked to make infer-
ences in the testing phase (Figur 4).
In the learning phase participants were provided with information about a causal system
with three binary variables. They were given qualitative information concerning the variables
and causal relations, as well as quantitative information using the experience sampling
method with data sheets (Rehder & Waldmann, 2017) which involves participants viewing
samples of data that manifest the statistical relations implied by the causal model. Each of
the experimental domains used a different causal structure, which was either a chain, common
cause, or common effect structure. The network parametrization of the structures was taken
from Rottman and Hastie (2016, Experiment 1A), which was also used to fit the original MS
Zu (Davis & Rehder, 2020).
In the testing phase participants responded to (conditional) probabilistic queries regarding
the causal systems. Each of the 3 testing phases consisted of three blocks with different levels
of time pressure implemented using response deadlines of 3, 9 Und 20 seconds (of which the
last one was intended to give participants ample time to respond). Each of these blocks con-
sisted of 27 trials each consisting of a different inference. These inferences were of the form
‘Variable A has value x, variable B has value y. What is the probability that variable C has
value z?'. Each of the three variables could have three states, one of the two binary values
or unknown, leading to 33 = 27 different inferences. All participants completed 27 trials per
domain and deadline condition, for a total of 27 × 3 × 3 = 243 Versuche. Participants responded on
a scale from 0% Zu 100%.
Out of the 43 participants in the dataset, 17 did the study online. The only noteworthy dif-
ference between the online and offline study was the response modality; participants in the lab
indicated a percentage by moving a joystick while online participants responded by moving
their cursor using a mouse or trackpad.
We will fit the BMS and MS to each participant and condition (response deadline × causal
Struktur) separately, this results in 43 × 3 × 3 = 387 sets of fitted parameters. In this way each
set of parameters is fitted to 27 responses on 27 different inferences of a participant.
We did not identify a closed-form likelihood function for the BMS. Darüber hinaus, the parame-
ters of the models consist of a combination of continuous (beta) and discrete (chain length)
Parameter. These considerations suggest a discontinuous or at least complex parameter
OPEN MIND: Discoveries in Cognitive Science
329
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
landscape. A parameter recovery study (Appendix A) supported this suspicion, but revealed
that using a parameter grid search (vgl. Maaß et al., 2021; Mestdagh et al., 2019) resulted in
correlations between true and estimated parameters consistently above .75 (see Method 2
Coarse grid in Appendix A), which is generally seen as good or excellent recovery (z.B.,
Anders et al., 2016; van Maanen et al., 2021; van Ravenzwaaij & Oberauer, 2009; White
et al., 2018). Darüber hinaus, the parameter recovery study provided assurance regarding the iden-
tifiability of the BMS (van Maanen & Miletić, 2021).
To fit the models using a grid search, we first simulate responses using the models with a
range of realistic parameters (siehe unten). These simulated responses were then saved in a grid.
Each cell of this grid represents the predictions of the model under a particular set of param-
eters. To compute how closely the simulated responses match empirical responses we use the
Probability Density Approximation method (PDA; Holmes, 2015; Turner & Sederberg, 2014)
on each grid cell. PDA computes a ‘synthetic’ likelihood through kernel density estimation
(Turner & Sederberg, 2014). The estimated parameters for a given condition and participant
are from the cell with the highest likelihood given the data. We apply this method separately to
each participant and 9 experimental conditions (3 levels of time pressure for each of the 3
causal structures) to obtain the optimal parameters for each.
To make sure that the grid contains the optimal parameters we set a wide parameter range.
The chain lengths were varied between [2, 4, …, 68, 70], which includes the chain lengths
found previously for reasoning tasks (Davis & Rehder, 2020) and the range of number of sam-
ples people are generally thought to generate ( Vul et al., 2014). For the Beta prior parameter,
we first included values for β from 0 Zu 1 with step size 0.1. Nächste, we included values for β > 1
based on the principle that the range of priors should be symmetric about the uniform prior.
Das ist, priors with β > 1 would need to differ from the uniform distribution as much as priors
with β < 1. To achieve this, we computed the total variation distance (Levin & Peres, 2017)
between the uniform distribution and each prior in the grid with a β < 1. Then we identified the
set of β > 1 that had the same total variation distance. This procedure resulted in the following
betas: β 2 [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.11, 1.26, 1.45, 1.73, 2.14, 2.83, 4.14,
7.35, Und 21.54]. For β = 0 the principle of symmetry about the uniform prior would lead us to
pick β = ∞. Jedoch, as using a Beta(∞, ∞) prior would lead to responses only at 50%, Wir
picked β = 100 stattdessen.
In sum, we used a grid of 35 (values for the chain length parameter ranging from 2 Zu 70) von
21 (values for the β parameter ranging from 0 Zu 100) covering a wide range of plausible
parameter values and simulated responses using (35 × 21 =) 735 different parameter combi-
nations. While Davis and Rehder (2020) also estimated the causal parameters (base rates and
causal strengths) of the causal structures that participants learned, we assume that participants
learned the information they were presented accurately (we discuss this point further in the
General Discussion). Hence with our setup the MS has only one free parameter (the chain
Länge). The BMS has the β parameter for the symmetric Beta prior as a second free parameter.
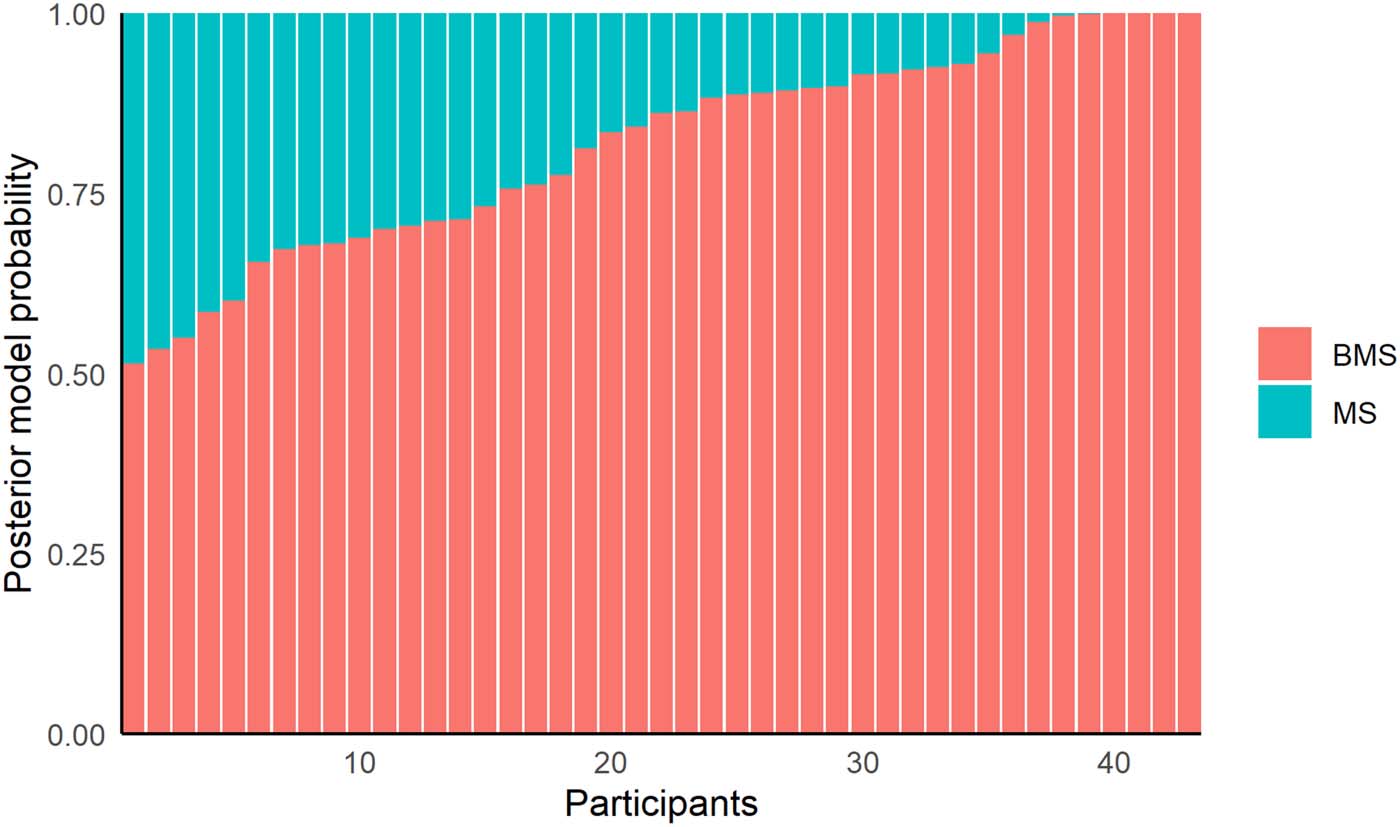
Overall fit. To quantify relative model performance of BMS to MS we computed BIC values for
each set of fitted parameters (Schwarz, 1978). BIC, as compared to AIC, typically penalizes
additional free parameters more strongly and so can be considered more conservative. We find
that for 82.9% of the optimized models the BMS has a lower BIC value than the MS (mean
ΔBIC = −29.6). Nächste, we computed the average BIC weights per participant as approximations
of posterior model probabilities (Neath & Cavanaugh, 2012; Schwarz, 1978; Wagenmakers &
Farrell, 2004). We find that for each participant the BMS has a higher posterior probability than
the MS (Figur 5).
OPEN MIND: Discoveries in Cognitive Science
330
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Figur 5. Posterior model probabilities per participant for the BMS and MS. Posterior model
probabilities are approximated using BIC weights.
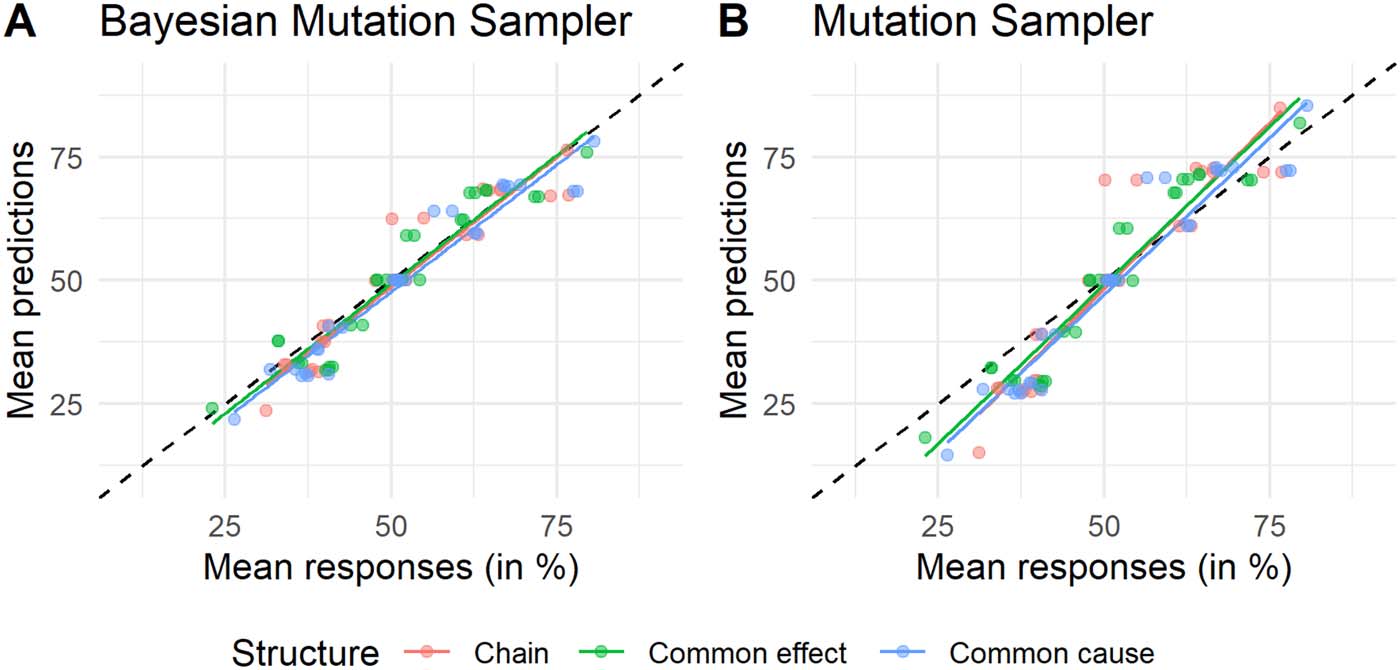
Mean predicted judgments. As discussed in the Introduction, the MS accurately predicts mean
responses on a variety of causal judgment tasks. To assess the mean predictions of the BMS we
computed the expected value of all predictions from the BMS with the best fitting parameters
of each participant. Speziell, per inference and per causal structure, we computed the aver-
age across participants of the predictions at each percentage point, resulting in an averaged
predicted distribution, and then computed the expected value of this distribution. We find that
the predictions closely follow the observed mean responses (Figur 6), indicating that the BMS
is a good account of mean responses. The BMS outperforms the MS in this regard (RMSEBMS =
2.74; RMSEMS = 7.51).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
.
/
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 6. Mean predictions of (A) the BMS and (B) the MS plotted against mean responses. Dots
and lines are colored based on the causal structure in the experiment. Each dot represents one of the
27 inferences. Each line represents a linear fit to the predicted and empirical means. Black dashed
diagonal lines indicate error free predictions.
OPEN MIND: Discoveries in Cognitive Science
331
The Bayesian Mutation Sampler
Kolvoort et al.
In addition to mean judgments, another important behavioral index
Variability of judgments.
is the variability of judgments (Kolvoort et al., 2021). Jedoch, getting a reasonable estimate
of the variability in judgments is often challenging as it requires the repeated elicitation of
comparable judgments (see Kolvoort et al., 2021). To obtain such repeated measurements
and to present results concisely a common practice is to collapse over symmetry in the
causal networks (z.B., Davis & Rehder, 2020; Kolvoort et al., 2021; Rehder, 2018; Rottman
& Hastie, 2016). The joint distribution of the causal networks in the experiment used here
were highly symmetric, allowing us to collapse over the terminal variables (z.B., P(Y = 1|X1 =
1, X2 = 0) = P(Y = 1|X1 = 0, X2 = 1)), over the presence or absence of variables by flipping
responses to the upper half of the response scale (z.B., P(Y = 1|X1 = 1, X2 = 1) = 1 − P(Y = 1|
X1 = 0, X2 = 0)), and over unknown variables (z.B., P(X1 = 1|Y = 1) = P(Y = 1|X2 = 1)). In
addition, since we did not find significant differences in parameters, we will collapse over
response deadline conditions. Endlich, we will collapse over the chain and common cause
network structures as these have an equivalent underlying normative distribution. Das tun wir
not use the common effect structure for this analysis nor for the analysis of distributions below,
since the small number of observations would lead to unreliable estimates of variability.
Collapsing resulted in 7 groups of inferences presented in Table 2 (see Appendix B for an
overview of all inferences in each group).
To index variability we use Gini’s Mean Difference (GMD; David, 1968; Yitzhaki, 2003),
defined as the average difference between any two observations. We use this non-parametric
index as judgments on causal reasoning tasks tend to not be normally distributed (Davis &
Rehder, 2020; Kolvoort et al., 2021, 2022; Rehder, 2018; Rottman & Hastie, 2016). To com-
pute the GMD of model predictions, we first computed averaged predicted distributions for
each participant and inference group (by averaging the predicted distributions over the dead-
line conditions, the chain and common cause networks, and the different inferences in each
inference group). We then drew 10,000 samples from these aggregated distributions which
we used to compute the GMD.
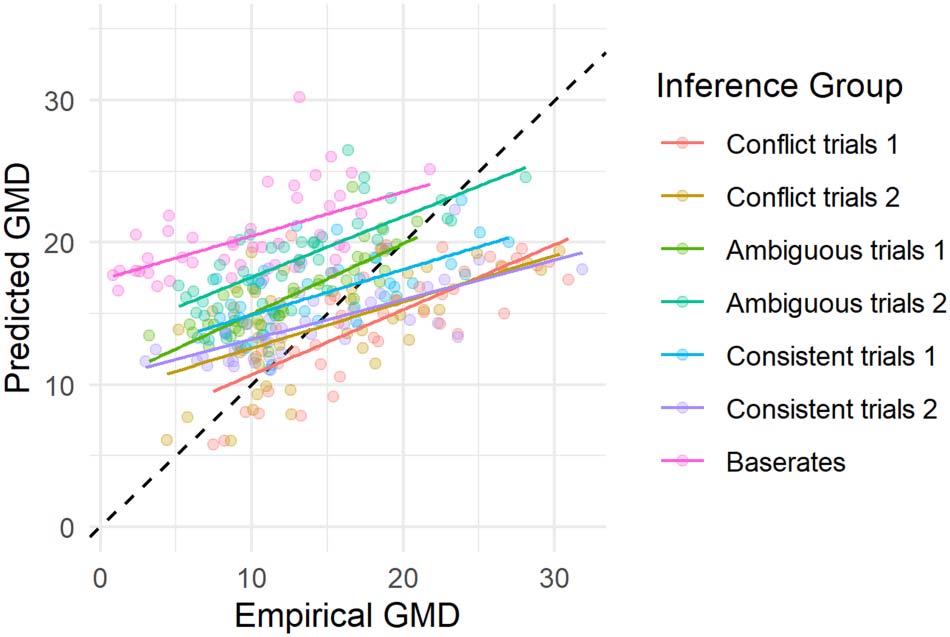
We find an empirical mean GMD of 13.8 indicating there is substantial variability in
responses. Both models predict mean variability to be higher (GMDBMS = 16.4, GMDMS =
19.2). The higher GMD for the MS is expected, because it predicts more extreme responses,
increasing variability. Although the average variability of the BMS is higher than the observed
variability, there are clear associations between the observed and predicted variability for each
inference group (Figur 7 und Tisch 3). Tisch 3 presents the correlation coefficients of the
predicted and empirical variability, for both BMS and MS.
Within inference groups, the BMS predicts differences in variability between participants
(Figur 7). Jedoch, the model does not perform well at predicting differences in variability
between inference groups. Zum Beispiel, it consistently predicts base rate judgments to be more
variable than they are, and it predicts that judgments in the conflict inferences 1 group are less
variable than they are. That the BMS does not perform well in predicting between inference
group variability might be due to that all different inferences are modelled with a single set of
model parameters. While there seems no a priori reason that people use different priors for
different inferences, it might be that the chain length differs based on the inference (sehen
Gershman & Guter Mann, 2014; Hertwig & Pleskac, 2010; Vul et al., 2014; Zhu et al., 2020).
When faced with a problem that is complex at first glance (z.B., an inference with conflicting
conditional information), people could decide to sample for a longer duration. We return to
this idea in the following sections. To get a better grasp of why some of the variability estimates
are off we regard full response distributions next.
OPEN MIND: Discoveries in Cognitive Science
332
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
/
.
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ö
P
E
N
M
N
D
ICH
:
ich
D
S
C
Ö
v
e
R
ich
e
S
ich
N
C
Ö
G
N
ich
T
ich
v
e
S
C
e
N
C
e
ich
Tisch 2. Grouping of inferences for variability and distributional analysis based on symmetry in chain and common cause causal network structures.
Group
1
Inference type
Conflict
Conditioning information
Two known variables
with different values
Queried variable
1: terminal variable
2: middle variable
Ambiguous
Only one known variable
1: adjacent to known
Consistent
Two known variables
with the same values
Base rates
No known variables
Variable
2: non-adjacent to
known variable
1: terminal variable
2: middle variable
–
2
3
4
5
6
7
Normative
response
75%
Obs. pro
participant
24
50%
75%
62.5%
75%
90%
50%
12
48
24
24
12
18
Example
P(X1 = 1|Y = 1, X2 = 0)
P(Y = 1|X1 = 1, X2 = 0)
P(X1 = 1|Y = 1)
P(X1 = 1|X2 = 1)
P(X1 = 1|Y = 1, X2 = 1)
P(Y = 1|X1 = 1 X2 = 1)
P(X2 = 1)
‘Queried variable’ refers to the variable that participants are asked to judge the probability of. ‘Terminal variable’ refers to either X1 or X2, and ‘middle variable’ to Y in
Figur 1. The variable names in the example column refer to the variables as presented in Figure 1. See Appendix B for a full list of inferences in each group.
3
3
3
T
H
e
B
A
j
e
S
ich
A
N
M
u
T
A
T
ich
Ö
N
S
A
M
P
l
e
R
K
Ö
l
v
Ö
Ö
R
T
e
T
A
l
.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
.
/
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Figur 7.
Scatterplot of empirical variability and variability predicted by the BMS (indexed by
Gini’s Mean Difference, GMD). Responses and predictions are collapsed over the common cause
and chain structures, the response deadlines, and into inference groups (see main text). Each dot
represents one participant. Black diagonal indicates perfect predictions. Colored lines indicate
mean linear trends per inference group.
Distributions. To better understand the predicted distributions and how they match observed
responses we present these distributions in Figure 8. Here the averaged best-fitting predictions
of BMS and MS are presented together with histograms of participant responses.
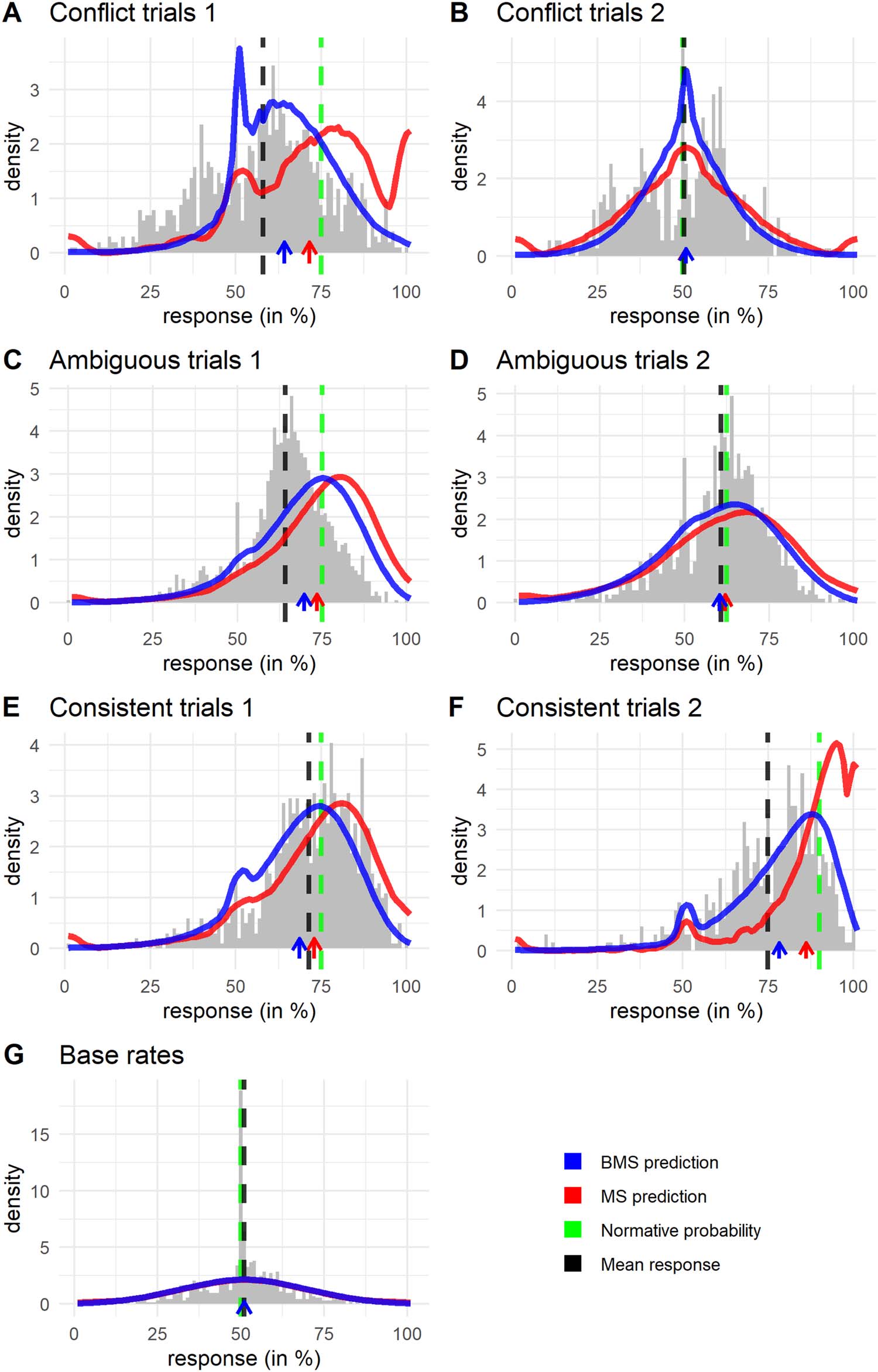
Erste, let us discuss the distributional problems of the MS brought to light in the first part of
this paper. The issue of extreme responses is visible relatively strongly in both the types of
conflict trials (Figure 8A and B). This can be expected, since conflict trials (where the condi-
tional information is conflicting), require the sampler to visit mixed variable states. These states
are harder to reach for the sampler, since the sampler is biased towards consistent, prototypical
Staaten. Hence the probability of a default extreme response is higher. Some extreme predicted
responses by the MS are also visible for the ambiguous and consistent trials (Figure 8C–F). Der
BMS does not produce any of these extreme responses. That there are fewer extreme responses
for the MS than our analysis in the first part would indicate is because the chain lengths we
found are higher than expected based on previous studies with the MS (Davis & Rehder, 2017,
Tisch 3.
Pearson correlations of predicted and empirical variability as indexed by GMD.
R
Conflict trials 1
Conflict trials 2
Ambiguous trials 1
Ambiguous trials 2
Consistent trials 1
Consistent trials 2
Base rates
BMS
.72
.58
.83
.74
.64
.68
.57
OPEN MIND: Discoveries in Cognitive Science
MS
−.19
.094
.4
.31
.37
.38
.38
334
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
.
/
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
Ö
P
M
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
ich
.
/
/
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
.
/
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 8. Observed and predicted response distributions. Blue and red solid-colored lines indi-
cate predictions based on model fits from the BMS and MS respectively, the arrows on the x-axis
indicate the mean prediction. Grey histogram represents participant responses with the black
dashed line indicating the mean. The green dashed line indicates the normative probability.
OPEN MIND: Discoveries in Cognitive Science
335
The Bayesian Mutation Sampler
Kolvoort et al.
2020). The second distributional issue we diagnosed of the MS, the lack of moderate conser-
vatism, is also clearly visible in Figure 8 (panels A, C, E, and F). We see that the main mode of
responses is at or more extreme than the normative probability. The BMS is more accurate in
predicting where the bulk of responses are. Taken together, the BMS resolves the principal
issues that the MS has in predicting where responses tend to be on the response scale.
The BMS is a clear improvement over the MS in predicting full response distributions and,
according to our knowledge, the only process-level model of causal probabilistic reasoning
that can satisfactorily account for response distributions. Jedoch, the predictions of the
BMS are not perfect and certain limitations come to light when we regard the distributions
for each inference type in more detail.
Figure 8A indicates that the BMS correctly predicts the mode of computed responses for
conflict inferences where the middle variable is queried (Conflict trials 1). Jedoch, Es
wrongly predicts very few responses to be below 50%. Inspecting individual responses, Wir
find that individual participants tended to respond on both sides of 50%. We observe this as
well for the conflict trials where a terminal variable is queried (Conflict Trials 2, Figure 8B),
hence it seems that the stimulus makes participants respond inconsistently due to the pres-
ence of conflicting cues. A substantial number of responses on this inference are possibly the
result of random guessing which is not captured by the BMS. Such random responding might
also explain why the frequency of responding at 50% is less than predicted. For the conflict
trials where a terminal variable is queried (Conflict trials 2, Figure 8B) we see that the spike of
responses at 50% is captured by the BMS prediction. What is not captured by the prediction
is that participants tended not to respond close to 50%. One possible explanation for this
observation is that participants rounded their responses to 50%. The reduced amount of
responses near 50% occurs for both types of conflict trials, so it might be that the tendency
to round to 50% is related to a participant’s uncertainty in their estimates (vgl. Kolvoort
et al., 2022).
For the ambiguous trials, we observe that the prediction seems to be quite accurate for
inference group 2 (Ambiguous trials 2, Figure 8D), but for group 1 (Ambiguous trials 1,
Figure 8C) participants are more conservative than predicted. Such a pattern could be
explained if participants sampled less, d.h., used a shorter chain of samples, to form a judgment
in response to stimuli in group 1 than for group 2. When chain lengths are shorter, the influ-
ence of the prior is stronger and so responses would be closer to 50%. In our modeling we
fixed the chain length over inference types. Jedoch, previous research has indicated that it is
possible that people adaptively change their desired number of samples as the estimated costs
and benefits of further sampling are dependent on the problem type (Gershman & Guter Mann,
2014; Hertwig & Pleskac, 2010; Vul et al., 2014; Zhu et al., 2020). Why might participants use
different chain lengths for these inferences? Remember that for these ambiguous trials the state
of one variable is given, while the state of the other non-queried variable is unknown. For the
first group of ambiguous inferences the given variable is adjacent to the queried one, and so
these stimuli may be considered as less ambiguous than group 2, where the given and queried
variable are separated by an unknown variable. The observation that responses to stimuli in
first group (Figure 8C) seem less variable than the second group (Figure 8D) is congruent with
this idea. Since the stimulus in group 1 is less ambiguous, participants might view it as easier
and so obtain fewer samples to form a judgment. A repeated measures ANOVA indicates that
response times are indeed significantly shorter for group 1 than for group 2 (M1 = 4.32 S, M2 =
4.62 S, F(39, 2891) = 14.73, P < .001, BF = 32.5), corroborating this explanation. This effect is
not captured in our predictions as we did not model a process by which participants might
decide to use different chain lengths.
OPEN MIND: Discoveries in Cognitive Science
336
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
For the consistent trials (Figure 8E and F) the BMS seems to capture the spread of responses
rather accurately. For the base rate trials, however, the BMS severely underpredicts the spike
of responses at 50% while capturing the rest of the variability quite accurately (Figure 8G).
Compared to the other inference types participants have a strong tendency to respond at
50%. These base rate trials can be considered to involve the most uncertainty for participants
compared to other inferences, since no conditioning information is provided. This uncertainty
could lead to default responses or ‘guessing’ at 50% (Kolvoort et al., 2021, 2022; Rottman &
Hastie, 2016). Upon viewing the stimulus participants might forego on sampling and instead
respond at 50%. This would indicate a mixture of processes, where prior to the sampling
process one might decide not to sample and instead respond in a default fashion. As we
did not specify any mixture of processes the large spike at 50% is not captured by the
BMS predictions here.
It is important to realize that we are putting up a very high bar when considering the ways
in which the predicted distributions do not exactly match participant responses. The modeling
of full response distributions is a complex endeavor as there are many processes and mecha-
nisms that likely affect distributions of judgements which traditionally would be filtered out by
taking the mean. In fact, many of the limitations of the BMS predictions just discussed point
towards the need to specify additional processes to match the empirical distributions more
accurately. We return to this point in the General Discussion, before doing so we first regard
the estimated parameter values.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
Estimated parameters. A summary of fitted BMS parameter per response deadline condition is
shown in Table 4. The overall median β parameter was 1.45, which is close to the uniform
distribution (β = 1) that is often considered the prototypical uninformative prior. For most par-
ticipants (79.1%) the mean β is larger than one, indicating they expected answers to be closer
to 50%, validating our choice to include values for β > 1 (vgl. Zhu et al., 2020). Higher values
for β lead participants to be more conservative in their responses. This could explain (a part of )
the substantial conservatism observed on this (Kolvoort et al., 2022) and other causal reason-
ing tasks. While no participant was fitted best by the upper bound of the grid (β = 100), we find
that in 5.94% of cases the best fitting β is zero, the lower bound of the grid. This indicates that
in only a small subset of cases the relative frequency method of generating judgments (as pro-
posed by the original MS) was used. As could be expected the prior used was not affected by
response deadlines (F(2, 336) = 1.04, p = .433, BFH1 = 0.036).
The average chain lengths we find fall within a range expected based on the literature. Zhu
et al. (2020) for instance found best fitting chain length for certain participants to be well over
Tisch 4.
deadline condition separately, ergebend 387 sets of parameters.
Summary of fitted BMS parameters based on fitting to each participant, Struktur, Und
β parameter
Chain length
ich
/
/
.
1
0
1
1
6
2
Ö
P
M
_
A
_
0
0
0
8
0
2
1
3
8
6
6
6
Ö
P
M
_
A
_
0
0
0
8
0
P
D
/
.
ich
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Median (SD) Minimum Maximum Median (SD) Minimum Maximum
1.73 (2.58)
40 (19.0)
21.5
70
0
8
Deadline
6 S
9 S
20 S
1.11 (2.77)
1.45 (3.14)
0
0
0
21.5
21.5
21.5
46 (19.5)
50 (20.4)
44.9 (19.7)
4
6
4
Gesamt
1.45 (2.83)
The β parameter refers to the fitted Beta(β, β) priors.
OPEN MIND: Discoveries in Cognitive Science
70
70
70
337
The Bayesian Mutation Sampler
Kolvoort et al.
Tisch 5.
Spearman correlations of mean fitted parameters and behavioral measures per participant.
Chain length
β
Response time
.344*
(3.29)
−.0974
(0.405)
Accuracy
.893***
(>100)
.00740
(0.341)
Conservatism
−.323*
(2.48)
.749***
(>100)
See main text for definitions of Accuracy and Conservatism. Numbers in brackets refer to Bayes
factors (BFH1, d.h., for the existence of a correlation), computed using the Bayes Factor package in
R using default settings (Morey & Rouder, 2014). Asterisks indicate p-values: *P < .05, **p < .01,
***p < .001.
200 in simple probability judgment tasks. While Davis and Rehder (2020) found a maximum
mean chain length of 28 for causal inference studies, the average best fitting chain length for
some causal intervention or categorization studies was above 60. There seems to be a trend of
increasing chain lengths for longer deadlines (Table 4). This would be consistent with the
hypothesis that participants sample longer when they have more time to respond. However,
a repeated measures ANOVA indicates that there is no statistical support for such an effect (F(2,
336) = 3.74, p = .121, BFH1 = 0.25). 14.0% of fitted chain lengths reached the maximum value
of 70. This reflects that larger chain lengths are more difficult to estimate, since the differences
in the predictions of the BMS become increasingly smaller as chain lengths increase (Appendix
A). While there is some uncertainty regarding the exact values of the higher chain lengths, the
median chain lengths we find are noticeably higher than found by Davis and Rehder (2020) for
experiments involving causal inference, as they found the best fitting chain lengths to range
from 4 to 28 in these types of tasks7.
BMS and behavioral measures. Lastly, we studied the relationship between the fitted parameters
and other behavioral measures to validate the BMS. As the BMS is a process model, it should
relate to behavioral measures not specified in the model itself. We looked at three important
behavioral measures: response times, accuracy, and conservatism. Response times here are
especially of interest as they are not part of the data used to fit the BMS. Accuracy was defined
as the absolute distance of responses from the normative answer and conservatism was
defined as the absolute distance of responses from 50%. For ease of interpreting the statistics,
we multiplied both accuracy and conservatism values with minus one, as by doing so higher
values indicate higher levels of accuracy and conservatism respectively. We computed the
mean fitted parameters and the means of these behavioral measures over all conditions per
participant and tested their relationships using Spearman correlations (Table 5).
We find that chain length is positively correlated with response times and strongly with
accuracy, while being negatively correlated with conservatism. These correlations all reflect
a higher task performance of individuals that sample for a longer duration: Firstly, as the chain
length is a direct reflection of the sampling duration, a correlation with response time is
expected. Secondly, longer chain lengths indicate more computed responses that get to the
normative answer as the effect of the starting point bias decreases, resulting in higher accuracy.
7 The uncertainty regarding the exact values of higher chain lengths does not affect the conclusion that we
found higher chain lengths, since if participants indeed used only few samples (smaller chain lengths) to make
judgments, our parameter recovery study indicates we would have recovered those parameter values accurately
(Appendix A).
OPEN MIND: Discoveries in Cognitive Science
338
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Finally, longer chain lengths also imply less influence of the prior, which is reflected in
responses being less conservative. This is also reflected by the strong positive correlation
between the β parameter and conservatism. Higher values of β imply the use of a prior that
has more probability mass near 50% which results in more conservative responses. In sum,
these correlations support the BMS model specification by showing expected relations
between the parameter estimates and behavior.
GENERAL DISCUSSION
The aim of this paper was to understand distributions of probabilistic causal judgments. In the
first part we diagnosed problems with the distributions of responses that a process model of
causal reasoning, the Mutation Sampler (MS), predicts. The two main problems we identified
were that the MS predicts a non-trivial number of extreme responses at 0 or 100 %, and that it
predicts the bulk of computed responses to be centered near the normative probability. Con-
trary to these predictions, data indicate that people actually refrain from using the extreme
ends of the response scale and that the bulk of their responses tends to lie in between the
normative answer and 50% (Kolvoort et al., 2021, 2022; Rehder, 2018; Rottman & Hastie,
2016). We traced these issues back to the process by which the MS forms judgments based
on samples and proposed to extend the MS by the incorporation of prior information into judg-
ments. In the second part of the paper, we formalized the idea of incorporating prior informa-
tion into judgments and presented the Bayesian Mutation Sampler (BMS). The BMS combines
the sampling process of the MS with the use of prior information. We fitted the BMS and MS to
data from a recent causal reasoning experiment to illustrate that the BMS provides a better
account of the data, and found that the BMS resolves the distributional problems associated
with the MS. Although the BMS predictions are not perfect, the model is able to account for a
lot of the variability we observe in causal judgments. To our knowledge the BMS is the only
computational (process-level) model of causal reasoning that is able to capture response dis-
tributions to this degree. This is not an easy feat, especially considering that the model uses
only two free parameters to predict full response distributions for multiple inference types.
These findings provide evidence for the notion that the variability observed in causal judg-
ments is due to a sampling mechanism. This is in line with findings implicating sampling being
the source of variability in children’s responses on causal learning tasks (Bonawitz et al., 2014)
Our formulation of the BMS entails some important theoretical commitments. We proposed
that participants have prior beliefs regarding likely (conditional) probabilities and that they
incorporate these beliefs into their judgments in Bayesian fashion. Amongst other reasons,
we motivated the use of priors by the observation that participants do not provide extreme
judgments. That is, we interpret the avoidance of the extremes of the response scale as a ratio-
nal adjustment to small sample sizes via the incorporation of prior information. However, there
are other plausible explanations for the observation that people avoid making extreme judg-
ments. One option would be that people avoid the extremes of the response scale due to a
response bias; e.g., participants could be reluctant to express the confidence that a judgment
of 0% or 100% might imply (e.g., DuCharme, 1970; Phillips et al., 1966). Another option
could be that people use a particular mapping of objective probabilities to subjective probabil-
ities, such as a probability-weighting function used in Prospect Theory (Tversky & Kahneman,
1992). The BMS posits that people avoid the extremes of a probabilistic response scale due to
their beliefs (encoded by priors) instead of this being the result of a particular mapping from
beliefs to a response scale. While we are not necessarily committed to the idea that participant
beliefs map straightforwardly onto a probabilistic response scale, we did not implement a
mapping function.
OPEN MIND: Discoveries in Cognitive Science
339
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
A different approach was used in the original MS paper, where the authors used a scaling
factor to map the probabilities computed by the MS to the response scale (Davis & Rehder,
2020). A free ‘scaling’ parameter s was used such that a predicted response = s * p, where p is
the probability generated by the MS. The MS combined with such a mapping function can
produce responses that fall outside the response scale and so we did not consider it to be a
proper account of the variability in causal judgments (Appendix C provides an illustration of
this effect). Including such a scaling parameter improves the fit of the MS, but it is still out-
performed by the BMS (Appendix C). Moreover, as the use of a (Beta) prior is theoretically
motivated the BMS is clearly the favored model.
We can consider the alternative explanations for conservatism mentioned earlier as other
theoretically motivated mechanisms that could map probabilities produced by the MS to a
response scale. In other words, a response bias related to a reluctance to express confidence
or the use of a probability-weighting function as in Prospect Theory could be assumed instead
of a Beta prior. These explanations could predict that responses are ‘pushed’ towards the mid-
dle of the response scale in a similar way as the incorporation of a symmetric prior does. Due
to this we cannot use the distribution of responses in the current experiment to distinguish
between these explanations. One possible approach to empirically verify the prior mechanism
proposed by the BMS would be to conduct an experiment in which one manipulates partic-
ipant beliefs about what the likely answers to a causal probabilistic query are. To manipulate
prior beliefs participants need to be presented with data. This data could be of various forms,
such as training data that imply extreme probabilities, fabricated responses from other partic-
ipants, or participants could be provided feedback on their own responses. If the BMS is cor-
rect we would expect participants to update their prior in light of this new data which in turn
would systematically affect their judgments. We suggest future research to run such experi-
ments to confirm the use of priors. As it currently stands, though, we maintain that the use
of priors is the most plausible explanation of the observed behavior as there are compelling
arguments in its favor that go beyond response mapping. There are the usual normative argu-
ments in favor of a Bayesian approach and people have been shown to reason in a Bayesian
manner (that is, using priors) in many other domains (see Oaksford & Chater, 2020; Parpart
et al., 2018; Vul et al., 2014; Zhu et al., 2020).
In all, our work contributes to a recent movement in the field of causal reasoning arguing
that that the variability observed on tasks reflects information of interest (Kolvoort et al., 2021;
O’Neill et al., 2022). Understanding the variability in responses and modeling full response
distributions can be a challenging task but it comes with important benefits (see O’Neill et al.,
2022). To promote future research in this direction the remainder of this paper discusses poten-
tial pitfalls and gains of such an approach and suggest promising directions of research into
causal judgments.
The Importance of Distributions
Important benefits of shifting the explanatory focus from mean responses to response distribu-
tions include the potential to ask more questions and providing safeguards against drawing
erroneous conclusions.
Asking more questions. Recent examples of using response distributions to better our under-
standing of causal reasoning include initial preliminary investigations by Rehder (2018) and
Rottman and Hastie (2016), and the more recent studies by Kolvoort et al. (2021) and O’Neill
et al. (2022). Using a novel experimental design Kolvoort et al. (2021) elicited repeated causal
judgments which allowed them to establish the presence of substantial within-participant
OPEN MIND: Discoveries in Cognitive Science
340
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
variability that differs per inference type. O’Neill et al. (2022) analyzed response distributions
of existing and new vignette-based experiments which led them to conclude that causal judg-
ments are often graded and multimodal. This result allowed them to assess theories of causal
reasoning and suggest improvements based on a graded concept of causation. Similarly in our
work, both predicted and empirical distributional phenomena informed the development of
the BMS. The observation that the MS predicts extreme responses and many responses near
the normative probability was crucial in determining how the MS could be improved. A shift
towards analyzing distributions will allow researchers to target more behavioral phenomena
and subsequently develop more comprehensive theories.
In addition to leading us to more questions, using distributions
Stop erroneous inferences.
instead of means as our explanatory target can help us to not draw erroneous conclusions.
It has become clear from the current work and recent investigations that the variability of
causal judgments does not just reflect noise and that these response distributions are often
multimodal and non-normal (Kolvoort et al., 2021; O’Neill et al., 2022; Rottman & Hastie,
2016). This entails that what we infer from statistical and cognitive models which characterize
only mean responses can be severely misleading. This can be illustrated by looking at what
would happen if we had merely modeled mean responses using the BMS. Figure 9 shows three
predicted distributions for a single inference of the BMS using different sets of parameters.
While the chain lengths range from 18 to 70 and the β parameter from 0.1 to 2.1, the mean
response for these distributions is the same. Hence the model would not be identified if we
were to only regard mean responses. Moreover, these distributions, though having the same
mean, imply a very different type of responding (cf. Anders et al., 2016). For instance, while it
is common to assume that most responses are near the expected value of a response distribu-
tion, Figure 9 shows that the BMS can produce varying densities of responses near the
expected value while keeping the expected value itself fixed. This is an issue related to model
identifiability (cf. van Maanen & Miletić, 2021) and it is quite common outside of the domain
of causal reasoning (for instance with models predicting response time distributions, e.g.,
Anders et al., 2016). For the BMS, increasing the chain length moves the expected value
towards the normative response, while increasing β moves the expected value of the predicted
distribution towards 50%. Hence for any percentage point Z that is between the normative
probability and 50%, there are an infinite number model parameter combinations that would
produce distributions with the expected value at Z. Due to this solely focusing on the mean
response can lead to drawing multiple erroneous conclusions. One wrong conclusion could
be that most responses lie near the mean predicted response, which is often not the case for
causal judgments (e.g., O’Neill et al., 2022). Relatedly, the amount of disagreement between
participants could be overestimated if one were to erroneously conclude that the grey predic-
tion in Figure 9 accurately captures group-level responses (compared to other predictions in
Figure 9).
To make sure researchers do not draw erroneous conclusions based on models that
overemphasize the importance of the central tendency of responses, O’Neill et al. (2022) rec-
ommend to plot histograms of response data regularly and to assess whether the underlying
distributional assumptions of their (statistical) models are met. This latter point is important, as
the standard linear models often assume equal variances over participants and conditions,
while we now know that this assumption is often violated in causal judgments (e.g., Kolvoort
et al., 2021; O’Neill et al., 2022).
Using generative models to target distributions. Another recommendation O’Neill et al. (2022)
give is for researchers to move towards modeling response distributions using a generative
OPEN MIND: Discoveries in Cognitive Science
341
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Illustration of BMS predicted response distributions of the inference P(X1 = 1|Y = 1, X2 =
Figure 9.
0) for 3 different sets of parameters using a chain causal structure with the same parametrization
as used in the experiments studied in this manuscript. 10,000 simulations were run to compute
each of the three distributions. Each of the distributions was smoothed using a kernel density
estimate as specified by the PDA method. CL refers to the chain length parameter, β refers to the
parameter for the Beta(β, β) prior. The vertical dashed line indicates the expected value of all
three distributions.
approach. This computational approach is becoming more widespread in psychological and
brain sciences (see for recent overviews, Ahn & Busemeyer, 2016; Forstmann et al., 2016;
Guest & Martin, 2021; Jarecki et al., 2020; Lee et al., 2019; Ratcliff et al., 2016; Turner
et al., 2017; Wilson & Collins, 2019). Generative modeling involves constructing computa-
tional models that embody theoretical assumptions about how behavior is generated (Haines
et al., 2020). This involves characterizing the psychological process that turns inputs (stimuli)
into outputs (behavior or judgments) in mathematical terms. The BMS (as well as MS) is a gen-
erative model of the process by which people generate causal probabilistic judgments by way
of sampling from a causal network (Davis & Rehder, 2020).
Generative modeling naturally leads researchers to focus on psychologically interpretable
parameters (such as the number of samples or type of prior information) instead of on estimat-
ing descriptive effects. Such descriptive effects are often defined using differences in mean
response between conditions and tested using standard parametric statistical tools (such as
t-tests, regressions, ANOVAs, etc.). However, we know that means often don’t capture
response distributions in a meaningful way and that this violates the assumptions of the stan-
dard parametric tests (see Haines et al., 2020). These descriptive effects could also be modeled
using ‘descriptive’ models that predict only mean responses (e.g., Rehder, 2018; Rottman &
Hastie, 2016), but this could lead one to draw erroneous conclusions as the mean response
could misguide researchers (see Figure 9).
Instead, generative modeling helps researchers to account for more than just averaged
behavior. When mathematically specifying the data-generating process a researcher has to
incorporate assumptions about the psychological processes that generate empirical data.
These assumptions should allow the model to generate predictions that mimic not just empir-
ical means, but empirical distributions.
While generative models can be used to characterize group-level behavior, often they are
implemented at the level of individual psychological processes. This allows for the fruitful
study of individual differences, which could help in assessing competing models of causal
OPEN MIND: Discoveries in Cognitive Science
342
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
reasoning (a good example can be found in Gerstenberg et al., 2021). We did not focus on
explaining such individual differences here, but the BMS can in principle explain inter-
individual variation by appealing to differences in how long people sample and the prior infor-
mation they use. Since it is a longstanding question in the field of causal judgments to what
extent the observed variability is due to within- or between-participant variability (Davis &
Rehder, 2020; Kolvoort et al., 2021; Rehder, 2018; Rottman & Hastie, 2016), this seems to
be an important direction for future research.
Related to individual differences, note that Davis and Rehder (2020) did not fix the causal
parametrization of the causal network in the MS, instead estimating the causal parameters (i.e.,
base rates of the causal variables and causal strengths) to account for participants not learning
an accurate representation of the causal network. Consequently, there is no strict one-to-one
correspondence between their results and ours. The justification for estimating causal param-
eters was that we cannot assume that participants’ representations actually conform to what
they are taught during the experiment about the causal networks. There is some force behind
this argument as it is unlikely that participants learn the qualitative and quantitative aspects of
the causal systems exactly as how they are presented to them. However, the current study was
not aimed at understanding such individual differences. As mentioned, the current implemen-
tation of the BMS could explain individual differences by appealing to differences in how
much people sample and the prior information they use. It might be that other individual fac-
tors need to be estimated to capture individual differences, such as individually learned causal
parameters or, for instance, individual subjective probability weighting functions (Tversky &
Kahneman, 1992) or differences in the order of processing of variables (Mistry et al., 2018).
Which factors explain individual differences in probabilistic causal judgments remains an
open question for now.
Overcoming Challenges in Studying Distributions: Extending the BMS
The study of full response distributions, possibly using generative process models, is a prom-
ising direction and will help advance our understanding of the cognitive processes responsible
for causal judgments. This type of work does, however, come with its own set of challenges.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Modeling the multitude of processes resulting in a response. One possible direction to improve the
BMS would be to adapt its core features. It could be that a different sampling mechanism (e.g.,
a Gibbs sampler instead of the MH algorithm; cf. Davis & Rehder, 2020) or differently shaped
prior could help explain more of the variability. However, our results seem to indicate that the
limitations of the BMS predictions are due to additional processes at play. That is, to capture
empirical response distributions more accurately we need to model these processes.
The existence of additional processes affecting responses is a big challenge in trying to
account for response distributions. There are a multitude processes that affect how judgments
are made. Examples of such processes are the rounding of estimates (e.g., Budescu et al.,
1988; Costello & Watts, 2014; Erev et al., 1994; Kleinjans & van Soest, 2014), guessing
(Kolvoort et al., 2022; Kong et al., 2007; Schnipke & Scrams, 1997), a general mixture of
multiple problem-solving strategies (Archambeau et al., 2022; Evans, 2008; van Maanen
et al., 2014, 2016) and ‘dynamic effects’ such as fatigue, boredom, and learning (e.g.,
Gunawan et al., 2022). All these processes affect participant’s judgments on experimental
tasks and partly determine the resulting response distribution.
The existence of all these additional processes is an important rationale in studying mean
judgments: averaging across many trials filters out supposed noise. However, when targeting
OPEN MIND: Discoveries in Cognitive Science
343
The Bayesian Mutation Sampler
Kolvoort et al.
response distributions with generative models this solution is not available. Instead, we need to
tackle the inherent complexity and develop theories and models explaining the target distri-
butional phenomena.
While there are many processes that can be modelled, we focus here on two that our results
indicated might play a large role in determining the observed distributions. The first is using a
mixture of strategies. One likely strategy that is consistent with our observations is a guessing
strategy. We observed varying peaks of responses at 50% which have been attributed to guess-
ing before (Kolvoort et al., 2021, 2022; Rottman & Hastie, 2016). A second alternative strategy
is that of adapting chain lengths based on the inference type one is confronted with. Such a
mechanism has been suggested before (e.g., Zhu et al., 2020) and could, for instance, explain
the difference in fit between the two types of ambiguous inferences (see Figure 8). While there
can be many other processes affecting responses, we hypothesize that these two are likely to
account for a substantial amount of the unexplained variability.
Modeling mixtures. People can employ a variety of strategies to perform a particular task and
so it is often assumed that observed behavior is the result of a mixture of such strategies
(Campbell & Xue, 2001; Coltheart et al., 2001; Couto et al., 2020; Donkin et al., 2013;
Dunlosky & Hertzog, 2001; Dutilh et al., 2011; Evans, 2008; Kahneman, 2011; Smith et al.,
1998; van Maanen et al., 2014; van Maanen & van Rijn, 2010; van Rijn et al., 2003). For
example, the dual-process framework of decision-making is built on the idea we can solve
problems in either a more intuitive/heuristic manner or in a more deliberative manner (Evans,
2008; Kahneman, 2011; Stanovich, 1999). Intuitive reasoning is characterized by being auto-
matic, fast and non-conscious, which is contrasted with deliberative reasoning that is more
rule-based, slow, analytic and controlled. We can see this in two ways related to the BMS.
One way is to consider the BMS to implement both intuitive and deliberative reasoning. If
sampling chains are short responses are most affected by the biased starting points (proto-
types), which can be seen as intuitive. When sample chains are long, the response is based
more on the learned statistical relationships and we can consider this deliberative. Another
way to look at this is to consider all sampling (e.g., as implemented by the BMS) as a delib-
erative way of reasoning. In this case, intuitive reasoning would be implemented by a wholly
different mechanism. For instance, a more heuristic manner by which participants could
respond on causal reasoning tasks would be by using a simple ‘tallying’ rule (Gigerenzer &
Gaissmaier, 2011; Kolvoort et al., 2022; Rottman & Hastie, 2016), which involves counting
positive cues (present variables) and subtracting negative cues (absent variables) to form a
judgment. Even simpler strategies would be to just guess 50% or respond randomly, which
is believed to happen on a subset of trials (Kolvoort et al., 2022; Kong et al., 2007; Schnipke
& Scrams, 1997).
There is evidence that participants use such simple strategies in causal judgment tasks. One
salient feature of response distributions in the probabilistic causal judgment literature are
spikes of responses at 50% and it has been found that the size of these spikes differs per infer-
ence type (Kolvoort et al., 2021; Rottman & Hastie, 2016). Our results are in line with these
findings. We found spikes of responses at 50% whose size depended on the inference type (see
Figure 8). The large spike at 50% for base rate judgments stands out the most as it is substan-
tially larger than the BMS would predict (Figure 8G).
We believe that this large spike at 50% for base rate judgments may reflect guessing or a
‘default’ response at 50%. In fact, spikes at 50% have previously been associated with uncer-
tainty in the response (Kolvoort et al., 2022; Rottman & Hastie, 2016). When participants are
uncertain or do not know how to respond they could employ their default response strategy
OPEN MIND: Discoveries in Cognitive Science
344
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
and respond at (or around) 50%. This reasoning might explain why the spike at 50% is highest
for base rate trials. For base rate trials the stimulus is most uncertain, as no information regard-
ing the other variables in the causal structure is given. Hence based on this uncertainty expla-
nation we would expect to see many such 50% responses for base rate queries.
While our modeling approach assumed that all responses were generated by way of muta-
tion sampling, it is likely that participants varied in how they responded and that in a subset of
trials they just guessed 50%. Additionally, for Conflict trials 1, in which the queried variable is
adjacent to two opposing cues, we found that individual participants responded on both sides
of 50%. This type of responding is consistent with a strategy of random responding.
If indeed the observed response distributions on causal judgment tasks are the result of a
mixture of strategies, then it appears that the mixture proportions are dependent on the infer-
ence type. One piece of evidence for this is that we found substantially larger spikes for base
rate inferences. More evidence come from previous studies, both Rottman and Hastie (2016)
and Kolvoort et al. (2022) concluded that the frequency of 50% responses depended on the
uncertainty that reasoners might have. That is, they found spikes to be smallest for consistent
inferences, larger for ambiguous inferences, and largest for inconsistent inferences. We also
observe this pattern in our data (Figure 8). These findings seem to point toward a mechanism
in which people resolve their uncertainty by responding using the middle of the response scale
(Kolvoort et al., 2022). It suggests that people adapt their response strategy based on an
uncertainty-related feature of the stimulus. People use the ‘guessing strategy’ more often when
there is a lot of uncertainty (e.g., a conflict or base rate trial) versus when there is not (e.g., a
consistent trial).
Adaptive chain lengths. Another potential source of variability that comes to light once we start
modeling the full response distributions is that possibility of variable chain lengths. That is, it
may be that the number of samples one considers for making a judgment, could differ per
inference type. We found that for the ambiguous trials, where the state of one variable was
unknown, participants were more conservative and responded more quickly when the known
variable was adjacent to the queried one. This is consistent with the effects of having a shorter
chain length. In the Results section we proposed that this might be due to these inferences
being less ambiguous leading to people thinking they can be relatively accurate without
needing to generate many samples.
While we could estimate the chain length separately for each inference type, a more prin-
cipled approach would be to determine why and how chain lengths differ and to incorporate
this into the BMS. Future research could focus on investigating this relation between stimulus
and chain length. Zhu et al. (2020) suggest that how much someone samples could be depen-
dent on problem complexity. This would be consistent with our ambiguity-based explanation.
Related to this idea, other researchers have proposed an adaptive scheme in which the costs
and benefits of samples are weighed to determine how many samples to generate (Gershman
& Goodman, 2014; Hertwig & Pleskac, 2010; Vul et al., 2014; Zhu et al., 2020). These seem
like fruitful ways to extend the BMS.
CONCLUSION
We studied the predictions of the MS, as it currently is the most promising process-level model
of causal reasoning, and found it has some shortcomings in explaining full response distribu-
tions. The original MS model was developed to implement four psychological principles that
apply to causal inference: we think about concrete cases, we make small adjustment to these
OPEN MIND: Discoveries in Cognitive Science
345
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
cases, we have a bias for prototypes, and we can only draw a limited number of samples. By
developing the BMS and showing its improved performance we have argued for an additional
principle to be added to this list: people make use of prior information. By adding this princi-
ple, and implementing it with the BMS, we showed it is possible to account for more distri-
butional phenomena in causal judgments. We hope this work spurs other researchers to focus
efforts on analyzing more than just mean responses as we believe this will improve our under-
standing of underlying cognitive mechanisms greatly.
AUTHOR CONTRIBUTIONS
Ivar R. Kolvoort: Conceptualization; Formal analysis; Methodology; Writing—Original draft;
Writing—Review & editing. Nina Temme: Formal analysis. Leendert van Maanen: Conceptu-
alization; Methodology; Writing—Original draft; Writing—Review & editing.
FUNDING INFORMATION
This work was supported by an Interdisciplinary Doctoral Agreement grant awarded to Leen-
dert van Maanen by the University of Amsterdam.
DATA AVAILABILITY STATEMENT
The experimental data analyzed during the current study are available in the OSF repository of
the original experimental study at https://osf.io/bz9vj/. Model code and helper functions to run
simulations with the BMS and MS are available at https://osf.io/xd9az/.
ETHICAL APPROVAL
The study was approved by the local ethics committee of the University of Amsterdam (nr.
2019-PML-10019).
REFERENCES
Ahn, W.-Y., & Busemeyer, J. R. (2016). Challenges and promises for
translating computational tools into clinical practice. Current
Opinion in Behavioral Sciences, 11, 1–7. https://doi.org/10
.1016/j.cobeha.2016.02.001, PubMed: 27104211
Ali, N., Chater, N., & Oaksford, M. (2011). The mental representa-
tion of causal conditional reasoning: Mental models or causal
models. Cognition, 119(3), 403–418. https://doi.org/10.1016/j
.cognition.2011.02.005, PubMed: 21392739
Anders, R., Alario, F. X., & van Maanen, L. (2016). The shifted wald
distribution for response time data analysis. Psychological
Methods, 21(3), 309–327. https://doi.org/10.1037/met0000066,
PubMed: 26867155
Archambeau, K., Couto, J., & van Maanen, L. (2022). Non-parametric
mixture modeling of cognitive psychological data: A new method
to disentangle hidden strategies. Behavior Research Methods.
https://doi.org/10.3758/s13428-022-01837-0, PubMed: 36219308
Bonawitz, E., Denison, S., Griffiths, T. L., & Gopnik, A. (2014).
Probabilistic models, learning algorithms, and response vari-
ability: Sampling in cognitive development. Trends in Cogni-
tive Sciences, 18(10), 497–500. https://doi.org/10.1016/j.tics
.2014.06.006, PubMed: 25001609
Bramley, N. R., Lagnado, D. A., & Speekenbrink, M. (2015). Con-
servative forgetful scholars: How people learn causal structure
through sequences of interventions. Journal of Experimental Psy-
chology: Learning, Memory, and Cognition, 41(3), 708–731.
https://doi.org/10.1037/xlm0000061, PubMed: 25329086
Budescu, D. V., Weinberg, S., & Wallsten, T. S. (1988). Decisions
based on numerically and verbally expressed uncertainties. Journal
of Experimental Psychology: Human Perception and Performance,
14(2), 281–294. https://doi.org/10.1037/0096-1523.14.2.281
Campbell, J. I. D., & Xue, Q. (2001). Cognitive arithmetic across
cultures. Journal of Experimental Psychology: General, 130(2),
299–315. https://doi.org/10.1037/0096-3445.130.2.299,
PubMed: 11409105
Cheng, P. W. (1997). From covariation to causation: A causal
power theory. Psychological Review, 104(2), 367–405. https://
doi.org/10.1037/0033-295X.104.2.367
Coenen, A., Rehder, B., & Gureckis, T. M. (2015). Strategies to
intervene on causal systems are adaptively selected. Cognitive
Psychology, 79, 102–133. https://doi.org/10.1016/j.cogpsych
.2015.02.004, PubMed: 25935867
Coltheart, M., Rastle, K., Holloway, R., Perry, C., & Ziegler, J.
(2001). DRC: A dual route cascaded model of visual word
recognition and reading aloud. Psychological Review, 108(1),
204–256. https://doi.org/10.1037/0033-295X.108.1.204,
PubMed: 11212628
OPEN MIND: Discoveries in Cognitive Science
346
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Costello, F., & Watts, P. (2014). Surprisingly rational: Probability
theory plus noise explains biases in judgment. Psychological
Review, 121(3), 463–480. https://doi.org/10.1037/a0037010,
PubMed: 25090427
Couto, J., van Maanen, L., & Lebreton, M. (2020). Investigating the
origin and consequences of endogenous default options in
repeated economic choices. PLoS One, 15(8), Article e0232385.
https://doi.org/10.1371/journal.pone.0232385, PubMed:
32790729
Dasgupta, I., Schulz, E., & Gershman, S. J. (2017). Where do
hypotheses come from? Cognitive Psychology, 96, 1–25.
https://doi.org/10.1016/j.cogpsych.2017.05.001, PubMed:
28586634
David, H. A. (1968). Gini’s mean difference rediscovered. Biome-
trika, 55(3), 573–575. https://doi.org/10.1093/biomet/55.3.573
Davis, Z. J., & Rehder, B. (2017). The causal sampler: A sampling
approach to causal representation, reasoning and learning. In 39th
Annual Meeting of the Cognitive Science Society: Computational
Foundations of Cognition, CogSci 2017 (pp. 1896–1901). The
Cognitive Science Society.
Davis, Z. J., & Rehder, B. (2020). A process model of causal reason-
ing. Cognitive Science, 44(5), Article e12839. https://doi.org/10
.1111/cogs.12839, PubMed: 32419205
Donkin, C., Nosofsky, R. M., Gold, J. M., & Shiffrin, R. M. (2013).
Discrete-slots models of visual working-memory response times.
Psychological Review, 120(4), 873–902. https://doi.org/10.1037
/a0034247, PubMed: 24015956
DuCharme, W. M. (1970). Response bias explanation of conserva-
tive human inference. Journal of Experimental Psychology, 85(1),
66–74. https://doi.org/10.1037/h0029546
Dunlosky, J., & Hertzog, C. (2001). Measuring strategy production
during associative learning: The relative utility of concurrent ver-
sus retrospective reports. Memory & Cognition, 29(2), 247–253.
https://doi.org/10.3758/BF03194918, PubMed: 11352207
Dutilh, G., Wagenmakers, E.-J., Visser, I., & van der Maas, H. L. J.
(2011). A phase transition model for the speed-accuracy trade-off
in response time experiments. Cognitive Science, 35(2), 211–250.
https://doi.org/10.1111/j.1551-6709.2010.01147.x, PubMed:
21428999
Erev, I., Wallsten, T., & Budescu, D. (1994). Simultaneous over-and
underconfidence: The role of error in judgment processes. Psy-
chological Review, 101(3), 519–527. https://doi.org/10.1037
/0033-295X.101.3.519
Evans, J. S. B. T. (2008). Dual-processing accounts of reasoning,
judgment, and social cognition. Annual Review of Psychology,
59(1), 255–278. https://doi.org/10.1146/annurev.psych.59
.103006.093629, PubMed: 18154502
Fernbach, P. M., & Erb, C. D. (2013). A quantitative causal model
theory of conditional reasoning. Journal of Experimental Psychol-
ogy: Learning Memory and Cognition, 39(5), 1327–1343. https://
doi.org/10.1037/a0031851, PubMed: 23565785
Forstmann, B. U., Ratcliff, R., & Wagenmakers, E.-J. (2016). Sequen-
tial sampling models in cognitive neuroscience: Advantages,
applications, and extensions. Annual Review of Psychology,
67(1), 641–666. https://doi.org/10.1146/annurev-psych-122414
-033645, PubMed: 26393872
Gershman, S. J., & Goodman, N. D. (2014). Amortized inference in
probabilistic reasoning. Proceedings of the Annual Meeting of the
Cognitive Science Society, 36, 517–522.
Gerstenberg, T., Goodman, N. D., Lagnado, D. A., & Tenenbaum,
J. B. (2021). A counterfactual simulation model of causal judgments
for physical events. Psychological Review, 128(5), 936–975.
https://doi.org/10.1037/rev0000281, PubMed: 34096754
Gigerenzer, G., & Gaissmaier, W. (2011). Heuristic decision
making. Annual Review of Psychology, 62, 451–482. https://doi
.org/10.1146/annurev-psych-120709-145346, PubMed:
21126183
Griffiths, T. L., & Tenenbaum, J. B. (2005). Structure and strength in
causal induction. Cognitive Psychology, 51(4), 334–384. https://
doi.org/10.1016/j.cogpsych.2005.05.004, PubMed: 16168981
Griffiths, T. L., & Tenenbaum, J. B. (2009). Theory-based causal
induction. Psychological Review, 116(4), 661–716. https://doi
.org/10.1037/a0017201, PubMed: 19839681
Guest, O., & Martin, A. E. (2021). How computational modeling
can force theory building in psychological science. Perspectives
on Psychological Science, 16(4), 789–802. https://doi.org/10
.1177/1745691620970585, PubMed: 33482070
Gunawan, D., Hawkins, G. E., Kohn, R., Tran, M.-N., & Brown,
S. D. (2022). Time-evolving psychological processes over
repeated decisions. Psychological Review, 129(3), 438–456.
https://doi.org/10.1037/rev0000351, PubMed: 35727307
Hagmayer, Y. (2016). Causal Bayes nets as psychological theories
of causal reasoning: Evidence from psychological research. Syn-
these, 193(4), 1107–1126. https://doi.org/10.1007/s11229-015
-0734-0
Hagmayer, Y., & Osman, M. (2012). From colliding billiard balls to
colluding desperate housewives: Causal Bayes nets as rational
models of everyday causal reasoning. Synthese, 189, 17–28.
https://doi.org/10.1007/s11229-012-0162-3
Haines, N., Kvam, P. D., Irving, L. H., Smith, C., Beauchaine, T. P.,
Pitt, M. A., Ahn, W.-Y., & Turner, B. M. (2020). Theoretically
informed generative models can advance the psychological
and brain sciences: Lessons from the reliability paradox.
PsyArXiv. https://doi.org/10.31234/osf.io/xr7y3
Hastings, W. K. (1970). Monte Carlo sampling methods using
Markov chains and their applications. Biometrika, 57(1), 97–109.
https://doi.org/10.1093/biomet/57.1.97
Hayes, B. K., Hawkins, G. E., Newell, B. R., Pasqualino, M., &
Rehder, B. (2014). The role of causal models in multiple judg-
ments under uncertainty. Cognition, 133(3), 611–620. https://
doi.org/10.1016/j.cognition.2014.08.011, PubMed: 25238316
Hemmer, P., Tauber, S., & Steyvers, M. (2015). Moving beyond
qualitative evaluations of Bayesian models of cognition. Psycho-
nomic Bulletin & Review, 22(3), 614–628. https://doi.org/10
.3758/s13423-014-0725-z, PubMed: 25233880
Hertwig, R., & Pleskac, T. J. (2010). Decisions from experience:
Why small samples? Cognition, 115(2), 225–237. https://doi.org
/10.1016/j.cognition.2009.12.009, PubMed: 20092816
Holmes, W. R. (2015). A practical guide to the Probability Density
Approximation (PDA) with improved implementation and error
characterization. Journal of Mathematical Psychology, 68–69,
13–24. https://doi.org/10.1016/j.jmp.2015.08.006
Holyoak, K. J., Lee, H. S., & Lu, H. (2010). Analogical and
category-based inference: A theoretical integration with Bayesian
causal models. Journal of Experimental Psychology: General,
139(4), 702–727. https://doi.org/10.1037/a0020488, PubMed:
21038985
Jarecki, J. B., Tan, J. H., & Jenny, M. A. (2020). A framework for
building cognitive process models. Psychonomic Bulletin &
Review, 27(6), 1218–1229. https://doi.org/10.3758/s13423-020
-01747-2, PubMed: 32632887
Jazayeri, M., & Shadlen, M. N. (2010). Temporal context calibrates
interval timing. Nature Neuroscience, 13(8), 1020–1026. https://
doi.org/10.1038/nn.2590, PubMed: 20581842
Kahneman, D. (2011). Thinking, fast and slow. Farrar, Straus, and
Giroux.
OPEN MIND: Discoveries in Cognitive Science
347
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
Kleinjans, K. J., & van Soest, A. (2014). Rounding, focal point
answers, and nonresponse to subjective probability questions.
Journal of Applied Econometrics, 29, 567–585. https://doi.org
/10.1002/jae.2321
Kolvoort, I. R., Davis, Z. J., van Maanen, L., & Rehder, B. (2021).
Variability in causal reasoning. In Proceedings of the 43rd Annual
Meeting of the Cognitive Science Society (pp. 1250–1256).
Kolvoort, I. R., Fisher, E. L., van Rooij, R., Schulz, K., & van Maanen,
L. (2022). Probabilistic causal reasoning under time pressure.
PsyArXiv. https://doi.org/10.31234/osf.io/ej26r
Kong, X. J., Wise, S. L., & Bhola, D. S. (2007). Setting the response
time threshold parameter to differentiate solution behavior from
rapid-guessing behavior. Educational and Psychological
Measurement, 67(4), 606–619. https://doi.org/10.1177
/0013164406294779
Krynski, T. R., & Tenenbaum, J. B. (2007). The role of causality in
judgment under uncertainty. Journal of Experimental Psychology:
General, 136(3), 430–450. https://doi.org/10.1037/0096-3445
.136.3.430, PubMed: 17696692
Lee, H. S., & Holyoak, K. J. (2008). The role of causal models in
analogical inference. Journal of Experimental Psychology: Learn-
ing, Memory, and Cognition, 34(5), 1111–1122. https://doi.org
/10.1037/a0012581, PubMed: 18763895
Lee, M. D., Criss, A. H., Devezer, B., Donkin, C., Etz, A., Leite, F. P.,
Matzke, D., Rouder, J. N., Trueblood, J. S., White, C. N., &
Vandekerckhove, J. (2019). Robust modeling in cognitive sci-
ence. Computational Brain and Behavior, 2(3–4), 141–153.
https://doi.org/10.1007/s42113-019-00029-y
Levin, D. A., & Peres, Y. (2017). Markov chains and mixing times.
American Mathematical Society. https://doi.org/10.1090/mbk/107
Lieder, F., & Griffiths, T. L. (2020). Resource-rational analysis:
Understanding human cognition as the optimal use of limited
computational resources. Behavioral and Brain Sciences, 43,
Article E1. https://doi.org/10.1017/S0140525X1900061X,
PubMed: 30714890
Lieder, F., Griffiths, T. L., & Goodman, N. D. (2012). Burn-in, bias,
and the rationality of anchoring. Advances in Neural Information
Processing Systems, 25, 2690–2798.
Lu, H., Yuille, A. L., Liljeholm, M., Cheng, P. W., & Holyoak, K. J.
(2008). Bayesian generic priors for causal learning. Psychological
Review, 115(4), 955–984. https://doi.org/10.1037/a0013256,
PubMed: 18954210
Maaß, S. C., de Jong, J., van Maanen, L., & van Rijn, H. (2021).
Conceptually plausible Bayesian inference in interval timing.
Royal Society Open Science, 8(8), Article 201844. https://doi
.org/10.1098/rsos.201844, PubMed: 34457319
Marchant, M., Toro-Hernandez, F., & Chaigneau, S. E. (2021).
Know your priors: Task specific priors reflect subjective expecta-
tions in Bayesian models of categorization. PsyArXiv. https://doi
.org/10.31234/osf.io/e6zhm
Marr, D. (1982). Vision: A computational investigation into the
human representation and processing of visual information. W. H.
Freeman.
Meder, B., Mayrhofer, R., & Waldmann, M. R. (2014). Structure
induction in diagnostic causal reasoning. Psychological Review,
121(3), 277–301. https://doi.org/10.1037/a0035944, PubMed:
25090421
Mestdagh, M., Verdonck, S., Meers, K., Loossens, T., & Tuerlinckx,
F. (2019). Prepaid parameter estimation without likelihoods.
PLoS Computational Biology, 15(9), Article e1007181. https://
doi.org/10.1371/journal.pcbi.1007181, PubMed: 31498789
Mistry, P. K., Pothos, E. M., Vandekerckhove, J., & Trueblood, J. S.
(2018). A quantum probability account of individual differences
in causal reasoning. Journal of Mathematical Psychology, 87,
76–97. https://doi.org/10.1016/j.jmp.2018.09.003
Morey, R. D., & Rouder, J. N. (2014). BayesFactor package for R
(0.9.12-4.3). https://cran.r-project.org/web/packages/BayesFactor
/index.html
Neath, A. A., & Cavanaugh, J. E. (2012). The Bayesian information
criterion: Background, derivation, and applications. Wiley Inter-
disciplinary Reviews: Computational Statistics, 4(2), 199–203.
https://doi.org/10.1002/wics.199
O’Neill, K., Henne, P., Bello, P., Pearson, J., & De Brigard, F. (2022).
Confidence and gradation in causal judgment. Cognition, 223,
Article 105036. https://doi.org/10.1016/j.cognition.2022
.105036, PubMed: 35092903
Oaksford, M., & Chater, N. (2020). New paradigms in the psychol-
ogy of reasoning. Annual Review of Psychology, 71, 305–330.
https://doi.org/10.1146/annurev-psych-010419-051132,
PubMed: 31514580
Park, J., & Sloman, S. A. (2013). Mechanistic beliefs determine
adherence to the markov property in causal reasoning. Cognitive
Psychology, 67(4), 186–216. https://doi.org/10.1016/j.cogpsych
.2013.09.002, PubMed: 24152569
Parpart, P., Jones, M., & Love, B. C. (2018). Heuristics as Bayesian
inference under extreme priors. Cognitive Psychology, 102,
127–144. https://doi.org/10.1016/j.cogpsych.2017.11.006,
PubMed: 29500961
Pearl, J. (2009). Causality. Cambridge University Press. https://doi
.org/10.1017/CBO9780511803161
Phillips, L. D., Hays, W. L., & Edwards, W. (1966). Conservatism in
complex probabilistic inference. IEEE Transactions on Human
Factors in Electronics, HFE-7(1), 7–18. https://doi.org/10.1109
/THFE.1966.231978
Ratcliff, R. (1978). A theory of memory retrieval. Psychological
Review, 85(2), 59–108. https://doi.org/10.1037/0033-295X.85
.2.59
Ratcliff, R., Smith, P. L., Brown, S. D., & McKoon, G. (2016).
Diffusion decision model: Current issues and history. Trends in
Cognitive Sciences, 20(4), 260–281. https://doi.org/10.1016/j
.tics.2016.01.007, PubMed: 26952739
Rehder, B. (2014). Independence and dependence in human causal
reasoning. Cognitive Psychology, 72, 54–107. https://doi.org/10
.1016/j.cogpsych.2014.02.002, PubMed: 24681802
Rehder, B. (2018). Beyond Markov: Accounting for independence
violations in causal reasoning. Cognitive Psychology, 103,
42–84. https://doi.org/10.1016/j.cogpsych.2018.01.003,
PubMed: 29522980
Rehder, B., & Burnett, R. C. (2005). Feature inference and the
causal structure of categories. Cognitive Psychology, 50(3),
264–314. https://doi.org/10.1016/j.cogpsych.2004.09.002,
PubMed: 15826612
Rehder, B., & Davis, Z. J. (2021). Testing a process model of causal
reasoning with inhibitory causal links. In Proceedings of the 43rd
Annual Meeting of the Cognitive Science Society (pp. 653–659).
Rehder, B., & Waldmann, M. R. (2017). Failures of explaining
away and screening off in described versus experienced causal
learning scenarios. Memory and Cognition, 45(2), 245–260.
https://doi.org/10.3758/s13421-016-0662-3, PubMed:
27826953
Rottman, B. M., & Hastie, R. (2014). Reasoning about causal rela-
tionships: Inferences on causal networks. Psychological Bulletin,
140(1), 109–139. https://doi.org/10.1037/a0031903, PubMed:
23544658
Rottman, B. M., & Hastie, R. (2016). Do people reason rationally
about causally related events? Markov violations, weak inferences,
OPEN MIND: Discoveries in Cognitive Science
348
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The Bayesian Mutation Sampler
Kolvoort et al.
and failures of explaining away. Cognitive Psychology, 87, 88–134.
https://doi.org/10.1016/j.cogpsych.2016.05.002, PubMed:
27261539
Sanborn, A. N., Heller, K., Austerweil, J. L., & Chater, N. (2021).
REFRESH: A new approach to modeling dimensional biases in
perceptual similarity and categorization. Psychological Review,
128(6), 1145–1186. https://doi.org/10.1037/rev0000310,
PubMed: 34516151
Schnipke, D. L., & Scrams, D. J. (1997). Modeling item response
times with a two-state mixture model: A new method of measur-
ing speededness. Journal of Educational Measurement, 34(3),
213–232. https://doi.org/10.1111/j.1745-3984.1997.tb00516.x
Schwarz, G. (1978). Estimating the dimensions of a model. The
Annals of Statistics, 6(2), 461–464. https://doi.org/10.1214/aos
/1176344136
Shafto, P., Kemp, C., Bonawitz, E. B., Coley, J. D., & Tenenbaum,
J. B. (2008). Inductive reasoning about causally transmitted prop-
erties. Cognition, 109(2), 175–192. https://doi.org/10.1016/j
.cognition.2008.07.006, PubMed: 18952205
Smith, E. E., Patalano, A. L., & Jonides, J. (1998). Alternative strat-
egies of categorization. Cognition, 65(2–3), 167–196. https://doi
.org/10.1016/S0010-0277(97)00043-7, PubMed: 9557382
Spirtes, P., Glymour, C., & Scheines, R. (2000). Causation, predic-
tion, and search. MIT Press. https://doi.org/10.7551/mitpress
/1754.001.0001
Stanovich, K. E. (1999). Who is rational? Psychology Press. https://
doi.org/10.4324/9781410603432
Steyvers, M., Tenenbaum, J. B., Wagenmakers, E.-J., & Blum, B.
(2003). Inferring causal networks from observations and interven-
tions. Cognitive Science, 27, 453–489. https://doi.org/10.1207
/s15516709cog2703_6
Tauber, S., Navarro, D. J., Perfors, A., & Steyvers, M. (2017).
Bayesian models of cognition revisited: Optimality aside and
letting data drive psychological theory. Psychological Review,
124(4), 410–441. https://doi.org/10.1037/rev0000052, PubMed:
28358549
Turner, B. M., Forstmann, B. U., Love, B. C., Palmeri, T. J., & van
Maanen, L. (2017). Approaches to analysis in model-based cog-
nitive neuroscience. Journal of Mathematical Psychology, 76,
65–79. https://doi.org/10.1016/j.jmp.2016.01.001, PubMed:
31745373
Turner, B. M., & Sederberg, P. B. (2014). A generalized,
likelihood-free method for posterior estimation. Psychonomic
Bulletin & Review, 21(2), 227–250. https://doi.org/10.3758
/s13423-013-0530-0, PubMed: 24258272
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory:
Cumulative representation of uncertainty. Journal of Risk and
Uncertainty, 5, 297–323. https://doi.org/10.1007/BF00122574
van Maanen, L., Couto, J., & Lebreton, M. (2016). Three boundary
conditions for computing the fixed-point property in binary
mixture data. PLoS One, 11(11), Article e0167377. https://doi
.org/10.1371/journal.pone.0167377, PubMed: 27893868
van Maanen, L., de Jong, R., & van Rijn, H. (2014). How to assess
the existence of competing strategies in cognitive tasks: A primer
on the fixed-point property. PLoS One, 9(8), Article e0106113.
https://doi.org/10.1371/journal.pone.0106113, PubMed:
25170893
van Maanen, L., & Miletić, S. (2021). The interpretation of
behavior-model correlations in unidentified cognitive models.
Psychonomic Bulletin & Review, 28(2), 374–383. https://doi.org
/10.3758/s13423-020-01783-y, PubMed: 32767046
van Maanen, L., van der Heiden, R. M., Bootsma, S. T., & Janssen,
C. P. (2021). Identifiability and specificity of the two-point visual
control model of steering. In Proceedings of the 43rd Annual
Meeting of the Cognitive Science Society (pp. 237–243).
van Maanen, L., & van Rijn, H. (2010). The locus of the Gratton
effect in picture–word interference. Topics in Cognitive Science,
2(1), 168–180. https://doi.org/10.1111/j.1756-8765.2009.01069.x,
PubMed: 25163629
van Ravenzwaaij, D., & Oberauer, K. (2009). How to use the
diffusion model: Parameter recovery of three methods: EZ,
fast-dm, and DMAT. Journal of Mathematical Psychology, 53(6),
463–473. https://doi.org/10.1016/j.jmp.2009.09.004
van Rijn, H., van Someren, M., & van der Maas, H. (2003).
Modeling developmental transitions on the balance scale task.
Cognitive Science, 27(2), 227–257. https://doi.org/10.1207
/s15516709cog2702_4
Vul, E., Goodman, N., Griffiths, T. L., & Tenenbaum, J. B. (2014).
One and done? Optimal decisions from very few samples. Cog-
nitive Science, 38(4), 599–637. https://doi.org/10.1111/cogs
.12101, PubMed: 24467492
Wagenmakers, E.-J., & Farrell, S. (2004). AIC model selection using
Akaike weights. Psychonomic Bulletin & Review, 11(1),
192–196. https://doi.org/10.3758/ BF03206482, PubMed:
15117008
Waldmann, M. R., & Hagmayer, Y. (2006). Categories and causal-
ity: The neglected direction. Cognitive Psychology, 53(1), 27–58.
https://doi.org/10.1016/j.cogpsych.2006.01.001, PubMed:
16497289
Welsh, M. B., & Navarro, D. J. (2012). Seeing is believing: Priors,
trust, and base rate neglect. Organizational Behavior and Human
Decision Processes, 119(1), 1–14. https://doi.org/10.1016/j
.obhdp.2012.04.001
White, C. N., Servant, M., & Logan, G. D. (2018). Testing the
validity of conflict drift-diffusion models for use in estimating
cognitive processes: A parameter-recovery study. Psychonomic
Bulletin & Review, 25(1), 286–301. https://doi.org/10.3758
/s13423-017-1271-2, PubMed: 28357629
Wilson, R. C., & Collins, A. G. E. (2019). Ten simple rules for the
computational modeling of behavioral data. eLife, 8, Article
e49547. https://doi.org/10.7554/eLife.49547, PubMed:
31769410
Yitzhaki, S. (2003). Gini’s mean difference: A superior measure of
variability for non-normal distributions. Metron, 61(2), 285–316.
https://doi.org/10.2139/ssrn.301740
Zhu, J.-Q., Sanborn, A. N., & Chater, N. (2020). The Bayesian
sampler: Generic Bayesian inference causes incoherence in
human probability judgments. Psychological Review, 127(5),
719–748. https://doi.org/10.1037/rev0000190, PubMed:
32191073
OPEN MIND: Discoveries in Cognitive Science
349
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
8
0
2
1
3
8
6
6
6
o
p
m
_
a
_
0
0
0
8
0
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3