PERSPECTIVE
Dynamical networks: Finding, measuring, Und
tracking neural population activity
using network science
Mark D. Humphries
Faculty of Biology, Medicine, and Health, University of Manchester, Manchester, Großbritannien
Schlüsselwörter: Graphentheorie, Network theory, Systems neuroscience, Calcium imaging, Multineuron
Aufnahmen, Neural ensembles
Keine offenen Zugänge
Tagebuch
ABSTRAKT
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
N
e
N
_
A
_
0
0
0
2
0
P
D
T
.
Systems neuroscience is in a headlong rush to record from as many neurons at the same time
as possible. As the brain computes and codes using neuron populations, it is hoped these
data will uncover the fundamentals of neural computation. But with hundreds, thousands,
or more simultaneously recorded neurons come the inescapable problems of visualizing,
describing, and quantifying their interactions. Here I argue that network science provides a
set of scalable, analytical tools that already solve these problems. By treating neurons as
nodes and their interactions as links, a single network can visualize and describe an
arbitrarily large recording. I show that with this description we can quantify the effects of
manipulating a neural circuit, track changes in population dynamics over time, Und
quantitatively define theoretical concepts of neural populations such as cell assemblies.
Using network science as a core part of analyzing population recordings will thus provide
both qualitative and quantitative advances to our understanding of neural computation.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
EINFÜHRUNG
Neurons use spikes to communicate (Rieke, Warland, de Ruyter van Stevninck, & Bialek,
1999). From this communication arises coding and computation within the brain; and so arises
all thought, perception, and deed. Understanding neural circuits thus hinges critically on un-
derstanding spikes across populations of neurons (Pouget, Beck, Ma, & Latham, 2013; Wohrer,
Humphries, & Machens, 2013; Yuste, 2015).
This idea has driven a technological arms race in systems neuroscience to record from
as many individual neurons at the same time as physically possible (Stevenson & Kording,
2011). Current technology, ranging from imaging of fluorescent calcium-binding proteins
(Chen et al., 2013; Dupre & Yuste, 2017; S. Peron, Chen, & Svoboda, 2015; S. P. Peron,
Freeman, Iyer, Guo, & Svoboda, 2015) and voltage-sensitive dyes (Briggman, Abarbanel, &
Kristan 2005; Bruno, Frost, & Humphries, 2015; Frady, Kapoor, Horvitz, & Kristan, 2016) Zu
large scale multielectrode arrays and silicon probes (Buzsáki, 2004; Jun et al., 2017), Jetzt
allows us to simultaneously capture the activity of hundreds of neurons in a range of brain
Systeme. These systems include such diverse systems as invertebrate locomotion, durch
zebrafish oculomotor control, to executive functions in primate prefrontal cortex. With the
data captured, the key questions for any system become: How do we describe these spike
Daten? How should we visualize them? And how do we discover the coding and computations
therein?
Zitat: Humphries, M. D. (2017).
Dynamical networks: Finding,
measuring, and tracking neural
population activity using network
Wissenschaft. Netzwerkneurowissenschaften,
1(4), 324–338. https://doi.org/10.1162/
netn_a_00020
DOI:
https://doi.org/10.1162/netn_a_00020
zusätzliche Informationen:
http://netwiki.amath.unc.edu/
VisComms
https://github.com/mdhumphries/
SpikeTrainCommunitiesToolBox
Erhalten: 9 Marsch 2017
Akzeptiert: 6 Juni 2017
Konkurrierende Interessen: The author has
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Mark D. Humphries
mark.humphries@manchester.ac.uk
Handling-Editor:
Olaf Sporns
Urheberrechte ©: © 2017
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
Networks of neural dynamics
Here I argue that network science provides a set of tools ideally suited to both describe the
data and discover new ideas within it. Networks are simply a collection of nodes and links:
nodes representing objects, and links representing the interactions between those objects. Das
representation can encapsulate a wide array of systems, from email traffic within a company,
through the social groups of dolphins, to word co-occurrence frequencies in a novel (Newman,
2003). By abstracting these complex systems to a network description, we can describe their
Topologie, compare them, and deconstruct them into their component parts. Darüber hinaus, we gain
access to a range of null models for testing hypotheses about a network’s structure and about
how it changes. I will demonstrate all these ideas below.
Erste, an important distinction. Networks capture interactions as links, but these links do
not necessarily imply physical connections. In manchen Fällen, such as the network of router-level
connections of the Internet or a power grid, the interaction network follows exactly a physical
Netzwerk. In somes cases, such as a Facebook social network, there is no physical connection
between the nodes. In anderen Fällen, of which neuroscience is a prime example, the interactions
between nodes are shaped and constrained by the underlying physical connections, but are
not bound to them. We shall touch on this issue of distinguishing interactions from physical
connections throughout.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
N
e
N
_
A
_
0
0
0
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
DESCRIBING MULTINEURON DATA AS A NETWORK
A network description of multineuron recording data rests on two ideas: The nodes are the neu-
rons, and the links are the interactions between the neurons (Figure 1A). Strictly speaking, Die
nodes are the isolated time series of neural activity, whether spike trains, calcium fluorescence,
or voltage-dye expression (with the usual caveats applied to the accuracy of spike-sorting for
electrodes or image segmentation and stability for imaging; Harris, Quiroga, Freeman, &
Schmied, 2016). An immediate advantage of a network formalism is that it separates the details
of choosing the interaction from the network topology itself—whatever measure of interaction
wir haben uns entschieden, the same topological analyses can be applied.
We are free to choose any measure of pairwise interaction we like; and indeed that choice
depends on what questions we want to ask of the data. Typical choices include cosine similar-
ity or a rectified correlation coefficient, as these linear measures are familiar, easy to interpret,
and not data-intensive. But with sufficient data we could also use nonlinear measurements
of interaction including forms of mutual information (Bettencourt, Stephens, Ham, & Brutto,
2007; Singh & Lesica, 2010) und Transferentropie (Nigam et al., 2016; Schreiber, 2000;
Thivierge, 2014). We could fit an Ising model, so estimating “direct” interactions while fac-
toring out other inputs (S. Yu, Huang, Singer, & Nikolic, 2008). We could even fit a model
to each neuron for the generation of its activity time series, such as a generalized linear
Modell (Pillow et al., 2008; Truccolo, Eden, Fellows, Donoghue, & Braun, 2005), and use the
fitted weights of the inputs from all other neurons as the interaction values in a network
(Gerhard, Pipa, Lima, Neuenschwander, & Gerstner, 2011). Zusätzlich, there is a large selec-
tion of interaction measures specific for spike trains (z.B., Lyttle & Fellous, 2011; van Rossum,
2001; Victor & Purpura, 1996), whose use in defining interaction networks has yet to be well
explored. And we should always be mindful that measures of pairwise interaction alone can-
not distinguish between correlations caused by common input from unrecorded neurons and
correlations caused by some direct contact between the recorded neurons.
Whatever measure of interaction we use, the important distinction is between whether
the interaction measurement is undirected (z.B., the correlation coefficient) or directed (z.B.,
Netzwerkneurowissenschaften
325
Adjacency matrix A
Eff = 0.74
C = 0.59
Weight matrix W
Eff = 0.14
C = 0.072
Networks of neural dynamics
A
Trial
start
C
F
D
P
0.08
0.06
0.04
0.02
20
10
0
ich
)
S
/
S
e
k
P
S
(
e
T
A
R
0
20
40
60
Time from trial start (S)
0.4
F
D
P
0.2
20
F
D
P
10
B
D
0
0
25
50
Degree
0
0
5
10
Strength
0
0
0.2
0.4
Weights
0.6
ich
T
N
e
C
ich
F
F
e
Ö
C
G
N
ich
R
e
T
S
u
C
l
0.1
0.05
0
E
j
C
N
e
C
ich
F
F
ich
E
l
A
B
Ö
G
N
l
ich
10
20
30
40
50
Neuron
e
S
A
e
R
C
e
D
×10-3
8
6
4
2
0
10
20
30
40
50
Deleted neuron
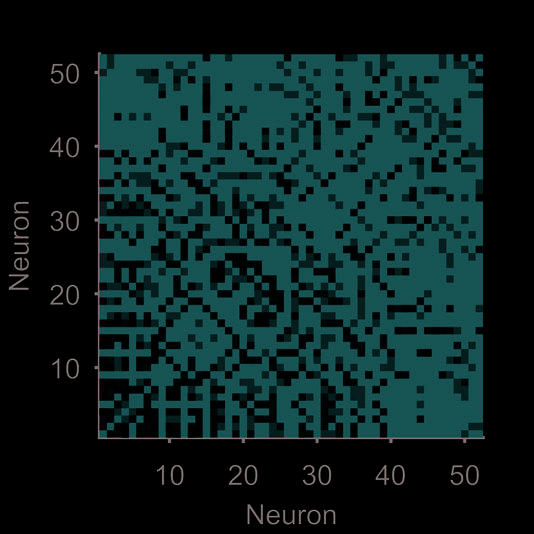
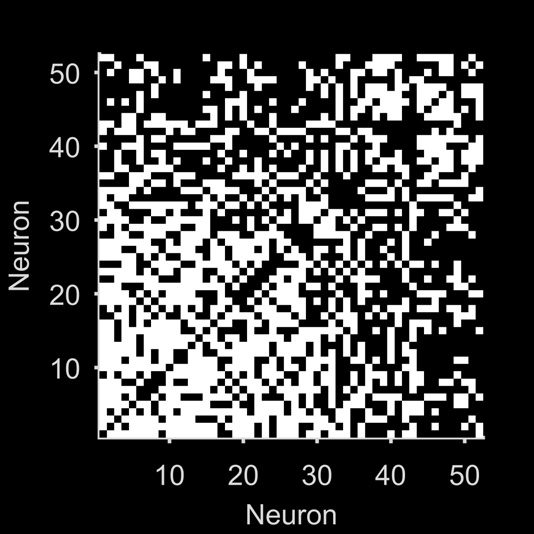
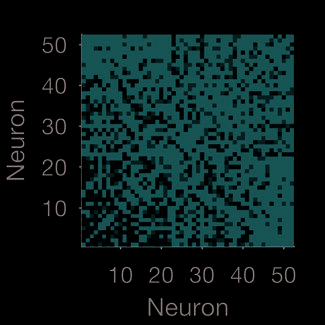
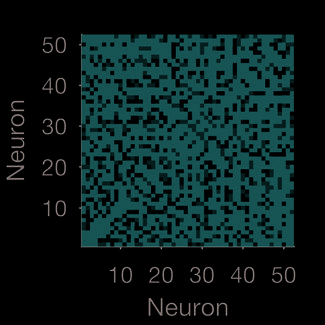
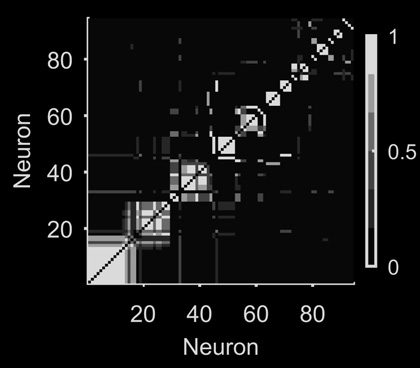
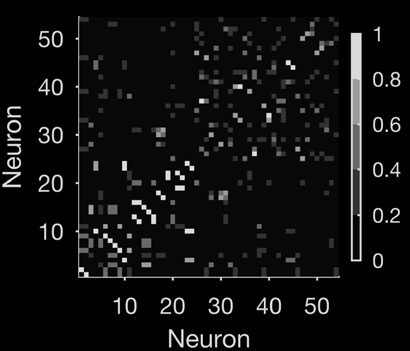
Figur 1. Quantifying neural population dynamics using network science. (A) Schematic of turning neural activity time series into a network.
Links: A raster plot of 52 simultaneously recorded neurons in rat medial prefrontal cortex, during a single trial of a maze navigation task. Rechts:
The corresponding network representation: Nodes are neurons, links indicate pairwise interactions, and their gray scale indicates the strength
of interaction. Top: Interactions here are rectified Pearson’s R (setting R < 0 to 0) between pairs of spike trains convolved with a Gaussian
(σ = 250 ms); two example convolved trains are plotted here. (B) Representations of the network in panel A: The adjacency matrix describes
the presence (black) or absence (white) of links; the weight matrix describes the strengths of those links. Neurons are ranked by total link
strength in descending order. Above each we give the global efficiency (E f f ) and average clustering coefficient (C), respectively measuring
the ease of getting from one node to another, and the density of links in the neighbourhood of one node. (C) Distributions of node degree (total
number of links per node), node strength (total weight of links per node), and link strength for the network in panel A. (D) Network clustering
fingerprint. A histogram of the weighted clustering coefficient for each neuron, measuring the ratio of weighted triangles to weighted triples
in which that neuron participates: The higher the ratio, the more strongly connected is the neighbourhood of that neuron. Some neurons
(e.g., 2, 5) have strongly connected neighbourhoods, implying a local group of correlated neurons. (E) Network efficiency fingerprint, given
by the decrease in the network’s global efficiency after deleting each neuron in turn. Neurons that strongly decrease the efficiency (e.g., 3) are
potential network hubs, mediating interactions between many neurons.
transfer entropy), and so whether we end up with an undirected or directed network as a result
(throughout this paper I consider only symmetric measures of interaction, and hence undi-
rected networks). And we end up with a weighted network (Newman, 2004). While much
of network science, and its use in neuroscience, is focused on binary networks whose links
indicate only whether an interaction between two nodes exists, any measurement of interac-
tion gives us a weight for each link (Figure 1B). Thresholding the weights to construct a binary
network inevitably loses information (Humphries, 2011; Zanin et al., 2012). Consequently,
multineuron recording data are best captured in a weighted network.
This weighted network of interactions between neurons need not map to any physical net-
work of connections between neurons. The synaptic connections between neurons in a circuit
shape and constrain the dynamics of those neurons, which we capture as population activity
in multineuron recordings. But interactions can change independently of the physical net-
work, both because the firing of a single neuron requires inputs from many other neurons, and
Network Neuroscience
326
0.6
0.5
0.4
0.3
0.2
0.1
0
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
Efficiency:
Reciprocal of the mean shortest path
length between all pairs of nodes;
path lengths are weighted. The
higher the efficiency, the shorter the
average path between a pair of
nodes.
Small-world network:
A network with both high clustering
of nodes and high efficiency.
because physical connections can be modulated on fast timescales, such as short-term plas-
ticity temporarily enhancing or depressing the strength of a synapse. Nonetheless, because
physical connections between neurons constrain their dynamics, so sustained changes in
interactions on timescales of minutes and hours are evidence of some physical change to
the underlying circuit (Baeg et al., 2007; Carrillo-Reid, Yang, Bando, Peterka, & Yuste, 2016;
Grewe et al., 2017; Laubach, Wessberg, & Nicolelis, 2000; Yamada et al., 2017).
The use of network science to describe interactions between neural elements has
been growing in cognitive neuroscience for a decade, and widely used to analyze EEG,
MEG, and fMRI time series data (Achard, Salvador, Whitcher, Suckling, & Bullmore, 2006;
Bassett & Bullmore, 2016; Bullmore & Sporns, 2009). Neuroimaging has long used the un-
fortunate term “functional networks,” with its connotations of causality and purpose, to de-
scribe the network of pairwise correlations between time series of neural activity. To avoid any
semantic confusion, and distinguish the networks of interactions from the underlying physi-
cal network, I will describe the network of single neuron interactions here as a “dynamical”
network.
What can we do with such dynamical networks of neurons? In the following I show how
with them we can quantify circuit-wide changes following perturbations and manipulations;
we can track changes in dynamics over time; and we can quantitatively define qualitative
theories of computational concepts.
CAPTURING POPULATION DYNAMICS AND THEIR CHANGES BY MANIPULATIONS
Applying network science to large-scale recordings of neural systems allows us to capture
their complex dynamics in a compact form. The existing toolbox of network science gives us
a plethora of options for quantifying the structure of a dynamical network. We may sim-
ply quantify its degree and strength distributions (Figure 1C), revealing dominant neurons
(Dann, Michaels, Schaffelhofer, & Scherberger, 2016; Nigam et al., 2016). We can assess the
local clustering of the dynamical network, the proportion of a neuron’s linked neighbours that
are also strongly linked to each other (Watts & Strogatz, 1998; Figure 1D), revealing the lock-
ing of dynamics among neurons (Bettencourt et al., 2007; Sadovsky & MacLean, 2013). We
can compute the efficiency of a network (Latora & Marchiori, 2001), a measure of how easily
a network can be traversed (Figure 1E), revealing how cohesive the dynamics of a popula-
tion are—the higher the efficiency, the more structured the interactions amongst the entire
population (Thivierge, 2014). We may define structural measures relative to a null model,
such as quantifying how much of a small-world the dynamical network is (Dann et al., 2016;
Gerhard et al., 2011; S. Yu et al., 2008). Our choice of quantifying measures depends on the
aspects of dynamics we are most interested in capturing.
Having compactly described the dynamics, we are well placed to then characterize the
effects of manipulating that system. Manipulations of a neural system will likely cause system-
wide changes in its dynamics. Such changes may be the fast, acute effect of optogenetic stim-
ulation (Boyden, 2015; Deisseroth, 2015; Miesenböck, 2009); the sluggish but acute effects of
drugs (Vincent, Tauskela, Mealing, & Thivierge, 2013); or the chronic effects of neurological
damage (Otchy et al., 2015). All these manipulations potentially change the interactions be-
tween neurons, disrupting normal computation. By comparing the dynamical networks before
and after the manipulation, one could easily capture the changes in the relationships between
neurons.
Network Neuroscience
327
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
There have been few studies examining this idea. Srinivas, Jain, Saurav, & Sikdar (2007)
used dynamical networks to quantify the changes to network-wide activity in hippocampus
caused by the glutamate-injury model of epilepsy, suggesting a dramatic drop in network clus-
tering in the epilepsy model. Vincent et al. (2013) used dynamical networks to quantify the
potential neuroprotective effects of drug preconditioning in rat cortex in vitro, finding increased
clustering and increased efficiency in the network over days, implying the drugs enriched the
synaptic connections between groups of neurons. Quantifying manipulations using network
science is an underexplored application, rich in potential.
TRACKING THE EVOLUTION OF DYNAMICS
Neural activity is inherently nonstationary, with population activity moving between differ-
ent states on a range of timescales, from shifting global dynamics on timescales of seconds
(Zagha & McCormick, 2014), to changes wrought by learning on timescales of minutes and
hours (Benchenane et al., 2010; Huber et al., 2012). For a tractable understanding of these
complex changes, ideally we would like a way describe the entire population’s dynamics with
as few parameters as possible. A recent example of such an approach is population coupling,
the correlation over time between a single neuron’s firing rate and the population average rate
(Okun et al., 2015). But with dynamical networks we can use the same set of tools above, and
more, to easily track changes to the population activity in time.
Figure 2 illustrates the idea of tracking nonstationary activity with data from a study by
Peyrache, Khamassi, Benchenane, Wiener, & Battaglia (2009). Rats were required to learn
rules in a Y-maze to obtain reward.
I use here a single session in which a rat learned the
rule “go to the cued arm” (Figure 2A); 52 simultaneously recorded neurons from medial pre-
frontal cortex were active in every trial of this session. As the rat learned the rule in this
session, and activity in medial prefrontal cortex is known to represent changes in behavioral
strategy (Durstewitz, Vittoz, Floresco, & Seamans, 2010; Karlsson, Tervo, & Karpova, 2012;
Powell & Redish, 2016), we might reasonably expect the population activity to evolve during
rule learning. Visualizing trial-by-trial changes using dynamical networks (built as in Figure 1A)
shows a stabilization of the interactions between neurons over trials (Figure 2B). Quantifying
this by correlating weight matrices on consecutive trials (Figure 2C) confirms there was a rapid
stabilization of neuron interactions at the start of this learning session. Plotting the total weight
or total number of links in the network over trials (Figure 2D) shows that this stabilization of
the dynamical network was not a simple consequence of a global stabilization of the interac-
tions between neurons. These analyses thus track potentially learning-induced changes in the
population activity of prefrontal cortex.
We can also use these data to illustrate the benefits we accrue from the null models in net-
work science. These models define the space of possible networks obtained by some stochas-
tic process. Classically, the null model of choice was the Erdos-Renyi random network, which
assumes a uniform probability of a link falling between any pair of nodes. As few if any
real-world networks can be described this way, more detailed null models are now available.
One common example is the configuration model (Chung & Lu, 2002; Fosdick, Larremore,
Nishimura, & Ugander, 2016), in which we assume connections between nodes are made
proportional to the number of links they already have. This model, applied to neural time se-
ries, is a null model for testing whether the existence of interactions between a pair of neurons
is simply a result of those neurons having many interactions. Other null model networks in-
clude the exponential random graph model (Robins, Pattisona, Kalisha, & Lushera, 2007), or
Network Neuroscience
328
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
A
B
Trial 1
Trial 5
Trial 20
d
r
a
w
e
r
e
v
i
t
a
u
m
u
C
l
20
10
0
C
W
f
o
n
o
i
t
a
e
r
r
o
C
l
0.6
0.4
0.2
0
Start
5 10 15 20 25
Trial
D
t
h
g
e
w
i
l
a
t
o
T
120
100
80
60
700
650
600
550
5 10 15 20 25
Trial
5
15
Trial
25
E
T
o
a
t
l
n
u
m
b
e
r
o
f
l
i
n
k
s
t
i
n
e
c
i
f
f
e
o
c
g
n
i
r
e
t
s
u
C
l
0.1
0.05
0
5
F
Data
)
%
(
g
n
i
r
e
t
s
u
c
l
Null Model
s
s
e
c
x
E
150
100
50
0
25
15
Trial
5
15
Trial
25
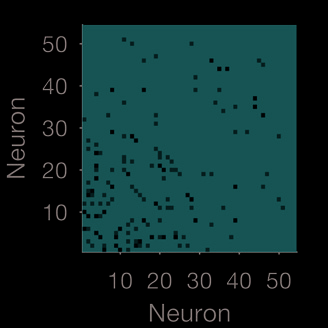
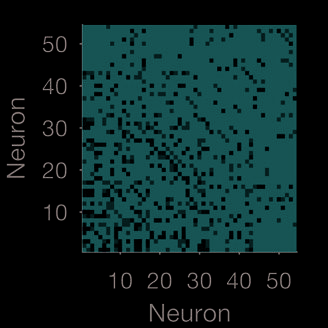
Figure 2. Tracking changes in neural population dynamics using network science. (A) Recordings
examined here are from one behavioral session of a Y-maze learning task. For this session, the rat had
to reach the end of the randomly cued arm to receive reward (schematic, top). This session showed
evidence of behavioral learning (bottom), with a sustained increase in reward accumulation after
Trial 10 (gray line). A trial lasted typically 70 s, running from the rat leaving the start position through
reaching the arm end and returning to the start position to initiate the next trial. The population
activity from a single trial is shown in Figure 1A. (B) Dynamical networks from trials 1, 5, and 20 of
that session. The top row plots the networks, with nodes as neurons and grayscale links indicating
the strength of pairwise interaction. The bottom row plots the corresponding weight matrix (ordered
by total node strength in Trial 1 throughout). The networks show a clear reorganization of inter-
actions between neurons during learning. (C) Tracking network stability. The correlation between
the weight matrix W at trial t and at trial t − 1. The dynamical network rapidly increased in similarity
over the first few trials. Gray line: behavioral learning trial. (D) Changes in total weight (red) and
total number of links (blue) over trials. (E) Clustering coefficient of the weighted network (“Data”)
on each trial; compared with the mean clustering coefficient over 20 null model weighted networks
per trial (“Null Model”). (F) Excess clustering in the data compared with the null model on each
trial (data in panel E expressed as a ratio: 100 × C
model). The variation across trials in the data
is well accounted for by the null model, suggesting the average local clustering did not change over
learning.
/C
data
the stochastic block model and its variants (Newman & Martin, 2014).
In general, network
null models allow us to test whether features of our dynamical networks exceed those
expected by stochastic variation alone.
We use the example of determining whether there is a change in the clustering of inter-
actions between neurons over this example learning session. Figure 2E plots the average
clustering coefficient for the dynamical networks, and we can see that it varies across tri-
als. We can compare this to a suitable null model; here I use a null model that conserves
node strength, but randomly reassigns the set of weights between nodes (Rubinov & Sporns,
2011). Plotting the average clustering coefficient for this null model on each trial shows that
the clustering in the data-derived dynamical networks is well in excess of that predicted by the
Clustering coefficient:
Ratio of weighted triangles to
weighted triples—incomplete
triangles—in the network.
Network Neuroscience
329
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
Motifs:
A specific pattern of connections
between a small number of nodes,
which includes at least one
connection for every node. For
example, in an undirected network,
for 4 nodes there are 5 possible
motifs.
null model: the interactions between groups of three neurons are more dense than predicted
by just their total interactions with all neurons.
But the null model also shows that the average local clustering does not change over
learning. The ratio of the data and model clustering coefficients is approximately constant
(Figure 2F), showing that trial-by-trial variation in clustering is largely accounted for by vari-
ations in the overall interactions between neurons (one source of these might be finite-size
effects in estimating the interactions on trials of different durations). So we can conclude that
changes over behavioral learning in this population of neurons reflected a local reorganiza-
tion (Figure 2B) and stabilization (Figure 2C) of interactions, but which did not change the
population-wide distribution of clustering.
The rich potential for tracking dynamics with the readily available metrics of network sci-
ence has not yet been tapped. As just demonstrated, with dynamical networks we can track
trial-by-trial or event-by-event changes in population dynamics. For long recordings of spon-
taneous activity, building dynamical networks in time windows slid over the recorded data
allows us to track hidden shifts underlying global dynamics (Humphries, 2011). On slower
timescales, we can track changes during development of neural systems, either using ex vivo
slices (Dehorter et al., 2011) or in vitro cultures (Downes et al., 2012; M. S. Schroeter,
Charlesworth, Kitzbichler, Paulsen & Bullmore, 2015). These studies of development have all
shown how maturing neuronal networks move from seemingly randomly distributed inter-
actions between neurons to a structured set of interactions, potentially driven by changes to
the underlying connections between them.
Other tools from network science could be readily repurposed to track neural population
dynamics. The growing field of network comparison uses distributions of network properties to
classify networks (Guimera, Sales-Pardo, & Amaral, 2007; Onnela et al., 2012; Przulj, 2007;
Wegner, Ospina-Forero, Gaunt, Deane, & Reinert, 2017). A particularly promising basis for
comparison is the distributions of motifs (or graphlets) in the networks (Przulj, 2007). Repur-
posed to track changes in dynamical networks, by comparing motif distributions between time
points, these would provide tangible evidence of changes to the information flow in a neural
system.
Ongoing developments in temporal networks (Holme, 2015) and network-based ap-
proaches to change-point detection algorithms (Barnett & Onnela, 2016; Darst et al., 2016;
Peel & Clauset, 2014) also promise powerful yet tractable ways to track neural population
dynamics. Temporal networks in particular offer a ranges of formalisms for tracking changes
In one approach, interaction networks for each slice of time
through time (Holme, 2015).
are coupled by links between the same node in adjacent time slices; this allows testing for
how groups of nodes evolve over time, constrained by their groups in each slice of time
(Bassett et al., 2011; Mucha, Richardson, Macon, Porter, & Onnela, 2010). A range of null
models are available for testing the evolution of networks in this time-slice representation
(Bassett et al., 2013). But such a representation requires coarse-graining of time to capture the
interactions between all nodes in each time slice. An alternative approach is to define a net-
work per small time step, comprising just the interactions that exist at each time step (Holme,
2015; Thompson, Brantefors, & Fransson, 2017), and then introduce the idea of reachability:
that one node is reachable from another if they both link to an intermediate node on different
time steps. With this representation, standard network measures such as path-lengths, clus-
tering, and motifs can be easily generalized to include time (Thompson et al., 2017). Thus, a
Network Neuroscience
330
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
network description of multineuron activity need not just be a frozen snapshot of interactions,
but can be extended to account for changes in time.
NETWORK THEORY QUANTITATIVELY DEFINES COMPUTATIONAL CONCEPTS OF
NEURAL POPULATIONS
The mathematical framework of networks can also provide precise quantitative definitions of
important but qualitative theories about neural populations. A striking example is the theory
of neural ensembles (Harris, 2005). An ensemble is qualitatively defined as a set of neurons
that are consistently coactive (Harris, 2005), thereby indicating they code or compute the
same thing. This qualitative definition leaves open key quantitative questions: What defines
coactive, and what defines consistent?
The network science concept of modularity provides answers to these questions. Many
networks are modular, organized into distinct groups: social networks of friendship groups,
or collaboration networks of scientists. Consequently, the problem of finding modules within
networks in an unsupervised way is an extraordinarily fecund research field (Fortunato & Hric,
2016). Most approaches to finding modules are based on the idea of finding the division of the
network that maximizes its modularity Q = {number of links within a module} − {expected
number of such links} (Newman, 2006). Maximizing Q thus finds a division of a network
in which the modules are densely linked within themselves, and weakly linked between
them.
Applied to dynamical networks, modularity defines neural ensembles (Billeh, Schaub,
Anastasiou, Barahona, & Koch, 2014; Bruno et al., 2015; Humphries, 2011): groups of neu-
rons that are more coactive with each other than with any other neurons in the population,
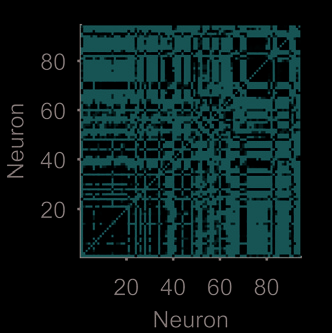
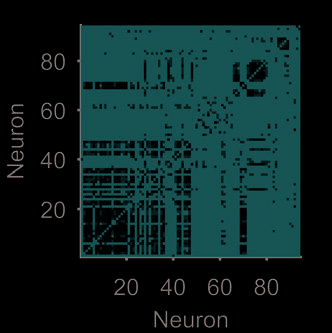
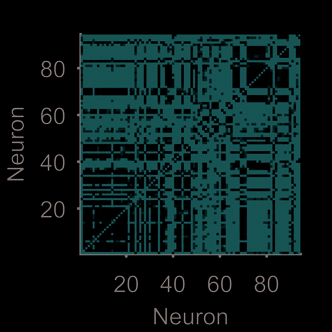
given the choice of pairwise interaction used. Figure 3 demonstrates this idea using an example
recording of 94 neurons from the motor circuit of the sea slug Aplysia during fictive locomo-
tion (Bruno et al., 2015). The weight matrix and network views in Figure 3A clearly indicate
some structure within the dynamical network. Applying an unsupervised module-detection
algorithm finds a high modularity division of the dynamical network (Figure 3B). When we
plot the 94 spike trains grouped by their modules in the dynamical network, the presence of
multiple ensembles is clear (Figure 3C).
With this modularity-based approach, we can also easily check how robust these ensembles
are to the choice of timescale of coactivity. When computing pairwise interactions, we often
have a choice of temporal precision, such as bin size or Gaussian width (Figure 1A): Choosing
small values emphasizes spike-time precision; large values emphasize covarying firing rates.
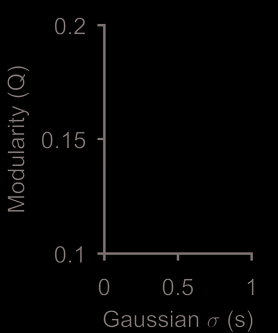
As shown in Figure 3D, we can also use Q to look for timescales at which the population
dynamics are most structured (Humphries, 2011): This view suggests a clear peak timescale at
which the ensembles are structured. Nonetheless, we can also see a consistent set of modules
at all timescales: The weight matrix W at the smallest and largest Gaussian width are simi-
lar (Figure 3E); and the majority of neurons are placed in the same group at every timescale
(Figure 3F). Modularity not only defines ensembles, but also lets us quantify their timescales
and find consistent structure across timescales.
The complexity of the population activity will determine whether a consistent set of
ensembles appears across timescales, or whether there are different ensembles at different
timescales (see Humphries, 2011, for more examples). We can see this when running the same
module-detection analysis on a session from the medial prefrontal cortex data (Figure 3G–I).
Network Neuroscience
331
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
A
D
G
0.2
B
i
w
e
g
h
t
E
H
(cid:1) = 0.05 s
(cid:1) = 1 s
(cid:1) = 0.1 s
(cid:1) = 0.05 s
(cid:1) = 0.5 s
(cid:1) = 1 s
C
F
I
)
Q
(
l
y
t
i
r
a
u
d
o
M
0.15
0.1
0
0.25
0.5
Gaussian (cid:1) (s)
s
a
m
e
e
n
s
e
m
b
e
(
p
)
l
l
C
u
s
t
e
r
e
d
i
n
s
a
m
e
e
n
s
e
m
b
e
(
p
)
l
l
C
u
s
t
e
r
e
d
i
n
Figure 3. Defining and detecting neural ensembles using network science.
(A) A dynamical
network of population dynamics during crawling in Aplysia. The weight matrix (top) and net-
work view (bottom) for a simultaneous recording of 94 neurons during 90 seconds from the ini-
tiation of crawling (from the experimental protocol of Bruno et al., 2015). Weights are rectified
Pearson’s R between pairs of neurons convolved with a Gaussian of σ = 0.306 s (using the
median interspike interval of the recording as an initial guide to timescale, as in Bruno et al.,
2015).
(B) Modules within the dynamical network. Colored nodes indicate different modules
found within the dynamical network using an unsupervised consensus module-detection algo-
rithm (Bruno et al., 2015). Placement of the modules reflects the similarity between them (Traud,
Frost, Mucha, & Porter, 2009). (C) Raster plot of the corresponding spike trains, grouped according
to the modules in panel B. The detection of multiple neural ensembles is evident. (D) Dependence
of the modular structure on the timescale of correlation. Smaller Gaussian σ detects precise
spike-timing; larger σ detects covariation in firing rates. Circle:
timescale used in panels A–C.
(E) Weight matrices for the smallest and largest timescale used for the Gaussian convolution.
Neurons are plotted in descending order of total weight in the shorter timescale.
(F) Stability
of modules over timescales. We plot here a confusion matrix, in which each is the proportion
of timescales for which that pair of neurons was placed in the same module. The majority of
neuron pairs were placed in the same module at every timescale. (G–I) Comparable analysis for
the medial prefrontal cortex data. (G) Dependence of Q on the timescale of correlation, for every
trial in one session (from Figure 2). Black: learning trial; red: prelearning trial; blue: postlearning
trial. (H) As for panel E, for the learning trial of the medial prefrontal cortex data. (I) As for panel F,
for the learning trial.
Network Neuroscience
332
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
For this cortical data there are modules present at every timescale, but no consistent timescale
at which the neural activity is most structured (Figure 3G–H). Consequently, there is not a
consistent set of modules across timescales (Figure 3I).
Such multiscale structure is potentially a consequence of the order-of-magnitude distribu-
tion in firing rates (Dann et al., 2016; Wohrer et al., 2013), for which more work is needed on
suitable measures of interaction. It may also indicate that some neurons are members of more
than one ensemble, which are active at different times during the recording. Consequently,
these neurons’ correlations with others will depend on the timescale examined. Examining
the detected modules for nodes that participate in more than one module (Guimera & Amaral,
2005; Guimera et al., 2007) may reveal these shared neurons. Clearly, such multiscale struc-
ture means that tracking changes in the structure of population activity should be done at a
range of timescales, and comparisons made based on similar timescales.
As a final step, we can now quantitatively define a Hebbian cell assembly (Holtmaat &
Caroni, 2016). By definition, a cell assembly is an ensemble of neurons that become coactive
because of changes to synaptic connections into and between them during learning (Carrillo-
Reid et al., 2016). Thus, by combining the ideas of tracking dynamical networks and of module
detection, we can test for the formation of assemblies: If we find dynamical network modules
that appear during the course of learning, then we have identified potential cell assemblies.
OUTLOOK
The dynamics of neural populations are emergent properties of the wiring within their microcir-
cuits. We can of course use network science to describe physical networks of the micro-
circuit too (Humphries, Gurney, & Prescott, 2006; Lee et al., 2016; M. Schroeter, Paulsen, &
Bullmore, 2017), gaining insight into the mapping from wiring to dynamics. But dynamical
networks need not map to any circuit. Indeed while dynamical networks are constrained by
their underlying physical connections, they can change faster than their corresponding phys-
ical networks. A clear example is with the actions of neuromodulators—these can increase
or decrease the effective strength of connections between neurons and the responsiveness
of individual neurons (Nadim & Bucher, 2014), so changing the dynamical network without
changing the underlying physical network. More broadly, rapid, global changes in brain state
can shift the dynamics of a neural population (Zagha & McCormick, 2014). Thus, dynamical
networks describing the simultaneous activity of multiple neurons capture the moment-to-
moment changes in population dynamics.
There are of course other analysis frameworks for visualizing and describing the activity
of large neural populations. The detection of neural ensembles is an unsupervised cluster-
ing problem, for which a number of neuroscience-specific solutions exist (Feldt, Waddell,
Hetrick, Berke, & Zachowski, 2009; Fellous, Tiesinga, Thomas, & Sejnowski, 2004; Lopes-
dos-Santos, Conde-Ocazionez, Nicolelis, Ribeiro, & Tort, 2011; Russo & Durstewitz, 2017).
Some advantages of network science here are that the detection of ensembles is but one ap-
plication of the same representation of the population activity; that a range of null models is
available for testing hypotheses of clustering; and that the limitations of module detection are
well established, allowing comparatively safe interpretation of the results (Fortunato & Hric,
2016; Good, de Montjoye, & Clauset, 2010). More generally, analyses of neural population
recordings have used dimension-reduction approaches in order to visualize and describe the
dynamics of the population (Cunningham & Yu, 2014; Pang, Lansdell, & Fairhall, 2016). As
discussed in Box 1, both network and dimension-reduction approaches offer powerful, com-
plementary views of complex neural dynamics.
Network Neuroscience
333
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
Box 1. Networks and dimension-reduction approaches
Dimension-reduction approaches to neural population recordings aim to find a com-
pact description of the population’s activity using many fewer variables than neurons
(Pang et al., 2016). Typical approaches include principal components analysis (PCA) and
factor analysis, both of which aim to find a small set of dimensions in which the
population activity can be described with minimal
information (Ahrens et al.,
2012; Bartho, Curto, Luczak, Marguet, & Harris, 2009; Briggman et al., 2005; Bruno et al.,
2015; Kato et al., 2015; Levi, Varona, Arshavsky, Rabinovich, & Selverston, 2005; Mazor
& Laurent, 2005; Wohrer et al., 2013). More complex variants of these standard approaches
can cope with widely varying timescales in cortical activity (B. M. Yu et al., 2009), or aim
to decompose multiplexed encodings of stimulus variables by the population’s activity into
different dimensions (Kobak et al., 2016).
loss of
Both network and standard dimension-reduction approaches have in common the starting
point of a pairwise interaction matrix. PCA, for example, traditionally uses the covariance
matrix as its starting point. Consequently, both approaches assume that the relationships be-
tween neurons are static over the duration of the data from which the matrix is constructed.
(This assumption is also true for dimension-reduction methods that fit generative models,
such as independent component analysis or Gaussian process factor analysis [B. M. Yu et al.,
2009], as fitting the model also assumes stationarity in the model’s parameters over the dura-
tion of the data.)
Where the approaches diverge is in their advantages and limitations. Dimension-reduction
approaches offer the advantage of easy visualization of the trajectories of the population
activity over time. This in turn allows for potentially strong qualitative conclusions, either
about the conditions under which the trajectories differ—such as in encoding different stimuli
(Kobak et al., 2016; Mazor & Laurent, 2005) or making different decisions (Briggman et al.,
2005; Harvey, Coen, & Tank, 2012)—or about the different states repeatedly visited by the
population during movement
(Ahrens et al., 2012; Bruno, Frost, & Humphries, 2017;
Kato et al., 2015; B. M. Yu et al., 2009). By contrast, there are not yet well-established ways of
drawing quantitative conclusions from standard dimension-reduction approaches, nor of how
to track changes in the population dynamics over time, such as through learning. Further,
while reducing the dimensions down to just those accounting for a high proportion of the
variance (or similar) in the population activity can remove noise, it also risks removing some
of the higher-dimensional, and potentially informative, dynamics in the population. Finally,
to date, most applications of dimension-reduction approaches have been based on just the
pairwise covariance or correlation coefficient.
As I have demonstrated here, network-based approaches take a different slant on simplifying
complex dynamics. The network description maintains a representation of every neuron, and
so potentially captures all dynamical relationships that might be removed by dimension re-
duction. It is simple to use any measure of pairwise interaction, without changing the analysis.
Quantitative analyses of either static (Figure 1) or changing (Figure 2) population activity are
captured in simple, compact variables. And we have access to a range of null models for test-
ing the existence of meaningful interactions between neurons and changes to those interac-
tions. However, interpreting some of these quantifying variables, such as efficiency, in terms of
neural activity is not straightforward. And it is not obvious how to visualize trial-by-trial pop-
ulation activity, nor how to draw qualitative conclusions about different trajectories or states
of the activity. Consequently, combining both network and dimension-reduction approaches
could offer complementary insights into a neural population’s dynamics (Bruno et al., 2015).
One motivation for turning to network science as a toolbox for systems neuroscience is
rooted in the extraordinarily rapid advances in recording technology, now scaling to hundreds
or thousands of simultaneously recorded neurons (Stevenson & Kording, 2011). Capturing
whole nervous systems of even moderately complex animal models will require scaling by
Network Neuroscience
334
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
further orders of magnitude (Ahrens et al., 2012; Lemon et al., 2015). And here is where net-
work science has its most striking advantage: These tools have been developed to address
social and technological networks of millions of nodes or more, so easily scale to systems
neuroscience problems now and in the foreseeable future.
This is not a one-way street. Systems neuroscience poses new challenges for network sci-
ence. Most studies in network science concern a handful of static or slowly changing data
networks. Neural populations have nonstationary dynamics, which change rapidly compared
with the temporal resolution of our recordings. And systems neuroscience analysis requires
quantitatively comparing multiple defined networks within and between brain regions, within
and between animals, and across experimental conditions—stimuli, decisions, and other ex-
ternal changes. More work is needed, for example, on appropriate null models for weighted
networks (Palowitch, Bhamidi, & Nobel, 2016; Rubinov & Sporns, 2011); and on appropriate
ways to regularise such networks, in order to separate true interactions from stochastic noise
(MacMahon & Garlaschelli, 2015). Bringing network science to bear on challenges in systems
neuroscience will thus create a fertile meeting of minds.
ACKNOWLEDGMENTS
I thank Silvia Maggi for reading a draft, Adrien Peyrache for permission to use the rat medial
prefrontal cortex data, and Angela Bruno and Bill Frost for permission to use the Aplysia pedal
ganglion data.
SUPPORTING INFORMATION
Visualizations and analyses here drew on a range of open-source MATLAB (Mathworks, NA)
toolboxes:
Brain Connectivity Toolbox (Rubinov & Sporns, 2010): https://sites.google.
com/site/bctnet/
Network vizualizations used the MATLAB code of Traud et al.
(2009), available here:
http://netwiki.amath.unc.edu/VisComms. This also the needs MatlabBGL
library: http://uk.mathworks.com/matlabcentral/fileexchange/10922-
matlabbgl. Mac OSX 64-bit users will need this version: https://dgleich.
wordpress.com/2010/07/08/matlabbgl-osx-64-bit/
Spike-Train Communities Toolbox (Bruno et al., 2015; Humphries, 2011): implement-
ing unsupervised consensus algorithms for module detection https://github.com/
mdhumphries/SpikeTrainCommunitiesToolBox
AUTHOR CONTRIBUTION
Mark D Humphries: Conceptualization; Formal Analysis; Investigation; Visualization; Writing
FUNDING INFORMATION
This work was funded by a Medical Research Council Senior Non-Clinical Fellowship (MR/
J008648/1), and a Medical Research Council research grant (MR/P005659/1).
Network Neuroscience
335
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
REFERENCES
Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore,
E. (2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. Journal of Neuroscience, 26(1), 63–72.
Ahrens, M. B., Li, J. M., Orger, M. B., Robson, D. N., Schier,
A. F., Engert, F., & Portugues, R.
(2012). Brain-wide neuronal
dynamics during motor adaptation in zebrafish. Nature, 485,
471–477.
Baeg, E. H., Kim, Y. B., Kim, J., Ghim, J.-W., Kim, J. J., & Jung,
M. W.
(2007). Learning-induced enduring changes in func-
tional connectivity among prefrontal cortical neurons. Journal of
Neuroscience, 27, 909–918.
Barnett, I., & Onnela, J.-P. (2016). Change point detection in cor-
relation networks. Scientific Reports, 6, 18893.
Bartho, P., Curto, C., Luczak, A., Marguet, S. L., & Harris, K. D.
(2009). Population coding of tone stimuli in auditory cortex:
Dynamic rate vector analysis. European Journal of Neuroscience,
30(9), 1767–1778.
Bassett, D. S., & Bullmore, E. T. (2016). Small-world brain networks
revisited. The Neuroscientist.
Bassett, D. S., Porter, M. A., Wymbs, N. F., Grafton, S. T., Carlson,
(2013). Robust detection of dynamic
J. M., & Mucha, P. J.
community structure in networks. Chaos, 23, 013142.
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
(2011). Dynamic reconfiguration of
Proceedings of the
J. M., & Grafton, S. T.
human brain networks during learning.
National Academy of Sciences, 108, 7641–7646.
Benchenane, K., Peyrache, A., Khamassi, M., Tierney, P. L.,
(2010). Coherent
Gioanni, Y., Battaglia, F. P., & Wiener, S. I.
theta oscillations and reorganization of spike timing in the
hippocampal-prefrontal network upon learning. Neuron, 66(6),
921–936.
Bettencourt, L. M. A., Stephens, G. J., Ham, M. I., & Gross, G. W.
(2007). Functional structure of cortical neuronal networks grown
in vitro. Physical Review E, 75(2. Pt. 1), 021915.
Billeh, Y. N., Schaub, M. T., Anastassiou, C. A., Barahona, M., &
Koch, C. (2014). Revealing cell assemblies at multiple levels of
granularity. Journal of Neuroscience Methods, 236, 92–106.
Boyden, E. S. (2015). Optogenetics and the future of neuroscience.
Nature Neuroscience, 18, 1200–1201.
Briggman, K. L., Abarbanel, H. D. I., & Kristan, W., Jr. (2005). Op-
tical imaging of neuronal populations during decision-making.
Science, 307(5711).
Bruno, A. M., Frost, W. N., & Humphries, M. D.
Bruno, A. M., Frost, W. N., & Humphries, M. D. (2017). A spiral
attractor network drives rhythmic locomotion. eLife, 6, e27342.
(2015). Modu-
lar deconstruction reveals the dynamical and physical building
blocks of a locomotion motor program. Neuron, 86, 304–318.
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10, 186–198.
Buzsáki, G. (2004). Large-scale recording of neuronal ensembles.
Nature Neuroscience, 7, 446–451.
Carrillo-Reid, L., Yang, W., Bando, Y., Peterka, D. S., & Yuste, R.
Imprinting and recalling cortical ensembles. Science,
(2016).
353, 691–694.
Chen, T.-W., Wardill, T. J., Sun, Y., Pulver, S. R., Renninger,
S. L., Baohan, A.,
(2013). Ultrasensitive
fluorescent proteins for imaging neuronal activity. Nature, 499,
295–300.
. . . Kim, D. S.
Chung, F., & Lu, L.
(2002). Connected components in random
graphs with given expected degree sequences. Annals of Combi-
natorics, 6, 124–145.
Cunningham, J. P., & Yu, B. M. (2014). Dimensionality reduction
for large-scale neural recordings. Nature Neuroscience, 17,
1500–1509.
Dann, B., Michaels,
J. A., Schaffelhofer, S., & Scherberger, H.
(2016). Uniting functional network topology and oscillations
in the fronto-parietal single unit network of behaving primates.
eLife, 5, e15719.
Darst, R. K., Granell, C., Arenas, A., Gómez, S., Saramäki, J., &
(2016). Detection of timescales in evolving
Fortunato, S.
complex systems. Scientific Reports, 6, 39713.
. . . Hammond, C.
Dehorter, N., Michel, F., Marissal, T., Rotrou, Y., Matrot, B., Lopez,
C.,
(2011). Onset of pup locomotion
coincides with loss of NR2C/D-mediated corticostriatal EPSCs
and dampening of striatal network immature activity. Frontiers
Cellular Neuroscience, 5, 24.
Deisseroth, K.
(2015). Optogenetics: 10 years of microbial
opsins in neuroscience. Nature Neuroscience, 18(9), 1213–
1225.
Downes, J. H., Hammond, M. W., Xydas, D., Spencer, M. C.,
Becerra, V. M., Warwick, K., . . . Nasuto S. J.
(2012). Emer-
gence of a small-world functional network in cultured neurons.
PLoS Computational Biology, 8(5), e1002522.
Dupre, C., & Yuste, R. (2017). Non-overlapping neural networks in
Hydra vulgaris. Current Biology, 27, 1085–1097.
Durstewitz, D., Vittoz, N. M., Floresco, S. B., & Seamans, J. K.
(2010). Abrupt transitions between prefrontal neural ensem-
ble states accompany behavioral transitions during rule learning.
Neuron, 66, 438–448.
Feldt, S., Waddell, J., Hetrick, V. L., Berke, J. D., & Zochowski,
(2009). Functional clustering algorithm for the analysis of
M.
dynamic network data. Physical Review E, 79, 056104.
Fellous, J. M., Tiesinga, P. H., Thomas, P. J., & Sejnowski, T. J.
(2004). Discovering spike patterns in neuronal responses. Journal
of Neuroscience, 24(12), 2989–3001.
Fortunato, S., & Hric, D. (2016). Community detection in networks:
A user guide. Physics Reports, 659, 1–44.
Fosdick, B. K., Larremore, D. B., Nishimura, J., & Ugander, J. (2016).
Configuring random graph models with fixed degree sequences.
arXiv:1608.00607
Frady, E. P., Kapoor, A., Horvitz, E., & Kristan, W. B., Jr. (2016). Scal-
able semisupervised functional neurocartography reveals canon-
ical neurons in behavioral networks. Neural Computation, 28(8),
1453–1497.
Network Neuroscience
336
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
Gerhard, F., Pipa, G., Lima, B., Neuenschwander, S., & Gerstner,
W. (2011). Extraction of network topology from multi-electrode
recordings: Is there a small-world effect? Frontiers in Computa-
tional Neuroscience, 5, 4.
Good, B. H., de Montjoye, Y.-A., & Clauset, A.
(2010). Perfor-
mance of modularity maximization in practical contexts. Physical
Review E, 81, 046106.
Grewe, B. F., Gründemann, J., Kitch, L. J., Lecoq, J. A., Parker, J. G.,
Marshall, J. D., . . . Schnitzer, M. J.
(2017). Neural ensemble
dynamics underlying a long-term associative memory. Nature,
543, 670–675.
Guimera, R., & Amaral, L. A. N. (2005). Cartography of complex
Journal of Statistical
networks: Modules and universal roles.
Mechanics, P02001.
Guimera, R., Sales-Pardo, M., & Amaral, L. A. N. (2007). Classes of
complex networks defined by role-to-role connectivity profiles.
Nature Physics, 3(1), 63–69.
Harris, K. D. (2005). Neural signatures of cell assembly organiza-
tion. Nature Reviews Neuroscience, 6, 399–407.
Harris, K. D., Quiroga, R. Q., Freeman, J., & Smith, S. L. (2016). Im-
proving data quality in neuronal population recordings. Nature
Neuroscience, 19, 1165–1174.
Harvey, C. D., Coen, P., & Tank, D. W.
(2012). Choice-specific
sequences in parietal cortex during a virtual-navigation decision
task. Nature, 484(7392), 62–68.
Holme, P. (2015). Modern temporal network theory: A colloquium.
European Physical Journal B, 88, 234.
Holtmaat, A., & Caroni, P. (2016). Functional and structural under-
pinnings of neuronal assembly formation in learning. Nature
Neuroscience, 19, 1553–1562.
Huber, D., Gutnisky, D. A., Peron, S., O’Connor, D. H., Wiegert,
J. S., Tian, L., . . . Svoboda, K.
(2012). Multiple dynamic rep-
resentations in the motor cortex during sensorimotor learning.
Nature, 484(7395), 473–478.
Humphries, M. D. (2011). Spike-train communities: Finding groups
of similar spike trains. Journal of Neuroscience, 31, 2321–2336.
Humphries, M. D., Gurney, K., & Prescott, T. J. (2006). The brain-
stem reticular formation is a small-world, not scale-free, network.
the Royal Society of London B: Biological
Proceedings of
Sciences, 273, 503–511.
Jun, J. J., Mitelut, C., Lai, C., Gratiy, S., Anastassiou, C., & Harris,
T. D.
(2017). Real-time spike sorting platform for high-density
extracellular probes with ground-truth validation and drift cor-
rection. bioRxiv:101030
Karlsson, M. P., Tervo, D. G. R., & Karpova, A. Y. (2012). Network
resets in medial prefrontal cortex mark the onset of behavioral
uncertainty. Science, 338, 135–139.
Kato, S., Kaplan, H. S., Schrödel, T., Skora, S., Lindsay, T. H.,
Yemini, E., . . . Zimmer, M. (2015). Global brain dynamics embed
the motor command sequence of caenorhabditis elegans. Cell,
163, 656–669.
Kobak, D., Brendel, W., Constantinidis, C., Feierstein, C. E., Kepecs,
(2016). Demixed prin-
Life, 5,
A., Mainen, Z. F., . . . Machens, C. K.
cipal component analysis of neural population data.
e10989.
Latora, V., & Marchiori, M.
(2001). Efficient behaviour of small-
world networks. Physical Review Letters, 87, 198701.
Laubach, M., Wessberg, J., & Nicolelis, M. A. (2000). Cortical en-
semble activity increasingly predicts behaviour outcomes during
learning of a motor task. Nature, 405(6786).
Lee, W.-C. A., Bonin, V., Reed, M., Graham, B. J., Hood, G.,
(2016). Anatomy and function of an ex-
Glattfelder, K., et al.
citatory network in the visual cortex. Nature, 532, 370–374.
Lemon, W. C., Pulver, S. R., Höckendorf, B., McDole, K., Branson,
K., Freeman, J., & Keller, P. J.
(2015). Whole-central nervous
system functional imaging in larval Drosophila. Nature Commu-
nications, 6, 7924.
Levi, R., Varona, P., Arshavsky, Y. I., Rabinovich, M. I., & Selverston,
A. I. (2005). The role of sensory network dynamics in generating
a motor program. Journal of Neuroscience, 25(42), 9807–9815.
Lopes-dos-Santos, V., Conde-Ocazionez, S., Nicolelis, M. A. L.,
Ribeiro, S. T., & Tort, A. B. L. (2011). Neuronal assembly detec-
tion and cell membership specification by principal component
analysis. PLoS ONE, 6(6), e20996.
Lyttle, D., & Fellous, J.-M.
(2011). A new similarity measure for
spike trains: Sensitivity to bursts and periods of inhibition. Jour-
nal of Neuroscience Methods, 199(2), 296–309.
MacMahon, M., & Garlaschelli, D. (2015). Community detection
for correlation matrices. Physical Review X, 5, 021006.
Mazor, O., & Laurent, G. (2005). Transient dynamics versus fixed
points in odor representations by locust antennal lobe projection
neurons. Neuron, 48(4), 661–673.
Miesenböck, G.
(2009). The optogenetic catechism. Science,
326(5951), 395–399.
Mucha, P. J., Richardson, T., Macon, K., Porter, M. A., & Onnela,
J.-P. (2010). Community structure in time-dependent, multiscale,
and multiplex networks. Science, 328(5980), 876–878.
Nadim, F., & Bucher, D. (2014). Neuromodulation of neurons and
synapses. Current Opinion in Neurobiology, 29, 48–56.
Newman, M. E. J. (2003). The structure and function of complex
networks. SIAM Review, 45, 167–256.
Newman, M. E. J. (2004). Analysis of weighted networks. Physical
Review E, 70, 056131.
Newman, M. E. J.
(2006). Finding community structure in net-
works using the eigenvectors of matrices. Physical Review E, 74,
036104.
Newman, M. E. J., & Martin, T. (2014). Equitable random graphs.
Physical Review E, 90, 052824.
Nigam, S., Shimono, M.,
Ito, S., Yeh, F.-C., Timme, N.,
Myroshnychenko, M., . . . Beggs, J. M.
(2016). Rich-club
organization in effective connectivity among cortical neurons.
Journal of Neuroscience, 36, 670–684.
Okun, M., Steinmetz, N. A., Cossell, L., Iacaruso, M. F., Ko, H.,
(2015). Diverse coupling of neu-
Barth, P., . . . Harris, K. D.
rons to populations in sensory cortex. Nature, 521, 511–515.
Onnela, J.-P., Fenn, D. J., Reid, S., Porter, M. A., Mucha, P. J.,
(2012). Taxonomies of networks
Fricker, M. D., & Jones, N. S.
from community structure. Physical Review E, 86, 036104.
Otchy, T. M., Wolff, S. B. E., Rhee, J. Y., Pehlevan, C., Kawai, R.,
Kempf, A., . . . Ölveczky, B. P. (2015). Acute off-target effects of
neural circuit manipulations. Nature, 528, 358–363.
Network Neuroscience
337
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Networks of neural dynamics
Palowitch, J., Bhamidi, S., & Nobel, A. B.
(2016). The contin-
uous configuration model: A null for community detection on
weighted networks. arXiv:1601.05630
Pang, R., Lansdell, B. J., & Fairhall, A. L. (2016). Dimensionality re-
duction in neuroscience. Current Biology, 26(14), R656–R660.
Peel, L., & Clauset, A. (2014). Detecting change points in the large-
scale structure of evolving networks. arXiv:1403–0989
Peron, S., Chen, T.-W., & Svoboda, K.
(2015). Comprehensive
imaging of cortical networks. Current Opinion in Neurobiology,
32, 115–123.
Peron, S. P., Freeman, J., Iyer, V., Guo, C., & Svoboda, K.
(2015).
A cellular resolution map of barrel cortex activity during tactile
behavior. Neuron, 86, 783–799.
Peyrache, A., Khamassi, M., Benchenane, K., Wiener, S. I., &
Battaglia, F. P. (2009). Replay of rule-learning related neural pat-
terns in the prefrontal cortex during sleep. Nature Neuroscience,
12, 916–926.
Pillow,
J. W., Shlens,
J., Paninski, L., Sher, A., Litke, A. M.,
Chichilnisky, E. J., & Simoncelli, E. P.
(2008). Spatio-temporal
correlations and visual signalling in a complete neuronal popu-
lation. Nature, 454, 995–999.
Pouget, A., Beck, J. M., Ma, W. J., & Latham, P. E.
(2013). Prob-
abilistic brains: Knowns and unknowns. Nature Neuroscience,
16(9), 1170–1178.
Powell, N. J., & Redish, A. D. (2016). Representational changes of
latent strategies in rat medial prefrontal cortex precede changes
in behaviour. Nature Communications, 7, 12830.
Przulj, N.
(2007). Biological network comparison using graphlet
degree distribution. Bioinformatics, 23, e177–e183.
Rieke, F., Warland, D., de Ruyter van Stevninck, R., & Bialek, W.
(1999). Spikes: Exploring the neural code. Cambridge, MA: MIT
Press.
Robins, G., Pattisona, P., Kalisha, Y., & Lushera, D. (2007). An in-
troduction to exponential random graph (p*) models for social
networks. Social Networks, 29, 173–191.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52,
1059–1069.
Rubinov, M., & Sporns, O. (2011). Weight-conserving characteri-
zation of complex functional brain networks. NeuroImage, 56,
2068–2079.
Russo, E., & Durstewitz, D. (2017). Cell assemblies at multiple time
scales with arbitrary lag constellations. eLife, 6, e19428.
Sadovsky, A. J., & MacLean, J. N.
(2013). Scaling of topologi-
cally similar functional modules defines mouse primary auditory
and somatosensory microcircuitry. Journal of Neuroscience, 33,
14048–14060.
Schreiber, T.
(2000). Measuring information transfer. Physical
Review Letters, 85, 461–464.
Schroeter, M., Paulsen, O., & Bullmore, E. T.
(2017). Micro-
connectomics: Probing the organization of neuronal networks at
the cellular scale. Nature Reviews Neuroscience, 18, 131–146.
Schroeter, M. S., Charlesworth, P., Kitzbichler, M. G., Paulsen, O.,
& Bullmore, E. T. (2015). Emergence of rich-club topology and
coordinated dynamics in development of hippocampal func-
Journal of Neuroscience, 35, 5459–
tional networks in vitro.
5470.
Singh, A., & Lesica, N. A. (2010). Incremental mutual information:
A new method for characterizing the strength and dynamics of
connections in neuronal circuits. PLoS Computational Biology,
6, e1001035.
Srinivas, K. V., Jain, R., Saurav, S., & Sikdar, S. K.
(2007). Small-
world network topology of hippocampal neuronal network is
lost, in an in vitro glutamate injury model of epilepsy. European
Journal of Neuroscience, 25, 3276–3286.
Stevenson, I. H., & Kording, K. P.
(2011). How advances in
neural recording affect data analysis. Nature Neuroscience, 14,
139–142.
Thivierge, J.-P. (2014). Scale-free and economical features of func-
tional connectivity in neuronal networks. Physical Review E, 90,
022721.
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static
to temporal network theory: Applications to functional brain con-
nectivity. Network Neuroscience, 1, 69–99. https://doi.org/10.
1162/netn_a_00011
Traud, A. L., Frost, C., Mucha, P. J., & Porter, M. A. (2009). Visual-
ization of communities in networks. Chaos, 19, 041104.
Truccolo, W., Eden, U. T., Fellows, M. R., Donoghue, J. P., & Brown,
(2005). A point process framework for relating neural
E. N.
spiking activity to spiking history, neural ensemble, and extrinsic
covariate effects. Journal of Neurophysiology, 93, 1074–1089.
van Rossum, M. C. (2001). A novel spike distance. Neural Compu-
tation, 13(4), 751–763.
Victor, J. D., & Purpura, K. P. (1996). Nature and precision of tem-
poral coding in visual cortex: A metric-space analysis. Journal of
Neurophysiology, 76(2), 1310–1326.
Vincent, K., Tauskela,
J.-P.
(2013). Altered network communication following a neuropro-
tective drug treatment. PloS ONE, 8, e54478.
J. S., Mealing, G. A., & Thivierge,
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-
world” networks. Nature, 393, 440–442.
Wegner, A. E., Ospina-Forero, L., Gaunt, R. E., Deane, C. M., &
(2017). Identifying networks with common organi-
Reinert, G.
zational principles. arXiv:1704.00387
Wohrer, A., Humphries, M. D., & Machens, C. (2013). Population-
wide distributions of neural activity during perceptual decision-
making. Progress in Neurobiology, 103, 156–193.
Yamada, Y., Bhaukaurally, K., Madarász, T.
J., Pouget, A.,
Rodriguez, I., & Carleton, A. (2017). Context- and output layer-
dependent long-term ensemble plasticity in a sensory circuit.
Neuron, 93, 1198–1212.e5.
Yu, B. M., Cunningham, J. P., Santhanam, G., Ryu, S. I., Shenoy,
K. V., & Sahani, M. (2009). Gaussian-process factor analysis for
low-dimensional single-trial analysis of neural population activ-
ity. Journal of Neurophysiology, 102, 614–635.
Yu, S., Huang, D., Singer, W., & Nikolic, D. (2008). A small world
of neuronal synchrony. Cerebral Cortex, 18, 2891–2901.
Yuste, R.
(2015). From the neuron doctrine to neural networks.
Nature Reviews Neuroscience, 16, 487–497.
Zagha, E., & McCormick, D. A.
(2014). Neural control of brain
state. Current Opinion in Neurobiology, 29, 178–186.
Zanin, M., Sousa, P., Papo, D., Bajo, R., García-Prieto, J., del Pozo,
F., . . . Boccaletti, S. (2012). Optimizing functional network rep-
resentation of multivariate time series. Scientific Reports, 2, 630.
Network Neuroscience
338
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
3
2
4
1
0
9
1
8
5
2
n
e
n
_
a
_
0
0
0
2
0
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3