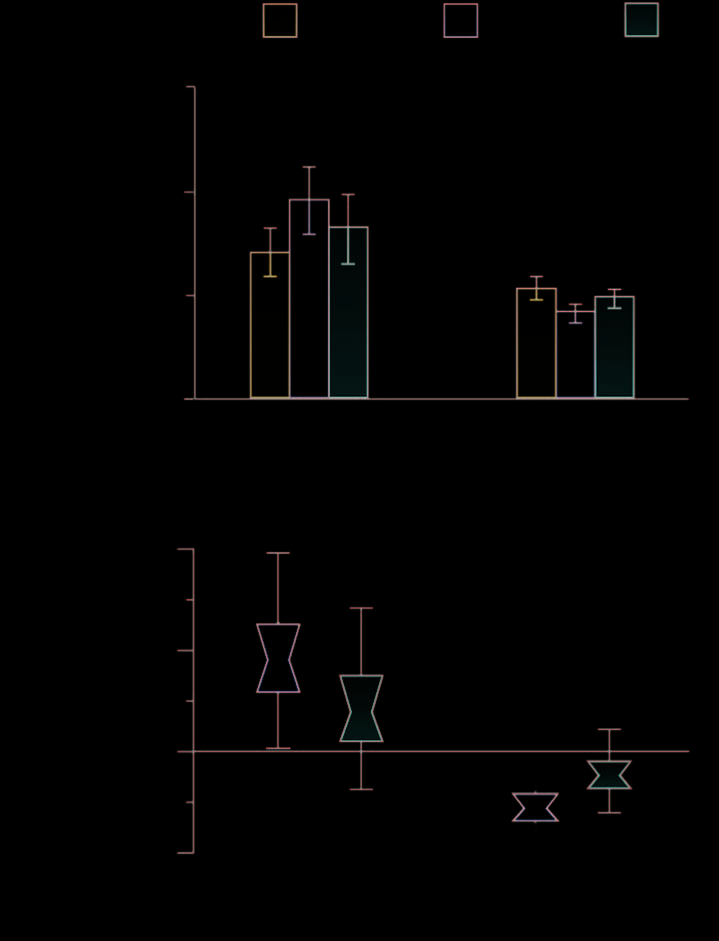Perceptual Integration for Qualitatively Different 3-D - Am MIT spezialisierte KI-Forschung

Perceptual Integration for Qualitatively Different 3-D
Cues in the Human Brain

Dicle Dövencioğlu1*, Hiroshi Ban1,2*, Andrew J. Schofield1,
and Andrew E. Welchman1

Abstrakt

■ The visual systemʼs flexibility in estimating depth is remark-
able: We readily perceive 3-D structure under diverse condi-
tions from the seemingly random dots of a “magic eye”
stereogram to the aesthetically beautiful, but obviously flat,
canvasses of the Old Masters. Noch, 3-D perception is often en-
hanced when different cues specify the same depth. This per-
ceptual process is understood as Bayesian inference that
improves sensory estimates. Despite considerable behavioral
support for this theory, insights into the cortical circuits in-
volved are limited. Darüber hinaus, extant work tested quantitatively
similar cues, reducing some of the challenges associated with
integrating computationally and qualitatively different signals.
Here we address this challenge by measuring fMRI responses
to depth structures defined by shading, binocular disparity,

and their combination. We quantified information about depth
configurations (convex “bumps” vs. concave “dimples”) in dif-
ferent visual cortical areas using pattern classification analysis.
We found that fMRI responses in dorsal visual area V3B/KO
were more discriminable when disparity and shading concur-
rently signaled depth, in line with the predictions of cue inte-
gration. Wichtig, by relating fMRI and psychophysical tests
of integration, we observed a close association between depth
judgments and activity in this area. Endlich, using a cross-cue
transfer test, we found that fMRI responses evoked by one
cue afford classification of responses evoked by the other. Das
reveals a generalized depth representation in dorsal visual cor-
tex that combines qualitatively different information in line with
3-D perception. ■

EINFÜHRUNG

Many everyday tasks rely on depth estimates provided by
the visual system. To facilitate these outputs, das Gehirn
exploits a range of inputs: from cues related to distance
in a mathematically simple way (z.B., binocular disparity,
motion parallax) to those requiring complex assumptions
and prior knowledge (z.B., shading, occlusion; Burge,
Fowlkes, & Banks, 2010; Kersten, Mamassian, & Yuille,
2004; Mamassian & Goutcher, 2001). These diverse
signals each evoke an impression of depth in their own
Rechts; Jedoch, the brain aggregates cues (Landy, Maloney,
Johnston, & Jung, 1995; Buelthoff & Mallot, 1988;
Dosher, Sperling, & Wurst, 1986) to improve perceptual
judgments (Knill & Saunders, 2003).

Here we probe the neural basis of integration, testing
binocular disparity and shading depth cues that are com-
putationally quite different. At first glance, these cues
may appear so divergent that their combination would
be prohibitively difficult. Jedoch, perceptual judgments
show evidence for the combination of disparity and shad-
ing (Lovell, Bloj, & Harris, 2012; Lee & Saunders, 2011;
Schiller, Slocum, Jao, & Wiener Würstchen, 2011; Vuong, Domini,

1University of Birmingham, 2Japan Society for the Promotion
of Science
*These authors contributed equally to this work.

& Caudek, 2006; Doorschot, Kappers, & Koenderink,
2001; Buelthoff & Mallot, 1988), and the solution to
this challenge is conceptually understood as a two-stage
Verfahren (Landy et al., 1995) in which cues are first ana-
lyzed quasi-independently followed by the integration
of cue information that has been “promoted” into com-
mon units (such as distance). Darüber hinaus, observers can
make reliable comparisons between the perceived depth
from shading and stereoscopic, as well as haptic, compar-
ison stimuli (Schofield, Rock, Sun, Jiang, & Georgeson,
2010; Kingdom, 2003), suggesting some form of com-
parable information.

To gain insight into the neural circuits involved in pro-
cessing 3-D information from disparity and shading, pre-
vious brain imaging studies have tested for overlapping
fMRI responses to depth structures defined by the two
Hinweise, yielding locations in which information from dis-
parity and shading converge (Nelissen et al., 2009; Georgieva,
Todd, Peeters, & Orban, 2008; Sereno, Trinath, Augath, &
Logothetis, 2002). Although this is a useful first step, Das
previous work has not established integration: Zum Beispiel,
representations of the two cues might be collocated within
the same cortical area, but represented independently. Von
Kontrast, recent work testing the integration of disparity
and motion depth cues, indicates that integration occurs in
higher dorsal visual cortex (area V3B/kinetic occipital [KO];
Ban, Preston, Meeson, & Welchman, 2012). This suggests a

© 2013 Massachusetts Institute of Technology Published under a
Creative Commons Attribution 3.0 Unportiert (CC–BY 3.0) Lizenz

Zeitschrift für kognitive Neurowissenschaften 25:9, S. 1527–1541
doi:10.1162/jocn_a_00417

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

F
/

T
T

ich
T
.

:
/
/

H
T
T
P
:
/
D
/
Ö
M
w
ich
N
T
Ö
P
A
R
D
C
e
.
D
S
F
ich
R
Ö
l
M
v
e
H
R
C
P
H
A
D
ich
ich
R
R
e
.
C
C
T
.
Ö
M
M
/
J
e
D
Ö
u
C
N
Ö
/
C
A
N
R
A
T
R
ich
T
ich
C
C
l
e
e
–
P
–
D
P
D
2
F
5
/
9
2
5
1
/
5
9
2
/
7
1
1
5
9
2
4
7
5
/
6
1
3
7
8
7
Ö
9
C
5
N
6
_
4
A
/
_
J
0
Ö
0
C
4
N
1
7
_
A
P
_
D
0
0
B
4
j
1
G
7
u
.
e
P
S
T
D
Ö
F
N
B
0
j
7
S
M
e
ICH
P
T
e
M
L
ich
B
B
e
R
R
A
2
R
0
2
ich
3
e
S

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

candidate cortical locus in which other types of 3-D infor-
mation may be integrated; Jedoch, it is not clear whether
integration would generalize to (ich) more complex depth
structures and/or (ii) different cue pairings.

Erste, Ban and colleagues (2012) used simple fronto-
parallel planes that can suboptimally stimulate neurons
selective to disparity-defined structures in higher portions
of the ventral ( Janssen, Vogels, & Orban, 2000) and dorsal
streams (Srivastava, Orban, De Maziere, & Janssen, 2009)
compared with more complex curved stimuli. It is there-
fore possible that other cortical areas (especially those in
the ventral stream) would emerge as important for cue
integration if more “shape-like” stimuli were presented.
Zweite, it is possible that information from disparity
and motion are a special case of cue conjunctions, Und
daher, integration effects may not generalize to other
depth signal combinations. Insbesondere, depth from dis-
parity and from motion have computational similarities
(Richards, 1985) and joint neuronal encoding (DeAngelis
& Uka, 2003; Anzai, Ohzawa, & Freeman, 2001; Bradley,
Qian, & Andersen, 1995) and can, grundsätzlich, support

metric (absolute) judgments of depth. Im Gegensatz, Die
3-D pictorial information provided by shading relies on
a quite different generative process that is subject to dif-
ferent constraints and prior assumptions (Thompson,
Fleming, Creem-Regehr, & Stefanucci, 2011; Fleming,
Dror, & Adelson, 2003; Koenderink & van Doorn, 2003;
Mamassian & Goutcher, 2001; Sun & Perona, 1998; Horn,
1975).

To test for cortical responses related to the integration
of disparity and shading, we assessed how fMRI re-
sponses change when stimuli are defined by different
Hinweise (Figure 1A). We used multivoxel pattern analysis
(MVPA) to assess the information contained in fMRI re-
sponses evoked by stimuli depicting different depth con-
figurations (convex vs. concave hemispheres to the left
vs. right of the fixation point). We were particularly inter-
ested in how information about the stimulus contained in
the fMRI signals changed depending on the cues used to
depict depth in the display. Intuitively, we would expect
that discriminating fMRI responses should be easier
when differences in the depicted depth configuration

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

T
T

F
/

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

Figur 1. Stimulus illustration and experimental procedures. (A) Links: Cartoon of the disparity and/or shading defined depth structure.
One of the two configurations is presented: bumps to the left, dimples to the right. Rechts: Stimulus examples rendered as red–cyan anaglyphs.
(B) Illustration of the psychophysical testing procedure. (C) Illustration of the fMRI block design. (D) Illustration of the vernier task performed by
participants during the fMRI experiment. Participants compared the horizontal position of a vertical line flashed (250 ms) to one eye against
the upper vertical nonius element of the crosshair presented to the other eye.

1528

Zeitschrift für kognitive Neurowissenschaften

Volumen 25, Nummer 9

were defined by two cues rather than just one (d.h., dif-
ferences defined by disparity and shading together
should be easier to discriminate than differences defined
by only disparity). The theoretical basis for this intuition
can be demonstrated based on statistically optimal dis-
crimination (Ban et al., 2012), with the extent of the
improvement in the two-cue case providing insight into
whether the underlying computations depend on the
integration of two cues or rather having colocated but
independent depth signals.

To appreciate the theoretical predictions for a cortical
area that responds to integrated cues versus colocated
but independent signals, first consider a hypothetical
area that is only sensitive to a single cue (z.B., shading).
If shading information differed between two presented
Reize, we would expect neuronal responses to change,
providing a signal that could be decoded. Im Gegensatz,
manipulating a nonencoded stimulus feature (z.B., dis-
Parität) would have no effect on neuronal responses,
meaning that our ability to decode the stimulus from
the fMRI response would be unaffected. Such a compu-
tationally isolated processing module is biologically
rather unlikely, so next, we consider a more plausible
scenario where an area contains different subpopulations
of neurons, some of which are sensitive to disparity and
others to shading. In this case, we would expect to be
able to decode stimulus differences based on changes
in either cue. Darüber hinaus, if the stimuli contained differ-
ences defined by both cues, we would expect decoding
performance to improve, where this improvement is pre-
dicted by the quadratic sum of the discriminabilities for
changes in each cue. This expectation can be understood
graphically by conceiving of discriminability based on
shading and disparity cues as two sides of a right-angled
triangle, where better discriminability equates to longer
side lengths; the discriminability of both cues together
equals the triangleʼs hypotenuse whose length is deter-
mined based on a quadratic sum (d.h., the Pythagorean
equation) and is always at least as good as the discrimina-
bility of one of the cues.

The alternative possibility is a cortical region that inte-
grates the depth cues. Under this scenario, we also
expect better discrimination performance when two cues
define differences between the stimuli. Wichtig,
Jedoch, unlike the independence scenario, when stimu-
lus differences are defined by only one cue, a fusion
mechanism is adversely affected. Zum Beispiel, if contrast-
ing stimulus configurations differ in the depth indicated
by shading but disparity indicates no difference, Die
fusion mechanism combines the signals from each cue
with the result that it is less sensitive to the combined
estimate than the shading component alone. Durch con-
sequence, if we calculate a quadratic summation predic-
tion based on MVPA performance for depth differences
defined by single cues (d.h., disparity; shading) we will
find that empirical performance in the combined cue
Fall (d.h., disparity + shading) exceeds the prediction

(Ban et al., 2012). Here we exploit this expectation to
identify cortical responses to integrated depth signals,
seeking to identify discrimination performance that is
“greater than the sum of its parts” due to the detrimental
effects of presenting stimuli in which depth differences
are defined in terms of a single cue.

Zu diesem Zweck, we generated random dot patterns (Feige-
ure 1A) that evoked an impression of four hemispheres,
two concave (“dimples”) and two convex (“bumps”). Wir
formulated two different types of display that differed
in their configuration: (1) bumps left–dimples right (von-
picted in Figure 1A) versus (2) dimples left–bumps right.
We depicted depth variations from (ich) binocular dis-
Parität, (ii) shading gradients, Und (iii) the combination
of disparity and shading. Zusätzlich, we employed a con-
trol stimulus (iv) in which the overall luminance of the
top and bottom portions of each hemisphere differed
(Ramachandran, 1988; disparity + binary luminance).
Perceived depth for these (deliberately) crude approxi-
mations of the shading gradients relied on disparity.
We tested for integration using both psychophysical
and fMRI discrimination performance for the component
Hinweise (ich, ii) with that for stimuli containing two cues (iii,
iv). We reasoned that a response based on integrating
cues would be specific to concurrent cue stimulus (iii)
and not be observed for the control stimulus (iv).

METHODEN

Teilnehmer

Twenty observers from the University of Birmingham
participated in the fMRI experiments. Of these, five were
excluded due to excessive head movement during scan-
ning, meaning that the correspondence between voxels
required by the MVPA technique was lost. Excessive
movement was defined as ≥4 mm over an 8-min run,
and we excluded participants if they had fewer than five
runs below this cut-off as there was insufficient data for
the MVPA. Generally, participants were able to keep still:
The average absolute maximum head deviation relative
to the start of the first run for included participants was
1.2 mm versus 4.5 mm for excluded participants. More-
over only one included participant had an average head
motion of >2 mm per run, and the mode of the head
movement distribution across participants was <1 mm. Six women and nine men were included; 12 right- handed. Mean age was 26 ± 1.2 (SEM ) years. Authors A.E.W. H.B. participated; all other participants were naive to the purpose of study. Four participants had taken part in Ban et al.ʼs (2012) Participants had normal or corrected-to-normal vision pre- screened for stereo deficits. Experiments approved by University Birmingham Science Engineer- ing Ethics Committee; observers gave written informed consent. Dövencioğlu al. 1529 D o w n l o a d e d f r o m l l > 0) and selected to the top 300 voxels as
data for the classification algorithm (Preston, Li, Kourtzi,
& Welchman, 2008). To minimize baseline differences
between runs we z-scored the response time course of
each voxel and each experimental run. To account for
the hemodynamic response lag, the fMRI time series
were shifted by two repetition times (4 Sek). Thereafter,
we averaged the fMRI response of each voxel across the
16 sec stimulus presentation block, obtaining a single test
pattern for the multivariate analysis per block. To remove
potential univariate differences (that can be introduced
after z-score normalization due to averaging across time
points in a block and grouping the data into train vs. test
data sets), we normalized by subtracting the mean of all
voxels for a given volume (Serences & Boynton, 2007),
with the result that each volume had the same mean
value across voxels and differed only in the pattern of
Aktivität. We performed multivoxel pattern analysis using
a linear support vector machine (SVMlight toolbox) clas-
sification algorithm. We trained the algorithm to dis-
tinguish between fMRI responses evoked by different
stimulus configurations (z.B., convex to the left vs. Zu
the right of fixation) for a given stimulus type (z.B., dis-

Parität). Participants typically took part in eight runs, jede
of which had three repetitions of a given spatial config-
uration and stimulus type, creating a total of 24 patterns.
We used a leave-one-run-out cross-validation procedure:
We trained the classifier using seven runs (d.h., 21 pat-
Seeschwalben) and then evaluated the prediction performance
of the classifier using the remaining, nontrained data (d.h.,
three patterns). We repeated this, leaving a single run out
im Gegenzug, and calculated the mean prediction accuracy across
cross-validation folds. Accuracies were represented in units
of discriminability (D

0) using the formula:

D 0 ¼ 2erfinvð2p−1Þ

ð1Þ

where erfinv is the inverse error function and p is the
proportion of correct predictions.

For tests of transfer between disparity and shading
Hinweise, we used a Recursive Feature Elimination method
(De Martino et al., 2008) to detect sparse discriminative
patterns and define the number of voxels for the SVM
classification analysis. In each feature elimination step,
five voxels were discarded until there remained a core
set of voxels with the highest discriminative power. To
avoid circular analysis, the Recursive Feature Elimination
method was applied independently to the training pat-
terns of each cross-validation fold, resulting in eight sets
of voxels (d.h., one set for each test pattern of the leave-
one-run-out procedure). This was done separately for
each experimental condition, with final voxels for the
SVM analysis chosen based on the intersection of voxels
from corresponding cross-validation folds. A standard
SVM was then used to compute within- and between-
cue prediction accuracies. This feature selection method
was required for transfer, in line with evidence that it
improves generalization (De Martino et al., 2008).

We conducted repeated-measures GLM in SPSS (IBM,
Inc., Armonk, New York) applying Greenhouse-Geisser correc-
tion when appropriate. Regression analyses were also
conducted in SPSS. Für diese Analyse, we considered the
use of repeated-measures MANCOVA (and found results
consistent with the regression results); Jedoch, Die
integration indices (defined below) we use are partially
correlated between conditions because their calculation
depends on the same denominator, violating the GLMʼs
assumption of independence. We therefore limited our
analysis to the relationship between psychophysical and
fMRI indices for the same condition, for which the psycho-
physical and fMRI indices are independent of one another.

Quadratic Summation and Integration Indices

We formulate predictions for the combined cue condi-
tion (d.h., disparity + shading) based on the quadratic
summation of performance in the component cue condi-
tionen (d.h., disparity, shading). As outlined in the Intro-
duktion, this prediction is based on the performance of

1532

Zeitschrift für kognitive Neurowissenschaften

Volumen 25, Nummer 9

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

F
/

T
T

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

introduced during fMRI measurement (scanner noise,
observer movement), colocated but independent re-
sponses can yield a positive index (see the fMRI simula-
tions by Ban et al., 2012 in their Supplementary Figure 3).
Daher, the integration index alone cannot be taken as
definite evidence of cue integration and therefore needs
to be considered in conjunction with the other tests. To
assess statistical significance of the integration indices,
we used bootstrapped resampling as our use of a ratio
makes distributions non-Normal, and thus a nonpara-
metric procedure more appropriate.

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

Figur 2. Psychophysical results. (A) Behavioral tests of integration.
Bar graphs represent the between-subject mean slope of the
psychometric function. *P < .05. (B) Psychophysical results as an integration index. Distribution plots show bootstrapped values: The center of the “bowtie” represents the median, the colored area depicts 68% confidence values, and the upper and lower error bars represent 95% confidence intervals. an ideal observer model that discriminates pairs of inputs (visual stimuli or fMRI response patterns) based on the optimal discrimination boundary. Psychophysical tests indicate that this theoretical model matches human per- formance in combining cues (Knill & Saunders, 2003; Hillis, Ernst, Banks, & Landy, 2002). To compare measured empirical performance in dis- parity + shading condition with the prediction derived from the component cue conditions, we calculate a ratio index (Ban et al., 2012; Nandy & Tjan, 2008) whose gen- eral form is Index ¼ CDþS p ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ þ C2 C2 D S −1 ð2Þ where CD, CS, and CD+S are sensitivities for disparity, shading, and the combined cue conditions, respectively. If the responses of the detection mechanism to the dis- parity and shading conditions (CD, CS) are independent of each other, performance when both cues are available (CD+S) should match the quadratic summation pre- diction, yielding a ratio of 1 and thus an index of zero. A value of less than zero suggests suboptimal detection performance, and a value above zero suggests that the component sources of information are not independent (Ban et al., 2012; Nandy & Tjan, 2008). However, a value above zero does not preclude the response of indepen- dent mechanisms: Depending on the amount of noise RESULTS Psychophysics To assess cue integration psychophysically, we measured observersʼ sensitivity to slight differences in the depth profile of the stimuli (Figure 1B). Participants viewed two shapes sequentially, and decided which had the greater depth (i.e., which bumps were taller or which dimples were deeper). By comparing a given standard stimulus against a range of test stimuli, we obtained psychometric functions. We used the slope of these functions to quantify observersʼ sensitivity to stimulus differences (where a steeper slope indicates higher sen- sitivity). To determine whether there was a perceptual benefit associated with adding shading information to the stimuli, we compared performance in the disparity condition with that in the disparity and shading condi- tion. Surprisingly, we found no evidence for enhanced performance in the disparity and shading condition at the group level, F(1, 14) < 1, p = .38. In light of previous empirical work on cue integration, this was unexpected (e.g., Lovell et al., 2012; Schiller et al., 2011; Vuong et al., 2006; Doorschot et al., 2001; Buelthoff & Mallot, 1988) and prompted us to consider the significant var- iability between observers, F(1, 14) = 62.23, p < .001, in their relative performance in the two conditions. In particular, we found that some participants clearly bene- fited from the presence of two cues; however, others showed no benefit and some actually performed worse relative to the disparity only condition. Poorer perfor- mance might relate to individual differences in the as- sumed direction of the illuminant (Schofield, Rock, & Georgeson, 2011); ambiguity or bistability in the inter- pretation of shading patterns (Wagemans, van Doorn, & Koenderink, 2010; Liu & Todd, 2004); and/or differ- ences in cue weights (Lovell et al., 2012; Schiller et al., 2011; Knill & Saunders, 2003; we return to this issue in the Discussion). To quantify variations between partici- pants in the relative performance in two conditions, we calculated a psychophysical integration index (ψ): ψ ¼ SDþS SD −1 ð3Þ Dövencioğlu et al. 1533 l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j / . 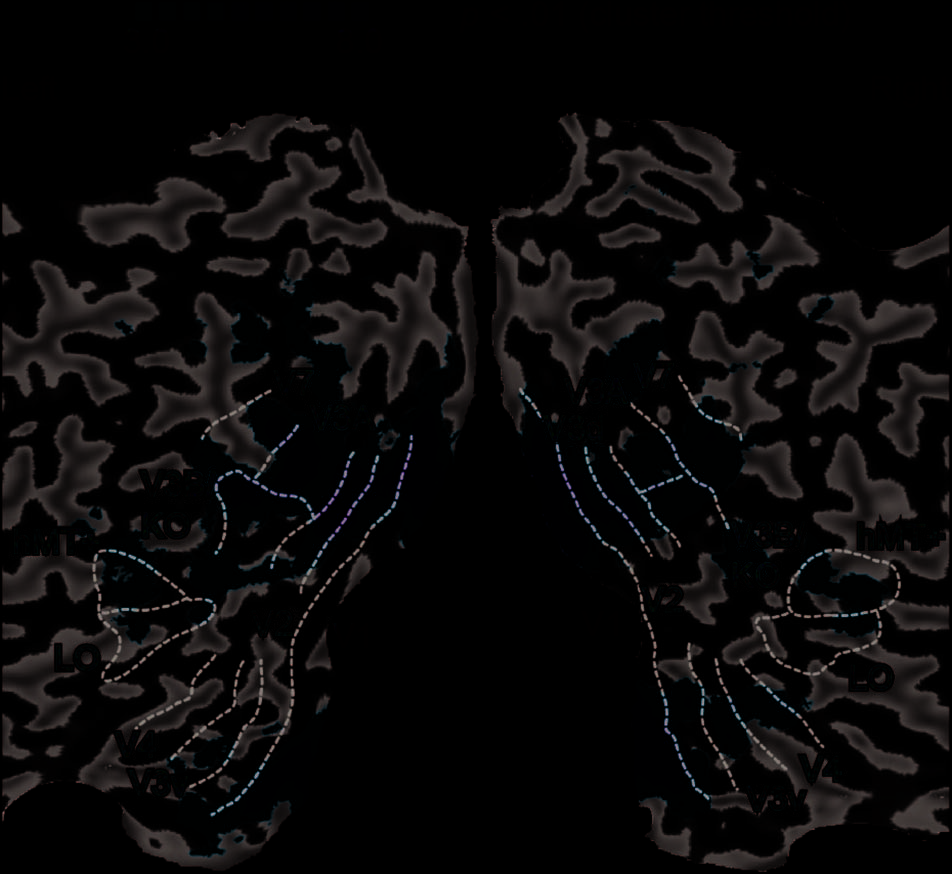t f u s e r o n 1 7 M a y 2 0 2 1 fMRI Measures Before taking part in the main experiment, each partici- pant underwent a separate fMRI session to identify ROIs within the visual cortex (Figure 3). We identified retino- topically organized cortical areas based on polar and eccentricity mapping techniques (Tyler et al., 2005; Tootell & Hadjikhani, 2001; DeYoe et al., 1996; Sereno et al., 1995). In addition, we identified area LO involved in object processing (Kourtzi & Kanwisher, 2001), the human motion complex (hMT+/ V5; Zeki et al., 1991), and the KO region, which is localized by contrasting motion-defined contours with transparent motion (Zeki et al., 2003; Dupont et al., 1997). Responses to the KO localizer overlapped with the retinotopically localized area V3B and were not consistently separable across participants and/or hemispheres (see also Ban et al., 2012) so we denote this region as V3B/KO. A representa- tive flatmap of the ROIs is shown in Figure 3, and Table 1 provides mean coordinates for V3B/KO. We then measured fMRI responses in each of the ROIs and were a priori particularly interested in the V3B/KO region (Ban et al., 2012; Tyler, Likova, Kontsevich, & Wade, 2006). We presented stimuli from four experimental condi- tions (Figure 1) under two configurations: (a) bumps to the left of fixation, dimples to the right or (b) bumps to the right, dimples to the left, thereby allowing us to contrast fMRI responses to convex versus concave stimuli. To analyze our data, we trained a machine learning classifier (SVM) to associate patterns of fMRI voxel activity and the stimulus configuration (convex vs. concave) that gave rise to that activity. We used the performance of the D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . 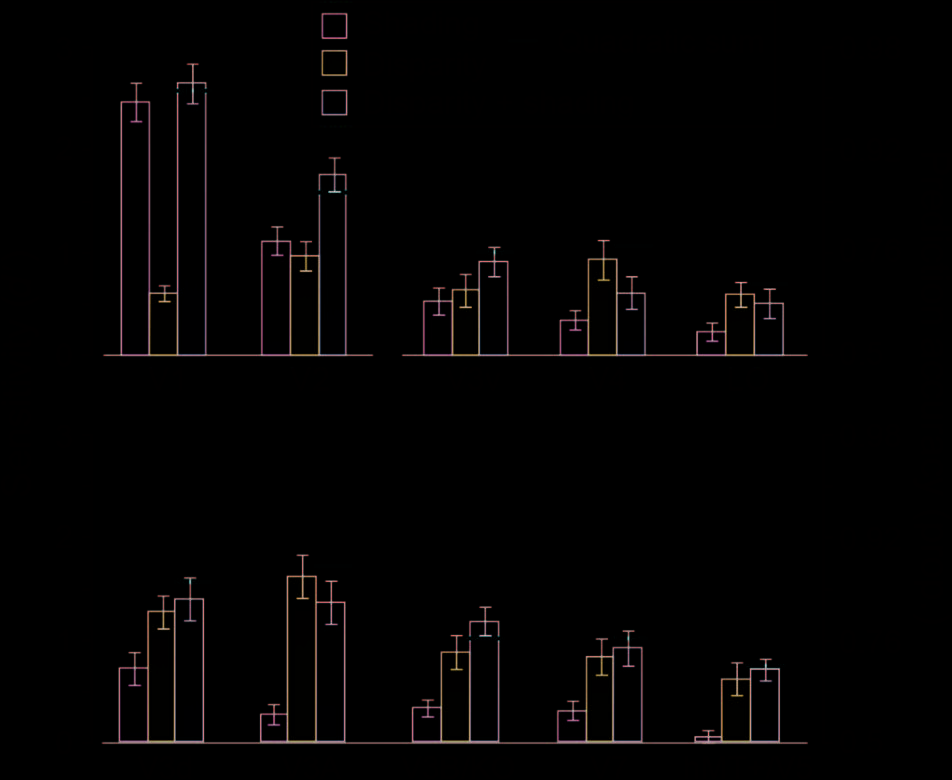f / t u s e r o n 1 7 M a y 2 0 2 1 Figure 4. Performance in predicting the convex versus concave configuration of the stimuli based on the fMRI data measured in different ROIs. The bar graphs show the results from the “single cue” experimental conditions, the “disparity + shading” condition, and the quadratic summation prediction (horizontal red line). Error bars indicate SEM. Figure 3. Representative flat maps from one participant showing the left and right ROIs. The sulci are depicted in darker gray than the gyri. Shown on the maps are retinotopic areas, V3B/KO, the human motion complex (hMT+/ V5), and LO area. The activation on the maps shows the results of a searchlight classifier analysis that moved iteratively throughout the measured cortical volume, discriminating between stimulus configurations. The color code represents the t value of the classification accuracies obtained. This procedure confirmed that we had not missed any important areas outside those localized independently. p where SD+S is sensitivity in the combined condition and SD is sensitivity in the disparity condition. This index is based on the quadratic summation test (Ban et al., 2012; Nandy & Tjan, 2008; see Methods) where a value above zero suggests that participants integrate the depth information provided by the disparity and shading cues when making perceptual judgments. In this instance we ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ assumed that SD ≈ Þ þ S 2 ðS 2 because our attempts to S D measure sensitivity to differences in depth amplitude defined by shading alone in pilot testing resulted in such poor performance that we could not fit a reliable psycho- metric function. Specifically, discriminability for the max- 0 = 0.3 ± 0.25 for imum presented depth difference was d 0 = 3.9 ± 0.3 for disparity, shading alone, in contrast to d that is, SD 2 ≫ SS 2. We used a clustering algorithm on ψ to determine whether our participants formed different subgroups. In particular, SPSSʼs two-step clustering algorithm (apply- ing Schwarzʼs Bayesian Criterion for cluster identifica- tion) indicated two subgroups: Participants with ψ >
0.1 were associated with cluster 1 and participants with
ψ < −0.1 with cluster 2; hereafter, we refer to these groups as good integrators (n = 7) and poor integrators (n = 8). By definition, these post hoc groups differed in the relative sensitivity to disparity and disparity + shading conditions (Figure 2). Our purpose in forming these groups, however, was to test the link between dif- ferences in perception and fMRI responses. 1534 Journal of Cognitive Neuroscience Volume 25, Number 9 classifier in decoding the stimulus from independent fMRI data (i.e., leave-one-run-out cross validation) as a measure of the information about the presented stimulus within a particular region of cortex. We could reliably decode the stimulus configuration in the four conditions in almost every ROI (Figure 4), and there was a clear interaction between conditions and ROIs, F(8.0, 104.2) = 8.92, p < .001. This widespread sensitivity to differences between convex versus concave stimuli is not surprising in that a range of features might modify the fMRI response (e.g., distribution of image intensities, contrast edges, mean disparity, etc.). The machine learning classifier may thus decode low-level image features, rather than “depth” per se. We were therefore interested not in overall prediction accuracies between areas (which are influenced by our ability to measure fMRI activity in different anatomical locations). Rather, we were interested in the relative performance between conditions, and whether this related to between- observer differences in perceptual integration. We there- fore considered our fMRI data subdivided based on the behavioral results (significant interaction between condi- tion and group [good vs. poor integrators]: F(2.0, 26.6) = 4.52, p = .02). First, we wished to determine whether fMRI decoding performance improved when both depth cues indicated depth differences. Prediction accuracies for the concurrent stimulus (disparity + shading) were statistically higher than the component cues in areas V2, F(3, 39) = 7.47, p < .001, and V3B/KO, F(1.6, 21.7) = 14.88, p < .001. To assess integration, we compared the extent of improve- ment in the concurrent stimulus relative to a minimum bound prediction (Figures 4 and 5, red lines) based on the quadratic summation of decoding accuracies for “single cue” presentations (Ban et al., 2012). This cor- responds to the level of performance expected if dis- parity signals and shading signals are collocated in a cortical area, but represented independently. If perfor- mance exceeds this bound, it suggests that cue repre- sentations are not independent, as performance in the “single” cue case was attenuated by the conflicts that result from “isolating” the cue. We found that perfor- mance was higher (outside the SEM) than the quadratic summation prediction in areas V2 and V3B/KO (Figure 5). However, this result was only statistically reliable in V3B/KO. 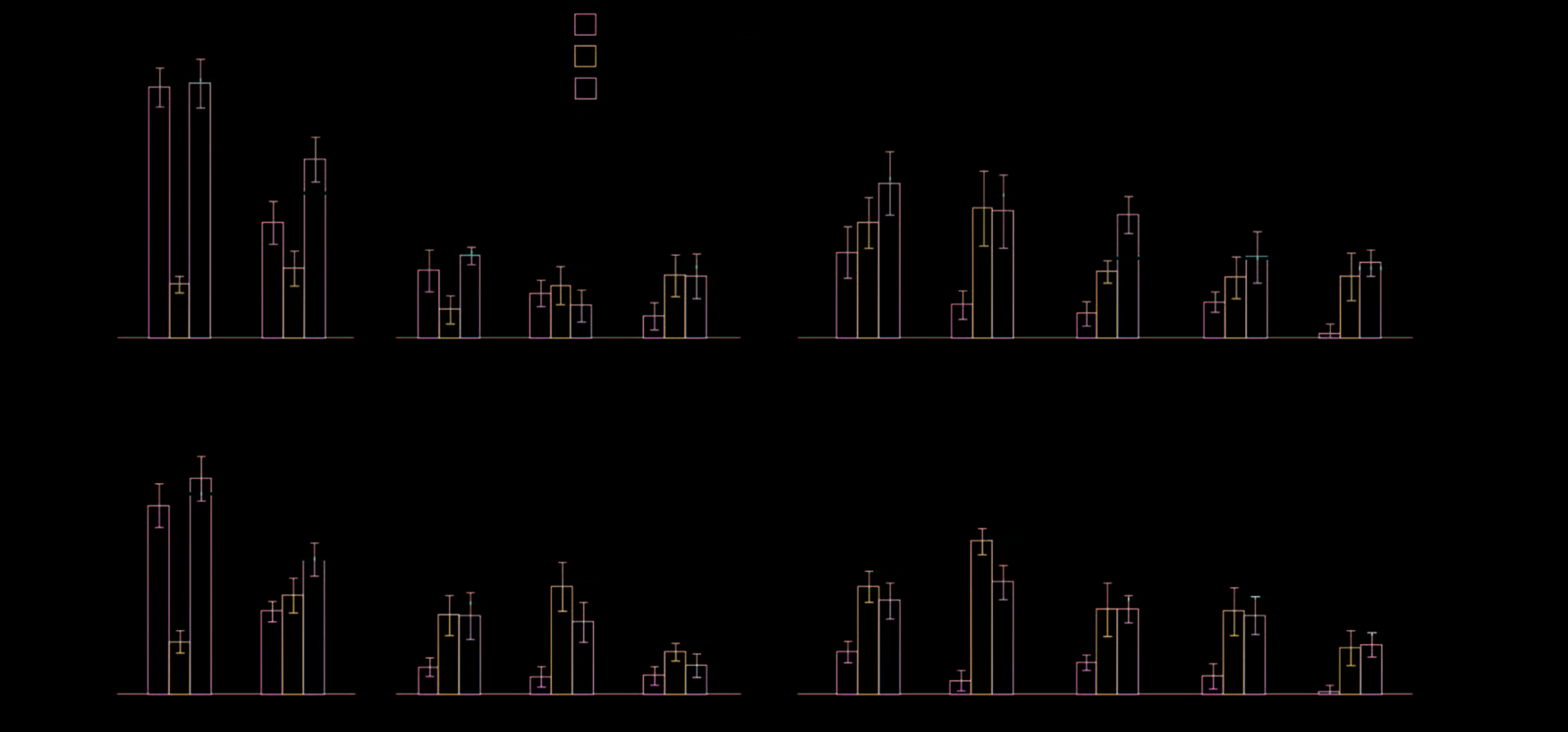Specifically in V3B/KO, there was a significant interaction between the behavioral group and experi- mental condition, F(2, 26) = 5.52, p = .01, with decod- ing performance in the concurrent (disparity + shading) condition exceeding the quadratic summation prediction for good integrators, F(1, 6) = 9.27, p = .011, but not for the poor integrators, F(1, 7) < 1, p = .35 (Figure 5). In V2, there was no significant difference be- tween the quadratic summation prediction and the mea- sured data in the combined cue conditions, F(2, 26) < 1, p = .62, nor an interaction, F(2, 26) = 2.63, p = .091. We quantified the extent of integration using a boot- strapped index (ϕ) that contrasted decoding perfor- mance in the concurrent condition (d D+S) with the quadratic summation of performance with “single” cues (d D and d S): 0 0 0 ϕ ¼ p d0 DþS ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ D2 þ d0 d0 S2 −1 ð4Þ Using this index, a value of zero corresponds to the performance expected if information from disparity D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t f . / u s e r o n 1 7 M a y 2 0 2 1 Figure 5. Prediction performance for fMRI data separated into the two groups based on the psychophysical results (“good” vs. “poor” integrators). The bar graphs show the results from the “single cue” experimental conditions, the “disparity + shading” condition, and the quadratic summation prediction (horizontal red line). Error bars indicate SEM. Dövencioğlu et al. 1535 that approximated luminance differences in the shaded stimuli but did not, per se, evoke an impression of depth. As the fMRI response in a given area may reflect low-level stimulus differences (rather than depth from shading), we wanted to rule out the possibility that improved decoding performance in the concurrent dis- parity + shading condition could be explained on the basis that two separate stimulus dimensions (disparity and luminance) drive the fMRI response. The quadratic summation test should theoretically rule this out; never- theless, we contrasted decoding performance in the concurrent condition versus the binary control (disparity + binary luminance) condition. We reasoned that if enhanced decoding is related to the representation of depth, superquadratic summation effects would be lim- ited to the concurrent condition. On the basis of a significant interaction between subject group and condi- tion, F(2, 26) = 5.52, p = .01, we found that this was true for the good integrator subjects in area V3B/KO: sensi- tivity in the concurrent condition was above that in the binary control condition, F(1, 6) = 14.69, p = .004. By contrast, sensitivity for the binary condition in the poor integrator subjects matched that of the concurrent group, F(1, 7) < 1, p = .31, and was in line with quadratic summation. Results from other ROIs (Table 2) did not suggest the clear (or significant) differences that were apparent in V3B/KO. As a further line of evidence, we used regression ana- lyses to test the relationship between psychophysical and fMRI measures of integration. Although we would not anticipate a one-to-one mapping between them (the fMRI data were obtained for differences between concave vs. convex shapes, whereas the psychophysical tests measured sensitivity to slight differences in the depth profile), our group-based analysis suggested a corre- spondence. We found a significant relationship between the fMRI and psychophysical integration indices in V3B/ KO (Figure 6B) for the concurrent (R = 0.57, p = .026) but not the binary luminance (R = 0.10, p = .731) con- dition. This result was specific to area V3B/KO (Table 3) and, in line with the preceding analyses, suggests a rela- tionship between activity in area V3B/KO and the percep- tual integration of disparity and shading cues to depth. As a final assessment of whether fMRI responses related to depth structure from different cues, we tested whether training the classifier on depth configurations from one cue (e.g., shading) afforded predictions for depth configura- tions specified by the other (e.g., disparity). To compare the prediction accuracies on this cross-cue transfer with baseline performance (i.e., training and testing on the same cue), we used a bootstrapped transfer index: T ¼ 2d0 T þ d0 d0 D S ð5Þ 0 where d ½ (d 0 D + d T is between-cue transfer performance and S) is the average within-cue performance. A 0 Figure 6. (A) fMRI based prediction performance as an integration index for the two groups of participants in area V3B/KO. A value of zero indicates the minimum bound for fusion as predicted by quadratic summation. The index is calculated for the “disparity + shading” and “disparity + binary shading” conditions. Data are presented as notched distribution plots. The center of the “bowtie” represents the median, the colored area depicts 68% confidence values, and the upper and lower error bars represent 95% confidence intervals. (B) Correlation between behavioral and fMRI integration indices in area V3B/KO. Psychophysics and fMRI integration indices are plotted for each participant for disparity + shading and disparity + binary luminance conditions. The Pearson correlation coefficient (R) and p value are shown. (C) The transfer index values for V3B/KO for the good and poor integrator groups. Using this index, a value of 1 indicates equivalent prediction accuracies when training and testing on the same cue versus training and testing on different cues. Distribution plots show the median, 68% and 95% confidence intervals. Dotted horizontal lines depict a bootstrapped chance baseline based on the upper 95th centile for transfer analysis obtained with randomly permuted data. and shading are collocated, but independent. We found that only in areas V2 and V3B/ KO was the integration index for the concurrent condition reliably above zero for the good integrators (Figure 6A; Table 2). To provide additional evidence for neuronal responses related to depth estimation, we used the binary lumi- nance stimuli as a control. We constructed these stimuli such that they contained a very obvious low-level feature 1536 Journal of Cognitive Neuroscience Volume 25, Number 9 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f / . t u s e r o n 1 7 M a y 2 0 2 1 Table 2. Probabilities Associated with Obtaining a Value of Zero for the fMRI Integration Index in the (i) Disparity + Shading Condition and (ii) Luminance Control Condition Disparity + Shading Disparity + Binary Luminance Cortical Area Good Integrators Poor Integrators Good Integrators Poor Integrators V1 V2 V3v V4 LO V3d V3A V3B/KO V7 hMT+/ V5 0.538 0.004 0.294 0.916 0.656 0.253 0.609 <0.001 0.298 0.315 0.157 0.419 0.579 0.942 0.944 0.890 1.000 0.629 0.595 0.421 0.999 0.607 0.726 0.987 0.984 0.909 0.999 0.327 0.844 0.978 0.543 0.102 1.000 0.628 0.143 0.234 0.961 0.271 0.620 0.575 Values are from a bootstrapped resampling of the individual participantsʼ data using 10,000 samples. Bold formatting indicates Bonferroni-corrected significance. value of one using this index indicates that prediction accuracy between cues equals that within cues. To provide a baseline for the transfer that might occur by chance, we calculated the transfer index on data sets for which we ran- domly shuffled the condition labels, such that we broke the relationship between fMRI response and the stimulus that evoked the response. We calculated shuffled transfer per- formance 1000 times for each ROI and used the 95th cen- tile of the resulting distribution of transfer indices as the Table 3. Results for the Regression Analyses Relating the Psychophysical and fMRI Integration Indices in Each ROI Cortical Area V1 V2 V3v V4 LO V3d V3A V3B/KO V7 hMT+/ V5 Disparity + Shading Disparity + Binary Luminance R −0.418 0.105 −0.078 0.089 0.245 0.194 0.232 0.571 0.019 0.411 p .121 .709 .782 .754 .379 .487 .405 .026 .946 .128 R −0.265 −0.394 0.421 −0.154 −0.281 −0.157 −0.157 0.097 −0.055 −0.367 p .340 .146 .118 .584 .311 .577 .577 .731 .847 .178 The table shows the Pearson correlation coefficient (R) and the signifi- cance of the fit as a p value for the “disparity + shading” and “disparity + binary luminance” conditions. cut-off for significance. We found reliable evidence for transfer between cues in area V3B/KO (Figure 6C) for the good, but not poor, integrator groups. Furthermore, this effect was specific to V3B/KO and was not observed in other areas (Table 4). Together with the previous ana- lyses, this result suggests a degree of equivalence between representations of depth from different cues in V3B/KO that is related to an individualʼs perceptual interpretation of cues. To ensure we had not missed any important loci of activity outside the areas we sampled using our ROI local- izers, we conducted a searchlight classification analysis (Kriegeskorte, Goebel, & Bandettini, 2006) in which we moved a small spherical aperture (diameter = 9 mm) through the sampled cortical volume performing MVPA on the difference between stimulus configurations for the concurrent cue condition (Figure 3). This analysis indicated that discriminative signals about stimulus dif- ferences were well captured by our ROI definitions. Our main analyses considered MVPA of the fMRI responses partitioned into two groups based on psycho- physical performance. To ensure that differences in MVPA prediction performance between groups related to the pattern of voxel responses for depth process- ing, rather than the overall responsiveness of different ROIs, we calculated the average fMRI activations (percent signal change) in each ROI for the two groups of partici- pants. Reassuringly, we found no evidence for statistically reliable differences between groups across conditions and ROIs (i.e., no ROI × Group interaction: F(3.3, 43.4) < 1, p = .637; no Condition × Group interaction: F(3.5, 45.4) < 1, p = .902; and no ROI × Condition × Group interaction: F(8.6, 112.2) = 1.06, p = .397). Moreover, limiting this analysis to V3B/KO provided no evidence Dövencioğlu et al. 1537 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j / t f . u s e r o n 1 7 M a y 2 0 2 1 Table 4. Probabilities Associated with the Transfer between Disparity and Shading Producing a Transfer Index above the Random (Shuffled) Baseline Cortical Area Good Integrators Poor Integrators V1 V2 V3v V4 LO V3d V3A V3B/KO V7 hMT+/ V5 0.247 0.788 0.121 0.478 0.254 0.098 0.295 <0.001 0.145 0.124 0.748 0.709 0.908 0.062 0.033 0.227 0.275 0.212 0.538 0.302 These p values are calculated using bootstrapped resampling with 10,000 samples. Bold formatting indicates Bonferroni-corrected significance. for a difference in the percent signal change between groups (i.e., no Condition × Group interaction: F(3.1, 40.3) < 1, p = .586). Furthermore, we ensured that we had sampled from the same cortical location in both groups by calculating the mean Talairach location of V3B/KO subdivided by groups (Table 1). This confirmed that we had localized the same cortical region in both groups of participants. To guard against artifacts complicating the interpreta- tion of our results, we took specific precautions during scanning to control attentional allocation and eye move- ments. First, participants performed a demanding vernier judgment task at fixation. This ensured equivalent atten- tional allocation across conditions, and, as the task was unrelated to the depth stimuli, psychophysical judgments and fMRI responses were not confounded and could not thereby explain between-subject differences. Second, the attentional task served to provide a subjective measure of eye vergence (Popple et al., 1998). In particular, partici- pants judged the relative location of a small target flashed (250 msec) to one eye, relative to the upper vertical nonius line (presented to the other eye; Figure 1D). We fit the proportion of “target is to the right” responses as a function of the targetʼs horizontal displacement. Bias (i.e., deviation from the desired vergence position) in this judgment was around zero suggesting that participants were able to maintain fixation with the required vergence angle. Using a repeated-measures ANOVA, we found that there were no significant differences in bias between Stim- ulus Conditions, F(1.5, 21.4) = 2.59, p = .109, Sign of Curvature, F(1, 14) = 1.43, p = .25, and no interaction, F(2.2, 30.7) = 1.95, p = .157. Furthermore, there were no differences in the slope of the psychometric functions: no effect of Condition, F(3, 42) < 1, p = .82, or Curvature, F(1, 14) < 1, p = .80, and no interaction, F(3, 42) < 1, p = .85. Third, our stimuli were constructed to reduce the potential for vergence differences: Disparities to the left and right of the fixation point were equal and opposite, a constant low spatial frequency pattern surrounded the stimuli, and participants used horizontal and vertical nonius lines to monitor their eye vergence. DISCUSSION Here we provide three lines of evidence that activity in dorsal visual area V3B/KO reflects the integration of dis- parity and shading depth cues in a perceptually relevant manner. First, we used a quadratic summation test to show that performance in concurrent cue settings im- proves beyond that expected if depth from disparity and shading are collocated but represented indepen- dently. Second, we showed that this result was specific to stimuli that are compatible with a 3-D interpretation of shading patterns. Third, we found evidence for cross-cue transfer. Importantly, the strength of these re- sults in V3B/KO varied between individuals in a manner that was compatible with their perceptual use of inte- grated depth signals. These findings complement evidence for the integra- tion of disparity and relative motion in area V3B/KO (Ban et al., 2012) and suggest both a strong link with perceptual judgments and a more generalized represen- tation of depth structure. Such generalization is far from trivial: Binocular disparity is a function of an objectʼs 3-D structure, its distance from the viewer and the separation between the viewerʼs eyes; by contrast, shading cues (i.e., intensity distributions in the image) depend on the type of illumination, the orientation of the light source with respect to the 3-D object, and the reflective properties of the objectʼs surface (i.e., the degree of Lambertian and Specular reflectance). As such disparity and shading pro- vide complementary shape information: They have quite different generative processes, and their interpreta- tion depends on different constraints and assumptions (Doorschot et al., 2001; Blake, Zisserman, & Knowles, 1985). Taken together, these results indicate that the 3-D representations in the V3B/KO region are not specific to specific cue pairs (i.e., disparity–motion) and generalize to more complex forms of 3-D structural information (i.e., local curvature). This points to an important role for higher portions of the dorsal visual cortex in comput- ing information about the 3-D structure of the surround- ing environment. Individual Differences in Disparity and Shading Integration One striking, and unexpected feature of our findings was that we observed significant between-subject variability in the extent to which shading enhanced performance, with 1538 Journal of Cognitive Neuroscience Volume 25, Number 9 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j / f . t u s e r o n 1 7 M a y 2 0 2 1 some participants benefitting, and others actually per- forming worse. What might be responsible for this varia- tion in performance? Although shading cues support reliable judgments of ordinal structure (Ramachandran, 1988), shape is often underestimated (Mingolla & Todd, 1986) and subject to systematic biases related to the estimated light source position (Mamassian & Goutcher, 2001; Sun & Perona, 1998; Curran & Johnston, 1996; Pentland, 1982) and light source composition (Schofield et al., 2011). Moreover, assumptions about the position of the light source in the scene are often esoteric: Most observers assume overhead lighting, but the strength of this assumption varies considerably (Thomas, Nardini, & Mareschal, 2010; Wagemans et al., 2010; Liu & Todd, 2004), and some observers assume lighting from below (e.g., 3 of 15 participants in Schofield et al., 2011). Our disparity + shading stimuli were designed such that the cues indicated the same depth structure to an observer who assumed lighting from above. Therefore, it is quite possible that observers experienced conflict between the shape information specified by disparity and that deter- mined by their interpretation of the shading pattern. Such participants would be “poor integrators” only inas- much as they failed to share the assumptions typically made by observers (i.e., lighting direction, lighting com- position, and Lambertian surface reflectance) when inter- preting shading patterns. In addition, participants may have experienced alternation in their interpretation of the shading cue across trials (i.e., a weak light-from-above assumption that has been observed quite frequently; Thomas et al., 2010; Wagemans et al., 2010); aggregating such bimodal responses to characterize the psychometric function would result in more variable responses in the concurrent condition than in the “disparity“ alone condi- tion, which was not subject to perceptual bistability. Such variations could also result in fMRI responses that vary between trials; in particular, fMRI responses in V3B/KO change in line with different perceptual interpretations of the same (ambiguous) 3-D structure indicated by shading cues (Preston, Kourtzi, & Welchman, 2009). This variation in fMRI responses could thereby account for reduced decoding performance for these participants. An alternative possibility is that some of our observers did not integrate information from disparity and shading because they are inherently poor integrators. Although cue integration both within and between sensory modal- ities has been widely reported in adults, it has a develop- mental trajectory and young children do not integrate signals (Gori, Del Viva, Sandini, & Burr, 2008; Nardini, Jones, Bedford, & Braddick, 2008; Nardini, Bedford, & Mareschal, 2010). This suggests that cue integration may be learnt via exposure to correlated cues (Atkins, Fiser, & Jacobs, 2001) where the effectiveness of learning can differ between observers (Ernst, 2007). Furthermore, although cue integration may be mandatory for many cues where such correlations are prevalent (Hillis et al., 2002), interindividual variability in the prior assumptions that are used to interpret shading patterns may cause some participants to lack experience of integrating shad- ing and disparity cues (at least in terms of how these are studied in the laboratory). These different possibilities are difficult to distinguish from previous work that has looked at the integration of disparity and shading signals and reported individual re- sults. This work indicated that perceptual judgments are enhanced by the combination of disparity and shading cues (Lovell et al., 2012; Schiller et al., 2011; Vuong et al., 2006; Doorschot et al., 2001; Buelthoff & Mallot, 1988). However, between-participant variation in such enhancement is difficult to assess given that low numbers of participants were used (mean per study = 3.6, max = 5), a sizeable proportion of whom were not naive to the purposes of the study. Here we find evidence for inte- gration in both authors H.B. and A.W., but considerable variability among the naive participants. In common with Wagemans et al. (2010), this suggests that interobserver variability may be significant in the interpretation of shading patterns in particular and integration more gen- erally, providing a stimulus for future work to explain the basis for such differences. Responses in Other ROIs When presenting the results for all the participants, we noted that performance in the disparity + shading con- dition was statistically higher than for the component cues in area V2 as well as in V3B/KO (Figure 3). Our sub- sequent analyses did not provide evidence that V2 is a likely substrate for the integration of disparity and shad- ing cues. However, it is possible that the increased de- coding performance—around the level expected by quadratic summation—is due to parallel representations of disparity and shading information. It is unlikely that either signal is fully elaborated, but V2ʼs more spatially extensive receptive fields may provide important infor- mation about luminance and contrast variations across the scene that provide signals important when interpret- ing shape from shading (Schofield et al., 2010). Previous work (Georgieva et al., 2008) suggested that the processing of 3-D structure from shading is primarily restricted in its representation to a ventral locus near the area we localize as LO (although Gerardin, Kourtzi, & Mamassian, 2010 suggested V3B/ KO is also involved and Taira, Nose, Inoue, & Tsutsui, 2001 reported wide- spread responses). Our fMRI data supported only weak decoding of depth configurations defined by shading in LO, and more generally across higher portions of both the dorsal and ventral visual streams (Figures 3 and 4). Indeed, the highest prediction performance of the MVPA classifier for shading (relative to overall decoding accura- cies in each ROI) was observed in V1 and V2, which is likely to reflect low-level image differences between stim- ulus configurations rather than an estimate of shape from shading per se. Nevertheless, our findings from V3B/KO Dövencioğlu et al. 1539 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f . t / u s e r o n 1 7 M a y 2 0 2 1 make it clear that information provided by shading contributes to fMRI responses in higher portions of the dorsal stream. Why then is performance in the “shading” condition so low? Our experimental stimuli purposefully provoked conflicts between the disparity and shading information in the “single cue” conditions. Therefore, the conflicting information from disparity that the viewed surface was flat is likely to have attenuated fMRI re- sponses to the “shading alone” stimulus. Indeed, given that sensitivity to disparity differences was so much great- er than for shading, it might appear surprising that we could decode shading information at all. Previously, we used mathematical simulations to suggest that area V3B/KO contains a mixed population of responses, with some units responding to individual cues and others fus- ing cues into a single representation (Ban et al., 2012). Thus, residual fMRI decoding performance for the shad- ing condition may reflect responses to nonintegrated processing of the shading aspects of the stimuli. This mixed population could help support a robust perceptual interpretation of stimuli that contain significant cue con- flicts: for example, the reader should still be able to gain an impression of the 3-D structure of the shaded stimuli in Figure 1, despite conflicts with disparity). In summary, previous fMRI studies suggest a number of locations in which 3-D shape information might be processed (Nelissen et al., 2009; Sereno et al., 2002). Here we provide evidence that area V3B/KO plays an important role in integrating disparity and shading cues, compatible with the notion that it represents 3-D struc- ture from different signals (Tyler et al., 2006) that are sub- ject to different prior constraints (Preston et al., 2009). Our results suggest that V3B/KO is involved in 3-D estimation from qualitatively different depth cues, and its activity may underlie perceptual judgments of depth. Acknowledgments The work was supported by the Japan Society for the Promotion of Science (H22,290), the Wellcome Trust (095183/Z/10/Z), the EPSRC (EP/F026269/1), and the Birmingham University Imaging Centre. Reprint requests should be sent to Andrew E. Welchman, School of Psychology, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK, or via e-mail: A.E.Welchman@ bham.ac.uk. REFERENCES Anzai, A., Ohzawa, I., & Freeman, R. D. (2001). Joint-encoding of motion and depth by visual cortical neurons: Neural basis of the Pulfrich effect. Nature Neuroscience, 4, 513–518. Atkins, J. E., Fiser, J., & Jacobs, R. A. (2001). Experience- dependent visual cue integration based on consistencies between visual and haptic percepts. Vision Research, 41, 449–461. Ban, H., Preston, T. J., Meeson, A., & Welchman, A. E. (2012). The integration of motion and disparity cues to depth in dorsal visual cortex. Nature Neuroscience, 15, 636–643. Belhumeur, P. N., Kriegman, D. J., & Yuille, A. L. (1999). The bas-relief ambiguity. International Journal of Computer Vision, 35, 33–44. Blake, A., Zisserman, A., & Knowles, G. (1985). Surface descriptions from stereo and shading. Image and Vision Computing, 3, 183–191. Bradley, D. C., Qian, N., & Andersen, R. A. (1995). Integration of motion and stereopsis in middle temporal cortical area of macaques. Nature, 373, 609–611. Buelthoff, H. H., & Mallot, H. A. (1988). Integration of depth modules - Stereo and shading. Journal of the Optical Society of America: A, 5, 1749–1758. Burge, J., Fowlkes, C. C., & Banks, M. S. (2010). Natural-scene statistics predict how the figure-ground cue of convexity affects human depth perception. Journal of Neuroscience, 30, 7269–7280. Curran, W., & Johnston, A. (1996). The effect of illuminant position on perceived curvature. Vision Research, 36, 1399–1410. De Martino, F., Valente, G., Staeren, N., Ashburner, J., Goebel, R., & Formisano, E. (2008). Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. Neuroimage, 43, 44–58. DeAngelis, G. C., & Uka, T. (2003). Coding of horizontal disparity and velocity by MT neurons in the alert macaque. Journal of Neurophysiology, 89, 1094–1111. DeYoe, E. A., Carman, G. J., Bandettini, P., Glickman, S., Wieser, J., Cox, R., et al. (1996). Mapping striate and extrastriate visual areas in human cerebral cortex. Proceedings of the National Academy of Sciences, U.S.A., 93, 2382–2386. Doorschot, P. C. A., Kappers, A. M. L., & Koenderink, J. J. (2001). The combined influence of binocular disparity and shading on pictorial shape. Perception & Psychophysics, 63, 1038–1047. Dosher, B. A., Sperling, G., & Wurst, S. A. (1986). Tradeoffs between stereopsis and proximity luminance covariance as determinants of perceived 3-D structure. Vision Research, 26, 973–990. Dupont, P., De Bruyn, B., Vandenberghe, R., Rosier, A. M., Michiels, J., Marchal, G., et al. (1997). The kinetic occipital region in human visual cortex. Cerebral Cortex, 7, 283–292. Ernst, M. O. (2007). Learning to integrate arbitrary signals from vision and touch. Journal of Vision, 7, 1–14. Fleming, R. W., Dror, R. O., & Adelson, E. H. (2003). Real-world illumination and the perception of surface reflectance properties. Journal of Vision, 3, 347–368. Georgieva, S. S., Todd, J. T., Peeters, R., & Orban, G. A. (2008). The extraction of 3-D shape from texture and shading in the human brain. Cerebral Cortex, 18, 2416–2438. Gerardin, P., Kourtzi, Z., & Mamassian, P. (2010). Prior knowledge of illumination for 3-D perception in the human brain. Proceedings of the National Academy of Sciences, U.S.A., 107, 16309–16314. Gori, M., Del Viva, M., Sandini, G., & Burr, D. C. (2008). Young children do not integrate visual and haptic form information. Current Biology, 18, 694–698. Grill-Spector, K., Kushnir, T., Hendler, T., & Malach, R. (2000). The dynamics of object-selective activation correlate with recognition performance in humans. Nature Neuroscience, 3, 837–843. Hillis, J. M., Ernst, M. O., Banks, M. S., & Landy, M. S. (2002). Combining sensory information: Mandatory fusion within, but not between, senses. Science, 298, 1627–1630. Horn, B. K. P. (1975). Obtaining shape from shading information. In P. H. Winston (Ed.), The psychology of computer vision (pp. 115–155). New York: McGraw Hill. 1540 Journal of Cognitive Neuroscience Volume 25, Number 9 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . t f / u s e r o n 1 7 M a y 2 0 2 1 Janssen, P., Vogels, R., & Orban, G. A. (2000). Three- dimensional shape coding in inferior temporal cortex. Neuron, 27, 385–397. Kersten, D., Mamassian, P., & Yuille, A. (2004). Object perception as Bayesian inference. Annual Review of Psychology, 55, 271–304. Kingdom, F. A. A. (2003). Color brings relief to human vision. Nature Neuroscience, 6, 641–644. Knill, D. C., & Saunders, J. A. (2003). Do humans optimally integrate stereo and texture information for judgments of surface slant? Vision Research, 43, 2539–2558. Koenderink, J. J., & van Doorn, A. J. (2003). Shape and shading. In L. M. Chalupa & J. S. Werner (Eds.), The visual neurosciences (pp. 1090–1105). Cambridge, MA: MIT Press. Kourtzi, Z., & Kanwisher, N. (2001). Representation of perceived object shape by the human lateral occipital complex. Science, 293, 1506–1509. Kriegeskorte, N., Goebel, R., & Bandettini, P. (2006). Information-based functional brain mapping. Proceedings of the National Academy of Sciences, U.S.A., 103, 3863–3868. Landy, M. S., Maloney, L. T., Johnston, E. B., & Young, M. (1995). Measurement and modeling of depth cue combination - In defense of weak fusion. Vision Research, 35, 389–412. Larsson, J., Heeger, D. J., & Landy, M. S. (2010). Orientation selectivity of motion-boundary responses in human visual cortex. Journal of Neurophysiology, 104, 2940–2950. Lee, Y. L., & Saunders, J. A. (2011). Stereo improves 3-D shape discrimination even when rich monocular shape cues are available. Journal of Vision, 11, Article 2. Liu, B., & Todd, J. T. (2004). Perceptual biases in the interpretation of 3-D shape from shading. Vision Research, 44, 2135–2145. Lovell, P. G., Bloj, M., & Harris, J. M. (2012). Optimal integration of shading and binocular disparity for depth perception. Journal of Vision, 12, 1–18. Mamassian, P., & Goutcher, R. (2001). Prior knowledge on the illumination position. Cognition, 81, B1–B9. Mingolla, E., & Todd, J. T. (1986). Perception of solid shape from shading. Biological Cybernetics, 53, 137–151. Nandy, A. S., & Tjan, B. S. (2008). Efficient integration across spatial frequencies for letter identification in foveal and peripheral vision. Journal of Vision, 8, 1–20. Nardini, M., Bedford, R., & Mareschal, D. (2010). Fusion of visual cues is not mandatory in children. Proceedings of the National Academy of Sciences, U.S.A., 107, 17041–17046. Nardini, M., Jones, P., Bedford, R., & Braddick, O. (2008). Development of cue integration in human navigation. Current Biology, 18, 689–693. Nelissen, K., Joly, O., Durand, J. B., Todd, J. T., Vanduffel, W., & Orban, G. A. (2009). The extraction of depth structure from shading and texture in the macaque brain. Plos One, 4, e8306. Pentland, A. P. (1982). Finding the illuminant direction. Journal of the Optical Society of America, 72, 448–455. Popple, A. V., Smallman, H. S., & Findlay, J. M. (1998). The area of spatial integration for initial horizontal disparity vergence. Vision Research, 38, 319–326. Preston, T. J., Kourtzi, Z., & Welchman, A. E. (2009). Adaptive estimation of three-dimensional structure in the human brain. Journal of Neuroscience, 29, 1688–1698. Preston, T. J., Li, S., Kourtzi, Z., & Welchman, A. E. (2008). Multivoxel pattern selectivity for perceptually relevant binocular disparities in the human brain. Journal of Neuroscience, 28, 11315–11327. Ramachandran, V. S. (1988). Perception of shape from shading. Nature, 331, 163–166. Richards, W. (1985). Structure from stereo and motion. Journal of the Optical Society of America: A, 2, 343–349. Schiller, P. H., Slocum, W. M., Jao, B., & Weiner, V. S. (2011). The integration of disparity, shading and motion parallax cues for depth perception in humans and monkeys. Brain Research, 1377, 67–77. Schofield, A. J., Rock, P. B., & Georgeson, M. A. (2011). Sun and sky: Does human vision assume a mixture of point and diffuse illumination when interpreting shape-from-shading? Vision Research, 51, 2317–2330. Schofield, A. J., Rock, P. B., Sun, P., Jiang, X. Y., & Georgeson, M. A. (2010). What is second-order vision for? Discriminating illumination versus material changes. Journal of Vision, 10. Serences, J. T., & Boynton, G. M. (2007). The representation of behavioral choice for motion in human visual cortex. Journal of Neuroscience, 27, 12893–12899. Sereno, M. E., Trinath, T., Augath, M., & Logothetis, N. K. (2002). Three-dimensional shape representation in monkey cortex. Neuron, 33, 635–652. Sereno, M. I., Dale, A. M., Reppas, J. B., Kwong, K. K., Belliveau, J. W., Brady, T. J., et al. (1995). Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science, 268, 889–893. Srivastava, S., Orban, G. A., De Maziere, P. A., & Janssen, P. (2009). A distinct representation of three-dimensional shape in macaque anterior intraparietal area: Fast, metric, and coarse. Journal of Neuroscience, 29, 10613–10626. Sun, J., & Perona, P. (1998). Where is the sun? Nature Neuroscience, 1, 183–184. Taira, M., Nose, I., Inoue, K., & Tsutsui, K. (2001). Cortical areas related to attention to 3-D surface structures based on shading: An fMRI study. Neuroimage, 14, 959–966. Thomas, R., Nardini, M., & Mareschal, D. (2010). Interactions between “light-from-above” and convexity priors in visual development. Journal of Vision, 10, 6. Thompson, W. B., Fleming, R. W., Creem-Regehr, S. H., & Stefanucci, J. K. (2011). Illumination, shading and shadows. Chapter 9 of Visual perception from a computer graphics perspective. Boca Raton, FL: Taylor and Francis. Tootell, R. B. H., & Hadjikhani, N. (2001). Where is “dorsal V4” in human visual cortex? Retinotopic, topographic and functional evidence. Cerebral Cortex, 11, 298–311. Tootell, R. B., Hadjikhani, N., Hall, E. K., Marrett, S., Vanduffel, W., Vaughan, J. T., et al. (1998). The retinotopy of visual spatial attention. Neuron, 21, 1409–1422. Tyler, C. W., Likova, L. T., Chen, C.-C., Kontsevich, L. L., & Wade, A. R. (2005). Extended concepts of occipital retinotopy. Current Medical Imaging Reviews, 1, 319–329. Tyler, C. W., Likova, L. T., Kontsevich, L. L., & Wade, A. R. (2006). The specificity of cortical region KO to depth structure. Neuroimage, 30, 228–238. Vuong, Q. C., Domini, F., & Caudek, C. (2006). Disparity and shading cues cooperate for surface interpolation. Perception, 35, 145–155. Wagemans, J., van Doorn, A. J., & Koenderink, J. J. (2010). The shading cue in context. i-Perception, 1, 159–177. Zeki, S., Perry, R. J., & Bartels, A. (2003). The processing of kinetic contours in the brain. Cerebral Cortex, 13, 189–202. Zeki, S., Watson, J. D., Lueck, C. J., Friston, K. J., Kennard, C., & Frackowiak, R. S. (1991). A direct demonstration of functional specialization in human visual cortex. Journal of Neuroscience, 11, 641–649. Dövencioğlu et al. 1541 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e d o u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 5 / 9 2 5 1 / 5 9 2 / 7 1 1 5 9 2 4 7 5 / 6 1 3 7 8 7 o 9 c 5 n 6 _ 4 a / _ j 0 o 0 c 4 n 1 7 _ a p _ d 0 0 b 4 y 1 g 7 u . e p s t d o f n b 0 y 7 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . f / u s e r o n 1 7 M a y 2 0 2 1 Perceptual Integration for Qualitatively Different 3-D image

PDF Herunterladen