Model Compression for Domain Adaptation through Causal Effect
Estimation
Guy Rotman∗, Amir Feder∗, Roi Reichart
Faculty of Industrial Engineering and Management, Technion, IIT, Israel
grotman@campus.technion.ac.il
feder@campus.technion.ac.il
roiri@technion.ac.il
Abstrakt
Recent improvements in the predictive quality
of natural language processing systems are of-
ten dependent on a substantial increase in the
number of model parameters. This has led to
various attempts of compressing such models,
but existing methods have not considered the
differences in the predictive power of various
model components or in the generalizability
of the compressed models. To understand the
connection between model compression and
out-of-distribution generalization, we define
the task of compressing language representa-
tion models such that they perform best in a
domain adaptation setting. We choose to ad-
dress this problem from a causal perspective,
attempting to estimate the average treatment
Wirkung (ATE) of a model component, wie zum Beispiel
a single layer, on the model’s predictions.
Our proposed ATE-guided Model Compres-
sion scheme (AMoC), generates many model
candidates, differing by the model components
that were removed. Dann, we select the best
candidate through a stepwise regression model
that utilizes the ATE to predict the expected
performance on the target domain. AMoC
outperforms strong baselines on dozens of do-
main pairs across three text classification and
sequence tagging tasks.1
1
Einführung
The rise of deep neural networks has transformed
the way we represent language, allowing models
to learn useful features directly from raw inputs.
Jedoch, recent improvements in the predictive
quality of language representations are often re-
lated to a substantial increase in the number of
model parameters. In der Tat, the introduction of the
Transformer architecture (Vaswani et al., 2017)
∗Authors contributed equally.
1Our code and data are available at: https://github
.com/rotmanguy/AMoC.
and attention-based models (Devlin et al., 2019;
Liu et al., 2019; Brown et al., 2020) have improved
performance on most natural language processing
(NLP) tasks, while facilitating a large increase in
model sizes.
Since large models require a significant amount
of computation and memory during training and
inference, there is a growing demand for com-
pressing such models while retaining the most
relevant information. While recent attempts have
shown promising results (Sanh et al., 2019), Sie
have some limitations. Speziell, they attempt
to mimic the behavior of the larger models without
trying to understand the information preserved or
lost in the compression process.
In compressing the information represented in
billions of parameters, we identify three main
Herausforderungen. Erste, current methods for model
compression are not interpretable. While the im-
portance of different model parameters is certainly
not uniform, it is hard to know a priori which
of the model components should be discarded
in the compression process. This notion of fea-
ture importance has not yet trickled down into
compression methods, and they often attempt to
solve a dimensionality reduction problem where
a smaller model aims to mimic the predictions of
the larger model. dennoch, not all parameters
are born equal, and only a subset of the informa-
tion captured in the network is actually useful for
generalization (Frankle and Carbin, 2018).
The second challenge we observe in model
compression is out-of-distribution generalization.
Typically, compressed models are tested for their
in-domain generalization. Jedoch, in reality the
distribution of examples often varies and is differ-
ent than that seen during training. Without testing
for the generalization of the compressed models
on different test-set distributions, it is hard to fully
assess what was lost in the compression process.
1355
Transactions of the Association for Computational Linguistics, Bd. 9, S. 1355–1373, 2021. https://doi.org/10.1162/tacl a 00431
Action Editor: Hai Zhao. Submission batch: 5/2021; Revision batch: 8/2021; Published 12/2021.
C(cid:13) 2021 Verein für Computerlinguistik. Distributed under a CC-BY 4.0 Lizenz.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The setting explored in domain adaptation pro-
vides us with a platform to test the ability of the
compressed models to generalize across-domains,
where some information that the model has learned
to rely on might not exist. Strong model perfor-
mance across domains provides a stronger signal
on retaining valuable information.
zuletzt, another challenge we identify in training
and selecting compressed models is confidence es-
timation. In trying to understand what gives large
models the advantage over their smaller competi-
tors, recent probing efforts have discovered that
commonly used models such as BERT (Devlin
et al., 2019), learn to capture semantic and syn-
tactic information in different layers and neurons
across the network (Rogers et al., 2021). Während
some features might be crucial for the model, oth-
ers could learn spurious correlations that are only
present in the training set and are absent in the
test set (Kaushik et al., 2019). Such cases have
led to some intuitive common practices such as
keeping only layers with the same parity or the top
or bottom layers (Fan et al., 2019; Sajjad et al.,
2020). Those practices can be good on average,
but do not provide model confidence scores or
success rate estimates on unseen data.
Our approach addresses each of the three main
challenges we identify, as it allows estimating
the marginal effect of each model component, Ist
designed and tested for out-of-distribution gen-
eralization, and provides estimates for each com-
pressed model performance on an unlabeled target
Domain. We dive here into the connection be-
tween model compression and out-of-distribution
generalization, and ask whether compression
schemes should consider the effect of individual
model components on the resulting compressed
Modell. Insbesondere, we present a method that
attempts to compress a model while maintain-
ing components that can generalize well across
domains.
Inspired by causal inference (Pearl, 1995), unser
compression scheme is based on estimating the
average effect of model components on the de-
cisions the model makes, at both the source and
target domains. In causal inference, we measure
the effect of interventions by comparing the differ-
ence in outcome between the control and treatment
groups. In our setting, we take advantage of the
fact that we have access to unlabeled target ex-
amples, and treat the model’s predictions as our
outcome variable. We then try to estimate the
effect of a subset of the model components, solch
as one or more layers, on the model’s output.
To do that, we propose an approximation of a
counterfactual model where a model component
of choice is removed. We train an instance of the
model without that component and keep every-
thing else equal apart from the input and output to
that component, which allows us to perform only a
small number of gradient steps. Using this approx-
imation, we then estimate the average treatment
Wirkung (ATE) by comparing the predictions of the
base model to those of its counterfactual instance.
Since our compressed models are very effi-
ciently trained, we can generate a large number of
such models per each source-target domain pair.
We then train a regression model on our training
domain pairs in order to predict how well a com-
pressed model would generalize from a source to
a target domain, using the ATE as well as other
Variablen. This regression model can then be ap-
plied to new source-target domain pairs in order
to select the compressed model that best supports
cross-domain generalization.
To organize our contributions, we formulate
three research questions:
1. Can we produce a compressed model that out-
performs all baselines in out-of-distribution
generalization?
2. Does the model component we decide to
remove indeed hurt performance the least?
3. Can we use the average treatment effect to
guide our model selection process?
In § 6 we directly address each of the three
research questions, and demonstrate the usefulness
of our method, ATE-guided model compression
(AMoC), to improve model generalization.
2 Previous Work
Previous work on the intersection of neural model
compression, domain adaptation, and causal in-
ference is limited, as our application of causal
inference to model compression and our discus-
sion of the connection between compression and
cross-domain generalization are novel. Jedoch,
there is an abundance of work in each field on
its own, and on the connection between domain
adaptation and causal inference. Since our goal
1356
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
is to explore the connection between compression
and out-of-distribution generalization, as framed
in the setting of domain adaptation, we survey the
literature on model compression and the connec-
tion between generalization, Kausalität, and domain
adaptation.
2.1 Model Compression
NLP models have been increased exponentially in
Größe, growing from less than a million parameters
a few years ago to hundreds of billions. Since the
introduction of the Transformer architecture, Das
trend has been strengthened, with some models
reaching more than 175 billion parameters (Braun
et al., 2020). Infolge, there has been a growing
interest in compressing the information captured
in Transformers into smaller models (Chen et al.,
2020; Ganesh et al., 2020; Sun et al., 2020).
Usually, such smaller models are trained us-
ing the base model as a teacher, with the smaller
student model learning to predict its output prob-
abilities (Hinton et al., 2015; Jiao et al., 2020;
Sanh et al., 2019). Jedoch, even if the student
closely matches the teacher’s soft labels, their
internal representations may be considerably dif-
ferent. This internal mismatch can undermine the
generalization capabilities originally intended to
be transferred from the teacher to the student
(Aguilar et al., 2020; Mirzadeh et al., 2020).
As an alternative, we try not to interfere or alter
the learned representation of the model. Compres-
sion schemes such as those presented in Sanh et al.
(2019) discard model components randomly. In-
stead, we choose to focus on understanding which
components of the model capture the information
that is most useful for it to perform well across
domains, and hence should not be discarded.
2.2 Domain Adaptation and Causality
Domain adaptation is a longstanding challenge
in machine learning (ML) and NLP, which deals
with cases where the train and test sets are drawn
from different distributions. A great effort has
been dedicated to exploit labels from both source
and target domains for that purpose (Daum´e III
et al., 2010; Sato et al., 2017; Cui et al., 2018;
Lin and Lu, 2018; Wang et al., 2018). Jedoch,
a much more challenging and realistic scenario,
also termed unsupervised domain adaptation, oc-
curs when no labeled target samples exist (Blitzer
et al., 2006; Ganin et al., 2016; Ziser and Reichart,
2017, 2018A, B, 2019; Rotman and Reichart, 2019;
Ben-David et al., 2020). In this setting, we have
access to labeled and unlabeled data from the
source domain and to unlabeled data from the
target, and models are tested by their performance
on unseen examples from the target domain.
A closely related task is domain adaptation
success prediction. This task explores the pos-
sibility of predicting the expected performance
degradation between source and target domains
(McClosky et al., 2010; Elsahar and Gall´e,
2019). Similar to predicting performance in a
given NLP task, methods for predicting domain
adaptation success often rely on in-domain per-
formance and distance metrics estimating the
difference between the source and target dis-
tributions (Reichart and Rappoport, 2007; Ravi
et al., 2008; Louis and Nenkova, 2009; Van Asch
and Daelemans, 2010; Xia et al., 2020). Während
these efforts have demonstrated the importance of
out-of-domain performance prediction, they have
not been made as far as we know in relation to
model compression.
Ist
As the fundamental purpose of domain adap-
tation algorithms
improving the out-of-
distribution generalization of learning models, Es
is often linked with causal inference (Johansson
et al., 2016). In causal inference we typically
care about estimating the effect that an inter-
vention on a variable of interest would have on
an outcome (Pearl, 2009). Kürzlich, using causal
methods to improve the out-of-distribution per-
formance of trained classifiers is gaining traction
(Rojas-Carulla et al., 2018; Wald et al., 2021).
In der Tat, recent papers applied a causal approach
to domain adaptation. Some researchers proposed
using causal graphs to predict under distribution
shifts (Sch¨olkopf et al., 2012) and to understand
the type of shift (Zhang et al., 2013). Adapting
these ideas to computer vision, Gong et al. (2016)
were one of the first to propose a causal graph
describing the generative process of an image
as being generated by a ‘‘domain’’. The causal
graph served for learning invariant components
that transfer across domains. Since that, the no-
tion of invariant prediction has emerged as an
important operational concept in causal inference
(Peters et al., 2017). This idea has been used to
learn classifiers that are robust to domain shifts
and can perform well on unseen target distribu-
tionen (Gong et al., 2016; Magliacane et al., 2018;
1357
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Rojas-Carulla et al., 2018; Greenfeld and Shalit,
2020).
Here we borrow ideas from causality to help
us reason on the importance of specific model
components, such as individual layers. Das ist,
we estimate the effect of a given model compo-
nent (denoted as the treatment) on the model’s
predictions in the unlabeled target domain, Und
use the estimated effect as an evaluation of the
importance of this component. Our treatment ef-
fect estimation method is inspired by previous
causal model explanation work (Goyal et al., 2019;
Feder et al., 2021), although our algorithm is very
anders.
3 Causal Terminology
Causal methodology is most commonly used in
cases where the goal is estimating effects on
real-world outcomes, but it can be adapted to
help us understand and explain what affects NLP
Modelle (Feder et al., 2021). Speziell, we can
think of intervening on a model and altering its
components as a causal question, and measure the
effect of this intervention on model predictions.
A core benefit of this approach is that we can
estimate treatment effects on model’s predictions
without the need for manually-labeled target data.
Borrowing causal methodology into our setting,
we treat model components as our treatment, Und
try to estimate the effect of removing them on our
model’s predictions. The predictions of a model
are driven by its components, and by changing
one component and holding everything else equal,
we can estimate the effect of this intervention. Wir
can use this estimation in deciding which model
component should be kept in the compression
Verfahren.
As the link between model compression and
causal inference was not explored previously, Wir
provide here a short introduction to causal infer-
ence and its basic terminology, focusing on its
application to our use case. We then discuss the
connection to Pearl’s do-operator (Pearl et al.,
2009) and the estimation of treatment effects.
Imagine we have a model m that classifies
examples to one of L classes. Given a set C
of K model components, which we hypothesize
might affect the model’s decision, we denote the
set of binary variables Ic = {Icj ∈ {0, 1}|j ∈
{1, . . . , K}}, where each corresponds to the in-
clusion of the component in the model, das ist,
if Icj = 1 then the j-th component (cj) is in the
Modell. Our goal is to assert how the model’s pre-
dictions are affected by the components in C. Als
we are interested in the effect on the class proba-
bility assigned by m, we measure this probability
for an example x, and denote it for a class l as
z(M(X))l and for all L classes as ~z(M(X)).
Using this setup, we can now define the ATE,
the common metric used when estimating causal
Effekte. ATE is the difference in mean outcomes
between the treatment and control groups, Und
using do-calculus (Pearl, 1995) we can define it
as follows:
Definition 1 (Average Treatment Effect (ATE))
The average treatment effect of a binary treatment
Icj on the outcome ~z(M(X)) Ist:
ATE(cj) =E
(cid:2)~z(M(X))|do(Icj = 1)(cid:3)
− E
(cid:2)~z(M(X))|do(Icj = 0)(cid:3) ,
(1)
where the do-operator is a mathematical opera-
tor introduced by Pearl (1995), which indicates
that we intervene on cj such that it is included
(do(Icj = 1)) or not (do(Icj = 0)) im Modell.
While the setup usually explored with do-
calculus involves a fixed joint-distribution where
treatments are assigned to individuals (or exam-
ples), we borrow intuition from a specialized case
where interventions are made on the process which
generates outcomes given examples. This type of
an intervention is called Process Control, Und
was proposed by Pearl et al. (2009) and further
explored by Bottou et al. (2013). This unique
setup is designed to improve our understanding of
the behavior of complex learning systems and
predict
the consequences of changes made to
the system. Kürzlich, Feder et al. (2021) gebraucht
it to intervene on language representation models,
generating a counterfactual representation model
through an adversarial training algorithm which
biases the representation model to forget infor-
mation about treatment concepts and maintain
information about control concepts.
In our approach we intervene on the j-th com-
ponent, by holding the rest of the model fixed and
training only the parameters that control the input
and output to that component. This is crucial for
our estimation procedure as we want to know the
effect of the j-th component on a specific model
Beispiel. This effect can be computed by compar-
ing the predictions of the original model instance
1358
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
to those of the intervened model (siehe unten).
This computation is fundamentally different from
measuring the conditional probability where the
j-th component is not in the model by estimating
E
(cid:2)~z(M(X))|Icj = 0(cid:3).
4 Methodik
We start by describing the task of compress-
they perform well on
ing models such that
out-of-distribution examples, detailing the domain
adaptation framework we focus on. Dann, we de-
scribe our compression scheme, designed to allow
us to approximate the ATE and responsible for
producing compressed model candidates. Endlich,
we propose a regression model that uses the ATE
and other features to predict a candidate model’s
performance on a target domain. This regression
allows us to select a strong candidate model.
4.1 Task Definition and Framework
To test the ability of a compressed model to
generalize on out-of-distribution examples, Wir
choose to focus on a domain adaptation setting. Ein
appealing property of domain adaptation setups is
that they allow us to measure out-of-distribution
performance in a very natural way by training on
one domain and testing on another.
In our setup, during training, we have access
to n source-target domain pairs (Si, Ti)N
i=1. Für
each pair we assume to have labeled data from the
source domains (LSi)N
i=1 and unlabeled data from
the the source and target domains (USi, UTi)N
i=1.
We also assume to have held-out labeled data
for all domains, for measuring test performance
(HSi, HTi)N
i=1. At test time we are given an unseen
domain pair (Sn+1, Tn+1) with labeled source data
LSn+1 and unlabeled data from both domains USn+1
and UTn+1, jeweils. Our goal is to classify
examples on the unseen target domain Tn+1 using
a compressed model mn+1 trained on the new
source domain.
1, . . . , mi
For each domain pair in (Si, Ti)N
i=1, we gen-
erate a set of K candidate models M i =
{mi
K}, differing by the model compo-
nents that were removed from the base model
mi
B. For each candidate, we compute the ATE and
other relevant features which we discuss in § 4.3.
Dann, using the training domain pairs, for which
we have access to a limited amount of labeled
target data, we train a stepwise linear regression
to predict the performance of all candidate models
In {M i}N
i=1 on their target domain. Endlich, at test
Zeit, after computing the regression features on
the unseen source-target pair, we use the trained
regression model to select the compressed model
(mn+1)∗ ∈ M n+1 that is expected to perform best
on the unseen unlabeled target domain.
While this task definition relies on a limited
number of labeled examples from some target do-
mains at training time, at test time we only use
labeled examples from the source domain and un-
labeled examples from the target. We elaborate
on our compression scheme, responsible for gen-
erating the compressed model candidates in § 4.2.
We then describe the regression features and the
regression model in § 4.3 and § 4.4, jeweils.
4.2 Compression Scheme
Our compression scheme (AMoC) assumes to
operate on a large classifier, consisting of an
encoder-decoder architecture, that serves as the
base model being compressed. In such models,
the encoder is the language representation model
(z.B., BERT), and the decoder is the task classifier.
Each input sentence x to the base model mi
B is
encoded by the encoder e. Dann, the encoded
sentence e(X) is passed through the decoder d to
compute a distribution over the the label space
L: ~z(mi
B(X)) = Sof tmax(D(e(X))). AMoC is
designed to remove a set of encoder components,
and can in principle be used with any language
encoder.
As described in Algorithm 1, AMoC generates
candidate compressed versions of mi
B. In each it-
eration it selects from C, the set containing subsets
of encoder components, a candidate ck ∈ C to be
removed.2 The goal of this process is to generate
many compressed model candidates, such that the
k-th candidate ck differs from the base model mi
B
only by the effect of the parameters in ck on the
model’s predictions. After generating these candi-
dates, AMoC tries to choose the best performing
model for the unseen target domain.
When generating the k-th compressed model of
the i-th source-target pair, we start by removing
all parameters in ck from the computational graph
of mi
B. Dann, we connect the predecessor of each
detached component from ck to its successor in
the graph, which yields the new mi
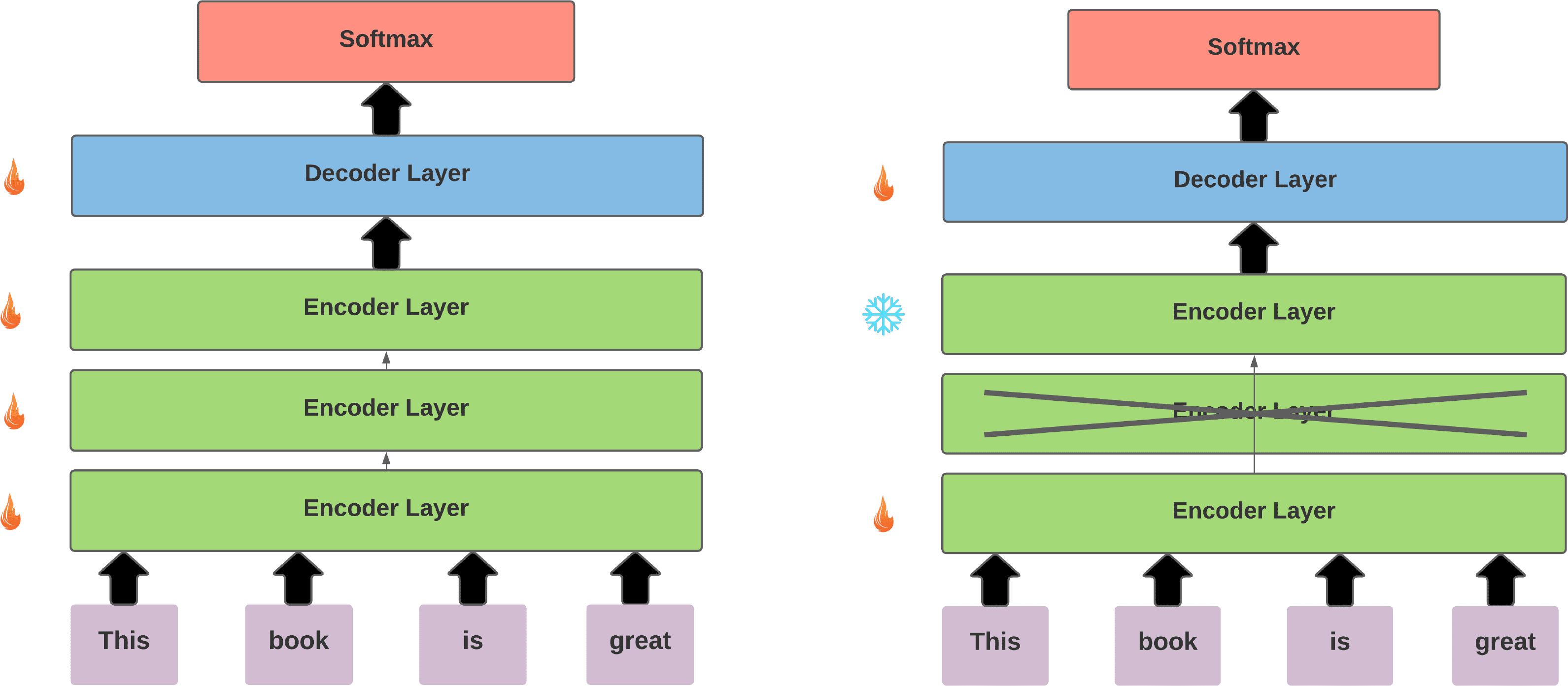
k (siehe Abbildung 1).
To estimate the effect of ck on the predictions of
2Zum Beispiel, if components correspond to layers, and we
wish to remove an individual layer from a 12-layer encoder,
then C = {{ich}|i ∈ {1, . . . , 12}}.
1359
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Algorithm 1 ATE-Guided Model Compression (AMoC)
Input: Domain pairs (Si, Ti)n+1
i=1 with Labeled source data
(LSi )n+1
i=1 , Unlabeled source and target data (USi , UTi )n+1
i=1 ,
Labeled held-out source and target data (HSi , HTi )N
i=1, Und
a set C of subsets of encoder components to be removed.
Algorithm:
1. For each domain pair in (Si, Ti)N
(A) Train the base model mi
(B) For ck ∈ C
i=1
B on LSi .
– Freeze all encoder parameters.
– Remove every component in ck from mi
B.
– Connect and unfreeze the remaining
components according to § 4.2.
– Fine-tune the new model mi
k on LSi for
one or more epochs.
– Compute [AT ESi (ck) Und [AT ET i (ck)
according to Eq. 2, using USi and UTi .
– Compute the remaining features in 4.3.
2. Train the stepwise regression according to Eq. 4, verwenden
all compressed models generated in step 1.
3. Repeat steps 1(A)-1(B) für (Sn+1, Tn+1) and choose
(mn+1)∗ with the highest expected performance
according to the regression model.
mi
B, we freeze all remaining model parameters in
mi
k and fine-tune it for one or more epochs, train-
ing only the decoder and the parameters of the
new connections between the predecessors and
successors of the removed components. An ad-
vantage of this procedure is that we can efficiently
generate many model candidates. Figur 1 Dämon-
strates this process on a simple architecture when
considering the removal of layer components.
Guiding our model selection step is the ATE
of ck on the base model mi
B. The generation of
each compressed candidate mi
k is designed to al-
low us to estimate the effect of ck on the model’s
Vorhersagen. In comparing the predictions of mi
B
to the compressed model mi
k on many exam-
ples, we try to mimic the process of generating
control and treatment groups. As is done in con-
trolled experiments, we compare examples that
are given a treatment, nämlich, encoded by the
compressed model mi
k, and examples that were
encoded by the base model mi
B. Intervening on
the example-generating process was explored pre-
viously in the causality literature by Bottou et al.
(2013); Feder et al. (2021).
Alongside the ATE, we compute other fea-
tures that might be predictive of a compressed
model’s performance on an unlabeled target do-
main, which we discuss in detail in § 4.3. Using
those features and the ATE, we train a linear step-
wise regression to predict a compressed model’s
performance on target domains (§ 4.4). Endlich,
at test time AMoC is given an unseen domain
pair and applies the regression in order to choose
the compressed source model expected to perform
best on the target domain. Using the regression,
we can estimate the power of the ATE in predict-
ing model performance and answer Question 3
of § 1.
In diesem Papier, we choose to focus on the removal
of sets of layers, as done in previous work (Fan
et al., 2019; Sanh et al., 2019; Sajjad et al., 2020).
While our method can support any other parameter
partitioning, such as clusters of neurons, we leave
this for future work. In the case of layers, to estab-
lish the new compressed model we simply connect
the remained layers according to their hierarchy.
Zum Beispiel, for a base model with a 12-layer
encoder and c = {2, 3, 7} the unconnected com-
ponents are {1}, {4, 5, 6} Und {8, 9, 10, 11, 12}.
Layer 1 will then be connected to layer 4, Und
layer 6 to layer 8. The compressed model will be
then trained for one or more epochs where only
the decoder and layers 1 Und 6 (using the original
indices) are fine-tuned. In times where layer 1 Ist
removed, the embedding layer is connected to the
first unremoved layer and is fine-tuned.
4.3 Regression Features
Apart from the ATE, which estimates the impact
of the intervention on the base model, we naturally
need to consider other features. In der Tat, without
any information on the target domain, predicting
that a model will perform the same as in the source
domain could be a reasonable first-order approx-
imation (McClosky et al., 2010). Auch, adding
information on the distance between the source
and target distributions (Van Asch and Daelemans,
2010) or on the type of components that were re-
moved (such as the number of layers) might also
be useful for predicting the model’s success. Wir
present here all the features we consider, Und
discuss their usefulness in predicting model per-
Form. To answer Q3, we need to show that
given all this information, the ATE is still pre-
dictive for the model’s performance in the target
Domain.
ATE Our main variable of interest is the av-
erage treatment effect of the components in ck
on the predictions of the model. In our compres-
sion scheme, we estimate for a specific domain
1360
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
T
A
C
l
/
l
A
R
T
ich
C
e
–
P
D
F
/
D
Ö
ich
/
.
1
0
1
1
6
2
/
T
l
A
C
_
A
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
T
l
A
C
_
A
_
0
0
4
3
1
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1: An example of our method with a 3-layer encoder when considering the removal of layer components.
(A) At first, the base model is trained (Alg. 1, step 1(A)). (B) The second encoder layer is removed from the base
Modell, and the first layer is connected to the final encoder layer. The compressed model is then fine-tuned for one
or more epochs, where only the parameters of the first layer and the decoder are updated (Alg. 1, step 1(B)). Wir
mark frozen layers and non-frozen layers with snowflakes and fire symbols, jeweils.
d ∈ {Si, T i} the ATE for each compressed model
mi
k by comparing it to the base model mi
B:
[AT Ed(ck) =
1
|Ud| X
x∈Ud
h~z(cid:0)mi
B(X)(cid:1) − ~z(cid:0)mi
k(X)(cid:1)ich
(2)
where the operator hi denotes the total variation
Distanz: A summation over the absolute values
of vector coordinates.3 As we are interested in the
effect on the probability assigned to each class by
the classifier mi
k, we measure the class probability
of its output for an example x, as proposed by
Feder et al. (2021).4
In our regression model we choose to include
the ATE of the source and the target domains,
[AT ESi(ck) (estimated on USi) Und [AT ET i(ck)
(estimated on UTi) , jeweils. We note that
in computing the ATE we only require the pre-
dictions of the models, and do not need labeled
Daten.
In-domain Performance A common metric for
selecting a classification model is its performance
3For a three class prediction and a single example, Wo
the probability distributions for the base and the compressed
models are (0.7, 0.2, 0.1) Und (0.5, 0.1, 0.4), jeweils,
[AT Ei(ck) = |0.7 − 0.5| + |0.2 − 0.1| + |0.1 − 0.4| = 0.6.
compute
sentence-level ATEs by averaging the word-level proba-
bility differences, and then average those ATEs to get the
final ATE.
tagging tasks, Wir
sequence
4Für
Erste
on a held-out set. In der Tat, in cases where we do
not have access to any information from the target
Domain, the naive choice is the best performing
model on a held-out source domain set (Elsahar
and Gall´e, 2019). Somit, for every ck ∈ C we
compute the performance of mi
k on HSi.
Domain Classification An important variable
when predicting model performance on an unseen
test domain is the distance between its training
domain and that test domain (Elsahar and Gall´e,
2019). While there are many ways to approximate
this distance, we choose to do so by training a
domain classifier on USi and UTi, classifying
each example according to its domain. We then
compute the average probability assigned to the
target examples to belong to the source domain,
according to the domain classifier:
\
P (Si|T i) =
1
|HTi| X
x∈HTi
P (Si|X),
(3)
where P (Si|X) denotes for an unlabeled target
example x, the probability that it belongs to the
source domain Si, based on the domain classifier.
Compression-size Effects We include in our
regression binary variables indicating the number
of layers that were removed. Naturally, we assume
that the larger the number of layers removed, Die
bigger the gap from the base model should be.
1361
4.4 Regression Analysis
In order to decide which ck should be removed
from the base model, we follow the process de-
scribed in Algorithm 1 for all c ∈ C and end up
with many candidate compressed models, differ-
ing by the model components that were removed.
As our goal is to choose a candidate model to be
used in an unseen target domain, we train a stan-
dard linear stepwise regression model (Hocking,
1976; Draper and Smith, 1998; Dubossarsky et al.,
2020) to predict the candidate’s performance on
the seen target domains:
Y = β0 + β1X1 + · · · + βmXm + ǫ,
(4)
where Y is performance on these target domains,
computed using their held-out sets (HTi)N
i=1, Und
X1, · · · , Xm are the set of variables described in
4.3, including the ATE. In stepwise regression
variables are added to the model incrementally
only if their marginal addition for predicting Y is
statistically significant (P < 0.01). This method
is useful for finding variables with maximal and
unique contribution to the explanation of Y . The
value of this regression is two-fold in our case
as it allows us to: (1) get a predictive model
that can choose a high quality compressed model
candidate, and (2) estimate the predictive power
of the ATE on model performance in the target
domain.
5 Experiments
5.1 Data
We consider three challenging data sets (tasks):
(1) The Amazon product reviews data set for sen-
timent classification (He and McAuley, 2016).5
This data set consists of product reviews and
metadata, from which we choose 6 distinct do-
mains: Amazon Instant Video (AIV), Beauty (B),
Digital Music (DM), Musical Instruments (MI),
Sports and Outdoors (SAO), and Video Games
(VG). All reviews are annotated with an integer
score between 0 and 5. We label > 3 reviews as
positive and < 3 reviews as negative. Ambiguous
reviews (rating = 3) are discarded. Since the data
set does not contain development and test sets, we
randomly split each domain into training (64%),
development (16%), and test (20%) sets.
(2) The Multi-Genre Natural Language In-
ference (MultiNLI) corpus for natural language
inference classification (Williams et al., 2018).6
This corpus consists of pairs of sentences, a
premise and a hypothesis, where the hypothesis
either entails the premise, is neutral to it or contra-
dicts it. The MultiNLI data set extends upon the
SNLI corpus (Bowman et al., 2015), assembled
from image captions, to 10 additional domains:
5 matched domains, containing training, devel-
opment and test samples and 5 mismatched,
containing only development and test samples.
We experiment with the original SNLI corpus
(Captions domain) as well as the matched version
of MultiNLI, containing the Fiction, Government,
Slate, Telephone and Travel domains, for a total
of 6 domains.
(3) The OntoNotes 5.0 data set (Hovy et al.,
2006), consisting of sentences annotated with
named entities, part-of-speech tags and parse
trees.7 We focus on the Named Entity Recogni-
tion (NER) task with 6 different English domains:
Broadcast Conversation (BC), Broadcast News
(BN), Magazine (MZ), Newswire (NW), Tele-
phone Conversation (TC), and Web data (WB).
This setup allows us to evaluate the quality of
AMoC on a sequence tagging task.
The statistics of our experimental setups are
reported in Table 1. Since the test sets of the
MultiNLI domains are not publicly available, we
treat the original development sets as our test
sets, and randomly choose 2,000 examples from
the training set of each domain to serve as the
development sets. We use the original splits of
the SNLI as they are all publicly available. Since
our data sets manifest class imbalance phenomena
we use the macro average F1 as our evaluation
measure.
For the regression step of Algorithm 1, we
use the development set of each target domain
to compute the model’s macro F1 score (for the
Y and the in-domain performance variables). We
compute the ATE variables on the development
sets of both domains, train the domain classifier
on unlabeled versions of the training sets and
\P (S|T ) on the target development set.
compute
5http://jmcauley.ucsd.edu/data/amazon/.
6https://cims.nyu.edu/∼sbowman/multinli/.
7https://catalog.ldc.upenn.edu/LDC2013T19.
1362
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Amazon Reviews
Amazon Instant Video
Beauty
Digital Music
Musical Instruments
Sports and Outdoors
Video Games
Train Dev
21K
112K 28K
37K
6K
174K 43K
130K 32K
Test
5.2K 6.5K
35K
9.2K 11K
1.5K 1.9K
54K
40K
Captions
Fiction
Government
Slate
Telephone
Travel
MultiNLI
Train Dev
550K 10K
75K
75K
75K
81K
75K
OntoNotes
2K
2K
2K
2K
2K
Test
10K
2K
2K
2K
2K
2K
Broadcast Conversation
Broadcast News
Magazine
News
Telephone Conversation
Web
Test
Train Dev
36K
173K 30K
26K
207K 25K
161K 15K
17K
878K 148K 60K
11K
92K
11K
50K
361K 48K
Table 1: Data statistics. We report the number of
sentences for Amazon Reviews and MultiNLI,
and the number of tokens for OntoNotes.
5.2 Model and Baselines
Model The encoder being compressed is the
BERT-base model (Devlin et al., 2019). BERT
is a 12-layer Transformer model Vaswani et al.
(2017); Radford et al. (2018), representing tex-
tual
inputs contextually and sequentially. Our
decoder consists of a layer attention mechanism
(Kondratyuk and Straka, 2019) which computes
a parameterized weighted average over the lay-
ers’ output, followed by a 1D convolution with
the max-pooling operation and a final Softmax
layer. Figure 1(a) presents a simplified version
of the architecture of this model with 3 encoder
layers.
Baselines To put our results in context of pre-
vious model compression work, we compare our
models to three strong baselines. Like AMoC,
the baselines generate reduced-size encoders.
These encoders are augmented with the same
decoder as in our model to yield the baseline
architectures.
The first baseline is DistilBERT (DB) (Sanh
et al., 2019): A 6-layer compressed version of
BERT-base,
trained on the masked language
modelling task with the goal of mimicking the
predictions of the larger model. We used its
default setting,
i.e., removal of 6 layers with
c = {2, 4, 6, 7, 9, 11}. Sanh et al. (2019) demon-
strated that DistilBERT achieves comparable
results to the large model with only half of its
layers.
Since DistilBERT was not designed or tested
on out-of-distribution data, we create an addi-
tional version, denoted as DB + DA. In this
version, the training process is performed on the
masked language modelling task using an unla-
beled version of the training data from both the
source and the target domains, with its original
hyperparameters.
We further add an additional adaptation-aware
baseline: DB + GR,
the DistilBERT model
equipped with the gradient reversal (GR) layer
(Ganin and Lempitsky, 2015). Particularly, we
augment the DistilBERT model with a domain
classifier, similar in structure to the task classifier,
which aims to distinguish between the unlabeled
source and the unlabeled target examples. By re-
versing the gradients resulting from the objective
function of this classifier, the encoder is biased to
produce domain-invariant representations. We set
the weights of the main task loss and the domain
classification loss to 1 and 0.1, respectively.
Another baseline is LayerDrop (LD), a pro-
cedure that applies layer dropout during training,
making the model robust to the removal of certain
layers during inference (Fan et al., 2019). During
training, we apply a fixed dropout rate of 0.5 for all
layers. At inference, we apply their Every Other
strategy by removing all even layers to obtain a
reduced 6-layer model.
Finally, we compare AMoC to ALBERT, a
recently proposed BERT-based variant designed
to mimic the performance of the larger BERT
model with only a tenth of its parameters (11M
parameters compared to BERT’s 110M parame-
ters) (Lan et al., 2020). ALBERT is trained with
cross-layer parameter sharing and sentence order-
ing objectives, leading to better model efficiency.
Unlike other baselines explored here, it is not
directly comparable since it consists of 12 layers
and was pre-trained on substantially more data. As
such, we do not include it in the main results ta-
ble (Table 2), and instead discuss its performance
compared to AMoC in Section 6.
1363
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
S\T
AIV
B
DM
MI
SAO
VG
AVG
AIV
B
DM
MI
SAO
VG
AVG
S\T
Captions
Fiction
Govern.
Slate
Telephone
Travel
AVG
Captions
Fiction
Govern.
Slate
Telephone
Travel
AVG
S\T
BC
BN
MZ
NW
TC
WB
AVG
BC
BN
MZ
NW
TC
WB
AVG
Base AMoC
DB
DB+DA DB+GR
LD
AIV
80.05
78.97
65.24
77.10
82.73
76.81
79.18
78.57
69.87
77.64
83.79
77.81
Base AMoC
64.44
67.99
80.16
82.70
71.10
71.53
84.16
86.43
78.56
84.73
82.07
76.50
69.23
69.52
54.96
63.26
73.66
66.13
DB
58.26
66.47
59.18
71.09
66.22
64.24
74.07
76.00
67.21
70.01
78.98
73.25
66.73
70.39
55.99
63.43
73.24
65.96
MI
DB+DA DB+GR
61.64
76.28
67.21
78.64
76.77
72.11
58.64
68.03
61.37
72.27
67.38
65.54
74.10
72.14
56.53
67.72
76.24
69.35
LD
61.43
71.87
63.13
72.44
70.59
67.89
Amazon Reviews
Base AMoC
82.14
75.49
DB
65.00
76.54
72.72
83.88
85.20
78.77
74.37
72.78
85.12
85.21
79.92
Base AMoC
69.52
69.76
83.21
83.73
63.83
70.94
72.71
70.08
82.61
75.42
82.23
74.30
63.83
55.75
69.87
69.62
64.81
DB
59.71
72.23
58.45
59.23
68.96
63.72
MNLI
B
DB+DA DB+GR
75.86
65.42
74.94
74.83
81.74
80.34
77.54
65.21
46.44
67.19
70.91
63.03
SAO
DB+DA DB+GR
71.62
79.57
65.29
71.39
79.12
73.40
58.96
72.11
61.75
58.30
70.18
64.26
LD
69.51
67.36
61.25
76.32
77.13
70.31
LD
62.97
77.29
62.79
66.10
73.83
68.60
Captions
Fiction
Base AMoC
DB
DB+DA DB+GR
LD
Base AMoC
58.37
58.92
DB
46.96
DB+DA DB+GR
57.37
46.04
LD
54.93
71.33
62.52
65.04
65.04
65.77
65.94
68.81
68.04
62.40
61.22
62.11
64.52
Base AMoC
53.26
52.83
62.94
66.76
65.59
65.22
65.53
65.02
63.07
63.62
60.11
61.10
39.04
44.45
37.58
40.03
36.54
39.53
DB
41.30
44.79
46.57
45.73
45.65
44.81
67.60
63.47
46.99
58.65
60.11
59.36
45.26
39.23
44.87
36.64
38.29
40.86
Slate
DB+DA DB+GR
52.96
64.13
62.89
56.35
60.96
59.46
42.23
45.70
45.42
44.68
47.08
45.02
Base AMoC
DB
BC
DB+DA DB+GR
74.25
66.56
72.23
42.63
28.47
56.83
71.06
62.00
70.26
41.78
27.58
54.54
Base AMoC
58.80
61.31
69.79
73.55
63.80
67.40
35.25
22.60
52.02
35.15
26.40
50.79
70.83
60.55
68.22
45.14
26.79
54.31
DB
58.44
70.51
63.04
36.73
23.64
50.47
70.11
61.76
70.16
39.18
25.17
53.28
70.29
62.06
41.20
21.32
26.97
44.37
NW
DB+DA DB+GR
57.75
71.26
63.64
35.58
27.57
51.16
46.95
58.80
50.33
20.83
20.61
39.50
63.27
54.68
55.39
59.77
55.41
57.70
LD
50.56
59.82
61.06
60.70
56.51
57.73
LD
65.61
54.76
63.57
29.64
21.97
47.11
LD
50.73
62.31
52.08
27.93
17.02
42.01
67.61
69.83
69.07
66.97
66.48
66.05
67.70
67.77
65.19
65.02
44.5
46.53
47.45
44.05
45.90
63.47
58.59
63.76
60.06
60.65
Telephone
46.75
43.58
46.76
42.94
45.21
Base AMoC
56.68
56.94
68.47
71.83
67.87
67.54
71.27
68.27
DB
41.22
41.66
43.73
45.21
69.57
66.83
66.31
66.12
42.30
42.82
OntoNotes
DB+DA DB+GR
58.35
67.70
65.39
59.39
64.35
63.04
45.53
44.52
45.88
39.50
45.86
44.26
Base AMoC
71.28
73.78
DB
70.76
71.47
80.85
53.08
40.39
63.91
67.32
79.54
52.37
40.68
62.24
Base AMoC
63.07
62.39
65.69
69.64
56.94
60.31
51.88
61.20
18.68
54.44
15.45
50.61
66.5
78.15
54.56
39.09
61.81
DB
58.19
61.45
54.61
50.73
18.36
48.67
BN
DB+DA DB+GR
70.94
58.22
66.41
79.34
51.69
40.35
61.75
59.67
68.92
19.80
30.79
47.48
TC
DB+DA DB+GR
59.53
64.68
55.51
49.78
15.38
48.98
59.31
64.98
63.37
36.48
7.64
46.36
60.44
62.07
61.91
56.67
59.20
LD
54.01
64.97
65.46
61.06
61.63
61.43
LD
66.46
61.29
75.07
42.16
33.55
55.71
LD
55.21
60.40
42.00
44.38
10.77
42.55
Base AMoC
76.02
77.66
76.60
77.10
60.09
74.30
81.10
74.05
63.88
75.15
82.43
74.82
Base AMoC
76.52
77.71
82.23
82.57
76.04
78.45
67.91
65.10
81.06
80.05
DM
DB+DA DB+GR
75.94
72.74
68.24
67.60
75.08
71.92
62.8
58.52
30.42
60.58
72.51
56.97
VG
DB+DA DB+GR
76.44
76.96
76.21
56.37
75.14
67.11
65.50
66.93
49.67
65.78
DB
67.12
65.42
50.01
58.51
71.21
62.45
DB
67.43
65.52
68.67
51.60
64.51
LD
71.92
69.94
52.67
64.60
76.01
67.03
LD
70.19
71.59
70.66
56.87
70.00
76.78
76.75
63.55
72.22
63.00
67.86
Base AMoC
59.35
59.51
69.71
73.41
72.95
71.46
74.24
70.31
72.16
65.47
72.07
67.75
Base AMoC
57.40
57.88
66.28
69.86
64.70
67.45
69.01
71.47
65.97
69.20
Govern.
DB
40.14
46.83
49.53
46.83
49.03
46.47
DB
42.86
46.98
48.67
46.19
47.30
DB+DA DB+GR
57.85
69.55
71.31
66.63
72.69
67.61
42.54
47.10
49.23
45.99
51.32
47.24
Travel
DB+DA DB+GR
54.84
66.52
66.99
57.94
65.53
43.64
46.81
48.58
46.92
42.94
LD
56.85
63.56
66.82
65.53
65.47
63.65
LD
54.88
62.36
63.09
61.79
61.76
67.17
64.67
46.40
62.36
45.78
60.78
Base AMoC
60.96
64.06
68.34
69.92
74.66
39.17
15.86
52.73
71.78
38.59
20.09
51.95
Base AMoC
47.42
48.90
50.14
51.34
44.78
48.25
50.52
52.23
35.36
36.50
MZ
DB+DA DB+GR
64.75
69.39
72.28
38.75
24.84
54.00
48.48
69.70
65.76
16.98
15.53
43.29
WB
DB+DA DB+GR
46.00
48.72
43.91
49.30
36.23
45.56
48.39
39.98
41.34
25.72
DB
63.44
68.71
71.86
41.94
22.84
53.76
DB
45.58
48.02
43.11
49.07
37.00
LD
53.78
60.87
64.82
33.81
13.52
45.36
LD
40.17
43.45
38.80
45.72
27.04
47.44
45.64
44.56
44.83
40.20
39.04
Table 2: Domain adaptation results in terms of macro F1 scores on Amazon Reviews (top), MultiNLI
(middle), and OntoNotes (bottom) with 6 removed layers. S and T denote Source and Target, respectively.
The best result among the compressed models (all models except from Base) is highlighted in bold. We
mark results that outperform the uncompressed Base model with an underscore.
5.3 Compression Scheme Experiments
While our compression algorithm is neither
restricted to a specific deep neural network ar-
chitecture nor to the removal of certain model
components, we follow previous work and focus
on the removal of layer sets (Fan et al., 2019, Sanh
et al., 2019; Sajjad et al., 2020). With the goal of
addressing our research questions posed in § 1,
we perform extensive compression experiments
on the 12-layer BERT by considering the removal
of 4, 6, and 8 layers. For each number of layers
removed, we randomly sample 100 layer sets to
generate our model candidates. To be able to test
our method on all domain pairs, we randomly split
these pairs into five 20% domain pair sets and train
five regression models, differing in the set used
for testing. Our splits respect the restriction that
no test set domain (source or target) appears in the
training set.
5.4 Hyperparameters
We implement all models using HuggingFace’s
Transformers package (Wolf et al., 2020).8 We
consider the following hyperparameters for the
uncompressed models: Training for 10 epochs
8https://github.com/huggingface/transformers.
1364
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(Amazon Reviews and MultiNLI) or 30 epochs
(OntoNotes) with an early stopping criterion ac-
cording to the development set, optimizing all
parameters using the ADAM optimizer (Kingma
and Ba, 2015) with a weight decay of 0.01 and a
learning rate of 1e-4, a batch size of 32, a window
size of 9, 16 output channels for the 1D convolu-
tion, and a dropout layer probability of 0.1 for the
layer attention module. The compressed models
are trained on the labeled source data for 1 epoch
(Amazon Reviews and MultiNLI) or 10 epochs
(OntoNotes).
The domain classifiers are identical
in ar-
chitecture to our task classifiers and use the
uncompressed encoder after it was optimized
during the above task-based training. These clas-
sifiers are trained on the unlabeled version of the
source and target training sets for 25 epochs with
early stopping, using the same hyperparameters as
above.
6 Results
Performance of Compressed Models Table 2
reports macro F1 scores for all domain pairs of
the Amazon Reviews, MultiNLI, and OntoNotes
data sets, when considering the removal of 6 lay-
ers, and Figure 2 provides summary statistics.
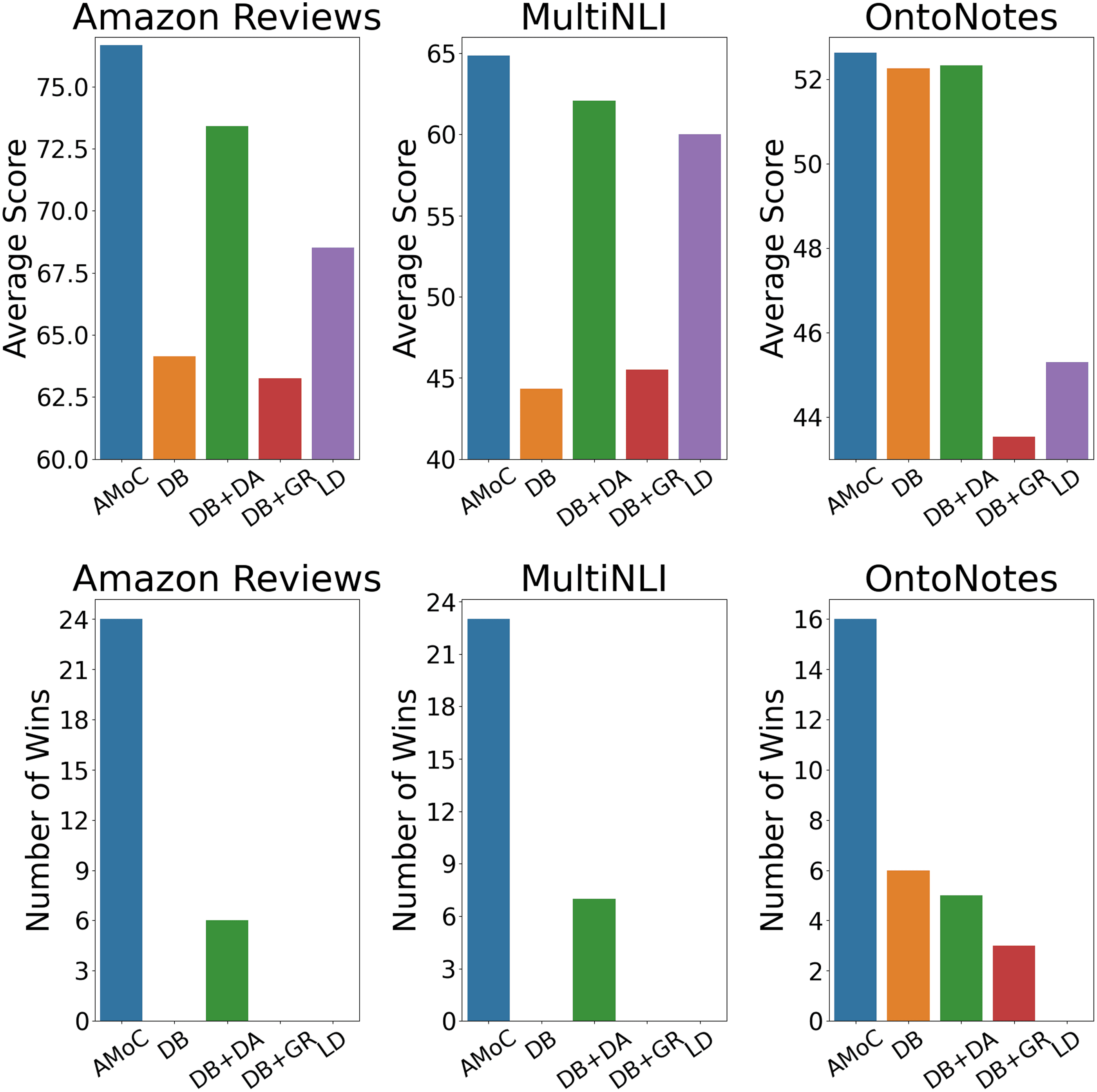
Clearly, AMoC outperforms all baselines in the
vast majority of setups (see, e.g., the lower graphs
of Figure 2). Moreover, its average target-domain
performance (across the 5 source domains) im-
proves over the second best model (DB + DA)
by up to 4.56%, 5.16%, and 1.63%, on Amazon
Reviews, MultiNLI, and OntoNotes, respectively
(lowest rows of each table in Table 2; see also
the average across setups in the upper graphs of
Figure 2). These results provide a positive answer
to Q1 of § 1, by indicating the superiority of
AMoC over strong alternatives.
DB+GR is overall the worst performing base-
line, followed by DB, with an average degradation
of 11.3% and 8.2% macro F1 score, respectively,
compared to the more successful cross-domain
oriented variant DB + DA. This implies that
out-of-the-box compressed models such as DB
struggle to generalize well to out-of-distribution
data. DB + DA also performs worse than AMoC
in a large portion of the experiments. These results
are even more appealing given that AMoC does
not perform any gradient step on the target data,
performing only a small number of gradient steps
Figure 2: Summary of domain adaptation results. Over-
all average score (top) and overall number of wins
(bottom) over all source-target domain pairs.
on the source data. In fact, AMoC only uses the
unlabeled target data for computing the regres-
sion features. Lastly, LD, another strong baseline
which was specifically designed to remove layers
from BERT, is surpassed by AMoC by as much as
6.76% F1, when averaging over all source-target
domain pairs.
Finally, we compare AMoC to ALBERT. We
find that on average ALBERT is outperformed
by AMoC by 8.8% F1 on Amazon Reviews,
and by 1.6% F1 on MultiNLI. On OntoNotes the
performance gap between ALBERT and AMoC
is an astounding 24.8% F1 in favor of AMoC,
which might be a result of ALBERT being an
uncased model, an important feature for NER
tasks.
Compressed Model Selection We next evalu-
ate how well the regression model and its variables
predict the performance of a candidate compressed
model on the target domain. Table 3 presents the
Adjusted R2, indicating the share of the variance
in the predicted outcome that the variables ex-
plain. Across all experiments and regardless of
the number of layers removed, our regression
model predicts well the performance on unseen
domain pairs, averaging an R2 of 0.881, 0.916,
and 0.826 on Amazon Reviews, MultiNLI, and
OntoNotes, respectively. This indicates that our
1365
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
# of removed Layers
6
8
4
Data set
Amazon Reviews 0.844 0.898 0.902
0.902 0.921 0.926
MultiNLI
0.827 0.830 0.821
OntoNotes
Average
0.881
0.916
0.826
Table 3: Adjusted R2 on the test set for each
type of compression (4, 6, or 8 layers) on each
data set.
regression properly estimates the performance of
candidate models.
Another support for this observation is that in
75% of the experiments the model selected by the
regression is among the top 10 performing com-
pressed candidates. In 55% of the experiments, it
is among the top 5 models. On average it performs
only 1% worse than the best performing com-
pressed model. Combined with the high adjusted
R2 across experiments, this suggests a positive
answer to Q2 of § 1.
Finally, as expected, we find that AMoC is
often outperformed by the full model. However,
the gap between the models is small, averaging
only in 1.26%. Moreover, in almost 25% of all
experiments AMoC was able to surpass the full
model (underscored scores in Table 2).
Marginal Effects of Regression Variables
While the performance of the model on data drawn
from the same distribution may also be indicative
of its out-of-distribution performance, additional
information is likely to be needed in order to
make an exact prediction. Here, we supplement
this indicator with the variables described in § 4.3
and ask whether they can be useful to select the
best compressed model out of a set of candidates.
Table 4 presents the most statistically significant
variables in our stepwise regression analysis. It
demonstrates that the ATE and the model’s per-
formance in the source domain are usually very
indicative of the model’s performance.
Indeed, most of the regression’s predictive
power comes from the model performance on
the source domain (F 1S) and the treatment effects
on the source and target domains (\AT ES, \AT ET ).
\P (S|T )) and the
In contrast, the distance metric (
\P (S|T ))
interaction terms (\AT ET ·
contribute much less to the total R2. The predic-
tive power of the ATE in both source and target
domains suggests a positive answer to Q3 of § 1.
\P (S|T ), F 1S ·
∆R2
∆R2
1.836 0.029
MultiNLI
β
OntoNotes
Amazon
∆R2
β
β
Variable
F 1S
0.435 0.603 −0.299 0.143 0.748 0.510
\AT ET −1.207 0.239 −0.666 0.413 117.5 0.202
\AT ES
0.557 0.232 125.9 0.072
\P (S|T ) −0.298 0.028 −0.652 0.061 15.60 0.052
\AT ET
\P (S|T )
·
F 1S
\P (S|T )
·
8 layers −0.137 0.001 −0.303 0.001 −3.145 0.001
6 layers −0.066 0
−0.146 0.007 −1.020 0.005
0.259 0
const
−0.560 0.007 −0.092 0.029 −115.8 0.004
0.187 0.004
1.027 0.043
0.472 0.004
−12.18 0
0.594 0
Table 4: Stepwise regression coefficients (β) and
their marginal contribution to the adjusted R2
(∆R2) on all experiments on both data sets.
7 Additional Analysis
7.1 Layer Importance
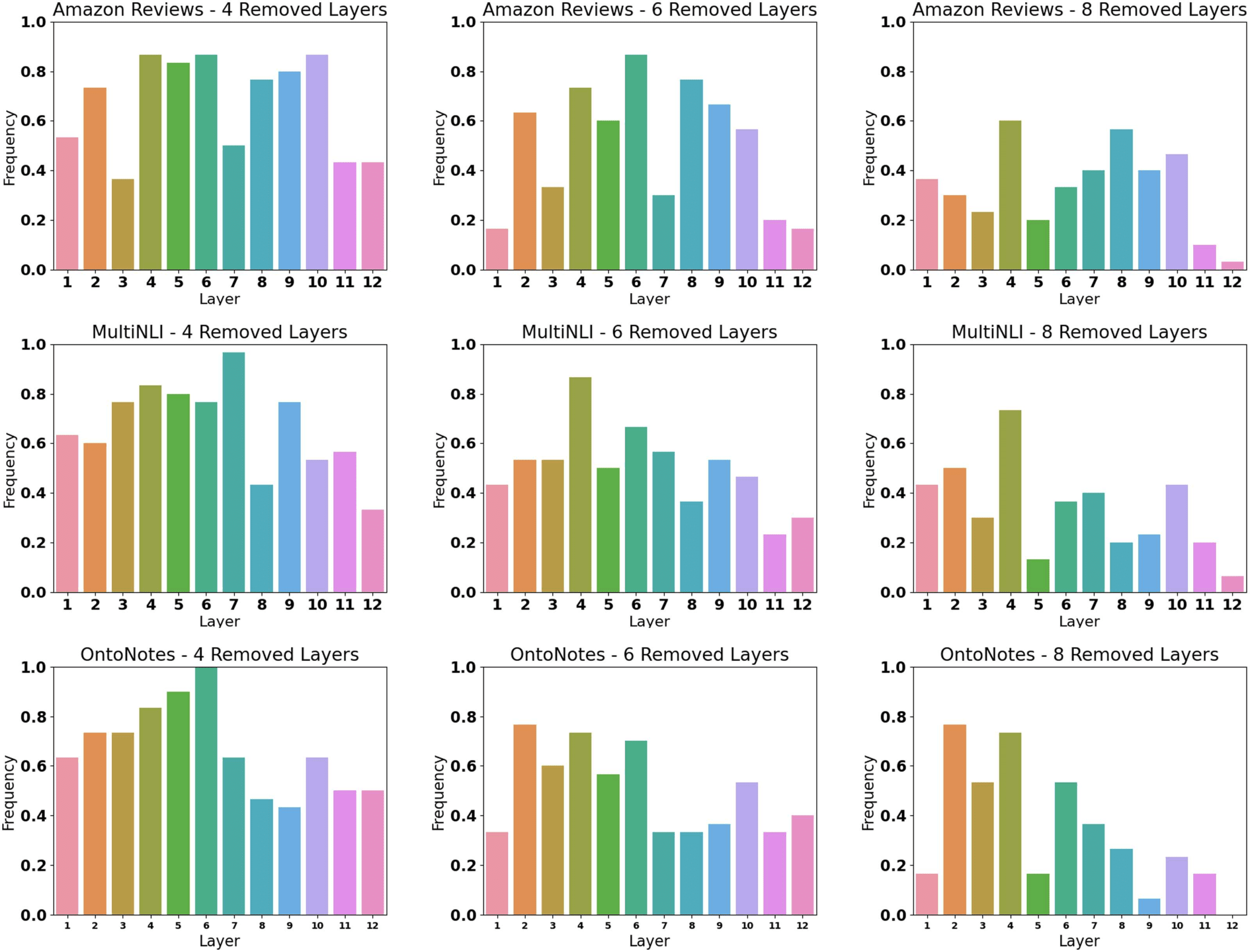
To further understand the importance of each
of BERT’s layers, we compute the frequency in
which each layer appears in the best candidate
model, namely, the model with the highest F1
score on the target test set, of every experiment.
Figure 3 captures the layer frequencies across
the different data sets and across the number of
removed layers.
The plots suggest that the two final layers, lay-
ers 11 and 12, are the least important layers with
average frequencies of 30.3% and 24.8%, respec-
tively. Additionally, in most cases layer 1 is ranked
below the other layers. These results imply that
the compressed models are able to better recover
from the loss of parameters when the external lay-
ers are removed. The most important layer appears
to be layer 4, with an average frequency of 73.3%.
Finally, we notice that a large frequency variance
exists across the different subplots. Such variance
supports our hypothesis that the decision of which
layers to remove should not be based solely on the
architecture of the model.
To pin down the importance of a specific layer
for a given base model, we utilize a similar regres-
sion analysis to that of § 6. Specifically, we train
a regression model on all compressed candidates
for a given source-target domain pair (in all three
tasks), adding indicator variables for the exclusion
of each layer from the model. This model asso-
ciates each layer with a regression coefficient,
which can be interpreted as the marginal effect
1366
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: Layer frequency at the best (oracle) compressed models when considering the removal of 4, 6, and 8
layers in the three data sets.
of that layer being removed on expected target
performance. We then compute for each layer
its average coefficient across source-target pairs
(Table 5, β column) and compare it to the frac-
tion of source-target pairs where this layer is not
included in the best possible (oracle) compressed
model (Table 5, P (Layer removed) column).
As can be seen in the table, layers that their re-
moval is associated with better model performance
are more often not included in the best performing
compressed models. Indeed, the Spearman’s rank
correlation between the two rankings is as high as
0.924. Such analysis demonstrates that the regres-
sion model used as part of AMoC not only selects
high quality candidates, but can also shed light on
the importance of individual layers.
7.2 Training Epochs
We next analyze the number of epochs required
to fine-tune our compressed models. For each
data set (task) we randomly choose for every
target domain 10 compressed models and cre-
ate two alternatives, differing in the number of
training epochs performed after layer removal:
One trained for a single epoch and another for
5 epochs (Amazon Reviews, MultiNLI) or 10
Layer Rank
1
2
3
4
5
6
7
8
9
10
11
12
¯β
0.0448
0.0464
0.0473
0.0483
0.0487
0.0495
0.0501
0.0507
0.0514
0.0522
0.0538
0.0577
P (Layer removed)
0.300
0.333
0.333
0.333
0.416
0.555
0.472
0.638
0.500
0.638
0.611
0.666
Table 5: Layer rank according to regres-
sion coefficients (β) and the probability
the layer was removed form the best com-
pressed model. Results are averaged across
all target-domain pairs in our experiments.
epochs (Ontonotes). Table 6 compares the av-
erage F1 (target-domain task performance) and
\AT ET differences between the two alternatives,
on the target domain test and dev sets, respec-
tively. The results suggest that when training for
1367
F1 Difference \AT ET Difference
Amazon Reviews
MNLI
OntoNotes
0.080
−0.250
2.940
0.011
0.003
−0.009
Table 6: F1 and ATE differences when training
AMoC after layer removal for multiple epochs
vs. a single epoch.
Overall Parameters Trainable Parameters Train Time Reduction
BERT-base
DistilBERT
110M
66M
AMoC
110M - 7M · L
110M
66M
7M · min{L, 12 − L}
+17M · 1
{1∈c}
×1
×1.83
×11
Table 7: Comparison of number of parameters and
training time between BERT-base, DistilBERT,
and AMoC when removing L layers. AMoC’s
number of trainable parameters is an upper bound.
more epochs on Amazon Reviews and MultiNLI
the difference in both the F1 and ATE are negligi-
ble. For OntoNotes (NER), in contrast, additional
training improves the F1, suggesting that further
training of the compressed model candidates may
be favorable for sequence tagging tasks such as
NER.
7.3 Space and Time Complexity
Table 7 compares the number of overall and
trainable parameters and the training time of
BERT, DistilBERT, and AMoC. Removing L
layers from BERT yields a reduction of 7L mil-
lion parameters. As can be seen in the Table,
AMoC requires training only a small fraction of
the overall parameters. Since we only unfreeze
one layer per each new connected component, at
the worst case our algorithm requires the training
of min{L, 12 − L} layers. The only exception is
in the case where Layer 1 is removed (1 ∈ c).
In such a case we unfreeze the embedding layer,
which adds 24 million trained parameters. In terms
of total training time (one epoch of task-based
fine-tuning), when averaging over all setups, a
single compressed AMoC model is ×11 faster
than BERT and ×6 faster than DistilBERT.
7.4 Design Choices
Computing the ATE Following Goyal et al.
(2019) and Feder et al. (2021), we implement
the ATE with the total variation distance be-
tween the probability output of the original model
and that of the compressed models. To verify
the quality of this design choice, we re-ran our
experiments where the ATE is calculated using
the KL-divergence between the same distribu-
tions. While the results in both conditions are
qualitatively similar, we did find a consistent
quantitative improvement of the R2 (average of
0.05 across setups) when considering our total
variation distance.
Regression Analysis Our regression approach
is designed to allow us to both select high-quality
compressed candidates and to interpret the im-
portance of each explanatory variable, including
the ATEs. As this regression has relatively few
features, we do not expect to lose significant
predictive power by choosing to focus on linear
predictors. To verify this, we re-ran our experi-
ments when using a fully connected feed-forward
network9 to predict
target performance. This
model, which is less interpretable than our re-
gression, is also less accurate: We have observed
an increased mean squared error of 1-3% with the
network.
8 Conclusion
We explored the relationship between model com-
pression and out-of-distribution generalization.
AMoC, our proposed algorithm, relies on causal
inference tools for estimating the effects of inter-
ventions. It hence creates an interpretable process
that allows to understand the role of specific model
components. Our results indicate that AMoC is
able to produce a smaller model with minimal loss
in performance across domains, without any use
of target labeled data at test time (Q1).
AMoC can efficiently train a large number of
compressed model candidates, that can then serve
as training examples for a regression model. We
have shown that this approach results in a high
quality estimation of the performance of com-
pressed models on unseen target domains (Q2).
Moreover, our stepwise regression analysis indi-
cates that the \AT ES and \AT ET estimates are
instrumental for these attractive properties (Q3).
As training and test set mismatches are com-
mon, we steered our model compression research
towards out-of-domain generalization. Besides
its realistic nature, this setup poses additional
modeling challenges, such as understanding the
proximity between domains, identifying which
9With one intermediate layer, same input feature as the
regression, and hyperparameters tuned on the development
set of each source-target pair.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1368
components are invariant to domain shift, and es-
timating performance on unseen domains. Hence,
AMoC is designed for model compression in
the out-of-distribution setup. We leave the design
of similar in-domain compression methods for
future work.
Finally, we believe that using causal methods
to produce compressed NLP models that can well
generalize across distributions is a promising di-
rection of research, and hope that more work will
be done in this intersection.
Acknowledgments
We would like to thank the action editor and
the reviewers, as well as the members of the
IE@Technion NLP group for their valuable feed-
back and advice. This research was partially
funded by an ISF personal grant No. 1625/18.
References
Gustavo Aguilar, Yuan Ling, Yu Zhang, Benjamin
Yao, Xing Fan, and Chenlei Guo. 2020.
Knowledge distillation from internal repre-
sentations. In Proceedings of the AAAI Con-
ference on Artificial Intelligence, volume 34,
pages 7350–7357. https://doi.org/10
.1609/aaai.v34i05.6229
Eyal Ben-David, Carmel Rabinovitz, and Roi
Reichart. 2020. PERL: Pivot-based domain
adaptation for pre-trained deep contextual-
ized embedding models. Transactions of the
Association for Computational Linguistics,
8:504–521. https://doi.org/10.1162
/tacl_a_00328
John Blitzer, Ryan McDonald, and Fernando
Pereira. 2006. Domain adaptation with struc-
In Proceed-
tural correspondence learning.
ings of
the 2006 Conference on Empirical
Methods in Natural Language Processing,
pages 120–128. https://doi.org/10.3115
/1610075.1610094
L´eon Bottou, Jonas Peters, Joaquin Qui˜nonero-
Candela, Denis X Charles, D Max Chickering,
Elon Portugaly, Dipankar Ray, Patrice Simard,
and Ed Snelson. 2013. Counterfactual reasoning
and learning systems: The example of compu-
tational advertising. The Journal of Machine
Learning Research, 14(1):3207–3260.
Samuel Bowman, Gabor Angeli, Christopher
Potts, and Christopher D. Manning. 2015. A
large annotated corpus for learning natural
the
language inference.
2015 Conference on Empirical Methods in
Natural Language Processing, pages 632–642.
https://doi.org/10.18653/v1/D15
-1075
In Proceedings of
Tom B. Brown, Benjamin Mann, Nick Ryder,
Melanie Subbiah,
Jared Kaplan, Prafulla
Dhariwal, Arvind Neelakantan, Pranav Shyam,
Girish Sastry, Amanda Askell, Sandhini
Agarwal, Ariel Herbert-Voss, Gretchen
Krueger, Tom Henighan, Rewon Child, Aditya
Ramesh, Daniel M. Ziegler,
Jeffrey Wu,
Clemens Winter, Christopher Hesse, Mark
Chen, Eric Sigler, Mateusz Litwin, Scott
Gray, Benjamin Chess, Jack Clark, Christopher
Berner, Sam McCandlish, Alec Radford, Ilya
Sutskever, and Dario Amodei. 2020. Language
models are few-shot learners. arXiv preprint
arXiv:2005.14165.
Daoyuan Chen, Yaliang Li, Minghui Qiu, Zhen
Wang, Bofang Li, Bolin Ding, Hongbo Deng,
Jun Huang, Wei Lin, and Jingren Zhou. 2020.
Adabert: Task-adaptive bert compression with
differentiable neural architecture search. In Pro-
ceedings of
the Twenty-Ninth International
Joint Conference on Artificial Intelligence,
IJCAI-20, pages 2463–2469. International Joint
Conferences on Artificial Intelligence Organi-
zation. Main track. https://doi.org/10
.24963/ijcai.2020/341
Wanyun Cui, Guangyu Zheng, Zhiqiang Shen,
Sihang Jiang, and Wei Wang. 2018. Transfer
learning for sequences via learning to collo-
cate. In International Conference on Learning
Representations.
Hal Daum´e III, Abhishek Kumar, and Avishek
Saha. 2010. Frustratingly easy semi-supervised
domain adaptation. In Proceedings of the 2010
Workshop on Domain Adaptation for Natural
Language Processing, pages 53–59.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of the 2019 Con-
ference of the North American Chapter of the
1369
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Association for Computational Linguistics: Hu-
man Language Technologies, Volume 1 (Long
and Short Papers), pages 4171–4186.
Norman R. Draper and Harry Smith. 1998. Applied
Regression Analysis, volume 326. John Wiley
& Sons. https://doi.org/10.1002
/9781118625590
Haim Dubossarsky, Ivan Vuli´c, Roi Reichart, and
Anna Korhonen. 2020. The secret is in the
spectra: Predicting cross-lingual task perfor-
mance with spectral similarity measures. In
Proceedings of the 2020 Conference on Empir-
ical Methods in Natural Language Processing,
pages 2377–2390. https://doi.org/10
.18653/v1/2020.emnlp-main.186
Hady Elsahar and Matthias Gall´e. 2019. To an-
notate or not? Predicting performance drop
under domain shift. In Proceedings of the 2019
Conference on Empirical Methods in Natural
Language Processing and the 9th Interna-
tional Joint Conference on Natural Language
Processing, pages 2163–2173. https://doi
.org/10.18653/v1/D19-1222
Angela Fan, Edouard Grave, and Armand Joulin.
2019. Reducing transformer depth on de-
mand with structured dropout. In International
Conference on Learning Representations.
Amir Feder, Nadav Oved, Uri Shalit, and Roi
Reichart. 2021. CausaLM: Causal model ex-
planation through counterfactual language mod-
els. Computational Linguistics, 47(2):333–386.
https://doi.org/10.1162/coli a 00404
Yaroslav Ganin, Evgeniya Ustinova, Hana
Ajakan, Pascal Germain, Hugo Larochelle,
Franc¸ois Laviolette, Mario Marchand, and
Victor Lempitsky. 2016. Domain-adversarial
training of neural networks. The Journal of
Machine Learning Research, 17(1):2096–2030.
Mingming Gong, Kun Zhang, Tongliang Liu,
Dacheng Tao, Clark Glymour, and Bernhard
Sch¨olkopf. 2016. Domain adaptation with
transferable components. In In-
conditional
ternational Conference on Machine Learning,
pages 2839–2848.
Yash Goyal, Amir Feder, Uri Shalit, and
Been Kim. 2019. Explaining classifiers with
causal concept effect (cace). arXiv preprint
arXiv:1907.07165.
Daniel Greenfeld and Uri Shalit. 2020. Robust
indepen-
learning with the Hilbert-Schmidt
dence criterion. In Proceedings of the 37th
International Conference on Machine Learn-
ing, volume 119 of Proceedings of Machine
Learning Research, pages 3759–3768. PMLR.
Ruining He and Julian McAuley. 2016. Ups
and downs: Modeling the visual evolution
of fashion trends with one-class collaborative
filtering. In Proceedings of
the 25th Inter-
national Conference on World Wide Web,
pages 507–517.
Geoffrey Hinton, Oriol Vinyals, and Jeffrey
Dean. 2015. Distilling the knowledge in a
neural network. In NIPS Deep Learning and
Representation Learning Workshop.
Jonathan Frankle and Michael Carbin. 2018.
The lottery ticket hypothesis: Finding sparse,
In International
trainable neural networks.
Conference on Learning Representations.
Ronald R. Hocking. 1976. A biometrics invited
paper. The analysis and selection of variables
in linear regression. Biometrics, 32(1):1–49.
https://doi.org/10.2307/2529336
Prakhar Ganesh, Yao Chen, Xin Lou,
Mohammad Ali Khan, Yin Yang, Deming
Chen, Marianne Winslett, Hassan Sajjad, and
Preslav Nakov. 2020. Compressing large-scale
transformer-based models: A case study on bert.
arXiv preprint arXiv:2002.11985.
Yaroslav Ganin and Victor Lempitsky. 2015.
Unsupervised domain adaptation by backpropa-
gation. In International Conference on Machine
Learning, pages 1180–1189. PMLR.
Eduard Hovy, Mitch Marcus, Martha Palmer,
Lance Ramshaw, and Ralph Weischedel. 2006.
Ontonotes: The 90% solution. In Proceedings of
the Human Language Technology Conference
of the NAACL, Companion Volume: Short Pa-
pers, pages 57–60. https://doi.org/10
.3115/1614049.1614064
Xiaoqi Jiao, Yichun Yin, Lifeng Shang, Xin
Jiang, Xiao Chen, Linlin Li, Fang Wang, and
Qun Liu. 2020. TinyBERT: Distilling BERT
1370
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
for natural language understanding. In Find-
the Association for Computational
ings of
Linguistics: EMNLP 2020, pages 4163–4174,
Online. Association for Computational Linguis-
tics. https://doi.org/10.18653/v1
/2020.findings-emnlp.372
Fredrik Johansson, Uri Shalit, and David Sontag.
2016. Learning representations for counterfac-
tual inference. In International Conference on
Machine Learning, pages 3020–3029.
Divyansh Kaushik, Eduard Hovy, and Zachary
Lipton. 2019. Learning the difference that
makes a difference with counterfactually-
augmented data. In International Conference
on Learning Representations.
Diederik P. Kingma and Jimmy Ba. 2015.
Adam: A method for stochastic optimiza-
tion. In International Conference on Learning
Representations.
Dan Kondratyuk and Milan Straka. 2019. 75
languages, 1 model: Parsing universal depen-
dencies universally. In Proceedings of the 2019
Conference on Empirical Methods in Natural
Language Processing and the 9th Interna-
tional Joint Conference on Natural Language
Processing, pages 2779–2795. https://doi
.org/10.18653/v1/D19-1279
Zhenzhong Lan, Mingda Chen, Sebastian
Goodman, Kevin Gimpel, Piyush Sharma, and
Radu Soricut. 2020. Albert: A lite BERT for
self-supervised learning of language representa-
tions. In International Conference on Learning
Representations.
Bill Yuchen Lin and Wei Lu. 2018. Neural
adaptation layers for cross-domain named en-
tity recognition. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing, pages 2012–2022.
Yinhan Liu, Myle Ott, Naman Goyal, Jingfei
Du, Mandar Joshi, Danqi Chen, Omer Levy,
Mike Lewis, Luke Zettlemoyer, and Veselin
Stoyanov. 2019. RoBERTa: A robustly opti-
mized bert pretraining approach. arXiv preprint
arXiv:1907.11692.
Annie Louis and Ani Nenkova. 2009. Performance
confidence estimation for automatic summa-
rization. In Proceedings of the 12th Conference
of the European Chapter of the ACL (EACL
2009), pages 541–548. Association for Compu-
tational Linguistics. https://doi.org/10
.3115/1609067.1609127
Sara Magliacane, Thijs van Ommen, Tom
Claassen, Stephan Bongers, Philip Versteeg,
and Joris M. Mooij. 2018. Domain adap-
tation by using causal
inference to predict
invariant conditional distributions. In Advances
in Neural Information Processing Systems,
pages 10846–10856.
David McClosky, Eugene Charniak, and Mark
Johnson. 2010. Automatic domain adaptation
for parsing. In Human Language Technolo-
gies: The 2010 Annual Conference of
the
North American Chapter of the Association
for Computational Linguistics, pages 28–36.
Association for Computational Linguistics.
Seyed Iman Mirzadeh, Mehrdad Farajtabar, Ang
Li, Nir Levine, Akihiro Matsukawa, and Hassan
Ghasemzadeh. 2020. Improved knowledge dis-
tillation via teacher assistant. In Proceedings of
the AAAI Conference on Artificial Intelligence,
volume 34, pages 5191–5198. https://doi
.org/10.1609/aaai.v34i04.5963
Judea Pearl. 1995. Causal diagrams for empirical
research. Biometrika, 82(4):669–688.
Judea Pearl. 2009. Causality, Cambridge Univer-
sity Press. https://doi.org/10.1093
/biomet/82.4.669
Judea Pearl. 2009. Causal inference in statistics:
An overview. Statistics Surveys, 3:96–146.
Jonas Peters, Dominik Janzing, and Bernhard
Schlkopf. 2017. Elements of Causal Inference:
Foundations and Learning Algorithms. The
MIT Press. https://doi.org/10.1214
/09-SS057
Alec Radford, Karthik Narasimhan, Time
Salimans, and Ilya Sutskever. 2018. Improv-
ing language understanding with unsupervised
learning. Technical report, OpenAI.
Sujith Ravi, Kevin Knight, and Radu Soricut.
2008. Automatic prediction of parser accu-
racy. In Proceedings of the 2008 Conference
on Empirical Methods in Natural Language
Processing, pages 887–896. https://doi
.org/10.3115/1613715.1613829
1371
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Roi Reichart and Ari Rappoport. 2007. An ensem-
ble method for selection of high quality parses.
In Proceedings of the 45th Annual Meeting of
the Association of Computational Linguistics,
pages 408–415.
Anna Rogers, Olga Kovaleva,
and Anna
Rumshisky. 2021. A primer in BERTology:
What we know about how BERT works. Trans-
actions of the Association for Computational
Linguistics, 8:842–866. https://doi.org
/10.1162/tacl_a_00349
Mateo Rojas-Carulla, Bernhard
Sch¨olkopf,
Richard Turner, and Jonas Peters. 2018. In-
variant models for causal
transfer learning.
The Journal of Machine Learning Research,
19(1):1309–1342.
Guy Rotman and Roi Reichart. 2019. Deep
contextualized self-training for low resource
dependency parsing. Transactions of
the
Association for Computational Linguistics,
7:695–713. https://doi.org/10.1162
/tacl_a_00294
Hassan Sajjad, Fahim Dalvi, Nadir Durrani,
and Preslav Nakov. 2020. Poor man’s BERT:
Smaller and faster transformer models. arXiv
preprint arXiv:2004.03844.
Victor Sanh, Lysandre Debut, Julien Chaumond,
and Thomas Wolf. 2019. Distilbert, a distilled
version of BERT: smaller, faster, cheaper and
lighter. In Proceedings of the 5th Workshop
on Energy Efficient Machine Learning and
Cognitive Computing in Advances in Neural
Information Processing Systems.
Motoki Sato, Hitoshi Manabe, Hiroshi Noji, and
Yuji Matsumoto. 2017. Adversarial training for
cross-domain universal dependency parsing. In
Proceedings of the CoNLL 2017 Shared Task:
Multilingual Parsing from Raw Text to Univer-
sal Dependencies. https://doi.org/10
.18653/v1/K17-3007
Bernhard Sch¨olkopf, Dominik Janzing, Jonas
Peters, Eleni Sgouritsa, Kun Zhang, and Joris
Mooij. 2012. On causal and anticausal learn-
ing. In Proceedings of the 29th International
Conference on International Conference on
Machine Learning, pages 459–466.
Zhiqing Sun, Hongkun Yu, Xiaodan Song, Renjie
Liu, Yiming Yang, and Denny Zhou. 2020.
MobileBERT: A compact task-agnostic BERT
for resource-limited devices. In Proceedings of
the 58th Annual Meeting of the Association for
Computational Linguistics, pages 2158–2170.
Association for Computational Linguistics.
Vincent Van Asch and Walter Daelemans. 2010.
Using domain similarity for performance esti-
mation. In Proceedings of the 2010 Workshop
on Domain Adaptation for Natural Language
Processing, pages 31–36.
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017.
In Advances
Attention is all you need.
in Neural Information Processing Systems,
pages 5998–6008.
Yoav Wald, Amir Feder, Daniel Greenfeld,
and Uri Shalit. 2021. On calibration and
out-of-domain generalization. arXiv preprint
arXiv:2102.10395.
Zhenghui Wang, Yanru Qu, Liheng Chen,
Jian Shen, Weinan Zhang, Shaodian Zhang,
Yimei Gao, Gen Gu, Ken Chen, and Yong
Yu. 2018. Label-aware double transfer learn-
ing for cross-specialty medical named entity
recognition. In Proceedings of the 2018 Con-
ference of the North American Chapter of the
Association for Computational Linguistics: Hu-
man Language Technologies, Volume 1 (Long
Papers), pages 1–15. Association for Compu-
tational Linguistics. https://doi.org/10
.18653/v1/N18-1001
Adina Williams, Nikita Nangia, and Samuel
Bowman. 2018. A broad-coverage challenge
corpus for sentence understanding through in-
ference. In Proceedings of the 2018 Conference
of the North American Chapter of the Asso-
ciation for Computational Linguistics: Human
Language Technologies, Volume 1 (Long Pa-
pers), pages 1112–1122. https://doi.org
/10.18653/v1/N18-1101
Thomas Wolf, Lysandre Debut, Victor Sanh,
Julien Chaumond, Clement Delangue, Anthony
Moi, Pierric Cistac, Tim Rault, R´emi Louf,
Morgan Funtowicz, Joe Davison, Sam Shleifer,
Patrick von Platen, Clara Ma, Yacine Jernite,
1372
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Julien Plu, Canwen Xu, Teven Le Scao,
Sylvain Gugger, Mariama Drame, Quentin
Lhoest,
and Alexander M. Rush. 2020.
Transformers: State-of-the-art natural language
processing. In Proceedings of the 2020 Con-
ference on Empirical Methods in Natural
Language Processing: System Demonstra-
tions, pages 38–45. Association for Compu-
tational Linguistics. https://doi.org/10
.18653/v1/2020.emnlp-demos.6
Mengzhou Xia, Antonios Anastasopoulos,
Ruochen Xu, Yiming Yang, and Graham
Neubig. 2020. Predicting performance for natu-
ral language processing tasks. In Proceedings of
the 58th Annual Meeting of the Association for
Computational Linguistics, pages 8625–8646.
Association for Computational Linguistics.
Kun Zhang, Bernhard Sch¨olkopf, Krikamol
Muandet, and Zhikun Wang. 2013. Do-
main adaptation under target and conditional
shift. In International Conference on Machine
Learning, pages 819–827.
Yftah Ziser and Roi Reichart. 2017. Neural
structural correspondence learning for domain
adaptation. In Proceedings of the 21st Con-
ference on Computational Natural Language
Learning (CoNLL 2017), pages 400–410.
https://doi.org/10.18653/v1/K17
-1040
for
Yftah Ziser and Roi Reichart. 2018a. Deep
pivot-based modeling
cross-language
cross-domain transfer with minimal guid-
ance. In Proceedings of the 2018 Conference
on Empirical Methods in Natural Language
Processing, pages 238–249. Association for
Computational Linguistics. https://doi
.org/10.18653/v1/D18-1022
Yftah Ziser and Roi Reichart. 2018b. Pivot based
language modeling for improved neural do-
main adaptation. In Proceedings of the 2018
Conference of the North American Chapter
of the Association for Computational Linguis-
tics: Human Language Technologies, Volume 1
(Long Papers), pages 1241–1251. Association
for Computational Linguistics. https://doi
.org/10.18653/v1/N18-1112
Yftah Ziser and Roi Reichart. 2019. Task re-
finement learning for improved accuracy and
stability of unsupervised domain adaptation. In
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 5895–5906. Association for Computa-
tional Linguistics. https://doi.org/10
.18653/v1/P19-1591
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
3
1
1
9
7
6
7
7
8
/
/
t
l
a
c
_
a
_
0
0
4
3
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1373