METHODEN
Network structural dependency in the human
connectome across the life-span
Markus D. Schirmer
1,2,3∗
, Ai Wern Chung4∗
, P. Ellen Grant4, and Natalia S. Rost1
1Stroke Division & Massachusetts General Hospital, J. Philip Kistler Stroke Research Center,
Harvard Medical School, Boston, MA, USA
2Computer Science and Artificial Intelligence Lab, Massachusetts Institute of Technology, Cambridge, MA, USA
3Department of Population Health Sciences, German Centre for Neurodegenerative Diseases (DZNE), Berlin, Deutschland
4Fetal-Neonatal Neuroimaging & Developmental Science Center, Division of Newborn Medicine,
Boston Children’s Hospital, Harvard Medical School, Boston, MA, USA
∗ Authors contributed equally
Keine offenen Zugänge
Tagebuch
Schlüsselwörter: Network dependency index, Subnetwork, Life-span, Rich club, Diffusion
ABSTRAKT
Principles of network topology have been widely studied in the human connectome. Von
particular interest is the modularity of the human brain, where the connectome is divided into
subnetworks from which changes with development, aging or disease can be investigated.
We present a weighted network measure, the Network Dependency Index (NDI), to identify
an individual region’s importance to the global functioning of the network. Wichtig, Wir
utilize NDI to differentiate four subnetworks (Tiers) in the human connectome following
Gaussian mixture model fitting. We analyze the topological aspects of each subnetwork
with respect to age and compare it to rich club-based subnetworks (rich club, feeder, Und
seeder). Our results first demonstrate the efficacy of NDI to identify more consistent, zentral
nodes of the connectome across age groups, when compared with the rich club framework.
Stratifying the connectome by NDI led to consistent subnetworks across the life-span,
revealing distinct patterns associated with age where, Zum Beispiel, the key relay nuclei and
cortical regions are contained in a subnetwork with highest NDI. The divisions of the human
connectome derived from our data-driven NDI framework have the potential to reveal
topological alterations described by network measures through the life-span.
Zitat: Schirmer, M. D., Chung, A. W.,
Grant, P. E., & Rost, N. S. (2019).
Network structural dependency in the
human connectome across the
life-span. Netzwerkneurowissenschaften, 3(3),
792–806. https://doi.org/10.1162/
netn_a_00081
DOI:
https://doi.org/10.1162/netn_a_00081
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00081
Erhalten: 26 Oktober 2018
Akzeptiert: 7 Februar 2019
EINFÜHRUNG
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Markus D. Schirmer
mschirmer1@mgh.harvard.edu;
mail@markus-schirmer.com
Handling-Editor:
Olaf Sporns
Urheberrechte ©: © 2019
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
Network theoretical principles have been readily applied to the human connectome to in-
vestigate its structural and functional organization. Typically, a brain network comprises of
nodes representing brain regions that are connected by edges representing either reconstructed
white matter pathways from diffusion-weighted magnetic resonance imaging (dMRI) or func-
tional correlations from functional MRI (fMRT). Außerdem, edges between two nodes may be
weighted to reflect the strength of the connection (Bullmore & Spurns, 2009; Fornito et al.,
2013). There has been an ongoing quest to identify the regions in brain networks that are
critical for efficient network functioning (sehen, z.B., Hagmann et al., 2008), as well as defining
modules, or sets of nodes, that distinguish themselves from other nodes in the connectome.
One network organizational principle that has been established in the human connectome is
the rich club (RC), a core subnetwork of brain regions that are strongly connected to form a
high-cost, high-capacity backbone. The RC has been shown to be critical for effective com-
munication in the connectome (van den Heuvel et al., 2012; Van Den Heuvel & Spurns, 2011)
and has been studied in healthy subjects (Grayson et al., 2014; Schirmer & Chung, 2018;
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
N
e
N
_
A
_
0
0
0
8
1
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Network structural dependency across the life-span
Diffusion-weighted magnetic
resonance imaging (dMRI):
Imaging method measuring the
motion and directionality of water
molecules from which to estimate
local biological structure.
Functional MRI:
Imaging method to determine
the temporal patterns of
blood-oxygenation levels.
Modules/subnetworks:
A subset of nodes and their
connecting edges of a network that,
based on some definition, Sind
separable from all remaining
nodes/edges.
Degree:
A nodal property, this is the number
of edges connected to a node.
Topological distance:
The distance between any two
nodes in a graph as defined by
the network’s topology.
Van Den Heuvel & Spurns, 2011; Zhao et al., 2015), with development (Ball et al., 2014), Und
in disease (Collin et al., 2014; Daianu et al., 2015; Ray et al., 2014). Although an important
topological aspect in brain networks, defining RC membership is not straightforward. Typically,
an RC regime is identified over a range of degrees where the RC coefficient is significantly
greater than a distribution of equivalent RC coefficients computed from random networks.
From this range, a single degree, k, is chosen, and nodes with a degree greater or equal to k
are deemed to form the RC subnetwork. The lack of consensus in choosing this k-th threshold
is in part due to the variations in network construction and weightings employed in the field,
leading to great variability in RC coefficients (Van Den Heuvel & Spurns, 2011). Als solche, Die
neuroscience community has yet to establish an optimal way of defining RC nodes.
In this work, we present an alternative for defining regions of the brain that are integral for
network efficiency, and which can be consistently identified across the life-span, basierend auf
NDI, network dependency index (Woldeyohannes & Jiang, 2018). First introduced in network
communication science for critical node detection, NDI quantifies a node’s importance as
defined by the impact on the network’s performance given the node’s failure (or removal) aus
the system; simply put, NDI measures the dependency of the network on any given node. It also
has the advantage of evaluating nodal importance by incorporating the network’s efficiency
for information transport as measured by topological distance. Ordering brain regions by NDI
then allows us to stratify the connectome into subnetworks according to nodal importance.
We present a comparative investigation between RC and NDI frameworks for detecting a core
subnetwork and their corresponding “peripheral” subnetworks. We demonstrate the efficacy
of NDI to identify more consistent, central nodes of importance in the human connectome by
applying our framework on a large, open-source, normal population from the NKI-Rockland
study with an age range of 4 Zu 85 Jahre. By doing so, we derive reference values evaluating
NDI with age from which to contextualize our findings with other literature in the field. Im
following sections, we describe both RC and our NDI framework to define a core subnetwork
from which to further stratify the entire connectome. In Results, we compare the core regions
detected by both frameworks and their corresponding network characteristics in relation to
Alter. We end with a discussion of our main NDI findings in comparison to the RC formalism.
MATERIALS AND METHODS
Study Design and Patient Population
In this work we utilize data from the NKI-Rockland life-span study (Nooner et al., 2012). Pre-
processed connectome data were obtained from the USC Multimodal Connectivity database
(http://umcd.humanconnectomeproject.org). MRI acquisition details are available elsewhere
(Brown et al., 2012). In brief, insgesamt 196 connectomes of healthy participants are com-
puted from 3T dMRI acquisitions (64 gradient directions; TR = 10,000 MS; TE = 91 MS; voxel
size = 2 mm3; b-value = 1,000 s/mm2). Following eddy current and motion correction, diffu-
sion tensors are modeled and deterministic tractography performed using fiber assignment by
; Mori et al., 1999). Regions of interest (ROIs) Sind
continuous tracking (angular threshold 45
based on the Craddock atlas (Craddock et al., 2012), ergebend 188 ROIs, and connections
are weighted by the number of streamlines connecting pairs of ROIs. Hier, we normalize each
connectome by the maximum streamline count for each subject so that the connection weights
wij within each subject are wij
(cid:2) [0,1].
◦
Tractography:
An algorithm that reconstructs
white-matter pathways by using
dMRI data, yielding tracts that
connect regions in the brain.
For part of our analysis, we divide the 196 participants into four age groups: U20 ≤ 20 Jahre,
20 Jahre < U40 ≤ 40 years, 40 years < U60 ≤ 60 years, and 60 years < O60 ≤ 80 years. Four
Network Neuroscience
793
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network structural dependency across the life-span
Table 1. NKI-Rockland life-span study cohort characterization and their stratification by age
(in years).
N
Age, mean (SD)
Sex, male; %
Overall
196
35.0 (20.0)
58.1
U20
53
13.8 (4.1)
54.7
U40
67
27.4 (5.9)
56.7
U60
47
47.4 (5.4)
72.3
O60
29
71.0 (6.8)
44.8
SD = Standard deviation.
subjects were above 80 years old (81, 82, 83, and 85 years). As there were only four subjects,
we included them in the O60 group. Table 1 characterizes the study cohort and groups.
The available connectivity matrices include both cortical and subcortical structures. Before
analysis, regions in the brainstem and cerebellum were removed from the network, resulting
in 170 nodes covering 46 bilateral, anatomical regions (see Table S1 in Supporting Information
for distribution of nodes by anatomical region).
Group and Cohort Connectomes
A group-averaged connectome of weighted matrices can be computed in two steps (Van Den
Heuvel & Sporns, 2011). First, we calculate a binarized, group-average adjacency matrix by
retaining edges that are present in at least 90% of the subjects in each group, thus preserv-
ing connections which can be reliably identified across the group/cohort. Weights are subse-
quently added to the group-averaged adjacency matrix by taking the average weight of each
connection across the group, generating a weighted group-averaged connectome Wgroup. In
addition to calculating a connectome for each age group, we also compute a cohort-based
connectome, Wcohort, across all 196 subjects.
Rich Club Framework
We utilize Wgroup to subsequently calculate the weighted RC parameter Φgroup(k) (Opsahl
et al., 2008), where k denotes the degree of a node. The RC parameter Φgroup(k) is normalized
relative to a set of comparable random networks of equal size and with similar connectivity
distribution. Here, we generate 1,000 random networks while preserving weight, degree, and
strength distributions of Wgroup (Rubinov & Sporns, 2010). For each of these random realiza-
tions of the graph, we calculate the weighted RC parameter Φ
rand(k). Finally, the normalized
weighted RC parameter is calculated as
Φnorm
group(k) =
Φnorm(k)
Φ
rand(k)
For this metric, Φnorm
group(k) > 1 denotes the presence of a richclub. In our analysis, we select
kgroup
max
: max(k), for which Φnorm
Gruppe(k) > 1,
as the degree of the RC nodes of a given group, which allows us to determine the RC members
with a degree of at least k.
For each group connectome, we first determine k
Gruppe
max , as imple-
Rich club subnetworks.
mented in the Brain Connectivity Toolbox (Rubinow & Spurns, 2010). Statistical significance
of Φnorm
Gruppe(k) > 1 is assessed by performing a right-sided t test for each k (P < 0.05 after
Bonferroni correction, where the number of tests equals the maximum degree within each
Strength:
A nodal property, this is the sum of
weights of the corresponding edges
that are connected to a node.
Network Neuroscience
794
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network structural dependency across the life-span
group connectome). After establishing the RC nodes, remaining nodes in the group connec-
tome were categorized according to their relationship to the RC subnetwork. All non-RC nodes
were identified as Feeders (F) if they were connected to an RC node, or Seeders (S) if they
shared no connection with an RC node (Schirmer & Chung, 2018).
Network Dependency Index Framework
The NDI score has recently been described in unweighted networks (Woldeyohannes & Jiang,
2018). Here, we extend their formalism for use in weighted networks. Given a connectivity
matrix Wgroup = {wij
} in a network G with n nodes, we first calculate the topological distance
matrix D between all node pairs using the inverse of the connection strength wij between
nodes i and j as an initial topological distance. The information measure (In)ij between nodes
i and j can then be calculated as 1/Dij, resulting in an information measure matrix In. As
a next step, we normalize In by the maximum information measure Imax = max(wij). Imax
can be defined for each connectivity matrix W individually; however, as we compare NDIs
across groups, we define it as the maximum of Imax across all 196 connectivity matrices. In
case of disconnected components, the maximum loss of information Imax thereby becomes
comparable across connectomes.
To determine the NDI of node m, we first create a subnetwork G-m, by removing node
m. We subsequently calculate (In
ij for all remaining node pairs (i,j) in G-m. If removal of
node m results in disconnected components, some path lengths may become infinite. For such
−m is assigned an
paths, the loss of information measure is set to 1. Finally, each node i ∈ G
accumulated loss in information measure
−m)
ΔIi = ∑
j
(In)ij
− (In
−m)
ij.
The NDI of node m is then given as the mean of ΔIi over all nodes i in G-m, where the closer
the value is to 1, the higher the information loss and subsequently the more important node
m is to the network. This analysis is then repeated for all nodes in the network, resulting in an
n-dimensional feature vector of NDI scores for the network.
For each group connectome, we calculate its NDI scores. We determine
NDI subnetworks.
regions of importance by ranking their NDI score from highest to lowest for comparison with
RC nodes. Additionally, we model the natural-log-transformed NDI of each group connec-
tome by using a Gaussian mixture model with g Gaussian distributions (GMMg). Using the
halfway point between the Gaussian centers, we define g + 1 subnetworks (with one additional
subnetwork for nodes with NDI = 0), referred to as Tiers, of decreasing NDI importance (from
Tier 1, …, g + 1, where Tier 1 contains nodes with greatest NDI scores).
Statistical Analysis
Network organization by age group. Our first analysis is to investigate the consistency and
distributions of NDI scores for each Tier in relation to richclub subnetworks. Consistency of
NDI across age groups is subsequently tested using Spearman’s rank correlation coefficient.
Additionally, to further assess this consistency, we generate confusion matrices, where nodal
assignments to subnetworks/Tiers are compared between age groups. To characterize the topol-
ogy of the subnetworks derived from each framework, we calculate three network measures
(Rubinov & Sporns, 2010), namely, transitivity (T), global efficiency (E), and assortativity (a).
Gaussian mixture model:
A probabilistic model comprised of
multiple Gaussian distributions that
can be used to represent overlapping
clusters in a population.
Transitivity:
A global measure of clustering,
representing the ratio of closed
triangles in relation to the total of
number possible in the network.
Global efficiency:
The ease at which to traverse
between any two nodes, and relates
to the inverse of the shortest
pathlength.
Assortativity:
Measure of preference of nodes to
connect to those with a similar
degree.
Network Neuroscience
795
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network structural dependency across the life-span
Age-dependent subnetwork trends within the cohort. We also investigate the associations of
each network measure with age in both RC- and NDI-defined subnetworks. To make the sub-
networks uniform across the age groups, we repeat the RC and NDI analyses by using the
population averaged connectome Wcohort. Furthermore, we apply the Wcohort defined subnet-
works from both frameworks to each subject’s individual connectome for analysis with age.
Associations are estimated by fitting a linear model to the subject-level data, given by
measure = m ∗ age + b,
with slope m and offset b. Additionally, we report the average strength and density for each
subnetwork in both RC and NDI frameworks with corresponding standard deviation.
Finally, we investigate NDI Tier assignment on a
Nodal NDI Tier assignment on subject level.
subject level. To do so, we calculate each subject’s nodal NDI labeling and then determine
the median Tier assignment of each node across 196 connectomes. Furthermore, we quantify
the corresponding variation as standard deviation.
All statistical analyses were performed using MATLAB. The code used to calculate the statis-
tics and generate the figures, as well as an implementation for computing NDI is available at
https://github.com/mdschirmer/NDI.
RESULTS
Network Organization by Age Group
Table 2 details the k
of corresponding regions determined to form the richclub subnetwork.
group
max computed from each group-averaged connectome and the number
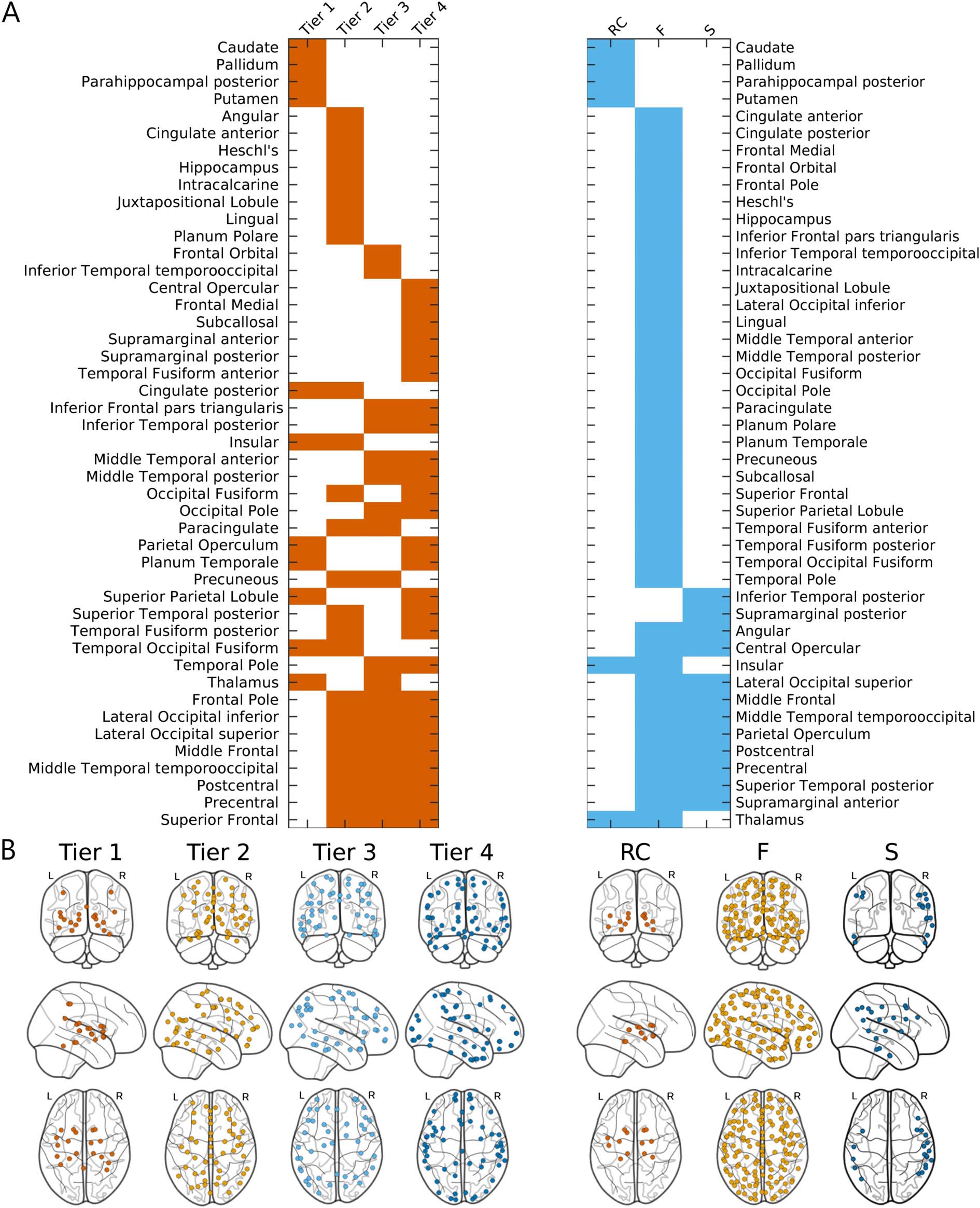
In some cases, the atlas assigns multiple nodes to the same anatomical label. Figure 1 shows
group
max shown in Table 2.
the richclub regions identified for each of our four age groups using k
It highlights 14 regions as belonging to the richclub across the life-span cohort, with 8 re-
gions appearing in at least three of the four age groups. These regions consist bilaterally of
the caudate, thalamus, pallidum, and parahippocampal posterior regions, as well as the right
putamen.
For NDI, the 10 regions with highest score are also indicated in Figure 1. Comparing NDI
across the four age groups demonstrates high consistency with an average Spearman’s correla-
tion coefficient of 0.98 ± 0.01, with the same correlation in degree sequences between group
connectomes.
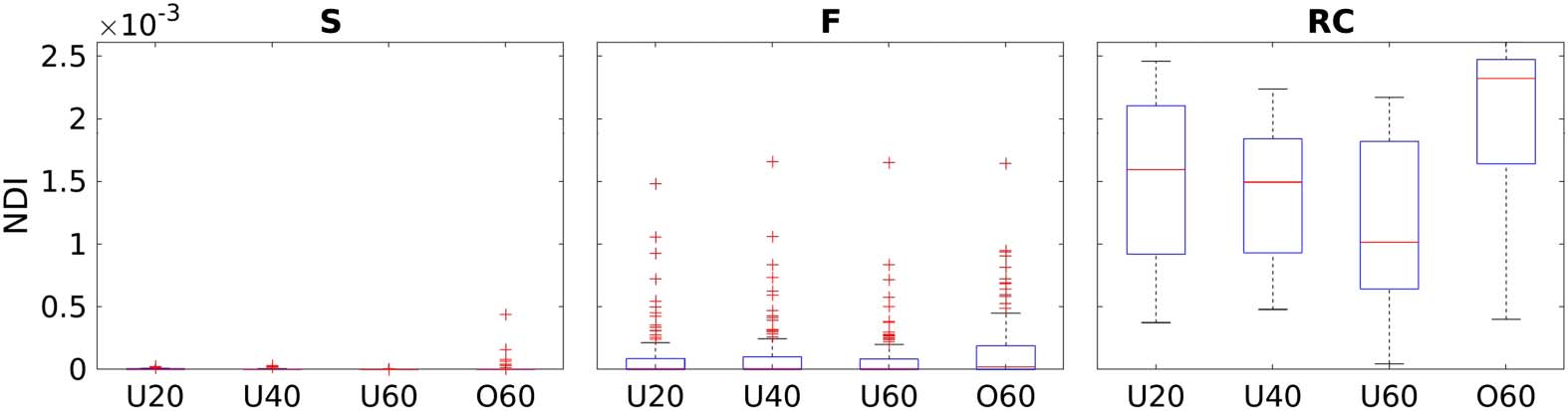
Using the subnetworks defined by the richclub, we investigate the NDI scores of RC, F,
and S. Figure 2 summarizes the NDI scores stratified by RC subnetworks and age groups. RC
nodes, on average, have the highest NDI scores of the group connectome, with lower scores
for F, followed by S regions.
Table 2. Normalized RC coefficient analysis of the four age groups, identifying the degree range
group
with Φnorm
max
group
max , and the corresponding number of nodes at k
group(k) significantly greater than 1, k
k-range
group
k
max
Number of nodes
U20
34–49
49
11
U40
36–48
48
10
U60
37–47
47
14
O60
39–53
53
5
796
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network structural dependency across the life-span
Figure 1. Richclub and the top 10 brain regions with highest NDI scores defined from the con-
nectome (Wgroup) for each age group.
Subnetwork Definition Using NDI
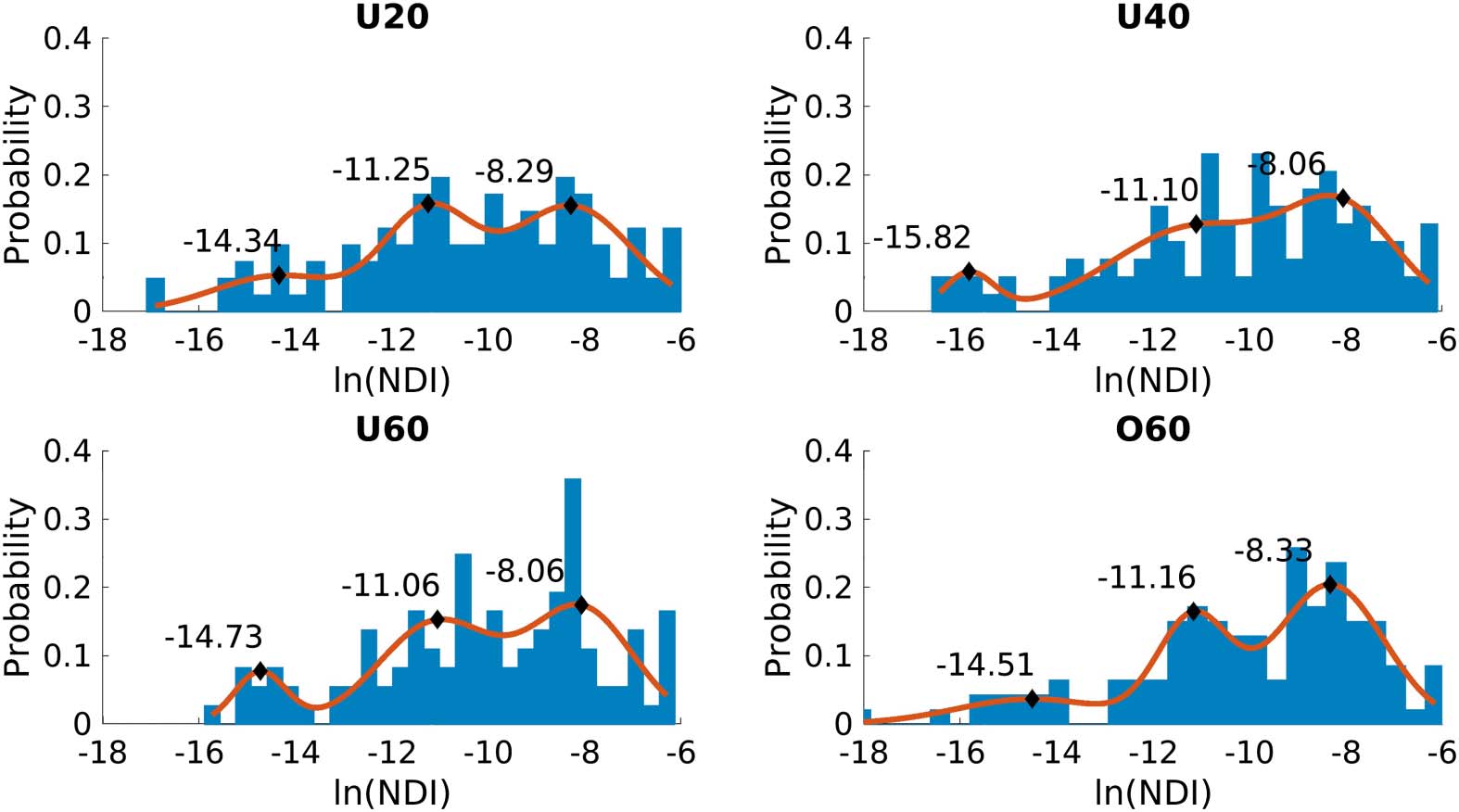
We observe that each group connectome’s NDI follows a mixture of normal distributions
after a natural log transform (Figure 3). Akaike information criterion and Bayesian informa-
tion criterion analysis both showed minima for g = 3, suggesting that three Gaussians de-
scribed the distribution best (see Figure S1 in Supporting Information) and was employed
for all further analysis. This resulted in four Tiers in our NDI framework. GMM3 fitted to
each of the distributions are shown in Figure 3. The average centers of the Gaussians across
all four Wgroup were −14.85 ± 0.67, −11.14 ± 0.08, and −8.19 ± 0.15. The halfway point be-
tween consecutive Gaussians (−13.00 and −9.66) divide the NDI distribution into three sec-
tions. Subsequently, with the inclusion of the NDI = 0 Tier, each node is assigned to one of
the four Tiers according to their NDI value for our analysis.
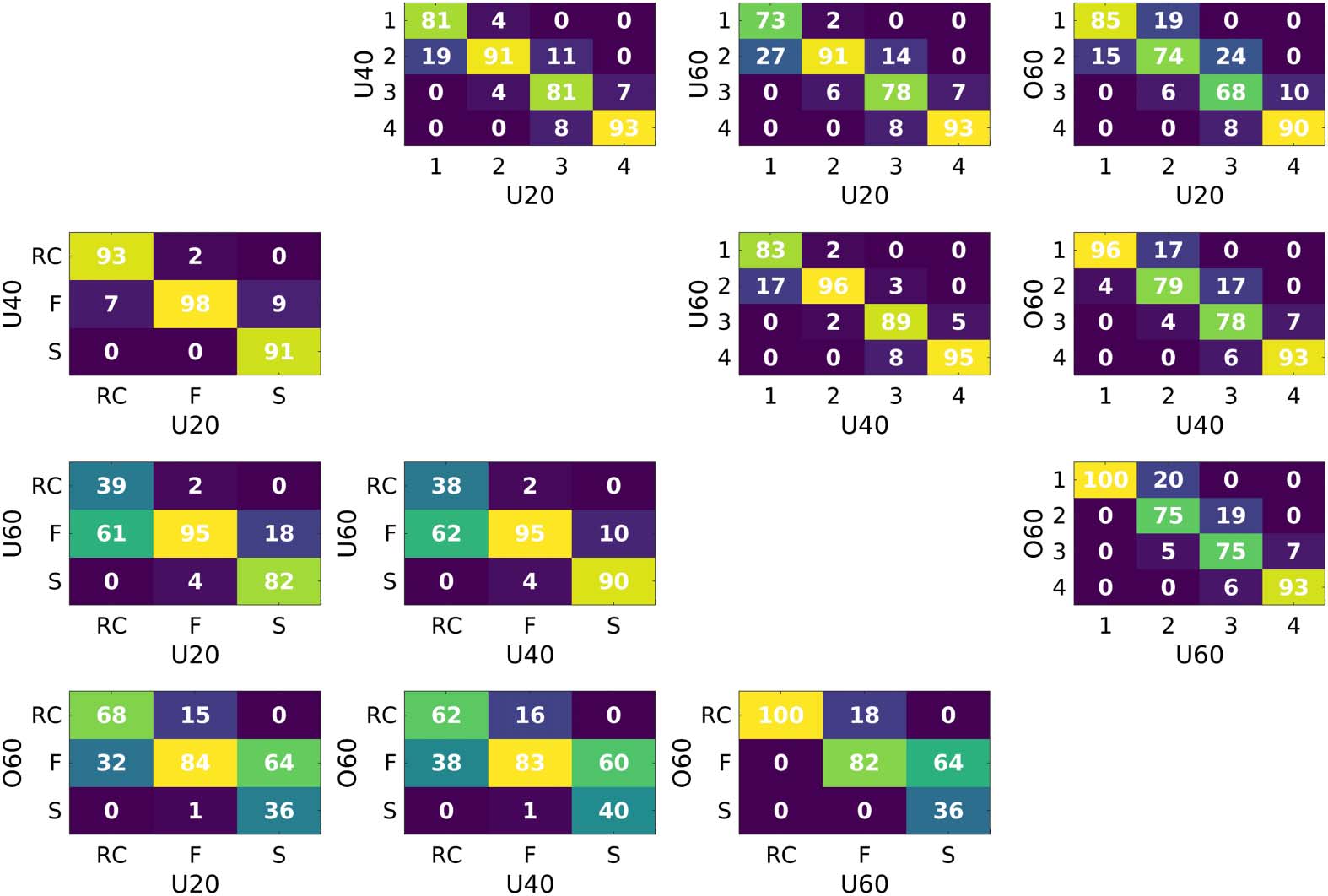
Figure 4 shows the confusion matrices assessing the stability of nodal assignment for both
NDI and richclub frameworks across age groups. On average, the largest variations in nodal
assignment to a different subnetwork is found with the RC framework (greater off-diagonal
percentages in RC confusion matrices, when compared with NDI).
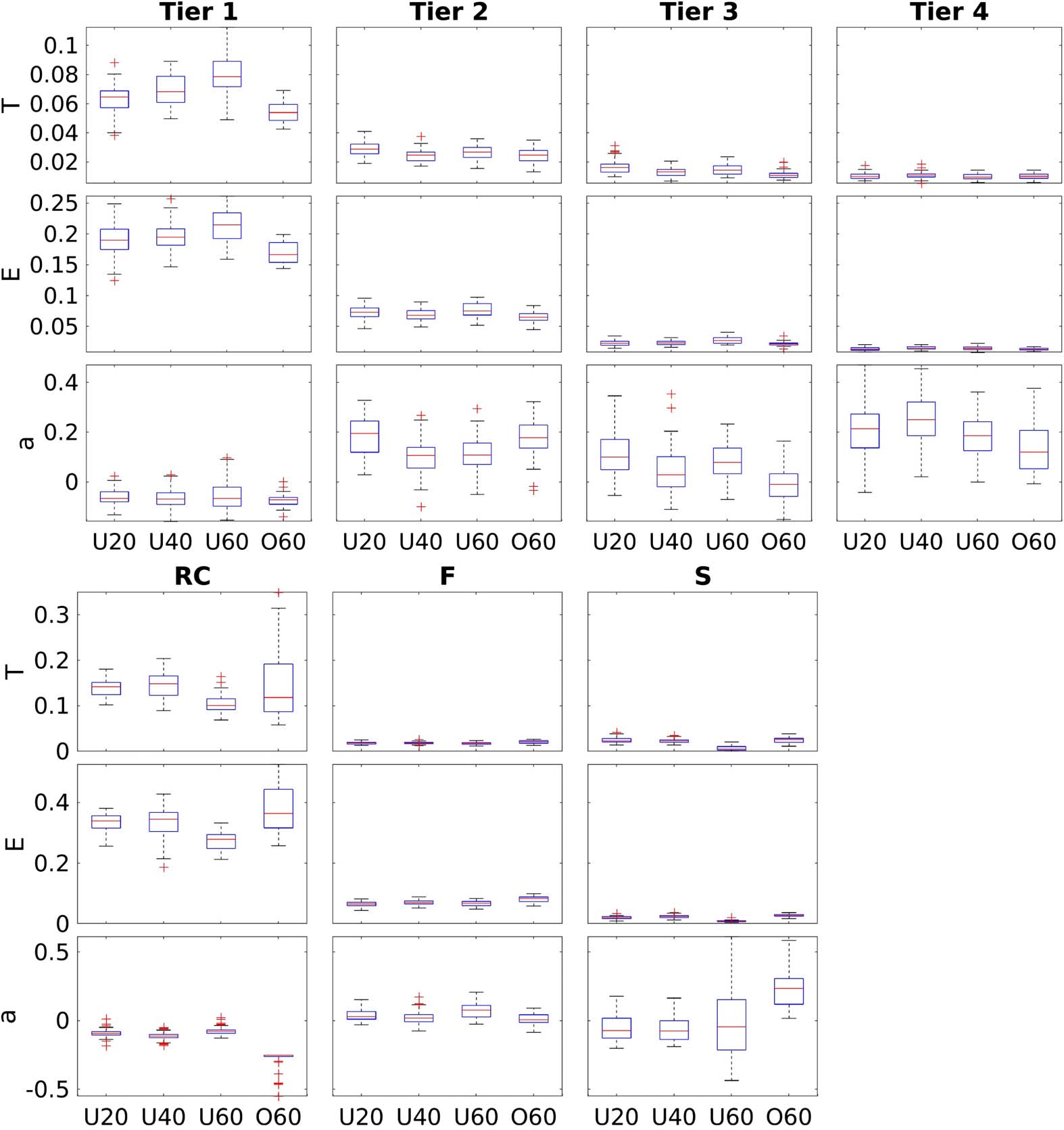
Network theoretical measures computed from the subnetworks derived via both the RC and
NDI frameworks are plotted in Figure 5.
Figure 2. A comparison of NDI scores stratified by RC subnetworks for each age group.
Network Neuroscience
797
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network structural dependency across the life-span
Figure 3. Natural log-transformed NDI distribution for each age group. Each distribution has a
GMM with three Gaussians fitted to it. The centers of these Gaussians are indicated by black dia-
monds, and the probability density function is shown in orange.
Age-Dependent Subnetwork Associations Within the Cohort
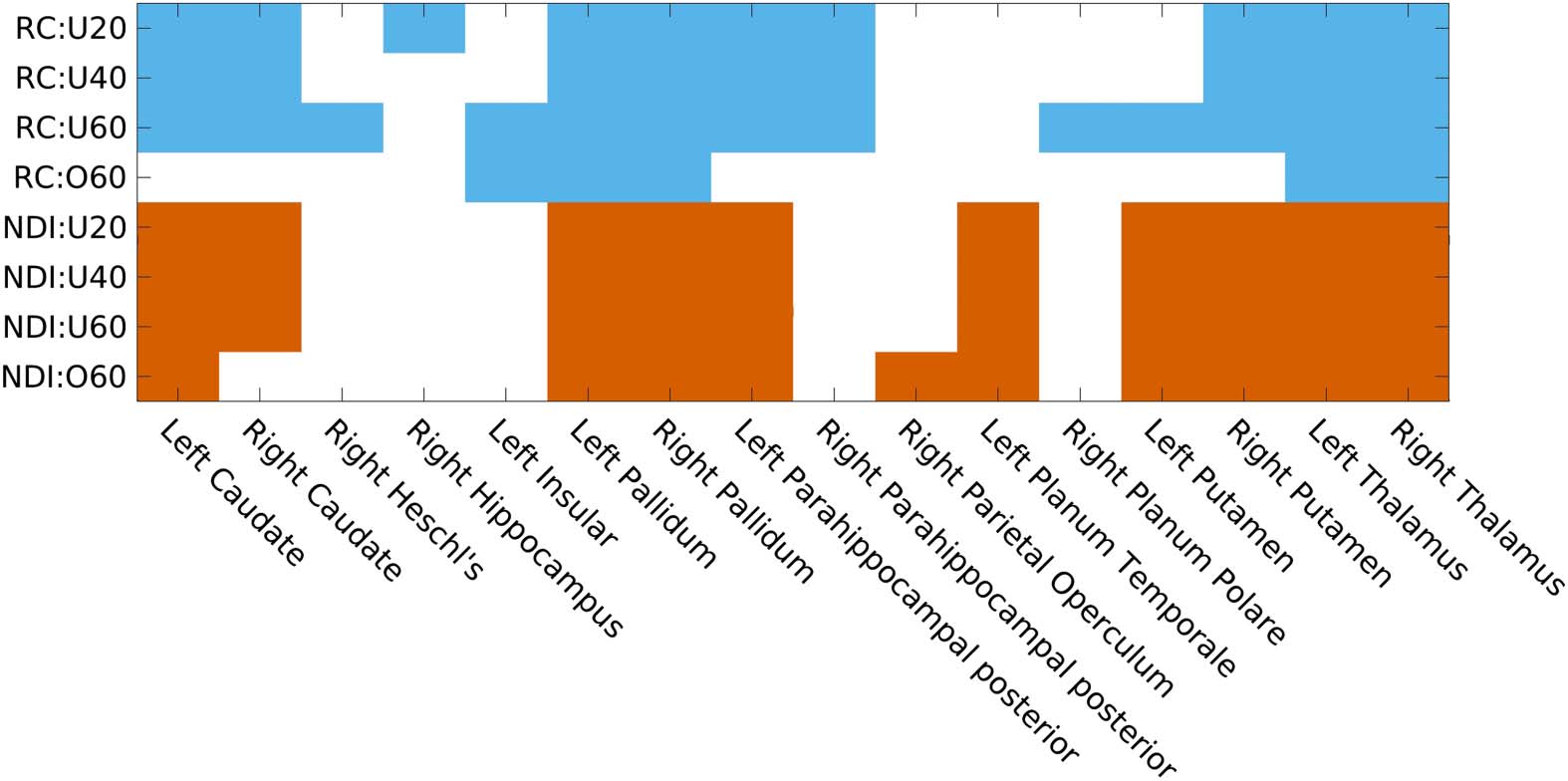
Figure 6 shows the regions stratified by subnetworks from Wcohort, as defined from NDI and
RC frameworks. NDI nodes were classified according to Gaussian means −14.76, −10.75,
and −7.93 for Tiers 1 to 3, respectively, and RC nodes were defined with kmax = 47.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Percentage of nodal assignment to subnetworks/Tiers between groups. The upper right
corresponds to comparisons using the NDI framework, whereas the lower left utilizes the RC
framework.
Network Neuroscience
798
Network structural dependency across the life-span
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Network measures stratified by age group for each of the investigated subnetworks. Top:
NDI-based subnetworks following their differentiation from fitting a GMM3 model, with decreasing
NDI from Tiers 1 to 4. Bottom: RC-based subnetworks, stratified by their connectivity profile with
respect to the richclub.
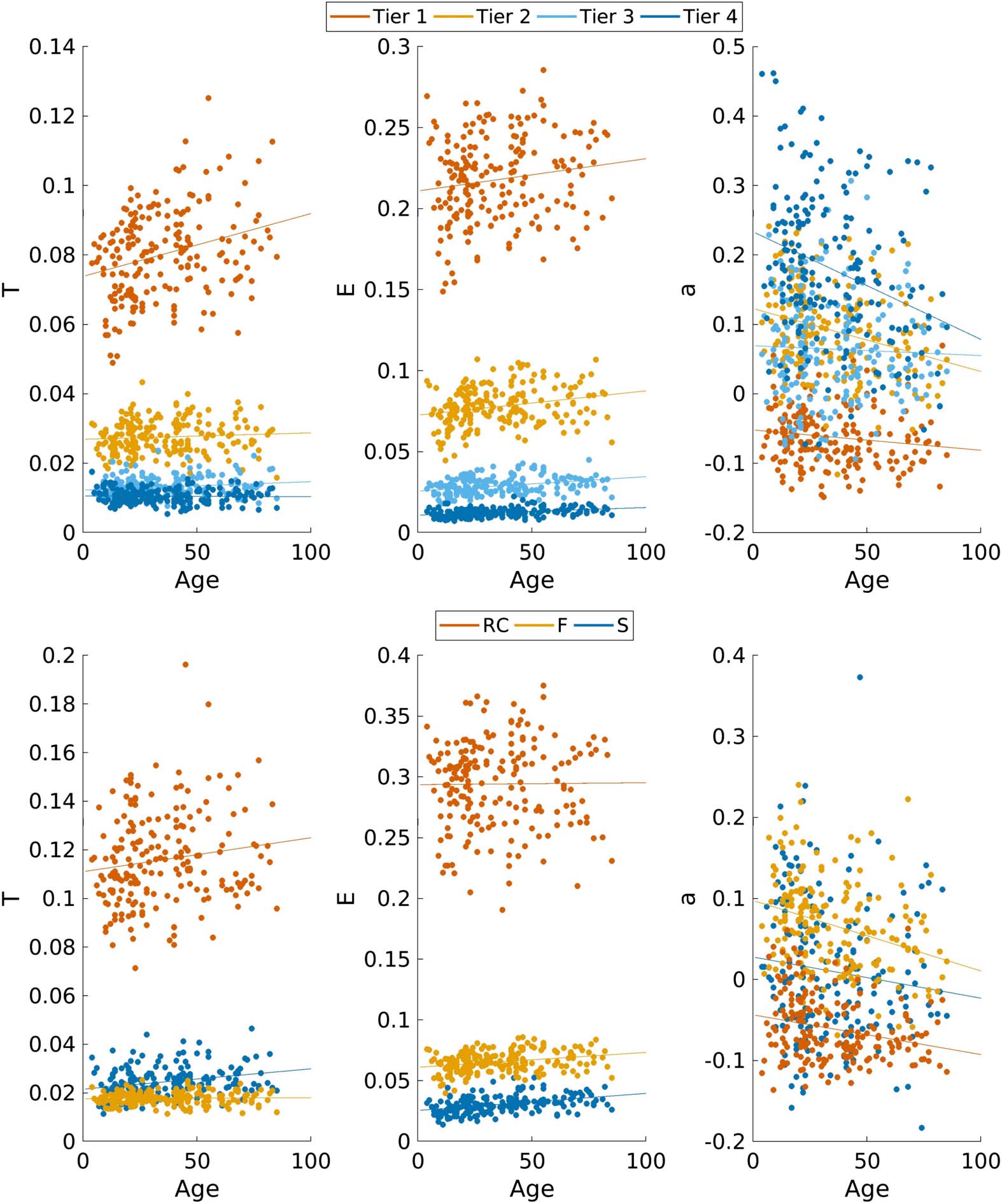
Figure 7 shows the association of network measures calculated from RC- and NDI-based
subnetworks with age. Subnetworks contained 20, 50, 44, and 56 nodes for Tier 1, 2, 3, and 4,
with 13, 137, and 20 nodes for RC, F, and S subnetworks, respectively. For both frameworks,
we see, on average, good separation of each subnetwork investigated in at least one of the
three network measures consistently across age. Global efficiency demonstrates the highest
separation between subnetworks in both frameworks, with RC and Tier 1 regions having the
highest levels of efficiency. We see clear differentiation between regions in the three remaining
subnetworks in the NDI framework (Tiers 2, 3, and 4), as well as between the two remaining
subnetworks in the RC framework (F and S). This separation between subnetworks can also
be observed in terms of transitivity, where Tiers 3 and 4, as well as F and S, overlap in part.
For assortativity, there is less of an overlap between subnetworks derived from NDI compared
with the RC framework.
Network Neuroscience
799
Network structural dependency across the life-span
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. NDI (left) and RC-derived (right) subnetworks from cohort-averaged connectome (Wcohort). (A) Assignments of cortical regions by
subnetwork for each framework, where corresponding left and right hemispheric anatomical regions were combined into a single label.
Regions are first ordered according to their unique membership in a subnetwork and then by increasing overlap. (B) Brain regions plotted by
subnetwork label for each framework (enlarged plots are in Figure S2 of Supporting Information).
Network Neuroscience
800
Network structural dependency across the life-span
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Network measures transitivity (T), efficiency (E), and assortativity (a) plotted against age
for NDI (top) and RC (bottom) subnetworks defined from the full cohort connectome (Wcohort).
Linear regression lines for each network measure and subnetwork are plotted. NDI Tiers show an
average strength of 0.25 ± 0.05, 0.44 ± 0.08, 1.45 ± 0.25, and 2.32 ± 0.33 with an average density
of 0.15 ± 0.02, 0.24 ± 0.03, 0.41 ± 0.05, and 0.78 ± 0.07 for Tiers 4, 3, 2, and 1, respectively.
RC subnetworks show an average strength of 0.33 ± 0.08, 2.04 ± 0.31, and 2.33 ± 0.33 with an
average density of 0.34 ± 0.05, 0.29 ± 0.03, and 0.91 ± 0.07 for RC, F, and S, respectively.
Fitted parameters of the linear regressions are summarized in Table 3. All subnetworks
show increasing efficiency with age, while assortativity decreases. In the RC-based sub-
networks, S decreases in transitivity, as does the Tier 4 subnetwork (NDI = 0). All other sub-
networks exhibit increasing transitivity with age.
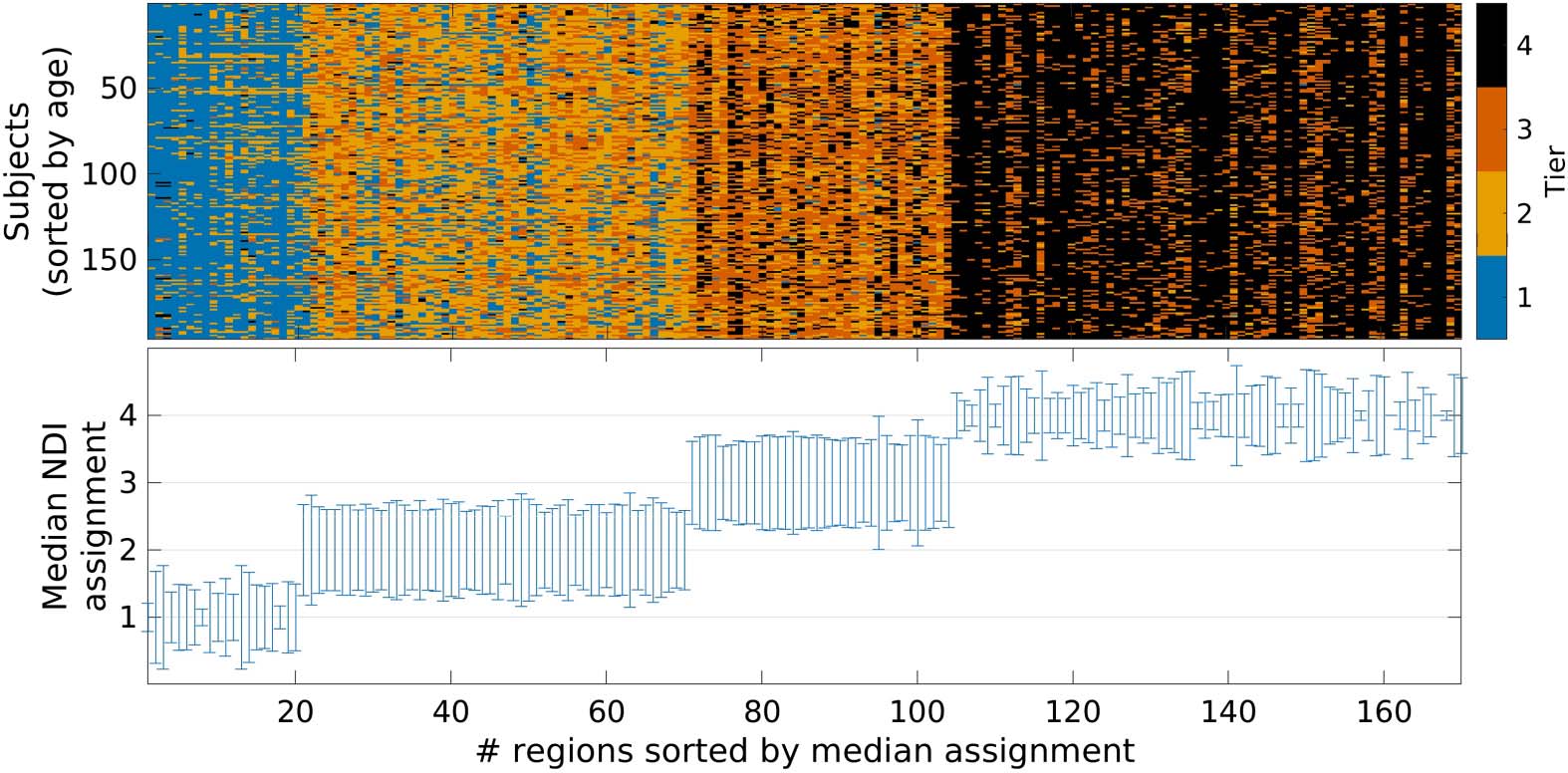
Figure 8 shows each node’s (region) NDI Tier as-
Nodal NDI Tier assignment on subject level.
signment for every subject, as well as the median assignment with corresponding variation
Network Neuroscience
801
Network structural dependency across the life-span
Table 3. Results of linear regression with slope m and offset b for transitivity (T), efficiency (E), and assortativity (a) with age from NDI- (1, 2,
3, 4) and richclub–based (RC, F, S) subnetworks. Statistically significant regression parameters are in bold (significance at p < 0.001, corrected
for multiple comparisons).
NDI
m
b
RC
m
b
1
1.42E-4
8.07E-2
RC
1.40E-4
1.11E-2
2
2.64E-5
2.88E-2
F
4.52E-6
1.77E-2
T
3
2.56E-5
1.29E-2
S
−8.39E-5
2.79E-2
4
−1.89E-6
1.06E-2
E
1
1.63E-4
2.19E-1
RC
1.59E-5
2.94E-1
2
1.63E-4
8.08E-2
F
1.22E-4
6.12E-2
3
1.08E-4
2.82E-2
S
1.40E-4
2.57E-2
4
1
4.70E-5 −3.18E-4
1.09E-2 −5.42E-2
RC
−4.90E-4
−4.35E-2
a
2
−1.00E-3
1.40E-1
F
−8.71E-4
9.77E-2
3
−4.09E-4
6.75E-2
S
−5.08E-4
2.79E-2
4
−1.55E-3
2.34E-1
(standard deviation) across all 196 subjects. Although some variation exists between Tier
assignments on the subject level, both plots indicate relative stability of these assignments
on the subject level.
DISCUSSION
In this work we extended the NDI metric into a novel framework to analyze weighted networks
and utilized the nodal indices to identify four distinct subnetworks in the human connectome.
Importantly, our subnetwork definition is data driven, without any manually chosen parame-
ters for a given connectome, and shows higher consistency across age groups compared with
RC-based subnetworks.
Investigating NDI, stratified by RC-based subnetworks, revealed generally higher NDI for
nodes that also belong to the richclub. This is to be expected, as the richclub has been shown
to be an integral part for effective information transport in networks. Feeders and Seeders have
lower NDI, where Seeders almost uniformly exhibit an NDI of zero. This is consistent with the
notion that these nodes are “local” or “peripheral” in the network. However, we observe that
some nodes belonging to Feeder regions exhibit higher importance for network functioning,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. NDI Tier assignments. Top: Assignment to the four NDI Tiers (color coded) for each node
and every subject. If an assignment of a given node is stable, the corresponding column will consist
of a single color. Subjects are ordered by age from youngest to oldest (top to bottom row). Bottom:
Median NDI Tier assignment for each node. Uncertainty is characterized as standard deviation
(minimum: 0; maximum: 0.98) of nodal assignment and indicated as error bars.
Network Neuroscience
802
Network structural dependency across the life-span
with NDI values that are comparable to richclub members. The richclub is often coined as a
backbone for information transport in brain networks. Although this aspect has been previously
shown, because of the limited assessment of richclub regions based simply on nodal degree
(a localized measure), their importance as a backbone structure is only partially interrogated.
NDI, however, investigates the relevance of each region for efficient information transport
within the entire brain network by incorporating topological distance information, a more
globally informed measure than nodal degree. In doing so, nodal NDI may be more reflective
of pathologies or structural changes that implicate entire pathways, making it advantageous
over simply counting the number of edges immediately appended to a node.
We observed that NDI followed a mixture of normal distributions after a natural log trans-
form. Here, we modeled the natural log-transformed NDI of each group connectome and the
cohort connectome into three distributions by using a Gaussian mixture model. By using the
halfway point between Gaussian centers (where the probability of a node belonging to either
one of the distributions is equal), we distinguish four different subnetworks. Importantly,
the Gaussian center estimations are consistent, whether computed by age groups or from the
cohort connectome. Furthermore, NDI demonstrated greater stability in identifying more re-
curring regions with higher NDI values in all four age groups than the RC framework (Figure 1).
However, the definition of richclub nodes, due to the lack of consensus on how to define it, is
variable. Nonetheless, NDI demonstrates greater stability, even if, for example, the number of
richclub nodes is fixed across age groups (see Supporting Information Figure S3). Stability in
identifying regions integral to brain architecture and functioning is desirable for comparative
purposes particularly given that they have been similarly detected across species, age, and
disease (Ball et al., 2014; Daianu et al., 2015; Grayson et al., 2014; Heuvel & Sporns, 2011;
Schirmer & Chung, 2018; van den Heuvel et al., 2013). This has led to a recent uptake in
employing a priori RC nodes for network analysis (Collin et al., 2016, 2014; van den Heuvel
et al., 2013; Wierenga et al., 2018). Utilizing these NDI subnetwork definitions and inves-
tigating their network topology with commonly used network measures, we observe distinct
patterns for each of the four subnetworks.
Our first analysis investigates age-associated changes in network measures by stratifying the
cohort according to age. In both frameworks we observe clear, mostly nonlinear patterns in
each subnetwork. Similar patterns have been observed previously, for example, with strength,
following an inverse U-shape for RC members (Zhao et al., 2015). However, the membership
of each region to a subnetwork (at the RC and Tier 1 level, for example) is not constant with
age group in this analysis. Although refinement and reassignment of region membership to any
subnetwork is possible, comparisons between age groups becomes difficult. In our second ex-
periment, we homogenized the regions that define the subnetworks in both frameworks by
utilizing the cohort connectome. Analyzing the trends of the investigated network measures
also showed significant patterns associated with age in each subnetwork for both framework.
Specifically, we observe a general increase in efficiency with age, most likely reflecting a re-
finement of the information transport within each subnetwork. It should be noted, however,
that whole connectome analyses have identified similar U-shape patterns as mentioned above,
warranting further investigation into the differences in network measures computed from sub-
networks versus the whole connectome. Assortativity shows a general decrease with age and
for all subnetworks, indicating that the connections between nodes of different degrees are
strengthened. Transitivity demonstrates mixed patterns for individual subnetworks. It generally
increases in RC and F subnetworks, as well as in Tiers 1, 2, and 3, indicative of a within-
subnetwork strengthening over age. However, for S and Tier 4, transitivity decreases, reflective
of less tightly integrated subnetworks. This may be the result of a distribution of the limited
Network Neuroscience
803
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
9
2
1
0
9
2
4
5
6
n
e
n
_
a
_
0
0
0
8
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network structural dependency across the life-span
that our NDI
resources in the brain, which favors preexisting, highly integrated regions. These results
suggest
framework defines organizations of age-associated network prin-
ciples of T, E, and a with good separation between subnetworks (Figure 7), indicative of more
highly modularized groupings of nodes, when compared with the RC framework, across the
ages.
Regarding the functional significance of the NDI-derived subnetworks, it can be clearly
noted that the gray matter regions (both subcortical nuclei and cortical regions) follow a
unique, largely nonredundant pattern (Figure 6). This is particularly noticeable in separation
of the Tier 1 regions from Tiers 2–4, given that the major components of the Tier 1 subnetwork
represent the key relay nuclei in the brain (such as thalamus or the basal ganglia represented
by caudate, pallidum, putamen) or cortical regions (such as insular, posterior cingulate gyrus)
responsible for processing and redistribution of essential information flow from the primary
(motor, sensory, language) cortex to the related association cortices and beyond. Greater over-
lap appears to exist between the cortical regions represented in Tiers 2–4, which potentially
reflects the redundancy necessary for operations involving larger and more complex clusters
of gray matter structures. This redundancy may serve to ensure the dynamic connectivity that
engages multiple brain functions necessary to sustain defined tasks. Future studies on the func-
tional topography of NDI-derived subnetworks should aim to elucidate the significance and
versatility of the tier-specific region interactions, as well as the potential influences that may
disrupt or enhance them.
There are some limitations to our study. For our framework, we employed three Gaussians
to model the NDI distributions based on our Akaike and Bayesian information criteria analysis.
While we observe good separation and consistent Gaussian centers across the cohort and four
age group connectomes, other choices may be valid depending on the dataset. Additionally,
other studies have employed alternative means to investigate versions of the richclub, such as
the participation coefficient, community and/or the distribution index (Grayson et al., 2014;
Van Den Heuvel & Sporns, 2011). Although these network measures are closely related to
NDI, the purpose of our work was not to use NDI as a direct measure of network topology,
but to differentiate and identify meaningful subnetworks in the connectome. However, NDI
can be utilized as a nodal measure to inform the impact of localized damage, for example, in
conditions such as stroke or brain tumors, and to study differences in network topology, which
will be the aim of future studies. Limitations in any life-span analysis include defining the age
groups in the cohort, and also how to standardize network estimates across subjects and/or
age groups. We utilized age groups to investigate potential changes in subnetwork definition
based on differences in the group connectome in the first part of the presented analysis. In
particular, subjects in the youngest age group (<20 years; U20) include biological changes
such as myelination which can modify the structural connectome globally, part of normal
development. The level in to subdivide by age during periods neurological develop-
ment (or aging) is not trivial. Therefore, this work we did focus on these developmental
stages, warranting dedicated, fine-grained studies U20 group. In terms standardizing
networks for richclub analysis a life-span study, identifying consistent RC nodes com-
plicated because lack consensus how choose degree parameter k. this
analysis, allowed framework, flexibility define subnetworks reflected by
for each group, or propagating from
the data, defining k
a cohort-averaged network all subjects. However, NDI consistently demonstrated greater
stability coherent when compared with frameworks. This also
holds true if other choices are used, example, fixing the
number across groups (see Supporting Information Figure S3).
group
max
Network Neuroscience
804
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
>