METHODEN
Inferring excitation-inhibition dynamics using a
maximum entropy model unifying brain
structure and function
Igor Fortel1
Anastasios Sidiropoulos6, Yichao Wu7, Ira Driscoll2, Dan Schonfeld1,8, and Alex Leow1,5
, Mitchell Butler1, Laura E. Korthauer2,3, Liang Zhan4, Olusola Ajilore5,
1Department of Bioengineering, University of Illinois at Chicago, Chicago, IL, USA
2Abteilung für Psychologie, University of Wisconsin–Milwaukee, Milwaukee, WI, USA
3Warren Alpert Medical School, Brown University, Providence, RI, USA
4Department of Electrical and Computer Engineering, University of Pittsburgh, Pittsburgh, PA, USA
5Department of Psychiatry, University of Illinois at Chicago, Chicago, IL, USA
6Department of Computer Science, University of Illinois at Chicago, Chicago, IL, USA
7Department of Math, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL, USA
8Department of Electrical and Computer Engineering, University of Illinois at Chicago, Chicago, IL, USA
Schlüsselwörter: Funktionale Konnektivität, Structural connectome, Ising model, Brain criticality,
Excitation-inhibition balance, Maximum entropy
ABSTRAKT
Neural activity coordinated across different scales from neuronal circuits to large-scale brain
networks gives rise to complex cognitive functions. Bridging the gap between micro- Und
macroscale processes, we present a novel framework based on the maximum entropy model
to infer a hybrid resting-state structural connectome, representing functional interactions
constrained by structural connectivity. We demonstrate that the structurally informed network
outperforms the unconstrained model in simulating brain dynamics, wherein by constraining
the inference model with the network structure we may improve the estimation of pairwise
BOLD signal interactions. Weiter, we simulate brain network dynamics using Monte Carlo
simulations with the new hybrid connectome to probe connectome-level differences in
excitation-inhibition balance between apolipoprotein E (APOE)-ε4 carriers and noncarriers.
Our results reveal sex differences among APOE-ε4 carriers in functional dynamics at
criticality; speziell, female carriers appear to exhibit a lower tolerance to network
disruptions resulting from increased excitatory interactions. In sum, the new multimodal
network explored here enables analysis of brain dynamics through the integration of structure
and function, providing insight into the complex interactions underlying neural activity such as
the balance of excitation and inhibition.
EINFÜHRUNG
The brain is a complex dynamical system whose functional properties are largely determined
by the characteristics of its neurons and patterns of synaptic connectivity, resulting in a bal-
ance of excitatory (E) and inhibitory (ICH) interactions. Zum Beispiel, if the number of neurons that
are coactivated from one signal is too high (increased excitation), the result is wide-scale acti-
vations and errant signal propagation across the brain’s subnetworks. Andererseits, wenn die
number of coactivated neurons is too low (increased inhibition), the propagation of the signal
Keine offenen Zugänge
Tagebuch
Zitat: Fortel, ICH., Diener, M., Korthauer,
L. E., Zhan, L., Ajilore, O., Sidiropoulos,
A., Wu, Y., Driscoll, ICH., Schonfeld, D., &
Leow, A. (2022). Inferring excitation-
inhibition dynamics using a maximum
entropy model unifying brain structure
and function. Netzwerkneurowissenschaften,
6(2), 420–444. https://doi.org/10.1162
/netn_a_00220
DOI:
https://doi.org/10.1162/netn_a_00220
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00220
Erhalten: 24 Juni 2021
Akzeptiert: 7 Dezember 2021
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Alex Leow
alexfeuillet@gmail.com
Handling-Editor:
Olaf Sporns
Urheberrechte ©: © 2021
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Criticality:
From physics, representing the state
of a dynamical system between order
and disorder.
Funktionale Konnektivität (FC):
Undirected measure describing the
statistical dependance between brain
regions based on blood oxygen
level–dependent (BOLD) Signale
from fMRI.
Pairwise maximum entropy model
(pMEM):
A maximum entropy model that takes
into account the average activity of a
node as well as pairwise interactions.
Ising model:
Network model in which node
activity is represented with binary
states and energy is computed based
on pairwise interactions.
Maximum entropy model (MEM):
A statistical model of data
representing the highest entropy that
satisfies the constraint of prior
Wissen.
(BOLD) signals extracted from fMRI
may diminish too quickly, limiting information transfer. The dynamical balance between exci-
tation and inhibition is important for adjusting neural input/output relationships in cortical net-
works and regulating the dynamic range of their responses to stimuli (Kinouchi & Copelli,
2006) as well as the optimal dynamic range where information capacity and transfer are max-
imized (Shew et al., 2011). This is the central thesis of the criticality hypothesis, a phenomenon
that suggests that neural networks and many aspects of brain activity self-organize into a
unique configuration, sometimes called a critical state (Wilting & Priesemann, 2019). This state
represents the transition of complex dynamical systems like the brain from order (balanced
excitation-inhibition) to disorder (disrupted excitation-inhibition balance) and has found appli-
cations in many scientific domains, including neuroscience and clinical neurology (Cocchi
et al., 2017; Hahn et al., 2017; Sornette, 2006; Tagliazucchi, 2017). Studies have demon-
strated that the cortex operates near criticality during neuronal signaling (Beggs & Plenz,
2003; Hahn et al., 2017; Shew et al., 2009), as well as in studies utilizing blood oxygen
level–dependent
Bildgebung (Haimovici et al., 2013;
Lombardi et al., 2017; Rabuffo et al., 2021; Tagliazucchi et al., 2012). Tatsächlich, there is growing
evidence from animal models and whole-cell recordings supporting the hypothesis that synap-
tic dysfunction leading to neuronal hyperexcitation may represent some of the earliest changes
in the progression of neurodegenerative disease like Alzheimer’s disease (AD; Busche &
Konnerth, 2016; Palop et al., 2007; Petrache et al., 2019; Ren et al., 2018). Jedoch, the major
challenge with early detection and intervention is that both normal aging and AD are associated
with alterations to neural structure and function (McDonald et al., 2009; Schuff et al., 1999). Das
includes regional hypometabolism (Chételat et al., 2013; Curiati et al., 2011), white matter (WM)
changes (Barrick et al., 2010; Michielse et al., 2010), Aβ deposition (Rodrigue et al., 2012; Rowe
et al., 2010), and disrupted resting-state functional connectivity (Damoiseaux et al., 2008; Sheline
et al., 2010; Wang et al., 2006). To improve our understanding of neurodegenerative diseases
(accounting for major factors such as age, Sex, or genetic phenotypes) and improve early
detection, we investigate a model that can integrate microscale principles at a connectome level
to bridge the gap between cell- to network-level degeneration. Jedoch, we acknowledge that
some abstraction is required in this strategy; in models of large-scale effects, physiological informa-
tion may be more abstract, and details of cellular processes potentially lost. While this may
seem counterintuitive from a biological perspective, it is necessary for describing higher-level
phenomena informed by MRI neuroimaging.
Zu diesem Zweck, in this paper we introduce a method based on statistical physics to jointly
model both brain structure and function via a pairwise maximum entropy model (pMEM).
Our framework is inspired by the Ising model representation of brain dynamics whereby
self-organized patterns of connectivity are formed through the spontaneous fluctuations of ran-
dom spins (Reichl & Luscombe, 1999). This model has been used to characterize complex
microscale dynamics of the human brain (Deco et al., 2008; Kadirvelu et al., 2017; Ostojic
& Brunel, 2011; Tkačik et al., 2015), as well as macroscale interactions (Ezaki et al., 2017;
Marinazzo et al., 2014; Nghiem et al., 2018; Niu et al., 2019; Nuzzi et al., 2020; Schneidman
et al., 2006). Unconstrained maximum entropy models (MEM) have been shown to accu-
rately represent spatiotemporal coactivations in neuronal spike trains (Roudi et al., 2009;
Schneidman et al., 2006; Shlens et al., 2006) as well as patterns of BOLD activity (Ashourvan
et al., 2017; Cocco et al., 2017; Ezaki et al., 2020; Watanabe et al., 2013). Tatsächlich, Zanoci et al.
(2019) recently showed that the Ising model captures collective neuronal behavior during
Wachsamkeit, light sleep, and deep sleep when both excitatory (E) and inhibitory (ICH) Neuronen
are modeled. Weiter, at the macroscale, Ashourvan et al. (2021) recently developed a max-
imum entropy–based framework that derives functional connectivity measures from
Netzwerkneurowissenschaften
421
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Structural connectome (SC):
Network representation of physical
connections in the brain. Nodes
represent brain regions. Edges
represent a measure of connectivity
between them.
APOE-ε4:
An allele representing one of the
strongest genetic risk factors for
developing Alzheimer’s disease
(AD).
intracranial EEG recordings; their findings suggest that structural connections in the brain give
rise to large-scale patterns of functional connectivity by promoting coactivation between con-
nected structures. Daher, MEM may be an ideal tool to model functional connectivity and ulti-
mately link microscale interactions (such as excitation and inhibition in neuronal circuits) Zu
the functional connectome (FC) captured through fMRI BOLD activity.
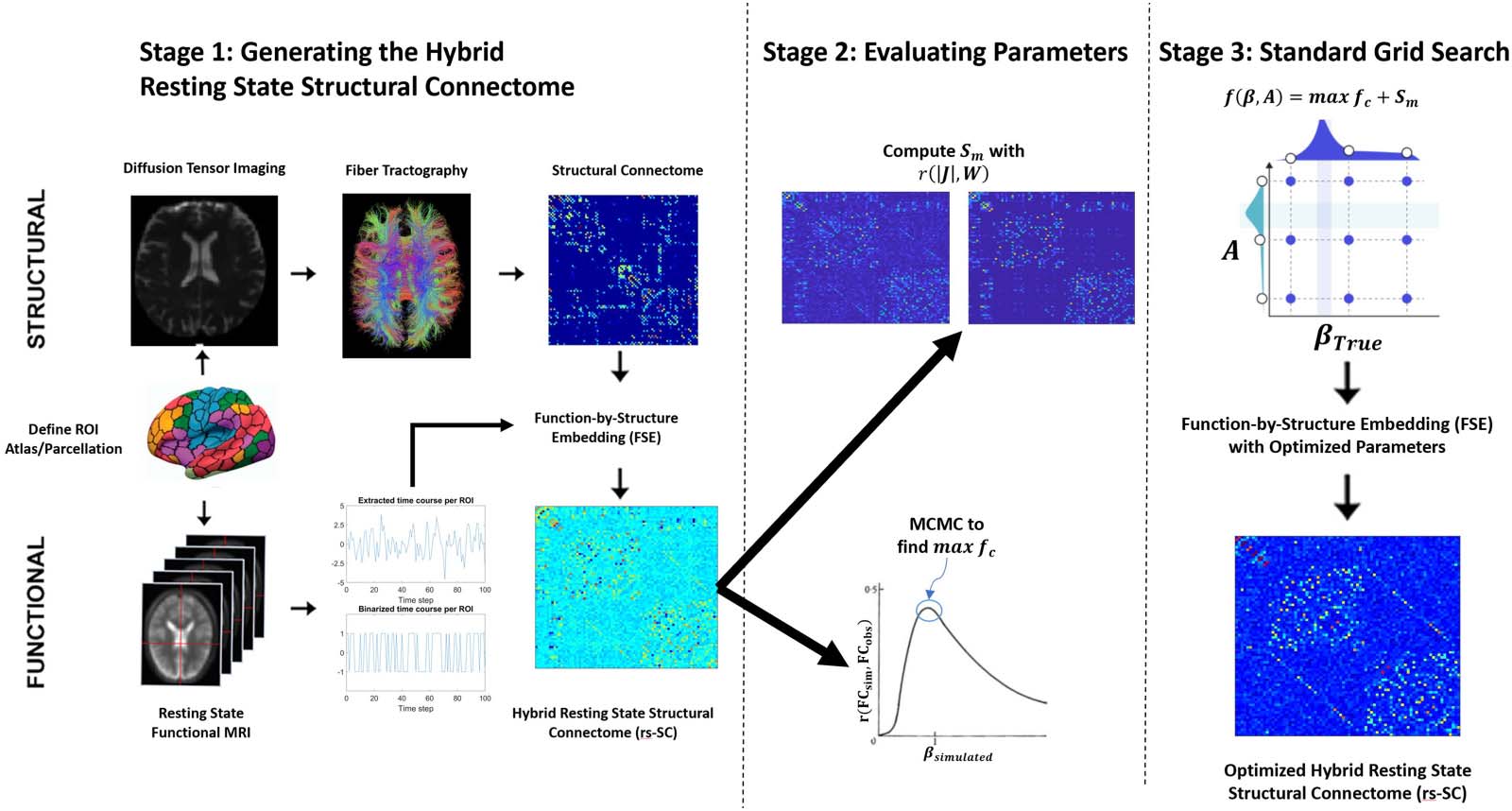
Described as a function-by-structure embedding (FSE), our model infers the organization of
functional connectivity from global activity patterns (d.h., simultaneously considering the activ-
ity of more than two brain regions) constrained to the structural connectome. We present a
robust numerical approach for our model, optimizing a constrained maximum likelihood esti-
mation. The use of a structural connectome to inform the modeling of BOLD activity is moti-
vated by a strong link between fMRI-based functional connectivity and white matter–based
structural connectivity (Bettinardi et al., 2017; Honey et al., 2009; Shen et al., 2015). Diese
studies suggest that models of functional dynamics should also be governed by the underlying
structure to include direct and indirect connections between brain regions. Daher, if our model
accurately describes large-scale brain activity patterns during rest, it will provide a much richer
representation of functional interactions governing global dynamics that may give rise to
hyperexcitation. With our framework we construct hybrid resting-state structural connectomes
(rs-SC) for a group of 76 middle-aged and cognitively intact individuals. These unique struc-
tural networks are informed by a spin-glass-like Ising model, whose dynamics resemble that of
traditional FC. We demonstrate that our new structurally informed networks can consistently
and accurately reconstruct observed BOLD correlations. Investigating macroscale brain
dynamics through the lens of statistical physics allows us to infer computationally the nature
of resting-state activity (corresponding to inhibition or excitation) and probe potential disrup-
tions to E/I balance that may lead to hyperexcitation and subsequent increased vulnerability to
neurodegeneration. To evaluate this phenomenon, we create subgroups of 38 Alter- and sex-
matched individuals based on whether one is a carrier of the apolipoprotein E (APOE)-ε4
allele, a well-known genetic risk factor of AD. Recent studies have shown that APOE-ε4
may contribute directly to early neuronal dysfunction, either directly via modification of the
excitation/inhibition balance or linked with amyloid deposition (Bi et al., 2020; Koelewijn
et al., 2019; Nuriel et al., 2017; Stargardt et al., 2015). Using our new hybrid rs-SC, we inves-
tigate the relationship between E/I balance and criticality in these two groups. We hypothesized
that because of a shift in E/I balance towards hyperexcitation, the female APOE-ε4 carrier group
would exhibit a lower tolerance to perturbations in the network when simulating brain dynam-
ics using Monte Carlo simulations of the Ising model as compared with the female noncarrier
Gruppe. Herein we aim to demonstrate that an increase in excitatory interactions at the connec-
tome level, identified using our new hybrid connectome, may provide new evidence of vulner-
ability among females to AD neuropathology due to disruptions in E/I balance.
ERGEBNISSE
Constructing a Function-by-Structure Embedding Using a Constrained Maximum Likelihood Estimation
In constructing the function-by-structure embedding (FSE), we begin with the unconstrained
pairwise maximum entropy model (pMEM) as described in the Methods section. The pMEM is
sometimes referred to as the inverse Ising model, where the pairwise interactions (represented
as Ji,J, with i and j representing regions of interest, ROIs, in the brain network) are inferred from
the observed data (BOLD time series). As the model assumes binary data, we binarized the
resting-state fMRI signals obtained from the 76 cognitively intact middle-aged subjects. Der
binarized activity pattern of N = 80 ROIs at time t (t = 1, 2, …, tmax; tmax = 236) is denoted
S(T ) = s1(T ), s2(T ), …, sN(T ) 2 {−1, +1}N. Note that tmax is determined as a result of the 8-min fMRI
Netzwerkneurowissenschaften
422
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Hamiltonian:
Equation representing the total
energy of the system.
scan time with TR = 2 S (see the Methods section). Here s1(T ) = ± 1 indicates that an ROI is
either active (+1) or inactive (−1). Erste, the time series goes through a z-score normalization
procedure, resulting in zero mean and unitary variance. To assess the sensitivity of our results
to thresholding, we tested thresholds of 0 and ±1 SD. The results of this assessment will be
presented in the section called Determining Parameters for Generating the Optimal Resting-
State Structural Connectome. For the unconstrained pMEM, we fit the following probability
distribution to all 76 subjects by maximizing a pseudolikelihood (see the Methods section):
Pr(S) = exp (−βH(S))/Z, where H sð Þ ¼ −
(cid:2) is the Hamiltonian
function describing the energy of the system, and Z ¼
Þ is the partition func-
tion. Hier, the spin configuration s is defined as the column vector s = [s1, s2, …, sN]tmax, Wo
si and sj are the spin states of region i and j, and Ji,j represents a pairwise interaction between
those regions. Traditionell, the Hamiltonian includes a term for external influences that we
assume to be zero for resting-state data. We use the unconstrained pMEM as a control for com-
parison purposes. In our approach, we hypothesized that the interaction Ji,j between two
regions should be directly linked back to the diffusion MRI-derived structural connectivity
between them as informed by tractography, so we add a constraint to the Hamiltonian function
as follows:
Ji;jsisj; with i; J 2 1; 2; …; k
½
P
D
s exp −βH sð Þ
P
H sð Þ ¼ −
X
ich
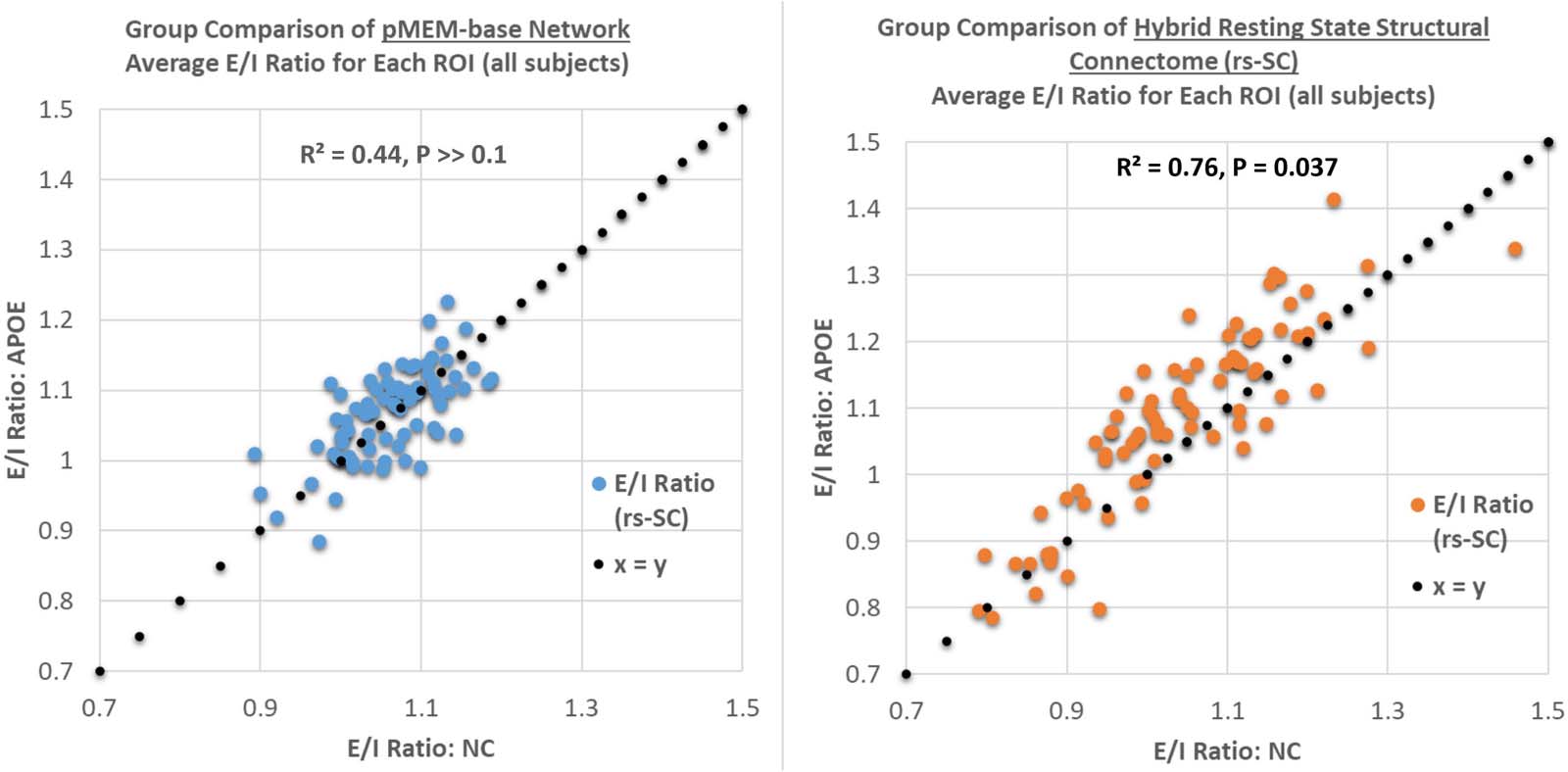
funktioniert. Umgekehrt, performing a similar computation of the E/I ratio on the rs-SC networks
results in a strong association between NC and APOE groups, with R2 = 0.76, as well as a
notable shift observed for all ROIs (d.h., globally). A paired t test between the groups results
in P = 0.037, suggesting a statistically significant group difference in the rs-SC networks
between NC and APOE groups, as evaluated with the E/I ratio that cannot be identified with
the unconstrained model. In sum, the results presented in this section indicate that the novel
rs-SC network constructed with the FSE framework can not only describe structural and func-
tional dynamics, but also probe brain dynamics that may not be captured using a similar
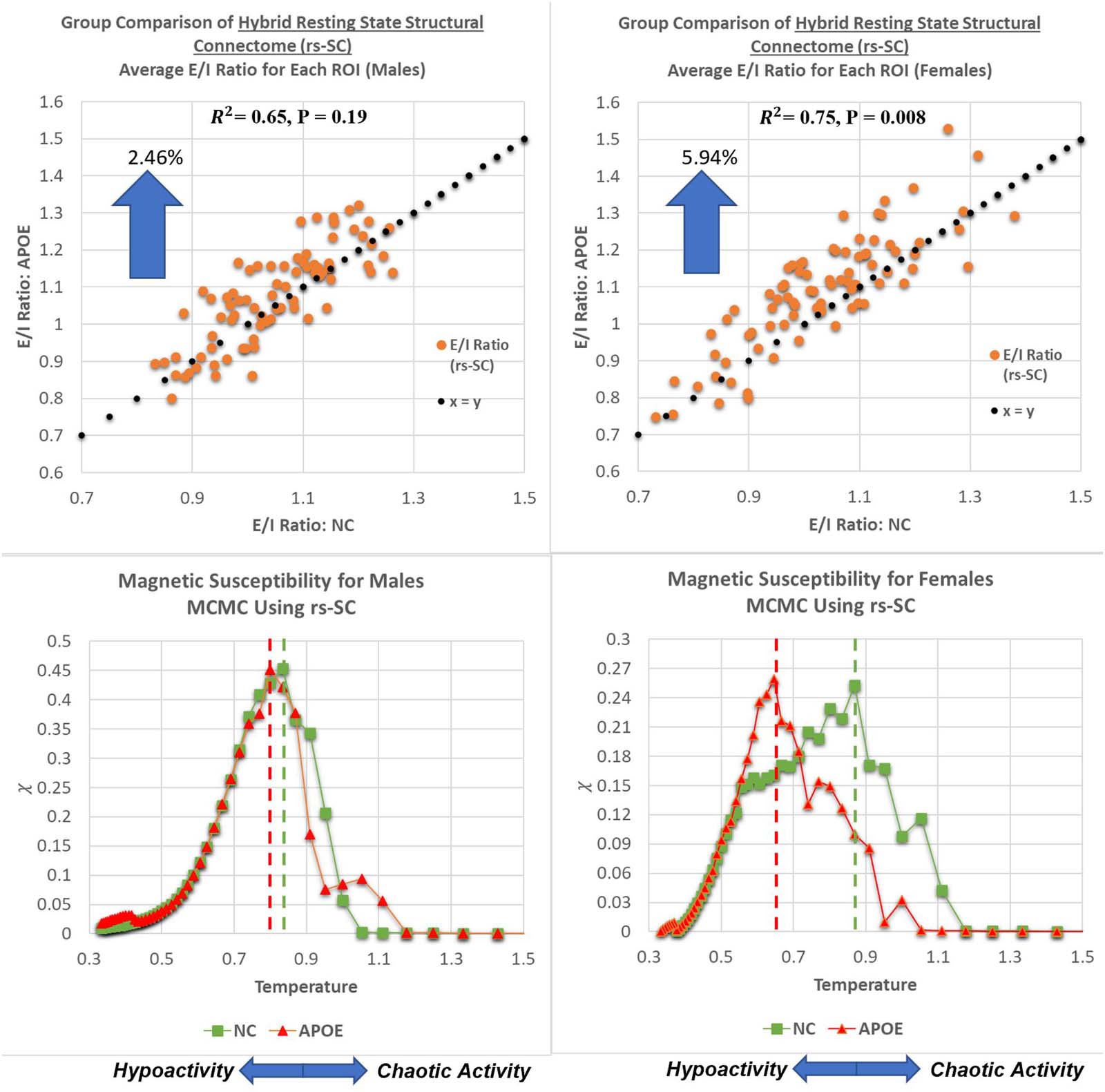
unconstrained methodology. Last, we compare the E/I ratio in a group comparison of males
and females (NC versus APOE) and present the results in the scatterplot of Figure 5. Beide
males and females exhibit a positive association between groups with R2 = 0.65 and R2 =
0.75, jeweils; Jedoch, only the female group has a statistically significant group
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4. Group comparison of the excitation-inhibition ratio for each brain region based on the unconstrained pairwise maximum entropy
model and the function-by-structure embedding. As described in the Methods section, the E/I ratio is simply the sum of positive edges divided
by the sum of negative edges for each ROI. Hier, we present a plot comparing the E/I ratio between the NC and APOE groups using the pMEM-
based network and our rs-SC network, computed and averaged at the ROI level. This results in a weak association with R2 = 0.44 for for the
pMEM-based network, and R2 = 0.76 for the rs-SC network, with paired t tests across all ROIs resulting in P >> 0.1 and P = 0.037, jeweils.
This suggests no statistically significant differences in E/I balance when using the unconstrained model; Jedoch, there is a statistically sig-
nificant difference in the two groups when using our structurally informed model. We note that numerically, an increase in group-averaged E/I
ratio would move a point (representing one ROI) above the x = y reference line, suggesting a shift in E/I balance towards hyperexcitation. A
tabular version of these results is included in the Supporting Information.
Netzwerkneurowissenschaften
428
Unifying brain structure and function using a maximum entropy model
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
Figur 5. Gender-based comparison of critical behavior and E/I balance. As described in the Methods section, the E/I ratio is simply the sum
of positive edges divided by the sum of negative edges for each ROI. In the top panels, we present plots comparing the E/I ratios between the
NC and APOE groups for males and females, computed and averaged at the ROI level. This results in a strong association with R2 = 0.65 für
Männer, and R2 = 0.75 for females with paired t tests across all ROIs resulting in P = 0.19 for males, and P = 0.008 for females. This suggests no
statistically significant differences in E/I balance for males; Jedoch, there is a statistically significant difference for females. We note that
numerically, an increase in group-averaged E/I ratio would move a point (representing one ROI) above the x = y reference line, vorschlagen
a shift in E/I balance towards hyperexcitation with increased risk of chaotic activity. Daher, for each ROI, we can quantify the shift in E/I balance
by computing delta ¼ 1− E=I
D
to evaluate the average change between NC and APOE groups; this yields a shift of 5.94% in the female
D
E=I
group between carriers and noncarriers, while in the male group it is 2.46% (approximately 2.4× difference between sexes). A tabular version
of these results is included in the Supporting Information.
Þ
Þ
APOE
NC
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Þ
NC
Þ
APOE
to evaluate the average change between NC and APOE groups. The males
difference with P = 0.008. Hier, we perform a calculation on group difference by computing
D
delta ¼ 1− E=I
D
E=I
have an average increase of 2.4% (averaged across all ROIs), while the females have an
average increase of 5.9% in E/I ratio (approximately 2.4x higher than the male group).
The raw values for each brain region are shared in Supplementary Table 1 for reference.
Criticality and Hyperexcitation in Female APOE-ε4 Carriers
In this study, our subjects are separated into two age- and sex-matched groups (NC and APOE).
One aspect of the link between APOE-ε4 and AD that has often been overlooked is that
Netzwerkneurowissenschaften
429
Unifying brain structure and function using a maximum entropy model
females with at least one ε4 allele are four times more likely to develop AD than males (Bretsky
et al., 1999; Jack et al., 2015; Payami et al., 1994). Daher, we use our framework to evaluate not
just group differences in criticality, but sex differences as well (22F/16M in each group). Als
previously mentioned, the brain criticality hypothesis suggests that neural networks self-
organize into a unique configuration between order and disorder. In the context of statistical
physics and the Ising model, this unique configuration occurs at some critical point (βcritical).
Hier, we again utilized MCMC simulations to generate a series of state configurations (±1)
resulting in an N × t matrix, where N = 80 ROIs, and t = 100,000 runs (see Methods). In
the previous section we used these states to compute a correlation between brain regions;
Jedoch, in this case we will evaluate the critical dynamics elucidated from the rs-SC net-
funktioniert. Speziell, we are interested in the phase transitions based on the positive edges of
die Netzwerke. The Ising model can be modified to model spin-glass behavior (full signed net-
arbeiten); Jedoch, this can lead to “frustration” in the simulations. Frustration describes a sce-
nario in which it is impossible to simultaneously minimize all the terms in the Hamiltonian. Als
ein Ergebnis, this generally leads to complex energy landscapes with many local minima. At low β,
the system can get stuck in the local minima without ever reaching a true equilibrium. In future
work we can investigate thermodynamic properties using the full signed network (spin-glass),
but here we proceed in evaluating the ferromagnetic phase transitions.
For each β, we compute the order parameter (magnetization) and the variance (susceptibil-
ität) with respect to βsimulated. Hier, we again compute average values over NC and APOE
groups to investigate potential group differences in critical behavior. As described in the
Methoden, β is the inverse temperature (T ) parameter used in the Boltzmann distribution, Und
thus when simulating dynamics to identify phase transitions, we interpret temperature as a
tolerance of the system when increased randomness is introduced. Performing Monte Carlo
simulations of the Ising model using our hybrid network for a range of temperatures is used
to identify a critical point, such that the system transitions from a hypoactive regime to a cha-
otic regime. Somit, the critical temperature is a measure of how much tolerance the system
has to increased perturbations. We present the phase diagrams for susceptibility in Figure 5 für
males and females, highlighting Tcritical for both groups (evaluated by the peak of susceptibil-
ität). It should be noted that β was simulated from 0.2 Zu 3.0 at increments of 0.05 (then plotted
against T ¼ 1
βÞ. We identified a more pronounced deviation between NC and APOE females
with Tcritical = 0.65 for the female APOE group as compared with Tcritical = 0.87 in the NC
Gruppe. Umgekehrt, Tcritical = 0.80 in the male APOE group as compared with Tcritical = 0.83
in the NC group. This suggests that the critical dynamics within the male group between
NC and APOE are more similar in nature than the dynamics observed within the female group
between NC and APOE. A lower critical temperature in the female carrier group suggests a
lower tolerance to network dysfunction as a result of an increase in excitatory interactions,
increasing vulnerability to chaotic activity. In sum, these results suggest that there is a link
between brain criticality and excitation-inhibition balance that can be identified via our
new connectome, demonstrating a disruption to this balance in APOE carriers (with a larger
effect in females).
Weiter, presented here are plots demonstrating a global evaluation of critical brain dynam-
ics. In the bottom panels, ferromagnetic susceptibility is shown for males and females, mit dem
dashed lines representing the critical point Tcritical = Tsimulated(max χ). These charts demon-
strate a more pronounced deviation between NC and APOE females with Tcritical = 0.65 für
the female APOE group as compared with Tcritical = 0.87 in the NC group. Umgekehrt, Tcritical
= 0.80 in the male APOE group as compared with Tcritical = 0.83 in the NC group. This suggests
that as the E/I balance shifts at global scale, the critical point also decreases because of an
Critical temperature:
Parameter describing the tolerance of
a system to increasing perturbations
(commonly used in physics to
identify loss of magnetic properties).
Netzwerkneurowissenschaften
430
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
increase in excitatory interactions. As described in the Methods section, a lower critical tem-
perature indicates a lower tolerance to network dysfunction, increasing vulnerability to cha-
otic activity.
DISKUSSION
Using a constrained maximum entropy model for our function-by-structure embedding (FSE),
we have developed here a novel resting-state structural connectome (rs-SC), unifying
connectome-level structure and function into a new spatiotemporal network. We constructed
rs-SC networks for 76 cognitively intact participants with a grid-search parameter optimization
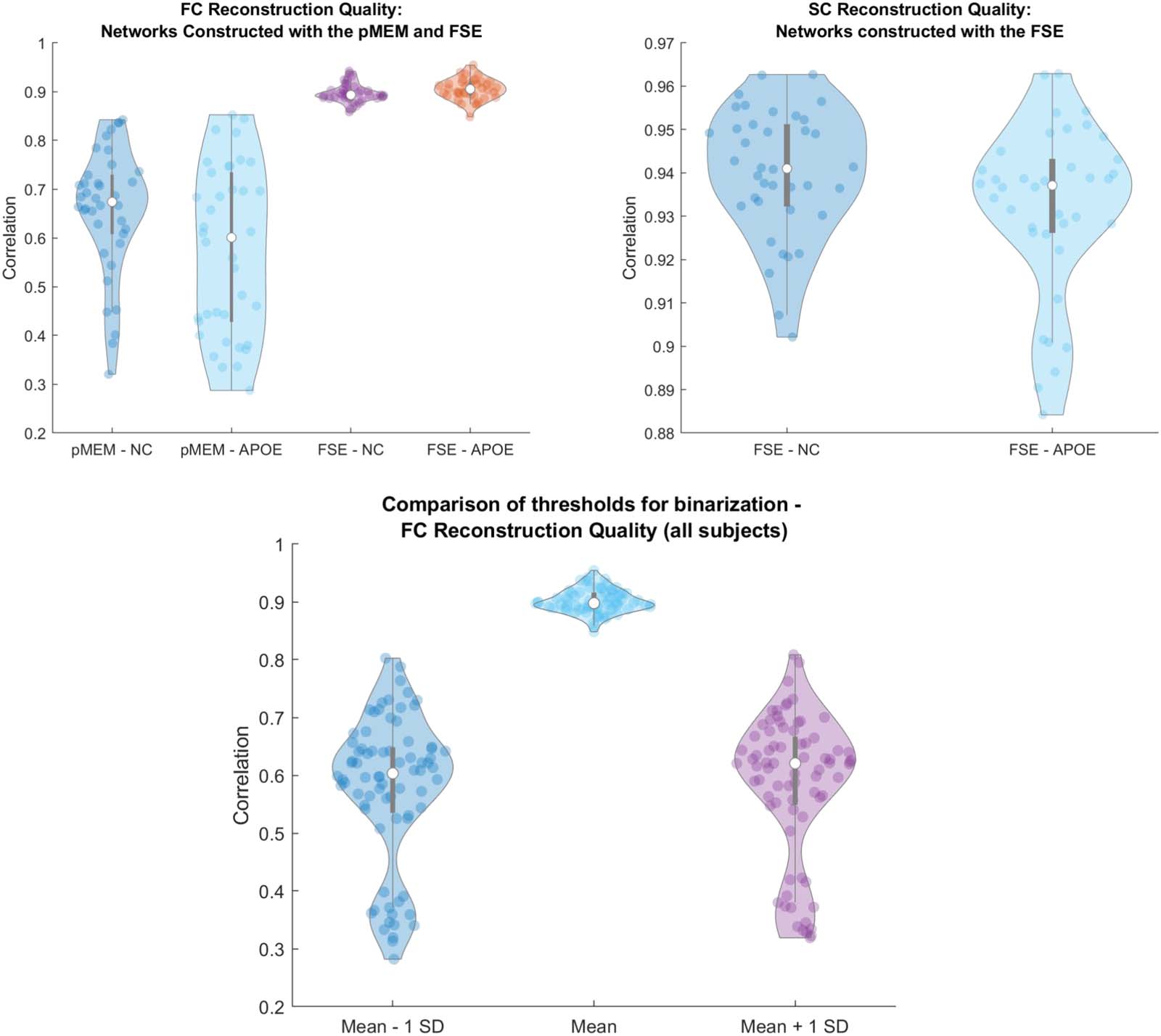
scheme. Somit, we demonstrate two important results: Erste, the underlying structure of the
rs-SC is as expected, strongly correlated with the empirical structural connectome (r > 0.9)
due to it being used as a constraint in the FSE framework. Zweite, and more importantly, Wir
demonstrated that it is possible to model the resting-state functional connectome based on a
model of spin products, accounting for indirect or higher order structural connectivity. Wir
acknowledge that when Ising dynamics are used to model neural firing patterns, these activa-
tions may amount to the collective behavior of a few neurons, and at the macro level of fMRI
imaging used in this study each voxel may be providing information as a result of thousands of
interacting neurons. Jedoch, simulation and empirical studies have demonstrated that
increases in excitatory neuronal activity amplify oscillations associated with the transient BOLD
response, while increasing inhibitory activity evokes an overall decrease in the BOLD signal
(Aksenov et al., 2019; Krishnan et al., 2018; Sotero & Trujillo-Barreto, 2007; Sten et al.,
2017). By grounding our macroscale methodology with models of microscale dynamics, Wir
bridge the gap between the two, hereby inferring the nature (excitatory or inhibitory) of structural
connectivity at rest. Weiter, the rs-SC can be used to simulate functional dynamics using Monte
Carlo simulations, reconstructing traditional functional correlation patterns (ravg = 0.9). Darüber hinaus
model quality and performance, we have also demonstrated that our rs-SC can distinguish
between female noncarriers and APOE-ε4 carriers (Alter- and sex-matched) using our
excitation-inhibition (E/I) Verhältnis. Our results demonstrate that modeling with the rs-SC reveals a
global shift of E/I balance for the APOE-ε4 carrier group. Given that APOE-ε4 carriers are at an
elevated risk for AD, the observed shift in E/I balance in this sample may be a result of disease
pathology. In many studies of AD, one critical feature that is often overlooked is that females with
at least one ε4 allele are four times more likely to develop AD than are males (Jack et al., 2015). A
comparison of group-averaged E/I ratio at the ROI level for each sex using the rs-SC (with new
optimization strategy) yielded a global shift in E/I balance towards hyperexcitation, in line with
our previous work (Fortel et al., 2020) and prior studies on sex differences related to the APOE
genotype (Aboud et al., 2013; Bi et al., 2020; Jiménez-Balado & Eich, 2021; Leung et al., 2012).
In future work, we may investigate in depth the relationship of our hybrid connectome with tra-
ditional measures of structural and functional connectivity in a larger cohort (with increased age
range), to investigate known sex differences and further evaluate our method.
Weiter, in this study, we observe significant differences in critical behavior between a
group of cognitively intact individuals with a genetic predisposition for late onset AD as com-
pared with age- and sex-matched noncarriers. Traditional structural and functional connectiv-
ity based on BOLD correlations were unable to separate the two groups (Fortel et al., 2020;
Korthauer et al., 2018). These results suggest that using a multimodal framework to unify struc-
ture and function can reveal underlying patters in brain dynamics that would otherwise not be
captured using traditional methods. Weiter, we endeavored to identify a link between E/I bal-
ance and criticality. As a result of increased positive interactions (increased deviation from an
E/I balance) in the hybrid connectome, simulations of brain dynamics using Monte Carlo
Netzwerkneurowissenschaften
431
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
simulations revealed a shift in criticality for female carriers compared with noncarriers of
APOE-ε4 that may suggest an increased vulnerability to AD neuropathology in female
APOE-ε4 carriers. We describe the critical temperature as a measure of tolerance in our mod-
eled system that we simulate in dynamical regimes spanning from highly ordered (d.h.,
hypoactive) to highly disordered. This is in line with studies of preclinical neural models that
have shown that networks operating at criticality exhibit an E/I balance as compared with
networks that have been over excited or overinhibited by a controlled chemical stimulus
(Heiney et al., 2019; Shew et al., 2011). Tatsächlich, many of the in vivo studies that have investigated
the criticality hypothesis and excitation-inhibition balance in neurodegenerative disorders
have relied on electroencephalography (EEG) or magnetoencephalography (MEG) Aufnahmen
(Bruining et al., 2020; Montez et al., 2009; Rajkumar et al., 2021; Stam et al., 2005), welche haben
inherent challenges with spatial resolution. By defining our activity states using both structural
and functional connectivity together, we are capable of analyzing patterns of activity across both
temporal and spatial scales, thereby improving the network inference and mitigating many chal-
lenges observed in unimodal and traditional analyses.
The results presented herein regarding E/I balance, criticality, and the APOE-ε4 genotype
also coincide with the current understanding of the microscale mechanisms underlying AD
pathology. A recent review article by Najm and colleagues explored the relationship among
APOE-ε4, loss of GABAergic interneurons, and dysfunctional brain networks in the context of
AD (Najm et al., 2019). Zusamenfassend, neurons responding to different factors (z.B., normal aging,
injury, or stress) break down APOE-ε4 proteins and produce fragments that trigger phosphor-
ylation of tau; this in turn disrupts mitochondrial function, leading to cell death. Destruction of
inhibitory neurons in this way can alter network activity and produce hyperexcitability in neu-
ral circuits long before clinically identifiable symptoms arise. This may help explain the known
associations of APOE-ε4 with memory deficits and severe epilepsy. In der Tat, several in vitro and
preclinical in vivo studies (cited by Najm et al., 2019) have demonstrated that intracellular
APOE-ε4 is toxic to GABAergic interneurons, particularly in the hippocampus.
Darüber hinaus, other authors have recently suggested that neuronal hyperexcitability may be
considered to be both a causal factor and a risk factor in the disease progression, even in
the preclinical phase (Hijazi et al., 2020; Paterno et al., 2020; Tok et al., 2021). While signif-
icant structural and functional degeneration is well established in AD (DeTure & Dickson,
2019), our framework incorporates both structural and functional connectivity in order to pro-
vide a new multimodal perspective of connectome-level interactions in a preclinical group of
individuals predisposed to AD. We acknowledge that our methodology is limited to insights
that may be gained from macroscale BOLD activity as opposed to direct measurements of
neuronal processes. That said, we reached a similar conclusion to independent studies of
underlying neural mechanisms in AD: Individuals with the APOE-ε4 allele (females in partic-
ular) have a higher risk of neurodegeneration due to an increase of excitatory activity in neural
circuits (Jiménez-Balado & Eich, 2021; Koutsodendris et al., 2022; Y. Li et al., 2016).
We note several limitations of this study. Erste, this study investigated only a small cross
section of healthy middle-aged individuals at increased risk of developing AD. Weiter, Die
parcellation used in the processing used an atlas with 80 Gehirnregionen, which may be con-
sidered too coarse. Additional research with a longitudinal cohort and higher resolution par-
cellation would help improve the generalizability of results, providing important validation
regarding within-subject variability, as well as broadening our understanding of longitudinal
alterations in brain dynamics. Zweite, when interpreted as a strictly nodal property, excitation-
inhibition balance may be best measured at a regional level using FDG PET or phosphorous
Bildgebung. Jedoch, as conceptualized in this study, the concept of E/I balance may directly
Netzwerkneurowissenschaften
432
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
relate to this notion of “criticality” in brain dynamics. Weiter, in this group of participants,
measurements of well-known biomarkers of Aβ and tau were not included in the protocol,
and thus we could not add this layer of validation. Future studies comparing additional imag-
ing modalities and biomarkers for validation and correlation purposes may be used to
strengthen the results and methodology presented in this study (in addition to more state-of-
the-art diffusion tensor imaging and fMRI imaging protocols). Weiter, in this study as we are
working with resting-state data processed with global signal regression (accounting for back-
ground and nonneural physiological noise), we model the BOLD activity assuming no external
influences; future work can incorporate external influences in the framework to account for
different interference scenarios.
It remains unclear whether the difference in criticality observed between the NC and APOE
groups is because the NC group (on average) contains more inhibitory interactions or whether
the APOE group has more excitatory interactions. Since we do not identify directionality in this
Studie, this question is left for future work. Zusätzlich, we have not performed an assessment
herein on the potential relationships between traditional structural and functional connectivity
Maßnahmen, and metrics obtained with our rs-SC. This may be explored in detail with future
investigations. Weiter, at the coarser spatial scale of human fMRI, there is evidence that the
strength of functional connectivity between regions is greatest for region pairs separated by
short physical distance and that connectivity strength decays rapidly as the Euclidean distance
between brain regions increases (Alexander-Bloch et al., 2013). Likewise, the extent of white
matter tract connectivity as measured with diffusion imaging also decays with distance. Wie-
immer, the inverse relationship between fMRI-based connectivity and distance is significant even
after controlling for the strong association between anatomical connectivity and functional
Konnektivität (Honey et al., 2009). In the future, the role of distance related to excitatory
and inhibitory interactions should be explored in greater depth. Further utilizing thermo-
dynamic principles, it should be investigated whether the rs-SC decays algebraically with a
distance d (d.h., J(D ) ∝ d −α) as well as what, wenn überhaupt, effect this distance decay would have on
critical brain dynamics. Given the complex inner workings of the brain, it is entirely plausible
that dynamics between brain regions at or near criticality rely on a balance between long- Und
short-range interactions. Wieder, this suggests that functional brain dynamics are governed by
the underlying structure of the networks. Daher, after decades of research studying the brain’s
individual components, from neurons to neuronal ensembles and large-scale brain regions,
conclusive evidence demonstrates the need for maps and models that incorporate interactions
among these components in order to better understand the brain’s ensemble dynamics, circuit
Funktion, and emergent behavior.
MATERIALS AND METHODS
Participants and MRI Data Acquisition
The cohort used in this work has been described in a previous study (Korthauer et al., 2018).
Teilnehmer (N = 76; all Caucasian) were selected based on APOE genotype from a larger
sample of 150 adults aged 40–60 (age = 49.9 ± 6.0 in years; 60 men). The University of
Wisconsin–Madison Biotechnology Center conducted the sequencing of the single nucleotide
polymorphisms (SNPs; rs7412, rs429358) making up the common ε2, ε3, and ε4 APOE geno-
types. Thirty-eight individuals out of the larger sample were APOE-ε4 carriers (either ε3/ε4 or
ε4/ε4). Somit, a subset of noncarriers (ε3/ε3 or e2/ε3) were age- and sex-matched, creating
equal groups (N = 38, 22 weiblich) of carriers (APOE) and noncarriers (NC). The following exclu-
sion criteria were used: (A) self-reported cognitive or memory complaints; (B) Mini–Mental State
Netzwerkneurowissenschaften
433
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Tisch 1. Demographic characteristics and screening measures. Values represent M(SD). DRS-2:
Mattis Dementia Rating Scale-2. MMSE: Mini–Mental State Examination. GDS: Geriatric
Depression Scale.
Alter (Jahre)
Sex (M:F)
Education (Jahre)
DRS-2 (total)
MMSE (total)
GDS (total)
ε4 carriers (N = 38)
50.8 (0.99)
non-ε4 carriers (N = 38)
50.9 (0.99)
16:22
15.4 (2.5)
139.9 (2.3)
28.5 (1.1)
1.8 (2.3)
16:22
15.2 (2.4)
139.9 (2.3)
28.8 (1.3)
2.4 (2.7)
Exam (MMSE; Folstein et al., 1975) score ≤ 24; (C) Mattis Dementia Rating Scale Second Edition
(DRS-2; Johnson-Greene, 2004) score ≤ 135; (D) Geriatric Depression Scale (GDS; Yesavage
et al., 1982) > 10; (e) history of central nervous system disease (z.B., Demenz, stroke, Parkinson’s
Krankheit, epilepsy, other neurological disease); (F ) history of severe cardiac disease (z.B., myo-
cardial infarction, coronary bypass surgery, angioplasty); (G) history of metastatic cancer; (H)
history of serious psychiatric disorder or substance use disorder; Und (ich) any contraindication
to MRI. MRI imaging was conducted on a GE Signa 3T scanner ( Waukesha, WI) with quad
split quadrature transmit/receive head coil. All participants provided written informed con-
sent, and were compensated financially for their participation; the imaging collection was
carried out in accordance with the guidelines set by the institutional review boards of the
University of Wisconsin–Milwaukee and Medical College of Wisconsin (Korthauer et al.,
2018). Demographic characteristics and screening measures for each group are presented
in Table 1.
All participants were screened for any contraindications to MRI. Imaging sessions lasted
75 min. To determine the structural and functional connectivity maps, multimodal imaging
(including T1-weighted MRI, resting-state fMRI, and diffusion weighted MRI) durchgeführt wurde.
For structural MRI imaging, a “spoiled-grass” (SPGR) sequence (axial acquisition: TR = 35 MS,
TE = 5 MS, flip angle = 45°, matrix = 256 × 256, FOV = 24 cm, NEX = 1) was obtained,
followed by a T2*-weighted functional scan with an echo-planar pulse imaging (EPI) sequence
(28 axial slices, 20 × 20 cm2 FOV, 64 × 64 Matrix, 3.125 mm × 3.125 mm × 4 mm voxels, TE =
40 MS, TR = 2,000 MS). The 8-min rs-fMRI scan was acquired while participants were under
task-free conditions (d.h., Ruhezustand). Zusätzlich, a 3-min, 30-s diffusion tensor imaging
sequence was acquired with a spin echo single shot, echo-planar imaging sequence with
sensitivity (SENSE = 2.5) encoding (2.2 mm isotropic voxels, 212 × 212 mm FOV, 96 ×
96 acquired matrix), TR/TE = 6,338/69 MS, 60 slices for whole-brain coverage. Diffusion gra-
dients were applied along 32 noncollinear directions at a b-factor of 700 s/mm2, including one
minimally weighted image with b = 0 s/mm2.
Processing of fMRI and Diffusion Tensor Imaging
Preprocessing of rs-fMRI images was performed using Analysis of Functional NeuroImages
(AFNI; Cox, 1996) and FMRIB Software Library (FSL; Smith et al., 2004) based on the rs-fMRI
preprocessing pipeline from the Human Connectome Project (HCP; Smith et al., 2013).
Detailed processing information steps can be found in prior work (Korthauer et al., 2018).
Netzwerkneurowissenschaften
434
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Diffusion tensor imaging data processing was carried out with the FSL. The B0 image was
skull-stripped using the brain extraction tool (Schmied, 2002), with the resulting mask applied
to the other images. Eddy current-induced distortions and subject movements were corrected
using FSL’s eddy tool (Andersson & Sotiropoulos, 2016). A probability distribution for fiber
direction was generated at each voxel using BEDPOSTX (Behrens et al., 2007; Behrens
et al., 2003), which was then used in probabilistic tractography. For individual subjects,
FreeSurfer cortical parcellation and subcortical segmentation was used, defining the 80 ROIs
(Dale et al., 1999; Fischl et al., 2002; Fischl et al., 2004). Affine registration with 6 degrees
of freedom using FLIRT registered the ROIs to MNI and diffusion space (Jenkinson et al.,
2002). For each ROI, the mean time course from the BOLD signal was extracted using
globale Signalregression (GSR) from the preprocessed rs-fMRI data prior to constructing the
functional connectivity matrix. The resulting zero-mean time courses for each ROI were then
correlated using Pearson correlations to generate a traditional functional connectivity matrix.
Probabilistic tractography was performed between pairs of ROIs using Probtrackx for esti-
mating the structural connectivity. The resulting matrix was then further normalized by
dividing each matrix row by the way-total for its corresponding seed ROI (Behrens et al.,
2007; Behrens et al., 2003).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Unconstrained Pairwise Maximum Entropy Model (pMEM)
This maximum entropy approach provides a way of quantifying the goodness of fit in models
that include varying degrees of correlations (Schneidman et al., 2006). At a microscale level
Zum Beispiel, a first-order model seeks to fit only the average firing rate of all neurons
recorded in the ensemble. A second-order model would seek to fit the average firing rate
and all pairwise correlations, with an nth-order model fitting all correlations up to and
including those between all n-tuples of neurons in the ensemble. At macroscale, Das
amounts to fitting the average BOLD activation rate of a brain region and all pairwise cor-
Beziehungen. Hier, the observed bold activation rate is determined through a binarization of the
BOLD time course. Daher, we construct unbiased predictions for the probabilities of func-
tional brain states by fitting a pairwise maximum entropy model (pMEM). Hier, in estimating
the probability distribution, it is necessary to use the distribution that maximizes the uncer-
tainty (z.B., entropy). To fit the pMEM, we must tune the first- and second-order interaction
parameters between ROIs such that the predicted activation and coactivation rates match the
observed data (the BOLD time series). An accurately fitted pMEM suggests that patterns of
functional activity can be estimated from each ROI’s independent activation rate combined
with the joint activation rates. Daher, the pMEM represents a model of fMRI BOLD dynamics
as a probabilistic process defined by underlying pairwise relationships between ROIs. In
constructing this model, we leverage the Ising model, a special case of a Markov random
field in which each ROI can exhibit two possible states s = ± 1. In this work, we first convert
our BOLD time series to z-scores, ensuring that our BOLD date is represented as zero-mean
with unitary variance, without altering the correlations between brain regions. As maximum
entropy models of neural activity are developed based on Ising dynamics, studies investigat-
ing pairwise interactions using BOLD time course data are binarized to define activation
Staaten (entweder +1 for active, or −1 for inactive) in both simulated and empirical fMRI-based
Studien (Ashourvan et al., 2021; Cofré et al., 2019; Ezaki et al., 2020; Ezaki et al., 2017; Gu
et al., 2018; Nghiem et al., 2018; Niu et al., 2019; Watanabe et al., 2013). We will show
how the binarization strategy may be validated using Monte Carlo simulations, whereby we
use the inferred interaction networks to reconstruct functional correlations. Our results will
Netzwerkneurowissenschaften
435
Unifying brain structure and function using a maximum entropy model
also show that for our network construction methodology, binarizing the z-scored time series
at zero provides better inference of functional interactions than ±1 SD.
We first begin by modeling the neural system using an energy-based formulation, nämlich
the Hamiltonian, as follows:
H sð Þ ¼ −
X
Ji;jsisj; where i; J 2 1; 2; …; k
½
(cid:2)
(8)
Hier, the spin configuration s is defined as the column vector s = [s1, s2, …sk]T, k is the number
of regions, si and sj are the spin states of region i and j, and Ji,j represents a pairwise interaction
between ROIs. Conceptually, if two regions are co-active or co-inactive, the pairwise interac-
tion is likely positive (excitatory), and if one region is active while the other is inactive, Die
pairwise interaction is likely negative (inhibitory). Here we assume that there is no external
influence (d.h., Ruhezustand). Weiter, unless otherwise stated, the summations in this manu-
script are for i < j to avoid double counting and exclude self-connections. The probability
of observing a specific configuration is given as the following Boltzmann distribution:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Pr sð Þ ¼ exp −βH sð Þ
ð
Þ=Z ;
(9)
where β is the inverse temperature, and Z is the partition function: Z ¼
P
ð
s exp −βH sð Þ
Þ.
The summation in the partition function is over all possible configurations of states. Similar to
other studies fitting pairwise models to neuronal firing data, a gradient ascent updating scheme
is used (Watanabe et al., 2013; Yeh et al., 2010). Estimating a parameter set that minimizes the
Kullback-Leibler (K-L) divergence between modeled and observed probability distributions is
equivalent to maximizing a log likelihood of the observed data (the empirical BOLD time
series). We note that a brute-force application of the maximum likelihood estimation requires
heavy computational costs with calculations over all 2N possible spin configurations for the
partition function (Nguyen et al., 2017). To overcome the intractability of the partition function
Z, we utilize a pseudolikelihood estimation method (Ezaki et al., 2017). Pseudolikelihood esti-
mation has been shown to converge to a maximum likelihood estimator for large sample sizes
(Besag, 1975).
The optimal interaction matrix J can thus be derived by maximizing the pseudolikelihood
function (Besag, 1975, 1977):
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
n
e
n
_
a
_
0
0
2
2
0
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Lpeusdo J; βð
Þ ¼
Y
Y
tmax
t¼1
k
(cid:3)
i¼1 Pr si tð Þj J;β; s−i tð Þ
(cid:4)
:
(10)
Pseudolikelihood substitutes the probability of observing the state vector s(t) by the product of
the conditional probability ep ¼ Pr si tð Þj J; β; s−i tð Þ
of observing a single element si (t ) while all
the other elements, denoted s−i(t), are fixed. Thus, we maximize the following log-
pseudolikelihood function as the following:
(cid:4)
(cid:3)
Network Neuroscience
‘ J; βð
Þ ¼
1
tmax
ln Lpseudo J; βð
Þ
(11)
436
Unifying brain structure and function using a maximum entropy model
0
¼
X
1
tmax
X
tmax
t¼1
@
ln
N
i¼1
(cid:5)
exp β
P
(cid:5)
exp β
P
N
k¼1 Ji;k sk tð Þ
(cid:6)
N
k¼1 Ji;k si tð Þsk tð Þ
(cid:5)
(cid:6)
P
þ exp −β
N
k¼1 Ji;k sk tð Þ
1
A:
(cid:6)
(12)
This probability distribution is derived based on the Boltzmann distribution under pseudo-
likelihood conditions. The numerator describes the energy of the system, while the denomi-
nator is the sum of all possible energies. Hence, there are only two terms in the denominator,
one positive and one negative since si(t ) is binary. The likelihood function may be simplified
further by setting Ci tð Þ ¼ β
m¼1 Ji;msm tð Þ, resulting in the following:
P
k
‘ J; βð
Þ ¼
1
tmax
X
tmax
t¼1
X
N
i¼1 Ci tð Þsi tð Þ − ln exp Ci tð Þ
ð
ð
Þ
Þ þ exp −Ci tð Þ
ð
Þ:
(13)
The gradient ascent procedure can now be constructed with respect to Ji,j by computing the
partial derivative of the log-pseudolikelihood as the following:
∂ ‘
∂ Ji;j
¼
1
X
tmax
tmax
t¼1
(cid:7)
Þ
β si tð Þsj tð Þ − sj tð Þ tanh Ci tð Þ
ð
(cid:8)
:
(14)
The updating scheme follows: Jnþ1
i;j
¼ Jn
i;j
þ γ ∂ ‘
∂ Ji;j
n. Here, n is the iteration number and γ is the
j
learning rate.
Monte Carlo Simulations for the Ising Model
All scripts were developed and executed in MATLAB R2018a on a Windows 10 machine with
Intel i7 CPU@ 2.8 GHz and 16 GB of RAM. We used a Markov chain Monte Carlo (MCMC)
method based on the metropolis algorithm to calculate the observables of the Ising model
using the networks inferred from the pMEM and FSE. Here we present the simulations per-
formed step by step:
(1) Define the parameters J (network inferred with pMEM or FSE), the number of runs t,
and a range of βsimulated.
(2) For each run randomly fix an si from the configuration and compute the Hamiltonian
(3)
H(si ).
If H sið Þ ≤ 0 or rand 0; 1ð
, flip the state. Note: The command rand(0, 1)
generates a random value between 0 and 1. Complete this for all elements in the
configuration.
(cid:5)
Þ ≤ exp H sið Þ
simulated
(cid:6)
β
(4) The final configuration of states is then used as the input for the next run.
(5) Concatenate all runs into an N × t array and compute the averages of the observables
(i.e., Pearson correlation < si sj >, magnetization |M|, susceptibility χ).
(6) Do this for all βsimulated.
Because of the computational cost, when performing MCMC simulations for the grid-search
parameter optimization we used t = 2,000 runs and βsimulated from 0.2 Zu 3.0 with increments of
0.2. For the control case based on pMEM, we used t = N × N × 10 runs with βsimulated from 1 Zu
20 with increments of 0.5. Last, when evaluating the thermodynamic properties magnetization
|M|, susceptibility χ using the rs-SC network, we use t = 100,000 with βsimulated from 0.2 Zu 3.0
Netzwerkneurowissenschaften
437
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
with increments of 0.05. The number of runs as well as range and increments of βsimulated were
selected based on the task performed to maximize algorithmic performance and to minimize
processing time. The upper and lower bound of these values was first empirically determined
to be containing the optimal range by simulations.
Phase Transition and Biological Motivation
The simplicity of the Ising model enables the prediction of cooperative behavior among a sys-
tem of biological elements wherein each element has two states, and the energy of the system
depends only on the state of each element and its neighbors. Darüber hinaus, the model parameters
and representative physical properties are readily amenable to biological interpretation in the
context of various complex systems. Zum Beispiel, a four-dimensional cellular automaton-like
Ising model has been previously developed to investigate transitions between normal, prolif-
erative, hypoxic, and necrotic states in the tumorigenesis processes (Durrett, 2013; Torquato,
2011). Ising-like models have also been implemented to estimate information transfer between
spins occurring on the human connectome (Marinazzo et al., 2014) or to assess differentially
expressed genes in cancer patients (X. Li et al., 2011), and even to model the joint expression
profiles of genes to reconstruct E. coli gene interaction pathways (Santhanam et al., 2009).
Somit, when we discuss a “phase transition,” it is a result of the interactions among many
Elemente, not from the specific nature of the individual units (be they ferromagnetic materials
or biological elements like neurons, protein chains, or genes).
To evaluate these transitions, we look to the average of activations over the whole network
(termed magnetization), which determines the ordering of the system. Magnetic susceptibility
is simply the variance of the magnetization. If all the binary spin states are aligned in the same
Richtung, a magnetization of ±1 corresponds to a configuration of complete order. The mag-
i¼1 < si>; Wo < : > represents the ensemble average
netization per site, defined as M =
and quantifies the mean tendency that si = 1 as opposed to si = −1, is taken across the brain
Regionen. The magnetic susceptibility is defined as χ ¼ 1
Þ (Landauer, 2009).
β
PN
D
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Hier, we consider brain networks positioned near a critical point between complete inac-
tivity (d.h., neuronal death) and random activity (as in epilepsy, Zum Beispiel). In a less extreme
sense, simulations of Ising dynamics can reveal a transition from a hypoactive state towards a
more chaotic state. As described in Equation 9, the behavior of the modeled system depends
on temperature. Jedoch, for a network of neurons or brain regions, there is no real concept of
“temperature.” Hence, when performing Monte Carlo simulations of the Ising model, we may
describe temperature (T ) as a “tolerance” of the system in the sense that the effect of the
T parameter injects additional randomness into the simulated dynamics of
the system.
Daher, for very low T (T < Tcritical), spontaneous MCMC spin flips are less probable, with the
spins in each configuration mostly aligned to contribute the minimum energy of the system.
For very high T (T > Tcritical), the magnetic ordering is completely lost as a result of a high
number of spontaneous spin flips; daher, the magnetization tends to zero, which can be used
to characterize the disordered (or chaotic) Phase. In the intermediate range of T where self-
organized criticality and second-order phase transitions occur, there is a point of maximal
fluctuations in the magnetization at T = Tcritical that corresponds to a peak in the magnetic
susceptibility (Chialvo, 2010). Daher, a system with lower critical temperature is suggestive
of a lower tolerance to perturbations in the network as determined via Monte Carlo simula-
tions of brain dynamics than is a higher critical temperature that would suggest a higher
tolerance.
Netzwerkneurowissenschaften
438
Unifying brain structure and function using a maximum entropy model
Parameter Optimization Using a Similarity Metric and Correlation Function
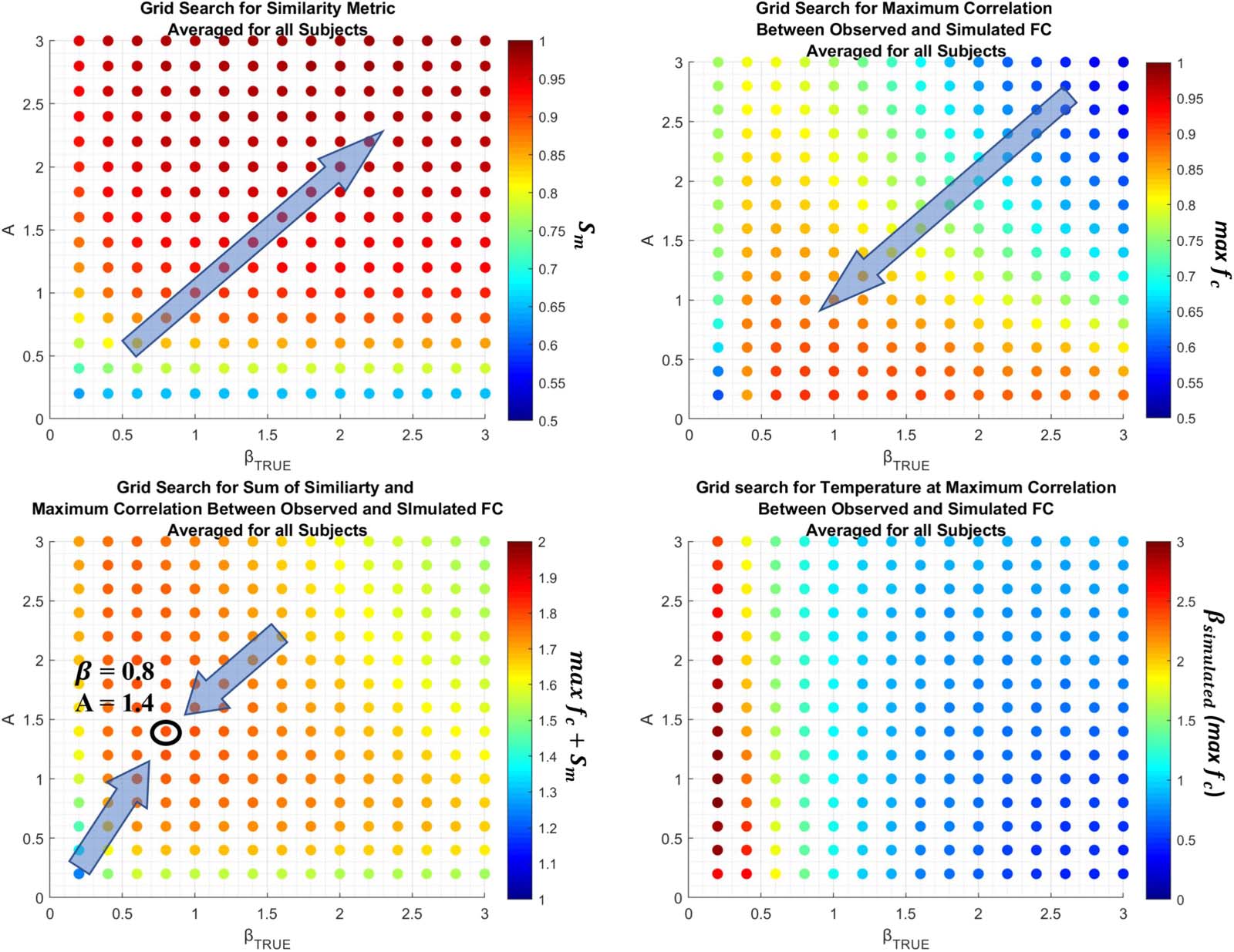
In this work, we use a grid-search optimization scheme to find the optimal parameters {β, A}.
The parameters are evaluated from 0.2 Zu 3.0 mit 0.2 increments for all 76 Teilnehmer.
With the FSE, J, we generate a correlation function max fc( β, A) by simulating the Ising
model with Monte Carlo simulations, computing a Pearson correlation between observed
and simulated functional connectivity for all βsimulated (aus 0.2 Zu 3.0 mit 0.2 increments).
Weiter, we compute a similarity metric Sm( β, A) via the correlation r (|Ji,J|, Wi,J) ∀ i, j to ensure
that jJi,jj ∝ Wi,J, the structural connectome. To identify the optimal parameters, we find A, β
such that f ( β, A) = max fc + Sm is maximized.
Excitation-Inhibition (E/I) Ratio
It is important to note that in using the terminology connectome-level excitation-inhibition
balance and hyperexcitation, we are not necessarily inferring directionality of these interac-
tions or measuring processes at a neuronal level. Eher, we used such terminology to bridge
the gap between microscale interactions (such as excitation and inhibition of neuronal circuits)
and the connectome-level changes that may occur because of such processes. Note that sim-
ilar terminologies have previously been adopted in several seminal studies that investigated
neuronal firing patterns using the Ising model (Schneidman et al., 2006; Tkačik et al.,
2013). To be clear, from a connectomics perspective, if several brain regions are identified
to have an increase in positive edges in the rs-SC, collectively, that would suggest a wider
spread pattern of coupling (d.h., more likely to exhibit a pattern of global coupling) that may
subserve hyperexcitation. It is in this context that we conceptualize the excitation-inhibition
(E/I) Verhältnis, a global (whole-brain) or local (ROI-level) estimation of E/I balance, computed as
the sum of positive edges divided by the sum of negative edges. Zum Beispiel, if an ROI in the
network has 45 positive edges and 34 negative edges, then the E/I ratio = 45
34, oder 1.32 (a value of
1 indicates perfect E/I balance).
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00220.
BEITRÄGE DES AUTORS
Igor Fortel: Konzeptualisierung; Formale Analyse; Untersuchung; Methodik; Software; Valida-
tion; Visualisierung; Writing – original draft; Writing – review & Bearbeitung. Mitchell Butler: Con-
ceptualization; Methodik; Writing – review & Bearbeitung. Laura E. Korthauer: Datenkuration;
Untersuchung; Methodik. Liang Zhan: Konzeptualisierung; Formale Analyse; Funding acqui-
sition; Methodik. Olusola Ajilore: Konzeptualisierung; Untersuchung. Anastasios Sidiropoulos:
Konzeptualisierung; Untersuchung. Yichao Wu: Konzeptualisierung; Untersuchung. Ira Driscoll:
Datenkuration; Untersuchung. Dan Schonfeld: Konzeptualisierung; Methodik; Aufsicht;
Validierung. Alex Leow: Konzeptualisierung; Formale Analyse; Akquise von Fördermitteln; Methodik;
Aufsicht; Validierung; Writing – review & Bearbeitung.
FUNDING INFORMATION
Alex Leow and Liang Zhan, Nationale Gesundheitsinstitute (https://dx.doi.org/10.13039
/100000002), Award ID: R01AG071243. Alex Leow, Yichao Wu, and Liang Zhan, National
Institutes of Health (https://dx.doi.org/10.13039/100000002), Award ID: R01MH125928.
Liang Zhan, Nationale Gesundheitsinstitute (https://dx.doi.org/10.13039/100000002), Award
Netzwerkneurowissenschaften
439
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
ID: U01AG068057. Liang Zhan, Nationale Wissenschaftsstiftung (https://dx.doi.org/10.13039
/100000001), Award ID: IIS2045848. Liang Zhan, Nationale Wissenschaftsstiftung (https://dx
.doi.org/10.13039/100000001), Award ID: IIS1837956.
VERWEISE
Aboud, O., Mrak, R. E., Boop, F. A., & Griffin, W. S. T. (2013). Epi-
lepsy: Neuroinflammation, neurodegeneration, and APOE geno-
type. Acta Neuropathologica Communications, 1(1), 41. https://
doi.org/10.1186/2051-5960-1-41, PubMed: 24252240
Aksenov, D. P., Li, L., Müller, M. J., & Wyrwicz, A. M. (2019). Role
of the inhibitory system in shaping the BOLD fMRI response.
N e u ro I m a g e , 2 0 1 , 11 6 0 3 4 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / J
.neuroimage.2019.116034, PubMed: 31326573
Alexander-Bloch, A. F., Vértes, P. E., Stidd, R., Lalonde, F., Clasen,
L., Rapoport, J., Giedd, J., Bullmore, E. T., & Gogtay, N. (2013).
The anatomical distance of functional connections predicts brain
network topology in health and schizophrenia. Hirnrinde,
23(1), 127–138. https://doi.org/10.1093/cercor/bhr388, PubMed:
22275481
Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated
approach to correction for off-resonance effects and subject move-
ment in diffusion MR imaging. NeuroImage, 125, 1063–1078.
https://doi.org/10.1016/j.neuroimage.2015.10.019, PubMed:
26481672
Ashourvan, A., Gu, S., Mattar, M. G., Vettel, J. M., & Bassett, D. S.
(2017). The energy landscape underpinning module dynamics in
the human brain connectome. NeuroImage, 157, 364–380.
https://doi.org/10.1016/j.neuroimage.2017.05.067, PubMed:
28602945
Ashourvan, A., Shah, P., Pines, A., Gu, S., Lynn, C. W., Bassett,
D. S., Davis, K. A., & Ein wenig, B. (2021). Pairwise maximum entropy
model explains the role of white matter structure in shaping emer-
gent activation states. Communications Biology, 4(1), 1-15.
https://doi.org/10.1038/s42003-021-01700-6, PubMed:
33594239
Barrick, T. R., Charlton, R. A., Clark, C. A., & Markus, H. S. (2010).
White matter structural decline in normal ageing: A prospective
longitudinal study using tract-based spatial statistics. Neuro-
Image, 51(2), 565–577. https://doi.org/10.1016/j.neuroimage
.2010.02.033, PubMed: 20178850
Beggs, J. M., & Plenz, D. (2003). Neuronal avalanches in neocortical
circuits. Zeitschrift für Neurowissenschaften, 23(35), 11167–11177. https://
doi.org/10.1523/ JNEUROSCI.23-35-11167.2003, PubMed:
14657176
Behrens, T. E. J., Berg, H. J., Jbabdi, S., Rushworth, M. F. S., &
Woolrich, M. W. (2007). Probabilistic diffusion tractography with
multiple fibre orientations: What can we gain? NeuroImage, 34(1),
144–155. https://doi.org/10.1016/j.neuroimage.2006.09.018,
PubMed: 17070705
Behrens, T. E. J., Woolrich, M. W., Jenkinson, M., Johansen-Berg,
H., Nunes, R. G., Clare, S., Matthews, P. M., Brady, J. M., &
Schmied, S. M. (2003). Characterization and propagation of uncer-
tainty in diffusion-weighted MR imaging. Magnetic Resonance in
Medicine, 50(5), 1077–1088. https://doi.org/10.1002/mrm
.10609, PubMed: 14587019
Besag, J. (1975). Statistical analysis of non-lattice data. Zeitschrift für
the Royal Statistical Society: Series D (The Statistician), 24(3),
179–195. https://doi.org/10.2307/2987782
Besag, J. (1977). Efficiency of pseudolikelihood estimation for sim-
ple Gaussian fields. Biometrika, 64(3), 616–618. https://doi.org
/10.2307/2345341
Bettinardi, R. G., Deco, G., Karlaftis, V. M., Van Hartevelt, T. J.,
Fernandes, H. M., Kourtzi, Z., Kringelbach, M. L., & Zamora-
López, G. (2017). How structure sculpts function: Unveiling
the contribution of anatomical connectivity to the brain’s spon-
taneous correlation structure. Chaos, 27(4), 047409. https://doi
.org/10.1063/1.4980099, PubMed: 28456160
Bi, D., Wen, L., Wu, Z., & Shen, Y. (2020). GABAergic dysfunction
in excitatory and inhibitory (E/I) imbalance drives the pathogen-
esis of Alzheimer’s disease. Alzheimer’s and Dementia, 16(9),
1312–1329. https://doi.org/10.1002/alz.12088, PubMed:
32543726
Bretsky, P. M., Buckwalter, J. G., Seeman, T. E., Müller, C. A., Poirier,
J., Schellenberg, G. D., Finch, C. E., & Henderson, V. W. (1999).
Evidence for an interaction between apolipoprotein E genotype,
Geschlecht, and Alzheimer disease. Alzheimer Disease and Associ-
ated Disorders, 13(4), 216–221. https://doi.org/10.1097
/00002093-199910000-00007, PubMed: 10609670
Bruining, H., Hardstone, R.,
Juarez-Martinez, E. L., Sprengers,
J., Avramiea, A.-E., Simpraga, S., Houtman, S.
J., Poil, S.-S.,
Dallares, E., Verehrung, S., Oranje, B., Matias Palva, J., Mansvelder,
H. D., & Linkenkaer-Hansen, K. (2020). Measurement of
excitation-inhibition ratio in autism spectrum disorder using crit-
ical brain dynamics. Wissenschaftliche Berichte, 10(1), 9195. https://doi
.org/10.1038/s41598-020-65500-4, PubMed: 32513931
Busche, M. A., & Konnerth, A. (2016). Impairments of neural circuit
function in Alzheimer’s disease. Philosophical Transactions of
the Royal Society B: Biological Sciences, 371(1700). https://doi
.org/10.1098/rstb.2015.0429, PubMed: 27377723
Chételat, G., Landeau, B., Salmon, E., Yakushev,
ICH., Bahri,
M. A., Mézenge, F., Perrotin, A., Bastin, C., Manrique, A.,
Scheurich, A., Scheckenberger, M., Desgranges, B., Eustache,
F., & Fellgiebel, A. (2013). Relationships between brain metabo-
lism decrease in normal aging and changes in structural and
functional connectivity. NeuroImage, 76, 167–177. https://doi
.org/10.1016/j.neuroimage.2013.03.009, PubMed: 23518010
Chialvo, D. R.
(2010). Emergent complex neural dynamics.
Nature Physics, 6(10), 744–750. https://doi.org/10.1038
/nphys1803
Cocchi, L., Gollo, L. L., Zalesky, A., & Breakspear, M. (2017). Crit-
icality in the brain: A synthesis of neurobiology, models and
Netzwerkneurowissenschaften
440
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Erkenntnis. Fortschritte in der Neurobiologie, 158, 132–152. https://doi
.org/10.1016/j.pneurobio.2017.07.002, PubMed: 28734836
Cocco, S., Monasson, R., Posani, L., & Tavoni, G. (2017). Func-
tional networks from inverse modeling of neural population
Aktivität. Current Opinion in Systems Biology, 3, 103–110.
https://doi.org/10.1016/j.coisb.2017.04.017
Cofré, R., Herzog, R., Corcoran, D., & Rosas, F. E. (2019). A com-
parison of the maximum entropy principle across biological spa-
tial scales. Entropy, 21(10), 1009. https://doi.org/10.3390
/e21101009
Cox, R. W. (1996). AFNI: Software for analysis and visualization of
functional magnetic resonance neuroimages. Computers and
Biomedical Research, 29(3), 162–173. https://doi.org/10.1006
/cbmr.1996.0014, PubMed: 8812068
Curiati, P. K., Tamashiro-Duran, J. H., Duran, F. L. S., Buchpiguel,
C. A., Squarzoni, P., Romano, D. C., Vallada, H., Menezes, P. R.,
Scazufca, M., Busatto, G. F., & Alves, T. C. T. F. (2011). Alter-
related metabolic profiles in cognitively healthy elders: Ergebnisse
from a voxel-based [18F]fluorodeoxyglucose-positron-emission
tomography study with partial volume effects correction. Ameri-
can Journal of Neuroradiology, 32(3), 560–565. https://doi.org/10
.3174/ajnr.A2321, PubMed: 21273352
Dale, A. M., Fischl, B., & Sereno, M. ICH. (1999). Cortical
surface-based analysis: ICH. Segmentation and surface reconstruc-
tion. NeuroImage, 9(2), 179–194. https://doi.org/10.1006/nimg
.1998.0395, PubMed: 9931268
Damoiseaux, J. S., Beckmann, C. F., Arigita, E. J. S., Barkhof, F.,
Scheltens, P., Stam, C. J., Schmied, S. M., & Rombouts, S. A. R. B.
(2008). Reduced resting-state brain activity in the “default net-
work” in normal aging. Hirnrinde, 18(8), 1856–1864.
https://doi.org/10.1093/cercor/bhm207, PubMed: 18063564
Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., & Friston, K.
(2008). The dynamic brain: From spiking neurons to neural
masses and cortical fields. PLoS Computational Biology, 4(8),
e1000092. https://doi.org/10.1371/journal.pcbi.1000092,
PubMed: 18769680
DeTure, M. A., & Dickson, D. W. (2019). The neuropathological
diagnosis of Alzheimer’s disease. Molecular Neurodegeneration,
14(1), 32. https://doi.org/10.1186/s13024-019-0333-5, PubMed:
31375134
Durrett, R. (2013). Cancer modeling: A personal perspective.
Notices of the AMS, 60(3), 304–309. https://doi.org/10.1090
/noti953
Ezaki, T., Fonseca dos Reis, E., Watanabe, T., Sakaki, M., &
Masuda, N. (2020). Closer to critical resting-state neural dynam-
ics in individuals with higher fluid intelligence. Kommunikation
Biology, 3(1), 1–9. https://doi.org/10.1038/s42003-020-0774-y,
PubMed: 32015402
Ezaki, T., Watanabe, T., Ohzeki, M., & Masuda, N. (2017). Energy
landscape analysis of neuroimaging data. Philosophical Transac-
tions of the Royal Society A: Mathematical, Physical and Engi-
neering Sciences, 375(2096), 20160287. https://doi.org/10.1098
/rsta.2016.0287, PubMed: 28507232
Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich, M.,
Haselgrove, C., Kouwe, A. van der, Killiany, R., Kennedy, D.,
Klaveness, S., Montillo, A., Makris, N., Rosen, B., & Dale,
A. M. (2002). Whole brain segmentation: Automated labeling
of neuroanatomical structures in the human brain. Neuron, 33(3),
341–355. https://doi.org/10.1016/S0896-6273(02)00569-X,
PubMed: 11832223
Fischl, B., van der Kouwe, A., Destrieux, C., Halgren, E., Ségonne,
F., Salat, D. H., Busa, E., Seidman, L. J., Goldstein, J., Kennedy,
D., Caviness, V., Makris, N., Rosen, B., & Dale, A. M. (2004).
Automatically parcellating the human cerebral cortex. Zerebral
Kortex, 14(1), 11–22. https://doi.org/10.1093/cercor/ bhg087,
PubMed: 14654453
Folstein, M. F., Folstein, S. E., & McHugh, P. R. (1975). “Mini–men-
tal state”: A practical method for grading the cognitive state of
patients for the clinician. Journal of Psychiatric Research, 12(3),
189–198. https://doi.org/10.1016/0022-3956(75)90026-6
Fortel, ICH., Diener, M., Korthauer, L. E., Zhan, L., Ajilore, O., Driscoll,
ICH., Sidiropoulos, A., Zhang, Y., Guo, L., Huang, H., Schonfeld, D.,
& Leow, A. (2019). Brain dynamics through the lens of statistical
mechanics by unifying structure and function. In D. Shen, T. Liu,
T. M. Peters, L. H. Staib, C. Essert, S. Zhou, P.-T. Yap, & A. Khan
(Hrsg.), Medical image computing and computer assisted interven-
tion – MICCAI 2019 (S. 503–511). Springer International Pub-
lishing. https://doi.org/10.1007/978-3-030-32254-0_56
Fortel, ICH., Korthauer, L. E., Morrissey, Z., Zhan, L., Ajilore, O.,
Wolfson, O., Driscoll, ICH., Schonfeld, D., & Leow, A. (2020). Con-
nectome signatures of hyperexcitation in cognitively intact
middle-aged female APOE-ε4 carriers. Hirnrinde, 30(12),
6350–6362. https://doi.org/10.1093/cercor/bhaa190, PubMed:
32662517
Gu, S., Cieslak, M., Baird, B., Muldoon, S. F., Grafton, S. T.,
Pasqualetti, F., & Bassett, D. S. (2018). The energy landscape
of neurophysiological activity implicit in brain network structure.
Wissenschaftliche Berichte, 8(1), 2507. https://doi.org/10.1038/s41598
-018-20123-8, PubMed: 29410486
Hahn, G., Ponce-Alvarez, A., Monier, C., Benvenuti, G., Kumar, A.,
Chavane, F., Deco, G., & Frégnac, Y. (2017). Spontaneous corti-
cal activity is transiently poised close to criticality. PLoS Compu-
tational Biology, 13(5), e1005543. https://doi.org/10.1371
/journal.pcbi.1005543, PubMed: 28542191
Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges
at criticality on a model of the human connectome. Physical
Review Letters, 110(17), 178101. https://doi.org/10.1103
/PhysRevLett.110.178101, PubMed: 23679783
Heiney, K., Ramstad, Ö. H., Sandvig, ICH., Sandvig, A., & Nichele, S.
(2019). Assessment and manipulation of the computational
capacity of in vitro neuronal networks through criticality in neu-
ronal avalanches. 2019 IEEE Symposium Series on Computa-
tional Intelligence (SSCI), 247–254. https://doi.org/10.1109
/SSCI44817.2019.9002693
Hijazi, S., Heistek, T., Scheltens, P., Mansvelder, H. D., Smit, A. B.,
& van Kesteren, R. E. (2020). Interneuron hyperexcitability as
both causal factor and risk factor in Alzheimer’s disease. Alzhei-
mer’s and Dementia, 16(S3), e040877. https://doi.org/10.1002
/alz.040877
Honey, C. J., Spurns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Verfahren
der Nationalen Akademie der Wissenschaften, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601
Netzwerkneurowissenschaften
441
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Jack, C. R., Wiste, H. J., Weigand, S. D., Knopman, D. S., Vemuri,
P., Mielke, M. M., Lowe, V., Senjem, M. L., Gunter, J. L.,
Machulda, M. M., Gregg, B. E., Pankratz, V. S., Rocca, W. A.,
& Petersen, R. C. (2015). Alter, Sex, and APOE ε4 effects on mem-
ory, brain structure, and β-amyloid across the adult life span.
JAMA Neurology, 72(5), 511–519. https://doi.org/10.1001
/jamaneurol.2014.4821, PubMed: 25775353
Jenkinson, M., Bannister, P., Brady, M., & Schmied, S. (2002).
Improved optimization for the robust and accurate linear registra-
tion and motion correction of brain images. NeuroImage, 17(2),
825–841. https://doi.org/10.1006/nimg.2002.1132, PubMed:
12377157
Jiménez-Balado, J., & Eich, T. S. (2021). GABAergic dysfunction,
neural network hyperactivity and memory impairments in human
aging and Alzheimer’s disease. Seminars in Cell and Develop-
mental Biology, 116, 146–159. https://doi.org/10.1016/j.semcdb
.2021.01.005, PubMed: 33573856
Johnson-Greene, D. (2004). Dementia Rating Scale-2 (DRS-2). Von
P. J. Jurica, C. L. Leitten, and S. Mattis: Psychological assessment
resources, 2001. Archives of Clinical Neuropsychology, 19,
145–147. https://doi.org/10.1016/j.acn.2003.07.003
Kadirvelu, B., Hayashi, Y., & Nasuto, S. J. (2017). Inferring structural
connectivity using Ising couplings in models of neuronal net-
funktioniert. Wissenschaftliche Berichte, 7(1), 1–12. https://doi.org/10.1038
/s41598-017-05462-2, PubMed: 28811468
Kinouchi, O., & Copelli, M. (2006). Optimal dynamical range of
excitable networks at criticality. Nature Physics, 2(5), 348–351.
https://doi.org/10.1038/nphys289
Koelewijn, L., Lancaster, T. M., Linden, D., Dima, D. C., Routley,
B. C., Magazzini, L., Barawi, K., Brindley, L., Adams, R., Tansey,
K. E., Bompas, A., Tales, A., Bayer, A., & Singh, K. (2019). Oscil-
l a t o r y h y p e r a c t i v i t y a n d h y p e r c o n n e c t i v i t y i n y o u n g
APOE-ɛ4 carriers and hypoconnectivity in Alzheimer’s disease.
eLife, 8, e36011. https://doi.org/10.7554/eLife.36011, PubMed:
31038453
Korthauer, L. E., Zhan, L., Ajilore, O., Leow, A., & Driscoll, ICH.
(2018). Disrupted topology of the resting state structural connec-
tome in middle-aged APOE ε4 carriers. NeuroImage, 178,
295–305. https://doi.org/10.1016/j.neuroimage.2018.05.052,
PubMed: 29803958
Koutsodendris, N., Nelson, M. R., Rao, A., & Huang, Y. (2022).
Apolipoprotein E and Alzheimer’s disease: Findings, hypotheses,
and potential mechanisms. Annual Review of Pathology: Mech-
anisms of Disease, 17(1). https://doi.org/10.1146/annurev
-pathmechdis-030421-112756, PubMed: 34460318
Krishnan, G. P., González, Ö. C., & Bazhenov, M. (2018). Origin of
slow spontaneous resting-state neuronal fluctuations in brain
Netzwerke. Verfahren der Nationalen Akademie der Wissenschaften,
115(26), 6858–6863. https://doi.org/10.1073/pnas.1715841115,
PubMed: 29884650
Landauer, D. P. (2009). A guide to Monte Carlo simulations in statis-
tical physics. Retrieved from https://www.amazon.com/Guide
-Monte-Simulations-Statistical-Physics/dp/0521768489. https://
doi.org/10.1017/CBO9780511994944
Leung, L., Andrews-Zwilling, Y., Yoon, S. Y., Jain, S., Ring, K., Dai,
J., Wang, M. M., Tong, L., Walker, D., & Huang, Y. (2012). Apo-
lipoprotein E4 causes age- and sex-dependent impairments of
hilar GABAergic interneurons and learning and memory deficits
in mice. PLoS ONE, 7(12), e53569. https://doi.org/10.1371
/zeitschrift.pone.0053569, PubMed: 23300939
Li, X., Feltus, F. A., Sun, X., Wang, J. Z., & Luo, F. (2011). Identifizieren
differentially expressed genes in cancer patients using a
non-parameter Ising model. Proteomics, 11(19), 3845–3852.
https://doi.org/10.1002/pmic.201100180, PubMed: 21761563
Li, Y., Sun, H., Chen, Z., Xu, H., Bu, G., & Zheng, H. (2016). Impli-
cations of GABAergic neurotransmission in Alzheimer’s disease.
Frontiers in Aging Neuroscience, 8, 31. https://doi.org/10.3389
/fnagi.2016.00031, PubMed: 26941642
Lombardi, F., Herrmann, H. J., & de Arcangelis, L. (2017). Balance
of excitation and inhibition determines 1/f power spectrum in
neuronal networks. Chaos, 27(4), 047402. https://doi.org/10
.1063/1.4979043, PubMed: 28456161
Marinazzo, D., Pellicoro, M., Wu, G., Angelini, L., Cortés, J. M., &
Stramaglia, S. (2014). Information transfer and criticality in the
Ising model on the human connectome. PLoS ONE, 9(4),
e93616. https://doi.org/10.1371/journal.pone.0093616,
PubMed: 24705627
McDonald, C. R., McEvoy, L. K., Gharapetian, L., Fennema-
Notestine, C., Hagler, D. J., Holland, D., Koyama, A., Brewer,
J. B., Dale, A. M., & Alzheimer’s Disease Neuroimaging Initia-
tiv. (2009). Regional rates of neocortical atrophy from normal
aging to early Alzheimer disease. Neurologie, 73(6), 457–465.
https://doi.org/10.1212/ WNL.0b013e3181b16431, PubMed:
19667321
Michielse, S., Coupland, N., Camicioli, R., Fuhrmann, R., Seres, P.,
Sabino, J., & Malykhin, N. (2010). Selective effects of aging on
brain white matter microstructure: A diffusion tensor imaging
tractography study. NeuroImage, 52(4), 1190–1201. https://doi
.org/10.1016/j.neuroimage.2010.05.019, PubMed: 20483378
Montez, T., Poil, S.-S., Jones, B. F., Manshanden, ICH., Verbunt, J. P. A.,
van Dijk, B. W., Brussaard, A. B., van Ooyen, A., Stam, C. J.,
Scheltens, P., & Linkenkaer-Hansen, K. (2009). Altered temporal
correlations in parietal alpha and prefrontal theta oscillations in
early-stage Alzheimer disease. Proceedings of the National Acad-
emy of Sciences, 106(5), 1614–1619. https://doi.org/10.1073
/pnas.0811699106, PubMed: 19164579
Najm, R., Jones, E. A., & Huang, Y. (2019). Apolipoprotein E4,
inhibitory network dysfunction, and Alzheimer’s disease. Molec-
ular Neurodegeneration, 14(1), 24. https://doi.org/10.1186
/s13024-019-0324-6, PubMed: 31186040
Nghiem, T.-A., Telenczuk, B., Marre, O., Hand, A., & Ferrari, U.
(2018). Maximum-entropy models reveal the excitatory and
inhibitory correlation structures in cortical neuronal activity.
Physical Review E, 98(1), 012402. https://doi.org/10.1103
/PhysRevE.98.012402, PubMed: 30110850
Nguyen, H. C., Zecchina, R., & Berg, J. (2017). Inverse statistical
problems: From the inverse Ising problem to data science.
Advances in Physics, 66(3), 197–261. https://doi.org/10.1080
/00018732.2017.1341604
Niu, W., Huang, X., Xu, K., Jiang, T., & Yu, S. (2019). Pairwise inter-
actions among brain regions organize large-scale functional con-
nectivity during execution of various tasks. Neurowissenschaften, 412,
190–206. https://doi.org/10.1016/j.neuroscience.2019.05.011,
PubMed: 31181368
Netzwerkneurowissenschaften
442
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
Nuriel, T., Angulo, S. L., Khan, U., Ashok, A., Chen, Q., Figueroa,
H. Y., Emrani, S., Liu, L., Herman, M., Barrett, G., Savage, V.,
Buitrago, L., Cepeda-Prado, E., Fung, C., Goldberg, E., Brutto,
S. S., Hussaini, S. A., Moreno, H., Small, S. A., & Duff, K. E.
(2017). Neuronal hyperactivity due to loss of inhibitory tone in
APOE4 mice lacking Alzheimer’s disease-like pathology. Natur
Kommunikation, 8(1), 1464. https://doi.org/10.1038/s41467-017
-01444-0, PubMed: 29133888
Nuzzi, D., Pellicoro, M., Angelini, L., Marinazzo, D., & Stramaglia,
S. (2020). Synergistic information in a dynamical model imple-
mented on the human structural connectome reveals spatially
distinct associations with age. Netzwerkneurowissenschaften, 4(3),
910–924. https://doi.org/10.1162/netn_a_00146, PubMed:
33615096
Ostojic, S., & Brunel, N. (2011). From spiking neuron models to
linear-nonlinear models. PLoS Computational Biology, 7(1),
e1001056. https://doi.org/10.1371/journal.pcbi.1001056,
PubMed: 21283777
Palop, J. J., Chin, J., Roberson, E. D., Wang, J., Thwin, M. T., Bien-Ly,
N., Yoo, J., Ho, K. O., Yu, G.-Q., Kreitzer, A., Finkbeiner, S.,
Noebels, J. L., & Mucke, L. (2007). Aberrant excitatory neuronal
activity and compensatory remodeling of inhibitory hippocampal
circuits in mouse models of Alzheimer’s disease. Neuron, 55(5),
697–711. https://doi.org/10.1016/j.neuron.2007.07.025,
PubMed: 17785178
Paterno, R., Casalia, M., & Baraban, S. C. (2020). Interneuron def-
icits in neurodevelopmental disorders: Implications for disease
pathology and interneuron-based therapies. European Journal
of Paediatric Neurology, 24, 81–88. https://doi.org/10.1016/j
.ejpn.2019.12.015, PubMed: 31870698
Payami, H., Montee, K. R., Kaye, J. A., Bird, T. D., Yu, C. E., Wijsman,
E. M., & Schellenberg, G. D. (1994). Alzheimer’s disease, apo-
lipoprotein E4, and gender. JAMA, 271(17), 1316–1317. https://
doi.org/10.1001/jama.1994.03510410028015, PubMed:
8158809
Petrache, A. L., Rajulawalla, A., Shi, A., Wetzel, A., Saito, T., Saido,
T. C., Harvey, K., & Ali, A. B. (2019). Aberrant excitatory–inhibitory
synaptic mechanisms in entorhinal cortex microcircuits during
the pathogenesis of Alzheimer’s disease. Hirnrinde, 29(4),
1834–1850. https://doi.org/10.1093/cercor/ bhz016, PubMed:
30766992
Rabuffo, G., Fousek, J., Bernard, C., & Jirsa, V. (2021). Neuronal
cascades shape whole-brain functional dynamics at rest. eNeuro,
8(5). https://doi.org/10.1523/ENEURO.0283-21.2021, PubMed:
34583933
Rajkumar, R., Régio Brambilla, C., Veselinović, T., Bierbrier, J.,
Wyss, C., Ramkiran, S., Orth, L., Lang, M., Rota Kops, E., Mauler,
J., Scheins, J., Neumaier, B., Ermert, J., Herzog, H., Langen, K.-J.,
Binkofski, F. C., Lerche, C., Shah, N. J., & Neuner, ICH. (2021).
Excitatory–inhibitory balance within EEG microstates and
resting-state fMRI networks: Assessed via simultaneous trimodal
PET–MR–EEG imaging. Translational Psychiatry, 11(1), 1-15.
https://doi.org/10.1038/s41398-020-01160-2, PubMed:
33462192
Reichl, L. E., & Luscombe, J. H. (1999). A modern course in statistical
Physik, 2nd edition [Book review]. American Journal of Physics,
67(12), 1285–1287. https://doi.org/10.1119/1.19118
Ren, S.-Q., Yao, W., Yan, J.-Z., Jin, C., Yin, J.-J., Yuan, J., Yu, S., &
Cheng, Z. (2018). Amyloid β causes excitation/inhibition imbal-
ance through dopamine receptor 1-dependent disruption of
fast-spiking GABAergic input in anterior cingulate cortex. Scien-
tific Reports, 8. https://doi.org/10.1038/s41598-017-18729-5,
PubMed: 29321592
Rodrigue, K. M., Kennedy, K. M., Devous, M. D., Rieck, J. R.,
Hebrank, A. C., Diaz-Arrastia, R., Mathews, D., & Park, D. C.
(2012). β-Amyloid burden in healthy aging: Regional distribution
and cognitive consequences. Neurologie, 78(6), 387–395. https://
d o i . org / 10 . 1 2 12 / W N L . 0 B 01 3 e 3 1 8 24 5 D 29 5 , P ub M ed :
22302550
Roudi, Y., Tyrcha, J., & Hertz, J. (2009). Ising model for neural data:
Model quality and approximate methods for extracting functional
Konnektivität. Physical Review E, 79(5), 051915. https://doi.org/10
.1103/PhysRevE.79.051915, PubMed: 19518488
Rowe, C. C., Ellis, K. A., Rimajova, M., Bourgeat, P., Pike, K. E.,
Jones, G., Fripp, J., Tochon-Danguy, H., Morandeau, L., O’Keefe,
G., Price, R., Raniga, P., Robins, P., Acosta, O., Lenzo, N.,
Szoeke, C., Salvado, O., Kopf, R., Martins, R., … Villemagne,
V. L. (2010). Amyloid imaging results from the Australian Imag-
ing, Biomarkers and Lifestyle (AIBL) study of aging. Neurobiology
of Aging, 31(8), 1275–1283. https://doi.org/10.1016/j
.neurobiolaging.2010.04.007, PubMed: 20472326
Santhanam, N., Dingel, J., & Milenkovic, Ö. (2009). On modeling
gene regulatory networks using Markov random fields. In 2009
IEEE Information Theory Workshop on Networking and Informa-
tion Theory (S. 156–160). IEEE. https://doi.org/10.1109/ITWNIT
.2009.5158562
Schneidman, E., Berry, M. J., Segev, R., & Bialek, W. (2006). Weak
pairwise correlations imply strongly correlated network states in
a neural population. Natur, 440(7087), 1007–1012. https://doi
.org/10.1038/nature04701, PubMed: 16625187
Schuff, N., Amend, D. L., Knowlton, R., Norman, D., Fein, G., &
Wiener Würstchen, M. W. (1999). Age-related metabolite changes and vol-
ume loss in the hippocampus by magnetic resonance spectros-
copy and imaging. Neurobiologie des Alterns, 20(3), 279–285.
https://doi.org/10.1016/s0197-4580(99)00022-6, PubMed:
10588575
Sheline, Y. ICH., Morris, J. C., Snyder, A. Z., Price, J. L., Yan, Z., D’Angelo,
G., Liu, C., Dixit, S., Benzinger, T., Fagan, A., Goate, A., & Mintun,
M. A. (2010). APOE4 allele disrupts resting state fMRI connectiv-
ity in the absence of amyloid plaques or decreased CSF Aβ42.
Zeitschrift für Neurowissenschaften, 30(50), 17035–17040. https://doi.org
/10.1523/JNEUROSCI.3987-10.2010, PubMed: 21159973
Shen, K., Hutchison, R. M., Bezgin, G., Everling, S., & McIntosh,
A. R.
(2015). Network structure shapes spontaneous func-
tional connectivity dynamics. Zeitschrift für Neurowissenschaften, 35(14),
5579–5588. https://doi.org/10.1523/JNEUROSCI.4903-14.2015,
PubMed: 25855174
Shew, W. L., Yang, H., Petermann, T., Roy, R., & Plenz, D. (2009).
Neuronal avalanches imply maximum dynamic range in cortical
networks at criticality. Zeitschrift für Neurowissenschaften, 29(49),
15595–15600. https://doi.org/10.1523/ JNEUROSCI.3864-09
.2009, PubMed: 20007483
Shew, W. L., Yang, H., Yu, S., Roy, R., & Plenz, D. (2011). Informa-
tion capacity and transmission are maximized in balanced
Netzwerkneurowissenschaften
443
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Unifying brain structure and function using a maximum entropy model
cortical networks with neuronal avalanches. Journal of Neurosci-
enz, 31(1), 55–63. https://doi.org/10.1523/ JNEUROSCI.4637
-10.2011, PubMed: 21209189
Shlens, J., Field, G. D., Gauthier, J. L., Grivich, M. ICH., Petrusca, D.,
Sher, A., Litke, A. M., & Chichilnisky, E. J. (2006). The structure of
multi-neuron firing patterns in primate retina. Journal of Neuro-
s c i en c e , 2 6 (3 2), 8 25 4 –8 2 6 6. h t t ps : / / d o i . o rg / 1 0. 1 5 2 3
/JNEUROSCI.1282-06.2006, PubMed: 16899720
Schmied, S. M. (2002). Fast robust automated brain extraction. Human
Brain Mapping, 17(3), 143–155. https://doi.org/10.1002/ hbm
.10062, PubMed: 12391568
Schmied, S. M., Beckmann, C. F., Andersson, J., Auerbach, E.
J.,
Bijsterbosch, J., Douaud, G., Duff, E., Feinberg, D. A., Griffanti,
L., Harms, M. P., Kelly, M., Laumann, T., Müller, K. L., Moeller, S.,
Petersen, S., Power, J., Salimi-Khorshidi, G., Snyder, A. Z., Vu, A. T.,
… WU-Minn HCP Consortium. (2013). Resting-state fMRI in the
Human Connectome Project. NeuroImage, 80, 144–168. https://
doi.org/10.1016/j.neuroimage.2013.05.039, PubMed: 23702415
Schmied, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F.,
Behrens, T. E. J., Johansen-Berg, H., Bannister, P. R., De Luca,
M., Drobnjak, ICH., Flitney, D. E., Niazy, R. K., Saunders, J., Vickers,
J., Zhang, Y., De Stefano, N., Brady, J. M., & Matthews, P. M.
(2004). Advances in functional and structural MR image analysis
and implementation as FSL. NeuroImage, 23, S208–S219. https://
doi.org/10.1016/j.neuroimage.2004.07.051 , PubMed:
15501092
Sornette, D. (2006). Critical phenomena in natural sciences: Chaos,
fractals, selforganization and disorder: Concepts and tools.
Springer Science & Business Media.
Sotero, R. C., & Trujillo-Barreto, N. J. (2007). Modelling the role of
excitatory and inhibitory neuronal activity in the generation of
the BOLD signal. NeuroImage, 35(1), 149–165. https://doi.org
/10.1016/j.neuroimage.2006.10.027, PubMed: 17234435
Stam, C. J., Montez, T., Jones, B. F., Rombouts, S. A. R. B., van der
Made, Y., Pijnenburg, Y. A. L., & Scheltens, P. (2005). Disturbed
fluctuations of resting state EEG synchronization in Alzheimer’s
Krankheit. Clinical Neurophysiology, 116(3), 708–715. https://doi
.org/10.1016/j.clinph.2004.09.022, PubMed: 15721085
Stargardt, A., Swaab, D. F., & Bossers, K. (2015). The storm before
the quiet: Neuronal hyperactivity and Aβ in the presymptomatic
stages of Alzheimer’s disease. Neurobiologie des Alterns, 36(1), 1–11.
https://doi.org/10.1016/j.neurobiolaging.2014.08.014, PubMed:
25444609
Sten, S., Lundengård, K., Witt, S. T., Cedersund, G., Elinder, F., &
Engström, M. (2017). Neural inhibition can explain negative
BOLD responses: A mechanistic modelling and fMRI study. Neu-
roImage, 158, 219–231. https://doi.org/10.1016/j.neuroimage
.2017.07.002, PubMed: 28687518
Tagliazucchi, E. (2017). The signatures of conscious access and its
phenomenology are consistent with large-scale brain communi-
cation at criticality. Consciousness and Cognition, 55, 136–147.
https://doi.org/10.1016/j.concog.2017.08.008, PubMed:
28846872
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3.
https://doi.org/10.3389/fphys.2012.00015, PubMed: 22347863
Tkačik, G., Marre, O., Mora, T., Amodei, D., Berry, M. J., II, & Bialek,
W. (2013). The simplest maximum entropy model for collective
behavior in a neural network. Journal of Statistical Mechanics: Der-
ory and Experiment, 2013(03), P03011. https://doi.org/10.1088
/1742-5468/2013/03/P03011
Tkačik, G., Mora, T., Marre, O., Amodei, D., Palmer, S. E., Berry,
M. J., & Bialek, W. (2015). Thermodynamics and signatures of
criticality in a network of neurons. Verfahren des Nationalen
Akademie der Wissenschaften, 112(37), 11508–11513. https://doi.org/10
.1073/pnas.1514188112, PubMed: 26330611
Tok, S., Ahnaou, A., & Drinkenburg, W. (2021). Functional neuro-
physiological biomarkers of early-stage Alzheimer’s disease: A
perspective of network hyperexcitability in disease progression.
Zeitschrift für Alzheimer-Krankheit. https://doi.org/10.3233/ JAD
-210397, PubMed: 34420957
Torquato, S. (2011). Toward an Ising model of cancer and beyond.
Physical Biology, 8(1), 015017. https://doi.org/10.1088/1478
-3975/8/1/015017, PubMed: 21301063
Wang, L., Zang, Y., Er, Y., Liang, M., Zhang, X., Tian, L., Wu, T.,
Jiang, T., & Li, K. (2006). Changes in hippocampal connectivity
in the early stages of Alzheimer’s disease: Evidence from resting
state fMRI. NeuroImage, 31(2), 496–504. https://doi.org/10.1016
/j.neuroimage.2005.12.033, PubMed: 16473024
Watanabe, T., Hirose, S., Wada, H., Imai, Y., Machida, T., Shirouzu,
ICH., Konishi, S., Miyashita, Y., & Masuda, N. (2013). A pairwise
maximum entropy model accurately describes resting-state
human brain networks. Nature Communications, 4, 1370.
https://doi.org/10.1038/ncomms2388, PubMed: 23340410
Wilting, J., & Priesemann, V. (2019). 25 years of criticality in
neuroscience—Established results, open controversies, novel
concepts. Aktuelle Meinung in der Neurobiologie, 58, 105–111.
https://doi.org/10.1016/j.conb.2019.08.002, PubMed: 31546053
Yeh, F.-C., Tang, A., Hobbs, J. P., Hottowy, P., Dabrowski, W., Sher,
A., Litke, A., & Beggs, J. M. (2010). Maximum entropy
approaches to living neural networks. Entropy, 12(1), 89–106.
https://doi.org/10.3390/e12010089
Yesavage, J. A., Brink, T. L., Rose, T. L., Lum, O., Huang, V., Adey,
M., & Leirer, V. Ö. (1982). Development and validation of a geri-
atric depression screening scale: A preliminary report. Zeitschrift für
Psychiatric Research, 17(1), 37–49. https://doi.org/10.1016/0022
-3956(82)90033-4, PubMed: 7183759
Zanoci, C., Dehghani, N., & Tegmark, M. (2019). Ensemble inhibi-
tion and excitation in the human cortex: An Ising-model analysis
with uncertainties. Physical Review E, 99(3), 032408. https://doi
.org/10.1103/PhysRevE.99.032408, PubMed: 30999501
Netzwerkneurowissenschaften
444
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
2
0
2
0
2
8
1
6
2
N
e
N
_
A
_
0
0
2
2
0
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3