Methoden - Am MIT spezialisierte KI-Forschung

Methoden

Large-scale directed network inference
with multivariate transfer entropy and
hierarchical statistical testing

Leonardo Novelli

, Patricia Wollstadt
4

, Pedro Mediano
1

Michael Wibral

, and Joseph T. Lizier

2,∗

1Centre for Complex Systems, Faculty of Engineering, The University of Sydney, Sydney, Australia
2Honda Research Institute Europe, Offenbach am Main, Deutschland
3Computational Neurodynamics Group, Department of Computing, Imperial College London, London, Großbritannien
Campus Institute for Dynamics of Biological Networks, Georg-August University, Göttingen, Deutschland
First authors contributed equally to this work.

∗

Keine offenen Zugänge

Tagebuch

Schlüsselwörter: Neuroimaging, Directed connectivity, Effective network, Multivariate transfer entropy,
Informationstheorie, Nonlinear dynamics, Statistical inference, Nonparametric tests

ABSTRAKT

Network inference algorithms are valuable tools for the study of large-scale neuroimaging
datasets. Multivariate transfer entropy is well suited for this task, being a model-free measure
that captures nonlinear and lagged dependencies between time series to infer a minimal
directed network model. Greedy algorithms have been proposed to efﬁciently deal with
high-dimensional datasets while avoiding redundant inferences and capturing synergistic
Effekte. Jedoch, multiple statistical comparisons may inﬂate the false positive rate and are
computationally demanding, which limited the size of previous validation studies. Der
algorithm we present—as implemented in the IDTxl open-source software—addresses these
challenges by employing hierarchical statistical tests to control the family-wise error rate and
to allow for efﬁcient parallelization. The method was validated on synthetic datasets
involving random networks of increasing size (up to 100 Knoten), for both linear and
nonlinear dynamics. The performance increased with the length of the time series, reaching
consistently high precision, recall, and speciﬁcity (>98% on average) für 10,000 Zeit
Proben. Varying the statistical signiﬁcance threshold showed a more favorable
precision-recall trade-off for longer time series. Both the network size and the sample size are
one order of magnitude larger than previously demonstrated, showing feasibility for typical
EEG and magnetoencephalography experiments.

EINFÜHRUNG

The increasing availability of large-scale, ﬁne-grained datasets provides an unprecedented op-
portunity for quantitative studies of complex systems. dennoch, a shift toward data-driven
modeling of these systems requires efﬁcient algorithms for analyzing multivariate time series,
which are obtained from observation of the activity of a large number of elements.

In the ﬁeld of neuroscience, the multivariate time series typically obtained from brain record-
ings serve to infer minimal (effective) network models which can explain the dynamics of the
nodes in a neural system. The motivation for such models can be, zum Beispiel, to describe a
causal network (Ay & Polani, 2008; Friston, 1994) or to model the directed information ﬂow

Zitat: Novelli, L., Wollstadt, P.,
Mediano, P., Wibral, M., & Lizier, J. T.
(2019). Large-scale directed network
inference with multivariate transfer
entropy and hierarchical statistical
testing. Netzwerkneurowissenschaften, 3(3),
827–847. https://doi.org/10.1162/
netn_a_00092

DOI:
https://doi.org/10.1162/netn_a_00092

zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00092
https://github.com/pwollstadt/IDTxl

Erhalten: 24 Januar 2019
Akzeptiert: 24 April 2019

Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.

Korrespondierender Autor:
Leonardo Novelli
leonardo.novelli@sydney.edu.au

Handling-Editor:
Olaf Sporns

Urheberrechte ©: © 2019
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz

Die MIT-Presse

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

in the system (Vicente et al., 2011) in order to produce a minimal computationally equivalent
Netzwerk (Lizier & Rubinow, 2012).

Informationstheorie (Cover & Thomas, 2005; Shannon, 1948) is well suited for the latter
motivation of inferring networks that describe information ﬂow as it provides model-free mea-
sures that can be applied at different scales and to different types of recordings. These mea-
sures, including conditional mutual information (Cover & Thomas, 2005) und Transferentropie
(Schreiber, 2000), are based purely on probability distributions and are able to identify non-
linear relationships (Paluš et al., 1993). Most importantly, information-theoretic measures al-
low the interpretation of the results from a distributed computation or information processing
Perspektive, by modeling the information storage, transfer, and modiﬁcation within the system
(Lizier, 2013). daher, information theory simultaneously provides the tools for building the
network model and the mathematical framework for its interpretation.

The general approach to network model construction can be outlined as follows: for any
target process (Element) in the system, the inference algorithm selects the minimal set of pro-
cesses that collectively contribute to the computation of the target’s next state. Every process
can be separately studied as a target, and the results can be combined into a directed network
describing the information ﬂows in the system. This task presents several challenges:

The state space of the possible network models grows faster than exponentially with
respect to the size of the network;
Information-theoretic estimators suffer from the “curse of dimensionality” for large sets
of variables (Paninski, 2003; Roulston, 1999);
In a network setting, statistical signiﬁcance testing requires multiple comparisons. Das
results in a high false positive rate (type I errors) without adequate family-wise error rate
Kontrollen (Dickhaus, 2014) or a high false negative rate (type II errors) with naive control
Verfahren;
Nonparametric statistical testing based on shufﬂed surrogate time series is computation-
ally demanding but currently necessary when using general information-theoretic esti-
mators (Bossomaier et al., 2016; Lindner et al., 2011).

Several previous studies (Faes et al., 2011; Lizier & Rubinow, 2012; Sun et al., 2015; Vlachos
& Kugiumtzis, 2010) proposed greedy algorithms to tackle the ﬁrst two challenges outlined
über (see a summary by Bossomaier et al., 2016, Sek 7.2). These algorithms mitigate the curse
of dimensionality by greedily selecting the random variables that iteratively reduce the uncer-
tainty about the present state of the target. The reduction of uncertainty is rigorously quantiﬁed
by the information-theoretic measure of conditional mutual information (CMI), which can also
be interpreted as a measure of conditional independence (Cover & Thomas, 2005). In partic-
ular, these previous studies employed multivariate forms of the transfer entropy, das ist, con-
ditional and collective forms (Lizier et al., 2008, 2010). Allgemein, such greedy optimization
algorithms provide a locally optimal solution to the NP-hard problem of selecting the most
informative set of random variables. An alternative optimization strategy—also based on con-
ditional independence—employs a preliminary step to prune the set of sources (Runge et al.,
2012, 2018). Despite this progress, the computational challenges posed by the estimation of
multivariate transfer entropy have severely limited the size of problems investigated in previous
validation studies in the general case of nonlinear estimators, Zum Beispiel, Montalto et al.
(2014) gebraucht 5 nodes and 512 Proben; Kim et al. (2016) gebraucht 6 nodes and 100 Proben;
Runge et al. (2018) gebraucht 10 nodes and 500 Proben. Jedoch, modern neural recordings
often provide hundreds of nodes and tens of thousands of samples.

Netzwerkneurowissenschaften

828

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

IDTxl:
The “Information Dynamics Toolkit
xl” is an open-source Python
package available on GitHub (sehen
zusätzliche Informationen).

Markovian with ﬁnite memory:
The present state of the target does
not depend on the past values of the
target and the sources beyond a
maximum ﬁnite lag l

These computational challenges, as well as the multiple testing challenges described above,
are addressed here by the implementation of rigorous statistical tests, which represent the main
theoretical contribution of this paper. These tests are used to control the family-wise error rate
and are compatible with parallel processing, allowing the simultaneous analysis of the targets.
This is a crucial feature, which enabled an improvement on the previous greedy algorithms.
Exploiting the parallel computing capabilities of high-performance computing clusters and
graphics processing units (GPUs) enabled the analysis of networks at a relevant scale for brain
recordings—up to 100 nodes and 10,000 Proben. Our algorithm has been implemented in
the recently released IDTxl Python package (the “Information Dynamics Toolkit xl”; Wollstadt
et al., 2019).

We validated our method on synthetic datasets involving random structural networks of
increasing size (also referred to as ground truth) and different types of dynamics (vector auto-
regressive processes and coupled logistic maps). Allgemein, effective networks are able to re-
ﬂect dynamic changes in the regime of the system and do not reﬂect an underlying structural
Netzwerk. dennoch, in the absence of hidden nodes (and other assumptions, including sta-
tionarity and the causal Markov condition), the inferred information network was proven to
reﬂect the underlying structure for a sufﬁciently large sample size (Sun et al., 2015). Experi-
ments under these conditions provide arguably the most important validation that the algorithm
performs as expected, and here we perform the ﬁrst large-scale empirical validation for non-
Gaussian variables. As shown in the Results, the performance of our algorithm increased with
the length of the time series, reaching consistently high precision, recall, and speciﬁcity (>98%
on average) für 10,000 time samples. Varying the statistical signiﬁcance threshold showed a
more favorable precision-recall trade-off for longer time series.

METHODEN

Deﬁnitions and assumptions

Let us consider a system of N discrete-time stochastic processes for which a ﬁnite number of
samples have been recorded (over time and/or in different replications of the same experiment).
Allgemein, let us assume that the stochastic processes are stationary in each experimental
time-window and Markovian with ﬁnite memory l
M. Further assumptions will be made for the
validation study. The following quantities are needed for the setup and formal treatment of the
algorithm and are visualized in Figure 1 and Figure 2:

Target process Y: a process of interest within the system (where Y = {Yt | t ∈ N}); Die
choice of the target process is arbitrary and all the processes in the system can separately
be studied as targets.

Source processes X i: the remaining processes within the system (where i = 1, . . . , N − 1 Und

X i = {Xi,T | t ∈ N}).

Sample number (or size) T: the number of samples recorded over time.
Replication number R: the number of replications of the same experiment (z.B., Versuche).
Target present state Yt: the random variable (RV) representing the state of the target at time t

(where t ≤ T), whose information contributors will be inferred.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Candidate target past Y

C
1/αmax.

J,S; Yt|Y

J,1; Yt|Y

2. Compute the maximum CMI value over candidates I∗
S

N,S) für jede
surrogate s = 1, . . . , S. Hier, n denotes the number of candidates and hence the number
of comparisons. The obtained values I∗
1 , . . . , I∗
S provide the (empirical) null distribution
of the maximum statistic (siehe Tabelle 1).

1,S, . . . , ICH(cid:5)

:= max(ICH(cid:5)

3. Calculate the p value for I∗

as the fraction of surrogate maximum statistic values that are

larger than I∗
I∗

is deemed signiﬁcant if the p value is smaller than αmax (d.h., the null hypothesis of
conditional independence for the candidate variable with the maximum CMI contribu-
tion is rejected at level αmax).

The variables and quantities used in the above algorithm are presented in Table 1. Der Schlüssel
goal in the surrogate generation is to preserve the temporal order of samples in the target time
series Yt (which is not shufﬂed) and preserve the distribution of the sources Cj while destroying
any potential relationships between the sources and the target (Vicente et al., 2011). This can
be achieved in multiple ways. If multiple replications (z.B., Versuche) are available, surrogate data is
generated by shufﬂing the order of replications for the candidate Cj while keeping the order of
replications for the remaining variables intact. When the number of replications is not sufﬁcient
to guarantee enough permutations, the embedded source samples within individual trials are
shufﬂed instead (see Chávez et al., 2003; Lizier et al., 2011; Verdes, 2005; Vicente et al., 2011;
and the summary by Lizier, 2014, Appendix A.5). Note that the generation of surrogates (Schritte
1-3) can be avoided when the null distributions can be derived analytically, Zum Beispiel, mit
Gaussian estimators (Barnett & Bossomaier, 2012).

The same test is performed during the selection of the variables in the candidate sources
S
ich

)

threshold

, . . . , In ≤ i

)

threshold

Ij ≤ i

(cid:3)

threshold

(cid:2)

= 1 −

= 1 − P (I1 ≤ i
N
∏
j=1
= 1 − P (I1 ≤ i
= 1 − (1 − v

threshold
)N

FPR

(1)

(2)

daher,

FPR

= 1 − (1 − αmax)1/N

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

Interessant, Gleichung 2 shows that the maximum statistic correction is equivalent to the
Dunn-Šidák correction (Šidák, 1967). Performing a Taylor expansion of Equation 2 around
αmax = 0 yields:

−

j−1
∏
k=0

(kn − 1)

(cid:5)J

(cid:4) αtarget
N

FPR

∞
∑
j=1

Truncating the Taylor series at j = 1 yields the ﬁrst-order approximation

FPR

≈

αmax
N

(3)

(4)

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

which coincides with the false positive rate resulting from the Bonferroni correction (Dickhaus,
2014). Darüber hinaus, since the summands in Equation 3 are positive for every j, the Taylor series
is lower bounded by any truncated series. Insbesondere, the false positive rate resulting from
the Bonferroni correction is a lower bound for the v
FPR (the false positive rate for a single
variable resulting from the maximum statistic test), das ist, the maximum statistic correction is
less stringent than the Bonferroni correction.

Let us now study the effect of the maximum statistic test on the family-wise error rate t
FPR
for a single target while accounting for all the iterations performed during the step-down

Netzwerkneurowissenschaften

835

Large-scale network inference with multivariate transfer entropy

test, (d.h., T
Wir haben:

FPR is the probability that at least one of the selected sources is a false positive).

FPR

N
∑
j=1
N
∑
j=1

P(“the source selected on step j is false positive”)
(cid:7)

(cid:6)

αj
max

= αmax

1 − αn
max
1 − αmax

daher,

FPR

≈ αmax

(5)

(6)

for the typical small values of αmax used in statistical testing (even in the limit of large n), welche
shows that αmax effectively controls the family-wise error rate for a single target.

The minimum statistic test is employed during the third main step of
Minimum statistic test.
the algorithm (pruning step) to remove the selected variables that have become redundant in
S
the context of the ﬁnal set of selected source past variables X
98% on average). (Beachten Sie, dass, while S = 1, 000 is minimal for αmax = 0.001,
recall was unchanged using S = 10, 000 for T = 100.) For longer time series (T = 10, 000),

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

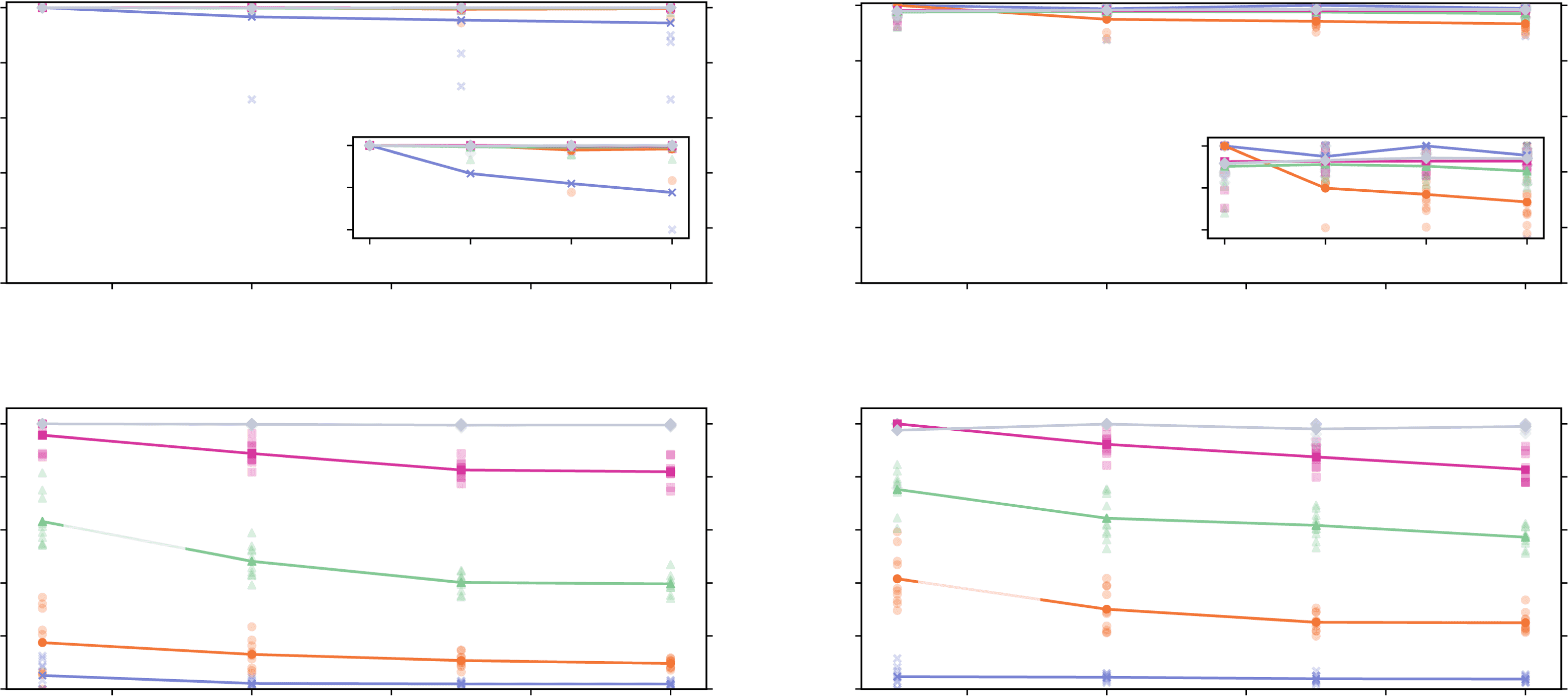
Figur 3. Precision (top) and recall (bottom) for different network sizes, sample sizes, and dynamics. Links: Vector autoregressive process;
Rechts: Coupled logistic maps. Each subplot shows ﬁve curves, corresponding to different time series lengths (T = 100, 300, 1,000, 3,000,
10,000). The results for 10 simulations from different initial conditions are shown (low-opacity markers) in addition to the mean values (solid
markers). All the random networks have an average in-degree N p = 3.

Netzwerkneurowissenschaften

839

Large-scale network inference with multivariate transfer entropy

high performance according to all measures was achieved for both the VAR and CLM pro-
Prozesse, regardless of the size of the network. The high precision and speciﬁcity are due to
the effective control of the false positives, in accordance with the strict statistical signiﬁcance
level αmax = 0.001 (the inﬂuence of αmax is further discussed in the following sections). Der
inference algorithm was therefore conservative in the classiﬁcation of the links.

Validation of False Positive Rate
The critical alpha level for statistical signiﬁcance αmax is a parameter of the algorithm that is
designed to control the number of false positives in the network inference. As discussed in
the Statistical Tests section in the Methods, αmax controls the probability that a target is a false
positive, das ist, that at least one of its sources is a false positive. This approach is in line with
the perspective that the goal of the network inference is to ﬁnd the set of relevant sources for
each node.

A validation study was carried out to verify that the ﬁnal number of false positives is consis-
tent with the desired level αmax after multiple statistical tests are performed. The false positive
rate was computed after performing the inference on empty networks, where every inferred
link is a false positive by deﬁnition (d.h., under the complete null hypothesis). The rate was
in good accordance with the critical alpha threshold αmax for all network sizes, as shown in
Figur 4.

fMRI data from the Human Connectome Project resting-state dataset

The false positive rate validation was replicated in a scenario where the null hypothesis
(sehen
held for real
zusätzliche Informationen). The ﬁndings are presented in the Supporting Information, together
with a note on autocorrelation. Vor allem, the results on fMRI data are in agreement with the
results on synthetic data shown in Figure 4.

False positive rate:
FP/(FP + TN).

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 4. Validation of false positive rate for a single target (T
FPR) on empty networks. The points
indicate the average false positive rate over 50 simulations of a vector autoregressive process
(T = 10,000). The horizontal marks indicate the corresponding 5th and 95th percentiles of the
expected range. These were computed empirically from the distribution of the random variable
(cid:10)Xj/N(cid:11), where Xj ∼ Binomial(N, αmax) are i.i.d. random variables, and the angular brackets in-
dicate the ﬁnite average over 50 repetitions. The 5th percentile for N = 10 and N = 40 Und
αmax = 10−3
are equal to zero and therefore omitted from the log-log plot. The identity function is
plotted as a reference (dashed line).

Netzwerkneurowissenschaften

840

Large-scale network inference with multivariate transfer entropy

Inﬂuence of Critical Level for Statistical Signiﬁcance

Given the conservative results obtained for both the VAR and CLM processes (Figur 3), A
natural question is to what extent the recall could be improved by increasing the critical alpha
level αmax and to what extent the precision would be negatively affected as a side effect.

In order to elucidate this trade-off, the analysis described above (Figur 3) was repeated for
increasing values of αmax, with results shown in Figure 5. For the shortest time series (T = 100),
increasing αmax resulted in a higher recall and a lower precision, as expected; auf dem anderen
Hand, for the longest time series (T = 10,000), the performance measures were not signiﬁcantly
affected. Interessant, for the intermediate case (T = 1,000), increasing αmax resulted in higher
recall without negatively affecting the precision.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 5.
Inﬂuence of statistical signiﬁcance threshold on network inference performance. Preci-
sion versus recall for different statistical signiﬁcance levels (αmax = 0.05, 0.01, 0.001), entsprechen-
ing to different colors. The plots summarize the results for different dynamics (Top: Vector autore-
gressive process; Bottom: Coupled logistic maps), different time series lengths (T = 100, 1,000,
10,000), and different network sizes (N = 10, 40, 70, 100, not distinguished). The arrows join
the mean population values for the lowest and highest signiﬁcance levels, illustrating the average
trade-off between precision loss and recall gain.

Netzwerkneurowissenschaften

841

Large-scale network inference with multivariate transfer entropy

Inference of Coupling Lags

So far, the performance evaluation focused on the identiﬁcation the correct set of sources
for each target node, regardless of the coupling lags. Jedoch, since the identiﬁcation of the
correct coupling lags is particularly relevant in neuroscience (see Wibral et al., 2013, Und
references therein), the performance of the algorithm in identifying the correct coupling lags
was additionally investigated.

Durch den Bau, a single coupling lag was imposed between each pair of processes (chosen
at random between one and ﬁve discrete time steps, as described in the Methods). The average
absolute error between the real and the inferred coupling lags was computed on the correctly
recalled sources and divided by the value expected at random (which is the average absolute
difference between two i.i.d. random integers in the [1, 5] interval). In line with the previous
results on precision, the absolute error on coupling lag is consistently much smaller than that
expected at random, even for the shortest time series (Figur 6). Außerdem, 1,000 Proben
were sufﬁcient to achieve nearly optimal performance for both the VAR and the CLM processes,
regardless of the size of the network. Note that as T increases and the recall increases, the lag
error can increase (vgl. T = 100 Zu 300 for the CLM process). This is perhaps because while the
larger T permits more weakly contributing sources to be identiﬁed, it is not large enough to
reduce the estimation error to make lag identiﬁcation on these sources precise.

Estimators

Given its speed, the Gaussian estimator is often used for large datasets or as a ﬁrst exploratory
step, even when the stationary distribution cannot be assumed to be Gaussian. The availability
of the ground truth allowed us to compare the performance of the Gaussian estimator and the
nearest-neighbor estimator on the nonlinear CLM process, which does not satisfy the Gaus-
sian assumption. Wie erwartet, the performance of the Gaussian estimator was lower than the
performance of the nearest-neighbor estimator for all network sizes (Figur 7).

The hierarchical tests introduced in the Methods section allow running the network infer-
ence algorithm in parallel on a high-performance computing cluster. Such parallelization is
especially needed when employing the nearest-neighbor estimator. Insbesondere, each target
node can be analyzed in parallel on a CPU (employing one or more cores) or a GPU, welche
is made possible by the CPU and GPU estimators provided by the IDTxl package (custom

Figur 6. Average absolute error between the real and the inferred coupling lags, relative to the value expected at random. Results for
different dynamics (Links: Vector autoregressive process; Rechts: Coupled logistic maps), different time series lengths (T = 100, 300, 1,000,
3,000, 10,000), and different network sizes (N = 10, 40, 70, 100). The error bars indicate the standard deviation over 10 simulations from
different initial conditions.

Netzwerkneurowissenschaften

842

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

Figur 7. Gaussian versus nearest-neighbor estimator on the coupled logistic maps process. The precision (links) and recall (Rechts) are plotted
against the network size and a ﬁxed time series length (T = 10,000 Proben). The results for 10 simulations from different initial conditions
are shown (low-opacity markers) in addition to the mean values (solid markers). The statistical signiﬁcance level αmax = 0.05 was employed;
an even larger gap between the recall of the estimators is obtained with αmax = 0.001.

OpenCL kernels were written for the GPU implementation). A summary of the CPU and GPU
run times is provided in the Supporting Information.

DISKUSSION

The algorithm presented in this paper provides robust statistical tests for network inference to
control the false positive rate. These tests are compatible with parallel computation on high-
performance computing clusters, which enabled the validation study on synthetic sparse net-
works of increasing size (10 Zu 100 Knoten), using different dynamics (linear autoregressive
processes and nonlinear coupled logistic maps) and increasingly longer time series (100 Zu
10,000 Proben). Both the network size and the sample size are one order of magnitude larger
than previously demonstrated, showing feasibility for typical EEG and MEG experiments. Der
results demonstrate that the statistical tests achieve the desired false positive rate and success-
fully address the multiple-comparison problems inherent in network inference tasks (Figur 4).

The ability to control the false positives while building connectomes is a crucial prerequisite
for the application of complex network measures, to the extent that Zalesky et al. (2016) con-
cluded that “speciﬁcity is at least twice as important as sensitivity (d.h., recall) when estimating
key properties of brain networks, including topological measures of network clustering, net-
work efﬁciency and network modularity.” The reason is that false positives occur more preva-
lently between network modules than within them, and the spurious intermodular connections
have a dramatic impact on network topology (Zalesky et al., 2016).

The trade-off between precision and recall when relaxing the statistical signiﬁcance thresh-
old was further investigated (Figur 5). When only 100 samples were used, the average recall
gain was more than ﬁve times smaller than the average precision loss. In our opinion, this result
is possibly due to the sparsity of the networks used in this study and suggests a conservative
choice of the threshold for sparse networks and short time series. The trade-off was reversed for
longer time series: Wann 1,000 samples were used, the average recall gain was more than ﬁve
times larger than the average precision loss. Endlich, für 10,000 Proben, high precision and
recall were achieved (>98% on average) for both the vector autoregressive and the coupled
logistic maps processes, regardless of the statistical signiﬁcance threshold.

For both types of dynamics, the network inference performance increased with the length of
the time series and decreased with the size of the network (Figur 3). This is to be expected since
larger systems require more statistical tests and hence stricter conditions to control the family-

Netzwerkneurowissenschaften

843

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

wise error rate (false positives). Konkret, larger networks result in wider null distributions
of the maximum statistic (d.h., larger variance), whereas longer time series have the opposite
Wirkung. daher, for large networks and short time series, controlling the false positives can
have a negative impact on the ability to identify the true positives, particularly when the effect
Größe (d.h., the transfer entropy value) is small.

Zusätzlich, the superior ability of the nearest-neighbor estimator over the Gaussian estima-
tor in detecting nonlinear dependencies was quantiﬁed. There is a critical motivation for this
comparison: the general applicability of the nearest-neighbor estimators comes at the price
of higher computational complexity and a signiﬁcantly longer run time, so that the Gaussian
estimator is often used for large datasets (or at least as a ﬁrst exploratory step), even when the
Gaussian hypothesis is not justiﬁed. To investigate such a scenario, the Gaussian estimator was
tested on the nonlinear logistic map processes: while the resulting recall was signiﬁcantly lower
than the nearest-neighbor estimator for all network sizes, it was nonetheless able to identify
over half of the links for a sufﬁciently large number (10,000) of time samples (Figur 7).

The stationarity assumption about the time series corresponds to assuming a single regime
of neuronal activity in real brain recordings. If multiple regimes are recorded, which is typical
in experimental settings (z.B., sequences of tasks or repeated presentation of stimuli interleaved
with resting time windows), different stationary regimes can be studied by performing the anal-
ysis within each time window. The networks obtained in different time windows can either
be studied separately and compared against each other or collectively interpreted as a single
evolving temporal network. To obtain a sufﬁcient amount of observations per window, multiple
replications of the experiment under the same conditions are typically carried out. Replica-
tions can be assumed to be cyclo-stationary and estimation techniques exploiting this property
have been proposed (Gómez-Herrero et al., 2015; Wollstadt et al., 2014); these estimators are
also available in the IDTxl Python package. The convergence to the (unknown) causal net-
work was only proven under the hypotheses of stationarity, causal sufﬁciency, and the causal
Markov condition (Sun et al., 2015). Jedoch, conditional independence holds under milder
assumptions (Runge, 2018) and the absence of links is valid under general conditions. Der
conditional independence relationships can, daher, be used to exclude variables in follow-
ing intervention-based causal experiments, making network inference methods valuable for
exploratory studies.

Tatsächlich, the directed network is only one part of the model and provides the scaffold over
which the information-theoretic measures are computed. daher, even if the structure of a
system is known and there is no need for network inference, information theory can still pro-
vide nontrivial insights on the distributed computation by modeling the information storage,
transfer, and modiﬁcation within the system (Lizier, 2013). This decomposition of the predic-
tive information into the active information storage and transfer entropy components is one
out of many alternatives within the framework proposed by Chicharro & Ledberg (2012). Ar-
guably, the storage-transfer decomposition reﬂects the segregation-integration dichotomy that
has long characterized the interpretation of brain function (Spurns, 2010; Zeki & Shipp, 1988).
Information theory has the potential to provide a quantitative deﬁnition of these fundamental
but still unsettled concepts (Li et al., 2019). Zusätzlich, information theory provides a new
way of testing fundamental computational theories in neuroscience, Zum Beispiel, predictive
coding (Brodski-Guerniero et al., 2017).

Als solche, information-theoretic methods should not be seen as opposed to model-based
approaches, but complementary to them (Friston et al., 2013). If certain physically motivated

Netzwerkneurowissenschaften

844

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

parametric models are assumed, the two approaches are equivalent for network inference:
maximizing the log-likelihood is asymptotically equivalent to maximizing the transfer entropy
(Barnett & Bossomaier, 2012; Cliff et al., 2018). Darüber hinaus, different approaches can be com-
bined; Zum Beispiel, the recent large-scale application of spectral DCM was made possible by
using functional connectivity models to place prior constraints on the parameter space (Razi
et al., 2017). Networks inferred using bivariate transfer entropy have also been employed to
reduce the model space prior to DCM analysis (Chan et al., 2017).

Abschließend, the continuous evolution and combination of methods show that network in-
ference from time series is an active ﬁeld of research and there is a current trend of larger valida-
tion studies, statistical signiﬁcance improvements, and reduction of computational complexity.
Information-theoretic approaches require efﬁcient tools to employ nearest-neighbor estimators
on large datasets of continuous-valued time series, which are ubiquitous in large-scale brain
Aufnahmen (calcium imaging, EEG, MEG, fMRT). The algorithm presented in this paper is com-
patible with parallel computation on high-performance computing clusters, which enabled the
study of synthetic nonlinear systems of 100 nodes and 10,000 Proben. Both the network size
and the sample size are one order of magnitude larger than previously demonstrated, bring-
ing typical EEG and MEG experiments into scope for future information-theoretic network
inference studies. Außerdem, the statistical tests presented in the Methods are generic and
compatible with any underlying conditional mutual information or transfer entropy estimators,
meaning that estimators applicable to spike trains (Spinney et al., 2017) can be used with this
algorithm in future studies.

ACKNOWLEDGMENTS

The authors acknowledge the Sydney Informatics Hub and the University of Sydney’s high-
performance computing cluster Artemis for providing the high-performance computing re-
sources that have contributed to the research results reported within this paper. Außerdem,
the authors thank Aaron J. Gutknecht for commenting on a draft of this paper, and Oliver Cliff
for useful discussions and comments.

SUPPORTING INFORMATION

The network inference algorithm described in this paper is implemented in the open-source
Python software package IDTxl (Wollstadt et al., 2019), which is freely available on GitHub
(https://github.com/pwollstadt/IDTxl). In diesem Papier, we refer to the current release (v1.0) Bei der
time of writing (doi:10.5281/zenodo.2554339).

The raw data used for the experiment presented in the Supporting Information (https://doi.
org/10.1162/netn_a_00092) is openly available on the MGH-USC Human Connectome Project
database (https://ida.loni.usc.edu/login.jsp).

ROLE INFORMATION

Leonardo Novelli: Konzeptualisierung; Data Curation; Formal Analysis; Untersuchung; Soft-
ware; Validierung; Visualisierung; Writing – Original Draft; Writing – Rezension & Editing. Patricia
Wollstadt: Konzeptualisierung; Software; Writing – Rezension & Editing. Pedro Mediano: Software;
Writing – Rezension & Editing. Michael Wibral: Konzeptualisierung; Funding Acquisition; Method-
ology; Software; Aufsicht; Writing – Rezension & Editing. Joseph T. Lizier: Konzeptualisierung;
Funding Acquisition; Methodik; Software; Aufsicht; Writing – Rezension & Editing.

Netzwerkneurowissenschaften

845

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

FUNDING INFORMATION

Joseph T. Lizier, Universities Australia/German Academic Exchange Service (DAAD) Australia-
Germany Joint Research Cooperation Scheme Grant: “Measuring Neural Information Synthe-
sis and Its Impairment,” Award Id: 57216857. Michael Wibral, Universities Australia/German
Academic Exchange Service (DAAD) Australia-Germany Joint Research Cooperation Scheme
Grant: “Measuring Neural Information Synthesis and Its Impairment,” Award Id: 57216857.
Joseph T. Lizier, Australian Research Council DECRA Grant, Award Id: DE160100630. Michael
Wibral, Deutsche Forschungsgemeinschaft (DFG) Grant, Award Id: CRC 1193 C04. Joseph T.
Lizier, Australian Research Council Discovery Grant, Award Id: DP160102742.

VERWEISE

Atay, F. M., & Karabacak, Ö. (2006). Stability of coupled map net-
works with delays. SIAM Journal on Applied Dynamical Systems,
5(3), 508–527.

Ay, N., & Polani, D. (2008). Information ﬂows in causal networks.

Advances in Complex Systems, 11(01), 17–41.

Barnett, L., Barrett, A. B., & Seth, A. K. (2009). Granger causality
and transfer entropy are equivalent for Gaussian variables. Phys-
ical Review Letters, 103(23), 238701.

Barnett, L., & Bossomaier, T. (2012). Transfer entropy as a log-

likelihood ratio. Physical Review Letters, 109(13), 138105.

Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov-
ery rate: a practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society. Serie B (Methodological),
57(1), 289–300.

Bossomaier, T., Barnett, L., Harré, M., & Lizier, J. T. (2016). An In-
troduction to Transfer Entropy. Springer International Publishing,
Chambridge, Vereinigtes Königreich.

Brodski-Guerniero, A., Paasch, G.-F., Wollstadt, P., Özdemir, ICH.,
Lizier, J. T., & Wibral, M. (2017). Information-theoretic evidence
for predictive coding in the face-processing system. The Journal
der Neurowissenschaften, 37(34), 8273–8283.

Chan, J. S., Wibral, M., Wollstadt, P., Stawowsky, C., Brandl, M.,
Helbling, S., . . . Kaiser, J. (2017). Predictive coding over the
lifespan: Increased reliance on perceptual priors in older adults—
a magnetoencephalography and dynamic causal modelling
Studie. bioRxiv Preprint, page 178095.

Chávez, M., Martinerie, J., & Le Van Quyen, M. (2003). Statistical
assessment of nonlinear causality: application to epileptic EEG
Signale. Journal of Neuroscience Methods, 124(2), 113–128.
Chicharro, D., & Ledberg, A. (2012). Framework to study dynamic
dependencies in networks of interacting processes. Physical Re-
view E, 86(4), 041901.

Cliff, O., Prokopenko, M., & Fitch, R. (2018). Minimising the
Kullback-Leibler divergence for model selection in distributed
nonlinear systems. Entropy, 20(2), 51.

Cover, T. M., & Thomas, J. A. (2005). Elements of Information The-

ory. John Wiley & Sons, Hoboken, NJ, USA, 2 edition.

Dickhaus, T. (2014). Simultaneous Statistical Inference. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Erd ˝os, P., & Rényi, A. (1959). On random graphs. Publicationes

Mathematicae Debrecen, 6, 290–297.

Faes, L., Nollo, G., & Porta, A. (2011). Information-based detec-
tion of nonlinear Granger causality in multivariate processes via

a nonuniform embedding technique. Physical Review E, 83(5),
051112.

Frenzel, S., & Pompe, B. (2007). Partial mutual information for cou-
pling analysis of multivariate time series. Physical Review Letters,
99(20), 204101.

Friston, K. J. (1994). Functional and effective connectivity in neu-
roimaging: a synthesis. Kartierung des menschlichen Gehirns, 2(1-2), 56–78.
Friston, K. J., Moran, R., & Seth, A. K. (2013). Analysing connectivity
with Granger causality and dynamic causal modelling. Current
Opinion in Neurobiology, 23(2), 172–178.

Garland, J., James, R. G., & Bradley, E. (2016). Leveraging infor-
mation storage to select forecast-optimal parameters for delay-
coordinate reconstructions. Physical Review E, 93(2), 022221.
Gómez-Herrero, G., Wu, W., Rutanen, K., Soriano, M., Pipa, G., &
Vicente, R. (2015). Assessing coupling dynamics from an ensem-
ble of time series. Entropy, 17(4), 1958–1970.

Granger, C. W. J. (1969). Investigating causal relations by econo-
metric models and cross-spectral methods. Econometrica, 37(3),
424–438.
Kim, P., Rogers,

(2016). Causation
entropy identiﬁes sparsity structure for parameter estimation
of dynamic systems. Journal of Computational and Nonlinear
Dynamics, 12(1), 011008.

J., & Bollt, E. M.

J., Sun,

Kraskov, A., Stögbauer, H., & Grassberger, P. (2004). Estimating mu-

tual information. Physical Review E, 69(6), 066138.

Li, M., Han, Y., Aburn, M. J., Breakspear, M., Poldrack, R. A., Shine,
J. M., & Lizier, J. T. (2019). Transitions in brain-network level
information processing dynamics are driven by alterations in neu-
ral gain. bioRxiv Preprint, page 581538.

Lindner, M., Vicente, R., Priesemann, V., & Wibral, M. (2011).
TRENTOOL: A Matlab open source toolbox to analyse informa-
tion ﬂow in time series data with transfer entropy. BMC Neuro-
Wissenschaft, 12, 119.

Lizier, J. T. (2013). The Local Information Dynamics of Distributed
Computation in Complex Systems. Springer Berlin, Heidelberg.
Lizier, J. T. (2014). JIDT: An information-theoretic toolkit for study-
ing the dynamics of complex systems. Frontiers in robotics and
AI, 1, 11.

Lizier,

J. T., Heinzle,

J., Horstmann, A., Haynes,

J.-D., &
Prokopenko, M. (2011). Multivariate information-theoretic mea-
sures reveal directed information structure and task relevant
changes in fMRI connectivity. Journal of Computational Neuro-
Wissenschaft, 30(1), 85–107.

Netzwerkneurowissenschaften

846

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
2
7
1
0
9
2
4
6
7
N
e
N
_
A
_
0
0
0
9
2
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Large-scale network inference with multivariate transfer entropy

Lizier, J. T., Prokopenko, M., & Zomaya, A. Y. (2008). Local infor-
mation transfer as a spatiotemporal ﬁlter for complex systems.
Physical Review E, 77(2), 026110.

Lizier, J. T., Prokopenko, M., & Zomaya, A. Y. (2010). Information
modiﬁcation and particle collisions in distributed computation.
Chaos, 20(3), 037109.

Lizier, J. T., Prokopenko, M., & Zomaya, A. Y. (2012). Local mea-
sures of information storage in complex distributed computation.
Information Sciences, 208, 39–54.

Lizier, J. T., & Rubinow, M. (2012). Multivariate construction of effec-
tive computational networks from observational data. Technisch
Report Preprint 25/2012, Max Planck Institute for Mathematics
in the Sciences.

Lorenz, H.-W. (1993). Chaotic dynamics in discrete-time economic
Modelle. In Nonlinear Dynamical Economics and Chaotic Motion
(pages 119–166). Springer, Berlin.

Montalto, A., Faes, L., & Marinazzo, D. (2014). MuTE: A MATLAB
toolbox to compare established and novel estimators of the
multivariate transfer entropy. PLoS ONE, 9(10), e109462.

Nichols, T., & Hayasaka, S. (2003). Controlling the familywise error
rate in functional neuroimaging: a comparative review. Statistical
Methods in Medical Research, 12(5), 419–446.

Paluš, M., Albrecht, V., & Dvoák, ICH. (1993). Information theoretic test
for nonlinearity in time series. Physics Letters A, 175(3-4), 203–209.
Paninski, L. (2003). Estimation of entropy and mutual information.

Neural Computation, 15(6), 1191–1253.

Razi, A., Seghier, M. L., Zhou, Y., McColgan, P., Zeidman, P.,
Park, H.-J., Spurns, O., Rees, G., & Friston, K. J. (2017). Groß-
scale DCMs for resting-state fMRI. Netzwerkneurowissenschaften, 1(3),
222–241.

Roulston, M. S. (1999). Estimating the errors on measured entropy
Information. Physica D: Nonlinear Phenomena,

and mutual
125(3-4), 285–294.

Rubinow, M., Spurns, O., van Leeuwen, C., & Breakspear, M. (2009).
Symbiotic relationship between brain structure and dynamics.
BMC Neuroscience, 10, 55.

Runge, J. (2018). Causal network reconstruction from time se-
Ries: from theoretical assumptions to practical estimation. Chaos,
28(7), 075310.

Runge, J., Heitzig, J., Petoukhov, V., & Kurths, J. (2012). Escaping
the curse of dimensionality in estimating multivariate transfer en-
tropy. Physical Review Letters, 108(25), 258701.

Runge, J., Nowack, P., Kretschmer, M., Flaxman, S., & Sejdinovic,
D. (2018). Detecting causal associations in large nonlinear time
series datasets. arXiv Preprint. arXiv: 1702.07007.

Schreiber, T. (2000). Measuring information transfer. Physical Re-

view Letters, 85(2), 461–464.

Schreiber, T., & Schmitz, A. (2000). Surrogate time series. Physica

D: Nonlinear Phenomena, 142(3-4), 346–382.

Shannon, C. E. (1948). A mathematical theory of communication.

Bell System Technical Journal, 27(3), 379–423.

Šidák, Z. (1967). Rectangular conﬁdence regions for the means of
multivariate normal distributions. Journal of the American Statis-
tical Association, 62(318), 626–633.

Sims, C. A. (1980). Macroeconomics and reality. Econometrica,

48(1), 1–48.

Spinney, R. E., Prokopenko, M., & Lizier, J. T. (2017). Transfer en-
tropy in continuous time, with applications to jump and neural
spiking processes. Physical Review E, 95(3), 032319.

Spirtes, P., Glymour, C., & Scheines, R. (1993). Causation, Pre-
diction, and Search, Volumen 81 of Lecture Notes in Statistics.
Springer New York.

Spurns, Ö. (2010). Networks of the Brain. MIT Press Cambridge,

MA.

Strogatz, S. H. (2015). Nonlinear Dynamics and Chaos. CRC Press,

Boca Raton, FL.

Sun, J., Taylor, D., & Bollt, E. M. (2015). Causal network inference by
optimal causation entropy. SIAM Journal on Applied Dynamical
Systeme, 14(1), 73–106.

Takens, F. (1981). Detecting strange attractors in turbulence. In
Rand, D. und Jung, L., editors, Dynamical Systems and Turbu-
lence, pages 366–381. Springer, Berlin.

Vakorin, V. A., Krakovska, Ö. A., & McIntosh, A. R. (2009). Con-
founding effects of indirect connections on causality estimation.
Journal of Neuroscience Methods, 184(1), 152–160.

Valdes-Sosa, P. A., Roebroeck, A., Daunizeau, J., & Friston, K. J.
(2011). Effective connectivity: inﬂuence, causality and biophysi-
cal modeling. NeuroImage, 58(2), 339–361.

Vejmelka, M., & Paluš, M. (2008). Inferring the directionality of cou-
pling with conditional mutual information. Physical Review E,
77(2), 026214.

Verdes, P. F. (2005). Assessing causality from multivariate time se-

Ries. Physical Review E, 72(2), 026222.

Vicente, R., Wibral, M., Lindner, M., & Pipa, G. (2011). Transfer
entropy—a model-free measure of effective connectivity for the
neurosciences. Journal of Computational Neuroscience, 30(1),
45–67.

Vlachos, ICH., & Kugiumtzis, D. (2010). Nonuniform state-space recon-
struction and coupling detection. Physical Review E, 82(1), 016207.
Wibral, M., Pampu, N., Priesemann, V., Siebenhühner, F., Seiwert,
H., Lindner, M., . . . Vicente, R. (2013). Measuring information-
transfer delays. PLoS ONE, 8(2), e55809.

Wollstadt, P., Lizier, J. T., Vicente, R., Finn, C., Martínez-Zarzuela,
M., Mediano, P., . . . Wibral, M. (2019). IDTxl: The Information
Dynamics Toolkit xl: a Python package for the efﬁcient analy-
sis of multivariate information dynamics in networks. Zeitschrift für
Open Source Software, 4(34), 1081.

Wollstadt, P., Martínez-Zarzuela, M., Vicente, R., Díaz-Pernas, F. J.,
& Wibral, M. (2014). Efﬁcient transfer entropy analysis of non-
stationary neural time series. PLoS ONE, 9(7), e102833.

Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear,
(2014). Time-resolved resting-state brain networks. Pro-
the National Academy of Sciences, 111(28),

M.
ceedings of
10341–10346.

Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel,
M. P., & Breakspear, M. (2016). Connectome sensitivity or speci-
ﬁcity: which is more important? NeuroImage, 142, 407–420.
Zeki, S., & Shipp, S. (1988). The functional logic of cortical connec-