METHODEN - Am MIT spezialisierte KI-Forschung

METHODEN

Guided graph spectral embedding: Application to
the C. elegans connectome

Miljan Petrovic

1,2

, Thomas A. W. Bolton

, Maria Giulia Preti

1,2

Raphaël Liégeois

, and Dimitri Van De Ville

1,2

1Institute of Bioengineering, École Polytechnique Fédérale de Lausanne, Campus Biotech, Genf, Schweiz
2Department of Radiology and Medical Informatics, University of Geneva, Genf, Schweiz

Schlüsselwörter: Spectral graph domain, Graph embedding, Low-dimensional
connectomics

Raum, Focused

Keine offenen Zugänge

Tagebuch

ABSTRAKT

Graph spectral analysis can yield meaningful embeddings of graphs by providing insight into
distributed features not directly accessible in nodal domain. Recent efforts in graph signal
processing have proposed new decompositions—for example, based on wavelets and
Slepians—that can be applied to ﬁlter signals deﬁned on the graph. In this work, we take
inspiration from these constructions to deﬁne a new guided spectral embedding that
combines maximizing energy concentration with minimizing modiﬁed embedded distance
for a given importance weighting of the nodes. We show that these optimization goals are
intrinsically opposite, leading to a well-deﬁned and stable spectral decomposition. Der
importance weighting allows us to put the focus on particular nodes and tune the trade-off
between global and local effects. Following the derivation of our new optimization criterion,
we exemplify the methodology on the C. elegans structural connectome. The results of our
analyses conﬁrm known observations on the nematode’s neural network in terms of
functionality and importance of cells. Compared with Laplacian embedding, the guided
Ansatz, focused on a certain class of cells (sensory neurons, interneurons, oder
motoneurons), provides more biological insights, such as the distinction between somatic
positions of cells, and their involvement in low- or high-order processing functions.

EINFÜHRUNG

Many aspects of network science relate to graph partitioning—the grouping of nodes in
subgraphs—and graph embedding—their representation in a low-dimensional space that ac-
counts for graph topology (Von Luxburg, 2007). Spectral graph theory motivates analytical
methods based on the eigenvectors of fundamental graph operators, such as the adjacency
and the Laplacian operators (Chung, 1997). Zum Beispiel, the well-known graph cut problem
can be convexly relaxed and solved by thresholding of the Laplacian eigenvector with the
smallest nonzero eigenvalue, known as the Fiedler vector (Fiedler, 1989). More recently, neu
approaches in graph signal processing have taken advantage of the Laplacian eigenvectors to
deﬁne the graph Fourier transform, which can then be used to process (d.h., ﬁlter) graph signals
in the spectral domain (Ortega, Frossard, Kovaˇcevi´c, Moura, & Vandergheynst, 2018; Schumann,
Narang, Frossard, Ortega, & Vandergheynst, 2013); the spectral graph wavelet transform by
Hammond, Vandergheynst, & Gribonval (2011) is one such example.

The Laplacian eigenvectors also provide a meaningful embedding by mapping nodes onto a
Linie, or higher dimensional representation, that minimizes distances between connected nodes

Zitat: Petrovic, M., Bolton, T. A. W.,
Preti, M. G., Liégeois, R., & Van De
Ville, D. (2019). Guided graph spectral
embedding: Application to the
C. elegans connectome. Netzwerk
Neurowissenschaften, 3(3), 807–826. https://
doi.org/10.1162/netn_a_00084

DOI:
https://doi.org/10.1162/netn_a_00084

zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00084

Erhalten: 29 November 2018
Akzeptiert: 12 Marsch 2019

Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.

Korrespondierender Autor:
Miljan Petrovic
miljan.petrovic@epﬂ.ch

Handling-Editor:
Olaf Sporns

Urheberrechte ©: © 2019
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz

Die MIT-Presse

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Guided graph spectral embedding

Graph:
Mathematical model of networks
including vertices (Knoten) and edges
connecting them.

Eigenvector:
A vector whose multiplication with
the given matrix produces a scaled
version of itself.

Laplacian:
Matrix describing a graph and
containing information on
smoothness of signals deﬁned on that
graph.

Eigenvalue:
The value of the scaling of an
eigenvector due to its multiplication
with a matrix.

Embedding:
Procedure of reducing
dimensionality of the data;
describing a dataset (graph) with less
memory requirements while
preserving important information.

Slepians:
Signals with maximally localized
structure in both time/vertex and
frequency domain.

(Belkin & Niyogi, 2003). Other well-known embedding techniques use different metrics for
distance in order to assess local graph properties, ranging from simple Euclidean distance in
locally linear embedding (Roweis, 2000), to shortest path in Isomap (Tenenbaum, 2000), tran-
sition probability (Shen & Meyer, 2008), or conditional probability of an edge in t-distributed
stochastic neighbor embedding (van der Maaten & Hinton, 2008). A time-dependent dynam-
ical similarity measure has also been introduced (Schaub, Delvenne, Lambiotte, & Barahona,
2018). Zusätzlich, efforts have been made to employ global properties of the graph, wie zum Beispiel
in Sammon mapping (Sammon, 1969), where a cost function including all pairwise distances
is optimized. In this manner, embedding is performed while taking in consideration both local
(neighborhood) and global (distant nodes) properties of the graph. Jedoch, these techniques
are not aware of the network at the mesoscale: One cannot guide the embedding by giving
a certain subgraph more importance while still preserving local features and global topology
characteristics.

In essence, the most powerful feature of graph spectral embedding is to effectively summa-
rize local structure across the graph into low-dimensional global patterns. This is achieved, für
Beispiel, with the recently introduced concept of graph Slepians; das ist, graph signals that are
bandlimited and take into account a subset of selected nodes. Konkret, two types of Slepian
designs that respectively optimize for energy concentration and modiﬁed embedded distance
have been introduced (Van De Ville, 2016; Van De Ville, Demesmaeker, & Preti, 2017B).

In this work, we further build on this framework by providing a simple way to guide analy-
ses with additional ﬂexibility. Guidance includes the selection of a given subgraph or group of
nodes to study, and the ability to specify the intensity of the focus set on these selected nodes.
With respect to graph Slepians, we hereby provide several extensions. Erste, we allow the se-
lection process to be weighted, so that the importance of a node can be gradually changed.
Zweite, we propose a new criterion that meaningfully combines the two existing ones; Das
Ist, we want to maximize energy concentration and minimize modiﬁed embedded distance at
die selbe Zeit. Dritte, as we detail below, these two criteria are counteracting, and hence, Wir
obtain stable solutions even at full bandwidth, where the original Slepian designs degenerate
numerically. Vierte, we show how this criterion can be rewritten as an eigenvalue problem of
an easy modiﬁcation of the adjacency matrix, which can be interpreted as reweighting paths
in the graph, and thus signiﬁcantly simpliﬁes the whole Slepian concept. The solution of the
eigendecomposition then deﬁnes the guided spectral domain, spanned by its eigenvectors.
We illustrate the proposed approach with a proof-of-concept on the Caenorhabditis elegans
(C. elegans) connectome. Through spectral embedding-based visualization, we observe the
effects of focusing on a speciﬁc cellular population made of sensory neurons, interneurons, oder
motoneurons, and we reveal trajectories of these neurons as a function of focus strength.

METHODEN

Essential Graph Concepts

We consider an undirected graph with N nodes, beschriftet 1, 2, . . . , N. The edge weights are
contained in the symmetric weighted adjacency matrix ˜A with nonnegative real-valued ele-
ments ˜ai,J, ich, j = 1, . . . , N. We also assume that the graph contains no self-loops; das ist, alle
diagonal elements ˜ai,i are zero. The degree matrix D is the diagonal matrix with elements
di,i = ∑N
j=1 ˜ai,J. The graph Laplacian is deﬁned as ˜L = D − ˜A and can be interpreted as a
second-order derivative operator on the graph. Hier, we use the symmetrically normalized
variants of the adjacency ˜A and graph Laplacian ˜L deﬁned as A = D
and L = I − A.

−1/2 ˜AD

−1/2

Netzwerkneurowissenschaften

808

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Guided graph spectral embedding

This normalization is often used in applications to emphasize the changes in topology and not
in nodal degree (De Lange, De Reus, & Van den Heuvel, 2014).

Let us deﬁne a graph signal as a vector of length N that associates a value with each node
(Shuman et al., 2013). One way to recognize the importance of the Laplacian and its eigen-
decomposition is to consider the smoothness of a graph signal x as

(cid:2)

Lx =

N
∑
ich,j=1

ai,J(xi − xj)2,

(1)

which sums squared differences between signal values on nodes that are connected, propor-
tionally to their link strength ai,J. The eigenvectors of L minimize this distance that is reﬂected
by the eigenvalues, sorted by convention increasingly as λ1 = 0 ≤ λ2 ≤ . . . ≤ λN. daher,
considering the eigenvectors associated with the smallest nonzero eigenvalues provides the
Laplacian embedding of the nodes that minimizes distance in a lower dimensional space
(Belkin & Niyogi, 2003). The eigenvector with the smallest nonzero eigenvalue is also known
as the Fiedler vector (Fiedler, 1989), which relates to the solution of the convex relaxation of
the graph cut problem (Von Luxburg, 2007).

daher, the eigendecomposition L = UΛU

of the graph Laplacian is the cornerstone
of spectral methods for graphs, as the eigenvectors {uk}, k = 1, . . . , N (columns of U) play
the role of graph Fourier components, and the associated eigenvalues {λk}, k = 1, . . . , N, von
frequencies (Chung, 1997). The graph Fourier transform (GFT) then provides the link between
a graph signal x and its spectral coefﬁcients given by vector ˆx:

(cid:2)

x = Uˆx, and ˆx = U

(cid:2)

Graph Slepians

In earlier work, the combination of the concepts of selectivity and bandwidth for graph
signals has been used to deﬁne “graph Slepians” (Tsitsvero, Barbarossa, & Di Lorenzo, 2016;
Van De Ville, 2016; Van De Ville et al., 2017B); das ist, bandlimited graph signals with max-
imal energy concentration in the subset of nodes S—a generalization of prolate spheroidal
wave functions that were proposed 50 years ago on regular domains to ﬁnd a trade-off be-
tween temporal and spectral energy concentrations (Slepian, 1978; Slepian & Pollak, 1961).
The presence or absence of a node in S is encoded by the diagonal elements of the selection
matrix S; das ist, we have Si,i = δi∈S , i = 1, . . . , N, where δ is the Kronecker delta. The Slepian
design then boils down to ﬁnding the linear combination of Laplacian eigenvectors, encoded
by spectral coefﬁcients ˆg, within the bandlimit W with maximal energy in S, reverting to the
Rayleigh quotient

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

μ = ˆg

(cid:2)

U
(cid:2)
ˆg

SUWˆg
ˆg

(2)

where W is a spectral selection matrix that has W ones on its diagonal followed by N − W
zeros. This problem can be solved by the eigendecomposition of the concentration matrix
C = W
SUW as C ˆgk = μk ˆgk, k = 1, . . . , W. The graph Slepians gk = U ˆgk, k = 1, . . . , W,
are orthonormal over the entire graph as well as orthogonal over the subset S; das ist, we have
(cid:2)
k gl = δk−l as well as g
G

(cid:2)
k Sgl = μkδk−l.

(cid:2)

For the purpose of this work, we introduce the set of bandlimited graph signals

BW = {X| ˆx = Wˆx} ,

Netzwerkneurowissenschaften

809

Guided graph spectral embedding

such that we can then rewrite the Slepian criterion of Equation (2) directly in the vertex
domain as

μ = g

(cid:2)

Sg
G(cid:2)G

s.t. g ∈ BW.

(3)

An alternative Slepian design was also proposed in Van De Ville et al. (2017B)—see also

Huang et al. (2018), modifying the Laplacian embedded distance of Equation (1) as follows:

ξ = g

1/2

(cid:2)

1/2
L

SL
G(cid:2)G

s.t. g ∈ BW.

(4)

(cid:2)

The Laplacian embedded distance x

Lx is a measure of smoothness of the vector x over
the graph, which is why eigenvectors of L with increasing eigenvalues are ordered according
to smoothness. Imposing the modiﬁcation with the selection matrix S focuses the smoothness
on a certain subgraph, notwithstanding how the signal behaves outside it. Gleichung (4) can
also be seen as a generalization of Laplacian embedding, since L
reverts to L for the
special case of S = I.

1/2

It is important to realize that the eigenvalues {μk} of the original design reﬂect the energy
concentration in the subset S, while the eigenvalues {ξk} of the alternative design correspond
to a modiﬁed embedded distance that can be interpreted as a “frequency value” localized in
S, in analogy to the global GFT case. Folglich, “interesting” eigenvectors correspond to
those with high μk, concentrated in the subset S, or low ξk, showing the main localized low-
frequency trends, jeweils. Jedoch, the eigendecompositions, taken individually, do not
necessarily lead to eigenvectors that combine both virtues.

Guiding Spectral Embedding Using a New Criterion

We hereby propose to further generalize the Slepian design in a number of ways. Erste, Wir
relax the selection matrix S to a cooperation matrix M with diagonal elements that can take
any nonnegative real values ml ≥ 0, l = 1, . . . , N. This allows to gradually change the impact
of a node on the analysis, between an enhanced (ml > 1), an unmodiﬁed (ml = 1), und ein
reduced (ml < 1) importance with respect to the selection matrix case. Second, we combine the criteria of both already existing Slepian designs by subtracting the modiﬁed embedded distance from the energy concentration: ζ = μ − ξ = g (cid:2) Mg − g (cid:2) 1/2 L g(cid:2)g ML 1/2 g s.t. g ∈ BW. (5) Third, we remove the bandlimit constraint and allow g to be any graph signal, which is an operational choice because of the joint optimization of both criteria, as will be illustrated and discussed later. Using the Taylor series approximation of the square root function, we derive L 1/2 in terms of the adjacency matrix A: 1/2 = (I−A)1/2 = I − L 1 2 A − 1 8 A 2 − 1 16 A 3 − . . . = I − ∞ ∑ k=1 ckA k, (6) (7) 810 Network Neuroscience l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 3 8 0 7 1 0 9 2 4 0 4 n e n _ a _ 0 0 0 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Guided graph spectral embedding (2k)! with ck = section. We can then further rewrite the internal part of the Criterion 5 as 22k(k!)2(2k−1) . Details on the series expansion are discussed in the Taylor Series M − (I − A)1/2 M(I − A)1/2 = (cid:2) ∞ ∑ k=1 ck (cid:3) MA k + A k M − (cid:4) ∞ ∑ k1=1 ∞ ∑ k2=1 (cid:5) ck1 ck2 k1MA k2. A (8) By convention, the associated eigenvalues are sorted in decreasing order. Based on the fact that eigenvalues of the symmetric normalized Laplacian are greater or equal to 0 and lower or equal to 2, one can derive mmax ≥ ζ1 ≥ ζ2 ≥ . . . ≥ −2mmax, where mmax is the highest cooperation value appearing in M, using bounds from Corollary 2.4 in Lu and Pearce (2000). In what follows, we will be considering the linear and quadratic approximations of the new criterion’s eigenvalues: (cid:2) (cid:2) (cid:2) g (cid:2) g MA+AM 2 g(cid:2)g MA+AM 2 ζ lin = ζ quad = (cid:3) g , M − AMA 4 (cid:3) g . + MA 2 2+A 8 g(cid:2)g (9) (10) Interestingly, the combination of both existing Slepian criteria leads to the emergence of the adjacency matrix A as the key player in our new formalism. In fact, when the cooperation matrix is the identity matrix, the criterion reverts to the eigendecomposition of A itself. Let us now interpret the impact of the cooperation weights: Obviously, an element ai,j of the adjacency matrix contains the weight of a direct path from i to j. 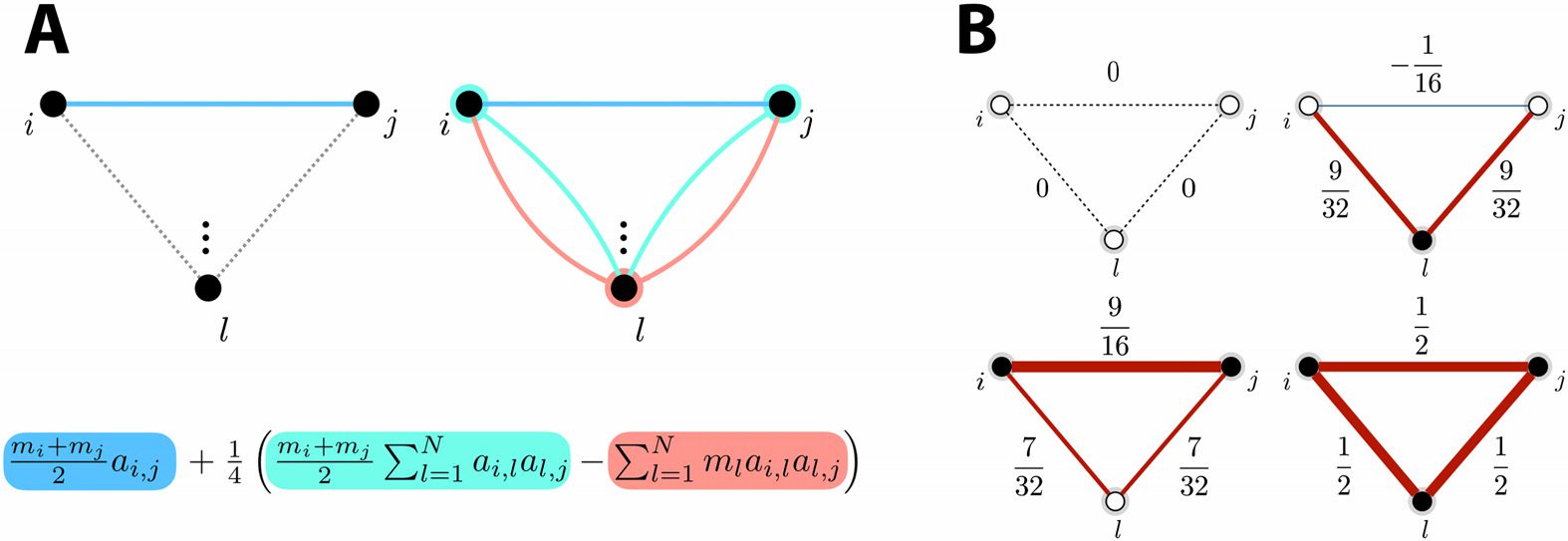The linear approximation lin reweights such a direct path with the average (mi + mj)/2 of the cooperation weights that ζ are attributed to nodes i and j, as illustrated in Figure 1A (left half). Notice that paths where only one node has a cooperation weight equal to 0 are still possible, as the other cooperation weight is then simply divided by 2. As for the quadratic approximation, it takes into account length-2 paths between nodes i and j. For instance, the sum of all length-2 paths between i and j can be read out from the squared adjacency matrix: [A 2]i,j = N ∑ l=1 ai,lal,j = (cid:6) (cid:7) , ai,·, a·,j where the inner product reveals the kernel interpretation of the length-2 walk matrix. Therefore, as illustrated in Figure 1A (right half), the term [MA 2 2 + A M]i,j = (mi + mj) N ∑ l=1 ai,l al,j reweights all length-2 paths by the summed cooperation weight between the start and end nodes, while subtracting the term [AMA]i,j = N ∑ l=1 ml ai,l al,j penalizes the path according to the cooperation weight of node l through which it passes. Network Neuroscience 811 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 3 3 8 0 7 1 0 9 2 4 0 4 n e n _ a _ 0 0 0 8 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Guided graph spectral embedding (A) In the case of two nodes i and j, the average of their cooperation weights yields Figure 1. the multiplying factor for ai,j (blue term). When a third node l is added, the difference between average cooperation weight between nodes i and j (light blue term), and the cooperation weight of node l (salmon term), multiplies the length-2 path and then also contributes to the output entry. (B) In an example three-node network, output entries for different examples where cooperation weights are either set to 0 (white nodes) or to 1 (black nodes). Edge thickness is proportional to the output entry weight. Red strokes denote positive edge values, while blue strokes highlight nega- tive edge values. All nonzero entries of the normalized adjacency matrix of the example network equal 1/2. k Analogously, the term A in the criterion introduces modiﬁcations of k-length paths in the graph. However, for k > N, reweighting reduces to modiﬁcations of lower length paths. Der
Cayley-Hamilton theorem implies that for every matrix A of size N × N, the matrix A
can
for k = 0, 1, . . . N − 1. By induction, Es
be written as a linear combination of matrices A
for every k > N can also be written as a linear combination of the same set of N
holds that A
matrices. Somit, modiﬁcations of paths longer than N − 1 can be seen as a linear combination
of additional modiﬁcations of paths of length 0 to N − 1.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

MATHEMATICAL CONSIDERATIONS

This section provides mathematical foundations supporting the methods and the results pre-
sented in this work. We start by discussing the link between the selection matrix and the
eigenspectrum associated with the energy concentration criterion, and the relationship with
the modiﬁed embedded distance criterion, using full bandwidth. Dann, we provide a formal
justiﬁcation of the Taylor series approximation of the square root matrix function used in Equa-
tion 6, and discuss the error associated with this approximation.

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Eigenspectrum Associated With the Energy Concentration Criterion
For full bandwidth, the concentration matrix is deﬁned as C = U
SU, where U is the matrix
whose columns are eigenvectors of the graph Laplacian, and S is a diagonal selection matrix.
Somit, the eigendecomposition of C is trivial: Its eigenvectors are the rows of U, und das
eigenvalues of C correspond to the diagonal entries of S, as can be seen from Figure 3A for
W = 279.

(cid:2)

Eigenspectrum Associated With the Modiﬁed Embedded Distance Criterion

We show that for full bandwidth, the number of zero eigenvalues of the modiﬁed embedded
distance matrix, denoted zλ, is lower bounded by the number of zeros on the diagonal of the

Netzwerkneurowissenschaften

812

Guided graph spectral embedding

selection matrix, denoted zS. To see this, consider the following decomposition of the modiﬁed
embedded distance matrix Cemb:

Cemb = L

1/2

1/2 =

N−zS
∑
k=1

sik

lik

l(cid:2)
ik

1/2

where ik is the index of the kth nonzero entry of the selection matrix S, and lik denotes the ikth
. From this expression, it can be seen that the rank of Cemb is
column vector of the matrix L
at most N − zS and hence, zλ ≥ zS. Equality holds when the set of vectors {lik
} dazugehörigen
to the nonzero entries of S are linearly independent. This is the case for connected graphs, als
any subset (with cardinality strictly less than N) of the columns of L
is linearly independent.
This relationship is observed in Figure 3B for W = 279.

1/2

Taylor Series of Matrix-Valued Functions

The Taylor expansion of L
of f (X) =

√

x evaluated around the point a = 1:

1/2

proposed in Equation 6 is derived using the scalar Taylor series

√

x = 1 +

∞
∑
k=1

tk(x − 1)k,

where tk = (−1)k−1(2k)!

22k(k!)2(2k−1) and x ∈ R, x > 0. The square root matrix of L then writes

1/2 = ULΛ1/2
L

(cid:2)
L U
L
1 + ∑∞

⎡

⎢
⎢
⎣

= UL

k=1 tk(λ1 − 1)k

⎤

⎥
⎥
⎦ U

(cid:2)
L

. . .

1 + ∑∞

k=1 tk(λN − 1)k

= UL(ICH +

∞
∑
k=1

tk(ΛL − I)k)U

(cid:2)
L .

Since the Laplacian and adjacency matrices are normalized, their eigenvalues verify ΛL =
I − ΛA and their eigenvectors are equal (UL = UA) when ordered following increasing and
decreasing eigenvalues, jeweils. The previous equation ﬁnally reduces to

1/2 = I + UA(

∞
∑
k=1

tk(−ΛA)k)U

(cid:2)
A

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

(−1)ktkUAΛk

(cid:2)
A

= I +

= I −

∞
∑
k=1
∞
∑
k=1

ckA

where ck =

(2k)!

22k(k!)2(2k−1), which is the expression used in Equation 6.

Truncation of the Taylor series of a function f (X) to a ﬁnite upper bound on k ≤ K leads to

an approximation error that can be estimated by the Lagrange form of the remainder

RK(X) =

F (K+1)(j)
(K + 1)!

(x − 1)K+1,

Netzwerkneurowissenschaften

813

Guided graph spectral embedding

Frobenius distance:
Square root of the sum of pointwise
squared differences between two
matrices.

bei dem die (K + 1)th derivative is evaluated at the point y found between x and 1. Auf dem anderen
Hand, since the eigenvectors forming UL are unit-norm vectors, the distance dK between a
ﬁnite sum approximation of L

and the true square root of the matrix is bounded as

1/2

dK = ||L

1/2 − (I −

K
∑
k=1

ckA

k)||F ≤

N
∑
i=1

|RK(λi)|,

Wo || · ||F denotes the Frobenius norm. In the case of a ﬁrst-order Taylor approximation
(K = 1), we get

d1 ≤

N
∑
i=1

| F (2)(yi)|
2!

(λi − 1)2.

The eigenvalues λi range from 0 Zu 2, and all contribute to the total approximation error
d1, with eigenvalues further from 1 contributing more. Since the second-order derivative of the
square root function increases as its argument approaches 0, the most contributing factors of
the error derive from Taylor approximation terms with near-zero eigenvalues. Somit, graphs
whose Laplacian spectrum exhibits higher eigengaps in the lower band tend to have lower
approximation error.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

Endlich, the Frobenius distance dK,M between the true proposed criterion M − L

1/2

and its approximation using a Kth-order Taylor approximation of L1/2

veriﬁes

dK,M ≤ dK||M||FdK,

Wo ||M||F corresponds to the Frobenius norm of the cooperation matrix. Somit, the upper
bound on dK,M reduces as the nodes are given less importance; das ist, when the cooperation
values get closer to 0.

ERGEBNISSE

The C. elegans worm is an intensely studied model organism in biology. Insbesondere, the wiring
diagram of its 302 neurons has been carefully mapped during a long and effortful study (White,
Southgate, Thomson, & Brenner, 1986). Hier, we use the graph that summarizes data from 279
somatic neurons (unconnected and pharyngeal neurons were excluded from the full diagram
von 302 Neuronen), and combined connectivity from chemical synapses and gap junctions (Chen,
Hall, & Chklovskii, 2006). The binary adjacency matrix Abin with edge weights 0 oder 1 has been
symmetrically normalized with the degree matrix D into A = D
, as described in
the Essential Graph Concepts section. We retrieved the type of each neuron (sensory neuron,
interneuron, or motoneuron) from the WormAtlas database (http://www.wormatlas.org/).

AbinD

−1/2

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

In their modeling work, Varshney, Chen, Paniagua, Hall, & Chklovskii (2011) studied net-
work properties of the worm connectome using different approaches, including Laplacian
embedding. Insbesondere, the topological view generated by mapping nodes on the ﬁrst two
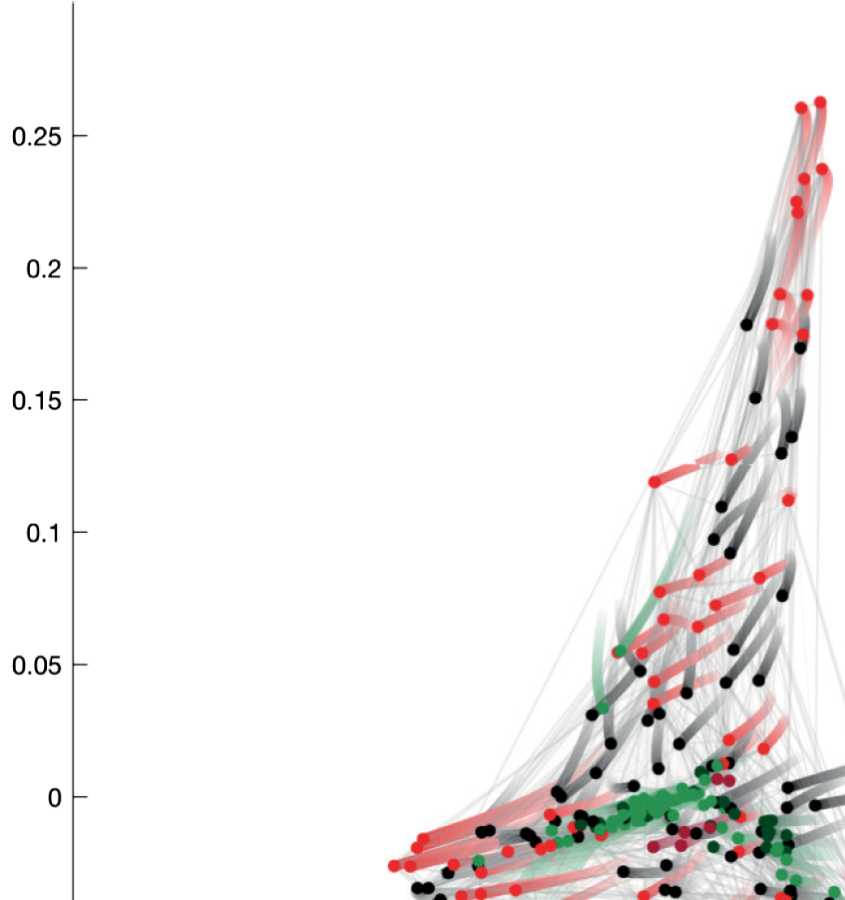
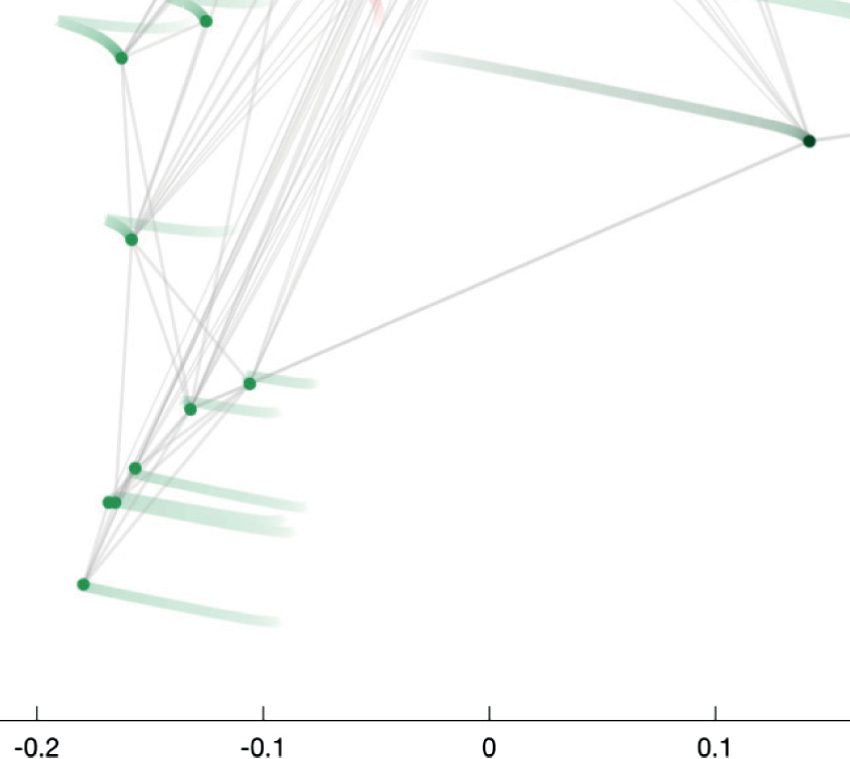
eigenvectors with smallest nonzero eigenvalues already reveals interesting network organiza-
tion (siehe Abbildung 2). The horizontal dimension (u2) mainly distinguishes the motoneurons from
the head (right green circles) and from the ventral cord (left green circles). The vertical dimen-
sion (u3) reﬂects information ﬂow from sensory neurons and interneurons of the animal’s head
(top) to the nerve ring and ventral cord circuitries (bottom).

Eigenvalues of Different Criteria

To illustrate the eigenvalues obtained with the existing Slepian designs, as well as the newly
proposed criterion, we considered the 128 motoneurons and “unselected” them by setting their

Netzwerkneurowissenschaften

814

Guided graph spectral embedding

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

Figur 2. Spectral embedding of the C. elegans connectome according to the eigenvectors of
the Laplacian matrix with second and third smallest eigenvalues. The purpose of this work is to
introduce guided spectral analysis; das ist, to indicate direction by selecting a subset of nodes, Und
to adjust the strength of the focus set on this subset. Each colored circle in the ﬁgure depicts one
C. elegans neuron. Light gray strokes link the cells that are connected by gap junctions or chemical
synapses. Labels and connectivity were retrieved from Varshney et al. (2011).

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

respective entries in S to 0. We applied the original, concentration-based Slepian design for
different bandwidths W = 100, 150, 200, 279, the latter corresponding to full bandwidth. Der
eigenvalues μk, which reﬂect energy concentration in the 151 remaining neurons, are shown
in Figure 3A. The characteristic behavior of classical Slepians is preserved for the graph vari-
ant; das ist, eigenvalues cluster around 1 Und 0 for well- and poorly concentrated eigenvectors,
jeweils, and the phase transition occurs more abruptly at higher bandwidth. For full band-
width, perfect concentration becomes possible, and the problem degenerates in retrieving two
linear subspaces of 151 Und 128 dimensions spanned by eigenvectors with concentration 1
Und 0, jeweils (see the Mathematical Considerations section for a proof on the number
of distinct eigenvalues). In practical terms, for high but not full bandwidth, the “interesting”

Netzwerkneurowissenschaften

815

Guided graph spectral embedding

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 3. Plots of eigenvalues obtained using different Slepian criteria: (A) energy concentration μ, (B) modiﬁed embedded distance ξ, Und
(C) our new proposed criterion ζ. For the ﬁrst two cases, in which the design depends on a bandwidth parameter, eigenvalue spectra are
plotted for W = 100, 150, 200, Und 279 with increasingly lighter blue or purple shades, jeweils. In the full-bandwidth case, the shaded
green areas highlight eigenvalues linked to optimal solutions of the respective criteria (see the Mathematical Considerations section for the
associated mathematical derivations). In the third case, equivalent μ and ξ eigenspectra are plotted in blue and purple on top of the ζ one.
The full ζ eigenspectrum is also compared with approximations obtained through Taylor series of increasing order (D), from linear to order
20, as depicted by increasingly darker brown curves. The two smaller plots are insets sampled at the start and at the end of the main plot,
jeweils.

eigenvectors with large concentration correspond to the part indicated by the green area on the
plot, and become numerically indistinguishable. A few indicative examples of Slepian vectors
across bandwidths are displayed in Supplementary Figure S1C (zusätzliche Informationen).

Nächste, we applied the modiﬁed Slepian design inspired by the Laplacian embedded distance.
As shown in Figure 3B, the eigenvalues ξk reﬂect the modiﬁed embedded distance, which we
now want to minimize. For increasing bandwidth (darker curves), its smallest values can be
made lower; Jedoch, the subset of nodes with Si,i entries set to 0 is also described by eigen-
vectors with small eigenvalues. This becomes even clearer at full bandwidth, a case for which
a subspace of 128 dimensions spanned by eigenvectors with a modiﬁed embedded distance
von 0 is retrieved, as indicated by the green area in Figure 3B and explicitly demonstrated in the
Mathematical Considerations section. Some examples of Slepians across bandwidths can be
seen in Supplementary Figure S1D (zusätzliche Informationen).

The degeneracies of the Slepian designs at full bandwidth are instructive about the opposing
effects of maximizing energy concentration and minimizing modiﬁed embedded distance; Das

Netzwerkneurowissenschaften

816

Guided graph spectral embedding

Ist, the subspaces indicated by the green areas in Figures 3A and 3B, which are optimal for
the corresponding criteria, are actually different ones, representing signals on sensory and
interneurons (151 Knoten) on the one hand, and on motoneurons (128 Knoten) auf dem anderen
Hand (compare Supplementary Figures S1C and S1D, ﬁrst rows; zusätzliche Informationen). Das
leads us to the eigenvalues ζk of the proposed criterion, as shown in Figure 3C (black curve).

The maximum eigenvalue peaks close to 1, a case reﬂecting jointly high equivalent μk (Blau
curve) and low equivalent ξk (purple curve); das ist, a high energy concentration at the same
time as a low modiﬁed embedded distance (low localized graph frequency) within S. The low
amount of such solutions shows that it is difﬁcult to conceal high energy concentration and
small modiﬁed embedded distance.

As values of ζk decrease, we ﬁrst observe a rise in modiﬁed embedded distance (eigen-
vectors remain reasonably concentrated within S, but rapidly exhibit a larger localized graph
frequency), and then a decrease of both μk and ξk, which indicates that eigenvectors become
less concentrated within the subset of interest. Afterwards, we observe a regime in which both
quantities are null at the same time; das ist, a subspace spanned by eigenvectors that are fully
concentrated outside S. Notice that this set of eigenvectors is now “pushed away” from the
meaningful low ξk ones, and lie in the middle of the spectrum. Endlich, the sign of ζk switches,
and the right-hand side of Figure 3C denotes eigenvectors of increasing concentration within
S and localized graph frequency, the latter effect dominating over the former.

Interessant, computing the eigenspectrum using a linear approximation of the criterion
Matrix (Figure 3D, light brown curve) leads to very similar results, which only slightly vary for
the largest eigenvalues. When the approximation order is increased up to 20 (increasingly dark
brown curves), this low error further diminishes, although a mild difference remains with the
ground truth. Inspection of the Slepian vectors related to several locations of the eigenspectrum
(Supplementary Figure S2, zusätzliche Informationen) conﬁrmed that the only salient differences
actually involved the ﬁrst Slepian vector (largest eigenvalue one).

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

Procrustes transform:
Geometric transform that changes
only the size and the overall position
of an object but not its shape.

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Topology Revealed by Guided Spectral Analysis

We now guide the spectral analysis to focus on the three different types of neurons. Für in-
Haltung, when focusing on the role of the sensory neurons, we gradually decrease the coopera-
tion weights of interneurons and motoneurons from 1 Zu 0. For each setting, we then visualize
the topology revealed by the guided analysis by projecting the nodes on the eigenvectors with
the second and third largest eigenvalues. We build the trajectory of each node through this
two-dimensional embedding, after applying the Procrustes transform (Schönemann, 1966) Zu
compensate for any irrelevant global transformations. As a complementary visualization, Notiz
that we provide the start, intermediate, and end points of each trajectory as separate ﬁgures in
Supplementary Figure S3 (zusätzliche Informationen). Endlich, k-means clustering was performed
on the nodes in focus at the end point embedding of trajectories, producing sets of clusters
given in Supplementary Figure S4 and Supplementary Tables 1–3 (see Supporting Information
for details). Example visualizations when resorting to different Slepian vectors are provided in
Supplementary Figure S5 (zusätzliche Informationen).

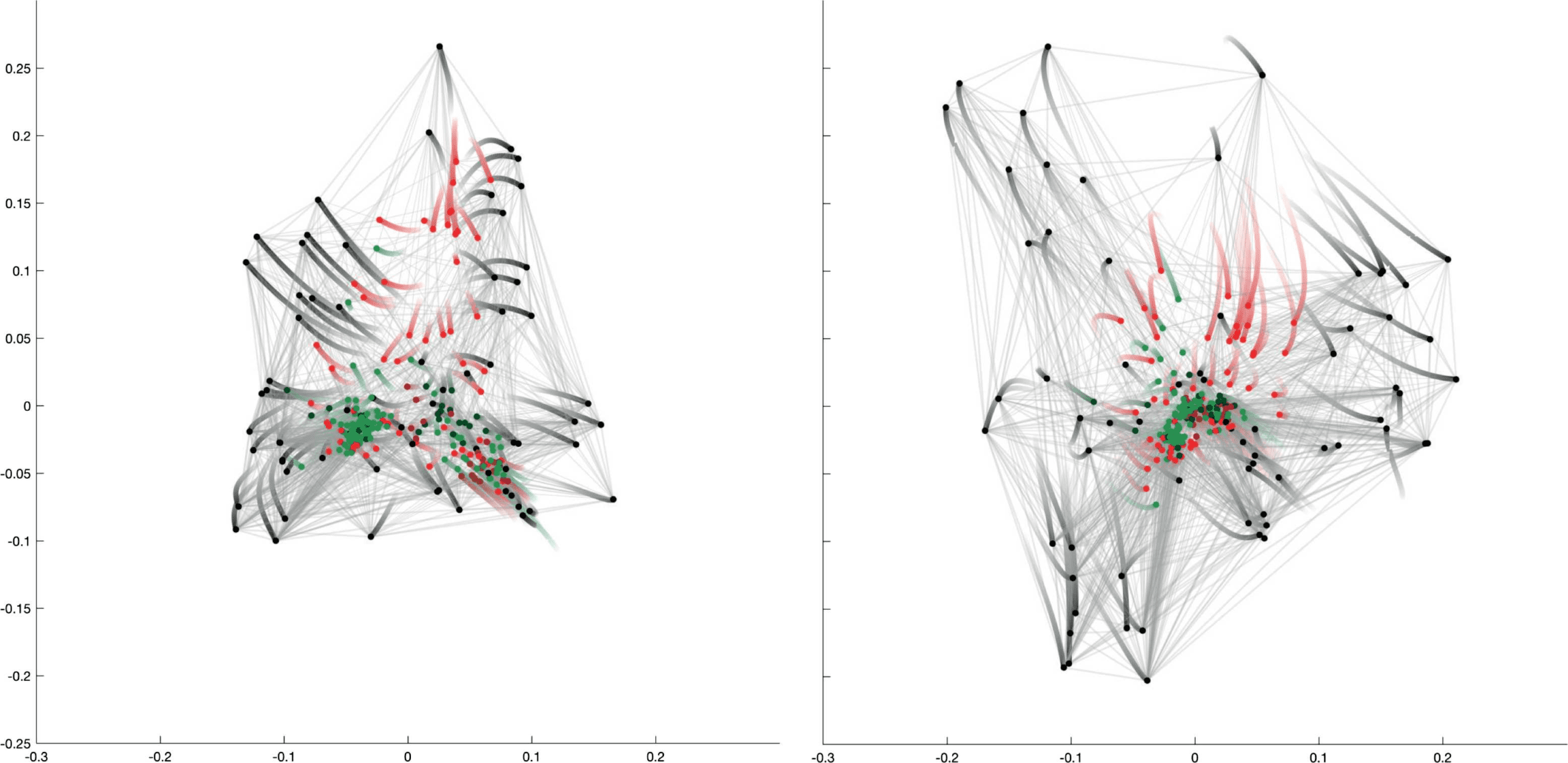
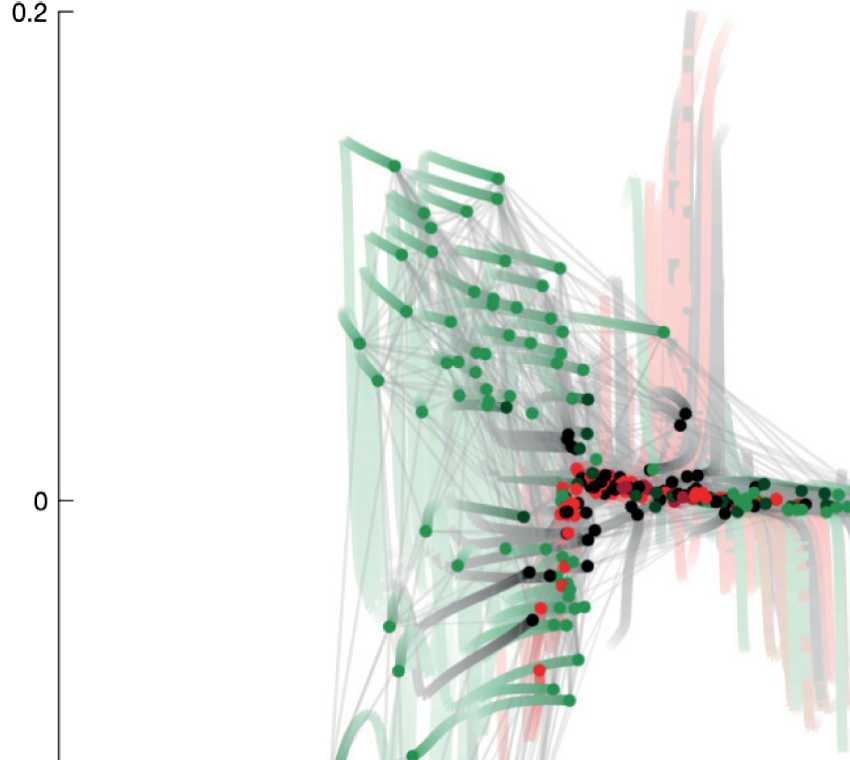
In Figures 4A and 4B, the trajectories are depicted when focusing on the sensory neurons
by attributing cooperation weights to the other types of neurons ranging from 1 Zu 0.5, Und
aus 0.5 Zu 0, jeweils. During the ﬁrst half (Figure 4A), the network organization is only
slightly altered with respect to the initial view of Figure 2; das ist, the sensory neurons move
slightly more to the periphery, while the interneurons and motoneurons move to the origin. In

Netzwerkneurowissenschaften

817

Guided graph spectral embedding

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

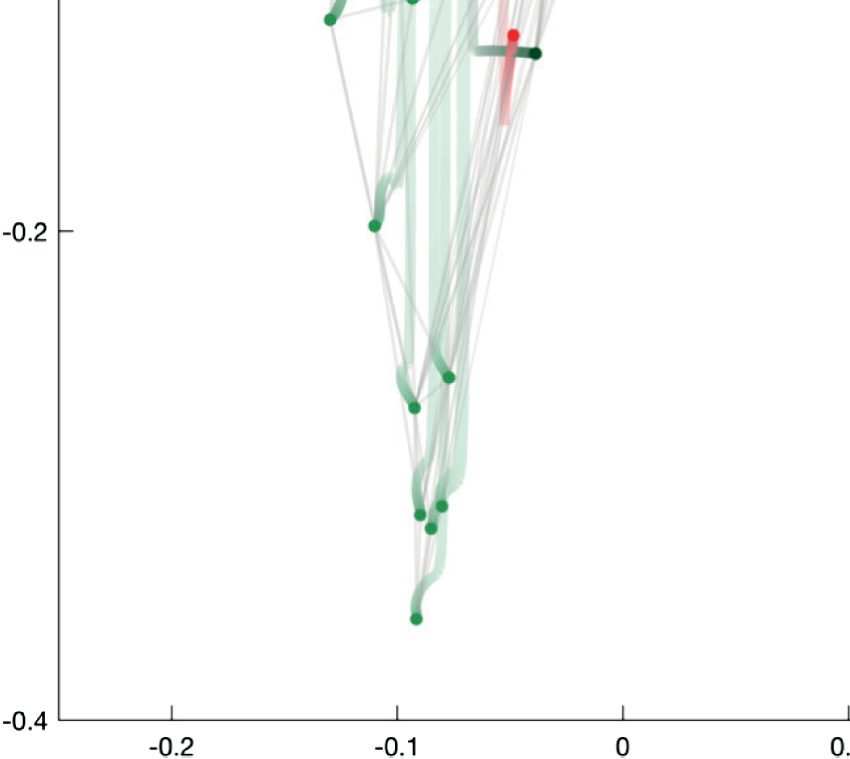
Figur 4. Focusing on the sensory neurons by reducing the cooperation weights of the interneurons and motoneurons (A) aus 1 Zu 0.5, Und
(B) aus 0.5 Zu 0. The trajectory of a neuron is represented by a color change from light to dark tones, and dots represent ﬁnal positions. Notiz
that the starting conﬁguration in (A) is identical to the representation in Figure 2. Cells are labeled according to Varshney et al. (2011).

the second part of the trajectory (Figure 4B), a major split occurs in the bottom right branch of
Figure 4A between the left and right versions of a whole series of neurons, while the bottom
left branch neurons move back to the center of the coordinate frame. The cell types found in
the top branch are amphid neurons, whereas the rest of the sensory neurons split into their
left and right counterparts located in the left and right bottom branches. The clusters found by
the k-means approach (see Supplementary Table 1, zusätzliche Informationen) include a group
of ﬁve bilateral amphid neurons (AWA, AWC, ASE, ASI, and AFD; cluster C3) and six other
clusters, two of which span the bottom left and right subbranches (clusters C5 and C2).

As described in the Guiding Spectral Embedding section, since paths through nodes with
cooperation weights set to 0 are still considered by the proposed criterion, the embedding
focusing on a particular subtype of neurons can still include functionally distinct cells as clearly
standing out in the visualization. Zum Beispiel, in addition to the above clustering of sensory
neurons in Figure 4B, we notice the segregation of the bilateral RIP interneurons towards the
left and the right branch. This shows that the embedding does not neglect nodes outside the
focus, even when their cooperation weight is set to 0.

In Figures 5A and 5B, we then focus on the interneurons by reducing the cooperation
weights of sensory neurons and motoneurons in two steps. Wie erwartet, the interneurons move
towards the periphery. Their organization does not seem to be dominated by left versus right
variants, as we found for sensory neurons, but rather by a set of well-deﬁned clusters related to
their functional involvement in the C. elegans neuronal circuitry (see Supplementary Table 2,
zusätzliche Informationen): In the ﬁrst quadrant, we ﬁnd the isolated AIA bilateral pair (cluster C4).

Netzwerkneurowissenschaften

818

Guided graph spectral embedding

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

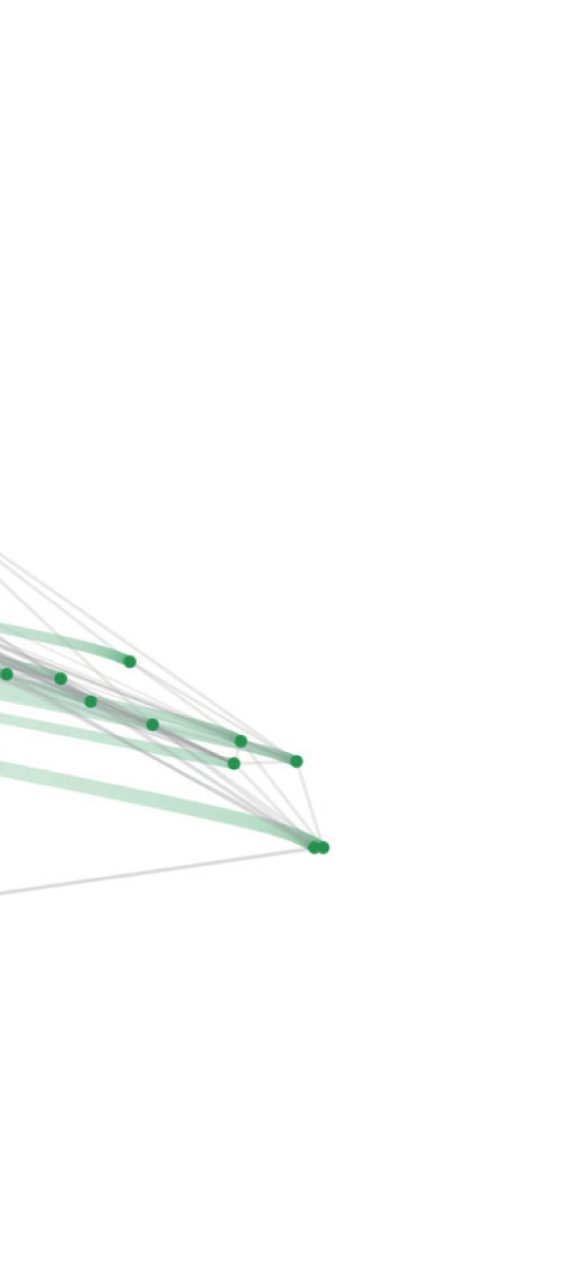
Figur 5. Focusing on the interneurons by reducing the cooperation weights of the sensory neurons and motoneurons (A) aus 1 Zu 0.5, Und
(B) aus 0.5 Zu 0. The trajectory of a neuron is represented by a color change from light to dark tones, and dots represent ﬁnal positions. Notiz
that the starting conﬁguration in (A) is identical to the representation in Figure 2. Cells are labeled according to Varshney et al. (2011).

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

Moving clockwise, a larger cluster of neurons includes the bilateral AIY, AIZ, AIN, AIB, RIA,
RIB, AUA, and the single neurons RIR and RIH (cluster C3). Next we ﬁnd a cluster including
AVE, AVK, RIG, PVT, DVA, and other neurons located closer to the origin of Figure 5 (clus-
ter C5), before reaching another large ensemble of neurons including the bilateral AVA, AVD,
LUA, PVC, PVW, and the single neuron PVR (cluster C6). Moving back upwards, cluster C1
contains the bilateral AVB, AVJ, BDU, the single neuron AVG, and PVPR, whose left counter-
part PVPL belongs to cluster C5, thus standing as the only bilateral pair of neurons split into
different clusters. Endlich, we reach the last group of cells containing the bilateral RIF, AVH,
AIM, PVQ, and AVF (cluster C2).

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Endlich, in Figures 6A and 6B, the organization of motoneurons is examined. Already in the
ﬁrst step (Figure 6A), when reducing the cooperation weights of the sensory and interneurons
aus 1.0 Zu 0.5, we observe much stronger changes than in the previous cases. Insbesondere, Die
initial organization completely collapses and the left branch of the motoneurons spreads out.
This branch then develops into a peripheral organization when further decreasing the coop-
eration weights (Figure 6B), with three main subsets of neurons and ambiguous positioning of
the cell DVB between the left and the right bottom branches. K-means clustering into optimal
cell groups captured this architecture into seven smaller clusters (Supplementary Table 3, Sup-
porting Information): Clusters C4 and C7 spanned top neurons, clusters C2 and C3 included the
bottom left branch neurons, and clusters C5 and C6 contained the bottom right branch cells.

Netzwerkneurowissenschaften

819

Guided graph spectral embedding

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 6. Focusing on the motoneurons by reducing the cooperation weights of the sensory neurons and interneurons (A) aus 1 Zu 0.5, Und
(B) aus 0.5 Zu 0. The trajectory of a neuron is represented by a color change from light to dark tones, and dots represent ﬁnal positions. Notiz
that the starting conﬁguration in (A) is identical to the representation in Figure 2. Cells are labeled according to Varshney et al. (2011).

DISKUSSION

Beyond Original Slepian Designs

The originality of our approach lies in providing a new and simple way to guide graph spec-
tral analysis. Inspired by graph Slepians, we propose a novel criterion that combines energy
concentration and modiﬁed embedded distance, taking into account cooperation weights that
can gradually increase or decrease the importance of selected nodes. The new criterion lets
the adjacency matrix emerge as the central graph operator, instead of the Laplacian, und ist
operational at full bandwidth.

This is surprising at ﬁrst sight, because neither of the conventional Slepian criteria is prac-
tical without the bandlimit constraint. For the energy concentration with binary cooperation
weights, as shown in Figure 3A for an illustrative example on the C. elegans connectome,
full bandwidth leads to two eigenvalues (1 Und 0), the dimensionality of the corresponding
subspaces being the number of nodes with cooperation weight 1 Und 0, jeweils. For the
modiﬁed embedded distance, as shown in Figure 3B, full bandwidth creates a subspace with
eigenvalue 0 of dimensionality equal to the number of nodes with cooperation weight 0. Dort-
Vordergrund, subtracting both criteria leads to opposing objectives; das ist, at full bandwidth, an energy
concentration of 1 encodes the subspace for nodes with weight 1, while a modiﬁed embedded
distance of 0 encodes the subspace for nodes with weight 0.

The obtained eigenspectrum for the new criterion, shown in Figure 3C, illustrates that only a
few eigenvectors are able to combine high energy concentration with low modiﬁed embedded

Netzwerkneurowissenschaften

820

Guided graph spectral embedding

Distanz, a counterbalance that can be further revealed by measuring μ and ξ separately
for these new eigenvectors. Such a large eigengap is also good news for numerical com-
putation of the leading eigenvectors for large graphs when relying upon efﬁcient large-scale
solvers (Lehoucq & Sorensen, 1996) implemented in widely available software libraries such
as ARPACK.

Intriguingly, the approximation error was already low using a linear approximation, and did
not noticeably decrease further, except for the ﬁrst Slepian vector, when resorting to higher or-
der terms (siehe Abbildung 3 and Supplementary Figure S2, zusätzliche Informationen). Modifying the
importance of a node via the corresponding cooperation value affects all-length paths through
that node according to the series expansion from Equation 8, where the power of A in each
term corresponds to the affected path length. Once we restrict the criterion to a linear approxi-
mation, the only paths whose importance is changed are those of length 1. This does not mean
that other paths are not included in the graph analysis, but rather that they are included with
their original (unmodiﬁed) effect on the topology. Low error of linear approximation suggests
that the highest percentage of topological importance of a node falls into the importance of
its length-1 paths. Weiter, a slightly higher error at eigenvectors with the highest ζ may be
explained similarly: Not modifying higher order paths produces greater error at these eigen-
vectors because of their increased relative importance, because high ζ eigenvectors tend to be
very smooth (even approaching a constant signal); daher, in order to even out the values at all
nodes in the process, one needs to “reach” far enough.

The proposed criterion should not be confused with the Sobolev norm that is sometimes
used to regularize graph signals (Mahadevan & Maggioni, 2006). Konkret, in the case of
M = I, our criterion of Equation 5 applied to g reverts to g
Lg, whereas the Sobolev
norm of g reads g
Lg. The difference in the sign of the second term introduces signiﬁ-
cantly distinct optimization goals regardless of the apparent similarity of the two expressions.

g − g

G + G

(cid:2)

As for future extensions of our approach, one could envisage to dig into the relationship
with graph uncertainty principles (Agaskar & Lu, 2013; Teke & Vaidyanathan, in press; Tsitsvero
et al., 2016), to consider statistical resampling for graphs (Pirondini, Vybornova, Coscia, & Van
De Ville, 2016), or to focus on the discovery of hierarchical graph structure (Arenas, Fernández,
& Gómez, 2008; Irion & Saito, 2014) by gradual reﬁnement of the subgraph. The design could
also be extended to directed graphs using recent extensions of spectral decompositions in this
Kontext (Mhaskar, 2018; Sandryhaila & Moura, 2013).

Gaining Insights on C. elegans

The application of our newly developed approach to the C. elegans connectome enabled us
to conﬁrm past ﬁndings from the literature, and to shed light on additional cellular targets
and groupings that may deserve further experimental analyses. At the level of sensory neurons
(Figur 4, Supplementary Figure S3A, and Supplementary Figure S4A; Supporting Informa-
tion), seven clusters were extracted, collectively accounting for the three branches evident in
Figur 4: the top branch made of 12 (including the thermosensor AFD) pairs of amphid neurons
(at y-coordinate greater than 0.04), and other cells split into the left and right bottom branches.
Interessant, one of the clusters found by k-means included ﬁve pairs of bilateral amphid neu-
rons: AWA and AWC involved in odortaxis (Bargmann, Hartwieg, & Horvitz, 1993; Li et al.,
2012), the thermosensor AFD (Mori & Ohshima, 1995), and ASE and ASI implicated in chemo-
taxis (Bargmann & Horvitz, 1991; Luo et al., 2014). These neurons act as low-order sensors,

Netzwerkneurowissenschaften

821

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Guided graph spectral embedding

whose extraction as a separate cluster inside the amphid group may suggest new information
worth further exploration.

The lower branches in Figure 4 split the neurons into their right and left counterparts, daher
extracting relevant somatic information. These neurons act as higher order sensing apparatus
as compared with amphid neurons: IL1 and OLQ have jointly been implicated in the worm
foraging response (Hart, Sims, & Kaplan, 1995); CEP and ADE are involved in the response
upon food sensing (Sawin, Ranganathan, & Horvitz, 2000); URX, URY, and OLL are linked
to the reproductive drive (Barrios, Ghosh, Fang, Emmons, & Barr, 2012), und so weiter. The split
between low- and high-order sensing is summarized in Figure 7A.

Further inspection of the branches (Supplementary Figure S6A, zusätzliche Informationen)
showed that the left-right segregation involved chemical synapses, but not gap junctions.
Auch, Supplementary Figure S5 (zweite Reihe, zusätzliche Informationen) shows that for higher
order Slepian vectors (fourth and ﬁfth), additional contributors emerge, such as the bilateral
PHA/PHB. This suggests that the approach ﬁnds different subgroups of higher order sensory
neurons depending on the choice of the embedding eigenvectors. The biological/functional
intepretation of the exact clusters asks for a more detailed analysis of the subgroups of neu-
rons. Endlich, the emergence of RIP interneurons in the embedding (Figur 4) points towards
an important role of the sensory neurons yet to be explained, possibly in connection with their
presynaptic inputs from IL1 (White et al., 1986).

Turning to interneurons (Figur 5, Supplementary Figure S3B, and Supplementary Figure S4B;
zusätzliche Informationen), we notice a trend of grouping neurons at the same command-chain
Ebene. Starting from the top of Figure 5, we ﬁnd AIA, AIB, AIY, and AIZ jointly known for their
role on locomotory behavior and acting as a ﬁrst-relay drives (Gray, Hill, & Bargmann, 2005;
Wakabayashi, Kitagawa, & Shingai, 2004). Moving clockwise, we ﬁnd RIA and RIB acting
as second-layer intermediates, and further on, neurons such as AVE, and in the next cluster
AVAL and AVD, all being command interneurons (Haspel, O’Donovan, & Hart, 2010; Hobert,
2003; Kawano et al., 2011). The trend of following the locomotory pathway clockwise in the
embedding space suggests that the approach targets relevant information about the neural sys-
tem. Jedoch, the exact compact clusters in Supplementary Figure S4B (Supporting Informa-
tion) need further elaboration. Some of the interesting ﬁndings worth exploring would be the
unexplained grouping of the scarcely studied RIR neuron (Hobert, Johnston, & Chang, 2002)
with the cluster of cells including AIB and AIY, or the grouping of PVR and LUA (Chalﬁe et al.,
1985; Wicks & Rankin, 1995) with locomotion-regulating neurons such as AVD and AVA.

Considering motoneurons (Figur 6, Supplementary Figure S3C, and Supplementary
Figure S4C), the embedding positions ﬁt somatic location (see Supplementary Figure S7): a spi-
ral beginning at the origin, turning right, then moving clockwise and ending in the top branch
follows the postero-anterior direction (zusätzliche Informationen). This conﬁrms that the approach
has extracted meaningful information. Jedoch, the exact split between the three branches as
well as the k-means clustering into the seven ensembles remains unclear, seit, from prelimi-
nary explorations, we ﬁnd both A-type and B-type cholinergic motoneurons and the inhibitory
D-type motoneurons in all clusters. Endlich, DVB deserves further attention (Schuske, Beg, &
Jorgensen, 2004) because of its isolated location between the two bottom branches.

In Figure 6B, two sensory nodes stick out the furthest away from the center; das ist, towards
the lower left and right branches of motoneurons. These are PVD and PHC neurons, responsible
for nociceptive mechano- and thermosensation, jeweils. The locations of these nodes in
the embedding may be linked to the fact that harmful nociceptive stimuli induce a locomotory

Netzwerkneurowissenschaften

822

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Guided graph spectral embedding

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 7. Summary of the main functions operated by the sensory neurons (A), interneurons (B), and motoneurons (C) unraveled by guided
spectral analysis. Clusters of neurons discussed in the Discussion section are delineated and color coded according to their main roles: Das
may be in sensing (thermosensation in red, olfactory sensation in yellow, chemosensation in green, and mechanosensation in blue), higher
order functions (reproduction in pink, food responses in brown), or locomotion (from ﬁrst cellular relays to effector motoneurons in increasingly
darker shades of gray). A gradient in the color coding indicates that more than one function is performed by neurons from a given cluster.
Neurons that could not be clearly related to the rest of the unraveled circuitry are encircled in white.

Netzwerkneurowissenschaften

823

Guided graph spectral embedding

response. As in the case of RIP interneurons emerging in the focused embedding of sensory
Neuronen, we once again conﬁrm the ability of the proposed approach to extract important
nodes even when their cooperation weight was initially set to 0.

Zusammenfassend, as illustrated in Figure 7, all three types of neurons found in the C. elegans
nematode could be arranged in a meaningful hierarchy thanks to the introduced guided graph
spectral embedding. Sensory neurons were separated between ﬁrst-order and higher order
sensors. Different levels of processing of motor functions were distinguished (see the gradient
from white to dark gray tones going clockwise in Figure 7B), with the eventual recruitment of
motoneurons, which have been separated on the basis of somatic location. Future analyses will
allow the study of different types of neurons through more elaborate combinations of focused
Knoten. Zusätzlich, it will be interesting to see whether future experimental work can shed light
on some of the neurons that were extracted here without being yet extensively documented in
the literature, such as AVKL or RIR.

Perspectives for Future Uses

The proposed graph embedding provides a simple, yet powerful approach to visualization and,
if combined with clustering techniques, to the extraction of meaningful subgraphs from any
graph-modeled dataset. In neuroimaging, focusing on a speciﬁc subgraph of interest (by setting
the appropriate cooperation values) can direct research onto clinically relevant concepts, solch
as the medial temporal lobe and limbic structures for human brain imaging studies comparing
healthy controls and Alzheimer patients (Krasuski et al., 1998). Be it using the structural or
the functional connectome for analyses (Contreras, Goñi, Risacher, Spurns, & Saykin, 2015),
features such as cluster size and/or the inclusion of speciﬁc nodes (Gehirnregionen) in a cluster
may become biomarkers for an early diagnosis or prediction of the disease.

Außerdem, graph modeling of the human brain is frequently employed to extract impor-
tant nodes/brain regions and to identify their topological roles, such as provincial/connector
hubs suggesting clinically signiﬁcant functional roles (van den Heuvel & Spurns, 2013). Do-
ing so requires the use of diverse node centrality measures, such as degree or betweenness
centrality. Andererseits, entries of the proposed Slepian eigenvectors may be interpreted
as higher order spectral centrality measures relative to the focused subgraph, and for the spe-
cial case M = I, the eigenvector corresponding to the highest positive eigenvalue reverts to
the eigenvector centrality (M. Newman, 2010). Somit, if clustering of a dataset based on the
proposed embedding coordinates reveals nodes distant from the rest of the graph, it is sug-
gested that those nodes exhibit a hub-like role when the focused subgraph is considered more
important than the rest of the graph. Zum Beispiel, the AIA pair in the discussed C. elegans
example emerges as a separate cluster in Figure 5 and Supplementary Figure S4B (Supporting
Information), where the focus is set on interneurons. Its role as a hub can be conﬁrmed by the
high number of connections to the set of amphid neurons, and a small number of connections
to the other cells, as compared with the rest of the interneurons. Identiﬁcation of hubs and/or
peripheral nodes with respect to other similar type nodes may lead to a better understanding
of the functional role of both neurons and brain regions, depending on the inspected dataset.

BEITRÄGE DES AUTORS

Miljan Petrovic: Untersuchung; Methodik; Validierung; Writing – Review & Editing. Thomas
Bolton: Formale Analyse; Visualisierung; Writing – Review & Editing. Maria Giulia Preti: Writing –
Rezension & Editing. Raphaël Liégeois: Methodik; Validierung; Writing – Review & Editing.
Dimitri Van De Ville: Konzeptualisierung; Formale Analyse; Writing – Original Draft; Writing –
Rezension & Editing.

Netzwerkneurowissenschaften

824

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Guided graph spectral embedding

FUNDING INFORMATION

Dimitri Van De Ville, CHIST-ERA IVAN project (http://dx.doi.org/10.13039/501100001942),
Award ID: 20CH21_174081. Dimitri Van De Ville, Schweizerischer Nationalfonds zur
Förderung der Wissenschaftlichen Forschung (http://dx.doi.org/10.13039/501100001711),
Award ID: 200021_175506. Dimitri Van De Ville, Bertarelli Foundation. Maria Giulia Preti,
Center for Biomedical Imaging (CIBM) of the Geneva–Lausanne Universities and the EPFL.

VERWEISE

Agaskar, A., & Lu, Y. M. (2013). A spectral graph uncertainty princi-
Bitte. IEEE Transactions on Information Theory, 59(7), 4338–4356.
Arenas, A., Fernández, A., & Gómez, S. (2008). Analysis of the
structure of complex networks at different resolution levels.
New Journal of Physics, 10(5), 053039.

Bargmann, C. ICH., Hartwieg, E., & Horvitz, H. R. (1993). Odorant-
selective genes and neurons mediate olfaction in C. elegans.
Cell, 74(3), 515–527.

Bargmann, C. ICH., & Horvitz, H. R. (1991). Chemosensory neurons
with overlapping functions direct chemotaxis to multiple chem-
icals in C. elegans. Neuron, 7(5), 729–742.

Barrios, A., Ghosh, R., Fang, C., Emmons, S. W., & Barr, M. M.
(2012). PDF-1 neuropeptide signaling modulates a neural circuit
for mate-searching behavior in C. elegans. Naturneurowissenschaften,
15(12), 1675.

Belkin, M., & Niyogi, P. (2003). Laplacian eigenmaps for dimen-
sionality reduction and data representation. Neural Computa-
tion, 15(6), 1373–1396.

Chalﬁe, M., Sulston, J. E., White, J. G., Southgate, E., Thomson,
J. N., & Brenner, S. (1985). The neural circuit for touch sensi-
tivity in Caenorhabditis elegans. Zeitschrift für Neurowissenschaften, 5(4),
956–964.

Chen, B. L., Hall, D. H., & Chklovskii, D. B. (2006). Wiring opti-
mization can relate neuronal structure and function. Verfahren
der Nationalen Akademie der Wissenschaften, 103(12), 4723–4728.
Chung, F. R. K. (1997). Spectral graph theory. Providence: amerikanisch

Mathematical Society.

Contreras, J. A., Goñi, J., Risacher, S. L., Spurns, O., & Saykin,
A. J. (2015). The structural and functional connectome and pre-
diction of risk for cognitive impairment in older adults. Current
Behavioral Neuroscience Reports, 2(4), 234–245. https://doi.org/
10.1007/s40473-015-0056-z

De Lange, S., De Reus, M., & Van den Heuvel, M. (2014). The lapla-
cian spectrum of neural networks. Frontiers in Computational
Neurowissenschaften, 7(189), 1–12.

Fiedler, M. (1989). Laplacian of graphs and algebraic connectivity.

Combinatorics and Graph Theory, 25, 57–70.

Gray, J. M., Hill, J. J., & Bargmann, C. ICH. (2005). A circuit for nav-
igation in Caenorhabditis elegans. Verfahren des Nationalen
Akademie der Wissenschaften, 102(9), 3184–3191.

Hammond, D. K., Vandergheynst, P., & Gribonval, R.

(2011).
Wavelets on graphs via spectral graph theory. Applied and Com-
putational Harmomic Analysis, 30(2), 129–150.

Hart, A. C., Sims, S., & Kaplan, J. M. (1995). Synaptic code for sen-
sory modalities revealed by C. elegans GLR-1 glutamate receptor.
Natur, 378(6552), 82.

Haspel, G., O’Donovan, M.

(2010). Moto-
neurons dedicated to either forward or backward locomotion in
the nematode Caenorhabditis elegans. Zeitschrift für Neurowissenschaften,
30(33), 11151–11156.

J., & Hart, A. C.

Hobert, Ö. (2003). Behavioral plasticity in C. elegans: Paradigms,

circuits, genes. Journal of Neurobiology, 54(1), 203–223.

Hobert, O., Johnston, R. J., Jr., & Chang, S. (2002). Left–right asym-
metry in the nervous system: The Caenorhabditis elegans model.
Nature Reviews Neurowissenschaften, 3(8), 629.

Huang, W., Bolton, T. A., Medaglia, J. D., Bassett, D. S., Ribeiro, A.,
& Van De Ville, D. (2018). A graph signal processing perspective
on functional brain imaging. Proceedings of the IEEE.

Irion, J., & Saito, N. (2014). Hierarchical graph Laplacian eigen
transforms. JSIAM Letters, 6, 21–24. https://doi.org/10.14495/
jsiaml.6.21

Kawano, T., Po, M. D., Gao, S., Leung, G., Ryu, W. S., & Zhen, M.
(2011). An imbalancing act: Gap junctions reduce the backward
motor circuit activity to bias C. elegans for forward locomotion.
Neuron, 72(4), 572–586.

Krasuski, J. S., Alexander, G. E., Horwitz, B., Daly, E. M., Murphy,
D. G., Rapoport, S. ICH., & Schapiro, M. B. (1998). Volumes of me-
dial temporal lobe structures in patients with alzheimer’s disease
and mild cognitive impairment (and in healthy controls). Bio-
logical Psychiatry, 43(1), 60–68. https://doi.org/10.1016/s0006-
3223(97)00013-9

Lehoucq, R. B., & Sorensen, D. C. (1996). Deﬂation techniques for
an implicitly restarted Arnoldi iteration. SIAM Journal on Matrix
Analysis and Applications, 17(4), 789–821.

Li, Z., Li, Y., Yi, Y., Huang, W., Yang, S., Niu, W., . . . Xu, T. (2012).
Dissecting a central ﬂip-ﬂop circuit that integrates contradictory
sensory cues in C. elegans feeding regulation. Nature Commu-
nications, 3, 776.

Lu, L.-Z., & Pearce, C. E. M. (2000). Some new bounds for singular
values and eigenvalues of matrix products. Annals of Operations
Forschung, 98(1–4), 141–148.

Luo, L., Wen, Q., Ren, J., Hendricks, M., Gershow, M., Qin, Y.,
. . . Zhang, Y. (2014). Dynamic encoding of perception, Erinnerung,
and movement in a C. elegans chemotaxis circuit. Neuron, 82(5),
1115–1128.

Mahadevan, S., & Maggioni, M. (2006). Value function approxi-
mation with diffusion wavelets and Laplacian eigenfunctions. In
Y. Weiss, B. Schölkopf, & J. C. Platt (Hrsg.), Advances in neural in-
formation processing systems 18 (S. 843–850). Cambridge, MA:
MIT Press.

Mhaskar, H. (2018). A uniﬁed framework for harmonic analysis of
functions on directed graphs and changing data. Applied and

Netzwerkneurowissenschaften

825

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Guided graph spectral embedding

Computational Harmonic Analysis, 44(3), 611–644. https://doi.
org/10.1016/j.acha.2016.06.007

Mori, ICH., & Ohshima, Y. (1995). Neural regulation of thermotaxis in

Caenorhabditis elegans. Natur, 376(6538), 344.

Newman, M. (2010). Netzwerke: An introduction. New York, New York:

Oxford University Press.

Newman, M. E. J. (2006). Finding community structure in networks
using the eigenvectors of matrices. Physical Review E, 74(3).
https://doi.org/10.1103/physreve.74.036104

Ortega, A., Frossard, P., Kovaˇcevi´c,

J. M., &
Vandergheynst, P. (2018). Graph signal processing: Overview,
Herausforderungen, and applications. Proceedings of the IEEE, 106(5),
808–828.

J., Moura,

Pirondini, E., Vybornova, A., Coscia, M., & Van De Ville, D.
(2016). Spectral method for generating surrogate graph signals.
IEEE Signal Processing Letters, 23(9), 1275–1278. https://doi.org/
10.1109/LSP.2016.2594072

Rousseeuw, P. J. (1987) Silhouettes: A graphical aid to the interpreta-
tion and validation of cluster analysis. Journal of Computational
and Applied Mathematics, 20, 53–65. https://doi.org/10.1126/
science.290.5500.2323

Roweis, S. T. (2000). Nonlinear dimensionality reduction by locally
linear embedding. Wissenschaft, 290(5500), 2323–2326. https://doi.
org/10.1016/0377-0427(87)90125-7

Sammon, J. (1969). A nonlinear mapping for data structure analy-
Schwester. IEEE Transactions on Computers, C-18(5), 401–409. https://
doi.org/10.1109/t-c.1969.222678

Sandryhaila, A., & Moura, J. M. F. (2013). Discrete signal pro-
cessing on graphs. IEEE Transactions on Signal Processing, 61(7),
1644–1656.

Sawin, E. R., Ranganathan, R., & Horvitz, H. R. (2000). C. elegans
locomotory rate is modulated by the environment through a
dopaminergic pathway and by experience through a serotonergic
pathway. Neuron, 26(3), 619–631.

Schaub, M. T., Delvenne, J.-C., Lambiotte, R., & Barahona, M.
(2018). Multiscale dynamical embeddings of complex networks.
Schönemann, P. H. (1966). A generalized solution of the orthogo-

nal procrustes problem. Psychometrika, 31(1), 1–10.

Schuske, K., Beg, A. A., & Jorgensen, E. M. (2004). The GABA
nervous system in C. elegans. Trends in den Neurowissenschaften, 27(7),
407–414.

Shen, X., & Meyer, F. G. (2008). Low-dimensional embedding of
fMRI datasets. NeuroImage, 41(3), 886–902. https://doi.org/10.
1016/j.neuroimage.2008.02.051

Schumann, D.

ICH., Narang, S. K., Frossard, P., Ortega, A., &
Vandergheynst, P. (2013). The emerging ﬁeld of signal processing
on graphs: Extending high-dimensional data analysis to networks
and other irregular domains. IEEE Signal Processing Magazine,
30(3), 83–98.

Slepian, D.

(1978). Prolate spheroidal wave-functions, Fourier-
Analyse, and uncertainty. Discrete case. Bell System Technical
Zeitschrift, 57(5), 1371–1430.

Slepian, D., & Pollak, H. Ö. (1961). Prolate spheroidal wave func-
tionen, Fourier analysis, and uncertainty. Bell System Technical
Zeitschrift, 40(1), 43–63.

Teke, O., & Vaidyanathan, P. P. (in press). Uncertainty principles
and sparse eigenvectors of graphs. IEEE Transactions on Signal
Processing.

Tenenbaum, J. B. (2000). A global geometric framework for non-
linear dimensionality reduction. Wissenschaft, 290(5500), 2319–2323.
https://doi.org/10.1126/science.290.5500.2319

Tsitsvero, M., Barbarossa, S., & Di Lorenzo, P. (2016). Signals on
graphs: Uncertainty principle and sampling. IEEE Transactions on
Signal Processing, 64(18), 4845–4860.

van den Heuvel, M. P., & Spurns, Ö. (2013). Network hubs in the
human brain. Trends in den Kognitionswissenschaften, 17(12), 683–696.
https://doi.org/10.1016/j.tics.2013.09.012

van der Maaten, L., & Hinton, G. (2008). Visualizing data using
t-SNE. Journal of Machine Learning Research, 9, 2579–2605.
Retrieved from http://www.jmlr.org/papers/v9/vandermaaten08a.
html

Van De Ville, D. (2016). Steering macro-scale network community

structure by micro-scale features. arXiv: 1603.05623

Van De Ville, D., Demesmaeker, R., & Preti, M. G. (2017A). Guid-
ing network analysis using graph Slepians: An illustration for the
C. elegans connectome. In Wavelets and sparsity xvii (Bd. 10394,
P. 103941Y).

Van De Ville, D., Demesmaeker, R., & Preti, M. G. (2017B). Wann
Slepian meets Fiedler: Putting a focus on the graph spectrum.
IEEE Signal Processing Letters, 24, 1001–1004. https://doi.org/
10.1109/LSP.2017.2704359

Varier, S., & Kaiser, M. (2011). Neural development features: Spatio-
temporal development of the Caenorhabditis elegans neuronal
Netzwerk. PLoS Computational Biology, 7(1), e1001044.

Varshney, L. R., Chen, B. L., Paniagua, E., Hall, D. H., & Chklovskii,
D. B. (2011). Structural properties of the Caenorhabditis elegans
neuronal network. PLoS Computational Biology, 7(2), e1001066.
Von Luxburg, U. (2007). A tutorial on spectral clustering. Statistics

and Computing, 17(4), 395–416.

Wakabayashi, T., Kitagawa, ICH., & Shingai, R. (2004). Neurons reg-
ulating the duration of forward locomotion in Caenorhabditis
elegans. Neuroscience Research, 50(1), 103–111.

White, J. G., Southgate, E., Thomson, J. N., & Brenner, S. (1986). Der
structure of the nervous system of the nematode Caenorhabditis
elegans. Philosophical Transactions of
the Royal Society of
London B: Biological Sciences, 314(1165), 1–340.

Wicks, S. R., & Rankin, C. H. (1995). Integration of mechanosen-
sory stimuli in Caenorhabditis elegans. Zeitschrift für Neurowissenschaften,
15(3), 2434–2444.

Netzwerkneurowissenschaften

826

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

F
/

3
3
8
0
7
1
0
9
2
4
0
4
N
e
N
_
A
_
0
0
0
8
4
P
D