BRIEF
Communicated by Mika Rubinov
Comparison of Different Generalizations of Clustering
Coefficient and Local Efficiency for Weighted
Undirected Graphs
Yu Wang
Eshwar Ghumare
eshwargorakhnath.ghumare@kuleuven.be
Laboratory for Cognitive Neurology, Department of Neurosciences, KU Leuven,
Leuven 3000, Belgien
Rik Vandenberghe
rik.vandenberghe@uzleuven.be
Laboratory for Cognitive Neurology, Department of Neurosciences, KU Leuven,
Leuven 3000, Belgien, and Alzheimer Research Centre, KU Leuven, Leuven
Institute for Neuroscience and Disease, KU Leuven, Leuven 3000, Belgien
Patrick Dupont
patrick.dupont@kuleuven.be
Laboratory for Cognitive Neurology, Department of Neurosciences, KU Leuven,
Leuven 3000, Belgien; Alzheimer Research Centre, KU Leuven, Leuven
Institute for Neuroscience and Disease, KU Leuven, Leuven 3000, Belgien; Und
Medical Imaging Research Center, KU Leuven and University Hospitals Leuven,
Leuven 3000, Belgien
Binary undirected graphs are well established, but when these graphs are
konstruiert, often a threshold is applied to a parameter describing the
connection between two nodes. daher, the use of weighted graphs is
more appropriate. In this work, we focus on weighted undirected graphs.
This implies that we have to incorporate edge weights in the graph mea-
sures, which require generalizations of common graph metrics. After re-
viewing existing generalizations of the clustering coefficient and the local
efficiency, we proposed new generalizations for these graph measures. To
be able to compare different generalizations, a number of essential and
useful properties were defined that ideally should be satisfied. We ap-
plied the generalizations to two real-world networks of different sizes.
Infolge, we found that not all existing generalizations satisfy all es-
sential properties. Außerdem, we determined the best generalization
for the clustering coefficient and local efficiency based on their properties
and the performance when applied to two networks. We found that the
best generalization of the clustering coefficient is CM,hm, defined in Miya-
jima and Sakuragawa (2014), while the best generalization of the local
Neural Computation 29, 313–331 (2017)
doi:10.1162/NECO_a_00914
C(cid:2) 2017 Massachusetts Institute of Technology.
Veröffentlicht unter Creative Commons
Namensnennung 3.0 Unportiert (CC BY 3.0) Lizenz.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
314
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
efficiency is EP
loc, proposed in this letter. Depending on the application and
the relative importance of sensitivity and robustness to noise, other gen-
eralizations may be selected on the basis of the properties investigated
in this letter.
1 Einführung
A complex system can be modeled as a graph or network, which is com-
posed of nodes and edges connecting them. Analysis over a wide range of
complex systems has led to a fundamental insight: many complex systems
often share certain topological characteristics, and these can be captured
by graph-theoretical metrics (Barabasi & Oltvai, 2004; Amaral & Ottino,
2004; Zhang & Horvath, 2005; Bullmore & Spurns, 2009; Fornito, Zalesky, &
Breakspear, 2013). The small-world topology for example, has been found in
many real-world networks (Er, Chen, & Evans, 2007; Opsahl & Panzarasa,
2009; Batalle et al., 2012; Vandenberghe et al., 2013), and is an indication of
the cost-efficiency of these networks.
While traditional graph analysis uses binary edges to enhance contrast
between strong and weak connections, there is an increasing demand for
using edge weight, which entails potentially important information. Incor-
porating edge weights in the graph analysis calls for generalizations of the
graph metrics. While some of these measures can be naturally generalized
to a weighted version (z.B., node degree to node strength), others cannot
be generalized in a straightforward way. The generalization of clustering
coefficient and local efficiency, used to quantify the small-world topology
(Watt & Strogatz, 1998; Achard and Bullmore, 2007; Batalle et al., 2012), Ist
far from trivial.
The clustering coefficient reflects the tendency that neighbors of a node
are also neighbors to each other (Rubinow & Spurns, 2010). The clustering
coefficient is high in small-world networks compared to random networks
(Watt & Strogatz, 1998). Local efficiency is a measure for the fault toler-
ance of the system: it measures how efficient the communication is between
neighbors of a node when that node is removed (Latora & Marchiori, 2003).
A small-world network features a local efficiency intermediate to that of
regular (lattice) and random network (Achard & Bullmore, 2007; Batalle
et al., 2012). The two measures are related in a way that the clustering coef-
ficient in an undirected network is found to be a reasonable approximation
of local efficiency (Latora & Marchiori, 2003).
Although it is straightforward to find the neighbors of a node, the ques-
tion of how to define their weighted surrogates is far from obvious. Several
generalizations have been proposed (Barrat, Barthelemy, Pastor-Satorras,
& Vespignani, 2004; Utopie, Saram¨aki, Kert´esz, & Kaski, 2005; Zhang &
Horvath, 2005; Saram¨aki, Kivel¨a, Utopie, Kaski, & Kertesz, 2007; Opsahl &
Panzarasa, 2009; Miyajima & Sakuragawa, 2014; Rubinow & Spurns, 2010).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
315
Different definitions capture slightly different aspects of the network, yet
some of the generalizations are not designed for fully weighted networks
(Rubinow & Spurns, 2010; Barrat et al., 2004; Onnela et al., 2005). Diese
generalizations require the removal of the weak or noisy connections be-
forehand. A preferable solution is to adapt the equations in such a way that
they can be used for a fully weighted network (Zhang & Horvath, 2005;
Saram¨aki et al., 2007; Opsahl & Panzarasa, 2009; Miyajima & Sakuragawa,
2014).
In this letter, we first define a number of essential and useful properties
that ideally should be satisfied when using a generalized graph measure
and explain how we will evaluate them. Then we review the existing gen-
eralizations, and we propose new generalizations for the local efficiency
for fully weighted undirected networks with no self-connections. Endlich,
we make a thorough comparison of the different generalizations and apply
them to two real-world networks.
2 Methoden
Assume an undirected weighted network with N nodes and an N × N ad-
jancy matrix A for which the (ich, J)th element ai j is 1 if an edge between i and j
exists and 0 ansonsten. In this work, we assume that no self-connections are
= 0. For a binary undirected network, the clustering coefficient
present: aii
for node i is given by
C(ich) =
1
− 1)
(ki
ki
(cid:2)
J,H
ai jaiha jh
,
(2.1)
with ki the degree of node i. The node degree ki is defined as the number of
nodes connected to node i. The local efficiency is defined as
Eloc
(ich) =
1
− 1)
(ki
ki
(cid:2)
J,H; J(cid:3)=h
ai jaih[d jh
(Ni
−1,
)]
(2.2)
in which Ni is the subgraph consisting of the neighbors of i excluding node
) is the length of the shortest path between nodes j and
i itself, and d jh
h containing only neighbors of i. If no path containing these neighbors is
found, d jh
) = ∞.
(Ni
(Ni
In a weighted network, we define the weight matrix W in which each
element represents the weight w
i j between node i and node j. All weights
are assumed to be positive. If no connection is present, the weight is 0.
In this work, we focus on networks without self-connections: ∀i, w
= 0.
ii
The node degree ki is calculated based on the presence of connections with
nonzero weights irrespective of the amplitude. In case of a fully connected
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
316
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
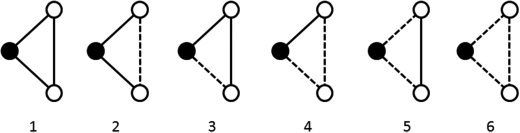
Figur 1: Six possible triangle configurations for node i filled in black. Normal
and dashed lines represent strong and weak edges, jeweils.
= N − 1. Der
weighted network with N nodes and no self-connections, ki
node strength, which takes into account the weight of the connection, Ist
defined by
=
si
(cid:2)
J
w
,
i j
Note that for a binary network in which w
i j
between nodes i and j and 0 ansonsten, si
= ki.
(2.3)
= 1 if a connection is present
2.1 Properties of Generalized Graph Measures. A generalization
Gw(W) of a binary graph measure Gb
(A) should ideally satisfy some prop-
erties. Some of these properties are essential, while others may depend on
the application. The essential properties are:
Das
• General versatility. If the input is given as a binary network, Die
output of the generalizations should give the same results as the
binary version: Gw = Gb when W = A (Miyajima & Sakuragawa,
2014).
• Continuity. The graph measure should be continuous,
Ist,
lim(cid:2)→0 Gw(W(cid:2) ) = Gw(W) in which W(cid:2) = W except for one connec-
tion weight, which differs by (cid:2) (Miyajima & Sakuragawa, 2014).
• Sensitivity. The graph measure should be able to make a distinction
between different cases for which the graph measure is designed.
Because the clustering coefficient and the local efficiency are defined
using triangles, we will evaluate the six possible cases in which the
weight is either low or high in one of the connections of the triangle
(siehe Abbildung 1).
• Robustness to noise. The graph measure Gw(W)(ich) for node i should
be robust when adding noise to the weights of the connections. Wenn
we assume a noise matrix ν, which represents additive noise on each
connection weight wν
i j, and define the mean relative error
i j
i j
(in percent) with respect to the noise-free measures as
= w
+ ν
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
317
(cid:4)(ν) = 100
N
(cid:3)
(cid:3)
(cid:3)
(cid:3)
N(cid:2)
i=1
Gw(W + ν)(ich) − Gw(W)(ich)
Gw(W)(ich)
(cid:3)
(cid:3)
(cid:3)
(cid:3) ,
(2.4)
then a small value of ||ν|| should lead to a small error value (cid:4)(ν).
Additional useful properties can be defined, but these properties de-
pend on the application under investigation and should not be considered
essential:
• Weight-scale invariance. The graph measure is invariant to a global
scale factor λ > 0 for all edges: Gw(λW) = Gw(W) (Miyajima &
Sakuragawa, 2014).
• Applicable to fully weighted networks. In some applications, it is ben-
eficial to avoid any thresholding of the weights of the connections
in a network. Infolge, every node is connected with every other
node, although the weights may be very small. A generalization of
the clustering coefficient and the local efficiency should be applicable
to such cases.
2.2 Generalizations. A good review of existing generalizations of the
clustering coefficient and local efficiency can be found in Miyajima and
Sakuragawa (2014). The authors investigated general versatility, weight-
scale invariance, and continuity. Hier, we investigate all criteria listed in
the previous section. We first give a short description of the different gen-
eralizations currently available.
Barrat et al. (2004) proposed a generalization by including the node
strength si and the weights of the connections from node i:
CB(ich) =
1
− 1)
(ki
si
(cid:2)
w
i j
+ w
2
J,H
ih
ai jaiha jh
.
(2.5)
If the network is fully weighted, CB(ich) = 1 for all nodes i.
Onnela et al. (2005) proposed a weighted clustering coefficient for node
i based on the weighted triangles, and this algorithm is used in the brain
connectivity toolbox (Rubinow & Spurns, 2010):
CO(ich) =
1
− 1)
(ki
ki
(cid:2)
(w
J,H
)1/3
w
w
i j
ih
jh
max(W )
.
(2.6)
Zhang and Horvath (2005) have defined, in their gene co-expression
network analysis, a clustering coefficient for node i for a fully weighted
Netzwerk. The original equation can be rewritten as (Saram¨aki et al., 2007):
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
(2.8)
(2.9)
318
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
CZ(ich) =
1
max(W )
(cid:4)
(cid:4)
w
i j
J,H
J,H; J(cid:3)=h
w
ih
w
i j
w
jh
w
ih
.
(2.7)
Holme, Park, Kim, and Edling (2007) have defined a similar definition
as the previous one except that in the denominator, J (cid:3)= h is not required:
CH (ich) =
1
max(W )
(cid:4)
J,H
(cid:4)
w
w
w
i j
w
ih
w
i j
ih
J,H
jh
.
Opsahl and Panzarasa (2009) proposed a generalization as
(cid:4)
COp(ich) =
(cid:4)
J,h f (w
, w
J,H; J(cid:3)=h f (w
i j
i j
)ai jaiha jh
ih
)ai jaih
, w
ih
.
): arithmetic mean
They proposed four methods to calculate f (w
i j
(COp,mean), geometric mean (COp,gm), and maximum (COp,max) and minimum
(COp,min) of the weights of the edges. We refer to the set of these four methods
by COp.
, w
ih
Miyajima and Sakuragawa (2014) extended the generalization of the
cluster coefficient of node i to the case of weighted directed networks using
different functions (multiplication, geometric mean, minimum, and har-
monic mean). The case of multiplication in the context of an undirected
network leads to the same generalization as the one from Holme et al.
(2007). For undirected networks, we give their other extensions below:
Geometric mean:
(cid:4)
(cid:5)(cid:6)
CM,gm(ich) =
(cid:4)
J,H
(cid:5)(cid:6)
J,H; J(cid:3)=h
w
w
i j
ih
w
jh
w
w
ih max(W )
i j
Minimum:
(cid:4)
CM,min(ich) =
Harmonic mean:
(cid:4)
J,h min(w
, w
J,H; J(cid:3)=h min(w
i j
, w
ih
, w
i j
jh
)
ih
)
(cid:4)
J,H; J(cid:3)=h
CM,hm(ich) =
(cid:4)
1w
i j
J,H; J(cid:3)=h
1w
i j
1
2
+ 1w
ih
2
+ 1
w
jh
1
2
+ 1w
ih
2
+ 1
max(W )
ai jaih
ai jaih
We refer to the set of these three methods by CM.
(2.10)
(2.11)
(2.12)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
319
A generalization of the local efficiency is given by Rubinov and Sporns
(2010):
ER
loc
(ich) =
1
− 1)
(ki
ki
(cid:2)
J,H; J(cid:3)=h
(w
w
ih[D
w
jh
(Ni
i j
−1)1/3,
)]
(2.13)
in which Ni is the subgraph consisting of the neighbors of i excluding node i
selbst, and dw
) is the shortest distance between nodes j and h containing
jh
only neighbors of i. The distance between nodes j and h in a weighted
network is defined as
(Ni
w
jh
D
=
(cid:2)
k,l
∈gW
j↔h
A
kl
,
1
w
kl
(2.14)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
j↔h the shortest weighted path between j and h. If no path containing
with gW
these neighbors is found, dw
jh
= ∞.
As is the case for the clustering coefficient, multiple generalizations can
be defined for the weighted local efficiency. We define three possible ex-
tensions that we compare with the current generalization ER
loc defined by
Rubinov and Sporns (2010).
The first alternative for the weighted local efficiency is given by
(cid:4)
EW
loc
(ich) =
1
max(W )
J,H; J(cid:3)=h
(cid:4)
((min(w
, w
i j
ih
(min(w
J,H; J(cid:3)=h
( ˜Ni
))3[dw
jh
))2
, w
i j
ih
)]−1
,
(2.15)
( ˜Ni
where dw
) is the adapted shortest distance between j and h. This adapted
jh
˜Ni
shortest distance was calculated as the shortest distance in the network
containing all neighbors of i excluding node i after replacing the weight of
edge ( J, H) to ˜w
jh:
˜w
jh
=
jh
w
w
w
i j
ih
(max(W ))3
.
(2.16)
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
˜Ni, dw
jh
( ˜Ni
) = ∞.
If no path containing nodes j and h is found in
Weighting by max(W ) makes the shortest distance invariant to the
weight scale.
The second alternative for the weighted local efficiency is given by
EP
loc
(ich) =
(cid:4)
J,H; J(cid:3)=h
(cid:4)
.w
w
i j
J,H; J(cid:3)=h
( ˜Ni
ih[dw
jh
.w
w
i j
ih
)]−1
,
(2.17)
320
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
and the third alternative, more closely related to the extension defined in
equation 2.13 Ist
NEIN
loc
(ich) =
1
max(W )1/3
(cid:4)
J,H
w1/3
i j
(cid:4)
w1/3
ih [dw
w1/3
i j
(N(cid:9)
ich
jh
w1/3
ih
J,H
)]−1
,
(2.18)
(N(cid:9)
ich
where dw
) is the adapted shortest distance between j and h. This adapted
jh
shortest distance was calculated as the shortest distance in the network N(cid:9)
ich
containing all neighbors of i excluding node i after replacing the weight of
edge ( J, H) Zu
w(cid:9)
jh
= w1/3
jh
.
If no path containing nodes j and h is found in N(cid:9)
ich, dw
jh
(2.19)
(N(cid:9)
ich
) = ∞.
2.3 Application to Two Real-World Networks. A number of essen-
tial (general versatility, continuity) and useful (weight-scale invariance and
applicability to fully weighted networks) properties are evaluated on a the-
oretical basis. The essential property sensitivity will be assessed by studying
the cases shown in Figure 1, while the fourth essential property robustness
to noise will be assessed using two real-world networks.
2.3.1 The Associative-Semantic Network. An empirical network was taken
to test the properties of the generalization. The associative-semantic net-
work is constructed from functional interactions between brain regions
activated during the associative-semantic task (Vandenberghe et al., 2013;
Wang et al., 2014) measured using fMRI. The network has 57 Knoten, welche
are mostly located in the left hemisphere. The data are taken from one el-
derly subject who participated in an fMRI measurement on a 3T Philips
System (Wang et al., 2014). The nodes were defined based on a previous
Experiment (Vandenberghe et al., 2013). Based on the average time series
in these nodes, partial correlations were calculated. The weight of the edge
between node i and j is calculated from the Fisher r-to-z transform zi j of the
partial correlation as
w
i j
= (2(cid:6)(|zi j
|) − 1)4,
(2.20)
Wo (cid:6) is the cumulative distribution function of the standard normal dis-
tribution. The weights are a measure of the functional interaction between
Gehirnregionen.
We will evaluate the robustness to noise of the different generalizations
by studying the situation in which we add noise to the Z-value (before the
transformation to weights) of each (nonzero) connection using a standard
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
321
normal distribution as noise model multiplied by some constant f > 0 Zu
model the amount of noise. After adding the noise, weights are calculated as
before using equation 2.20. We will study the case of f = 0.001, 0.01, Und 0.1
corresponding to different levels of noise ranging from weak to strong noise.
The average error will be calculated over 10 noise realizations.
Since this is a fully weighted network, we will also calculate the correla-
tion of the different versions of the clustering coefficient and local efficiency
between this fully weighted network and the soft-thresholded network
(thresholded such that the density is 80%, 60%, oder 40%). Often a thresh-
old is used to remove connections with low weight. This is referred to as
the creation of soft-thresholded weighted networks. We hypothesize that
weighted graph measures calculated for the original weighted network and
for the soft-thresholded weighted network are highly correlated, especially
when the density of the latter network is high.
2.3.2 The Resting State fMRI Network. The second network is a functional
connectivity network constructed from correlations between regional fMRI
times series, measured in 638 nodal locations from 27 gesunde Freiwillige
scanned in resting state on a Siemens 3T scanner. The details of this exper-
iment can be found in Crossley et al. (2013). The data of this network are
publicly available.1 Unfortunately, the connection strengths (expressed as
Z-scores) were already thresholded, and as a result, only the connections
with Z > 0.6 were available. daher, we can only study the robustness
to noise in this case. We will do this in the same way as the first real-
world network, including the transformation of Z-values to weights using
equation 2.20.
3 Ergebnisse
3.1 General Versatility. All the generalizations of the clustering coeffi-
cient, except CH, lead to the same equation in the case of binary undirected
Netzwerke, as can be easily seen from equations 2.5 Zu 2.7 Und 2.9 Zu 2.12,
where w
= ki. The generalization CH does not show
i j
general versatility because in the denominator, there is no requirement that
the two sides of a triangle should be different (d.h., when the triplet is not a
triangle but a line).
= 0 oder 1 and si
= ai j, ai j
The generalization of the local efficiency, introduced in equation 2.13,
does not show general versatility because of the power − 1
3 of the distance
compared to −1 in the binary case. Im Gegensatz, the generalizations of the
local efficiency proposed in this letter—equations 2.15, 2.17, and 2.18—do
show general versatility.
1https://sites.google.com/site/bctnet/datasets as GroupAverage_rsfMRI_matrix
.mat.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
322
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
Tisch 1: General Versatility and Continuity for Fully Weighted Networks of the
Different Generalizations.
Method General Versatility Continuity
CB
CO
CZ
CH
COp,mean
COp,gm
COp,max
COp,min
CM,gm
CM,min
CM,hm
ER
loc
EW
loc
EP
loc
NEIN
loc
Ja
Ja
Ja
NEIN
Ja
Ja
Ja
Ja
Ja
Ja
Ja
NEIN
Ja
Ja
Ja
NEIN
NEIN
Ja
Ja
NEIN
NEIN
NEIN
NEIN
Ja
Ja
Ja
NEIN
Ja
Ja
Ja
The results of each generalization for this criterion are summarized in
Tisch 1.
3.2 Continuity. The node degree ki is a discontinuous function for a
weighted network since any node with a nonzero weight is considered a
neighbor irrespective of the amplitude. This implies that the value for the
node degree ki will differ with 1 between the case in which an arbitrary
small weight is present for an edge between nodes i and j and the case in
which this edge is not present (d.h., has zero weight). Infolge, CB, CO, Und
ER
loc are not continuous. COp is also not continuous since in the numerator,
only closed triangles will contribute, no matter how small the weight of the
third connection in the triangle is and the contribution depends only on the
weights of the two other connections in the triangle. The other extensions—
CZ, CH, CM, EW
loc—are all continuous.
loc
The results of each generalization for this criterion are summarized in
loc, and EZ
, EP
Tisch 1.
3.3 Sensitivity. In Table 2, we show how far each generalization is able
to detect differences between each of the six possible cases shown in Figure 1
for the clustering coefficient and the local efficiency. We have given a weak
connection the value 0.1 and a strong connection the value 1 while assuming
that max(W ) = 1.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
323
Tisch 2: Sensitivity of the Clustering Coefficient and Local Efficiency for the
Cases Presented in Figure 1.
Number of Different
Values (max = 6) Minimum Maximum
1
4
4
4
1
1
1
1
2
2
4
4
5
5
2
1
0.1
0.1
0.0165
1
1
1
1
0.3162
0.1
0.1818
0.1
0.0001
0.001
0.4642
1
1
1
0.5
1
1
1
1
1
1
1
1
1
1
1
Method
CB
CO
CZ
CH
COp,mean
COp,gm
COp,max
COp,min
CM,gm
CM,min
CM,hm
ER
loc
EW
loc
EP
loc
NEIN
loc
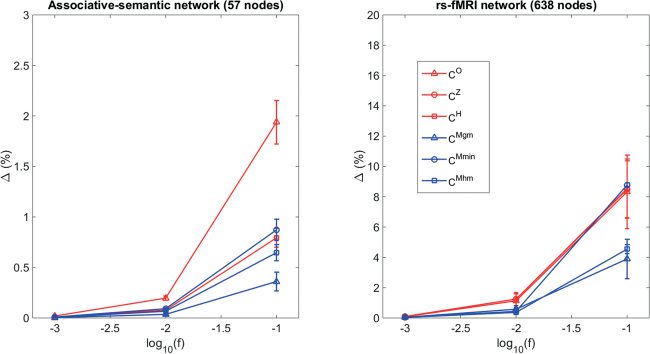
3.4 Robustness to Noise. When adding different amounts of gaussian
noise to both real-world networks, we observe that the generalizations CM,gm
and CM,hm of the clustering coefficient perform best for both networks across
all levels of noise used in this study with a mean error within 5%. Most of
the other generalizations also perform reasonably well, with mean errors
innerhalb 10% (siehe Abbildung 2).
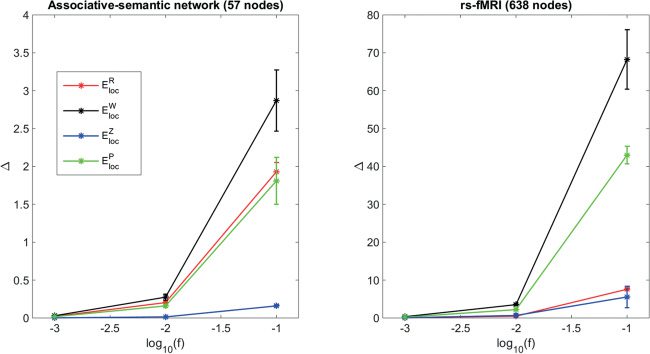
All generalizations of the local efficiency have an acceptable mean error
(d.h., less than 5%) in both networks when noise is not too large (siehe Abbildung 3).
Jedoch, when noise increases, only EZ
loc have mean errors below
10% in both networks.
loc and ER
3.5 Weight-scale Invariance and Applicability to Fully Weighted Net-
funktioniert. Weight-scale invariance is satisfied for all generalizations of the
clustering coefficient as can be derived mathematically by multiplying ev-
ery weight by a factor λ and observing that the result is independent of this
loc, EP
factor. The generalizations of the local efficiency EW
loc, and EZ
loc also show
weight-scale invariance, but this is not the case for ER
loc.
From equation 2.5 for CB and equation 2.9 for COp, we see that for fully
weighted networks, the clustering coefficient equals 1 for all nodes, Und
therefore we consider these generalizations not suitable for fully weighted
Netzwerke (siehe Tabelle 3). All other generalizations for the clustering coefficient
and the local efficiency can be used for fully weighted networks.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
324
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
Figur 2: Mean relative error (cid:4) of the robustness to noise of the clustering
coefficient for different generalizations as a function of the amount of gaussian
noise for the associative-semantic network (links) and the resting-state fMRI
Netzwerk (Rechts) on the nonzero connections. The noise fraction f is defined
as the factor that is multiplied with samples from the standard normal noise
distribution. In the left panel, the lines of CZ and CH almost coincide, and this is
also the case for CO, CZ, and CH in the right panel.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3: Mean relative error (cid:4) of the robustness to noise of the local efficiency
for different generalizations as a function of the amount of gaussian noise for the
associative-semantic network (links) and the resting-state fMRI network (Rechts).
The noise fraction f is defined as the factor that is multiplied with samples from
the standard normal noise distribution.
Generalizations of Clustering Coefficient and Local Efficiency
325
Tisch 3: Weight Scale Invariance and Applicability to Fully Weighted Networks
of the Different Generalizations.
Weight Scale
Invariance Weighted Networks
Suitable for Fully
Ja
Ja
Ja
Ja
Ja
Ja
Ja
Ja
Ja
Ja
Ja
NEIN
Ja
Ja
Ja
NEIN
Ja
Ja
Ja
NEIN
NEIN
NEIN
NEIN
Ja
Ja
Ja
Ja
Ja
Ja
Ja
Method
CB
CO
CZ
CH
COp,mean
COp,gm
COp,max
COp,min
CM,gm
CM,min
CM,hm
ER
loc
EW
loc
EP
loc
NEIN
loc
Tisch 4: Summary of the Main Findings.
Property
Clustering Coefficient
Local Efficiency
General versatility
Continuity
Sensitivitya
Robustness to noiseb
CM,hm, CM,gm, CM,min, CZ, CB, CO,
COp,gm, COp,mean, COp,max, COp,min
CM,hm, CM,gm, CM,min, CZ, CH
CM,hm, CZ, CH, CO, CM,gm, CM,min,
COp,gm, COp,mean, COp,max, COp,min, CB
CM,gm, CM,hm, CZ, CH, CM,min, CO
Weight scale invariance All generalizations
Applicable to fully
weighted networks
CM,hm, CM,gm, CM,min, CZ, CH, CO
loc, EW
EP
loc, NEIN
loc
loc, EW
EP
loc, EW
EP
loc, NEIN
loc
loc, NEIN
loc, ER
loc
loc, EW
loc
loc, EP
NEIN
loc, ER
loc, NEIN
loc, EW
EP
loc
All generalizations
Notiz: The generalizations listed satisfy the property or are ranked according to
Leistung.
aListed based on their overall ranking (siehe Tabelle 2) from best to worst.
bListed based on their overall ranking (see Figures 2 Und 3) from best to worst.
A summary table with the main findings for the essential and useful
properties is given in Table 4.
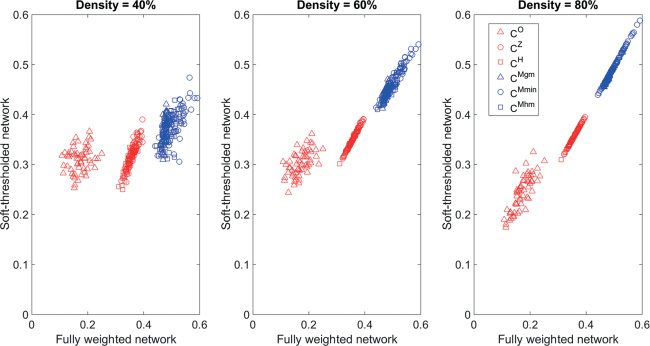
3.6 Soft-Thresholded Weighted Networks. For generalizations of the
clustering coefficient that can be applied to fully weighted networks, Wir
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
326
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
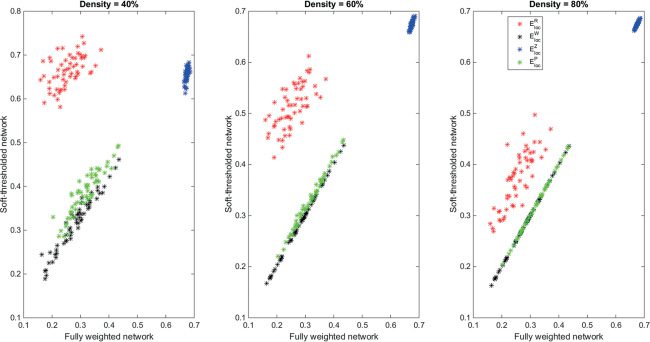
Figur 4: Scatter plot of the nodal clustering coefficient for different generaliza-
tions for nodes in the fully weighted network and the soft-thresholded weighted
associative-semantic network.
Tisch 5: Correlation between the Clustering Coefficient or Local Efficiency Cal-
culated in Each Node for the Fully Weighted Network and the Soft-Thresholded
Weighted Network in the Associative-Semantic Network.
Density (%)
40
60
80
CO
CZ
CH
CM,gm
CM,min
CM,hm
ER
loc
EW
loc
EP
loc
NEIN
loc
0.21
0.91
0.91
0.52
0.71
0.55
0.51
0.97
0.92
0.65
0.57
1.00
1.00
0.85
0.97
0.92
0.68
1.00
0.99
0.89
0.81
1.00
1.00
0.96
1.00
1.00
0.82
1.00
1.00
0.98
compared the values obtained in a fully weighted network with those ob-
tained in a soft-threshold network. Since we have only unthresholded data
for the associative-semantic network, the analysis is limited to this net-
arbeiten. The hypothesis is that there will be a high correlation between both
Fälle, especially when the density of the soft-thresholded network is high.
In Abbildung 4 und Tisch 5, the results are shown for different soft-threshold
Werte.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
327
Figur 5: Scatter plot of the nodal local efficiency for different generalizations
for nodes in the fully weighted network and the soft-thresholded weighted
associative-semantic network.
Zweite, we performed the same analysis for the generalizations of the
local efficiency. The results are shown in Figure 5 und Tisch 5.
4 Diskussion
In this letter, we have defined a set of essential and useful properties that
should ideally be satisfied for a generalization of a graph measure when
extending from a binary network to a (völlig) weighted network. Wir haben
compared all of these properties for the generalizations for the clustering
coefficient and the local efficiency found in the literature, as well as for new
generalizations. Some of the generalizations are especially suited in the case
von (völlig) weighted undirected graphs.
4.1 Essential Properties of Generalizations of Binary Graph Measures.
Generalizations from binary graph measures that are applicable to (völlig)
weighted graphs should ideally satisfy a number of properties. These prop-
erties can be subdivided into essential properties and useful properties.
The latter class of properties depends on the application and should be
considered relevant only in those applications.
The first essential property is general versatility, which refers to the fact
that when applying the generalization on a binary graph, the result should
be the same as the corresponding binary graph measure. This property is
not satisfied for the generalization CH of the clustering coefficient and the
generalization ER
loc of the local efficiency. The second essential property is
continuity, which means that an infinitesimal small change in one of the
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
328
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
weights should lead to an infinitesimal small change in the graph mea-
Sicher. This is not the case for CB, CO, and COp, and it is also not satisfied
for ER
loc. Important to note is that expressions for the local clustering coeffi-
cient CO (see equation 2.6) and the local efficiency ER
loc (see equation 2.13),
currently used in the brain connectivity toolbox in case of weighted undi-
rected graphs, are not satisfying continuity (Onnela et al., 2005; Rubinow &
Spurns, 2010). The third essential property is sensitivity to capture differ-
ent cases for which the graph measures are designed. We have evaluated
this property by looking at six possible cases for a simple triangle since
both clustering coefficient and local efficiency are based on triangles. Wir
found that the most sensitive generalizations for the clustering coefficient
are CO, CZ, CH, and CM,hm, which could distinguish four of six cases. Der
best generalizations for the local efficiency are EW
loc, which were able
to distinguish five of six cases. The fourth essential property is robustness
to noise. We have investigated the robustness against different amounts of
gaussian noise for two different real-world networks of different sizes. Wir
found that CM,gm and CM,hm were the most robust generalizations for the
clustering coefficient and EZ
loc are the most robust generalizations
for the local efficiency.
loc and ER
loc and EP
4.2 Useful Properties of Generalizations of Binary Graph Measures.
Weight-scale invariance means that the graph measure is invariant to a
global scale factor for all edges. In manchen Fällen, only relative connection
strengths can be determined, and this property is especially useful in such
Fälle. All generalizations of the clustering coefficient and the local efficiency
are weight-scale-invariant except the generalization ER
loc for the local effi-
ciency. Außerdem, all generalizations of the local efficiency can be applied
to fully weighted networks. This is also the case for most generatlizations
of the clustering coefficient except for CB and COp.
4.3 Fully Weighted Undirected Graphs. Most studies on graphs in
neuroscience are related to binary undirected graphs (Spurns, Honey, &
K ¨otter, 2007; He et al., 2007; Er, Chen, & Evans, 2008; Van Wijk, Stam, &
Daffertshofer, 2010; Vandenberghe et al., 2013). These graphs have either a
connection or not between a pair of nodes, and they are easy to analyze.
Jedoch, in order to obtain a binary graph, some measure of connectivity
(often continuous) between nodes needs to be calculated and then thresh-
olded on either amplitude or significance. The results of this procedure
critically depend on the threshold used and do not take into account the
strength of the connection. Infolge, true connections that do not sur-
vive the threshold are removed, while false connections may sometimes be
enthalten. An alternative is the use of weighted graphs. In order to avoid
taking into account spurious noisy connections, a soft threshold is some-
times applied, which removes these connections. The other connections
are weighted (Wang, Li, Metzak, Er, & Woodward, 2010; van den Heuvel,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
329
Mandl, Stam, Kahn, & Pol, 2010). This reduces the problem described above
but does not solve it completely. The advantage of fully weighted graphs is
that no thresholding is required and all connections are taken into account
(Mumford et al., 2010). The weight should then reflect not only the strength
of the actual underlying biological connection but also the probability of
being a true connection. daher, it might be necessary to apply a transfor-
mation from connection strength (z.B., defined by the (partial) correlation
between two nodes in fMRI based functional networks) to weights. In case
of the associative-semantic network, we have shown that the generaliza-
tions that are applicable to fully weighted networks show a high correlation
with the network, which is soft-thresholded, especially when the density of
the latter is high.
4.4 Choice of the Best Generalization. The choice of the best general-
ization is not always easy. The essential requirements of general versatility
and continuity can be proven mathematically, and they are completely in-
dependent of the application. The relative importance of the two other
essential properties, sensitivity and robustness to noise, depend on the ap-
plication and most likely requires a trade-off between these two properties.
In this study, we have tried to quantify sensitivity based on the values ob-
tained for six possible triangles and robustness to noise by evaluating the
behavior when adding different amounts of gaussian noise. Based on our
results, we propose that the best generalization of the clustering coefficient
is CM,hm, which is more robust to noise compared to CZ. The choice of the
best generalization of the local efficiency is EP
loc, but if robustness to noise
is very important, NEIN
loc can be selected; sensitivity, Jedoch, will clearly be
lower compared to EP
loc. If the noise in an application is nongaussian, a simi-
lar approach, as we have shown, can be taken for the noise model, welches ist
more appropriate for the application. Satisfying the useful properties can be
important but depends on the application. Despite the difficulty in selecting
the optimal generalization, we believe that readers can use the assessment
of all properties for all generalizations to a select the best generalization for
the application under study.
5 Abschluss
In this letter, we have focused on the comparison of different generaliza-
tions for the clustering coefficient and local efficiency to the case of (völlig)
weighted networks by looking at different properties of these graph mea-
sures and studying the performance in two real-world networks of different
sizes. The best generalization of the clustering coefficient is CM,hm, defined
in Miyajima and Sakuragawa (2014), while the best generalization of the
local efficiency is EP
loc proposed in our work. Depending on the application
and the relative importance of sensitivity and robustness to noise, andere
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
330
Y. Wang, E. Ghumare, R. Vandenberghe, and P. Dupont
generalizations may be selected on the basis of the properties investigated
in this letter.
Danksagungen
This work was supported by Research Foundation Flanders (FWO;
G0660.09 and G0A0913N to R.V. and P.D.), KU Leuven (OT/12/097 to R.V.
and P.D.), Federaal Wetenschapsbeleid belspo (IAP-VII P7/11), and Sticht-
ing voor Alzheimer Onderzoek (SAO11020 and 13007). Y.W. has a grant
from the Chinese Scholarship Council, and R.V. is a senior clinical inves-
tigator. We thank both reviewers for their constructive comments, welche
greatly improved the letter.
Verweise
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economical brain functional
Netzwerke. PLoS Computational Biology, 3(2), e17.
Amaral, L. A., & Ottino, J. M. (2004). Complex networks. European Physical Journal
B—Condensed Matter and Complex Systems, 38, 147–162.
Barabasi, A.-L., & Oltvai, Z. N. (2004). Network biology: Understanding the cell’s
functional organization. Nature Reviews Genetics, 5, 101–113.
Barrat, A., Barthelemy, M., Pastor-Satorras, R., & Vespignani, A. (2004). The architec-
ture of complex weighted networks. Verfahren der Nationalen Akademie der Wissenschaften
of the United States of America, 101, 3747–3752.
Batalle, D., Eixarch, E., Figueras, F., Mu ˜noz-Moreno, E., Bargallo, N., Illa, M., . . .
Gratacos, E. (2012). Altered small-world topology of structural brain networks
in infants with intrauterine growth restriction and its association with later neu-
rodevelopmental outcome. NeuroImage, 60, 1352–1366.
Bullmore, E., & Spurns, Ö. (2009). Complex brain networks: Graph theoretical anal-
ysis of structural and functional systems. Nat. Rev. Neurosci., 10, 186–198.
Crossley N. A., Mechelli, A., Vrtes, P. E., Winton-Brown, T. T., Patel, A. X., Ginestet,
C. E., . . . Bullmore, E. T. (2013). Cognitive relevance of the community structure
of the human brain functional coactivation network. Proc. Natl. Acad. Sci. USA,
110, 11583–11588.
Fornito, A., Zalesky, A., & Breakspear, M. (2013). Graph analysis of the human
connectome: Promise, progress, and pitfalls. NeuroImage, 80, 426–444.
Er, Y., Chen, Z. J., & Evans, A. C. (2007). Small-world anatomical networks in the
human brain revealed by cortical thickness from MRI. Cereb. Kortex, 17(10), 2407–
2419.
Er, Y., Chen, Z., & Evans, A. (2008). Structural insights into aberrant topological
patterns of large-scale cortical networks in Alzheimer’s disease. Journal of Neuro-
Wissenschaft, 28, 4756–4766.
Holme, P., Park, S. M., Kim, B. J., & Edling, C. R. (2007). Korean university life in a
network perspective: Dynamics of a large affiliation network. Physica A: Statistical
Mechanics and Its Applications, 373, 821–830.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Generalizations of Clustering Coefficient and Local Efficiency
331
Latora, V., & Marchiori, M. (2003). Economic small-world behavior in weighted
Netzwerke. European Physical Journal B—Condensed Matter and Complex Systems, 32,
249–263.
Miyajima, K., & Sakuragawa, T. (2014). Continuous and robust clustering coefficients for
weighted and directed networks. arXiv:1412.0059
Mumford, J. A., Horvath, S., Oldham, M. C., Langfelder, P., Geschwind, D. H.,
& Poldrack, R. A. (2010). Detecting network modules in fMRI time series: A
weighted network analysis approach. NeuroImage, 52, 1465–1476.
Utopie, J.-P., Saram¨aki, J., Kert´esz, J., & Kaski, K. (2005). Intensity and coherence of
motifs in weighted complex networks. Phys. Rev. E, 71, 065103.
Opsahl, T., & Panzarasa, P. (2009). Clustering in weighted networks. Social Networks,
31, 155–163.
Rubinow, M., & Spurns, Ö. (2010). Complex network measures of brain connectivity:
Uses and interpretations. NeuroImage, 52, 1059–1069.
Saram¨aki, J., Kivel¨a, M., Utopie, J.-P., Kaski, K., & Kertesz, J. (2007). Generalizations
of the clustering coefficient to weighted complex networks. Physical Review E, 75,
027105.
Spurns, O., Honey, C. J., & K ¨otter, R. (2007). Identification and classification of hubs
in brain networks. PloS One, 2(10), e1049.
van den Heuvel, M. P., Mandl, R. C., Stam, C. J., Kahn, R. S., & Pol, H. E. H. (2010).
Aberrant frontal and temporal complex network structure in schizophrenia: A
graph theoretical analysis. Zeitschrift für Neurowissenschaften, 30(47), 15915–15926.
Van Wijk, B. C., Stam, C. J., & Daffertshofer, A. (2010). Comparing brain networks
of different size and connectivity density using graph theory. PLoS One, 5(10),
e13701.
Vandenberghe, R., Wang, Y., Nelissen, N., Vandenbulcke, M., Dhollander, T., Sunaert,
S., & Dupont, P. (2013). The associative-semantic network for words and pictures:
Effective connectivity and graph analysis. Brain Lang., 127(2), 264–272.
Wang, L., Li, Y., Metzak, P., Er, Y., & Woodward, T. S. (2010). Age-related changes
in topological patterns of large-scale brain functional networks during memory
encoding and recognition. NeuroImage, 50, 862–872.
Wang, Y., Nelissen, N., Adamczuk, K., De Weer, A.-S., Vandenbulcke, M., Sunaert,
S., . . . Dupont, P. (2014). Reproducibility and robustness of graph measures of the
associative-semantic network. PloS One, 9(12), e115215.
Watt, D. J., & Strogatz, S. H. (1998). Collective dynamics of small-world networks.
Natur, 393(6684), 440–442.
Zhang, B., & Horvath, S. (2005). A general framework for weighted gene co-
expression network analysis. Statistical Applications in Genetics and Molecular Bi-
ology, 4(1), 1–43.
Received August 27, 2015; accepted September 5, 2016.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
9
2
3
1
3
2
0
1
5
4
0
4
N
e
C
Ö
_
A
_
0
0
9
1
4
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3