BRIEF
Communicated by S. Sathiya Keerthi
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
Michael Hopkins
michael.hopkins@manchester.ac.uk
Steve Furber
steve.furber@manchester.ac.uk
School of Computer Science, APT Group, University of Manchester,
Manchester M13 9PL, VEREINIGTES KÖNIGREICH.
Simulation of neural behavior on digital architectures often requires the
solution of ordinary differential equations (ODEs) at each step of the
Simulation. For some neural models, this is a significant computational
burden, so efficiency is important. Accuracy is also relevant because so-
lutions can be sensitive to model parameterization and time step. Diese
issues are emphasized on fixed-point processors like the ARM unit used
in the SpiNNaker architecture. Using the Izhikevich neural model as
an example, we explore some solution methods, showing how specific
techniques can be used to find balanced solutions.
We have investigated a number of important and related issues, wie zum Beispiel
introducing explicit solver reduction (ESR) for merging an explicit ODE
solver and autonomous ODE into one algebraic formula, with benefits for
both accuracy and speed; a simple, efficient mechanism for cancelling the
cumulative lag in state variables caused by threshold crossing between
time steps; an exact result for the membrane potential of the Izhikevich
model with the other state variable held fixed. Parametric variations of
the Izhikevich neuron show both similarities and differences in terms
of algorithms and arithmetic types that perform well, making an overall
best solution challenging to identify, but we show that particular cases
can be improved significantly using the techniques described.
Using a 1 ms simulation time step and 32-bit fixed-point arithmetic
to promote real-time performance, one of the second-order Runge-Kutta
methods looks to be the best compromise; Midpoint for speed or Trape-
zoid for accuracy. SpiNNaker offers an unusual combination of low en-
ergy use and real-time performance, so some compromises on accuracy
might be expected. Jedoch, with a careful choice of approach, results
comparable to those of general-purpose systems should be possible in
many realistic cases.
1 Einführung
In computational neuroscience, most neuron models are specified in the
form of ordinary differential equations (ODEs) or occasionally partial
Neural Computation 27, 2148–2182 (2015)
doi:10.1162/NECO_a_00772
C(cid:2) 2015 Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 3.0 Unportiert (CC BY 3.0) Lizenz
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2149
differential equations (PDEs), which are themselves usually reduced to
ODEs for efficient solution. The state variables within the equation model
the internal state of the neuron at any particular point in time, und das
ODE describes its dynamic behavior. The state variables are initialized at
the start of the simulation, and then the evolution of the neuron behavior is
computed by solving the ODE at each time point, taking into account state
variables and input history. There is a voluminous literature on the numer-
ical solution of initial value ODEs going back at least to the work of Euler in
1770 (Bashforth & Adams, 1883; Runge, 1895; Heun, 1900; Kutta, 1901; Eu-
ler, 1913; Gear, 1971; Lambert, 1973, 1991; Hall & Watt, 1976; Butcher, 2003).
A large variety of methods are available, and many trade-offs exist among
the three key performance measures of accuracy, stability and efficiency
(the last being defined in our context as “time taken per neural update”).
This letter aims to assess the options and find practical solutions that
are biased toward a particular set of circumstances while, wir hoffen, Auch
highlighting some more general principles and possibilities. In order to get
a balance between breadth and depth of analysis within space constraints,
we have chosen to look only at the Izhikevich model with a limited set of
variations in parameterization, input behavior, and initial conditions. Wir
hope that some of the ideas and methods will be useful more widely. Der
set of circumstances we focused on here are
1. 32-bit fixed-point arithmetic
2. Run-time efficiency as a primary motivation
3. The Izhikevich neural model
The first two requirements stem from the need to execute on the ARM968
processor used in the SpiNNaker architecture described in Furber, Galluppi,
Temple, and Plana (2014), which does not contain a hardware floating-
point unit, and the challenging aim of simulating large-scale neural models
in real time. The third requirement arises because the Izhikevich model is
widely used and provides a large number of realistic neural behaviors while
remaining manageable in terms of computational load. The continuous part
of the Izhikevich ODE model is defined in Izhikevich (2003) als:
dV
dt
dU
dt
= 140 + (5 + 0.04V )V − U + ICH,
= a(bV − U ),
(1.1)
(1.2)
where V represents a notional membrane voltage in mV, U represents a di-
mensionless membrane recovery variable, I is the input current to the neu-
ron in nA, and a and b are dimensionless parameters that define the dynamic
behavior of the recovery variable in terms of timescale and the sensitivity
to subthreshold fluctuations in V, jeweils. A second part of the model
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2150
M. Hopkins and S. Furber
defines the discontinuity that occurs when V hits the firing cutoff of the
neuron,
V → c,
U → U + D,
(1.3)
(1.4)
c being the postspike reset value for V and d being the postspike offset for
U. Thirty mV appears to be the defacto standard cutoff value for this pa-
rameterization of the model, and we have also chosen to use it. As Touboul
(2009) showed, the solution can be very sensitive to this value, und da
is an argument that it is therefore an important fifth parameter. Looking
at our results compared to Touboul, we do not appear to suffer from this
sensitivity in any case. It’s interesting to observe in Figure 1f of Touboul
that there seems to be a “clear patch” where bifurcation behavior is much
reduced around the 30 mV cutoff value. Perhaps this has contributed to the
common choice of this value.
The presence of this discontinuity in the state variables will be seen
to have an effect on both the solution methods that are most appropriate
and the refinements required to approximate continuous time when the
simulation is computed at discrete time points. It should be noted that many
current neural models have a similar discontinuity property (usually called
integrate-and-fire models). Izhikevich (2003) showed that by choosing {A,
B, C, D} appropriately, one can reproduce many realistic types of neural
behavior. Other studies that look at the options for numerical solution of
this type of equation are Humphries and Gurney (2007) and Touboul (2010).
In the following sections, we show that in the context being considered,
some ODE solution methods are more effective than others in terms of their
balance between efficiency and accuracy and that techniques can be used to
improve solutions by appropriately taking into account the specific nature
of the SpiNNaker simulation system and arithmetic hardware.
2 Classes of ODE Methodologies and Examples Chosen
A convenient way to consider the variety of methods available for solv-
ing initial value ODEs is to categorize them according to the nature of the
Algorithmus. A first consideration is explicit versus implicit. Implicit solvers
require the solution of a set of inherently nonlinear equations at each time
Punkt, usually via iterative algorithms—though direct solutions using lin-
earized approximations are possible in some cases. They provide desirable
properties in terms of improved stability when encountering the stiff nu-
merical behavior that can occur when solving neural ODEs. Stiffness in the
context of ODEs is explained in Butcher (2003): “These systems are charac-
terised by very high stability, which can turn into very high instability when
approximated by standard numerical methods” (P. 27).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2151
This extra numerical stability does not come for free, as it is significantly
more expensive computationally and therefore not of interest to us taking
into account our aim of real-time computation with limited computational
power. Im Gegensatz, explicit solvers use values already available or readily
computable and then predict the value(S) of the state variable(S) at the next
time point using a direct algebraic formula. Explicit solvers vary widely in
their stability characteristics.
Another consideration is fixed versus adaptive step size. Fixed step size
uses a constant time step for moving the simulation forward, whereas adap-
tive step size makes decisions on step size based on the nature of the solution
at each time point. Adaptive step size provides desirable properties for all of
the usual numerical requirements of accuracy, efficiency, and stability and
should always be considered if feasible. Jedoch, due to key aspects of the
simulation of large-scale neural systems on the SpiNNaker architecture,
the complexity and overhead of moving away from the underlying fixed
time-step behavior of the system as a whole make the global use of adaptive
time steps infeasible. In the spirit of practicality, we have therefore worked
with fixed time-step behavior in this study (apart from the reference results
used for comparison). It is important to keep this in mind when looking
at results, as it has an inevitable impact on the accuracy and stability of
Lösungen.
The order of a method expresses how quickly the prediction error im-
proves as step size reduces, but the exact implication of order differs de-
pending on the method being considered. Zum Beispiel, higher order should
reduce prediction error in general, but for some methods, stability will in-
crease while for others it will reduce. It needs to be borne in mind that the
sophisticated mathematical analysis underlying these results in most cases
assumes exact arithmetic. This can make actual behavior quite different
from the formal expectations, as highlighted in the following sections.
Butcher (2003) provides a helpful breakdown of the most commonly used
numerical algorithms into the following three dimensions: multistep—use
previous values of the state variables; multistage—calculate first deriva-
tives at multiple points between the current and next time point; Und
multiderivative—use higher derivatives calculated at the current time
Punkt. Example explicit methods relevant to our requirements are the fol-
lowing (for details see Gear, 1971; Lambert, 1973):
• Multistep: Linear multistep methods—Adams-Bashforth in simplest
bilden
• Multistage: Runge-Kutta
• Multiderivative: Taylor series and Parker-Sochacki
The basic Euler method is the simplest example of all three types and
Also, in a sense, defines the origin in this 3D space. Auch, hybrid methods
that combine features of some or all of the types are possible. A detailed
discussion of these potentially interesting hybrids is beyond the scope of
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2152
M. Hopkins and S. Furber
this letter, but some possibilities are mentioned later. An algorithm that does
not fit neatly into this scheme is the extrapolation method; the best-known
example is the Gragg-Bulirsch-Stoer (see Lambert, 1973; Drücken Sie, Teukolsky,
Vetterling, & Flannery, 1992; Stewart & Bair, 2009). This is probably the
first choice when very accurate solutions for smoothly behaving systems
are required, but it is not recommended when discontinuities in the state
variables are expected or when the derivative calculations are nontrivial.
We therefore restrict initial consideration to the following explicit, fixed
time step solution methods: Linear Multistep, Runge-Kutta, Taylor Series,
and Parker-Sochacki.
All are families of methods that provide different orders. For the Runge-
Kutta methods of order 2 and higher, there is an infinite variety of algorithms
for each order adjusted by free parameters that define the explicit equations
to be calculated. These considerations are expressed in the form of a Butcher
tableau, the most comprehensive description of which is given by Butcher
(2003). Rechnerisch, the Runge-Kutta methods require one derivative
calculation per order per state variable. The Taylor series method is sim-
ilar to Runge-Kutta in this respect but unique in analytical form for each
Befehl, as is Parker-Sochacki. The relevant explicit linear multistep method
(Adams-Bashforth) requires only one derivative calculation per state vari-
able independent of order, making it potentially very efficient.
In order to keep the numerical investigation manageable, we further trim
the methods being considered. The Parker-Sochacki method uses truncated
Picard iteration to compute a Maclaurin series and has already been suc-
cessfully applied to the Izhikevich model, unter anderen (for details of how
these methods fit together, see Stewart & Bair, 2009). It offers many op-
portunities for extra sophistication by, Zum Beispiel, automatically adapting
to provide a required level of accuracy and naturally expressing power
Serie, rational and transcendental functions using iterative polynomial op-
erations. It certainly deserves further study, but an initial analysis of the
computations required makes it clear that it is unlikely to be competitive in
terms of efficiency here and so has not been considered further.
The Adams-Bashforth method has great potential in terms of efficiency,
but the stability is poor, especially for higher orders, and in the presence of
stiff behavior, it is unlikely to converge reliably with realistic time steps. In-
corporating it into predictor-corrector algorithms with an Adams-Moulton
corrector and the local extrapolation technique sometimes called Milne’s
method increases stability significantly but also computational load (sehen
Lambert, 1991, for details of this combination and his Figures 4.1 Und 4.2
for a before-and-after comparison). Furthermore it requires extra mem-
ory to retain past values—the local fast memory that would be required
is at a premium in the SpiNNaker chip—and will not cope well with the
discontinuities in the state variables without extra administration code and
related overhead.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2153
So the final methods that are evaluated and compared with each other
and against a reference solution computed using the sophisticated ODE
solver available in the Mathematica environment (Wolfram Research, 2014)
are the Runge-Kutta and Taylor series.
3 Specifics and Implications of Fixed-Point Architecture
Compared to a standard numerical computation environment where
floating-point types and operations are available, working with fixed-point
arithmetic and the various constraints that come with it can be a challenge.
Historically, fixed-point arithmetic has usually been carried out using hand-
coded transformations of integer arithmetic (for an example of this in a
closely related context, see Jin, Furber, & Wald, 2008). A benefit of this
approach is that custom types can be generated for specific problems, Und
key arithmetic operations can be optimized for speed, including the use
of assembly language where appropriate. Jedoch, it makes the code sig-
nificantly harder to write, read, and maintain and is prone to hard-to-find
bugs. It is therefore not considered ideal for large-scale software engineer-
ing where ideas and code need to be shared between groups, especially
when those groups may contain more neuroscientists, mathematicians, Und
engineers than computer scientists. Glücklicherweise, the recent draft standard
TR18037 ISO/IEC (2008) offers a well-defined solution to this quandary by
types and arithmetic operations that use fixed-point arithmetic, while al-
lowing C code that looks very similar to that using the usual floating-point
types and operations and with all the required manipulations carried out
automatically by the compiler. This draft standard has been implemented
in the GCC development tool chain since the 4.7 release—currently for the
ARM target only. As the SpiNNaker architecture is based on ARM, we can
transparently apply this approach for our numerical work, and so the rest
of this letter works under this assumption unless stated otherwise. Unser
chosen default type is defined in the ISO draft as accum—a 32-bit signed
type with 16 integer bits and 15 fractional bits (s16.15) that allows efficient
arithmetic operations on the ARM processor.
With this consideration dealt with, the other important issues are
numerical—in particular, overflow, underflow, and quantization/rounding
Fehler. As discussed briefly in the previous section, most standard results on
accuracy and stability for ODE solvers are based on exact arithmetic. Sogar
for double precision floating point, we are a long way from this ideal case,
and in our target 32-bit architecture using the s16.15 type, other issues will
come into play. Work has been done to look specifically at the effect of round-
ing error on initial value ODEs (in Gill, 1951; Henrici, 1962; Babuˇska, Pr´ager,
& Vit´asek, 1966; Kahan, 1965; Vit´asek, 1969; Higham, 1996), but much of
the recent work is in the context of floating-point arithmetic, which has
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2154
M. Hopkins and S. Furber
different properties from fixed point—in particular, the various compen-
sated summation schemes recommended for floating-point algorithms (sehen,
e.g. section 4.3 of Higham, 1996) are of no benefit in fixed-point calculations.
The earliest three references are exceptions, with Gill (1951) providing
the detail of an ingenious mechanism for applying the traditional fourth-
order Runge-Kutta method in fixed-point arithmetic while minimizing the
effect of rounding errors in the calculation. Henrici (1962) provides an
analysis and examples of statistical distributions of rounding errors for
a number of explicit algorithms. Kapitel 2 Und 3 of Babuˇska et al. (1966)
provide an analysis of both fixed-point and floating-point errors in rela-
tion to ODE solutions with examples. Although details vary a great deal
between their examples and methods, a characteristic V-shaped pattern oc-
curs where the error reduces as step size is reduced until the point where
roundoff/quantization causes the error to rise again as step size is reduced
weiter. The slopes of this pattern depend on details of the equation and
whether floating-point or fixed-point arithmetic is being used.
Though interesting and relevant to some of our results, a thorough math-
ematical analysis of the difference between the two types of arithmetic is
outside the scope of this letter. One thing that has become apparent, Wie-
immer, is that the sensitivity to rounding error is difficult to characterize
analytically because the same algorithm can be implemented differently in
terms of, Zum Beispiel, the choice and ordering of interim variables, and this
in itself can make a significant difference to the accuracy of final results.
Our search for the best algorithm in each case was entirely manual and
clearly not provably optimal. Within that context, Jedoch, it was relatively
thorough, looking at a large number of possible equation factorizations and
orderings for variables and operations. Even with this limited approach,
significant differences were found between options that were identical if
considered in terms of their algebraic definition. We hope this has at least
demonstrated the potential of the approach. Work has been done on au-
tomating this process by Martel (2009), Darulova et al. (2013), and Gao,
Bayliss, and Constantinides (2013), and this would appear to be a poten-
tially fruitful way to proceed. We would add a note of caution to the ef-
fect that fixed-point types require very firm prior knowledge in order to
turn the process over to an automated method—in particular, strict guar-
antees that variables within algorithms will not overflow or underflow the
representable range in any possible use case—and that these are sometimes
more difficult to provide than might at first seem to be the case.
The key numerical details of working with the accum s16.15 type on an
ARM target are:
1. Absolute values < 0.000031 become zero.
2. Absolute values ≥ 65,536 wrap around (saturated types are available
but are much slower).
3. Precision is absolute rather than relative as with floating point.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2155
4. Division is very slow (due partly to details of the ARM instruction
set) and should be avoided.
5. There is no native transcendental function library (though one is
being developed in our group).
As might be expected, these points have a direct impact on the algorithms
that we are discussing here and will be referred back to when considering
implementations and results.
4 Implementation Details
The system language for SpiNNaker is ANSI C, and so this is the language
used for the implementation. An API was developed that provides a general
but also efficient interface between the neural model API and the ODE
solvers that might be of interest. A plug-in architecture was chosen that
provides the ability to test new algorithms while also promoting efficiency
in regard to such issues as compiler optimizations, memory access patterns,
and the use of registers. After some consideration, we arrived at a structure
similar to the one used in chapter 16 of Press et al. (1992) but focused on
our particular needs.
The API refers to a generic REAL type, which can be instantiated at
compile time to any type of interest—in our case, accum, long accum, float,
and double. This allows end-to-end comparison of all models and algorithms
with one type definition in a header file.
The ODE solver API includes the ability to internally reduce the solution
step size independent of the overall simulation time step. This is a useful
mechanism for increasing accuracy for a linear cost in efficiency if required.
The solver type is in general sent as a function pointer within the code in
order to be changed easily and is therefore ideal for comparative work.
However, the price to be paid for this generality is the time taken to de-
reference the pointer at each call. For production code, this overhead can
be reduced, with each successive specialization allowing the compiler to
shave off instructions required for the solve routine. This can be specialized
further if one knows in advance how many state variables will be in a neuron
definition by hard-coding the inner loops in the solver. Some examples of
the efficiency gains are given in section 7.
Another possibility for speed improvement that is orthogonal to the spe-
cializations just described is the use of static inline functions. Using this
technique, code is defined in the header file rather than the source file sim-
ilar to the usual use of templates in C++. Although the software package is
now rather less clean in terms of build and delivery, this technique allows
the compiler further optimization opportunities—in particular, code opti-
mizations across source files that would normally be compiled separately
and linked at build time. The efficiency benefits of this approach are also
discussed in section 7.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2156
M. Hopkins and S. Furber
An important idea that arose while considering implementation was the
following. As in any particular case we are working with a fixed step size,
explicit solver and known ODE, the calculations at any given time step
can be described algebraically instead of algorithmically, the normal imple-
mentation method. This can then be manipulated to, for example, simplify
and find common terms, which will reduce the computational overhead
and allow the compiler to find more optimizations. We have called this
explicit solver reduction (ESR), and it turns out that not only does it en-
able efficiency gains, but also the reduction chosen can help fixed-point
arithmetic retain more precision and avoid overflow and underflow condi-
tions and therefore improve accuracy as well. We give more details in the
examples. We call these quasi–closed form solutions as they approximate
closed-form solutions. Other software engineering benefits are that the use
of static inline functions is no longer required, as all relevant compiler opti-
mizations can now be done in the single source file where the computation
is defined and any given method/neuron combination can be delivered
pretested.
A broadly similar approach has been proposed recently by Stimberg,
Goodman, Benichoux, and Brette (2014). Although we have independently
come to the conclusion that there are benefits in combining the ODE and
solver into an algebraic equation, the motivation and the methods used are
different. For them, the emphasis is on a general mechanism for describing
models, easy testing of new ideas, and automatic code generation; for us,
it has been seen as an algebraic method of finding the best computational
trade-off between accuracy and efficiency, while simultaneously taking into
account the particular constraints of fixed-point arithmetic.
Like most other neurally inspired ODEs, the Izhikevich model is au-
tonomous, meaning that the equations make no explicit mention of the
time variable on the right-hand side; they are a function of neural param-
eters and values of the state variables only without time being referenced.
This allows Taylor series methods to be implemented algebraically in ad-
vance for any number of state variables using an elegant approach described
by Alsaker (2009). This means that these solver/neuron combinations can
be converted to quasi–closed form solutions directly with all the benefits
described previously.
5 Specifics of Neural Context
Previous work has used different default time steps, usually either 0.1 ms or
1 ms. The default on SpiNNaker was chosen as 1 ms to facilitate biological
real-time performance. As a result, most of the comparison work uses this
time step unless stated otherwise. Over time, this may change in order to
achieve more accuracy for ODE solutions and integration of synapses with
short time constants, and so some results will also be shown at 100 μs for
comparison.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2157
A particular feature of many neural ODEs is the discontinuity present
when a neuron state variable hits the cutoff and fires. In the case of the
Izhikevich model, both state variables have their values instantaneously
changed at this point. This generates two requirements for numerical
solutions:
1. A solution method that is not troubled by these discontinuities
2. A mechanism to correct for the threshold-crossing point being be-
tween time steps
The first has already been discussed. The second we describe here as time
quantization (TQ) and requires some more thought.
Correct handling of TQ should be dealt with by any comprehensive
ODE solution code, but naıve codes will ignore the issue and treat the
cutoff point as the next time step after the threshold has been crossed. It is
not hard to see that this will inevitably introduce a cumulative lag into the
progress of the state variables. Assuming a random uniform distribution
of the crossing point between time steps would imply that this approach
accumulates an expected lag of 1/
2 time step every time the neuron fires.
An improvement is possible, but this requires more processing and so must
be done efficiently. The simplest method is to add some time to the first
evolution of the state variables after the neuron has fired in order to allow it
to catch up the lost time. The obvious value to choose would be the expected
value of this loss: 1/
2 time step so that the first solve after the firing event
receives a time value of 11/
2 time steps. This removes the expected bias and
provides a maximum error of 1/
2 time step, a standard deviation for the
jitter introduced into the spike timing of about 0.29 time step, and a mean
absolute deviation of 1/
4 time step. This simple scheme performs quite well
and has low overhead. More sophisticated schemes are available, but the
most accurate ones require some form of iteration (e.g., Newton-Raphson in
section 3.2 of Stewart and Bair, 2009) and would therefore be too expensive
to consider given our challenging real time target.
More accurate direct solutions usually require some form of interpola-
tion for the time progress of the state variables between time steps. This
is a promising approach, but interpolation inevitably requires at least one
arithmetic division, which is very expensive on the ARM processor, and so
a technique is needed that approximates the ideal form of interpolation but
uses no divisions. We describe a simpler scheme that is based on trigono-
metric arguments and requires the assumption of linear behavior between
the prethreshold and postthreshold time point. The time step is divided into
three sections and, depending on where the crossing point is calculated to
have occurred, the midpoint of that section is chosen for the next time step
(see Figure 1). This again removes the expected bias and provides a max-
imum error of 1/
6 time step, a jitter standard deviation of approximately
0.096 time step, and a mean absolute deviation of 1/
12 time step using an
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2158
M. Hopkins and S. Furber
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
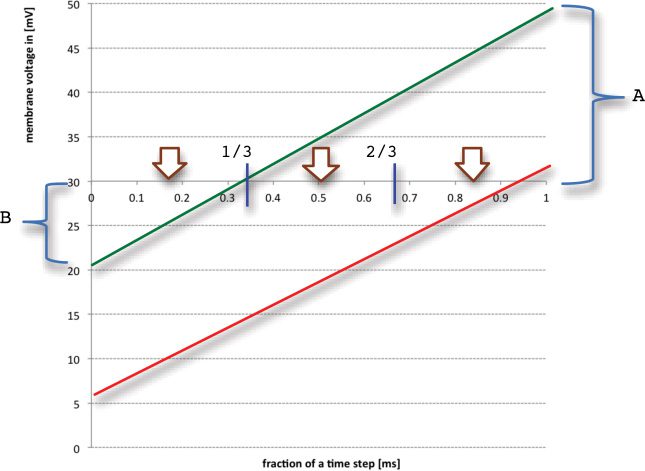
Figure 1: TQ3 correction scheme. The three arrows show the center points of the
three sectors, which are expectations over the unknown distribution of threshold
crossing time given that it happened in one of the three sectors. So these are
used as the best estimate once the sector has been inferred from the pre- and
post-threshold state variable value (here in mV). The green line shows a state
variable trajectory that spikes at the end of the first third and the values of A
and B used in the sample calculation. The red line shows one that spikes in the
last third.
expected1 computational load of
2 × subtract + 1.67 × (multiply + compare),
(5.1)
which is significantly lower than a linear interpolation in its simplest pre-
computable form:
Divide + 2 × multiply + 2 × subtract + addition.
(5.2)
The calculation is carried out as shown in Figure 1, and the code snippet
that follows, here using a cutoff of 30 mV and 1 ms time step with the
previous point at 0 and current point at 1. For the green line, the brackets
show A = 20 and B = 9 → spiked in the first third (just) and for the red line
A = 2 and B = 24 → spiked in the last third:
1The first (multiply + compare) operation is always called, and the second is called in
two-thirds of cases.
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2159
In the comparisons shown later, this scheme is described as TQ3 and the
previous simpler scheme as TQ1. Other types of scheme can come about
as an automatic result of locally adaptive time steps that are designed to
make the solvers more stable just prior to a spike event. These have been
investigated briefly with promising results and are mentioned in section 8.
It should be noted that due to the current clock-driven simulation in-
frastructure on SpiNNaker, we can currently deliver spikes on the time
grid chosen only when the simulation is run. TQ is therefore only an at-
tempt to avoid the lag that would otherwise accumulate in state variable
trajectories, without being able to make the spike timings themselves more
precise—although this is still going to be beneficial over a long simula-
tion. As Hansel, Mato, Meunier, and Neltner (1998) pointed out, the usual
benefits of higher-order methods will be reduced by this limitation unless
some method of interpolating the spike timings themselves can be imple-
mented. This is something that deserves further investigation in terms of
both which neural models and which solvers are most susceptible; recur-
rently connected populations are likely to be particularly sensitive. One
possible solution under investigation is to use the interpolation method to
put a time stamp on a spike when it is sent and therefore recover something
like the full potential of using smaller time steps.
6 Accuracy Results
Even with the trimmed-down selection of methods described, it would be
easy to generate a quantity of data that are difficult to summarize. For
example, the solver methods chosen are families rather than individuals,
the four parameters in the Izhikevich model allow a very large range of
behavior, there are four arithmetic types (32-bit: floating point ⇒float; fixed
point⇒accum, 64-bit: floating point⇒double; fixed point⇒long accum) and at
least two time steps of interest, and the neuron can be stimulated in different
ways, for example. To avoid this explosion of information, a number of
decisions have been taken:
(cid:2)
One reference neuron type has been chosen for most evaluation, with
limited results for two other examples. It is described by Izhike-
vich as regular spiking and uses the following parameters: a = 0.02,
b = 0.2, c = −65 mV, d = 8. V and U are initialized at −75 mV and 0,
respectively.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2160
M. Hopkins and S. Furber
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
The reference result in each case uses the sophisticated ODE solver in
Mathematica, which automatically uses adaptive time steps and han-
dles threshold crossing and stiffness transparently. We have enforced
25 decimal place arithmetic to ensure high accuracy.
Two time steps are used: 1 ms for most evaluations and some at
100 μs.
The two 32-bit arithmetic types are focused on: accum and float. If the
64-bit types (double and long accum) demonstrate particular behavior,
they are referred to specifically.
Two different stimulations are used. The neuron initially receives no
input; then (1) at 60 ms, a 4.775 nA DC current is delivered and
sustained (DC input) or (2) at 50 ms, an exponentially decaying input
with a time constant of 8 ms (giving a total charge of (cid:6)80 pC) is
injected and then every 50 ms thereafter (synaptic input). Once the
initial transient settles, these values provide a spike rate of about
10 Hz, exact interspike intervals of 100 ms that can then be easily
compared to the reference. The DC input is a more rigorous test of
the accuracy performance of the ODE solvers.
Results are in the form of graphs that show (1) the membrane voltage
V against the reference from 50 to 350 milliseconds and (2) accumu-
lated lags measured in milliseconds for the times of the nth spike com-
pared to the reference over the first 2 seconds of the simulation (for
the more difficult DC input only; all methods perform quite well for
the synapse input simulation). In the membrane voltage graphs, the
focus should be on the spike timings and the shape of the subthresh-
old behavior as opposed to the height of V before spiking, as the
latter is mainly a function of the time sampling interval chosen for
producing the graphs.
A naming scheme for identifying any particular result is the following:
Method-order(type)-ODE or ESR-TQ-Time step in μs-arithmetic type
To give an example, RK-3(Heun)-ODE-TQ1-1000-accum means “Runge-
Kutta 3rd order with Heun parameters implemented as an algorithmic ODE
solver with the simple time quantization correction at 1 ms time step using
the accum arithmetic type.” For ODE solvers, results from the use of static
inline functions are not shown separately as they should have an effect only
on efficiency, not accuracy.
Solver methods chosen for investigation are the following:
Euler ≡ Runge-Kutta 1st order ≡ Taylor Series 1st order: This is the
simplest explicit solver available and the default choice in a number
of neural software packages.
Runge-Kutta 2nd order: This is a family of solvers, and so three of the
most commonly used members are chosen. The names of this family
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2161
Table 1: Second-Order Runge-Kutta Solver Definitions.
a2
1
2/
3
1/
2
Name
Trapezoid/improved Euler
Ralston/Heun
Midpoint/improved polygon/modified Euler
are often confused in the literature and so will be referred to as in
section 4.3 of Lambert (1973), where they are parameterized by a2 as
shown in Table 1 and we shall use the names in bold.
Runge-Kutta 3rd order: Another family of solvers and this time with two
free parameters. They are generally not confused in the literature and
so we refer to them by their common names: Kutta, Heun, Lotkin. As
these are inevitably going to be less efficient, we do not investigate
them as thoroughly as the second-order methods.
The Runge-Kutta second- and third-order methods can be implemented
using ESR or in the standard ODE solver framework. There is much theory
related to which member of each family of methods is supposed to be
superior, with the choice dependent on how this superiority is assessed. For
example, the Ralston second-order method and Lotkin third-order method
have their free parameters chosen in order to minimize local truncation
error. However, in the presence of finite precision and other implementation
details of actual algorithms, it seems that these theoretical results do not
necessarily translate into actual benefits.
Taylor Series second- and third-order methods are implemented using
ESR and the equations that arise out of the Alsaker (2009) approach.
We have also briefly investigated the methods of Chan and Tsai (2010),
which combine Runge-Kutta methods with higher derivatives, with inter-
esting results. The second-order method (which we call CT-2-ESR) produces
an identical equation to TS-2-ESR and so is equivalent. The third-order
method is new.
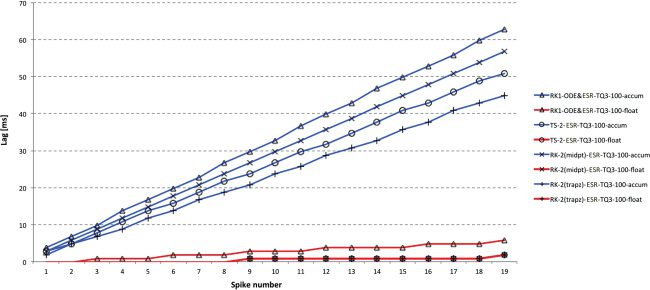
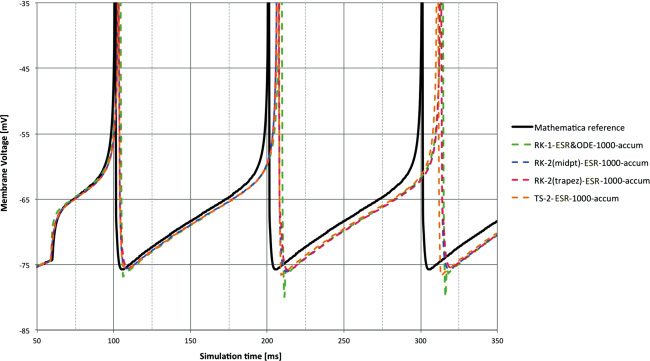
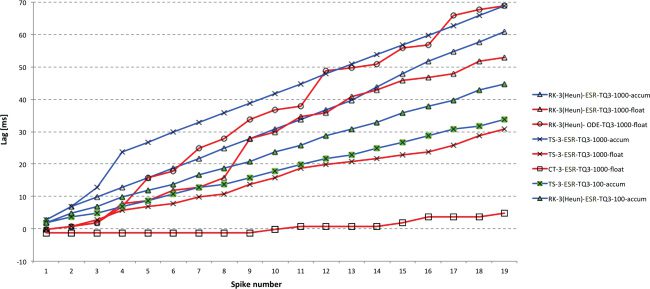
6.1 First- and Second-Order methods. Figures 2 and 3 gives a compar-
ison of the spike lags compared to the reference for the first- and selected
second-order methods using the DC input and the two 32-bit types (accum
use blue lines; float use red lines). Note that each graph uses a different
y-scale to provide the best precision.
Unsurprisingly, RK1 (=Euler=TS1) is the poorest performer. Of the
second-order methods, RK-2 (trapezoid) is a clear winner with accum and
equally best with float. Clearly the use of float improves performance over
accum here (and in all subsequent results). TS-2 is average but appears to be
more susceptible to random numerical errors, as evidenced by the appar-
ent variation around the linear lag trends produced by the RK methods. At
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2162
M. Hopkins and S. Furber
Figure 2: Spike lag for DC input at 1 ms time step with accum and float types
using blue and red, respectively. Float clearly outperforms accum and RK-1
= Euler is the worst-performing solver, although TS-2 performs surprisingly
poorly by comparison with float, the apparent random variation almost certainly
caused by numerical issues in one of the interim calculations. RK-2 (Trapezoid)
is clearly best for accum and approximately equally best for float.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
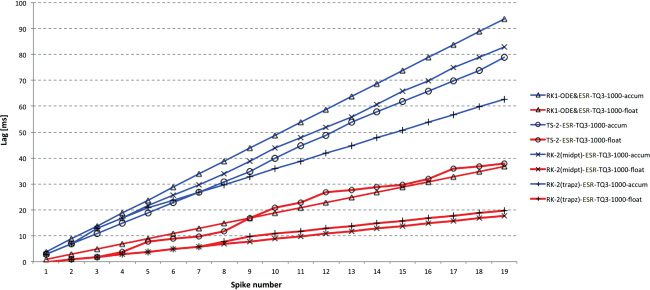
Figure 3: Spike lag for DC input at 100 μs time step with accum and float types
using blue and red, respectively. Float now outperforms accum more clearly and
RK-1 = Euler is now consistently the worst performer. RK-2 (trapezoid) is again
best for accum and equally best for float. Any of the RK-2 float results at 100 μs
are likely to be acceptable for high-quality simulations.
100 μs, improved lag performance (about 45% better) with the same approx-
imate ordering is present with accum. With float, all the methods perform
very well and identically, apart from RK-1, which is not as good.
Despite being designed to minimize, local truncation error, RK-2 (Ral-
ston) is less accurate than the other two RK-2 algorithms with accum and
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2163
identical with the other three types. As it is also slower, we have not shown
these results and focus on the others from here on. The ODE versions of
the ESR algorithms shown here are all slightly less accurate for accum and
usually identical for the other types.
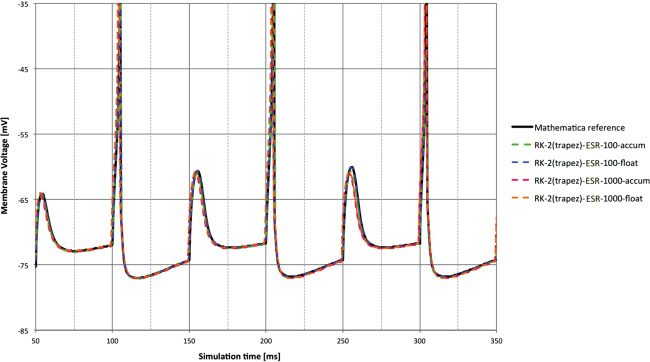
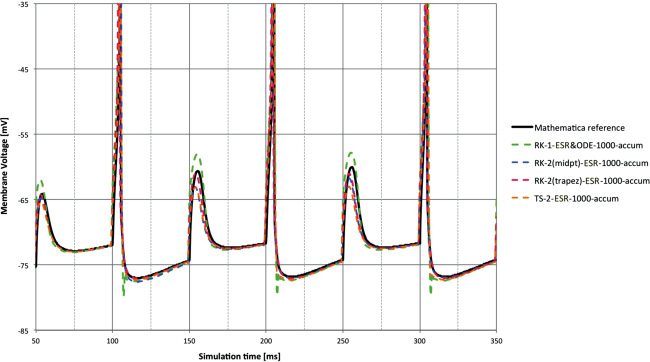
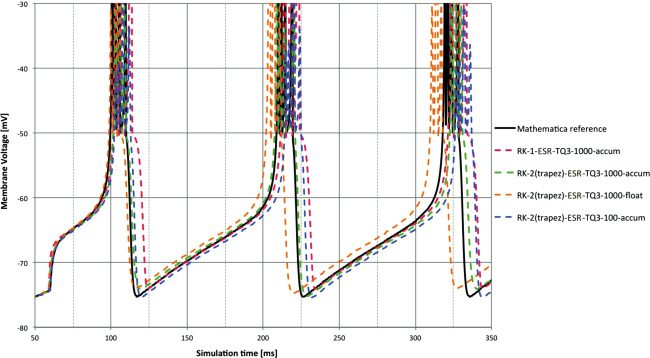
The next two sets of Figures 4 and 5, and 6 and 7 (one for each input
of the stimulation types), show detail from the membrane voltages (i.e.,
state variable V) against the reference from 50 to 350 ms. The first in each
set compares different solvers at 1 ms time step and with accum type. The
second shows the effect of changing time step and 32-bit type with the RK-2
(trapezoid)-ESR solver.
The lags measured in the previous figures can be seen in the membrane
voltages, but over the short timescale used, the separation between the
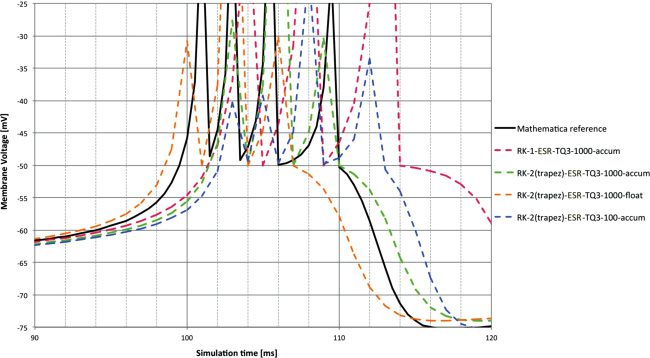
methods is not clear. RK-1 shows an undershoot after the spike event. This
is explained by the fact that Euler is in simple terms a linear extrapola-
tion and so will inevitably overshoot a state variable trajectory that con-
tains a substantial second-order component that is heading in the opposite
direction—as the initial recovery after a spike will be for the membrane
voltage state variable in most integrate-and-fire models.
The comparative benefits from reduced time step and floating point are
shown clearly in Figure 5. The benefit of float at 1 ms is clear (orange versus
red), and float at 100 μs is very difficult to distinguish from the reference. An
interesting comparison is between float at 1 ms and accum at 100 μs (orange
versus green). The former is likely to be faster, but the significantly better
performance suggested by the lag plots is apparent.
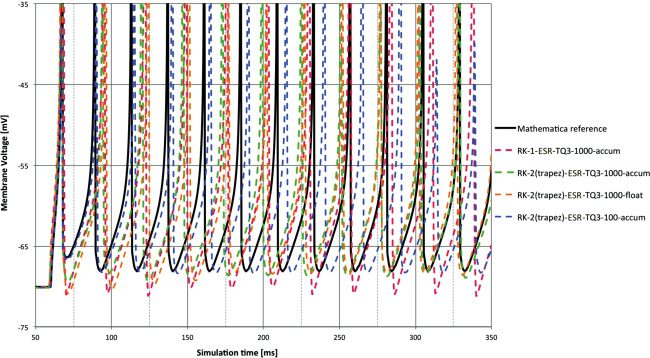
The synaptic input is an easier test, and the lag performance is seen as
very similar between the methods. RK-1 still shows overshoot after a spike
event in Figure 6. The various methods follow the pulse at 150 and 250 ms
with varying degrees of fidelity.
With RK-2 (trapezoid) the benefits of shorter time step and floating point
are less clear with the synaptic input in Figure 7.
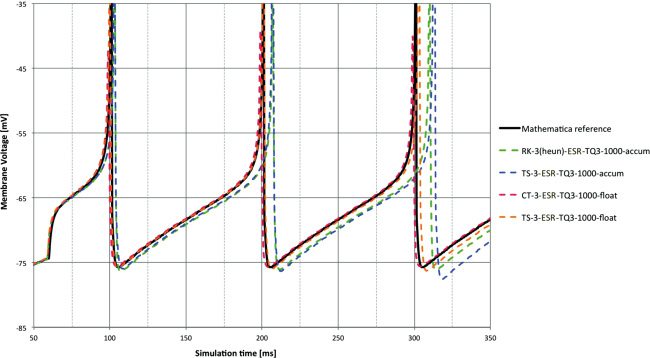
6.2 Third-Order Methods. For comparison, a selection of third-order
methods is also shown despite the extra computational load that will in-
evitably result. (See Figures 8 and 9.)
It was quite a surprise to see how badly the standard third-order methods
performed at 1 ms time step, even with the 64-bit types. Of the Runge-Kutta
third-order order methods, only RK-3 (Heun) provides reliable solutions on
the DC input, and even then they are less accurate than the second-order
methods. With accum, only the ESR methods worked at all. Previous ex-
perience with ODE solvers has shown an incremental improvement with
increased order up to fifth and sixth order, as predicted by analytical results
in standard texts. However, this experience has usually been with adaptive
time-step algorithms and double-precision floating point.
Some diagnostics were therefore required to investigate an initial hy-
pothesis of underflow or overflow (or both), and for this, a range-checking
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2164
M. Hopkins and S. Furber
Figure 4: Membrane voltage for DC input at 1 ms time step and accum type
compared to reference. The spike lags measured in Figure 2 are clear. Note the
overshoot after the spike with the RK-1 solver.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
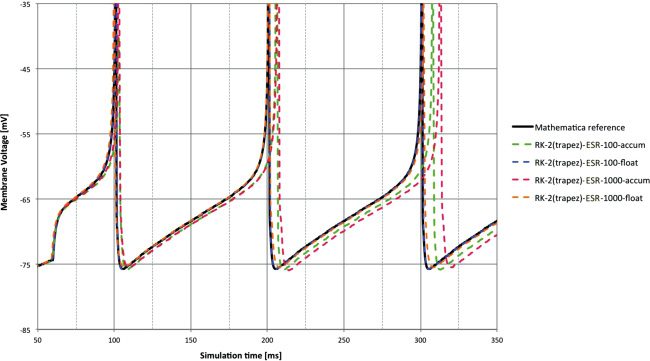
Figure 5: Membrane voltage for DC input. RK-2 (Trapezoid) ESR solver with
different 32-bit arithmetic types and time steps compared to reference. The
100 μs and float combination is difficult to distinguish from the reference, and
even at 1 ms, float provides good performance—significantly better than accum
at 100 μs.
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2165
Figure 6: Membrane voltage for synaptic input at 1 ms time step and accum
type compared to reference. Clearly this is an easier task than DC input, with all
methods giving relatively good performance except some overshoot behavior
from RK-1 = Euler.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7: Membrane voltage for synaptic input. RK-2 (Trapezoid) ESR solver
with different 32-bit types and time steps compared to reference. A good per-
formance in all cases, with the 100 μs results difficult to distinguish from the
reference.
2166
M. Hopkins and S. Furber
Figure 8: Spike lag for DC input for various third-order combinations of solver
and time step, with accum and float types using blue and red, respectively. A
surprisingly poor set of results, especially for float in some cases, caused by
numerical issues discussed in the text. CT-3 gives excellent performance at 1 ms
in this case with little efficiency penalty compared to RK-2 solvers.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: Membrane voltage for DC input at 1 ms time step with various third-
order combinations of solver and arithmetic type. Poorer-than-expected perfor-
mance is again shown here. CT-3 (and to a lesser extent TS-3) with float are a
good match to the reference.
macro was formulated that could print out values of selected state vari-
ables or intermediate values internal to the algorithms if they got either
very small or very large. This macro works for all arithmetic types and can
be removed in one place for speed testing. It shows that with the higher-
order RK methods, intrastep predictions and derivatives calculated during
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2167
(and particularly toward the end of) a time step can become enormous just
before a spike event. One reason that the higher-order RK methods suf-
fer more from this phenomenon is that they make predictions or calculate
derivatives later in the time step than lower-order methods, where these
effects become rapidly more prevalent near a spike. Plotting high-order
derivatives of the reference solution show very large values in these cases,
which will either overflow the arithmetic type or violate assumptions made
when assessing local error behavior in the presence of exact arithmetic. In
essence, the membrane voltage exhibits superexponential behavior near
cutoff that can not be modeled well when a relatively large fixed time step
is used in the solution, and the higher-order methods suffer more as they
attempt to track these very large high-order derivatives. With 100 μs time
step, no problems were seen with any of the algorithms.
Methods that locally switch to smaller time steps when close to spikes
have been investigated briefly and show promising results. They clearly
improve the performance of the third-order methods described here with
a small speed penalty and give an opportunity to get a better estimate of
threshold-crossing time than TQ3 if formulated correctly. It may be worth-
while to pursue these ideas further, as they will be of some benefit to all
solvers if the speed penalty can be made small enough.
Although the Runge-Kutta methods are widely considered to be the
method of choice where singularities are likely to be encountered in the
solutions (see, e.g., chapter 16 of Press et al., 1992), some have mentioned
the dangers of applying the higher-order versions in such cases (p. 232
of Gear, 1971, and p. 21 of Enright, Higham, Owren, & Sharp, 1995). We
conclude that this, in combination with the restriction of a fixed time step
that is too large to allow effective tracking of the superexponential behavior
near to a spike and, to a lesser extent, finite precision issues, are the causes
for the higher-order methods being so ineffective here.
6.3 Other Izhikevich Neuron Types. In Figures 10 to 12, we show some
comparison of membrane voltages against reference result for the RK-1 and
RK-2 (Trapezoid) solvers (the latter with different time steps and arithmetic
types) on two other types of Izhikevich neuron using the DC input.
The types chosen are:
1. Chattering ⇒ {a = 0.02, b = 0.2, c = −50, d = 2}
2. Fast Spiking ⇒ {a = 0.1, b = 0.2, c = −65, d = 2}
Both of these neuron types are going to be harder for the ODE solvers to
deal with because of higher rates of change relative to the fixed time step.
For the Chattering neuron, these high rates of change come in clusters; for
the Fast Spiking neuron, the rate of spiking is just uniformly higher for a
given input.
With the Chattering neuron, it is clearly far more difficult to assess the
detail of the spiking behavior when clusters of spikes are being generated.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2168
M. Hopkins and S. Furber
Figure 10: Membrane voltage for DC input with varying solver setups and
arithmetic types compared to reference. Chattering neuron (zoomed time axis
to show more detail). Both leading and lagging behavior present with only the
100 μs result providing four spikes per burst as reference. RK-1 = Euler is the
worst performer
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 11: Membrane voltage for DC input with varying solver setups
and arithmetic types compared to reference. Chattering neuron over normal
timescale. This is clearly a challenging task and no clear winner. The 100 μs re-
sult produces the correct number of spikes per burst but starts to lag reference.
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2169
Figure 12: Membrane voltage for DC input with varying solver setups and
arithmetic types compared to reference. Fast Spiking neuron. The 1 ms results
all lag more than the 100 μs accum result. RK-1 = Euler gives overshoot and the
worst lag.
Figure 10 zooms in on the time between 90 ms and 120 ms to improve clarity
for the first cluster. Only RK-2 (Trapezoid) at 100 μs time step manages to
match the four spikes produced by the reference solver, albeit with some
lag. The 1 ms solvers all produce three spikes, with RK-2 (Trapezoid)-float
clearly leading and RK-1-accum clearly lagging. Figure 11 on the usual time
axis shows some patterns that are present in the lag behavior that differ from
those seen on the reference neuron. Although the worst lag is RK-1-accum as
before, RK-2 (Trapezoid) at 100 μs time step is not much better and appears
to be getting worse as time goes on, which is a surprise as it works well
with the reference neuron. The tendency for RK-2 (Trapezoid)-float to lead
the others is also shown here, but it seems to be leading too much, at least
over the first 350 ms. Perhaps surprisingly, the best performer in terms of
overall lag seems to be the RK-2 (Trapezoid)-accum at 1 ms time step.
For the Fast Spiking neuron in Figure 12, the story is a little simpler.
All the 1 ms time step results lag the reference results with RK-1 worst,
then RK-2 (Trapezoid)-float and RK-2 (Trapezoid)-accum quite similar. RK-2
(Trapezoid)-accum at 100 μs stands apart as lagging far less—about 10 ms
by the twelfth spike. Clearly the smaller time step deals better with the
higher spike rate, which is not surprising.
6.4 Discussion of Accuracy Results. In all of the cases tested, the 64-bit
types produce results similar or identical to the 32-bit float type, and so
no separate figures have been produced. This suggests that no significant
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2170
M. Hopkins and S. Furber
benefits would accrue in these cases, and therefore the computation and
storage cost of 64-bit types are not currently justified.
It is worth noting that for synaptic input (which looks on the face of it to
be the more realistic case), the use of accum and 1 ms does not have much of a
penalty associated with it even for the simpler methods. However, although
neurons in a realistic network could be receiving inputs from (in some cases
in the auditory system) a single synapse, more commonly it would be up to
1000 synapses or more, and for the latter case, the summation of these inputs
at realistic spike rates and 1 ms time step would converge asymptotically on
DC input with gaussian noise. This makes the case for the more challenging
input type in terms of simulating actual behavior. Results in Mainen and
Sejnowski (1995) and Brette and Guigon (2003) suggest that some aperiodic
variation around a DC component could be a good deterministic test signal
in future work. As we mention later, simulating realistic amounts of pseudo-
random input noise and analyzing output distributions in the presence of
this noisy input would be closer still to a realistic use case.
Clearly, to find the best ODE solver, one needs to work with a realistic
set of neural behaviors. From the brief analysis of two other common types
in the previous section, it seems that a solver that works well on one neuron
type does not necessarily transfer that superior performance to other types.
Although useful as another demonstration of performance characteristics,
it should be remembered that the other two neuron types are a harder
challenge and that these spike rates are less likely in spiking neural networks
that match realistic behavior in much of the brain (though they can exist
transiently or in certain areas). In any case, the complex interaction between
neuron type, time step, arithmetic type, solver algorithm, and even exact
ordering of arithmetic operations make a definitive statement difficult to
reach here. Some patterns are, however, present. The second-order methods
generally improve on RK-1, in some cases significantly. A more complete
investigation would require the capability to script and automate test cases
in order to search the various parameter spaces more thoroughly.
The almost linear nature of some of the spike lag plots might lead one to
believe that a simple correction could be applied in order to bring this line
back onto the x-axis. However, the observed lag is a complex and nonlinear
function of input dynamics and neuron definition among other things,
and solving this problem would be computationally more challenging than
simply moving to a better solver.
7 Efficiency Results
The results in Table 2 show the time taken for a SpiNNaker board running
at 200 MHz to carry out 10,000 neuron updates in a simple loop, divided
by 10,000. The synaptic input scheme is used with 1 ms time step. After
the initial transient, the spiking rate (cid:6)10 Hz so that discrete state updates
are in correct relative proportion. The timing is corrected to remove the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2171
Table 2: Cost in μs per Neuron Update with TQ1 Correction.
accum float
long accum double
RK-1 (≡Euler; ODE≡ESR)
RK-2 (MidPoint)-ESR
RK-2 (Trapezoid)-ESR
RK-2 (Ralston)-ESR
TS-2-ESR ≡ CT-2-ESR
RK-2 (MidPoint)-ODE gen driver
RK-2 (MidPoint)-ODE gen driver S.I.
RK-2 (MidPoint)-ODE spec driver
RK-2 (MidPoint)-ODE spec driver S.I.
RK-2 (Trapezoid)-ODE gen driver
RK-2 (Trapezoid)-ODE gen driver S.I.
TS-3-ESR
RK-3 (Heun)-ESR
RK-3 (Heun)-ODE spec driver
RK-3 (Heun)-ODE spec driver S.I.
CT-3-ESR
0.56
0.86
0.97
1.07
0.93
2.33
1.36
1.63
0.89
2.37
1.32
2.19
1.50
2.16
1.26
1.86
3.99
6.97
7.67
8.29
6.81
8.91
7.68
8.21
7.24
9.46
8.21
13.46
11.43
10.47
11.57
11.12
6.48
12.54
13.41
15.87
13.22
14.41
CompErr
13.67
12.61
14.42
CompErr
28.30
21.96
21.85
20.35
28.40
6.35
11.23
12.30
13.52
10.90
13.64
11.95
13.01
11.66
14.50
12.87
21.84
18.78
21.33
19.06
15.80
Notes: The static inline functions are denoted S.I.; general ODE drivers with
function pointers are denoted gen driver; the most specialized drivers are
denoted spec driver. CompErr means that a compiler error caused a build
failure.
overhead of code required for generating input, collecting and counting
spikes, and other administrative functions. The time per update therefore
refers only to the cost of computation and memory access and movement
specific to each algorithm. The compiler flag -Ofast is used, and thumb
code is disabled to promote speed above other considerations and allow
the compiler to perform as many optimizations as possible.2 No manual
adjustment of assembly code is used, though preliminary investigations
have shown potential for this to improve performance, for example, in the
case where the multiplication of different fixed-point types might deliver
improved accuracy. Floating-point operations on the ARM968 processor are
carried out by software library functions.
For the ODE solver results, we have a number of comparisons available
for the same methods: (1) implemented either as either normal C source or
static inline functions in the header files (these are denoted S.I.) and (2) the
difference between the most general ODE driver that uses function pointers
(gen driver) and the most specialized one that explicitly codes the algorithm
and avoids inner loops by knowing that two state variables are present (spec
driver). CompErr means that a compiler error does not allow that build to
complete.
2The compiler used is the gcc 4.7.3 cross compiler from Mac OS X to arm-none-eabi.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2172
M. Hopkins and S. Furber
7.1 Discussion of Efficiency Results. With RK-1 as the reference and
for the moment considering only accum results, the extra cost of a second-
order method is between 54% and 91% for ESR, between 59% and 143%
for ODE in static inline form, and between 191% and 323% for ODE using
function pointers and general loops over state variables. Clearly the ESR is
effective here as well as in terms of accuracy. The static inline results show
that the compiler makes effective use of the optimizations allowed across
source files that would not otherwise be possible. The fastest second-order
method is RK-2 (Midpoint)-ESR. The two fastest third-order methods cost
125% and 168%.
For float, the relative costs differ somewhat. On average, the solution
takes 6.6 times longer, though the relative penalty is uniformly less for the
general ODE results, presumably because they were worse in the first place.
The faster second-order methods are generally slightly slower relative to
RK-1, and the ordering among them is approximately the same except that
now, TS-2-ESR is now the smallest penalty at 71%, though RK-2 (Midpoint)-
ESR is not far behind at 75%.
Adding TQ3 correction costs typically about 0.025 to 0.05 μs. This is per-
haps larger than expected because the correction is calculated only when a
spike occurs—approximately once for every 100 updates, which suggests
that the cost of each TQ3 correction is about 5 μs. Removing TQ correction
altogether provides a useful efficiency gain for two reasons: (1) as the fixed
time step is now always known in advance, this simplifies the optimal ESR
form, leading to less computation, and (2) one indirect memory access is
no longer required. For example, the cost of one neuron update for RK-2
(MidPoint)-ESR reduces to 0.73 μs for accum, a 15% improvement. As the
algorithm gets simpler, another threshold is reached where such gains be-
come even greater, presumably because the compiler finds it increasingly
easy to optimize the use of registers. An example is a stripped-down ver-
sion of RK-1 with accum where all code related to TQ is removed. The time
per update becomes 0.45 μs, a 20% gain over the standard TQ1 version.
8 Conclusion and Ideas for Further Work
Perhaps with an innovative technology like SpiNNaker, which offers an un-
expected combination of very low energy use and real-time performance,
it should not be a surprise if some trade-offs need to be made. A com-
parison with neural solver frameworks that work with double-precision
floating-point arithmetic, adaptive time steps, high-order/implicit solvers,
and sophisticated threshold-crossing algorithms will inevitably show some
differences in terms of state variable trajectories and spike timings. How-
ever, with a careful choice of solver and TQ approach, even just the use of
float instead of accum with either fewer neurons per core (or, equivalently,
performance that is slower than real time) will provide a performance that is
very close to these much more energy-intensive systems, which themselves
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2173
offer only some tiny fraction of real-time performance. Other possibilities
such as order adaptivity and within-step time adaptivity are discussed be-
low. As with almost everything in the area of mathematical computation, an
informed choice of where to be in the {accuracy, speed} space needs to be
made, and we hope that this study helps to elucidate some of the trade-offs.
The Izhikevich neuron model creates membrane voltage trajectories that
are super exponential near to the spike with large high-order derivatives,
and the spike events are discontinuities. These will always provide a chal-
lenge to explicit fixed time-step algorithms with time steps that are signifi-
cant relative to the rate of change, as they try to track the sudden increase
and inevitably lag. This is the main cause of the lagging shown in the accu-
racy result, and the failure of the higher-order methods to improve on the
lower-order ones at 1 ms time step.
Although full time-step adaptivity has been ruled out for this study, some
other options are possible. Parker-Sochacki offers a form of order adaptivity,
adding higher-order terms as necessary, and this has been investigated
briefly here in the context of adding higher-order terms in the Taylor series
solvers—in our case, up to fourth order. It is easy to achieve in this case,
as each higher-order update to the state variable can be simply added to
the previous one. Current results are promising but variable and so have
not been reported in detail yet. It is likely that the decision on when to
add higher-order terms is the key to success for this approach, and this
requires further study. It is also likely that the higher-order terms will be
more difficult to calculate in the presence of numerical errors. A similar
approach could be used for Runge-Kutta solvers, but it would inevitably
be more expensive computationally or at least much more complex.
Another possibility that shows promise is limited time-step adaptivity,
where at certain points, the solver divides its own internal time step by an
integer d and then repeats the solve d times before returning the updated
neuron to the system. This will obviously create a “d times” overhead, but
only at points where it is needed—near spikes where the derivatives get
very large—and so is unlikely to generate a significant overhead for the
simulation as a whole. As with order adaptivity, the key will be making an
effective and robust decision about when to carry it out. Initial experiments
show useful improvements for all solvers at relatively modest cost, for
example, making the third-order methods more stable.
A simple mechanism for removing the accumulated lag caused by ig-
noring the actual time of a threshold crossing has been proposed and im-
plemented. The simplest, TQ1, has little overhead and removes the 1/
2 time
step bias. A more complex one, TQ3, adds only a small extra overhead and
provides significantly more accurate post spike transitions with a mean ab-
solute deviation of 1/
12 time step. Allowing the size of the time step to be
adaptive near spikes for better accuracy and stability, as discussed above,
provides a different mechanism for measuring the threshold-crossing time
at essentially no extra cost. At the moment, however, neither of these
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2174
M. Hopkins and S. Furber
mechanisms will deliver spikes between time steps. As the SpiNNaker
system evolves, it may be that certain ground rules change; for example,
event-driven rather than clock-driven behavior might become possible (see,
e.g. section 2.3 of Brette et al., 2007).
Both accuracy and efficiency results are sensitive to exact implementa-
tions of the algorithms. Obviously the compiler reorders instructions ac-
cording to the optimization scheme. In this work, it has been commonly
found that the simple reordering of one subtraction in an algorithm that has
eighty mathematical operations in total can make a significant difference,
especially to accuracy and for the 32-bit types. Also, the neatest algebraic
reductions are not always the ones that produce the best accuracy (with ac-
cum in particular), but they do usually produce the best efficiency. Clearly,
the optimization of a particular solution requires art and experimentation
as well as science. (See Martel, 2009; Darulova et al., 2013; and Gao et al.,
2013, for ideas about how the process could be made more scientific.)
Other neuron models will provide different challenges and opportu-
nities. Complex behavior (e.g., the Hodgkin-Huxley model) will almost
certainly require higher-order methods and possibly implicit solvers, with
consequences for neuron update performance and the number of neurons
that can be supported per core in real time. An effective application of
Parker-Sochacki for this model is shown in Stewart and Bair (2009) and the
approach may be of wider interest.
Of course, the ideal is to have closed-form solutions (or at least close
approximations) for the state variable trajectories as available with, for
example, the current-based leaky integrate-and-fire (LIF) neuron. As our
ODE is autonomous, the integral is separable, and so a standard solution
technique is available:
(cid:2)
(cid:2)
= f (V ) ⇒
dt =
dV
dt
dV
f (V )
(8.1)
The general requirement for knowing the membrane voltage at the end of
the next time step is then the solution of integral equations of the following
form, with the unknown in this case being Vnext:
timestep =
(cid:2)
Vnext
Vnow
1
f (V ) dV.
(8.2)
Some progress has been made on such solutions for one state variable in
the Izhikevich equations if the other state variable is kept fixed over the time
step. As Humphries and Gurney (2007) showed, this assumption, leads to
an exact solution for the U state variable. Using a further assumption, they
also show a solution for the V state variable with a slightly more complex
version of the Izhikevich equations than ours. We have found an analytical
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2175
solution for our simpler version, which may not have yet appeared in the
literature and is given below, where t is in milliseconds and I is in nanoamps:
⎛
⎛
Vnext = −5
√
α tan
⎝2
√
α
⎝−
(cid:6)
(cid:5)
γ√
α
0.5 tan−1
√
α
⎞
⎞
− 0.1t
⎠
⎠ − 62.5.
(8.3)
and
α = I − U − 16.25, γ = 0.2V + 12.5.
Clearly, α will be negative in many cases, leading to the need for complex
arithmetic and using the real part of the solution (which appears to always
have zero imaginary part anyway). This does suggest that an even simpler
form may be available, but we have not yet found it.
Of course, the extra computation required for the above may not be
justified if holding one state variable fixed over the time step in order
to solve the other introduces more error than the exact solution removes.
Finding a solution for the coupled 2D system of integral equations for both
V and U is the real answer, but it has so far proved elusive and may not be
possible. It is almost certain that if such a solution exists, it will require the
use of transcendental functions and complex numbers, which reinforces the
need for a fast and accurate library of such operations for fixed-point types
to be available.
It is likely that the ESR will be useful anywhere that the ODE is au-
tonomous and an explicit solver can be used. We have shown that carefully
implemented algorithms can be both more accurate and faster than the most
heavily optimized general solver of the same kind with static inline func-
tion optimization. The fact that the neuron solver code can be delivered
pretested and in standard compiled library + header form also provides
software engineering advantages.
Due to time and space limitations, we have looked at only a small se-
lection of Izhikevich parameters (and therefore neuron behaviors) in this
study, and so it cannot be considered an exhaustive analysis. We hope that
the examples we chose show trends that can be extrapolated to more general
conclusions, but of course it is possible that unseen pathological cases exist.
Even a small sample of two other neuron types within the compass of the
Izhikevich parameterization has shown some different patterns from the
reference neuron results. One way to achieve better coverage is to automate
the testing mechanism. This was partially implemented for the study within
the main C event loop running on the SpiNNaker board, but to achieve it
comprehensively, the ability to script testing mechanisms on a host would
be ideal. At the moment, this is not straightforward using the fixed-point
types because they only cross-compile to an ARM target with no operating
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2176
M. Hopkins and S. Furber
system. If these types could be supported on the host machine—or,
alternatively, within a scriptable emulator environment—then validation
over larger example spaces in particular would become much easier. It
would also facilitate testing with stochastic inputs, which are very likely
in actual use cases, leading to output measures based upon differences
between distributions of spikes or spike intervals using, for example,
Kullback-Leibler information-theoretic measures, with the reference neu-
ron providing the reference output distribution.
Hybrids between multistep, multistage, and multiderivative methods
exist and can be reasoned about using the approach of general linear meth-
ods as shown in chapter 5 of Butcher (2003), who mentions some of the
better-known examples: the Rosenbrock and Obreshkov methods. The ex-
tent to which these hybrid methods can find a better balance between
accuracy and efficiency while retaining stability and remaining within our
nominal constraints of fixed 1 ms time step and accum arithmetic type
has not yet been fully explored, but the potential is there—particularly
those combining multistage and multiderivative approaches (usually called
Obreshkov or Turan methods). The methods discussed in Chan and Tsai
(2010) should be worthwhile investigating further as they allow an algebraic
combination of our Taylor series and Runge-Kutta solutions for potentially
better accuracy at minimal extra overhead. Initial tests have been very
promising, with CT-3-ESR being by far the most accurate algorithm at 1 ms
time step (except for the accum type, where numerical underflow sabotages
accuracy in all the algorithm orderings so far investigated) while also being
the fastest third-order algorithm for floating-point types. (For related work
see Shintani, 1972; Mitsui, 1982; and Ono & Yoshida, 2004.)
At the current time and on the basis of the limited set of tests so far
carried out on Izhikevich neuron types, the best trade-off between speed
and accuracy—using the accum type and 1 ms time step to facilitate real-
time operation—looks to be one of the RK2-ESR solver methods; Midpoint
for speed or Trapezoid for accuracy.
Appendix: An Example of ESR
This appendix shows an example of the ESR, from an original definition of
the ODE and explicit solver algorithm, through a reduction to constituent
common terms, and ending up in C source code. The analysis and reduction
is carried out using Mathematica. We start with a definition of the Izhikevich
equation as derivatives with regard to V and U as follows:
ODEV (V, U ) = I − U + (( 0.04V + 5)V + 140),
ODEU(V, U ) = a(bV − U ).
Next we define an explicit ODE solver formula. In this case, it will be
the Runge-Kutta second-order midpoint method (sometimes also called
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2177
modified Euler):
V → V + h ODEV
U → U + h ODEU
(cid:9)
V + h
2
(cid:9)
V + h
2
ODEV (V, U ), U + h
2
ODEV (V, U ), U + h
2
(cid:10)
ODEU(V, U )
(cid:10)
ODEU(V, U )
,
.
Combining these generates algebraic formulase equivalent to running the
RK-2 (Midpoint) ODE solver with the Izhikevich ODE system. So for the
next value of V and U, we have:
V → V + h(140 + I − U − h
2
a(−U + bV )
+ (V + h
2
(5 + 0.04(V + h
2
U → U + ah(−U − h
2
(140 + I − U + (5 + 0.04V )V ))
(140 + I − U + (5 + 0.04V )V )))),
a(−U + bV )
+ b(V + h
2
(140 + I − U + (5 + 0.04V )V ))).
Even for a relatively simple second-order ODE solver, these equations are
quite unwieldy. As the order increases, they rapidly become unmanage-
able in this form. Fortunately, there are many ways of simplifying them
and finding common terms, typically either automatically using the alge-
braic manipulation commands available in Mathematica, by inspection, or
usually a combination of the two. Considerations are:
(cid:2)
(cid:2)
(cid:2)
(cid:2)
Maximizing the number of common terms among the state variables
to minimize computational load
For fixed-point types, ensuring that interim variables have values
that minimize the possibility of under- or overflow, around 2.0 for
accum
In general, choosing interim calculations that minimize truncation or
roundoff errors
Orderings of arithmetic operations can have an effect on both ac-
curacy and speed (though this is due to the C compiler later in the
chain)
One choice of common terms is described by the set of Mathematica
substitutions given below. These were arrived at after experimenting with a
range of different possibilities. It provides the RK-2 (Midpoint)-ESR solver
that is both the fastest and most accurate among a number tested so far
across a range of arithmetic types and therefore seems to be close to optimal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
n
e
c
o
_
a
_
0
0
7
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2178
M. Hopkins and S. Furber
within the limited testing regime:
(cid:11)
140 + I − U → θ , θ + (5 + 0.04V )V → α,
H
2
α + V → η, − h
2
A(−U + bV ) → β
(cid:12)
.
Applying this substitution to the two equations for the state variable up-
dates produces the following expressions:
V → V + H(β + (0.04η + 5)η + θ ),
U → U + Ah(bη + β − U ).
Translating these into C code gives the following:
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2179
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 13: Histograms from sample of state and computational interim vari-
ables for RK-2 (Midpoint)-ESR-TQ3-double over 2 seconds of simulation using
1 ms time step, DC input and TQ3 adjustment (other setups produce similar
results).
To indicate typical values used by the state and interim variables in
this form, the histograms in Figure 13 show samples from 2 seconds of
simulation of the reference neuron using 1 ms time step with the DC input
and TQ3.
C code that implements the core of several of the ESR solvers described
in the letter is available at http://www.mitpressjournals.org/doi/suppl
/10.1162/NECO_a_00772.
Danksagungen
We thank Dave Lester and Jamie Knight for discussions about fixed-point
issues and static inline function optimisations; Sergio Davies, Luis Plana,
2180
M. Hopkins and S. Furber
Steve Temple, and Simon Davidson for their initial guidance through
the SpiNNaker architecture and development environment for M.H.; Jim
Garside for looking at assembly output to identify optimization opportu-
nitäten; Patrick Camilleri for help with LaTeX; and the reviewers for helpful
comments and references.
The research leading to these results has received funding from
EPSRC (the U.K. Engineering and Physical Sciences Research Council
grants EP/G015740/1 and EP/G015775/1), ARM Ltd, the European Re-
search Council under the European Unions Seventh Framework Pro-
gramme (FP7/2007-2013) / ERC grant agreement 320689 and the EU
Flagship Human Brain Project (FP7-604102).
Verweise
Alsaker, C. A. (2009). Solving systems of differential equations using the Taylor series.
(Tech. Rep.). South Dakota School of Mines and Technology.
Babuˇska, ICH., Pr´ager, M., & Vit´asek, E. (1966). Numerical processes in differential equations.
New York: SNTL/Wiley Interscience.
Bashforth, F., & Adams, J. C. (1883). An attempt to test the theories of capillary action by
comparing the theoretical and measured forms of drops of fluid with an explanation of
the method of integration employed in construction the tables which give the theoretical
forms of such drops. Cambridge: Cambridge University Press.
Falten, R., & Guigon, E. (2003). Reliability of spike timing is a general property of
spiking model neurons. Neural Computation, 15, 279–308.
Falten, R., Rudolf, M., Carnevale, T., Hines, M., Beeman, D., Bower, J., Diesmann,
M., . . . & Hand, A. (2007). Simulation of networks of spiking neurons: A re-
view of tools and strategies. J. Comput. Neurosci., 23, 349–398.
Butcher, J. C. (2003). Numerical methods for ordinary differential equations. New York:
Wiley.
Chan, R. P. K., & Tsai, A. Y. J. (2010). On explicit two-derivative Runge-Kutta methods.
Numerical Algorithms, 53, 171–194.
Darulova, E., Kuncak, V., Saha, ICH., & Majumdar, R. (2013). Synthesis of fixed-point
Programme (Tech. Rep.). Lausanne: Ecole Polytechnique F´ed´erale de Lausanne.
Enright, W. H., Higham, D. J., Owren, B., & Sharp, P. W. (1995). A survey of the explicit
Runge-Kutta method (Tech. Rep. 94-291). Toronto: Universität von Toronto.
Euler, L. (1913). De integratione aequationum differentialium per approximationem.
Opera Omina, ser. 1, 11, 424–434.
Furber, S. B., Galluppi, F., Temple, S., & Plana, L. A. (2014). The SpiNNaker project.
Proceedings of the IEEE, 102, 652–665.
Gao, X., Bayliss, S., & Constantinides, G. (2013). SOAP: Structural optimization of
arithmetic expressions for high-level synthesis. In Proceedings of the International
Conference on Field-Programmable Technology (S. 112–119). Piscataway, NJ: IEEE.
Gear, C. W. (1971). Numerical initial value problems in ordinary differential equations.
Oberer Saddle River, NJ: Prentice Hall.
Gill, S. (1951). A process for the step-by-step integration of differential equations in an
automatic digital computing machine. Mathematical Proceedings of the Cambridge
Philosophical Society, 47(1), 96–108.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Accuracy and Efficiency in Fixed-Point Neural ODE Solvers
2181
Hall, G., & Watt, J. M. (Hrsg.) (1976). Modern numerical methods for ordinary differential
Gleichungen. Oxford: Clarendon Press.
Hansel, D., Mato, G., Meunier, C., & Neltner, L. (1998). On numerical simulations of
integrate-and-fire neural networks. Neural Computation, 10, 467–483.
Henrici, P. (1962). Discrete variable methods in ordinary differential equations. New York:
Wiley.
Heun, K. (1900). Neue Methoden zur approximativen Integration der Differential-
gleichungen einer unabh¨angigen Ver¨anderlichen. Z. Math. Phys., 45, 23–38.
Higham, N. J. (1996). Accuracy and stability of numerical algorithms. Philadelphia:
SIAM.
Humphries, M. D., & Gurney, K. (2007). Solution methods for a new class of simple
model neurons. Neural Computation, 19, 3216–3225.
ISO/IEC. (2008). TR18037 Programming languages—C – Extensions to support embedded
processors. (Tech. Rep.). Genf: International Organization for Standardization.
Izhikevich, E. M. (2003). Simple model of spiking neurons. IEEE Trans. on Neural
Netzwerke, 14, 1569–1572.
Jin, X., Furber, S. B., & Wald, J. V. (2008). Efficient modelling of spiking neural
networks on a scalable chip multiprocessor. In Proceedings of the IJCNN 2008 (S.
2812–2819). New York: Springer.
Kahan, W. (1965). Further remarks on reducing truncation errors. Comm. ACM, 8, 40.
Kutta, M. W. (1901). Beitrag zur n¨aherungsweisen Integration totaler Differential-
gleichungen. Z. Math. Phys., 46, 435–453.
Lambert, J. D. (1973). Computational methods in ordinary differential equations. Neu
York: Wiley.
Lambert, J. D. (1991). Numerical methods for ordinary differential systems: The initial
value problem. New York: Wiley.
Mainen, Z. F., & Sejnowski, T. J. (1995). Reliability of spike timing in neocortical
Neuronen. Wissenschaft, 268(5216), 1503–1506.
Martel, M. (2009). Enhancing the implementation of mathematical formulas for fixed-
point and floating-point arithmetics. Formal Methods in System Design, 35, 265–278.
Mitsui, T. (1982). Runge-Kutta type integration formulas including the evaluation of
the second derivative: Teil 1. Publ. RIMS, Kyoto Univ., 18, 325–365.
Ono, H., & Yoshida, T. (2004). Two-stage explicit Runge-Kutta type methods using
derivatives. Japan J. Indust. Appl. Math., 21, 361–374.
Drücken Sie, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. (1992). Numerical
recipes in C (2nd ed.). Cambridge: Cambridge University Press.
Runge, C.D.T. (1895). ¨Uber die numerische Aufl ¨osung von Differentialgleichungen.
Math. Ann., 46, 167–178.
Shintani, H. (1972). On explicit one-step methods utilizing the second derivative.
Hirsohima Math. J., 2, 353–368.
Stewart, R. D., & Bair, W. (2009). Spiking neural network simulation: Numerical
integration with the Parker-Sochacki method. J. Comput. Neurosci., 27, 115–133.
Stimberg, M., Guter Mann, D. F. M., Benichoux, V., & Falten, R. (2014). Gleichung-
oriented specification of neural models for simulations. Frontiers in Neuroinfor-
matics, 8(6).
Touboul, J. (2009). Importance of the cutoff value in the quadratic adaptive integrate-
and-fire model. Neural Computation, 21, 2114–2122.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2182
M. Hopkins and S. Furber
Touboul, J. (2010). On the simulation of nonlinear bidimensional spiking neuron
Modelle. Neural Computation, 23, 1704–1742.
Vit´asek, E. (1969). The numerical stability in solution of differential equations. Conf.
on Numerical Solution of Differential Equations, 109, 87–111.
Wolfram Research (2014). Mathematica (Ausführung 10.0 Hrsg.). Champaign, IL: Wolfram
Forschung.
Received October 31, 2014; accepted June 4, 2015.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
2
7
1
0
2
1
4
8
2
0
1
9
6
2
1
N
e
C
Ö
_
A
_
0
0
7
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3