BRIEF
Communicated by Karl Friston
A Minimum Free Energy Model of Motor Learning
B. A. Mitchell
brian_a_mitchell@engineering.ucsb.edu
Department of Computer Science, Universität von Kalifornien, Santa Barbara,
Santa Barbara, CA 931056, USA.
N. Lauharatanahirun
nina.lauharatanahirun.civ@mail.mil
Human Research and Engineering Directorate, The CCDC Army Research
Laboratory, Aberdeen Proving Ground, MD 21005, USA., and Annenberg School
for Communication, University of Pennsylvania, Philadelphia, PA 19104, USA.
J. Ö. Garcia
javier.o.garcia.civ@mail.mil
Human Research and Engineering Directorate, The CCDC Army Research
Laboratory, Aberdeen Proving Ground, MD 21005, USA., and Department of
Bioengineering, University of Pennsylvania, Philadelphia, PA 19104, USA.
N. Wymbs
nwymbs@gmail.com
Department of Physical Medicine and Rehabilitation, Johns Hopkins Medical
Institution, Baltimore, MD 21205, USA.
S. Grafton
stgrafton@ucsb.edu
Department of Psychological Brain Sciences, Universität von Kalifornien,
Santa Barbara, Santa Barbara, CA 931056, USA.
J. M. Vettel
jean.m.vettel.civ@mail.mil
Department of Psychological Brain Sciences, Universität von Kalifornien, Santa Barbara,
Santa Barbara, CA 931056, USA.; Human Research and Engineering Directorate,
The CCDC Army Research Laboratory, Aberdeen Proving Ground, MD 21005,
USA.; and Department of Bioengineering, University of Pennsylvania,
Philadelphia, PA 19104, USA.
L. R. Petzold
petzold@engineering.ucsb.edu
Department of Computer Science and Department of Mechanical Engineering,
Universität von Kalifornien, Santa Barbara, Santa Barbara, CA 931056, USA.
Neural Computation 31, 1945–1963 (2019) © 2019 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01219
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
N
e
C
Ö
_
A
_
0
1
2
1
9
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1946
B. Mitchell et al.
Even highly trained behaviors demonstrate variability, which is corre-
lated with performance on current and future tasks. An objective of mo-
tor learning that is general enough to explain these phenomena has not
been precisely formulated. In this six-week longitudinal learning study,
participants practiced a set of motor sequences each day, and neuroimag-
ing data were collected on days 1, 14, 28, Und 42 to capture the neu-
ral correlates of the learning process. In our analysis, we first modeled
the underlying neural and behavioral dynamics during learning. Our re-
sults demonstrate that the densities of whole-brain response, task-active
regional response, and behavioral performance evolve according to a
Fokker-Planck equation during the acquisition of a motor skill. We show
that this implies that the brain concurrently optimizes the entropy of a
joint density over neural response and behavior (as measured by sam-
pling over multiple trials and subjects) and the expected performance
under this density; we call this formulation of learning minimum free
energy learning (MFEL). This model provides an explanation as to how
behavioral variability can be tuned while simultaneously improving per-
formance during learning. We then develop a novel variant of inverse re-
inforcement learning to retrieve the cost function optimized by the brain
during the learning process, as well as the parameter used to tune vari-
ability. We show that this population-level analysis can be used to derive
a learning objective that each subject optimizes during his or her study.
In this way, MFEL effectively acts as a unifying principle, allowing users
to precisely formulate learning objectives and infer their structure.
1 Einführung
Motor learning in biological systems is defined as a change in the capacity
to behave based on experience and practice. The change in behavioral ca-
pacity is typically described in terms of improved performance. Jedoch,
it has become increasingly apparent that an additional important property
of movement is persistent performance variability despite extensive train-
ing. In der Tat, there exists an extensive number of motor control studies of
birdsong, locomotion, and limb control demonstrating the extent to which
movement variability influences and is influenced by performance and
learning (Haar, Donchin, & Dinstein, 2017; Wu, Miyamoto, Castro, Lvecsky,
& Schmied, 2014; Olveczky, Andalman, & Fee, 2005; Kao, Doupe, & Brainard,
2005; Tumer & Brainard, 2007).
An important theme throughout this letter is that even in learned, highly
stereotyped behaviors, there exists variability in the expression of these be-
haviors within and across subjects. The presence of systematic variability
in behaviors that have been heavily trained poses a problem for under-
standing how these systems learn. Even in the case where the behavior is
generated by a stochastic system, the learning objective cannot simply be a
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
N
e
C
Ö
_
A
_
0
1
2
1
9
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Minimum Free Energy Model of Motor Learning
1947
single performance variable such as error minimization (accuracy) or maxi-
mal speed; this would result in behavior with zero variability and suggests
that a more general framework for characterizing learning objectives is nec-
essary to explain a putative aspect of motor learning.
To address this need, we present an approach that tracks dynamic
changes of performance (in our study, movement time) while also captur-
ing performance variability in terms of a free energy functional of density
Dynamik. Gleichzeitig, we characterize the evolving dynamics of neu-
ral activity, whose variability is also described as a property of a density
Funktion. Neural activity is based on fMRI blood oxygen level dependent
(BOLD) measurements recorded as subjects learn a set of finger sequences
practiced at different training intensities. The goal of this work is to de-
termine how the joint brain-behavior densities evolve as a function of the
amount of training.
We show that the dynamics of the density over global (all brain regions)
and localized (the task-active regions) brain-behavior pairs follow a Fokker-
Planck partial differential equation (FPE). (We use the term density as
shorthand for probability density function in this work.) The FPE is a fun-
damental aspect of the physical sciences for both classical and quantum
mechanics (Kadanoff, 2000; Leal, 2012; Landauer & Lifshitz, 1965). With re-
spect to the neurosciences, the FPE is the population-level version of the
drift-diffusion equation often used to model decision making (Heekeren,
Marrett, Bandettini, & Ungerleider, 2004; Forstmann et al., 2008) und hat
also been used to model stochastic neuronal dynamics (Harrison, David,
& Friston, 2005). The advantage of this joint brain-behavior density frame-
work is that it offers a potential explanation of the nature of behavioral vari-
ability and how it is tuned during learning. A strength of this explanation
is that it is grounded in the dynamics of the underlying neural activity. To
the best of our knowledge, the combined modeling of neural activity and
behavior is a novel extension of past work on motor variability (Haar et al.,
2017; Wu et al., 2014; Olveczky et al., 2005).
The introduction of this joint brain-behavior framework provides a pre-
cise formulation of the learning objective that gives rise to the observed
variability. Speziell, we show that the optimization of a popular objec-
tive in the reinforcement learning and optimal control literature (Haarnoja,
Tang, Abbeel, & Levine, 2017) also yields dynamics that follow the FPE. Das
objective is so named because it contains two terms: expected performance of
the brain-behavior density and its entropy. We refer to this framework as min-
imum free energy learning (MFEL). The consequences of this finding are
twofold. Erste, it suggests an appropriate definition of behavioral variabil-
ity as the entropy of the brain-behavior density. Nächste, it suggests a way to
recover the parameters of the MFEL objective to infer the performance ob-
jective optimized, as well as the manner in which variability is tuned during
learning.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
N
e
C
Ö
_
A
_
0
1
2
1
9
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1948
B. Mitchell et al.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
N
e
C
Ö
_
A
_
0
1
2
1
9
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
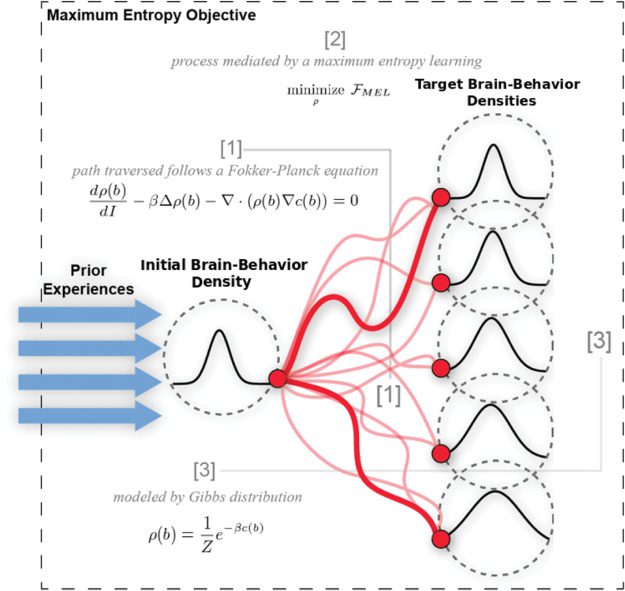
Figur 1: Overview of the findings of this work. Previous experience is em-
bodied in the initial brain-behavior density before any learning. Based on the
form of the dynamics of this density (red lines, [1]), this density is modeled as
a Gibb’s distribution ([3]). The eventual target of these dynamics is largely in-
fluenced by the temperature parameter, β. This coefficient tunes the entropy of
the brain-behavior density, as shown by the minimum free energy objective [2].
Using a novel variant of inverse reinforcement learning, we retrieve the
cost function optimized during motor learning, as well as the parameter
tuning the entropy of the brain-behavior density (siehe Abbildung 1).1 This allows
us to relate the population-level analysis performed to infer these objects
to learning on the individual level. Insbesondere, we show that the MFEL
framework is appropriate to characterize individual learning by showing
that individuals optimize the same objective as the population of subjects.
1
The appeal to reinforcement learning is meant to highlight the connection between
our method and the control of neural systems. Tatsächlich, the method presented in the online
supplement is a generic approach to parameter estimation for density dynamics following
the Fokker-Planck equation.
A Minimum Free Energy Model of Motor Learning
1949
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
N
e
C
Ö
_
A
_
0
1
2
1
9
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
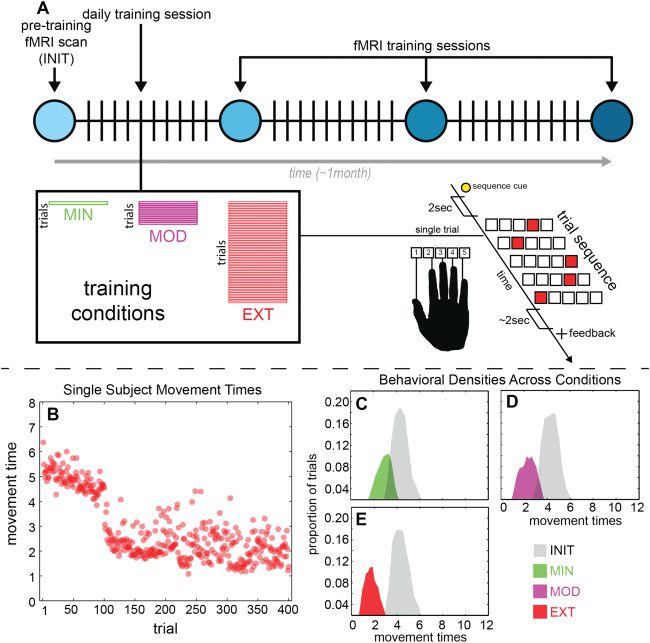
Figur 2: (A) Schematic summarizing the DSP task as well as the experimental
Design. (B) Example movement times for a single subject in the EXT condition.
Each scanning session consists of 100 Versuche, and each point gives the perfor-
mance on a single trial. Movement time variability persists even with the highest
training intensity and duration. (C–E) Evolution of movement time densities for
EXT (panel E), MOD (panel D), and MIN (panel C) conditions with INIT shown
in gray.
2 Methoden
2.1 Experimental Design. The motor sequence training protocol oc-
curred over a six-week period with four MRI scanning sessions spaced two
weeks apart on days 1, 14, 28, Und 42 (siehe Abbildung 2). On day 1 of the exper-
imental protocol, the participants completed their first MRI session, scan
1, and the experimenter installed the training module on the participant’s
personal laptop and explained how to use it for at-home training sessions.
1950
B. Mitchell et al.
Behavioral measurements were taken during these at-home training ses-
sionen, and interspersed throughout this training regimen, neuronal mea-
surements were taken using fMRI BOLD. Participants were required to do
the training for a minimum of 10 out of the 14 days in each two-week period
between the subsequent scanning sessions. All participants completed the
full training regimen; none completed fewer than 10 full training sessions.
In their at-home training sessions, participants practiced a set of 10-
element sequences using their right hand. Sequences were presented us-
ing a horizontal array of five square stimuli, and the key responses were
mapped from left to right, such that the thumb corresponded to the leftmost
stimulus and the pinky finger corresponded to the rightmost stimulus (sehen
Figur 2). A square highlighted in red served as the target stimulus, und das
next square in the sequence was highlighted immediately after each cor-
rect key press. If an incorrect key was pressed, the sequence was paused at
the error and restarted upon the appropriate key press. Participants had an
unlimited amount of time to respond and complete each trial.
Each practice trial began with the presentation of a sequence-identity cue
that identified one of six sequences. These six sequences were presented
with three different levels of exposure in order to acquire data over a larger
range of learning stages while controlling for the effect of scanning day. Der
two extensively trained (EXT) sequences were identified with a colored cir-
cle (cyan for sequence A and magenta for B), and they were each practiced
für 64 trials during every at-home training session. The two moderately
trained (MOD) sequences were identified by triangles (red for sequence C
and green for D) and each practiced for 10 trials in every session. The two
minimally trained (MIN) sequences were identified by black outlined stars
(filled with orange for sequence E and white for F) and practiced for only
1 trial each during the at-home training sessions. Participants were given
feedback every 10 trials that reported the number of error-free sequences
and the mean time required to complete them.
2.2 Data Collection. Twenty-two right-handed participants (13 Frauen
Und 9 men; mean age, 24 Jahre) volunteered and provided informed con-
sent in writing in accordance with the guidelines of the Institutional Re-
view Board of the University of California, Santa Barbara. All had normal
or corrected vision and no history of neurological disease or psychiatric dis-
orders. We excluded 2 Teilnehmer; one participant failed to complete the
Experiment, and the other exhibited excessive head motion (persistent head
motion greater than 5 mm during the MRI scanning).
During each of the four MRI scanning sessions, we collected functional
echo planar imaging data while participants performed 300 trials of the self-
paced motor sequence task. Unlike the at-home practice sessions, partici-
pants completed an equal number of trials for each of the three exposure
types. Der 50 trials for each sequence type were grouped in blocks of 10 tri-
als of the same sequence type (10 MIN, 10 MOD, 10 EXT), and the blocks
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
N
e
C
Ö
_
A
_
0
1
2
1
9
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
A Minimum Free Energy Model of Motor Learning
1951
were randomly ordered across the five BOLD runs. After each block of 10,
participants received feedback about the number of error-free sequences
and mean reaction time to complete the sequences.
Because sequence production was self-paced, the number of scanned
TRs varied between subject and session. In order to collect event-related
fMRI data, the intertrial interval ranged between 0 Und 6 S (Durchschnitt von 5 S).
The number of sequence trials performed during each scan session was the
same for all subjects with the exception of two abbreviated sessions due to
technical problems. In each of these two cases, the scanning protocol was
stopped short, so that four of the normally acquired five runs were com-
pleted. Data from these sessions are included in our analysis.
2.3 fMRT-Datenanalyse. Functional imaging data processing and anal-
ysis were performed using statistical parametric mapping (SPM8, Wellcome
Department of Cognitive Neurology). Raw functional data were realigned,
coregistered to the native T1 (using the first mean image as the base image
for all functional scans), normalized to the MNI-152 template with a resliced
resolution of 3 × 3 × 3 mm, and then smoothed with a kernel of 8 mm full
width at half-maximum.
BOLD response was modeled for each subject using a single design ma-
trix with parameters estimated using a general linear model (GLM). Ein
event-related design was used to model sequence-specific activity patterns.
Trial onset is signaled by the presentation of the sequence identity cue and
is presented 2 s prior to the initial discrete sequence production (DSP) tar-
get stimulus. Neural activity in this case reflects both the preparation and
production of learned sequences. The design matrix for each subject was
constructed using separate factors for each scan session (pretraining, train-
ing sessions 1–3), exposure condition (MIN, MOD, and EXT), and repetition
(new or repeated trial). A trial is coded as a repeated event if the previous
trial was the exact same sequence and the previous trial had been performed
correctly. Error trials and repeated trials that followed error trials were mod-
eled using a separate column in the design matrix. Blocking variables were
used to account for nonspecific session effects for each scan run.
The full-factorial design option in SPM was used to perform higher-
level mixed-effects group analysis. Skill-specific longitudinal effects were
modeled using a single factor (12 levels: one for each exposure condi-
tion and session). Training intensity, das ist, the cumulative number of
training trials performed, was used for model factor levels: pretraining
(MIN/MOD/EXT), MIN during training scans 1 Zu 3, MOD during train-
ing scans 1 Zu 3, and EXT during training scans 1 Zu 3. We were primarily
interested in analyzing BOLD dynamics with respect to training intensity.
Um dies zu tun, a contrast was developed at the group level where the main ef-
fect of training intensity, over all sequences, scanning sessions, and types of
training intensity, was calculated using a one-sample t-test and corrected for
multiple comparisons using family-wise error (FWE) correction (P < 0.05).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1952
B. Mitchell et al.
Based on the previous literature on motor learning, we focused our anal-
ysis on nine sensorimotor regions, including the postcentral gyrus, supple-
mentary motor area, and lateral occipital cortices (Mattar et al., 2018). To
investigate neural activation within these areas during the task, we con-
structed a mask image representing the intersection of each brain region
as indicated by the Harvard-Oxford atlas and the group level contrast of
training intensity that was FWE corrected. This ensured that we analyzed
the task-active voxels within the sensorimotor regions that were common
across the group, and then we extracted an average time series for each in-
dividual from each region for each training intensity. This provided a ma-
trix that was 24 (subjects) × 9 (sensorimotor regions) × 3 (training intensity
MIN, MOD, and EXT).
The estimated beta weights reflect a group-level GLM contrast that re-
flects the main effect of training intensity across all sequences, scanning,
sessions, and types of training intensity. This map was the result from a one-
sample t-test corrected for multiple comparisons using a family-wise-error
(FWE) correction with a p-value threshold of 0.05. The higher-level group
mixed-effects model was estimated using all but one subject, and from this,
the identified local optima were used to extract mean beta weights from the
remaining subject. Mean beta weights were extracted using a spherical ROI
(6 mm radius) centered on each local optimum. We performed this proce-
dure for each of the 20 subjects, so that the displayed amplitudes correspond
to the overall mean of the left-out-subjects’ beta weights.
The brain regions outside the sensorimotor system were defined based
on task active voxels in the group-level contrast, reflecting the main effect
of training intensity across all sequences, scanning sessions, and types of
training intensity. A mask image was constructed that represented the in-
tersection of each Harvard-Oxford anatomical region and the group-level
task activation image, and then the mask was applied to each subject’s im-
age. For each subject, the mean of the extracted, nonzero voxels within each
region for each subject and each condition was computed.
3 Results
In our longitudinal study of motor learning, participants (N = 20) per-
formed a discrete sequence production task for six weeks where we var-
ied the amount of practice across a set of six sequences. Neural responses
(BOLD activity) were recorded to obtain baseline neural responses while
the participants were first being exposed to the sequences (INIT). As shown
in Figure 2A, participants then completed at-home training sessions where
two of the sequences were trained extensively (64 trials per session; EXT),
two were trained moderately (10 trials per session; MOD), and two mini-
mally (1 trial per session; MIN). Performance was measured by movement
time to complete the sequence where the subjects were instructed to pri-
oritize perfect accuracy over completing the movement sequences faster.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Minimum Free Energy Model of Motor Learning
1953
Across the four imaging sessions (with two weeks’ separation between
each), whole-brain analysis was conducted to identify brain regions acti-
vated during sequence production for each training intensity condition.
Beta values (derived from modeling BOLD activity using a GLM) from
whole brain analysis were extracted using the Harvard-Oxford atlas. Den-
sity estimates were constructed from histograms of beta values using evenly
spaced bins over the support of the distribution. These distributions were
constructed using measurements taken from all subjects, trials, and brain
regions for a given condition (INIT, MIN, MOD, or EXT).
3.1 Behavioral Variability Persists during Motor Learning. First, we
examine behavioral performance during a motor learning task as a function
of training intensity. Across all participants and all training intensity con-
ditions, there was a reduction in movement time during the motor learning
task (see Figures 2C to 2E). A significant decrease in average movement time
across all training intensity conditions relative to the initial training session
was observed (see Figure 2C; MIN versus INIT, M = 1.88, SD = 0.63, t(df) =
139.83, p < 0.0001; MOD versus INIT, M = 2.49, SD = 0.75, t(df) = 96.86, p <
0.0001); EXT versus INIT, M = 3.04, SD = 0.71, t(df) = 74.65, p < 0.0001),
with average performance on sequences in the EXT condition showing the
greatest reduction in movement times relative to initial training. In fact, al-
ternative hypotheses were rejected using t-tests when all pairs of the four
conditions were compared with each other rather than just comparing MIN,
MOD, and EXT conditions with INIT (p-values were less than 0.0001). This
demonstrates that the exposure of individuals to more intense training will
improve their performance as defined by the average movement time.
In addition to improved average performance, motor learning is char-
acterized by the persistence of behavioral variability. We refer to this vari-
ability as the entropy of the behavioral density. This definition is formally
justified in section 3.3. The experimental data (Figure 2B) suggest that an-
alyzing the dynamics of the density over movement times, and its entropy
in particular, may help to explain the origin of this variability and allow us
to understand its evolution over time.
To this point, the evolution of the movement time densities as a func-
tion of training intensity is shown in Figures 2C, 2D, and 2E. Notably, the
entropy in the movement time density does not decrease to zero with in-
creased training intensity. We relate this result to past work where even
highly trained, stereotyped behaviors retain a certain amount of variabil-
ity when executed (Haar et al., 2017; Wu et al., 2014; Olveczky et al., 2005;
Kao et al., 2005; Tumer & Brainard, 2007). The fact that the entropy of the
movement time density after high training intensity is nonzero suggests
that learning has at least two objectives: improved average performance
and tuning the entropy of the density. This follows from the fact that simply
optimizing for average performance would result in deterministic behav-
ior (i.e., a movement time density with zero entropy). This is not to say that
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1954
B. Mitchell et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
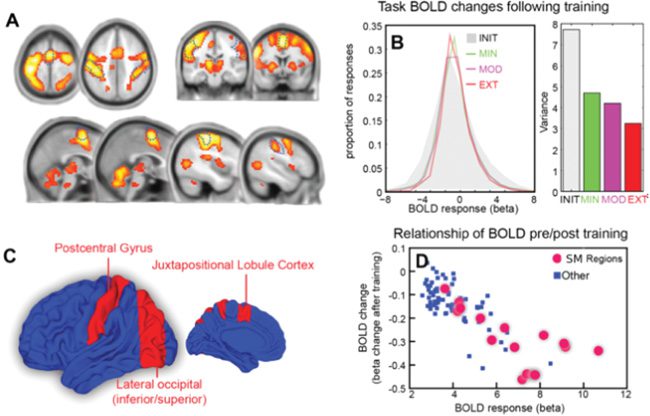
Figure 3: (A) Global task-active beta coefficients illustrated on axial, sagittal,
and coronal slices (FWE < 0.05). (B) Global density of beta coefficients (left)
and the variances of the densities for each training intensity. (C) Sensorimotor
(SM) brain regions (red) and all other brain regions (blue). (D) Change in beta
coefficient with training intensity plotted against initial beta coefficient for SM
regions (red) and all other task-active regions (blue).
behavioral variability is intentionally preserved by the brain, but it may be
that there is a minimum amount of noise in the execution of movements
that cannot be further refined. Yet even in this case, in order to accurately
model motor learning, this persistent noise must be mathematically formu-
lated and incorporated into the model.
3.2 Motor Learning Follows Fokker-Planck Dynamics. To examine the
dynamics of the neural substrates of motor learning across all regions in-
volved in sequence production, BOLD beta values from task-dependent
brain regions were extracted using the Harvard-Oxford atlas. In Figure 3,
the densities of BOLD beta values are plotted to demonstrate the changes
in global brain dynamics across the different training intensity conditions.
There was a decrease in the entropy of the BOLD density relative to initial
training, but similar to behavioral performance results, this entropy remains
nonzero at the highest training intensity (see Figure 3B; INIT, M = 0.19, SD =
2.78; MIN versus INIT, M = 0.007, SD = 2.16, Levene = 6.47, p = 0.012; MOD
versus INIT, M = 0.0168, SD = 2.05, Levene = 8.50, p = 0.004); EXT versus
INIT, M = 0.086, SD = 1.81, Levene = 15.14, p = 0.0001).
A Minimum Free Energy Model of Motor Learning
1955
Importantly, brain regions that are implicated in sensorimotor function
are more sensitive to these dynamics than other task-relevant brain areas.
This is shown in Figure 3D, where the change in the beta coefficient with in-
creased training intensity is plotted against the initial beta coefficient, and a
two-dimensional Kolmogorov-Smirnov test distinguishes these two groups
of brain regions with p-value of 0.00031. This result also holds at the individ-
ual level for all but four subjects (with p-values of 0.05926, 0.11123, 0.18631,
and 0.11049, respectively).
Naively, this decreasing entropy seen at the global scale might be ex-
plained by a minimization of extraneous and error-prone movements and a
refinement of movements to more efficiently execute each sequence. But the
dynamics of the movement time density in Figures 2C, 2D, and 2E suggest
that the influence of training intensity is more subtle. Simply optimizing
for performance (movement time) would result in deterministic behavior.
The fact that even expert behavior on EXT sequences is probabilistically
distributed suggests that a different model of learning is required.
To better visualize the relationship between neural activity and move-
ment time, we plot the brain-behavior density as it evolves with increased
training intensity in Figure 4. A partial differential equation (PDE) that cap-
tures the dynamics shown is the Fokker-Planck equation (FPE), which is
given by
dρ(b)
dI
− β(cid:4)ρ(b) − ∇ · (ρ(b)∇c(b)) = 0,
(3.1)
where b is the 2-tuple containing the random variables for neural activity
and behavior, ρ(b) is the probability density over brain-behavior pairs, (cid:4) is
the Laplacian operator, ∇· is the divergence operator, c(b) is a cost function,
β is the diffusion coefficient, and I is the training intensity. This equation can
be understood as shifting an initial value of ρ(b) (corresponding to the INIT
condition) in the direction specified by ∇c(b) while producing diffusion,
the direction and rate of which is specified by β (we relate the diffusion of
ρ(b) to entropy in the next section). We have defined the evolution of the
density with respect to training intensity, though the FPE is typically used
to characterize the evolution of a density with respect to time. Since we have
also defined training intensity as the number of exposures of a subject to a
sequence, assuming each exposure takes a fixed amount of time, these two
approaches can be seen as equivalent.
In the case of the DSP task presented in this work, the cost function is the
mathematical representation of the motivation each subject has to improve
his or her respective performance on the task. Put simply, ρ(b) performs
steepest descent on c(b) to improve performance and change the shape of
ρ(b), while the diffusion term tunes the entropy of ρ(b). The incorporation
of this function into the FPE framework not only gives insight into the dy-
namics of the brain-behavior densities (goodness-of-fit tests are provided
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1956
B. Mitchell et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
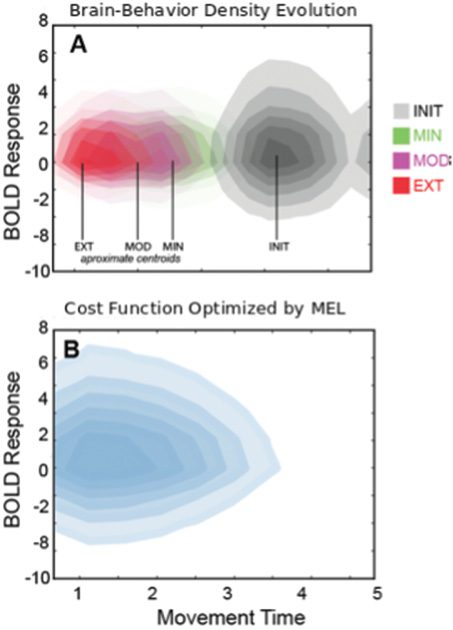
Figure 4: (A) Evolution of the brain-behavior densities with increased train-
ing intensity. (B) The cost function optimized during MFEL as derived from
population-level analysis.
in the supplement), but also the rate at which the brain-behavior densities
converge to an expert state during learning. In the supplement, we show
that the solution of the FPE converges to steady state exponentially fast,
explaining the exponential improvement seen in the subjects’ behavioral
performance.
Previous work in neuroscience and physics has demonstrated that the
use of Fokker-Planck dynamics is a biologically appropriate model for
explaining stochastic neuronal dynamics (Harrison et al., 2005). While a
majority of prior work has primarily focused on using the FPE to model
stochastic changes in neuronal networks, this study extends this line of re-
search to explain the neurobehavioral dynamics of motor learning through
training. Specifically, we extend the use of the FPE to show that it applies to
A Minimum Free Energy Model of Motor Learning
1957
jointly model the BOLD response and behavior of subjects, a result that does
not necessarily follow from past work on neuronal dynamics. In the context
of motor learning, the FPE provides a mathematical framework to precisely
define the source of and mechanism for tuning behavioral variability: both
derive from diffusion of the brain-behavior density.
3.3 Fokker-Planck Dynamics Are Generated via Free Energy Opti-
mization. While the FPE may capture the dynamics of the brain-behavior
density during learning, it is not clear how these dynamics relate to the
problem solved by the subjects. In fact, the FPE suggests a popular frame-
work as a model for the learning problem solved by the subjects. To pro-
ceed further, though, we require a model of the brain-behavior density.
The steady-state distribution of the Fokker-Planck equation is the Gibbs
distribution,
ρ(b) = 1
Z
−βc(b),
e
(3.2)
where Z is a normalizing constant and β is a temperature parameter. This
distribution also appears in the literature under the name “maximum en-
tropy distribution.” There are many ways to interpret this name, but per-
haps the most direct is to begin with an optimization problem. Consider the
objective
FMFEL = Eρ[c] − βH[ρ],
(3.3)
where H is the entropy of ρ, Eρ is the expectation operator with respect to
the brain-behavior density ρ, and c is the cost as defined in the previous
section. Equation 3.3 is actually a specific example of a more general ex-
pression (Ortega & Braun, 2010, 2013). In particular, c may be redefined as
a generic “potential” or “energy,” φ. In its current form with φ interpreted
as a cost, this equation is commonly used for policy optimization meth-
ods in reinforcement learning and control engineering (Kappen, Gomez, &
Opper, 2012; van den Broek, Wiegerinck, & Kappen, 2010; Braun, Ortega,
Theodorou, & Schaal, 2011) and can be related to models of neural systems
as optimizing prediction errors (Adams, Shipp, & Friston, 2013). By setting
φ to be the negative log-likelihood of the data, equation 3.3 can also be used
to derive the evidence lower bound (ELBO), used for variational inference.
This objective can be incorporated into the following optimization problem:
minimize
ρ
FMFEL.
(3.4)
If a brain-behavior density is found by optimizing this expression in a par-
ticular way, then its dynamics follow the Fokker-Planck equation (see the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1958
B. Mitchell et al.
supplement for derivation). Because the dynamics of the brain-behavior
density follow a Fokker-Planck equation during motor learning, equation
3.4 is also a good model of the optimization problem that accounts for the
neural changes during learning. This connection formalizes the intuition
given in the previous section: motor learning proceeds by simultaneous op-
timization of expected cost and the brain-behavior density. We refer to this
model as minimum free energy learning (MFEL) throughout the rest of this
letter.
The MFEL model implies that behavioral variability is tuned by adjust-
ing the entropy of the brain-behavior density (i.e., tuning β). For example, if
the entropy of the brain-behavior density is increased along the behavioral
coordinate, then samples from this density are going to be more variable.
Given empirical examples of the evolution of the brain-behavior density,
though, it is not immediately clear how to estimate the cost function, c(b),
or the temperature parameter, β. These objects are retrieved in the next sec-
tion (the methods for doing so are presented in the supplement), and the use
of the MFEL framework as a model for motor learning is further validated.
3.4 Each Subject Learns the Same Optimal Behavior. The objective
given in equation 3.4 represents a rule governing how the population of
subjects learns. But when analyzing the learning procedure of individual
subjects, both the structure of the brain-behavior density and its dynam-
ics might seem quite different from those presented in Figure 4. In order to
validate the utility of the population-level analysis for modeling learning
within individual subjects, we first inferred the structure of the cost func-
tion optimized during motor learning. To do this, we developed a novel
approach to inverse reinforcement learning (IRL) in order to compute an
explicit representation of the cost function. One class of IRL methods, called
maximum entropy IRL (MEIRL), attempts to infer c(b) given samples from
p∗
(b) has the form of the Gibb’s distribution. One strat-
egy for finding c(b) in this case is to use a gradient-based method to optimize
the negative log likelihood of the samples (Finn, Levine, & Abbeel, 2016).
This approach is not ideal in the case of the data presented here because
the optimization scheme does not necessarily preserve the Fokker-Planck
dynamics observed during learning. Instead, we would like to develop a
method that not only retrieves c(b) but does so in a way that is consistent
with the dynamics of neural learning.
(b), assuming that p∗
The method we develop relies on the modification of a popular method
used to simulate the FPE. Briefly, this method simulates the FPE by solving
a sequence of optimal transport problems. That is, one can simulate the FPE
by, at every time step t, evolving pt (b) to pt+1(b) by finding the pt+1(b) that
is as close as possible to pt (b) while still reducing the value of equation 3.3.
Since for our data, pt+1(b) is known (i.e., it is either the empirical densities
for the MIN, MOD, or EXT conditions), we simply need to solve the optimal
transport problem between pt (b) and pt+1(b). The cost function optimized
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Minimum Free Energy Model of Motor Learning
1959
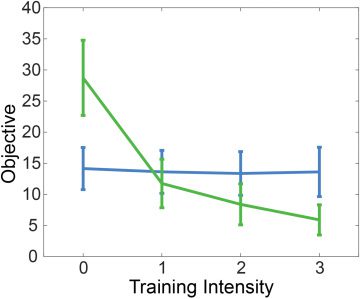
Figure 5: The value of the population-level objective for each subject plotted
against training intensity (green) compared with a null model (blue). The null
model was generated by shuffling data across conditions, within each subject’s
data set. The brain-behavior density for each subject is evaluated using the
MFEL objective, where the cost function is derived from a population-level anal-
ysis. This plot demonstrates that individual subjects optimize the population-
level objective.
in moving from pt (b) to pt+1(b) can be retrieved from the solution of these
optimal transport problems (see the supplement for full derivation).
The cost function returned by our method is shown in Figure 4. The cost
function is approximately convex, and this result implies, given the MFEL
model, that the optimal brain-behavior density is always achieved and this
density is unique. With respect to tuning behavioral variability, this theoret-
ical guarantee indicates that there is an optimal level of variability (i.e., an
optimal value for the entropy of the brain-behavior density). This follows
from the fact that this cost function includes β from equation 3.2. So in ef-
fect, it includes information on the cost function being optimized, as well
as the target variability.
Finally, in Figure 5, we present evidence demonstrating that each sub-
ject optimizes a similar objective. Using the cost function derived from
the population-level analysis (shown in the bottom plot of Figure 4) in
the objective in equation 3.4, we computed this objective using the brain-
behavior densities for each individual subject. The curves presented in
Figure 5 demonstrate exponential improvement in this objective with in-
creased training intensity. Moreover, we note that nearly every subject
demonstrated strictly monotonic improvement in this objective with in-
creased training intensity. These results suggest that the estimate of the ob-
jective given in equation 3.4 is not only a good representation of population-
level learning but also of learning that takes place within the individual.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1960
4 Discussion
B. Mitchell et al.
In this letter, we presented a minimum free energy model of motor learning.
We have taken a popular objective from the engineering and statistics com-
munity, equation 3.4, and shown that it has a strong biological foundation.
This connection between biology and engineering follows from the evolu-
tion of the empirical brain-behavior density according to a Fokker-Planck
equation. We show how learning is characterized as evolving with training
intensity and analyze the full density of observed responses (behavioral and
neuronal) to justify this perspective. In doing so, we are able to connect a
number of seemingly disparate schools of thought: the brain as a controller,
inference engine, and dynamical system (Friston, 2010; Friston, Mattout,
& Kilner, 2011; Friston, Samothrakis, & Montague, 2012). Optimization of
equation 3.4 is commonly used to perform policy optimization for control
systems. This problem is equivalent to the one solved during variational
Bayesian inference, where the cost (c) is interpreted as a negative log like-
lihood and a KL divergence is minimized between estimated and actual
posterior densities. And we show that if equation 3.4 is solved in a partic-
ular manner, the dynamics follow the FPE. The ability of the MFEL to act
as a unifying principle across these three schools of thought allows us to
lend support to the theory of learning in the brain as performing Bayesian
inference. The brain-behavior densities for a given training intensity can be
interpreted as posterior densities where responses are sampled from these
densities. The fact that this kind of inference is performed by optimizing the
entropy of Bayesian beliefs about responses speaks to the close connection
between the minimum free energy and Occam’s principles.
The fundamental finding that motor learning can be modeled with an
FPE explains why it proceeds exponentially fast, as well as suggests a new
approach to solving the IRL problem. Many different approaches to IRL
have been taken, but it is not clear how any of them relate to the dynamics
of learning. This raises issues related to the accuracy of the cost function
retrieved, especially in the case where the solution is not unique. Our ap-
proach, based on optimal transport, is both novel and has a clear connec-
tion with the biology of learning. While optimal transport has been used
for Bayesian inference, it has not been used for IRL (Moselhy & Marzouk,
2012). More important, we are able to use the population-level inferences
and show that individual subjects also optimize the population-level objec-
tive. We are thus able to give both theoretical and empirical support for the
use of our variant of IRL.
Another conclusion following from the observed learning dynamics is
that samples from the brain-behavior density become less variable with in-
creased training intensity. This can be interpreted as a kind of inflexibility, a
concept that has been studied from a number of different perspectives pre-
viously, including a network scientific perspective (Bassett et al., 2011, 2013;
Khambhati, Mattar, Wymbs, Grafton, & Bassett, 2018; Reddy et al., 2018),
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Minimum Free Energy Model of Motor Learning
1961
aging (Berry et al., 2016) and neural systems at the cellular and circuit lev-
els (Fusi, Asaad, Miller, & Wang, 2007). With respect to artificial controllers
fit using the MFEL objective, this inflexibility manifests as an inability of
learned policies to handle nonstationary environments (i.e., a cost function
that changes with time; Mitchell & Petzold, 2018). It is not clear, though,
that inflexibility in organic neural controllers fit using the MFEL objective
would be a direct consequence of exposing subjects to increased training
intensity.
One complication that might arise involves the ability of organic neural
systems to maintain multiple skills at once, though it is currently an open
problem to train artificial neural network controllers to do the same (Kirk-
patrick et al., 2017). Inflexibility is not necessarily problematic in the case
of a stationary environment. Inflexibility must thus take into account the
size of the space of skills a neural controller has learned and the probabil-
ity of the environment to transition away from this space. Further work is
required to combine these ideas with the models of MFEL presented in this
letter.
The study of individual differences with respect to the MFEL model pre-
sented in this letter is another interesting avenue for future research. We
showed in Figure 5 that individual subjects largely demonstrate exponen-
tial improvement in the population-level objective with increased training
intensity. Within this population of subjects, though, there is a nonzero vari-
ance over the learning rate (i.e., the value λ, if the value of the objective
over intensity decays like e−λI). From the models presented in this letter, it
is not immediately clear how to relate MFEL models of individual learning
to MFEL models at the population level. A Bayesian approach may be fruit-
ful, where brain-behavior densities of individual subjects are assumed to
belong to a family of densities with a common prior. In this case, one would
expect to be able to analyze the population-level cost function to provide in-
sight into learning the entire task and learning dynamics in general, as has
been done in this work. Further insight could be drawn based on the struc-
ture of individual cost functions, though. For example, such insight would
include a better understanding of why some individuals tend to have more
variable behaviors than others.
References
Adams, R. A., Shipp, S., & Friston, K. J. (2013). Predictions not commands: Active
inference in the motor system. Brain Struct. Funct., 218, 611–643.
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson, J. M., & Grafton,
S. T. (2011). Dynamic reconfiguration of human brain networks during learning.
Proceedings of the National Academy of Sciences, 108(18), 7641–7646.
Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha, P. J., & Grafton,
S. T. (2013). Task-based core-periphery organization of human brain dynamics.
PLoS Computational Biology 9(9).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1962
B. Mitchell et al.
Berry, A. S., Shah, V. D., Baker, S. L., Vogel, J. W., O’Neil, J. P., Janabi, M., . . . Jagust, W.
J. (2016). Aging affects dopaminergic neural mechanisms of cognitive flexibility.
Journal of Neuroscience 36(50), 12559–12569.
Braun, D. A., Ortega, P. A., Theodorou, E., & Schaal, S. (2011). Path integral con-
trol and bounded rationality. In Proceedings of the IEEE Symposium on Adaptive
Dynamic Programming and Reinforcement Learning (pp. 202–209). Piscataway, NJ:
IEEE.
Finn, C., Levine, S., & Abbeel, P. (2016). Guided cost learning: Deep inverse optimal
control via policy optimization. In Proceedings of the International Conference on
Machine Learning. arXiv:1603.00448v3
Forstmann, B. U., Dutilh, G., Brown, S., Neumann, J., von Cramon, D. Y., Rid-
derinkhof, K. R., & Wagenmakers, E. J. (2008). Straitum and pre-SMA facilitate
decision-making under time pressure. PNAS, 105(45), 17538–17542.
Friston, K. (2010). The free-energy principle: A unified brain theory? Nat. Rev. Neu-
rosci., 11, 127–138.
Friston, K., Mattout, J., & Kilner, J. (2011). Action understanding and active inference.
Biol. Cybern., 104, 137–160.
Friston, K., Samothrakis, S., & Montague, R. (2012). Active inference and agency:
Optimal control without cost functions. Biol. Cybernetics, 106, 523–541.
Fusi, S., Asaad, W. F., Miller, E. K., & Wang, X. J. (2007). A neural circuit model of
flexible sensori-motor mapping: Learning and forgetting on multiple timescales.
Neuron 54(2), 319–333.
Haar, S., Donchin, O., & Dinstein, I. (2017). Individual movement variability mag-
nitudees are explained by cortical neural variability. Journal of Neuroscience, 37,
9076–9085. doi:10.1523/JNEUROSCI.1650-17.2017.
Haarnoja, T., Tang, H., Abbeel, P., & Levine, S. (2017). Reinforcement learning with deep
energy-based policies. arXiv:1702.08165v2.
Harrison, L. M., David, O., & Friston, K. J. (2005). Stochastic models of neuronal
dynamics. Phil. Trans. R. Soc. 360, 1075–1091.
Heekeren, H. R., Marrett, S., Bandettini, P. A., & Ungerleider, L. G. (2004). A general
mechanism for perceptual decision-making in the human brain. Nature, 431, 859–
862.
Kadanoff, L. P. (2000). Statistical physics: Statics, dynamics and renormalization. Singa-
pore: World Scientific.
Kao, M. H., Doupe, A. J., & Brainard, M. S. (2005). Contributions of an avian
basal ganglia-forebrain circuit to real-time modulation of song. Nature, 433, 638–
643.
Kappen, H. J., Gomez, Y., & Opper, M. (2012). Optimal control as a graphical model
inference problem. Machine Learning, 87, 159–182.
Khambhati, A. N., Mattar, M. G., Wymbs, N. F., Grafton, S. T., & Bassett, D. S. (2018).
Beyond modularity: Fine-scale mechanisms and rules for brain network recon-
figuration. NeuroImage, 166, 385–399.
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Desjardins, G., Rusu, A. A.,
. . . Hadsell, R. (2017). Overcoming catastrophic forgetting in neural networks.
Proceedings of the National Academy of Sciences, 114(13), 3521–3526.
Landau, L. D., & Lifshitz, E. M. (1965). Quantum mechanics. New York: Elsevier.
Leal, G. L. (2012). Advanced transport phenomena. doi:10.1017/CBO9780511800245
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Minimum Free Energy Model of Motor Learning
1963
Mattar, M. G., Wymbs, N. F., Bock, A. S., Aguirre, G. K., Grafton, S. T., & Bassett,
D. S. (2018). Predicting future learning from baseline network architecture.
NeuroImage, 172, 107–117.
Mitchell, B. A., & Petzold, L. R. (2018). Control of neural systems at multiple scales
using deep reinforcement learning. Scientific Reports, 8, 10721.
Moselhy, A. T. E., & Marzouk, Y. M. (2012). Bayesian inference with optimal maps.
Journal of Computational Physics, 231(23), 7815–7850.
Olveczky, B. P., Andalman, A. S., & Fee, M. S. (2005). Vocal experimentation in the ju-
venile songbird requires a basal ganglia circuit. PLoS Biology. doi:10.1371/journal
.pbio.0030153
Ortega, P. A., & Braun, D. A. (2010). A minimum relative entropy principle for learn-
ing and acting. J. Artif. Int. Res., 38, 475–511.
Ortega, P. A., & Braun, D. A. (2013). Thermodynamics as a theory of decision-making
with information-processing costs. Proc. R. Soc. A, 469, 2153.
Reddy, P. G., Mattar, M. G., Murphy, A. C., Wymbs, N. F., Grafton, S. T., Satterth-
waite, T. D., & Bassett, D. S. (2018). Brain state flexibility accompanies motor-skill
acquisition. NeuroImage 171, 135–147.
Tumer, E. C., & Brainard, M. S. (2007). Performance variability enables adaptive plas-
ticity of “crystallized” adult birdsong. Nature, 450(7173), 1240–1244. doi:10.1038
/nature06390
van den Broek, J. L., Wiegerinck, W. A. J. J., & Kappen, H. J. (2010). Risk-sensitive
path integral control. In Proceedings of the Association for Uncertainty in Artificial
Intelligence. AUAI Press.
Wu, H. G., Miyamoto, Y. R., Castro, L. N. G., Lvecsky, B. P., & Smith, M. A. (2014).
Temporal structure of motor variability is dynamically regulated and predicts
motor learning ability. Nature Neuroscience, 17(2), 312–321. doi:10.1038/nn.3616
Received March 15, 2019; accepted May 9, 2019.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
1
1
0
1
9
4
5
1
8
6
4
3
6
4
n
e
c
o
_
a
_
0
1
2
1
9
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3