Wie geht es Feynman - Am MIT spezialisierte KI-Forschung

Wie geht es Feynman
Diagramme funktionieren?

James Robert Brown
Universität von Toronto

Einführung

1.
Feynman-Diagramme (im Folgenden FDs) sind mittlerweile ikonisch. Wie Bilder von den Bohr
Atom, Jeder weiß, dass sie etwas Wichtiges mit der Physik zu tun haben.
Diejenigen, die in der Quantenfeldtheorie arbeiten, Stringtheorie, und andere esoterische
Die Bereiche der Physik nutzen sie ausgiebig. Trotzdem, Es ist alles andere als klar, was
sie sind oder wie sie funktionieren. Sind sie bloße Rechenwerkzeuge?? Sind das welche?-
wie Bilder der physischen Realität? Sind sie Vorbilder in irgendeiner interessanten Hinsicht??
Oder spielen sie eine andere Rolle??

Man kann mit Sicherheit sagen, dass sie mit einer Art Berechnungstool verknüpft sind, aber danach
dass es alles andere als klar ist. Wenn Sie mich fragen, wie ich von Toronto nach Montreal komme,
Ich könnte auf zwei Arten antworten: (1) Ich könnte dir sagen, dass du nach Norden fahren sollst, bis du dort ankommst
die Hauptautobahn, Biegen Sie dann rechts ab und fahren Sie etwa fünf Stunden lang weiter, oder
(2) Ich könnte Ihnen eine Karte geben und Ihnen sagen, wo Sie sich gerade darauf befinden. Beide
Wege bieten die Informationen, um Sie erfolgreich nach Montreal zu bringen. Die Karte in
Die zweite Methode ist eindeutig ein Modell; Die Anweisung in der ersten Methode lautet
ganz sicher nicht. Was ich argumentieren werde, ist, dass Feynman-Diagramme sehr ähnlich sind
(1) obwohl es sehr ähnlich aussieht (2). Mit anderen Worten, Es sind keine Bilder oder
Beschreibungen der Realität, Sie sind auch keine Vorbilder im vernünftigen Sinne. Sie spielen
eine andere Art von Rolle in der Physik.

Ich hatte viele angenehme und produktive Gespräche zum Thema FDs mit Michael Stöltzner und Mauro
Dorato, während wir den Sommer verbrachten 2012 in Bielefeld. Michaels Schüler, Jim Talbert schrieb
Eine gute These, die uns den Anfang bereitete. Vielen Dank auch an Letitia Meynell für einige hilfreiche Gespräche
und vor allem, weil er ernsthafte ästhetische Überlegungen in das Thema eingebracht hat, und an Adrian
Wüthrich für sein hervorragendes neues Buch, Die Entstehung der Feynman-Diagramme, von dem ich
viel gelernt und viel gekniffen. Adrian, Letitia, Mauro, Michael, und ich machte einen ersten Versuch
dieses Thema auf einer gemeinsamen Sitzung beim Treffen der European Philosophy of Science Association
in Helsinki, August 2013. Ich bin dem Publikum dort für die wertvolle Diskussion dankbar.

Perspektiven auf die Wissenschaft 2018, Bd. 26, NEIN. 4
© 2018 vom Massachusetts Institute of Technology

doi:10.1162/posc_a_00281

423

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

424

Wie funktionieren Feynman-Diagramme??

Es ist eine allgemein anerkannte Wahrheit, wie Jane Austen sagen würde, Das
alles kann für alles andere stehen. In Stolz und Vorurteil Elizabeth Bennet
und Herr. Darcy repräsentiert Geschlechterverhältnisse und Klassenspannungen in Regency
England. Beim Abendessen, Jemand sagt, ein Salzstreuer stehe für Napoleon
Der Kartoffelsalat repräsentiert La Grande Armée. Das gleiche Salz und der gleiche Salat
von einer anderen Person verwendet, um ein Wasserstoffatom zu modellieren; sie spielen das jeweilige
Rollen von Elektron und Kern. Fügen Sie den Pfeffer als zweites Elektron im Orbit hinzu
um den Salat herum und wir haben ein Heliummodell. Wenn wir eine ausreichende Menge nehmen
liberale Sichtweise, Dann kann von Feynman-Diagrammen wohl kaum eine Rede sein
Darstellung oder Modellierung der physischen Realität. Zum Beispiel, Das könnte ich vorschreiben
Feynmans erstes Diagramm steht für Napoleon und sein zweites für Kutusow.
Natürlich, Das ist albern und wird wahrscheinlich nichts Nützliches dabei herausbringen – aber es könnte sein
getan werden, Darum geht es. Die Frage ist viel interessanter, wann
Wir legen eine angemessene Einschränkung fest und fordern eine geeignete Art von
Ähnlichkeit. Ich kann nicht sagen, worin diese Ähnlichkeit besteht, da es keinen Konsens darüber gibt
die Art der Ähnlichkeiten in Modellen überhaupt. Aber ich gehe davon aus, dass es eine gibt
Es gibt einen klaren Unterschied zwischen den beiden Möglichkeiten, den ich später besprechen werde:
Feynman-Diagramme können typische Modelle oder Darstellungen sein, auf dem einen
Hand, oder sie könnten etwas ganz anderes sein, auf dem anderen.

Ich werde zunächst einige Hintergrundannahmen erwähnen. Erste, Ich werde
etwas dogmatisch eine weitgehend realistische Sichtweise einnehmen. Manchmal könnte es so sein
gezwungen, spezifisch auf die Details des Realismus einzugehen, aber zum größten Teil meine
Die Standardposition ist eine ziemlich verbreitete Ansicht dieser Angelegenheit. Zweite, angenommen
Standardquantentheorie, wie es normalerweise verstanden wird. Folglich, ein paar von meinen
Ansprüche sind möglicherweise unvereinbar mit, sagen, Böhmische Mechanik. Ziel ist es
FDs in einem weiten Rahmen verstehen, der allgemein akzeptiert wäre,
ein Rahmen, der die normale Glaubwürdigkeit nicht übersteigt.

Es gibt eine Reihe von Fragen zum Verständnis von FDs. Wie
Sind sie zum ersten Mal entstanden?? Wie haben sie sich entwickelt, sodass sie praktisch nützlich waren?
in QED? Wie wurden sie auf die Quantenchromodynamik und andere ausgeweitet?
Felder? Dies sind historische Fragen und wurden in der ausführlich diskutiert
ausgezeichnete Bücher von Kaiser (2005), Schweber (1994), und Wüthrich (2010).
Ich interessiere mich mehr für philosophische Fragen darüber, wie FDs aktuell sind-
häufig eingesetzt und warum sie erfolgreich sind.

Wenn ich sage: „Derzeit verwendet," Jedoch, Ich sollte beachten, dass FDs möglicherweise vorhanden sind
Auf ihren Weg nach draußen. Es sind neue Techniken auf den Markt gekommen, die scheinen
leistungsfähiger und könnte FDs als Standardberechnungsmethode ersetzen
in naher Zukunft.1 In diesem Fall, Ich würde dann etwas darüber diskutieren

1. Ein guter Ausgangspunkt ist Bern et al (2012). Siehe auch Brito (http://arxiv.org/abs/1012.4493v2)
für eine Rezension, Brito et al (http://arxiv.org/abs/hep-th/0501052v2) für eine wichtige Vorrunde
Ergebnis, und Arkani-Hamid (arXiv:1012.6030v1 [hep-th]) für wichtige Anwendungen.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

425

Figur 1. Einfaches Feynman-Diagramm: Elektron-Positron-Wechselwirkung. (Die Zeit läuft
von links nach rechts.)

nach 70 Jahre fruchtbarer Dienste sind bald passé. Egal; Die
Die Natur von FDs bleibt philosophisch interessant, auch wenn wir es nur versuchen
alten Techniken einen Sinn geben.2

2. Grundeigenschaften
Es gibt eine Reihe von Regeln für die Erstellung von FDs. Im Großen und Ganzen werde ich das tun
Bleib bei QED, wobei die relevanten Teilchen Fermionen sind (Elektronen e−,
Positronen e+) und Bosonen (Photonen γ) die miteinander interagieren können.
Diagramme stellen die verschiedenen Arten dar, wie Interaktionen stattfinden können. Zum Beispiel-
reichlich, Ein Elektron und ein Positron vernichten sich gegenseitig und tun dies
Sie erzeugen ein Photon, was wiederum ein weiteres Elektron und Positron erzeugt
(Figur 1).

Der Ausdruck „Feynman-Diagramm“ ist etwas allgemein gehalten. Es deckt oft ab
Sowohl die Diagramme als auch der Prozess der Erstellung des mathematischen Beispiels-
Druck, der mit den Diagrammen verbunden ist. Es gibt, Jedoch, eindeutige Regeln
für jede. Der Prozess der Konstruktion des mathematischen Ausdrucks
mit einem Diagramm ist, nicht überraschend, bekannt als „die Feynman-Regeln“. Ich werde
Erklären Sie beides kurz, Beginnend mit den Diagrammen.

Zur Darstellung von QED-Prozessen werden drei Symbole verwendet: durchgezogene gerade Linien für
die Fermionen, Wellenlinien für Photonen, und Punkte oder Eckpunkte für die Interaktion.
Ein Elektron im Anfangszustand wird durch eine durchgezogene Linie mit einem Pfeil dargestellt
, aber im Endzustand wird es dargestellt durch
zeigt auf den Scheitelpunkt,
eine Linie mit einem Pfeil, der vom Scheitelpunkt weg zeigt,
. Ein Positron drin
die Initiale (endgültig) Der Status kehrt die Richtung der Pfeile um. Ein Photon im
Anfangs- oder Endzustand wird dargestellt, jeweils, durch eine Wellenlinie, die a trifft
. An einen Scheitelpunkt sind immer drei Linien angeschlossen
Scheitel,

oder

2. Ich sollte erwähnen, dass ich mich vor einigen Jahren im Rahmen einer Studie kurz mit diesem Thema befasst habe
Allgemeine Darstellung von Diagrammen in der Wissenschaft (Braun 1996). Mein Bericht über FDs in diesem Artikel war
von Meynell kritisiert (2008) und Wüthrich (2010). Der vorliegende Aufsatz ist ein Versuch dazu
tiefer in das Thema eintauchen. Meine Überzeugungen darüber, wie FDs funktionieren, bleiben weitgehend erhalten, etwas zu
meine Überraschung, Ich hoffe jedoch, dass sie etwas anspruchsvoller und besser verteidigt sind.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

426

Wie funktionieren Feynman-Diagramme??

Figur 2. Zwei Diagramme zweiter Ordnung des Compton-Effekts. (Die Zeit läuft von links
nach rechts.)

Figur 3. Einige Diagramme 4. Ordnung des Compton-Effekts.

Es: ein Boson, ein Fermion zeigt nach innen, und ein weiteres Fermion weist darauf hin.
Die Ordnung einer FD ist die Anzahl der darin enthaltenen Eckpunkte. Figur 1 über, zum Beispiel,
ist zweite Ordnung. Je höher die Reihenfolge, je größer die Komplexität und desto mehr
Terme in der entsprechenden Reihe.3 Zeichnen Sie für einen bestimmten Prozess einen FD mit dem niedrigsten Wert
Befehl. In der niedrigsten Reihenfolge kann es mehr als eine geben, Daher ist es wichtig zu zeichnen
alles möglich. Der Grund dafür ist Feynmans besondere Art, Quan zu praktizieren-
Tum-Mechanik, das ist die Summe aller möglichen Prozesse. Daher, für in-
Haltung, Für den Compton-Effekt gibt es zwei Diagramme zweiter Ordnung (Figur 2).
Beide haben den gleichen Eingang (ein Photon und ein Elektron) und das
gleiche Ausgabe (ein Photon und ein Elektron). Das Elektron zwischen den beiden ver-
tices ist ein virtuelles Elektron. Seine Existenz ist sehr kurzlebig, also nicht
gegen das Energie-Zeit-Unschärfeprinzip verstoßen. Auf der Linken, ein Photon und
Elektron werden vernichtet; Es entsteht ein virtuelles Elektron; es wiederum ist annihi-
zugunsten eines Elektrons und eines Photons. Auf der rechten Seite, ein Photon und elektr-
Ein Tron tauscht ein virtuelles Elektron aus und erzeugt ein Elektron und ein Photon.

Der nächste Schritt besteht darin, Diagramme höherer Ordnung zu zeichnen, beginnend mit allem Möglichen
4Diagramme th-Ordnung (vier Interaktionsknoten). Ein Elektron, zum Beispiel,
könnte ein virtuelles Photon emittieren und absorbieren. Die nächste Figur (Figur 3) zeigt an
einige der Möglichkeiten. Grundsätzlich zeichnen wir weiter in höherer Ordnung
Diagramme; es gibt keine Grenzen. In der Praxis, Natürlich, Wir hören nach einer Weile auf, seit
Das Überschreiten eines bestimmten Punktes hat keine messbaren Konsequenzen.

3. Die Terminologie ist nicht einheitlich. Einige Autoren verwenden „1. Ordnung“ für Diagramme mit zwei
Eckpunkte, „2. Ordnung“ für Diagramme mit vier Eckpunkten, und so weiter. Folglich, einige ca-
Wenn man auf Formulierungen wie „Effekt 2. Ordnung“ stößt, ist dies angebracht.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

427

Figur 4. Diagrammelemente entsprechend den Feynman-Regeln.

Der nächste Schritt besteht darin, die Reihe der mathematischen Terme zu konstruieren
den Elementen jedes Diagramms zugeordnet. Freeman Dyson
spielte insbesondere bei der Entwicklung von QED und FDs eine große Rolle. Dyson
(1949) erwies sich als entscheidendes Ergebnis, das die Diagramme und die Mathematik verbindet
Bedingungen: Zwischen ihnen besteht eine Eins-zu-Eins-Entsprechung. Hier sind einige
der expliziten Regeln zum Aufstellen der mathematischen Ausdrücke.

1.
2.

Für jeden Scheitelpunkt (wie in Abbildung 4(A)) schreibe also ga
Für jedes interne Photon mit Impuls k (wie in Abbildung 4(B)) schreiben
i − gαβ/k2+iε
Für jedes innere Elektron mit Impuls p (wie in Abbildung 4(C))
schreibe i/p/ − m + iε (wobei p/ eine Instanz der Schrägstrichnotation ist,
eine Abkürzung für eine lange Formel, die ich hier nicht aufführe)
Für jedes externe Elektron (wie in Abbildung 4(D)) schreib uns(P)

Addieren Sie die Begriffe. Tun Sie dies für jedes Diagramm. Endlich, wir fügen alles hinzu
Terme aus allen Diagrammen und berechnen Sie das Endergebnis, M, welche (Wann
kariert) gibt uns die Wahrscheinlichkeit des Ereignisses.

Dies sind nur einige der vielen Regeln. Einige davon überspringe ich
sind ziemlich wichtig; zum Beispiel, sie beinhalten Überlegungen zur Symmetrie
und die Anforderung, dass der Impuls an jedem Scheitelpunkt erhalten bleibt. Was ich
enthalten haben, Jedoch, sollte für meine Zwecke ausreichen, was heißt
Geben Sie einen Bericht über drei Dinge: ein FD, die Störungsreihe associ-
mit der FD abgestimmt, und der mit der Perturba verbundene physikalische Prozess-
tionsreihe und damit zur FD. Dieser Prozess des Zeichnens von Diagrammen und
Die Zuweisung mathematischer Begriffe ist irgendwann beendet. Der Beitrag-
Die von Diagrammen höherer Ordnung ausgehende Information nimmt rapide ab, so typisch-
Tatsächlich wird die Serie ziemlich bald abgebrochen.

3. Feynmans Verständnis
Was hielt Feynman von FDs?? Hat er sie fotografiert?
physikalische Prozesse oder Geräte zur Verfolgung von Berechnungen,
oder vielleicht eine Kombination aus beidem? Es ist alles andere als klar.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

428

Wie funktionieren Feynman-Diagramme??

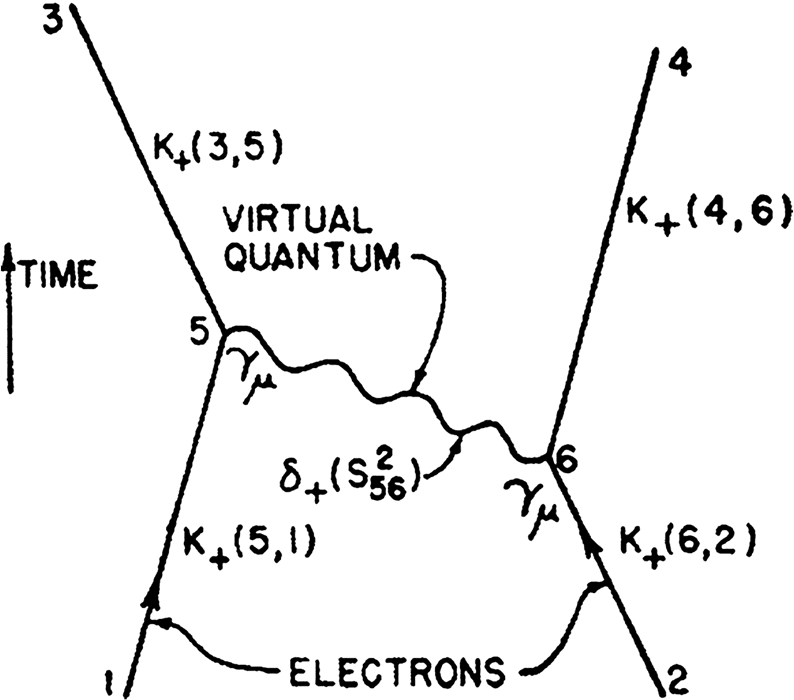
Figur 5. Feynmans erstes veröffentlichtes Diagramm (Feynman, 1949A, 1949B).

Freeman Dyson kannte Feynman gut und verbrachte viele Stunden mit ihm
Ende der 1940er Jahre diskutierte er seinen Ansatz zur QED. Natürlich, das tut nicht
garantieren, dass er Feynman richtig verstanden hat, aber es ging ihm gut
Position, um dies richtig zu machen. Dyson kam es zu dieser Zeit so vor, als ob Feynman
nutzte seine Diagramme, um ein Bild physikalischer Vorgänge zu vermitteln.

In Feynmans Theorie entspricht der Graph einer bestimmten Matrix
Element betrachtet wird, nicht nur als Rechenhilfe, aber als
Bild des physikalischen Prozesses, der zur Entstehung dieser Matrix führt
Element. Zum Beispiel, Eine Elektronenlinie, die x1 mit x2 verbindet, stellt die dar
mögliche Entstehung eines Elektrons bei x1 und seine Vernichtung bei x2,
zusammen mit der möglichen Entstehung eines Positrons bei x2 und seiner
Vernichtung bei x1. (Dyson 1949, P. 496)

In den 1960ern, Jedoch, Feynman schien eine andere Meinung zu vertreten. In einem (n
Interview mit Charles Weiner, Feynman scheint zu leugnen, dass FDs im Spiel sind
in keiner Weise ein Abbild oder Modell der Realität, sondern vielmehr ein Hilfsmittel zur Berechnung
und nichts weiter.

Feynman: Ich kann Ihnen nicht sagen, wann ich sie zum ersten Mal geschrieben habe. [ … ] Ich wahrscheinlich
Ich habe Diagramme erstellt, die mir beim Nachdenken helfen sollen [Störungsausdrücke].
[ … ] Es handelte sich wahrscheinlich nicht um eine bestimmte Erfindung, sondern nur um eine Art Erfindung
eine Kurzschrift, mit der ich mir selbst beim Nachdenken half, was nach und nach
Für einige Diagramme wurden spezielle Regeln entwickelt. [ … ]

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

429

Wiener Würstchen: Um Ihnen zu helfen, körperlich zu denken? Mit anderen Worten, Du warst
im Physischen sehen—
Feynman: NEIN, mathematische Ausdrücke. Mathematische Ausdrücke.
Ein Diagramm, das beim Aufschreiben der mathematischen Ausdrücke hilft. (Zitiert
in Wüthrich 2010, P. 6)

Dies sind sehr unterschiedliche Berichte über FDs, die von Feynman selbst stammen.
Hat er seine Meinung geändert?? War ihm die Spannung zwischen diesen beiden bewusst?
Ansichten? Es ist nicht entscheidend, dass wir wissen, was er über das Thema dachte. Aber
Es bedeutet jedoch, dass wir uns nicht an den Ersteller von FDs als unantastbaren Menschen wenden können
Autorität, die unfehlbar sagen konnte, wie diese Dinge damals waren
wie sie heute funktionieren sollen oder wie sie funktionieren sollen.

Die Probleme

4.
FDs sind für die Berechnung hilfreich, Aber tun sie etwas darüber hinaus??
Die wichtigsten philosophischen Fragen im Zusammenhang mit Feynman-Diagrammen sind folgende:

1. Sind FDs Bilder der physischen Realität?
2. Stellen FDs dar? (in jedem Sinne) physikalische Prozesse?
3.

Wenn FDs keine physischen Objekte oder Prozesse darstellen, was machen Sie
tun und warum sie damit erfolgreich sind?

Zu den anspruchsvolleren Ansichten, die ich für falsch halte, gehört Adrian Wüthrich
und Letitia Meynell. Wüthrich behauptet, dass FDs „gleichzeitig funktionieren können-
notwendigerweise als idealisierte Darstellung der untersuchten Phänomene und als
Werkzeug zur Ableitung von Aussagen über diese Phänomene“ ( Wüthrich 2010,
P. 13). Letitia Meynell (2008) stellt eine ähnliche Behauptung auf, dass FDs beides sein können
rechentechnisch nützlich und in einem wichtigen Sinne repräsentativ. Mein
Die Antwort ist bei beiden gleich: Werkzeug? - Ja. Ideale Darstellung? - NEIN.

5. Bilder der physischen Realität
Ich werde nicht versuchen, „Bild“ zu definieren,Aber nehmen Sie es als verstanden. Fotos und
Zeichnungen, die ihren Zielen sehr ähnlich sind, sind offensichtliche Beispiele. Sie
kann abstrakter sein und dennoch Bilder sein (Denken Sie an ein Picasso-Gemälde),
aber es ist unwahrscheinlich, dass es eine scharfe Grenze zwischen Bildern und anderem gibt
Formen der Darstellung. Mit dieser groben Charakterisierung des Bildes im Hinterkopf,
wir können fragen: Sind FDs Bilder der physischen Realität, insbesondere von Quanten
Systeme?

Auf den ersten Blick mag es so scheinen. Freeman Dyson (wie ich oben zitiert habe), In
sein berühmtes Papier, das die Theorien von Tomonaga vereinheitlichte, Schwinger, Und
Feynman, schrieb, „In Feynmans Theorie entspricht der Graph a
Das jeweilige Matrixelement wird betrachtet, nicht nur als Rechenhilfe,

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

430

Wie funktionieren Feynman-Diagramme??

sondern als Abbild des physikalischen Prozesses…“ (Dyson 1949, P. 496). FDs
werden als Prozesse in Raum und Zeit dargestellt; In der Tat, Sie erschienen zum ersten Mal
in Feynmans Artikel mit dem Titel „A Space-time Approach…“ und sie sehen so aus
Wolkenkammerspuren. Es gibt sogar eine interessante Ähnlichkeit mit dem Knoten
Diagramme und die zu ihrer Darstellung verwendeten Notationen. Schließlich der Analsex-
Ogy bricht zusammen, aber es ist aufschlussreich, sie zu vergleichen, was ich tun werde
momentan.

Eine Reihe von Leuten hat Einwände gegen die Idee erhoben, dass FDs Bilder davon seien
physische Objekte oder Prozesse. Einer dieser Einwände basiert auf einem bekannten
Merkmal der Quantenmechanik, nämlich, die Nichtexistenz von Flugbahnen. In
einen früheren Artikel zu diesem Thema, den ich geschrieben habe,

Feynman-Diagramme sehen aus wie Wolkenkammerbilder, und sie sind
oft als Raum-Zeit-Diagramme bezeichnet. Das führt zur Verwirrung. Tatsächlich,
Die Diagramme bilden überhaupt keine physikalischen Prozesse ab. Stattdessen, Sie
stellen Wahrscheinlichkeiten dar (Genau genommen, Wahrscheinlichkeitsamplituden). Der
Das Argument dafür ist sehr einfach. In der Quantenmechanik (wie immer
verstanden) Die Heisenberg-Unsicherheitsrelationen implizieren, dass nein
Teilchen könnten gleichzeitig einen Ort und einen Impuls haben,
Das heißt, es gibt keine Flugbahnen, Wege, durch
Freizeit. Daher können die Linien in einem Feynman-Diagramm keine Darstellungen sein
von Teilchen und ihren tatsächlichen Wegen durch die Raumzeit. (Braun 1996,
S. 265–67)

Dieser Punkt ist sicherlich nicht neu; Bohr schaffte es zuerst bei Feynman
Präsentation in 1948 seines Berichts über QED. Feynman, es scheint, War
vollkommen bewusst; er behauptete nichts anderes. Diese Ablehnung von FDs als
Bilder von Bewegung in Raum und Zeit scheinen insofern richtig zu sein, aber die
Die Schlussfolgerung, dass es sich bei FDs lediglich um Berechnungswerkzeuge handelt, ist noch nicht gerechtfertigt
wurde zu Recht kritisiert (Meynell 2008; Wüthrich 2010). Es gibt
weitere Darstellungsmöglichkeiten zu berücksichtigen (zuletzt von Stöltzner
2017).

Bevor man an ganz unterschiedlichen Orten sucht, es lohnt sich darüber nachzudenken
Ähnlichkeit oder Fehlen davon in einem bestimmten physikalischen Beispiel. Der Compton
Wirkung, über die Wechselwirkung von Licht mit Elektronen, war einer der
wichtigsten Entdeckungen in der Entwicklung der Quantenmechanik
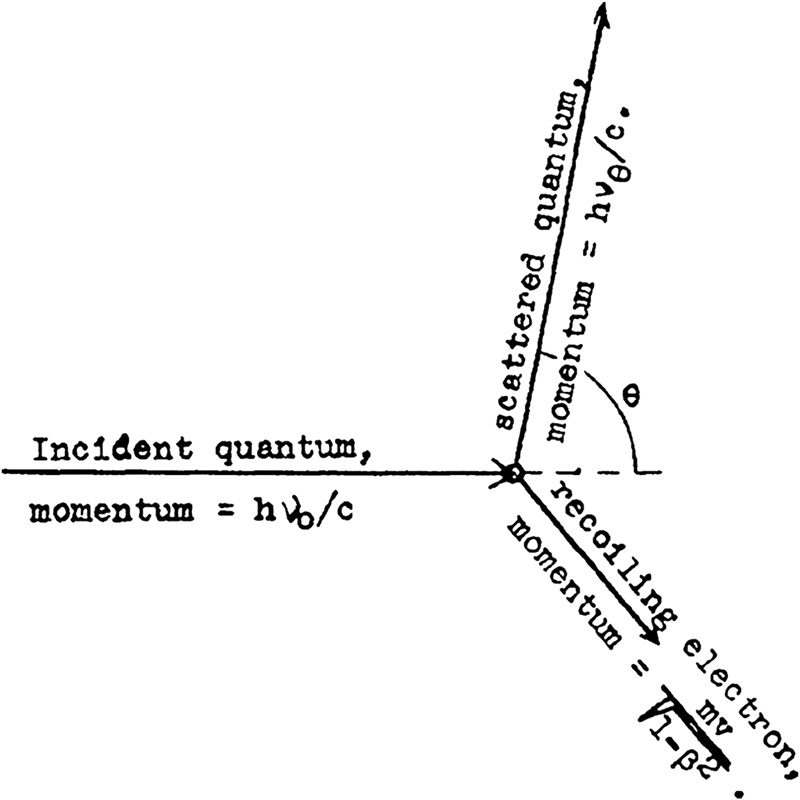
(Compton 1923). Figur 6 ist das Diagramm, das in Compton’s erschien
originaler Artikel.

Als dieses Diagramm veröffentlicht wurde 1923, Heisenbergs Prinzip hatte
noch nicht am Tatort angekommen. Zu dieser Zeit wäre es als angenommen worden
schematisches Bild des tatsächlichen physikalischen Prozesses, wie er im Weltraum abläuft.
Andere Diagramme aus dieser Zeit sind ziemlich gleich. Es ist interessant
um sie mit zeitgenössischen FDs des Compton-Effekts zu vergleichen (Figur 7).

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

431

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

Figur 6. Comptons Originaldiagramm (Compton 1923).

Als Darstellungen, sie sehen ähnlich aus, und so sollten sie beide gedacht werden
als Bilder physikalischer Prozesse oder keines von beiden sollte es sein. In der Tat,
Aus dem bereits genannten Grund sollte dies auch nicht der Fall sein – die Quantenmechanik ist in-
kompatibel mit Flugbahnen durch die Raumzeit. Im Fall des Compton
Effekt-Diagramm (Figuren 6 Und 7 [links]) Wir gehen davon aus, dass es sich um ein Bild davon handelt
physikalischer Vorgang, aber der Fehler, Flugbahnen anzunehmen, ist harmlos, seit
Das Bild macht keine ernsthafte Arbeit. Wir sollten nicht den gleichen Fehler machen
die FD-Version (Figur 7 [Rechts]), da das Diagramm nur instrumentell ist
die entsprechenden Berechnungen durchführen.

Ein zweiter Einwand dagegen, dass FDs Bilder des physischen Bereichs sind, wird begründet
über ihren Einsatz virtueller Teilchen. Im Mai FDs, Darin wird ein Prozess dargestellt
konnte in keiner Weise beobachtet werden, Weil, zum Beispiel, es verstößt gegen die

Figur 7. Zwei zeitgenössische Diagramme des Compton-Effekts: Ein Standarddiagramm
(links), und ein Feynman-Diagramm (Rechts). (Die Zeit läuft von links nach rechts.)

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

432

Wie funktionieren Feynman-Diagramme??

Energieeinsparung. Jedoch, wenn dieser Vorgang weniger als eine vorgegebene Zeitspanne dauert
Zeit (d.h., verletzt nicht die Zeit-Energie-Unschärferelation), dann ist es
Die Existenz ist logisch nicht ausgeschlossen. Eine Reihe von Kritikern argumentieren, dass dies der Fall sei
virtuelle Einheiten existieren nicht. Vor diesem Hintergrund sind zwei Haltungen möglich
Einspruch. Einer davon ist, dass die Physik die Verwendung virtueller Teilchen ablehnen sollte.
Das andere ist, dass sie zwar genutzt werden dürfen, wir aber ihre bloße Bedeutung erkennen sollten
instrumenteller oder fiktionaler Natur sein. In beiden Fällen, Diagramme mit virtuellen
Entitäten bilden kein Bild der Realität ab. Natürlich, Dieser Einwand dagegen, dass FDs pic-
tures ist nur so gut wie der Einwand gegen virtuelle Teilchen, aber der Fall
gegen sie ist stark. Wir werden diese Argumente nicht wiederholen, aber stattdessen
Verweisen Sie die Leser auf eine Auswahl aus der Literatur. Sehen, zum Beispiel, Bunge
(1970) oder Teller (1995).

Es gibt einen dritten Einwand, schwächer als die anderen, aber erwähnenswert-
ing. FDs gehen von einer Teilcheninterpretation der QED aus. Eine solche Interpretation
ist alles andere als offensichtlich richtig und viele würden es bestreiten. Der Punkt, Wie-
immer, ist, dass FDs vollkommen gut funktionieren würden, selbst wenn ein solches Teilchen inter-
Prätation ist falsch. Also, wenn FDs Bilder wären, es wären Bilder davon
Punktteilchen, aber wenn keine Punktteilchen existieren, dann wären es immer noch FDs
erfolgreich. Trotzdem, Ihr Erfolg wäre ein Rätsel.

6. Kostenlose Körperdiagramme
Es gibt eine interessante Analogie zu sogenannten Freikörperdiagrammen (Auch
sogenannte Kraftdiagramme).4 Wir beginnen mit der tatsächlichen körperlichen Situation,
was vielleicht sichtbar ist, oder ein ziemlich realistisches Diagramm oder Foto. Dann wir
Zeichne ein Freikörperdiagramm. Normalerweise ist dies ein separates Diagramm, aber es könnte sein
dem realistischen Bild überlagert werden. Endlich, Orientierung am Diagramm,
Wir hängen Zahlen an und verwenden sie in den entsprechenden zu lösenden Gleichungen
irgendein interessantes Problem.

Beginnen Sie mit einem Kind auf einer Rutsche. Nehmen wir an, dass die Rutsche reibungslos ist,
Der Winkel der Rutsche zum Boden beträgt 45°, und die Masse des Kindes ist
25 Kg. Wir wollen die Beschleunigung a des Kindes wissen. (Figur 8)

Es gibt eine einfache Möglichkeit, dies zu tun. Das Freikörperdiagramm zeigt
alle Kräfte. Die Kraft aufgrund der Schwerkraft Fgravity wird in eine Kraft aufgelöst, die ist
normal Fnormal zum Schlitten und eine Kraft entlang des Schlittens Fslide. Der letzte von
das ist Fslide = Fgravity × sin 45. Da F = ma, die Kraft Fgravity = mg =
25 × 9.8 Newton. Daher, die Kraft auf das Kind beträgt Fslide = 25 × 9.8 × Sünde
45 = 173 Newton. Folglich, die Beschleunigung des Kindes auf der Rutsche
ist a = F/m = 173/25 = 6.9 m/s2.

4. Wüthrich (2010, P. 14) verwendet ein ähnliches Beispiel, zieht aber den gegenteiligen Schluss,

behauptet, es sei einem FD ähnlich.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

433

Figur 8. Kind auf Folie und Freikörperdiagramm zur Darstellung der Kräfte.

Das Argumentationsmuster ist einfach:

physikalisches System (oder realistisches Bild)
↓
Freikörperdiagramm
↓
Mathematik

Wenn FDs analog zu Freikörperdiagrammen wären, dann würde das Muster
ähnlich sein:

physikalisches System (oder realistisches Bild)
↓
Feynman-Diagramm
↓
Mathematik

Natürlich, Es gibt eine offensichtliche Diskrepanz. Im typischen Beispiel
Basierend auf der klassischen Physik haben wir ein klares Verständnis der Physik-
isches System in dem Sinne, dass wir wissen, wie man ein Freikörperdiagramm zeichnet
nachdem ich es mir angesehen habe (oder ein realistisches Bild) und wir wissen es durch Sehen
das eigentliche System, wie man Zahlen an die Elemente des Freien anfügt
Körperdiagramm. Dies können wir im Quantenfall nicht tun. Stattdessen, Wir
werden mit etwas Geheimnisvollem konfrontiert. Anstelle eines unabhängigen
zugängliches physikalisches System, Wir haben wirklich wenig oder gar keine Ahnung davon, wie diese aussehen
Prozesse funktionieren. Wir haben kaum oder keine Ahnung, wie das System aussehen könnte oder
wie die FDs damit verknüpft sein könnten. Anstelle des Diagramms oben, Die
Die Situation scheint eher so zu sein:

Unzugängliches physisches System
↓
Feynman-Diagramm ↔ Mathematik

Die Feynman-Regeln sagen uns, wie wir FDs mit der Mathematik verknüpfen können, aber dort
ist keine Führung durch das physikalische System. Tatsächlich, ein erhebliches Problem
wird deutlich. Welcher link, wenn überhaupt, Gibt es zwischen der Welt und
FDs? Warum sollten wir glauben, dass irgendein FD überhaupt einen Bezug zur Realität hat?

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

434

Wie funktionieren Feynman-Diagramme??

Wir könnten uns eine realistische Darstellung oder ein realistisches Bild vorstellen? Es scheint, dass FDs
sind lediglich eine Hilfestellung bei der Berechnung. Die Feynman-Regeln behalten den Überblick
der Mathematik durch Nutzung der FDs. Dies hat die Fragen ordentlich beantwortet-
tion, Wie funktionieren FDs?? Dennoch stellt es uns vor ein großes Rätsel, was wir können
als Dilemma ausdrücken.

Ein Freikörperdiagramm vermittelt zwischen der Realität (oder realistisches Bild davon
Wirklichkeit) und der mathematische Bereich, mit dem wir messbar rechnen
Mengen. Es sind drei unabhängig voneinander zugängliche Einheiten beteiligt: Die
physikalisches System, Das Diagramm, und die Mathematik. Mit einem FD gibt es
nur zwei, das Diagramm und die Mathematik. Wir könnten ein drittes Element bekommen
indem man die FD doppelte Aufgaben übernehmen lässt: Wir gehen davon aus, dass es sich um ein realistisches Bild handelt
Realität und dass es einem freien Körperdiagramm ähnelt. Oder wir könnten zufrieden sein
wobei es nur zwei Komponenten gibt, das Diagramm und die Mathematik.
Wenn wir den ersten Weg nehmen, Wir stoßen auf das anerkannte Problem von Vio-
Definition des Unschärfeprinzips, da Elektronen, und andere elementare Par-
Ticles haben keine Flugbahnen. Wenn wir den zweiten Weg wählen, dann haben wir nein
Zusammenhang zwischen FD und Realität. Es wäre ähnlich, als hätte man ein kostenloses
Körperdiagramm ohne Ahnung, was es darstellt, das ist, keine Verbindung zu
die Welt überhaupt. Das ist unser Dilemma.

7. Darstellungen
Bilder der physischen Realität sind nicht die einzige Möglichkeit zur Darstellung. Könnte FDs
Seien Sie Darstellungen des physischen Bereichs auf abstraktere Weise?
Bilder, Natürlich, einen Bereich bilden; Sie können ihren Zielen sehr ähnlich sein
oder sie können eher schematisch sein. Aber es gibt Formen der Darstellung
sind in keiner Weise Bilder. Zum Beispiel, Möglicherweise handelt es sich um einen periodischen Prozess
dargestellt durch eine Sinuskurve (Figur 9), was wiederum dargestellt werden könnte
durch eine Taylor-Reihe:

sinx ¼ x − x3=3! x5=5! − x7=7! …

Vielleicht repräsentieren FDs physikalische Prozesse auf diese abstraktere Weise, wie ein
Taylor-Reihe. Das, Ich finde, ist Wüthrichs Ansicht.

…es muss klargestellt werden, dass Feynman Diagramme erstellt (sicherlich von
die Zeit, als Dyson die Diagramme systematisierte) sind nicht klassisch
Darstellungen von Streuereignissen. Sie repräsentieren Letztere
relevante Aspekte auf eine abstraktere Art und Weise darzustellen: Sie zeigen die Zusammenhänge
zwischen den Schöpfungs- und Vernichtungsereignissen, und diese Zusammenhänge
werden als Vakuumerwartungswerte des Feldes verstanden
Betreiber. ( Wüthrich 2010, P. 31)

Letitia Meynell hat ausführlich für eine solche Darstellung argumentiert (Meynell 2008).
Sie erkennt das Argument an, dass FDs dies im gewöhnlichen Sinne nicht können

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

435

Figur 9. Sinuskurve.

seien Bilder von physikalischen Prozessen, behaupten aber, dass es sich dabei um Repräsentanten handeln könnte-
Dennoch auf einer etwas abstrakteren Ebene. Zu diesem Zweck entwickelt sie
und wendet die ästhetischen Ansichten von Kendall Walton auf Fiktionen und Make an-
glauben. Der entscheidende Unterschied, den sie anwendet, ist der zwischen „Denotation“
und „Repräsentation“. Ersteres bezieht sich auf etwas, Letzteres auf etwas
nicht. Sie kommt zu dem Schluss, dass FDs tatsächlich Rechengeräte sind, aber dass sie
sind auch Darstellungen physikalischer Vorgänge. „…wir spielen eine Art Make-
Glauben Sie mit den Diagrammen, die es einem ermöglichen, sich das Subatomare vorzustellen
Reich" (Meynell 2008, P. 55). Könnte es sein, dass FDs Berechnungswerkzeuge sind?
und stellen physikalische Prozesse in einem sehr abstrakten Sinne dar? Ich werde betrügen-
Ich denke über einige Vorschläge nach, aber zuerst, eine kurze Diskussion über die Art der Anwendung
Mathematik.

8. Wie verbindet sich die Mathematik mit der Welt??5
Nehmen wir zwei unterschiedliche Bereiche an: man ist ein mathematischer Bereich, welches ist
reich genug, um das Zweite darzustellen, ein physischer Bereich. Wir suchen uns einen aus
Aspekt der physischen Welt und finden Sie eine ähnliche mathematische Struktur
repräsentiere es. Zum Beispiel, Das Gewicht wird auf einer numerischen Skala dargestellt. Der
Hauptphysikalische Beziehungen zwischen Objekten, deren Gewicht bestimmt wird, sagen,
durch einen Schwebebalken, sind, dass einige mehr Gewicht haben als andere und das
wenn Objekte kombiniert werden, Ihr gemeinsames Gewicht ist größer als bei beiden
ihre individuellen Gewichte. Das Gewicht kann dann durch eine beliebige Mathematik dargestellt werden-
matische Struktur, wie zum Beispiel die positiven reellen Zahlen, in denen es ein gibt
Größer-als-Beziehung, die mit der physikalischen Größer-als-Beziehung übereinstimmt, und ein
Additionsrelation, die zur physikalischen Kombinationsrelation passt.

Allgemeiner, eine mathematische Darstellung eines Nichtmathematischen
Bereich tritt auf, wenn ein Homomorphismus zwischen einem relationalen System vorliegt

5. Dieser Abschnitt ist von Brown übernommen (2008).

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

436

Wie funktionieren Feynman-Diagramme??

P und ein mathematisches System M. P wird aus einer Domäne D und rela bestehen-
tionen R1, R2, … auf dieser Domäne definiert; M besteht ebenfalls aus einer Domäne
D* und Beziehungen R*1, R*2, … auf dieser Domain. Ein Homomorphismus ist ein
Abbildung von φ von D auf D*, die die Struktur in geeigneter Weise bewahrt
Weg. Betrachten Sie ein vereinfachtes Beispiel. Sei D eine Menge von Körpern mit Gewicht,
sei D* = R, die Menge der reellen Zahlen; Außerdem, seien ≼ und ⊕ die
Beziehungen von physikalischem Gewicht gleich oder kleiner als und physikalischer Zusammensetzung.
Die Beziehungen ≤ und + sind die üblichen Beziehungen auf reellen Zahlen gleich oder
kleiner als und Addition, jeweils. Die beiden Systeme, Dann, sind P = hD,
≼, ⊕i und M = hR, ≤, +ich. Den Körpern werden dann Nummern zugeordnet
(A, B, … 2 D) durch den Homomorphismus φ: D → R, was die beiden erfüllt
Bedingungen:

(1)

(2)

a ≼ b → φ dass Þ ≤ φ bð Þ

φ a ⊕ b

Þ ¼ φ zu Þ þ φ bð Þ:

In reinem Englisch, (1) sagt, dass wenn a das gleiche oder weniger wiegt als b, dann ist die
Die mit a verknüpfte reelle Zahl ist gleich oder kleiner als die Zahl asso-
zitiert mit b, Und (2) sagt, dass die Zahl mit dem Gewicht verbunden ist
des kombinierten Objekts a ⊕ b ist gleich der Summe der assoziativen Zahlen-
getrennt mit den Objekten verbunden. Mit anderen Worten, die Beziehungen, die bestehen
zwischen physischen Körpern werden in den mathematischen Bereich kodiert und
Gibt es Beziehungen zwischen reellen Zahlen?. Eines der Objekte
kann beliebig herausgegriffen werden (aber meist mit Blick auf die Bequemlichkeit) Zu
als Einheitsgewicht dienen, u, so dass φ(u) = 1.

Der entscheidende Punkt ist, dass die Mathematik auf die physische Welt anwendbar ist
Bereitstellung von Modellen oder Analogien, nicht durch direktes Beschreiben von Dingen. Streng
Apropos, Masse ist keine Zahl und Kraft ist kein Vektor, aber sie sind
dargestellt durch reelle Zahlen und Vektoren, jeweils. Das Gemeinsame
Der Ausdruck „eine mathematische Beschreibung der Realität“ ist irreführend, wenn er bedeutet
nichts anderes als die Mathematik, die von einer Theorie in diesem Analogon verwendet wird-
ische Art und Weise.

Die physische Verbindung zweier Körper mit Gewicht, wie oben beschrieben,
wird durch die Addition zweier reeller Zahlen dargestellt. Aber die Einbettung
Homomorphismus ist nicht immer so einfach wie in diesem Fall. Das Relativistische
Addition zweier Geschwindigkeiten, Zum Beispiel, ist durch eine Obergrenze begrenzt
auf ihre Gelenkgeschwindigkeit. Es ist aufschlussreich, den Unterschied zu bedenken.

Stellen Sie sich einen Ball vor, der mit der Geschwindigkeit W in einem Flugzeug nach vorne geschleudert wird
Fliegen mit der Geschwindigkeit V relativ zum Boden. Nehmen Sie W und V als Geschwindigkeiten an,
nicht die Zahlen, die sie darstellen, genau wie wir Gewicht unterschieden haben
ihre repräsentierenden Zahlen. Wie oben beschrieben, Wir assoziieren reelle Zahlen

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

437

mit diesen Geschwindigkeiten: Phi (W ) = w und φ (V ) = v. In der Newtonschen Physik ist die
Die Zusammensetzung der Geschwindigkeiten nimmt eine einfache und vertraute Form an: Phi(W ⊕ V ) =
Phi(W ) + Phi (V ) = w + v. Jedoch, in der relativistischen Physik die Zusammensetzung
der Geschwindigkeiten ist komplizierter:6

φ W⊕V

Þ ¼

φ Wð

Þ þ φ Vð Þ

φ Wð

1 þ

Þ (cid:2) φ Vð Þ
c2

¼ w þ v
1 þ wv
c2

Der Übergang von der galiläischen zur relativistischen Geschwindigkeitsaddition sollte leicht möglich sein
folgen, Auch wenn Letzteres eine Abweichung vom gesunden Menschenverstand darstellt. Das ist
nicht immer der Fall. Oft, nach einer anfänglichen Assoziation zwischen dem Physischen
Reich und das Mathematische, es bleibt noch viel offen. Wir haben
Es ist noch nicht möglich, die gesamte Bandbreite der Konsequenzen der anfänglichen Assoziation zu entdecken.
Möglicherweise sind größere mathematische Innovationen erforderlich. Aber wir haben genug gesagt
über die Anwendung der Mathematik auf den physikalischen Bereich, um unsere Stellung zu beziehen
Problem klar.

Mit dieser Darstellung der Mathematik hinter uns, wir können jetzt klarer
Beschreiben Sie das Problem der FDs wie folgt: Stellen FDs das physische System dar?
P oder das mathematische System M? Das ist, wenn FDs etwas darstellen,
dann was? Repräsentieren sie das Physische?, oder das Mathematische, beide,
oder keines von beiden? Ich werde argumentieren, dass die richtige Antwort weder das eine noch das andere ist. Vor
Ich komme dazu, ein kurzer Exkurs, um die Bühne zu bereiten.

9. Divergente Serie
Die von QED verwendete Störungsreihe konvergiert nicht. Dies wurde bewiesen
vor langer Zeit von Dyson (1952). Es ist, Jedoch, eine asymptotische Reihe, so wird es
arbeiten in dem Sinne, dass sie nützliche Antworten für Näherungen niedriger Ordnung geben,
aber es wird irgendwann abweichen, wenn mehr Begriffe einbezogen werden. Daher, Die Mathematik-
Die mathematische Darstellung der QED ist in einem wichtigen Sinne nicht konsistent.
Das bedeutet, dass FDs keine konsistente Darstellung von irgendetwas sein können
in der physischen Welt. Sie könnten immer noch eine Darstellung davon sein, vielleicht,
ist pragmatisch nützlich, aber nicht „verständlich“.

Eine Erklärung zu divergenten Reihen könnte nützlich sein. Ein einfacher Ex-
8 þ …=
,
Ein Beispiel für eine konvergente Reihe ist die Reihe
da es gleich ist 1, eine endliche Zahl. Die Serie 1+ 2+ 3+ 4+ … ist divergent;
die Summe ergibt offensichtlich Unendlich, ebenso wie die Serie
3 þ …=
.

n ¼ 1 þ 1
=

2n ¼ 1
=

4 þ 1
=

2 þ 1
=

2 þ 1

P∞
1

6. Beachten Sie, dass der Bereich von φ in beiden Fällen unterschiedlich ist. Sei N die Menge aller
mögliche Geschwindigkeiten im Newtonschen Fall, wir haben φ : N → R, während im Einsteinschen Fall,
mit E die Menge der möglichen Geschwindigkeiten, wir haben φ : E → (−c, C), da c eine Grenze für jeden Rahmen von ist
Referenz.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

438

Wie funktionieren Feynman-Diagramme??

Die Störungsreihe der QED ist divergent, aber asymptotisch, welche
bedeutet, dass wir es nach ein paar Begriffen abschneiden können und ein nützliches Ergebnis erhalten, endlich
Antwort. Divergente Reihen sind, gelinde gesagt, zwielichtig. Der große Mathe-
Der Mathematiker Abel nannte sie das Werk des Teufels und sagte, sie sollten gemieden werden.
Seit seiner Zeit, Jedoch, Mathematiker haben sich damit vertraut gemacht
ihre Verwendung, eine Verwendung, die durchaus fruchtbar geworden ist.

Trotz ihres Nutzens, die Divergenz der Störungsreihe macht
selbst der folgende bescheidene Versuch einer repräsentativen Darstellung ist unmöglich.

Bitte verstehe: Diese Feynman-Diagramme sind rein symbolischer Natur;
Sie stellen keine Teilchenbahnen dar (wie Sie sie vielleicht sehen, sagen,
ein Blasenkammerfoto). Die vertikale Dimension ist die Zeit, Und
Horizontale Abstände entsprechen nicht den physischen Trennungen. … All die
Diagramm sagt ist: „Es gab einmal ein Elektron und ein Positron; Sie
ein Photon ausgetauscht; dann gab es ein Elektron und ein Positron
wieder." (Griffiths 1987, P. 59. Zitiert bei Wüthrich 2010, P. 3)

Der Autor will (schon richtig) um die Leser davor zu warnen, naiv zu sein
FDs; sie repräsentieren keine Vorgänge in Raum und Zeit. Jedoch, er tut
sagen, „Es gab einmal ein Elektron und ein Positron; Sie tauschten ein Photon aus;
dann gab es wieder ein Elektron und ein Positron.“ Sogar das könnte sein
zu viel sagen, wie die folgenden Überlegungen nahelegen.

Ich möchte nun zwei Dinge zusammenfassen, die zuvor erwähnt wurden:
Zuerst, Dysons Argument für die Eins-Eins-Korrespondenz zwischen Diagrammen
und Reihenterme, und zweitens, Dysons Beweis, dass die Serie divergent ist. Zu sein
präzise,

1. Zwischen Diagrammen und Reihen besteht eine Eins-zu-eins-Entsprechung

Bedingungen.

2. Die Serie divergiert.
3. Daher, Die Reihe kann keine physikalischen Daten kohärent und korrekt darstellen-

ischer Prozess.

4. daher, Diagramme können keinen physikalischen Prozess darstellen (dh, kann nicht

in jedem vernünftigen Sinne des Begriffs darstellen).

10. Flussdiagramme
Wir brauchen eine andere Denkweise über FDs. Ich schlage vor, dass sie es sind
Flussdiagramme. Um das klarzustellen, Ich muss zunächst zwei Arten von Strömungen unterscheiden
Diagramme: beschreibend und präskriptiv. Ein präskriptives Flussdiagramm ist kein
Modell eines physikalischen Systems oder Prozesses. Stattdessen handelt es sich um eine Reihe von Regeln, instruk-
tionen, oder Befehle. Im Gegensatz, ein beschreibendes Flussdiagramm ist (zumindest typ-
isch) ein Modell oder eine Darstellung eines Prozesses. Hier sind zwei einfache
Illustrationen.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Vorgeschriebenes Flussdiagramm: Ein Rezept

Beschreibendes Flussdiagramm: Verdauung

Perspektiven auf die Wissenschaft

439

Den Backofen vorheizen und zwei Backbleche einfetten

↓

Zucker verrühren, Mehl, Eier, Milch,
und Kokos in einer großen Schüssel

↓

In die gefetteten Pfannen füllen
↓

Backe für 35 Minuten um 190 C
↓

Abkühlen lassen
↓

Stapeln Sie die beiden Schichten und decken Sie sie ab
mit Schokoladenglasur

Mund
↓

Rachen
↓

Speiseröhre
↓

Magen
↓

Dünndarm
↓

Dickdarm
↓

Rechts (Ausscheidung)

Es bedarf nur eines kurzen Nachdenkens, um einen großen Unterschied zu erkennen. Das Beschreibende
Flussdiagramm ist eine Beschreibung der Realität (eine angebliche Beschreibung, Natürlich; es ist
fehlbar). Wie Darstellungen gehen, es ist völlig unkompliziert. Im Gegensatz,
Das Rezept versucht nicht einmal, die Realität darzustellen oder zu modellieren; es sagt uns, wie es geht
etwas erreichen.

Unter Berücksichtigung der deskriptiv-vorschreibenden Unterscheidung, ein FD ist, Ich würde
vorschlagen, ein präskriptives Flussdiagramm. Es handelt sich um eine Reihe von Befehlen. Es ist (implizit)
eine Reihe von Anweisungen zum Zuweisen von Gleichungen zu physikalischen Prozessen. Wüthrich
schlägt etwas Ähnliches vor, Man nennt sie „Algorithmen“.

Dass die mathematischen Ausdrücke M auf ein Diagramm reduziert werden können,
von Dyson als „grafische Darstellung der Matrix“ beschrieben
Elemente,„ könnte die Notwendigkeit, lange aufzuschreiben, überflüssig machen
In manchen Fällen handelt es sich um einen Integralausdruck, aber das ist überhaupt nicht das Wichtigste
Funktion der Diagramme. Diese Visualisierung des Mathematischen
Ausdrücke sind zweitrangig. Eher, die wichtigste Funktion des
Diagramme sind die grafischen Regeln zum Verbinden von Scheitelpunkten und
anschließende Übersetzung in eine mathematische Ausdrucksform an
Algorithmus, um alle Matrixelemente ungleich Null zu finden, und diese allein.
(Wüthrich 2010, P. 155)

In gewisser Weise könnte sogar ein Rezept als „repräsentiert“ bezeichnet werden-
stationär: Die Realität sieht so aus, dass das Rezept (über) für einen Schokoladenkuchen schon

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

440

Wie funktionieren Feynman-Diagramme??

Das Ergebnis ist ein Schokoladenkuchen. Nicht alle Rezepte funktionieren. Besonders aussichtslos ist dies
Rezept von Macbeth: "Auge von Newt, und Froschzehe / Fledermauswolle, und Zunge von
Hund, / Addergabel, und Blindwurmstich, / Eidechsenbein, und Howlets Flügel,
/ Für einen Zauber mächtigen Ärgers, / Wie eine höllische Brühe, die brodelt und blubbert.“ Als
Reize gehen, es hat keine Kraft. Was das Zubereiten einer Suppe zum Mittagessen angeht – fragen Sie nicht einmal.

11. Abschließende Bemerkungen
Wir müssen über drei Dinge nachdenken: die physische Welt, das Mathematische
Bereich, der die physische Welt darstellt oder modelliert, und FDs, was scheint
existieren unabhängig von den anderen beiden. Die entscheidende Frage betrifft den Status
dieser Diagramme. Sind sie Modelle des physischen Bereichs?? Wenn ja, wie machen Sie das
Modell? Wenn sie nicht repräsentativ sind, Was ist dann ihre Beziehung zu beiden?
der physikalische Bereich und der mathematische Bereich? Meine Antwort war das
FDs sind in keinem nennenswerten Sinne beschreibend oder repräsentativ. Stattdessen,
es sind Rezepte, Anleitung zum Aufschreiben der Störung
Reihe, die ein mathematisches Modell der Realität ist. Die Unterscheidung zwischen de-
Skriptive und präskriptive Flussdiagramme scheinen dies gut zu erfassen.

Also, was dann visualisiert wird? Ich denke, die Antwort ist einfach diese: FDs
sind geometrische Darstellungen von Wahrscheinlichkeitsfunktionen. Es sind keine Bilder
von Phänomenen. Wir sollten die Visualisierung der Technik nicht verwechseln
zur Konstruktion der Störungsreihe mit einer Visualisierung des Physischen
durch die Störungsreihe modellierter Prozess.

Verstehen ist ein nebulöses und subjektives Konzept. Ein Raumzeitdiagramm
Die Darstellung eines physikalischen Prozesses liefert oft ein beträchtliches Verständnis dessen, was ist
geht weiter. FDs scheinen diese Art von Verständnis zu vermitteln. Aber es ist eine Illustration-
sion. Sie sind wunderbar in dem, was sie tun, aber sie erklären nichts und sie
bieten nichts, um die Funktionsweise der Natur zu verstehen.

FDs sind hervorragende Werkzeuge, die bei Berechnungen helfen. Sie sind nicht mehr als
Das. Es sind keine Bilder, sie repräsentieren nichts, und das tun sie nicht
bieten einen Einblick in die Quantenwelt. Josef Jauch was right
als er sich vor langer Zeit beschwerte:

Die pragmatische Tendenz der modernen Forschung hat dies oft verdeckt
Unterschied zwischen dem Wissen über den Gebrauch einer Sprache und dem Verstehen
die Bedeutung seiner Konzepte. Es gibt überall viele Studenten, die
haben ihre Prüfungen in Quantenmechanik mit Bestnoten bestanden
ohne wirklich zu verstehen, was das alles bedeutet. Oft ist es sogar
schlimmer als das. Anstatt wie ein Papagei die Quantenmechanik zu lernen
Mode, Sie können auf diese Weise nur bestimmte Annäherungen lernen
Techniken (wie etwa die Störungstheorie, Feynman-Diagramme oder Dispersion
Beziehungen), was sie dann glauben lässt, dass diese Techniken nützlich sind
sind identisch mit der konzeptionellen Grundlage der Theorie. ( Jauch 1968, P. v)

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspektiven auf die Wissenschaft

441

Verweise
Arkani-Hamid, N., J. Bourjaily, F. Cachazoc, A. Hodgesd und J. Schwarzdorn.
2010. „Eine Anmerkung zu Polytopen zur Streuamplituden,„arXiv:1012.6030v1
[hep-th] 29 Dezember.

Braun, James Robert. 1996. „Illustration und Schlussfolgerung.“ Pp. 250–268
in Bildwissen: Historische und philosophische Probleme bezüglich
der Einsatz von Kunst in der Wissenschaft. Herausgegeben von B. Absolvent. Toronto: Universität
Toronto Press.

Braun, James Robert. 2008. Philosophie der Mathematik: Ein zeitgenössischer
Einführung in die Welt der Beweise und Bilder. London und New York:
Routledge.

Bunge, Mario. 1970. „Virtuelle Prozesse und virtuelle Teilchen: Real
für Theoretische Physik, 3(6):

oder fiktiv?” Internationale Zeitschrift
507–508.

Bern, Z., Lance J. Dixon und David A. Kosovo. 2012. „Schleifen, Bäume, Und

die Suche nach neuer Physik.“ Wissenschaftlicher Amerikaner, 306(5): 34–41.

Compton, A. H. 1923. „Eine Quantentheorie der Streuung von Röntgenstrahlen

durch Lichtelemente,„Körperliche Überprüfung, 21(5): 483–502.

Dyson, F. J. 1949. „Die Strahlungstheorien von Tomonaga, Schwinger, Und

Feynman.“ Körperliche Überprüfung, 75(3): 486–502.

Dyson, F. J. 1952. „Divergenz der Störungstheorie in der Quantenelektrotechnik-

Dynamik,„Körperliche Überprüfung, 85(4): 631–632.

Feynman, R. P. 1949A. „Raum-Zeit-Ansatz für Quantenelektro-

Dynamik." Körperliche Überprüfung, 76(6): 769–789.

Feynman, R. P. 1949B. „Die Theorie der Positronen,„Körperliche Überprüfung, 76(6):

749–759.

Griffiths, David. 1987. Einführung in Elementarteilchen. New York:

Wiley.

Jauch, J. 1968. Grundlagen der Quantenmechanik. New York: Addison

Wesley.

Kaiser, D. 2005. Theorien auseinander ziehen: Die Streuung von Feynman-Diagrammen

in Nachkriegsphysik. Chicago: Die University of Chicago Press.

Meynell, Letitia. 2008. „Warum Feynman-Diagramme repräsentieren.“ International

Studium der Wissenschaftsphilosophie, 22(1): 39–59.

Schweber, S. S. 1994. QED und die Männer, die es geschafft haben: Dyson, Feynman,

Schwinger, und Tomonaga. Princeton: Princeton University Press.

Stöltzner, M. 2017. „Feynman-Diagramme als Modelle.“ Das Mathematische

Geheimdienstler, 46–54, DOI 10.1007/s00283-017-9716-z.

Erzähler, Paul. 1995. Eine interpretative Einführung in die Quantenfeldtheorie.

Princeton: Princeton University Press.

Wüthrich, Adrian. 2010. Die Entstehung der Feynman-Diagramme. Dordrecht,

London: Springer.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
Ö
S
C
_
A
_
0
0
2
8
1
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

442

Wie funktionieren Feynman-Diagramme??

Zusätzliche Ressourcen
Britto, Ruth. 2010. „Schleifenamplituden in Eichtheorien: Moderne Analytik

Ansätze." http://arxiv.org/abs/1012.4493v2

Britto, Ruth, Freddy Cachazo, Bo Feng, und Edward Witten. 2005. "Direkte
Beweis der Rekursionsbeziehung auf Baumebene in der Yang-Mills-Theorie.“ http://
arxiv.org/abs/hep-th/0501052v2

das Regt, Henk. 2014. „Visualisierung als Werkzeug zum Verstehen.“ Perspektiven

über Wissenschaft, 22(3): 377–396.

Harré, R. 1988. Analysieren der Amplituden. Pp. 59–71 in Philosophical Found-
Daten der Quantenfeldtheorie. Herausgegeben von H. R. Brown und R. Harré.
Oxford: Clarendon Press.

Brutto, Ari. 2012. „Bilder und Pädagogik: Die Rolle von Diagrammen in
Feynmans frühe Vorlesungen,„Studien in Geschichte und Philosophie der Moderne
Physik, 43: 184–194.

Die Tafel, L. 1981. „Eine Widerlegung des konvergenten Realismus.“ Philosophie der Wissenschaft,

48(1): 19–49.

Mattuck, Richard. 2012. Ein Leitfaden zu Feynman-Diagrammen im Vielteilchensystem

Problem, 2nd ed., New York: Dover.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
P
Ö
S
C
/
A
R
T
ich
C
e
–
P
D