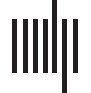FOKUS-FUNKTION:
Topological Neuroscience
Replays of spatial memories suppress topological
fluctuations in cognitive map
1
Andrey Babichev
, Dmitriy Morozov
2
, and Yuri Dabaghian
1,3
1Department of Computational and Applied Mathematics, Rice University, Houston, TX, USA
2Lawrence Berkeley National Laboratory, Berkeley, CA, USA
Department of Neurology, The University of Texas McGovern Medical School, Houston, TX, USA
3
Schlüsselwörter: Learning and memory, Hippocampal replays, Transient networks, Zigzag homology
theory
Keine offenen Zugänge
Tagebuch
ABSTRAKT
The spiking activity of the hippocampal place cells plays a key role in producing and
sustaining an internalized representation of the ambient space—a cognitive map. Diese
cells do not only exhibit location-specific spiking during navigation, but also may rapidly
replay the navigated routs through endogenous dynamics of the hippocampal network.
Physiologically, such reactivations are viewed as manifestations of “memory replays”
that help to learn new information and to consolidate previously acquired memories by
reinforcing synapses in the parahippocampal networks. Below we propose a computational
model of these processes that allows assessing the effect of replays on acquiring a robust
topological map of the environment and demonstrate that replays may play a key role in
stabilizing the hippocampal representation of space.
ZUSAMMENFASSUNG DES AUTORS
In this manuscript, we use methods of zigzag homology theory to study the physiological role
of the replays—the hippocampal networks endogenous activity that recapitulates the activity
of the place cells during exploration of the environment. Insbesondere, we demonstrate that
deterioration of the hippocampal spatial memory map caused by excessive transience of
synaptic connections may be mitigated by spontaneous replays. The results help to
understand how transient information about local spatial connectivity may stabilize at a large
scale, and shed light on the separation between faster and slower memory processing in the
complementary (hippocampal and neocortical) learning systems.
EINFÜHRUNG
Spatial awareness in mammals is based on an internalized representation of the environment—
a cognitive map. In rodents, a key role in producing and sustaining this map is played by the
hippocampal place cells, which preferentially fire action potentials as the animal navigates
through specific domains of a given environment—their respective place fields. Remarkably,
hippocampal place cells may also activate due to the endogenous activity of the hippo-
campal network during quiescent wake states (Johnson & Redish, 2007; Pastalkova, Itskov,
Amarasingham, & Buzsáki, 2008) or sleep (Ji & Wilson, 2007; Louie & Wilson, 2001; Wilson
& McNaughton, 1994). Zum Beispiel, the animal can preplay place cell sequences that rep-
resent possible future trajectories while pausing at “choice points” (Papale, Zielinski, Frank,
Jadhav, & Redish, 2016), or replay sequences that recapitulate the order in which the place
Zitat: Babichev, A., Morozov, D., &
Dabaghian, Y. (2019). Replays of spatial
memories suppress topological
fluctuations in cognitive map. Netzwerk
Neurowissenschaften, 3(3), 707–724. https://
doi.org/10.1162/netn_a_00076
DOI:
https://doi.org/10.1162/netn_a_00076
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00076
Erhalten: 19 Juli 2018
Akzeptiert: 18 Dezember 2018
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Yuri Dabaghian
dabaghian@gmail.com
Handling-Editor:
Paul Expert
Urheberrechte ©: © 2018
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
N
e
N
_
A
_
0
0
0
7
6
P
D
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Memory replays suppress fluctuations in cognitive map
Hippocampal place cells:
Cells that fire in specific restricted
locations in the environment—their
respective place fields. It is believed
that a cognitive map of a given
environment emerges from the
combined activity of place cells.
cells have fired during previous exploration of the environment (Foster & Wilson, 2006;
Hasselmo, 2008). Darüber hinaus, spontaneous replays are also observed during active navigation,
when the hippocampal network is driven both by the idiothetic (body-derived) inputs and by
the network’s autonomous dynamics (Carr, Jadhav, & Frank, 2011; Dragoi & Tonegawa, 2011;
Jadhav, Kemere, Deutsch, & Frank, 2012; Jadhav, Rothschild, Roumis, & Frank, 2016; Karlsson
& Frank, 2009).
Cognitive map:
An internal neural representation
of the environment, used by the
Tiere (z.B., birds and mammals)
to orient in space, to plan spatial
navigation strategies, path integrate,
und so weiter. It is generally accepted
that the hippocampus plays a key
role in producing and sustaining
cognitive maps.
Neurophysiologically, place cell replays are viewed as manifestations of the animal’s
“mental explorations” (Babichev & Dabaghian, 2018; Dabaghian, 2016; Hopfield, 2010;
Zeithamova, Schlichting, & Preston, 2012), which help constructing the cognitive maps and
consolidating memories (Ego-Stengel & Wilson, 2010; Gerrard, Kudrimoti, McNaughton, &
Barnes, 2001; Girardeau, Benchenane, Wiener, Buzsáki, & Zugaro, 2009; Girardeau & Zugaro,
2011; Roux, Hu, Eichler, Stark, & Buzsáki, 2017). Although the detailed mechanisms of these
phenomena remain unknown, it is believed that replays may reinforce synaptic connections
that deteriorate over extended periods of inactivity (Sadowski, Jones, & Mellor, 2011, 2016;
Singer, Carr, Karlsson, & Frank, 2013).
The activity-dependent changes in the hippocampal network’s synaptic architecture occur
at multiple timescales (Bi & Poo, 1998; Fusi, Asaad, Müller, & Wang, 2007; Karlsson & Frank,
2008). Insbesondere, statistical analyses of the place cells’ spiking times indicate that place cells
exhibiting frequent coactivity tend to form short-lived “cell assemblies”—commonly viewed
as functionally interconnected groups of neurons that form and disband at a timescale be-
tween tens of milliseconds (Atallah & Scanziani, 2009; Bartos, Vida, & Jonas, 2007; Buzsáki,
2010; Harris, Csicsvari, Hirase, Dragoi, & Buzsáki, 2003) to minutes or longer (Billeh, Schaub,
Anastassiou, Barahona, & Koch, 2014; Goldman-Rakic, 1995; Hiratani & Fukai, 2014; Kuhl,
Shah, DuBrow, & Wagner, 2010; Murre, Chessa, & Meeter, 2013; Russo & Durstewitz, 2017;
Zenke & Gerstner, 2017), that is to say the functional architecture of this network is constantly
changing. In our previous work (Babichev & Dabaghian, 2017A, 2017B; Babichev, Morozov,
& Dabaghian, 2018) we used a computational model to demonstrate that despite the rapid
rewirings, such a “transient” network can produce a stable topological map of the environ-
ment, provided that the connections’ decay rate and the parameters of spiking activity fall into
the physiological range (Arai, Brandt, & Dabaghian, 2014; Basso, Arai, & Dabaghian, 2016;
Dabaghian, Mémoli, Frank, & Carlsson, 2012). Below we adopt this model to study the role
of the hippocampal replays in acquiring a robust cognitive map of space. Konkret, Wir
demonstrate that reinforcing the cell assemblies by replays helps to reduce instabilities in the
large-scale representation of the environment and to reinstate the correct topological structure
of the cognitive map.
THE MODEL
General Description
The topological model of spatial learning rests on the insight that the hippocampus produces
a topological representation of spatial environments and of mnemonic memories—a rough-
and-ready framework that is filled with geometric details by other brain regions (Dabaghian,
Brandt, & Frank, 2014). This approach, backed up by a growing number of experimental
(Alvernhe, Sargolini, & Poucet, 2012; Fenton, Csizmadia, & Müller, 2000; Gothard, Skaggs, &
McNaughton, 1996; Knierim, Kudrimoti, & McNaughton, 1998; Leutgeb et al., 2005; Moser,
Kropff, & Moser, 2008; Touretzky et al., 2005; Wills, Lever, Cacucci, Bürger, & O’keefe,
2005; Yoganarasimha, Yu, & Knierim, 2006) and computational (Chen, Gomperts, Yamamoto,
& Wilson, 2014; Curto & Itskov, 2008; Petri et al., 2014) Studien, and allows using a powerful
Netzwerkneurowissenschaften
708
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
N
e
N
_
A
_
0
0
0
7
6
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Memory replays suppress fluctuations in cognitive map
arsenal of methods from algebraic topology, in particular persistent (Carlsson, 2009; Lum
et al., 2013; Singh et al., 2008) and zigzag (Carlsson & De Silva, 2010; Carlsson, De Silva, &
Morozov 2009) homology theory techniques, for studying structure and dynamics of the hip-
pocampal map. Insbesondere, the approaches developed in Arai et al. (2014); Babichev, Cheng,
& Dabaghian (2016); Babichev, Ji, Mémoli, & Dabaghian (2016); Basso et al. (2016); Dabaghian
et al. (2012); Hoffman, Babichev, & Dabaghian (2016) help to explain how the information
provided by the individual place cells combines into a large-scale map of the environment,
to follow how the topological structure of this map unfolds in time, and to evaluate the con-
tributions made by different physiological parameters into this process. It was demonstrated,
Zum Beispiel, that the ensembles of rapidly recycling cell assemblies can sustain stable quali-
tative maps of space, provided that the network’s rewiring rate is not too high. Otherwise the
integrity of the cognitive map may be overwhelmed by topological fluctuations (Babichev &
Dabaghian, 2017A, 2017B; Babichev et al., 2018).
Mathematically, the method is based on representing the combinations of coactive place
cells in a topological framework, as simplexes of a specially designed simplicial complex
(Figure 1A and 1B). Each individual simplex σ schematically represents a connection (z.B.,
an overlap) between the place fields encoded by the corresponding place cells’ coactivity. Der
full set of such simplexes—the coactivity simplicial complex T —incorporates the entire pool
of connections encoded by the place cells in a given environment E, and hence represents the
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
N
e
N
_
A
_
0
0
0
7
6
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1. Basic notions of the hippocampal physiology in the context of the topological model.
(A) Im Folgenden, we simulate rat’s navigation in a square-shaped environment E with a hole in the
Mitte. The curves γ1, γ2, and γ3 represent a few short segments of a physical trajectorynavigated by
the rat. The place fields—the regions where the corresponding place cells become active—densely
cover the environment, forming a place field map ME . An exemplary place field is represented by
a highlighted cluster of blue dots in the top left corner of the environment. The right segment of the
environment shows a highlighted pair, a triple and a quadruple of the overlapping place fields; Die
remaining place fields are dimmed into background. (B) Simplexes that correspond to overlapping
place fields: a single vertex corresponds to place field (or a single active cell); a link between two
vertexes represents a pair of overlapping place fields (or a pair of coactive cells); three overlapping
place fields (or a triple of coactive place cells) correspond to a triangle, und so weiter. (C) A collection
of simplexes forms a simplicial complex, which schematically represents the net structure of the
place field map. Shown is a fragment of a two-dimensional (2D) coactivity complex with simplicial
paths Γ1, Γ2, and Γ3 that represent the physical paths γ1, γ2, and γ3 shown on the left. The classes of
equivalent simplicial paths describe the topological structure of the coactivity complex: the number
of topologically inequivalent, contractible simplicial paths such as Γ1 and Γ2, defines the number
of pieces, b0, of the coactivity complex (see Methods). The number of topologically inequivalent
paths contractible to a one-dimensional (1D) loop defines the number b1 of holes and so forth
(Hatcher, 2002). (D) A schematic representation of a replayed sequence of place cells, shown over
the corresponding place fields. The colored ticks in the top left corner schematically represent a
sequence of spikes replayed within a short time window w.
Netzwerkneurowissenschaften
709
Memory replays suppress fluctuations in cognitive map
topological structure of the cognitive map of the navigated space (Best, White, & Minai, 2001;
O’Keefe & Dostrovsky, n.d.).
Topological Structure of the Coactivity Complex
The topological structure of the coactivity complex provides a convenient framework for rep-
resenting spatial information encoded by the place cells. Zum Beispiel, the combinations of
the cells ignited during the rat’s moves along a physical trajectory γ, or during a mental re-
play of such a trajectory, is represented by a “simplicial path”—a chain of simplexes Γ =
{σ1, σ2, . . . , σk} that qualitatively represents the shape of γ. A simplicial path that loops onto
itself represents a closed physical rout; a pair of topologically equivalent simplicial paths rep-
resent two similar physical paths and so forth (Abbildung 1C).
The net structure of the simplicial paths running through a given simplicial complex T
can be used to describe its topological shape. Konkret, the number of topologically dis-
tinct (counted up to topological equivalence) closed paths that contract to zero-dimensional
vertexes—the zeroth Betti number b0(T )—enumerates the connected components of T ; Die
number of topologically distinct paths that contract to closed chains of links—the first Betti
number b1(T )—counts its holes and so forth (sehen (Aleksandrov, 1965; Hatcher, 2002); Und
Methoden).
Dynamics of the Coactivity Complexes
In der Praxis, the coactivity complexes can be designed to reflect particular physiological prop-
erties of the cell assemblies. Zum Beispiel, the time course of the simplexes’ appearance may
reflect the dynamics of the cell assemblies’ formation (Babichev & Dabaghian, 2017A, 2017B;
Babichev et al., 2018; Hoffman et al., 2016), or the details of the place cell activity mod-
ulations by the brain waves (Arai et al., 2014; Basso et al., 2016) und so weiter. Insbesondere, A
population of forming and disbanding cell assemblies can be represented by a set of appearing
and disappearing simplexes, das ist, by a “flickering” coactivity complex F studied in Babichev
& Dabaghian (2017A, 2017B) and Babichev et al. (2018). There it was demonstrated that if a
cell assembly network rewires sufficiently slowly (tens of seconds to a minute timescale), Dann
the “topological shape” of the corresponding coactivity complex remains stable and equiva-
lent to the topology of the simulated environment E shown on Figure 1A, as defined by its Betti
numbers bk(F ) = bk(E ) = 1, k = 0, 1 (see Methods). Physiologically, this implies that cell
assemblies’ turnover at the intermediate and the short memory timescales does not prevent
the hippocampal network from producing a lasting representation of space, despite perpetual
changes of its functional architecture (Wang et al., 2006).
Insbesondere, the model (Babichev et al., 2018) predicts that cell assembly network pro-
duces a stable topological map if the connections’ mean lifetime exceeds τ ≥ 150−200 s,
which corresponds to the Hebbian plasticity timescale (Billeh et al., 2014; Goldman-Rakic,
1995; Hiratani & Fukai, 2014; Russo & Durstewitz, 2017; Zenke & Gerstner, 2017). For no-
ticeably shorter τ, the topological fluctuations in the simulated hippocampal map are too
strong and a stable representation of the environment fails to form. Zum Beispiel, in the case
of the place field map shown on Figure 2A, the connections’ proper lifetime is about τ = 50 S
and the corresponding coactivity complex is unstable: its Betti numbers frequently exceed the
physical values (bk(F ) > bk(E )), implying that F may split into several disconnected pieces,
each one of which may contain transient gaps, holes, and other topological defects that do not
correspond to the physical features of the environment.
Netzwerkneurowissenschaften
710
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
N
e
N
_
A
_
0
0
0
7
6
P
D
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Memory replays suppress fluctuations in cognitive map
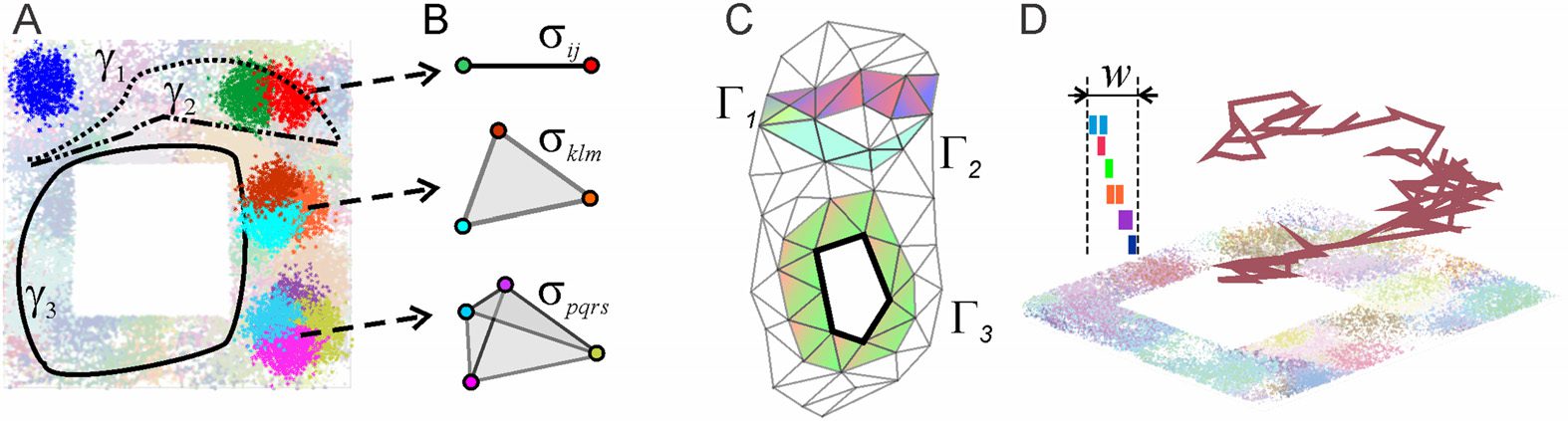
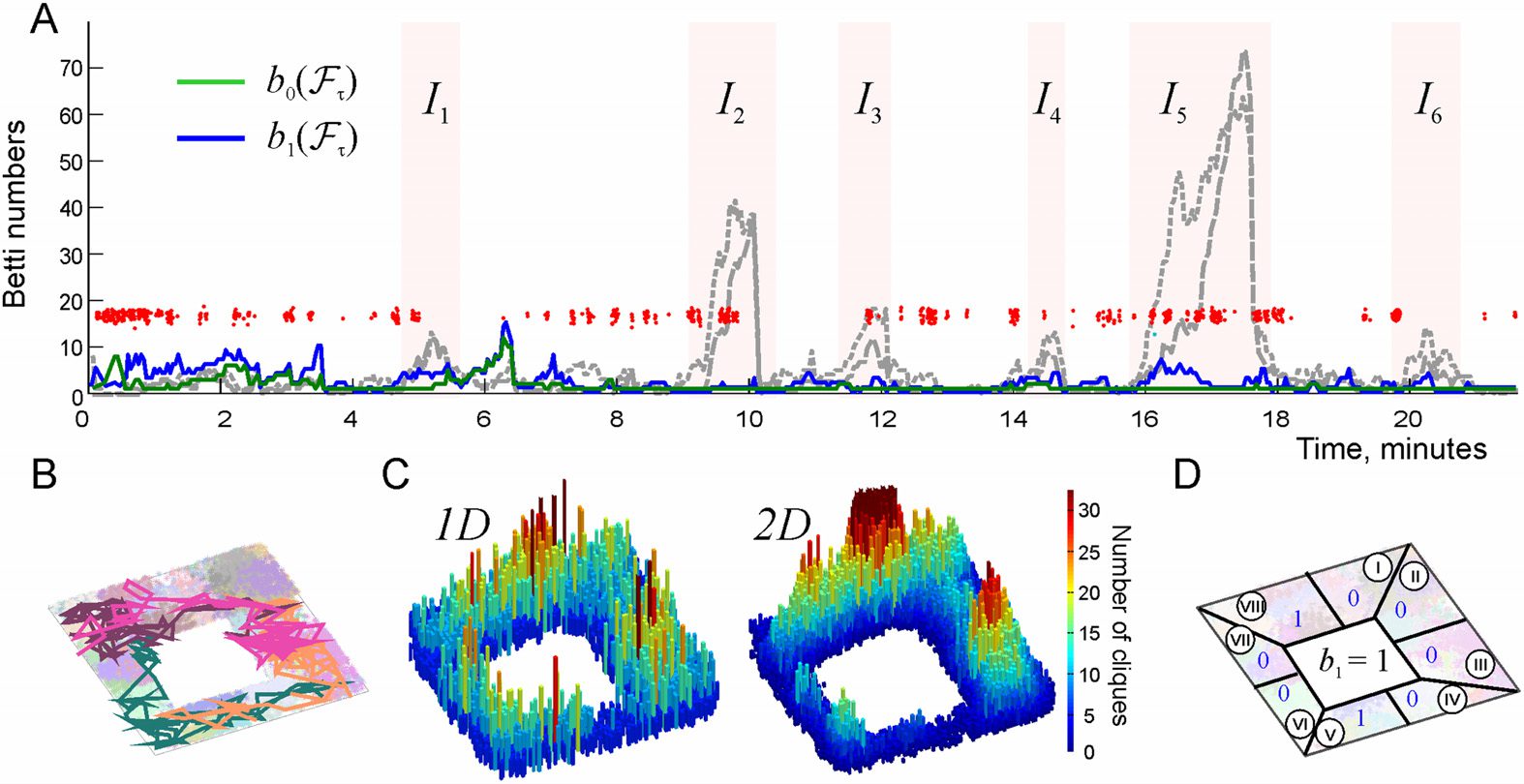
Figur 2. Topological fluctuations in a rapidly decaying coactivity complex in absence of replays.
(A) The green and the blue lines show, jeweils, the zeroth and the first Betti numbers, b0(Fτ)
and b1(Fτ) (see Methods), as functions of time. For most of the time, both Betti numbers remain
small, (cid:3)b0(Fτ)(cid:4) ≈ 2.5 ± 2.1 Und (cid:3)b1(Fτ)(cid:4) ≈ 2.8 ± 2.2, indicating a few disconnected fragments of
the coactivity complex Fτ and a few spurious holes in them. The rapid increase of the Betti numbers
during short “instability intervals” I1, . . . , I6 (highlighted by the pink background) indicate periods
of strong topological fluctuations in Fτ. (B) A segment of the simulated trajectory taken between the
16th and 18th minute shows that the animal spends time before and during the instability period I5
in a particular segment of the arena. During this time, the connections over the unvisited segments
of E start to decay (here the connections’ mean proper lifetime is τ = 50 S), as a result of which
the coactivity complex Fτ fractures into a large number of disconnected pieces riddled in holes,
which explains the splash of b0(Fτ) and b1(Fτ). (C) Spatial histograms of the links (d.h., Zentren
of the pairwise place field overlaps, left panel) and of the three-vertex simplexes (d.h., centers of
triple place field overlaps, right panel) present in Fτ during the instability period I5. The simplexes
concentrate over the northeast corner of the environment, whereas the populations of simplexes
over the south and the southwestern parts thin out. (D) The “local” Betti number b1 (blue numerals)
computed separately for the eight sectors of the environment (circled Roman numerals) indicate that
the holes emerge in all the “abandoned” parts, Zum Beispiel, sector IV contains 5 holes and sector
V contains 16 holes, und so weiter. The global Betti number computed at about 16th minute for the
entire complex, b1(Fτ) = 21, is shown in the middle.
For most of the time, these defects are scarce (bk(F ) < 5, Figure 2A) and may be viewed
as topological irregularities that briefly disrupt otherwise functional cognitive map. Indeed,
from the physiological perspective, it may be unreasonable to assume that biological cogni-
tive maps never produce topological inconsistencies—in fact, admitting small fluctuations in a
qualitatively correct representation of space may be biologically more effective than spending
time and resources on acquiring a precise and static connectivity map, especially in dynam-
ically changing environments. However, during certain periods, the topological fluctuations
may become excessive, indicating the overall instability of the cognitive map. The origin of
such occurrences is clear: if, for example, the animal spends too much time in particular parts
of the environment, then the parts of F that represent the unvisited segments of space begin
to deteriorate, leaving behind holes and disconnected fragments (Figure 2B– 2D). Outside of
these “instability periods,” when the rat regularly visits all segments of the environment, most
place cells fire recurrently, thus preventing the coactivity complex F from deteriorating.
Although this description does not account for the full physiological complexity of synaptic
and structural plasticity processes in the cell assembly network, it allows building a qualitative
Network Neuroscience
711
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
Hippocampal cell assemblies:
Transient, functionally
interconnected groups of place
cells that exhibit frequent coactivity.
The organized activity of cells in
the hippocampal and cortical
assemblies is believed to underlie
learning and memory mechanisms.
model that connects the animal’s behavior, the parameters describing deterioration of the
hippocampal network’s functional architecture and the large-scale topological properties of
the cognitive map. This, in turn, provides a context for testing the effects produced by the
place cell replays, for example, their alleged role in acquiring and stabilizing memories by
strengthening the connections in parahippocampal networks (Colgin, 2016; Sadowski et al.,
2011, 2016). To test these hypotheses, we adopted the topological model (Babichev et al.,
2018) so that the decaying connections in the simulated hippocampal cell assemblies can be
(re)established not only by the place cell activity during physical navigation but also by the
endogenous activity of the hippocampal network, and studied the effect of the latter on the
structure of the hippocampal map, as outlined below.
Implementation of the Coactivity Complexes
Implementation of the coactivity complexes is based on a classical model of the hippocampal
network, in which place cells ci are represented as vertexes vi of a “cognitive graph” G, while
the connections between pairs of coactive cells are represented by the links, ςij = [vi, vj] of
this graph (Babichev, Cheng, & Dabaghian, 2016; Burgess & O’keefe, 1996; Muller, Stead,
& Pach, 1996). The assemblies of place cells ς = [c1, c2, . . . , cn]—the “graphs of synaptically
interconnected excitatory neurons,” according to Buzsáki (2010)—then correspond to fully in-
terconnected subgraphs of G, that is, to its maximal cliques (Babichev, Cheng, & Dabaghian,
2016; Babichev et al., 2016; Hoffman et al., 2016). Since each clique ς, as a combinato-
rial object, can be viewed as a simplex spanned by the same set of vertexes (see Supplemental
Figure 6 in Basso et al., 2016), the collection of cliques of the graph G defines a clique simplicial
complex (Jonsson, 2008), which proves to be one of the most successful implementations of
the coactivity complex. In previous studies (Babichev, Cheng, & Dabaghian, 2016; Babichev
et al., 2016; Basso et al., 2016; Hoffman et al., 2016), we demonstrated that in absence of decay
(τ = ∞), such a complex T effectively accumulates information about place cell coactivity
at various timescales, capturing the correct topology of planar and voluminous environments.
If the decay of the connections is taken into account (τ < ∞), then the topology of the “flick-
ering” coactivity complex F remains stable for sufficiently small rates, but if τ becomes too
small, the topology of F may degrade. A question arises, whether the replays can slow down
its deterioration, as the biological considerations suggest.
Dynamics of the Coactivity Graph
Physiologically, place cell spiking is synchronized with the components of the extracellular lo-
cal field potential—the so-called brain waves that also define the timescale of place cell coac-
tivity (Buzsaki, 2006). Specifically, two or more place cells are considered coactive if they
fire spikes within two consecutive θ-cycles—approximately 150–250 ms interval (Mizuseki,
Sirota, Pastalkova, & Buzsáki, 2009)—a value that is also suggested by theoretical studies (Arai
et al., 2014). In the following, this period will define the shortest timescale at which the func-
tional connectivity of the simulated hippocampal network can change. For example, a new
link ςij = [vi, vj] in the coactivity graph will appear, if a coactivity of the cells ci and cj was
detected during a particular 2θ period. In absence of coactivity, the links can also disappear
with probability
p0(t) =
1
τ
e−t/τ,
(1)
where t is the time measured from the moment of last spiking of both cells ci and cj and
the parameter τ defines the mean lifetime of the synaptic connections in the cell assembly
network. In the following, τ will be the only parameter that describes the deterioration of the
Network Neuroscience
712
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
synaptic connections within the cell assemblies (Babichev et al., 2018). We will therefore use
the notations Gτ and Fτ to refer, respectively, to the flickering coactivity graph with decaying
connections and to the resulting flickering coactivity complex with decaying simplexes.
Replays of Place Cell Sequences
Replays of place cell sequences:
The endogenous activities in
the hippocampal network that
recapitulate sequential place cell
firing during physical exploration of
an environment. Spontaneous replays
are observed during sleep, quiescent
wakeful states, and active navigation.
It is believed that replays mark
animals exploration and retrieval of
the learned spatial information by
“cuing” the hippocampal network.
Replays of place cell sequences may in general represent both spatial and nonspatial memories.
In the following, we simulate only spatial replays by constructing simplicial paths that represent
previously navigated trajectories. Specifically, we select chains of connections that appeared
in the coactivity graph Gτ at the initial stages of navigation and reactivate them at the later
replay times tr, r = 1, 2, . . . , Nr (Kudrimoti, Barnes, & McNaughton, 1999; O’Neill, Senior, &
Csicsvari, 2006). To replay a trajectory originating at a given timestep ti, we randomly select a
coactivity link ς(i)
kl ∈ Gτ(ti) that is active within that time window; this link then gives rise to
a sequence of joined links, randomly selected among the ones that activate at the consecutive
time steps, ς(i+1)
, . . .. Since there are typically several active links at every moment, this
procedure allows generating a large number of replay trajectories. The physiological duration
of replays—typically about 100–200 ms (Colgin, 2016)—roughly corresponds to the coactivity
window widths, that is, to the timesteps in which the coactivity graph evolves; we therefore
“inject” the activated links into a particular coactivity window tr in order to simulate rapid
replays.
lm , ς(i+2)
mn
After a simplicial trajectory is replayed, the injected links begin to decay and to (re)activate
in the course of the animal’s moves across the environment, just as the rest of the links. Most
of these “reactivated” links simply rejuvenate the existing connections in Gτ. However, some
injections instantaneously reinstate decayed connections and produce an additional popula-
tion of higher order cliques, which affect the topological properties of the coactivity complex
Fτ, and hence—according to the model—of the cognitive map. As mentioned previously, hip-
pocampal replays are believed to enable spatial learning by stimulating inactive connections,
by slowing down their decay, and by reinforcing cell assemblies’ stability (Carr et al., 2011;
Ego-Stengel & Wilson, 2010; Girardeau et al., 2009; Girardeau & Zugaro, 2011; Jadhav et al.,
2012; Sadowski et al., 2016). In the model’s terms, this hypothesis translates as follows: the
additional influx of rejuvenated simplexes provided by the replays should qualitatively im-
prove the topological structure of the flickering coactivity complex, slow down deterioration
of its simplexes, suppress its topological defects, and, in general, help to sustain its topological
integrity. In the following, we test this hypothesis by simulating different patterns of the place
cell reactivations and quantifying the effect that this produces on the simulated cognitive map.
RESULTS
Initial Testing
The effect produced by the replays on the cognitive map depends on the parameters of the
model: the selection of replayed trajectories, the injection times, the frequency of the replays,
and so forth. To start the simulations, we selected Ns = 80 different replay sequences originat-
ing at Ni = 25 moments of time, ti, i = 1, . . . , Ni, between 20 and 200 s of navigation (the initial
interval Iinit). During this period, the trajectory covers the arena more or less uniformly: a typ-
ical 25-s-long segment of a trajectory extends across the entire environment and contains on
average about ls = 100 links (Supporting Information Figure S1). As a result, the corresponding
simplicial paths traverse the full coactivity complex Fτ, and one would expect that replaying
these paths should help to suppress the topological defects in F . To verify this prediction, we
replayed the resulting pool of G-link sequences within the main instability period I5 by using
Network Neuroscience
713
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
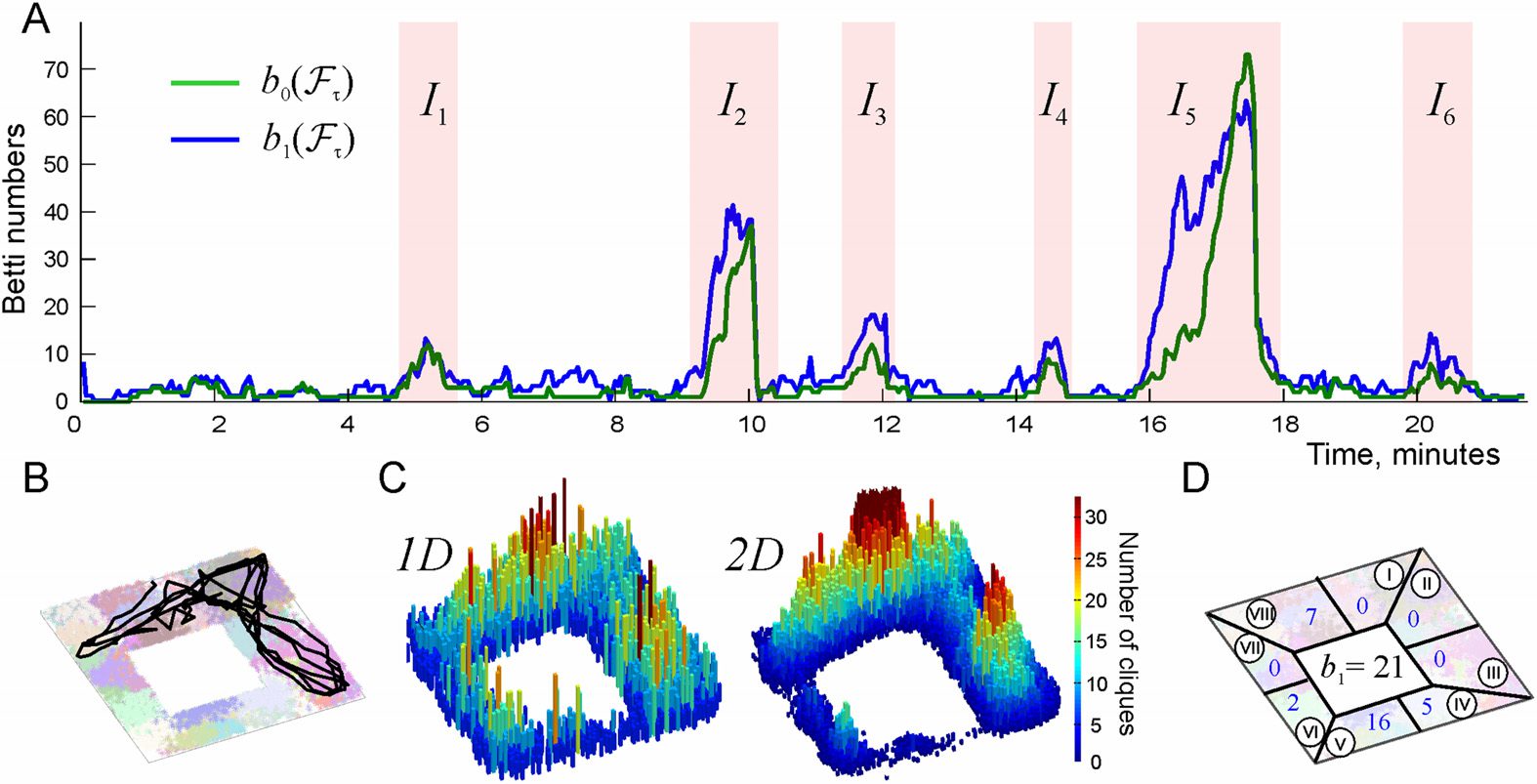
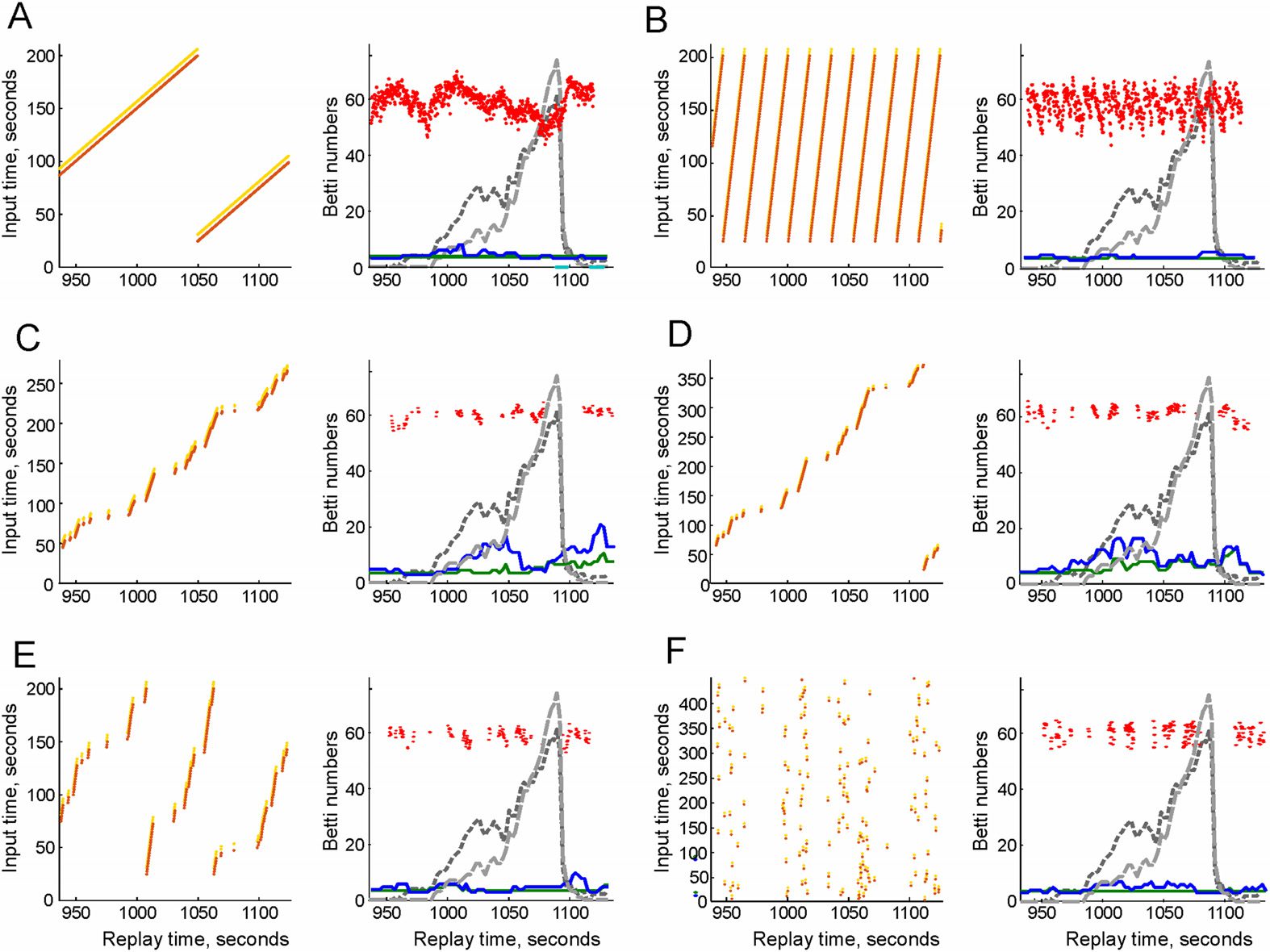
Figure 3. Suppressing topological fluctuations by reactivation of simplexes. (A) During the insta-
bility period I5 (approximately between 15.5 and 18.5 min) the topological fluctuations in the coac-
tivity complex become very strong, with the Betti numbers soaring at b0(Fτ) ≈ 65 and b1(Fτ) ≈ 75.
(B) If all the reactivated links are injected into the coactivity complex at once, at a moment preced-
ing the peak of the Betti numbers (marked by a vertical red dashed line), the fluctuations in the
coactivity complex are immediately suppressed. However, as the connection decay takes over, the
fluctuations kick back, reaching the original high values in under a minute. (C) Five consecutive
replays, marked by five vertical red dashed lines, produce a more lasting effect, reducing the Betti
numbers to smaller values (cid:3)b0(Fτ)(cid:4) ≈ 3 and (cid:3)b1(Fτ)(cid:4) ≈ 7 over the remainder of the instability
period. (D) More frequent replays (once every 2.5 s, vertical dashed lines) nearly suppress the topo-
logical fluctuations, producing the average values (cid:3)b0(Fτ)(cid:4) ≈ 1.2 and (cid:3)b1(Fτ)(cid:4) ≈ 3, that is, leaving
only a couple of spurious loops in Fτ.
different approaches and tested whether this can suppress the topological fluctuation
(Figure 3A).
In the first scenario, all replay chains were injected into the connectivity graph Gτ at once,
in the middle of the instability period I5 (Figure 3B). As a result of such a “massive” instan-
taneous replay, the topological fluctuations are initially suppressed but then they quickly re-
bound, producing about the same number of spurious 0D loops (i.e., the cognitive map remains
as fragmented as before) and an even higher number of 1D loops that mark spurious holes in
the cognitive map (Supporting Information Movie 1). In other words, our model suggests that a
single “memory flash” fails to correct the deteriorating memory map even at a short timescale,
which suggests that more regular replay patterns are required.
Indeed, if the same set of replay sequences is uniformly distributed into Nr = 5 con-
secutive groups inside the instability period I5 (one group per 36 s, Ns/Nr = 16 chains
of links each), then the topological fluctuations in the coactivity complex Fτ subside more
and over a longer period (see Figure 3C and Supporting Information Movie 2). If the re-
plays are produced even more frequently (every 9 s, i.e., about 20 replays total, Ns/Nr ≈ 4
chains of links injected per replay) then the topological fluctuations in I5 are essentially fully
suppressed over the entire environment (Figure 3D, Supporting Information Figure 2 and
Supporting Information Movie 3).
One can draw two principal observations from these results: first, that spontaneous reac-
tivation of connections at the physiological timescale can qualitatively alter the topological
structure of the flickering coactivity complex, and, second, that the temporal pattern of replays
plays a key role in suppressing the topological fluctuations in the cognitive map.
Implementation of the Replays
Electrophysiological data shows that the frequency of the replays ranges between 0.1 Hz in ac-
tive navigation to 0.4 Hz in quiescent states and 4 Hz during sleep (Colgin, 2016; Jadhav et al.,
2012; O’Neill et al., 2006; Sadowski et al., 2016). Since we model spatial learning taking place
Network Neuroscience
714
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
during active navigation, we implemented replays at the maximal rate of 0.4 Hz, which corre-
sponds to no more than one replay event over 10 consecutive coactivity intervals. Second, we
took into account the fact that, in complex environments, the hippocampus may replay a few
sequences simultaneously. For example, on the Y-track (O’Neill et al., 2006) two simultaneous
replay sequences can represent the two prongs of the Y. In open environments, there may be
more simultaneously replayed sequences; however, we used the most conservative estimate
and replayed two different sequences at each replay moment tr.
In the simplest scenario, we injected pairs of sequences into the coactivity graph Gτ with a
constant delay of about ΔT = ti − tr ≈ 14 min after their physical onset, which placed them
inside of the instability period I5 (Figure 4A). In response, the topological fluctuations in the
coactivity complex Fτ significantly diminished. In fact, the zeroth Betti number (the number
of the disconnected components) regained its physical value b0(Fτ) = 1, indicating that the
replays helped to pull the fragments of the cognitive map together into a single connected
piece. The first Betti number (the number of holes) remains on average close to its physical
value, (cid:3)b1(Fτ)(cid:4) = 1.5, exhibiting occasional fluctuations, Δb1 = ±2.2.
As mentioned above, the occasional islets separating from the main body of the simplicial
complex or a few small holes appearing in it for a short period should be viewed as topolog-
ical irregularities rather than signs of topological instability. We therefore base the following
discussion on addressing only the qualitative differences produced by the replays on the topol-
ogy of the cognitive map: whether replays can prevent fracturing of the complex into multiple
pieces and rapid proliferation of spurious loops in all dimensions. From such perspective, our
results demonstrate that translational replays at a physiological rate can effectively restore the
correct topological shape of the cognitive map, which illustrates functional importance of the
replay activity.
Since the replays are generated by the endogenous activity of the hippocampal network, the
relative temporal order of the replayed sequences can be altered, that is, the replay times tr can
be spread wider or denser than their “physical” origination times ti. The effect of the replays will
be, respectively, weaker or stronger than in the case of translational delay because of the cor-
responding changes of the sheer number of the reactivated links. However, one can factor out
the direct contribution of the replays’ volume and study more subtle effects produced specifi-
cally by the replay’s temporal organization. To this end, we split the replay period I5 into a set
5 , I2
of NR shorter subintervals, I1
, and then replayed the sequences of links originating
from the initial 3-min interval Iinit within each subinterval In
5 , n = 1, 2, . . . , NR. Since only two
sequences are replayed within every coactivity window, the total number of the (re)activated
sequences remains the same as in the delayed replay case, even though the source interval
Iinit is compressed NR-fold in time. Thus, the difference between the effects produced by the
“compressed” replays will be due solely to the differences in their temporal reorganizations.
5 , . . . I NR
5
The results illustrated in Figure 4B demonstrate that the compressed replays suppress the
topological fluctuations more effectively. For example, the repeated replay in a sequence of
20-s intervals (NR = 9 fold compression) not only restores the correct value of the zeroth
Betti number, b0(Fτ) = 1, but also drives the average number of noncontractible simpli-
cial loops close to physical value, (cid:3)b1(Fτ)(cid:4) = 1.2 ± 1. In other words, Fτ almost regains its
topologically correct shape, with an occasional spurious hole appearing for less than a sec-
ond. Physiologically, these results suggest that time-compressed, repetitive “perusing” through
memory sequences helps to prevent deterioration of global memory frameworks better than
simple “orderly” recalls.
Network Neuroscience
715
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Suppressing the topological fluctuations by replays. In all cases, the injection diagram
on the left relates the times when the place cell sequences were originally produced (vertical axis)
to the times when they are replayed (horizontal axis). Each yellow and brown dot corresponds to
a replayed sequence. On the right panel, the replay times are marked by red dots, with the ver-
tical scatter proportional to the simulated speed of the animal. The resulting zeroth Betti number
(b0(Fτ), green line) and the first Betti number (b1(Fτ), blue line) are shown in the foreground, and
the original, unstable Betti numbers (without replays) are shown in the background (dark and light
dashed gray lines, respectively). (A) A simple translational replay of a couple of sequences repeated
over a 3-min period (between 20 and 200 s), with a ΔT = 14-min delay. The zeroth Betti number
regains its physical value, b0(Fτ) = b0(E ) = 1, indicating that cognitive map reconnects into one
piece. The first Betti number fluctuates near the physical value b1(Fτ) = 1.5 ± 2.2, indicating that
nearly all spurious holes are closed. (B) Compressed replay: a 3-min period is replayed repeatedly
over several consecutive 20-s intervals. Here the zeroth Betti number remains correct, b0(Fτ) = 1,
and the fluctuations of the first Betti number reduce farther, b1(Fτ) = 1.2 ± 1. (C) Modulating
the replay times by slow move periods (v < 15 cm/s) produces sparser replays. As a result, the
topological fluctuations in the case of uncompressed, speed-modulated delayed replays increase,
b0(Fτ) = 4.2 ± 1.9, b1(Fτ) = 8.2 ± 3.4. (D) Small compressions (up to 300 s replayed over ∼ 150
second period, same delay) may intensify the fluctuations: b0(Fτ) = 5.9 ± 2.4, b1(Fτ) = 9.2 ± 4.1.
(E) Further compression of the replays improves the results, b0(Fτ) = 1.1 ± 1.4, b1(Fτ) = 1.7 ± 2,
although the variations of b1(Fτ) remain high compared with the cases in which the replays are
not modulated by the speed. (F) Random replays reduce the fluctuations even further: the coactiv-
ity complex acquires the correct zeroth Betti number b0(Fτ) = 1 (the map becomes connected),
producing occasional spurious loops, b1 = 1.4 ± 1.2, that is, occasional topological irregularities.
Speed Modulation of the Replays
Since replays are mostly observed during quiescent periods and slow moves (O’Neill et al.,
2006; O’Neill, Senior, Allen, Huxter, & Csicsvari, 2008), we studied whether such “low-speed”
replays will suffice for suppressing the topological fluctuations in the cognitive map. Specifi-
cally, we identified the periods when the speed of the animal falls below 15 cm/sec (which, in
Network Neuroscience
716
Memory replays suppress fluctuations in cognitive map
our simulations happens during 14% of time (see Supporting Information Figure 3 and Koene
& Hasselmo, 2008; Nádasdy, Hirase, Czurkó, Csicsvari, & Buzsáki, 1999), and replayed the
place cell sequences only during these periods.
It turns out that although the resulting slow motion replays can stabilize the topological
structure of the simulated cognitive map, the effect strongly depends on their temporal organi-
zation. Specifically, in the simple delayed replay scenario, the topological fluctuations remain
significantly higher than without speed modulation (Figure 4C and Movie 4, Supporting In-
formation). On average, the coactivity complex contains about a dozen spurious loops: it
remains split in a few pieces, (cid:3)b0(Fτ)(cid:4) = 4.2, that together contain (cid:3)b1(Fτ)(cid:4) = 8.2 holes
on average. This is a natural result—one would expect that speed restrictions will dimin-
ish the number of the injected active connections and hence that Fτ will degrade more. A
slightly compressed replay (4 min of activity replayed over 3-min period) does not improve
the result: both the number of disconnected components and the number of holes in them
increase (cid:3)b0(Fτ)(cid:4) = 5.9, (cid:3)b1(Fτ)(cid:4) = 9.2 (Figure 4D). However, if the replays are com-
pressed further, the average number of disconnected components is significantly reduced: for
the threefold compression shown on Figure 4E, the mean values are (cid:3)b0(Fτ)(cid:4) = 1.1 and
(cid:3)b1(Fτ)(cid:4) = 1.7, that is, the encoded map approaches the quality of the maps produced with
unrestricted replays.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Replays suppress topological fluctuations over the entire navigation period. (A) The time
dependence of the Betti numbers b0(Fτ) and b1(Fτ) (the green and the blue line respectively) in
presence of the replays. The topological fluctuations that previously overwhelmed the map during
the “instability intervals” (shown in the background by two dashed gray lines, see Figure 2A) are
now nearly fully suppressed. The replay moments, tr, marked by the red dots, are modulated by
speed, v < 15 cm/s. (B) Several examples of replayed trajectories over the navigated environment
are shown in different colors (see also Supporting Information Figure 1). (C) Spatial histograms of
the centers of the links (left panel) and of the three-vertex simplexes (right panel) during the in-
stability period I5 in presence of the replays. The populations of simplexes over the south and the
southwestern parts of the environment in presence of the replays have increased compared to the
case shown on Figure 2C, which suppresses spurious topological loops in the coactivity complex.
(D) The Betti numbers b1 computed for the eight sectors of the environment are also significantly
reduced, indicating that the topological fluctuations are suppressed both locally and globally. The
deviations of b1 from 0 in the sectors V and VIII are due to boundary effects at the sector’s edges that
do not affect the global value b1(Fτ) = 1. All zeroth Betti numbers, both local and global, assume
correct values b0 = 1 and are not shown.
Network Neuroscience
717
Memory replays suppress fluctuations in cognitive map
The effectiveness of the latter scenario can be explained by noticing that replay compression
brings the activities that are widely spread in physical time into close temporal vicinities during
the replays. In other words, in compressed replays, a wider variety of connections is activated
at each tr: the real-time separation between activity patterns shrinks. This helps to reduce or
eliminate the temporal “lacunas” in place cell coactivity across the entire hippocampal net-
work and hence to prevent spontaneous deterioration of its parts. In physiological terms, this
implies that the compressed replays of the place cell patterns are less constrained by the phys-
ical temporal scale of the rat’s navigational experiences, which leads to a more even activation
of the connections in the network and helps to prevent the memory map’s fragmentation.
To test this idea, we amplified this effect by shuffling the order of the replayed sequences
and by randomizing the injection diagram, thus enforcing a nearly uniform pattern of injected
activity across the simulated population of cell assemblies. This indeed proved to be the most
effective replay strategy: as shown on Figure 4F, such replay patterns restore the topological
shape of the coactivity complex, allowing only occasional holes: (cid:3)b0(Fτ)(cid:4) = 1, (cid:3)b1(Fτ)(cid:4) ≈
1.4 ± 1.2 (Supporting Information Movie 5). Thus, the model suggests that “reshuffling” the
temporal sequence of memory replays helps to sustain memory framework better than orderly
recollections, occurring in natural past-to-future succession. The effect of random replays of
the place cell sequences over the entire simulated navigation period shown in Figure 5 clearly
illustrates the importance of replays for rapid encoding of topological maps: the fluctuations in
the cognitive map are uniformly suppressed (for the original values of the Betti numbers during
all six instability periods without replays see Table 1 in Methods).
DISCUSSION
The model discussed above suggests that replays of place cell activity help to learn and to sus-
tain the topological structure of the cognitive map. The physiological accuracy of the replay
simulation can be increased ad infinitum, by incorporating more and more parameters into
the model. In this study we use only a few basic properties of the replays, which, however,
capture several key functional aspects of the replay activity. First, the model implements an
effective feedback loop, in which the onset of topological instabilities in the flickering coac-
tivity complex Fτ triggers the replays that restore its integrity. Indeed, the cell assemblies’ (and
the corresponding simplexes’) decays intensify as the animal’s exploratory movements slow
down and visits to particular segments of the environment become less frequent. On the other
hand, low-speed periods define temporal windows during which the simulated replays are in-
jected into the network, which work to suppress the topological instabilities. Second, the model
allows controlling the replays’ temporal organization independently from the other parameters
or neuronal activity and exploring the replays’ contribution into acquiring and stabilizing the
cognitive maps. The results demonstrate that in order to strengthen the decaying connections
in the hippocampal network effectively, the replays must (1) be produced at a sufficiently high
rate that falls within the physiological range and (2) distribute without temporal clustering, in
a semi-random order.
An important aspect of the obtained results is a separation of the timescales at which dif-
ferent types of topological information is processed. On the one hand, rapid turnover of the
information about local connectivity at the working memory timescale is represented by quick
recycling of the cell assemblies and rapid spontaneous replays of the learned sequences. On
the other hand, the large-scale topological structures of the cognitive map, described by the in-
stantaneous homological characteristics of the coactivity complex, emerge at the intermediate
memory timescale. Thus, the model suggests that the characteristic timescale of the topological
Network Neuroscience
718
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
loops’ dynamics is by an order of magnitude larger than the timescale of fluctuations at the cell
assembly level. This observation provides a functional perspective on the role played by the
place cell replays in learning: by reducing the fluctuations, replays help separating the fast and
the slow information processing timescales and hence to extract stable topological information
that can be used to build a long-term, qualitative representation of the environment. This sepa-
ration of timescales corroborates with the well-known observation that transient information is
rapidly processed in the hippocampus and then the resulting memories are consolidated and
stored in the cortical areas, but at slower timescales and for longer periods.
METHODS
Topological Glossary
For the reader’s convenience, we briefly outline the key topological terms and concepts used
in this paper.
.
.
1
2
1
, ci1
, υj1
, . . . , cid
, . . . , υjk
∈ Σ and σ(d2)
as a line segment, σ(2)
An abstract simplex of order d is a set of (d + 1) elements, for example, a set of coactive
cells, σ(d) = [ci0
] or a set of place fields, σ(d) = [υj0
]. The subsets
of σ(d)
are its subsimplexes. Subsimplexes of maximal dimensionality (d − 1) are referred
to as facets of σ(d)
An abstract simplicial complex Σ is a family of abstract simplexes closed under the over-
lap relation: a nonempty overlap of any two simplexes σ(d1)
∈ Σ is a
and σ(d2)
subsimplex of both σ(d1)
Geometrically, simplexes can be visualized as d-dimensional polytopes: σ(0)
as a triangle, σ(3)
σ(1)
as a point,
as a tetrahedron, and so forth. The cor-
responding geometric simplicial complexes are multidimensional polyhedra that have
a shape and a structure that does not change with simplex deformations, for example,
disconnected components, holes, cavities of different dimensionality, and so on. This
structure, commonly referred to as topological (Aleksandrov, 1965), is identical in a ge-
ometric simplicial complex to and in the abstract complex built over the vertexes of the
geometric simplexes. Thus, abstract simplicial complexes may be viewed as structural
representations of the conventional geometric shapes.
Topological properties of the simplicial complexes are established based on algebraic
analyses of chains, cycles and boundaries.
2
A chain α(d)
is a formal combination d-dimensional simplexes with coefficients from an
algebraic ring or a field. Intuitively, they can be viewed, for example, as the simplicial paths
described in The Model section. Such combinations permit algebraic operations: they can be
added, subtracted, and multiplied by a common factor, and so forth. As a result, the set of all
chains of a given simplicial complex, C(Σ), also forms an algebraic entity, for example, if the
chains’ coefficients form to a field, then C(Σ) forms a vector space.
A boundary of a chain, ∂α(d)
, is a formal combination of all the facets of the α-chain,
with the coefficients inherited from α and alternated so that the boundary of ∂α(d)
vanishes,
∂2α(d) = 0. This universal topological principle—boundary of a boundary is a null set—can
be illustrated on countless examples, for example, by noticing that the external surface of a
triangular pyramid σ(3)
—its geometric boundary—has no boundary itself.
Cycles generalize the previous example—a generic cycle z is a chain without a boundary,
∂z = 0. Intuitively, cycles correspond to agglomerates of simplexes (e.g., simplicial paths) that
Network Neuroscience
719
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
loop around holes and cavities of the corresponding dimension. Note however, that although
all boundaries are cycles, not all cycles are boundaries.
Homologies are two cycles, z1 and z2, that are equivalent, or homologous, if they differ
by a boundary chain. The set of equivalent cycles forms a homology class. If the chain
coefficients come from a field, then the homology classes of d-dimensional cycles form
a vector space Hd(Σ). The dimensionality of this vector space is the d-th Betti number of
the simplicial complex Σ, bd(Σ) = dim Hk(Σ), which counts the number of independent
d-dimensional holes in Σ.
Flickering complexes F (t) consist of simplexes that may disappear or (re)appear, so that
the complex as a whole may grow or shrink from one moment to another (see Figure 2
in Babichev et al., 2018),
F (t1) ⊆ F (t2) ⊆ F (t3) ⊇ F (t4) ⊆ F (t5) ⊇ . . . .
Computing the corresponding Betti numbers, bk(F (t)), requires a special technique—
Zigzag persistent homology theory that allows tracking cycles in F on moment-to-
moment basis (Babichev et al., 2018; Carlsson & De Silva, 2010; Carlsson et al., 2009).
A clique in a graph G is a set of fully interconnected vertices, that is, a complete subgraph
of G. Combinatorially, cliques have the same key property as the abstract simplexes: any
subcollection of vertices in a clique is fully interconnected. Hence a nonempty overlap
of two cliques ς and ς(cid:10)
, which implies that cliques may
be formally viewed as abstract simplexes and a collection of cliques in a given graph
G produces its clique simplicial complex Σ(G) (Jonsson, 2008). In particular, the clique
coactivity complexes Tς is induced from the coactivity graphs G (Babichev et al., 2016;
Basso et al., 2016; Hoffman et al., 2016) and the flickering clique complexes Fτ are con-
structed using coactivity graph with flickering connections Gτ, (Babichev & Dabaghian,
2017a, 2017b; Babichev et al., 2018). Note however, that the topological analyses ad-
dress the topology of the coactivity complexes, rather than the network topology of G.
is a subclique in both ς and ς(cid:10)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Spike Simulations
The environment shown on Figure 1A is simulated after typical arenas used in typical electro-
physiological experiments. Over the navigation period Ttot = 30 min, the trajectory covers the
environment uniformly. The maximal speed of the simulated movements is vmax = 50 cm/s,
with the mean value ¯v = 25 cm/s. The firing rate of a place cell c is defined by
λc(r) = fce
− (r−rc)2
2s2
c
where fc is the maximal firing rate and sc defines the size of the place field centered at rc
(Barbieri et al., 2004). In addition, spiking is modulated by the θ-oscillations—a basic cycle
of the extracellular local field potential in the hippocampus, with the frequency of about 8 Hz
(Arai et al., 2014; Huxter, Senior, Allen, & Csicsvari, 2008; Mizuseki et al., 2009). The simulated
ensemble contains Nc = 300 virtual place cells, with the typical maximal firing rate f = 14 Hz
and the typical place field size s = 20 cm.
The Statistics of the Betti Numbers
The values during instability periods without replays is provided in Table 1. Note that all values
differ significantly from the Betti numbers exhibited by the coactivity complexes with replays
(see Results).
Network Neuroscience
720
Memory replays suppress fluctuations in cognitive map
Table 1. Betti number statistics for the six instability periods (Figures 2) without replays: the mean
¯bk and the variance Δbk, for k = 0, 1.
¯
b0
Instability period
I1
7.7
I2
17.9
I3
7.1
I4
5.5
I5
27.8
I6
5.7
¯
b1
8.2
28.7
14.2
8.9
34.9
7.7
Δb1
4.3
11.1
3.8
4.4
21.2
3.1
Δb0
4.2
9.8
3.8
3.4
19.8
3.8
ACKNOWLEDGMENTS
This document was prepared as an account of work sponsored by the United States Govern-
ment. While this document is believed to contain correct information, neither the United States
Government nor any agency thereof, nor the Regents of the University of California, nor any of
their employees, makes any warranty, express or implied, or assumes any legal responsibility
for the accuracy, completeness, or usefulness of any information, apparatus, product, or pro-
cess disclosed, or represents that its use would not infringe privately owned rights. Reference
herein to any specific commercial product, process, or service by its trade name, trademark,
manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recom-
mendation, or favoring by the United States Government or any agency thereof, or the Regents
of the University of California. The views and opinions of authors expressed herein do not
necessarily state or reflect those of the United States Government or any agency thereof or the
Regents of the University of California.
This manuscript has been authored by an author at Lawrence Berkeley National Labora-
tory under Contract No. DE-AC02-05CH11231 with the U.S. Department of Energy. The U.S.
Government retains, and the publisher, by accepting the article for publication, acknowledges,
that the U.S. Government retains a non-exclusive, paid-up, irrevocable, world-wide license to
publish or reproduce the published form of this manuscript, or allow others to do so, for U.S.
Government purposes.
AUTHOR CONTRIBUTIONS
Andrey Babichev: Formal analysis; Investigation; Software; Validation; Visualization. Dmitriy
Morozov: Methodology; Software. Yuri Dabaghian: Conceptualization; Data curation; Formal
analysis; Funding acquisition; Investigation; Methodology; Project administration; Resources;
Software; Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Yuri Dabaghian, National Science Foundation (http://dx.doi.org/10.13039/100000001), Award
ID: 1422438. Dmitriy Morozov, Department of Energy, Office of Science (http://dx.doi.org/
10.13039/100006132), Contract ID: DE-AC02-05CH11231.
REFERENCES
Aleksandrov, P.(1965). Elementary concepts of topology. NewYork: Ungar.
Alvernhe, A., Sargolini, F., & Poucet, B. (2012). Rats build and
update topological representations through exploration. Animal
Cognition, 15(3), 359–368.
Arai, M., Brandt, V., & Dabaghian, Y. (2014). The effects of theta
precession on spatial learning and simplicial complex dynam-
ics in a topological model of the hippocampal spatial map. PLoS
Computational Biology, 10(6), e1003651.
Network Neuroscience
721
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Memory replays suppress fluctuations in cognitive map
Atallah, B. V., & Scanziani, M. (2009). Instantaneous modulation
of gamma oscillation frequency by balancing excitation with
inhibition. Neuron, 62(4), 566–577.
Carr, M. F., Jadhav, S. P., & Frank, L. M. (2011). Hippocampal replay
in the awake state: A potential substrate for memory consolida-
tion and retrieval. Nature Neuroscience, 14(2), 147–153.
Babichev, A., Cheng, S., & Dabaghian, Y. A. (2016). Topological
schemas of cognitive maps and spatial learning. Frontiers in
Computational Neuroscience, 10, 18.
Chen, Z., Gomperts, S. N., Yamamoto, J., & Wilson, M. A. (2014).
Neural representation of spatial topology in the rodent hip-
pocampus. Neural Computation, 26(1), 1–39.
Babichev, A., & Dabaghian, Y. (2017a). Persistent memories in
transient networks. In Emergent Complexity from Nonlinearity, in
Physics, Engineering and the Life Sciences (pp. 179–188). Cham,
Switzerland: Springer.
Babichev, A., & Dabaghian, Y. (2017b). Transient cell assembly net-
works encode stable spatial memories. Scientific Reports, 7(1),
3959.
Babichev, A., & Dabaghian, Y. A. (2018). Topological schemas of
memory spaces. Frontiers in Computational Neuroscience, 12, 27.
Babichev, A., Ji, D., Mémoli, F., & Dabaghian, Y. A. (2016). A
topological model of the hippocampal cell assembly network.
Frontiers in Computational Neuroscience, 10, 50.
Babichev, A., Morozov, D., & Dabaghian, Y. (2018). Robust spatial
memory maps encoded by networks with transient connections.
PLoS Computational Biology, 14(9), e1006433.
Barbieri, R., Frank, L. M., Nguyen, D. P., Quirk, M. C., Solo, V.,
Wilson, M. A., & Brown, E. N. (2004). Dynamic analyses of in-
formation encoding in neural ensembles. Neural Computation,
16(2), 277–307.
Bartos, M., Vida, I., & Jonas, P.
(2007). Synaptic mechanisms of
synchronized gamma oscillations in inhibitory interneuron net-
works. Nature Reviews Neuroscience, 8(1), 45–56.
Basso, E., Arai, M., & Dabaghian, Y. (2016). Gamma synchroniza-
tion influences map formation time in a topological model of
spatial learning. PLoS Computational Biology, 12(9), e1005114.
Best, P. J., White, A. M., & Minai, A. (2001). Spatial processing in
the brain: the activity of hippocampal place cells. Annual Review
of Neuroscience, 24(1), 459–486.
Bi, G.-Q., & Poo, M.-M. (1998). Synaptic modifications in cultured
hippocampal neurons: Dependence on spike timing, synaptic
strength, and postsynaptic cell type. Journal of Neuroscience,
18(24), 10464–10472.
Billeh, Y. N., Schaub, M. T., Anastassiou, C. A., Barahona, M., &
Koch, C. (2014). Revealing cell assemblies at multiple levels of
granularity. Journal of Neuroscience Methods, 236, 92–106.
Burgess, N., & O’keefe, J. (1996). Cognitive graphs, resistive grids,
and the hippocampal representation of space. The Journal of
General Physiology, 107(6), 659–62.
Buzsaki, G. (2006). Rhythms of the Brain. Oxford, UK: Oxford
University Press.
Buzsáki, G. (2010). Neural syntax: Cell assemblies, synapsembles,
and readers. Neuron, 68(3), 362–385.
Carlsson, G. (2009). Topology and data. Bulletin of the American
Mathematical Society, 46(2), 255–308.
Carlsson, G., & De Silva, V. (2010). Zigzag persistence. Foundations
of Computational Mathematics, 10(4), 367–405.
Carlsson, G., De Silva, V., & Morozov, D. (2009). Zigzag persis-
tent homology and real-valued functions. In Proceedings of the
Twenty-Fifth Annual Symposium on Computational Geometry
(pp. 247–256).
Colgin, L. L. (2016). Rhythms of the hippocampal network. Nature
Reviews Neuroscience, 17(4), 239–49.
Curto, C., & Itskov, V. (2008). Cell groups reveal structure of stim-
ulus space. PLoS Computational Biology, 4(10), e1000205.
Dabaghian, Y.
(2016). Maintaining consistency of spatial infor-
mation in the hippocampal network: A combinatorial geometry
model. Neural Computation, 28(6), 1051–1071.
Dabaghian, Y., Brandt, V. L., & Frank, L. M.
(2014). Recon-
ceiving the hippocampal map as a topological template. Elife,
3, e03476.
Dabaghian, Y., Mémoli, F., Frank, L., & Carlsson, G. (2012). A
topological paradigm for hippocampal spatial map formation
using persistent homology. PLoS Computational Biology, 8(8),
e1002581.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dragoi, G., & Tonegawa, S.
future place
cell sequences by hippocampal cellular assemblies. Nature,
469(7330), 397–401.
(2011). Preplay of
Ego-Stengel, V., & Wilson, M. A. (2010). Disruption of ripple-
impairs spatial
associated hippocampal activity during rest
learning in the rat. Hippocampus, 20(1), 1–10.
Fenton, A. A., Csizmadia, G., & Muller, R. U. (2000). Conjoint con-
trol of hippocampal place cell firing by two visual stimuli: I. The
effects of moving the stimuli on firing field positions. The Journal
of General Physiology, 116(2), 191–210.
Foster, D. J., & Wilson, M. A. (2006). Reverse replay of behavioural
sequences in hippocampal place cells during the awake state.
Nature, 440(7084), 680–683.
Fusi, S., Asaad, W. F., Miller, E. K., & Wang, X.-J. (2007). A neu-
ral circuit model of flexible sensorimotor mapping: Learning and
forgetting on multiple timescales. Neuron, 54(2), 319–333.
Gerrard, J. L., Kudrimoti, H., McNaughton, B. L., & Barnes, C. A.
(2001). Reactivation of hippocampal ensemble activity patterns
in the aging rat. Behavioral Neuroscience, 115(6), 1180–1192.
Girardeau, G., Benchenane, K., Wiener, S. I., Buzsáki, G., & Zugaro,
M. B.
(2009). Selective suppression of hippocampal ripples
impairs spatial memory. Nature Neuroscience, 12(10), 1222–3.
Girardeau, G., & Zugaro, M. (2011). Hippocampal ripples and memory
consolidation. Current Opinion in Neurobiology, 21(3), 452–459.
(1995). Cellular basis of working memory.
Goldman-Rakic, P. S.
Neuron, 14(3), 477–485.
Gothard, K. M., Skaggs, W. E., & McNaughton, B. L. (1996). Dy-
namics of mismatch correction in the hippocampal ensemble
code for space: Interaction between path integration and envi-
ronmental cues. Journal of Neuroscience, 16(24), 8027–8040.
Harris, K. D., Csicsvari, J., Hirase, H., Dragoi, G., & Buzsáki, G.
(2003). Organization of cell assemblies in the hippocampus.
Nature, 424(6948), 552–556.
Hasselmo, M. E. (2008). Temporally structured replay of neural ac-
tivity in a model of entorhinal cortex, hippocampus and post-
subiculum.European Journal of Neuroscience, 28(7), 1301–1315.
Network Neuroscience
722
Memory replays suppress fluctuations in cognitive map
Hatcher, A. (2002). Algebraic Topology. Cambridge, UK: Cambridge
UP.
Hiratani, N., & Fukai, T.
Interplay between short-and
long-term plasticity in cell-assembly formation. PloS One, 9(7),
e101535.
(2014).
Hoffman, K., Babichev, A., & Dabaghian, Y. (2016). A model of to-
pological mapping of space in bat hippocampus. Hippocampus,
26(10), 1345–1353.
Hopfield,
J.
J.
Proceedings of
1648–1653.
(2010). Neurodynamics of mental exploration.
the National Academy of Sciences, 107(4),
Huxter, J. R., Senior, T. J., Allen, K., & Csicsvari, J. (2008). Theta
phase–specific codes for two-dimensional position, trajectory
and heading in the hippocampus. Nature Neuroscience, 11(5),
587–94.
Jadhav, S. P., Kemere, C., German, P. W., & Frank, L. M.
(2012).
Awake hippocampal sharp-wave ripples support spatial memory.
Science, 336(6087), 1454–1458.
Jadhav, S. P., Rothschild, G., Roumis, D. K., & Frank, L. M. (2016).
Coordinated excitation and inhibition of prefrontal ensembles
during awake hippocampal sharp-wave ripple events. Neuron,
90(1), 113–127.
Ji, D., & Wilson, M. A. (2007). Coordinated memory replay in
the visual cortex and hippocampus during sleep. Nature Neu-
roscience, 10(1), 100–107.
Johnson, A., & Redish, A. D. (2007). Neural ensembles in CA3 tran-
siently encode paths forward of the animal at a decision point.
Journal of Neuroscience, 27(45), 12176–12189.
Jonsson,
J.
(2008). Simplicial Complexes of Graphs (Vol. 3).
New York: Springer.
Karlsson, M. P., & Frank, L. M. (2008). Network dynamics under-
lying the formation of sparse, informative representations in the
hippocampus. Journal of Neuroscience, 28(52), 14271–14281.
Karlsson, M. P., & Frank, L. M. (2009). Awake replay of remote
experiences in the hippocampus. Nature Neuroscience, 12(7),
913–18.
Knierim, J. J., Kudrimoti, H. S., & McNaughton, B. L. (1998). In-
teractions between idiothetic cues and external landmarks in the
control of place cells and head direction cells. Journal of Neuro-
physiology, 80(1), 425–446.
Koene, R. A., & Hasselmo, M. E. (2008). Reversed and forward
buffering of behavioral spike sequences enables retrospective
and prospective retrieval in hippocampal regions CA3 and CA1.
Neural Networks, 21(2-3), 276–288.
Kudrimoti, H. S., Barnes, C. A., & McNaughton, B. L. (1999). Re-
activation of hippocampal cell assemblies: Effects of behavioral
state, experience, and EEG dynamics. Journal of Neuroscience,
19(10), 4090–4101.
Kuhl, B. A., Shah, A. T., DuBrow, S., & Wagner, A. D. (2010).
Resistance to forgetting associated with hippocampus-mediated
reactivation during new learning. Nature Neuroscience, 13(4),
501–506.
Leutgeb, J. K., Leutgeb, S., Treves, A., Meyer, R., Barnes, C. A.,
McNaughton, B. L., . . . Moser, E. I. (2005). Progressive transfor-
mation of hippocampal neuronal representations in “morphed”
environments. Neuron, 48(2), 345–358.
Louie, K., & Wilson, M. A. (2001). Temporally structured replay of
awake hippocampal ensemble activity during rapid eye move-
ment sleep. Neuron, 29(1), 145–156.
Lum, P. Y., Singh, G., Lehman, A., Ishkanov, T., Vejdemo-Johansson,
M., Alagappan, M., . . . Carlsson, G. (2013). Extracting in-
sights from the shape of complex data using topology. Scientific
Reports, 3, 01236.
Mizuseki, K., Sirota, A., Pastalkova, E., & Buzsáki, G. (2009). Theta
oscillations provide temporal windows for local circuit com-
putation in the entorhinal-hippocampal loop. Neuron, 64(2),
267–280.
Moser, E. I., Kropff, E., & Moser, M.-B. (2008). Place cells, grid cells,
and the brain’s spatial representation system. Annual Review of
Neuroscience, 31, 69–89.
Muller, R. U., Stead, M., & Pach, J. (1996). The hippocampus as a cog-
nitive graph. The Journal of General Physiology, 107(6), 663–694.
Murre, J. M., Chessa, A. G., & Meeter, M. (2013). A mathematical
model of forgetting and amnesia. Frontiers in Psychology, 4, 76.
Nádasdy, Z., Hirase, H., Czurkó, A., Csicsvari, J., & Buzsáki, G.
(1999). Replay and time compression of recurring spike se-
quences in the hippocampus. Journal of Neuroscience, 19(21),
9497–9507.
O’Keefe, J., & Dostrovsky, J. (n.d.). The hippocampus as a spatial
map: Preliminary evidence from unit activity in the freely-moving
rat. Brain Research, 171–175.
O’Neill, J., Senior, T., & Csicsvari, J. (2006). Place-selective firing of
CA1 pyramidal cells during sharp wave/ripple network patterns
in exploratory behavior. Neuron, 49(1), 143–155.
O’Neill, J., Senior, T. J., Allen, K., Huxter, J. R., & Csicsvari, J. (2008).
Reactivation of experience-dependent cell assembly patterns in
the hippocampus. Nature Neuroscience, 11(2), 209–15.
Papale, A. E., Zielinski, M. C., Frank, L. M., Jadhav, S. P., & Redish,
A. D. (2016). Interplay between hippocampal sharp-wave-ripple
events and vicarious trial and error behaviors in decision making.
Neuron, 92(5), 975–982.
Pastalkova, E., Itskov, V., Amarasingham, A., & Buzsáki, G. (2008).
Internally generated cell assembly sequences in the rat hippo-
campus. Science, 321(5894), 1322–1327.
Petri, G., Expert, P., Turkheimer, F., Carhart-Harris, R., Nutt, D.,
Hellyer, P. J., & Vaccarino, F. (2014). Homological scaffolds of
brain functional networks. Journal of The Royal Society Interface,
11(101), 20140873.
Roux, L., Hu, B., Eichler, R., Stark, E., & Buzsáki, G. (2017). Sharp
wave ripples during learning stabilize the hippocampal spatial
map. Nature Neuroscience, 20(6), 845–853.
Russo, E., & Durstewitz, D. (2017). Cell assemblies at multiple time
scales with arbitrary lag constellations. Elife, 6, e19428.
Sadowski, J. H., Jones, M. W., & Mellor, J. R. (2011). Ripples make
waves: Binding structured activity and plasticity in hippocampal
networks. Neural Plasticity, 2011, 960389.
Sadowski, J. H., Jones, M. W., & Mellor, J. R. (2016). Sharp-wave
ripples orchestrate the induction of synaptic plasticity during
reactivation of place cell firing patterns in the hippocampus.
Cell Reports, 14(8), 1916–1929.
Singer, A. C., Carr, M. F., Karlsson, M. P., & Frank, L. M. (2013).
Hippocampal SWR activity predicts correct decisions during
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
723
Memory replays suppress fluctuations in cognitive map
the initial
1163–1173.
learning of an alternation task. Neuron, 77(6),
Singh, G., Memoli, F., Ishkhanov, T., Sapiro, G., Carlsson, G., &
Ringach, D. L. (2008). Topological analysis of population activ-
ity in visual cortex. Journal of Vision, 8(8), 11–18.
Touretzky, D. S., Weisman, W. E., Fuhs, M. C., Skaggs, W. E.,
Fenton, A. A., & Muller, R. U. (2005). Deforming the hippocam-
pal map. Hippocampus, 15(1), 41–55.
Wang, Y., Markram, H., Goodman, P. H., Berger, T. K., Ma, J., &
Goldman-Rakic, P. S. (2006). Heterogeneity in the pyramidal
network of the medial prefrontal cortex. Nature Neuroscience,
9(4), 534–42.
Wills, T. J., Lever, C., Cacucci, F., Burgess, N., & O’keefe, J. (2005).
Attractor dynamics in the hippocampal representation of the
local environment. Science, 308(5723), 873–876.
Wilson, M. A., & McNaughton, B. L. (1994). Reactivation of hip-
pocampal ensemble memories during sleep. Science, 265(5172),
676–679.
Yoganarasimha, D., Yu, X., & Knierim,
(2006). Head di-
rection cell representations maintain internal coherence dur-
ing conflicting proximal and distal cue rotations: Comparison
with hippocampal place cells. Journal of Neuroscience, 26(2),
622–631.
J.
J.
Zeithamova, D., Schlichting, M. L., & Preston, A. R. (2012). The hip-
pocampus and inferential reasoning: Building memories to nav-
igate future decisions. Frontiers in Human Neuroscience, 6, 70.
Zenke, F., & Gerstner, W.
(2017). Hebbian plasticity requires
compensatory processes on multiple timescales. Philosophi-
cal Transactions of the Royal Society B: Biological Sciences,
372(1715).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
3
7
0
7
1
0
9
2
4
1
4
n
e
n
_
a
_
0
0
0
7
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
724