FOKUS-FUNKTION:
Neue Trends in der Connectomics
Estimating the impact of structural directionality:
How reliable are undirected connectomes?
Penelope Kale
1,2
3
, Andrew Zalesky
, and Leonardo L. Gollo
1,2
1QIMR Berghofer Medical Research Institute, Australia
2University of Queensland, Australia
3Melbourne Neuropsychiatry Centre and Department of Biomedical Engineering, University of Melbourne, Australia
Schlüsselwörter: Directionality, Connectome, Structural connectivity, Graphentheorie, Hubs, False positives
Keine offenen Zugänge
Tagebuch
ABSTRAKT
Directionality is a fundamental feature of network connections. Most structural brain
networks are intrinsically directed because of the nature of chemical synapses, welche
comprise most neuronal connections. Because of the limitations of noninvasive imaging
Techniken, the directionality of connections between structurally connected regions of the
human brain cannot be confirmed. Somit, connections are represented as undirected, Und
it is still unknown how this lack of directionality affects brain network topology. Using six
directed brain networks from different species and parcellations (cat, mouse, C. elegans,
and three macaque networks), we estimate the inaccuracies in network measures (Grad,
betweenness, clustering coefficient, path length, global efficiency, participation index,
and small-worldness) associated with the removal of the directionality of connections. Wir
employ three different methods to render directed brain networks undirected: (A) remove
unidirectional connections, (B) add reciprocal connections, Und (C) combine equal numbers
of removed and added unidirectional connections. We quantify the extent of inaccuracy in
network measures introduced through neglecting connection directionality for individual
nodes and across the network. We find that the coarse division between core and peripheral
nodes remains accurate for undirected networks. Jedoch, hub nodes differ considerably
when directionality is neglected. Comparing the different methods to generate undirected
networks from directed ones, we generally find that the addition of reciprocal connections
(false positives) causes larger errors in graph-theoretic measures than the removal of the
same number of directed connections (false negatives). These findings suggest that
directionality plays an essential role in shaping brain networks and highlight some
limitations of undirected connectomes.
ZUSAMMENFASSUNG DES AUTORS
Most brain networks are inherently directed because of the nature of chemical synapses,
which comprise most neuronal connections. Jedoch, owing to limitations of non-invasive
Techniken, the human connectome is represented without directionality. To better
understand the effects of directionality on graph-theoretic measures of anatomical networks,
we compare brain networks across species when directionality is neglected, and find that
hubs become vulnerable. Darüber hinaus, the addition of few false-positive reciprocal connections
is more detrimental to network measures than the removal of the same number of directed
false-negative connections. Our results suggest that directionality plays an essential role in
shaping brain networks and highlight some limitations of undirected connectomes.
Zitat: Kale, P., Zalesky, A., & Gollo,
L. L. (2018). Estimating the impact of
structural directionality: How reliable
are undirected connectomes?
Netzwerkneurowissenschaften, 2(2), 259–284.
https://doi.org/10.1162/netn_a_00040
DOI:
https://doi.org/10.1162/netn_a_00040
zusätzliche Informationen:
https://doi.org/10.1162/netn_a_00040
Erhalten: 14 Juli 2017
Akzeptiert: 19 Dezember 2017
Konkurrierende Interessen: Die Autoren haben
erklärte, dass keine konkurrierenden Interessen bestehen
existieren.
Korrespondierender Autor:
Leonardo L. Gollo
leonardo.l.gollo@gmail.com
Handling-Editor:
Olaf Sporns
Urheberrechte ©: © 2018
Massachusetts Institute of Technology
Veröffentlicht unter Creative Commons
Namensnennung 4.0 International
(CC BY 4.0) Lizenz
Die MIT-Presse
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Undirected network:
A network describing the presence
(or the strength) of a relationship
between nodes for which the edges
are represented in the absence of
information about the directionality
of the connection.
Graphentheorie:
A branch of mathematics concerned
with the study of networks (graphs).
It provides various quantitative
measures that are used to describe
the topological organization of
Netzwerke.
EINFÜHRUNG
Connectomes provide a comprehensive network description of structural brain connectivity
(Spurns, Tononi, & Kötter, 2005). Large-scale connectomes mapped in humans are typically
represented and analyzed as undirected networks, because of the inability of noninvasive con-
nectome mapping techniques to resolve the directionality (afferent or efferent) of white matter
fibers. Reducing an inherently directed network such as the connectome to an undirected
network is a simplification that may introduce inaccuracies in graph-theoretic analyses. Für
Beispiel, the flow of action potentials along an axon is mostly only ever in one direction, Und
thus analyses of information flow are critically dependent on connection directionality. Das
study aims to systematically and comprehensively characterize the impact of representing and
analyzing connectomes as undirected networks.
At the neuronal level, the connections between nodes (Neuronen) are given by synapses, Und
the great majority of them are chemical, which have distinctive pre- and postsynaptic terminals
determining the direction of neurotransmitter flux (Kandel, Schwartz, Jessell, Siegelbaum, &
Hudspeth, 2000). This structural feature of chemical synapses emphasizes the importance of
directionality for the connections, and therefore for the whole network. Invasive techniques to
map connectomes such as tract tracing (Kötter, 2004; Dong, 2008; Scannell, Verbrennungen, Hilgetag,
O'Neil, & Jung, 1999; Spurns, Honey, & Kötter, 2007) or electron microscopy (Achacoso &
Yamamoto, 1992; White, Southgate, Thomson, & Brenner, 1986) can detect the directionality
of the connections. Umgekehrt, human connectomes are currently mapped with noninva-
sive tractography methods performed on diffusion-weighted magnetic resonance imaging data
(Assaf & Basser, 2005; Hagmann et al., 2008; Tournier, Calamante, & Connelly, 2012). Während
methods for improving the quality of diffusion-based connectomes have advanced in recent
Jahre, and numerous tractography algorithms have been developed to reconstruct axonal
fiber bundles, they cannot provide any information about the directionality of the connec-
tionen. daher, analyses of the human connectome, as well as modeling studies that use the
human connectivity matrix, are compromised by the lack of information regarding direction-
ality, which is one of the most fundamental features of complex networks.
In the absence of directionality, networks are considered undirected and therefore the con-
nections only represent the existence of a relationship between nodes. This is the case for scien-
tific coauthorship networks (Newman, 2004), film actor networks (Watt & Strogatz, 1998), Und
functional networks defined by symmetric functions such as the Pearson correlation (Biswal,
Zerrin Yetkin, Haughton, & Hyde, 1995) or the phase locking value (Aydore, Pantazis, & Leahy,
2013). Among others, studies of tractography-derived human brain networks have revealed a
variety of important features such as hub regions (van den Heuvel & Spurns, 2013), modularity
and clustering (Spurns, 2011; Spurns & Betzel, 2016), small-worldness (Bassett & Bullmore,
2006; Medaglia & Bassett, 2017), core-periphery structure (Hagmann et al., 2008), und das
existence of a rich club (van den Heuvel & Spurns, 2011). These topological properties are
not specific to the human brain. Comparisons across many species have recapitulated these
Merkmale (Betzel & Bassett, 2016; Harriger, van den Heuvel, & Spurns, 2012; Towlson, Vértes,
Ahnert, Schafer, & Bullmore, 2013; van den Heuvel, Bullmore, & Spurns, 2016). Jedoch, Die
topological characteristics of connectomes, as well as many other graph-theoretic measures,
are affected by the directionality of connections (Rubinow & Spurns, 2010).
When directionality cannot be identified, undirected representations of connectomes are
incomplete. Undirected networks inform the presence of a relationship between two brain
Netzwerkneurowissenschaften
260
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Unidirectional connection:
An edge in a directed graph denoting
a connection from one node to
another in a single direction.
False positive connection:
A connection that is spuriously
represented in a connectivity matrix
without the existence of an
underlying link. False positive
connections often occur because of
errors associated with the inference
of connections. In undirected
Netzwerke, we use the expression false
positive connection to refer to a
unidirectional connection that is
represented as an undirected link,
which is often assumed to be a
bidirectional connection.
False negative connection:
A connection that is not represented
in a connectivity matrix given the
existence of an underlying link. False
negative connections often occur
because of errors associated with the
inference of connections. In
undirected networks, we use the
expression false negative connection
to refer to a unidirectional
connection that is not represented as
an undirected link.
Bidirectional connection:
An edge in a directed graph denoting
a reciprocal connection between two
Knoten.
Regionen. But these networks lack information about the asymmetry of this relationship. Für
Beispiel, if a directed network is represented as an undirected network, unidirectional con-
nections are either present, which can be interpreted as a spurious addition of a reciprocal
connection (false positives), or overlooked (false negatives). More specifically, if a unidirec-
tional connection exists from node u to v, but not from v to u, then the undirected represen-
tation of this connection is either (A) an undirected connection between u and v, which can
be construed as admitting a false positive from node v to u; oder, (B) absence of an undirected
connection between u and v, which can be construed as a false negative from node u to v. In
either case, a potential error (false positive or false negative) is introduced to the undirected
Netzwerk.
Beyond the effect of directionality, connectomes also contain errors in the balance between
overlooked and spurious connections owing to imprecisions in currently available mapping
Techniken (Calabrese, Badea, Cofer, Qi, & Johnson, 2015; Donahue et al., 2016). Obwohl
both error types impact the network topology, spurious (false positive) connections introduce
inaccuracies in a few graph-theoretic measures (network clustering, efficiency, and modularity)
in different connectomes that are at least twice as large as those found with the same number
of overlooked (false negative) connections (Zalesky et al., 2016). This finding indicates that
the importance of specificity is much greater than sensitivity for general connectivity in which
false positives could be any absent connection and false negatives, any present connection.
Jedoch, the impact of representing a directed connection as undirected, welche, for practical
Zwecke, is typically indistinguishable from a bidirectional connection, is currently unknown.
daher, when directed networks are mapped with techniques that cannot infer directionality,
it is important to establish what undirected representation is the most detrimental with respect
to directionality: admitting spurious reciprocal connections (false positives) or overlooking
unidirectional connections (false negatives).
Darüber hinaus, the effect of directionality on the identification of network hubs may also be im-
portant, as hubs play an important role for normal brain function (Miši´c et al., 2015; van den
Heuvel, Kahn, Goñi, & Spurns, 2012) as well as in neuropsychiatric disorders (Bassett et al.,
2008; Crossley et al., 2014; Fornito, Zalesky, & Breakspear, 2015). But how are these highly
connected regions affected by directionality? Does the classification of nodes into hubs still
hold if directionality is taken into account? Außerdem, to what extent do graph-theoretic
measures at the node level remain valid? The characterization of the human brain as an undi-
rected network is often overlooked and requires investigation.
The aim of this study is to understand the limitations of analyzing inherently directed con-
nectomes as undirected networks. Beginning with directed connectomes of the macaque, cat,
mouse, and Caenorhabditis elegans (C. elegans), we study how seven graph-theoretic mea-
sures are affected as we progressively modify unidirectional connections, either deleting them
or making them undirected. More specifically, we consider three schemes to progressively
eliminate directionality information: removing unidirectional connections (creating false neg-
atives), adding reciprocal connections to existing unidirectional connections (creating false
positives), and removing one unidirectional connection for each reciprocal connection added,
thus preserving the density and mean degree of the original network. We show how essential
network features, such as the identification and classification of hubs, are affected by pertur-
bations in directionality. Darüber hinaus, we quantify how graph-theoretic measures are affected
at both the node and the network level and determine whether false positive or false nega-
tive unidirectional connections are more detrimental to the characterization of graph-theoretic
Maßnahmen.
Netzwerkneurowissenschaften
261
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Structural connectivity:
A description of the presence (Und
potentially directionality and weight)
of anatomical connections (z.B.,
synapses or axonal tracts) zwischen
(brain network) nodes such as
cortical areas or neurons.
Parcellation:
A segmentation of the brain into
individually defined parcels; diese
parcels often refer to cortical
Bereiche, the nodes of macroscale
connectomes.
MATERIALS AND METHODS
Connectivity Data
Following a comparative connectomics approach (van den Heuvel et al., 2016), we analyzed
structural connectivity data from several species and various parcellations including three
macaque connectomes, a cat and mouse connectome, and a C. elegans nervous system con-
nectome (Figur 1). Each network possesses a different number of nodes, proportion of uni-
directional connections, modularity, and network density (see Supplementary Table 1, Kale,
Zalesky, & Gollo, 2018). Crucially, these networks include information on the directionality of
connections (all networks are directed) obtained through invasive techniques that have differ-
ent proportions of connection reciprocity (Garlaschelli & Loffredo, 2004). Among the meso-
and macroscale connectomes, nodes represent cortical regions and the directed connections
represent axons or white matter fibers linking these regions via chemical synapses. In the case
of the microscale C. elegans connectome, nodes represent neurons, the directed connections
represent chemical synapses, and the electrical synapses (or gap junctions) are bidirectional
connections.
To accommodate the analysis of such a wide range of directed connectomes, the strength
of connections was disregarded (for the cat and mouse connectomes) to make each network
binary. This procedure allowed us to characterize all connectomes using the same methods
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
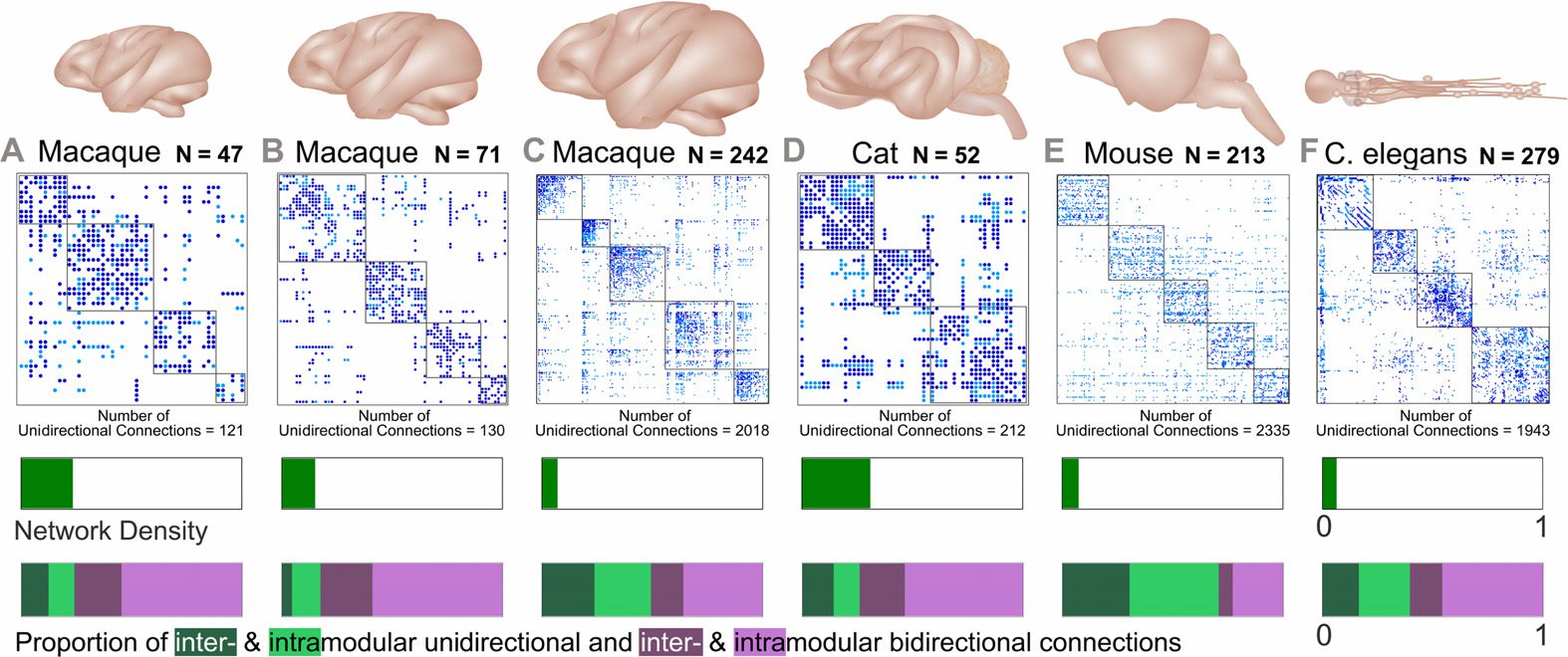
Figur 1. The six connectomes analyzed in this study. Brain and connectome for three different
parcellations of the macaque cortex (A) nodes N = 47 (Honey et al., 2007), (B) N = 71 (Jung,
1993), Und (C) N = 242 (Harriger et al., 2012), as well as three additional species including a (D)
cat (Scannell et al., 1999), (E) mouse (Dong, 2008), Und (F) C. elegans (White et al., 1986; Varshney
et al., 2011). The connectomes represent connectivity matrices with rows and columns denoting
Gehirnregionen (or nodes), and the elements within the matrices denoting the presence (filled) or ab-
sence (blank) of a connection between two regions. Unidirectional connections are highlighted in
light blue (with the number of unidirectional connections stated below each connectome) und das
nodal regions are arranged into modular communities. The bars below each connectome display
the density of each network (A = 0.234, B = 0.15, C = 0.07, D = 0.308, E = 0.073, F = 0.063)
and the proportion of unidirectional and bidirectional connections. The latter is segmented to
display the proportion of unidirectional connections between modules (dark green: A = 0.123,
B = 0.046, C = 0.238, D = 0.142, E = 0.304, F = 0.165) and within modules (light green: A =
0.117, B = 0.129, C = 0.255, D = 0.117, E = 0.404, F = 0.232) separately, as well as the proportion
of bidirectional connections between modules (dark purple: A = 0.214, B = 0.236, C = 0.147,
D = 0.21, E = 0.064, F = 0.147) and within modules (light purple: A = 0.547, B = 0.59, C =
0.359, D = 0.536, E = 0.229, F = 0.457).
Netzwerkneurowissenschaften
262
Estimating the impact of structural directionality
for binary and directed networks as a first step to understand the role of directionality in struc-
tural brain networks. Other high-quality weighted connectomes can be used in future studies
(Bezgin, Vakorin, van Opstal, McIntosh, & Bakker, 2012; G˘am˘anu¸t et al., 2017; Markov et al.,
2012; Shih et al., 2015; Ypma & Bullmore, 2016). As recently reported, the combination of
both directionality and weight can be crucial to uncover relationships between structural con-
nectivity and univariate brain dynamics (Sethi, Zerbi, Wenderoth, Fornito, & Fulcher, 2017).
The first macaque network (with number of nodes N = 47 and connec-
Macaque networks.
tions E = 505, Figure 1A), used in a study by Honey, Kötter, Breakspear, and Sporns (2007),
follows the parcellation scheme of Felleman and Van Essen (1991) including the visual and
sensorimotor cortex, and motor cortical regions. Relevant data were collated in the CoCoMac
database (Modha & Singh, 2010) following the procedures of Kötter (2004) and Stephan
et al. (2001), and translated to the brain map using coordinate independent mapping (Kötter
& Wanke, 2005; Stephan, Zilles, & Kötter, 2000).
The second macaque connectome (N = 71 and E = 746, Figure 1B) was derived from a
whole cortex model generated by Young (1993) with regions of the hippocampus and amygdala
eliminated. The parcellation was based mostly on the scheme by Felleman and Van Essen
(1991), except for the fields of the superior temporal cortex (Yeterian & Pandya, 1985). Yeterian
and Pandya (1985) utilized an autoradiographic technique (radioactively labeled amino acids)
to establish the existence and trajectory of fibers.
The final macaque connectome (N = 242 and E = 4, 090, Abbildung 1C) was generated by
Harriger et al. (2012). This network comprises anatomical data from over 400 tract tracing
studies collated in the CoCoMac database (Modha & Singh, 2010) following the procedures
of Kötter (2004) and Stephan et al. (2001), focusing on the right hemisphere with all sub-
cortical regions removed as well as regions without at least one incoming and one outgoing
connection.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
.
T
The data collated for the CoCoMac database used a range of tracer substances (with antero-
grade, retrograde, or bidirectional transport properties) and methods (as discussed in Stephan
et al., 2001). Each contributing study must discern a source and target for the connection. Wenn die
reciprocal direction had not been tested for, the connection was assumed to be unidirectional.
Some connections have been confirmed to be unidirectional, Zum Beispiel, the connection from
V2 to FST; see Boussaoud, Ungerleider, and Desimone (1990). Regarding macaque connec-
tomes, Felleman and Van Essen (1991) have also suggested that the reciprocity of connections
may vary between individuals.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The cat matrix is a connectome reconstructed by Scannell et al. (1999) Und
Cat network.
curated from a database of thalamo-cortico-cortical connections from a large number of pub-
lished studies in the adult cat. The parcellation was based on a previous scheme by Reinoso-
Suarez (1984) and adapted by Scannell, Blakemore, und Jung (1995). Areas ALG, SSF, SVA,
DP, Amyg, and 5m were discarded (and some regions grouped) to create a weighted network
(N = 52 and E = 818, Figure 1D). This connectome was generated from the available data
across numerous studies. It is noted that each study used a different type of anterograde and/or
retrograde tracer, methodology, and parcellations. Some connections lacked data on the
existence of a reciprocal direction between brain regions (these were left as unidirectional),
and all connections between the cortex and thalamus were assumed to be reciprocal.
Netzwerkneurowissenschaften
263
Estimating the impact of structural directionality
Mouse network. We obtained the mouse connectome (N = 213 and E = 2, 105, Figure 1E)
from the Allen Mouse Brain Connectivity Atlas generated by Dong (2008). The major advan-
tage of this connectome is that the connectivity data, obtained at a cellular level (axons and
synaptic terminals), are generated for the whole mouse brain. daher, alle 469 individual
experiments use the same anterograde tracer and consistent techniques. Each brain is ap-
plied to a 3D template, which itself is averaged across 1,231 brain specimens, and the regions
are matched against the Allen reference atlas (Dong, 2008). We thresholded this dense and
weighted network using the disparity filter (Serrano, Boguná, & Vespignani, 2009), maintain-
ing only connections with a p value smaller than 0.05. Thresholding was performed such that
the resulting network was binary.
The C. elegans nervous system matrix (N = 279 and E = 1, 943,
C. elegans network.
Figure 1F) was collated by Varshney, Chen, Paniagua, Hall, and Chklovskii (2011), and includes
data mapped by White, Southgate, Thomson, and Brenner (1986) using electron microscopy,
in addition to various other sources (Durbin, 1987; Hall & Russell, 1991; White, Southgate,
Thomson, & Brenner, 1976). This microscale connectome is composed of a directed chemical
synapse network and an undirected gap junction network. Although gap junctions may possess
directionality, this has not yet been demonstrated in C. elegans. For the purpose of analysis,
the connections from the gap junction network were treated as bidirectional connections.
Perturbed Networks
To investigate the effects of directionality on the characteristics of the brain, each empiri-
cal connectome was altered by progressively removing connection directionality information,
generating a spectrum of perturbed networks. This spectrum comprised the empirical connec-
tome at one end, and a fully undirected representation of the connectome at the opposite end.
For this purpose, the empirical networks were considered to be approximately the ground-truth
connectomes for a given parcellation. Figur 2 illustrates the three different approaches used
to generate perturbed networks for the macaque (N = 47) connectome. The empirical connec-
tome is shown in Figure 2A, and the unidirectional connections of this network are shown in
Figure 2B. Perturbed networks (Figures 2C–E) were generated by altering the directionality or
presence of the unidirectional connections. In this example, we only show the extreme case in
which all information about connection directionality is removed, yielding a fully undirected
perturbed network.
For further analyses we present three schemes that were developed to progressively elim-
inate connection directionality information from the empirical connectomes, yielding per-
turbed networks that increasingly resembled undirected networks.
The first perturbed network was generated by removing a
False negative perturbed networks.
fixed number of randomly chosen unidirectional connections, leading to a connectome with
false negative unidirectional connections (FN network, Figure 2C). The perturbed network was
undirected in the extreme case when all unidirectional connections were removed. This pertur-
bation assumes that unidirectional connections are weaker in strength (weight) relative to their
bidirectional counterparts, and thus unidirectional connections are most vulnerable to elimi-
nation with weight-based thresholding procedures (Rubinow & Spurns, 2010). Such threshold-
ing is commonly used to eliminate weak connections obtained with tractography, welche sind
often attributed to noise or error (Maier-Hein et al., 2017). Als Beispiel, the majority of
the weighted mouse connectome is composed of unidirectional connections (57%), and they
Netzwerkneurowissenschaften
264
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
T
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
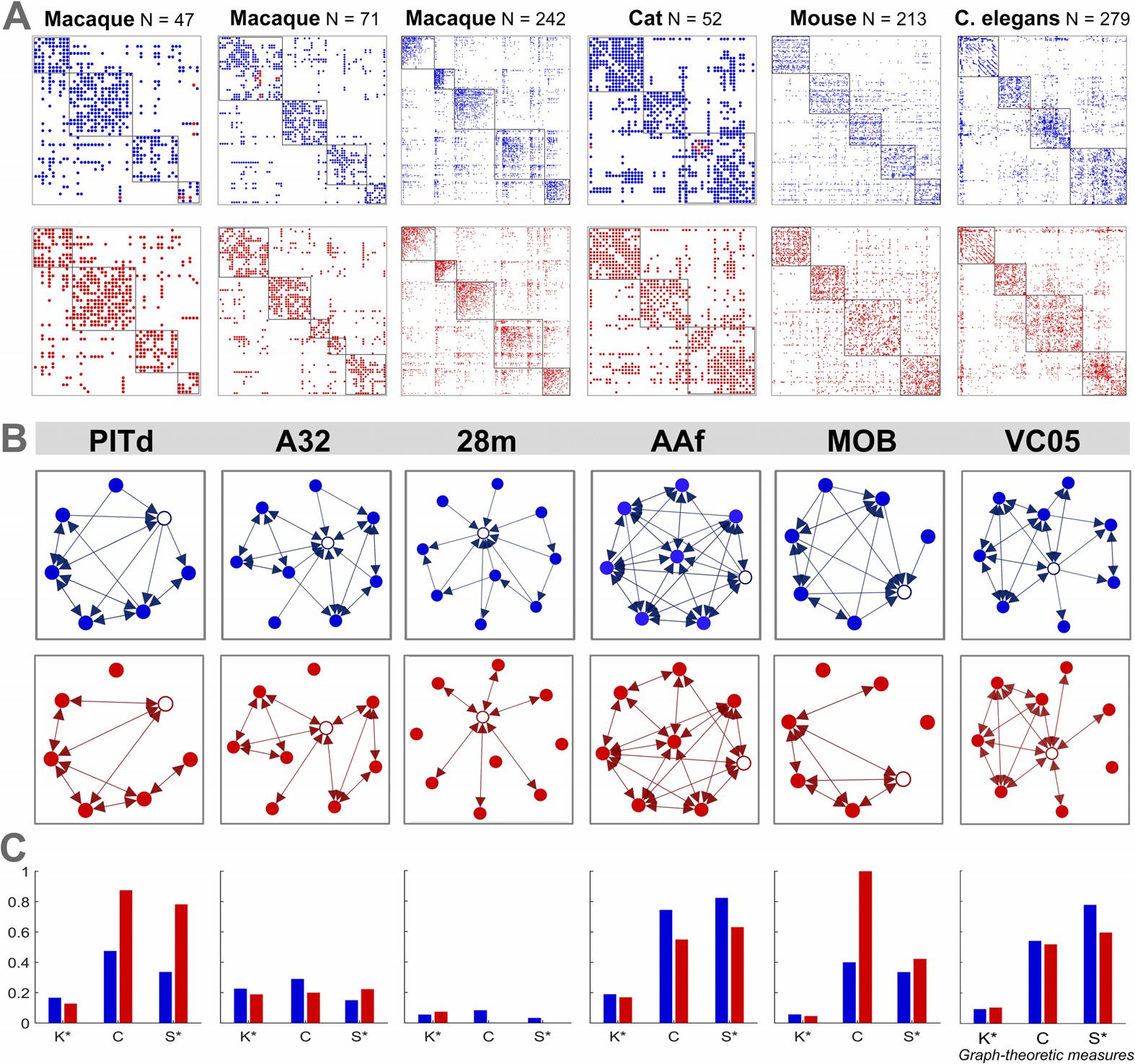
Figur 2. Structural connectome for the macaque N = 47 cortex and perturbed undirected vari-
ants, with an exemplar subnetwork. Subnetwork (top) encompassing the PITd region (white node)
and neighboring nodes, the adjacency matrix (Mitte), and the entire network (bottom) für (A)
macaque empirical connectome with the community modules outlined in red; (B) unidirectional
connections of the connectome; (C) connectome with unidirectional connections removed (false
negative network); (D) connectome with reciprocal connections added to unidirectional connec-
tionen (false positive network); (E) connectome with one randomly selected reciprocal connection
added to a unidirectional connection for each randomly selected unidirectional connection re-
In each connectome, the connections linking PITd (dorsal
moved (density-preserving network).
posterior inferotemporal) to the rest of the network are colored orange.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
T
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
are also weaker than the bidirectional connections. The mean of the strength of unidirectional
connections is 0.066, whereas the mean strength of bidirectional connections is 0.165, welche
is significantly weaker (P < 10−45
, Welch’s t test).
If the weight of a unidirectional connection exceeds the
False positive perturbed networks.
weight-based threshold, the connection will be represented in the perturbed network as an
undirected connection (i.e., a unidirectional connection from node u to v becomes an undi-
rected connection between nodes u and v). In this case, the undirected connection is treated as
a bidirectional connection, and thus construed as a false positive. To model this case, we gen-
erated perturbed networks by adding reciprocal connections to a fixed number of randomly
chosen existing unidirectional connections, leading to a perturbed network with false posi-
tive reciprocal connections (FP network, Figure 2D). In the extreme case when all reciprocal
connections were added, the perturbed network effectively became an undirected network.
Finally, to preserve basic properties of the empirical
Density-preserving perturbed networks.
connectome, an additional perturbed connectome termed the density-preserving network was
generated (DP network, Figure 2E). In this perturbed connectome, for each reciprocal con-
nection added to a unidirectional connection, another unidirectional connection is removed
(at randomly selected locations). The DP network has an equal number of false negative and
Network Neuroscience
265
Estimating the impact of structural directionality
positive connections and also preserves the mean degree of the empirical connectome, but
not the degree of each node.
To generate undirected perturbed networks, we progressively applied one of the above
three schemes to randomly chosen unidirectional connections in the empirical connectomes
until a desired proportion of connections were changed. We generated perturbed networks
in which 5%, 10%, 20%, and 100% of directed connections were altered (eliminated or the
reciprocal connection added). This process was repeated for multiple trials to generate an
ensemble of perturbed networks. Ensemble averages for all graph-theoretic measures were
then computed. Each perturbed network was associated with a rewiring scheme (FN, FP, and
DP) and a proportion of changed connections. Supplementary Table 2 (Kale et al., 2018)
provides the details of the proportion of unidirectional connections altered in the perturbed
networks and other relevant parameters used for each analysis.
The perturbed networks can comprise isolated nodes that are not connected to any other
nodes (see Supplementary Figure 1, Kale et al., 2018). Isolated nodes are more likely to occur
in the FN perturbed networks, potentially having a greater impact on graph-theoretic measures
as more connections are changed. Therefore, in cases where only a subset of unidirectional
connections are modified (<100%), the trials that cause nodes to become disconnected are
rejected.
Network Measures
Connectome analyses were performed using a range of common graph-theoretic network mea-
sures (da Fontoura Costa, Rodrigues, Travieso, & Villas Boas, 2007). These measures enable the
quantitative comparison of connectomes across species and neuroimaging techniques while
remaining computationally inexpensive (Rubinov & Sporns, 2010). Furthermore, the graphi-
cal properties of cortical systems have previously been associated with functional connectivity
and evolutionary adaptations in behavior and cognition (Bullmore & Sporns, 2012; van den
Heuvel et al., 2016). For each empirical connectome and associated perturbed network, we
computed several graph-theoretic measures (see Supplementary Table 3, Kale et al., 2018),
using the Brain Connectivity Toolbox (Rubinov & Sporns, 2010). Graph-theoretic measures for
directed networks were used in all cases where applicable.
The degree of each node was calculated as the sum of the in- and out-
Measures of centrality.
degree, or the sum of all directed connections connecting that node to the rest of the network
(Rubinov & Sporns, 2010). Network centrality identifies nodes that act as important points of
information flow between regions. We used a betweenness centrality measure, defined as the
fraction of all the shortest paths between regions that pass through a particular node (Freeman,
1978). The participation index or coefficient describes the proportion of intra- and intermod-
ular connections linking each node (Guimera & Amaral, 2005a). As shown in Supplementary
Table 3 (Kale et al., 2018), we used the out-participation index with the Louvain algorithm
(Blondel, Guillaume, Lambiotte, & Lefebvre, 2008) to define network modules (Rubinov &
Sporns, 2010). Further details about module delineation are provided below.
Measures of functional segregation. We calculated the clustering coefficient, a measure de-
scribing the proportion of a node’s neighbors that are connected to each other (Fagiolo, 2007).
In undirected networks it is calculated as the probability that two connections (linking three
nodes) will be closed by a third connection to form a triangle. In directed networks, however,
Network Neuroscience
266
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
n
e
n
_
a
_
0
0
0
4
0
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Estimating the impact of structural directionality
a set of three nodes can generate up to eight different triangles. The function utilized in this
study, clusteringcoef_bd (Rubinov & Sporns, 2010), takes this into account.
A path is defined as a sequence of nodes and connections
Measures of functional integration.
that represent potential routes of information flow between two brain regions. In a directed net-
work, connections comprising a path must be arranged such that the head of one connection
always precedes the tail of the subsequent connection. The characteristic path length for each
network was calculated as the average shortest distance between all pairs of nodes (Watts &
Strogatz, 1998). We also calculated the global efficiency of each network as the average nodal
efficiency, which is the reciprocal of the harmonic mean of the shortest path length between
all pairs of nodes (Latora & Marchiori, 2001).
Lastly, we measured the small-world characteristics of each network
Small-worldness.
(Watts & Strogatz, 1998). For each node and for the network (see Supplementary Table 3, Kale
et al., 2018), the small-world index was classified as the clustering coefficient divided by the
characteristic path length of the network, with a comparison to a directed random network,
makerandCIJ_dir (Rubinov & Sporns, 2010), unless otherwise stated (Humphries & Gurney,
2008). This index combines local and global topological properties and has been linked to
network efficiency (Bassett & Bullmore, 2006).
Community detection and modularity. We generated consensus matrices to describe the com-
munity structure of each empirical connectome (Lancichinetti & Fortunato, 2012). Specifically,
100 runs of the Louvain modularity algorithm (Blondel et al., 2008) were performed to gen-
erate a set of modular decompositions for each empirical connectome. The different runs did
not necessarily yield identical decompositions because of degeneracy of the solution space
and the stochastic nature of the algorithm. A consensus modularity matrix was determined
for the 100 decompositions such that each element in the consensus matrix stored the propor-
tion of runs for which a particular pair of nodes comprised the same module. The consensus
modularity matrix was then thresholded (retaining values >0.4), Und 100 runs of the Louvain
algorithm were performed on the thresholded consensus matrix. This process was iterated
until the consensus matrix converged and did not change between successive iterations. Der
macaque N = 47 network required a greater number of iterations before a consistent com-
munity structure could be achieved (macaque N = 47: 408, macaque N = 71: 2, macaque
N = 242: 5, cat: 4, mouse: 36, C. elegans: 2).
For the perturbed networks with all unidirectional connections altered, a single consen-
sus matrix and consistent modularity was obtained for the FN and FP networks. For the rank
correlation-coefficient analyses, the modularity for each perturbed network remained the same
as that assigned to the associated empirical connectome. These perturbed networks only had
a small percentage of unidirectional connections altered (5%). With these measures we in-
tended to isolate the effect of directionality on the ranking of nodes by each graph-theoretic
messen, Und, daher, used the empirical consensus modularity for the (participation index)
calculations on each type of perturbed network.
For DP networks with 100% of connections altered, a consensus matrix was obtained for
each trial (see Supplementary Table 2 for more details; Kale et al., 2018). For other perturbed
networks where 5%, 10%, Und 20% of unidirectional connections are altered, consensus mod-
ularity matrices were obtained for each run (50 runs; see Supplementary Table 2, Kale et al.,
2018) and for each type of network (FN, FP, and DP).
Netzwerkneurowissenschaften
267
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Classification of Highly Connected Regions
Core nodes were determined using the core-periphery algorithm, function core_periphery_dir
from the Brain Connectivity Toolbox (Rubinow & Spurns, 2010), with gamma = 1, which sub-
divides all nodes in the network into either core or periphery groups of similar size. Hubs
were defined as regions with a degree at least one standard deviation above the mean (Spurns
et al., 2007), and super hubs were classified as those with a degree of at least 1.5 standard
deviations above the mean (see Figure 4A for an example). Super hubs were defined to evalu-
ate the robustness of hub nodes to the progressive removal of connection directionality. More
specifically, we aimed to assess whether super hubs would be demoted to hubs or nonhub
nodes as directionality information was lost.
We tested the resilience of the classification of nodes belonging to the core of the network,
or the set of hubs and super hubs. For each perturbed network, the accuracy of the classifica-
tion of nodes into each of these three groups (core, hubs, and super hubs) was compared with
the empirical connectomes. For each group, the accuracy, or matching index, A was com-
puted taking into account the number of nodes with common classification and the number of
mismatched nodes that had a different classification between the empirical and the perturbed
Netzwerke. More precisely, A was given by the simple matching index:
A =
C
C + (Ne − C) + (Nb − C)
,
(1)
where C was the number of overlapping nodes within the same group between the empirical
and perturbed networks; Ne was the number of nodes within this group for the empirical
connectome; and Nb was the number of nodes within this group for the perturbed network.
This measure of accuracy attained a minimum of 0 when there was no overlap between the
connectomes and a maximum of 1 for a perfect overlap.
The participation index can be used to classify nodes, and has been applied to hubs (Guimera
& Amaral, 2005B). Hubs with large participation index connect areas from different modules.
Supplementary Table 4 (Kale et al., 2018) lists the regions classified as hubs for each empirical
Netzwerk, as either connector (with a participation index Y > 0.35) or provincial (Y ≤ 0.35)
hubs. Consistent with other studies (Sporns et al., 2007), node degree (as the sum of the in-
and out-degree) was used to define the set of hubs based on their topological role within the
Netzwerk.
Quantifying Changes in Network Measures
To investigate changes in node-specific features between the empirical connectomes and cor-
responding perturbed networks, we developed a measure to quantify the change in the ranking
of nodes. Nodes can be ranked with any of a number of graph-theoretic measures. The rank-
shift index (RSI) represents the sum of the absolute value of the difference between the ranking
of the empirical (E) and perturbed (B) matrices for each node, divided by the maximum pos-
sible difference (D) in which the ranks of the network are reversed:
RSI = ∑N
i=1
|Ei − Bi|
D
.
(2)
An RSI of 0 indicates no change, and an index of 1 indicates a complete inversion in the rank
Befehl (siehe Abbildung 5). Node-level changes were also measured by the Spearman rank correlation
(Spearman, 1904) and Kendall coefficient (Kendall, 1938).
Netzwerkneurowissenschaften
268
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
ERGEBNISSE
To understand the effects of neglecting connection directionality on the structural properties of
connectomes, we compared several directed brain networks across multiple species, inkl-
ing three macaque connectomes (with different parcellation schemes), a cat, a mouse, und ein
C. elegans connectome. The characteristics of each of these networks were analyzed using a
range of network measures: Grad, betweenness centrality, clustering coefficient, character-
istic path length, global efficiency, participation index, and small-world index.
We altered unidirectional connections according to one of three schemes (see Methods)
to progressively eliminate information about connection directionality. We then quantified
the inaccuracies in graph-theoretic measures admitted through this loss of directionality infor-
mation. We begin with the density-preserving (DP) scheme and consider the extreme case in
which all unidirectional connections are eliminated, resulting in an undirected network.
In
besondere, we compare the network characteristics of selected regions of interest (ROIs) across
the empirical connectomes and single-trial DP counterparts (Figur 3). These ROIs (shown as
the red matrix entries in Figure 3A) occupy peripheral locations in the network topology and
have low degree, and the subnetwork of the local neighborhood surrounding each ROI can
be clearly represented (Abbildung 3B). From the empirical to the DP subnetworks, unidirectional
connections are eliminated and made bidirectional, resulting in changes to graph-theoretic
measures characterizing these regions. Figure 3C illustrates the relative graph-theoretic metrics
at these exemplar regions for the empirical and DP subnetworks. Although the mean degree
of the DP network is preserved, at the node level, the degree may increase or decrease de-
pending on whether the unidirectional connections surrounding the node of interest received
more false positive or false negative alterations. Likewise, clustering and small-worldness also
exhibit trial-dependent changes based on how the neighbors of these exemplar regions and
the whole network topology are affected.
Highly Connected Regions
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
T
/
Connector hubs:
A highly connected hub region
that has a substantial density of
connections with regions from other
modules.
Provincial hubs:
A highly connected hub region
that has a substantial density of
connections with regions belonging
to the same module.
Connectivity across brain regions and connections is heterogeneously distributed. Hub nodes
are identified as the most connected neural regions, and have enhanced importance in in-
formation integration for cognitive functions (van den Heuvel & Spurns, 2013). Hub nodes
can be further classified based on their participation index as either provincial or connector
hubs, depending on their level of intra- versus intermodule connectivity (Guimera & Amaral,
2005B; Sporns et al., 2007). Provincial hubs, with a high intramodule degree and low partici-
pation index, are thought to facilitate modular segregation. Umgekehrt, connector hubs, mit
a higher participation index, are thought to assist with intermodular integration (Rubinow &
Spurns, 2010). When hub regions are more densely connected among themselves than to
other nodes they form a “rich club,” consisting of a central but costly backbone of path-
ways that serve an important role in global brain communication (Aerts, Fias, Caeyenberghs,
& Marinazzo, 2016; Colizza, Flammini, Serrano, & Vespignani, 2006; van den Heuvel et al.,
2012). Somit, alterations to directionality at hub nodes influence the network activity ob-
served in functional connectivity. But how is the identification and characteristics of these
highly significant hub regions affected when directionality is modified?
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Inaccuracies may be introduced to node-specific graph-theoretic measures as connection
directionality information is lost. By comparing the empirical connectomes to correspond-
ing perturbed networks with all unidirectional connections eliminated according to the DP
scheme, we see that peripheral, core, and hub nodes are all impacted (Figur 4). Even the
Netzwerkneurowissenschaften
269
Estimating the impact of structural directionality
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3. Graph-theoretic measures for a specific region of interest from each empirical and
density-preserving connectome. (A) Empirical (Blau) and density-preserving (Rot, an illustrative sin-
gle trial with 100% of unidirectional connections altered) connectomes. Nodal regions are arranged
into modular communities and the connections connecting the region of interest to the rest of the
network in the empirical connectome are colored red. (B) Labels for each region of interest (top),
and subnetworks of the local neighborhood around each region of interest (white node). (C) Graph-
theoretic measures at the selected brain region for the empirical and density-preserving networks.
Graph-theoretic measures are as follows: K = degree, C = clustering coefficient, and S = small-
world index (S→
ich ). *Normalized by the maximum value of that measure across all nodes in their
respective network. PITd: dorsal posterior inferotemporal, A32: anterior cingulate area 32, 28M:
medial entorhinal cortex, AAF: anterior auditory field, MOB: main olfactory bulb, VC05: ventral
cord neuron 5.
Grad, a fundamental network characteristic, is affected in these perturbed networks, als
shown in Figure 4A for each cortical area in the macaque N = 47 connectome.
In partic-
ular, the degree of some hub and super-hub nodes falls below the threshold used for their
classification in the empirical connectome. This implies that hub nodes identified based on
degree can be inaccurate when directionality within the network is neglected or unknown.
To further investigate this, we redefined core, hub, and super-hub nodes for each perturbed
Netzwerk, and calculated their accuracy according to the empirical connectome. Figure 4B
shows the percentage of nodes that retain the same classification for core, hub, and super-
hub nodes across all perturbed networks. We find that the estimation of core nodes from the
Netzwerkneurowissenschaften
270
Estimating the impact of structural directionality
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
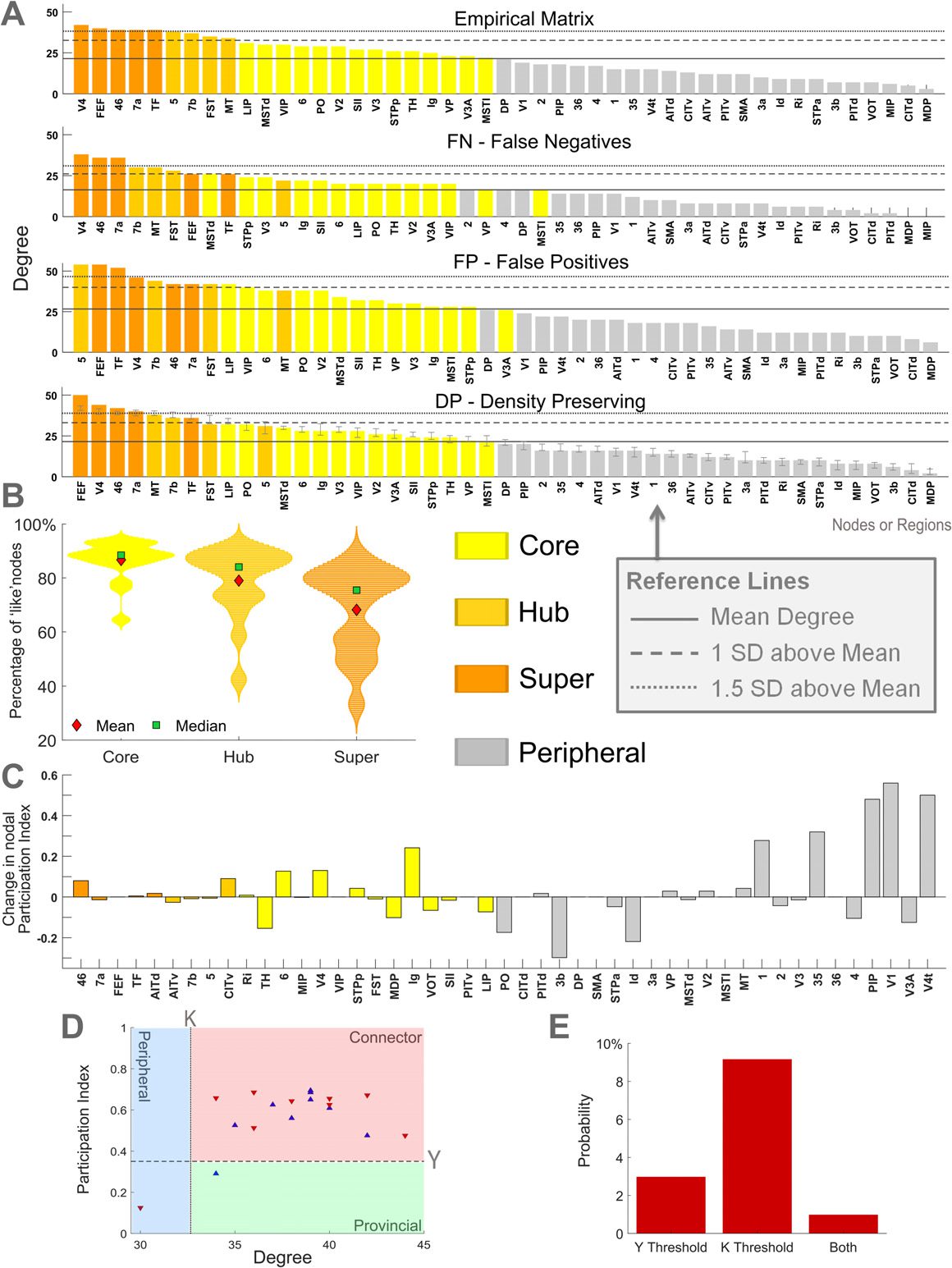
Figur 4.
Identification of hubs, changes in graph-theoretic measures at the node level, Und
(A) Cortical areas of the macaque N = 47 connectome
provincial/connecter hub classification.
sorted by degree for the empirical and each perturbed network. Hubs are defined as nodes that have
a total degree (in-degree plus out-degree) mindestens 1 standard deviation above the mean, and super
hubs are defined as nodes that have a degree at least 1.5 standard deviations above the mean.
The density-preserving results are from an illustrative single trial and show the standard deviation
in degree for each node (über 1,000 Versuche).
(B) Percentage of core, hub, and super-hub nodes
across the perturbed networks of all six connectomes that retain correct classification according
to their empirical connectome (as the mean over 1,000 Versuche).
(C) Change in the participation
index of each brain region from the empirical macaque N = 47 connectome to an illustrative case
of the density-preserving network. (D) Identification and classification of hub nodes for the empir-
isch (Blau) macaque N = 47 connectome and an illustrative case of the density-preserving (Rot)
Netzwerk. The dotted line represents the hub definition based on the degree, and the dashed line
represents the subclassification of hubs as either connector (Y > 0.35) or provincial (Y ≤ 0.35),
based on the participation index. (E) Mean probability (across all connectomes over 1,000 Versuche)
that hub nodes will cross over either, oder beides, of the threshold lines following density-preserving al-
terations in directionality, resulting in a classification that is inconsistent with the empirical connec-
tomes. (A–E) Each perturbed network has 100% of unidirectional connections altered. Hub nodes
are defined in the empirical network and retain the same definition in the perturbed networks.
Netzwerkneurowissenschaften
271
Estimating the impact of structural directionality
perturbed networks was the most accurate compared with the empirical connectomes (mean =
86.7%). Jedoch, the estimation of hubs and super hubs is less precise (mean = 79% Und
68.2%, jeweils). The accuracy of nodes belonging to core, hub, and super-hub was tested
with paired sample t tests and found to be significantly different. Core (including results from
all connectomes and each type of perturbed network) versus hubs P = 0.0027, core versus
super hubs P = 0.00001, and hubs versus super hubs P = 0.003. In Supplementary Figure 2
(Kale et al., 2018) these results are shown for each type of perturbed network and connectome
separately.
A recent study in the mouse brain (Sethi et al., 2017) showed a strong correlation between
the in-degree characteristics of a brain region and its resting-state functional MRI dynamics.
We therefore sought to investigate in- and out-degree separately. Supplementary Figures 3A
and 3B (Kale et al., 2018) display the in- and out-degree of all cortical regions in the macaque
N = 47 empirical connectome and perturbed networks. In this case, the delineation of hubs
and super-hub nodes depends on the directed degree, and therefore a different set are identified
in Figures 2A and 2B (Kale et al., 2018). Jedoch, because of the methodology for generating
the perturbed networks, the resulting in- and out-degree of each node becomes equal. Das ist
Weil (Wann 100% of unidirectional connections are altered) the only remaining connec-
tions in each case (FN, FP, or DP) are represented as bidirectional, and therefore each region
has the same number of incoming connections as it has outgoing connections. Previous stud-
ies in the cat connectome have found that high in-degree nodes also show (on average) a high
out-degree as well. In this connectome, 66% of rich-club nodes (defined by the summed de-
gree) had a higher in-degree than out-degree (de Reus & van den Heuvel, 2013). A comparison
across the connectomes analyzed in this study (Supplementary Figure 3C, Kale et al., 2018)
showed that four out of six sets of hub regions had a higher mean in-degree than out-degree.
The mouse connectome, Jedoch, was an interesting case for which all hub regions had a
much larger out-degree.
Nächste, we investigate the classification of hubs based on the participation index. In compar-
ison to peripheral regions, the participation index of hub nodes is more resilient as illustrated
in Figure 4C as the change for each region from the empirical macaque N = 47 connec-
tome to a (typical) DP example network. Because peripheral nodes have a low degree, Die
alterations in directionality may affect a larger proportion of these connections. daher,
peripheral regions often show greater change in the participation index than both core and
hub nodes. As illustrated in Supplementary Figure 4 (Kale et al., 2018), this also occurs for
other graph-theoretic measures.
The relationship between participation index and degree for the set of hub nodes (defined
in the empirical connectome) are displayed in Figure 4D for the empirical macaque N = 47
connectome and an illustrative DP network. Directionality alterations to the network cause
changes in these measures, both of which were used to define and classify the set of hubs in the
empirical connectome. Als solche, some of these regions in the DP network exceed the degree
and participation index thresholds (degree K = 1 SD above the mean and Y = 0.35), resulting
in misclassifications according to the empirical network. Across all connectomes, hub nodes
are more likely to lose their classification based on degree, indicating that the definition of
hubs based on the degree is on average 3.5 times more vulnerable to changes in directionality
in comparison to the misclassification of hubs based on the participation index (Figure 4E and
Supplementary Figure 5, Kale et al., 2018). Supplementary Figure 6 (Kale et al., 2018) displays
the number of core, hub, and super hubs across the connectomes (A: mean, B: individually),
as defined in the empirical and each perturbed network.
Netzwerkneurowissenschaften
272
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
T
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
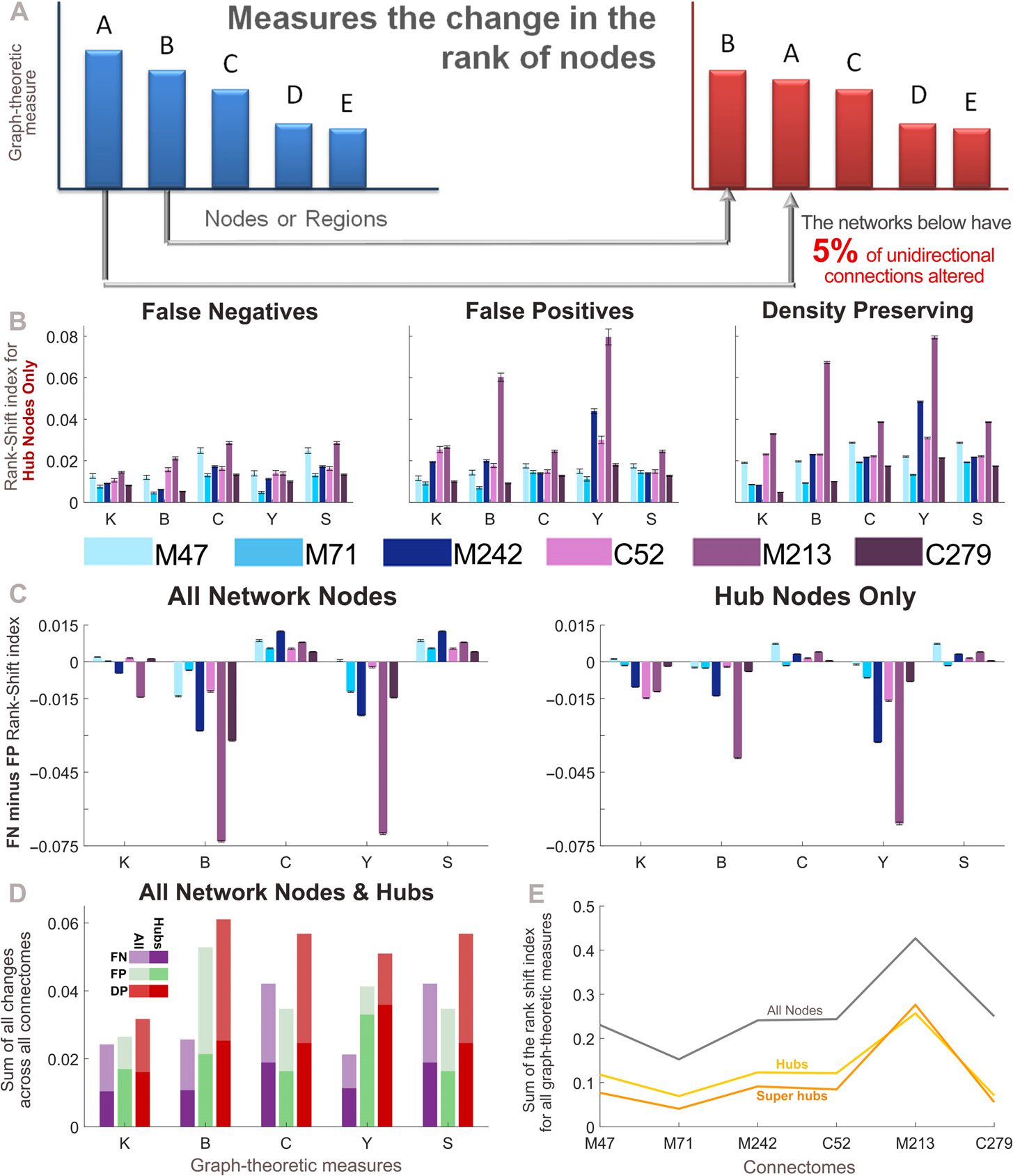
Quantifying the Errors in Node Rank When Directionality Is Lost
All the results presented thus far have pertained to perturbed networks in which all unidi-
rectional connections are altered, yielding perturbed networks that are effectively undirected.
Nächste, we investigate the impact of losing only a small proportion of connection direction-
ality information. Zu diesem Zweck, we generate perturbed networks in which the proportion of
unidirectional connections altered is 5%. Changes in node-specific network measures were
quantified using the rank-shift index (RSI, see Methods). This measure calculates the change in
the ranking of nodes by a specific graph-theoretic measure from the empirical to the perturbed
Netzwerke (see Figure 5A). We first focus on the set of hub nodes for each connectome, finding
that differences in the RSI can be seen across perturbed networks and graph-theoretic mea-
sures (Figure 5B; super-hub results were similar). Figure 5C directly compares the effects of the
FN and FP connections (perturbations) on the graph-theoretic measures, first across all nodes
in the network, and then for the set of hub nodes. It can be seen that the FP connections con-
sistently have a greater effect on the betweenness centrality and participation index, wohingegen
the clustering coefficient and small-worldness are more affected by the FN connections. Für
hub nodes, the RSI shows that the degree is also more affected by FP connections.
The RSI calculation is similar to the Spearman rank correlation coefficient (Spearman, 1904)
and Kendall rank coefficient (Kendall, 1938) at the network level. Supplementary Figure 7
(Kale et al., 2018) pertains to analyses repeated with these similar, yet alternative, Maßnahmen
and should be compared with Figures 5B and 5C. Regardless of the measure used, the overall
trends in the data between Figures 5B and 5C and Supplementary Figure 7 are consistent.
Directly comparing each of the methods for altering directionality (Figure 5D), we find that
the DP networks showed the greatest RSI across almost all measures. Across connectomes the
summed RSI for all graph-theoretic measures were quite similar (Figure 5E). Insbesondere,
the mouse connectome, which has the largest proportion of unidirectional connections (sehen
Figur 1 and Supplementary Table 1), showed larger differences for the same percentage of
altered connections.
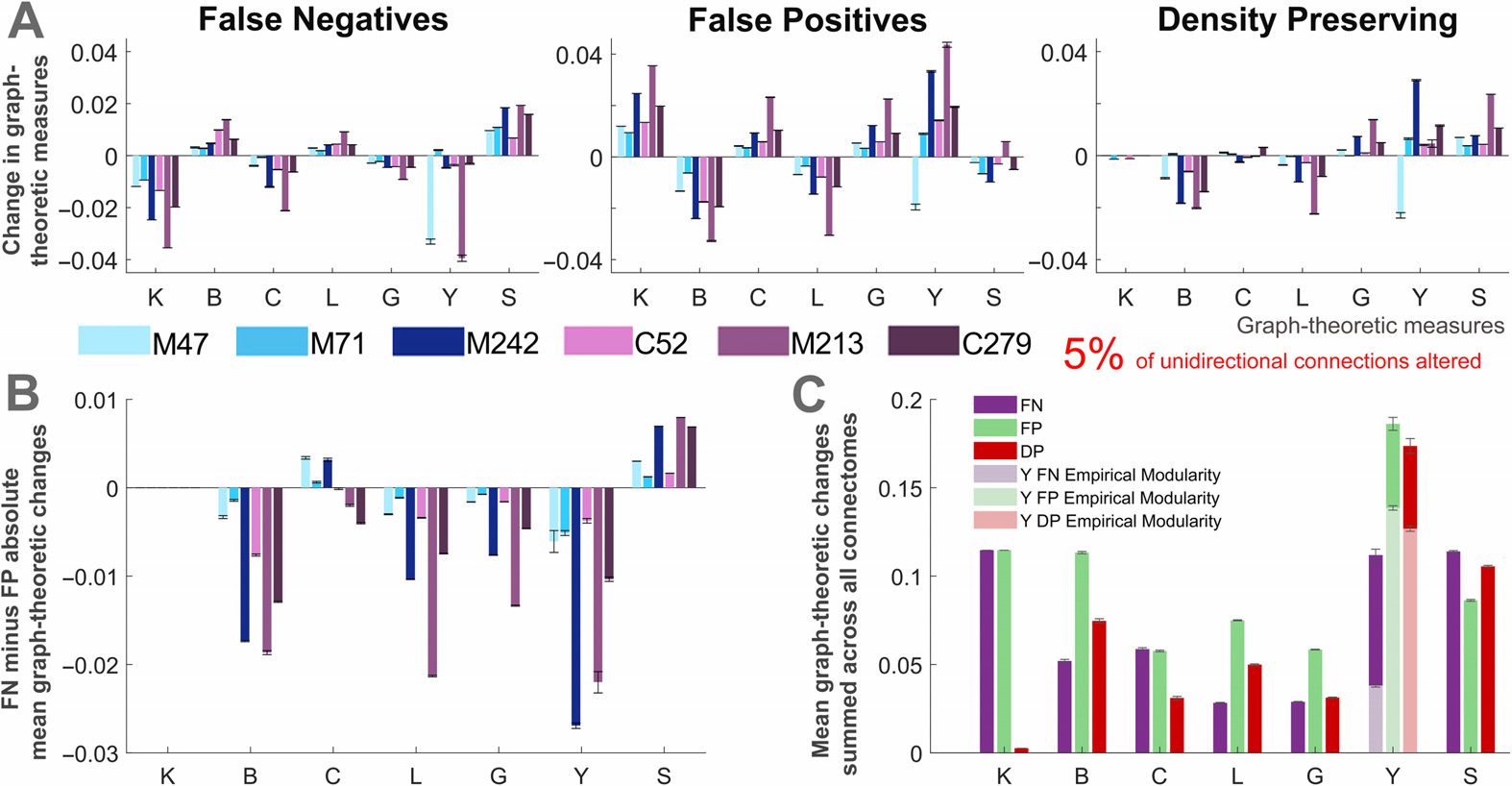
Quantifying the Importance of Directed Connections in the Whole Network
We next considered the mean changes in graph-theoretic measures in the whole network
caused by the loss of directionality. We focus our analysis on perturbed networks with al-
Im
terations to a small percentage of the unidirectional connections (5%; siehe Abbildung 6).
initial two perturbed connectomes, false negative and false positive alterations have oppo-
site effects on network measures (Figure 6A). The changes in betweenness (B), characteristic
path length (L), and global efficiency (G) are directly dependent on the degree (K), as these
connections facilitate a shorter route between nodes. The effects pertaining to clustering (C),
participation index (Y), and small-world index (S) are more complex because they depend on
whether the changes increase or decrease the interneighbor or the intermodular connectivity.
Aside from the mean degree (which is preserved in the DP networks), the effects on graph-
theoretic measures were mostly similar across the FP and DP perturbed networks. To better
understand the role of unidirectional connections, we next compare how false positive and
false negative modifications affect the mean graph-theoretic measures of networks (Figure 6B).
When it is not possible to distinguish the directionality of the connections, is it better to assume
that they are bidirectional or to disregard unidirectional connections?
In the case where a subset of connections is altered,
for most graph-theoretic mea-
sures the false positive unidirectional connections were more detrimental. It can be seen in
Netzwerkneurowissenschaften
273
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
/
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 5. Nodal changes measured by the Rank-Shift Index. (A) The rank-shift index quantifies the
change in the rank of nodes from the empirical connectome to the perturbed network when they
are ordered by a particular graph-theoretic measure. More specifically, it calculates the sum of the
difference between graph-theoretic values for each node in the empirical and perturbed matrices,
divided by the maximum potential difference that could exist between these two networks (where a
value of 0 indicates no change, and a value of 1 indicates the maximum change). See Methods for
further explanation. (B) Rank-shift index of hub nodes across all perturbed networks, for each graph-
theoretic measure. (C) Difference in the rank-shift index between the false negative and false positive
networks for all nodes (links), and hub nodes (Rechts). A positive value indicates that the false negative
connections cause greater changes in the ranking of nodes, whereas a negative value indicates the
same for false positive connections. (D) Rank-shift index for each graph-theoretic measure summed
across all connectomes. (E) Rank-shift index values summed across all graph-theoretic measures for
each density-preserving connectome. (B–E) Results correspond to the mean over 50 trials for which
5% of randomly selected unidirectional connections are modified in each perturbed network (Fehler
bars show the standard error of the mean). Graph-theoretic measures are as follows: K = degree,
B = betweenness centrality, C = clustering coefficient, Y = participation index, and S = small-
world index (S→
). M47: the macaque connectome with 47 Knoten, M71: macaque N = 71, M242:
ich
macaque N = 242, C52: cat, M213: mouse, C279: C. elegans.
Netzwerkneurowissenschaften
274
Estimating the impact of structural directionality
Figur 6. Relative changes in mean graph-theoretic measures for perturbed networks. (A) Changes
in mean graph-theoretic measures across all connectomes and each type of perturbed network.
(B) Difference between the changes in mean graph-theoretic measures for the false negative and
false positive networks. (C) Mean changes in graph-theoretic measures for each of the perturbed
Netzwerke, summed across all connectomes. Two separate modularity inputs are used the partici-
pation index calculations for the perturbed networks: the consensus modularity of the empirical
Netzwerke (light colors) and the new modularity assignments for each generated perturbed network
(A–C) All results correspond to perturbed networks with 5% of randomly selected
(dark colors).
unidirectional connections modified. The results represent the mean of these networks over 50 tri-
als, and describe the change in the mean graph-theoretic measure (from the empirical to perturbed
Netzwerk) normalized by the mean of the empirical network (error bars show the standard error
of the mean). Graph-theoretic measures are as follows: K = degree, B = betweenness centrality,
C = clustering coefficient, L = characteristic path length, G = global efficiency, Y = participation
index, and S = small-world index (S→
, changes in this measure are presented as the mean over
1,000 Versuche). M47: the macaque connectome with 47 Knoten, M71: macaque N = 71, M242:
macaque N = 242, C52: cat, M213: mouse, C279: C. elegans.
Supplementary Figure 8 (Kale et al., 2018) that this trend remains robust as the proportion of
unidirectional connections is increased (Zu 10% Und 20%). Jedoch, the error present in each
graph-theoretic measure is predictably increased. With the exception of the small-worldness
and degree, the FP perturbed networks consistently show the greatest changes in the mean
graph-theoretic measures (Figure 6C and Supplementary Figures 8C and 8F, Kale et al., 2018).
The participation index is the only measure directly affected by the modularity of the networks.
The changes in mean graph-theoretic measures are emphasized across connectomes in
Supplementary Figure 9 (Kale et al., 2018). In the FN and FP networks, the changes for each
graph-theoretic measure depend on the degree and proportion of unidirectional connections.
Noch einmal, the degree is correlated with the global efficiency and inversely correlated with
the characteristic path length and betweenness. Darüber hinaus, the clustering coefficient is also
correlated with the changes in degree, but this is caused by the elimination of triangles from
false negatives and addition of triangles from false positives.
DISKUSSION
Über 10 years ago, Sporns et al. (2005) proposed an influential coordinated research strat-
egy to map the human connectome, which motivated and guided many researchers. A lot of
Netzwerkneurowissenschaften
275
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
progress has been made towards this goal with the development of diffusion-weighted imaging
and tractography methods, enabling the reconstruction of several descriptions of the human
connectome (Assaf & Basser, 2005; Goulas et al., 2014). Jedoch, much more research is
needed to achieve an accurate, reliable, and standardized representation of connectivity in
das menschliche Gehirn. It must also be acknowledged that the methods of collation and reconstruc-
tion for these large datasets, including diffusion imaging and tract tracing, can give rise to errors
and inconsistencies in the data, as discussed elsewhere (Calabrese et al., 2015; Donahue et al.,
2016; G˘am˘anu¸t et al., 2017). Beyond this, several parcellation schemes have been proposed
for the human connectome (Cloutman & Ralph, 2012; de Reus & van den Heuvel, 2013;
Glasser et al., 2016; Honnorat et al., 2015), which can each have different effects on the char-
acterization of the network (Zalesky et al., 2010). Außerdem, the inability to resolve con-
nection directionality noninvasively, which was originally classified as a crucial task (Spurns
et al., 2005), has remained surprisingly overlooked. Without improvements in neuroimaging
Techniken, directionality can only be indirectly estimated for the human connectome, für
Beispiel, investigating effective connectivity (Friston, 2011; Stephan, Tittgemeyer, Knösche,
Moran, & Friston, 2009). With current macroscale connectome mapping techniques, connec-
tion directionality cannot be explicitly resolved.
Hier, we quantified the impact of disregarding directionality in connectome analysis. Specif-
isch, we estimated the inaccuracies in brain networks quantified by graph-theoretic measures
following modifications to the unidirectional connections in connectomes of different species
and parcellations.
Our analyses indicate that several network measures are susceptible to error when direc-
tionality is lost. Graph-theoretic measures are affected at both the individual-node and the
network level, as is the definition of hubs. Across all networks analyzed, those with a larger
proportion of unidirectional connections were more extensively affected by the loss of connec-
tion directionality. This proportion is closely related to the parcellation, as finer parcellations
tend to have a larger proportion of unidirectional connections. We have also compared three
different schemes to generate undirected networks, which showed that the addition of recip-
rocal connections to a subset of existing connections (false positives) is more detrimental to
graph-theoretic measures than the removal of unidirectional connections (false negatives).
Error in the Classification of Hub Nodes
Heterogeneity in cortical regions plays an important role in structural brain networks: Highly
connected hub regions support integration of functionally and structurally segregated brain
Regionen (Miši´c et al., 2015; van den Heuvel et al., 2016; van den Heuvel et al., 2012). At these
Regionen, neuronal dendrites have larger spine density (Scholtens, Schmidt, de Reus, & van den
Heuvel, 2014; van den Heuvel & Spurns, 2013) and increased transcription of metabolic
genes (Fulcher & Fornito, 2016). Darüber hinaus, hub nodes have high wiring cost and demand for
metabolic resources, meaning their connections are more likely to become structurally dam-
aged and symptomatic in a wide range of neuropsychiatric disorders (Crossley et al., 2014;
Fornito et al., 2015; Fulcher & Fornito, 2016). Zum Beispiel, the increased vulnerability of
hubs in Alzheimer’s disease could be explained by excessive neuronal activity at these regions
(de Haan, Mott, van Straaten, Scheltens, & Stam, 2012; Kitsak et al., 2010; Raj, Kuceyeski, &
Wiener Würstchen, 2012). Somit, the correct identification and classification of hub regions is crucial
to understanding the effects of their normal functioning (van den Heuvel & Spurns, 2013) Und
dysfunction (Fornito et al., 2015) within the brain network.
Netzwerkneurowissenschaften
276
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
T
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Our results indicate that a proportion of hubs and super-hub nodes of the human con-
nectome are vulnerable to misclassification because the directionality of connections is not
verfügbar. Insbesondere, the classification of super-hub nodes was found to have a significant
lower accuracy than hub nodes. As a caveat, we need to be aware that this measure is sensitive
to noise because the number of super-hub nodes in some of the connectomes is limited.
Hubs were also classified as either connector or provincial based on their level of intramod-
ule versus intermodule connectivity (Guimera & Amaral, 2005B; van den Heuvel & Spurns,
2011). Previous studies have found that targeted attacks on connector hubs have a widespread
effect on network dynamics because of their role in functional integration, whereas attacks on
provincial hubs produce a more localized effect within communities (Honey & Spurns, 2008).
It has been hypothesized that such localized damage would cause specific clinical deficits,
whereas damage to connector hubs would cause complex, distributed dysfunction through-
out the network (Fornito et al., 2015). We found that alterations to unidirectional connections
lead to multiple errors in the classification of hub regions. Hubs were more likely to be de-
fined incorrectly based on degree (losing their classification) rather than the participation index
(changing classification between connector and provincial).
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Effect of False Positive and False Negative Connections
Diffusion-weighted and diffusion tensor imaging allow detailed reconstructions of the struc-
tural human brain network (Iturria-Medina, Sotero, Canales-Rodríguez, Alemán-Gómez, &
Melie-García, 2008; Van Essen et al., 2013). Depending on the data and specific tractog-
raphy algorithms used, crossing fiber geometries can give rise to two types of errors during
network reconstruction: absent connections (false negatives) and spurious connections (false
positives; Dauguet et al., 2007; Jbabdi & Johansen-Berg, 2011). These errors cannot be com-
pletely eliminated from the reconstructed network; Jedoch, when there are multiple subjects,
a group threshold can be used to minimize these errors and achieve a balance between the
exclusion of false positives and false negatives (de Reus & van den Heuvel, 2013; Roberts,
Perry, Roberts, Mitchell, & Breakspear, 2017).
In a recent study, these two types of errors were investigated in undirected connectomes,
where false negative connections were generated by pruning existing connections and false
positive connections were generated by connecting pairs of unconnected nodes (Zalesky et al.,
2016). False positive connections were at least twice as detrimental as false negatives to the
estimation of common graph-theoretic measures: clustering coefficient, network efficiency,
and modularity. This has been attributed to the modular topology of the network (Spurns &
Betzel, 2016). Because nodes within the same module are likely to have a higher connec-
tion density, false negative connections were more likely to occur within modules and to be
more redundant to network topology. Umgekehrt, false positive connections were more likely
to occur between modules, introducing shortcuts that have a greater impact on the graph-
theoretic metrics of the network. Here we investigated the impact of perturbations to a sub-
set of unidirectional connections, which were about half intramodular and half intermodular.
Despite the similarity of this analysis, here we generated false negative connections by remov-
ing existing unidirectional connections and false positive connections by adding the reciprocal
connections and making them bidirectional.
Our results also show that false positive connections were overall more detrimental than
false negatives. This occurs for betweenness, path length, global efficiency, and participa-
tion index. Vor allem, the small-world index and the clustering (for some connectomes) Sind
Netzwerkneurowissenschaften
277
Estimating the impact of structural directionality
exceptions, in which false negative directed connections are more detrimental than false pos-
itives. For these measures, the removal of directed connections reduces the number of closed
three-node motifs in the network, which may be more detrimental. These findings suggest
that graph-theoretic measures are overall more susceptible to addition of shortcuts introduced
by false positive connections. A simple and immediate recommendation that follows from
our results is that connectomes should be thresholded stringently to maximize specificity at
the cost of sensitivity. This recommendation is very straightforward to implement and does
not require the development of any new methodologies. In the mouse as well as other con-
nectomes that have weaker unidirectional connections, a more stringent thresholding would
create more false negative unidirectional connections and avoid many false positive unidirec-
tional connections that are more detrimental for network measures. Our findings also suggest
that the development of future connectome mapping methodologies should place more im-
portance on specificity. In this way, our work can inform and guide the development of future
tractography algorithms.
Connectome Mapping and Directionality Estimation
the reconstruction of
the macroscopic human connectome, parcellation schemes
Für
nodes or regions up to more than 105
range from less than 102
(sehen, Zum Beispiel, Aleman-
Gomez, 2006; Glasser et al., 2016; Hagmann et al., 2007; Salvador, Suckling, Schwarzbauer,
& Bullmore, 2005; Tzourio-Mazoyer et al., 2002; van den Heuvel, Stam, Boersma, & Pol,
2008). The choice of parcellation can affect several local and global topological parameters
of the network, lowering the reliability of comparisons between connectomes (Zalesky et al.,
2010). The parcellation also affects the proportion of unidirectional connections, as coarser
parcellations correspond to larger brain regions that are more likely to have reciprocal connec-
tionen. Zum Beispiel, three of the connectomes can be considered coarse parcellations and have
a relatively small proportion of unidirectional connections (macaque N = 47, N = 71, and cat
connectomes). dennoch, even for these connectomes, the identification of hubs and their
graph-theoretic measures can result in inaccuracies due to loss of connection directionality.
We have used connectomes from various species and parcellations that were obtained using
different techniques. These factors make it a complex task to compare and interpret some
subtle features of the results across all connectomes. dennoch, the consistency of most
results across connectomes suggests that they reflect general properties of brain networks and
are largely independent from the techniques used to obtain these connectomes. Somit, Sie
are also expected to be valid in other connectomes.
Effect of Connectome Structure on Brain Dynamics
Although the problem of directionality is a recurrent topic in connectomics, with few ex-
ceptions (Négyessy, Nepusz, Zalányi, & Bazsó, 2008; Rosen & Louzoun, 2014), most work
has focused on identifying the directionality of the interactions from the dynamics of nodes.
The directionality of the interactions of nodes in motifs and networks is paramount to shap-
ing the dynamics of systems (Bargmann & Marder, 2013). The dynamics of small circuits
or network motifs can be substantially altered by subtle differences in connectivity patterns.
Zum Beispiel, the presence of a single reciprocal connection can amplify the synchroniza-
tion due to resonance (Gollo & Breakspear, 2014; Gollo, Mirasso, Spurns, & Breakspear,
2014); the presence of triangles (Schleifen) can increase metastability (Gollo & Breakspear, 2014)
or multistability (Levnaji´c, 2011) due to frustration. Darüber hinaus, the presence of an inhib-
itory feedback can cause anticipated synchronization between neurons (Matias, Gollo, Carelli,
Netzwerkneurowissenschaften
278
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
T
/
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
.
/
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Mirasso, & Copelli, 2016) or cortical regions (Matias et al., 2014). Naturally, this susceptibility
of the dynamics to structural perturbations goes beyond network motifs, affecting the dynam-
ics of the whole network (Eguíluz, Pérez, Borge-Holthoefer, & Arenas, 2011; Esfahani, Gollo,
& Valizadeh, 2016; Gollo, Zalesky, Hutchison, van den Heuvel, & Breakspear, 2015; Hu,
Trousdale, Josi´c, & Shea-Brown, 2012).
A basic and influential manner of summarizing the dynamics of brain networks corresponds
to functional connectivity (Biswal et al., 1995). Functional connections correspond to linear
correlations between pairs of regions. These functional connections are symmetric and undi-
rected (Friston, 2011). Disambiguating the directionality of connections between pairs of cor-
tical regions has been a priority in the field (Friston, 2011; Friston, Harrison, & Penny, 2003),
as this directionality can reveal causal interaction between regions, or how they effectively
interagieren (Friston et al., 2017). Außerdem, a number of methods have been proposed and
utilized to determine the causal interactions between nodes (Friston, Moran, & Seth, 2013),
or to reconstruct the underlying network structure from the network dynamics (Ching & Tam,
2017; Deng, Deng, Yu, Guo, & Wang, 2016; Friston et al., 2013; López-Madrona, Matias,
Pereda, Canals, & Mirasso, 2017; Napoletani & Sauer, 2008; Stam, Nolte, & Daffertshofer,
2007; Tajima, Yanagawa, Fujii, & Toyoizumi, 2015; Timme, 2007; Vicente, Wibral, Lindner,
& Pipa, 2011; Wei, Liao, Yan, Er, & Xia, 2017). A better understanding of the relationship
between directionality in network structure and dynamics may aid in determining causal
interactions (Stephan et al., 2009).
At the network level, it is important to distinguish the roles of in- and out-degree in affecting
brain dynamics. A recent study found strong relationships between the structural connectivity
of a region and its BOLD (blood oxygen level dependent) signal dynamics (Sethi et al., 2017).
Außerdem, several graph-theoretic measures showed stronger correlations to the network
Dynamik (resting-state functional MRI) when directionality was taken into account. Brain re-
gions receiving more input (larger in-degree) required longer integration time to process and
combine all these inputs, which is consistent with the attributed function of rich-club associa-
tion areas (Heeger, 2017), and also supports the notion of a hierarchy of timescales recapitu-
lating the anatomical hierarchy of brain structure (Chaudhuri, Knoblauch, Gariel, Kennedy, &
Wang, 2015; Cocchi et al., 2016; Gollo, Roberts, & Cocchi, 2016; Gollo et al., 2015; Kiebel,
Daunizeau, & Friston, 2008; Murray et al., 2014). Gesamt, these findings highlight the impor-
tance of the directionality of the structural connectivity to understand brain dynamics.
Despite intensive efforts, the structure-function relationship remains far from elucidated,
and the issue of inferring directionality in undirected anatomical connectomes has yet to be
addressed. Here we have focused on characterizing the effect of directionality on brain struc-
ture via graph-theoretic measures, and future work will characterize how perturbations to the
directionality of connections influence network dynamics.
CONCLUSIONS
Connectomes are inherently directed networks. The majority of noninvasive techniques for
mapping connectomes are unable to resolve connection directionality,
thereby yielding
undirected approximations in which truly unidirectional connections are either overlooked
or rendered bidirectional. We found that the inability to resolve connection directionality
can introduce substantial error to the estimation of topological descriptors of brain networks,
particularly with respect to the classification and identification of hubs. We analyzed the ef-
fect of progressively eliminating connection directionality information in six directed connec-
tomes that were mapped with invasive techniques capable of resolving afferent and efferent
Netzwerkneurowissenschaften
279
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
T
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
connections (C. elegans, mouse, cat, and three macaque networks). We demonstrated that
the identification of the most connected hubs is especially affected by the loss of connection
directionality. We also found that the addition of reciprocal unidirectional connections (false
positives) is more detrimental to the estimation of most topological measures than removal of
unidirectional connections (false negatives). Our findings underscore the need for noninvasive
connectome mapping techniques that can (A) provide estimates of connection directionality
Und (B) yield relatively sparse and highly specific fiber maps that preference false negatives
over false positives. Given that most topological properties have been found to be recapitu-
lated across directed (macaque) and undirected (menschlich) connectomes, at least qualitatively,
resolving the directionality of human connectomes in the future will most likely not result in
a radical reappraisal of human brain network organization, but it will enable a more accurate
characterization of the human connectome.
ACKNOWLEDGMENTS
We would like to sincerely thank Madeleine Flynn, QIMR Berghofer Medical Research
Institut, for her illustrations (Figur 1 brain/nervous system images).
BEITRÄGE DES AUTORS
Penelope Kale: Formale Analyse; Untersuchung; Ressourcen; Visualisierung; Writing – original
Entwurf; Writing – review & Bearbeitung. Andrew Zalesky: Konzeptualisierung; Validierung; Writing –
Rezension & Bearbeitung. Leonardo L. Gollo: Konzeptualisierung; Akquise von Fördermitteln; Methodik;
Projektverwaltung; Ressourcen; Aufsicht; Validierung; Writing – original draft; Writing –
Rezension & Bearbeitung.
FUNDING INFORMATION
Leonardo L. Gollo, National Health and Medical Research Council (http://dx.doi.org/10.
13039/501100000925), Award ID: APP1110975. Andrew Zalesky, National Health and Med-
ical Research Council (http://dx.doi.org/10.13039/501100000925), Award ID: APP1047648.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
T
.
VERWEISE
Achacoso, T., & Yamamoto, W. (1992). AY’s neuroanatomy of
C. elegans for computation. Boca Raton, FL: CRC Press.
chical organization of human cortical networks in health and
schizophrenia. Zeitschrift für Neurowissenschaften, 28, 9239–9248.
Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016).
Brain networks under attack: Robustness properties and the
impact of lesions. Gehirn, 139(12), 3063–3083.
Aleman-Gomez, Y. (2006). IBASPM: Toolbox for automatic parcel-
lation of brain structures. In 12th Annual Meeting of the Organ-
ization for Human Brain Mapping, June 11–15, 2006, Florence,
Italien.
Assaf, Y., & Basser, P. J. (2005). Composite hindered and restricted
model of diffusion (CHARMED) MR imaging of the human brain.
NeuroImage, 27, 48–58.
Aydore, S., Pantazis, D., & Leahy, R. M. (2013). A note on the phase
locking value and its properties. NeuroImage, 74, 231–244.
Bargmann, C. ICH., & Marder, E. (2013). From the connectome to
brain function. Nature Methods, 10, 483–490.
Bassett, D. S., & Bullmore, E. (2006). Small-world brain networks.
The Neuroscientist, 12, 512–523.
Bassett, D. S., Bullmore, E., Verchinski, B. A., Mattay, V. S.,
(2008). Hierar-
Weinberger, D. R., & Meyer-Lindenberg, A.
Betzel, R. F., & Bassett, D. S.
NeuroImage, 160, 73–83.
(2016). Multi-scale brain networks.
Bezgin, G., Vakorin, V. A., van Opstal, A. J., McIntosh, A. R., &
Bakker, R.
(2012). Hundreds of brain maps in one atlas: Reg-
istering coordinate-independent primate neuro-anatomical data
to a standard brain. NeuroImage, 62, 67–76.
Biswal, B., Zerrin Yetkin, F., Haughton, V. M., & Hyde, J. S. (1995).
Functional connectivity in the motor cortex of resting human
brain using echo-planar MRI. Magnetic Resonance in Medicine,
34, 537–541.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Zeitschrift
of Statistical Mechanics: Theory and Experiment, 2008, P10008.
Boussaoud, D., Ungerleider, L. G., & Desimone, R. (1990). Path-
ways for motion analysis: Cortical connections of the medial
superior temporal and fundus of the superior temporal visual
areas in the macaque. Zeitschrift für Vergleichende Neurologie, 296,
462–495.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
280
Estimating the impact of structural directionality
Bullmore, E., & Spurns, Ö. (2012). The economy of brain network
organization. Nature Reviews Neurowissenschaften, 13, 336–349.
Calabrese, E., Badea, A., Cofer, G., Qi, Y., & Johnson, G. A. (2015).
A diffusion MRI tractography connectome of the mouse brain
and comparison with neuronal tracer data. Hirnrinde, 25,
4628–4637.
Chaudhuri, R., Knoblauch, K., Gariel, M.-A., Kennedy, H., &
Wang, X.-J. (2015). A large-scale circuit mechanism for hierar-
chical dynamical processing in the primate cortex. Neuron, 88,
419–431.
Ching, E. S., & Tam, H. (2017). Reconstructing links in directed
networks from noisy dynamics. Physical Review E, 95, 010301.
Cloutman, L. L., & Ralph, L. (2012). Connectivity-based structural
and functional parcellation of the human cortex using diffusion
imaging and tractography. Frontiers in Neuroanatomy, 6, 34.
Cocchi, L., Sale, M. V., Gollo, L. L., Glocke, P. T., Nguyen, V. T.,
Zalesky, A., . . . Mattingley, J. B. (2016). A hierarchy of timescales
explains distinct effects of local inhibition of primary visual
cortex and frontal eye fields. eLife, 5, e15252.
Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, A. (2006).
Detecting rich-club ordering in complex networks. Natur
Physik, 2, 110–115.
Crossley, N. A., Mechelli, A., Scott,
J., Carletti, F., Fuchs, P. T.,
McGuire, P., & Bullmore, E. T. (2014). The hubs of the human
connectome are generally implicated in the anatomy of brain
disorders. Gehirn, 137, 2382–2395.
da Fontoura Costa, L., Rodrigues, F. A., Travieso, G., & Villas Boas,
P. R. (2007). Characterization of complex networks: A survey of
measurements. Advances in Physics, 56, 167–242.
Dauguet, J., Peled, S., Berezovskii, V., Delzescaux, T., Warfield,
S. K., Born, R., & Westin, C.-F. (2007). Comparison of fiber tracts
derived from in-vivo DTI tractography with 3D histological neu-
ral tract tracer reconstruction on a macaque brain. NeuroImage,
37, 530–538.
de Haan, W., Mott, K., van Straaten, E. C., Scheltens, P., & Stam,
C. J. (2012). Activity dependent degeneration explains hub vul-
nerability in Alzheimer’s disease. PLoS Computational Biology,
8, e1002582.
de Reus, M. A., & van den Heuvel, M. P. (2013). The parcellation-
based connectome: Limitations and extensions. NeuroImage,
80, 397–404.
Deng, B., Deng, Y., Yu, H., Guo, X., & Wang, J.
(2016). Depen-
dence of inter-neuronal effective connectivity on synchrony dy-
namics in neuronal network motifs. Chaos, Solitons & Fractals,
82, 48–59.
Donahue, C.
Jbabdi, S., Hernandez-
Fernandez, M., Behrens, T. E., Dyrby, T. B., . . . Van Essen,
D. C.
(2016). Using diffusion tractography to predict corti-
cal connection strength and distance: A quantitative compari-
Zeitschrift für Neurowissenschaften, 36,
son with tracers in the monkey.
6758–6770.
J., Sotiropoulos, S. N.,
Dong, H. W. (2008). The Allen reference atlas: A digital color brain
atlas of the C57Bl/6J male mouse: John Wiley & Sons Inc.
Durbin, R. M.
(1987). Studies on the development and organisa-
tion of the nervous system of Caenorhabditis elegans (Doctoral
dissertation, University of Cambridge, Cambridge, Vereinigtes Königreich).
Eguíluz, V. M., Pérez, T., Borge-Holthoefer, J., & Arenas, A. (2011).
Structural and functional networks in complex systems with
delay. Physical Review E, 83, 056113.
Esfahani, Z. G., Gollo, L. L., & Valizadeh, A. (2016). Stimulus-
dependent synchronization in delayed-coupled neuronal net-
funktioniert. Scientific Reports, 6.
Fagiolo, G.
(2007). Clustering in complex directed networks.
Physical Review E, 76, 026107.
Felleman, D. J., & Van Essen, D. C. (1991). Distributed hierarchi-
cal processing in the primate cerebral cortex. Hirnrinde, 1,
1–47.
Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connectomics
of brain disorders. Nature Reviews Neurowissenschaften, 16, 159–172.
(1978). Centrality in social networks conceptual
Freeman, L. C.
clarification. Social Networks, 1, 215–239.
Friston, K., Moran, R., & Seth, A. K. (2013). Analysing connectivity
with Granger causality and dynamic causal modelling. Current
Opinion in Neurobiology, 23, 172–178.
Friston, K., Preller, K. H., Mathys, C., Cagnan, H., Heinzle, J.,
Razi, A., & Zeidman, P. (2017). Dynamic causal modelling re-
visited. NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.
02.045
Friston, K. J. (2011). Functional and effective connectivity: Eine Rezension.
Gehirnkonnektivität, 1, 13–36.
Friston, K. J., Harrison, L., & Penny, W.
(2003). Dynamic causal
modelling. NeuroImage, 19, 1273–1302.
Fulcher, B. D., & Fornito, A. (2016). A transcriptional signature of
hub connectivity in the mouse connectome. Verfahren der
Nationale Akademie der Wissenschaften, 113, 1435–1440.
G˘am˘anu¸t, R., Kennedy, H., Toroczkai, Z., Van Essen, D.,
Knoblauch, K., & Burkhalter, A. (2017). The mouse cortical inter-
areal network reveals well defined connectivity profiles and an
ultra dense cortical graph. bioRxiv:156976
Garlaschelli, D., & Loffredo, M. ICH. (2004). Patterns of link reciprocity
in directed networks. Physical Review Letters, 93, 268701.
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., . . . Jenkinson, M. (2016). A multi-
modal parcellation of human cerebral cortex. Natur, 536(7615),
171–178.
Gollo, L. L., & Breakspear, M. (2014). The frustrated brain: Aus
dynamics on motifs to communities and networks. Philosophical
Transactions of the Royal Society B, 369, 20130532.
Gollo, L. L., Mirasso, C., Spurns, O., & Breakspear, M. (2014).
Mechanisms of zero-lag synchronization in cortical motifs. PLoS
Computational Biology, 10, e1003548.
Gollo, L. L., Roberts,
(2016). Mapping
how local perturbations influence systems-level brain dynamics.
arXiv:160900491
J. A., & Cocchi, L.
Gollo, L. L., Zalesky, A., Hutchison, R. M., van den Heuvel, M., &
Breakspear, M. (2015). Dwelling quietly in the rich club: Gehirn
network determinants of slow cortical fluctuations. Philosophical
Transactions of the Royal Society B, 370, 20140165.
Goulas, A., Bastiani, M., Bezgin, G., Uylings, H. B., Roebroeck,
A., & Stiers, P. (2014). Comparative analysis of the macroscale
structural connectivity in the macaque and human brain. PLoS
Computational Biology, 10, e1003529.
Netzwerkneurowissenschaften
281
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Guimera, R., & Amaral, L. A. N. (2005A). Cartography of com-
plex networks: Modules and universal roles. Journal of Statistical
Mechanics: Theory and Experiment, 2005, P02001.
Guimera, R., & Amaral, L. A. N. (2005B). Functional cartography
of complex metabolic networks. Natur, 433, 895–900.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Spurns, Ö. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6, e159.
Hagmann, P., Kurant, M., Gigandet, X., Thiran, P., Wedeen, V. J.,
Meuli, R., & Thiran, J.-P. (2007). Mapping human whole-brain
structural networks with diffusion MRI. PloS ONE, 2, e597.
Hall, D. H., & Russell, R. L. (1991). The posterior nervous system
of the nematode Caenorhabditis elegans: Serial reconstruction of
identified neurons and complete pattern of synaptic interactions.
Zeitschrift für Neurowissenschaften, 11, 1–22.
Harriger, L., van den Heuvel, M. P., & Spurns, Ö. (2012). Rich club
organization of macaque cerebral cortex and its role in network
communication. PloS ONE, 7, e46497.
Heeger, D. J. (2017). Theory of cortical function. Proceedings of
the National Academy of Sciences, 114, 1773–1782.
Honey, C. J., Kötter, R., Breakspear, M., & Spurns, Ö. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy
of Sciences, 104, 10240–10245.
Honey, C. J., & Spurns, Ö. (2008). Dynamical consequences of le-
sions in cortical networks. Kartierung des menschlichen Gehirns, 29, 802–809.
Honnorat, N., Eavani, H., Satterthwaite, T. D., Gur, R. E., Gur, R. C.,
& Davatzikos, C. (2015). GraSP: Geodesic graph-based segmen-
tation with shape priors for the functional parcellation of the
Kortex. NeuroImage, 106, 207–221.
Hu, Y., Trousdale, J., Josi´c, K., & Shea-Brown, E. (2012). Motiv
statistics and spike correlations in neuronal networks. BMC
Neurowissenschaften, 13, P43.
Humphries, M. D., & Gurney, K.
(2008). Network “small-world-
ness”: A quantitative method for determining canonical network
equivalence. PloS ONE, 3, e0002051.
Iturria-Medina, Y., Sotero, R. C., Canales-Rodríguez, E. J., Alemán-
Gómez, Y., & Melie-García, L. (2008). Studying the human
brain anatomical network via diffusion-weighted MRI and graph
theory. NeuroImage, 40, 1064–1076.
Jbabdi, S., & Johansen-Berg, H. (2011). Tractography: Where do we
go from here? Gehirnkonnektivität, 1, 169–183.
Kale, P., Zalesky, A., & Gollo, L. L.
(2018). Supplemental mate-
rial for “estimating the impact of structural directionality: Wie
reliable are undirected connectomes?” Network Neuroscience,
2(2), 259–284. https://doi.org/10.1162/netn_a_00040
Kandel, E. R., Schwartz, J. H., Jessell, T. M., Siegelbaum, S. A., &
(2000). Principles of neural science. New York,
Hudspeth, A.
New York: McGraw-Hill.
Kendall, M. G.
(1938). A new measure of rank correlation.
Biometrika, 30, 81–93.
Kiebel, S. J., Daunizeau, J., & Friston, K. J. (2008). A hierarchy of time-
scales and the brain. PLoS Computational Biology, 4, e1000209.
Kitsak, M., Gallos, L. K., Havlin, S., Liljeros, F., Muchnik, L., Stanley,
H. E., & Makse, H. A. (2010). Identification of influential spread-
ers in complex networks. Nature Physics, 6, 888–893.
Kötter, R. (2004). Online retrieval, Verarbeitung, and visualization
of primate connectivity data from the CoCoMac database.
Neuroinformatics, 2, 127–144.
Kötter, R., & Wanke, E.
(2005). Mapping brains without coordi-
nates. Philosophical Transactions of the Royal Society of London
B: Biological Sciences, 360, 751–766.
Lancichinetti, A., & Fortunato, S. (2012). Consensus clustering in
complex networks. Scientific Reports, 2, 336.
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
Netzwerke. Physical Review Letters, 87, 198701.
Levnaji´c, Z.
(2011). Emergent multistability and frustration in
phase-repulsive networks of oscillators. Physical Review E, 84,
016231.
López-Madrona, V. J., Matias, F. S., Pereda, E., Canals, S., &
Mirasso, C. R. (2017). On the role of the entorhinal cortex in
the effective connectivity of the hippocampal formation. Chaos,
27, 047401.
Maier-Hein, K. H., Neher, P. F., Houde,
J.-C., Côté, M.-A.,
Garyfallidis, E., Zhong, J., . . . Ji, Q. (2017). The challenge of
mapping the human connectome based on diffusion tractogra-
phy. Nature Communications, 8, 1349.
Markov, N. T., Ercsey-Ravasz, M., Ribeiro Gomes, A., Lamy, C.,
Magrou, L., Vezoli, J., . . . Gariel, M. (2012). A weighted and
directed interareal connectivity matrix for macaque cerebral
Kortex. Hirnrinde, 24, 17–36.
Matias, F. S., Gollo, L. L., Carelli, P. V., Bressler, S. L., Copelli, M.,
& Mirasso, C. R.
(2014). Modeling positive Granger causality
and negative phase lag between cortical areas. NeuroImage, 99,
411–418.
Matias, F. S., Gollo, L. L., Carelli, P. V., Mirasso, C. R., & Copelli,
M. (2016). Inhibitory loop robustly induces anticipated syn-
chronization in neuronal microcircuits. Physical Review E, 94,
042411.
Medaglia, J. D., & Bassett, D. S. (2017). Network analyses and
nervous system disorders. arXiv:170101101
Miši´c, B., Betzel, R. F., Nematzadeh, A., Goñi,
J., Griffa, A.,
Hagmann, P., . . . Spurns, Ö. (2015). Cooperative and competi-
tive spreading dynamics on the human connectome. Neuron, 86,
1518–1529.
Modha, D. S., & Singh, R. (2010). Network architecture of the
long-distance pathways in the macaque brain. Verfahren der
Nationale Akademie der Wissenschaften, 107, 13485–13490.
Murray, J. D., Bernacchia, A., Freedman, D. J., Romo, R., Wallis,
intrin-
J. D., Cai, X.,
sic timescales across primate cortex. Naturneurowissenschaften, 17,
1661–1663.
(2014). A hierarchy of
. Lee, D.
.
.
Napoletani, D., & Sauer, T. D. (2008). Reconstructing the topology
of sparsely connected dynamical networks. Physical Review E,
77, 026103.
Négyessy, L., Nepusz, T., Zalányi, L., & Bazsó, F. (2008). Conver-
gence and divergence are mostly reciprocated properties of the
connections in the network of cortical areas. Verfahren der
Royal Society of London B: Biological Sciences, 275, 2403–2410.
(2004). Coauthorship networks and patterns of
scientific collaboration. Proceedings of the National Academy of
Wissenschaften, 101, 5200–5205.
Newman, M. E.
Netzwerkneurowissenschaften
282
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
/
T
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Raj, A., Kuceyeski, A., & Wiener Würstchen, M. (2012). A network diffusion model
of disease progression in dementia. Neuron, 73, 1204–1215.
Reinoso-Suarez, F.
(1984). Connectional patterns in parietotem-
porooccipital association cortex of the feline cerebral cortex. In
Cortical integration: Basic archicortical and cortical association
levels of neural integration, IBRO monograph series, Bd. 11
(S. 255–278). New York, New York: Raven Press.
Roberts, J. A., Perry, A., Roberts, G., Mitchell, P. B., & Breakspear,
(2017). Consistency-based thresholding of the human con-
M.
nectome. NeuroImage, 145, 118–129.
Rosen, Y., & Louzoun, Y. (2014). Directionality of real world net-
works as predicted by path length in directed and undirected
graphs. Physica A: Statistical Mechanics and Its Applications,
401, 118–129.
Rubinow, M., & Spurns, Ö. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52,
1059–1069.
Salvador, R., Suckling, J., Schwarzbauer, C., & Bullmore, E. (2005).
Undirected graphs of frequency-dependent functional connec-
tivity in whole brain networks. Philosophical Transactions of the
Royal Society of London B: Biological Sciences, 360, 937–946.
Scannell, J. W., Blakemore, C., & Jung, M. P. (1995). Analysis of
connectivity in the cat cerebral cortex. Zeitschrift für Neurowissenschaften,
15, 1463–1483.
Scannell, J. W., Verbrennungen, G., Hilgetag, C., O'Neil, M., & Jung, M. P.
(1999). The connectional organization of the cortico-thalamic
system of the cat. Hirnrinde, 9, 277–299.
Scholtens, L. H., Schmidt, R., de Reus, M. A., & van den Heuvel,
M. P. (2014). Linking macroscale graph analytical organization
to microscale neuroarchitectonics in the macaque connectome.
Zeitschrift für Neurowissenschaften, 34, 12192–12205.
Serrano, M. Á., Boguná, M., & Vespignani, A. (2009). Extracting the
multiscale backbone of complex weighted networks. Proceed-
ings of the National Academy of Sciences, 106, 6483–6488.
Sethi, S. S., Zerbi, V., Wenderoth, N., Fornito, A., & Fulcher, B. D.
(2017). Structural connectome topology relates to regional BOLD
signal dynamics in the mouse brain. Chaos, 27, 047405.
Shih, C.-T., Spurns, O., Yuan, S.-L., Su, T.-S., Lin, Y.-J., Chuang,
C.-C., . . . Chiang, A.-S. (2015). Connectomics-based analysis of
information flow in the Drosophila brain. Aktuelle Biologie, 25,
1249–1258.
Spearman, C. (1904). The proof and measurement of association
between two things. American Journal of Psychology, 15, 72–101.
Spurns, Ö. (2011). The human connectome: A complex network.
Annalen der New York Academy of Sciences, 1224, 109–125.
Spurns, O., & Betzel, R. F. (2016). Modular brain networks. Jährlich
Rezension der Psychologie, 67, 613–640.
Spurns, O., Honey, C. J., & Kötter, R.
(2007).
Identification and
classification of hubs in brain networks. PloS ONE, 2, e1049.
Spurns, O., Tononi, G., & Kötter, R.
(2005). The human connec-
tome: A structural description of the human brain. PLoS Compu-
tational Biology, 1, e42.
Stam, C. J., Nolte, G., & Daffertshofer, A. (2007). Phase lag index:
Assessment of functional connectivity from multi channel EEG
and MEG with diminished bias from common sources. Human
Brain Mapping, 28, 1178–1193.
Stephan, K. E., Kamper, L., Bozkurt, A., Verbrennungen, G. A., Jung, M. P.,
& Kötter, R. (2001). Advanced database methodology for the col-
lation of connectivity data on the macaque brain (CoCoMac).
Philosophical Transactions of the Royal Society of London B:
Biological Sciences, 356, 1159–1186.
Stephan, K. E., Tittgemeyer, M., Knösche, T. R., Moran, R. J., &
(2009). Tractography-based priors for dynamic
Friston, K.
causal models. NeuroImage, 47, 1628–1638.
J.
Stephan, K. E., Zilles, K., & Kötter, R.
(2000). Coordinate–
independent mapping of structural and functional data by objec-
tive relational transformation (ORT). Philosophische Transaktionen
of the Royal Society of London B: Biological Sciences, 355,
37–54.
Tajima, S., Yanagawa, T., Fujii, N., & Toyoizumi, T. (2015). Un-
in consciousness by cross-
tangling brain-wide dynamics
embedding. PLoS Computational Biology, 11, e1004537.
Timme, M. (2007). Revealing network connectivity from response
Dynamik. Physical Review Letters, 98, 224101.
Tournier, J., Calamante, F., & Connelly, A.
(2012). MRtrix: Diffu-
sion tractography in crossing fiber regions. International Journal
of Imaging Systems and Technology, 22, 53–66.
Towlson, E. K., Vértes, P. E., Ahnert, S. E., Schafer, W. R., &
Bullmore, E. T. (2013). The rich club of the C. elegans neuronal
connectome. Zeitschrift für Neurowissenschaften, 33, 6380–6387.
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M. (2002). Automated
anatomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
NeuroImage, 15, 273–289.
van den Heuvel, M. P., Bullmore, E. T., & Spurns, Ö. (2016). Com-
parative connectomics. Trends in den Kognitionswissenschaften, 20, 345–361.
van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Spurns, Ö. (2012).
High-cost, high-capacity backbone for global brain communi-
cation. Verfahren der Nationalen Akademie der Wissenschaften, 109,
11372–11377.
van den Heuvel, M. P., & Spurns, Ö. (2011). Rich-club organiza-
Zeitschrift für Neurowissenschaften, 31,
tion of the human connectome.
15775–15786.
van den Heuvel, M. P., & Spurns, Ö. (2013). Network hubs in the
human brain. Trends in den Kognitionswissenschaften, 17, 683–696.
van den Heuvel, M. P., Stam, C. J., Boersma, M., & Pol, H. H. (2008).
Small-world and scale-free organization of voxel-based resting-
state functional connectivity in the human brain. NeuroImage,
43, 528–539.
Van Essen, D. C., Schmied, S. M., Barch, D. M., Behrens, T. E., Yacoub,
E., Ugur-Auto, K., & WU-Minn HCP Consortium. (2013). The WU-
Minn Human Connectome Project: An overview. NeuroImage,
80, 62–79.
Varshney, L. R., Chen, B. L., Paniagua, E., Hall, D. H., & Chklovskii,
D. B. (2011). Structural properties of the Caenorhabditis elegans
neuronal network. PLoS Computational Biology, 7, e1001066.
Vicente, R., Wibral, M., Lindner, M., & Pipa, G. (2011). Transfer
entropy—A model-free measure of effective connectivity for the
neurosciences. Journal of Computational Neuroscience,30, 45–67.
Watt, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-
world” networks. Natur, 393, 440–442.
Netzwerkneurowissenschaften
283
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
T
/
.
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Estimating the impact of structural directionality
Wei, Y., Liao, X., Yan, C., Er, Y., & Xia, M. (2017). Identifizieren
topological motif patterns of human brain functional networks.
Kartierung des menschlichen Gehirns, 38, 2734–2750.
White, J. G., Southgate, E., Thomson, J. N., & Brenner, S.
(1976).
The structure of the ventral nerve cord of Caenorhabditis elegans.
Philosophical Transactions of the Royal Society of London B:
Biological Sciences, 275, 327–348.
White, J. G., Southgate, E., Thomson, J. N., & Brenner, S.
(1986).
The structure of the nervous system of the nematode Caenorhab-
ditis elegans. Philosophical Transactions of the Royal Society of
London B: Biological Sciences, 314, 1–340.
Yeterian, E. H., & Pandya, D. N. (1985). Corticothalamic connec-
tions of the posterior parietal cortex in the rhesus monkey. Zeitschrift
of Comparative Neurology, 237, 408–426.
Jung, M. P. (1993). The organization of neural systems in the pri-
mate cerebral cortex. Proceedings of the Royal Society of London
B: Biological Sciences, 252, 13–18.
Ypma, R.
J., & Bullmore, E. T.
(2016). Statistical analysis of
tract-tracing experiments demonstrates a dense, complex cor-
tical network in the mouse. PLoS Computational Biology, 12,
e1005104.
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel,
M. P., & Breakspear, M. (2016). Connectome sensitivity or speci-
ficity: Which is more important? NeuroImage, 142, 407–420.
Zalesky, A., Fornito, A., Harding, ICH. H., Cocchi, L., Yücel, M.,
Pantelis, C., . . . Bullmore, E. T. (2010). Whole-brain anatomi-
cal networks: Does the choice of nodes matter? NeuroImage,
50, 970–983.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
T
/
e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D
l
F
/
/
/
/
0
2
0
2
2
5
9
1
0
9
2
1
7
5
N
e
N
_
A
_
0
0
0
4
0
P
D
/
.
T
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Netzwerkneurowissenschaften
284