Esteban Maestre, Rafael Ram´ırez, - Am MIT spezialisierte KI-Forschung

Esteban Maestre, Rafael Ram´ırez,
Stefan Kersten, and Xavier Serra
Music Technology Group
Universität Pompeu Fabra
122 – 140 Tanger
Barcelona 08018 Spanien
{esteban.maestre, rafael.ramirez,
stefan.kersten, xavier.serra}@upf.edu

Expressive Concatenative
Synthesis by Reusing
Samples from Real
Performance Recordings

The manipulation of sound properties such as
zeitliche Koordinierung, Amplitude, Timbre, and pitch by different
performers and styles is an important fact not to
be missed when approaching instrumental sound
synthesis. Expressive music performance studies
the manipulation of such sound properties in an
attempt to understand expression, so that it can be
applied to sound synthesis for obtaining expressive
instrumental sound in the shape of a synthetic
Leistung.

During the past few years, the availability
of technology for high-fidelity sound synthesis
based on samples has pushed the consolidation
of sample-based concatenative synthesizers as the
most popular and flexible mean of reconstruct-
ing the sound of traditional musical instruments
(Schwarz 2006). Recent implementations (Bonada
and Serra 2007; Lindemann 2007) have yielded
high-quality sound synthesis and often offer a wide
range of synthesis parameters, including some re-
lated to expression, normally concerning either
a note or the transition between two successive
notes. Jedoch, these parameters must in most
of cases be tuned manually, which is extremely
time consuming and requires considerable effort
and knowledge from the user. Im Idealfall, Ausdruck-
related parameters should be tuned automatically
by the synthesis system by applying some prior
knowledge about the expressive transformations a
particular musician introduces when performing a
Stück.

In the past, such knowledge has been tradition-
ally obtained by empirically studying real expressive
performance recordings (z.B., Repp 1992; Todd 1992;
Friberg et al. 1998), and more recently, by applying
machine-learning techniques (z.B., Widmer 2001;
Lopez de Mantaras and Arcos 2002; Ramirez, Hazan,
and Maestre 2006a, 2006B). Machine-learning ap-
proaches to expressive-performance modeling reside

Computermusikjournal, 33:4, S. 23–42, Winter 2009

on top of a symbolic representation to which
machine-learning techniques can be applied. Das
symbolic representation can be easier to obtain,
as it is for the case of excitation-instantaneous
musical instruments (z.B., piano), or more difficult
to obtain, as is the case for excitation-continuous
musical instruments (z.B., wind or bowed-string in-
Instrumente). In excitation-continuous instruments,
both excitation and control of the sound-production
mechanisms are achieved by continuous mod-
ulations; daher, the extraction of symbolic-level
information requires the analysis of the recorded
audio stream instead of measuring note durations or
dynamics from MIDI-like representations.

Here we describe an approach to the expressive
synthesis of jazz saxophone melodies that reuses
audio recordings and carefully concatenates note
Proben. The aim is to generate an expressive audio
sequence from the analysis of an arbitrary input
score using a previously induced performance model
and an annotated saxophone note database extracted
from real performances. We push the idea of using
the same corpus for both inducing an expressive
performance model and synthesizing sound by
concatenating samples in the corpus. daher,
a connection between the performers’ instrument
sound and performance characteristics is kept during
the synthesis process.

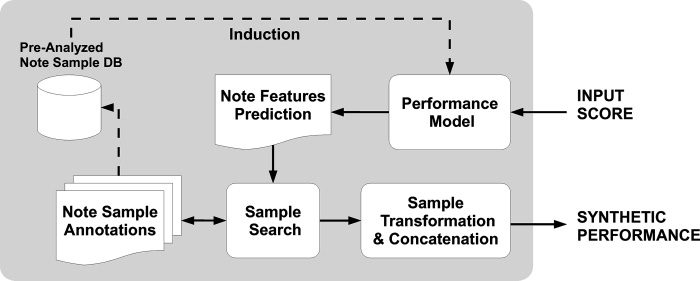
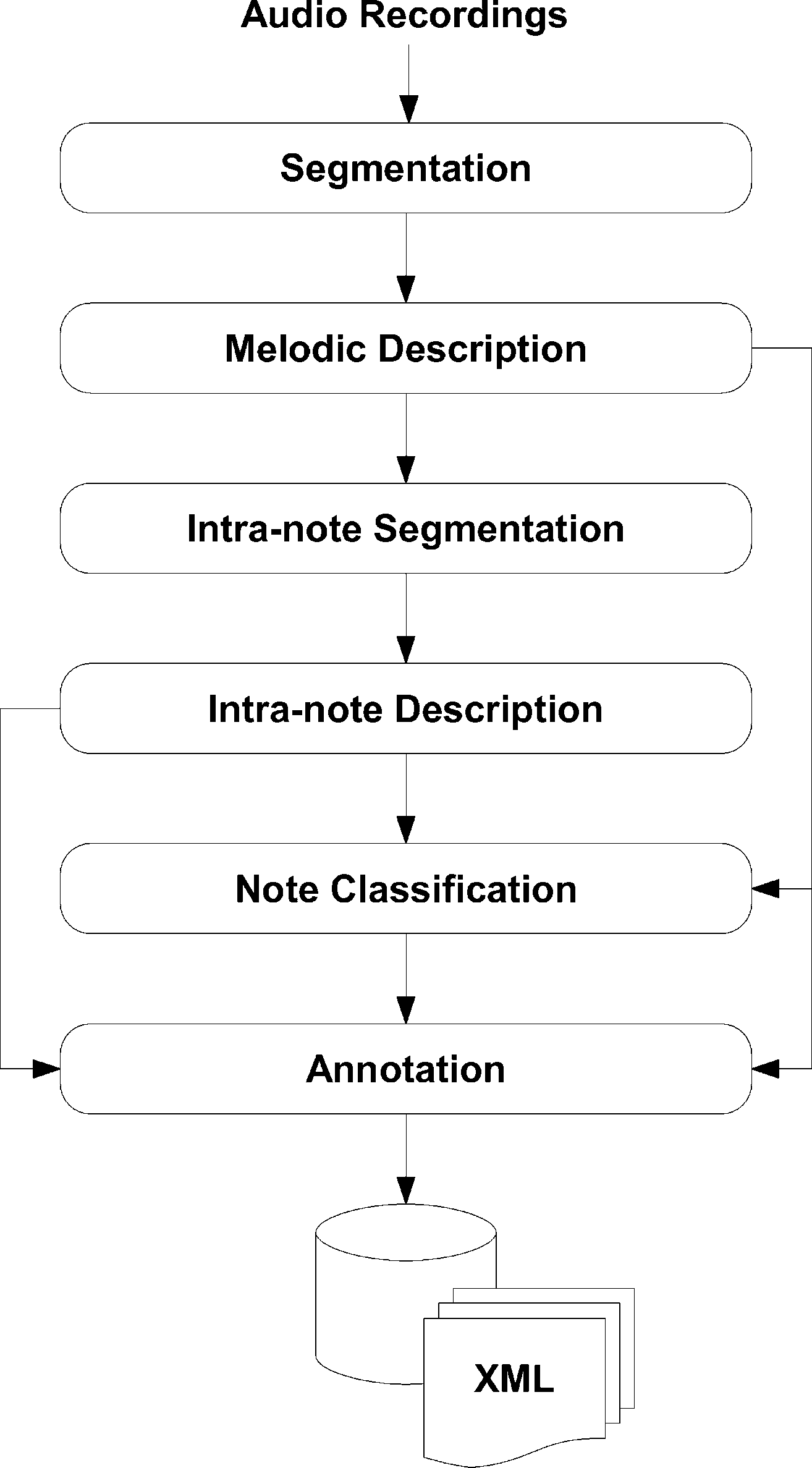
The architecture of our system, depicted in
Figur 1, can be briefly summarized as follows. Erste,
given a set of expressive performance recordings, Wir
obtain a description of the audio by carrying out seg-
mentation and characterization at different temporal
levels (Notiz, intra-note, note-to-note transition) Und
build an annotated database of pre-analyzed note
segments for later use in the synthesis stage. A
performance model is trained using inductive logic-
programming techniques by matching the score to
the description of the performances obtained while
constructing the database. For synthesizing expres-
sive audio, the input score is first analyzed, and a set

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 1. Schematic view
of the system architecture.

of descriptors is extracted. From such a description,
the performance model obtains an enriched score
including expression–related parameters. Endlich,
by considering the enriched score, the most suit-
able note samples from the database are retrieved,
transformed, and concatenated. This article presents
an extended description of an off-line audio anal-
ysis/synthesis application based on previous work
(Maestre et al. 2006; Ramirez, Hazan, and Maestre
2006B; Ramirez et al. 2007).

The rest of the article is organized as follows.

The next section describes related work, aus
sample-based concatenative synthesis to expressive
performance modeling. The following sections
present the audio analysis carried out to annotate
our database of performance recordings, und das
details of the database-construction process. Nächste,
we reveal the insights of building the expressive
performance model from the database annotations.
Dann, we present the audio synthesis methods,
giving special emphasis to the sample search.
Endlich, we present some conclusions and state
further work for future improvements.

Related Work

Sample-Based Concatenative Synthesis

Sample-based concatenative synthesis is an emerg-
ing approach to sound generation based on con-
catenating short audio excerpts (Proben) von einem
database to achieve a desired sonic result given a
target description (z.B., a score) or sound (Schwarz

2000). Although sampling cannot be strictly con-
sidered as a sound-synthesis technique, it provides,
in terms of sound quality and realism, one of
the most successful approaches for reproducing
real-world musical sound (Bonada and Serra 2007).
The main reason is that the naturalness of sounds
is maintained, because the audio slices used for
concatenation are actual samples collected from
realistic contexts to which just some meaningful
sound transformations need to be applied, both to
smooth concatenations and to match the input spec-
ification given ad hoc distance metrics. Darüber hinaus,
for greater database sizes, it is more probable that
a closely matching sample will be found, so the
need to apply transformations is reduced (Schwarz
2006). The samples can be non-uniform—i.e., Sie
can comprise any duration from a sound snippet,
through an entire instrumental note, up to a whole
Phrase. Even though it is customary to consider
homogeneous sizes and types of samples, and some-
times a sample is just a short time window of the
signal used in conjunction with some spectral anal-
yses and overlap-add synthesis (Schwarz 2007), Wir
approach the synthesis of melodies by concatenating
note samples, each one corresponding to an entire
performed note of arbitrary duration.

Apart from the transformations to be applied to
the retrieved samples, which might end up resulting
in a degradation of the sound quality when the target
features and the retrieved sample are far apart given
a particular distance metric, the way in which the
most convenient sequence of samples is selected
from the database is important when trying to
maintain the feeling of sound continuity. This issue

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

has been treated from an optimization perspective
in general-purpose, concatenative-synthesis appli-
cations for music and speech, where not just the
descriptions of the samples are considered, but also
their context (Hunt and Black 1996; Aucouturier
and Pachet 2006). In our work, we have similarly
placed emphasis on respecting the sample’s original
context during the retrieval stage.

Concatenative sound synthesis (CSS) has been

used and studied for some time, with its first
applications found in the early text-to-speech (TTS)
synthesis systems, which transform input text
into speech sound signals (Klatt 1983; Prudon 2003).
Although speech synthesis and music synthesis have
different objectives (intelligibility and naturalness
vs. expressivity and musical flexibility), ähnlich
principles can be found in speech synthesis and
musical sound synthesis, and thus important parts
of the methodology have traditionally been shared
(Sagisaka 1988; Beller et al. 2005). Although used
for strictly musical purposes in many different
ways, only recently has sample-based CSS has been
formally defined in a purely musical context.

According to Schwarz (2007), one of the main

applications of corpus-based CSS is high-level
instrument synthesis, where natural-sounding tran-
sitions can be synthesized by selecting samples
from matching contexts. This is a particularly chal-
lenging issue for the case of excitation-continuous
Instrumente (z.B., wind instruments). Some rele-
vant implementations have appeared recently, aus
which we will briefly review those that resulted
the most inspiring or closely related for the work
presented in this article. For a comprehensive review
of CSS, we refer the reader to Schwarz (2006).

One of the most important and broad contribu-
tions to the topic of CSS is Schwarz’s PhD disserta-
tion (2004). In addition to formally defining several
important aspects involved and unifying concepts,
this work introduces a general-purpose, corpus-
based system based on data-driven unit selection.
In his general framework, the target specification
is obtained from either a symbolic score or audio
analysis as a sequence of descriptor values. In our
Fall, we introduce an expressivity component when
constructing an enhanced symbolic score, generated
as an enrichment of an input musical score, von

means of performance knowledge induced from
the database itself. In our system, selection of the
best sample sequence is accomplished by distance
functions and a path-search sample-selection al-
gorithm, including some constraint-satisfaction
Techniken. One of the extensions that we introduce
is that the knowledge of our expressive-performance
modeling component has been induced from the
synthesis database itself, and therefore there is a
strong connection between the expressivity and syn-
thesis modules of our system. Daher, we could make
the “corpus-based” term also cover the induced
expressive performance model.

Staying on the musical side but particularly
closer to the speech, we find the singing-voice syn-
thesizer developed by Bonada and Loscos (2003) Und
Bonada and Serra (2007). This system, developed
over several years, has become the most successful
singing voice commercial synthesizer: Yamaha’s
Vocaloid (www.vocaloid.com). The system, based
on phase-vocoder techniques and spectral concate-
nation, searches the most convenient sequence of
diphonemes (Proben) of an annotated database of
singing voice excerpts, recorded at different tempi
and dynamics, to render a virtual performance out
of the lyrics and an input score. Although based
on complex articulation-oriented concatenation
constraints, sample selection relies on a full search
of sample candidates, examining the context of two
score notes. Traits of the original voice and articu-
lation characteristics are impressively retained after
transformations, owing to a refined source-filter
spectral model. Jedoch, the expressive possibili-
ties are limited to manual editing of some pitch and
dynamics curves, or adding pre-defined transforma-
tion templates for including expressive resources.
In diesem Artikel, we use explicit expressivity knowl-
edge induced from the synthesis corpus, and we
later automatically apply it when selecting and
transforming samples.

The approach introduced by Lindemann (2007),
referred to as reconstructive phrase synthesis (RPM),
achieves musical expressivity through a blend of
functional additive synthesis and phrase-oriented
parametric concatenative synthesis that can be
used both off-line from a score, and real-time from
standard MIDI performance controls. This approach

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

has resulted in a successful commercial appli-
cation of concatenative sound synthesis: Synful
(www.synful.com). Slow-varying harmonic compo-
nents are directly predicted from the input score
or controls via spectral nonlinear prediction based
on neural networks. Dann, an annotated database
containing the rapidly varying components of a
selection of the most representative phrases is
searched to get the most appropriate sequence of
samples taking into account local contexts spanning
several notes. Those rapidly varying components
are added to the low-frequency ones to form the
harmonic part of the sound. Noisy elements, Auch
stored in the database, are added on top of the
concatenated harmonic sound. Although the results
obtained for excitation-continuous instruments are
impressive, especially in attacks and transitions,
this system again lacks an explicit high-level ex-
pressive component representing the deviations or
nuances that a particular performer introduces in
particular contexts.

Expressive Performance Modeling

Understanding and formalizing expressive music
performance is an extremely challenging problem
that in the past has been studied from different
perspectives (z.B., Seashore 1936; Gabrielsson 1999;
Bresin 2002). The main approaches to empirically
studying expressive performance have been based on
statistical analysis (z.B., Repp 1992), mathematical
modeling (e.g. Todd 1992), and analysis-by-synthesis
(z.B., Friberg et al. 1998). In each of these approaches,
a human is responsible for devising a theory or
mathematical model that captures different aspects
of expressive performance. The theory or model is
later tested on real performance data to determine
its accuracy. Kürzlich, machine-learning-based
approaches have been proposed. The most related
work was undertaken by Arcos, de Mantaras, Und
Serra (1997), Lopez de Mantaras and Arcos (2002),
Ramirez, Hazan, and Maestre (2006A, 2006B), Und
Ramirez et al. (2008).

Arcos, de Mantaras, and Serra (1997) and Lopez de

Mantaras and Arcos (2002) report on SaxEx, a per-
formance system capable of generating expressive

solo performances in jazz. Their system is based on
case-based reasoning, a type of analogical reasoning
where problems are solved by reusing the solutions
of similar, previously solved problems. To generate
expressive solo performances, the case-based rea-
soning system retrieves, from a memory containing
expressive interpretations, those notes that are sim-
ilar to the input inexpressive notes. Jedoch, Dort
is no analysis at the intra-note level, which means
that the note’s instantaneous amplitude and timbre
is not considered.

Ramirez et al. (2008) explore and compare dif-
ferent machine-learning techniques for inducing
both an interpretable expressive performance model
(characterized by a set of rules) and a generative
expressive performance model. Based on this, Sie
describe a performance system capable of generat-
ing expressive monophonic jazz performances and
providing “explanations” of the expressive transfor-
mations it performs. This work extends the work
of Ramirez, Hazan, and Maestre (2006A, 2006B) von
incorporating inter-note analysis of the expressive
recordings in the machine-learning and synthesis
components.

Traditionell, research in expressive performance
using machine-learning techniques has focused on
classical solo piano music (Widmer 2001) bei dem die
tempo of the performed pieces is not constant and
melody alterations are not permitted. (In classical
Musik, melody alterations are often considered
performance errors.) Daher, in such works, Die
focus is on global tempo and energy (loudness)
transformations. We are interested in note-level
timing and energy transformations as well as in
melody ornamentations that are a very important
expressive resource in jazz. Darüber hinaus, we deal with
the saxophone as an example of an excitation-
continuous instrument.

Dealing with excitation-continuous musical
instruments in particular, we find several relevant
studies also very relevant to the work presented
Hier. In Canazza et al. (2004), the authors present
an approach to modify the expressive content of
a performance in a gradual way among different
moods. They use a linear model to carry out the
alterations based on previous segmentation, Und
they modify the melodies at both the symbolic and

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

audio-signal levels. Stattdessen, we aim here to model
the expressivity of particular performers by picking
up notes from their own performance recordings and
applying rules discovered from the same data.

Trumpet performance is studied in Dannenberg,
Pellerin, and Derenyi (1998) by computing amplitude
descriptors, and the statistical analysis techniques
used for analyzing trumpet envelopes led the authors
to find significant envelope groupings, an approach
that is similar to the database annotation that we
use. Nachher, they extended the work to a system
that combined instrument and performance models
(Danneberg and Derenyi 1998), although the authors
did not take into account duration, onset deviation,
or ornamentations. The authors followed a similar
line in Dubnov and Rodet (1998), who perform
analysis of sound behavior as it occurs in the course
of an actual performance of several solo works
to build a model capable of reproducing aspects
of sound textures originating in the performer’s
expressive inflections. Jedoch, these models are
devised after a preliminary statistical analysis
rather than being induced from the training data,
possibly because of the difficulties in parameterizing
continuous data from real-world recordings.

Simon et al. (2005) introduce the use of con-
catenative synthesis for obtaining, given an input
MIDI score, a new performance from a monophonic
recording and its MIDI transcription. Their use
of a recorded melody is interesting, as is their
methodology for searching samples (single notes or
pairs of notes), but the system lacks any expressive
knowledge to be applied.

Preliminary results of the work we present in
this article were introduced in Maestre et al. (2006),
where the authors built a concatenative synthe-
sizer for rendering jazz saxophone melodies from
a database of recorded performances and an ex-
pressivity model induced from the same database
that is used for synthesis. Although promising
results were achieved, issues like context-aware
expressivity knowledge induction and sample
selection needed to be further improved. Hier
we extend the work with significant improve-
ments in sample selection and by giving a more
detailed description of each part of the whole
System.

Audio Analysis

In diesem Abschnitt, we give the details of the methods we
used for the analysis of the recordings of expressive
Aufführungen. Erste, a set of low-level descriptors
is computed for each frame. Dann, we perform
note segmentation using low-level descriptor values
and fundamental-frequency estimation. Using note
boundaries and low-level descriptors, we perform
energy-based intra-note segmentation, hintere
intra-note-segment amplitude-envelope character-
ization, and a transition description. This infor-
mation will be used for both modeling expressive
performance and annotating the sample database
used later in the synthesis stage. Audio analysis data
obtained with these methods has already been used
for expressive-performance rule induction (Ramirez,
Hazan, and Maestre 2006a), intra-note feature pre-
diction (Ramirez, Hazan, and Maestre 2005), Und
genetic programming-based expressive-performance
modeling (Ramirez et al. 2008).

The contents of the section can be summarized
as follows. Erste, we present the audio description
scheme we followed. Dann, the procedures for
melodic description, musical analysis, and intra-
note/inter-note segmentation and description are
detailliert.

Description Scheme

To define a structured set of audio descriptors
able to provide information about the expressivity
introduced in the performance, we define and
extract descriptors related to different temporal
Waage. Some features are defined as instantaneous
or related to an analysis frame, such as energy,
fundamental frequency, Spektralschwerpunkt, Und
spectral tilt. We also obtain intra-note/inter-note
segment features, d.h., descriptors attached to a
certain intra-note segment (Attacke, sustain and
release segments, considering the classical ADSR
model of, z.B., Bernstein and Cooper [1976], oder
transition segment). After observing the shape of the
energy envelope of our recorded notes, we realized
that most of the notes did not present a clear decay
segment but rather a fairly constant-slope sustain
segment. Daher, we decided not to consider decay and

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 2. Schematic view
of the melodic-description
Verfahren. Note onsets are
extracted based on the
study of energy and
fundamental frequency.

sustain segments separately, but just a linear sustain
segment with variable slope. Endlich, Note features
or descriptors attached to a certain note are also
extracted. We considered that the proposed features
set up a simple but concise scheme for representing
the typical expressive nuances in which we are
interested, adapted to our application context. Für
the complete list of descriptors, siehe Tabelle 1 im
“Database Construction” section, subsequently.

Melodic Description

The first step once the low-level descriptors have
been extracted for each frame is to get a melodic de-
scription of the audio phrases consisting of the exact
onset and duration of notes, along with the corre-
sponding MIDI equivalent pitch. We base our melody
transcription on the extraction of two different onset
streams, the first based on energy, and the second
based on fundamental frequency. Energy onsets are
first detected following a band-wise algorithm that
uses psychoacoustic knowledge (Klapuri 1999). In
ein zweiter Schritt, fundamental-frequency transitions
are also detected. Endlich, both results are merged
to find note boundaries (siehe Abbildung 2). We compute
note descriptors using the note boundaries and the
low-level descriptors values. The low-level descrip-
tors associated with a particular note segment are
computed by averaging the frame values within this
note segment. Pitch histograms are used to compute
the pitch note of each note segment. An extended
explanation of the methods we use for melodic
description can be found in Gomez et al. (2003).

Musical Analysis

It is widely recognized that expressive performance
is a multilevel phenomenon and that humans per-

form music considering a number of abstract musical
structures. After having computed the note descrip-
tors, and as a first step toward providing an abstract
structure for the recordings under study, we decided
to use Narmour’s (1990) theory of perception and
cognition of melodies to analyze the performances.
The implication/realization model proposed by
Narmour is a theory of perception and cognition of
melodies. The theory states that a melodic musical
line continuously causes listeners to generate
expectations of how the melody should continue.
The nature of these expectations in an individual
are motivated by two types of sources: innate and
gelernt. According to Narmour, on the one hand, Wir
are all born with innate information that suggests
to us how a particular melody should continue. An
die andere Hand, learned factors are due to exposure
to music throughout our lives and familiarity with
musical styles and particular melodies. Nach
to Narmour, any two consecutively perceived notes
constitute a melodic interval, and if this interval
is not conceived as complete, it is an implicative
interval, d.h., an interval that implies a subsequent
interval with certain characteristics. That is to
sagen, some notes are more likely than others to
follow the implicative interval. Two main principles
recognized by Narmour concern registral direction
and intervallic difference. The principle of registral
direction states that small intervals imply an
interval in the same registral direction (a small
upward interval implies another upward interval
and analogously for downward intervals), and large
intervals imply a change in registral direction (a large
upward interval implies a downward interval and
analogously for downward intervals). The principle
of intervallic difference states that a small (five
semitones or less) interval implies a similarly sized
interval (plus or minus two semitones), and a large
interval (seven semitones or more) implies a smaller

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 3. Prototypical
Narmour structures.

Figur 4. Narmour analysis
of All of Me.

interval. Based on these two principles, melodic
patterns or groups can be identified that either
satisfy or violate the implication as predicted by
the principles. Such patterns are called structures
and are labeled to denote characteristics in terms of
registral direction and intervallic difference.

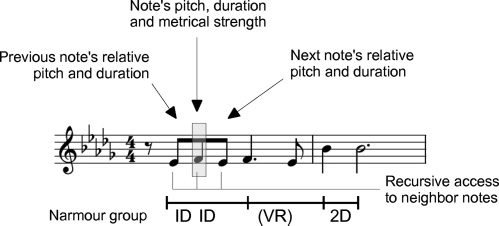
Figur 3 shows prototypical Narmour structures.

A note in a melody often belongs to more than
one structure. Daher, a description of a melody as
a sequence of Narmour structures consists of a list
of overlapping structures. We parse each melody in
the training data to automatically generate an im-
plication/realization analysis of the pieces. Figur 4
shows the analysis for a fragment of a melody.

Extraction of Intra-Note and Transition Features

Once we segment the audio signal into notes, Wir
perform a characterization of each of the notes in
terms of its internal features, and of each of the
note-to-note transitions based on the intra-note
features extracted for both notes involved in the
Übergang.

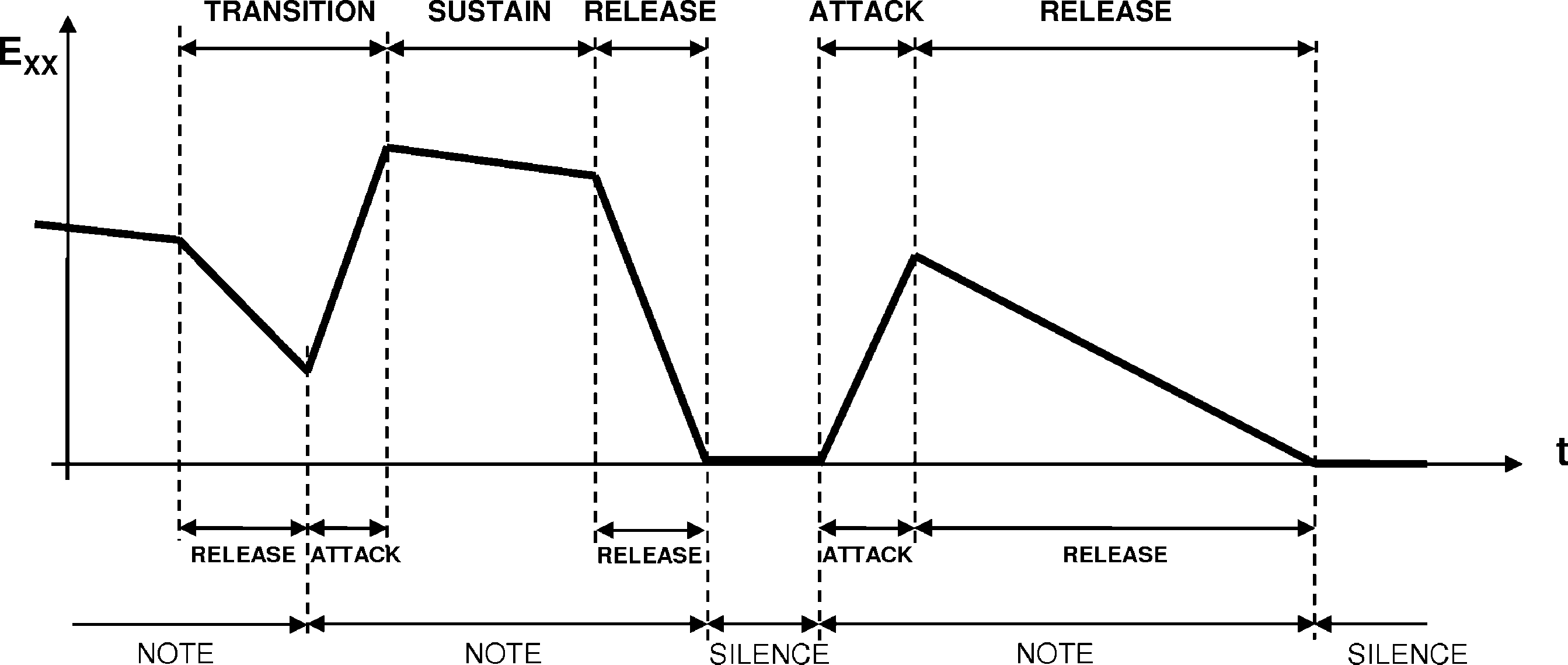
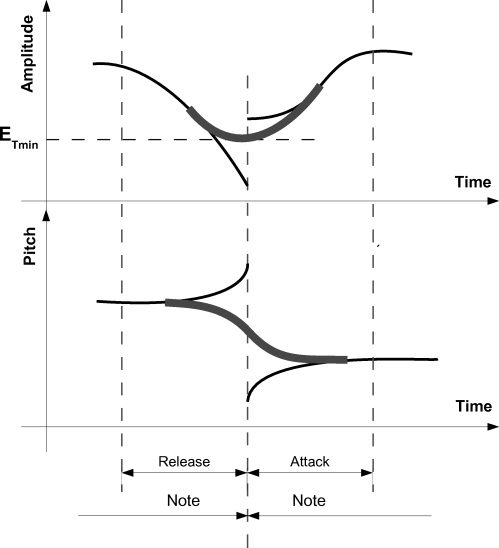
The intra-note segmentation method is based
on the study of the energy envelope contour of the
Notiz. Once onsets and offsets are located, we study
the instantaneous energy values of the analysis
frames corresponding to each note. This study is
carried out by analyzing the envelope curvature and
characterizing its shape to estimate the limits of
the intra-note segments under consideration. Der
model used is schematically represented in Figure 5.
To extract the limits of the three characteristic
segments, we perform automatic search by looking
for the energy envelopes’ second-derivative extrema
in a way similar to that presented in Jensen (1999).
Jedoch, in Jensen, partial amplitude envelopes
are modeled for isolated sounds. Hier, we instead
analyze the global energy envelope of notes in

their musical context, considering two (attack and
release) or three (Attacke, aufrechterhalten, and release) linear
segments, depending on the appearance of sustain
segment. Transition segments are considered as
including release and attack segments of adjacent
notes. We described in detail and evaluated the
procedure for carrying out intra-note segmentation
in Maestre and Gomez (2005).

Once we have found the intra-note segment
limits, we describe each one by its duration (absolute
and relative to note duration), start and end times,
initial and final energy values (absolute and relative
to note maximum), and slope. We also extract two
spectral descriptors corresponding to the sustain
segment: spectral centroid and spectral tilt (Peeters
2004). These are computed as an average along the
sustain segment, or else as a single value at the
end of the attack segment when a sustain segment
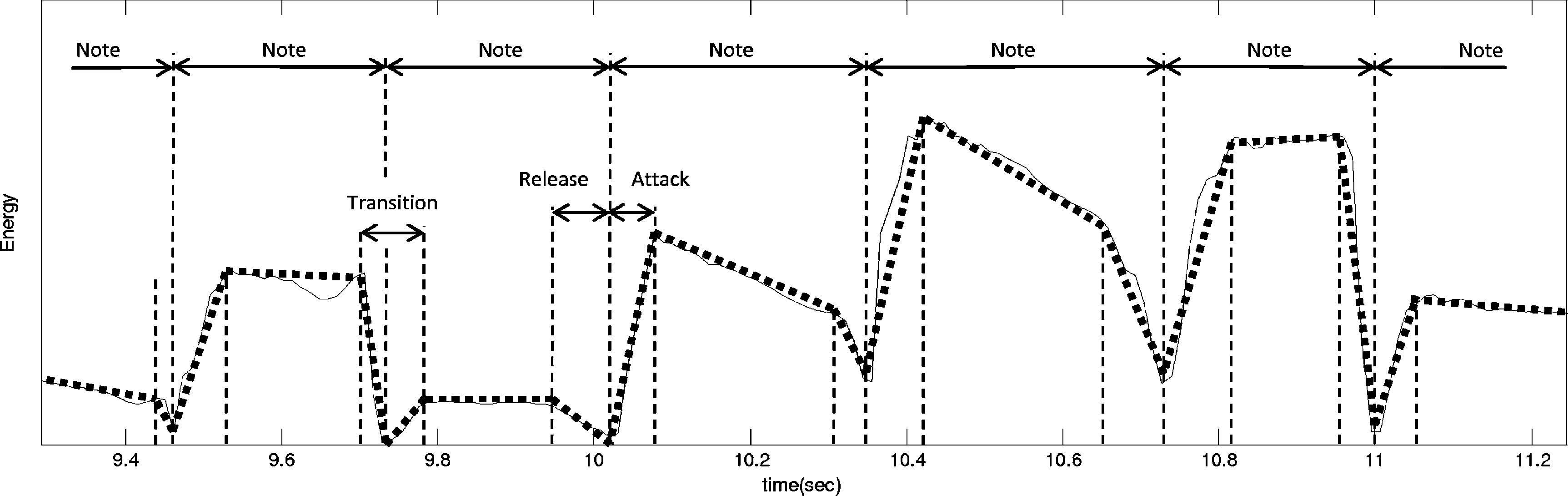
has not been detected. Figur 6 shows the linear
approximation of energy envelope of a real excerpt
obtained by using the methods presented here.

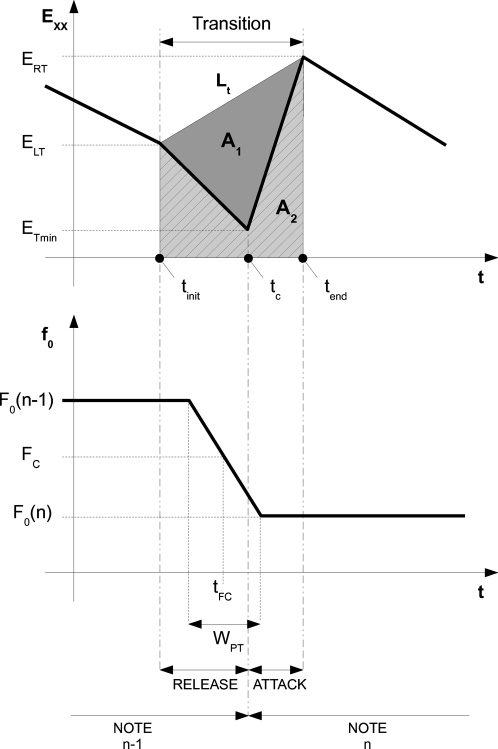
To characterize note detachment, we also extract
some features of the note-to-note transitions describ-
ing how two notes are detached. For two consecutive
notes, we consider the transition segment starting at
the beginning of the first note’s release and finishing
at the end of the following note’s attack. Both the
energy envelope and the fundamental-frequency
contour (schematically represented by E XX and f0
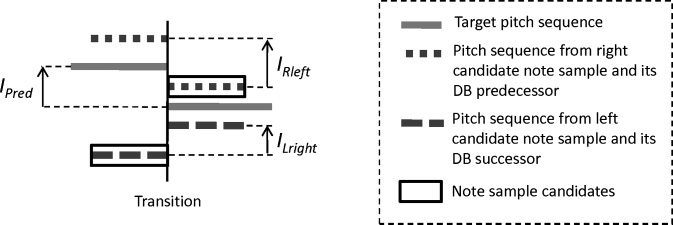
in Abbildung 7) during transitions are studied to extract
descriptors related to articulation. We measure the
energy envelope minimum position tc (see also
Figur 7) with respect to the transition duration
as Equation 1. This descriptor has proven useful
when reconstructing amplitude envelopes during
transitions.

ETPOSmin

tc
tend − tinit

(1)

We then compute a legato descriptor as described

nächste. Erste, we join start and end points on the
energy-envelope contour by means of a line Lt

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 5. Schematic view
of the energy-envelope-
based intra-note
segmentation that is used
in this work.

Figur 6. Energy envelope
of a real excerpt with
intra-note segment and
transition limits depicted,
where the linear
approximation has been
superimposed.

Figur 5

Figur 6

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

representing the smoothest (least detached) case of
articulation. Dann, we compute both the area A2
below the energy envelope and the area A1 between
the energy envelope and the joining line Lt and
define our legato descriptor as shown in Equation 2.
The legato descriptor has a value of 0.0 when it
is smoothest and 1.0 when it is most detached. In
Maestre and Gomez (2005), we evaluate the validity
of this descriptor.

LE G =

A1
A1 + A2

(cid:2)

tend
tinit

(Lt(T) − E XX(T))dt
(cid:2)
Lt(T)dt

tend
tinit

(2)

After observing fundamental-frequency contours
from the recordings, pitch transitions are considered
to be linear for this study (see lower part Figure
7), being characterized by measuring width and
translation with respect to the position of the
energy-envelope minimum and the transition

Länge. (Portamento transitions, d.h., transitions
incurring pitch glides significantly slower than
the linear pitch transitions in our study, are not
berücksichtigt, as they are not present in the recordings
used for constructing the database.) Pitch-transition
center time tF C and width WP T are measured by
finding the boundaries of pitch steps, studying
pitch derivatives along the transition. To do so, Wir
followed an approach analogous to the one followed
for describing the energy envelope of a note: Wir
characterize pitch contour by three linear segments
using automatic segmentation adapted from the
method introduced in Maestre and Gomez (2005).
Pitch-transition center time tF C is estimated as the
midpoint of the pitch step width WP T. Pitch-step
width WP T enriches a legato descriptor in terms of
fundamental-frequency description, and it is also
used for helping in the final concatenation step
during the synthesis stage.

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Computermusikjournal

Figur 7. Schematic view
of the transition-segment
characterization.

Figur 8. Datenbank
construction steps. Once
the melodic description
has been obtained,
intra-note and transition

segment annotations are
attached to each note
sample together with their
melodic description.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Database Construction

Although currently employed in a synthesis con-
Text, the database used in this work was recorded
for analysis purposes. Previous studies carried out
by the authors focused on studying timing and dy-
namics deviations occurring during jazz saxophone
performances at different tempi (Gomez et al. 2003),
obtaining significant results. Later, we found it inter-
esting to apply the obtained expressive-performance
models for audio synthesis (Ramirez, Hazan, Und
Maestre 2006a, 2006B). In addition to using the au-
dio recordings for inducing expressive performance
Modelle, we also aim at exploring the possibilities
of using the performance-recordings database for

rendering new performances using concatenative
synthesis. Such a possibility became one of the key
points of the methodology introduced by this work.
An important issue here is the fact that dynamics or
timbre nuances and ornamentations were not given
any emphasis during the recordings (the performer
was able to freely use such resources in each con-
Text), which led us to be able induce expressivity
knowledge with no constraints, making the analysis
extensible to any performance recording.

We used an audio database consisting of four
jazz standards played by a professional musician
at eleven different tempi around the nominal one.
Most phrases were repeated to test consistency
among performances. The jazz standards recorded
were Body and Soul, Once I Loved, Like Someone
in Love, and Up Jumped Spring—approximately 1.5
hours of recording distributed among approximately
5,000 notes. The different steps followed for the
construction of the database are sketched in Figure 8.
Out of the performance recordings, we carry
out both segmentation into notes and a melodic

Maestre et al.

description for each phrase. Dann, starting from the
note segmentation, we perform intra-note segmen-
tation into attack, sustain or release segments for
each note, thus also obtaining the note-to-note tran-
sition limits. Intra-note segments and transitions
are then characterized in a fourth step, following
also the techniques for audio analysis outlined
previously. Dann, we classify notes based on their
context in the performance, and also based on their
amplitude envelope and timbral features. Endlich,
we store audio files of recorded phrases along with
their corresponding XML annotation files including
segmentation and extracted features for each note
at the different temporal levels considered in the
Analyse.

Note Classiﬁcation

We group notes in two different steps. Erste, Wir
classify notes from the recorded phrases into four
different articulation classes, depending on their
Kontext, by looking at the adjacent segments.
Referring to the note under consideration as n
and to a silence as to SIL, the four classes are (1)
SIL–n–SIL, (2) SIL–n–NOTE, (3) NOTE–n–SIL, Und
(4) NOTE–n–NOTE. This information will be used as
a strict constraint during the sample-retrieval stage
to match the original articulation context of the
notes used for synthesizing the output performance.
Once the expressive component predicts the output
note sequence, the resulting articulation group for
each note is used for fulfilling this requirement. Wir
observed notable improvements in the synthesis
results when forcing the sample-search algorithm to
strictly match the articulation group.

As a second step, we divide, for each set of notes
corresponding to one of the four articulation groups,
all notes (as segmented from the recordings) into
several clusters. This is done by characterizing each
note by a set of intra-note features representing the
internal structure of the note. The set of intra-note
features consists of the note’s attack level, aufrechterhalten
Dauer (relative to the duration of the note), aufrechterhalten
slope, Spektralschwerpunkt, and spectral tilt. Das ist,
each performed note is characterized by the tuple
(AtackLev, SustDur, SustSlo, SpecCen, SpecTilt).
These intra-note features provide an amplitude and

timbre description for each note in the database.
Based on this note characterization, we apply k-
means clustering to group together notes that are
likely to be perceptually similar. The choice of the
value for k was chosen according to the predictive
accuracy of the classifiers described later in the
section entitled “Transition Level Prediction”: k = 2
for articulation groups SIL–n–SIL, SIL–n–NOTE, Und
NOTE–n–NOTE, and k = 3 for group NOTE–n–SIL.
We also consider transformations consisting of
alterations to the melody (as specified in the score) von
introducing or suppressing notes. Daher, we annotate
the notes in the recordings to indicate whether a
note alters the melody. We have categorized these
transformations as consolidations, fragmentations,
and ornamentations. A consolidation represents the
agglomeration of multiple score notes into a single
performed note, a fragmentation represents the
performance of a single score note as multiple notes,
and an ornamentation represents the insertion of one
or several short notes between two performed notes.

Database Annotation Overview

Tisch 1 summarizes the descriptors attached to
each note in the database. The table shows a logical
grouping of descriptors, as well as the context in
which each descriptor is used in our system.

Expressive Performance Modeling

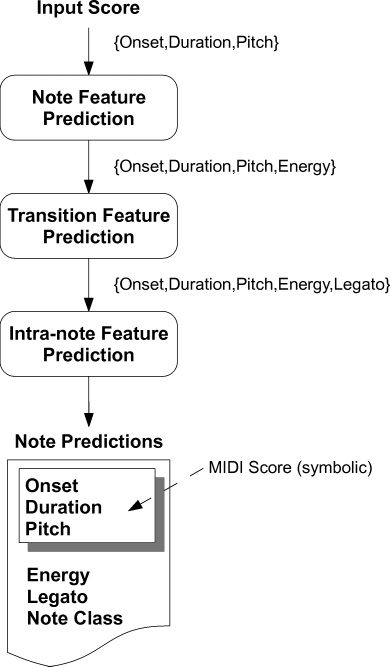
In diesem Abschnitt, we describe our inductive approach
to learning expressive-performance models for
different expressiveness-related dimensions such
as duration transformation, onset, Energie, melody
alteration (z.B., ornamentations), inter-note transi-
tionen, and/or note-class estimation. Diese Modelle
are applied at different stages to automatically
synthesize expressive audio. Erste, ornamentation
and rhythm variation relative to the input score are
predicted, together with the note’s mean energy.
Dann, subsequent predictions (transition level and
intra-note level) are performed for each of the notes
present in the obtained sequence (siehe Abbildung 9).
Note that the term “prediction” here does
not refer to any anticipation of future notes in

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Tisch 1. Database Annotation Overview

Logical Group

Descriptor Name

Short Name Type (Einheiten)

Context Usage

Notiz
Classiﬁcation Modeling

Expression Concatenative

Melody/Dynamics Pitch

Onset time
Duration
Alteration
Mean Energy

Pitch
Tonne
Dauer
Alt
EnergyM

Context

Timbre

Intra-Note

Classification

MetStr

Metrical Strength
Narmour group (Pos 1) Nar1
Narmour group (Pos 2) Nar2
Narmour group (Pos 3) Nar3
Articulation group
Duration (previous)
Duration (nächste)
Pitch (previous)
Pitch (succ)

ArtGroup
PrevDur
NextDur
PrevPitch
NextPitch

Mean spectral centroid
Mean spectral tilt

SpecCen
SpecTilt

AttackLev

Attack level
Sustain relative duration SustDur
SustSlo
Sustain slope
LegLeft
Legato (previous)
LegRight
Legato (nächste)
tc
Note change time
tinit
Transition init time
tend
Transition end time
WPT
Pitch step width time
tpc
Pitch step center time
Clus

Cluster number

real (Hz)
real (Sek)
real (Sek)
Label
real (dB)

Label
Label
Label
Label
Label
real (Sek)
real (Sek)
real (Hz)
real (Hz)

X
real (Hz)
real (dB/oct) X

X
real (dB)
real (Verhältnis)
X
real (dB/sec.) X
real (Verhältnis)
real (Verhältnis)
real (Sek)
real (Sek)
real (Sek)
real (Sek)
real (Sek)

Label

X
X
X
X
X

X
X
X
X
X
X
X
X
X

X
X

X
X
X
X
X

Synthesis

X
X
X

X
X

X
X
X
X
X

die Performance, but rather to the output of
our performance model, which “predicts” the
expressiveness-related dimensions as relative to
the input score. A more detailed description of the
model induction process can be found in Ramirez,
Hazan, and Maestre (2006B).

Training Data

The training data used to induce the expressive per-
formance model is the data described in the section
entitled “Database Construction”—monophonic
recordings of jazz standards performances at dif-
ferent tempi. Each note in the musical score is

characterized by a set of features representing the
musical context in which the note appears. Das
set of features consists of the note’s pitch, Dauer,
and metrical strength; relative pitch and duration of
the neighboring notes (d.h., previous and following
notes); and the Narmour structures to which the
note belongs (siehe Abbildung 10). Daher, each score note is
contextually characterized by the tuple (Pitch, Dauer,
MetStr, PrevPitch, PrevDur, NextPitch, NextDur,
Nar1, Nar2, Nar3).

Zusätzlich, each performed note is characterized

by a set of intra-note and transition features. Der
intra-note and transition features represent the
internal structure of a note, specified as intra-note

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 9. Overview of the
learning task.

Figur 10. Overview of the
note’s musical context
characterization.

the nodes of the tree, the algorithm tests logical
predicates. This provides the advantages of both
propositional decision trees (d.h., efficiency and
pruning techniques), the use of first-order logic (d.h.,
increased expressiveness), and the possibility of
including background knowledge in the learning
Verfahren. The increased expressiveness of first-order
logic not only provides a more elegant and efficient
specification of the musical context of a note, but it
provides a more accurate predictive model (Ramirez,
Hazan, and Maestre 2006b).

Temporal sequencing of notes is captured by
including a predicate succ(X, Y) in the learning pro-
Prozess. The predicate succ(X, Y) means “the successor
of X is Y.” Note that succ(X, Y) also means “X is the
predecessor of Y.” The succ(X, Y) predicate allows
the specification of arbitrarily sized note contexts by
chaining a number of successive notes: succ(X1, X2),
succ(X2, X3) . . . , succ(Xn−1, Xn), where Xi (1 ≤ i ≤ n)
is the note of interest.

Note-Level Prediction

At the note level, we are interested in predicting
duration transformation, onset deviation, Energie
Variation, and any note alterations (z.B., orna-
mentations). These expressive transformations are
respectively represented by the parameters duration,
onset, Energie, and alteration. Duration is expressed
as a percentage of the note score duration (z.B., A
value of 1.1 represents a prediction of 10% Länge-
ening for a particular note). Onset is expressed as a
fraction of a quarter note (z.B., 0.2 represents a delay
in onset of 0.2 of a quarter note). Energy is expressed
as a percentage of a predefined average energy
value extracted from the whole set of recordings.

and transition characteristics extracted from the
audio signal. These consist of the note’s attack level,
sustain relative duration, sustain slope, amount of
legato with respect to the previous note, amount
of legato with respect to the following note, mean
Energie, Spektralschwerpunkt, and spectral tilt. Das ist,
each performed note is characterized by the tuple
(AttackLev, SustDur, SustSlo, LegLeft, LegRight,
EnergyM, SpecCen, SpecTilt).

Algorithm

To obtain the expressive performance models, Wir
apply inductive logic programming techniques, In
particular Tilde’s inductive algorithm (Blockeel
et al. 1998). Tilde’s algorithm can be considered as a
first-order logic extension of the C4.5 decision-tree
Algorithmus: Instead of testing attribute values at

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Tisch 2. Correlation Coefﬁcient (CC), Relative
Absolute Error (RAE), and Root Relative Squared
Error (RRSE) for the Duration, Onset, and Energy
Models

Tisch 3. Correctly Classiﬁed Instances (CCI),
Relative Absolute Error (RAE), and Root Relative
Squared Error (RRSE) for the Melody-Alteration
Modell

90.02
80.37
79.80

RAE
(%)

70.12
45.25
36.61

RRSE
(%)

87.45
76.96
71.52

Onset
Duration
Energy

Alteration assumes one of the following classes:
consolidation, fragmentation, ornamentation, Und
none. By applying the Tilde inductive logic pro-
gramming algorithm (see the previous section), Wir
learn a predicate definition (d.h., a set of first-order
rules) for each of the expressive transformations.
The accuracies obtained by applying inductive logic
programming techniques to the data are higher than
the accuracies obtained by other machine-learning
Techniken, including support vector machines,
(propositional) decision trees, k-nearest neighbor,
and artificial neural networks. Details of the re-
sulting models, which were evaluated by means of
10-fold cross validation, can be found in Ramirez,
Hazan, and Maestre (2006B).

Transition-Level Prediction

At the inter-note level, we are interested in predict-
ing the type of transition (legato/staccato) zwischen
two neighboring notes. Um dies zu tun, we assign each
performed note to a one of four articulation groups
depending on whether the note is preceded/followed
by silence or a note. For the group of notes preceded
and followed by a silence (d.h., SIL–n–SIL), es gibt kein
need to predict any type of transition; for the groups
of notes preceded by a note (d.h., NOTE–n–SIL and
NOTE–n–NOTE), we predict the transition with
the previous note; and for the groups followed by
a note (d.h., SIL–n–NOTE and NOTE–n–NOTE), Wir
predict the transition with the subsequent note. Der
transition-level prediction consists then of a real
number in [0, 1], mit 0 representing a maximum
staccato transition and 1 representing a maximum

CCI (%)

RAE (%)

RRSE (%)

Melody alteration

80.37

45.25

56.96

legato transition. Tisch 2 shows the obtained corre-
lation coefficient (CC), and relative absolute error
(RAE) for the legato prediction model. The RAE is a
relative measure of the average absolute prediction
error and the average absolute deviation of the real
performance data values from their mean.

From the results shown in Table 2, we can see
how the models involving silences (NOTE–n–SIL
and SIL–n–NOTE) show a CC and RAE consistently
higher than those not involving silences (NOTE–n–
NOTE). One possible cause for this difference would
simply appear to be related to inherent limitations of
the learning task: it might remain more “difficult”
to model legato in NOTE–n–SIL and SIL–n–NOTE
transitions. Jedoch, we attribute the observed
difference to database sparseness: the space is less
populated with NOTE–n–SIL and SIL–n–NOTE
transitions than with NOTE–n–NOTE transitions,
so a smaller set of examples (z.B., a less rich variety
of context parameters) is used when training the first
two models, keeping the accuracy from reaching
equivalent levels.

Intra-Note Level Prediction

For each of the articulation groups described above
(d.h., SIL–n–SIL, SIL–n–NOTE, NOTE–n–SIL, Und
NOTE–n–NOTE), we are interested in predicting
several intra-note properties, z.B., attack level.
We apply k-means clustering to all the notes in a
particular articulation group using the intra-note
Merkmale. This divides the notes within a particular
articulation group into a set of clusters, jede
containing notes with similar intra-note features.
For each articulation group, we train a classifier
Das, given the musical context of a note, predicts
a cluster. Tisch 3 shows the number of clusters

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 11. Overview of the
audio-synthesis engine.

considered and the ratio of correctly classified
instances for each articulation group. Wir haben
selected the number of classes based on comparing
their relative classification accuracies.

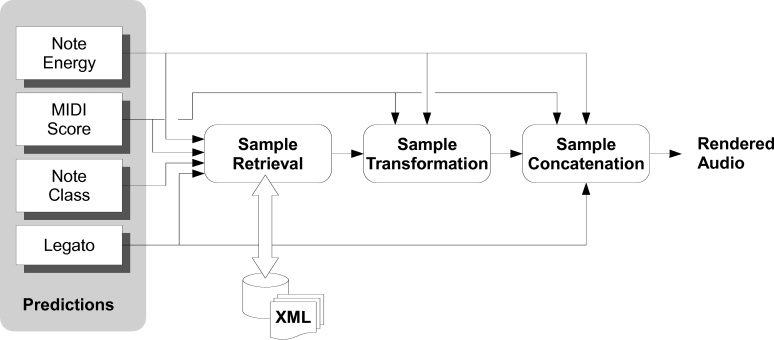
Audio Synthesis

The system generates the audio sequence based on
the predictions of the expressive performance model
and the annotated sample database. An overview
of the process is illustrated in Figure 11. Erste, Die
expressive-performance modeling component is fed
with the input score, and a prediction of an enriched
note sequence is obtained (see the previous section).
For each note in the new sequence, a candidate
list containing possible matching samples from the
database is generated. Dann, the best note sample
sequence is determined by paying attention both
to the “cost” of the transformations to be applied
(as explained subsequently) and also to the concate-
nations involved. Selected samples are analyzed in
the spectral domain, and a representation of their
spectral regions (Bonada and Loscos 2003; Laroche
2003) is extracted. Such a representation allows us
to apply phase-vocoder techniques for time, Bin-
plitude, and frequency transformations, along with
equalizations needed in the concatenations.

For the synthesis part of this work, we adapted a

generic concatenative-synthesis framework cur-
rently being developed at Music Technology

Group (GenConcatSynth) and being used in dif-
ferent sample-based synthesis applications. Notes
(Proben) are transformed to fit the predicted note
characteristics applying global note amplitude trans-
Formation, pitch shift, and non-linear time stretch
for matching, jeweils, Dynamik, fundamental
frequency, and duration of the target sequence. Nach
Das, samples are concatenated by means of ampli-
tude, pitch, and spectral-shape interpolation applied
to the resulting note transitions to obtain a smooth
reconstruction from release and attack segments of
adjacent notes. Amplitude reconstruction is carried
out by taking into account the legato prediction
coming from the expressive-performance modeling
component.

Sample Retrieval

The output of the expressive performance-modeling
component carries time (onset and duration),
fundamental-frequency (pitch), and dynamics
(Energie) information at a global note level. In einem
subsequent step, the note-class prediction (cluster)
containing information about energy envelope and
spectral shape is provided, along with a predic-
tion of the legato feature for each of the involved
transitions. With this information, the best pos-
sible combination of notes from the database is
determined.

We recall here the recurrent problem of database

sparseness in sample-based systems for which

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

high-dimensional descriptions are attached to each
sample. We used four songs—each one played at
eleven different tempi, implying lower coverage
in pitch-related dimensions than in duration and
timbre-related features. Even though we did not
formally check how populated the different areas
of the feature space are, we devised a clustering
step during database analysis and a further cluster
prediction step prior to synthesis to avoid pre-
dictions in too high-dimensional of a space. Der
advantage of compacting information by means of
such a classification and class-prediction process is
that a set of dimensions potentially causing sparse-
ness in the feature space (z.B., energy-envelope or
timbral features) are instead modeled as areas in
such the space from which note samples will be
retrieved, mostly based on dimensions for which
interpolation is available. This therefore implies a
constrained high-dimensional prediction, ensuring
that interpolation is not needed for all dimensions,
because an actual sample will be retrieved and no
transformations will be applied in the dimensions
used in this dual “classification–class prediction”
Verfahren. Daher, a number of other features (those
used for distance computation within the predicted
cluster) configure a space for which interpolation is
indeed performed (z.B., global energy, Dauer, oder
pitch transformation).

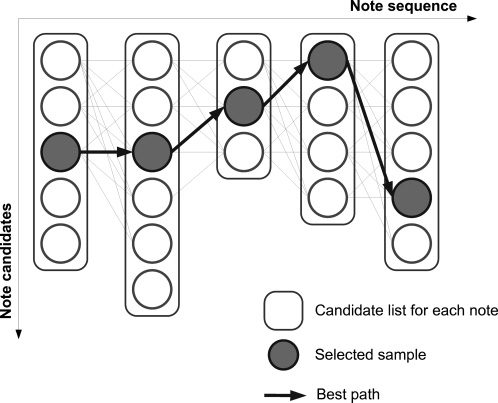
Jetzt, an overview of the sample-retrieval pro-
cess is given. Erste, a list of all possible candidates
for each note in the sequence is generated, bei-
tending to the constraints given by database note
classification (see subsequent discussion). Dann, A
computational “cost” is computed for every pos-
sible path, considering the limitations of involved
sample transformations and concatenations. Es ist
important to clarify here that by “cost” we do not
refer to computational efficiency, but to a distance
between samples (see the next section) that provides
an estimation of the potential degradation of candi-
date samples when transforming and concatenating
ihnen. The most suitable combination of samples is
found as the notes belonging to the path presenting
the minimum total cost (siehe Abbildung 12 and the sec-
tion entitled “Computation of Costs”). Depending
on the computation requirements, the candidate
lists may be truncated by attending to pre-computed

Figur 12. Illustration of
the path search. Once the
candidate sample list is
generated for each note, alle
possible paths are
searched, and the path
presenting the minimum
total cost is selected.

transformation and applying some thresholds. Wir
use dynamic programming techniques, by means
of the so-called Viterbi algorithm (Viterbi 1967) Zu
speed up the search.

Candidate Sample List Generation

Based on the articulation class of each of the
notes in such an output sequence, and also on the
predicted note class (cluster), a list containing all
possible candidates from the database is generated.
Candidates must match the articulation class and
must also belong to the predicted class cluster. Mit
the goal of reducing the number of computations
needed during the search (especially for large
databases or long sequences with no silence in
between notes), the candidate list might be truncated
by pre-computing sample transformation costs
(see the next section) and retaining the n best
candidates.

Computation of Costs

A set of heuristic formulas adapted to our
application context has been devised for satisfying
our needs for cost computation during the sample-
retrieval stage. It remains difficult to formally assess

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

the quality and validity of such a set of ad hoc cost
formulas. Even though we aimed at designing them
as general and independent of the algorithms used,
some consideration was given to a subjective quality
measure of the techniques available for transforma-
tion (see for instance the duration-transformation
and frequency-transformation costs). Darüber hinaus, Wir
carried out a manual calibration of applied weights
by listening to synthesis results for a set of ad hoc
input scores by supervising sample retrieval and
transformation processes. Letzten Endes, a formal
calibration of cost formulas and weights would
need of an extensive set of perceptual listening
tests.

The total path cost CP is computed in Equation 3

as a weighted sum of two components: the to-
tal sample transformation cost CT and the total
concatenation cost CC.

CP = wTCT + wCCC

(3)

Transformation Cost

We compute the total transformation cost CT as the
sum of the transformation costs for each of the NS
note samples of the path. We obtain the estimation
of the transformation cost from a weighted sum of
three different sub-costs (Gleichung 4): the duration
transformation cost CD, the frequency transforma-
tion cost CF , and the energy transformation cost CE .

CT =

NS(cid:3)

i=1

wDCD(ich) + wF CF (ich)(ich) + wE CE (ich)

(4)

The duration transformation cost CD is computed
as a weighted average of time-stretch transformation
costs CTS, computed from the time-stretch factor
FTS values to be applied along the note sample to
match the predicted duration. This is expressed in
Gleichung 5, where Nf corresponds to number of
frames of the database sample. Time stretching is
not applied linearly for the whole note, but rather
according to a variable-shape function. The shape of
such functions can vary to avoid stretching critical
Abschnitte, such as attack or release segments. (Ihre
limits are annotated.) For weighting, we use the
time-stretch transformation cost CTS itself, so that

high values penalize the total cost.

CD =

(cid:4)

NS
i=1 C2
TS(ich)
N
i=1 CTS(ich)

(5)

In Equation 6, a logarithmic function is used
for computing the time-stretch transformation cost
CTS to make its value equal to unity for time-
stretch factors of 2 oder 0.5. This decision is based
on prior knowledge on the quality of our time-
stretch transformation algorithm (see next section),
assuming near-lossless time-stretch transformations
for stretching factors of 0.5–2.

CTS = |log2(FTS)|

(6)

For the frequency transformation cost CF , wir gebrauchen
a logarithmic function that depends on the relation
of the fundamental frequencies expressed in Hz, als
it is expressed in Equation 7. A transposition of one
octave up or down would correspond to a cost of
unity. Wieder, the decision adapting the cost formula
to arbitrary limits of transposition transformation
(one octave) is based on prior knowledge of the
quality of the pitch-shifting technique that we used
(See the next section).

(cid:6)

(cid:5)
(cid:5)
(cid:5)
(cid:5)log2

CF =

(cid:7)(cid:5)
(cid:5)
(cid:5)
(cid:5) . . . .

F0 Pred
F0 DB

(7)

The energy transformation cost CE is computed
from the relation of the predicted mean energy E Pr ed
and the mean energy of the database sample E DB
expressed in a linear scale (RMS), using again a
logarithmic function for which a global amplitude
transformation of ±12dB would correspond to a cost
of unity (Gleichung 8).
(cid:5)
(cid:5)
(cid:5)
(cid:5)log2

(cid:7)(cid:5)
(cid:5)
(cid:5)
(cid:5) . . . .

(8)

(cid:6)

CE = 1
2

EPred
EDB

Concatenation Cost

The concatenation cost CC of the path is computed
as a sum of all NC involved sample-to-sample
concatenations. Wieder, we compute it as a weighted
sum of three sub-costs: the legato cost CL, Die
interval cost CI , and the continuity cost CP , als

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 13. Illustration of
the intervals involved in
the interval cost
Berechnung.

expressed in Equation 9:

Sample Transformation

CC =

NC(cid:3)

i=1

wLCL(ich) + wICI (ich) + wP CP (ich))

(9)

For computing the legato cost CL, taking into
account that its value ranges from zero to unity,
we use the difference between the predicted value
LEGPr ed and a pre-computation of the legato de-
scriptor LEGDBr ec resulting from concatenating
the two samples involved in the transition into
consideration (Gleichung 10).

CL = |LE GPred − LE GDBrec|

(10)

We compute an interval cost CI of the notes
involved in the transition (siehe Abbildung 13) as expressed
in Gleichung 11:

(cid:5)
(cid:5)
(cid:5)
(cid:5)

CI =

|IPred − ILright| + |IPred − IRleft|
IPred

(cid:5)
(cid:5)
(cid:5)
(cid:5)

(11)

Hier, IPr ed corresponds to the target interval, IRlef t
corresponds to interval from the candidate sample
at the right side of the transition to its predecessor
sample in the database, and ILright corresponds to
interval from the candidate sample at the left side
of the transition to its successor sample in the
database.

Endlich, we reward sample choices for which notes

that were consecutive in the database recordings
appear as consecutive in the synthesis sequence,
by including a continuity cost CP . This cost is set
to zero if such a condition is satisfied, and unity
ansonsten.

Once the best sequence of note samples has been
determined, samples are analyzed in the spectral
Domain, obtaining a frame representation array
based on spectral peaks and harmonic regions.
Using spectral-processing techniques based on the
phase-vocoder (Amatriain et al. 2002; Bonada and
Loscos 2003; Laroche 2003), each retrieved note
is transformed in terms of amplitude, pitch, Und
duration to match the target description given at the
output of the performance model.

To match the energy prediction, a note global-
energy transformation is applied to the sample as
a global amplitude transformation, weil das
energy-envelope quality, Spektralschwerpunkt, Und
spectral tilt are already represented by the note
Klasse (cluster) prediction. (See the previous section
entitled “Transition Level Prediction.”)

Dann, a pitch transformation is applied to the
sample by shifting harmonic regions of the spectrum
by an amount equal to the fundamental frequency
ratio between the retrieved sample and the value
appearing in the sample sequence, preserving
spectral shape (Laroche 2003).

In a final step, a duration transformation is
carried out by applying a time stretch with vari-
able stretch-factor values along the note’s length.
The frame insertion/dropping rate is not con-
stant along the note, as it is governed by an ad
hoc function constructed from the intra-note seg-
mentation annotations. This prevents inserting or
dropping frames outside the limits of the sustain
segment so that blurring of attacks or transitions is
avoided. The fundamental frequency and spectral
shape of the new frames are obtained by linearly

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 14. Amplitude and
pitch corrections applied
during the transition-
reconstruction stage. Der
value ETmin is adjusted to
match the legato
prediction for such a
Übergang.

interpolation (Bonada and Loscos 2003) while
maintaining overall energy.

Abschluss

We have presented an approach to synthesizing
expressive jazz-saxophone performances that is
based on concatenating note samples (Aufnahmen
of notes). We used a set of expressive saxophone
recordings both for training the performance model
and for constructing the database used for synthesis.
We have carried out tests synthesizing pieces in the
training set and pieces not included in the training
set and obtained promising results. The presence
of subtle timbral and loudness discontinuities in
the synthesized pieces has led us to consider using
samples of transitions in our future work. Es ist
always difficult to evaluate formally a model that
captures subjective knowledge, as is the case with
an expressive music synthesis model. The ultimate
evaluation may consist of listening to the resulting
synthesized pieces.

Further work includes studying pitch contour to
model portamento-like transitions and pitch mod-
ulations (z.B., Vibrato) occurring within a sustain
segment. Darüber hinaus, owing to the difficulties of eval-
uating the synthesized performance’s expressivity
and naturalness, we must carry out more extended
auditory tests to be able to tune and improve our
System. This work should be considered as a step
toward a methodology for the automatic creation
of both the performance model and the sample
database needed to carry out expressive synthesis.
The application of the proposed methodology to
other instruments, together with the exploration of
other classification techniques, can only inspire the
expansion and further improvement of high-level,
sample-based instrumental sound synthesis.

Danksagungen

The authors would like to thank Emilia G ´omez,
Maarten Grachten, and Amaury Hazan for data
preprocessing; and Jordi Janer, Jordi Bonada, Und
Merlijn Blaauw for their work in the sound-synthesis
Rahmen.

interpolating the surrounding frames (Amatriain
et al. 2002).

Sample Concatenation

Endlich, sample concatenation is performed by
restoring the possible amplitude, pitch, and timbre
discontinuities occurring within the resulting tran-
sitions in the neighborhood of the junction point
between each pair of consecutive notes (d.h., those
with no silence in between them). On one side,
amplitude and pitch contours are reconstructed
(siehe Abbildung 14) by means of smoothing curves (Wir
use cubic splines) spanning several frames. Für
the case of amplitude reconstruction, the shape of
the curve is adapted by means of controlling the
minimum energy value ETmin so that it matches the
prediction of legato (its value is computed following
the procedure outlined in the previous section,
“Extraction of Intra-Note and Transition Features”)
coming from the expressive-performance modeling
component. Timbre discontinuities are smoothed
around the junction point by spectral-shape

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Verweise

Amatriain, X., et al. 2002. “Spectral Processing.” In U.
Zoelzer, Hrsg. DAFX Digital Audio Effects. New York:
Wiley, S. 373–438.

Arcos, J., R. de Mantaras, and X. Serra. 1997. “SaxEx:
A Case-Based Reasoning System for Generating Ex-
pressive Musical Performances.” Proceedings of the
1997 International Computer Music Conference. San
Francisco, Kalifornien: International Computer Music
Association, S. 329–336.

Aucouturier, J. J., and F. Pachet. 2006. “Jamming with

Plunderphonics: Interactive Concatenative Synthesis of
Music.” Journal of New Music Research 35(1):35–50.
Beller, G., et al. 2005. “A Hybrid Concatenative Synthesis
System on the Intersection of Music and Speech.”
Proceedings of 2005 Joun ´ees d’Informatique Musicale.
Lyon, Frankreich: GRAME, S. 41–45.

Bernstein, A. D., and E. D. Cooper. 1976. “The Piecewise
Linear Technique of Electronic Music Synthesis.”
Journal of the Audio Engineering Society 24(6):446–
454.

Blockeel, H., L. De Raedt, and J. Ramon. 1998. “Top-
down Induction of Clustering Trees.” Proceedings
of the 15th International Conference on Machine
Learning. San Francisco, Kalifornien: Morgan Kaufmann,
S. 55–63.

Bonada , J., and A. Loscos. 2003. “Sample-Based Singing

Voice Synthesis Based in Spectral Concatenation.” Pro-
ceedings of the 2003 Stockholm Music and Acoustics
Conference. Stockholm: KTH, S. 439–442.

Bonada, J., and X. Serra. 2007. “Synthesis of the Singing
Voice by Performance Sampling and Spectral Models.”
IEEE Signal Processing Magazine 24(2):67–78.

Bresin, R. 2002. “Articulation Rules for Automatic Music
Performance.” Proceedings of the 2001 International
Computermusikkonferenz. San Francisco, Kalifornien:
International Computer Music Association, S. 294–
297.

Canazza, S., et al. 2004. “Modelling and Control of

Expressiveness in Music Performance.” Proceedings of
the IEEE 92(4):686–701.

Danneberg, R. B., and I. Derenyi. 1998. “Combining

Instrument and Performance Models for High Quality
Music Synthesis.” Journal of New Music Research
27(3):211–238.

Dannenberg, R. B., A. Pellerin, and I. Derenyi. 1998.

“A Study of Trumpet Envelopes.” Proceedings of the
1998 International Computer Music Conference. San
Francisco, Kalifornien: International Computer Music
Association, S. 57–61.

Dubnov, S., and X. Rodet. 1998. “Study of Spectro-

Temporal Parameters in Musical Performance, Mit
Applications for Expressive Instrument Synthesis.”
Verfahren der 1998 IEEE International Conference
on Systems Man and Cybernetics. Piscataway, Neu
Jersey: Institute of Electrical and Electronics Engineers,
S. 1091–1094.

Friberg, A., et al. 1998. “Musical Punctuation on the

Microlevel: Automatic Identification and Performance
of Small Melodic Units.” Journal of New Music
Forschung 27(3):217–292.

Gabrielsson, A. 1999. “The Performance of Music.” In D.
Deutsch, Hrsg. The Psychology of Music, 2nd ed. Neu
York: Academic Press, S. 501–602.

Gomez, E., et al. 2003. “Melodic Characterization of

Monophonic Recordings for Expressive Tempo Trans-
formations.” Proceedings of the 2003 Stockholm
Music and Acoustics Conference. Stockholm: KTH,
S. 203–206.

Hunt, A. J., and A. W. Black. 1996. “Unit Selection in
a Concatenative Speech Synthesis System Using a
Large Speech Database.” Proceedings of the 1996 IEEE
International Conference on Acoustics, Speech, Und
Signal Processing. Piscataway, New Jersey: Institute of
Electrical and Electronics Engineers, S. 373–376.
Jensen, K. 1999. “Envelope Model of Isolated Musical

Sounds.” Proceedings of the 1999 DAFx (Digital Audio
Effects) Conference. Trondheim, Norwegen, S. 35–40.
Klapuri, A. 1999. “Sound Onset Detection by Applying
Psychoacoustic Knowledge.” Proceedings of the 1999
IEEE International Conference on Acoustics, Speech
and Signal Processing. Piscataway, New Jersey: Institut
of Electrical and Electronics Engineers, S. 3089–3092.
Klatt, D. H. 1983. “Review of Text-to-Speech Conversion
for English.” Journal of the Acoustics Society of
Amerika 82(3):737–793.

Laroche, J. 2003. “Frequency-Domain Techniques for

High-Quality Voice Modification.” Proceedings of the
2003 DAFx (Digital Audio Effects) Conference. London:
Queen Mary, University of London, S. 328–332.
Lindemann, E. 2007. “Music Synthesis with Recon-

structive Phrase Modeling.” IEEE Signal Processing
Magazine 24(2):80–91.

Lopez de Mantaras, R., and J. L. Arcos. 2002. “AI and

Musik, from Composition to Expressive Performance.
AI Magazine 23(3):43–57.

Maestre, E., and E. Gomez. 2005. “Automatic Character-
ization of Dynamics and Articulation of Monophonic
Expressive Recordings.” Proceedings of the 118th AES
Convention. New York: Audio Engineering Society,
paper number 6364.

Maestre et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M

J
.

2
0
0
9
3
3
4
2
3
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Maestre, E., et al. 2006. “Using Concatenative Synthesis
for Expressive Performance in Jazz Saxophone.” Pro-
ceedings of the 2006 International Computer Music
Conference. San Francisco, Kalifornien: International
Computer Music Association, S. 219–222.

Narmour, E. 1990. The Analysis and Cognition of Basic
Melodic Structures: The Implication Realization
Modell. Chicago, Illinois: University of Chicago Press.

Peeters, G. 2004. “A Large Set of Audio Features for

Similarity and Classification.” CUIDADO IST Project
Bericht. IRCAM.

Prudon, R. 2003. “A Selection/Concatenation TTS

Synthesis System.” PhD Thesis, LIMSI, Universität
Paris XI.

Ramirez, R., A. Hazan, and E. Maestre. 2005. “Intra-
Note Features Prediction Model for Jazz Saxophone
Performance.” Proceedings of the 2005 International
Computermusikkonferenz. San Francisco, Kalifornien:
International Computer Music Association, S. 373–
376.

Ramirez, R., A. Hazan, and E. Maestre. 2006A. “A Tool

for Generating and Explaining Expressive Music Perfor-
mances of Monophonic Jazz Melodies.” International
Journal on Artiﬁcial Intelligence Tools 15(4):673–691.
Ramirez, R., A. Hazan, and E. Maestre. 2006B. “A Data
Mining Approach to Expressive Music Performance
Modeling.” In V. A. Petrushin and L. Khan, Hrsg.
Multimedia Data Mining and Knowledge Discovery.
London: Springer, S. 362–379.

Ramirez R., et al. 2007. “Performance-based Interpreter
Identification in Saxophone Audio Recordings.” IEEE
Transactions on Circuits and Systems for Video
Technologie 7(3):356–364.

Ramirez, R., et al. 2008. “A Genetic Rule-based Expressive
Performance Model for Jazz Saxophone.” Computer
Musikjournal 32(1):338–350.

Repp, B. H. 1992. “Diversity and Commonality in Music
Performance: An Analysis of TimingMicrostructure

in Schumann’s Traumerei.” Journal of the Acoustical
Gesellschaft von Amerika 92(5):2546–2568.

Sagisaka, T. 1988. “Speech Synthesis by Rule Using an
Optimal Selection of Non-Uniform Synthesis Units.”
Verfahren der 1988 IEEE International Conference
on Acoustics, Speech, and Signal Processing. Piscat-
weg, New Jersey: Institute of Electrical and Electronics
Engineers, S. 679–682.

Schwarz, D. 2000. “A System for Data-Driven Concatena-
tive Sound Synthesis.” Proceedings of the 2000 DAFx
(Digital Audio Effects) Conference. Verona: Universität
of Verona, S. 97–102.

Schwarz, D. 2004. “Data-Driven Concatenative Sound

Synthesis.” PhD Thesis, University of Paris VI, Frankreich.
Schwarz, D. 2006. “Concatenative Sound Synthesis: Der
Early Years.” Journal of New Music Research 35(1):3–22.
Schwarz, D. 2007. “Corpus-Based Concatenative Synthe-
sis.” IEEE Signal Processing Magazine 24(2):92–104.
Seashore, C. E., Hrsg. 1936. Objective Analysis of Music
Performance. Iowa City: University of Iowa Press.
Simon, ICH., et al. 2005. “Audio Analogies: Creating New

Music from an Existing Performance by Concatenative
Synthesis.” Proceedings of the 2005 International
Computermusikkonferenz. San Francisco, Kalifornien:
International Computer Music Association, S. 65–
72.

Todd, N. 1992. “The Dynamics of Dynamics: A Model of
Musical Expression.” Journal of the Acoustical Society
of America 91(6):3540–3550.

Viterbi, A. J. 1967. “Error Bounds for Convolutional
Codes and an Asymptotically Optimum Decoding
Algorithm.” IEEE Transactions on Information Theory
13(2):260–269.

Widmer, G. 2001. “Discovering Strong Principles of

Expressive Music Performance with the PLCG Rule
Learning Strategy.” Proceedings of the 12th European
Conference on Machine Learning (ECML’01). Berlin:
Springer-Verlag, S. 552–563.

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
3
4
2
3
1
8
5
5
3
9
4
/
C
Ö
M