DEVELOPMENT,

DISCOURAGEMENT, OR

DIVERSION? NEW EVIDENCE ON

THE EFFECTS OF COLLEGE

REMEDIATION POLICY

Judith Scott-Clayton

(Korrespondierender Autor)

Community College Research

Center

Teachers College

Columbia University
New York, New York 10027

scott-clayton@tc.columbia.edu

Olga Rodriguez

Teachers College

Columbia University
New York, New York 10027

orodriguez@tc.columbia.edu

Abstrakt
Half of all college students will enroll in remedial course-
work but evidence of its effectiveness is mixed. Using a
regression-discontinuity design with data from a large
urban community college system, we make three contri-
butions. Erste, we articulate three alternative hypotheses
regarding the potential impacts of remediation. Zweite,
in addition to credits and degree completion we exam-
ine several underexplored outcomes, including initial
Einschreibung, grades in subsequent courses, und posten-
treatment proficiency test scores. Endlich, we exploit rich
high school background data to examine impact hetero-
geneity by predicted dropout risk. We find that remedial
assignment does little to develop students’ skills. Aber
we also find little evidence that it discourages initial en-
rollment or persistence, except for a subgroup we iden-
tify as potentially misassigned to remediation. Stattdessen,
the primary effect of remediation appears to be diver-
sionary: students simply take remedial courses instead
of college-level courses. These diversionary effects are
largest for the lowest-risk students.

4

doi:10.1162/EDFP_a_00150
© 2015 Association for Education Finance and Policy

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

1. EINFÜHRUNG
Remedial education, or “developmental” education as it is called in the field,
may be the most widespread and costly intervention aimed at addressing a
perceived lack of preparation among incoming college students.1 Remedial
courses, which do not count towards degree completion, are intended to help
students master the skills needed for successful progression toward their de-
gree goals. Half of all undergraduates will take one or more remedial courses
while enrolled.2 At community colleges, remedial credits represent approxi-
mately 10 percent of all credits earned, suggesting that the cost of remediation
may be nearly $4 billion per year in this sector alone.3 Previous research, primarily relying on regression-discontinuity (RD) anal- yses comparing students just above and below remedial test score cutoffs, has found mixed evidence at best regarding whether assignment to remediation ac- tually improves student outcomes (Bettinger and Long 2005, 2009; Calcagno and Long 2008; Boatman and Long 2010; Martorell and McFarlin 2011; Dadgar 2012; Hodara 2012). But remediation is not going away, and if anything, Re- mediation policies trend towards becoming stricter over time (Hughes and Scott-Clayton 2011). Policy makers may be cautious in their interpretations of the existing research on remediation for two reasons: Zuerst, lingering uncertainty about the generalizability of prior findings to other contexts, particularly to lower- ability students who may not be represented in local RD estimates; zweite, the reality that remediation may serve other purposes beyond simply developing students’ college readiness. Zum Beispiel, an unadvertised but implicit function of remedial assignment may be to signal students about their likelihood of college completion; it may be efficient to both the student and the institution to realize this and adjust their investments sooner rather than later. Darüber hinaus, regardless of its effectiveness in remediating skill deficiencies, remediation may still serve as an expedient form of student tracking. Even if remediated students never make it to college-level coursework, students in both remedial and college-level courses may learn more during their three semesters of 1. We use the terms “remedial” and “developmental” interchangeably throughout the paper. 2. Estimate based on Beginning Postsecondary Students (BPS): 2009 transcript data (NCES 2012; tables accessed via QuickStats at nces.ed.gov/datalab/quickstats/createtable.aspx). 3. Credit attainment estimates based on BPS: 2009 transcript data (NCES 2012), which indicate an average of two remedial courses (roughly six “equated” credits) and sixty total credits earned within six years among first-time beginning students entering public two-year colleges. The Delta Cost Project (2012) estimates total expenditures of roughly $12,957 per full-time equivalent student per
Jahr, implying a per-credit cost of roughly $540 (since full-time is defined as 24 credits per year). This in turn implies the cost of remediation is roughly $3,200 per community college entrant (nicht
per remediated student). With over 1.2 million first-time students entering community colleges
annually, this suggests national costs of nearly $4 Milliarden jährlich.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

5

THE EFFECTS OF COLLEGE REMEDIATION POLICY

attendance (the average, in our sample) than if they were all grouped in already-
crowded college courses.

Our study makes three primary contributions. Erste, we articulate three al-
ternative hypotheses regarding the functions of remediation: as development
for future coursework, discouragement from further study, or simply a diver-
sion onto a separate track. Zweite, using rich administrative data on 100,000
students at six institutions within a large, urban community college system
(LUCCS), we utilize a regression discontinuity approach (comparing students
just above and below remedial test score cutoffs) to examine several outcomes
underexplored in the prior literature, including the initial decision to enroll,
grades in subsequent college courses in the same subject, and post-treatment
scores on a proficiency exam required in order to earn any degree.4 Finally, Wir
explore impact heterogeneity using a novel new approach that gets us beyond
the usual local nature of RD estimates: Because the placement test scores used
for the RD are quite noisy, we use rich high school background data to iden-
tify students with varied levels of prior predicted dropout risk who all scored
around the placement test cutoff.

Our findings affirm prior research indicating that assignment to remedi-
ation does not develop students’ skills sufficiently to increase their rates of
college success (Calcagno and Long 2008; Martorell and McFarlin 2011). An
die andere Hand, neither does remedial assignment appear to be a significant
discouragement to student progress, except for one group we identify as po-
tentially misassigned to remediation—students who passed a more difficult
writing test, but just barely failed a significantly easier reading test. Among
other negative effects, this group experienced an 8 percentage point increase
in the likelihood of dropping out.

Gesamt, the primary effect of remediation appears to be diversionary: stu-
dents generally enroll and persist at the same rates but simply take remedial
courses instead of college-level courses. Although our conceptual framework
suggests diversion is not necessarily a bad thing, our findings provide some
reason for concern. Erste, we find that potentially one quarter of students
diverted from college-level courses in math, and up to 70 percent of those
diverted in reading, would have earned a B or better in the relevant college
course. Weiter, our analysis of impacts by prior predicted dropout risk sug-
gests that diversionary effects are largest for the lowest-risk students, and we
fail to find positive effects for any risk subgroup.

The remainder of the text proceeds as follows: in section 2, we describe
our conceptual framework and review the prior literature. In section 3, Wir
describe our empirical strategy. In section 4 we present our main results and

4. The system requested anonymity as a condition of providing access to the data.

6

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

F

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

specification checks. Abschnitt 5 explores heterogeneous effects by test type and
prior predicted dropout risk. Abschnitt 6 concludes.

2. CONCEPTUAL FRAMEWORK AND PRIOR LITERATURE
The increasing availability of large-scale administrative data sets makes it in-
creasingly feasible for researchers to examine dozens of outcomes for any
given intervention. Carefully delineating a program’s potential mechanisms
is thus essential to identifying the key outcomes of interest and interpret-
ing the resulting pattern of estimates. Prior research has described several
purposes that remedial coursework might serve within an institution. We cat-
egorize these potential functions into three broad hypotheses, nämlich, Das
remediation serves as (1) skill development that prepares students for future
college-level courses, (2) a discouragement that stigmatizes students and sends
a signal about their probability of college success, oder (3) a diversion that steers
students out of college-level courses and reduces heterogeneity within class-
Räume. These functions may or may not be intentional and are not mutually
exclusive. Im Folgenden, we describe each hypothesis and summarize the
relevant causal research in context.

The Developmental Hypothesis

Prior research has documented low levels of preparation among recent cohorts
of high school graduates (Greene and Forster 2003). At open-access institu-
tionen, remedial coursework is intended to develop underprepared students’
skills so that they have the opportunity to pursue college success regardless of
prior preparation (RP Group 2007). In der Tat, this central function is expressed
in terminology—many institutions and researchers now eschew the traditional
term “remedial education” in favor of the more optimistic “developmental ed-
ucation.” In this view, developmental education is an investment—compared
with how they might have fared without remediation, these students may ex-
perience an initial negative setback as they delay some college coursework but
should reap benefits over the longer term. These longer term benefits should
most directly include improved performance in college-level courses, welche
may in turn lead to greater persistence and higher rates of degree completion
and/or transfer.

Three prior evaluations of remedial education provide evidence on the
developmental mechanism by examining whether remediated students even-
tually complete more college-level credits, persist for longer, and/or complete
degrees or transfer at higher rates than similar students who took the most
direct path. The first quasi-experimental study of remediation, by Bettinger
and Long (2009), provides the most encouraging evidence in support of the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

7

THE EFFECTS OF COLLEGE REMEDIATION POLICY

developmental hypothesis. They take advantage of seemingly arbitrary varia-
tion in placement test cutoff policies across two- and four-year campuses in
Ohio, using distance to college as an instrument for students’ probability of
remediation. They find some important positive impacts: Students who were
more likely to be remediated (by virtue of the cutoff policy at the nearest school)
were more likely to complete a bachelor’s degree in four years. They also find
those remediated in English were less likely to drop out in their first year.
Andererseits, mixed with these positive effects, they also find some sig-
nificant negative impacts. Zum Beispiel, remediated students in both English
and math completed significantly fewer total credits, and those remediated in
math were more likely to drop out in their first year.

Two subsequent studies using an RD approach, comparing students just
above and below test score cutoffs for remediation within institutions, find little
evidence to support the development hypothesis. A study using data from over
100,000 two-year entrants in the state of Florida found no impact on retention,
degree completion, transfer, or completion of college credits for students near
the cutoff (Calcagno and Long 2008). Martorell and McFarlin (2011), WHO
studied over 250,000 students in Texas public two- and four-year colleges,
find that assignment to remediation decreased the probability of completing
additional years of college and reduced credit accumulation, with no impact
on degree attainment.

It is worth noting that the prior literature has not fully explored one set
of outcomes particularly relevant to the development hypothesis: grades in
subsequent college-level coursework in the remediated subject. If remedia-
tion improves students’ performance in the college-level courses that directly
follow remediation, this alone might justify the intervention, even without
broader impacts on credits or graduation, which may be asking too much of a
fairly narrow treatment. Natürlich, grades can be a tricky outcome to examine
causally because many students simply never reach college-level coursework.
Two prior studies examine whether remediated students have a higher likeli-
hood of ever completing a college-level course in the relevant subject (Calcagno
and Long 2008; Dadgar 2012). These studies find no effect, but potential im-
pacts higher in the grade distribution are unexplored. Boatman and Long
(2010) take a different approach, examining grades only for students who at-
tempted a college-level course—although these comparisons do not have a
causal interpretation because they are conditional on a post-treatment out-
kommen (ever taking a college-level course).5 In order to examine grades while
preserving our causal identification strategy, we examine binary outcomes

5. They find no effects of remediation versus those assigned directly to college level in math or reading,
but find that those assigned to lower levels of writing remediation have higher grades (if they ever
take a college-level course) than those assigned to higher levels of writing remediation.

8

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

F

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

such as whether or not a student ever earned a B or better or C or better in the
first college-level course in the relevant subject (where those never taking the
course are entered as zeros).

The Discouragement Hypothesis
Martorell and McFarlin’s (2011) finding that assignment to remediation nega-
tively impacts college persistence suggests the presence of discouragement or
stigma effects. This is consistent with evidence on the impact of test score
performance labels at the high school level, indicating that being labeled
as a poor performer discourages students from enrolling in college (Papay,
Murnane, and Willett 2011). Via this mechanism, an assignment to remedia-
tion may send a message to students that they are not “college material.” This
is in line with Burton Clark’s (1960) description of a “cooling out” process
in higher education, in which obstacles encountered by the student in college
serve to gradually diminish their degree aspirations. Students assigned to re-
mediation may, as a result, be less likely to enroll, or may end up dropping
out sooner even if they do enroll. Note that although discouragement is typ-
ically framed as an undesirable potential side effect, it is possible to take a
more agnostic view: A remedial assignment may simply give students a signal
about their preparation that causes them to rationally reevaluate the benefits
of enrollment or persistence.6

Allowing for potential discouragement effects has several implications for
our study. Erste, it highlights the importance of tracking students from the
point that they receive their first test scores, not only after they enroll. Whereas
all of the prior remediation studies look for negative impacts on persistence or
completion conditional on enrollment, ours joins just one other recent study
in examining whether there are any effects on college enrollment between the
time of the first test and initial course registration. Martorell, McFarlin, Und
Xue (2015), using the same Texas data as in the Martorell and McFarlin (2011)
Studie, find no significant effect on initial enrollment in either direction. Gegeben
the variation in remedial testing and assignment procedures across systems,
our study will help establish whether this finding generalizes to a different
Kontext.

Zweite, the discouragement hypothesis implies that some students as-
signed to remediation may be negatively affected even if they never actually
enroll in or complete remediation. With the exception of Martorell, McFar-
lin, and Xue (2015), prior research typically uses remedial assignment policy
as an instrumental variable for actual remedial course-taking (Calcagno and

6. This is also in line with Manski’s (1989) model of college education as experimentation, in which

the dropout decision is the result of new information regarding skills and preferences.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

9

THE EFFECTS OF COLLEGE REMEDIATION POLICY

Long 2008; Bettinger and Long 2009; Martorell and McFarlin 2011). But un-
less one is willing to assume away any direct effects of the remedial label, nur
the reduced-form effect of remedial assignment can be credibly established.
We thus focus primarily on reduced-form effects of remedial assignment.

Endlich, the discouragement hypothesis highlights the importance of con-
sidering heterogeneous effects when evaluating remedial policies: Some stu-
dents may be discouraged, whereas other students may do better than they
would otherwise. One potential limitation of any RD study is that the esti-
mated effects are local to students scoring near remedial cutoffs (das ist, Die
highest-ability remediated students). Defenders of the developmental model
may legitimately argue that higher-ability students might be the most sensitive
to discouragement effects and least likely to benefit from developmental in-
struction, implying that lower-ability students might experience more positive
Effekte. Martorell and McFarlin (2011) are able to examine RD effects sepa-
rately for cohorts with higher and lower cutoffs and find less negative (but not
positive) effects when the marginal student is of lower measured ability.

Recent RD studies have also explored the effects of assignment to lower
levels of remediation (Boatman and Long 2010; Dadgar 2012; Hodara 2012).
These studies compare students just above and below test score cutoffs for
longer versus shorter (or more versus less intensive) remedial sequences,
rather than comparing those above and below the threshold for college-level
coursework. These studies have also found less negative effects, with a smat-
tering of some positive effects of assignment to lower remedial levels. Das
pattern is consistent either with less negative effects for lower-ability students,
or simply reflects a different bundle of treatment (Zum Beispiel, it may be that
discouragement effects apply equally to remediated students regardless of level
but those at lower levels get a larger “dose” of the developmental mechanism).
Our study provides a new means of exploring heterogeneous effects in RD
designs: Although the placement test scores used for assignment are often
assumed to be a measure of ability, they are in fact quite noisy and error-
prone (ACT, Inc. 2006; Scott-Clayton 2012). This implies that even around
the cutoff there is variation in student ability. We use rich demographic and
background data on high school achievement to predict students’ pretreatment
risk of dropping out of college. We then run our RD analysis separately for
subgroups based on this index of dropout risk.

The Diversion Hypothesis

A third possible view of remediation is neither as optimistic as the development
hypothesis nor as pessimistic as the discouragement hypothesis. Under the
diversion hypothesis, the primary role of remediation is simply for institutions
to sort students of different ability onto different course tracks. The goal in this

10

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

case need not be to prepare remediated students for future coursework but
simply to maximize learning gains for both remediated and nonremediated
students for as long as they remain enrolled (welche, in our sample, is an
average of three semesters). While research on K–12 education largely finds
that low-achieving students learn more when they are placed in heterogeneous
classrooms (Peterson 1989; White et al. 1996; Burris, Heubert, and Levin
2006), some studies have found that tracking may be beneficial, or at least not
harmful, to students of lower ability (Figlio and Page 2002; Zimmer 2003).

Darüber hinaus, there is strong evidence of peer effects in higher education
(Sacerdote 2001; Zimmerman 2003; Winston and Zimmerman 2004; Car-
rell, Fullerton, and West 2009), raising the concern that allowing too many
underprepared students into college-level courses might depress the achieve-
ment of the better-prepared. While Carrell, Fullerton, and West (2009) find
that positive peer effects for low-achieving students outweigh negative effects
for high-achieving students, it is not obvious their results (in the context of the
UNS. Air Force Academy) would extrapolate to community college students.
Endlich, if college-level courses are already at capacity, then allowing too many
students into college-level coursework might depress achievement because of
overcrowding, regardless of whether or not the ability mix shifts.

The prior causal research on remediation has not been designed to examine
impacts on nonremediated students, and our study is no different on this
dimension. Like prior research, we are able to examine diversion by looking at
the relative impact on total credits (including both remedial and college-level
courses) versus college-level credits—a diversion story suggests there may be
no effect on the former but negative effects on the latter. Both Calcagno and
Long (2008) and Martorell and McFarlin (2011) find evidence of diversion
Effekte. Trotzdem, a potential outcome under the diversion hypothesis is
that even if remediated students never make it to college level coursework, Sie
may learn more in their remedial courses than they would have otherwise. Das
suggests that one should examine some direct measures of learning beyond
simply credits and credentials. Martorell and McFarlin (2011) find no impact
on labor market outcomes, though their estimates are too noisy to rule out
modest effects in either direction. We extend the literature on this front by
examining post-assignment scores on a proficiency exam that is required of
all students in order to graduate.

3. EMPIRICAL STRATEGY
Institutional Context

Our analysis focuses on first-time degree-seeking students who were admitted
to any of the six community colleges in a single LUCCS between Fall 2001 Und

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

11

THE EFFECTS OF COLLEGE REMEDIATION POLICY

Fallen 2007.7 Over the period under study in this report, the LUCCS utilized two
different exams for placement in math. Aus 2001 Zu 2004 the LUCCS utilized
a single-score math exam that was developed in-house. Seit 2004, the LUCCS
has utilized scores from the COMPASS R(cid:2)
numerical skills/pre-algebra module
as well as the algebra module for remedial placement.8 For reading/writing
placement, over the entire period the LUCCS used the COMPASS R(cid:2)
reading
exams as well as a writing exam that the LUCCS adapted slightly from the stan-
dard COMPASS R(cid:2)
writing module (and which the LUCCS grades in-house).
As in many systems, students are exempted from the placement exams
if they score above a certain level either on the SAT, ACT, or on a standard-
ized state high school exam. Approximately 20 percent of entering students
were exempt from placement testing in math, and approximately 25 Prozent
were exempt in English for the cohorts under study. These exempt students
are excluded from the analysis. All students who are not exempted from
placement testing must take the relevant placement exam(S) prior to initial
enrollment.9 The retesting policy is strict—students may not retake a place-
ment exam until they have completed either a remedial course or at least twenty
hours of documented participation in an alternative intervention, which might
include a workshop or regular tutoring.

Each year, the LUCCS central office establishes minimum cut scores for
access to college-level courses that apply to all of the LUCCS institutions,
although schools are free to establish higher cutoffs, and some schools in
some years were allowed to have lower cutoffs on the writing exam on a pilot
basis. We determined the cutoff policies in place at each college in each year
by examining information from college course catalogs and following up with
institutional administrators if necessary. We also checked these stated cutoffs
against the actual course-taking patterns by test score that we can observe in
our data.

Students are encouraged but not required to begin their remedial course-
work immediately upon enrollment. Although they may be able to access
some college-level courses before completing remediation, many college-level
courses require freshman composition in particular as a prerequisite. More-
über, students must pass college-level freshman composition and at least one
credit-bearing math course in order to earn any degree, so a student can-
not graduate without successfully exiting remediation. Although relatively few
students in the LUCCS who are assigned to a remedial course circumvent

of the several four-year institutions that are part of the same urban public college system.

7. We are then able to track these individuals if they transfer within these six institutions or to any
8. The COMPASS R(cid:2)
9. This is in contrast to Texas’s system, analyzed in Martorell and McFarlin (2011), in which students

suite is a product of ACT, Inc.

could delay their placement exam until after enrollment.

12

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

that placement to enroll in a college-level course, this does not imply that
all students follow their remedial assignment. As we will show subsequently,
many students who are assigned to remediation never actually take a remedial
course, whereas others who test out of remediation may nonetheless take a
remedial course (in manchen Fällen, math/science majors have higher remedial
cutoffs than the institution-level cutoff we use in our analyses).

Data and Sample

The data for this analysis were provided under a restricted-use agreement
with the LUCCS. All students are followed for three years after they were
first tested (we can also look at longer-term outcomes for some cohorts). Wir
can track students’ credits, grades, and degree outcomes even if they transfer
to another public two- or four-year institution within the same urban public
college system.10 Our data include information on all placement exam admin-
istrations, so we are able to identify and utilize the scores from the students’
first-test attempt. Endlich, our sample includes tested students even if they ulti-
mately did not enroll at any of the LUCCS institutions, enabling us to examine
whether remedial placement may impact the enrollment decision itself.

Tisch 1 provides descriptive information on the full sample of test-takers
and main subsamples for the analysis. Column 1 shows that among all test-
takers during this time period, 72 percent were assigned to remedial math,
72 percent were assigned to remedial writing, Und 38 percent were assigned to
remedial reading. Gesamt, etwa 90 percent were assigned to reme-
diation in one or more subjects.11 This proportion has generally been flat or
declining over the sample timeframe except for discrete and substantial jumps
when new tests or new cutoffs were implemented.

It is important to note that the LUCCS entrants are not typical of commu-
nity college entrants nationally, with the exception of their gender composition
(57 percent female). Nationally, über 60 percent of entrants identify as non-
Hispanic white students, the average age is 23.6 Jahre, and during the relevant
time period just under 30 percent of community college entrants received Pell
Grants.12 In contrast to these national figures, the LUCCS student body reflects
the diversity of its urban environment: 34 percent identify their race/ethnicity
as Hispanic, 28 percent identify as non-Hispanic black, 14 percent identify
as non-Hispanic white, 11 percent identify as Asian/Pacific Islander, Und
7 percent identify as another race/ethnicity. Nearly half received Pell Grants

10. Bedauerlicherweise, students who transfer to private institutions, for-profit institutions, or public insti-

tutions outside the urban area are not captured in our data.

11. These rates are higher than those observed in the system overall (in which roughly 82 percent are
assigned to remediation in at least one subject), Weil 20 Zu 25 percent of entrants are exempt
from testing in each subject.

12. Authors’ calculations using the BPS: 2003–04 data set (NCES 2012).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

F

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

13

THE EFFECTS OF COLLEGE REMEDIATION POLICY

)
S
T
P
4
±

(

)
S
T
P
4
±

(

)
S
T
P
4
±

(

l

e
P
M
A
S

J

T
C
e
B
u
S

j
N
A

ich

N
Ö
ich
T
A
D
e
M
e
R
Ö
N

S
R
e
k
A
T
–
T
S
e
T

2
5
7
.
0

0
0
0
.
0

2
4
4
.
0

0
4
8
.
0

3
8
6
.
0

6
7
7
0

.

0
0
0
1

.

1
8
4
0

.

0
0
0
1

.

9
6
5

.

0

3
7
5
0

.

0
6
6
0

.

3
0
3
0

.

1
5
8
0

.

1
6
5

.

0

3
9
7
0

.

2
9
7
0

.

8
1
4
0

.

0
0
0
1

.

0
8
5

.

0

0
0
0
0

.

0
0
0
0

.

0
0
0
0

.

0
0
0
0

.

2
6
5

.

0

0
2
7
.
0

9
1
7
.
0

8
7
3
.
0

1
0
9
.
0

8
7
5
.
0

8
0
4
.
0
2

4
0
1

.

1
2

1
4
9

.

0
2

2
1
7

.

1
2

2
0
1

.

0
2

5
8
5
.
1
2

6
5
1
.
0

6
0
3
.
0

1
3
3
.
0

2
8
0
.
0

8
6
0
.
0

9
2
4
.
0

3
4
6
.
0

8
2
7
.
1

3
4
3
.
3
7

1
3
5
.
2
1

4
3
9
.
0

0
9
3
.
0

2
7
5
.
0

0
6
1
.
0

7
8
7
.
0

3
5
3
.
0

6
1
1
0

.

3
0
3
0

.

5
6
3

.

0

8
0
1

.

0

2
6
0

.

0

0
4
5
0

.

6
8
5
0

.

2
8
1
2

.

4
0
7

.

2
7

2
4
6
1
1

.

7
0
9
0

.

3
1
3
0

.

2
0
6
0

.

1
6
1
0

.

6
7
7
0

.

1
3
3
0

.

6
7
1
0

.

0
9
2
0

.

3
0
3

.

0

6
0
1

.

0

1
6
0

.

0

4
1
5
0

.

9
7
5
0

.

9
6
2
2

.

6
2
5

.

3
7

8
5
1
2
1

.

3
1
9
0

.

6
9
2
0

.

4
3
5
0

.

1
3
1
0

.

4
7
7
0

.

9
5
3
0

.

4
3
1
0

.

2
8
2
0

.

4
5
3
0

.

6
0
1
0

.

6
6
0

.

0

7
3
5
0

.

3
4
5
0

.

8
2
7
2

.

3
4
3

.

3
7

9
0
5
1
1

.

1
0
9
0

.

5
8
2
0

.

2
8
5
0

.

4
7
1

.

0

9
2
7
0

.

1
6
3
0

.

3
3
2
0

.

0
8
2
0

.

1
3
2

.

0

6
1
1

.

0

7
6
0

.

0

6
2
4
0

.

3
5
6
0

.

8
3
8
1

.

5
0
7

.

5
7

2
5
4
4
1

.

2
4
9
0

.

4
9
3
0

.

5
5
4
0

.

3
1
1

.

0

7
3
8
0

.

2
9
3
0

.

2
4
1
.
0

2
8
2
.
0

3
4
3
.
0

6
0
1
.
0

7
6
0
.
0

7
2
5
.
0

1
5
5
.
0

4
6
6
.
2

8
5
5
.
3
7

7
3
7
.
1
1

4
0
9
.
0

4
9
2
.
0

9
6
5
.
0

0
7
1
.
0

7
3
7
.
0

6
6
3
.
0

.
D
T
S
e
G
e

l
l

Ö
C
G
N
ich
T
ich
R

W
v
e
D
Ö
T

.
D
T
S
e
G
e

l
l

ich

Ö
C
G
N
D
A
e
R
v
e
D
Ö
T

D
e
N
G
S
S
A

ich

D
e
N
G
S
S
A

ich

.
D
T
S
e
G
e

l
l

Ö
C

.
D
E

v
e
D
j
N
A

Ö
T

D
e
N
G
S
S
A

ich

l

e
A
M
e
F

l

Ö
Ö
H
C
S
H
G
H

ich

C
ich
N
A
P
S
H
N
Ö
N

ich

–

C
ich
N
A
P
S
H
N
Ö
N

ich

–

,
e
T
ich
H
W

,
k
C
A
B

l

Ö
N
ich
T
A
L

e
G
A

R
e
D
N
A
S
ICH

l

C
fi
ich
C
A
P

N
A
S
A

ich

e
C
A
R
R
e
H
T
Ö

l

A
C
Ö
L
M
Ö
R
F

D
e
T
A
u
D
A
R
G

ich

j
T
ich
R
Ö
N
M
e
G
A
u
G
N
A
L

ich

ich

)
G
N
S
S
M
N
Ö
N

–

l

,
e
A
C
S
0
0
1
–
0
(

A
P
G
S
H

ich

ich

)
G
N
S
S
M
N
Ö
N
(

–

S
T
ich
N
U
P
e
R
P

e
G
e

l
l

Ö
C
S
H

ich

ich

)
G
N
S
S
M
N
Ö
N
(

–

j
R
T
N
E

T
A

l
l

e
P

D
e
v
ich
e
C
e
R

ich

ich

)
G
N
S
S
M
N
Ö
N
(

–

j
R
T
N
E

T
A

T
N
e
D
N
e
P
e
D

A
T
A
D

l
l

e
P

ich

G
N
S
S
M

ich

A
T
A
D
j
C
N
e
D
N
e
P
e
D
G
N
S
S
M

ich

ich

e
C
ich
Ö
H
C
T
S
1

S

ich

e
G
e

l
l

Ö
C

R
A
e
j
–
R
u
Ö
F

A
P
G
S
H
S
A
H

T
N
e
M

l
l

Ö
R
N
e

D
e
j
A
e
D

l

S
R
A
e
Y

.
D
T
S
e
G
e

l
l

Ö
C

,
H
T
A
M
v
e
D
Ö
T

D
e
N
G
S
S
A

ich

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

,
S
ich
S
j
l
A
N
A
G
N
D
A
e
R

ich

,
S
ich
S
j
l
A
N
A
G
N
D
A
e
R

ich

G
N
ich
T
ich
R

W
D
e
S
S
A
P

G
N
ich
T
ich
R

W
D
e

l
ich

A
F

S
ich
S
j
l
A
N
A
H
T
A
M

N

ich

ich

N
Ö
ich
T
A
D
e
M
e
R

l
l

A

l

e
P
M
A
S
S
S
j
l
A
N
A

ich

j
B

S
N
A
e
M
e
P
M
A
S

l

.

l

1
e
B
A
T

14

Judith Scott-Clayton and Olga Rodriguez

,
S
ich
S
j
l
A
N
A
G
N
D
A
e
R

ich

,
S
ich
S
j
l
A
N
A
G
N
D
A
e
R

ich

G
N
ich
T
ich
R

W
D
e
S
S
A
P

G
N
ich
T
ich
R

W
D
e

l
ich

A
F

S
ich
S
j
l
A
N
A
H
T
A
M

N

ich

ich

N
Ö
ich
T
A
D
e
M
e
R

l
l

A

.
D
e
u
N
ich
T
N
Ö
C

.

l

1
e
B
A
T

)
S
T
P
4
±

(

)
S
T
P
4
±

(

)
S
T
P
4
±

(

l

e
P
M
A
S

J

T
C
e
B
u
S

j
N
A

ich

N
Ö
ich
T
A
D
e
M
e
R
Ö
N

S
R
e
k
A
T
–
T
S
e
T

7
8
7
.
0

0
4
8
.
0

7
8
5
.
0

5
8
3
.
0

9
1
3
.
0

8
6
2
.
0

1
7
1
.
0

8
5
2
.
0

5
4
7
.
0

8
2
6
.
0

1
9
5
.
0

8
1
4
.
0

6
3
1
.
0

0
8
1
.
0

5
0
2
.
0

5
1
6
.
0

3
6
4
.
3

7
4
3
.
1
3

7
0
6
.
7
2

9
0
2
.
0

7
9
1
.
0

4
7
3
,
1

9
9
8
.
2
4

3
7
7
0

.

8
3
8

.

0

8
7
5
0

.

2
5
3
0

.

0
9
2

.

0

0
4
2
0

.

3
6
1
0

.

1
5
2
0

.

7
7
4
0

.

8
0
4
0

.

0
8
3
0

.

6
5
2
0

.

4
8
0
0

.

2
1
1
0

.

3
5
2
0

.

4
3
6
0

.

1
5
3
3

.

2
6
7
9
2

.

7
0
5
2
2

.

0
3
1
0

.

6
1
1

.

0

9
4
0

,

7

1
1
6

.

1
4

9
8
7
0

.

6
6
8

.

0

3
3
5
0

.

1
8
4
0

.

2
8
3
0

.

7
1
3
0

.

7
1
2
0

.

9
7
1
0

.

1
1
6
0

.

9
1
5
0

.

2
9
4
0

.

4
6
3
0

.

5
1
1
0

.

5
5
1
0

.

4
4
2
0

.

1
0
6
0

.

3
0
5
3

.

6
3
0
3
3

.

1
1
8
6
2

.

2
7
1
0

.

7
5
1
0

.

4
2
7

,

8
1

5
4
0

.

2
4

3
4
7
0

.

5
2
8
0

.

1
8
5
0

.

2
4
3
0

.

7
7
2

.

0

9
2
2
0

.

8
5
1
0

.

1
4
2
0

.

4
0
5
0

.

4
2
4

.

0

8
9
3
0

.

4
8
2
0

.

0
8
0
0

.

9
0
1
0

.

5
4
2
0

.

5
4
6
0

.

9
4
2
3

.

7
6
9
8
2

.

2
7
0
2
2

.

6
2
1

.

0

4
1
1

.

0

2
4
3

,

0
9

9
9
8

.

1
4

7
3
8
0

.

6
8
8
0

.

5
9
1
0

.

2
4
6
0

.

6
3
5

.

0

9
6
4
0

.

3
6
3
0

.

2
0
0
0

.

6
5
8
0

.

2
4
7

.

0

0
2
7
0

.

6
9
5
0

.

0
2
2
0

.

4
9
2
0

.

1
9
1
0

.

6
1
5
0

.

2
8
8
3

.

9
0
0
9
3

.

4
0
5
7
3

.

5
1
3

.

0

2
0
3

.

0

2
9
5

,

7

9
8
7

.

4
4

0
5
7
.
0

9
2
8
.
0

7
4
5
.
0

7
6
3
.
0

9
9
2
.
0

9
4
2
.
0

6
7
1
.
0

9
1
2
.
0

4
3
5
.
0

1
5
4
.
0

5
2
4
.
0

0
1
3
.
0

2
9
0
.
0

4
2
1
.
0

0
4
2
.
0

5
3
6
.
0

7
9
2
.
3

1
6
7
.
9
2

7
4
3
.
3
2

2
4
1
.
0

9
2
1
.
0

0
5
2
,
0
0
1

7
2
4
.
2
4

3

ich

N
/
w
H
T
A
M

.
v
e
D
k
Ö
Ö
T

3

ich

N
/
w
D
e

l
l

Ö
R
N
E

ich

j
l
e
T
A
D
e
M
M

ich

D
e

l
l

Ö
R
N
E

3

ich

N
/
w
H
T
A
M
e
G
e

l
l

Ö
C
k
Ö
Ö
T

H
T
A
M
e
G
e

l
l

Ö
C
D
e
S
S
A
P

H
T
A
M
e
G
e

l
l

Ö
C
N

ich

H
T
A
M
e
G
e

l
l

Ö
C
N

ich

R
e
H
G
H

ich

R
Ö
C

R
e
H
G
H

ich

R
Ö
B

3

ich

N
/
w
H
S

ich
l

G
N
E

e
G
e

l
l

Ö
C
k
Ö
Ö
T

3

ich

N
/
w
G
N
D
A
e
R

ich

.
v
e
D
k
Ö
Ö
T

H
S

ich
l

G
N
E

e
G
e

l
l

Ö
C
D
e
S
S
A
P

3

ich

N
/
w
e
e
R
G
e
D
D
e
N
R
A
E

R
Ö

D
e
R
R
e
F
S
N
A
R
T

3

ich

N
/
w
A
B
R
Ö

A
A

D
e
N
R
A
E

3
R
A
e
Y

F
Ö

D
N
E

T
A

D
e

l
l

Ö
R
N
E

l
l
ich
T
S

3

R
A
e
Y

j
B

T
u
Ö
D
e
P
P
Ö
R
D

3

ich

N
/
w
D
e

l
l

Ö
R
N
e

S
M
R
e
T

F
Ö

R
e
B
M
u
N

3

N

ich

D
e
S
S
A
P

S
T
ich
D
e
R
C
D
e
T
A
u
Q
E

.
T
Ö
T

3

N

ich

D
e
S
S
A
P

S
T
ich
D
e
R
C
e
G
e

l
l

Ö
C

.
T
Ö
T

3

ich

N
/
w
E
P
C
k
Ö
Ö
T

3

ich

N
/
w
E
P
C
S
S
A
P

3

ich

N
/
w
e
R
Ö
C
S
T
S
e
H
G
H
E
P
C

ich

e
z
ich
S
e
P
M
A
S

l

H
S

ich
l

G
N
E

H
S

ich
l

G
N
E

e
G
e

l
l

Ö
C
N

ich

e
G
e

l
l

Ö
C
N

ich

R
e
H
G
H

ich

R
Ö
C

R
e
H
G
H

ich

R
Ö
B

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

15

THE EFFECTS OF COLLEGE REMEDIATION POLICY

at entry, and more than half identified as speaking a primary language other
than English.13 The LUCCS entrants, bei 21.6 Jahre alt, are also younger than
the national average, likely reflecting the fact that the LUCCS offers very few
vocational/technical certificate programs.14

Tisch 1 indicates that a substantial proportion of students—17 percent
overall—who take a placement test at one of the LUCCS colleges never en-
roll (or at least still had not enrolled three years after their first test).15 Das
highlights the importance of looking at initial enrollment as a margin that
could be affected by remedial assignment. The average student enrolled for
3.3 semesters over three years, and nearly two thirds (64 Prozent) had dropped
out (not enrolled, no degree) at the end of the three-year follow-up period.16
An additional 24 percent were still enrolled at one of the LUCCS colleges, Und
the remainder (12 Prozent) had either completed a degree or transferred to a
local public four-year institution. Endlich, table 1 indicates that approximately
13 percent of tested students had taken and passed a college proficiency exam
(CPE) required for graduation, and those who took the exam scored an average
von 42 points (out of 72 möglich, mit 34 required to pass). It should be noted
that with such a low proportion of the sample taking this test, our ability to
examine overall impacts on learning is substantially limited (because some
students whose learning is impacted may never take this test).

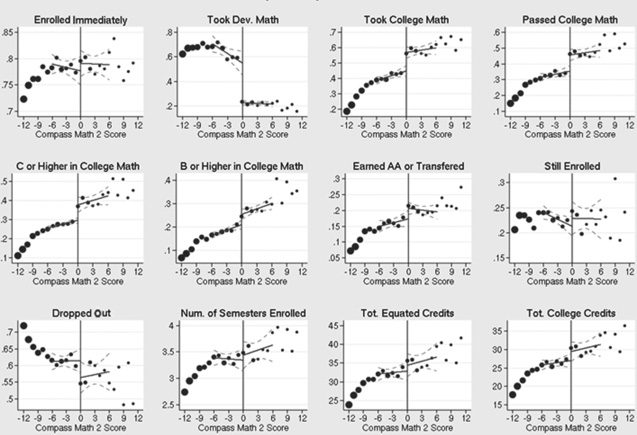
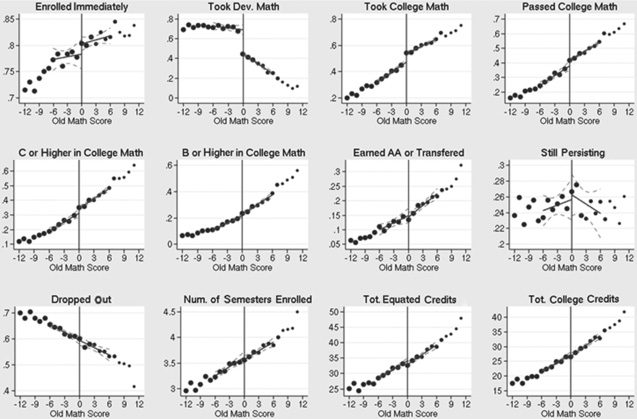
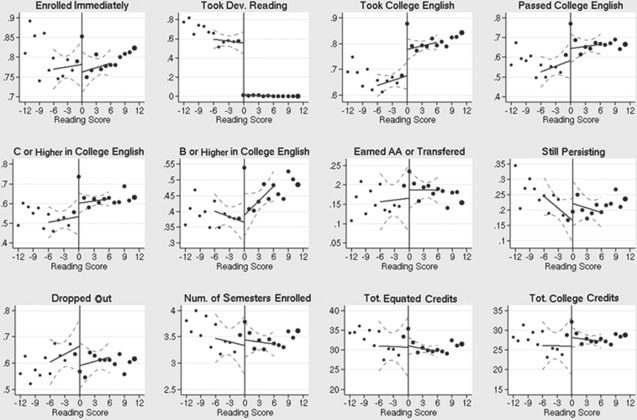
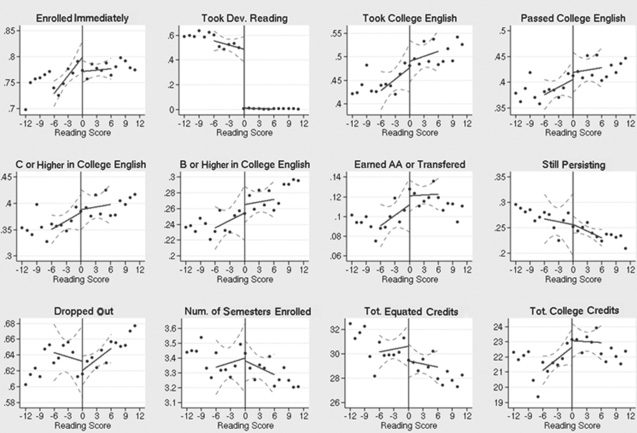
Some of the outcomes in table 1 that will be a focus of our RD analysis merit
additional explanation. To examine impacts on actual achievement in college-
level courses in the relevant subject, we have created composite outcomes, solch
as “Passed College Math,” or “Earned B or Higher in College Math,” that take
a value of one if the individual ever took the course and received the relevant
grade, and zero otherwise (including those who never took the course, took
it but dropped out, or took and finished it but received less than the relevant
grade). We use a parallel strategy to construct the composite outcome “Ever
Passed the CPE.” Using these composite outcomes allows us to sidestep the
selection bias that would result if we were to limit our comparison to only
those who took the course/test. It does have implications for the interpretation
of those results, however—an issue that we will return to later.

13. This measure of language minority status is derived from self-reported native language and country

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

of origin as indicated on the college application.

14. These differences are likely to also apply to the LUCCS versus the statewide Texas sample examined
in Martorell and McFarlin (2011) as well as to the LUCCS versus the statewide Florida sample
examined in Calcagno and Long (2008), because the LUCCS sample covers only a single urban
area rather than an entire state system. Although these studies do not report all of these same
demographic characteristics, certainly along race/ethnicity our sample has a significantly higher
minority population.

15. Note that for a small proportion of students who took a placement exam while still enrolled in high

Schule, the three-year follow-up period does not begin until after high school graduation.

16. Students who transferred to private or out-of-state institutions cannot be distinguished from

dropouts in our data.

16

Judith Scott-Clayton and Olga Rodriguez

In the case of the CPE, we also look for “impacts” on the CPE score for
those students who did actually take the test. These estimates are not strictly
causal because they are computed conditional on taking the test, which is itself
an outcome of interest. dennoch, if there is no impact on the probability
of taking the exam, the potential for selection bias in the score estimates is
limited. (In the case of college grades, we do not examine conditional impacts
because the probability of taking a college level course is so clearly impacted.)

Identification Strategy
Tisch 1 provides mean outcome levels for those students assigned to remedia-
tion in any subject, as well as means for those not assigned to any remediation
(including students who were exempt from testing). Although comparisons
between these two groups may provide useful context, they are unlikely to have
any causal interpretation; students who score lower on placement exams are
likely to do worse on average than those who score more highly, regardless of
the effect of remediation.

Following prior literature by Calcagno and Long (2008) and Martorell and
McFarlin (2011), we utilize a RD design to identify the causal effect of reme-
dial assignment for those students who score near the cutoff. The intuition
underlying the approach is simple: If we assume the underlying relationship
between test scores and future outcomes is continuous and nothing other than
the placement policy varies discontinuously at the cutoff, then we may attribute
any observed discontinuity in outcomes at the cutoff to the placement policy.
Zum Beispiel, although we might expect degree completion to be positively
related to test scores, there is no reason other than the placement policy to
expect a discontinuous jump (or dropoff) in this relationship at the test score
cutoff.

This intuition can be formalized using Rubin’s (1974) potential outcomes
Rahmen, following Imbens and Lemieux (2008). We would like to compare
an individual’s potential outcome if they are assigned to remediation, denoted
as Y(1), to that individual’s potential outcome if they are not assigned to remedi-
ation, denoted as Y(0). Assignment to remediation is determined by whether
or not the test score, X, is above or below some cutoff, C. The fundamental
problem of causal inference is that we can never observe both Y(1) and Y(0)
for a single individual. As long as the relationship between potential outcomes
and test scores is continuous, Jedoch, then we may define a causal effect:

βRD = lim

x→c − E [Y|X = x] − lim

x→c + E [Y|X = x].
Mit anderen Worten, the RD estimator is simply the difference between
two regression functions at the cutoff, where one function is estimated by

(1)

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

17

THE EFFECTS OF COLLEGE REMEDIATION POLICY

approaching the cutoff from below and the other is estimated by approaching
the cutoff from above. Even if there is a systematic relationship between test
scores and outcomes, as long as this relationship is continuous, es gibt kein
reason to expect the limits in equation 1 to differ except because of the dif-
ference in remedial assignment. The estimated RD impact is “local” to the
cutoff, meaning the estimate only applies to individuals near the cutoff, unless
further assumptions are made.

There are multiple ways to estimate βRD in practice. We follow Imbens
and Lemieux (2008) by focusing primarily on a local linear estimation that
is limited to a narrow bandwidth around the cutoff. The generic specification
takes the form:

Yi = α + b1(Abovei ) + B 2(ScoreDis tan cei ∗ Abovei ∗ CollegeFE )

+ B 2(ScoreDis tan cei ∗ Bel owi ∗ CollegeFE )

+ Xi δ + CollegeFE + CohortFE + εi ,

(2)

where Y is an outcome (measured over three years of follow-up, unless other-
wise indicated) such as ever enrolled, number of semesters enrolled, number
of credits accumulated, or whether the student ever completed a degree or
transferred; Above is a binary indicator of whether or not the student scored
above the relevant cutoff in that institution, Jahr, and subject; ScoreDistance is
the difference between the student’s actual score and the relevant cutoff score
in that institution, Jahr, and subject; X is a vector of individual-level covariates
including binary indicators for gender, race/ethnicity, language minority sta-
tus, whether or not the student graduated from a local high school, sowie
continuous measures of age and years since high school graduation; CollegeFE
is a vector of college fixed effects, important because the treatment assignment
is determined by the particular policies of each college; and CohortFE is a vec-
tor of test cohort fixed effects. Note the coefficient on ScoreDistance is allowed
to vary both across institutions, as well as above and below the cutoff.

The rationale for a local linear approach is that the alternative global meth-
ods focus energy on estimating the relationship between the test score and
outcomes for ranges of the score that are far from the cutoff and which thus
may provide little information about the regression function at the cutoff. Als
bandwidth is restricted to be closer to the cutoff, higher order terms in the
regression function become less necessary and in fact may lead to excessive
sensitivity around the cutoff. dennoch, we test the robustness of our results
to variations in bandwidth as well as the addition of quadratic terms and also
examine graphical plots of the data as a check on the specification.

18

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

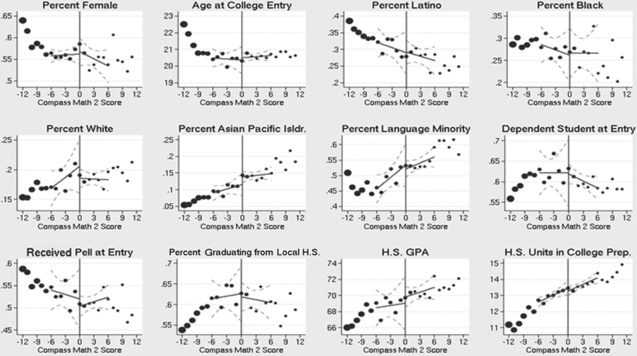
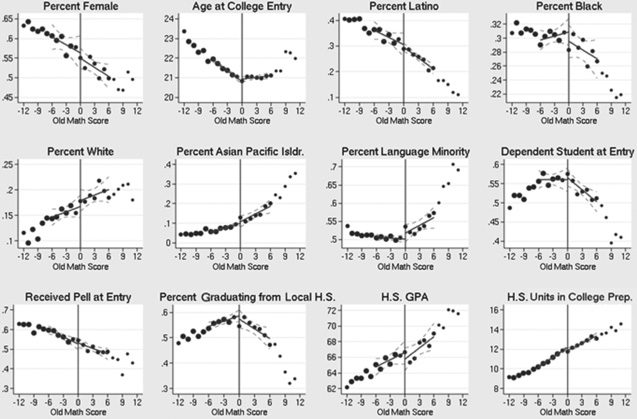
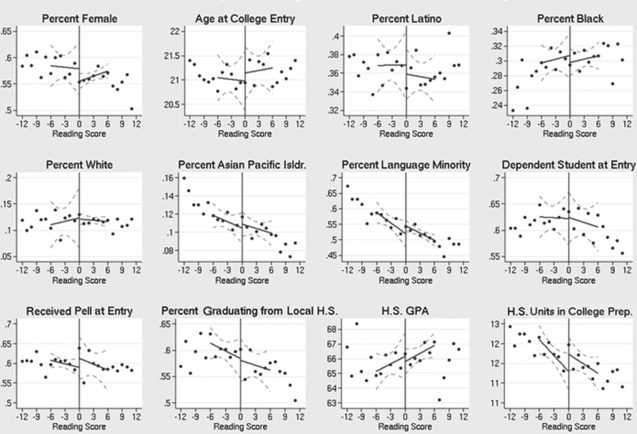
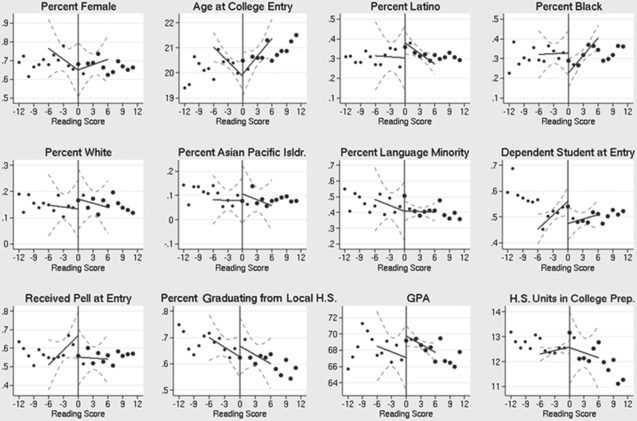
Because of variations in the test format across subjects and over time,
and because of differences in where the cutoffs are placed at each school,
the precise estimating equation is different for math and English. In math,
because two different tests were in place over the time period, we further
separate the ScoreDistance controls depending upon whether the student took
the old or the new test:

Yi = α + b1(Abovei ) + B 2(OldScoreDis tan cei ∗ Abovei ∗ CollegeFE )

+ B 2(OldScoreDis tan cei ∗ Bel owi ∗ CollegeFE )

+ B 2(NewScoreDis tan cei ∗ Abovei ∗ CollegeFE )

+ B 2(NewScoreDis tan cei ∗ Bel owi ∗ CollegeFE )

+ Xi δ + CollegeFE + CohortFE + εi .

(3)

In equation 3, note that the cohort fixed effects absorb the main effects
of test version. Zusätzlich, for those cohorts who took the new math test,
the Above and ScoreDistance variables are based on the cutoffs for the more
stringent of the two math modules (algebra) and the sample is restricted
to those students who passed the easier of the two math modules (numerical
skills/pre-algebra).17 The resulting β1 is (nearly) equivalent to running separate
RDs within each college and test version, and then taking the weighted average
of the impact estimates.18 We also show results separately by test version,
because the cutoffs for the two exams fell at different points in the ability
distribution.

To be placed into college-level English, students are required to pass both
a reading test and a more difficult writing test. The writing test is the stronger
determinant of college-level placement, because the majority of those near the
cutoff in reading would fail the writing test anyway. Bedauerlicherweise, Jedoch,
the writing test is graded on a limited 0–12 scale with each score unit repre-
senting a potentially large difference in underlying ability. Darüber hinaus, this final
scale represents the sum of scores from two exam graders who are encouraged
to agree on their scores, resulting in a discontinuous distribution of scores
around the cutoff of 7.

Daher, we undertake two analyses in English, both focused on students
scoring near the reading test cutoff. Erste, we limit the sample to those who

17. Students must pass both math modules to be placed directly into college-level classes, although
in practice the vast majority of students who are near the cutoff on the easier module fail the
harder module. Mit anderen Worten, the cutoff policy on the harder (algebra) module is the primary
determinant of college-level versus remedial assignment.

18. With the minor difference that the pooled regression in equation 3 restricts the college fixed effects

and student covariates to have the same effect across cohorts/test version.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

19

THE EFFECTS OF COLLEGE REMEDIATION POLICY

failed the writing exam and look at the impact of being assigned to remedi-
ation in reading plus writing instead of writing alone. Zweite, we limit the
sample to those who passed the writing exam and look at the impact of being
assigned to remediation in reading versus being assigned to college-level En-
glish. Although this is a relatively rare occurrence (nur 19 percent of those who
passed the writing exam failed the easier reading exam), our large sample still
generates sufficient power to identify meaningful impacts.19 Moreover, Das
latter analysis enables us to say something about the impact of remediation
for students whose test scores may be an underestimate of their true ability
(conditional on passing the writing exam, the likelihood that a failing score on
the reading exam results is a “mistake” increases). For both of these analyses,
the estimating equation follows equation 2 where Above and ScoreDistance are
both computed from the reading score.

Endlich, as noted earlier, all of our analyses focus on estimating the effect of
remedial assignment rather than the effect of enrollment in remediation per
se. This stands in contrast to prior studies which have used an instrumental
variables or “fuzzy” regression discontinuity design in which cutoff-based re-
medial assignments are used as an instrument for actual remedial enrollment
(Calcagno and Long 2008; Martorell and McFarlin 2011). A key assumption
needed to justify such an approach is that remedial assignment has no effect
on future outcomes except through its effect on remedial enrollment. In vielen
contexts including the LUCCS, Jedoch, this assumption is unlikely to hold.
Zum Beispiel, a student assigned to remediation may opt not to enroll at all. A
student who enrolls may find his access to college-level coursework restricted,
and will not be able to graduate, even if he never enrolls in a remedial course.
Daher, we maintain that the assignment itself is the relevant treatment (never-
theless, someone willing to make the necessary assumptions can still ballpark
the instrumental variable estimates by dividing any of our impact estimates by
our estimated “first stage” impacts on remedial enrollment).

4. FULL SAMPLE RESULTS
Graphical Analysis and Specification Checks

We begin by presenting graphical evidence to support the RD assumptions.
Erste, we plot the distributions of the test scores to check for discontinuities
in the density at the cutoff. Discontinuities in the density at the cutoff may
suggest either that students are systematically sorting themselves around the
cutoff (this is more of a concern in contexts that allow for retesting) or that
some sample selection is taking place after students learn their scores (wieder

19. We refer to the writing exam as “harder” than the reading exam purely based on the empirical

observation that students are much more likely to fail writing than reading.

20

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

Figur 1. Distributions of Test Scores Relative to School-Year-Specific Cutoffs. Top left hand figure:
A. Distribution of Math Scores Relative to Cutoff (Old Test); Bottom left hand figure: B. Distribution
of Algebra Scores Relative to Cutoff (New Test); Top right hand figure: C. Distribution of Reading
Scores, Failed Writing; Bottom right hand figure: D. Distribution of Reading Scores, Passed Writing.
Notes: The old math test was a single test, whereas the new math test has two modules. The harder
of the two modules, algebra, is the most common determinant of college-level versus remedial
placement in math. The sample in panel B is restricted to those who passed the easier math
module.

this is more of a concern in contexts in which researchers may not have data
on students who never enroll). In any case, we see little visual evidence of
any discontinuities in the four distributions presented in figure 1. For each
distribution we run McCrary (2008) tests for discontinuities in the density
and find none (results available upon request).

Zweite, we examine graphical plots of several pretreatment covariates by
test score in figures 2–5, and run the corresponding regressions to test for
discontinuities (in math, although we show plots for the old and new math
tests separately, we run a single pooled regression in the form of equation 3
except with each covariate as the dependent variable, no covariates included
in the regression, and the regression bandwidth restricted to ±6 points). Der
regressions confirm what the graphs suggest: no systematic differences in
covariates around the cutoff. The only covariate for which we find a statistically
significant difference is for high school preparatory units around the math
cutoff; the regression indicates those below the cutoff have 0.34 zusätzlich
high school preparatory units (p = 0.03), although a single significant (but still
substantively small) difference among the dozen of covariates tested provides
little cause for concern.

Endlich, we examine graphical plots of several key outcomes by test score for
visual evidence of discontinuities at the cutoff, shown in figures 6–9. Gesamt,

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

21

THE EFFECTS OF COLLEGE REMEDIATION POLICY

Figur 2. Covariates by Test Score Relative to the Cutoff, Old Math Test.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 3. Covariates by Algebra (“Math 2”) Score Relative to the Cutoff, New Math Test.

the graphs provide little indication that assignment to remediation affects
the initial enrollment decision or the number of semesters enrolled over the
subsequent three years. There is some hint of possible negative effects on
degree/transfer mirrored by possible positive effects on dropout. The clearest
pattern coming out of these graphs is that those scoring just below the cutoffs
are substantially more likely to take remedial coursework, and somewhat less
likely to take, pass, or do well in college-level coursework in the relevant subject.
As noted earlier, the effect of assignment to remediation on the likelihood
of actually taking a remedial course is far less than 100 Prozent. In math,

22

Judith Scott-Clayton and Olga Rodriguez

Figur 4. Covariates by Reading Test Score, for Those Who Failed Writing.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

Figur 5. Covariates by Reading Test Score, for Those Who Passed Writing.

assignment to remediation increases the likelihood of taking a remedial math
course by about 27 percentage points, and assignment to reading remediation
increases the likelihood of taking a reading course by 45 Zu 55 percentage points,
depending upon the specification. The higher compliance rate in English than
math is due to two factors: (1) some majors have higher major-specific remedial
cutoffs in math, so some students may take remedial courses even though they

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

23

THE EFFECTS OF COLLEGE REMEDIATION POLICY

Figur 6. Outcomes by Old Math Test Score (2001–2004 Cohorts).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 7. Outcomes by New Math Test Score (2004–2007 Cohorts).

score above the institution-specific cutoff, Und (2) more college courses require
freshman composition (the first college-level English course) as a prerequisite
than require any college-level math course as a prerequisite. These differences
in compliance are important to keep in mind when interpreting the different
patterns of results for remedial math and remedial reading assignments.

24

Judith Scott-Clayton and Olga Rodriguez

Figur 8. Outcomes by Reading Score for Those Who Failed Writing.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

F

/

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

.

F

Figur 9. Outcomes by Reading Score for Those Who Passed Writing.

Main Results

Assignment to Remedial versus College-Level Math

Main results from the analysis of remedial math assignment are presented
in table 2. Our main specification utilizes a local linear regression with a
bandwidth of ±6 points. To test the sensitivity of our results we also show
results with and without covariates, with a narrower local linear specification,

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

25

THE EFFECTS OF COLLEGE REMEDIATION POLICY

and with a wider bandwidth that includes quadratic terms for all of the test
score distance variables. Gesamt, the estimated effects are highly robust across
these alternative specifications.

We find little evidence of discouragement effects on initial enroll-
ment. Although the results indicate assignment to math remediation has
a small, statistically significant negative effect on immediate enrollment
(–2 percentage points), this fades out such that there is no impact on whether
students enroll within three years. Daher, students assigned to remediation
may delay enrollment but it does not appear to discourage them from en-
rolling ultimately. Darüber hinaus, some students who delay enrollment may in fact
have been recruited into non-credit skills remediation programs. Zum Beispiel,
the LUCCS offers several intensive non-credit college transition programs for
improving math and English skills, and students recruited into these programs
may defer formal enrollment but still remain attached to the institution (Das
is essentially a form of pre-enrollment remediation and offers another reason
why we would not want to assume the only students impacted by remedial
assignment are those who enroll in a formal remedial course).

Nor do we find any indication of either development or discouragement
effects post enrollment. Assignment to remediation has little influence, NEIN-
ther positive or negative, on degree completion, degree/transfer, persistence,
dropout, or semesters enrolled. Weiter, we find no evidence that students
learned more in remediation, as measured by outcomes on a standardized
proficiency exam required in order to earn a two- or four-year degree. Wir finden
no impact on rates of taking or passing the college exit exam, and for the
17 percent of these students who took the exam, we find no impact on their
scores (unfortunately, as noted earlier, we cannot examine impacts on learning
for students who never take the test).20

The only outcomes for which we see a consistent pattern of impacts are
those relating to the specific courses students take—assignment to math re-
mediation increases the probability of taking remedial math by 27 Prozentsatz
points, and decreases the probability of taking college level math by about
8 percentage points. Ähnlich, those assigned to math remediation were 5
percentage points less likely to pass college-level math, 4 percentage points
less likely to ever earn a C or better, Und 2 percentage points less likely to ever
earn a B or better in college-level math. If one is willing to assume the impacts
on the B-or-better outcome result purely from the reduction in college-level

20. The impacts on proficiency test scores are not strictly causal because they are conditional on a
post-treatment outcome (taking the exam). Wenn, Jedoch, we make the assumption that any impact
of treatment on test-taking is monotonic across individuals, then the fact that there is no overall
impact on test-taking enables us to interpret the score differences—or lack thereof—causally (sehen,
z.B., Lee 2009, who shows that under this monotonicity assumption, selection bias goes to zero as
the impact of treatment on the probability of selection goes to zero).

26

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

F

/

e
D
u
e
D
P
A
R
T
ich
C
e
–
P
D

l

F
/

/

/

/

/

1
0
1
4
1
6
8
9
6
5
8
e
D
P
_
A
_
0
0
1
5
0
P
D

F

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Judith Scott-Clayton and Olga Rodriguez

ich

H
T
D
w
D
N
A
B
e
D
W

ich

ich

H
T
D
w
D
N
A
B
w
Ö
R
R
A
N

S
e
T
A
ich
R
A
v
Ö
C
Ö
N

N
Ö
ich
T
A
C
fi
C
e
P
S

ich

ich

N
A
M

ich

N
Ö
ich
T
A
D
e
M
e
R
H
T
A
M
Ö
T

T
N
e
M
N
G
S
S
A

ich

F
Ö

S
T
C
e
F
F
E

:
S
T
l
u
S
e
R
N
A
M

ich

.

l

2
e
B
A
T

)
E
S
(

B

)
E
S
(

B

)
E
S
(

B

)
E
S
(

B

e
M
Ö
C
T
u
Ö

∗

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗

)
1
1
0
.
0
(

)
9
0
0
.
0
(

1
2
0
.
0
−

3
1
0
.
0
−

)
2
1
0
.
0
(

7
5
2
.
0

)
3
1
0
.
0
(

)
3
1
0
.
0
(

)
2
1
0
.
0
(

)
1
1
0
.
0
(

)
8
0
0
.
0
(

)
9
0
0
.
0
(

)
2
1
0
.
0
(

1
8
0
.
0
−

8
4
0
.
0
−

0
4
0
.
0
−

9
1
0
.
0
−

5
0
0
.
0
−

4
0
0
.
0
−

0
1
0
.
0
−

)
3
1
0
.
0
(

5
1
0
.
0

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗

)

4
1
0

.

0

(

9
7
2

.

0

)

5
1
0

.

0

(

)

5
1
0

.

0

(

)

4
1
0

.

0

(

)

2
1
0

.

0

(

)

0
1
0

.

0

(

5
7
0
0
−

.

9
5
0
0
−

.

0
5
0
0
−

.

3
2
0

.

0
−

1
0
0

.

0
−

)

1
1
0

.

0

(

2
0
0

.

0

)

3
1
0

.

0

(

6
1
0
0
−

.

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗
∗

)

5
1
0
0

.

(

3
1
0
0

.

)

1
1
0

.

0

(

4
7
2

.

0

)

2
1
0

.

0

(

)

2
1
0

.

0

(

)

1
1
0

.

0

(

)

0
1
0
0

.

(

)

8
0
0

.

0

(

)

9
0
0

.

0

(

)

1
1
0
0

.

(

)

2
1
0
0

.

(

7
7
0
0
−

.

1
5
0
0
−

.

5
4
0
0
−

.

3
2
0

.

0
−

2
0
0
0
−

.

1
0
0
0
−

.

9
0
0

.

0
−

1
1
0
0

.

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗
∗
∗

∗
∗

)

1
1
0
.
0
(

3
7
2
.
0

H
T
A
M
v
e
D

k
Ö
Ö
T

)

2
1
0
.
0
(

)

2
1
0
.
0
(

)

1
1
0
.
0
(

)

0
1
0
.
0
(

)

8
0
0
.
0
(

)

9
0
0
.
0
(

)

1
1
0
.
0
(

7
7
0
.
0
−

0
5
0
.
0
−

3
4
0
.
0
−

1
2
0
.
0
−

2
0
0
.
0
−

2
0
0
.
0
−

8
0
0
.
0
−

)

2
1
0
.
0
(

0
1
0
.
0

H
T
A
M
L
C
N

ich

R
e
H
G
H

ich

R
Ö
C
D
e
N
R
A
E

H
T
A
M
L
C
N

ich

R
e
H
G
H

ich

R
Ö
B
D
e
N
R
A
E

D
e
R
R
e
F
S
N
A
R
T

R
Ö

A
A

D
e
N
R
A
E

A
A

D
e
N
R
A
E

G
N
ich
T
S
S
R
e
P

ich

l
l
ich
T
S

T
u
Ö

D
e
P
P
Ö
R
D

H
T
A
M

l

e
v
e

l
–

e
G
e

l
l

Ö
C

D
e
S
S
A
P

H
T
A
M

l

e
v
e

l
–

e
G
e

l
l

Ö
C

k
Ö
Ö
T

)

3
1
0

.

0

(

)

1
1
0

.

0

(