Data-driven Cross-lingual Syntax:
An Agreement Study with Massively
Multilingual Models
Andrea Gregor de Varda
University of Milano-Bicocca
a.devarda@campus.unimib.it
Marco Marelli
University of Milano-Bicocca
m.marelli@unimib.it
Massively multilingual models such as mBERT and XLM-R are increasingly valued in Nat-
ural Language Processing research and applications, due to their ability to tackle the uneven
distribution of resources available for different languages. The models’ ability to process multiple
languages relying on a shared set of parameters raises the question of whether the grammatical
knowledge they extracted during pre-training can be considered as a data-driven cross-lingual
grammar. The present work studies the inner workings of mBERT and XLM-R in order to test
the cross-lingual consistency of the individual neural units that respond to a precise syntactic
phenomenon, das ist, number agreement, in five languages (English, Deutsch, French, Hebrew,
Russian). We found that there is a significant overlap in the latent dimensions that encode
agreement across the languages we considered. This overlap is larger (A) for long- vis-`a-vis short-
distance agreement and (B) when considering XLM-R as compared to mBERT, and peaks in the
intermediate layers of the network. We further show that a small set of syntax-sensitive neurons
can capture agreement violations across languages; Jedoch, their contribution is not decisive in
agreement processing.
1. Einführung
Massively multilingual models (MMMs) such as multilingual BERT (mBERT, Devlin
et al. 2019) and XLM-RoBERTa (XLM-R, Conneau et al. 2020A) are transformer-based
language representation models trained simultaneously on multilingual text in several
languages (104 Und 100, jeweils). They do not involve any architectural changes
with respect to their monolingual counterparts (BERT and RoBERTa), nor any reliance
on any explicit cross-lingual signal. MMMs reach impressive performance scores in
tasks involving zero-shot cross-lingual transfer, a procedure that entails the fine-tuning
of the model on supervised data in a language L1 and its application to a different
Action Editor: Byron Wallace. Einreichung erhalten: 27 Juni 2022; revised version received: 24 September
2022; zur Veröffentlichung angenommen: 12 Oktober 2022.
https://doi.org/10.1162/coli a 00472
© 2023 Verein für Computerlinguistik
Published under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International
(CC BY-NC-ND 4.0) Lizenz
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
language L2, with no additional training.1 This procedure has been shown to be success-
ful across a variety of languages and downstream tasks (Pires, Schlinger, and Garrette
2019; Wu and Dredze 2019; Dufter and Sch ¨utze 2020; Liu et al. 2020; Lauscher et al. 2020;
see Doddapaneni et al. 2021 für eine Rezension). Although performance levels tend to be pos-
itively correlated with the typological similarity between the two languages (Lauscher
et al. 2020), zero-shot cross-lingual transfer yields surprising results in languages
written in different scripts (Pires, Schlinger, and Garrette 2019) and with little or no
(Karthikeyan et al. 2020); (Conneau et al. 2020B) vocabulary overlap. With only a
subset of the world’s languages being properly represented in the evolving language
technologies, the distribution of resources available for NLP researchers is extremely
asymmetrical (Joshi et al. 2020). Massively multilingual models represent an attempt
to temper the effects of this imbalance by exploiting the knowledge that can be shared
across languages.
The performance of MMMs in the transfer tasks hints at the possibility that their
internal representations might be inherently cross-lingual (Pires, Schlinger, and Garrette
2019; Dufter and Sch ¨utze 2020; Guarasci et al. 2022). Dufter and Sch ¨utze (2020) argue
that mBERT multilingualism might be due to its finite number of dimensions, welche
forces it to exploit common structures to compress representations across languages.
The question of whether a multilingual model induces a shared representational space
where abstract cross-linguistic regularities are encoded through a common set of pa-
rameters is remindful of the debate on the neural underpinning of linguistic knowledge
in multilingual individuals (see Dhar and Bisazza [2021] for similar considerations). In
besondere, the problem is reminiscent of the question of whether the neural resources
allocated to different languages in a multilingual brain overlap (at least partially, sehen
Perani et al. 1998; Abutalebi, Cappa, and Perani 2001; Perani and Abutalebi 2005; Grün
2008) or involve functionally independent neural populations (Kim et al. 1997; Tham
et al. 2005; Tan et al. 2011; Xu et al. 2017). If we consider the possibility of looking
at artificial neural networks as a different “species” (Cummins and Schwarz 1988;
McCloskey 1991), in a fashion that reminds us of the study of animal models, the study
of the representations produced by these networks might offer novel insights into the
space of possible solutions to the cognitive question mentioned above.
A modest but increasing number of findings is contributing to the question of
whether MMMs develop a data-driven universal grammar through an analysis of their
internal states. A study targeting mBERT vector representations has shown that syntac-
tic trees can be retrieved from its intermediate representational subspaces, with these
subspaces being approximately shared across languages (Chi, Hewitt, and Manning
2020). These intermediate subspaces can be used in machine translation, by identifying
the nearest neighbor in different representation spaces given a sentence in a source
language and a set of candidates in a target language (Pires, Schlinger, and Garrette
2019). Other studies have performed representational similarity analysis comparing
encoded sentences in different languages; while most results suggested that MMMs
develop a cross-lingual space in the intermediate layers (Conneau et al. 2020B; Del and
Fishel 2021; Muller et al. 2021), as shown by converging similarity between sentence
representations in deeper layers of the networks, contrasting results have documented
an opposed pattern when sentence representations are obtained through CLS pooling
instead of mean-pooling (Singh et al. 2019, although see Del and Fishel 2021 for a case
against the CLS pooling strategy).
1 Where L1 and L2 are typically a resource-rich and resource-poor language, jeweils.
262
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
The work we reviewed insofar targeted vector representations as a whole, neglect-
ing the role of the individual parameters in the embeddings. Jedoch, while research
in NLP used to largely overlook the single dimensions in the neural representations,
a recent research line is starting to investigate the linguistic properties encoded in
individual neurons and attention weights (see for instance Karpathy, Johnson, Und
Fei-Fei 2015; Li et al. 2015; Radford, Jozefowicz, and Sutskever 2017; Tang et al. 2017;
Kementchedjhieva and Lopez 2018; Bau et al. 2018; Dalvi et al. 2019A; Lakretz et al.
2019; Pinter, Marone, and Eisenstein 2019; Serrano and Smith 2019). Aiming to ex-
tend this line of analysis to a multilingual setting, we isolated the contribution of the
individual neurons in mBERT and XLM-R, defined as dimensions in the deep latent
Darstellungen. While most studies assessing the models’ cross-lingualism considered
phrasal representations as a whole, without discerning between semantic and syntactic
properties (Pires, Schlinger, and Garrette 2019; Liu et al. 2020; Del and Fishel 2021),
we restricted our study to number agreement, a structure-dependent phenomenon. Es
has been shown that BERT captures syntactic features in the intermediate
layers
(Jawahar, Sagot, and Seddah 2019), which are the same that show the highest repre-
sentational similarity across languages in the multilingual model (Del and Fishel 2021).
This layer-wise convergence of syntactic and cross-lingual knowledge in (M)BERT in-
spired our choice to constrain our study to a structural linguistic feature. The general
question of whether MMMs represent patterns that generalize across languages is
hereby framed as an inquiry into the cross-lingual stability of the neural units that
encode number agreement.
6, 9
(cid:75)
(cid:74)
2. Related Work
A productive research line in computational linguistics has focused on the analysis of
the linguistic features learned by neural language models. This line of analysis aimed
at testing whether sequence processing networks were able to construct hierarchical
representations of the linguistic input, or either relied on local heuristics without ac-
quiring core knowledge of different grammatical phenomena. A popular trend within
this framework relied on the large-scale unsupervised training of a language model,
and the fine-grained evaluation of the probabilities it assigned to different linguistic
units in a controlled setting as a “behavioral” correlate of its ability to capture the
regularities of a given language. Along this line of work, numerous studies have used
long-distance number agreement as a way of probing the networks’ ability to encode
structure-dependent relationships (Linzen, Dupoux, and Goldberg 2016; Bernardy and
Lappin 2017; Gulordava et al. 2018; Kuncoro et al. 2018; Marvin and Linzen 2018;
Goldberg 2019; van Schijndel, Mueller, and Linzen 2019; Lasri, Lenci, and Poibeau 2022).
While all the previous studies evaluated the models on their native tasks, Lakretz et al.
(2019) presented an ablation-based study of the inner mechanisms that underlie number
agreement processing in LSTMs at the single neuron level, showing that a very sparse
set of specialized units carried number features from the subject to the verb across the
intervening material. In ähnlicher Weise, Finlayson et al. (2021) have used causal analysis
to implicate specific neurons in transformer models.
With the debut of multilingual models, the previous studies were replicated in
different languages, showing that mBERT successfully captures syntax-sensitive agree-
ment patterns (Bacon and Regier 2019; Mueller et al. 2020). Jedoch, these experiments
limited their focus on the analysis of mBERT’s predictive behavior, overlooking the
functioning of its internal processes. A complementary line of analysis has investigated
263
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
how multilingual models encode other linguistic attributes in their internal represen-
tations. Zum Beispiel, Gonen, Ravfogel, and Goldberg (2022) have shown that gender
information is encoded in both language-specific and language-neutral subspaces in the
embeddings of mBERT. Außerdem, Antverg and Belinkov (2021) have investigated
the cross-lingual consistency in the units of mBERT and XLM-R that responded to
different morphological features, showing that there is a significant overlap in the
latent dimensions that encode attributes such as gender, Zeitform, and number. Ähnlich,
Stanczak et al. (2022) have probed the same models in 43 languages, and on a variety
of morphosyntactic categories. Jedoch, while these two studies have investigated the
encoding of number in MMMs, they have not investigated number agreement, das ist,
the structural relationship that is instantiated between a subject and a verb in a well-
formed sentence. To fill this research gap, we tested whether the processes that underpin
number agreement computation across languages could be ascribed to an overlapping
set of latent dimensions in the structural embeddings of the models.
3. Materials and Methods
3.1 Language Models
Our experiments were performed utilizing the native masked language modeling com-
ponent of mBERT and XLM-R. The configurations of the models were left unaltered
with respect to their original releases (Devlin et al. 2019; Conneau et al. 2020A). Im Par-
besonders, we relied on the multilingual version of BERTBASE (cased) and on XLM-RBASE.
The two networks share an analogous structural configuration: They are composed of
12 layers, 12 self-attention heads, and a hidden size of 768. Jedoch, while mBERT is
jointly trained with a masked language modeling and a next sentence prediction (NSP)
objective, XLM-R drops the latter component, and increases the amount of training
Daten. The networks did not undergo any fine-tuning nor adaptation process, as they
were used as out-of-the-box masked language models. We did not mask any word
throughout this work.
3.2 Materials
The agreement data was obtained from the CLAMS dataset2 (Mueller et al. 2020), A
cross-linguistic resource for the syntactic evaluation of word prediction models. CLAMS
comprises subject-verb agreement challenge sets for English, Deutsch, French, Russian,
and Hebrew, constructed by means of artificial grammars. Note that in abstract terms
these languages encode agreement patterns in a similar way, das ist, through a form of
morphological inflection that links subject and verb on account of their grammatical
number. For the sake of simplicity, out of the seven syntactic constructions covered
in the original dataset we only included simple agreement and long-distance VP-
coordination (henceforth short- and long-distance agreement; siehe Abbildung 1). We selected
these two conditions as they represent the settings with the shortest and the longest
dependency length between the subject and the verb, jeweils. While in short-
distance agreement the two constituents are immediately adjacent, in long-distance
2 Publicly available at https://github.com/aaronmueller/clams.
264
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
(1)
(2)
(A)
(B)
The author
*The author
smiles
smile
knows
knows
viele
viele
anders
anders
foreign
foreign
languages
languages
Und
Und
likes
wie
Zu
Zu
betrachten
betrachten
The author
*The author
(A)
(B)
Fernsehen
Fernsehen
zeigt an
zeigt an
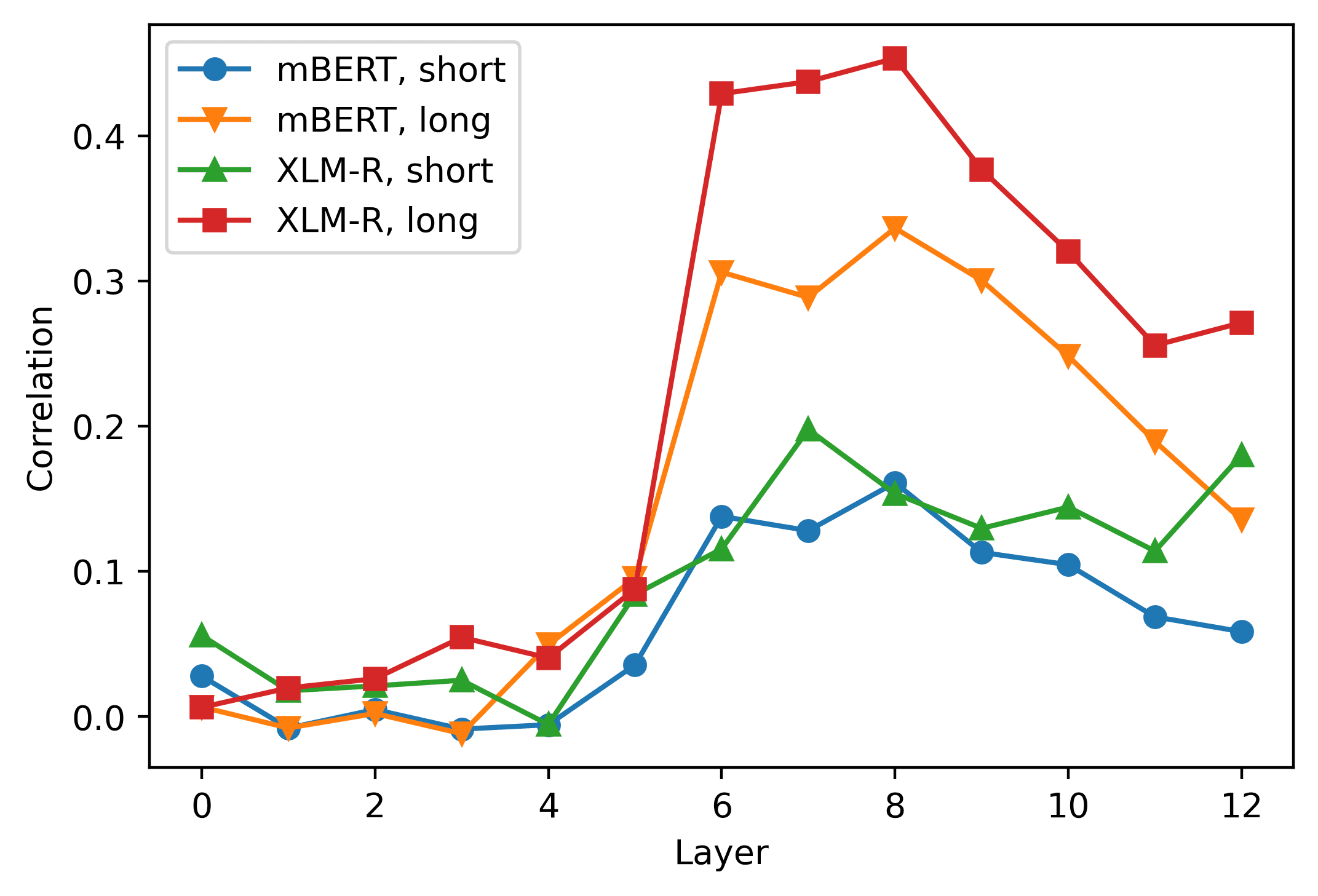
Figur 1
English examples of grammatical (A) and ungrammatical (B) sentences in the simple agreement
(1) and long-distance VP-coordination (2) Bedingungen.
agreement they are separated by a large amount of intervening verbal material (nämlich,
the VP projection of the main phrase and the coordinating conjunction).
3.3 Verfahren
In order to identify the most relevant units with respect to the agreement task, Wir
adopted the Linguistic Correlation Analysis (LCA) procedure (Dalvi et al. 2019A,B),
a supervised method based on linear classification. The first step of LCA consists of
extracting the neuron activations from the model in response to the input words. Dann,
a logistic classifier is trained to predict a label (in our case, the grammaticality of
the sentence obtained by including the word in the phrasal context) from the overall
internal state of the model, with cross-entropy loss and elastic net regularization as
additional loss term (Zou and Hastie 2005), with λ1 = λ2 = 0.001. The trained weights
of the classifier are used as a measure of the relevance of the corresponding units with
respect to the linguistic property being investigated (d.h., the binary label of grammat-
ical acceptability); this allows sorting the neurons according to the absolute value of
their respective weights. In our study, we restricted our analyses to the activations in
response to the verb that should instantiate an agreement relationship with the subject
(z.B., smiles/*smile, likes/*like in Figure 1). As a result of this choice, we trained the logistic
classifiers with the verb representations as input. In the case of multi-token verbs,
the activations corresponding to the two tokens were averaged, following Dalvi et al.
(2019A).
Probing classifiers have the undeniable advantage of being a flexible analysis tech-
nique that can help researchers understand the roles and dynamics of the hidden
components of a network and diagnose potential problems (Alain and Bengio 2016).
Jedoch, several shortcomings of probing classifiers have been highlighted in the liter-
ature. Zum Beispiel, it has been emphasized that the probing framework might highlight
correlations between the representations generated by a language model and a given
linguistic property, but it does inform us on the role of this property in the predictions
of the model (Belinkov and Glass 2019; Belinkov 2022). Antverg and Belinkov (2021)
have proposed a methodology to rank individual neurons in language models without
the need for an external probe. This procedure involves the computation of the average
network activation q(z) for every categorical label z ∈ Z; Dann, a simple element-wise
subtraction between the centroids of each category is calculated to assess the differential
role of each neuron across classes. The ranking is then obtained by sorting the neurons
according to their absolute value in the vector difference. It has been shown that probe-
free rankings better identify neural units that are actually used by the language mod-
els, as demonstrated through selective interventions (Antverg and Belinkov 2021). In
265
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
order to complement the results we obtained with the linear probing, and to offset the
limitations that are inherent in the probing framework, we also experiment with such a
probeless method.3
The ranking processes were performed independently for (A) each ranking method
(linear and probeless), (B) each model (mBERT and XLM-R), (C) each agreement condition
(long- and short-distance), Und (D) each individual language considered, in einem 2 × 2 ×
2 × 5 design which allowed us to derive 40 distinct rankings. In all cases, the classifier
was trained and tested on two subsets of the original data (80% train, 20% test). In
order to license meaningful comparisons on the performances of the classifiers across
languages, we downsampled all the short-distance challenge sets to 280 Artikel (224 im
training and 56 in the test set), and the long-distance datasets to 800 Artikel (640 Ausbildung,
160 test). All the procedures described above were implemented with the NeuroX toolkit
(Dalvi et al. 2019B), a Python package to perform interpretation and analysis of deep
neural networks.
Once the neuron ranking was obtained, we evaluated the cross-lingual consistency
in the set of neural units computing agreement across languages. Um dies zu tun,
we assessed the intersection between the top 100 neurons independently selected in
each language.4 In practice, we did not test the statistical significance of the cross-
lingual overlap at the level of the whole architecture, since the estimate of our test
would have been biased by the sequential flow of information within the network. Der
cross-lingual congruence of the neural units processing syntactic agreement could be
overestimated if one does not take into account the fact that similar processes with
a comparable degree of structural abstraction are likely to be processed in the same
layers. Intuitively, a dimension in the first layer of XLM-R or mBERT embeddings is less
likely to occupy a high position in the neuron ranking, since it is already known that
syntactic features are processed in the intermediate layers of the architecture (Jawahar,
Sagot, and Seddah 2019); because the probability associated with a given size of a set
intersection is critically dependent on the size of the population from which the sets are
sampled, a conservative approach to avoid a type-1 error is to consider a single layer
as the reference population. Daher, we previously searched for the layers that were more
relevant in the computation of cross-lingual agreement, and then evaluated the cross-
lingual overlap in the within-layer neural population. The statistical significance of the
resulting intersection size was computed through the super exact test (Wang, Zhao,
and Zhang 2015), a procedure for computing the distributions of multi-set intersections
based upon combinatorial theory.
4. Ergebnisse
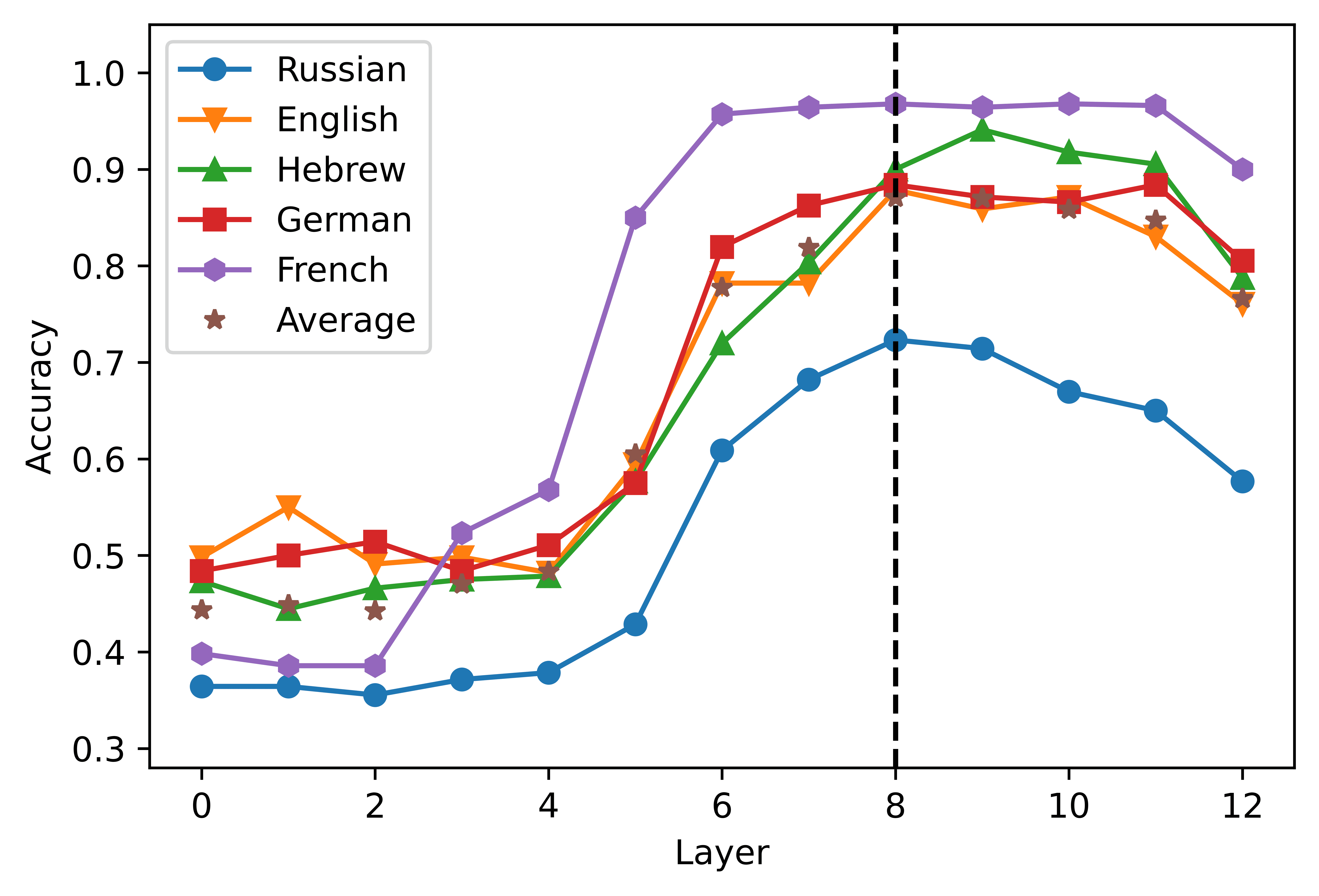
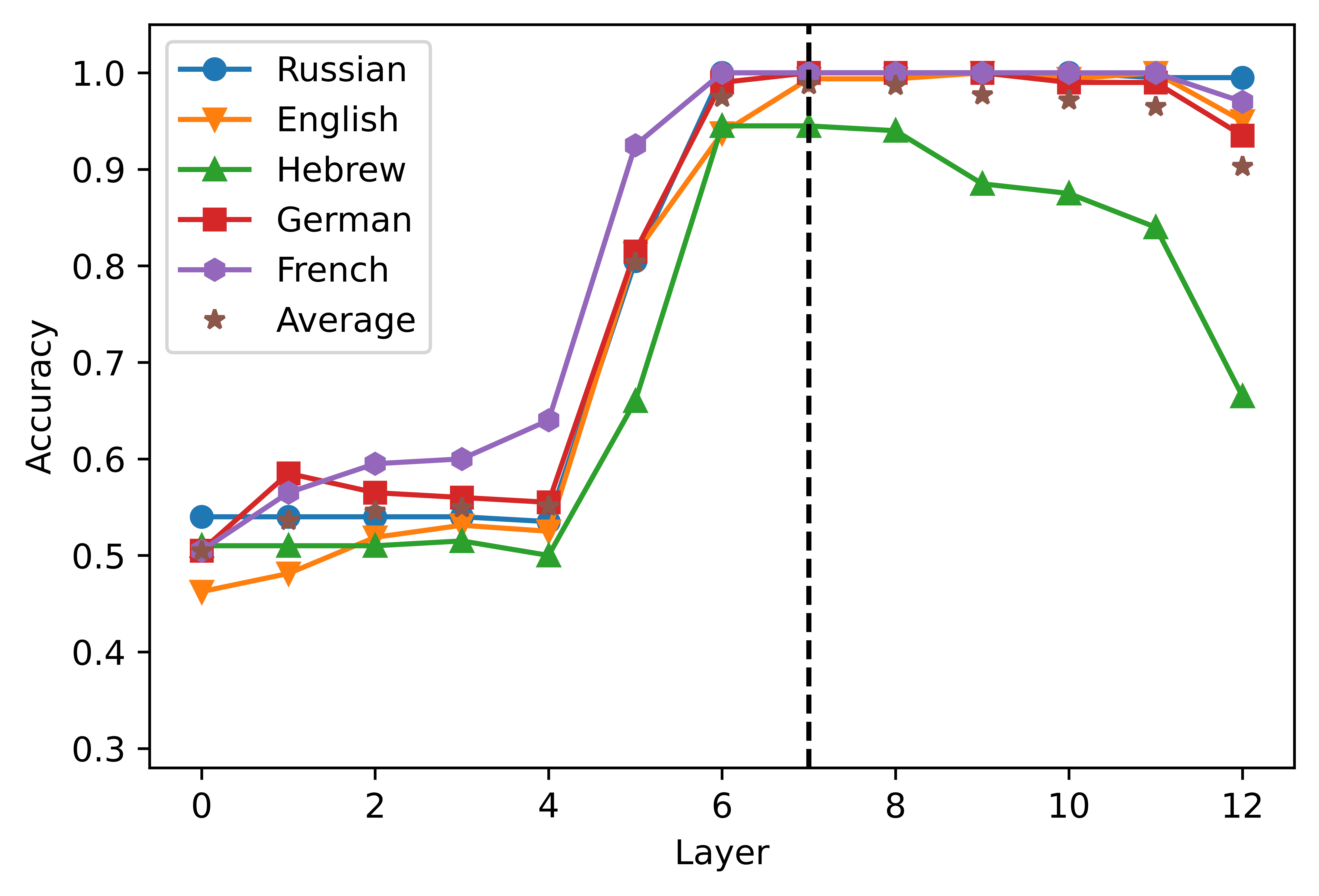
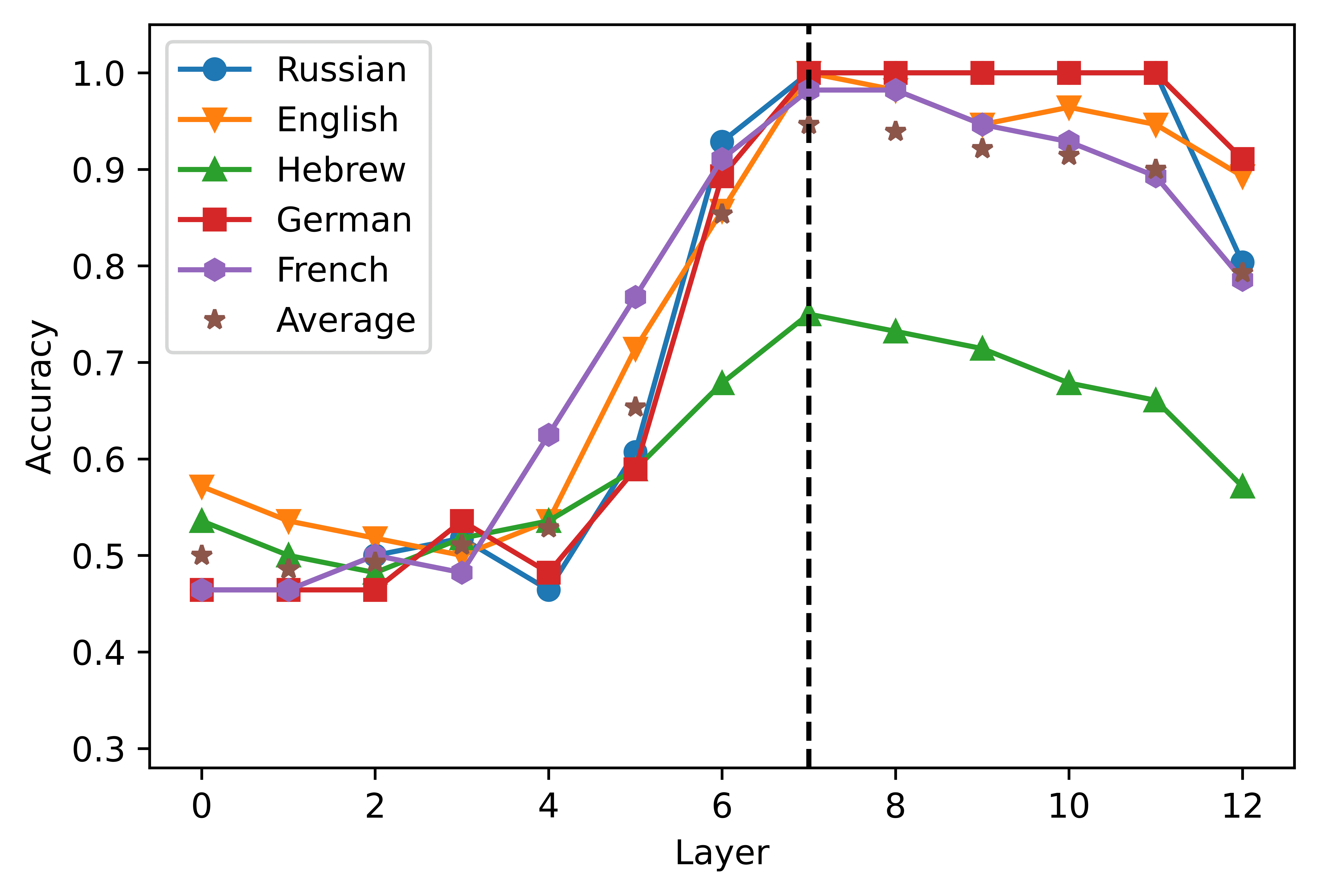
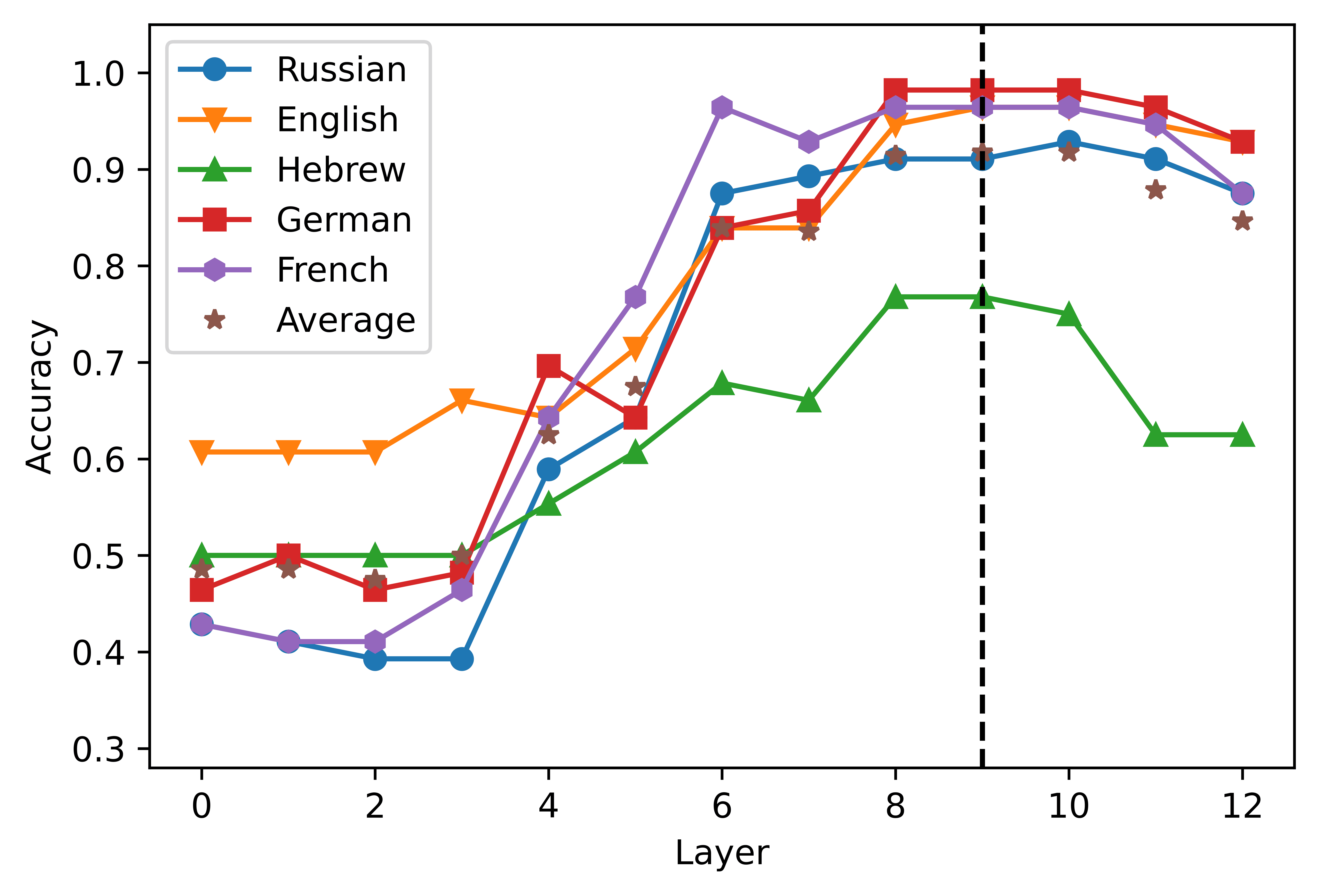
4.1 Layer-wise Analyses
In order to restrict our intersection analysis to a pre-specified layer, we first analyzed
the performance of a classifier trained to predict the grammaticality label in response to
each layer’s activation. The results are summarized in Figure 2. In the case of mBERT,
3 We thank an anonymous reviewer for the suggestion.
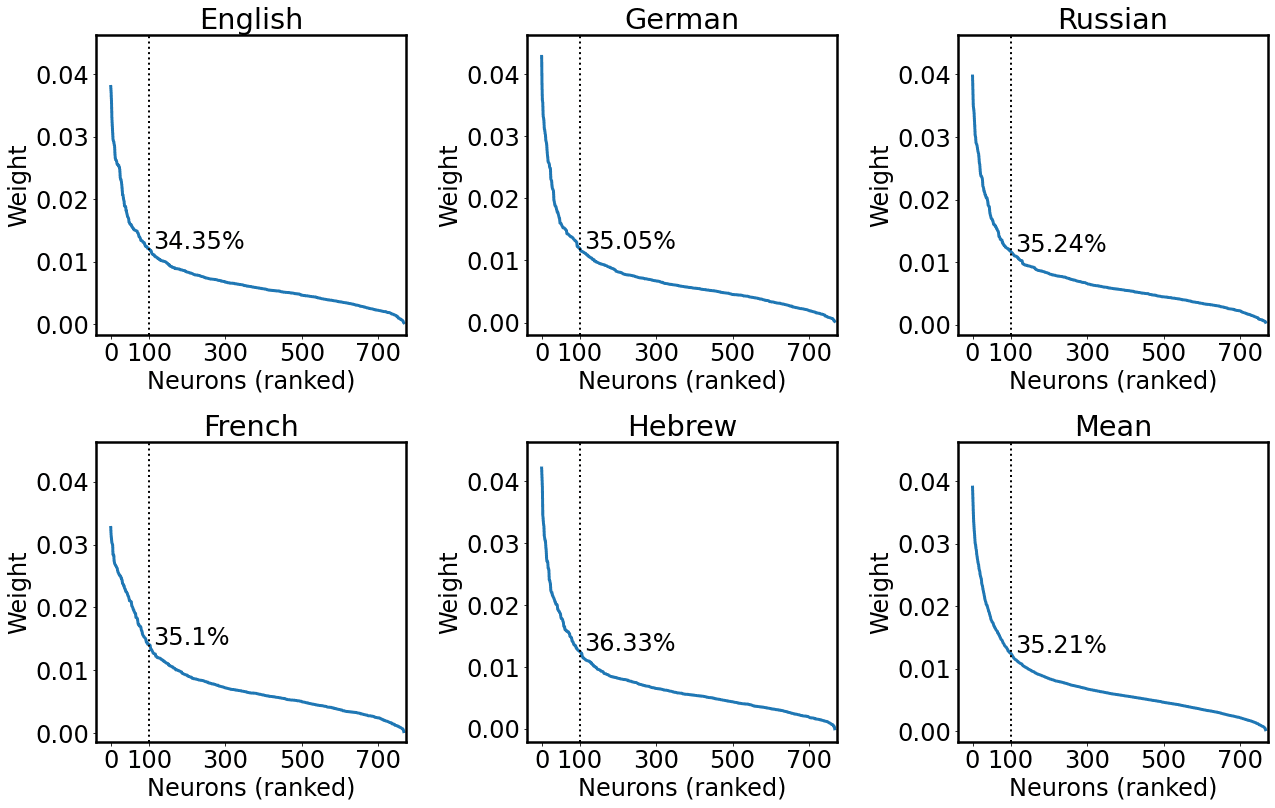
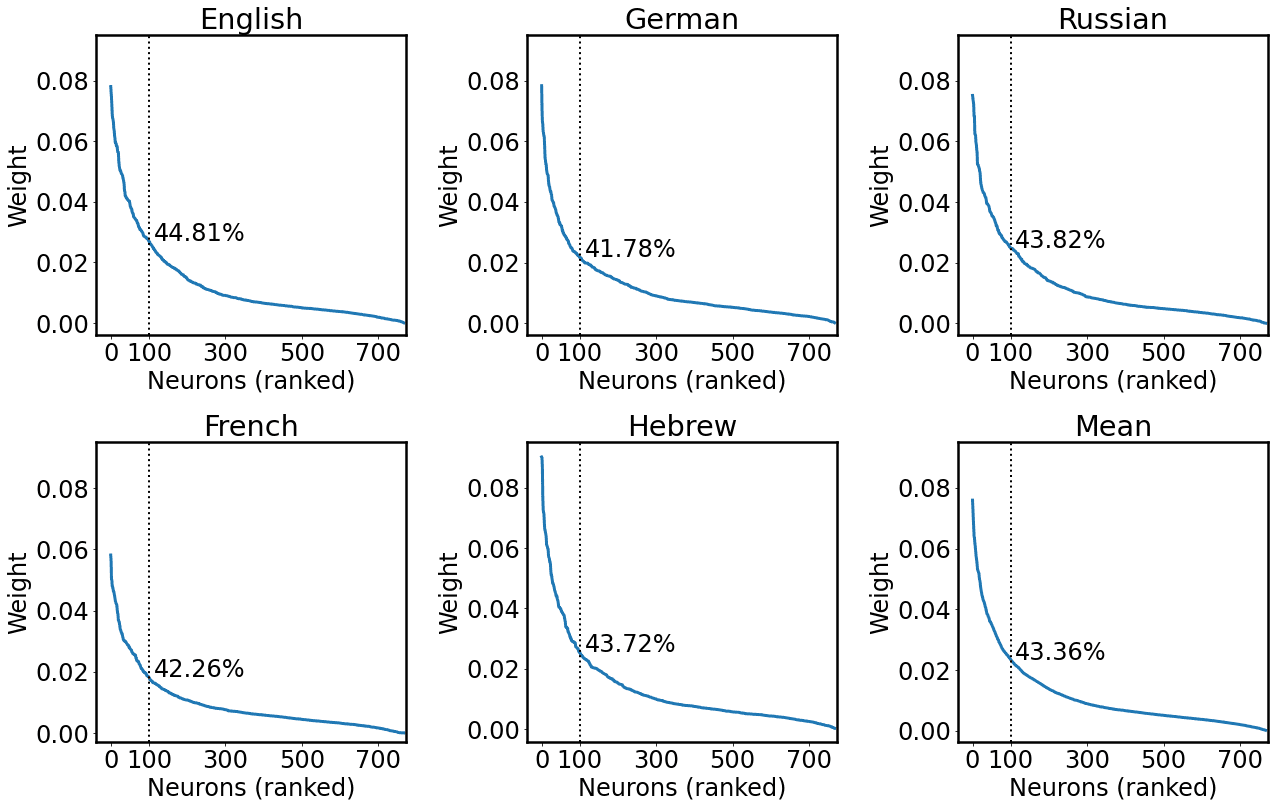
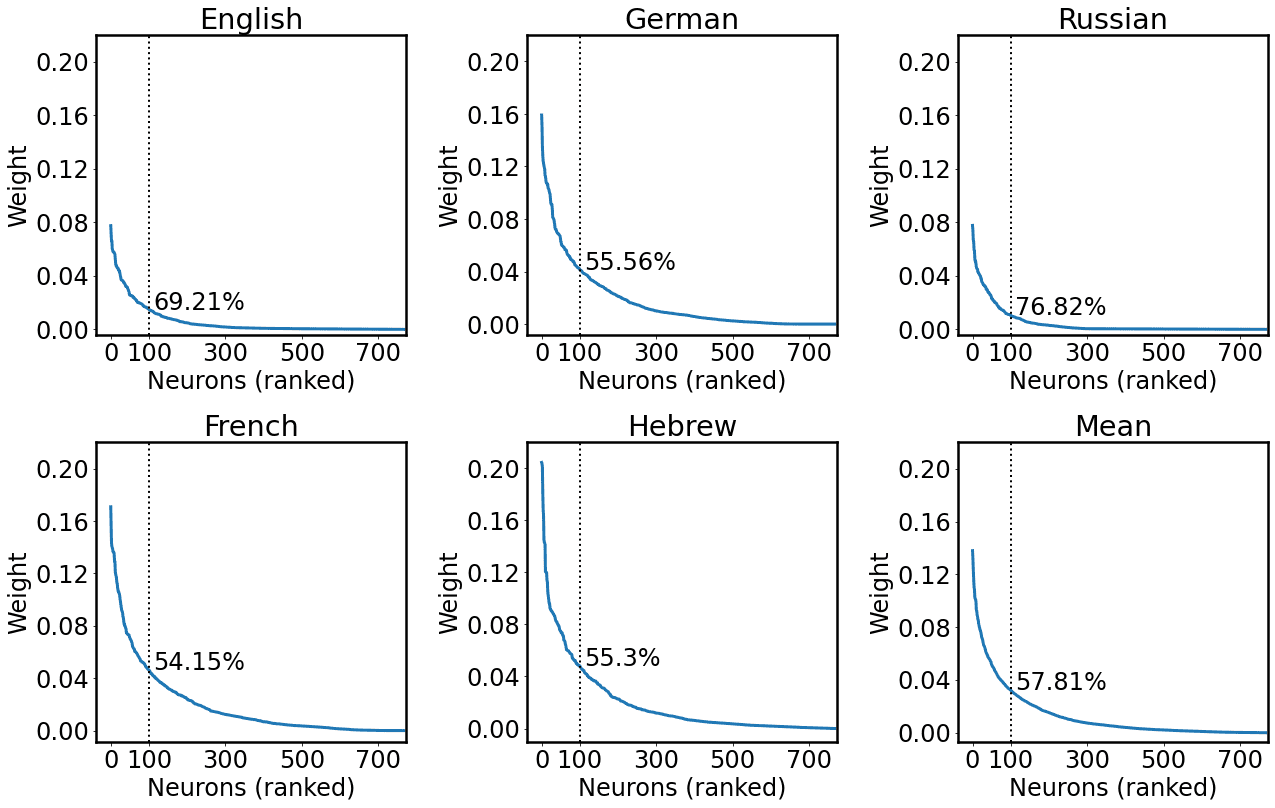
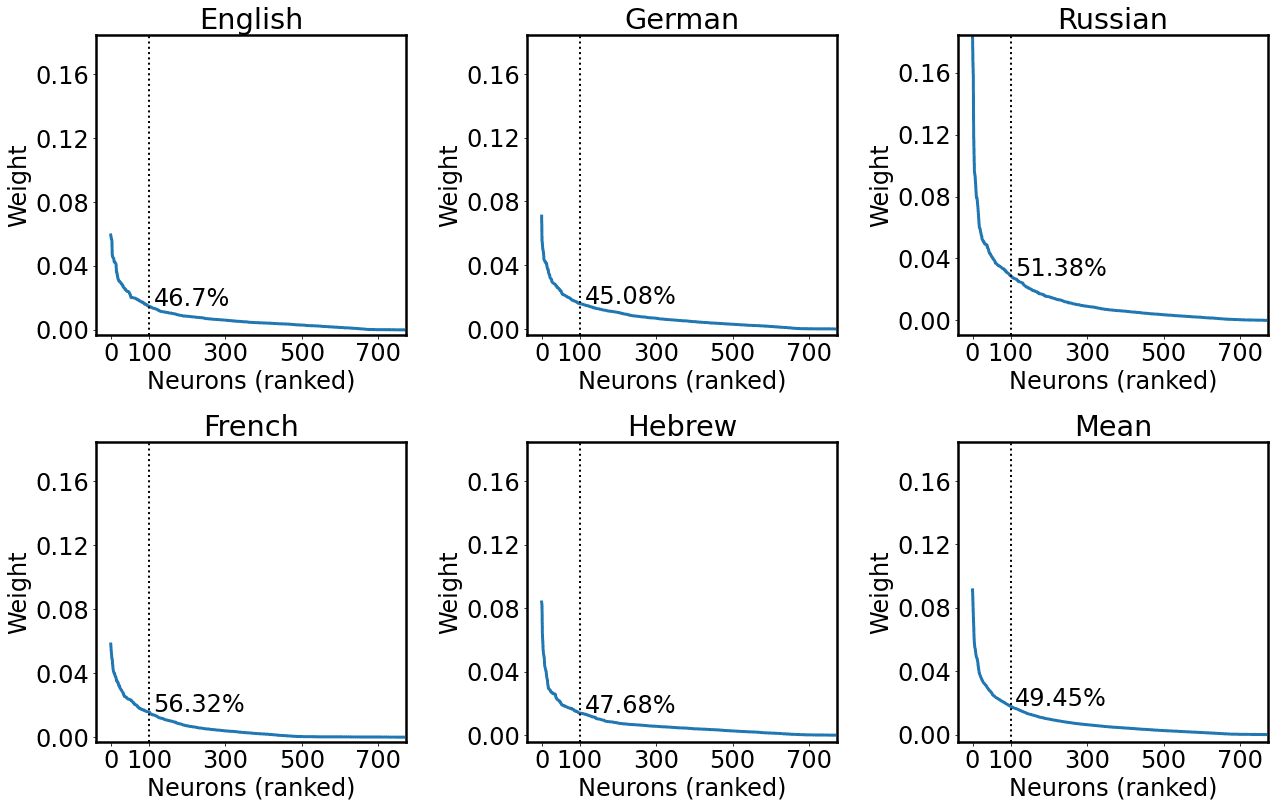
4 We considered 100 units as Antverg and Belinkov (2021); Jedoch, following an anonymous reviewer’s
suggestion, we analyzed post hoc the ratio of weight mass that could be ascribed to these neurons. Der
top 100 units contribute to a substantial proportion of the weight mass of the layer (on average 45.46%),
while constituting only the 13.02% of the layer units (N = 768). We report a detailed analysis in
Appendix 1.
266
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
(A) Short-distance agreement, mBERT
(B) Long-distance agreement, mBERT
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(C) Short-distance agreement, XLM-R
(D) Long-distance agreement, XLM-R
Figur 2
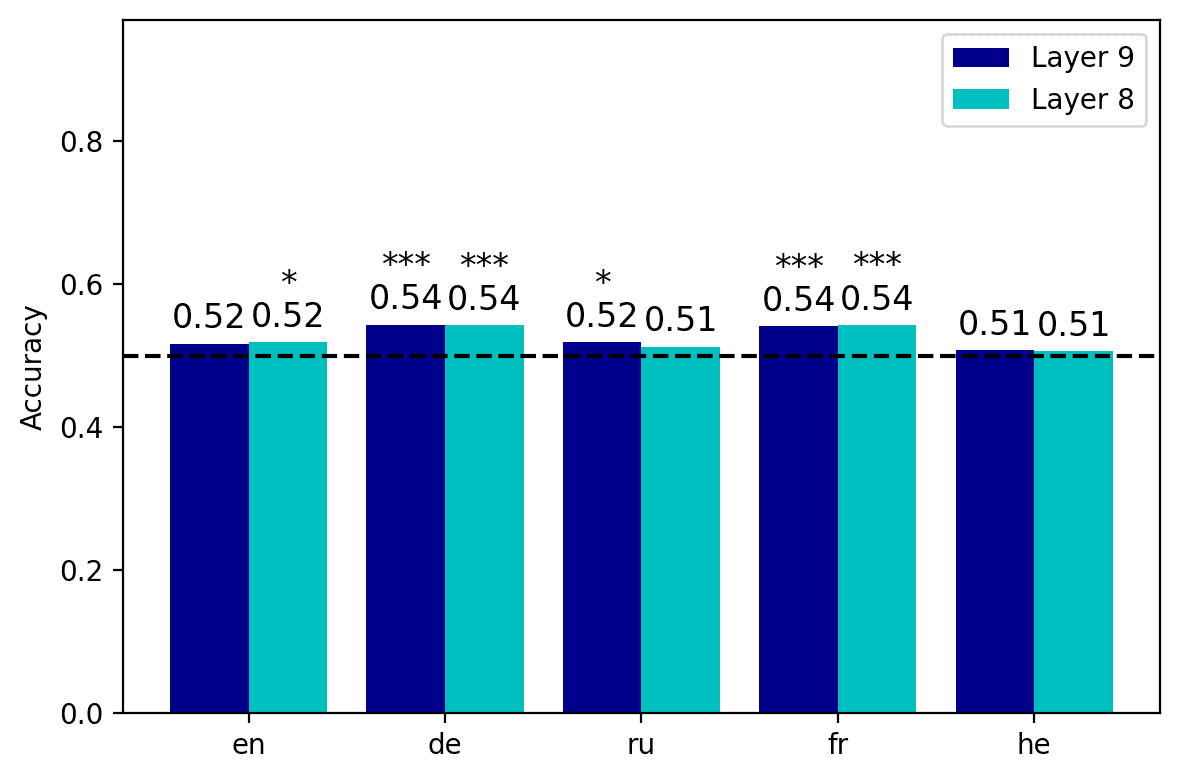
Layer-wise performance of the logistic classifier. The layer 0 includes the embedding layer
Darstellungen. The vertical dashed line indicates the peak of the average accuracy obtained by
the classifiers in the five languages considered.
the highest average accuracy scores in the short- (2A) and the long-distance (2B) con-
ditions were obtained from the activations of the eighth (0.8707) and ninth (0.9505)
layer, jeweils. XLM-R showed a higher degree of congruence across conditions,
since the highest scores were obtained in the seventh layer both in the short- (0.8089,
2C) and in the long-distance datasets (0.98775, 2D). A clear pattern that emerges from
the graphs is that the accuracy curve is highly dependent on the language considered.
In the case of short-distance agreement, mBERT’s performance in Russian falls 0.1474
points below the average; in the long-distance condition, the performance levels in
Hebrew is 0.0880 points lower than the mean. The classifiers built upon the XLM-R
representations perform consistently worse in Hebrew, where their performance levels
Sind 0.1661 Und 0.0420 points below average in the short- and in the long-distance con-
ditions, jeweils. These results corroborate the finding that mBERT does not learn
equally high-quality representations for its 104 languages (Wu and Dredze 2020), Und
extends this observation to XLM-R. The relatively poor performance scores obtained in
Hebrew and Russian are also consistent with the results of the standard predictive tests
obtained by Mueller et al. (2020), where mBERT’s accuracy in the agreement tasks was
noticeably lower in the two languages written in non-Latin scripts. dennoch, Die
pattern of performance across layers seems to be stable across languages and models:
predictably, the activations extracted from the most shallow layers are not a solid basis
267
Computerlinguistik
Volumen 49, Nummer 2
for the detection of grammatical violations; the classification accuracy increases in the
intermediate layers of the network, and declines in the deepest layers.
4.2 Intersections
4.2.1 Linguistic Correlation Analysis Rankings. Building upon these results, we confined
our multi-set intersection analyses to the layers that achieved the best results in the
classification task, nämlich, the seventh layer for XLM-R, and the eighth and the ninth
layer for mBERT (short- and long-distance agreement, jeweils). The results of
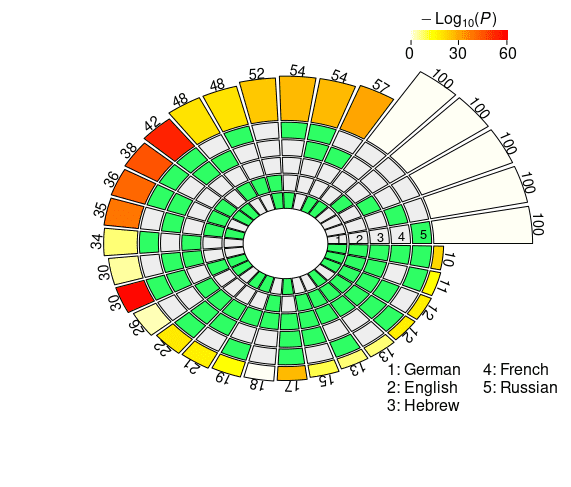
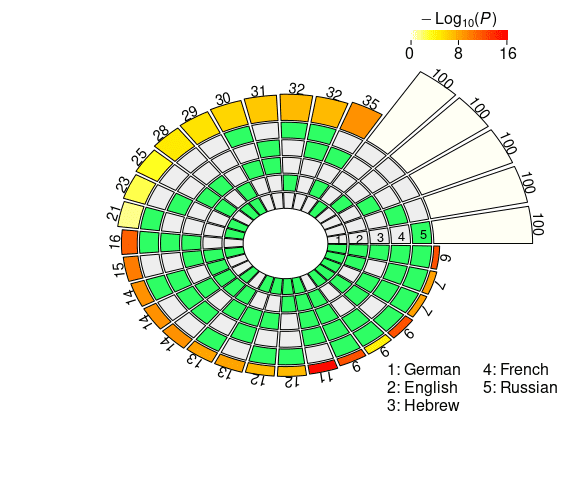
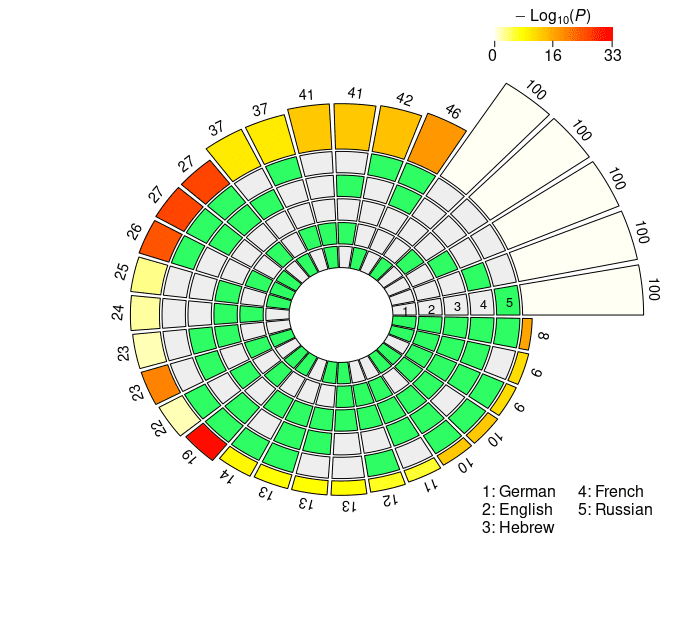
the super exact test on the cross-lingual neural overlap are depicted in Figure 3, Und
(A) Short-distance, layer 8, mBERT
(B) Long-distance, layer 9, mBERT
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(C) Short-distance, layer 7, XLM-R
(D) Long-distance, layer 7, XLM-R
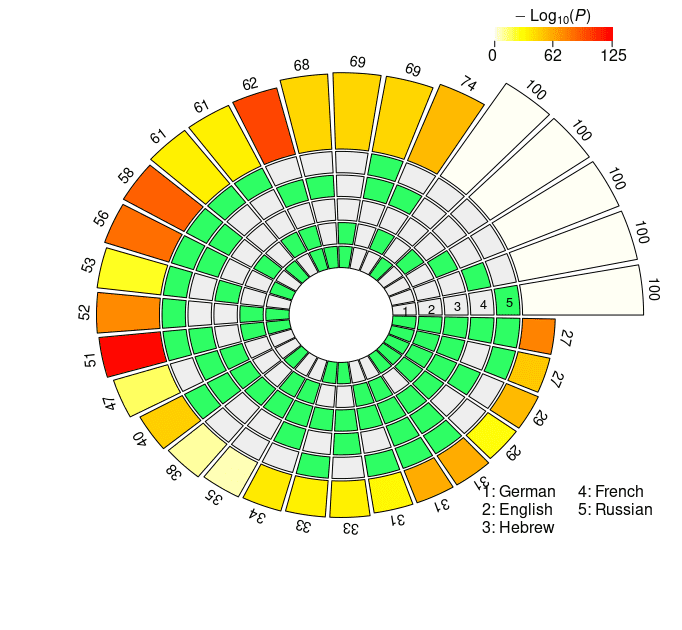
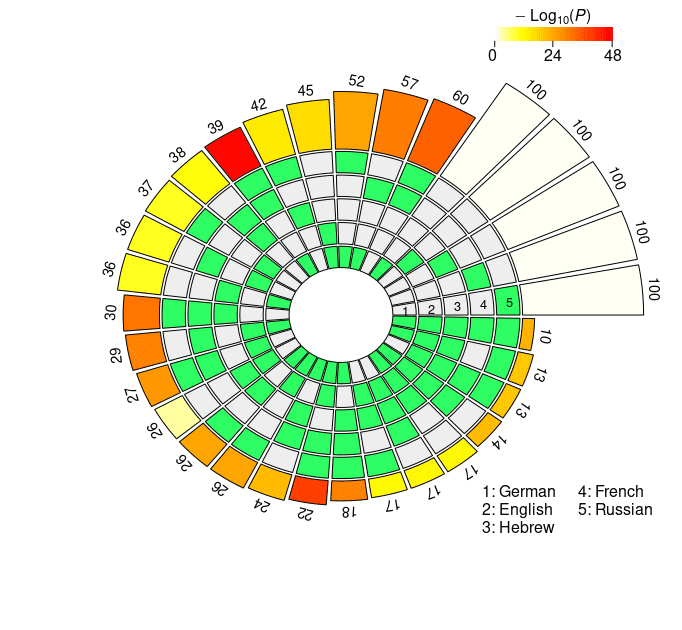
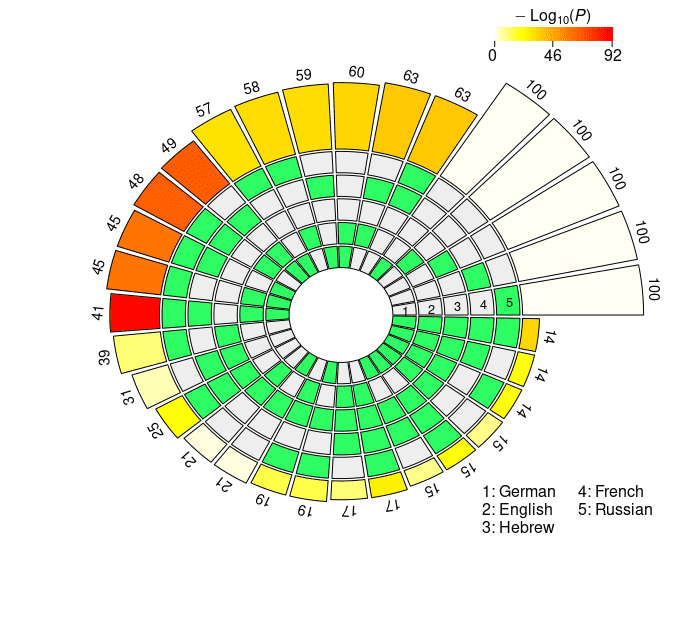
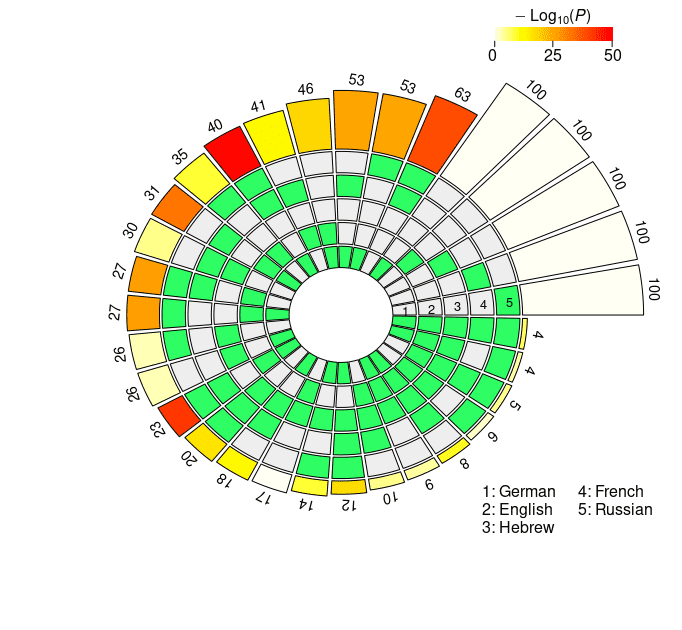
Figur 3
Set intersections of the top 100 neural units responsible for subject-verb agreement in the two
Bedingungen. The five concentric rings in the middle represent the five sets of top neurons relative
to each language, and the individual sections indicate the presence (Grün) or the absence (grau)
of the sets in each intersection. Each circular sector corresponds to a particular configuration of
set intersections. Zum Beispiel, a sector with the first and the last segment highlighted in green
corresponds to the German ∩ Russian intersection. The height of the bars in the outer layer is
proportional to the intersection sizes, which are made explicit by the numbers on the top. Der
color intensity of the bars represents the log-transformed p-value significance of the
intersections, as computed with the super exact test. The white bars on the right of the diagrams
are not associated with FE and statistical significance, and they simply report the number of
considered units for each language (N = 100). The segments are ordered counterclockwise by
intersection size.
268
de Varda and Marelli
Data-driven Cross-lingual Syntax
reported in detail in Appendix 2 (Tables 2, 3 for mBERT; Tables 4, 5 for XLM-R). Alle
two-, three-, four-, and five-way combinations show an overrepresentation of the set
intersection relative to the random expectation. This overrepresentation is statistically
significant in all but four intersections (out of 104); in the case of mBERT, the statistical
significance of the fold enrichment (FE; d.h., the ratio between observed and expected
overlap5) exceeds the conventional threshold of α = .05 in the En6 ∩ He and De ∩ He
cases in the short-distance condition, and He ∩ Fr in the long-distance condition. Der
only combination with p > .05 in the intersections based on XLM-R is En ∩ He; vor allem,
Hebrew is present in all the non-significant intersections.
In the case of the mBERT short-distance agreement results, the two-, three-, Und
four-way intersections associated with the highest fold enrichment are En ∩ Fr, En ∩ Fr
∩ Ge, and En ∩ Fr ∩ De ∩ Ru, jeweils (see Figure 3a). These three combinations
have in common the absence of the Hebrew set, and the presence of the English and
the French sets. On average, the pairwise set intersections in the case of short-distance
agreement comprise 24.9 Einheiten; a striking number of 39 units is found in the En ∩ Fr
intersection (FE = 2.9952, p = 5.84 · 10–13). Remarkably, three neurons survived all the
five-way set intersections, occupying a high position in all the five language-specific
rankings (FE = 104.3677, p = 3.39 · 10–6). In the case of long-distance agreement, Die
highest fold enrichment for each N2 . . . 4-way intersection is found in Fr ∩ Ru, Fr ∩ En
∩ Ge, and Fr ∩ En ∩ De ∩ Ru, with Hebrew being again the absent language in the
three combinations and French appearing in all of them (see Figure 3b). The average
pairwise intersection size is 28.4; the five-way intersection in the long-distance condition
includes four neurons, with FE = 139.1569 and p = 1.01 · 10–10. Gesamt, Vereinbarung-
related information displays a greater degree of convergence in the long- vis-`a-vis the
short-distance condition. In der Tat, in the former case intersection sizes are consistently
bigger, and associated with higher FE (on average, the FE for the pairwise intersections
Ist 1.8893 in the short-distance condition, Und 2.1811 in the long-distance condition).
The results obtained by XLM-R mirror the ones derived from mBERT: Long-
distance agreement is characterized by larger intersections in the top-100 neuron rank-
ings, showing signs of a stronger cross-lingual alignment. In der Tat, the average pairwise
FE is 2.1965 in the short-distance condition, Und 3.3333 in the long-distance condition.
The N2 . . . 4-way intersections with highest FE in the short-distance condition are En ∩
Fr, He ∩ Fr ∩ Ru, and De ∩ En ∩ Fr ∩ Ru (see Figure 3c); in the long-distance condition,
the combinations that share the highest number of neurons are De ∩ Fr, De ∩ Fr ∩ Ru,
and De ∩ En ∩ Fr ∩ Ru (see Figure 3d). While Hebrew appears in one top combination
in the short-distance condition, most of the best scoring intersections do not include it.
The number of neurons that are present in the top-100 sets across all five languages is
remarkably high: In the short-distance condition, we found six cross-lingual neurons
(FE = 208.7354, p = 3.87 · 10–13), whereas in the long-distance condition the number rises
to ten (FE = 347.8924, p = 1.29 · 1023, by far the highest FE score we obtained in our
Studie). The overall congruence in the neural units responding to agreement violations
is stronger in XLM-R with respect to mBERT; this disparity is particularly evident in the
long-distance condition, where the neurons surviving through the five-way intersection
are more than double.
5 With the observed overlap being equal, higher-degree set intersections—which have lower expected
overlap—will have higher FE.
6 For readability purposes, the set of the top 100 units selected for a given language is reported with the
ISO 639-1 code of that language (English: En; Deutsch: Von; Russian: Ru; French: Fr; Hebrew: Er).
269
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
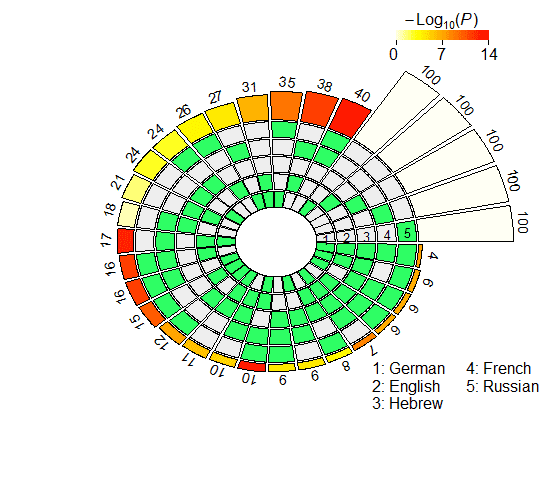
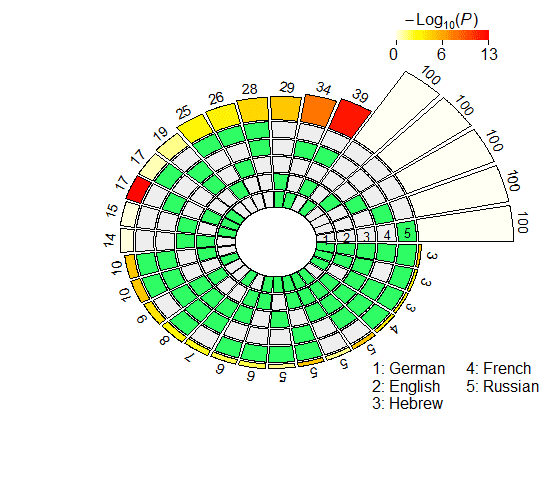
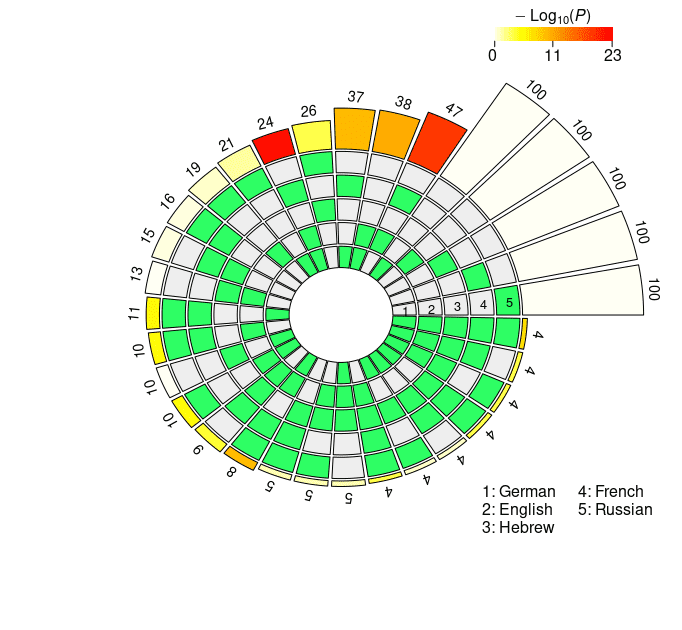
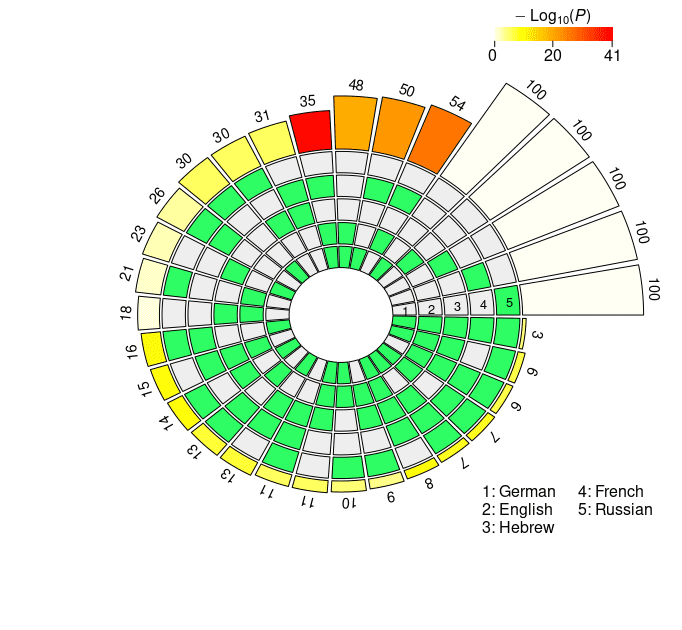
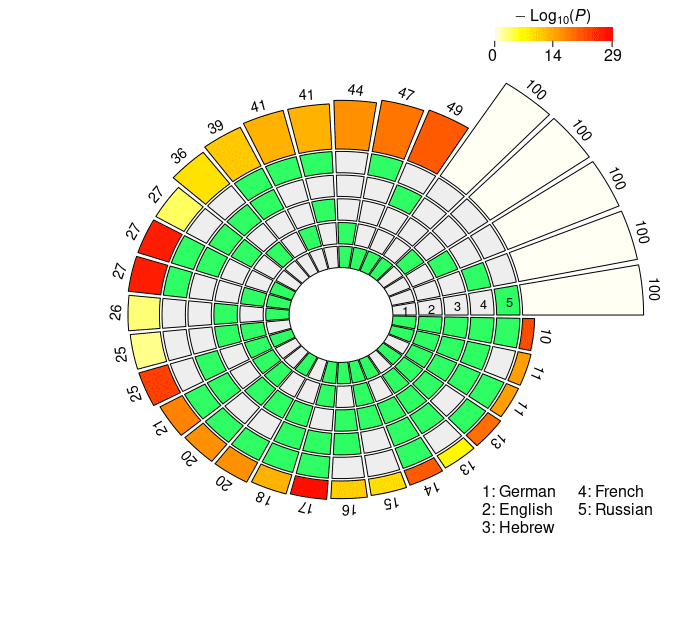
4.2.2 Probeless Rankings. As with the LCA method, we restricted our multi-set analyses to
the individual units populating the seventh layer in the case of XLM-R, and the eighth
and ninth layers for mBERT (long- and short-distance agreement). The results of the
super exact test based on the probeless rankings are graphically depicted in Figure 4,
and reported in detail in Appendix 2 (Tables 6, 7 for mBERT; Tables 8, 9 for XLM-R).
From a qualitative standpoint, the results obtained with the probeless ranking method
are analogous to those described in the previous section. Intersection sizes show a
general overrepresentation of units with respect to what would be expected by chance;
In der Tat, when considering short-distance agreement, in all the set intersections the size
of the observed overlap exceeds the size of the expected overlap by a significant margin
with the exception of very few combinations, most of which include the Hebrew set
(mBERT: En ∩ He; XLM-R: Fr ∩ Ru, He ∩ Fr, En ∩ He, De ∩ He, De ∩ He ∩ Ru, De ∩
He ∩ Fr). In the long-distance condition there are no exceptions to this trend, mit dem
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
(A) Short-distance, layer 8, mBERT
(B) Long-distance, layer 9, mBERT
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(C) Short-distance, layer 7, XLM-R
(D) Long-distance, layer 7, XLM-R
Figur 4
N2 . . . 5-way intersection statistics derived from the rankings obtained with the probeless
method.
270
de Varda and Marelli
Data-driven Cross-lingual Syntax
FE associated with all intersections being statistically significant, regardless of model
type. Noch einmal, intersection sizes tend to be bigger in the long-distance condition,
showing signs of a stronger representational alignment across languages. Restricting
our focus to pairwise overlap, the average FE is higher in the long-distance intersection
Daten (mBERT, short: 2.7421; mBERT, long: 3.2947; XLM-R, short: 1.8586; XLM-R, long:
4.416). Außerdem, the cross-lingual overlap is more pronounced when considering
the embeddings of the RoBERTa-based encoder (see above), in line with the LCA-based
results.
In the case of mBERT, the intersections with the highest overrepresentation of the
fold for each degree are En ∩ Fr, En ∩ Fr ∩ De, En ∩ Fr ∩ De ∩ He (short-distance), Und
Fr ∩ Ru, Fr ∩ Ru ∩ De, Fr ∩ Ru ∩ De ∩ En (long-distance). In the case of XLM-R, Die
intersections with the highest FE are En ∩ Fr, En ∩ Fr ∩ De, En ∩ Fr ∩ De ∩ Ru (beide
long- and short-distance). While Hebrew appears in one top combination in the short-
distance condition (mBERT), all the other best scoring intersections do not include it; An
die andere Hand, they all include the French set, in line with the results obtained with the
linear classifier.
5. Diskussion
Number agreement is a syntactic phenomenon that crucially relies on a proper parse
of the structure of a sentence. In all five languages we considered, number agreement
is made explicit through a form of morphological inflection that links subject and verb
by virtue of their syntactic relationship and their shared grammatical number. Gegeben
the similarity of the underlying grammatical process, a truly multilingual neural model
should display some degree of cross-lingual consistency in the neural units computing
Vereinbarung. Our analyses showed that indeed there is a correspondence in the encoding
of agreement patterns across languages, not only in terms of the layer-wise convergence
of information, but also in terms of the organization of the neural units within a single
layer. In the layer-wise analyses, a linear classifier built upon both mBERT and XLM-R
embeddings was able to detect syntactic anomalies from the intermediate layers of the
Netzwerk. The classification accuracy decreased in the deepest layers of the networks, In
line with results obtained with monolingual models (Jawahar, Sagot, and Seddah 2019);
crucially, this quadratic concave trend was coherent across the languages included
in our study. The structural alignment of different language pairs was susceptible to
systematic differences affecting in particular Hebrew, a low-resource language that
also obtains lower performance scores in layer-wise classification. We speculate that
this difference in results might be due, at least in part, to the typological relations
between the languages included in our study. In der Tat, English, Deutsch, French, Und
Russian are Indo-European languages. Hebrew, andererseits, is a Semitic lan-
guage belonging to the Afroasiatic family,7 despite exhibiting some Indo-European
influences (Zuckermann 2006). Außerdem, differently from the others, Hebrew is a
language characterized by a templatic morphology: Verbs and nouns can be inflected
by modifying a consonantal root, adding vowels between the consonants. Somit, A
linear segmentation of the input into sub-word units (as the one underlying mBERT and
XLM-R tokenizers) might not capture the full morphological complexity of the words
(Klein and Tsarfaty 2020). This entails that two inflected forms of the same root might
not share any sub-word token more frequently than in languages with concatenative
7 Following the Omniglot classification of languages at https://omniglot.com/writing/langfam.htm.
271
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
morphological systems, making agreement computations more difficult and based on
representational properties that are different from the other considered languages. Wir
thus speculate that the weaker correspondence in the neural unit processing agreement
in Hebrew might be motivated by these typological and morphological differences.
Despite a certain degree of language specificity in the intersection patterns, Die
independent selection of language-specific relevant units can nonetheless identify a
shared substrate underlying number agreement processing. Across model types and
ranking methods, the size of this shared substrate is consistently larger with increased
distance between the two hierarchically dependent words, as evidenced by the higher
FE in the long-distance condition. The greater distance between subject and verb, als
well as the contingent introduction of attractors between them, makes the task of
word prediction more difficult, as evidenced by standard predictive tests (Mueller et al.
2020). Somit, the comparison between the results obtained in the two agreement con-
ditions suggests that cross-lingual alignment is favored by more complex sentence
Darstellungen. A possible objection to this observation lies in the fact that both the
training and the test set in the long-distance condition comprised more items than in
the short-distance condition (see Section 3.3). This asymmetry in training data might
have resulted in a more precise ranking in the long-distance case, which in turn could
have identified more efficiently the cross-lingual components in the network. To rule
out this possible confound, we repeated all our analyses after downsampling the long-
distance set,8 and still found a more consistent unit-level convergence with increased
distance between the two interdependent constituents (see Appendix 3). Another factor
that influenced the cross-lingual convergence of syntactic information was model type:
The intersection sizes derived from the XLM-R-based ranks were much larger than the
ones obtained from its predecessor, regardless of the neuron ranking algorithm (in line
with previous results on probing with MMMs, see Antverg and Belinkov [2021] Und
Stanczak et al. [2022] for similar results). The two models are minimally different: Der
main attributes that distinguish them are the larger amount of training data and the
absence of the NSP objective in XLM-R. This suggests that the NSP loss is not a crucial
determinant of cross-lingual convergence, and that more trained and better performing
multilingual models have stronger language-neutral internal components (see also Del
and Fishel 2021).
From a methodological standpoint, the qualitative convergence in the results ob-
tained with LCA and the probeless ranking method shows that our findings are not
biased by the inherent limitations of the probing framework, such as the conflation
between the information learned by the model and by the probe (Antverg and Belinkov
2021). In der Tat, the main outcomes of our study—such as the greater cross-lingual con-
vergence in long- versus short-distance agreement and the stronger alignment in the
RoBERTa-based encoder—are robust regardless of the neuron ranking method applied.
6. Follow-up: The Depth of the Cross-lingual Syntax
In the previous sections, we started from the implicit assumption that the most relevant
layers for computing agreement within a single language would show the highest con-
sistency in their inner organization across languages. In the present follow-up study, Wir
8 We chose to rule out this confound a posteriori instead of performing our analyses on balanced sets from
the beginning in order to derive more precise estimates for the log-distance condition, where more data
were available.
272
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
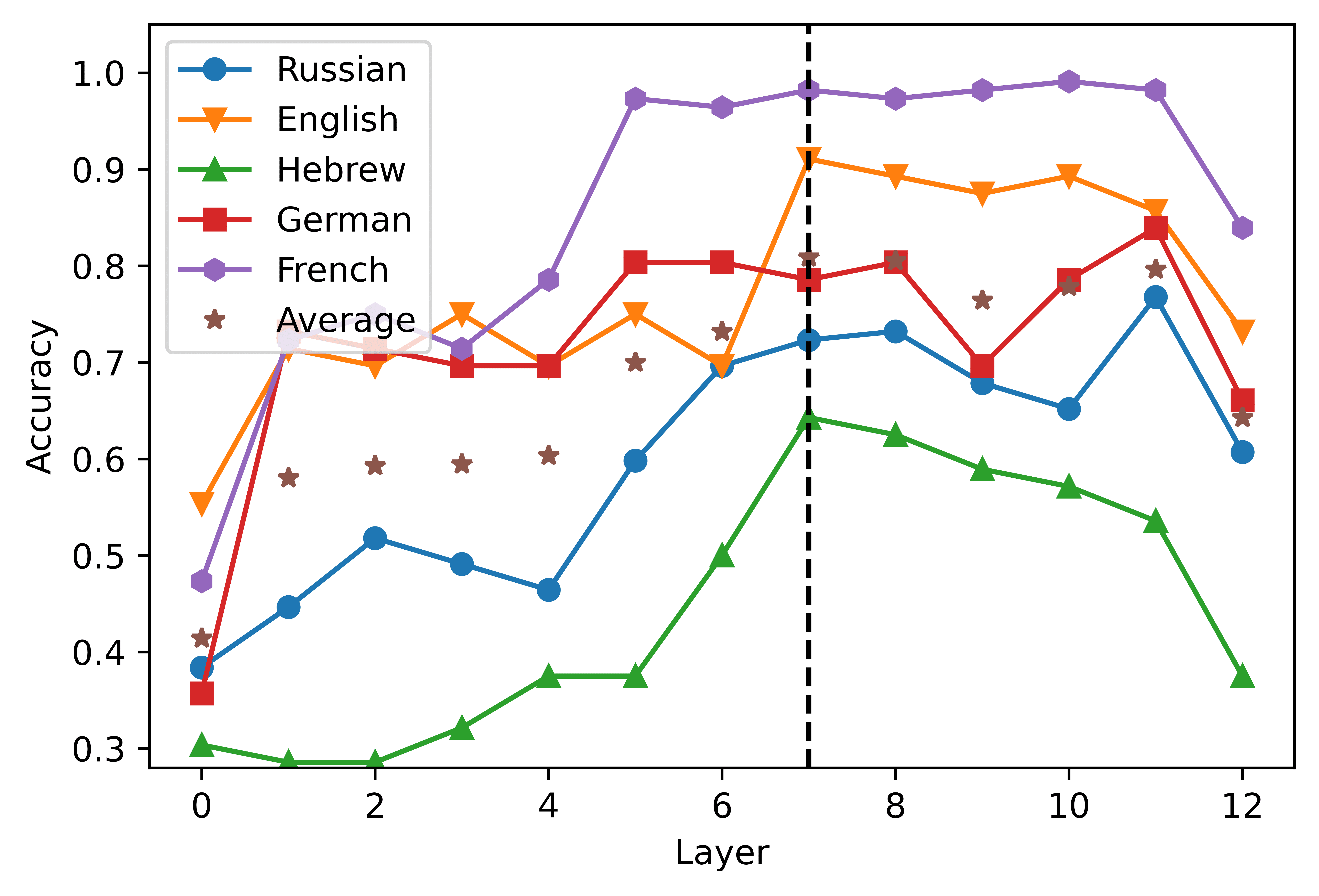
empirically tested this premise. Erste, we examined the weights assigned by the linear
classifiers to the highest scoring individual neurons across layers, and their dispersion
across languages (6.1). Dann, as a control, we also analyzed the layer-wise correla-
tions between the weight matrices learned by the classifiers in the five different lan-
guages9 (6.2).
6.1 Top Neurons Across Layers
Whereas in our previous experiments we adopted a maximally conservative approach
by extracting five language-specific independent neuron rankings for each condition,
here we used a more exploratory procedure by jointly searching for relevant cross-
lingual neurons in each layer. We reasoned that a cross-lingual neuron responding to
agreement should satisfy two necessary conditions. Erste, it should have, on average, A
high impact on the prediction of the grammaticality label. Zweite, the measures of that
neuron’s impact in the five languages considered should be comparable: Its relevance
should not be driven by a subset of the languages, but rather be cross-linguistically
stable. Following this line of reasoning, we operationalized the cross-lingual relevance
of each unit with respect to the task by averaging the absolute value of its weights
learned by the five language-specific classifiers. This procedure allowed us to construct
a global, language-neutral ranking of the neurons. Dann, for each layer, we considered
the neural unit with the highest average weight, and observed the relative standard
deviation of its value across languages. We performed our analyses independently for
short- and long-distance agreement, and for either model type.
(cid:74)
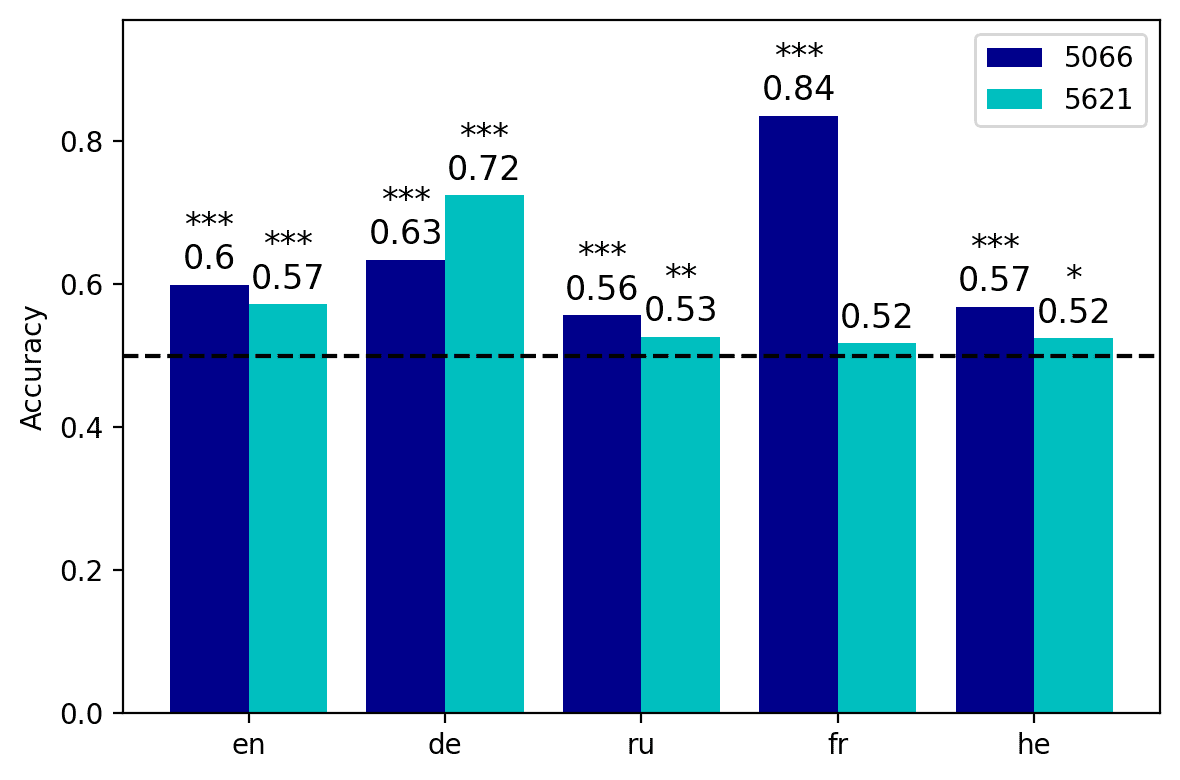
The results of our follow-up tests are depicted in Figure 5. The general pattern that
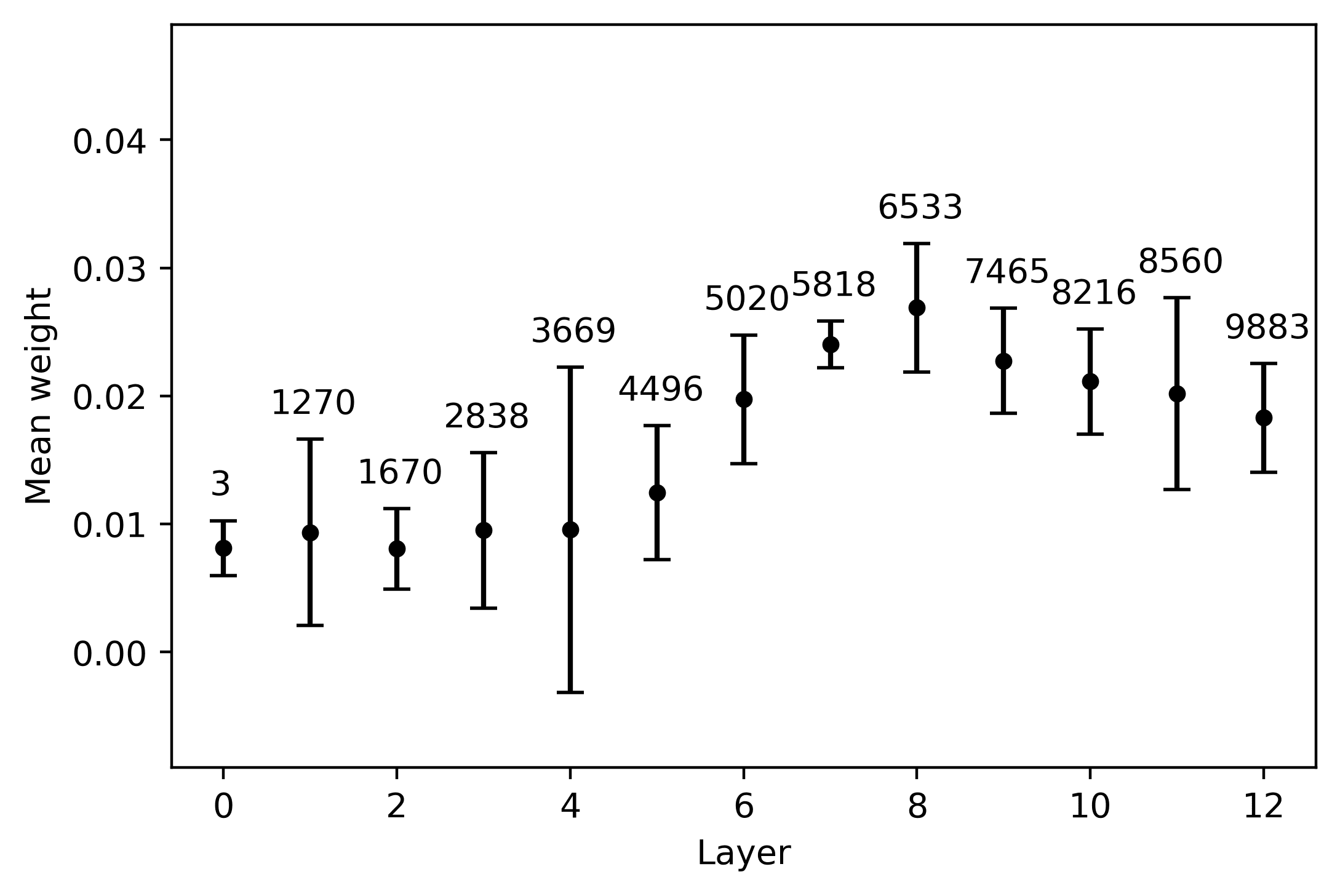
clearly emerges from the four plots is an initial increase in average weight, welches ist
steeper in the long-distance condition; the average weights then decrease in the last
layers. The growth in the average weight is associated with a contingent reduction
in the cross-lingual measure of dispersion, as indicated by the error bars. In the case
8, 9
of mBERT, this rise in the average weight reaches its peak in the intermediate
(cid:75)
layers. In the short-distance condition, the highest weight is obtained in the eighth
layer by neuron 6533 (5A); this neuron’s weights also exhibit a contained amount of
variation across languages (although the top neurons in the embedding and in the
seventh layer display an even smaller amount of dispersion). The best candidate cross-
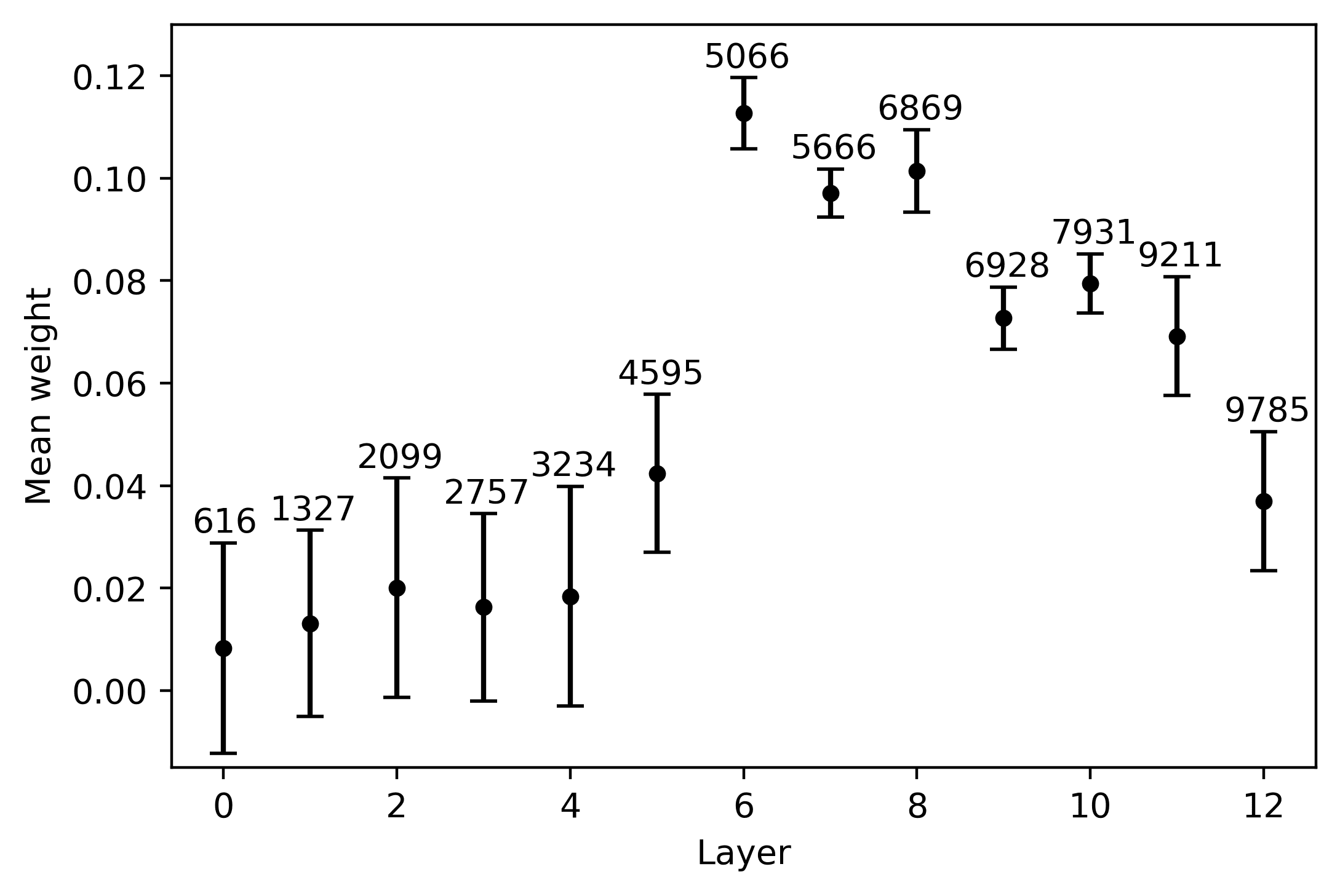
lingual neuron is easier to identify in the long-distance condition: Neuron 7674 im
ninth layer exhibits at the same time the two preconditions identified above, being both
the one with the highest weight and the one with the lowest cross-lingual deviation
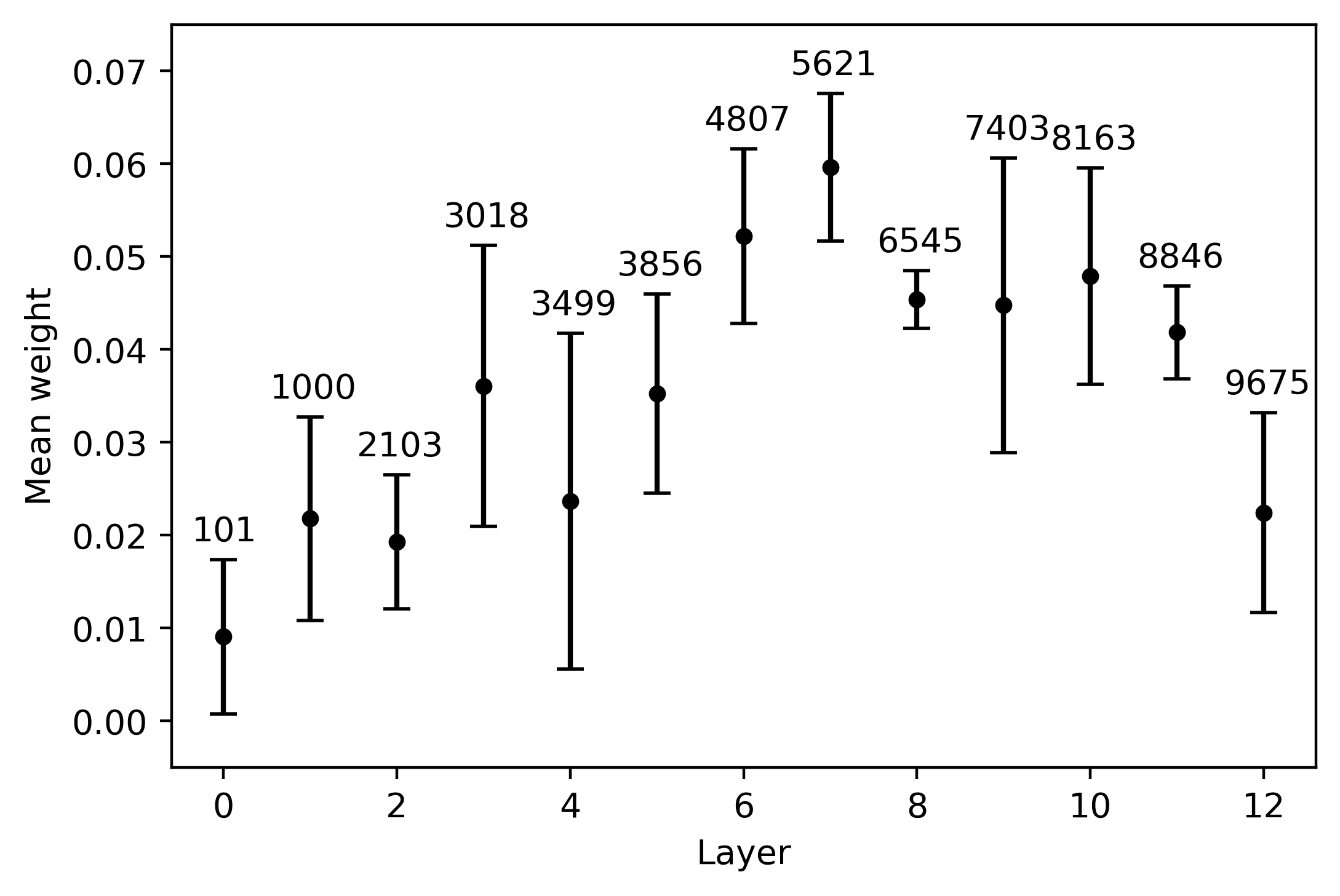
(5B). XLM-R neurons behave in an analogous way, but reach their maximal cross-lingual
convergence in earlier layers. In the short-distance condition, the highest mean weight
is obtained in the seventh layer by neuron 5621 (5C); this neuron also displays contained
cross-lingual variation, although the weights of neuron 6545 in the eighth layer are more
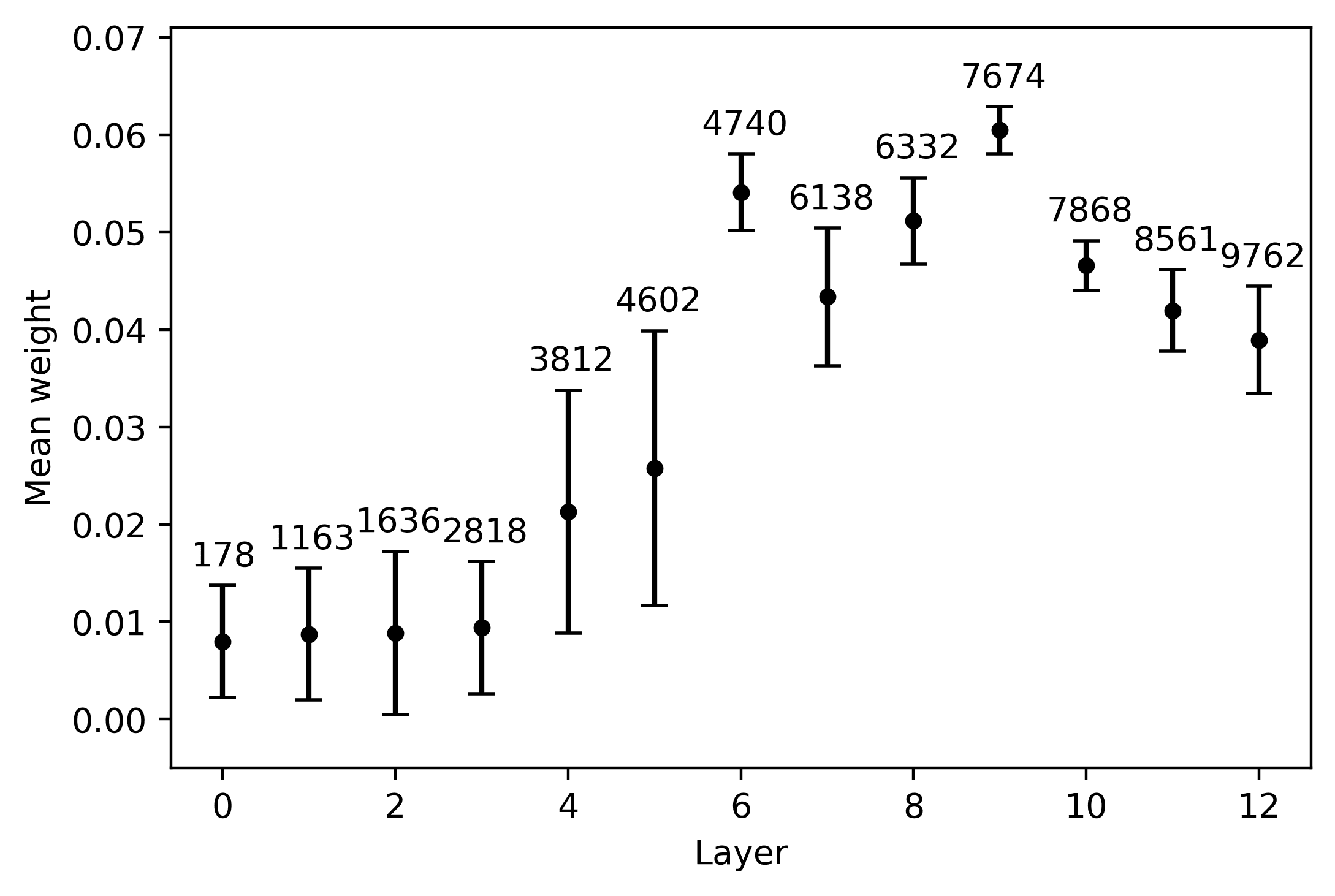
stable across languages. In the long distance condition, neuron 5066 in the sixth layer is
the most relevant agreement-responding unit (5D); while neurons 5666, 6928, Und 7931
are slightly more stable across languages, 5066 clearly marks the weight peak. Im
case of XLM-R, the weight-by-layer growth curve is steeper if compared with mBERT,
especially in the long-distance condition: While the weights of the top neurons in the
first five layers are close to zero and highly variable across languages, from the sixth
layer we have an almost sudden increment.
9 We thank the anonymous reviewers for the suggestion.
273
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
(A) Short-distance, mBERT
(B) Long-distance, mBERT
(C) Short-distance, XLM-R
(D) Long-distance, XLM-R
Figur 5
Mean weight of each layer’s top neuron, averaged over five languages. The error bars indicate
the relative standard variation of the weight across the five languages, rescaled by a 102 factor
for readability purposes. The numbers annotated over the error bars specify the ID of the neuron
whose metrics are depicted in the graph. Note that the y axis scale varies across plots, um zu
highlight the layer-wise progression of the average weights.
6.2 Correlation Between Weight Matrices Across Layers
In the previous section, we considered the individual units of each layer that were
assigned the highest average weight by the linear classifier, in order to draw conclusions
about the layer-wise encoding of agreement across languages. This approach allowed
us to identify a set of individual units that are cross-lingually associated with number
Vereinbarung; Jedoch, this procedure neglects the vast majority of the network’s units.
Somit, as a sanity check, we also analyzed the cross-lingual correlation between the
weights assigned by the linear classifiers to the neurons of each layer. The weights of the
classifier are supposed to reflect the relevance of each unit with respect to the linguistic
property being investigated, nämlich, grammatical agreement. Daher, a cross-lingual
correlation in the classifier weights reflects how similarly two given languages encode
agreement relations. Differently from our previous results, this analysis considers all
the neural units within a layer, and not only the top neurons. Following our previous
results, we predicted an increase in cross-lingual weight correlation in the first layers
of the networks, followed by a plateau in the intermediate layers, and a final decrease
toward the deepest layers of the models.
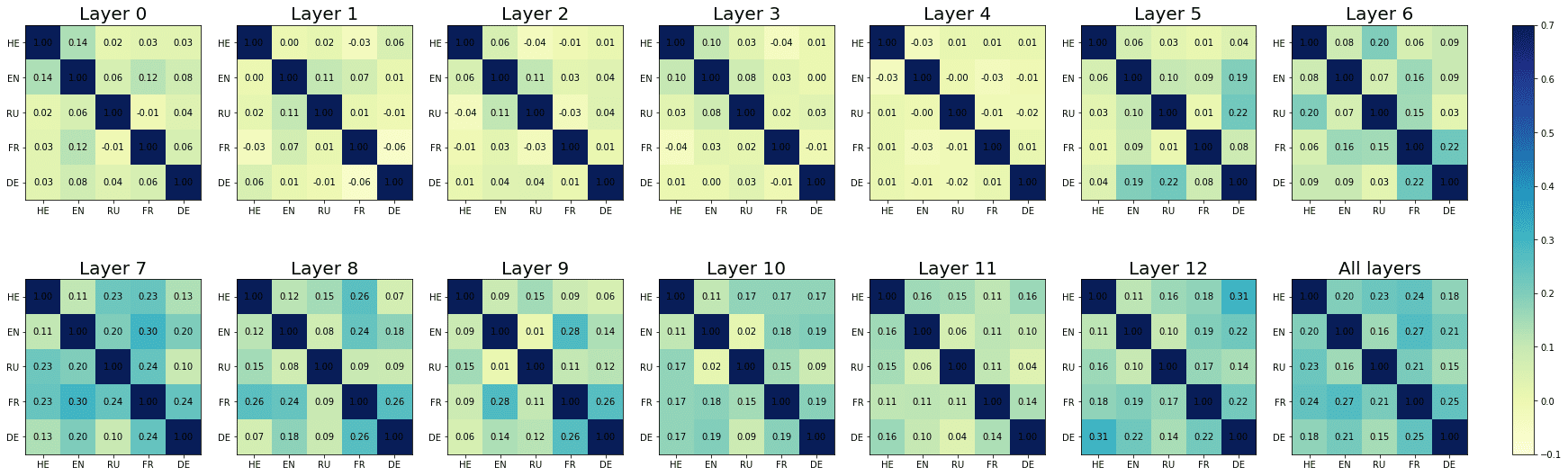
The layer-wise results of our weight correlation analysis are reported in Figure 6;
note that each point in the plot reflects the average weight correlation obtained across
274
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Figur 6
Layer-wise progression of cross-lingual weight correlations, grouped by model and condition.
the ten combinations of language pairs. All the pairwise correlations are reported in
detail in Appendix 4 (Figur 10). The results of the correlation analyses are largely con-
sistent with what we reported in the previous section. Across model types and condi-
tionen, the cross-lingual correlation in the weight matrices (henceforth CCWM) erhöht sich
in the intermediate layers of the models, reaching its peak in the seventh (XLM-R, short-
distance agreement) and eighth layer (mBERT, short- and long-distance agreement;
XLM-R, long-distance agreement). Dann, the CCWM progressively decreases toward
the deepest layers of the models. While the localization of the correlation peaks does
not coincide exactly with the weight maxima identified in § 6.1, from a qualitative
standpoint the layer-wise progression of the CCWM is mostly coherent with our previ-
ous observations, when considering the effects of both agreement condition and model
type. In der Tat, the increase in CCWM is steeper (A) when considering long- as opposed
to short-distance dependencies, Und (B) when analyzing XLM-R as opposed to mBERT
embeddings.
Taken together, these layer-wise patterns strengthen our previous findings in two
ways. Erste, they confirm the premise of our first experiment concerning the layer-wise
flow of cross-lingual syntactic information within the network, supporting our choice
to constrain our tests to the middle layers of the network. Zweite, they clearly show
that there is a cross-lingual convergence in the encoding of grammatical structures in
the middle-to-deep layers of the networks. This means that MMMs such as mBERT and
XLM-R progressively develop a cross-lingual space where language-neutral individual
units respond to similar grammatical structures in different languages. Gesamt, diese
results are consistent with the view that identifies the first layers of an MMM as a
multilingual encoder (Del and Fishel 2021), where syntactic features are progressively
elaborated and converge toward the same units in the middle-to-deep layers. Dann, Die
subsequent decline is coherent with the view of MMMs as the stacking of two sub-
Netzwerke: a multilingual encoder followed by a task-specific decoder, which has little
importance in the transfer (Muller et al. 2021).
6.3 Single Neurons Encode Grammatical Structures
In § 6.1, we identified four candidate cross-lingual neurons. These units were assigned
on average a high weight by the linear classifier, and their relevance was characterized
275
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Computerlinguistik
Volumen 49, Nummer 2
by a reduced variation across languages. In diesem Abschnitt, we studied their individual
behavior in response to well-formed and agreement-violating sentences. More precisely,
we tested whether their activation patterns alone were sufficient and necessary to predict
the grammaticality of such sentences. To do so, we assessed whether (A) the activations
of those units alone could predict agreement violations, Und (B) the activations of their
respective layers could predict grammaticality when these units were zeroed out. To
increase the generalizability of our results, we measured their responses to agreement
in another condition of the CLAMS dataset, across a Prepositional Phrase (z.B., “The
surgeons behind the architect *smiles/smile”). This condition was chosen as it falls
between the long-distance VP coordination and the short-distance condition in terms of
the distance between subject and verb. A total of 11,200 sentences from this condition10
were selected and divided in a train and a test set (80% train, 20% test). Dann, Wir
extracted the activations of the models in the verb position, Und (A) selected the output
of the four units identified in the previous section (Neuronen 7674 Und 6533 in the case of
mBERT, and neurons 5066 Und 5621 for XLM-R), oder (B) zeroed out their activations in the
layers output. In the former case (A), we used the output of each of these neurons taken
singularly as a predictor in a logistic regression model, with the dummy-coded label of
grammatical acceptability as dependent variable. We then computed the classification
accuracy in the test set, and assessed the statistical significance of our results against
chance level with a binomial test. As an additional baseline, we also randomly sampled
30 neural units from the corresponding layers in the two models (layers 8 Und 9 für
mBERT, Und 7 Und 6 for XLM-R), and evaluated their average accuracy in predicting the
grammaticality label on the same dataset.11 In the second case (B), we used as predictors
in the logistic regression models all the layer units except for the neuron of interest;
we then compared the results obtained with the full layer embedding with the results
obtained with the ablated layer by means of a McNemar test, a statistical test utilized
on paired nominal data.
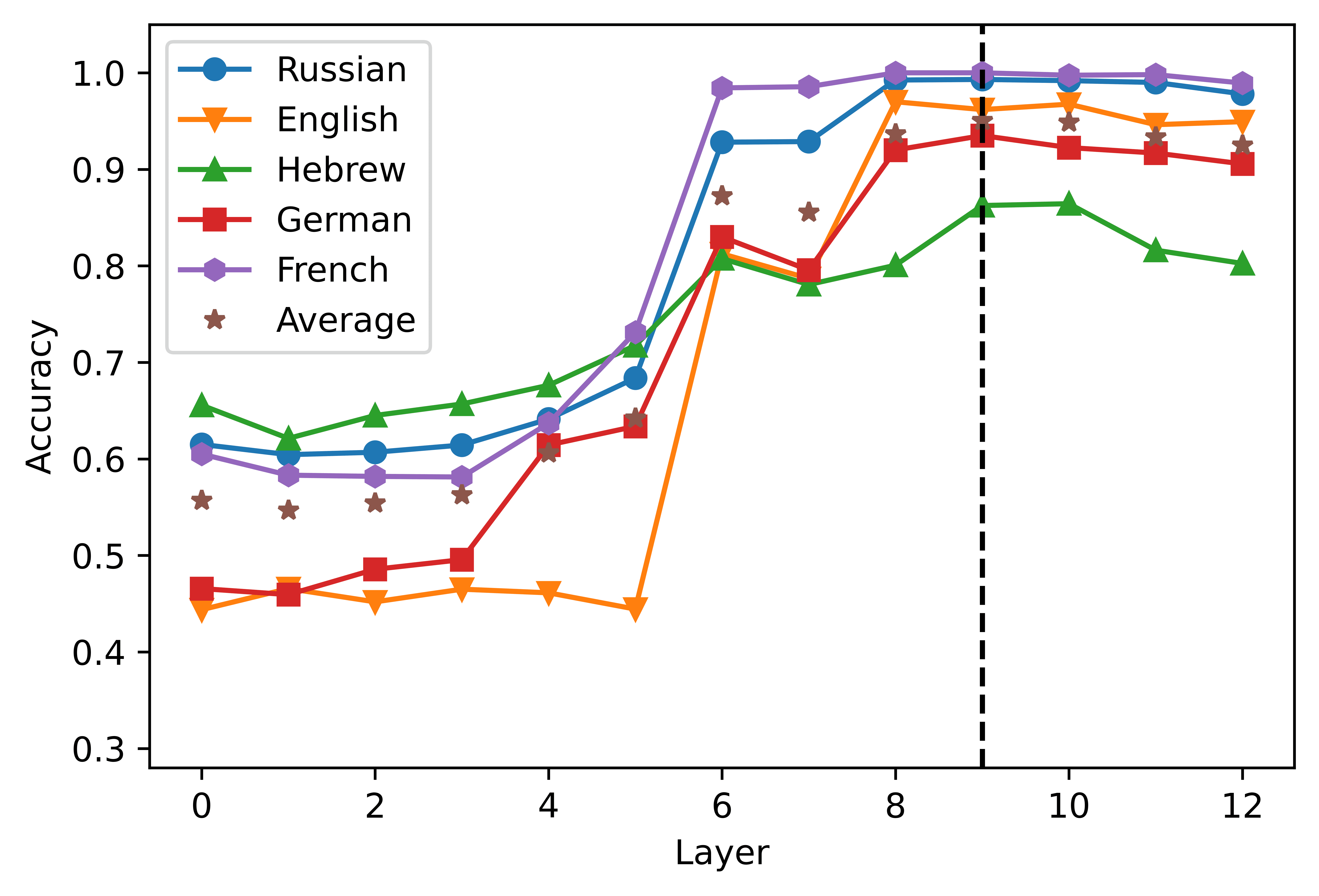
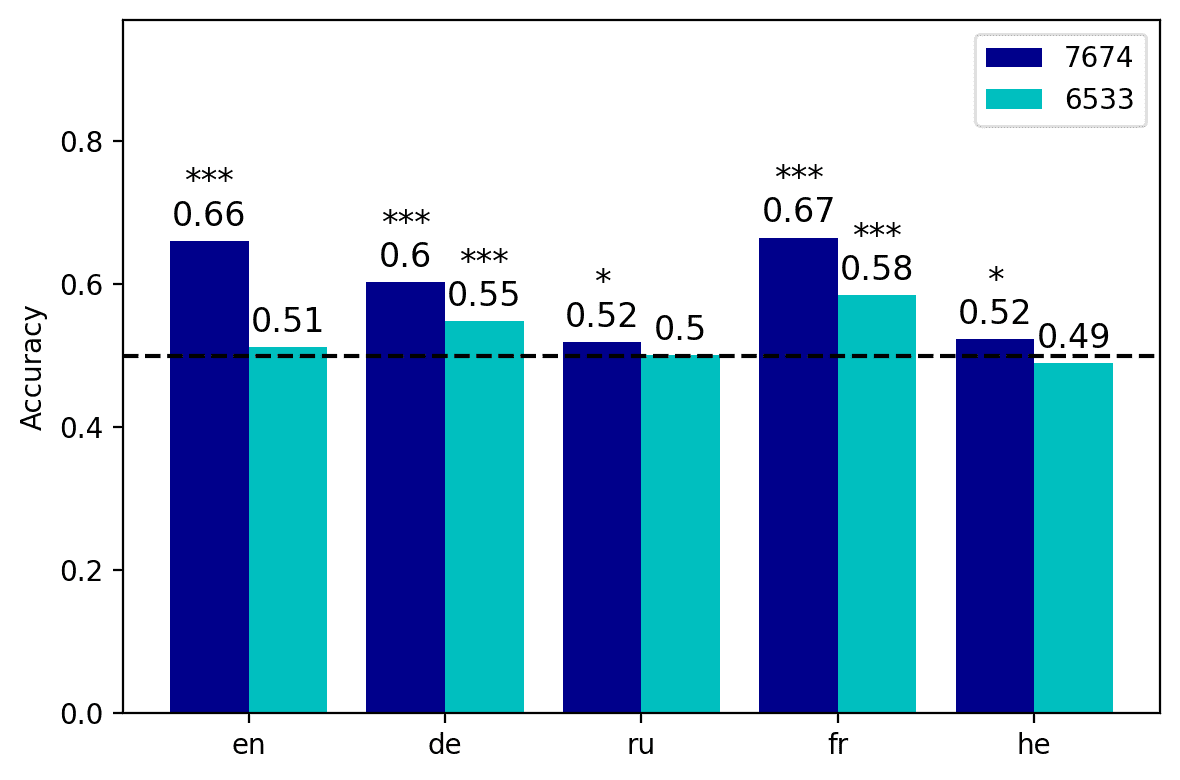
6.3.1 Single Neurons Are Sufficient to Compute Agreement. The results of our experiment
are reported in Figure 7. Gesamt, the neurons that we identified in the previous section
were significantly predictive of grammaticality across languages, providing a sanity
check for our procedure. In the case of mBERT, the activation of neuron 7674, welche
had been singled out in the long-distance condition, was sufficient to significantly
classify sentences as agreement-violating in all the languages considered, with an av-
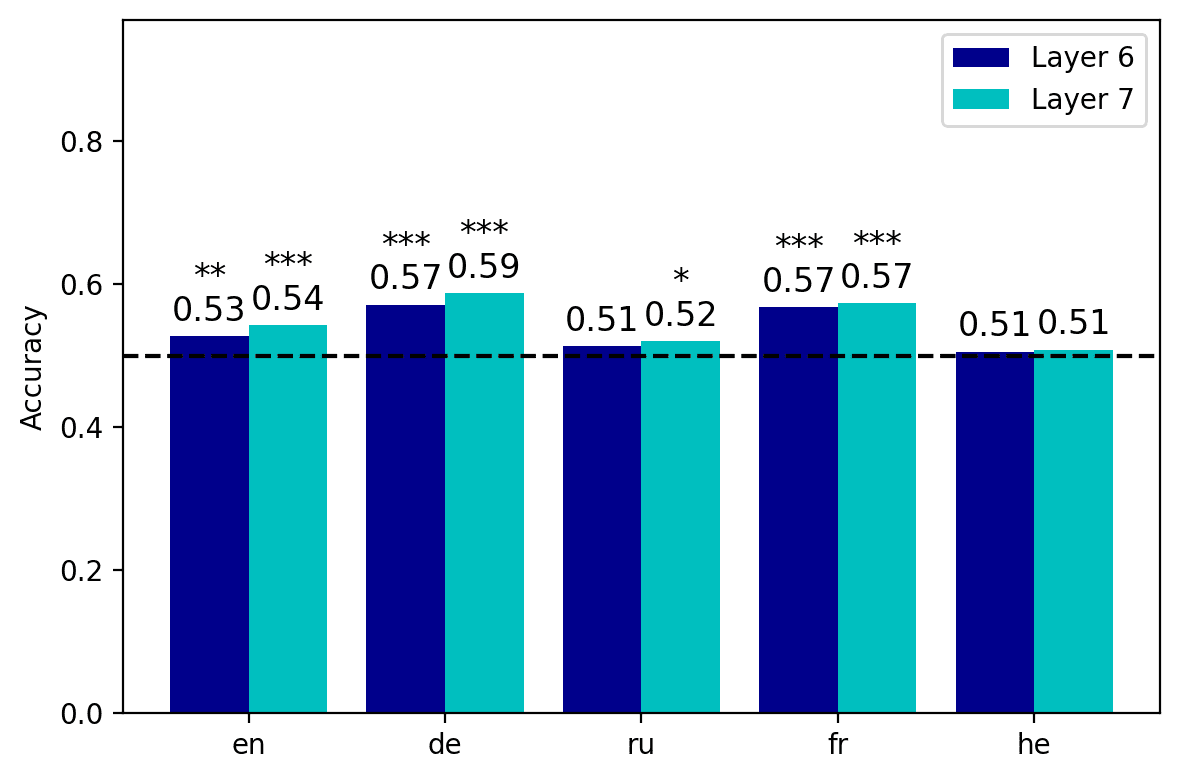
erage accuracy of 0.59 (7A). Nicht überraschend, accuracy was lower in the Russian and
Hebrew datasets, but nonetheless the performance levels were still above chance. Der
activation of neuron 6533 achieved a rather inferior performance, as it reached statistical
significance only in German and French, with an average cross-lingual accuracy of 0.53.
As in all the tests we reported so far, the results obtained with XLM-R were more
solid, as both neuron 5066 Und 5621 were significant predictors of grammaticality in all
languages (7B), with the exception of neuron 5621 in French, which was only marginally
significant (p = 0.056). The logistic classifier based on neuron 5066 achieved an average
accuracy of 0.64; vor allem, its output alone was sufficient to reach an accuracy level of
0.84 in French. Similarly to mBERT, the neuron identified in the short-distance condition
(5621) was less strongly associated with the label in most languages, but it still obtained
10 The number of instances was chosen to match the smallest challenge set (in Hebrew) for cross-lingual
comparability.
11 We thank an anonymous reviewer for the suggestion.
276
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
(A) mBERT, cross-lingual neurons
(B) XLM-R, cross-lingual neurons
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
l
ich
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
C
Ö
l
ich
_
A
_
0
0
4
7
2
P
D
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(C) mBERT, random neurons
(D) XLM-R, random neurons
Figur 7
Accuracy of the classifiers based on the neurons identified in Section 6 (top row) and average
performance obtained by 30 units randomly sampled from the same layer (bottom row),
grouped by language. The asterisks indicate the statistical significance of the results against
chance level, with p < 0.001***, p < 0.01**, p < 0.05*.
an average accuracy of 0.57. If compared to randomly sampled units from the same
layers, which in theory could be expected to respond to similar linguistic phenomena,
the neurons extracted with our procedure were generally more effective in predicting
the well-formedness of a sentence. Across both model types, the neurons identified
in the long-distance condition (7674 and 5066) consistently outperformed in classifi-
cation accuracy the randomly sampled units extracted from their respective layers,
with the only exception the Russian data, where the outcomes were comparable. Once
again, the results in the short-distance condition are less clear-cut. In the case of mBERT,
neuron 6533 outperformed the randomly sampled baseline only in German and French,
but when considering the RoBERTa-based transformer, neuron 5621 outperformed the
baseline in all the languages but French. However, it should be noted that the neurons
that we randomly sampled from the relevant layers generally obtained above-chance
performance scores in the classification task, suggesting that number agreement com-
putations are spread out across the middle layers of the network.
6.3.2 Single Neurons Are not Necessary to Compute Agreement. Once verified that the
four interlingual neurons we singled out in § 6.1 were sufficient to capture agreement
277
Computational Linguistics
Volume 49, Number 2
Table 1
Comparison of the results of the classifier obtained with the full layer and the ablated layer.
The first two columns indicate the language and the agreement condition where the units were
identified (see § 6.1). The following five columns specify the results obtained with mBERT, and
in particular the target neuron that was zeroed out, the respective layer, the accuracy obtained
with the full layer embedding, the accuracy obtained with the ablated layer, and the statistical
significance of the McNemar test. The last five columns report the same indexes, but relative to
the XLM-R model. *In contrasting the accuracy of the full and the ablated layer, the standard χ2
calculation was used instead of the binomial test, as the number of observations per cell in the
contingency table was higher than 25.
mBERT
XLM-R
Language Cond.
Neuron L
Acc
French
French
English
English
Hebrew
Hebrew
Russian
Russian
German
German
Short
Long
Short
Long
Short
Long
Short
Long
Short
Long
6533
7674
6533
7674
6533
7674
6533
7674
6533
7674
8
9
8
9
8
9
8
9
8
9
1.0000
1.0000
0.9464
0.9549
0.9013
0.8933
0.9821
0.9754
1.0000
1.0000
Accabl
1.0000
1.0000
0.9451
0.9558
0.9013
0.8942
0.9821
0.9754
1.0000
1.0000
p
Neuron L
Acc
1.0000
1.0000
0.2500
0.6250
1.0000
0.6880
1.0000
1.0000
1.0000
1.0000
5621
5066
5621
5066
5621
5066
5621
5066
5621
5066
7
6
7
6
7
6
7
6
7
6
1.0000
1.0000
0.9527
0.9049
0.8710
0.8299
0.9254
0.8777
1.0000
1.0000
Accabl
1.0000
1.0000
0.9527
0.9040
0.8705
0.8326
0.9259
0.8790
1.0000
1.0000
p
1.0000
1.0000
1.0000
0.7540
1.0000*
0.4170
1.0000
0.6640
1.0000
1.0000
violations with an above-chance performance, we aimed to test whether their contribu-
tion was necessary for the task. The results of these analyses are summarized in Table 1.
As can be seen in the table, the ablation of the candidate cross-lingual units did not show
a significant impact on the results obtained by the classifiers in any of the languages
considered in the analyses, regardless of model type. This result is largely consistent
with our previous observation that number agreement processing is not restricted to a
small number of specialized units in multilingual transformer models, but it is encoded
with redundancy in the network’s embeddings. While the activation patterns of the
neurons we set apart in our cross-lingual search do encode agreement to a significant
extent, their role is not decisive in agreement processing.
6.4 Testing in an Unseen Language
In the previous section, we tested the four candidate interlingual neurons we identified
in § 6.1 in a novel condition of the CLAMS dataset, showing that our selection procedure
was robust to small changes in the sentential structure of the agreement data. To further
assess the cross-lingual abilities of those units, we further extended the analyses to
measure their predictive power in detecting agreement violations in an unseen language,
that is, Italian. Since the CLAMS dataset did not include any other language beyond the
ones that we had previously considered, we artificially created a new agreement dataset
in a rule-based fashion, and replicated our previous analyses in this dataset.
6.4.1 Dataset Creation and Analyses. To generate an agreement dataset in Italian, we
started from a set of 2 determiners (definite and indefinite; D), 20 nouns (N), 20 verbs
(10 transitive, 10 intransitive; V), and 15 temporal prepositional modifiers (M). Then,
we created a corresponding plural set for each of D, N, and V (Dp, Np, Vp). Starting
278
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
from those samples, we created four agreement conditions by computing the Cartesian
products between the three sets:12
(a)
(b)
(c)
(d)
Singular agreement: D × N × V
Plural agreement: Dp × Np × Vp
Violated singular agreement: D × N × Vp
Violated plural agreement: Dp × Np × V
where each condition consisted of 800 items. We then inserted one modifier sampled
from M after the nouns, to increase the distance between subject and verb to an amount
comparable to the CLAMS condition we used in § 6.3 (across a Prepositional Phrase).
Conditions (a) and (b) were then merged and labeled as grammatical, whereas condi-
tions (c) and (d) were codified as ungrammatical. This method allowed us to generate
3,200 labeled sentences, which were then divided in a train (80%) and a test set (20%).
Following our previous procedures, we used the two transformer models to extract
their internal activations in the verb position; then, we selected from the obtained
embeddings the output of the four candidate cross-lingual units (mBERT: 6533, 7674;
XLM-R: 5621, 5066). We then trained four different logistic regression models—one for
the output of each neuron—in the training set data, and evaluated their accuracy in
the test set. Beside contrasting the model accuracy against chance level with a binomial
test, we implemented a second baseline with 30 neural units randomly sampled from
the same layers as the target neurons.
6.4.2 Results. The neural units that we consider in this study were generally successful
in detecting agreement violations in Italian. When considering mBERT, the neuron
identified in the short-distance condition (6533) reached an accuracy score of 0.57 (p =
0.0001); the unit that had been singled out in the long-distance condition (7674) obtained
an accuracy of 0.52, although the binomial test was not significant (p = 0.1258). On
the other hand, both the units that were identified in the XLM-R model significantly
outperformed chance level (5621: 0.60, p = 1.56 · 10–7; 5066: 0.64, p = 1.63 · 10–13). The
randomly sampled units obtained instead a rather inferior performance in the Italian
test set, with the exception of the sample based on the ninth layer of mBERT (mBERT,
layer 8: 0.53, p = 0.0525; mBERT, layer 9: 0.53, p = 0.0446; XLM-R, layer 7: 0.54, p = 0.0219;
XLM-R, layer 6: 0.51, p = 0.3319). Taken together, these results strengthen the validity of
our methodology, showing that the neural units that were associated with agreement
in a set of languages can successfully capture the same property in a different language
which did not concur in the unit selection.
The performance of individual neurons in predicting well-formedness demon-
strates that explicit knowledge emerges in a quasi-symbolic format in the neural units
we identified in the previous experiment. Interestingly, simply training a transformer
model on a masked language modeling objective on multilingual data causes the
emergence of syntax-sensitive units that respond to the same linguistic phenomenon in
different languages. The knowledge encoded in these units is also sufficiently abstracted
12 Note that the agreement relationship between D and N was set to always be grammatical, so that the only
structure-dependent relationship that could be violated was subject-verb number agreement.
279
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 49, Number 2
from the low-level features of the input that can be captured even in settings that
differ from the one employed during unit selection, both in terms of agreement condi-
tions (across a Prepositional Phrase) and languages (Italian). However, the comparison
with randomly sampled neurons further shows that while some units are particularly
responsive to agreement violations, this grammatical phenomenon is encoded with
redundancy in the network’s embeddings. Indeed, other randomly sampled dimensions
in the activation matrix still respond to the same structure-dependent relationship,
although with lower levels of association with the label (see Dalvi et al. [2020] for an
analysis of redundancy in transformer language models). This finding is congruent with
the layer ablation results, where we showed that the activation patterns of the target
neurons were not necessary to reach near-perfect accuracy in the classification task.
7. Conclusion
This study presents the first single-neuron analysis aimed at assessing the cross-lingual
nature of mBERT and XLM-R agreement processing mechanisms. Our findings are in
line with the view that the very large neural capacity in MMMs leads to multilingual
representations that have both language-neutral and language-specific components (see
also Doddapaneni et al. 2021; Gonen, Ravfogel, and Goldberg 2022). While the majority
of the networks’ units shows a heterogeneous cross-lingual relevance, several neurons
in the structural embeddings of mBERT and XLM-R respond to syntactic features in two
or more languages. We argue that those neurons can be considered as the implementa-
tional substrate that supports number agreement computations across languages. The
independent neuron rankings, while far from being identical, display an above-chance
level of cross-lingual consistency. This consistency is stronger for long- vis-`a-vis short-
distance agreement, suggesting that more complex structures tax more strongly the
language-neutral components of the networks. Our results are also informative in terms
of model comparison: While most research efforts considered a single model—generally
mBERT—when assessing the eventual cross-lingual nature of its representations (Singh
et al. 2019; Chi, Hewitt, and Manning 2020; Dufter and Sch ¨utze 2020; Muller et al.
2021; Guarasci et al. 2022, although see Del and Fishel 2021), our results contrast two
prominent MMMs, showing that the RoBERTa-based transformer excels in cross-lingual
alignment. With respect to the previous literature, our study is novel in that it measures
the convergence of cross-lingual signal in the syntactic domain. Previous studies often
used a coarse-grained approach to cross-lingual coherence; indeed, the emergence of
an interlingual space was often measured as the layer-wise progression of sentence
similarity scores across languages, thus conflating syntactic and semantic features (e.g.,
Singh et al. 2019; Del and Fishel 2021; but see Chi, Hewitt, and Manning 2020). In
this study, we extended the previous findings by showing that even when narrow-
ing the scope of our analyses to subtle structure-dependent phenomena, the mod-
els consistently allocate an overlapping set of resources to similar processes across
languages. In the Introduction, we mentioned how the study of the convergence of
information in a multilingual neural model could inform the debate on the neural
underpinnings of linguistic knowledge in multilingual individuals. In that respect, our
study shows that the optimal solution that naturally emerges from priorless sequence
processing networks is a partial overlap of resources, which is dependent on the typo-
logical similarity between languages.
The very existence of language-neutral components in mBERT and XLM-R shows
that the models address the high surface inconsistency of the multilingual input through
280
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
strong generalization—hence, leveraging truly multilingual knowledge. Once acknowl-
edged that the representation space exploited by MMMs is multilingual in nature, the
study of their predictive behavior could provide us with unique insights into the struc-
tural symmetries that are instantiated across languages, and inform us on the nature of
language as a system beyond the surface discrepancies shown by single languages. We
hope that this investigation will pave the way to future studies inspecting the MMMs’
learned representation spaces to acquire novel knowledge on the properties that are
shared across languages and language families.
8. Limitations and Further Directions
This study showed that number agreement is partly encoded by a language-neutral
set of parameters in the structural embeddings of mBERT and XLM-R. However, two
important caveats must be made. First, the syntactic relationship we analyze is a circum-
scribed expression of the variety of grammatical phenomena that characterize natural
languages. While restricting our analyses to a specific class of grammatical instances
increases the experimental control over our study, it should be noted that the gener-
alizability of our findings to other linguistic structures should be properly assessed in
future research. Second, the phenomenon we investigate is expressed in our language
sample in a rather consistent way, when analyzed in abstract terms: Subject and verb
are paired through a form of morphological inflection—which is mainly concatenative
in four out of the five languages considered—on account of their structural dependency
and their grammatical number. We leave for future research an assessment of whether
our results hold when considering a more typologically diverse language sample that
conveys agreements relationships in fundamentally different ways.
Appendix 1. Weight Mass Analyses
In § 4, we considered the number of top 100 units that were shared among two or
more languages to draw conclusions on the neuron-level cross-lingual convergence
of agreement information in the networks. However, the threshold we used, while
congruent with previous research (Antverg and Belinkov 2021), needs to be motivated.
In particular, it is necessary to ensure that the top neurons that are considered in the
analyses effectively account for a sufficiently ample proportion of the weight mass. In
other words, it is critical to verify that (a) the weight distribution is sufficiently skewed
to motivate the selection of N top neurons, and (b) N = 100 is a sensible threshold
that includes the most relevant units, and does not include too many of the non-
relevant ones. To verify these premises, we plot the weight distribution of the different
model × condition × language combinations, and examine the ratio of the cumulative
weight mass13 accounted for by the top 100 units. The outcomes of these analyses are
summarized in Figure 8. As can be clearly seen from the figure, the weight distributions
are highly skewed, with a small number of units that are assigned high weights, and a
long right tail of less relevant neurons. In general, 100 neurons—which only constitute
13.02% of the layer units—contribute to a substantial proportion of the weight mass
of the layer (on average 45.46%). This proportion is lower when considering mBERT
13
(cid:80)100
(cid:80)768
i=1 wi
j=1 wj
281
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 49, Number 2
(a) Short-distance, mBERT, layer 8
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
(b) Long-distance, mBERT, layer 9
Figure 8
Weights (y axis) associated by the linear classifier to the individual units (x axis) of the relevant
layers. The percentage superimposed on the graph indicates the cumulative weight mass
accounted for by the top 100 units in each individual language.
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
282
de Varda and Marelli
Data-driven Cross-lingual Syntax
(c) Short-distance, XLM-R, layer 7
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(d) Long-distance, XLM-R, layer 7
(short-distance: 35.21%; long-distance: 43.36%) as opposed to XLM-R (short-distance:
49.45%; long-distance: 57.81), and with short- as opposed to long-distance dependencies
between subject and verb (see above). This suggests that both model type and subject-
verb distance contribute to the sparseness of the encoding of the phenomenon under
scrutiny, with XLM-R and long-distance dependencies causing the emergence of fewer
specialized units that respond to agreement violations, and mBERT and short-distance
agreement promoting more distributed and possibly redundant encoding patterns.
However, despite a certain amount of variability across models and conditions, 100
units generally contribute to a large amount of the weight mass, justifying a posteriori
the choice of our threshold.
283
Computational Linguistics
Volume 49, Number 2
Appendix 2. Super Exact Test Results in Detail
2.1. Linguistic Correlation Analysis
Table 2
Results of the super exact test relative to all N2 . . . 5-way intersections of the top 100 neurons in
the short-distance agreement condition (mBERT, LCA).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
28
26
19
25
39
14
17
34
15
29
8
10
6
9
10
5
7
6
17
5
4
3
5
3
5
3
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
2.1504
1.9968
1.4592
1.9200
2.9952
1.0752
1.3056
2.6112
1.1520
2.2272
4.7186
5.8982
3.5389
5.3084
5.8982
2.9491
4.1288
3.5389
10.027
2.9491
18.1194
13.5895
22.6492
13.5895
22.6492
104.3677
p
1.21 · 10–05
1.17 · 10–04
4.47 · 10–02
3.34 · 10–04
5.84 · 10–13
4.28 · 10–01
1.34 · 10–01
3.03 · 10–09
3.10 · 10–01
3.54 · 10–06
2.29 · 10–04
4.68 · 10–06
6.33 · 10–03
3.50 · 10–05
4.68 · 10–06
2.59 · 10–02
1.30 · 10–03
6.33 · 10–03
1.58 · 10–13
2.59 · 10–02
6.82 · 10–05
1.38 · 10–03
2.59 · 10–06
1.38 · 10–03
2.59 · 10–06
3.39 · 10–06
284
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Table 3
Long-distance agreement condition (mBERT, LCA).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
40
24
18
26
38
21
35
27
24
31
9
16
8
10
16
12
9
15
17
11
6
6
10
6
7
4
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
3.0720
1.8432
1.3824
1.9968
2.9184
1.6128
2.6880
2.0736
1.8432
2.3808
5.3084
9.4372
4.7186
5.8982
9.4372
7.0779
5.3084
8.8474
10.0270
6.4881
27.1791
27.1791
45.2985
27.1791
31.7089
139.1569
p
8.85 · 10–14
8.90 · 10–04
8.03 · 10–02
1.17 · 10–04
3.64 · 10–12
1.13 · 10–02
6.17 · 10–10
3.90 · 10–05
8.90 · 10–04
2.51 · 10–07
3.50 · 10–05
2.50 · 10–12
2.29 · 10–04
4.68 · 10–06
2.50 · 10–12
5.83 · 10–08
3.50 · 10–05
3.59 · 10–11
1.58 · 10–13
5.54 · 10–07
7.95 · 10–08
7.95 · 10–08
1.22 · 10–14
7.95 · 10–08
2.00 · 10–09
2.12 · 10–08
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
285
Computational Linguistics
Volume 49, Number 2
Table 4
Short-distance agreement condition (XLM-R, LCA).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
32
30
31
32
35
25
21
23
28
29
16
14
13
14
9
12
13
12
14
15
9
7
7
9
11
6
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
2.4576
2.3040
2.3808
2.4576
2.6880
1.9200
1.6128
1.7664
2.1504
2.2272
9.4372
8.2575
7.6677
8.2575
5.3084
7.0778
7.6677
7.0779
8.2575
8.8474
40.7686
31.7089
31.7089
40.7686
49.8283
208.7354
p
6.13 · 10–08
9.74 · 10–07
2.52 · 10–07
6.13 · 10–08
6.17 · 10–10
3.34 · 10–04
1.14 · 10–02
2.22 · 10–03
1.21 · 10–05
3.54 · 10–06
2.50 · 10–12
4.68 · 10–10
5.51 · 10–09
4.68 · 10–10
3.50 · 10–05
5.84 · 10–08
5.51 · 10–09
5.84 · 10–08
4.68 · 10–10
3.59 · 10–11
7.79 · 10–13
2.01 · 10–09
2.01 · 10–09
7.79 · 10–13
1.69 · 10–16
3.87 · 10–13
286
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Table 5
Long-distance agreement condition (XLM-R, LCA).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
54
34
30
48
48
18
54
57
26
52
22
36
13
15
42
19
21
38
35
13
12
17
30
11
12
10
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
4.1472
2.6112
3.3040
3.6864
3.6864
1.3824
4.1472
4.3776
1.9968
3.9936
12.9761
21.2337
7.6677
8.8474
24.7726
11.2067
12.3863
22.4133
20.6438
7.6677
54.3582
77.0074
135.8955
49.8283
54.3582
347.8924
p
5.84 · 10–28
3.03 · 10–09
9.74 · 10–07
2.94 · 10–21
2.94 · 10–21
8.04 · 10–02
5.84 · 10–28
1.12 · 10–31
1.18 · 10–04
1.28 · 10–25
4.42 · 10–20
6.28 · 10–43
5.51 · 10–09
3.59 · 10–11
1.29 · 10–54
4.90 · 10–16
1.07 · 10–18
1.07 · 10–46
4.33 · 10–41
5.51 · 10–09
2.04 · 10–18
9.49 · 10–29
1.52 · 10–60
1.69 · 10–16
2.04 · 10–18
1.29 · 10–23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
287
Computational Linguistics
Volume 49, Number 2
2.2. Probeless
Table 6
Short-distance agreement condition (mBERT, probeless).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
26
30
31
21
54
18
30
50
23
48
11
13
9
15
16
14
13
10
35
11
6
7
7
6
8
3
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
1.9968
3.3040
2.3808
1.6128
4.1472
1.3824
3.3040
3.8400
1.7664
3.6864
6.4881
7.6677
5.3084
8.8474
9.4372
8.2575
7.6677
5.8982
20.6438
6.4881
27.1791
31.7089
31.7089
27.1791
36.2388
104.3677
p
1.18 · 10–04
9.74 · 10–07
2.52 · 10–07
1.14 · 10–02
5.84 · 10–28
8.04 · 10–02
9.74 · 10–07
2.19 · 10–23
2.22 · 10–03
2.94 · 10–21
5.55 · 10–07
5.51 · 10–09
3.5 · 10–05
3.59 · 10–11
2.5 · 10–12
4.68 · 10–10
5.51 · 10–09
4.69 · 10–06
4.33 · 10–41
5.55 · 10–07
7.95 · 10–08
2.01 · 10–09
2.01 · 10–09
7.95 · 10–08
4.28 · 10–11
3.39 · 10–06
288
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Table 7
Long-distance agreement condition (mBERT, probeless).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
60
42
38
37
36
26
52
57
36
45
30
27
17
17
39
26
24
26
29
17
13
18
22
13
14
10
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
4.608
3.2256
2.9184
2.8416
2.7648
1.9968
3.9936
4.3776
2.7648
3.4560
17.6947
15.9253
10.027
10.027
23.0031
15.3354
14.1558
15.3354
17.1049
10.027
58.888
81.5373
99.6567
58.888
63.4179
347.8924
p
1.21 · 10–35
1.7 · 10–15
3.64 · 10–12
2.14 · 10–11
1.18 · 10–10
1.18 · 10–04
1.28 · 10–25
1.12 · 10–31
1.18 · 10–10
2.92 · 10–18
2.29 · 10–32
1.64 · 10–27
1.59 · 10–13
1.59 · 10–13
1.25 · 10–48
5.85 · 10–26
5.94 · 10–23
5.85 · 10–26
1.02 · 10–30
1.59 · 10–13
2.19 · 10–20
5.93 · 10–31
3.45 · 10–40
2.19 · 10–20
2.09 · 10–22
1.29 · 10–23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
289
Computational Linguistics
Volume 49, Number 2
Table 8
Short-distance agreement condition (XLM-R, probeless).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
16
26
15
19
47
13
21
37
10
38
5
10
5
9
11
4
4
10
24
5
4
4
8
4
4
4
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
1.2288
1.9968
1.1520
1.4592
3.6096
0.9984
1.6128
2.8416
0.7680
2.9184
2.9491
5.8982
2.9491
5.3084
6.4881
2.3593
2.3593
5.8982
14.1558
2.9491
18.1194
18.1194
36.2388
18.1194
18.1194
139.1569
p
2.12 · 10–01
1.18 · 10–04
3.11 · 10–01
4.48 · 10–02
3.12 · 10–20
5.54 · 10–01
1.14 · 10–02
2.14 · 10–11
8.71 · 10–01
3.64 · 10–12
2.59 · 10–02
4.69 · 10–06
2.59 · 10–02
3.5 · 10–05
5.55 · 10–07
8.78 · 10–02
8.78 · 10–02
4.69 · 10–06
5.94 · 10–23
2.59 · 10–02
6.82 · 10–05
6.82 · 10–05
4.28 · 10–11
6.82 · 10–05
6.82 · 10–05
2.13 · 10–08
290
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Table 9
Long-distance agreement condition (XLM-R, probeless).
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
69
53
47
61
74
35
61
68
38
69
40
58
31
34
56
33
33
52
62
29
31
31
51
27
29
27
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
5.2992
4.0704
3.6096
4.6848
5.6832
2.6880
4.6848
5.2224
2.9184
5.2992
23.593
34.2098
18.2845
20.054
33.0301
19.4642
19.4642
30.6709
36.5691
17.1049
140.4253
140.4253
231.0223
122.3059
131.3656
939.3093
p
3.46 · 10–49
8.92 · 10–27
3.12 · 10–20
5.01 · 10–37
6.89 · 10–58
6.17 · 10–10
5.01 · 10–37
1.49 · 10–47
3.64 · 10–12
3.46 · 10–49
1.36 · 10–50
1.77 · 10–91
4.77 · 10–34
2.78 · 10–39
2.17 · 10–86
1.66 · 10–37
1.66 · 10–37
1.22 · 10–76
4.19 · 10–102
1.02 · 10–30
2.94 · 10–63
2.94 · 10–63
1.99 · 10–125
1.26 · 10–52
7.23 · 10–58
5.53 · 10–78
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
291
Computational Linguistics
Volume 49, Number 2
Appendix 3. Long-distance Condition Downsampled
(a) Long-distance agreement, mBERT
(b) Long-distance agreement, XLM-R
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
(c) Long-distance, layer 9, LCA, mBERT
(d) Long-distance, layer 7, LCA, XLM-R
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(e) Long-distance, layer 9, probeless, mBERT
(f) Long-distance, layer 7, probeless, XLM-R
Figure 9
Layer-wise performance of the logistic classifier (top) and N2 . . . 5-way intersection statistics
obtained with LCA (middle) and probeless ranking (bottom) on the downsampled long-distance
agreement data.
292
de Varda and Marelli
Data-driven Cross-lingual Syntax
In this section, we report the results we obtained by downsampling the long-
distance condition to match the number of items available in the short-distance
dataset—224 in the training (80%) and 56 in the test set (20%). Given the rather limited
number of instances available in this condition, we decided to report in the article the
results obtained with the larger dataset. Nonetheless, because we also comment on the
short- vs. long-distance comparison, it is necessary to rule out the possible confound
of the different amount of training data.14 The peak of performance is obtained in the
same layers as in the non-downsampled analyses (layers 9 and 7 for mBERT and XLM-R,
respectively, see Figure 9a, 9b). The multi-set intersection analysis also shows a coherent
pattern of results with respect to what we reported above. Indeed, in the case of mBERT
the N2 . . . 4-way intersections with the highest FE are Fr ∩ Ru, Fr ∩ Ru ∩ (En ⊕ De),
and Fr ∩ En ∩ De ∩ Ru, with Hebrew being absent in three combinations and French
appearing in all of them (see Figure 9c, Table 10). Similarly, in the case of XLM-R the
highest FE is obtained in De ∩ Fr, De ∩ Ru ∩ (En ⊕ Fr), and Fr ∩ En ∩ De ∩ Ru (Figure 9d,
Table 11). Crucially, intersection sizes are consistently bigger in the downsampled long-
distance condition (Figure 9c, 9d) than in the short-distance condition (Figure 3a,3a)
across both model types.
Table 10
Downsampled long-distance condition, mBERT.
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
46
22
23
37
41
24
42
37
25
41
13
27
12
11
27
14
13
26
23
13
9
10
19
10
9
8
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
3.5328
1.6896
1.7664
2.8416
3.1488
1.8432
3.2256
2.8416
1.9200
3.1488
7.6677
15.9252
7.0779
6.4881
15.9252
8.2575
7.6677
15.3354
13.5660
7.6677
40.7686
45.2985
86.0671
45.2985
40.7686
278.3139
14 We thank the anonymous reviewers for bringing this issue to our attention.
p
3.11 · 10–19
5.20 · 10–03
2.22 · 10–03
2.14 · 10–11
1.27 · 10–14
8.90 · 10–04
1.70 · 10–15
2.14 · 10–11
3.34 · 10–04
1.27 · 10–14
5.51 · 10–09
1.64 · 10–27
5.84 · 10–08
5.54 · 10–07
1.64 · 10–27
4.68 · 10–10
5.51 · 10–09
5.85 · 10–26
1.69 · 10–21
5.51 · 10–09
7.79 · 10–13
1.23 · 10–14
3.36 · 10–33
1.23 · 10–14
7.79 · 10–13
3.13 · 10–18
293
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 49, Number 2
Table 11
Downsampled long-distance condition, XLM-R.
Intersection
Degree Obs. overlap
Exp. overlap
FE
Fr ∩ Ru
He ∩ Ru
He ∩ Fr
En ∩ Ru
En ∩ Fr
En ∩ He
De ∩ Ru
De ∩ Fr
De ∩ He
De ∩ En
He ∩ Fr ∩ Ru
En ∩ Fr ∩ Ru
En ∩ He ∩ Ru
En ∩ He ∩ Fr
De ∩ Fr ∩ Ru
De ∩ He ∩ Ru
De ∩ He ∩ Fr
De ∩ En ∩ Ru
De ∩ En ∩ Fr
De ∩ En ∩ He
En ∩ He ∩ Fr ∩ Ru
De ∩ He ∩ Fr ∩ Ru
De ∩ En ∩ Fr ∩ Ru
De ∩ En ∩ He ∩ Ru
De ∩ En ∩ He ∩ Fr
De ∩ En ∩ He ∩ Fr ∩ Ru
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
5
54
34
30
48
48
18
54
57
26
52
22
36
13
15
42
19
21
38
35
13
12
17
30
11
12
10
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
13.0208
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
1.6954
0.2208
0.2208
0.2208
0.2208
0.2208
0.0287
2.9952
3.1488
2.0736
3.1488
2.7648
1.9200
3.6096
3.7632
1.9968
3.3792
10.6168
12.3863
11.7965
7.6677
15.9252
11.7965
9.4372
15.9252
14.7456
8.8474
49.8283
63.4179
77.0074
58.8880
49.8283
347.8924
p
5.85 · 10–13
1.27 · 10–14
3.90 · 10–05
1.27 · 10–14
1.18 · 10–10
3.34 · 10–04
3.12 · 10–20
2.62 · 10–22
1.18 · 10–04
2.59 · 10–17
9.22 · 10–15
1.07 · 10–18
2.39 · 10–17
5.50 · 10–09
1.64 · 10–27
2.39 · 10–17
2.50 · 10–12
1.64 · 10–27
1.94 · 10–24
3.59 · 10–11
1.69 · 10–16
2.09 · 10–22
9.49 · 10–29
2.19 · 10–20
1.69 · 10–16
1.29 · 10–23
294
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Appendix 4. Pairwise Correlations in the Weight Matrices
(a) Short-distance, mBERT
(b) Long-distance, mBERT
(c) Short-distance, XLM-R
(d) Long-distance, XLM-R
Figure 10
Pairwise correlation coefficients between the weights learned by the classifiers, divided by layer,
condition, and model type.
295
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 49, Number 2
References
Abutalebi, Jubin, Stefano F. Cappa, and
Daniela Perani. 2001. The bilingual brain
as revealed by functional neuroimaging.
Bilingualism: Language and Cognition,
4(2):179–190. https://doi.org/10.1017
/S136672890100027X
Alain, Guillaume and Yoshua Bengio. 2016.
Understanding intermediate layers using
linear classifier probes. arXiv preprint
arXiv:1610.01644.
Antverg, Omer and Yonatan Belinkov. 2021.
On the pitfalls of analyzing individual
neurons in language models. In
International Conference on Learning
Representations.
Bacon, Geoff and Terry Regier. 2019. Does
BERT agree? Evaluating knowledge of
structure dependence through agreement
relations. arXiv preprint arXiv:1908.09892.
Bau, Anthony, Yonatan Belinkov, Hassan
Sajjad, Nadir Durrani, Fahim Dalvi, and
James Glass. 2018. Identifying and
controlling important neurons in neural
machine translation. In International
Conference on Learning Representations.
Belinkov, Yonatan. 2022. Probing classifiers:
Promises, shortcomings, and advances.
Computational Linguistics, 48(1):207–219.
https://doi.org/10.1162/coli_a_00422
Belinkov, Yonatan and James Glass. 2019.
Analysis methods in neural language
processing: A survey. Transactions of the
Association for Computational Linguistics,
7:49–72. https://doi.org/10.1162
/tacl a 00254
Bernardy, Jean Philippe and Shalom Lappin.
2017. Using deep neural networks to learn
syntactic agreement. Linguistic Issues in
Language Technology. https://doi.org
/10.33011/lilt.v15i.1413
Chi, Ethan A., John Hewitt, and Christopher
D. Manning. 2020. Finding universal
grammatical relations in multilingual
BERT. In Proceedings of the 58th Annual
Meeting of the Association for Computational
Linguistics, pages 5564–5577. https://doi
.org/10.18653/v1/2020.acl-main.493
Conneau, Alexis, Kartikay Khandelwal,
Naman Goyal, Vishrav Chaudhary,
Guillaume Wenzek, Francisco Guzm´an,
´Edouard Grave, Myle Ott, Luke
Zettlemoyer, and Veselin Stoyanov. 2020a.
Unsupervised cross-lingual representation
learning at scale. In Proceedings of the 58th
Annual Meeting of the Association for
Computational Linguistics, pages 8440–8451.
https://doi.org/10.18653/v1/2020
.acl-main.747
296
Conneau, Alexis, Shijie Wu, Haoran Li, Luke
Zettlemoyer, and Veselin Stoyanov. 2020b.
Emerging cross-lingual structure in
pretrained language models. In Proceedings
of the 58th Annual Meeting of the Association
for Computational Linguistics,
pages 6022–6034. https://doi.org/10
.18653/v1/2020.acl-main.536
Cummins, Robert and George Schwarz. 1988.
Radical connectionism. The Southern
Journal of Philosophy, 26(5):43. https://doi
.org/10.1111/j.2041-6962.1988
.tb00462.x
Dalvi, Fahim, Nadir Durrani, Hassan Sajjad,
Yonatan Belinkov, Anthony Bau, and
James Glass. 2019a. What is one grain of
sand in the desert? Analyzing individual
neurons in deep NLP models. In
Proceedings of the AAAI Conference on
Artificial Intelligence, pages 6309–6317.
https://doi.org/10.1609
/aaai.v33i01.33016309
Dalvi, Fahim, Avery Nortonsmith, Anthony
Bau, Yonatan Belinkov, Hassan Sajjad,
Nadir Durrani, and James Glass. 2019b.
Neurox: A toolkit for analyzing individual
neurons in neural networks. In Proceedings
of the AAAI Conference on Artificial
Intelligence, pages 9851–9852. https://
doi.org/10.1609/aaai.v33i01
.33019851
Dalvi, Fahim, Hassan Sajjad, Nadir Durrani,
and Yonatan Belinkov. 2020. Analyzing
redundancy in pretrained transformer
models. In Proceedings of the 2020
Conference on Empirical Methods in Natural
Language Processing (EMNLP),
pages 4908–4926. https://doi.org/10
.18653/v1/2020.emnlp-main.398
Del, Maksym and Mark Fishel. 2021.
Establishing interlingua in multilingual
language models. ArXiv, abs/2109.01207.
Devlin, Jacob, Ming-Wei Chang, Kenton Lee,
and Kristina Toutanova. 2019. BERT:
Pre-training of deep bidirectional
transformers for language understanding.
In Proceedings of the 2019 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long and Short
Papers), pages 4171–4186.
Dhar, Prajit and Arianna Bisazza. 2021.
Understanding cross-lingual syntactic
transfer in multilingual recurrent neural
networks. In Proceedings of the 23rd Nordic
Conference on Computational Linguistics
(NoDaLiDa), pages 74–85.
Doddapaneni, Sumanth, Gowtham Ramesh,
Anoop Kunchukuttan, Pratyush Kumar,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
and Mitesh M. Khapra. 2021. A primer on
pretrained multilingual language models.
arXiv preprint arXiv:2107.00676.
Dufter, Philipp and Hinrich Sch ¨utze. 2020.
Identifying necessary elements for BERT’s
multilinguality. arXiv preprint
arXiv:2005.00396. https://doi.org/10
.18653/v1/2020.emnlp-main.358
Finlayson, Matthew, Aaron Mueller,
Sebastian Gehrmann, Stuart Shieber, Tal
Linzen, and Yonatan Belinkov. 2021.
Causal analysis of syntactic agreement
mechanisms in neural language models. In
Proceedings of the 59th Annual Meeting of the
Association for Computational Linguistics and
the 11th International Joint Conference on
Natural Language Processing (Volume 1: Long
Papers), pages 1828–1843. https://doi
.org/10.18653/v1/2021.acl-long.144
Goldberg, Yoav. 2019. Assessing BERT’s
syntactic abilities. CoRR, abs/1901.05287.
Gonen, Hila, Shauli Ravfogel, and Yoav
Goldberg. 2022. Analyzing gender
representation in multilingual models.
In Proceedings of the 7th Workshop on
Representation Learning for NLP,
pages 67–77. https://doi.org/10.18653
/v1/2022.repl4nlp-1.8
Green, David W. 2008. Bilingual aphasia:
Adapted language networks and their
control. Annual Review of Applied
Linguistics, 28:25–48. https://doi.org
/10.1017/S0267190508080057
Guarasci, Raffaele, Stefano Silvestri,
Giuseppe De Pietro, Hamido Fujita, and
Massimo Esposito. 2022. BERT syntactic
transfer: A computational experiment on
Italian, French and English languages.
Computer Speech & Language, 71:101261.
https://doi.org/10.1016/j.csl.2021
.101261
Gulordava, Kristina, Piotr Bojanowski,
´Edouard Grave, Tal Linzen, and Marco
Baroni. 2018. Colorless green recurrent
networks dream hierarchically. In
Proceedings of the 2018 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long Papers),
pages 1195–1205. https://doi.org/10
.18653/v1/N18-1108
Jawahar, Ganesh, Benoˆıt Sagot, and Djam´e
Seddah. 2019. What does BERT learn about
the structure of language? In Proceedings of
the 57th Annual Meeting of the Association for
Computational Linguistics, pages 3651–3657.
https://doi.org/10.18653/v1/P19-1356
Joshi, Pratik, Sebastin Santy, Amar Budhiraja,
Kalika Bali, and Monojit Choudhury. 2020.
The state and fate of linguistic diversity
and inclusion in the NLP world. In
Proceedings of the 58th Annual Meeting of the
Association for Computational Linguistics,
pages 6282–6293. https://doi.org/10
.18653/v1/2020.acl-main.560
Karpathy, Andrej, Justin Johnson, and Li
Fei-Fei. 2015. Visualizing and
understanding recurrent networks. arXiv
preprint arXiv:1506.02078.
Karthikeyan, K., Wang Zihan, Stephen
Mayhew, and Dan Roth. 2020.
Cross-lingual ability of multilingual BERT:
An empirical study. In International
Conference on Learning Representations.
Kementchedjhieva, Yova and Adam Lopez.
2018. ‘Indicatements’ that character
language models learn English
morpho-syntactic units and regularities. In
Proceedings of the 2018 EMNLP Workshop
BlackboxNLP: Analyzing and Interpreting
Neural Networks for NLP, pages 145–153.
https://doi.org/10.18653/v1/W18
-5417
Kim, Karl H. S., Norman R. Relkin,
Kyoung-Min Lee, and Joy Hirsch. 1997.
Distinct cortical areas associated with
native and second languages. Nature,
388(6638):171–174. https://doi.org
/10.1038/40623, PubMed: 9217156
Klein, Stav and Reut Tsarfaty. 2020. Getting
the ##life out of living: How adequate are
word-pieces for modelling complex
morphology? In Proceedings of the 17th
SIGMORPHON Workshop on Computational
Research in Phonetics, Phonology, and
Morphology, pages 204–209. https://doi
.org/10.18653/v1/2020.sigmorphon
-1.24
Kuncoro, Adhiguna, Chris Dyer, John Hale,
Dani Yogatama, Stephen Clark, and Phil
Blunsom. 2018. LSTMs can learn
syntax-sensitive dependencies well, but
modeling structure makes them better. In
Proceedings of the 56th Annual Meeting of the
Association for Computational Linguistics
(Volume 1: Long Papers), pages 1426–1436.
https://doi.org/10.18653/v1/P18-1132
Lakretz, Yair, Germ´an Kruszewski, Theo
Desbordes, Dieuwke Hupkes, Stanislas
Dehaene, and Marco Baroni. 2019. The
emergence of number and syntax units in
LSTM language models. In Proceedings of
NAACL-HLT, pages 11–20. https://doi
.org/10.18653/v1/N19-1002
Lasri, Karim, Alessandro Lenci, and Thierry
Poibeau. 2022. Does BERT really agree?
Fine-grained analysis of lexical
dependence on a syntactic task. In Findings
297
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Computational Linguistics
Volume 49, Number 2
of the Association for Computational
Linguistics: ACL 2022, pages 2309–2315.
https://doi.org/10.18653/v1/2022
.findings-acl.181
Lauscher, Anne, Vinit Ravishankar, Ivan
Vuli´c, and Goran Glavaˇs. 2020. From zero
to hero: On the limitations of zero-shot
language transfer with multilingual
Transformers. In Proceedings of the 2020
Conference on Empirical Methods in Natural
Language Processing (EMNLP),
pages 4483–4499. https://doi.org/10
.18653/v1/2020.emnlp-main.363
Li, Jiwei, Xinlei Chen, Eduard Hovy, and
Dan Jurafsky. 2015. Visualizing and
understanding neural models in NLP.
arXiv preprint arXiv:1506.01066.
https://doi.org/10.18653/v1/N16
-1082
Linzen, Tal, Emmanuel Dupoux, and Yoav
Goldberg. 2016. Assessing the ability of
LSTMs to learn syntax-sensitive
dependencies. Transactions of the Association
for Computational Linguistics, 4:521–535.
https://doi.org/10.1162/tacl_a_00115
Liu, Zihan, Genta Indra Winata, Andrea
Madotto, and Pascale Fung. 2020.
Exploring fine-tuning techniques for
pre-trained cross-lingual models via
continual learning. arXiv preprint
arXiv:2004.14218.
Marvin, Rebecca and Tal Linzen. 2018.
Targeted syntactic evaluation of language
models. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing, pages 1192–1202.
https://doi.org/10.18653/v1/D18-1151
McCloskey, Michael. 1991. Networks and
theories: The place of connectionism in
cognitive science. Psychological Science,
2(6):387–395. https://doi.org/10.1111
/j.1467-9280.1991.tb00173.x
Mueller, Aaron, Garrett Nicolai, Panayiota
Petrou-Zeniou, Natalia Talmina, and Tal
Linzen. 2020. Cross-linguistic syntactic
evaluation of word prediction models. In
Proceedings of the 58th Annual Meeting of the
Association for Computational Linguistics,
pages 5523–5539. https://doi.org/10
.18653/v1/2020.acl-main.490
Muller, Benjamin, Yanai Elazar, Benoˆıt Sagot,
and Djam´e Seddah. 2021. First align, then
predict: Understanding the cross-lingual
ability of multilingual BERT. In Proceedings
of the 16th Conference of the European Chapter
of the Association for Computational
Linguistics: Main Volume, pages 2214–2231.
https://doi.org/10.18653/v1/2021
.eacl-main.189
298
Perani, Daniela and Jubin Abutalebi. 2005.
The neural basis of first and second
language processing. Current Opinion in
Neurobiology, 15(2):202–206. https://
doi.org/10.1016/j.conb.2005.03.007,
PubMed: 15831403
Perani, Daniela, Eraldo Paulesu, Nuria
Sebastian Galles, Emmanuel Dupoux,
Stanislas Dehaene, Valentino Bettinardi,
Stefano F. Cappa, Ferruccio Fazio, and
Jacques Mehler. 1998. The bilingual brain.
Proficiency and age of acquisition of the
second language. Brain: A Journal of
Neurology, 121(10):1841–1852. https://
doi.org/10.1093/brain/121.10.1841,
PubMed: 9798741
Pinter, Yuval, Marc Marone, and Jacob
Eisenstein. 2019. Character eyes: Seeing
language through character-level taggers.
In Proceedings of the 2019 ACL Workshop
BlackboxNLP: Analyzing and Interpreting
Neural Networks for NLP, pages 95–102.
https://doi.org/10.18653/v1/W19-4811
Pires, Telmo, Eva Schlinger, and Dan
Garrette. 2019. How multilingual is
multilingual BERT? In Proceedings of the
57th Annual Meeting of the Association for
Computational Linguistics, pages 4996–5001.
https://doi.org/10.18653/v1/P19-1493
Radford, Alec, Rafal Jozefowicz, and Ilya
Sutskever. 2017. Learning to generate
reviews and discovering sentiment. arXiv
preprint arXiv:1704.01444.
Serrano, Sofia and Noah A. Smith. 2019. Is
attention interpretable? In Proceedings of the
57th Annual Meeting of the Association for
Computational Linguistics, pages 2931–2951.
https://doi.org/10.18653/v1/P19-1282
Singh, Jasdeep, Bryan McCann, Richard
Socher, and Caiming Xiong. 2019. BERT is
not an interlingua and the bias of
tokenization. In Proceedings of the 2nd
Workshop on Deep Learning Approaches for
Low-Resource NLP (DeepLo 2019),
pages 47–55. https://doi.org/10
.18653/v1/D19-6106
Stanczak, Karolina, Edoardo Ponti, Lucas
Torroba Hennigen, Ryan Cotterell, and
Isabelle Augenstein. 2022. Same neurons,
different languages: Probing
morphosyntax in multilingual pre-trained
models. In Proceedings of the 2022
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies,
pages 1589–1598. https://doi.org/10
.18653/v1/2022.naacl-main.114
Tan, Li Hai, Lin Chen, Virginia Yip, Alice
H. D. Chan, Jing Yang, Jia-Hong Gao, and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
de Varda and Marelli
Data-driven Cross-lingual Syntax
Wai Ting Siok. 2011. Activity levels in the
left hemisphere caudate–fusiform circuit
predict how well a second language will
be learned. Proceedings of the National
Academy of Sciences, 108(6):2540–2544.
https://doi.org/10.1073/pnas
.0909623108, PubMed: 21262807
Tang, Zhiyuan, Ying Shi, Dong Wang, Yang
Feng, and Shiyue Zhang. 2017. Memory
visualization for gated recurrent neural
networks in speech recognition. In 2017
IEEE International Conference on Acoustics,
Speech and Signal Processing (ICASSP),
pages 2736–2740. https://doi.org/10
.1109/ICASSP.2017.7952654
Tham, Wendy W. P., Susan J. Rickard Liow,
Jagath C. Rajapakse, Tan Choong Leong,
Samuel E. S. Ng, Winston E. H. Lim, and
Lynn G. Ho. 2005. Phonological processing
in Chinese-English bilingual biscriptals:
An fMRI study. NeuroImage, 28(3):579–587.
https://doi.org/10.1016/j.neuroimage
.2005.06.057, PubMed: 16126414
van Schijndel, Marten, Aaron Mueller, and
Tal Linzen. 2019. Quantity doesn’t buy
quality syntax with neural language
models. In Proceedings of the 2019 Conference
on Empirical Methods in Natural Language
Processing and the 9th International Joint
Conference on Natural Language Processing
(EMNLP-IJCNLP), pages 5831–5837.
https://doi.org/10.18653/v1/D19-1592
Wang, Minghui, Yongzhong Zhao, and Bin
Zhang. 2015. Efficient test and
visualization of multi-set intersections.
Scientific Reports, 5:16923.
https://doi.org/10.1038/srep16923,
PubMed: 26603754
Wu, Shijie and Mark Dredze. 2019. Beto,
bentz, becas: The surprising cross-lingual
effectiveness of BERT. In Proceedings of the
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International Joint Conference on Natural
Language Processing (EMNLP-IJCNLP),
pages 833–844. https://doi.org/10
.18653/v1/D19-1077
Wu, Shijie and Mark Dredze. 2020. Are all
languages created equal in multilingual
BERT? In Proceedings of the 5th Workshop on
Representation Learning for NLP,
pages 120–130. https://doi.org/10
.18653/v1/2020.repl4nlp-1.16
Xu, Min, Daniel Baldauf, Chun Qi Chang,
Robert Desimone, and Li Hai Tan. 2017.
Distinct distributed patterns of neural
activity are associated with two
languages in the bilingual brain. Science
Advances, 3(7):e1603309.
https://doi.org/10.1126
/sciadv.1603309, PubMed: 28706990
Zou, Hui and Trevor Hastie. 2005.
Regularization and variable selection
via the elastic net. Journal of the Royal
Statistical Society: Series B (Statistical
Methodology), 67(2):301–320.
https://doi.org/10.1111
/j.1467-9868.2005.00503.x
Zuckermann, Ghil’ad. 2006. A new vision for
Israeli Hebrew: Theoretical and practical
implications of analyzing Israel’s main
language as a semi-engineered
Semito-European hybrid language. Journal
of Modern Jewish Studies, 5(1):57–71.
https://doi.org/10.1080
/14725880500511175
299
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
l
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
9
2
2
6
1
2
1
2
5
5
6
5
/
c
o
l
i
_
a
_
0
0
4
7
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3