Compressing Large-Scale Transformer-Based Models:
A Case Study on BERT

Prakhar Ganesh1∗, Yao Chen1∗, Xin Lou1, Mohammad Ali Khan1,
Yin Yang2, Hassan Sajjad3, Preslav Nakov3, Deming Chen4, Marianne Winslett4
1Advanced Digital Sciences Center, Singapur
2College of Science and Engineering, Hamad Bin Khalifa University, Qatar
3Qatar Computing Research Institute, Hamad Bin Khalifa University, Qatar
4University of Illinois at Urbana-Champaign, USA
{prakhar.g,yao.chen,lou.xin,mohammad.k}@adsc-create.edu.sg,
{yyang,hsajjad,pnakov}@hbku.edu.qa, {dchen,winslett}@illinois.edu

Abstrakt

Pre-trained Transformer-based models have
achieved state-of-the-art performance for vari-
ous Natural Language Processing (NLP) tasks.
Jedoch, these models often have billions
of parameters, and thus are too resource-
hungry and computation-intensive to suit low-
capability devices or applications with strict
latency requirements. One potential remedy
for this is model compression, which has at-
tracted considerable research attention. Hier,
we summarize the research in compressing
Transformers, focusing on the especially pop-
ular BERT model. Insbesondere, we survey the
state of the art in compression for BERT, Wir
clarify the current best practices for compress-
ing large-scale Transformer models, and we
provide insights into the workings of various
Methoden. Our categorization and analysis also
shed light on promising future research direc-
tions for achieving lightweight, accurate, Und
generic NLP models.

1

Einführung

Sentiment analysis, paraphrase detection, machine
reading comprehension, question answering, Text
summarization—all these Natural Language Pro-
Abschließen (NLP) tasks benefit from pre-training a
large-scale generic model on an enormous corpus
such as a Wikipedia dump and/or a book collec-
tion, and then fine-tuning for specific downstream
tasks, wie in der Abbildung gezeigt 1. Earlier solutions fol-
lowing this methodology used recurrent neural
Netzwerke (RNNs) as the base model, Zum Beispiel,
ULMFiT (Howard and Ruder, 2018) and ELMo

∗Both authors contributed equally to this research.

pre-trained Transformers

(Peters et al., 2018), but more recent methods
use the Transformer architecture (Vaswani et al.,
2017), which relies heavily on the attention
mechanism.
Popular

include
BERT (Devlin et al., 2019), GPT-2 (Radford et al.,
2019), XLNet (Yang et al., 2019), MegatronLM
(Shoeybi et al., 2019), Turing-NLG (Rosset,
2020), T5 (Raffel et al., 2020), and GPT-3 (Braun
et al., 2020). These Transformers are—for exam-
Bitte, BERT, when first released, improved the state
of the art for eleven NLP tasks by sizable margins
(Devlin et al., 2019). Jedoch, Transformers are
also bulky and resource-hungry: Zum Beispiel,
GPT-3 (Brown et al., 2020), a recent large-scale
Transformer, has over 175 billion parameters.
Models of this size incur high memory consump-
tion, computational overhead, and energy. Der
problem is exacerbated when we consider devices
with lower capacity (z.B., smartphones), and ap-
plications with strict latency constraints, (z.B.,
interactive chatbots).

To put things in perspective, a single training
run for GPT-3 (Brown et al., 2020), one of the
most powerful and heaviest Transformer-based
Modelle, trained on a total of 300 billion tokens,
costs well above 12 million USD (Floridi and
Chiriatti, 2020). Darüber hinaus, fine-tuning or even
inference with such a model on a downstream task
cannot be done on a GPU with 32GB memory,
which is the capacity of Tesla V100, one of the
most advanced data center GPUs.

Instead it requires access to high-performance
GPU or multi-core CPU clusters, which often
means a need to access cloud computing with high
computation density, such as the Google Cloud

1061

Transactions of the Association for Computational Linguistics, Bd. 9, S. 1061–1080, 2021. https://doi.org/10.1162/tacl a 00413
Action Editor: Andre Filipe Torres Martins. Submission batch: 4/2021; Revision batch: 6/2021; Published 9/2021.
C(cid:3) 2021 Verein für Computerlinguistik. Distributed under a CC-BY 4.0 Lizenz.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

BERT (Devlin et al., 2019). Although the com-
pression methods discussed here can be extended
to Transformer-based decoders and multilingual
Transformer models, we restrict our discussion to
BERT in order to be able to provide more detailed
insights into the various methods that we compare.
Our study is timely, seit (ich) the use of
Transformer-based BERT-like models has grown
dramatically, as demonstrated by current leaders
of various NLP tasks such as language under-
Stehen (Wang et al., 2018), machine reading
comprehension (Rajpurkar et al., 2016, 2018),
maschinelle Übersetzung (Machacek and Bojar, 2014),
summarization (Narayan et al., 2018), und so weiter;
(ii) many researchers are left behind as they
do not have expensive GPUs (or a multi-GPU
setup) with a large amount of GPU memory, Und
thus cannot fine-tune and use the large BERT
model for relevant downstream tasks; Und (iii) AI-
powered devices such as smartphones would ben-
efit tremendously from an on-board BERT-like
Modell, but do not have the capability to run it. In
addition to summarizing existing techniques and
best practices for BERT compression, we point out
several promising future directions of research
for compressing large-scale Transformer-based
Modelle.

2 Breakdown and Analysis of BERT

Bidirectional Encoder Representations from Trans-
formers, or BERT (Devlin et al., 2019), ist ein
Transformer-based model (Vaswani et al., 2017)
pre-trained on large corpora from Wikipedia and
the Bookcorpus dataset (Zhu et al., 2015) us-
ing two training objectives: (ich) Masked Language
Modell (MLM), which helps it learn the context in a
Satz, Und (ii) Next Sentence Prediction (NSP),
from which it learns the relationship between two
Sätze. Subsequent Transformer architectures
have further improved the training objective in
various ways (Lan et al., 2020; Liu et al., 2019B).
Im Folgenden, we focus on the original BERT
Modell.

BERT decomposes the input sentence(S) into
WordPiece tokens (Wu et al., 2016). Speziell,
WordPiece tokenization helps improve the rep-
resentation of the input vocabulary and reduce
its size, by segmenting complex words into sub-
Wörter. These subwords can even form new words
not seen in the training samples, thus making the

Figur 1: Pre-training large-scale models.

Platform (GCP), Microsoft Azure, Amazon Web
Dienstleistungen (AWS), und so weiter, and results in a high
monetary cost (Floridi and Chiriatti, 2020).

One way to address this problem is through
model compression, an intricate part of deep learn-
ing that has attracted attention from both research-
ers and practitioners. A recent study by Li et al.
(2020C) highlights the importance of first training
over-parameterized models and then compressing
ihnen, instead of directly training smaller models,
to reduce the performance errors. Although most
methods in model compression were originally
proposed for convolutional neural networks (CNNs)
(pruning, quantization, knowledge distillation,
usw.) (Cheng et al., 2018), many ideas are di-
rectly applicable to Transformers. There are also
methods designed specifically for Transformers
(z.B., attention head pruning, attention decompo-
sition, replacing Transformer blocks with an RNN
or a CNN), which we will discuss in Section 3.
Unlike CNNs, a Transformer model has a rela-
tively complex architecture consisting of multiple
parts such as embedding layers, self-attention,
and feed-forward layers (details introduced in
Abschnitt 2). Daher, the effectiveness of different
compression methods can vary when applied to
different parts of a Transformer model.

Several recent surveys have focused on pre-
trained representations and large-scale Transformer-
based models (Qiu et al., 2020; Rogers et al.,
2020; Wang et al., 2020A). Jedoch, to the best
of our knowledge, no comprehensive, systematic
study has compared the effectiveness of different
model compression techniques on Transformer-
based large-scale NLP models, even though a
variety of approaches for compressing such mod-
els have been proposed. Motivated by this, Hier
we offer a thorough and in-depth comparative
study on compressing Transformer-based NLP
Modelle, with a special focus on the widely used

1062

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

tence of length 256, and then we collected the
results in Figure 3. The top graph in the figure
compares the model size as well as the theoretical
computational requirements (measured in millions
of FLOPs) of different parts of the model. Der
bottom two graphs track the model’s run-time
memory consumption as well as the inference
latency on two representative hardware setups.

We conducted our experiments using Nvidia
Titan X GPU with 12GB of video RAM and
Intel Xeon E5-1620 CPU with 32 GB of system
Erinnerung, which is a commonly used server or
workstation configuration. All data was collected
using the PyTorch profiling tool.

Clearly, the parts consuming the most memory
in terms of model size and executing the high-
est number of FLOPs are the FFN sub-units. Der
embedding layer is also a substantial part of the
model size, due to the large vector size (H) gebraucht
to represent each embedding vector. Note that it
has zero FLOPs, since it is a lookup table that in-
volves no arithmetic computations at inference
Zeit. For the self-attention sub-units, we further
break down the costs into multi-head self-attention
layers and the linear (d.h., fully connected) lay-
ers before and after them. The multi-head self-
attention does not have any learnable parameters;
Jedoch, its computational cost is non-zero due
to the dot products and the softmax operations.

The linear layers surrounding each attention
layer incur additional memory and computational
overhead, though it is relatively small compared
to the FFN sub-units. Note that the input to the at-
tention layer is divided among various heads, Und
thus each head operates in a lower-dimensional
Raum (H/A). The linear layer before attention is
roughly three times the size of that after it, seit
each attention has three inputs (key, value, Und
query) and only one output.

The theoretical computational overhead may
differ from the actual inference cost at run-time,
which depends on the hardware that the model
runs on. Wie erwartet, when running the model
on a GPU, the total run-time memory includes
memory both on the GPU side and on the CPU
Seite, and it is greater than for a model running
solely on a CPU due to duplicate tensors present
on both devices for faster processing on a GPU.

The most notable difference between the theo-
retical analysis and the run-time measurements on
a GPU is that the multi-head self-attention layers
are significantly more costly in practice than in

Figur 2: BERT model flowchart.

model more robust to out-of-vocabulary (OOV)
Wörter. BERT further inserts a classification token
([CLS]) before the input tokens, and the output
corresponding to this token is used for classifica-
tion tasks that target the entire input. For sentence
pair tasks, the two sentences are packed together
by inserting a further separator token ([SEP])
between them.

BERT represents each WordPiece token with
three vectors, nämlich, its token, segment, and posi-
tion embeddings. These embeddings are summed
together and then passed through the main body of
the model (d.h., the Transformer backbone), welche
produces the output representations that are fed
into the final, application-dependent layer (z.B., A
classifier for sentiment analysis).

As shown in Figure 2, the Transformer back-
bone consists of multiple stacked encoder units,
each with two major sub-units: a self-attention
sub-unit and a feed forward network (FFN)
sub-unit, both with residual connections. Jede
self-attention sub-unit consists of a multi-head
self-attention layer, and fully connected layers be-
fore and after it. An FFN sub-unit exclusively
contains fully connected layers. The architecture
of BERT can be specified using the following three
hyper-parameters: number of encoder units (L),
size of the embedding vector (H), and number of
attention heads in each self-attention layer (A). L
and H determine the depth and the width of the
Modell, whereas A is an internal hyper-parameter
that affects the number of contextual relations that
each encoder can focus on. The authors of BERT
provided two pre-trained models:

• BERTBASE (L = 12; H = 768; A = 12);

• BERTLARGE (L = 24; H = 1024; A = 16).

We conducted various experiments with the
BERTBASE model by running inference on a sen-

1063

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 3: Breakdown analysis of BERTBASE.

theory. This is because the operations in these
layers are complex, and are implemented as sev-
eral matrix transformations followed by a matrix
multiplication and a softmax. Darüber hinaus, GPUs
are designed to accelerate certain operations, Und
thus can implement linear layers faster and more
efficiently than the more complex attention layers.
When we compare the run-time performance
on a CPU, where the hardware is not specialized
for linear layer operations, the inference time as
well as the memory consumption of all the linear
layers shoots up more compared to the multi-head
self-attention. Daher, on a CPU, the behavior of run-
time performance is similar to that of theoretical
computations. The total execution time for a single
example on a GPU (57.1 MS) is far superior as
compared to a CPU (750.9 MS), as expected. Der
execution time of the embedding layer is largely
independent of the hardware on which the model
is executed (since it is just a table lookup) und es
is relatively small compared to the other layers.

The FFN sub-units are the bottleneck of the whole
Modell, which is consistent with the results from
the theoretical analysis.

3 Compression Methods

Because of BERT’s complex architecture, no ex-
isting compression method has focused on every
single aspect of the model: self-attention, linear
layers, embedding size, model depth, und so weiter.
Stattdessen, each compression method applies to cer-
tain components of BERT. Below, we consider
the compression methods that offer model size
reduction and speedup at inference time, eher
than during the training procedure.

3.1 Quantization

Quantization refers to reducing the number of
unique values required to represent model weights
and activations, which allows to represent them

1064

to adjust the quantized weights. Figur 4 shows an
example of na¨ıve linear quantization, quantization
noise, and the importance of quantization-aware
Ausbildung. For BERT, QAT has been used to
perform fixed-length integer quantization (Zafrir
et al., 2019; Boo and Sung, 2020), Hessian-based
mixed-precision quantization (Shen et al., 2020),
adaptive floating-point quantization (Tambe et al.,
2020), and noise-based quantization (Fan et al.,
2021). Endlich, it has been observed that the em-
bedding layer is more sensitive to quantization
than the other encoder layers, and thus that it re-
quires more bits in order to maintain the model
accuracy (Shen et al., 2020).

3.2 Pruning

Pruning refers to identifying and removing redun-
dant or less important weights and/or components,
which sometimes even makes the model more ro-
bust and better-performing. Darüber hinaus, pruning is
a commonly used method of exploring the lottery
ticket hypothesis in neural networks (Frankle and
Carbin, 2019), which has also been studied in the
context of BERT (Chen et al., 2020B; Prasanna
et al., 2020). Pruning methods for BERT largely
fall into two categories, which we explore below.

Unstructured Pruning. Unstructured pruning,
also known as sparse pruning, prunes individual
weights by locating the set of the least impor-
tant weights in the model. The importance of the
weights can be judged by their absolute values,
by the gradients, or by some custom-designed
measurement (Gordon et al., 2020; Mao et al.,
2020; Guo et al., 2019; Sanh et al., 2020; Chen
et al., 2020B). Unstructured pruning could be
effective for BERT, given the latter’s massive
amount of fully-connected layers. Unstructured
pruning methods include magnitude weight prun-
ing (Gordon et al., 2020; Mao et al., 2020; Chen
et al., 2020B), which simply removes weights
that are close to zero, movement-based pruning
(Sanh et al., 2020; Tambe et al., 2020), welche
removes weights that move towards zero dur-
ing fine-tuning, and reweighted proximal pruning
(RPP) (Guo et al., 2019), which uses itera-
tively reweighted (cid:2)1 minimization followed by the
proximal algorithm for decoupling pruning and
error back-propagation. Since unstructured prun-
ing considers each weight individually, the set
of pruned weights can be arbitrary and irregular,
which in turn might decrease the model size, Aber

Figur 4: Quantization.

using fewer bits, to reduce the memory footprint,
and to lower the precision of the numerical calcula-
tionen. Quantization may even improve the runtime
memory consumption as well as the inference
speed when the underlying computational device
is optimized to process lower-precision numerical
Werte, Zum Beispiel, tensor cores in newer gener-
ations of Nvidia GPUs. Programmable hardware
such as FPGAs can also be specifically optimized
for any bitwidth representation. Quantization of
intermediate outputs and activations can further
speed up the model execution (Boo and Sung,
2020).

Quantization is applicable to all model weights
as the BERT weights reside in fully connected
layers (d.h., the embedding layer, the linear layers,
and the FFN sub-units), which have been shown
to be quantization-friendly (Hubara et al., 2017).
The original BERT model provided by Google
represents each weight by a 32-bit floating point
number. A na¨ıve approach is to simply truncate
each weight to the target bitwidth, which often
yields a sizable drop in accuracy as this forces
certain weights to go through a severe drift in
their value, known as quantization noise (Fan
et al., 2021).

A possible way around this issue is to identify
these weights and then not to truncate them during
the quantization step in order to retain the model
accuracy. Zum Beispiel, Zadeh et al. (2020) als-
sumed Gaussian distribution in the weight matrix
and identified the outliers. Dann, by not quan-
tizing these outliers, they were able to perform
post-training quantization without any retraining
requirements.

A more common approach to retaining the
model accuracy is Quantization-Aware Training
(QAT), which involves additional training steps

1065

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 5: Various pruning methods including structured pruning by (A) pruning number of encoder units (L), (B)
pruning embedding size (H), (C) pruning number of attention heads (A), sowie (D) unstructured pruning.

with negligible improvement in runtime memory
or speed, unless executed on specialized hardware
or with specialized processing libraries.

Structured Pruning. Unlike unstructured prun-
ing, structured pruning focuses on pruning struc-
tured blocks of weights (Li et al., 2020A) or even
complete architectural components in the BERT
Modell, by reducing and simplifying certain nu-
merical modules:

• Attention Head Pruning. As we have seen
über, the self-attention layer incurs consid-
erable computational overhead at inference
Zeit; yet, its importance has often been ques-
tioned (Kovaleva et al., 2019; Tay et al.,
2020; Raganato et al., 2020). Tatsächlich, es hat
been shown that high accuracy is possible
with only 1–2 attention heads per encoder
unit, even though the original BERT model
hatte 16 attention heads (Michel et al., 2019).
Randomly pruning attention heads during the
training phase has also been proposed, welche
can create a model that is robust to vari-
ous numbers of attention heads, and thus a
smaller model can be directly extracted for
inference based on the required deployment
requirements (Hou et al., 2020).

• Encoder Unit Pruning. Another structured
pruning method aims to reduce the number
of encoder units L by pruning the less impor-
tant layers. Zum Beispiel, layer dropout drops
encoder units randomly or with a pre-defined
strategy during training. If the layers are
dropped randomly, a smaller model of any

desired depth can be extracted during infer-
enz (Fan et al., 2020; Hou et al., 2020).
Ansonsten, a smaller model of fixed depth is
erhalten (Sajjad et al., 2020; Xu et al., 2020).
As BERT contains residual connections for
every sub-unit, using an identity prior to
prune these layers has also been proposed
(Lin et al., 2020).

• Embedding Size Pruning. Similarly to en-
coder unit pruning, we can reduce the size of
the embedding vector (H) by pruning along
the width of the model. Such a model can
be obtained by either training with adaptive
width, so that the model is robust to such
pruning during inference (Hou et al., 2020),
or by removing the least important feature
dimensions iteratively (Khetan and Karnin,
2020; Prasanna et al., 2020; Tsai et al., 2020;
Lin et al., 2020).

Figur 5 shows a visualization of various forms

of structured pruning and unstructured pruning.

3.3 Knowledge Distillation

Knowledge Distillation refers to training a smaller
Modell (called the student) using outputs (aus
various intermediate functional components) von
one or more larger pre-trained models (called the
Lehrer). The flow of information can sometimes
be through an intermediate model (commonly
known as teaching assistants) (Ding and Yang,
2020; Sun et al., 2020B; Wang et al., 2020C).
In the BERT model, there are multiple inter-
mediate results that the student can potentially

1066

Figur 6: Knowledge distillation. Student models can be formed by (A) reducing the encoder width, (B) reduzierend
the number of encoders, (C) replacing with a BiLSTM, (D) replacing with a CNN, or some combination thereof.

learn from, such as the logits in the final layer,
the outputs of the encoder units, and the atten-
tion maps. Darüber hinaus, there are multiple forms of
loss functions that can be adapted for this pur-
pose such as cross-entropy loss, KL divergence,
MAE, und so weiter. While knowledge distillation
is most commonly used to train student models
directly on task-specific data, recent results have
shown that distillation during both pre-training
and fine-tuning can help create better performing
Modelle (Song et al., 2020). An overview of var-
ious forms of knowledge distillation and student
models is shown in Figure 6. Based on what the
student learns from the teacher, we can categorize
the existing methods as follows:

Distillation from Output Logits. Ähnlich zu
knowledge distillation for CNNs (Cheng et al.,
2018), the student can directly learn from the
output logits (d.h., from soft labels) of the final
softmax layer in BERT. This is done to allow the
student to better mimic the output of the teacher
Modell, by replicating the probability distribution
across various classes.

While knowledge distillation on output logits
is most commonly used to train smaller BERT
Modelle (Sun et al., 2019; Sanh et al., 2019; Jiao
et al., 2020; Zhao et al., 2019B; Cao et al., 2020;
Sun et al., 2020B; Song et al., 2020; Mao et al.,
2020; Li et al., 2020B; Ding and Yang, 2020;
Noach and Goldberg, 2020), the student does
not need to be a smaller version of BERT or
even a Transformer, and can follow a completely
different architecture. Below we describe the two
commonly used replacements:

• Replacing the Transformer with a BiLSTM, Zu
create a lighter backbone. Recurrent models
such as BiLSTMs process words sequen-
tially instead of simultaneously attending to

each word in the sentence like Transformers
do, resulting in a smaller runtime memory
requirement. Both can create bidirectional
Darstellungen, and thus BiLSTMs can be
considered a faster alternative to Transform-
ers (Wasserblat et al., 2020). Compressing to
a BiLSTM is typically done directly for a spe-
cific NLP task (Mukherjee and Awadallah,
2020). Since these models are trained from
scratch on the task-specific dataset without
any intermediate guidance, various methods
have been proposed to create additional syn-
thetic training data using rule-based data
augmentation techniques (Tang et al., 2019;
Mukherjee and Awadallah, 2020) or to col-
lect data from multiple tasks to train a single
Modell (Liu et al., 2019A).

• Replacing the Transformer with a CNN, Zu
take advantage of massively parallel compu-
tations and improved inference speed (Chia
et al., 2018). While it is theoretically pos-
sible to make the internal processing of an
encoder parallel, where each parallel unit
requires access to all the inputs from the
previous layer as an encoder unit focuses
on the global context, this setup is computa-
tionally intensive and cost-inefficient. Unlike
Transformers, each CNN unit focuses on lo-
cal context, Und, unlike BiLSTMs, CNNs do
not operate on the input sequentially, welche
makes it easier for them to divide the compu-
tation into small parallel units. Es ist möglich
to either completely replace the Transformer
backbone with a deep CNN network (Chen
et al., 2020A), or to replace only a few encoder
units to balance performance and efficiency
(Tian et al., 2019).

1067

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Distillation from Encoder Outputs. Each en-
coder unit in a Transformer model can be viewed
as a separate functional unit. Intuitively, the out-
put tensors of such an encoder unit may contain
meaningful semantic and contextual relationships
between input tokens, leading to an improved rep-
resentation. Following this idea, we can create
a smaller model by learning from an encoder’s
outputs. The smaller model can have a reduced
embedding size H, a smaller number of encoder
units L, or a lighter alternative that replaces the
Transformer backbone.

• Reducing the number of heads H yields
more compact representations in the student
(Zhao et al., 2019B; Sun et al., 2020B; Jiao
et al., 2020; Li et al., 2020B). One chal-
lenge is that the student cannot directly learn
from the teacher’s intermediate outputs, fällig
to different sizes. To overcome this, the stu-
dent also learns a transformation, which can
be implemented by either down-projecting
the teacher’s outputs to a lower dimension
or by up-projecting the student’s outputs to
the original dimension (Zhao et al., 2019B).
Another possibility is to introduce these
transformations directly into the student
Modell, and later to merge them with the ex-
isting linear layers to obtain the final smaller
Modell (Zhou et al., 2020A).

• Reducing the number of encoder units L
forces each encoder unit in the student to
learn from the behavior of a sequence of mul-
tiple encoder units in the teacher (Sun et al.,
2019; Sanh et al., 2019; Sun et al., 2020B;
Jiao et al., 2020; Zhao et al., 2019B; Li et al.,
2020B). Further analysis into various details
of choosing which encoder units to use for
distillation is provided by Sajjad et al. (2020).
Zum Beispiel, preserving the bottom encoder
units and aggressively distilling the top en-
coder units yields a better-performing student
Modell, which indicates the importance of the
bottom layers in the teacher model. Während
most existing methods create an injective
mapping from the student encoder units to
the teacher, Li et al. (2020B) instead proposed
a way to build a many-to-many mapping for
a better flow of information. One can also
completely bypass the mapping by combin-
ing all outputs into one single representation
vector (Sun et al., 2020A).

• It is also possible to use encoder outputs to
train student models that are not Transform-
ers (Mukherjee and Awadallah, 2020; Tian
et al., 2019). Jedoch,when the student model
uses a completely different architecture, Die
flexibility of using internal representations is
rather limited, and only the output from the
last encoder unit can be used for distillation.

Distillation from Attention Maps. An atten-
tion map refers to the softmax distribution output
of the self-attention layers and indicates the
Zu-
contextual dependence between the input
kens. It has been proposed that attention maps
in BERT can identify distinguishable linguistic
Beziehungen, Zum Beispiel,
identical words across
Sätze, verbs and corresponding objects, oder
pronouns and corresponding nouns (Clark et al.,
2019). These distributions are the only source
of inter-dependency between input tokens in a
Transformer model, and thus by replicating these
distributions, a student can also learn such linguis-
tic relations (Sun et al., 2020B; Jiao et al., 2020;
Mao et al., 2020; Tian et al., 2019; Li et al., 2020B;
Noach and Goldberg, 2020).

A common method of distillation from atten-
tion maps is to directly minimize the difference
between the teacher’s and the student’s multi-head
self-attention outputs. Similarly to distillation
from encoder outputs, replicating attention maps
also faces a choice of mapping between the teacher
and the student, as each encoder unit has its own
attention distribution. Previous work has also pro-
posed replicating only the last attention map in
the model to truly capture the contextual depen-
dence (Wang et al., 2020C). One can attempt an
even deeper distillation of information through
intermediate attention outputs such as key, query,
and value matrices, individual attention head out-
puts, key–query, and value–value matrix products,
und so weiter, to facilitate the flow of information
(Wang et al., 2020C; Noach and Goldberg, 2020).

3.4 Matrix Decomposition

The computational overhead in BERT mainly con-
sists of large matrix multiplications, both in the
linear layers and in the attention heads. Daher, von-
composing these matrices can significantly impact
the computational requirements for such models.

Weight Matrix Decomposition. The compu-
tational overhead of the model can be reduced

1068

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figur 7: Attention decomposition.

Figur 8: Dynamic inference acceleration.

through weight matrix factorization, welche re-
places the original A × B weight matrix by the
product of two smaller ones (A × C and C × B).
The reduction in model size and runtime memory
use is sizable if C (cid:4) A, B. The method can be
applied to the linear layers (Noach and Goldberg,
2020; Mao et al., 2020), or to the embedding
Matrix (Lan et al., 2020; Tambe et al., 2020).

Attention Decomposition.
It has been shown
that computing attention over the entire sentence
makes a large number of redundant computations
(Tay et al., 2020; Cao et al., 2020). Daher, es hat
been proposed to do it in smaller groups, by either
binning them using spatial locality (Cao et al.,
2020), magnitude-based locality (Kitaev et al.,
2020), or an adaptive attention span (Tambe
et al., 2020). Darüber hinaus, since the outputs are
calculated independently, local attention methods
also enable a higher degree of parallel processing
and individual representations can be saved dur-
ing inference for multiple uses. Figur 7 zeigt an
an example of attention decomposition based on
spatial locality.

It has been also proposed to reduce the atten-
tion computations by projecting the key–query
matrix into a lower dimensionality (Wang et al.,
2020B) or by only calculating the softmax of the
top-k key-query product values in order to further
highlight these relations (Zhao et al., 2019A).

Since the multi-head self-attention layer con-
tains no weights, these methods only improve the
runtime memory costs and execution speed, Aber
do not reduce the model size.

3.5 Dynamic Inference Acceleration
Besides directly compressing the model, manche
methods focus on reducing the computational

overhead at inference time by catering to indi-
vidual input examples and dynamically changing
the amount of computation. Figur 8 shows a visu-
alization of two such methods, which we discuss
below.

Early Exit Ramps. One way to speed up infer-
ence is to create intermediary exit points in the
Modell. Since the classification layers are the least
parameter-extensive part of BERT, separate clas-
sifiers can be trained for each encoder unit output.
This allows the model to have dynamic inference
time for various inputs. Training these separate
classifiers can be done either from scratch (Xin
et al., 2020; Zhou et al., 2020B; Tambe et al., 2020)
or by distilling the output of the final classifier
(Liu et al., 2020).

Progressive Word Vector Elimination. Ein-
other way to accelerate inference is by reducing
the number of words processed at each encoder
Ebene. Since we only use the final output corre-
sponding to the [CLS] token (defined in Section 2)
as a representation of the complete sentence, Die
information of the entire sentence must have fused
into that one token. Goyal et al. (2020) observed
that such a fusion cannot be sudden, and that it
must happen progressively across various encoder
levels. We can use this information to lighten the
later encoder units by reducing the sentence length
through word vector elimination at each step.

3.6 Other Methods

Besides the aforementioned methods, es gibt
also several one-of-a-kind methods that have been
shown to be effective for reducing the size and the
inference time of BERT-like models.

1069

Parameter Sharing. ALBERT (Lan et al.,
2020) uses the same architecture as BERT, Aber
with weights shared across all encoder units,
which reduces memory consumption signifi-
cantly. Darüber hinaus, ALBERT enables training
larger and deeper models: While BERT’s per-
formance peaks at BERTLARGE (performance of
BERTXLARGE drops significantly), ALBERT keeps
improving until the far larger ALBERTXXLARGE
Modell (L = 12; H = 4096; A = 64).

Embedding Matrix Compression. The embed-
ding matrix is the lookup table for the embedding
layer, which is about 21% of the size of the
complete BERT model. One way to compress it
is by reducing the vocabulary size V , welches ist
about 30k in the original BERT model. Recall
from Section 2 that the vocabulary of BERT is
learned using a WordPiece tokenizer, which relies
on the vocabulary size to figure out the degree
of fragmentation of the words in the input text.
A large vocabulary size allows for better repre-
sentation of rare words and for more adaptability
to out-of-vocabulary words. Jedoch, even with
a 5k vocabulary size, 94% of the tokens match
those created using a 30k vocabulary size (Zhao
et al., 2019B). Daher, the majority of the words that
appear frequently enough are covered even with
a small vocabulary size, which makes it reason-
able to decrease the vocabulary size to compress
the embedding matrix. Another alternative is to
replace the existing one-hot vector encoding with
a ‘‘codebook’’-based one, where each token is
represented using multiple indices from the code-
Buch. The final embedding of the token can then
be calculated as the sum of the embeddings present
in all these indices (Prakash et al., 2020).

Squeezing. Weight
Weight
squeezing
(Chumachenko et al., 2020) is a compression
method similar to knowledge distillation, Wo
the student learns from the teacher. Jedoch,
instead of learning from intermediate outputs
as in knowledge distillation, the weights of the
teacher model are mapped to the student through
a learnable transformation, and thus the student
learns its weights directly from the teacher.

4 Effectiveness of Compression Methods

In diesem Abschnitt, we compare the performance of
several BERT compression techniques based on

their model size and speedup, as well as their
accuracy or F1 score on various NLP tasks. Wir
chose work whose results are either on the Pareto
frontier (Deb, 2014) or representative for each
compression technique mentioned in the previous
section.

4.1 Datasets and Evaluation Measures

From the General Language Understanding Eval-
uation (GLUE) benchmark (Wang et al., 2018)
and the Stanford Question Answering Dataset
(SQuAD) (Rajpurkar et al., 2016), we use the
following most common tasks: MNLI and QQP
for sentence pair classification, SST-2 for sin-
gle sentence classification, and SQuAD v1.1 for
machine reading comprehension. Following the
official leaderboards, we report the accuracy for
MNLI, SST-2, and QQP, and F1 score for SQuAD
v1.1. In an attempt to quantify the results on a sin-
gle scale, we also report the absolute drop in
performance with respect to BERTBASE, aver-
aged across all tasks for which the authors have
reported results.

We further report speedup on both GPU and
CPU devices, collected directly from the original
Papiere. For papers that report speedup, we also
mention the target device on which is was cal-
culated, and for such that do not, we run their
models on our own machine and we perform in-
ference on the complete MNLI-m test set (verwenden
a batch size of 1) with machine configurations as
detailed in Section 2. We also report the model
size with and without the embedding matrix, seit
for certain application scenarios, where the mem-
ory constraints for model storage are not strict,
the parameters of the embedding matrix can be
ignored as it has negligible run-time cost (sehen
Abschnitt 2). As no previous work has reported the
drop in runtime memory, and as many papers that
we compare to use probabilistic models that cannot
be easily replicated without their code, we could
not perform direct runtime memory comparisons.

4.2 Comparison and Analysis

Tisch 1 compares various BERT compression
Methoden. While some compress only part of the
Modell, for uniformity, we report size and speedup
for the final complete models after compression.
Daher, certain values might not match exactly what
is reported in the original papers.

1070

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

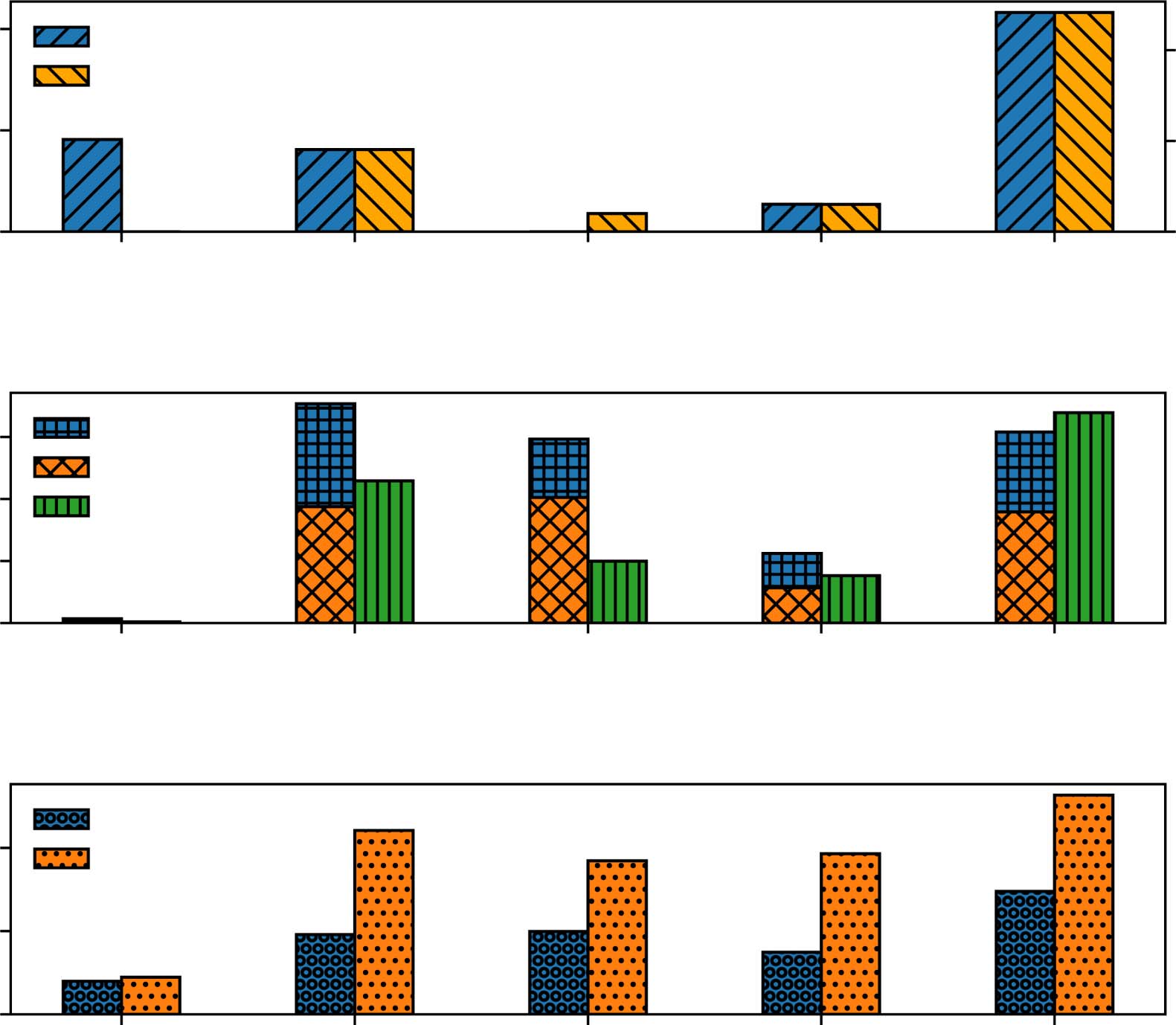
Methoden

Provenance

Target Model Size
Avr.
Device w/ emb w/o emb GPU CPU MNLI QQP SST-2 SQD Drop

Accuracy/F1

Speedup

–

–
–
–

88.9 91.8

BERTBASE

Quantization

1X
1X
1X
1X
1X
1X
–

1X
1X
1X
1X
1X
1X
–

Structured
Pruning

Unstructured
Pruning

KD from
Output Logits

84.6 89.2 93.5 88.5
83.9
83.7
–

(Devlin et al., 2019)
(Shen et al., 2020) S
(Zadeh et al., 2020) S
(Guo et al., 2019) A
(Chen et al., 2020B) S
(Sanh et al., 2020) S
(Lin et al., 2020) S
(Khetan and Karnin, 2020) A
(Song et al., 2020) A,S
(Liu et al., 2019A)† S
(Chen et al., 2020A) A,S
KD from Attn. (Wang et al., 2020C) A

100% 100%
–
15% 12.5%
–
10.2%
5.5%
–
67.6% 58.7%
–
48.9%∗ 35.1%∗
–
3%
23.8%
–
60.7%
50%
–
–
39.1% 38.8% 2.93x‡ 2.76x‡ 83.4
–
22.8% 10.9% 6.25x 7.09x
–
V100
8.6x‡
3.3% 10.7X
24.1%
V100
4.8% 19.5x∗
7.4%
–
V100
50% 1.94x 1.73x
60.7%
P100
(Sanh et al., 2019) A
50% 1.94x 1.73x
60.7%
CPU
4.7x‡
23.1% 24.8% 3.9x‡
(Sun et al., 2020B)† A
Pixel
9.3x‡
(Jiao et al., 2020) A,S
6.4% 9.4X
13.3%
K80
1.8% 25.5x‡ 22.7x‡
(Zhao et al., 2019B) A
1.6%
–
(Noach and Goldberg, 2020) S Titan V 60.6% 49.1% 0.92x 1.05x
100% 100% 3.14x 3.55x
100% 100% 1.25X
100% 100% 2.5X
8.8% 1.2x‡
10.7%
40.0% 37.3%
1X
31.2% 12.4% 5.9x‡
7.6%
5.7%
1.3%

0.0
92.6 88.3 −0.6
−0.9
–
–
–
0.0
88.5
83.1 89.5 92.9 87.8 −0.63
79.9 −4.73
–
79.0 89.3
−1.0
–
90.9 86.7 −1.86
−0.6
88.6 92.9
–
−3.03
78.6 88.6 91.0
–
−2.06
81.6 88.7 91.8
–
−0.1
84.0 91.0 92.0
–
82.2 88.5 91.3 86.9 −1.73
92.8 90.0 −0.16
83.3
–
−1.0
–
82.5 89.2 92.6
– −12.3
71.3
82.2
–
−0.13
84.8 89.7 92.4
–
87.1 −0.76
82.6 90.3
–
1.28x‡ 83.9 89.2 93.4
−0.26
3.1x‡
−1.1
83.8
92.1
1.2x‡
84.3 89.6 90.3 89.3 −0.58
−0.7
83.5 88.9 92.8
1X
–
8.7x‡
−0.96
82.0 90.4 92.0
–
−2.6
–
–
82.0
3.9% 1.94x 1.73x
4.7x‡
6.1% 3.9x‡
92.6 90.0 −0.23
83.3
–
−1.53
–
84.4 89.8 88.5
–
0.9% 1.83X

Matrix
Decomposition (Cao et al., 2020) S
(Xin et al., 2020) S
Dynamic
(Goyal et al., 2020) S
Inference
Param. Teilen (Lan et al., 2020) A
(Mao et al., 2020) S
Pruning
(Hou et al., 2020) S
with KD
(Zadeh et al., 2020) S
Quantization
(Sun et al., 2020B)† A
with KD
(Tambe et al., 2020) S
Compound

V100
P100
K80
–
–
K40
CPU
Pixel
TX2

Multiple KD
combined

–
–

–

–

Tisch 1: Evaluation of various compression methods. ∗ indicates models using task-specific sizes or
speedups; average values are reported in such cases. † represents models that use BERTLARGE as the
teacher model. ‡ represents speedup values that we calculated. Empty cells in the speedup columns
are for papers that do not describe the detailed architecture of their final compressed model. A marks
models compressed in a task-agnostic setup, d.h., requiring access to the pre-training dataset. S indicates
models compressed in a task-specific setup. V100 is Nvidia Tesla V100; P100 is Nvidia Tesla P100;
K80 is Nvidia Tesla K80; Titan V is Nvidia Titan V; K40 is Nvidia Tesla K40; CPU is Intel Xeon E5;
TX2 is Nvidia Jetson TX2; and Pixel is Google Pixel Phone.

Quantization and Pruning. Quantization is
well suited for BERT, and it can outperform
other methods in terms of both model size and
accuracy. As shown in Table 1, it can compress
BERT to 15% Und 10.2% of its original size, mit
accuracy drop of only 0.6% Und 0.9%, bzw-
aktiv, across various tasks (Shen et al., 2020;
Zadeh et al., 2020). This can be attributed to its
architecture-invariant nature, as it only reduces
the precision of the weights, but preserves all
original components and connections. Unstruc-
tured pruning also shows performance that is on
par with other methods. It compresses BERT to
67.6% of its original size, without any loss in

accuracy, possibly due to the regularization effect
of pruning (Guo et al., 2019). Jedoch, almost all
existing work in unstructured pruning freezes the
embedding matrix and focuses only on pruning the
weight matrices of the encoder. This makes ex-
treme compression difficult—for example, sogar
mit 3% weight density in encoders, the total
model size still remains at 23.8% of its original
Größe (Sanh et al., 2020), and yields a sizable drop
in accuracy/F1 (4.73% on average).

While both quantization and unstructured prun-
ing reduce the model size significantly, none of
them yields actual run-time speedups on a stan-
dard device. Stattdessen, specialized hardware and/or

1071

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

libraries are required, which can do lower-bit
arithmetic for quantization and an optimized im-
plementation of sparse weight matrix multipli-
cation for unstructured pruning. Jedoch, diese
methods can be easily combined with other com-
pression methods as they are orthogonal from an
implementation viewpoint. Below, we discuss the
performance of compounding multiple compres-
sion methods.

Structured Pruning. As discussed in Section 3,
structured pruning removes architectural compo-
nents from BERT, which can also be seen as
reducing the number of hyper-parameters that
govern the BERT architecture. While Lin et al.
(2020) pruned the encoder units (L) and reduced
the model depth by half with an average accuracy
drop of 1.0%, Khetan and Karnin (2020) took
it a step further and systematically reduced both
the depth (L) as well as the width (H, A) of the
Modell, compressing to 39.1% of the original size
with an average accuracy drop of only 1.86%. Von-
tailed experiments by Khetan and Karnin (2020)
also show that reducing all hyper-parameters in
harmony, instead of focusing on just one, yields
better performance.

Model-Agnostic Distillation. Applying distil-
lation from output
logits only allows model-
agnostic compression and gives rise to LSTM/
CNN-based student models. While methods exist
that try to train a smaller BERT model (Song et al.,
2020), this category is dominated by methods that
replace Transformers with lighter alternatives. Es
has been shown that a BiLSTM student model
can yield significantly better speedup (Liu et al.,
2019A) compared to a Transformer-based student
model of comparable size (Song et al., 2020). Chen
et al. (2020A) demonstrated the fastest model in
this category, a NAS-based CNN model, with only
2.06% average drop in accuracy. Gesamt, diese
methods achieved high compression ratio, Aber
they paid a heavy price: sizable drop in accuracy.
This could be because the total model size is not
a true indicator of how powerful their compres-
sion is, as the model size is dominated by the
embedding matrix.

Zum Beispiel, while the total size of the student
model of Liu et al. (2019A) Ist 101 MB, nur 11
MB is the size of their BiLSTM model, und das
remaining 90 MB are just the embedding ma-
trix. Daher, we can conclude that, similarly to un-

structured pruning, ignoring the embedding matrix
can hurt the practical deployment of such models
on devices with strict memory constraints.

Distillation from Attention Maps. Wang et al.
(2020C) were able to reduce BERT to 60.7% its
original size, with only 0.1% loss in accuracy on
average, just by doing deep distillation on the at-
tention layers. For the same student architecture,
Sanh et al. (2019) used all other forms of dis-
tillation (d.h., output logits and encoder outputs)
together and still faced an average accuracy loss
von 1.73%. Clearly, the intermediate attention maps
are an important distillation target.

Combining Multiple Distillations. Combining
multiple distillation targets can yield an even better
compressed model. Jiao et al. (2020) created a stu-
dent model with smaller H and L hyper-parameter
Werte, compressing the model size to 13.3% Und
achieving a 9.4x speedup on a GPU (9.3x on
a CPU), while only facing a drop of 1.0% In
accuracy. Zhao et al. (2019B) extended the idea
and created an extremely small BERT student
Modell (1.6% of the original size, ∼ 25x faster)
with H = 48 and vocabulary size |V | = 4, 928
(BERTBASE has H = 768 Und |V | = 30, 522).
The model lost 12.3% accuracy to pay for its size.

Matrix Decomposition and Dynamic Inference
Acceleration. While weight matrix decomposi-
tion helps reduce the size of the weight matrices
in BERT, it creates deeper and fragmented mod-
els, which hurts the execution time (Noach and
Goldberg, 2020). Andererseits, methods that
implement faster attention and various forms of
dynamic speedup do not change the model size,
but instead provide faster inference. Zum Beispiel,
Cao et al. (2020) showed that attention calculation
across the complete sentence is not needed for
the initial encoder layers, and they were able to
achieve ∼ 3x speedup with only 0.76% drop in
accuracy. For applications where latency is the
major constraint, such methods can be suitable.

Structured Pruning vs. Distillation. Während
structured pruning attempts to iteratively prune
the hyper-parameters of BERT, distillation starts
with a smaller model and tries to train it us-
ing knowledge directly from the original BERT.
Jedoch, both of them end up with a similar
compressed model, and thus it is interesting to
compare which path yields better results. As can

1072

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

be noted from Table 1, for the same compressed
model with L = 6, the drop in accuracy for the
model of Lin et al. (2020) is smaller compared to
that of Sanh et al. (2019). Jedoch, this is not a
completely fair comparison, as Sanh et al. (2019)
did not use attention as a distillation target. Wann
we compare other methods, we find that Jiao
et al. (2020) was able to beat Khetan and Karnin
(2020) in terms of both model size and accuracy.
This shows that structured pruning outperforms
student models trained using distillation only on
encoder outputs and output logits, but fails against
distillation on attention maps. This further indi-
cates the importance of replicating attention maps
in BERT.

Pruning with Distillation. Similarly to com-
bining multiple distillation methods, it is also
possible to combine pruning with distillation, als
this can help guide the pruning towards removing
the less important connections. Mao et al. (2020)
combined distillation with unstructured pruning,
while Hou et al. (2020) combined distillation with
structured pruning. When compared with only
structured pruning (Khetan and Karnin, 2020), Wir
see that Hou et al. (2020) achieved both a smaller
model size (12.4%) and also a smaller drop in
accuracy (0.96%).

Quantization with Distillation. Similarly to
pruning, quantization is also orthogonal in imple-
mentation to distillation, and can together achieve
better performance than either of them individu-
ally. Zadeh et al. (2020) attempted to quantize an
already distilled BERT model (Sanh et al., 2019)
to four bits, thus reducing the model size from
60.2% Zu 7.5%, with an additional accuracy drop
of only 0.9% (1.73% Zu 2.6%). Ähnlich, Sun
et al. (2020B) attempted to quantize their model
to eight bits, which reduced their model size from
23% Zu 5.25%, with only a 0.07% additional drop
in accuracy.

Compounding Multiple Methods Together.
As we have seen in this section, different meth-
ods of compression target different parts of the
BERT architecture. Note that many of these meth-
ods are orthogonal in implementation, similarly
to the work we discussed on combining quantiza-
tion and pruning with distillation, and thus it is
possible to combine them. Zum Beispiel, Tambe
et al. (2020) combined multiple forms of com-
pression methods to create a truly deployable lan-

guage model for edge devices. They combined
parameter sharing, embedding matrix decompo-
sition, unstructured movement pruning, adaptive
floating-point quantization, adaptive attention
Spanne, dynamic inference speed with early exit
ramps, and other hardware accelerations to suit
their needs. Jedoch, as we noticed in this section,
these particular methods can reduce the model size
significantly, but they cannot drastically speed up
the model execution on standard devices. Während
the model size is reduced to only 1.3% of its orig-
inal size, the speedup obtained on a standard GPU
is only 1.83x, with an average drop of 1.53% In
terms of accuracy. With specialized accelerators,
the authors eventually pushed the speedup to 2.1x.

4.3 Practical Advice

Based on the experimental results we have dis-
cussed in this section, below we attempt to give
some practical advice to the reader on what to use
for specific applications:

• Quantization and unstructured pruning can
help reduce the model size, but they do noth-
ing to improve the runtime inference speed
or the memory consumption, unless executed
on specialized hardware or with specialized
processing libraries. Andererseits, Wenn
executed on proper hardware, these meth-
ods can provide tremendous boost in terms
of speed with negligible loss in performance
(Zadeh et al., 2020; Tambe et al., 2020; Guo
et al., 2019). Daher, it is important to recognize
the target hardware device before deciding to
use such compression methods in practical
applications.

• Knowledge distillation has shown great af-
finity to a variety of student models and its or-
thogonal nature of implementation compared
to other methods (Mao et al., 2020; Hou et al.,
2020) means that it is an important addition
to any form of compression. More specif-
isch, distillation from self-attention layers
(if possible) is an integral part of Transformer
compression (Wang et al., 2020C).

• Alternatives such as BiLSTMs and CNNs
have an additional advantage in terms of
execution speed when compared to Trans-
formers. Daher, for applications with strict
latency constraints, replacing Transformers

1073

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

with alternative units is a better choice. Modell
execution can also be sped up using dynamic
inference methods, as they can be incorpo-
rated into any student model with a skeleton
that is similar to that of Transformers.

• A major takeaway of our discussion above is
the importance of compounding various com-
pression methods together to achieve truly
practical models for edge environments. Der
work of Tambe et al. (2020) is a good exam-
ple of this, as it attempts to compress BERT,
while simultaneously performing hardware
optimizations in accordance with their cho-
sen compression methods. Daher, combining
compression methods that complement each
other is generally a better idea than com-
pressing a single aspect of the model to its
extreme.

5 Open Issues and Research Directions

From our analysis and comparison, we con-
clude that traditional model compression methods
such as quantization and pruning are beneficial
for BERT. Techniques specific to BERT also
yield competitive results, Zum Beispiel, variants of
knowledge distillation and methods that reduce the
number of architectural hyper-parameters. Solch
methods also offer insights into BERT’s work-
ings and the importance of various layers in its
architecture. We see multiple avenues for future
Forschung:

1. A very prominent feature of most BERT
compression methods is their coupled na-
ture across various encoder units, sowie
the inner architecture. Jedoch, some layers
might be able to handle more compression.
Methods compressing each layer indepen-
dently (Khetan and Karnin, 2020; Tsai et al.,
2020) have shown promising results, Aber
remain under-explored.

2. The Transformer backbone that forces the
model to be parameter-heavy makes com-
pression challenging. Existing work in re-
placing the Transformer by Bi-LSTMs and
CNNs has yielded extraordinary compression
ratios, but with a sizable drop in accuracy.
This suggests further exploration of more
complex variations and hybrid Bi-LSTM/
CNN/Transformer models (Tian et al., 2019).

3. Many methods for BERT compression only
work on specific parts of the model. Wie-
immer, we can combine such methods to
achieve better results. We have seen in
Abschnitt 4 that compound compression meth-
ods perform better than their individual coun-
terparts (Tambe et al., 2020; Hou et al., 2020),
and thus more exploration in combining var-
ious existing methods is needed.

Danksagungen

This publication was made possible by NPRP
grant NPRP10-0208-170408 from the Qatar Na-
tional Research Fund (a member of Qatar Foun-
dation). This work is also partially supported by
the National Research Foundation, Prime Min-
ister’s Office, Singapur, under its Campus for
Research Excellence and Technological Enter-
prise (CREATE) Programm. The findings herein
reflect the work, and are solely the responsibility
von, the authors.

Verweise

Yoonho Boo and Wonyong Sung. 2020. Fixed-
point optimization of transformer neural net-
arbeiten. In Proceedings of the IEEE International
Conference on Acoustics, Speech and Signal
Processing, ICASSP ’20, pages 1753–1757.

Tom Brown, Benjamin Mann, Nick Ryder,
Melanie Subbiah, Jared D. Kaplan, Prafulla
Dhariwal, Arvind Neelakantan, Pranav Shyam,
Girish Sastry, Amanda Askell, Sandhini
Agarwal, Ariel Herbert-Voss, Gretchen
Krueger, Tom Henighan, Rewon Child, Aditya
Ramesh, Daniel Ziegler, Jeffrey Wu, Clemens
Winter, Chris Hesse, Mark Chen, Eric
Sigler, Mateusz Litwin, Scott Gray, Benjamin
Chess, Jack Clark, Christopher Berner, Sam
McCandlish, Alec Radford, Ilya Sutskever, Und
Dario Amodei. 2020. Language models are
few-shot learners. In Advances in Neural In-
formation Processing Systems, Volumen 33 von
NeurIPS ’20, pages 1877–1901.

Qingqing Cao, Harsh Trivedi, Aruna Balasubra-
manian, and Niranjan Balasubramanian. 2020.
DeFormer: Decomposing pre-trained trans-
formers for
In
Proceedings of the 58th Annual Meeting of

faster question answering.

1074

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

the Association for Computational Linguistics,
ACL ’20, pages 4487–4497.

Daoyuan Chen, Yaliang Li, Minghui Qiu, Zhen
Wang, Bofang Li, Bolin Ding, Hongbo Deng,
Jun Huang, Wei Lin, and Jingren Zhou. 2020A.
AdaBERT: Task-adaptive BERT compression
with differentiable neural architecture search. In
Proceedings of the Twenty-Ninth International
Joint Conference on Artificial Intelligence,
IJCAI 2020, pages 2463–2469. https://doi
.org/10.24963/ijcai.2020/341

Tianlong Chen, Jonathan Frankle, Shiyu Chang,
Sijia Liu, Yang Zhang, Zhangyang Wang, Und
Michaelg Carbin. 2020B. The lottery ticket hy-
pothesis for pre-trained BERT networks. In
Proceedings of the 34th Conference on Neural
Information Processing Systems, NeurIPS ’20,
pages 1753–1757, Vancouver, Kanada.

Yu Cheng, Duo Wang, Pan Zhou, and Tao
Zhang. 2018. Model compression and acceler-
ation for deep neural networks: The principles,
progress, and challenges. IEEE Signal Process-
ing Magazine, 35(1):126–136. https://doi
.org/10.1109/MSP.2017.2765695

Yew Ken Chia, Sam Witteveen, and Martin
Andrews. 2018. Transformer to CNN: Label-
scarce distillation for efficient text classifica-
tion. In Proceedings of
the Compact Deep
Neural Network Representation with Industrial
Applications Workshop, Montr´eal, Kanada.

Artem Chumachenko, Daniil Gavrilov, Nikita
Balagansky, and Pavel Kalaidin. 2020. Weight
squeezing: Reparameterization for extreme
compression and fast inference. arXiv:2010.
06993.

Kevin Clark, Urvashi Khandelwal, Omer Levy,
and Christopher D. Manning. 2019. What does
BERT look at? An analysis of BERT’s atten-
tion. In Proceedings of the ACL Workshop
BlackboxNLP: Analyzing and Interpreting
Neural Networks for NLP, BlackboxNLP’19,
pages 276–286. Florence, Italien. https://doi
.org/10.18653/v1/W19-4828

Kalyanmoy Deb. 2014. Multi-objective optimiza-
tion. In Search Methodologies, pages 403–449.
Springer. https://doi.org/10.1007/978
-1-4614-6940-7 15

Jacob Devlin, Ming-Wei Chang, Kenton Lee, Und
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
Verständnis. In Proceedings of the 2019 Con-
ference of
the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, NAACL-HLT
’19, pages 4171–4186, Minneapolis, MN, USA.

Lifang Ding

and Yujiu Yang.

2020.
SDSK2BERT: Explore the specific depth with
specific knowledge to compress BERT. In
Proceedings of the IEEE International Con-
ference on Knowledge Graph,
ICKG ’20,
pages 420–425. https://doi.org/10.1109
/ICBK50248.2020.00066

Angela Fan, Edouard Grave, and Armand Joulin.
2020. Reducing transformer depth on demand
with structured dropout. In Proceedings of
the 8th International Conference on Learn-
ing Representations, ICLR ’20, Addis Ababa,
Ethiopia.

Angela Fan, Pierre Stock, Benjamin Graham,
Edouard Grave, R´emi Gribonval, Herv´e J´egou,
and Armand Joulin. 2021. Training with quanti-
zation noise for extreme model compression. In
Proceedings of the 10th International Confer-
ence on Learning Representations, ICLR ’21.

Luciano Floridi and Massimo Chiriatti. 2020.
GPT-3: Its nature, scope, limits, and conse-
quences. Minds and Machines, 30(4):681–694.
https://doi.org/10.1007/s11023-020
-09548-1

Jonathan Frankle and Michael Carbin. 2019.
The lottery ticket hypothesis: Finding sparse,
trainable neural networks. In Proceedings of
the 7th International Conference on Learning
Darstellungen, ICLR ’19, New Orleans, LA,
USA.

Mitchell Gordon, Kevin Duh, and Nicholas
Andrews. 2020. Compressing BERT: Study-
ing the effects of weight pruning on transfer
learning. In Proceedings of the 5th Workshop on
Representation Learning for NLP, RepL4NLP
’20, pages 143–155. https://doi.org/10
.18653/v1/2020.repl4nlp-1.18

Saurabh Goyal, Anamitra Roy Choudhury,
Saurabh Raje, Venkatesan Chakaravarthy,

1075

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Yogish Sabharwal, and Ashish Verma. 2020.
PoWER-BERT: Accelerating BERT infer-
ence via progressive word-vector elimination.
the International Con-
In Proceedings of
ference on Machine Learning,
ICML ’20,
pages 3690–3699.

Fu-Ming Guo, Sijia Liu, Finlay S. Mungall, Xue
Lin, and Yanzhi Wang. 2019. Reweighted
large-scale language
proximal pruning for
representation. arXiv:1909.12486.

Lu Hou, Zhiqi Huang, Lifeng Shang, Xin Jiang,
Xiao Chen, and Qun Liu. 2020. DynaBERT:
Dynamic BERT with adaptive width and depth.
In Advances in Neural Information Processing
Systeme, Volumen 33 of NeuIPS ’20.

Olga Kovaleva, Alexey Romanov, Anna Rogers,
and Anna Rumshisky. 2019. Revealing the
dark secrets of BERT. In Proceedings of the
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International Joint Conference on Natural
Language Processing, EMNLP-IJCNLP ’19,
pages 4365–4374, Hongkong, China.

Zhenzhong Lan, Mingda Chen, Sebastian
Guter Mann, Kevin Gimpel, Piyush Sharma, Und
Radu Soricut. 2020. ALBERT: A lite BERT for
self-supervised learning of language represen-
tations. In Proceedings of
the 8th Interna-
tional Conference on Learning Representations,
ICLR ’20, Addis Ababa, Ethiopia.

Jeremy Howard and Sebastian Ruder. 2018. Uni-
versal
language model fine-tuning for text
classification. In Proceedings of the 56th An-
nual Meeting of the Association for Computa-
tional Linguistics, ACL ’18, pages 328–339,
Melbourne, Australia. https://doi.org/10
.18653/v1/P18-1031

Bingbing Li, Zhenglun Kong, Tianyun Zhang,
Ji Li, Zhengang Li, Hang Liu, and Caiwen
Ding. 2020A. Efficient transformer-based large
scale language representations using hardware-
friendly block structured pruning. In Findings
of the Association for Computational Linguis-
Tics: EMNLP 2020, pages 3187–3199.

Itay Hubara, Matthieu Courbariaux, Daniel
Soudry, Ran El-Yaniv, and Yoshua Bengio.
2017. Quantized neural networks: Training neu-
ral networks with low precision weights and
activations. The Journal of Machine Learning
Forschung, 18(1):6869–6898.

Xiaoqi Jiao, Yichun Yin, Lifeng Shang, Xin Jiang,
Xiao Chen, Linlin Li, Fang Wang, and Qun Liu.
2020. TinyBERT: Distilling BERT for natural
In Proceedings of
language understanding.
Die 2020 Conference on Empirical Methods
in Natural Language Processing: Findings,
EMNLP ’20, pages 4163–4174. https://doi
.org/10.18653/v1/2020.findings-emnlp
.372

Ashish Khetan and Zohar Karnin. 2020. schu-
BERT: Optimizing elements of BERT. In Pro-
ceedings of the 58th Annual Meeting of the
Verein für Computerlinguistik,
ACL’20, pages 2807–2818. https://doi
/10.18653/v1/2020.acl-main.250

Nikita Kitaev, Lukasz Kaiser, and Anselm
Levskaya. 2020. Reformer: The efficient trans-
ehemalig. In Proceedings of the International
Conference on Learning Representations, ICLR
’20, Addis Ababa, Ethiopia.

Jianquan Li, Xiaokang Liu, Honghong Zhao,
Ruifeng Xu, Min Yang, and Yaohong Jin.
2020B. BERT-EMD: Many-to-many layer
mapping for BERT compression with earth
Die
mover’s distance.
2020 Conference on Empirical Methods in
Natural Language Processing, EMNLP ’20,
pages 3009–3018.

In Proceedings of

Zhuohan Li, Eric Wallace, Sheng Shen, Kevin Lin,
Kurt Keutzer, Dan Klein, and Joey Gonzalez.
2020C. Train big, then compress: Rethinking
model size for efficient training and inference
of transformers. In Proceedings of the Interna-
tional Conference on Machine Learning, ICML
’20, pages 5958–5968.

Zi Lin, Jeremiah Liu, Zi Yang, Nan Hua, Und
Dan Roth. 2020. Pruning redundant mappings
in transformer models via spectral-normalized
identity prior. In Findings of the 2020 Confer-
ence on Empirical Methods in Natural Lan-
guage Processing, pages 719–730. https://
doi.org/10.18653/v1/2020.findings
-emnlp.64

Linqing Liu, Huan Wang, Jimmy Lin, Richard
Socher, and Caiming Xiong. 2019A. MKD: A

1076

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

multi-task knowledge distillation approach for
pretrained language models. arXiv:1911.03588.

Brussels, Belgien. https://doi.org/10
.18653/v1/D18-1206

Weijie Liu, Peng Zhou, Zhiruo Wang, Zhe Zhao,
Haotang Deng, and Qi Ju. 2020. FastBERT:
A self-distilling BERT with adaptive infer-
ence time. In Proceedings of the 58th Annual
Meeting of the Association for Computational
Linguistik, ACL ’20, pages 6035–6044.

Yinhan Liu, Myle Ott, Naman Goyal, Jingfei
Von, Mandar Joshi, Danqi Chen, Omer Levy,
Mike Lewis, Luke Zettlemoyer, and Veselin
Stoyanov. 2019B. RoBERTa: A robustly opti-
mized BERT pretraining approach. arXiv:1907.
11692.

Matous Machacek and Ondrej Bojar. 2014. Re-
the WMT14 metrics shared task.
sults of
In Proceedings of
the Ninth Workshop on
Statistical Machine Translation, WMT ’14,
pages 293–301, Baltimore, MD, USA. https://
doi.org/10.3115/v1/W14-3336

Yihuan Mao, Yujing Wang, Chufan Wu, Chen
Zhang, Yang Wang, Quanlu Zhang, Yaming
Yang, Yunhai Tong, and Jing Bai. 2020.
LadaBERT: Lightweight adaptation of BERT
through hybrid model compression. In Pro-
ceedings of the 28th International Conference
on Computational Linguistics, COLING ’20,
pages 3225–3234.

Paul Michel, Omer Levy, and Graham Neubig.
2019. Are sixteen heads really better than
eins? In Advances in Neural Information Pro-
cessing Systems, Volumen 32 of NeurIPS ’19,
pages 14014–14024, Vancouver, BC, Kanada.

Subhabrata Mukherjee and Ahmed H. Awadallah.
2020. XtremeDistil: Multi-stage distillation
In Pro-
for massive multilingual models.
ceedings of
the 58th Annual Meeting of
the Association for Computational Linguis-
Tics, ACL ’20, pages 2221–2234. https://doi
.org/10.18653/v1/2020.acl-main.202

Shashi Narayan, Shay B. Cohen, and Mirella
Lapata. 2018. Don’t give me the details,
just the summary! Topic-aware convolutional
neural networks for extreme summarization.
Die 2018 Conference on
In Proceedings of
Empirical Methods
in Natural Language
Processing, EMNLP ’18, pages 1797–1807,

Matan Ben Noach and Yoav Goldberg. 2020.
Compressing pre-trained language models by
matrix decomposition. In Proceedings of the
1st Conference of the Asia-Pacific Chapter of
the Association for Computational Linguistics
and the 10th International Joint Conference on
Natural Language Processing, AACL-IJCNLP
’20, pages 884–889.

Matthew Peters, Mark Neumann, Mohit Iyyer,
Matt Gardner, Christopher Clark, Kenton Lee,
and Luke Zettlemoyer. 2018. Deep contextu-
alized word representations. In Proceedings of
Die 2018 Conference of the North American
the Association for Computa-
Chapter of
tional Linguistics: Human Language Tech-
nologies, NAACL-HLT ’18, pages 2227–2237,
New Orleans, LA, USA. https://doi.org
/10.18653/v1/N18-1202

Prafull Prakash, Saurabh Kumar Shashidhar,
Wenlong Zhao, Subendhu Rongali, Haidar
Khan, and Michael Kayser. 2020. Compress-
ing transformer-based semantic parsing models
using compositional code embeddings. In Find-
Die 2020 Conference on Empirical
ings of
Methods in Natural Language Processing,
https://doi.org/10
Seiten
.18653/v1/2020.findings-emnlp.423

4711–4717.

Sai Prasanna, Anna Rogers, and Anna Rumshisky.
2020. When BERT plays the lottery, all tick-
ets are winning. In Proceedings of the 2020
Conference on Empirical Methods in Nat-
ural Language Processing, EMNLP ’20,
https://doi.org/10
Seiten
.18653/v1/2020.emnlp-main.259

3208–3229.

XiPeng Qiu, TianXiang Sun, YiGe Xu, YunFan
Shao, Ning Dai, and XuanJing Huang. 2020.
Pre-trained models for natural language pro-
Abschließen: A survey. Science China Technological
Wissenschaften, 63(10):1872–1897. https://doi
.org/10.1007/s11431-020-1647-3

Alec Radford, Jeffrey Wu, Rewon Child, David
Luan, Dario Amodei, and Ilya Sutskever. 2019.
Language models are unsupervised multitask
learners. OpenAI Blog, 1(8):9.

Colin Raffel, Noam Shazeer, Adam Roberts,
Katherine Lee, Sharan Narang, Michael

1077

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Matena, Yanqi Zhou, Wei Li, und Peter J. Liu.
2020. Exploring the limits of transfer learning
with a unified text-to-text transformer. Zeitschrift
of Machine Learning Research, 21:1–67.

Victor Sanh, Thomas Wolf, and Alexander Rush.
2020. Movement pruning: Adaptive sparsity by
fine-tuning. In Advances in Neural Information
Processing Systems, Volumen 33 of NeurIPS ’20.

Alessandro Raganato, Yves Scherrer,

Und
J¨org Tiedemann. 2020. Fixed encoder self-
attention patterns in transformer-based machine
Übersetzung. In Findings of
the Association
für Computerlinguistik: EMNLP 2020,
pages 556–568. https://doi.org/10.18653
/v1/2020.findings-emnlp.49

Pranav Rajpurkar, Robin Jia, and Percy Liang.
2018. Know what you don’t know: Unanswer-
able questions for SQuAD. In Proceedings of
the 56th Annual Meeting of the Association
für Computerlinguistik, ACL ’18,
Seiten
784–789, Melbourne, Australia.
https://doi.org/10.18653/v1/P18-2124

Pranav Rajpurkar,

Jian Zhang, Konstantin
Lopyrev, and Percy Liang. 2016. SQuAD:
100,000+ questions for machine comprehension
of text. In Proceedings of the 2016 Conference
on Empirical Methods in Natural Language
Processing, EMNLP ’16, pages 2383–2392,
Austin, TX, USA. https://doi.org/10
.18653/v1/D16-1264

Anna Rogers, Olga Kovaleva,

and Anna
Rumshisky. 2020. A primer in BERTology:
What we know about how BERT works. Trans-
actions of the Association for Computational
Linguistik, 8:842–866. https://doi.org
/10.1162/tacl a 00349

Corby Rosset. 2020. Turing-NLG: A 17-billion-
parameter language model by Microsoft. Mi-
crosoft Research Blog, 2:13.

Hassan Sajjad, Fahim Dalvi, Nadir Durrani,
and Preslav Nakov. 2020. Poor man’s BERT:
Smaller and faster transformer models. arXiv:
2004.03844.

Victor Sanh, Lysandre Debut, Julien Chaumond,
and Thomas Wolf. 2019. DistilBERT, a dis-
tilled version of BERT: smaller, faster, cheaper
and lighter. In Proceedings of the 5th Work-
shop on Energy Efficient Machine Learning
and Cognitive Computing, Vancouver, Kanada.
https://doi.org/10.1609/aaai.v34i05
.6409

Sheng Shen, Zhen Dong, Jiayu Ye, Linjian
Ma, Zhewei Yao, Amir Gholami, Michael W.
Mahoney, and Kurt Keutzer. 2020. Q-BERT:
Hessian based ultra low precision quantization
of BERT. In Proceedings of the AAAI Confer-
ence on Artificial Intelligence, Volumen 34 von
AAAI ’20, pages 8815–8821.

Mohammad Shoeybi, Mostofa Patwary, Raul
Puri, Patrick LeGresley, Jared Casper, Und
Bryan Catanzaro. 2019. Megatron-LM: Train-
ing multi-billion parameter language models
using model parallelism. arXiv:1909.08053.

Kaitao Song, Hao Sun, Xu Tan, Tao Qin,
Jianfeng Lu, Hongzhi Liu, and Tie-Yan Liu.
2020. LightPAFF: A two-stage distillation
framework for pre-training and fine-tuning.
arXiv:2004.12817.

Siqi Sun, Yu Cheng, Zhe Gan, and Jingjing
Liu. 2019. Patient knowledge distillation for
BERT model compression. In Proceedings
of the 2019 Conference on Empirical Meth-
ods in Natural Language Processing and the
9th International Joint Conference on Natural
Language Processing, EMNLP-IJCNLP ’19,
pages 4314–4323, HongKong,China. https://
doi.org/10.18653/v1/D19-1441

Siqi Sun, Zhe Gan, Yuwei Fang, Yu Cheng,
Shuohang Wang, and Jingjing Liu. 2020A.
Contrastive distillation on intermediate repre-
sentations for language model compression. In
Verfahren der 2020 Conference on Empir-
ical Methods in Natural Language Processing,
EMNLP ’20, pages 498–508, https://doi
.org/10.18653/v1/2020.emnlp-main.36

Zhiqing Sun, Hongkun Yu, Xiaodan Song, Renjie
Liu, Yiming Yang, and Denny Zhou. 2020B.
MobileBERT: A compact task-agnostic BERT
for resource-limited devices. In Proceedings
of the 58th Annual Meeting of the Associa-
tion for Computational Linguistics, ACL ’20,
pages 2158–2170.

Thierry Tambe, Coleman Hooper, Lillian
Pentecost, Tianyu Jia, En-Yu Yang, Marco
Donato, Victor Sanh, Paul Whatmough,

1078

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Alexander M Rush, David Brooks, and Gu-
Yeon Wei. 2020. EdgeBERT: Sentence-level
energy optimizations for latency-aware multi-
task NLP inference. arXiv:2011.14203.

Raphael Tang, Yao Lu,

and Jimmy Lin.
2019. Natural language generation for effec-
tive knowledge distillation. In Proceedings
of the 2nd Workshop on Deep Learning Ap-
proaches for Low-Resource NLP, DeepLo ’19,
pages 202–208, Hongkong, China. https://
doi.org/10.18653/v1/D19-6122

Yi Tay, Dara Bahri, Donald Metzler, Da-Cheng
Juan, Zhe Zhao, and Che Zheng. 2020. Synthe-
sizer: Rethinking self-attention in transformer
Modelle. arXiv:2005.00743.

James Yi Tian, Alexander P. Kreuzer, Pai-Hung
Chen, and Hans-Martin Will. 2019. WaL-
DORf: Wasteless language-model distillation
on reading-comprehension. arXiv:1912.06638.

Henry Tsai, Jayden Ooi, Chun-Sung Ferng,
Hyung Won Chung, and Jason Riesa. 2020.
Finding fast transformers: One-shot neural ar-
chitecture search by component composition.
arXiv:2008.06808.

Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017. Bei-
tention is all you need. In Proceedings of
the 31st International Conference on Neural
Information Processing Systems, NIPS ’17,
pages 6000–6010, Long Beach, CA, USA.

Alex Wang, Amanpreet Singh, Julian Michael,
Felix Hill, Omer Levy, and Samuel Bowman.
2018. GLUE: A multi-task benchmark and
analysis platform for natural language under-
Stehen. In Proceedings of the 2018 EMNLP
Workshop BlackboxNLP: Analyzing and Inter-
preting Neural Networks for NLP, Blackbox-
NLP ’18, pages 353–355, Brussels, Belgien.
https://doi.org/10.18653/v1/W18-5446

Shirui Wang, Wenan Zhou, and Chao Jiang.
2020A. A survey of word embeddings based
on deep learning. Computing, 102(3):717–740.

Sinong Wang, Belinda Li, Madian Khabsa,
Han Fang, and Hao Ma. 2020B. Linformer:
Self-attention with linear complexity. arXiv:
2006.04768. https://doi.org/10.1007
/s00607-019-00768-7

Wenhui Wang, Furu Wei, Li Dong, Hangbo Bao,
Nan Yang, and Ming Zhou. 2020C. MiniLM:
Deep self-attention distillation for task-agnostic
compression of pre-trained transformers. In
Advances in Neural Information Processing
Systeme, Volumen 33 of NeurIPS ’20.

Moshe Wasserblat, Oren Pereg, and Peter Izsak.
2020. Exploring the boundaries of low-resource
BERT distillation. In Proceedings of the Work-
shop on Simple and Efficient Natural Language
Processing, SustaiNLP ’20, pages 35–40.
https://doi.org/10.18653/v1/2020
.sustainlp-1.5

Yonghui Wu, Mike Schuster, Zhifeng Chen,
Quoc V. Le, Mohammad Norouzi, Wolfgang
Macherey, Maxim Krikun, Yuan Cao, Qin
Gao, Klaus Macherey, Jeff Klingner, Apurva
Shah, Melvin Johnson, Xiaobing Liu, Łukasz
Kaiser, Stephan Gouws, Yoshikiyo Kato, Taku
Kudo, Hideto Kazawa, Keith Stevens, George
Kurian, Nishant Patil, Wei Wang, Cliff Young,
Jason Smith, Jason Riesa, Alex Rudnick,
Oriol Vinyals, Greg Corrado, Macduff Hughes,
and Jeffrey Deanand. 2016. Google’s neu-
ral machine translation system: Bridging the
gap between human and machine translation.
arXiv:1609.08144.

Ji Xin, Raphael Tang, Jaejun Lee, Yaoliang Yu,
and Jimmy Lin. 2020. DeeBERT: Dynamic
early exiting for accelerating BERT inference.
In Proceedings of the 58th Annual Meeting of
the Association for Computational Linguistics,
ACL ’20, pages 2246–2251. https://doi
.org/10.18653/v1/2020.acl-main.204

Canwen Xu, Wangchunshu Zhou, Tao Ge, Furu
Wei, and Ming Zhou. 2020. BERT-of-Theseus:
Compressing BERT by progressive module re-
placing. In Proceedings of the 2020 Conference
on Empirical Methods in Natural Language
Processing, EMNLP ’20, pages 7859–7869.

Zhilin Yang, Zihang Dai, Yiming Yang, Jaime
Carbonell, Russ R. Salakhutdinov, and Quoc
V. Le. 2019. XLNet: Generalized autoregres-
sive pretraining for language understanding.
In Advances in Neural Information Process-
ing Systems, Volumen 32 of NeuIPS ’19,
pages 5753–5763.

Ali H. Zadeh,

Isak Edo, Omar Mohamed
Awad, and Andreas Moshovos. 2020. GOBO:

1079

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Quantizing attention-based NLP models for low
latency and energy efficient inference. In Pro-
ceedings of the 53rd Annual IEEE/ACM In-
ternational Symposium on Microarchitecture,
MICRO ’20, pages 811–824. https://doi
.org/10.1109/MICRO50266.2020.00071

Ofir Zafrir, Guy Boudoukh, Peter Izsak, Und
Moshe Wasserblat. 2019. Q8BERT: Quantized
8bit BERT. In Proceedings of the 5th Work-
shop on Energy Efficient Machine Learn-
ing and Cognitive Computing, Vancouver,
Kanada. https://doi.org/10.1109/EMC2
-NIPS53020.2019.00016

Guangxiang Zhao, Junyang Lin, Zhiyuan Zhang,
Xuancheng Ren, Qi Su, and Xu Sun. 2019A.
transformer: Concentrated
Explicit
attention through explicit selection. arXiv:
1912.11637.

sparse

Sanqiang Zhao, Raghav Gupta, Yang Song, Und
Denny Zhou. 2019B. Extreme language model
compression with optimal subwords and shared
projections. arXiv:1909.11687.

Denny Zhou, Mao Ye, Chen Chen, Tianjian Meng,
Mingxing Tan, Xiaodan Song, Quoc Le, Qiang
Liu, and Dale Schuurmans. 2020A. Go wide,
then narrow: Efficient training of deep thin
Netzwerke. In Proceedings of the International
Conference on Machine Learning, ICML ’20,
pages 11546–11555.

Wangchunshu Zhou, Canwen Xu, Tao Ge,
Julian McAuley, Ke Xu, and Furu Wei. 2020B.
BERT loses patience: Fast and robust infer-
ence with early exit. In Advances in Neural
Information Processing Systems, Volumen 33 von
NeurIPS ’20.

Yukun Zhu, Ryan Kiros, Rich Zemel, Ruslan
Salakhutdinov, Raquel Urtasun, Antonio
Torralba, and Sanja Fidler. 2015. Aligning
books and movies: Towards story-like visual
explanations by watching movies and reading
books. In Proceedings of the IEEE Interna-
tional Conference on Computer Vision, ICCV
’19, pages 19–27, Seoul, Korea. https://
doi.org/10.1109/ICCV.2015.11

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

e
D
u

/
T

A
C
l
/

l

A
R
T
ich
C
e
–
P
D

F
/

D
Ö

ich
/

.

1
0
1
1
6
2

/
T

l

A
C
_
A
_
0
0
4
1
3
1
9
6
4
0
0
6

/

/
T

l

A
C
_
A
_
0
0
4
1
3
P
D

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1080

PDF Herunterladen