ARTIKEL
Communicated by Jeremy Manning
The Discrete and Continuous Brain: From Decisions
to Movement—And Back Again
Thomas Parr
thomas.parr.12@ucl.ac.uk
Karl J. Friston
k.friston@ucl.ac.uk
Wellcome Trust Centre for Neuroimaging, Institute of Neurology,
University College London, WC1N 3BG, VEREINIGTES KÖNIGREICH.
To act upon the world, creatures must change continuous variables such
as muscle length or chemical concentration. Im Gegensatz, decision making
is an inherently discrete process, involving the selection among alterna-
tive courses of action. In diesem Artikel, we consider the interface between
the discrete and continuous processes that translate our decisions into
movement in a Newtonian world—and how movement informs our de-
cisions. We do so by appealing to active inference, with a special focus on
the oculomotor system. Within this exemplar system, we argue that the
superior colliculus is well placed to act as a discrete-continuous interface.
Interessant, when the neuronal computations within the superior col-
liculus are formulated in terms of active inference, we find that many as-
pects of its neuroanatomy emerge from the computations it must perform
in this role.
1 Einführung
The nervous system faces a dual challenge in shaping behavior. To in-
duce changes in the external world, it is necessary to contract muscles
or secrete chemicals. Such processes necessarily involve the manipula-
tion of continuous variables—muscle length or chemical concentration.
Zusätzlich, animals must make decisions. To do so, they must entertain
several different possible courses of action, or policies. Letzten Endes, Sie
must select one of these actions or policies that are necessarily discrete.
We draw on recent work that considers the interactions between the neu-
ronal processing of discrete and continuous quantities (Friston, Parr, &
de Vries, 2017). To make this more concrete, we focus on the oculomotor
System. Sampling the visual world entails decisions about where to look
and the implementation of these decisions by contraction of the extraocular
muscles.
We use perceptual inference performed by the networks supporting eye
movements as a way of motivating and illustrating the theoretical challenge
Neural Computation 30, 2319–2347 (2018) © 2018 Massachusetts Institute of Technology.
Veröffentlicht unter Creative Commons
doi:10.1162/neco_a_01102
Namensnennung 4.0 Unportiert (CC BY 4.0) Lizenz.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2320
T. Parr and K. Friston
we want to address. Jedoch, the treatment we offer generalizes to any sys-
tem that involves the physical implementation of categorical decisions. Der
ideas presented in this article complement previous treatments of cognitive
Zeit (VanRullen & Koch, 2003), including the notion of a perceptual mo-
ment (Allport, 1968; Shallice, 1964; Stroud, 1967) and the suggestion that
brain oscillations act as discrete clocks to support this type of computation
(Buschman & Müller, 2009, 2010). They also resonate with recent develop-
ments in machine learning (Linderman et al., 2017) and some of the prob-
lems faced in modern robotics (Cowan & Walker, 2013; Schaal, 2006). In
short, the coupling of categorical decision making and dynamic perception
(and motor control) raises some deep questions about the temporal schedul-
ing of perception (and action).
Oscillatory rhythms in measured brain activity have been linked to cycli-
cal perceptual processes (Buzsaki, 2006), with theta and alpha cycles as the
most popular hypothesized units of perceptual time (VanRullen, 2016). In
endorsement of this, the timing of processing relative to the phase of cer-
tain oscillations appears to be important (Buzsáki, 2005). While there is
some controversy concerning the frequency of the perceptual clock, an ad-
vantage to focusing on the oculomotor system is that we can evade this
issue. The frequency of spontaneous saccadic sampling is around 4 Hz,
allowing us to commit to a theta rhythm. Conveniently, this is the fre-
quency often associated with attentional and central executive (Entscheidung)
functions (Chelazzi, Müller, Duncan, & Desimone, 1993; Duncan, Station, &
Shapiro, 1994; Hanslmayr, Volberg, Wimber, Dalal, & Greenlee, 2013; Lan-
dau & Fries, 2012; VanRullen, 2013), as opposed to sensory processes asso-
ciated with faster frequencies (Drewes & VanRullen, 2011; Dugué, Marque,
& VanRullen, 2011; Ergenoglu et al., 2004; van Dijk, Schoffelen, Oostenveld,
& Jensen, 2008).
The oculomotor system is a distributed network that includes brain stem,
cortical, and subcortical regions (Parr & Friston, 2017A). An important point
of contact between the cortical oculomotor networks and those in the brain
stem is the superior colliculus (Raybourn & Keller, 1977), found in the mid-
Gehirn. This structure receives a dual input from the cortex (Fries, 1984) Und
the basal ganglia (Hikosaka & Wurtz, 1983) and provides an important in-
put to the brain stem oculomotor nuclei. Im Folgenden, we argue that
the connectivity implied by active inference is consistent with a role for the
superior colliculus as an interface between the discrete and continuous pro-
cessing of the oculomotor system.
This article is organized as follows. In section 2, we review the princi-
ples of active inference, their application to discrete and continuous state
Räume, and the relationship between the two. In section 3, we relate the
computational anatomy implied by active inference to the neuroanatomy of
oculomotion. In section 4, we illustrate oculomotor behavior, and its neural
correlates, through simulation. Abschnitt 5 presents the discussion, and sec-
tion 6 concludes.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2321
2 Active Inference
2.1 Principles of Active Inference. Active inference is the process of
minimizing variational free energy through action and perception (Fris-
Tonne, Samothrakis, & Montague, 2012; Friston, Daunizeau, Kilner, & Kiebel,
2010). The imperative to maintain a low free energy stems from the self-
evidencing (Hohwy, 2016) nature of living systems. If an organism samples
sensory input (z.B., blood pressure, pH, and temperature) compatible with
life, this constitutes evidence for its existence as the sort of thing it is. Es ist
intuitively sensible that living creatures should act so that they experience
such sensations.
In more formal terms, the adaptive fitness of a creature’s phenotypic state
or trait “just is” the probability of a creature being in that state. This prob-
ability can be treated as model evidence by associating the creature with a
model and its sensory exchange with the world with phenotypic or char-
acteristic states. By casting exchange with the world in terms of a random
dynamical system, it is fairly straightforward to show that the states that
constitute the creature must, on average, increase model evidence; somit
self-evidencing. (See Friston, 2013, for details.)
Active inference formalizes this notion by casting behavior as free-
energy-minimizing or self-evidencing processes. Perception follows from
recognizing or inferring the causes of sensory input by optimizing proba-
bilistic representations with respect to free energy. Crucially, these causes
include our own actions. This means action selection can be treated as
“planning is inference” (Attias, 2003; Botvinick & Toussaint, 2012). Zusamenfassend,
perceptual inference underlies action, active sensing informs perception,
and both serve to minimize free energy or maximize model evidence.
Mathematically, the relationship between free energy and model evi-
dence can be expressed through Jensen’s inequality:
ln p(j)
(cid:2) (cid:3)(cid:4) (cid:5)
log evidence
= ln
(cid:2)
(cid:6)
Eq(θ )
(cid:7)
P(j, θ )
Q(θ )
(cid:6)
ln
P(j, θ )
Q(θ )
(cid:7)
(cid:5)
≥ Eq(θ )
(cid:3)(cid:4)
Jensen’s inequality
=
−F
negative free energy
.
This equation shows that the evidence associated with observations, j (d.h.,
sensory data) for a given system is always greater than or equal to the nega-
tive free energy. The free energy is a function of two things. The first is a gen-
erative model, P(j, θ ), that describes how sensory data are generated from
latent (“hidden”) Variablen, θ . The second is an arbitrary (“recognition”)
distribution, Q(θ ), that becomes an approximate posterior when the free en-
ergy is minimized (Dayan, Hinton, Neal, & Zemel, 1995; Friston, 2009):
Q(θ ) ≈ p(θ |j) ⇔
δF
δq(θ )
= 0.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2322
T. Parr and K. Friston
To ensure that free energy minimization is tractable, this distribution is
often assumed to factorize into several marginal distributions. This is re-
ferred to as a mean-field approximation (Feynman, 1998). Although orig-
inally introduced to solve problems in physics, it appears to be consistent
with the anatomical separation of processing streams in the brain (Friston
& Buzsáki, 2016). Zum Beispiel, the division of visual processing into dorsal
(“where”) and ventral (“what”) streams (Ungerleider & Haxby, 1994) sug-
gests that the brain factorizes beliefs about these variables, implementing
something like a mean-field approximation. The approximation takes the
bilden
Q(θ ) =
(cid:8)
ich
Q(θ
ich).
If we substitute this into the expression for the free energy above and then
take the variational derivative with respect to these marginals, we find the
optimal value for this distribution (Beal, 2003):
Q(θ
ich) ∝ exp
(cid:13)
Q(θ \i) =
J(cid:6)=i
(cid:9)
(cid:10)
Eq(θ \i)
(cid:11)(cid:12)
ln p(j, θ )
Q(θ
J )
⎫
⎪⎬
⎪⎭
⇔
δF
δq(θ
ich)
= 0.
(2.1)
This solution is common to variational inference about discrete and contin-
uous data and is key to understanding the rest of this article. To apply it in
each of these domains, we must consider that the form of the probabilistic
generative model is encoded by p(j, θ ). In the remainder of this section, Wir
show how this simple equation can be applied to inference in discrete and
continuous state-space models, allowing us to address the general problem
of oculomotor control in terms of neuronal (variational) message passing
(Dauwels, 2007; Winn, 2004).
This inference problem is illustrated as a Bayesian network in Figure 1.
We first address inferences about the upper part of this network that selects
target fixation locations. We then consider how these inform beliefs about
sensory data and generate changes in the external world.
2.2 Deciding Where to Look. The first computations we address are
those that mediate decisions about where to look. Decisions involve the se-
lection of one from several alternatives—in our example, saccadic targets.
Als solche, (Markov) decision processes are a natural form for the genera-
tive model because they are defined on discrete state spaces (FitzGerald,
Schwartenbeck, Moutoussis, Dolan, & Friston, 2015; Friston, FitzGerald,
Rigoli, Schwartenbeck, O’Doherty, et al., 2016; Friston, FitzGerald, Rigoli,
Schwartenbeck, & Pezzulo, 2017; Friston et al., 2015; Friston et al., 2013;
Friston et al., 2014; Friston, Lin, et al., 2017; Friston, Parr, et al., 2017; Friston,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2323
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
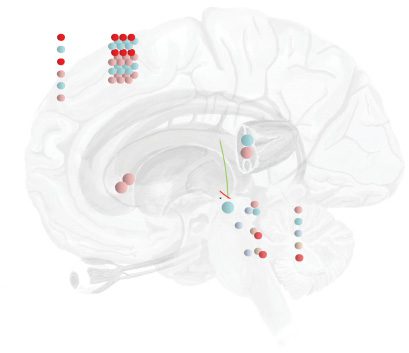
Figur 1: From decisions to eye movements. This figure shows the form of a
generative model (unfilled circles) that generates predictions about visual and
proprioceptive data, ˜y, from the policy, π , discrete hidden states, sτ , continuous
hidden causes, ˜v, and continuous hidden states, ˜x, that the brain believes are in
play. The filled circles indicate the generative process that describes how data
are generated by physical processes in the external world. Superscripts refer to
the left or right eye. Subscripts indicate modalities (θ = angular position; ω =
angular velocity; V indicates vision). Note that action, A, of the extraocular mus-
cles (EOM) induces changes in angular velocity (d.h., accelerations) and that the
generative model assumes only one gaze direction despite the fact that the gen-
erative process allows for each eye to move independently. This is based on the
generative model and process in Parr and Friston (2018), but extends it with the
addition of a discrete level. Figur 2 provides more detail on the mathematical
specification of these types of models.
Rosch, Parr, Price, & Bowman, 2017; Mirza, Adams, Mathys, & Friston, 2016;
Parr & Friston, 2017C, 2017D; Schwartenbeck, FitzGerald, Mathys, Dolan,
Wurst, et al., 2015). Our latent variables are the hidden states of the world,
S, that represent fixation locations. Each policy, π (course of action), Das
2324
T. Parr and K. Friston
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
Figur 2: Discrete and continuous generative models. (A) This graphic shows
a Markov decision process in factor graph form (Loeliger et al., 2007). Blue
squares indicate probability distributions (factors of the generative distribu-
tion). Below, these factors are expressed in terms of probability matrices. “Cat”
denotes a categorical distribution. The implicit mean-field factorization of the
approximate distribution, Q, is shown. (B) This shows the equivalent structure
for a continuous state-space model. Heuristically, we can think of these (gener-
ative) models as an algorithm that generates data. This would involve drawing
, ˜v ), and using these variables
variables from their prior distributions (z.B., π , s1
, ˜x) from conditional distributions. Fi-
to sample dependent variables (z.B., s2
schließlich, the data ( ˜o, ˜y) can then be generated from the likelihood. Zusamenfassend, a gen-
erative model is just a probabilistic specification of how data are caused. Notiz
that the prior mean for ˜v is derived from the outcomes of the discrete model.
See the main text and Figure 1 for an explanation of the variables.
can be pursued is represented as a competing model. As time progresses,
hidden states undergo transitions that depend on the state at the previous
Zeit. The transition between control states depends on the policy pursued.
In our example, this means that the sequence of fixation locations is de-
termined by the policy. Each state gives rise to an outcome, Ö. We use the
notation ˜o = [o1
, . . . , oT ]T to describe the sequence of outcomes through
Zeit. The outcome we are interested in here corresponds to “where I am
looking.” Figure 2a shows graphically how one can factorize this kind of
Modell.
, o2
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2325
The form of this generative model implies that we must perform a
Bayesian model selection to decide on the best policy (sequence of saccades)
to pursue. To do so, we define prior beliefs about the probability of each
Politik. Active inference mandates the selection of policies that minimize
free energy. Jedoch, free energy is a function of outcomes, which are not
known for future time steps. The solution to this is to select policies that
minimize the expected free energy. To convert the expected free energy for
each policy to a probability distribution (that sums to one), we use a softmax
(normalized exponential) Funktion, σ (·):
(cid:18)
P(π ) = σ
−γ
(cid:19)
G(π, τ )
(cid:20)
G(π, τ ) = −E ˜Q
(cid:6)
τ >t
P(oτ , sτ |π )
Q(sτ |π )
ln
,
(cid:7)
= DKL [Q(oτ |π )||P(oτ )] + EQ(sτ |π ) [H[P(oτ |sτ )]] .
To account for future outcomes, we have used the (posterior predictive) dis-
tribution ˜Q(oτ , sτ |π ) = P(oτ |sτ )Q(sτ |π ). The γ parameter is an inverse tem-
perature parameter (associated with dopaminergic signaling) that weights
how sensitive the prior is to differences in the expected free energy of poli-
cies. The above equation can be expressed in linear algebraic form as (Fris-
Tonne, FitzGerald, Rigoli, Schwartenbeck, & Pezzulo, 2017):
(cid:18)
π
0
= σ
−γ
(cid:20)
Gπ τ
,
(cid:19)
τ >t
Gπ τ = oπ τ · (ln oπ τ − ln C)
(cid:2)
(cid:5)
(cid:3)(cid:4)
ςπτ
+ H · sπ τ .
To perform inferences within these types of models, we apply equation 2.1,
substituting in our discrete variables.
Q(sτ |π ) ∝ exp
(cid:9)
(cid:12)
EQ(s\τ |π )[ln P( ˜o, ˜s|π )]
(cid:9)
ln P(oτ |sτ ) + EQ[ln P(sτ |sτ −1
= exp
, π )] + EQ[ln P(sτ +1
|sτ , π )]
(cid:12)
.
Expressing these distributions as vectors (and matrices) of their sufficient
Statistiken, we can write
ln sπ τ = ln A · oτ + ln Bπ τ −1sπ τ −1
+ ln Bπ τ · sπ τ +1
.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2326
T. Parr and K. Friston
It is then straightforward to construct a biologically plausible gradient as-
cent scheme with this solution as its fixed (attracting) Punkt:
sπ τ = σ (vπ τ ),
επ τ = ln A · oτ + ln Bπ τ −1sπ τ −1
˙vπ τ = επ τ ,
+ ln Bπ τ · sπ τ +1
− ln sπ τ .
(cid:21)
If we want to estimate a hidden state from this, we can use a Bayesian model
average over policies. This gives sτ =
π ππ · sπ τ and completes our spec-
ification of the Bayesian belief updates required for categorical inference
and decision making. For outcomes not yet observed, we can perform a
Bayesian model average over oπ τ = Asπ τ to get a posterior predictive dis-
tribution, oτ . As we will see in section 2.3, this will act as our prior for a
(lower-level) generative model of continuous states like forces and velocity.
2.3 Moving the Eyes. At the level of biological effectors (glands and
muscles) and sensory receptors, the variables the nervous system must
deal with are continuous. Mit anderen Worten, to enact a selected policy, es ist
necessary to map categorical representations to the physical world with
continuous states and time. Muscles generate continuous forces, while pho-
toreceptors signal light intensity. This means that there must be a generative
model that maps the abstract, discrete outcomes from the generative (MDP)
model above, to continuous data (Friston, Parr, et al., 2017).
Hier, we consider how predictions about the next saccades are realized.
An MDP outcome, representing fixation location, corresponds to one of sev-
eral discrete saccadic targets, defined in continuous coordinates (v ). If we
associate each target location with the attracting (fixed) points of some con-
tinuous oculomotor dynamics, the prediction from the MDP effectively de-
fines an equilibrium point that will attract the subsequent eye movement
(vgl. the equilibrium point hypothesis; Feldman, 2009). If there is some un-
certainty about the particular location of the target, we can specify the pre-
dicted target location through a Bayesian model average of each location
ηm associated with a discrete outcome hypothesis or model, M:
P(v|Ö) = N(η, (cid:11)v ),
(cid:19)
η =
om · ηm.
M
The ensuing location now plays the role of a latent or hidden cause that
predicts the dynamics of continuous latent variables, ˙x (eye position, angu-
lar velocity), and observable sensory data, j (vision and proprioception).
The probability distributions that constitute the dynamic generative model
are provided in Figure 2b. As in discrete state-space models, we use the tilde
notation to indicate a trajectory. Hier, Jedoch, the trajectory is represented
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2327
as a vector of generalized motion (Friston, Trujillo-Barreto, & Daunizeau,
2008), ˜x = [X, X(cid:7), X(cid:7)(cid:7) . . .]T . We will use x[ich] to refer to the ith order motion.
Using equation 2.1, but substituting latent variables x and v, we can write
Q(X[ich]) ∝ exp
Q(v [ich]) ∝ exp
(cid:12)
(cid:9)
Eq( ˜v )Q( ˜x\i)[ln p( ˜y, ˜x, ˜v )]
(cid:12)
(cid:9)
Eq( ˜v\i)Q( ˜x)[ln p( ˜y, ˜x, ˜v )]
,
.
Under the Laplace approximation (Friston, Mattout, Trujillo-Barreto, Ash-
burner, & Penny, 2007), the precision of these distributions depends only
on the mean. This means we only need to optimize the mean explicitly. Als
this will be the maximum of the distribution, we can evaluate the above
equations at their means and perform a generalized gradient ascent (Fris-
Tonne, Stephan, Li, & Daunizeau, 2010):
˙μ[ich]
X
− μ[i+1]
X
=
v − μ[i+1]
˙μ[ich]
v
=
∂
∂μ[ich]
X
∂
∂μ[ich]
v
ln p(j, ˜μx, ˜μv ),
ln p(j, ˜μx, ˜μv ).
The expressions on the left ensure that when the gradient is zero, the motion
of the mean is equal to the mean of the motion. We can supplement these
Gleichungen, which mediate perceptual inference, with a differential equation
equipping the system with low-level reflexes (d.h., the actions that cause
contractions of the extraocular muscles) (Adams, Shipp, & Friston, 2013).
These also minimize free energy but can be thought of as fulfilling predic-
tions about sensory data by changing the external world:
˙a =
∂
∂a
ln p(j, ˜μx, ˜μv )
Figur 3 (left lower panel) shows these equations for the generative model
in Figure 2b.
2.4 Ascending Messages. To recap, we have specified both discrete and
continuous state-space models. We have shown how predictions of the for-
mer model can play the role of (empirical) prior beliefs in the latter. Der
final thing to specify is the process by which the continuous state-space
model informs the discrete model. Mit anderen Worten, what sort of evidence
is passed from the continuous to the discrete part of the (active) inference
scheme? In brief, the discrete part of the generative model provides prior
constraints on the continuous part, while the continuous part reciprocates
with Bayesian model evidence for the discrete hypotheses entertained by
the discrete part to enable Bayesian belief updating. This updating entails
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2328
T. Parr and K. Friston
Figur 3: The anatomy of oculomotion. This schematic illustrates the depen-
dencies between the variables in the equations described in the main text and
summarized on the left. It does so in the form of a neural network with popula-
tions of neurons assigned to plausible anatomical locations. There is a remark-
able degree of neuroanatomical plausibility to these assignments, including a
common laminar origin for cortical projections to the striatum, superior collicu-
lus, and higher-order thalamic nuclei. Zusätzlich, a dual cortico-subcortical
input to the colliculus is necessitated by this scheme, as are the excitatory-
inhibitory connections of the direct pathway through the basal ganglia. Der
equations in the box on the top left describe variational message passing in a
Markov decision process. The bottom box gives the Bayesian filtering equations
of the sort usually associated with predictive coding. The middle box expresses
the descending messages derived from Bayesian model averaging and the as-
cending messages that result from model reduction. We have not shown the
neuronal representation of the C matrix, encoding preferences. In previous pa-
pers, we show that this is likely to be represented in the mapping from higher
cortical areas (Friston, Rosch, et al., 2017), such as the dorsolateral prefrontal
Kortex, an area that houses representations that endure over a longer temporal
scale (Parr & Friston, 2017D) and connects to the frontal eye fields.
the selection of alternative hypotheses (outcomes) that constitute empirical
priors at the continuous level.
To adjudicate between these hypotheses, we need to compute the pos-
terior probabilities over each outcome (z.B., target fixation). We give an ab-
breviated outline of this (Bayesian model reduction) procedure here (for a
more technical account, see Friston, Litvak, et al., 2016). Given that the only
differences between discrete hypotheses are their priors, we can use Bayes’
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2329
rule to write the posterior odds ratio between the full and reduced model,
cancelling the likelihood terms:
P( ˜v| ˜y, om)P( ˜y|om)
P( ˜v| ˜y, Ö)P( ˜y|Ö)
= p( ˜v|om)
P( ˜v|Ö)
We can replace the posteriors here with those that we compute using the
Bayesian filtering approach outlined above. Rearranging this, we get
P( ˜y|om)Q( ˜v|om) = p( ˜v|om)
P( ˜v|Ö)
Q( ˜v|Ö)P( ˜y|Ö).
Integrating both sides with respect to the hidden cause gives
P( ˜y|om) = p( ˜y|Ö)
(cid:22)
P( ˜v|om)
P( ˜v|Ö)
Q( ˜v|Ö)d ˜v.
As the free energy approximates the negative log evidence, this can be
rewritten as
F(om) = F(Ö) − ln
(cid:22)
P( ˜v|om)
P( ˜v|Ö)
Q( ˜v|Ö)d ˜v
Vor allem, this means that the free energy of any hypothesis, M, can be cal-
culated from the free energy of the full outcome model without having to
explicitly compute the posteriors associated with the latent variables in m.
This is a slightly technical point that from a computational perspective, af-
fords a very simple and efficient form of Bayesian model comparison. In
other words, the evidence for different hypotheses or models at the dis-
crete level can be computed directly and easily from the sufficient statistics
of posterior beliefs encoded at the continuous level. In terms of neurobiol-
Ogy, this speaks to the biological possibility of belief propagation from the
continuous to the discrete domains.
To convert the evidence for each model back to discrete time, we inte-
grate the model evidence (free energy) over the time period corresponding
to one theta cycle. This is then combined with the prior over the model to
give a vector (E) that can be passed through a softmax function to give the
posterior over each outcome model, rτ (Friston, Parr, et al., 2017). This plays
the role of a discrete observation or outcome from the point of view of the
MDP (siehe Abbildung 3).
This concludes our technical description of belief propagation between
discrete and continuous parts of a generative model. A worked example
of how this sort of belief propagation of message passing could work in
the brain is provided in the final section (using the update equations in
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2330
T. Parr and K. Friston
Figur 3). To motivate the interpretation of these simulations, we now con-
sider the basic neurobiology of the oculomotor system and how its compu-
tational architecture could support belief propagation of this sort.
3 The Computational Anatomy of Oculomotion
In section 2, we described the problem the brain faces in making discrete de-
cisions about where to look and the continuous inferences required to real-
ize and update these decisions. We outlined the computations mandated by
active inference in solving these problems, with a special focus on the mes-
sage passing between discrete and dynamic domains. In diesem Abschnitt, we as-
sociate these computations with their neurobiological substrates. While this
assignment is speculative, it is constrained by both the anatomy of message
passing and the presence (or absence) of connections in the brain. Figur 3
shows the consistency between the computational anatomy of oculomotion
and the networks known to support oculomotor function. Im Folgenden,
we describe the cortical, subcortical, and brain stem components of this net-
arbeiten (Parr & Friston, 2017A). This section concludes with an analysis of the
superior colliculus, a structure uniquely placed to translate discrete deci-
sions into target locations in a continuous state space.
3.1 Hirnrinde. The cerebral cortex is a laminar structure, mit
layer-specific projections and terminations (Felleman & Van Essen, 1991).
The connectivity implied by inference using a Markov decision process
closely resembles this pattern (Friston, Rosch, et al., 2017). Speziell, Die
inference scheme we have described involves several distinct types of vari-
ables that receive messages from a subset of the other variables. This im-
plies a stereotyped pattern of connectivity between these groups (or layers)
of computational units. Consistent with cortical laminae, external input tar-
gets only one layer. Outputs of different types arise from defined popula-
tionen. In diesem Abschnitt, we use known neuroanatomy to constrain the assign-
ment of computational units to their appropriate laminae.
Layer IV of the cortex receives ascending connections from lower areas
(Shipp, 2007), or from first-order thalamic nuclei. The computational units
that receive this input are the error units, επ τ , suggesting that these occupy
this layer. This also implies that rτ , the subcortical projection to layer IV,
is likely to be represented by neurons in first-order thalamic relay nuclei,
such as the lateral geniculate nucleus (Herkenham, 1980). Layer III gives
rise to ascending connections. These are not shown here but would arise
from neurons encoding the state sτ at that hierarchical level (Friston, Rosch,
et al., 2017). For simplicity, we consider a single cortical area, the frontal eye
field, omitting the parietal (Corbetta et al., 1998; Gaymard, Lynch, Ploner,
Condy, & Rivaud-Péchoux, 2003; Parr & Friston, 2017B; Shipp, 2004) Und
Hinterhaupt (Bruce & Tsotsos, 2009) contributions to this system.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2331
Layer V of the cortex has several subcortical targets (Kasper, Larkman,
Lübke, & Blakemore, 1994; Ojima, Murakami, & Kishi, 1996). It is the layer
that houses the pyramidal cells of Betz in the motor cortex that project to
lower motor neurons in the spinal cord. Zusätzlich, layer V gives rise to
projections to the second-order thalamic nuclei, such as the pulvinar, Die
superior colliculus, and the basal ganglia (Fries, 1985; Hübener & Bolz, 1988;
Shipp, 2007). As Figure 3 zeigt an, units encoding oπ τ send messages to all
of these anatomical homologues. They participate in the evaluation of the
expected free energy in the striatum, the model averaging of continuous
time models by the superior colliculus, and Bayesian model reduction by
the thalamus. That the Eτ units of the thalamus receive cortical projections
from layer V suggests that these neurons must be located in second-order
thalamic nuclei (Crick & Koch, 1998; Rockland, 1998; Sherman, 2007).
3.2 Basal Ganglia. Wie oben beschrieben, the basal ganglia receive input from
cortical layer V, encoding predictions about discrete outcomes. This input,
in addition to a signal from the error units, ςπ τ , is used to compute the ex-
pected free energy, Gπ , of each policy. The basal ganglia are well recognized
to be involved in policy evaluation (Gurney, Prescott, & Redgrave, 2001; Ja-
hanshahi, Obeso, Rothwell, & Obeso, 2015). Most of the cortical inputs to
the basal ganglia target the striatum (Alexander & Crutcher, 1990; Shipp,
2017), implying the expected free energy is represented by medium spiny
neurons in this structure. These give rise to inhibitory GABAergic projec-
tions to the substantia nigra pars reticulata, which itself projects to the supe-
rior colliculus (Hikosaka & Wurtz, 1983). This direct pathway connectivity
is remarkably consistent with the influence of Gπ on π and π on ˜εv . The lat-
ter influence is in the Bayesian model averaging over expected outcomes to
generate a prior mean, ˜η, for the implementation of the policy in continu-
ous time. The output nuclei of the basal ganglia participate in an additional
Bayesian model averaging of hidden states. This is mediated by modulatory
projections (via thalamic relays) to superficial layers of the cortex (Haber &
Calzavara, 2009; McFarland & Haber, 2002).
3.3 The Brain Stem. The brain stem is the source of the cranial nerves
to the extraocular muscles. This suggests that brain stem structures engage
in continuous message passing. We have previously demonstrated that the
anatomy of this message passing is not only consistent with the connectivity
of the brain stem, but also that it reproduces electrophysiological responses
in these structures, and the same deficits as in neurological patients when
lesioned (Parr & Friston, 2018). Zusätzlich, these nerves carry propriocep-
tive information from the muscles (Cooper & Daniel, 1949; Cooper, Daniel,
& Whitteridge, 1951), while the midbrain receives optic nerve fibers from
the retinotectal pathway (Linden & Perry, 1983). Given beliefs about the
current position and velocity of the eyes, ˜μx, it is possible to make predic-
tions about the resulting sensory input (Adams, Perrinet, & Friston, 2012;
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2332
T. Parr and K. Friston
Friston, Adams, Perrinet, & Breakspear, 2012; Perrinet, Adams, & Friston,
2014). This induces a sensory prediction error ˜εy that is minimized by ac-
tion. This implies that the midbrain and pontine nuclei responsible for sig-
nals to the extraocular muscles must contain neurons that broadcast these
Fehler. As the brain stem nuclei form the nodes of the network engaged in
continuous inference, they must receive input from the region mapping de-
cisions into this space. The obvious candidate for this region is the superior
colliculus.
3.4 The Superior Colliculus. The superior colliculus is the interface
between the forebrain and brain stem networks. It is the recipient of cor-
tical (Hanes & Wurtz, 2001) and basal ganglia projections (Hikosaka &
Wurtz, 1983; siehe Abbildung 4) and is intimately connected to the oculomotor
system within the brain stem (Sparks, 2002). Als solche, it sits at the anatom-
ical boundary between the discrete and continuous networks. It is found
in the dorsal midbrain, at the same level as the oculomotor nucleus. Wie
the cortex, it is a laminar structure, with different electrophysiological re-
sponses in different subsets of cells. There are three broad groups of these
Neuronen, as illustrated in Figure 4. These are the burst, fixation, and buildup
cells (Ma, Graybiel, & Wurtz, 1991; Munoz & Wurtz, 1995A).
We have previously argued (Parr & Friston, 2018) that these groups cor-
respond to three different types of computational unit. Burst cells, welche
fire at the start of a saccade, have the properties we would expect from neu-
rons signaling visual prediction error, ˜εy. This is consistent with the fact
that a subset of retinal ganglion cells synapses within the colliculus and
that some collicular cells respond to visual stimuli (Mays & Sparks, 1980;
Wurtz & Mohler, 1976). Fixation neurons are active during fixations, Und
we have associated these with the expectation neurons encoding target fix-
ation locations, ˜μv . Consistent with the computational anatomy of Figures
3 Und 4, it is this group that projects to the brain stem centers for saccade
Generation (Gandhi & Keller, 1997).
Buildup neurons show a pattern of activation consistent with a pop-
ulation encoding (Anderson, Keller, Gandhi, & Das, 1998; Lee, Rohrer, &
Sparks, 1988). A traveling hill of excitation moves from a peripheral loca-
tion toward the rostral pole of the colliculus during a saccade (Munoz &
Wurtz, 1995B). At a population level, these neurons can be thought of as
expressing a prediction error between a target fixation and the current eye
Position, ˜εv (Sparks, 1986). The movement toward the pole, representing the
foveal location, can be thought of as encoding the reduction in prediction
error as the eye moves closer to its target. That this occurs at the population
level suggests that buildup neurons individually code for discrete spatial
Regionen.
The discretized encoding of continuous variables by these units is
consistent with their computational role, evaluating the difference be-
tween ˜η, parameterizing competing hypothetical models, and the estimated
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2333
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
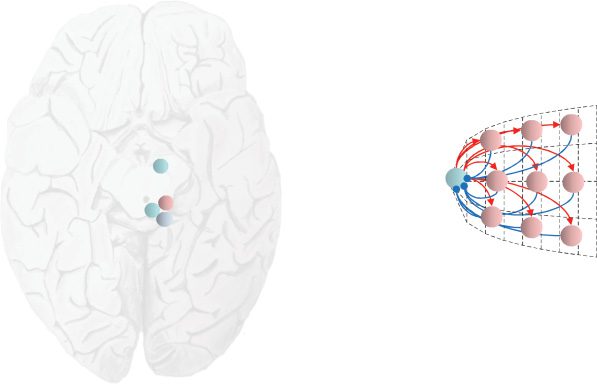
Figur 4: The discrete-continuous interface. This schematic shows the connec-
tivity between the neuronal populations in the superior colliculus in greater
detail. The transverse section through the midbrain allows us to depict the ter-
minations in the optic tectum from the optic nerve. We also illustrate the to-
pographical arrangement of the fixation (rostral pole) and buildup (distributed
throughout) cells, and the connectivity between these implied by our formula-
tion. Note that burst neurons are the most dorsal, with buildup neurons found
more ventrally. As the schematic shows, this would be consistent with the pro-
posed extrinsic (between regions) Konnektivität, as each population is oriented
toward the regions it is connected to. The intrinsic (within region) connectiv-
ity between buildup and fixation neurons is shown on the right, conforming
to the known retinotopy of the colliculus (Paré, Crommelinck, & Guitton, 1994;
Quaia, Aizawa, Optican, & Wurtz, 1998). The angles indicate the coordinates of
the visual field represented at each point in the colliculus.
position in continuous coordinates, ˜μv . Speziell, each neuron may en-
code the prediction error associated with a particular hypothesis, ˜ηm, mit
activity weighted by the prior probability of that hypothesis om. Der Konverter-
sion from discrete to continuous coordinates then simply requires that the
connection strengths between these neurons and the fixation neurons at the
pole vary with distance. The inhibitory connections (Munoz & Istvan, 1998)
from buildup to fixation neuron should be stronger if the anatomical dis-
tance between the two is greater. Zusammenfassend, electrophysiological proper-
ties corroborate the neuroanatomical evidence that the superior colliculus is
the discrete-continuous interface of the oculomotor system, and the topog-
raphy of buildup and fixation neurons hints at the computational mecha-
nisms that map between them. We next use the neurobiological pointers
2334
T. Parr and K. Friston
established in this section to interpret simulated oculomotor control in
terms of established electrophysiological responses in the oculomotor
System.
4 Simulations
Our aim in performing these (minimal) simulations is to illustrate the in-
teractions between the discrete and continuous domains of the oculomotor
System. Als solche, we chose a simple behavioral paradigm with three pos-
sible fixation locations (links, Rechts, and center). We then set the prior pref-
erences (through the C matrix) so that proprioceptive data are preferred
that are consistent with central fixation initially, then with leftward fixa-
tion, rightward fixation, and finally central fixation again. This is consistent
with the instruction to look at a sequence of targets at each of these loca-
tionen. The structure of the model we used is as depicted in Figure 1. Der
continuous part employs the belief that the eyes are drawn toward an at-
tracting location, and this is implemented by an action that has the effect
of a Newtonian torque. The details of this can be found in Parr and Fris-
Tonne (2018) and are very closely related to those in previous formulations of
oculomotion (Adams et al., 2012; Friston, Adams, et al., 2012; McSpadden,
1998; Perrinet et al., 2014). The discrete part is formally similar to that used
in Mirza et al., 2016 and Parr and Friston (2017B, 2017C).
Figur 5 shows the results of simulating active vision in this model. Cru-
cially, this type of simulation allows us to show what is happening at dif-
ferent neuroanatomical locations simultaneously and gives a sense of the
functional interaction of these areas. The results are presented in the form
of raster plots, as if we had recorded from single neurons in each of the
simulated brain areas. Representations in the cortex and basal ganglia up-
date on a theta cycle (4 Hz), while superior colliculus buildup cells trans-
late this into continuous time for collicular fixation neurons. These induce
(via brain stem circuits) changes in eye position, as shown in the simulated
electro-oculography trace. Note that these neurons vary continuously with
eye position, unlike the neurons in the discrete compartments, which en-
code the probability of an alternative fixation point.
Intuitively, we can see how the mapping from discrete to continuous oc-
curs. Bei 250 MS, the cortex updates its representations. These cause the ex-
pected free energy under each policy to change, inducing updates in the
striatum. Through the direct pathway, this causes inhibition in the substan-
tia nigra pars reticulata, resulting in the selection of a new policy (“look
right”). A Bayesian model average over outcomes then results in the selec-
tion of superior collicular buildup neurons that represent the error between
the current belief about eye position (given by the fixation neurons) Und
the anticipated rightward location. These then induce changes in the fix-
ation neuron activity. During the next 100 MS, as the eyes move to fulfill
this belief, we can see the resolution of the prediction error in the superior
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2335
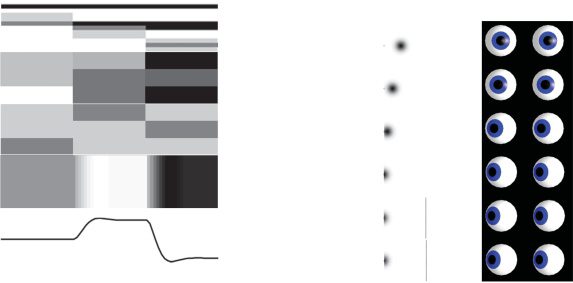
Figur 5: Simulated electrophysiological responses. This figure shows the elec-
trophysiological responses we would expect to observe under the process the-
ory associated with active inference. Auf der Linken, we show neuronal firing rates
(representing approximate posterior beliefs), depicted in the form of a raster
plot. These are synchronized across all of the neurons shown. Darker colors in-
dicate a greater firing rate. In the cortex (frontal eye field), we show neurons
representing the possible fixation targets. The first three rows indicate the neu-
rons representing left, center, and right at the first discrete time step (τ = 1).
These three options are then replicated in the next three rows, but reporting
the second time step. The third and fourth steps are similarly represented. In
the striatum, direct pathway medium spiny neurons (dMSN) represent the ex-
pected free energy of each of the three policy options (saccade right, saccade
center, and saccade left). These then inhibit their corresponding neurons in the
substantia nigra pars reticulata that represent the posterior beliefs about these
policies. Note the inversion of striatal activity in the substantia nigra as a re-
sult of this inhibition. We show the activity of a superior collicular (SC) fixation
neuron to illustrate neuronal firing representing a continuous variable, mit dem
horizontal electro-oculography trace below to depict the movement of the eyes.
The right panel shows simulated activity across the superior collicular buildup
layer during a saccade, with the corresponding eye positions. Population activ-
ity is depicted in terms of a gaussian intensity where the distance between the
mean and the collicular pole is equal to the prediction error (as in Parr & Friston,
2018).
colliculus buildup layer through the movement of the hill of activity toward
the pole.
5 Diskussion
5.1 Message Passing and Inference. Variational message passing is
not the only local message passing scheme that has been associated with
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2336
T. Parr and K. Friston
neuronal signaling. Belief propagation (Pearl, 2014) is one alternative. Der
message passing under this approach is perfectly consistent with the free
energy principle, as the requisite messages can be shown to minimize the
Bethe free energy (Yedidia, Freeman, & Weiss, 2005). Jedoch, although at-
tempts have been made to link belief propagation to neural signaling (Jardri
& Denève, 2013), the resulting architectures turn out to be more complicated
than the equivalent variational schemes. The primary reason for this is the
recursive computation of such messages. Each message is derived from an-
other message rather than from posterior beliefs about each variable. Vari-
ational messages passed from one population of neurons are derived from
the posterior beliefs represented by these neurons, mapped through a set
of synaptic weights. This means that the same set of neurons can be used
to compute multiple different messages. Im Gegensatz, a recursive scheme
requires streams of forward and backward messages that do not directly
interagieren.
A further possibility is that the messages we have described might be
computed through sampling, or Monte Carlo, approaches (Hastings, 1970).
One argument against this is that these methods tend to take much longer
to converge. In a biological setting (requiring online inference), this means
that animals would spend more time in surprising states (associated with
a lower model evidence). Zusamenfassend, while Monte Carlo approaches may
achieve a greater accuracy, they induce a larger (path integral of the) frei
energy than variational approaches.
5.2 Physiology and Behavior. The approach we have described here is
capable of reproducing a wide range of physiological and behavioral phe-
nomena in the oculomotor system and more generally. In the context of the
oculomotor system, we have previously shown that the signals we have
simulated bear a close resemblance to those measured in brain stem nuclei
(Parr & Friston, 2018). Most striking, we found that simulated collicular
buildup neuron responses qualitatively reproduced single-unit recordings
published in the experimental literature (Munoz & Wurtz, 1995B).
Lesions to these models induce similar behavioral syndromes to those
found in neurological patients with damage to the associated neu-
roanatomy. By disrupting neuronal message passing (i.e. inducing discon-
nection syndromes; Geschwind, 1965), we have simulated visual neglect
(Parr & Friston, 2017B) and internuclear ophthalmoplegia (Parr & Friston,
2018). The white matter disconnections associated with these syndromes
are the superior longitudinal fasciculus (Doricchi & Tomaiuolo, 2003) Und
the medial longitudinal fasciculus (Virgo & Plant, 2017), jeweils. Der
locations of these synthetic lesions constrain the computational anatomy,
and their nature endorses the notion that the brain engages in variational
inference.
Allgemeiner, models based on active inference have a high degree
of face validity, in that they reproduce a wide range of neurobiological
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2337
phenomena. These range from single cell responses, including place fields
(Friston, FitzGerald, Rigoli, Schwartenbeck, & Pezzulo, 2017) and mid-
brain dopamine activity (Friston et al., 2014), to evoked responses, inkl-
ing those associated with classic working memory tasks (Parr & Friston,
2017D). They have been used to generate behaviors as diverse as exploration
(Friston et al., 2015; Mirza et al., 2016), handwriting (Friston, Mattout, &
Kilner, 2011), eye-blink conditioning (Friston & Herreros, 2016), habit for-
mation (FitzGerald, Dolan, & Friston, 2014), communication (Friston &
Frith, 2015), and insight (Friston, Lin, et al., 2017). In addition to these the-
oretical accounts, active inference has been used pragmatically to model
behavior and to characterize individuals according to the parameters of
their prior beliefs (Adams, Bauer, Pinotsis, & Friston, 2016; Mirza, Adams,
Mathys, & Friston, 2018; Schwartenbeck & Friston, 2016).
5.3 Generalizations. The issues described in this article generalize be-
yond eye movements. Any neurobiological system that needs to make de-
cisions and implement these via some physical effector must solve the
problem we have described here. This is vital for (but not exclusive to)
Rede, locomotion, and autonomic regulation. Language is made up of dis-
crete units (phonemes, Wörter, Sätze) that are expressed as continuous
changes in auditory frequencies generated by contraction of the laryngeal
(and pharyngeal) muscles (Simonyan & Horwitz, 2011). Walking involves
taking a series of discrete steps, each of which requires a careful coordina-
tion of skeletal muscles (Ijspeert, 2008; Winter, 1984). Interoceptive states are
frequently divided into discrete dichotomies including fed versus fasting
(Kalsbeek, la Fleur, & Fliers, 2014; McLaughlin & McKie, 2016; Roh, Song,
& Kim, 2016), diastole versus systole, and sympathetic versus parasympa-
thetic (McDougall, Münzberg, Derbenev, & Zsombok, 2014; Owens, Fris-
Tonne, Low, Mathias, & Critchley, 2018). Each of these induces continuous
changes in enzyme activity, blood pressure, or smooth muscle contractions.
The form of the variational message passing will be very similar for each
of these processes, but the variables represented will differ. This suggests a
similar pattern of cortico-subcortical connectivity, but differing regions of
Kortex, and different subcortical components.
In diesem Artikel, we have chosen to focus on a fairly concrete problem:
deciding where to look and how to do this. For more abstract decisions,
perhaps at higher hierarchical levels in the brain (Badre, 2008; Badre &
D'Esposito, 2009; Christoff, Keramatian, Gordon, Schmied, & Mädler, 2009;
Rasmussen, 1985), it may be necessary to integrate beliefs across multiple
modalities. A challenge for future work is to incorporate the set of beliefs
that constitute an emotional state, as emotions are often thought to con-
tribute to “irrational” behaviors. It is not always easy to intuit how such
behaviors might be Bayes optimal.
One line of research into these issues frames them as questions about in-
teroceptive inference (Ondobaka, Kilner, & Friston, 2017; Seth, 2013; Seth
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2338
T. Parr and K. Friston
& Friston, 2016). Given beliefs about (abstract) variables that have both in-
teroceptive and exteroceptive sensory consequences, it becomes clear that
policies must minimize expected free energy in both domains. For exam-
Bitte, a belief that a predatory animal is present implies that the sympathetic
nervous system should be active, but also that visual data are consistent
with the presence of said animal. Anatomically, these dependencies are con-
sistent with the sensory and autonomic targets of the amygdala (LeDoux,
Iwata, Cicchetti, & Reis, 1988; Ressler, 2010). A tachycardia then carries
(weak) evidence for the presence of a scary animal and could influence pol-
icy selection even in the absence of exteroceptive evidence. This suggests a
framework in which an emotional state may influence decision making in
an apparently irrational way that is entirely compatible with the formula-
tion we have described here.
5.4 Future Directions. We hope to further the ideas in this work both
theoretically and empirically. Two important theoretical issues need to be
addressed in greater depth than we have space for here. The first is a thor-
ough comparison of alternative message-passing schemes in relation to
their anatomical and physiological plausibility. The second is a general-
ization of the inferences required for oculomotor decisions (and their mo-
toric implementation) to other systems. While the ideas we have presented
are generally applicable, it will be necessary to specify the generative mod-
els required to solve locomotive, autonomic, and abstract decision-making
problems. Endlich, although the computational anatomy we have proposed
has a high degree of face validity, it will be necessary to establish its predic-
tive validity.
One way to do so would be to use computational fMRI (Schwartenbeck,
FitzGerald, Mathys, Dolan, & Friston, 2015), fitting this model to oculomo-
tor behavior, and looking for brain regions that show activity patterns con-
sistent with the simulated neuronal responses. We hypothesize that these
regions will match the computational anatomy illustrated in Figure 3. Ein
alternative would be to use single-unit responses from each brain area
recorded during an oculomotor task. One could then compare each simu-
lated neuronal response to each recording and construct a confusion matrix
of the evidence for each synthetic signal in each region. We would expect a
greater evidence for each signal that we have associated with each region
über.
6 Abschluss
In diesem Artikel, we have described the discrete and continuous message pass-
ing that must be performed in an oculomotor system that realizes a se-
quence of saccadic fixations. We have illustrated the remarkable consistency
between the belief propagation or message passing implied by active infer-
ence and the anatomy of the oculomotor system. This accounts for several
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2339
neuroanatomical observations, including the dual input from frontal eye
fields and the substantia nigra to the superior colliculus, and the common
laminar origin of axons that target the striatum, second-order thalamus,
and midbrain tectum. Endlich, we simulated electrophysiological responses
as saccadic targets are selected and as the eyes move to implement that
saccade. This shows, functionally, how the superior colliculus is uniquely
positioned to act as the interface between the discrete and continuous
oculomotor systems.
Software Note
Although the generative model changes from application to application,
the belief updates described in this article are generic and can be imple-
mented using standard routines (here spm_MDP_VB_X.m). These routines
are available as Matlab code in the SPM academic software: http://www
.fil.ion.ucl.ac.uk/spm/. Simulations of the sort reported above can be re-
produced (and customized) via a graphical user interface by typing in >>
DEM and selecting the ‘visual foraging’ demo.
Danksagungen
T.P. is supported by the Rosetrees Trust (award 173346). K.J.F. is a Wellcome
Principal Research Fellow (088130/Z/09/Z). We are grateful to two anony-
mous reviewers for their helpful suggestions.
Disclosure Statement
We have no disclosures or conflict of interest.
Verweise
Adams, R. A., Bauer, M., Pinotsis, D., & Friston, K. J. (2016). Dynamic causal mod-
elling of eye movements during pursuit: Confirming precision-encoding in V1
using MEG. NeuroImage, 132, 175–189.
Adams, R. A., Perrinet, L. U., & Friston, K. (2012). Smooth pursuit and visual occlu-
sion: Active inference and oculomotor control in schizophrenia. PLoS ONE, 7(10),
e47502. doi:10.1371/zeitschrift.pone.0047502
Adams, R. A., Shipp, S., & Friston, K. J. (2013). Predictions not commands: Ac-
tive inference in the motor system. Brain Structure and Function, 218(3), 611–643.
doi:10.1007/s00429-012-0475-5
Alexander, G. E., & Crutcher, M. D. (1990). Functional architecture of basal ganglia
circuits: neural substrates of parallel processing. Trends in den Neurowissenschaften, 13(7),
266–271. doi:10.1016/0166-2236(90)90107-L
Allport, D. A. (1968). Phenomenal simultaneity and the perceptual moment hy-
pothesis. British Journal of Psychology, 59(4), 395–406. doi:10.1111/j.2044-8295.1968
.tb01154.x
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2340
T. Parr and K. Friston
Anderson, R. W., Keller, E. L., Gandhi, N. J., & Das, S. (1998). Two-dimensional
saccade-related population activity in superior colliculus in monkey. Zeitschrift für
Neurophysiologie, 80(2), 798.
Attias, H. (2003). Planning by Probabilistic Inference. In Proceedings of the 9th Int. Work-
shop on Artificial Intelligence and Statistics. Society for Artificial Intelligence and
Statistics.
Badre, D. (2008). Kognitive Kontrolle, hierarchy, and the rostro–caudal organization
of the frontal lobes. Trends in den Kognitionswissenschaften, 12(5), 193–200. doi:10.1016/J
.tics.2008.02.004
Badre, D., & D'Esposito, M. (2009). Is the rostro-caudal axis of the frontal lobe hierar-
chical? Nature Reviews Neurowissenschaften, 10, 659. doi:10.1038/nrn2667. https://www
.nature.com/articles/nrn2667#supplementary-information
Beal, M. J. (2003). Variational algorithms for approximate Bayesian inference. Ph.D. dis-
sertation, University of London.
Botvinick, M., & Toussaint, M. (2012). Planning as inference. Trends Cogn. Sci., 16(10),
485–488.
Bruce, N. D. B., & Tsotsos, J. K. (2009). Saliency, attention, and visual search: Ein
information theoretic approach. Journal of Vision, 9(3), 1–24. doi:10.1167/9.3.5
Buschman, T. J., & Müller, E. K. (2009). Serial, covert, shifts of attention dur-
ing visual search are reflected by the frontal eye fields and correlated with
population oscillations. Neuron, 63(3), 386–396. doi:10.1016/j.neuron.2009.06
.020
Buschman, T. J., & Müller, E. K. (2010). Shifting the spotlight of attention: Beweis
for discrete computations in cognition. Grenzen der menschlichen Neurowissenschaften, 4, 194.
doi:10.3389/fnhum.2010.00194
Buzsáki, G. (2005). Theta rhythm of navigation: Link between path integration and
landmark navigation, episodic and semantic memory. Hippocampus, 15(7), 827–
840. doi:10.1002/hipo.20113
Buzsáki, G. (2006). Rhythms of the brain. New York: Oxford University Press.
Chelazzi, L., Müller, E. K., Duncan, J., & Desimone, R. (1993). A neural basis for visual
search in inferior temporal cortex. Natur, 363(6427), 345–347.
Christoff, K., Keramatian, K., Gordon, A. M., Schmied, R., & Mädler, B. (2009). Pre-
frontal organization of cognitive control according to levels of abstraction. Gehirn
Forschung, 1286, 94–105. doi:10.1016/j.brainres.2009.05.096
Cooper, S., & Daniel, P. M. (1949). Muscle spindles in human extrinsic eye muscles.
Gehirn, 72(1), 1–24. doi:10.1093/brain/72.1.1
Cooper, S., Daniel, P. M., & Whitteridge, D. (1951). Afferent impulses in the oculo-
motor nerve, from the extrinsic eye muscles. Journal of Physiology, 113(4), 463–474.
doi:10.1113/jphysiol.1951.sp004588
Corbetta, M., Akbudak, E., Conturo, T. E., Snyder, A. Z., Ollinger, J. M., Drury, H.
A., . . . Shulman, G. L. (1998). A common network of functional areas for attention
and eye movements. Neuron, 21(4), 761–773. doi:10.1016/S0896-6273(00)80593-0
Cowan, L. S., & Walker, ICH. D. (2013). The importance of continuous and discrete ele-
ments in continuum robots. International Journal of Advanced Robotic Systems, 10(3),
165. doi:10.5772/55270
Crick, F., & Koch, C. (1998). Constraints on cortical and thalamic projections: the no-
strong-loops hypothesis. Natur, 391, 245. doi:10.1038/34584
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2341
Dauwels, J. (2007). On variational message passing on factor graphs. In Proceedings
of the IEEE Internatinal Sympoisum on Information Theory. Piscataway, NJ: IEEE.
Dayan, P., Hinton, G. E., Neal, R. M., & Zemel, R. S. (1995). The Helmholtz machine.
Neural Computation, 7(5), 889–904.
Doricchi, F., & Tomaiuolo, F. (2003). The anatomy of neglect without hemianopia: A
key role for parietal–frontal disconnection? Neuroreport, 14(17), 2239–2243.
Drewes, J., & VanRullen, R. (2011). This is the rhythm of your eyes: The phase of on-
going electroencephalogram oscillations modulates saccadic reaction time. Jour-
nal of Neuroscience, 31(12), 4698.
Dugué, L., Marque, P., & VanRullen, R. (2011). The phase of ongoing oscillations me-
diates the causal relation between brain excitation and visual perception. Zeitschrift
der Neurowissenschaften, 31(33), 11889.
Duncan, J., Station, R., & Shapiro, K. (1994). Direct measurement of attentional dwell
time in human vision. Natur, 369(6478), 313–315.
Ergenoglu, T., Demiralp, T., Bayraktaroglu, Z., Ergen, M., Beydagi, H., & Uresin,
Y. (2004). Alpha rhythm of the EEG modulates visual detection performance in
humans. Kognitive Gehirnforschung, 20(3), 376–383. doi:10.1016/j.cogbrainres.2004
.03.009
Feldman, A. G. (2009). New insights into action-perception coupling. Exp. Brain Res.,
194(1), 39–58.
Felleman, D. J., & Van Essen, D. C. (1991). Distributed hierarchical processing in the
primate cerebral cortex. Hirnrinde, 1(1), 1–47.
Feynman, R. P. (1998). Statistical mechanics: A set of lectures. New York: Avalon
Veröffentlichung.
FitzGerald, T. H. B., Dolan, R. J., & Friston, K. J. (2014). Model averaging, op-
timal inference, and habit formation. Grenzen der menschlichen Neurowissenschaften, 8, 457.
doi:10.3389/fnhum.2014.00457
FitzGerald, T. H., Schwartenbeck, P., Moutoussis, M., Dolan, R. J., & Friston, K.
(2015). Active inference, evidence accumulation, and the urn task. Neural Com-
put, 27(2), 306–328. doi:10.1162/NECO_a_00699
Fries, W. (1984). Cortical projections to the superior colliculus in the macaque mon-
key: A retrograde study using horseradish peroxidase. Journal of Comparative Neu-
rology, 230(1), 55–76. doi:10.1002/cne.902300106
Fries, W. (1985). Inputs from motor and premotor cortex to the superior colliculus of
the macaque monkey. Behavioural Brain Research, 18(2), 95–105. doi:10.1016/0166
-4328(85)90066-X
Friston, K. (2009). The free-energy principle: A rough guide to the brain? Trends in
Cognitive Sciences, 13(7), 293–301. doi:10.1016/j.tics.2009.04.005
Friston, K. (2013). Life as we know it. JR Soc. Interface, 10(86), 20130475.
Friston, K., Adams, R. A., Perrinet, L., & Breakspear, M. (2012). Perceptions as hy-
potheses: Saccades as experiments. Grenzen in der Psychologie, 3, 151. doi:10.3389
/fpsyg.2012.00151
Friston, K., & Buzsáki, G. (2016). The functional anatomy of time: What and when in
das Gehirn. Trends in den Kognitionswissenschaften, 20(7), 500–511. doi:10.1016/j.tics.2016.05.001
Friston, K. J., Daunizeau, J., Kilner, J., & Kiebel, S. J. (2010). Action and behav-
ior: A free-energy formulation. Biological Cybernetics, 102(3), 227–260. doi:10.1007
/s00422-010-0364-z
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2342
T. Parr and K. Friston
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., O’Doherty, J., & Pezzulo, G.
(2016). Active inference and learning. Neuroscience and Biobehavioral Reviews, 68,
862–879. doi:10.1016/j.neubiorev.2016.06.022
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., & Pezzulo, G. (2017). Active
inference: A process theory. Neural Computation, 29(1), 1–49. doi:10.1162/NECO
_a_00912
Friston, K. J., & Frith, C. D. (2015). Active inference, communication and hermeneu-
Tics. Kortex, 68, 129–143. doi:10.1016/j.cortex.2015.03.025
Friston, K., & Herreros, ICH. (2016). Active inference and learning in the cerebellum.
Neural Computation, 28(9), 1812–1839. doi:10.1162/NECO_a_00863
Friston, K. J., Lin, M., Frith, C. D., Pezzulo, G., Hobson, J. A., & Ondobaka, S. (2017).
Active inference, curiosity and insight. Neural Computation, 29, 2633–2683.
Friston, K. J., Litvak, V., Oswal, A., Razi, A., Stephan, K. E., van Wijk, B. C. M., . . .
Zeidman, P. (2016). Bayesian model reduction and empirical Bayes for group
(DCM) Studien. NeuroImage, 128(Suppl. C), 413–431. doi:https://doi.org/10
.1016/j.neuroimage.2015.11.015
Friston, K., Mattout, J., & Kilner, J. (2011). Action understanding and active inference.
Biological Cybernetics, 104(1–2), 137–160. doi:10.1007/s00422- 011-0424-z
Friston, K., Mattout, J., Trujillo-Barreto, N., Aschenbrenner, J., & Penny, W. (2007). Varia-
tional free energy and the Laplace approximation. NeuroImage, 34(1), 220–234.
Friston, K. J., Parr, T., & de Vries, B. (2017). The graphical brain: Belief propaga-
tion and active inference. Netzwerkneurowissenschaften, 1, 381–414. doi:10.1162/NETN
_a_00018
Friston, K., Rigoli, F., Ognibene, D., Mathys, C., Fitzgerald, T., & Pezzulo, G.
(2015). Active inference and epistemic value. Cognitive Neuroscience, 6(4), 187–214.
doi:10.1080/17588928.2015.1020053
Friston, K. J., Rosch, R., Parr, T., Price, C., & Bowman, H. (2017). Deep temporal
models and active inference. Neuroscience and Biobehavioral Reviews, 77, 388–402.
doi:10.1016/j.neubiorev.2017.04.009
Friston, K., Samothrakis, S., & Montague, R. (2012). Active inference and agency:
Optimal control without cost functions. Biological Cybernetics, 106(8), 523–541.
doi:10.1007/s00422-012-0512-8
Friston, K., Schwartenbeck, P., Fitzgerald, T., Moutoussis, M., Behrens, T., & Dolan,
R. (2013). The anatomy of choice: Active inference and agency. Frontiers in Human
Neurowissenschaften, 7(598). doi:10.3389/fnhum.2013.00598
Friston, K., Schwartenbeck, P., FitzGerald, T., Moutoussis, M., Behrens, T., & Dolan,
R. J. (2014). The anatomy of choice: Dopamine and decision-making. Philosoph-
ical Transactions of the Royal Society B: Biological Sciences, 369(1655), 20130481.
doi:10.1098/rstb.2013.0481
Friston, K., Stephan, K., Li, B., & Daunizeau, J. (2010). Generalised filtering. Mathe-
matical Problems in Engineering, 2010.
Friston, K. J., Trujillo-Barreto, N., & Daunizeau, J. (2008). DEM: A variational treat-
ment of dynamic systems. NeuroImage, 41(3), 849–885. doi:10.1016/j.neuroimage
.2008.02.054
Gandhi, N. J., & Keller, E. L. (1997). Spatial distribution and discharge characteris-
tics of superior colliculus neurons antidromically activated from the omnipause
region in monkey. Journal of Neurophysiology, 78(4), 2221.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2343
Gaymard, B., Lynch, J., Ploner, C. J., Condy, C., & Rivaud-Péchoux, S. (2003).
The parieto-collicular pathway: Anatomical location and contribution to saccade
Generation. Europäisches Journal für Neurowissenschaften, 17(7), 1518–1526. doi:10.1046/j.1460
-9568.2003.02570.X
Geschwind, N. (1965). Disconnexion syndromes in animals and man. II. Gehirn, 88(3),
585.
Gurney, K., Prescott, T. J., & Redgrave, P. (2001). A computational model of action
selection in the basal ganglia. ICH. A new functional anatomy. Biological Cybernetics,
84(6), 401–410. doi:10.1007/PL00007984
Haber, S. N., & Calzavara, R. (2009). The cortico-basal ganglia integrative net-
arbeiten: The role of the thalamus. Brain Research Bulletin, 78(2), 69–74. doi:10.1016
/j.brainresbull.2008.09.013
Hanes, D. P., & Wurtz, R. H. (2001). Interaction of the frontal eye field and superior
colliculus for saccade generation. Journal of Neurophysiology, 85(2), 804.
Hanslmayr, S., Volberg, G., Wimber, M., Dalal, Sarang S., & Greenlee, Mark W.
(2013). Prestimulus oscillatory phase at 7 Hz gates cortical information flow and
visual perception. Aktuelle Biologie, 23(22), 2273–2278. doi:10.1016/j.cub.2013.09
.020
Hastings, W. K. (1970). Monte Carlo sampling methods using Markov chains and
their applications. Biometrika, 57, 97–109. doi:10.1093/biomet/57.1.97
Herkenham, M. (1980). Laminar organization of thalamic projections to the rat neo-
Kortex. Wissenschaft, 207(4430), 532.
Hikosaka, O., & Wurtz, R. H. (1983). Visual and oculomotor functions of monkey
substantia nigra pars reticulata. IV. Relation of substantia nigra to superior col-
liculus. Journal of Neurophysiology, 49(5), 1285.
Hohwy, J. (2016). The self-evidencing brain. Noûs, 50(2), 259–285. doi:10.1111
/nous.12062
Hübener, M., & Bolz, J. (1988). Morphology of identified projection neurons in layer 5
of rat visual cortex. Neurowissenschaftliche Briefe, 94(1), 76–81. doi:https://doi.org/10.1016
/0304-3940(88)90273-X
Ijspeert, A. J. (2008). Central pattern generators for locomotion control in animals and
robots: Eine Rezension. Neural Networks, 21(4), 642–653. doi:https://doi.org/10.1016
/j.neunet.2008.03.014
Jahanshahi, M., Obeso, ICH., Rothwell, J. C., & Obeso, J. A. (2015). A fronto-striato-
subthalamic-pallidal network for goal-directed and habitual inhibition. Nat. Rev.
Neurosci., 16(12), 719–732. doi:10.1038/nrn4038
Jardri, R., & Denève, S. (2013). Circular inferences in schizophrenia. Gehirn, 136(11),
3227–3241. doi:10.1093/brain/awt257
Kalsbeek, A.,
la Fleur, S., & Fliers, E. (2014). Circadian control of glucose
metabolism. Molecular Metabolism, 3(4), 372–383. doi:https://doi.org/10.1016
/j.molmet.2014.03.002
Kasper, E. M., Larkman, A. U., Lübke, J., & Blakemore, C. (1994). Pyramidal neurons
in layer 5 of the rat visual cortex. ICH. Correlation among cell morphology, intrinsic
electrophysiological properties, and axon targets. Journal of Comparative Neurol-
Ogy, 339(4), 459–474. doi:10.1002/cne.903390402
Landauer, A. N., & Fries, P. (2012). Attention samples stimuli rhythmically. Current
Biology, 22(11), 1000–1004. doi:10.1016/j.cub.2012.03.054
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2344
T. Parr and K. Friston
LeDoux, J. E., Iwata, J., Cicchetti, P., & Reis, D. J. (1988). Different projections of the
central amygdaloid nucleus mediate autonomic and behavioral correlates of con-
ditioned fear. Zeitschrift für Neurowissenschaften, 8(7), 2517–2529.
Lee, C., Rohrer, W. H., & Sparks, D. L. (1988). Population coding of saccadic eye
movements by neurons in the superior colliculus. Natur, 332(6162), 357–360.
Linden, R., & Perry, V. H. (1983). Massive retinotectal projection in rats. Brain Re-
suchen, 272(1), 145–149. doi:https://doi.org/10.1016/0006-8993(83)90371-2
Linderman, S., Johnson, M., Müller, A., Adams, R., Blei, D., & Paninski, L. (2017).
Bayesian learning and inference in recurrent switching linear dynamical systems.
In Proceedings of the 20th International Conference on Artificial Intelligence and Statis-
Tics. PMLR. http://proceedings.mlr.press
Loeliger, H. A., Dauwels, J., Hu, J., Korl, S., Ping, L., & Kschischang, F. R. (2007). Der
factor graph approach to model-based signal processing. Proceedings of the IEEE,
95(6), 1295–1322. doi:10.1109/JPROC.2007.896497
Ma, T. P., Graybiel, A. M., & Wurtz, R. H. (1991). Location of saccade-related neu-
rons in the macaque superior colliculus. Experimentelle Hirnforschung, 85(1), 21–35.
doi:10.1007/BF00229983
Mays, L. E., & Sparks, D. L. (1980). Dissociation of visual and saccade-related re-
sponses in superior colliculus neurons. Journal of Neurophysiology, 43(1), 207.
McDougall, S. J., Münzberg, H., Derbenev, A. V., & Zsombok, A. (2014). Central con-
trol of autonomic functions in health and disease. Frontiers in Neuroscience, 8, 440.
doi:10.3389/fnins.2014.00440
McFarland, N. R., & Haber, S. N. (2002). Thalamic relay nuclei of the basal gan-
glia form both reciprocal and nonreciprocal cortical connections, linking multiple
frontal cortical areas. Zeitschrift für Neurowissenschaften, 22(18), 8117–8132.
McLaughlin, J. T., & McKie, S. (2016). Human brain responses to gastrointesti-
nal nutrients and gut hormones. Current Opinion in Pharmacology, 31, 8–12.
doi:https://doi.org/10.1016/j.coph.2016.08.006
McSpadden, A. (1998). A mathematical model of human saccadic eye movement. Ph.D.
dissertation, Texas Tech University.
Mirza, M. B., Adams, R. A., Mathys, C. D., & Friston, K. J. (2016). Scene construc-
tion, visual foraging, and active inference. Frontiers in Computational Neuroscience,
10(56). doi:10.3389/fncom.2016.00056
Mirza, M. B., Adams, R. A., Mathys, C., & Friston, K. J. (2018). Human visual explo-
ration reduces uncertainty about the sensed world. PLoS ONE, 13(1), e0190429.
doi:10.1371/zeitschrift.pone.0190429
Munoz, D. P., & Istvan, P. J. (1998). Lateral inhibitory interactions in the intermediate
layers of the monkey superior colliculus. Journal of Neurophysiology, 79(3), 1193–
1209.
Munoz, D. P., & Wurtz, R. H. (1995A). Saccade-related activity in monkey superior
colliculus. ICH. Characteristics of burst and buildup cells. Journal of Neurophysiology,
73(6), 2313.
Munoz, D. P., & Wurtz, R. H. (1995B). Saccade-related activity in monkey superior
colliculus. II. Spread of activity during saccades. Journal of Neurophysiology, 73(6),
2334–2348.
Ojima, H., Murakami, K., & Kishi, K. (1996). Dual termination modes of corticotha-
lamic fibers originating from pyramids of layers 5 Und 6 in cat visual cortical
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2345
Bereich 17. Neurowissenschaftliche Briefe, 208(1), 57–60. doi:https://doi.org/10.1016/0304
-3940(96)12538-6
Ondobaka, S., Kilner, J., & Friston, K. (2017). The role of interoceptive inference
in theory of mind. Brain and Cognition, 112, 64–68. doi:https://doi.org/10.1016
/j.bandc.2015.08.002
Owens, P., Friston, K. J., Low, D. A., Mathias, C. J., & Critchley, H. D. (2018). Inves-
tigating the relationship between cardiac interoception and autonomic cardiac
control using a predictive coding framework. Autonomic Neuroscience: Basic and
Klinisch, 210, 65–71. doi:10.1016/j.autneu.2018.01.001
Paré, M., Crommelinck, M., & Guitton, D. (1994). Gaze shifts evoked by stimulation
of the superior colliculus in the head-free cat conform to the motor map but also
depend on stimulus strength and fixation activity. Experimentelle Hirnforschung,
101(1), 123–139.
Parr, T., & Friston, K. J. (2017A). The active construction of the visual world. Neuropsy-
chologia, 104, 92–101. doi:http://dx.doi.org/10.1016/j.neuropsychologia.2017
.08.003
Parr, T., & Friston, K. J. (2017B). The computational anatomy of visual neglect. Cere-
bral Cortex, 28, 1–14. doi:10.1093/cercor/bhx316
Parr, T., & Friston, K. J. (2017C). Uncertainty, epistemics and active inference. Zeitschrift
of The Royal Society Interface, 14(136), 20170376.
Parr, T., & Friston, K. J. (2017D). Working memory, attention, and salience in active
inference. Wissenschaftliche Berichte, 7(1), 14678. doi:10.1038/s41598-017-15249-0
Parr, T., & Friston, K. J. (2018). Active inference and the anatomy of oculomotion.
Neuropsychologie, 111, 334–343 doi:10.1016/j.neuropsychologia.2018.01.041
Pearl, J. (2014). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible In-
Referenz. Amsterdam: Elsevier Science.
Perrinet, L. U., Adams, R. A., & Friston, K. J. (2014). Active inference, eye move-
ments and oculomotor delays. Biological Cybernetics, 108(6), 777–801. doi:10.1007
/s00422-014-0620-8
Quaia, C., Aizawa, H., Optican, L. M., & Wurtz, R. H. (1998). Reversible inactivation
of monkey superior colliculus. II. Maps of saccadic deficits. Journal of Neurophys-
iology, 79(4), 2097.
Rasmussen, J. (1985). The role of hierarchical knowledge representation in decision-
making and system management. IEEE Transactions on Systems, Man, and Cyber-
netics, SMC-15(2), 234–243. doi:10.1109/TSMC.1985.6313353
Raybourn, M. S., & Keller, E. L. (1977). Colliculoreticular organization in primate
oculomotor system. Journal of Neurophysiology, 40(4), 861.
Ressler, K. J. (2010). Amygdala activity, fear, and anxiety: Modulation by stress. Bio-
logical Psychiatry, 67(12), 1117–1119. doi:10.1016/j.biopsych.2010.04.027
Rockland, K. S. (1998). Convergence and branching patterns of round, type
2 corticopulvinar axons. Zeitschrift für Vergleichende Neurologie, 390(4), 515–536.
doi:10.1002/(WISSENSCHAFT)1096-9861(19980126)390:4<515::AID- CNE5>3.0.CO;2-3
Roh, E., Song, D. K., & Kim, M.-S. (2016). Emerging role of the brain in the home-
ostatic regulation of energy and glucose metabolism. Experimental Molecular
Medicine, 48, e216. doi:10.1038/emm.2016.4
Schaal, S. (2006). Dynamic movement primitives-a framework for motor control
in humans and humanoid robotics. In H. Kimura, K. Tsuchiya, A. Ishiguro,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2346
T. Parr and K. Friston
& H. Witt (Hrsg.), Adaptive motion of animals and machines (S. 261–280): Berlin:
Springer.
Schwartenbeck, P., FitzGerald, T. H. B., Mathys, C., Dolan, R., & Friston, K. (2015).
The dopaminergic midbrain encodes the expected certainty about desired out-
comes. Hirnrinde, 25(10), 3434–3445. doi:10.1093/cercor/bhu159
Schwartenbeck, P., FitzGerald, T. H., Mathys, C., Dolan, R., Wurst, F., Kron-
bichler, M., & Friston, K. (2015). Optimal inference with suboptimal mod-
els: Addiction and active Bayesian inference. Med. Hypotheses, 84(2), 109–117.
doi:10.1016/j.mehy.2014.12.007
Schwartenbeck, P., & Friston, K. (2016). Computational phenotyping in psychiatry: A
worked example. eNeuro, 3(4), ENEURO.0049-0016.2016. doi:10.1523/ENEURO
.0049-16.2016
Seth, A. K. (2013). Interoceptive inference, emotion, and the embodied self. Trends in
Cognitive Sciences, 17(11), 565–573. doi:10.1016/j.tics.2013.09.007
Seth, A. K., & Friston, K. J. (2016). Active interoceptive inference and the emotional
Gehirn. Philosophical Transactions of the Royal Society B: Biological Sciences, 371(1708),
20160007. doi:10.1098/rstb.2016.0007
Shallice, T. (1964). The detection of change and the perceptual moment hypoth-
esis. British Journal of Statistical Psychology, 17(2), 113–135. doi:10.1111/j.2044
-8317.1964.tb00254.x
Sherman, S. M. (2007). The thalamus is more than just a relay. Aktuelle Meinung in
Neurobiology, 17(4), 417–422. doi:https://doi.org/10.1016/j.conb.2007.07.003
Shipp, S. (2004). The brain circuitry of attention. Trends in den Kognitionswissenschaften, 8(5),
223–230. doi:http://dx.doi.org/10.1016/j.tics.2004.03.004
Shipp, S. (2007). Structure and function of the cerebral cortex. Aktuelle Biologie, 17(12),
R443–R449. doi:10.1016/j.cub.2007.03.044
Shipp, S. (2017). The functional logic of corticostriatal connections. Brain Structure
and Function, 222(2), 669–706. doi:10.1007/s00429-016-1250-9
Simonyan, K., & Horwitz, B. (2011). Laryngeal motor cortex and control of speech in
humans. Neuroscientist, 17(2), 197–208. doi:10.1177/1073858410386727
Sparks, D. L. (1986). Translation of sensory signals into commands for control of sac-
cadic eye movements: Role of primate superior colliculus. Physiological Reviews,
66(1), 118.
Sparks, D. L. (2002). The brainstem control of saccadic eye movements. Nat. Rev.
Neurosci., 3(12), 952–964.
Stroud, J. M. (1967). The fine structure of psychological time. Annalen von New York
Akademie der Wissenschaften, 138(2), 623–631. doi:10.1111/j.1749-6632.1967.tb55012.x
Ungerleider, L. G., & Haxby, J. V. (1994). “What” and “where” in the human brain.
Aktuelle Meinung in der Neurobiologie, 4(2), 157–165. doi:http://dx.doi.org/10.1016
/0959-4388(94)90066-3
van Dijk, H., Schoffelen, J.-M., Oostenveld, R., & Jensen, Ö. (2008). Prestimulus os-
cillatory activity in the alpha band predicts visual discrimination ability. Zeitschrift
der Neurowissenschaften, 28(8), 1816.
VanRullen, R. (2013). Visual attention: A rhythmic process? Aktuelle Biologie, 23(24),
R1110–R1112. doi:https://doi.org/10.1016/j.cub.2013.11.006
VanRullen, R. (2016). Perceptual cycles. Trends in den Kognitionswissenschaften, 20(10), 723–735.
doi:10.1016/j.tics.2016.07.006
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The Discrete and Continuous Brain
2347
VanRullen, R., & Koch, C. (2003). Is perception discrete or continuous? Trends in Cog-
nitive Sciences, 7(5), 207–213. doi:10.1016/S1364-6613(03)00095-0
Virgo, J. D., & Plant, G. T. (2017). Internuclear ophthalmoplegia. Practical Neurology,
17(2), 149–153.
Winn, J. M. (2004). Variational message passing and its applications. Citeseer.
Winter, D. A. (1984). Biomechanics of human movement with applications to the
study of human locomotion. Critical Reviews in Biomedical Engineering, 9(4), 287–
314.
Wurtz, R. H., & Mohler, C. W. (1976). Organization of monkey superior colliculus:
Enhanced visual response of superficial layer cells. Journal of Neurophysiology,
39(4), 745–765.
Yedidia, J. S., Freeman, W. T., & Weiss, Y. (2005). Constructing free-energy approxi-
mations and generalized belief propagation algorithms. IEEE Transactions on In-
formation Theory, 51(7), 2282–2312.
Received December 4, 2017; accepted March 6, 2018.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
0
9
2
3
1
9
1
0
4
7
4
6
4
N
e
C
Ö
_
A
_
0
1
1
0
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3