ARTIKEL
Communicated by Anthony Neville Burkitt
Single Circuit in V1 Capable of Switching Contexts During
Movement Using an Inhibitory Population as a Switch
Doris Voina
dvoina@uw.edu
Applied Mathematics, Universität Washington, Seattle, WA 98195 USA.
Stefano Recanatesi
stefano.recanatesi@gmail.com
Department of Physiology and Biophysics, Universität Washington,
Seattle, WA 98195, USA.
Brian Hu
brian.hu@kitware.com
Allen Institute for Brain Science, Seattle, WA 98109 USA.
Eric Shea-Brown
etsb@uw.edu
Applied Mathematics, Universität Washington, Seattle, WA 98195, USA.
Stefan Mihalas
stefanm@alleninstitute.org
Applied Mathematics, Universität Washington, Seattle, WA 98195, USA., Und
Allen Institute for Brain Science, Seattle, WA 98109, USA.
As animals adapt to their environments, their brains are tasked with pro-
cessing stimuli in different sensory contexts. Whether these computa-
tions are context dependent or independent, they are all implemented in
the same neural tissue. A crucial question is what neural architectures can
respond flexibly to a range of stimulus conditions and switch between
ihnen. This is a particular case of flexible architecture that permits multi-
ple related computations within a single circuit.
Hier, we address this question in the specific case of the visual system
circuitry, focusing on context integration, defined as the integration of
feedforward and surround information across visual space. We show that
a biologically inspired microcircuit with multiple inhibitory cell types
can switch between visual processing of the static context and the mov-
ing context. In our model, the VIP population acts as the switch and mod-
ulates the visual circuit through a disinhibitory motif. Darüber hinaus, the VIP
population is efficient, requiring only a relatively small number of neu-
rons to switch contexts. This circuit eliminates noise in videos by using
Neural Computation 34, 541–594 (2022)
https://doi.org/10.1162/neco_a_01472
© 2022 Massachusetts Institute of Technology
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
542
D. Voina et al.
appropriate lateral connections for contextual spatiotemporal surround
modulation, having superior denoising performance compared to circuits
where only one context is learned. Our findings shed light on a minimally
complex architecture that is capable of switching between two naturalis-
tic contexts using few switching units.
1 Einführung
Our brains are unique in their ability to adapt to the context in which stim-
uli appear. Animals face the problem of processing visual stimuli rapidly
and efficiently while adapting to different contexts every time they transi-
tion to a new environment (z.B., from jungle to savanna, from the shores of
a river to underwater). A classic example of adaptation to different contexts
is discussed in Barlow’s “efficient coding hypothesis” (Barlow, 1961), welche
proposes that sensory systems encode maximal information about environ-
ments with different statistics (Olshausen & Field, 1996A, 1996B). In diesem
and other cases, when context changes, neural circuits switch from previ-
ous strategies of feature representation to new ones that are better adapted
to the statistical properties of the new context. How the neuronal circuitry
of the brain is organized to account for the multitude of contexts animals
may encounter has not been established (Yang, Cole, & Rajan, 2019). Im Par-
besonders, when do we need separate circuits for different contexts, and when
can single circuits be modulated to switch among multiple contexts (Gozzi
et al., 2010; Koganezawa, Kimura, & Yamamoto, 2016; Zhou et al., 2017;
Cardin, 2019; Mante, Sussillo, Shenoy, & Newsome, 2013; Cohen, Dunbar, &
McClelland, 1990; Yang et al., 2019)? Our aim is to identify a biologically
constrained network that is capable of switching contexts and to infer the
building blocks required for such switching. In constructing such a net-
arbeiten, we will only discuss and include the structural and functional detail
needed for the switching of contexts.
We focus on a concrete setting in which rapid context switching is ap-
parent. This is mouse V1, which responds differently to inputs when the
animal is running (moving condition) compared to when it is stationary
(static condition) (Niell & Stryker, 2010; Fu et al., 2014). When the animal
transitions from standing still to running, visually evoked firing rates sig-
nificantly increase. Zum Beispiel, in one experimental setting, the firing rate
of neurons in layers II/III of area V1 more than doubled (Niell & Stryker,
2010), while in layer V of V1, noise correlations between pairs of neurons
were substantially reduced (Dadarlat & Stryker, 2017).
While an enormous diversity of cell types has been characterized (Tasic
et al., 2018), in this work we focus on the three primary classes of inhibitory
interneurons—vasoactive intestinal peptide (VIP), somatostatin (SST), Und
parvalbumin (PV)—and one class of long-range projecting excitatory neu-
rons: the pyramidal neurons (PYR) as shown in Figure 1a (Fu et al., 2014;
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
543
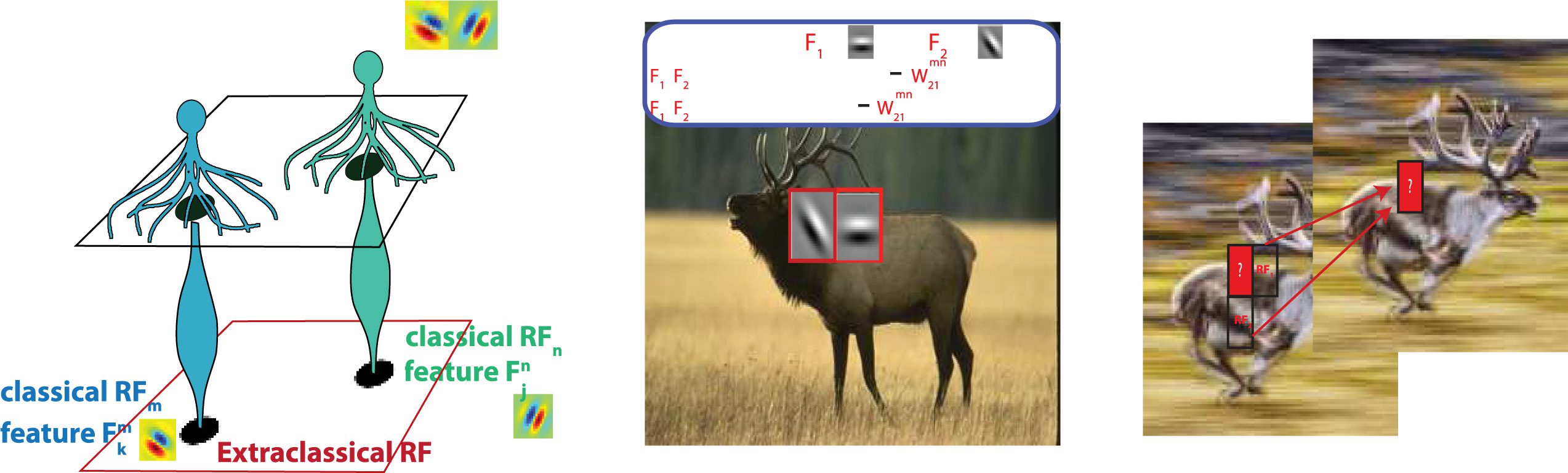
Figur 1: (A) Schematic of circuit involving VIP, SST, PV, and PYR groups of neu-
rons. When VIP are silent, PYR are self-excitatory, while SST and PV inhibit PYR.
When VIP are active, they inhibit the PYR while also creating a disinhibitory mo-
tif given by VIP-SST-PYR. The potential connection from PYR to VIP explored
in this article is marked with a dotted arrow. (B) Processing of two input types
(z.B., Bilder, videos) happens using two separate networks for each type of in-
put, each having N units with 2N2 weights in total to learn. (C) Processing of
two input types can be done with one circuit: a switching circuit with N units
adapted to one of the contexts and M switching units that turn on when the
other context is presented. We may want M << N, with N2 + 2NM connections
to learn (assuming switching units are not interconnected). When the number of
switching units required in a switching circuit is small, fewer connections need
to be learned; more specifically, if M < N/2 ⇒ N2 + 2MN < 2N2. This general-
izes well to a range of circuits, including in the case of sparse connectivities, as
often presented throughout the article.
Cardin, 2018; Rudy, 2011; Pfeffer, Xue, He, Huang, & Scanziani, 2013).
VIP is an inhibitory population of neurons that is strongly modulated by
running (Fu et al., 2014). In our simplified model of the circuit, VIP neurons
act in a switch-like manner: they are silent when animals are static but start
firing when animals are running, inhibiting SST cells and hence releasing
PYR cells from SST inhibition. The disinhibition of PYR cells is not uniform,
but rather a complex pattern that is dependent on the particular PYR cell
response. We will show that the switch can be effective only if PYR cells pro-
vide input information to the VIP cells. Although this simple model does
not capture all the physiological responses of VIP neurons, we believe the
model captures the crux of the disinhibitory switching computation at the
expense of biological realism.
We study this circuit using a model in which the contextual informa-
tion is stored in the lateral connections between neurons (Iyer, Hu, &
Mihalas, 2020). Each neuron receives information about the visual scene
from feedforward connections (which can be arbitrary in this model) and
complements this with surround information provided by nearby neurons.
The connections are dependent on the statistics of the environment; more
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
544
D. Voina et al.
precisely, they depend on the frequency of co-occurrence in the environ-
ment of the features which the neurons represent. These connections are
most useful if the information from the feedforward connections is cor-
rupted (e.g., by occlusions).
Importantly, the contextual information via lateral connections comes
not only from the spatial surround but also from the past. Synaptic de-
lays introduce a constraint on the available information each neuron gets.
During the static condition, past surround information matches present in-
formation, and thus there is no temporal variability of the context. During
movement, this no longer holds; neighboring features now also vary tem-
porally, which changes the co-occurrence frequency; hence, the statistics of
the moving context are different. We aim to find connection strengths from
the switching VIP units that, during movement, modulate firing rates and
neuronal correlation structure to adapt and enhance the encoding of visual
stimuli when the moving context is turned on. Although throughout the ar-
ticle, we focus on the visual circuit and the switching role of the VIP neural
population, these results can be generalized to circuits processing multiple
contexts, and thus their applicability has broader scope. In section 3, we list
several other biological examples of circuits processing multiple contexts.
Understanding switching circuits may also further aid efforts to de-
sign both flexible and efficient artificial neural architectures. This research
area has benefited from bio-inspired architectures and algorithms like elas-
tic weight consolidation (Kirkpatrick, Pascanu, & Hadsel, 2017), intelli-
gent synapses (Zenke, Poole, & Ganguli, 2017), iterative pruning (Mallya
& Lazebnik, 2018), leveraging prior knowledge through lateral connec-
tions (Rusu et al., 2016), task-based hard attention mechanism (Serra, Suris,
Miron, & Karatzoglou, 2018), and block-modular architecture (Terekhov,
Montone, & O’Regan, 2015), for example, to enable sequential learning by
eliminating “catastrophic forgetting” (where previously acquired memo-
ries are overwritten once new tasks are learned). We hypothesize that a few
switching units akin to VIP can be incorporated as part of the hidden lay-
ers to enable context modulation. This makes such a switching circuit ar-
chitecture (see Figure 1c) more efficient than employing separate circuits
for the different contexts (see Figure 1b) because switching circuits have
fewer connections to learn.1 We hope such a circuit architecture will inspire
next-generation flexible artificial nets that can process stimuli in changing
contexts.
1
In general, if N is the number of neurons per location, L is the number of locations,
and C is the number of connections per neuron, then the total number of connections in a
circuit is NLC. Two identical circuits have 2NLC connectivities, while a switching circuit
has NLC + LM(cin
, cout are
the number of connections to and from the switching units, respectively. When M (cid:3) N
+ cout ) which is true
and cin
for circuits with small M, cin
+ cout ), where M is the number of switching (VIP) units and cin
, cout < C, then 2NLC > NLC + LM(cin
+ cout ) ⇔ NC > M(cin
, cout .
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
545
1.1 Article Outline. In section 2.1, we first detail a model introduced in
Iyer et al. (2020) that describes neuronal connections and firing rates of a
circuit adapted to static visual scenes (Bilder). We next extend this model
to the case of circuits adapted to moving visual scenes (videos). These cir-
cuits are attuned to the statistical regularities of movement and take into
account constraints of biological networks, like synaptic delay. We are able
to map these two circuit models to the V1 circuit, consisting of PYR, SST,
and PV neuron populations. We thus obtain two different networks with
full cell-type specifications achieving optimal context integration for static
and moving contexts, jeweils. In section 2.2 we detail the data sets and
procedures used to quantify connectivities and firing rates in these two cir-
cuits. In section 2.3, we go on to describe a circuit that can switch between
neuronal activity in static circuit and neuronal activity in the moving circuit
by virtue of adding a single population, the VIP. We find that VIP projec-
tions to SST and PYR are not enough to shift activity during movement,
but that we need a feedback connection from the PYR to the VIP (section
2.4). The resulting circuit is the minimally complex circuit resembling V1
we have found to switch contexts. In section 2.5, we describe how this cir-
cuit switches using only a small number of VIP units. We follow up on these
results in section 2.6, where we use this switching circuit to obtain better re-
constructions of videos in conditions of high noise. Endlich, we evaluate the
new switching circuit architecture with data from V1 that confirms some of
the model’s predictions (siehe Sektion 2.7).
2 Ergebnisse
2.1 Theoretical Models of Processing Visual Information in Static and
Moving Contexts. We first introduce two models of visual processing in
the V1 in the static and moving contexts where the circuits implementing
the computations perform optimal inference and are adapted to the statis-
tical regularities of the contexts through the lateral connections between
Neuronen.
2.1.1 Model of Visual Processing in the Static Context. To study optimal con-
text integration in the static condition (where the visual input is static im-
Alter), we take as a starting point a model proposed by Iyer et al. (2020)
where model neurons respond to a patch in the visual space—the classical
receptive field—but this response is modulated by a larger region of space—
the extraclassical receptive field. The extraclassical receptive field contribu-
tion is determined by nearby local receptive fields providing indirect input
from a larger area of visual space (see Figure 2a). Speziell, interneuron
interactions providing extraclassical information from the surround via lat-
eral connections (siehe Sektion 4.1) complement intrinsic neuronal responses
to classical receptive fields to determine firing rates.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
546
D. Voina et al.
Figur 2: (A) Neurons receive stimulus input from a patch in space at position n,
their classical receptive field (RFn), but also from surrounding patches in space
(z.B., the patch at position m) through interactions with other neurons. Diese
neurons are connected by weights Wmn
that depend on the statistical regular-
jk
ities of natural scenes. (B) When features F1 and F2 at positions m, n occur to-
gether often in natural scenes, then Wmn
21 is strong; when F1 and F2 occur together
by chance, without significant correlation, Wmn
21 is close to 0. (C) Spatiotemporal
surround for motion processing. Due to synaptic delay, context integration uses
surrounding patches that are also (cid:2)t ms in the past to assess the features in the
present frame.
Starting from the assumption that firing rates of a population of neu-
rons encode the probability of specific features being present in a given lo-
cation of the image, we consider a probabilistic framework that includes
probability of feature occurrence and feature co-occurrence, which we can
then map to an equation involving firing rates of neurons and weights (sehen
section 4.1). Allgemein, a feature j, denoted by F j, describes a specific pat-
tern that neurons are most attuned to, which can vary from simplistic, wie
Gabor filters, to complex, like faces or objects that are robust to stimulus
transformations such as scale and position changes. In more detail, for neu-
rons responding to Fn
J (feature j at patch n in visual space), we define fn
j to
be the steady-state firing rate due to the classical receptive field and rn
j to
be the (overall) steady-state firing rate taking into account the extraclassi-
cal receptive field contribution. The probabilistic assumption stated above
is such that fn
|In) by the following relation,
j relates to the probability p(Fn
J
fn
J
= g(P(Fn
J
|In)),
(2.1)
(cid:2)
j p(Fn
J
where g is a monotonically increasing function, in is a patch n in visual space,
|In) = 1. For simplicity, we fix g to be the identity, leaving the
Und
|In), neu-
relaxation of this linear assumption for future work. With fn
J
rons tuned for distinct features respond differently to the same patch in in
= p(Fn
J
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
547
visual space depending on how well its corresponding feature is repre-
gesendet. Operationally, to compute fn
j in response to an image, we first chose
a basis of features, Zum Beispiel, features obtained by approximating spa-
tial receptive fields from recorded neurons in V1. We then preprocessed the
Bild (siehe Sektion 4.2), convolved the image with feature j and normalized
the result such that the sum over all features is 1 at each spatial position,
and finally considered the patch in of the normalized convolution.
Once fn
J
= p(Fn
J ) = p(Fn
j is computed, we can continue assuming that neuronal firing
rates contain information about feature occurrence in the surround, Also
|i1, i2, . . . , In, . . .), where i1, i2, . . . , im are surrounding
that rn
J
patches of in. We can then use Bayes’ rule to express this probability in terms
of feature probability at patch in and at surrounding locations im (see sec-
tion 4.1 for a detailed calculation) and finally map the resulting equations
to neurobiological quantities (siehe Sektion 4.1). Zusammenfassend, these operations
yield that the firing rates rn
j of neurons are the result of modulating the
classical receptive field firing rate fn
j by extraclassical receptive field in-
formation from the surround, which is a linear function of other neurons’
classical receptive field firing rates, fm
k . These firing rates are weighed by
the lateral connections Wstatic, representing the prior information about the
statistical regularities of natural images. After ignoring terms that are due
to higher-order modulation of the surround (siehe Sektion 4.1), speziell
neurons from the surround having surround modulation of their own, Wir
obtain the following firing rates (see Figure 2a) as explained in detail in
section 4.1:
(cid:3)
rn
J
≈ fn
J
◦
1 +
(cid:5)
Wmn
k j fm
k
,
(cid:4)
M,k
with the weights expressed as
Wmn
k j
=
∩ Fn
P(Fm
J )
k
k )P(Fn
P(Fm
J )
− 1 =
(cid:8)fm
k
(2.2)
− 1,
(2.3)
(cid:9)
, fn
J
(cid:8)fm
k
(cid:9)
all images
(cid:9)
(cid:8)fn
J
all images
all images
(cid:2)
k j fm
M,k Wmn
where Fn
is a Gabor-like feature n at location j that we will illustrate
J
shortly, the symbol ∩ denotes the co-occurrence of two features, and ◦ is
the Hadamard product, the element-wise multiplication between tensors
j and 1 +
fn
k . Weiter, fn
j is the evoked firing rate due to the clas-
sical receptive field of neurons firing for feature Fn
j is the firing
rate of neurons firing for feature Fn
j using information from classical and
is over neurons with
extraclassical receptive fields. The sum
receptive fields at different locations m, responsive to features k. Endlich,
Wmn
is the connectivity in the static context between neurons responsive to
k j
J , and rn
M,k Wmn
k j fm
k
(cid:2)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
548
D. Voina et al.
k and Fn
J . We define Wstatic ≡ {Wmn
}
features Fm
M,N,k, j as the connectivity ap-
plied to static visual scenes. Assuming that weights only connect neurons
with nonoverlapping receptive fields, the resulting weights are sparse (sehen
section 4.2).
k j
From a computational perspective, the organism cannot measure the
feature probabilities and joint probabilities in equations 2.1 Und 2.3 di-
rectly, but these can be estimated given our defined neural code as the
= in ∗ F j, and as the
convolutions between image and feature, P(Fn
J
∩ F j ) =
cross-correlations between classical receptive field firing rates, P(Fk
∗ f j. By mapping these probabilistic statements on feature occurrence to
fk
neurobiological quantities that capture firing rates and weights, we have
obtained a circuit that does approximate context integration, extracting in-
formation through priors embedded in the neural connectivities. While the
start of the model is Bayes optimal via equations 4.12 Und 4.14, a set of ap-
proximations is needed to keep the circuit simple.
|In) = fn
J
There are multiple possible mappings from the probabilistic framework
to the neurobiological circuit (Iyer et al., 2020), but the current correspon-
dence is straightforward and yields successful predictions from data, solch
as like-to-like connectivity, as detailed below. When a pair of features is
frequently co-occurring, weights between neurons preferential for these
features are strong and positive (see Figure 2b). Im Gegensatz, when two
features are unlikely to co-occur in the same image, the connectivity is
strong and negative. Overall occurrence probabilities of individual features
normalize the co-occurrence probabilities so that the weights express the
co-occurrence of features over and above chance. Co-occurrence probabil-
ities of features are then averaged over many natural scenes so that the
corresponding weights Wstatic capture the statistical regularities of natural
environments.
2.1.2 Model of Visual Processing in the Moving Context. We next show how
the framework above can be applied to the moving context. While equa-
tionen 2.2 Und 2.3 show how connectivity and firing rates can be optimized
to account for spatially co-occurring features—features that appear at the
same moment in time but in different locations of the visual field—we
now extend these equations to account for temporal co-occurring features—
features that occur at nearby moments in time at different locations of the
visual field.
In more detail, context is generally integrated from (cid:2)t in the past
due to synaptic delay (see Figure 2c), and weights are proportional to
co-occurrence probabilities of neighboring features that are also separated
by a time window (cid:2)T. This is a direct generalization of the model in Iyer
et al. (2020) to the time domain and includes synaptic delay as a biologi-
cally motivated constraint. The extended model can capture how local cir-
cuit connectivity is shaped by spatiotemporal correlations across receptive
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
549
fields and across time windows characteristic of biological processes like
synaptic delay. The firing rate during the moving context is (see sections
4.1 Und 4.2):
⎛
⎞
rn,T
J
≈ fn,T
J
◦
⎝1 +
(cid:4)
M,k
Wmn,(cid:2)T
k j
fm,t−(cid:2)T
k
⎠ ,
with the weights expressed as
Wmn,(cid:2)T
k j
=
k
P(Fm,T
P(Fm,T
k
∩ Fn,t−(cid:2)T
)P(Fn,t−(cid:2)T
J
J
)
)
− 1 =
(cid:8)fm,T
(cid:9)
k
, fn,t−(cid:2)T
J
(cid:9)
(cid:8)fn,t−(cid:2)T
all videos
(cid:9)
all videos
J
(cid:8)fm,T
k
all videos
(2.4)
− 1,
(2.5)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
where we apply an analogous notation as for equations 2.2 Und 2.3, the only
difference being the additional t, (cid:2)T, t − (cid:2)t superscripts that denote the
time coordinate for the features, firing rates, and weights. Wmoving ≡ Wnm,(cid:2)T
is the connectivity in the moving context between neurons responsive to
features Fm,T
and Fn,t−(cid:2)T
whose activation is separated by a time delay (cid:2)T.
Note that the expression for Wnm,(cid:2)T
as shown in equation 2.5 also holds for
the static context when we use static visual input to compute the weights,
such that ft = ft−(cid:2)t for all t, (cid:2)T.
k j
k j
k
J
We have introduced a model of visual processing where feedforward
and lateral connections between neurons serve different roles. Die seitliche
connections between neurons perform unsupervised learning of the proba-
bility of co-occurrence of visual features that the neurons represent. For the
purpose of this study, the feedforward connections can be arbitrary, Und
the microcircuit described here can be at any level of processing. This sep-
aration of the roles for the feedforward and lateral connections allows for
an easy implementation of both supervised and unsupervised learning in
deep networks (Hu & Mihalas, 2018).
Hier, we show how this model can integrate information from the sur-
round using these within-layer connectivities in both static and moving
Staaten. Jedoch, integration of these two contexts results in two distinct cir-
cuits needed to perform visual processing under different conditions (statisch
versus moving). The model optimally integrates context in the Bayes sense,
meaning it uses priors on the co-occurrence of features in natural scenes
when integrating information from the surround. These priors reflect the
known statistical regularities of the environment (Simoncelli, 2003; Barlow,
1961; Marr, 1982) and weigh the surround contributions appropriately. Wir
are then able to map this model formalism to the circuit architecture in V1
described above while specifying steady-state network weights and acti-
vationen, as well as cell type functionality. This model emphasizes robust
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
550
D. Voina et al.
coding and applies best in conditions of high noise, where parts of the vi-
sual scene are missing due to occlusions or are corrupted, and thus where
context information may play a critical role. We next describe our model of
visual processing in detail.
2.2 Modeling Firing Rates and Weights in Networks Responding to
Images and Videos. We next describe two separate circuits capable of do-
ing optimal context integration in each of the moving and static contexts.
We characterize these two circuits through the connectivities Wstatic and
Wmoving, computed by using images and videos in training data sets and
applying formulas 2.3 Und 2.5. Once the corresponding connectivities are
specified, we can further characterize the static and moving circuits by
their neural activations. Im Folgenden, we elaborate, section by section,
on the algorithm we implemented to compute the static and the moving
weights.
2.2.1 Data Set and Feature Preparation. We applied our framework for pro-
cessing static images and videos to different benchmark data sets, chosen
to address differences in the statistics of visual features across conditions:
during viewing of static images (static condition) and during viewing of
videos that contain motion (moving condition). For the static condition, Wir
gebraucht 300 selected grayscale images of the BSDS data set (Martin, Fowlkes,
Tal, & Malik, 2001) (see Figure 3a) while for videos, the BSDS data set is pre-
processed through a smaller sliding window that travels along the image to
reproduce motion (see Figure 3b and section 4.4). Although in general the
sliding window can move in any direction (see Figures S1 to S2 for results
in diesem Fall), here we constrained it to move solely in the horizontal direc-
tion to roughly approximate flow of images across the (sideways-facing)
eyes of mice during forward movement. We have not used a generic data
set of natural videos since most videos in such data sets contain limited
movement of objects, humans, or animals rather than movement of sections
of an environment that would mimic the visual experience of a running
Tier.
We generated a dictionary of features (filters) based on a parameter-
ized set of models derived from recordings in V1 (Durand et al., 2016).
This contains 18 filters with gaussian subfields (see Figure 3d) at differ-
ent relative intensities and orientations. We added filters containing a tem-
poral dimension—spatiotemporal filters—to obtain a set of 34 filters. Unser
spatiotemporal filters consist of two frames (see Figure 3e) and represent a
temporal shift by several pixels in the horizontal direction, dazugehörigen
to the direction of movement and amount of displacement of the sliding
window in the videos described above.
To more easily illustrate and interpret our model, we first tested our
framework on a different, synthetic context. We analyzed a simplified 9 × 9
world of horizontal and vertical bars moving up and down as well as
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
551
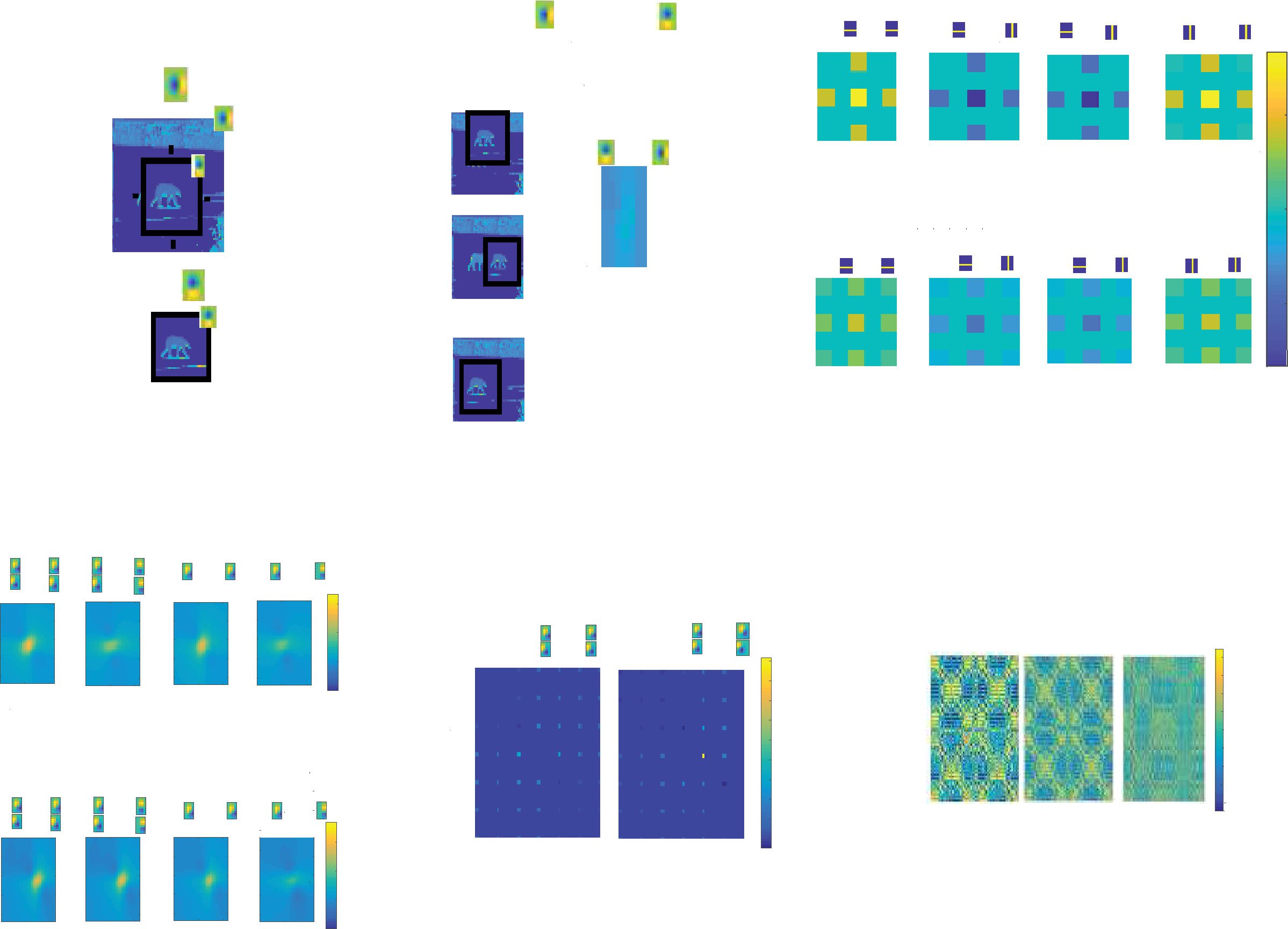
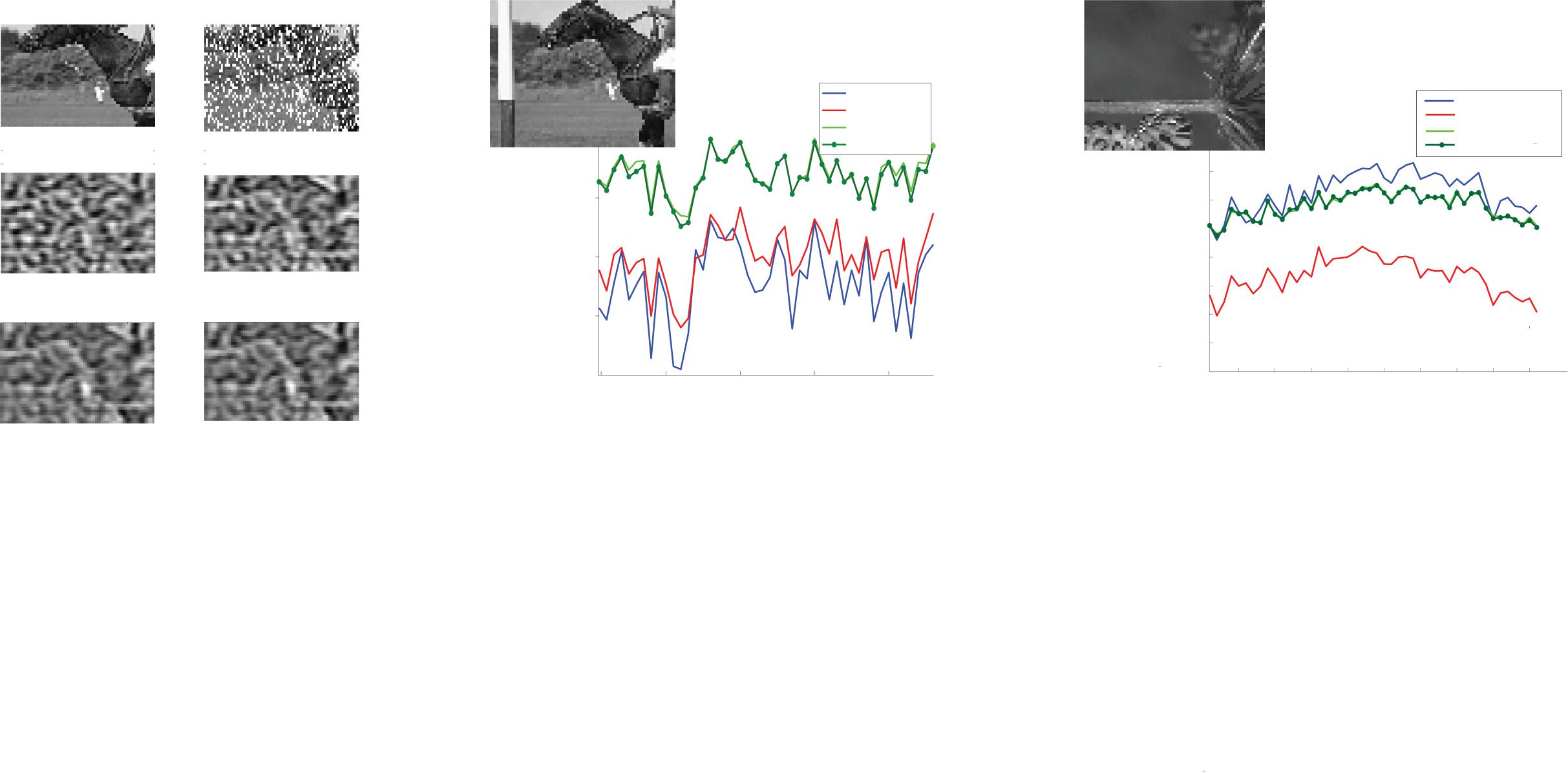
Figur 3: (A) Sample images from the BSDS data set. Images of animals, menschlich
faces, landscapes, buildings, and so on are used. (B) Sliding window on images
from the BSDS data set so that the appearance of movement is achieved. Shown
by the red arrow is how much the window has moved from frame 1 to frame
4. Allgemein, movement of sliding window is random and in any direction, Aber
we focus on horizontal movement in the case of natural videos. (C) Images of
horizontal and vertical bars (über) and how the bars move in videos (below).
(D) Eighteen filters: ON, OFF, ON/OFF with two gaussian subfields, anders
subfields dominating, at different intensities and orientations. Color bars show
the different intensities of pixels. (e) Example of a spatiotemporal filter com-
prising two frames. Spatiotemporal filters are added to the 18 original filters to
make up a total of 34 filters. The filter shown here over two frames captures a
45 deg bar moving to the left and is obtained by translating the original filter by
three pixels. Color bars show the different intensities of pixels to the left. (F) Two
filters for the simplistic “bar world” comprising a horizontal and a vertical bar,
jeweils.
left and right (see Figure 3c). This simple data set has only two features,
horizontal bars and vertical bars (see Figure 3f), but movement can be in
any of the four orthogonal directions.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
2.2.2 Computing the Weights Wstatic, Wmoving. The firing rates f due to the
classical receptive field represent feature probabilities (see equation 2.1 mit
G(X) = x) and were computed by the following sequence of operations: pre-
processing inputs and filters (siehe Sektion 4.2), convolving the image or video
frames with the respective sets of filters, rectifying, and then normalizing
so that all firing rates fm
k lie in the interval between 0 Und 1 and sum up to
1 across all features k. To find the weights for static and moving contexts,
Wstatic and Wmoving, we fixed (cid:2)T. After convolving ft
in accordance
k and ft−(cid:2)T
J
552
D. Voina et al.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4: (A) To obtain the weight matrix, we first take the convolution of video
, i ∗ Fj). We then consider
frames with features from the feature basis (z.B., i ∗ Fk
the convolution of these convolved image frames to detect feature co-occurrence
∗ f j). (B) Schematic of how weights are represented. Normalized con-
(z.B., fk
volutions between patches separated by the same spatial and temporal dis-
tances are averaged and stored in the corresponding entry of the weight matrix.
(C) Top: Static weights for the data set of images of bars. Bottom: Moving weights
for the data set of videos of bars. (D) Static weights (über) and moving weights
(below) for the data set of natural images/videos during horizontal motion
nur. (e) Sparse versions of slices from the static and moving weights for the
data sets of natural images/videos during horizontal motion. Weights between
neurons whose receptive fields are not at certain preselected, sufficiently far
apart locations in the visual space were discarded to satisfy the constraint that
patches are independent. (F) The full (nonsparse) tensors Wstatic, Wmoving, Und
Wmoving − Wstatic, ordered first by spatial position, then by filter.
with equations 2.3 Und 2.5 and following the procedure outlined in Figures
4a and 4b, we obtained a high-dimensional tensor that characterizes the
connections between each pair of cell types (k, J) at each position in the im-
Alter. Using the feature Fk
j as a proxy for a cell “type,” the resulting tensor
is four-dimensional, with dimensions: cell type of the source, cell type of
the target, and relative spatial position of the source and target in x and y
directions.
Context-Dependent Computations in a V1 Local Circuit
553
,n2
, j2
,n4
, j2
= (cid:2)n3
Wann (cid:2)n1
= Wn3
j1
2.2.3 Simplifications to Weights. We make three simplifications to reduce
the number of parameters in this tensor (siehe Sektion 4.2): (1) we assume
translational invariance so that only the relative position of two filters is
− (cid:2)n4); (2) the model is designed
− (cid:2)n2
relevant (Wn1
j1
to compute connections to neurons that receive independent observations;
daher, we only consider connections between neurons whose receptive fields
are sufficiently far apart (d.h., at least half a receptive field apart); (3) as sta-
tistical dependencies in natural images decay with distance, we limit the
spatial extent of connectivity to three times the size of the classical recep-
tive field. Figures 4c and 4d show several 2D slices through this tensor,
corresponding to a specific cell source and target, as well as the full static
and moving weights (see Figure 4f) ordered by spatial position and feature
type (see also Figure S1a). Figure 4c serves to provide some intuition as to
what these weights represent and how they are structured: in the data set
of bars, horizontal feature F1 frequently occurs or is absent together with
other horizontal features F1 at neighboring locations, which leads Wstatic
Zu
have positive values. Umgekehrt, horizontal feature F1 occurs always when
vertical feature F2 is absent, und umgekehrt, leading to negative weights
Wstatic
12
(see Figure 4c).
, Wstatic
21
11
2.2.4 Characterizing Wmoving in the Case of Two Different Video Statistics.
In the generation of the video data set we use a sliding window to enforce
controlled and comparable statistics between the moving and static con-
texts. When the sliding window is free to move in all directions, the mov-
ing weights tend to be weaker in absolute value, which holds for the simple
data set of bars (see Figure 4c), and the weights generated from the data set
of natural images and videos (see Figures S1a to S1b). This effect is due to
the weaker statistical dependence of features separated by the time win-
dow (cid:2)T. Feature co-occurrence, and thus connectivity, is affected by the
distortions during movement, like change of orientation of objects or ap-
pearance or disappearance of objects in the visual scene. Moving weights in
this case are approximately smoothed-out versions of the static weights (sehen
Figures S1a to S1b). In these conditions, as the information from surround
is less reliable, the feedforward input plays a more important role during
Bewegung.
k and Fn+(S,0),t−(cid:2)T
In the case when the sliding window moves s pixels horizontally in (cid:2)T
time steps, Fn,T
actually coincide so that their probability
of co-occurrence is maximized. This means that for horizontal movement,
peaks s pixels from the center for any feature Fk and Wn,n+(S,0),(cid:2)T
Wmoving
kk
is strong (see Figures 4d to 4e). Results for natural videos below are for
horizontal movement, although the same general conclusions hold when
movement is allowed in any direction (see Figure S2).
Endlich, using Wstatic, Wmoving and applying equations 2.2 Und 2.4 we ob-
kk
k
tain the corresponding firing rates r in both static and moving contexts.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
554
D. Voina et al.
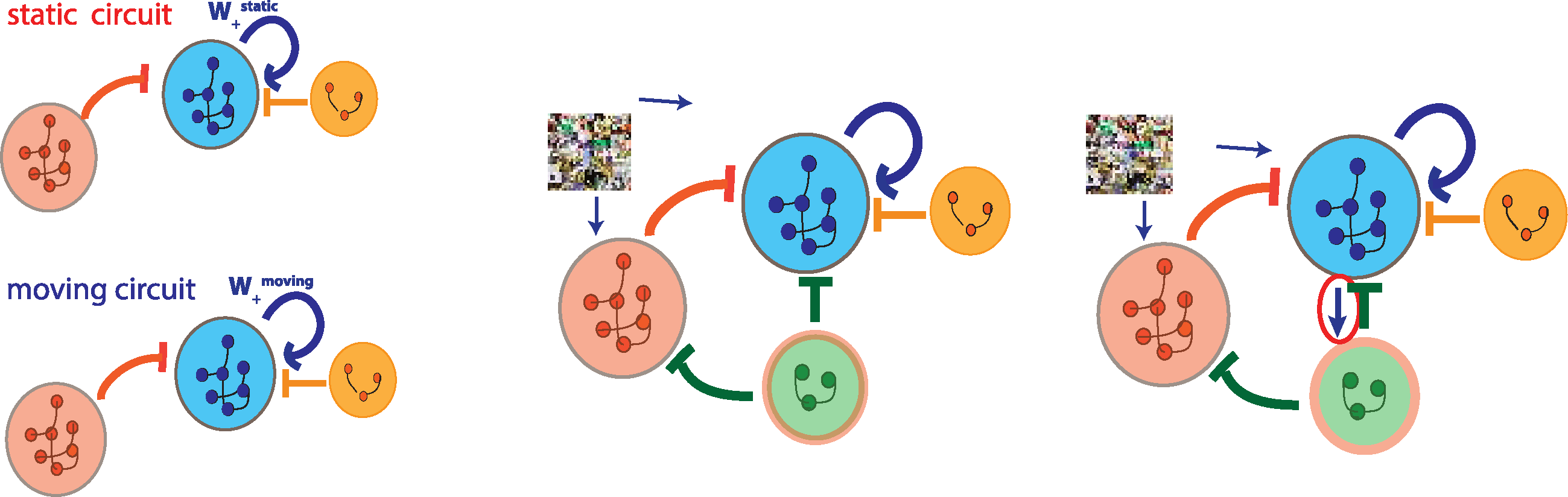
Figur 5: (A) Two separate circuits for optimal visual processing of static (top)
and moving contexts (bottom), jeweils. (B) The proposed switching circuit
with the VIP population approximates the static circuit when the VIP are silent
and the animal is static, and approximates the moving circuit when the VIP
are active and the animal is moving. (C) Previous circuit, but with a feedback
connection added from the PYR population to the VIP.
2.3 Implementing a Switching Circuit. Having two just defined opti-
mal connectivities, Wstatic and Wmoving, for the static and moving contexts,
we next consider whether a single circuit involving the cell types described
über (VIP, PYR, SST, and PV) can respond optimally in these two contexts
and switch between them. We additionally seek the computational princi-
ples behind the minimally complex circuit (d.h., the circuit with fewest con-
nections) for such a switching circuit. Speziell, we ask whether a circuit
with optimal weights for the static context can switch to produce nearly op-
timal activities in the moving context, via projections from a set of switching
Einheiten. In such a circuit, every PYR neuron approximates Bayesian inference,
combining classical receptive field information with information from the
surround to estimate feature probability.
We start by rewriting the model described by equations 2.2 Und 2.4 In
vector form to obtain the following firing rates:
rt,static = ft ◦ (1 + Wstaticft ),
rt,moving = ft ◦ (1 + Wmovingft ).
(2.6)
(2.7)
Assuming, as discussed above, that the activation of the VIP neural popula-
tion implements the switch between contexts, we want the switching circuit
to reproduce the firing rates given by equation 2.6 when the VIP neurons are
silent in the static context, and the firing rates given by equation 2.7 Wann
the VIP neurons are active in the moving context (see Figures 5a and 5b).
We next explain how rstatic, rmoving above can be modeled as the firing rates
of the PYR neurons.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
555
When the VIP are silent, the only groups of neurons active are PV, SST,
and PYR. This circuit is equivalent to one without any VIP connections,
reproducing firing rates of PYR given by equation 2.6 when the animal is
statisch. PYR neurons contribute to integrating surround information through
excitatory projections and receive inhibitory feedback from SST interneu-
rons (Braitenberg & Schuz, 1991). PV implements a normalization of the
PYR population in our model, consistent with data on their connectivity
(Jiang et al., 2015; Pfeffer et al., 2013). Empirically it has been shown these
neurons receive the average inputs of the PYR neurons whose receptive
fields overlap with their classical receptive fields and project back equally
(Pfeffer et al., 2013). In our model, this normalization applies to the clas-
sical receptive field f, as described in section 4.1. As for the role of PYR
and SST, given that PYR are excitatory and SST are inhibitory and that
Wstatic = Wstatic
, it is natural to map the positive component of the
−
static weights, Wstatic
, to the connections within the PYR population, Und
the negative component of the static weights, Wstatic
, to the inhibitory con-
−
nections from SST to PYR. Somit, we obtain the following:
+ + Wstatic
+
rt,static = ft ◦ (1 + Wstaticft ) = ft ◦ (1 + Wstatic
+
ft + Wstatic
−
ft )
(2.8)
can be mapped to
rt,static = ft ◦ (1 + Wstaticft ) = ft ◦ (1 + WPYR→PYRft + WSST→PYRft ),
(2.9)
where WX→Y denotes the weights that connect neuronal populations X (Die
source) and Y (the target).
On the other hand when VIP are active, PYR firing rates ought to repro-
duce the activity given by equation 2.7. We make the simplifying assump-
tions that the switch from static to moving can happen instantaneously and
that the VIP switch is binary. When the animal initiates movement and the
VIP turns on, the model circuit should approximate the optimal response
of PYR neurons resulting from the Wmoving connectivities, within a circuit
where the four neuronal populations interact (see Figure 5b). For VIP mod-
ulation of PYR (which is either direct or through the SST) that gives rise to
the optimal firing rates in the moving context, we have that
rt,moving = ft ◦ (1 + Wmovingft−(cid:2)T )
(2.10)
is mapped to
rt,moving = ft ◦ (1 + Wstaticft−(cid:2)T + VIP contribution).
(2.11)
Daher, the switch in the circuit occurs as VIP neurons modulate SST and
PYR neurons and make PYR switch firing rates from rstatic to rmoving. Wir
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
556
D. Voina et al.
now proceed to find the unknown connectivities from VIP to PYR and from
VIP to SST that cause this to occur within the circuit (see Figures 5b and 5c).
2.4 In the Absence of Feedback to VIP Neurons, the Circuit Is Unable
to Switch from Static to Moving Conditions. We attempt to describe the
computational principles of the minimal switching circuit inspired by the
V1 circuitry whose main structure and logic were described in Fu et al.,
(2014). After adding the switching population VIP, the goal is to find con-
nectivities from VIP to the other two neuronal populations (PYR, SST) Das
would account for the PYR firing rates that yield optimal representation in
the moving context. With the VIP contribution, the firing rate of PYR neu-
rons can be expressed as (siehe Sektion 4.5)
rt,moving = ft ◦ (1 + Wstaticft−(cid:2)T + WSST→PYRWVIP→SSTft−(cid:2)T,VIP
+ WVIP →PYRft−(cid:2)T,VIP),
(2.12)
where ft, ft−(cid:2)t are firing rates due to the classical receptive field at times
t and t − (cid:2)t and inferred from the data set of natural videos as outlined
in sections 2.1 Und 4.2, ft,VIP are the intrinsic firing rates of the VIP at time
T, and rt,moving is the firing rate during the moving context with the extra-
classical receptive field contribution. Hier, WSST→PYR are weights from SST
to PYR, WVIP→SST are weights from VIP to SST, and WVIP →PYR are weights
from VIP to PYR. VIP neurons project to PYR neurons directly via weights
WVIP→PYR and indirectly via the SST population. The effects of the indirect
pathway VIP-SST-PYR can be captured by taking the product of connectiv-
ities, yielding WSST→PYRWVIP→SST . The three unknown variables are then
ft,VIP, WVIP→SST, and WVIP →PYR, but since we assume ft,VIP is constant in
time t, this tensor can be combined with the connectivities to form the ef-
fective parameters
α = WVIP→SST ft−(cid:2)T,VIP
F
Und
β = WVIP→PYRft−(cid:2)T,VIP
F
(2.13)
(2.14)
and hence reduce the number of unknowns and simplify notation. Our ob-
jective is to have firing rates in the switching circuit be as closely matched
as possible to the firing rates in the separate moving circuit with Wmoving:
rmoving,t = ft ◦ (1 + Wmovingft−(cid:2)T )
≈ ft ◦ (1 + Wstaticft−(cid:2)T + WSST→PYRf
β
α + F
).
(2.15)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
557
This amounts to minimizing the loss function defined by the approximation
error Eswitch,1 over the variables fα, fβ
:
fα ,fβ Eswitch,1
min
= min
fα ,fβ
1
N
(cid:4)
F
(cid:13)(Wmoving − Wstatic)f − WSST →PYRf
α − f
β (cid:13)F,
(2.16)
Wo (cid:13) · (cid:13)F is the Frobenius norm of a tensor, for all f (firing rates due to
classical receptive fields) corresponding to video frames, and N is a nor-
malization factor, the number of video frames in our data set. f is inferred
through our model from the data sets of video frames and features using
|In) = in ∗ F j and thus is a known quantity throughout the opti-
fn
J
mization. Wichtig, since ft,VIP are firing rates and hence ft,VIP ≥ 0, while
WSST→PYR ≤ 0, WVIP→SST ≤ 0, and WVIP→PYR ≤ 0, we have that fα, fβ ≤ 0,
and WSST→PYRfα ≥ 0.
= p(Fn
J
and fβ
This is a high-dimensional constrained optimization problem with the
loss function defined as in equation 2.16, which we solved by means of a
gradient descent method using the gradient-based Adam optimizer, imple-
mented in PyTorch.2 The weights fα
as defined in equations 2.13 Und
2.14 are unknown and learned by stochastic gradient descent (SGD), while
Wmoving, Wstatic, WSST→PYR ≡ [Wstatic]− are fixed. Finding the global mini-
mum of the loss function is difficult, but the main goal is to find weights
that give a small enough error Eswitch,1 instead and later test these on a
specific task to demonstrate that the optimal moving circuit can be approx-
imated successfully (siehe Sektion 2.6). We assessed the stability of our opti-
mization by modifying several learning parameters—for example, learning
rate (ranging from 0.001 Zu 0.1) and optimization algorithm (SGD, AdaGrad,
RMSProp, Adam)—and checking the generalization error on a small num-
ber of frames (50) that were not used during training.
Regardless of hyperparameters, our optimization procedure did not find
weights that together approximate the moving circuit significantly better
than the static circuit. Mit anderen Worten, adding VIP neurons in an attempt to
switch contexts does not lead to a significantly better approximation of the
moving circuit than having no VIPs. This result holds for both the simple
data set of horizontal and vertical bars and for the more complex data set
of natural images and videos (see Figures 6b and 6c).
In order to understand the origin of this failure, we mathematically an-
≈ 0, Dann
alyzed the circuit at hand. Analytically, if the loss is small Eswitch,1
(Wmoving − Wstatic)f ≈ WSST→PYRfα + fβ
, where f is unique to each image
in the data. The left side becomes a term that varies across a wide range
2
The tensor weights are very high-dimensional so that the least-squares method and
variations thereof have failed due to the high memory requirements.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
558
D. Voina et al.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 6: (A) Goal: Instead of two separate circuits for visual processing of static
and moving contexts, the proposed circuit approximates the static circuit when
the VIP are silent and the animal is static and the moving circuit when the VIP
are active and the animal is moving. (B) Generalization/validation error found
during the optimization to minimize the functional Eswitch,1 for the data sets of
static and moving bars does not converge. (C) Generalization/validation error
found during the optimization to minimize the functional Eswitch,1 for the data
sets of natural images and videos converges, but the norm of the loss function
decreases by only ≈ 25%. (D) Circuit as in panel a, but with a feedback connec-
tion added from the PYR population to the VIP. (e) Training error (Blau) Und
generalization/validation error (Rot) found during the optimization to mini-
mize the functional Eswitch,2 (movement approximation error) for the data sets
of natural images and videos converges to yield a relatively small error. (F) Der
movement approximation error for various circuit architectures: the static cir-
cuit with no VIP switching units, the circuit depicted in panel a without PYR to
VIP feedback, and the circuit depicted in panel d.
of video frames, while the right side is a constant term incorporating the
weights we are solving for: fα, fβ
. This suggests that the failure of our op-
timization procedure to yield weights that approximate the moving circuit
results from the VIP having no stimulus dependence.
We conclude that the circuit switching between static and moving con-
texts must be more complex than the simple circuit here, which has only
Context-Dependent Computations in a V1 Local Circuit
559
outgoing projections from VIP. Below, we introduce recurrent connections
that make the VIP input dependent and overcome the limitations above.
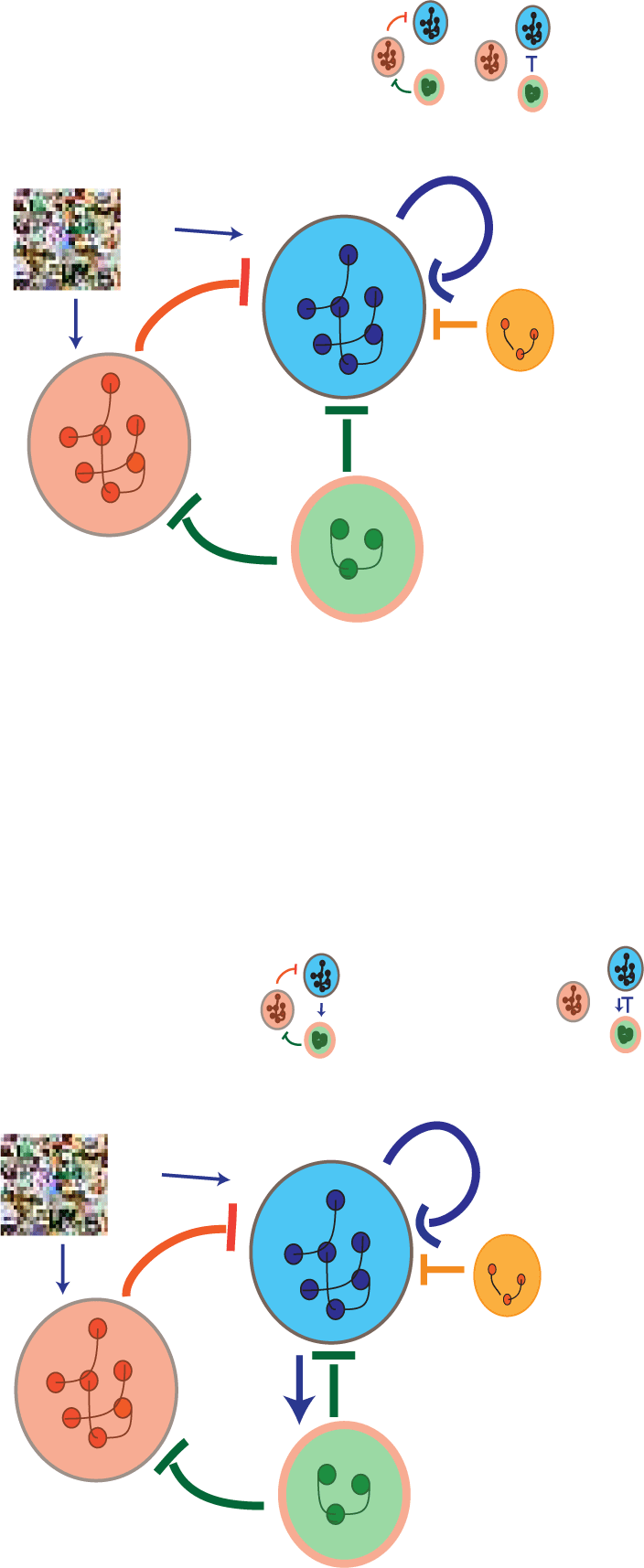
2.5 VIP Circuit with Feedback from the PYR Cells Can Switch Context
Integration from Static to Moving Conditions. Above we showed that
a minimal switching circuit with only outgoing projections from the VIP
units is insufficient to switch between the two contexts. Somit, we added
a connection between PYR and VIP, such that the VIP group of neurons
has access to information about the visual input through PYR (siehe Abbildung
5C). In this case we can approximate the firing rate of PYR during move-
ment as follows, using the same conventions and assumptions as before (sehen
section 4.5):
rmoving,t = ft ◦ (1 + Wstaticft−(cid:2)T + WSST→PYRWVIP→SSTWPYR→VIPft−(cid:2)T +
+ WVIP →PYRWPYR →VIPft−(cid:2)T ).
(2.17)
We remind the reader that f is the contribution to the firing rate of the
classical receptive field, and WX→Y are the weights from population X of
neurons to population Y of neurons, where X, Y are the PYR, SST, VIP neu-
rons. In addition to the fixed Wstatic and Wmoving, we also fix WSST →PYR =
[Wstatic]−. A schematic of the underlying circuit model, along with the cor-
responding formula for the firing rate of PYR, is shown in Figure 6d.
We would like to find the three unknown weights WVIP→PYR,
WVIP→SST , and WPYR→VIP to best achieve the approximation:
rmoving,t = ft ◦ (1 + Wmovingft−(cid:2)T )
≈ ft ◦ (1 + Wstaticft−(cid:2)T + WSST→PYRWVIP→SSTWPYR→VIPft−(cid:2)T +
+ WVIP→PYRWPYR→VIPft−(cid:2)T ).
(2.18)
We denote the approximated expression of equation 2.18 by rapprox. Das
approximation rapprox ≈ rmoving amounts to minimizing the loss function
defining the movement approximation error Eswitch,2:
Eswitch,2
= 1
N
(cid:4)
F
(cid:13)(Wmoving − Wstatic)f − WSST→PYRWVIP→SSTWPYR→VIPf −
− WVIP→PYRWPYR→VIPf(cid:13)F,
(2.19)
for all N frames whose corresponding classical receptive field firing rate is f.
In the case of simple images and videos of bars, we consider W · f to be the
regular matrix vector multiplication, while in the case of natural scenes, Wir
perform the convolution operation W ∗ f. Applying convolution for natural
images and videos fits with the assumption we have applied for the PYR,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
560
D. Voina et al.
SST populations that weights between neurons are translationally invari-
ant, and further reduces the number of parameters.
To solve this high-dimensional optimization problem, we set up, as in
section 2.4, an optimization problem with the loss function being the aver-
age Frobenius norm as defined in equation 2.19. Weights to and from VIP
are unknown (WVIP→SST, WVIP→PYR, and WPYR→VIP) and learned by SGD,
while Wmoving − Wstatic, WSST→PYR are fixed. Wichtig, Dale’s law is en-
forced (WVIP→SST, WVIP→PYR ≤ 0, WPYR→VIP ≥ 0) for biological realism.
To find how many switching units are needed, we varied the number of
VIP neurons, which was equivalent to varying the dimensionality of ten-
sors WVIP→SST, WVIP→PYR, and WPYR→VIP. We found the smallest number of
switching neurons VIP that enabled the loss (see equation 2.19) to be min-
imized. We first considered the simple image/video data set, which was
9 × 9 with horizontal and vertical bars. In this case, the loss was minimized
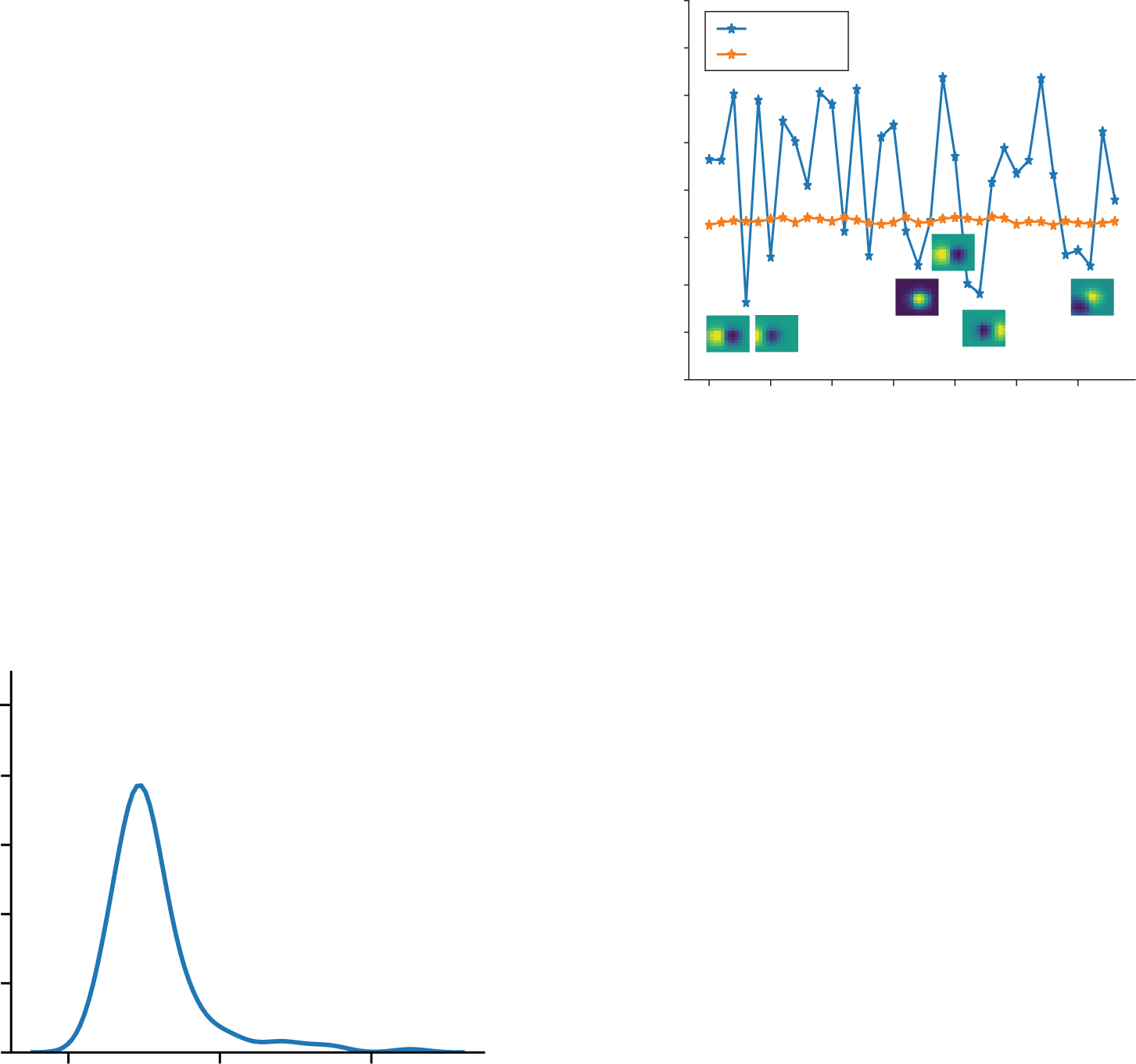
with at least 20 VIP neurons (see Figure 7a). For comparison, es gibt 162
PYR and SST neurons, one for each filter and pixel in the image or frame. Als
increasing the number of VIP units further does not decrease the loss func-
tion, we conclude that for the case of bar-like images, having 20 switching
units is enough.
Zweite, in the distinct case of more complex stimuli like images and
videos of natural scenes, the movement approximation error in equation
2.19 was minimized when the number of VIP units is 34 per unit space,
which matches the number of units in the PYR and SST population. Wie-
immer, the approximation error was already significantly minimized with
nur 5 VIP units per unit space, without any significant improvement af-
ter adding more units (see Figure 7b). Varying the dimensionality of spatial
components of the tensors (see Figure S4) we were solving for (WVIP→SST ,
WVIP→PYR, WPYR→VIP) and the synaptic delay (cid:2)t for sparse weights W that
account for patch independence, we obtained the same qualitative results.
Our results also hold for nonsparse weights, as shown in Figure S5a. Fixing
the number of VIP units to 5 per unit space, we find that the approximated
firing rate of equation 2.18 matches rmoving compared to the rstatic firing rates
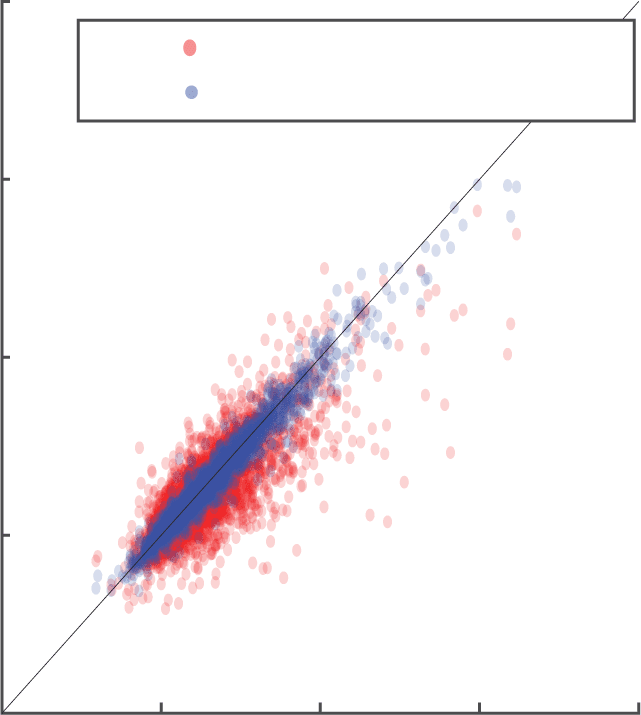
of a circuit without VIP units (see Figure 7c). We conclude that for the spe-
cific parameters chosen in Figure 7b, the ratio of PYR to switching VIP units
Ist 34/5 = 6.9, so that the switching operation requires relatively few units,
a fact we return to in the context of the underlying biology below.
All in all, we have shown that a switching circuit with relatively few
numbers of switching VIP units and appropriate feedback connections can
be implemented to achieve visual processing during the static and moving
contexts, and for both a simple synthetic data set of bars and a biologically
relevant data set of natural images and videos.
2.6 Context-Dependent Visual Processing with Extraclassical Recep-
tive Fields Leads to Denoising. According to our theory (siehe Sektion 4.1),
the moving circuit achieves optimality of visual processing for videos, Die
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
561
Figur 7: (A) Adding VIP switching units to the circuit processing videos of
bars approximates the activity to that of the optimal circuit for moving con-
text for this simple data set. Jedoch, no more than 20 VIPs are needed in
üben, compared to the 162 PYR and SST cells. (B) Adding VIP switching
units to the circuit processing natural videos approximates the activity to that
of the optimal circuit for moving context for the naturalistic data set. Wie-
immer, no more than 5 VIPs per unit space are needed in practice, compared to
Die 34 PYR and SST cells per unit space. The parameters chosen for this opti-
mization are (cid:2)t = 2 and dim(WVIP→SST ) = dim(WVIP→PYR) = 34 × N f2
× 3 × 3,
dim(WPYR→VIP) = N f2
× 34 × 3 × 3, where N f2 is the variable number of VIP
Einheiten. (C) A random subset of activities corresponding to different video frames,
filters, spatial positions for the static, moving, and approximated moving cir-
cuit. Red dots for activities for moving circuit (rmoving) versus activities for static
circuit (rstatic); blue dots for activities for moving circuit versus activities for ap-
proximated switching circuit (rapprox). Activities are computed using weights
mit 5 VIP units/unit space. Activities chosen for the approximated switching
circuit are able to better estimate the activities in the moving circuit in compar-
ison to the ability of the activities in the static circuit to estimate the activities in
the moving circuit.
static circuit achieves optimality of processing for static images, and we
have found appropriate connectivities to and from a population of switch-
ing units—VIP—that can approximate either circuit in a model of V1, Die
switching circuit. Wir haben, Jedoch, not yet assessed the performance of
these circuits on specific visual processing tasks. We pursue this here for
the task of denoising. Speziell, we ask how well (1) extra-classical re-
ceptive field contributions from the static or moving circuits (see Figure 5a)
can improve reconstructions of noisy images and videos and (2) ob
the switching circuit can achieve the same level of performance as the sep-
arately optimized moving circuit when processing videos. We focus on re-
constructions of video frames and the superior performance of the moving
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
562
D. Voina et al.
and switching circuits for processing moving contexts, although we also
mention the comparably high performance of the static circuit and implic-
itly that of the switching circuit responding to static scenes, for processing
static contexts.
To reconstruct a visual scene during movement, our brain uses informa-
tion from the present but also time-delayed surround information, both of
which can be inaccurate or incomplete. We use Wmoving to weigh the past
surround information, as these weights encapsulate the cross-correlational
structure between features of the past and the present, thereby informing
which features are more or less likely. We note that during motion, verwenden
Wstatic to weigh surround information may still be better than using no sur-
round information at all: if movement in the videos is slow enough or (cid:2)t is
small, features are smooth and Wstatic and Wmoving are highly correlated.
To apply our models to the task of denoising, we apply gaussian white
noise or salt and pepper noise ξ to the original frames X of the videos (sehen
Figure 8a) and compute firing rates in the circuits in response to the noisy
frames X + ξ . The firing rates are expressed as
rno EXC(T) = ft,
(2.20)
rstatic(T) = ft ◦ (1 + Wstaticft−(cid:2)T ),
rmoving(T) = ft ◦ (1 + Wmovingft−(cid:2)T ),
(2.22)
rapprox(T) = ft ◦ (1 + Wstaticft−(cid:2)T + WSST→PYRWVIP→SST WPYR→VIPft−(cid:2)T +
(2.21)
+ WVIP→PYRWPYR→VIPft−(cid:2)T ).
(2.23)
We denote “EXC” throughout the figures and text to represent the extraclas-
sical receptive field contribution. Somit, rno EXC is the firing rate due to only
the feedforward pathway, with no lateral connections, and thus without
any extraclassical, surround modulation. In the case of rstatic (rmoving), Wstatic
(Wmoving) weights are the lateral connections applied that weigh the extra-
classical receptive field information from the past surround. While Wstatic
are nonoptimal weights to compute the firing rate, Wmoving are optimal for
inferring features in noisy conditions as described below (siehe Sektion 4.1).
Endlich, rapprox results from lateral connections from our switching circuit
with connections to and from VIP.
For each image frame X, we computed the corresponding firing rate r
via equations 2.20 Zu 2.23 to obtain a tensor with entries for every filter and
spatial position of X. We then deconvolved r for each filter F j (siehe Sektion
4.6) along its corresponding dimension to obtain the “reconstructed” frame
X(cid:16):
X + ξ → r → X
(cid:16).
(2.24)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
563
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
N
e
C
Ö
_
A
_
0
1
4
7
2
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 8: (A) Example of a reconstructed frame for each condition/circuit ar-
chitecture: no EXC, static EXC, moving EXC, approximated EXC. (B) Average
correlation coefficients between reconstructed noisy frames and reconstructed
noiseless frames for one video in our data set. Hier, reconstruction benefits from
surround contextual information. (C) Same as panel a but in this case, the gen-
eral inequality that holds on average ρ(rno EXC), ρ(rstatic) < ρ(rmoving) ≈ ρ(rapprox)
breaks down and r(rno EXC) ≈ r(rmoving). (d) Average correlation coefficient over
all frames and all videos after salt and pepper noise was added to the video
frames. The probability is 0.2 each pixel is changed to white and 0.2 each pixel is
changed to black, and (cid:2)t = 2 (frames). The moving and approximated EXC av-
erage correlation coefficients are higher than for static EXC or no EXC (p-value
< 0.05 using the Wilcoxon rank-sum test for all relevant comparisons). Inset:
Correlation coefficients in time, averaged across videos. (e) Same as panel d for
gaussian white noise with 0.5 standard deviation. (cid:2)t = 2 (frames). p < 0.05 for
all relevant comparisons, Wilcoxon rank-sum test. (f) Average correlation coeffi-
cient over frames and videos as noise level is varied. Top: Salt and pepper noise
is varied; Down: Gaussian white noise SD is varied.
Although there are ways for a biological circuit to do more accurate recon-
structions (e.g., via learning weights), we have chosen a simple reconstruc-
tion approach that does not require additional assumptions here (e.g., the
circuit does not know the structure of the noise or the input), as described
in section 4.6.
We compare the quality of reconstructions from the four circuit models
above. The baseline for these comparisons is the reconstruction of a noise-
less image frame (ξ = 0), where the extraclassical contribution does not
564
D. Voina et al.
provide any additional information. (Note that this reconstruction X(cid:16)
is not
the same as the original frame X, as all feature information not included in
the filters is lost in the initial convolution of the image frame to get r). We de-
note by ρ(·) a metric of the quality of the reconstruction. This takes the firing
rate r as input and generates the Pearson correlation coefficient between the
reconstruction X(cid:16)
and the baseline reconstruction described above as out-
put. The metric ρ for a video frame with noise ξ is
ρ(r) = Corr(X
(cid:16)
ξ , X
(cid:16)
ξ =0) =
(X(cid:16)
ξ − ¯X(cid:16)
(cid:13)Xξ − ¯Xξ (cid:13)
ξ ) · (X(cid:16)
ξ =0
(cid:13)Xξ =0
2
− ¯X(cid:16)
− ¯Xξ =0
ξ =0)
(cid:13)
2
,
(2.25)
where · is the dot product and ¯X, ¯X(cid:16) are the means of the image and recon-
struction, respectively. The upper limit for correlation coefficient is 1 when
there is no noise in the image or frame (see Figure 8f).
Thus equipped, we ask which circuit architecture gives rise to neural
activity best suited for decoding visual scenes in noisy conditions. Fig-
ure 8a shows reconstructions of a video frame using different such circuit
architectures. We expect ρ(rno EXC), ρ(rstatic) < ρ(rmoving), ρ(rapprox) on aver-
age, as Wmoving are the optimal lateral connections as defined above. How-
ever, the exact relationship between ρ(rno EXC), ρ(rstatic), ρ(rmoving), ρ(rapprox)
depends on the exact correlational structure of the frames for each video.
Some videos match our prediction that ρ(rmoving) is maximized (see Figure
8b), while other videos do not (see Figure 8c). Specifically, there are videos
where surround modulation is not effective, which appears to be due to the
presence of independent features where the information in the extraclassi-
cal receptive field does not aid image reconstruction.
On average throughout the videos, rmoving and rapprox yield the best
reconstructions (dark and light green bars), displaying the highest cross-
correlation coefficients ρ between the noiseless reconstruction (the base-
line) and the reconstructed frames (see Figure 8d). Figures 8d and 8e show
this holds true when adding to the original frames either salt and pepper
noise, when we varied the proportion of pixels occluded, or gaussian white
noise, when we varied the standard deviation of the normal distribution of
noise. The relation ρ(rno EXC), ρ(rstatic) < ρ(rmoving) ≈ ρ(rapprox) is robust to
the amount of noise added to the frames (see Figure 8f), whether for salt
and pepper noise or gaussian noise. This holds true both when the com-
plete set of 34 spatiotemporal filters is used (see Figure S10a) and when only
the set of 18 filters with no temporal component is used (see Figure S10b).
As expected, the addition of filters with a temporal component improves
the reconstruction performance in all four circuit architectures presented
(see Figure S10c). Furthermore, reconstruction performance for images in
the static condition is maximized on average using Wstatic to weigh the sur-
round so that ρ(rno EXC), ρ(rmoving), ρ(rapprox) < ρ(rstatic) on average (see Fig-
ure S9). This shows that the moving circuit is best used for processing noisy
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
565
video frames and that the static circuit (or switching circuit with VIP silent)
is ideally used for processing images at the highest performance.
Thus, the switching circuit provides reconstruction performance compa-
rable to a dedicated moving circuit for videos and comparable to a ded-
icated static circuit for images. In the case of videos, this is because the
switching circuit reproduces firing rates that are close enough to rmoving to
improve reconstruction fidelity. The correlation coefficients found between
noiseless baseline reconstructions and reconstructions due to the moving
and switching circuits, respectively, present almost perfect overlap (light
and dark green curves in Figures S10a and S10b). In sum, we conclude that
the extraclassical receptive field contribution in the moving circuit and ap-
proximated switching circuit generates neural activity that can be decoded
to produce more accurate frame reconstructions in videos. To produce the
most accurate image reconstructions, the VIP neurons in the switching cir-
cuit must be silent so that the network implements the static circuit.
2.7 Experimental Evidence of VIP Role in Movement-Related Visual
Coding. When we examine the weights W to and from the VIP we have
inferred in our model, we find that there are a few equally correct solutions
for the optimization problem, equation 2.19, due to the multiple local min-
ima of the movement approximation error. One of the possible solutions we
found matched experimental data showing that in various layers of V1, the
VIP-to-SST connection is strong compared to other connections, specifically
the VIP-to-PYR connection (see Figure S6). Interestingly, this property arose
only when including weights from SST to VIP in the circuit, consistent with
experiments (Pfeffer et al., 2013, found the connection probability/strength
from SST to VIP to be strong). Including this connection in our circuit and
rewriting the circuit equations as in equation 4.24, we obtain a new set of
connectivity patterns and activities so that we can now compare predictions
of our model switching circuit to the extensive empirical evidence from the
literature.
Importantly, we have not meticulously explored the set of all possible so-
lutions from the optimization problem, equation 2.19, and, further, the op-
timization may allow additional constraints to the switching circuit while
still admitting solutions. Acknowledging this, we now study both the con-
nectivity and activity of the switching circuit with an additional SST to VIP
connection.
2.7.1 Connectivity. We find that our model produces connectivity pat-
terns that are largely consistent with empirical findings, as we describe
next. Connection weights in the model can be interpreted as correspond-
ing to a combination of connection probabilities and connection strengths
in the data, as these have been shown to correlate well (Cossell et al., 2015).
Regarding the connection from the VIP to SST, experimental data on con-
nectivity in the visual cortex from Pfeffer et al. (2013) has shown that in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
566
D. Voina et al.
layer 4 of V1, the average connection probability from VIP to SST is dou-
ble the connection probability from VIP to PYR (0.625 compared to 0.351),
while in layer 5, VIP to SST is five times more probable (0.625 compared
to 0.125) (Pfeffer et al., 2013). A recent study by Campagnola et al. (2021)
has confirmed the relative paucity of VIP-to-PYR connections as compared
to VIP-to-SST connections throughout all layers, for example finding 3 out
of 52 VIP-to-PYR versus 5 out of 33 VIP to SST interarea L2/3 connections
(Campagnola et al., 2021). VIP-to-SST connections are also stronger than
VIP-to-PYR throughout all the layers: 0.32 compared to 0.28 as found by
Jiang et al. (2015) and 0.3 compared to 0.21 as found by Campagnola et al.
(2021).
We next examine the distribution of connectivity patterns in our compu-
tational model, as displayed in Figures 9a and 9b, and compare these model
findings with experimental results. As found empirically, VIP-to-PYR con-
nections in our model are sparser than VIP-to-SST connections, with a large
peak at 0 in the connectivity histogram, in addition to being on average
weaker (0.38 versus 0.47 for average weights in our model). Despite their
sparsity, our model predicts a long tail to the distribution of VIP-to-PYR
connection strengths. In addition, our model also predicts very high vari-
ability of WVIP→PYR connection strengths averaged with respect to the filter
(which represents the postsynaptic cell type) as shown in Figure 9c. The
strong connections correspond to the vertically oriented filters, as detailed
below. We conclude that our model agrees with previous measurements
and makes further predictions on the V1 microcircuit connectivity when
including weights from SST to VIP.
We next inquire whether the synapses encode the contextual statistics by
probing like-to-like connectivity both between PYR neurons and between
VIP and PYR populations of neurons (see section 4.9). We find that while
there is like-to-like connectivity between PYR neurons as found by Iyer et al.
(2020), this effect is largely absent between the VIP and PYR. To further ex-
amine the pattern of connectivity from the VIP, we correlate both WVIP→PYR
and WVIP→SST to Wmoving/static and Wmoving − Wstatic, because these latter
weights reflect the statistical regularities of the static and moving contexts.
We obtain that after averaging over presynaptic filters (N f2) and the spa-
tial receptive fields, WVIP→PYR correlates positively with Wmoving − Wstatic
(0.41, p-value < 0.02, two-sided t-test); while WVIP→SST also correlates pos-
itively, the correlation coefficient is weaker and not statistically significant.
Similarly, the convolution WPYR→VIP→PYR ≡ WVIP→PYR ∗ WPYR→VIP also cor-
relates positively with Wmoving − Wstatic (0.15, p-value < 0.01, two-sided
t-test).
Analyzing the
average postsynaptic weights Wmoving − Wstatic,
WVIP→PYR, WPYR→VIP→PYR more specifically, we find that the strongest
connections are for inhibited postsynaptic units corresponding to ver-
tical or diagonal filters. Looking at the strongest inhibitory weights for
WVIP→PYR, for example (see Figure 9c), we find that 6/10 correspond to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
567
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: (a–c) Analysis of model connectivities WVIP→SST , WVIP→PYR. (a) His-
togram of the absolute value of connectivities for WVIP→PYR showing a mean of
0.31. (b) Histogram of the absolute value of connectivities for WVIP→SST showing
a mean of 0.4. (c) Average connectivity per filter, corresponding to the postsy-
naptic cell type, for WVIP→PYR (blue) and WVIP→SST (orange). Filters for postsy-
naptic units corresponding to the strongest conectivities are displayed to show
what units are strongly inhibited during movement. (d–f) Data analysis of VIP
population activity in calcium imaging data. (d) Dimensionality ratio (partic-
ipation ratio measure) during periods of spontaneous activity between move-
ment and static conditions across CRE lines. (e) Histogram of the modulation
of dimensionality (statistics relative to the blue bar in panel d). (f) Activity (dff
signal) ratio during periods of natural images viewing between movement and
static conditions across CRE lines.
postsynaptic vertical filters and 9/10 to either vertical or diagonal post-
synaptic filters. For Wmoving − Wstatic and WPYR→VIP→PYR, 7 out of 10 such
filters are vertical or diagonal (see Figure S11). We note also that the average
connection strength of Wmoving − Wstatic for postsynaptic vertical filters is
−5) compared to that for horizontal filters
negative and stronger (−5.4 · 10
−6). This can be interpreted as follows: our videos feature horizontal
(2 · 10
movement, hence the spatiotemporal co-occurrence for vertical features
in particular will be distorted during the moving context; this results in
weaker Wmoving weights overall when the postsynaptic cell responds to
vertical filters and thus Wmoving − Wstatic weights are strongly negative on
average for such filters. The overall positive correlation of Wmoving − Wstatic
with WVIP→PYR, WPYR→VIP→PYR determines that postsynaptic units tuned
568
D. Voina et al.
for vertical features will be more strongly inhibited through these connec-
tions when switching from static to moving contexts. This phenomenon
is more prevalent for WVIP→PYR where more of the strongest connections
(9/10) are driven at least in part by inhibition of vertically tuned units, and
in contrast with Wstatic and even Wmoving, where the strongest inhibitory
connections are mostly for horizontally tuned units (5/5 and 5/5, respec-
tively, of top inhibitory filters are either horizontal or diagonal) while
Wstatic, Wmoving connections for vertically tuned units are mostly excitatory
(on average, 1.4 · 10
−5, respectively).
−4 and 8.7 · 10
2.7.2 Activity. We next study the consistency of activity patterns pro-
duced by our model with respect to empirical data. Published experimen-
tal findings provide strong evidence that the VIP inhibitory population
acts to modulate the visual circuitry in a movement-dependent manner
(Niell & Stryker, 2010; Pfeffer et al., 2013; Fu et al., 2014). Very recent
results show that VIP neurons respond synergistically to stimuli mov-
ing front to back during locomotion, a conjunction expected during lo-
comotion in a natural environment for mice, with a preference for low
but nonzero contrasts (Millman et al., 2020). Such movement-modulated
activity matches the one required in our models, although we have not en-
dowed the VIP units with specific feature selectivity. Additionally, we per-
form a set of new analyses of experimental data in the context of our model.
These draw both on the literature and on the Allen Brain Observatory
(http://observatory.brain-map.org/visualcoding, 2016), which contains in
vivo physiological activity in the mouse visual cortex, featuring representa-
tions of visually evoked calcium responses from GCaMP6-expressing neu-
rons in selected cortical layers, visual areas, and Cre lines. The data set
contains calcium activations across multiple experimental conditions, and
here we focus on periods of spontaneous activity, natural images, and
drifting gratings.
Our model of the switching circuit shows that the relative number of
VIP neurons required to switch between moving and static contexts is low
when compared to the number of PYR or SST neurons (see Figures 7a and
7b). This number qualitatively matches the relative abundance of neurons
in the three populations. Excitatory neurons PYR are more abundant than
inhibitory ones (roughly 80% to 20%), and VIP are a minority of inhibitory
cells. Moreover, the existing VIP cells recorded in the Allen Observatory
do not appear to exploit substantially more degrees of freedom (as mea-
sured by their relative dimensionality) than other cell populations (see Fig-
ure S10a), consistent with a small number of effective VIP “units.”
We now highlight two aspects of VIP neural activity that are directly
related to our model and justify the choice of VIP as switching units
whose activities are modulated by the locomotion state of the animal. First,
VIP activity dimensionality is significantly modulated across the moving
and static conditions during periods of spontaneous activity, as shown in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
569
Figures 9d and 9e. To extract such dimensionality modulation, we consid-
ered periods of spontaneous activity in the recordings and divided the sta-
tistical distribution of the animal’s speed, for each experimental session,
into four quartiles. We then computed the average dimensionality, or partic-
ipation ratio (PR; see section 4.8) for each recording in each quartile, which
we define here as the (lower) dimension of a subspace where the data of ac-
tivations can be represented while retaining some meaningful properties of
the original data. We define the dimensionality modulation to be the ratio
between the average dimensionality distribution within the highest quartile
(movement condition) and the average within the first quartile (static con-
dition). Such ratio is displayed in Figure 9e. The dimensionality of the VIP
population is significantly modulated by movement, while in other popu-
lations, the same quantity was not significantly different across moving and
static conditions (see Figure 9d). The histogram of such statistics is shown
in Figure 9e.
Second, we analyzed evoked activity during the animals’ viewing of
natural scenes. We performed a calcium signal modulation analysis and
found that for this stimulus set, the activity was strongly modulated for
the VIP population and less so for other neural populations (see Figure
9f) across moving and static conditions assessed via the quartile method
just described. This further confirms the stronger VIP modulation across
the moving-static conditions. Further pieces of experimental evidence are
presented in Figure S12.
Finally, we analyzed the activities of VIP and PYR neuron populations.
Similar to Niell and Stryker (2010), we find the activity of the PYR during
the moving condition to be higher than the stationary condition on average
(0.066 versus 0.074, p-value < 0.01). However, our PYR population activity
does not double during locomotion compared to periods of stationarity, as
in Niell and Stryker (2010). More recent studies, however, have reproduced
the relation between excitatory neuronal activity in mouse visual cortex and
running but have observed a much weaker relation (Millman et al., 2020,
Figure 5e).
We conducted further analysis to infer the tuning properties of the PYR
and the VIP. This was achieved by considering a wavelet family (e.g.,
Daubechies), taking the two-dimensional discrete wavelet transforms of
the video frames in our data, regarding the corresponding average wavelet
transforms as features, and finally performing a linear regression or GLM
against VIP or PYR activities with the average wavelet transforms as the
independent variables (see section 4.9). We find that most PYR neurons are
tuned to horizontal features, and much less to vertical features. Because VIP
neurons in our model only get input from the PYR, while the top-down in-
put activating VIP is described simply by the binary term st, VIP acquires
the same preferential selectivity to horizontal features over and above that
to vertical features (see Figure S13 and section 4.9 for details). This is counter
to what we would expect if the VIP were capable of detecting the horizontal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
570
D. Voina et al.
movement in our data set by exhibiting preferential selectivity toward ver-
tical features within their receptive fields instead of through the ad hoc bulit
in switch term st. We conclude the simplification used by employing a bi-
nary term st in equation 4.27 prevents us from observing a more realistic
VIP activation pattern that would deviate from the PYR pattern and pro-
vide further insight. This points to an important direction for future and to
more detailed modeling expanding on our current simplified model.
Altogether these comparisons provide further support for our modeling
assumptions and for the role of VIP neurons in visual coding across static
and moving conditions. We conclude that our switching circuit model re-
produces the global pattern of interactions via VIP that we expect, approxi-
mating the static and moving circuits, synchronal with VIP activation. Fur-
ther analysis of future data sets, as examined in section 3, will guide next
steps of circuit modeling.
3 Discussion
We have introduced a computational model for V1 circuitry that uses mul-
tiple cell types to integrate contextual information into local visual process-
ing, during two different—static and moving—contexts. We have identified
a need for recurrence, leading to the architecture of a switching circuit with
bidirectional, learned connections to a switching population (here, the VIP
cell class). Beyond V1 and biological circuit modeling, this circuit may be
useful in searching for artificial neural network (ANN) architectures that
can operate in different contexts and switch effectively between them.
Our model connects to a body of recent empirical studies elucidating
V1 neural cell types and network logic. First, Niell and Stryker (2010) have
established that as the speed of mice increases, the circuit increases spik-
ing overall and changes the frequency content of local field potentials. Po-
tentially, distinct activity patterns during locomotion could be attributed
to effects from eye movements; however, Niell and Stryker provide evi-
dence against this hypothesis. These findings prompt us to model the net-
work as a switching circuit that adapts its activity as the state of the animal
changes from static to moving. Later studies have focused on the connection
strengths for excitatory and inhibitory neurons: neurons display like-to-like
connectivity (Cossell et al., 2015; Ko et al., 2011), whereby neurons with sim-
ilar orientation tuning have a higher probability of connecting and display
stronger connections on average. Pfeffer et al. (2013) describe the V1 cir-
cuit logic by using transgenic mouse lines expressing fluorescent proteins
or Cre-recombinase, providing a consistent classification of cell populations
across experiments. Three large nonoverlapping classes of molecularly dis-
tinct interneurons that interact via a simple connectivity scheme were iden-
tified: PV, SST, and VIP inhibitory neurons. In particular, PV inhibit one
another, SST avoid one another and inhibit all other types of interneurons,
and VIP preferentially inhibit SST cells.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
571
Another important development made by Fu et al. (2014) has estab-
lished that locomotion activates VIP neurons independent of visual stim-
ulation and predominantly through nicotinic inputs from basal forebrain.
This study was the first to propose the existence of a cortical circuit for the
enhancement of visual response by locomotion, describing a modulation of
sensory processing by behavioral state. These studies motivate us to choose
VIP as switching units and to map the positive and negative weights of our
model to connectivities between different neuronal populations. Finally, an-
other study suggests that differentiated network response during locomo-
tion can be advantageous for visual processing (Dadarlat & Stryker, 2017):
an increase in firing rates can enhance the mutual information between vi-
sual stimuli and single neuron responses over a fixed window of time, while
noise correlations decrease across the population, which further improves
stimulus discrimination. The authors hypothesize that cortical state modu-
lation due to locomotion likely increases visually pertinent information en-
coded in the V1 population during times when visual information changes
rapidly, such as during movement.
At least one study (Dipoppa et al., 2018) has disputed the findings of
Neill and Stryker and of Fu et al., finding contrary evidence to the disin-
hibitory model. Experiments with the light on and visual stimuli present
showed that locomotion increased both SST responses to large stimuli and
VIP responses to small stimuli. However, the authors note that rerunning
the measurements in darkness reproduced results from Fu et al., reinforc-
ing the assumption that our model operates in conditions of poor visibility
and high noise.
There is a vast literature on models of efficient coding starting with Bar-
low (1961) and Attneave (1954). (For a great description of this literature,
see Chalk, Marre, & Tkaˇcik, 2018.) On one extreme, if the signal-to-noise
ratio is high and additional constraints (e.g., sparsity) are introduced, such
models emphasize redundancy reduction (Olshausen & Field, 1996a; Rao
& Ballard, 1999; Harpur & Prager, 1996; Comon, 1994; Bell & Sejnowski,
1995; Zemel, 1993; Dayan, Hinton, Neal, & Zemel, 1995). At the other ex-
treme, if the signal-to-noise ratio is low, such models emphasize robust cod-
ing (Karklin & Simoncelli, 2011; Doi & Lewicki, 2014). We use a theoretical
framework that emphasizes robust coding and that we have selected be-
cause of its generality. It starts with an assumption on neuronal activation
functionality (i.e., firing rates of neurons encode the probability of specific
features being present in a given location of the image). This model de-
scribes local circuit interactions needed for integration of information from
surrounding visual stimuli in noisy conditions for an arbitrary represen-
tation. The model matches multiple empirical findings—for example that
statistical regularities of natural images give rise to like-to-like local circuit
connectivities, as observed experimentally (Cossell et al., 2015; Ko et al.,
2011). However, in different contexts the model predicts different functional
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
572
D. Voina et al.
lateral interactions. Therefore, we looked at circuits that can implement
multiple functional interactions in one circuit.
Our model also relates to other switching circuits reported in the experi-
mental literature. For example, selective inhibition of a subset of neurons in
central nucleus of the amygdala (CeA) led to decreased conditioned freez-
ing behavior and increased cortical arousal as visualized by fMRI (Gozzi
et al., 2010). This therefore identifies a circuit that can shift fear reactions
from passive to active. Another study has unraveled the cellular identity of
the neural switch that governs the alternative activation of aggression and
courtship in Drosophila fruit flies (Koganezawa et al., 2016). While these
studies detail circuits responsible for switching behaviors, there are circuits
switching between contexts: from detection of weak visual stimuli to dis-
crimination after adaptation in mice (Ollerenshaw, Zheng, Millard, Wang, &
Stanley, 2014); from high-response firing during active whisker movement,
to low response when no tactile processing is initiated (Zhou et al., 2017);
from odor attraction in food-deprived larva switching to odor aversion in
well-fed larva (Vogt et al., 2020).
In contrast to this rich body of experimental studies, there are relatively
few computational models proposed so far that explain switching of cir-
cuits (Yang et al., 2019). We may compare our V1 circuit to the recurrent
circuits using FORCE learning, where a single unit or a few units project
their feedback onto a recurrent neural net and momentarily disrupt chaotic
activity to enable training. VIP units in our model precisely resemble such
output units providing feedback in the FORCE framework, but it is unclear
how far this analogy goes and to what extent the framework in Sussillo and
Abbott (2009) is helpful in understanding V1 circuitry.
Another interesting example of a circuit with flexible, context-dependent
behavior has been proposed by Mante et al. (2013), where prefrontal cortex
(PFC) activity is modulated by the presence of a visual cue signaling which
feature (color versus direction) the animals must integrate in a random-dots
decision task. PFC functionality in this task has been modeled using a re-
current neural network (RNN) that takes the direction of motion, color of
random dots, and visual cue as input and outputs the appropriate, reward-
generating direction to saccade. This suggests the RNN enacts a potentially
new mechanism for selection and integration of context-dependent inputs,
with gating possible because the representations of the inputs and the up-
coming choice are separable at the population level, even though they are
deeply entangled at the single neuron level. The architecture of the model
RNN proposed in this study is simpler than what we have laid out while
also attaining high flexibility. There are important differences between the
framework outlined in this article and our work. First, it is unclear what the
number of weights in the network might be for the circuit in Mante et al.
(2013) to be multitasking. One of our main motivations has been to achieve
a switching circuit with few added units and weights, so that the circuit
has fewer weights to learn than two separate circuits processing the two
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
573
contexts independently. It is unclear if this potential advantage holds in the
case of Mante et al. Second, our circuit adapts to the statistics of both static
and moving scenes and yields firing rates that are optimal for visual pro-
cessing in either context. In the case of Mante et al., the circuit does not
change momentary input processing when the context changes; it simply
adapts its dynamics to integrate the appropriate feature and initiate the ac-
tion that will be rewarded. Context takes on different meanings in these two
instances: in our model, context is given by the statistical regularities of a
certain environment, static or moving and in Mante et al., context refers
to an input cue that changes the goals and reward dependencies of ac-
tions within the task. Importantly, we have focused on switching circuits
that modulate their responses to different sensory contexts, as opposed to
different input cues and behaviors. It is unclear whether identical or dif-
ferent mechanisms for switching apply in the case of sensory processing
or action selection, when the animal changes scene statistics or behaviors,
respectively.
Although our model is faithful to some aspects of the biology of V1
circuits, it has several limitations. First, it has been reported that during
animal locomotion, firing rates of neurons more than double, at least in lay-
ers II/III of V1. Our firing rates are normalized to sum to one across fea-
tures and cannot reproduce a doubling occurring uniformly over features.
Second, the model does not reproduce a few experimental findings as re-
ported in Ayaz, Saleem, Scholvinc, and Carandini (2013) and Keller et al.
(2020). For instance, locomotion does not increase spontaneous activity as
found by sequentially showing, to the static and moving circuits, images
where every pixel takes on a constant value or images with gaussian white
noise (0.13 versus 0.11 mean static, moving activity for constant pixel im-
ages; 0.063 versus 0.53 mean static, moving activity for gaussian white noise
images/videos). Similar to Keller et al., the firing rate due to the cross-
oriented surround is only slightly higher than the firing rate due to the iso-
oriented surround (0.087 versus 0.085, p-value < 0.015; see Figure S14 for
stimuli shown to the circuits). However, locomotion does weaken signals
conveying surround suppression as reported in Ayaz et al. through the in-
hibition of the SST population by the VIP.
Moreover, another study (Dadarlat & Stryker, 2017) reported that noise
correlations are reduced during motion, but this does not occur in our
model. Further, we model VIP as a switch that is off during the static condi-
tion and has an activation during locomotion dependent on input images,
whereas data show VIP activity is modulated at a finer scale and correlates
strongly with speed (Fu et al., 2014). In addition, VIP switching units in our
model turn on based on perfect knowledge of whether the animal is static
or moving, rather than based on more subtle time-varying visual or mo-
tor features. Furthermore, data from Ko et al. (2011), Pfeffer et al. (2013),
Jiang et al. (2015), Hofer et al. (2011), Lefort, Tomm, Floyd Sarria, and Pe-
tersen (2009), Thomson, West, Wang, and Bannister (2002), and Cauli et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
574
D. Voina et al.
(1997) on connection probabilities and strengths between neuron popula-
tions present a richer, more complex picture than our simplified circuit.
There is wide-ranging connectivity to and from PV, there are strong connec-
tions from PYR to SST in most layers, and the weights from SST to VIP are
strong (in terms of both connection probability and strength across layers),
details that our simplified model cannot describe. Enabling weights from
SST to VIP showed that we can similarly infer weights to and from VIP so
that we are able to approximate the circuit during the moving condition (see
Figures S6a and S6b). However, there are still many more potential connec-
tivity structures between neuron populations our model does not describe.
From a computational perspective, our model makes several simplifi-
cations in describing context integration in circuits tuned to the statistical
regularities of natural scenes. These include approximating a product with
a sum in equation 4.12 and ignoring higher-order surround modulation go-
ing from equation 4.6 to 4.8. Furthermore, our equations have omitted terms
explicitly describing feedback from higher-order areas. Top-down input to
the VIP that mediates increase of local PYR activity has been reported, for
example, in Zhang et al. (2014), Wilmes and Clopath (2019), Hertäg and
Sprekeler (2019), Batista-Brito, Zagha, Ratliff, & Vinck (2018), and Wall et al.
(2016). In our model, terms modulating the VIP firing rate causing the neu-
ronal population to have a switch-like behavior have been essentially en-
capsulated into the binary st variable in equation 4.27. Despite the fact that
incorporating cell type-specific contributions of top-down feedback in our
model is an avenue of clear importance to relate to recent experimental
findings, we leave this to future work. For simplicity, we have also limited
the basis set of filters to one that extracts information about oriented edges
in natural scenes. However, the computation of the extraclassical receptive
fields need not be intrinsically limited to simple cells responding to Gabor-
like filters but can be extended to encompass neurons responding to more
complex features in areas beyond V1. Switching circuits can occur more
generally, including in somatosensory and auditory cortices, where some
of the same neuronal populations interact using similar circuit logic (Niell
& Stryker, 2010; Bigelow, Morrill, Dekloe, & Hasenstaub, 2019). Populations
of neurons in general switching circuits can respond to diverse stimuli (e.g.,
the VIP in auditory cortex are activated by punishment in Pi et al., 2013).
The theoretical framework here did not make assumptions regarding the
completeness of the basis. Instead, it focuses specifically on interactions out-
side the classical receptive field. Prior work of Olshausen (2013), Olshausen
and Field (1996a, 1996b, 1997), and Lewicki and Sejnowski (2000) have dis-
cussed extensively the benefits of overcomplete bases. The key feature in
our model is the normalization of the activity of the neurons in patch, not
the orthogonality or completeness of the basis (indeed, 34 filters used here
are not orthogonal). In our model, the interactions outside the classical re-
ceptive field of a cell are expressed exclusively on the representations by
the cells with classical receptive fields in that location. As such, features
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
575
not represented in an incomplete basis will be ignored in the context calcu-
lations. We use a relatively simple linear model for the classical receptive
field formation. If there are nonlinear interactions in the classical receptive
field, the model can be expanded to represent covariance of neuronal ac-
tivities rather than covariance of projections on a linear filter; however, the
analysis of such an extension is beyond the scope of the current study.
Here, we showed how a biologically inspired switching mechanism can
enable a network to efficiently process stimuli in two different conditions.
Most artificial neural networks (ANNs) suffer from what has been termed
catastrophic forgetting, by which previously acquired memories are over-
written once new tasks are learned. Conversely, humans and other animals
are capable of transfer learning—the ability to use past information without
overwriting previous knowledge. Proposed solutions to this problem, like
elastic weight consolidation or intelligent synapses, are discussed in Kirk-
patrick et al. (2017), Zenke et al. (2017), and Mallya, Davis, and Lazebnik
(2018). When applied to a narrow condition of learning new contexts, our
work adds a switching mechanism based on the connections among differ-
ent cell types in V1. This may open new doors to artificial neural networks
with analogous switching architectures.
4 Methods
4.1 A Theory of Optimal Integration of Static Context in Images. A
theory of optimal context integration, first outlined in Iyer et al. (2020),
describes a probabilistic framework for inferring features at particular
locations of an image given the features at surrounding locations. The
probabilities of these feature occurring and co-occurring are then mapped
to elements of a biological circuit (firing rates, weights).
4.1.1 Neuronal Code. We assume the firing rate of neurons to be a func-
tion of the probability of a feature being present at a specific location of the
image:
fm
k,X
= g(p(Fm
k
|iX )),
(4.1)
where fm
k,X represents the firing rate due to the classical receptive field of
a neuron coding for feature Fk at location m in response to image iX and g
is a monotonic function. For every image and every location, we impose a
normalization over features:
(cid:4)
k
p(Fm
k
|iX ) =
(cid:4)
k
−1(fm
g
k,X ) = 1.
(4.2)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
576
D. Voina et al.
Thus, the sum over probabilities of features adds up to 1. Throughout
the article, we assume g(y) = y, although the model may be applied with
other monotonic functions as well.
4.1.2 Probabilistic Framework. We subdivide the image X into N patches
that correspond to the classical receptive fields of neurons. Thus, we have
p(Fm
k
|iX ) = p(Fm
k
|i1
X
, i2
X
X ).
, . . . , iN
(4.3)
We will assume from this point forward that the firing rates are in response
to an image X (iX) but omit the subscript X to simplify the notation.
We first look at the simple case where there are only two patches: the
classical receptive field (patch im) and the surround, which is part of the
extraclassical receptive field (patch in). We will take into account other
surrounding patches later when we perform an order expansion from
|i1, i2, . . . , iN ). The aim in the simple case with two
p(Fm
k
patches is to infer to what extent feature Fk at patch im, denoted by Fm
k , is
present given information from both the classical receptive field and the sur-
rounding extraclassical receptive field. Using Bayes’ rule and simple prob-
abilistic relations, we sum over all possible features Fm
|im, in) to p(Fm
k
j in patch im to get
p(Fm
k
|im, in) =
(cid:4)
j
p(Fm
k
|im, in, Fn
j )p(Fn
j
|im, in).
(4.4)
We can simplify the above relation by assuming the surround contribu-
tion from in does not contain higher-order surround information; instead,
j ) ≈
it includes only data from the classical receptive field: p(Fm
k
p(Fm
j ). Our previous probabilistic statement, equation 4.4, thus
k
becomes
|im, in, Fn
|im, Fn
p(Fm
k
|im, in) =
(cid:4)
j
p(Fm
k
|im, Fn
j )p(Fn
j
|im, in).
Using Bayes’ rule for the first term,
p(Fm
k
|im, Fn
j ) =
p(Fn
j
|Fm
k
p(Fn
j
, im)p(Fm
k
|im)
|im)
,
equation 4.5 becomes
p(Fm
k
|im, in) = p(Fm
k
|im)
(cid:4)
j
p(Fn
j
p(Fn
j
|im, Fm
k )
|im)
p(Fn
j
|im, in).
(4.5)
(4.6)
(4.7)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
577
Assuming that we can ignore higher-order contributions due to surround
modulation (i.e., the surround modulation of the surround), we can make
|im, Fm
the following simplifications: p(Fn
j ), and
j
|in). This way, patch in is in the surround of patch im and
p(Fn
j
modulates the firing rate due to im, but we are not concerned about the fur-
ther effect in has on im. Then equation 4.6 thus becomes
|im, in) ≈ p(Fn
j
k ) ≈ p(Fn
|im) ≈ p(Fn
k ), p(Fn
j
|Fm
j
p(Fm
k
|im, Fn
j ) =
p(Fn
j
∩ Fm
p(Fn
k )p(Fm
k
j )p(Fm
k )
|im)
.
(4.8)
The original equation, 4.4, becomes
p(Fm
k
|im, in) = p(Fm
k
|im)
p(Fn
j
1 +
k ) − p(Fn
∩ Fm
j )p(Fm
p(Fn
k )
j )p(Fm
k )
(cid:5)
(cid:3)
(cid:4)
j
⎛
p(Fn
j
|in) ⇔ (4.9)
⎞
p(Fm
k
|im, in) = p(Fm
k
|im)
⎝1 +
(cid:4)
p(Fn
j
j
k ) − p(Fn
∩ Fm
j )p(Fm
p(Fn
k )
j )p(Fm
k )
p(Fn
j
⎠ .
|in)
(4.10)
The last equivalence holds because we have assumed in equation 4.2 that
all probabilities sum to 1.
We can now go from two patches to N patches that cover the entire im-
age: i1, i2, . . . , iN. We further assume that each patch provides independent
information to a neuron coding for Fm
k so that we obtain
p(Fm
k
|i) = p(Fm
k
|i1, i2, . . . , iN )
⎛
= p(Fm
k
|im) ·
N(cid:10)
n(cid:17)=m
(cid:4)
p(Fn
j
⎝1 +
j
k ) − p(Fn
∩ Fm
j )p(Fm
p(Fn
k )
j )p(Fm
k )
⎞
p(Fn
j
⎠ .
|in)
(4.11)
If the contribution from each patch is very small, we can ignore the higher-
i(1 + xi) ≈ 1 +
order terms in equation 4.11 and apply the approximation
(cid:2)
(cid:11)
i xi for xi
(cid:3) 1:
p(Fm
k
|i) = p(Fm
k
|i1, i2, . . . , iN )
⎛
= p(Fm
k
|im) ·
⎝1 +
(cid:4)
(cid:4)
p(Fn
j
n,n(cid:17)=m
j
k ) − p(Fn
∩ Fm
j )p(Fm
p(Fn
k )
j )p(Fm
k )
⎞
p(Fn
j
|in)
⎠. (4.12)
4.1.3 Mapping from the Probabilistic Framework to a Neural Network. Using
a simple neural code with g(x) = x, so that the firing rate represents the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
578
D. Voina et al.
probability of feature presence, we obtain a simple mapping to a network
of neurons. We denote
p(Fm
k
Wmn
k j
=
∩ Fn
j ) − p(Fm
k )p(Fn
j )
k )p(Fn
j )
p(Fm
=
∩ Fn
p(Fm
j )
k
k )p(Fn
p(Fm
j )
− 1
(4.13)
and map Wmn
entially to features Fm
k j to the synaptic weight between neurons responding prefer-
k and Fn
j , respectively. Then equation 4.12 becomes
⎛
⎞
p(Fm
k
|i) = p(Fm
k
|im) ·
⎝1 +
(cid:4)
(cid:4)
n,n(cid:17)=m
j
Wmn
k j p(Fn
j
⎠ .
|in)
(4.14)
|im),
We can also map firing rates to probabilities: rm
k
where rm
k is the firing of the neuron with receptive field at patch m and most
responsive to feature Fk, and fm
k is the firing rate of the same neuron due to
just the classical receptive field im. As we recognize below, inferring these
firing rates from our image and video data sets requires rectification and
normalization so that f and r can be interpreted as probabilities.
|i) and fm
k
= p(Fm
k
= p(Fm
k
The formula for synaptic weight can be expressed based on average ac-
tivities of cells, when X spans a comprehensive set of natural images:
Wmn
k j
=
(cid:8)rm
(cid:9)X
k rn
j
(cid:9)X
(cid:9)X(cid:8)rn
j
(cid:8)rm
k
− 1.
(4.15)
These weights can be achieved using Hebbian learning in an unsupervised
manner. To avoid writing implicit equations for the firing rates, which are
difficult to solve, and to make the computation tractable in practice without
requiring learning, we use an approximation that requires only f, the firing
rates due to the classical receptive fields:
Wmn
k j
≈
(cid:8)fm
(cid:9)X
k fn
j
(cid:9)X
(cid:9)X(cid:8)fn
j
(cid:8)fm
k
− 1.
(4.16)
Finally, the probabilistic equations, 4.12 to 4.14, outlined above can be
rewritten in terms of biologically relevant quantities like firing rates and
synaptic weights by applying the appropriate mappings,
rm
k
= 1
Lm fm
k
(cid:10)
⎛
⎝1 +
(cid:4)
n,n(cid:17)=1
j
⎞
Wmn
k j fn
j
⎠ ,
(4.17)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
579
or, more simply,
rm
k
≈ 1
Lm fm
k
⎛
⎝1 +
(cid:4)
(cid:4)
n,n(cid:17)=m
j
⎞
Wmn
k j fn
j
⎠ ,
(4.18)
when lateral connections given by Wmn
k j all sum up together to have a multi-
plicative effect. Here Lm is a normalization coefficient for patch im since we
require
(cid:4)
k
rm
k
= 1
and thus denote
Lm =
(cid:4)
k
·
fm
k
N(cid:10)
n(cid:17)=m
⎛
⎝1 +
(cid:4)
j
⎞
⎠ .
Wmn
k j fn
j
(4.19)
(4.20)
As outlined in Iyer et al. (2020), this can be implemented in a network in
which a set of neurons responsible for normalization have a divisive effect
on the neurons, are patch-specific (have a classical receptive field of similar
size to the neurons), inhibit equally all the neurons in their image patch,
are untuned to features in the visual space, and receive inputs equal to the
average of the inputs of the neurons in the patch.
4.2 Computing the Synaptic Weights. To compute weights according
to equation 4.16, we first compute fn
k , the firing rates due to the classical re-
ceptive field for every image X in a large data set. Initially, we preprocess
the image: we convert the image to grayscale, subtract the mean, and nor-
malize the image to have a maximum value of 1. Similarly, we preprocess
the filters so the mean of each is 0. fk is the result of convolving X with fea-
ture k, rectifying and then normalizing so that at each location n, the sum
over features k of firing rates fn
k is equal to 1. Rectification ensures that firing
rates are nonnegative, while normalization further ensures we can interpret
f as probabilities. We average these firing rates over all images X in the data
set to obtain (cid:8)fn
(cid:9)X for each feature k. The feature co-occurrence probability
k
given by (cid:8)fm
(cid:9)X in the numerator for the synaptic weight formula is then
, fn
j
k
computed by further pairwise convolution of firing rates due to the classi-
cal receptive field for each possible pair of filters in the basis set and each
image in the data set and then averaged over all images.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
580
D. Voina et al.
For a data set of videos, formula 4.16 becomes
Wm,n,(cid:2)t
,k2
k1
=
(cid:8)fm,t
k
(cid:9)
j
, fn,t−(cid:2)t
(cid:9)
(cid:8)fn,t−(cid:2)t
frames
(cid:9)
frames
j
(cid:8)fm,t
k
frames
− 1.
(4.21)
The feature co-occurrence probability given by (cid:8)fm,t
frames is com-
puted by convolution of firing rates due to the classical receptive field at
different frames (t and t − (cid:2)t) for each video and averaged over all videos
and video frames. The assumption here is that extraclassical effects are de-
layed by a time (cid:2)t that corresponds to the time between movie frames or,
biologically, corresponds to the synaptic delay.
, fn,t−(cid:2)t
(cid:9)
k
j
,n2
, j2
,n4
, j2
− (cid:2)n2
= (cid:2)n3
when (cid:2)n1
We first assume translational invariance so that only the relative posi-
− (cid:2)n4. The
= Wn3
tion of two filters is relevant: Wn1
j1
j1
assumption that weights act with translational invariance allows rewriting
the connectivities as simply a function of the distance, in image space, be-
tween the receptive field centers of the two neurons. Second, the mathemat-
ical validity of our probabilistic framework relies on the assumption that
patches in the visual space, representing receptive fields of neurons, con-
tain independent information. To reconcile this assumption with our em-
pirically derived weights, we only consider connections between neurons
whose receptive fields are sufficiently far apart, regardless of their corre-
sponding feature identity. This leads to the use of sparse weights for mov-
ing and static contexts (see Figure 4e), where the only nonzero weights we
allow in W are spatially farther apart than a minimum distance, which is
half of the receptive field size. More precisely, for every feature k, synaptic
weights from target filters were sampled in steps of 0.5× the receptive field
size at three distances in each direction around (0,0), so that we have synap-
tic weights on a (7 × 7) grid (three connections to the left/up + 3 connec-
tions to the right/down + self-connection = 7). Instead of using these sparse
weights after sampling, we could have also rescaled the original, nonsparse
weights by a scalar α so that (cid:13)Wstatic/moving (sparse) − αWstatic/moving(cid:13) ≈ 0.
Searching over possible values of α, we find α ≈ 1/50. We choose, however,
to work with sparse weights or test our results on the original nonsparse
weights without worrying about the rescaling by α. Although results pre-
sented in this study are largely for sparse weights, we have checked that
the main results also hold when using full connectivity, at least for small
(cid:2)t ∈ {1, 2} (see Figure S6a). Further, assuming that the contribution due
to context integration decays as the filters are spatially farther and farther
apart, we can limit the weights in space to three times the size of the clas-
sical receptive field. Sample synaptic weights obtained using this proce-
dure are shown in Figure 4e (and Figures 4d and 4f without the sampling of
weights).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
581
4.3 Constructing the Feature Space for Natural Images and Videos.
We chose a basis of spatial filters that was constructed as outlined in Iyer
et al. (2020). This is done by averaging approximations of spatial receptive
field sizes from 212 recorded neurons in V1 (Durand et al., 2016). This set
of filters is our first feature space and consists of four classes of spatial RFs
observed experimentally: ON (1 feature), OFF (1 feature), and two versions
of ON/OFF neurons (8 features each, for a total of 16), with the first ver-
sion having a stronger ON subfield and the second a stronger OFF subfield.
Each subfield was modeled as a 2D gaussian with a standard deviation of
σ = 0.5× average subfield size, which was measured to be 4.8 degrees for
the OFF subfield and 4.2 degrees for the ON subfield. The relative orienta-
tion between two subfields for each ON/OFF class was varied uniformly
in steps of 45 degrees, from 0 to 315 degrees. Also for the ON/OFF class,
the relative distance between the centers of the ON and OFF subfields was
chosen to be 5 degrees, which equates to roughly 2σ . According to the data,
the amplitude of the weaker subfield is chosen to be half that of the stronger
subfield, whose highest amplitude was chosen to be unity. These two sub-
fields are then combined additively to form a receptive field whose size is
7 degrees (the distance between the two subfields plus σ ). The set of 18 fea-
tures is shown in Figure 3d.
We then added 16 more filters with a temporal component, for a total
of 34 filters. These filters have two frames with the first frame being one of
the ON/OFF filters. The second frame is the ON/OFF filter in the previous
frame shifted 3 pixels to the left, which matches the distance the sliding
window moves every frame to generate the video. Such a spatiotemporal
filter is shown in Figure 3e.
4.4 Data Sets of Natural and Synthetic Images and Videos.
4.4.1 Natural Images and Videos. For the data set of images, we used the
Berkeley Segmentation Dataset (BSDS) training and test data sets (Martin
et al., 2001). The training data set consists of 200 images of animals, human
faces, landscapes, buildings, and so on and is used compute the weights
Wstatic. This same training set is then employed to construct the data set of
200 videos where a sliding window moves across the image for each frame
of the video. In the simple case, the sliding window (167 × 167) moves 3
pixels per frame in the horizontal direction across the image (321 × 481 or
481 × 321), from left to right for 50 frames (see Figure 3b). The sliding win-
dow may also move in any random direction, resulting in different statis-
tics of the video data set and hence different Wmoving. This different data set
of videos is generated by choosing any pixel in the image and moving the
sliding window toward it in smaller increments until that pixel is reached; a
new pixel is then chosen from the image until the maximum limit of frames
in the video (50 frames). Results from this different data set are shown in
Figures S1 and S2. We further get 100 images from the BSDS test set to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
582
D. Voina et al.
generate the corresponding 100 videos and use in the optimization problem.
These video frames are provided as input to the optimizer that minimizes
the loss functions Eswitch,1 and Eswitch,2 to find fα
for Eswitch,1 and WVIP→SST ,
WVIP→PYR, and WPYR→VIP for Eswitch,2. For both optimization problems, we
set 50 frames aside from these 100 videos to compute the generalization
error during the minimization procedure.
, fβ
In order to generate the numbers in Figure 8, another set of 100 videos
generated from BSDS testing data set is altered by adding gaussian and salt-
and-pepper noise of different parameters to each frame. The resulting noisy
video frames are used to establish the ability of the switching circuit to do
visual processing of stimuli with better reconstruction capability than the
circuit implementing the static extraclassical receptive field or without extr-
aclassical receptive field (see section 2.6). Gaussian white noise has standard
deviation σ = 0.5 for reconstructions in Figure 8e, while salt-and-pepper
noise turns pixels black or white with probability p = 0.2 each, for recon-
structions in Figures 8d and 8f. Parameters σ and p are varied (σ ∈ [0.5, 3],
p ∈ [0.05, 0.3]) in Figure 8f.
4.4.2 Synthetic Data Sets of Images and Videos of Horizontal and Vertical Bars.
This simple synthetic data set consists of 18 images of horizontal and ver-
tical bars (9 horizontal, 9 vertical). Images are 9 × 9, each image having a
bar at a different location. Videos consist of bars moving in any direction
one pixel at a time: left or right (for horizontal bars) and up or down (for
vertical bars).
4.5 Deriving an Equation for PYR Firing Rate Consistent with V1 Cir-
cuit Architecture. Let f be the firing rate due to the classical receptive field,
r the firing rate incorporating extraclassical receptive field information, and
W X→Y the weights between neuronal populations X, Y. We can write ap-
proximated expressions for firing rates of PYR, SST, VIP neurons at time t:
Case a: When there is no feedback connection from PYR to VIP:
rt
PYR
= ft
PYR
◦ (1+WPYR→PYRrt−1
PYR
+ WSST→PYRrt−1
SST
+ WVIP→PYRrt−1
VIP)
rt
SST
= ft
SST
+ WVIP→SST rt
VIP
rt
VIP
= st · ft
VIP
.
(4.22)
(4.23)
(4.24)
Case b: When there is feedback from PYR to VIP:
rt
PYR
= ft
PYR
· (1 + WPYR→PYRrt−1
PYR
+ WSST→PYRrt−1
SST
+ WVIP→PYRrt−1
VIP)
(4.25)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
rt
SST
= ft
SST
+ WVIP→SST rt
VIP
rt
VIP
= st · WPYR→VIPrt
PYR
,
583
(4.26)
(4.27)
where ft
VIP of equation 4.24 is the intrinsic firing rate of VIP and st
is a binary variable that takes the value 1 during the moving condi-
tion and 0 during the static condition. For the analysis of the firing
rate during movement, we assume st = 1. Equations 4.22 and 4.25,
expressing the firing rate rt
PYR of the PYR population, assume the extr-
aclassical receptive field contribution given by lateral connections has
a multiplicative effect on the feedforward activities fPYR. This multi-
plicative gain is the result of mapping from the probabilistic frame-
work of equations 4.14 and 4.18 and their analogs for the moving
circuit activities and weights. This results in the network doing op-
timal inference of visual features via PYR firing rates as expressed in
equations 4.22 and 4.25, and as detailed in section 2.1. The VIP firing
rate rVIP expression involves a binary gating term that switches based
on state (static or moving), a simplification of what has been found
empirically. The model could incorporate a term fVIP into expression
4.27 describing VIP firing rates driven independently from PYR such
+ fVIP, but this change would not alter
that rt
our main results. Finally, only the interneuron connections with the
longest synaptic delay are assumed to be noninstantaneous (connec-
tions to and from PYR), while other connections are presumed to
occur at a much faster timescale (connections between inhibitor neu-
rons). Biologically, PYR are assumed to carry out computations by us-
ing dendritic trees, as outlined in Poirazi, Brannon, and Mel (2003),
while SST and VIP are more spatially compact than PYR (Gouwens
et al., 2019). Hence, synaptic delays between PYR and other neuron
populations are longer than between other populations.
= st · WPYR→VIPrt
PYR
VIP
Making the appropriate substitutions in equations 4.22 and 4.25, we get
the PYR firing rates, for case a,
rt
PYR
= ft
◦ [1 + WPYR→PYRrt−1
PYR
+ WSST→PYR(ft−1
SST
+ WVIP→SST ft−1
VIP) +
PYR
+ WVIP→PYRft−1
VIP]
and for case b,
rt
PYR
= ft
PYR
◦ [1 + WPYR→PYRrt−1
PYR
+ WSST→PYR(ft−1
+ WVIP→PYRWPYR→VIPrt−1
SST
PYR].
+ WVIP→SST WPYR→VIPrt−1
PYR) +
(4.28)
(4.29)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
584
D. Voina et al.
We can ignore further recurrence due to additional extraclassical receptive
field contributions by making the approximation rt−1
PYR. We are thus
PYR
ignoring contextual surround modulation that is itself subject to surround
influence—a “higher order” surround modulation—and instead consider
only the classical receptive field response from surround neurons. These
terms are small since this additional contribution is a linear combination of
fif j, fif jfk, . . . where fi are classical receptive field firing rates of neuron i
and 0 ≤ fi
= ft−1
≤ 1.
Additionally, we assume PYR and SST receive the same input so that
SST . With these simplifications and dropping the subscript PYR for
= ft
ft
PYR
clarity, the equations for rt
PYR become, for case a,
rt = ft ◦ (1 + WPYR→PYRft−1 + WSST→PYRft−1
+ WSST→PYRWVIP→SST fVIP + WVIP→PYRfVIP),
(4.30)
which leads to
rt = ft ◦ (1 + WPYR→PYRft−1 + WSST→PYRft−1 + WSST→PYRf
β
α + f
),
(4.31)
where
α ≡ WVIP→SST fVIP
f
and
β ≡ WVIP→PYRfVIP
f
while for case b,
rt = ft ◦ (1 + WPYR→PYRft−1 + WSST→PYRft−1
+ WSST→PYRWVIP→SST WPYR→VIPft−1
+ WVIP→PYRWPYR→VIPft−1).
(4.32)
(4.33)
(4.34)
During the static condition, there is no contribution from the VIP and ft =
ft−1 so the firing rate becomes
rstatic = f ◦ (1 + WPYR→PYRf + WSST→PYRf).
(4.35)
However, we know from our theoretical framework that the firing rate dur-
ing the static context can be written as
rstatic = f ◦ (1 + Wstaticf),
(4.36)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
585
where Wstatic has been computed from the data set(s) of images and is
a function of the average feature co-occurrence probability for pairs of
spatial features. Therefore, we can consider a simple mapping that as-
signs WPYR→PYR and WSST→PYR to known weights: WPYR→PYR = Wstatic
and
+
WSST→PYR = Wstatic
is the negative
component of Wstatic. The unknowns of equation 4.37 corresponding to the
V1 circuit model with PYR-to-VIP connections are thus only three sets of
weights to and from VIP: WVIP→SST , WVIP→PYR, WPYR→VIP.
is the positive and Wstatic
, where Wstatic
−
−
+
Finally, the equation for the firing rate of PYR neurons during the moving
condition that we focus on throughout the article (with PYR projecting to
VIP) becomes
rt = ft ◦ (1 + Wstatic
+
ft−1 + Wstatic
−
ft−1
+ Wstatic
− WVIP→SST WPYR→VIPft−1 + WVIP→PYRWPYR→VIPft−1)
= ft ◦ (1 + Wstaticft−1 +
+ WSST→PYRWVIP→SST WPYR→VIPft−1 +WVIP→PYRWPYR→VIPft−1).
(4.37)
4.6 Reconstructions from Noisy Videos Using Firing Rates and Opti-
mal Synaptic Weights of Different Circuit Architectures. To gain insight
into how optimal synaptic weights can facilitate decoding of information
present in the neuronal activity, we reconstructed natural image frames
from videos using four distinct circuits. The firing rates in these circuits are
described by the following equations:
rno EXC(t) = ft,
(4.38)
rstatic(t) = ft ◦ (1 + Wstaticft−(cid:2)t ),
rmoving(t) = ft ◦ (1 + Wmovingft−(cid:2)t ),
(4.40)
rapprox(t) = ft ◦ (1 + Wstaticft−(cid:2)t + WSST→PYRWVIP→SST WPYR→VIPft−(cid:2)t (4.41)
(4.39)
+ WVIP→PYRWPYR→VIPft−(cid:2)t ).
(4.42)
The first equation above describing rno EXC relies solely on the feedforward
information where no extraclassical receptive field contribution is included.
The next two expressions restate how the firing rates for the static and
moving circuits require contributions from the extraclassical receptive fields
through lateral connections Wstatic, Wmoving, reflective of the statistical regu-
larities of images/videos. Equation 4.42 describes the switching circuit we
have implemented and characterized above and should approximate the
firing rate in the moving circuit when VIP are active: rmoving ≈ rapprox.
The reconstruction was performed as follows. For any noisy input image
X + ξ , where ξ is some random variable representing a noisy process, we
calculated the effective firing rate (activity) r of neuron/feature k at location
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
586
D. Voina et al.
n using equations 4.38 to 4.42. To reconstruct image frames from firing rates,
we convolved the firing rates computed with the inverses of the filters in
our basis set. More specifically, the activity rk corresponding to filter k was
convolved with the inverse of k, which was obtained by flipping k about
the horizontal and vertical axes. These convolutions for all filters were then
averaged to obtain the final reconstruction.
We then performed the reconstruction for the same image frame X with-
out any noise added. We assessed the denoising capability of our circuits
by computing the Pearson correlation coefficient ρ between the reconstruc-
tion of X + ξ and the reconstruction of X. The latter is a baseline for our
comparisons, as there is no noise to remove from the image frame through
extraclassical surround modulation. The Pearson correlation coefficient ρ is
a function of the activity r of different circuit architectures and is discussed
and compared across circuits in section 2.6.
Two further issues merit further discussion. First, if the spectral content
of the noise and image frame is known, a Wiener deconvolution can be ap-
plied, which minimizes the mean square error between the estimated re-
construction and the original frame. Such a Wiener deconvolution would
minimize the impact of deconvolved noise at frequencies with poor signal-
to-noise ratio. However, we assume here that interpretation of signals is
done without access to knowledge of this spectral content, but rather imple-
menting a naive reconstruction as would be optimal in the noise-free limit.
Second, given the presence of extraclassical surround contribution, the de-
convolution operation may be more complex than the simple, filter by filter,
convolution with the inverse filter FT . Specifically, the inverse may contain
information about the cross-correlation of features. Again we work in the
simplifying limit in which this is not the case. We do not exclude, however,
the possibility that the biological circuit may apply a more complex recon-
struction (e.g., via learning weights), an interesting avenue to explore in
future work.
4.7 Like-to-Like Connectivity for PYR and VIP Populations. In addi-
tion to interneuron connectivity discussed in section 2.7, PYR connection
probability as a function of the difference in orientation tuning (see Figures
S2c and S2d) qualitatively matches the same graph reported experimentally
(Ko et al., 2011). This like-to-like connectivity, with neurons responding to
similar features (orientations) more strongly connected, holds true for both
static (shown in Iyer et al., 2020) and moving weights (shown in Figures S2c,
S2d, and S3). Another feature concerns the amplitude of static and moving
weights, which decreases with distance from the classical receptive field,
with lower weights on average between neurons whose classical receptive
fields are far away. Figure S2 shows the dependence of the maximum, min-
imum, and average positive and negative synaptic weights on the distance
between neuronal receptive fields. Assuming an exponential spatial decay
of weights with distance and using the first two points in the plot displaying
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
587
decreasing distance dependence in the mean positive static weights curve
= 0.8×
(see Figure S2a), we computed the spatial constants Dstatic/moving
the classical receptive field size. This is in accordance with past findings
(Angelucci and Bressloff, 2006; Iyer et al., 2020), suggesting that the near
surround extends over a range similar in size to the classical receptive field.
We further study the inferred connections to and from the VIP to es-
tablish whether these weights reflect the contextual statistics of static and
moving states. We first inferred whether there is like-to-like connectivity
between VIP and PYR populations by building a similarity matrix of di-
mension number of VIP neurons × number of PYR neurons that measures
response similarity between VIP and PYR neuronal populations. Each en-
try of this response similarity matrix is computed by taking the Pearson
correlation between the GLM coefficients found above (see section 2.7) for
each VIP neuron and each PYR neuron, respectively. We next built, from our
× 34 × 3 × 3 tensor WVIP→PYR used for convolution, a matrix of connec-
N f2
tivities of dimension number of VIP neurons × number of PYR neurons.
Finally, taking the Pearson correlation coefficient between the response
similarity matrix and the matrix of connectivities yields a statistically
significant but very low correlation coefficient (−0.01, p-value < 0.01,
Kolmogorov-Smirnov test). We conclude that while like-to-like connectivity
is present between PYR neurons, this phenomenon is not prevalent between
VIP and PYR populations.
4.8 Measuring Dimensionality with the Participation Ratio. We aim
to characterize the dimensionality of the distribution of population vector
responses representing neural activity. Across many trials, these popula-
tion vectors populate a cloud of points. The dimensionality is a weighted
measure of the number of axes explored by that cloud,
Dim(C) = (TrC)2
TrC2
(cid:2)
(cid:2)
i
= (
i
,
λ
i)2
λ2
i
(4.43)
where C is the covariance matrix of the matrix of neural activations and
λ
i is the ith eigenvalue of the covariance matrix C. Dim(C) measures the
dimensionality of neural activity of our network and is termed the partici-
pation ratio. The eigenvectors of the covariance matrix C are the axes of our
cloud of points representing activity in neural space. If the neural activi-
ties are independent and all have equal variance, all the eigenvalues of the
covariance matrix have the same value and Dim(C) = N. Alternatively, if
the components are correlated so that the variance is evenly spread across
M dimensions, only M eigenvalues would be nonzero and Dim(C) = M. For
other correlation structures, this measure interpolates between these two
regimes and, as a rule of thumb, the dimensionality can be thought as cor-
responding to the number of dimensions required to explain about 80% of
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
588
D. Voina et al.
the total population variance in many settings (Mazzucato, Fontanini, & La
Camera, 2016; Gao et al., 2020; Litwin-Kumar, Harris, Axel, Sompolinsky,
& Abbott, 2017).
4.9 Inferring the Tuning Properties of VIP and PYR Neurons. We fur-
ther study the activation patterns of units in our switching circuit model
by inferring the tuning properties of VIP and PYR units. To achieve this,
we first choose a wavelet family that will determine our features and dif-
fers from the basis approximating spatial receptive fields in V1 from sec-
tion 4.3. We chose the Daubechies 4 wavelet family with a mother wavelet
of length 15 pixels, as shown in Figure S13a. We then consider the 2D dis-
crete wavelet transforms of our video frames to obtain the approximation,
horizontal detail, vertical detail, and diagonal detail coefficients (wavelet
transforms), respectively, for each frame. The goal is to use the averages of
these coefficients as the independent variables of a linear regression or GLM
that models VIP or PYR activations.
To achieve this, we first reduce the dimensionality of the wavelet trans-
forms obtained above by considering 100 = 10 × 10 patches of size 5 × 5
that tile wavelet transforms of each video frame. Averaging over the spatial
component of these patches, we obtain three sets of 10 × 10 coefficients (for
the horizontal, vertical, and diagonal detail, respectively) that will be the
independent variables of the linear regression or GLM. For each PYR/VIP
neuron, we can regress its activity for every video frame against the 300
(= 3 × 10 × 10) coefficients we have inferred,
a = C · x,
(4.44)
where a ∈ Rno. frames=4700
is the activity of a neuron (for every 4700
frames), C ∈ Rno. frames×no. regressors(300) is the matrix of regressors, and x ∈
Rno. coefficients=no. regressors contains the unknowns that will determine the tun-
ing of each neuron.
We obtain that most PYR neurons are tuned to horizontal features, and
much less so to vertical features (data not shown). Using either a linear re-
gression or a GLM with a Poisson distribution yields qualitatively similar
results. Because VIP neurons in our model only get input from the PYR,
while the top-down input activating VIP is described simply by the binary
term st, we obtain that VIP acquires the same preferential selectivity to hor-
izontal features to the detriment of vertical features (see Figure S13d). VIP
neurons are tuned to horizontal features with an average regression coeffi-
cient of 0.65, while they are tuned to vertical features with an average re-
gression coefficient of 0.015 (using the results from the linear regression).
This runs counter to our expectation that VIP is capable of detecting hor-
izontal movement in our data set by exhibiting preferential selectivity to-
ward vertical features within their receptive fields, analogous to empirical
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
589
results in Millman et al. (2020). Clearly, the simplification we have made
by employing a binary term st in equation 4.27 prevents us from observ-
ing a more realistic VIP activation pattern that would deviate from the PYR
pattern and provide further insights. We leave the more detailed modeling
expanding our current simplified model in this direction to future work.
Code
Source code is available in ModelDB (McDougal et al., 2017) at http://
modeldb.yale.edu/267120.
Acknowledgments
We gratefully acknowledge the support of the Swartz Foundation Cen-
ter for Theoretical Neuroscience at the University of Washington, and of
NIH training grant 5 R90 DA 033461-08. We are grateful to Matthew Far-
rell and Kameron Harris for their helpful comments in producing the final
manuscript. We thank Paul G. Allen, the founder of the Allen Institute for
Brain Science, for his vision, encouragement, and support.
References
Angelucci, A., & Bressloff, P. C. (2006). Contribution of feedforward, lateral and
feed-back connections to the classical receptive field center and extra-classical
receptive field surround of primate V1 neurons. In S. Martinez-Conde (Ed.),
Progress in brain research, vol. 2006 (pp. 93–120). Amsterdam: Elsevier. 10.1016/
S0079-6123(06)54005-1
Ayaz, A., Saleem, A. B., Scholvinc, M. L., & Carandini, M. (2013). Locomotion con-
trols spatial integration in mouse visual cortex. Current Biology, 23, 890–894.
10.1016/j.cub.2013.04.012, PubMed: 23664971
Attneave, F. (1954). Some informational aspects of visual perception. Psychological
Review, 61(3). 10.1037/h0054663, PubMed: 13167245
Barlow, H. (1961). Possible principles underlying the transformation of sensory mes-
sages. In W. A. Rosenblith (Ed.), Sensory communication (pp. 217–234). Cambridge,
MA: MIT Press.
Batista-Brito, R., Zagha, E., Ratliff, J. M., & Vinck, M., (2018). Modulation of
cortical circuits by top-down processing and arousal state in health and dis-
ease. Current Opinion in Neurobiology, 52, 172–181. 10.1016/j.conb.2018.06.008,
PubMed: 30064117
Bell A. J., & Sejnowski T. J., (1995). An information-maximization approach to blind
separation and blind deconvolution. Neural Computation, 7, 1129–1159. 10.1162/
neco.1995.7.6.1129, PubMed: 7584893
Bigelow, J., Morrill, R. J., Dekloe, J., & Hasenstaub, A. R. (2019). Movement and VIP
interneuron activation differentially modulate encoding in mouse auditory cor-
tex. eNeuro, 6(5). 10.1523/ENEURO.0164-19.2019, PubMed: 31481397
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
590
D. Voina et al.
Braitenberg V., & Schüz, A. (1991). Anatomy of the cortex: Statistics and geometry. Berlin:
Springer-Verlag.
Campagnola, L., Seeman, S. C., Chartrand, T., Kim, L., Hoggarth, A., Gamlin, C.,
. . . Jarsky, T. (2021). Local connectivity and synaptic dynamics in mouse and human
neocortex. https://www.biorxiv.org/content/10.1101/2021.03.31.437553v2
Cardin J., (2018). Inhibitory interneurons regulate temporal precision and correla-
tions in cortical circuits. Trends Neurosci., 41, 689–700. 10.1016/j.tins.2018.07.015,
PubMed: 30274604
Cardin J., (2019). Functional flexibility in cortical circuits. Current Opinion in Neuro-
biology, 58, 175–180. 10.1016/j.conb.2019.09.008, PubMed: 31585330
Cauli, B., Audinat, E., Lambolez, B., Angulo, M. C., Ropert, N., Tsuzuki, M., . . .
Rossier, J. (1997). Molecular and physiological diversity of cortical nonpyrami-
dal cells. J. Neurosci., 17(10), 3894–3906. 10.1523/JNEUROSCI.17-10-03894.1997,
PubMed: 9133407
Chalk, M., Marre, O., &Tkaˇcik, G. (2018). Toward a unified theory of efficient, pre-
dictive, and sparse coding. In Proceedings of the National Academy of Science USA,
115(1), 186–191. 10.1073/pnas.1711114115
Cohen, J. D., Dunbar, K., & McClelland, J. L. (1990). On the control of automatic pro-
cesses: A parallel distributed processing account of the Stroop effect. Psychological
Review, 97, 332–361. 10.1037/0033-295X.97.3.332, PubMed: 2200075
Comon, P. (1994). Independent component analysis, a new concept? Signal Process-
ing, 36, 287–314. 10.1016/0165-1684(94)90029-9
Cossell, L., Iacaruso, M. F., Muir, D. R., Houlton, R., Sader, E. N., Ko, H., . . .
Mrsic-Flogel, T. D. (2015). Functional organization of excitatory synaptic strength
in primary visual cortex. Nature, 518(7539), 399–403. 10.1038/nature14182,
PubMed: 25652823
Dadarlat, M. C., & Stryker, M. P. (2017). Locomotion enhances neural encoding of
visual stimuli in mouse V1. Journal of Neuroscience, 37(14), 3764–3775. 10.1523/
JNEUROSCI.2728-16.2017, PubMed: 28264980
Dayan, P., Hinton, G. E., Neal, R. M., & Zemel, R. S. (1995). The Helmholtz machine.
Neural Computation, 7, 889–904. 10.1162/neco.1995.7.5.889, PubMed: 7584891
Dipoppa, M., Ranson, A., Krumin, M., Pachitariu, M., Carandini, M., & Harris,
K. D. (2018). Vision and locomotion shape the interactions between neuron
types in mouse visual cortex. Neuron, 98, 602–615. 10.1016/j.neuron.2018.03.037,
PubMed: 29656873
Doi, E., & Lewicki, M. S.
(2014). A simple model of optimal population
coding for sensory systems. PLOS Comput. Biol., 10(8), e1003761. 10.1371/
journal.pcbi.1003761, PubMed: 25121492
Durand, S., Iyer, R., Mizuseki, K., de Vries, S., Mihalas, S., & Reid, R. C. (2016). A
comparison of visual response properties in the lateral geniculate nucleus and
primary visual cortex of awake and anesthetized mice. J. Neurosci., 36(48), 12144–
12156. 10.1523/JNEUROSCI.1741-16.2016, PubMed: 27903724
Fu, Y., Tucciarone, J. M., Espinosa, J. S., Sheng, N., Darcy, D. P., Nicoll R. A., . . .
Stryker, M. P. (2014). A cortical circuit for gain control by behavioral state. Cell,
156, 1139–1152.
Gao, P., Trautmann, E., Yu, B., Santhanam, G., Ryu, S., Shenoy, K., & Ganguli, S.
(2020). A theory of multineuronal dimensionality, dynamics and measurement. https:
//www.biorxiv.org/content/early/2017/11/05/214262
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
591
Gouwens, N. W., Sorensen, S. A., Berg, J., Lee, C., Jarsky, T., Ting, J.,
.
Koch, C. (2019). Classification of electrophysiological and morphological neu-
ron types in the mouse visual cortex. Nat. Neurosci., 22(7), 1182–1195. 10.1038/
s41593-019-0417-0, PubMed: 31209381
.
.
Gozzi, A., Jain, A., Giovanelli, A., Bertollini, C., Crestan, V., Schwarz, A. J., . . . Bi-
fone, A. (2010). A neural switch for active and passive fear. Neuron, 67, 656–666.
10.1016/j.neuron.2010.07.008, PubMed: 20797541
Harpur, G. F., & Prager, R. W.
low entropy cod-
ing in a recurrent network. Network, 7, 277–284. 10.1088/0954-898X_7_2_007,
PubMed: 16754387
(1996). Development of
Hertäg, L., & Sprekeler, H. (2019). Amplifying the redistribution of somatodendritic
inhibition by the interplay of three interneuron types. PLOS Comput. Biol., 15(5),
e1006999. doi:10.1371/journal.pcbi.1006999
Hofer S. B., Ko, H., Pichler, B., Vogelstein, J., Ros, H., Zeng, H., . . . Mrsic-Flogel,
T. D. (2011). Differential connectivity and response dynamics of excitatory and
inhibitory neurons in visual cortex. Nature Neuroscience, 14, 1045–1052. 10.1038/
nn.2876, PubMed: 21765421
Hu, B., & Mihalas, S. (2018). Convolutional neural networks with extra-classical receptive
fields. https://arxiv.org/abs/1810.11594v1
Iyer, R., Hu, B., & Mihalas, S. (2020). Contextual integration in cortical and convolu-
tional neural networks. Front. Comput. Neurosci., April 23, 31.
Jiang, X., Shen, S., Cadwell, C. R., Berens, P., Sinz, F., Ecker, A. S., . . . Tolias, A. S.
(2015). Principles of connectivity among morphologically defined cell types in
adult neo-cortex. Science, 350 (6264), aac9462. 10.1126/science.aac9462
Karklin, Y., & Simoncelli, E. P. (2011). Efficient coding of natural images with a popu-
lation of noisy linear-nonlinear neurons. In J. Shawe-Taylor, R. Zemel, P. Bartlett,
F. Pereira, & K. Q. Weinberger (Eds.), Advances in neural information processing sys-
tems, 24 (pp. 999–1007). Red Hook, NY: Curran. 26273180
Keller, A. J., Dipoppa, M., Roth, M. M., Caudill, M. S., Ingrosso, A., K. D.
Miller, & Scanziani M. A. (2020). Disinhibitory circuit for contextual modulation
in primary visual cortex. https://www.biorxiv.org/content/10.1101/2020.01.31
.929166v2.
Kirkpatrick, J., Pascanu, R., & Hadsel, R. (2017). Overcoming catastrophic forget-
ting in neural networks. PNAS, 114(13), 3521–3526. 10.1073/pnas.1611835114,
PubMed: 28292907
Ko, H., Hofer, S. B., Pichler, B., Buchanan, K. A., Sjostro, P. J., & Mrsic-Flogel, T.
D. (2011). Functional specificity of local synaptic connections in neocortical net-
works. Nature, 473(7345), 87–91, 5. 10.1038/nature09880, PubMed: 21478872
Koganezawa, M., Kimura, K., & Yamamoto, D. (2016). The neural circuitry that func-
tions as a switch for courtship versus aggression in drosophila males. Current
Biology, 26, 1395–1403. 10.1016/j.cub.2016.04.017, PubMed: 27185554
Lefort, S., Tomm, C., Floyd Sarria, J. C., & Petersen, C. C. H. (2009). The excitatory
neuronal network of the C2 barrel column in mouse primary somatosensory cor-
tex. Neuron, 61, 301–316. 10.1016/j.neuron.2008.12.020, PubMed: 19186171
Lewicki, M. S., & Sejnowski, T. J. (2000). Learning overcomplete representa-
tions, Neural Computation, 12, 337–365. 10.1162/089976600300015826, PubMed:
10636946
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
592
D. Voina et al.
Litwin-Kumar, A., Harris, K. D., Axel, R., Sompolinsky, H., & Abbott, L. F. (2017).
Optimal degrees of synaptic connectivity. Neuron, 93, 1153–1164.e7. 10.1016/
j.neuron.2017.01.030, PubMed: 28215558
Mallya, A., Davis, D., & Lazebnik, S. (2018). Piggyback: Adapting a single network
to multiple tasks by learning to mask weights. In Proceedings of the European Con-
ference on Computer Vision. Berlin: Springer.
Mallya, A., & Lazebnik, S. (2018). PackNet: Adding multiple tasks to a single network
by iterative pruning. In Proceedings of the Conference on Computer Vision and Pattern
Recognition. Piscataway, NJ: IEEE.
Mante, V., Sussillo, D., Shenoy, K. V., & Newsome, W. T. (2013). Context-dependent
computation by recurrent dynamics in prefrontal cortex. Nature, 503, 78–84.
10.1038/nature12742, PubMed: 24201281
Marr, D. (1982). Vision: A computational investigation into the human representation and
processing of visual information. San Francisco: Freeman.
Martin, D., Fowlkes, C., Tal, D., & Malik, J. (2001). A database of human segmented
natural images and its application to evaluating segmentation algorithms and
measuring ecological statistics. In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition. Piscataway, NJ: IEEE.
Mazzucato, L., Fontanini, A., & La Camera, G. (2016). Stimuli reduce the dimension-
ality of cortical activity. Front. Syst. Neurosci., 10, 11. 10.3389/fnsys.2016.00011,
PubMed: 26924968
McDougal, R. A., Morse, T. M., Carnevale, T., Marenco, L., Wang, R., Migliore, M.,
. . . Hines, M. L. (2017). Twenty years of ModelDB and beyond: Building essential
modeling tools for the future of neuroscience. J. Comput. Neurosci., 42(1), 1–10.
10.1007/s10827-016-0623-7, PubMed: 27629590
Millman, D. J., Ocker, G. K., Caldejon, S., Kato, I., Larkin, J. D., Lee, E. K., . . . de
Vries, E. J. (2020). VIP interneurons in mouse primary visual cortex selectively en-
hance responses to weak but specific stimuli eLife, 9, e55130. 10.7554/eLife.55130,
PubMed: 33108272
Niell, C. M., & Stryker, M. P.
(2010). Modulation of visual responses by
behavioral state in mouse visual cortex. Neuron, 65(4), 472–479. 10.1016/
j.neuron.2010.01.033, PubMed: 20188652
Ollerenshaw, D. R., Zheng, H. J. V., Millard, D. C., Wang, Q., & Stanley, G. B. (2014).
The adaptive trade-off between detection and discrimination in cortical repre-
sentations and behavior. Neuron, 81, 1152–1164. 10.1016/j.neuron.2014.01.025,
PubMed: 24607233
Olshausen, B. A. (2013). Highly overcomplete sparse coding. In Proceedings of SPIE
(vol. 8651). Bellingham, WA: SPIE.
Olshausen, B. A., & Field, D. J. (1996a). Emergence of simple-cell receptive field prop-
erties by learning a sparse code for natural images. Nature, 381(6583), 607–609.
10.1038/381607a0
Olshausen, B. A., & Field, D. J. (1996b). Natural image statistics and efficient coding.
Network, 7(2), 333–339, 5. 10.1088/0954-898X_7_2_014
Olshausen, B. A., & Field, D. J. (1997). Sparse coding with an overcomplete basis set:
A strategy employed by V1? Vision Res., 37, 3311–3325. 10.1016/S0042-6989(97)
00169-7, PubMed: 9425546
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Context-Dependent Computations in a V1 Local Circuit
593
Pfeffer, C. K., Xue, M., He, M., Huang, Z. J., & Scanziani, M. (2013). Inhibition of
inhi bition in visual cortex: The logic of connections between molecularly distinct
interneurons. Nat. Neurosci., 16, 1068–1076. 10.1038/nn.3446, PubMed: 23817549
Pi, H. J., Hangya, B., Kvitsiani, D., Sanders, J., Huang, Z. J., & Kepecs, A. (2013).
Cortical interneurons that specialize in disinhibitory control. Nature, 503, 521–
524. 10.1038/nature12676, PubMed: 24097352
Poirazi, P., Brannon, T., & Mel, B. W. (2003). Pyramidal neuron as two-layer neural
network. Neuron, 37, 989999. 10.1016/s0896-6273(03)00149-1
Rao, R. P. N., & Ballard, D. H. (1999). Predictive coding in the visual cortex: A func-
tional interpretation of some extra-classical receptive-field effects. Nature Neuro-
science, 2(1). 10.1038/4580, PubMed: 10195184
Rudy, B. (2011). Three groups of interneurons account for nearly 100% of neo-
cor tical GABAergic neurons. Dev. Neurobiol., 71(1), 45–61. 10.1002/dneu.20853,
PubMed: 21154909
Rusu, A. A., Rabinowitz, N. C., Desjardins, G., Soyer, H., Kirkpatrick,
J.,
Kavukcuoglu, K., . . . Hadsell, R. (2016). Progressive neural networks. arXiv:1606.
04671.
Serra, J., Suris, D., Miron, M., & Karatzoglou, A. (2018). Overcoming catastrophic
forgetting with hard attention to the task. In Proceedings of the 35th International
Conference on Machine Learning (pp. 4548–4557).
Simoncelli, E.
(2003). Vision and the statistics of
the visual environment.
Current Opinion in Neurobiology, 13, 144–149. 10.1016/S0959-4388(03)00047-3,
PubMed: 12744966
Sussillo, D., & Abbott, L. F., (2009). Generating coherent patterns of activity from
chaotic neural networks. Neuron, 63, 544–557. 10.1016/j.neuron.2009.07.018,
PubMed: 19709635
Tasic, B., Yao, Z., Graybuck, L. T., Smith, K. A., Nguyen, T. N., & Bertagnolli, D. (2018).
Shared and distinct transcriptomic cell types across neocortical areas. Nature, 563,
72–78. 10.1038/s41586-018-0654-5, PubMed: 30382198
Terekhov, A. V., Montone, G., & O’Regan, J. K. (2015). Knowledge transfer in deep
block-modular neural networks. In S. Wilson, P. Verschure, A. Mura, & T. Prescott
(Eds.), Lecture Notes in Computer Science: Vol. 9222. Biomimetic and Biohybrid Sys-
tems. Living Machines. Cham: Springer. 10.1007/978-3-319-22979-927
Thomson, A. M., West, D. C., Wang, Y., & Bannister, A. P. (2002). Synaptic con-
nections and small circuits involving excitatory and inhibitory neurons in lay-
ers 2–5 of adult rat and cat neocortex: Triple intracellular recordings and bio-
cytin labelling in vitro. Cerebral Cortex, 12(9), 936–953. 10.1093/cercor/12.9.936,
PubMed: 12183393
Vogt, K., Zimmerman, D. M., Schlichting, M., Hernandez-Nuñez, L., Qin, S., Mala
con, K., . . . Samuel, D. T. (2020). Internal state configures olfactory behavior and early
sensory processing in Drosophila larva. 10.1101/2020.03.02.973941.
Wall, N. R., De La Parra, M., Sorokin, J. M., Taniguchi, H., Huang, Z. J., & Call-
away, E. M. (2016). Brain-wide maps of synaptic input to cortical interneu-
rons. Journal of Neuroscience, 36(14), 4000–4009. 10.1523/JNEUROSCI.3967-15,
PubMed: 27053207
Wilmes, K. A., & Clopath, C. (2019). Inhibitory microcircuits for top-down plas-
ticity of sensory representations. Nature Communications, 10, art. 5055. 10.1038/
s41467-019-12972-2, PubMed: 31699994
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
594
D. Voina et al.
Yang, G. R., Cole, M. W., & Rajan, K. (2019). How to study the neural mechanisms
of multiple tasks. Current Opinion in Behavioral Sciences, 29, 134–143. 10.1016/
j.cobeha.2019.07.001, PubMed: 32490053
Zemel, R. S. (1993). A minimum description length framework for unsupervised learning,
PhD thesis, University of Toronto.
Zenke, F., Poole, B., & Ganguli, S. (2017). Continual learning through synaptic intel-
ligence. In Proceedings of the International Conference on Machine Learning Research,
70, (pp. 3987–3995).
Zhou, T., Zhu, H., Fan, Z., Wang, F., Chen, Y., Liang, H., . . . Hu, H. (2017). History
of winning remodels thalamo-PFC circuit to reinforce social dominance. Science,
357, 162–168. 10.1126/science.aak9726, PubMed: 28706064
Received January 6, 2021; accepted September 21, 2021.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
4
3
5
4
1
1
9
8
9
4
6
6
n
e
c
o
_
a
_
0
1
4
7
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3