ARTIKEL
Communicated by Nick Hardy
Stimulus-Driven and Spontaneous Dynamics
in Excitatory-Inhibitory Recurrent Neural
Networks for Sequence Representation
Alfred Rajakumar
aar653@nyu.edu
Courant Institute of Mathematical Sciences, New York University,
New York, New York 10012, USA.
John Rinzel
rinzel@cns.nyu.edu
Courant Institute of Mathematical Sciences and Center for Neural Science,
New York University, New York, New York 10012, USA.
Zhe S. Chen
zhe.chen@nyulangone.org
Department of Psychiatry and Neuroscience Institute, New York University
School of Medicine, New York, New York 10016, USA.
Recurrent neural networks (RNNs) have been widely used to model se-
quential neural dynamics (“neural sequences”) of cortical circuits in cog-
nitive and motor tasks. Efforts to incorporate biological constraints and
Dale’s principle will help elucidate the neural representations and mech-
anisms of underlying circuits. We trained an excitatory-inhibitory RNN
to learn neural sequences in a supervised manner and studied the rep-
resentations and dynamic attractors of the trained network. The trained
RNN was robust to trigger the sequence in response to various input sig-
nals and interpolated a time-warped input for sequence representation.
Interessant, a learned sequence can repeat periodically when the RNN
evolved beyond the duration of a single sequence. The eigenspectrum
of the learned recurrent connectivity matrix with growing or damping
modes, together with the RNN’s nonlinearity, were adequate to gener-
ate a limit cycle attractor. We further examined the stability of dynamic
attractors while training the RNN to learn two sequences. Zusammen, unser
results provide a general framework for understanding neural sequence
representation in the excitatory-inhibitory RNN.
1 Einführung
Sequentially activated neuronal activities (“neural sequences”) are univer-
sal neural dynamics that have been widely observed in neural assemblies
Neural Computation 33, 2603–2645 (2021) © 2021 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01418
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2604
A. Rajakumar, J. Rinzel, and Z. Chen
of cortical and subcortical circuits (Fujisawa, Amarasingham, Harrison, &
Buzsaki, 2008; Long et al., 2010; Harvey, Coen, & Tank, 2012; Buzsaki & Tin-
gley, 2018; Adler et al., 2019; Hemberger, Shein-Idelson, Pammer, & Laurent,
2019). Sequence-based neural dynamics have been proposed as a common
framework for circuit function during spatial navigation, motor learning,
Erinnerung, and decision-making tasks (Sussillo, 2014). Neural sequential ac-
tivity can be driven by sensory or motor input, such as in the rodent hip-
pocampus, rodent primary motor cortex, and premotor nucleus HVC of
song birds; neural sequences can be driven by intrinsic dynamics during
the task period in the absence of sensory or motor input. Such sequential
dynamics could potentially be implemented using feedforward or recur-
rent architectures (Goldman, 2009; Cannon, Kopell, Gardner, & Markowitz,
2015).
Biological networks are strongly recurrent. daher, nonlinear recur-
rent neural networks (RNNs) have been developed for modeling a wide
range of neural circuits in various cognitive and motor tasks (Mante, Sus-
sillo, Shenoy, & Newsome, 2013; Sussilo, Churchland, Kaufman, & Shenoy,
2015; Rajan, Harvey, & Tank, 2016; Barak, 2017; Goudar & Buonomano,
2018; Yang, Joglekar, Lied, Newsome, & Wang, 2019; Kao, 2019; Mack-
wood, Naumann, & Sprekeler, 2021; Bi & Zhou, 2020; Zhang, Liu, & Chen,
2021). Jedoch, biological constraints were only recently considered in
RNN models (Lied, Yang, & Wang, 2016; Ingrosso & Abbott, 2019; Xue,
Halassa, & Chen, 2021), whereas in other work (Murphy & Müller, 2009), bi-
ological constraints were considered only in the linear recurrent system. In
allgemein, RNNs have been treated as black boxes, and their mechanisms and
high-dimensional computations are difficult to analyze (Sussillo & Barak,
2013; Ceni, Ashwin, & Livi, 2019).
In diesem Artikel, we used an excitatory-inhibitory nonlinear RNN to model
neural sequences. Extending previous modeling efforts (Rajan et al., 2016;
Hardy & Buonomano, 2018; Orhan & Ma, 2019), we explicitly incorporated
Dale’s principle and excitatory-inhibitory (E/I) balance into the RNN and
studied its stimulus-driven and spontaneous dynamics. Neural sequences,
as a special form of dynamical attractors, can be viewed as an alternative to
fixed points for storing memories (Rajan et al., 2016). Generalized Hopfield-
type neural networks can store patterns in limit cycles (Deshpande & Das-
gupta, 1991). Jedoch, to our best knowledge, limit cycle dynamics have
not been well studied in the context of excitatory-inhibitory RNN.
Neural dynamics during online task behavior is referred to as a transient
Zustand, whereas the neural dynamics during the offline state (in the absence
of stimulus input) is often described as the steady or stationary state, welche
can also play important roles in brain functions (such as memory replay).
Based on extensive computer simulations for learning one or two neural se-
quences, we discovered and studied the stability of limit cycles encoded by
the excitatory-inhibitory RNN while evolving in the stimulus-free sponta-
neous state (“steady state”). Our combined theoretical and computational
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2605
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
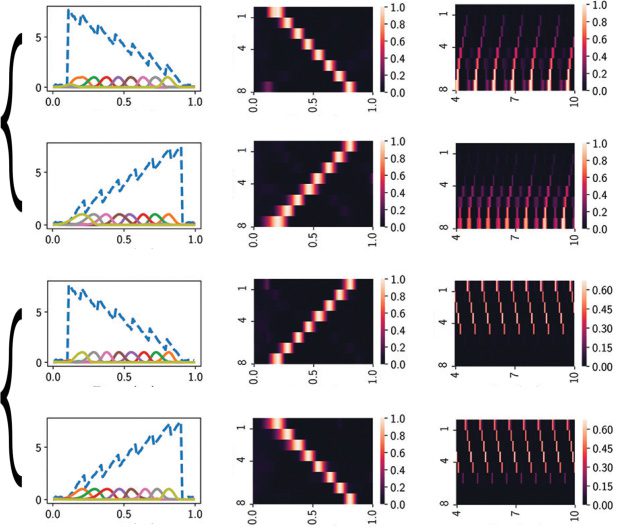
Figur 1: (A) Schematic of an excitatory-inhibitory recurrent neural network
(RNN) characterized a fully recurrent connectivity matrix Wrec. All neurons in
the RNN receive a time-varying input signal (scaled by Win) and produce a par-
tial sequence in the neuronal readout. The readout is assumed to be the subset
of excitatory neurons (scaled by Wout). (B,c) Several versions of input signals.
(B) An exponentially decaying signal 6e−3(t−0.1) (links) and modulated sinusoidal
signal 6e−3(t−0.1)(1 + 0.3 cos(10π (t − 0.1))) (Rechts). (c) A linear function (links) Und
a modulated sawtooth signal (Rechts). (D) Target neural sequence represented by
eight readout neurons. Rechts: The sequential neural activation is shown as a
heat map, where the values of each row are normalized between 0 Und 1.
analyses provide a framework to study sequence representation in neural
circuits in terms of excitatory-inhibitory balance, network connectivity, Und
synaptic plasticity.
2 Excitatory-Inhibitory RNN
In a basic RNN (see Figure 1a), the network receives an Nin-dimensional
input u(T) and produces an Nout-dimensional output z(T). We assumed the
2606
A. Rajakumar, J. Rinzel, and Z. Chen
neural state dynamics (which can be interpreted as the latent current or
activity as in a rate model), X(T), follows
τ ˙x = −x + Wrecr + Winu + σ ξ,
(2.1)
where τ denotes the time constant; ξ denotes additive N-dimensional gaus-
sian noise, each independently drawn from a standard normal distribution;
σ 2 defines the scale of the noise variance; Win ∈ RN×Nin denotes the matrix of
connection weights from the inputs to network units and Wrec is an N × N
× N matrix of
matrix of recurrent connection weights, and Wout is an Nout
connection weights from the network units to the output.
The network state of RNN is described by the N-dimensional dynamical
system over time. The neuronal firing rate vector r is defined by a nonlinear
function φ(X), which can be either a rectified linear function or a softplus
Funktion,
(cid:2)
r = φ(X) =
[X]+ = max{X, 0}
softplus(X) = log(1 + ex)
,
(2.2)
where the rectified linear function is a piecewise linear function, wohingegen
the softplus function is continuous and differentiable function. The rectified
linear unit (ReLU) is scale invariant and favors sparse activation. Addition-
ally, it can alleviate the saturation or vanishing gradient problem as can oc-
cur for a sigmoid activation function (Glorot, Bordes, & Bengio, 2011). Für
both ReLU and softplus functions, the nonlinearity is defined component-
wise for the vector x. Furthermore, the output z is given by
z = Woutr.
In a scalar form, equation 2.1 is described by
τ dxi
dt
= −xi
+
N(cid:3)
j=1
wrec
i j r j
+ win
i u + σ ξ
ich
,
and the output component z(cid:7) ((cid:7) = 1, . . . , Nout) is given by
z(cid:7) =
N(cid:3)
i=1
wout
(cid:7)i ri
.
(2.3)
(2.4)
(2.5)
The RNN dynamics is nonlinear due to the function φ(X). Generally, Wir
can rewrite equation 2.1 as a nonlinear mapping function G: ˙x = G(X, u),
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2607
with the first-order derivative (Jacobian) defined as
∇xG(X, u) = − 1
τ I + 1
τ Wrecdiag{Phi(cid:4)
(X)}
(2.6)
where the derivative φ(cid:4)
< 1 is a nonnegative logistic sigmoid
function in the case of softplus function, whereas the derivative of ReLU
is defined by a Heaviside step function. In the scalar case, we have
(x) = ex
1+ex
∂Gi(x, u)
∂x j
= − 1
τ
δ
i j
+ 1
τ
wrec
i j
φ(cid:4)
(x j ),
(2.7)
where δ
i j
= 1 if i = j and 0 otherwise.
In a special case when φ(·) is an identity function, the firing rate dynam-
ics is reduced to a linear dynamical system,
τ ˙r = −r + Wrecr + Winu + σ ξ,
(2.8)
where the eigenvectors of Wrec determine N basis patterns of neurons, and
the associated eigenvalues determine the pattern propagation (Murphy &
Miller, 2009). For instance, the eigenvalues {λ
, . . . , λN} of Wrec with positive
1
real part correspond to patterns that can self-amplify by routing through
the network (if not dominated by the leakage rate, −1). In the special case
where equation 2.8 has no noise and external input, the firing rate mode
decays exponentially with a time constant proportional to τ /(1 − Re{λ
i
}).
Biological neuronal networks consist of excitatory and inhibitory neu-
rons. Local cortical circuits have varying degrees of connectivity and spar-
sity depending on the nature of the cell types: excitatory-to-excitatory (EE),
inhibitory-to-excitatory (IE), excitatory-to-inhibitory (EI), and inhibitory-
to-inhibitory (II) connections (Murphy & Miller, 2009). We imposed the fol-
lowing biological constraints on our excitatory-inhibitory RNN:
• The ratio of the number of excitatory to inhibitory neurons is around
4:1 according to Dale’s principle: Nexc
Ninh
= 4
1 , where N = Nexc
+ Ninh.
• The dimensionality of the input signal is 1, Nin
= 1; for ease of
}N×1 has only positive
interpretation, we assumed that Win = {win
i
elements.
• Wrec = {wrec
(cid:5)
i j
EE IE
II
EI
(cid:4)
}N×N has EE, EI, IE, and II connections as follows:
. Both EE and EI connections were from presynaptic exci-
tatory neurons, and therefore their weights were positive, whereas IE
and II connections were from presynaptic inhibitory neurons and had
negative weights. No self-connection was assumed for Wrec; namely,
all diagonal elements {wrec
ii
} are zeros.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2608
A. Rajakumar, J. Rinzel, and Z. Chen
• The output sequences are direct (scaled) readout of Nout neurons from
}Nout×N is
= 8, and we constrained Wout
× Nout diagonal matrix,
the excitatory neuron population. Therefore, Wout = {wout
(cid:7)i
a partial identity matrix. Here, Nout
such that its upper block contained an Nout
namely, wout
(cid:7)i
= 0, ∀(cid:7) (cid:6)= i.
For the ith postsynaptic neuron in the sequence output, we define its net
excitatory and inhibitory currents as follows:
Iexc
i
=
Iinh
i
=
(cid:3)
j∈exc
(cid:3)
j∈inh
wrec
i j,EEr j
,
wrec
i j,IEr j
,
(2.9)
= [x j]+ = max(x j
where r j
presynaptic neuron, and wrec
within Wrec, respectively.
, 0) denotes the neuronal firing rate of the jth
i j,EE and wrec
i j,IE represent the EE and IE weights
2.1 Computer Simulation Setup. For a relatively simple computational
= 1)
task, we assumed that the input was a one-dimensional signal (i.e., Nin
and set N = 100. According to Dale’s principle, we assumed that the EE, EI,
IE, and II connections were represented as 80 × 80, 20 × 80, 80 × 20, and
20 × 20 submatrices, respectively.
We have considered different forms of input signals u(t) lasting 900 ms
during the 1 s task period (see Figures 1b and 1c), which could be ei-
ther sinusoidal modulated on an exponential carrier (single sequence case)
or sawtooth functions on a linear increasing/decreasing carrier (two se-
quences case). The continuous-time model was numerically implemented
in discrete time by Euler’s method. For each input signal, we set dt =
= 100, resulting in a simulation trial duration of ∼ 1 s. We
10 ms and Ntime
have also tried smaller dt (e.g., 2 ms and 5 ms) and obtained similar re-
sults. However, the simulation sample size became much larger and signif-
icantly increased the computational cost. Therefore, our default setup was
dt = 10 ms.
The output has the same duration as the input signal. The desired read-
out of the RNN was a neural sequence (see Figure 1d); each neuronal activa-
tion was sparse in time and had 5% overlap between its neighbor activation.
In the simulations here, we used the first eight excitatory neurons’ firing
= 8). The number
rates as the readout for the sequence output (i.e., Nout
= 20, and the input signals were generated with added
of trials was Ntrials
independent additive gaussian noise (zero mean and variance 0.01).
2.2 RNN Training with Gradient Descent. We initialized the RNN
weights as follows. The input weights Win were drawn from a uniform
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2609
distribution [−0.1, 0.1]; the recurrent weights Wrec was first initialized with
a gamma distribution gamma(2, 0.0495) (mean 0.099, variance 0.0049) while
ensuring all the diagonal values were zeros. Furthermore, we rescaled the
recurrent weight matrix to obtain a spectral radius around 0.99 and ensured
the sum of excitatory elements the same as the sum of the inhibitory ele-
ments to keep the E/I balance. Finally, the output weights Wout had a di-
agonal structure, with diagonal values drawn from a uniform distribution
[−0.1, 0.1] while keeping the nontarget neuron connections as zeros. We did
not impose additional constraints on the connection weights.
The training procedure was the same as in Song et al. (2016) and briefly
described here. We used the cost function
E = 1
Ntrials
Ntrials(cid:3)
n=1
Ln
=
1
NtrialsNoutNtime
Ntrials(cid:3)
Nout(cid:3)
Ntime(cid:3)
n=1
(cid:7)=1
t=1
(cid:6)
Merror
t(cid:7)
(zt )(cid:7) − (ztarget
t
)(cid:7)
(cid:7)
2,
(2.10)
where the error mask Merror
is a matrix of ones and zeros that determines
whether the error in the (cid:7)th output at time t should be taken into account.
During training, we used the batch size as the same as Ntrials
= 20.
t(cid:7)
In addition, we imposed an L2-norm regularization on the firing rates
and the sum of L1-norms of connection weights onto E. We used the stochas-
tic gradient descent (SGD) algorithm with default learning rate parameter.
The gradient was computed effectively by backpropagation through time
(BPTT). The vanishing gradient problem was alleviated using the regular-
ization techniques discussed in Song et al. (2016). The RNN implementation
was adapted based on the Python package (https://github.com/frsong/
pycog), with modifications for task design, network architecture, and op-
timization. To avoid overfitting, in addition to the training trials, we also
monitored the cost function of an independent validation data set. We con-
cluded the trained network achieved convergence when the mean-squared
error between the network output and the target out was sufficiently small
or their correlation coefficient was sufficiently high (e.g., R2 > 0.95). Der
standard choice of hyperparameters is shown in Table 1. Jedoch, the re-
sults reported here are not sensitive to the hyperparameter configuration.
2.3 Eigenspectrum Analysis. For a linear dynamical system (z.B., equa-
tion 2.8), the real part of the eigenvalue is responsible for the decay or
growth of oscillation. daher, the dynamical system becomes unstable
in the presence of even a single eigenvalue with a positive real component.
Jedoch, for an RNN with ReLU activation, the analysis of dynamics is
more complex (see appendixes A and B).
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2610
A. Rajakumar, J. Rinzel, and Z. Chen
Tisch 1: Hyperparameters Used for RNN Training.
Parameter
L1 weight regularization for weights
driven noise variance
input noise variance σ 2
In
gradient mini-batch size
validation mini-batch size
unit time constant τ
learning rate
max gradient norm
Setup
2
(0.01)2
(0.01)2
20
1000
50 MS
0.01
1
The stability of the dynamic system described by the excitatory-
inhibitory RNN is strongly influenced by the recurrent connection matrix
Wrec (Brunel, 2000; Rajan & Abbott, 2006). Since Wrec is generally asymmet-
ric, and each column of the matrix has either all positive or all negative
Elemente, it will produce a set of complex conjugate pairs of eigenvalues
(possibly including purely real eigenvalues) from eigenvalue decomposi-
tion Wrec = U(cid:3)U−1, where the column vectors of matrix U are the eigen-
vectors and the diagonal elements of (cid:3) denote the eigenvalues. Generally,
Wrec is nonnormal (unless all submatrices are symmetric and EI and IE con-
nections are identical); as a result, its eigenvectors are not orthogonal (Gold-
man, 2009; Murphy & Müller, 2009).
For the leakage matrix (Wrec − I), each eigenmode determines the cor-
responding response, and each mode is labeled by a complex eigenvalue,
whose real part corresponds to the decay rate and imaginary part is propor-
tional to the frequency of the oscillation. Take the delta pulse of input as an
Beispiel: its response can be described by a sinusoid with an exponential
envelope, where the real part of the eigenvalue λ of Wrec determines the rate
of exponential growth or decay (Goldman, 2009). Re{λ} > 1 implies expo-
nential growth; Re{λ} < 1 corresponds to exponential decay; Re{λ} = 1 de-
notes no decays (i.e., pure harmonic oscillatory component); and Re{λ} = 0
corresponds to decay with the intrinsic time constant. The magnitude of
the imaginary part of eigenvalue |Im{λ}| determines the frequency of the
sinusoidal oscillation, with a greater value representing a faster oscillation
frequency (see Figure 2a).
An alternative way to examine the network connectivity matrix Wrec is
−1, where Q is a unitary ma-
through the Schur decomposition, Wrec = QTQ
trix whose columns contain the orthogonal Schur mode and T is an upper
triangular matrix that contains the eigenvalues along the diagonal. The tri-
angular structure of T can be interpreted as transforming an RNN into a
feedforward neural network, and the recurrent matrix Wrec corresponds to
a rotated version of the effective feedforward matrix T, which defines self-
connections and functionally feedforward connections (FFC) of the neural
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2611
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
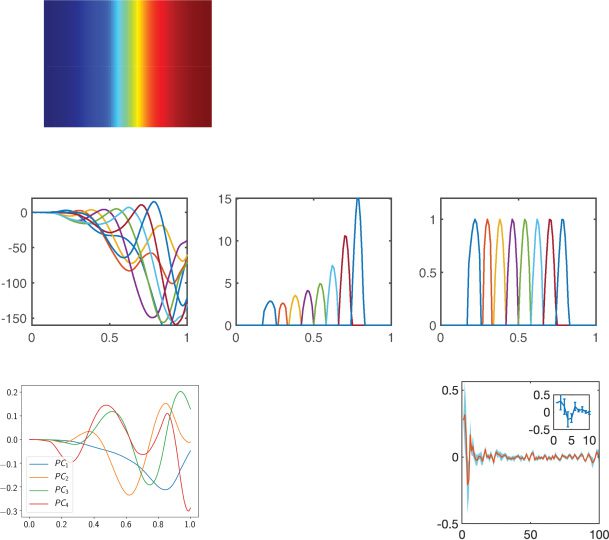
Figure 2: (a) Eigenvalues in the complex plane. (b) The eigenspectrum of
(Wrec − I)/τ , with each dot representing the real or complex-valued eigenvalue
(based on ReLU nonlinearity). (c) The neural state dynamics consisted of a set of
driven harmonic oscillators aligned in time, with time-varying amplitude and
frequency. Different colors represent individual components {xi(t)} or {ri(t)}.
The traces of {xi(t)} were first mapped to firing rates {φ(xi(t))} and then mapped
to the output sequence {z(cid:7)(t)}. (d) Extracted four principal components (PCs)
derived from 100-dimensional x(t). (e) Rotation dynamics extracted from 100-
dimensional x(t) during the trial period ([0, 1] s), with each trace representing
one computer simulation trial. The origin represents the initial point, and the
arrow indicates the time direction. (f) Applying the Schur decomposition to
Wrec and visualizing the connection strengths of effective feedforward matrix
} (upper diagonal) with respect to the neuron index gap j − i. Shaded
T = {Ti j
area shows SEM. The inset shows the first 10 elements.
network (Goldman, 2009). For a normal matrix, the Schur basis is equiva-
lent to the eigenvector basis. However, unlike eigenvalue decomposition,
the Schur decomposition produces the simplest (yet nonunique) orthonor-
mal basis for a nonnormal matrix.
2612
3 Results
A. Rajakumar, J. Rinzel, and Z. Chen
3.1 Sequences Are Generated by Superposition of Driven Har-
monic Oscillators. To avoid local minima, we trained multiple excitatory-
inhibitory RNNs with different random seeds, hyperparameters, and initial
conditions in parallel. In each condition, we trained at least five networks
and selected the suboptimal solution with the smallest cost function. De-
pending on the learning rate parameter and the input-output setup, the
excitatory-inhibitory RNN converged relatively slowly (typically > 105
Epochen) to obtain a good solution.
Upon training the excitatory-inhibitory RNN, we examined the learned
representation in the RNN dynamics. By examining the temporal trajecto-
ries of x and φ(X) that were associated with the readout neurons, we found
that the RNN behaved approximately as a collection of driven (wachsend
or damping) harmonic oscillators with time-varying frequencies (see Fig-
ure 2c). In the trained RNN, some readout neurons had large negative am-
plitudes in xi(T) because of the lack of constraint—this could be seen in the
net excitatory and net inhibitory input to each target neuron (see equa-
tion 2.9). By examining the eigenspectrum plane of (Wrec − I)/τ (see Fig-
ure 2b), the maximum imaginary frequency was around 0.125 radian/s
(equivalently 0.125/2π ≈ 0.02 Hz), which produced one oscillator at the
same timescale of time constant τ = 50 MS. Each generalized harmonic os-
cillator was associated with an eigenmode that has nonzero imaginary parts
regardless of whether the real part is positive, negative, or zero. The maxi-
mum peaks of the harmonic oscillators were temporally aligned to form a
neural sequence. The peaks and troughs of the generalized harmonic oscil-
lators were controlled by the time-varying excitation and inhibition levels
in the RNN, and the spacing between the neighboring peaks determined
the span of sequential activation.
In the case of RNN dynamics, the neural state will become unstable if
all components of xi(T) are positive simultaneously (d.h., all neurons fire
together). Since this phenomenon rarely happens, the RNN could reach sta-
ble dynamics when a few of the xi(T) components were positive (d.h., neu-
rons fire sparsely). Allgemein, it is difficult to derive mathematical solutions
to high-dimensional time-varying nonlinear dynamical systems (see equa-
tion 2.1). In the case of RNN with threshold-linear (ReLU) Einheiten, the sys-
tem is piecewise linear, and we can derive the analytic solutions of two and
three-dimensional systems (see appendixes A and B, jeweils). In these
low-dimensional systems, the phase space contains regions where neuronal
activation is either linear or zero. Wichtig, the system is time-varying,
and the stability of RNN dynamics may change from moment to moment
in the phase space. Jedoch, it may be possible to construct dynamic tra-
jectories, such as fixed points or periodic orbits in higher-dimensional sys-
tems by patching the eigenmodes across the “switch boundaries” (although
we did not implement the patching procedure, only fixed points but not
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2613
periodic orbits were found in our simulations of the two- and three-
dimensional systems; see appendixes A and B).
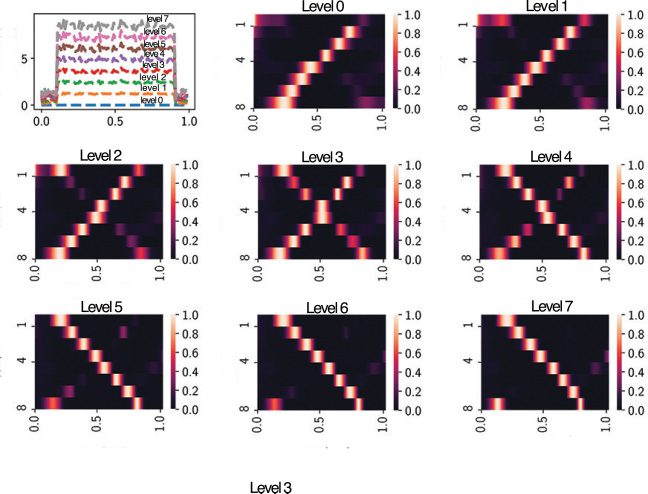
In light of principal component analysis (PCA), we found that the 100-
dimensional neural state trajectory x(T) was usually embedded in a lower-
dimensional space (see Figure 2d), with five to six components explaining
mehr als 90% variance. Each principal component (PC) behaved like an
oscillator that was intrinsically related to the presence of complex eigen-
values in Wrec. To further examine the oscillator structure in the simulated
neural dynamics, we also applied the polar decomposition (see appendix
C) to high-dimensional x(T) (similar to the rotation jPCA method as shown
in Churchland et al., 2012) and visualized the two-dimensional projection
in the rotation plane (see Figure 2e). Interessant, we also found rotation
dynamics on the single simulation trial basis while projecting the data onto
the eigenvectors associated with jPCA.
Allgemein, it is difficult to infer any structure from the eigenspectrum
of Wrec alone. We further applied the Schur decomposition to Wrec and
computed the effective feedforward matrix T, which is an upper diago-
nal matrix (siehe Sektion 2.3). To examine the relative feedforward connection
strengths between neurons, we plotted Ti j with respect to the neuron index
difference ( j − i). Interessant, we found relative large strengths between
the first eight Schur modes (see Figure 2f). Furthermore, on average, jede
mode excited its nearby modes but inhibited modes that were farther away.
Because of Dale’s principle, Wrec is nonnormal; the nonnormal dynamics in
RNNs may offer some benefits such as extensive information propagation
and expressive transients (Ganguli, Hug, & Sompolinsky, 2008; Kerg et al.,
2019; Orhan & Pitkow, 2020).
3.2 Robustness to Tested Input and Time Warping. Once the RNN was
trained, we found that the output sequences are robust to qualitative modi-
fications to the original input signal. Speziell, the same output sequences
were produced in response to different input signals, with varying forms of
Amplitude, frequency, or waveform (see examples in Figure 3a).
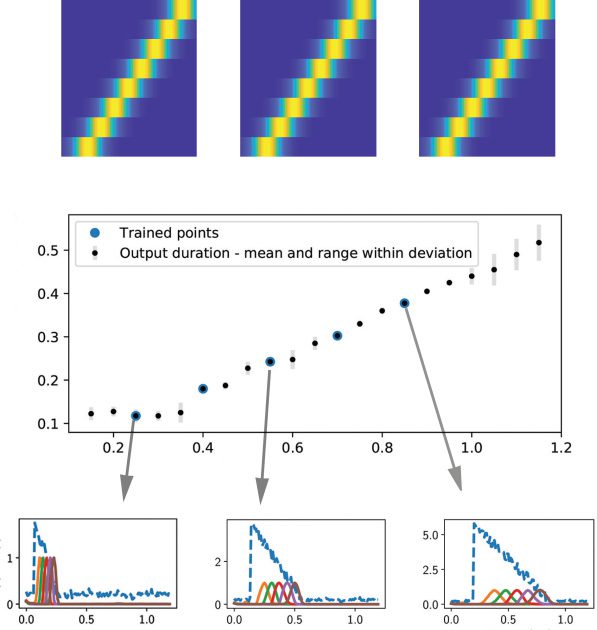
We further tested the generalization or invariance of RNNs in sequence
representation with respect to temporal scaling of the inputs. Speziell,
we trained the RNN in a task of mapping five different inputs to five
different scaled versions of output sequences. Each sequence was repre-
sented by sequential activation of five excitatory neurons. The five input
signals were temporally scaled versions of each other. Similarly, the five
output sequences were also temporally scaled versions of each other (sehen
Figure 3b). We then tested whether the trained RNN can learn to interpo-
late or extrapolate in response to the unseen scaled version of input signals.
In each test condition, we created five random realizations and computed
the error bar for each output sequence duration. The results are shown
in Figures 3b and 3c. Speziell, the RNN generalized very well by an
approximately linear interpolation but extrapolated poorly in the case of
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2614
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
Figur 3: (A) In the testing phase, the neural sequence out of the trained
excitatory-inhibitory RNN was robust to the exact waveform or amplitude of
the tested input signal (white trace in the inset). The RNN was trained on one
input signal and tested on the other two input signals. (B) Temporal scaling in-
variance of the sequences. Five input-output pairs with different durations were
trained together. Each input-output pair is a temporally scaled version of each
andere (d.h., 25%, 40%, 55%, 70%, Und 85% scaled versions of the original 1 s du-
ration). In each case, the durations of input and output were scaled by the same
scaling factor. Three scaled versions (25%, 55% Und 85%) are illustrated in pan-
els c, D, and e, jeweils. The dashed blue trace represents a noisy version of
u(T), and the remaining solid traces represent the sequential activations of five
output neurons: z1−5(T). We trained the excitatory-inhibitory RNN five times,
each with a different random seed. The mean of the output duration for each
scaling factor was shown by the black dots in panel a, and the actual output
duration was highlighted with a larger blue dot. The range (Mittelwert ± SD) of the
RNN output duration for each tested scaling factor is shown by a gray error bar.
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2615
short-scaled input (z.B., 0.1 Und 0.2). Our finding here was also consistent
with the recent results of RNN without biological constraints, in which
temporal scaling of complex motor sequences was learned based on pulse
inputs (Hardy, Goudar, Romero-Sosa, & Buonomano, 2018) or on time-
varying sensory inputs (Goudar & Buonomano, 2018).
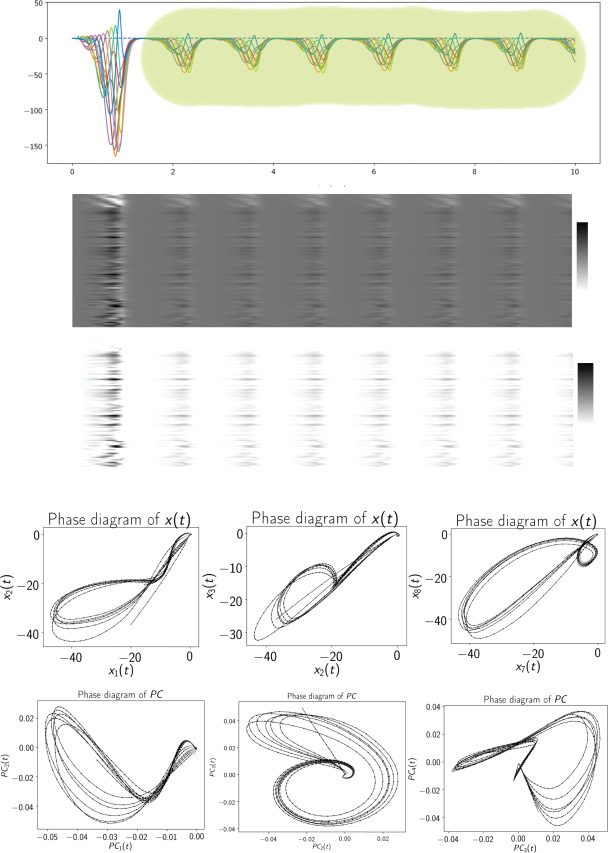
3.3 Limit Cycle in the Steady State. After examining the RNN dy-
namics during the task period, we further investigated the dynamics of
trained RNNs in the steady state: for a long-duration, stimulus-free time
course well beyond the duration of a trained sequence. During the steady
Zustand, the RNN dynamics was driven by spontaneous and recurrent net-
work activity. If one or more growing complex eigenmodes are activated,
the network may exhibit associated spontaneous oscillations. Interessant,
we found that the RNN sequence generator was able to produce a stable
high-dimensional dynamic attractor (see Figure 4a). Das ist, the neural dy-
namics xi(T) and xk(T) (k (cid:6)= i) form a constant phase shift in their activa-
tion strengths, thereby forming a limit cycle and seen as a closed orbit in
two-dimensional projections of phase portrait (see Figure 4b). Letting Pss(X)
denote steady-state probability distribution of x, we define a potential func-
tion of the nonequilibrium system as follows:
U (X) = − log P(X, t → ∞) = − log Pss
.
(3.1)
Vor allem, the limit cycle was embedded not only in the eight sequence
readout neurons (d.h., z1(T) through z8(T)), but also in the remaining 92 neu-
rons. To visualize the low-dimensional representations, we applied PCA to
100-dimensional x(T) during the training trial period ([0,1] S) and then pro-
jected the steady-state activations onto the dominant four-dimensional PC
subspaces. Wieder, we observed stable limit cycles in the PC subspace.
Since the limit cycle was embedded in the high-dimensional neural
state dynamics, it is difficult to derive theoretical results based on any
existing mathematical tools (z.B., the Hopf bifurcation theorem). The dy-
namic attractors in the steady state are fully characterized by equation 2.1
and the N × N matrix Wrec. To date, limited analysis of periodic behav-
ior was obtained for the RNN, except for two-dimensional cases (Jouf-
froy, 2007; Bay, Lepsoy, & Magli, 2016). To understand the conditions of
limit cycles in the excitatory-inhibitory RNN, we decomposed Wrec into
a symmetric and a skew-symmetric component and made further low-
dimensional approximation (see appendix D). Speziell, the symmetric
matrix produces a spectrum with only real eigenvalues, whereas the skew-
symmetric matrix produces a spectrum with only imaginary eigenvalues.
Furthermore, we projected the N-dimensional x(T) onto a two-dimensional
eigenvector space. Under some approximations and assumptions, we could
numerically simulate limit cycles based on the learned weight connection
matrix Wrec (Susman, Brenner, & Barak, 2019).
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2616
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
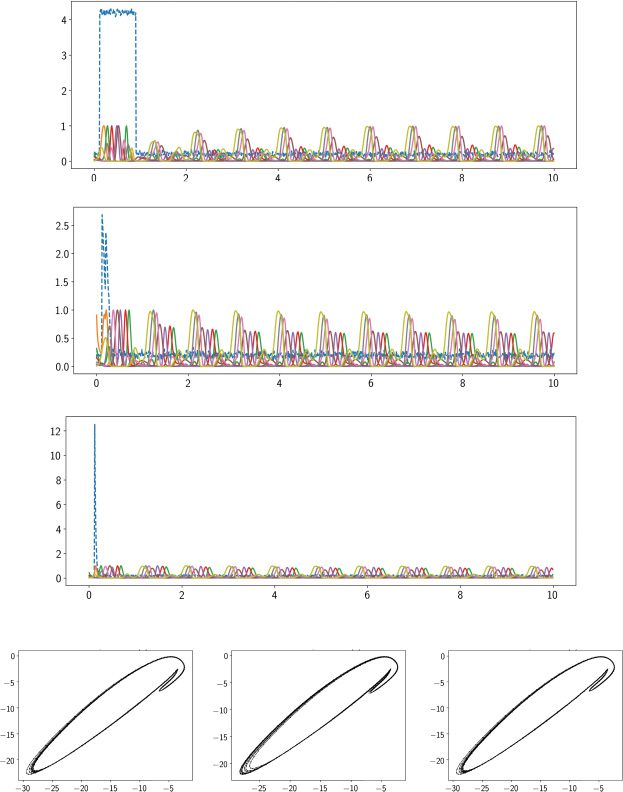
Figur 4: A trained excitatory-inhibitory RNN produced a limit cycle attrac-
tor in the steady state. (A) Output sequence shown as a heat map during t ∈
[0, 10] S, where the shaded area indicated the steady state. (B) Heat maps of
neural activity x(T) (top panel) and firing rate r(T) (bottom panel) of 100 neu-
rons. (c) Illustration of two-dimensional phase diagrams at different subspaces
of {x1(T), x2(T), x3(T), x7(T), x8(T)}. (D) Illustration of two-dimensional phase dia-
grams at the vector spaces spanned by the first four dominant principal com-
ponents (PCs): {PC1(T), PC2(T), PC3(T), PC4(T)}.
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2617
Limit cycle attractors were frequently observed in our various testing
Bedingungen. During training, we varied the sequence duration, the input
waveform, and the number of neurons engaging in the output sequence;
we frequently found a limit cycle attractor in the steady state. By observing
equation 2.9, it is noted that the relative E/I balance is required for the reac-
tivation of sequence output: too much inhibition would suppress the neu-
ronal firing because of below-threshold activity. For each xi(T), if the level
of net inhibition was greater than the level of net excitation, the ith neuron
would not be able to fire even though the memory trace was preserved in
the high-dimensional attractor.
3.4 Impact of Wrec on Dynamic Attractors. The stability of the limit
cycle attractor can be studied by theoretical analysis or numerical (pro-
turbation) Analyse. To study how the change in Wrec affects the stability
of dynamic attractors, we conducted a perturbation analysis on the con-
nection weights. Erste, we scaled the recurrent weight matrix according
(cid:8)
(cid:9)
, a2
, a4
, a3
EE de-
, where Wrec
a1Wrec
EE
a3Wrec
EI
to the functional blocks as follows,
a2Wrec
IE
a4Wrec
II
fines the excitatory-to-excitatory connectivity, Wrec
IE defines the inhibitory-
to-excitatory connection strength, and Wrec
II defines the disinhibition among
inhibitory neurons; {a1
} are four positive scalars. A scaling factor
greater (or smaller) als 1 implies scaling up (or down) the degree of ex-
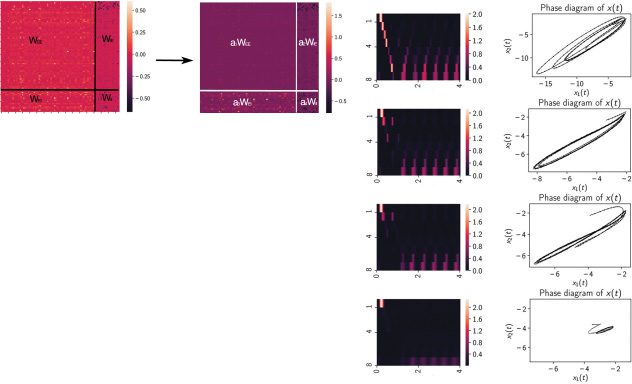
citation and inhibition. Speziell, we found that the limit cycle dynamics
was robust with respect to EI and II scaling and was most sensitive to the EE
scaling (see Figure 5b). Scaling the whole matrix together would scale up or
down the eigenspectrum, thereby affecting the stability. These results sug-
gest that the excitatory-inhibitory RNN is only stable with balanced E/I, Die
excitatory network by itself is unstable, and stabilized only by the feedback
inhibition. Additionally, when scaling down EE connections, Wir fanden das
the amplitude of the limit cycle (d.h., X(T) activation amplitude) reduced with
decreasing scaling factor a1 (see Figure 5c), until converging to a fixed point,
suggesting that emergence of limit cycle behavior is via a Hopf bifurcation
of the network.
Nächste, we imposed a sparsity constraint onto the learned Wrec. We ran-
domly selected a small percentage of connection weights and set them ze-
ros and examined the impact on the dynamic attractor. Since Wrec
EE was most
sensitive to the dynamics, we gradually increased the percentage from 5%,
Zu 10%, 15%, Und 20%, and set randomly chosen entries of Wrec
EE to zeros.
Infolge, the neural sequential activation was reduced during both in-
task and steady-state periods (see Figure 5d). Vor allem, the limit cycle was
still present even when 5% Zu 15% of Wrec
EE elements were zeros, vorschlagen
that the dynamic attractor was robust to sparse coding. Vor allem, the ampli-
tude of x(T) gradually decreased with increasing sparsity level. Wann 20%
of Wrec
EE elements were zeros, the limit cycle converged to a fixed point.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2618
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
, Wrec
, Wrec
IE
= 1. IE: a2 was varied while fixing a1
Figur 5: Robustness of recurrent connectivity matrix that preserved the limit
cycle attractor in the steady state. (A) The recurrent connectivity matrix Wrec
EI , and Wrec
was divided into four blocks. The four submatrices Wrec
II
EE
were scaled with four scaling factors a1, a2, a3, and a4, jeweils. We examined
the range of these scaling factors so that the dynamic attractor remained stable
as a limit cycle and beyond which the dynamic attractor became unstable or
converged to a fixed point. (B) The range of scaling factor that the limit cycle was
=
preserved under different conditions. EE: a1 was varied while fixing a2
= 1. EI: a3 was varied while
a4
= 1. EE and
= a3
fixing a1
= a4 were
EI: a1
= a4 were varied
varied together while fixing a1
together. (c) The amplitude of limit cycle gradually decreased with decreasing
EE . Only the phase diagram of {x1(T), x2(T)} is shown for
scaling factor a1 of Wrec
illustration, but similar observations also held for other state variable pairs. Top
and bottom rows correspond to the noisy and noiseless conditions, jeweils.
(D) The transient and steady-state responses while setting the sparsity of Wrec
EE to
5%, 10%, 15%, Und 20%. The heat maps of z1:8(T) and phase portraits x1(T) versus
x2(T) are shown in the left and right columns, jeweils.
= a2
= 1. IE and II: a2
= a3
= a2
= a3 were varied together while fixing a2
= 1. II: a4 was varied while fixing a1
= a4
= 1. Gesamt: a1
= a3
= a4
= a3
= a2
= a4
= a3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2619
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 6: Computer setup for learning two neural sequences. The first column
shows the two input-output patterns {u(T), z1−8(T)}. Note that inputs 1 Und 2,
as well as output sequences 1 Und 2 are mirror images of each other. The sec-
ond column shows the {z1−8(T)} in the normalized heat maps. The third column
shows the heat maps of {z1−8(T)} in the steady-state period. (A) Setup 1. (B) Setup
2: swapped input-output pairs of setup 1.
3.5 Extension to Learning Two Sequences. RNNs have been also used
to learn multiple sequences (Rajan et al., 2016; Hardy & Buonomano, 2018).
Nächste, we extended the RNN task from learning one sequence to two se-
quences. For simplicity, we used a mirror image setup such that the same
amplitude or power was shared between two inputs and between two out-
puts (siehe Abbildung 6). In setup 1, we mapped two input signals to two equal-
duration outputs, one forward-ordered and one reverse-ordered sequence,
using the same readout neurons. The input signal consisted of a combi-
nation of linear input and a sawtooth component, plus additive gaussian
noise. In setup 2, we reversed the input-output mapping and swapped
the output sequence 1 and output sequence 2. In both setups, we used
= 20 for each input (total 40 Versuche) and added the variability (solch
Ntrials
2620
A. Rajakumar, J. Rinzel, and Z. Chen
as the sinusoidal frequency of the input, the timing of the trigger, and net-
work noise) at each trial. After training the RNN, we examined the transient
and steady-state responses of eight readout neurons.
During the transient response period ([0, 1] S), similar to the previ-
ously demonstrated single-sequence condition, the RNN showed robust
sequence responses and was insensitive to the exact input waveform. In
order to examine the effect of the input magnitude on the trained RNN,
we fed DC input signals with different levels for a duration of 0.8 S (sehen
Figure 7a) and observed the network output. Depending on the magnitude
of DC input, the output sequence was a superposition of two output se-
quences (see Figures 7b and 7i). This result suggests that the bimodal RNN
output was determined by the level of internal excitability in x(T), welche
was contributed from the DC input (see equation 2.1). At a certain level, Die
system reached a state that simultaneously produced two sequence out-
puts (see Figures 7e, 7F, and 7j). The coactivation of two sequences suggests
a symmetric (or asymmetric) double-well potential landscape, and the bi-
ased activation of one of two sequences is influenced by the control DC
Eingang, suggesting a kind of biased competition. The intermediate cases ap-
pear as transients during the competition. To visualize the N-dimensional
Dynamik, we projected x(T) onto the two-dimensional jPCA subspace, Und
observed an ∞-shaped trajectory (see Figure 7k for level 3). The change
in spiraling direction (first clockwise, then counterclockwise) of the phase
portrait reflected the push-pull force in the bistable state.
Interessant, the steady-state output with zero input showed only one
of the output sequences (sequence 2 in both setups shown in Figure 6,
where U (xseq2) < U (xseq1) in the potential landscape). To investigate the tol-
erance of the dynamic attractor to interference, we further fed the variants
of input signals to the trained excitatory-inhibitory RNN at random timing
during the steady-state period. It was found that the reactivation of output
sequence could be triggered by a transient excitatory input, leveling up the
excitability in x(t). Interestingly, the transient input triggered one of two se-
quences and then switched back to the stable state (see Figures 8a and 8b),
suggesting that the trained RNN was not in a state with bistable attractors.
In our computer simulations and perturbation analyses, we didn’t observe
the coexistence of two stable limit cycles, yet the single stable limit cycle
showed a high degree of robustness to various transient input signals. We
may envision two periodic orbits, one stable and the other unstable, coex-
isting in the system (see Figure 8d). One such example is described by the
following two-dimensional system equations,
dx1
dt
dx2
dt
= x1(x2
1
+ x2
2
− 1)(x2
1
+ x2
2
− 2) − x2
,
= x2(x2
1
+ x2
2
− 1)(x2
1
+ x2
2
− 2) + x1
,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2621
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
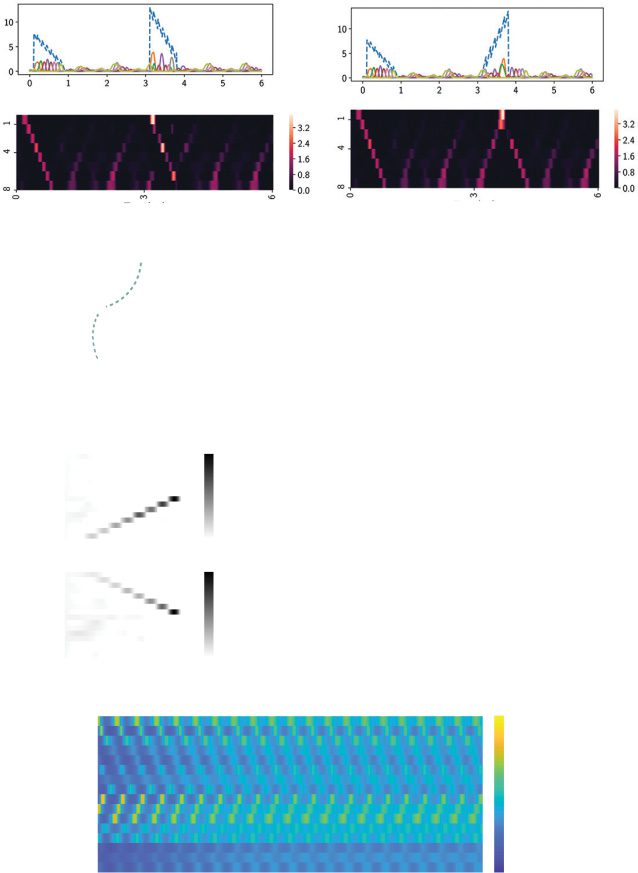
Figure 7: Readout neuronal sequences change in response to different levels of
the DC input during the transient response period ([0, 1] s). DC input was sent to
the trained RNN using setup 1 shown in Figure 6. (a) Illustration of eight differ-
ent levels of DC inputs (the mean input u(t) ∈ {0, 1, 2, . . . , 7}) for t ∈ [0.1, 0.9] s).
(b)–(i) Normalized heat maps of output sequences {z1(t), z2(t), . . . , z8(t)} in re-
sponse to varying levels of DC input. Note that the transition occurred at
levels 3 and 4, where both sequences were clearly visible. (j) Activation of
{x1(t), x2(t), . . . , x8(t)} at level 3. (k) Two-dimensional projection of single-trial
x(t) activation at level 3 onto the first two PC subspaces from jPCA. The origin
represents the initial point, and the arrow indicates the time direction.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2622
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8: (a) Two test input signals were presented at two periods ([0, 1] s
and [3, 4] s, respectively) for the pretrained RNN. The eight readout neurons’
activations {r1−8(t)} were shown by the heat map at the bottom. Note that
the second input triggered the learned forward sequence (at around 3 s) and
then switched back to the stable reverse sequence in the steady state. (b) The
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2623
= 1 is stable, but the
which contain two periodic orbits (the circle x2
1
outer circle is unstable); the trajectories in between are repelled from the
unstable cycle and attracted to the stable one.
+ x2
2
In both setups 1 and 2, the output of readout neurons (units #1–8) were
orthogonal to each other for representing two sequences. Next, we consid-
ered a different setup (setup 3), in which we set Nout = 16, where units #1–
8 represented the output of sequence 1, and units #9–16 represented the
output of sequence 2 (see Figure 8e). Therefore, readout neurons have or-
thogonal representations for these two sequences. Upon learning these two
sequences, we again examined the phase portraits of x(t) during the steady
state. Interestingly, in this new setup, the RNN dynamics also exhibited
a stable limit cycle attractor (see Figure 8f). This stable limit cycle attrac-
tor simultaneously represented the partial forward- and reverse-ordered
sequences, with opposite rotation directions in the phase portrait (see
Figures 8f and 8g). Therefore, the two orthogonal output sequences learned
independently can be coactivated in the steady state, and any two-
dimension combination from {x1
} would also form a periodic os-
, . . . , x16
cillator in the two-dimensional phase space. However, the coactivation of
forward and reverse sequences still appeared as a single limit cycle (with a
shorter period compared to Figures 8a and 8b).
Finally, we investigated whether the period of limit cycle attractor
changed with respect to different inputs. First, using the RNN shown in
Figure 6 as an example, we fed various input signals to the trained RNN
and found qualitatively similar limit cycles (see Figure 9a), suggesting the
invariance property of the RNN-encoded limit cycle with respect to the new
input. Second, using the temporally scaled inputs (as shown in Figure 3),
we fed the various scaled input signals to the trained RNN and again found
→ t2
1 and t(cid:4)
second input triggered a mixed representation of forward sequence and reverse
sequence (at around 3.6 s), and then switched back to the stable reverse se-
quence. (c) Schematic illustration of perturbation of a stable limit cycle. Time
→ t3 progresses on the limit cycle of a unperturbed system,
trajectory t1
whereas a perturbed system is driven away from the limit cycle (t(cid:4)
→ t(cid:4)
3)
1
by an impulsive signal between t(cid:4)
2 and then relaxes back to the limit cy-
cle. (d) Phase portraits of two periodic orbits, one being stable (red solid line)
and the other unstable (red dashed line). The arrows represent the vector field
, ˙x2). (e) Computer simulation setup 3: Units #1–8 represent sequence 1 acti-
( ˙x1
vation, whereas units #9–16 represent sequence 2 activation. Heat maps show
the r(t) activation upon completion of RNN training. Blue traces represent the
corresponding input u(t). (f) Phase portraits of limit cycle attractor in the steady
state with u(t) = 0. The phase portrait x1 versus x2 displays a limit cycle projec-
tion with clockwise direction, whereas the phase portrait x16 versus x15 displays
a limit cycle projection with counterclockwise direction. Open circles represent
the initial point. (g) Heat map of x1−16(t) during the steady-state period.
→ t(cid:4)
2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2624
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: (a) Three examples of u(t) and sequence output {z(t)} during the task
period ([0, 1] s) and steady state ([1, 10] s) for the RNN shown in Figure 6.
(b) Three examples of phase diagrams of x1(t) versus x2(t) during the steady
state under different task input settings for the RNN shown in Figure 3.
the limit cycle was invariant to the task input signal’s period and wave-
form (Figure 9b). Together, these results suggest that once the excitatory-
inhibitory RNN was trained, the dynamic attractor properties during the
steady state were fully determined by the eigenspectrum of Wrec, and the
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2625
period of limit cycle attractor was invariant to the amplitude, waveform, or
frequency of the transient input signals.
4 Discussion
4.1 Relation to Other Work. RNNs are capable of generating a rich class
of dynamical systems and attractors (Trischler & D’Eleuterio, 2016; Pollock
& Jazayeri, 2020). Dynamics of excitatory-inhibitory RNN has been stud-
ied in the literature (Brunel, 2000; Murphy & Miller, 2009). Murphy and
Miller (2009) used mean field theory to study the linear recurrent dynamics
of excitatory-inhibitory neuronal populations and studied the steady-state
response with balanced amplification mechanisms. However, since their
neural network is linear, no limit cycle attractor can arise from the assumed
linear dynamical system. To model neural sequences, Gillett, Pereira, and
Brunel (2020) used mean field theory to derive a low-dimensional descrip-
tion of a sparsely connected linear excitatory-inhibitory rate (and spik-
ing) network. They found that a nonlinear temporally asymmetric Hebbian
learning rule can produce sparse sequences.
Most RNN modeling work for brain functions has focused on repre-
sentations and dynamics during the task period (or transient state), yet
has ignored the stimulus-absent steady state. It remains unclear how the
steady-state dynamics are related to the task-relevant dynamics and how
they further contribute to the task. In the literature, the analysis of limit
cycles for nonlinear RNN dynamics has been limited to two-dimensional
systems (Jourffroy, 2007; Bay et al., 2016; Trischler & D’Eleuterio, 2016).
To our best knowledge, no result was available for the existence of
excitatory-inhibitory RNN in a high-dimensional setting. Our computer
simulation results have shown the emergence of limit cycles from the
trained excitatory-inhibitory RNN while learning the sequence tasks. How-
ever, no theoretical results have been derived regarding the sufficient or
necessary condition. Our computer simulations were built on supervised
learning and gradient descent for learning neural sequences, which is close
in spirit to prior work (Namikawa & Tani, 2009) that they used an Elman-
type RNN structure to learn multiple periodic attractors and the trained
RNN could embed many attractors given random initial conditions.
It is possible to show the existence of periodic orbits or limit cycles in a
content-addressable memory (CAM) network with an asymmetric connec-
tion weight matrix, where the neural firing patterns are binary (Folli, Gosti,
Leonetti, & Ruocco, 2018; Susman et al., 2019). However, the CAM networks
in previous studies did not consider temporal dynamics.
Upon learning neural sequences, we found that the excitatory-inhibitory
RNN exhibited a rotation dynamics in the population response (by jPCA).
This rotation dynamics can be robustly recovered in the single-trial data.
Our finding is consistent with a recent independent finding while reex-
amining the neuronal ensemble activity of the monkey’s motor cortex
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2626
A. Rajakumar, J. Rinzel, and Z. Chen
(Lebedev et al., 2019). In our case, the rotation dynamics analysis was ap-
plied to the complete population, whereas Lebedev’s study was applied
only to the sequence readout neurons. Notably, it was shown that rotational
patterns can be easily obtained if there are temporal sequences in the pop-
ulation activity (Lebedev et al., 2019).
4.2 Dynamic Attractors and Memories. Synaptic efficacy is fundamen-
tal to memory storage and retrieval. The classical RNN used for associative
memory is the Hopfield network, which can store the patterns via a set of
fixed points. The weight connection matrix in the Hopfield network is sym-
metric, thereby yielding only real positive eigenvalues. However, memo-
ries stored as time-varying attractors of neural dynamics are more resilient
to noise than fixed points (Susman et al., 2019). The dynamic attractor is
appealing for storing memory information as it is tolerant to interference;
therefore, the limit cycle mechanism can be useful to preserve time-varying
persistent neuronal activity during context-dependent working memory
(Mante, Sussillo, Shenoy, & Newsome, 2013; Schmitt et al., 2017).
In the excitatory-inhibitory RNN, the stability of a dynamic system is
defined by the recurrent connectivity matrix, which can further affect In-
trinsically generated fluctuating activity (Mastrogiuseppe & Ostojic, 2017).
According to dynamical systems theory, stability about a set-point is related
to the spectrum of the Jacobian matrix (i.e., local linear approximation of the
nonlinear dynamics) (Sussillo & Barak, 2013). For a general Jacobian matrix,
the spectrum consists of a set of complex eigenvalues. The real part of this
spectrum defines the system’s stability: a system is stable only if all eigen-
values have negative real parts, whereas the imaginary part of the spec-
trum determines the timescales of small-amplitude dynamics around the
set-point, but not stability (Susman et al., 2019).
In the special case, the unconstrained RNN (i.e., without imposing Dale’s
principle) can be approximated and operated as a line attractor (Seung,
1996), although the approximation of line attractor dynamics by a nonlin-
ear network may be qualitatively different from the approximation by a
linear network. Additionally, strong nonlinearity can be used to make mem-
ory networks robust to perturbations of state or dynamics. Linearization
around some candidate points that minimize an auxiliary scalar function
|G(x)|2 (kinematic energy) may help reveal the fixed and slow points of
high-dimensional RNN dynamics (Sussillo & Barak, 2013; Kao, 2019; Zhang
et al., 2021). However, efficient numerical methods to analyze limit cycle at-
tractors of RNNs remain unexplored.
It has been found that our trained excitatory-inhibitory RNN can trigger
the neural sequence based on a wide range of input signals, representing
one possible mechanism of memory retrieval. This is analogous to remem-
bering a sequence of a phone number triggered by a name, where the form
of name presentation may vary. The sequence readout is also robust to noise
and system perturbation. During the steady state, the steady-state RNN
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2627
dynamics displayed either forward or reverse sequences, reminding us of
rodent hippocampal memory replay during the offline state (Foster & Wil-
son, 2006; Diba & Buzsaki, 2007).
Multistability is an important property of RNNs (Cheng, Lin, & Shih,
2006; Ceni, Ashwin, Livi, & Oostlethwaite, 2020). For a general class of
N-dimensional RNN with (k-stair) piecewise linear activation functions,
RNNs can have (4k − 1)N equilibrium points, and (2k)N of them are locally
exponentially stable (Zeng, Huang, & Zheng, 2010). Recently, it has been
shown that a two-dimensional gated recurrent units (GRU) network can
exhibit a rich repertoire of dynamical features that includes stable limit cy-
cles, multistable dynamics with various topologies, Andronov-Hopf bifur-
cation, and homoclinic orbits (Jordan, Sokol, & Park, 2019). However, their
RNN allows self-connections and does not impose excitatory-inhibitory
constraints. While training the excitatory-inhibitory N-dimensional RNN
to learn two sequences, we found that memory retrieval is dominated by a
single memory pattern within one stable limit cycle attractor (see Figures 8a
and 8b). However, reactivation of two sequence patterns can be obtained by
using orthogonal neuronal representations (see Figures 8e to 8g). The topics
of coexistence of bi- or multistability and the mechanism of bistable switch-
ing between two limit cycles or between a limit cycle and fixed points would
require further theoretical and simulation studies.
4.3 Hebbian Plasticity versus Backpropagation. Supervised learning
algorithms have been widely used to train RNNs (Werbos, 1988; Jaeger,
2001; Maass, Natschläger, & Markram, 2002; Sussilo & Abbott, 2009; Song
et al., 2016). We have used the established BPTT algorithm to train the
excitatory-inhibitory RNN, where synaptic modification was applied to all
synaptic connections based on gradient descent. In addition, it is possible
to introduce a partial synaptic weight training mechanism on the recurrent
weight matrix (Rajan et al., 2016; Song et al., 2016).
The supervised learning algorithms (e.g., BPTT or FORCE) assume an
error-correction mechanism (Werbos, 1988; Sussilo & Abbott, 2009). How-
ever, how error backpropagation mechanisms can be implemented in the
brain remains debatable (Lillicrap et al., 2020). In contrast, Hebbian plastic-
ity represents an alternative yet more biologically plausible rule for learning
sequential activity in the brain (Fiete, Senn, Wang, & Hahnloser, 2010; Gillett
et al., 2020). More important, the brain is likely to use a continual learning
strategy for multiple tasks (Kirkpatrick et al., 2017; Zenke, Poole, & Ganguli,
2017; Yang et al., 2019; Duncker, Driscoll, Shenoy, Sahani, & Sussillo, 2020),
such as multiple sequences. Distributing resources of synaptic weights and
readout neurons in RNNs is crucial for continual learning. Recently, it has
been shown that neural sequences in the mouse motor cortex could reacti-
vate faster during the course of motor learning (Adler et al., 2019). Eigen-
value analysis of recurrent weight matrix Wrec can provide new insight into
such neural plasticity (see Figure 10 for a toy example illustration).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
2628
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
Figure 10: (a) Hinton diagram of 5×5 connection matrix Wrec for one inhibitory
and four excitatory neurons. The white and black represent the positive and
negative value, respectively. The size of the square is proportional to the ab-
solute value of the connection weights. The eigenspectrum of Wrec consists
of one real and two pairs of complex conjugate eigenvalues {−0.99, 1.22 ±
j2.42, −0.73 ± j0.29}. Weight perturbation by slightly enhancing the local E-E
connectivity while keeping I-E connection unchanged leads to a new eigenspec-
trum {−0.99, 1.39 ± j2.43, −0.90 ± j0.57}. (b) Two growing or decaying modes
of harmonic oscillators emerge from the superposition of real and complex
eigenmodes. The eigenmode in blue oscillates faster after synaptic plasticity.
(c) Activation of two readout neurons (in red and blue) after ReLU transforma-
tion. After synaptic weight perturbation, the red-blue neuron sequence activa-
tion shifts earlier.
Biologically inspired Hebbian learning has been proposed for sequence
learning (Fiete et al. 2010; Panda & Roy, 2017). For instance, a generalized
Hebbian synaptic plasticity rule has been proposed with the following form
(Koulakov, Hromadka, & Zador, 2009),
˙wrec
i j
= (cid:11)
1rir j
wrec
i j
− (cid:11)
wrec
i j
,
2
(4.1)
where the first term describes the generalized correlation between the
presynaptic firing ri and postsynaptic firing r j, and the second term
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
n
e
c
o
_
a
_
0
1
4
1
8
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2629
< 1 denotes the learning rate,
2 denotes the weight-decaying coefficient. In the discrete form, equa-
describes a weight decay component; 0 < (cid:11)
and (cid:11)
tion 4.1 is rewritten as
1
i j (t + (cid:12)t) = (cid:11)
1ri(t)r j(t)wrec
wrec
(cid:10)
(cid:11)
=
i j (t)(cid:12)t + (1 − (cid:11)
(cid:11)
(cid:12)t)wrec
i j (t)
2
1ri(t)r j(t)(cid:12)t + 1 − (cid:11)
(cid:12)t
2
wrec
i j (t)
= χ (t)wrec
i j (t),
(4.2)
(cid:12)t > 0 is a positive time-varying scaling factor (assuming that (cid:11)
1ri(T)r j(T)(cid:12)T + 1 −
Wo (cid:12)t denotes the discrete time bin, and χ (T) = (cid:11)
(cid:11)
2 Und (cid:12)T
2
are sufficiently small). Note that this generalized Hebbian plasticity has
a multiplicative form and preserves the excitatory or inhibitory sign of
synaptic weights. As the multiplicative rule implies, the change in synaptic
weights is proportional to the absolute value of the synaptic weight. Das
type of multiplicative rule can lead to a log-normal distribution of synaptic
strengths (Loewenstein, Kuras, & Rumpel, 2011; Buzsaki & Mizuseki, 2014).
A future research direction will focus on how heterosynatpic Hebbian/
non-Hebbian plasticity influences the existing neural sequence represen-
tation or, gleichwertig, the eigenspectrum of recurrent weight matrix.
4.4 Limitation of Our Work. The excitatory-inhibitory RNN provides a
framework to investigate the dynamics of biological neural networks. Wie-
immer, it still has several important limitations. Erste, our computer simula-
tions could not fully capture the constraints in the biological system. Für
Beispiel, the unconstrained x(T) showed strongly negative amplitudes in
the time course, raising the issue of plausibility in terms of subthreshold
synaptic activity. One possible solution is to bound the xi(T) amplitude by
their net E and I contributions,
τ dxi
dt
= −xi
+ (Iexc
ich
− xi)
(cid:3)
j∈exc
wrec
i j r j
+ (Iinh
ich
− xi)
(cid:3)
j∈inh
wrec
i j r j
+ win
i u + σ ξ
ich
,
(4.3)
welche, Jedoch, may make the learning unstable or slower. Zweite, Die
computational task used in our simulations was very simple, and the net-
work size was relatively small. Generalization of our empirical observations
to a more complex setting would require further investigations. Dritte, lim-
ited insight can be derived from a learned large weight matrix. Jedoch,
it is possible to impose additional recurrent connectivity constraint onto
the RNN while conducting constrained optimization; this additional con-
straint can potentially improve the expressivity and interpretability of RNN
(Kerg et al., 2019). Vierte, it should be noted that computer simulations,
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2630
A. Rajakumar, J. Rinzel, and Z. Chen
albeit useful, could not provide a rigorous mathematical proof regarding
the stability or sufficient condition for limit cycle attractors. One type of
mathematical analysis in the future work can study the Hopf bifurcation via
AUTO (Roussel, 2019). Speziell, this would require linearization of the
high-dimensional nonlinear dynamical system around the fixed points, fol-
lowed by computation of complex conjugate eigenvalues. Endlich, it remains
unclear whether we can construct a line attractor excitatory-inhibitory RNN
that produces a neural sequence by hand-tuning the network connectiv-
ität (result not shown: we have succeeded in constructing a simple RNN
with a ring structure of 6 excitatory-inhibitory units to generate a periodic
oscillator).
5 Abschluss
Zusammenfassend, we trained an excitatory-inhibitory RNN to learn neural se-
quences and study its stimulus-driven and spontaneous network dynamics.
Dale’s principle imposes a constraint on the nonnormal recurrent weight
matrix and provides a new perspective to analyze the impact of excitation
and inhibition on RNN dynamics. Upon learning the output sequences, Wir
found that dynamic attractors emerged in the trained RNN, and the limit
cycle attractors in the steady state showed varying degrees of resilience to
noise, interference, and recurrent connectivity. The eigenspectrum of the
learned recurrent connectivity matrix with growing or damping modes
Combined together with the RNN’s nonlinearity, are adequate to generate
a limit cycle attractor. By theoretical analyses of the approximate linear sys-
tem equation, we also found conceptual links between the recurrent weight
matrix and neural dynamics. Despite the task simplicity, our computer sim-
ulations provide a framework to study stimulus-driven and spontaneous
dynamics of biological neural networks and further motivate future theo-
retical work.
Appendix A: Solving Equation for the Two-Dimensional
Dynamical System
For simplicity of analysis, let us consider a rectified linear function and a
noiseless condition,
τ ˙x = −x + Wrecφ(X) + Winu,
(A.1)
where φ(X) = [X]+. It could be observed that equation A.1 is nonlinear and
hence highly difficult and complicated to solve by analytical means for large
dimensions of x(T). Jedoch, the ReLU activation results in nonlinearity.
Depending on the sign of each of the components of x ∈ RN, we obtain 2N
different linear equations.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2631
For x(T) ∈ R2, equation A.1 may be split into 22 = 4 different conditions
, wie folgt:
depending on the sign of individual component of x =
(cid:8)
(cid:6)
x1 x2
(cid:9) (cid:8)
(cid:7)(cid:11)
(cid:9)
(cid:9)
(cid:8)
(cid:9)
(cid:8)
− 1
wrec
11
wrec
21
wrec
12
− 1
wrec
22
x1
x2
+
win
1
win
2
u
τ , where x1
> 0, x2
> 0,
(cid:9) (cid:8)
(cid:9)
(cid:8)
− 1
wrec
11
wrec
21
0
−1
−1
wrec
12
− 1
0 wrec
22
(cid:9) (cid:8)
−1
0
0 −1
x1
x2
x1
x2
x1
(cid:9) (cid:8)
x2
(cid:8)
(cid:9)
+
+
(cid:9)
(cid:8)
(cid:9)
+
win
1
win
2
win
1
win
2
win
1
win
2
(cid:9)
(cid:9)
(A.2)
u
τ , where x1
> 0, x2
≤ 0, (A.3)
u
τ , where x1
≤ 0, x2
> 0, (A.4)
u
τ , where x1
≤ 0, x2
≤ 0.
(A.5)
dx1
dt
dx2
dt
(cid:9)
(cid:9)
(cid:9)
(cid:8)
(cid:8)
(cid:8)
dx1
dt
dx2
dt
dx1
dt
dx2
dt
dx1
dt
dx2
dt
= 1
τ
= 1
τ
= 1
τ
= 1
τ
(cid:8)
(cid:8)
(cid:8)
Equations A.2 through A.5 may be simply rewritten as
˙x = Ax + Bu,
(A.6)
τ Win and A is different depending on whether x1,2
where B = 1
≤ 0.
x1,2
Without loss of generality, we assume that the input u(T) has an expo-
> 0 oder
nential decaying form as follows:
(cid:2)
u(T) =
0,
c1e−c2(t−ts ),
Wenn 0 ≤ t < ts if t ≥ ts, where c1 and c2 are two positive constants. A more generalized form of u(t) = the following derivation. (cid:12) c1 cos(βt + β 0)e−c2 (t−ts ) is also valid for (A.7) To examine the dynamics of linear differential equation A.6, we apply eigenvalue decomposition to matrix A, AV = V Z, where (cid:7) (cid:6) v1 v2 = V = (cid:9) (cid:8) v v 11 12 v v 21 22 and Z = (cid:8) ζ 1 0 (cid:9) . 0 ζ 2 (A.8) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 1 0 2 6 0 3 1 9 6 3 3 8 9 n e c o _ a _ 0 1 4 1 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 2632 A. Rajakumar, J. Rinzel, and Z. Chen Here, v1 and v2 denote two eigenvectors of A, and ζ sponding eigenvalues, respectively. 1 and ζ 2 are their corre- Furthermore, we assume that v1 and v2 are linearly independent of each other, and for arbitrary x = (cid:7)(cid:11) (cid:6) x1 x2 , we have x = p1v1 + p2v2 = V p, where p = (cid:6) (cid:7)(cid:11) . p1 p2 In light of equations A.6, A.8, and A.9, we have V ˙p = V Zp + Bu. Multiplying V −1 on both sides of the equation A.10 yields ˙p = Zp + V −1Bu. Let m = V −1B = (cid:6) m1 m2 (cid:7)(cid:11) ˙p1 ˙p2 = ζ 1 p1 = ζ 2 p2 + m1u(t), + m2u(t). ; then equation A.11 is rewritten as (A.9) (A.10) (A.11) (A.12) (A.13) Note that ζ 1 and x2. , ζ 2 , m1 , m2 are different depending on the algebraic signs of x1 Solving linear equations A.12 and A.13 further yields ⎧ ⎨ ⎩ pi(t) = 0, 0 ≤ t < ts (cid:16) eζ mi c1 i(t−ts ) − e−c2(t−ts ) (cid:17) , t ≥ ts for i = 1, 2. From A.9, x(t) is rewritten as (cid:8) (cid:9) (cid:8) x1(t) x2(t) = (cid:9) v v 11 12 p1(t) + (cid:9) (cid:8) v v 21 22 p2(t). (A.14) (A.15) For each of four quadrants of [x1 , x2], the eigenvalues can be calculated as follows: • When x1 > 0, x2
> 0, we have the determinant
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
+ 1
ζ − wrec
11
−wrec
21
−wrec
12
ζ − wrec
22
+ 1
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
= 0.
(A.16)
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2633
This further implies
− wrec
ζ 2 + (2 − wrec
11
ζ 2 + 2ζ + (1 − wrec
12
22 )ζ + (1 + wrec
21 ) = 0
wrec
11
wrec
22
− wrec
12
wrec
21
− wrec
11
− wrec
22 ) = 0 Und
(A.17)
because of wrec
11
roots:
= wrec
22
= 0. Solving equation A.17 yields two complex
(cid:19)
ζ ++
1,2
= −1 ±
wrec
12
wrec
21
,
(A.18)
where wrec
imaginary. Let ω =
iω.
wrec
12 has the opposite signs from wrec
21 is purely
21 so that
√
−1, so we have ζ ++
= −1 ±
−wrec
1,2
12
21 and i =
wrec
wrec
12
(cid:20)
• For all three other cases, das ist, when x1
0, x2
> 0, or when x1
≤ 0, x2
≤ 0, or when x1
≤ 0 in light of equation A.17, Wir haben
> 0, x2
≤
(cid:20)
ζ 2 + 2ζ + 1 = 0,
(A.19)
as either wrec
11
the solutions as
= wrec
21
= 0 and/or wrec
12
= wrec
22
= 0. We further derive
ζ +−
1,2
= ζ −+
1,2
= ζ −−
1,2
= −1.
Zusammenfassend, for a two-dimensional system equation, the solution is
given as
(cid:2)
−1 ±
−1,
ζ
1,2
=
(cid:20)
wrec
12
wrec
21
,
if x1
> 0, x2
ansonsten.
> 0
(A.20)
daher, the solution can be either real or a pair of conjugate complex
Werte.
Seit {x1(T), x2(T)} are potentially changing the quadrant location, Sie
will influence the percentage of neuron activation (entweder 100%, 50%, oder 0%)
in a time-varying manner. daher, the superposition of the eigenmodes
will change in both stimulus-driven and spontaneous network dynamics.
To help visualize the vector field in two-dimensional space, we used the
softplus activation function (as a continuous approximation to ReLU) Und
randomized Wrec to examine the existence of fixed points or limit cycles.
An example of phase portrait is shown in Figure 11a. Although a fixed point
could be found, we did not find any closed orbit or periodic solution in four
orthants.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2634
A. Rajakumar, J. Rinzel, and Z. Chen
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 11: (A) Phase portrait of a two-dimensional (2D) dynamical system based
= 3. A fixed point was
on the softplus activation function, where wrec
12
found around (−2, 0). (b–d) Phase portraits of a three-dimensional (3D) dynam-
ical system based on the softplus activation function. Arrows represent the vec-
tor field.
= −2, wrec
21
Appendix B: Solving Equation for the Three-Dimensional
Dynamical System
For x ∈ R3, equation A.1 can be split for 23 = 8 different cases depending
on the algebraic sign of individual components. For notation simplicity,
we omit the superscript in wrec
i j in the remaining
derivation:
⎡
i j and replace it with w
⎤
⎤
⎡
⎤
⎡
⎤
⎡
w
⎥
⎦ = 1
⎥
τ
⎢
⎣
⎢
⎢
⎣
dx1
dt
dx2
dt
dx3
dt
− 1
11
w
w
21
31
12
− 1
w
w
22
w
32
> 0, x2
w
33
> 0, x3
w
w
x1
x2
x3
⎥
⎦
⎢
⎣
13
23
− 1
> 0
where x1
⎥
⎦ +
⎢
⎣
win
1
win
2
win
3
⎥
⎦
,
u
τ
(B.1)
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2635
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
⎡
⎢
⎢
⎣
dx1
dt
dx2
dt
dx3
dt
dx1
dt
dx2
dt
dx3
dt
dx1
dt
dx2
dt
dx3
dt
dx1
dt
dx2
dt
dx3
dt
dx1
dt
dx2
dt
dx3
dt
dx1
dt
dx2
dt
dx3
dt
dx1
dt
dx2
dt
dx3
dt
⎤
⎥
⎦ = 1
⎥
τ
⎤
⎥
⎦ = 1
⎥
τ
⎤
⎥
⎦ = 1
⎥
τ
⎤
⎥
⎦ = 1
⎥
τ
⎤
⎥
⎦ = 1
⎥
τ
⎤
⎥
⎦ = 1
⎥
τ
− 1
w
⎤
⎥
⎦ = 1
⎥
τ
w
⎡
⎢
⎣
11
w
w
21
31
0
0
−1
12
− 1
w
22
w
32
> 0, x2
> 0, x3
w
13
w
23
− 1
0
−1
0 w
> 0, x2
w
33
≤ 0, x3
⎡
⎤
w
12
− 1 w
w
⎥
⎦
⎢
⎣
22
w
13
23
⎤
⎡
⎥
⎦
⎢
⎣
≤ 0
⎤
⎡
⎥
⎦
⎢
⎣
x1
x2
x3
x1
x2
x3
⎤
⎡
⎥
⎦ +
⎢
⎣
⎤
⎡
⎥
⎦ +
⎢
⎣
⎤
⎥
⎦
⎤
⎥
⎦
win
1
win
2
win
3
win
1
win
2
win
3
,
u
τ
,
u
τ
> 0
⎤
⎡
⎥
⎦ +
⎢
⎣
x1
x2
x3
⎤
⎥
⎦
,
u
τ
win
1
win
2
win
3
32
≤ 0, x2
33
> 0, x3
⎡
⎤
> 0
⎤
⎡
⎥
⎦
⎢
⎣
⎥
⎦ +
⎢
⎣
0
0
−1
0
0 −1
where x1
⎡
− 1
w
⎢
⎣
11
w
w
21
31
where x1
⎡
−1
0 w
0
⎢
⎣
where x1
⎡
− 1
w
⎢
⎣
11
w
w
21
31
x1
x2
x3
x1
x2
x3
x1
x2
x3
⎤
⎥
⎦
⎤
⎥
⎦
⎤
⎥
⎦
win
1
win
2
win
3
win
1
win
2
win
3
win
1
win
2
win
3
,
u
τ
,
u
τ
,
u
τ
> 0, x2
w
12
− 1
where x1
⎡
−1
0 w
0
⎢
⎣
22
w
0
0
−1
≤ 0, x3
⎤
⎡
≤ 0
⎤
⎡
⎥
⎦
⎢
⎣
⎥
⎦ +
⎢
⎣
13
w
23
− 1
32
≤ 0, x2
w
where x1
⎡
−1
0
0 −1
0
⎢
⎣
where x1
⎡
−1
0
0 −1
0
⎢
⎣
0 w
33
≤ 0, x2
⎤
0
0
0 −1
where x1
≤ 0, x2
> 0, x3
⎤
⎡
≤ 0
⎤
⎡
⎥
⎦
⎢
⎣
⎥
⎦ +
⎢
⎣
≤ 0, x3
⎤
⎡
> 0
⎡
⎥
⎦
⎢
⎣
⎥
⎦ +
⎢
⎣
x1
x2
x3
≤ 0, x3
≤ 0
⎤
⎥
⎦
,
u
τ
win
1
win
2
win
3
Equations B.1 through B.8 may be simply rewritten as
˙x = Ax + Bu,
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
(B.2)
(B.3)
(B.4)
(B.5)
(B.6)
(B.7)
(B.8)
(B.9)
2636
A. Rajakumar, J. Rinzel, and Z. Chen
(cid:6)
(cid:7)(cid:11)
where x =
on whether x1,2,3
x1 x2 x3
, B = 1
> 0 or x1,2,3
τ Win and the exact form of matrix A depends
≤ 0.
Similar to the derivation shown in appendix A, applying eigenvalue de-
composition to matrix A yields
AV = V Z,
Wo
(B.10)
(cid:6)
v1 v2 v3
(cid:7)
=
V =
⎡
⎢
⎣
v
v
v
11
12
13
v
v
v
21
22
23
v
v
v
31
32
33
⎤
⎥
⎦ and Z =
⎡
⎢
⎣
ζ
1
0
0
0
ζ
2
0
⎤
⎥
⎦ ,
0
0
ζ
3
, v2
} are the eigenvectors of A and {ζ
Wo {v1
1
sponding eigenvalues, respectively.
(cid:7)(cid:11)
, v3
(cid:6)
Wieder, we express x =
x1 x2 x3
as a linear combination of eigenvectors,
, ζ
2
, ζ
3
} are their corre-
x = p1v1
+ p2v2
+ p3v3
= V p,
where p =
(cid:6)
(cid:7)(cid:11)
.
p1 p2 p3
In light of equations B.9, B.10, and B.11, Wir haben
˙p = Zp + V
−1Bu,
Let m = V −1B =
(cid:6)
m1 m2 m3
(cid:7)(cid:11)
. We further obtain
⎧
⎪⎪⎨
⎪⎪⎩
˙p1
˙p2
˙p3
= ζ
1 p1
= ζ
2 p2
= ζ
3 p3
+ m1u(T)
+ m2u(T)
+ m3u(T)
,
(B.11)
(B.12)
(B.13)
a decoupled form of equations B.1 through B.8. Note that ζ
1
(cid:6)
, m3 are different depending on the algebraic sign of
x1 x2 x3
m1
, m2
Solving the linear differential equation B.13 yields
, ζ
2
(cid:7)(cid:11)
.
, ζ
3
,
⎧
⎪⎨
⎪⎩
pi(T) =
0, 0 ≤ t < ts (cid:16) eζ mi c2 i(t−ts ) − e−q(t−ts ) (cid:17) , t ≥ ts, (B.14) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 1 0 2 6 0 3 1 9 6 3 3 8 9 n e c o _ a _ 0 1 4 1 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Dynamics in Excitatory-Inhibitory Recurrent Neural Networks 2637 and equation B.11 is rewritten as ⎤ ⎡ ⎥ ⎦ = ⎢ ⎣ ⎡ ⎢ ⎣ x1(t) x2(t) x3(t) v v v 11 12 13 ⎤ ⎥ ⎦ p1(t) + ⎤ ⎥ ⎦ p2(t) + ⎡ ⎢ ⎣ v v v 21 22 23 ⎤ ⎥ ⎦ p3(t). ⎡ ⎢ ⎣ v v v 31 32 33 (B.15) Depending on the values of {x1 , x2 , x3 }, we can compute the eigenvalues as follows: > 0, x2
> 0, x3
> 0, we have the following 3 × 3 determinant
• When x1
Matrix:
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
ζ − w
+ 1
−w
11
−w
21
−w
31
12
+ 1
ζ − w
22
−w
32
−w
13
−w
ζ − w
23
+ 1
33
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
(cid:18)
= 0.
(B.16)
From w
11
= w
22
= w
33
= 0, we further derive
ζ 3 + 3ζ 2 + ζ (3 − w
w
+ (1 − w
w
23
12
31
12
w
21
− w
− w
w
− w
31
w
32)
13
w
w
13
21
− w
32
23
23
w
− w
w
21
− w
w
31) = 0.
13
12
32
(B.17)
The analytic solution of cubic equation B.17 is available, but this equa-
tion does not have ζ = −1 as one of its roots, unlike the remaining
cases discussed. The eigenvalues for other cases shown in equations
B.2 to B.9 are discussed in the sequel.
> 0, x3
≤ 0, from equation B.17, Wir haben
> 0, x2
• When x1
ζ 3 + 3ζ 2 + ζ (3 − w
12
w
21) + (1 − w
12
w
21) = 0
(B.18)
13
23
= w
= 0, which is assumed in this case. It is noted
because of w
that ζ = −1 is one of the roots satisfying equation B.18. Rewriting
equation B.18 in a factorized form, (ζ + 1)(ζ 2 + 2ζ + (1 − w
21)) =
0, we obtain the solutions
√
w
12
ζ = −1 or − 1 ±
w
w
12
21
.
• When x1
> 0, x2
≤ 0, x3
> 0, solving equation B.17 yields
√
ζ = −1 or − 1 ±
w
w
13
31
.
• When x1
≤ 0, x2
> 0, x3
> 0, solving equation B.17 yields
√
ζ = −1 or − 1 ±
w
w
23
32
.
(B.19)
(B.20)
(B.21)
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2638
A. Rajakumar, J. Rinzel, and Z. Chen
• For all other remaining cases, nämlich, when x1
≤ 0, x2
≤ 0, or when x1
> 0, x3
≤ 0, we have the solutions as
when x1
≤ 0, x2
x1
≤ 0, x2
≤ 0, x3
> 0, x2
≤ 0, x3
≤ 0, x3
≤ 0, oder
> 0, or when
ζ = −1.
(B.22)
daher, the solutions can contain one real and a pair of conjugate com-
plex values.
Examples of phase portraits of three-dimensional dynamical system for
two selected hyperoctants are shown in Figures 11b to 11d. We have exam-
ined and simulated both E-E-I (two excitatory and one inhibitory neurons)
and E-I-I (one excitatory and two inhibitory neurons) setups.
Appendix C: jPCA via Polar Decomposition
The jPCA method has been used to reveal rotational dynamics of neuronal
population responses (Churchland et al., 2012). Let’s assume that the data
are modeled as a linear time-invariant continuous dynamical system of the
bilden
˙x = Mx,
(C.1)
where the linear transformation matrix M is constrained to be skew-
symmetric (d.h., M(cid:11) = −M). The jPCA algorithm projects high-dimensional
data x(T) onto the eigenvectors of the M matrix, and these eigenvectors arise
in complex conjugate pairs. Given a pair of eigenvectors {v
}, the kth
k
− ¯v
jPCA projection plane axes are defined as uk,1
k and uk,2
k)
k
(where j =
, ¯v
k
= j(v
−1).
+ ¯v
= v
√
k
The solution to continuous-time differential equation C.1 is given by
X(T) = eMtx(0), where the family {eMt} is often referred to as the semi-group
generated by the linear operator M. Since M is skew-symmetric, eM is or-
thogonal; daher, it can describe the rotation of the initial condition x(0)
im Laufe der Zeit. We apply eigenvalue decomposition to the real skew-symmetric
matrix M, so that M = U(cid:3)U−1, Wo (cid:3) is a diagonal matrix whose en-
versucht {λ
}N
i=1 are a set of (zero or purely imaginary) eigenvalues. daher,
ich
we have eMt = Ue(cid:3)tU−1. By taking the powers of the diagonal matrix (cid:3), Wir
have
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
∞(cid:3)
eMt = U
((cid:3)T)k
k!
−1
U
1T
k=0
⎛
eλ
0
…
0
⎜
⎜
⎜
⎜
⎝
= U
0
eλ
2T
…
0
· · ·
· · ·
. . .
· · ·
⎞
⎟
⎟
⎟
⎟
⎠
0
0
…
eλNt
−1
U
(C.2)
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2639
in which each eigenmode defines the natural frequency of oscillation.
In addition, Wir haben
X(T + τ ) = eM(t+τ )X(0) = eMτ
X(T),
(C.3)
which implies that for any time pairs {T, T + τ }, their activations are sepa-
rated by a constant phase shift eMτ
. In a two-dimensional space, assuming
(cid:9)
(cid:8)
that the orthogonal matrix eMτ has the form of
cos θ − sin θ
cos θ
sin θ
, this or-
thogonal matrix corresponds to a rotation around the origin by angle θ .
Upon time discretization (assuming dt = 1), we have the discrete analog
of equation C.1,
X(T + 1) = (ICH + M)X(T).
(C.4)
Beachten Sie, dass (ICH + M) is a first-order Taylor’s series approximation to the or-
thogonal transformation Q = eM.
Alternativ, we can directly solve a discrete dynamical system of the
vector autoregressive (VAR) process form x(T + 1) = Qx(T) over the space
of orthogonal Q matrices. Mathematically, we have previously shown that
this is equivalent to solving the following constrained optimization prob-
lem (Nemati, Linderman, & Chen, 2014):
∗ = arg min
Q
Q
(cid:16)|A − Q|(cid:16)2
F
, subject to QQ
(cid:11) = I,
(C.5)
T )(XtX(cid:11)
T )
Wo (cid:16) · (cid:16)F denotes the matrix Frobenius norm and A = (Xt+1X(cid:11)
−1
represents the least square solution to the unconstrained problem x(T + 1) =
Ax(T). The solution to the above constrained optimization is given by the
orthogonal matrix factor of celebrated polar decomposition of matrix A,
nämlich, A = QP (Higham, 1986).
From polar decomposition, if λ
k correspond to the eigenvalue and
eigenvector of matrix M, jeweils, Dann 1 + λ
k will correspond to
the approximate eigenvalue and eigenvector of matrix Q. Das ist, the jPCA
eigenvectors span the same space as the eigenvectors of the polar decom-
position factor Q.
k and v
k and v
Appendix D: Low-Dimensional Approximation of Limit
Cycle Attractor
Given an arbitrary real-valued square matrix Wrec, we can decompose it
into the sum of a symmetric matrix ˜W1
1 and a skew-symmetric matrix
˜W2
= ˜W(cid:11)
= − ˜W(cid:11)
2 :
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2640
A. Rajakumar, J. Rinzel, and Z. Chen
= Wrec
Wrec
+ W(cid:11)
rec
2
+ ˜W2
.
+ Wrec
− W(cid:11)
rec
2
(D.1)
≡ ˜W1
Applying eigenvalue decomposition to the N × N matrix ˜W1, we use the
first two dominant eigenvectors u and v to approximate ˜W1:
˜W1
≈ λ
1uu
(cid:11) + λ
2vv
(cid:11),
(D.2)
> λ
2
> 0 denotes the eigenvalues, Und (cid:16)u(cid:16) = (cid:16)v(cid:16) = 1, u(cid:11)v =
where λ
1
v(cid:11)u = 0. The vectors u and v represent the dominant principal component
(PC) subspaces.
We further approximate ˜W2 with the following form,
˜W2
≈ ρ(uv
(cid:11)
(cid:11) − vu
),
where ρ is a constant such that
ρ = arg min
λ
(cid:16) ˜W2
− λ(uv
(cid:11)
(cid:11) − vu
.
)(cid:16)2
F
(D.3)
(D.4)
√
In light of equations D.2 and D.3, we define pu = u(cid:11)x/
N and pv =
v(cid:11)x/
N as two linear projections of N-dimensional x onto the vector spaces
u and v, jeweils. In the steady state (d.h., u(T) = 0), equation A.1 is
rewritten as
√
τ ˙x = −x + Wrecφ(X).
Multiplying u(cid:11)
(or v(cid:11)
) to the both sides of equation D.5 yields
τ ˙pu ≈ −pu + (λ
τ ˙pv ≈ −pv + (λ
1u
2v
(cid:11)
(cid:11) + ρv
(cid:11)
(cid:11) − ρu
)φ/
)φ/
√
√
N,
N.
(D.5)
(D.6)
(D.7)
daher, we can examine the phase portrait of the approximate dynamical
system in the two-dimensional (pu-pv) Raum.
According to Susman et al. (2019), linear stability theory predicts that the
solutions of equations D.6 and D.7 converge onto the u-v plane, so we can
√
express x = puu + pvv. Let qu = u(cid:11)φ/
N; equations D.6
and D.7 can be rewritten as
N and qv = v(cid:11)φ/
√
τ ˙pu ≈ −pu + λ
τ ˙pv ≈ −pv + λ
1qu + ρqv,
2qv − ρqu.
(D.8)
(D.9)
Based on an approximation of activation function φ, the approximate two-
dimensional dynamical system equations D.8 and D.9 can be numerically
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2641
Figur 12: Numerical simulation of a stable limit cycle based on an approx-
imate two-dimensional dynamical system in the (pu, pv) plane. Hier, we used
= 1.51, ρ = 3. A stable limit cycle attractor was observed for a wide
λ
1
range of ρ. Color represents the time direction.
= 1.96, λ
2
simulated given arbitrary initial conditions (Susman et al., 2019). An ex-
ample of stable limit cycle simulated on the (pu, pv) plane is shown in
Figur 12.
In Figures 4c and 4d, we demonstrated that once high-dimensional x
forms a limit cycle attractor, its lower-dimensional PCA projection also
forms a limit cycle.
Danksagungen
We thank Vishwa Goudar for valuable feedback. This work was par-
tially supported by NIH grants R01-MH118928 (Z.S.C.) and R01-NS100065
(Z.S.C.) and an NSF grant CBET-1835000 (Z.S.C).
Verweise
Adler, A., Zhao, R., Schienbein, M. E., Yasuda, R., & Gan, W. B. (2019). Somatostatin-
expressing interneurons enable and maintain learning-dependent sequential ac-
tivation of pyramidal neurons. Neuron, 102, 202–216.
Bay, A., Lepsoy, S., & Magli, E. (2016). Stable limit cycles in recurrent neural net-
funktioniert. In Proceedings of IEEE International Conference on Communications. Piscat-
weg, NJ: IEEE. doi:10.1109/ICComm.2016.7528305
Barak, Ö. (2017). Recurrent neural networks as versatile tools of neuroscience re-
suchen. Curr. Opin. Neurobiol., 46, 1–6.
Bi, Z., & Zhou, C. (2020). Understanding the computation of time using neural net-
work models. In Proc. Natl. Acad. Sci. USA, 117, 10530–10540.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2642
A. Rajakumar, J. Rinzel, and Z. Chen
Brunel, N. (2000). Dynamics of networks of randomly connected excitatory and in-
hibitory spiking neurons. J. Physiol. Paris, 94, 445–463.
Buzsaki, G., & Mizuseki, K. (2014). The log-dynamic brain: How skewed distribu-
tions affect network operations. Nat. Rev. Neurosci., 15, 264–278.
Buzsaki, G., & Tingley, D. (2018). Space and time: The hippocampus as a sequence
generator. Trends in den Kognitionswissenschaften, 22, 853–869.
Cannon, J., Kopell, N., Gardner, T., & Markowitz, J. (2015) Neural sequence genera-
tion using spatiotemporal patterns of inhibition. PLOS Comput. Biol., 11, e1004581.
Ceni, A., Ashwin, P., & Livi, L. (2019). Interpreting recurrent neural networks behavior
via excitable network attractors. arXiv:1807.10478v6.
Ceni, A., Ashwin, P., Livi, L., & Oostlethwaite, C. (2020). The echo index and multi-
stability in input-driven recurrent neural networks. Physica D: Nonlinear Phenom-
ena, 412, 132609.
Cheng, C-Y., Lin, K-H., & Shih, C-W. (2006). Multistability in recurrent neural net-
funktioniert, SIAM Journal on Applied Mathematics, 66, 1301–1320.
Churchland, M. M., Cunningham, J. P., Kaufman, M. T., Foster, J. D., Nuyujukian, P.,
Ryu, S. ICH., & Shenoy, K. V. (2012). Neural population dynamics during reaching.
Natur, 487, 51–56.
Deshpande, V., & Dasgupta, C. (1991). A neural network for storing individual pat-
terns in limit cycles. J. Phys. A Math. Gen., 24, 5105–5119.
Diba, K., & Buzsaki, G. (2007). Forward and reverse hippocampal place-cell se-
quences during ripples. Nat. Neurosci., 10, 1241–1242.
Duncker, L., Driscoll, L. N., Shenoy, K. V., Sahani, M., & Sussillo, D. (2020).
Organizing recurrent network dynamics by task-computation to enable con-
tinual learning. In H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, & H.
Lin (Hrsg.), Fortschritte in der Verarbeitung von neuronalen Informationsverarbeitungssystemen, 33. Red Hook, New York:
Curran.
Fiete, ICH. R., Senn, W, Wang, C. Z. H., & Hahnloser, R. H. R. (2010). Spike-time-
dependent plasticity and heterosynaptic competition organize networks to pro-
duce long scale-free sequences of neural activity. Neuron, 65, 563–576.
Folli, V., Gosti, G., Leonetti, M., & Ruocco, G. (2018). Effect of dilution in asymmetric
recurrent neural networks. Neural Networks, 104, 50–59.
Foster, D. J., & Wilson, M. A. (2006). Reverse replay of behavioural sequences in
hippocampal place cells during the awake state. Natur, 440, 680–683.
Fujisawa, S., Amarasingham, A., Harrison, M. T., & Buzsaki, G. (2008). Behavior-
dependent short-term assembly dynamics in the medial prefrontal cortex. Natur
Neurowissenschaften, 11, 823–833.
Ganguli, S., Hug, D., & Sompolinsky, H. (2008). Memory traces in dynamical sys-
Systeme. In Proc. Natl. Acad. Sci. USA, 105, 18970–18975.
Gillett, M., Pereira, U., & Brunel, N. (2020). Characteristics of sequential activity in
networks with temporally asymmetric Hebbian learning. In Proc. Natl. Acad. Sci.
USA, 117, 29948–29958.
Glorot, X., Bordes, A., & Bengio, Y. (2011). Deep sparse rectifier networks. In Proceed-
ings of the Fourteenth International Conference on Artificial Intelligence and Statistics,
15, 315–323.
Goldman, M. S. (2009). Memory without feedback in a neural network. Neuron, 61,
621–634.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2643
Goudar, V., & Buonomano, D. V. (2018). Encoding sensory and motor patterns as
time-invariant trajectories in recurrent neural networks. eLife, 7, e31134.
Hardy, N. F., & Buonomano, D. V. (2018). Encoding time in feedforward trajectories
of a recurrent neural network model. Neural Computation, 30, 378–396.
Hardy, N. F., Goudar, V., Romero-Sosa, J. L., & Buonomano, D. V. (2018). A model
of temporal scaling correctly predicts that motor timing improves with speed.
Naturkommunikation, 9, 4732.
Harvey, C. D., Coen, P., & Tank, D. W. (2012). Choice-specific sequences in parietal
cortex during a virtual-navigation decision task. Natur, 484, 62–68.
Hemberger, M., Shein-Idelson, M., Pammer, L., & Laurent, G. (2019). Reliable se-
quential activation of neural assemblies by single pyramidal cells in a three-
layered cortex. Neuron, 104, 353–369.
Higham, N. J. (1986). Computing the polar decomposition with applications. SIAM
J. Sci. Stat. Comput., 7, 1160–1174.
Ingrosso, A., & Abbott, L. F. (2019). Training dynamically balanced excitatory-
inhibitory networks. PLOS One, 14, e0220547.
Jaeger, H. (2001). The “echo state” approach to analyzing and training recurrent neural
Netzwerke (GMD Technical Report 148). St. Augustin: German National Research
Center for Information Technology.
Jordan, ICH. D., Sokol, P. A., & Park, ICH. M. (2019). Gated recurrent units viewed through the
lens of continuous time dynamical systems. arXiv:1906.01005.
Jouffroy, G. (2007). Design of simple limit cycles with recurrent neural networks for
oscillatory control. In Proceedings of Sixth International Conference on Machine Learn-
ing and Applications. doi:10.1109/ICMLA.2007.99
Kao, J. C. (2019). Considerations in using recurrent neural networks to probe neural
Dynamik. J. Neurophysiol, 122, 2504–2521.
Kerg, G., Goyette, K., Touzel, M. P., Gidel, G., Vorontsov, E., Bengo, Y., & Die-
joie, G. (2019). Non-normal recurrent neural network (nnRNN): Learning long
time dependencies while improving expressivity with transient dynamics. In
H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fuchs, & R. Gar-
nett (Hrsg.), Fortschritte in der Verarbeitung von neuronalen Informationsverarbeitungssystemen, 32. Red Hook, New York:
Curran.
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Gardens, G., Rusu, A. A.,
. . . Hadsell, R. (2017) Overcoming catastrophic forgetting in neural networks. In
Proc. Natl. Acad. Sci. USA, 114, 3521–3526.
Koulakov, A., Hromadka, T., & Zador, A. M. (2009). Correlated connectivity and the
distribution of firing rates in the neocortex. Zeitschrift für Neurowissenschaften, 29, 3685–3694.
Lebedev, M. A., Ossadtchi, A., Mühle, N. A., Urpi, N. A., Cervera, M. R., & Nicolelis,
A. L. (2019). Analysis of neuronal ensemble activity reveals the pitfalls and short-
comings of rotation dynamics. Sci. Rep., 9, 18978.
Lillicrap, T. P., Stantoro, A., Marris, L., Akerman, C. J., & Hinton, G. E. (2020), Back-
propagation and the brain. Nat. Rev. Neurosci., 21, 335–346.
Loewenstein, Y., Kuras, A., & Rumpel, S. (2011). Multiplicative dynamics underlie
the emergence of the log-normal distribution of spine sizes in the neocortex in
vivo. Zeitschrift für Neurowissenschaften, 31, 9481–9488.
Long, M. A., Jin, D. Z., & Fee, M. S. (2010). Support for a synaptic chain model of
neuronal sequence generation. Natur, 468, 394–399.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2644
A. Rajakumar, J. Rinzel, and Z. Chen
Maass, W., Natschläger, T., & Markram, H. (2002). Real-time computing without sta-
ble states: A new framework for neural computation based on perturbations. Neu-
ral Computation, 14, 2531–2560.
Mackwood, Ö. H., Naumann, L. B., & Sprekeler, H. (2021). Learning excitatory-
inhibitory neuronal assemblies in recurrent networks. eLife, 10, e59715. https://doi.
org/10.7554/eLife.59715
Mante, V., Sussillo, D., Shenoy, K., & Newsome, W. T. (2013). Context-dependent
computation by recurrent dynamics in prefrontal cortex. Natur, 503, 78–84.
Mastrogiuseppe, F., & Ostojic, S. (2017). Intrinsically-generated fluctuating activity
in excitatory-inhibitory networks. PLOS Comput. Biol., 13(4), e1005498.
Murphy, B. K., & Müller, K. D. (2009). Balanced amplification: A new mechanism of
selective amplification of neural activity patterns. Neuron, 61, 635–648.
Namikawa, J., & Tani, J. (2009). Building recurrent neural networks to implement
multiple attractor dynamics using the gradient descent method. Advances in Ar-
tificial Neural Systems, 2009, 846040.
Nemati, S., Linderman, S. W., & Chen, Z. (2014). A probabilistic modeling approach for
uncovering neural population rotational dynamics. COSYNE abstract.
Orhan, A. E., & Ma, W. J. (2019). A diverse range of factors affect the nature of neural
representations underlying short-term memory. Nat. Neurosci., 22, 275–283.
Orhan, A. E., & Pitkow, X. (2020). Improved memory in recurrent neural networks
with sequential non-normal dynamics. In Proc. Int. Conf. Learning Representations.
ICLR.
Panda, P., & Roy. K. (2017). Learning to generate sequences with combination of Heb-
bian and non-Hebbian plasticity in recurrent spiking neural networks. Frontiers
in Neursoscience, Dezember 12.
Pollock, E., & Jazayeri, M. (2020). Engineering recurrent neural networks from task-
relevant manifolds and dynamics. PLOS Computational Biology, 16, e1008128.
Rajan, K., & Abbott, L. F. (2006). Eigenvalue spectra of random matrices for neural
Netzwerke. Physical Review Letters, 97, 188104.
Rajan, K., Harvey, C. D., & Tank, D. W. (2016). Recurrent network models of sequence
generation and memory. Neuron, 90, 128–142.
Roussel, M. R. (2019). Bifurcation analysis with AUTO. Nonlinear dynamics. Morgan
& Claypool.
Schmitt, L., Wimmer, R. D., Nakajima, M., Happ, M., Mofakham, S., & Halassa, M. M.
(2017). Thalamic amplification of cortical connectivity sustains attentional con-
trol. Natur, 545, 219–223.
Seung, H. S. (1996). How the brain keeps the eyes still. In Proc. Natl. Acad. Sci. USA,
93, 13339–13344.
Lied, H. F., Yang, G. R., & Wang, X. J. (2016). Training excitatory-inhibitory recur-
rent neural networks for cognitive tasks: A simple and flexible framework. PLOS
Comput. Biol., 12, e1004792.
Susman, L., Brenner, N., & Barak, Ö. (2019). Stable memory with unstable synapses.
Naturkommunikation, 10, 4441.
Sussillo, D. (2014). Neural circuits as computational dynamical systems. Curr. Opin.
Neurobiol., 25, 156–163.
Sussillo, D., & Abbott, L. F. (2009). Generating coherent patterns of activity from
chaotic neural networks. Neuron, 63, 544–557.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dynamics in Excitatory-Inhibitory Recurrent Neural Networks
2645
Sussillo, D., & Barak. Ö. (2013). Opening the black box: Low-dimensional dynamics
in high-dimensional recurrent neural networks. Neural Computation, 25, 626–649.
Sussillo, D., Churchland, M. M., Kaufman, M. T., & Shenoy, K. V. (2015). Ein neuronaler
network that finds a naturalistic solution for the production of muscle activity.
Naturneurowissenschaften, 18, 1025–1033.
Trischler, A. P., & D’Eleuterio, G. M. T. (2016). Synthesis of recurrent neural networks
for dynamical system stimulation. Neural Networks, 80, 67–78.
Werbos, P. J. (1988). Generalization of backpropagation with application to a recur-
rent gas market model. Neural Networks, 1, 339–356.
Xue, X., Halassa, M. M., & Chen, Z. (2021). Spiking recurrent neural networks represent
task-relevant neural sequences in rule-dependent computation. bioRxiv preprint. https:
//www.biorxiv.org/conten
Yang, G. R., Joglekar, M. R., Lied, H. F., Newsome, W. T., & Wang, X. J. (2019). Aufgabe
representations in neural networks trained to perform many cognitive tasks. Bereits-
ture Neuroscience, 22, 297–306.
Zeng, Z., Huang, T., & Zheng, W. X. (2010). Multistability of recurrent neural net-
works with time-varying delays and the piecewise linear activation function.
IEEE Trans. Neural Networks, 21, 1371–1377.
Zenke, F., Poole, B., & Ganguli, S. (2017). Continual learning through synaptic intel-
ligence. In Proceedings of International Conference on Machine Learning (S. 3978–
3995). PMLR.
Zhang, X., Liu, S., & Chen, Z. (2021). A geometric framework for understanding dynamic
information integration in context-dependent computation. bioRxiv preprint. https:
//biorxiv.org/cgi/content/short/2
Received December 16, 2020; accepted April 8, 2021.
l
D
o
w
N
o
A
D
e
D
F
R
o
M
h
T
T
P
:
/
/
D
ich
R
e
c
T
.
M
ich
T
.
/
e
D
u
N
e
c
o
A
R
T
ich
c
e
–
P
D
/
l
F
/
/
/
/
3
3
1
0
2
6
0
3
1
9
6
3
3
8
9
N
e
c
o
_
A
_
0
1
4
1
8
P
D
.
/
F
B
und
G
u
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3