ARTIKEL

Communicated by Ruoyu Sun

Critical Point-Finding Methods Reveal Gradient-Flat
Regions of Deep Network Losses

Charles G. Frye
cfrye59@gmail.com
Redwood Center for Theoretical Neuroscience and Helen Wills Neuroscience Institute,
Universität von Kalifornien, Berkeley, CA 94720, USA.

James Simon
james.simon@berkeley.edu
Redwood Center for Theoretical Neuroscience and Department of Physics,
Universität von Kalifornien, Berkeley, CA 94720, USA.

Neha S. Wadia
neha.wadia@berkeley.edu
Andrew Ligeralde
ligeralde@berkeley.edu
Redwood Center for Theoretical Neuroscience and Biophysics Graduate Group,
Universität von Kalifornien, Berkeley, CA 94720, USA.

Michael R. DeWeese
deweese@berkeley.edu
Redwood Center for Theoretical Neuroscience, Helen Wills Neuroscience Institute,
Department of Physics, and Biophysics Graduate Group, Universität von Kalifornien,
Berkeley, CA 94720, USA.

Kristofer E. Bouchard
kebouchard@lbl.gov
Redwood Center for Theoretical Neuroscience and Helen Wills Neuroscience Institute,
Universität von Kalifornien, Berkeley, CA 94720, USA; and Biological Systems and
Engineering Division and Computational Research Division, Lawrence Berkeley
National Lab, Berkeley, CA 94720, USA.

Despite the fact that the loss functions of deep neural networks are highly
nonconvex, gradient-based optimization algorithms converge to approx-
imately the same performance from many random initial points. Eins
thread of work has focused on explaining this phenomenon by numer-
ically characterizing the local curvature near critical points of the loss
Funktion, where the gradients are near zero. Such studies have reported

M.D. and K.B. contributed equally to the work.

Neural Computation 33, 1469–1497 (2021) © 2021 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01388

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1470

C. Frye et al.

that neural network losses enjoy a no-bad-local-minima property, in dis-
agreement with more recent theoretical results. We report here that the
methods used to find these putative critical points suffer from a bad local
minima problem of their own: they often converge to or pass through
regions where the gradient norm has a stationary point. We call these
gradient-flat regions, since they arise when the gradient is approximately
in the kernel of the Hessian, such that the loss is locally approximately
linear, or flat, in the direction of the gradient. We describe how the pres-
ence of these regions necessitates care in both interpreting past results
that claimed to find critical points of neural network losses and in de-
signing second-order methods for optimizing neural networks.

1 Einführung

Large neural networks are surprisingly easy to optimize (Sun, 2019), von-
spite the substantial nonconvexity of the loss as a function of the parameters
(Goodfellow & Vinyals, 2014). Insbesondere, it is usually found that chang-
ing the random initialization has no effect on performance, wenngleich
it can change the model learned by gradient-based optimization methods
(Garipov, Izmailov, Podoprikhin, Vetrov, & Wilson, 2018). Understanding
the cause of trainability from random initial conditions is critical for the
development of new architectures and optimization methods, which must
otherwise just hope to retain this favorable property based on heuristics.

One possible explanation for this phenomenon is based on the station-
ary points of gradient-based optimization methods. These methods are sta-
tionary when the gradient of the loss function is 0, at the critical points of
the loss. Critical points are classified by their Morse index, or the degree
of local negative curvature (d.h., the relative number of dimensions in pa-
rameter space along which the curvature is negative). Seit, among all crit-
ical points, gradient descent methods only converge to those points with
index 0 (Lee, Simchowitz, Jordanien, & Recht, 2016), which includes local min-
ima, it has been argued that large neural networks are easy to train because
their loss functions for many problems only have local minima at values of
the loss close to or at the global optimum. This is known as the “no-bad-
local-minima” property. Previous work (Dauphin et al., 2014; Pennington
& Bahri, 2017) has reported numerical evidence for a convex relationship
between index and loss that supports the hypothesis that neural network
loss functions have the no-bad-local-minima property: for low values of the
loss, only low values of the index were observed, whereas for high values
of the loss, only high values of the index were observed. Jedoch, mehr
recent theoretical work has indicated that there are in fact bad local minima
on neural network losses in almost all cases (Ding, Li, & Sun, 2019).

The validity of the numerical results depends on the validity of the crit-
ical point-finding algorithms, and the second-order critical point-finding

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1471

algorithms used in Dauphin et al. (2014) and Pennington and Bahri (2017)
are not in fact guaranteed to find critical points in the case where the Hes-
sian is singular. In this case, the second-order information used by these
critical point-finding methods becomes unreliable.

Neural network loss Hessians are typically highly singular (Sagun, Evci,
Güney, Dauphin, & Bottou, 2017), and poor behavior of Newton-type crit-
ical point-finding methods has been reported in the neural network case
(Coetzee & Stonick, 1997), casting doubt on the completeness and accuracy
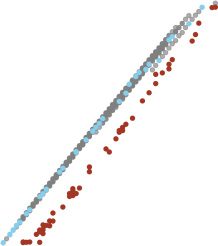
of the results in Dauphin et al. (2014) and Pennington and Bahri (2017). Frye,
Wadia, DeWeese, and Bouchard (2019) verified that second-order methods
can in fact find high-quality approximate critical points for linear neural
Netzwerke, for which the analytical form of the critical points is known (Baldi
& Hornik, 1989), providing ground truth. Insbesondere, the two-phase con-
vergence pattern predicted by the classical analysis of Newton methods
(Nocedal & Wright, 2006) is evident: a linear phase followed a short, local
superlinear phase (see Figure 1A). The superlinear convergence is visible
in the “cliffs” in the blue traces in Figure 1A, where the convergence rate
suddenly improves. With a sufficiently strict cutoff on the gradient norms,
the correct loss-index relationship obtained analytically (see Figure 1B, gray
points) is shared by the points obtained numerically (see Figure 1B, light
blue points). With an insufficiently strict cutoff, the loss-index relationship
implied by the observed points is far from the truth (see Figure 1B, dark red
points)

Bedauerlicherweise, good performance on linear networks does not guaran-
tee good performance on nonlinear networks. When applied to a nonlinear
Netzwerk, even with the same data, the behavior of these Newton methods
changes dramatically for the worse (see Figure 1C). No runs exhibit super-
linear convergence, and the gradient norms at termination are many orders
of magnitude larger. These are not the signatures of a method converging to
a critical point, even though gradient norms are sometimes still under the
thresholds reported in Pennington and Bahri (2017) and Frye et al. (2019)
(no threshold reported in Dauphin et al. (2014)). This makes it difficult to de-
termine whether the putative loss-index relationship measured from these
critical points (see Figure 1D) accurately reflects the loss-index relationship
at the true critical points of the loss function.

In diesem Artikel, we identify a major cause of this failure for second-order
critical point-finding methods: gradient-flat regions, where the gradient is ap-
proximately in the kernel of the Hessian. In these regions, the loss function
is locally approximately linear along the direction of the gradient, ob
or not the gradient is itself small, as would be the case near a true criti-
cal point. After introducing critical point finding methods in section 2.1,
we define gradient flatness in section 2.2 and explain in section 2.3, mit
a low-dimensional example, why it is problematic for second-order meth-
Odds: gradient-flat points can be “bad local minima” for the problem of find-
ing critical points. We further define a numerical index of approximate

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1472

C. Frye et al.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 1: Newton methods that find critical points on a linear network fail on a
nonlinear network. (A, B) Newton-MR on a linear autoencoder applied to mul-
tivariate gaussian data, as in Frye et al. (2019). (A) Squared gradient norms of
the loss L, as a function of the parameters θ , across iterations of Newton-MR,
colored by whether, after the first of early termination or 1000 Epochen, kariert
gradient norms are below 1e-8 (Blau) or not (orange). (B) The loss and Morse
index of putative and actual critical points, with ground truth. The Morse index
is defined as the fraction of negative eigenvalues. Analytically derived critical
points in gray, points from the end of runs that terminate below a squared gra-
dient norm of 1e-8 in light blue, and points from trajectories stopped early, once
they pass a squared gradient norm of 1e-2, in dark red. (C, D) As in panels A and
B, on the same network architecture and data, but with Swish (Ramachandran,
Zoph, & Le, 2017) nonlinear activations instead of identity activations. (D) Loss
and Morse index of putative critical points. Points with squared gradient norm
above 1e-8 in orange, those below 1e-8 in blue. Analytical expressions for critical
points are not available for this nonlinear network.

Gradient-Flat Regions of Deep Network Losses

1473

gradient flatness, R, based on the size of the residual of the least-squares
Newton solution. We then provide evidence that gradient-flat regions are
encountered when applying the Newton-MR algorithm1 to a deep neural
network loss (see sections 3 and A.5). Außerdem, we show that though
gradient-flat regions need not contain actual critical points, the loss-index
relationship looks strikingly similar to that reported in Dauphin et al. (2014)
and Pennington and Bahri (2017), suggesting that these previous studies
may have found gradient-flat regions, not critical points. Endlich, we note
the implications of gradient-flatness for the design of second-order methods
for use in optimizing neural networks: in the presence of gradient-flatness,
approximate second-order methods, like K-FAC (Martens & Grosse, 2015)
and Adam (Kingma & Ba, 2014) may be preferable to exact second-order
methods even without taking computational cost into account.

2 Gradient-Flat Points Are Stationary Points for Second-Order

Methoden

In diesem Abschnitt, we first define critical points and second-order critical point-
finding methods for the benefit of readers less familiar with these concepts.
Then we introduce and define gradient-flat points and explain why they
are problematic for second-order critical point-finding methods, mit dem
help of a low-dimensional example to build intuition. In numerical settings
and in high dimensions, approximately gradient-flat points are also impor-
tant, and so we define a quantitative index of gradient-flatness based on
the residual norm of the Newton update. Connected sets of these numeri-
cally gradient-flat points are gradient-flat regions, which cause trouble for
second-order critical point-finding methods.

2.1 Second-Order Critical Point-Finding Methods Rely on the Hes-
sian Matrix. Critical points are of interest because they are points where
the first-order approximation of a function f at a point2x + δ based on the
local information at x,

F (X + δ) ≈ f (X) + ∇ f (X)

(cid:4)δ,

(2.1)

is constant, indicating that they are the stationary points of first-order op-
timization algorithms like gradient descent and its accelerated variants. Von
“stationary point,” we mean a point at which the proposed updates of an
iterative algorithm are zero.

1

The code used in our experiments is available at https://github.com/charlesfrye/

autocrit.
2

Note that for a neural network loss function, the variable we take the gradient with
respect to, here x, is the vector of parameters, θ , not the data, which is often denoted with
an x.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1474

C. Frye et al.

In searching for critical points, it is common to use a linear approxima-
tion to the behavior of the gradient at a point x + p given the local informa-
tion at a point x:

∇ f (X + P) ≈ ∇ f (X) + ∇ 2 F (X)P.

(2.2)

Because these methods rely on a quadratic approximation of the original
function f , represented by the Hessian matrix of second partial derivatives,
we call them second-order critical point-finding methods.

The approximation on the right-hand side is constant whenever p is an
element of ker ∇ 2 F (X), where ker M is notation for the kernel of a matrix
M—the subspace that M maps to 0. When ∇2 f (X) is nonsingular, this is only
satisfied when p is 0, so if we can define an update rule such that p = 0 iff
∇ f (X) = 0, Dann, for nonsingular Hessians, we can be sure that our method
is stationary only at critical points.

In a Newton-type method, we achieve this by selecting our step by solv-
ing for the zeroes of this linear approximation, das ist, the Newton system,

0 = ∇ f (X) + ∇ 2 F (X)P,

which has solution

p = −∇ 2 F (X)

+∇ f (X),

where the matrix M+
is the Moore-Penrose pseudoinverse of the matrix
M, obtained by performing the singular value decomposition, inverting the
nonzero singular values, and recomposing the SVD matrices in reverse or-
der. The Newton update p is zero iff ∇ f (X) Ist 0 for a nonsingular Hessian,
for which the pseudoinverse is simply the inverse. For a singular Hessian,
the update p is zero iff ∇ f (X) is in the kernel of the pseudoinverse. Beachten Sie, dass
if the Hessian is constant as a function of x, the linear model of the gradient
is exact and this algorithm converges in a single step.

Within the vicinity of a critical point, this algorithm converges extremely
quickly (Nocedal & Wright, 2006), but the guarantee of convergence is
strictly local. Practical Newton methods in both convex optimization (Boyd
& Vandenberghe, 2004) and nonlinear equation solving (Nocedal & Wright,
2006; Izmailov & Solodov, 2014) often compare multiple possible choices of
p and select the best one according to a “merit function” applied to the gra-
dients, which has a global minimum for each critical point. Such algorithms
have broader guarantees of global convergence. A common choice for merit
function is the squared norm,

G(X) = 1
2

(cid:5)∇ f (X)(cid:5)2.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1475

In gradient norm minimization (McIver & Komornicki, 1972), another
second-order critical point-finding method, we optimize this merit function
directly. The gradients of this method are

∇g(X) = ∇ 2 F (X)∇ f (X),

and so it is also a second-order critical point-finding method.

As with Newton methods, in the invertible case, the updates are zero iff
∇ f (X) Ist 0. In the singular case, the updates are zero if the gradient is in
the Hessian’s kernel. Because this method is framed as the minimization
of a scalar function, it is compatible with first-order optimization methods,
which are more commonly implemented and better supported in neural
network libraries.

2.2 At Gradient-Flat Points, the Gradient Lies in the Hessian’s Kernel.
Second-order critical point-finding methods, by the preceding argument,
can guarantee convergence to critical points when the Hessian is nowhere
singular. Jedoch, neural network Hessians are generally singular, espe-
cially in the overparameterized case (Sagun et al., 2017; Ghorbani, Krish-
nan, & Xiao, 2019), meaning the kernel is nontrivial, and so neither class of
methods can guarantee convergence to critical points. In this case, Newton’s
method can diverge, oscillate, or behave chaotically (Griewank & Osborne,
1983). The addition of merit function–based upgrades can remove these be-
haviors, but it cannot guarantee convergence to critical points (Powell, 1970;
Griewank & Osborne, 1983). The gradient norm minimization method, rein-
vented for use on neural network loss functions in Pennington and Bahri
(2017), was previously proposed and this flaw pointed out twice in the
field of chemical physics: once in the 1970s—proposed (McIver & Komor-
nicki, 1972) and critiqued (Cerjan & Müller, 1981) and again in the 2000s—
proposed simultaneously (Angelani, Leonardo, Ruocco, Scala, & Sciortino,
2000; Broderix, Bhattacharya, Cavagna, Zippelius, & Giardina, 2000) Und
critiqued (Doye & Wales, 2002).

What are the stationary points, besides critical points, for these two
method classes in the case of singular Hessians? It would seem at first that
they are different: for gradient norm minimization, when the gradient is
in the Hessian’s kernel; for Newton-type methods, when the gradient is in
the Hessian’s pseudoinverse’s kernel. Tatsächlich, Jedoch, these conditions are
identical due to the Hessian’s symmetry,3 and so both algorithms share a
broad class of stationary points.

These stationary points have been identified previously, but nomen-
clature is not standard. Doye and Wales, studying gradient norm

3

In der Tat, the kernel of the pseudoinverse is equal to the kernel of transpose, as can
be seen from the singular value decomposition, and the Hessian is equal to its transpose
because it is symmetric. See Strang (1993).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1476

C. Frye et al.

minimization, call them nonstationary points (Doye & Wales, 2002), seit
they are nonstationary with respect to the function f , while Byrd et al.,
studying Newton methods, call them stationary points (Byrd, Marazzi, &
Nocedal, 2004), since they are stationary with respect to the merit function
G. To avoid confusion between these incommensurate conventions or with
the stationary points of the function f , we call a point where the gradient
lies in the kernel of the Hessian a gradient-flat point. This name was chosen
because a function is flat when its Hessian is 0, meaning every direction is in
the kernel, and so it is locally flat around a point in a given direction when-
ever that direction is in the kernel of the Hessian at that point. Note that be-
cause 0 ∈ ker for all matrices, every critical point is also a gradient-flat point,
but the reverse is not true. When we wish to explicitly refer to gradient-
flat points that are not critical points, we will call them strict gradient-flat
points. At a strict gradient-flat point, the function is, along the direction of
the gradient, locally linear up to second order.

An alternative view of gradient-flat points is based on the squared gra-
dient norm merit function. All gradient-flat points are stationary points of
the gradient norm, which may in principle be local minima, maxima, oder
saddles, while the global minima of the gradient norm are critical points.
When they are local minima of the gradient norm, they can be targets of
convergence for methods that use first-order approximations of the gra-
dient map, as in gradient norm minimization and Newton-type methods.
Strict gradient-flat points, Dann, can be “bad local minima” of the gradient
norm, and therefore prevent the convergence of second-order root-finding
methods to critical points, just as bad local minima of the loss function can
prevent convergence of first-order optimization methods to global optima.
Note that Newton methods cannot be demonstrated to converge only
to gradient-flat points (Powell, 1970). Außerdem, Newton convergence
can be substantially slowed when even a small fraction of the gradient is
in the kernel (Griewank & Osborne, 1983). Below we will see that while a
Newton method applied to a neural network loss sometimes converges to
and almost always encounters strict gradient-flat points, the final iterate is
not always either a strict gradient-flat point or a critical point.

2.3 Convergence to Gradient-Flat Points Occurs in a Low-Dimensional
Quartic Example. The difficulties that gradient-flat points pose for Newton
methods can be demonstrated with a polynomial example in two dimen-
sionen, plotted in Figure 2A. Below, we will characterize the strict gradient-
flat (orange) and critical (Blau) points of this function (see Figure 2A). Dann
we will observe the behavior of a practical Newton method applied to it
(see Figures 2B and 2C) and note similarities to the results in Figure 1.
We will use this simple, low-dimensional example to demonstrate princi-
ples useful for understanding the results of applying second-order critical
point-finding methods to more complex, higher-dimensional neural net-
work losses.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1477

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 2: Stationarity of and convergence to a strict gradient-flat point on a
quartic function. (A) Critical and strict gradient-flat points of quartic f (X, j)
(defined in equation 2.3). Central panel: F (X, j) plotted in color (black, low val-
ues; Weiß, high values), along with the direction of the Newton update p as
A (notably nonsmooth) vector field (Rot). Stationary points of the squared gra-
dient norm merit function g are indicated: strict gradient-flat points in orange,
the critical point in blue. Top and bottom panels: The value (top) and squared
gradient norm (bottom) of f as a function of x value with y fixed at 0. Der
x-axis is shared between panels. (B) Performance and trajectories of Newton-MR
(Roosta, Liu, Xu, & Mahoney, 2018) on equation 2.3. Runs that terminate near a
strict gradient-flat point are in orange, while those that terminate near a critical
point are in blue. Central panel: Trajectories of Newton-MR laid over f (X, j).
X- and y-axes are shared with the central panel of panel A. Initial values in-
dicated with scatter points. Top and bottom panels: Function values (top) Und
squared gradient norms (bottom) of Newton-MR trajectories as a function of
iteration. The x-axis is shared between panels.

1478

C. Frye et al.

As our model function, we choose

F (X, j) = 0.25×4 − 3×2 + 9X + 0.9y4 + 5y2 + 40.

(2.3)

√

√

It is plotted in Figure 2A, central panel. This quartic function has
two affine subspaces of points with nontrivial Hessian kernel, defined by
√
[±
2, j]. The kernel points along the x direction and so is orthogonal to
this affine subspace at every point. As a function of y,
f is convex, mit
one-dimensional minimizers at y = 0. The strict gradient-flat points occur
2, 0],
at the intersections of these two sets: one strict gradient-flat point at [
which is a local minimum of the gradient norm, and one at [−
2, 0], welche
is a saddle of the same (see Figure 2A, orange points, all panels). Im
vicinity of these points, the gradient is, to first order, constant along the x-
axis, and so the function is locally linear or flat. These points are gradient-
flat, but neither is a critical point of f . The only critical point is located at
the minimum of the polynomial, bei [−3, 0] (see Figure 2A, blue point, alle
panels), which is also a global minimum of the gradient norm. The affine
subspace that passes through [−
2, 0] divides the space into two basins
of attraction, loosely defined, for second-order methods: one with initial
x-coordinate x0
2, for the critical point of f and the other for the strict
gradient-flat point. Note that the vector field in the central panel shows up-
date directions for the pure Newton method, which can behave extremely
poorly in the vicinity of singularities (Powell, 1970; Griewank & Osborne,
1983), often oscillating and converging very slowly or diverging.

< − √ √ Practical Newton methods use techniques like damping and line search to improve behavior (Izmailov & Solodov, 2014). To determine how a prac- tical Newton method behaves on this function, we focus on the case of Newton-MR (Roosta, Liu, Xu, & Mahoney, 2018), which uses the MR-QLP (Choi, Paige, & Saunders, 2011) solver4 to compute the Newton update and backtracking line search with the squared gradient norm merit function to select the step size. Pseudocode for this algorithm is provided in sec- tion A.3. This method was found to perform better than a damped Newton method and gradient norm minimization on finding the critical points of a linear autoencoder in Frye et al. (2019). These numerical and computational advantages of Newton-MR do not change the attraction of the method to gradient-flat points.5 Results are qualitatively similar for damped Newton methods with a squared gradient norm merit function. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 4 5 MR-QLP, short for MINRES-QLP, is a Krylov subspace method akin to conjugate gra- dient but specialized to the symmetric, indefinite, and ill-conditioned case, which makes it well suited to this problem and to neural network losses. Assumption 4 of the convergence proof for Newton-MR in Roosta et al. (2018), the gradient-hessian nullspace property, is effectively a statement that the function has no gradient-flat points. Precisely: their constant ν tends to the boundary value of 0 as the function approaches gradient-flatness; this causes the convergence time to increase without bound. Gradient-Flat Regions of Deep Network Losses 1479 The results of applying Newton-MR to equation 2.3 are shown in Figure 2B. The gradient-flat point is attracting for some trajectories (orange), while the critical point is attracting for others (blue). For trajectories that approach the strict gradient-flat point, the gradient norm does not converge to 0 but converges to a nonzero value near 10 (orange trajectories; see Figure 2B, bottom panel). This value is typically several orders of magnitude lower than the initial point, and so would appear to be close to 0 on a linear scale that includes the gradient norm of the initial point. Since log-scaling of loss functions is uncommon in machine learning, as losses do not always have minima at 0, second-order methods approaching gradient-flat points can appear to converge to critical points if typical methods for visually assessing convergence are used. Two interesting and atypical behaviors are worth noting. First, the tra- jectories tend to oscillate in the vicinity of the gradient-flat point and con- verge more slowly (see Figure 2B, central panel, orange lines). Updates from points close to the affine subspace where the Hessian has a kernel, and so have an approximate kernel themselves, sometimes jump to points where the Hessian does not have an approximate kernel. This suggests that when converging toward a gradient-flat point, the degree of flatness will change iteration by iteration. Second, some trajectories begin in the nominal basin of attraction of the gradient-flat point but converge to the critical point (see Figure 2B, central panel, blue points with x-coordinate > −
2). Das
is because the combination of backtracking line search and large proposed
step sizes means that occasionally, very large steps can be taken, based on
nonlocal features of the function. In der Tat, backtracking line search is a lim-
ited form of global optimization, and the ability of line searches to change
convergence behaviors predicted from local properties on nonconvex prob-
lems is known (Nocedal & Wright, 2006). Since the backtracking line search
is based on the gradient norm, the basin of attraction for the true critical
Punkt, which has a lower gradient norm than the gradient-flat point, is much
enlarged relative to that for the gradient-flat point. This suggests that New-
ton methods using the gradient norm merit function will be biased toward
finding gradient-flat points that also have low gradient norm.

√

2.4 Approximate Gradient-Flat Points and Gradient-Flat Regions.
Analytical arguments focus on exactly gradient-flat points, where the Hes-
sian has an exact kernel and the gradient is entirely within it. In numerical
settings, it is almost certain no matrix will have an exact kernel due to finite
precision. For the same reason, the computed gradient vector will generi-
cally not lie entirely within the exact or approximate kernel. Jedoch, nu-
merical implementations of second-order methods will struggle even when
there is no exact kernel or when the gradient is only partly in it, and so a
numerical index of flatness is required. This is analogous to the requirement
to specify a tolerance for the norm of the gradient when deciding whether
to consider a point an approximate critical point or not.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1480

C. Frye et al.

Calculating an index of gradient-flatness would seem to require addi-
tional computation on top of the application of the critical point-finding al-
gorithm. Stattdessen, we quantify the degree of gradient-flatness of a point by
means of the relative residual norm (R) and the relative co-kernel residual
norm (rH) for the Newton update direction p, two quantities that are calcu-
lated in the normal process of iteratively computing a Newton update using
a minimum residual solver like MR-QLP (Paige & Strakos, 2002). The resid-
ual norm r is used to detect convergence on nonsingular systems, während die
co-kernel residual norm rH is used to detect convergence on singular sys-
Systeme. In the absence of numerical issues, one or the other will be small
once the solver terminates (Choi et al., 2011, Sek 2.4). See section A.4 for
definitions.

Both r and rH compare the magnitude of the Newton system residual
H p − g to the magnitude of g, where H and g are the current Hessian and
gradient. When r is at its minimal value of 0, the residual is 0 and the New-
ton update is a perfect solution to the Newton system, H p = g. If r is close
to its maximal value of 1, then the residual is large relative to the gradient
and p is a poor solution to the Newton system. If at the same time the value
of rH is small, the gap between H p and −g is almost entirely in the kernel
of H, which can occur only when g is itself almost entirely in the kernel of
H. daher, the combination of a high value of r and a low value of rH at
a point indicates that the gradient is largely (but not necessarily entirely) In
the kernel; we call such a point an approximate gradient-flat point.

There are multiple reasonable numerical indices of flatness besides the
definition above. Zum Beispiel, the Hessian-gradient regularity condition in
Roosta et al. (2018), which is used to prove convergence of Newton-MR,
would suggest creating a basis for the approximate kernel of the Hessian
and projecting the gradient onto it. Alternativ, one could compute the
Rayleigh quotient of the gradient with respect to the Hessian. Our method
has the advantage of being computed as part of the Newton-MR algo-
rithm. It furthermore avoids diagonalizing the Hessian or the specification
of an arbitrary eigenvalue cutoff and relies on numerically stable techniques
(Choi et al., 2011). The Rayleigh quotient can be computed with only one
Hessian-vector product, plus several vector-vector products, so it might be
a superior choice for larger problems where computing a high-quality in-
exact Newton step is computationally infeasible.

We summarize the different classes of points under consideration in
terms of the squared norm of the gradient at the point, (cid:5)G(cid:5)2, and the residual
norms r and rH in Table 1. We set εc to 1e-8, which is sufficient for approxi-
mate critical points to have the same loss and index as exact critical points
for a linear neural network (Frye et al., 2019). We set the values of εr and εg
Zu 0.1 and 5e-4, meaning that we consider a point approximately gradient-
flat when the value of rH is below 5e-4 while the value of r is above 0.9.
We emphasize that numerical issues for second-order critical point-finding
methods can arise even when the degree of gradient-flatness is small.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1481

Tisch 1: Criteria for Determining the Class of a Point.

Exact critical point
Approximate critical point
Gradient-flat point
Approximate gradient-flat point
Strict gradient-flat point
Approximate strict gradient-flat point

(cid:5)G(cid:5)2

0
< εc ≥ εc ≥ 0 > 0
≥ εc

R

rH

0
≥ 0
1

0
≥ 0
0
> 1 − εg < εr 0 > 1 − εg < εr 1 Under this relaxed definition of gradient-flatness, there will be a neigh- borhood of approximate gradient-flat points around a strict, exact gradient- flat point for functions with Lipschitz-smooth gradients and Hessians. Furthermore, there might be connected sets of non-null Lebesgue mea- sure that all satisfy the approximate gradient-flatness condition but none of which satisfy the exact gradient-flatness condition. We call both of these gradient-flat regions. 3 Gradient-Flat Regions Are Common on Deep Network Losses To determine whether gradient-flat regions are responsible for the poor behavior of Newton methods on deep neural network (DNN) losses demonstrated in Figure 1, we applied Newton-MR to the loss of a small, two-hidden-layer, fully connected autoencoder trained on 10k MNIST im- ages downsized to 4 × 4, similar to the downsized data sets in Dauphin et al. (2014) and Pennington and Bahri (2017). We found similar results on a fully connected classifier trained on the same MNIST images via the cross- entropy loss (see section A.5) and another classifier trained on a very small subset of 50 randomly labeled MNIST images, as in (Zhang, Bengio, Hardt, Recht, & Vinyals, 2016, see section A.6). We focused on Newton-MR be- cause we found that a damped Newton method like that in Dauphin et al. (2014) performed poorly, as reported for the XOR problem in Coetzee and Stonick (1997), and furthermore that there was insufficient detail to repli- cate (Dauphin et al., 2014) exactly. We denote the network losses by L and the parameters by θ . See section A.1 for details on the networks and data set and section A.2 for details on the critical point-finding experiments. Gradient norms observed in these experiments appear in Figure 3A. We found that after 500 iterations, 14% of runs terminated with squared gra- dient norm below the cutoff in Frye et al. (2019) and so found approxi- mate critical points (blue). Twice as many runs terminated above that cutoff but terminated in a gradient-flat region (28%, orange), while the remainder were above the cutoff but were not in a gradient-flat region at the final iter- ation (black). As in the experiments on the nonlinear autoencoder applied to the multivariate gaussian data (see Figure 1C), all of the runs terminated l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1482 C. Frye et al. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3: Critical point-finding methods more often find gradient-flat regions on a neural network loss. (A) Squared gradient norms across the first 100 it- erations of Newton-MR for 100 separate runs on an autoencoder loss. Gradi- ent norms were flat after 100 iterations. See section A.1 for details. Runs that terminate with squared gradient norm below 1e-8, at a critical point, in blue. Runs that terminate above that cutoff and with r above 0.9, in a gradient-flat re- gion, in orange. All other runs in black. Asterisks indicate trajectories in panel B. (B) The relative residual norm r, an index of gradient-flatness, for the approx- imate Newton update computed by MR-QLP at each iteration (solid lines) for three representative traces. Values are local averages with a window size of 10 iterations. Raw values are plotted with reduced opacity underneath. Top: non- flat, noncritical point (black). Middle: flat, noncritical point (orange). Bottom: flat, critical point (blue). (C) Empirical cumulative distribution functions for the final (top) and maximal (bottom) relative residual norm r observed during each run of Newton-MR. Values above the cutoff for approximate gradient-flatness, r > 0.9, in orange. Observations from runs that terminated below the cutoff for
critical points, (cid:5)∇L(θ )(cid:5)2 < 1e-8, indicated with blue ticks. (D) Loss and index for the maximally gradient-flat points obtained during application of Newton-MR. Points with squared gradient norm below 1e-8 in blue. Other points colored by their gradient-flatness: points above 0.9 in orange, points below in black. Only points with squared gradient norm below 1e-4 shown. Gradient-Flat Regions of Deep Network Losses 1483 with squared gradient norms over 10 orders of magnitude greater than the typical values observed after convergence in the linear case (<1e-30; see Figure 1A). The relative residual norm for the Newton solution, r, is an index of gradient-flatness (see section 2.4 and appendix A.4 for details). The values of r for every iteration of Newton-MR are shown for three representative traces in Figure 3B. In the top trace, r is close to 0, indicating that the iter- ates are not in a gradient-flat region (r (cid:9) 0.9, black). Newton methods can be substantially slowed when even a small fraction of the gradient is in the kernel (Griewank & Osborne, 1983) and can converge to points that are not gradient-flat (Byrd, Marazzi, & Nocedal, 2004). By contrast, in the middle trace (orange), the value of r approaches 1, indicating that almost the en- tirety of the gradient is in the kernel. This run terminated in a gradient-flat region, at effectively an exactly gradient-flat point. Further, the squared gradient norm at 500 iterations, 2e-5, is multi- ple orders of magnitude higher than the cutoff necessary for approximate critical points to approximate the loss and index of exact critical points, 1e-8 (Frye et al., 2019). The norm at these points is, however, much smaller than the minimum observed during optimization of this loss (squared gra- dient norms between 1e-4 and 5e1), indicating the presence of noncritical gradient-flat regions with very low gradient norm. Critical point-finding methods that disqualify points on the basis of their norm but have too loose of a cutoff (e.g., those used in Dauphin et al., 2014; Pennington & Bahri, 2017) will both converge to and accept these points, even though they need not be near true critical points, as demonstrated in Frye et al. (2019). In the bottom trace (blue), the behavior of r is the same, while the gradient norm drops much lower, to 3e-13, suggesting convergence to a gradient-flat re- gion around a critical point that has an approximately singular Hessian. Not all traces exhibit such simple behavior for the value of r. In many traces, the value of r oscillates from values close to 1 to middling values, indicating that the algorithm is bouncing in and out of one or more gradient- flat regions (see section A.5 for examples, on a classifier). This can occur when the final target of convergence given infinite iterations is a gradient- flat point, as in the example in section 2.3. We found that 99 of 100 traces included a point where at least half of the gradient was in the kernel, according to our residual measure, while 89% of traces included a point that had a residual greater than 0.9, and 50% in- cluded a point with r > 0.99 (see Figure 3C, bottom). This demonstrates that
there are many regions of substantive gradient-flatness, in which second-
order critical point-finding methods could be substantively slowed.

The original purpose of applying these critical point-finding methods
was to determine whether the no-bad-local-minima property held for this
loss function and, more broadly, to characterize the relationship at the
critical points between the loss and the local curvature, summarized via
the Morse index. If we look at either the points found after 500 Iterationen

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1484

C. Frye et al.

(results not shown; see section A.5 for an example on a classifier) or the it-
erates with the highest gradient-flatness (see Figure 3D), we find that the
qualitative features of the loss-index relationship reported previously are
recreated: convex shape, small spread at low index that increases for higher
index, no minima or near-minima at high values of the loss. Jedoch, unser
analysis suggests that the majority of these points are not critical points but
either strict gradient-flat points (orange) or simply points of spurious or
incomplete Newton convergence (black). The approximately critical points
we do see (Blau) have a very different loss-index relationship: their loss is
equal to the loss of a network that has constant output equal to the mean
of the data, and their index is low but not 0. This suggests that the results
presented in Dauphin et al. (2014) and Pennington and Bahri (2017) are not
evidence of the reported loss-index relationship at critical points of neural
network losses.

4 Diskussion

We observed that gradient-flat regions, where the gradient is nearly in the
approximate kernel of the Hessian, are a prevalent feature of some pro-
toypical neural network loss surfaces. The networks used in this article are
very small relative to practical networks for image recognition and natural
language processing, which have several orders of magnitude more param-
eters. Jedoch, increasing parameter count tends to increase the singular-
ity of loss Hessians (Sagun et al., 2017), and so we expect there to be even
greater gradient-flatness for larger networks. The gradient-flat regions were
discovered by second-order critical point-finding algorithms, which are at-
tracted to these regions as bad local minima of the squared norm of the
gradient of the loss. We measured approximate gradient-flatness using the
norm, R, of the residual of the least-squares solution to the Newton system.
We comment on these observations below.

4.1 Implications of Gradient-Flatness for Identification of Critical
Points. The strategy of using gradient norm cutoffs to determine whether
a point is near enough to a critical point for the loss and index to match the
true value is natural. Jedoch, in the absence of guarantees on the smooth-
ness of the behavior of the Hessian (and its spectrum) around the critical
Punkt, the numerical value sufficient to guarantee correctness is unclear.
The observation of gradient-flat regions at extremely low gradient norm
and the separation of these values, in terms of loss-index relationship, aus
the bulk of the observations suggest that there may be spurious targets of
convergence for critical point-finding methods even at such low gradient
norm. Alternativ, they may in fact be near real critical points, and so in-
dicate that the simple, convex picture of loss-index relationship painted by
the numerical results in Dauphin et al. (2014) and Pennington and Bahri
(2017) is incomplete.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1485

Our results motivate a revisiting of those numerical results, as do re-
cent analytical results demonstrating that bad local minima do exist for al-
most all neural network architectures and data sets (see Ding et al., 2019,
for a helpful table of positive and negative theoretical results regarding lo-
cal minima). Looking back at Figure 4 of Dauphin et al. (2014), we see that
their nonconvex Newton method, a second-order optimization algorithm
designed to avoid saddle points by reversing the Newton update along di-
rections of negative curvature, appears to terminate at a gradient norm of
Befehl 1. This is only a single order of magnitude lower than what was ob-
served during training. It is likely that this point was either in a gradient-flat
region or otherwise had sufficient gradient norm in the Hessian kernel to
slow the progress of their algorithm. This suggests that second-order meth-
ods designed for optimization, which use the loss as a merit function, eher
than norms of the gradient, can terminate in gradient-flat regions. In diesem
Fall, the merit function encourages convergence to points where the loss,
rather than the gradient norm, is small, but it still cannot guarantee conver-
gence to a critical point. Dauphin et al. (2014) do not report a gradient norm
cutoff, among other details needed to recreate their critical point-finding
experiments, so it is unclear to which kind of points they converged. Wenn,
Jedoch, the norms are as large as those of the targets of their nonconvex
Newton method, in accordance with our experience with damped Newton
methods and that of Coetzee and Stonick (1997), then the loss-index rela-
tionships reported in their Figure 1 are likely to be for gradient-flat points,
rather than critical points.

Pennington and Bahri (2017), who used the gradient norm minimiza-
tion method to find critical points, report a squared gradient norm cutoff of
1e-6. This cutoff is right in the middle of the bulk of values we observed,
and which we labeled gradient-flat regions and points of spurious conver-
gence, based on the cutoff in Frye et al. (2019), which separates a small frac-
tion of runs from this bulk. This suggests that some of their putative critical
points were gradient flat points. Their Figure 6 shows a disagreement be-
tween their predictions for the index, based on a loss-weighted mixture of
Wishart and Wigner random matrices and their observations. We specu-
late that some of this gap is due to their method of recovering approximate
gradient-flat points rather than critical points.

It is notable that the loss-index relationship we observe for gradient-flat
points (in Figures 3D and 4D) resembles that reported by Dauphin et al.
(2014) and Pennington and Bahri (2017): it is convex, with loss increas-
ing as index increases. This overall shape is also observed for points sam-
pled along the trajectory of gradient descent on a linear network (see Frye
et al., 2019, Figure 2D) and so may in some sense be a property of generic
points on neural network loss surfaces. This suggests that there may in-
deed be critical points that have this convex loss-index relationship but that
previous attempts may or may not have found them due to becoming stuck
in gradient-flat regions.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1486

C. Frye et al.

Gradient-flatness will cause trouble for all second-order critical point-
finding methods, which rely on a quadratic approximation that becomes
infinitely bad in the presence of gradient-flatness. Note that first-order
Methoden, despite their popularity in optimization, are inapplicable to this
problem since they are attracted to minima, rather than generic critical
points.6

Other types of critical point-finding methods are not necessarily at-
tracted to gradient-flat regions. In principle, higher-order methods, based
on higher-order approximations, could be applied to the problem of finding
critical points. Jedoch, these methods suffer from much increased com-
putational complexity, and the development and analysis of practical im-
plementations, even for the convex case, is a matter of ongoing research
(Nesterov, 2018). Newton homotopy methods, first used on neural net-
works in the 1990s (Coetzee & Stonick, 1997), then revived in the 2010s (Bal-
lard et al., 2017; Mehta, Zhao, Bernal, & Wales, 2018), which are popular in
algebraic geometry (Bates, Haunstein, Sommese, & Wampler, 2013), might
auch genutzt werden. Jedoch, singular Hessians still cause issues for homotopy-
based methods: for a singular Hessian H, the curve to be continued by the
homotopy becomes a manifold with dimension 1 + corank(H), and orienta-
tion becomes more difficult. This can be avoided by removing the singular-
ity of the Hessian, Zum Beispiel, by the randomly weighted regularization
method in Mehta, Chen, Tang, and Hauenstein (2018). While these tech-
niques may make it possible to find critical points, they fundamentally alter
the loss surface, limiting their utility in drawing conclusions about other
features of the loss. Insbesondere, in the time since the initial resurgence
of interest in the curvature properties of neural network losses sparked by
Dauphin et al. (2014), the importance of overparameterization for optimiza-
tion of, and generalization by, neural networks has been identified (Li, Ding,
& Sun, 2018; Poggio, Liao, & Banburski, 2020). Large overparameterized
networks have more singular Hessians (Sagun et al., 2017), and so the dif-
ference between the original loss and an altered version with an invertible
Hessian is greater. Wichtig, in a more overparameterized network, Die
prevalence of gradient-flat regions should increase, since the Hessian kernel
covers an increasingly large subspace.

4.2 Implications of Gradient-Flatness for Optimization. While our fo-
cus in the work explored in this article was on the behavior of second-order
critical point-finding methods, second-order methods for optimization also
rely on the Hessian and so are affected by gradient-flatness.

6

In der Tat, applying first-order optimization tools to the problem of minimizing the gra-
dient norm results in the second-order method gradient norm minimization, as discussed
in section 2.1.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1487

Our observation of singular Hessians at low gradient norm suggests
that some approximate saddle points of neural network losses may be de-
generate (as defined in Jin, Ge, Netrapalli, Kakade, & Jordanien, 2017) Und
non-strict (as defined in Lee et al., 2016). These points need not be local
minima; they are effectively “local minima up to at least second order.” Ac-
cording to the analyses in Jin et al. (2017) and Lee et al. (2016), gradient de-
scent may converge to these points. Jedoch, in two cases, we observe the
lowest-index saddles at low values of the loss (see Figures 3 Und 4) and so
these analyses still predict that gradient descent will successfully reduce the
loss, even if it does not find a local minimum. In the third case, an overpa-
rameterized network (siehe Abbildung 5), we do observe a bad local minimum, als
predicted in Ding et al. (2019) for networks capable of achieving 0 Ausbildung
Fehler.

Even in the face of results indicating the existence of bad local minima
(Ding et al., 2019), it remains possible that bad local minima of the loss are
avoided by initialization and optimization strategies. For example ReLU
networks suffer from bad local minima when one layer’s activations are all
0 or when the biases are initialized at too small of a value (Holzmüller &
Steinwart, 2020), but careful initialization and training can avoid the issue.
Our results do not directly invalidate this hypothesis, but they do call the
supporting numerical evidence into question. Our observation of gradient-
flat regions on almost every single run suggests that while critical points
are hard to find and may even be rare, regions where gradient norm is ex-
tremely small are neither. For non-smooth losses, such as those of ReLU
networks or networks with max-pooling, whose loss gradients can have
discontinuities, critical points need not exist, but gradient-flat regions may.
In der Tat, in manchen Fällen, the only differentiable minima in ReLU networks are
also flat (Laurent & von Brecht, 2017).

Sagun et al. (2017) emphasize that when the Hessian is singular ev-
erywhere, the notion of a basin of attraction is misleading, since targets
of convergence form connected manifolds and some assumptions in theo-
rems guaranteeing first-order convergence become invalid (Jin et al., 2017),
though with sufficient, if unrealistic, overparameterization, convergence
can be proven (Von, Zhai, Poczos, & Singh, 2019). They speculate that a
better approach to understanding the behavior of optimizers focuses on
their exploration of the sublevel sets of the loss. Our results corroborate
that speculation and further indicate that this flatness means using second-
order methods to try to accelerate exploration of these regions in search
of minimizers is likely to fail: the alignment of the gradient with the Hes-
sian’s approximate kernel will tend to produce extremely large steps for
some methods, or no acceleration and even convergence to nonminimizers,
for others.

Our observation of ubiquitous gradient-flatness further provides an
alternative explanation for the success and popularity of approximate

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1488

C. Frye et al.

second-order optimizers for neural networks, like K-FAC (Martens &
Grosse, 2015), which uses a layerwise approximation to the Hessian. Diese
methods are typically motivated by appeals to the computational cost
of even Hessian-free exact second-order methods and their brittleness in
the stochastic (nonbatch) setting. Jedoch, exact second-order methods
are justified only when the second-order model is good, and at an exact
gradient-flat point, the second-order model can be infinitely bad, in a sense,
along the direction of the gradient. Approximations need not share this
Eigentum. Even more extreme approximations, like the diagonal approxi-
mations in the adaptive gradient family, such as AdaGrad (Duchi, Hazan,
& Singer, 2011) and Adam (Kingma & Ba, 2014), behave reasonably in
gradient-flat regions: they smoothly scale up the gradient in the directions
in which it is small and changing slowly, without making a quadratic model
that is optimal in a local sense but poor in a global sense.

Gesamt, our results underscore the difficulty of searching for critical
points of singular nonconvex functions, including deep network loss func-
tionen, and shed new light on other numerical results in this field. In diesem
setting, second-order methods for finding critical points can fail badly by
converging to gradient-flat points. This failure can be hard to detect unless
it is specifically measured. Außerdem, gradient-flat points are generally
places where quadratic approximations become untrustworthy, and so our
observations are relevant for the design of exact and approximate second-
order optimization methods as well.

Appendix

A.1 Networks and Data Sets

A.1.1 Data Sets. For the experiments in Figure 1, 10,000 16-dimensional
gaussian vectors with mean parameter 0 and diagonal covariance with
linearly spaced values between 1 Und 16 were generated and then mean-
centered.

For the experiments in Figures 3 Und 4, 10,000 images from the MNIST
data set (LeCun, Cortes, & Burges, 2010) were cropped to 20 × 20 Und
rescaled to 4 × 4 using PyTorch (Paszke et al., 2019), then z-scored. Das war
done for two reasons: (1) to improve the conditioning of the data covariance,
which is very poor for MNIST due to low variance in the border pixels, Und
(2) to reduce the number of parameters n in the network, as computing a
high-quality inexact Newton solution is O(n2). Nonlinear classification net-
works trained on this downsampled data could still obtain accuracies above
90%, better than the performance of logistic regression (≈87%).

For the experiments in Figure 5, 50 random images of 0s and 1s from the
MNIST data set were PCA-downsampled to 32 dimensions using sklearn
(Pedregosa et al., 2011). This provided an alternative approach to improving

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1489

the conditioning of the data covariance and reducing the parameter counts
in the network. The labels for these images were then shuffled.

A.1.2 Networks. All networks, their optimization algorithms, und das
critical point-finding algorithms were defined in the autograd Python pack-
Alter (Maclaurin, 2016). For the experiments in Figure 1, two networks were
trained: a linear auto-encoder with a single, fully connected hidden layer of
4 units and a deep non-linear auto-encoder with two fully connected hidden
layers of 16 Und 4 units with Swish (Ramachandran et al., 2017) activations.
Performance of the critical point-finding algorithms was even worse for net-
works with rectified linear units (results not shown) as reported by others
(Pennington and Bahri, persönliche Kommunikation). Nonsmooth losses need
not have gradients that smoothly approach 0 near local minimizers, so it
is only sensible to apply critical point finding to smooth losses (see Lau-
rent & von Brecht, 2017). The nonlinear auto-encoder used (cid:6)
2 regulariza-
tion. Neither network had biases. All auto-encoding networks were trained
with mean squared error.

For the experiments in Figure 3, a fully connected autoencoder with two
hidden layers of 8 Und 16 Einheiten, with Swish activations and biases, was used.
This network had no (cid:6)

2 regularization.

For the experiments in Figure 4, a fully connected classifier with two
hidden layers of 12 Und 8 Einheiten, with Swish activations and biases, was used.
This network had (cid:6)
2 regularization, since the cross-entropy loss with which
it was trained can otherwise have critical points at infinity.

For the experiments in Figure 5, a fully connected classifier with two hid-
den layers of 32 Und 4 Einheiten, with Swish activations, was used. This network
had no biases. This network also used (cid:6)
2 regularization and was trained
with the cross-entropy loss. Networks were trained to near-perfect training
Leistung: 48 Zu 50 correctly classified examples out of 50.

A.2 Critical Point-Finding Experiments. The code for all of our exper-

iments is available at https://github.com/charlesfrye/autocrit.

For all critical point-finding experiments, we followed the basic proce-
dure pioneered in Dauphin et al. (2014) and used in Pennington and Bahri
(2017) and Frye et al. (2019). Erste, an optimization algorithm was used to
train the network multiple times. For the results in Figure 1, this algorithm
was full-batch gradient descent, while for the remainder of the results, Das
algorithm was full-batch gradient descent with momentum (learning rates
0.1 in both cases; momentum 0.9 in the latter).

The parameter values produced during optimization were then used as
starting positions for Newton-MR. Following Pennington and Bahri (2017)
and based on the arguments in Frye et al. (2019), we selected these initial
points uniformly at random with respect to their loss value.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1490

C. Frye et al.

Newton-MR (Roosta et al., 2018) computes an inexact Newton update
with the MR-QLP solver (Choi et al., 2011) and then performs backtracking
line search based on the squared gradient norm. For pseudocode of the
equivalent exact algorithm, see section A.3.

The MR-QLP solver has the following hyperparameters for determin-
ing stopping behavior: maximum number of iterations (maxit), maximum
solution norm (maxxnorm), relative residual tolerance (rtol), and condition
number limit (acondlim). We set maxit to be equal to the number of pa-
rameters, since with exact arithmetic, this is sufficient to solve the Newton
System. We found that the maxxnorm and acondlim parameters did not affect
stopping behavior, which was driven by the tolerance rtol. For Figure 1,
we used a tolerance of 1e-10. For Figures 3 Und 4, we used a tolerance of
5e-4, based on the values for the relative residuals found after maxit iter-
ations on test points. See section A.4 for details about the relative residual
stopping criterion. We do not provide pseudocode for this algorithm (Choi
et al., 2011).

The backtracking line search has the following hyperparameters: α, Die
starting step size; β, the multiplicative factor by which the step size is re-
duziert; and ρ, the degree of improvement required to terminate the line
suchen. We set these hyperparameters to α := 0.1, β := 0.5, and ρ := 0.1. Fur-
thermore, in backtracking line search for Newton methods, it is important
to always check a unit step size in order to attain superlinear convergence
(Nocedal & Wright, 2006). So before running the line search, we also check
unit step size with a stricter ρ(cid:10)

:= 0.5.

On termination of the critical point-finding algorithm, the loss and in-
dex must be calculated. The index is defined analytically as the fraction of
negative eigenvalues, but numerical errors make this infeasible for highly
singular matrices, which have many eigenvalues that are close to but not
exactly 0. We use the same cutoff verified in Frye et al. (2019): eigenvalues
greater than or equal to -1e-5 are considered nonnegative.

A.3 Newton-MR Pseudocode. The pseudocode in algorithm 1 defines
an exact least-squares Newton method with exact line search. To obtain
the inexact Newton-MR algorithm, the double argmin to determine the up-
date direction p should be approximately satisfied using the MR-QLP solver
(Choi et al., 2011) and the argmin to determine the step size α should be ap-
proximately satisfied using Armijo-type backtracking line search. For de-
tails, see Roosta et al. (2018).

A.4 Relative Residual and Relative Co-Kernel Residual. The quan-
tities referred to in this article as the relative residual norm r and co-
kernel residual norm rH were introduced in Paige and Strakos (2002) für die
quantification of the performance of minimum residual Krylov subspace
Methoden. r measures the size of the error of an approximate solution to
the Newton system. Introducing the symbols H and g, for the Hessian and

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1491

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

gradient at a query point, the Newton system may be written 0 = H p + G,
and r is then

R(P) =

(cid:5)H p + G(cid:5)
(cid:5)H(cid:5)F(cid:5)P(cid:5) + (cid:5)G(cid:5)

,

Wo (cid:5)M(cid:5)F of a matrix M is its Frobenius norm. Since all quantities are
nonnegative, r is nonnegative; because the denominator bounds the numer-
ator, by the triangle inequality and the compatibility of the Frobenius and
Euclidean norms, r is at most 1. For an exact solution of the Newton system
p∗
) Ist 0, the minimum value, while r(0) Ist 1, the maximum value. Notiz
that small values of (cid:5)P(cid:5) do not imply large values of this quantity, seit (cid:5)P(cid:5)
goes to 0 when a Newton method converges toward a critical point, while
r goes to 0.

, R(p∗

When g is partially in the kernel of H, the Newton system is unsatisfi-
able, as g will also be partly in the co-image of H, the linear subspace into
which H cannot map any vector. In this case, the minimal value for r will
no longer be 0. The optimal solution for (cid:5)H p + G(cid:5) instead has the property
that its residual is 0 once restricted to the co-kernel of H, the linear subspace
orthogonal to the kernel of H. This co-kernel residual can be measured by
applying the matrix H to the residual vector H p + G. After normalization, Es
becomes

rH (P) =

(cid:5)H(H p + G)(cid:5)
(cid:5)H(cid:5)F(cid:5)H p + G(cid:5)

.

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1492

C. Frye et al.

Wieder, by the compatibility of the Frobenius and Euclidean norms, we have
that the numerator is less than the denominator, and so rH is bounded be-
zwischen 0 Und 1. Note that this value is also small when the gradient lies
primarily along the eigenvalues of smallest magnitude. On each internal
iteration, MR-QLP checks whether either of these values is below a toler-
ance level—in our experiments, 5e-4—and if either is, it ceases iteration.
With exact arithmetic, either one or the other of these values should go to 0
within a finite number of iterations given by the dimension of p; with inex-
act arithmetic, they should just become small. We determined the tolerance
level 5e-4 by executing the maximum number of iterations and checking
the size of the residual on a number of candidate runs. See Choi et al. (2011)
for details. Less than 5% of Newton steps were obtained from the kernel
residual going below the tolerance, indicating that almost all points of the
loss surface had an approximately unsatisfiable Newton system.

A.5 Replication of Results from Section 3 on MNIST MLP. We re-
peated the experiments whose results are shown in Figure 3 on the loss
surface of a fully connected classifier on the same modified MNIST data
set (details in section A.1). We again found that the performance of the
Newton-MR critical point-finding algorithm was poor (see Figure 4A) Und
that around 90% of runs encountered a point with gradient-flatness above
0.9 (see Figure 4C, bottom row). Jedoch, we observed that fewer runs ter-
minated at a gradient-flat point (see Figure 4C, top row), vielleicht weil
the algorithm was bouncing in and out of gradient-flat regions (siehe Abbildung
4B, top and bottom rows), rather than because of another type of spuri-
ous Newton convergence. If we measure the loss-index relationship at the
maximally gradient-flat points (see Figure 4D), we see the same pattern as
in Figure 3D. This also holds if we look at the loss and index of the points
at termination (results not shown).

A.6 Replication of Results from Section 3 on Binary MNIST Sub-
set Memorization. We repeated the experiments whose results are shown
in Abbildung 3 on the loss surface of a fully connected classifier on a small sub-
set of 50 0s and 1s from the MNIST data set (details in section A.1). In diesem
setting, the network is overparameterized, in that it has a hidden layer al-
most as wide as the number of points in the data set (32 versus 50) und hat
more parameters than there are points in the data set (1160 versus 50). Es
is also capable of achieving 100% accuracy on this training set, which has
random labels, as in Zhang et al. (2016). We again observe that the majority
of runs do not terminate with squared gradient norm under 1e-8 (33 out of
50 runs) and a similar fraction (31 out of 50 runs) encounter gradient-flat
points (see Figures 5A and 5C, bottom panel). The loss-index relationship
looks qualitatively different, as might be expected for a task with random
labels. Notice the appearance of a bad local minimum: the blue point at in-
dex 0 and loss ln(2).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Gradient-Flat Regions of Deep Network Losses

1493

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D

/

l

F
/

/

/

/

3
3
6
1
4
6
9
1
9
1
6
3
7
0
N
e
C
Ö
_
A
_
0
1
3
8
8
P
D

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 4: Gradient-flat regions also appear on an MLP loss. (A) Squared gra-
dient norms across the first 100 iterations of Newton-MR for 60 separate runs
on an MLP loss (see section A.1 for details). Runs that terminate with squared
gradient norm below 1e-8 in blue. Runs that terminate above that cutoff and
with r above 0.9, in orange. All other runs in black. Asterisks indicate trajecto-
ries in panel B. (B) The relative residual norm r, for the approximate Newton
update computed by MR-QLP at each iteration for three representative traces.
Values are local averages with a window size of 10 Iterationen. Raw values are
plotted with reduced opacity underneath. Top: nonflat, noncritical point (black).
Mitte: flat, noncritical point (orange). Bottom: nonflat, critical point (Blau).
(C) Empirical cumulative distribution functions for the final (top) and maxi-
mal (bottom) relative residual norm r. Values above the cutoff for approximate
gradient-flatness, r > 0.9, in orange. Observations from runs that terminated
below the cutoff for critical points, (cid:5)∇L(θ )(cid:5)2 < 1e-8, indicated with blue ticks. (D) Loss and index for the maximally gradient-flat points obtained during ap- plication of Newton-MR. Colors as in top-left; only points with squared gradient norm below 1e-4 shown. 1494 C. Frye et al. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / Figure 5: Gradient-flat regions also appear on an overparameterized loss. (A) Squared gradient norms across 500 iterations of Newton-MR for 50 sep- arate runs on the loss of an overparameterized network (see section A.1 for details). Runs that terminate with squared gradient norm below 1e-8 in blue. Runs that terminate above that cutoff and with r above 0.9, in orange. All other runs in black. Asterisks indicate trajectories in panel B. (B) The relative residual norm r, for the approximate Newton update computed by MR-QLP at each it- eration for three representative traces. Values are local averages with a window size of 10 iterations. Raw values are plotted with reduced opacity underneath. Top: nonflat, noncritical point (black). Middle: flat, noncritical point (orange). Bottom: flat, critical point (blue). (C) Empirical cumulative distribution func- tions for the final (top) and maximal (bottom) relative residual norm r. Values above the cutoff for approximate gradient-flatness, r > 0.9, in orange. Observa-
tions from runs that terminated below the cutoff for critical points, (cid:5)∇L(θ )(cid:5)2 < 1e-8, indicated with blue ticks. (D) Loss and index for the points found after 500 iterations of Newton-MR. Colors as in top-left; only points with squared gradient norm below 1e-4 shown. f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Gradient-Flat Regions of Deep Network Losses 1495 Acknowledgments We thank Yasaman Bahri, Jesse Livezey, Dhagash Mehta, Dylan Paiton, and Ryan Zarcone for useful discussions. C.F. and A.L. were supported by the National Science Foundation Graduate Research Fellowship Program un- der grant DGE 1752814. N.W. was supported by the Google PhD Fellow- ship. A.L. was supported by a National Institutes of Health training grant, 5T32NS095939. M.R.D. was supported in part by the U.S. Army Research Laboratory and the U.S. Army Research Office under contract W911NF-13- 1-0390. K.B. was funded by a DOE/LBNL LDRD, Deep Learning for Science (PI, Prabhat). References Angelani, L., Leonardo, R. D., Ruocco, G., Scala, A., & Sciortino, F. (2000). Saddles in the energy landscape probed by supercooled liquids. Physical Review Letters, 85(25), 5356–5359. Baldi, P., & Hornik, K. (1989). Neural networks and principal component analysis: Learning from examples without local minima. Neural Networks, 2(1), 53–58. Ballard, A. J., Das, R., Martiniani, S., Mehta, D., Sagun, L., Stevenson, J. D., & Wales, D. J. (2017). Energy landscapes for machine learning. Phys. Chemistry Chemical Physics, 19, 12585–12603. Bates, D. J., Haunstein, J. D., Sommese, A. J., & Wampler, C. W. (2013). Numerically solving polynomial systems with Bertini (software, environments and tools). Philadel- phia: Society for Industrial and Applied Mathematics. Boyd, S., & Vandenberghe, L. (2004). Convex optimization. New York: Cambridge Uni- versity Press. Broderix, K., Bhattacharya, K. K., Cavagna, A., Zippelius, A., & Giardina, I. (2000). Energy landscape of a Lennard-Jones liquid: Statistics of stationary points. Phys- ical Review Letters, 85(25), 5360–5363. Byrd, R. H., Marazzi, M., & Nocedal, J. (2004). On the convergence of Newton iterations to non-stationary points. Mathematical Programming, 99(1), 127–148. doi:10.1007/s10107-003-0376-8 Cerjan, C. J., & Miller, W. H. (1981). On finding transition states. Journal of Chemical Physics, 75(6), 2800–2806. doi:10.1063/1.442352 Choi, S.-C. T., Paige, C. C., & Saunders, M. A. (2011). MINRES-QLP: A Krylov sub- space method for indefinite or singular symmetric systems. SIAM Journal on Sci- entific Computing, 33(4), 1810–1836. Coetzee, F., & Stonick, V. L. (1997). 488 solutions to the XOR problem. In M. C. Mozer, M. I. Jordan, & T. Petsche (Eds.), Advances in neural information processing systems, 9 (pp. 410–416). Cambridge, MA: MIT Press. Dauphin, Y., Pascanu, R., Gülçehre, Ç., Cho, K., Ganguli, S., & Bengio, Y. (2014). Iden- tifying and attacking the saddle point problem in high- dimensional non-convex optimiza- tion. CoRR, abs/1406.2572. Ding, T., Li, D., & Sun, R. (2019). Sub-optimal local minima exist for almost all over- parameterized neural networks. arXiv:1911.01413. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1496 C. Frye et al. Doye, J. P. K., & Wales, D. J. (2002). Saddle points and dynamics of Lennard-Jones clusters, solids, and supercooled liquids. Journal of Chemical Physics, 116(9), 3777– 3788. Du, S. S., Zhai, X., Poczos, B., & Singh, A. (2019). Gradient descent provably optimizes over-parameterized neural networks. In Proceedings of the Interna- tional Conference on Learning Representations. https://openreview.net/forum?id= S1eK3i09YQ. Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res., 12, 2121–2159. Frye, C. G., Wadia, N. S., DeWeese, M. R., & Bouchard, K. E. (2019). Numerically re- covering the critical points of a deep linear autoencoder. arXiv:1901.10603. Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D., & Wilson, A. G. (2018). Loss surfaces, mode connectivity, and fast ensembling of DNNs. arXiv:1802.10026. Ghorbani, B., Krishnan, S., & Xiao, Y. (2019). An investigation into neural net op- timization via Hessian eigenvalue density. In Proceedings of Machine Learning Research. Goodfellow, I. J., & Vinyals, O. 2014. Qualitatively characterizing neural network opti- mization problems. CoRR, abs/1412.6544. Griewank, A., & Osborne, M. R. (1983). Analysis of Newton’s method at irregular singularities. SIAM Journal on Numerical Analysis, 20(4), 747–773. Holzmüller, D., & Steinwart, I. 2020. Training two-layer RELU networks with gradient descent is inconsistent. arXiv:2002.04861. Izmailov, A. F., & Solodov, M. V. 2014. Newton-type methods for optimization and vari- ational problems. New York: Springer. Jin, C., Ge, R., Netrapalli, P., Kakade, S. M., & Jordan, M. I. 2017. How to escape saddle points efficiently. CoRR, abs/1703.00887. Kingma, D. P., & Ba, J. 2014. Adam: A method for stochastic optimization. arXiv:1412.6980. Laurent, T., & von Brecht, J. (2017). The multilinear structure of ReLU networks. arXiv:1712.10132. LeCun, Y., Cortes, C., & Burges, C. 2010. MNIST handwritten digit database. http:// yann.lecun.com/exdb/mnist, 2. Lee, J. D., Simchowitz, M., Jordan, M. I., & Recht, B. 2016. Gradient descent only con- verges to minimizers. In V. Feldman, A. Rakhlin, & O. Shamir, (Eds.), Proceedings of the 29th Annual Conference on Learning Theory (vol. 49, pp. 1246–1257). Li, D., Ding, T., & Sun, R. 2018. On the benefit of width for neural networks: Disappearance of bad basins. arXiv:1812.11039. Maclaurin, D. 2016. Modeling, inference and optimization with composable differentiable procedures. PhD diss., Harvard University. Martens, J., & Grosse, R. 2015. Optimizing neural networks with Kronecker-factored ap- proximate curvature. arXiv:1503.05671. McIver, J. W., & Komornicki, A. (1972). Structure of transition states in organic re- actions: General theory and an application to the cyclobutene-butadiene isomer- ization using a semiempirical molecular orbital method. Journal of the American Chemical Society, 94(8), 2625–2633. Mehta, D., Chen, T., Tang, T., & Hauenstein, J. D. 2018. The loss surface of deep linear networks viewed through the algebraic geometry lens. arXiv:1810.07716. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Gradient-Flat Regions of Deep Network Losses 1497 Mehta, D., Zhao, X., Bernal, E. A., & Wales, D. J. 2018. Loss surface of XOR artificial neural networks. Physical Review E, 97(5). Nesterov, Y. 2018. Implementable tensor methods in unconstrained convex optimiza- tion (Technical Report 2018005). Center for Operations Research and Economet- rics Université catholique de Louvain. https://ideas.repec.org/p/cor/louvco/ 2018005.html. Nocedal, J., & Wright, S. (2006). Numerical optimization (2nded. ). New York: Springer. Paige, C. C., & Strakos, Z. 2002. Residual and backward error bounds in minimum residual Krylov subspace methods. SIAM Journal on Scientific Computing, 23(6), 1898–1923. doi:10.1137/s1064827500381239 Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., . . . Chintala, S. (2019). PyTorch: An imperative style, high-performance deep learning library. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’AlchéBuc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems, 32 (pp. 8024–8035). Red Hook, NY: Curran. Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., . . . Duchesnay, E. (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12, 2825–2830. Pennington, J., & Bahri, Y. 2017. Geometry of neural network loss surfaces via ran- dom matrix theory. In Proceedings of the International Conference on Learning Repre- sentations. Poggio, T., Liao, Q., & Banburski, A. 2020. Complexity control by gradient descent in deep networks. Nature Communications, 11(1). doi:10.1038/s41467-020-14663-9 Powell, M. J. 1970. A hybrid method for nonlinear equations. Numerical methods for non- linear algebraic equations. Ramachandran, P., Zoph, B., & Le, Q. V. 2017. Searching for activation functions. arXiv:1710.05941. Roosta, F., Liu, Y., Xu, P., & Mahoney, M. W. 2018. Newton-MR: Newton’s method with- out smoothness or convexity. arXiv:1810.00303. Sagun, L., Evci, U., Güney, V. U., Dauphin, Y., & Bottou, L. 2017. Empirical analysis of the Hessian of over-parameterized neural networks. CoRR, abs/1706.04454. Strang, G. 1993. The fundamental theorem of linear algebra. American Mathematical Monthly, 100(9), 848. doi:10.2307/2324660 Sun, R. 2019. Optimization for deep learning: Theory and algorithms. arXiv:1912.08957. Zhang, C., Bengio, S., Hardt, M., Recht, B., & Vinyals, O. 2016. Understanding deep learning requires rethinking generalization. CoRR, abs/1611.03530. Received March 23, 2020; accepted January 11, 2021. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 3 6 1 4 6 9 1 9 1 6 3 7 0 n e c o _ a _ 0 1 3 8 8 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3

PDF Herunterladen