ARTIKEL
Communicated by Ruben Moreno-Bote
Heterogeneous Synaptic Weighting Improves Neural Coding
in the Presence of Common Noise
Pratik S. Sachdeva
pratik.sachdeva@berkeley.edu
Redwood Center for Theoretical Neuroscience and Department of Physics,
Universität von Kalifornien, Berkeley, Berkeley, CA 94720 USA., and Biological
Systems and Engineering Division, Lawrence Berkeley National Laboratory,
Berkeley, CA 94720, USA.
Jesse A. Livezey
jlivezey@lbl.gov
Redwood Center for Theoretical Neuroscience, Universität von Kalifornien, Berkeley,
Berkeley, CA 94720, USA., and Biological Systems and Engineering Division,
Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA.
Michael R. DeWeese
deweese@berkeley.edu
Redwood Center for Theoretical Neuroscience, Department of Physics, and Helen
Wills Neuroscience Institute, Universität von Kalifornien,
Berkeley, Berkeley, CA 94720 USA.
Simultaneous recordings from the cortex have revealed that neural ac-
tivity is highly variable and that some variability is shared across neu-
rons in a population. Further experimental work has demonstrated that
the shared component of a neuronal population’s variability is typically
comparable to or larger than its private component. In der Zwischenzeit, an abun-
dance of theoretical work has assessed the impact that shared variability
has on a population code. Zum Beispiel, shared input noise is understood
to have a detrimental impact on a neural population’s coding fidelity.
Jedoch, other contributions to variability, such as common noise, can
also play a role in shaping correlated variability. We present a network
of linear-nonlinear neurons in which we introduce a common noise in-
put to model—for instance, variability resulting from upstream action
potentials that are irrelevant to the task at hand. We show that by apply-
ing a heterogeneous set of synaptic weights to the neural inputs carrying
the common noise, the network can improve its coding ability as mea-
sured by both Fisher information and Shannon mutual information, sogar
in cases where this results in amplification of the common noise. Mit
a broad and heterogeneous distribution of synaptic weights, a popula-
tion of neurons can remove the harmful effects imposed by afferents that
Neural Computation 32, 1239–1276 (2020) © 2020 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01287
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1240
P. Sachdeva, J. Livezey, and M. DeWeese
are uninformative about a stimulus. We demonstrate that some nonlinear
networks benefit from weight diversification up to a certain population
Größe, above which the drawbacks from amplified noise dominate over the
benefits of diversification. We further characterize these benefits in terms
of the relative strength of shared and private variability sources. Endlich,
we studied the asymptotic behavior of the mutual information and Fisher
information analytically in our various networks as a function of popula-
tion size. We find some surprising qualitative changes in the asymptotic
behavior as we make seemingly minor changes in the synaptic weight
distributions.
1 Einführung
Variability is a prominent feature of many neural systems: neural responses
to repeated presentations of the same external stimulus typically vary from
trial to trial (Shadlen & Newsome, 1998). Außerdem, neural variability
often exhibits pairwise correlations, so that pairs of neurons are more (oder
weniger) likely to be co-active than they would be by chance if their fluctua-
tions in activity to a repeated stimulus were independent. These so-called
noise correlations (which we also refer to as “shared variability”) have been
observed throughout the cortex (Averbeck, Latham, & Pouget, 2006; Cohen
& Kohn, 2011), and their presence has important implications for neural
coding (Zohary, Shadlen, & Newsome, 1994; Abbott & Dayan, 1999).
If the activities of individual neurons are driven by a stimulus shared by
all neurons but corrupted by noise that is independent for each neuron (Also-
called private variability), then the signal can be recovered by simply aver-
aging the activity across the population (Abbott & Dayan, 1999; Ma, Beck,
Latham, & Pouget, 2006). If instead some variability is shared across neu-
rons (d.h., there are noise correlations), naively averaging the activity across
the population will not necessarily recover the signal, no matter how large
the population (Zohary et al., 1994). An abundance of theoretical work has
explored how shared variability can be either beneficial or detrimental to
the fidelity of a population code (relative to the null model of only private
variability among the neurons), depending on its structure and relationship
with the tuning properties of the neural population (Zohary et al., 1994; Ab-
bott & Dayan, 1999; Yoon & Sompolinsky, 1999; Sompolinsky, Yoon, Kang,
& Shamir, 2001; Averbeck & Lee, 2006; Cohen & Maunsell, 2009; Cafaro &
Rieke, 2010; Ecker, Berens, Tolias, & Bethge, 2011; Moreno-Bote et al., 2014;
Nogueira et al., 2020).
One general conclusion of this work highlights the importance of the ge-
ometric relationship between noise correlations and a neural population’s
signal correlations (Averbeck et al., 2006; Hu, Zylberberg, & Shea-Brown,
2014). To illustrate this, the mean responses of a neural population across
a variety of stimuli (d.h., those responses represented by receptive fields or
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1241
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1: Private and shared variability. (A) The geometric relationship between
neural activity and shared variability. Black curves denote mean responses to
different stimuli. Variability for a specific stimulus (black dot) may be private
(links), geteilt (Mitte), or take on the structure of differential correlations (Rechts).
The red arrow represents the tangent direction of the mean stimulus response.
(B) Schematic of the types of variability that a neural population can encounter.
The variability of a neural population contains both private components (z.B.,
synaptic vesicle release, channel noise, thermal noise) and shared components
(z.B., variability of presynaptic spike trains, shared input noise). Shared variabil-
ity can be induced by the variability of afferent connections (which is shared
across a postsynaptic population) or inherited from the stimulus itself. Fur-
thermore, shared variability is shaped by synaptic weighting. (C) Estimates of
the private variability contributions to the total variability of neurons (N = 28)
recorded from auditory cortex of anesthetized rats. Diagonal line indicates the
Identität. Figure reproduced from Deweese and Zador (2004).
tuning curves) can be examined in the neural space (see Figure 1a, black
curves). The correlations among the mean responses for different stimuli
specify the signal correlations for a neural population (Averbeck et al.,
2006). Private variability exhibits no correlational structure, and thus its
1242
P. Sachdeva, J. Livezey, and M. DeWeese
relationship with the signal correlations is determined by the mean neural
activity and the individual variances (see Figure 1a, links). Shared variability,
Jedoch, may reshape neural activity to lie, Zum Beispiel, orthogonal to the
mean response curve (see Figure 1a, Mitte). In the case of Figure 1a, mid-
dle, neural coding is improved (relative to private variability) weil das
variability occupies regions of the neural space that are not traversed by the
mean response curve (Montijn, Meijer, Lansink, & Pennartz, 2016). Shared
variability can also harm performance, Jedoch. Recent work has identi-
fied differential correlations—those that are proportional to the products of
the derivatives of tuning functions (see Figure 1a, Rechts)—as particularly
harmful to the performance of a population code (Moreno-Bote et al., 2014).
While differential correlations are consequential, they may serve as a small
contribution to a population’s total shared variability, leaving “nondifferen-
tial correlations” as the dominant component of shared variability (Kohn,
Coen-Cagli, Kanitscheider, & Pouget, 2016; Montijn et al., 2019; Kafashan
et al., 2020).
The sources of neural variability, and their respective contributions to the
private and shared components, will have a significant impact on shaping
the geometry of the population’s correlational structure, and therefore its
coding ability (Brinkman, Weber, Rieke, & Shea-Brown, 2016). Zum Beispiel,
private sources of variability such as channel noise or stochastic synaptic
vesicle release could be averaged out by a downstream neuron receiving in-
put from the population (Faisal, Selen, & Wolpert, 2008). Jedoch, sources
of variability shared across neurons, such as the variability of presynaptic
spike trains from neurons that synapse onto multiple neurons, would in-
troduce shared variability and place different constraints on a neural code
(Shadlen & Newsome, 1998; Kanitscheider, Coen-Cagli, & Pouget, 2015).
Insbesondere, differential correlations are typically induced by shared input
noise (d.h., noise carried by a stimulus) or suboptimal computations (Beck,
Ma, Pitkow, Latham, & Pouget, 2012; Kanitscheider et al., 2015).
Past work has examined the contributions of private and shared sources
to variability in cortex (Arieli, Sterkin, Grinvald, & Aertsen, 1996; Deweese
and Zador, 2004). Speziell, by partitioning subthreshold variability of
a neural population into private components (synaptic, thermal, channel
noise in the dendrites, and other local sources of variability) and shared
components (variability induced by afferent connections), it was found that
the private component of the total variability was quite small, während die
shared component can be much larger (see Figures 1b and 1c). Daher, neural
populations must contend with the large shared component of a neuron’s
variability. The incoming structure of shared variability and its subsequent
shaping by the computation of a neural population is an important con-
sideration for evaluating the strength of a neural code (Zylberberg, Pouget,
Latham, & Shea-Brown, 2017).
Moreno-Bote et al. (2014) demonstrated that shared input noise is detri-
mental to the fidelity of a population code. Hier, we instead examine
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1243
sources of shared variability, which do not necessarily result in differen-
tial correlations (they do not appear as shared input noise) and thus can be
manipulated by features of neural computation such as synaptic weight-
ing. We refer to these noise sources as “common noise” to distinguish them
from the special case of shared input noise (Vidne et al., 2012; Kulkarni &
Paninski, 2007). Zum Beispiel, a common noise source could include an up-
stream neuron whose action potentials are noisy in the sense that they are
unimportant for computing the current stimulus. Common noise, Weil
it is manipulated by synaptic weighting, can serve as a source of nondiffer-
ential correlations (see Figure 1a, Mitte), thereby having either a beneficial
or a harmful impact on the strength of the population code. We aim to better
elucidate the nature of this impact.
We consider a linear-nonlinear architecture (Paninski, 2004; Karklin &
Simoncelli, 2011; Pillow, Paninski, Uzzell, Simoncelli, & Chichilnisky, 2005)
and explore how its neural representation is affected by both a common
source of variability and private noise sources affecting individual neurons
unabhängig. This simple architecture allowed us to analytically assess
coding ability using both Fisher information (Abbott & Dayan, 1999; Yoon
& Sompolinsky, 1999; Wilke & Eurich, 2002; Wu, verstopft, & Amari, 2001)
and Shannon mutual information. We evaluated the coding fidelity of both
the linear representation and the nonlinear representation after a quadratic
nonlinearity as a function of the distribution of synaptic weights that shape
the shared variability within the representations (Adelson & Bergen, 1985;
Emerson, Korenberg, & Citron, 1992; Sakai & Tanaka, 2000; Pagan, Simon-
celli, & Rust, 2016). We find that the linear stage representation’s coding
fidelity improves with diverse synaptic weighting, even if the weighting
amplifies the common noise in the neural circuit. In der Zwischenzeit, the nonlin-
ear stage representation also benefits from diverse synaptic weighting in a
regime where common noise may be amplified, but not too strongly. More-
über, we found that the distribution of synaptic weights that optimized the
networks performance depended strongly on the relative amount of pri-
vate and shared variability. Insbesondere, the neural circuit’s coding fidelity
benefits from diverse synaptic weighting when shared variability is the
dominant contribution to the variability. Zusammen, our results highlight the
importance of diverse synaptic weighting when a neural circuit must con-
tend with sources of common noise.
2 Methoden
The code used to conduct the analyses described in this article is publicly
available on Github (https://github.com/pssachdeva/neuronoise).
2.1 Network Architecture. We consider the linear-nonlinear architec-
ture depicted in Figure 2. The inputs to the network consist of a stimulus
s along with common (gaussian) noise ξ
C. The N neurons in the network
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1244
P. Sachdeva, J. Livezey, and M. DeWeese
Figur 2: Linear-nonlinear network architecture. The network takes as its in-
puts a stimulus s and common noise ξ
C. A linear combination of these quan-
tities is corrupted by individual private noises ξ
P,ich. The output of this linear
stage is then passed through a nonlinearity gi((cid:3)) to produce a “firing rate” ri.
The weights for the linear stage of the network, v
ich, can be thought of
as synaptic weighting. Wichtig, the common noise is distinct from shared
input noise because it is manipulated by the synaptic weighting.
i and w
take a linear combination of the inputs and are further corrupted by inde-
pendent and identically distributed (i.i.d.) private gaussian noise. Daher, Die
output of the linear stage for the ith neuron is
(cid:3)
ich
= v
Ist + w
ich
σ
C
ξ
C
+ σPξ
P,ich
,
(2.1)
P,i is the private noise, v
where ξ
and private noise terms are scaled by positive constants σ
linear combination is passed through a nonlinearity gi((cid:3)
can be thought of as a firing rate.
i are the weights, and the common
C and σP. The noisy
ich) whose output ri
i and w
Daher, the network-wide computation is given by
r = g(vs + wσ
C
ξ
C
+ σPξP),
(2.2)
where g((cid:3)) is an element-wise application of the network nonlinearity.
2.2 Measures of Coding Strength. In order to assess the fidelity of the
population code represented by (cid:3) or r, we turn to the Fisher information and
the Shannon mutual information (Cover & Thomas, 2012). The former has
largely been used in the context of sensory decoding and correlated vari-
ability (Abbott & Dayan, 1999; Averbeck et al., 2006; Kohn et al., 2016) while
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1245
the latter has been well studied in the context of efficient coding (Attneave,
1954; Barlow, 1961; Glocke & Sejnowski, 1997; Rieke, Warland, de Ruyter van
Steveninck, & Bialek, 1999).
The Fisher information sets a limit by which the readout of a popula-
tion code can determine the value of the stimulus. Formally, it sets a lower
bound to the variance of an unbiased estimator for the stimulus. In terms
of the network architecture, the Fisher information of the representation r
(oder (cid:3)) quantifies how well s can be decoded given the representation. Für
gaussian noise models with stimulus-independent covariance, the Fisher
information is equal to the linear Fisher information (LFI):
ILFI(S) =
T
∂f(S)
∂s
(cid:4)−1(S)
∂f(S)
∂s
,
(2.3)
where f(S) Und (cid:4)(S) are the mean and covariance of the response (Hier, r or
(cid:3)) to the stimulus s. In anderen Fällen, the LFI serves as a lower bound for the
Fisher information and thus is a useful proxy when the Fisher information
is challenging to calculate analytically. The estimator for ILFI is the locally
optimal linear estimator (Kohn et al., 2016).
The Shannon mutual information quantifies the reduction in uncertainty
of one random variable given knowledge of another:
(cid:2)
ICH[S, F] =
dsdf p(S, F) log
(cid:3)
(cid:4)
.
P(S, F)
P(S)P(F)
(2.4)
Earlier work demonstrated that the Fisher information provides a lower
bound for the Shannon mutual information in the case of gaussian noise
(Brunel & Nadal, 1998). Jedoch, more recent work has revealed that the
relationship between the two is more nuanced, particularly in the cases
where the noise model is nongaussian (Wei & Stocker, 2016). Daher, Wir
supplement our assessment of the network’s coding ability by measuring
the mutual information, ICH[S, R], between the neural representation r and the
stimulus s. As with the Fisher information, the mutual information is often
intractable but fortunately can be estimated from data. Speziell, Wir
employ the estimator developed by Kraskov and colleagues, which uses
entropy estimates from k-nearest neighbor distances (Kraskov, Stögbauer,
& Grassberger, 2004).
2.3 Structured Weights. The measures of coding strength are a function
of the weights that shape the interaction of the stimulus and noise in the net-
arbeiten. Daher, the choice of the synaptic weight distribution affects the calcu-
lation of these quantities. We first consider the case of structured weights
in order to obtain analytical expressions for measures of coding strength.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1246
P. Sachdeva, J. Livezey, and M. DeWeese
Structured weights take on the form
⎛
⎞
T
w =
⎝ 1 · · · 1
(cid:7) (cid:8)(cid:9) (cid:10)
N/k times
2 · · · 2
(cid:7) (cid:8)(cid:9) (cid:10)
N/k times
⎠
· · · k · · · k
(cid:7) (cid:8)(cid:9) (cid:10)
N/k times
.
(2.5)
Speziell, the structured weight vectors are parameterized by an integer k
that divides the N weights into k homogeneous groups. The weights across
the groups span the positive integers up to k. Wichtig, larger k will only
increase the weights in the vector. Daher, in the above scheme, increased “di-
versity” can be achieved only by increasing k, which will invariably result
in an amplification of the signal to which the weight vector is applied. Im
case that k does not evenly divide N, each group is repeated (cid:2)N/k(cid:3) mal,
except the last group, which is only repeated N − (N − 1) · (cid:2)N/k(cid:3) mal (Das
Ist, the last group is truncated to ensure the weight vector is of size N).
Zusätzlich, we consider cases in which k is of order N, Zum Beispiel, k =
N/2. Allowing k to grow with N ensures that typical values for the weights
grow with the population size. This contrasts with the case in which k is a
constant, such as k = 4, which sets a maximum weight value independent
of the population size.
2.4 Unstructured Weights. While the structured weights allow for an-
alytical results, they possess an unrealistic distribution of synaptic weight-
ing. Daher, we also consider the case of unstructured weights, in which
the synaptic weights are drawn from some parameterized probability
distribution:
v ∼ p(v; θv); w ∼ p(w; θw).
(2.6)
We calculate both information-theoretic quantities over many random
draws from these distributions and observe how these quantities behave
as some subset of the parameters θ is varied. Insbesondere, we focus on the
log-normal distribution (Iyer, Menon, Buice, Koch, & Mihalas, 2013), welche
has been found to describe the distribution of synaptic weights well in slice
electrophysiology (Song, Sjöström, Reigl, Nelson, & Chklovskii, 2005; Sar-
gent, Saviane, Nielsen, DiGregorio, & Silver, 2005). Speziell, the weights
take on the form
w ∼ (cid:7) + Lognormal(M, σ ),
(2.7)
Wo (cid:7) > 0. For a log-normal distribution, an increase in μ will increase
the distribution’s mean, median, and mode (see Figure 3e, inset). Daher, M
as a parameter acts similar to k for the structured weights in that increased
weight diversity must be accompanied by an increase in their magnitude.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1247
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
= σ 2
C
Figur 3: Network coding performance of the linear stage representation. Hier,
= 1. Fisher information is shown on the top row
the noise variances are σ 2
P
and mutual information on the bottom row. (A, B) Structured weights. Linear
Fisher information and mutual information are shown as a function of the pop-
ulation size, N, across different levels of weight heterogeneity, kw (indicated by
color). (C, D) Linear fisher information and mutual information are shown as
a function of weight heterogeneity, kw, for various population sizes, N. (e, F)
Unstructured weights. Linear Fisher information and mutual information are
shown as a function of the mean of the log-normal distribution used to draw
common noise synaptic weights. Information quantities are calculated across
1000 random drawings of weights: solid lines depict the means while the shaded
region indicates one standard deviation. Inset: The distribution of weights for
various choices of μ. Increasing μ shifts the distribution to the right, increasing
heterogeneity.
3 Ergebnisse
We consider the network’s coding ability after both the linear stage ((cid:3)) Und
the nonlinear stage (R). Mit anderen Worten, the linear stage can be considered
the output of the network assuming each of the functions gi((cid:3)
ich) is the iden-
tity. Außerdem, due to the data processing inequality, the qualitative con-
clusions we obtain from the linear stage should apply for any one-to-one
nonlinearity.
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1248
P. Sachdeva, J. Livezey, and M. DeWeese
3.1 Linear Stage. The Fisher information about the stimulus in the
linear representation can be shown to be (see appendix A.1.1 for the
derivation)
(cid:13)
IF (S) = 1
σ 2
P
|v|2
σ 2
P
=
(cid:14)
σ 2
P
/σ 2
C
(cid:13)
(cid:14)
(cid:13)
|v|2 +
(σ 2
P
|v|2|w|2 − (v · w)2
C ) + |w|2
/σ 2
σ 2
/σ 2
P
C
/σ 2
(σ 2
P
+ |w|2 sin2 θ
C ) + |w|2
,
(cid:14)
(3.1)
(3.2)
which is equivalent to the linear Fisher information in this case. In equation
3.2, θ refers to the angle between v and w. The mutual information can be
expressed as (see appendix A.1.2 for the derivation)
ICH[S, (cid:3)] = 1
2
(cid:15)
1 + σ 2
(cid:16)
S IF (S)
.
log
(3.3)
For the case the mutual information, we have assumed that the prior distri-
bution for the stimulus is gaussian with zero mean and variance σ 2
S .
Examining equation 3.2 reveals that increasing the norm of v without
changing its direction (das ist, without changing θ ) will increase the Fisher
Information, while increasing the norm of w without changing its direction
will either decrease or maintain information (seit 0 ≤ sin2 θ ≤ 1). Addi-
tionally, if v and w become more aligned while leaving their norms un-
changed, the Fisher information will decrease (since sin2 θ will decrease).
This decrease in Fisher information is consistent with the observation that
alignment of v and w will produce differential correlations. If v and w are
changed in a way that modulates both their norm and direction, the impact
on Fisher information is less transparent.
To better understand the Fisher information, we impose a parameterized
structure on the weights that allows us to increase weight diversity without
decreasing the magnitude of any of the weights. This weight parameteriza-
tion, which we call the structured weights, is detailed in section 2.3. Wir
chose this parameterization for two reasons. Erste, we desired a scheme in
which an increase in diversity must be accompanied by an amplification of
common noise. We chose this behavior so that any improvement in coding
ability can only be explained by the increase in diversity rather than a po-
tential decrease in common noise. Zweite, we desired analytic expressions
for the Fisher information as a function of population size, which is possible
with this form of structured weights.
Under the structured weight parameterization, Gleichungen 3.1 Und 3.3 can
be explored by varying the choice of k for both v and w (we refer to them
as kv and kw, jeweils). It is simplest and most informative to exam-
ine these quantities by setting kv = 1 while allowing kw to vary, as ampli-
fying and diversifying v will only increase coding ability for predictable
Gründe dafür (this is indeed the case for our network) (Shamir & Sompolinsky,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1249
2006; Ecker et al., 2011). While increasing kw will boost the overall amount
of noise added to the neural population, it also changes the direction of the
noise in the higher-dimensional neural space. Daher, while we might expect
that adding more noise in the system would hinder coding, die Beziehung
between the directions of the noise and stimulus vectors in the neural space
also plays a role.
We first consider how the Fisher information and mutual information
are affected by the choice of kw. In the structured regime, we have
|v|2 = N,
v · w = N
k
|w|2 = N
k
k(cid:17)
i=1
k(cid:17)
i=1
i = N(k + 1)
2
,
i2 = N(k + 1)(2k + 1)
6
,
which allows us to rewrite equation 3.1 als
IF (S) = IF = N
2σ 2
P
12(σ 2
P
/σ 2
/σ 2
C ) + N(k2 − 1)
C ) + N(2k2 + 3k + 1)
6(σ 2
P
(3.4)
(3.5)
(3.6)
(3.7)
.
The form of the mutual information follows directly from plugging equa-
tion 3.7 into equation 3.3.
The analytical expressions for the structured regime reveal the asymp-
totic behavior of the information quantities. Neither quantity saturates as a
function of the number of neurons, N, except in the case of kw = 1 (see Fig-
ures 3a and 3b). In this regime, increasing the population size of the system
also enhances coding fidelity. Außerdem, both quantities are monotoni-
cally increasing functions of the common noise synaptic heterogeneity, kw
(see Figures 3c and 3d), implying that decoding is enhanced despite the fact
that the amplitude of the common noise is magnified for larger kw. Our ana-
lytical results show linear and logarithmic growth for the Fisher and mutual
Information, jeweils, as one might expect in the case of gaussian noise
(Brunel & Nadal, 1998). These qualitative results hold for essentially any
choice of (σ
In the case of kw = 1, the signal and common noise are aligned perfectly
in the neural representation. Daher, the common noise becomes equivalent in
form to shared input noise. As a consequence, we observe the saturation of
both Fisher information and mutual information as a function of the neural
Bevölkerung. This saturation implies the existence of differential correlations,
consistent with the observation that information-limiting correlations occur
under the presence of shared input noise (Kanitscheider et al., 2015).
, σP, σ
C).
S
The structured weight distribution we described allows us to derive ana-
lytical results, but the limitation to only a fixed number of discrete synaptic
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1250
P. Sachdeva, J. Livezey, and M. DeWeese
weight values is not realistic for biological networks. Daher, we use unstruc-
tured weights, described in section 2.4, in which the synaptic weights are
drawn from a log-normal distribution. In this case, we estimate the linear
Fisher information and the mutual information over many random draws
according to w
∼ (cid:7) + Lognormal(M, σ 2). We are primarily concerned with
ich
varying μ, as an increase in this quantity uniformly increases the mean, me-
dian, and mode of the log-normal distribution (see Figure 3e, inset), akin to
increasing kw for the structured weights.
Our numerical analysis demonstrates that increasing μ increases the av-
erage Fisher information and average mutual information across popula-
tion sizes (see Figures 3e and 3f: bold lines). Zusätzlich, the benefits of
larger weight diversity are felt more strongly by larger populations (see Fig-
ures 3e and 3f: different colors).
In the structured weight regime, our analytical results show that weight
heterogeneity can ameliorate the harmful effects of additional information-
limiting correlations induced by common noise mimicking shared input
noise. They do not imply that weight heterogeneity prevents differential
correlations, as the common noise in this model is manipulated by synap-
tic weighting, in contrast with true shared input noise. For unstructured
weights, we once again observe that larger heterogeneity affords the net-
work improved coding performance, despite the increased noise in the sys-
tem. Zusammen, these results show that linear networks could manipulate
common noise to prevent it from causing induced differential correlations.
Jedoch, neural circuits, which must perform other computations that may
dictate the structure of the weights on the common noise inputs, can still
achieve good decoding performance provided that the circuits’ synaptic
weights are heterogeneous.
3.2 Quadratic Nonlinearity. We next consider the performance of the
network after a quadratic nonlinearity gi(X) = x2 for all neurons i. This non-
linearity has been used in a neural network model to perform quadratic dis-
criminant analysis (Pagan et al., 2016) and as a transfer function in complex
cell models (Adelson & Bergen, 1985; Emerson et al., 1992; Sakai & Tanaka,
2000). Außerdem, we chose this nonlinearity because we were able to cal-
culate the linear Fisher information analytically (as an approximation to the
Fisher information); see appendix A.3 for a numerical analysis with an ex-
ponential nonlinearity. Jedoch, the mutual information is apparently not
analytically tractable; we performed a numerical approximation using sim-
ulated data.
3.2.1 Linear Fisher Information. An analytic expression of the linear Fisher
information is calculated in appendix A.1.3. Its analytic form is too compli-
cated to be restated here, but we will examine it numerically for both the
structured and unstructured weights. The qualitative behavior of the Fisher
information depends on the magnitude of the common variability (σ
C) Und
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1251
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
= σ
C
= 5, σ
C
= 1). (C) Normalized Fisher information. For a choice of σ
Figur 4: Linear Fisher information after quadratic nonlinearity in a network
with structured weights. (A) Fisher information as a function of population size
= 1, das ist, private and common noise have equal variances.
when σ
P
Solid lines denote constant k while dashed lines denote k scaling with popu-
lation size. (B) Same as panel a, but for a network where private variance dom-
inates (σ
P,
P
the Fisher information is calculated for a variety of kw (y-axis) and divided
by the maximum Fisher information (across the kw, for the choice of σ
P). Für
a given σ
P, the normalized Fisher information is equal to one at the value of
kw, which maximizes decoding performance. (D) Behavior of the Fisher infor-
mation as a function of synaptic weight heterogeneity for various population
= 1). (e) Same as panel d, but for networks where private variance
= σ
sizes (σ
C
P
= 1). (F) The coefficient of the linear term in the asymp-
= 5, σ
dominates (σ
C
P
totic series of the Fisher information at different levels of private variability. Bei
kw = 1, 2, the coefficient of N is exactly zero.
private variability (σP) in a more complicated fashion than the linear stage,
which depends on these variables primarily through their ratio σ
/σP. Daher,
C
we separately consider how common and private variability affect coding
efficacy under various synaptic weight structures.
As before, we first consider the structured weights with kv set to 1 while
= 1 (d.h., equal
only varying kw. We start with the special case where σP = σ
C
private and common noise variance). Hier, the Fisher information satu-
rates for both kw = 1 and kw = 2, but increases without bound for larger kw
(see Figure 4a). We can also consider the case where the structured weight
heterogeneity grows in magnitude with the population size (d.h., kw is a
1252
P. Sachdeva, J. Livezey, and M. DeWeese
function of N). In this scenario, the Fisher information is much smaller and
saturates (see Figure 4a, gestrichelt).
The information saturation (or growth) for various kw can be under-
stood in terms of the geometry of the covariance describing the neural
population’s variability. Information saturation occurs if the principal
eigenvector(S) of the covariance align closely (but not necessarily exactly)
with the differential correlation direction, F(cid:6)
, while the remaining eigenvec-
tors quickly become orthogonal to f(cid:6)
as population size increases (Moreno-
Bote et al., 2014; see appendix A.2 for more details). When kw = 1, the com-
mon noise aligns perfectly with the stimulus, and so the principal eigen-
vector of the covariance aligns exactly with f(cid:6)
(as in Figure 1a, Rechts). Wann
kw > 1, the principal eigenvector aligns closely, but not exactly, with the dif-
ferential correlation direction. Jedoch, when kw = 2, the remaining eigen-
vectors become orthogonal quickly enough for information to saturate. Das
does not occur when kw > 2. The case of kw ∼ O(N), meanwhile, is slightly
anders. Hier, the variances of the covariance matrix scale with population
Größe, so that the neurons simply exhibit too much variance for any meaning-
ful decoding to occur. Jedoch, we believe that it is unreasonable to expect
that the synaptic weights of a neural circuit scale with the population size,
making this scenario biologically implausible.
When private variability dominates, we observe qualitatively different
finite network behavior (σP = 5; see Figure 4b). For N = 1000, both kw = 1
and kw = 2 exhibit better performance relative to larger values of kw (von
Kontrast, the case with kw ∼ O(N) quickly saturates). We note that, unsur-
prisingly, the increase in private variability has decreased the Fisher infor-
mation for all cases we considered compared to σP = 1 (compare the scales
of Figures 4a and 4b). Our main interest, Jedoch, is identifying effective
synaptic weighting strategies given some amount of private and common
variability.
The introduction of the squared nonlinearity produces qualitatively dif-
ferent behavior at the finite network level. In contrast with Figure 3, In-
creased heterogeneity does not automatically imply improved decoding.
Tatsächlich, there is a regime in which increased heterogeneity improves Fisher
Information, beyond which we see a reduction in decoding performance
(see Figure 4d). If the private variability is increased, this regime shrinks
or becomes nonexistent, depending on the population size (see Figure 4e).
Außerdem, entering this regime for higher private variability requires
smaller kw (d.h., less weight heterogeneity).
The results shown in Figures 4d and 4e imply that there exists an inter-
esting relationship among the network’s decoding ability, its private vari-
ability, and its synaptic weight heterogeneity kw. To explore this further, Wir
examine the behavior of the Fisher information at a fixed population size
(N = 1000) as a function of both σP and kw (see Figure 4c). To account for the
fact that an increase in private variability will always decrease the Fisher
Information, we calculate the normalized Fisher information: for a given
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1253
choice of σP, each Fisher information is divided by the maximum across
a range of kw values. Daher, a normalized Fisher information allows us to
determine what level of synaptic weight heterogeneity maximizes coding
fidelity, given a particular level of private variability σP.
Figure 4c highlights three interesting regimes. When the private variabil-
ity is small, the network benefits from larger weight heterogeneity on the
common noise. But as the neurons become noisier, the “Goldilocks zone” in
which the network can leverage larger noise weights becomes constrained.
When the private variability is large, the network achieves superior coding
fidelity by having less heterogeneous weights, despite the threat of induced
differential correlations from the common noise. Between these regimes,
there are transitions for which many choices of kw result in equally good
decoding performance.
It is important to point out that Figures 4a to 4e capture only finite
network behavior. daher, we extended our analysis by validating the
asymptotic behavior of the Fisher information as a function of the pri-
vate noise by examining its asymptotic series at infinity (see Figure 4f). Für
kv = 1, 2, the coefficient of the linear term is zero for any choice of σP, im-
plying that the Fisher information always saturates. Zusätzlich, when the
common noise weights increase with population size (d.h., kw ∼ O(N)), Die
asymptotic series is always sublinear (not shown in Figure 4f). Daher, Dort
are multiple cases in which the structure of synaptic weighting can induce
differential correlations in the presence of common noise. Increased hetero-
geneity allows the network to escape these induced differential correlations
and achieve linear asymptotic growth. If kw becomes too large, Jedoch, Die
linear asymptotic growth begins to decrease. Once kw scales as the popula-
tion size, differential correlations are once again significant.
Nächste, we reproduce the analysis with unstructured weights. As before,
we draw 1000 samples of common noise weights from a shifted log-normal
distribution with varying μ. The behavior of the average (linear) Fischer
information is qualitatively similar to that of the structured weights (sehen
Figur 5). There exists a regime for which larger weight heterogeneity im-
proves the decoding performance, beyond which coding fidelity decreases
(see Figure 5a). If the private noise variance dominates, this regime begins
to disappear for smaller networks (see Figure 5b). Daher, with very noisy
Neuronen, the coding fidelity of the network is improved when the synaptic
weights are less heterogeneous (and therefore smaller).
To summarize these results, we once again plot the normalized Fisher in-
Formation (this time, normalized across choices of μ and averaged over 1000
samples from the log-normal distribution) for a range of private variabili-
Krawatten (see Figure 5c). The heat map exhibits a similar transition at a specific
level of private variability. At this transition, a wide range of μ’s provide
the network with similar decoding ability. For smaller σP, we see behavior
comparable to Figure 5a, where there exists a regime of improved Fisher
Information. Beyond the transition, the network performs better with less
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1254
P. Sachdeva, J. Livezey, and M. DeWeese
Figur 5: Linear Fisher information after quadratic nonlinearity, unstructured
weights. In contrast to Figure 4, panels a and b are plotted on a log scale. (A) Lin-
ear Fisher information as a function of the mean, M, of the log-normal distribu-
tion used to draw the common noise synaptic weights. Solid lines denote means,
while shaded regions denote one standard deviation across the 1000 Zeichnungen
of weights from the log-normal distribution. (B) Same as panel a but for net-
= 1). (C) Normalized
works in which private variability dominates (σ
P
linear Fisher information. Same plot as Figure 4c, but the average Fisher infor-
mation across the 1000 samples is normalized across μ (akin to normalizing
across kw).
= 5, σ
C
diverse synaptic weighting, though it becomes less stringent as σP increases.
The behavior exhibited by this heat map is similar to Figure 4c but contains
fewer uniquely identifiable regions. This may imply that the additional re-
gions in Figure 4c are an artifact of the structured weights.
The amount of the common noise will also affect how the network be-
haves and what levels of synaptic weight heterogeneity are optimal. Für
Beispiel, consider a network with private noise variability set to σP = 1.
When common noise is small, the Fisher information is comparable among
various choices of synaptic weight diversity (see Figure 6a). When the com-
mon noise dominates, Jedoch, the network benefits strongly from diverse
weighting (see Figure 4b), though it is punished less severely for having
kw scale with N (see Figure 6b, gestrichelt; compare to Figure 4b). Diese
observations are true at finite population size. As before, the Fisher informa-
tion saturates for kw = 1, 2 and kw ∼ O(N), no matter the choice of common
noise variance.
We calculated the normalized Fisher information across a range of com-
mon noise strengths to determine the optimal synaptic weight distribution.
The results for structured weights and unstructured weights are shown
in Figures 6c and 6d, jeweils. While they strongly resemble Figures
4c and 5c, they exhibit opposite qualitative behavior. As before, es gibt
three identifiable regions in Figure 6c, each divided by abrupt transitions
where many choices of kw are equally good for decoding. For small common
noise, the coding fidelity is improved with less heterogeneous weights, Aber
as the common noise increases, the network enters the Goldilocks regions.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1255
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 6: The relationship among common noise, private noise, and synaptic
weight heterogeneity. (A, B) Fisher information as a function of population size,
N, when common noise contribution is drowned out by private noise (A) Und
= 1) (B). Solid lines indicate constant kw, while
common noise dominates (σ
P
dashed lines refer to kw that scales with N. (C, D) Normalized Fisher informa-
tion as a function of common noise for structured weights (C) and unstructured
weights (D). For unstructured weights, each Fisher information is calculated by
averaging over 1000 networks with their common noise weights drawn from
the respective distribution. (e) The value of kw that maximizes the network’s
Fisher information for a given choice of σ
C. The maximum is taken over
kw ∈ [1, 10]. (F) The value of μ that maximizes the average Fisher information
über 1000 draws for a given choice of σ
P and σ
P and σ
C.
1256
P. Sachdeva, J. Livezey, and M. DeWeese
After another abrupt transition near σ
C
greatly improved by heterogeneous weights.
≈ 0.34, the network performance is
Daher, common noise and private noise seem to have opposite impacts
on the optimal choice of synaptic weight heterogeneity. When private noise
dominates, the Fisher information is maximized under a set of homoge-
neous weights, since coding ability is harmed by amplification of common
noise. When common noise dominates, the network coding is improved
under diverse weighting: this prevents additional differential correlations
and helps the network cope with the punishing effects on coding due to the
amplified noise.
How should we choose the synaptic weight distribution within the ex-
tremes of private or common noise dominating? We assess the behavior of
the Fisher information as both σP and σ
C are varied over a wide range. Für
the structured weights, we calculate the choice of kw that maximized the
network’s Fisher information (within the range kw ∈ [1, 10]; see Figure 6e).
For the unstructured weights, we calculate the choice of μ that maximizes
the network’s average Fisher information over 1000 drawings of w from the
log-normal distribution specified by μ (see Figure 6f).
Figures 6e and 6f reveal that the network is highly sensitive to the val-
ues of σP and σ
C. Figure 6e exhibits a bandlike structure and abrupt transi-
tions in the value of kw, which maximizes Fisher information. This bandlike
structure would most likely continue to form for smaller σP if we allowed
kw > 10. One might expect that the bandlike structure is due to the artifi-
cial structure in the weights; Jedoch, we see that Figure 6f also exhibits
these types of bands. Note that the regime of interest for us is when private
variability is a smaller contribution to the total variability than the common
variability. When this is the case, Figures 6e and 6f imply that a population
of neurons will be best served by having a diverse set of synaptic weights,
even if the weights amplify irrelevant signals.
Zusammen, these results highlight how the introduction of the nonlinearity
in the network reveals an intricate relationship among the amount of shared
variability, private variability, and the optimal synaptic weight heterogene-
ität. Our observations that the network benefits from increased synaptic
weight heterogeneity in the presence of common noise are predicated on the
size of the network (see Figures 4a and 4b and 6a and 6b) and the amount
of private and shared variability (see Figures 4c, 6C, and 6d). Insbesondere,
when shared variability is the more significant contribution to the overall
variability, the coding performance of the network benefits from increased
heterogeneity, whether the weights are structured or unstructured (see Fig-
ures 6e and 6f). This implies that in contrast to the linear network, there exist
regimes where increasing the synaptic weight heterogeneity beyond a point
will harm coding ability (see Figures 4d and 4e and 5a and 5b), demonstrat-
ing that there is a trade-off between the benefits of synaptic weight hetero-
geneity and the amplification of common noise it may introduce.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1257
Figur 7: Mutual information computed by applying the KSG estimator on
data simulated from the network with quadratic nonlinearity and structured
weights. The estimates consist of averages over 100 data sets, each containing
100,000 Proben. Standard error bars are smaller than the size of the markers.
(A) Mutual information as a function of common noise weight heterogeneity for
various population sizes N. We consider smaller N than in the case of Fisher in-
formation as computation time becomes prohibitive for larger dimensionalities.
= 0.5. (B) The behavior of mutual information for various choices
Hier, σ
P
= 0.5. (C) The behavior of mutual information for various choices
of σ
= 0.5.
of σ
= σ
C
P, while σ
C, while σ
C
P
3.2.2 Mutual Information. When the network possesses a quadratic non-
linearity, the mutual information I[S, R] is far less tractable than for the linear
Fall. daher, we computed the mutual information numerically on data
simulated from the network, using an estimator built on k-nearest neigh-
bor statistics (Kraskov et al., 2004). We refer to this estimator as the KSG
estimator.
We applied the KSG estimator to 100 unique data sets, each contain-
ing 100,000 samples drawn from the linear-nonlinear network. We then
estimated the mutual information within each of the 100 data sets. The com-
putational bottleneck for the KSG estimator lies in finding nearest neigh-
bors in a kd-tree, which becomes prohibitive for large dimensions (∼20), Also
we considered much smaller population sizes than in the case of Fisher in-
Formation. Außerdem, the KSG estimator encountered difficulties when
samples became too noisy, so we limited our analysis to smaller values of
(σP, σ
C). Due to these constraints, we are only able to probe the finite net-
work behavior of the mutual information.
Our results for the structured weights are shown in Figure 7. When uti-
lizing estimators of mutual information from data, caution should be taken
before comparing across different dimensions due to bias in the KSG esti-
mator (Gao, Ver Steeg, & Galstyan, 2015). Daher, we restrict our observations
to within a specified population size. Erste, we evaluated the mutual infor-
mation for various population sizes (N = 8, 10, 12, 14) in the case where
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1258
P. Sachdeva, J. Livezey, and M. DeWeese
σ
= σP = 0.5. Observe that, as before, the mutual information increases
C
with larger weight heterogeneity (kw; see Figure 7a). The improvement in
information occurs for all four population sizes.
Decreasing the private variability increases mutual information (see Fig-
ure 7b). Jedoch, the network sees a greater increase in information with
diverse weighting when σP is small. This is consistent with the small σP
regime highlighted in Figure 4c: the smaller the private variability, the more
the network benefits from larger synaptic weight heterogeneity. Ähnlich,
decreasing the common variability increases mutual information (see Fig-
ure 7c). If the common variability is small enough (z.B., σ
= 1), then larger
C
kw harms the encoding. Daher, when the common noise is small enough, Die
amplification of noise that results when kw is increased harms the network’s
encoding. It is only when the common variability becomes the dominant
contribution to the variability that the diversification provided by larger kw
improves the mutual information.
As for the unstructured weights, we calculated the mutual information
ICH[S, R] über 100 synaptic weight distributions drawn from the aforemen-
tioned log-normal distribution. For each synaptic weight distribution, Wir
applied the KSG estimator to 100 unique data sets, each consisting of 10,000
Proben. Daher, the mutual information estimate for a given network was
computed by averaging over the individual estimates across the 100 Daten
sets. With this procedure, we explored how the mutual information behaves
as a function of the private noise variability, common noise variability, Und
mean of the log-normal distribution.
Similar to the normalized Fisher information, we present the normal-
ized mutual information as a function of the private and common vari-
ances (siehe Abbildung 8). For a given σP or σ
C, the mutual information is
calculated across a range of μ ∈ [−1, 1]. The normalized mutual informa-
tion is obtained by dividing each individual mutual information by the
maximum value across the μ. Daher, for a given σP, the value of μ whose
normalized mutual information is 1 specifies the log-normal distribution
that maximizes the network’s encoding performance. As private variabil-
ity increases, the network benefits more greatly benefits diverse weighting
(larger μ; see Figure 8a). As common variability increases, the network once
again prefers more diverse weighting. If the common variability is small
enough, Jedoch, the network is better suited to homogeneous weights
(see Figure 8b). daher, the analysis using the unstructured weights
largely corroborates our findings for the structured weights shown in
Figur 7.
Daher, these results highlight that there exist regimes where neural cod-
ing, as measured by the Shannon mutual information, benefits from in-
creased synaptic weight heterogeneity. Außerdem, similar to the case of
the linear Fisher information, the improvement in coding occurs more sig-
nificantly when shared variability is large relative to private variability.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1259
Figur 8: Normalized mutual information for common and private variability.
For a given μ, 100 networks were created by drawing common noise weights
w from the corresponding log-normal distribution. The mutual information
shown is the average across the 100 Netzwerke. For a specified network, the mu-
tual information was calculated by averaging KSG estimates over 100 simuliert
data sets, each containing 10,000 Proben. Endlich, for a choice of (σ
C), mu-
P
tual information is normalized to the maximum across values of μ. (A) Normal-
= 0.5).
ized mutual information as a function of μ and private variability (σ
C
(B) Normalized mutual information as a function of μ and common variability
(σ
= 0.5).
, σ
P
4 Diskussion
We have demonstrated in a simple model of neural activity that if synap-
tic weighting of common noise inputs is broad and heterogeneous, cod-
ing fidelity is actually improved despite inadvertent amplification of
common noise inputs. We showed that for squaring nonlinearities, Dort
exists a regime of heterogeneous weights for which coding fidelity is max-
imized. We also found that the relationship between the magnitude of pri-
vate and shared variability is vital for determining the ideal amount of
synaptic heterogeneity. In neural circuits where shared variability is dom-
inant, as has been reported in some parts of the cortex (Deweese & Zador,
2004), larger weight heterogeneity results in better coding performance (sehen
Figure 6e).
Why are we afforded improved neural coding under increased synaptic
weight heterogeneity? An increase in heterogeneity, as we have defined it,
ensures that the common noise is magnified in the network. Gleichzeitig
Zeit, Jedoch, the structure of the correlated variability induced by the
common noise is altered by increased heterogeneity. Previous work has
demonstrated that the relationship between signal correlations and noise
correlations is important in assessing decoding ability; Zum Beispiel, the sign
rule states that noise correlations are beneficial if they are of opposite sign
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1260
P. Sachdeva, J. Livezey, and M. DeWeese
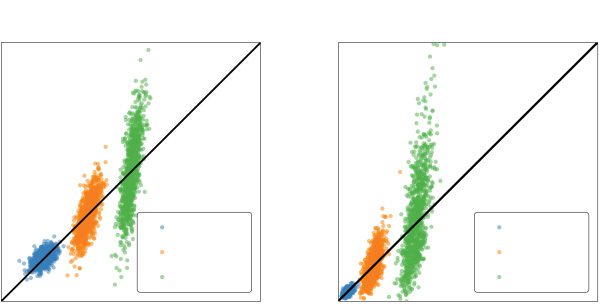
Figur 9: The benefits of increased synaptic weight heterogeneity. (A) The re-
sponses of a pair of neurons against the signal space, taken after the linear stage.
Colors indicate different choices of kw (while kv = 1). Each cloud contains 1000
sampled points. (B) Same as panel a, but responses are taken after the quadratic
nonlinearity.
as the signal correlation (Hu et al., 2014). Geometrically, the sign rule is a
consequence of the intuitive observation that decoding is easier when the
noise correlations lie perpendicular to the signal manifold (Averbeck et al.,
2006; Zylberberg, Cafaro, Turner, Shea-Brown, & Rieke, 2016; Montijn et al.,
2016).
Zum Beispiel, consider the correlated activity for two neurons in the net-
work against their signal space (see the black lines in Figures 9a and 9b) as a
function of kw. Note that the signal space is linear. After the linear stage, Die
larger weight heterogeneity pushes the cloud of neural activity to lie more
orthogonal to the signal space. Gleichzeitig, the variance becomes ob-
servably larger due to the magnification of the common noise (siehe Abbildung
9A). Wichtig, note that the variability for kw = 1 lies parallel to the sig-
nal space, signifying the presence of differential correlations. The correlated
variability after the nonlinear stage is similar in that orthogonality to the sig-
nal space increases with kw. There is a notable difference: squaring the linear
stage ensures nonnegative activities, thereby limiting the response space.
Daher, for large enough kw, the rectification manifests strongly enough that
the network enters a regime where increased heterogeneity harms decod-
ing. These figures only demonstrate the relationship between a pair of neu-
rons, while the collective correlated variability structure ultimately dictates
decoding performance. They do, Jedoch, shed light on how the distribu-
tion of synaptic weights can radically shape the common noise and thereby
the overall structure of the shared variability.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1261
The linear stage of the network constitutes a noisy projection of two sig-
nals (one of which is not useful to the network) in a high-dimensional space.
Daher, we can assess the entire population by examining the relationship
between the projecting vectors v and w. We might expect that improved
decoding occurs when these signals are farther apart in the N-dimensional
Raum (Kanerva, 2009). For a chosen kv, this occurs as kw is increased when
the weights are structured. When the weights are unstructured, the average
angle between the stimulus and weight vectors is large as either μv or μw in-
creases. Increased heterogeneity implies access to a more diverse selection
of weights, thus pushing the two signals apart. From this perspective, Die
nonlinear stage acts as a mapping on the high-dimensional representation.
Given that no noise is added after the nonlinear processing stage in the net-
funktioniert, if the nonlinearities were one-to-one, the data processing inequality
would ensure that the results from the linear stage would hold. But as we
observed earlier, the nonlinear stage benefits from increased heterogeneity
only in certain regimes. Daher, the behavior of the nonlinearity is important:
the application of the quadratic nonlinearity restricts the high-dimensional
space that the neural code can occupy, and thus limits the benefits of diverse
synaptic weighting. Validating and characterizing these observations for
other nonlinearities (such as an exponential nonlinearity or a squared rec-
tified linear unit) and within the framework of a linear-nonlinear-Poisson
cascade model will be interesting to pursue in future studies. For exam-
Bitte, we performed a simple experiment numerically assessing the behavior
of the linear Fisher information under an exponential nonlinearity. We ob-
served that synaptic weight heterogeneity benefits coding, but information
may saturate for a wide range of kw (see appendix A.3). Daher, the choice of
nonlinearity may affect the coding performance in the presence of common
noise.
In this work, we considered the coding ability of a network in which
a stimulus is corrupted by a single common noise source. Jedoch, cor-
tical circuits receive many inputs and must likely contend with multiple
common noise inputs. Daher, it is important to examine how our analysis
changes as the number of inputs increases. Naively, the neural circuit could
structure weights to collapse all common noise sources on a single sub-
Raum, but this strategy will fail if the circuit must perform multiple tasks
(z.B., the circuit may be required to decode among many of the inputs us-
ing the same set of weights). Außerdem, there are brain regions in which
the dimensionality is drastically reduced, such as cortex to striatum (10 Zu
1 reduction) or striatum to basal ganglia (300 Zu 1 reduction; Bar-Gad, Mor-
ris, & Bergman, 2003; Seger, 2008). In these cases, the number of inputs may
scale with the size of the neural circuit. In such an underconstrained sys-
tem, linear decoding will be unable to properly extract estimates of the rel-
evant stimulus. This implies that linear Fisher information, which relies on a
linear decoder, may be insufficient to judge the coding fidelity of these
Populationen. Daher, future work could examine how the synaptic weight
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1262
P. Sachdeva, J. Livezey, and M. DeWeese
distribution affects neural coding with multiple common noise inputs. Das
includes the case when the number of common noise sources is smaller than
the population size or when they are of similar scale, the latter of which
may require alternative coding strategies (Davenport, Duarte, Eldar, & Ku-
tyniok, 2012; Garfinkle & Hillar, 2019).
It may seem unreasonable that the neural circuit possesses the ability to
weight common noise inputs. Jedoch, excitatory neurons receive many
excitatory synapses in circuits throughout the brain. Some subset of com-
mon inputs across a neural population will undoubtedly be irrelevant for
the underlying neural computation, even if these signals are not strictly
speaking “noise” and could be useful for other computations. Daher, diese
populations must contend with common noise sources contributing to their
overall shared variability and potentially hampering their ability to encode
a stimulus. Our work demonstrates that neural circuits, armed with a good
set of synaptic weights, need not suffer adverse impacts due to inadver-
tently amplifying potential sources of common noise. Stattdessen, broad, het-
erogeneous weighting ensures that common noise sources will project the
signal and noise into a high-dimensional space in such a way that is bene-
ficial for decoding. This observation is in agreement with recent work that
explored the relationship between heterogeneous weighting and degrees
der synaptischen Konnektivität (Litwin-Kumar, Harris, Axel, Sompolinsky, & Ab-
bott, 2017). Außerdem, synaptic input, irrelevant on one trial, may be-
come the signal on the next: heterogeneous weighting provides a general,
robust principle for neural circuits to follow.
We chose the simple network architecture in order to maintain analytic
tractability, which allowed us to explore the rich patterns of behavior it
exhibited. Our model is limited, Jedoch. It is worthwhile to assess how
our qualitative conclusions hold with added complexity in the network.
Zum Beispiel, interesting avenues to consider include the implementation
of recurrence, spiking dynamics, and global fluctuations. Zusätzlich, diese
networks could also be equipped with varying degrees of sparsity and in-
hibitory connections. Wichtig, the balance of excitation and inhibition in
networks has been shown to be vital in decorrelating neural activity (Renart
et al., 2010). Past work has explored how to approximate both information-
theoretic quantities studied here in networks with some subset of these fea-
tures (Beck, Bejjanki, & Pouget, 2011; Yarrow, Challis, & Seriès, 2012). Daher,
analyzing how common noise and synaptic weighting interact in more com-
plex networks is of interest for future work.
We established correlated variability structure in the linear-nonlinear
network by taking a linear combination of a common noise source and pri-
vate noise sources (though our model ignores any noise potentially carried
by the stimulus). This was sufficient to establish low-dimensional shared
variability observed in neural circuits. As a consequence, our model as de-
vised enforces stimulus-independent correlated variability. Recent work,
Jedoch, has demonstrated that correlated variability is in fact stimulus
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1263
dependent. Such work used both phenomenological (Lin, Kabel, Carandini,
& Harris, 2015; Franke et al., 2016) and mechanistic (Zylberberg et al., 2016)
models in producing fits to the stimulus-dependent correlated variability.
These models all share a doubly stochastic noise structure, stemming from
both additive and multiplicative sources of noise (Goris, Movshon, & Si-
moncelli, 2014). It is therefore worthwhile to fully examine how both ad-
ditive and multiplicative modulation interact with synaptic weighting to
influence neural coding. Zum Beispiel, Arandia-Romero et al. (2016) Dämon-
strated that such additive and multiplicative modulation, modulated by
overall population activity, can redirect information to specific neuronal
assemblies, increasing information for some but decreasing it for others.
Synaptic weight heterogeneity, attuned by plasticity, could serve as a mech-
anism for additive and multiplicative modulation, thereby gating informa-
tion for specific assemblies.
A Appendix
A.1 Calculation of Fisher and Mutual Information Quantities.
A.1.1 Calculation of Fisher Information, Linear Stage. All variability after
the linear stage is gaussian; daher, the Fisher information can be expressed
als (Abbott & Dayan, 1999; Kay, 1993)
(cid:6)
IF (S) = f
(cid:6)
(S)T (cid:4)−1(S)F
(cid:15)
(S) + 1
2
Tr
(cid:4)(cid:6)
(S)(cid:4)−1(S)(cid:4)(cid:6)
(cid:16)
(S)(cid:4)−1(S)
.
(A.1)
Our immediate goal is to calculate f(S), the average response of the linear
stage, Und (cid:4), the covariance between the responses. The output of the ith
neuron after the linear stage is
(cid:3)
ich
= v
Ist + w
ich
σ
C
ξ
C
+ σPξ
P,ich
,
so that the average response as a function of s is
fi(S) = (cid:9)(cid:3)
ich
(cid:10) = v
Ist.
(cid:6)
F(S) = vs ⇒ f
(S) = v,
Daher,
Und
(cid:9)(cid:3)
ich
(cid:3)
J
(cid:10) = (cid:9)(v
= v
v
ich
Ist + w
ich
js2 + w
σ
C
ξ
C
w
ich
J
+ σPξ
+ σ 2
σ 2
P
C
P,ich)(v
,
δ
i j
js + w
σ
C
ξ
C
J
+ σPξ
P, J )(cid:10)
(A.2)
(A.3)
(A.4)
(A.5)
(A.6)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1264
so that
(cid:9)
i j
= (cid:9)(cid:3)
ich
(cid:3)
(cid:10) − (cid:9)(cid:3)
ich
J
(cid:10)(cid:9)(cid:3)
(cid:10)
J
= σ 2
P
δ
i j
+ w
w
ich
σ 2
C
J
⇒ (cid:4) = σ 2
P I + σ 2
C wwT .
P. Sachdeva, J. Livezey, and M. DeWeese
(A.7)
(A.8)
(A.9)
Notice that the covariance matrix does not depend on s, so the second term
in equation A.1 will vanish. Das tun wir, Jedoch, need the inverse covariance
matrix for the first term:
(cid:4)−1 = 1
σ 2
P
(cid:18)
I −
σ 2
C
+ σ 2
C
σ 2
P
|w|2
(cid:19)
wwT
.
Somit, the Fisher information is
(cid:18)
vT
I −
(cid:14)
(cid:13)
σ 2
P
/σ 2
C
IF (S) = 1
σ 2
P
= 1
σ 2
P
(cid:19)
v
|w|2
wwT
σ 2
C
+ σ 2
C
(cid:13)
|v|2|w|2 − (v · w)2
C ) + |w|2
σ 2
P
|v|2 +
(σ 2
P
/σ 2
(A.10)
(A.11)
(A.12)
(cid:14)
.
A.1.2 Calculation of Mutual Information, Linear Stage. The mutual infor-
mation is given by
(cid:2)
ICH[S, (cid:3)] =
D(cid:3)dsP[S]P[(cid:3)|S] log
(cid:2)
(cid:2)
P[(cid:3)|S]
P[(cid:3)]
= H[(cid:3)] +
dsP[S]
D(cid:3)P[(cid:3)|S] log P[(cid:3)|S].
(A.13)
(A.14)
Note that P[(cid:3)] and P[(cid:3)|S] are both multivariate gaussians. Der (differential)
entropy of a multivariate gaussian random variable X with mean μ and
covariance (cid:4) is given by
H[X] = 1
2
log (det (cid:4)) + N
2
(1 + log(2π )).
(A.15)
daher, by the gaussianity of the involved distributions,
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
P[(cid:3)|S] =
(cid:20)
1
σ N−1
P
(2π )N(σ 2
P
(cid:21)
+ σ 2
C
|w|2)
(cid:18)
× exp
− 1
2σ 2
P
((cid:3) − vs)T
I −
(cid:19)
(cid:22)
((cid:3) − vs)
(A.16)
σ 2
CwwT
+ σ 2
C
|w|2
σ 2
P
Heterogeneous Synaptic Weighting under Common Noise
1265
P[(cid:3)] =
(cid:20)
1
(2π )Nσ 2N−4
P
κ
(cid:23)
− 1
2
(cid:13)
(cid:3)T
exp
σ 2
P I + σ 2
S vvT + σ 2
C wwT
Wo
κ = (σ 2
P
+ σ 2
C
|w|2)(σ 2
P
+ σ 2
S
|v|2) − σ 2
C
S (v · w)2.
σ 2
Daher,
H[(cid:3)] = 1
2
(cid:13)
log
σ 2N−4
P
κ
(cid:14)
+ N
2
(1 + log(2π ))
(cid:14)−1 (cid:3)
(cid:24)
,
(A.17)
(A.18)
(A.19)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
Und
(cid:2)
D(cid:3)P[(cid:3)|S] log P[(cid:3)|S] = − 1
2
− N
2
log(σ 2N−2
P
(σ 2
P
+ σ 2
C
|w|2))
(1 + log(2π )),
(A.20)
which is notably independent of s. Daher, the integral over s will marginalize
weg. We are left with
(cid:18)
(cid:19)
ICH[S, (cid:3)] = 1
2
log
(cid:13)
log
= 1
2
P
κ
+ σ 2
C
(cid:14)
S IF (S)
P (σ 2
σ 2
1 + σ 2
|w|2)
.
(A.21)
(A.22)
A.1.3 Calculation of Linear Fisher Information, Quadratic Nonlinearity. Wir
repeat the calculation of the first section, but after the nonlinear stage. In
this case, we consider a quadratic nonlinearity. Instead of the Fisher infor-
mation, we calculate the linear Fisher information (since it is analytically
tractable). The output of the network is
ri
= (v
= v 2
Ist + w
ich
i s2 + w2
+ σPξ
σ
ξ
C
C
+ σ 2
ξ 2
σ 2
P
C
C
ich
P,ich)2
ξ 2
P,ich
+ 2sv
w
σ
C
ξ
C
ich
ich
+ 2sv
σPξ
ich
P,ich
+ 2w
σ
C
σPξ
C
ich
ξ
P,ich
.
(A.23)
Daher, the average is then
fi(S) = (cid:9)ri
(cid:10) = v 2
i s2 + w2
ich
σ 2
C
+ σ 2
P
,
(A.24)
(A.25)
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1266
P. Sachdeva, J. Livezey, and M. DeWeese
was impliziert
(cid:9)ri
(cid:10)(cid:9)r j
(cid:10) = (v 2
i s2 + w2
ich
+ s2σ 2
+ σ 2
σ 2
C
+ v 2
= σ 4
P
ich
P (v 2
w2
J
ich
+ s2σ 2
C (v 2
+ v 2
J
J
P )(v 2
J ) + σ 2
ich ) + s4v 2
w2
j s2 + w2
C (w2
σ 2
v 2
J
P
ich
ich
σ 2
C
+ σ 2
P )
+ w2
J )
+ σ 4
C
w2
ich
w2
J
.
Nächste, the covariate can be written as
(cid:9)rir j
(cid:10) = σ 4
P
+ s2σ 2
+ v 2
P (v 2
ich
+ 3σ 4
C
P
J ) + σ 2
w2
J
C (w2
σ 2
v
+ 4s2σ 2
C
ich
w2
ich
+ w2
v
ich
J
w
ich
C (v 2
ich
J ) + s2σ 2
.
w
J
+ s4v 2
ich
v 2
J
The off-diagonal terms of the covariance matrix are then
(cid:9)rir j
(cid:10) − (cid:9)ri
(cid:10)(cid:9)r j
(cid:10) = 2σ 4
C
w2
ich
w2
J
+ 4s2σ 2
C
v
ich
v
J
w
ich
w
.
J
(A.26)
(A.27)
w2
J
+ v 2
J
w2
ich )
(A.28)
(A.29)
Endlich, the variance of ri (the diagonal terms of the covariance matrix) Ist
given by
Var(ri) = (cid:9)r2
ich
= 3σ 4
P
(cid:13)
(cid:10)2
(cid:10) − (cid:9)ri
+ 6s2σ 2
P
v 2
ich
+ 6σ 2
P
σ 2
C
(cid:14)
2
w2
ich
+ 6s2σ 2
C
v 2
ich
w2
ich
+ s4v 4
ich
+ 3σ 4
C
w4
ich
(A.30)
−
i s2 + w2
v 2
w4
ich
σ 2
ich
C
+ 4s2σ 2
C
+ σ 2
P
+ 2σ 4
P
w2
ich
v 2
ich
= 2σ 4
C
+ 4s2σ 2
P
v 2
ich
+ 4σ 2
P
σ 2
C
w2
ich
.
(A.31)
(A.32)
Daher, the total covariance, which takes the variance into consideration, Ist
(cid:9)
i j
= δ
i j
(cid:13)
2σ 4
P
+ 4σ 2
P (s2v 2
ich
(cid:14)
w2
ich )
+ σ 2
C
+ 4s2σ 2
C
v
ich
v
J
w
ich
w
J
+ 2σ 4
C
w2
ich
w2
J
.
(A.33)
In vector notation, this can be expressed as
(cid:4) = 2σ 4
P I + 4σ 2
P s2diag(V) + 4σ 2
P
C diag(W) + 4s2σ 2
σ 2
C XXT + 2σ 4
CWWT ,
Wo
V = v (cid:12) v,
W = w (cid:12) w,
X = v (cid:12) w,
(A.34)
(A.35)
(A.36)
(A.37)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1267
Wo (cid:12) indicates the Hadamard product (element-wise product). We now
proceed to the linear Fisher information:
(cid:6)
ILFI(S) = f
(S)T (cid:4)(S)
(cid:6)
−1f
(S).
(A.38)
We start by calculating the inverse covariance matrix, which we will achieve
with repeated applications of the Sherman-Morrison formula (Sherman &
Morrison, 1950). We can write
(cid:4)−1 = (M + 2σ 4
−1
C WWT )
−1 − M−1(2σ 4
1 + 2σ 4
= M
CWWT )M−1
CWT M−1W
2σ 4
C
C WT M−1W
= M
−1 −
1 + 2σ 4
−1WWT M
−1,
M
Wo
−1 ≡
M
(cid:13)
2σ 4
P
−
+ 4σ 2
P s2v 2
ich
σ 4
P
+ 2s2σ 2
C
σ 2
P
(cid:14)−1 δ
i j
w2
ich
+ 4σ 2
σ 2
P
C
s2σ 2
C
(cid:17)
ich
v 2
ich
+ 2s2v 2
ich
w
w
J
(cid:14) (cid:25)
J
ich
σ 2
P
σ 2
P
v
v
ich
w2
ich
w2
ich
+ 2σ 2
C
w2
ich
+ 2s2v 2
ich
+ 2σ 2
C
+ 2s2v 2
J
(cid:26) .
+ 2σ 2
C
w2
J
×
(cid:13)
σ 2
P
Beachten Sie, dass
(cid:6)
F
(S) = 2sV,
so the Fisher information is
(cid:18)
ILFI(S) = 4s2
VT M
−1V −
2σ 4
C
C WT M−1W
1 + 2σ 4
(cid:18)
= 4s2
VT M
−1V −
2σ 4
C
C WT M−1W
1 + 2σ 4
VT M
−1WWT M
−1V
(cid:13)
VT M
−1W
(cid:14)
2
(cid:19)
.
(A.44)
(A.45)
To facilitate the matrix multiplications, we will define the following nota-
tion:
{v, w}
=
M,N
(cid:17)
σ 2
P
ich
v m
ich
+ 2s2v 2
ich
wn
ich
+ 2σ 2
C
.
w2
ich
(A.46)
(A.39)
(A.40)
(A.41)
(A.42)
(A.43)
(cid:19)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1268
Daher,
P. Sachdeva, J. Livezey, and M. DeWeese
VT M
−1V = 1
2σ 2
P
(cid:17)
σ 2
P
ich
v 4
ich
+ 2s2v 2
ich
w2
ich
+ 2σ 2
C
(cid:18)
(cid:17)
−
s2σ 2
C
σ 2
P
+ 2s2σ 2
C
σ 4
P
{v, w}
2,2
σ 2
P
ich
(cid:19)
2
w
v 3
ich
ich
+ 2σ 2
+ 2s2v 2
C
ich
w2
ich
(A.47)
= 1
2σ 2
P
{v, w}
4,0
−
s2σ 2
C
σ 2
P
+ 2s2σ 2
C
σ 4
P
{v, w}
2,2
{v, w}2
3,1
.
(A.48)
Außerdem,
WT M
−1W = 1
2σ 2
P
{v, w}
0,4
−
s2σ 2
C
σ 2
P
+ 2s2σ 2
C
σ 4
P
{v, w}
2,2
{v, w}2
1,3
(A.49)
Und, finally,
VT M
−1W = 1
2σ 2
P
{v, w}
2,2
−
s2σ 2
C
σ 2
P
+ 2s2σ 2
C
σ 4
P
{v, w}
2,2
{v, w}
1,3
{v, w}
.
3,1
(A.50)
Inserting this expression into equation A.45 and simplifying, we can write
the Fisher information as
ILFI(S) = 4s2
(cid:25)
1
σ 2
P
{v, w}
4,0
−
2s2σ 2
C
{v,w}
σ 2
C
+2s2σ 2
P
σ 2
P
2,2
{v, w}2
3,1
+
σ 4
P
+σ 2
P (σ 4
C
σ 2
σ 4
P
C
{v,w}
{v,w}
2,2
+2s2σ 2
C
+2s2σ 6
{v,w}
C ({v,w}
2,2 )+2s2σ 6
−2{v,w}
C ({v,w}
2,2
1,3
0,4
0,4
{v,w}
{v,w}
3,1 )
2,2
−2{v,w}2
1,3 )
(cid:26)
. (A.51)
A.2 Information Saturation and Differential Correlations. In section
3.2.1, we observed that the Fisher information saturates in particular in-
stances of the nonlinear network. Speziell, for the nonlinear network,
Fisher information saturates for kw = 1 and kw = 2, but not for kw > 3. Ad-
ditionally, Fisher information saturates for kw ∼ O(N). To understand why
we observe saturation in some cases and not others, it is helpful to exam-
ine the eigenspectrum of the covariance matrix (cid:4) describing the neural re-
sponses. Hier, we rely on an analysis in the supplement of Moreno-Bote
et al. (2014).
The linear Fisher information can be written in terms of the eigenspec-
trum of (cid:4) als
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1269
ILFI = f
(cid:6)T (cid:4)−1f
(cid:6)
(cid:17)
= f
(cid:6)
(cid:6)T f
k
cos2 θ
σ 2
k
k
,
(A.52)
(A.53)
k is the kth eigenvalue and θ
where σ 2
k is the angle between the kth eigenvec-
tor and f(cid:6). We consider the cases in which ILFI saturates with the population
size N. Erste, note that the squared norm of the tuning curve derivative f(cid:6)T f(cid:6)
will scale as O(N), since there are N terms in the sum. This implies that the
summation must shrink at least as fast as O(1/N) for information to satu-
rate. This implies that any eigenvalues scaling as O(1) must have their cor-
responding cosineangles shrink faster than O(1/N). If there are O(N) solch
eigenvalues, they must shrink faster than O(1/N2).
In the case of kw = 1, one eigenvalue grows as O(N) while the others
remain constant (see Figure 10a, links). In der Zwischenzeit, the cosine-angles of the
constant eigenvalues are effectively zero. This case is the easiest to under-
stand: the principal eigenvector aligns with f(cid:6) while all other directions are
effectively orthogonal to f(cid:6). For kw ≥ 1, Jedoch, two eigenvalues grow as
Ö(N) while the others grow as O(1) (see Figure 10a, middle and right). In
this case, the behavior of the cosine-angles corresponding to the constant
growth eigenvalues varies depending on kw.
As in Moreno-Bote et al. (2014) we split up equation A.53 into two
groups: those with eigenvalues that scale as O(N), denoted by the set SN,
and those that scale as O(1), denoted by the set S1:
ILFI = f
(cid:6)T f
(cid:17)
m∈SN
cos2 θm
σ 2
M
+ F
(cid:6)
(cid:6)T f
(cid:17)
n∈S1
cos2 θn
σ 2
N
.
(A.54)
The left sum contains one term when kw = 1 and two terms when kw > 1.
Information saturation is dictated by the right sum, which we call Rkw :
=
Rkw
(cid:17)
n∈S1
cos2 θn
σ 2
N
.
(A.55)
The addends of Rkw correspond to the O(1) eigenvalues, whose eigenvec-
tors must have cosine-angles that vanish more quickly than O(1/N) seit
there are O(N) such eigenvalues. Wie erwartet, for kw = 1, R1 quickly van-
ishes (see Figure 10a: gray line). We observe similar behavior for kw = 2:
the summation R2 eventually vanishes as well (see Figure 10b: red line).
Jedoch, for kw > 2, this no longer occurs: the cosine-angles scale to zero
slowly enough that R3 approaches a constant value (thereby preventing in-
formation saturation). Daher, going to larger kw ensures that the majority of
the eigenvectors of (cid:4) do not become orthogonal to f(cid:6)
quickly enough for
information saturation to occur.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1270
P. Sachdeva, J. Livezey, and M. DeWeese
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
Figur 10: Characterizing the scaling of the eigenvalues and the shrinking of
the cosine-angles for the nonlinear stage covariance. (A) Behavior of the largest
3 for the cases of kw = 1, 2, 3. The aspect ratio is
three eigenvalues σ 2
chosen so that unit steps on each axis appear of equal length. (B) The behavior
of cosine-angle sum Ri corresponding to the constant-growth eigenvalues, für
each of kw = 1, 2, 3. The inset depicts the same curves, but on a log-log scale.
2 , and σ 2
1 , σ 2
In the case of kw ∼ O(N), Jedoch, the behavior of the covariance matrix
is different. Recall that the covariance matrix takes on the form
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
(cid:4) = 2σ 4
P I + 4σ 2
P s2diag(V) + 4σ 2
P
Cdiag(W) + 4s2σ 2
σ 2
C XXT + 2σ 4
CWWT .
(A.56)
The dominant contribution to the covariance matrix is 2σ 4
scaling of the trace of (cid:4) Ist
C WWT . Daher, Die
Heterogeneous Synaptic Weighting under Common Noise
1271
Tr[(cid:4)] ∼ Tr[WWT ] = Tr[(w (cid:12) w)(w (cid:12) w)T ].
= (w (cid:12) w)T (w (cid:12) w)
N(cid:17)
(cid:14)
(cid:13)
i2
∼
i=1
2 ∼ O(N5).
(A.57)
(A.58)
(A.59)
Since the trace of the covariance matrix is equal to the sum of the eigen-
Werte, some subset of the eigenvalues can scale as O(N5) sowie. Tatsächlich,
all eigenvalues scale at least as O(N), with the largest eigenvalue scaling as
Ö(N5). In this scenario, the Fisher information must saturate because the
cosine-angle can at most scale to a constant. In plainer terms, the variances
of the covariance matrix scale so quickly that the differential correlation
direction is irrelevant. We interpret this behavior as the neurons simply ex-
hibiting too much variance for any meaningful decoding to occur. Notiz,
Jedoch, that the saturation can be avoided if the behavior of f(cid:6)
, which we
assumed scales as O(N), instead scales more quickly. This can occur, für
Beispiel, when kv ∼ O(N). Jedoch, it is unreasonable to expect that the
synaptic weights of a neural circuit scale with the population size, Herstellung
this scenario biologically implausible.
A.3 Linear Fisher Information under an Exponential Nonlinearity.
The application of an exponential nonlinearity to the output of the linear
stage gi((cid:3)
ich) implies that the output of the network r = g((cid:3)) follows
a multivariate log-normal distribution (since the linear stage is gaussian).
The linear stage is described by the distribution
ich) = exp((cid:3)
(cid:3) ∼ N (M, (cid:4)L),
μ = vs,
(cid:4)L = σ 2
P I + σ 2
C wwT .
(A.60)
(A.61)
(A.62)
The multivariate log-normal distribution has first- and second-order statis-
tics given by
(cid:23)
E [R]ich
= exp
M
ich
(cid:24)
(cid:9)L
ii
,
+ 1
2
(cid:23)
(cid:16)
(cid:15)
ri j
Var
= exp
M
ich
+ M
J
+ 1
2
(cid:25)
(cid:26)(cid:24) (cid:25)
(cid:26)
(cid:9)L
ii
+ (cid:9)L
j j
exp((cid:9)L
i j ) − 1
.
(A.64)
(A.63)
Daher, the mean activity and its derivative with respect to s are given by
fi(S) = exp
(cid:23)
1
2
+ v
σ 2
P
Ist + 1
2
(cid:24)
σ 2
C
w2
ich
,
(A.65)
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1272
P. Sachdeva, J. Livezey, and M. DeWeese
Figur 11: The behavior of linear Fisher information for an exponential non-
linearity as a function of population size. Colors denote different choices of kw.
Inset shows the same plot but on a regular scale.
(cid:6)
ich (S) = v
F
i exp
(cid:23)
1
2
+ v
σ 2
P
Ist + 1
2
(cid:24)
σ 2
C
w2
ich
.
(A.66)
These equations provide us the tools to calculate the linear Fisher infor-
mation. The inversion of the covariance matrix (see equation A.64) is not
tractable, but we can proceed numerically.
We calculated the linear Fisher information numerically under the same
conditions as in Figure 4a, but with kw = 1, . . . , 5 and for a wider range
of population sizes. In Abbildung 11, we plot the linear Fisher information as
a function of N for these choices of kw. We observe that for large enough
N, synaptic weight heterogeneity results in improved coding performance.
Jedoch, we also observe what appears to be saturation of the Fisher infor-
mation. Since we cannot write the Fisher information as a function of N, Wir
cannot validate this observation analytically. This does, Jedoch, vorschlagen
that the choice of nonlinearity can have a dramatic impact on the behavior
of the linear Fisher information.
Danksagungen
We thank Ruben Coen-Cagli for useful discussions. P.S.S. was supported
by the Department of Defense through the National Defense Science and
Engineering Graduate Fellowship Program. J.A.L. was supported through
the Lawrence Berkeley National Laboratory-internal LDRD “Deep Learn-
ing for Science” led by Prabhat. M.R.D. was supported in part by the U.S.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1273
Army Research Laboratory and the U.S. Army Research Office under Con-
tract No. W911NF-13-1-0390.
Verweise
Abbott, L. F., & Dayan, P. (1999). The effect of correlated variability on the accuracy
of a population code. Neural Computation, 11(1), 91–101.
Adelson, E. H., & Bergen, J. R. (1985). Spatiotemporal energy models for the
perception of motion. Journal of the Optical Society of America A, 2(2), 284–
299.
Arandia-Romero, ICH., Tanabe, S., Drugowitsch, J., Kohn, A., & Moreno-Bote, R. (2016).
Multiplicative and additive modulation of neuronal tuning with population ac-
tivity affects encoded information. Neuron, 89(6), 1305–1316.
Arieli, A., Sterkin, A., Grinvald, A., & Aertsen, A. (1996). Dynamics of ongoing ac-
tivity: Explanation of the large variability in evoked cortical responses. Wissenschaft,
273(5283), 1868–1871.
Attneave, F. (1954). Some informational aspects of visual perception. Psychological
Rezension, 61(3), 183.
Averbeck, B. B., Latham, P. E., & Pouget, A. (2006). Neural correlations, Bevölkerung
coding and computation. Nature Reviews Neurowissenschaften, 7(5), 358.
Averbeck, B. B., & Lee, D. (2006). Effects of noise correlations on information encod-
ing and decoding. Journal of Neurophysiology, 95(6), 3633–3644.
Bar-Gad, ICH., Morris, G., & Bergman, H. (2003). Information processing, dimensional-
ity reduction and reinforcement learning in the basal ganglia. Progress in Neuro-
biology, 71(6), 439–473.
Barlow, H. B. (1961). Possible principles underlying the transformation of sensory
messages. Sensory Communication, 1, 217–234.
Beck, J., Bejjanki, V. R., & Pouget, A. (2011). Insights from a simple expression for lin-
ear Fisher information in a recurrently connected population of spiking neurons.
Neural Computation, 23(6), 1484–1502.
Beck, J. M., Ma, W. J., Pitkow, X., Latham, P. E., & Pouget, A. (2012). Not noisy, just
wrong: The role of suboptimal inference in behavioral variability. Neuron, 74(1),
30–39.
Glocke, A. J., & Sejnowski, T. J. (1997). The “independent components” of natural scenes
are edge filters. Sehforschung, 37(23), 3327–3338.
Brinkman, B. A., Weber, A. ICH., Rieke, F., & Shea-Brown, E. (2016). How do efficient
coding strategies depend on origins of noise in neural circuits? PLOS Computa-
tional Biology, 12(10), e1005150.
Brunel, N., & Nadal, J.-P. (1998). Mutual information, Fisher information, and pop-
ulation coding. Neural Computation, 10(7), 1731–1757.
Cafaro, J., & Rieke, F. (2010). Noise correlations improve response fidelity and stim-
ulus encoding. Natur, 468(7326), 964.
Cohen, M. R., & Kohn, A. (2011). Measuring and interpreting neuronal correlations.
Naturneurowissenschaften, 14(7), 811.
Cohen, M. R., & Maunsell, J. H. (2009). Attention improves performance primarily
by reducing interneuronal correlations. Naturneurowissenschaften, 12(12), 1594.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
N
e
C
Ö
_
A
_
0
1
2
8
7
P
D
.
/
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
1274
P. Sachdeva, J. Livezey, and M. DeWeese
Cover, T. M., & Thomas, J. A. (2012). Elements of information theory. Hoboken, NJ:
Wiley.
Davenport, M. A., Duarte, M. F., Eldar, Y. C., & Kutyniok, G. (2012). Introduction to
compressed sensing. In Y. Eldar& G. Kutyniok (Hrsg.), Compressed sensing: Theory
and applications (S. 1–64). Cambridge: Cambridge University Press.
Deweese, M. R., & Zador, A. M. (2004). Shared and private variability in the auditory
Kortex. Journal of Neurophysiology, 92(3), 1840–1855.
Ecker, A. S., Berens, P., Tolias, A. S., & Bethge, M. (2011). The effect of noise corre-
lations in populations of diversely tuned neurons. Zeitschrift für Neurowissenschaften, 31(40),
14272–14283.
Emerson, R. C., Korenberg, M. J., & Citron, M. C. (1992). Identification of complex-
cell intensive nonlinearities in a cascade model of cat visual cortex. Biological Cy-
Bernetik, 66(4), 291–300.
Faisal, A. A., Selen, L. P., & Wolpert, D. M. (2008). Noise in the nervous system. Natur
Reviews Neuroscience, 9(4), 292.
Franke, F., Fiscella, M., Sevelev, M., Roska, B., Hierlemann, A., & da Silveira, R. A.
(2016). Structures of neural correlation and how they favor coding. Neuron, 89(2),
409–422.
Gao, S., Ver Steeg, G., & Galstyan, A. (2015). Efficient estimation of mutual informa-
tion for strongly dependent variables. In Proceedings of the Eighteenth International
Conference onArtificial Intelligence and Statistics (S. 277–286).
Garfinkle, C. J., & <, C. J., (2019). On the uniqueness and stability of dictionaries
for sparse representation of noisy signals. IEEE Transactions on Signal Processing,
67(23), 5884–5892.
Goris, R. L., Movshon, J. A., & Simoncelli, E. P. (2014). Partitioning neuronal vari-
ability. Nature Neuroscience, 17(6), 858.
Hu, Y., Zylberberg, J., & Shea-Brown, E. (2014). The sign rule and beyond: Bound-
ary effects, flexibility, and noise correlations in neural population codes. PLOS
Computational Biology, 10(2), e1003469.
Iyer, R., Menon, V., Buice, M., Koch, C., & Mihalas, S. (2013). The influence of synap-
tic weight distribution on neuronal population dynamics. PLOS Computational
Biology, 9(10), e1003248.
Kafashan, M., Jaffe, A., Chettih, S. N., Nogueira, R., Arandia-Romero, I., Harvey, C.
D., Drugowitsch, J. (2020). Scaling of information in large neural populations reveals
signatures of information-limiting correlations. bioRxiv:2020.01.10.90217.
Kanerva, P. (2009). Hyperdimensional computing: An introduction to computing
in distributed representation with high-dimensional random vectors. Cognitive
Computation, 1(2), 139–159.
Kanitscheider, I., Coen-Cagli, R., & Pouget, A. (2015). Origin of information-limiting
noise correlations. Proceedings of the National Academy of Sciences, 112(50), E6973–
E6982.
Karklin, Y., & Simoncelli, E. P. (2011). Efficient coding of natural images with a pop-
ulation of noisy linear-nonlinear neurons. In J. Shawe-Taylor, R. S. Zemel, P. L.
Bartlett, F. Pereira, & K. Q. Weinberger (Eds.), Advances in neural information pro-
cessing systems, 24 (pp. 999–1007). Red Hook, NY: Curran.
Kay, S. M. (1993). Fundamentals of statistical signal processing. Upper Saddle River, NJ:
Prentice Hall.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
n
e
c
o
_
a
_
0
1
2
8
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Heterogeneous Synaptic Weighting under Common Noise
1275
Kohn, A., Coen-Cagli, R., Kanitscheider, I., & Pouget, A. (2016). Correlations and
neuronal population information. Annual Review of Neuroscience, 39, 237–256.
Kraskov, A., Stögbauer, H., & Grassberger, P. (2004). Estimating mutual information.
Physical Review E, 69(6), 066138.
Kulkarni, J. E., & Paninski, L. (2007). Common-input models for multiple neural
spike-train data. Network: Computation in Neural Systems, 18(4), 375–407.
Lin, I.-C., Okun, M., Carandini, M., & Harris, K. D. (2015). The nature of shared cor-
tical variability. Neuron, 87(3), 644–656.
Litwin-Kumar, A., Harris, K. D., Axel, R., Sompolinsky, H., & Abbott, L. (2017). Op-
timal degrees of synaptic connectivity. Neuron, 93(5), 1153–1164.
Ma, W. J., Beck, J. M., Latham, P. E., & Pouget, A. (2006). Bayesian inference with
probabilistic population codes. Nature Neuroscience, 9(11), 1432.
Montijn, J. S., Liu, R. G., Aschner, A., Kohn, A., Latham, P. E., & Pouget, A. (2019).
Strong information-limiting correlations in early visual areas. bioRxiv:842724.
Montijn, J. S., Meijer, G. T., Lansink, C. S., & Pennartz, C. M. (2016). Population-level
neural codes are robust to single-neuron variability from a multidimensional cod-
ing perspective. Cell Reports, 16(9), 2486–2498.
Moreno-Bote, R., Beck, J., Kanitscheider, I., Pitkow, X., Latham, P., & Pouget, A.
(2014). Information-limiting correlations. Nature Neuroscience, 17(10), 1410.
Nogueira, R., Peltier, N. E., Anzai, A., DeAngelis, G. C., Martínez-Trujillo, J., &
Moreno-Bote, R. (2020). The effects of population tuning and trial-by-trial vari-
ability on information encoding and behavior. Journal of Neuroscience, 40(5), 1066–
1083.
Pagan, M., Simoncelli, E. P., & Rust, N. C. (2016). Neural quadratic discriminant anal-
ysis: Nonlinear decoding with V1-like computation. Neural Computation, 28(11),
2291–2319.
Paninski, L. (2004). Maximum likelihood estimation of cascade point-process neural
encoding models. Network: Computation in Neural Systems, 15(4), 243–262.
Pillow, J. W., Paninski, L., Uzzell, V. J., Simoncelli, E. P., & Chichilnisky, E. (2005).
Prediction and decoding of retinal ganglion cell responses with a probabilistic
spiking model. Journal of Neuroscience, 25(47), 11003–11013.
Renart, A., De La Rocha, J., Bartho, P., Hollender, L., Parga, N., Reyes, A., & Harris, K.
D. (2010). The asynchronous state in cortical circuits. Science, 327(5965), 587–590.
Rieke, F., Warland, D., de Ruyter van Steveninck, R., & Bialek, W. S. (1999). Spikes:
Exploring the neural code. Cambridge, MA: MIT Press.
Sakai, K., & Tanaka, S. (2000). Spatial pooling in the second-order spatial structure
of cortical complex cells. Vision Research, 40(7), 855–871.
Sargent, P. B., Saviane, C., Nielsen, T. A., DiGregorio, D. A., & Silver, R. A. (2005).
Rapid vesicular release, quantal variability, and spillover contribute to the pre-
cision and reliability of transmission at a glomerular synapse. Journal of Neuro-
science, 25(36), 8173–8187.
Seger, C. A. (2008). How do the basal ganglia contribute to categorization? Their roles
in generalization, response selection, and learning via feedback. Neuroscience and
Biobehavioral Reviews, 32(2), 265–278.
Shadlen, M. N., & Newsome, W. T. (1998). The variable discharge of cortical neu-
rons: Implications for connectivity, computation, and information coding. Journal
of Neuroscience, 18(10), 3870–3896.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
n
e
c
o
_
a
_
0
1
2
8
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1276
P. Sachdeva, J. Livezey, and M. DeWeese
Shamir, M., & Sompolinsky, H. (2006). Implications of neuronal diversity on popu-
lation coding. Neural Computation, 18(8), 1951–1986.
Sherman, J., & Morrison, W. J. (1950). Adjustment of an inverse matrix corresponding
to a change in one element of a given matrix. Annals of Mathematical Statistics,
21(1), 124–127.
Sompolinsky, H., Yoon, H., Kang, K., & Shamir, M. (2001). Population coding in neu-
ronal systems with correlated noise. Physical Review E, 64(5), 051904.
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., & Chklovskii, D. B. (2005). Highly non-
random features of synaptic connectivity in local cortical circuits. PLOS Biology,
3(3), e68.
Vidne, M., Ahmadian, Y., Shlens, J., Pillow, J. W., Kulkarni, J., Litke, A. M., Paninski,
L. (2012). Modeling the impact of common noise inputs on the network activity
of retinal ganglion cells. Journal of Computational Neuroscience, 33(1), 97–121.
Wei, X.-X., & Stocker, A. A. (2016). Mutual information, Fisher information, and ef-
ficient coding. Neural Computation, 28(2), 305–326.
Wilke, S. D., & Eurich, C. W. (2002). Representational accuracy of stochastic neural
populations. Neural Computation, 14(1), 155–189.
Wu, S., Nakahara, H., & Amari, S.-I. (2001). Population coding with correlation and
an unfaithful model. Neural Computation, 13(4), 775–797.
Yarrow, S., Challis, E., & Seriès, P. (2012). Fisher and Shannon information in finite
neural populations. Neural Computation, 24(7), 1740–1780.
Yoon, H., & Sompolinsky, H. (1999). The effect of correlations on the Fisher informa-
tion of population codes. In M. J. Kearns, S. A. Solla, & D. A. Cohn (Eds.), Ad-
vances in neural information processing systems, 11 (pp. 167–173). Cambridge, MA:
MIT Press.
Zohary, E., Shadlen, M. N., & Newsome, W. T. (1994). Correlated neuronal discharge
rate and its implications for psychophysical performance. Nature, 370(6485), 140.
Zylberberg, J., Cafaro, J., Turner, M. H., Shea-Brown, E., & Rieke, F. (2016). Direction-
selective circuits shape noise to ensure a precise population code. Neuron, 89(2),
369–383.
Zylberberg, J., Pouget, A., Latham, P. E., & Shea-Brown, E. (2017). Robust informa-
tion propagation through noisy neural circuits. PLOS Computational Biology, 13(4),
e1005497.
Received September 25, 2019; accepted February 24, 2020.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
7
1
2
3
9
1
8
6
4
9
4
1
n
e
c
o
_
a
_
0
1
2
8
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3