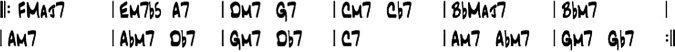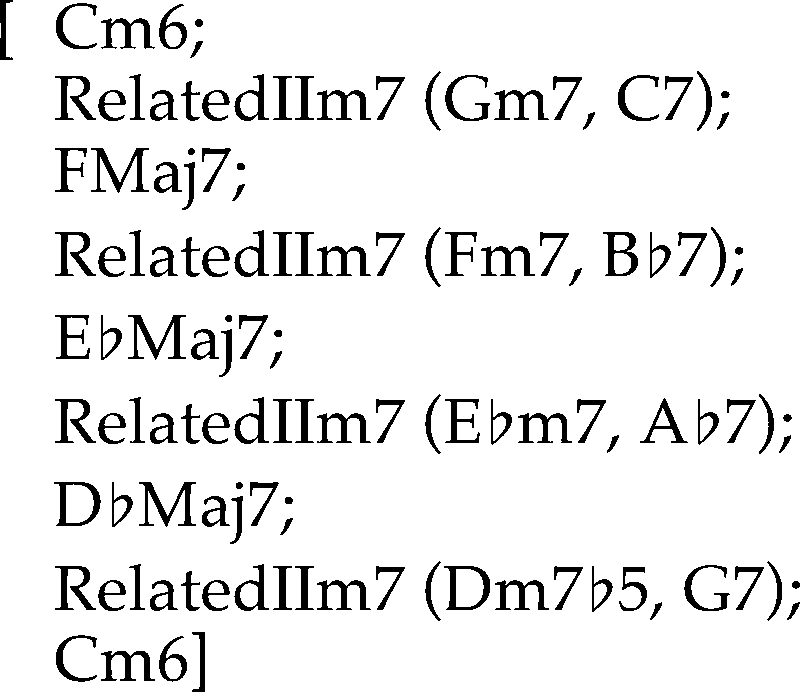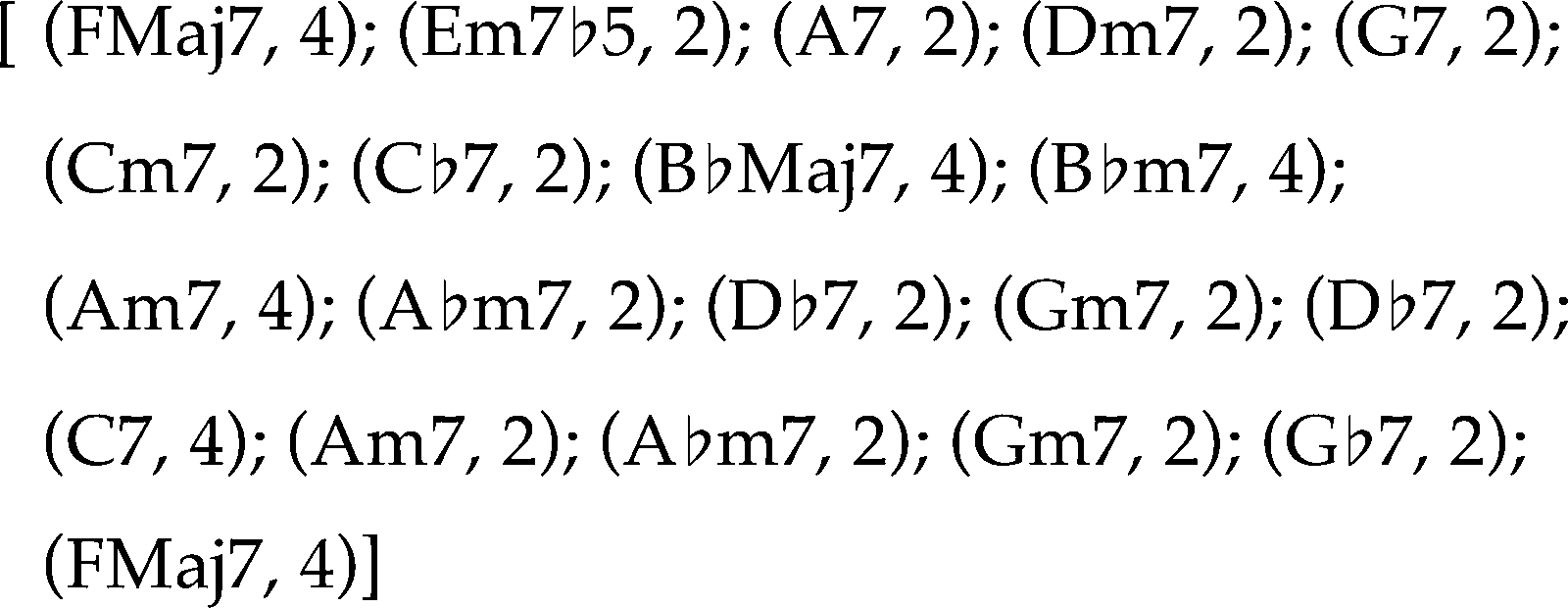Andrew Choi
131 Shawnee Place Southwest
Calgary, Alberta, Canada T2Y 1X1
andrew@sixthhappiness.ca
Jazz Harmonic Analysis
as Optimal Tonality
Segmentation
When asked to improvise over the chord changes
of a tune, jazz musicians, either by an intuitive
or formal process, perform an analysis to obtain a
harmonic road map that guides them through the
possibilities of what notes and scales to play. Der
purpose of this harmonic analysis is to discover
and understand underlying structures in the chord
changes. A notation often used in jazz theory texts
(z.B., Nettles and Graf 1997; Jaffe 2009) to represent
this harmonic structure identifies a segmentation
of the chord changes, the key center (or tonality) von
each segment, and the harmonic function of each
chord with respect to its key center and other chords.
Performing such an analysis is a fundamental step
if jazz improvisation is to be simulated by software.
It is also an interesting and important problem to
be considered on its own for the implementation
of jazz compositional and teaching tools. Das
article presents a formulation of and an algorithm
for the harmonic analysis of jazz chord sequences.
Some familiarity with jazz harmony or traditional
harmony is assumed.
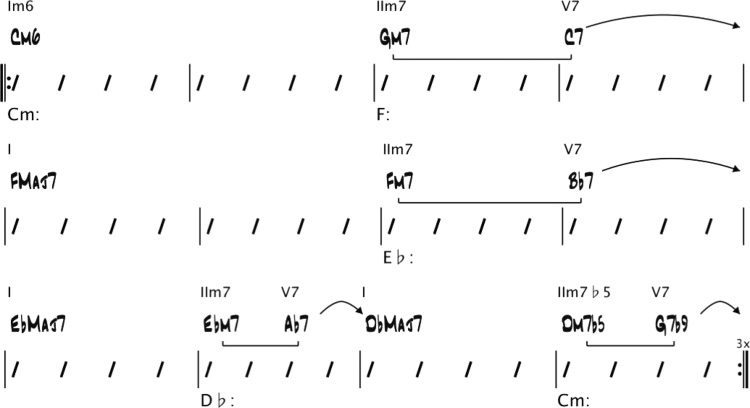
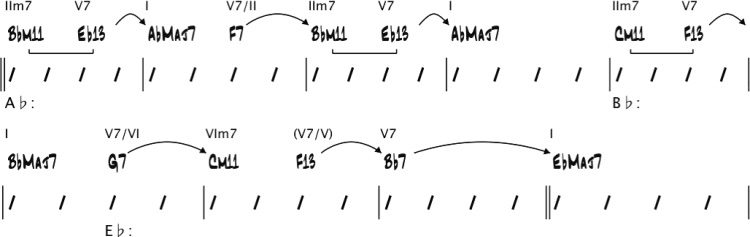
Here is an example of the intended kind of
Analyse. Consider the chord changes for Miles
Davis’s Solar in Figure 1.
These chord changes will be the input given to
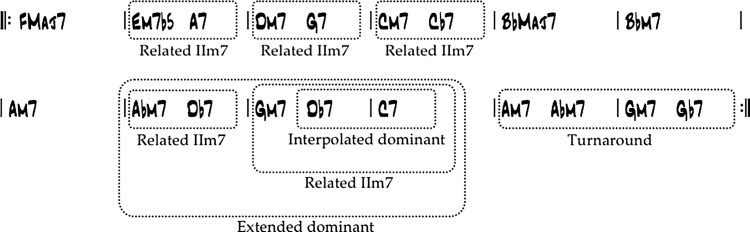
the harmonic analysis algorithm. The output of the
algorithm is an annotated chord chart, as shown in
Figur 2.
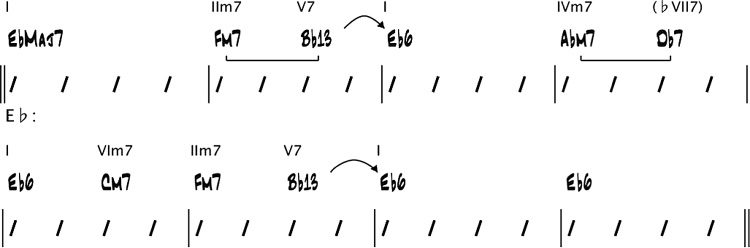
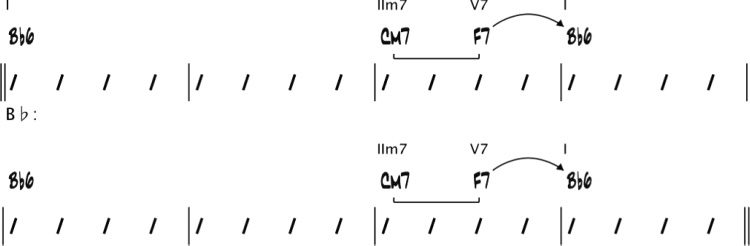
Key centers are shown below the bars: Der Schlüssel
center of bars 1 Und 2 is C minor, that of bars 3–6
is F major, that of bars 7–9 is E(cid:2) major, und so weiter.
Arrows and brackets represent dominant resolutions
and related minor seventh chords (d.h., the related
IIm7s), jeweils (Nettles and Graf 1997). (Diese
will be explained further in the section “Structural
Analysis.”) Roman numeral chord symbols above
the chords indicate their harmonic functions with
respect to their key centers. Zum Beispiel, the Dm7(cid:2)5
and G7(cid:2)9 chords in bar 12 function as IIm7(cid:2)5 and V7
chords, jeweils, resolving to the root of the key
Computermusikjournal, 35:2, S. 49–66, 2011
C(cid:2) 2011 Massachusetts Institute of Technology.
center C minor. Once this analysis is performed, Die
information it provides can be used by a musician
to determine what notes to play over the chord
changes. This is the subject of numerous jazz theory
texts and method books (z.B., Levine 1995; Pass
1996).
This representation of the result of harmonic
analysis has sound theoretical basis and is well
understood by jazz musicians. It facilitates direct
comparison to analyses performed manually, Und
allows analysis algorithms to be evaluated objec-
tively and compared with one another, since corpora
of analyses of jazz standards are available in the
Literatur (Mehegan 1959, 1962, 1964, 1965; Coker
1987).
The main innovation of the harmonic analysis
algorithm presented in this article results from
the observation that chord functions and harmonic
structures (such as dominant resolutions and re-
lated IIm7s) are completely determined by a given
segmentation and choice of key centers. Harmonic
analysis can therefore be formulated and solved
algorithmically as a tonality segmentation problem.
This formulation and a solution for it in the form of
a dynamic programming algorithm are the subject
of this article.
Related Work
Previous studies related to the subject of this
article can be categorized into the following areas:
grammar-based and rule-based harmonic analysis
of jazz chord sequences, harmonic analysis of tonal
Musik, jazz improvisation systems, and jazz theory.
Grammar-Based and Rule-Based Harmonic
Analysis of Jazz Chord Sequences
Formal grammar has been used in the study of jazz
chord sequences for some time. Steedman (1984)
proposes a context-sensitive grammar as a generative
Choi
49
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1. Chord changes
for Solar.
Figur 2. A harmonic
analysis of Solar.
Figur 1.
Figur 2.
model of variations of twelve-bar blues changes by
chord substitution. The use of formal grammar for
harmonic analysis, Jedoch, is problematic because
no grammar that encompasses all possible chord
changes will likely be found. It is also unclear
how modulations can be described by grammar
rules because “there seem to be no constraints on
modulation: a theme can modulate to any new key”
(Johnson-Laird 2002, P. 429).
Pachet (1991) proposes a production rule system
for harmonic analysis of jazz chord sequences. A
rule-based system has the same weakness as a
grammar-based system in that it cannot derive a
suitable analysis when its set of rules does not
include those required to analyze a given tune. Für
Beispiel, the system is used to determine whether
the chord changes of Solar are in the form of a blues.
Lacking a rule for the general form of these changes,
it “produces an analysis which is not what a human
would do” (Pachet 2000). Mouton and Pachet (1995)
suggest that a symbolic, rule-based method can
benefit from a softer decision model by integrating
numerical techniques, but offer no concrete proposal
as to how this can be applied to harmonic analysis.
The algorithm presented in this article incorporates
symbolic knowledge in jazz theory and treats
tonality segmentation as an optimization problem,
and not one of “parsing” the chord sequences. Der
sample analysis of Solar generated by this algorithm
(siehe Abbildung 2) demonstrates that a chord sequence
can indeed be analyzed fully with such a technique.
daher, with respect to harmonic analysis in the
sense taught by jazz theory texts, it is unnecessary
to determine whether a tune such as Solar is a
blues, although it is crucial to find a good tonality
segmentation for it.
Scholz, Dantas, and Ramalho (2005) extend
Pachet’s method by additional processing on gaps:
segments of the chord sequence for which no
pattern rules apply. After patterns are identified,
gaps are merged with neighboring segments when
certain conditions are met. Both their and Pachet’s
50
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
methods determine tonality segmentation for a
chord sequence by the breaks among adjacent
patterns detected by their sets of rules. If tonality
segmentation is viewed as an optimization problem,
such methods represent greedy algorithms (Corman,
Leiserson, and Rivest 2009) in the sense that they
make locally optimal choices in hopes that these
will lead to globally optimal segmentations. Der
tonality segmentation algorithm in this article
explicitly models the conditions under which
modulations may occur and solves the optimization
problem directly, using dynamic programming. In
the formulation given herein, the quality of the
tonality segmentation completely determines that
of a harmonic analysis.
Harmonic Analysis of Tonal Music
Much work has also been done in harmonic analysis
of tonal music, where the objective is to determine
the harmonic structure in a sequence of musical
notes. Algorithms proposed for this type of analysis
make decisions based on numerical as well as
symbolic information. Numerical algorithms for
harmonic analysis typically introduce cost and
distance functions and formulate the analysis
problems as optimization problems. Daher, Die
algorithm of this article has more in common with
them than rule- and grammar-based algorithms
for chord sequences. Temperley and Sleator (1999)
propose an analysis algorithm based on well-
formedness rules and preference rules, adapted
from A Generative Theory of Tonal Music (Lerdahl
and Jackendoff 1983). The well-formedness rules
define a solution space while the preference rules
define a scoring system for the solutions. Ihre
harmonic analysis problem is then formulated as an
optimization problem—one of finding the shortest
path in a directed graph, which is solved using
dynamic programming.
Pardo and Birmingham (2002) extend Temperley
and Sleator’s method by also taking chord qualities
of segments into consideration. They present results
of experiments that evaluate the performance of
their algorithm and consider heuristic versions, als
well as an optimal version, of the search algorithm.
Illescas, Rizo, and I ˜nesta (2007) show how chord
functions and cadences can be incorporated into
preference rules. Stronger cadences are given higher
scores, causing analyses that contain them to be
bevorzugt. Their technique shows how relationships
among consecutive chords and their functions
can be reflected in the preference rules. Ihre
harmonic analysis problem is then also formulated
as a shortest path problem and solved by dynamic
programming.
Jazz Improvisation Systems
Numerous research papers and theses have been
written about computer-music systems that gen-
erate jazz improvisations in various forms (z.B.,
Ramalho, Rolland, Ganascia 1999; Klein 2005).
Jedoch, in these studies the problem of harmonic
analysis only receives limited attention, and tech-
niques are primarily borrowed from already-existing
efforts. Interactive music systems for jazz improvisa-
tion apply machine learning techniques to generate
improvisation from training data input by users
(Pachet 2003; Thom 2003). Without a harmonic
analysis component, these systems can only play
tunes on which they have been trained, and can only
apply or adapt learned lines. Keller and colleagues
(2006) design and implement a GUI learning tool
that allows its user to “compose an improvisation”
by choosing lines to play against each chord (oder
group of chords) in a chart from a library. It also
does not perform harmonic analysis and leaves the
decision of which scales to use to its users. All of
these systems will benefit from a more complete
solution for the problem of harmonic analysis of
chord sequences, such as the one presented in this
Artikel.
Jazz Theory
The notation for representing harmonic analysis
used in the introduction has been taught at least as
far back as the 1980s at the Berklee College of Music
(Nettles and Ulanowsky 1987) and elsewhere (Jaffe
1983). Not all jazz musicians and teachers agree on
Choi
51
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
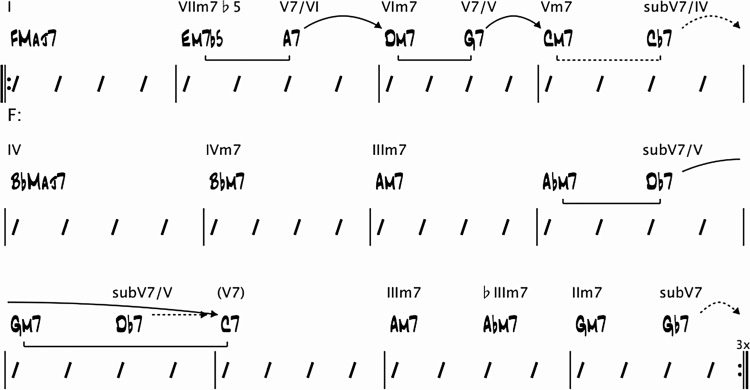
Figur 3. Dominant
resolution and deceptive
Auflösung.
the importance of formal harmonic analysis, Und
there is, Natürlich, an immense body of knowledge
on different approaches to jazz improvisation. Most
will agree, Jedoch, that the study of harmonic
analysis is necessary for understanding how and
why jazz harmony works. It is also essential for
computer simulation of jazz improvisation with
explainable and reproducible results.
Jazz theory texts generally describe elements
of harmonic analysis by example and define them
informally. Speziell, there is no concrete model
for modulations, nor is there a systematic procedure
for constructing an analysis from a given set of
chord changes. A contribution of this article is the
formalization of these concepts and descriptions
into a mathematical model that can be operated on
by computer.
Structural Analysis
The harmonic analysis algorithm operates in two
Schritte: a structural analysis step which converts
a chord sequence into a list of analysis elements
(defined subsequently) and a tonality segmentation
step which partitions this list into segments of
different key centers.
In this section the structural analysis algorithm
and the data representation for the resulting har-
monic structure are described. This description
begins with a review of the following elements
of jazz theory: dominant resolutions, harmonic
rhythm, substitute dominants, related IIm7s, ex-
tended dominants, turnarounds, and interpolated
dominants (Nettles and Graf 1997; Jaffe 2009).
Review of Jazz Harmony
the IMaj7 chord. (Four-note diatonic chords are
prevalent in jazz-related contexts, so in a major key
the I chord is usually IMaj7, and in a minor key
the Im chord is usually Im7 or ImMaj7. The I6 and
Im6 chords can also be used as the I and Im chords,
respectively.) Zum Beispiel, in F major, the primary
dominant is C7, which resolves to FMaj7. In a major
key, the secondary dominants are the VI7, VII7,
I7, II7, and III7 chords, which are also denoted by
V7/II, V7/III, V7/IV, V7/V, and V7/VI, jeweils.
They are expected to resolve to the diatonic chords
IIm7, IIIm7, IVMaj7, V7, and VIm7, jeweils. In F
major, the secondary dominants are D7 (resolves to
Gm7), E7 (resolves to Am7), F7 (resolves to B(cid:2)Maj7),
G7 (resolves to C7), and A7 (resolves to Dm7).
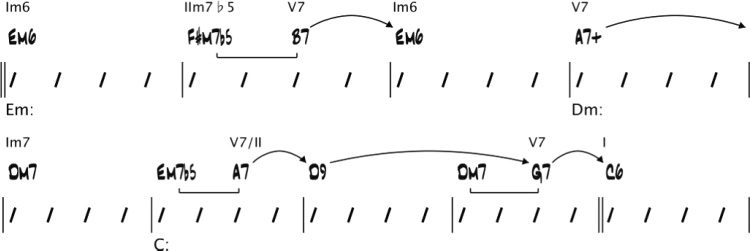
A primary or secondary dominant resolving to
the expected diatonic chord a perfect fifth below
creates a dominant resolution, which is annotated
in a harmonic analysis by a solid arrow (bars 2 Und 3
in Abbildung 3).
A dominant chord that does not resolve to the
expected diatonic chord often represents a deceptive
Auflösung. A deceptive resolution is not represented
by an arrow in a harmonic analysis, but by a
parenthesized roman numeral chord (bars 1 Und 4
in Abbildung 3). Note that deceptive resolutions are
difficult to represent and analyze using grammar
rules.
For simplicity, tunes to be analyzed are assumed
to be composed of sections whose lengths in bars
are multiples of four, with four beats to a bar. Der
metrical structure (Lerdahl and Jackendoff 1983)
of every four bars of a chord sequence is given by
the grid in Figure 4. The majority of jazz standards
satisfy this assumption. For tunes that do not, andere
means of deducing the metrical structure must be
gebraucht, which will not be covered here.
Stronger beats are ones with higher numbers. Har-
The primary dominant is the V7 chord of a given
key. In a major key it is expected to resolve to
monic rhythm is the pattern of accents created by
the chord changes. Certain harmonic elements are
52
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 4. Four-bar metrical
Struktur.
Figur 5. Substitute
dominant resolutions and
related IIm7s.
Figur 4.
Figur 5.
identified by interaction between harmonic rhythm
and metrical structure. A dominant resolution is
heard only when a dominant chord on a weaker beat
resolves to its target chord on a stronger beat. In
Figur 3, the dominant chords C7 and A7 occur on
weaker beats compared to the FMaj7 and B(cid:2)Maj7
chords into which they resolve.
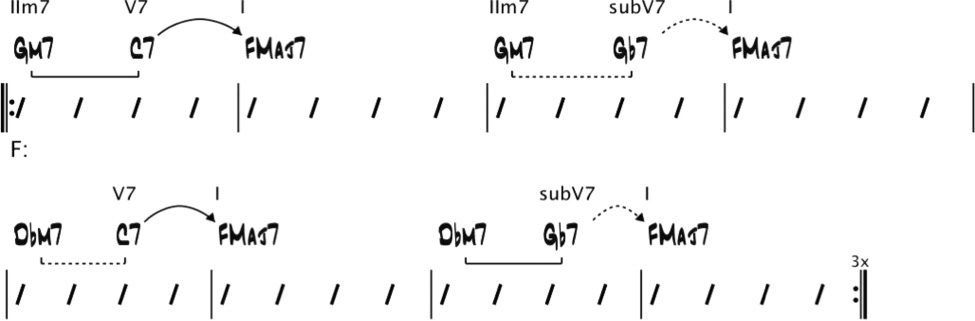
The tritone substitution for a dominant chord
is the dominant chord whose root is a (cid:3)IV interval
below (or equivalently, A (cid:2)V interval above) Die
first chord’s root. These substitute dominants can
be used in place of the corresponding primary
and secondary dominant chords. In a major key, Die
substitute dominants are the (cid:2)II7, (cid:2)III7, (cid:2)V7, Und (cid:2)VI7
chords, which are also denoted by subV7, subV7/II,
subV7/IV, and subV7/V, jeweils. The chords IV7
(subV7/III) Und (cid:2)VII7 (subV7/VI) will only function
as substitute dominants in rare situations (Nettles
and Graf 1997). Substitute dominant resolutions are
annotated in a harmonic analysis by dotted arrows
(G(cid:2)7 resolving to FMaj7 in Figure 5).
The related IIm7 of a dominant chord is the
minor seventh chord (or a minor seventh flatted
fifth chord for minor tonalities) whose root is a
perfect fourth below the dominant chord’s root.
Any dominant chord may be preceded by its related
IIm7, or its tritone substitution’s related IIm7. In
a harmonic analysis, this is annotated by a solid
bracket (or dotted bracket, jeweils) under the
two chords (siehe Abbildung 5). Harmonic rhythm must
also be taken into consideration in the detection of
related IIm7s: the related IIm7 and the dominant
chord must be on a stronger beat and a weaker beat,
jeweils. (This applies regardless of whether a
tritone substitution is used for the dominant chord
and whether the IIm7 chord is the related IIm7 of
the dominant chord or its tritone substitution.)
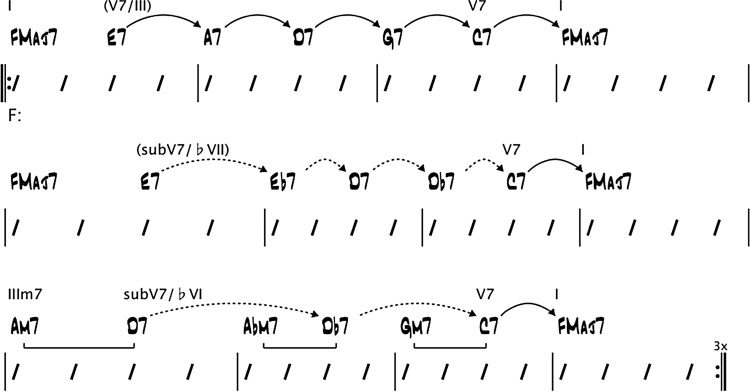
An extended dominant (also called sequential
dominant and substitute sequential dominant)
is a series of dominant chords each resolving
(deceptively) to the next one. It is represented by a
series of arrows in a harmonic analysis (bars 1–4 in
Choi
53
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 6. Examples of
extended dominants.
Figur 6). Only the first and last dominant chords are
labeled with roman numeral chords. An extended
dominant may also be composed of a combination
of dominant and substitute dominant resolutions
(bars 5–8 in Figure 6). It may also contain related
IIm7s (bars 9–12 in Figure 6).
A turnaround is an idiomatic progression of
(typically) four chords occurring at the end of a
section, replacing an extended duration of a tonic
chord. Many turnarounds cannot be analyzed by
the usual rules. Because their chord progressions
are so distinctive, Jedoch, the structural analysis
algorithm can recognize them by looking up an
internal library of turnarounds. An example of a
turnaround in F major is the two bars | Am7 A(cid:2)m7
| Gm7 G(cid:2)7 |. The library of turnarounds used in the
current implementation of the structural analysis
algorithm contains 13 turnarounds extracted from
the collections of tunes in Appendix D of Coker
(1987).
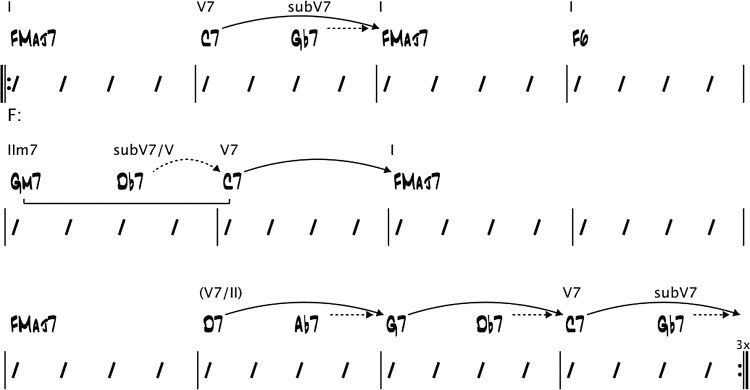
An interpolated dominant is a substitute domi-
nant chord that is inserted into a larger structure. Es
always resolves to the chord that follows it, whose
root is a (cid:2)II interval below its own root. That target
chord must be part of a larger structure. It may be
the target of a dominant resolution (the FMaj7 chord
in bar 3 in Abbildung 7). The interpolated dominant is
depicted with a straight dotted arrow connecting
it to its target. It may be the dominant chord of
a related IIm7-dominant chord pair (the C7 chord
in bar 6 in Abbildung 7). Or, it may be the second or
subsequent dominant chord in, or the final target
von, an extended dominant (the chords G7, C7, Und
FMaj7 in bars 11, 12, Und 1 in Abbildung 7).
Structural Analysis Algorithm
The structural analysis algorithm and the data
structure it generates are now described. Consider
the variation of the blues progression in Figure 8.
Figur 9 shows its harmonic analysis. Beachten Sie, dass
the entire chord sequence is composed of a single
segment with a F major key center.
The structural information that needs to be
extracted from the chord sequence to generate the
harmonic analysis above is represented by boxes in
Figur 10.
Each chord, turnaround, interpolated dominant,
related IIm7, or extended dominant is represented by
an analysis element (AE). (AEs are representations
of basic elements of jazz theory used in harmonic
Analyse; contrast them with “analysis objects” in
Pachet [2000] which represent such elements as
well as high-level concepts such as “shapes” and
song forms.) The output of the structural analysis
algorithm is simply a list of AEs, das ist, an AE
list. Each chord is represented by a chord AE. A
54
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 7. Examples of
interpolated dominants.
Figur 8. A blues
progression.
Figur 7.
Figur 8.
turnaround AE contains an AE list, the elements of
which are chord AEs. An interpolated dominant AE
contains AEs for the substitute dominant chord and
its target chord. A related IIm7 AE contains AEs for
the IIm7 chord and the “V7”; the latter may be the
dominant chord to which the IIm7 chord is related
or that dominant chord’s tritone substitution, oder
an interpolated dominant whose target chord is a
suitable dominant chord. An extended dominant
AE contains an AE list; each of its elements may
be a chord AE that represents a dominant chord, ein
interpolated dominant AE, or a related IIm7 AE.
Note that dominant resolutions, substitute
dominant resolutions, and deceptive resolutions
are not represented explicitly in the data structure.
AEs that represent dominant chords, related IIm7s,
extended dominants, and turnarounds ending in
dominant chords resolve (normally or deceptively)
to the AEs that follow them. Zum Beispiel, Die
AEs corresponding to bars 2 (Em7(cid:2)5 A7), 3 (Dm7
G7), Und 8 (A(cid:2)m7 D(cid:2)7) in Abbildung 9 all function as
dominants that resolve to the AEs that follow them,
jeweils. The AE corresponding to bar 4 (Cm7
C(cid:2)7) is a substitute dominant that resolves to the
B(cid:2)Maj7 chord in bar 5. The related IIm7 (welche
contains an interpolated dominant) in bars 9 Und 10
(Gm7 D(cid:2)7 C7) resolves deceptively to Am7, the first
chord of the turnaround in bars 11 Und 12.
Here is the structural analysis algorithm.
Input: an AE list of input chords.
Output: an AE list representing the result of the
Analyse.
1.
Scan the input AE list for turnarounds;
for each one found, replace the chord AEs in it
with a turnaround AE.
2.
Scan the AE list for related IIm7s (*); für
each one found, replace the two AEs forming
the related IIm7 with a related IIm7 AE.
3.
(*); for each one found, replace the AEs in it
with an extended dominant AE.
Scan the AE list for extended dominants
Choi
55
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 9. A harmonic
analysis of the blues
progression.
Figur 10. Structural
information in the blues
progression.
Figur 9.
Figur 10.
Scan the AE list for interpolated domi-
4.
nants at its top level; for each one found, replace
the two AEs in it with an interpolated dominant
AE.
identified when they are part of a larger structure.
Clearly the running time of the structure analysis
algorithm is a linear function of the number of input
chords.
(*) When looking for a dominant chord in
step 2 Und 3, take into account that it may be
preceded by an interpolated dominant chord
and construct an interpolated.
The four passes of the algorithm detect
turnarounds, related IIm7s, extended dominants,
and top-level interpolated dominants, jeweils.
Note that the algorithm cannot scan for interpolated
dominants all in one step because they can only be
Note also that the structural analysis algorithm
does not detect dominant chords in blues pro-
gressions and special situations where they do
not create a dominant or deceptive resolution.
These will be handled by the tonality segmentation
Algorithmus.
The input to the structural analysis algorithm is
a list of chord AEs constructed from the input chord
sequence. The duration of each chord, measured in
beats, is also stored in the chord AE. The following
56
Computermusikjournal
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
list represents the chord sequence of the sample
blues progression.
From this representation the starting beat of each
chord can be deduced, which enables us to check
harmonic rhythm requirements when locating
related IIm7s. Here is the output generated for this
input by the structural analysis algorithm.
“Am7 A(cid:2)m7 Gm7 G(cid:2)7” in the chord sequence.
The presence of the turnaround “Am7 A(cid:2)m7 Gm7
G(cid:2)7” also implies that the current key center
is either F major or F minor. This information
will be used to define the cost of a turnaround
in the subsequent “Cost Function for Segments”
section.
Because of this, the structural analysis algorithm
here can also be applied as it is to chord sequences
containing tonality changes. The output generated
by the structural analysis algorithm for the tune
Solar, Zum Beispiel, whose analysis is given in Figure
2, is as follows.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Chord AEs are listed by just the names of the
chords. In actual implementation each chord’s
starting beat and duration are stored with the
chord to make it easy to check harmonic rhythm
requirements for dominant resolutions and generate
the harmonic analysis output.
An important observation is that the structural
analysis algorithm does not require prior knowledge
of the key center to work. Interpolated dominants,
related IIm7s, and extended dominants can be
identified without knowing the underlying tonality.
Also in practice, chord progressions in turnarounds
are so distinctive that they can be identified by
deducing the key centers from the matched chords.
For example the turnaround library contains the
pattern “IIIm7 (cid:2)IIIm7 IIm7 (cid:2)II7”, which will match
The key centers are needed to generate the roman
numeral chords in the analysis output. Jedoch,
this operation is only performed when the tonality
segmentation algorithm is complete, at which time
the key centers are known.
Tonality Segmentation
Conceptually, the tonality segmentation algorithm
is quite simple. It divides the AE list generated by
the structural analysis algorithm into segments and
assigns a key center to each segment. Its goal is to
divide the AE list at positions where modulations
occur in the represented chord sequence, und zu
assign key centers to the segments that “best
explain” each chord’s harmonic function with
respect to the key center of its segment (to be
quantified by a cost function below). Diese beiden
aspects of the algorithm will be discussed in
“Validity Conditions for Segments” and “Cost
Function for Segments,” respectively. Erste, the use
of dynamic programming for tonality segmentation
is described.
Choi
57
A Dynamic Programming Algorithm for
Tonality Segmentation
Let a0, a1, . . . , an−1 be the AE list output of the
structural analysis algorithm. Each ai, 0 ≤ i < n, is a
top-level AE on the AE list. For example, for the AE
list for Solar, n = 9, a0 is the chord AE for Cm6, a1 is
the related IIm7 AE for Gm7 and C7, a2 is the chord
AE for FMaj7, and so on.
A segmentation of the AE list into m segments is
represented by indexes p0, p1, . . . , pm such that 0 =
p0 < p1 < · · · < pm = n. The i-th segment contains
the AEs api , api +1, . . . , api+1−1, for 0 ≤ i < m. The
objective of the algorithm is to find a segmentation
with minimal cost, where the cost of a segmentation
is defined as follows. Let dk
i, j be the cost (described
later) of assigning the key center k to the segment
ai, ai+1, . . . , aj, where 0 ≤ i ≤ j < n, k ∈ K, and K is
the set of all possible major and minor keys. Let d∗
i, j
be the minimal cost of dk
i, j among all keys, i.e.,
d∗
i, j for 0 ≤ i ≤ j < n can be determined in n2 |K|
operations. Because |K| is constant (24, if 12 major
keys and 12 minor keys are considered), this step
takes O(n2) time. The values of ci for 0 ≤ i < n can
also be computed in O(n2) time in the order of
increasing index i. A standard technique in dynamic
programming is used to record the index j that
results in the minimal cost in each step so that the
minimal segmentation can be recovered after cn−1
has been computed.
This formulation of tonality segmentation makes
the assumptions that changes in tonality do not
occur within the AEs and that the tonality of each
segment is independent of those of past and future
segments. In practice these assumptions do not
hinder the discovery of the “correct” segmentation.
The structural analysis algorithm can thus be viewed
as a normalization step performed on the input
chord sequences so that the tonality segmentation
algorithm can process them more easily.
d∗
i, j
= min
k∈K
dk
i, j
Then the cost of the segmentation p0, p1, . . . , pm
is given by
M(m− 1) +
(cid:2)m−1
i=0
d∗
pi , pi+1−1
where M is a constant that represents the cost
of a modulation. The choice of its value will be
discussed subsequently.
A minimal-cost segmentation can be found using
dynamic programming. Let ci be the minimal cost
for segmenting a0, a1, . . . , ai, for 0 ≤ i < n. Then,
(cid:3)
ci =
d∗
0,0
min
(cid:4)
d∗
0,i, mini
j=1
(cid:4)
cj−1 + d∗
j,i
(cid:5)(cid:5)
+ M
if i = 0
if i > 0
Cost Function for Segments
To complete the description of the tonality seg-
mentation algorithm, dk
ich, J, the cost for choosing k
as the key center for the segment ai, ai+1, . . . , aj
needs to be defined. Zum Beispiel, one would expect
d“F major”
to have a small value for the AE list in the
1,2
given example, because the segment a1, a2 (Gm7 C7,
FMaj7) corresponds to the most common cadence in
F major. Let
(cid:3)
dk
ich, J
=
ich, j is true
tk
if sk
ich, J
∞ otherwise
Das ist, apart from the initial condition, the minimal
cost of analyzing the first i AEs is given by either
the cost of analyzing all of them in one key center,
or the minimum of the sum of the minimal cost
of analyzing the first j AEs, that of analyzing
the remaining i − j AEs in one key center, Und
the cost of a modulation, over all possible values
of j—whichever is smaller. Given the values of
ich, J, für 0 ≤ i ≤ j < n and k ∈ K, the values of
dk
for all 0 ≤ i ≤ j < n and k ∈ K. The quantities sk
i, j
and tk
i, j play the roles that well-formedness rules and
preference rules do in Temperley and Sleator (1999),
respectively. That is, sk
i, j defines a space of all valid
solutions, and tk
i, j assigns costs to these solutions
to reflect their respective quality; the optimization
problem is then one of finding a valid solution with
minimal cost. The cost measure tk
i, j is defined to
be the sum of costs associated with the harmonic
58
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
Table 1. Chord Categories and Costs
Category
Major Key Chords
Minor Key Chords
Cost
Root
Diatonic excluding root
and primary dominant
Primary dominant
Substitute primary dominant
Secondary dominant
Substitute secondary dominant
Blues
Modal interchange
Diminished
Unknown
Im7
IMaj7
IIm7, (cid:2)IIIMaj7, IVm7,
IIm7, IIIm7, IVMaj7,
Vm7, (cid:2)VIMaj7, (cid:2)VII7
VIm7, VIIm7(cid:2)5
–5
–4
V7
V7
(cid:2)II7
(cid:2)II7
–3
VI7, (cid:2)VII7, I7, II7, (cid:2)III7, IV7 –2
VI7, VII7, I7, II7, III7
(cid:2)II7, II7, (cid:2)V7, (cid:2)VI7, VII7
(cid:2)III7, (cid:2)V7, (cid:2)VI7, IV7, (cid:2)VII7
–1
0
IV7
—
Im7, IIm7(cid:2)5, (cid:2)IIIMaj7, IVm7, Vm7, (cid:2)VIMaj7, (cid:2)VII7 —
0
0
Any diminished chord
∞
Chords not listed above
Any diminished chord
Chords not listed above
–6
functions of each of the AEs ai, ai+1, . . . , aj with
respect to the key center k according to Table 1.
For example, a1 in the given example, a related
IIm7 with chords Gm7 and C7, functions as a
primary dominant in F major (as explained subse-
quently), and contributes a cost of –4 to segments
that contain it. The cost assigned to each category
indicates how much the presence of an AE in that
category supports the choice of the key center. That
is, the presence of a root is better evidence in support
of the key center than a “diatonic” chord (as defined
in Table 1, which excludes the root and the primary
dominant), which is in turn better evidence than
a primary dominant, and so on. Note that minor
keys do not have blues or modal interchange chords,
indicated by empty entries in Table 1.
These cost values are chosen by trial and error
through experiments conducted on the collection of
tunes in Appendix D of Coker (1987). They follow
our intuition on the degrees to which chords in these
different categories reflect the presence of a given
key center. The tonality segmentation algorithm
appears to be robust with respect to variations in the
cost values as long as relative rankings among the
categories are preserved.
To determine the category of a chord AE, its
roman numeral chord with respect to k is computed
and looked up in the appropriate column of Table 1.
The category of an interpolated dominant AE is that
of its target chord. The category of a related IIm7 AE
is that of its “V7” AE. The category of an extended
dominant AE is that of its last AE. The cost of a
turnaround depends on the key centers it implies,
which are determined when it is detected by the
structural analysis algorithm. Its cost is 0 if k is one
of those key centers and ∞ otherwise. For example,
the cost of the turnaround “Am7 A(cid:2)m7 Gm7 G(cid:2)7”
is 0 if k is F major or F minor, and ∞ otherwise.
The values of tk
i, j, 0 ≤ i ≤ j < n, and k ∈ K can be
computed in O(n2) time:
(cid:3)
tk
i, j
=
category cost of ai from table 1 if i = j
tk
i, j−1
+ tk
j, j
otherwise
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
The cost of a modulation, M, is assigned a
value larger than that of any segment. That is, let
M > −tk
0,n−1 for all k ∈ K. Because of this, the tonality
segmentation algorithm will always minimize the
number of modulations (under the constraint of
the validity conditions to be discussed) sowie
find an assignment of key centers to the segments
that correspond to the best analysis of harmonic
functions of all the AEs.
Validity Conditions for Segments
To complete the definition of dk
ich, j to be
the validity of analyzing the segment ai, ai+1, . . . , aj
in key center k. It is defined as a logical conjunction
of four conditions:
ich, J, define sk
sk
ich, J
= r k
ich, J
∧ f k
ich, J
∧ uk
ich, J
∧ ek
ich, J
Choi
59
Figur 11. Bridge of tune
31A.
A valid segment is assumed to always contain a
root AE of key center k. Let r k
ich, j be true if and only
if the segment ai, ai+1, . . . , aj contains a root AE in
key k.
Auch, a valid segment is assumed not to end in
a dominant chord. Let f k
ich, j be true if and only if aj
is not an AE of a category in DOM in key k, Wo
DOM = {Primary dominant, Secondary dominant,
Substitute primary dominant, Substitute secondary
dominant}.
Each AE in the segment must have a known
harmonic function in key k. Let uk
ich, j be true if and
only if all of ai, ai+1, . . . , aj have known categories in
Tisch 1 with respect to key k.
It is easy to verify that each of r k
ich, J, and uk
ich, J
can be computed in O(n2) time for all 0 ≤ i ≤ j < n
and k ∈ K.
i, j, f k
Validity of a Segment Due to Subsegments
i, j causes the validity of
The final condition ek
analyzing the segment ai, ai+1, . . . , aj in key k to be
affected by whether subsegments embedded in it
can be analyzed as modulations to keys related to k.
In other words, ek
i, j is true if and only if the segment
ai, ai+1, . . . , aj contains no modulation to a related
key that prevents it from being analyzed completely
in key k. A key is related to key k if the former’s
tonic chord has one of the harmonic functions in
k listed in Table 1. A related key is specified by a
roman numeral interval optionally followed by the
letter ‘m’ (for minor keys). For example, the related
keys (cid:2)VI and IIIm of F major are D(cid:2) major and A
minor, respectively. Using this notation, the related
keys of a major key are IIm, IIIm, IV, VIm, Im, (cid:2)III,
IVm, Vm, and (cid:2)VI and those of a minor key are IIm,
(cid:2)III, IVm, Vm, and (cid:2)VI.
Modulations to keys unrelated to k are already
1,4
i, j. For example, in the
detected by the use of uk
analysis of Solar in Figure 2, analysis of the segment
containing the AEs a1 (Gm7 C7), a2 (FMaj7), and a3
(Fm7 B(cid:2)7) in F major cannot extend into a4 (E(cid:2)Maj7)
because E(cid:2)Maj7 has no valid harmonic function in F
major. Thus, the value of u“F major”
is false. Note also
that because a3 functions as a substitute secondary
dominant in F major and as a primary dominant
in E(cid:2) major, the cost assignments in Table 1 will
associate it with the latter key center after the
modulation from F major to E(cid:2) major is detected.
As an example of a tune with a modulation
to a related key, consider tune 31a in Appendix
D of Coker (1987). This tune begins with an A
section with a key center of B(cid:2) major, played twice.
It then modulates to E(cid:2) major in the bridge, as
shown in Figure 11. This is followed by a repeat of
the A section (in B(cid:2) major). The bridge contains a
turnaround “E(cid:2)6 Cm7 Fm7 B(cid:2)13” that implies an
E(cid:2) major tonality. Because this turnaround does not
have a valid harmonic function in B(cid:2) major, the
modulation to E(cid:2) major in the bridge is detected in
the same way a modulation to an unrelated key is
detected, as described above, using uk
i, j.
Now consider tune 31b in Appendix D of Coker
(1987). It begins with an A section in F major,
played twice. It then modulates to B(cid:2) major in
the bridge, shown in Figure 12. This is followed
by a variation of the A section (also in F major).
The bridge is composed of only two types of AEs,
60
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 12. Bridge of tune
31b.
chord AE B(cid:2)6 and related IIm7 AE Cm7 F7. Because
these AEs have valid harmonic functions in F
major, using only the mechanisms described so
far, the bridge will also be analyzed in F major,
leaving the modulation to B(cid:2) major undetected.
The use of ek
i, j enables the tonality segmentation
algorithm to detect modulations within segments
even when these modulations do not contain AEs
that distinguish them from the tonal centers of the
enclosing segments.
The design of ek
i, j presents a challenge because
if the condition is too selective, the algorithm will
miss subsegments that are in fact modulations
to related keys; if it is too indiscriminate, the
algorithm will detect superfluous modulations.
Therefore, ek
i, j is defined in such a way that allows
experimentation and fine tuning. The chord charts
with tonality segmentation in Appendix D of Coker
(1987) are then used in experiments to determine its
final definition, which is presented herein. A future
extension to the tonality segmentation algorithm
can include a statistical model for modulations and
select parameters for defining ek
using a set of training data.
i, j automatically
Let gk
i, j(r k, sc, st, sp), for 0 ≤ i ≤ j < n and k ∈ K,
be the validity of analyzing segment ai, ai+1, . . . , aj
in the key k with respect to whether it contains
subsegments that can be identified as modula-
tions according to a criterion specified by the tuple
(r k, sc, st, sp). That is, gk
i, j(r k, sc, st, sp) is true if and
only if no subsegment of a certain type (specified
by (r k, sc, st, sp)) occurs within it, which would
invalidate the analysis of the entire segment in k.
The first parameter r k is a related key of k. The
precise definitions of sc, st, and sp will be given
herein. Intuitively, the parameters sc and st provide
a test for determining whether a subsegment has
the characteristics of a modulation (e.g., being long
enough, or containing AEs of the right categories).
The parameter sp specifies the allowable positions
of a subsegment in ai, ai+1, . . . , aj. The complete
list of values for (r k, sc, st, sp) that the tonality seg-
mentation algorithm considers is given in Table 2.
Then ek
i, j is simply the logical conjunction of the
values of gk
i, j(r k, sc, st, sp) over all these sets of
values.
Certain related keys such as IV and VIm are
“more related” to the original major key than
others. Subsegments in these related keys need to
be more prominent before they are identified as
modulations. Under certain conditions (see “type
C,” subsequently), these subsegments must be
eight bars or longer to be identified as modulations.
Subsegments in “less related” keys, such as (cid:2)III
and (cid:2)VI, are identified as modulations more easily.
For example, in a segment in the key of F major,
a short two-bar subsegment of, say, an E(cid:2)7 chord
followed by an A(cid:2)Maj7 chord, is already identified
as a modulation.
According to how easily subsegments analyzed in
them are identified as modulations, related keys are
divided into three types as follows.
Type A – (cid:2)III and (cid:2)VI of a major or minor key
Type B – Im, IIm, IIIm, IVm, and Vm of a major
key; IIm and Vm of a minor key
Type C – IV, and VIm of a major key; IVm of a
minor key
Choi
61
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Table 2. List of All Related Keys, Subsegment Categories, Subsegment Tests, and Subsegment
Positions Considered by the Tonality Segmentation Algorithm
Related Key (r k)
Subsegment Categories(sc) Subsegment Test (st) Subsegment Position(sp)
Type
For major key k
(cid:2) III
(cid:2) VI
Im
IIm
IIIm
IVm
Vm
IV
IV
VIm
VIm
scsimple
scsimple
scsimple
scsimple
scsimple
scsimple
scsimple
sclong
scshor t
sclong
scshor t
stsimple
stsimple
stsimple
stsimple
stsimple
stsimple
stsimple
stlong
stshor t
stlong
stshor t
ANY
ANY
E P
E P
E P
E P
E P
ANY
E P
ANY
E P
A
A
B
B
B
B
B
C
C
C
C
For minor key k
Related Key (r k) Subsegment Categories(sc) Subsegment Test (st) Subsegment Position (sp) Type
(cid:2) III
stsimple
(cid:2) VI
stsimple
stsimple
IIm
stsimple
Vm
stlong
IVm
stshor t
IVm
scsimple
scsimple
scsimple
scsimple
sclong
scshor t
ANY
ANY
E P
E P
ANY
E P
A
A
B
B
C
C
These types have increasingly stringent require-
ments for subsegments analyzed in their related
keys to be identified as modulations. Each type
has its own criterion (or criteria) for identifying
modulations.
A subsegment in a related key of type A is
detected by setting the parameters sc, st, and sp to
sc = scsimple = {Root, Primary dominant},
st = stsimple = dur (h, l) ≥ 8, and
sp = ANY
respectively, where dur (h, l) denotes the total du-
ration (in number of quarter notes) of the AEs in
the subsegment ah, ah+1, . . . , al. In other words, a
passage in a related key of type A must be at least
two bars long to be considered a modulation. The
subsegment ah, ah+1, . . . , al is identified as a modu-
lation if, when analyzed in the related key r k, each
AE in ah, ah+1, . . . , al is of a category in sc, the test
st evaluates to true, and (1) at least one AE of the
subsegment is in the Root category and (2) the sub-
segment does not end in an AE of a category in DOM.
Conditions (1) and (2) are always added regardless
of the values of r k, sc, st, and sp. For example, in
the key of F major, the subsegment |E(cid:2)7|A(cid:2)Maj7| is
identified as a modulation in the related key (cid:2)III. So
are |A(cid:2)Maj7|A(cid:2)Maj7| and |F7|B(cid:2)7|E(cid:2)7|A(cid:2)Maj7|, but
not |Bm(cid:2)7|E(cid:2)7| (violates condition [1]), |A(cid:2)Maj7|E(cid:2)7|
(violates condition [2]), or |B(cid:2)(cid:2)7|A(cid:2)Maj7| (category of
B(cid:2)(cid:2)7 not in sc).
The value ANY for the parameter sp means that
the subsegment ah, ah+1, . . . , al may appear anywhere
within the segment in question, and therefore
represents a null test.
Related keys of type B are “more related” to the
original key k than those of type A. Subsegments in
them are identified as modulations when they are
immediately preceded or followed by a modulation
to yet another key center. They are not identified
as modulations when they appear in the middle of a
segment in key k, however. As an example of modu-
lations to related keys of type B, consider the analysis
62
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13. Bridge of
Yardbird Suite.
of the bridge of tune 73 (Yardbird Suite) in Appendix
D of Coker (1987), shown in Figure 13. Its first three
bars form a segment with a key center of E minor.
Its last three bars (and the A section that follows,
only the first bar of which is shown) form a segment
with a key center of C major. Although bars 4 and 5
can be analyzed in C major, they satisfy the criterion
specified below (including being preceded by a seg-
ment with another key center, E minor). They are
therefore detected as a separate segment with a key
center of D minor, a related key of C major of type B.
Note also that if the Em6 chords in bars 1 and 3 (no
harmonic function in C major) are changed to Em7
chords (diatonic chords in C major), the entire bridge
will be analyzed in C major because bars 4 and 5
occur in the middle of a segment with a key center of
C major.
Modulations to related keys of type B are detected
by setting the parameters sc, st, and sp to
sc = scsimple,
st = stsimple, and
sp = E P
The value of E P for parameter sp specifies that
the subsegment ah, ah+1, . . . , al must appear at an
endpoint of the segment ai, ai+1, . . . , aj. That is, an
additional test is performed which evaluates to true
if and only if h = i ∨ l = j.
Chords in the related keys of type C are most re-
lated to k. Two sets of criteria are needed to correctly
handle the different ways in which modulations in
these related keys may appear. Longer subsegments
in these related keys are identified as modulations
regardless of where they are in the original segment.
Such subsegments will contain AEs belonging to
more categories. The settings for sc, st, and sp to
identify these modulations are
sc = sclong = {Root, Diatonic} ∪ DOM
st = stlong = dur (h, l) ≥ 32 ∧ 4 · r dur (h, l)
≥ odur (h, l), and
sp = ANY
where r dur (h, l) and odur (h, l) denote the total
durations (in number of quarter notes) of root AEs
and other AEs in the subsegment ah, ah+1, . . . , al,
respectively. The modulation from F major in the
A section to B(cid:2) major in the bridge in tune 31b
in Appendix D of Coker (1987; see Figure 12) is
detected by these parameter settings.
Shorter subsegments in related keys of type C
are also detected as modulations when they are
immediately preceded or followed by a modulation
to another key center. The corresponding settings
for sc, st, and sp are
sc = scshor t = {Root, Primary dominant},
st = stshor t = dur (h, l) ≥ 8 ∧ 2 · r dur (h, l)
≥ odur (h, l) ∧ odur (h, l) > 0, Und
sp = E P
Als Beispiel, tune 33 (Jeepers Creepers) In
Appendix D of Coker (1987) begins with two repeats
of an A section in the key of E(cid:2) major, followed by the
bridge shown in Figure 14, then followed by another
time through the A section. Bar 5 and the first half of
bar 6 of the bridge are analyzed in B(cid:2) major because
B(cid:2)Maj7 has no valid harmonic function in E(cid:2) major.
The first four bars can be analyzed in E(cid:2) major as
Choi
63
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
e
D
u
/
C
Ö
M
J
/
l
A
R
T
ich
C
e
–
P
D
F
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
C
Ö
M
_
A
_
0
0
0
5
6
P
D
.
J
F
B
j
G
u
e
S
T
T
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figur 14. Bridge of Jeepers
Creepers.
Figur 15. Chord changes
for Solar represented by
key centers and roman
numeral chords.
Figur 14.
Figur 15.
a continuation of the segment containing the A
section. Jedoch, they are not, because they are
detected by the settings for sc, st, and sp above and
analyzed as a separate segment with a key center of
A(cid:2) major.
It can be shown that the computation of ek
ich, j for all
0 ≤ i ≤ j < n and k ∈ K requires O(n2) time. Given k,
for each combination of r k, sc, st, and sp, categorize
the AEs a0, a1, . . . , an−1 with respect to the related
key r k. Identify all maximal spans in it for which:
each AE is of a category in sc, st is true, at least
one AE in the Root category is present, and the
category of the last AE is not in DOM. Intuitively,
a segment ai, ai+1, . . . , aj can only be valid for
sp = ANY if i and j are in the same maximal span
or gap between maximal spans, since any proper
subsegment it contains that overlaps a maximal
span will invalidate it. (A proper subsegment of a
segment is one that is [strictly] shorter than the
segment.) Additionally, the segment ai, ai+1, . . . , aj
can only be valid for sp = E P if i and j are in the
same maximal span or gap between maximal spans,
or each of them is in a gap between maximal spans.
This ensures that no proper subsegment at its two
endpoints overlaps a maximal span, which will
invalidate it. Therefore let z0, z1, . . . , zn−1 be integer
labels assigned to the AEs such that two AEs have
the same odd (or even) label if and only if they belong
to the same span (respectively, gaps between spans).
Then it can be shown that
gk
i, j(r k, sc, st, sp)
(cid:3)
zi =zj
zi =zj ∨ (zi mod 2=0 ∧ zj mod 2=0) if sp= E P
if sp= ANY
=
This completes the description of the tonality seg-
mentation algorithm. Note that the time complexity
of the harmonic analysis algorithm is O(n2).
Evaluation of the Tonality Segmentation Algorithm
The performance of the tonality segmentation al-
gorithm is evaluated using the entire collection of
tunes in Appendix D of Coker (1987). These tunes
contain a wide variety of types of modulations and
compositional and harmonic devices and demon-
strate the general applicability of the harmonic
analysis algorithm. The chord changes of the tunes
are given by key centers and roman numeral chords.
For example, the chord changes for Solar (see Figure
1) are represented as in Figure 15. The key centers
below the roman numeral chords represent how a
64
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
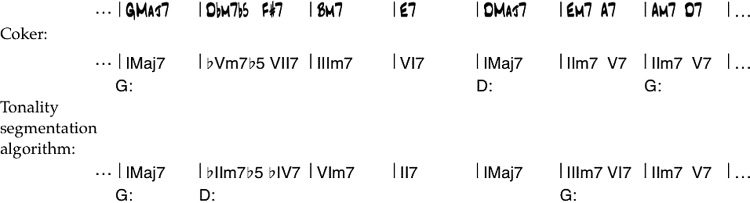
Figure 16. Example of
different segmentation due
to handling of dominants.
musician might perform tonality segmentation for
the tune. They provide a benchmark against which
the output of the tonality segmentation algorithm
can be compared.
This representation is converted into an ordinary
chord chart (such as the one in Figure 1), and then
used as input for the structural analysis algorithm
and tonality segmentation algorithm. The resulting
segmentation and original segmentation are then
compared.
Among the 78 tunes in that collection, 57 receive
exactly the same segmentation by both Coker and
the tonality segmentation algorithm. An additional
13 (tunes 7, 12, 27, 28, 29, 33, 53, 63, 69, 70, 73,
78, and 82) have identical sequences of key centers,
but different assignment of dominant chords to
consecutive segments. An example of this type of
discrepancy is shown in Figure 16, which results
from the requirement of the tonality segmentation
algorithm to end segments with AEs that do not
function as dominant chords. Dominant chords at
the boundary of two segments often play dual roles
in the two key centers and it is simpler and more
consistent to associate them with the chords into
which they resolve.
Among the eight remaining tunes, in five (20, 23,
36, 52, and 62) the tonality segmentation algorithm
detects more segments than those given by Coker
(1987). For example, the tonality segmentation
algorithm determines that tune 23 (Charlie Parker’s
Blues for Alice) contains one bar in F major, four
bars in B(cid:2) major, two bars in A(cid:2) major, and five bars
in F major. Coker considers the entire tune to be in
F major. Both analyses are in some sense “correct.”
The tonality segmentation algorithm omits some
segments in the other three tunes (3, 25, and 54).
These segments are too short or fail to satisfy the
criteria (they do not contain a root AE of the key
center, for example) to be detected by the algorithm.
An OCaml (Leroy 2008) implementation of
the structural analysis and tonality segmentation
algorithms and test data can be downloaded from
the Web page www.sixthhappiness.ca/jazz-harmonic
-analysis.
Summary
A new algorithm for harmonic analysis of jazz chord
sequences has been described. It views harmonic
analysis as a problem of segmenting the input chord
sequences and determining the key centers of the
segments. This representation is natural and com-
monly used by jazz musicians. More importantly,
it allows modulations in the chord sequences to
be modeled explicitly. The harmonic analysis prob-
lem can then be formulated mathematically and
solved by dynamic programming as an optimization
problem. Jazz theory knowledge is incorporated
into the algorithm to specify and solve the tonality
segmentation problem. Once the segments and
key centers are determined, structural information
can be recovered from straightforward detection of
well-understood elements of jazz theory such as
dominant resolutions, harmonic rhythm, substitute
dominants, related IIm7s, extended dominants,
turnarounds, and interpolated dominants. The algo-
rithm can be used in software that simulates jazz
improvisation and for implementation of composi-
tional and teaching tools. An example of the latter is
a GUI tool called T2G, which was used to generate
the analyses in this article (see Figures 2, 3, 5–7, 9,
and 11–14). T2G is also available for download at
the URL given at the end of the previous section.
Choi
65
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Future work on the tonality segmentation problem
can focus on algorithm evaluation and comparison
using more comprehensive test data sets, and im-
proved models of modulations (including the use of
statistical models).
References
Coker, J. 1987. Improvising Jazz. New York: Simon &
Schuster.
Corman,T. H., C. E. Leiserson, and R. L. Rivest. 2009.
Introduction to Algorithms. 3rd ed. Cambridge, Mas-
sachusetts: MIT Press.
Illescas, P. R., D. Rizo, and J. M. I ˜nesta. 2007. “Harmonic,
Melodic, and Functional Automatic Analysis.” In Pro-
ceedings of International Computer Music Conference,
pp. 165–168.
Jaffe, A. 1983. Jazz Theory. Dubuque, Iowa: Wm. C. Brown
Company Publishers.
Jaffe, A. 2009. Jazz Harmony. 3rd ed. Rottenburg: Advance
Music.
Johnson-Laird, P. N. 2002. “How Jazz Musicians Impro-
vise.” Music Perception 19(3):415–442.
Keller, R. M., et al. 2006. “A Computational Frame-
work Enhancing Jazz Creativity.” In Proceedings of
European Conference on Artificial Intelligence (pages
unnumbered).
Mehegan, J. 1964. Jazz Improvisation 3. New York:
AMSCO Music Publishing.
Mehegan, J. 1965. Jazz Improvisation 4. New York:
AMSCO Music Publishing.
Mouton, R., and F. Pachet. 1995. “The Symbolic vs. Nu-
meric Controversy in Automatic Analysis of Music.” In
Proceedings of the Workshop on Artificial Intelligence
and Music, International Joint Conference on Artificial
Intelligence, pp. 32–39.
Nettles, B., and R. Graf. 1997. The Chord Scale Theory
and Jazz Harmony. Rottenburg: Advance Music.
Nettles, B., and A. Ulanowsky. 1987. Harmony 1–4.
Boston, Massachusetts: Berklee College of Music.
Pachet, F. 1991. “A Meta-Level Architecture Applied to
the Analysis of Jazz Chord Sequences.” In Proceedings
of International Computer Music Conference, pp.
266–269.
Pachet, F. 2000. “Computer Analysis of Jazz Chord
Sequences: Is Solar a Blues?” In E. Miranda, ed. Readings
in Music and Artificial Intelligence. Amsterdam:
Harwood Academic Publishers, pp. 85–113.
Pachet, F. 2003. “The Continuator: Musical Interaction
With Style.” Journal of New Music Research 32(3):333–
341.
Pardo, B., and W. P. Birmingham. 2002. “Algorithms for
Chordal Analysis.” Computer Music Journal 26(2):27–
49.
Pass, J. 1996. Joe Pass on Guitar. Miami, Florida: Warner
Klein, J. 2005. “A Pattern-based Framework for Computer-
Brothers Publications.
aided Jazz Improvisation.” Diploma Thesis, Me-
dia Computing Group, Computer Science Depart-
ment, Rheinisch-Westf ¨alische Technische Hochschule
Aachen University.
Lerdahl, F., and R. Jackendoff. 1983. A Generative Theory
of Tonal Music. Cambridge, Massachusetts: MIT Press.
Leroy, X. 2008. The Objective Caml System Release
3.11 Documentation and User’s manual. Paris: In-
stitut National de Recherche en Informatique et en
Automatique.
Levine, M. 1995. The Jazz Theory Book. Petaluma,
California: Sher Music Company.
Mehegan, J. 1959. Jazz Improvisation 1. New York:
AMSCO Music Publishing.
Mehegan, J. 1962. Jazz Improvisation 2. New York:
AMSCO Music Publishing.
Ramalho, G. L., P. Y. Rolland, and J. G. Ganascia. 1999.
“An Artificially Intelligent Jazz Performer.” Journal of
New Music Research 28(2):105–129.
Scholz, R., V. Dantas, and G. Ramalho. 2005. “Automating
Functional Harmonic Analysis: The Funchal System.”
In Proceedings of the Seventh IEEE International
Symposium on Multimedia, pp. 759–764.
Steedman, M. 1984. “A Generative Grammar for Jazz
Chord Sequences.” Music Perception 2:52–77.
Temperley, D., and D. Sleator. 1999. “Modeling Meter and
Harmony: A Preference-Rule Approach.” Computer
Music Journal 23(1):10–27.
Thom, B. 2003. “Interactive Improvisational Music
Companionship: A User-Modeling Approach.” User
Modeling and User-Adapted Interaction 13(1–2):133–
177.
66
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
5
2
4
9
1
8
5
5
6
5
3
/
c
o
m
_
a
_
0
0
0
5
6
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3